Nou Biaix, 34

Revista de la FEEMCAT i de la SCM

Juny 2014

ubiaixno

número 34

sumari

Consell de Redacció: Manel Sol / Josep Lluís Solé (coords.)

Marianna Bosch

Joan Carles Ferrer

Joan Miralles

Josep Pla

Romà Pujol

Manuel Udina

Juanjo Cárdenas (responsable pàgina web)

© dels autors dels articles

Coediten:

Federació dEntitats per a ’’lEnsenyament de les Matemàtiques (FEEMC AT )

Campus de Montilivi, edifici P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com sites.google.com/site/noubiaix

Fotografia de la coberta: Vol dabscisses ’ Abel Feliu Masachs IES Rafael de Campalans, Anglès Concurs del 2011 Categoria de batxillerat al Periodicitat: semestr

Preu d‘exemplar ordinari: 12 € Nombre d‘exemplars: 1.700

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Publicacions i Edicions de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430

Fax: 934 035 531 comercial.edicions@ub.edu www.publicacions.ub.edu

57 64 3

Editorial 10 23 32 41

articles

Introducció als desenvolupaments de deter minades superfícies reglades des de l’anàlisi matemàtica

Xavier Gelada Serrat

El problema dels ponts de Köningsberg. Idees per a l’aula

Mireia López Beltran i Pura Fornals Sánchez

Jocs d’estratègia i el currículum escolar

Guido Ramellini

Les taules de multiplicar a través d’imatges

Maria Bras-Amorós

seccions

Per pensar d’un minut a una hora

Jordi Deulofeu

Construint matemàtiques

Anton Aubanell

El racó del MMAC A

Josep Rey i Manuel Udina

El racó del Cesire- Creamat

editorialeditorial

Unavegadaméstenimlasatisfacciódefer-vosarribarunnouexemplardelarevista. Éselquefacincdel’etapa Noubiaix.Enaquestsmoments,sensepretendre-ho,ens veiemforçatsaferalgunscanvis.EnJosepPla,quevaserundelsimpulsorsd’aquest projecteiquehaestatalseudavanttotaquesttemps,hadeciditdeixarlacoordinació, peròseguiràcol·laborantambnosaltrescomamembredelconsellderedacció.En Joseppottenirlasatisfacciód’haverassolitsobradamentelsobjectiusambquèva néixeraquestapublicació.Desd’aquesteslínies,iennomdetotelconsellderedacció, livolemagrairtotelseuesforçientusiasme,elsqualshanfetpossiblequelarevista siguielquearaés.

ElnourepresentantdelaSCMques’ocuparàdelacoordinacióseràenJosepLluísSolé.Li donemlabenvingudaaaquestanovaresponsabilitatilitransmetemelsuportilacol·laboraciódetotl’equipdepersonesqueparticipemenlarealitzaciódelarevista.

TambéensdiuadéuenClaudiAlsina,col·laboradorentusiasta,quehamantingutlasecció «Sabiesque...»desdeldesembrede 2005.Ennomdetotelconsellderedacció,isegurque tambéeneldetotselslectors,livolemtransmetrel’agraïmentpelsseusarticles,queenshan fetgaudiriaprendrealllargdetantsanys.

Totsaquestscanvis,però,noafectenlalíniadelarevista.Volemserunpuntdetrobadaentre elscol·lectiusdelsdiferentsnivellsd’educaciómatemàticaaCatalunya,desdelabàsicafins alauniversitat,unmitjàperatransmetreicompartirexperiències,reflexionsiinquietuds.Els mestresielsprofessorsdematemàtiquessomespecialmentactius.Volemmostrar-hopera queensserveixid’estímulifacilitilamilloradelanostratascadiàriaalesaules.Aprofitem aquestesreflexionsperanimar-vosafer-nosarribararticlesamblesvostresidees.

Comanovetatenaquestnúmeros’inicienduesnovesseccions.D’unase’nfaràcàrrecl’Anton Aubanell,professorbenconegutperlasevadilatadacarreraprofessional,iesdirà«Construint matemàtiques».L’Antonesvajubilarel 19 dedesembrepassativaferladarreraclasse dedidàcticaalaFacultatdeMatemàtiques.Classequeesvaconvertirenunemotiuacte d’homenatge,enelqualfouacompanyatpertotselsamicsquevanpoderassistir-hi.Ellva llegirunamagníficacartaadreçadaaunprofessornovellsuggerint-liunsconsellscoma professorexperimentatqueés,isavicoms’hafetalllargdetantsanyscomadocent.Enshi parladelafelicitatilapassiód’ensenyarmatemàtiques.L’hemvolgudapublicarcomainici delasevaseccióperquè,se’nsdubte,resultaràd’interèstantaperalsnovellscomperals veterans.

Del’altraseccióse’nfaràcàrrecelgrupdeprofessorsdelMMACAiesdirà«ElracódelMuseu deMatemàtiquesdeCatalunya».Encadanúmerodelarevistaensexplicaranlesideesque hihaaldarrered’undelsmòdulsdelmuseu.Aquestprimerracó,escritperenManelUdina

ienJosepRey,estàdedicatapresentar-nossituacionssorprenentslligadesal’encaixde poliedres,donant-lilaformad’undiàlegsobrealgunesvariantsdelproblemadelpríncep Rupert.

El31 dedesembrepassatvafinalitzarelperíodedelmandatdelaJuntadelaFEEMCAT,presididaperlaIolandaGuevara.Elrelleul’harecollitl’associaciódeGironaAdemgiilapresidenta seràlaVictòriaOliu.Desd’aquesteslíniesvolemagrairalajuntapresididaperlaIolandatota lafeinafetaielsuportquesemprehandonatalprojectedel Noubiaix.D’altrabanda,donem moltsànimsalaVictòriaielseuequip,elsqualsjahancomençatatreballar.Publiquemles cartesrespectivesd’acomiadamentidepresentació.

Pelquefaalsarticles,enpresentemundeprimària,escritperlaMariaBras,enelqualensdóna ideessobrel’úsdelesimatgesperapromourel’aprenentatgedelestaulesdemultiplicar d’unamaneravivencial,aixícomfaevidentlarelaciódelamatemàticailarealitat.

Enelnivelldesecundària,laPuraFornalsilaMireiaLópezplantegennovessituacionsque serveixenperalaintroducciódelesmatriusilessevesoperacions,enespecialladelproducte, apartirdelconegutproblemadelspontsdeKöningsberg.D’aquestamaneraaconsegueixen captarl’interèsdelsseusalumnesimillorar-neelsresultats.Enunaltrearticle,enXavier Geladaensfaveurequeenelnostreentornestemenvoltatsdecossosgeomètricsconstruïts ambsuperfíciesreglades.Ensensenyacomtrobarlessevesequacionsilacomplementarietat entrelageometriadiferencialilageometriaclàssicabasadaenelregleielcompàs.

Eltreballd’enGuidoRamelliniensproposal’úsdejocsd’estratègiaambalumnesdequalsevol edat,unrecursmoltapropiatperaldesenvolupamentdelescompetènciesmatemàtiques. Tambéfal’anàlisidelesideesmatemàtiquesquehihadarreredecadaundelsjocsque presenta.

Amésdelesnovesseccionsqueushemanunciat,seguimcomptantamblesqueja erenhabituals:«Perpensarunminut»d’enJordiDeulofeu,i«ElracódelCreamat»del Cesire-Creamat.Atotsellselsagraïmlasevacol·laboració.

CanvideJuntaalaFEEMCAT

Ambl’inicidel’anys’haproduïtuncanvialaJuntadelaFEEMCATtalcomestàestablertals estatuts.Uspresentemlescartesd’acomiadamentidepresentaciódelespresidentessortint ientrant,respectivament.

Comiatdelapresidentasortint

UsparlaIolandaGuevaraCasanovapresidentadelaFEEMCATdurantelperíode 2011-2013, quevaformarequipamblaMarionaPetitVila(secretària)iambenPacoMorenoRigall(tresorer).

VamaccediralacoordinacióseguintlarotacióquemarquenelsestatutsdelaFederació, rellevantl’equipdel’APaMMs,constituïtperlaCarmeAymerichPadilla(presidenta),enLluís MoraCañellas(secretari)ilaBertaVilaJofré(tresorera).

Elgenerdel 2011,laMariona,enPacoijoéremrespectivamentsecretària,tresoreripresidenta del’ABEAM.EnPacoijodesdelnovembrede 2005ilaMarionaenelsdarrersanys,jaqueen elsprimersvaser-hoenGerardRomoGarrido.

Durantelprimersmesosdel 2011 vamentendrequeestaralcapdavantdelesduesjuntes,la delaFEEMCATiladel’ABEAMeraunatascainabastable.Caliaunanovajuntaperal’ABEAM. Eljulioldel 2011,l’ABEAMtenianovajunta:MireiaLópezBeltrán(presidenta),PuraFornals Sánchez(secretària)iJoanaVillalongaPons(tresorera).

Volemagrairdesd’aquílasevabonapredisposicióperassumirelscàrrecsilatascarealitzada desdelseunomenament.

Lajuntasortint,laconstituíemtrespersonesambunasòlidaformaciómatemàtica,laMariona ijollicenciadesenmatemàtiques,ienPacoenfísiques,quehemdedicatlanostraprofessió aladocènciaenmatemàtiquesperòquedesdelcomençamentdelesnostrestrajectòries professionalshemcreguteneltreballassociatiuienelsequipsperavançarenelcamídela milloradelapràcticadocentidelaimplicaciódel’alumnatenelseuaprenentatge.

ComamembresdelajuntadelaFEEMCAT 2011-2013hemcontinuatelqueerenlesgrans líniesdelafederació,lacoordinacióentrelesquatreassociacions(ADEMGI,APMCM,APaMMs iABEAM)ialavegadalacoordinacióamblaFESPM.

El Femmatemàtiques éselprojectedemésenvergaduraqueesduatermedesdelaFEEMCAT. Aquestconcurs,basatenlaresoluciódeproblemes,éselqueensfamésvisiblescoma federacióenescolesicentresdesecundària,enorganismesientitatsdelmóneducatiu,perquè hemaconseguitfitesdeparticipaciódemésdevuitmilalumnes.Caldirqueelmèritésdeles quatreassociacionsidelsseusrespectiuscoordinadorsque,anydarrereany,deformamolt autònomaiprofessional,organitzenlesdiferentsfasesterritorialsilafinaldeformarotativa.

Sipassemllistad’algunsdelstemesquehemimpulsatalcapdavantdelaFEEMCAT,seguint unordremésomenyscronològiccitaríemelssegüents:enprimerlloc,l’apostapels Tallers d’Anemx + matemàtiques,adreçatsaalumnesde4td’ESOambunacertadestresaigustper

lesmatemàtiques,aldarrertrimestresdelcurs2010-2011.Enelscursossegüentselprojecte s’haanatconsolidantfinsaarribaralsquatretallersdelcurs2013-2014,queapleguengairebé uncentenard’alumnesde4td’ESO,totiquehemperduteltalleral’APMCM,quecaldrà recuperarenelsproperscursos.

Alssetembres,lescitesanualsdelesJornadesd’Ensenyamentdelesmatemàtiques,convocatòriaconjuntadelaSCMiXEIXialaqualdesdel2011s’hivaafegirAl-Khwarizmi.Cadaany untemad’interèsdeciditentrelesquatresocietatsconvocants:L’avaluacióal’aula(2011),La divulgaciódelesmatemàtiques(2012)iL’afabetitzacióestadística(2013).

Desprésdeltreballderepresainovaredacciódelesbasesdurantelcurs2011-2012,la convocatòriaconjunta(FEEMCAT,XEIX,Al-Khwarizmi)delpremibiennalMariaAntòniaCanals(MAC)enlesedicions2012i2014.

Laconsolidaciódel NouBiaix comarevistaconjuntadelaFEEMCATilaSCMquel’any2013 haaconseguitelsdosexemplarsanualsqueesproposavaeneldocumentdefusióambla SCM,signateldesembredel2010.

LaparticipacióenelProgramadeformaciócientífica,tecnològicaimatemàtica(CTM),de formaincipientelcurs2012-2013ideformamésàmpliaitemàticaelcurs2013-2014.Enguany s’hanimpartittallers-xerradesaBarcelona,Girona,LleidaiTarragonasobreelsdiferentsàmbits enquèestreballadesdelaFEEMCATolessevesassociacions:Femmatemàtiques,Anemx+ matemàtiques,Fotografiamatemàtica,Úsdelahistòriaal’auladematemàtiquesirevistes sobreensenyamentiaprenentatgedematemàtiques.

Eljulioldel2012esvaconstituirelcomitèorganitzadordel’OlimpíadaMatemàtica2014 queconvocacadaanylaFESPM.Així,eldesembredel2012,laFEEMCATvapresentarelseu projecteformald’organització,quevaseraprovatperlajuntadelaFESPM.

Eljulioldel2013vamconvocar,conjuntamentamblaSCM,unconcurspúblicperacobrir duesvacantsdeprofessoratdelprojecteEstalmatCatalunya.Enlamateixalínia,hemdonat suportalseminarianualestataldeprofessorsd’EstalmatquesecelebraaBarcelonaelsdies4, 5i6d’abrildel2014iquetindràtrentaplacesobertesalprofessoratdeCatalunyaquevulgui participaralessessionsdelsdies4i5.

Volemesmentartambél’estretacol·laboracióambelCREAMAT,enreconeixementdegrups detreball,suportal’organitzaciódelesJornadesConjuntes,peticióperaformarpartdeljurat del vídeoMat,suportenelCTM...itambéamblaSCM,amblaqualcompartimel NouBiaix,les JornadesConjuntes,elsProblemesal’Esprint,EstalmatCatalunya...

Finsaquíhemfetunamiradaenpositiudelpassatmésproper;nohemesmentantels problemesderivatsdel’agreujamentdelacrisieconòmica,delarepercussióenelsconvenis ilessubvencions.Enaquestaspectehemaconseguitsortirendavantamblacol·laboració delaSCM,delaFMEdelaUPC,delDepartamentdeDidàcticadelaMatemàticadelaUAB, delDepartamentd’Ensenyament,idelaFundacióCellex,queenshandonatsuportihan reconegutlanostratasca.Somconscientsquealgunesqüestionshanquedatpendentsique d’altresespodenmillorar.Confiemenlanovajuntaperfer-ho.Elsdonemelnostresuporti elsdesitgemmoltasortenaquestanovaiemocionanttasca.

PresentaciódelanovapresidentadelaFEEMCAT

EmdicVictòriaOliuiSubiranasiagafoelrelleudelaIolandaGuevaraenlapresidènciade laFEEMCATperalperíodedel 2014al 2016,seguintlarotacióquemarquenelsestatutsdela Federació,aquestavegadaperencàrrecdelajuntadel’ADEMGI(Associaciód’Ensenyantsde MatemàtiquesdeGirona).

PrimerdetotvullagrairalaIolanda,alaMarionaiaenPaco,presidenta,secretàriaitresorerde lajuntaanterior,totelsuportqueensestandonantperfermésfàcilelcanvidecàrrecs,tanta micomalaSílviaMargelíiaenRaülFernández,novasecretàriainoutresorer,respectivament.

VullagrairalaSílvia,aenRaül,aenXavi,al’ImmaiaenPepusquehaginacceptatformar equipambmi.Gràcies,equip!Tambévullmostrarelmeuagraïmental’AntonAubanell,ala MariaÀntoniaCanals,al’ElisabetSaguer,al’actualjuntadel’ADEMGIiatotselscompanysi amicsquem’hanfetcostatim’hananimataemprendreaquestaresponsabilitat.

SócllicenciadaenmatemàtiquesperlaUniversitatdeBarcelona,sòciadelaSCMdesque vaigacabarlallicenciaturaisòciadel’ADEMGIdesdelasevafundació.Sócprofessorade matemàtiquesal’institutdelaBisbald’Empordàdesdelcurs 1986/1987.Heestatvocaldediferentsjuntesdel’ADEMGIicoordinadoradelFemMatemàtiquesdurantunabonacolla d’edicions.Heampliatlamevaformacióinicialparticipantendiversoscursosdeformació, grupsICEijornades.HeelaboratmaterialsperacursostelemàticsdelDepartamenttreballant enequipambaltrescompanysiheestatformadoradecursospresencialsitelemàticsdel Departament.

M’heinteressatpertotesleseinesalmeuabastquem’hansemblatútilsperamillorarla tascadocentinohedubtatmaiaprovardiferentsmetodologiesaclasse,ihepreparatels meuspropismaterials,sobretotambeinesdigitals.Peraixòemvaigformarenlautilització d’entornsvirtualsd’aprenentatgeiarasócmoltfandeMoodleiGeoGebraiutilitzoelsmeus propiscursosMoodlecomasuportaladocènciapresencial.

Elcurs 2010/2011 vaiggaudird’unallicènciad’estudisgràciesalaqualvaigpoderposaren ordreelsmaterialsqueteniaicrear-nedenous.Lamevacol·lecciód’objectesd’aprenentatge iitinerarisdematemàtiquesperasecundàriaestrobaadisposiciódetotelprofessoraten l’aplicacióARC(AplicaciódeRecursosalCurrículum).

TambéheparticipatenelprojecteEstalmat-Catalunyadesdelseuiniciiimparteixotallers peralprojecte«Anempermésmatemàtiques»aGirona.

LanovajuntadelaFEEMCATijomateixa aixònomésespotferenequip estemcomençant lanostrapresidènciaambànimdeserveialcol·lectiud’ensenyantsdematemàtiquesde Catalunya,desdelsmestres,passantpelsprofessorsd’institut,finsalsdocentsuniversitaris, amblavistaposadaenlamilloradel’aprenentatgedelesmatemàtiquesperpartdetotsels estudiantsdeCatalunya,nensinenes,adolescentsijoves,quesónelfuturdelnostrepaísila raódeserdelsnostresesforços.

Perpoderduratermeaquestsobjectius,alanovajuntaestemutilitzantleseinesd’Internet, pàginaweb,Facebook,Twittericorreuelectrònic,pertaldecontinuarteixintlaxarxaque ensfacilitilacomunicacióil’intercanvi,enspermetitenirl’orellaposadaenlesinquietudsde

lacomunitateducativaiestaralcorrentdetoteslesactivitatsorganitzadesperlaFEEMCAT iperlaFederacióEspanyoladeprofessorsdematemàtiques(FESPM).Usesperematotsa lanovapàginawebperquènecessitemlesvostresopinionsielvostresuport.Aquestaés l’adreça:www.feemcat.org

Finsaramateix!

articl artices les

rticles

Introduccióals desenvolupamentsde determinadessuperfícies regladesdesde l’anàlisimatemàtica

XavierGeladaSerrat

InstitutBoscdelaComad’Olot xgelada@xtec.cat

Resum Abstract

Elscossosgeomètricsdeterminatspersuperfícies regladesdesenvolupables,comelcilindretallatper plansoblics,elconoblicdebasecircularo interseccionsvàriesd’aqueststipusdesòlids,estan semprepresentsenl’entornquotidiàatravésde múltiplesàmbitsdelconeixementcoml’art, l’arquitecturaoeldissenyindustrial.Enelsentitmés ampli,l’aplicabilitatd’aquestesestructuresenla societatactualés,pertant,fonamental.Malgrattot, lesfontsd’informaciódisponiblessobrel’estudi d’aquestsdesenvolupamentsestanorientats, bàsicament,alaconstrucciógeomètricaambreglei compàsoalageneraciód’imatgesdigitals,sense deduiroexplicitarl’equaciódelstraçats.Pertant,el queespreténenaquestarticleésiniciarl’exploració d’aquestesequacionsidelsresultatssignificatiusque se’npuguinderivaratravésdel’anàlisimatemàtica, percontribuiralasevadifusió.D’aquestamanera,la geometriadiferencialiladeregleicompàs,lluny d’excloure’s,escomplementenmeravellosamentbé, enaquestcas,peraunmillorconeixementde determinadessuperfícies isomètriquesalpla.

Geometricalbodiesdeterminedbydevelopableruled surfacessuchasacylindercutbyobliqueplanes,an obliqueconewithacircularbase,andmultipleother intersectionsofsuchsolidbodiesareconstantlymade presentinoureverydaylivesbyseveralknowledge disciplinessuchasart,architectureandindustrial design.Inawidersense,theapplicabilityofsuch structuresinpresentsocietyisthereforeessential. However,theonlyavailablesourcesofinformationon thestudyofsuchdevelopmentsaremainlygearedto eithergeometricalconstructionofthe ruler-and-compassnature,ortogeneratingdigital images,thuspayingnoattentiontothedeductionor explanationoftheirunderlyingequations.Thisiswhy themainpurposeofthisarticleliesinintroducingthe explorationofsuchequationsandthesignificantresults whichderivefromthemthroughmathematical analysis,inordertomakethemmorefamiliartoawider audience.Inthisway,bothdifferentialgeometryand ruler-and-compassgeometry,farfromexcludingone another,complementeachotherwonderfully,andlead toabetterunderstandingofcertain isometric-to-the-planesurfaces.

Lafinalitatd’aquestarticleésiniciarl’estudid’algunscossosgeomètricsconstituïtspersuperfíciesregladesdesenvolupables,centrant-seenlesequacionsquedeterminenelstraçats alplaatravésdel’anàlisimatemàtica.Iparal·lelament,mostrartantlabellesadelsconceptes

geomètricsimplicatscomlasevaindubtableaplicabilitatenl’artilaciència.L’arquitectura, eldissenyindustrialolesartsaplicadesal’esculturasónalgunsdelsnombrososàmbitsdel coneixementenquèapareixenaquestesformes.Acontinuacióesmostrenobjectesrealsque n’exemplifiquenalgunes:

Cilindre tallat per un pla oblic

Fig. 1. Imatge esquerra: Conductes de climatització. Palau Sant Jordi (Barcelona). Colze segmentat de 90º.

Portal volcànic

Fig. 2. Imatge dreta: Escultura de Josep Guinovart Bertran, titulada(Olot). Suport central constituït per cilindres simètricament seccionats.

Con

oblic de base circular

Fig.3.Reduccionscòniquesobliqüesdebasesparal·leles,utilitzadescomaelementsd'unióintermèdiaentre duespecesdediferentdiàmetre.D'aplicaciógeneralen conductesdecaptaciódepolsienespecialencanonadesdetransportpneumàticdematerialsipartícules.1

Fig. 4. Accessori de bany. Penjador de braç cònic oblic, truncat i amb bases circulars no paral·leles.

1.ImatgescedidesperEstudiSicília(Girona)iperMetal·lúrgicaRos(SantJaumedeLlierca,Girona).

Interseccions

Fig. 5. Font pública. Població de l'Escala (Girona). Intersecció perpendicular de cilindres de diferent diàmetre i eixos secants.

Fig.6.Entroncamentspantaló.Intersecciósimètricade dosconductescònicsrectesd'igualdiàmetreieixossecants,formantunanglede60º.Sortidasuperiorcentral cilíndricadediferentdiàmetre.D'aplicacióenxarxesde canonadesdecaptaciódepolsitransportpneumàtic.2 2

Algunsd’aquestsobjecteshanestatconstruïtsapartirdedesenvolupaments,mentreque d’altresno.Però,almargedelatecnologiaemprada,qualsevolproducteconstituïtper aqueststipusdecossosgeomètricspotsersusceptibledeserfabricatmitjançanteltraçat geomètricdecorbesalpla.

Pelquefa,específicament,alstraçatsdelsdesenvolupamentsdesuperfíciesregladesisomètriquesalpla,labibliografiaexistentestàorientada,bàsicament,al’úsdelregleielcompàso alageneraciód’imatgesdigitals,perònopasaladeduccióanalíticadelesequacionsqueels determinen.Ésjustamentaquestal’òpticaapartirdelaqualespreténcomençarafer-neun estudi,queenaquestarticlesecentraràenelcilindretallatperunplaoblic:

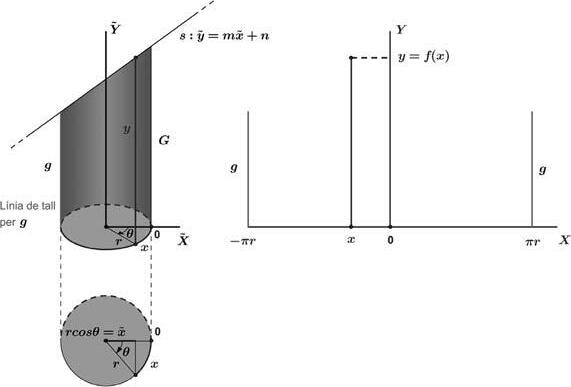
Figura 7. Plantejament analític del desenvolupament del cilindre tallat per un pla oblic.

2.ImatgescedidesperEstudiSicília(Girona)iperMetal·lúrgicaRos(SantJaumedeLlierca,Girona).

Enlafiguras’observaque,amesuraquevaria θ ∈ [ π, π],esrecorrelabasedelcilindre obtenintaixídiferentsarcsdelongitud x (negatiusper θ ∈ [ π, 0) ipositiusper θ ∈ (0, π], atèsque x = r · θ ).Acadascundelsvalors x licorresponunaúnicaaltura y ,demaneraque enstrobemdavantunafunció y = f (x ) quecaltrobar.

Projectantortogonalmentelsegmentradienl’eix X estéqueperacadavalor x s’obtéun valor x = r cos θ = r cos x r ,talcommostralafigura.Isiconsideremlarecta s : y = mx + n, determinadaperladiagonalmajordelaseccióel·lípticaentallarelcilindreperunplaoblic, ésclarque y (x )= y (x ) quan x = r cos x r ⇒ y (x )= y r cos x r = m

Pertant,noméscaltrobarelpendentil’ordenadaal’origende s.Mirantlafiguraésclarque m = G g 2r i n = g + G 2 ,on g i G sónlesalturesmínimaimàxima,respectivament.Aleshores, y (x )= G g 2r · r cos x r + g + G 2 ⇒ y = f (x )= 1 2 g + G +(G g) cos x r ,x ∈ [ π r, π r ] .

Fentelgràficdelafuncióobtenimeldesenvolupamentdeformaràpidaienqualsevolpunt:

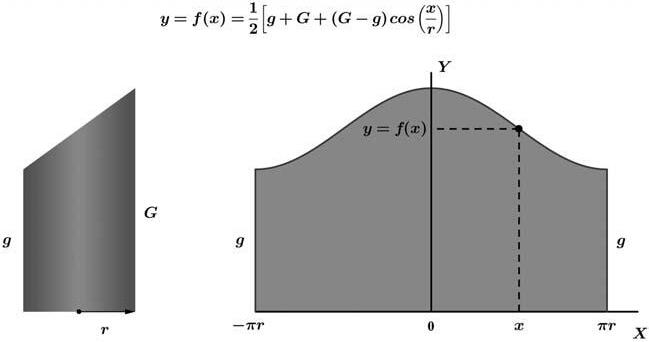
Figura 8. Funció i desenvolupament del cilindre tallat per un pla oblic.

Elsavantatgesd’haverobtingutl’equaciódeltraçatenrelacióambelmaneigdelregleiel compàssónmoltsivariats:3 d’entradaenspermetrealitzareldesenvolupamentambuna granrapidesaiprecisió,amésdepodertreballardeformagenèricaambqualsevolcilindretallatperunplaoblic4 enfunciódelsparàmetres r , g i G.Amés,l’expressióanalítica y = f (x )

3.Aquestaafirmaciónopreténmenystenirenabsolutlageometriaderegleicompàs.Alcontrari,la geometriaclàssicadel’antigaGrècia,malauradamentoblidadadurantbonapartdelsegle XX perla«matemàtica moderna»,ésundelspilarsimprescindiblesperedificaraquesttipusdeconeixement.

4.Comamostra,espotferúsdel’aplicació Desenvolupament_Cilindre_Seccionat_Analitic.html Perobtenirlacalaccediral’adreçaelectrònicadel’aplicaciówebARChttp://apliense.xtec.cat/arc(oatravésdelareferència 2 delabibliografia),iferlacercapertítol(ElCilindreSeccionat )operautor(XavierGeladaSerrat).Finalment,calclicar enl’ítem«AplicacionsenGeoGebraiExcelassociadesalesactivitats».

ensdiuquelacorbadescritaésunasinusoide,llunyd’unapossibleprimerapercepcióqueel desenvolupamentpodriaadquirirunperfiltriangular.

Peròl’obtenciód’aquestaequaciótambéindueixdeformanaturalacalcularlasuperfíciedel sòlidilalongituddelasecciómitjançantelcàlculintegral:

Superfície del sòlid

Atèsquelamètricaesmanté,lasuperfícielateraldelcilindretallatperunplaoblicseràdonadaperl’àreadelseudesenvolupament,ésadir:

Calassenyalarque,enelcasdelcilindretallatperunplaoblic,se’npotobtenirlasuperfície lateralsensel’úsd’integrals.Observemlafigurasegüent:

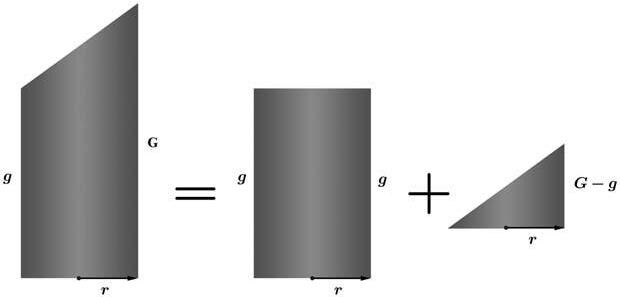
Figura 9. Descomposició geomètrica del cilindre tallat per un pla oblic.

Lasuperfícielateraldelcilindretallatperunplaoblic(Sup.Lat.)ésigualalasumadelasuperfície lateraldelcilindre S1 ilasuperfícielateraldelapartseccionada S2 ⇒ Sup.Lat. = S1 + S2 . Ésevidentque S2 éslameitatdelasuperfícielateraldelcilindrequedeterminai,pertant:

Sup.Lat. = 2 π rg + 2 π r (G g) 2 = 2 π rg + π rG π rg = π r (g + G) queésl’expressióobtingudaamblaintegral.

Coméslògic,aquesttipusderesolucióperdescomposiciónoéspossibleenlamajoriadels cossosgeomètricslimitatspersuperfíciescorbes,encaraquesiguindesenvolupablesalpla, peròaixònorestal’interèsderelacionarambdósprocediments,pelfetd’estartanallunyats l’undel’altre.

Siesvoltenirencomptelesbasesinferiorisuperiorenelcàlculdelasuperfícieconsiderant elcilindreseccionattapat,caldràafegir-nelesàrees:

Àreadelabasecircular = π r 2

Encanvi,l’àreadel’altrabaseseràdonadaperunaseccióel·lípticad’equacióreduïda x 2 a2 + y 2 b2 = 1.Observantlafigura3ésclarqueelsemieixmajorés

ielmenorés b = r .

Així,l’equacióreduïdadelaseccióel·lípticaés

Percalcularl’àreaquedelimitarelacionaremlafunció g (x ) quedeterminalameitatsuperior dequalsevolel·lipsealllargdelseueix 2a amblafunció c (x ) delasemicircumferència superiordediàmetrel’eix 2a.Totiqueaquestarelacióésperfectamentconeguda(relació d’afinitat),ésadientraonar-la:

Aïllantla y designepositiudel’equaciógenèricareduïda x 2 a2 + y 2 b2 = 1 s’obté g (x )= = y = b a √a2 x 2 , x ∈ [ a,a].L’expressiódelradicalobeeixalafunciódelasemicircumferènciasuperiordediàmetre 2a descrita.Pertant,estélarelaciód’afinitat g (x )= b a c (x ).En altresparaules,laimatgedelafuncióel·lípticaperacadavalor x ésladelacircumferència multiplicadapelfactor b a ,talcommostralafigurasegüent:

10. Relació d afinitat entre l el·lipse i la circumferència principal. ’’

Figura

Perdir-hodeformaplaneraiintuïtiva,unael·lipseespotinterpretarcomlacircumferència tangentexteriordediàmetrel’eixmajor(circumferènciaprincipaldel’el·lipse),comprimida deformahomogèniaiortogonalmental’eixesmentat.

Conseqüentment,l’àread’unael·lipseés,deformaraonada:

expressióàmpliamentconeguda.

Enelcasdelcilindretallatperunplaoblic,tenimquel’àreadelaseccióel·lípticaés,pertant,

Finalment,doncs,lasuperfícietotaldelcilindretallatperunplaoblicambelsparàmetresque esmostrenenlesfigures 1, 2 i3,tenintencomptetantlabasecircularcomlaseccióel· líptica,és:

quesiesvolespotexpressarcom:

ésadir:

Sup.Total = π r (sumadelesaltures + sumadelssemieixos) interpretantlacircumferènciacomuncasparticulard’el·lipsedediàmetresiguals.

Longitud del traçat

Atèsquelamètricaentreelsòlidieldesenvolupamentesmanté,lalongituddelaseccióel·líptica,quedenotaremperLong.,éslamateixaquelalongituddeltraçatdeldesenvolupament.

D’unabanda,podemutilitzarlafunciódeduïdarespectealtraçatdeldesenvolupament y = f (x )= 1 2 g + G +(G g) cos x r , x ∈ [ π r, π r ] queesmostraenlafigura8;de l’altra,lafunciódelameitatsuperiordel’el·lipse g (x )= y = b a √a2 x 2 , x ∈ [ a,a] (figura 10),queunavegadasubstituïdeslesexpressionsde a i b anteriorss’escriucom:

Així,lalongituddelaseccióel·lípticaLong.éslamateixatantenlacorbade f (x ) comenlade g (x ) dobladasimètricamentrespecteal’eixmajor(jaquerepresentalameitatdel’el·lipse).I comquelesduesfuncionssóndeclasse C 1 icontínuesalseudomini,podemescriure:

Arabé,ni 1 +(f (x ))2 ni 1 +(g (x ))2 tenenprimitivesexpressablesambfuncions simples,peròaixònoimpedeixpodercalcularamblaprecisiódesitjadalesintegralsamb paràmetresconcretsmitjançantmètodesnumèricsd’integracióvaris(fórmulesdeNewtonCotes,laQuadraturadeGauss...).Lamultiplicitatdeprogramarilliured’integraciónumèrica, almarged’elaborarprogramespropis,permetobtenirambfacilitatresultatsràpidsiprecisos.

Aixòés,justament,elquefaremenuncasrealal’apartatsegüent,queensserviràtambéper ail·lustrarelscontingutsteòricsdesenvolupats.

Aplicació de la teoria a un objecte concret

Tornantalprincipideldocument,hitrobemobjectesconcretscomaexemplesdecossos geomètricsdeterminatspersuperfíciesregladesdesenvolupables.Aplicaremlateoriaenel colzede 90◦ ide80 cmdediàmetre5 situatalapartcentraldelaimatgesegüent,queconstitueixpartdelsistemadeclimatitzaciódelPalauSantJordideBarcelona:

Figura 11

Sienshifixem,elcolzeestàformatpercincpeces:la 2,3i4sóncilindrestallatsperdosplans oblicsdeformasimètrica.Encanvi,la 1 ila5sóncilindrestallatsperunsolplaoblicque, acoblats,formarientambéunsolcilindretallatperdosplansoblicssimètrics.Pertant,encara queelcolzeestiguiformatpercincpeces,diemqueestàformatperquatreelements,jaque n’hihatresdecompletsiundeseccionatperlameitat.

Lalongitudde AB éspròximaa48cm,demaneraquesuposaremperraonspràctiquesque, efectivament, AB = 48cm.Amés,totselsplansoblicstallenelscilindresambelmateixangle α,jaqueelselementssónidèntics(lespeces 1 i5formen,juntes,unaltreelementidènticals altres).Enaquestsentit,observemque,enpassard’unapeçaal’altrapercadaunió,acumulemduesvegadesl’angle α icomqueelcolzeestàformatperquatreunions,entotalgiremun angle 2α · 4 = 8α,quehadeser 90◦ ⇒

Pertant,aplicanttrigonometriaelementalal’alçat AA B B del’elementdelaimatgetenimla relació:

Així,jatenimlesmidesdel’elementque,persimetria,éseldobledelcilindretallatperunpla oblicquehemestudiat.Utilitzantlanotaciódelateoriapodemescriure: 2 g ≈ 16,17402 cm, 2 G = 48cmi r = 40 cm ⇒ g ≈ 8,08701 cm, G = 24cmi r = 40 cm,que,aplicatsalafunció deldesenvolupamentsuperior, y = f (x )= 1 2 g + G +(G g) cos x r ,x ∈ [ π r, π r ]

donenlafigura:

12. Funció i desenvolupament d'un element del colze.

Unaspected’interèsquanesfanmilersdecolzescomeldelaimatgeésconèixerlalongitud necessàriadelasoldaduraperafabricar-lo.6 Nomésperlesunionsentrelescincpecesqueel formen,senseconsiderarlasoldaduralateralperformarlapeçaensi,calcalcularl’expressió

6.Segonslatecnologiadisponibleilafuncióquehad’acomplir,s’utilitzendiferentsprocedimentspera formariunirlespecesd’uncolze:pertipusvarisdesoldadura,utilitzantcèrcolsperaunirlespestanyes,engrapant-les, acoblant-lesúnicamentperembotició...Enaquestcas,suposaremques’hafetúsdelasoldaduraperaassegurarla màximaestanquitat.

Figura

4 · long.,jaqueestàcompostadequatreunions.Utilitzarem f (x ) encomptesde g (x ) (equació delaseccióel·líptica),jaque g (x ),ambaquestesdadesconcretes,derivaenunaexpressió quelamajoriad’integradorsnumèricsnosóncapaçosd’avaluar.

Pertant,lalongituddelasoldaduradelcolze,únicamententreelselements,és 1.015,18cm = = 10,1518m,aproximadament.

Vallapenacomentarqueaqueststipusdedesenvolupamentsnosoleniniciar-seapartir delssegmentslaterals 2g (alturamenor)o 2G (alturamajor),comenlafigura5anterior(que s’iniciaen 2g),jaqueaixòimplicariaunefectepocestèticenelconjuntdelcolzeperquèles soldadureslateralsdecadapeças’alternarienenelssegments 2g i 2G (o g i G peralespeces 1 i5)o,encaraqueesreordenessin,esformariasempreunalíniadiscontínuadesoldadura. Lafigurasegüentil·lustraundesenvolupamentdelcolze,apartird’unaplanxarectangular, queproduiriaaquestefectenodesitjat:

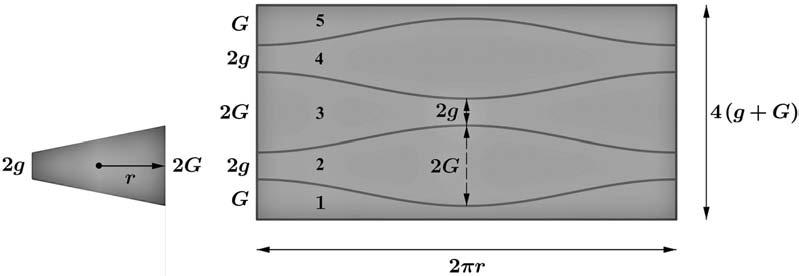
13. Desenvolupament no usual del colze a partir d'una planxa rectangular.

Perevitaraquestproblema,esdesenvolupenlespecesapartirdel’alturamitjanaentrela mínimailamàxima,ésadir, 2g + 2G 2 = g + G enelscasdelselements(2,3i4)i g + G 2 enles pecesextremes(1 i5),meitatsd’unelement.

Lafigurasegüentreflecteixlamaneracomhabitualmentesdesenvoluparienlespecesdel colze:

7.Elcàlculnumèricd’integracióespotobtenirambprogramarilliurecomGeoGebraoambl’integrador WolframAlpha R ,entremoltsd’altres.Peròtambépotsermoltinteressantutilitzarprogramarid’elaboraciópròpia ifinsitotfer-homanualment,acotantl’expressiódel’error.

Figura

Figura 14. Desenvolupament habitual del colze a partir d'una planxa rectangular.

Enaquestaconfiguració,lafunciódeltraçatsuperiordel’element 2 ésdonadaperla

mateixafunció y = f (

,peròambeldominidefinit

, 4

],talcomes reflecteixenlesfigures 12 i 13.

Observemquetotselsaltrestraçatsdelespecessóndeterminatsperlamateixafuncióola simètricarespecteal’eixhoritzontal.

D’aquestamanera,enelcolzeespodenalineartoteslessoldadureslateralsformantunalínia contínua,adiferènciadelquepassaenlesfigures 12 i 13.

Enl’argotpropidel’àmbitdelaplanxisteria,lacaldereriailametal·lúrgiaengeneral,el desenvolupamentdel’element 2 (delimitatencolortaronja)s’anomena lasardineta,una denominaciófrancamentencertadaibonica.Totselsaltreselementsprenen,també,aquesta formapeculiar(lespeces 1 i5representen mitjasardineta).

Pertant,l’equacióqueexpressaeltraçatdeldesenvolupamentd’unapeçaqualsevold’un colze,siguionode 90◦ ,dedimensionsgenèriquesésdeterminadaperl’expressió: y = f (x )= 1 2 g + G +(G g) cos x r eneldomini x ∈ π r 2 , 3π r 2 .

Òbviament,totselscàlculssobrelasuperfícieilalongitudques’hanfetamb f (x ) enel domini x ∈ [ π r, π r ] sónidènticsutilitzant f (x ) eneldomini x ∈ πr 2 , 3πr 2 ,jaque l’amplituddelsdosdominisés 2πr icoincideixambelperíodedelafunció.Esdeixacoma propostad’activitatperallectorlacomprovaciód’aquestesigualtatsiqueelsextremsdel domini, π r 2 i 3π r 2 ,sónabscissesdepuntsd’inflexió.

Continuantambl’aplicacióconcretaalcolzede 90◦ quehemtractatfinsara,sivolem conèixerlalongitudtotaldelasoldadura,alalongituddelasoldaduradelesunions 4 · long. ≈ 10,1518mcaldràafegir-hilalongituddelessoldadureslateralsqueformen cadapeça.Enlafigura7quedaclarquelalongituddelasoldaduralateralés4 (g + G) ≈ ≈ 4 · 32,08701 = 128,34804cm.Pertant,lalongitudtotaldelasoldaduranecessàrianomés peraferelcolzedelaimatgeés,aproximadament, 11,435metres.

Enrelacióamblasuperfície,noméscalconsiderar,peracadaelementdelcolze,l’expressió 2 Sup.Lat. = 2π r (g + G) perquècadascunestàformatperdoscilindressimètricstallats obliquamentisensetapes.Iatèsqueelcolzeestàconstituïtperquatreelements(cinc peces),lasuperfícietotaldelcolzeésdonadaper8 Sup.Lat. = 8π r (g + G).Substituintles dadesconcretes,obtenimquelasuperfícienecessàriadeplanxa,d’ungruixdeterminat,per aelaborarelcolzeés:8

Consideracions finals

Elscontingutsd’aquestarticlerepresentenl’evoluciónaturalenl’aprofundimentmatemàtic d’unapartconcretadelallicènciad’estudisretribuïda MatemàtiquesiRealitat (2011),9 concedidapelDepartamentd’EnsenyamentdelaGeneralitatdeCatalunya.Concretament, implicaunacontinuïtatdecaràctertècnicdel’element ElCilindreSeccionat,alqualtambé s’hipotaccediratravésdel’aplicaciówebARChttp://apliense.xtec.cat/arcfentlacerca,per exemple,pertítoldel’elementoperautor.

Comaaplicacionsinteractivesespecífiqueshihados applets enGeoGebra:d’unabanda, Desenvolupament_Cilindre_Seccionat_Analitic.html i,del’altra, Simetria_Desenvolupament_ Cilindre_Seccionat_html,dinsl’arxiu«AplicacionsenGeoGebraiExcelassociadesalesactivitats».

Bibliografia

Departamentd’Ensenyament.GeneralitatdeCatalunya. CurrículumiOrganització [enlínia]. GeneralitatdeCatalunya.http://phobos.xtec.cat/edubib/intranet[consulta:30.7.2012].

Gelada,X.(2011). Matemàtiquesirealitat:Connexionsatravésdelaresoluciódeproblemesiel desenvolupamentd’activitatsinterdisciplinàries [enlínia].Barcelona:GeneralitatdeCatalunya. http://www.xtec.cat/web/innovacio/recercaed/llicencies/cercador[consulta: 26.8.2012].

Gomis,J.(1996). CurvasysuperficiesenDiseñodeIngeniería.València:ServiciodePublicaciones delaUniversidadPolitécnicadeValencia.

8.Calesmentarqueenelcàlculnos’haincorporatlasuperfíciedelespestanyesdecadapeçaperquè representenunasuperfícieaddicionalpocsignificativaenrelacióambeltotal.Malgrataixò,ésimprescindible tenir-lesencompteeneltraçatperpoderfabricarelcolze.

9.Referència 2 delabibliografia.

Olave,A.(2004). Manualprácticodedesarrollosdecalderería.Barcelona:EdicionesCeac.

Ortega,J.(1990). Introduccióal’anàlisimatemàtica.Bellaterra:ServeidePublicacionsdela UniversitatAutònomadeBarcelona.

MireiaLópezBeltran UniversitatPompeuFabra iICEUniversitatPolitècnicadeCatalunya mireia.lopez@gmail.com

PuraFornalsSánchez

INSFrancescMaciàdeCornellàdeLlobregat pfornals@gmail.com

Resum Abstract

AprofitemelproblemadelspontsdeKöningsberg perplantejaral’alumnatunasituació contextualitzadaqueenspermettreballar diferentsaspectes,curricularsono,deles matemàtiques.Amés,seguintdirectamentelfil històricdelproblemaespotveurecomd’una situacióprousenzillaespodendeduirgrans resultatsmatemàticsqueenspermetenintroduir altresaspectesambmésfacilitat. Laintroducció,perpartd’Euler,d’unsistemade notacióquepermetsimplificarelplantejamentila resoluciódelproblemadelsponts(començantper unproblemaméssenzill,obrintlapossibilitatde novesformesderepresentació...)facilitala comprensiódelasituacióperpartdel’alumnatili obrel’oportunitatd’atrevir-searesoldrealtres situacionssimilars,amblasatisfacció personalqueaixòsuposa.

D’altrabanda,laintroducciódelanotació matricialidelesoperacionsambmatrius,sobretot elproducte,suposaunadificultatafegidaa l’alumnat.Ambaquestplantejament,aconseguim queaugmentielseuinterèsi,pertant,lamillora delsresultats. Elferservirlateoriadegrafsnocomportacap complicacióafegida,ansalcontrari,l’alumnatho veucomunamanerapràcticaderepresentar situacionsrealsqueenfacilitalalecturaila interpretacióposteriors.Pertant,totinoser curricularasecundària,ésuna bonaeinaaintroduir.

WetaketheproblemoftheBridgesofKoningsbergto presenttostudentsacontextualsituationthat allowsustoworkondifferentaspects,curricularor not,ofmathematics.Also,followingondirectlyfrom thehistoricalproblem,itcanbeseenhow,froma quitesimplesituation,majormathematicalresults thatallowustointroduceotheraspectsmoreeasily canbededuced.

Theintroduction,byEuler,ofanotationsystemthat makesitpossibletosimplifyandsolvetheproblemof theBridges(startingwithaneasierproblem,opening upthepossibilityofnewformsofrepresentation...) facilitatesunderstandingbystudentsofthesituation andgivesthemtheopportunitytodaretosolveother similarsituations,achievingpersonalsatisfaction. Furthermore,theintroductionofmatrixnotation andmatrixoperations,especiallytheproduct,gives anaddeddifficultyforstudents.Withthisapproach, wemanagedtoincreasetheirinterestandthus improvetheresults.

Theuseofgraphtheoryinvolvesnofurther complication;onthecontrary,studentsseeitasa practicalwaytorepresentrealsituationsfacilitating subsequentreadingandinterpretation.Therefore, althoughnotpartofthehighschoolcurriculum,itis agoodtooltointroduce.

Introducció

Proposaralsnostresalumneslaresoluciódesituacionsencontextosricsisignificatiusés undelsreptesquetenimelsprofessorsdelesdiferentsetapeseducatives.Elproblemadels pontsdeKöningsbergésunasituaciómoltrica,jaqueenspermettreballarunagrandiversitat d’aspectes:

1.Elcontexthistòricreal.

2.Laresolucióhistòrica.

3.Generalitzem?

4.Dibuixosd’unsoltraç.

5.Elsgrafs.

6.Elproductedematrius.

1.Elcontexthistòricreal

ElproblemadelspontsdeKöninsbergenspermetportaral’aulaunproblemarealsense haverdesimplificarl’enunciatoriginal.Aixòfaqueelsalumnespercebin,perunabandala matemàticacomunaeinaqueserveixperadonarrespostaasituacionsplantejadesenlavidaquotidiana,iperunaaltrabandaqueveginlamatemàticacomunaàreadeconeixement queesvacreantapartirderesoldresituacionsconcretes.Tambéhipodemafegirlavessant humanaipresentarelmatemàticquehihadarreredelsraonamentsidelscàlculs.Araque tenimelsordinadorsielsprojectorsal’aula,ésrelativamentsenzillmostrarelsdiferents matemàticsanantdirectamentalasevabiografia.Aixípodemmostrar-nelaimatge,parlar dellloconvanéixeridel’èpocaenquèvaviure.

Enelguardonatarticle«ThetruthaboutKöningsberg»,HopkinsiWilson(2004)ensexpliquen nosesapdelcertcomlivaarribaraEuleraquestproblema,peròs’hatrobatcorrespondència ambCarlLeonhardGottliebEhler,alcaldedeDanzig,antigaPrússia(actualGdanskaPolònia), a 130 quilòmetresdeKonigsberg,onparlavendelproblemadelsponts.

Enunciatdelproblema

Acontinuaciódoneml’enunciatqueEulermateixvaescriureenunacartadatadael 13de marçde 1736:

M’hanplantejatunproblemasobreunaillaalaciutatdeKöningsberg,envoltadaperun riutravessatpersetponts,iemvanpreguntarsialgúpodiatravessarelspontsseparats enunpasseigdemaneraquecadapontestravessinomésunavegada(HopkinsiWilson, 2004).

Iamésafegeixquehaestatinformatqueencaraningúl’hademostratnihamostratqueaixò noéspossible.PeraEuleraquestproblemaera«banal»,peròlicridal’atenció,jaqueveuque enlasevaresoluciónecessitanovestècniquesienespecialcreuquepotserunproblema quepertanyiala geometriadelaposició quehaviaintroduïtLeibniz.

2.Laresolucióhistòrica

Undelsinteressosdidàcticsd’aquestproblemaéselfetques’hadedemostrarqueelcamí buscatnoexisteix.Noésgairehabitualqueenlesnostresclassesplantegemalsalumnes problemesenquèhagindeprovarquealgunacosanoéspossible.Enaquestaproposta resseguiremlaresolucióhistòricaqueproposaEuler.2

Totelmeumètodeesbasaenlaformaparticularmentconvenientenquèl’encreuament delpontespotrepresentar.Peraixò,utilitzoleslletresmajúsculesA,B,C,D3 pera cadascunadelesregionsdeterraseparadespelriu.SiunviatgervadesdeAfinsaB pelpont a o b,hoescricAB onlaprimeralletrarepresentalaregióqueelviatgerestà deixantilasegonalletra,laregióonarribadesprésdecreuarelpont.

(...)ABDC,ques’hadeprendreenelsentitqueelviatger,començantenA,travessaaB,va aD,ifinalmentarribaaC(Biggs etal., 1986,p.4).

D’aquestamanera,argumentaquesielpasseighadepassarpercadaundelssetpontsuna inomésunavegada,aleshoreslarutapotserrepresentadapervuitlletres,demaneraque «leslletresAiBestanl’unaalcostatdel’altraduesvegades,jaquehihadosponts, a i b, connectantlesregionsAiB».

Perintentartrobarsiexisteixunaseqüènciadevuitlletresquecompleixielsrequisitsde lletresadjacentsapropiats,redueixelproblemaaestudiarunasolaregióA,ambunnombre indeterminatdeponts(fig. 2).Primerestudialasituacióambunpont,desprésambtres

1.ImatgeextretadeHopkinsiWilson, 1986.

2.EnlaURLdeEuler, 1736podeutrobarlaversióoriginalenllatí.EnHopkinsiWilson, 1986,tambéen digital,podeutrobarunresumenanglèsforçadetallatdelprocésdeltreballd’Euler.EnBiggs etal., 1986,3-8,podeu trobarlatraducciódeltreballal’anglès.

3.VegeuFig. 1

Fig.1

Fig.2

ponts,perconclourequesielnombredepontsésimparell,aleshoreselnombredelletresA quehihad’haveralaseqüènciaserialameitatd’aquestnombredepontsmésun.

NotemqueEulernofaservircapllenguatgealgebraicenaquestaargumentació,quees podriareduira:sitenimunnombredeponts k imparell,aleshoreslalletrahad’aparèixer k +1 2 vegades.

Comqueenelnostreproblemaelnombredepontsquearribaacadaregióésimparell,no enscalampliarl’estudi.ComquealaregióAhiarriben5ponts,aleshoreslalletraAhade sortirtresvegadesicomquealesregionsB,CiDhiarribentrespontsatotestres,aleshores cadascunad’aquestestreslletreshadesortirduesvegades.Entotal,nou,i«aixònopotser enunaseqüènciadevuitlletres».D’aquestamanera,conclouqueelpasseigdemanatnoes potferatravésdelssetpontsdeKöningsberg.

Finsitotmésendavanteneltext,recullaquestainformacióenunataula:

Fig.3.Euler,1736.

Enunacartadatadael3d’abrilde 1736,Eulerexposaque«comqueaquesttipusdesoluciótépocarelacióamblesmatemàtiques,noentencperquèesperesunmatemàticpera realitzar-la,mésquequalsevol,jaquelasolucióestàbasadanomésenlaraó,ielseudescobrimentnodepèndecapprincipimatemàtic»(HopkinsiWilson, 1986).

Potseraquestasensaciódepocamatemàticaéselqueelvaportaraplantejar-seiresoldreel problemageneral.

3.Generalitzem?

Eltextd’Eulerestàorganitzatenparàgrafsnumerats.Apartirdeldesèparàgraf,comença elraonamentperalcasgeneraliperaixòenprimerllocnecessitacontinuarl’anàlisientre elspontsielnombredevegadesquesurtunalletraalaseqüència,peròaraampliantaun nombredepontsparell.

Peranaril·lustrantelmètodegeneral,proposaunaltreexempleambméselementsqueel delssetpontsdeKöningsberg,concretamentamb7regionsi 15ponts:

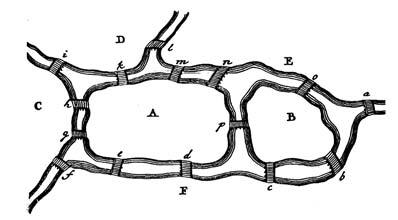
Aquestpasageneralitzartambéésunaeinadidàcticamoltpotentque,enaquestcas,sorgeix delmateixtexthistòricdel’autor.

4.Dibuixosd’unsoltraç

Nopodemoblidarmencionarlarelaciód’aquestproblemaambelsdibuixosd’unsoltraç (fig.5).

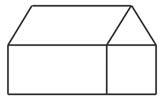
Apartirderepassareltreballoriginald’Euler,nopodemdeixardefernotarquenohihacap referènciaalconceptedegraf.Capdelessevesrepresentacions(fig. 1, 2 i4)ésproperaala pròpiadelsgrafs.Noobstantaixò,l’atribucióaEulerdel’autoriadelconcepteésàmpliament acceptada.Amés,eltextamblaresoluciódelproblemadelspontsdeKöningsberges consideraque«involucralaformulaciódediversosdelsconceptesbàsicsdelateoriade grafs»(Biggs etal., 1986).Senseaquestproblema,elsorígensdelsgrafsnomésespodrien relacionarambdivertimentsinfantilscomelpresentatenaquestapartat.

5.Elsgrafs

Elconceptedegrafnoéscurricularasecundària,però,talcomindicaCastrillón(2009),les sevesideespodensertreballadesambalumnesd’aquestgrau.L’autor,amés,destacaque lesideesqueenvoltenelconceptedegrafsónsenzilles,sensequeaixònidellunysignifiqui pobresaenelscontinguts.

EnFornalsiLópez, 2013esdescriuambdetalleltreballquelesautoresportematerme dinsdelprojecteEstalmat4 enlesduessessionsqueesduenatermeambelsalumnesde segonany.Enlaprimerasessióestreballalaintroduccióalconceptedegrafapartirdela

4.www.estalmat.org

Fig.4

Fig.5

presentaciódeldiagramadevolsdelacompanyiaVueling.Tambéespresenta,apartir d’exercicisconcrets,unvocabularimínimsobregrafs.

Enlasegonasessióescomençaambunadiscussiósobreelsdibuixosd’unsoltraçiles característiquesquefanpossiblequeaquestrequerimentespuguicomplirono.Aquest escalfamentserveixperatreballardespréselproblemadelspontsdeKöningsberg.Ambels alumnesestreballalaresolucióhistòricaques’hapresentatal’apartat 2.

L’objectiudelessessionséstreballarambgrafsenaquellessituacionsenquèaquestaeina matemàticaenspotajudararesoldre-les.Unadelessituacions,quecreiemqueésmoltenriquidora,ésdonaruncontextalproductedematriustalcompresentaremenl’apartatsegüent.

6.Elproductedematrius

DesprésdepresentarelproblemadelspontsdeKöningsbergiintroduirlaresolucióhistòrica d’Euler,s’instaelsalumnesareflexionarsobreelcomentari:«Totelmeumètodeesbasaenla formaparticularmentconvenientenquèl’encreuamentdelpontespotrepresentar».Després delaintroducciódelsgrafsalasessióanterior,esdemanaalsalumnesquerepresentinla situaciódelproblemamitjançantungrafqueelsajudiaseguirelraonamentd’Euler.

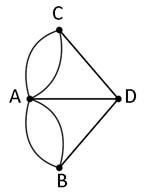
Fig.6.GrafproblemadelspontsdeKöningsberg.

Aquestatascanocomportagairesproblemesperalsalumnesmésenllàd’adonar-sequeno hihaunúnicgrafcorrecte.Lamajoriadelsgrafsquedibuixensóncomelmostratalafigura6.Noacostumenaincorporar-hielsnomsdelsponts.Siesfes,ensquedariaelgrafsegüent:

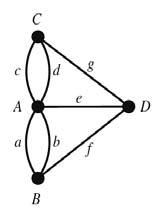
Uncopacabadalaresoluciódelproblema,esdemanaquecomptindequantesmaneres diferentspodemanardelaregióCalaregióDpassantexactamentperdosponts.Elsalumnes trobenlesduespossibilitatsilesrepresentemambundiagramasemblantalsegüent:

Fig.7

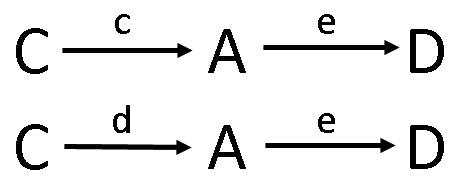
Totseguit,introduïmelconceptedematriuassociadaaungrafapartird’unexempleiels demanemqueescriguinlamatriuassociadaalgrafqueellshandibuixat.Sensegairesdificultats,trobenquelamatriudemanadaés:

Acontinuació,calculem M2 il’anomenem N.Tenimque M2 = N =

Abansjaelshemdefinitproductedematrius.

Iaraelsdemanemsipodentrobarunainterpretaciódelterme n34 = 2 quehantrobatapartir decalcular:

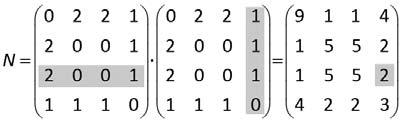
Notemquesónelscaminsdesegonordre(passantperdosponts)peranardeCaD,ésadir:

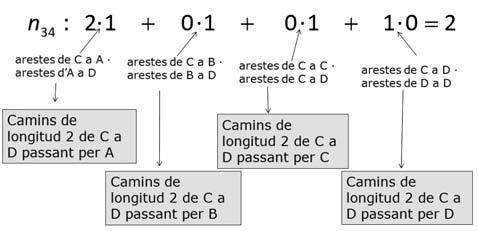
Fig.115

5.InterpretacióbasadaenlatrobadaaTicó, 2000

Fig.8

Fig.9

Fig.10

Perconsolidarelconcepte,espotescollirunaltreelement,comperexemple n14 :

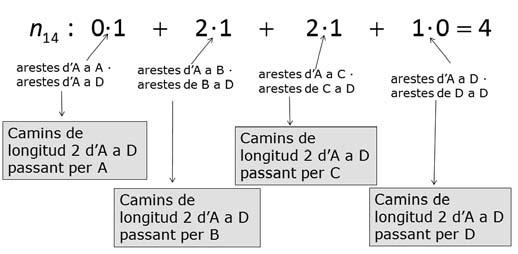
Tambéespotplantejaralrevés,talcomhofemaEstalmat(FornalsiLópez, 2013).Partint d’unamatriuinicialreferidaavolsentrediferentsciutats,elsfemcalcularlaquantitatde maneresquehihaperfercadarecorregutambdosvols(unaescala)iaixítrobenelsvalors delamatriualquadratsensesaber-ho.Desprésintentendeduirquinesoperacionscalfer perarribar-hiapartirdelamatriuiniciali,enlamajoriad’ocasions,algunalumnehoacaba descobrint.Ésdesprésquanfemaparèixerelprocésalgèbricdelproductedematrius,uncop treballatelproblemadelsponts.

Peral’alumnatdelbatxilleratsocial,resultamésassequibleaquestprocediment,jaque ladefiniciódeproductecomaaplicaciólinealresultantdelacomposiciódeduesaltres aplicacionslinealshabitualmentelsresultamoltpocengrescador.Finsitotespodenproporcionarenllaços6 apàginesenlesqualsespot«practicar»elrecorregutproposatalproblema delspontsialtressituacionsderivades,relaxantaixílatensióhabitualenunamatèriacomles matemàtiques.

7.Conclusions

Apartirdelesdiferentsexperiènciesdutesatermeendiferentsgrups(projecteEstalmat, 2ndebatxillerat,cursdematemàtiques 1rd’Enginyeria,màsterdeformaciódelprofessorat) s’hapogutapreciarlariquesadeconceptesiprocedimentsqueespodentreballarapartir delproblemadelspontsdeKöningsberg.Enaquesttreballhemintentatapuntar,totique demaneramoltresumida,aquellsaspectesqueespodendural’aula.Tambéhemprocurat pararmésatencióenaquellsaspectesquecreiemquepodenserdemésinterèspelnostre alumnat:elraonamentdelpropiEuler,larepresentaciómitjançantungrafd’unasituació concreta,lamatriuassociadaambunagrafilarelacióentreelproductedematriusiels caminsdesegonordre.

6. Laaventuradelsaber (RTVE).Capítulo6Euler[revisat: 19/07/2013]

http://www.rtve.es/aventura/universo-matematico/webcap6/index.html

ProyectoDescartes 2D.Materialesdidácticos.Bloquetallerdematemáticas:LospuentesdeKöningsberg: [revisat 19/07/2013]

http://recursostic.educacion.es/descartes/web/materiales_didacticos/rompecabezas/PuentesKoningsberg. htm

Fig.12

Elsresultatsques’obtenenambaquestmaterialsorprenenperlabonaacceptacióperpart del’alumnatiperlesgranspossibilitatsqueelsobredavantd’altressituacionsquelipuguem plantejar,augmentantclaramentelseuinterèsperlesmatemàtiquesengeneral.

Bibliografia

Biggs,N.,Lloyd,E.,Wilson,R.(1986). GraphTheory,1736-1936.Oxford:UniversityPress.

Castrillón,M.(2009).Grafosyalgunasamenidadestopológicas.DinsA.PéreziM.Sánchez (coord.), Matemáticasparaestimulareltalento:actividadesdelproyectoEstalmat (p. 19-34). Sevilla(Espanya):SociedadAndaluzadeEducaciónMatemáticaThales.

Euler,L.(1736).Solutioproblematisadgeometriamsituspertinentis. CommentariiAcademiae ScientiarumImperialisPetropolitanae,8, 128-140.

URL:http://www.math.dartmouth.edu/~euler/docs/originals/E053.pdf(revisat: 19/07/2013).

Fornals,P.,López,M.(2013).Pero,¿porquénoscomplicamostantoparaenseñarcómo multiplicardosmatrices?UnaaproximaciónapartirdelproblemadelospuentesdeKöningsberg.Dins ActasXVIJornadaparaelAprendizajeyEnseñanzadelasMatemáticas(JAEM). Palma. (Pendentdepublicació).

Hopkins,B.,Wilson,R.J.(2004).TheTruthAboutKönigsberg. TheCollegeMathematicsJournal, 35,pp. 198-207.

URL:http://www.maa.org/sites/default/files/pdf/upload_library/22/Polya/hopkins.pdf(revisat: 23/12/2013).

Recursosweb

Ticó,T.(2000).PasseigmatemàticperCatalunya.Llicènciaretribuïdacurs 1999-2000.URL: http://www.xtec.cat/sgfp/llicencies/199900/resums/ttico.html(revisat: 19/07/2013).

Jocsd’estratègiaiel currículumescolar

GuidoRamellini InstitutBoscdelaComad’Olot

Resum Abstract

L’enfocamentcompetencialde l’ensenyamentdelesmatemàtiquesobre unnouespaiperalautilitzaciódidàctica delsjocsd’estratègia,quepodencontribuir aldesenvolupamentdelesquatre dimensionsindicadesenelsdocumentsdel Departamentd’Ensenyamentdela GeneralitatdeCatalunya:Resolucióde problemes,RaonamentiProva,Connexions iComunicació,iRepresentació. Elsjocsd’estratègiaresponentambéal reptedetreballarmaterialsqueestiguina l’abastdetotamenad’alumnatide permetrequecadascúpuguiconstruir-se unrecorregutd’aprenentatgecoherent ambelsseusinteressosilasevacapacitat.

Partintdetresexemples(Torresd’Hanoi, GranotesiGripausiJocdelesFitxes), l’articleanalitzatambélesmatemàtiques queestanamagadesasotad’un apropamentlúdiciaparentmentsenzill. Pensemqueésinteressantdonara professoratialumnatocasionspera profunditzarautònomamentelscontinguts idescobrirelplaerdelainvestigació.

Thecompetenceapproachtoteaching mathematicsopensupanewspaceforthe educationaluseofstrategygames.Theycan contributetothedevelopmentofthefour dimensionsmentionedindocumentsfromthe DepartmentofEducationoftheGeneralitat deCatalunya:ProblemSolving,Reasoning andProof,Connectionsand Communication,andRepresentation. Strategygamesrespondtothechallengeof providingactivitieswithinanystudent’s reach.Theyalsoofferanopportunitytobuild alearningpathtailoredtotheirowninterests andabilities.

Furthermore,throughthreegames(Hanoi Towers,FrogsandToads,andFormand Value),thearticleexaminesthemathematics hiddenunderadeceptivelysimpleandfun approach.Wethinkitisinterestingtogive teachersandstudentstheopportunitytogo moredeeplyintothecontentand autonomouslydiscoverthepleasureof research.

Logicisinvinciblebecauseinordertocombatlogicitisnecessarytouselogic P.BOUTROUX

AlesexposicionsitallersdelMMACAienelscursetsdeformacióquefaig,soloambla PuraFornals,treballoelsjocsd’estratègiacomunaeinaperadesenvoluparelpensament matemàticdelprofessoratidel’alumnat.

Elplaerlúdicilaconnexióamblalògicabàsicahanfetquecapdocent,desecundàriaode primària,esqueixéspeltempsqueelsdedicava,peròsempreemquedavaunamicademalaconsciènciaperhaversortitdelcurrículumidelesexigènciesdeformaciómésexplícites.

Enquinllocdelcurrículumespodencol·locarelsjocsd’estratègia?L’habilitatdecàlcul necessàriaésmoltreduïda,encaraquelligadaalcàlculmental,quevoldríemméspracticata l’aula.D’altrabanda,elconeixementnecessariperadissenyarestratègiesguanyadoresiel llenguatgeperaexpressar-lessónforçacomplexosdeformular.

Acabemlligantaquestàmbitalaresoluciódeproblemes,perraonsdemètoded’apropament oprocedimentals.

Moltspedagogsressaltenelvalordidàcticdeljoc;dePiagetaVygotsky,deBatesonaBruner: noméscalescollir.Peròensinteressamésanalitzarenaquestcontextelsdocumentsdel Departamentd’Educació(2013).

Enlesquatredimensionsquefocalitza:Resoluciódeproblemes,Raonamentiprova,ConnexionsiComunicació,iRepresentació,trobemcompetènciesbàsiquesqueespodenestimular atravésdelsjocsd’estratègia.

Unaaltracoincidènciaquetroboambelsdocumentsesmentatsésladeproposaractivitats queinvolucrentotl’alumnatiprovoquenaprenentatgesegonslescapacitatsdecadascú.

Enaquestaòptica,lafacilitatperapropar-sealesactivitatslúdiquesilasimplicitatdeles reglesfanquetothompuguienfrontar-s’hi.

Aunsegonnivellpodríemcol·locarlacapacitatd’observarlessituacionsclauqueesrepeteixen enunjoc,esbossosd’estratègies:elsmovimentsguanyadorsielspassosenfalsoelscercles viciosos...oalgunesreincidènciesentrejocsdiferents,aparentmentllunyans,isomorfismes queesfanevidentsquanassumimelqueelcitatdocumentdelDepartamentd’Ensenyament (2013)indicacomagradaciómésaltad’adquisiciódecompetènciesiintentemtrobarles estratègiesguanyadores,expressadesenunllenguatgemínimamentrigorós,peraplicarlesenaltrescontextos.

Transversalmentaaquestsnivellsd’adquisiciódecompetènciesespecífiques,estaremtreballantcosestanimportantscomaralamotivació,laclassificació,elcanvidelpuntdevista, l’assumpcióielrespectedereglesirelacions,lacol·laboració,lacomunicació,lainvestigació...

Abansdepassaramostrarenl’òpticacompetencialunsexemplesdejocsd’estratègia,tots prouconeguts,m’agradariareivindicarlaintel·ligènciadelscompanysicompanyesque, desdel’ensenyament,faanysqueesdediquenaeducarjugant,convençutsdelaconnexió potentqueexisteixentrejociaprenentatge.

ElpremiGonzaloSánchezVázquezalsvalorshumansdel’ensenyament,quelaFSPMha conceditalmestreCoquePazosdurantlesJAEMdeMallorca,n’éselmillorhomenatge.

1.LesTorresdeBrahmaoTorresd’Hanoi (fig. 1)

Figura1.LesTorresdeBrahmaoTorresd’Hanoi.

Ésunjocforçaconegutiambbonespotencialitatsdidàctiques,comhodemostraunmagnífic articledeLuisBalbuena(2006).

Uncopenteseslesregles,simples,tothomhipotjugar.

Espotjugarenlíniaa:http://www.xtec.cat/~jjareno/activitats/hanoi/hanoi.htmo http://hanoitower.mkolar.org/Hanoi.html

Abansd’arribaralplantejamentfinal:Quinéselnombremínimdemovimentspertraslladar unatorrede n discos?,esdescobreixenalgunescosesinteressants:

• Siunrepteetsemblamassacomplicat,planteja’tunasituacióméssimple.Enaquest cas,començaambmenyspeces,perexemple 2 discos.

Elquecomptasónlespreguntesqueetvasfent: Quantsmovimentshenecessitat?

Enquinpalheposatelprimerdisc?

• Abansdepassararesoldreelreptedelatorrede3discos,not’oblidis,permassafàcil,del reptede latorred’unsoldisc iunsolmoviment.

• Inot’oblidisd’anotar:per 1 disc ⇒ 1 moviment;per 2 discos ⇒ 3moviments;per3discos ⇒ 8moviments;...

• Jaambelreptedelatorrede4discos,unapartdel’alumnathauràvistque,perpoder construirsobreelpalClatorrede4,hauràhagutdeconstruirsobreelpalBlatorrede3 discosisobreelClade 2.Iaixòtémoltaveureamb l’estratègiaguanyadora.

• Així,amb n torres,abansdecomençarjapucsabersobrequinpalhaurédemoureelprimer discperquèlatorrede n discosesconstrueixisobreelpalC,iestalviarmoviments.

Bonapartdel’alumnatpodràarribaracomptarelnombredemovimentsnecessarisper a 1-5torres(1,3,7, 15i31)iunapartexpressaràlaseqüènciadientque,afegintundisc cadavegada,anemaugmentantde 2,4,8i 16moviments.Jahasortitlarelacióambles potènciesde2 itothompodràvalorarquelatorrede6discosnecessitaràunmínimde63 movimentsperpassardelpalAalpalC.Quanalgunmésespavilatarribaràaexpressarlaregla 2n 1,moltshoentendranientendrantambél’avantatged’aquestamanerad’expressar l’estratègia,quenodemanasumarelspassosanteriors.

RecuperatelmagníficconteoriginarideltempledeBrahmaidelasevatorrede64discos, trobaremquecoincideixambelcontedel’inventordelsescacs(enl’últimacaselladeltauler s’haurandeposar 263 gransd’arròs,peròentoteltaulern’hihaurà 263 + 262 + 2

+ 26

+ 2

, osigui, 264 1).

Sipersatisferl’apostaambl’inventordelsescacscaldria 200 vegadeslaproducciómundial decereals,perferelsmésde 18milionsdemilionsdemilionsdemoviments,alritmed’un discperminut,seriennecessarisquasi3,5milionsdemilionsd’anys.Comveieu,faltatemps perquès’acabielmón!

Del’articledeLuisBalbuena(2006)espodentreuremoltesidees:

• ElnombretotaldemovimentspossiblesdibuixaunfractalanomenatTriangledeSierpinski ielsmovimentsguanyadorssegueixenelcostatdretdeltriangle.

Vamaprofitaraixòperacrear,dinsdelprogramaRecercaenAcció(2011),unasimulació quevampresentar,juntamentambalmaterialmanipulable,al’exposiciódelMMACAal CentreSociald’UnnimaSabadell(gener-novembre 2012).

Forçajocsd’estratègiaidematemàgiafanservirels nombresbinaris.Potserelmésfamós éselNim,quelagentdelMMACAutilitzemperlesfiresenlaversió Marienbad :

• 15pals(repartitsen4grups: 1,3,5,7);

• Cadajugadorpottreureacadajugadaelnombredepalsquevoldelmateixgrup;

• Eljugadorqueprenl’últimpalperd.

Entornaremaparlarmésendavant.

2.Granotesigripaus (fig. 2) Figura2.Granotesigripaus.

Normalments’hijugaamb3o4granotesielmateixnombredegripaus,posatsenlescaselles d’untaulerqueamésaméstéunacasellabuidaperpodermourelespeces.

Lesfitxespodenavançarosaltar(nomésunapeça)perocuparlacasellabuidainoespot tornarenrere.

Moltsenzilldejugar,perònotantderesoldre.

Alcapd’unsquantsintents,escomencenareconèixersituacionsquerepresentenun obstacleinsuperableiques’hand’evitar.Resoldreunavegadaelreptenosignificahaver entèsl’estratègiaguanyadoraicaljugar-himésvegadesperarribaraconsolidar-la.

Abansdeplantejar-nosquinéselnombremínimdemovimentsper n granotesi n gripaus, ésinteressantobservaratentamentlasimetriaeneldesenvolupamentdeljoc.

Aquítambéésmillorcomençarambunnombrereduïtdepeces,registrantdemanera ordenadaelsmovimentsqueesfan:

1 granota(g)i 1 gripau(G):Avançag;[SaltaG];Avançag 2 granotes(g)i 2 gripaus(G):Ag;SG;AG;Sg;[*];Sg;AG;SG;Ag 3granotes(g)i3gripaus(G):Ag;SG;AG;Sg;Sg;Ag;SG;[SG];SG;Ag;Sg;Sg;AG;SG;Ag

Aquestreculldedades,queespotferambunfulldecàlcul,dónamoltesindicacions; evidencia:

• comelsmovimentsdelespecessónsimètrics(l’elementcentraldelasimetriaestàposat entre[*]):

exemple(amb 2 gi 2 G):A,S,A,SS,A,S,A

• comlasimetriaesmantéintroduintlavariabledegranotesigripaus:

exemple(amb 2 gi 2 G):Ag,SG,AG,SgSg,AG,SG,Ag

Iaquestadoblesimetria(moviments,peces)ésmantéaugmentantelnombredepeces (i,òbviament,demovimentsperintercanviarposicionsdegranotesigripaus).

• Ésinteressant,comapascapaldescobrimentdelafórmulaquerelacionaelnombrede movimentsieldegranotes,anotarlasumademovimentsd’AvançadesiSalts: n = 1: A = 2, S = 1 Tot = 3 n = 4: A = 8, S = 16Tot = 24 n = 2: A = 4, S = 4Tot = 8 n = 5: A = 10, S = 25Tot = 35 n = 3: A = 6, S = 9 Tot = 15 ···

Simiremelsmovimentstotals,éspossiblequealgúarribiaformular: m = (n + 1)2 1 ⇒ m = n2 + 2n + 1 1 = n2 + 2n

Simiremelsmovimentd’AvançamentiSalt,trobaremAn = 2n iSn = n2

Figura3.Variacionsdelnombredesalts(S),avançades(A)imovimentstotals(T) enrelacióalnombredepecesdeljoc.

Unabonaanàlisideljocestrobaenlafitxadelacol·leccióJuegosdeIngenio(2003).

Espotjugarenlíniaa:http://www.xtec.cat/~jjareno/activitats/granotes/granotes.htm http://akidsheart.com/math/mathgames/leapfrog.htm

3.Eljocdelesfitxes

Elvaigdescobrirenl’ediciód’estiud’undiariitalià,quans’ompleelbuitdenotíciesampliant lasecciódepassatemps.

Elcàlculil’estratègiaquedemanasónproufàcils,peròlacombinaciódelsdospotresultar motivadoraperal’alumnatdeprimària,aixíquehemincorporataquestreptealanostra col·lecciódematerialsiconstrucciód’unmòdulperalesexposicions.

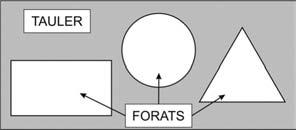
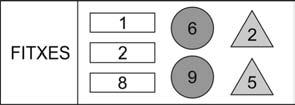
Figures4i5.Tauleripecesdeljocdelesfitxes.

Elrepteconsisteixaobtenirdeterminatsvalorsencadaforatdeltauler,posant-hilesfitxes necessàriesitenintencomptequeunafitxaposadaenunforatdelamateixaformadoblael seuvalor.Perexemple(fig.6):

Aquestreptecorrespona:RECTANGLE: 12 (2 × 2 + 2 + 6)

CERCLE: 19 (9 × 2 + 1)

TRIANGLE: 18(5 × 2 + 8).

Hemelaboratunadotzenad’aquestsreptes,queespodenproposarambmaterialsde diferentsqualitats(dimensions,disseny,consistència,pes...)perdural’aula,atallersdeleses-

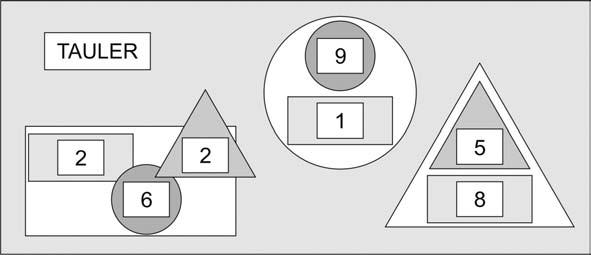
Figura6.Exempledesoluciód’unreptedeljocdelesfitxes.

colesodelMMACAoaexposicionsifires,ambbonaacollidatantdelpúblicescolarcomdel públicengeneral.

MarcusDuSatoy(2012)fareferènciaalsproblemesNP-complets,osigui,aquellsenquè«hiha unnombreimmensdesolucionspossibles».Ésadir,noespotarribaradissenyarunalgoritme queensdonitoteslessolucions.DuSatoy(2012)diuque,siestrobésaquestalgoritme,seria elmateixperatotselsproblemesd’aquesttipus.Altext,l’autorposal’exempledelspartits defutbolidelescomplicacionsquevaprovocarpassard’unasituació:PARTITGUANYAT = = 2 punts;EMPATAT = 1 punt,al’actual:PARTITGUANYAT = 3punts;EMPATAT = 1 punt. Calcularquinsresultatsdetotselspartitsdetotselsequipsserienfavorablesalnostreequip perfer-loguanyarlalligas’hatransformatenunproblemaNP-complet.

Aquestalecturaemvacanviarlapercepcióqueteniadeljocdelesfitxes,jaquedecopemva semblarque,rereunenfocamentsimple,amagavaunesmatemàtiquesmoltméscomplexes.

Quèsabem?

• Elvalormínimquepodensumartoteslesfitxesuncopcol·locadesésde33(sicapfitxaés enunforatdelamateixaforma)ielmàxim,naturalment,66(toteslesfitxeshandoblatel seuvalor).

• Col·locantoportunamentlesfitxespodemobtenirtotselsvalorsentre33i66.

• Moltsvalorsespodenobtenirambmésd’unacombinaciódefitxes(el66evidentmentno. Però:iel33?).

Suposoque,finsaquí,podríemintentarcalcularquantespossiblescombinacionsesdonen, encaraquesiguinmoltes(mésde 2.000)ieltreballprouavorrit.

Però,quanintroduïmelsvalorsquecorresponenacadaforat,lacosacanviaiNOtotesles combinacionspossiblesperobtenirlasumadelsvalorsdelsforatsseranacceptables.

Tindremsolucionsúniquesomúltiplesoimpossibles.

Perexemple:hihauràmoltesmaneresd’obteniruntotalde44:1

1 R = foratrectangular; C = foratcirculari T = forattriangular r = fitxesrectangulars; c = fitxescircularsi t = fitxestriangulars

R15(c9 + r 1 = 2 + r 2 = 4); C 17(t 5 + c6 = 12); T 12 (r 8 + t 2 = 4) R6(r 1 = 2 + r 2 = 4); C 17(t 5 + c6 = 12); T 21 (r 8 + c9 + t 2 = 4) R11 (t 5 + r 1 = 2 + r 2 = 4); C 12 (c6 = 12); T 21 (r 8 + c9 + t 2 = 4) R6(r 1 = 2 + r 2 = 4); C 25(r 8 + t 5 + c6 = 12); T 13(c9 + t 2 = 4) etc.

Noméscanviantdeforatelsvalorsquenodoblenespodenobteniraltresvariants,comenel casdesuma = 33.

Peròhihaurànomésunasolucióperfer:

Icapperfer: R20; C 10 i T 14.

Podríempreveuresihihacaracterístiquesgeneralscomunesatoteslescombinacionsimpossibles?Iquantesn’hihaurà?

Vistaixí,elmòdulsemblatenirtotselsrequisitsquedemanaunproblemaNP-complet.

ÉsevidentqueaquestaanàlisiestàdirigidaalprofessoratifinsitotnoaTOTelprofessorat, sinóaaquell(e)scompany(e)squetinguinganesd’investigarelterrenyqueenvoltalanostra feinadeprofessors.

Tornantal’alumnat,quèpodemesperarcomaactitudiadquisiciódesprésd’untreballamb elsjocsd’estratègia?

RecordeulanostraversióMarienbaddelNimilessevesregles?

Són 15pals(repartitsen4grupsde 1,3,5,7pals);cadajugadorpottreureacadajugadael nombredepalsquevoldelMATEIXGRUP;eljugadorqueprenl’últimpalperd.Doncs:

LaImprobableAlíciaploriquejavadavantdelGat:

«Heperdutundelspalsqueemvasdonar!Justamentara,quehaviaentèscompodia guanyarqualsevoladversari...»

«Quinasortquehastingut! lireplicavaelGat .Aratensunnoujocpercomprovarsi lestevesestratègiesencarasónvalides.Ivésambcompte:noéselmateixsielpalperdut éselquetotsolformavaungrupoelqueanavaambelsaltres.Amigameva,ésaraquan comencenrealmentaentrarenjoclesmatemàtiques...»

Idientaixò,elGatvacomençaradesaparèixer.Jas’esfumavaelsomriuremisteriósdel Gat,queunsomriurenomenysmàgicesformavaalsllavisdel’Alícia,mentredinselseu capanavaanalitzantlesvariantsd’unjocquetornavaaserunrepte.Iperaellasola!»2

Perquè,comdeiaJohnBelushi:«Whenthegoinggetstough,thetoughtgetgoing!».

GràciesalaPurailaFinaperrevisarformaicontinguts.

2.DedicatalToni,alumnede6èdeprimàriadelCEIPElPolvorí,quevatenirlapossibilitatd’escollirentre l’opciómésfàcil idolça desubstituirelpalperdutdelNimquelihaviaregalatambelpald’unpolool’elaboració denovesestratègiesperaljocamb 14pals.Opciómésdifícil,naturalment,iambelgustsalatdelasuor.

Bibliografia

Departamentd’Educació(2013):http://www20.gencat.cat/docs/Educacio/Home/Departament /Publicacions/Col_leccions/Competencies_basiques/competencies_mates_primaria.pdf; http://www 2 0 .gencat.cat/docs/Educacio/Home/Departament/Publicacions/Col_leccions/ Competencies_basiques/competencies_mates_ESO.pdf

Balbuena,L.(2006).LasTorresdeHanoiyelMandatodeBrahma. Sigma, 28,83-94.

Recercaenacció(2011).Matemàtiquesalavista.http://www.recercaenaccio.cat/agaur_reac/ AppJava/ca/diari/20120110-missatge-1-les-.jsp.

Diversosautors.(2003).RanasySapos.Dins JuegosdeIngenio (fitxa34).Barcelona:OrbisFabbri.

DuSatoy,M.(2012).Elsecretodelarachaganadora.Dins Losmi5teriosdelosnúmer6s (p. 192-196).Barcelona:Acantilado.

Lestaulesdemultiplicar atravésd’imatges

MariaBras-Amorós1 UniversitatRoviraiVirgili

Resum Abstract

Proposemunconjuntd’activitatsdirigides aungrupd’alumnesquejaconeguinles taulesdemultiplicariestrobinenel procésdememoritzar-les.Espreténdonar unaprenentatgevivencialdelestaulesde multiplicarifacilitar-nelamemoritzacióa travésd’imatges,almateixtempsque intentemconferiral’infantunamirada matemàticainumèricadelarealitat.

Someactivitiesareproposedforagroupof studentswhoalreadyknowthe multiplicationtablesandareintheprocess ofmemorizingthem.Thegoalistoprovide anexperientiallearningofthemultiplication tablesfacilitatingtheirmemorization throughimages,whileconferringonthe infantamathematicalandnumericalview ofreality.

1. Desenvolupament

• Sortiremalpatidel’escolaoaalgunpuntpropericomptaremquantesfinestrestél’escola.Sil’ordenamentdelesfinestresnoésendistribuciórectangular,aleshoresbuscarem algunedificidel’entorn.Motivaremqueelsalumnesdedueixinperellsmateixosque espotcomptarunconjuntd’objectesordenatsendistribuciórectangularutilitzantel producte.

Silaprimeraexplicaciónolapodemferambunexempledefinestres,convébuscarun altreexempleenquèelsobjectessiguinmínimamentgrans.Peraexemplesposteriors japodremutilitzaraltresobjectesméspetitscomelstimbresolesbústies.

• Proposaremalsinfantsquefacinunacercaforadel’escola,enelseutempslliure,de distribucionsrectangulars perl’arquitecturadelseuentorniquen’aportinimatgesa laclasse.Interessaquesiguinimatgesd’espaisexteriors,accessiblesperaqualsevol companyi,preferiblement,espaisqueresultinfamiliarsaunamajoriadelsinfants.

• Uncopaportadeslesimatgesalaclasse,demanaremalsinfantsqueensexpliquind’on éscadaimatgeiquinsobjectescomptemi,òbviament,aquinproductecorresponi ambquinresultat.

• Podensorgirdubtesinteressants,comenelscasossegüents: Quelescolumnesnosiguinequiespaiades.

Figura1.Finestresdel’escolaSt.PereNolasc,aSt.AndreudePalomar.

Figura2.TimbresdelaCasaBlocaSt.AndreudePalomar.

Queelsobjectesdecadafilasiguindiferents.

Queelrectanglenosiguipla.

Quelafigurageomètricadibuixadanosiguiunrectangle, sinó,simplement,unparal·lelogram.

Figura3.AjuntamentdeSt.AndreudePalomar.

Figura4.MiradordeSt.JeroniaMontserrat.

Figura5.Torredela Miranda,aCornellà.

• Entrelesimatgesquerepeteixenproductes,espotferunaselecciópervotacionso, simplement,prioritzantperalgundelscriterissegüents:

imatgesquesiguinmésfamiliars, imatgesenquèelrectanglesiguimésclar, imatgesquepermetinnorepetirtantelsmotius(quenototsiguinfinestres,per exemple).

• Amblesimatgesaportadespodemcomençaraconstruirlestaulesdemultiplicar damuntd’unacartolinaounpaperd’embalar.

Primerdibuixaremlagraellaperpoderomplir-ladesprés(figura6a).

Suggerimnodesenvoluparlatauladel’1 niladel 10 enaquestaactivitat,aixícom tampocelprimerniúltimproductedecadataula,corresponentamultiplicarper 1 iper 10.Latauladel’1 potresultarconfusaenelcontextqueplantegem.D’altrabanda,no treballaremlatauladel 10 perquèconvéqueelnombred’imatgestreballadesnosigui massaextens,pertaldefacilitar-nelamemorització.

(a)

(b)

(c)

Figura6.Construcciódeltauler.

Podemutilitzarl’espaidelataulacorresponentalsproductesomesosperaferunmarc iescriure-hielsnombresdel’1 al 10 ielsmúltiplesde 10,que,defet,sónelsvalorsque correspondrienalesrespectivescaselles.

Peromplirlataulaposaríem,perexemple,enelllocdel 2 × 4,unafotografiad’una finestraamb8vidresdistribuïtsen4rengleresde 2 vidrescadascuna.Posaremla mateixaimatgeper 2 × 4queper4 × 2.Aixíseràmésfàcilvisualitzarlacommutativitat ihihauràmenysimatgesamemoritzar.

• Identifiquemambelsalumneslesdistribucionsrectangularsquefalten(figura6b).

• Deixemunsdiespertalqueelsalumnesaportinlesimatgesquefaltenpercompletarla taulaobéfemunasortidaperl’entornimmediatdel’escola,ambl’objectiudetrobar-les.

• Completemlataulailapodempenjaralaparetdelaclasse(figura6c).

• Paral·lelament,plastificaremunacòpiadecadafoto(duplicantlesfotosqueno corresponguinanombresquadrats),demaneraqueensquedinuntotalde64cartes (figura7a).

Ambaquestescartesproposemunsquantsjocsperacabardefamiliaritzarelsalumnesamb lesimatges.Elsmateixosinfantspodeninventaraltresjocs.

Peraalgunsdelsjocsseràmillordividirlaclasseengrupsdequatreosisalumnes,demanera queaniràbétenirunesquantesbarallesdecartes.

• Jocsimple. Ambtoteslescartesgiradescapperavall,lesanemdestapantunaaunai hemd’endevinarquinproducteésiambquinresultat.Amesuraquelesanemdestapant podemanar-lescol·locantenuntaulerbuit(figura7b).

• Jocdememòriadeferparelles(o memory ). Podemjugaraljocclàssicambdues petitesmodificacions(figura7c):

Perpoderquedar-nosunaparella,abanshemdedirdequinamultiplicacióestracta iambquinresultat.

Lescartescorresponentsaquadratsenslespodemquedarsensehaver-losdetrobar parella(perquènoentenen!).

• Dòmino. Estractadeldòminoclàssic,peròenquècadafitxaésrepresentadaperuna multiplicació.Seràmésfàcilsitraiemlescartesrepetides.El6 × 3elpodríemencadenar ambel3 × 7iaquestambel7 × 2,etc.(figura7d).

Demanaremquecadajugador,abansdejugarcapcarta,diguidequinamultiplicació estractaiquinn’éselresultat.

Perdonarunpapermésrellevantalsquadrats,podemimposarquelescartescorresponentsaquadratsobliguinaferungiralacadenadecartes.

Tambépodemintentarveurequinaéslacadenamésllargaquepodemfer.

Figura7.Jocsdecartes.

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

• Jocdelestresparelles. Esreparteixen6cartesacadaparticipantil’objectiuésobtenir tresparellesdecartesiguals.Siaconseguimunacartacorresponentaunquadrat,ella solajacomptacomaparella(figures7ei7f).

Almighihauràduespilesamblescartesquequedinsensehaver-serepartit:unapila capperamuntil’altracapperavall.Fentunaronda,elsjugadorspodenoptarperagafar laprimeracartavisibledelapilaqueestàcapperamuntolaprimeranovisibledela pilaqueestàcapperavall.Desprésn’handedeixarunadevisiblealapilaqueestàcap peramunticantardequinamultiplicacióestractaiambquinresultat.Siunjugador s’equivocaperduntorn.

Sienalgunmomentesbuidalapilaqueestàcapperavall,aleshoresesparteixl’altra pilaperlameitatise’nfanduesdenoves.

Guanyaelprimerjugadorqueobtétresparelles.

• Bingo. Cadaparticipants’hadeferunallistade6nombresdelsquesurtinalataula (quèsignificaqueunnombresurtialataula?)iensenyar-laalscompanys.Aleshoreses posentoteslescartesdinsunabossaderoba.Fentunaronda,cadaparticipanthade treureunacarta(figura7g)ideixar-laalmigoaunllocvisiblepertotselsparticipants. Elsparticipantshaurandefixar-sesitenenalasevallistaelvalordelamultiplicació corresponentalacarta.Guanyaelprimerparticipantlallistadelqualcorrespontotaa valorsquehananatsortint.Elsaltresparticipantsfaranlacomprovació.Siunparticipant esproclamaguanyadorerròniament,quedaeliminatfinsalapartidasegüent.

Desprésd’haverjugatunesquantesvegades,elsjugadorshauriendedescobrirquehi hanombresmésbonsperposaralallistaqued’altres.Elsmillorssónelsquetenenmés divisorsmenorsque 10.Perexemple,el49 nomésésrepresentatperunacartai,per tant,noésgairebonaopció.Encanvi,el63ésrepresentatperduescartesoel 24és representatper4cartes,queésmoltmillor.

• Finalment,tambéproposemquelescartess’utilitzinquans’hagid’escolliralgunalumne perferalgunacosadeldiaadiadel’auladelamanerasegüent:Esposentotesles cartesdinsunabossaderobaicadaalumneentreuuna.S’esculll’alumnequetreuun productemésalt.Sielproductemésalteltenenrepetitmésd’unalumne,aleshores aniremrepetintentreelsempatatsfinsquenomésenquediun(figura7h).

2. Objectius

• Pretenemdonarunaprenentatgevivencialdelestaulesdemultiplicarifacilitar-nela memoritzacióatravésd’imatges.Peraixòconvétreballarambimatgesfamiliarspera l’infanti,preferiblement,imatgesqueesvisualitzinquotidianament.

• Intentemconferiral’infantunamiradamatemàticainumèricadel’entorn.

• Incentivemlainquietudperlarecercadefetsmatemàticsdelarealitat.

• Visualitzemfàcilmentlacommutativitatdelproducteperlasimetriadelataula.

3. Ampliació

• Podemaprofitarl’activitatperaintroduirelconceptedenombre quadrat.

• Tambépodemaprofitarperaintroduirelconceptedenombreprimerdesdelaperspectivadelsgrecs,comanombrequenoadmetuna representaciórectangular.Peraixò ésconvenientnohaveromplertlatauladel’1

Referències

Canals,M.A.(2009).NombresioperacionsII,volum 109 de Dossiers.AssociaciódeMestres RosaSensat.

Canals,M.A.(2009).Primersnombresiprimeresoperacions,volum 101 de Dossiers.Associació deMestresRosaSensat.

Giménez,J.,Girondo,L.(1990). Càlculal’escola:reflexionsipropostes.Barcelona:Graó.

Dedicatòria i agraïments

AquesttreballvadedicatalaMariaTeresaOlivaBastéiatotalasevafamília,quen’hanestat lafontd’inspiració.Agraïmlacol·laboraciódelaBibliotecaIgnasiIglésias-CanFabra.

Nota sobre les imatges

Toteslesimatgesdel’articlehanestatfetesperl’autoraalbarrideSantAndreudeBarcelonaexceptelaimatgedelaTorredelaMiranda,alParcdeCanMercaderdeCornellà,extretadelapàginawebhttp://commons.wikimedia.org/wiki/File:Torre_de_la_Miranda,_Cornell%C3%A0 de_Llobregat-2.JPG?uselang=caideladeSantJeroni,aMontserrat,extretadelapàginaweb http://www.shbarcelona.com/blog/en/a-day-trip-to-montserrat.

seccions seccions rcions

pensar per pensar d’un minut a una hora

JordiDeulofeu

DepartamentdeDidàcticadelaMatemàtica idelesCiènciesExperimentals UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

Dedicaréelmeuarticleapetitsigrans,segonscomesmiri,problemesdenombresi començaréambalgunesqüestionselementals,paraulaquenosempreéssinònimade simple,delqueconeixemcomadivisibilitat.Sovint,quanestreballaaquesttema,tanta finalsdeprimàriacomal’inicidel’ESO,lestasquesproposadesalsalumnessecentrenen exercicisperadeterminardivisorsomúltiplesd’unnombreilestècniquesperafer-ho,obé trobarelm.c.d.i/oelm.c.m.apartirdeladescomposiciód’unnombreenfactorsprimers. Comamolt,esfanalgunsproblemesestàndardd’aplicaciód’aquestsconceptes,sensetenir encomptequelafinalitatdeltreballsobreladivisibilitatnoéstantladefercàlculs,sinólade conèixerelsnombresilessevesrelacions,aixícomlespropietatsqueesderivendelaseva descomposicióenfactorsprimers.Pertant,elscàlculscaldràfer-losquansiguinecessariper aresoldreundeterminatproblema,jaque,sinohihaproblemesperresoldre,quinsentit tenentotsaquestscàlculs?

Perexemple,talcomm’explicavafaunsdiesenDavidBarba,apropòsitd’unaactivitatquela CecíliaCalvohaviatreballatambelsseusalumnesd’ESO,enllocdedemanar-losquecalculin elsdivisorsdetalitalnombre,perquènoproblematitzemlaqüestióielsfemlapregunta (problema 1):quinéselnombrededuesxifresquetémésdivisors?Aixòés,almeuentendre, apropar-seaaquellaideatansuggerent,iqueheesmentatmésd’unavegada,queens proposaval’amicPauloAbrantes:generaral’aulaunambientderesoluciódeproblemes.A vegadesnocalplantejar«grans»problemesiunaqüestiócomlaproposadapotesdevenirel motorperatreballarnombrososaspectessobreelsnombresiladivisibilitat.

Noésgairedifícild’imaginarqueenresoldreelproblemaanterioresfaranunapiladecàlculs dedivisors,peròaméscaldràanalitzarl’estructuradeladescomposiciódelsnombresen factorsprimersi,endefinitiva,pensarenlesrelacionsdedivisibilitat.Latascaanterioresva ferenunasessiód’exercitacióperconvertirl’exercicidetrobarelsdivisorsdecertsnombres (trobaD(24),D(27),D(36)iD(52))enunreptemésgeneral,plantejatdemaneracol· laborativa, repartintelsnombresentreelsdiferentsgrupsiresolentelproblemaenunaposadaencomú final.Amésdepassar-homoltbé,elsalumnesnosolamentvantrobarunapiladedivisors, sinóquevanpoderreflexionarsobreperquèunsentenienmoltsialtresmoltpocs.

Ésclarque,apartirdelapreguntaanterior,enpodensorgird’altres(problema 2):quins nombresdeduesxifrestenenunadescomposicióambnomésunfactorprimer?,laqual cosaenspotportaraparlardelespotències;obé(problema3):quinsnombrestenen unadescomposicióenquètotselsfactorsprimersnomésapareixenunavegada?Sinous n’heuadonat,proveuquèpassaambl’anyactual, 2014,elseuanteriorielposterior(les descomposicionsdel 2012 idel 2016tenenunaestructuradiferent),iuspodeuplantejarsi aixòpassagairesovinto,ditd’unaaltramanera,quanvapassarperdarreravegadaiquan tornaràapassar.Cadascúdecidiràsienaquesttipusdetreballesvolrestringiranombres deduesxifres,detresomésgrans,ifinsaquinpuntésinteressanttrobar-lostots.Aquesta ésunadelestasquesquetenimcomaprofessors:determinarladificultatdelrepteque proposemalsnostresalumnesidecidirfinsonvolemarribar.

Seguintambelmateixtema,peròpensantennombresmésgrans,aquíteniuunparellde problemescuriosos,elprimerdelsqualsvaigtenirl’ocasiódetreballarambelsamicsdel Garraf,enelquartberenarmatemàticorganitzataVilanovaperenPepSalesienJoanGómez, el 22 denovembrede 2013,alqualemvanconvidar:

Problema4:Quinéselnombremésgrandesetxifres,totesdiferents,queésdivisibleper cadascunadelesxifresqueelformen?Tingueuencomptequenopothaver-hielzeroique aixòjaenspermeteliminaralgunaaltraxifra.

Seguintambnombresgrans,aquíenteniuunaltredeproucuriós:

Problema5:Amblesxifresdel’1 al 9,formemunnombredenouxifrestotesdiferents. Quinhadeseraquestnombre(onombressihihamésd’unasolució)siquanescrivimla primeraxifra(s’enténquecomencemaescriureelnombreperl’esquerra)elnombreha deserdivisibleper 1;quanescrivimlasegona,elnombrededuesxifresquearatenimhade serdivisibleper 2;quanescrivimlatercera,elnombrehadeserdivisibleper3,iaixífinsal final,enquèobtindremunnombredenouxifres,quehadesermúltiplede 9?Perexemple, elnombre 123456789 noéssolució,jaque 1234noésdivisibleper4, 1234567noésdivisible per7,i 12345678nohoésper8.

Problema6:Unproblemasimilaral’anteriorseriaconstruir,comabans,unnombredenou xifrestotesdiferents,fent-hod’esquerraadreta,peròdemaneraqueelssuccessiusdivisors, queenelprimercaserenelsnombresdel’1 al 9 ordenats,arahaguessindeserelsnombres corresponentsaladarreraxifraescrita.

Tésentitplantejarelsmateixosproblemes emrefereixoalsproblemes5i6 ,peròtenint encomptequeanemformantelnombrecomençantperlaxifradeladretaiprocedimcapa l’esquerra?Perquè?

Seguintambl’úsdelesnouxifres,usproposounaconegudarecreaciómatemàtica,d’una certadificultat,laresoluciódelaqualensremettambéaqüestionsdedivisibilitat,jaquesi intentemresoldre-laemprantnomésassaigierrorésdifícilarribaralasolució.L’hetreballat sovintaEstalmatitambéenunconcursderecreacionsmatemàtiquesdelaSetmanade laCiènciade 2013al’institutRoviraiFornsdeSantaPerpètua,dinselmarcdelprojecte Tàndem, ambargumentsinteressantsdelsalumnesperexplicarcomhan trobatlasolució, queésúnica.

Problema7:Situarelsnombresdel’1 al 9 enlescasellesdelataulasegüentdemanera queescompleixinlesigualtatsdelstresproductesindicats(s’enténquenoespotrepetircap dígit):

Deixemladivisibilitat,peròseguimambelsnombres,iconsideremaquellsqueexpressen quantitatsenormes.Aquestcurss’haposatenmarxaelmàsterinteruniversitarideformació delprofessoratdesecundàriadematemàtiques,enelqualparticipenlesdiferentsuniversitats catalanesquefinsaraimpartienelmàster(UAB,UB,UOC,UPCiUPF).Lalliçóinauguralla vaimpartirenJosepPla,que,enunamagníficaconferència,ensvaparlardel’existènciaen matemàtiquesatravésdecinccontes,alfinaldecadascundelsqualsvapresentarunseguit deqüestionsiproblemes.

Apropòsitdelprimerconte,laconegudallegendadel’inventordelsescacs,desprésde mostrar-noselnombrequecorresponalnombretotaldegransdeblatqueresultade fer 264 1,unmagníficexemplardevintxifres: 18.446.744.073.709.551.615,enJosepva reflexionarsobrelasevaexistència:existeixentotsaquestsgransdeblat?Hanexistitmai?

Podemparlard’unaexistènciareal mónfísic id’unad’ideal mónmatemàtic ?També ensvapresentaralgunesqüestionsqueusproposoacontinuació:

Problema8:Observaeltempsquetriguesacomptarelssuccessiusnombres.Quanttemps trigariesacomptartotselsgransdeblat?Aquesttempséssuperioroinferioral’edatde l’univers?

Problema 9:Imagina’tqueescriuselsnombresunacontinuaciódel’altre,començantper 1 iacabantpelnostrenombredevintxifres.Quantesxifreshauràsd’escriure?Quansblocsde DINA4,decentfullscadascun,escritsperlesduescares,necessitaries?

Siencaranousheumarejatambaquestsnombresimmensos,penseuenaltresquantitats querequereixinnombressemblants,jasiguiapartirdesituacionsdelarealitat,comper exempleelnombred’Avogadro(6,02214179 × 1023 ),ensituacionsdejocsd’atzar(dequantes maneresespodenordenarles52 cartesd’unabaralla?)oensituacionsmatemàtiques,com perexemplelasegüent:quinéselnombremésgranquepodeuescriureemprantnoméstres xifres?Totsaquestsnombresqueheutrobatsónmajorsomenorsqueelnostreprotagonista?

Comnopodiaserd’unaaltramanera,acabaréambunproblemadenombresnaturalsqueem vanproposarlaMartaBeriniil’AntoniGomà.Ésforçasenzill,peròajudaareflexionarsobre elsignificatdelesxifresqueconstitueixenunnombre,especialmentperquè,comveureu enllegirl’enunciat,aquestsignificatpotserdivers,inosempreéssenzillfercompatibles diferentssignificats.

Problema 10:Suposeuqueescriviuunnombrede n xifres:quinhadeserelnombresi volemquelaprimeraxifra(ladel’esquerra)indiquielnombredezerosquetéelnombre quehemescrit,lasegonaxifraindiquielnombred’uns,laterceraelnombrededososiaixí successivament.Perexemple, 2020 compleixlescondicions,jaquetédoszeros,capu,dos

dososicaptres.Compodeusuposar,hihauràmésd’unnombrequecompleixiaquestes condicions;peròn’hihamoltsopocs?Unavegadatrobats,sabríeujustificarquenon’hiha capaltre?

Finsaquíl’articled’avui.Esperoretrobar-vosenelpropernúmerodelarevistaiusprometo queenaquestaocasióeltemanoseranelsnombresnaturals,nipetitsnigrans.

Cartaaquicomençaen l’oficid’ensenyar matemàtiques

Benvolgutamic,benvolgudaamiga:

Estàscomençantenunaprofessióenlaqualpotssermoltfeliç!Ensenyarmatemàtiquespot serunadelesaventuresmésapassionantsdelatevavida.Tindràselprivilegidetransmetre aaltrespersonesalgunsdelsconeixementsmésformidablesquehacreatl’ésserhumà,els ajudaràsadescobrir-nelabellesainterna,l’encantdelsseusreptesilasevautilitatpera analitzar,interpretaripreveureelmónqueensenvolta.

Agraeixotenirl’oportunitatd’adreçar-teaquestacartapercompartirambtualgunesdeles cosesquem’agradariahaveraprès(notincclard’haver-lesapreses!)alllargdelsanysen quèheexercitl’oficid’ensenyarmatemàtiques.Jaséqueunesquantesideesescritesenun papernopodensubstituirelseguitd’experiènciesqueaniràsvivintalesaulesiqueaniran construint-tecomadocent,peròcrecqueamim’haurienestatútilsidesitjariaquetambé te’nfossinatu.Gràciesperdedicar-hiunsminutsallegir-les!

Amesuraquehanpassatelsanysheanatessentmésconscientqueunadelesresponsabilitats mésgransquetéundocentésadministrarbéeltempsdelsseusalumnes.Acadaclasse, ungrupdejovesposaalestevesmansundelsbénsmésvaluososqueté:elseutemps. Aprofita’l,noperfermoltescoses,sinóperfer-lesmoltbé!

Bensegurquehihauràdificultats,desencisos,dubtes,pors...nototseràfàcil,perònodeixis maiqueaquestsmalsmomentsetrobinlesganesd’ensenyarmatemàtiques,lail·lusióper motivarelsalumnes.Mostraaquestentusiasme,perquès’encomana!Moltsdiesetsortiràde dins,peròhihauràdiesdifícils.Aquestsdiestambémostra’tentusiastaiacabaràssentint-te’n.

Intentaquelasuccessiódeclassesnosiguimonòtona.Particularitzalaclasse.Cadadiapotser especial:unaefemèride,unaideanovaqueavuitractarem,unproblemamoltinteressant,un materialsorprenent,unadinàmicadetreballdiferent...Intentaintroduircanvisenlesteves classes,noreprodueixisautomàticamentlamaneracometvarenensenyar,experimenta

possiblesmillores,noetconformisafer,cursrerecurs,toteslescosesdelamateixamanera, introdueixnousrecursossensepressaperòsensepausa...elsteusalumnest’hoagrairanitu etmantindràsprofessionalmentjove!

Tinguesencomptequecadanenonena,noionoiaésdiferent.Téelseucaràcter,lesseves aficions,elseuentornfamiliar...Adinsdelestevesclassesnoexisteixaixòque,avegades, s’anomena«l’alumnat»,existeixenalumnesconcrets,cadascunicadascunaamblesseves capacitatsilessevesemocions,amblessevesporsilessevesil·lusions,ambelsseuspunts fortscomaestudiantilessevesdificultats...evitalesvaloracionsgenerals,intentaentendre acadauiindividualitzaeltracte.Sempret’agrairanunasalutaciópelpassadís,unamirada afectuosa,uncopal’esquena,unafelicitaciópersonaloladiscrecióenunavíssobreaquell aspectequecalmillorar.

Gestionabéelserrorsdelsteusidelestevesalumnes.Tinguesencompteque,ensituació d’aprenentatge,l’errornoésunfracàs,sinóunmissatgequecalsaberllegirperconvertir-lo enunaoportunitatdemillorar.Sietprecipitesdonantal’errord’unalumneod’unaalumna unacàrregamoltnegativaperdràsl’ocasiódetreure’nprofit.Ajudaqueellmateixoella mateixaeldescobreixiielcorregeixi.Tupotsdetectarl’error,perònooblidisquel’autèntica correcció,laquearribaalfonsdel’aprenentatge,tansolslapotfercadaalumne.

Igestionabéelsteuspropiserrors.Noexisteixlaclasseperfecta!Quansurtisdeclassenoet desesperissinohaanatbé.Nitotdepèndetu,nitotelquefacisseràsempreencertat.Tothom s’equivoca:tindràsunaerradamatemàticaofaràsuncomentariinadequatopreguntaràsa quinohauriesdepreguntaronovaloraràsallòquehauriesdevalorar...peròaprendràsdels teuserrorsi,sielsassumeixesambnaturalitat,tambén’aprendranelsteusalumnesilesteves alumnes.

Avegadeshauràsfettotelquehaspogut(iencaraunamicamés!)idespréslescosesno anirancomvoldries;avegadeselsresultatsnoserantanbonscomesperavesonot’acabaràs d’entendreambalgun/aalumne/a,perònoetdesanimisfàcilment.Reflexiona,aprèn,intenta millorarigaudeixdetoteslescosesquesíquesurtenbé,aquellaprenentatgequehaquedat benclar,aquellsalumnesquemostrenmoltd’interès,aquellgrupqueestàmillorant...Mai t’instal·liseneldesànimoenlaqueixafàcilacurtterminiperòerosionantallargtermini (fes-hopelsteusilestevesalumnesperòsobretotfes-hopertu!).Cercaconstantmentraons peramantenirunaactitudpositiva,especialmentquanetcostitrobar-ne!

Pelquefaal’avaluació,tinguesunamiradaàmpliainoprenguiscomareferèncialateva experiènciapersonalolestevescapacitats.Deixaclareslesreglesdejocelprimerdiai sigues-hicoherentalllargdelcurs.Elsteusalumnesacceptaranquesiguismésdur/aomés tou,perònoquesiguisarbitrari.

Coneixelcurrículum,perònote’lprenguiscomunanormatancada,sinócomunaporta obertaalainnovació.Planifica,programa,perònosiguisesclaudelsteusplans.Elsdocuments podenajudar,peròlarealitatésl’aula.Adapta’t,siguesflexible.Siutilitzesllibredetextno deixisquet’ofeguiipensaque,avegades,elsllibresproposendefertantescosesquenodeixentempsperfer-lesbé.Ami,elsprimersanys,emvaserútilportarundiarioncontrolava eltempsqueanavadedicantacadatemai,ambunparelldelínies,descriviaquèhaviafeta classeiquèhaviaquedatpendentperalapropera.

Procuraprojectarunavisióaplicadaifuncionaldelesmatemàtiquesalmateixtemps queajudesadescobrir-nelabellesaintrínseca,l’estructura,lametodologia,elpensament matemàtic.Utilitzadiversostipusderecursosipresentaofesdescobrirlesideesmatemàtiques dediferentsmaneres.Aixíarribaràsalsdiversosestilsd’aprenentatge.

Pensaque,engranmesura,fermatemàtiquesésferproblemes,perònovulguisfermoltsproblemes,avegadesésmésuntemadequalitatquedequantitat.Potsercalfermenys problemesperfer-losmillor,convidantaexplicarl’enunciat,aexplicitarelpladeresolució,a contrastaropinions,aplantejaralternativesi,sobretot,donanttempsperquècadaalumne hientri,eltreballi,se’lfaciseu.Sicorremmassapodemtrobar-nosexplicantboniques resolucionsdeproblemesquel’alumneencaranis’haplantejat.Fentproblemesaclasse valoramoltelteusilencipernotrepitjarlafeinaquecalquefacil’alumne.Responapreguntes ambnovespreguntesquesuggereixindireccionsd’avenç,peròdeixaquefacielseucamí. Nolirobisl’èxitd’arribaralasolucióambelsseuspropismitjans.Itinguesencompteque laresoluciód’unproblemanoacabaquans’obtélasolució:convidaaanalitzarelprocés seguit,abuscaralternatives,acontrastaropinions...Laresoluciód’unbonproblemade matemàtiquesaclasseésunaaventuraalaqualcalatorgarimportància,donant-hitemps, immergint-loenunclimaderaonamentcompartit,promoventlaconversaivalorantmoltla feinafeta.

I,parlantdeproblemes...tinguesencompteque,inevitablement,algundiahihauràun conflicte!Nopateixis!Elconflicteésnaturalentoteslescomunitatshumanes.Not’ha d’importarelconflicte,elquet’had’importaréssaber-logestionarbé:prendistància,pren-te temps,not’hoprenguiscomunassumptepersonal...Noetquedisnomésamblamiradade l’alumnequeetdesafiaoqueetmenysprea,buscalamiradadelsalumnesilesalumnesque volenaprendre,quet’estandientquevalorenelteuesforç...nofosqueunaactitudnegativa t’impedísveuremoltesactitudspositives.

Evitaquecapalumnesesentiexclòsdelesmatemàtiques.Demostra-liquetensconfiançaen lessevespossibilitats,celebraefusivamentelsseusèxitsmatemàticsireconeixelseuesforç encaraquenoacabidedonarfruit.Noperdiscapoportunitatdefelicitarenveualtai,quan siguinecessari,avisaorecriminaenveubaixa.

Forma’tcontínuament:treballaenequipiintentanocaminarsol,documenta’t,experimenta, assisteixatrobadesprofessionals,buscal’acompanyamentd’altresdocents,comenteui reflexioneusobreallòqueushafuncionatiallòquenohaanattanbé,obrelesportesdela tevaclasseaaltrescol·leguesi,sientensoportunitat,assisteixalessevesclasses,escoltaels teusalumnesilestevesalumnesillegeixlessevescares...totaixòaniràrefinantipolintles tevescapacitatscomaprofessoripensaquesempretindràsmoltperaprendreiquesovint, malgratquehaginpassatelsanys,etsentiràscomunprofessornovell.

I,detantentant,miraenrereivaloraamborgulltotelcamíquehasfet,totelquehasaprèsi totelquehasensenyatalsteusalumnes!

Moltasortamic/amiga!Quesiguismoltfeliç!

mmaca el racó del mmaca

Encaixantpoliedres:diàlegsobrealgunes

variantsdelproblemadelpríncepRupert

JosepRey,ManuelUdina

Elseditorsdel NouBiaix enshanencarregatunanovasecciófixadelarevista,enlaqual comentaremalgunsdelsmòdulsdelesexposicionsdelMMACA(MuseudelesMatemàtiques deCatalunya).Enaquestaocasióvolemparlardelmòdul«Encaixarpoliedres»perquè,toti quepotsernoésundelsquecridamésl’atenció,enshapermèstrobarlligamsambaltres qüestionsd’interès.Teniraquestmaterialal’abastdelesmansensfaaprendreimillorarla intuïciógeomètrica.

Laprimeraideavaserpartird’uncubdefustasenseunadelescaresimirard’encaixar-hi altrespoliedresregulars,commésgransmillor.Trobarquinssónelsmésgransvaserpera nosaltresunrepte,il’estudiquen’hemhagutdeferensil·lustrasobrealgunespropietatsdel cubquepotsernosóngaireconegudes.Al’escritlidoneml’habitualformadediàlegentre duespersonesAiB.

Tetràedre

A.Comencempeltetràedre.

B.Eltetràedreté4caresquesóntrianglesequilàters.D’entradapodríempreguntar-nos compodemposar(inscriure)untriangleequilàter,commésgranmillor,dinsdelcub.

A.Ladimensiómésgrandelcubésladiagonalinterior,queuneixdosvèrtexsoposats. Arabé,siféssimcoincidiraquestadiagonalambuncostatdeltriangle,aquestsortiria foradelcub,seriamassagran(fig.1).

B.Amés,nopassariaperlacara,jaqueladimensiómàximadelacaraéslasevadiagonal, queésméspetita.

A.Podemcomençar,doncs,mirantsiaquestadiagonaldelacarapotseruncostatdel trianglequevoleminscriureenelcub.

B.Efectivament,siunavegadadibuixadaunad’aquestesdiagonalsd’unacaradelcub ensfixemenunvèrtexd’aquestacaraquenoestiguialadiagonaldibuixada,idonant lavoltaaaquestvèrtexcompletemuntriangleamblesdiagonalsapropiadesdeles duescaresadjacents,obtindremuntriangleequilàterbengran(fig. 2).

A.Sí,senyor!Espodria,ara,continuarconstruinteltetràedre?

B.Sí,sí,noméscalunircadaundelsvèrtexsd’aquesttriangleambelvèrtexoposata aquellalqualhemdonatlavolta.Fixa’tquetambéanemseguintdiagonalsdecares delcubi,pertant,aquesttetràedretétoteslesarestesigualsiconseqüentmentles caressóntrianglesequilàters(fig.3).

A.Ésd’interèsfernotarqueelvolumd’aquesttetràedreés 1/3delvolumdelcub.La diagonald’unacaradelcubunitatval √2,l’alturadeltriangleequilàterseria √6/2,iper tantl’àreadelacaradeltetràedreserà:

ielvolumd’aquesttetràedremàximserà:

B.Iéscuriósveurel’expressiódesatisfacciódelvisitantquanaconsegueixencaixarel tetràedreenelcub.Moltesvegadeshoestanintentantforçaestona,ifinsquenofan coincidirl’arestaambladiagonalsemblaquenopuguientrar.

Octàedre.L’octàedredeRupert

A.Estudiemaral’octàedre.

B.Elspuntsmitjansdelescaresdelcubpodrienserelssisvèrtexsd’unoctàedreregular,i quedariabenencaixatenelcub.Aquestoctàedretindriaunaarestameitatdel’aresta deltetràedreanterior,ésadir, √2/2,itindriaunvolumiguala 1/6delcub.

Figura 1

Figura 2

Figura 3

A.Peròjaesveuqueésunoctàedremassapetit.Defet,potreposarsobreunacarasense tocarlesaltres.Segurqueespodentrobaroctàedresmésgransinscritsenelcub.

B.Podríemintentarquesiguinlesarestesdel’octàedreinosolamentelsvèrtexsquese situïnenlescaresdelcub.Potserpodríemfercoincidiralgunacaradel’octàedreamb unasecciótriangulardelcub.

A.Sideixemreposarl’octàedresobreunacara,elpodemveurecomunantiprisma(així comenunprismarectelesbasessóndospolígonsparal·lelsiambcareslaterals rectangulars,enunantiprismaelspolígonsbaseestangiratsuncertangleunen relacióambl’altreilescareslateralssóntriangles).Atèsqueelcubtéseccionsquesón trianglesequilàters(generadesperunplaperpendicularaunadiagonal),unamanera deveureunapossibleinserciódel’octàedreenelcubseriaposarelcubverticalment segonsunadelessevesdiagonalsiquelesduescareshoritzontalsdel’octàedre coincideixinambseccionstriangularsregularsdelcub(fig.4i5).

B.Defet,comeneltetràedre,lestresarestesd’unacaradel’octàedresesituarienenuna secciótriangularcomdonantlavoltaaunvèrtexdelcub.

A.Ilacaraoposadadel’octàedreescorrespondriaambelvèrtexoposatdelcubiuna altrasecciótriangulardelcub.Ambaquestsdostrianglesjatindríemelssisvèrtexsde l’octàedreensisdelesarestesdelcub(lesquetenenundelsextremsenelsvèrtexs superioriinferior)ilessisaresteshoritzontalsdel’octàedreenlessiscaresdelcub.

B.Ensproposemcalcular,donatuncubd’aresta 1,quinaserial’alçadaaquècalferles duesseccionstriangularsigualsiparal·lelesperquèl’antiprismaresultantsiguiun octàedreregular.

A.Consideremelcubambunadiagonalvertical.Ambduesseccionsaigualdistànciadels vèrtexssuperioriinferiorobtenimdostrianglesequilàtersqueespodenconsiderar comlescaressuperioriinferiord’unantiprisma(quetambéésunoctàedre).Plantegem quequalsevoldelessisarestesquevand’unacaraal’altrafentcomunaziga-zaga siguiigualqueelcostatdeltriangleseccióperaconseguirquel’octàedresiguiregular.

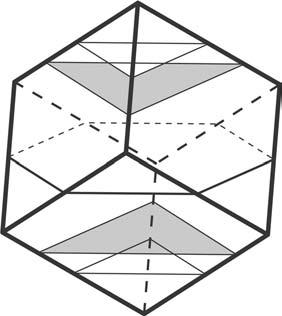
4

Figura

B.Arautilitzaremcoordenades.Enunareferènciaamborigenelvèrtexinferiordelcub (d’arestaunitat)ielseixoscoincidentsamblesarestesquesurtend’aquestvèrtex,que seriael(0,0,0)(elvèrtexsuperiorseriaelpunt(1,1,1)),untriangleestariaformatpels punts(t ,0,0),(0,t ,0)i(0,0,t )il’altrepelspunts(1 t ,1,1),(1,1 t ,1)i(1,1,1 t ).Posem lacondició d ((t ,0,0),(0,t ,0))= d ((t ,0,0),(1,1,1 t ));queportaa 2t 2 = 2(t-1)2 + 1,id’aquí t = 3/4,amblaqualcosal’arestadel’octàedreseria 3√2/4,superioraladel’octàedrede l’inicidelaconversa.

A.AquestresultatcoincideixamblasoluciódelproblemadelpríncepRupert,iendóna unasoluciómésexplicativa,perquèprecisaquinaésladireccióenquèelcubmòbil hauriadetravessarelfix(ladirecciódeladiagonaldel’octàedreencaixat)(fig.6).

ElproblemadelpríncepRupert

ElpríncepRupert(1619-1682),comtedelRin,vaapostar(iguanyar)queespodiafer passaruncubatravésd’unforatfetenunaltrecubd’igualsdimensions.Elproblema vaserresoltperWallissuposantqueladireccióenquèelcubtravessaelfixcoincideix ambunadelesdiagonalsdelcub(ivadeterminarquelasoluciós’obteniaambel cubquetépercaraelquadratmàximqueespotinscriureenl’hexàgonprojecció delcubsobreunplaperpendicularaladiagonal.Ésunexerciciveurequeelcostat d’aquestquadratperalcubd’aresta 1 val √6 √2 (aprox. 1,03).

Perextensió,elproblemadelpríncepRupertproposatrobarelcubmésgranque podria«travessar»uncubdedimensionsdonades.Gairebécentanysdesprésdela soluciódeWallis,PeterNieuwland(1764-1794)vatrobaruncubmésgranqueel deWallisquecompleixlescondicionsdelproblema,ielcostatdelqualés 3√2 4 ,que téunvaloraproximatde 1,06.Enaquestcas,ladireccióenquèaquestcubsolució travessaelcubfixnoésbenbélad’unadiagonaldelcub,sinólaquecorrespona unadiagonaldel’octàedremésgranqueespotencaixarenelcub.

Defet,trobarelquadratmàximinscriptibleenelcubésunproblemaequivalent aldelpríncepRupert.Lademostracióqueelquadratmésgranéseldelcostat esmentatespotferambalgunscàlculsdegeometriaanalítica,iespottrobarenla webhttps://www.fme.upc.edu/arxius/el_full/fulls-antics/061/solucio_cub.pdf

B.Uncopconstruïtaquestoctàedreveiemquenoésfàcilencaixar-lodinselcubperquè costatrobarl’orientacióambquèl’hemdecol·locar.Peròjustamentaixòéselquefa queelmòdulsiguimésatractiuperalvisitant.

Figura 5

Figura 6

A.Elfetqueelvalordel’arestadel’octàedrecoincideixiambelresultatdelproblemadel príncepRupertensconvençquehemtrobatl’octàedredevolummàximinscriptible (oencaixable)enelcubperquèlesarestesdel’octàedreformentresquadratsinscrits enelcub,ipertantaquestoctàedrel’anomenaremoctàedredeRupert.

B.Podemdeixarcomaexercicidemostrarqueelvolumdel’octàedredeRupertésuna micamésgranquelameitatdelvolumdelcub.(Podeucomprovarqueelvolumde l’octàedredeRupertcorresponentalcubunitatés 9/16).

A.Doncssíquehihemguanyatdesd’1/6,queéselvolumdelprimeroctàedreque havíemconsiderat!Fixem-nosenunaltreaspecteremarcabledel’octàedredeRupert encaixat:quanfemlasecciódelcubqueformaunhexàgonregular(seccióambun plaquepassapelcentredelcubiésperpendicularaladiagonalesmentadaabans), l’octàedretambéquedaseccionatperunhexàgonregularconcèntricambeldelcub (fig.7i8).

7

8

B.Haquedatbenbonic.Hemaconseguitposarnomaunoctàedre.Vallapenaacabar deveurelarelaciódelcubidel’octàedredeRupertambalgunsdibuixoscomentats.

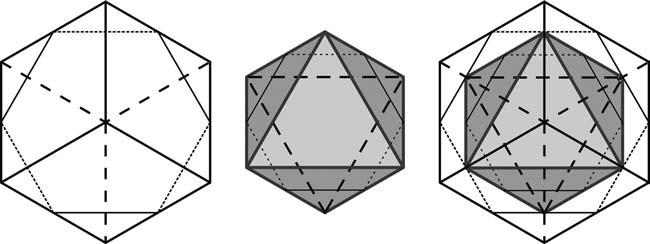
9

Descripciódelesfigures9,10i11

Figura 10 Figura 11

• Lafigura9éslaprojecciódelcubsobreunplaperpendicularaunadiagonalqueensdóna l’hexàgondecostatsgruixutsdeldibuix.Hihadibuixattambél’hexàgonqueuneixelspunts mitjansdelesarestesdelprimerhexàgon.

Figura

Figura

Figura

• Lafigura10éslaprojecciód’unoctàedresobreunplad’unacara,quetambéésunhexàgon regular.

• Lafigura11mostraaquestesduesprojeccionscombinadesquanteniml’octàedredeRupert encaixatenelcub.Espodenveurequatrehexàgonsenprogressiógeomètrica,queesdetallen acontinuació:

L’hexàgonexteriordibuixatambcostatsgruixutséslaprojecciód’uncubenunplaperpendicular aunadelessevesdiagonals.Elcostatdel’hexàgon(peralcubunitat)seria √6 3 .L’hexàgonque uneixelspuntsmitjansdelscostatsdelprimerhexàgoncorresponalaprojecciódelasecció hexagonaldelcubqueuneixelspuntsmitjansdelesarestescentrals.Comqueaquesthexàgon ésenunplaparal·lelaldelaprojecció,lesmidesdelscostatsd’aquestsegonhexàgonsóniguals a √2 2 .

Eltercerielquarthexàgonscorresponenalsdelafigura10.Elterceruneixtambéelspunts mitjansdel’hexàgonanterioricorresponalaprojecciódel’octàedredeRupertsobreelpla esmentat.Elsdostrianglesequilàtersdibuixatsunintvèrtexsalternatiusd’aquesthexàgon corresponenalesprojeccionsdelescareshoritzontalsdel’octàedre,ilamidad’undelscostats d’aqueststriangles(queéselvalordel’arestadel’octàedre)és 3√2 4 .Elscostatsd’aquesttercer hexàgonsónlaprojecciódelesarestesdelaziga-zagadel’octàedreimesuren √3 2 √2 2 = √6 4 .

Finalment,elquarthexàgoncorresponalasecciódel’octàedrepelspuntsmitjansdelesarestes del’antiprisma.Lamidad’uncostatd’aquesthexàgonseràlameitatdel’arestadel’octàedre,és adir, √6 4 √3 2 = 3 4 √2 2 .Hemobtingutquatrehexàgonsenprogressiógeomètricaderaó √3 2 que enshanpermèsapreciaralgunsdetallsdel’octàedredeRupertidelasevainsercióenelcub.

Dodecàedreiicosàedre

A.Araestudiemeldodecàedre.

B.Semblauncasméssenzill,perquèésclarqueundodecàedreregularquecompleixi queladistànciaentrearestesoposadessigui 1 téunencaixnaturalenelcubunitatque facoincidirtresparellsd’arestesparal·lelesalesarestesdelcubpassantclaramentpel puntmitjàdelescaresdelcubinosemblaquepuguiballargaire,perquèestàfixaten tresdireccions(fig. 12).

A.Sí;siescol·locaenladirecciócorrectaquedabenencaixat,peròs’observaquesise’l posaenunaaltradirecciósíqueballai,comabans,podemtornaraposartantelcub comeldodecàedreverticalmentsobreunvèrtex,amblaqualcosahihasisarestesdel dodecàedrequeestanendosplansparal·lelsihoritzontalsipermetriarecolzarlestres arestesinferiorsenlescaresinferiorsdelcub,amblaqualcosaesveuclaramentque eldodecàedrededistànciaentrearestesoposades 1 queda«petit».

B.Podem,doncs,fercréixereldodecàedredemaneraquetambélesarestesdelpla superiortoquinlescaressuperiorsdelcubialeshores,comenelcasdel’octàedrede Rupert,escompliràqueelplaquetallaelcubenunhexàgonregular(paral·lelament alesseccionsesmentades)tambéseccionaeldodecàedreenunhexàgonregular concèntricambl’anterior(fig. 13).

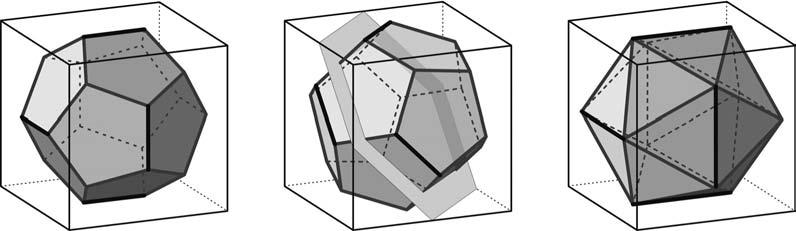
A.Potserseriaexageratanomenaraquestdodecàedre«deRupert»,peròésmésgran quel’anterior(lesarestesd’aquestsónun3%mésgrans).Observemquelesseccions horitzontalsquecontenenlesarestesquetoquenlescaresdelcubsóntambé hexàgons,enaquestcasirregulars.

B.Aquestaformad’encaixareldodecàedreenelcubespotdescriureaixí:Quanposemel dodecàedreambunadiagonalvertical,quedentrescaresadaltitresabaix.Elscostats oposatsalvèrtexsuperior(inferior)delstrespentàgonsquehicoincideixenqueden enunplahoritzontal.Lessisarestesd’aquestspentàgonssónlesquetocaranlessis caresdelcub(endosplansparal·lelsequidistantsdelcentredelcub).Lesaltressiscaresdeldodecàedreformenlafranjacentralquequanseseccionapelspuntsmitjans delesarestesdónalaseccióhexagonalques’haesmentatabans.

A.Araseriallargd’explicar,peròaquestaconfiguraciódesisarestesdel’octàedretambé latrobemenunaltredelsmòduls(«vestirpoliedres»)del’exposició.Podríemparlar-ne enunaaltraocasió.

B.Iperacabar,quèpodemdirdel’icosàedre?

A.Lasolució«natural»ésl’únicaquehemconsiderat.Hemconstruïtl’icosàedreamb distànciaentrearestesoposades 1,ihihatresparellsd’arestesparal·lelsalstresparells d’arestesdelcubd’aresta 1,quesesituaranpassantpelspuntsmitjansdecadacara (fig. 14).

B.Doncshopodemdeixaraquí.

Figura 12

Figura 13

Figura 14

creamat el racó del cesire-creamat

Contingutsclau.SEPiPIM,unaoportunitatperpensar-hi

Alcurs 2011-2012,elDepartamentd’Ensenyamentvaimpulsarlaimplementacióales escolesd’educacióprimàriadelSEP(SuportEscolarPersonalitzat).L’objectiueraintroduir canvisorganitzatiusimetodològicsperoferirsuportindividualitzatpertald’aconseguir, mitjançantaquestreforçespecial,quecapalumnes’endarrereixienelseusaprenentatges bàsicscomprometentelseuprogrés.

Aquestcurs 2013-2014,al 1rcursd’ESO,s’haimplantatelPIM(ProgramaIntensiudeMillora), adreçataalumnatquearribaalasecundàriaambdèficitsenaquestsaprenentatges.Aquest programaproposalaformaciódegrupsd’alumnesreduïtsiflexiblesis’adreçaespecialment areforçarlesàreesdellenguaimatemàtiques.Sónduespropostesorientadesal’atencióde ladiversitatambl’objectiudegarantirunassolimentsuficientdelescompetènciesbàsiques.

Aquestmarcorganitzatiuenelqualenssituemplanteja,entred’altres,algunespreguntes directes:Quèhemdetreballarenaquesteshores?Comhohemdefer?Intentarem,en aquestescrit,presentaralgunesorientacionspertrobarrespostesdesdel’àmbitdeles matemàtiques.

Ésmoltfàcil,enunasituacióaixí,prioritzarl’enfortimentdeldominidecertesmecàniques iconceptesmoltbàsics,especialmentcentratsenelcàlcularitmètic,totpensantquesi l’alumnenose’nsurtamblesrutinesclàssiquesdecàlculnopodràavançariquedaràsempre endarrerit.Aquestavisióesfonamentaenlaideaquelamecanitzacióésprèviaalraonament, mentreque,enrealitat,elraonamenthauriadesustentarlamecanització.Éscertquecalcular ensdóna,fentunjocdeparaules,operativitat.Peròelnostreobjectiuésmésampli:ajudar afercréixerlacompetènciamatemàticageneraldel’alumnat.Convertiraquesttempsde treballméspersonalitzatenuntempsd’exclusivamecanitzaciórepetitivasignificaperdre unabonaoportunitatperareforçareldesenvolupamentreald’aquestacompetència,que noméss’assoleixmostrantquelesmatemàtiquesdonenrespostesaproblemessorgitsdel nostreentornidonantl’oportunitatdepensariargumentar.

Apartird’aquestavisióméscomplexadelsobjectiusquevolemassolirretornaremalesdues preguntesbàsiques:Quinscontingutsprioritzem?Comelstreballem?

Dedicareml’apartatsegüentalaprimeradelesduespreguntes.Alasegona,donaríemuna resposta«deprincipisgenerals»:fer-hodelamateixamaneraqueatoteslesclasses,incorporantelsprocessos(resoluciódeproblemes,raonamentiprova,comunicacióirepresentació

iconnexions).Tenir-losencomptemarcaunalíniametodològicaquebasal’assolimentdels aprenentatgesenlapròpiaactivitatconstructivadel’alumnat.

Contingutsclau

Destriarelscontingutsclauensobligaaprendredecisionsalvoltantdetreseixos:

• Ferunaselecció,ambcriteri,d’aquellscontingutsquepodensermésnecessarisperacontinuaravançant.

• Seqüenciar-los,deformaacurada,tenintencomptelaprogressióconceptualiladificultat.

• Establirelgraud’aprofundimentalquals’had’arribarambcadaalumneiencadamoment.

DesdelCesire-Creamathemelaboratunconjuntdedocumentsd’acompanyamentalSEP dematemàtiquesquevolendonarorientacionsconcretesalsdosprimerseixosdedecisió esmentats:triaiordenació.Latriadecontingutss’hafetambelcriteridedestacaraquells que,perlessevescaracterístiquesilasevainterrelacióambd’altres,sinoestanprouassolits, podendificultarelprogrésdel’alumne.Encapmomenthihalaintenciód’assenyalaruns contingutsque«s’handefer»odonarlaideaqueespotprescindirdelsquenosónalallista. Nomésésunallistafocalitzadora.

LadocumentaciódelSEPs’agrupaperetapesicicles:educacióinfantil,cicleinicialdeprimària, ciclemitjàiciclesuperior.Acadagruptrobem,bàsicament,tresdocuments:

• Unapresentaciógeneral.

• Unallistadecontingutsquepreténassenyalaraquellsquesónclauenunaedatdeterminada.

• Undocumentambpropostesd’activitatsperajudaradesenvolupar-los.

AquestsdocumentspodensertambéorientadorsperalprofessoratimplicatenelPIM, especialmentelsdeciclesuperior,jaqueelsdosprogramescomparteixenunmateix propòsit.

Podeuconsultaraquestadocumentacióal’enllaçsegüent:http://goo.gl/vTSYN

Noés,però,l’únicafontperajudaralapresadedecisionssobrecontinguts.Unaaltra d’interessantsónelsdocumentsde Competènciesbàsiquesdel’àmbitmatemàtic,ontrobareu unataulaquerelacionacontingutsclauamblescompetènciesmatemàtiquesdescritesal propidocument,ungràficqueelsinterrelacionaiunasegonataulaqueelsfacorrespondreals diferentsblocsdelcurrículum.Elstrobaremalsannexosdecadadocument.Peraltemaque tractemenaquestarticlepotserespecialmentinteressantmirarelsdeldocumentdeprimària (http://goo.gl/VzKx0K),delqualmostremeldiagramadeconnexionsentrecontingutsclaua lafigura 1.

Nombres

Nombres. Relacions entre nombres

Sistema de numeració

Significat de les operacions

Càlcul

Obtenció, representació i interpretació de dades estadístiques

Fenòmens aleatoris

Mesura

Transformacions geomètriques

Patrons

Equivalència

Taules i gràfics

Figures geomètriques

Relacions espacials

Geometria

Estadística i probabilitat

Figura1.Diagramadeconnexionsentrecontingutsclauaprimària.

Font:Competènciesbàsiquesdel’àmbitmatemàtic.Identificacióidesplegamental’educacióprimària.

Tenirencompteaquestesconnexionspotserd’especialinterèsperenfrontar-seaunaltre delsproblemesbàsicsquetenimenelnostrediaadiaal’aula:establirunequilibrientre l’amplituddecontingutsclauatreballarieltempsdisponibleperaconseguir-ho.Sienuna mateixaactivitatconnectemmésd’uncontingutclau,apartirdelessevesinterrelacionsno tansolspossibilitaremaquestequilibrisinóquetambépodremcrearperalnostrealumnat unespaiamblacalmanecessàriaperapoder,apartirdelessevesexperiènciesencontextos adequats,construirelseupropiconeixementmatemàticidesenvoluparlasevacompetència personal.

Nopodemacabarsenseconvidar-vosavisitarelsespaisdedicatsalSEPialPIMalportal educatiudelDepartamentd’Ensenyament,laXTEC,onpodreuampliarlainformaciói,sobretot,trobarrecursosperaconcretaraquestsprogramesal’aula.

L’equipdelCesire-Creamat

LaFEEMCAT(Federaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesaCatalunya),la SCM(SocietatCatalanadeMatemàtiques),laRealAcademiadeCienciasanuncienla i convocatòria peral’admissióenelseu

projecteESTALMATaCatalunya (DeteccióiestímuldeltalentprecoçenatemàtMiques)

Dotzenapromoció2014-2016

Objectiudelprojecte:fomentarl’aficióil’habilitatespecialenmatemàtiquesdenoisinoiesque viuenaCatalunyaiamb datadenaixementl’anyl’2001oany2002.

Activitats:Totselsdissabtesdelperíodelectiudelscursos2014-2015i2015-2016,de10ha13ha laFacultatdeMatemàtiquesiEstadística(FME)delaUPC,aBarcelona.

Procésdeselecció:

La selecciódel grupde 2nois i noies que 5participaranenelprojectetéduesfases:

1.

2. Testd’aptitud: eldissabte31demaigde2014ales10halesciutatsdeBarcelona,Girona, LleidaiReus.

Entrevistapersonal ambelsparesotutorsielsnois/espreseleccionats/des.

Inscripció:

Lamare,elpareotutorlegalhaurand’omplirunquetrobaranalapàginawebdel’orformulari ganització,www.estalmat.org.Veuranquehihaunenllaçespecialperalsdetallsd’aquestaconvocatòria,iunaltreenllaçonpodranllegirinformaciódetalladadelprojecteaCatalunya.

Termini: ’. del1finsal30demaigde2014

Aquestesactivitatsserangratuïtes peralsnoisinoiesseleccionats,elsparesotutorsdelsquals s’haurandecomprometreaportar-losirecollir-losaleshoresesmentades. Lleida).

Dadesqueesdemanen: nomidatadenaixementdel’alumne/ainteressat/daaparticiparenel projecteESTALMAT,adreça,correuelectrònic,númerodetelèfondecontacteicentreescolaron estudiadurantelcurs2013-2014.

aquinapoblaciódesitjarienferlaprova (Barcelona,Reus,Gironao Caldràqueindiquin

Lallistad’inscritsielsdetallsdelarealitzaciódelaprovadeseleccióes web podranconsultaral www.estalmat.org,promoció201-201.Tambéespotdemanarinformaciósobreel dotzena 46 procésd’inscripcióaNúriaFuster,SocietatCatalanadeMatemàtiques(telèfon:933248583; la correuelectrònic@iec.). :scmcat

PremiMariaAntòniaCanals2014

LaFederaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesaCatalunya(FEEMCAT),laSocietat BaleardeMatemàtiquesSBM-XEIXilaSocietatd’EducacióMatemàticadelaC.V.« Al-Kwhrizm āī » convoquenelPremi«MariaAntòniaCanals» 2014,peraprojectesd’innovacióeducativarealitzatsen algun/sdelstrescursosanteriorsalaconvocatòria.Elsprojecteshand’estardirigitsal’ensenyament delamatemàticaenelsnivellseducatiussegüents:educacióinfantil(0-6),educacióprimària(6-12), educaciósecundària(12-18),iuniversitària.

Potoptaralpremiqualsevolprofessionaldel’ensenyament,desdel’escolabressolfinsalauniversitat, semprequefaciservirelcatalàenqualsevoldelessevesvariants.

Nopodranoptaralpremitreballsjapublicatsopremiatsenaltresconcursos.

Elsprojecteshandeserpresentatsensuportinformàtic(Word,OpenOffice,PDF),ambunaextensió d’entre 10 i40 pàginescomamàxim(Arial 11 adobleespai).

Lapresentaciódelprojecteconstaràdelsapartatssegüents:

• Resumde5a 10 línies,redactatsencatalà,ambArial 11 adobleespai.

• Exposiciódelsobjectiusidelcontextenquès’hadesenvolupat.Referènciesemprades(webs,textos...)

• Descripciódel’experiènciaidelsmaterialsusats.

• Unamostradelesproduccionsdel’alumnat(fotografies,produccionsescanejades...)

• Conclusionsireflexiófinalsobreelquèharepresentatelprojectepelquefaal’aprenentatge matemàticdel’alumnatimplicatenelprojecte.

• Document,apartdel’anterior,quecontinguilesindicacionssegüents: nomicognomsdelsautors; adreçapostalielectrònica,itelèfondelsautors; NIFdelsautors; unadeclaraciósignadapelsautorsqueeltreballésinèditinohaestatpremiatenaltresconcursos.

S’atorgaràunsolpremipernivelleducatiu,dotatamb600 e i,siescau,mencionsespecialsalstreballs quehomereixincitant-losal’actadeljuratifacilitant-neladifusió.

Elspremispodenrestardesertsonoésseradjudicats.

Elterminidelliuramentdelstreballsfinalitzaràel31dejuliolde2014

Elveredicteseràcomunicatpersonalmentalsguanyadorsiellliuramentesfaràenunactepúblic.

Lessocietatsconvocantsesreserveneldretalapublicaciódelsprojectespremiats.Aquestapublicació potseralarevista NouBiaix oenformatdellibreod’altresquepuguinsermésescaientsenfunciódel tipusdetreballpremiat.

Lessocietatsescomprometenadivulgarelspremisiadonaral’autorl’oportunitatdepresentarelseu treballenlesjornadesrespectives.

Eljuratestaràformatperunmembredesignatpercadasocietat,unmembredelconsellderedaccióde larevista NouBiaix iunespecialistaendidàcticadelamatemàticaambveuivot,ielsecretarid’unade lestressocietatsconvocants,ambveuisensevot,queactuaràdesecretari.

Elguanyadorescomprometaferconstarelguardóenulteriorspublicacions.

Elstreballss’hand’adreçarindistintamenta:premi.mantoniacanals@gmail.comobéalesseusdeles societats:

FEEMCAT

PremiM.AntòniaCanals CampusdeMontilivi,edificiP-IV 17071 Girona

SocietatBaleardeMatemàtiquesSBM-XEIX

PremiM.AntòniaCanals c/MartíRubí,37,alts. 07141 SaCabaneta(Marratxí)

Societatd’EducacióMatemàticadelaCV Al-Kwhrizm āī

PremiM.AntòniaCanals

Apartatdecorreus: 22045

46071 València

Normes per a la presentació de contribucions

1.Larevista NouBiaix acceptaperalasevapublicaciócontribucionsoriginalsrelacionadesamb experiènciesdidàctiques,activitatsd’ensenyamentiaprenentatge,escritsd’opinió,dedivulgació id’investigacióenelcampdelamatemàticaielseuensenyamentenqualsevolnivelleducatiu.

2.Lescontribucionsrebudesseransotmesesaunaavaluacióprèviaacàrrecdedosespecialistes reconeguts.L’acceptaciódelapublicacióserànotificadadirectamental’autorambunaindicació deladataaproximadadepublicació.Encasqueunacomunicaciónofosacceptada,tambése n’enviarànotificació.

3.Peralapresentaciódetreballsoriginals,l’autortrametràal’adreçanoubiaix@gmail.comunarxiu, preferiblementenWord,ambundocumentadobleespaiiambmargesamplis(65caràctersper línia).Elsgràfics,diagramesifigureshaurandeseroriginals(nofotocopiats).Elsarxiusgràficses presentaranenformatepsotifiambunaresolucióde300dpia135mmd’amplada.

4.Lacontribucióhauràd’incloureeltítol,elnomdel’autoroautors,lasevaadreçaprofessional completailasevaadreçaelectrònica.S’adjuntaràunresumnomésllargde300paraulesencatalà ianglès.Alfinaldeldocuments’inclouràobligatòriamentlabibliografiaperordrealfabèticde cognoms,d’acordamblanormativaAPA;exemples:

Articles

Albertí,M.(2002).LesMatemàtiquesdesd’unaperspectivacultural:Etnomatemàtiques. Biaix, 20,6-25.

Llibres

Godino,J.,Font,V.(2003). Razonamientoalgebraicoparamaestros.Granada:Universidadde Granada.

Capítolsdellibres

Edo,M.,Revelles,S.(2004).Situacionesmatemáticaspotencialmentesignificativas.DinsM.Antóni B.Moll(ed.), EducaciónInfantil.OrientacionesyRecursos(0-6años) (p.410/103-410/179). Barcelona:Praxis.

Actesdecongressos

Morales,M.,Font,V.,Planas,N.(2004).Estudiomicroetnográficoentornoaunconocimiento matemáticosituado.DinsA.Franzéialtres(ed.), ActasdelaIReuniónCientíficaInternacional sobreEtnografíayEducación (CD-ROM).València:Germanía,PolisPaideia.

Pàginesweb

Ibanyez,A.,Paolu,N.,Pedreira,J.(2007).RelojBinariodesobremesa,aMicrosiervos. http://www.microsiervos.com/archivo/gadgets/reloj-binario-sobremesa.html

5.Lescontribucionsacceptadesquedaranenpropietatde NouBiaix ipodranserimpresessense autoritzacióexpressadel’autor.Peralasevareproducciótotaloparcial,sen’hauràdesol·licitar l’autoritzacióa NouBiaix.Encasdetreballspresentatsperdiferentsautors,s’enténqueelprimer autortélaconformitatdelsaltres.

6.Elsarticlesespublicaranenllenguacatalana.Nomésestraduiranalcatalàlescontribucions acceptadesrealitzadesperautorsnoresidentsalsPaïsosCatalans.

7.Elsautorsesresponsabilitzarandelcomplimentdelesnormesestablertesperal’autoritzacióde lareproducciódematerialprocedentd’altresfontsbibliogràfiques.

8.Elsarticlestindranunaextensiód’entre6i12pàginesdetext ésadir,untotalmàximde12.000 caràcters ,incloseslesnotesapeudepàgina.Podrananaracompanyatsd’il·lustracions,sempre quenosuperinl’extensiódeduespàgines.Endefinitiva,totcomplet quaneltextcontingui quadres,figures,fotografies,gràfics,mapes,etc. nopodràsuperar,encapcas,les15pàgines.