BSCM, 33-2

BUTLLET Í

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 33 ● Número 2 ● Desembre 2018

BARCELONA 2018

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques filialdel’Institutd’EstudisCatalans

CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament

perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

Imprèsa Open Print,SL

ISSN:0214-316-X

DipòsitLegal:B19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprografia ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.2,2018

Índex

CarlesBarril,SílviaCuadradoiJordiRipoll Modelsmatemàticsendinàmicadepoblacions....................................87

AgustíReventós GaspardMonge.....................................................................111

NarcísSayolsiSebastiàXambó Codiscorrectorsd’errorsicriptografiapostquàntica............................147

Englishsummaries.....................................................................173

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.2,2018.Pàg.87–109. DOI:10.2436/20.2002.01.81

Modelsmatemàticsendinàmicadepoblacions

CarlesBarril,SílviaCuadradoiJordiRipoll

Resum: Ladinàmicadepoblacions,comelseunomindica,estudial’evoluciódela midailacomposiciódelespoblacions.Enaquestarticlepresentemunreculldels principalsmodelsmatemàticsquedescriuenladinàmicadepoblacionsbiològiques. Primerament,faremunaintroduccióhistòricaalamatèriatotdescrivintdiferents problemesenecologia,demografiaiepidemiologia,aixícomleseinesitècniques matemàtiquesemprades.Seguidament,descriuremunanovaformulacióentermes d’equacionsambretardqueestableixunmarcgeneralrigorósperalamodelització matemàticadeladinàmicadepoblacions.

Paraulesclau: biologiamatemàtica,poblacionsestructurades,equacionsambretard, equacionsenderivadesparcials.

ClassificacióMSC2010: 92D25,35Q92,47N20.

Labiologiamatemàticaésladisciplinaques’encarregadeproporcionar modelsieinesmatemàtiquesperaentendreprocessosbiològics.Enl’actualitat s’ocupad’unagranvarietatdetemes,peròlesprimeresinteraccionsentre biologiaimatemàtiquesvantenirllocenelcontextdela dinàmicadepoblacions, queéslabrancadelabiologiamatemàticaquetéperobjectel’estudide l’evoluciódelamidadelespoblacionsilasevacomposició.Començaremfentneunbreurepàshistòric(vegeu,peramésinformació,[3, 11, 9, 33, 45, 50]). Totiqueelsmodelspresentatsenaquesttreballsón,enlanostraopinió, moltrepresentatiusdelahistòriadeladinàmicadepoblacions,degutal grandesenvolupamentenelsúltimsanysd’aquestadisciplina,unadescripció exhaustivadelamatèriaaniriamésenllàdel’objectiud’aquestarticle.

1Ladinàmicadepoblacionsanterioralseglexx

Elquepodríemconsiderarelprimerproblemaendinàmicadepoblacionsva serelproposatperLeonardodePisa,mésconegutcomaFibonacci,enelseu llibre Liberabaci,publicatel1202:

CarlesBarril,SílviaCuadradoiJordiRipoll

Unhometéunaparelladeconillsenunlloctancat.Esvoldriasaberquantes parellesméss’obtenendelaprimeraparella,enunany,silanaturad’aquests conillséstalqueengendrenunanovaparellacadamesicomencenaserfèrtils apartirdelsegonmesdevida.

Sianomenem un elnombredeparellesdeconillsjovesi vn eldeparelles adultes,alcomençamentdelmes n,aleshoreselproblemaanteriordonalloca lesrelacionsderecurrència

Aixòequivalal’equacióderecurrència

,apartir delaqualFibonaccivaconstruirlafamosasuccessióqueportaelseunomi queambelsanyss’haobservatqueapareixdemanerafreqüentalanatura. Existeixfinsitotunarevistacientífica, TheFibonacciQuarterly,quepublica articlesrelacionatsambaquestasuccessió.

Tenim,doncs,queelprimeríssimproblemadedinàmicadepoblacionsja consideravaduesvariablesindependents(discretes):tempsiedat.

DesprésdeFibonacci,lahistòriadeladinàmicadepoblacionshad’esperar cincseglesperquèesplantegiunnouproblema,totiqueentremigesvanfer gransaportacionsalamatemàtica,coméseldesenvolupamentmoderndel càlculdiferencial.

VaserLeonhardEulerquiel1748publicàelllibre Introductioinanalysin infinitorum [22],on,alcapítolsobreexponencialsilogaritmes,inclouexemples dedinàmicadepoblacionscomelsegüent:

Silapoblaciód’unacertaregióaugmentaanualmentenunatrentenaparti inicialmenthihavia 100000 habitants,voldríemsaberlapoblaciódesprésde 100 anys.

Estractad’unexempled’unapoblacióambcreixementgeomètricilaresposta és P100 = 1 + 1 30 100100000.

L’any1760publicàals proceedings del’AcadèmiadeCiènciesdeBerlínel treball«Recherchesgénéralessurlamortalitéetlamultiplicationdugenre humain»,onesplantejaelproblemadetrobarladistribucióenedatsd’una poblaciósotacerteshipòtesis[23,24]:

Sianomenem Pn lapoblaciól’any n i Bn elnombredenaixementsl’any n, Eulervasuposarquelapoblaciócreixgeomètricament,ésadir, Pn+1 = λPn, (1) iqueelquociententreelnombredenaixementsilapoblacióésconstant: Bn = mPn. (2)

Notemqueaquestesdueshipòtesisimpliquenqueelnombredenaixements creixgeomètricamentiamblamateixataxa: Bn+1 = λBn. (3)

Denotantper lk laproporciódenounatsqueencarasónviusl’any k isuposant queningúsobreviumésde100anys,Euleresplantejasi,coneguts Bn, Pn i lk, podemconèixerquantsindividushihaacadagrupd’edat.Tenim,fentservir reiteradament(1)i(3),

Dividintper λ100P0 obteniml’anomenada equaciód’Euler

Suposantconegutselsnaixementsilapoblacióenundeterminatany, Bn, Pn i, pertant,elparàmetre m = Bn/Pn =···= B0/P0,iconegudeslesprobabilitats desupervivència lk, k ≥ 1,l’equaciód’Eulerenspermettrobar λ

Tenintencomptequedurantl’any n elnombred’individusnascuts l’any n k queencarasónviusés

laproporciód’individusd’edat k és

Aquestaproporcióésconstanti,pertant,lapiràmided’edatnocanviaambel tempsiesdiuquelapoblacióés estable

Totiquel’equació (1) vaserproposadaperEuler,esconeixcoma modelde Malthus enreferènciaaThomasMalthus,qui,l’any1798,vapublicar AnEssay onthePrincipleofPopulation [42],que,totigenerarunagrancontrovèrsiaen elmomentdelasevapublicació,vatenirunagraninfluènciaenlesteories econòmiquesdelsegle xix,aixícomeneldesenvolupamentdelateoriade l’evolució.Efectivament,tantCharlesDarwincomAlfredRussellWallacevan afirmarqueelllibredeMalthuselshaviainspiratperaformularlateoria del’evolucióperselecciónatural,laqual,descobertapelsdoscientíficsde maneraindependent,foupublicadademaneraconjuntaenunarticlepresentat alaLinneanSocietydeLondres[12].LatesideMalthusalseullibreésquela poblaciócreixdemanerageomètrica(oexponencial),mentrequeelsrecursos necessarisperadonarsuportalapoblaciócreixendemaneraaritmètica,cosa quedonallocalques’haconegutcoma catàstrofemalthusiana. Malthusvaconsiderarunapoblacióhomogènia(totselsindividussón idèntics)d’unasolaespècie,aïlladaotancada(nohihamigracions),gran(pertal denegligirfactorsestocàstics)ienunhàbitatinvariant(laquantitatderecursos nocanviadegutafactorsexternsnialamateixapoblació).Performularel

CarlesBarril,SílviaCuadradoiJordiRipoll

model,denotemper x(t) lamidadelapoblació(nombretotald’individus)a temps t.Totique x(t) ésdefetdiscreta,comques’estàsuposantunapoblació moltgran,esconsidera x(t) unafunciórealdelavariablereal t.Donatqueno hihamigració,lamidadelapoblaciócanvianomésdegutanaixementsimorts i,pertant,lataxadecanvienlamidadelapoblacióseràlafertilitat(taxa per capita denaixements)menyslamortalitat(taxa percapita demorts).Atèsque s’estàsuposantquel’hàbitatnocanvia,aquestesduestaxesnodependrandel tempsnidelapoblaciómateixa.Denotantper β lafertilitatiper µ lamortalitat tenim

x (t) = (β µ)x(t),x(0) = x0. (5)

Elparàmetre r := β µ éslataxa percapita decreixement(odecreixement) exponencialirepelnomdeparàmetremalthusià.Enfunciódelapoblació inicial x0 ≥ 0,l’evoluciódelapoblacióvedonadaper

x(t) = ert x0, (6) queéslasoluciódelproblemadevalorinicial (5).Lapoblaciós’extingirà, romandràconstantocreixeràil limitadamentdepenentdesi r< 0, r = 0 o r> 0,respectivament.Equivalentment,definintlaquantitat R0 := β µ ,tenimel mateixresultatsi R0 < 1, R0 = 1o R0 > 1,respectivament. R0,queéslataxade fertilitatperl’esperançadevida1/µ,donaelnombreesperatdedescendents quetécadaindividualllargdelasevavida;vegeu[4].

LeshipòtesisconsideradesperMalthussobrelapoblaciópodenservàlides peracertesespèciesenunperíodedetempssuficientmentcurt,peralesquals s’observaefectivamentuncreixementexponencial.Noobstant,lahipòtesique lataxadecreixementd’unapoblacióésproporcionalalamidadelapoblació (modellineal)éspocrealistaaescalesdetempsmésgrans.

Anysméstard,el1838,Pierre-FrançoisVerhulstpublicaeltreball«Notice surlaloiquelapopulationsuitdanssonaccroissement»,onproposa,donant-li elnomde equaciólogística,elmodel

x (t) = r 1 x(t) K x(t),x(0) = x0, (7)

onlataxa percapita decreixementdelapoblaciójanoésconstantcomen elmodeldeMalthus,sinóquedepèndemaneradecreixentdelapoblació: r(x) := r 1 x K amb r> 0.Enefecte, r éselvalormàximdelafunciór(x), ques’anul.lapera x = K iesfanegativaquan x>K.Notemquesilapoblació éspetitaaleshoreslapoblaciótéuncreixementexponencial(x ≈ rx),mentre quequanlapoblaciótéunvalorpropera K,pràcticamentnocanvia(x ≈ 0).

Lasolucióde(7)enfunciódelapoblacióinicialés

x(t) = Kx0 x0 + (K x0)e rt , (8) d’onpodemveurequeperaunapoblacióinicial x0 > 0,lapoblaciós’acosta a K quaneltemps t tendeixainfinit. K equivalalacapacitatdecàrregade

lapoblacióperquèrepresentalamidamàximasostenibledelapoblació.Així doncs,elmodellogístic1 prediu,silapoblacióinicialéspetita,creixement exponencialseguitd’undecreixementenlataxadecreixementquaneltemps avançademaneraquelapoblaciós’acostaallímit K.

2Ladinàmicadepoblacionsdelseglexx

EltreballdeVerhulstvainspirarmoltsdelsinvestigadorsquedesenvoluparien ladinàmicadepoblacionsdecomençamentsdelsegle xx.Und’ellsvaserel matemàticitaliàVitoVolterra,aquielseufuturgendreibiòlegmaríUmberto D’Anconademanàsierapossibleestudiarmatemàticamentlesvariacions poblacionalsobservadesenunapoblaciódepeixos.D’Ancona(vegeu[10, 1]) teniadadessobreelpercentatgetotaldecapturesdecondrictis(taurons, rajades...)sobreeltotaldepeixoscapturatsdurantunperíodealvoltantdela PrimeraGuerraMundial.

PercentatgedecapturesdecondrictisalportdelmarAdriàticFiume(Rijeka,Croàcia) 1914191519161917191819191920192119221923 11.9%21.4%22.1%21.2%36.4%27.3%16.0%15.9%14.8%10.7%

D’Anconavaobservarl’augmentd’aquestsdepredadors,queenaquellmomentnoesconsideravencomestibles,durantlaguerraicreiaqueeradegut aladisminuciódelapescaenaquestperíode.Elseuraonamenteraque,en pescarmenys,hihaviaméspresesiperaixòelnombredecondrictisaugmentava.Sorprenentment,però,semblavaqueelnombredepreses,encomptes d’augmentar,haviadisminuïtquanespescavamenys.Pertald’entendrecom aquestadisminuciódelapescapodiaafectarlespoblacionsdepeixosvademanarajutaVolterra.EnrespostaaD’Ancona,Volterrapublicàl’any1926 eltreball«Variazioniefluttuazionidelnumerod’individuiinspecieanimali conviventi»[54].

ElmateixmodelproposatperVolterravaseranalitzatdemaneraindependent(enuncontextdiferent)perAlfredLotkael1920al’article[38]iel1925a lasevaobra,publicadaprimerambeltítol TheElementsofPhysicalBiology [39] iposteriormentambeltítol ElementsofMathematicalBiology [41]iperaixòes coneixcoma modeldeLotkaiVolterra.Passemaraadescriure’l.

Denotemper x(t) i y(t) elnombredepresesidepredadorsatemps t, respectivament.Sesuposaque,enabsènciadedepredadors,lespresesexperimentenuncreixementmalthusiàambtaxadecreixement r> 0,mentreque, enabsènciadepreses,elsdepredadorss’extingeixendemaneraexponencial ambtaxademortalitat µ> 0.Tambésesuposaqueladinàmicad’aquestes poblacionsvindràdonadanomésperlesinteraccionsentrepresesidepredadors,demaneraquelasupervivènciadelsdepredadorsdepèndelaquantitat depresesilespresesalavegadatenennoméselsdepredadorscomafactorde

1 Noésdeltotclar,peròsemblaqueelnomde logística téaveureambelslogaritmes (M.Iannelli,comunicaciópersonal).Així,perexemple,de x = 1/(1 + e t ) obtenimlarelació inversa t = ln(x/(1 x))

CarlesBarril,SílviaCuadradoiJordiRipoll

control.Lataxadepredaciós’obtédelques’anomena lleid’acciódemasses,que estableixqueelnombredetrobadesentrepresesidepredadorsésproporcional alproductedelespoblacionsrespectives.Suposantqueunafracció a detotes lestrobadesésefectiva(eldepredadormatalapresa),elnombredepreses consumidespelsdepredadorsperunitatdetempsés axy.Aixòs’anomena respostafuncionaldetipusI.Elnombredenousdepredadorsperunitatde tempsserà αaxy,on α denotalataxadeconversió(habilitatdelsdepredadors deconvertirlespresesentaxa percapita decreixementperalpredador).Amb totsaquestsingredientspodemescriurejaelmodeldeLotkaiVolterra

x (t) = rx(t) ax(t)y(t), y (t) =−µy(t) + αax(t)y(t). (9)

Aquestsistematédosequilibris (0, 0) i µ αa , r a .Si x ≠ 0, y ≠ 0esté (µ αax) x x + (r ay) y y = 0 o,equivalentment, d dt (ln(xµ y r ) αax ay) = 0, perlaqualcosaesté xµ y r eαax eay = K peraqualsevolconstantpositiva K.Tenim,doncs,quelafunció F(x,y) := xµ y r eαax eay ésunaintegralprimeradelsistema,ésadir,lesòrbitesde (9) estan contingudesalsconjuntsdenivellde F .Aquestescorbesdenivellsóntancades alvoltantdel’equilibri µ αa , r a [10, 1]i,pertant,lessolucionsde (9) són periòdiques.

Figura 1: Simulacionsnumèriquesdelretratdefaseidelessolucions alllargdeltempsenunsistemaLotka-Volterra.

PertaldecompararlessolucionsdelseumodelamblesdadesdeD’Ancona, Volterracalcula ˆ x i ˆ y,lesmitjanesenunperíode T ,delespoblacionsdepreses

idepredadors,respectivament,idemostraque ˆ x = 1 T T 0 x(t)dt = µ αa , ˆ y = 1 T T 0 y(t)dt = r a .

Ésadir,lesmitjanesdelnombredepresesidelnombrededepredadorsenun períodesónindependentsdelescondicionsinicialsiigualsalespoblacionsen equilibri.

Volterraconsideràelsefectesdelapesca,afegintalesequacions (9) un termeperamodelitzarlescaptures,quesuposàproporcionalsalespoblacions respectivesiamblamateixaintensitatperatotesdues: x (t) = rx(t) ax(t)y(t) εx(t), y (t) =−µy(t) + αax(t)y(t) εy(t). (10)

Peraquestsistema,lesmitjanessón

a ,laqualcosaexplica lesdadesdeD’Ancona:undecreixementmoderatdelapesca(reduccióde ε) augmentaenmitjanaelnombrededepredadors,mentrequedisminueixel nombredepreses.

Comcomentàvemanteriorment,AlfredLotkavaarribaralesmateixes conclusionsqueVolterra,pensantenreaccionsquímiquesienunapoblació deplantesiherbívors.Peròabansd’interessar-seperaixò,Lotkahaviafet contribucionsmoltimportantsenaltresaspectesdeladinàmicadepoblacions, enparticularendemografia.Elsanys1907i1911publicaelstreballs[37] i[47](elsegonconjuntamentambF.R.Sharpe),onestudialadinàmicade poblacionsestructuradesperl’edat.Desconeixedordelstreballsd’Eulersobre aquesttema,Lotkaproposaelmateixmodelperòconsideranteltempsil’edat comavariablescontínues(vegeutambé[35,32,52]).

Considerantunapoblaciódefemelles(defet,alseuarticle,SharpeiLotka considerenunapoblaciódemascles),denotemper B(t) lataxadenaixementsa temps t,ésadir,elnombretotaldenaixementsperunitatdetemps,per F(a) laprobabilitatdesobreviurefinsaedat a ≥ 0,iper β(a) lataxadefertilitatde lesfemellesd’edat a (nombremitjàdefillesperunitatdetempsiperfemella enl’intervalinfinitesimal [a,a + da]).

Aleshores,jaquelesfemellesd’edat a atemps t hannascutatemps t a, tenimqueelnombredefemellesnascudesentreeltemps t a i t a + da queencarasónvivesatemps t és B(t a)F(a)da.Aquestesfemellestenen β(a)B(t a)F(a)da fillesperunitatdetempsiobteniml’equacióderenovació (odeVolterra)següent:

B(t) = t 0 β(a)B(t a)F(a)da + F(t),t ≥ 0, (11) onelprimertermedeladretaensdonaelnombredenaixementsdefilles defemellesnascudesenl’intervaldetemps [0,t] ielsegonterme F(t) són

CarlesBarril,SílviaCuadradoiJordiRipoll

elsnaixementsdegutsalesfemellesjapresentsalapoblacióatemps t = 0. L’equacióintegral(11)ésequivalenta

B(t) = ∞

β(a)B(t a)F(a)da,t ≥ 0, (12)

sisuposemunahistòriadenaixementsconeguda B(θ) = φ(θ), θ ≤ 0.Noti’s quel’edatmàximadelsindividusd’unapoblacióespotsuposarfinitaopotencialmentinfinita.Buscantunasolucióexponencial, B(t) = beλt , b> 0, d’aquestaequacióintegral,Lotkaobtél’anomenada equaciócaracterísticade Lotka

= ∞

β(a)e λaF(a)da, (13) queéslaversiócontínuadel’equaciód’Euler(4).

Pera λ real,elcostatdretde (13) ésunafunciódecreixentde λ quetendeix a +∞ quan λ →−∞ ia0quan λ →+∞.Pertant,hihaunúnicvalorreal λ∗ quesatisfà(13)que,amés,seràpositiusiinoméssi

R0 := ∞ 0 β(a)F(a)da> 1.

Aquestaquantitatéselfamósnúmeroreproductiubàsic(lanotacióvaser introduïdaperDubliniLotkael1925,[21])is’interpretacomelnombreesperat defillesquetécadaindividudelapoblacióalllargdelasevavida.

SharpeiLotka[47]vanenunciarqueelnombredenaixementsperunitatde tempssatisfà

B(t) ∼ beλ∗t quan t →+∞ amb b unaconstantpositiva.

AixòvaserdemostratdemanerarigorosaperW.Fellerel1941[25]ies coneixcoma teoremafonamentaldelademografia. Tenintencomptequelapoblaciótotalatemps t és

P(t) = ∞

B(t a)F(a)da, tenimquel’estructuraenedatdelapoblació(distribuciónormalitzadad’edats) vedonadaper

B(t a)F(a) P(t) quetendeixa

aF(a)

aF(a)da quenodepèndeltemps(nideladistribucióinicialdelapoblació)i,pertant, esté,comenelcasdiscretd’Euler,elqueLotkaanomenà poblacióestable:la piràmided’edatsmantélamateixaformaalllargdeltemps,peròlapoblació totalcreixodecreixexponencialment.

Unamaneraalternativadeformularaquestmodelvaserproposadaper A.G.McKendrickel1926[44]iméstardperH.vonFoerster[55]ivadonar llocal’anomenada equaciódeMcKendrick-vonFoerster,quevaserlaprimera equacióenderivadesparcialsdeladinàmicadepoblacionsestructurades.

Denotantper n(a,t) ladensitatd’individusd’edat a atemps t iper µ(a) la taxa percapita demortalitataedat a tenim

n(a + ∆t,t + ∆t) n(a,t) =−µ(a)n(a,t)∆t, (14)

ésadir,elsindividusd’edat a atemps t tindranedat a + ∆t quanhapassat untemps ∆t il’úniccanvienelnombred’individusvindràdonatpelsquehan mortdurantl’interval (t,t + ∆t).Dividint (14) per ∆t ifentellímit ∆t → 0 suposantque n ésdiferenciablerespectea a i t obtenim

nt (a,t) + na(a,t) =−µ(a)n(a,t). (15)

McKendrickvaespecificarque(pera t>a)

n(a,t) = n(0,t a)e a 0 µ(s)ds , perònovadefinircapcondicióinicialnicapcondiciódefrontera.Peradescriureelmodelcomplet,denotantper β(a) lataxadefertilitataedat a,tenimque elsnaixementsvenendonatsperlacondiciódefrontera(nolocal)aedatzero

B(t) = n(0,t) = ∞ 0 β(a)n(a,t)da. (16)

Sidenotemper n0(a) ladistribucióinicialdelapoblació,tenimqueelmodel completserà

nt (a,t) + na(a,t) =−µ(a)n(a,t), n(0,t) = ∞ 0 β(a)n(a,t)da, n(a, 0) = n0(a). (17)

Perveurel’equivalènciaentreelsmodelsdeMcKendrick-vonFoersteriSharpeLotkaresolem(17)pelmètodedelescaracterístiquesiobtenim

n(a,t) = 

n(0,t a)e a 0 µ(s)ds a<t, n(a t, 0)e a a t µ(s)ds a ≥ t.

Substituintaquestaexpressióalacondiciódefrontera(16)escrivim

n(0,t) = ∞ 0 β(a)n(a,t)da = = t 0 β(a)n(0,t a)e a 0 µ(s)ds da+ + ∞ t β(a)n(a t, 0)e a a t µ(s)ds da. (18)

CarlesBarril,SílviaCuadradoiJordiRipoll

Definint F(a) := e a 0 µ(s)ds ifentuncanvidevariablealsegonsumand,espot escriure(18)com

n(0,t) = t 0 β(a)n(0,t a)F(a)da + ∞ 0 β(a + t)n(a, 0) F(a + t) F(a) da,

queésl’equacióderenovació(11)amb n(0,t) = B(t). Desdelpuntdevistabiològic,elmodellineal (17) suposaquelestaxes vitals β i µ sónparàmetresintrínsecsdelsistemainotenenencomptelacompetènciaentreelsindividuspelsrecursos,quesónlimitats.Aquestalimitació vaserconsideradaperGurtiniMacCamyel1974a[28],onvanintroduirtaxes vitalsdependents,apartdel’edat,delamateixapoblació.Igualqueenelcas del’equaciólogística (7),aixòdonallocaunmodelnolinealquepermetqueel creixementdelapoblaciósiguiautoregulatperlamateixapoblació:

nt (a,t) + na(a,t) =−µ(a,P(t))n(a,t),P(t) = ∞ 0 n(a,t)da,

n(0,t) = ∞ 0 β(a,P(t))n(a,t)da,

n(a, 0) = n0(a).

Enaquestmodel,lainfluènciadeles condicionsambientals enelsindividus delapoblacióesresumeixenunasolaquantitat,queéslapoblaciótotal. Altresautors,comperexempleM.Iannelliel1995(vegeu[34]),hanconsiderat aquestmateixmodelperòperaedatmàximafinitaisuposantquelainfluència ambientalvedonadaperunacol.lecciófinitademidesdelapoblacióambun pes,ésadir, S(t) = ∞ 0 γi(a)n(a,t)da,per i = 1,...,m

Unagranvarietatdemodelsnolinealsambdependènciaenedatvanaparèixerposteriorment.Podríemdirquelateoriadeladinàmicadepoblacions estructuradesperl’edatvaquedarmoltbenrecollidaperG.F.Webbales referències[57, 56].Webbestudiaunmodelnolinealmoltgeneralperala densitatrespectedel’edat a de m tipusogrupsd’individus:

Dn(a,t) =G(n( ,t))(a), n(0,t) =B(n( ,t)), n(a, 0) = n0(a), (20)

on Dφ(a,t) := limh→0+ φ(a+h,t+h) φ(a,t) h ésla«derivadadireccional»enladirecciódelvector (1, 1) deladensitatvectorialdepoblacióatemps t ≥ 0, n(·,t) pertanyal’espaideBanach X := L1((0, ∞); Rm) equipatamblanorma ||φ||= m i=1 ∞ 0 |φi(a)| da.Enelsistema (20),perunabandahiteniml’operador G : X → X,ques’anomena funciód’envelliment ipotinclouretermes relacionatsamblamortalitatiamblestransicionsentretipusogrupsd’individus,iperl’altrabanda,hiteniml’operador B : X → Rm,ques’anomena funció denaixements idonaelnombredenounatsdecadatipusperunitatdetemps.

Peracabaraquestaexposicióhistòrica,volemdestacarquenogairelluny d’aquestsmodelsecològicshihatotaunaclassedemodelsendinàmicade

poblacionsqueconstituixenelques’anomena epidemiologiamatemàtica.Els primerstreballsqueesconeixenenaquestcampsónelsdeDanielBernoullisobrelainoculaciódelaverola[7](gairebéquarantaanysabansdeldescobriment delesvacunes,atribuïtaEdwardJenner,1798)ielsdeRonaldRosssobrela malària[46].Rossvaserundelsprimersdeformularunmodelcompartimental, donatqueconsideravaunapoblaciódemosquitsiunad’humans,itambéva serundelsprimersdeparlard’unllindardel’epidèmiaquemésendavant s’anomenà númeroreproductiubàsic (nombreesperatd’infeccionsproduïdes perunindividutípicdelapoblacióal’inicidel’epidèmia)iqueésl’equivalent delnúmero R0 definitanteriormentenelcontextecològic.

Hihaunaclassedemodelsepidèmicsquetambéconsiderenl’edatperò enelsentitdeltempstranscorregutdesdelmomentenquèunindividu contrauunamalaltiainfecciosa(edatdelainfecció).L’articledeW.O.Kermack iA.G.McKendrickdel1927[36]haesdevingutunclàssicdel’epidemiologia matemàticaquehaestatcitatunainfinitatdevegades.Pertaldeferjustícia, caldestacarqueaquestarticleesconeixprincipalmentpelfamósmodelSIR (sistemasimplificatd’EDOs),peròque,enrealitat,estudiaunmodelmésgeneral tenintencomptel’edatdelainfecció.

ElmodelclàssicdeKermack-McKendrickdescriul’evoluciódelbrotepidèmicd’unamalaltiainfecciosaonelsnaixementsilesmortspercausesnaturals sónnegligitsi,pertant,lamidadelapoblacióesmantéconstant.Lapoblacióesdivideixentresgrups:individus susceptibles (d’adquirirlamalaltia), densitatd’individus infectats respectedel’edatd’infecció(podentransmetre lamalaltia),iindividus recuperats (elsquehansuperatlamalaltiaiarasón immunespermanentment,perexemple)ievolucionasegons:

S (t) =−

β(τ)i(τ,t)dτ · S(t), it (τ,t) + iτ (τ,t) + γ(τ)i(τ,t) = 0, i(0,t) = τ† 0 β(τ)i(τ,t)dτ · S(t), R (t) = τ† 0 γ(τ)i(τ,t)dτ, (21) ambcondicionsinicials S(0) = S0, i(θ, 0) = i0(θ), R(0) = R0,ion τ ∈ [0,τ†] ésl’edatdelainfecció, β(τ) éslataxadetransmissiódelamalaltiai γ(τ) ésla taxaderecuperació,vegeu[36, 34].Enelcasquelestaxes β, γ siguinconstants, llavors,integrantrespecteal’edatdelainfecciól’equacióenderivadesparcials a(21),obtenimelfamóssistemad’equacionsdiferencialsordinàriesSIR: S (t) =−βI(t)S(t),I (t) = βI(t)S(t) γI(t),R (t) = γI(t), amb I(t) = τ† 0 i(τ,t)dτ (nombretotald’infectatsatemps t).

Finsaquíhemexposateldesenvolupamenthistòricdeladinàmicadepoblacionsaprofundintespecialmentenlespoblacionsestructuradesperl’edat, jaquepodríemdirquetotmodeldedinàmicadepoblacionsconsideraimplícitamentl’edatdelsindividus,donatquel’edatnoésresmésqueeltemps

CarlesBarril,SílviaCuadradoiJordiRipoll

transcorregutdesdelmomentdelnaixementdelsindividus.Enresum,la cronologiadelateoriadelespoblacionsestructuradesperl’edatcomença essencialmentambEuler[23],passantperLotka[37, 47, 40],Feller[25],McKendrick[44],vonFoerster[55],GurtiniMacCamy[28],iconclousubstancialment ambWebb[56,57].

Paradoxalment,l’edatésunavariablemassasenzillaperadescriureamb detallelsprocessosfisiològicsdelespoblacions.Aixòfaque,depenentdel tipusdeproblemabiològicquevulguemanalitzarpotserconvenientclassificar elsindividussegonsalgunamesurabiomètrica,encomptes(oamés)del’edat, perexempleestructurarlapoblacióperlamidaenpoblacionscel.lulars.Els primersquevanconsiderarpoblacionsestructuradesfisiològicamentvanser Fredrickson etal. [51, 26, 27],Bell etal. [6, 5, 2]iSinkoiStreifer[48, 49]; vegeu[29]peramésdetalls.Elmodelméssenzilld’unapoblacióestructurada perlamidadelsindividusvaseranalitzatperVanSicklea[53].Aquestmodel, queésuncasparticulardelsmodelsintroduïtspelsgrupsd’investigadors citatsanteriorment,suposaqueelsnounatstenentotsunamida ε> 0ique ladensitatrespectedelamida x ≥ ε atemps t, n(x,t) evolucionasegons (vegeu[43]peraladeducciódelmodel):

nt (x,t) + (g(x)n(x,t))x =−µ(x)n(x,t), g(ε)n(ε,t) = ρ ∞ ε β(x)n(x,t)dx, n(x, 0) = n0(x), (22)

on g(x)> 0éslataxa percapita decreixementindividual,ésadir, x (t) = g(x(t)), µ(x) éslataxa percapita demortalitatamida x, β(x) éslataxa per capita defertilitatamida x,i ρ éslaprobabilitatdelsnounatsdesobreviure durantel nurserystage.VegeuHeijmansiMetz[31]peraunamillorad’aquest modellineal.

Enlaproperaseccióesveuràcomtotsaquestsmodelsestructuratsper l’edatoperunavariablefisiològicamésgeneral,quefinsarahanestatdescrits entermesdetaxesinstantàniesdecanvii,pertant,ambequacionsdiferencials, espodendescriureambunanovaformulaciódesenvolupadaperO.Diekmann, M.GyllenbergiJ.Metz,iH.Thiemeialtrescol.laboradors(1986–actualitat),que esténigeneralitzalajafamosaequaciódeVolterra (12) afegint-hiunrecurs dinàmicqueésconsumitpelsindividusdelapoblació.Aquestateoriavaser iniciadaambelllibre[43]idesenvolupadaposteriormentalstreballs[17, 14, 15,13]i[20,19,16],entred’altres.

3Formulaciódeladinàmicadepoblacionsusantequacions ambretard

Peraestudiarladinàmicad’unapoblaciódesd’unpuntdevistamecanicistacal considerarelcomportamentdelsseusindividus.Unindividuparticularactuarà d’unamaneraoaltraenfunciódelessevescaracterístiquesidel’ambientenel qualviu.Ésoportú,pertant,estructurarlapoblaciódeformaques’agrupinels

individusquesónanàlegs.Enaquestsentit,cadaindividuestàdotatd’un estat individual (tambéanomenat estat-i)iesconsiderenequivalentselsindividusque comparteixenelmateixestat.L’estat-i éslavariabled’estructuradelapoblació ipotferreferènciatantavariablesinternesdel’individu(coml’edat,lamida,el fenotip,l’estatd’alertaoelquesiguiqueensinteressi)comavariablesexternes (comlaposicióenunhàbitatdonat).Alseutorn,esdefineixl’estatpoblacional (tambéanomenat estat-p)comladensitatpoblacionalrespectedel’estat-i dels seusindividus.

Clàssicamentladinàmicadepoblacions,comhemvistalesseccionsanteriors,haconsideratl’estat-p comlavariabledependentdelproblema.La formulacióambretardesdiferenciaenaquestpuntperquè,enllocdeconsiderarl’estat-p,utilitzala històriadelsnaixements.Aquestavariabledescriucom hanestatelsnaixementsenelpassat,ienconcretespotutilitzarperasaber quantsindividusd’estatindividual x estavennaixent τ unitatsdetempsen elpassat.Enparticular,siconeixemla històriadenaixements icomsónles trajectòriesdecadaindividuperl’espaid’estats-i desdelmomentenquèneix finsalpresent,aleshorespodemrecuperarladensitatpoblacionalalpresent, ésadir,l’estat-p

Comhemdit,perasabercomvarial’estat-i d’unindividuenuninstantno n’hihaproudeconèixerl’estat-i del’individuenaquellinstant.Apartd’aquestavariabletambécalsaberquinaésla condicióambiental enaquellinstant. Remarquemquen’hihaprouambla condicióambiental instantàniaiqueno calconèixercomeral’ambientenelpassat.Aixòésaixíperquèl’efectequeha tingutl’ambientdelpassatenl’individuestàcontingutimplícitamentenelseu estat-i actual.Notemtambéquela condicióambiental ésunavariableglobalen elsentitqueéslamateixaperatotselsindividus.Ésl’efectequetél’ambient sobreelsdiferentssubjecteselquepotvariar.Perexemple,potpassarquecerta fontd’alimentnoméssiguiaccessiblealsindividuspetitsoqueelsindividus gransnosiguinperseguitspelsdepredadors.L’ambient,però,éselqueés.

Siesconeixla condicióambiental alllargdeltemps,aleshoresespotescriureunaequacióderenovacióoequaciódeVolterraperala històriade naixements.Lapoblació,però,téunimpactesobrel’ambient,jasiguiperquè consumeixrecursosoperquècontamina,laqualcosaimpedeixconèixer, a priori,comseràl’ambient.La condicióambiental és,defet,unavariabledel sistemaquedepèntantdela condicióambiental enelpassatcomdela històriadenaixements.Aixís’arribaaunsistemadeduesequacionsambretard acoblades.L’objectiud’aquestaseccióésdonarunaexpressióexplícitadel sistemaanteriorentermesdequatreingredientsfenomenològics.Elprimer ingredientcontéinformaciósobrecomevolucional’estat-i d’unindividua travésdel’espaid’estatsindividuals,i,pertant,téencompteprocessoscom eldesenvolupament,elcreixement,elmovimentolasupervivència.Elsegon ingredientincloutotelqueestàrelacionatamblareproducciódelsindividus. Elterceringredientdescriul’impactequetéunindividusobrel’ambientmentre queelquartdescriucomvariaelmedienabsènciadepoblació.Totsquatre ingredientss’especificaranformalmentquansiguinecessari.

Delsindividusalapoblació

Comencemintroduint Ω comelconjuntdetotsels estatsindividuals admissibles.Elselementsde Ω depenentantdelques’estàmodelitzantcomdel nivelldedetalldelmodel.Perexemple,siesteminteressatsenlamidadels individus,podemoptarperunmodelmoltsenzill,enquè Ω ={petit, gran} operunmodelunamicamésricenelqualesdistingeixenelsindividusen funciódelasevamassacorporal,demaneraque Ω = R+.Finsitotespodrien classificarelsindividusenfunciódediversesmesuresbiomètriques.Perexemple,sivolguéssimestudiarunapoblaciód’aus,podriaserrellevantdistingirels ocellsenfunciódelamidadelbecidelalongituddelesales.Enaquestcas prendríem Ω = R2 +.

Deformasimilar,consideremelconjuntdetotesles condicionsambientals admissiblesieldenotemambelsímbol E.Deformamésomenysgeneral,es potdirqueladinàmicad’unapoblacióestàdeterminadaperdosfactors:els recursosdequèdisposailesamenacesalesqualsestàexposada.Enaquest sentit,elconjuntde condicionsambientals hauriadereflectiraquestainformacióiobviaraltrescaracterístiquesambientalssupèrfluescom,perexemple, laposiciódelsplanetesalfirmament(notem,però,queaquestainformació seriaimportantsiestudiéssimunapoblaciód’astrònomsiastrònomes,ofins itotsiconsideréssimunapoblaciód’escarabatspiloters,delsqualssesap ques’orientenamblesestrelles).Enelcasquelapoblaciónomésdepengui d’untipusderecurs, E potanar,enfunciódelasimplicitatdelmodel,desd’un conjuntdedoselementscom {poc, molt} aunconjuntcontinucom R+ que reflecteixilaconcentraciódelrecursenelmedi.Siestinguésencomptela distribucióespacialdelsindividus,aleshoreselselementsde E serienfuncions queespecificarienlaconcentracióderecursencadaposició.

3.1Dinàmicapoblacionaldonatelmedi:teorialineal

Pertaldeplantejarelsistemadinàmiccomencemsuposantquela condició ambiental estàdonadaperatottemps.Ésadir,consideremunafunció E : R → E talque E(t) denotal’ambientdelsistemaal’instant t

Primeringredient Sigui uE (t,s,ξ,ω) laprobabilitatqueunindividuamb estat individual ξ ∈ Ω enl’instant s tinguiun estat-i continguta ω ⊂ Ω en l’instantposterior t sabentquela condicióambiental vedonadaper E entre s i t.

Perdefinicióestéque uE (s,s,ξ,ω) és1si ξ ∈ ω i0encascontrari,laqual cosaespotescriureformalmentutilitzantladeltadeDiraccom uE (s,s,ξ,ω) = δξ (ω).Observi’stambéquelaprobabilitatqueunindividuamb estatindividual ξ al’instant s segueixiviual’instantposterior t és uE (t,s,ξ, Ω) ≤ 1.A mésamés,comqueladinàmicad’unindividunomésdepèndelseu estat-i a l’instant s ideles condicionsambientals entre s i t,esconclouquelesequacions deChapman-Kolmogorov(vegeu[29])sesatisfan,ésadir,peratot τ ∈ (s,t)

uE (t,s,ξ,ω) = Ω uE (t,τ,η,ω)uE (τ,s,ξ,dη). (23)

Observemque E noméscalqueestiguidefinidaentre τ i t alprimerfactor delaintegralientre s i τ enelsegon.D’araendavantutilitzarem,coma normanotacional,queelsubíndex E enunafuncióquedepèndeduesvariables temporalsindicaquelafunciónomésestàafectadaperlapartde E definida entreaquestesduesvariables.

Segoningredient Sigui β(ξ, E,ω) elnombreesperatdedescendentsdirectes nascutsen ω ⊂ Ω perunitatdetempsqueprodueixunindividuamb estatindividual ξ ∈ Ω sabentquela condicióambiental instantàniaés ˜ E.

Combinantelsingredients β i uE espotdefinir

1 E (t,s,ξ,ω) := Ω

E (t,s,ξ,dη) (24)

comelnombreesperatdenounatsamb estat-i continguta ω ⊂ Ω queestan naixentperunitatdetempsal’instant t iquesóndescendentsdirectes(fillsi fillesnomés)d’unindividuamb estatindividual ξ ∈ Ω al’instant s,sabentque la condicióambiental entre s i t ésladonadaper E

Apartirdelsignificatdelafunció β1 E éspossibleconstruirunsistema dinàmicperales històriesdelsnaixements.Elsistemaprenlaformad’una equacióderenovació,is’obtéobservantqueelsnounatsqueestannaixent alpresentsónnecessàriamentdescendentsdirectesd’individusnascutsal passat.Així,elnombreesperatdenounatsamb estat-i continguta ω ⊂ Ω que estannaixentperunitatdetempsal’instant t,magnitudquedenotemcom a B(t,ω),s’obté«sumant»elsdescendentsdirectesdelesdiferentscohorts d’edatnascudesalpassat.Ladescripcióanteriors’escriuformalmentcom

B(t,ω) = ∞ 0 Ω β1 E (t,t a,ξ,ω)B(t a,dξ)da. (25)

Observemqueéspossiblerecuperarlamesurapoblacionalenuninstant t siesconeixlahistòriade B finsal’instant t.Noméscalseguirladinàmica delsindividusdesdelmomentenquèneixenfinsal’instant t,laqualcosaés possiblesiesdisposadelprimeringredientdelmodel.Enefecte,sidenotem amb m(t,ω) laquantitatd’individusquehihad’estat-i continguta ω ⊂ Ω a l’instant t,tenim

m(t,ω) = ∞ 0 Ω uE (t,t a,ξ,ω)B(t a,dξ)da. (26)

3.2Dinàmicapoblacionaliambiental:teorianolineal

Consideremaraqueelsindividusdelapoblaciópodenalterarla condició ambiental,demaneraqueaquestadeixadeserindependentdelapoblació. L’efecteconcretquetenenelsindividussobrel’ambientésunaltreingredient delmodel.

CarlesBarril,SílviaCuadradoiJordiRipoll

Terceringredient Sigui γ(ξ, ˜ E) lataxadecanviqueexperimentaelmediquan la condicióambiental és ˜ E degutalesaccionsd’unindividud’estatindividual ξ.Ensreferimalafunció γ coml’alteracióambiental percapita.

«Sumant»l’alteracióambientalqueprovocacadaindividud’unapoblacióobtenimlataxadecanviambientaldegutalapoblacióenconjunt.Denotemaquesta taxaamblalletra g ienshireferimcoml’alteracióambientalpoblacional.Formalment,si m éslamesurapoblacionali E ésla condicióambiental,l’alteració ambientalpoblacionalvedonadaper

˜ E,m) :=

˜ E)m(dη). (27)

Notemqueimplícitamentestemsuposantquecadaindividuafectal’ambient deformaindependent.Això,però,noésunarestricciósinóunaconseqüència delfetquelainformacióquedeterminaelcomportamentd’unindividuestà contingudaala condicióambiental.Enaquestsentit,siesprodueixeninteraccionsdirectesentreindividusdiferents(depredació,cooperació,aparellament, etc.),aleshoresla condicióambiental haderecollirelsdetallspertinentsdela distribuciópoblacionalpertaldereflectiraquestesinteraccions.Defet,elque passaenaquestessituacionsésquel’ambientefectiud’unindividunonomés contérecursosaliensalapoblaciósinótambéelementsdelamateixapoblació.

Amésamésdelscanvisambientalsprovocatsperlapoblació,elmedi tambépotmanifestarunadinàmicaintrínseca.Aquestéseldarreringredient delmodel.

Quartingredient Sigui g0( ˜ E) lataxadecanviqueexperimentaelmediquan la condicióambiental és E degutacausesalienesalapoblació.

Ambaquestainformacióéspossibledonarunaequaciódiferencialperala condicióambiental.Sinohihacapindividuenlapoblaciómodelitzada,aleshores l’alteracióambientalpoblacionalésnul.lail’equaciódiferencialéssimplement

(t) = g0(E(t)).

Engeneral,silamesurapoblacionalestàdescritaperunafunció m(t),esté

E (t) = g0(E(t)) + g(E(t),m(t)). (28)

Comhemvistenl’apartatanterior,lamesurapoblacional m(t) espotescriure entermesdelahistòriadenaixementsfinsal’instant t utilitzantl’equació (26). Pertant,l’equació (28) relacionaladinàmicadelsnaixementsambladinàmica ambiental,laqualcosaacoblalesequacions (25) i (28).D’aquestamaneras’obté unsistemanolinealambretardqueinvolucraunaequacióderenovaciói unaequaciódiferencialambretard.Prenent t> 0i θ ≤ 0,demaneraque t es

E

potpensarcomuninstantdelfutur(posteriora0)i θ comuninstantdel passat(anteriora0),elproblemaenqüestiós’escriucom

B(t,ω) = t −∞ Ω β1 E (t,τ,ξ,ω)B(τ,dξ)dτ,

E (t) = g0(E(t))+ Ω γ(η,E(t)) ∞ 0 Ω uE (t,t a,ξ,dη)B(t a,dξ)da,

B(θ,ω) = φ1(θ,ω),

E(θ) = φ2(θ), (29)

on φ1 i φ2 sónleshistòriesinicialsde B i E.Observemquecomavariables d’estatestemagafanthistòriestantdelestaxesdenaixementcomdela condició ambiental.Observemtambéquel’equacióderenovacióperalafunció B pot ferqueaquestapresentidiscontinuïtats,mentrequel’equaciódiferencialamb retardsuggereixquelafunció E éscontínua.Peraquestsmotiusprenemcoma espaidefasedelsistemadinàmicdefinitper(29)l’espai

L1((−∞, 0); M(Ω)) × C((−∞, 0]; E),

on M(Ω) denotaelconjuntdemesuresdefinidessobreelconjunt Ω irecordem quelacondicióambientalprenvalorsalconjunt E.Coméshabitualenequacionsambretard,unasolució (B(t, ),E(t)) de (29) defineixunpuntd’aquest espaid’estatsmitjançant Bt (θ) := B(t + θ, ·), Et (θ) := E(t + θ)

Notemtambéquesilahistòriade B finsal’instant s ésdonadaper φ,de maneraque B(τ,ω) := φ(τ,ω) peratot τ ≤ s,aleshores (25) espotreescriure com

B(t,ω) = t s Ω β1 E (t,σ,ξ,ω)B(σ,dξ)dσ + F(t,ω), (30)

on F(t,ω) éslataxadenaixementsdenounatsamb estat-i continguta ω ⊂ Ω quesóndescendentsdirectesd’individusqueal’instant s jaexistien, i.e.,

F(t,ω) := s −∞ Ω β1 E (t,σ,ξ,ω)φ(σ,dξ)dσ = = 0 −∞ Ω β1 E (t,s a,ξ,ω)φ(s a,dξ)da. (31)

Enresum,elsistema (29) espotinterpretarcomunaextensiódel’equació (25), quealseutornésunageneralitzaciódel’equaciódeVolterra(12).

Finalmentvolemacabaraquestateoriaabstractadepoblacionsambun exempleil.lustratiui,alhora,entenedor.Consideremunapoblacióestructurada perl’edat,demaneraque Ω = [0, ∞).Suposemquelacondicióambientalésun escalarquerepresentalaconcentraciódenutrients,demaneraque E= [0, ∞). Perdeterminarelprimeringredientfemlahipòtesiquelataxademortalitat

CarlesBarril,SílviaCuadradoiJordiRipoll

ésunafuncióquedepèndel’edatidelaconcentraciódenutrients µ(a,E).En símbolstenimque

uE (t,s,ξ,ω) = e t s µ(ξ+τ s,E(τ))dτ δξ+t s (ω). (32)

Peralsegoningredient,prenem β(η, ˜ E,ω) = β0(η, ˜ E)δ0(ω),laqualcosa significaquequanlacondicióambientalés E,unindividud’edat η téunataxa defertilitat β0(η, ˜ E) ila δ deDirac δ0 apareixdemaneranaturaljaquetotsels individusneixenambedatzero.

Peralterceringredient,suposemqueelconsumdenutrientsperpartd’un individuésproporcionalalaconcentraciódenutrientsiindependentdela sevaedat,demaneraque γ(η, ˜ E) =−c ˜ E, c> 0.

Peralquartingredient,suposemqueelsnutrientss’estangenerantauna taxaconstant r> 0iquenoesdegradendeformanatural,demaneraque g0(E) = r .Totsaquestsingredients,usant (32), (24) ilesformesespecialsde lesfuncions β i γ a(29),donenllocalsegüentsistemanolinealambretard

B(t,ω) = t −∞ [0,∞) β0(ξ + t τ,E(t))e t τ µ(σ τ,E(σ))dσ B(τ,dξ)dτδ0(ω), E (t) = r cE(t) [0,∞) ∞ 0 [0,∞) e t t a µ(σ t+a,E(σ))dσ δξ+a(dη)B(t a,dξ)da,

B(θ,ω) = φ1(θ,ω),

E(θ) = φ2(θ).

(33)

Observemquelaprimeraequacióésdelaforma B(t,ω) = b(t)δ0(ω).Considerantqueaixòesdonaperaqualsevoltemps(cosaraonablejaquetotsels individusneixenambedatzero),lesequacionsdinàmiquesdelsistemaanterior esdevenen:

b(t)δ0(ω) = t −∞ β0(t τ,E(t))e t τ µ(σ τ,E(σ))dσ b(τ)dτδ0(ω), E (t) = r cE(t) ∞ 0 e t t a µ(σ t+a,E(σ))dσ b(t a)da.

(34)

Siaméssuposemqueelrecurstéunadinàmicaràpidaiqueestàenunestat quasiestacionari(i.e. E (t) ≈ 0),llavorspodemrelacionarlapoblaciótotal,que recordemquevedonadaper P(t) = ∞ 0 e t t a µ(σ t+a,E(σ))dσ b(t a)da,amb elmateixrecurs:

E(t) = r cP(t)

ialeshores(34)esredueixaunasolaequacióderenovació

b(t) = t −∞ β0 t τ, r cP(t) e t τ µ σ τ, r cP(t) dσ b(τ)dτ,

queésequivalental’equacióderenovaciódelmodelnolinealdeGurtini MacCamy(19)ambfuncions β i µ adequades.

Certament,l’exempleanteriorésprousenzillperapoder-lotractardirectamentutilitzantlaformulacióambequacionsenderivadesparcials.Noobstant això,quanelsestatsdelsindividussónméscomplicats(vegeu,perexemple[30] i[18]onelsindividusestanestructuratsperlamidai[8]onestéencomptela concentracióintracel.lulard’unaproteïna),llavorslaformulacióambretardno nomésensajudaaplantejarelmodelentermesdepropietatsbàsiquesdels individus,sinóquetambéenspermetferunaanàlisimésrigorosasobreel comportamentasimptòticdelessolucionsentorndelsestatsestacionaris.

Agraïments

ElsautorshanrebutparcialmentelsuportdelMinisterideCiènciaiInnovació,referènciesMTM2017-84214-C2iMTM2014-52402-C3,idel’Agènciade Gestiód’AjutsUniversitarisideRecerca-GeneralitatdeCatalunya,referència 2017-SGR-1392.

Referències

[1] Allen,L.J.S. AnIntroductiontoMathematicalBiology.UpperSaddleRiver, NJ:PearsonPrenticeHall,2007.

[2] Anderson,E.C.;Bell,G.I.;Petersen,D.F.;Tobey,R.A. «Cellgrowthand divisionIV.Determinationofvolumegrowthrateanddivisionprobability». Biophys.J.,9(1969),246–263.

[3] Bacaër,N. AShortHistoryofMathematicalPopulationDynamics.Londres: Springer-VerlagLondon,Ltd.,2011.

[4] Barril,C.;Calsina,À.;Ripoll,J. «Apracticalapproachto R0 incontinuous-timeecologicalmodels». Math.MethodsAppl.Sci.,specialissuepaper (2017). DOI:10.1002/mma.4673.

[5] Bell,G.I. «CellgrowthanddivisionIII.Conditionsforbalancedexponentialgrowthinamathematicalmodel». Biophys.J.,8(4)(1968),431–444.

[6] Bell,G.I.;Anderson,E.C. «CellgrowthanddivisionI.Amathematicalmodelwithapplicationstocellvolumedistributionsinmammalian suspensioncultures». Biophys.J.,7(4)(1967),329–351.

[7] Bernoulli,D. «Essaid’unenouvelleanalysedelamortalitécauséepar lapetitevérole,etdesavantagesdel’inoculationpourlaprévenir». Mem. Math.Phys.Acad.R.Sci. (1766),1–45.

[8] Borges,R.;Calsina,À.;Cuadrado,S.;Diekmann,O. «Delayequation formulationofacyclin-structuredcellpopulationmodel». J.Evol.Equ., 14(4–5)(2014),841–862.

CarlesBarril,SílviaCuadradoiJordiRipoll

[9] Brauer,F.;Castillo-Chávez,C. MathematicalModelsinPopulationBiologyandEpidemiology.NovaYork:Springer-Verlag,2001.(TextsinAppliedMathematics;40)

[10] Braun,M. DifferentialEquationsandTheirAplications.AnIntroductiontoAppliedMathematics.NovaYork:Springer-Verlag,1975.(AppliedMathematicalSciences;15)

[11] Britton,N.F. EssentialMathematicalBiology.Londres:Springer-Verlag London,Ltd.,2003.(SpringerUndergraduateMathematicsSeries)

[12] Darwin,C.;Wallace,A.R. «Onthetendencyofspeciestoformvarieties; andontheperpetuationofvarietiesandspeciesbynaturalmeansof selection». JournaloftheProceedingsoftheLinneanSociety.Zoology,3 (1858),45–62.

[13] deRoos,A.M.;Diekmann,O.;Getto,P.;Kirkilionis,M.A. «Numerical equilibriumanalysisforstructuredconsumerresourcemodels». Bull.Math. Biol.,72(2)(2010),259–297.

[14] Diekmann,O.;Getto,P.;Gyllenberg,M. «StabilityandbifurcationanalysisofVolterrafunctionalequationsinthelightofsunsandstars». SIAMJ. Math.Anal.,39(4)(2007/08),1023–1069.

[15] Diekmann,O.;Gyllenberg,M. «Abstractdelayequationsinspiredby populationdynamics».A: FunctionalAnalysisandEvolutionEquations. Basilea:Birkhäuser,2008,187–200.

[16] Diekmann,O.;Gyllenberg,M.;Huang,H.;Kirkilionis,M.;Metz,J.A.J.; Thieme,H.R. «Ontheformulationandanalysisofgeneraldeterministic structuredpopulationmodels.II.Nonlineartheory». J.Math.Biol.,43(2) (2001),157–189.

[17] Diekmann,O.;Gyllenberg,M.;Metz,J. «Physiologicallystructuredpopulationmodels:towardsageneralmathematicaltheory».A: Mathematics forEcologyandEnvironmentalSciences.Berlín:Springer,2007,5–20.(Biol. Med.Phys.Biomed.Eng.)

[18] Diekmann,O.;Gyllenberg,M.;Metz,J.A.J.;Nakaoka,S.;deRoos,A.M. «Daphniarevisited:localstabilityandbifurcationtheoryforphysiologically structuredpopulationmodelsexplainedbywayofanexample». J.Math. Biol.,61(2)(2010),277–318.

[19] Diekmann,O.;Gyllenberg,M.;Metz,J.A.J.;Thieme,H.R. «Onthe formulationandanalysisofgeneraldeterministicstructuredpopulation models.I.Lineartheory». J.Math.Biol.,36(4)(1998),349–388.

[20] Diekmann,O.;Gyllenberg,M.;Thieme,H.R. «Semigroupsandrenewal equationsondualBanachspaceswithapplicationstopopulationdynamics».A: DelayDifferentialEquationsandDynamicalSystems.Berlín: Springer,1991,116–129.(LectureNotesinMath.;1475)

[21] Dublin,L.I.;Lotka,A.J. «Onthetruerateofnaturalincrease». J.Amer. Statist.Assoc.,20(151)(1925),305–339.

[22] Euler,L. Introductioinanalysininfinitorum.Tomusprimus.Lausana:apud Marcum-MichaelemBousquet&Socies,1748.

[23] Euler,L. «Recherchesgénéralessurlamortalitéetlamultiplicationdu genrehumain». Mémoiresdel’AcadémiedessciencesdeBerlin,16(1760), 144–164.

[24] Euler,L. «Ageneralinvestigationintothemortalityandmultiplication ofthehumanspecies». Theoret.PopulationBiol.,1(3)(1970),307–314. [TraduïtperNathaniBeatriceKeyfitz]

[25] Feller,W. «Ontheintegralequationofrenewaltheory.» Ann.Math.Statistics,12(1941),243–267.

[26] Fredrickson,A.G.;Ramkrishna,D.;Tsuchiya,H.M. «Statisticsand dynamicsofprocaryoticcellpopulations». Math.Biosci.,1(1967),327–374.

[27] Fredrickson,A.G.;Tsuchiya,H.M. «Continuouspropagationofmicroorganisms». AIChEJ.,9(4)(1963),459–468.

[28] Gurtin,M.E.;MacCamy,R.C. «Non-linearage-dependentpopulation dynamics». Arch.RationalMech.Anal.,54(1974),281–300.

[29] Gyllenberg,M. «Mathematicalaspectsofphysiologicallystructured populations:thecontributionsofJ.A.J.Metz». J.Biol.Dyn.,1(1)(2007), 3–44.

[30] Heijmans,H.J.A.M. «Thedynamicalbehaviouroftheage-size-distribution ofacellpopulation».A: TheDynamicsofPhysiologicallyStructuredPopulations.Berlín:Springer,1986,185–202.(LectureNotesinBiomath.;68)

[31] Heijmans,H.J.A.M.;Metz,J.A.J. «Smallparametersinstructured populationmodelsandtheTrotter-Katotheorem». SIAMJ.Math.Anal., 20(4)(1989),870–885.

[32] Iannelli,M.;Martcheva,M.;Milner,F.A. Gender-StructuredPopulation Modeling:MathematicalMethods,Numerics,andSimulations.Filadèlfia,PA: SocietyforIndustrialandAppliedMathematics(SIAM),2005.(Frontiersin AppliedMathematics;31)

[33] Iannelli,M.;Milner,F. AnIntroductiontoMathematicalPopulationDynamics.AlongthetrailofVolterraandLotka.Cham:Springer,2014. (Unitext-LaMatematicaperil3 + 2;79)

[34] Iannelli,M.;Milner,F. TheBasicApproachtoAge-StructuredPopulationDynamics.Models,MethodsandNumerics.Dordrecht:Springer,2017. (LectureNotesonMathematicalModellingintheLifeSciences)

[35] Inaba,H. Age-StructuredPopulationDynamicsinDemographyandEpidemiology.Singapur:Springer,2017.

[36] Kermack,W.O.;McKendrick,A.G. «Acontributiontothemathematical theoryofepidemics». Proc.Roy.Soc.LondonSer.A,115(1927),700–721.

[37] Lotka,A.J. «Relationbetweenbirthratesanddeathrates». Science, 26(653)(1907),21–22.

CarlesBarril,SílviaCuadradoiJordiRipoll

[38] Lotka,A.J. «Analyticalnoteoncertainrhythmicrelationsinorganic systems». Proc.Natl.Acad.Sci.USA,6(7)(1920),410–415.

[39] Lotka,A.J. TheElementsofPhysicalBiology.Baltimore:Williams&Wilkins Co.;Londres:Baillière,Tindall&Cox,1925.

[40] Lotka,A.J. «Onanintegralequationinpopulationanalysis». Ann.Math. Statist.,10(2)(1939),144–161.

[41] Lotka,A.J. ElementsofMathematicalBiology.NovaYork:DoverPublications,Inc.,1956.[Republicaciósensesobresortirdelaprimeraedició publicadasotaeltítol: TheElementsofPhysicalBiology [39]]

[42] Malthus,T. AnEssayonthePrincipleofPopulation.Londres:J.Johnson, 1798.

[43] Metz,J.A.J.;Diekmann,O. (ed.). TheDynamicsofPhysiologicallyStructuredPopulations.Berlín:Springer,1986.(LectureNotesinBiomathematics;68)

[44] M’Kendrick,A.G. «Applicationsofmathematicstomedicalproblems». Proc.EdinburghMath.Soc.,40(1926),98–130.

[45] Murray,J.D. MathematicalBiology.Berlín:Springer-Verlag,1989.(Biomathematics;19)

[46] Ross,R. ThePreventionofMalaria.Londres:JohnMurray,1911.

[47] Sharpe,F.R.;Lotka,A.J. «Aprobleminage-distribution». Philos.Mag.(6), 21(124)(1911),435–438.

[48] Sinko,J.W.;Streifer,W. «Anewmodelforage-sizestructureofapopulation». Ecology,48(6)(1967),910–918.

[49] Sinko,J.W.;Streifer,W. «Applyingmodelsincorporatingage-sizestructureofapopulationto Daphnia». Ecology,50(4)(1969),608–615.

[50] Thieme,H.R. MathematicsinPopulationBiology.Princeton,NJ:Princeton UniversityPress,2003.(PrincetonSeriesinTheoreticalandComputational Biology)

[51] Tsuchiya,H.M.;Fredrickson,A.G.;Aris,R. «Dynamicsofmicrobial cellpopulations».A: AdvancesinChemicalEngineering.Vol.6.NovaYork; Londres:AcademicPress,1966,125–206.

[52] Tuljapurkar,S. «Stablepopulationtheory».A: TheNewPalgraveDictionaryofEconomics.Londres:PalgraveMacmillanUK,2008,1–7.

[53] VanSickle,J. «Analysisofadistributed-parameterpopulationmodel basedonphysiologicalage». J.Theoret.Biol.,64(3)(1977),571–586.

[54] Volterra,V. «Variazioniefluttuazionidelnumerod’individuiinspecieanimaliconviventi». MemoriedellaRealeAccademiaNazionaledei Lincei(6),2(1926),31–113.

[55] vonFoerster,H. «Someremarksonchangingpopulations».A: TheKineticsofCellularProliferation.NovaYork:Grune&Stratton,1959,382–407.

[56] Webb,G.F. «Nonlinearsemigroupsandage-dependentpopulationmodels». Ann.Mat.PuraAppl.(4),129(1981),43–55(1982).

[57] Webb,G.F. TheoryofNonlinearAge-DependentPopulationDynamics.Nova York:MarcelDekker,Inc.,1985.(MonographsandTextbooksinPureand AppliedMathematics;89)

CarlesBarril,SílviaCuadrado

DepartamentdeMatemàtiques

UniversitatAutònomadeBarcelona

EdificiC,FacultatdeCiències 08193,CerdanyoladelVallès,Barcelona {carlesbarril,silvia}@mat.uab.cat

JordiRipoll

Departamentd’Informàtica,MatemàticaAplicadaiEstadística

UniversitatdeGirona Av.LluísSantaló,s/n 17003,Girona jripoll@imae.udg.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.2,2018.Pàg.111–145. DOI:10.2436/20.2002.01.82

GaspardMonge

AgustíReventós

Resum: Aquestarticlevolseruntributal’obradeMongeenelcampdelageometria diferencialdecorbesisuperfíciesenelsdos-centsanysdelasevamort.Desprésd’un breurecordatoridelasevabiografia,enscentremenelsseustreballssobreevolutes decorbesal’espaiisobretotenelnaixementdeleslíniesdecurvaturaenunarticle dedicataltransportdeterres.Analitzemendetallelfull xv delessevesfamoses Feuillesd’analyse ifemunbreucomentaridelarestadelsseustreballssobregeometria diferencial.AcabemambunanotadeJosepLluísSolésobreundelsamicsibiògrafde Monge:FrançoisArago.

Paraulesclau: Monge,corbes,superfícies,evolutes,líniesdecurvatura.

ClassificacióMSC2010: 53A04,53A05,01A50.

1Introducció

El28dejuliold’aquestany2018s’hacomplertdos-centsanysdelamortdel grangeòmetraGaspardMonge(1746–1818).Intentarédonarunavisióresumida delasevavidaiobracentrant-me,però,nomésenelstreballsdegeometria diferencial,jaquel’obraglobaldeMongeésimmensaiabraçadesdelaquímica, alameteorologia,lamecànica,etc.

GaspardMonge(1746–1818).

AgustíReventós

AMongese’lpotconsiderar,juntamentambEuleriGauss,comelfundadordelageometriadiferencialdecorbesisuperfícies.Tambése’lconsidera creadordelateoriadederivadesparcialsdesegonordre,queellsempreestudiavalligadesaproblemesgeomètrics,peròquehantingutposteriorment tantaimportànciaenaltrescamps.

Elstreballssobrelavidail’obradeMongeescritsperpersonesqueel coneixiendirectamentiquesónmoltcompletssónelsdelsseusdeixebles CharlesDupin[T7],de1819,ieldeFrançoisArago[T1],de1846.

EltreballdeDupinestitula Essaihistoriquesurlesservicesetlestravaux scientifiquesdeGaspardMonge.Desprésd’unaprimerapartbiogràficaconté elscapítolssegüents:«Géométriepureetdescriptive»,«Géométrieanalytique»,«Géométrieappliquéeauxarts»,«Géométrieappliquéeàlaméchanique», «Physique:Attractionmoléculaire»,«Optique»,«Météorologie»,«Technologie: Feutrage»,«Chimiegénérale»,«Artschimiques:Métallurgie»,«Économiedomestique:FrabricationdesfromagesdeLodézan»,«OuvragesetMémoires publiésparG.Monge»,«MonumentàerigerenhonneurdeMonge»,«Listede souscripteurs».

Comveieu,hipodeutrobarlallistaexhaustivadelespublicacionsdeMonge ielsseusdiversoscampsd’interès,inclososelsformatges!1 DupintambéfaunretratdeMongequeenspotajudaraacostar-nosal personatge([T7,p.150]):

Ilétaid’unehautestature,laforcephysiquesemontraitdansseslargesmuscles, commelaforcemoralesepeignaitdanssonregardvasteetprofond.Safigure étaitlargeetraccourciecommelafacedulion.[...]Désqu’ilparlait,oncroyait voirunautrehomme...,unfeunouveaubrillaitdanssesyeux.

[Eraalt,laforçafísicaesveiaenelsseusllargsmuscles,comlaforçamorales reflectiaenlasevamiradavastaiprofunda.Lasevafiguraeraamplaiescurçada comlacarad’unlleó.[ ]Quanparlava,homcreiaveureunaltrehome...,un focnoubrillavaenelsseusulls.]

Eltreballd’Arago2 foullegital’Académiedessciencesel1846,constade 157pàgines,is’hiveuentotmomentlagranestimaqueAragosentiaper Monge.Donamoltainformacióinteressant,perlaproximitattemporal,sobre laRevolucióFrancesailacampanyad’Egipte.

1 Dupinvadedicarelseuprimerllibre, Développementsdegéometrie [A1],de1813,aMonge posantcomasubtítol PourfairesuitealaGéométrieDescriptiveetalaGéométrieAnalytiquede M.Monge,idient:

MONILLUSTREMAÏTRE,JevousdédiemonpremierOuvragedansungenreoùjedois toutàvosleçons;vosencouragementsm’ontengagédanslacarrièreaplanieparvos travaux[ ]

[IL LUSTREMESTRE,usdedicolamevaprimeraObrasobreuntemaenelqualhodectota lesvostreslliçons;elsvostresencoratjamentsm’hancompromèsenlacarreraaplanada pelsvostrestreballs[...]]

2PersaberméssobreArago,vegeulasecció8,escritaperJosepLluísSoléClivillés.

Aixímateixhemconsultatelselogisfúnebresdedosdelsseusprimersalumnesal’Écolepolytechnique,N.Guyon[T10]iB.Brisson[T3],delmateix1818.

Tambésónd’interèselselogisqueel1849dedicaaMongeeldirectorde l’escoladeBeaune,F.Ravailhe[T12].Estractadel’escolaonvaestudiarMonge depetit.AquestselogisestandedicatsalafilladeMonge,Émilie,enaquell momentMadameMareyMonge,jaques’haviacasatambNicolas-JosephMarey el1789.Elmotiuésquel’esposadeMongehaviallegatalcol.legideBeaunela quantitatde3000francsperdotard’unabecaanuall’alumnemésdistingiten matemàtiquesdurantl’any.Elpremil’entregavenelsfillsd’Émilie.

Unaobramoltdocumentadaés Ungrandfrançais.Mongefondateurde l’Écolepolytechnique [T5],deLouisdeLaunay(1933).Aprofundeixmoltenla relacióentreMongeiNapoleóilestasquesdeMongecomapresidentdelSenat. Peròl’autorqueméshaestudiatMonge,unsanysméstard(1951),éssens dubteRenéTatona L’œuvrescientifiquedeMonge [T16].Ésl’obradefinitiva sobreeltema.

Trobareumésdetallssobrelavida,obra,deixeblesicontinuadorsdeMonge alesnotesbiogràfiquesdeStruik[T15].Tambéal’articlequeSergescuva escriureel1946ambmotiudelbicentenaridelnaixementdeMonge[T14].

AltresreferènciessónelsarticlesdeBrunoBelhoste«GaspardMonge:Urgencesrevolutionnairesetutopie»[T2](1989),deJoséJ.Etayo«Lasbasesdela GeometríaDiferencial»[T8](1993),ideRémiLangevin«GaspardMonge,de laplancheàdessinauxlignesdecourbure»[T11](2002).Tambéhihaunamolt bonainformacióalaViquipèdia.

Lesllistesbibliogràfiquesquetanquenaquestarticle,tantlaqueesrefereix alstreballsdeMongecomladelstreballssobreMonge,nosónexhaustivesi fanreferèncianomésalesobresqueheconsultat.Heprocurat,aixòsí,quea lallistadetreballsdeMongeapareguintotselsrelacionatsamblageometria diferencial,peròlesfronteresmatemàtiquessóndifuses.

2Breubiografia

GaspardMongeneixel9demaigdel1746aBeaune.Vaserelprimerdelstres fillsdeJacquesMonge,uncomerciantquevaportarunavidadeprivacionsper poderportarelsfillsal’escola,concretamentalCollèged’OratoriensdeBeaune.

El1762Gaspardacabaelsestudisdefilosofia,físicaimatemàtiquesa Beaune.AmbnoméssetzeanysésnomenatprofessordefísicaaLió.Segons Ravailhe[T12],elseupareelvaacomiadardient:«Fillmeu,recordaqueentota circumstànciadeusrespectealsteussuperiorsiexemplealsteusinferiors».

El1764faunplànoldetallatdeBeaunequeofereixalamunicipalitat.El coroneldeVignan,segoncomandantdel’ÉcoleroyaledugéniedeMézières,3 sapapreciareltreballiproposaalseuautord’anaraMézières.

3 L’escolad’enginyersdeMézièresvaserfundadael1748pelcavallerdeChastillon,pertal deformarenginyersmilitarsexpertsenfortificacions.Vaagafardeseguidagranreputació.Les matemàtiquesilafísicaerenensenyadespelsprestigiososprofessorsiabatsBossutiNollet.

Hientra,peròcomaalumnedesegonacategoria,destinatauntallerannex. Semblaqueaquíjatreballaambdovellesdeguix,cosaquepotserl’influiràen elsseustreballsposteriorssobreeltalldepedres.

Pertalderesoldreproblemespràcticsdefortificacionsinventa,quantenia aproximadamentunsdinouanys,la geometriadescriptiva.Comqueaquests coneixementspodiencaureenmansdel’enemic,seliordenade«nerien divulguerniverbalementniparécrit».4 Novapoderexplicaraquestescoses finsal1794,quanesvacrearl’Écolenormale.Aixòvaserpocdesprésdel9de termidor,5 quanlaConvencióNacional(règimpolíticquevagovernarFrança del1792al1795)vasentirlanecessitatdereorganitzarlainstrucciópública.

El1768passade répétiteur 6 aprofessoraMézièresiel1771esfacàrrec delsensenyamentsdematemàtiquesifísica.Aquestanyfaunprimerviatge aParís,onconeixCondorcet,d’AlembertiVandermonde;aquestúltimtindrà unpaperimportantdurantlaRevolucióiexerciràinfluènciasobreMonge. Vegeu«Monge,géomètreetJacobin»,deJ.Chapelon[T4].El1772ésnomenat correspondant al’Académiedessciencesperuntribunalformatperd’Alembert, BossutiCondorcet.

Escasael1777ambMarie-CatherineHuart,víduaHorbon,ambquitétres filles,Émilie,LouiseiAdélaïde.7

El14degenerdel1780Mongeéselegitgeòmetraadjuntdel’Académie dessciences,ensubstituciódeVandermonde.Aixòliexigeixestar-seaParís almenyscincmesosperany.Durantaquestsperíodesajudaval’abatBossut enelsseuscursosalLouvre.Esvadedicaralafísicailaquímica,vatreballar ambLavoisier,publicantmemòriessobrelasíntesidel’aigua,temademodaa l’època.

El1783morÉtienneBézout,queexerciad’examinadordelsalumnesde marina,iMongeésnomenatperaaquestcàrrec.Aixòelfaabandonardefinitivamentl’ÉcoleroyaledugéniedeMézières,jaquehaviadeviatjarmolt.Va rebredel’Écoleunapensióde1000lliuresperany.

QuanesclatalaRevolucióFrancesa,Mongeésundelscientíficsmésconeguts,probablementméspelsseustreballsdefísicaiquímicaquecomamatemàtic.Ocupadiversosllocsdedireccióalclubdelsjacobins,iformapartdela comissiódepesosimesuresperintroduirelsistemamètricdecimal.8

4Diversosautorsposenendubteaquestaafirmaciód’Arago. 5Diadel’arrestdeRobespierre,27dejulioldel1794.

6S’estavaambelsalumnesalessalesd’estudiajudant-losambelstreballsgràfics.Repetiael quehaviaexplicatelprofessor.

7 Napoleó,enelseudesterramentaSantaHelena,vadirqueMongehaviaofertlessevesfilles enmatrimonialsprimerssoldatsferitsendefensadeFrança,peròArago,desprésd’unaconversa ambl’esposadeMonge,hodesmenteixoalmenyshomatisa.

8 Mongejaparticipàenlacomissióquel’Académiecreàel1789perestudiarunplaperala uniformitzaciódelspesosimesures,laqualaconsellàlapropostadeTalleyrandal’Assemblée Nationalel1790,enlaqualexposenelsavantatgesdetriarlalongituddelpèndolquebat unsegonenelparal.lel45comaunitatdemesura.El1791lapropostajahacanviat:esdecideix quelanovaunitatsiguiunafracciódelmeridià,iqueesfarannovesmesuresdelmeridiàde ParísentreDunkerqueiBarcelona(l’Académienecessitafer-senecessàriaenelsconvulsostemps revolucionaris).MongeiMeusniersónencarregatsdemesurarlesbasesdelatriangulació,però

Afinalsdel17929 éselegit,perl’Assemblea,ministredelaMarina,càrrec queexercirànomésfinsal’abrildel1793.Elsetembredel1793ésencarregat, juntamentambVandermondeiBerthollet,d’organitzarlafabricaciódel’acer, pertald’accelerarlafabricaciód’armes.Publica Descriptiondel’artdefabriquer lescanons comamanualperalesfàbriques.

L’11demarçdel179410 elComitèdeSalutPúblicacreaunacomissióformadaperJacques-ÉliLamblardie,GaspardMongeiLazareCarnotamblamissió d’organitzaruna«écolecentraldetravauxpublics».Finalments’inaugurael21 dedesembreambseualPalaisBourbon.L’1desetembredel1795l’escolacanviadenom,passaadir-seÉcolepolytechniqueis’ubicaal’HôteldeLassay.Es consideraMongecomelseuprincipalfundadoriimpulsor.Lasevaexperiència devintanysal’ÉcoleroyaledugéniedeMézièresvaserfonamental.

Mongevaserl’ànimadel’École.Envaserdirectordel1796al1799.Vivia rodejatdelsseusalumnes,aquinodubtavad’ajudarentotelquepodia, inclúsoposant-seal’emperador.Avuidiaésuniversalmentreconegutcomun granprofessor.Taton[T16],alapàgina367,citaparaulesdeJomard,undels alumnesdeMonge:

Quandildécrivaitunesurfaceilladessinaitdesesmans...etl’engendraitavec ungesteéloquentdemaniereàlarendrepalpable;[ ]ilavaitl’artderendre simplesleschoseslespluscompliquéesetclaireslesplusobscures. nocompliranaquestatascajaqueMeusnier,generaldel’exèrcit,morel1793enelsetgede Mainz,iMongeésnomenatministre.

Tambéel1793,elgovernrevolucionarisuprimeixperelitismel’Académie,peròconstitueix una«Comissiontemporairedespoidsetmesures»enlaqualhihaMonge.Senseesperarels resultatsdelesmedicionsdeDelambreiMéchain,s’acordael1795definirunmetreprovisional, basatenlesmesuresdelmeridiàfetesperLaCaillequarantaanysabans.Mongecol laboraenels càlculscorresponents.

Finalment,el1798,unanovacomissióestudialesdadesaportadesperDelambreiMéchaini encaraqueMongehifigura,tampocpotparticipar-hi,jaqueacompanyaNapoleóaEgipte.

Unareferènciamoltbonasobreaquestahistòriaapassionantés:AntonioE.Ten(1996), Medirel Metro,InstitutodeEstudiosDocumentaleseHistóricossobrelaCiencia,UniversitatdeValència. [PeudepàginaescritperJosepLluísSolé.]

9 El13d’agostdel1792Lluís xvi ésdetingutisubstituïtperunconsellformatperministres elegitsperl’Assemblea.

10«21ventôse,an ii»,amblanotaciódel’època.

Écolepolytechnique,de1805a1976.

AgustíReventós

[Quandescriviaunasuperfícieladibuixavaamblessevesmans...il’engendrava ambungesteloqüentperfer-lapalpable;[...]tenial’artdefersimpleslescoses méscomplicadesiclareslesmésfosques.]

EntreelsdeixeblesdeMongedestaquemCharlesdeTinseaud’Amondans (1748–1822)iJeanBaptisteMeusnier(1754–1793),quejavanseralumnes seusaMézières.CitemtambéSylvestreLacroix(1765–1843),JeanBaptiste JosephFourier(1768–1830),MichelAngeLancret(1774–1807),JosephDiez Gergonne(1771–1859),André-MarieAmpère(1775–1836),SophieGermain (1776–1831)(ambnomfals),PierreCharlesFrançoisDupin(1784–1873),LouisLégerVallée(1784–1864),Jean-VictorPoncelet(1788–1867),MichelChasles (1793–1880),ThéodoreOlivier(1793–1853),BenjaminOlindeRodrigues(1795–1851),GabrielLamé(1795–1870),AdhémarBarrédeSaint-Venant(1797–1886), etc.

Mongevasertambéundelsprincipalsinspiradorsdel Journaldel’Écolepolytechnique. 11 Elprimerarticledelprimervolumdel Journal,aparegut el1794,ésdeMongeiestitula«Stéréotomie»[M8].L’estereotomiaésl’art detallariacoblarlespecesdepedraofusta,pertaldeconstruirelements arquitectònicscomaraarcs,mènsules,tramsd’escales,etc.

Lesprimerestreslíniesdiuen:

Lagéométriedescriptiveestl’artdereprésentersurdesfeuillesdedessinsqui n’ontquedeuxdimensions,lesobjetsquienonttrois,etquisontsusceptibles d’unedéfinitionrigoureuse.

[Lageometriadescriptivaésl’artderepresentarsobreelsfullsdedibuixque notenenmésqueduesdimensions,elsobjectesqueentenentres,iquepoden serdefinitsrigorosament.]

ElsapuntsdeclassedeMongeapareixenendiversesnotesposteriorsdel Journal,signadesperEisenmaniambelmateixtítolgenèricde«Stéréotomie»[A3].

EnaquestaèpocaMongevacomençaraparlaralsseusalumnesde geometria analítica perreferir-sealquefinsalmoments’anomenavasimplement àlgebra aplicadaalageometria. 12

El1796vaaItàliacomamembred’unacomissióquehaderecollir«les monumentsd’artetdesciencequelestraitésdepaixaccordaientauxarmées françaisesvictorieuses».ComdiuLouisdeLaunay[T5],unsaqueigorganitzat.

11 A http://gallica.bnf.fr/ark:/12148/cb34378280v/date.r=journal+ecole podeu trobarelsvolumsentreelsanys1794i1938.

12 Lacroix,enelseu Traitéélémentairedecalculdifférentieletdecalculintégral [A8],de1797, perreferir-sealstreballsdeMongeonaquestutilitzaderivadesparcialspergenerarsuperfícies, comperexemple«Surl’expressionanalytiquedelagénérationdessurfacescourbes»[M6],diu: «VoyezsaGéométrieAnalytique».PeraquestmotiuesconsideraaquestllibredeLacroixcomel primerlloconapareixaquestaexpressióde geometriaanalítica (pàgina504delaquartaedició deBachelierde1828).

A[T5]podeutrobarinformaciósobreelscinccomboisambobresd’artque esvanorganitzar.TornaaParísel1797iésnomenatdirectordela«pauvre Écolepolytechnique»,comdiuellmateix,queestavaenhoresbaixes.Encara faràunsegonviatgeaRomamotivatperl’assassinatdelgeneralDuphot, queelDirectoriliencarregainvestigar.IpercomminarelpapaPius vi a abandonarelpodertemporal.ElPapaabandonaRomael20defebrerdel1798. AquestaestadacoincideixambelspreparatiusdelacampanyadeNapoleóa Egipte.

SegonsArago,Napoleós’haviasentitmoltbentractatpelministredemarina Mongequanelleraunjoveoficiald’artilleria.AixòvafernéixerunaamistatentreMongeiNapoleó,quiinsisteixfortamentperquèl’acompanyialacampanya d’Egipte.UnaamistatenlaqualNapoleómanavaiMongeobeïa.

EstrobaambNapoleóaMaltael9dejunydel1798.L’illaésconquerida el10dejunyiel13dejunyjas’hicreentretzeescolesprimàriesiunaescola centralperensenyarmatemàtiques,astronomia,etc.

UncopaEgiptevaambNapoleófinsaRamanieh,onsesepareniMonge remuntaelNilambBerthollet.Sónatacatspelsturcsielsmamelucs,però salvatsfinalmentperlestropesfranceses.13 Ésllavors,el20dejulioldel1798, queNapoleódiudavantlapiràmidedeGizehlacèlebrefrase:«Soldats,duhaut decesmonuments,quarantesièclesvouscontemplent!».

PosteriormentNapoleócreal’Institutd’Egipteienconfialapresidènciaa Monge.14 Prenparttambéenl’expedicióaSíria,peròesposamalaltitorna aParísambNapoleól’octubredel1799.FanelviatgedeFréjusaParísen cotxedesiscavallsBerthollet,MongeiNapoleó.SegonsArago,lagents’estranyavadeveureNapoleóencompanyiadeduespersonesmalvestides(feia gairebédosanysqueerenforadecasa).Eldesembredelmateixanyésnomenat senador.

El1803acompanyaNapoleóperBèlgicaielnorddeFrança.Tornant,és nomenatperalasenadoriadeLieja.Semblaquenohoacceptadegairebon grat,jaqueenunacartaalasevadonaperjustificarlasevaabsènciacomenta que«LePremierConsulatantfaitpourmoiquejedoisfairecequejepuis pourlui».Hifallarguesestadesentre1803i1805,anyenquèNapoleódona al’ÉcolepolytechniqueunestatusmilitarilasituaalamuntanyadeSanta GenovevaaParís.

Delmaigdel1806alsetembredel1807éspresidentdelSenatdel’emperador,irepunadonacióqueellmateixhaviasol.licitatenfavordeBertholletde centmilfrancs,amblaqualcompraelcastelldeBierre,alaBorgonya. NomenatcomptedePéluse,el1808,rependotaciódiversespropietatsa Westfàlia.

13 ElbutlletíoficialdelcombatfamenciódelabravuradeMongeiBerthollet.Peròaquestúltim esvaomplirlesbutxaquesdepedresperanaralfonsdelriuinosercapturatimutilatpels ferotgesmamelucs.Moltsd’aquestsmamelucsesvanacabarposantposteriormentalcostatde Napoleó.

14 Delprocésverbal(Arago[T1]): lecitoyenMonge,president;lecitoyenBonaparte,vice-président, pourlepremiertrimestre;etlecitoyenFourier,secrétaireperpétuel. Sobrelacampanyad’Egipte vegeu GaspardMongeetl’expeditiond’Égypte,deJean-BaptisteSansondePongerville[T6].

El1809,començantasentir-secansat,deixaambrecançal’Écolepolytechnique;perònolarelaciócientíficaquehitenia,jaqueentre1810i1816encara podemtrobara Correspondancesurl’Écoleimpérialepolytechnique setnotes moltbreusdeMonge,potserlamésimportantdelesqualsés«Surleséquations différentiellesdescourbesduseconddegré»[M17].

El1813intentaorganitzarlaresistènciacontraelsinvasors(Àustria,Rússia iPrússia).Elfebrerdel1814,dosmesosabansqueNapoleófosdesterrata Elba,peltractatdeFontainebleau,destrueixpartdelsseusdocumentsdela Revolució,enparticularlacorrespondènciaambNapoleó,i,fugintdel’enemic, abandonaParísel29demarç.

QuantornaaParísel1816,desprésd’haverestatamagatuntemps,veu destruirlasevaobra:l’Écolepolytechniqueésprimersuprimidaidesprés reorganitzada,ésexclòsdel’Académiedessciences,15 etc.Morel28dejuliol del1818.Elsalumnesdel’Écolepolytechniquenovantenirautoritzacióper assistiralsfuneralsdeMonge,quenovarebrecaphomenatgeoficial,però vanaprofitarelprimerdiadesortidaperanar-seainclinarsobrelatombadel fundadordelasevaescola.

3Memòriasobrelesevolutes

ComentemacontinuacióelqueesconsideracomelprimerarticledeMonge[M7].El22degenerdel1769Mongevaescriureal’abatCharlesBossut peraexplicar-liqueestavatreballanten«développées»decorbesdedoble curvatura.16

Enréfléchissantdernièrementsurcequiarriveàplusieurssurfacescourbesque l’onfaitmouvoirlesunessurlesautrespourengendrerdesépicycloïdessur toutessortesdesurfaces,jesuisparvenuàtrouverlesdéveloppéesdescourbes àdoublecourbure.[Taton[T16,p.166]]

[Reflexionantdarreramentsobreelquepassaadiversessuperfíciescorbes queesfanmourelesunessobrelesaltresperengendrarepicicloidessobre tottipusdesuperfícies,hearribatatrobarlesevolutesdelescorbesdedoble curvatura.]

Recordemquela développée o evoluta d’unacorbaplanaéslacorbaque s’obtécomaenvolventdelessevesnormals.Equivalentment,éslacorbaqueté lapropietatqueuncordillembolicatsobreella,endesembolicar-se,generala corbadonada.Mongegeneralitzaaquestaconstruccióal’espaiexigintqueen desenvoluparelcordillesvagimantenintsempresobrelasuperfícieformada perlestangentsalacorba(la desenvolupabletangencial).

15 TothomvaveurelagreuinjustíciaqueesfeiaambMonge,iCauchyvaserduramentcriticat pelfetd’acceptarelllocvacant.

16 Ambl’expressió corbesdedoblecurvatura esrefereixacorbesguerxes(noplanars)del’espai. Lesduescurvaturesserienenllenguatgeactuallacurvaturailatorsió.

Développante o Involuta

x(0)

y(s)

Développée o Evoluta

y(0)

Figura 1: Evolutesiinvolutes.

Concretament,l’evoluta d’unacorba x(s) del’espaiésunaaltracorba y(s) (la développante o involuta)talque x(s) estàcontingudaaladesenvolupable tangencialde y(s) ilatangenta y(s) pertanyalplanormala x(s) enelpunt corresponent.Desenrotllantuncordillprèviamentembolicata y(s),mantenintloenlasuperfíciedelestangents,obtenim x(s). Eljunydel1769vaaparèixerunsumaridelsseusresultatsal Journal encyclopèdique,editataBouillonperPierreRousseau,queesconsideracomla primerapublicaciódeMonge.17 Eltreballcompletesvasotmetreal’Académie dessciencesdeParísl’octubredel1770iesvallegirdavantl’Académiel’agost del1771,perònoesvapublicarfinsal1785ambeltítol«Mémoiresurles développées,lesrayonsdecourbure,etlesdifferentsgenresd’inflexionsdes courbesàdoublecourbure»;vegeu[M7]ilespàgines392–420de[M18].

Aquestarticlecomençaaixí:

Toutcequel’onafaitjusqu’àpresentsurlesDéveloppéesdescourbesen generalsereduitàavoirtrouvécellesdescorbesplanes[ ]Jemepropose dedémontrerdansceMémoirequ’unecourbe,planeouàdoublecourbure auneinfinitédedéveloppées,toutesadoublecourbure,àl’exceptiond’une seulepourchaquecourbeplane,etdedonnerlamanièredetrouverleséquationsdetelledecescourbesqu’onvoudra,étantdonnéesleséquationsdela développante.

[Totelques’hafetfinsarasobrelesevolutesdecorbesengeneralesredueix ahavertrobatlesdelescorbesplanes[...]Emproposodemostrarenaquesta Memòriaqueunacorba,planaodedoblecurvatura,téunainfinitatd’evolutes, totesdedoblecurvatura,ambl’excepciód’unasolaperacadacorbaplana, idonarlamaneradetrobarlesequacionsd’aquestescorbes,donadesles equacionsdelainvoluta.]

17 Vegeul’articledeRenéTaton«LapremièrenotemathématiquedeGaspardMonge»[T17],on esreprodueixaquestescrit.

AgustíReventós

Lafigura2mostraunacorbaplanaialgunesdelessevesevolutes,que,com javaobservarMonge,estansobrelasuperfíciepolar,ésadir,lasuperfície regladaformadaperrectesquepassenpelscentresdecurvaturaitenenla direcciódelabinormalcorresponent.

Evolutes

Superfíciepolar

Tangental’evoluta, ortogonalalacorba

2: Evolutesisuperfíciepolar.

VeiemcomintrodueixMongel’eixpolar.Començaobservantquelesnormals enunpuntnosingulard’unacorbaal’espaiestanenunpla.Enaquestpla estrobaunarectaqueellanomena«eix»,queésellímitdelaintersecció d’aquestplaambelplacorresponentaunaltrepuntdelacorba,infinitament pròxim.Ésadir,cadapunt P delacorbatéelseu«eix».Sihomtraçauna perpendiculardesde P al’eixcorresponenta P ianomenem Q elpeud’aquesta perpendicular, Q seràelcentredecurvatura, PQ elradidecurvatura,ila inversadelalongitud PQ,lacurvatura.

ComdiuGirbau[A6],d’aquestamaneras’estableixclaramentperprimer coplanocióde curvatura d’unacorbaal’espai.

La torsió hiapareiximplícitament.18 Ambnotacióactuall’eixpolarcorresponentalpuntdeparàmetre s delacorba γ(s) éslarecta

r(u) : γ(s) + ρ(s)N(s) + uB(s), on ρ(s) éselradidecurvaturai N(s), B(s) elsvectorsnormalprincipali binormal,respectivament.

Launiódetotesaquestesrecteséslasuperfíciereglada

ϕ(s,u) = γ(s) + ρ(s)N(s) + uB(s), anomenada superfíciepolar associadaalacorba γ(s).Mongelacalculaala secció xx del’articleitrobaqueéslasuperfícieenvolventdelafamíliadeplans 18 ElconceptedetorsióvaserdefinitivamentestablertméstardperLancreta«Mémoiresur lescourbesadoublecourbure»[A9],peròhaviaestatusatjaperLacroixa[A8].L’anomenaven segonaflexió o segonacurvatura.Elnomde torsió provédeLouisL.Vallée.

Corbaplana

Figura

normals.Ésadir,veuqueelplatangentaaquestasuperfícieenqualsevoldels seuspuntscoincideixambundelsplansdelafamíliadeplansnormals.

Demostratambéqueaquestasuperfícieés desenvolupable, 19 veientque lessevesgeneratrius,elseixospolars,sóntangentsalacorbaformadapels centresdelesesferesosculatrius.

AquestacorbadelscentresésanomenadaperMonge arêtederebroussement,nomquepodríemtraduirper arestaderetrocés o eixderegressió,dela superfíciepolar,ivedonadaper

γ(s) + ρ(s)N(s) + ρ (s) τ(s) B(s),

on τ(s) éslatorsióde γ(s) (suposadanonul.la).Mongelacalculaalasecció xxii del’article.

Elspuntsd’aquestaarestanoformenpartdelasuperfície(sónpunts singulars),quequeda,doncs,divididaenduesparts.

TotaixòhofaMongeambargumentsgeomètricscomaratallarunplaamb el«següent»,etc.,jaqueaquestasuperfícieés,comhemdit,l’envolventdels plansnormals.

L’esferaosculatriu20 laintrodueixaixíalasecció xxiv:

[ ]danstoutecourbeàdoublecourburetroisélémentsconsécutifssont toujoursàégalesdistancesd’uncertainpoint,etpeuvent,parconséquent,être regardéscommeplacéssurlasurfaced’unemêmesphèredontcepointestle centre.

[[ ]entotacorbadedoblecurvaturatreselementsconsecutiusestansempre alamateixadistànciad’uncertpunt,ipoden,perconsegüent,servistoscom situatssobrelasuperfícied’unamateixaesferaquetéaquestpuntcoma centre.]

Delscàlculsanteriorsesdedueixqueelradidel’esferaosculatriués

R(s) = ρ(s)2 + ρ (s) τ(s) 2 .

Tambéesveuquelacorbaformadapelscentresdecurvaturad’unacorba (projecciód’aquestacorbasobrel’eixpolar)nopotserunaevolutadela

19 Unasuperfícieregladaesdiu desenvolupable silesrectesquelaformensóntangentsauna corba(eixderegressió).Equivalentment,sónlessuperfíciesregladesambcurvaturadeGauss zerooencaraunaaltraequivalència:sónlessuperfíciesregladestalsqueelplatangentés constantalllargdelesgeneratrius.

20 ThéodoreOlivier(1793–1853),alumnedel’Écolepolytechnique,estudialesesferesosculatrius il’ordredecontacted’aquestesambleshèlixs,vegeu«Delacourbureetlaflexiond’unecourbea doublecourbure»[A12].Ésconegutpelsseusmodelsdesuperfíciesqueestallen,superfícies formadespercordesimetall,queenmoure’spermetenestudiarlacorbaintersecció.Vegeu TheodoreOlivierThree-DimensionalGeometryStringModels,unàlbumeditatpelCanadaScience andTechnologyMuseum.

AgustíReventós

corbadonadaamenysqueaquestasiguiplana.Enaquestcastenimlaclàssica evoluta,unacorbalestangentsdelaqualsónnormalsalacorbadonada.

Donadaunacorba x(s) Mongeesproposa,alasecció xxv,trobartotesles corbes y(s) (lesevolutesde x(s))talsquelestangentsa y(s) pertanyenal planormalde x(s).Ésadir,voltrobarlescorbesquesiesdesenvolupenpel mètodedelcordilldonen x(s)

Ambnotacióactuals’obté

y(s) = x(s) + ρ(s) N(s) + cot α(s)B(s) ,

on ρ(s) éselradidecurvatura, N(s), B(s) lanormalprincipalilabinormal de x(x),i

α(s) = s 0 τ(t)dt + c,

amb τ(s) latorsió.

Cadavalorde c corresponaunadelesinfinitesevolutesdelacorba x(s). Si τ = 0,unadelesevolutesésplanailesaltressónhèlixssobreelcilindre ortogonalalpladelacorba.

Quanparladels diferentsgèneresd’inflexió,alasecció xxx,esrefereixalfet quelacurvaturailatorsióespodenanul.lar.Hodiuaixí:

[ ]ilpeutarriverouquetroisélémentsconsécutifsd’unemêmecourbeà doublecourburesetrouvendansunmêmeplan,ouquedeuxdeceséléments sointenlignedroit.Ilsuitdelàquelescourbesàdoublecourburepeuvent avoirdeuxespècesd’inflexions:lapremièrealieulorsquelacourbedevient plane,etnousl’appellerons simpleinflexion;laseconde,quenousappellerons doubleinflexion,alieulorsquelacourbedevientdroitedansundesespoints.

[[ ]potpassarquetreselementsconsecutiusd’unamateixacorbadedoble curvaturaestrobinenunmateixpla,oquedosd’aquestselementsestiguin alineats.Sesegueixd’aixòquelescorbesdedoblecurvaturapodentenirdos tipusd’inflexions:laprimeraesdonaquanlacorbaesdevéplana,inosaltres l’anomenarem inflexiósimple;lasegona,queanomenarem inflexiódoble,télloc quanlacorbaesdevérectaenundelsseuspunts.21]

Capalfinaldel’article,alasecció xxxiii,trobal’expressióexplícitadelradi decurvaturadelacorba(amblasevanotació y = ϕx, z = ψx) [1 + (ϕ x )2 + (ψ x )2]3/2 (ϕ x )2 + (ψ x )2 + (ψ x ϕ x ϕ x ψ x )2 que,posant σ(s) = (s,ϕ(s),ψ(s)),noésmésque ρ(s) = σ (s) 3 σ (s) ∧ σ (s)

21 Comésbensabut,silacurvaturaészeroenuninterval,lacorbaésrectaenaquestinterval, isilatorsióészeroenuninterval,lacorbaésplanaenaquestinterval.Peròlacurvaturaila torsióespodenanul.larnomésenunsolpunt(puntd’inflexió)illavorslacorbanoésrectani planaalvoltantd’aquestpunt.

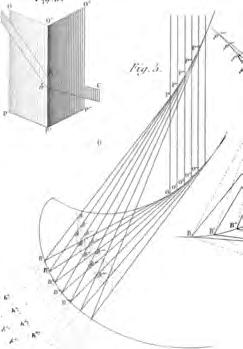
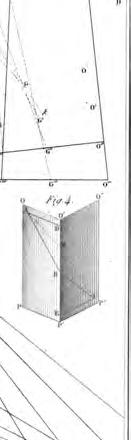
Figura 3: DetalldelaplanxaquetancaaquestarticledeMonge.

4Ombresipenombres

L’11degenerdel1775Mongepresentaal’Académieeltreball«Mémoiresur lespropriétésdeplusieursgenresdesurfacescourbes,particulièrementsur cellesdessurfacesdéveloppables,avecuneapplicationàlathéoriedesombres etdespénombres»[M1],quenoespublicafinsal1780.

Enaquestamemòriadonal’avuibenconegudaequaciódelplatangenten funciódedeterminadesderivadesparcials,quedenotaper p i q,notacióque haperduratfinsal’actualitat.Itambél’equaciódiferencialdelessuperfícies desenvolupables, rt s2 = 0,onara r , s, t sónlesderivadessegones.Observeu queaquestaexpressiónomésdiuquelacurvaturadeGaussészerojaqueés eldeterminantdelasegonaformafonamental.Elproblema i d’aquestl’article estàdedicatatrobarl’equaciógeneraldelessuperfíciesdesenvolupables.En donatressolucionsialgunscorol.laris.

Elproblema ii consisteixatrobarlessuperfíciestalsquelarelacióentre l’àread’unapartqualsevold’ellesilasevaprojecció[sobreunpla]ésconstant.Òbviament,amblamateixanotacióqueanteriorment,hadepassarque 1 + p2 + q2 siguiconstanti,pertant,que p siguifuncióde q.

Acontinuacióintrodueixla théoriegénéraledesombresetdespénombres Donaunadefinicióprecisad’ombraipenombrasuposantprimerquehihaun puntdellumiuncosopacquelatapaisuposantdesprésquelallumprové d’unasuperfície.Demostraqueenaquestcasl’ombra«pura»estàdelimitada perunasuperfíciedesenvolupablecircumscritaalavegadaalessuperfícies delcoslluminósidelcosopac.Donaunadefinicióintuïtivadepenombra idemostraqueestàdeterminadaperunaaltrasuperfíciedesenvolupable parcialmentcircumscritatambéalessuperfíciesdelscossosopacilluminós.

AgustíReventós

Ladiferènciaentreaquestasuperfícieilaprimeraésquel’arestaderetrocés (arêtederebroussement)estrobaentreelsdoscossosienelprimercasels doscossossónalmateixcostatd’aquestaaresta.Aquestesdemostracionsles presentasensefercapcàlcul.

Posacomaexempleelcasdedoscossosesfèrics,comelsdelafigura4.

4: Ombresipenombres.

Elproblema iii d’aquestarticleconsisteixatrobar,peraunasuperfície donada,l’equaciódelacorbaintersecciód’aquestasuperfícieambunconcircumscritalamateixa,devèrtexunpuntdonat.Estàestudiant,doncs,ombres ipenombresenelcasparticularenquèelcoslluminósesredueixaunpunt. Actualmentesdiuqueaquestacorbaéslacorbageneradoradelcontorno corbageneratriu.Estàcaracteritzadaperlacondiciódeserelvectornormala lasuperfíciesobreaquestacorbaperpendicularencadapuntalarectadeterminadaperaquestpuntielpuntdellum.Monge,al’articlequecomentarema continuació,[M2],endiu corbadecontornaparent. L’article[M1]acabaambunparelldeproblemessobreelmateixtema.El problema iv s’ocupadetrobarlasuperfíciecònicaambvèrtexdonatque passaperunacorbadonada,ienelproblema v estableixlesequacionsdeles superfíciesqueenvoltenl’ombrailapenombrad’uncosopacil.luminatperun coslluminós.

5Teoriadeltransport

EnaquestaseccióestudiemundelsarticlesmésimportantsdeMonge,«Mémoiresurlathéoriedesdéblaisetdesremblais»[M2],de1781.22

22 AquestarticleestàmoltbenestudiatperÉtienneGhysa[T9].ComentaGhysque,comenaltres treballsdeMonge,esbarrejaaquílateoriailapràctica.Mongeparteixd’unproblemapràctic,

Cos lluminós

Cosopac

Penombra

Ombra

Penombra

Figura

Aquestarticlecomençaparlantdeltransportdeterres.

Lorsqu’ondoittransporterdesterresd’unlieudansunautre,onacoutumede donnerlenomde Déblai auvolumedesterresquel’ondoittransporter,etle nomde Remblai àl’espacequ’ellesdoiventoccuperaprèsletransport.

[Quans’handetransportarterresd’unllocaunaltre,estéelcostumd’anomenar déblai elvolumdeterresques’hadetransportar,ianomenar remblai l’espai quehand’ocupardesprésdeltransport.]

Icontinuacomentantque,comqueelpreudeltransportd’unamolèculaés proporcionalalseupesial’espaiquerecorre,elpreutotaldeltransportha deserproporcionalalasumadelsproductesdelesmolècules(elsseuspesos) multiplicadacadascunaperl’espairecorregut,itambéquedonatel déblai i el remblai enfiguraiposició,noésindiferentqueunamolèculadel déblai siguitransportadaaunllocoaltredel remblai.S’had’aconseguirquelasuma d’aquestsproductessiguilamínimapossiblepertaldeminimitzarelpreudel transport.

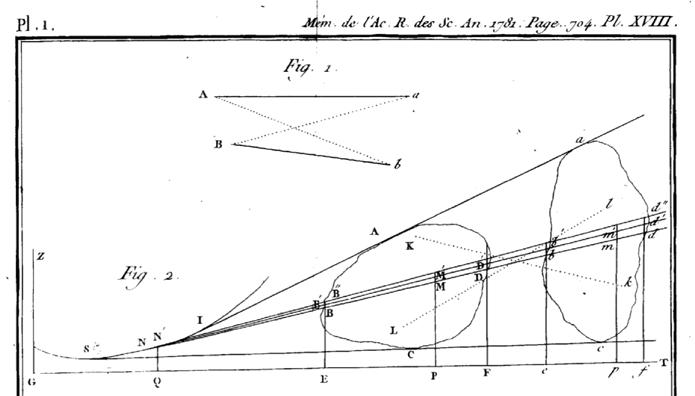
Figura 5: DibuixdeMongedel déblai iel remblai.Lesrectesdeterminen unaàreaigualsobrecadafigura, ABD = abd.Sóntangentsaunacorba. BD had’anara bd.

Aquestproblemahadonatllocala teoriadeltransport,moltusadatambé eneconomia.Enllenguatgeactualestractademinimitzarunaintegraldeltipus

D F(x,y) (x,y) dxdy,

on D ésel déblai i F latransformacióentre déblai i remblai

queenrealitatnoacabaderesoldre,peròqueliserveixdemotivacióiquedonallocaimportants desenvolupamentsteòrics.

AgustíReventós

Fetaaquestaintroducció,Mongedivideixlamemòriaenduesparts:elcas delplaielcasdel’espai.

Dimensió2

Desprésd’observarquelestrajectòriesseguidesperlesmolèculesnoespoden tallar,jaquelasumadedistàncies Ab + Ba ésmajorque Aa + Bb,tornaa repetirl’enunciatpelpla:

6: Transportenelpla.

Donadesduesàreesiguals,trobarelcamíquehadeseguircadamolècula delaprimeraielpuntonhad’arribardelasegonapertalque,quans’han transportattotselspunts,lasumadelsproductesdecadamolècula(elseupes) perl’espaiqueellaharecorregutsiguimínim.Suposapersimplificarquela densitatésuniforme.23

Primerargumentaquesiunarectatallael déblai iel remblai deixantaun mateixcostatàreesiguals,lesmolèculesdelaprimeraregióhand’anaraparar alesdelasegona.24 EneldibuixdeMonge(figura5),laregió ABD had’anarala regió abd (sempreutilitzamajúsculesperal déblai iminúsculesperal remblai). Iconclouque,dividintel déblai iel remblai enunainfinitatdepetitsrombes, cadascundelsrombesdel déblai hadesertransportatsobreelcorresponent rombedel remblai.Iqueésindiferentenquinordrelesmolèculesdelprimer esdistribueixensobreelsegon.

Introdueixcoordenadesidonaunafórmulaperaladirecciódecadamolècula.Latècnicaconsisteixatransformarlafamíliabiparamètricaderectes y = ax + b enunafamíliauniparamètricaenimposarqueaquestesrectes tallin,delmateixcostat, déblai i remblai enregionsd’àreaigual.

Sil’envolventd’aquestafamíliauniparamètricaderectesestàal’esquerra del déblai,lessevestangentstallenel déblai iel remblai ensegments BD i bd, respectivament.Enaquestcaselques’hadeferéstransportarelsegment BD sobreelsegment bd

S’adona,però,que,comquetrajectòriesdepuntspròximsespodentallar,i aixònodonariaunmínim,calquelacàustica25 queesformacomaenvolvent delscaminsestrobimésenllàdel déblai respectedel remblai omésenllàdel remblai respectedel déblai.

23 ComremarcaÉtienneGhysa[T9],Mongenoespreocupaperl’existènciadesolucionsdel problemad’extremalsqueesproposaresoldre.Tampocs’ocupadesi,donadesduesregions diferentsdelpladelamateixaàrea,hihaunatransformacióqueportal’unasobrel’altra.

24 Aquestaafirmaciónoéscertaengeneral,elmateixMongehoreconeixmésendavant,quan diu«lasolutionprécedénteestillusoire».

25 Mongeutilitzalaparaula càustica,paraulaquearaesreservaal’envolventderajosdellum.

Figura

Uncopconeixladirecciód’unamolèculaqualsevol(lestangentsal’envolvent),jaésfàciltrobarelpreudeltransport.

Alasecció xiv tractaelcasenquèlesrutesdelesmolèculesestansubjectes apassarperpuntsdeterminats,comperexemplepontssobreriusoportesen elsmurs.Quantspontshihauriad’haver?Peròsienelproblemademinimitzar eltransporthientraelpreudelsponts,eltemaescomplica!Aixíacabala primerapartdel’article.

Dimensió3

Lasegonapart,dedicadaalproblemadeltransportendimensió3,comença donantelsprincipisdegeometriasobreelsqualsesfonamentaranlesidees posteriors.

Laprimeraobservacióésfonamental26 ifareferènciaafamíliesbiparamètriquesderectes: sipercadapuntd’unplahipassaunarectadel’espaideterminadaperunacertalleiiprenemunad’aquestesrectes,llavorsentrelesrectes infinitamentpròximesaaquestanomésn’hihadues,genèricament,quela tallen.27

Iposal’exemplesegüent.Prenemunarectaexterioralpladonatipercada puntdelplahitracemlaperpendicularaaquestarecta.

Figura 7: Lesrectes AA i BB determinen,cadascunad’elles,unpla amb OA;encanvi, CC no.

Noméshihaduesdireccionsquefanquerectesinfinitamentpròximesa unadedonadaestallin(enparticularestiguinenunpla):lesdeterminades

26 Lamentablementésfalsa.Ocertanoméssotadeterminadescondicions.ÉtienneGhysremarca a[T9]quelafibraciódeHopfn’ésuncontraexemple.Lafamíliaderectesde R3 quetallenel pla z = z0 ambvectortangenten (x,y,z0) donatper (xz0 + y,yz0 x,z2 0 + 1) notécap parelladerectescoplanàries,nianivellinfinitesimal.Nopodenser,pertant,lesnormalsauna superfície.Vegeulanotadelapàgina132.

27Enllocdefamíliabiparamètricaderectestambéesparlade congruènciaderectes

pelplaformatperlarectadonadailarectaexterior(estallenal’infinit)iles determinadespelplaperpendicularalarecta.

Acontinuacióendonaunademostracióquepreténsergeneralperòaquesta demostraciófalla,jaquesuposaqueunaequaciódesegongrautésempre arrelsreals.ÉscuriósqueMongenofacicapcomentarisobreaixò,tretquela paraula«généralement»quandiu«cetteéquationduseconddegrénedonne généralementquedeuxvaleurs»espuguiinterpretarensentitampli.

Ialasecció xx s’hitrobajaengermenelteoremadeMonge:

Ilsuitde-làquedanslesystèmededroitesdontils’agitonpeuttoujours passerdedeuxmanièresdifferentesd’unequelconquedecesdroitesàune autreinfinimentproche,quisoitavecelledansunmêmeplane:celaposé,de l’unequelconquedecesdroites,passonseneffetàl’unedecellesquilacoupe, ensuiteetdanslemêmesens,àcellequicoupelasecond,de-lààcellequidans lemêmesensecoupelatroisième;ilestévidentqu’encontinuantainsidesuite nousparcourronsunesurfacedéveloppable.

[D’aixòesdedueixqueenelsistemaderectesenqüestiósempreespot passardeduesmaneresdiferentsd’unaqualsevold’aquestesrectesaunaaltra d’infinitamentpropera,queestiguiambellaenunmateixpla:ditaixò,d’una qualsevold’aquestesrectes,passemefectivamentaunad’aquestesquelatallen, acontinuacióienelmateixsentitalaquetallalasegona,d’aquíalaqueen elmateixsentittallalatercera;ésevidentquesicontinuemd’aquestamanera recorreremunasuperfíciedesenvolupable.]

Quangeneralitzemaquestresultatalafamíliabiparamètricaderectes formadaperlesnormalsaunasuperfícieobtenimunapartdelteoremade Monge.Aixòéselquefaalasecció xxi: lesnormalsaunasuperfíciesónles interseccionsdeduessuccessionsdesuperfíciesdesenvolupablestalsquecada superfíciedelaprimerasuccessiótallatoteslesdelasegonaenlíniesrectesien anglesrectesirecíprocament

Iara,alasecció xxii,quereprodueixoíntegrament,ésquanensfanotar queaquíestanapareixent,encaraquenohosembli,leslíniesdecurvatura!El resultatd’aquestaobservacióéselfamósteoremadeMonge: lesnormalsauna superfíciesobreleslíniesdecurvaturaformenunasuperfíciedesenvolupable.

Quoiquecettepropositionnesembleavoirqu’unrapportéloignéaveclabelle théoriedesrayonsdecourburedessurfacescourbesqu’adonnéeM.Euler,dans lesMémoiresdel’AcadémiedeBerlin,année1760;28 cependant,sij’oseparler ainsi,ellecomplèteletravaildecetillustreGéomètresurcettematière:car lesdeuxpointsoùchaquenormaleestcoupéeparlesdeuxnormalesvoisines sontprécisémentlesextrémitésdesdeuxrayonsdeplusgrandeetdemoindre courbure,ensortequelesintersectionsdelasurfacecourbeaveclessurfaces développablesquicomposentlapremièresuitesont,leslignesdemoindre courburedelasurfaceetquelesintersectionsaveclessurfacesdéveloppables quicomposentl’autresuitesontleslignesdeplusgrandecoubure.

28Esrefereixa[A4].

[Encaraqueaquestaproposiciónosemblatenirgaireaveureamblabellateoria delsradisdecurvaturadelessuperfíciescorbesquevadonarelsenyorEuler, alesMemòriesdel’AcadèmiadeBerlín,l’any1760;noobstantaixò,sise’m permetdir-ho,completal’obrad’aquestil lustregeòmetrad’aquestamanera: comqueelsdospuntsoncadanormaléstalladaperlesduesnormalspròximes sónprecisamentelsextremsdelsdosradisdemajorimenorcurvatura,de maneraquelesinterseccionsdelasuperfíciecorbaamblessuperfíciesdesenvolupablesquecomponenlaprimeraseqüènciasónleslíniesdemenorcurvatura delasuperfícieiquelesinterseccionsamblessuperfíciesdesenvolupablesque componenl’altrasuccessiósónleslíniesdemajorcurvatura.]

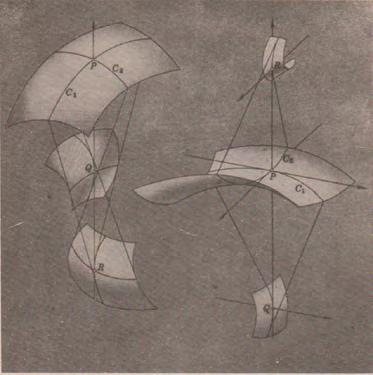
8

Alasecció xxv donal’expressiódelsradisdecurvaturaapartirdeles consideracionsquehafetiveuquecoincideixambladonadaperEuler.Ala secció xxvi donalesequacionsdeleslíniesdecurvatura.Iaixòjanohova ferEuler.Alasecció xxvii trobalesevolutesdelasuperfíciedonada:llocs geomètricsdelscentresdemajorimenorcurvaturadelasuperfície.Ala secció xxix estudiabreumentles líniesdelcontornaparent enrelacióamb aquestessuperfícies.

Alasecció xxxi donal’elementd’àreaencoordenadesprincipals.Enelseu llenguatgetrobal’àreadel«quadrat»formatperduescorbes«consecutives»de majorcurvaturaambduescorbes«consecutives»demenorcurvatura.Troba també,alasecciósegüent,elvolumdelsòlidformatperaquestquadratiles normalsalasuperfícieenelsseuspunts.

29 Lafiguradel’esquerrarepresentaunasuperfícieenlaqueelsdosradisdecurvaturaprincipal tenenelmateixsigne;lesevolutesestanenelmateixcostatrespectedelasuperfície.Lafigura deladretarepresentaunasuperfícieenlaqueelsdosradisdecurvaturaprincipaltenensignes oposats;lesevolutesestanencostatsoposatsrespectedelasuperfície.Enelsdoscasos,seguint lanormalfinsa ρ1 o ρ2 (radisdecurvaturaprincipal)trobemduesevolutesdelasuperfície.Les normalsalasuperfíciesóntangentsalesevolutes.

Figura

: DibuixdeStruik[T15,p.108].29

Finsalasecció xxxiv noretornaalproblemade déblai i remblai.Aplicant totselsresultatsanteriorsarribaalaconclusióquelesrutesdelesmolècules, queserancomenelcasplalíniesrectes,handeserlesinterseccionsde duessuccessionsdesuperfíciesdesenvolupablestalsquecadasuperfíciedela primerasuccessiótallitoteslesdelasegonaenanglesrectes;iaquestasituació escorresponambelquesucceeixamblesnormalsaunasuperfície,comhavist alasecció xxi,demaneraquepotdirque lestrajectòriesquehandeseguirles molèculesdelprimervolumperarribaraomplirelsegonhandeserlesnormals aunamateixasuperfíciecorba.

Idonal’equaciódiferenciald’aquestasuperfície.ComfanotarÉtienneGhys, ésenaquestesequacionsonapareixperprimercoplafamosaequacióde Monge-Ampère,unaequacióenderivadesparcialsdesegonordrequenoésni linealniquasilinealperòqueéslinealenelhessiàilesderivadessegones.Sila superfícieés z = z(x,y) escompleix

peradeterminadesfuncions F , G, H.

Iacabareconeixentquelasoluciód’aquestproblemaestàmoltllunyde poderseraplicadaalapràctica,jaquehiintervenenmoltesmésvariables,les molèculesnoespodentransportarenlíniarecta,etc.30

6 Fullsd’anàlisi,full XV

EnaquestaseccióestudiaremleslíniesdecurvaturatalcomhovaferMongeal full xv delesseves Feuillesd’analyse [M11],titulat Desdeuxcourburesd’une surfacecourbe.Peròtoteslesideesestanal’articlesobre déblai i remblai [M2]. LaideadeMongeéstansimplecomintentarcopiarperasuperfíciesla construcciódel’envolventdelesnormalsconsideradaperacorbesplanes: l’evolutad’unacorbaespotconsiderarcomlacorbaques’obtéentallar normalsalacorbadonadaenpunts infinitamentpròxims.Quanelsclàssics parlendepuntsinfinitamentpròxims,comaraenelcasdelesnormalsque estemcomentant,volendirtallarlanormalalacorba α(s) enelpunt α(0) amblanormalalacorbaenelpunt α(∆s),iacontinuaciópassarallímitquan ∆s tendeixazero.

30 Dupinvatractaraquesttemadel déblai iel remblai el1813a[A1]iel1822a[A2](totala tercerapartdel’obra,unesseixantapàgines,estàdedicadaaaquesttema;estitula Surletracé desroutesdanslesdéblaisetlesremblais)tractantd’aclarir,ampliarijustificarpuntsdèbilsde l’articledeMonge.Consideracasosenquèelterrenynoésplaiobtésolucionsenslesqualsles trajectòriesdelesmolèculesnosónrectes.

Elproblemaésquesiconsideremduesnormalsaunasuperfícieenpunts infinitamentpròximspotpassarqueaquestesduesnormalsnoestallin,jaque duesrectesal’espainormalmentnoestallen.

Tambélaidead’infinitamentpròxims’haderetocarenelsentitqueara tenimmoltesmaneresdiferentsd’acostar-nosaunpuntdonat.Éselmateix problemaquehihaquanpassemdel’estudidederivadesdefuncionsd’una variableafuncionsdeduesvariables.

Totaixòesresoldelamanerasegüent.Suposemunasuperfíciedonadaper lagràficad’unafunció z = z(x,y) quepassaperl’origen O = (0, 0, 0) amb platangent z = 0.Prenemunacorba γ(x) = (x,y(x),z(x,y(x))) sobrela superfíciequepassiper O quan x = 0.

Voldríemtallarlarectanormalalasuperfícieenelpunt γ(x) amblarecta normalalasuperfícieenelpunt O = γ(0),queéslarecta x = y = 0.Aquestes rectespotsernoestalleni,pertant,elquefaremseràtallarlanormalala superfícieen γ(x) ambelsplans x = 0i y = 0.

Obtenimcomapuntsdetall

0, ∗,z + x p , ∗, 0,z + y q ,

on p, q sónlesderivadesprimeresde z enelpuntcorresponent.Elsasterics sónquantitatsquetendeixenazeroamb x inoenscalen.

Sivolemqueenellímitlesrectesestallin,lestercerescomponentsd’aquestspuntshandecoincidir(handecoincidirelspunts,peròamblestercerescomponentsjan’hihaprou).AplicantlaregladeL’Hôpitalirecordant que p(0) = q(0) = 0,tenim lim x→0 x p(x) = 1 r + sy , lim x→0 y(x) q(x) = y s + ty ,

on r , s, t sónlesderivadessegonesde z enelpunt x = 0.Pertant,hadeser 1 r + sy = y s + ty , ésadir, sy 2 + (r t)y s = 0.

Aquestaésl’equaciódelesdireccionsprincipals: lesdireccionssobrelesquals t’hasd’aproximaraunpuntpertalquelesnormalsestallin. Comqueelproductedelesarrelsd’aquestaequaciódesegongraués 1, aquestesdireccionssónortogonals.Observemqueeldiscriminantd’aquesta equacióéspositiu.

Sirepetiml’argumentquehemusatpercalcularlesdireccionsprincipalsa l’origen,peròaratreballantsobreunpuntarbitrari P ,obteniml’equaciógeneral deleslíniesdecurvatura.

Teorema. L’equaciódiferencialdeleslíniesdecurvaturad’unasuperfíciedonadacomagràficade z = z(x,y) és

Observemquelasegonaitercerafilessónelscoeficientsdelaprimerai segonaformesfonamentals.

Nota. Donemuncontraexempleal’afirmaciódeMongedelapàgina127, onafirmaque,donadaunarectad’unafamíliabiparamètricaderectes,n’hi haduesd’infinitamentpròximesquelatallen.Peraaixòrepetimelscàlculs d’aquestaseccióperalafamíliabiparamètricaderectesformadaperaquelles rectesquetallenelpla z = 1ambvectordirector (x + y,y x, 2),ésadir,les rectes

(x,y, 1) + (x + y,y x, 2)

Aquestafamílias’obtéapartirdelafibraciódeHopf,comindicaÉ.Ghysa[T9].

Consideremunacorba (t,y(t), 1),definidaperavalorspetitsde t,amb y(0) = 0.Lesrectesdelafamíliainicialquepassenperaquestacorbatallenel pla x = 0enunpuntquetéperterceracomponent 1 2t t + y(t) , itallenelpla y = 0enunpuntquetéperterceracomponent 1 2y(t) y(t) t .

Sivolemqueenellímitlarectadelafamíliatallil’eix z,queéstambéunarecta delafamília(i,pertant,quesiguicoplanàriaambellacomdeiaMonge),s’ha decomplir lim t→0 t t + y(t) = lim t→0 y(t) y(t) t .

Obtenim,perL’Hôpital, 1 1 + y = y y 1 , equacióquenotésoluciósobreelsreals.

Ésadir,talcomhemcomentatalanota26(pàgina127),lafamíliaderectes donadanotécapparelladerectescoplanàries,nianivellinfinitesimal.Nosón lesrectesnormalsaunasuperfície.

Figura 9: Lafoliaciódonadapelsplansortogonalsaaquestesrectesno ésintegrable.

7Altrestreballs

ComentembreumentalgunstreballsmésdeMongesobregeometriadiferencial.

El1783publica«Suruneméthoded’intégrerleséquationsauxdifférences ordinaires»[M3],oneslimitaadonaralaprimerapàginaunmètodeperresoldreequacionsdiferencialsiaplicar-loadiversessituacions,comararesoldrela típicaequaciódelessuperfíciesminimals31 (1 + q2)r 2pqs + (1 + p2)t = 0, queatribueixaM.leChevalierdeBorda,atrobarlíniesdecurvatura,etc.

Del1784és«Surlecalculintégraldeséquationsauxdifférencespartielles»[M5].Estractad’untreballmoltextensontornaaintegrarl’equació diferencialdelessuperfíciesminimals,recordantnovamentM.leChevalierde Borda.Elmètoded’integraciódeMongeésmilloratméstardperLegendrea«Mémoiresurl’integrationdequelqueséquationsauxdifférencespartielles»[A10], ontambécorregeixalgunserrorscomesosperMonge.

Elmateixany1784estudialageneraciódesuperfíciesipublicaessencialmentlamateixamemòria«Surl’expressionanalytiquedelagénérationdes surfacescourbes»aTorí[M6]iaParís[M4].

AlamemòriadeToríresoltresproblemesqueconsisteixenaexpressarque unasuperfíciecorbaestàgeneradaper:1)Uncerclequeesmoudemanera queelseuplasiguisempreperpendicularalacorbarecorregudapelscentres. 2)Uncerclequeesmoud’unamaneraqualsevol.3)Unacorbaqualsevol constantdeformaqueesmoud’unamaneraqualsevolal’espai.

AladeParís,mésdetalladaiextensa,resolexactamentaqueststresmateixos problemesméselsegüent: expressarqueunasuperfíciecorbaestàgenerada perunacorbaplanaqueesmoudemaneraqueelplaquelacontéesmanté

31 Superfícesd’àreamínimaambvoradonada.Estancaracteritzadespelfetdetenircurvatura mitjanazero.

perpendicularalescorbesrecorregudespertotselsseuspunts.Deseguida diuqueaquestessuperfíciesespodendefinircomlessuperfíciesgenerades perunacorbaplanaquanelseuplagirasenselliscarsobreunasuperfície desenvolupable.Aquestessuperfíciesrebenavuielnomde superfíciesdeMonge iestancaracteritzadesperquèleslíniesdecurvatura(lesmàximesomínimes) sóngeodèsiques.32 Mongedemostraquesobreunalíniadecurvatural’altra curvaturaésconstant.

El1795publica«Surleslignesdecourburedelasurfacedel’Ellipsoïde» [M9],utilitzantlesequacionsgeneralsdeleslíniesdecurvatura,quehavia estudiata«Mémoiresurlathéoriedesdéblaisetdesremblais»[M2].Obté

Axyy 2 + y (x2 Ay 2 B) xy = 0, amb A = a2(b2 c2) b2(a2 c2) ,B = a2(a2 b2) a2 c2 , on a, b, c sónelssemieixosdel’el lipsoide.Ideseguidaintegral’equacióiveu queestractad’unasecciócònicadeltipus y 2 = βx2 + γ,percertesconstants β, γ ques’hand’ajustar.Pertant,estractad’unacònicaconcèntricaamb l’el.lipsoidequeseràunael.lipseounahipèrbolasegonselsignede β.Observem queaquestacònicaéslaprojecciósobreelpla z = 0deleslíniesdecurvatura.

Figura 10: Líniesdecurvaturadel’el.lipsoide[M18].

32 Recordemqueleslíniesdecurvaturatenentorsiógeodèsicazeroiquesobrelesgeodèsiques latorsióilatorsiógeodèsicacoincideixen.Pertant,unageodèsicailíniadecurvaturaésplana.A partird’aquíespotrecuperarelresultatdeMongeambrelativafacilitat.

Posteriormentreprodueixaqueststreballsalasecció xvi d’Applicationde l’analyseàlagéométrie [M18].

Laideaésintentarferunarcdepedra,comaraunaporta,peròdemanera quelacorbasuportnosiguiunarcdecircumferènciasinóunarc,perexemple, d’el.lipse.Elpicapedrerhadetallarlespedresquevanasobred’aquestarcde maneraques’acoblinbéentreelles,ielspicapedrerspiquenenlíniesrectes, demaneraquejaesveuquelapedrahad’estartalladacomunasuperfície reglada,peròelquenoéstanevidentésquehagidesertambédesenvolupable.

Mongehodiuaixí:

S’ilétoitquestiondevoûterunspacecirconscritenprojectionhorizontalepar uneellipse,onnepourroitpasdonneràlavoûteunesurfaceplusconvenable quecelledelamoitiéd’uneellipsoïde[...]etensupposantquecettevoûte dûtêtreexécutéenpierresdetaille,ilfaudraitqueladivisionenvoussoirs fûtopéréeaumoyendeslignesdecourbure[ ]etquelesjointsfussentles surfacesdéveloppablesnormalesàlavoûte.

[Siestractésdeferunavoltasobreunespaicircumscritenprojeccióhoritzontal perunael.lipse,noespodriadonaralavoltaunasuperfíciemésadequadaque ladelameitatd’unel.lipsoide[ ]isuposantqueaquestavoltas’executésen pedrestallades,serianecessariqueladivisióendovellesesfespermitjàdeles líniesdecurvatura[ ]iquelesjuntesfossinlessuperfíciesdesenvolupables normalsalavolta.]

Comentaqueenaquellmoments’estanconstruintlessalesperalsconsellsde lalegislaturaiquelamillorformaquese’lspotdonarésl’el.lípticaiqueestigui cobertaperunel lipsoide.Llavorsesposarialatribunad’oradorsjustsotaun delspuntsumbilicalsdelavolta.Iespodriadecorarl’espaiposantcolumnes seguintleslíniesdecurvatura.Is’imaginatambédosllumsd’aranyapenjant delsumbilicals!

Al’articledeJ.Sakarovitch«GaspardMongefounderof“Constructive Geometry”»[T13],esreprodueixlafigurasegüent(figura11),queatribueixa Leroy,1844.33 Esveulavoltael.lipsoidalamblespedressuperiorsodovelles acobladesentreellesperpendicularmentalasuperfíciequelesaguanta.

El1801espubliquenles Feuillesd’analyseappliquéeàlagéométrieàl’usage del’Écolepolytechnique [M11],peròlesprimeresnotesambaquestnomper alsestudiantsdel’Écolepolytechniquesóndel1795.Elsalumnesanomenaven aquestllibre«LegrosMonge».

Enunanotadel1799,«Descourbesàdoublecourbure»[M19],escomplementenqüestionssobrelescorbesdedoblecurvaturaquefaltenales Feuilles. Aquestarticleacabaambunanotaapeudepàginad’Hachette,34 quediu:

33 Elllibre iv del Traitédestéréotomie deLeroy(1780–1854)[A11]esdiu«CoupedesPierres», itéunaseccióqueestitula«Voûteenellipsoïdeàtroisaxesinégaux.Emploideslignesde courbure».EldibuixquereprodueixSakarovitchéslaplanxa44de[A11].

34 JeanNicolasPierreHachettevaserundelsmésimportantsimpulsorsdel Journaldel’École polytechnique.Vacol.laborarestretamentambMongesobretotenl’estudiilesaplicacionsde lageometriadescriptiva.Vaestudiarelsradisdecurvaturadelessuperfíciesa«Dequelques propriétésdesrayonsdecourbured’unesurface»[A7].

136 (Leroy, 1844, pp. 366-367) in their courses on stereotomy, the wish to see the theory of stone assembly revive mortarless architecture (cf. Sakarovitch 1998, p. 311). One must however observe that this did not happen. We have not been able to find any examples or any mortarless architectural works involving new surfaces or vaults involving intradoses with complex surfaces assembled according to the lines of curvature.

4: The lines of curvature as generalized ellipses

“The families of the lines of curvature can be regarded as generalized ellipses: choosing a pair of umbilical points not diametrically opposite, we attach the ends of a thread of sufficient length to them and pull it toward a point P of the ellipsoid. The various positions that P can assume on the ellipsoid trace out a line of curvature”; (Hilbert 1952, p. 188).

CetécritpourrasuppléeràcequimanquesurlesCourbesàdoublecourbure danslesfeuillesd’analyseappliquéeàlagéométrie,queleC.en Mongeafait imprimerpourlesélèvesdel’Écolepolytechnique.

[Aquestescritpodràsuplirelquemancasobrelescorbesdedoblecurvatura ales Feuillesd’analyseappliquéeàlagéométrie,queelciutadàMongehafet imprimirperalsalumnesdel’Écolepolytechnique.]

Edicionsposteriorsdeles Feuilles,fetesapartirdel1807,portavenpertítol Applicationdel’analysealagéométrie.Liouvillevatenircuradelacinquena edició,de675pàgines,quevacorregiricomentar,vegeu[M18].Alasecció6 hemestudiatelfull xv

AquestaediciódeLiouvilleestàcompostadevint-i-setseccions,dedicades totesalquepodríemanomenardemaneragenèrica generaciódesuperfícies Perexemple:«x.Delasuperfícieengendradapelmovimentd’unalíniarecta paral.lelaaunplafixat»,«xii.Superfíciesdesenvolupables»,«xvii.Delageneraciódelasuperfíciecorbaenlaqualtotesleslíniesd’unadelescurvatures estanenplansparal.lelsaunpladonat»,«xx.Delasuperfíciecorbaenlaqual elsdosradisdecurvaturasónsempreigualsidesignescontraris»,«xxii.De lasuperfíciecorbaqueenvoltaunasuccessiód’esferesderadivariableicentressobreunacorbaqualsevol»,«xxiii.Article[M12]»,«xxiv.Article[M13]», «xxv.Article[M14]»,«xxvi.Article[M15]»,«xxvii.Article[M7]».

AcontinuacióLiouvillereprodueixlamemòriaimmortaldeC.F.Gauss traduïdaalfrancèsambeltítol«Recherchessurlathéoriegéneraldessurfaces courbes»[A5].Iacabaambunesfamosessetnotes:«i.Sobrelescorbesdedoble curvatura»,«ii.Expressionsdiversesdeladistànciadedospuntsinfinitament

Figure

Figure 5 : ellipsoid vault using lines of curvature In (Leroy 1844)

Figura 11: Dovellessobreel lipsoide.

pròximsidelacurvaturageodèsicadeleslíniessobreunasuperfície»,«iii.Teoremasobrelaintegraciódeleslíniesgeodèsiques»,«iv.Sobreelteorema deGausssobreelproductedelsdosradisdecurvaturaprincipalsencada puntd’unasuperfície»,«v.Deltraçatgeogràficdesuperfícies,lesunessobre lesaltres»,«vi.Extensióalcasdetresdimensionsdelaqüestiódeltraçat geogràfic»,«vii.Sobrel’equaciódelescordesvibrants».

El1802Mongepublica«Mémoiresurlasurfacecourbedonttoutesles normalessonttangentesàlasurfaced’unemêmesphère»[M12],onintrodueix elnomdecorba característica dient:

C’estàcettecourbe,donttouteslessurfacessoumisesàlamêmegénération sontpourainsidirecomposées,35 qu’onauraitdûconsacrerlenomde génératrice;maiscemotestdéjàemployédansunsensquin’estpastoujoursle mêmequecelui-ci:j’aidonccrunécessairedemeservird’unmotnouveau,et j’ainommécettecourbe caractéristique.

[Ésaaquestacorba,delaqualtoteslessuperfíciessotmesesalamateixa generacióestanperaixídircompostes,queselihauriad’haverassignatelnom de generatriu;peròaquestnomjas’utilitzaenunsentitquenoéselmateix queaquestd’aquí:hecregut,doncs,necessariservir-med’unanovaparaula,i heanomenataquestacorba característica.]

Veu,entrealtrescoses,queunasuperfíciequesatisfàleshipòtesisdeltítol éstalquel’esferaéselllocgeomètricdelscentresd’unadelessevescurvatures. Ampliaaquesttipusderesultatscanviantl’esferaperunasuperfíciecònica arbitràriaa«Surlasurfacecourbedonttouteslesnormalessonttangentesà unemêmesurfaceconiqueàbasearbitraire»[M13],publicatjustacontinuació del’anterior.

El1805,apareixelllibredeMongeiHachette, Applicationdel’algèbreala géométrie [M21],quereculldiversostreballsdeMonge.Defet,jael1802havien publicatunarticleambelmateixnomal Journaldel’Écolepolytechnique [M20], basedelllibreposterior.Abansdecomençardiu(observeulesdatessegonsel noucalendariimposatperlaRevolucióFrancesa):

AVERTISSEMENT

LésÉlevesdel’Écolepolytechniqueonttrouvéjusqu’apresentleprécisdes leçonssurl’applicationdel’AlgèbreàlaGéométrie,danslesFeuillesd’analyse de Monge,etleMémoiresurlessurfacesduseconddegré,impriméenl’an10 dansleJournaldel’École.TouslesexemplairesdeceMémoire,tirésàpartlors delapublicationduJournal,ayantétédistribués,MM.MONGEetHACHETTEon proposédeleremplacerparunouvrageayantpourtitre:«Surfacesdupremier etseconddegré»,leConseild’instruction,danssaséancedu19pluviosean13, aarrétéquecetOuvrageseroitimprimépourl’École.

[Elsalumnesdel’Écolepolytechniquehantrobatfinsaraelsapuntsdeles lliçonssobrel’aplicaciódel’àlgebraalageometria,ales Feuillesd’analysede Monge,ialaMemòriasobrelessuperfíciesdesegongrau,impresal’any10 35 Abanshaposat,comaexempled’aquestacorba,elsmeridiansdelessuperfíciesderevolució.

alarevistadel’Escola.Haventestatdistribuïtstotselsexemplarsd’aquesta Memòria,impresosperseparatquanesvapublicarel Journal,elssenyors MONGEiHACHETTEhanproposatreemplaçar-laperunaobraquetépertítol: «Surfacesdupremieretseconddegré»,elConseild’Instruction,enlasevasessió del19pluviósany13,hadonatpermísperquèaquestaobrasiguiimpresaper l’Escola.]

Elllibreestàcompostdelesvuitseccionssegüents:«i.Equacionsd’unpunt», «ii.Equacionsdelalíniarecta»,«iii.Equacionsdelpla»,«iv.Problemesrelatius arectesiplans»,«v.Canvisdecoordenades»,«vi.Delcentreidelsplans diametralsd’unasuperfície»,«vii.Superfíciesdesegongrau»,«viii.Superfícies desegongrauquanlescoordenadesdelcentresónal’infinit».

El1806publicadosarticlesllargsconsecutiusal Journaldel’Écolepolytechnique.Elstítolssónexplícitsdelseucontingut,elprimerestitula«Surla surfacecourbedonttouteslesnormalessonttangentesàunemêmesurfacedéveloppablequelconque»[M14],itocaelmateixtemaqueenelsanteriors[M12] i[M13],ielsegon«Delasurfacecourbequienveloppel’espaceparcourupar unesphèrevariablederayon,etdontlecentreparcourtunecourbeàdouble courburequelconque»[M15].Estudia,doncs,tubs.

El1807enviaal’Écolepolytechniqueunabreusoluciódelproblemade trobarunasuperfíciedesenvolupablequetinguicomaarestaderetrocés unacorbadonada,queHachettereculla Correspondancesurl’Écoleimpériale polytechnique [M16].Tambéd’aquestanyéslanotaconjuntaambHachette «Surlathéoriedesombresetdelaperspective;surlespointsbrillantsdes surfacescourbes»[M22].Defineixen puntbrillant comelpuntdelasuperfície quereflecteixunraiglluminóscapal’ulldel’espectador.Nohihacapfórmula, nomésconsideracionsgeomètriques.

El1810enviaunanotaal’Écoletitulada«Surleséquationsdifférentielles descourbesduseconddegré»[M17].Diuqueplantejar-seaquestproblemaper acorbesdegrauarbitrarilisembla«uneenterpriseinutile».Peròque,perla sevaimportància,vallapenafer-hoperalescorbesdesegongrau.Comque lessevesequacionssón

posant

comaequaciódiferencialdetoteslescorbesdesegongrau.

El1811espublicalasevafamosa Géométriedescriptive [M10],onhihaun capítoltitulat«Desplanstangentsetdesnormalesauxsurfacescourbes»,en elqualesparladecanons,del’enemic,etc.Ésmoltcuriósl’esperitpatriòtic quedestil.lalaintroducció.

Pourtirerlanationfraçaisedeladépendanceoúelleaétéjusqu’àprésentde l’industrieétrangère,ilfautpremièrementdirigerl’educationnationaleversla connaisancedesobjetsquiexigentdel’exactitud[...]et,àcetégard,ilaut l’avouer,nousavonsbeaucoupàpuiserchezlesnationsétrangères.

C’estd’abordenfamiliarisantavecl’usagedelaGéométriedescriptivetous lesjeunesgensquiontdel’intelligence,tantceuxquiontunefortuneacquise, afinqu’unjourilssoientenétatdefairedeleurscapitauxunemploiplusutile etpoureuxetpourl’État,queceuxmêmesquin’ontd’autrefortunequeleur éducation,afinqu’ilspuissentunjourgrandprixàleurtravail.

[Pertreurelanaciófrancesadeladependènciaquehatingutfinsaradela indústriaestrangera,caldirigirprimerl’educaciónacionalcapalconeixement d’objectesquerequereixenexactitud[ ]i,enaquestsentit,hohemdeconfessar,tenimmoltaaprofitardelesnacionsestrangeres.

Enprimerllocfamiliaritzanttotselsjovesambintel.ligènciaenl’úsdela geometriadescriptiva,tantelsquetenenfortunaadquirida,perquèundia estiguinencondicionsdeferdelsseuscapitalsunúsmésútilperaellsipera l’Estat,comaquellsquenotenenmésfortunaquelasevaeducació,demanera queundiapuguindonarmésvaloralseutreball.]

Esperoqueaquesttreballapropielsfutursalumnesdegeometriadiferencial delesnostresuniversitatsalafiguradeMongeialcontextenquèesvainiciar l’estudidecorbesisuperfícies.

8FrançoisAragó

perJosepLluísSolé

PerconèixerlavidadeF.Aragó36 (1786–1853)usrecomanemambentusiasme l’autobiografiatitulada Històriadelamevajoventut (col leccióPopularBarcino, núm.155),publicadaperEditorialBarcino(1937),reimprèsperArtífexCultural, Palma(2000),queredactàquan,comdiuellmateix,jaeravelliestavamalalt. Esllegeixcomunamagníficanovel.lad’aventures.

Enelllibreensparladelasevainfantesaalpobled’Estagell,alRosselló,i lasevaadolescènciaaPerpinyà.Tambédelapreparaciódel’examend’ingrés al’Écolepolytechnique,estudiantensolitariobresdeLegendre,Lacroixi Garnier...examenquefeuaTolosa,davantd’untribunalpresiditperMonge, queprimerelrebéambdesconfiança.L’examenduràdueshoresiacabàamb l’abraçadadeMonge,impressionatpelsconeixementsdeljoveAragó.

Enshiexplical’ambientdel’Écolepolytechnique,lligadaalsmoments políticsdifícilsdelaFrançadelaprimeradècadadelsegle xix.Allíconeguéifeu amistatambLaplace.Juntambaltresestudiantsesnegàasignareldocument d’adhesióalaproclamaciódeNapoleócomaemperador,iperaixòelgeneral Lacuée,directordel’École,proposàlasevaexpulsió.NapoleódemanàaLacuée

36 Enaquestasecciós’harespectatlagrafiadelcognomambaccentempradaperJosepLluís Solé.

quinllocdelapromocióocupavaAragó,ienveurealallistaqueeraelprimer digué:«Ah,sihaguessinestatalacua!...SenyorLacuée,deixeu-hocórrer...».

El1804founomenatsecretaridel’ObservatorideParísrecomanatper Poisson,professordeljoveAragóalapolytechnique.DemanàaLaplace,directordel’Observatori,reprendrelesmesuresdelmeridiàdeParísaEspanya, interrompudesperlamortdeMéchain.

Encaraquetrossosd’aquestmeridiàhavienestatobjectededistintescampanyesdemesuraanteriors(Picard,Cassini i,Cassini ii,LaHire,Maraldi...),quan l’AssembleaNacionaldecidí(1791)establirunpatródemesuraquepoguésser acceptatpertoteslesnacions,l’Acadèmiaproposàtornaramesurarelmeridià deParís,peròaquestavegadanonomésenterritorideFrança,sinóarribar finsaBarcelona(elmeridiàdeParísentraalMediterranialaplatjad’Ocata,al Maresme).Delambrefoul’encarregatdemesurarlapartnord,deDunquerkea Rodés,iMéchain,lapartsud,deRodésaBarcelona.Lesmesurescomençarenel diaabansdelapresadelaBastilla,ilahistòriad’aquestacampanyacientífica, fetaenmomentsconvulsos,mereixunaexplicacióapart.

El1801,Méchain,directordel’ObservatorideParís,demanàprolongar lesmesuresdelmeridiàdeBarcelonaalesBalears(elmeridiàdeParístalla saDragonera,ideixal’illadeMallorcatotalmentallevantseu).Perfer-ho, proposàtriangularlacostadeCastellóiValènciaperpoderferelsaltaEivissa iFormentera,id’allíalaserradeTramuntanadeMallorca.El1803Méchain començàelstreballs,peròmoríelsetembredel1804sensepoderacabarelseu encàrrec.

F.AragóiJ.-B.Biotforen,doncs,comissionatsperacabarlesmesuresde Méchain,isónlesanècdotesd’aquestaexpedició,iniciadaaprincipisdel1806, lesqueocupenlagranpartdelllibretquehemesmentatalprincipi.Enshi explicalasevaestadaalcimdeldesertdeValènciadurantsismesosintentant visualitzarelturódesCampVell,aEivissa,a150kmdedistància.Lestrobades iamistatambelsbandolersdepropdeCullera,alsuddeValència;lapersecució d’unamantgelósaSagunt;l’estadaalaMoladeFormentera,enunacasaque encaraavuiexisteix,ilaconstrucciód’unacabanadepedraalcimdelaMola des’Esclop,sobreAndratx,últimvèrtexdeldarrertriangle,hisóndescritsamb moltaamenitat.

AlaMolades’Esclopelsorprenguél’aixecamentcontraNapoleó(1808). Avisatque,comqueelpoblecreiaqueeraunespia,elpujavenamatar,fugí vestitdepastoriesrefugiàaPalma.AllífoutancatalcastelldeBellver,d’on escapà,ipujàaunvaixellqueelportàaAlger.EmbarcàcapaFrança,peròun corsarideRosescapturàelvaixell,iAragó,sensedonar-seaconèixerifent-se passarpercatalà,foutancatalaciutadelladeRosesiaPalamós.Alliberat, unvaixelll’haviadeportaraMarsella,peròunatempestadesviàelvaixella Bugia,alescostesalgerianes,on,desprésd’unviatgearriscat,poguéarribar alconsolatfrancèsd’Alger.Allís’embarcàenunvaixelldebanderaalgeriana, iarribàfinalmentaMarsellaeljunydel1809,evitantelbloqueigdelaflota anglesa.Totaixòamblallibretad’observacionsamagadaalasevaroba!

Unanydesprés(1809)fouelegitmembredel’Acadèmia,peraunavacanta laqualtambéaspiravaD.Poisson,quehaguéd’esperartresanysapoder-hi accedir.Eneldarrercapítolde Memòriesdelamevajoventut ensexplicala sevaactivitatcomaacadèmic,finsalseunomenamentcomasecretariperpetu el1830,ilasevarenúncialaplaçadeprofessordel’Écolepolytechniqueafavor deFourier.

Nodescriuremenaquestesnotesdecaràcterbiogràficl’obracientífica d’Aragó,peròsíquevolemassenyalarquenoabandonàelseucompromís polític.FoumembredelgovernprovisionaldelaSegonaRepública,sorgida desprésdelaRevoluciódel1848,elqualestablíelsufragiuniversalil’abolició del’esclavitudaFrança.Comaministredelaguerraidemarinavasuprimirels càstigscorporalsal’armadaimilloràeltractealsmariners(vegeuelcapítol6 delllibredeP.Murdin FullMeridianofGlory,NovaYork,SpringerBussiness Media,2000).

QuanNapoleó iii restablíl’imperiel1851,Aragóesretiràdelavidapolítica, peròlipermeterencontinuarsentdirectordel’Observatorifinsqueesretiràa Estagellel1853.

Agraïments

AgraeixoaJosepLluísSoléClivillésqueenshagicediteltextsobreFrançois Arago,aixícomlaredacciódelpeudepàgina8.IaDavidMarínqueemva ajudarenelscàlculssobrelafibraciódeHopf.

TreballsdeMonge

[M1] Monge,G. «Mémoiresurlespropriétésdeplusieursgenresdesurfaces courbes,particulièrementsurcellesdessurfacesdéveloppables,avec uneapplicationàlathéoriedesombresetdespénombres». Mémoiresde MathématiqueetdePhysique[MémoiresdesSavantsÉtrangers],9(1780), 382–440.

[M2] Monge,G. «Mémoiresurlathéoriedesdéblaisetdesremblais». Histoire del’Académieroyaledessciences [París](1781),666–704.

[M3] Monge,G. «Suruneméthoded’intégrerleséquationsauxdifférences ordinaires,lorsqu’ellessontélevées,etdanslescasoùleursintégrales complètessontalgébriques». Mémoiresdel’Académiedessciencesde Paris (1783),719–724.

[M4] Monge,G. «Mémoiresurl’expressionanalytiquedelagénérationdes surfacescourbes». Histoiredel’Académieroyaledessciences.Mémoires deMathématiqueetdePhysique [París](1784),85–117.

[M5] Monge,G. «Surlecalculintégraldeséquationsauxdifférencespartielles». MémoiresdeMathématiqueetdePhysique[MémoiresdesSavants Étrangers] (1784),118–192.

AgustíReventós

[M6] Monge,G. «Surl’expressionanalytiquedelagénérationdessurfaces courbes». Mémoiresdel’AcadémieroyaledessciencesdeTurin (1784), 19–33.

[M7] Monge,G. «Mémoiresurlesdéveloppées,lesrayonsdecourbure,etles differensgenresd’inflexionsdescourbesàdoublecourbure». Mémoires présentéspardiverssavantsàl’Académiedessciencesdel’Institutde France, x (1785),511–550.[Vegeutambé[M18,392–420]]

[M8] Monge,G. «Stéréotomie». Journalpolytechnique ou Bulletindutravail, 1ercahier(1794),1–15.

[M9] Monge,G. «Surleslignesdecourburedelasurfacedel’ellipsoïde». Journaldel’Écolepolytechnique ou Bulletindutravail,2ecahier(1795), 145–165.[Reproduïtalasecció xvi,p.139,de[M18]]

[M10] Monge,G. Géométriedescriptive.Leçonsdonnéesauxécolesnormales, l’an3delaRépublique.París:Baudouin,1799.[N’hihamoltesedicions,perexempleunadeKlostermannde1811iunadeJacquesGabay de1989]

[M11] Monge,G. Feuillesd’analyseappliquéeàlagéométrieàl’usagedel’École polytechnique.París:Baudouin,1801.[ÉditionsJacquesGabayenfauna reimpressióel2008]

[M12] Monge,G. «Mémoiresurlasurfacecourbedonttouteslesnormales sonttangentesàlasurfaced’unemêmesphère». Journaldel’École polytechnique,11ecahier, iv (1802),28–58.

[M13] Monge,G. «Surlasurfacecourbedonttouteslesnormalessonttangentesàunemêmesurfaceconiqueàbasearbitraire». Journaldel’École polytechnique,11ecahier, iv (1802),59–86.

[M14] Monge,G. «Surlasurfacecourbedonttouteslesnormalessonttangentesàunemêmesurfacedéveloppablequelconque». Journaldel’École polytechnique,13ecahier, vi (1806),1–40.

[M15] Monge,G. «Delasurfacecourbequienveloppel’espaceparcouruparune sphèrevariablederayon,etdontlecentreparcourtunecourbeàdouble courburequelconque». Journaldel’Écolepolytechnique,13ecahier, vi (1806),41–59.

[M16] Monge,G. «Trouverl’équationdelasurfacedéveloppable,quiapour arétederebroussementunecourbeàdoublecourbure,dontonconnaît l’équationuniqueauxdifférencesordinaires?».A: Hachette,J.N.P. (ed.). Correspondancesurl’Écoleimpérialepolytechnique (Avril1804–Mars1808).Vol. i.París:Klostermann,1807,209–211.

[M17] Monge,G. «Surleséquationsdifférentiellesdescourbesdusecond degré».A: Hachette,J.N.P. (ed.). Correspondancesurl’Écoleimpériale polytechnique (Janvier1809–Mars1813).Vol. ii.París:Klostermann, 1810,51–54.

[M18] Monge,G. Applicationdel’analyseàlagéométrie.5aed.,revisada, corregidaianotadaperJ.Liouville.París:Bachelier,1850.[1aed.,1807]

[M19] Monge,G.;Hachette,J.N.P.,«Descourbesàdoublecourbure.(Extrait desOuvragesduC.en GaspardMonge.)» Journaldel’Écolepolytechnique ou Bulletindutravail,6ecahier, ii (1799),345–363.

[M20] Monge,G.;Hachette,J.N.P. «Applicationd’àlgebreàlagéométrie». Journaldel’Écolepolytechnique,11ecahier, iv (1802),143–170.

[M21] Monge,G.;Hachette,J.N.P. Applicationdel’algèbrealagéométrie.Des surfacesdupremieretseconddegré,al’usagedel’Écolepolytechnique. París:Bernard,1805.

[M22] Monge,G.;Hachette,J.N.P. «Surlathéoriedesombresetdela perspective;surlespointsbrillantsdessurfacescourbes».A: Hachette, J.N.P. (ed.). Correspondancesurl’Écoleimpérialepolytechnique (Avril 1804–Mars1808).Vol. i.París:Klostermann,1807,295–305.

TreballssobreMonge

[T1] Arago,F. «BiographiedeGaspardMonge». Mémoiresdel’Académiedes sciencesdel’InstitutdeFrance, xxiv (1854), i–clvii.[Llegitalasessió públicadel’11demaigde1846]

[T2] Belhoste,B. «GaspardMonge:Urgencesrevolutionnairesetutopie». CahiersduMouvementuniverseldelaresponsabilitéscientifique(MURS), 17(1989),55–75.

[T3] Brisson,B. NoticehistoriquesurGaspardMonge.París:Plancher,Éditeur duManueldesBraves,1818.

[T4] Chapelon,J. «Monge,géomètreetJacobin». LaPensée,NouvelleSérie, 13(1947).

[T5] deLaunay,L. Ungrandfrançais.Mongefondateurdel’Écolepolytechnique.París:ÉditionsPierreRoger,1933.

[T6] dePongerville,J.-B.S. GaspardMongeetl’expeditiond’Égypte.París: ChallamelAiné,éditor,1860.

[T7] Dupin,Ch. Essaihistoriquesurlesservicesetlestravauxscientifiquesde GaspardMonge.París:Bachelier,1819.

[T8] Etayo,J.J. «LasbasesdelaGeometríaDiferencial». HistoriadelaMatemáticaenelsiglo xix (2a parte).Cursdeconferènciesdurantelsmesos defebreraabrildel1993.RealAcademiadeCienciasExactas,Físicasy Naturales,1993,171–190.

[T9] Ghys,É. «GaspardMonge.Lemémoiresurlesdéblaisetlesremblais».A: ImagesdesMathématiques (2012),1–24.[Articleadjuntal’obra«Gaspard Monge,lebeau,l’utileetlevrai»,disponiblea http://images.math. cnrs.fr/Gaspard-Monge]

[T10] Guyon,N. ÉlogefunèbredeM.Monge,comptedePeluze.París:Plancher, ÉditeurduManueldesBraves,1818.

AgustíReventós

[T11] Langevin,R. «GaspardMonge,delaplancheàdessinauxlignesde courbure».A: Delaméthode.Besançon:Press.Univ.Franc-Comtoises, 2002,127–154.(Colloq.Sémin.)

[T12] Ravailhe,F. ÉlogedeGaspardMonge.Beaune:ImprimeriedeBlondeauDejussieu,1849.

[T13] Sakarovitch,J. «GaspardMongefounderof“ConstructiveGeometry”». A: ProceedingsoftheThirdInternationalCongressonConstructionHistory. Cottbus:BrandenburgUniversityofTechnology,2009,1293–1300.

[T14] Sergescu,P. «LebicentenairedeGaspardMonge». Rev.HistoireSci.Appl., 1(2)(1947),162–170.

[T15] Struik,D.J. GeometríaDiferencialClásica.Madrid:Aguilar,1970.[Traduccióde LecturesonClassicalDifferentialGeometry.Cambridge,Mass.: Addison-WesleyPress,Inc.,1950]

[T16] Taton,R. L’œuvrescientifiquedeMonge.París:PressesUniversitairesde France,1951.

[T17] Taton,R. «LapremièrenotemathématiquedeGaspardMonge(juin 1769)». Rev.HistoireSci.Appl.,19(2)(1966),143–149.

Altres

[A1] Dupin,Ch. Développementsdegéométrie,AvecdesApplicationsàla stabilitédesVaisseaux,auxDéblaisetRemblais,auDéfilement,àl’Optique, etc.;ouvrageapprouvéparl’InstitutdeFrance,pourfairesuiteala GéométrieDescriptiveetalaGéométrieAnalytiquedeM.Monge.París:M. V.Courcier,Imprimeur-LibrairepourlesMathématiques,1813.

[A2] Dupin,Ch. Applicationsdegéométrieetdeméchaniquealamarine, auxpontsetchausses,etc.,pourfairesuiteaux«Développementsde géométrie».París:Bachelier,successeurdeM.V.Courcier,1822.

[A3] Eisenman.«Stéréotomie». Journalpolytechnique ou Bulletindutravail, 2ecahier(1795),100–106;3ecahier(1795),440–442;4ecahier(1796), 619–622.

[A4] Euler,L. «Recherchessurlacourburedessurfaces». Mémoiresdel’AcadémiedessciencesdeBerlin,16(1767),119–143.[Publicattambéa Opera Omnia,Serie1,28(1955),1–22]

[A5] Gauss,C.F. «Disquisitionesgeneralescircasuperficiescurvas». CommentationesSocietatisRegiaeScientarumGottingensisRecentioresClassis Mathematicae, vi (1828),99–146.[Presentatel8d’octubredel1827]

[A6] Girbau,J. Memoriasobreelconcepto,métodoyfuentesdelageometría diferencial.Barcelona:1973.[Apunts]

[A7] Hachette,J.N.P. «Dequelquespropriétésdesrayonsdecourbured’une surface».A: Hachette,J.N.P. (ed.). Correspondancesurl’Écoleimpériale

polytechnique (Avril1804–Mars1808).Vol. i.París:Klostermann,1807, 213–218.

[A8] Lacroix,S.F. Traitéélémentairedecalculdifférentieletdecalculintégral 3vol.París:Duprat,1797–1800.[N’hihadiversesedicionsposteriors,editadesperBachelier,París.Laquecitemeneltextde1810éseditadaper ChezCourcier,iportaelsubtítol«Secondeédition,revueetaugmentée»]

[A9] Lancret,M.A. «Mémoiresurlescourbesadoublecourbure».A: Mémoiresprésentéspardiverssavantsàl’Académiedessciencesdel’Institutde France, i (1802),416–454.[Llegitel6deflorealdel’any10]

[A10] Legendre,A.-M. «Mémoiresurl’integrationdequelqueséquationsaux différencespartielles». Histoiredel’Académieroyaledessciences,París (1789),309–351.[Llegitl’1desetembrede1787]

[A11] Leroy,C.F.A. Traitédestéréotomie,comprenantlesapplicationsde lagéométriedescriptiveàlathéoriedesombres,laperspectivelinéaire,la gnomonique,lacoupedespierresetlacharpente.París:Bachelier,1844.

[A12] Olivier,T. «Mémoiredegéométrie.Delacourbureetlaflexiond’une courbeadoublecourbure». Journaldel’Écoleroyalepolytechnique, 24ecahier,15(1835),61–92.

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.2,2018.Pàg.147–171. DOI:10.2436/20.2002.01.83

Codiscorrectorsd’errorsicriptografiapostquàntica NarcísSayolsiSebastiàXambó

Resum: RevisitemelsistemacriptogràficdeclaupúblicadeMcEliece,introduït faquarantaanys,ambl’ajudaderecursosdesenvolupatsrecentment:unamillora deldescodificadordePeterson-Gorenstein-Zierlerperalscodiscorrectorsd’errors alternants;unsistemadecomputaciósimbòlicaiunpaquetd’utilitatsfuncionalsper alscàlculsempratsenladefinició,codificacióidescodificaciódecodiscorrectors d’errors,totprogramatenPython,iunapàginawebquedonaaccéslliurealsmaterials generatspelprojecte.L’interèsprincipaldelsistemadeMcEliecerauenelfetqueés uncandidatseriósperaunestàndarddecriptografiapostquàntica.

Paraulesclau: criptografiapostquàntica,codisalternants,computaciósimbòlica, programarilliure.

ClassificacióMSC2010: 11T71,68-04,68W30,94A60.

Pròleg

Comqueelsautorsd’aquestarticlenosomexpertsencriptografia,abansde resenssemblaconvenientcomentarquèenshaportataescriure’l.

Elcontexthaestateltreball,iniciatlatardordel2015,perdissenyariprogramar PyECC,unentornquepermetilaconstrucció,codificacióidescodificació decodiscorrectorsd’errorsiposar-loalalliuredisposiciódelpúblic,totpensantbàsicamentenestudiants,docentsiinvestigadors.Elnuclid’aquestentorn ésunpaquetdeclassesifuncionsdePython1 queanomenemCC(vegeu[46]).

Inicialmentlaideafouigualarlafuncionalitatdelpaquet Wiris/cc descrit a[56],unentorndesenvolupatafidepoderrealitzarlestasquescomputacionalsesmentadesperalscodiscorrectorstractatsenaquelltext.Peròaviatens vanconvèncerquepodíemanarmésenllàendiversesdireccions.Unad’elles, queharesultatserunbontestpera PyECC,foulaimplementaciód’unprototip rudimentaridelsistemacriptogràficdeclaupúblicadescrita[32].

1 https://ca.wikipedia.org/wiki/Python

AquestestudidelsistemadeMcElieceensportàainteressar-nosperlaseva evoluciódesqueesvapublicarfaquarantaanysfinsal’actualitat.Elresultatés quesegueixsent,comveurem,unadeleslíniesmésprometedoresenunhoritzóde criptografiapostquàntica,locucióintroduïdael2003perD.J.Bernstein (vegeu[41])perdesignarparadigmescriptogràficsquegaranteixinprotecció contraqualsevolginydecomputació,actualofutur,incloent-hielssistemesde computacióquàntica(peraunaintroducciógeneralalacomputacióquàntica, vegeu,perexemple,[45];peraunaavaluaciórecentdelapossibleevolucióde l’enginyeriadesistemesdecomputacióquànticaidelssistemesde criptografia quàntica,vegeu[17, 16]ilanotaalfinaldelasecció5).Aquestfetenssemblaquetéunagranimportància,jaqueelsestàndardscriptogràficsusatsen l’actualitatnoofereixenaquestesgaranties.Perexemple,elssistemesbasats enladificultatdefactoritzarnúmerosenters,comaraelsistemaRSA,2 resultenextremamentvulnerablesalacomputacióquànticaacausadela(baixa) complexitatpolinòmicadel q-algorismedeShorperfactoritzarnúmerosenters (vegeu[45,§8]).

Engranmesura,elcontingutd’aquesttreballescorresponambeldela conferència[47]programadaenlaJornadadeTeoriadeNombrescelebrada el7d’octubredel2017alDepartamentdeMatemàticadelaUniversitatde Lleida.3 Tanmateix,eldesigd’augmentar-nel’assequibilitatenshaimpulsata incorporarforçamésdetallsdelsqueespodencomunicarenunapresentació oral,iaintroduirvariacionsenl’ordreexpositiuperaconseguirqueelpendent delalecturasiguitansuaucomsiguipossible.

Alaprimeraseccióesdescriuenbreumentelsingredientsd’unsistemacriptogràficdeclaupúblicaiambmésdetall,alasegonasecció,elsqueconcorren enunsistemadeMcEliece.Totseguits’exposen,alatercerasecció,lesgeneralitatsquenecessitemsobrecodiscorrectorsd’errors,incloent-hielsdetalls específicssobreelscodisd’unsistemadeMcEliece(codisdeGoppaclàssics binaris).Alesseccionsquartaicinquenaestracten,respectivament,l’evolució delssistemesdeMcElieceielgraudeseguretatcriptogràficaqueofereixen. L’apèndixAcontéunabreunotíciasobre PyECC,ienparticularsobreelseu úsiinstal lació,ial’apèndixBesdonenelsdetallsmésrellevantssobrela implementacióusant PyECC d’unsistemadeMcEliece.

1Criptografiadeclaupública

Enun sistemacriptogràfic,unmissatge M és encriptat enun criptograma C ambunafunció Ek quedepènd’unparàmetre k anomenat claud’encriptació: C = Ek(M).

2Vegeu https://ca.wikipedia.org/wiki/RSA. 3 Seminari«Cargols2017»,organitzatpelGrupdeRecercaenCriptografiaiGrafs, http://www. cig.udl.cat/

La descodificació Dk (C) corresponentesrealitzamitjançantunafunció Dk , tambédepenentd’unparàmetre k (claudedesencriptació),ielprimerrequisit fonamentalésques’hadecomplirlarelació

k (C) = Dk (Ek(M)) = M.

Amés,lesfuncions E i D s’handepodercalculareficientment.

Pertalqueespuguiverificarl’equació (1), k i k hand’estarrelacionadesi, pertant,unusuariemissoriunusuarireceptorhandecompartirinformació adientsobre k i k .L’intercanvid’aquestainformaciódemaneraquealtresusuarisnohipuguinaccedirésl’anomenat problemadedistribuciódeclaus.Unpas cabdalenlasoluciód’aquestproblemafoul’esquemadeDiffieiHellman[22] publicatel1976.Segonsafirmenenelresumelsseusautors:«lesnecessitats detelecomunicacióhandonatllocalanecessitatdenoustipusdesistemes criptogràficsqueminimitzinlanecessitatdedisposardecanalsdedistribució declausseguresiqueproporcioninl’equivalentaunasignaturaperescrit. Aquestarticlesuggereixmaneresderesoldreaquestsproblemesactualment oberts».Unadelesmaneresqueproposenésladels sistemescriptogràficsde claupública,«quepermetenlatransmissiód’informaciópercanalsinsegurs sensecomprometrelaseguretatdelsistema».

Enunsistemacriptogràficde claupública,comaraeldeMcEliece,cada usuaritéunaclaud’encriptació pública iunaclaudedesencriptació privada (o secreta).Abansd’entrarenmésdetalls,il.lustrembreumentelfuncionament enelcasdelfamiliarsistemaRSA.Publicatel1978perRivest,ShamiriAdleman[44],endescrivimelfuncionamentacontinuació(comareferènciageneral, vegeu[20]).

Totusuaridisposadelasevaclauenunapartprivadaiunapartpública.La partprivadaestàformadaperdosnúmerosprimers p i q,ilaclaupública, pelproducte n = pq iperunnúmeronatural k primeramb (p 1)(q 1). L’encriptacióquefaunaltreusuaridelmissatge M (quepodemsuposarqueés unnúmeroenternonegatiuinferiora n)s’obtéperlafórmula

C = M k mod n, (2) iladescodificacióamb

C k mod n, (3) on k ésl’inversde k mòdul (p 1)(q 1).Larelació (1) enaquestcassignifica que

M kk = M mod n, (4)

laqualésunaconseqüènciadirectaderesultatselementalsd’aritmèticamodulariperalsqualsellectorpotconsultar[20,§3.3.1].Adonem-nosqueun sistemaRSAéssegursemprequelafactoritzaciódenúmerosentersgrans siguiunproblemadifícil.

D

(1)

2Ingredientsd’uncriptosistemadeMcEliece

Elsingredients generals d’aquestprotocold’encriptaciósónelssegüents:

• F = Fq,uncosfinitdecardinal q (aquíelcasmésimportantserà F = Z2).

• k,unnúmeroenterpositiu.Delselementsdel’espai F k endirem missatges.

• n>k,unnúmeroenter.Delselementsdel’espai F n endirem missatgesde transmissió otambé missatgesdecanal.Si x ∈ F n,posarem |x| per denotarelnombredecomponentsnonul lesde x idiremqueésel pes de x.

Aquestsingredientssónpúblicsihomsuposaquequalsevolusuaridel protocolpotgenerarmissatgesimissatgesdetransmissió,iquepotenviar qualsevolmissatgedetransmissióaqualsevolaltreusuari.

Cadausuaritambéhadedisposardemitjanspergenerarelsobjectes iefectuarelscàlculsadientsalseupaperd’emissororeceptor.Totseguit descrivimaquestsobjectesioperacionssegonsqueestractidegenerarclaus (clauprivadaiclaupública)pertald’esdevenirunusuarireceptor,d’encriptari enviarunmissatgeenelcasd’unusuariemissor,odedesencriptarunmissatge rebutenelcasd’unreceptor.

Generaciódeclaus. Una clauprivada,quedenotarem {G,S,P },estàformada pertresmatriusd’elementsde F :

• G,matriu k × n derang k.

• S,matriu k × k invertibleseleccionadaaleatòriamentsegonsladistribució uniforme.

• P ,matriu n × n depermutacióseleccionadaaleatòriament,tambésegons ladistribucióuniforme.

Lapropietatmésdecisivadelamatriu G peraunusuarireceptorésqueha d’existirunafunció

D : X → F n , on X ⊆ F n , quegaudeixidelapropietatsegüent,on t ésunnúmeroenterpositiuprefixat: (∗) Peratot u ∈ F k itot e ∈ F n amb |e|≤ t,escompleix

x = uG + e ∈ X i D(x) = uG.

D’aquestafunció D endirem descodificador,iensreferiremalapropietat anteriordientque D potcorregirfinsa t errors.Delselementsde X esdiuque sónvectors descodificables.

Enprincipi,cadausuaripottenirelseupropidescodificador,enelsentitque l’algorismeempratpercalcular D,ilasevaimplementació,podenserprivats peralsusuarisquehodesitgin.Tanmateix,caldirqueunsistemacompletha d’incorporarundescodificadorqueserveixiperatothom(descodificador per

defecte),iqueenprincipiésraonablepensarquetotselsusuarispodenser emissorsireceptors.

Lateoriafonamentalqueusaremperalaconstrucciódedescodificadors apropiatséslateoriadecodiscorrectorsd’errors.

La claupública corresponentalaclauprivada {G,S,P } ésunparell {G ,t} definitcomsegueix:

• G = SGP ,queésunamatriu k × n.

• Unnúmeroenterpositiu t quesatisfà (∗).

Protocold’encriptació. Elprotocolquehadeseguirunusuariquevolencriptar ienviarunmissatge u al’usuariambclaupública {G ,t} constadedospassos:

• Generacióaleatòriad’unvectordetransmissió e depes t.

• Tramesadelvector x = uG + e = uSGP + e

Protocoldedesencriptació. Constadequatrepassosquenomésuseninformació privadadelreceptorielvector x enviatperl’emissor:

• Càlculde y = xP 1,demaneraque y = (uS)G + eP 1 .

• Càlculde x = D(y).Comque P ésunamatriudepermutació, |eP 1|=|e|= t

i,pertant,aquestaoperacióestàbendefinida,jaque D corregeixfinsa t errors.Elresultatés x = (uS)G.Ésadir, x ésunacombinaciólineal delesfilesde G ambcoeficients u = uS.

• Comque G térang k, u quedaunívocamentdeterminatper x iespot obtenirresolentelsistemad’equacionslineals x = u G,onlaincògnita éselvector u .

• Càlculde u = u S 1.Missatgerebutcorrectament!

Peralsaspectescomputacionalsd’aquestsingredients,vegeu:A.2«Aritmèticamodular»,A.3«Polinomisirreductibles»,A.4«Construcciódecossosfinits», A.5«Vectorsimatrius»,iA.6«UtilitatsperalsistemaMcEliece».

3CodisdeGoppaclàssics

Enelquesegueix,posem F(k,n) perdenotarlesmatriusd’ordre k×n formades ambelementsd’uncos F .

Codislineals:conceptesbàsicsinotacions Uncodi(lineal)detipus [n,k] sobre Fq ésunsubespaivectorial C dedimensió k de F n q .Enparticulars’hade complir k ≤ n.Diemque n i k sónla longitud ila dimensió de C,respectivament, iescrivim C ∼ [n,k].La taxadetransmissió de C éselquocient R = k/n

NarcísSayolsiSebastiàXambó

Unamatriu G detipus k × n esdiuqueésuna matriugeneradora de C silessevesfilesformenunabasede C.Donadaunamatriu G detipus k × n, posem G perdenotarelsubespaivectorialgeneratperlesfilesde G.Ésun

codidetipus [k ,n],on k éselrangde G.Enelcasque G siguiunamatriu generadorade C,llavors G = C.

Si G ésunamatriugeneradoradelcodi C ∼ [n,k],l’aplicaciólineal f : F k q → F n q , u uG,ésinjectivailasevaimatgeés C.Del’aplicació f esdiuqueésun

codificador de C,isi u ∈ F k q , x = f(u) ésla codificació de u.

Exemple(elcodideHammingbinari [7, 4]). x = uG,on

1000111 0100110 0010101 0001011

Elscodislinealstambéespodendescriuremitjançantelquepodemanomenar construcciódual.Sigui H unamatriudetipus r × n isuposemqueelseurang és r .Llavors

CH ={x ∈ Fn : xHT = 0}= ker HT

ésuncodilineal [n,n r].Delamatriu H esdiuqueésuna matriudecontrol de CH .Ésclarquepodemformarunamatriugeneradorade CH escollintuna basedeker HT .

Exemple. Lamatriu

=

ésunamatriudecontroldelcodideHamming [7, 4].Enefecte,siposem R perdenotarlasubmatriuformadaperlestresdarrerescolumnesde G,llavors G = (I4|R), H = (RT |I3),i

GHT = (I4|R) R I3 = R + R = 0

Pertant, C = G ⊆ ker HT ,quedefetésunaigualtatperquèelsdostermesde lainclusiótenendimensió4.

Remarca. Unamatriugeneradoradelaforma G = (Ik|R) esdiuqueés sistemàtica respectedelescomponents1,...,k,jaque x = uG = (u|uR) iaixòpermet recuperar u comlesprimeres k componentsde x.Enaquestcas,unargument similaraldel’exempleanteriorenspermetconcloureque H = ( RT |In k) és unamatriudecontrolde G .Remarquemque H = (RT |In k) enelcasbinari. Laconstrucciódualadmetlageneralitzacióquedescrivimacontinuaciói queusaremperconstruirelscodisdeGoppaclàssics.Sigui F = Fq i F = Fqm , on m ésunnúmeroenterpositiu.Sigui H unamatriudetipus r × n amb

componentsde F isuposemqueelseurangés r .Llavorspodemdefinirelcodi lineal/F

CH,F = CH ∩ F n ={x ∈ F n : xHT = 0}.

Pertrobarunamatriudecontrol H (sobre F )d’aquestcodi,podemprocedir delamanerasegüent.Sigui H lamatriusobre F obtingudasubstituintcada element β de H perlacolumnadeles m componentsde β relativamenta unabasede F sobre F ,demaneraque H ∈ F(rm,n).Finalment,sigui H el resultatdesuprimirlesfilesde H quesóncombinaciólinealdelesanteriors, H ∈ F(r ,n).Delaconstruccióesdesprènque

CH,F = CH = CH

i,pertant, dim CH = n r .Atèsque r ≤ mr ,resultaque k ≥ n r .També escompleixque r ≥ r o k ≤ n r (vegeu,perexemple,[56,prop.4.1]).Pera unexempleconcretdecàlculde H , H, r i k,vegeuA.7.

Un descodificador d’uncodi C ésunaaplicacióexhaustiva g : F n → C E (uniódisjunta),on E ésunconjuntde«missatgesd’error»,quecompleix g(x) = x peratot x ∈ C.

Elconjunt g 1(C) ⊆ F n éseldels vectorsdescodificables,mentrequeelconjunt F n g 1(C) = g 1E éselconjuntdels vectorserronis.Undescodificador és complet si g 1(C) = F n (casenelqual E=∅).

Diemqueeldescodificador g té capacitatcorrectora t si g(y) = x peratot vector y ∈ F n talque |y x|≤ t.

Siposem B(x,t) ={y ∈ Fn : |y x|≤ t} (d’aquestconjuntesdiuqueés la boladeHamming decentre x iradi t),aleshorestenimque ∪x∈C B(x,t) ⊆ g 1(C) i g(B(x,t)) ={x}

CodisdeGoppabinaris Percompletarlaconstrucciód’unsistemadeMcEliece, l’ingredientmésimportantqueensfaltaésunamatriugeneradorabinària G quecompleixilacondició (∗) delapàgina150.Dediquemelquerestad’aquesta seccióadescriurecomesresolaquestproblema.Peralaconstruccióefectiva delesmatrius S i P ,vegeuA.6.

SibééscertqueelsistemainicialdeMcElieceésbinari,ladescripciódels codisdeGoppaclàssicslafaremsobreuncosfinit F qualsevol.Preparemaixí elterrenyperpoderconsiderarvariacionsdelsistemaoriginalintroduïdes posteriormentsenseque,defet,representicapdificultatteòricaaddicional.

Sigui,doncs, F = Fq uncosfinit(F = Z2 enelcasbinari).Escollimun númeroenterpositiu m iposem F = Fqm .Escollimelementsdistints α = α1,...,αn ∈ F ,cosaqueimplica n ≤ qm,iunpolinomi p ∈ F[T] degrau r ≥ 1 talque p(αj ) = 0(j = 1,...,n).Finalmentposem hj = 1/p(αj ) (j = 1,...,n)i Γ = Γ (p, α) := CH,F ,on

Diemque Γ ésel codideGoppaclàssic associata p i α.Comqueelnombre defilesde H és r ,i F tégrau m sobre F , k = dim Γ (p, α) compleix,pelqueja hemdit,que n r ≥ k ≥ n rm.Amés,resultaque Γ corregeix t omenys errors,on t éslapartenterade r/2[56,p.191].Enelcasbinari, Γ corregeix r omenyserrorssi p notéarrelsmúltiples[56,exerciciP.4.7,p.194].Defet,en aquestcasescompleixque Γ (p, α) = Γ (p2 , α) i,pertant,aquestcodicorregeix t errorssi t ≤ r .Peraunexempledetallat,vegeuA.8.

Descodificadors ElscodisdeGoppaclàssicssónuncasespecialdelsanomenats codisalternants.L’interèsd’aquestscodisnoraunomésenelfetqueels constructorsdecodisdeGoppaclàssicssónespecialitzacionsdelsconstructors decodisalternants,sinóqueelscodisalternantsadmetendescodificadorsgeneralseficientsqueproporcionenbonsdescodificadorsperalscodisdeGoppa clàssicsi,enparticular,peralscodisdeGoppaclàssicsbinaris.

Elpaquest PyECC inclouimplementacionsdelsdosdescodificadorsprincipalsperacodisalternants:eldeBerlekamp-Massey-Sugiyama(BMS)ielde Petterson-Gorenstein-Zierler(PGZ).Vegeul’exempleA.9.

4EvoluciódelssistemesdeMcEliece

ElcontextenquèMcEliecevaproposarelseusistemavaserelcreatpels treballsdeDiffieiHellman[22],enquèvanintroduirlanociódesistema criptogràficdeclaupública;deMerkleiHellman[33],enquèvanproposar elsistemabasatenladificultatdel’anomenat problemadelamotxilla, 4 i sobretotdeRivest,ShamiriAdleman[44],enquèvanproposarelcelebrat sistemaRSAbasatenladificultatdefactoritzarnúmerosenters(vegeu§1). ElsistemadeMcEliecefouelprimersistemadeclaupúblicabasatenlateoria delscodisalgebraicsquehaviaintroduïtGoppael1970[28],iqueaquíen diem codisdeGoppaclàssics (enelmarcdelscodisdeGoppagenerals,es corresponenambelscodisdegènere0).5 Esmentemtambéqueelsparàmetres escollitsperMcElieceperil.lustrardiversosaspectesdelseusistemavanser [n,k] = [1024, 524] i t = 50,quegarantienunaseguretatdemésde60bits, considerablefaquarantaanys,peròno,comveuremalasecciósegüent,enles circumstànciesactuals.

UnamodificaciódelsistemadeMcEliecevaserproposadaperNiederreiter el1986[37].Laclauprivadad’aquestsistemaésunaterna {H,S,P } dematrius binàriesdetipus n × (n k), (n k) × (n k) i n × n,respectivament.Aquestes matriushandesatisferlescondicionssegüents: H ésunamatriudecontrol d’uncodideGoppaclàssicbinari Γ ∼ [n,k] (ésadir, y ∈ Γ siinomés si yHT = 0)quecorregeix t errors, S ésunamatriunosingularescollida aleatòriamentsegonsladistribucióuniforme,i P ésunamatriudepermutació,

4 Vegeu https://ca.wikipedia.org/wiki/Problema de la motxilla,ontambéesdocumentalarupturad’aquestsistemael1982perShamir.

5 McEliecenocital’articledeGoppai,encanvi,remetalespàgines179–180i193–194de[31].

tambéescollidaaleatòriamentsegonsladistribucióuniforme.Laclaupública corresponentéselparell {H ,t},on H = PHS.Elsmissatges u sónvectors binarisdelongitud n ipes t.Elmissatgeencriptatés x = uH = uPHS. Elreceptorrecupera u delamanerasegüent:(1)calcula s = xS 1 = uPH; (2)comqueconeix H,pottrobar u = uP = D(s, x) ambundescodificador D apropiat(algorismedePatterson[39],queavuiconvéveurecomunavariant delsdescodificadorsestàndardBMSoPGZ),i(3)comqueconeix P ,pottrobar u = u P 1,queéselmissatgeenviat.Elsvalorsdelsparàmetresenlail.lustració inicialeren [n,k] = [1024, 644], t = 38.Peralageneracióeficientdemissatges depes t ilongitud n,vegeu[48].

Enl’estudidelssistemesdeMcElieceiNiederreiterpresentatalamemòria d’habilitaciódeSendrierde2002[49],s’afirma:«Desprésdevintanysd’esforços [icitaunadotzenallargadetreballs],capcriptoanàlisihapogutrompreaquests sistemes».Comveurem,aquestaapreciaciósegueixessentvàlida.

ElproblemademodificarelssistemesdeMcElieceiNiederreiterperpoder funcionarambclauspúbliquessubstancialmentmenorsésconsideratper Gaborita[26].Serveixin,comail.lustraciódelresultat,lesdadessegüents: peralongituds2047i4095,sónsuficientsclauspúbliquesde12KBi20KB, respectivament.Peramésdetallsdecomestavenlescosesfaunadècada, ésrecomanablel’article[24].Peralsautors,«lacriptografiabasadaenteoria decodisésunaalternativainteressantalacriptografiabasadaenteoriade nombres»,jaque«moltesdelesfuncionscriptogràfiquesbàsiques[ ]es podenrealitzarambconceptesdeteoriadecodis».

Tambécalesmentarl’article[12],queentred’altresqüestionsproposanous paràmetresperalssistemesdeMcElieceiNiederreiterqueassoleixenbons nivellsdeseguretatcontratotselsatacsconegutsiamblongitudsdelesclaus considerablementmenors.Amés,s’afirmaque«elscomputadorsquànticsno aportenmilloressignificativesalapotènciadelsatacsmésenllàdepossibles milloresgenèriquesderivadesdel’algorismedeGroveri,pertant,l’esquema criptogràficdeMcElieceésundelscandidatsinteressantsperalacriptografia postquàntica»(peral’algorismedeGrover,podeuconsultarperexemple[45, §5]).

Sibélanociódecriptografiapostquànticavaserintroduïda,comjas’hadit, el2003,alnostreentendrel’inicimésvisibleesprodueixquanalapublicació delmagníficmanualdecriptografiaconvencional[29]vaseguir,unanymés tard,ladelvolum[10].Enaquestvolum,elprimerd’aquestnouenfocament delacriptografia,ésimportantl’articleintroductorideD.J.Bernstein[7],que enparticularpresentaelsquatreparadigmesconsideratsmésprometedors. Amésdelacriptografiabasadaencodis(articled’OverbeckiSendrier[38]), esconsiderentambésistemesbasatsenpolinomisdediversesvariables,en reticlesde Rn (vegeu[53]peraunarticlerecentsobrelaqüestió),ienfuncions hash.Enl’articledeBernsteintotjustesmentat,trobemelquepodriaser el leitmotiv delacriptografiapostquàntica:«Nohihajustificaciópersaltar del’afirmació“elscomputadorsquànticsdestrueixenRSA,DSAiECDSA”a l’afirmació“elscomputadorsquànticsdestrueixenlacriptografia”.Hihamoltes

classesimportantsdesistemescriptogràficsmésenllàdeRSA,DSAiECDSA». Defet,enl’articled’OverbeckiSendrierllegim:«Passadestresdècades,s’han hagutd’ajustarunamicaelsparàmetres,perònoesconeixcapatacque representiunaamenaçaseriosa[alssistemesdeMcEliece],nitansolselsd’un computadorquàntic».

Aquestesapreciacionss’hanrepetit,ifinsitotreforçat,enelsdarrersanys. Esmentemunamostradetreballsenquès’aprofundeixendiversesdireccions: [15],[13](aquestarticleproposanousparàmetresperaconseguirunbonnivell deseguretatdavantdetotselsatacsconeguts),[3],[34],[36](tesidoctoral), [40](unaaltratesidoctoral,enlaqualesrevitalitzenelscodisdeSrivastava generalitzats,iambimplementacionsefectives),[43],[54]i[21].

Entotaaquestadècadapostquàntica,unpioneratenirencompteés D.J.Bernstein,quejahemcitatidelqualenrecomanemlapàginaweb:[6]. TambévallapenaconsultarlapàginaquepublicaambT.Lange,[41],iseguir laconferènciaPQC2018,enfocadaaaconseguirunaestandarditzaciódels protocolscriptogràficspostquànticsidelaqualpodeutrobarinformacióa[19].

5Seguretatcriptogràficad’unsistemadeMcEliece

ElmateixMcEliecea[32]consideràlaqüestiódelaseguretatquepodiaoferir elseusistema.Enunplanteiggeneral,homsuposaqueunespia,diguem-ne E, haaconseguitelvectorencriptat x enviatperunusuariiqueconeixlaclau públicadeldestinatari,ésadir, G = SGP i t.Quinespossibilitatstéd’obtenir elmissatgeinicial u?

Intentardescodificar x = uG + e usantlamatriuconeguda G noespot considerarprometedor,si k éssuficientmentgran,jaqueelproblemade descodificarcodislineals [n,k] ésNP-complet(cf.[5]).

L’altreatacquevaconsiderarMcEliecealseusistemaésméssorprenent. L’espiapotseleccionar k coordenadesde x aleatòriament.Sitésort,cap d’aquestescoordenadesseràerròniaipodràdeterminar u resolentelsistema d’equacionslineals x = uG ,on x éselvectorformatamblescoordenades de x seleccionadesi G éslasubmatriude G formadaamblescolumnescorresponentsalsíndexsde x.Sinotésort,algunadelesentradesseleccionades seràerròniaielsistemanotindràsolució.Aquestatacésmésseriósdelque podriasemblaraprimeravista.Enefecte,decidirsielsistema x = uG és compatible,itrobarlasoluciósienté,comportaunnombred’operacionsde l’ordrede k3,mentrequelaprobabilitatd’escollir k coordenadesnoerròniesés

k ,

demaneraqueelnombred’operacionsquel’espiahad’esperarferpertenir èxitéssuperiora k3/(1 t/n)k.Ambelsparàmetresdelail.lustracióde McEliece,aixòcomportaunesforçnoinferiora264 operacions,unfetque podemexpressardientqueassoleixunaseguretatde64bits(relativamenta l’atacenqüestió).

Figura 1: GraudeseguretatenbitsdelsistemadeMcElieceenfuncióde lataxadetransmissió R = k/n iperalongituds n = 2l (l = 10,..., 13) delcodi.Comagraudeseguretatesprenellogaritmeenbase2del nombred’unitatsdecomputació(factordetreball)del’atacmésfort conegut.

Lafigura1,adaptadadelafigura6.2de[49],resumeixelgraudeseguretat delsistemadeMcElieceaprincipisd’aquestsegle.Hihemafegitleslínies depuntspertaldepoder-locompararambelgraudeseguretatqueacabemde comentar.Veiemque,tenintencomptetotselsatacs,elsparàmetresoriginals garanteixen63bitsdeseguretat,iqueambunataxaunamicasuperior(0.625en llocde524/1024 = 0.512)esté,perlamateixalongitud,unaseguretatde 64bits,enremarcablecoincidènciaambl’anàlisiinicial.

Sendriertambéremarcaque,sibéelsdossistemestenenavantatgespel quefaalafacilitatd’implementació,lasevaclaupúblicaésrelativamentgran. Tambéanunciaunresultatquecalconsiderarimportant,jaquefinsaleshores nos’haviaaconseguittrobar:unesquemadesignaturadigitalbasatenMcEliece.

Lesreferènciesquesegueixenposendemanifestqueaquestsresultatsde Sendriersobreelgraudeseguretatcontinuenessencialmentvigents,sovint ambvariacionspelquefaalscodisemprats:[50,52,23,2,27,11,1].

Enl’article[2]esconsignenlesrecomanacionsinicialsdelprojectePQCRYPTO,jaesmentat,pelquefaalaconfiançaenlaseguretatdelssistemes,més quenopasenl’eficiència.Perexemple,peralssistemesdeMcEliecebasatsen codisdeGoppaclàssicsbinaris,elsparàmetresqueesproposensón n = 6960, k = 5413i t = 119perassolir128bitsdeseguretat.Laseguretatde128bits ésinferiorals172bitsquedonaelrecomptedeMcEliecequehemcomentat abans,laqualcosas’explicapelfetqueenlesestimacionsestenenencompte totselsatacsconegutsques’havienimaginatfinsaaquellmoment.Peramés detallssobreelsistemadeMcElieceproposatperBernstein etal.,itambésobre unavariantdelMcEliece-Niederreiter,vegeu[18].

Acabemlaseccióambunesreferènciessobreprogressosencomputació quànticaquepodenajudaraentendreperquèaquestrecurs,finsitotambtota lapotènciaimaginableenelfutur,potsernopotarribarasertanpoderóscom s’haestimatenmomentspassatsiquemoltprobablementmaiseràsuficient pertrencaralgunsdelssistemesquecomeldeMcEliecetenentotelpotencial deserrealmentpostquàntics:[17,9,8,14].

Tanmateix,calesmentarqueeltreballpionerdeShor[51]vacontribuir apromoureelcampdelacriptografiaquàntica,l’objetiudelaqualésusar lespropietatsquàntiquesdelssistemesperdissenyarsistemescriptogràfics. Peraunadescripcióelementald’aquestssistemes,vegeu[16]ilabibliografia corresponent.Peraunavisiógeneral,queincloularelacióamblacriptografia postquàntica,vegeu[55,18]ielsjacitats[10,8,11].

AIntroduccióaPYECC

L’arquitecturade PyECC esbasaenunajerarquiadeclassesdePythongestionadamitjançantunpaquetdefuncionsqueliserveixd’interfície.Peralsdetalls sobreaquestaarquitectura,aixícomsobrelainstal lacióiús,vegeu[46].Enla restad’aquestapèndixs’exposenunesconsideracionsgeneralsdestinadesa il.lustrar-neelfuncionament.

A.1Valorsinoms

Totobjectecreatamb PyECC téunnomperdefecte.Perexemple, Zn(6) crea l’anell Z6 ielseunomés Z6.Podemoptarperdonar-liunnom,posem ’A’, amblasintaxi Zn(6,’A’).Lallistasegüentmostralasevaflexibilitat(emprem elssímbols -> perindicarqueelvalorqueelssegueixéseldel’expressió anterior):

Zn(6)

-->Z6::Ring

A=Zn(6)

A

-->Z6::Ring

Z6=Zn(6,’A’)

Z6

-->A::Ring

A=Zn(6,’A’)

A

-->A::Ring

Unaltreexempleésquel’anelldepolinomis A[X] sobrel’anellanomenat A es potcrearamb polynomial_ring(A),iespotoptarperdonaraltresnomsala indeterminadaialmateixanelldepolinomis:

A=Zn(6) polynomial_ring(A) -->[Z6[X]::Ring,X::Z6[X]]

A=Zn(6,’A’) polynomial_ring(A)

-->[A[X]::Ring,X::A[X]] polynomial_ring(A,’t’)

-->[A[t]::Ring,t::A[t]] polynomial_ring(A,’t’,’P’) -->[P::Ring,t::P] polynomial_ring(A,name=’P’) -->[P::Ring,X::P]

Convencionssimilarssónvàlidesperalacreaciód’extensionsdecossoso d’anells,comesveuràenelsexemplesquesegueixen.

A.2Aritmèticamodular

Engeneral, Zn(n) creal’anell Zn = Z/(n),ienparticularelcosde n elements quan n ésprimer.Si A i B sónanellsconstruïtsiexisteixunhomomorfisme «canònic»de A a B,laimatgede a ∈ A a B peraquesthomomorfismees denota a»B

A=Zn(17)

#Projeccióde3aA a=3>>A

-->3::Z17

#Ordredel’elementa order(a)

-->16

#Ordrede3mòdul17 order(3,17)

-->16

#Potènciesdea,vistescomenters [lift(a**j)forjinrange(17)]

-->[1,3,9,10,13,5,15,11,16,14,8,7,4,12,2,6,1]

#Potènciesde3mòdul17 [3**j%17forjinrange(17)]

-->[1,3,9,10,13,5,15,11,16,14,8,7,4,12,2,6,1]

#Potènciesdea vector([a**jforjinrange(17)])

-->[1,3,9,10,13,5,15,11,16,14,8,7,4,12,2,6,1]::Vector[Z17]

A.3Polinomisirreductibles

Peralaconstrucciódelamatriu G d’unaclauprivadadeMcElieceésnecessària l’elecciód’unpolinomimònicirreductible p degrau t sobre F = Fq (t ésel segonelementdelaclaupública).Atalfitenimlafunció p=get_irreducible_polynomial(F,t)

Comqueaquestafuncióiteralaseleccióaleatòriad’unpolinomi p mònicde grau t mentre p nosiguiirreductible,ésimportantconèixerlaprobabilitat que p siguiirreductible.Elresultatésqueaquestaprobabilitatés ∼ 1/t coma

NarcísSayolsiSebastiàXambó

conseqüènciadela fórmuladeGauss quedonaelnombre Iq(t) depolinomis mònicsirreductiblesdegrau t sobre Fq: Iq(t) = 1 t d|t µ(t/d)qd = qt t +···

Defet,laprobabilitatesmentadaés Iq(t)/qt = 1 t +··· ,jaque qt éselnombre depolinomismònicsdegrau t.Vegeulafigura2enlaqualesmostralaprimera cel.lad’un notebook deJupyter(Nb)quecontécodi PyECC percalcular Iq(t) i tabular-neunsquantsvalors.

A.4Construcciódecossosfinits

Lacreaciódecossos(ianells)finitsespotfercomenl’exemplesegüent.

#Creaciódelcosbinari

K=Zn(2)

#CreaciódelcosF=F8comaK[X]/(f=X^3+X+1),amba=Xmodf [F,a]=extension(K,[1,0,1,1],’a’,’F’)

Si A ésunanelljaconstruïti C = [1,a1,...,ar ] ésunallistad’elementsde A ambprimerelement1, PyECC creal’anell

B = A[X]/(f = Xr + a1Xr 1 +···+ ar 1X + ar ),

iensemsfal’assignació x = X mod f ,ambl’expressió [B,x]=extension(A,C,’x’,’B’)

Comjas’haditabans,l’anelldepolinomis P = A[X] espotcrearambl’expressió [P,X]=polynomial_ring(A,’X’)

Uncopcreat P ,si f = Xr + a1Xr 1 +···+ ar 1X + ar ∈ P ,l’expressió [B,x]=extension(A,f,’x’,’B’) téelmateixvalorquel’expressió [B,x]=extension(A,C,’x’,’B’) d’abans.

A.5Vectorsimatrius

Sigui A unanelli n unnúmeroenterpositiu.Lafunció v=vector(A,n) crea elvectornuldelongitud n ambcoeficientsdel’anell A.Si a ∈ A i0 ≤ j< n,l’expressió v[j]=a assigna a alacomponent j-èsimade v,isi a és unallistad’elementsde A, vector(a) latrasformaenunvector.Anàlogament,l’expressió M=matrix(A,k,n) crealamatriunul.lade k filesi n columnes,iespotassignarl’element a ∈ A alacasella (i,j) ambl’expressió M[i,j]=a.Si a1,...,ak sónllistesdelongitud n d’elementsde A,l’expressió matrix([a1 ,...,ak ]) lestransformaenlacorresponentmatriu k × n

A.6UtilitatsperalsistemaMcEliece

DelsingredientsqueentrenenunsistemadeMcEliece,hemvistcomespot construir G alasecció3.Acontinuacióesmostracompodemconstruirles matrius P i S.

Lafunció permutation_matrix(n) creaunamatriudepermutació d’ordre n escollidauniformement.Enlaimplementaciós’usenlesfuncions ZZ(),quecreal’anelldelsnúmerosenters,i permutation(n),quesubministraunapermutacióaleatòria,uniformementdistribuïda,delconjunt N= [0, 1,...,n 1].

defpermutation_matrix(n):

N=list(range(n))

p=permutation(n)

P=matrix(ZZ(),n,n) forjinrange(n):

P[j,p[j]]=1 returnP

Adonem-nosquel’expressió P[j,p[j]]=1 posaun1alafila j,columna p[j]

Lafunció rd_GL(n,F) creaunamatriude F(n) invertibleescollidauniformement.Estàdefinidadelamanerasegüent: defrd_GL(n,F=Zn(2)):

a=rd_nonzero(F)

A=matrix([[a]]) for_inrange(2,n+1):

A=rd_extend(A) returnA

Lapartcentraléslafunció rd_extend(A),quecrea,donadaunamatriuinvertible A ∈ F(k),unamatriuinvertible B ∈ F(k + 1) quesegueixladistribució uniformesi A télamateixapropietat.Comqueelvalorinicialde A ésclarament unaseleccióuniformed’unamatriuinvertiblede F(1),la iteració produeixuna matriuinvertiblede F(n) distribuïdauniformement.

Ladefinicióde rd_extend(A) estàinspiradaenelsenzillalgorisme recursiu deD.Randallpublicata[42].Primerseseleccionaunvectornonulde longitud k + 1iesposa r perindicarl’índexdelasevaprimeracomponentno nul.la.Lalínia rd_insert(A,r) creaprimerunamatriude F(k,k + 1) inserint unacolumnaaleatòriad’elementsde F entrelescolumnesd’indexs r 1i r de A,desprésenfaunamatriuinvertiblede F(k + 1) afegintunaprimerafila de0ambun1enlaposiciód’índex r ,ifinalmentmultiplicaelresultatperla matriuobtingudadelamatriuidentitat Ik+1 persubstituciódelaseva r -èsima filapelvector v.Totcomptat,alafiresultaladefiniciósegüent:

defrd_extend(A): k=ncols(A);F=K_(A) v=rd_nonzero_vector(F,k+1) r=0

forjinrange(k+1): ifv[j]!=0: r=j;break

A=rd_insert(A,r) x=v[r]

forjinrange(r+1,k+1):

A[:,j]=A[:,j]+A[:,r]*v[j]

A[:,r]=x*A[:,r] returnA

Enllocdedonaraquíunaexplicaciómésdetallada,quepodeutrobara[46], enssemblamésadientil lustrarlaconstruccióenelcasdematriusinvertibles de F(2).Inicialmenttenimunelementaleatorinonul a ∈ F i v pottenirunade lesduesformessegüents: v = [b,y] o v = [0,b] (b,y ∈ F , b = 0).Enelprimer cas,l’explicacióquehemdonatesconcreta(posant x ∈ F )enl’expressió

xa by 01 = by xbxy + a

Enelsegoncas,resultal’expressió(posant x ∈ F )

Laprimeraexpressiódonatoteslesmatriusinvertiblesde F(2),laprimerafiladelesqualstéunelementnonulenlaprimeraposició.Elnombre dematriusaixíobtingudesés m0 = q2(q 1)2.Lasegonaexpressiódonales matriusinvertiblesde F(2),laprimerafiladelesqualscomençaamb0.El nombred’aquestesmatriusés m1 = q(q 1)2,iésimmediatcomprovarque m0 + m1 = (q2 1)(q2 q),queéselcardinaldelgruplineal GL(2,F).Això provaqueelselementsd’aquestgrupapareixenuniformementquanesgeneren pelprocedimentexplicat.

A.7Càlculdematriusgeneradores

Lafunció blow(H,F) calcula H ilafunció prune(H ) eliminalesfilesquesón combinaciólinealdelesanteriors,demaneraquealfinaldelprocéstenimuna matriudecontrol H

n=7;r=2

K=Zn(2)

[F,a]=extension(K,[1,0,1,1],’a’,’F’)

R1=[1,1,1,1,1,1,1]

R2=[1,a,a**2,a**3,a**4,a**5,a**6]

HH=matrix(F,[R1,R2]) prune(blow(HH,F)) --> [[1111111] [0010111] [0101110] [1001011]]

Aixòmostraqueladimensiódelcodiés7 4 = 3.Adonem-nosqueles componentsde1 ∈ F respectedelabase {1,a,a2} de F sobre K són [1, 0, 0], demaneraquelamatriu blow(HH,F),queésdetipus6×7,téduesfilesdezeros ipertantl’efectede prune(blow(HH,F)) éssimplementeliminaraquestes duesfiles.

A.8ExempledecodideGoppa

#UncodideGoppa[19,12]sobreF5 F5=Zn(5)

#CreaciódelcosF25,ambgeneradorxtalquex**2-2=0 [F25,x]=extension(F5,[1,0,-2],’x’,’F25’)

#Creaciódel’anelldepolinomisF25[T] [A,T]=polynomial_ring(F25,’T’)

#ConjuntdelselementsnonulsdelcosF25 #[1:]excloul’elementd’índex0,queés0>>F25 a=Set(F25)[1:]

#Creaciód’unpolinomip p=T**6+T**3+T+1

#Llistad’elementsdeaquenosónarrelsdep a=[tfortinaifevaluate(p,t)!=0] n=len(a) -->19

#CreaciódelcodiCdeGoppaassociatapia C=Goppa(p,a)

#LamatriudecontroldeCs’obtéambl’expressióH_(C) H=blow(H_(C),F5) n-rank(H) -->12

Enl’exempleanterior, p tésisarrels(2,2,3,4, a + 2,4a + 2)i,pertant,la longituddelcodiés25 1 5 = 19.Elrangde H resultaser7i,pertant, k = 12.

A.9Descodificació

L’exemplequesegueixésunacontinuaciódel’exempleanterioriil.lustrauna descodificacióambPGZ.

#Generaciód’unvectord’erroraleatoridepes3 e=rd_error_vector(Z5,n,3)

-->e=[0,1,0,0,0,3,0,4,0,0,0,0,0,0,0,0,0,0,0]

#DescodificaciódeeambPGZ PGZ(e,C)

-->PGZ:Errorpositions[1,5,7],errorvalues[1,3,4] [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]::Vector[Z5]

A.10EntornsJupyter

Acabemaquestaseccióveientunexempledelfuncionamentde Jupyter 6

6 http://jupyter.org/

Referint-nosalafigura2,laprimeralíniaésuncomentariquecontéeltítol del notebook.Amblacomandadelasegonalínia, fromPyECCimport *,es carregaelpaquet PyECC.Enladefiniciódelafunció irr(q,m), divisors i mu_moebius sónfuncionsde PyECC quecalculenlallistaordenadadedivisors de m ielvalor µ(m//d) delafunciódeMöbiusperalquociententerde m per d,quocientqueenPythons’expressa m//d (calremarcarqueelvalorde l’expressió m/d ésunnúmerodecimal).Elresultatde show(M) ésequivalenta lataulasegüent.

Figura 2: Imatgedelaprimeracel.lad’un notebook deJupyterque mostralafunció irr(q,t) de PyECC quecalculaelnombredepolinomis irreductiblesmònicsdegrau t sobre Fq,aixícomlesexpressionsper obtenirelsvalorsdelataula1.

1234567 21236918 3381848116312 4620602046702340 51040150624258011160 721112588336019544117648 8281681008655243596299592 93624016201180888440683280

Taula 1: Valorsde irr(q,t) pera1 ≤ t ≤ 7i q ≤ 9.

BImplementaciód’unprototipdesistemadeMcEliece

Seguirempasapasunexemplemoltsenzillquehauriadesersuficientper il lustrarelsdiversospassosdelprocediment.

#0.Inici.ImportemPyECCidefinimZ2ambnom’K’ fromPyECCimport * K=Zn(2,’K’)

Codisicriptografia

#1.ConstruïmF32ambgeneradora [F,a]=extension(K,get_irreducible_polynomial(K,5),’a’,’F’)

#2.Generemaleatòriamentunpolinomimònicirreductible #degrau3deF[T] p=get_irreducible_polynomial(F,3,’T’) show(p)--> T**3+(a**4+a**3+a**2+a)*T**2+(a**4+a**3)*T+a**2+a::F[T]

#3.CreemelcodideGoppadepolinomip**2sobre #elselementsnonulsdeF(expressióX[1:]) #Corregeixdeg(p)=3errors X=Set(F)

C=Goppa(p**2,X[1:])

#4.Matriusdecontrol/Fi/K HH=H_(C) H1=blow(HH,F) show(shape(HH)) -->(6,31) show(shape(H1)) -->(30,31) show(rank(H1)) -->15

#5.Matriugeneradora/K,G.Veiemquek=16 G=transpose(kernel(H1)) show(shape(G)) -->(16,31)

#6.MatriuSdelaclauprivada;K_(G)ésK,jaqueC/K. #Sésunamatriubinària16x16. S=rd_GL(K_(G),nrows(G)) show(det(S)) -->1

#7.MatriuP(entera)delaclauprivada.det(P)potser1o-1 P=permutation_matrix(ncols(G)) show(det(P)) -->1

#8.Claupública(G1,t) G1=S*G*P show(shape(G1)) -->(16,31) t=nrows(H_(C))//2 -->3

#9.Encriptaciód’unvectoraleatoriu

u=rd_vector(F,nrows(G1))

-->[0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1] x=u*G1-->

[0,0,0,0,1,1,1,1,1,1,0,0,0,0,1,0,0,1,0,0,0,0,1,1,0,1,0,0,1,0,1] e=rd_error_vector(F,len(x),t)-->

[0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0] x1=x+e-->

[0,0,0,0,1,1,1,1,1,1,0,1,0,0,1,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,1]

#10.Desencriptació.LainversadePéslasevatransposada y=x1*transpose(P)-->

[0,0,1,1,1,0,1,1,0,0,0,1,0,0,1,1,0,0,1,0,1,1,1,1,0,0,0,0,1,0,0] x2=PGZ(y,C)-->#uSG

[0,0,0,1,1,0,1,1,0,0,0,1,0,0,1,1,0,0,1,0,0,1,1,1,0,1,0,0,1,0,0] u1=solve_linear_system(transpose(G),transpose(x2)) u1=transpose(u1)

-->[1,0,0,1,0,0,1,1,1,0,1,0,0,1,0,0] u1/S

-->[0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1] u

-->[0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1]

Sigles

AKEAuthenticatedKeyExchange7

BMSBerlekamp-Massey-Sugiyamadecodingalgorithm

CAKECode-basedAlgorithmforKeyEncapsulation

DSADigitalSignatureAlgorithm

ECDSAEllipticCurveDigitalSignatureAlgorithm

HQCHammingQuasi-CyclicCodes

ICTInformationandCommunicationsTechnology

IEEEInstituteofElectricalandElectronicsEngineers

IND-CCAIndistinguishabilityunderChosenCiphertextAttack

IND-CPAIndistinguishabilityunderChosenPlaintextAttack

INRIAInstitutNationaldeRechercheenInformatique etenAutomatique

ISITInternationalSymposiumonInformationTheory

KEMKeyEncapsulationMechanism

LDPCLow-densityParity-checkCodes

MDPCModerate-densityParity-CheckCodes

NISTNationalInstituteofStandardsandTechnology

PGZPeterson-Gorenstein-Zierlerdecodingalgorithm

RLCERandomLinearCodeEncryption

WCCWorkshoponCodesandCryptography

7Vegeu[30]peramoltsaltresacrònimsrelacionats.

Agraïments

LaJornadadeTeoriadeNombresesmentadamésamuntfouunimportant estímulperalsautors,elsqualsescomplauenaagrairlainvitaciódelsorganizadors(AnaRío,JosepM.MiretiJordiGuàrdia)ilabenvolençadelsparticipants aescoltarlasevaconferència.GràciesaRafelFarréiSantiagoMolina,coautors delsarticles[25]i[35],respectivament,jaquelaprogramaciódelsalgorismes ques’hitractenvarepresentarunpasimportanteneldesenvolupamentde PyECC.Elnostreagraïmenttambéalrevisordel’articlepelsseussuggeriments, quehancomportatunamilloradelaversióoriginal.

Referències

[1] Aragon,N.;Gaborit,P.;Hauteville,A.;Tillich,J.-P. «Improvement ofgenericattacksontheranksyndromedecodingproblem».2017. https://hal.archives-ouvertes.fr/hal-01618464.

[2] Augot,D.;Batina,L.;Bernstein,D.J.;Bos,J.;Buchmann,J.; Castryck,W.;Dunkelman,O.;Güneysu,T.;Gueron,S.;Hülsing,A.; Lange,T.;Mohamed,M.S.E.;Rechberger,C.;Schwabe,P.;Sendrier,N.; Vercauteren,F.;Yang,B.Y. «Initialrecommendationsoflong-termsecurepost-quantumsystems».PQCRYPTOICT-645622-Horizon2020,2015. https://pqcrypto.eu.org/docs/initial-recommendations.pdf.

[3] Barbier,M.;Barreto,P.S.L.M. «KeyreductionofMcEliece’scryptosystem usinglistdecoding».A: Kuleshov,A.;Blinovsky,V.M.;Ephremides,A. (ed.). InternationalSymposiumofInformationTheory(ISIT).SantPetersburg:IEEE,2011,2657–2661.

[4] Barreto,P.S.L.M.;Gueron,S.;Güneysu,T.;Misoczki,R.;Persichetti,E.;Sendrier,N.;Tillich,J.-P. «CAKE:Code-basedalgorithmforkeyencapsulation».A: CryptographyandCoding.Cham:Springer,2017,207–226. (LectureNotesinComput.Sci.;10655)

[5] Berlekamp,E.R.;McEliece,R.J.;vanTilborg,H.C.A. «Ontheinherent intractabilityofcertaincodingproblems». IEEETrans.InformationTheory, IT-24(3)(1978),384–386.

[6] Bernstein,D.J. «Indexofformalscientificpapers». https://cr.yp.to/ papers.html.

[7] Bernstein,D.J. «Introductiontopost-quantumcryptography».A: PostQuantumCryptography.Berlín:Springer,2009,1–14.

[8] Bernstein,D.J. «Isthesecurityofquantumcryptographyguaranteed bythelawsofphysics?».2017. https://sidechannels.cr.yp.to/qkd/ holographic-20160326.pdf.

[9] Bernstein,D.J.;Biasse,J.-F.;Mosca,M. «Alow-resourcequantumfactoringalgorithm».A: Post-QuantumCryptography.Cham:Springer,2017, 330–346.(LectureNotesinComput.Sci.;10346)

[10] Bernstein,D.J.;Buchmann,J.;Dahmen,E. (ed). Post-QuantumCryptography.Berlín:Springer,2009.

[11] Bernstein,D.J.;Lange,T. «Post-quantumcryptography». Nature,549 (2017),188–194.

[12] Bernstein,D.J.;Lange,T.;Peters,C. «Attackinganddefendingthe McEliececryptosystem».A: Post-QuantumCryptography.Berlín:Springer, 2008,31–46.(LectureNotesinComput.Sci.;5299)

[13] Bernstein,D.J.;Lange,T.;Peters,C. «WildMcElieceincognito».A: PostQuantumCryptography.Heidelberg:Springer,2011,244–254.(Lecture NotesinComput.Sci.;7071)

[14] Bernstein,D.J.;Yang,B.Y. «Asymptoticallyfasterquantumalgorithms tosolvemultivariatequadraticequations».2017. https://cr.yp.to/ papers/groverxl-20171215.pdf

[15] Biswas,B. «Implementationalaspectsofcode-basedcryptography».Tesi doctoral.ÉcolePolytechniqueiINRIA,2010.

[16] Cameron,P.J. «Notesoncryptography». http://www.maths.qmul.ac.uk/ ∼pjc/notes/crypt.pdf.

[17] Campbell,E.T.;Terhal,B.M.;Vuillot,C. «Thesteeproadtowards robustanduniversalquantumcomputation».Preprint,2016. https:// arxiv.org/abs/1612.07330.

[18] Chen,L.[etal.] «ReportonPost-QuantumCryptography».NISTIR8105. NationalInstituteofStandardsandTechnology,U.S.Departmentof Commerce,2016. https://nvlpubs.nist.gov/nistpubs/ir/2016/NIST.IR. 8105.pdf.

[19] CSRC(ComputerSecurityResourceCenter).«Post-QuantumCryptography2018». https://csrc.nist.gov/Projects/Post-Quantum-Crypto graphy.[PrimeraconferènciadenormalitzaciódelPQCorganitzadapel CentredeRecursosperalaSeguretatInformàtica-NIST]

[20] Delfs,H.;Knebl,H. IntroductiontoCryptography.PrinciplesandApplications.2aed.Berlín:Springer,2007.(InformationSecurityandCryptography)

[21] Deneuville,J.-C.;Gaborit,P.;Zémor,G. «Ouroboros:asimple,secure andefficientkeyexchangeprotocolbasedoncodingtheory».A: PostQuantumCryptography.Cham:Springer,2017,18–34.(LectureNotesin Comput.Sci.;10346)

[22] Diffie,W.;Hellman,M.E. «Newdirectionsincryptography». IEEETrans. InformationTheory,IT-22(6)(1976),644–654.

[23] Dinh,H.;Moore,C.;Russell,A. «McElieceandNiederreitercryptosystems thatresistquantumFouriersamplingattacks».A: AdvancesinCryptology— CRYPTO2011.Heidelberg:Springer,2011,761–779.(LectureNotesin Comput.Sci.;6841)

[24] Engelbert,D.;Overbeck,R.;Schmidt,A. «AsummaryofMcEliece-type cryptosystemsandtheirsecurity». J.Math.Cryptol.,1(2)(2007),151–199.

[25] Farré,R.;Sayols,N.;Xambó-Descamps,S. «OnPGZdecodingofalternant codes».Preprint,2017. https://arxiv.org/abs/1704.05259.

[26] Gaborit,P. «Shorterkeysforcode-basedcryptography».A: Proceedings ofWorkshoponCodesandCryptography.França:WCC2005,2005,81–90.

[27] Gaborit,P.;Ruatta,O.;Schrek,J. «Onthecomplexityoftheranksyndromedecodingproblem». IEEETrans.Inform.Theory,62(2)(2016), 1006–1019.

[28] Goppa,V.D. «Anewclassoflinearcorrectingcodes». ProblemyPeredaˇci Informacii,6(3)(1970),24–30.[Enrus]

[29] Katz,J.;Lindell,Y. IntroductiontoModernCryptography.BocaRaton, FL:Chapman&Hall/CRC,2008.(Chapman&Hall/CRCCryptographyand NetworkSecurity)

[30] Lee,J.;Park,C.S. «Anefficientauthenticatedkeyexchangeprotocolwitha tightsecurityreduction».2008. https://eprint.iacr.org/2008/345.pdf.

[31] McEliece,R.J. TheTheoryofInformationandCoding:AMathematical FrameworkforCommunication.Mass.;Londres;Amsterdam:AddisonWesleyPublishingCo.,Reading,1977.(EncyclopediaofMathematicsand itsApplications;3)

[32] McEliece,R.J. «Apublic-keycryptosystembasedonalgebraiccodingtheory». TheDeepSpaceNetworkProgressReport [JetPropulsionLaboratory]. 42–44(1978),NASACode310.10.67-11,114–116.

[33] Merkle,R.C.;Hellman,M.E. «Hidinginformationandsignaturesin trapdoorknapsacks». IEEETrans.InformationTheory,IT-24(5)(1978), 525–530.

[34] Misoczki,R.;Tillich,J.-P.;Sendrier,N.;Barreto,P.S.L.M. «MDPCMcEliece:NewMcEliecevariantsfrommoderatedensityparity-checkcodes».2012. https://eprint.iacr.org/2012/409.pdf

[35] Molina,S.;Sayols,N.;Xambó-Descamps,S. «Abootstrapforthe numberof Fqr -rationalpointsonacurveover Fq».Preprint,2017. https://arxiv.org/abs/1704.04661.

[36] Niebuhr,R. «Attackinganddefendingcode-basedcryptosystems».Tesi doctoral,FachbereichInformatikderTechnischenUniversitätDarmstadt, 2012.

[37] Niederreiter,H. «Knapsack-typecryptosystemsandalgebraiccodingtheory». ProblemsControlInform.Theory/ProblemyUpravlen.Teor.Inform., 15(2)(1986),159–166.

[38] Overbeck,R.;Sendrier,N. «Code-basedcryptography».A: Post-Quantum Cryptography.Berlín:Springer,2009,95–145.

[39] Patterson,N.J. «ThealgebraicdecodingofGoppacodes». IEEETrans. InformationTheory,IT-21(1975),203–207.

[40] Persichetti,E. «Improvingtheefficiencyofcode-basedcryptography». Tesidoctoral.NovaZelanda:UniversityofAuckland,DepartmentofMathematics,2012.

[41] Post-quantumcryptography https://pqcrypto.org/

[42] Randall,D. «Efficientgenerationofrandomnonsingularmatrices».Informetècnicnúm.UCB/CSD-91-658.Berkeley(EUA):UniversityofCalifornia atBerkeley,1991.

[43] Repka,M.;Zajac,P. «OverviewoftheMcEliececryptosystemandits security». TatraMt.Math.Publ.,60(2014),57–83.

[44] Rivest,R.L.;Shamir,A.;Adleman,L. «Amethodforobtainingdigital signaturesandpublic-keycryptosystems». Comm.ACM,21(2)(1978), 120–126.

[45] Rué,J.;Xambó,S. «Introducciómatemàticaalacomputacióquàntica». ButlletídelaSocietatCatalanadeMatemàtiques,28(2)(2013),183–231.

[46] Sayols,N.;Xambó-Descamps,S. «PyECC:APythonpackagefortheconstruction,codinganddecodingoferror-correctingcodes».2015–2018. https://mat-web.upc.edu/people/sebastia.xambo/PyECC.html.

[47] Sayols,N.;Xambó-Descamps,S. «AlternantcodesandtheMcEliece cryptosystem».ConferènciapronunciadaalaJornadadeTeoriade Nombres(UniversitatdeLleida,2017). https://mat-web.upc.edu/people/ sebastia.xambo/PyECC/s-CryptoLleida-7-10-2017.pdf

[48] Sendrier,N. «Efficientgenerationofbinarywordsofgivenweight».A: Proceedingsofthe5thIMAConferenceonCryptographyandCoding.Londres: Springer-Verlag,1995,184–187.

[49] Sendrier,N. «Cryptosystèmesàclépubliquebaséssurlescodescorrecteursd’erreurs».Mémoired’habilitationàdirigerdesrecherches.París: UniversitéPierreetMarieCurie,Paris6;Rocquencourt:InstitutNational deRechercheenInformatiqueetAutomatique,2002.

[50] Sendrier,N. «Ontheuseofstructuredcodesincodebasedcryptography». A: CodingTheoryandCryptographyIII.Contactforum.KoninklijkeVlaamseAcademievanBelgiëvoorWetenschaeppenenKunsten,2009,59–68.

[51] Shor,P.W. «Algorithmsforquantumcomputation:discretelogarithms andfactoring».A: 35thAnnualSymposiumonFoundationsofComputer Science.LosAlamitos,CA:IEEEComput.Soc.Press,1994,124–134.[Per obtenirunaversiórevisadaiampliadad’aquestarticle,vegeu:«Polynomialtimealgorithmsforprimefactorizationanddiscretelogarithmsona quantumcomputer». SIAMJ.Comput.,26(5)(1997),1484–1509]

[52] Tillich,J.-P. «ThedecodingfailureprobabilityofMDPCcodes».Preprint, 2018. https://arxiv.org/abs/1801.04668

[53] Wang,J. «QuantumresistantrandomlinearcodebasedpublickeyencryptionschemeRLCE».A: Proceedings2016IEEEInternationalSymposiumon InformationTheory(ISIT).IEEE,2016,2519–2523.

[54] Wang,J. «DecodinggeneralizedReed-Solomoncodesanditsapplication toRLCEencryptionschemes».Preprint,2017. https://arxiv.org/abs/ 1702.07737.

[55] «Quantumcryptography».A:Wikipedia. https://en.wikipedia.org/wiki/ Quantum cryptography

[56] Xambó-Descamps,S. BlockError-correctingCodes.AComputationalPrimer. Berlín:Springer-Verlag,2003.(Universitext)

NarcísSayols DepartamentESAII

UPC,EdificiK2M

c.JordiGirona, 1–3 08034 Barcelona,Spain narcis.sayols@upc.edu

SebastiàXambó DepartamentdeMatemàtiques

UPC,EdificiOMEGA

c.JordiGirona, 1–3 08034 Barcelona,Spain sebastia.xambo@upc.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.2,2018.Pàg.173–174

Englishsummaries

CarlesBarril,SílviaCuadradoandJordiRipoll

Mathematicalmodelsinpopulationdynamics

Populationdynamicsstudiestheevolutionofsizeandcompositionofpopulations.Inthisarticlewepresentacompilationofthemainmathematicalmodels describingthedynamicsofbiologicalpopulations.Westartwithahistorical introductiontothesubjectshowingdifferentproblemsinecology,demography andepidemiology,aswellasthetoolsandmathematicaltechniquesused.Then wedescribeanewformulationintermsofdelayequationsthatestablishes athoroughgeneralframeworkforthemathematicalmodelingofpopulation dynamics.

Keywords: mathematicalbiology,structuredpopulations,delayequations,partialdifferentialequations.

MSC2010SubjectClassification: 92D25,35Q92,47N20.

AgustíReventós GaspardMonge

Thisarticleseekstopaytribute,200yearsafterhisdeath,toMonge’sworkin thefieldofdifferentialgeometryofcurvesandsurfaces.Afterabriefreminder ofhisbiography,wefocusonhisworkonevolutesofcurvesinspaceand especiallyontheoriginofthelinesofcurvature,inanarticlededicatedto transportofland.TheFeuille xv ofhisfamous Feuillesd’analyse isanalyzed indetailandabriefcommentismadeontherestofhisworksindifferential geometry.Weattachanote,byJosepLluísSolé,aboutoneofMonge’sfriends andhisbiographer:FrançoisArago.

Keywords: Monge,curves,surfaces,evolutes,linesofcurvature.

MSC2010SubjectClassification: 53A04,53A05,01A50.

NarcísSayolsandSebastiàXambó

Error-correctingcodesandpost-quantumcryptography

Theforty-yearoldMcEliecepublic-keycrypto-systemisrevisitedwiththe helpofrecentlydevelopedresources:animprovedPeterson-Gorenstein-Zierler decoderforalternanterror-correctingcodes;asymboliccomputationsystem andapackageoffunctionalutilitiesforthecomputationsinvolvedindefining, codinganddecodingerror-correctingcodes,fullyprogrammedinPython;and awebpagewithfree-accesstothematerialsgeneratedbytheproject.Themain interestoftheMcEliecesystemstemsfromitbeingaseriouscandidatefora post-quantumcryptographystandard.

Keywords: post-quantumcryptography,alternantcodes,symboliccomputation, freesoftware.

MSC2010SubjectClassification: 11T71,68-04,68W30,94A60.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorialpercorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2010.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX,preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespot obteniralespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Fem notarqueenaquestapublicaciós’utilitzapreferentmentelpuntperaseparar decimals,enllocdelacomarecomanadaperl’IEC,perapoderfacilitarla comprensiódelesexpressionsmatemàtiques.Pertald’accelerarelprocésde producció,espregaalsautorsquesegueixinlesindicacionscontingudesenel documentd’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateix,modificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcas,el Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Lapropietatintel.lectualdelsarticlesésdelsrespectiusautors.

Elsautors,enelmomentdelliurarelsarticlesal Butlletí perasol.licitar-ne lapublicació,acceptenelstermessegüents:

—ElsautorscedeixenalaSCM(filialdel’Institutd’EstudisCatalans)els dretsdereproducció,comunicaciópúblicaidistribuciódelsarticlespresentats peraserpublicatsal Butlletí.

—ElsautorsresponendavantlaSCMdel’autoriail’originalitatdelsarticles presentats.

—Ésresponsabilitatdelsautorsl’obtenciódelspermisosperalareproducciódetotelmaterialgràficinclòsenelsarticles.

—LaSCMestàexemptadetotaresponsabilitatderivadadel’eventual vulneraciódedretsdepropietatintel.lectualperpartdelsautors.

CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigitaldelseu articleiunexemplarimprèsdelnúmerodel Butlletí enelqualespubliqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

Pelquefaalaprotecciódedadespersonals,l’Institutd’EstudisCatalans(IEC) compleixelqueestableixelReglamentgeneraldeprotecciódedadesdelaUnió Europea(Reglament2016/679,del27d’abrilde2016).Deconformitatamb aquestanorma,s’informaque,ambl’acceptaciódelesnormesdepublicació, elsautorsautoritzenquelessevesdadespersonals(nomicognoms,dadesde contacteidadesdefiliació)puguinserpublicadesenelcorresponentvolum del Butlletí.

Aquestesdadesseranincorporadesauntractamentqueésresponsabilitat del’IECamblafinalitatdegestionaraquestapublicació.Únicaments’utilitzaranlesdadesdelsautorsperagestionarlapublicaciódel Butlletí ino serancedidesatercers,niesproduirantransferènciesatercerspaïsosoorganitzacionsinternacionals.Uncoppublicatel Butlletí,aquestesdadeses conservarancomapartdelregistrehistòricd’autors.Elsautorspodenexercir elsdretsd’accés,rectificació,supressió,oposició,limitacióeneltractament iportabilitat,adreçant-seperescrital’Institutd’EstudisCatalans(carrerdel Carme,47,08001Barcelona),obéenviantuncorreuelectrònical’adreça dades.personals@iec.cat,enquès’especifiquidequinapublicacióestracta.

Comitèeditorial

JuliàCufí(editorencap) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona jcufi@mat.uab.cat

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona fagella@maia.ub.es

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

AntoniGuillamon DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya antoni.guillamon@upc.edu

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta)

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

MarcNoy

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

AgustíReventós

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

JoanSaldaña

Dep.d’Informàtica,Mat.AplicadaiEstadística UniversitatdeGirona joan.saldana@udg.edu

MartaSanz-Solé

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona marta.sanz@ub.edu

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies i Butlletídela SocietatCatalanadeMatemàtiques.Elssocisdela SCM reben,gratuïtament, aquestesduespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

President:XavierJarqueiRibera

Vicepresident:EnricVenturaiCapell

Adjuntadelavicepresidència:IolandaGuevaraiCasanova

Secretari:AlbertRuiziCirera

Tresorera:NatàliaCastellanaiVila

Vocals:AlbertAvinyóiAndrés,MartaBeriniiLópez-Lara,Abraham delaFuentePérez,NúriaFagellaiRabionet,JosepGranéiManlleu, CarlesRomeroiChesa,ManelUdinaiAbelló

Delegatdel’IEC:PilarBayeriIsant

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.