BSCM, 30-1

BUTLLETÍ

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 30 ● Número 1 ● Juny 2015

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques

filialdel’Institutd’EstudisCatalans CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

ImprèsaLimpergraf,SL PolígonindustrialCanSalvatella CarrerdeMogoda,29-31 08210BarberàdelVallès

ISSN:0214-316-X DipòsitLegal:B.19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprografia ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.1,2015

Índex

CarlesM.Cuadras

ElllegatdeGalton,Pearson,Fréchetid’altres: commesurariinterpretarl’associacióestadística..................................5

XavierMoraiMariaOliver

Eleccionsmitjançantelvotd’aprovació.ElmètodedePhragmén ialgunesvariants....................................................................57

Englishsummaries.....................................................................103

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.1,2015.Pàg.5–56. DOI:10.2436/20.2002.01.58

ElllegatdeGalton,Pearson,Fréchetid’altres: commesurariinterpretarl’associacióestadística

CarlesM.Cuadras

Resum: Presentementrespartselsconceptesdecorrelacióid’associacióestadística, començantperlanociódecorrelaciódeGalton,milloradaperPearson.Utilitzemcom ail.lustraciólesdadesclàssiquesdeGaltoniPearsonsobreheretabilitatdeparesi fillsrespecteal’estatura.Lasegonapartexplicacoms’hand’estudiarlesmateixes dadesdesd’unaperspectivamultivariant(anàlisidecorrelaciócanònicaidecorrespondències).UtilitzemtambédadesdeFisher.Mostremcompodemassociardades detipusgeneralmitjançantdistàncies.Latercerapartladediquemalesdistribucions bivariants.Presentemlateoriadefuncionsivalorspropisperadosnuclis,ques’aplica aldesenvolupamentdiagonald’unadistribucióbivariant,incloent-hielsdesenvolupamentscontinusentermesd’integrals.Proposemunafamíliadecòpulescanòniques, quepermetgenerardistribucionsbivariants.

Paraulesclau: dadesdeGaltoniPearson,correlacióintraclàssica,correlaciócanònica, anàlisidecorrespondències,associacióbasadaendistàncies,operadorsintegrals, distribucionsambmarginalsdonades,funcionscanòniques.

ClassificacióMSC2010: 62H20,60E05.

Part I:Estadísticaclàssica

1Introduccció

Desdesemprehemvolgutesbrinarlacausad’unfenomen.Perquès’haproduïtunincendi?Quèhaprovocatunaguerra?Quinaéslaprincipalcausadel càncerdepulmó?Perquèuncantanttééxit?Enalgunespartsdelafísicai lamecànica,elbinomicausa-efecteésbenconegut.Sovintlesrelacionsentre variablesobservablesimesurablessóndeterministesiespodenexpressar ambunarelaciófuncional y = f(x),quelligaunavariabledependent y amb unad’independent x.Aquestarelacióésmoltimportantibenestudiadaen matemàtiquesialtresciènciesexactes.Peròenbiologia,economia,sociologia, meteorologia,etc.,aningúseliacudiriaimaginarquepuguiexistirunarelació

tanexactaentreduesvariables.Perexemple,lapressióarteriald’unapersona térelacióambelpes,peròlarelacióés«imprecisa».

Compodemrelacionarduesvariables?Enprincipipodemsuposar y = f(x) + e,on f(x) representalapartdeterministai e lapartaleatòriadecada observació y.Altramentdit,

observació = model + error, entenentper«error»ladesviaciódelmodel.Aleshoresésnaturalqueens plantegemcomcalmesuraraquestarelaciómitjançantuncoeficiententre0 i1,demaneraqueelvalor0signifiquimancaderelacióielvalor1espugui interpretarcomquehiharelacióperfecta,matemàticamentparlant.1

Aleshoresesplantejaladeterminaciódelafunció f ilanaturalesadela desviació e,sovintinterpretadacomunavariablealeatòriaambdistribució normal.

2Galtonielcoeficientdecorrelació

L’any1886FrancisGalton[37],contemporanideMendelicosídeDarwin,es vaplantejarlatascademesurarobjetivamentlarelacióentreduesvariables observadessobreunamateixapoblació,afidedonarunaprovacientíficadela teoriadel’evolució.Aleshoresvatenirlaideagenialdeproposarelcoeficient decorrelació r ,quevail.lustraramblesdadesde n = 205famílies.Vaanotar lesvariablessegüents:

X1 = alçadadelpare,Y1 = alçadadelfill, X2 = alçadadelamare,Y2 = alçadadelafilla

D’entradaGaltonvatrobarqueelsparesielsfillseren,engeneral,mésaltsque lesmaresilesfilles,ésadir,hihaviadadesdeduespoblacions.Encertadament vaintuirqueelcoeficientdecorrelacióhauriadeserunamesurad’associació vàlidaperaunasolapoblació.Defet,quanbarregemduespoblacions,espoden presentarparadoxes(vegeulasecció7).Pertant,Galtonvadecidirintroduir unacorreccióconsistentaaugmentarl’alçadadelesdones.Concretament,va considerarlesvariables

X = (X1 + 1.08X2)/2,Y = Y1 o Y = 1.08Y2, on,peracada X,lavariable Y potprendretantsvalorscomfillsifillesteniael matrimoni,obtenint n = 934parellesd’observacions.Lavariable X repelnom de mid-parent iencaraavuidias’utilitzaenantropologia.

1 Gairebémaisabremsielmodelrepresentatperlafunció f éselcorrecte.Unmodelésuna simplificaciódelarealitat.M.Chaslesvadir:«Lageometriaésl’artderaonarbésobrefigures falses».

ElllegatdeGalton,Pearson,Fréchetid’altres

Amblacorrecciódemultiplicarper1 08l’alçadadecadadona,Galtonva tractarlesdadescomsitinguésnomésunapoblació[41].Lataula1il lustra algunesdades.Lafamília18té3fillsicapfilla.La102té3fillsi3fillesila198 té4fillsi1filla.

FamíliaPareMareGènereFill/Filla 187873166 5-64 5-64

1026966170-68.5-68

1026966265-63-62.5

19865 560168-68-67-67

19865.560262

Taula1: Exemplededadessobrealçades(enpolzades)deparesifills obtingudesperGaltonel1886.

Elcoeficientdecorrelacióéselquocient r = Sxy /(Sx Sy ),on Sxy ésla covariànciai Sx , Sy sónlesdesviacionstípiquesdelesvariables X, Y .Elvalor absolutd’aquestcoeficientésinvariantpertransformacionslinealsdeles variablesisatisfà |r |≤ 1.Vaserproposatel1895perK.Pearson,amblaqual cosamilloràlainvenciódeGalton.2

Galtonvaobtenir r = 0 50,queindicavaunacertarelacióentreparesi fillsrespecteal’alçada.Aleshoresvarepresentarlesdadesenundiagrama (figura1),vadibuixaraullunarectad’ajustivaafirmarquel’alçadad’unfill eraaproximadament2/3del’alçadadelspares(variablemid-parents).

Larecta y = a + bx quemillors’ajustaalesdades,enelsentitdelsmínims quadrats,on a i b sóntalsque n i=1 (yi a bxi)2 ésmínima, éslarectaderegressió,queés y = y + b(x x), on b = Sxy /S 2 x , (1) essent x i y lesmitjanesdelesvariablesi b elcoeficientderegressióopendent delarectaderegressió.Aquestarectadescriuelmodelabansesmentat,ésa dir,lafunció f(x) éslineal.Alasecciósegüentparlaremdel’origendelterme regressió.

2 EldescobrimentdelcoeficientdecorrelacióésdescritperGalton(queteniaunabonavisió matemàtica)a MemoriesofMyLife.Elcoeficient r apareiximplícitamententreballsdeGaussi Bravaissobreladistribuciónormalbivariant.K.Pearson,aquihemd’atribuirlaformulacióactual, vaproposar(comtambéhoproposariaHilbert)unateoriadelarelativitat.Lasevadefinicióde coeficientdecorrelació esbasaenl’estructurad’espaivectorialdelesvariablesaleatòries.Tot ilaimportànciadelcoeficientdecorrelació,l’estadísticSigmundSchott(1928)vaafirmar:«És moltlamentablequelacomplicadafonamentaciómatemàticadelcàlculdelacorrelacióilaseva prolixaresolucióaritmèticaexcloguinpersemprelapossibilitatd’aplicarenalguncasconcret aquestnotableprocediment».

Mitjana

Galton n = 934 Pearson n = 1078

Mid-parentsFills PareFill

69.2069.23 67.2068.16

Desviaciótípica 1.802.58 2.722.74

Correlació/regressió r = 0.50 b = 0.71 r = 0.51 b = 0.52

Taula2: Mitjanes,desviacionstípiquesicoeficentdecorrelacióiregressióqueresultendelesdadesoriginalsdeGaltonidePearson-Lee.Dades enpolzades;67.2polzadessón170.7cm.,68.16polzadessón173cm.

Exemple. Lataula2contéalgunsresultatsestadísticsperalesdadesdeGalton(n = 934)idePearson-Lee(n = 1078),publicadesl’any1903[53]ique comentaremalasecció8.

3Laregressióalamitjania

Elcoeficientderegressió b = 0.71(taula2)vadonarpeuaGaltonperafirmar quehihaviauna«regressióalamitjania».Altramentdit,enpredir y donat x, s’esperavaqueunparealt,l’alçadadelqualerasuperioralamitjana,tindria fillstambéalts,perònotantcomelpare.Ésadir,elfill(ofilla)estariamés apropdelamitjanaqueelseuprogenitor.Demanerasimilar,unparebaix tindriatendènciaatenirfillsbaixosperònotantcomelpare.

Aquestnotablefet,quedónanomalterme modelderegressió (totique regressió ésepistemològicamentincorrecte),semblaparadoxal.Perònohoésen sentitbiològic.Sielsparesaltstinguessinfillsmésalts,alageneraciósegüent elsfillsencarahoserienmés,ialcapdemoltesgeneracionshihauriagegants. Delamateixamanera,sielsparesbaixostinguessinfillsmésbaixos,alallarga hihaurianans.Tampochihaparadoxaestadística,atèsquesiajuntemtotsels fills,lamitjanaesrecuperaisihiharegressiódinsd’unafamília,non’hihaa lapoblació.

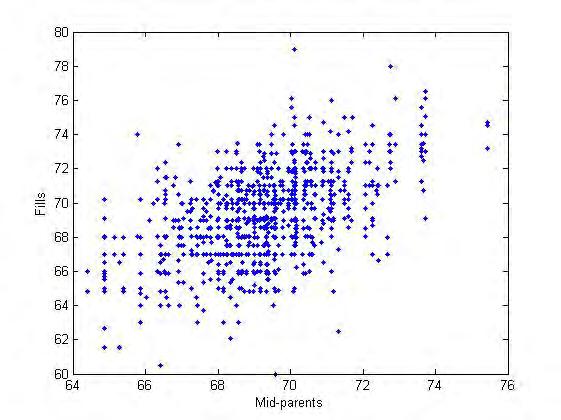
Figura1: Diagramaquerepresental’alçadacombinadadepareimare sobreladelsfillsifilles,pera934observacionsobtingudesperGalton.

4Correlaciómúltiple

Elcoeficientdecorrelacióenlaformaquearaelconeixemvaserelaborat perK.Pearson.Podemgeneralitzarlacorrelaciósimple r ,vàlidaperadues variables,definintlacorrelaciómúltiple R.Donadaunavariableresposta Y i p variablesexplicatives X1,...,Xp,elcoeficient R esdefineixcomlacorrelació simpleentre Y i Y ,essent Y = b0 + b1X1 +···+ bpXp lacombinaciólinealque millors’ajustaa Y enelsentitqueelscoeficients bi verifiquen

E(Y Y)2 = E(Y b0 b1X1 bpXp)2 ésmínima.

Escalculamitjançant

R2 = r R 1r,

on R éslamatriu p × p decorrelacionsentrelesvariables X,i r éselvector amblescorrelacionsdelavariable Y ambcadascunadeles X.

Exemple. PeralesdadesdeGalton,si Y ésl’alçadadelpare(odelamare), X1 i X2 sónlesalçadesdefillifilla,obtenim:

rpare = 0.5457 0.5067 , rmare = 0.3650 0.3808 , R = 10.5419 0.54191 .

Elscoeficientsdecorrelaciómúltipledelparesobrefill/fillaidelamare sobrefill/filla,són:

Rpare = 0.6067,Rmare = 0.4249. Curiosament,respecteal’alçada,hihamésinfluènciadelpare.

5Unsofismasobrelacorrelació

Plantegemunaparadoxaaparentosofismasobrelacorrelació.Suposemque X i Y sónduesvariablescorrelacionadessobrelamateixapoblació,ambvariàncies σ 2 x i σ 2 y ,respectivament.Denotemper σxy lacovariànciaiper ρxy elcoeficientdecorrelació.Entotselscasossuposemqueelsparàmetressón poblacionals.

Consideremaraunamostraaleatòriasimplede X demida n.Ésadir, considerem X1,...,Xn variablesindependents,igualmentdistribuïdesambla mateixadistribucióque X.

Lavariànciadelamitjanamostral Xn = (X1 +···+ Xn)/n és σ 2 x /n ila covariànciaentre Xn i Y és

cov(Xn,Y) = 1 n cov(X1 +···+ Xn,Y) = 1 n nσxy = σxy .

Pertant,atèsque ρxy = σxy /(σx σy ),elcoeficientdecorrelacióentre Xn i Y és cor(Xn,Y) = σxy (σx /√n)σy = √nρxy

Enstrobemquesi n ésprougran,podríemtenir √nρxy > 1.Perexemple, si ρxy = 0.5i n> 4aleshores √nρxy > 1.Aixòcontradiulapropietatqueel coeficientdecorrelaciómaisuperaelvalor1.Tornaremacomentaraquesta aparentirregularitatmésendavant.3

6Eltotpotsermésgranquelasumadelesparts

Silesvariables X estanincorrelacionadesduesadues,ésadir,lamatriudecorrelacionsés R = I (identitat),aleshores R2 = r 2 1 +···+ r 2 p ,essent r1,...,rp les correlacionssimplesde Y ambcadascunadelesvariables X.Engeneralles X estancorrelacionadesihomesperariaque R2 <r 2 1 +···+ r 2 p ,atèsquenohi haredundànciaenlasumadequadratsperòsíen R2.Noobstantaixò,hiha situacionsrealson

Elcas p = 2vaserestudiatperHamiltoniRoutledge[40, 56].Enelcas general,Cuadras[9]vademostrarqueladesigualtat (2),quepodemescriure coma R2 = r R 1r > r r,ésequivalenta

essent rZi , i = 1,...,p,lescorrelacionssimplesentrelavariableresposta Y iles componentsprincipals Z1,...,Zp,i λ1,...,λp,elsvalorspropisde R.Recordem quelescomponentsprincipals Zi sónlescombinacionslinealsdelesvariables X ambvariànciamàximacondicionadaaquesiguinincorrelacionades.Aquestes variànciessónprecisamentelsvalorspropisde R

Atèsqueelsprimersvalorspropissónmésgransque1ielsúltims,més petits,tenimque (2) esverificasi Y téunacorrelacióaltaamblescomponents principalsdemenorvariància(figura2).Pertant,éserronicreurequevariables correlacionadessónredundants.

Moltrelacionadaamb (2) éslapossibilitatd’augmentarlescorrelacions simplesperòque,sorprenentment,disminueixilacorrelaciómúltiple.Consideremlamatriudecorrelacions R dequatrevariables X idosvectors r1, r2 que contenenlescorrelacionsambles X deduesvariablesdependents Y1, Y2.

3 Algunsestadísticsdestacatsvannecessitarhores,finsitotdies,atrobarunaexplicacióa aquestdesconcertantsofismasobrelacorrelació.

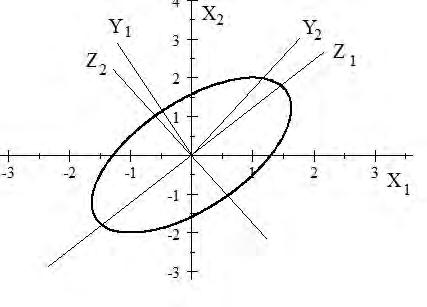
Figura2: Lavariabledependent Y1 segueixladirecciódelasegona componentprincipal Z2,perpendicularaladireccióprincipaldeles dades,representadaperlaprimeracomponentprincipal Z1.

Comquelescorrelacionssimplessónmésgranspera Y1,s’esperariaquetambé hosiguilacorrelaciómúltiple.Noobstantaixò,esverifica R2 1 = r1R 1r1 = 0.483 <R2 2 = r2R 1r2 = 0.688.

L’explicaciód’aquestaanomaliaeslasegüent: r1 ésunvectorambdirecció (mesuradaperl’angle)pròximaalsúltimsvectorspropisde R,mentreque r2 segueixunadireccióméssemblantalsprimersvectorspropis.Altramentdit, Y1 estariamésinfluïdaperlesduesúltimescomponentsprincipals,mentre que Y2 estariamésrelacionadaamblesduesprimeres.Vegeulafigura2,amb nomésduesvariables X,peròigualmentil.lustrativa.Laconseqüènciadetot aixóésqueelcostumdedescartarvariables X poccorrelacionadesamb Y podriaserinadequat.Peramésdetalls,vegeu[10,59].

7Fal.làciaecològica

Examinemlafigura3,querepresentaelriscdecàncerrespectealconsumde caloriesperadiferentspaïsos.Considerantnoméslesmitjanesdecadapaís (cerclenegre),veiemqueelriscaugmentaambelconsumdecalories.Però examinantcadapaísperseparat(cerclesblancsagrupats),veiemqueelrisc disminueixsiaugmental’alimentació.Lacorrelacióés,defet,negativa,peròsi agrupempoblacions,apareixunafalsacorrelaciópositiva.L’anomenada fal.làcia ecològica esdeualfetd’ajuntarpoblacionsdiferentsiaplicarlacorrelació, ignorantqueaquestcoeficientnomésespotutilitzaracadapoblacióperseparat.

Exemples. Peraunamalaltiahereditària,esvadetectarunacertacorrelació positivaentrel’edat X d’aparicióenelpareil’edat Y d’aparicióenelfill[42].

Enrealitat X i Y sónindependents,il’edatd’aparicióenelfillnotéresaveure ambladelpare.Lafalsacorrelacióeradegudaaquehihadosgens A i B,quees presentenambprobabilitats pA i pB iquecausenlamateixamalaltia.Ésadir, lesedatsobservadesprovenendeduespoblacionsdiferents.Si X i Y (igualment distribuïdescondicionadesacadagen)tenenmitjanes E(X|A) = E(Y |A) = µA i E(X|B) = E(Y |B) = µB ianàlogamentvariàncies σ 2 A i σ 2 B ,depenentdelgen causant A o B,lesesperancesmatemàtiquesdelesvariablesobservades X i Y , elsseusquadratsielproducte XY són:

E(X) = E(Y) = pAµA + pB µB , E(X2) = E(Y 2) = pA(µ2 A +

=

Operant,obtenimlesvariàncies: var(X) = var(Y) = pA

Demanerasimilar,lacovariànciaés cov(X,Y) = pApB (µA µB )2.Elcoeficient decorrelacióés,doncs,

Concretament,si pA = pB = 1/2, σ

,iladiferència |µA µB | entrelesduesmitjanesval2σ ,aleshoresobtenim ρxy = 0.5,totiqueles variables X i Y sónindependentsacadapoblació.

Unaltreexempleapareixenelpolèmicllibre TheBellCurve,deBerrstein iMurray,publicatel1994.Enaquesttractats’afirmaqueelsblancssónmés intel.ligentsqueelsnegres.Enconseqüència,argumentenelsautors,elsblancs tambéseransuperiorsenunaaltrahabilitatmesuradaperunavariable H,que espuguiquantificariqueestiguicorrelacionadapositivamentamblaintelligència I.Pertant,afid’escollirentreunblanciunnegreperencarregar-se d’unafeina(pilotarunaaeronau,perexemple),queesfariamillorsil’habilitat mesuradamitjançant H ésalta,siambdóscandidatstenenelmateixcoeficient d’intel.ligència,aleshoreselvalorde H enelblancseràmésaltqueenelnegre. Pertant,seriaconvenientproposarelcandidatblanc.L’argumentació,fruitde barrejarduespoblacions,ésfalsa,comvadenunciarKaplan[46].Ésmés,per aunamateixa I,elnegretindriaunvalor H mésaltqueelblanc,compodem apreciaralafigura4,quecontélesduesrectesderegressió,ipertantelnegre estariaméscapacitatperalafeina.Demaneramésprecisa,suposemlamateixa habilitatmitjanade H enblancsinegres, E(H|B) = E(H|N) = 100,peròuna certasuperioritatenintel.ligència: E(I|B) = 100, E(I|N) = 90.Silesdesviacions típiquessónigualsa15ielcoeficientdecorrelacióentre H i I és0.6,aleshores lesprediccions(utilitzantlesrectesderegressió)indicarienlasuperioritatdel negresobreelblanc:

Blanc H = 100 + 0.6 × (105 100) = 103,

Negre H = 100 + 0 6 × (105 90) = 109

Figura3: Fal.làciaecològica.Lacorrelacióconsiderantnoméslesmitjanes delespoblacions(cerclesnegres)éspositiva.Peròlacorrelaciódintrede cadapoblació(cerclesblancsagrupats)ésnegativa.

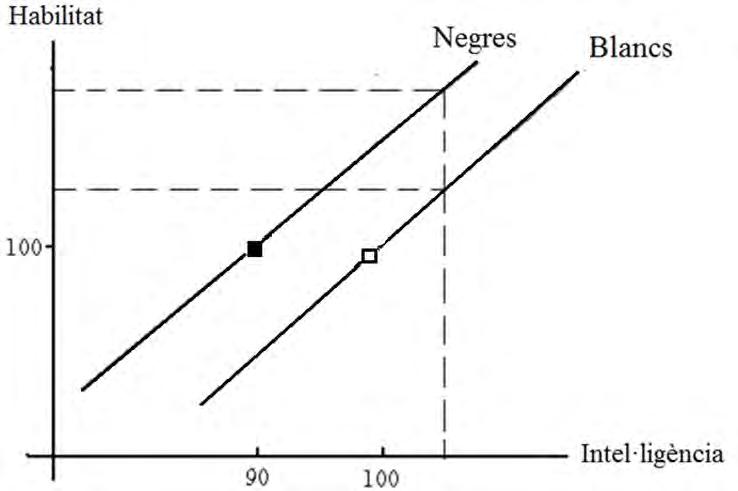
Figura4: Suposantquelaintel.ligènciasiguisuperiorenelsblancs,si unnegretéelmateixcoeficientd’intel ligènciaqueunblanc,aleshores elsuperariaenunaaltrahabilitatcorrelacionadaamblaintel.ligència. Equivocadament,a TheBellCurve s’afirmaelcontrari.

8Méssobrelacorrelació

8.1Raódecorrelació

QuanK.Pearsonvadefinirelcoeficientdecorrelacióenlasevaformaactual, deseguidadeuriaveurequelesdadesdeGaltonnoresponienperfectament aladefinició.Enefecte,peracadavalorde X (variablemid-parent),tenim 1,2omésvalorsde Y ,perquèunaparellapottenirmésd’unfill.Amés,si bépodemsuposarquelesalçadesdelsparessónindependents,lesdelsfills estancorrelacionadesdintredecadafamília.Defet,el1903,K.Pearson[53]va efectuarelscàlculsambnovesdadesivaconsiderar n = 1078famíliesamb nomésunodosfills.Vaobteniruncoeficientdecorrelació r = 0.51entrepare ifillvaró(vegeulataula2).

PodemestudiarlesdadesdeGaltonconsiderantunmodellineal yij = µ + βixi + eij ,i = 1,...,k,j = 1,...,ni, (3) on yij ésl’alçadadelfill j delafamília i, µ ésunamitjanageneral, βi és elcoeficientderegressióperalafamília i corresponentaunmid-parent xi. Elterme eij ésladesviaciódelmodel,ireflecteixelfetqueelsfillsd’una mateixafamílianotenenlamateixaestatura.Sigui µH l’estimaciópermínims quadratssuposantquetotesles βi són0.Aquestaestimacióéslamitjana generaldeles yij .Denotemper R2 H = i,j (yij µH )2 lasumadequadrats residual.Siguin µ, βi, i = 1,...,k,lesestimacionssenseimposarrestriccions isigui R2 0 = i,j (yij µ + βixi)2 lasumadequadratsresidual.Tenimque R2 0 ≤ R2 H ,atèsque R2 H ésunmínimrestringit.Aleshores r 2 = 1 R2 0 R2 H (4)

ésuncoeficientqueindicaelgrauderelaciólinealentre X i Y .Veiemfàcilment quesielmodelésperfecte(nohihadesviació eij ),aleshores r 2 = 1.Perales dadesdeGalton, r coincideixambelcoeficientdecorrelació,ipertant r = 0 50. Plantegemaraunmodelgeneral

yij = g(xi) + eij ,i = 1,...,k,j = 1,...,ni, on g ésunafunciópossiblementnolineal.Sisuposem g = 0,l’estimacióde µ ilasumadequadratsresidual R2 H sónlesmateixesd’abans.L’estimacióno restringidade g(xi) éslamitjanacorresponentalgrup i.Aplicantlamateixa mesurad’ajust,obtenim

η2 = 1

k i=1 ni n S 2 i S 2 Y ,

on n = n1 +···+ nk, S 2 i éslavariànciaperalafamília i, S 2 Y éslavariància global.Escompleix η2 ≥ r 2.Sinohihadesviaciódelmodelnolineal,ésadir, S 2 i = 0,aleshores η2 = 1.Enlesaplicacionscalcomparar η amb r

Consideremlaconegudadescomposiciódelavariabilitatenl’anàlisidela variància, anova (vegeu[57]),

essent y lamitjanageneral, y i lamitjanadelgrup i.Escriurem QT = QE + QD, onlesquantitats QT , QE , QD sónlessumesdequadratstotals,entregrupsi dintredegrups.Aleshorestambépodemexpressarlaraódecorrelacióper

Exemple. PeralesdadesdeGaltonobtenim η = 0 58,unindiciclarderelacióno lineal,jaque η = 0.58éssignificativamentmésgranque r = 0.50.Possiblement siguidegutalesrepeticionsdelsvalorsdelsparesquetenenmésd’unfill. PeròPearsonvacomentarqueeradegutaunamaneraamateurd’obtenirles dades[58].Defet,Pearsonvatreballaramb1078famíliesiunesdadesmés benobservadesimillorajustadesalsconceptesde correlació i regressió.Va obtenir η = 0.52,fetqueindicaunabonarelaciólineal,jaqueladiferència entre η = 0 52i r = 0 51noéssignificativa.

Sidividimper n elstermesde(5)obtenim 1 n k i=1 ni j=1 (yij y)2 =

(yij y i )2 , (6)

queseriaunaversióestadísticadeladescomposiciódelavariànciad’unavariablealeatòria.Ésadir,donatunparelldevariables (X,Y),ladescomposició (6) éslaversió anova de var(Y) = var[E[Y |X]] + E[var[Y |X]], (7) on Y |X representalavariable Y condicionadaa X.Lacorbaderegressiódela mitjanaéslamillorcorbaqueajusta Y enfuncióde X,ésadir, y = E[Y |X = x]. Elgraudeconcentraciódelesobservacions (x,y) de (X,Y) alllargd’aquesta corbaés η2 = 1 E[var[Y |X]] var(Y) .

8.2Correlacióintraclàssica

Quinaéslacorrelacióentregermansperaunacaracterísticafísicacoml’alçada? Larespostanos’obtémitjançantelcoeficientdecorrelacióordinari,atèsque nopodemdisposardelsvalorsdelsgermansenparellesordenades (x,y). Suposemelmodel yij = µ + Ai + eij ,i = 1,...,k,j = 1,...,ni,

on Ai ésunamenadevariablealeatòriatalque E(Ai) = 0i var(Ai) = σ 2 A pera tota i.Suposemlescondicionsusualsd’independènciacompletaentreles Ai, eij itambéquevar(eij ) = σ 2

Esdefineixlacorrelacióintraclàssica ρI comlaquehihaentreduesobservacions yij i yij dintredelmateixgrup(ofamília).Esdemostrafàcilment[57] que ρI = σ 2 A/(σ 2 A + σ 2).

Siguin QA i QR lessumesdequadratsentregrupsidintredegrups(quantitatsqueabanshemindicatper QE i QD).Dividintpelsgrausdellibertat corresponents,consideremlesmitjanes QA = QA k 1 , QR = QR n k , essent n = n1 +···+ nk.Segons[33],unaestimacióde ρI és ρI = QA QR QA + (n0 1)QR , (8)

on n0 = n k i=1 n2 i /n /(k 1).

Relacionemara ρI amblaraódecorrelació η2.Amblapresentnotació, tenintencompteque QA/QR = η2/(1 η2),ésfàcilveurequelacorrelació intraclàssicaés

ρI = (n 1)η2 (k 1) (n kn0 + n0 1)η2 + (n0 1)(k 1)

Adiferènciade η,lacorrelacióintraclàssica ρI ésuncoeficientestadísticdel qualnohihaversióprobabilística.

Exemple. Peralesdades(nobalancejadesamb ni > 1)deGalton,aplicant (8), obtenim n0 = 5.23i ρI = 0.38,queindicaunacertacorrelacióintraclàssica entrelesalçadesdegermansigermanes.

8.3Laperspectivabayesiana

Ésoportúcomentaraquílacondiciófonamentaldelametodologia anova:la independènciaestocàsticailaigualtatdevariànciesdeltermed’error.Així,en elmodel anova d’unsolfactor,

yij = µ + αi + eij ,i = 1,...,k,j = 1,...,ni,

suposemladistribuciónormal Nni (0,σ 2Ini ) peracadasuccessió eij , j = 1,...,ni.Aquestahipòtesiésdiscordantambl’enfocamenttípicamentbayesià, quesuposalesmostresambdistribucióconjunta«intercanviable».Altrament dit,ladistribuciódecadascunadeles ni observacions yij és(condicionalment acadagrup)lamateixa,peròladistribucióconjuntaéssimètrica.

ElllegatdeGalton,Pearson,Fréchetid’altres 17

Peralleugerirlanotació,denotem ni per n iels ni errorsper x1,...,xn

Aleshores:

(x1,...,xn) ∼ (xj1 ,...,xjn ),

on (j1,...,jn) ésunapermutacióde (1,...,n).Elsímbol ∼ significa«mateixa distribucióque».

SegonselteoremadeBrunodeFinetti,ladensitatconjuntaprenlaforma[5]

p(x1,...,xn) = Iα n j=1 f(xj |α)π(α)dα,

on f(xj |α) ésunamenademodelestadísticonelparàmetre α provéde l’observaciód’unavariablelatentambsuportl’interval Iα idensitatdeprobabilitat π(α).Ladistribuciódelsvalors x1,...,xn sónindependentssiels condicionemaunvalorfixde α.Suposantquelavariànciaésconstant σ 2 , indicantlamitjanacondicionadaper µ(α) = R xf(x|α)dx,lamitjanaglobal d’unerror x és a = Iα µ(α)π(a)dα.Amés,siposem A = Iα µ(α)2π(α)dα, elvaloresperatdelproductededoserrors x i x ésprecisament

Iα R2 xx f(x|α)f(x |α)π(α)dαdxdx = A.

Comquelavariànciaés σ 2 + A a2,fàcilmentesdemostraquelacorrelació entredoserrorsés

ρ = A a2 σ 2 + A

Sisuposem α fixambprobabilitat1(enfocamentclàssic),obtenim A = a2 i ρ = 0.

Aplicantaquestenfocamentbayesià,atèsquenoconeixem π(α),unmodel raonableseriasuposarque (x1,...,xn) segueixladistribuciónormalsimètrica Nn(0, Σ),ilamatriudecovariànciesés

Aquestadistribucióésintercanviableipressuposa(dintred’ungrup)una mateixacorrelació ρ peracadaparellad’observacions(oerrors)diferents. Engeneral,unbayesiàpostularia ρ ≠ 0iunclàssicconsiderarialarestricció ρ = 0,queenelcasdenormalitatimplicariaindepèndenciacompletaentreles observacions.Éscorrecteelmodelrestringit?Afortunadamentperal’estadística clàssica,Wilks[60]vademostrarqueeltestFdeFisher-Snedecoréstambévàlid ambdadesnormalsequicorrelacionades,ésadir,enelcasquesigui ρ ≠ 0. Araéselmomentderesoldreelsofismedelasecció5,onlacorrelació entre Xn i Y semblavaquepodiasermésgranque1.Elparanyconsistiaa

prendre X1,...,Xn independents.L’acciód’obtenirunamostraaleatòriasimple, tanusualenestadística,ésincorrectasi X estàcorrelacionadaamb Y .Hem d’admetre,doncs,que X1,...,Xn nosónindependents.

Ditaixò,hihamaneresdiferentsdeveureque |cor(Xn,Y)|≤ 1.Perexemple, sisuposemelmodeld’equicorrelació,queimplicaqueles n variables X són intercanviablesinopasindependents,aleshores cov(Xi,Xj ) = σ 2 x ρ, i ≠ j.Per tant, var(Xn) = [nσ 2 x + n(n 1)σ 2 x ρ]/n2 , ielcoeficientdecorrelacióés

cor(Xn,Y) = √nρxy 1 + (n 1)ρ , quemaipotsuperarelvalor1.

Part II:Estadísticamultivariant

Elsmètodesdelesduesseccionssegüentsespodentrobarambdetalla[8, 15].

9Anàlisidecorrelaciócanònica

Lacorrelaciómúltipleentre Y i X1,...,Xp éslamàximacorrelacióentre Y iuna combinaciólinealde X1,...,Xp.Lageneralització,proposadaperHotelling,4 consideradosvectorsaleatoris X = (X1,...,Xp) i Y = (Y1,...,Yq),idetermina lescombinacionslineals[44]

U = Xa = a1X1 +···+ apXp,V = Yb = b1Y1 +···+ bqYq,

detalmaneraquelacorrelacióentre U i V siguimàxima,on a = (a1,...,ap) i b = (b1,...,bq) sóndosvectors.

Indiquemper S11 i S22 lesmatriusdecovariànciesmostralsde X i Y,respectivament(elcaspoblacionaltéuntractamentmoltsemblant).Sigui S12 la matriu p × q amblescovariànciesdelesvariables X amblesvariables Y.Tenim aleshoreslasupermatriu S = (Sij ),

XY

X S11 S12

Y S21 S22

on S21 = S12.Si S11 = (sij ),aleshores var(U) = p i,j=1 aiaj sij = a S11a,i anàlogamentvar(V) = b S22b icov(U,V) = a S12b.

4 H.Hotellingvaintroduirl’anàlisidecorrelaciócanònicael1936,enunintentderelacionar aptitudsfísiquesimentals.Elmètodetindriaunagraninfluènciaenanàlisifactorial,anàlisidecorrespondències,anàlisidiscriminant,anàlisicanònicadepoblacionsialtresmètodes multivariants.

Podemsuposarquevar(U) = var(V) = 1.Aleshoreselproblemaequivala:

maximitzar a S12b restringita a S11a = 1, b S22b = 1.

Lasoluciónoésúnicaielsvectorsdecoeficients a i b quecompleixenaquesta condiciósónelsvectorscanònics.Lamáximacorrelacióentre U i V ,combinacionslinealsde X i Y,repelnomdeprimeracorrelaciócanònica r1.Clarament, r1 = 0si X ésindependentde Y,i r1 = 1sihihaunarelaciólinealentreels dosvectors.Pertant, r1 téunpaperdestacatenlamesuradel’associacióentre X i Y.

Si U1 = Xa1, V1 = Yb1 éslaprimeraparelladevariablescanòniques,definim U2 = Xa2, V2 = Yb2 comlaparelladevariables(tambécombinacionslinealsde X i Y)incorrelacionadesamb U1 i V1.Aleshores r2 = cor(U2,V2) éslasegona correlaciócanònica.Anàlogamentobtenimlaterceraisegüentsvariablesi correlacionscanòniques,quesatisfanlescondicionsd’optimitzacióesmentades adalt.

Podemformularunaexpressióconjuntaperalsvectorscanònics ai i bi utilitzantladescomposiciósingulard’unamatriu.Suposantque p ≥ q,sigui m = min{p,q}= q iconsideremlamatriu p × q Q = S 1/2 11 S12S 1/2

Calculemladescomposiciósingular Q = UDs V ,on U ésunamatriu p × q ambcolumnesortonormals, V ésunamatriu q × q ortogonali Ds ésuna matriudiagonalambelsvalorssingularsde Q .Altramentdit, U U = Iq, V V = V V = Iq, Ds = diag(s1,...,sm).Aleshoreselsvectorscanònicsilescorrelacions canòniquessón ai = S 1/2 11

Formalment: Ui = Xai, Vi = Ybi, ri = si = cor(Ui,Vi), i = 1,...,m,ésadir,les correlacionscanòniquessónelsvalorssingularsde Q . Cadaparelladevariablescanòniquestécorrelaciómàxima,imantélacondiciód’ortogonalitat,ésadir,

cor(Ui,Vi) = ri, cor(Ui,Uj ) = cor(Vi,Vj ) = cor(Ui,Vj ) = 0si i ≠ j. Amésescompleixlarelaciórecursivasegüententreelsvectorscanònics:

Exemple. PeralesdadesdeGalton,podemconsiderarlesquatrevariables

X1 = alçadadelpare,Y1 = alçadadelfill, X2 = alçadadelamare,Y2 = alçadadelafilla

Volemrelacionar (Y1,Y2) amb (X1,X2).Atèsquenecessitemquaternescompletes,hemseleccionatfamíliesambalmenysunfilliunafilla,prenentlamitjana

quanhihamésd’undescendent.Obtenim n = 150ilesmatriusdecovariàncies:

S11 = 6.96540.4516 0 45165 3950 , S12 = 3.17592.7013 1 86971 7857 , S21 = 3 17591 8697 2.70131.7857 , S22 = 4 86242 4138 2.41384.0804 .

Elsdosvectorscanònicsielsvalorssingularssón:

a1 = (0.3050;0.2312) , b1 = (0.2742;0.2642) ,s1 = 0.71, a2 = (0.2265; 0.3646) , b2 = (0.4648; 0.5265) ,s2 = 0.038.

Laprimeracorrelaciócanònicaés r1 = 0.71ilesprimeresvariablescanòniques són:

U1 = 0 3050X1 + 0 2312X2,V1 = 0 2742Y1 + 0 2642Y2

Lacorrelacióhaaugmentatde0.50a0.71.Defet r1 = 0.71ésunamesura globald’associacióentrelesestaturesdeparesifills. Resultainteressantconstatarqueelcàlculdelacorrelacióentre U1 = 0 3050X1 + 0 2312X2 ilavariablemid-parent (X1 + 1 08X2)/2(peròconsiderant elconjuntcompletdeles934dadesinicials)dóna r = 0.995,unvalormolt elevat.Veiemquelavariablemid-parentempradaperGaltonafidereduir diferènciesentreparesimaresésgairebéequivalentalaprimeravariable canònica.

Definimaraunamesuraglobald’associacióentreelsvectorsaleatoris X = (X1,...,Xp) i Y = (Y1,...,Yq).Ensituacionspràctiquesinteressatrobaruna mesurad’associacióentreduesmatriusdedades n×p i n×q.Unabonamesura esbasaenlalambdadeWilks,queesfaservirperdecidirsiunahipòtesiés certaohauriadeserrebutjada.

Sigui f(x,θ) unmodelestadísticqueconsisteixenunadensitatdeprobabilitatindexadaperunparàmetre θ ∈ Θ.Donadaunamostraaleatòriasimplede mida n lafunciódeversemblançaés

L(x1,...,xn; θ) = f(x1,θ) ×···× f(xn,θ).

L’estimaciómàxim-versemblantde θ (proposadaperR.A.Fisher)éselvalor θ quemaximitza L(x1,...,xn; θ).Plantegemunahipòtesinul la H0 sobreelparàmetre θ,queespotformularcomunarestricciósobreelconjunt Θ.Escriurem H0 : θ ∈ Θ0 ⊂ Θ.Sigui θ0 l’estimaciómàxim-versemblantde θ dins Θ0.Tenim aleshoresduesfuncionsdeversemblança.Laraódeversemblançaéselquocient

λ = L(x1,...,xn; θ0)/L(x1,...,xn; θ).

Atèsqueelnumeradorésunmàximrestringit,clarament0 ≤ λ ≤ 1.Unvalor de λ pròxima1indicariaquelesduesversemblancessónsemblantsianiriaa

ElllegatdeGalton,Pearson,Fréchetid’altres 21

favorde H0.Sotaunmodelregularisuposant H0 certa,l’estadístic χ2 =−2 ln λ convergeixenlleialadistribuciókhiquadratsi n →∞,propietatquepermet decidirsobrel’acceptacióoelrebuigde H0.Sovint,enanàlisimultivariant,la raódeversemblançaestàrelacionadaamblalambdadeWilks,queesdefineix comelquocientdedeterminants Λ = det(A)/ det(A + B),on A i B sónmatrius deWishartestocàsticamentindependents.

Enelcasdedosvectors X i Y normalsmultivariants,laindependència estocàsticaentreambdósvectorsesformulaplantejantlahipòtesi H0 : Σ12 = 0,on Σ12 éslamatriu p × q quecontélescovariànciespoblacionalsentre lesvariablesdecadavector.Esdemostraquelaraódeversemblança λ està relacionadaamb

=|S|/(|S11||S22|) = (1 r 2 i ) ×···× (1 r 2 m),

on S éslasupermatriudecovariàncies (p + q) × (p + q).Sota H0,aquesta Λ segueixladistribuciólambdadeWilksiverifica Λ = λ2/n.Comque Λ pròxima a1afavoreixlahipòtesinul.lad’independènciaentre X i Y,resultaraonable definirlamesurad’associacióglobalsegüent: AW = 1 Λ = 1 m i=1 (1 r 2 i ), (10)

on m = min{p,q}.Aleshores AW val0encasd’independènciaestocàstica (suposantnormalitat)ival1sihihaunarelaciólinealentre X i Y.Perales dadesdeGaltonobtenim AW = 0 5060.

10Anàlisidecorrespondències

Podemtambéestudiarl’associacióentrelesalçadesdeparesifillsdefinint intervalsdeclasseperalesvariablesiaplicantanàlisidecorrespondències,5 mètodemultivariantquepermetvisualitzarlesfilesicolumnesd’unataulade contingència N = [nij ],d’ordre I × J.Aquestmètode,amblacontribucióprèvia deR.A.Fisherid’altres,vaesdevenirpopularambl’obradeJ.-P.Benzécri.6 Vegeu[4,39].

Denotemper P lamatriudecorrespondènciesiper r, c elstotalsmarginals delessevesfilesicolumnes:

P = 1 n N, r = P1J , c = P 1I ,

5 L’anàlisidecorrespondèncieshaestatdescobertaperdiversosautorsambplantejaments diferents.H.O.Hirschfeld(1935)iR.A.Fisher(1940)vanserelspioners.DesprésK.Maung (1941)varelacionarelsresultatsdeFisher(donarvalorsavariablescategòriquesquemaximitzen lacorrelació)ambl’anàlisidecorrelaciócanònicadeHotelling.J.-P.Benzécrilidonariauna interpretaciógeomètrica,contingudaenelsseusdosllibressobre L’analysedesdonnées,publicats el1973.ElmètodeesdifondriaapartirdelesobresdeL.Lebartid’altres,ienespecialde M.Greenacre,publicadesindependentmentel1984.

6 ConvidatperJ.Torrens-Ibern,J.Robert,deixebledeBenzécri,vadonarel1974aBarcelona uncurssobreanàlisidecorrespondències.

essent n = nij i 1I , 1J elsvectorsambunsdedimensions I, J,respectivament.Podeminterpretar N comelresumdelesrelacionsentreduesmatrius X i Y dedadesbinàriesquerelacionendosconjuntsdevariablescategòriques(possiblementordinals)amb I i J categories.Siconsideremlesmatrius diagonals Dr = diag(r) i Dc = diag(c),quecontenenlesfreqüènciesrelatives marginalsperfilesipercolumnes,esverifica

X X = nDr , Y Y = nDc , X Y = nP = N

Recordemque,donadaunamostra x = (x1,...,xn) ,podemexpressar lavariànciaper s2 = n 1x x (n 11 x)2,on 1 éselvectorcolumnaamb n uns.D’unamanerasimilar,unamatriudecovariànciesés n 1X X x x ,on x = n 1X 1 éselvectordemitjanes.Enelnostrecaselvector(columna)de mitjanesdeles I variablesfilaés r = n 1X 1.Anàlogamentperales J columnes. Pertant,lesmatriusdecovariànciesperalesvariablesfiles,columnes,ientre filesicolumnessón

S11 = Dr rr , S22 = Dc cc , S12 = P rc .

Siaravolemdonarvalorsalescategoriesdelesvariables,demaneraqueles correlacionssiguinmàximes,aplicant (9) icalculantladescomposiciósingular, obtenim

D 1/2 r (P rc )D 1/2 c = UDs V , (11) on Ds ésmatriudiagonalambelsvalorssingulars,quecoincideixenambles correlacionscanòniques.Elsvectorscanònicssón

ai = D 1/2 r ui, bi = D 1/2 c vi,i = 1,...,K = min{I,J}, quematricialmentpodemexpressarper

A = D 1/2 r UDs , B = D 1/2 c VDs

Lamultiplicacióaladretaper Ds noalteralescorrelacions.Escompleixenles relacionssegüentsentrelescoordenadesdefilesidecolumnes

A = D 1 r PBD 1 s , B = D 1 c P AD 1 s . (12)

Consideremaraelsperfilsdelesfiles (pi1/ri,...,piJ /ri),quepodeminterpretarcomles«probabilitatscondicionades»deles J columnesaunafila i determinada.Definimunadistància(alquadrat)entreelsperfilsdeduesfiles i, i , δ2 ii = J j=1 (pij /ri pi j /ri )2 cj . (13)

Siduesfilestenenelmateixperfilaleshores δ2 ii = 0.Aquestadistànciaesconeix ambelnomde khiquadrat

ElllegatdeGalton,Pearson,Fréchetid’altres

Esdefineixla inèrcia o variabilitatgeomètrica comlamitjanaponderadade lesdistàncieskhiquadratentrefiles:

Vδ ésunamesuradedispersiódelesdades,versiómultivariantdelavariància.

Esdemostraque Vδ = K k=1 s2 k = χ2/n,on si, i = 1,...,K = min{I,J},sónels valorssingularsde (11) i χ2 ésl’estadístickhiquadratpercontrastarlahipòtesi d’independènciaentrefilesicolumnesde N,ésadir, H0 : pij = pi × p j ,on pij éslaprobabilitatconjuntai pi·, p·j sónlesprobabilitatsmarginals.

Amés,lesdistàncieseuclidianes(alquadrat)entrelesfilesdelamatriu A = D 1/2 r UDs coincideixenamblesdistàncieskhiquadratentrefiles.Lesdues primerescoordenades (ai1,ai2) proporcionenunarepresentacióòptimaen dimensiódos,enelsentitquelasevavariabilitatgeomètrica,considerantnomés duescoordenades,ésmàximaival Vδ(2) = 2 k=1 s2 k ,queengeneralaportauna proporcióaltadelavariabilitattotal Vδ = K k=1 s2 k

Anàlogamentpodemdefinirelperfildelescolumnesiunadistànciakhiquadratentrecolumnes.Aleshoreslamatriu B = D 1/2 c VDs contélescoordenades euclidianesperaunarepresentaciódelescolumnes.

D’altrabanda,lesrelacions (12),recíproquesentre A i B,demostrenque lescoordenades (ail) delesfilessónlesmitjanes,ponderadespelsperfils delesfiles,delescoordenades (bjl) delescolumnes.Anàlogamentpera lescoordenadesdelescolumnes.Perexemple,cadaprimeracoordenadadeles filesverifica

ai1 = 1 s1 b11 pi1

ianàlogamentlescolumnes.Peròaquestamitjanabaricèntricanoésperfecta (perraonsgeomètriques,elspunts ai nopodensermitjanesdels bj irecíprocament).Hiha,pertant,unfactordilatador1/s1 > 1.Unaconseqüènciaimportant d’aquestarelacióésquepodemrepresentarconjuntament,enunmateixgràfic, lesfilesicolumnesd’unatauladecontingència I × J

Exemples. AgrupemlesdadesdeGaltoniformemintervalsdeclasseperales alçadesdemid-parentsifills.Peralesalçadesdelsparesesconsiderenelscinc intervals:

finsa66,(66, 68],(68, 70],(70, 72], mésde72, l’últimindicatalafigura5per«◦74».Enelcasdelsfillshihamésvariabilitati esconsiderenelssetintervals:

finsa64,(64, 66],(66, 68],(68, 70],(70, 72],(72, 74], mésde74, l’últimindicatenelgràficper« 76».Creuantaquestsintervalsobtenimuna tauladecontingènciaquerepresentemperanàlisidecorrespondènciessimples.

Veiemclaramentl’associació,jaquelesalçadesdelsparessónpròximesales delsfills,enelsentit,perexemple,quelesalçadesentre68i70delsfillssón mitjanesponderadesdelesalçadesdelspares,ielvalorquepredominaés precisamentla«probabilitatcondicionada»al’interval (68, 70] delspares.La variabilitatgeomètricadelgràfic(dimensió2)representael96%delavariabilitat total(dimensió4).Elprimervalorsingularoprimeracorrelaciócanònicaés0.49, valormoltsemblantalacorrelació r = 0.50ques’obtéamblesdadesoriginals.

Lataula3(esquerra)ésunataula4 × 4quecontédadesdefreqüències obtingudesperGaltonsobre n = 1000individus,classificatssegonselcolor delsulls(1blau,2verdogris,3grisfosc,4castanyfosc)deparesifills.Convé tenirencomptequearalesvariablessóncategòriquesinopodemcalcularel coeficientdecorrelacióclàssic.Lafigura6(esquerra)éselresultatdel’anàlisi decorrespondènciessimples.L’associacióentreparesifillsrespectealcolor delsullsésnotable.Lavariabilitatgeomètricaésel86.7%delavariabilitattotal. Laprimeracorrelaciócanònicaés r1 = 0 39.

Figura5: Representacióperanàlisidecorrespondènciesdelesfiles(midparents)icolumnes(fills),d’unatauladecontingència5 × 7resultatde distribuirenintervalsdelongitud2lesdadesdeGalton,querelacionen lesestaturesdeparesifills.Elvalor70represental’intervaldeclasse de68a70.

10.1Associacióentaulesd’ordresuperior

Lataula3(dreta)ésunataula2 × 2 × 2quecontédadesdefreqüènciesobtingudesperGaltonsobre n = 5008individus,classificatssegonselcolor(claro fosc)delsulls,tenintencompteelcolordelsullsdelsparesielsavis.Galton vaconsiderar78famíliesambmoltsfills,pertanthiharelació(enelsentit

decorrelacióintraclàssica)entregermansigermanes.Aratenimtresvariables categòriques,queespodenrepresentaraplicantanàlisidecorrespondències ordinarialatauladeBurt,taulasimètricaquecontélesfreqüènciescombinant lesvariables.Aquesttipusderepresentacióesconeixperanàlisidecorrespondènciesmúltiples[15, 39].Lafigura6(dreta)representalesfreqüències defills,paresiavisd’acordambelcolordelsulls.LaseparacióentrecolorCi colorF,quealseutornestanagrupats,mostraquehihaassociacióentrecolor iparentesc.

Figura6: Anàlisidecorrespondènciessimples(esquerra)idecorrespondènciesmúltiples(dreta),delcolorsdelsulls.Classificacionsifreqüències obtingudesperGaltonde1000individus(esquerra)ide5008individus (dreta).

Taula3: ClassificacióifreqüènciesobtingudesperGaltonde1000individus(esquerra)i5008individus(dreta),segonselcolordelsulls, considerantquatrecolors(esquerra)icolorclarofosc(dreta),iambel registretambédelcolordelsullsdelsseusparesiavis.

Intentemaramesurarl’associacióestadísticaentrefills,paresiavisrespecte delcolordelsulls.Enprimerllochemd’especificarunmodel.Siguin pijk les probabilitats,on i,j,k ∈{1, 2} sónelsíndexsperafill,pareiavi.Perexemple,

p111 éslaprobabilitatqueunfilltinguielsullsclars,aixícomelseupareielseu avi.L’estimacióés p111 = 1928/5008.Posem pij· = pij1 + pij2 ianàlogament pi k, p jk, pi ,etc.Especifiquemaraunmodel.Enteoria,elméscorrecteseria suposarquehihavuitprobabilitats pijk quesumen1.Peròestadísticament nopodemdecidirlasevavalidesaperquèhihatantsparàmetreslliurescom observacions.Lesestimacionsdels pijk donarienfreqüènciesesperades npijk quecoincidirienamblesobservades(l’estadístickhiquadratseria χ2 = 0).Hem d’afinarunamicamés.Suposaremqueelcolordelsullsdelsfillsésindependent entreparesifills,entreavisifillsientreavisipares.Entermesdeprobabilitats:

Peralesdadesdelataula3(dreta),eltestperaaquestahipòtesiaplicantla raódeversemblançadónaunakhiquadratde χ2 =−2 ln λ = 16 8ambungrau dellibertat,bastantsignificativai,pertant,rebutgemquehihaindependència entrefillsipares,etc.Lesdadestampocs’ajustenaunmodelgenèticcombinant dosal.lels.Defet,elmodelcorrectenoelconeixem(vegeulanotaalpeudela pàgina6).Acceptem,doncs,elsparàmetres pij·, pij·, p·jk comaprobabilitats genèriques,queesdesviendelmodeldetreballformatpelsproductes pi ×p j , etc.

Consideremaraelmodeld’independènciacompleta:elcolordelsullsde fills,paresiavisésindependent.Entermesdeprobabilitats:

Aquestmodelésunarestricciódel’anterior.Atèsquelakhiquadratés χ2 = 2 ln λ = 868.3ambdosgrausdellibertat,moltsignificativa,elmodels’hauria derebutjar.Tambépodemafirmarqueelmodelanterior(χ2 = 16 8)s’ajusta moltmilloralesdadesobservades.Comcalmesuraraquestajust,interpretat entermesd’associació?

Acceptemelvalorkhiquadratdividitpelsgrausdellibertatcomunadistància entrefreqüènciesobservadesiesperades,ésadir,unamesuradeladesviació delmodelcorresponent.Aplicant(4)obtenim

θ = 1 16.8 868 3/4 = 0 9226

Elgraud’associacióglobal(relatiualsdosmodels)quehihaentrelestres generacionsrespectealcolor(clarofosc)delsullsésalt.

Elcasgeneraldetaulesdecontingència J1 ×···× Jq éssemblant.Larepresentaciódelesvariablescategòriqueslapodemferaplicantl’anàliside correspondènciesmúltiples.Aleshorescalestablirdosmodels,undegeneral, l’altremésrestringit,ladesviaciódelqualexpressiladependènciaglobal.Aplicantelmateixprocediment,obtindremunamesuradedependènciarelativa. Usualmentelscàlculsesfanaplicantmodelslog-lineals[15],atèsqueprenent logaritmes,elsproductesesdevenensumes.

10.2Alternativesal’anàlisidecorrespondències

Quanlesfreqüènciesnoformenunataula I×J sinoqueprovenende I poblacions multinomialsindependents,aleshoresésmésadequada ladistànciadeHellinger entreperfils[23],seguintelplantejamentdegutaRao[54]:

Hihaaltresalternativesqueresponenalnomd’anàlisinosimètric,d’anàlisi log-ràtio,etc.Totesespodenunificarparametritzantladistància,quedepèn dedosparàmetres0 ≤ α, β ≤ 1,per

vegeu[19].Aleshoreslescoordenadesdelesfilesidelescolumness’obtenena partirdeladescomposiciósingular:

on M(α) = [mα ij ], Hc = I 1r .Lataula4resumeixelsdiferentsmètodes, ambelsacrònimsCA(anàlisidecorrespondències),HD(anàlisiambdistància Hellinger[54]),LR(anàlisilog-ràtio[1]),NSCA(anàlisidecorrespondències nosimètriques).Engeneral,lescoordenadesdelesfilessón A = D 1/2 r UDs ilesdelescolumnes, B = Dβ 1 c VDs .Lamatriucentradora Hc = I 1r ,que premultiplicaa (15),noapareixa (11) perquènoafectalessolucionsCAiNSCA. Larepresentacióendimensió2ésunaformageomètricad’explicarunapartde lainèrcia Vδ = s2 i ,on s1,s2,... sónelsvalorssingulars.

EnelmètodeCA,lainèrciaéselcoeficientdecontingènciadePearsoniestà lligatalakhiquadratperataulesdecontingència.SiconsideremHD,aleshores lainèrciatéaveureambelcoeficientd’afinitatdeMatusita,quemesurael graudeconcordànciaentreduesdensitats.LainèrciaenelmètodeNSCAestà relacionadaambelcoeficientdeGoodman-Kruskal,quemesuralapredictibilitat delescolumnesdonadeslesfiles.Pertant,NSCAésadequatsilescolumnes fanelpaperdevariablesrespostailesfiles,devariablespredictores.Finalment, LAésútilperadadescomposicionals[1](elsvalorsdecadafilasónpositiusi sumenunaquantitatfixa).

Hihaencaramésmètodes[38],algunsbasatsenfreqüènciesacumulades[12]. PeròelmètodeCAéselmésracionalielquemillorrespectalespropietatsde lesprobabilitats.Vegeu[22]peraunaperspectivageneral.

Coordenadesfiles,columnes

SVD,inèrcia

Mètode

CA(Benzécri,Greenacre)

Taula4: Quatremètodesperrepresentarlarelacióentredosconjunts devariablescategòriques.

11Associacióestadísticaambdadesgenerals

Femunaulladaalataula5,quecombinaundels Reportsdelarecercaa Catalunya(1996–2002),publicatperl’IEC,iunataulaextretade[7].Ladiagonal contéelnombred’articlesdematemàtiquesiestadísticapublicatspercada paíssensecol.laboracióambelsaltrespaïsosdelallista.Sobreladiagonalhi haelnombred’articlespublicatsambautorsd’altrespaïsos.Lapartpersota deladiagonalindicalarelaciócomercial(1siésimportant,0sinohoés). Perexemple,Espanya(incloent-hiCatalunya)hapublicat10560articles,dels quals8597tenenautorsespanyolsicapdelsaltrespaïsosdelallista,692amb coautorsd’EUA,473ambFrança,etc.;iEspanyahamantingutambelsEUAuna relaciócomercialimportant(valor1).

Hihaassociacióestadísticaentrecol.laboraciócientíficairelaciócomercial? Vegemunamanerageneraldemesurar-la.

EUAEsp.Fran.R.U.Ital.Alem.Can.JapóXinaRuss. EUA 634466922281250716422812273910391773893

Espanya 1859747334735227816369104177

França 1117155532916884496269167606

RegneUnit 11112585490810480213339365

Itàlia 011013197677290169120512

Alemanya 1111116588499350408984

Canadà 1001007927228601204

Japó 100000120001371193

Xina 100000113914064

Rússia 00000000118213

Taula5: Nombred’articlespublicatsambautorsd’unsolpaís(diagonal)iambautorsd’altrespaïsos(sobreladiagonal).Relaciócomercial significativaentrepaïsos(sotaladiagonal).

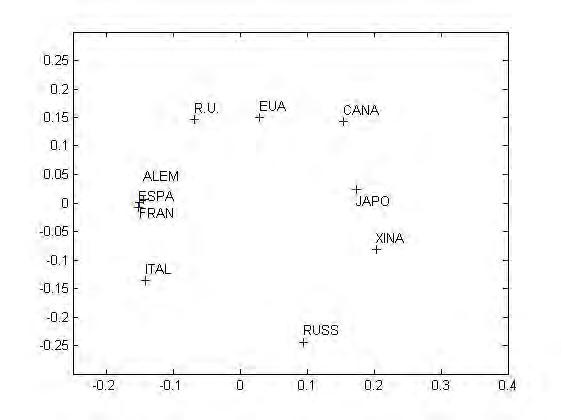
Figura7: RepresentacióRMDSdedeupaïsostenintencomptelacollaboraciócientíficailarelaciócomercial.

Sigui Ω ={ω1,...,ωn} unconjuntfinitamb n objectesoindividus.Suposem queperalgunprocedimentpodemdefinirunamesuradedissimilaritato distància δ : Ω×Ω → R+ entrecadaparellad’objectes: δij = δ(ωi,ωj ).Suposem que δ éssimètricainonegativa: δij = δji ≥ δii = 0.Obtenimaleshoresuna matriu n × n dedistàncies ∆x = (δij ).

Suposaremqueaquestamatriudedistàncieséseuclidiana.Ésadir,existeix unaconfiguraciódepunts x1,..., xn ∈Rp,ambcoordenades xi = (xi1,...,xip) , i = 1,...,n,detalmaneraque δ2 ij = (xi xj ) (xi xj ).Tenim,doncs,queles coordenadesdelselementsde Ω formenunamatriu n × p,quedenotarem per X = [xij ],detalmaneraqueladistànciaeuclidianaentrecadaparellade files i, j coincideixambladistànciainicial δij

Afidesabersi ∆x éseuclidiana,sigui In lamatriuidentitati 1n elvector d’uns.Ésbenconegutqueunamanerad’obtenir X (quenoésúnica)apartir de ∆x ,consisteixatrobarprimerlesmatrius Ax =− 1 2 ∆(2) x i Gx = Hc Ax Hc , on ∆(2) x = (δ2 ij ) i Hc = In (1/n)1n1n éslamatriudecentrat.Seguidament calculemladescomposicióespectral Gx = UΛ2 x U ,queproporcionalamatriu decoordenades X = UΛx .Aleshores ∆x ésunamatriudedistàncieseuclidianes siinoméssi Gx ésunamatriusemidefinidapositiva(elsvalorspropissónno negatius).

Suposantqueelsvalorspropiscontingutsenlamatriudiagonal Λ2 x estan disposatsenordredecreixent,lesmatrius X i U contenenlescoordenades principalsiestàndard,respectivament,dels n individusenrelacióambles distàncies ∆x .Aquestprocediment,conegutperanàlisidecoordenadesprincipals[8, 15],permetferunarepresentaciógràficadels n individusendimensió reduïda(usualment2)prenentlesprimerescoordenadesprincipals,ésadir,les

duesprimerescolumnesde X.Elresultatéssemblantal’anàlisidecorrespondències,quedefetseriaunaanàlisidecoordenadesprincipalsponderat.Hem dedir,però,queaquívolemrelacionaraquestescoordenadesambunsegon conjuntdedadesobservadessobreelmateixconjunt Ω.

Considerem,doncs,unaltreconjuntdedadesambobservacionssobreels mateixos n individus,ique,mitjançantunadistànciaodissimilaritatapropiada, podemobtenirunasegonamatriudedistàncies ∆y ,delaqualcalculem Ay ia continuació Gy = VΛ2 y V ,comhemfetabans.Sielsvalorspropisaladiagonal de Λ2 y estanordenats,lescoordenadesprincipalsde Ω respectea ∆y són Y = VΛy .Lescoordenadesestàndardsónles n filesde V

Ambaquestescoordenades,l’associacióentreelsdosconjuntsdedadeses potplantejarquantificantl’associacióentrelesmatrius X(n × p) i Y(n × q). Tenintencomptequesónmatriuscentrades(lamitjanadecadacolumnaés0), plantegemaraunmodelmatricialquegeneralitzi (1).Seguintelplantejament iniciata[14],elmodelés Y = XB + Ξ,essent B unamatriu p × q deparàmetres i Ξ unmatriu n × q dedesviacionsaleatòries.

L’estimacióde B pelcriteridelsmínimsquadratsés B = (X X) 1X Y ila matriudeprediccióés Y = XB = PY,on P = X(X X) 1X éslamatriude projecció.Òbviament,nohihacaprelacióentre X i Y si B = 0,mentrequela relacióésperfectasi Y = Y.

Eneltestdelahipòtesi H0 : B = 0,sigui E = (Y Y) (Y Y) la«matriuerror». De P2 = P obtenim E = Y Y Y Y.Denotemper H = Y Y la«matriuhipòtesi». Clarament Y Y = H + E.Atèsque Y ésunamatriucentrada,tenimque Y Y és proporcionalaunamatriudecovariàncies.Tenim,doncs,laversiómatricialde ladescomposiciódelavariabilitatenduesparts:ladegudaalahipòtesiila degudaaladesviaciódelahipòtesi(error).

Apliquemaraelcriteridelaraódeversemblança,enaquestcasequivalenta lalambdadeWilks, W = det(E)/ det(E + H).Valorsde W propersa0indiquen quelahipòtesi H0 hauriadeserrebutjadai,pertant, B ≠ 0

Enelnostrecontextdematriusdecoordenadesprincipals,tenim Y = VΛy aixícom Y = PY = UU VΛy .Pertant, E = Λy (I V UU V)Λy laqualcosa implica E + H = Y Y = Λy V VΛy = Λ2 y .Obtenim W = det(I V UU V).

D’altrabanda,d’acordamb (9),lescorrelacionscanòniques ri entreles columnesde X ilesde Y satisfanl’equació Y X(X X) 1X Yvi = r 2 i Y Yvi,ésa dir, Hvi = r 2 i (E + H)vi,on vi éselcorresponentvectorpropi.Aixòimplica Evi = (1 r 2 i )(E + H)vi.Pertant,podemexpressar W entermesdecorrelacions canòniques: W = (1 r 2 1 )×···×(1 r 2 m),on m = min(p,q).Trobemlamateixa mesurad’associació AW = 1 W quehemobtingutabans,vegeu (10),peròara peradadesgenerals. AW val0sinohiharelacióentreelsdosconjuntsde dades,ival1sihihaunarelaciólinealenelsentitquelesmatriusdedistàncies defineixenespaisequivalents.

Exemple. Consideremlataula5ilamatriudesimilaritat S = (sij ),on sij = 1sihiharelaciócomercialsignificativa, sij = 0encascontrari.Larelació comercialinternadecadapaísésmoltintensa,pertantconvindremque sii = 3.

ElllegatdeGalton,Pearson,Fréchetid’altres

Consideremtambélamatriu T = (tij ),onperadospaïsos i i j definim tij = nij / min{ni,nj },essent nij elnombred’articlespublicatsencol laboració. Elsnombres ni, nj sóneltotald’articlespublicatspelspaïsos i i j.Enelcas d’EspanyaiEUAtenim s12 = 1, t12 = 692/8597 = 0.0805.Transformantles similaritatsendistàncies(alquadrat)

δ2 ij (x) = 2(1 sij ),δ2 ij (y) = 2(1 tij ),

tenimque Gx = Hc SHc = UΛ2 x U i Gy = Hc THc = VΛ2 y V .Consideremles coordenadesprincipals UΛx i VΛy iprenemlesduesprimerescolumnesde U i de V.Denotemaquestesduesmatriusdecoordenadesestàndardper U2 i V2. Fentunaanàlisidecorrelaciócanònica,aplicant (9) iatèsque S11 i S22 són matriusidentitat,obtenim Q = U2V2,quetédosvalorssingularsocorrelacions canòniques r1 = 0 9182, r2 = 0 6437.Pertant, AW = 0 9081,queindicauna bonaassociacióentrecol laboraciócientíficaicomercial.

Podemtriaraltrescoeficientsambpropietatssemblants,comaraelproducte r 2 i ,queenaquestcasdonariaunvalorbastantbaix[14].Peròperdiverses raons, AW ésmillor,comesdemostraeneltractamentilacomparaciód’imatges hiperespectrals[31].

Lafigura7éselresultatd’aplicarla relatedmetricscaling [27],tècnicaque permetrepresentarelspaïsostenintencomptelesduesmatriusdesimilaritats considerades.Consisteixadiagonalizarlamatriu

G = Gx + Gy 1 2 (G1/2 x G1/2 y + G1/2 y G1/2 x ),

icalcularlescoordenadesprincipalsconjuntes.Podemveureque G = Gx + Gy enelcasd’ortogonalitatdelesconfiguracionsique G = Gx = Gy enelcasque lesmatriusdedistàncies ∆x , ∆y coincideixin.Larepresentacióespotfertambé aplicantunatècnicaconegudaper multiplefactoranalysis [35],quediagonalitza Gx +Gy i,pertant,ignoralaredundànciaentrelesduesmatrius,perquèprendre lasumaimplícitamentsuposaortogonalitat,ésadir, U V = 0.Considerant G1/2 x G1/2 y + G1/2 y G1/2 x estenenencomptelescorrelacionsentrecoordenades, contingudesenelsproductes U V i V U,iesgaudeixd’algunesdelespropietats deladistànciadeMahalanobis(vegeulasecció13.2).

12MANOVAbasatendistàncies

Suposemquetenim k ≥ 2conjuntsdedadesprovinentsdelespoblacions Ω1,..., Ωk,obtingutsobservant p variablesquantitatives.Enelmodel manova d’unavia,sigui T = B + W ladescomposiciódelamatriudeproductescreuats «total»ensumade«entregrups»i«dintregrups»,vegeu (5),partintde ni observacionsprovinentsde Ωi.Afidecontrastarlahipòtesi: H0 : Ω1 =···= Ωk, encasdenormalitatmultivariantihomogeneïtatdecovariàncies,tenimque W i B fanelpaperde E i H,il’estadísticclàssicperdecidirsobre H0 éslalambda deWilks:

W = det(W)/ det(B + W).

Pertractarambdadesgenerals,suposemquemitjançantunafunciódistància δ entreobservacionsobtenimlesmatriusd’intradistàncies ∆11,..., ∆kk,i lesmatriusd’interdistàncies ∆12,..., ∆k 1k.Lamatriudedistànciesglobalés ∆ Calculantcoordenadesprincipals(nocentrades)peracadamatriudedistàncies, igeneralitzantlaigualtat (1/n) i(xi x)2 = (1/2n2) i j (xi xj )2,obtenim lesmatrius p × p següents:

queverifiquen T = B + n k g=1 n 1 g Wg .Pertant,tenimque tr(T) = tr(B) + n k g=1 n 1 g tr(Wg ).

Calculantlesmitjanesdelesdistàncies(alquadrat),aplicant (14) amb pes1/n,podemobtenirlavariabilitatgeomètricapera ∆ iperala ∆ii decada població Ωi separadament.D’aquestamanera,peradadesgeneralsitreballant nomésambdistàncies,éspossibledescompondrelavariabilitatgeomètrica Vδ (total) = Vδ (entre) + k i=1 ni n Vδ (dintre i), (16)

queseriaunageneralitzacióde (6).Aleshoresuntestperdecidirsihiha diferènciessignificativesentreles k poblacions,podriaestarbasatenelquocient γ = Vδ (entre)/Vδ (total);vegeu[14].

Recentment,M.Andersonid’altres,amblatècnicaanomenada permanova, hancontinuatelmateixenfocamentambdadesdepenentdedosomésfactors (incloent-hiinteraccions),totiquelajustificacióteòricaésencarainsuficient.

Hihaunaversióprobabilísticade (16),relacionadaamb (7).Consideremun vectoraleatori X quetéperdensitatlamixtura f(x) = w1f1(x) +···+ wkfk(x), ontoteslesdensitatstenenelmateixsuport S.Suposemqueexisteixuna representació ψ : S → E,on E ésunespaieuclidià(odeHilbertseparable).

Aleshoreslavariabilitatgeomètricade X,respecteaunadistància δ,definida coma[30]

Vδ(X) = 1 2 S×S δ2(x, y)f(x)f(y)dx dy (17) verifica

Vδ(X) = V(µ1,...,µk) + k i=1 wiVi,

essent V(µ1,...,µk) = 1 2 k i,j=1 wiδ2(µi,µj )wj = k i=1 wiδ2(µi,µ),on µi = Ei[ψ(X)], δ2(µi,µj ) =||µi µj ||2 , µ = w1µ1 +···+ wkµk.Lavariabilitat geomètrica Vi éslade(17)peròcanviant f per fi;vegeu[21].

13Mésconceptesmultivariants

13.1Correlacióintraclàssicamultivariant

Consideremdenoulacorrelacióintraclàssica (8).Defet,ladefinicióunivariant decorrelacióentreduesobservacions yij i yij éspràcticaperòconvencional. Mésaviathemd’acceptarque ρI ésunamesurad’homogeneïtatentrelesmostres d’unmateixgrupofamília.Desd’aquestaperspectiva,resultaraonabledefinir unamesuradecorrelacióintraclàssicamultivariantentrelesobservacionsd’una mateixasubpoblacióquandisposemde k subpoblacions.

Enelmodel manova esmentatabans,sigui T = B + W,iconsiderem n0 = n k i=1 n2 i /n /(k 1).Lamesuraproposada,quegeneralitza(8),és

ΦI = tra(B)/(k 1) tra(W)/(n k) tra(B)/(k 1) + (n0 1) tra(W)/(n k) . (18)

Mésgeneralment,relacionant (16) amblestracesde B i W,unadefinicióde correlacióintraclàssica peradadesgenerals,treballantambunadistància δ entreobservacions,seria:

ΦI = Vδ (entre)/(k 1) k i=1( ni n )Vδ (dintre i)/(n k) Vδ (entre)/(k 1) + (n0 1) k i=1( ni n )Vδ (dintre i)/(n k) .

Exemple. Peralesdadesdeflorsiris,formadesperlesespèciesIrissetosa,Iris versicoloriIrisvirginica,empradesperR.A.Fisherperil.lustrarl’anàlisidiscriminant[15],tenim k = 3, n1 = n2 = n3 = 50.Pertant, n0 = 50.Aplicant (18), obtenim ΦI = 0.907.Hiha,pertant,unabonahomogeneïtatentrelesflors dintredecadaespècie.

13.2Fal.làciaecològicamultivariant

Lafal.làciaecològicaambduesvariables(figura3)espotinterpretarenelsentit quelesdadesglobalssegueixenunadirecció,gairebéperpendicularaladirecció delesdadesdecadasubpoblació.

Afidedetectarlafal.làciaambdadesrelativamentcomplicades,suposem duespoblacionsambvectorsdemitjanes µi = (µi1,...,µip) , i = 1, 2,imatriu decovariàncies(comuna) Σ = [σij ].LadistànciadeMahalanobisentreles duespoblacionsesdefineixper (µ1 µ2) Σ 1(µ1 µ2).Aquestadistància(al quadrat)ésinvariantpertransformacionslinealsdelesvariables,téencompte lescorrelacionsiapareixdemaneranaturalenmoltsmodelsmultivariants.

Sisuposemquelesvariablesestanincorrelacionades, Σ seriadiagonal,ila distànciadeMahalanobisesdevindria

(µ1 µ2) [diag(Σ)] 1(µ1 µ2) = p j=1 (µ1j µ2j )/σ 2 j ,

queesconeixper distànciadePearson.

Aleshores,tenintencompteque R2 = r R 1r i r r sónformalmentsimilarsaunadistànciadeMahalanobisidePearson,respectivament,entre r i 0, (2)suggereixladesigualtat

(µ1 µ2) Σ 1(µ1 µ2)>(µ1 µ2) [diag(Σ)] 1(µ1 µ2). (19)

CuadrasiFortiana[28]provenque (19) espresentasiladirecciódelsegment queuneixelspunts µ1 i µ2 ésessencialmentortogonalaladireccióprincipal (comuna)delesdadesdecadasubpoblació,queésdonadaperlesprimeres componentsprincipals(variablescombinaciólinealambmàximavariabilitat). Pertant,lafal.làciaecològicaestariarelacionadaambladesigualtat(19).

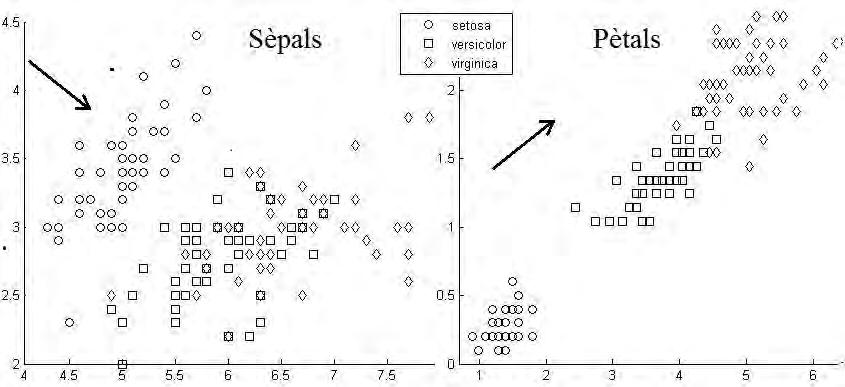
Figura8: Representaciódetresespèciesdeflorsdelgènere Iris,segonslongitudiampladadesèpalsidepètals.Peralssèpals,ladistànciadeMahalanobispredominasobreladePearson,ielscentres delespoblacionssegueixenunadirecciógairebéortogonalalaprincipaldelesdadesdecadaespècie.Peralspètals,ladistànciadePearsonpredominasobreladeMahalanobisielscentresdelespoblacions segueixenlamateixadireccióquelaprincipaldelesdades.

Exemple. Lafigura8il.lustralafal.làciaamblesdadessobreflorsdelesespècies Irissetosa,versicolorivirginica,consideradesalaseccióanterior.Lafigura8 (esquerra)representalestresespèciessegonslongitudiampladadesèpals delaflor.Lataula6(esquerra)contélesdistànciesdeMahalanobis(asobre deladiagonal),quepredominensobrelesdePearson(asotadeladiagonal).

Aleshoresladirecciódelscentresdelespoblacionsésgairebeortogonalala direccioprincipaldelesdades,i,pertant,hihafal làciaecològica.Amés,les correlacionsajuntantlescentcinquantaobservacionssónnegatives,peròles correlacionsdintredecadaespèciesónpositives.Tambéalafigura8(dreta), utilitzantaralongitudiampladadelspètals,observemelcontrari,ipertantno hihafal.làcia.LesdistànciesdeMahalanobis,taula6(centre),sónméspetites quelesdePearsoniladirecciódelscentresdelesespèciesésgairebélamateixa queladelesdadesdecadaespècie.Aixòconcordaamblescorrelacions,que resultentotespositivesconsiderantlescentcinquantaobservacions,itambé calculant-lesperacadaespècieperseparat.

Noresultatanfàcilvisualitzarlafal.làciaconsiderantlesquatrevariables. Aleshoresésquanresultaútilladesigualtat (19).Aquestaescompleixcomparant setosa amb versicolor iamb virginica.D’acordamblataula6(dreta),lasumade lesdistànciesdeMahalanobisidePearson,considerantlongitudsiamplades desèpalsipètals,dóna286 7i277 0,respectivament.Mahalanobispredomina sobrePearsoni,pertant,hihafal làciaecològicaensentitmultivariant.

Sèpals Pètals Sèpalsipètals

Iris set.vers.virg. set.vers.virg. set.vers.virg. setosa –14 921 6 –48 2112 –89 8179 versicolor 7.0–1.61 70.1–14.0 77.1–17.2 virginica 11.21.96– 16620.7– 17722.7–

Taula6: DistànciesdeMahalanobis(sobreladiagonal)iPearson(sotala diagonal),entretresespèciesdeflorsdelgènere Iris,considerantsèpals, pètalsilesquatremesuresjuntes.

13.3Coeficientsd’asimetriaicurtosi

Siguin x1,..., xn lesobservacionsde p variablessobreunapoblació.Denotem per x elvectordemitjanesiper S lamatriu p × p decovariàncies.Considerant elsproductesescalarsdeMahalanobis dij = (xi x) S 1(xj x),sónmesures multivariantsd’asimetriaicurtosi(proposadesperK.V.Mardia)lesquantitats

Enelcasdedistribuciónormalmultivariant Np(µ, Σ),elsvalorspoblacionals són β1 = 0i β2 = p(p + 2). Enlamateixalíniadelasecció12,suposemdadesgenerals(possiblement mixtes),descritesperunamatriu n×n dedistàncies ∆.Calculemlacorresponent matriudeproductesinterns G = UΛ2U ,queproporcionalamatriudecoordenadesprincipals X = UΛ.Aleshores,posant (aij )(m) = (am ij ),lageneralització, entermesdedistàncies,delesmesuresd’asimetriaicurtosiés: β1 = n1n[(GG )(3)]1n, β2 = n tra[(GG )(2)],

on G = UΛ 2U éslainversageneralitzadade G.Elsvalorsteòricsdereferència serien β1 = 0i β2 = m(m + 2),on m éselnombredecoordenadesprincipals, ésadir,elnombredecolumnesde X

Exemples. AmblesdadesdeGaltons’obtenen b1 = 0.04i b2 = 9.0,quesón bastantsemblantsalsvalorsteòrics β1 = 0i β2 = 8delanormalbivariant.Per alescinquantaflorsdel’espècie Irisvirginica,s’obté b1 = 3.15i b2 = 24.3, essentelsvalorsteòrics β1 = 0i β2 = 24encasdemultinormalitat.Lesdades tenenasimetriaiunacurtosimoltproperaalanormal.Peralataula5(part superior),siconsideremlesduesprimerescoordenadesprincipalscalculades sobrelamatriu T (secció11),obtenim β1 = 2.2i β2 = 5.9,queesdesvienuna micade β1 = 0i β2 = 8.

Part III:Distribucionsbivariantsambmarginals donades

14ClassesdeFréchet-Hoeffding

QuanK.PearsonvaestudiarlesdadesdeGaltonsobreestaturesdeparesi fills,aixícomlessevespròpiesdades(ambA.Lee)[53],vatenirmoltacura d’ajustar-lesaunadistribuciónormalbivariant.Aquestadistribucióvaserun modelmatemàticqueresumiacorrectamentlesdadesobservades.Pertant,una altramanerad’abordarl’associacióestadísticaconsisteixautilitzarlateoriade distribucionsbivariantsambmarginalsdonades,queestàrelacionadaambla teoriadecòpules.

Suposemque H(x,y) = P[X ≤ x,Y ≤ y] éslafunciódedistribucióconjuntadelvectoraleatori (X,Y),definitsobreunespaideprobabilitats (Ω, A,P). Lesdistribucionsmarginalssón F i G essent

F(x) = P[X ≤ x] = H(x, ∞),G(y) = P[Y ≤ y] = H(∞,y).

Consideraremque H ∈F(F,G),essent F(F,G) laclassedefuncionsdedistribucióbivariantsambmarginals F i G.Unexemplededistribucióbivariant H0 ∈F(F,G) és H0(x,y) = F(x)G(y),quecorresponalcasd’independència estocàstica.

Fréchet[36]vaintroduirlesfuncions H i H+ següents:

H (x,y) = max{F(x) + G(y) 1, 0},H+(x,y) = min{F(x),G(y)}, ivademostrar7 ladesigualtat

H (x,y) ≤ H(x,y) ≤ H+(x,y).

7 Quanel1977,alabibliotecadelSeminariMatemàticdeBarcelona,vaigconsultarelnúmero corresponenta1951delarevistaonFréchetvapublicarelseufonamentalarticle,elsplecsestaven sensetallar.Eldocumentnohaviaestatconsultatabans.Percert,ésunacoincidènciaqueelsúnics funcionarisperoposiciódelSeminariMatemàtic—l’eminentanalistaF.Sunyer-Balaguer(1967)i C.M.Cuadras(1974–1979)—erendeFigueres(Girona).

Aleshoreslesfuncions H ,H+ ∈F(F,G),anomenades cotesinferior i superior deFréchet-Hoeffding,verifiquen:

H = H F(X) = 1 G(Y) (q.s), H = H+ F(X) = G(Y) (q.s).

Aixósignificaquesiladistribucióés H ,hihadependènciafuncionalnegativa (Y ésfunciódecreixentde X).Siladistribucióés H+,hihadependènciafuncional positiva(Y ésfunciócreixentde X).

Exemple. Suposemqueduesvariables X i Y mesurenelmateixfenomenperò seguintprocedimentsdiferentsiquehihaunarelaciónolinealentre X i Y . Sidisposemde n parelles (xi,yi),aleshorespodemaplicaralgunmodelde regressió.Peròsinomésdisposemdeladistribuciódecadavariableperseparat, larelació F(x) = G(y) potresoldreelproblema.Comail.lustració,suposem que F(x) = (x 1)2 si1 ≤ x ≤ 2, G(y) = [1 e (y 2)/(1 e 2) si2 ≤ y ≤ 4. De y = G 1(F(x)) obtenim y = 2 ln[1 (1 e 2)(x 1)2].Tanmateix enunasituaciópràcticahauremdetreballaramblesfuncionsdedistribució empíriques Fn(x) i Gn(y),comenelcasdelamesuradeldiàmetred’unbacteri, seguintdosprocedimentsdiferents(analitzadordepartículesicitometria). A[45],seguintaquestprocediment,elsautorsobtenenpolinomisdesegon grauperadiversesclassesdebacteris.Perexemple,pera E.coli obtenen y = 8.74x2 6.71x + 2.08,on y (quevade0.7 × 10 3 finsa1.3 × 10 3)ésel diàmetreenmicresi x (quevade0 35 × 10 3 finsa0 65 × 10 3)ésunamesura defluxcitomètricqueproporcionaunanalitzadordepartícules.

14.1CorrelacionsdeHoeffding

Hoeffding[43]vademostrarquelacovariància,siexisteix,espotcalcularen termesdelesfuncionsacumulatives H, F i G,aplicant cov(X,Y) = R2 [H(x,y) F(x)G(y)]dxdy. (20)

Aleshores,sidenotemper ρ elcoeficientdecorrelacióperaladistribució H,es compleixladesigualtat

ρ ≤ ρ ≤ ρ+,

essent ρ i ρ+ elscoeficientsdecorrelaciócorresponentsalescotes H i H+.

Exemple. Sidesconeixemladistribucióconjuntade X i Y (comal’exemple anterior),lescorrelacionsmàximaimínimaquepodemobtenir,fixadesles marginals,són ρ+ i ρ .Perexemple,si X ésuniformesobre (0, 1), F(x) = x, 0 <x< 1,i Y ésexponencial, G(y) = 1 e y , y> 0,aleshores ρ+ = √3/2i ρ =−√3/2.

14.2Desenvolupamentsdiagonals

D’acordamb (11),enunmodelbivariantdiscret,onelrangdelesvariablesés numerable,podemexpressarladensitatdeprobabilitatconjunta pij comuna suma pij = ric

, on {sn} sónvalorssingulars,quefanelpaperdecorrelacionscanòniques.

L’anàlisidecorrespondènciesseriauncasfinitdeldesenvolupamentdiagonal quepresentemtotseguit.

SuposemqueladerivadadeRadon-Nikodym dH(x,y)/dF(x)dG(y) existeixiquelamesura dH ésabsolutamentcontínuarespectea dF × dG.Ésadir, podemexpressar H integrantrespectea dF(x)dG(y).Améssuposemqueel coeficientdecontingènciadePearson Φ2,definitcom

Φ2 + 1 = b a d c [dH(x,y)]2/[dF(x)dG(y)],

ésfinit.Aleshorespodemobtenireldesenvolupament:

dH(x,y) = dF(x)dG(y) 

1 + n≥1 ρnan(x)bn(y)

. (21)

Silesdensitatsconjuntaimarginals(respectedelamesuradeLebesgue) són h(x,y), f(x) i g(y),llavorspodemescriureeldesenvolupament (21) com h(x,y) = f(x)g(y) 

1 + n≥1

nan(x)bn(y)

(22)

Aleshores {an(x)}, {bn(y)},anomenadesfuncionscanòniques,sónconjuntsdefuncionsortonormals,quesóncompletsrespectede f i g.D’altra banda

E[an(X)] = E[bn(Y)] = 0,E[an(X)bm(Y)] = ρnδmn, essent ρn l’enèsimacorrelaciócanònicaentre X i Y .Les an(X), bm(Y) sónles variablescanòniques.Eldesenvolupamentdiagonal (22) vaserintroduïtper Lancaster[47].

Disposantlescorrelacionscanòniquesenordredescendent,aleshores ρ1 és laprimeracorrelaciócanònicaiéslamàximacorrelacióentreunafuncióde X i unafuncióde Y

ρ1 = supcor(α(X),β(Y)).

Esverifica0 ≤ ρ1 ≤ 1iespotprovarque ρ1 = 0siinoméssi X i Y són estocàsticamentindependents.AmésRényi[55]vademostrarque ρ1 ésl’única mesuradedependènciaqueverificasetpostulatsproposatsperellmateix.Per trobar ρ1,vegeu[52].Sitenim n mostres (xi,yi),unprocedimentpràcticperestimar ρ1 consisteixaaplicaranàlisidecorrelaciócanònica(secció9)apotències de xi ide yi,ésadir,relacionar (xi,x2 i ,....,xm i ) amb (yi,y 2 i ,...,y m i )

Exemple. Unelementde F(F,G),queapareixsovintalesaplicacionsienla construcciódemodelsbivariants,ésladistribucióFGM(degudaaFarlie,Gumbel iMorgenstern),quedepèndelparàmetre θ,

Hθ (x,y) = F(x)G(y){1 + θ[1 F(x)][1 G(y)]}, 1 ≤ θ ≤ 1

Elcoeficientdecorrelacióés ρ = θ/3.Aquestcoeficientverifica 1/3 ≤ ρ ≤ 1/3 iéstalque |θ/3| éslaprimeracorrelaciócanònica.Defet,nomésn’hihauna,i laFGMseriaelcasméssenzilldedesenvolupamentdiagonal.

14.3Còpules

Sigui (U,V) unvectoraleatoriambvalorssobre I2,essent I = [0, 1].Unacòpula ésunafunciódedistribució C(u,v) ambmarginalsuniformes (0, 1).Pertant, C(u,v) verifica

C(0,v) = C(u, 0) = 0,C(u, 1) = u,C(1,v) = v.

Elcasd’independènciaentre U i V corresponalacòpula C0(u,v) = uv.Les cotesdeFréchet-Hoeffdingsón

C (u,v) = max{u + v 1, 0},C+(u,v) = min{u,v}.

Peratotacòpula C esverifica

C (u,v) ≤ C(u,v) ≤ C+(u,v),u,v ∈ I. (23)

LescòpulessónimportantspelteoremadeSklar,quediuqueatotadistribució H lipodemassociarunacòpula CH talque H(x,y) = CH (F(x),G(y)) Pertant,n’hihaprouaestudiarcòpulespergenerardistribucionsbivariants. Perexemple,lafamíliadecòpules

Cθ (u,v) = uv[1 + θ(1 u)(1 v)], 1 ≤ θ ≤ 1, (24) generaladistribucióFGM.Noméshemdesubstituir u i v per F(x) i G(y). Lescòpules,tambéanomenades funcionsdedependència o representacionsuniformes,capturenl’associaciód’unparell (U,V) iengeneral,aplicant elteoremadeSklar,descriuenl’associaciódequalsevolparelldevariables aleatòries (X,Y)

Permesurarl’associacióentre X i Y ambdistribucióconjunta H icòpula C, homutilitzaelscoeficientsdecorrelació ρS deSpearmani τ deKendall,quees defineixenper

Totique ρS i τ estandefinitsentermesdecòpules,tenensentitperaqualsevol distribucióconjunta H(x,y).Ambduesmesuresd’associacióverifiquen:

1. Sóninvariantsrespectedetransformacionsestrictamentcreixentsde X i Y .

2. τ = ρs = 0si H = H0 (independènciaestocàstica).

3. τ = ρs =−1si H = H (cotainferiordeFréchet-Hoeffding).

4. τ = ρs =+1si H = H+ (cotasuperiordeFréchet-Hoeffding).

Numèricament ρs i τ sónsemblants.S’hanestudiatmoltlesrelacionsentre ρS i τ,lamésconegudadelesqualsés

1 ≤ 3τ 2ρS ≤ 1.

Generalmentesfaservir τ siespotcalcularfàcilmentamblacòpulatriada (casdelesanomenadescòpulesarquimedianes).Esfaservir ρS sielseucàlcul resultamésassequiblequeelde τ.

Exemples. PeraladistribucióFGM,ambcòpula (24),s’obté ρS = θ/3i τ = 2θ/9. Espotdonarelcasque ρS valgui0peròlesvariablessiguindependents.Per exemple:

C(u,v) = uv + (2u 1)u(1 u)(2v 1)v(1 v)/2, noéslacòpulaindependència,però ρS = 0.Amésamés,enaquestexemple tambéés τ = 0.

UnaltreexempleenseldónaladistribuciódePlackett,ques’aplicacom aalternativaalanormalbivariant.Aquestadistribucióapareixenelcontext del’estudideladependènciaentaulesdecontingència2 × 2iesdefineixcom a H(x,y) ambmarginals F(x) i G(y),detalmaneraque

θ = H(x,y)[1 F(x) G(y) + H(x,y)] [F(x) H(x,y)][(G(y) H(x,y))] ésconstantperatot x, y.Elparàmetre θ> 0mesuraladepèndència.Hi haindependènciaestocàsticasi θ = 1.Suposemaraquelesdistribucions marginalssóndeCauchy,distribucióquenotémoments(lamitjanailavariància noexisteixen).Aleshoresnopodemcalcularelcoeficientdecorrelaciólineal dePearson,però,emprantlacòpulacorresponent,podemcalcularlarhode Spearman,queperaladistribuciódePlackettés

θ = θ + 1 θ 1 2θ (θ 1)2 log(θ).

Finsaquíhemresumitelsaspectesmésbàsicsdelesdistribucionsamb marginalsdonadesilessevescòpules.Peraunestudiamplid’aquesttema, vegeu[51].

Silamodelitzaciódelesdadesbivariantslapodemdescriuremitjançantuna còpula,tenimuncamíidoniperesbrinareltipusd’associacióentrelesvariables. Peròhihamoltesfamíliesdecòpules:simètriques,arquimedianes,max-estables,

ElllegatdeGalton,Pearson,Fréchetid’altres 41

singulars,etc.Recentmentestendeixaidentificarprimerl’estructurad’una còpulapartintdelesdades[48]idespréstriarlacòpulaescaient.

Lesseccionssegüentscontenenresultatsqueresumeixentresarticles[13, 17,20]sobrecòpules.

15Lacovariànciaentreduesfuncions

Sigui (X,Y) unvectoraleatoriambfunciódedistribució H imarginals F i G. Vegemprimerduesgeneralitzacionsde (20) ideldesenvolupament (21).D’una bandatenimque

cov(α(X),β(Y)) = R2 [H(x,y) F(x)G(y)]dα(x)dβ(y), suposantquelesfuncions α i β verifiquenlescondicionsd’existènciadela variància[3,11].D’altrabandatenimque

H(x,y) F(x)G(y) = n≥1 ρn b a M1(x,s)dan(s) d c M2(t,y)dbn(t), (25)

on M1(x,y) = min{F(x),F(y)}− F(x)F(y), M2(x,y) = min{G(x),G(y)}− G(x)G(y);vegeu[12].

Convéobservarque (25) ésundesenvolupamentdelafunciódedistribucióen termesdecorrelacionscanòniquesicotesdeFréchet.Defet,esteminteressatsa trobarlescorrelacionsilesfuncionscanòniquesenelcasdecòpules.Altrament dit,hemdetrobarfuncions φ1 i φ2 talsque

ρ = supcor(φ1(U),φ2(V)). (26) Peraaquestfiensseràútilelresultatsegüent.

Teorema1. Siguin C, C∗ duescòpulescorresponentsadosvectorsaleatoris (U,V) i (U ∗,V ∗).Si α(u) i β(v) sónfuncionsdevariacióafitadadefinides sobre I = [0, 1],aleshores

cov(α(U),β(V)) cov(α(U ∗),β(V ∗)) = I I [C(u,v) C∗(u,v)]dα(u)dβ(v).

Enparticular,lacovariànciaentre α(U) i β(V) és

cov(α(U),β(V)) = I I [C(u,v) uv]dα(u)dβ(v), (27)

ilavariànciade α(U) és

var[α(U)] = I I [min{u,v}− uv]dα(u)dα(v). (28)

Apartird’arasuposaremque (U,V) ésintercanviable.Altramentdit,la còpula C(u,v) ésunafunciósimètrica.Aleshorespodemsuposar φ1 = φ2 a(26).Elproblemaesredueixatrobar ρ i φ detalmaneraque

ρ = supcov(φ(U),φ(V))/ var[φ(U)].

16Operadorsintegrals

Consideremunacòpula C,lacotasuperior min{u,v},quedenotemper M,ila còpulad’independència uv,queanomenem Π.Tenimque C ≺ M enelmateix sentitquea (23).Aleshoresésclarquealesintegralsde (27) i (28) hiintervenen elsnuclissimètrics K = C Π i L = M Π,queverifiquen K ≺ L.

Definimacontinuacióelsoperadorsintegralsielsproductesescalarsrelacionatsambunacòpula C.Advertimquefemservirelmateixsímbol K per alnucliiperal’operadorintegralassociat.Suposaremquetoteslesfuncions pertanyenalconjunt B defuncionsdevariacióafitadaal’interval I = [0, 1]. Sabemque B ⊂ L2(I)

Definició2. L’operadorintegral K sobre B és

Kϕ(u) = I K(u,v)dϕ(v).

Demanerasimilardefinim Lϕ i Tϕ essent T = aK + bL

K i L proporcionenlacovariànciailavariància,respectivament.Elsoperadors integralstambéserveixenperresoldreequacionsdiferencials.

Exemple. Considereml’equació y + f(x) = 0, y(0) = y(1) = 0,on f(x) és unafunciócontínuaal’interval (0, 1).Espotprovarquelasolucióés y(x) = I L(x,s)dF(s),essent F(x) unaprimitivade f(x) i L(s,t) = min{s,t}− st

Definició3. Elproducteescalargeneralitzatentrelesfuncionsintegrables φ, ϕ de B és

(φ,Kϕ) = I2 K(u,v)dφ(u)dϕ(v).

Demanerasimilar,definim (φ,Lϕ), (φ,Tϕ) i (Kφ,Lϕ).

Definició4. L’operador K és L-compactesiperatotasuccessió L-afitada {φn}, enelsentitque (φn,Lφn) ésfinit,lasuccessió {Kφn} contéunasubsuccessió convergent {Kφn(i)}.Ésadir, Kφn(i) → φ∗,enelsentitqueexisteix φ∗ talque Kφn(i) φ∗ L → 0quan i →∞

Sónbenconegudeslespropietatsdelsoperadorsal’espai L2(I) quan K és generali L ésl’operadoridentitat.Peròaquí L,quepermettrobarlavariància, noéslaidentitat.

Lespropietatssegüentsespodendemostraraplicant (27) i (28) iadaptant propietatsconegudesenelcasque L siguil’operadoridentitat.

1.Elsoperadorsintegrals K i L sónlinealsisatisfan (φ,Lφ) ≥ max{(φ,Kφ), 0}≥ 0.

Pertant, L ésdefinitpositiuielproducteescalar (φ,Lϕ) defineixlanorma φ L = [(φ,Lφ)]1/2 .

2. K ésdeHilbert-Schmidt, i.e., I2 K(u,v)2 dudv< ∞.

3.L’operadorintegral K és L-compacte.

4. Si K éslineali L-compacte,aleshores T = aK + bL éstambécompacteper aqualsevolparelladeconstants a,b ∈ R.

Clarament,sicanviem K = C Π per L = M Π,lespropietatsanteriors segueixenessentvàlides,atèsque L éstambéladiferènciadeduescòpules.

17Anàlisigeneralitzadadefuncionspròpies

Vegemaraalgunsresultatssobrefuncionspròpiesivalorspropisrelacionats ambelsoperadors K i L

Definició5. Unafunciópròpiageneralitzadade K respectede L éslaparella (φ,λ),on φ ésunafunciói λ ésunnombrereal,talsque I K(u,v)dφ(v) = λ I L(u,v)dφ(v), (29)

uniformementen u ∈ I.Hoexpressemper Kφ = λLφ.

Exemple. Siguilacòpula Fλ = λM + (1 λ)Π.Aleshores K = Fλ Π = λ(M Π).

Pertant, Kφ = λLφ on L(s,t) = min{s,t}−st i φ ésqualsevolfuncióintegrable sobrel’interval (0, 1)

Si (φ,λ) ésunaparellapròpia(funcióivalorpropi)de K respectede L, amb λ ≠ 0,tenimque (φ,Kφ) (φ,Lφ) = λ. (30)

Noésfàcilprovarelcontrari:si (φ,λ) satisfà (30) uniformementen u ∈ I, aleshoresésunaparellapròpiaquesatisfà(29).

Presentemacontinuacióalgunespropietatsdelesparellespròpies.Aquí K L, K i T sónnormesdelsoperadors K i T .

Teorema6. Sigui K L = sup |(ξ,Kξ)/(ξ,Lξ)|, K = sup |(ξ,Kξ)/(ξ,ξ)| i T = sup |(ξ,Tξ)/(ξ,ξ)|,essent ξ ≠ 0,on T = aK + bL, a,b ∈ R.Si α i β són duesfuncionsde B,aleshores:

1.Si K ésdefinitpositiu, (α,Kβ) ≤ min{ K L α L β L, K α β } (31)

2.Engeneral, |(α,Tβ)|≤ T α β . (32)

Ambl’ajutd’aquestteoremaesdemostraqueexisteixalmenysunvalor propi,queenelnostrecassignificaqueexisteixlamàximacorrelaciócanònica. Elteoremasegüentésbenconegutquan L ésl’operadoridentitat.Enelnostre

contextdedosoperadorsgeneratspercòpules,lademostraciócanviabastanti noésfàcil.8

Teorema7. K téalmenysunvalorpropirespectede L. Comenelcasclàssic(on L éslaidentitat),lademostracióconsisteixaprovar queelvalorpropi,quesempreexisteix,és

λ1 = sup ξ≠0 (ξ,Kξ)/(ξ,Lξ). (33)

Peròaquí L noéslaidentitatilademostraciónecessitaincorporaralgunes innovacions[17].

Araquesabemquehihavalorspropis,mencionemalgunespropietats.

1.Si λ ésunvalorpropi,aleshores λ ≤ λ1 ≤ 1,on λ1 esdefineixa(33).

2. Si ψ i ψ∗ sónfuncionspròpiesambvalorspropis λ ≠ λ∗,aleshores (ψ,Kψ∗) = (ψ,Lψ∗) = 0.

3. Sigui {ψn,λn} unconjuntdeparellespròpiestalsque (ψn,Lψn)> 0.Si {ψn,λn} ésinfinitnumerable,aleshoreslimn→∞ λn = 0.

4. Sigui {ψn,λn} unconjuntdeparellespròpiestalsque (ψn,Lψn)> 0. Definim

Φn(u) = I L(u,s)dψn(s). (34)

Esverifica Φn(0) = Φn(1) = 0, Φn =−ψn ilafunciócontínua Φn té diversoszerosa I.

RecordemaraelteoremadeMercer[2].Si A(s,t) éselnuclid’unoperador integralcontinu,simètricidefinitnonegatiu,i {ψn,λn} éselconjuntnumerable deparellespròpies,onels λn sónpositiusi ψn ésunsistemaortonormal, aleshores

A(s,t) = n≥1 λnψn(s)ψn(t), (35) onlasèrieconvergeixabsolutamentiuniformementen s, t

Si A ésl’operadorambnucli L(u,v) = min{u,v}− uv,iconsideremlesfuncions hn(x) = x 0 ψn(s)ds,podemobtenirunasuccessióortogonaldevariables aleatòries,quepermetdesenvolupar U (iengeneralqualsevolvariable X)en sèriedeltipus X = n≥1 dnhn(X),onlaconvergènciaésenmitjanaquadràtica. Vegeu[16,24,26].

Exemple. Suposem U ambdistribucióuniformesobre (0,1). Aleshores min{s,t}− st = n≥1 λnψn(s)ψn(t),essent ψn(x) =√2sin(nπx), λn = 1/(nπ)2 , hn(x) = [√2/(nπ)][1 cos(nπx)]

Enelcasdedosoperadorsintegrals K i L,eldesenvolupamentensèrie (35) presentaalgunesmodificacions.

8 Donadesduesmatriussimètriques A i B,lasegonadefinidapositiva,noésimmediatprovar quehihaalmenysunvalorpropide A respectede B (un λ talque Av = λBv),senseferúsde matriusinversesnideterminants,conceptesquenopodemaplicar(engeneral)treballantamb operadorsintegrals.

Teorema8. Sigui {ψn,λn} elconjuntnumerabledeparellespròpiesde K respectede L,talsque (ψn,Lψn) = 1.Suposemque K i L sóndosoperadorsintegrals continus,simètrics,essent L definitpositiu.Aleshoresésvàlideldesenvolupament

enelsentitque K(u,v) n i=1 λi I L(u,s)dψi(s) I L(t,v)dψi(t)2 2 → 0 si n → ∞,uniformementen u,v ∈ I.Amés,si {λn} ésinfinitnumerable,escompleix que limn→∞ λn = 0.

Ressaltemqueelsvalorspropispodensernegatiusiqueperacertescòpules, eldesenvolupament(36)podriaserunaintegralenllocd’unasèrie.

Sifemúsdelafunció(34),veiemfàcilmentque K(u,v) = n≥1 λnΦn(u)Φn(v). (37)

Exemple. Consideremlacòpula

C(u,v) = uv + u(1 u)v(1 v) + (2u 1)u(1 u)(2v 1)v(1 v)/2.

Si K(u,v) = C(u,v) uv i L(u,v) = min{u,v}− uv,elsvalorspropisde K respectea L són λ1 = 1/3i λ2 = 1/10.Esverifica K = 1 3 Lψ1 ⊗ ψ

Lψ2 ⊗

2L, essent ψ1(u) = √3(1 2u) i ψ2(u) = √5(6u2 6u + 1) lescorresponents funcionspròpies.

18Anàlisicanònica

Apliquemaraaquestesquemaalescòpules.Elresultatsegüentrelacionales parellespròpiesamblesfuncionsicorrelacionscanòniques.

Teorema9. Sigui (U,V) unvectoraleatoriquetéperdistribuciólacòpula C. Suposemque φ : I → R ésunafunciótalque var[φ(U)] ésfinita.Consideremels operadorsintegrals K = C Π i L = M Π.Esverifica:

1.Elcoeficientdecorrelacióentre φ(U) i φ(V) és cor(φ(U),φ(V)) = (φ,Kφ) (φ,Lφ) , (38) essent (φ,Kφ) = cov(φ(U),φ(V)), (φ,Lφ) = var[φ(U)]

2. Si φ ésunafunciópròpiade K respectea L,aleshores φ ésunafunció canònicai (φ,Kφ)/(φ,Lφ) = ρ éslacorresponentcorrelaciócanònica.

Pertant,apartirde(36),podemexpressarlacòpula C per

C = Π + n≥1

ρnLφn ⊗ φnL, (39) queseriaunavariantde(25).

Tenintencomptepropietatsgeomètriquesbasadesenladistànciakhi quadrat (13),vegeu[16, 29],podemdefinirladimensiód’unacòpulacom lacardinalitatdelconjunt {λn} devalorspropisde K respectea L.

Tenimaleshores:

1.Còpuladedimensió0:éslacòpulaindependència Π(u,v) = uv.

2.Còpuladedimensió1:unexempleéslacòpulaFGM,definidaa(24).

3.Còpuladedimensió2:unexempleés

C2(u,v) = uv +θ1u(1 u)v(1 v)+θ2(2u 1)u(1 u)(2v 1)v(1 v), (40) on (θ1,θ2) pertanyaunaregiócontingudaa [ 2, 2] × [ 1, 2]

4. Còpuladedimensióinfinitanumerable:unexempleéslacòpulaAMH(Ali, MikhailiHaq):

AMHθ (u,v) = uv/[1 θ(1 u)(1 v)], 1 ≤ θ ≤ 1 (41)

5. Còpuladedimensiócontínua,ésadir,infinitanonumerable:unexemple éslacòpuladeCuadras-Augé:

CAθ (u,v) = (uv)1 θ (min{u,v})θ , 0 ≤ θ ≤ 1 (42)

Aquestacòpulapresentaunanovetatimportantenlateoriadelesfuncions pròpies,tradicionalmentbasadaenelsupòsitqueelsvalorspropisformenun conjuntnumerable.Sobreaixòenparlaremalasecciósegüent.

18.1Ajustd’unacòpulaperunaaltradeconeguda

Unproblemadelescòpules(idelsmodelsengeneral),ésquenosempresabem quinaéslaquepodemajustaralesdadesobservades.Suposemquetenimdues còpules: CM ,lacòpulaquefemservircomunmodel,i CT ,lacòpula«veritable», laqueveritablementsegueixenlesnostresdadesbivariants. Suposemqueeldesenvolupamentcanònic

dCM (u,v) = dudv + n ρnAn(u)duBn(v)dv

de CM existeixiésconeguda,essent An i Bn funcionscanòniquesunitàries (mitjana0ivariància1).Ensinteressaaproximar CT perunacombinaciólineal finitadecorrelacionsifuncionscanòniques.Ditambmésprecisió,volemobtenir l’aproximació(vegeu[25])

dCM (u,v) dudv 1 + k i=1 ciAi(u)Bi(v),

on c1,...,ck sóncoeficientsrealsqueminimitzenl’expressió

dCM (u,v) dudv dudv k i=1 ciAi(u)Bi(v)

2 dudv. (43)

Teorema10. Suposem (U,V) ∼ CT .Elscoeficientsqueminimitzen (43) són ci = ρi,essent

ρi = cor(Ai(U),Bi(V)),i = 1,...,k.

L’avantatged’aquestprocedimentésclar:coneixemlesfuncionscanòniques Ai i Bi i,pertant,podremcalcular(mitjançantestimacióestadística)les correlacionsentrelesparelles Ai(U) i Bi(V) respectedelaveritablecòpula CT , queéslaquesegueixenlesnostresdades,peròqueengeneraldesconeixem.

θ

1 0.27110.02170.0055 0.2710 0.1817 0.1815

0 5 0 14890 00800 0017 0 1489 0 0995 0 0995

0.5 0.19240.02230.00320.19240.12880.1286

1 0.47830.23230.02610.47840.33330.3335

Taula7: AproximaciódelacòpulaAMH(modelcertperòdesconegut) perunacòpulaconegudaquetédimensiódos.L’ajustésforçaboiels coeficientsdecorrelaciórhoitausóngairebéelsmateixos.

Exemple. Unaaproximacióendimensió1consisteixautilitzarlacòpula (24) LaFGMésunmodelmoltutilitzatenestadística,totiquedónaunajustpobre. Unaaproximacióbastantmillorserialacòpula (40) (ounaversióambdimensió superior).Suposem,perexemple,quelacòpulaAMH,definidaa (41),ésla CT ,i quel’aproximemperlacòpula(40),quefaelpaperdemodel CM .Calculant a = max u,v∈I |CT (u,v) CM (u,v)|, obtenimvalorspetits,ésadir,unbonajust,depenentdelparàmetre θ dela còpulacorrectaAMH.Amés,lescorrelacionsdeSpearmaniKendalldonen pràcticamentelmateix.Lataula7mostraelsvalorsdelscoeficientsdel’aproximació,expressatsentermesdecorrelacionscanòniques,on ρ1 coincideixamb larhodeSpearmanperalacòpula C2

Arabé,sireduïmladimensiód’unacòpulaeliminanttermesdeldesenvolupamentdiagonal (36),ode (37),hemdetenirencomptequenosempre obtenimunanovacòpula.Demanerasimilar,enanàlisidecorrespondències, quanrepresentemlesfilesicolumnesendimensiódos,elgràficpodriareflectir unataulaambvalorsnegatius.

19Dimensiócontínua

Consideremelcasdeparellespròpies (φ,λ) onlafunció φ ténorma0.Això significa,enelnostrecontext,tractarambvariablesaleatòriesnoconstants peròambvariància0.Peròaquestasuposiciófatrontollarlateoriadelsvalors propis.Abansdeseguir,comentemalgunesdiferènciesamblateoriaordinària delsoperadorsaplicatsafuncionsquenosónconstants.

1. Lesfuncionspròpiescorresponentsaunmateixvalorpropigenerenun subespaidedimensiófinita.Silanormaés0hauremdeconsiderarvalors propisambmultiplicitatinfinita.

2. De Kφ = λφ,deduïmquelesfuncionspròpiesordinàriessóncontínues a I = [0, 1].Aratenim Kϕ = λLφ ipodemtrobarfuncionscontínuesa trossosambdiscontinuïtatsdesalt.

3. Lesfuncionsesnormalitzensegons (φ,Lφ) = 1.Arahemdeconsiderar elcas (φ,Lφ) = 0.Aleshoressuposaremqueexisteixunafamíliade funcions {φε} detalmaneraque (φε,Lφε)> 0iamés

ε = λ> 0, enelsentitque Kφε(u)/Lφε(u) → λ uniformementen u ∈ I

4. Elconjunt Sλ devalorspropisésfinitoinfinitnumerable.Enaquest nouescenari,elsvalorspropisde K respectea L podenconstituirun conjunt Sλ nonumerable.Perexemple, Sλ podriaserunintervalquetéla potènciadelcontinu.

Exemple. Definim φε(u) = 1si u ∈ (1 ε, 1], φε(u) = 0enaltrecas,on ε> 0ésarbitràriamentpetit.Siguin φ l’indicadorde {u = 1} i L = M Π, K = M 1/2Π1/2 Π.Espotprovar(vegeu[12, 16])que (φε,Lφε) = ε(1 ε), (φε,Kφε) = (1 ε)3/2 (1 ε)2,pertant, limε→0 Kφε/Lφε = 1/2.Tenimque (φ, 1/2) ésunaparellapròpiade K respectea L detalmaneraque (φ,Kφ) = (φ,Lφ) = 0.

Ressaltemquelesfuncionspròpiesdenorma0podencoexistiramblesde normapositiva.

20Còpulesambpartsingular

Unafamíliageneralquecontécòpulesambdimensiófinita,numerableocontínua,és

Dθ (u,v) = min{u,v}Gθ (max{u,v}), on θ ésunparàmetrei Gθ ésunafunciódelaqualparlaremtotseguit.Un membred’aquestafamíliaésla CAθ ,definidaa (42),queéslamitjanageomètrica delescòpules M i Π.Tenimque CA0 = Π i CA1 = M.Aixídoncs θ ésuna mesuradedependència.

Aquestafamília,introduïdaperCuadrasiAugé[18],haestatestudiadai aplicadaa[32, 49, 51]iad’altrestreballs.Téunapartsingular,jaque: P[U = V] = θ/(2 θ).Defet,si δA representalafuncióindicadoradel’esdeveniment A, ladensitatés

fθ (u,v) = (1 θ) max{u,v} θ δ{u≠v} + θu1 θ δ[u=v}, (44)

respectedelamesura µ = λ2 + λ1,essent λ2 lamesuradeLebesguesobre R2 i λ1 lamateixamesuraconcentradaa {u = v}.LarhodeSpearmanilataude Kendallde CAθ són: ρS = 3θ/(4 θ) i τ = θ/(2 θ).

Exemple. Lafamília CAθ s’hautilitzatperdefiniruníndexd’estabilitatfinancera,anomenat«Cuadras-Augéindex»;vegeu[6].Comentem,però,unasituació méssenzilla:ladistribuciódelssousdelesparellesd’unapoblació.Siguin (X,Y) elssousdel’homeiladonaquesónparella.Elsdossouspodenser independents,peròhihalapossibilitatquesiguiniguals(casfreqüentenprofessorsifuncionaris).SuposemquelesfuncionsdedistribuciósóndePareto: F(x) = 1 (m0/x)α si x ≥ m0, G(y) = 1 (m0/y)β si y ≥ m0,on m0 representaelsoumínimi α i β sónparàmetrestalsque2 <α<β.Observemquela mitjanade X ésmésgranquelade Y ,iquesielparàmetre β tendeixainfinit,el soumitjàtendeixalmínim m0.Podemprendre CAθ comacòpularelacionada ambladistribucióconjunta H(x,y) de (X,Y),onelssousmínimimàxim correspondrienalsvalors0i1,respectivament.Peròladensitat (44) de (U,V) indicaqueelssousigualstenenmésprobabilitatamesuraqueaugmenten. Considerem,doncs, (1 U, 1 V).Esfàcilveurequelacòpulaés

CS (u,v) = u + v 1 + CAθ (1 u, 1 v).

Pera CS tambéelssousmínimimàximcorresponenalsvalors0i1.Ladensitat adoptal’expressió

gθ (u,v) = (1 θ) max{1 u, 1 v} θ

Araelssousaltstenenmenysprobabilitatdecoincidir.

AplicantelteoremadeSklar(secció14.3),lafunciódedistribucióconjunta, possiblemodelpera (X,Y),és H(x,y) = CS (F(x),G(y)),ésadir, H(x,y) = 0 si x,y<m,i

H(x,y) = 1 (m0/x)α (m0/y)β + CAθ ((m0/x)α,(m0/y)β) si x,y ≥ m0

Continuantamblateoria,afidetrobarelsvalorsilesfuncionspròpies peralsnuclis K = CAθ Π i L = M Π,definimpera0 ≤ γ ≤ 1i ε> 0 arbitràriamentpetit,lafunció

γ,ε(x) =

0si x<γ, 1si γ ≤ x<γ + ε, ε/(γ + ε) si x ≥ γ + ε,

quetéperlímitlafuncióindicadora φγ (x), lim ε→0 Hγ,ε(x) = φγ (x) = 1si x = γ, 0si x ≠ γ.

Presentemaraladescomposicióenvalorsifuncionspròpiesde K respecte a L.Elresultatsegüentespotprovaraplicantteoriadefuncionsgeneralitzades. Aquífeml’anàlisisobreelsnuclis Kθi = M θi Π1 θi Π, i = 1, 2.Observemque L = M Π = K1

Teorema11. Si 0 ≤ θ1 <θ2 ≤ 1,elconjuntdeparellespròpiesde Kθ1 respecte a Kθ2 estàformatper (φγ ,λγ ) on

γ =Hγ,0,λγ = (θ1/θ2)γ

Tenintaraencomptequelesparellespròpiessónfuncionsicorrelacions canòniques,obtenimelresultatsegüent.

Teorema12. Elconjuntdefuncionsicorrelacionscanòniquesdelafamília CAθ és (φγ ,θγ1 θ ), 0 ≤ γ ≤ 1.

Pertant,elconjuntdecorrelacionscanòniquesésunintervalquetéla potènciadelcontinu.Lesvariablescanòniquestenen,enellímit,variància0, peròlescorrelacionscanòniquessónpositives.Unaconseqüènciadelteorema anterioréselresultatsegüent.

Corol.lari13. Lamàximacorrelacióperalafamília CAθ éselparàmetre θ, essent H1 lafunciócanònica,on H1 ésladistribuciódeHeaviside.

Laprovaque θ éslamàximacorrelacióapareixprimera[12].Recordemque lamàximacorrelació,introduïdaperH.Gebeleinel1941,ésl’únicamesurade dependènciaquecompleixelspostulatsdeRényi[55].Pertant, θ ésunabona mesuradedependènciaperaaquestafamília.

Consideremacontinuaciólasèrie (36),construïdasuposantquelesfuncions pròpiestenennorma1.Peròaralanormaés0ilasèrieesdevéunaintegral. Lasuccessiódecorrelacionscanòniquesés,enaquestcontext,unafunció,en generalcontínua.

Definició14. Unafunciódecorrelaciócanònicaésunafuncióintegrable fθ : I → I,quesatisfà I fθ (ρ)dρ ≤ 1.

Teorema15. LacòpulaCuadras-Augéespotexpressarentermesdeldesenvolupamentdiagonalcontinu

CAθ (u,v) = uv + 1 max{u,v} θρ1 θ (u/ρ)(v/ρ)dρ.

Engeneral,lafamília Dθ (u,v) = min{u,v}Gθ (max{u,v}) admeteldesenvolupamentintegral

Dθ (u,v) = uv + 1 max{u,v} fθ (u)(u/ρ)(v/ρ)dρ, (45) on fθ (ρ) = Gθ (ρ) ρGθ (ρ) ésunafunciódecorrelaciócanònica.

21Còpulescanòniques

Elterme max{u,v} queapareixa (45) verifica max{u,v}= uv/ min{u,v}. Doncsbé,si C ésunacòpula,engeneral

uv + 1 uv/C(u,v) fθ (ρ)(u/ρ)(v/ρ)dρ

tambéhoés.Defet Π/C espodriasubstituirperqualsevolquocientdedues còpules.

Encaraambmésgeneralitat,podemobtenirlafamília (46),delaqual (47) seriauncasparticular.

Teorema16. Sigui fθ unafunciódecorrelaciócanònicaindexadaper θ ∈ I Definimlesfuncions Fθ (ρ) = [fθ (ρ)/ρ2]dρ i Gθ (ρ) =−ρFθ (ρ) + ρFθ (1) + ρ.

Peraquocientsadequats Q deduescòpules,ladescomposicióintegral (45) permetgenerarlafamíliadecòpulescanòniques

Cθ = Π × Gθ (Q)/Q. (46)

Enparticular,si Q = Π/M,obtenimlafamília

Dθ (u,v) = min{u,v}Gθ (max{u,v}), (47)

on Gθ : I → I ésunafunciócreixentcontínuadetalmaneraque Gθ (ρ)/ρ és decreixentdins (0, 1]

fθ Gθ Q Família

0 ρC/Π Independència 11 Π/C Qualsevolcòpula

θθ + ρθ Π/M Fréchet θρ2 θρ2 +(1+θ)ρ Π/AMH1 Farlie-Gumbel-Morgenstern θρ2/[θ + ρθ]2 ρ/[θ + ρθ]FGM 1/Π Ali-Mikhail-Haq

θρ1 θ ρ1 θ Π/M

Cuadras-Augé fθ (ρ)Gθ (ρ) Π/M

Durante

θρ θρ log(ρ) + ρ Π/W Novafamília(48)

Taula8: Algunescòpulesgeneradesperfuncionscanòniquesieldesenvolupamentdiagonalenversióintegral.

Lataula8descriualgunesconstruccions,on θ = 1 θ.LesfamíliesFarlieGumbel-Morgenstern(FGM),Ali-Mikhail-Haq(AMH)hanestatdescritesabans, vegeu (24), (41).LafamíliadeFréchetéslamitjanaponderadadelacotasuperior ilaindependència:

Fθ (u,v) = θ min{u,v}+ (1 θ)uv.

D’altrabanda, Dθ de (47) vaserdefinidaperCuadrasiAugé[18]iestudiadaper Durante[34].Ésinteressantobservarquesi Q = Π/M,ladensitat (44) adopta laformasimètrica

fθ (u,v) = (1 θ)(1/Q)θ δ{u≠v} + θ(Q)1 θ δ{u=v}

Finalment,amb fθ (ρ) = θρ i Q = Π/W ,on W éslacòpula W(u,v) = [u 2 + v 2 1] 1/2,obtenimlanovafamíliadecòpules

NC(u,v) = uv[1 θ log(uv/W(u,v))]. (48)

Exemple. Sovintvolemdescriureunfetrealquehaestatobservatdesdediversesperspectives.Comail.lustració,sigui θ1 laprobabilitatd’unesdeveniment A, comaral’eficàciad’untractamentmèdic.Realitzem n1 provesindependents isigui L1(x1,θ1) = n x1 θx1 1 (1 θ1)n1 x1 lafunciódeversemblança,on x1 éslafreqüènciaobservadade A.L’estimadormàximversemblantde θ1 ésla freqüènciarelativa x1/n1.

Suposemaraque θ1 ésunparàmetrealeatoriambdistribucióuniforme (0, 1) Laversemblança,sotaaquestaperspectivabayesiana,és L(x1) = 1 0 n x1 θx1 1 (1 θ1)n1 x1 dθ1.

Consideremdosexperimentsindependentssotaelsqualsobtenimles freqüènciesrelatives x1/n1 i x2/n2 peraestimar θ1, θ2.Suposemque θ1 i θ2 sóndescripcionsd’unmetaparàmetre θ,tambéaleatori,queensdonariala «veritable»probabilitatde A encondicionsideals.(Imaginemqueuntractamentmèdics’haestudiatendoscentresdiferents.)Suposemqueladistribució conjuntade (θ1,θ) ésunacòpula(FGM,Plackettounacòpulacanònica),i anàlogamentlade (θ2,θ).Laversemblançade θ és

L(x1,x2|θ) = 2 i=1 1 0 n xi θ

i|θ)dθi,

on p(θi|θ) ésladensitatde θi condicionadaa θ iqueescalculaapartirdela còpula.Ladistribució apriori de θ ésuniformea (0, 1).Aplicantelteoremade Bayes,ladensitat aposteriori delmetaparàmetreés

p(θ|x1,x2) =

L(x1,x2|θ) 1 0 L(x1,x2|θ)dθ .

Uncoptenim p(θ|x1,x2) podemprendrelamoda(olamitjana)comuna estimaciódelaprobabilitat θ;vegeu[50].

Resumint,lateoriadecòpules,ienparticularlescòpulescanòniques,defineixenunaclasseàmpliademodelsprobabilísticsque,correctamentutilitzats, descriuenisintetitzenl’associacióestadísticad’unconjuntdedadesbivariants.

Referències

[1] Aitchison,J.;Greenacre,M. «Biplotsofcompositionaldata». J.Roy. Statist.Soc.Ser.C,51(4)(2002),375–392.

[2] Ash,R.B. InformationTheory.NovaYork:DoverPublications,Inc.,1990. Reediciócorregidadel’originalde1965.

[3] Beare,B.K. «AgeneralizationofHoeffding’slemma,andanewclassof covarianceinequalities». Statist.Probab.Lett.,79(5)(2009),637–642.

[4] Benzécri,J.-P. L’analysedesdonnées.II.L’analysedescorrespondances 2aed.París:Dunod,1976.

[5] Bernardo,J.M. «Unaintroduccióal’estadísticabayesiana». Butlletídela SocietatCatalanadeMatemàtiques,17(1)(2002),7–64.

[6] Cherubini,U.;Mulinacci,S.;Gobbi,F.;Romagnoli,S. Dynamiccopula methodsinfinance.NovaYork:Wiley,2011.

[7] Cox,T.F.;Cox,M.A.A. MultidimensionalScaling.Londres:Chapman& Hall,1994.(MonographsonStatisticsandAppliedProbability;59)

[8] Cuadras,C.M. MétodosdeAnálisisMultivariante.Barcelona:PPU,1991.

[9] Cuadras,C.M. «Interpretinganinequalityinmultipleregression». Amer. Statist.,47(4)(1993),256–258.

[10] Cuadras,C.M. «Increasingthecorrelationswiththeresponsevariable maynotincreasethecoefficientofdetermination:aPCAinterpretation».A: NewTrendsinProbabilityandStatistics.Vol.3.Utrecht:VSP,1995,75–83.

[11] Cuadras,C.M. «Onthecovariancebetweenfunctions». J.Multivariate Anal.,81(1)(2002),19–27.

[12] Cuadras,C.M. «Correspondenceanalysisanddiagonalexpansionsin termsofdistributionfunctions». J.Statist.Plann.Inference,103(1–2) (2002),137–150.

[13] Cuadras,C.M. «Continuouscanonicalcorrelationanalysis». Research LettersintheInformationandMathematicalSciences,8(2005),97–103.

[14] Cuadras,C.M. «Distance-basedassociationandmulti-sampletestsfor generalmultivariatedata».A: AdvancesinMathematicalandStatistical Modeling.Boston:Birkhäuser,2008,61–71.(Stat.Ind.Technol.)

[15] Cuadras,C.M. NuevosMétodosdeAnálisisMultivariante.Barcelona:CMC Editions,2014.

[16] Cuadras,C.M. «Nonlinearprincipalandcanonicaldirectionsfromcontinuousextensionsofmultidimensionalscaling». OpenJ.Stat.,4(2)(2014), 132–149.

[17] Cuadras,C.M. «Contributionstothediagonalexpansionofabivariate copulawithcontinuousextensions». J.MultivariateAnal.,139(2015), 28–44.

[18] Cuadras,C.M.;Augé,J. «Acontinuousgeneralmultivariatedistributionanditsproperties». Comm.Statist.A—TheoryMethods,10(4)(1981), 339–353.

[19] Cuadras,C.M.;Cuadras,D. «Aparametricapproachtocorrespondence analysis». LinearAlgebraAppl.,417(1)(2006),64–74.

[20] Cuadras,C.M.;Cuadras,D. «Eigenanalysisonabivariatecovariance kernel». J.MultivariateAnal.,99(10)(2008),2497–2507.

[21] Cuadras,C.M.;Cuadras,D. «Partitioningthegeometricvariabilityin multivariateanalysisandcontingencytables».A: ClassificationandMultivariateAnalysisforComplexDataStructures.Heidelberg:Springer,2011, 237–244.(Stud.ClassificationDataAnal.KnowledgeOrgan.)

[22] Cuadras,C.M.;Cuadras,D. «Aunifiedapproachforthemultivariate analysisofcontingencytables». OpenJ.Stat.,5(2015),223–232.

[23] Cuadras,C.M.;Cuadras,D.;Greenacre,M.J. «Acomparisonofdifferent methodsforrepresentingcategoricaldata». Comm.Statist.Simulation Comput.,35(2)(2006),447–459.

[24] Cuadras,C.M.;Cuadras,D.;Lahlou,Y. «Principaldirectionsofthe generalParetodistributionwithapplications». J.Statist.Plann.Inference, 136(8)(2006),2572–2583.

[25] Cuadras,C.M.;Díaz,W. «AnothergeneralizationofthebivariateFGM distributionwithtwo-dimensionalextensions». ActaComment.Univ.Tartu. Math.,16(1)(2012),3–12.

[26] Cuadras,C.M.;Fortiana,J. «Acontinuousmetricscalingsolutionfora randomvariable». J.MultivariateAnal.,52(1)(1995),1–14.

[27] Cuadras,C.M.;Fortiana,J. «Visualizingcategoricaldatawithrelatedmetricscaling».A: Blasius,J.;Greenacre,M. (ed.). VisualizationofCategorical Data.NovaYork:AcademicPress,1998,365–376.

[28] Cuadras,C.M.;Fortiana,J. «Theimportanceofgeometryinmultivariate analysisandsomeapplications».A: Statisticsforthe21stCentury.Nova York:Dekker,2000,93–108.(Statist.TextbooksMonogr.;161)

[29] Cuadras,C.M.;Fortiana,J.;Greenacre,M. «Continuousextensionsof matrixformulationsincorrespondenceanalysis,withapplicationstothe FGMfamilyofdistributions».A: Heijmans,R.D.H.;Pollock,D.S.G.; Satorra,A. (ed.). InnovationsinMultivariateStatisticalAnalysis.Dordrecht: KluwerAc.Publ.,2000,101–116.

[30] Cuadras,C.M.;Fortiana,J.;Oliva,F. «Theproximityofanindividualto apopulationwithapplicationsindiscriminantanalysis». J.Classification, 14(1)(1997),117–136.

[31] Cuadras,C.M.;Valero,S.;Cuadras,D.;Salembier,P.;Chanussot,J. «Distance-basedmeasuresofassociationwithapplicationsinrelating hyperspectralimages». Comm.Statist.TheoryMethods,41(13–14)(2012), 2342–2355.

[32] Dobrowolski,E.;Kumar,P. «SomepropertiesoftheMarshall-Olkinand generalizedCuadras-Augéfamiliesofcopulas». Aust.J.Math.Anal.Appl., 11(1)(2014),13p.

[33] Donner,A.;Wells,G. «Acomparisonofconfidenceintervalmethodsfor theintraclasscorrelationcoefficient». Biometrics,42(2)(1986),401–412.

[34] Durante,F. «Anewfamilyofsymmetricbivariatecopulas». C.R.Math. Acad.Sci.Paris,344(3)(2007),195–198.

[35] Escofier,B.;PagèsJ. Analysesfactoriellessimplesetmultiples.París: Dunod,1990.

[36] Fréchet,M. «Surlestableauxdecorrélationdontlesmargessontdonnées». Ann.Univ.Lyon.Sect.A.(3),14(1951),53–77.

[37] Galton,F. «Regressiontowardsmediocrityinhereditarystature». J.of theAnthropologicalInstitute,15(1886),246–263.

[38] Goodman,L.A. «Correspondenceanalysis,associationanalysis,andgeneralizednonindependenceanalysisofcontingencytables:Saturatedand unsaturatedmodels,andappropriategraphicaldisplays».A: Cuadras,C. M.;Rao,C.R. (ed.). MultivariateAnalysis:FutureDirections2.Amsterdam: Elsevier,1993,265–294.

[39] Greenacre,M.J. TheoryandApplicationsofCorrespondenceAnalysis. Londres:AcademicPress,Inc.[HarcourtBraceJovanovich,Publishers], 1984.

[40] Hamilton,D. «Sometimes R2 >r 2 yx1 + r 2 yx2 .Correlatedvariablesarenot alwaysredundant». Amer.Statist.,41(2)(1987),129–132.

[41] Hanley,J.A. «“Transmuting”womenintomen:Galton’sfamilydataon humanstature». Amer.Statist.,58(3)(2004),237–243.

[42] Harris,H.;Smith,C.A.B. «Thesib-sibageofonsetcorrelationamong individualssufferingfromahereditarysyndromeproducedbymorethan onegene». Ann.Eugenics,14(1949),309–318.

[43] Hoeffding,W. «MasstabinvarianteKorrelationtheorie». SchriftenMath. Inst.Univ.Berlin,5(1940),181–233.

[44] Hotelling,H. «Relationsbetweentwosetsofvariates». Biometrika,28 (3–4)(1936),321–377.

[45] Julià,O.;Comas,J.;Vives-Rego,J. «Second-orderfunctionsarethesimplestcorrelationsbetweenflowcytometriclightscatterandbacterialdiameter». JournalofMicrobiologicalMethods,40(1)(2000),57–61.

[46] Kaplan,J. «AstatisticalerrorinTheBellCurve». Chance,10(1997),20–21.

[47] Lancaster,H.O. «Thestructureofbivariatedistributions». Ann.Math. Statist.,29(1958),719–736.

[48] Li,B.;Genton,M.G. «Nonparametricidentificationofcopulastructures». J.Amer.Statist.Assoc.,108(502)(2013),666–675.

[49] Mai,J.-F.;Scherer,M. «EfficientlysamplingexchangeableCuadras-Augé copulasinhighdimensions». Inform.Sci.,179(17)(2009),2872–2877.

[50] Moreno,E.;Vázquez-Polo,F.J.;Negrín,M.A. «ObjectiveBayesianmetaanalysisforsparsediscretedata». Stat.Med.,33(21)(2014),3676–3692.

[51] Nelsen,R.B. AnIntroductiontoCopulas.2aed.NovaYork:Springer,2006. (SpringerSeriesinStatistics)

[52] Papadatos,N.;Xifara,T. «Asimplemethodforobtainingthemaximal correlationcoefficientandrelatedcharacterizations». J.MultivariateAnal., 118(2013),102–114.

[53] Pearson,K.;Lee,A. «Onthelawsofinheritanceinman:I.Inheritanceof physicalcharacters». Biometrika,2(1903),357–462.

[54] Rao,C.R. «AreviewofcanonicalcoordinatesandanalternativetocorrespondenceanalysisusingHellingerdistance». Qüestiió(2),19(1–3)(1995), 23–63.

[55] Rényi,A. «Onmeasuresofdependence». ActaMath.Acad.Sci.Hungar., 10(1959),441–451.

[56] Routledge,R.D. «Whenstepwiseregressionfails:correlatedvariables someofwhichareredundant». Internat.J.Math.Ed.Sci.Tech.,21(3)(1990), 403–410.

[57] Scheffé,H. TheAnalysisofVariance.NovaYork:JohnWiley&Sons; Londres:Chapman&Hall,1959.

[58] Wachsmuth,A.;Wilkinson,L.;Dallal,G.E. «Galton’sbend:apreviously undiscoverednonlinearityinGalton’sfamilystatureregressiondata». Amer.Statist.,57(3)(2003),190–192.

[59] Waller,N.G. «Thegeometryofenhancementinmultipleregression». Psychometrika,76(4)(2011),634–649.

[60] Wilks,S.S. «Samplecriteriafortestingequalityofmeans,equalityofvariances,andequalityofcovariancesinanormalmultivariatedistribution». Ann.Math.Statistics,17(1946),257–281.

Departamentd’Estadística

FacultatdeBiologia

UniversitatdeBarcelona Av.Diagonal,643 08028Barcelona ccuadras@ub.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.1,2015.Pàg.57–101. DOI:10.2436/20.2002.01.59

Eleccionsmitjançantelvotd’aprovació. ElmètodedePhragménialgunesvariants

XavierMoraiMariaOliver

Resum: S’estudiendiversesvariantsd’unmètodederepresentacióproporcionalque EdvardPhragménvaproposarafinalsdelsegle xix.Cadaelectorexpressalasevaopinió mitjançantunvotd’aprovació,onindicatoteslesopcionsquelisemblenadients.Les opcionspodensercandidatsindividuals,comsuposavaPhragmén,obécandidatures departitqueofereixenmúltiplesrepresentantscadascuna.Donatunconjuntdevots d’aquesttipusiunnombreprefixatd’escons,estractaderepartiraquestsesconsentre lesdiferentscandidaturesdemaneraqueelresultatsiguielmésrepresentatiupossible. Elpresentestudiprestaunaatencióespecialaunapropietatdemonotoniaquedemana quel’addiciód’aprovacionsafavord’unacandidaturanopuguiproduirunadisminució delnombred’esconsquelisónassignats.Enlavariantbàsica,onelsesconss’assignen mitjançantunprocedimentseqüencial,aquestamonotoniaescompleixenelcasde candidatsindividuals,perònoenelcasdecandidaturesdepartit.Tambés’exploren breumentunesvariantsdirectes,onelsesconss’assignentotsd’unavegadamitjançant alguncriteriadientd’optimització.Aquestesvariantssemblenmillorsdesdelpuntde vistadelamonotonia,peròpresentenunproblemademultiplicitatdesolucionsquefa necessarialguncriteriaddicionaldeselecció.

Paraulesclau: representacióproporcional,votd’aprovació,llistesobertes,Edvard Phragmén.

ClassificacióMSC2010: 91B12.

1Introducció

Suposemqueungrupde1000individusvolelegirquatrepersonesquerepresentintotelgrup,incloent-hinosolamentlesopinionsielspuntsdevista majoritaris,sinótambé,enladegudaproporcióienlamesuraquesiguipossible, toteslesaltresopinionsielsaltrespuntsdevista.Escomptaambvuitcandidats, a, b, c, d, e, f, g, h,iesdemanaacadamembredelgrupqueindiqui

AquestarticleésunaversióméselaboradadeltreballdefidegraudeMatemàtiquesrealitzat elcurs2011–2012alaUniversitatAutònomadeBarcelonaperMariaOliversotaladireccióde XavierMora.

quinsd’aquestscandidatslisemblenacceptablesperareflectirlasevaopinió. Imaginemquelesrespostesdels1000individusesreparteixendelamanera següent: 250: a, b, c, d;250: b, c, e;200: e, f, g, h;200: a, e, f;100: a, c, e, f. (1)

Quinssónelsquatrerepresentantsmésadequats?

Aquestéselproblemaqueesplantejaenl’eleccióderepresentantsmitjançantllistesobertesnoordenades.Enaquestarticleensocuparemd’elljuntamb unageneralitzacióenquèlesopcionssobrelesqualss’expressal’electorno sónelscandidatsindividuals,sinóunescandidaturescol lectivescadascunade lesqualspotproporcionarmúltiplesrepresentants.Enaquestescenaritambé potpassarquel’electortrobiacceptablemésd’unad’aquestescandidatures. Suposem,perexemple,queunpaísvolelegirunparlamentde135diputats iqueesdemanaacadaelectorqueindiquiquinesdelescandidaturesque presentenelspartitslisemblenprouoportunesdesdelseupuntdevista.Cada candidaturaofereixtantscandidatscomesconshihaalparlament.Imaginem queelselectorsvotencomsegueix,on A, B, C, D, E, F, G denotenlescandidatures corresponentsalsdiferentspartitsilesxifresindiquencentenarsdemilers d’electors:

6: A;8: A, B;2: B, C;2: B, C, D;3: C, D; 3: C, E;2: E;4: F;2: F, G;2: G. (2)

Quantsdiputatss’hand’assignaracadacandidatura?

Aquestaformadevotenquèl’electorindicatoteslesopcionsquelisemblen adientss’anomena votd’aprovació. Òbviament,unvotd’aquesttipusdóna mésinformacióquenopasunvotonnomésespermetindicarunasolaopció.A conseqüènciad’això,elsresultatspodenreflectirmillorlesveritablesopinions delselectors(quehoaconsegueixinonodependràdel’algorismeutilitzat).Una altraconseqüènciamoltpositivaésques’evitaencertamesuraelproblema delvotútil:l’electornotéresaperdresiinclouenelseuvotlesopcions querealmentprefereix,possiblementacompanyadesd’altresopcionsmenys preferidesperòambméspossibilitatsd’èxit.1

Enlaformatradicionaldevotquedemanaacadaelectorunasolaopció,habitualments’acceptatambécomavàlidelvotenblanc.Tanmateix,elsignificat d’aquestúltimnoésgensclar:enprincipi,tantpotsignificarelrebuigdetotes lesopcionsplantejades,coml’acceptaciódequalsevold’elles.Ambelvotd’aprovació,encanvi,aquestsdossignificatsoposatsquedenperfectamentseparats: elprimercascorresponanoaprovarcapopció,mentrequeelsegoncorrespon aaprovar-lestotes.

Enllocdelvotd’aprovació,espotplantejard’usarel votpreferencial,on amésd’indicarlesopcionsquelisemblenadients,l’electorlesordenatambé perordredepreferència.Defet,elvotpreferencialentermesdecandidats individualss’utilitzaperal’eleccióderepresentantsenelmètodedel vot

1 Lesnoteslesposemenparàgrafssagnatsambuncosdelletraméspetit,laqualcosafacilita decontinuarlalectura.

únictransferible.Comveuremmésavall,però,aquestmètodepresentacerts problemes—demancademonotoniarespectealcontingutdelsvots—quefan interessantd’estudiarunesaltresvies.

Enprincipi,tambéserienpossiblesaltresformesdevotquenoconsiderarem aquí,comaraquetambéespuguinexpressarpreferènciesentrelesopcionsno aprovades,obéquenoméss’expressinpreferènciesentrelesdiversesopcions, senseespecificarquinesd’aquestescomptenambl’aprovaciódel’elector.En certscontextos,elterme«votpreferencial»esrefereixaaquestaúltimaforma devot.Peròenelcontextdel’eleccióderepresentantséshabitualentendre aquesttermeenelsentitquehemdit,ésadir,comunvotd’aprovaciójuntamb unaordenaciódelesopcionsaprovades.

Mésconcretament,aquestarticlegiraràalvoltantd’unmètodequevaser proposatafinalsdelsegle xix pelmatemàticsuecEdvardPhragmén.Elmètode enqüestiócombinaideesdelvotúnictransferibleidelmètodedeD’Hondt, laqualcosaensportaràarevisarabansaquestsantecedents.

Talcomjahemditmésamunt,enssituaremenunmarcgeneralenquè lesopcionsqueaproval’electornosónnecessàriamentcandidatsindividuals, sinóquepodensercandidaturescol lectivesacadascunadelesqualsestracta d’assignaruncertnombrederepresentants.Defet,aquesttreballestàespecialmentmotivatperaquestapossibilitat,laqualseriaadienteneleccionsd’àmbit extens,onelselectorsdifícilmentconeixendirectamentelscandidats,itambé enescenarisondominaladisciplinadepartit.Lapropostaquelesopcionssobre lesqualss’expressil’electorsiguinlescandidaturescol lectivespresentades pelspartitstambéhaestatfetarecentmentperaltresautorsenelcontextdel votpreferencial[23].

L’articleestàestructuratdelamanerasegüent:Lesseccions2–6introdueixen lesdiversesideesiantecedentsqueensinteressen.Enlasecció7estudiem detalladamentlavariantbàsicadelmètodedePhragmén,laqualtreballaamb votsd’aprovacióiassignaelsesconsmitjançantunprocedimentseqüencial.Tal comhemdit,però,enssituemenelmarcgeneraldecandidaturescol lectives. Unamicainesperadament,veuremqueenelcasgeneralfallaunapropietatde monotoniaquesíqueescompleixenelcasdecandidaturesindividuals.Enla secció8explorembreumentlesvariantsdirectes,onelsesconss’assignentots d’unavegadamitjançantalguncriteriadientd’optimització.Segonscomentarem, hihaindicisqueaquestesvariantssíquetenenlapropietatdemonotonia.A canvi,però,enstrobemambunproblemademultiplicitatdesolucionsque fanecessarialguncriteriaddicionaldeselecció.L’articlesesuplementaamb dosapèndixsquerecullen,respectivament,unabreunotabiogràficasobre EdvardPhragméniunaclassificaciódelesdiversesvariantsqueaquestautor vaconsiderardelseumètode.

2Representacióproporcionalambpartitsosense

2.1 L’objectiugeneraldelarepresentacióproporcionaléselegirunconjunt derepresentantsonlesdiversesopinionsipuntsdevistaestiguinpresentsen

lamateixaproporcióqueatotalasocietat[24, 51].El1789,mesosabansdela RevolucióFrancesa,HonoréGabrielRiquetti,comtedeMirabeau,hocomparava amblarepresentacióqueunmapafad’unterritori,oncertamentconvéqueles longitudsiàreesdelmapasiguintanproporcionalsalesdelterritoricomsigui possible[24,§117].

Perintentarassoliraquestobjectiu,sovintesdemanaalselectorsqueescullinuna,inomésuna,delescandidaturespresentadespelspartitspolítics.Fet això,estractaderepartirelsesconsdelparlamententreaquestescandidatures assignantacadascunad’ellesunnombred’esconstanproporcionalalsvots obtingutscomsiguipossible.Comqueelsnombresenqüestiósónenters, lesdesviacionsrespectealaproporcionalitatexactasóninevitables.Aquestes desviacionsesdevenenespecialmentimportantsquanelnombred’esconsque esreparteixenéspetit,compassasovintcomaresultatd’unadivisióencircumscripcionsterritorials.Totplegatdónallocaunadiversitatdereglesde repartiment,entrelesqualsdestaquenladeJeffersoniD’HondtiladeWebster iSainte-Laguë,queserandiscutidesambmésdetalla§5.

Tanmateix,totaixòsuposaquecadaelectors’identificaambunainomés unadelespropostesquepresentenelspartits.Aquestahipòtesipotestarmolt allunyadadelarealitat,laqualcosapotcomportarresultatsdesencertats.

2.2 Enaquestarticleensinteressemenprocedimentsalternatiusbasatsen formesmésobertesdevotquenorequereixenunaclassificacióprèviadels candidatsenclassesdisjuntes.Talcomveurem,totiaixòencaraespotmirar derespectarelprincipiderepresentacióproporcional.

Tanmateix,noserveixpasqualsevolprocediment.Perexemple,suposem queesvolenelegir n representantsapartird’uncertconjuntprouamplide candidats.Unpossibleprocedimentésdemanaracadaelectorquedoniuna llistadels n candidatsquemésliagradenideclararelegitsels n candidatsque obtinguinmésvots.

Aquestprocedimentpotsemblarforçanatural,peròelcertésqueésmolt llunydel’idealdelarepresentacióproporcional.Suposem,perexemple,que n = 4iqueelsvotssóncommostremacontinuació:

75: a, b, c, d;25: e, f, g, h. (3) Ésadir,75electorscoincideixenaseleccionarelscandidats a, b, c, d,mentreque25electorscoincideixenaseleccionarelscandidats e, f, g, h.Aplicantel procedimentquehemdit,resultarienelegitselscandidats a, b, c, d.Tanmateix, perlamaneraenquès’havotatésobviquel’electoratestàclaramentdividiten dossectorsquetenenunapresènciarespectivadel75%i25%.Encanvi,enel conjuntescollitaquestsdossectorstenenunapresènciarespectivadel100% i0%.

Certament,l’idealdelarepresentacióproporcionaldemanaelegircoma representantstrescandidatsdelconjunt X ={a, b, c, d} iundelconjunt Y = {e, f, g, h},jaque75/25 = 3/1.

2.3 Enl’exempleprecedent,elfetqueesreconeguilasimilitudentreelselementsde X perunabandaielsde Y perunaaltraéspossibleperquèelselectors hanseleccionatmésd’uncandidat.Sinomésn’haguessinseleccionatun,llavors nohihauriacappistasobrelarelaciódesimilitudentrecandidats.

Amésamés,pertaldecapturaraquestarelaciódelamillormanerapossible, éspreferiblenoforçarl’electoradonarcapnombreconcretdecandidats.Per exemple,sihiha75electorsques’identifiquenambqualsevoldelscandidats delconjunt X ={a, b, c, d, e, f} icapaltre,i25electorsques’identifiquen ambqualsevoldelsde Y ={g, h} icapaltre,llavorselfetdedemanar-los queseleccioninexactamentquatrecandidatsnopermetràalspartidarisde X inclouretotselsseuspreferits,alhoraqueobligaràelspartidarisde Y aincloure algunelementde X enlasevallista,laqualcosadesdibuixaràlaparticióque hiharealmententre X i Y .Encanvi,sise’lspermetseleccionarunnombre arbitraridecandidats,llavorslavotaciópotposardemanifestaquestapartició. Evidentment,perquèquedireflectidadelamillormanerapossiblecalquecada electorincloguitotselscandidatsquelisemblenbé.Ésperaixòque enelvot d’aprovacióésessencialpermetrequel’electorindiquitoteslesopcionsqueli semblenadients.Perdescomptat,tambécalquerealmentexisteixiunapartició deltipusqueestemdient.Totaixòésaplicabletambéaunaparticióenmésde duesclasses.

Enl’exemple (3) ésmoltclaraladivisióendospuntsdevistadiferents.Però engeneralpotpassarcoma (1),onlarelaciódesimilitudentrecandidatsnoés pastanclara.Comhohemdeferenuncasaixí?

3Elvotúnictransferible

3.1 Elmètodemésconegutqueaplicalaideaderepresentacióproporcional senserequeriralselectorsqueespronunciïnperunsolpartitésel votúnic transferible.Aquestmètodeutilitzaelvotpreferencial(enelsentitquehem dita§1,ésadir,unvotd’aprovaciójuntambunaordenaciódelesopcions aprovades).Enprincipi,lesopcionsqueesconsiderensónelscandidatsindividuals,independentmentdesipertanyenaunpartitounaltre,idefet, independentmentdesiestandefinitsunspartitsono.Totiaixò,s’aconsegueix unefectederepresentacióproporcional,laqualcosavoldirqueaquestmètode detectad’algunamaneralessimilitudsentrecandidatsapartirdelsvotsdels electors.

Elmètodedelvotúnictransferibles’associanormalmental’advocatanglès ThomasHare,queelvaproposarel1857ivaobtenirungranressòatravés delfilòsofialeshoresmembredelparlamentanglèsJohnStuartMill.Detota manera,l’anyanteriorhaviaestatutilitzatjaaDinamarca,onelmatemàticdanès CarlChristoferGeorgAndræ,llavorsministredeFinancesdelseupaís,l’havia proposatindependentment.Iencaraabans,lamateixaideal’haviautilitzatel 1840aAustràliaRowlandHill,ifinsitotel1819aAnglaterraThomasWright Hill,paredel’anterior.

XavierMoraiMariaOliver

Elmètodedelvotúnictransferibleparteixdelprincipiquecadadiputat hauriaderepresentarelmateixnombred’electors.Aquestnombred’electorsper diputats’anomena quota inosaltresl’anomenem q.Elseuvaloresfixadesdel principiis’usadelamanerasegüent:mentrequedinméscandidatsqueescons perassignar,elquedeterminaqueuncandidatsiguielegitésquereuneixi —enelsentitquedeseguidaconcretarem—unnombredevotssuperior,oentot casigual,alaquota q.

D’araendavant w i n representen,respectivament,elnombred’electorsi elnombrederepresentantsques’hand’elegir.HareiAndræpreniencoma quota q elquocient w/n =: q0 il’objectiuerasuperaroigualaraquestvalor. El1868,però,l’advocatanglèsHenryRichmondDroopvaproposardeprendre q iguala w/(n + 1) =: qD irequerirqueelnombredevotssuperiestrictament aquestvalor.Elvalor q0 repelnomde quotasimple,o quotadeHare,i qD esconeixcoma quotadeDroop.Noteuqueenelcasextrem n = 1,ésadir, l’elecciód’unsolrepresentantcomúperatothom,laquotadeHarecorrespona lanociód’unanimitat,mentrequeladeDroopcorresponalanociódemajoria absoluta.

Lamaneradereunirelsvotsrequeritsconsisteixafigurarcomaprimera opcióenlabutlletad’unelector,oalternativament,figurar-hipersotad’altres candidatsquejahanobtingutunescóoquenopodenarribaraobtenir-necap. Tanbonpuntuncandidatassoleixlaquota,seliassignaunescóicadascundels votssobrantséstransferitalcandidatqueelsegueixenlabutlleta.Quannohiha capcandidatqueassoleixilaquota,llavorss’eliminaelqueenaquellmomentté menysvots;sienaquestmomentrestentantscandidatscomescons,aleshores aquestscandidatsresultenelegitsindependentmentdelsvotsambquècomptin ifinalitzaelprocediment;altrament,cadascundelsvotsdelcandidateliminat éstransferitalcandidatsegüentenlabutlleta.Enl’apartatquesegueixho il lustremambunparelld’exemples.

Perserexactes,Drooppreniacomaquotaasuperaroigualarelprimerenter N estrictamentsuperiora w/(n + 1).Queunnombreenter(devots)superio igualiaquestvalor N ésexactamentequivalentasuperarestrictamentelvalor w/(n + 1).Tanmateix,ambelsnombresfraccionarisdevotsquesorgiran mésavall,aquestesduescondicionsnosónexactamentequivalents.D’altra banda,aquestadistinciótambéafectalaquantitatexactadevotsqueestransferiran.Sobreaquestesqüestions,seguiremIrwinMannenrequerirquesesuperi estrictamentlaquota w/(n + 1) ialmateixtempstransferirtotl’excéssobre aquestaquantitat[56,p.271–272].

3.2 Vegemambmésdetallunparelld’exemples.Consideremprimeruncas similara(3)peròambvotspreferencials:

75: a > b > c > d;25: e > f > g > h. (4)

Suposemquevolemelegir n = 4representants.LaquotadeDroopés100/(4 + 1) = 20.Pertant,resultenelegitsdirectamenttant a com e.Enelcasde a sobren 55vots,elsqualspassena b;aquestresultaelegitiencarasobren35vots,els

qualspassena c;aquesttambéresultaelegit,peròels15votsquearasobreni passena d nosónsuficientsperquèaquestúltimcandidatobtinguiunescó.En elcasde e,noméssobren5vots,elsqualspassena f peròtambésóninsuficients peradonar-liunescó.Entotal,haresultatelegitelconjuntderepresentants següent: {a, b, c, e},queincloutresmembresdelconjunt X ={a, b, c, d} iundel conjunt Y ={e, f, g, h},talcomdemanalanociódeproporcionalitat.

Consideremaral’exemplesegüent,onhiha96electors:

Suposemquevolemelegir n = 3representants.LaquotadeDroopés96/(3 + 1) = 24.Pertant,resultaelegitdirectamentelcandidat a.Els10votsqueli sobrena a passena b,queresultaelegititransfereix6vots;comque10dels 30votsquehaviaobtingut b donaven c comaopciósubseqüentielsaltres20 donaven a,jaelegit,idesprés d,ésraonablemantenirlaproporcionalitati passar2dels6votssobrantsa c ielsaltres4a d.Comaresultatd’aixòqueda elegit d,peròno c.Pertant,resultaelegitelconjuntderepresentantssegüent: {a, b, d}.Noteuqueaquestconjuntincloudosmembresdelconjunt X ={a, b} i nomésundelconjunt Y ={c, d},laqualcosaestàd’acordambelfetqueels vots(5)espodenveureenlaforma

54: X > Y;42: Y > X. (6)

Encanvi,sienshaguéssimguiatnomésperlesprimeresopcionsdelsvots (5) haguéssimelegitnomésunmembrede X idosde Y.

Enconsideraraltresexemples,opetitesvariacionsdelsprecedents,sesuscitendeseguidacertesqüestionssecundàriesquerequereixenreglesaddicionals enlesqualsnoentraremisobrelesqualshihadiversesvariants.

3.3 Enelcasespecial n = 1—unsolrepresentantcomúperatots—elvot únictransferibleprenlaformaquedescrivimacontinuació,laqualesconeix coma votalternatiu [56,p.193–195].

Siuncandidatfiguracomaprimeraopcióenmésdelameitatdelsvots, aleshoresresultaelegit.Encascontrari,s’eliminaelcandidatquetémenysvots icadascund’aquestsvotsestransfereixalcandidatqueocupaelllocsegüent delallistaenelvot.Fetaixò,estornaamirarsialguncandidatreuneixmésde lameitatdelsvots,enelqualcasresultaelegit.Sinon’hihacapquecompleixi aquestacondició,aleshoresesprocedeixnovamentaeliminarelquetémenys votsiatransferirelsseusvots.Aquestprocésesrepeteixsuccessivamentfins queresultielegituncandidat.Atotaixòcalafegirqueencadavoltaesrevisael nombretotaldevotspertaldecomptarnoméselsqueencaracontenenalgun candidatnoeliminat.

Aquestprocedimentesconeixtambécoma«doblevoltainstantània»(instant runoffvoting),peròaquestnomnoésgaireencertat,jaqueengeneralpoden sernecessàriesmésdeduesvoltes.

3.4 Totiqueelprocedimentdelvotúnictransferibleestàclaramentinspirat enlaideaderepresentacióproporcional,segonscomesmiri,lasevaproporcionalitatnoésgensclara:quèésproporcionalaquè?LaregladeJeffersoni D’Hondtialtresreglessimilarsderepartimentresponenclaramentaunintent queelnombred’esconsassignatsaunpartitsiguitanproporcionalalnombre devotsobtingutscomsiguipossible.Peròaquínitansolsestandefinitsels partits.Iencaraquehoestiguessin,tampocestariagensclarquèvoldirel nombredevotsobtinguts.

Tanmateix,encertessituacionss’evidencial’existènciad’unapropietat realmentrelacionadaamblaproporcionalitat.Concretament,estractadelcas enquèundeterminatnombre v d’electorscoincideixenaencapçalarlaseva llistadepreferènciesperunmateixconjunt X decandidats,enunordreoun altre.Aquestsvotsespodeninterpretarcomafavorablesalconjunt X.Segonsel criterideproporcionalitatdeDroop —vegeu,perexemple,[36,§3.1]—,si v> mqD amb m enter,llavorshauriend’obtenirunescóalmenys m candidatsdel conjunt X,semprequeaquestconjuntcontinguiefectivamenttantscandidats. Elcomplimentd’aquestcriteriperpartdelvotúnictransferibleelvaposaren relleuel1984MichaelDummett[15,p.282–283](vegeutambé[58,55]).

L’exemplesegüent,tretde[24,§204],mostral’interèsd’aquestapropietat: S’hand’elegircincrepresentantsapartirdels100votssegüents:51: a > b > c > d > e;17: f > g > h > i > j;17: g > f > h > i > j;15: h > f > g > i > j

Aquestsvotsespodenveureenlaforma51: X;49: Y amb X ={a, b, c, d, e} i Y ={f, g, h, i, j},demaneraquel’idealdelarepresentacióproporcionaldemana tresrepresentantsdelconjunt X idosdelconjunt Y.LaquotadeDroopval qD = 100/6 = 50/3,demaneraqueescompleix51 > 3qD i49 > 2qD .D’acord amblapropietatqueacabemdecomentar,elvotúnictransferiblebasatenla quotadeDroopdónaelresultatdesitjat.Encanvi,laquotasimple q0 = w/n = 20 dónadosrepresentantsde X itresde Y

3.5 Elvotúnictransferibles’utilitzasobretotenpaïsosdela Commonwealth Enlasevaversióméstradicional,ques’usaperexempleenleseleccionsal parlamentirlandès[27],lestransferènciesdevotentrecandidatsesfanmaterialment,transportantlesbutlletesd’unabandaal’altra.Aixòposaenevidència elfetquecadaelectorquedaassignataundiputatenconcret. Tanmateix,tél’inconvenientque,engeneral,segonsquinesbutlletessón transferides,potsortirelegituncandidatounaltre(vegeu,perexemple,[56, p.272–273]).Aquestproblemas’arreglaencertesversionsméselaboradeson larepresentaciód’unelectorpotquedardistribuïdaentrediversosdiputats. Unmètoded’aquesttipusésutilitzatdesde1984perla RoyalStatisticalSociety al’horad’elegirelsmembresdelseu Council [22].

3.6 Malgrattotaixò,elvotúnictransferibletéundefectegairebéinacceptable. Suposemqueambunsvotsconcretsresultaseleccionatundeterminatcandidat x.Imaginemqueaquestsvotsexperimentenuncanviquenomésactua enelsentitd’afavoriraquestcandidat x.Tothomestaràd’acordquedesprés

d’aquestcanvihauriadecontinuarseleccionat x.D’aquestapropietatendirem monotonia (respectealcontingutdelsvots).Doncsbé,elvotúnictransferible nolacompleix!Totseguitendonaremunexempleamb n = 1.Segonselque hemvistmésamunt,aixòsignificaqueaquestdefecteestàpresentjaenel conegutmètodedeladoblevoltaperal’elecciód’unsolrepresentant,elqual s’utilitza,perexemple,enleseleccionspresidencialsfranceses.

Vetaquíunexemple.S’had’elegirunsolrepresentantihihatrescandidats a, b, c.Suposemqueelselectorsexpressenlespreferènciessegüents:

LaquotadeDroopés100/2 = 50.Comquenohihacapcandidatquelasuperi amblesprimerespreferènciesdelselectors,espassaaeliminarelqueenté menys,queresultaserelcandidat c,amb30vots.Aquestsvotspassena a,que enreuneix66i,pertant,resultaelegit.Suposemaraqueelsdarrersdeuelectors canviend’opinióensentitfavorablea a:enllocde b > a > c,aravoten a > b > c. Aquestcanvitambéportaal’eliminaciód’uncandidat,peròaraelqueresulta eliminatés b,amb24vots,iaquestsvotspassena c,queenreuneix54i,per tant,resultaelegit.Aixídoncs,elcandidat a hadeixatdeserelegittotiqueels votshanvariatclaramentafavorseu.

Aquestdefectedelvotúnictransferibleésassenyalata[13]i[7,p.38](vegeu també[59]).Davantdemancancesinesperadescomaquesta,elsdefensorsd’un mètode—enaquestcaselvotúnictransferible—solenargumentarquees tractadefetsmoltpocfreqüents.Detotamanera,elqueacabemdeveure nohauriadepassarmai.Siunavariacióclaramentfavorableaundeterminat candidatfaqueaquestdeixidesortirelegit,voldirquealmenysundelsdos resultats—abansodesprésdelavariació—ésincorrecte.

Arrand’aquestsfenòmens,MichaelDummett,elmateixqueel1984havia posatenrelleuelcomplimentdelcriterideproporcionalitatdeDroop,afirmava el1992queelvotúnictransferibleéselsegonmètodemésdolentdesprésdel votuninominal,onnomésespermetindicarunasolaopció[16,p.110–111].

Respecteaaquestaqüestióésmoltinteressantlacontribuciófetael1987 perDouglasWoodall[57].Aquestautorvademostrarlaimpossibilitatmatemàticad’unmètodebasatenelvotpreferencialquecombinilespropietats deproporcionalitatimonotoniaqueestemconsiderantambunesaltresque tambésónpresentsenelvotúnictransferible.Laprimerad’aquestespropietats addicionalsdemanasimplementquesielselectorseslimitenaindicaruna solaopció,resultinelegideslesopcionsmésvotades.L’altrarequereixque lesopcionsmenyspreferidesd’unabutlletamainoajudinniperjudiquinles méspreferides.Aquestaúltimacondicióésproudesitjable,jaquealtrament elselectorsespodenveureconduïtsaometreofalsejarlessevesveritables preferències.LademostracióquedónaWoodalldelaimpossibilitatesmentada consisteixsimplementaposarunexempleconcretonl’aplicaciódelesdiverses propietatspermetarribaraunacontradicció.

Peramésdetallssobreelmètodedelvotúnictransferible,remetemellector a[56,p.267–279].

XavierMoraiMariaOliver

4Candidaturescol.lectives

4.1 Talcomhemditenlaintroducció,enelquesegueixadoptemunmarc generalonlesopcionssobrelesqualss’expressal’electorsónconjuntsde candidatsindividuals.Aquestsconjunts,queanomenarem candidatures, són elsmateixosperatotselselectorsipodenestarreduïtsaunsolcandidat, enelqualcasesrecuperaelplantejamentoriginal.

Lescandidaturescol.lectivespodenserfixadesenelplantejamentdela votació.Aquestseriaelcasdelesllistestancadesquepresentenelspartitso coalicionselectorals,llevatqueaquítenimlaintencióquel’electornohagide limitarelseuvotaescollir-nenomésuna.

Tanmateix,lescandidaturescol.lectivestambépodensorgirdemanera espontàniaquanesvotaentermesdecandidatsindividuals.Així,enlavotació (3) espodenveurecomacandidaturescol.lectiveselsconjunts X ={a, b, c, d} i Y ={e, f, g, h}.Encanvi,enlavotació

65: a, b, c, d;15: a, f, h;20: e, f, g, h (8) hauríemdeprendre X1 ={a}, X2 ={b, c, d}, Y1 ={e, g} i Y2 ={f, h}.Entermesd’aquestsconjunts,aquestaúltimavotacióesveuenlaformasegüent:

65: X1, X2;15: X1, Y2;20: Y1, Y2. (9)

Quanlescandidaturessorgeixendemaneraespontàniatotiqueesvotaentermesdecandidatsindividuals,elsdiversoselementsd’unamateixa candidaturasesolenqualificarde clons.

Enelmarcgeneralqueintroduïm,una assignaciód’escons eslimitaa especificarquantsesconsrepcadacandidatura i.Aquestnombrel’anomenarem ni.Elseuvalornopotsuperarencapcaselnombredecandidatsindividualsqueformenlacandidaturaenqüestió.D’aquestvalormàximendirem la capacitat delacandidatura i,il’anomenarem νi.Enelcasdecandidatures reduïdescadascunaaunsolcandidatindividualtenim νi = 1peratota i.Enel casdellistesdepartits’acostumaaentendreque νi = n peratota i.

Unaassignaciód’esconsenelsentitqueacabemdedirnoacabadedeterminarquinscandidatsconcretsresultenelegits.Aaquestefecte,hihadiverses possibilitats.Unad’aquesteséssimplementferunsorteig.Unaaltraésutilitzarunordreprefixatdinsdecadacandidatura,talcomfanelspartitsenel sistemadellistestancades.Finalment,espotconsiderarlapossibilitatque l’electortambéexpressipreferènciesentrecandidatsindividuals,enelqualcas correspondràbasar-seenaquestainformació.

Detotamanera,enelquesegueixensocupemnomésdelaprimerapart delproblema,ésadir,ladeterminaciódelnombred’esconsquerepcada candidatura.

4.2 Quanesvotaentermesdecandidatsindividualsperòexisteixunaagrupaciód’aquestsenpartitsiunslídersreconegutsdinsdecadapartit,aleshoresel

votd’aprovaciódónapeualesanomenadesestratègiesde decapitació [8,p.25, 50,56].Sielsseguidorsd’undeterminatpartitaprovensistemàticamenttots elsseuscandidats,aleshoresunspocsvotsqueaprovinlamateixallistallevat delslíderspodenaconseguirqueaquestsúltimsnoresultinelegits.

Enrigor,aixòdependràdelmètodeques’utilitziperdeterminarelscandidats elegits.Peròjaesveuavenirquetotselsmètodesraonablestindranaquest problema,ielmètodedePhragménqueutilitzaelvotd’aprovaciónon’és unaexcepció.Davantd’això,Phragménvaproposarunescertesvariacionsque utilitzenelvotpreferencial(vegeul’apèndixB).

Tanmateix,desdelmomentquetenensentitlesestratègiesdedecapitació voldirquehihaunescandidaturescol.lectivesbendefinides,demaneraquees potplantejarlavotacióentermesd’aquestescandidaturescol lectives,illavors desapareixlaqüestiódeladecapitació.

5LaregladeJeffersoniD’Hondtilessevesalternatives

5.1 LaregladeJeffersoniD’Hondtilessevesalternativescorresponenalcas enquèelselectorsvotenentermesdecandidaturescol.lectivesperòeslimiten aindicar-nenomésuna.D’altrabanda,tambésuposenquecadacandidatura potarribaraproporcionar n representants.D’aquestescenariendiremapartir d’arael casuninominalnolimitat.

Enaquestescenari,elprincipideproporcionalitatdemanaqueelsnombres d’esconsassignats ni siguinproporcionalsalsnombresdevotsobtinguts,que d’araendavantserandenotatsper wi.

Laproporcionalitatexactaladonarienelsvalorssegüents,queanomenarem quotesexactes:

i I denotaelnombredecandidatures.Noteuquelesquotesexactess’obtenena partirdelsnombresdevots wi totdividint-losperlaquantitat q0 = w/n.Més amunt,enelcontextdelvotúnictransferible,ensreferíemaaquestaúltima quantitatcoma«quotasimple».Aquíusaremunaaltraterminologiaonaquesta quantitat,icertesalternativesquedeseguidaveurem,rebenelnomde divisor.

Peròengenerallesquotesexactesnoserannombresenters,demaneraque caldecidircomarrodonir-lespertaldedesviar-sedelaproporcionalitattan poccomsiguipossible.

Unapossibilitatmoltnaturaléslaregladeles restesmajors, queconsisteix a assignard’entradatantsesconscomdiguilapartenteradelaquotaexacta,i desprésdonar-neundemésalspartitsambrestesmésgrans.

5.2 Tanmateix,enl’esperitdelprincipideproporcionalitatésméspropi procedirdelamanerasegüent: trobarundivisor q demaneraque,enformar elsquocients wi/q iarrodonirelseuvalorperdefecte,lasumadelsnombres

XavierMoraiMariaOliver

entersobtingutssiguiexactament n (laqualcosarequereix q ≤ q0).Aquesta reglavaserproposadael1882perl’advocatbelgaVictorD’Hondt.Norantaanys abans,ThomasJeffersonhaviaproposatexactamentlamateixareglaambmotiu delrepartimentterritorialdelsesconsdelacambrabaixadelsEstatsUnits d’Amèrica.D’acordambaixò,d’araenendavantendirem regladeJeffersoni D’Hondt.

Encaraquealapràcticaésmoltpocfreqüent,devegadeshipothaverempats quedoninllocaindecisions.Perexemple,amblaregladeJeffersoniD’Hondt enstrobemambproblemesal’horaderepartirdosesconsentredospartitsque hanobtingut,respectivament, w = (2000, 1000) vots.Pera q ∈ (1000, 2000) lespartsenteresde wi/q són (1, 0),mentrequepera q ≤ 1000són (2, 1),i capd’aquestsdosrepartimentsdónauntotaldedosescons.Tanmateix,per adadesmoltproperesobtenimtantelrepartiment n = (2, 0),perexemple pera w = (2001, 999),comelrepartiment n = (1, 1),perexemplepera w = (1999, 1001).Davantd’això,enelcasproblemàtic w = (2000, 1000) ésnaturaladmetrequalsevold’aquestsdosrepartiments.Engeneral,admetrem, doncs,lapossibilitatdemésd’unasolució.Enrelacióambaixòiamblaregla deJeffersoniD’Hondt,resultaconvenientredefinirlapartenterad’unnombre real z demaneraquequan z siguienters’admetinllavorstantelmateixvalor z com z 1.Ambaquestafinalitatfaremúsdelanotaciósegüent:

z = l’entermésgraninferiora z,si z noésenter; obé z obé z 1,si z ésenter. (12)

Equivalentment, z ésqualsevolenterquesatisfacilesdesigualtats

z ≤ z ≤ z + 1. (13)

Perparlarambtotapropietathauríemdeconsiderar z comunconjunti escriure k ∈ z enllocde k = z ;tanmateix,peralsnostrespropòsitsserà suficientsuposarques’hafetunaeleccióconcretadelvalorde z sempreque z siguienter.

Amésdelaformulacióquen’hemdonatmésamunt,laregladeJeffersoni D’Hondtespotreformulardelesdiversesmaneresequivalentsquerecullel resultatsegüent:

Teorema5.1. Siguin w = (w1,...,wI ) unsnombresrealspositiusi n = (n1,...,nI ) unsnombresentersnonegatiusrestringitsasumarunvalordonat n.Les condicionssegüentssóntotesequivalents:

(a) Existeixunnombrerealpositiu q talque ni = wi/q peratota i

(b) ni éselnombredevegadesque wi figuracomanumeradorenels n quocients mésgransdelaforma wi/k amb i = 1, 2,...,I i k = 1, 2,...

(c) n s’obtérecursivamentprocedintdelamanerasegüent:Pera n = 0 esposa ni = 0 peratota i.Elpasde n a n + 1 esfaincrementant ni a ni + 1 pera una i qualsevolquemaximitzilaquantitat wi/(ni + 1)

(d)mini wi/ni ≥ maxi wi/(ni + 1)

(e) n maximitzalaquantitat mini wi/ni,iamés,minimitzaelnombredevalors de i querealitzenelmínimqueapareixenaquestaúltimaexpressió.

Elquocient wi/ni queapareixalsapartats(d)i(e)espotveurecomelpreu, envots,quelicostacadaescóalacandidatura i.Desd’aquestpuntdevista, lesdesviacionsrespectealaproporcionalitatnosónmésquediferènciesenel preudecadaescóperalesdiferentscandidatures.Lacaracterització(e)del resultatprecedentcorrespon,doncs,adirquelescandidaturesmésafavorides siguintanpocafavoridescomsiguipossible,iqueamés,elnombred’aquestes candidaturessiguielméspetitpossible.Enelcashabituald’absènciad’empats entreelsquocients wi/k,aquestacaracterització,quealeshoresesredueixal primercriteriquehiapareix,vaserposadaenrelleuel1901perLéonRouyer,i tambéel1910perMauriceEquer.Lacaracteritzaciógeneral,vàlidaenpresència d’empats,esdemostraa[36,§2].

Enllocdelquocient wi/ni,ésinteressantconsiderartambéelseuinvers ni/wi.Aquestensdónalafracciód’escóquecorresponacadascundels electorsquehanvotatlacandidatura i.Ditd’unaaltramanera,ensmesuralaquantitatderepresentacióqueobtécadascund’aquestselectors.Des d’aquestpuntdevista,lacaracterització(e)delteorema5.1ensdiuquelaregla deJeffersoniD’Hondtminimitzalarepresentaciódelselectorsmésrepresentats.

5.3 Enllocd’arrodonirelsquocients wi/q perdefecte,comfalareglade JeffersoniD’Hondt,tambéhihaaltresopcions.Enparticular,ésmoltnatural l’arrodonimental’entermésproper(queadmetduespossibilitatsenelcasde valorssemienters).Elresultatéslareglade WebsteriSainte-Laguë: trobarun divisor q demaneraque,enformarelsquocients wi/q iarrodonir-losal’enter mésproper,lasumadelsnombresentersobtingutssiguiexactament n. Aquesta reglavaserproposadaperDanielWebsterel1832enelcontextdelrepartiment territorial,iperAndréSainte-Laguëel1910enelcontextqueaquíensocupa d’assignarunnombrederepresentantsacadacandidaturasegonselsvots obtinguts.

Mésconcretament,Sainte-Laguëhivaarribarcomaresultatdebuscarla manerademinimitzarlasumadelsquadratsdelesdiferènciesderepresentació entreelselectors.Segonshemditmésamunt,larepresentacióqueobtéun electorquehavotatlacandidatura i éselquocient ni/wi delnombred’escons querepaquestacandidaturapelnombred’electorsquel’hanvotat.Silaproporcionalitatfosperfecta,totsaquestsquocientsserieniguals,ivaldrien,per tant, n/w.Enconseqüència,s’anul larialaquantitatsegüent,queexpressemen duesformesquesónexactamentequivalents:

= i wi ni wi n w 2 = 1 2w i,j wiwj ni wi nj wj 2 . (14)

XavierMoraiMariaOliver

Entermesestadístics, n/w i γ/w nosónaltracosaquelamitjanaivariànciade lesrepresentacionsdelselectors,ésadir,delsnombres ni/wi repetitscadascun amblafreqüència wi.Doncsbé,Sainte-Laguëvademostrarqueelcriteride minimitzarlasuma γ portavaalareglaquehemenunciatmésamunt:

Teorema5.2. LaregladerepartimentdeWebsteriSainte-Laguëésl’únicaque minimitzalasuma γ delsquadratsdelesdiferènciesderepresentacióentreels electors.

LaregladeWebsteriSainte-Laguëaconsegueixmillorsresultatsquelade JeffersoniD’Hondtpelmotiuquelesdesviacionsrespectealaproporcionalitat depenendelamidadelspartits.Mésconcretament,amblaregladeJeffersoni D’Hondtocorrequelesdesviacions δi = ni nwi/w tendeixenaserpositives peralspartitsgrans,ésadir,peravalorsgransde wi/w,inegativesper alspetits.Aquestefecte,quetéuncaràcterprobabilístic,adquireixespecial importànciaquanelterritoriestàdividitenmoltescircumscripcions,jaque aleshoresesprodueixunefecteacumulatiu.Encanvi,laregladeWebsteri Sainte-Laguëésmoltmésequilibradadesd’aquestpuntdevista.

PeramésdetallssobrelaregladeJeffersoniD’Hondtilessevesalternatives, remetemellectora[36]i[49].

6Lacorrespondènciaderepresentació

6.1 Elsmètodesderepresentacióproporcionalnoeslimitenadecidirquins candidatsesconverteixenendiputats;darrered’aquestadecisióhihatambé unaespecificació—simésnopotencial—dela correspondènciaderepresentació, ésadir,lacorrespondènciaentreelectorsirepresentants,laquals’ha d’amotllaralesrestriccionsipossiblespreferènciesexpressadespelselectors. Laproporcionalitatqueesvoldriaaconseguiresrefereixalesquantitatsde representantsid’electorsqueesposenencorrespondència.Laideaésqueel quocientd’aquestesduesquantitatshauriadeserelmateixperaqualsevol sectordelasocietat.Unaaltramaneradeveure-hoésquecadaelectorhauriadetenirassignadalamateixaquantitatderepresentants.Comquehiha moltsmenysrepresentantsqueelectors,alapràcticaaquestaquantitatde representantsperelectorseràunafracciómoltpetitadelaunitat.Peròelque importanoésaixò,sinóquetotselselectorstinguinunsvalors«commésiguals millor»d’aquestavariable.D’araendavantenshireferiremcomla(quantitat de) representació obtingudaperl’electorenqüestió.

Quanelsvotseslimitenaescollirunasolacandidatura,comhemconsiderat enlaseccióprecedent,llavorscadaelectorquedarepresentatpelsdiputats quehagiobtingutlacandidaturaescollida,iaquestsdiputatsesreparteixen apartsigualsentretotselselectorsquehanvotataquestacandidatura.Per tant,cadaelectorquehaoptatperlacandidatura i obtéunarepresentacióigual a ni/wi,onrecordemque ni denotaelnombred’esconsobtingutsperaquesta candidaturai wi,elnombred’electorsquehihanoptat.

Talcomjahemdit,lesversionsméstradicionalsdelvotúnictransferible assignenacadaelectorunsolrepresentantobécap.Enaquestescenari,el principid’igualtatentreelectorstambéportaarepartircadarepresentantaparts igualsentreelselectorsalsqualsésassignat.Laproporcionalitat(aproximada) delmètodederivadelfetquecadaescórequereixunnombred’electorssuperior alaquotaiqueelsvotssobrantssóntransferitsaaltrescandidats.

Jahemdittambéqueenlesversionsméselaboradesdelvotúnictransferible larepresentaciód’unelectorsolquedardistribuïdaentrediversosdiputats.A continuacióconsideraremambmésdetallaquesttipusdecorrespondències entreelectorsirepresentants,jaquetambéapareixenenelsmètodesqueestudiarem.D’altrabanda,lesconsideraremnomésenelmarcdelvotd’aprovació, queéselqueutilitzenaquestsmètodes.Enaquestcas,larestriccióqueha decomplirlacorrespondènciaderepresentacióésmoltclara:l’assignacióde representantsaunelectornoméspotutilitzarelscandidatsqueellhaaprovat.

6.2 Totseguitconcretemlamanerad’especificarunacorrespondènciade representació.

Sovintdescriuremelsvotsmitjançantunaenumeraciófreqüencial.Ésadir, queenllocdedonarelsvotsunaun,diremquantselectorshanvotatd’unao unaaltramanera(defet,éselquehemfetdesdelprincipiendonarexemples devotacions).Lesmaneresdevotarlesanomenarem opinions, ielnombre d’electorsquehanexpressatl’opinió k l’anomenarem uk.Siestemenumerant elsvotsunaun,llavors uk = 1peraqualsevol k.Perareferir-nosalselectors quehanexpressatl’opinió k,totsovintdiremsimplement«elselectors k».

Peraespecificarelcontingutdelsvotsd’aprovació,utilitzaremunavariable binàriaindexadaper i i k: aik val1sielselectors k aprovenlacandidatura i;en cascontrarival0.Alternativament,hoexpressaremtambéescrivint k √ i en elprimercas,i k √ i enelsegon.Elconjuntdecandidaturesaprovadespels electors k eldenotarem Ak.Aquestconjuntelsuposaremsemprenobuit.Dit d’unaaltramanera,noméstindremencompteelsvotsqueaprovenalguna candidatura.Elnombretotaldevotsenconsideracióés

Elnombred’aprovacionsobtingudesperlacandidatura i és

(16)

D’altrabanda,elnombredecandidaturesaprovadespelselectors k és

(17)

Lanotacióquehemintroduïtfinsaquíesreferiaalesdadesdelproblema. Parlemaradelesincògnites.Totgiraalvoltantdelacorrespondènciade

XavierMoraiMariaOliver

representació,laqualespecificaremmitjançantunavariablereal,positivao nul la,indexadatambéper i i k;aquestavariableladenominarem xik ielseu valordónalafracciódelacandidatura i queésassignadaacadaelectorde l’opinió k.Elnombred’esconsobtingutsperlacandidatura i és ni = k xikuk. (18)

D’altrabanda,lasuma

k = i xik (19)

dónalaquantitatderepresentacióqueobtécadaelectordel’opinió k. Lesrestriccionsquetenimsónlessegüents.Enprimerlloc,lesfraccionsde representacióhandeserpositivesonul.les: xik ≥ 0, peraqualssevol i,k. (20)

Ensegonlloc,larepresentaciódecadaelectors’haderestringiralescandidaturesqueellaprova: xik = 0, sempreque aik = 0. (21)

Entercerlloc,elnombred’esconsqueobtéunacandidaturahadeserenter,no negatiu,iinferioroigualalasevacapacitat νi (§4): ni ∈ Z, 0

Finalment,calqueelnombretotald’esconssiguieldesitjat:

(22)

Noteuquelarestricció (21) permetlimitarlasuma (18) alselectors k que aprovenlacandidatura i,iunacosasimilarpassaamblasuma(19):

i = k√ i xikuk, (24)

k = i | k√ i xik (25)

Envistade (18) o (24),ésclarquesitoteslesquantitats uk esmultipliquen perunamateixaconstantitoteslesquantitats xik esdivideixenperaquesta mateixaconstant,aleshoress’obtéelmateixrepartiment (ni).Pertant,elque importanosónelsvalorsconcretsde uk i xik,sinólessevesproporcions respectives,ésadir,elsquocients uk/u i xik/xi .

L’objectiuqueestractad’aconseguirésquelesrepresentacions rk siguin commésigualsmillorperatoteslesopinions k.Comésbensabut—vegeu, perexemple,[36,§5]—aixòadmetdiversesinterpretacions,lesqualsdonaran llocamètodesdiferents.

6.3 Lanociódecorrespondènciaderepresentacióapareixtambéenelstreballs deMonroe[35]idePotthoffiBrams([47],[5,ch.6]).Entrelesdiversespossibilitatsqueexplorenaquestsautors,s’hipottrobarunaidead’algunamanera dualalaprecedent:minimitzarunamesuradelamancaderepresentativitat (misrepresentation),ésadir, i,k(1 aik)xikuk,sotalesrestriccions (20), (22), (23) iunaaltraqueimposaunamateixaquantitatpredeterminadaderepresentació rk peraqualsevol k (acanvid’aixònos’imposapaslarestricció (21),iper tantnovalenni (24) ni (25),sinósolament (18) i (19)).Envirtutde (18) i (23), aquestplantejamentequivalamaximitzarlarepresentativitat i,k aikxikuk sotalescondicionsesmentades.

6.4 Suposemperunmomentquenohihaguéslarestricció (22),ésadir, queelsnombresd’escons ni poguessinserfraccionarisiprendrequalsevol valorentre0i n.Suposemtambéquecadaelectorhaaprovatalmenysuna candidatura.Enaquestescondicionsnohihaobstacleperaaconseguirqueles representacions rk siguinexactamentiguals(icoincideixin,pertant,amb n/w). Enefecte,peracadaopinió k espodentrobarfàcilmentunes xik quecompleixin lescondicions(20)–(21)itinguincomasumaelvalor n/w.

Sielselectors k hanaprovatmésd’unacandidatura,aleshoresaquesta assignaciódevalorsales xik espotferdemoltesmaneresdiferents.Davant d’això,elmésnaturaléstractardelamateixamaneratoteslescandidatures aprovadesperunsmateixoselectors.Ésadir,amblanotacióquehemintroduït a (17),prendre xik = (n/w)/σk peraqualsevol i talque k √ i (i xik = 0per aqualsevol i talque k √ i).Elsnombres(fraccionaris)d’esconsqueresulten peracadacandidaturasón ni = (n/w) k√ i uk/σk.Aquestsnombressón exactamentproporcionalsalesquantitats wi = k√ i uk σk

(26) lesqualscomptenelsvotsqueobtécadacandidaturaquancadavotesreparteix apartsigualsentretoteslescandidaturesquehisónaprovades.

Aixídoncs,enelsupòsitque ni/n poguésprendrequalsevolvalorfraccionarientre0i1,aleshoresposant ni/n = wi/w s’aconsegueixalhorauna representacióigualdetotselselectorsiuntractamentigualdelesdiverses candidatures.Totiqueelsupòsitqueconsideremcontradiularestricciódels ni avalorsenters,homs’hiacostacadavegadamésenellímit n →∞ sempreque lescandidaturestinguincapacitatmàxima νi = n. Ésraonable,doncs,demanar queenaquestlímitelquocient ni/n s’acostialvalor wi/w.

Peravalorsfinitsde n ocandidaturesindividuals(νi = 1)lesduescondicions d’igualtatdequèparlàvemfaunmoment—entreelectorsientrecandidatures— fàcilmentdeixendepoder-secomplirsimultàniament.

Davantd’això,ésnaturalpensaraimplementarlarestriccióanombres entersmitjançantalgunaregladerepartimententer,comaraladeJeffersoni D’HondtoladeWebsteriSainte-Laguë,aplicadaalesquantitats wi

XavierMoraiMariaOliver

Defet,D’Hondtproposavaunareglad’aquestamenaperatractarelsvots «mixtos»,ésadir,elsquecombinavencandidatsdediferentspartits.Adiferència delquenosaltresconsiderem,unvotd’aquesttipuscombinadiversospartitsen unesproporcionsnonecessàriamentiguals,jaquepotcontenirméscandidats d’unpartitqued’unaltre.Enaquestcontextésraonableprocedircomproposava D’Hondt([10,p.25–30],[11,p.32–33,43–49]),ésadir,quecadavotd’aquest tipussiguidividitentreelspartitsenqüestióenproporcióalsrespectiusnombres decandidats(laqualcosacorresponasubstituir (26) perunaexpressiómés generaldelaforma wi = k√ i αikuk amb i | k√ i αik = 1).Aquestareglatambé estàclaramentenunciadaa[2,princip IV].

Tanmateix,elquevolexpressarunvotd’aprovaciónoéspasunadivisióen partsiguals,sinósimplementunconjuntdepossibilitatsacceptables,laqual cosapermetdonarpreferènciaal’objectiufonamentald’aconseguirqueles representacions rk siguincommésigualsmillor.Aquestaéslaideaessencial delmètodedePhragmén,elqualestudiaremdetalladamentenlesproperes seccions.

Elmalencertd’aplicarunaregladerepartimententeralesquantitats wi és especialmentacusatenelcasdecandidaturesindividuals,ésadir,ambla restricció ni ∈{0, 1}.Enefecte,enaquestcasqualsevolreglaraonablede repartimententerd’acordambunesquantitatsdonadesesredueixaseleccionar els n valorsmésgransd’aquestesquantitats.Sihoapliquemal’exemple (3) amb lesquantitats (26) —itambéamblesquantitats (16)—aleshoressurtenelegits elsquatrecandidatsmésvotats,laqualcosaéstotalmentcontràriaal’esperit delarepresentacióproporcional.

6.5 Encontradelplantejamentqueestemfentespotobjectarquevoler especificarquindiputatrepresentacadaelectorésunautopia,imésencarasi larepresentaciód’unelectorlarepartimentrediversosdiputats.Alapràctica, l’únicqueimportaésquinscandidatssónelegitsdiputats.Aixòésbencert.Però calrecordarqueparlemdevotsonespodenaprovardiversescandidatures.En aquestcontext,elproblemadedecidirquinrepartimentd’esconsésmésadient perarepresentarelconjuntdel’electoratnoéspassenzill.Enl’esperitdela representacióproporcional,elquetocaferésconsiderarlacorrespondència detallada (xik) ibuscarlaquedoniunesrepresentacions (rk) mésequitatives, enalgunsentitounaltrequecaldràespecificar.

Unproblemaanàlegquepotajudaraentendreelqueensocupaéselsegüent: enllocd’electorsalsqualscaldonarrepresentació,tenimungrupdepersones quenecessitenalimentació;enllocdecandidats,tenimalimentsdediversos tipus,elsqualsmesuremambunaunitatcomuna(quepodriacorrespondre, perexemple,aundeterminatcontingutenergètic).Decadaalimentn’hiha undeterminatnombreenterd’unitats,ielconsumquese’nfacitambéhade serunnombreenterd’unitats(sis’encetaunaunitatllavorscalconsumir-la tota).L’objectiuésrepartirunaquantitattotaldeterminada n d’alimentsd’una maneracommésequitativamillor,totrespectantlarestricciódecadapersona alsalimentsqueelladigui.

L’analogiaesdevindriaméscompletasisuposéssimquedarrerecadaaliment hihaalgú,elseufabricant,quetéespecialinterèsqueesconsumeixiaquell alimentinoelsaltres,laqualcosaintentaaconseguirmitjançantpublicitati potsertambémitjançantalguncanvienl’alimentquel’acostimésalsgustos existents.

6.6 Unacorrespondènciaderepresentaciópotsermostradasobreelpaper mitjançantelqueendiremun diagramaderectangles, queésunavariaciódel quefaPhragména[43,p.89–90].Lafigura1endónaunexemple.

Figura1: Diagramaderectanglesd’unacorrespondènciaderepresentació.

Labasedelafiguraestàdivididaentantssegmentscomopinions k s’han manifestat.Asotadecadasegmenthemindicatlacorresponentllistade candidaturesaprovades.Elsegment k téunalongitudproporcionala uk,el nombred’electorsquehanmanifestataquellaopinió.Asobredelsegment k hiha tantsrectanglescomcandidatures i donenrepresentacióaaquestselectors.En cadarectangles’indicaaquinacandidaturacorrespon;aquíhofemmitjançant uncodidecolors.L’alturadelrectangle ik ésproporcionala xik.Pertant,l’àrea d’aquestrectangleésproporcionala xikuk,il’àreatotaldelsrectanglesdela candidatura i ésproporcionalalnombred’esconsobtinguts.D’altrabanda,la sumadelesalturesdelsrectanglesquehihaasobredelsegment k dónala representació rk queobtécadaelectord’aquestaopinió.

XavierMoraiMariaOliver

7ElmètodedePhragmén.Variantseqüencial

EnaquestaseccióestudiemafonslaformabàsicadelmètodedePhragmén, queaquestautorvapresentarenelsanys1894–1899[39, 40, 42, 43].Abansi desprésd’aquestesdates,Phragménvaconsiderardiversesvariacionssobre eltema,delesqualsdonemunaclassificacióenl’apèndixB.Adiferènciade Phragmén,queconsideravanoméselcasdecandidaturesindividuals,nosaltres enssituaremenelmarcgeneralenquèlesopcionssobrelesqualss’expressa l’electorpodensercandidaturescol lectives,cadascunadelesqualsofereixun determinatnombredecandidatsindividuals.

7.1 LaformabàsicadelmètodedePhragméntéuncaràcterseqüencial:encada pass’assignaunescóaalgunacandidaturaiaquestescóesreparteix,enparts nonecessàriamentiguals,entreelselectorsquel’hanaprovat.

Comveuremdeseguida,laideadebuscarlamàximaproporcionalitat possibles’enténenunsentitqueéscomúamblaregladeJeffersoniD’Hondt. Defet,italcomveuremmésavall,enelcasuninominalnolimitatelmètodede PhragménesredueixalaregladeJeffersoniD’Hondt.

Suposem,demoment,quelescandidaturessónindividuals.Doncsbé,el primerescós’assignaalcandidatquehareunitmésaprovacions.Aquestprimer escósíqueesreparteixapartsiguals;elsreceptorssóntotselselectorsque hanaprovatelditcandidat.Comqueestractadelcandidatmésaprovat,la representacióqueobtécadaelectoréslaméspetitapossible. Elsegüentescó s’assignaràaunaltrecandidatiesrepartiràdemaneraquetotselselectors quel’aprovenigualinlarepresentacióacumuladapercadascund’ellsfinsaquell moment.Elcandidatqueseseleccionaéselquefaqueaquestarepresentació acumuladasiguicomméspetitamillor. Noteuqueelselectorsquenoaproven aquestsegoncandidats’hanquedatamblarepresentacióquetenien,quepotser nul.lasitampochavienaprovatelprimercandidat.Elsegüentescóseselecciona ireparteixd’acordambelmateixprincipi,iaixísuccessivament.

Enelcasdecandidaturescol lectives,l’únicadiferènciaésque cadacandidaturapotcontinuarrebentesconsmentrenoarribialasevacapacitat νi

Vegemcomesconcretaaixòenunexemple(extretdelsarticlesdePhragmén).Suposemques’hand’elegirtresrepresentants,quehihasiscandidats a, b, c, p, q, r,iqueelsvotssónelssegüents:

1034: a, b, c;90: a, b, q;47: a, p, q;519: p, q, r. (27)

Segonselquehemdit,elprimerescóelrepelcandidat a,queéselquetotalitzamésaprovacions,ésadir,1034+90+47 = 1171.Cadaelectorquel’haaprovat repunapartalíquotad’aquestescó,ésadir,1/1171 = 0 854 10 3 escons.

Vegemaraquincandidatobtéelsegonescó.Elcandidat b haestataprovat pelselectorsdelesopinions abc i abq,elsqualsjatenenrepresentació,tots ellslamateixa,atravésde a.Pertant,sielnouescóésassignata b,esrepartirà uniformemententreaquests1034 + 90 = 1124electors,cadascundelsquals

elevaràlasevarepresentacióen1/1124 = 0 890 · 10 3 escons,iarribarà,per tant,a0.854 · 10 3 + 0.890 · 10 3 = 1.744 · 10 3 escons.Demanerasimilar, sielnouescóésassignata c,aleshoresesrepartiràapartsigualsentreels 1034electorsdel’opinió abc,cadascundelsqualselevaràlasevarepresentació en1/1034 = 0.967 10 3 escons,iarribarà,pertant,a0.854 10 3+0.967 10 3 = 1.821 · 10 3 escons.Consideremaralapossibilitatd’assignarelsegonescóal candidat p.Aquestésaprovatpelselectors apq,quejatenenrepresentacióa travésde a,itambépels pqr,queencaranotenenrepresentació.Segonshem dit,sil’assignema p,elnouescóhadeserrepartitdemaneraqueigualila representaciódetotsaquestselectors.Peracalcularaquestarepresentació finalcomuna ρ hemderesoldrel’equació519 ρ + 47 (ρ 0.854 · 10 3) = 1,que dóna

ρ = 47 × 0.854 · 10 3 + 1 (519 + 47) = 1 838 10 3 (28)

Uncàlculsimilarperalcandidat q ensdiuqueenaquestcaselselectors abq, apq i pqr quedarientotsellsambunarepresentacióiguala1 703 · 10 3 escons. Finalment,enelcasdelcandidat r,aprovatnoméspelselectors pqr,s’obté queaquestselectorsobtindrienunarepresentacióde1/519 = 1 927 10 3 escons.Recopilant,lescincpossibilitatsd’assignaciódelsegonescóelevenla representaciódelselectorsmésafavoritsalsvalorssegüents: b:1.744 10 3 , c:1.821 · 10 3 , p:1.838 · 10 3 , q:1.703 · 10 3 , r:1.927 · 10 3.Pertant,elsegon escóésassignatalcandidat q,queminimitzalarepresentacióacumuladafins arapelsseuselectors.

Passem,finalment,aconsiderareltercerescó.Enaquestmoment,elselectors abc tenencadascun0 854 · 10 3 escons,iels abq, apq i pqr tenencadascun 1.703 · 10 3 escons.Mitjançantunscàlculsanàlegsalsdelparàgrafprecedent, s’obtéqueeltercerescóhadeserassignatalcandidat b,elqualdeixaels electors abc i abq ambunarepresentacióde1.812 · 10 3 escons.

Eldiagramaderectanglesdelacorrespondènciaobtingudaéselquehem donatcomexemplealafigura1.

TalcomfanotarPhragmén[43,p.299–300],cadavegadaqueesconsideraun candidatconcretilasevadistribucióentreelselectors,elproblemaésanàleg aladistribuciód’unaunitatdevolumd’uncertlíquidentreunsrecipients cilíndricsquepotserjacontenenaltreslíquidsdelamateixadensitat.Cada recipient k téunabased’àrea uk inomésadmetelslíquids i talsque k √ i. D’altrabanda,totselsrecipientsqueadmetenellíquid i estancomunicatsentre si,demaneraquequans’hiabocaunaunitatdevolumdellíquid i,lagravetat faqueaquestesdistribueixiambunmateixnivellsuperiorentotsaquests recipients.

7.2 Entermesmatemàtics,esparteixde n = 0iladistribuciónul la,ielpas de n a n + 1esfadelamanerasegüent:peracadacandidatura i queencarano haesgotatlasevacapacitat νi,esconsideralarepresentaciótotalquereunirien elselectorsqueaprovenaquestacandidaturaenelsupòsitd’assignar-liaquest

nouescó,ésadir,larepresentacióquejatenenméselnouescó,iesdivideix pelnombretotald’aquestselectors: ρ(n+1) i = k√ i uk r (n) k + 1 wi . (29)

Unvalormésomenyselevatd’aquestquocientvoldirqueelselectorsenqüestió resultarienmésomenysbeneficiatsenelcasdeseleccionarlacandidatura i EnelmateixesperitquelaregladeJeffersoniD’Hondt,ésadir,queelselectors mésafavoritshosiguincommenysmillor,Phragménproposad’assignarel nouescóaunacandidatura i queminimitziaquestquocient(sotalacondició queencaranohagiesgotatlasevacapacitat νi).Sin’hihamésd’una,aleshores consideremadmissiblequalsevold’aquestes. Enelquesegueixensreferirema aquestacandidaturamitjançantlanotació ı n+1 iescriurem ρn+1 enllocde ρ(n+1) ı n+1 ; d’altrabanda,tambéconvindremaposar ρ0 = 0.Elnouescódelacandidatura escollida ı n+1 esreparteixentreelsseuselectorsdetalmaneraquetotsells assoleixinlarepresentació ρn+1.Talcomveuremdeseguida,aixòs’aconsegueix mitjançantl’actualitzaciósegüentdelrepartiment xik: x(n+1) ik x(n) ik =

n+1 r (n) k , si i = ı n+1 i k √ i ; 0, encascontrari. (30)

Multiplicantaquestesquantitatsper uk isumantsobre k,veiemqueefectivamentelsincrements x(n+1) ik x(n) ik totalitzenexactamentunescó.D’altrabanda, sumant(30)sobre i s’obtéque

r (n+1) k r (n) k =

n+1 r (n) k , si k √ ı n+1; 0, encascontrari. (31)

D’aixòesdedueixelquehavíemanunciatmésamunt: elselectors k quehan aprovat ı n+1 assoleixentotsells r (n+1) k = ρn+1.Mésgeneralment,unaaplicació reiteradade (31) portaalaconclusiósegüent(onconsidereml’índex n enlloc de n + 1):

Proposició7.1. Peraqualsevol n ≥ 0 escompleix r (n) k = ρm,on m éselmàxim índex,anterioroiguala n,talque k haaprovatlacandidatura ı m;si k noha aprovatcapdelescandidatures ı 1,..., ı n,llavors r (n) k = ρ0 = 0.Ésadir:

r (n) k = ρm, on m = max {0}∪{p ∈ Z | 1 ≤ p ≤ n,k √ ı p} (32)

Eleccionsmitjançantelvotd’aprovació

Enelsparàgrafsprecedentshemdonatpersuposatquelasuccessió (ρn | n = 0, 1, 2,...) nodecreixencapmoment.Sitinguéssim ρn+1 <ρn,llavors deixariadesercertque ρn+1 foslarepresentaciódelselectorsmésafavoritsen aquellmoment,talcomsuposàvem.D’altrabanda,algunadelesquantitatsque apareixenalsegonmembrede (30) i (31) llavorspodriasernegativa,laqual cosapodriaportaravalorsnegatiusde x(n) ik ,quenosónadmissibles.Totaixò quedadescartatambelresultatsegüent.

Proposició7.2. ρn+1 ≥ ρn peraqualsevol n ≥ 0.Enelcas n = 0 ladesigualtat ésestricta.

Prova. Procediremperinducció.Peragilitzarelllenguatge,escriurem i enlloc de¯ ı n+1.Pera n = 0tenim,efectivament,

Perapassarde n a n + 1noméscalnotarque

n+

onladarreradesigualtatésconseqüènciaimmediatadeladefinicióde ρn,i l’anteriorésconseqüènciadelahipòtesid’induccióatravésde(32). ✷

Proposició7.3. ρn = max k r (n) k .

Prova. Combinantlaproposició7.2amblaigualtat (32) s’obtéladesigualtat r (n) k ≤ ρn peraqualsevol k.D’altrabanda, (32) tambéensdiuque r (n) k és iguala ρn peralselectors k quehanaprovat¯ ı n. ✷

Totiqueengeneralladesigualtat ρn+1 ≥ ρn noésestricta,escompleix sempreelfetsegüent:

Proposició7.4. Cadaelectorrepunafraccióestrictamentpositivadecada candidaturaqueellhaaprovatiqueharesultatescollida.

Prova. Comencemperobservarquen’hihaprouambconsiderarcandidats individuals,jaqueunacandidaturacol lectivaequivalaunconjuntdecandidatsindividualsquevansemprejunts.Lademostracióseràpercontradicció. Suposemelcontraridelquevolemdemostrar:l’escó (n + 1)-èsimésassignat auncertcandidat i amblaparticularitatquehihaunselectors quehavien aprovataquestcandidatperònorebenrepresentacióatravésd’ell.Sipassa aixòvoldirque,abansd’assignaraquestescó,elselectors jahavienassolit laquantitatderepresentacióquearaobtenentotselsquehanaprovat i.Ésa dir, r (n) = ρn+1. Suposemqueelselectors hanassolitaquestarepresentació enserassignatl’escó m-èsim,demaneraquetenim r (m 1) <r (m) = ρn+1.

XavierMoraiMariaOliver

Combinantelsresultatsprecedents,se’ndedueixque r (m 1) <r (n).D’altra banda,perauna k arbitràriatenimladesigualtatnoestricta r (m 1) k ≤ r (n) k . Aquestsfetsenspermetenescriureque

ρm ≤ ρ(m) i = k√ i uk r (m 1) k + 1 wi < k√ i uk r (n) k + 1 wi = ρ(n+1) i = ρn+1. (35)

Tanmateix,laproposició7.3permetdeduirtambéladesigualtatcontrària ρm ≥ r (m) = ρn+1, demaneraqueefectivamenthemarribataunacontradicció. ✷

Observació. Enllocde (29),Phragmén—vegeu,perexemple,[42,p.191]— expressa ρ(n+1) i mitjançantlafórmulasegüent,quederivade (29) enintroduirhi(32):

ρ(n+1) i = w(n,1) i ρ1 + w(n,2) i ρ2 +···+ w(n,n 1) i ρn 1 + w(n,n) i ρn + 1 w(n,1) i + w(n,2) i +···+ w(n,n 1) i + w(n,n) i + w(n,0) i , (36)

on,peracada m = 1, 2,...,n, w(n,m) i representaelnombretotaldelselectors queaprovenelscandidats i i ı m perònocapdelscandidats ı p amb m<p ≤ n, id’altrabanda, w(n,0) i representaelnombretotaldelselectorsqueaproven i perònocapdels¯ ı p amb p = 1, 2,...,n.

7.3 Acontinuacióconsideremelnombretotald’esconsquereuneixunconjunt X decandidatures.Enrelacióambaixòusaremlanotaciósegüent,on calrecordarque Ak representaelconjuntdecandidaturesaprovadespels electors k:

Proposició7.5. Peraqualsevolconjunt X decandidaturesescompleixladesigualtatsegüent: nX ≤ ρn wX .

Prova.

onhempartitde (18),hemtingutencompteque xik = 0sinoésque i ∈ Ak,i hemusatlesdesigualtatsqueesdedueixende (19)–(20) idelaproposició7.3.✷

(37)

(38)

(39)

Corol.lari7.6. Elnombred’esconsquerepunacandidatura i compleixla desigualtatsegüent: ni ≤ ρn wi.

Proposició7.7. Sigui X unconjuntarbitraridecandidatures.Mentre nX no arribaalasevacapacitatmàxima i∈X νi, escompleixsempreladesigualtat següent: nX + 1 ≥ ρn uX .

Prova. Suposemladesigualtatcontrària,ésadir, nX + 1 <ρn uX . (40)

Sigui i qualsevolcandidaturade X amb ni <νi. Veuremqueladesigualtat precedentimplicaria ρ(n+1) i <ρn,encontradiccióambelfetque ρn ≤ ρn+1 ≤ ρ(n+1) i .Enefecte,partintde(29),podemescriure

ρ(n+1) i = k√ i,Ak≠X uk

. (41)

Arabé,elsegontermedeldenominadornoésaltreque uX .D’altrabanda,el segontermedelnumeradorestàacotatsuperiormentper nX ;enefecte, k | Ak=X uk r (n) k = j∈X k | Ak=X u

Finalment,lesrepresentacions r (n) k queapareixenenelprimertermedelnumeradorespodenacotartotesellesper ρn.Pertant,escompleixladesigualtat ρ(n+1) i ≤

+ nX + 1 k√ i,A

(43)

quecombinadaamblahipòtesi(40)dóna ρ(n+1) i <ρn ✷

7.4 Enaquestapartatensocupemd’unparelld’escenarisespecials.Elprimer éselcasuninominalnolimitat.Recordi’squeelcaràcteruninominalvoldirque cadaelectoraprovaunasolacandidatura.Pertant,lespossiblesopinionses corresponenamblesdiferentscandidatures,ipera X ={i} lesquantitats uX i wX definidesper (38) i (39) sónigualsentresiicoincideixenambla wi dela secció5.D’altrabanda,elcaràcternolimitatvoldirquecadacandidatura i té capacitat νi = n,ésadir,quepotarribaraproporcionar n representants.En aquestescondicionslesproposicions7.5i7.7ensdiuenque wi ni + 1 ≤ ρn ≤ wi ni . (44)

D’acordamblacaracterització(d)delteorema5.1,aixòenspermetarribarala conclusiósegüent:

Proposició7.8. Enelcasuninominalnolimitatl’algorismedePhragménes redueixalaregladeJeffersoniD’Hondt.

XavierMoraiMariaOliver

Valadirquetambéésfàcilarribardirectamentalacaracterització(c) delteorema5.1.Enefecte,enlescondicionsqueestemconsiderant,lesdesigualtats (42) i (43) pera X ={i} esconverteixenenigualtatsienlasegona d’ellesdesapareixenelsprimerstermesdelnumeradorideldenominador.Això estableixlaigualtat ρ(n+1) i = (ni + 1)/wi peraqualsevol i. Pertant,l’escó (n + 1)-èsims’assignaaunacandidatura i queminimitziaquestaquantitat,és adir,quemaximitzi wi/(ni + 1), talcomcontemplalaconegudaformulació recursivadelaregladeJeffersoniD’Hondt.

Consideremaraelcasqueenpodemdiruninominaltotalmentlimitat:cada electoraprovaunasolacandidaturadecapacitat1.Enaltresparaules,cada electoraprovaunsolcandidatindividual.Enaquestcas,tenim ρ(n+1) i = 1/wi semprequeelcandidat i encaranohagiestatelegit.Pertant,s’arribaala conclusiósegüent:

Proposició7.9. Enelcasenquècadaelectoreslimitaaaprovarunsolcandidat individual,elmètodedePhragménesredueixaseleccionarels n candidatsmés votats.

7.5 Acontinuacióensocupemdelaimportantqüestiódela monotoniarespectealcontingutdelsvots.Enelcasdelvotd’aprovacióestractasimplement que,sinovariaresmés,l’addiciód’aprovacionsafavord’unacandidaturano puguiproduirmaiunadisminuciódelsesconsquelisónassignats.Totique Phragménesrefereixdiversesvegadesaaquestaqüestiócomamotivaciódel seumètode,laveritatésqueencapmomentnodemostradetalladamentqueel seuprocedimentiteratiutinguiaquestapropietat.Totseguitdemostraremque ésefectivamentaixíenelcasdecandidaturesindividuals,perònoenelcasde candidaturescol lectives.

Proposició7.10. Enelcasdecandidaturesindividuals,ésadir, νi = 1 pera tota i,elprocedimentiteratiudePhragméntélapropietatdemonotoniarespecte alcontingutdelsvots.

Prova. Acontinuacióanomenarem i elcandidatenqüestióiusaremunatitlla perindicarlesquantitatscorresponentsalsnousvots.D’acordamblahipòtesi que i repaprovacionsaddicionalsiquenovariaresmés,escompleix

uk ≥ uk, sempreque k √ i. (45)

Suposemqueambelsvotsoriginalselcandidatenqüestióresultavaelegit peral’escó (n + 1)-èsim,ésadir,que i = ı n+1.Peraaconseguirelnostre objectiu,n’hihaprouambveureque,ambelsnousvots,siaquestcandidatno surtelegitperaunescóanterior,llavorssurtelegitforçosamentperal’escó (n + 1)-èsim.Comquesuposemquelesaprovacionsdelsaltrescandidatssón exactamentlesmateixesqueenelsvotsoriginals,lahipòtesiqueelcandidat i nohasortitelegitperacapescóanteriorimplicaquenohihacapvariació enlesquantitats ρ1,...,ρn ipertanten r (n) k ,itampocen ρ(n+1) j pera j ≠ i Envistad’això,elnostreobjectiuesredueixademostrarque ˜ ρ(n+1) i ≤ ρ(n+1) i .

Partintde (29) idel’expressióanàlogaambelsvotsmodificats,iteninten compteque wi = k√ i uk ianàlogamentpera ˜ wi,se’ndedueixsuccessivament que

onelsignedelsegonmembreésnegatiuozerojaque r (n) k = ρm peralguna m ≤ n, id’altrabanda ρ(n

Enelcasdecandidaturescol.lectivesl’addiciód’aprovacionsafavord’una potcomportarunadisminuciódelnombred’esconsquelisónassignats.Per exemple,pera n = 3ielsvots

4: A;7: B;1: A, B;16: A, C;4: B, C, (47) elmètodedePhragméndónadosesconsa A,peròsiundelsvotsquenomés aproven B passaaaprovartambé A (demaneraqueelscoeficientsesdevenen respectivament4,6,2,16,4)aleshores A obténomésunsolescó(l’assignació successivad’esconsés ABAABA enelprimerescenarii ACBAAB enel segon).

Unaltreexempleinteressantéselsegüent,ontambéconsiderem n = 3:2

10: A;3: B;12: C;21: A, B;6: B, C. (48)

Enaquestcas,elmètodedePhragméntambédónadosesconsa A,peròsiels votsqueaprovennoméslacandidatura A s’incrementenenunaunitat(passanta ser11enllocde10)aleshores A obténomésunsolescó(l’assignaciósuccessiva d’esconsés ACABAC… enelprimerescenarii ABCABA… enelsegon).

Talcomhemditmésamuntenrelacióambelvotúnictransferible,lamanca demonotoniaésundefectepocmenysqueinacceptable.Alasecció8veurem queaquestproblemapodriadesaparèixerencertesvariantsdelmètodede Phragmén.

7.6 Elresultatsegüentestableixunapropietatdel’estildelcriterideproporcionalitatdeDroop.Ésunageneralitzaciód’unresultatqueésbenconegut peralaregladeJeffersoniD’Hondt[36,prop.3.1].Lademostraciótambéserà anàloga.Recordi’sde (38) que uX voldirelnombred’electorsqueaproven exactamentundeterminatconjunt X decandidatures.

Proposició7.11(contingudaa[28,sats13.5,(ii)]). Si uX >mqD,amb qD = w/(n + 1) i m ≤ i∈X νi,aleshores nX ≥ m

2AquestexempleenshaestatassenyalatpelprofessorSvanteJanson.

XavierMoraiMariaOliver

Prova. Laproposició7.5,aplicadaa Xc , elconjuntcomplementaride X,ens garanteixladesigualtatsegüent:

n nX ≤ ρn wXc ≤ ρn(w uX ). (49)

D’altrabanda,l’acotacióinferiorqueestemsuposantsobre uX ilaidentitat w = (n + 1)qD impliquenque

w uX <qD (m + 1 m). (50)

Apartird’aquíprocediremperreduccióal’absurd.Suposemquenotinguéssim nX ≥ m sinóladesigualtatcontrària nX <m 1.Combinant-laamb (49) i (50) s’obtèque1/ρn <qD.Usantnovamentlahipòtesid’acotacióinferiorde uX , se’ndedueixque1/ρn <uX /m. Tanmateix,laproposició7.7ensasseguraque ρn ≤ (nX + 1)/uX .Pertant,enresultaque nX + 1 >m,ésadir nX ≥ m. ✷

7.7Elcasdeduescandidatures

Consideremduescandidatures A i B.Siguin α, β, ζ lesfraccionsdel’electoratque aprovenrespectivamentnoméslacandidatura A,nomésla B,ototesdues A i B (tenim,doncs, α + β + ζ = 1).Lesquantitatsderepresentacióperelectorque obtenenrespectivamentaqueststrestipusd’electorsserandenotadesaquíper rn, sn, tn,on n indicaelnombred’esconsenjoc;elsnombresd’esconsque rebenrespectivament A i B serandenotatsper pn, qn (pn + qn = n).Comque tn corresponalselectorsqueaproventant A com B,laproposició7.1ensassegura que tn = ρn,mentreque rn = ρm1 i sn = ρm2 amb m1,m2 ≤ n i max(m1,m2) = n. Envirtutdelaproposició7.2se’ndedueixque tn = max(rn,sn).D’altrabanda, lareglaquedetermina (rn+1,sn+1) apartirde (rn,sn) espotescriureenla forma

(rn+1,sn+1) = (rn,sn), si rn ≤ sn; (rn,sn), si rn ≥ sn, (51) on r0 = s0 = 0i rn i sn vénendonatsperlesfórmules

rn = αrn + ζtn + 1 α + ζ ,sn = βsn + ζtn + 1 β + ζ . (52)

Enelcas rn = sn admetemlesduespossibilitats,laqualcosadónalloca múltiplessolucions.Elnombred’esconsobtingutspercadacandidaturasegueix elprocéssegüent:

(pn+1,qn+1) = (pn + 1,qn), si rn+1 >rn; (pn,qn + 1), si sn+1 >sn. (53)

Ésnaturalpreguntar-secomdepenen pn, qn de α, β, ζ i n.Pera ζ = 0,enquè laregladePhragménesredueixaladeJeffersoniD’Hondt,lacaracterització(a) delteorema5.1implicaque pn/n → α i qn/n → β quan n →∞

Prova.Tenintencompte (13),lacaracterització(a)delteorema5.1enspermet escriure ni ≤ wi/q ≤ ni + 1.Isumantaquestesdesigualtatssobre i s’obté que n ≤ w/q ≤ n + I,on I denotaelnombredecandidatures.D’aquestes desigualtatsesdedueixd’unabandaque ni ≤ (n + I)wi/w id’altrabandaque ni + 1 ≥ nwi/w.Pertant, wi/w 1/n ≤ ni/n ≤ (n + I)wi/nw,d’onesdedueix elresultatdesitjat:limn→∞ ni/n = wi/w

Pera ζ> 0elcomportamentasimptòticde fn = pn/n quan n →∞ noéspas tansenzill.D’entrada,noésclarque fn = pn/n convergeixisemprecapaun límit.Ditaixò,lesexploracionsnumèriquessemblenindicartalconvergència pera«quasitotaparella»devalorsde α i β.Ellímit f∞ seriasemblantalque indicalafigura2,onhemrepresentatladependènciade f1200 respectea α i β

Elvalorde f1200 estàindicatperlaintensitatdegris:elcolorblanccorrespon alvalor0ielnegrealvalor1.Elvalorde f1200 ésconstantencadascundels lòbulsques’observenenlafigura.3 Ellòbulmésextens,situatalmig,correspon alvalor1/2.Elssegüentsenextensió,situatsabandaibandadel’anterior, corresponenalsvalors1/3i2/3.Mésenllà,n’hihadosmésquecorresponen alsvalors1/4i3/4.Tambésen’observenproubéunsaltresdemésprimsque corresponenalsvalors1/5,2/5,3/5i4/5.

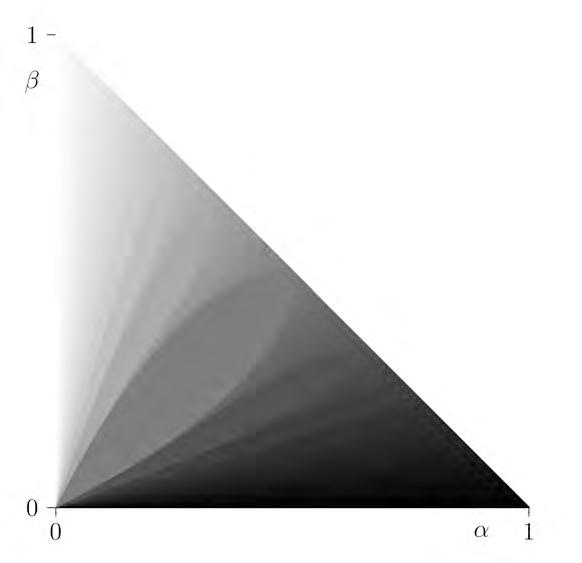
Figura2: Comportamentasimptòticdelavariantbàsicadelmètodede Phragménperaduescandidatures.Dependènciade f1200 respectede α i β.

3 Malauradament,esprodueixunail.lusióòpticaqueexageralocalmentelscontrastos.Vegeu, perexemple,WikiRadiography,2010,Machbandsandotheropticalillusions, http://www. wikiradiography.com/page/Mach+bands+and+other+Optical+Illusions.Tanmateix,sies cobreixlafigurallevatd’unapartcontingudaenunsollòbul,aleshoresespercepunaintensitat uniformedegris.

XavierMoraiMariaOliver

1/5 2/5 3/5 4/5

1/2 1/3 2/3

1/4 3/4

Figura3: Dependènciade f1200 respecte α pera ζ = 0 376.

Talcomsuggereixlafigura3,pera ζ> 0fixada,ladependènciade f∞ respectede α tindriauncaràctersimilaralafunciódeCantor[14],ambla particularitatqueaquícadaracionaltindriacomaantiimatgeunintervalde mesurapositiva.

Enqualsevolcas,elfetque f∞ siguiconstantenaquestslòbulsésunamica indesitjable.Fixem-nos,perexemple,enellòbulcentralon f∞ = 1/2.Talcomestàdelimitat,resultaqueelsesconsesreparteixenuniformemententre A i B tant pera (α,β,ζ) = (0.374, 0.25, 0.376) compera (α,β,ζ) = (0.25, 0.374, 0.376), totiqueenelprimercaselnombred’electorsqueaprovennoméslacandidatura A éssuperiorgairebéun50%alnombredelsqueaprovennomésla candidatura B,iqueenelsegoncaspassaexactamental’inrevés.Enllocd’això, ésmésraonable,segonshemargumentatal’apartat6.4,repartirelsescons proporcionalmenta α + ζ/2i β + ζ/2—queenlafigura3corresponauna rectadesde (0,ζ/2) finsa (1 ζ, 1 (ζ/2))

Aquestfenomennodesapareixpasambunnombrefinitd’escons.Perexemple,peraqualsevolvalorparellde n escontinuaobtenintunrepartimenta partsigualsperalsvalorsde (α,β,ζ) donatsenelparàgrafprecedent(ipera totselsvalorsintermedis).

8Variantsdirectes.Algunesperspectives

8.1 Elprocedimentquehemestudiatenlaseccióanteriorassignaelsesconsde manerasuccessiva;encadapasesmantenenlesassignacionsanteriorsielnou escós’assignademaneraqueesminimitzilarepresentaciódelselectorsmés afavorits.Enllocd’això,tambéespodenrepartirtotselsesconsdecopprestant atencióalaquantitatderepresentacióqueobtenenelsdiferentselectorsi mirantdeminimitzarladesigualtatentreells.Aquestsmètodeselsanomenem variantsdirectes

Talcomrecullelteorema5.1—quanafirmaquesónequivalentselsseus apartats(c)i(e)—,enelcasuninominalnolimitatelcriterideminimitzarla representaciódelselectorsmésafavoritsdónaelmateixresultattantsies procedeixseqüencialmenttotmantenintlesassignacionsanteriorscomsi esconsiderendirectamenttotselsesconsquehihaperrepartir.

Tanmateix,aquestaequivalènciadeixadesercertaquanelselectorsnoes limitenaaprovarunasolacandidatura.Enaquestcas,larestricciódemantenir lesassignacionsanteriorspotimpedird’accediraaltresrepartimentsque redueixenencaraméslarepresentaciódelselectorsmésafavorits.Considerem, perexemple,elsvotsd’aprovaciósegüentsreferentsatrescandidatsindividuals:

2: b;2: a, b;1: c;3: a, c. (54)

Pera n = 1,l’assignaciósuccessivaesredueixaunsolpas,demaneraque certamentcoincidiràambl’assignaciódirecta.L’objectiudeminimitzarlarepresentaciódelselectorsmésafavoritsportaaassignarl’escóalcandidatmés aprovat,enaquestcas a,iarepartiraquestcandidatapartsigualsentretots elselectorsquel’hanaprovat.Pera n = 2,lavariantd’assignaciósuccessiva buscaquinaltrecandidatcomplementamillorlarepresentaciójaassignada a a,iarribaalaconclusióqueés b.Encanvi,l’assignaciódirectanomanté necessàriamentelcandidat a,sinóqueesplantejadenoucomminimitzar ladesigualtatderepresentaciómitjançantdosrepresentants.Enaquestcas, ésobviquelamilloreleccióenaquestsentités b, c,laqualpermetdonarla mateixarepresentacióatotselselectors.

Talcomesveudeseguidaambaquestexemple, lesvariantsdirectesno seranpasmonòtonesrespectealnombred’escons n.Ésadir,queunaugment delnombrederepresentantsques’hand’elegirpotcomportarqueuncandidat concretpassideserelegitanoser-ho.Aquestfenomen,delmateixtipusquela coneguda paradoxad’Alabama [49,§9.4–9.7],ésforçaindesitjable.Tanmateix, enlapràcticaelnombrederepresentantsques’hand’elegirésunaquantitat prefixada,demaneraqueaquestamancademonotonianoéstangreu.

Engeneralnoespotaconseguirquetotselselectorstinguinexactamentla mateixaquantitatderepresentació.Davantd’això,ésnaturalmirardeminimitzaralguníndexquemesuriladesigualtatdelesquantitatsqueobtenenels diferentselectors.

Tambééscert,però,quenohihapasunasolamanerademesurarla desigualtatd’unrepartiment.

XavierMoraiMariaOliver

Finsaraenshembasatenelvalormàximdelesfraccionsqueobtenenels diferentselectors,ésadir, maxk rk.Aquestaquantitatnoésbenbéunamesura dedesigualtat,peròbastarestar-lielvalormitjà,ésadir, n/w,perobtenir uníndexques’anul.lanomésenelcasd’unrepartimenttotalmentequitatiu. Aquestíndexvedonat,doncs,per

(55)

Detotamanera,comqueelsvalorsde n i w ensvénendonats,enllocdeminimitzaraquestadiferència µ podemminimitzarsimplementelvalorde maxk rk.

Alternativament,podemprendrecomamesuradedesigualtatlavariància delesrepresentacionsqueobtenenelsdiferentselectors.Al’apartat5.3jahem considerataquestpuntdevistaenelcasuninominalnolimitat,elqualhemvist quedónallocalaregladeWebsteriSainte-Laguë.Enelcasgeneral,lavariància vedonadaperlesfórmulessegüents,quegeneralitzen(14):

(56) (laigualtatentreambduesexpressionsescomprovafàcilmentdesenvolupant elsquadratsiusantelfetque

).

Laideademinimitzarlavariànciadelesrepresentacionsapareixjaenun treballdePhragménpublicatel1896[42](bastantanterior,pertant,altreball deSainte-Laguë,quedatade1910).Mésconcretament,Phragménvaconsiderar aquestcriterienelcasdecandidaturesindividualsisotaunarestriccióespecial, ésadir,quecadacandidatelegitsiguirepartitdelamateixamaneraentretots elselectorsquel’hanaprovat.Mitjançantunexemplevamostrarqueaquesta restricciócomportaunamancademonotoniarespectealcontingutdelsvots, ésadir,queuncandidatpotdeixardeserelegitaconseqüènciaderebre mésaprovacions[42,p.186–188].Tanmateix,tambévaferveurequesies prescindeixd’aquestarestriccióaleshoressíquehihamonotoniarespecteal contingutdelsvots[42,p.188].

PeròPhragménconsideravanoméselcasdecandidaturesindividuals. Al’apartat7.5hemvistcomelpasdecandidaturesindividualsacandidaturescol.lectivesfeiadesaparèixeraquestapropietatdemonotoniaenlavariant seqüencial.Tanmateix,lesexploracionsnumèriquessemblenindicarque les variantsdirectesescomportariendemaneramonòtonarespectealcontingut delsvotsnosolamentenelcasdecandidaturesindividuals,sinótambéenelcas generaldecandidaturescol lectives. Enrelacióambaixòcalprecisarquequan hihamultiplicitatdesolucionselquevariariademaneramonòtonanoésel nombred’esconsquereplacandidaturaenqüestióenunasolucióconcreta, sinóelseuvalormàximalllargdetoteslessolucions.

Malauradament,aquestapossiblebonapropietatdelesvariantsdirectesve acompanyadapercertsinconvenients.Elprimerésladificultatdecàlcul,jaque

somdavantd’unproblemad’optimitzacióquerequereixalgorismesbastant méscomplexosqueeld’assignaciósuccessiva.

Elsegoninconvenientéslamultiplicitatdesolucions.Considerem,per exemple,elsegüentcasdeduescandidaturesprovinentdel’apartat7.7:

374: A;250: B;376: A, B. (57)

Pera n = 10,l’algorismeseqüencialdónacomaresultatelrepartiment (nA,nB) = (5, 5).Encanvi,lesvariantsdirectesdonenquatrepossibilitats,ésadir: (nA,nB) = (4, 6),(5, 5),(6, 4),(7, 3).Enefecte,resultaquetotsaquestsrepartimentspermetenaconseguirunarepresentaciótotalmentequitativa.Aixòésaixí perquèhihaungrannombred’electorsqueacceptenserrepresentatstantper A comper B.Perpocqueesprodiguinlesaprovacionsadiversescandidaturesper partd’unmateixelector,elnombrederepartimentsdiferentsques’obtenen amblesvariantsdirectescreixmoltfàcilmentambelnombredecandidatures iambelnombretotald’escons.

8.2 Enl’exempleprecedent,elresultatseqüencial (5, 5) noescorresponamb elfetquehihabastantsméselectorspartidarisd’A quede B.Enaquestsentit podriasermésindicatelrepartiment (6, 4) quetrobementreelsresultats directes.Noobstantaixò,lamateixalògicaqueenshaportataaquestrepartimenttambéensportaalrepartiment (4, 6),elqualnos’adiugensal’esmentat predominidepartidarisd’A.D’algunamaneraenshempassatdellarg.

Davantd’això,esfanecessarialguncriteriaddicionalperaseleccionar adequadamententreelsdiversosrepartimentsqueproporcionaelcriterid’optimitzaciódirecta.Unamaneradefer-hopodriaserlasegüent.Talcomhem comentatal’apartat6.4,elsvotsqueaprovendiversescandidaturestambé podrienserdividitsapartsigualsentreaquestes.Siesprocedeixd’aquesta manera,aleshoresanemapararareglescomlesdeJeffersoniD’Hondtide WebsteriSainte-Laguë,onlamultiplicitatderepartimentseslimitaacasosmolt singulars(d’igualtatexactaentrecertsnombresdevotsoelsseusmúltiples); acanvid’això,s’estàrenunciantaminimitzartotelpossibleladesigualtatde representacióentreelsdiferentselectors.Doncsbé,estractariadesituar-seen unpuntintermedionencaraesminimitzéstotelpossibleladesigualtatperò s’obtinguésnomésunrepartiment(oelsmenyspossibles).Mésconcretament, espodriencombinarelsdostractamentsmitjançantunparàmetre θ ∈ [0, 1] (onentendremque θ = 1corresponadividircadavotpercompletentreles candidaturesaprovadesenaquestvot)iescollirunvalord’aquestparàmetre ons’assoleixinalhoraelsdosobjectiusesmentats.

Elsmètodesqueapliquenaquestaideaelsanomenem variantsdirectes relaxades

Enl’exemple (57) aquestprocedimentseleccionaelrepartiment (nA,nB) = (6, 4) quemésamuntassenyalàvemcomamésplausible.Aquestrepartimentés l’únicqueresultaòptimquan θ superaelvalor0.670.D’altrabanda,permetuna representaciótotalmentequitativafinsa θ = 0 798.Persobred’aquestúltim

XavierMoraiMariaOliver

valorjanoéspossibleunarepresentaciótotalmentequitativa,peròl’assignació (6, 4) encaraminimitza µ i γ finsa θ = 1.

Engeneral,però,elresultatdelesvariantsdirectesrelaxadespotdependre dequinamesuradedesigualtats’utilitza.D’altrabanda,tambépotdiferirdel repartimentqueminimitzaladesigualtatpera θ = 1.

Així,enl’exemple (1) amb n = 4resultenelegitselscandidats a, c, e, f obé a, b, c, e segonsques’utilitzirespectivament µ obé γ.Tanmateix,pera θ = 1 ambduesmesuresdedesigualtatdonencomaòptimelsegond’aquestsdos conjunts.

Pelquefaal’exemple (2) amb n = 135,s’obtéelrepartiment n = (40, 22, 19, 8, 14, 20, 12) tantenelcasde µ comenelcasde γ.Encanvi,pera θ = 1 aquestesduesmesuresdedesigualtatdonen,respectivament,elsrepartiments (40, 23, 18, 8, 14, 20, 12) i (40, 22, 18, 9, 14, 20, 12).

Aquestsresultatss’hanobtingutmitjançantelprogramarid’optimització CPLEX[26].Tanmateix,lagranmultiplicitatdesolucionsnodeixadeseruna fontd’incertesa,demaneraqueunestudimésconclusiuhauriadecomençar permillorarelprocedimentdecàlcul.

9Conclusions

Elvotd’aprovaciópermetqueelselectorsdoninmésinformacióqueambelvot uninominal.Enconseqüència,elsresultatspodenreflectirmillorlesdiverses opinionsdelselectors.Tanmateix,perquèsiguiaixícalenprocedimentsmés laboriososqueelshabituals.

Lesopcionsquesónobjected’aprovaciópodensercandidatsindividuals obécandidaturescol.lectives.Elcasdecandidatsindividualsésapropiaten eleccionsapetitaescala,onelselectorstenenunaconeixençapersonalitzada delscandidats.Encanvi,eneleccionsd’abastampliésmésadientquelesopcions peraprovarsiguinlescandidaturescol.lectivespresentadespelspartits.En aquestcas,l’objectiuésdeterminarquantsesconshaderebrecadacandidatura.

Afinalsdelsegle xix Phragménvaproposarunmètodeiteratiuques’estén fàcilmentalcasdecandidaturescol lectives.Tanmateix,enaquestcasapareixen algunsfenòmensindesitjables,comaralamancademonotoniarespecteal contingutdelsvotsiunatendènciaaigualarmésdelcompteelsnombres d’esconsquerebenlesdiferentscandidatures.

Hihaindicisqueaquestsproblemesespodrienresoldremitjançantcertes variantsques’hanapuntatenaquestarticleiqueconvindriaestudiarmés detingudament.

Totsaquestsmètodessónméscomplicatsdelquehomvoldria.Tanmateix, elseugraudecomplicacióéscomparableacertesvariantsdelmètodedevot únictransferiblequesónutilitzadesperalgunsestatsiinstitucions.

Enrelacióambaixò,Phragménafirmavaelsegüent: totelqueéscorrecte espotfertambéfàcilmentcomprensible,encaraqueperaconseguir-hopotfer faltatempsifeina;amés,elpúblicengeneralapreciamillorelsresultatsqueles teories [41].

ANotabiogràfica [9,6,19,21]

EdvardPhragménvanéixerl’any1863aÖrebro(Suècia)ivamorirel1937a Estocolm.ElseunomcompleteraLarsEdvardPhragmén.Desdelsegle xvii els seusavantpassatsperlíniamasculinahaviensigutpastorsprotestants,peròel seupare,LarsPhragmén(1832–1920),vatrencarambaquestatradicióiesva dedicaralesmatemàtiques.

Seguintaquestspassos,el1882EdvardPhragménvaingressaralaUniversitat d’Uppsalapercursarestudisdematemàtiques.L’anysegüent,però,vaoptar perl’escolasuperior(högskola)d’Estocolm,onnos’obteniacapmenadetítol peròhihaviaunambientd’estudimoltautènticidesinteressat.Enparticular, l’influentprofessorGöstaMittag-Lefflerlideravaunarecercacapdavanteraen anàlisimatemàtica[12, 20].Apartird’aquellmateixany1883,Phragménva contribuiraaquestarecercaambdiversostreballs[6].

Aprincipisdel’any1888,Mittag-LefflervaconfiaraPhragménelcàrrecde secretarideredacciódelarevista ActaMathematica,unatascaquePhragménva desenvoluparmoltaconsciència.Tantvaseraixíqueafinalsdelmateixany vadetectarcertserrorsenunamemòriad’HenriPoincarésobreelproblema delstrescossoslaqualjahaviaestatescollidaguanyadorad’unimportant concurs,convocatpelreiÒscarIIdeSuèciaiNoruegaambmotiudelseu seixantèaniversari[9, 1].Elserrorsenqüestióerenrealmentseriosos,fins alpuntqueMittag-Lefflervadecidiraturarl’edicióirecuperarunesquantes còpiesquejas’haviendistribuïtenformaimpresa.Poincaréesvaveureobligat afercanvissubstancialsenlamemòriaiacostejarlesdespesesoriginades, lesqualssuperavenambescreixl’importdelpremi.Enlaversiódefinitiva,que novaserpublicadafinsal1890,Poincaréexpressavaaixíelseuagraïmenta Phragmén[46,p.5]:

JedoisbeaucoupdereconnaissanceàM. Phragmén quinonseulementarevules épreuvesavecbeaucoupdesoin,maisqui,ayantlulemémoireavecattentionet enayantpénétrélesensavecunegrandefinesse,m’asignalélespointsoùdes explicationscomplémentairesluisemblaientnécessairespourfaciliterl’entière intelligencedemapensée.Jeluidoislaformeélégantequejedonneaucalcul de Sm i etde T m i àlafindu§12.C’estmêmeluiqui,enappelantmonattention surunpointdélicat,m’apermisdedécouvriretderectifieruneimportante erreur.

Elfetd’havercorregitlamemòriadePoincarévadonarmoltdeprestigi aPhragmén,queeldesembrede1889obteniaelgraudellicenciat(filosofie licentiat )al’Universitatd’Uppsala.Elfebrerde1890vasernomenatprofessor associat(docent )dematemàtiquesimecànicaal’escolasuperiord’Estocolm,i elsetembrede1892vaesdevenir-hiprofessord’anàlisimatemàticasuperior, succeintenaquestaplaçaSofiaKovalevskaya,quehaviamortelfebrerde1891 d’unapneumonia.

EdvardPhragmén (retratprocedentdel’InstitutMittag-Leffler; fotògraf:HermanHamnqvist).

Enelperíode1892–1895Phragménvaformarpartdelsòrgansdegovernde l’escola.Enaquellmomenthihaviamoltapolèmicajaquealgunsprofessors, entreellselrectorOttoPettersson,queeraprofessordequímica,proposaven quel’escolaatorguéstítolsacadèmics,mentrequeunsaltress’hioposaven, entreellsMittag-LeffleriPhragmén.Aquesttemavadominarunesaccidentades eleccionsarectorquevantenirlloceldesembrede1894igenerde1895,en lesqualsesvabarrejartambélaqüestiódequiteniadretdevotenelclaustre. Defet,esvaarribaravotartresvegades.Lasegonahauriadonatelcàrreca Phragmén.Tanmateix,elresultatdefinitiuvaserlareelecciód’OttoPettersson. Ambellielsseussuccessors,l’escolavaevolucionarprogressivamentcapa l’atorgamentdetítolsacadèmics.

Alhoraquecontinuavatreballantenelstemesmésclàssicsd’anàlisimatemàtica,Phragménesvainteressarcadavegadamésenaltrestemesmésaplicats.

Entreelsqualshihaelquehemtractatenelpresentarticle:comelegirunconjunt derepresentantsquanelselectorss’expressenmitjançantvotsd’aprovacióo preferencials.Lasevaprimerapropostasobreaquestproblemadatademarç de1893[37]ivaserpresentadaenelmarcdel’entitat StudenterochArbetare —EstudiantsiTreballadors—,laqualteniacomaobjectiulacol.laboracióentre elsintel.lectualsilaclasseobrera.Phragménvacontinuarestudiantelproblema enquatrepublicacionsquevanaparèixerdel’any1894al1899[39, 40, 42, 43].

Posteriorment,hivacontribuirtambédesdeduescomissionsestatalsdeles qualsvaformarpartelsanys1902–1903i1912–1913[50, 48].Entreaquestes duescomissions,l’any1906tambéhivaferunanovaaportacióambmotiu d’uninformesobreeltemaquehaviademanatlacomissiófinlandesaperala reformaelectoral[44,45].

Lacomissióreialsuecade1902–1903sobreelsdretsdevotenlasevaprimerareunió. D’esquerraadreta:SixtenG.vonFriesen,CarlO.Moberg,IvarMånssoniTrää, AxelAsker,ChristoferJohanRappe,GustafJ.G.A.Berg, J.ElofBiesèrt,L.EdvardPhragméniEmilSvensén (StockholmsStadsmuseum,imatgeSSMD000156;fotògraf:AntonBlomberg[32]).

CalnotarquepocsdiesdesprésdelapresentaciódePhragménesmentada enl’associaciód’EstudiantsiTreballadors,elmateixGöstaMittag-Lefflerdonavaunaconferènciasobreeltemadelarepresentacióproporcionaldavant l’associaciósuecad’economistes[33].Amés,el1906vaescriurel’informepera lacomissiófinlandesaquejahemesmentat[34].Altresmatemàticsdel’entorn dePhragménquevanprestaratencióaltemadelarepresentacióproporcional sónIvarBendixson[2,3,4],AndersLindstedt[30,31]iErnstLindelöf[29].

XavierMoraiMariaOliver

ElsnomsdePhragméniLindelöfestanassociatsauncelebratresultat d’anàlisicomplexaid’equacionsenderivadesparcialsquegeneralitzaala vegadaelprincipidelmàximielteoremadeCauchyiLiouville.Aquestresultat datade1908iesténuntreballprevidePhragménde1904(vegeu[6]).

Unaltrecampquevaatraurel’atenciódePhragmén,iquefinalmentva absorbir-lofortament,vaserlamatemàticaactuarial,uncamponhihavia llavorsmoltademandaienelqualtambévaestarocupatelmateixMittagLeffler[9, 21].UnmomentcrucialenlavidadePhragménvaserl’inicidel’any 1904,quan,desprésd’havertreballatcomaactuariicomainspectorestatal d’assegurances,vaesdevenirdirectorgenerald’unnouorganismed’inspecciód’assegurances(1904–1908)[21].Phragméns’haviaimaginatqueaquest càrrecpodiasercompatibleamblasevadedicacióacadèmica,peròlarealitatva serunaaltraielmaigde1905vadeixardefinitivamentlaplaçadeprofessora l’escolasuperiord’Estocolm.Posteriorment,vapresidirl’AssociacióSuecad’Actuaris(1909–1934,comasuccessordeMittag-Leffler),vaformarpartdelconsell directiudelal’AssociacióSuecad’Assegurances(1912–1935)ivapresidirel conselldirectiudelaSocietatAnònimaEstataldeReassegurances(1914–1937).

BDiversesvariantsconsideradesperPhragmén

LespropostesdePhragménsobrerepresentacióproporcionalinclouenuna diversitatdevariants.Aquestesespodenclassificarenduesgransclasses,1i2, quecorresponenessencialmentalsmètodes«primer»i«segon»dePhragmén enlaterminologiade[8](onaqueststermessónaplicatsconcretamentales variants1.2i2.1).

1.Procedimentsdequotapreestablerta.

Aquestsprocedimentsespodenconsiderarcomavariantsdelmètodedevot únictransferible.Comaquest,comencenperestablirlaquota,ésadir,elnombre devotsquecalreunirperassignarunescó.Tambécoincideixenambelvotúnic transferibleenlaideadetransferirelsexcedentsalsaltrescandidatsindicats enlesbutlletes.Elsesconss’assignensuccessivament,fixant-sesempreenel candidatquereuneixmésvots,originalsotransferits.Tanmateix,sienalgun moments’escauquecapcandidatarribaalaquota,aleshores no esprocedeix aeliminarelcandidatquetémenysvots,sinóqueesrelaxalacondicióde superaroigualarlaquotainicial.Enparticular,enelcasdevolerelegirunsol representantaquestsprocedimentsescullensempreelmésvotat.

1.1.Variantpreferencialinicial (1893)[37, 38] Aquestaprimeraproposta consideravanomésvotspreferencials.LaquotautilitzadaésinicialmentlaquotadeDroop,peròsienalgunmoments’escauquecapcandidatarribaala quota,aleshoresaquestaesdisminueixcomsiesvolguésunrepresentantmés. DemaneramoltsimilaracomjahaviaproposatJ.B.GregoryaTasmàniapels voltsde1880([56,p.273],[28,§12.1.4]),quanuncandidatsuperalaquotai

obtéunescó,l’excedentesreparteixperigualentretotselsvotsqueteniaaquell candidatidecadavotestransfereixlafraccióexcedentalsegüentcandidat.

1.2.Variantdetipusrestesmajors (introduïdaseguramententre1893i1894). S’exposaa[8,§A.b,p.47–50].Abandadeconsiderarvotsd’aprovació,es diferenciadelavariantprecedentpelfetqueutilitzalaquotasimpledeHarei quequancapcandidatarribaalaquotaaleshoresseseleccionaelcandidatque enaquellmomentreuneixmésvots.Enelcasdellistesdepartitesredueixal mètodedelesrestesmajors.GustafEneströmvaarribarindependentmenta aquestamateixaideael1896arrandevolersimplificarlavariant2.1[17,18].

1.3.Variantfinal (1906)[44, 45]. Tambéutilitzalaquotasimple,peròla quantitatdevotsqueesbescanviaperunescósolserinferioralaquota. Concretament,si v representaelnombredevotsenqüestió,lapartquees bescanviaperunescóés v/(k+1) on k ésl’únicentertalque kq0 <v ≤ (k+1)q0. Aquestaespecificaciócorresponalaversiódefinitiva[45];enlaversióanterior queesdónaa[44]laquotasimpleesrecalculacadavegadaentermesdel nombredevotsquerestenactiusielnombred’esconsencaranoassignats.

1.4.Variantsquedistingeixendosgrausd’aprovació [8, 44, 45] Enprevenció delesestratègiesdedecapitació(apartat4.2)Phragménvasuplementarles duesvariantsprecedentsamblapossibilitatqueelvotantdistingeixidosgraus d’aprovació(laqualcosaespotconsiderarcomunaformaespecialdevot preferencial).Quanesvotaaixí,llavorselscandidatssecundarisd’unvotno entrenenjocfinsquenohaginestatseleccionatstotselscandidatsprimaris d’aquellvot.

2.Procedimentsd’optimització.

Aquestsprocedimentsmirendeminimitzarladesigualtatderepresentació entreelsdiferentselectors.

2.1.Variantseqüencial (1894–1899)[39, 40, 42, 43]. Éslaquenosaltresestudiemalasecció7.Consideravotsd’aprovacióiassignaelsesconsdemanera successiva.Cadaescós’assignademaneraqueenaquellmomentesminimitzi unacertamesuradeladesigualtatderepresentacióentreelsdiferentselectors.

2.2.Variantsdirectes (1896) Elsesconsnos’assignendemanerasuccessiva, sinóqueesdistribueixentotsd’unavegadademaneraqueesminimitzialguna mesuraespecificadadeladesigualtatderepresentacióentreelsdiferents electors.Engeneral,ladeterminaciód’aquestadistribuciórequereixalgorismes d’optimitzacióméscomplexosqueelsalgorismesd’assignaciósuccessiva.Tot iaixò,Phragménvaadoptaraquestpuntdevistadirecteoglobalenalguna ocasió,comaraa[42,p.184,188].Nosaltrestambél’adoptemalasecció8.

2.3.Variantpreferencialrelativa (1895)[40,§7] Aquestapropostaconsistia asubstituirunvotpreferencialdelaforma a > b > c > d > e perunvot d’aprovaciódelaforma a, b, c, d, e mésunafraccióespecificada,comara1/10, repartidaapartsigualsentrelesllistes a, b, c, d; a, b, c; a, b; a.

2.4.Variantpreferencialabsoluta (1903–1913) Utilitzaelprocedimentseqüencial,peròelsvotspreferencialssóntractatsambelcaràcter«absolut» següent(quegeneralitzalaideadelavariant1.4):elcandidat (k + 1)-èsim d’unvotpreferencialnoentraenjocfinsquenohanestatseleccionatsels k candidatsanteriors.Enunaprimeraversió,lainformaciópreferencialesreduïa adistingirdosgrausd’aprovació[8,p.56,62–64],peròdesprésesvaadmetre unaordenacióqualsevoldelscandidatsaprovats[48,p.47–54].Aquestaversió generalhaviaestatconsideradajael1910perNoreTenow[54].L’algorisme finalesdescriutambéa[28,§12.3.5,13].Adiferènciadelsmètodesdevotúnic transferible,enelcas n = 1noesredueixalvotalternatiu(apartat3.3),sinó aelegirelcandidatquerepmésvotsdeprimeraopció.Tanmateix,coincideix ambunadeterminadavariantdelvotúnictransferible—l’anomenatmètodede Gregoryinclusiu—sis’esculladequadamentlaquotad’aquestúltimil’ordre delestransferències[28,sats13.1].

Aquestavariantésmonòtonarespecteavariacionsdelsvotsafavord’un determinatcandidat.Tanmateix,nocompleixelcriterideproporcionalitatde Droop.Pertaldegarantiraquestúltim,l’any2002OlliSalmivaproposaruna modificaciómitjançantcertselementsdelvotúnictransferible[52, 53].Aquesta modificacióhaestatestudiadadetalladamentperDouglasWoodall[60],que endistingeixduesversionsidemostraquetotesduescompleixenelcriteride proporcionalitatdeDroop.UnaltreestudienaquestadireccióéseldeRoss Hyman[25].Tanmateix,enelcas n = 1aquestesmodificacionsesredueixen alvotalternatiu,laqualcosaimplicalaindesitjablemancademonotoniaque hemcomentatal’apartat3.6.

Lavariantpreferencialabsolutavaacabarformantpartdelsistemaelectoral suec,onvaserintroduïdael1921iencarahiéspresentactualment[28,§13.10, C.2.3].Tanmateix,noafectaelnombred’esconsquesónassignatsacada candidatura,sinónomésquinscandidatsconcretsrebenaquestsescons.De fet,l’electorhad’optarperunasolacandidatura,totiquepotvariarfinsa uncertpuntlallistaordenadadecandidats.Elnombred’esconsqueobté cadacandidaturaesdeterminavainicialmentmitjançantlaregladeJeffersoni D’Hondt,peròel1952aquestavasersubstituïdaperunacertamodificacióde laregladeWebsteriSainte-Laguë.Peramésdetallsremetemellectora[28].

Agraïments

ElsautorsvolemmanifestarelnostreagraïmentalsenyorMikaelRågstedt, bibliotecaridel’InstitutMittag-Leffler,perhaver-nosajudatalocalitzardiversos documents.TambéestemmoltagraïtsalsenyorMikaelAbrahamsson,biblio-

tecaridelCentredeCiènciesMatemàtiquesdelaUniversitatdeLund,pelseu ajutaobtenircòpiesdediversostreballsdePhragménid’altresautors.Els professorsMagnusFontesiJoachimKockenshanajudattambéenlatraducció detextosnòrdics.Moltesgràciesatotsdos.Tambévolemdonarlesgràcies alaprofessoraRosaCamps,laqualenshaajudataentendrelesideesde Phragméniaresoldrediversesqüestionstècniques.Finalment,agraïmtambé elscomentarisdelsprofessorsAureliAlabertiSvanteJanson,elsqualsenshan permèsmillorarelcontingutendiversospunts.

Referències

[1] Barrow-Green,J. Poincaréandthethreebodyproblem.Providence:AmericanMathematicalSociety;Londres:LondonMathematicalSociety,1997. (HistoryofMathematics;11)

[2] Bendixson,I. Regeringensförslagtillproportionelltvalsättochdessverkningar.Framställningochkritik.Estocolm:NordiskaBokhandeln,1905.

[3] Bendixson,I. «Rösträttsfrågan».Conferènciadonadael2denovembre de1906enl’associacióStockholmsHögskolasStudentföreningen.Resum manuscritdelaconferènciaideladiscussió,segonsnotesd’AdolfLarsson: Estocolm,KungligaBiblioteket,GöstaMittag-Lefflerpapper,L62:55,núm.6.

[4] [Bendixson,I.]«Promemoriaröranderegeringensproportionellavalmetod,afenantiproportionalist». FrisinnadeLandsföreningensMeddelanden (Estocolm),núm.52(8)(1907).

[5] Brams,S.J. Mathematicsanddemocracy.Designingbettervotingand fair-divisionprocedures.Princeton:PrincetonUniversityPress,2008.

[6] Carleman,T. «L.E.Phragméninmemoriam». ActaMath.,69(1)(1938), XXXI–XXXIII.

[7] Carstairs,A.M. AShortHistoryofElectoralSystemsinEurope.Londres: GeorgeAllen&Unwin,1980.

[8] Cassel,C.G. ProportionellaVal.Systematiskframställning.ApèndixI de[50].Estocolm:IsaacMarcus’Boktryckeri-Aktiebolag,1903.

[9] Cramér,H. «LarsEdvardPhragmén:Minnesteckning». KungligaSvenska VetenskapsakademiensÅrsbok (1958),279–301.Reproduïta LevnadsteckningaröverKungligaSvenskaVetenskapsakademiensLedamöter,9(Estocolm:Almqvist&Wiksell,1962),255–277.

[10] [D’Hondt,V.] LaReprésentationProportionnelledesPartis,parunélecteur. Brussel.les:Bruylant-Christophe,1878.

[11] D’Hondt,V. SystèmePratiqueetRaisonnédeReprésentationProportionnelle.Gant:J.S.VanDooselaere;Brussel.les:C.Muquardt,1882.

[12] Domar,Y. «MatematiskforskningunderStockholmshögskolasförsta decennier».Univ.Stockholm,1981.Reproduïta http://www2.math.su.se/ matematik/Historia/Historia.pdf.Traduccióanglesa:«Mathematical researchduringthefirstdecadesoftheUniversityofStockholm». http://www2.math.su.se/matematik/Historia/Histeng.pdf.

[13] Doron,G.;Kronick,R. «Singletransferablevote:anexampleofaperverse socialchoicefunction». AmericanJournalofPoliticalScience,21(1977), 303–311.

[14] Dovgoshey,O.;Martio,O.;Ryazanov,V.;Vuorinen,M. «TheCantor function». Expo.Math.,24(1)(2006),1–37.

[15] Dummett,M.A.E. VotingProcedures.Oxford:ClarendonPress,1984.

[16] Dummett,M.A.E. «Towardsamorerepresentativevotingsystem:The PlantReport». NewLeftRev.,I/194(1992),98–113.

[17] Eneström,G.H. Cartaal’editor. Aftonbladet (23febrer1896).

[18] Eneström,G.H. «Omaritmetiskaochstatistiskametoderförproportionellaval». ÖfversigtafKongligaVetenskaps-AkademiensFörhandlingar, 53(1896),543–570.

[19] Englund,K. «LEdwardPhragmén». SvensktBiografisktLexikon,29 (1995–1997),303–306.Reproduïta http://sok.riksarkivet.se/sbl/ artikel/7271.

[20] Gårding,L. MatematikochMatematiker.MatematikeniSverigeföre1950. Lund:LundUniversityPress,1994.Traduccióanglesa: Mathematicsand mathematicians.MathematicsinSwedenbefore1950.Providence:AmericanMathematicalSociety;Londres:LondonMathematicalSociety,1998. (HistoryofMathematics;13)

[21] Hagberg,J. «SvenskaAktuarieföreningen100år.Aktuarierisvensk försäkring». NordiskForsikringstidskrift,4(2005),377–385.

[22] Hill,I.D. «ElectionmethodforCouncil».RoyalStatisticalSociety(1995). http://www.rss.org.uk/site/cms/contentviewarticle.asp?article= 1005

[23] Hill,I.D. «Partylistsandpreferencevoting». VotingMatters,29(2011), 15–19.

[24] Hoag,C.G.;Hallett,Jr.,G.H. ProportionalRepresentation.NovaYork: Macmillan,1926.

[25] Hyman,R. «Divisormethodproportionalrepresentationinpreferenceballotelections». VotingMatters,28(2011),15–30.

[26] IBM.«CPLEXOptimizer.High-performancemathematicalprogramming solverforlinearprogramming,mixedintegerprogramming,and quadraticprogramming». http://www-01.ibm.com/software/commerce/ optimization/cplex-optimizer/index.html

[27] IrelandGovernment. DepartmentoftheEnvironment,Heritageand LocalGovernment. GuidetoIreland’sPR-STVElectoralSystem. http://www. environ.ie/en/LocalGovernment/Voting/PublicationsDocuments/File DownLoad,1895,en.pdf.

[28] Janson,S. ProportionellaValmetoder. http://www2.math.uu.se/∼svante/ papers/sjV6.pdf,2012–2014.

[29] Lindelöf,E. «Utkasttillettpåproportionalitetsidéengrundadtvalsätt, jämteförklaringochmotiveringafdeprincipersomliggatillgrundför detsamma».Manuscritde1906.Estocolm:KungligaBiblioteket:Gösta Mittag-Lefflerpapper,L62:55,núm.3.

[30] Lindstedt,A. «Promemoriaangåendemetoderförproportionellaval». Estocolm:KungligaBoktryckeriet,1906.

[31] Lindstedt,A. «Förslagtillmetodförproportionellaval».Estocolm:KungligaBoktryckeriet,1906.

[32] Millqvist,V. «Rösträttskommittén». Idun.IllustreradTidningförKvinnan ochHemmet,15(45)(1902),719–720.

[33] Mittag-Leffler,M.G. «Proportionellaval».Conferènciadonadael16de marçde1893enl’associacióNationalekonomiskaFöreningen.Referència: NationalekonomiskaFöreningensFörhandlingar,1893(1893),p.44.

[34] Mittag-Leffler,M.G. [«ResultatetavengranskningavA.Lindstedts ochE.Phragménsförslagtillproportionellvalmetod»].Informedirigital MinisterideJustíciadeFinlàndia.Manuscritde1906.Estocolm:Kungliga Biblioteket:GöstaMittag-Lefflerpapper,L62:55,núm.2.

[35] Monroe,B.L. «Fullyproportionalrepresentation». AmericanPolitical ScienceReview,89(1995),925–940.

[36] Mora,X. «LaregladeJefferson-D’Hondtilessevesalternatives». MatMat, 2013(4),34p. http://mat.uab.cat/matmat/PDFv2013/v2013n04.pdf.

[37] Phragmén,E. «Omproportionellaval».Conferènciadonadaenl’associació StudenterochArbetare(1893).Resum: StockholmsDagblad (14març1893).

[38] Phragmén,E. «Öfverproportionellaval».Contingut:Quatretaulesamb comentaris,13pàginesimpreses, circa 1893,nomdel’autoritítolescrits allapis.InstitutMittag-Leffler,Biblioteket,Sep.Coll.,Sv.9[Phragmén].

[39] Phragmén,E. «Suruneméthodenouvellepourréaliser,danslesélections,lareprésentationproportionnelledespartis». ÖfversigtafKongliga Vetenskaps-AkademiensFörhandlingar,51(3)(1894),133–137.

[40] Phragmén,E. ProportionellaVal.Envaltekniskstudie.Estocolm:LarsHökerbergs,1895.(SvenskaSpörsmål;25)

[41] Phragmén,E. Cartaal’editor. Aftonbladet (23febrer1896).

[42] Phragmén,E. «Surlathéoriedesélectionsmultiples». ÖfversigtafKongliga Vetenskaps-AkademiensFörhandlingar,53(1896),181–191.

[43] Phragmén,E. «Tillfråganomenproportionellvalmethod». StatsvetenskapligTidskrift,2(1899),297–308(núm.2,88–98).

[44] Phragmén,E. «Utkasttillföreskrifterbeträffandevalavriksdagsmäni andrakammarenochderassuppleanter».Estocolm:KungligaBoktryckeriet, 1906.

[45] Phragmén,E. «Promemoriabeträffandeenförenkladformafdenafundertecknadföreslagnavalmetoden».Manuscritde1906.Estocolm:Kungliga Biblioteket:GöstaMittag-Lefflerpapper,L62:55,núm.4.

[46] Poincaré,H. «Surleproblèmedestroiscorpsetleséquationsdela dynamique». ActaMath.,13(1890),A3–A270.

[47] Potthoff,R.F.;Brams,S.J. «Proportionalrepresentation:Broadeningthe options». JournalofTheoreticalPolitics,10(1998),147–178.

[48] Proportionsvalkommittén[vonFriesen,S.;Appelberg,G.;Bendixson, I.;Phragmén,E.]. Betänkandeangåendeändringarigällandebestämmelser omdenproportionellavalmetoden.Estocolm:IsaacMarcus’BoktryckeriAktiebolag,1913.

[49] Pukelsheim,F. Proportionalrepresentation.Apportionmentmethodsand theirapplications.Cham:Springer,2014.

[50] Rösträttskommittén[Asker,A.;Berg,G.J.G.A.;Biesèrt,J.E.;von Friesen,S.G.;Månsson,I.;Moberg,C.O.;Phragmén,L.E.;Rappe,C. J.;Svensén,E.;Cassel,C.G.] Betänkandemedförslagtillproportionellt valsättvidvaltillRiksdagensandrakammarejämtevissaändringari regeringsformenochriksdagsordningen.Estocolm:Hæggström,1903.

[51] RoviraiVirgili,A. ElsSistemesElectorals.Barcelona:Barcino,1932.2aed: Barcelona,Ed.Undarius,1977.

[52] Salmi,O. «D’Hondtwithoutlists». ElectionMethodsMailingList. http:// lists.electorama.com/pipermail/election-methods-electorama.com/ 2002-September/073943.html,2002.Vegeutambé ibidem 2002-August/ 073862.html, 2002-November/074151.html, 2002-November/106914.html i 2003-August/108863.html.

[53] Salmi,O. «Henkilökohtainensuhteellinenvaali». http://www.uusikaupunki. fi/∼olsalmi/vaalit/henkkoht.html,2004.

[54] Tenow,N.B. «Enproportionellrangmetod,afseddattpådeproportionellavalensområdeutgöraenmotsvarighettilldenvanligaformenför majoritetsvalienmansvalkretsar». StatsvetenskapligTidskrift,13(1910), 317–325.

[55] Tideman,T.N. «Thesingletransferablevote». JournalofEconomicPerspectives,9(1995),27–38.

[56] Tideman,T.N. CollectiveDecisionsandVoting.Ashgate,2006.

[57] Woodall,D.R. «Animpossibilitytheoremforelectoralsystems». Discrete Math.,66(1–2)(1987),209–211.

[58] Woodall,D.R. «Propertiesofpreferentialelectionrules». VotingMatters, 3(1994),8–15.

[59] Woodall,D.R. «Monotonicity.Anin-depthstudyofoneexample». Voting Matters,4(1995),5–7.

[60] Woodall,D.R. «QPQ,aquota-preferentialSTV-likeelectionrule». Voting Matters,17(2003),1–7.

XavierMora

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona Catalonia,Spain xmora@mat.uab.cat

MariaOliver

DepartamentdeTecnologiesdelaInformacióilesComunicacions UniversitatPompeuFabra Catalonia,Spain maria.oliverp@upf.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.1,2015.Pàg.103–104

Englishsummaries

CarlesM.Cuadras

ThelegacyofGalton,Pearson,Fréchetandothers:Howtomeasureandinterpret statisticalassociation

Alongthreeparts,wepresenttheconceptsofcorrelationandstatisticalassociation,startingwithGalton’snotionofcorrelation,improvedbyPearson.As anillustration,weusetheclassicdataofGaltonandPearsononheritability ofparentsandchildrenregardingthestature.Thesecondpartexplainshow tostudythesamedatafromamultivariateperspective(canonicalcorrelation analysis,correspondenceanalysis).WealsousedatafromFisher.Weshowhow toassociategeneraldatasetswithdistances.Thethirdpartisdevotedtothe bivariatedistributions.Wepresentthetheoryofeigenfunctionsandeigenvaluesfortwokernels,whichisappliedtothediagonalexpansionofabivariate distribution,includingcontinuousexpansionsintermsofintegrals.Wepropose afamilyofcanonicalcopulas,whichcangeneratebivariatedistributions.

Keywords: Galton‘sandPearson’sdata,intraclasscorrelation,canonicalcorrelation,correspondenceanalysis,associationbasedondistances,integral operators,distributionswithgivenmarginal,canonicalfunctions.

MSC2010SubjectClassification: 62H20,60E05.

XavierMoraandMariaOliver

Electionsbymeansofapprovalvoting.Phragmén’smethodandsomevariants ofit

Westudycertainvariantsofamethodforproportionalrepresentationthat wasproposedattheendofthenineteenthcenturybyEdvardPhragmén.Every electorexpresseshisopinionbymeansofanapprovalballot,whereheindicates alltheoptionsthathedeemssuitable.Theoptionscanbeindividualcandidates, asitwasconsideredbyPhragmén,orpartycandidatureswhichcanprovide severalrepresentativeseach.Givenasetofvotesofthiskindandaprefixed numberofseats,theaimistodistributetheseseatsamongthecandidaturesso astoachieveasmuchrepresentativenessaspossible.Thisworkpaysspecial attentiontoaconditionofmonotonicitywhichrequiresthataddingapprovals infavourofacertaincandidaturecannotresultinitsgettingasmallernumber ofseats.Inthebasicvariant,whereseatsareassignedbymeansofasequential procedure,suchamonotonicityholdsinthecaseofindividualcandidatesbut notinthegeneralcase.Webrieflyexplorealsosomedirectvariants,whereseats areassignedallatoncebymeansofasuitableoptimizationcriterion.These variantsseemtobebetterfromthepointofviewofmonotonicity.However,they sufferfromaproblemofmultiplicityofsolutionsthatcallsforasupplementary criteriontochooseamongthem.

Keywords: proportionalrepresentation,approvalvoting,openlists,Edvard Phragmén.

MSC2010SubjectClassification: 91B12.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorial,percorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2010.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX, preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespotobtenira lespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Femnotarque enaquestapublicaciós’utilitzapreferentmentelpuntperaseparardecimals, enllocdelacomarecomanadaperl’IEC,perpoderfacilitarlacomprensióde lesexpressionsmatemàtiques.Pertald’accelerarelprocésdeproducció,es pregaalsautorsquesegueixinlesindicacionscontingudeseneldocument d’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateixmodificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcasel Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Elsautorsdelsarticlespublicatsal Butlletí enreteneneldretdecòpia (copyright)iautoritzenl’IECadifondre’ls,tantatravésdelapublicacióimpresa commitjançantelsportalsdigitalspropisod’altresambquès’estableixinels convenisoportunsaaquestefecte.Ésresponsabilitatdelsautorsassegurar queesdisposadelsdretsdereproducciódelsgràficsidelesfiguresquehi apareguin.CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigital delseuarticleiunexemplarimprèsdelnúmerodel Butlletí enelquales publiqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

JuliàCufí(editorencap)

Comitèeditorial

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona jcufi@mat.uab.cat

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàticaAplicadaiAnàlisi UniversitatdeBarcelona fagella@maia.ub.es

JosepMariaFont

Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona jmfont@ub.edu

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

JorgeMateu

DepartamentdeMatemàtiques UniversitatJaumeI mateu@mat.uji.es

MarcNoy

DepartamentdeMatemàticaAplicadaII UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàticaAplicadaI UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

AgustíReventós

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

MartaSanz-Solé

Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona marta.sanz@ub.edu

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies i Butlletídela SocietatCatalanadeMatemàtiques.Elssocisdela SCM reben,gratuïtament, aquestesduespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

President:XavierJarqueiRibera

Vicepresident:EnricVenturaiCapell

Adjuntadelavicepresidència:IolandaGuevaraiCasanova

Secretari:AlbertRuiziCirera

Tresorera:NatàliaCastellanaiVila

Vocals:NúriaFagellaiRabionet,JosepGranéiManlleu,Agustí ReventósiTarrida,CarlesRomeroiChesa,OriolSerraiAlbó,Esther Silberstein,ManelUdinaiAbelló

Delegatdel’IEC:JoanGirbauiBadó

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.

El Butlletí de la Societat Catalana de Matemàtiques publica, en llengua catalana, exposicions matemàtiques de qualitat, que puguin interessar a un nombre elevat de lectors. Es donarà prioritat a aquells treballs en què destaquin la claredat d’exposició i l’interès general del tema. El Butlletí està obert a tots els camps de la matemàtica i també als aspectes matemàtics de les ciències experimentals, la tecnologia, l’economia, etc., així com a altres àrees, com la història, la didàctica i la filosofia, sempre que els treballs tinguin un component matemàtic important. També tenen cabuda al Butlletí aquells articles que desenvolupin un aspecte significatiu de la problemàtica de la professió matemàtica al nostre país.

El Butlletí publica un volum a l’any, dividit en dos números, que es trameten gratuïtament a tots els socis. El Butlletí es publica també en format electrònic. L’edició electrònica del Butlletí pot obtenir-se des del portal de revistes científiques en línia de l’IEC o al servidor http://scm.iec.cat.

La correspondència administrativa s’ha d’adreçar a la Societat Catalana de Matemàtiques.

Editor en cap

Julià Cufí

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Comitè editorial

Bartomeu Coll

Dep. de Matemàtiques i Informàtica

Universitat de les Illes Balears

Núria Fagella

Dep. de Matemàtica Aplicada i Anàlisi

Universitat de Barcelona

Josep Maria Font

Dep. de Probabilitats, Lògica i Estadística

Universitat de Barcelona

Armengol Gasull

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Gábor Lugosi

ICREA i Departament d’Economia

Universitat Pompeu Fabra

Societat Catalana de Matemàtiques

Carrer del Carme, 47 - 08001 Barcelona tel. 933 248 583 - fax 932 701 180

scm@iec.cat - http://scm.iec.cat

Editora adjunta

Rosa Camps

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Jorge Mateu

Departament de Matemàtiques

Universitat Jaume I

Marc Noy

Departament de Matemàtica Aplicada II

Universitat Politècnica de Catalunya

Francesc Planas

Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya

Agustí Reventós

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Marta Sanz-Solé

Dep. de Probabilitats, Lògica i Estadística Universitat de Barcelona