Minimal surfaces

A mathematical concept linking black holes to bubbles

A minimal surface is a surface that is described to locally minimise its area. As confusing as the definition is for minimal surfaces, it can be more easily understood by comparing it to shapes we are familiar with, such as soap bubbles.

When blowing soap bubbles, a loop is dipped into soapy water and a flat film can be seen stretching across the loop when lifted from the bubble solution. This film takes the simplest shape possible, a perfectly flat surface with no bumps. It naturally minimises surface tension and also minimises area. Imagine if the flat circle gained bulges, each bulge would add unnecessary surface area. Once blown, a perfect sphere is created. Here we once again witness the tendency for nature to form efficient shapes. A sphere has the least surface area for a given volume.

This is the starting point for understanding minimal surfaces, though a soap bubble is still not a minimal surface, since the air pressure within the bubble stops it from collapsing from the opposite force of its surface tension, which wants to form a flat plane. In comparison, the flat plane of the dipped loop is a minimal surface, as it does not need to account for any additional force a spherical bubble has that prevents it from collapsing into the minimal surface area possible. The effect of air pressure can be seen by gently blowing on the flat surface of the dipped loop. The added force disrupts the surface but as soon as you stop, it goes back to the flat plane.

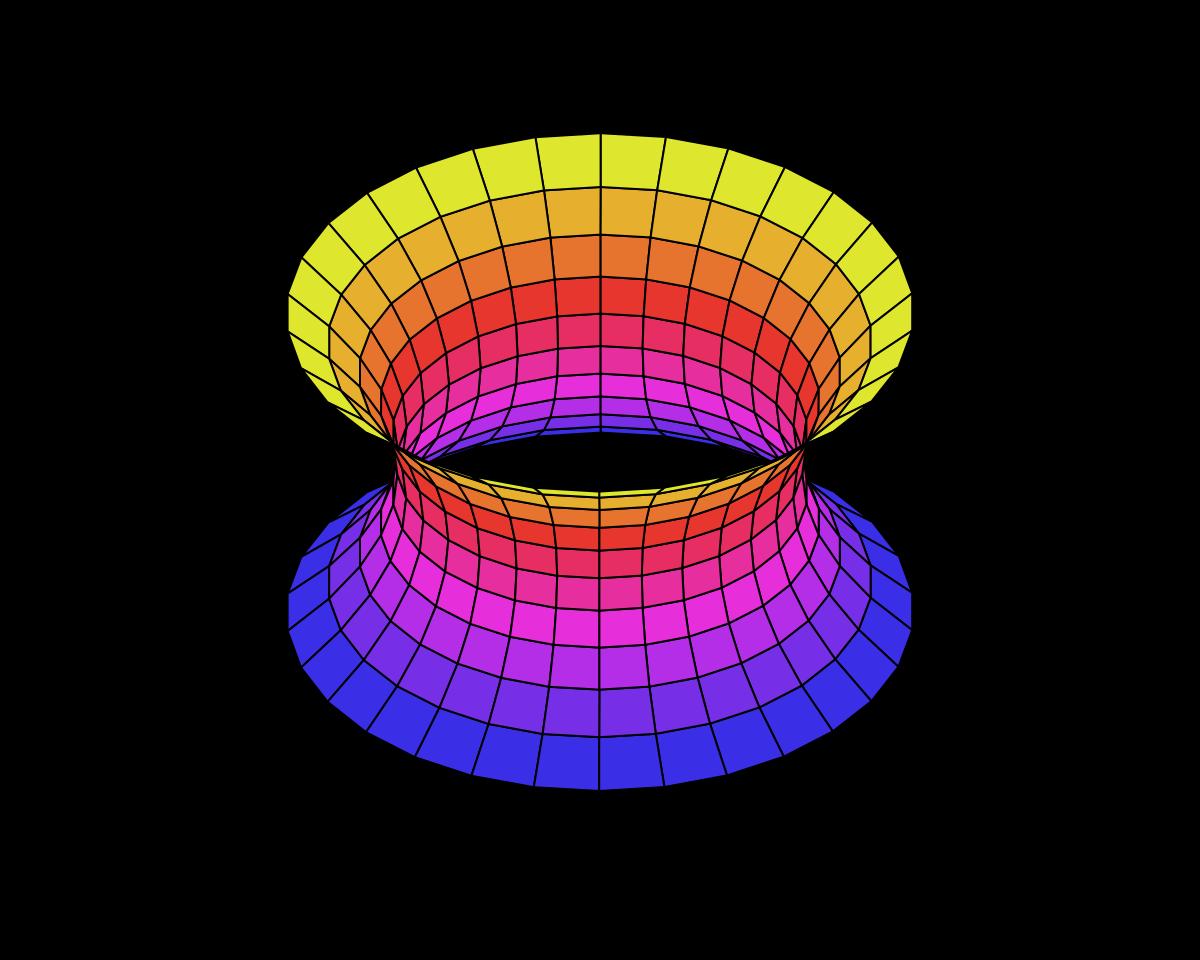
It was Leonardo da Vinci who first started studying soap films but it was mathematicians of the 18th century, Leonhard Euler and Joseph-Louis Lagrange who had taken up the subject of minimal surfaces and discovered two others from the surface shapes were called the catenoid (left) and the helicoid (right) The catenoid can be formed by dipping two rings in soapy water and joining the films to form a tube shape. One might initially assume that a cylinder will be formed, since at any point on a ring to another identical ring, a straight line would be the shortest length required to cross that distance. However, the catenoid is formed, which is essentially a cylinder which tapers in at the center before broadening back out symmetrically.

Now, finally going back to the original definition of locally minimising area, a minimal surface is essentially a surface that whenever you define a boundary upon it, the area within that boundary has the minimal surface it can have. Another

definition explains that a minimal surface, like a catenoid, occupies the least area when bounded by a closed space. The thin middle allows a catenoid to occupy less space than a cylinder.

Minimal surfaces has its foundations in theoretical mathematics but it ties in with relativity and quantum mechanics. What is particularly interesting is how Black Holes have been theorised to display Marginally trapped surfaces around their event horizon which create a hypersurface that are constructed of quasi-minimal surfaces. Closed trapped surfaces are a concept used in black hole solutions of general relativity which describe the inner region of an event horizon.

This surface is one where light is not moving away from the black hole. The event horizon is the boundary marking the limits of a black hole. The apparent horizon is a surface that is the boundary between light rays that are directed outwards and moving outwards and those directed outward but moving inward. The apparent horizon is also an example of a minimal hypersurface, linking the theory of black holes to minimal surfaces and the Plateau problem, raised by Joseph-Louis Lagrange in 1760 but is named after Joseph Plateau who experimented with soap films. This problem encompasses the finding of surfaces with a minimal area enclosed by a given curve in three dimensions. The mathematics associated with this is extremely complicated and has no easy summary. If you are interested I strongly recommend you delve deep within the many papers published analysing this idea

circular heli coid catenoid