Challenge—Community Center Design
A town named Willingdon has just decided to create a community center dedicated to helping people in the town. The mayor of the community is searching for young , creative, and brilliant architects who can build a community center in Willingdon. Your challenge is to design an original model of a community center that can serve the needs of citizens using three-dimensional shapes. The mayor will need to see your plans, measurements, and a model to consider using your design. The community center must stand up on its own and should include the use of at least 3 different three-dimensional shapes.
The mayor of Willingdon has added some requirements for the model community center building that you’re creating. Not only must the structure stand up on its own and use at least 3 three-dimensional figures, the mayor has requested that the building must also have a volume between 300 cm³ and 500 cm³ and that the surface area of your model structure be between 340 cm² and 700 cm². In addition, you may use glue sticks and tape to assemble your model community center building using cardstock provided by the teacher.
State the Challenge in your own words—what do you have to do?
What are the specifications for the challenge (what the design must do or possess)?
What are the constraints for the challenge (the limitations, typically time and materials)?
Knowledge and Skill Builders (KSBs)
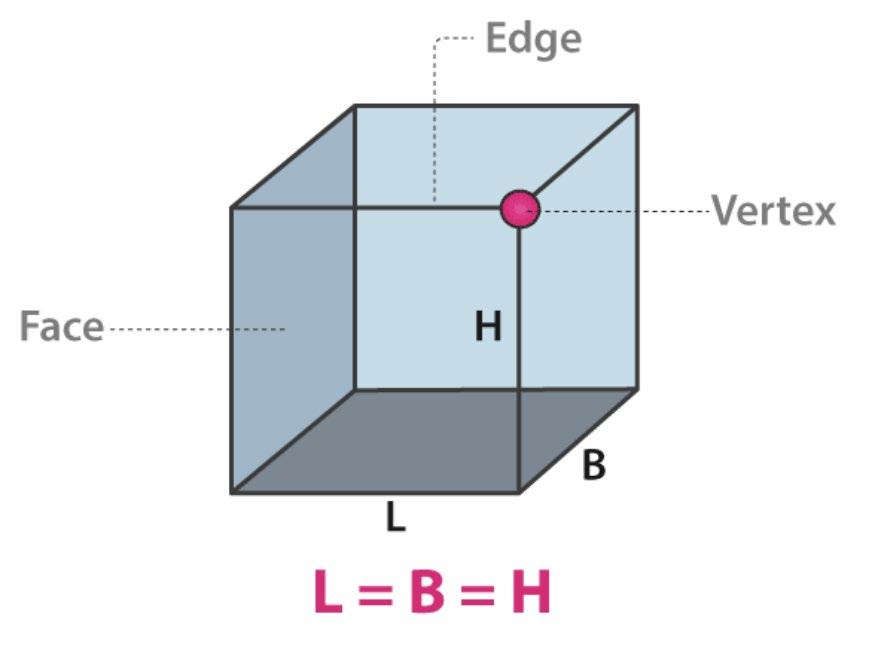
KSB1—Cubes
Cubes are a special case of a rectangular prism where are sides are the same length
The volume of the cube is L x B x H. The surface area of a face is L x B, B x H, or L x H depending on which face you are considering.
What would be volume of a cube where L = B = H = 3 cm? What would the surface area be?
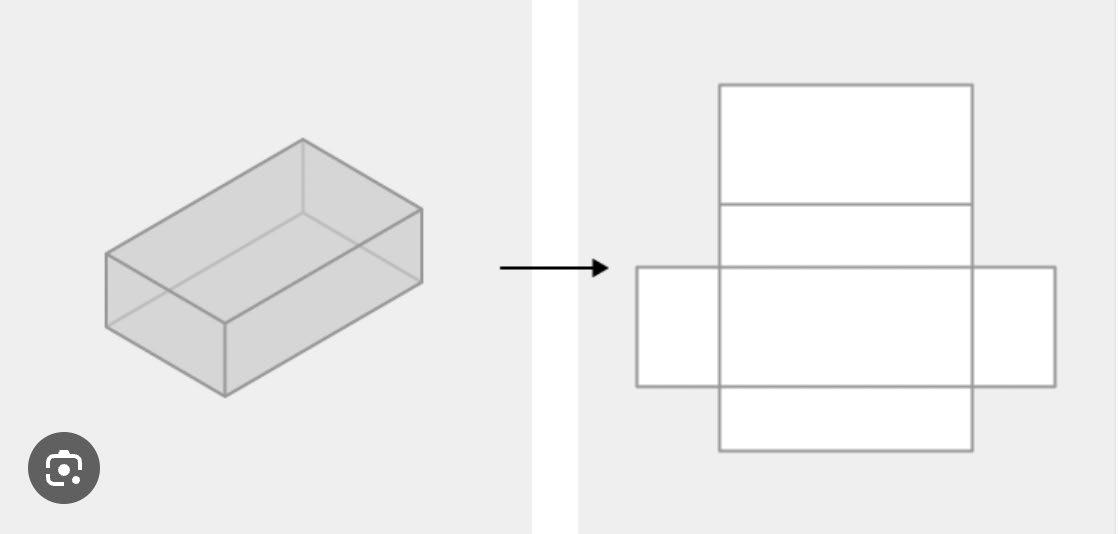
Constructing a Cube. Creating a net that can be folded into a cube.
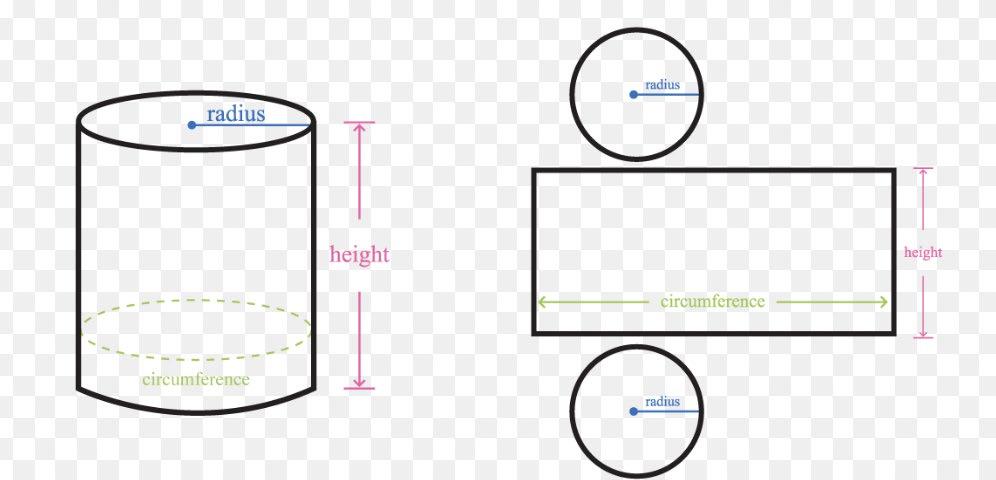
KSB2 Constructing a cylinder.
A cylinder is basically a circle that is extended. Imagine a circle on the ground and then you lifted it up So, it looks like this. And what it looks like unfolded
The volume of the cylinder is the area of the base, ���� = �������� 2 , times the height Now the surface is interesting as it the circumference times the height plus the areas of both ends. The
circumference 2πr. What would the surface area of a cylinder with a radius of 2 cm and a height of 5 cm be?
What would the volume of the cylinder be?
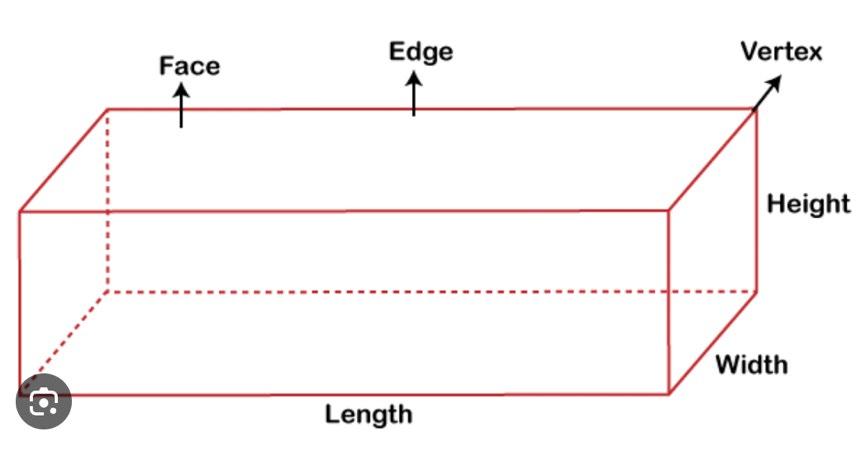
KSB3—Constructing a Rectangular Prism
Just as a cylinder is a circular base that is extruded, so is a rectangular prism. The base can be a rectangle, a square (special case).
So, the volume is easy, Length x Height x Width. If the length were 20 cm, the width 5 cm and the height 10 cm, what is the volume?
The surface area is a bit trickier There are six faces, two of each plane are identical (e. g. top and bottom, ends). What would the surface area of the rectangular prism be?
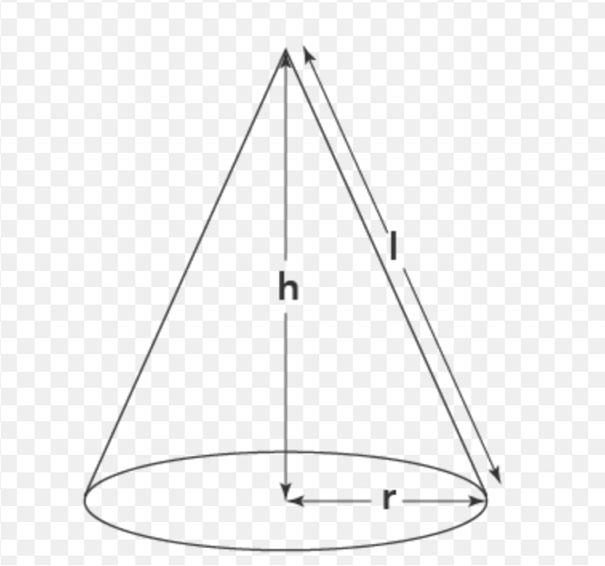
KSB 4 Constructing a Cone
Here is a picture of a cone with different dimensions indicated.
You remember that the volume of a cylinder is the area of the base (πr2) times the height (h). Well, the volume of a cone is one-third that value. When you see a cone, it is difficult to imagine that the volume just one-third that of a cylinder. This is one of the reasons coneshaped containers have great appeal (to whom).
So, V = 1/3 (πr2 h).
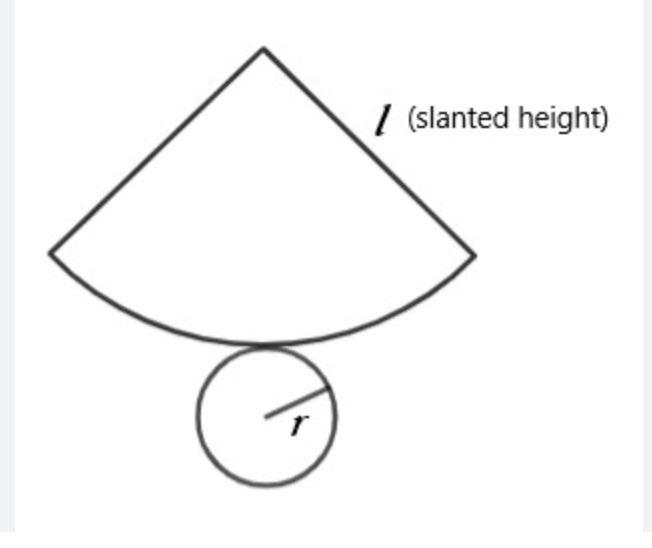
The surface area of the sloped side (lateral surface area) is not intuitive.
The lateral surface area (LSA) is LSA = (πr) √ (r2 + h2)
And the base surface area is simply πr2 .
Other Geometric Solids
You could research and investigate pyramids, spheres and hemispheres. And if you want to do so, include your research findings here It is very challenging to construct spheres and hemispheres.
Alternative Designs
Let’s get back to the challenge. Make sketches of possible designs just what you think of for a Community Center using at least three of the basic geometric forms. If the community center is to have specific functions, you may want to think about which geometric form is best for that function (e.g. shelter, theatre). You can also think about stacking forms for different purposes.
Best (Optimum) Design Choice
Which one did you like the best? Why?
Creating your Design Solution
Now you have to determine the sizes you want. Remember that when you attach shapes, the area of the attachment decreases the total surface area. Based on your sketch, show the calculations you are doing to figure out the optimum dimensions. Be sure to check on the total volume and very importantly, the total surface area. Include a sketch of each component to go along with the calculations. You may need to adjust dimensions.
Build it!
Make your solution Take a picture and paste here.
Test and Evaluate
Did it meet the specifications? Prove it!