PRINCIPIOS DE COSMOGRAFÍA

COSMOGRAFÍA PRINCIPIOS DE

PRINCIPIOS DE COSMOGRAFÍA

ARTURO MANUEL MONFORTE OCAMPO

PRINCIPIOS DE COSMOGRAFÍA

Editada y producida por

Derechos reservados conforme a la ley.

D.R. © Arturo Manuel Monforte Ocampo, 2013

Primera edición: mayo de 2013

Queda prohibida la reproducción parcial o total de esta obra por cualquier procedimiento sin la autorización de los titulares del copyright.

Producción editorial:

HELIOS Comunicación

Av. Insurgentes Sur 4411 edificio 7, departamento 3 Col. Tlalcoligia 14430 México, D.F.

Impreso en México en los talleres de Drokers Impresiones de México, S.A. de C.V.

Av. Insurgentes No. 100 304-O Col. Juárez Delegación Cuauhtémoc 06600, México, D.F. Tiro: 500 ejemplares.

Expreso mi agradecimiento a las empresas Servicios de Ingeniería en Vía Terrestre, S.C., Consultores y Constructores Escalante, S.A. de C.V., Freyssinet de México, S.A. de C.V., Construcciones JALO, S.A. de C.V. y PICIE, S.A. de C.V., por su amistoso y desinteresado apoyo.

ÍNDICE

CAPÍTULO I. GENERALIDADES

1. Círculos de una esfera .....................................................................

2. Eje y polos

3. Distancias esféricas ..........................................................................

4. Zonas .................................................................................................

5. Ángulo entre una recta y un plano ................................................

6. Ángulos diedros ...............................................................................

7. Ángulos esféricos .............................................................................

8. Triedros .............................................................................................

9. Triángulos esféricos .........................................................................

10. Coordenadas esféricas ...................................................................

11. Fórmulas trigonométricas

12. La elipse ...........................................................................................

13. La parábola

CAPÍTULO II. DEFINICIONES

1. La astronomía ...................................................................................

2. Los astros

3. Ramas de la astronomía ..................................................................

4. Cosmografía

5. Importancia de la astronomía ........................................................

CAPÍTULO III. ROTACIÓN APARENTE DEL CIELO

..........

1. La esfera celeste

2. Movimiento diurno .........................................................................

3. Rotación de la Tierra

4. El metro .............................................................................................

CAPÍTULO IV. COORDENADAS GEOGRÁFICAS .............

1. Longitud y latitud

2. Arco-tiempo .....................................................................................

Ejercicios propuestos

CAPÍTULO V. COORDENADAS HORIZONTALES

1. Horizonte ..........................................................................................

2. Acimut y altura

Ejercicios propuestos ...........................................................................

CAPÍTULO VI. COORDENADAS ECUATORIALES ...........

1. Definiciones ......................................................................................

2. Coordenadas ecuatoriales ...............................................................

3. Altura del polo ..................................................................................

4. Más sobre el movimiento diurno ...................................................

5. Comparación de los dos sistemas de coordenadas ......................

Ejercicios propuestos

CAPÍTULO VII. MEDIDA DEL TIEMPO

1. Tiempo solar medio .........................................................................

2. Tiempo sideral

...........................................................................

CAPÍTULO VIII. MEDIDA DE LAS COORDENADAS

ECUATORIALES

1. Triángulo astronómico ....................................................................

2. Anteojo ecuatorial

3. Obtención de las coordenadas ecuatoriales .................................. a partir de las horizontales

4. Otro método para obtener las coordenadas ecuatoriales

5. Las coordenadas horizontales deducidas de las ecuatoriales .....

6. Distancia angular entre dos astros .................................................

Ejercicios propuestos

CAPÍTULO IX. POSICIÓN DE UN PUNTO GEOGRÁFICO

1. Relación entre la hora y la longitud de un lugar ...........................

2. Determinación de la longitud

3. Determinación de la latitud ............................................................

Ejercicios propuestos

CAPÍTULO X. LAS ESTRELLAS

1. Las estrellas .......................................................................................

2. Las constelaciones ............................................................................

3. Reglas para reconocer constelaciones ...........................................

4. Magnitudes aparentes ......................................................................

5. Evolución de las estrellas y su clasificación ...................................

CAPÍTULO XI. EL SOL

1. Movimiento anual aparente del Sol ...............................................

2. La eclíptica

3. Precesión de los equinoccios ..........................................................

4. Nutación

5. Traslación de la Tierra .....................................................................

6. Movimiento helicoidal del Sol

7. Zonas geográficas .............................................................................

8. El día y la noche

9. Distancia cenital meridiana del Sol ...............................................

10. Calendario

11. Calor del Sol en la Tierra...............................................................

12. Estaciones

13. Climas de México ..........................................................................

Ejercicios propuestos

CAPÍTULO XII. LA LUNA ...................................................

1. Movimiento propio de la Luna

2. Fases de la Luna ................................................................................

3. Lunación

4. Edad de la Luna ................................................................................

5. Fiestas movibles

6. Rotación de la Luna .........................................................................

7. Libraciones

8. Relación entre las revoluciones siderales terrestre y lunar, y la sinódica lunar ..................................................................

9. Eclipses ..............................................................................................

Ejercicios propuestos ...........................................................................

CAPÍTULO XIII. LOS PLANETAS

1. Clasificación .....................................................................................

2. Movimientos aparentes ...................................................................

3. Movimientos reales

4. Explicación de los movimientos aparentes ...................................

5. Distancia de los planetas al Sol

6. Fases de los planetas ........................................................................

7. Satélites

Ejercicios propuestos ...........................................................................

CAPÍTULO XIV. BREVE DESCRIPCIÓN

DE LOS PLANETAS DEL SISTEMA SOLAR

1. Mercurio ...........................................................................................

2. Venus

3. Tierra .................................................................................................

4. Marte

5. Planetoides entre Marte y Júpiter ...................................................

6. Júpiter

7. Saturno ..............................................................................................

8. Urano .................................................................................................

9. Neptuno

CAPÍTULO

XV. COMETAS

1. Características ..................................................................................

2. Visibilidad

3. Composición ....................................................................................

4. Masa

5. Órbitas ...............................................................................................

6. Cometas notables .............................................................................

CAPÍTULO XVI. ASTROLITOS

1. Meteoritos o estrellas fugaces .........................................................

2. Visibilidad .........................................................................................

3. Origen................................................................................................

4. Leónidas ............................................................................................

5. Aerolitos

6. Choques con la Tierra .....................................................................

CAPÍTULO

XVII.

EL UNIVERSO ........................................

1. Las estrellas

2. Vía Láctea ..........................................................................................

3. La metagalaxia

4. Historia del conocimiento del Universo .......................................

5. Primeros conocimientos

Ejercicios propuestos ...........................................................................

CAPÍTULO

XVIII. TEMAS DIVERSOS................................

1. Paralaje de un astro

2. Acerca del Sol ..................................................................................

3. Aberración de la luz

4. Fuerza de gravitación de la Luna ....................................................

5. Cosmología .......................................................................................

6. Eras geológicas

7. Agujeros negros................................................................................

8. Tamaños aparentes

9. Algoritmo para calcular el día de la semana .................................

10. Velocidad de escape

11. Giovanni Papini .............................................................................

CAPÍTULO XIX. PRONTUARIO DE INFORMACIÓN GENERAL

1. Unidades de temperatura y conversiones .....................................

2. Fórmulas útiles y equivalencias ......................................................

3. Dimensiones de los planetas del Sistema Solar, en km, y su número de satélites .......................................................................

4. Dimensiones .....................................................................................

5. Distancias entre astros .....................................................................

6. Velocidades de traslación

7. Ángulos de paralaje .........................................................................

8. Semidiámetros aparentes

9. Edad estimada ..................................................................................

10. Temperaturas del Sol y sus planetas

11. Algunas propiedades de los planetas ...........................................

TABLAS

.........................................................................

Tabla I. Posiciones geográficas de las principales ciudades mexicanas .............................................................................

Tabla II. Hora sideral

Tabla III. Catálogo de estrellas (coordenadas en 1950) ...................

Tabla IV. Catálogo de estrellas (coordenadas en 2011)

Tabla V. Coordenadas ecuatoriales del Sol en 1946 .........................

Tabla VI. Epacta (año gregoriano)

Tabla VII. Número N para calcular la edad de la Luna ...................

Tabla VIII. Reglas para el uso del calendario perpetuo ...................

Tabla IX. Calendario para el siglo XX

Tabla X. Para el calendario juliano .....................................................

Tabla XI. Para el calendario gregoriano

Tabla XII. Domingo de Pascua en el calendario gregoriano (siglos XVI a XIX)

Tabla XIII. Domingo de pascua en el calendario gregoriano (siglos XX y XXI)

Tabla XIV. Fechas recientes de conjunciones y oposiciones ...........

BIBLIOGRAFÍA

PRÓLOGO

Un día de mediados de 2011, platicaba con el muy distinguido ingeniero Modesto Armijo Mejía acerca de las materias que se impartían en las escuelas preparatorias mexicanas hace más de 40 años; en particular, conversábamos de la materia de Cosmografía. Le comenté que siendo estudiante de preparatoria en la Universidad de Yucatán me tocó utilizar como libro de texto El Universo. Nuevas Lecciones de Cosmografía , escrito en 1947 por el ingeniero yucateco Joaquín Ancona Albertos, libro que yo deseaba obtener para releerlo, y que no lo encontraba ni en la propia Universidad de Yucatán, a lo que me respondió el ingeniero Armijo, que fue amigo del ingeniero Ancona Albertos, que él tenía un ejemplar.

En efecto, unos días después me obsequió el mismísimo libro que yo había llevado como texto en la preparatoria en 1963, lo que mucho le agradecí. Después de hojearlo y recordar los temas tan interesantes que trata el libro, decidí escribir sobre esta rama de la astronomía, a fin de compartir con mis amigos, y sobre todo con aquellos que no tuvieron la oportunidad de cursar la materia, los conocimientos que esta disciplina permite adquirir sobre el Universo y nuestro

Sistema Solar. Por supuesto, este trabajo también lo haré llegar a jóvenes estudiantes que no tienen ahora la oportunidad de cursar la materia en la preparatoria, toda vez que ya no se imparte.

Este trabajo solamente pretende ser una humilde aportación de conocimientos de varios temas que capacitarán al lector para determinar las coordenadas horizontales, ecuatoriales o eclípticas que permitan localizar y observar astros a simple vista o con telescopio. También podrá el lector conocer las propiedades, características y antigüedad de los cuerpos celestes del Sistema Solar, como nuestro astro rey, la Luna, los planetas y planetoides, los cometas y los astrolitos. Será capaz de calcular la fecha exacta de cada fase de la Luna, de saber cuándo habrá Luna llena en cualquier mes y año, y cuándo acaecerá la Semana Santa de cualquier año. También podrá entender, entre otros fenómenos, los eclipses solares y lunares, totales y parciales.

Consideré conveniente incluir un esbozo acerca de los conocimientos y descubrimientos de los primeros astrónomos de la historia, así como algunas frases célebres de grandes personajes como epígrafe en cada capítulo. También decidí anotar

algunas reflexiones filosóficas elaboradas por el escritor italiano Giovanni Papini (1881-1956), con gran sentido del humor, acerca de la astronomía y el Universo.

He incluido en algunos capítulos problemas prácticos acompañados del desarrollo de sus soluciones, así como otros para que resuelva el lector, a fin de que se ejercite en la obtención de respuestas a diversos problemas, si así lo desea. De estos últimos se proporcionan las soluciones al final del libro.

En cuanto al perfil que debe tener el lector para comprender los conceptos asentados, bastan los conocimientos de matemáticas y de geometría bien adquiridos en la preparatoria.

Ha sido mi intención hacer amigable este trabajo; es por eso que se imprimió con letra lo suficientemente grande para que nadie, o casi nadie, requiera anteojos para leerlo. También se preparó

con márgenes amplios en los cuatro bordes, con el objetivo de que sea de lectura cómoda, e incluso para hacer algunas anotaciones.

Es mi más ferviente deseo que los lectores de este libro lo encuentren claro, útil, que se interesen en los temas y también que se pongan a resolver los ejercicios propuestos. Con eso me sentiría muy satisfecho y se cumplirían todas mis expectativas generadas en el momento en que decidí escribirlo.

Conozco bien a mis amigos y sé que muchos de ellos se adentrarán en todos los capítulos, y me temo que posiblemente me harán ver errores cometidos en el tratamiento de algunos temas, lo cual obviamente no me dará mucho gusto, aunque sí lo apreciaré enormemente. Arturo Manuel Monforte Ocampo

CAPÍTULO I

Generalidades

Dadme un punto de apoyo y levantaré el mundo. Arquímedes (287-212 A. C.)

Círculos de una esfera

Si se corta una esfera por un plano en cualquier posición, la sección obtenida es un círculo (véase figura I.1). Así, las líneas ABA’C, DEFD, PBP’B’P, GHIG y KLRK son circunferencias.

Se llama círculo máximo a aquel cuyo plano pasa por el centro de la esfera. Si el plano no pasa por el centro, determina un círculo menor. Los círculos de una esfera tienen las siguientes propiedades:

1. Por dos puntos cualesquiera de la superficie de la esfera puede trazarse sólo un círculo máximo, a menos que esos dos puntos sean los extremos de un diámetro, en cuyo caso pueden trazarse por ellos infinidad de círculos máximos.

2. Todos los círculos máximos de una esfera son iguales.

Figura I.1

3. Todo círculo máximo divide a una esfera en dos partes iguales que se llaman hemisferios.

4. Dos círculos máximos se dividen mutuamente en partes iguales.

5. Por tres puntos de la superficie de una esfera sólo puede hacerse pasar una circunferencia, que en general corresponderá a un círculo menor.

Eje y polos

El eje de un círculo cualquiera obtenido de una esfera es el diámetro de ésta, perpendicular al plano de dicho círculo. Los polos de un círculo son los puntos en que su eje toca la superficie de la esfera. Todos los círculos cuyos planos son paralelos tienen el mismo eje y los mismos polos. Si dos círculos máximos son perpendiculares entre sí, cada uno pasa por los polos del otro. Si un

círculo máximo pasa por los polos de un círculo menor, divide a éste en dos partes iguales; así, en la figura I.1, el círculo máximo PBP’B’P corta en dos partes iguales cada uno de los círculos DEFD, GHIG, JKLJ y ABA’B’. Si un círculo máximo y uno menor se cortan oblicuamente, se dividen uno a otro en partes desiguales: la diferencia entre las dos partes de cada uno es tanto mayor, cuanto más lejos del centro de la esfera se halle el plano del círculo menor (véase figura I.2).

Distancias esféricas

La distancia entre dos puntos de una superficie esférica es el arco de la circunferencia máxima que pasa por ellos y se mide en grados, lo que se logra uniendo ambos puntos al centro de la esfera; así se obtienen los dos radios. El ángulo que forman, al igual que el arco, se llama distancia angular entre los dos puntos. Todos los puntos de la circunferencia de un círculo cualquiera de la esfera, perpendicular al eje, equidistan de cada polo del círculo, y esta distancia se llama distancia polar del círculo. Por ejemplo, la distancia polar de un círculo máximo vale 90 grados.

Zonas

I.2

Se llama zona esférica, o zona, a la parte de la superficie de una esfera comprendida entre las circunferencias de dos círculos paralelos. Estas circunferencias son las bases de la zona. Si uno de los planos paralelos es tangente a la esfera, la zona obtenida es un casquete (véase figura I.3).

Figura

Casquete polar

Zona templada del norte

Zona tórrida

I.3

En nuestro planeta existen la zona tórrida, las zonas templadas y los casquetes polares.

Ángulo entre una recta y un plano

Es el ángulo a que forma la recta con su proyección ortogonal sobre el plano (véase figura I.4).

I.4 A a B Perpendicular al plano

Proyección de AB

Ángulos diedros

Si se cortan dos planos, la abertura comprendida entre los dos se llama ángulo diedro o sólo diedro. Los dos planos son las caras del diedro y su inter-

sección es la arista. Si desde un punto cualquiera de la arista se trazan rectas perpendiculares a ésta en cada cara, el ángulo diedro es el formado por dichas rectas (véase figura I.5).

I.5

Ángulos esféricos

La abertura comprendida entre dos arcos de circunferencia máxima que parten de un mismo punto de la superficie de una esfera se llama

I.6 A B O P P’

Figura

Figura

Figura

Figura

ángulo esférico. El punto (P) se llama vértice del ángulo esférico. El ángulo se mide trazando desde el centro de la esfera los radios de ambas circunferencias máximas sobre el círculo máximo perpendicular a aquéllas. En la figura I.6 las circunferencias máximas son PAP’ y PBP’; el círculo máximo perpendicular a ellas es el OAB. El ángulo esférico se mide con el ángulo plano AOB.

Triedros

Son las figuras formadas por tres planos que concurren en un mismo punto: el vértice (véase figura I.7). Las intersecciones de cada dos planos son las aristas. Los ángulos planos que forman cada dos aristas son las caras del triedro, y los ángulos que forman cada dos caras son los ángulos diedros.

forman el triedro correspondiente al triángulo esférico (véase figura I.8). Cada lado del triángulo tiene la misma medida que la cara respectiva del triedro y cada ángulo del triángulo mide lo mismo que el diedro al que corresponde.

Triángulos esféricos

Un triángulo esférico es la porción de la superficie de una esfera comprendida entre tres arcos de círculo máximo que se cortan dos a dos. Los puntos de intersección de los arcos son los vértices, y los arcos de vértice a vértice, los lados. Si los vértices se unen con el centro de la esfera, sus radios

Los ángulos de un triángulo esférico suman más de 180° y menos de 540°. Un triángulo esférico puede tener dos de sus ángulos, o aun los tres, rectos u obtusos. Un triángulo esférico se llama birrectángulo o trirrectángulo, según tenga dos ángulos rectos o los tres.

Si dos círculos máximos de una esfera pasan por los polos de un tercero (véase figura I.6), forman con él dos triángulos birrectángulos que tienen un lado común, como sucede con los triángulos APB y AP’B.

Figura I.7

Figura I.8

Los ángulos PAB y PBA son rectos. En efecto, por ejemplo, el ángulo PAB es igual que el arco opuesto PB, que a su vez es igual al ángulo POB = 90°. Además, a PA y PB se les llama cuadrantes.

Si en una esfera se trazan dos círculos máximos

PAP’ y EAB perpendiculares entre sí (véase figura I.9), la esfera queda dividida en cuatro husos iguales. Si se traza un tercer círculo máximo PBP’ perpendicular a la intersección de los dos primeros, la superficie esférica queda dividida en ocho triángulos trirrectángulos iguales, cuyos lados son todos cuadrantes.

y por ende perpendicular a él, al que llamaremos círculo de las ordenadas. Sea M, una de las intersecciones de los círculos, el origen. Para determinar la posición de un punto A de la superficie esférica, se hace pasar por él un círculo máximo que contenga los polos P y P’ del círculo de las abscisas, y sea N el punto donde corta a éste. Se miden los arcos MN y NA, así se obtienen la abscisa y la ordenada esférica del punto A. El arco MN corresponde al ángulo MON y el arco NA es igual al ángulo NOA.

Coordenadas esféricas

En la figura I.10, sea el círculo máximo XMX’M’X el círculo de las abscisas, y PMP’M’P otro círculo máximo que pasa por los polos P y P’ del primero

Fórmulas trigonométricas

Conviene que recordemos aquí dos propiedades trigonométricas de los triángulos esféricos:

1. En todo triángulo esférico, los senos de los lados son proporcionales a los de los ángulos opuestos. Si designamos como A, B y C los án-

Figura I.9

Figura I.10

gulos y como a, b, y c los lados respectivamente opuestos, esta propiedad se expresa mediante la fórmula:

sen a = sen b = sen c (1)

sen A sen B sen C

2. En todo triángulo esférico, el coseno de un lado es igual al producto de los cosenos de los otros dos lados, más el producto de los senos de los mismos lados por el coseno del ángulo que forman. Esta propiedad se expresa con la fórmula:

cos a = cos b cos c + sen b sen c cos A (2)

La elipse

Es importante estudiar esta figura plana, por ser la que describen los astros del Sistema Solar en su movimiento de traslación alrededor de otros astros del propio sistema.

La elipse es el lugar geométrico de un punto P que se mueve de tal manera que la suma de sus distancias a dos puntos fijos F y F’ es una constante igual a 2a, donde a es el semieje mayor de la elipse.

Se puede dibujar una elipse (véase figura I.11) fijando los extremos de un hilo de longitud AA’ = 2a en dos puntos fijos F y F’ llamados focos, que

Figura I.11

B (0,b)

B’ (0,-b) A(a,0)

A’ (-a,0)

distan entre sí FF’ = 2c. A continuación se lleva el hilo tenso, con la punta de un lápiz, a todas las posiciones posibles en torno de F y F’. Los segmentos PF y PF’ son los radios vectores de un punto P cualquiera de la elipse.

La elipse tiene dos ejes de simetría: la recta AA’, que pasa por los focos (eje mayor), y la recta BB’ (eje menor), perpendicular y bisectriz de la línea FF’. La intersección O de ambos ejes es el centro de la elipse, y los extremos A, A’, B y B’ son sus vértices. La longitud del semieje menor es b. Cada uno de los radios vectores de los extremos B y B’ del eje menor es igual al semieje mayor a , que representa la distancia media de todos los puntos de la elipse a uno cualquiera de sus focos.

Se llama excentricidad de la elipse a la relación c/a (semidistancia focal dividida entre semieje mayor). Su achatamiento es la relación (a – b)/a. Una elipse es más alargada mientras mayor sea su excentricidad o su achatamiento. Cuando la elipse es circular, su excentricidad vale 0, ya que los focos coinciden con el centro; además, su achatamiento es nulo.

La ecuación de la elipse es + = 1 y se deduce de la siguiente manera:

F’P + FP = 2a, por definición; entonces:

{(x – c)2 + y2}1/2 + {(x + c)2 + y2}1/2 = 2a

Elevando al cuadrado ambos términos y simplificando:

a (x2 + 2cx + c2 + y2)1/2 =

Elevando al cuadrado y simplificando:

De acuerdo con la figura I.11, FB = FB’ = a, por lo que a2 – c2 = b2

∴ x2b2 + y2a2 = a2b2

Dividiendo entre a2b2 nos queda la ecuación de la elipse:

x2 + y2 = 1 a2 b2

La parábola

Es el lugar geométrico de un punto P que se mueve de tal modo que equidista siempre de una recta y de un punto, ambos fijos. La recta DD’ (véase figura I.12) se llama directriz, el punto F foco, y la distancia de cada punto P de la parábola al foco se llama radio vector

La parábola tiene un eje de simetría que es la perpendicular AX a la directriz (pasando por el foco) y un vértice V en que la curva corta a su eje; éste está situado en el punto medio de la distancia FA del foco a la directriz.

I.12

La ecuación de la parábola es y 2 = 4 px . De acuerdo con la figura I.12, PF = {(x – p)2 + y2}1/2 y PN = x + p

Entonces, [(x – p)2 + y2]1/2 = x + p

∴ (x – p)2 + y2 = (x + p)2

Simplificando se obtiene la ecuación de la parábola: y2 = 4px

Figura

CAPÍTULO II

Definiciones

Educad a los niños y no será necesario castigar a los hombres. PitágorAs (585-495 A. C.)

La astronomía

La astronomía estudia los astros, sus movimientos tanto aparentes como reales, sus distancias, dimensiones, estructura y condiciones físicas, así como las acciones mutuas que ejercen unos sobre otros por atracción y por sus radiaciones, su historia probable y su evolución futura.

Los astros

Los cuerpos celestes que estudia la astronomía y que genéricamente se denominan astros son:

1. La Tierra.

2. El Sol.

3. La Luna.

4. Los planetas, incluyendo sus satélites.

6. Los meteoritos, cuerpos diminutos que viajan alrededor del Sol y que penetran en la atmósfera terrestre y producen las estrellas fugaces.

7. Las estrellas, cuerpos análogos al Sol.

8. Las nebulosas, grandes masas de gas y de polvo que flotan en el espacio y que se muestran al telescopio como nubecillas informes.

9. Las galaxias, conjuntos inmensos de soles y nebulosas que constituyen verdaderos universos análogos a aquél del que formamos parte (Vía Láctea), pero que por su enorme distancia sólo se revelan a los telescopios como débiles manchitas difusas.

5. Los cometas o astros cabelludos, que giran en torno al Sol como los planetas, aunque difieren de ellos por su estructura y forma de movimientos.

Los astros anteriores pueden agruparse así:

• El Sistema Solar, es decir: el Sol, los planetas, satélites, cometas y meteoritos.

• La galaxia o sistema de estrellas y nebulosas al que pertenece el Sistema Solar.

• La metagalaxia o conjunto de sistemas análogos a nuestra galaxia.

Ramas de la astronomía

Son cuatro las ramas de la astronomía:

1. La astronomía práctica, que da métodos adecuados para la deducción de los datos empleados en las otras ramas de la astronomía y, en particular, para medir el tiempo y determinar la situación geográfica de un punto cualquiera de la Tierra.

2. La astronomía de posición o astrometría, que enseña procedimientos rigurosos para calcular las posiciones presentes, pasadas y futuras de los astros, y para predecir fenómenos celestes; también para medir los astros, sus distancias y las velocidades reales de sus movimientos.

3. La astrofísica, que estudia las características físicas de los astros, especialmente de los externos al Sistema Solar, para conocer su temperatura, la naturaleza y condiciones de sus atmósferas, de sus superficies y de sus interiores, así como sus dimensiones, distancias y movimientos reales.

4. La cosmogonía, que estudia la evolución del Universo, así como el nacimiento, el desarrollo

y el fin probable de cada uno de los astros que lo integran.

Cosmografía

Se encarga de la descripción del Universo; abarca todas las ramas de la astronomía y expone sus conclusiones sin detallar ni profundizar en los métodos, aunque los esboza con claridad suficiente para que pueda aquilatarse el valor de los conocimientos astronómicos; es un estudio elemental de la astronomía. Su objetivo fundamental es mirar el Universo en conjunto para comprender la posición que en él ocupa el ser humano.

Importancia de la astronomía

La regularidad del movimiento aparente de los astros, como el movimiento diurno de las estrellas, las salidas y puestas del Sol, la sucesión de las fases de la Luna, entre otros, ha llevado al ser humano a saber medir el tiempo. El primero de tales fenómenos es el único medio de regular los relojes. Dichos acontecimientos también han sido los únicos medios para guiar a los viajeros en el mar y en el desierto, y son el mejor recurso en las operaciones topográficas y geodésicas para fijar la posición de cada lugar, así como para la construcción de mapas de la superficie terrestre. El estudio de la astronomía ha enseñado al ser humano la existencia de las leyes naturales, inmutables, y lo ha librado de la creencia supersticiosa de que cuanto ocurre en el mundo es producto del azar o del capricho de los dioses.

CAPÍTULO III

Rotación aparente del cielo

El gran libro de la Naturaleza está escrito en símbolos matemáticos. gAlileo gAlilei (1564-1643)

La esfera celeste

Las estrellas o soles son cuerpos luminosos por sí mismos diseminados en el espacio moviéndose en diferentes direcciones con velocidades enormes que alcanzan decenas y aun centenares de kilómetros por segundo. A simple vista, todas nos parecen igualmente lejanas; además, se hallan tan enormemente distantes de nosotros, que sus movimientos nos pasan inadvertidos. Para entender esto recuérdese que si vemos pasar un avión, su movimiento parece tanto más lento cuanto más alto pase. Así, las estrellas nos parecen fijas y a la misma distancia, como si estuvieran adheridas a la superficie de una esfera hueca en cuyo centro estuviéramos nosotros.

Esta esfera ideal se llama esfera celeste.

La distancia angular de dos astros es el ángulo de las visuales dirigidas a ellos, o el arco de círculo

máximo de la esfera celeste comprendido entre las posiciones de dichos astros.

Movimiento diurno

A pesar de que las estrellas se mueven independientemente en el espacio, están tan lejos que la distancia angular entre dos de ellas no ha variado desde que el ser humano las comenzó a observar hace decenas de siglos. Sin embargo, si comparamos la posición de una estrella cualquiera con algún punto fijo de la Tierra, como el borde de una pared alta, descubriremos un movimiento de los astros con relación a la pared. Si vemos astros y pared hacia el Oriente, en pocos minutos las estrellas irán subiendo; si miramos hacia el Occidente, las veremos bajar y desaparecer detrás de la pared.

Viendo hacia el Norte, notaremos que las estrellas muy altas se mueven de derecha a izquierda, es decir, de Oriente a Poniente; en cambio, las muy bajas se moverán de izquierda a derecha; veremos que cada una describe una circunferencia en sentido inverso al de las manecillas del reloj, en torno de un punto llamado polo celeste norte.

Las estrellas “cercanas” al polo completan su circunferencia y podemos verlas tanto cuando pasan encima de él, como cuando se desplazan por debajo. Estas estrellas se llaman circumpolares. Respecto a las estrellas cuya distancia aparente al polo es muy grande, una parte de su trayectoria circular queda por debajo de la Tierra, y por tanto fuera del alcance de nuestra observación, por lo que salen y se ponen todos los días, lo mismo que el Sol. La observación atenta y continua de este movimiento de las estrellas ha permitido descubrir las siguientes leyes:

1. Todas las estrellas se mueven en el mismo sentido, de Oriente a Occidente, en la parte superior de su curso.

2. Cada estrella describe en el cielo una circunferencia con movimiento uniforme.

3. Las circunferencias que describen las estrellas pertenecen todas a planos paralelos, por lo que tienen un eje y polo comunes (véase “Eje y polos”, capítulo I). El eje de todos los círculos paralelos que describen las estrellas se llama eje del mundo, y sus extremos, polos celestes. El que nos queda enfrente cuando tenemos el Oriente a la derecha se llama polo norte; el opuesto,

polo sur. El polo celeste norte es visible desde cualquier punto del territorio mexicano; el polo sur es invisible.

4. Las estrellas emplean el mismo tiempo en dar cada vuelta completa. Este tiempo es el día sideral, que es muy constante. Medido en nuestro reloj común, dura 23 horas 56 minutos y 4 segundos, casi 4 minutos menos que el día solar, a cuyo ritmo se acomodan nuestros relojes.

El movimiento diurno de las estrellas se puede hacer patente en una fotografía de larga exposición que se tome con una cámara fija dirigida hacia el polo celeste norte. Cada estrella deja marcado un arco de círculo, o éste completo si la exposición dura lo que el día sideral. Si la exposición dura una hora, el arco marcado es de 15 grados.

Rotación de la Tierra

El movimiento diurno se explica considerando que la Tierra gira sobre sí misma, alrededor de un eje fijo que pasa por su centro en sentido inverso al del movimiento aparente del cielo, es decir, de Occidente a Oriente, o lo que es lo mismo, en el sentido de las manecillas del reloj, si se observa desde el polo celeste sur. La recta que llamamos antes eje del mundo es la prolongación del eje de rotación de la Tierra. El centro de la esfera celeste es el de nuestro planeta, y si nos parece tenerlo en los ojos es porque el radio terrestre es prácticamente nulo si se compara con las distancias a que se hallan las estrellas.

Aunque más adelante se tratará la traslación de la Tierra, conviene adelantar aquí únicamente que su órbita alrededor del Sol es también en el sentido dextrorso (el de las manecillas del reloj) si se observa desde el polo celeste sur.

El radio medio de la Tierra es de 6,371.23 km; la estrella menos lejana dista 40 millones de millones (billones) de kilómetros de nuestro planeta. Si tratamos de indicar en escala gráfica estas dos longitudes, entenderemos por qué el eje del mundo pasa por nuestros ojos.

Supongamos (en la figura III.1) que el círculo grande es la esfera celeste y que el pequeño concéntrico es nuestro planeta (T). Si estamos en la Ciudad de México, cuyas coordenadas geográficas son latitud N 19° 26’ 05”, longitud WG 99° 07’

54”, cuyo cenit es Z y su horizonte H-H, y nos movemos hacia el Norte, de modo que el cenit sea ahora Z’ con el horizonte H’-H’, el eje del mundo irá formando con el horizonte un ángulo cada vez más grande –inicialmente α y después β– (véase figura III.1), lo que nos irá permitiendo ver un mayor número de estrellas circumpolares.

Si llegáramos al Polo Norte, todas las estrellas parecerían moverse sobre círculos paralelos al horizonte, entendiendo por “todas”, las del hemisferio boreal, ya que no veríamos ninguna del austral. Si salimos de nuestra localidad hacia el Sur, cada vez veremos menos estrellas circumpolares; al llegar al Ecuador, el horizonte coincidirá con el eje del mundo y ya no veremos estrellas circumpolares; todos los astros permanecerán medio día sobre el horizonte y medio día debajo. Más al Sur ya no se vería el Polo Norte y el Polo Sur aparecería sobre el horizonte, tanto más alto cuanto más avancemos. Las estrellas circumpolares, cada vez más numerosas, se verán al Sur girando en el mismo sentido de las manecillas del reloj.

El metro

Antiguamente, hasta antes de 1789, había una gran cantidad de medidas de longitud, por lo que la Convención Nacional de París, con objeto de establecer uniformidad, decidió en 1789 crear un sistema único, el sistema métrico, y que la unidad de longitud fuese función de las dimensiones de nuestro planeta. Esa unidad, llamada metro, sería la diezmillonésima parte del cuadrante del me-

Figura III.1

ridiano terrestre (considerando que el diámetro ecuatorial de la Tierra es de 12,756 km, y el polar de 12,714 km, el promedio resulta de 12,735 km, que multiplicados por π dan 40,008 km, y que divididos entre 4 dan 10,002 km, es decir, aproximadamente 10’002,000 m).

Se encargó el proyecto a Méchain y Delambre, quienes midieron el arco de meridiano entre Dunkerque, en el extremo norte de Francia, y Barcelona, España. Esta distancia, del orden de 880 km, fue extrapolada para obtener la correspondiente a un cuadrante de meridiano. Finalmente, el metro patrón resultó una quinta

parte de milímetro menor que la diezmillonésima parte del cuadrante del meridiano; aunque el error es pequeño, la definición anterior de metro resulta errónea, por lo que para evitar problemas, se modificó por la expresión: “el metro es la longitud, a 0° C, de una regla metálica llamada Metro Patrón Internacional, que se conserva en la Oficina de Pesos y Medidas de París.”

La definición que implantó en 1983 la Oficina Internacional de Pesos y Medidas, y que permanece vigente, es: “El metro es la distancia que recorre la luz en el vacío durante un lapso de 1/299’792,458 de segundo.”

CAPÍTULO IV

Coordenadas geográficas

Longitud y latitud

Asumamos que la Tierra es una esfera de cerca de 13,000 km de diámetro que gira sobre sí misma en el sentido de las manecillas del reloj si la observáramos desde el Polo Sur, dando cada vuelta completa en un día sideral.

Los puntos P y P’ de la figura IV.1, en los que el eje de rotación corta la superficie de la esfera, son los polos terrestres Norte y Sur, respectivamente.

El círculo máximo EmE’ perpendicular al eje de rotación es el Ecuador, y determina en el planeta dos hemisferios: el boreal, que contiene al Polo Norte, y el austral, que contiene al Polo Sur. Los círculos máximos –como el PMmP’– que pasan por los polos, es decir, que tienen como diámetro común el eje de rotación, se llaman meridianos. Figura IV.1

Lo que es afirmado sin pruebas puede ser negado sin pruebas. euClides (325-265 A. C.)

Meridiano de Greenwich

La posición de un punto M cualquiera de la superficie terrestre se determina por sus coordenadas, tomando como círculos de referencia el Ecuador y el meridiano del Observatorio Astronómico de Greenwich, cerca de Londres (figura IV.2, p. 129, meridiano rojo). Volviendo a la figura IV.1, la abscisa esférica Om se llama longitud y la ordenada mM, latitud. Así, la longitud geográfica de M es el ángulo esférico OPM que forma su meridiano con el de Greenwich, y su latitud es el ángulo que forma la vertical del lugar con el plano del Ecuador, o bien, el valor en grados del arco mM.

La longitud se mide de 0° a 180° de uno y otro lado del Meridiano de Greenwich, considerando positivas (Este) las de los lugares situados al oriente de este meridiano y negativas (Oeste) las de aquellos que se ubiquen al poniente. También se suele expresar la longitud en tiempo, para lo cual se divide el círculo del Ecuador en 24 arcos iguales que se llaman horas, cada hora en 60 minutos y cada minuto en 60 segundos; los segundos se dividen en decimales.

La latitud se cuenta de 0° a 90° del Ecuador a los polos, con signo (+) en el hemisferio boreal y (−) en el austral. La Tabla I, al final de este libro, proporciona las coordenadas geográficas de las principales ciudades de México.

Arco-tiempo

Para convertir arco en tiempo o viceversa es necesario considerar que el círculo del Ecuador

se divide en 360° o 24 horas, y que cada arco de una hora equivale a la vigésima cuarta parte de 360°, esto es, 15°. Puesto que tanto la hora como el grado se dividen en 60 minutos, cada minuto de tiempo abarca 15 minutos de arco, y cada segundo de tiempo abarca 15 segundos de arco. Así, para convertir en arco una longitud expresada en tiempo, basta multiplicar por 15 esta última expresión.

Ejemplo 1. Expresar en arco 6 h 36 min 31.6 s.

Solución. 6 h × 15 = 90°

36 min × 15 = 540’ = 9°

31.6 s × 15 = 474” = 7’ 54”

Respuesta. 99° 07’ 54”

Ejemplo 2. Expresar en tiempo 99° 07’ 54”

Solución. 99°/15 = 6 h y sobran 9° = 540’

547’/15 = 36 min y sobran 7’ = 420”

474”/15 = 31.6 s

Respuesta. 6 h 36 min 31.6 s

Ejercicios propuestos

1. Expresar en arco la longitud geográfica de 7 h 42 min 18 s.

2. Expresar en tiempo un arco de Ecuador de 37° 29’ 45”.

3. Expresar en tiempo la longitud geográfica de la localidad del lector o de la más próxima que aparezca en la tabla I.

CAPÍTULO

V

Coordenadas horizontales

Horizonte

Se llama vertical de un lugar a la dirección del hilo de la plomada o de la caída libre de un cuerpo pesado; es normal a la superficie del agua en reposo.

La vertical de un punto toca la esfera celeste en dos puntos opuestos: el cenit, sobre nuestra cabeza, y el nadir.

Divide las dificultades que examines en tantas partes como sea posible, para su mejor solución. desCArtes (1596-1650)

Horizonte aparente

Todo plano que contiene la vertical de un lugar es un plano vertical; todo plano perpendicular a la vertical es un plano horizontal. El horizonte racional es el plano horizontal que pasa por el centro de la esfera celeste y tiene por eje la vertical del lugar, y por polos el cenit y el nadir. Podemos considerar que el horizonte racional es tangente a la Tierra en el punto de observación, o que pasa por nuestros ojos o por el centro de la Tierra, de- Figura V.1

pendiendo de las necesidades del problema que se estudie.

Cuando el horizonte racional se traza tangente a la superficie de la Tierra, se llama horizonte matemático; cuando se le hace pasar por el centro de la Tierra se llama geocéntrico o astronómico. Los círculos menores de la esfera celeste paralelos al horizonte racional se llaman almicántaras.

El horizonte aparente es el círculo que vemos a nuestro alrededor cuando estamos en alta mar o en una llanura extensa sin accidentes del terreno. Es la línea de contacto del cono de nuestra visual con la superficie de la Tierra (véase figura V.1).

El plano vertical que contiene al eje del mundo, y que por ende pasa por los polos, se llama meridiano astronómico (véase figura V.2); su

intersección con la superficie de la Tierra es el meridiano geográfico del punto de observación. En consecuencia, el meridiano astronómico pasa por el lugar de observación. La intersección del meridiano astronómico con el horizonte racional es una recta que se llama meridiana y es tangente al meridiano geográfico; va de Norte a Sur o viceversa. El plano vertical perpendicular a la meridiana se llama primo vertical; por definición, pasa por el cenit y por la línea Este-Oeste.

El extremo de la meridiana situado para nosotros, que estamos en el hemisferio boreal, en la región de las estrellas circumpolares, es el Norte o Septentrión; el opuesto es el Sur o Mediodía.

La intersección del primo vertical con el horizonte racional toca la esfera celeste en dos puntos,

vertical

Esfera celeste (al centro está la Tierra)

Figura V.2

Meridiano astronómico

Meridiana

Horizonte racional

Esfera celeste

situado cada uno a 90° del Norte o del Sur: el Este, Oriente, Orto o Levante queda a la derecha de un observador que mira hacia el Norte, y el Oeste, Poniente, Ocaso u Occidente queda en la región opuesta. El Norte, Sur, Este y Oeste son los puntos cardinales. Ya vimos cómo determinar la posición de un punto sobre el planeta a través de las coordenadas geográficas. Ahora, para fijar la posición de un astro en la esfera celeste, se usan varios sistemas de coordenadas.

Acimut y altura

El sistema de coordenadas horizontales (véase figura V.3) tiene como círculo de abscisas el horizonte racional, con origen en el extremo sur de la

meridiana. Se cuenta de 0° a 360° desde el extremo sur y en sentido dextrorso, es decir, el de las manecillas de un reloj colocado sobre una mesa con la carátula hacia arriba, y se llama acimut. Para el caso de la figura V.3 es el ángulo SOa mayor de 180° marcado con arco punteado.

El círculo de las ordenadas es el meridiano; se mide la ordenada, que se conoce como altitud de un astro o altura sobre el horizonte o elevación, a partir del horizonte racional. Así, la altitud de un astro

A (véase figura V.3) es el ángulo AOa que forma la visual dirigida al astro con el horizonte racional. Se mide de 0° a 90° del horizonte al cenit. Si el astro está abajo del horizonte, su altitud es negativa. Suele usarse también la distancia cenital ZA, complemento de la altura, que se mide de 0° a 180°

Figura V.3

sobre el círculo máximo vertical que pasa por el astro, con el cenit como origen.

En vez del acimut suele usarse el rumbo, que se mide de 0° a 90°, desde el Norte o desde el Sur y en uno u otro sentido. El número de grados y sus fracciones se escribe entre dos letras, que señalan el origen y el sentido de la medición. Por ejemplo, el rumbo S 24° 35’ W equivale a un acimut de 24° 35’; el rumbo N 72° 05’ W equivale a un acimut de 107° 55’. En operaciones topográficas suele tomarse como origen del acimut el extremo norte de la meridiana, conservando el sentido dextrorso.

Las coordenadas horizontales de un astro se pueden medir con el teodolito, que se compone esencialmente de dos círculos graduados, como puede observarse en la figura V.4.

Los círculos, uno horizontal y el otro vertical, son llamados limbos (figura V.4). El primero, H, gira alrededor de un eje vertical OZ y está graduado de 0° a 360°, en sentido dextrorso. El segundo, J, gira alrededor de un eje horizontal y está graduado de 0° a 180°, con un anteojo astronómico de poco aumento, cuyo eje óptico AB define la visual dirigida al astro que se observa. La visual se determina con auxilio de la retícula, constituida por dos hilos cruzados en ángulo recto en el interior del anteojo, uno de los cuales es horizontal.

El anteojo puede colocarse en cualquier posición sin que el eje OZ pierda su verticalidad, y su eje AB describe sobre los limbos del teodolito sendos ángulos que pueden determinarse con las

graduaciones. Si hacemos coincidir el eje óptico con la meridiana y miramos al Norte poniendo en ceros previamente las graduaciones de ambos limbos, al mover el anteojo para dirigir una visual a una estrella, su eje óptico describirá sobre el limbo horizontal el ángulo NOE que, aumentado en 180°, nos dará el acimut de la estrella. Sobre el limbo vertical, el ángulo DO’B será su altura sobre el horizonte. El complemento ZO’B de ese ángulo será la distancia cenital de la estrella.

Figura V.4

Ejercicios propuestos

1. Si la distancia cenital de un astro es de 8° 21’ , ¿cuál es su altura sobre el horizonte?

2. Si la distancia cenital de un astro es de 118° 50’ , ¿cuál es su altura sobre el horizonte?

3. Decir cuál es el acimut de un astro, si su rumbo es:

a) N 67° 39’ E

b) S 22° 18’ E

c) N 42° 42’ W

4. Obtener el rumbo S-W del inciso a); N-W del b); S-E del c) de un astro si su acimut es de:

a) 39° 20’ 34”

b) 101° 30’ 00”

c) 359° 59’ 59”

CAPÍTULO VI

Coordenadas ecuatoriales

Definiciones

Se llama ecuador celeste al círculo máximo de la esfera celeste perpendicular al eje del mundo; es prolongación del Ecuador terrestre. Dado que para fines prácticos el centro de la esfera celeste está en nuestros ojos, por ellos pasa también el ecuador celeste.

Todo círculo menor de la esfera celeste perpendicular al eje del mundo es un paralelo. Los círculos máximos que contienen el eje del mundo son círculos horarios.

Si admitimos que la Tierra y el cielo son dos esferas concéntricas (véase figura VI.1), con eje y polos comunes, un mismo círculo máximo perpendicular al eje común determina en ambas Figura VI.1

El verdadero conocimiento es saber que sabemos lo que sabemos, y saber que no sabemos lo que no sabemos.

NiColás CoPérNiCo (1473-1543)

el ecuador. Los círculos máximos que contienen al eje común son, en la Tierra, meridianos, y en el cielo, círculos horarios. Debido a la rotación de la Tierra, cada meridiano coincide sucesivamente, durante un día, con todos los círculos horarios.

Coordenadas ecuatoriales

El sistema de coordenadas ecuatoriales para determinar la posición de un astro tiene como círculo de las abscisas el Ecuador, y como origen el punto vernal (γ). Este punto se determina de la siguiente manera: observando diariamente la posición del Sol en el globo celeste, se encuentra que en un año le ha dado una vuelta completa al cielo sobre un círculo máximo que recibe el nombre de eclíptica,

cuya inclinación respecto al ecuador celeste es de 23° 27’ (véase figura VI.2).

La intersección γγ’ de la eclíptica con el Ecuador es la línea de los equinoccios, y sus extremos, los equinoccios. Uno de ellos, γ, donde el Sol corta al Ecuador al pasar del hemisferio austral al boreal, es el punto vernal o equinoccio de primavera, que sirve de origen a este sistema de coordenadas ecuatoriales. El punto γ’ es el equinoccio de otoño. El círculo horario que los contiene es el coluro de los equinoccios.

El círculo de las ordenadas es el coluro de los equinoccios. La abscisa esférica γPAa = γa = áng γOa se llama ascensión recta, y la ordenada aA = áng aOA se denomina declinación. La ascensión recta se mide de 0° a 360°, aunque con más frecuencia de 0 h a 24 h a partir del punto vernal, en sentido opuesto al movimiento diurno, es decir, en el mismo sentido de las manecillas del reloj mirando desde el Polo Sur hacia el Polo Norte.

La declinación es el arco aA del círculo horario que pasa por el astro, medido del Ecuador a éste, en grados, con signo positivo en el hemisferio boreal y negativo en el austral. En vez de la declinación, suele tomarse la distancia polar PA, contada en grados, desde el Polo Norte hasta el astro, y se le conoce como codeclinación; se le asigna siempre signo positivo.

También se utiliza el ángulo horario, similar a la ascensión recta, que es el diedro que forma el círculo horario de un astro con el meridiano del lugar de observación. Se mide sobre el arco

Figura VI.2

Coluro de los equinoccios

de ecuador que interceptan ambos círculos, en horas corridas de 0 a 24, a partir del meridiano del lugar y en el mismo sentido del movimiento diurno, es decir, en sentido contrario al de las manecillas del reloj, mirando hacia el Polo Norte desde el Polo Sur. Si el astro no ha pasado por el meridiano, puede medirse su ángulo horario en sentido opuesto, con signo negativo.

Altura del polo

Supongamos de nuevo que la Tierra y el cielo son dos esferas concéntricas (véase figura VI.3) y que aquélla es un punto en el centro de éste. Sea PP’ el eje del mundo, EFWF’ el Ecuador, OZ la vertical del lugar y NESW el horizonte racional. La altura

del Polo Norte sobre el horizonte del lugar es el ángulo NOP que el eje del mundo forma con el horizonte. La latitud geográfica del lugar es el ángulo FOZ que la vertical OZ forma con el Ecuador; estos dos ángulos son iguales (lados respectivamente perpendiculares). Así, en un lugar dado, la altura del polo sobre el horizonte es igual a la latitud geográfica del lugar. También, la latitud del lugar es precisamente la declinación del cenit.

Más sobre el movimiento diurno

Un paralelo celeste cuya distancia polar sea igual a la latitud geográfica del lugar, y que en consecuencia toca el horizonte en N (véase figura VI.4), define un casquete boreal con el Polo Norte en el

Figura VI.3

Figura VI.4

centro, en el que se hallan comprendidas las estrellas circumpolares para esa latitud. Lo mismo puede decirse de otro paralelo similar pero en la parte austral, el cual define un casquete austral cuyas estrellas circumpolares no podemos ver. La zona intermedia tiene estrellas que salen y se ponen. En efecto, una estrella A dentro del casquete boreal, cuya distancia polar sea menor que la latitud geográfica del lugar de observación, describe su circunferencia diurna completa sobre el horizonte en sentido opuesto al de las manecillas del reloj y pasa por el meridiano del lugar dos veces: encima y debajo del polo. Esto sucede en el casquete austral, aunque en México no podemos ver sus estrellas circumpolares. Las estrellas de la zona intermedia salen y se ponen, ya que los paralelos que describen cortan el horizonte y por lo tanto son visibles en la parte superior de su curso e invisibles en la inferior.

Cada estrella culmina (alcanza su posición más alta) cuando pasa por el meridiano del lugar. En la figura VI.4, la recta NS es la meridiana (recuérdese que la meridiana es la intersección del meridiano astronómico del lugar con el horizonte racional) y EW la línea Este-Oeste. Las estrellas situadas sobre el ecuador, como la B, salen por el punto E, exactamente al Este, y se ponen por el W, precisamente al Oeste, y como el horizonte corta al ecuador en dos partes iguales, entonces de la salida a la puesta transcurre medio día sideral o sidéreo.

Una estrella C situada en la parte boreal de la zona intermedia sale por el punto m y se pone por

el m’, hacia el norte del primo vertical, y como su paralelo queda dividido por el horizonte en partes desiguales, de la salida a la puesta transcurre más de la mitad del día sidéreo: un tiempo tanto más largo cuanto mayor sea la declinación de la estrella.

Para un observador situado en el Polo Norte, todas las estrellas del hemisferio celeste boreal parecen describir circunferencias paralelas al horizonte, porque el eje del mundo es vertical; las estrellas del hemisferio austral le son perpetuamente invisibles.

Comparación de los dos sistemas de coordenadas

Las coordenadas horizontales de un astro varían continuamente a causa del movimiento diurno; al salir una estrella, su altura sobre el horizonte es nula y su distancia cenital es de 90°; cuando culmina, su altura es máxima y su distancia cenital es mínima (recuérdese que aunque culmina, no necesariamente pasa por el cenit) y ambos arcos se miden entonces sobre el meridiano (hay que recordar que el meridiano pasa por el lugar de observación y por el Norte y Sur). En este mismo instante el acimut es de 0° o de 180°, según que la estrella culmine al sur o al norte del cenit; así, las coordenadas horizontales de un astro fijan la posición de éste, en un instante dado, con relación al horizonte y al meridiano del lugar; de aquí que al medirlas deba anotarse la hora de la observación.

En cambio, la ascensión recta y la declinación no varían, a causa del movimiento diurno, por lo cual sirven para fijar la posición de cada astro con relación al ecuador y al coluro de los equinoccios.

Estas coordenadas también varían, aunque muy lentamente, por causas distintas del movimiento diurno y que estudiaremos más adelante.

Conviene apuntar que el ángulo horario de un astro (ángulo formado por su círculo horario y el meridiano del lugar) es nulo en el momento de su culminación.

3. ¿Cuál es la distancia cenital del polo celeste norte en un lugar cuya latitud geográfica es de 19° 26’ 05”?

4. Si la latitud geográfica de un punto es de 20° 56’ 17”, ¿a qué distancia del cenit corta el meridiano del lugar al ecuador celeste?

5. Si la latitud geográfica de un lugar es +20°, diga entre qué límites de declinación se hallan: a) las estrellas circumpolares, b) las que salen y se ponen, c) las que están sobre el horizonte medio día sideral, d) las que permanecen sobre el horizonte más de 12 horas, y e) las que no pueden verse desde ese lugar.

Ejercicios propuestos

1. ¿Cuál es la declinación del polo celeste boreal y cuál la del austral?

2. ¿Cuál es la ascensión recta del punto vernal?

6. Consultando la tabla III, elija una estrella que se encuentre en cada uno de los casos del ejercicio 5.

CAPÍTULO VII

Medida del tiempo

Si mis teorías hubieran resultado falsas, los estadounidenses dirían que yo era un físico suizo; los suizos, que era un físico alemán; y los alemanes, que era un astrónomo judío. Albert eiNsteiN (1879-1955)

Tiempo solar medio

Como consecuencia de la rotación de la Tierra, todos los astros participan del movimiento diurno aparente del cielo, pero si se compara el lapso que transcurre entre dos culminaciones sucesivas de una estrella (lapso llamado día sideral y que mide aproximadamente la duración de una vuelta completa de la Tierra sobre sí misma) con el tiempo que transcurre entre dos culminaciones sucesivas del Sol, se verá que este último dura unos cuatro minutos más. El tiempo que transcurre entre dos culminaciones sucesivas del Sol se llama día solar verdadero, el cual no es rigurosamente constante, por lo que se adopta como unidad de medida del tiempo el valor medio de los días solares, con el

nombre de día solar medio o, simplemente, día medio. El día medio se divide en 24 horas, la hora en 60 minutos, el minuto en 60 segundos y el segundo en partes decimales. Este es el tiempo medio que mide nuestro reloj común.

El día solar verdadero se cuenta a partir de la media noche, o instante del paso inferior del Sol por el meridiano del lugar. Para fijar el inicio del día medio, hay que imaginar un Sol medio, ficticio, cuyo movimiento aparente tuviese la velocidad media del Sol verdadero: el día medio se cuenta a partir de la media noche media o instante en que el Sol medio pasa por la parte inferior del meridiano. El día así medido se llama día civil, y el tiempo que marca un reloj con arreglo a él, tiempo civil.

En un instante dado, los relojes de dos lugares no situados sobre el mismo meridiano geográfico marcan distinta hora civil. Por necesidades de orden práctico, se ha convenido dividir la Tierra en 24 husos horarios de 15° cada uno, y en acomodar los relojes de todo el huso a la hora civil de su meridiano central. De este modo, se desprecian las diferencias en tiempo que no llegan a una hora, y de un huso al inmediato la diferencia es de una hora exacta. El primer huso horario es el que tiene como meridiano central el de Greenwich. En México se usa la hora del meridiano de 90° WG, excepto en los estados de Nayarit, Sinaloa, Sonora, Baja California y Baja California Sur, donde se usa la del meridiano 105° WG. El tiempo así medido se llama tiempo legal u oficial. La tabla I proporciona en su columna “Δ”, para distintas localidades del país, la diferencia entre la hora oficial y la hora civil, de modo que restando esa diferencia a la hora

Ejemplo. Determinar la hora civil en la Ciudad de México cuando oficialmente son las 21:00 h.

Solución. La tabla I da en su columna “Δ” la diferencia entre la hora legal u oficial y la hora civil. Para la Ciudad de México la diferencia es de 36 min 31.6 s; así, hora oficial–hora civil = 36 min 31.6 s. Entonces, hora civil = hora oficial–36 min 31.6 s = 20 h 23 min 28.4 segundos.

Respuesta. 20 h 23 min 28.4 s.

oficial que marca nuestro reloj, obtenemos la hora civil.

Tiempo sideral

Se llama día sideral al lapso comprendido entre dos culminaciones sucesivas del punto vernal. El día sideral es un poco más breve que el solar, unos cuatro minutos menos. En efecto, sea T la Tierra (véase figura VII.1) animada del movimiento de rotación alrededor de su eje y de traslación en derredor del Sol en las direcciones indicadas por las flechas (vista desde el Norte, como es el caso de la figura VII.1, la Tierra gira en sentido contrario a las manecillas del reloj y se traslada alrededor del Sol en ese sentido contrario; vista desde el Sur, la Tierra gira en el sentido de las manecillas del

Figura VII.1

reloj, y se traslada alrededor del Sol también en el sentido de las manecillas del reloj). Si el Sol, S, se encuentra en el meridiano de un lugar, L, al mismo tiempo que un astro, A, en una fecha cualquiera, 24 horas siderales después, cuando la Tierra haya girado 360° sobre sí, la estrella A estará nuevamente en el meridiano T’L’, y el Sol parecerá haberse desplazado, debido a la traslación de la Tierra. El tiempo que tarda ésta en girar ese pequeño ángulo alrededor de su eje representa el exceso del día solar verdadero sobre el día sidéreo.

Como el ángulo TST’ es igual que el L’T’L’’, resulta que la traslación de la Tierra de T a T’ en un día es igual al ángulo que debe girar después de terminada una rotación entera para que se complete el día solar verdadero. Si llamamos τ al tiempo que tarda la Tierra en girar el ángulo

L’T’L’’, o lo que tarda en recorrer el arco TT’, puede escribirse la siguiente igualdad: día solar verdadero = día sideral + τ

El valor de τ es de 3 min 56.555 s, casi 4 min. Así, la hora sideral es 10 segundos más breve (4 min/día × 60 s/1 min × 1 día/24 h = 10 s/h) que la solar. Se ha diseñado un reloj sideral que mide el tiempo sideral; cuenta las horas corridas de 0 a 24 y marca 0 en el instante de la culminación del punto vernal. En otro instante cualquiera, el ángulo horario del punto vernal se mide con este reloj, de modo que en cualquier instante la hora sideral es el ángulo horario del punto vernal. Si se coloca un reloj sideral cuya carátula coincida con el plano

del ecuador celeste y de frente al Polo Norte, su horario señala hacia el punto vernal.

Aproximadamente, la hora sideral coincide con la hora civil media al iniciarse el día 22 de septiembre de cada año; a partir de esa fecha se adelanta los 3 min 56.555 s (3.9426 min) ya mencionados por día, respecto de la hora civil. Son casi 4 min que hacen dos horas por mes y 24 horas por año. Así, al iniciarse el día 1 de enero siguiente, es decir, a la hora civil cero (no a la hora oficial cero) del primer día de cada año, el reloj sideral marca las 6 h 34 min, aproximadamente, porque habiendo transcurrido 100 días desde el 22 de septiembre anterior, se ha adelantado ya 6 h 34 min (8 días de septiembre, 31 días de octubre, 30 días de noviembre y 31 días de diciembre hacen 100 días × 3.9426 min = 394.26 min = 6 h 34 min).

Para obtener la hora sideral aproximada en un momento cualquiera de otra fecha distinta, añadiremos a esas 6 h 34 min los días transcurridos del año multiplicados por 3.9426 min, más la hora civil del momento considerado.

Ejemplo 1. Calcular la hora sideral aproximada en Mérida, Yucatán, el día 15 de mayo de cualquier año, a las nueve de la noche, hora oficial. Solución. A partir del 1 de enero han transcurrido 31+28+31+30+14 = 134 días, que multiplicados por 3.9426 min arrojan un adelanto de 8 h 48 min, que sumadas a las 6 h 34 min dan un adelanto total del reloj sideral de 15 h 22 minutos.

Si la hora oficial es 21 h 00 min, al consultar la tabla I obtenemos para Mérida una diferencia de –1 min 29.7 s, que restada a la hora oficial da: 21 h 00 min –(–1 min 29.7 s)

= 21 h 1.5 minutos.

Entonces, la hora sideral buscada es 15 h 22 min + 21 h 1.5 min = 36 h 23.5 min – 24 h = 12 h 23.5 minutos.

La tabla II permite calcular la hora sideral con una aproximación de una décima de minuto.

Ejemplo 2. Hacer el mismo cálculo del ejemplo 1 para el año 2012, utilizando la tabla II.

Solución. De acuerdo con la tabla II, Ts = T +

To + Tf + Th – L, donde:

Ts = hora sideral; T = hora oficial; To, Tf y Th = datos tomados de las tablas A, B y C; L = longitud del lugar, menos 6 horas.

Entonces, procedamos al cálculo:

T = 21 h 00 min

To = 14 h 36.3 min + 0.1 min por cada cuatrienio que pase del año 1951. Así, son 15 cuatrienios que multiplicados por 0.1 min arrojan

1.5 min, que sumados a las 14 h 36.3 min

dan To = 14 h 37.8 min.

Tf = 0 h 55.2 min; Th = 3.45 min;

Long = 89° 37’ 25” = 89° 37.4167’ = 5 h 56 min + 2.5 min = 5 h 58.5 min.

Entonces, L = long – 6 h =5 h 58.5 min –

6 h = –1.5 min.

Así, Ts = 21 h 00 min + 14 h 37.8 min + 0 h 55.2 min + 0 h 3.45 min – (–1.5 min) = 35 h

97.95 min = 36 h 38 min –24 h = 12 h 38 min.

Ejercicios propuestos

1. Calcular la hora civil en Puebla, Puebla, cuando oficialmente son las 12:00 h.

2. Por el método de la sección “Tiempo sideral”, calcular la hora sideral aproximada cuando oficialmente sean las 19:00 h en Tepic, Nayarit, del 21 de marzo.

3. Calcular la hora sideral para Tepic, Nayarit, cuando oficialmente sean las 19:00 h del 21 de marzo de 2013 (utilizar la tabla II).

CAPÍTULO VIII

Medida de las coordenadas ecuatoriales

Si he hecho descubrimientos invaluables, ha sido más por tener paciencia que por cualquier otro talento. isAAC NewtoN (1642-1721)

Triángulo astronómico

Se llama triángulo astronómico (véase figura VIII.1) al de la esfera celeste cuyos vértices son el cenit Z, el Polo Norte N y el astro A que se observa. Sus lados son la distancia cenital ZA del astro, la distancia cenital ZP del polo o colatitud del lugar de observación y la distancia polar PA o codeclinación del astro. Sus ángulos son el ángulo horario ZPA (arco ZA) del astro, el PZA, que es igual a 180° menos el acimut del astro, si éste se observa después de su culminación, o el acimut menos 180° si se observa antes de que alcance el meridiano, y el ángulo paraláctico PAZ.

Figura VIII.1

La figura VIII.1 permite establecer la siguiente ecuación:

Eγ = γa + Ea, donde:

Eγ = ángulo horario EPγ del punto vernal, que expresado en tiempo es la hora sideral en el momento de la observación.

γa = ángulo γPa o ascensión recta de la estrella.

Ea = ángulo EPa = ángulo horario de la estrella.

Entonces, en un instante dado, la hora sideral

T es la suma de la ascensión recta α de un astro cualquiera y del ángulo horario H de éste, es decir:

T = α + H (1)

Anteojo ecuatorial

Es un anteojo montado en un mecanismo que permite seguir el movimiento diurno aparente del cielo mediante una sola rotación en torno del eje principal del instrumento (véase figura VIII.2).

Este eje AB, llamado eje polar, es paralelo al eje de rotación de la Tierra, es decir, forma con el horizonte un ángulo igual a la latitud geográfica del lugar y apunta al polo celeste del norte o al sur si el instrumento está instalado en el hemisferio austral. El eje polar lleva un círculo H perpendicular a AB, y por lo tanto es paralelo al ecuador celeste; está dividido en horas y sus fracciones para poder leer el ángulo horario del astro que se observa.

En el extremo B del eje polar va montado el eje de declinación CE, que puede moverse describien-

do un plano perpendicular a AB. En el extremo C del eje de declinación va montado el anteojo FG, de modo que a su vez pueda moverse describiendo un plano perpendicular a CE. El eje CE lleva un círculo D que coincide siempre, cualquiera que sea la posición del anteojo, con el círculo horario del astro observado, y está dividido en grados y sus fracciones para medir la declinación del astro, o bien, su distancia polar.

Cuando el anteojo está en la posición que indica la figura VIII.2, esto es, paralelo al eje polar del instrumento, y viendo hacia arriba, su eje óptico queda exactamente dirigido al polo celeste, y los dos círculos, el ecuatorial y el de declinación, marcan 0. Si se dirige el anteojo hacia un astro, en el círculo ecuatorial H se lee el ángulo horario y

Figura VIII.2

en el D la declinación o la distancia polar. Una vez colocada una estrella en el cruce de los hilos de la retícula, o simplemente en el centro del campo del anteojo, se le puede dar seguimiento moviendo el instrumento únicamente en torno del eje polar y no en torno del de declinación. El ángulo constante que durante el movimiento forman los ejes AB y FG es la distancia polar del astro que se observa; en cada instante, el círculo ecuatorial del instrumento marcará el ángulo horario. Para obtener este resultado, el anteojo debe girar en torno de su eje polar con movimiento perfectamente uniforme, idéntico al movimiento diurno del cielo, y para el efecto está provisto de un mecanismo de relojería impulsado por pesas o energía eléctrica.

La disposición del anteojo ecuatorial permite tomar fotografías con exposiciones que duran el tiempo que sea necesario.

Con este anteojo podemos medir las coordenadas de un astro: su declinación se lee directamente en el círculo D; su ascensión recta la obtenemos restando el ángulo horario que da el círculo H a la hora sideral que se tiene en el momento de la observación, con base en la fórmula (1) del apartado anterior.

Si tomamos de un catálogo la ascensión recta de una estrella y medimos su ángulo horario en el anteojo ecuatorial, obtendremos la hora sidérea por medio de la fórmula (1).

Ahora, si deseamos localizar una estrella de coordenadas conocidas, podemos deducir H = T – α y colocamos el instrumento de modo que en

su círculo ecuatorial H se lea el ángulo horario H y en el círculo D la declinación del astro.

Obtención de las coordenadas ecuatoriales a partir de las horizontales

En el triángulo astronómico de la figura VIII.1 tenemos que:

cos PA = cos ZP cos ZA+sen ZP sen ZA cos PZA

Con base en la trigonometría plana o esférica, sabemos que el seno de un ángulo o de un arco de círculo es el coseno de su complemento y viceversa, y que los cosenos de dos ángulos suplementarios son iguales y de signo contrario. Entonces, considerando que PA = codeclinación o 90° – declinación (δ) del astro; ZP = distancia cenital del polo = 90° – latitud (φ) del lugar; ZA = distancia cenital del astro = 90° – altitud (a) del astro; PZA = 180° – acimut (U) o acimut (U) –180°, la ecuación anterior queda como:

cos(90°– δ) = cos(90°– φ)cos(90°– a) + sen(90°–φ)sen(90°– a)cos(180°–U), o bien, cos(90°– δ) = cos(90°– φ)cos(90°– a) + sen(90°–φ)sen(90°– a)cos(U – 180); entonces:

sen δ = sen φ sen a + cos φ cos a (– cos U)

sen δ = sen φ sen a – cos φ cos a cos U (2)

Con la expresión anterior podemos obtener la declinación δ en función de las coordenadas horizontales y de la latitud geográfica. Para obte-

ner ahora la ascensión recta α bastaría obtener el ángulo horario H y recurrir a la ecuación (1) de este capítulo. Veamos:

Por el triángulo astronómico, sabemos que:

Sen ZPA/sen ZA = sen PZA/sen PA, esto es,

Sen H/sen (90° – a) = sen (180° – U)/sen (90° – δ), es decir,

Sen H/cos a = sen U/cos δ, de donde:

Sen H = cos a sen U/cos δ, y entonces, ya conocido H, α = T – H

Existen catálogos de estrellas en los que se refieren las coordenadas ecuatoriales de miles de ellas para una época determinada. En la tabla IV pueden hallarse las coordenadas de las estrellas más brillantes del cielo para 2011.

En la tabla número III pueden verse las coordenadas para 1950, que se incluyen con fines ilustrativos para observar la diferencia entre ellas. Comparando ambas, se encuentra que sus coordenadas difieren unos cuantos minutos-tiempo y minutos-ángulo.

Otro método para obtener las coordenadas ecuatoriales

Ascensión recta

Si en la fórmula (1) de este capítulo se asume H = 0, resulta que T = α, por lo que se puede obtener la ascensión recta de un astro con sólo observar la hora sideral de su paso por el meridiano. Para ello, existe en los observatorios el anteojo meridiano, un instrumento cuyo anteojo carece de

movimiento acimutal y se halla situado de modo que, girando en torno de un eje horizontal, describe el plano meridiano; es decir, el único limbo graduado que tiene es vertical y coincide con el meridiano. Un hilo vertical en su retícula traza en el cielo el meridiano astronómico.

Declinación

La declinación de un astro es igual a la latitud geográfica del lugar de observación, más o menos la distancia cenital del astro en el momento de su culminación, según ésta ocurra al norte o al sur del cenit (véase figura VIII.3).

Supongamos que el astro culmina al norte del cenit. Se tiene entonces que EA = EZ + ZA, esto es, δ = φ + Z (Z es la distancia cenital del astro). Si el astro B culmina al sur del cenit, entonces EB = EZ – ZB, o bien, δ = φ – Z.

CAPÍTULO

Figura VIII.3

Ocurrirá en ocasiones que al aplicar la fórmula anterior el resultado sea negativo, porque la distancia cenital del astro observado C sea mayor que la latitud geográfica del lugar de observación, lo cual significará que se ha elegido un astro del hemisferio austral cuya declinación es negativa.

Así, la declinación de un astro puede obtenerse por la fórmula:

δ = φ ± Z (3)

debiendo usarse el signo (+) para los astros que culminan al norte del cenit y (–) para los que culminen al sur. Si en la ecuación (3) se supone Z = 0, resulta que δ = φ, lo que demuestra que sólo pasan por el cenit aquellos astros cuya declinación es igual a la latitud geográfica del lugar.

Las coordenadas horizontales deducidas de las ecuatoriales

Puede ocurrir que se necesite saber con anticipación la altura y el acimut de un astro para un instante dado. Para resolver este problema es necesario conocer la latitud del lugar, la hora sideral de la observación, que puede deducirse de la oficial (“Tiempo sideral”, del capítulo VII) y las coordenadas ecuatoriales del astro que se considere, que supondremos tomadas de un catálogo.

En el triángulo astronómico (véase figura VIII.1) tenemos:

cos ZA = cos PZ cos PA + sen PZ sen PA cos ZPA, esto es,

cos (90°– a) = cos (90°– φ) cos (90°– δ) + sen(90°–φ) sen (90°– δ) cos H

sen a = sen φ sen δ + cos φ cos δ cos H (4)

En la expresión anterior falta conocer H (ángulo horario), el cual se puede obtener con la fórmula H = T – α.

Conocida ya la altura sobre el horizonte, sólo nos falta conocer el acimut, para lo cual hacemos lo siguiente:

sen ZPA/sen ZA=sen PZA/senPA (5)

donde:

ZPA = H

ZA = 90° – a

PZA = 180 – U si ya culminó o U – 180° si no ha culminado.

PA = 90° – δ, entonces:

sen H/cos a = sen PZA/cos δ, por lo que

sen PZA = sen H cos δ/cos a (6)

Obtenido el ángulo PZA, que en el caso de la figura VIII.1 (triángulo astronómico) es el rumbo NW del astro, puede deducirse fácilmente el acimut.

Ejemplo. Determinar en qué punto del cielo veremos la estrella Sirio, si queremos observarla desde Tonanzintla, Puebla, un 16 de marzo a las 8 de la noche (Sirio es la estrella más brillante del firmamento).

Datos. De la tabla I, las coordenadas geográficas de Tonanzintla son: φ = 19° 01’ 58’’ = 19.033°; long WG = 98° 18’ 50’’ = 6 h 33 min 15.33 s. De la tabla III, la ascensión recta α de Sirio es de 6 h 42 min 57 s y la declinación δ es de –16° 38’ 44’’ = –16.646°.

Solución. Debemos calcular la altura sobre el horizonte y el acimut o el rumbo para encontrar Sirio en la fecha y hora señaladas. Para ello, tenemos que calcular primero el ángulo horario de la estrella: hora oficial = 20:00 h; hora civil = hora oficial – valor tabla I = =20 h 00 min – 0 h 33 min = 19 h 27 min. Hora sideral, T = 6 h 34 min + (31 días ene. + 28 días feb. + 16 días mar.) × 3.9425 min/día + 19 h 27 min = 6 h 34 min + 295.7 min+19 h 27 min = 30 h 57 min – 24 h = 6 h 57 min.

Entonces, de acuerdo con la ecuación (1) de este capítulo, el ángulo horario, H, de Sirio vale: H = T – α = 6 h 57 min – 6 h 43 min = 14 min, que equivalen a 3.5°.

La altura sobre el horizonte la podemos calcular con la ecuación (4): sen a = senφsenδ + cosφcosδcosH = = sen19.03°sen(–16.646°)+cos19.03°cos (–16.646°)cos3.5° = = –0.093 + 0.904 = 0.811.

Así, a = 54.19° = 54° 11.4’’, esto es, distancia cenital = 35.41°

Téngase en cuenta que Sirio tiene una declinación negativa, por lo que es austral, es decir, se verá al Sur. Además, ya se obtuvo que su ángulo horario es positivo (+3.5°), y como se mide en el sentido del movimiento diurno a partir del meridiano del lugar, entonces ya culminó, por lo que se le verá por el Oeste y por el Sur, es decir, en el cuadrante SW.

Ahora obtengamos el acimut o el rumbo aplicando la ecuación (6): sen PZA = sen H cos δ/cos a = sen 3.5° cos (–16.646°)/cos 54.19° = 0.061 × 0.958/0.585 = 0.100; entonces PZA = 5.739° = 5° 44’ 20’’, que es el acimut buscado y es también el rumbo S 5° 44’ 20’’ W. Con éste y con la altura de 54° 11’ 24’’ se encontrará fácilmente a Sirio.

Como se comentó, este ejemplo fue resuelto con las coordenadas de Sirio correspondientes a 1950, de la tabla III. Si se utiliza la tabla IV, los resultados son: rumbo = S 4° 58’ 48’’ W y altura = 54° 06’, que no representan una diferencia importante con los valores obtenidos antes.

Distancia angular entre dos astros Sea (véase figura VIII.4) PP’ el eje del mundo; EE’ el Ecuador, y A y B dos astros cuyas coordenadas ecuatoriales se conocen.

En el triángulo PAB, tanto PA como PB son las codeclinaciones de los astros estudiados; el ángulo comprendido entre ellos, APB, es la diferencia de sus ascensiones rectas, esto es, APB = αB – αA.

La distancia angular entre los dos astros, lado AB, se puede calcular por la ecuación:

cos AB = cosPA cosPB+senPA senPB cosAPB = = senδA senδB + cosδA cosδB cos(αB – αA)

Ejercicios propuestos

Las respuestas de estos ejercicios se obtuvieron con las coordenadas de las estrellas para 1950 (tabla III). Se deja al lector el cálculo con las coordenadas para 2011 de la tabla IV.

1. Calcular la hora sideral cuando el ángulo horario de Sirio es de 2 h 17 minutos.

2. Calcular la hora sidérea cuando el ángulo horario de La Cabra (Capella, α de Aurigæ o Cochero) es de 22 h 42 minutos.

3. ¿Qué ángulos se deben marcar en los círculos de un anteojo ecuatorial para localizar Cástor en el instante en que el reloj sideral marque 9 h 25 minutos?

4. ¿A qué distancia cenital culmina Sirio si la latitud geográfica del lugar es de a) 21°; b) en la Ciudad de México.

5. Calcular las coordenadas horizontales de Sirio para las ocho de la noche (hora oficial) del 14 de mayo en Mérida, Yucatán.

6. Calcular la distancia angular entre Aldebarán y Arturo.

Figura VIII.4

CAPÍTULO

IX

Posición de un punto geográfico

Relación entre la hora y la longitud de un lugar

La diferencia de longitudes geográficas entre dos lugares es igual a la diferencia, en un instante dado, entre las horas siderales o civiles medias entre los dos lugares. Para demostrarlo, consideremos la figura IX.1 que muestra el plano de los ecuadores terrestre (círculo interior) y celeste (círculo exterior). Sean OA, OZ y OZ’ las intersecciones del Ecuador con los meridianos de Greenwich y de dos lugares dados, Ciudad de México y Mérida, por ejemplo. La diferencia de longitudes es el ángulo ZOZ’ que forman los meridianos de los dos lugares = AOZ – AOZ’.

Figura IX.1 S

Tengo una pregunta que a veces me tortura: estoy loco yo, o los locos son los demás. Albert eiNsteiN (1879-1955)

Z’ M’ M

Por otra parte, si γ es el punto vernal, las horas siderales de M y M’ están dadas por los ángulos

γOZ y γOZ’; la diferencia entre dichas horas es γOZ’ – γOZ = ZOZ’, que es también la diferencia de longitudes.

Si S es la posición del Sol medio en el instante considerado, el ángulo SOZ es la hora civil media de M, y SOZ’ la hora civil media de M’, de modo que la diferencia entre ambas es nuevamente el ángulo ZOZ’ que mide la diferencia de longitudes.

Así, considerando que la longitud de la Ciudad de México es de 99° 07’ 54’’ y la de Mérida es de 89° 37’ 25’’, la diferencia entre ellas es de 9° 30’ 29’’ que convertida a tiempo es de 38 min 1.93 s, que es la diferencia de sus horas civiles medias (no oficiales) y de sus horas siderales.

Determinación de la longitud

De la sección anterior, para determinar la longitud de un lugar se compara su hora civil en un instante dado con la de un lugar de longitud conocida. Para obtener tal hora civil, se obtiene primero la hora sideral del lugar con el siguiente procedimiento: se espera el paso por el meridiano de una estrella de ascensión recta conocida; entonces H = 0 y por consiguiente, de la ecuación (1) del capítulo VIII, T = α. Así, la hora civil puede deducirse de la hora sideral, invirtiendo el procedimiento tratado en “Tiempo sideral” del capítulo VII.

El otro lugar de hora y longitud conocidas podría ser el Meridiano de Greenwich u otro cualquiera de longitud y hora civil conocidas.

Ejemplo. Un topógrafo que tiene su reloj arreglado a la hora del meridiano 90° WG observa un 3 de febrero en un punto del estado de Puebla el paso por el meridiano de la estrella Betelgeuse, cuando su reloj marca las 8 h 32 min de la noche. ¿Cuál es la longitud geográfica del lugar?

Solución. En el momento de la observación, la hora sideral es igual que la ascensión recta de la estrella: 5 h 52 min (tabla III). Para calcular la hora civil hay que considerar que para el 3 de febrero han transcurrido ya 33 días del año, que a 3.9426 minutos por día, dan 130.1 min = 2 h 10 min de adelanto del reloj sideral, sobre las 6 h 34 min que ya tenía el 1 de enero. Así, la hora sideral está adelantada 8 h 44 min respecto a la civil media. Entonces, la hora civil en el momento de la observación es la sideral menos su adelanto, es decir, 5 h 52 min – 8 h 44 min = – 2 h 52 min + 24 h = 21 h 08 minutos

Puesto que el reloj marca como tiempo oficial las 8 h 32 min en tiempo del meridiano de 90° WG, la diferencia de horas: 21 h 08 min – 20 h 32 min = 0 h 36 min es la diferencia de longitudes; así, 36 min, que equivalen a 540’ = 9°, dan una longitud geográfica de 90° + 9° = 99°.

Determinación de la latitud

La fórmula (3) del capítulo VIII establece que δ = φ±Z, donde δ es la declinación de una estrella

dada, φ es la latitud del lugar de observación y Z es la distancia cenital de la estrella en el momento de su culminación. Entonces, la latitud del lugar en el momento de la culminación de la estrella es igual a su declinación, menos o más su distancia cenital (menos cuando culmina al norte del cenit y más cuando culmina al sur).

Ejemplo. El topógrafo del ejemplo anterior, al observar el paso por el meridiano de la estrella

Betelgeuse, anotó su distancia cenital, que fue de 11° 30’ al sur del cenit. ¿Cuál es la latitud del lugar?

Solución. Como la estrella culminó al sur del cenit, la fórmula aplicable es φ = δ + Z.

Así, la latitud del lugar de observación es la suma de la declinación de la estrella (7° 23’ 50’’, tabla III) y de la distancia cenital, es decir, φ = 18°54’

Ejercicios propuestos

Nota: Las respuestas de los ejercicios 3 y 4 se obtuvieron con las coordenadas de las estrellas para

1950 (tabla III). Se deja al lector el cálculo con las coordenadas para 2011 de la tabla IV.

1. Decir la diferencia entre las horas civiles medias, en un instante dado, entre a) México, D.F. y Hermosillo, Sonora; b) decir también la diferencia entre sus horas oficiales.

2. Decir la diferencia entre las horas siderales, en un cierto instante, entre Mérida, Yucatán y La Paz, Baja California Sur.

3. En un punto del estado de Michoacán, un topógrafo que tiene su reloj arreglado a la hora del meridiano de 90° WG observa el paso de la estrella Rigel por el meridiano, cuando su reloj marca las 20 h 58 min. Si la observación se hizo un 16 de enero, ¿cuál es la longitud geográfica del lugar? Utilizar la tabla III.

4. El mismo topógrafo del ejercicio anterior observa que la altura de Rigel sobre el horizonte en el momento de su culminación, al sur del cenit, es de 61° 33’. ¿Cuál es la latitud geográfica del lugar? Utilizar la tabla III.

CAPÍTULO X

Las estrellas

Me pregunto si las estrellas se iluminan con el fin de que, algún día, cada uno pueda encontrar la suya.

ANtoiNe de sAiNt-exuPéry (1900-1944)

Las estrellas

Las estrellas son astros excesivamente alejados de nosotros que emiten luz propia; a causa de su lejanía, aun con los telescopios más potentes, los vemos como puntos luminosos. A simple vista se nota que unas estrellas son más brillantes que otras y que algunas son rojizas, otras blancas y otras anaranjadas.

Una estrella es una masa gaseosa, por lo general de forma esférica o ligeramente elipsoidal si está animada de movimiento de rotación o, de otra forma, si por la atracción de alguna masa próxima tiene alguna protuberancia dirigida hacia dicha masa.

A simple vista se pueden distinguir las estrellas de los planetas por el centelleo de su luz, tanto

más notable cuanto más cerca del horizonte se encuentre la estrella.

En los tiempos de Hiparco y Ptolomeo se clasificaron las estrellas en seis grupos: se asignó a las más brillantes la magnitud 1 y a las que están en el límite de visibilidad la magnitud 6. Actualmente, la clasificación es más amplia y comprende estrellas visibles a simple vista y otras que sólo se pueden ver con telescopios potentes. El número total de estrellas de nuestro sistema estelar ha sido estimado en cuatrocientos mil millones.

Algunas estrellas cambian de brillo periódicamente o con irregularidad, por lo que se conocen como estrellas variables; la periodicidad con que lo hacen puede variar de unas cuantas horas (novas)

a varios años. Se cree que la variabilidad es debida a pulsaciones, contracciones o vibraciones de los propios astros.

Las constelaciones

En el capítulo III “La esfera celeste” se vio que debido a las enormes distancias de las estrellas respecto a nuestro Sistema Solar, las distancias angulares entre dos estrellas dadas cambian con tal lentitud que todas se nos presentan hoy como se veían cuando el hombre comenzó a observarlas, hace decenas de siglos. Así, fue posible desde la Antigüedad clasificar las estrellas por grupos notables que se llaman asterismos o constelaciones. Los antiguos seres humanos veían en ellas figuras de animales, de hombres u objetos que recordaban personajes o escenas mitológicas, y designaban cada estrella por la posición que ocupaba en la figura: el Hombro de Orión, el Ojo del Toro.

En la actualidad, las constelaciones conservan sus nombres, y sus estrellas se designan, en orden decreciente de su brillo, por las letras del alfabeto griego; así, la más brillante es alfa (α), la que le sigue es beta (β) y así sucesivamente, aunque, debido a que las estrellas cambian de brillo, a veces el orden alfabético ya no corresponde al de magnitud.

Como cada constelación tiene muchas estrellas, en ocasiones se agota el alfabeto griego y entonces se usa el latino y después números. En los observatorios es común designar las estrellas por el número que le corresponde en algún catálogo,

independientemente de la constelación a la que pertenecen, o por sus coordenadas ecuatoriales para una época determinada. También las estrellas más notables tienen su nombre propio.

Reglas para reconocer las constelaciones

Lo mejor para reconocer las constelaciones es buscarlas directamente en el cielo, para lo que puede ayudar una carta. Debe tenerse presente que, siendo el día sideral casi cuatro minutos más corto que el día solar medio, si cada noche anotamos la hora civil o la legal del paso de una estrella por el meridiano, veremos que adelanta su culminación cuatro minutos diarios, lo que hace una hora en 15 días, dos en un mes y 24 en un año. Así pues, el grupo de constelaciones que está a la vista a una hora dada, por ejemplo a las 21:00 h, va cambiando como si la esfera celeste tuviera, además de su movimiento diurno, otro del mismo sentido que le hiciera dar una vuelta completa en un año. De este modo, para conocer toda la esfera celeste se necesita un año de observaciones; en dos observaciones, con seis meses de intervalo, se verán constelaciones completamente distintas, salvo en el casquete circumpolar, donde aparecerán siempre las mismas, aunque en posición inversa.

Debe recordarse que en cualquier instante veremos pasar por el meridiano, o en su posición más alta, aquellas estrellas cuya ascensión recta sea igual a la hora sideral en que se les observe (véase

CAPÍTULO X.

en el capítulo VIII, “Triángulo astronómico”, y en el capítulo IX, “Determinación de la longitud”).

Para reconocer las estrellas notables, conviene calcular la hora sidérea del momento en que se les va a observar, y buscar en la tabla III las que tienen una ascensión recta igual a la hora calculada; ésas estarán culminando. Aquéllas cuya ascensión recta sea menor, habrán pasado ya por el meridiano, y aquéllas otras cuya ascensión recta sea mayor que la hora sideral, estarán aún hacia el Oriente.

En la región boreal hay tres constelaciones notables que pueden servir de guía para reconocer las demás: la Osa Mayor, Casiopea y la Osa Menor. Esta última es toda circumpolar para casi todo el territorio mexicano, y sólo algunas de sus estrellas no lo son para algunos estados del sur. En cambio, las otras dos constelaciones se ven en cualquier época del año.

La Osa Mayor se compone principalmente de siete estrellas con magnitud visual menor que 3 (véase figura X.1, p. 129), de las cuales cuatro forman aproximadamente un trapecio; las otras tres siguen a las primeras formando una figura que se parece a la cola de un cometa. Las dos estrellas que en el movimiento diurno van por delante son α y β; su distancia angular es de 5°, es decir, se hallan casi sobre un mismo círculo horario. La distancia polar de α es de unos 28° y es más cercana al polo norte que β.

Prolongando la línea βα un poco más de cinco veces su longitud sobre su propia dirección, se encuentra la Estrella Polar, que es la más cercana

al Polo Norte entre las perceptibles a simple vista. Por eso a las estrellas α y β de la Osa Mayor se les llama los punteros.

La Estrella Polar, que es α de la Osa Menor, es el extremo de la cola de esta constelación, que se parece a la Osa Mayor; como ésta, consta de siete estrellas principales dispuestas también en forma de un trapecio seguido de una cola, aunque con menores dimensiones aparentes. A principios de enero, hacia las nueve de la noche, la Osa Menor se extiende por debajo de la Estrella Polar y es difícilmente perceptible. A esa hora la Osa Mayor está saliendo a la derecha.

Cuando la Osa Mayor no está a la vista, puede encontrarse la Estrella Polar por medio de Casiopea, grupo de seis estrellas, de las cuales las cinco más brillantes parecen una letra M o W, de brazos muy abiertos (véase figura X.2, p. 129); cerca de las tres delanteras, formando con ellas un cuadro, se halla la sexta, menos brillante que las demás. De las dos delanteras, la segunda es α, la más brillante de la constelación; la primera es β. La línea que une la más brillante con la más débil, es decir, la diagonal del cuadro ya mencionado, prolongada cinco veces, pasa cerca de la Estrella Polar.

La ascensión recta de la estrella delantera β de Casiopea es casi nula, por lo que la línea que une a la Estrella Polar con β es aproximadamente el coluro de los equinoccios. El mismo círculo horario, del otro lado del Polo Norte, pasa entre las estrellas γ y δ (tercera y cuarta del trapecio de la Osa Mayor), cuyas ascensiones rectas son casi de

12 horas (180°). Así, estimando a simple vista el ángulo horario de β de Casiopea, o de γ y δ de la Osa Mayor, se puede conocer aproximadamente la hora sideral.

A partir de estas tres constelaciones es fácil reconocer otras; por ejemplo, la cola de la Osa Mayor, prolongada, conduce a Arturo, estrella α del Boyero (véase figura X.3, p. 130).

Otra constelación que ayuda a reconocer asterismos es Orión (véase figura X.4, p. 130). Está al sur del Cochero, sobre la línea del ecuador, y se halla muy alta al empezar la noche, durante los primeros meses del año. Se compone de un gran trapecio con dos estrellas de primera magnitud: Betelgeuse y Rigel, en medio del cual se hallan tres muy brillantes: el Cinto de Orión, grupo conocido también como las Tres Marías o los Tres Reyes. La línea de estas tres estrellas, prolongada hacia el sureste, conduce a Sirio, el α del Can Mayor, que es el astro más brillante de todas las estrellas. Prolongada en sentido contrario, conduce a Aldebarán, que es el α del Toro.

Magnitudes aparentes

Desde tiempos muy remotos, los observadores del cielo clasificaron las estrellas en seis tipos según su luminosidad aparente (el primer tipo correspondía a las más brillantes y el sexto a las que estaban en el límite de visibilidad), a los que asignaron magnitudes, en forma tal que el paso de una magnitud a la otra era por simple vista y no por una diferencia constante de bri-

llo (diferencia constante de brillo es el exceso de brillo de una estrella respecto al de otra de magnitud inferior). En el siglo XIX, Hershel y Arago hicieron mediciones fotométricas de las magnitudes y llegaron a la conclusión de que la luz que percibimos de una estrella de primera magnitud es 100 veces más brillante que otra de sexta magnitud.

Así, si llamamos b al brillo de una estrella de sexta magnitud y r a la diferencia de brillo de una magnitud a otra inmediata, entonces br será la intensidad de brillo de una de quinta magnitud, br² la de una de cuarta magnitud, y así sucesivamente hasta llegar a una estrella de primera magnitud, que tendrá una intensidad de brillo igual a br⁵. Además, de acuerdo con lo antes asentado: br⁵ = 100 b, donde: r = 2.512

Este número se conoce como constante de Pogson, pues Norman Pogson propuso que la unidad de magnitud correspondiera a una diferencia de intensidad igual a 2.512. Así, el brillo de una estrella de primera magnitud es 2.512 veces el brillo de una de segunda, y el brillo de ésta es 2.512 veces el brillo de una de tercera, y así sucesivamente.

Si designamos como I la intensidad de brillo de una estrella, y como I c la de otra que se toma como término de comparación, y sus respectivas magnitudes son m y m c , la razón de brillo es:

I = 2.512 (m c − m) I c

Entonces, log I I c = (m c − m) log 2.512, y

m – m c = 2.5 log I c I (1)

Esta ecuación indica la diferencia de magnitud entre las estrellas, en función de la razón de sus brillos. Si se determinan las razones de brillo de una serie de estrellas, tomando una de éstas como término de comparación, se puede determinar una escala de magnitudes con la ecuación anterior, siempre que se conozca la magnitud m c de la estrella de comparación que fija el punto cero de tal escala. La magnitud m c se ha fijado por convención internacional, de manera que la magnitud 1 corresponda a un término medio del brillo de las 21 estrellas que en la Antigüedad fueron llamadas estrellas de primera magnitud.

De acuerdo con la ecuación (1), las magnitudes se expresan no sólo por números enteros, sino también por fraccionarios y negativos. Así, por ejemplo, si una estrella E tiene una intensidad de brillo cinco veces mayor que la correspondiente a una de magnitud m c = 1, resulta de la ecuación (1) que:

mE = m c + 2.5 log I c 51 c = 1 + 2.5 log 1 5 = –0.75

Puede notarse que una estrella tendrá una magnitud menor mientras mayor brillo posea. Sirio, la más brillante de las estrellas, tiene una magnitud visual de –1.58 y el Sol una de –26.7, es decir, tiene un brillo de casi un billón de veces mayor que el de una estrella de magnitud 1, de

acuerdo con esta convención. La Luna, en plenilunio, tiene una magnitud visual de −12.55.

Evolución de las estrellas y su clasificación

Evolución estelar

Es la secuencia de cambios que experimenta una estrella a lo largo de su existencia. Durante mucho tiempo se pensó que las estrellas eran enormes bolas de fuego perpetuo.

En el siglo XIX, Kelvin y Helmholtz pensaban que las estrellas extraían su energía de la gravedad, y que por consiguiente se contraían gradualmente. Este hecho habría permitido que el Sol mantuviera su luminosidad durante sólo unas decenas de millones de años, lo que no concordaba con la edad de la Tierra estimada por los geólogos, que es de varios miles de millones de años. En 1920, Eddington propuso la energía nuclear como alternativa. La energía nuclear es aquella que se libera como resultado de una reacción nuclear que puede tener lugar mediante la fisión (división de núcleos atómicos pesados) o por fusión (unión de núcleos atómicos muy livianos). En las reacciones nucleares se libera una gran cantidad de energía, debido a que ocurre una ligera pérdida de masa de las partículas involucradas en el proceso.

Hoy se sabe que la vida de las estrellas está regida por esos procesos nucleares. Así, la evolución estelar puede describirse como una batalla entre dos fuerzas: la gravitatoria, que desde la

formación de una estrella a partir de una nube de gas tiende a comprimirla y a conducirla al colapso gravitatorio, y la nuclear, que tiende a oponerse a esa contracción por medio de la presión térmica resultante de las reacciones nucleares. Finalmente gana la batalla la gravedad, ya que en algún momento la estrella no tendrá más combustible nuclear que emplear.

Distancias de las estrellas

La determinación de la distancia de una estrella respecto a la Tierra se efectúa con su ángulo de paralaje, que se define como aquel con el que sería visto el radio de la órbita de la Tierra alrededor del Sol desde esa estrella. Recuérdese que al tratarse de un astro del Sistema Solar, el ángulo de paralaje es el ángulo con el que sería visto el radio de la Tierra (véase, en capítulo XVIII, “Paralaje de un astro”).

A, mucho más lejana, de modo que puedan considerarse paralelas las líneas TA y T’A. El ángulo 2λ es la suma de los ángulos α y β, y es el doble del ángulo de paralaje de la estrella. Una vez conocido el ángulo de paralaje λ de una estrella, se puede determinar su distancia de la Tierra.

Vamos a suponer que λ de una determinada estrella es igual a 1’’ y que en la figura X.6, S es el Sol, ST el radio de la órbita terrestre, E una estrella y SET = 1’’.

Para determinar el ángulo de paralaje de una estrella puede procederse como sigue: en dos posiciones de la Tierra, T y T’, con intervalo de seis meses, se miden los ángulos α y β que forman las direcciones de las visuales TE y T’E (véase figura X.5) con la dirección con que se ve otra estrella

Entonces: sen 1” = ST ET

En ángulos muy pequeños, en vez del seno puede tomarse el ángulo en radianes, de la siguiente manera:

ET = ; pero

sen 1” = 1” = 1” × × = 4.848 × 10–6

∴ ET = = 3.0837 × 1013 km

o bien, ET = 30,837 × 109 km

Figura X.5

Figura X.6

Esta distancia es llamada parsec (la sílaba par, de paralaje y la sílaba sec, de segundo). Es fácil comprender que mientras mayor sea el paralaje de una estrella, más cercana estará a la Tierra. El mayor ángulo de paralaje estelar que se conoce es de 0.76’’, y corresponde a la estrella más cercana a nuestro planeta, que es α Centauri.

Unidades de distancia

A fin de no manejar números muy grandes, para expresar la distancia de las estrellas a la Tierra se utiliza como unidad el año luz que, como ya vimos, es la distancia recorrida por la luz en un año. Así, el año luz es igual a 9,456 × 109 km . En astronomía se usa también el parsec; si se divide lo que vale un parsec en km (30,837 × 109), entre lo que vale un año luz en km (9,456 × 109), se obtiene: 1 parsec = 3.261 años luz

Tipos de estrellas

Hay muchos tipos de estrellas en el Universo, desde las enanas hasta las supergigantes:

• Protoestrella. Es una estrella en estado de evolución, un cúmulo de gas que ha colapsado desde una nube molecular gigantesca. Esta fase dura unos 100,000 años, durante los cuales la gravedad y la presión se van incrementando, hasta que la protoestrella colapsa.

• T Tauri. Son estrellas en un estado de evolución previo a convertirse en una estrella de secuencia principal (véase siguiente viñeta). La fase T Tauri ocurre al final de la fase protoestrella,

cuando la gravedad es su fuente de energía.

Este tipo de estrellas no tiene la presión o temperatura suficiente en su núcleo para generar fusión nuclear.

• Estrella de secuencia principal. De este tipo es la gran mayoría de las estrellas de nuestra galaxia y del Universo. La secuencia principal es la fase en que una estrella quema hidrógeno en su núcleo mediante fusión nuclear. La mayor parte de las estrellas pasan 90% de su vida en la región denominada “secuencia principal” del diagrama de Hertzsprung-Russell, que muestra el resultado de muchas observaciones sobre la relación existente entre la luminosidad de una estrella y su tipo espectral (coloración). Un ejemplo de estrella de secuencia principal es nuestro Sol. La masa de estas estrellas varía de 0.08 veces la masa total del Sol a 100 veces ésta.

• Gigante roja. Esta fase se da cuando una estrella ha consumido todo el hidrógeno de su núcleo, lo que provoca que la fusión nuclear se vea interrumpida y la estrella no pueda ya generar presión; esto causa que se contraiga y vea reducido su tamaño. Las gigantes rojas llegan a tener una masa de hasta diez mil veces la del Sol.

• Nova. Es una explosión (fusión termonuclear) causada por la acumulación de hidrógeno en la superficie de una estrella enana blanca (véase siguiente ítem). La enorme cantidad de energía liberada produce un destello muy brillante de corta duración (días), lo que dio origen al nombre de nova, ya que los astrónomos anti-

guos veían la aparición de una estrella “nueva”. Cuando la explosión es muy notable, incluso a simple vista, en lugares de la esfera celeste donde no se había detectado antes nada en particular, se denomina supernova.

• Enana blanca. Es un remanente estelar que se genera cuando una estrella de masa menor que 10 masas solares ha agotado su combustible nuclear; 97% de las estrellas que conocemos, incluido el Sol, pasará por esta etapa. Las enanas blancas y las enanas rojas son las más abundantes en el Universo. Puesto que en el núcleo de una enana blanca ya no se producen reacciones termonucleares, la estrella no tiene ninguna fuente de energía que equilibre la gravitación, por lo que se va comprimiendo debido a su propio peso. Las enanas blancas emiten solamente energía térmica almacenada, y por ello tienen luminosidades muy débiles.

• Enanas rojas. Junto con las enanas blancas, estas estrellas son las más comunes del Universo. Su diferencia respecto a las estrellas de secuencia principal consiste en que tienen poca masa y son mucho más frías que, por ejemplo, el Sol.

• Estrellas supergigantes. Son las más grandes del Universo; llegan a tener entre 10 y 50 veces la masa del Sol, y su diámetro puede ser hasta de mil veces el diámetro de éste; consumen a un ritmo muy rápido el hidrógeno de su núcleo, por lo que mueren jóvenes y detonan, con lo que generan una supernova, proceso por el cual se desintegran completamente.

Las supernovas producen destellos de luz muy intensos que pueden durar desde semanas hasta meses, para después decrecer en brillo paulatinamente hasta desaparecer por completo.

CAPÍTULO XI

El Sol

Cuando el Sol se eclipsa para desaparecer, se ve mejor su grandeza. séNeCA (55 A. C.-39 d. C.)

Movimiento anual aparente del Sol

Para comenzar, se puede afirmar que el radio del Sol equivale a 109.3 radios terrestres, es decir, es de 696,860 km. El diámetro aparente del Sol es de 32’ 35’’ en perigeo, y de 31’ 31’’ en apogeo, lo que da un diámetro medio aparente de 32’ 03’’. Asimismo, la distancia de la Tierra al Sol es de 23,439 radios terrestres, es decir, 149.5 millones de kilómetros.

Ya vimos que respecto de la hora civil media determinada por el movimiento diurno del Sol, cada estrella anticipa cuatro minutos diarios su paso por el meridiano. Si pudiéramos ver simultáneamente el Sol y las estrellas, cada día veríamos el primero un poco más hacia el Oriente respecto a las estrellas. Si la observación se hace viendo las estrellas que siguen inmediatamente al Sol

en su ocaso, o las que le preceden en la aurora, se comprobará que en un año el Sol le da una vuelta completa al cielo, pasando sucesivamente sobre las 12 constelaciones siguientes, llamadas zodiacales:

1. Aries (cordero)

2. Taurus (toro)

3. Gemini (gemelos)

4. Cancer (cangrejo)

5. Leo (león)

6. Virgo (virgen)

7. Libra (balanza)

8. Escorpio (escorpión)

9. Sagittarius (sagitario)

10. Capricornus (capricornio)

11. Aquarius (acuario)

12. Piscis (piscis)

Para estudiar con precisión el movimiento anual del Sol, es necesario medir diariamente sus coordenadas ecuatoriales; se verá que su ascensión recta crece continuamente de 0 a 24 horas durante el año, y que su declinación, nula el 21 de marzo, se hace primero boreal y crece hasta 23° 27’ el 21 de junio; decrece luego y se anula hacia el 22 de septiembre, para hacerse negativa enseguida, alcanzar hasta –23° 27’ el 21 de diciembre, y luego decrecer hasta anularse nuevamente el 21 de marzo. En la tabla VI están anotadas, a manera ilustrativa, las coordenadas ecuatoriales del Sol que fueron observadas en el año 1946.

La eclíptica

Marcando diariamente la posición del Sol por medio de sus coordenadas ecuatoriales, se halla que al cabo de un año le ha dado una vuelta completa al cielo sobre un círculo máximo que se llama eclíptica. Una franja de una amplitud total de unos 8°, que es el Zodiaco, contiene a la eclíptica y a las 12 constelaciones mencionadas en la sección anterior. La oblicuidad de la eclíptica (véase figura XI.1) es el diedro EγS que forma con el ecuador, y mide 23° 27’. El diámetro QQ’ de la esfera celeste, perpendicular al plano de la eclíptica, es el eje de ésta, y los puntos Q y Q’ son sus polos.

La intersección γγ’ de la eclíptica con el ecuador es la línea de los equinoccios, y sus extremos, los equinoccios. Uno de ellos (γ), por donde el Sol corta al ecuador al pasar del hemisferio austral al boreal, es el punto vernal o equinoccio de prima-

vera, que sirve de origen al sistema de coordenadas ecuatoriales; el otro (γ’), por donde el Sol vuelve al hemisferio austral, es el equinoccio de otoño; el círculo horario que los contiene es el coluro de los equinoccios. Los puntos S y S’ de la eclíptica en donde el Sol alcanza sus declinaciones máximas se llaman solsticio de verano, el del norte, y de invierno, el del sur. El círculo horario que los contiene es el coluro de los solsticios.

Los paralelos celestes que pasan por los solsticios se llaman trópicos: de Cáncer el del norte, y de Capricornio el del sur. Los paralelos que pasan por los polos de la eclíptica son: círculo polar ártico el boreal, y círculo polar antártico el austral.

Se llaman círculos de latitud aquellos máximos de la esfera celeste que pasan por los polos de la eclíptica.

Figura XI.1

La eclíptica se usa para un tercer sistema de coordenadas celestes que se llaman longitud y latitud celestes; la primera se mide a partir del punto vernal, en el mismo sentido del movimiento anual aparente del Sol, y la latitud a partir de la eclíptica. Así, la longitud celeste del Sol crece continuamente de 0° a 360° en el curso de un año; su latitud celeste permanece siempre nula.

Precesión de los equinoccios

Midiendo la declinación del Sol unos días antes y después de su paso del hemisferio austral al boreal, es posible determinar la posición exacta del punto vernal. Una larga serie de observaciones permite darse cuenta de que este punto no se halla rigurosamente fijo en la esfera celeste, sino que tiene un desplazamiento muy lento, en sentido retrógrado (opuesto al del desplazamiento anual del Sol), sobre la eclíptica. Este desplazamiento recibe el nombre de precesión de los equinoccios, y es de 50.26’’ por año. Dividiendo los 360° de la eclíptica entre la precesión, resulta que el punto vernal le da una vuelta completa a la eclíptica en 25,786 años. La precesión, entre otros, tiene los efectos siguientes:

1. Adelanta el instante del equinoccio de la primavera, ya que el punto vernal le sale al encuentro al Sol cuando a éste aún le faltan 50.26’’ para dar una vuelta completa a la eclíptica. Se llama año sideral al tiempo que emplea el Sol en dar una vuelta completa sobre el Zodiaco; dura 365.2564 días solares medios, es decir, 365 días,

6 horas, 9 minutos y 9.5 segundos. Se llama año trópico al tiempo que transcurre entre dos pasos sucesivos del Sol por el equinoccio de la primavera; en virtud de la precesión es menor que el año sideral, y dura 365.2422 días solares medios, esto es, 365 días, 5 horas, 48 minutos y 45.8 segundos. Este es el año propiamente dicho, o lapso después del cual se repiten las estaciones.

2. Reduce el día sideral en 0.00833 s, fracción que representa la diferencia entre el tiempo que dura la rotación de la Tierra y el lapso que transcurre entre dos culminaciones sucesivas del punto vernal.

3. Modifica continuamente las coordenadas ecuatoriales y eclípticas de las estrellas “fijas” (los astros errantes son: el Sol, la Luna, los planetas, los cometas, etc., con excepción de las estrellas). Las longitudes aumentan casi constantemente a razón de 50.26’’ por año; las latitudes se alteran poco.

4. Hace retroceder los signos del Zodiaco que, como ya vimos, son cada una de las partes iguales en que esta zona celeste se halla dividida por círculos de latitud a partir del punto vernal (recuérdese que los círculos de latitud son aquellos círculos máximos que pasan por los polos de la eclíptica). En tiempos de Hiparco (150 a. C.), el punto vernal se hallaba sobre la constelación Aries, y por eso se llamaba así el signo de la primavera. Desde entonces ha retrocedido unos 30° y se halla en la conste-

lación de los Peces, y como se sigue llamando Aries al signo de la primavera, ahora Tauro se halla sobre la constelación de Aries, y así sucesivamente.

Nutación

Además de la precesión, que es un retroceso secular continuo y uniforme del punto vernal, la posición de este punto se halla sujeta a una variación periódica y más rápida: la nutación, debida a la atracción lunar (véase capítulo XVIII, “Fuerza de gravitación de la Luna”), que consiste en la oscilación del equinoccio de una y otra parte de su posición media en un periodo de 18 años y ocho meses. Se llama equinoccio medio para una época t a la posición que tendría el punto vernal en la época t si no estuviese sujeto más que a la precesión. Se llama equinoccio aparente a la posición que realmente tiene el punto vernal en la época t, por efecto de la nutación.

Las coordenadas medias, ecuatoriales o eclípticas de un astro en la época t están referidas al equinoccio medio como origen; sus coordenadas aparentes, al equinoccio verdadero. La definición del día sideral se refiere al equinoccio medio; si se refiriese al aparente no sería constante, debido a la nutación.

Traslación de la Tierra

El desplazamiento anual del Sol en el Zodiaco, de Occidente a Oriente, es una apariencia debida al movimiento real de traslación de la Tierra alrede-

dor del Sol, que es también de Occidente a Oriente, es decir, en el sentido de las manecillas del reloj si se observa desde el polo celeste sur. Sea S (véase figura XI.2) el Sol y T, T₁, T₂, T₃, hasta llegar a T₁₁ diversas posiciones de la Tierra sobre su órbita o curva que describe alrededor del Sol.

Piscis

Acuario

Capricornio

Sagitario

Escorpión

Tauro

Géminis

Leo

Virgo

XI.2

El día del equinoccio de la primavera, 21 de marzo, cuando la Tierra está en T, el Sol se proyecta sobre el signo de Aries; un mes después la Tierra se ha trasladado a T₁, recorriendo 30° sobre su órbita, y el Sol se proyecta sobre el signo de Tauro. Al cabo de un año, cuando la Tierra vuelve a T, el Sol parecerá haber recorrido todo el Zodiaco en sentido igual del movimiento real de la Tierra.

Así, la eclíptica es el plano de la órbita terrestre; su inclinación se debe a que el eje de rotación de

CAPÍTULO

Figura

Aries

Libra

Cáncer

la Tierra forma con el plano de su órbita un ángulo de 66° 33’, con lo que el Ecuador terrestre y la eclíptica forman el diedro complementario, es decir, de 23° 27’.

La órbita de la Tierra no es una circunferencia en cuyo centro se halle el Sol, sino que es una elipse poco excéntrica, en uno de cuyos focos se

XI.3

Solsticio de verano

Figura XI.4

halla el centro del Sol. Para darse una idea de la excentricidad de la elipse trazada por la órbita de la Tierra, baste decir que (véase figura XI.3) e = OF/OA = 0.017. Por lo tanto, si se dibujase una elipse con el semieje mayor de 60 cm, cada foco distaría 1 cm del centro (OF = 0.017 × 60 cm = 1 cm). Así, la elipse dibujada parecería una circunferencia. Cabe agregar que la distancia media de la Tierra al Sol es de 149’504,201 kilómetros. Por lo antes visto, la distancia de la Tierra al Sol es variable, lo que se reconoce por las variaciones del diámetro aparente de su disco, el cual es máximo a principios de enero y mínimo a principios de julio, lo que indica que la distancia entre los dos astros es máxima (apogeo) en julio y mínima (perigeo) en enero. Si para el hemisferio norte, donde está México, hace más calor en julio que en enero, es porque a mediados de

Equinoccio de primavera

Órbita de la Tierra Tierra

Equinoccio de otoño

Solsticio de invierno

Figura

año la inclinación del eje de rotación de nuestro planeta hace que el hemisferio norte se encuentre vuelto hacia el Sol, mientras que en enero sucede lo contrario (véase figura XI.4).

Movimiento helicoidal del Sol

La traslación de la Tierra produce la apariencia del desplazamiento del Sol en el Zodiaco, y hace que crezcan de manera continua su ascensión recta y su longitud, lo que a su vez es causa de que el día solar sea mayor que el sideral, y de que haya un cambio continuo de las constelaciones que están a la vista a una hora dada de la noche; en efecto, con seis meses de intervalo, la Tierra se halla en dos puntos diametralmente opuestos de su órbita, con lo que las constelaciones están diametralmente opuestas en el cielo.

Además, la inclinación del eje de rotación de la Tierra respecto del plano de su órbita hace variar la declinación del Sol; la combinación de los dos movimientos de la Tierra hace que el movimiento diurno del Sol no se verifique con la sencillez de aquél de las estrellas; así, en lugar de describir diariamente un mismo paralelo, el Sol describe una especie de hélice que se va enrollando en la esfera celeste, de Sur a Norte desde el 21 de diciembre hasta el 21 de junio, y de Norte a Sur del 21 de junio al 21 de diciembre. Cada día, el recorrido del Sol se produce sensiblemente sobre distinto paralelo. Esto hace cambiar continuamente los puntos por donde sale, culmina y se pone, así como el tiempo que permanece sobre el horizonte.

El 21 de marzo, cuando su declinación es nula, el Sol se halla sobre el Ecuador; sale exactamente por el Este y se pone por el Oeste; permanece sobre el horizonte durante la mitad de su recorrido diurno, y el día es igual a la noche. A medida que la declinación crece y el Sol se interna en el hemisferio boreal, los puntos de salida y ocaso van quedando más al norte del primo vertical, y el día va creciendo en detrimento de la noche, es decir, que amanece más temprano y anochece más tarde. El 21 de junio, cuando el Sol alcanza su declinación máxima en el solsticio de verano, el día es máximo y la noche mínima. Después, la declinación empieza a decrecer: los puntos de salida y ocaso del Sol vuelven hacia el Sur, y el día va disminuyendo mientras la noche aumenta. El 22 de septiembre, en el equinoccio de otoño, el Sol sale de nuevo por el Este y se pone por el Oeste, y el día es igual a la noche. Después, el Sol pasa al hemisferio austral: sale y se pone al sur del primo vertical, y el día va disminuyendo mientras se alarga la noche, hasta el 21 de diciembre en que el Sol alcanza, en el solsticio de invierno, su declinación negativa máxima, y el día es mínimo. A partir de esta fecha el Sol emprende su viaje helicoidal hacia el Norte, para salir de nuevo por el Este el día 21 de marzo siguiente; los mismos fenómenos se repiten indefinidamente.

Zonas geográficas

Ya vimos que se llaman trópicos los paralelos terrestres cuya latitud es igual a la declinación máxi-

ma del Sol (23° 27’): de Cáncer el del norte, y de Capricornio el del sur (véase figura XI.5, p. 130).

Los países que cruza el Trópico de Cáncer, del océano Atlántico hacia el este, son: Mauritania, Mali, Argelia, Níger, Libia, Chad, Egipto, Arabia Saudita, Emiratos Árabes Unidos, Omán, India, Bangladesh, Birmania, China, Taiwán, Hawai (Estados Unidos), México y Bahamas.

Los países cruzados por el Trópico de Capricornio, partiendo del Meridiano de Greenwich hacia el oeste, son: Brasil, Paraguay, Argentina, Chile, Polinesia Francesa, Tonga, Australia, Madagascar, Mozambique, Sudáfrica, Botsuana y Namibia.

Son círculos polares los paralelos terrestres cuya latitud es igual al complemento de la declinación máxima del Sol (66° 33’): Ártico el del norte y Antártico el del sur. Estos círculos se corresponden con los del mismo nombre de la esfera celeste.

Los trópicos y los círculos polares dividen la superficie de la Tierra en cinco zonas: la tórrida, que se extiende entre los dos trópicos; dos zonas templadas, boreal y austral, comprendida cada una entre el trópico y el círculo polar, y dos casquetes glaciales, limitados alrededor de cada polo por el círculo polar respectivo. Así, para todo punto de la zona tórrida, el Sol pasa por el cenit dos veces al año, cuando la declinación del Sol se hace igual a la latitud del lugar. Fuera de la zona tórrida, el Sol culmina siempre al sur del cenit en el hemisferio boreal y siempre al norte en el austral.

Para todo punto de cualquiera de los casquetes glaciales, el Sol se hace circumpolar desde que su

declinación es igual al complemento de la latitud del lugar. En el polo, el Sol permanece seis meses sobre el horizonte.

El día y la noche

El lapso comprendido entre la salida y la puesta del Sol es el día de luz o día artificial, o simplemente el día; la noche es el tiempo durante el cual el Sol permanece debajo de nuestro horizonte y nos hallamos, en consecuencia, sumergidos en la sombra de la Tierra.

Siempre hay un hemisferio terrestre alumbrado por el Sol y otro, el opuesto, situado en la sombra, y se dice hemisferio porque la distancia entre la Tierra y el Sol es tan grande en comparación con los diámetros de ambos astros, que la línea de contacto de la superficie terrestre con el cono de los rayos solares puede considerarse un círculo máximo cuyo plano es perpendicular a la recta que une los centros de los dos astros. Este círculo máximo se llama círculo de iluminación

Los días de los equinoccios (declinación nula) el círculo de iluminación pasa por los polos terrestres y divide en partes iguales el Ecuador y todos los paralelos; el día dura lo mismo que la noche en todo el planeta, y de ahí el nombre de equinoccios de esas fechas.

Después del inicio de la primavera, la Tierra avanza sobre su órbita conservando siempre su eje de rotación paralelo a sí mismo, salvo el débil movimiento angular de la precesión, pero inclinado respecto al plano de la órbita y, en consecuencia,

presenta al Sol su polo norte y un casquete alrededor de este punto.

Si en un instante dado la declinación del Sol es el ángulo EOS (véase figura XI.6), el círculo de iluminación I-I’ forma con el eje PP’ el ángulo POI = EOS, y para todos los puntos cuya distancia al Polo Norte sea menor que el arco IP, el Sol no se pone ya; es circumpolar. El Ecuador también, que es un círculo máximo, queda dividido en partes iguales por el círculo de iluminación, y ahí el día sigue siendo igual a la noche, pero cualquier otro paralelo queda dividido en partes desiguales, correspondiendo la mayor al día, en el hemisferio norte, y a la noche, en el hemisferio sur.

En el hemisferio boreal, el arco diurno mAt del paralelo trazado por un punto A, irá creciendo en detrimento del nocturno, a medida que crezca

la declinación, porque se va ampliando el ángulo POI, y la cuerda mt se va alejando del centro Q del paralelo; entonces el día crece en detrimento de la noche a medida que avanza el año. En las zonas tórrida y templada alcanza su máximo el 21 de junio, solsticio de verano, cuando es máxima la declinación del Sol.

Después, disminuye al mismo tiempo que crece la noche, hasta que se igualan de nuevo el 22 de septiembre, día del equinoccio de otoño. Además, la diferencia entre los arcos diurno y nocturno del paralelo es tanto mayor en una fecha dada, cuanto mayor es la latitud del punto A, porque es mayor también la distancia RQ de la cuerda mt al centro Q del paralelo; así, en la misma fecha, el día artificial es tanto más largo cuanto mayor es la latitud del lugar.

En la zona tórrida, la diferencia entre el día y la noche es siempre pequeña; en la zona templada es grande cerca del solsticio de verano; en el círculo polar, el 21 de junio a media noche el Sol toca el horizonte por el Norte, sin ponerse; más al Norte, en un punto B del casquete glacial, hay día continuo mientras la declinación del Sol EOS = POI sea mayor que la distancia PB del lugar al Polo Norte. En el mismo polo hay día continuo de seis meses: se asoma el Sol por el horizonte el día del equinoccio de la primavera, cuando el círculo de iluminación coincide con el eje de la Tierra, y sube luego dando vueltas alrededor del horizonte en forma de hélice hasta el 21 de junio, en que comienza a bajar en igual forma, para trasponer

Figura XI.6

el horizonte el 22 de septiembre y desaparecer por seis meses.

En el hemisferio austral, después del 21 de marzo, el arco diurno m’Ct’ del paralelo descrito por un punto C es menor que el nocturno, esto es, el día dura menos que la noche. Con razonamientos análogos a los que acabamos de hacer, se demuestra que en un lugar dado el día decrece del 21 de marzo al 21 de junio y crece luego hasta el 22 de septiembre, en que vuelve a ser igual a la noche; también se demuestra que en una fecha dada el día artificial es tanto más corto, cuanto más al sur se halle el punto C. En la zona tórrida, la diferencia entre el día y la noche es siempre pequeña; en la zona templada, la diferencia es grande en las proximidades del 21 de junio, que ahí resulta un solsticio de invierno; en el mismo círculo polar, el 21 de junio el Sol quedará debajo del horizonte sin asomarse, y no lo hará hasta cerca del medio día del 22, hacia el Norte y por breve tiempo; más al Sur, en un punto D del casquete glacial, habrá noche continua mientras la declinación del Sol permanezca mayor que la distancia DP’ del punto al Polo Sur. En el mismo polo, la noche durará seis meses, del 21 de marzo al 22 de septiembre. Después de esta fecha, la Tierra presenta al Sol el Polo Sur y un pequeño casquete alrededor de éste (véase figura XI.7); todos los fenómenos descritos antes se repiten, pero en orden inverso: en el hemisferio boreal el día va disminuyendo y la noche creciendo desde el 22 de septiembre hasta el 21 de diciembre, y al revés del 21 de diciembre

al 21 de marzo. En una fecha dada, el día artificial es tanto más corto cuanto mayor sea la latitud del lugar, y hay noche continua en el casquete glacial desde que el punto de observación rebase el círculo I-I’.

En el hemisferio austral el día crece del 22 de septiembre al 21 de diciembre, y decrece desde esa fecha hasta el 21 de marzo, en que vuelve a ser igual a la noche; el día es tanto más largo que la noche, en una fecha dada, mientras mayor sea, en valor absoluto, la latitud del lugar, y hay día continuo para los puntos del casquete glacial cuya distancia al Polo Sur sea menor que la declinación del Sol.

Distancia cenital meridiana del Sol Sea A (véase figura XI.8) un punto geográfico situado al norte del Trópico de Cáncer, en que el Sol

Figura XI.7

culmina siempre al sur del cenit, a una distancia igual a la latitud geográfica del lugar, menos la declinación del Sol.

sur también aplican las deducciones anteriores, y el lector puede hacer como ejercicio los razonamientos respectivos.

Calendario

Trópico de Cáncer

Trópico de Capricornio

Se tiene que: ZAS = ZOS = EOZ – EOS.

Llamando Z a la distancia cenital meridiana del Sol (ZAS), δ a su declinación (EOS) y φ a la latitud del lugar (EOZ), se tiene que: Z = φ – δ

Si el punto geográfico estuviera en la zona tórrida, también sería válida la fórmula anterior si el Sol culminase al sur del cenit, es decir, si su declinación fuera menor que la latitud del lugar. Si el Sol culmina al norte del cenit, la fórmula se invierte (Z = δ – φ). La misma fórmula Z = φ – δ nos indica que cuando se igualen la declinación del Sol y la latitud del lugar, el Sol pasará por el cenit. Para un punto geográfico del hemisferio

El año civil es un periodo convencional que abarca cierto número exacto de días solares medios y que tiende a concordar con el año trópico, que es el que rige la sucesión de las estaciones. Los distintos procedimientos ideados para realizar esta concordancia se llaman calendarios. A continuación se mencionan los que han dado origen al que rige actualmente.

Calendario romano

Este calendario se estableció en el año 753 a. C. por Rómulo; constaba de 304 días distribuidos en 10 meses:

Figura

Aproximadamente en el año 690 a. C., Numa

Pompilio añadió 51 días para tener 12 lunaciones en el año, que fueron repartidos en dos meses: Januarius y Februarius. Más tarde se trató de concordar el año civil con el curso de las estaciones, y para ello se intercaló cada dos años, entre el 23 y 24 de febrero, un mes de 22 días llamado Mercedonius; así, el año civil resultó de 366 días en promedio, mayor que el año trópico; esta situación, aunada al poco cuidado que se tenía para redactar el calendario, llegó a producir gran confusión en el cómputo de los años romanos.

Calendario juliano

En el año 45 a. C., el emperador Julio César impuso un nuevo calendario que por encargo suyo arregló

Sosígenes de Alejandría. Sabiendo que el año trópico dura exactamente 365 días y un cuarto, Julio

César dispuso que se contasen los años comunes de 365 días y que se añadiera un día más cada cuatro años. El día adicional se intercaló entre el 24 y el 25 de febrero; como el 24 se llamaba día sexto antes de las calendas de marzo, el día adicional se llamó bis sexto, por lo que los años respectivos se llaman bisiestos. Se cambió el nombre del mes quintilis por el de julio, y en tiempos del emperador Augusto se cambió el de sextilis por su nombre y se le asignaron 31 días, para que no tuviera menos que julio; los demás meses se dispusieron tal como se conservan hoy en día.

El Concilio de Nicea, reunido en 325 d. C., adoptó para la cristiandad el calendario juliano,

pero se siguieron contando los años con origen en la época de la fundación de Roma. No fue hasta el año 580 que se empezó a contar el tiempo con origen en el año de nacimiento de Cristo; Dionisio Exiguus, monje que vivía en Roma aproximadamente en el año 580, afirmó que el Mesías vino al mundo en el año 754 de la fundación de Roma, y aunque cálculos posteriores indican que se equivocó, sigue aceptándose la fecha indicada, ya que los relatos evangélicos no fijan ninguna fecha al nacimiento de Cristo.

Adoptada la era cristiana, se convino en contar como bisiestos todos los años cuyas dos últimas cifras fueran múltiplo de 4.

Calendario gregoriano

Como ya se vio, el Concilio de Nicea, al adoptar el calendario juliano, dispuso que la Pascua se celebrase el domingo inmediato siguiente a la primera Luna llena de la primavera, y se fijó para el inicio de ésta el 21 de marzo, fecha en que cayó el equinoccio en el año del concilio. Sin embargo, como el año juliano era de 365.25 días y el año trópico es de 365.2422, se tenía un error de 365.2500 – 365.2422 = 0.0078 días por año, que acumulado acabó por poner una diferencia importante entre el año civil y el año trópico. En efecto, en 1582 habían pasado 1,257 años después del concilio, de modo que el error era de 1,257 × 0.0078 = 9.8 días y el equinoccio de la primavera, en vez de caer el 21 de marzo, cayó el 11 del mismo mes, lo que amenazaba a que la Pascua no se celebrase

inmediatamente después de la primera Luna llena de la primavera. Entonces, el papa Gregorio XIII suprimió 10 días al año 1582, y dispuso que el día siguiente al jueves 4 de octubre fuese el viernes 15 de octubre, es decir, que para obtener el calendario gregoriano, se sumaban 10 días al juliano, mientras que para obtener el juliano, se restaban 10 días al gregoriano. Además, como el error del año juliano acumula tres días en 400 años, se estipuló que de los años finales de siglo (1600, 1700, 1800, etcétera), sólo fueran bisiestos los que resultasen múltiplos de 400. Así, el año 1600 fue bisiesto, los años 1700, 1800 y 1900 no lo fueron a pesar de ser múltiplos de 4, y el 2000 sí lo fue; asimismo, no serán bisiestos los años 2100, 2200 ni 2300, pero sí lo será el 2400, y así sucesivamente.

Este calendario fue adoptado por los países católicos de Europa: Italia, Francia y España (y sus colonias), Portugal, Hungría y Polonia; posteriormente, a fines del siglo XVII, por Alemania, Holanda, Dinamarca y Suiza; a mediados del siglo XVIII, por Inglaterra y Suecia. Rusia continuó usando el juliano hasta 1918 y Rumania hasta 1919, años en que adoptaron el gregoriano; China lo adoptó desde febrero de 1912.

Una curiosidad histórica en cuanto a los calendarios es que Miguel de Cervantes Saavedra (1547-1616) y William Shakespeare (1564-1616) murieron el mismo día, no obstante que el primero falleció el 23 de abril de 1616 (en realidad falleció el 22, pero fue enterrado el 23), y el segundo el 3 de mayo de 1616, con lo que la diferencia es

de 10 días. La razón de ello es que en ese año, España ya había adoptado el calendario gregoriano, mientras que Gran Bretaña lo hizo en 1753.

Otro dato interesante está contenido en un párrafo del libro Historia de la Independencia de México, 1810-1824, del escritor ruso M. S. Alperovich, que dice:

A mediados de 1812, las autoridades coloniales lograron en cierta medida que se estabilizara la situación en México. Por ejemplo, el 20 de julio de ese año (1 de agosto de acuerdo con el calendario ruso entonces vigente), A. Y. Dashkov informaba a N. P. Rumiantzev, canciller del imperio ruso, que según los últimos datos, el levantamiento continuaba, y que la situación de los insurgentes mejoraba día tras día...1

Se ve que en 1812 la diferencia entre los calendarios juliano y gregoriano era ya de 12 días; en efecto, entre los años 325 d. C. y 1812 habían transcurrido 1,487 años, que multiplicados por 0.0078 dan por resultado 11.6 días ≈ 12 días.

Aunque ningún país utiliza actualmente el calendario juliano, procede comentar que la diferencia entre éste y el gregoriano es de 13 días desde el año 1991, y que será de 14 días a partir del año 2119, y así sucesivamente, 1 día más cada 128 años.

Calor del Sol en la Tierra

El calor recibido por una superficie es proporcional al coseno del ángulo de incidencia de la fuente;

en este caso el ángulo de incidencia es la distancia cenital del Sol. Entonces, un lugar recibe tanto más calor cuanto más cerca esté el Sol del cenit. En un día dado, el máximo calor recibido ocurre cuando el Sol pasa por el meridiano, ya que su distancia cenital es mínima. En el curso del año, el calor recibido es máximo en la fecha en que la distancia cenital meridiana del Sol es mínima: en la zona tórrida esto ocurre cuando éste pasa por el cenit; en las zonas templada y glacial del norte, el 21 de junio, y en las regiones templada y glacial del sur, el 21 de diciembre.

Por otra parte, mientras mayor es el día de luz en un lugar, mayor es la cantidad de calor que recibe. Además, el calor recibido por la Tierra varía en razón inversa del cuadrado de la distancia al Sol; sin embargo, la variación debida a esta causa es poco perceptible, ya que tal distancia cambia relativamente poco: de 147 millones de kilómetros a 152 millones de kilómetros, es decir, un 3.4 por ciento.

La influencia de la atmósfera es importante; la hora de calor máximo en un día y el día de calor máximo en un año no coinciden con la hora ni con el día en que cierto lugar recibe el máximo de calor, lo cual se debe a la atmósfera, ya que rodea y cubre a la Tierra como una capa, retiene una gran cantidad del calor recibido, y lo va liberando poco a poco por radiación. El aire absorbe cierta cantidad del calor que recibe, en función del espesor de la capa atmosférica atravesada por los rayos solares y de la cantidad de vapor de agua que

contenga el aire. Después del mediodía, durante unas dos horas, el aire recibe una cantidad de calor mayor que la que pierde por radiación, y la temperatura se eleva de forma continua; después de ello sucede lo contrario y la temperatura baja hasta el día siguiente, a la hora en que el Sol sale de nuevo y vuelve a calentar la atmósfera. Así, el calor máximo ocurre unas dos horas después del mediodía, y el mínimo al salir el Sol.

Por un efecto análogo se retardan los días de calor máximo y mínimo en el curso del año. En el hemisferio boreal, el mínimo de calor no se siente el 21 de diciembre, sino a mediados de enero; aumenta luego la temperatura hasta fines de julio, en que alcanza su máximo en las zonas templada y fría, y disminuye después hasta enero. En las zonas templada y fría del Sur sucede lo contrario: el calor máximo se siente en enero y el mínimo en julio. En la zona tórrida el día de calor máximo llega tres o cuatro semanas después del paso del Sol por el cenit; las variaciones de temperatura son poco sensibles pues varía poco la distancia cenital meridiana del Sol y los días son casi de igual duración durante todo el año.

Estaciones

La inclinación del eje de rotación de la Tierra respecto al eje de su órbita provoca que el año se divida en cuatro épocas llamadas estaciones, que inician al pasar el Sol por los equinoccios y por los solsticios: la primavera, el 20 o 21 de marzo, cuando el Sol pasa por el punto vernal o equinoccio de

primavera; el verano, el 21 o 22 de junio, cuando el Sol pasa por el solsticio de verano; el otoño, el 22 o 23 de septiembre; y el invierno, el 21 o 22 de diciembre. Estas son las estaciones en la zona templada del norte. En la del sur, las fechas son en orden inverso: el 21 de marzo comienza el otoño; el 21 de junio, el invierno; el 22 de septiembre, la primavera; y el 21 de diciembre, el verano. En la zona tórrida las estaciones son poco marcadas. En el Ecuador puede decirse que hay dos veranos, que empiezan los días de los equinoccios, y dos inviernos, que empiezan los días de los solsticios, aunque la temperatura varía muy poco. En los casquetes glaciales la temperatura es siempre muy baja, y lo que determina las diferencias de temperatura es el fenómeno de días y noches continuos.

Climas de México

La temperatura en un punto geográfico no sólo depende de su latitud y de la duración del día, sino de muchas otras variables de las cuales la más importante es su altura sobre el nivel del mar. La temperatura del aire en un mismo punto va descendiendo uniformemente conforme la altura va aumentando hasta 20 km de elevación; de ahí que existan las nieves perpetuas en la cima de los montes muy elevados y la temperatura templada de que gozan ciertos lugares a pesar de su escasa latitud, como ocurre en gran parte de la Mesa Central de México.

El territorio mexicano abarca dos zonas: la tórrida y la templada, entre los 15° y los 32° de latitud

boreal. La temperatura es extremosa en toda la parte norte del país, situada en la zona templada, con fuertes calores en el verano y fríos rigurosos en el invierno. Los climas de México son los más variados del mundo y están determinados por la altura sobre el nivel del mar, que divide al territorio en tres zonas: caliente, templada y fría.

La tierra caliente va desde el nivel del mar hasta 1,600 m de altitud. Los primeros 800 m tienen clima tórrido y abarcan todas las costas, en un ancho de 50 a 60 km, comprendiendo los estados de Yucatán, Campeche, Quintana Roo, Tabasco, el Istmo de Tehuantepec (Veracruz, Oaxaca y Chiapas) y las costas de los demás estados que dan al Golfo de México y al Océano Pacífico. La temperatura media anual en estas tierras bajas es de 25° a 28° C, con un mínimo de 15° C y un máximo de más de 40° C, especialmente en el Valle del Balsas, en el sur de Yucatán y en las costas del Golfo de Tehuantepec.

La tierra templada o zona subtropical va de los 1,500 a los 2,500 msnm y comprende la mayor parte de los estados del centro del país, así como parte de los estados de Coahuila, Nuevo León, Veracruz, Chiapas, Oaxaca, Guerrero, Jalisco, Sinaloa y Sonora, en que el clima es templado, bastante uniforme, sin grandes calores ni fríos excesivos. Excepcionalmente ha caído nieve en la Ciudad de México, en la de Puebla y en algunos otros puntos de la Mesa Central.

La tierra fría se extiende por encima de los 2,500 msnm y tiene una temperatura media anual

de 5° a 10° C. La ciudad de Toluca y otras poblaciones de los estados de México, Puebla y Tlaxcala pertenecen a esta categoría. Por arriba de los 4,300 msnm solamente sobresalen las cimas de algunos montes como el Pico de Orizaba, el Popocatépetl y el Iztaccíhuatl, donde reina un clima glacial enteramente análogo al de los casquetes polares.

Ejercicios propuestos

1. Decir cuál es la declinación de una estrella que en su movimiento diurno describe el Trópico de Cáncer.

2. Calcular las fechas en que pasa el Sol por el cenit de la Ciudad de México.

3. Decir en qué fecha del mes de mayo la distancia cenital meridiana del Sol es de 5° al sur del meridiano en Mérida, Yucatán.

4. Decir cuál es la ascensión recta y cuál la declinación de los equinoccios.

5. Decir la ascensión recta y la declinación de cada uno de los polos de la eclíptica.

1. Alperovich, M. S., Historia de la Independencia de México, 18101824. Grijalbo, 1967, p. 156.

CAPÍTULO XII

La Luna

Un hombre es como la Luna: con una cara obscura que a nadie enseña. mArk twAiN (1835-1910)

Movimiento

propio de la Luna

La Luna es el astro más cercano a la Tierra, alrededor de la cual gira; es su satélite, nombre con que se conoce a los astros que giran alrededor de los planetas. Al igual que el Sol, la Luna se desplaza sobre las constelaciones zodiacales, pero más rápido; las recorre todas en poco más de 27 días, lo que hace que su paso por el meridiano se retarde cerca de una hora diaria; este desplazamiento es de Occidente a Oriente, es decir, en el mismo sentido que la Tierra se traslada alrededor del Sol (en el sentido de las manecillas del reloj, mirando de Sur a Norte).

La órbita de la Luna es una elipse y la Tierra es uno de sus focos; la excentricidad de esta elipse es de 0.055, más del triple de aquélla de la órbita terrestre alrededor del Sol. La distancia media

desde la Tierra hasta la Luna es de 384,600 km, es decir, 60.3 veces el radio medio de la Tierra, lo que significa que tal distancia es 389 veces menor que la distancia de la Tierra al Sol. Cabe aquí anotar que el radio de la Luna es de 0.273 el radio de la Tierra, es decir, de 1,741 kilómetros.

En una hora, el desplazamiento medio de la Luna, de unos 33’, es casi igual a su propio disco, y en un día es de 13° 11’, por lo cual es fácilmente observable (el diámetro aparente medio de la Luna es de 31’ 05’’; en perigeo es de 33’ 28.8’’ y en apogeo, de 29’ 23.2’’). Si una noche la Luna está cerca de determinadas estrellas, la siguiente noche, a la misma hora, se habrá corrido considerablemente hacia el Este. La distancia angular de la Luna al Sol (elongación de la Luna) crece alrededor de 12° diarios.

Si se miden diariamente las coordenadas ecuatoriales de la Luna durante un mes (o sus coordenadas eclípticas), podrá comprobarse que da la vuelta al Zodiaco sobre un círculo máximo que forma con la eclíptica un ángulo cuyo valor medio es de 5° 08’ 48’’ que se llama inclinación de la órbita lunar (véase figura XII.1). La intersección del plano de la órbita con el de la eclíptica es la

línea de los nodos, y sus extremos son los nodos, que pueden ser: ascendente, el punto en que la Luna corta a la eclíptica a su paso del hemisferio austral al boreal, y descendente, el opuesto.

Los nodos tienen un movimiento bastante rápido de retroceso: cuando el nodo ascendente coincide con el punto vernal, la inclinación de la órbita lunar sobre el ecuador alcanza un máximo de 28° 35’ 48’’; nueve años y medio después, cuando el nodo descendente llega al punto vernal, la inclinación es mínima: 18° 18’ 12’’.

08’ 48’’

Línea de los nodos

Órbita lunar

Figura XII.1

Eclíptica

El tiempo que tarda la Luna en dar una vuelta completa sobre el Zodiaco es el mes sideral; dura 27 días 7 h 43 min 11.5 s y es el tiempo que se lleva para volver al círculo de latitud de una misma estrella. El mes trópico es el tiempo que tarda la Luna en pasar dos veces sucesivas por el círculo de latitud del punto vernal; a causa de la precesión de los equinoccios, es algo más corto que el mes sideral, y dura 27 días 7 h 43 min y 4.7 s. El mes draconítico es el lapso que transcurre entre dos pasos de la Luna por un mismo nodo. A causa de

Plenilunio

Cuarto creciente

Cuarto menguante

Novilunio

XII.2

Novilunio

CAPÍTULO

Figura

la retrogradación de estos puntos, es menor aun que el mes trópico y dura 27 días 5 h 5 min 35.8 s. Todos estos lapsos son algo variables, ya que el movimiento de la Luna sobre su órbita no es uniforme, de modo que las definiciones anteriores son valores medios.

Los movimientos de traslación de la Tierra alrededor del Sol, y de la Luna alrededor de la Tierra, hacen que la trayectoria de nuestro satélite en el espacio sea más complicada: al seguir a la Tierra, la Luna describe en torno del Sol una curva ondulada, siempre cóncava hacia el astro central (véase figura XII.2). Conviene agregar que la velocidad media de traslación de la Tierra es de 29.7 km/s (107,000 km/h), y la de la Luna, de 1 km/s (3,600 km/h).

Fases de la luna

En la figura XII.3 la Tierra se representa con T, y se localiza en el centro de la órbita lunar ABCDEFGH, y el Sol, a la derecha de la figura, se sitúa tan lejos que los rayos luminosos que envía son prácticamente paralelos entre sí. Entonces la Luna queda dividida en dos hemisferios: el iluminado y el oscuro.

Cuando está en conjunción (entre el Sol y la Tierra) es invisible, porque nos muestra su hemisferio oscuro; además, sale en pleno día, junto con el Sol y se llama luna nueva o novilunio. Al día siguiente de la conjunción se le ve por la tarde, al Poniente, poco antes de la puesta del Sol y poco después; tiene forma de cuerno muy delgado, con las puntas hacia el Oriente.

Segunda cuadratura o cuarto menguante

En oposición

En conjunción

Primera cuadratura o cuarto creciente

Figura XII.3

A medida que la Luna avanza sobre su órbita alrededor de la Tierra, va creciendo hasta que en la primera cuadratura, siete días después de la conjunción, vemos la mitad iluminada; es el cuarto creciente y en esta fase la Luna culmina (está en su mayor altura respecto al horizonte) al ponerse el Sol. En las noches siguientes el Sol se pone antes de que la Luna culmine, ya con más de medio disco iluminado.

Quince días después de la conjunción, la Luna está en oposición (la Tierra queda entre ella y el Sol), nos presenta su hemisferio totalmente iluminado y está a la vista durante toda la noche, ya que sale a la puesta del Sol y se pone en la madrugada: es la Luna llena o plenilunio.

Los siguientes días sale después de la puesta del Sol, cada noche más tarde; el retardo es de unos 50 minutos diarios y va decreciendo su parte iluminada. Cuando se halla en su segunda cuadratura sale a la media noche y vemos medio disco iluminado: es el cuarto menguante, y ocurre 22 días después de la conjunción. Posteriormente se le puede ver en la madrugada y en la mañana, con los cuernos mirando al Occidente. Cabe agregar que al novilunio y al plenilunio se les designa con el nombre de sizigias.

Durante los días que preceden y siguen a una conjunción, se ve el cuerno delgado de la Luna, brillante, y el resto débilmente iluminado por un resplandor gris, conocido como luz cenicienta. La causa es la reflexión de la luz solar, provocada por la Tierra, y sólo es perceptible en la proximidad de

una conjunción. Además, da la impresión de que la parte iluminada es de un diámetro mayor que la parte restante del disco (véase figura XII.4), lo cual se debe a que un disco negro parece menor que uno blanco de igual diámetro.

Lunación

El lapso que transcurre entre dos conjunciones sucesivas de la Luna con el Sol se llama revolución sinódica, mes lunar o lunación. La traslación de la Tierra hace que la lunación sea más larga que el mes sideral.

En la figura XII. 5, sea S el Sol, T la Tierra y L la Luna, estando en conjunción ésta. Al cabo de un mes sideral, la Tierra ha descrito sobre su órbita un arco TT’ de unos 27°, y la Luna, después de dar una vuelta completa sobre su órbita, en el mismo

Figura XII.4

sentido de traslación de la Tierra, se halla en L’ , en un punto tal que la recta T’L’ es paralela a TL; así, en apariencia la Luna ha vuelto a proyectarse sobre las mismas estrellas que 27 días antes, pero el Sol se ha corrido unos 27° hacia el Oriente. Entonces, para que la Luna vuelva a quedar en conjunción, es necesario que describa aún sobre su órbita el arco L’L’’, de igual amplitud angular que el arco TT’, para lo cual necesita aproximadamente dos días y cinco horas. La lunación dura 29.53 días = 29 días 12 horas 44 minutos 2.8 segundos, que son casi exactamente 29 días y medio. En un año sideral hay exactamente un mes sideral más que el número de meses sinódicos: 13.369 meses siderales y 12.369 lunaciones.

Edad de la Luna

Se llama edad de la Luna en una fecha dada al número de días transcurridos desde el último novilunio, de modo que en el propio novilunio la edad es cero; en el cuarto creciente es siete, en

el plenilunio es 14, en el cuarto menguante es 22 y en el plenilunio es 29. Es de señalarse que en la Antigüedad, el sabio Metón descubrió que las fases de la Luna se repiten en las mismas fechas del año cada 19 años; por ello se conoce como Ciclo de Metón

La epacta de un año cualquiera es la edad de la Luna el último día (31 de diciembre) del año anterior. Por ejemplo, la epacta del año 1900 fue de 29, que es el valor máximo que puede alcanzar; su valor mínimo es cero. Ahora bien, suponiendo un año de 365 días y la lunación de 29.5 días, resulta que ese año tiene 12 lunaciones y 11 días; en efecto, 29.5 × 12 = 354 días, y faltan 11 para completar el año. Así, conocida la epacta de un año, bastará añadirle 11 unidades para obtener la del siguiente.

Partiendo ahora de que la epacta del año 2000 fue de 24, sumándole 11 se obtiene 35, y quitando 30 días por una lunación, queda 5, que fue la epacta de 2001. La de 2002 fue de 5 + 11 = 16. La de 2003 fue de 16 + 11 = 27. La de 2004, 27 + 11 = 38 – 30 = 8, etcétera.

Entonces, la epacta de 2019 sería la misma que la del 2000, esto es 24. En la tabla VI puede obtenerse la epacta de todos los años comprendidos entre el 1500 y el 2999. Las seis primeras columnas son los años intermedios entre cada siglo, y las siguientes son las de inicio de siglo. Por ejemplo, si se desea conocer la epacta de 2004, se entra en la columna 12 correspondiente a 2000 y se busca su intersección con la fila correspondiente al año cuatro. El resultado es ocho.

Figura XII.5

Para encontrar la edad de la Luna en cualquier fecha, se suma la epacta a la fecha del mes, si se trata de enero o marzo; en febrero o abril, a esa suma se añade una unidad. En general, la cifra por añadir según el mes es la siguiente:

Mes Ene. Feb. Mar. Abr. May. Jun.

Núm. 0 1 0 1 2 3

Mes Jul. Ago. Sep. Oct. Nov. Dic.

Núm 4 5 7 7 9 9

Si el año es bisiesto, se agrega una unidad a partir de marzo. Por supuesto, si el resultado es 30 o más, se restará 30 cuantas veces sea necesario. A continuación explicaremos a qué se debe el número de cada mes. Es fácil comprender que si se trata de enero, simplemente se suma la epacta con la fecha del mes:

• Enero: epacta + fecha del mes.

• Febrero: epacta + fecha + 1, porque enero tiene 31 días.

• Marzo: epacta + fecha. En efecto, enero + febrero = 59 días; dos lunaciones = 2 × 29.5 = 59 días, por lo que la diferencia es cero.

• Abril: epacta + fecha + 1, porque enero + febrero + marzo = 90 días; tres lunaciones = 3 × 29.5 = 88.5 días, por lo que la diferencia es 1.5 días.

• Mayo: epacta + fecha + 2, porque enero + febrero + marzo + abril = 120 días y las cuatro

lunaciones = 4 × 29.5 = 118 días, y la diferencia es 2.

• Junio: epacta + fecha + 3, porque enero + febrero + marzo + abril + mayo = 151 días, mientras que las cinco lunaciones = 5 × 29.5 = 147.5, y la diferencia es 3.5 días.

• Diciembre: epacta + fecha + 9, porque enero + febrero + marzo + … + noviembre = 334 días, mientras que las 11 lunaciones = 11 × 29.5 = 324.5, y la diferencia es 9.5 días.

Ejemplo. Calcular la edad de la Luna el 10 de diciembre de 2011.

Solución. La epacta de 2011 = 25; 25 + 10 + 9 = 44; 44 – 30 = 14.

Así, el 10 de diciembre de 2011 la edad de la Luna fue de 14, es decir, hubo Luna llena.

Para obtener la fecha de un mes en que la Luna tenga determinada edad, se procede a la inversa: a la edad propuesta, aumentada en 30 cuando sea necesario, se le restan la epacta y el número del mes, y se resta 1 si el año es bisiesto.

Ejemplo. Obtener la fecha de abril de 2012 en la que la edad de la Luna fue 14, es decir, luna llena.

Solución. La epacta de 2012 = 6. Entonces, 14 – 6 –1 (número del mes) – 1 (año bisiesto)

CAPÍTULO

= 6. Así, la Luna llena se presentó el 6 de abril de 2012, y fue la primera de la primavera de ese año.

Fiestas movibles

Por decreto del Concilio de Nicea, la Iglesia católica celebra la Pascua de Resurrección el domingo siguiente a la primera Luna llena de primavera, tomándose siempre como fecha del equinoccio o inicio de la estación el 21 de marzo, y como edad de la Luna llena, 14. Es, lo más pronto, el 22 de marzo, y lo más tarde el 25 de abril. Así, para saber la fecha en que se celebrará la Pascua de un año dado, se calcula la fecha de la primera Luna llena de la primavera de ese año; a continuación, se obtiene el día de la semana en que cae la fecha obtenida, y entonces es posible determinar la fecha del domingo siguiente.

Para obtener el día de la semana en que cae cualquier fecha del siglo XX, se utiliza el calendario perpetuo de la tabla IX, que se explica en la tabla VIII. Veamos cómo se aplica: en primer lugar se entra con la fecha del mes, se sube verticalmente y se anota el número que aparece en la fila “cifra”; a continuación se entra con el mes y también se sube para anotar el número que indica la fila “cifra”. Lo mismo se hace con los últimos dos dígitos del año. Al resultado se resta 7 o el mayor múltiplo de 7 que contenga; se lleva el número obtenido a la tabla IX, fila “Cifras” y arriba se encuentra el día buscado de la semana.

Si se trata de otro siglo cualquiera, además de sumar las cifras tal como ya se explicó, se suma otra cifra tomada, según sea el caso, de las tablas X u XI.

Ejemplo. Averiguar en qué día de la semana cayó el 6 de abril de 2012 referido en el ejemplo anterior, y en qué fecha cayó el domingo de Pascua de Resurrección.

Solución.

Entramos con la fecha 6 (tabla VII) y en cifra hallamos un 6.

Entramos con abril (tabla VII) y en cifra encontramos un 6.

Entramos con el año 12 (tabla VII) y en cifra hallamos un 1.

Entramos en la tabla VII-bis con los dos primeros dígitos de 2012 y encontramos arriba un 6.

La suma da 19

A la suma de los números anteriores se resta el múltiplo de 7 más próximo y menor que 19, esto es, 14, con lo que se obtiene 5, que en la tabla VII corresponde a viernes. Como habíamos visto, el 6 de abril de 2012 fue el primer plenilunio de la primavera, y como cayó en viernes, entonces el domingo de Pascua de Resurrección, es decir, el domingo de la Semana Santa mayor, fue el 8 de abril de 2012. De la misma forma puede recurrirse, para obtener el día de la semana en que cae cualquier fecha, al algoritmo que se presenta en

el capítulo XVIII, “Algoritmo para calcular el día de la semana”.

En la tabla XII puede obtenerse la fecha del Domingo de Pascua de cualquier año de los siglos XX y XXI, la cual se explica por sí sola. Asimismo, en la tabla XIII puede averiguarse la fecha en que cayó el Domingo de Pascua a fines del siglo XVI y en los siglos XVII, XVIII y XIX.

Rotación de la Luna

En su traslación alrededor de la Tierra, la Luna gira sobre sí pero, a diferencia de la Tierra, que muestra al Sol sucesivamente todos los puntos de su superficie, la Luna le presenta a la Tierra constantemente el mismo hemisferio. Así, su rotación dura un tiempo igual que su revolución sideral. En efecto (véase figura XII.6), sea T la Tierra, y L y L’ dos posiciones de la Luna en su órbita; estando en L, su contorno aparente es AB; cuando se desplaza

y llega a L’ ese contorno aparente es A’B’, que forma con AB el ángulo A’L’A’’, que es igual a LTL’ (lados respectivamente perpendiculares). El primer ángulo es la rotación y el segundo la traslación; por tanto, la duración de la rotación de la Luna es exactamente igual a la de su traslación alrededor de la Tierra, y por eso presenta a la Tierra siempre el mismo hemisferio.

Libraciones

En el curso de una revolución sideral de la Luna, se logra ver una extensión superficial mayor que la de un hemisferio lunar, como si estuviese nuestro satélite animado de ligeros balanceos de Este a Oeste y de Norte a Sur; ello se debe a la excentricidad de su órbita, a la inclinación de su eje de rotación respecto a la eclíptica y al movimiento de rotación de la Tierra. Estos movimientos aparentes, que se conocen como libraciones, son tres: libración en longitud, libración en latitud y libración diurna.

Libración en longitud

Se debe a que el movimiento de rotación de la Luna es uniforme, mientras que su velocidad angular no lo es. En efecto, dado que la Tierra ocupa uno de los focos de la órbita lunar, la velocidad angular de la Luna no es uniforme, sino que es máxima en el perigeo y mínima en el apogeo, ya que se ajusta a la ley de las áreas; de ello resulta que un mismo punto de la Luna no puede quedar, con respecto a nosotros, en idéntica dirección en todo el curso de una rotación.

Figura XII.6

En efecto, en la figura XII.7 supóngase que

T es la Tierra en un foco de la órbita elíptica lunar y que P es un punto de la superficie de la Luna, situado exactamente en la línea TL de los centros. Cuando el vector TL haya barrido la cuarta parte de la órbita, el radio del punto P habrá girado 90° y estará dirigido según L’P’, por lo que desde la Tierra dicho punto parecerá ha-

berse desplazado hacia el Oriente, en el mismo sentido que la Luna.

Cuando la Luna se encuentre en L’’, el mismo punto volverá a estar en la línea de los centros, y cuando llegue a L’’’ el radio estará nuevamente desviado de la línea de los centros y lo veremos desplazado hacia el Occidente.

Debido a esta libración, parece que nuestro satélite tuviera un balanceo de Oriente a Occidente, gracias al cual se logra ver la superficie convexa correspondiente a la de un huso de 7 grados.

Libración en latitud

Se debe a la inclinación del eje de rotación de la Luna respecto al plano de su órbita y a la eclíptica. Dicho eje forma un ángulo de 88° 30’ con el plano de la eclíptica; además, la órbita lunar tiene una inclinación de 5° 08’ 48’’ con respecto a la eclíptica, por lo que el ángulo que forma el eje de rotación de la Luna con el plano de su órbita es (véase figura XII.8):

90° – (88° 30’ – 5° 09’) = 6° 21’

Figura XII.7

Figura XII.8

Entonces, no sólo pueden verse el polo norte y el polo sur de la Luna, sino que también se logra ver 6° 21’ más allá del polo sur; algo similar ocurre con la Tierra, debido a la inclinación de la eclíptica con respecto al plano del Ecuador, en que queda iluminada una franja de 23° 27’ más allá del polo boreal al inicio del verano, y otra franja de igual amplitud al inicio del invierno.

Esta libración es una especie de cabeceo de Norte a Sur en un tiempo que no es exactamente igual a una revolución sideral, ya que es de 27.2 días (recordar que el mes sideral dura 27 días 7 h 43 min y 11.5 s = 27.3217 días. El mes trópico, o tiempo que tarda la Luna en pasar dos veces sucesivas por el punto vernal es de 27 días 7 h

43 min 4.7 s = 27.3216 días; y el mes draconítico, o tiempo que transcurre entre dos pasos sucesivos

de la Luna por un mismo nodo, es de 27 días 5 h 5 min 35.8 s = 27.2122 días).

Libración diurna

Esta libración obedece a que el radio terrestre no es de longitud despreciable respecto a nuestra distancia de la Luna. Considérese en la figura

XII.9 a un observador colocado en un punto O de la Tierra que esté viendo un punto P de la Luna en el momento en que ésta sale por el horizonte (parte izquierda de la figura). Si P está en la línea de los centros, visto desde O parecerá estar afuera de dicha línea, hasta que la Luna pase por el meridiano, momento en que el punto P se verá sobre la línea de los centros. Al ir acercándose la Luna al Poniente, el punto P se verá nuevamente desplazado de la línea de los centros. El valor de

Figura XII.9

esta libración es casi de 1°, valor aproximado a su ángulo de paralaje.

Debido a las libraciones, se puede ver 9% más que la mitad de la superficie de la Luna, es decir, se puede ver 59%, por lo que sólo se desconoce 41% de ella.

Relación entre las revoluciones

siderales lunar y terrestre y la sinódica lunar

Observando la figura XII.10 puede verse que en una revolución sinódica de la Luna, la Tierra recorre un arco de a° y su satélite uno de 360°; para recorrer este último la Luna tarda t días, siendo t el mes sideral. Para recorrer 360° + a° tarda t’ días, donde t’ es el mes sinódico o lunar.

Por otra parte, la Tierra recorre 360° en T días, donde T es el año sideral, y recorre a° en t’ días; por lo tanto:

= , de donde a° = ; sustituyendo en (1):

donde t = mes sideral

T = año sideral

T’ = mes sinódico

Eclipses

Se puede definir un eclipse como la ocultación total o parcial de un cuerpo celeste por la interposición de otro; ese cuerpo puede ser luminoso como el Sol u opaco como nuestro planeta o la Luna. Si ésta nos oculta el Sol, hay eclipse de Sol; si la Tierra impide que la luz del Sol llegue a nuestro satélite, hay eclipse de Luna. Analicemos primero los eclipses de Luna.

XII.10

Así, =

Eclipses de Luna

Longitud del cono de sombra de la Tierra

Dado que la Tierra es un cuerpo opaco, intercepta la luz del Sol y proyecta un cono de sombra for-

Figura

mado por las tangentes exteriores comunes a los dos astros y cuyo eje es la prolongación de la línea de los centros (véase figura XII.11). Las tangentes interiores comunes determinan un tronco de cono, en cuya parte central está el cono de sombra; el diámetro menor de éste es la recta BD que une los puntos de tangencia. La región comprendida entre las tangentes comunes interiores y exteriores constituye la penumbra, porque sólo llega ahí una parte de los rayos del Sol.

En la figura XII.11, ST es la línea que une el centro S del Sol con el centro T de la Tierra; también ST es el plano de la eclíptica, que es perpendicular al plano de la figura; BDV es un corte del cono de sombra; EBV y FDV son cortes de la sección de penumbra. Cuando la Luna penetra en la penumbra, su brillo disminuye. Después de haber entrado al cono de sombra, aunque no se vuelve completamente invisible, su disco toma un tinte rojizo que se percibe perfectamente a pesar

de su débil resplandor. Con base en la propia figura XII.11, veamos cómo calcular la longitud

TV del cono de sombra proyectado por la Tierra:

Comparando los triángulos semejantes ASV y BTV, se puede escribir:

TV/TB = SV/SA

Si designamos a TV y ST como h y d, respectivamente, y llamamos R y r a los radios del Sol y de la Tierra, la ecuación anterior resulta:

h/r = (d + h)/R

al despejar h, resulta que:

h = rd/(R – r)

sustituyendo R por 109.3 r y d por 23,439 r (véase capítulo XI, párrafo 1), se tiene que:

Figura XII.11

h = 23,439 r²/108.3 r = 216.4 r

lo que significa que la longitud del cono de sombra es mucho mayor que la distancia de la Luna a la Tierra, que es de 60.3 r (véase primer apartado de este capítulo), es decir, que la Luna puede interferir en dicho cono de sombra y en la penumbra.

Diámetro de la sombra

Para calcular el diámetro de la sección de sombra a la distancia de la Tierra a la Luna, consideremos la figura XII.12, en la que T es el centro de la Tierra y LNM es un arco de la órbita lunar.

Considerando el triángulo MNV como rectángulo en N y comparándolo con TBV se tiene:

MN/MV = TB/TV, de donde:

MN = TB (MV/TV)

TB = r, TV = 216.4 r, MV = TV – TM = 216.4 r – 60.3 r = 156.1 r

entonces, MN = 156.1 r²/216.4 r = 0.72 r

Ahora bien, el radio de la Luna r’ vale 0.273 del radio de la Tierra, es decir, r’ = 0.273 r, o lo que es lo mismo r = r’/0.273; entonces:

MN = 0.72 r’/0.273 = 2.64 r’

Así, la Luna cabe muy bien dentro del cono de sombra. De lo anterior se infiere que si la órbita de la Luna tuviese la misma inclinación que la eclíptica, habría eclipse de Luna en cada oposición; pero como esos dos planos forman un ángulo de 5° 08’ 48’’, en sus oposiciones la Luna puede encontrarse al norte o al sur de la eclíptica. Para que haya eclipse es preciso que la latitud de la Luna sea tal que se introduzca en el cono de sombra.

Condición de latitud de la Luna para que se eclipse

En la figura XII.12 supóngase, como se dijo para la XII.11, el plano de la eclíptica apoyado en TV y perpendicular al plano de la figura. La latitud de L,

Figura XII.12

centro de la Luna (recuérdese que se llama latitud a la ordenada del sistema de coordenadas eclípticas: en capítulo XI, véase “La eclíptica”), en el instante en que su disco es tangente al cono de sombra, es el ángulo MTL. Para que en la oposición haya eclipse de Luna, su latitud debe ser menor que la suma de los ángulos MTN y NTL, es decir:

Latitud de la Luna < (ángulo MTN

+ ángulo NTL) (1)

El ángulo NTL es el semidiámetro aparente de la Luna, cuyo valor medio es de 15’ 33’’.

El triángulo MTN puede considerarse rectángulo en M, sin error significativo; entonces:

tan MTN = = = 0.012

∴ ángulo MTN = 41’ 2.7’’

Sustituyendo en (1) este valor y el del semidiámetro aparente de la Luna, se obtiene que la latitud del centro de la Luna no debe exceder los 56’ 36’’ para que haya eclipse.

Puesto que la distancia de la Tierra a la Luna es variable, el ángulo MTN y el semidiámetro aparente de nuestro satélite también lo son. Por ello, el ángulo MTL (latitud del centro de la Luna) oscila entre 62’ 41’’ y 51’ 21’’; si la latitud es mayor que 62’ 41’’ no hay eclipse; si es menor que 51’ 21’’ seguramente hay eclipse; si su valor queda adentro de tal rango, hay duda.

Para que haya un eclipse total, la Luna debe penetrar totalmente dentro del cono de sombra. Para esto se necesita que el valor de la latitud del centro sea igual o menor que 51’ 21’’ menos el semidiámetro aparente, es decir, que sea igual o menor que 51’ 21’’– 15’ 33’’ = 35’ 48’’.

Figura XII.13

Eclipses de Sol

Los eclipses de Sol ocurren cuando, al encontrarse la Luna entre el Sol y la Tierra, el disco lunar oculta total o parcialmente el del Sol. Para esto, la Luna debe estar en conjunción y su latitud no debe ser

Figura XII.14

Penumbra T L

Penumbra T L

mayor que cierto límite, como se verá más adelante. A diferencia de los eclipses de Luna, que son visibles simultáneamente en todo un hemisferio, el Sol sólo se eclipsa para los lugares de la Tierra situados en el cono de sombra que proyecta la Luna; si este cono toca a la Tierra (véase figura XII.13) hay eclipse total; para los puntos situados en la penumbra el eclipse será parcial; también será parcial si sólo la penumbra toca a la Tierra (véase figura XII.14).

Longitud del cono de sombra. De la figura XII.15 y considerando que los triángulos LBV y SAV son semejantes, se tiene que:

= , donde r’ es el radio de la Luna y R el del Sol

Dado que LT es variable por la excentricidad de la órbita lunar, y que oscila entre 56 y 64 radios terrestres, también la longitud del cono de sombra varía entre 57 y 59 radios terrestres (se deja al lector el ejercicio de demostrarlo). Así, en ciertas condiciones la sombra de la Luna llega a tocar la superficie de la Tierra, y habrá eclipse total de Sol para esa zona.

Latitud de la Luna para que ocurra eclipse de Sol

Si el plano de la órbita lunar alrededor de la Tierra fuese el mismo que el de la órbita terrestre alrededor del Sol, habría eclipse en el momento de la conjunción siempre y cuando la distancia

Figura XII.15

de la Luna a la Tierra fuese menor que la longitud del cono de sombra. Debido a la inclinación de la órbita lunar sobre la eclíptica, para que haya eclipse de Sol se requiere que en la conjunción la latitud del centro de la Luna sea menor que el ángulo STL (véase figura XII.16), que corresponde al momento en que la Luna se hace tangente a la línea AB.

De acuerdo con la figura XII.16, se tiene que :

ángulo STL = ángulo STA + ángulo ATC + ángulo CTL (3)

ángulo STA = semidiámetro aparente del Sol = 16’ 01.5’’(véase en capítulo XI “Movimiento anual aparente del Sol”)

El ángulo TCB es exterior al triángulo ATC, por lo que:

ángulo TCB = ángulo ATC + ángulo CAT, de donde:

ángulo ATC = ángulo TCB – ángulo CAT.

Ahora bien, el ángulo TCB = ángulo de paralaje de la Luna = 57’ 2.7’’ y el ángulo CAT = ángulo de paralaje del Sol = 8.8’’; entonces,

ángulo ATC = 56’ 53.9’’

ángulo CTL = semidiámetro aparente de la Luna = 15’ 33’’ (véase en capítulo XII “Movimiento propio de la Luna”)

sustituyendo en (3),

ángulo STL = 16’ 01.5’’ + 56’ 53.9’’ + 15’ 33’ = 1° 28’ 28’’

Todos los ángulos considerados son valores medios, así que en realidad, el valor del ángulo STL varía entre 1° 24’ y 1° 34’; por consiguiente, si el ángulo STL es menor que 1° 24’, seguramente hay eclipse; si es mayor, no lo hay. Si el ángulo STL está comprendido entre estos dos valores, hay duda y es necesario hacer los cálculos para cada caso particular.

Como ya se comentó, ocurre en ocasiones, precisamente en plenilunio, que la Luna se eclipsa:

Figura XII.16

una sombra de color cobrizo la va invadiendo de Oriente a Poniente hasta cubrirla toda (eclipse total) o hasta cierto límite (eclipse parcial), para retirarse luego, hasta que la Luna recupera todo su brillo. Tal situación ocurre cuando la oposición tiene lugar cerca de la línea de los nodos, ya que, como se calculó antes, la latitud necesaria de la Luna para que penetre en el cono de sombra de la Tierra es de 51’ 21’’. Recuérdese que la latitud de la Luna (ordenada respecto a la eclíptica) varía de 0° 0’ 0’’ en los nodos, a 5° 08’ 48’’ que es su latitud máxima. Puesto que el cono de sombra es más ancho que el diámetro de la Luna, ésta puede introducirse en él y eclipsarse por completo, para lo cual es preciso que la oposición se produzca en uno de los nodos o muy cerca, es decir, que la latitud de la Luna sea de 35’ 48’’; si ocurre un poco más lejos, la Luna sólo penetra parcialmente en la sombra, y hay eclipse parcial, durante el cual la Luna no se hace completamente invisible porque la luz solar, al atravesar la atmósfera terrestre, se refracta y llega a la Luna, aunque muy disminuida en intensidad y enrojecida, lo cual produce el color cobrizo.

Un eclipse lunar puede durar hasta cuatro horas, aunque la fase total no dura más de dos.

Los eclipses de Sol suceden durante la conjunción de la Luna con el Sol si ésta ocurre muy cerca de uno de los nodos de la órbita lunar, de acuerdo con los cálculos anteriores. El Sol es cubierto o tapado por la Luna, que al ir avanzando sobre su órbita, va produciendo en el disco solar una esco-

tadura absolutamente negra, limitada por un arco de círculo, que da al resto del Sol la forma de una hoz que va decreciendo hasta desaparecer (eclipse total) o hasta cierto límite (eclipse parcial), y en ambos casos crece luego con los cuernos en sentido opuesto.

A veces llega un momento en que se juntan las extremidades de los cuernos y queda visible un anillo completo del disco del Sol, en torno de una sombra circular y absolutamente negra que es la Luna.

Cuando el eclipse es total, se observan fenómenos interesantes: el cielo adquiere tonos rojizos al principio; luego, cuando la Luna cubre por completo al Sol, la temperatura desciende notoriamente; la oscuridad es suficiente para ver brillar estrellas y planetas; del disco negro emergen la corona solar y las protuberancias o llamas del Sol, de vivo color rojo; los pájaros van en busca de sus nidos.

Un eclipse de Sol puede durar, en todas sus fases, hasta cuatro y media horas. La fase total no llega a ocho minutos; la fase anular puede llegar a 12 minutos.

Ejercicios propuestos

1. Calcule la epacta de los años 2013 y 2016 (bisiesto).

2. Obtenga la edad de la Luna el 24 de diciembre de 2013.

3. ¿En qué fase estará la Luna el 21 de marzo de 2014?

4. ¿En qué día del mes de mayo de 2015 habrá Luna llena?

5. Diga en qué fecha del año 2020 será el domingo de Pascua de Resurrección.

6a. Demuestre que no puede haber eclipse de Sol el 10 de mayo de 2014.

6b. ¿Puede haber eclipse de Luna el 31 de diciembre de 2018?

CAPÍTULO XIII

Los planetas

Este bellísimo sistema compuesto por el Sol, los planetas y los cometas no pudo menos que haber sido creado por consejo y dominio de un ente poderoso e inteligente. El Dios supremo es un ser eterno, infinito, absolutamente perfecto. isAAC NewtoN (1642-1721)

Clasificación

Hace varios milenios que el ser humano supo diferenciar las estrellas de otros astros, ya que mientras aquéllas permanecen prácticamente fijas éstos tienen posiciones variables con respecto a las primeras. Los griegos llamaron planetas a estos astros “errantes”.

Los planetas, a diferencia de las estrellas, carecen de luz propia; la reciben del Sol y la reflejan.

A pesar de que los astros se parecen a simple vista a las estrellas, se distinguen de ellas porque: a) ordinariamente no presentan centelleo; b) la

distancia angular entre ellos, o entre cada uno de ellos y las estrellas, no es constante; c) observados con telescopio tienen forma de disco, mientras que las estrellas parecen puntos brillantes sin diámetro aparente.

Hasta 2006 se consideraba que el Sistema Solar contaba con nueve planetas (véase cuadro).

El 24 de agosto de 2006, durante la reunión en Praga de la International Astronomical Union, los casi dos mil quinientos científicos participantes acordaron dejar de considerar a Plutón como planeta regular, y lo declararon planeta enano, por

Nombre Diámetro ecuatorial (km)

lo que se estableció que el Sistema Solar está compuesto por ocho planetas. Cabe agregar que Plutón fue descubierto en 1930 por el estadounidense Clyde Tombaugh (1906-1997). En su eliminación influyó notablemente el descubrimiento por Brown, en 2003, del cuerpo celeste 2003-UB313 situado a 14,550 millones de kilómetros de nuestro planeta y con un diámetro de 3,000 km, es decir, mayor que Plutón.

La definición de planeta aprobada por unanimidad en Praga obedece a tres categorías:

1. Un planeta es un cuerpo celeste que está en órbita alrededor del Sol, que tiene suficiente masa para tener gravedad propia que supere las fuerzas rígidas de un cuerpo, de manera que asuma una forma equilibrada hidrostática, es decir, que sea esférica, y que haya despejado de cuerpos celestes las inmediaciones de

su órbita, ya sea aspirándolos o arrojándolos fuera de ella.

2. Un cuerpo celeste que está en órbita alrededor del Sol, que no ha despejado las inmediaciones de su órbita y que no es un satélite, se considera un planeta enano.

3. Todos los demás objetos que orbitan alrededor del Sol son considerados “cuerpos pequeños del Sistema Solar”.

Plutón no cumple con la condición de haber limpiado su órbita de otros cuerpos celestes, ya que atraviesa el Cinturón de Kuiper, compuesto por una gran cantidad de pequeños cuerpos celestes.

Entre las órbitas de Marte y Júpiter, separadas entre sí unos 550 millones de kilómetros, orbitan más de 18,000 asteroides, de los cuales el mayor es Ceres (diámetro = 960 km), considerado planeta enano, al igual que Plutón. Fue descubierto en 1801 por Giuseppe Piazzi.

En cuanto a su distancia de la Tierra, los planetas se clasifican en interiores y exteriores; los primeros son aquellos cuyas órbitas están contenidas en la órbita terrestre, como Mercurio y Venus; los exteriores son los demás. Con la excepción de Urano y Neptuno, los demás se perciben a simple vista, lo que hizo fácil que los observadores de la Antigüedad estudiaran sus movimientos aparentes, aunque de manera imperfecta, y no tardaron en reconocer una gran irregularidad en sus trayectorias, como su cambio de dirección en sentido

opuesto durante ciertas épocas. A los planetas interiores los llamaron también inferiores porque en su recorrido zodiacal no se apartan mucho del Sol, de modo que siempre se les ve bajos con relación al horizonte. A los exteriores les llamaron superiores porque se alejan del Sol hasta cualquier distancia angular, de modo que se les puede ver muy altos o cerca del cenit a cualquier hora de la noche.

Movimientos aparentes

Los movimientos aparentes de los planetas no son en un solo sentido como los del Sol y de la Luna, sino que describen primero un arco directo, es decir, del mismo sentido que el movimiento anual del Sol; después parecen detenerse algún tiempo, y luego recorren un arco retrógrado, esto es, hacia el Occidente. Después de otra estación emprenden de nuevo el arco directo y continúan indefinidamente en la misma forma. El arco directo es siempre más amplio que el retrógrado, por lo que todos los planetas acaban por dar una vuelta completa al cielo sobre el Zodiaco, en sentido directo, aunque en tiempos muy diferentes: los planetas inferiores dan cada vuelta completa al Zodiaco en un año cada uno, por seguir de cerca al Sol; los superiores la dan más lentamente: Marte, en cerca de dos años; Júpiter, en casi 12; Saturno, en algo menos de 30 años.

Los movimientos aparentes de los planetas están en estrecha relación con el Sol. Cada planeta superior pasa por el punto medio del arco directo cuando está en conjunción con el Sol, y por el

medio del arco retrógrado cuando está en oposición. Los planetas inferiores, que se apartan poco del Sol, no pueden nunca hallarse en oposición, pero quedan dos veces en conjunción: en el punto medio del arco directo (conjunción superior) y en el punto medio del arco retrógrado (conjunción inferior). Así, los planetas inferiores no pueden verse sino en las tardes, poco después de ponerse el Sol, y se dice que son vespertinos; o en las madrugadas, poco antes de la salida del Sol, y se dice que son matutinos.

La elongación (distancia angular del Sol) máxima o digresión de Mercurio varía de 18° a 28°, de modo que no puede ponerse más de dos horas después que el Sol, ni anticiparse más de ese tiempo a su salida.

La digresión de Venus es de unos 47° y puede ponerse hasta poco más de tres horas después que el Sol, o anticipársele en su salida ese mismo tiempo.

En cambio, los planetas superiores en la oposición salen a la puesta del Sol, se ponen a la salida de éste y culminan a media noche. Aunque los cinco planetas (Mercurio, Venus, Marte, Júpiter y Saturno) brillan siempre como las estrellas más notorias, su fulgor varía según las posiciones que ocupan respecto del Sol: los superiores alcanzan su mayor brillantez en la oposición, mientras que los inferiores brillan más en las proximidades de su digresión, poco antes y poco después de su conjunción inferior. El que mayor brillo alcanza es Venus, cuando su elongación es de unos 39°,

lo que ocurre unos 35 días antes y después de su conjunción inferior.

Asimismo, utilizando el telescopio, el diámetro aparente de un planeta superior es máximo en la oposición y mínimo en la conjunción con el Sol; el de un planeta inferior es máximo en la conjunción inferior y mínimo en la superior.

Se llama revolución sideral de un planeta a la media de los lapsos que transcurren entre dos pasos sucesivos del planeta por el círculo horario de una misma estrella. Es de 88 días para Mercurio, de 225 días para Venus, de 1.88 años para Marte, de cerca de 12 años para Júpiter y de cerca de 30 años para Saturno.

Se llama revolución sinódica de un planeta al promedio de los lapsos que transcurren entre dos conjunciones o entre dos oposiciones sucesivas del Sol, si se trata de un planeta superior, y entre dos conjunciones (inferiores o superiores) si se trata de uno inferior. Es de 116 días para Mercurio, de 584 días para Venus, de 780 días para Marte, de 399 días para Júpiter y de 378 días para Saturno.

Como ya se dijo, los lapsos anteriores son un promedio de muchos años. Así, por ejemplo, entre 1939 y 1948 las revoluciones sinódicas de Marte fueron el 23 de julio de 1939, el 10 de octubre de 1941 (lapso = 810 días), el 5 de diciembre de 1943 (lapso = 786 días), el 13 de enero de 1946 (770 días) y el 17 de febrero de 1948 (765 días). El promedio de estos cuatro lapsos es de 782.75 días, cercano a los 780 días dados para Marte.

Durante cada revolución sinódica los planetas describen un arco directo y uno retrógrado, y aunque los intervalos son algo variables puede decirse que Mercurio avanza unos 95 días y retrocede 21. Venus avanza 540 días y retrocede 44. Marte avanza 705 días y retrocede 75. Júpiter avanza 278 días y retrocede 121. Saturno avanza 245 días y retrocede 134.

Con la información anterior y con la fecha conocida de alguna de las posiciones notables de un planeta (véase la Tabla XIV), el lector podrá conocer la época en que ocurrirán las demás y por consiguiente saber cuál es la más favorable para la observación de cada planeta. Por ejemplo, sabiendo que Marte estuvo en oposición el 3 de marzo de 2012, volverá a estarlo en dos años y 50 días, esto es, el 22 de abril de 2014. Esta fecha es sólo aproximada, ya que los dos años y 50 días es un valor promedio a largo plazo. De cualquier modo, el resultado es útil para saber cuáles son las épocas favorables para la observación de cada planeta.

Movimientos reales

Los planetas, al igual que la Tierra, giran en órbitas elípticas con un foco común ocupado por el centro del Sol. Existen en el Sistema Solar, además de los ocho planetas descritos, más de 18 mil cuerpos celestes muy pequeños, a los que se les da el nombre de asteroides o planetoides y cuyas órbitas se hallan, en general, entre las de Marte y Júpiter; los principales se llaman Ceres, Palas, Juno y Vesta; no presentan disco sensible ni con buenos telescopios.

Como se ha señalado, se descubrió recientemente el planetoide 2003-UB313, lo que influyó en gran medida para que Plutón dejara de ser considerado planeta.

Explicación de los movimientos aparentes

Consideremos primero el movimiento heliocéntrico de Venus; suponiendo fijos al Sol en S y a la Tierra en T (véase la figura XIII.1), aceptemos que Venus describe alrededor del Sol una circunferencia VV’V’’V’’’.

cambia la posición del planeta respecto de las estrellas vecinas. Al ir de V’ a V’’’, pasando por V’’, su movimiento aparente será directo, y en V’’ pasará por la conjunción superior. Como su distancia a la Tierra es máxima, ofrecerá su tamaño aparente mínimo; al ir de V’’’ a V’ su movimiento aparente será retrógrado, y en el punto medio V pasará por la conjunción inferior a la mínima distancia de la Tierra y ofrecerá su diámetro aparente máximo, pero no su brillo máximo, ya que incluso será imperceptible a causa de la luz del Sol, pero poco antes y poco después de esta conjunción sí tendrá su brillo máximo.

Desde la Tierra se le verá oscilar de una y otra parte del Sol, sin apartarse más que el ángulo STV’. En los puntos de tangencia V’ y V’’’ el planeta parecerá estacionario, debido a que un pequeño arco de la órbita se confunde con la tangente y no

En virtud de la traslación de la Tierra, el Sol parecerá desplazarse sobre el Zodiaco en sentido directo, llevándose consigo la órbita del planeta, lo que alarga el arco directo de éste y acorta el retrógrado, pero sin ninguna otra modificación en las apariencias: cuando Venus se halla en su máxima elongación occidental en V (véase figura XIII.2), desde T el Sol y el planeta se ven proyectados en los puntos s y v del Zodiaco, y la elongación de Venus es el ángulo sTv. Algún tiempo después, la Tierra se ha trasladado a T’ y los puntos s y v del Zodiaco se ven sobre las direcciones T’s y T’v, paralelas respectivamente a Ts y Tv a causa de la inmensa distancia de las estrellas; el Sol se ve ahora proyectado en s’, de modo que ha tenido un desplazamiento zodiacal sT’s’. Al mismo tiempo, Venus se ha trasladado a V’, recorriendo sobre su órbita un arco VV’, mayor que el TT´ (la velocidad de órbita de Venus es mayor que la de la Tierra);

Figura XIII.1 V’’

desde T’ se le ve proyectado en v’, por lo que ha tenido un desplazamiento zodiacal vT’v’, mayor que el sT’s’ del Sol, pero del mismo sentido, es decir, directo, y se ha aproximado al astro central, ya que su elongación es ahora el ángulo s’T’v’, menor que el sT’v o el sTv.

zará a retroceder. En efecto, durante la digresión su distancia al Sol es el ángulo sTv; algún tiempo después, habiendo recorrido la Tierra el arco TT’ y Venus el VV’, mayor que el TT’, el Sol habrá tenido un desplazamiento zodiacal sT’s’, y Venus otro, vT’v’, de sentido opuesto, es decir, retrógrado, y el movimiento continuará en este sentido hasta unos 20 días después de la conjunción inferior, en que ocurrirá la estación y el cambio de sentido.

Después de la conjunción superior, Venus pasará al oriente del Sol, se hará vespertino y continuará avanzando sobre el Zodiaco más rápidamente que el Sol; se alejará de él cada vez más, hasta llegar a la digresión oriental en el punto de tangencia V (véase figura XIII.3), donde su velocidad de avance será igual a la del Sol, para ir disminuyendo luego la distancia angular entre los dos astros hasta que unos 20 días antes de la conjunción inferior Venus se estacionará y empe-

Consideremos ahora el movimiento de Marte como ejemplo de planeta exterior. Como primera idea, supongamos fijos al Sol en S (véase figura XIII.4) y a la Tierra en T, mientras Marte describe

Figura XIII.2

Figura XIII.3

la circunferencia MM’M’’M’’’; el planeta se hallará en conjunción en M (recuérdese que conjunción es cuando quedan en medio el planeta o el Sol; en este último caso es conjunción superior y el planeta está en su punto más lejano de la Tierra. Oposición es cuando la Tierra queda en medio), se hallará en oposición en M’’, y en cuadratura en M’ y en M’’’, cuando el ángulo Sol-Tierra-Marte sea de 90°. Estos serían los puntos de estación, porque el arco directo lo recorrería Marte de M’’’ a M’ con el punto medio en la conjunción M y el retrógrado de M’ a M’’’, con el punto medio en la oposición M’’. Pero el movimiento de la Tierra alarga el arco directo y disminuye el retrógrado porque el desplazamiento aparente que resulta en el Sol arrastra la órbita de Marte en un sentido igual al del primero y opuesto al del segundo. Así, las estaciones no se producen en las cuadraturas,

sino que se acercan a la oposición, que queda de todos modos en el punto medio del arco retrógrado.

Veamos ahora una explicación geométrica de los avances y retrocesos: estando el Sol en S (véase figura XIII.5), la Tierra en T y Marte en M, el planeta se hallará en la cuadratura oriental; el Sol se proyectará sobre un punto s del Zodiaco y Marte sobre otro m, y su elongación será el ángulo recto sTm. Algún tiempo después, habiendo recorrido la Tierra un arco TT’ y Marte el MM’, menor que el TT’, las nuevas posiciones del Sol y de Marte sobre el Zodiaco serán s’ y m’. Trazando T’s y T’m, paralelas a Ts y Tm, veremos que el Sol ha tenido un movimiento zodiacal sT’s’ y Marte otro mT’m’ del mismo sentido que el anterior,

Figura XIII.5

Figura XIII.4

XIII.6

esto es, directo pero menor, de modo que el planeta está yendo hacia la conjunción, después de la cual continuará aún el movimiento directo hasta algo después de la cuadratura occidental. En ésta (véase figura XIII.6), estando la Tierra en T, la elongación de Marte será el ángulo recto sTm; un tiempo después, al recorrer la Tierra el arco TT’ y Marte el MM’, menor que el TT’, las nuevas posiciones zodiacales de los dos astros observados serán s’ y m’; el Sol parecerá haber tenido el desplazamiento directo sT’s’ y Marte, el desplazamiento retrógrado mT’m’.

La elongación de Marte es ahora s’T’m’, mayor que el ángulo recto sTm; el planeta está cerca de la

oposición, que queda en el punto medio del arco retrógrado.

Distancia de los planetas al Sol

La distancia media de la Tierra al Sol, es decir, la longitud del semieje mayor de su órbita, es de unos 149.5 millones de kilómetros. Esta distancia se conoce como unidad astronómica (ua) y sirve para expresar las distancias a que se encuentran todos los astros del sistema solar. Las distancias medias de los planetas al Sol expresadas en ua son las siguientes, incluida la del planeta enano Ceres (mencionado al inicio del capítulo):

Planeta

Distancia al Sol (ua)

La serie de Bode nos permite obtener números muy aproximados a estas distancias, lo cual nos

CAPÍTULO

Figura

permite obtener una regla mnemotécnica bastante eficaz. En efecto, se anota un 0 y a continuación una progresión geométrica que empieza con 3 y cuya razón es 2:

0 3 6 12 24 48 96 192 384

A continuación se suman 4 unidades a cada número, con excepción de los tres últimos, y se dividen los resultados entre 10. Se obtiene así la serie:

Fases de los planetas

Al carecer de luz propia y sólo brillar por la luz del Sol, los planetas presentan fases. Consideremos primero un planeta inferior P (véase figura XIII.7) y supongamos al Sol en S y a la Tierra en T.

Los términos de la serie corresponden aproximadamente a las distancias, en ua, de Mercurio, Venus, Tierra Marte, Ceres, Júpiter, Saturno y Urano, pero no a la de Neptuno, que sería la única excepción.

Durante la conjunción inferior, el planeta P muestra a la Tierra su lado oscuro y podemos llamarle planeta nuevo; es invisible por ello, además de que pasa de día sobre el horizonte. Algunos días después la superficie del planeta ya es visible en la Tierra, en forma de hoz, hasta que ocurre su digresión occidental, en que el planeta alcanza su cuarto creciente. Ya en la conjunción superior el planeta es lleno aunque invisible, porque se pierde entre los rayos del Sol. En la segunda parte de la revolución sinódica se repiten los fenómenos anteriores.

Los mejores días para observar Mercurio son los de los cuartos creciente y menguante, es decir, cuando está en digresión, ya que es cuando menos estorba la luz solar. En cuanto a Venus, alcanza su brillo máximo cuando se halla a unos 39° del Sol, como 35 días antes y después de la conjunción, cuando su fase es análoga a la de la Luna en su quinto día.

Los planetas exteriores presentan también fases, aunque incompletas y muy poco sensibles. En primer lugar, el planeta es lleno tanto en oposición como en conjunción, ya que tanto desde T (véase figura XIII.8) como desde T’’ vemos su hemisferio iluminado y sólo cerca de las cuadraturas puede verse desde la Tierra T’’ una parte aob

Figura XIII.7

del hemisferio oscuro, tanto más pequeña cuanto más lejano es el planeta. En efecto, el ángulo aob del huso oscuro vuelto hacia la Tierra es igual al ángulo SoT’, y mientras mayor sea la distancia So menor será ese ángulo, toda vez que el lado ST’ es constante. En rigor, de los planetas exteriores sólo

Marte presenta fases sensibles, aunque la parte alumbrada de su disco es siempre de más de siete octavos de su disco total.

Tierra. Mercurio y Venus no tienen satélites; la Tierra tiene a la Luna. Marte tiene dos: Deimos y Fobos, tan pequeños que sólo son perceptibles con telescopios potentes. Júpiter tiene 63, de los cuales los cuatro principales, llamados Io, Europa, Ganimedes y Calixto pueden verse con anteojos de mediana potencia. Saturno tiene 200, siendo Titán el mayor de ellos, y es el único que cuenta con una atmósfera importante; su diámetro es mayor que el de Mercurio. Urano tiene 27, de los cuales los dos más grandes son Titania y Oberón. Neptuno tiene 13, siendo Tritón el más grande.

En general, los satélites se mueven alrededor de sus planetas en el mismo sentido que éstos en torno al Sol, sentido que es igual al de la traslación de la Tierra; sin embargo, algunos se mueven en sentido contrario, como tres de Júpiter, uno de Saturno, cuatro de Urano y uno de Neptuno.

Saturno lleva consigo, además de sus satélites, un sistema de anillos concéntricos, brillantes, separados por intervalos circulares oscuros. Estos anillos, constituidos por partículas de hielo y minerales, y con dimensiones que varían desde unas cuantas micras hasta algunos metros, pueden verse con anteojos de poca potencia.

Satélites

Alrededor de algunos planetas del Sistema Solar se mueven satélites , astros que giran en torno a los planetas, como la Luna alrededor de la

Ejercicios propuestos

1. Explicar gráficamente el retroceso de Venus desde poco antes hasta poco después de su conjunción inferior.

Figura XIII.8

2. Explicar gráficamente el avance de Marte desde poco antes hasta poco después de su conjunción.

3. Sabiendo que la luz recorre 300,000 km por segundo, ¿cuánto tiempo tarda en llegar del Sol a la Tierra?, ¿cuánto del Sol a Neptuno?

CAPÍTULO XIV

Breve descripción de los planetas del Sistema Solar

La verdad matemática prefiere palabras simples, ya que el lenguaje de la verdad es simple en sí mismo. tyCho brAhe (1546-1601)

Mercurio

Es el planeta más cercano al Sol; no es visible en sus conjunciones debido a la luz del Sol, pero cuando está en digresión es perceptible a simple vista, y por ser ésta de 29°, sólo puede verse unas dos horas antes de la salida del Sol y dos horas después de su ocaso. Su distancia media al Sol es de 0.39 ua o 58 millones de kilómetros. El radio de Mercurio es 0.38 del radio terrestre, su densidad es de 5.4 y la atracción de su superficie es 0.41 de la terrestre. La temperatura superficial mínima es de 90 K, mientras que la máxima es de 700 K (para

las unidades de temperatura, véase el apartado primero del capítulo XIX).

La órbita de Mercurio es la más excéntrica de los planetas del Sistema Solar; está inclinada 7° sobre la eclíptica. Su excentricidad es de 0.20, lo que da una diferencia de 24 millones de kilómetros entre la distancia afélica (distancia máxima al Sol) y la perihélica (distancia mínima al Sol) del planeta, que produce una variación notable de la temperatura superficial.

La revolución sideral de Mercurio es de 88 días; la sinódica, de 116 días. La velocidad de su órbita

es de 48 km/s. Su rotación dura 58.7 días. No tiene satélites.

El aspecto telescópico de Mercurio cuando está cerca de la elongación máxima es semejante al de la Luna en cuarto creciente: medio disco brillante, en el que se ven manchas grises sobre el planeta y, en mayor acercamiento, se observa una gran cantidad de cráteres (véase figura XIV.1, p. 131).

Así como la Luna produce eclipses de Sol en algunas conjunciones, también Mercurio en alguna conjunción inferior llega a proyectarse sobre el Sol como un punto negro y lo cruza. Este fenómeno se conoce como tránsito de Mercurio, y el más reciente ocurrió el 8 de noviembre de 2006 (véase figura XIV.2, p. 131); el más próximo ocurrirá el 9 de mayo de 2016.

Venus

Es el planeta de mayor albedo, que es la razón entre la cantidad total de la luz del Sol reflejada por un cuerpo esférico en todas direcciones y la cantidad de luz que recibe; su albedo es de 0.59. Es tan brillante que a veces es perceptible a simple vista en pleno día. La temperatura media en la superficie es de unos 750 K. En la figura XIV.3 (p. 131) puede verse una fotografía del planeta.

La distancia media de Venus al Sol es de 0.72 ua.

Su digresión es de 47°, por lo que sólo se le puede ver unas tres horas antes de la salida del Sol o de su ocaso.

La órbita de Venus es la menos excéntrica de los planetas solares: 0.007, por lo que puede con-

siderarse circular; su inclinación es de 3.5° sobre la eclíptica. Su revolución sideral es de 225 días; la sinódica, de 584 días. Su rotación es de sentido contrario a la de la Tierra y demás planetas, y dura más que su año sideral: 243 días.

El radio de Venus es de 6,052 km, su masa es 0.82 de la terrestre, su densidad es de 0.88 y la atracción en su superficie es 0.85 de la de la Tierra. Este planeta cuenta con amplias llanuras y muchos volcanes.

Venus tiene una muy densa atmósfera que imposibilita cualquier observación directa de la superficie del planeta; los cielos de este planeta son atravesados por imponentes conglomerados nubosos. El espesor de dicha atmósfera es de 70 km y está compuesta en 96.5% por dióxido de carbono, 3.4% de nitrógeno y el resto por argón, dióxido de azufre, vapor de agua, helio, neón y oxígeno.

Al igual que el tránsito de Mercurio, ocurre periódicamente el tránsito de Venus, fenómeno exclusivo de estos dos planetas por ser interiores. Como ya se ha tratado, sólo se produce cuando, además de estar en conjunción inferior, el planeta se encuentra muy cerca de la línea de los nodos. Los tránsitos de Venus son raros pero periódicos: a los 122 años de un tránsito ocurre otro que se repite ocho años después; transcurren luego otros 105 años para que se pueda observar uno más, el cual se repite a los ocho años, periodo después del cual vuelve a observarse un nuevo tránsito a los 122 años. Los últimos tránsitos observados de

Venus fueron en junio de 2004 y el 5 de junio de 2012, y los próximos serán en 2117 y en 2125.

En la figura XIV.4 (p. 132) puede verse la secuencia de fotografías del tránsito de Venus en junio de 2004 durante su cruce por el Sol, y en la figura XIV.5 (p. 132) se observa el tránsito del 5 de junio de 2012.

Tierra

Nuestro planeta tiene un diámetro medio de 12,742 km. Los 5/7 de su superficie, es decir, unos 360 millones de kilómetros cuadrados, están ocupados por las aguas oceánicas. La forma de la Tierra puede considerarse esférica, aunque para mayor exactitud es la de un elipsoide de revolución, teniendo en cuenta el achatamiento polar.

Alrededor de la superficie terrestre se encuentra la atmósfera, compuesta por gases como oxígeno, nitrógeno, dióxido de carbono, hidrógeno, helio, argón, etc., cuyas proporciones varían con la altitud. Las capas inferiores del aire son las más densas y se enrarecen con la altura. A unos 10 km no tienen la densidad necesaria para que sea posible la vida humana, y hasta aquí esta capa gaseosa se llama troposfera (espesor de 5 km en los polos y de 13 km en el Ecuador). Las capas superiores se denominan estratosfera. En la figura XIV.6 de la página 132 pueden verse las capas que componen nuestra atmósfera, así como la variación de la temperatura con la altura sobre el nivel del mar.

Como se vio, la revolución o año sideral de la Tierra dura 365.2564 días, mientras que la revo-

lución sinódica toma 365.2422 días. La excentricidad de su órbita es de 0.017 y su distancia media al Sol es de 1 ua, esto es, 149.5 millones de kilómetros. La rotación de nuestro planeta alrededor de su eje toma 23 h 56 min 03 segundos.

La densidad de la Tierra es de 5.52, que excede a la de las rocas superficiales que es de 2.5 a 3.0, por lo que seguramente en el interior del globo terrestre existen materiales con densidad mayor, por ejemplo, de 7.7 como el hierro, de 13.6 como el mercurio, etcétera.

La masa de la Tierra es de 5.975 × 1024 kg (la de Sol es 333,420 veces mayor, es decir, de 1.99 × 1030 kg).

En la figura XIV.7 de la página 133 puede verse una fotografía de nuestro planeta tomada el 4 de enero de 2012 desde un satélite de la NASA.

Marte

Junto con Mercurio, Venus, Júpiter y Saturno, este planeta fue conocido desde la Antigüedad y nombrado “el planeta rojo” al presentar esa coloración, que hoy se sabe se debe a la presencia de arena, rica en hierro oxidado, que existe en sus amplios desiertos. El planeta aparece registrado en el Almagesto, un tratado de astronomía escrito en el siglo II de nuestra era por Claudio Ptolomeo, de Alejandría. La rotación de Marte dura 24 h 37 min 22.6 s y su distancia media al Sol es de 1.52 ua. Su revolución sideral es de 687 días y la sinódica, de 780 días; la excentricidad de su órbita es 0.093. Tiene dos satélites: Deimos y Fobos. En la figu-

ra XIV.8 (p. 134) puede verse una fotografía de Marte, y en la parte superior central, el polo norte. El diámetro de Marte es un poco mayor que el radio terrestre, ya que es de 6,787 km; su órbita tiene una inclinación de 1° 44’ respecto a la eclíptica. Marte recibe menor cantidad de luz y de calor del Sol que la Tierra (cerca de la mitad) debido a que su distancia al astro central es mayor que la de nuestro planeta.

Puesto que la inclinación del ecuador de Marte sobre el plano de su órbita es de 25° 11’ (casi igual a la oblicuidad de la eclíptica) debe de tener estaciones parecidas a las nuestras, aunque de mayor duración, por ser el año marciano más largo que el terrestre.

La atmósfera de Marte, que en los polos tiene un espesor de 8 km y en el ecuador de 15 km, está compuesta principalmente de los siguientes elementos: dióxido de carbono, 95% (Tierra, 0.04%), nitrógeno, 2.7% (Tierra, 78%); argón, 1.6% (Tierra, 0.9%); oxígeno, 0.13% (Tierra, 21%); agua, 0.03% (Tierra, 0.4%) y neón, 0.00025% (Tierra, 0.002%). El dióxido de carbono, el más abundante en la atmósfera de Marte, se congela en los polos durante el invierno y se evapora en la primavera. Ello se nota claramente en las observaciones del planeta durante tales estaciones, ya que las dimensiones de la parte blanca de los polos cambian en forma importante.

Marte no presenta fases como Mercurio o Venus; ni siquiera se le ve como media luna. Su fase más notable se observa cuando está en cuadratura,

que es cuando tiene un aspecto semejante a la fase lunar dos o tres días antes del plenilunio (véase figura XIV.9, p. 134).

Telescópicamente, Marte presenta brillantes manchas blancas en sus polos, que con los cambios de estaciones aumentan o disminuyen; esas manchas se deben a la nieve de los casquetes polares, que está sujeta a variaciones análogas a los polos de la Tierra. También se observan en el planeta grandes manchas oscuras llamadas mares y otras más chicas denominadas lagos, que por lo general están unidas por líneas delgadas, casi rectas, que han sido llamadas canales, que son cauces de ríos antiguos muy amplios que fluyeron hace millones de años.

En cuanto a la creencia antigua de que en Marte existe vida, se sabe que desde antes de que las misiones del programa Viking de la NASA llegaran a Marte, en 1976, la mayoría de los astrónomos habían abandonado la esperanza de encontrar vida. Ya sabían que el planeta no tenía sistemas de canales ni agua superficial, que había muy poco oxígeno en su atmósfera y que no existían cambios estacionales de vegetación. Con la esperanza de que alguna forma de vida microbiológica hubiera sobrevivido a la fecha, el Viking iba preparado con experimentos diseñados para detectar actividad biológica. En la figura XIV.10 (p. 134) puede verse una fotografía tomada por la misión Viking.

Los tres experimentos biológicos del Viking supusieron alguna similitud básica entre las

hipotéticas bacterias marcianas y las de la Tierra. Un primer experimento de intercambio de gases ofreció un caldo nutriente para cualquier organismo presente en una muestra de suelo marciano y rastreaba gases que señalaran alguna actividad metabólica; otro experimento agregó al suelo componentes con contenido de carbón radiactivo, para esperar resultados que señalaran que los supuestos organismos marcianos habían ingerido o inhalado el carbón. El tercer experimento consistió en agregar a una muestra de suelo y atmósfera marcianos dióxido de carbono radiactivo, después retirarlo y probar el suelo, calentándolo, para ver si algún organismo había absorbido el dióxido.

Al principio, parecía que los tres experimentos habían dado señales positivas. Sin embargo, estudios subsecuentes muy cuidadosos condujeron a que los resultados podían ser explicados por reacciones químicas inorgánicas (sin vida). Así, no se tiene evidencia clara de vida, ni siquiera microbiana, en la superficie de Marte.

El 25 de mayo de 2008 llegó a Marte la misión Phoenix Mars Lander y sus hallazgos sugieren que existió agua líquida en su superficie. En 2010, científicos de la UNAM y de la NASA, al analizar las muestras obtenidas en tal misión, descubrieron compuestos orgánicos que abren la posibilidad de que exista vida microorgánica. Se tendrán que esperar los resultados de la misión de 2012 para saber si tales compuestos son de origen biológico o abiótico. Hasta el momento de

la edición de este libro, la NASA no ha publicado resultados, y al parecer no han sido exitosos los intentos de detectar señales por parte del equipo enviado.

Planetoides entre Marte y Júpiter

A fines del siglo XVI, considerando la gran distancia que existe entre Marte y Júpiter (550 millones de kilómetros), Kepler sospechó de la existencia de un planeta cuya órbita estuviera entre las de tales planetas; lo buscó, mas no lo encontró.

No fue hasta 1801 que el astrónomo italiano Piazzi descubrió un planetoide al que llamó Ceres; un año más tarde, Olbers descubrió el planetoide Pallas; en 1804 fue descubierto Juno por Harding. En 1807 Olbers descubrió otro planetoide, el más brillante de todos, al que llamó Vesta, que llega a ser perceptible a simple vista, al igual que Ceres. En 1846 Encke descubrió Astrea y desde 1847 el número fue aumentando; raro era el año en que no se descubrían dos o tres más. En 1954 el número era ya de 1,500, y a la fecha es de alrededor de 18,000. En la página 135, figura XIV.11, puede verse una fotografía de Ceres, y en la figura XIV.12 de la misma página, otra de Vesta.

El más reciente descubrimiento fue en 2005, cuando un grupo de astrónomos polacos encontró un planetoide doble, al que llamaron Lundia; el diámetro de cada uno es de 6 km y están separados 35 km; giran cada uno en torno del otro cada 15 horas, de modo que se eclipsan cada 7.5 horas.

Júpiter

En el cielo, este planeta se ha distinguido de las estrellas desde tiempos remotos. Su brillo es inferior al de Venus, pero llama la atención cuando su distancia a la Tierra es mínima, al estar en oposición; su albedo es de 0.44. Es el planeta más grande del Sistema Solar, con un diámetro de 142,800 km, es decir, 11 veces el de la Tierra. Su densidad es de 1.33, cuatro veces menor que la de la Tierra, lo que indica que una gran parte de su volumen está constituido por materia que se encuentra todavía en estado gaseoso.

Júpiter recorre su órbita en 11.86 años, con una excentricidad de 0.048, y su revolución sinódica dura 399 días. Su rotación dura 9 h 50 min 30 s y su distancia media al Sol es de 5.2 ua. Su ecuador está inclinado 3° 05’ con respecto al plano de su órbita, por lo que prácticamente no tiene estaciones ni variaciones en la duración de los días, con excepción de los polos.

Visto con un telescopio de mediana potencia, Júpiter aparece surcado por unas nueve bandas paralelas al ecuador y entre sí (véase figura XIV.13, p. 135), las que llegan a variar en su forma en unas cuantas horas, debido a la presencia de gases en su atmósfera, que está compuesta por hidrógeno en 87% y por helio en casi 13%; contiene además metano, amoniaco y vapor de agua, que sumados no alcanzan 0.1 por ciento.

En 1979, la sonda Voyager 1 descubrió que este planeta posee un sistema de anillos muy tenue, que no es visible desde la Tierra. El anillo prin-

cipal tiene unos 6,400 km de ancho y un espesor de 10 kilómetros.

Júpiter tiene 66 satélites; los cuatro mayores fueron descubiertos por Galileo en 1610, quien los denominó Io, Europa, Ganimedes y Calixto, con diámetros respectivos de 4,000, 3,430, 5,800 y 4,830 kilómetros.

En marzo de 1979, las sondas espaciales Voyager 1 y 2 descubrieron anillos del planeta, con un espesor óptico muy reducido. En 1989 apareció una mancha de color rojizo de contornos bien definidos, la cual es una tormenta de diámetro mayor que el de la Tierra y de duración posiblemente perpetua (ha durado más de 130 años) que alcanza velocidades de hasta 500 km/h (véase en la p. 135 figura XIV.14, parte inferior).

Saturno

Este planeta fue conocido desde la remota antigüedad, lo mismo que Venus, Marte y Júpiter, por ser perceptible a simple vista como una estrella amarillenta de primera magnitud. Se ve surcado por bandas como las de Júpiter, aunque no tan notorias. La duración de su rotación es incierta por no tener superficie visible y por girar su atmósfera en diferentes periodos en cada latitud. Así, se conoce en forma aproximada, aceptándose 10 h 45 min 45 s. Su albedo es de 0.46.

El diámetro ecuatorial de Saturno es de 120,536 km y el polar de 108,728 km. Gravita en una órbita elíptica de 0.056 de excentricidad y su distancia media al Sol es de 9.539 ua. Su revolu-

ción sideral es de 29.48 años y la sinódica dura 378 días.

La densidad de este planeta es de 0.72 debido a que tiene grandes masas de gases y nubes que reflejan la luz del Sol. En efecto, su atmósfera contiene 90% de hidrógeno y 5% de helio; el resto consiste en amoniaco y metano. En noviembre de 2007 se detectaron tormentas que duraron casi ocho meses. En diciembre de 2010 una enorme tormenta duró 200 días y rodeó el planeta (véanse manchas blancas en la parte superior de la figura XIV.15, p. 136).

Saturno presenta anillos que lo rodean (véanse figuras XIV.15, XIV.16 y XIV.17 en pp. 135 y 136) y Galileo los vio en 1610. En 1680, Cassini observó que eran dos anillos concéntricos, separados por una raya negra conocida como división de Cassini (véase figura XIV.16, p. 136). Con un telescopio potente se distinguen tres anillos principales: el A, el B y el C (véase figura XIV.17, p. 136); entre los dos primeros se encuentra la división de Cassini. El anillo exterior A es menos brillante que el B; entre A y F hay una finísima división conocida como división de Encke . El anillo C es mucho menos luminoso que el A. Hacia el exterior de F hay aún dos anillos que son más oscuros que éste.

Los anillos están compuestos de partículas de hielo y algunos minerales, con dimensiones que varían de unas cuantas micras a varios metros. Saturno cuenta con 200 satélites, de los cuales el mayor es Titán, con un diámetro de 5,160 km, es decir, más grande que el planeta Mercurio;

además, es el único satélite del Sistema Solar que cuenta con una atmósfera importante.

Urano

Este planeta, a diferencia de los ya tratados (que fueron conocidos desde épocas inmemoriales), fue descubierto por Herschel en 1781; gira alrededor del Sol a una distancia media de 19.19 ua con una excentricidad de 0.046. No se percibe a simple vista, ya que brilla como una estrella de sexta magnitud.

El diámetro de Urano es de 51,118 km y su densidad es de 1.24. Recorre su órbita en 84 años y su revolución sinódica dura 369.16 días.

Visto con telescopio es de color verdoso y tiene algunas bandas como las de Saturno (véase figura XIV.18, p. 137). En 1977 se descubrió que tiene un sistema de anillos, aunque tenues y oscuros. Su atmósfera está constituida en 84% por hidrógeno, 14% por helio y 2% por metano. Su rotación dura 17 h 14 minutos.

Urano tiene 27 satélites, de los cuales los más grandes son Titania y Oberón.

Neptuno

Este planeta fue descubierto por el francés Urbain Jean Joseph Le Verrier en 1846, al observar que la órbita teórica de Urano sufría perturbaciones y que las provocaba algún cuerpo celeste. Luego de hacer sus cálculos basados en la ley de Newton, anunció la posición ocupada por el astro perturbador, con lo que los astrónomos alemanes Galle

y Encke encontraron dicho astro, que más tarde fue llamado Neptuno.

El razonamiento matemático de Le Verrier fue que si Urano se separaba una cierta distancia de su órbita, entonces en las épocas de máxima perturbación debía estar cerca del cuerpo o planeta perturbador y la masa de éste debía ser proporcional al efecto producido, de acuerdo con la distancia asignada por la ley de Bode. En el supuesto de que esta distancia no coincidiera con la de Bode –en efecto, no coincide–, bastaba suponer una masa distinta.

Encke le escribió a Le Verrier así:

Permítame, señor, felicitarlo sinceramente por el admirable descubrimiento con el que usted ha enriquecido a la astronomía. Su nombre quedará vinculado a la más brillante prueba que pueda imaginarse de la atracción universal.

El procedimiento seguido por Le Verrier sirvió más tarde a los astrónomos estadounidenses

Lowell y Pickering para descubrir Plutón.

La rotación de Neptuno tarda 16 h 6 min 36 s; su diámetro es de 49,528 km. Recorre una elipse que es casi una circunferencia (su excentricidad es de 0.009) a una distancia media del Sol de 30.071 ua, en 164.8 años. Tiene una revolución sinódica de 367.5 días. Su atmósfera está compuesta en 85% por hidrógeno, 13% helio y 2% metano.

Neptuno tiene 13 satélites, de los cuales el más grande es Tritón. Brilla como un astro de octava magnitud, con una coloración azulosa (véase figura XIV.19, p. 137; se ven cuatro de sus satélites).

Tiene un sistema de anillos tenue, semejante al de Júpiter, que fue descubierto parcialmente en 1968 y plenamente en 1989 por la sonda espacial Voyager 2.

CAPÍTULO XV

Cometas

No sé qué armas serán usadas en la Tercera Guerra Mundial, pero sé que en la cuarta serán palos y piedras. Albert eiNsteiN (1879-1955)

Características

Los cometas son astros que giran, como los planetas, alrededor del Sol de acuerdo con la Ley de Gravitación Universal; difieren de los planetas por su estructura y porque sus órbitas son, en general, más alargadas. Las de los planetas son poco excéntricas, aunque las de varios planetas menores tienen mayor excentricidad.

Por lo que se refiere a su aspecto, existen los grandes cometas que se perciben a simple vista y los muy pequeños que sólo pueden verse con telescopio; éstos son los más numerosos.

Los grandes cometas constan por lo regular de núcleo, cabellera y cauda (véase figura XV.1, p. 137). El núcleo, que en algunos alcanza a ser tan brillante como Venus, se ve rodeado por la

cabellera, que es nebulosa, redonda y cuyo brillo disminuye del núcleo hacia la periferia, en forma tan gradual que a veces es imposible distinguir la frontera entre el núcleo y la cabellera. La cauda o cola parece una prolongación de la cabellera y se extiende a grandes distancias, de modo que llega a abarcar 90° o más en el cielo; es tan tenue que no empaña el brillo de las estrellas sobre las que se proyecta.

En general, la cauda permanece opuesta al Sol, sobre la prolongación del radio vector de la órbita del cometa (véase figura XV.2, p. 137).

Los cometas telescópicos o pequeños tienen el aspecto de una nebulosidad redonda o alargada en forma de puro a causa de una pequeña cauda que, al contrario de lo que ocurre en los grandes come-

tas, suele dirigirse hacia el Sol. El núcleo es poco perceptible, por lo que la característica principal de este tipo de cometas es la cabellera.

Cuando se aproxima al Sol, un cometa puede ver fraccionado su núcleo en dos o más partes; ha habido cometas que al fraccionarse dejan esparcidas en su órbita porciones sólidas que al cruzar la atmósfera terrestre se ven como estrellas errantes o fugaces.

Conforme los cometas van cumpliendo con sus órbitas y pasando cerca del Sol, también van sublimando su material ( sublimar: pasar directamente un cuerpo del estado sólido al gaseoso) y perdiéndolo consecuentemente, con lo que disminuye su magnitud. Después de cierto número de órbitas el cometa se habrá apagado y se convertirá en un asteroide, ya que no podrá recuperar masa.

Los cometas causaban en la Antigüedad admiración y temor: lo primero por su gran tamaño aparente y por su brillo; temor, porque a causa de su aumento gradual de brillo y dimensiones aparentes conforme llega al perihelio (distancia más cercana al Sol) se pensaba que chocaría con nuestro planeta.

Visibilidad

Caracteriza a los cometas el lapso limitado en que permanecen visibles, generalmente de unos días o unas semanas. Sin embargo, el periodo de visibilidad de algunos es amplio. De éstos puede citarse el gran cometa de 1811, que fue visible a

simple vista durante 260 días; apareció en marzo de 1811 y fue visible hasta junio, que fue cuando se perdió de vista por su cercanía al Sol; reapareció nuevamente en agosto y en septiembre pasó a 1.1 ua del Sol; finalmente desapareció en noviembre; se estimó que su núcleo medía entre 30 y 40 km; su periodo orbital es de más de 3,000 años.

Otros ejemplos de larga duración son: a) el cometa de 1865, que fue observado durante un año; b) el cometa Brooks, observado en 1889 y en 1890 durante 556 días; también fue visto en 1896, 1903 y 1911, por lo que su periodo era de siete años; en 1918 ya no se le vio y no se ha vuelto a observar; c) el cometa 1927 IV, que pudo observarse durante cuatro años.

Composición

Los cometas están compuestos de agua, hielo seco, amoniaco, metano, hierro, magnesio, sodio y silicatos. Los núcleos de los cometas llegan a tener diámetros de varias decenas de kilómetros. Al acercarse al Sol, el núcleo se calienta y una parte se sublima, los gases se proyectan hacia atrás y ello motiva la formación de la cola, que se puede extender millones de kilómetros. Se estima que en promedio un cometa puede pasar unas dos mil veces cerca del Sol antes de sublimarse completamente. A lo largo de su trayectoria, un cometa va dejando grandes cantidades de pequeños fragmentos de material, que penetran en la atmósfera terrestre en forma de estrellas fugaces cuando nuestro planeta atraviesa su órbita.

Masa

La masa de los cometas es muy pequeña. En efecto, no hay refracción (cambio de dirección de una onda al pasar de un medio material a otro) en la cabellera; la cola y el núcleo son transparentes, no proyectan sombra sobre el disco del Sol cuando pasan entre éste y la Tierra, y no perturban las órbitas de los planetas ni de sus satélites.

La mejor prueba de la pequeñísima densidad de los cometas es su transparencia, ya que las estrellas pueden verse a través de ellas. Se ha determinado que la masa del cometa más grande tiene sólo un cienmilésimo de la masa terrestre. El cometa Halley tiene una masa de 1 2 × 1014 de la masa de la Tierra.

Órbitas

A diferencia de las órbitas de los planetas, las de los cometas son muy alargadas y pueden ser cerradas o abiertas. Puesto que tienen masas muy pequeñas, casi no influyen gravitatoriamente en los planetas. Por el contrario, el Sol y los planetas gigantes Júpiter y Saturno alteran con frecuencia las órbitas de los cometas; una de estas alteraciones es la captura de cometas por parte de los planetas, que los transforman en cometas de periodo más corto del que tenían. Así, por ejemplo, Júpiter tiene una familia de más de 60 cometas cuyo afelio (punto de su órbita más lejano al Sol) se localiza cerca de la órbita de este planeta. También Saturno, Urano y Neptuno tienen familia de cometas.

Las órbitas cerradas son elípticas de gran excentricidad alrededor del Sol y se pueden observar cada vez que vuelven a estar cerca de él, y por eso se les llama cometas periódicos

Las órbitas abiertas son hiperbólicas o parabólicas; los cometas con estas órbitas aparecen una sola vez; surgen de las profundidades del espacio, se acercan al Sol y se alejan, para luego desaparer por siempre.

Las órbitas cometarias tienen muy distintas inclinaciones sobre el plano de la eclíptica. Algunas de ellas presentan una inclinación mayor de 90°, por lo que los cometas que las poseen se mueven en sentido retrógrado, por ejemplo, el cometa Halley.

Cometas notables

Entre los más famosos cometas pueden citarse los siguientes:

Encke. Es el de menor periodo de todos los conocidos: 3.3 años; fue descubierto en 1819 por el astrónomo alemán Johann Encke. Apenas es visible a simple vista y ha sido observado en sus últimos pasos por el perihelio en 2000, 2003, 2007 y 2010.

Biela. El astrónomo austriaco Wilhelm von Biela determinó su órbita en 1826, aunque ya había sido visto en 1772 y 1805. Por malas condiciones de visibilidad no se le volvió a ver hasta 1845, ya fraccionado en dos. Cuando volvió a aparecer en 1852 las dos partes estaban 10 veces más separadas. En 1877, en que debía volver a presentarse, se

observó durante seis horas una hermosa lluvia de estrellas. No se le ha vuelto a ver desde entonces.

Halley. Es grande y brillante, con periodicidad de 75 a 76 años en promedio, que fue determinada en 1705 por el astrónomo inglés Edmund Halley, aunque fue observado por chinos y caldeos en 240 a.C. En mayo de 1910, la Tierra pasó a través de su

cauda, que llegó a abarcar una extensión de 180°, es decir, todo el cielo, de Este a Oeste. Durante su más reciente aparición en 1986, se convirtió en el primer cometa observado por naves espaciales, con lo que se encontró que está compuesto de polvo, materiales no volátiles y sólo una pequeña parte de su superficie está cubierta de hielo.

CAPÍTULO IV. Coordenadas geográficas

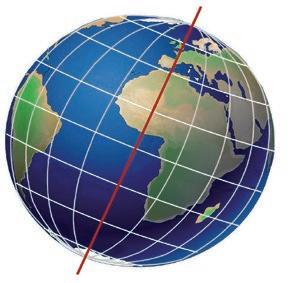
CAPÍTULO X. Las estrellas

(Benetnasch, Alkaid)

80 (Alcor)

(Mizar)

(Alioth)

(Megrez)

(Phekda, Phad)

(Merak)

Osa Menor (UMi)

(Pherkad)

(Kochab)

(Yildum, Pherkard)

(Polaris, Polar)

(Dubhe)

Osa Mayor (UMa)

Osa

Figura IV.2

Figura X.1

Figura X.2

Cisne Lira

Dragón

Meridiano

Casiopea

CAPÍTULO X. Las estrellas

Mirfak

Capela

Cástor

Pólux

Géminis

Can Menor

Auriga

El Nath

Aldebarán

Betelgueuse

Triángulo de invierno

Sirio

Can Mayor

Adhara

Almak

Perseo

Pléyades

Híades

Tauro

1 2

6 7 3 45

Orión

Menkar en la Ballena Cursa

Eridano

Rigel

Liebre

CAPÍTULO XI. El Sol

Eje de la Tierra

Círculo Ártico

Trópico de Cáncer

Ecuador

Trópico de Capricornio

Círculo Antártico

Figura X.3

Figura X.4

Figura XI.5

Arcturus -0.1

Alkaid 1.9

Alioth 1.8

Dubhe 1.8

CAPÍTULO XIV. Breve descripción de los planetas del Sistema Solar

Figura XIV.1

Figura XIV.3

Figura XIV.2

Mercurio

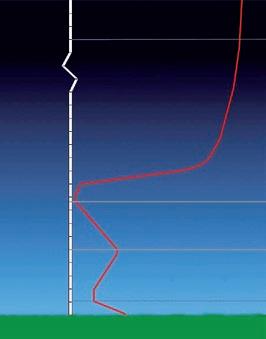
CAPÍTULO XIV. Breve descripción de los planetas del Sistema Solar

Figura XIV.6

Figura XIV.5

Figura XIV.4

Troposfera Estratosfera

Mesosfera

Exosfera

CAPÍTULO XIV. Breve descripción de los planetas del Sistema Solar

Figura XIV.7

CAPÍTULO XIV. Breve descripción de los planetas del Sistema Solar

Figura XIV.8

Figura XIV.9

Figura XIV.10

CAPÍTULO

XIV. Breve descripción de los planetas del Sistema Solar

Figura XIV.13

Figura XIV.14

Figura XIV.11

Figura XIV.12

CAPÍTULO XIV. Breve descripción de los planetas del Sistema Solar

Figura XIV.16

Figura XIV.17

División Cassini División Encke

A Anillo F

Figura XIV.15

CAPÍTULO XIV. Breve descripción de los planetas del Sistema Solar

CAPÍTULO XV. Cometas

Figura XIV.19

Figura XV.1

Figura XV.2

Figura XIV.18

CAPÍTULO XVI. Astrolitos

Figura XVI.3

Figura XVI.2

Figura XVI.4

Península de Yucatán

Cráter de Chicxulub Cenotes

CAPÍTULO XVII. El Universo

Figura XVII.1

Figura XVII.2

Sistema Solar

CAPÍTULO XVII. El Universo

Figura XVII.3

CAPÍTULO XVIII. Varios temas

Figura XVIII.9

Figura XVIII.8

Figura XVIII.10

CAPÍTULO XVIII. Varios temas

Figura XVIII.11

Figura XVIII.12 FIGURAS

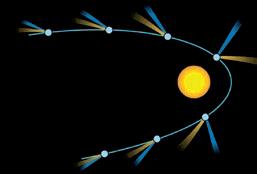
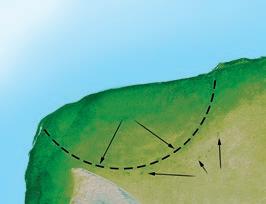
CAPÍTULO XVIII. Varios temas

Figura XVIII.14

Figura XVIII.13

Figura XVIII.19

Norteamérica

Océano Panthalassa

Océano

Sudamérica

CAPÍTULO XVIII. Varios temas

Figura XVIII.21

Figura XVIII.20

Triásico Hace 200 millones de años

Ecuador

Mar Tethys

Laurasia

CAPÍTULO XVI

Astrolitos

Un charlatán que no cree un poco en sus propias imposturas no es un buen charlatán. JeAN-Pierre lumiNet

Meteoritos o estrellas fugaces

Si se observa el cielo sin nubes y sin Luna, es común ver de manera repentina un punto luminoso que recorre muy rápidamente cierta trayectoria y desaparece; ese punto se conoce como meteorito, astrolito o estrella fugaz, aunque no se trata de ninguna estrella. Si el fenómeno se repite a cortos intervalos, se dice que hay lluvia de estrellas.

Visibilidad

Si un fragmento de materia extraterrestre penetra en nuestra atmósfera, la resistencia que le opone el aire hace disminuir su velocidad y cambiar de dirección, y la obliga a seguir una perpendicular a la órbita terrestre. El calor producido por la fricción eleva la temperatura del cuerpo hasta los 4,000° C,

lo vuelve incandescente, volatiliza los fragmentos pequeños y oxida los grandes. Por su incandescencia, dichos fragmentos se hacen visibles durante segundos o fracciones de segundo.

Origen

Hasta mediados del siglo XIX, se creía que los meteoritos eran fenómenos atmosféricos que se originaban en las capas superiores de la atmósfera. Con observaciones cuidadosas, los astrónomos notaron que en ciertas épocas del año estos cuerpos parecían proceder de regiones definidas del cielo. Pronto surgió una teoría, ya confirmada, según la cual se trata de “enjambres” de corpúsculos que circulan alrededor del Sol siguiendo órbitas elípticas que al cruzar la atmósfera terres-

tre (véase figura XVI.1) se hacen visibles por su incandescencia.

Como se mencionó en el capítulo anterior, al desaparecer el cometa Biela después de su desdoblamiento, debía reaparecer en 1877; sin embargo, en vez de ello, se observó una copiosa lluvia de estrellas fugaces que duró seis horas; se estimó en 14,000 el número de estelas meteóricas. Con ello se confirmó que los fragmentos cometarios y de asteroides son la causa principal de que existan los meteoritos. Sin embargo, de acuerdo con los estudios que se han realizado en muchos astrolitos, al parecer algunos de ellos provienen de la Luna y otros de Marte.

En noviembre de 1799 se observó una lluvia de estrellas de abundancia excepcional, que se

repitió en igual forma en noviembre de 1833. Ello hizo pensar en una periodicidad de 34 años; en noviembre de 1866 se volvió a contemplar una hermosa lluvia de estrellas; el número de meteoritos se estimó en 5,000 por hora. En noviembre de 1899 se repitió el fenómeno, aunque con menor intensidad, y en 1932 disminuyó notablemente el número de estrellas fugaces. Así, la periodicidad variaba entre 34 y 33 años.

En 1866, los astrónomos compararon los elementos de la órbita del cometa Tempel-Tuttle con los del “enjambre” de noviembre, y encontraron gran analogía entre ellos; de este modo descubrieron que posiblemente una gran cantidad de fragmentos giraba en torno del Sol y que cada 33 años cruzaban la órbita terrestre, para dar

Figura XVI.1

Enjambre de meteoritos

Sol Tierra

CAPÍTULO

origen al fenómeno. Posteriormente se confirmó que los cometas se disgregan y que los fragmentos que forman el núcleo se separan, pero continúan describiendo órbitas parecidas a las del cometa del que provienen. Si su órbita cruza la atmósfera terrestre, al ocurrir la intersección de sus órbitas se presenta la abundancia de estrellas fugaces.

Leónidas

Las leónidas son lluvias de meteoros que se producen cada año, entre el 15 y el 21 de noviembre, y alcanzan un máximo de intensidad cada 33 años. Estos eventos son llamados tormentas cuando superan el millar de meteoritos por hora. Muestran este pico de actividad debido a que el polvo del cometa Tempel-Tuttle no está distribuido homogéneamente a lo largo de su órbita. Las leónidas deben su nombre al hecho de que estas estrellas fugaces dan la apariencia (sólo es apariencia) de provenir de la constelación del León.

En 1966, la tormenta de leónidas registró 100,000 meteoritos por hora, mientras que en 1933 sólo había registrado 200 por hora. El 18 de noviembre de 1999 se observó en Europa una tormenta de varios miles de meteoritos por hora. En 2001, es decir, sólo dos años después, ocurrió una tormenta con un máximo de 1,500 meteoritos por hora.

Aerolitos

Como ya se mencionó, los corpúsculos que cruzan nuestra atmósfera se vuelven incandescentes

o se volatilizan y caen en la superficie de nuestro planeta en forma de polvo muy fino o en fragmentos con dimensiones de varios metros; a estos últimos se les llama aerolitos. A los meteoritos que hacen explosión al cruzar la atmósfera se les da el nombre de bólidos; la explosión, acompañada de un fuerte ruido, se debe a la existencia de gases interiores.

Los fragmentos que se han encontrado en nuestro planeta tienen un aspecto exterior rugoso y oxidado, semejante al de una piedra calcinada. En ninguno de los astrolitos encontrados hasta ahora se han hallado elementos desconocidos.

El aerolito mayor del mundo es el llamado Ahnighito, encontrado en Groenlandia, que se puede contemplar en el Museo de Historia Natural de Nueva York; su peso es de 37 toneladas, con una dimensión media de 6 metros. En el Palacio de Minería de la Ciudad de México se conservan tres aerolitos que se encuentran entre los más grandes que se conocen, y pesan 14, 6.7 y 3.3 toneladas.

Las estrellas fugaces brillan a unos 150 km de altura y desaparecen a los 60; su velocidad inicial es de 70 km/s y la final es de 30.

Choques con la Tierra

El 30 de junio de 1908, día en que el cometa Pons Wineck había estado muy próximo a la Tierra, ocurrió un fenómeno impresionante en la región de Krasnoyarsk, Siberia (latitud 60° 20’ N, longitud 102° 17’ E); se percibió un gran ruido

como cañoneo y los sismógrafos registraron violentos temblores. Una expedición científica que en 1921 exploró esa región encontró más de 300 cráteres de diversas dimensiones, causados por la caída de aerolitos. La región estaba devastada y los árboles incinerados.

En Arizona existe una oquedad (cráter Barringer) en forma de embudo (véase figura XVI.2 en p. 138) de 1,200 m de diámetro y 170 m de profundidad, debido a la caída de un aerolito de unos 50 m de diámetro medio, que se encontró a 200 m de profundidad. Ello ocurrió hace 50,000 años, durante el periodo Pleistoceno (véase capítulo XVIII); el cuerpo viajó a 12 kilómetros por segundo.

El cráter de Chicxulub es una enorme depresión de impacto cuyo centro se halla en la población costera de Chicxulub, Yucatán (véanse figuras XVI.3 y XVI.4, p. 138); mide 180 km de diámetro, con una profundidad de 900 m. Su gran tamaño impidió que fuera descubierto hasta 1978.

Una persona parada en su centro, ubicado en la población costera de Chicxulub, en Yucatán, no puede ver los bordes del cráter, pues quedan fuera del horizonte. Se estima que el bólido que lo formó medía 10 km de diámetro, que cruzó la atmósfera a una velocidad de 54,000 km/h y se destrozó con el golpe; la explosión resultante debe de haber sido del orden de 200,000 gigatones de energía, equivalente a 10,000 millones de veces la potencia de la bomba atómica de Hiroshima.

El cráter de Chicxulub fue descubierto en 1978 por Antonio Camargo y Glenn Penfield, geofísicos que trabajaban en la exploración de petróleo; pudieron demostrar que se trata de una depresión de impacto al obtener muestras de cuarzo chocado (cuarzo con estructura desplazada a lo largo de planos cristalográficos, que sólo puede darse después de estar sometido a muy elevadas presiones. Se descubrió durante ensayos subterráneos con bombas nucleares, en que se dan las condiciones de presión necesarias para que se forme; su presencia es uno de los indicios que se usan para determinar si una estructura se ha producido por un impacto meteorítico o por actividad volcánica, ya que esta última no genera tales presiones).

También se obtuvieron muestras de tectitas, iridio (un metal escaso en la Tierra, pero abundante en meteoritos y asteroides) y platino como metal asociado. Los estudios mostraron que estas estructuras datan de finales del periodo Cretácico, hace 65 millones de años, fecha de la extinción de los dinosaurios.

Recientemente se reafirmó la hipótesis de que el impacto de Chicxulub es el responsable de la extinción masiva del Cretácico Terciario. La emisión de polvo y partículas podría haber cubierto toda la superficie de la Tierra durante unos 10 años y creado un medio de vida difícil para los seres vivos.

La producción de dióxido de carbono provocada por el choque y la destrucción de rocas carbonatadas habría causado un dramático efecto

invernadero. Otra consecuencia es que el polvo de la atmósfera habría impedido que la luz solar llegara a la superficie de la Tierra, lo que disminuyó grandemente la temperatura. La fotosíntesis habría quedado interrumpida.

En marzo de 2010, cuatro decenas de expertos de Europa, Estados Unidos, Canadá, Japón

y México confirmaron en la revista Science que la extinción masiva de hace 65 millones de años, que terminó con los dinosaurios en la Tierra, fue originada por el impacto de un asteroide que causó la depresión de Chicxulub.

Se tiene incertidumbre sobre la procedencia de tal asteroide.

CAPÍTULO XVII

El Universo

Mi intención es demostrar que la máquina celestial no es como un ser divino, sino como un reloj. JohANN kePler (1571-1630)

Las estrellas

La estrella más próxima al Sistema Solar es la componente C de α de Centauro, que dista del Sol 263,000 ua, es decir, 40 billones de kilómetros, distancia que la luz recorre en 4.16 años. Así, puede decirse que esa estrella dista de nosotros 4.16 años luz. Nótese que año luz es una medida de longitud, no de tiempo. Un avión que viaja a 900 km/h (equipos estándar comerciales) necesitaría volar durante cinco millones de años para recorrer esa distancia. Una esfera con centro en el Sol y con radio de 16 años luz (150 billones de kilómetros) sólo abarca 48 estrellas de los miles de millones que se conocen.

Vía Láctea

En noches sin Luna y sin nubes puede observarse fácilmente una ancha faja blanca, de forma

irregular, que rodea todo el cielo a manera de un cinturón, y aproximadamente sobre un círculo máximo de la esfera celeste; es la Vía Láctea, que pasa al Norte sobre Casiopea y el Cisne. Cerca de Deneb se divide en dos ramas que pasan entre Vega y Altair; después de cortar el ecuador, se interrumpe y termina una de las ramas cerca de Antares. La otra pasa sobre Sagitario y Escorpión, hasta la Cruz del Sur; de allí vuelve al Norte sobre el Navío Argos, pasa cerca del Can Mayor, vuelve a cortar el ecuador para pasar al hemisferio boreal entre Orión de un lado y el Can Menor y los Gemelos del otro, y vuelve sobre el Cochero y Perseo hasta Casiopea.

A simple vista, la Vía Láctea parece una nube brillante. Galileo, que fue el primero en utilizar el telescopio, notó que está constituida por una gran

cantidad de estrellas pequeñísimas y muy apiñadas. Otros astrónomos, con el paso del tiempo, encontraron que el espacio ocupado por las estrellas tiene la forma de un elipsoide de revolución muy achatado, como una lente biconvexa (véase figura XVII.1, p. 139). Al conjunto de estrellas y astros que ocupan ese espacio de forma lenticular se le llama galaxia, la cual contiene a la Vía Láctea, que a su vez contiene al Sistema Solar (véase figura XVII.2, p. 139).

Se estima que la Vía Láctea tiene un diámetro de 100,000 años luz y que contiene 400,000 millones de estrellas. Se mueve en su órbita a una velocidad de 965,000 kilómetros por hora.

La metagalaxia

Nuestra galaxia no es la única en el Universo; se han fotografiado millones de sistemas análogos que aparecen como manchitas alargadas en forma de puro, con una condensación central en torno a la cual se notan frecuentemente brazos en forma de espiral. Un ejemplo de esto es la gran nebulosa de Andrómeda (véase figura XVII.3, p. 140), que es una de las galaxias más próximas al Sistema Solar; dista de la nuestra 800,000 años luz.

Hay otras que se encuentran a millones de años luz. Todas las galaxias, inclusive la nuestra, tienen movimiento de rotación alrededor de un eje perpendicular al plano mayor de ellas. La rotación de nuestra galaxia arrastra al Sol y a las estrellas vecinas con una velocidad estimada en 200 km/s, y les hace dar cada vuelta completa en 200 millones

de años. Este periodo se llama año cósmico. Además, las galaxias se hallan animadas por rápidos movimientos de traslación que las hacen apartarse unas de otras con velocidades fantásticas, tanto mayores cuanto más distantes se hallan, como si el Universo se estuviera expandiendo.

Historia del conocimiento del Universo

Los primeros observadores del firmamento no tenían idea de la naturaleza de los astros ni de las distancias que de ellos nos separan; creían que la Tierra es inmóvil; la mayoría de los pueblos la veían como un disco redondo, del que cada uno creía ocupar el centro. Todos los pueblos primitivos pensaban que los astros eran movidos por los dioses, o bien, los confundían con los dioses mismos. Los eclipses eran atribuidos a monstruos o dioses del mal que pretendían devorar a los dioses buenos del Sol o de la Luna, y era un deber de los hombres ayudar a éstos haciendo ruido y disparando dardos al cielo. Los mayas creían que nuestro planeta estaba sostenido por cuatro dioses llamados bacaob (plural de bacab), “los que están de pie”.

Primeros conocimientos

A pesar de las creencias antiguas, apoyadas en las supersticiones y en la ignorancia, los pueblos primitivos tuvieron conocimientos astronómicos notables, ya que esta ciencia se hizo necesaria para la navegación y para la medición del tiempo. Pueblos muy antiguos conocieron con bastante aproximación la duración del año y de la luna-

ción. Parece que los chinos fueron los primeros en aprender a predecir los eclipses. El eclipse de Sol más antiguo del que se tiene noticia fue el observado por los chinos 2,137 años antes de la era cristiana. La primera observación de un eclipse de Luna, hecha por los caldeos, fue en el año 720 antes de Cristo. La división del Zodiaco en doce partes iguales se atribuye a los egipcios. Los magos de Babilonia llegaron a conocer los movimientos aparentes de los planetas, y se valieron de ellos para predecir los destinos humanos, con lo que sentaron las bases de la astrología, que había de dar nacimiento a la astronomía.

Pitágoras (Grecia, siglo VI a.C.)

Pitágoras enseñó que la Tierra es esférica y que gira sobre sí misma de Occidente a Oriente, lo que produce la apariencia del movimiento diurno de los astros. Fue el primero en reconocer que la estrella del alba, Lucifer, y el lucero de la tarde, Vésper, son el mismo planeta (Venus).

Aristarco (Grecia, 310 a 230 a.C.)

Considerado el primer astrónomo, Aristarco intentó determinar la distancia de la Tierra al Sol en función de la distancia de la Tierra a la Luna.

Observó cuidadosamente (véase figura XVII.4) el tiempo que había entre la conjunción N y el cuarto creciente L’, y entre éste y el plenilunio P. El primer intervalo debe ser más corto que el segundo, porque la Luna alcanza su cuarto creciente en L’ , cuando el ángulo TL’S es de 90°, poco antes de estar en L, en cuadratura, cuando el ángulo recto es el LTS.

Aristarco concluyó con sus mediciones que el primer intervalo era 12 horas más corto que el segundo y, por tanto, que la Luna recorría el arco LL’ en la mitad, es decir, seis horas; como conocía la velocidad angular del desplazamiento, obtuvo el valor del ángulo L’TL. Ahora bien, este ángulo es igual al TSL’ , por lo que pudo construir un triángulo semejante al TL’S y ver cuántas veces cabe TL’ en TS. Además encontró que el Sol está 20 veces más lejos que la Luna.

El método es bueno, pero no era posible que Aristarco, a simple vista, determinara con precisión el instante en que la Luna aparece exactamente como un semicírculo, porque la superficie del astro es rugosa y porque el Sol no es un foco luminoso puntual, sino una esfera con un diámetro de casi el doble del de la órbita lunar. En realidad, la Luna recorre el arco L’L en menos de 18 min. En función de la velocidad angular del desplazamiento de la Luna puede deducirse trigonométricamente que el Sol está 348 veces más lejos que nuestro satélite. En efecto, si el arco L’L es recorrido por la Luna en casi 18 min, podemos conocer el ángulo L’TL. La velocidad angular del desplazamiento de la Luna es:

w = = = 13.1763°/d

= 0.00915°/min

∴ ángulo L’TL = 0.00915 × 18 = 0.1647°

y TS = = 348 TL’

Exactamente, el factor es 388.7

Sin embargo, los conocimientos de Aristarco ensancharon los estrechos límites del mundo antiguo, pues Platón suponía que el Sol estaba dos veces más lejos que la Luna. Pero Aristarco es célebre, sobre todo, por su concepción del sistema del mundo, que es el mismo que enseñaba Copérnico

18 siglos más tarde. Según este sistema, el centro del mundo no es la Tierra sino el Sol, alrededor del cual giran los planetas (heliocentrismo).

Eratóstenes (Alejandría, Egipto, ca. 250 a. C.)

Es célebre por su determinación del radio de la Tierra. Sabía que en Syene (Asuán, Egipto), a mediodía, el día del solsticio de verano en que el Sol alcanza su máxima declinación boreal, los cuerpos no hacen sombra y los rayos solares penetran hasta el fondo de los pozos más profundos, ya que el Sol se encuentra en el cenit. Ese día, Eratóstenes midió en Alejandría la distancia cenital ZAS del Sol (véase figura XVII.5) y la encontró igual a un cincuentavo de circunferencia, es decir, 7° 12’ = 7.2°.

Admitiendo que Syene (B) se hallase exactamente al sur de Alejandría (A), esto es, que un círculo máximo pasara por ambas ciudades, ese ángulo medía la amplitud del arco de meridiano AB, ya que, a causa de la gran distancia del Sol, las dos visuales AS y BS son paralelas y los ángulos ZAS y AOB son iguales. Sabía, además, que la distancia entre las dos poblaciones era de 5,000 estadios (en la Antigüedad el estadio utilizado correspondía a 600 pies, esto es, 182.9 m), deduciendo que la vuelta entera de la Tierra (longitud del meridiano) se podía obtener aplicando una regla de tres simple, es decir, 7° 12’ es a 5,000 estadios como 360° es a dicha longitud del meridiano. Así, obtuvo que la circunferencia de la Tierra es de 250,000 estadios, equivalentes a 45,725 km. En realidad es de 40,000 kilómetros.

Hiparco (Grecia, ca. 150 a. C.)

Inventó la Trigonometría, ideó el sistema de coordenadas geográficas, hizo un catálogo de estrellas, descubrió la precesión de los equinoccios y halló un método matemático para predecir eclipses. Inventó y construyó instrumentos astronómicos. Plinio, escritor romano, científico y naturalista (23-79 d. C.), dos siglos más tarde dijo que “Hiparco no habría hecho mejor sus predicciones si hubiera participado en las decisiones de la Naturaleza”.

Claudio Ptolomeo (Alejandría, 150 a. C.)

Escribió el libro Sintaxis, que ha pasado a la posteridad con el nombre de Almagesto que le dieron los árabes. En él se encierran todos los conocimientos astronómicos de la época; se utilizó durante cator-

ce siglos como el mejor libro en materia científica. Prueba la esfericidad de la Tierra pero objeta las ideas de Pitágoras y Aristarco acerca del movimiento de la Tierra, es decir, creía en el sistema geocéntrico. Decía que si la Tierra se moviese abandonaría tras sí todos los cuerpos, incluso el aire, y acabaría por salirse de la esfera celeste. Además, que su rotación provocaría un viento del Este tan intenso que arrasaría cuanto se hallase en la superficie terrestre.

Nicolás Copérnico (Polonia, 1473-1543)

Demostró el sistema heliocéntrico, supuso circulares las órbitas de los planetas y de la Luna. Determinó satisfactoriamente la duración del año trópico, lo que sirvió setenta años después para introducir en el calendario la reforma gregoriana.

Tycho Brahe (Dinamarca, 1546-1601)

Construyó un sistema mixto con las siguientes bases:

1. Los planetas –excepto la Tierra, que no se mueve– describen órbitas circulares alrededor del Sol.

2. El Sol, con todo su cortejo de planetas, describe en un año y en torno de la Tierra, que está fija en el centro del mundo, una órbita circular excéntrica.

3. Las estrellas se hallan fijas en una esfera que gira alrededor de la Tierra, de Oriente a Occidente, dando cada vuelta completa en un día sideral.

Figura XVII.5

Tycho Brahe es célebre por su descubrimiento de una estrella nueva que apareció en 1572 y por sus estudios sobre los movimientos de los planetas, tan precisos que años más tarde sirvieron a su discípulo Kepler para el establecimiento de las leyes del movimiento elíptico.

Galileo Galilei (Italia, 1564-1643)

Construyó un telescopio y lo empleó por primera vez en la historia para mirar el cielo. Descubrió las manchas del Sol y fue un convencido del sistema heliocéntrico. El Santo Oficio de Roma le prohibió que enseñase las teorías de la inmovilidad del Sol y de la movilidad de la Tierra, que se consideraban heréticas por contradecir los textos sagrados. Después de obedecer por algún tiempo, Galileo escribió su libro Sistemi del Mondo Ptolemaico et Copernicano, en el que de nuevo adujo pruebas a favor del sistema heliocéntrico; fue entonces

condenado por la Inquisición romana a retractarse y a prisión perpetua. Después de retractarse ante cardenales inquisidores, murmuró: “Y, sin embargo, se mueve”.

Johannes Kepler (Alemania, 1571-1630)

Estableció las siguientes leyes:

Primera. Cada planeta describe una elipse, en uno de cuyos focos se encuentra el centro del Sol.

Segunda. Las áreas descritas por el radio vector que corresponde a cada planeta son proporcionales a los tiempos empleados en describirlas.

Demostración: Se define la velocidad angular del Sol como el ángulo descrito en un día sideral por el radio vector que une los centros del Sol y de la Tierra. Sean AB y CD (véase figura XVII.6) dos arcos descritos por el movimiento aparente del Sol, cada uno en un día sideral y en diferentes épocas del año. Llamemos V y V’ a los ángulos

ATB y CTD, y R y R’ las distancias respectivas del Sol a la Tierra.

Puesto que la elipse es poco excéntrica y los arcos mencionados muy pequeños, los sectores

ATB y CTD pueden considerarse circulares y de radios constantes R y R’.

Sus áreas son:

A = π R²V/360° y A’ = π R’²V’/360°

Figura XVII.6

Entonces, A/A’ = R²V/ R’²V’ (1)

La observación demuestra que las distancias angulares son proporcionales a los cuadrados de los diámetros aparentes, es decir, inversamente proporcionales a los cuadrados de las distancias.

Así, V/V’= R’²/R², por lo que

R²V = R’²V’

Entonces, de la ecuación 1, A/A’ = 1, es decir,

A = A’

Dado que A y A’ son definidas ambas en un tiempo igual a un día sideral, es fácil deducir que las áreas descritas por el radio vector que va del centro del Sol al de la Tierra son proporcionales a los tiempos empleados en describirlas.

Como consecuencia se tiene que, dado que en los sectores de igual área mientras menor es el radio mayor es el arco, la velocidad aparente del Sol es máxima en el perigeo (enero) y mínima en el apogeo (julio), o, lo que es lo mismo, la velocidad real de la Tierra es máxima en el perihelio y mínima en el afelio. Así, crece continuamente del 5 de julio al 2 de enero, y decrece del 2 de enero al 5 de julio.

Tercera. Los cuadrados de los tiempos de las revoluciones siderales de los planetas son proporcionales a los cubos de sus distancias medias al Sol.

Llamando D y D₁ a las distancias medias de dos planetas al Sol, y T y T₁ a los tiempos que emplean en recorrer sus respectivas órbitas, la tercera ley queda expresada por la siguiente ecuación:

= Si el segundo planeta considerado es la Tierra, entonces T₁ es un año sideral de nuestro planeta, que tomaremos como unidad de tiempo, y D₁ es una unidad astronómica (1 ua), por ser la distancia media de la Tierra al Sol, es decir, 149.5 millones de kilómetros.

Así, la fórmula anterior se reduce a:

T² = D³

La expresión anterior permite calcular lo que dura la revolución sideral de un planeta si se conoce su distancia media al Sol, y viceversa.

Ejemplo. Calcular el tiempo de revolución sideral de Venus, sabiendo que su distancia media al Sol es de 0.72 u.a.

Solución. De acuerdo con la tercera ley de Kepler, tenemos que: T² = 0.72³, de donde T = 0.618 año sideral = 0.618 × 365.2564 = 225.7 días.

Así, Venus se toma 225.7 días en dar una vuelta al Sol.

Las leyes de Kepler se han hecho extensivas a los movimientos de los cometas, y también a los casos de ciertas estrellas que giran en torno de otras.

Isaac Newton (Inglaterra, 1642-1721)

Newton se propuso relacionar los movimientos de los planetas con las leyes de la mecánica, toda vez que Kepler estableció empíricamente las leyes de los movimientos de los planetas sin tratar de averiguar el porqué de ellas. Newton retomó el principio de la inercia de la materia, que un siglo antes había establecido Galileo, al afirmar que si un cuerpo se mueve sin que se ejerza en él fuerza alguna, dicho cuerpo se desplazará en línea recta y con velocidad constante. Entonces, Newton pensó que si los planetas describen elipses cerradas en torno del Sol, es porque una fuerza los atrae hacia el astro central. De la tercera ley de Kepler dedujo que la fuerza gravitacional del Sol es inversamente proporcional al cuadrado de la distancia a que se halla cada planeta. Demostró que la fuerza de gravedad terrestre que hace caer los cuerpos hacia el centro de la Tierra es la misma que mantiene a la Luna en su órbita, como la tensión centrípeta de un hilo mantiene la piedra de una honda sobre su órbita circular, impidiendo que se salga por la tangente.

Después enunció su Ley de la Gravitación

Universal: dos partículas materiales se atraen con una fuerza dirigida sobre la recta que las une, y que varía en razón directa de las masas de las dos

partículas, e inversa del cuadrado de su distancia, es decir:

= , en donde:

F = fuerza de atracción m = masa de un cuerpo a = distancia al centro de atracción

Newton desarrolló su Ley de la Gravitación

Universal considerando que la fuerza que tiende a producir el movimiento de un cuerpo hacia otro que lo atrae puede considerarse una fuerza centrípeta cuyo valor depende de la masa m del móvil, de su velocidad v y de su distancia a al centro de atracción.

Según las leyes de la mecánica, esa fuerza atractiva central F es, tratándose del movimiento circular uniforme,

F =

El valor de v = elevado al cuadrado y sustituido en la ecuación anterior conduce a:

F =

Para otro móvil (u otro planeta) de masa m₁, cuya distancia al Sol sea a₁ y tenga una revolución sideral de duración t₁, la fuerza centrípeta es :

F1 =

Dividiendo la última ecuación entre la penúltima:

= De acuerdo con la tercera Ley de Kepler, t₁²/t² = a₁³/a³; entonces:

= Newton encontró que la atracción que un cuerpo ejerce es el resultado de las atracciones ejercidas por todas sus moléculas, y actúa desde el centro de gravedad del cuerpo. En una esfera homogénea, el centro de gravedad se confunde con el centro de la figura; tratándose de los astros, todo es como si los centros se atrajesen directamente. Cuando dos astros están sujetos a su gravitación mutua, el sistema que forman tiene un centro de gravedad, que es el punto C (véase figura XVII.7) situado sobre la recta que une sus centros de figura; dicha recta queda dividida por C en partes inversamente

proporcionales a las masas M y m de los dos astros, y uno y otro describen sendas elipses en torno de ese centro de gravedad.

Si uno de los astros es de masa insignificante en comparación con la del otro, el centro de gravedad del sistema coincide prácticamente con el del más pesado, y es el menor el que se mueve en torno del mayor. En nuestro Sistema Solar, la masa del Sol es enormemente mayor que la de todos los planetas juntos, y por eso es el centro de los movimientos; sin embargo, cada planeta atrae a cada uno de los otros y es atraído por ellos, de lo que resultan perturbaciones, es decir, desviaciones respecto de las elipses ideales que había supuesto Kepler. Edmund Halley, inglés contemporáneo de Newton, aplicó la Ley de Newton a los movimientos de los cometas y logró predecir la reaparición de uno, que hoy lleva su nombre.

Newton dio cuenta del movimiento de precesión de los equinoccios como un bamboleo de la Tierra causado por la acción gravitatoria del Sol y de la Luna sobre el ensanchamiento ecuatorial. Con la Ley de Gravitación de Newton, Le Verrier descubrió en 1846 el planeta Neptuno.

Figura XVII.7

Albert Einstein (Alemania, 1879-1955)

Enunció en 1905 la Teoría Especial, y en 1915 la Teoría General de la Relatividad, con las que resolvió problemas pendientes de la Ley de Gravitación de Newton, como el de la acción a distancia, es decir, que un cuerpo pueda atraer a otro sin nada que se les interponga o los una de cierta forma. Newton mismo vio esa dificultad, por lo que había enunciado su ley diciendo: “Los cuerpos celestes se comportan como si se atrajeran.” Otros dos problemas pendientes que tanto preocuparon a los físicos y que Einstein resolvió eran 1) el hecho de que la gravitación fuese proporcional a la masa, es decir, a la materia inerte, y 2) que se ejerciese por igual entre dos cuerpos la gravitación, aunque otro se interpusiera entre ellos. Sólo se dirá aquí, de acuerdo con Einstein, que el movimiento de los astros en sus respectivas órbitas no se debe a una fuerza, sino a la curvatura del espacio; que espacio y tiempo se consideran dos modalidades

de un solo concepto, es decir, que el tiempo es la cuarta dimensión de las cosas; que el espacio es finito, aunque ilimitado, y que es una hiperesfera cuyo radio aumenta continuamente.

Ejercicios propuestos

1. Tomando 19.2 ua como distancia media de Urano al Sol, calcúlese la duración de la revolución sideral del planeta.

2. Sabiendo que el cometa Halley pasa por las proximidades del Sol cada 76 años, calcular su distancia media al astro central.

3. Considerando la solución del ejercicio anterior y sabiendo que la distancia mínima del cometa al Sol es de 0.587 ua, averiguar a qué distancia máxima puede llegar (apoyarse en el apartado 12 del capítulo I, “La elipse”), y cuál es la última órbita planetaria que rebasa.

CAPÍTULO XVIII

Temas diversos

Paralaje de un astro

El ángulo de paralaje de un astro del Sistema Solar, respecto a un punto B de la Tierra, es el ángulo con el que un observador situado en el centro de ese astro vería el radio terrestre TB. Si el astro se encuentra en el horizonte del punto B, el ángulo BAT se llama ángulo de paralaje horizontal (véase figura XVIII.1).

Si el astro se encuentra en otra posición (véase figura XVIII.2), el ángulo BA’T se llama ángulo de paralaje de altura.

Conocido el ángulo de paralaje horizontal de un astro, se puede determinar su distancia a la Tierra. Sea S el Sol, T la Tierra y TA el radio terrestre

El hombre encuentra a Dios detrás de cada puerta que la ciencia logra abrir. Albert eiNsteiN (1879-1955)

Figura XVIII.1

visto desde el centro del Sol con un ángulo de 8.8’’

(véase figura XVIII.3).

Si se dibuja un arco de circunferencia con radio ST y centro en S, la cuerda AT se confunde con el arco que subtiende, y dado que la razón entre la circunferencia completa y el arco AT es igual que la razón entre 360° y 8.8’’, tenemos que:

∴ ST = = 23,439 radios terrestres

A

XVIII.2

XVIII.3

el radio de la Tierra, r, es de 6,378.39 km, por lo que: ST = 149.5 millones de kilómetros.

Relación entre el ángulo de paralaje de altura y el horizontal Por la forma de la órbita de la Tierra alrededor del Sol, la distancia entre ambos astros varía a lo largo del año; el valor del ángulo de paralaje del Sol dado en líneas anteriores, 8.8’’, es sólo el valor medio del ángulo de paralaje horizontal ecuatorial.

Figura

Figura

Figura XVIII.4

Para un lugar determinado, ese ángulo depende de la altura del Sol sobre el horizonte. En efecto, sean S y S’ (véase figura XVIII.4) dos posiciones del Sol en un mismo día: una cuando llega al horizonte del observador O, y otra cuando se ha elevado sobre dicho horizonte.

El ángulo TSO o ángulo p es el ángulo de paralaje horizontal y el TS’O o ángulo p’ es el ángulo de paralaje de altura. En el triángulo OTS’ se tiene que:

= = (nótese que z es la distancia cenital del Sol), entonces,

= , por lo que sen p’ = sen z además, sen p = = entonces sen p’ = sen p sen z

Los ángulos p y p’ son muy pequeños, por lo que pueden, expresados en radianes, sustituir a sus senos, así:

Obtención del ángulo de paralaje

Determinemos el ángulo de paralaje de un astro del Sistema Solar. Supóngase a dos observadores situados en un mismo meridiano, lo más distantes posible entre sí, y que simultáneamente midan las distancias cenitales ZOL y Z’O’L (véase figura XVIII.5).

Del cuadrilátero LOTO’, se tiene que:

p’+p’’+(180 – z’)+OTO’+(180 – z’’) = 360° (recuérdese que la suma de los ángulos de un polígono = 180(n – 2)).

Ángulo OTO’ = φ’+φ’’ (latitudes de O y O’).

∴ p’ + p’’ = z’ + z’’ – (φ’+φ’’)

De acuerdo con la ecuación (1), p’ = p sen z’ y p’’ = p sen z’’

p’= p sen z (1) Figura XVIII.5

∴ p sen z’ + p sen z’’ = z’ + z’’ – (φ’+φ’’), de donde

p = Contando con esta expresión, Lalande y Lacaille determinaron la paralaje horizontal de la Luna. El primero se situó en Berlín (long 13° E) y el segundo en El Cabo (long 18° E), es decir, en meridianos muy cercanos; obtuvieron que p = 57’ 02’’, valor que casi no ha sido modificado.

Ejemplo. Calcular la distancia Tierra-Luna sabiendo que el ángulo de paralaje horizontal de la Luna es de 57’ 02’’.

Solución. = = 378.7

A pesar de su generalidad, este procedimiento no puede emplearse para obtener el ángulo de paralaje horizontal del Sol, debido a su valor tan pequeño.

Acerca del Sol Dimensiones

El radio de un astro supuesto esférico se deduce fácilmente cuando se conocen su semidiámetro aparente y su ángulo de paralaje. En efecto, sean C el Sol y C’ la Tierra (véase figura XVIII.6); si unimos sus centros C y C’ y trazamos las tangentes CB y C’A, así como los radios CA y C’B, resulta que el ángulo CC’A es el semidiámetro aparente del Sol y el ángulo C’CB es el ángulo de paralaje horizontal del Sol. Entonces:

∴ TL = = 60.3 r; r = 6,378.39 km

∴ TL = 384,616 kilómetros

C’B = CC’ sen C’CB y CA = CC’ sen CC’A

Así, =

XVIII.6

Figura

Los ángulos C’CB y CC’A son muy pequeños, por lo que podemos asimilarlos a sus senos; así, la fórmula anterior queda: = Llamando R al radio del Sol y r al radio de la Tierra, P a la paralaje horizontal C’CB del Sol y d al semidiámetro aparente CC’A del Sol, resulta:

= ∴ R = r

Si se quiere el radio relativo, hacemos r = 1, y obtenemos que:

R = El semidiámetro aparente d del Sol es de 16’ 01.5’’. El valor de su paralaje P es de 8.8’’. Dividiendo el primero entre el segundo:

R = = 109 radios terrestres

Rotación

Si se observa el Sol con un telescopio, se le ven unas manchas oscuras pequeñas, de formas muy variables; si se sigue el movimiento de una de ellas durante varios días, se encontrará que describe sobre el disco solar una semielipse muy achatada, que es la proyección, sobre el plano del disco solar, de la circunferencia que la mancha describe sobre la superficie esférica del Sol.

Las manchas se modifican constantemente y algunas llegan a desaparecer antes de alcanzar el borde del disco, aunque otras duran lo suficiente para que se pueda estudiar su vuelta completa. Se ha observado que el Sol gira sobre sí mismo en sentido directo, y que en su región ecuatorial una mancha tarda cerca de 14 días a la vista y 27.3 días entre dos pasos consecutivos por el meridiano central del Sol, que es la duración de su rotación sinódica.

∴ R=109 × 6,378 = 696,860 kilómetros

Así, el diámetro del Sol es de 1’393,720 kilómetros.

Deduzcamos a continuación que el Sol emplea 25 días para dar una vuelta, que es su rotación sideral. En efecto, si estando la Tierra en T (véase figura XVIII.7) se ve una mancha en a sobre la visual dirigida al centro del disco solar, días después la rotación del Sol la arrastrará en sentido directo (el mismo sentido de rotación de la Tierra), mientras la Tierra va recorriendo su órbita en igual sentido, aunque con velocidad angular mucho menor.

La mancha, después de dar una vuelta completa, deberá recorrer todavía el arco ab, igual en amplitud al que ha descrito la Tierra en 27.3 días

(véase sección anterior), para volverla a ver en b.

Así, la mancha ha recorrido 360°+26.9° = 386.9°.

Admitiendo que la rotación del Sol es de velocidad uniforme, los arcos recorridos serán proporcionales al tiempo, es decir,

S a b T T’

Figura XVIII.7

= , de donde

x = 25.4 días

En la figura XVIII.7 se ha supuesto que el plano del ecuador solar coincide con el de la eclíptica; el achatamiento de las elipses aparentes descritas

por las manchas ha permitido deducir que el plano del ecuador solar forma con el de la eclíptica un ángulo de 7° 10.5’, aunque ello modifica poco el resultado.

La rotación del Sol no es de igual duración en toda su superficie; no gira como lo haría un cuerpo sólido. Las manchas próximas a su ecuador dan una vuelta completa en 25 días, pero mientras más lejos estén de éste, mayor tiempo requieren para completar una revolución. A 30° del ecuador emplean 26 días; más lejos del ecuador ya no aparecen manchas, aunque el análisis espectral ha permitido estudiar la rotación del Sol en esas regiones y ha revelado que es tanto más lenta, cuanto más cerca de los polos se encuentren los puntos considerados. A 45° del ecuador, la rotación dura más de 27.5 días; a los 80°, más de 35 días. La velocidad de rotación del Sol es de 2 km/s en el ecuador.

Aspecto telescópico

La superficie del Sol, que parece uniforme cuando se le mira con un cristal ahumado, presenta un aspecto moteado si se le observa con telescopio. Se le han distinguido las siguientes capas:

1. Fotosfera. Es la capa brillante, emisora de luz y calor, formada por una gran cantidad de partículas brillantes que se encuentran a un mismo nivel. Su espesor es de unas decenas de kilómetros. El aspecto moteado de la superficie se debe a las partículas denominadas “granos de arroz”, que se observan fácilmente en la región central del disco.

2. Capa inversora. Al elevarse los vapores de la fotosfera, pierden calor y forman otra capa de unos mil kilómetros de espesor llamada capa inversora.

3. Cromosfera. Existe otra capa de vapores incandescentes, de unos 10,000 kilómetros de espesor, más elevada que la fotosfera y que la capa inversora; está formada por hidrógeno, calcio y helio, y es de color rosa. Los gases de esta capa descienden y se mezclan con las dos capas inferiores. La capa inversora y la cromosfera constituyen la atmósfera solar y sólo pueden observarse con el telescopio al principio y al fin de un eclipse total de Sol, aunque casi todos sus fenómenos pueden estudiarse en cualquier momento con el espectroscopio, que es un instrumento que se utiliza para medir las propiedades de la luz, separando las diferentes componentes de un espectro óptico. La cromosfera está siempre en violenta agitación y lanza hacia el exterior enormes llamas que suelen alcanzar centenares de miles de kilómetros de altura, y que se llaman protuberancias (véase figura XVIII.8, p. 141).

4. Corona. La corona es la envoltura del Sol con una densidad muy pequeña (un billón de veces menor que la de la atmósfera terrestre) que se eleva a grandísima altura, alrededor de un millón de kilómetros. Al igual que la capa inversora y la cromosfera, la corona sólo puede observarse durante los eclipses totales de Sol (véase figura XVIII.9, p. 141).

La corona no se extiende uniformemente ni es homogénea en su estructura; sus contornos son irregulares y se esfuman. Desde su base hasta su parte más alta se pueden distinguir largos haces de rayos. La forma de la corona varía según que el Sol esté en el periodo de máxima o mínima aparición de manchas (véase la sección “Manchas solares”, adelante); en el máximo, los penachos se extienden con regularidad, es decir, el contorno exterior es visiblemente circular; en el mínimo, los penachos de la región ecuatorial se extienden hasta alcanzar una longitud igual a tres o cuatro diámetros solares. La corona es tan luminosa en su base que su brillo casi iguala en intensidad al de la Luna en plenilunio.

Aurora boreal

En ocasiones ocurren auroras polares (boreal y austral), que son un fenómeno en forma de brillo o luminosidad que aparece en el cielo nocturno (véase figura XVIII.10, p. 141). Sucede en las zonas polares, aunque puede aparecer en otras partes del mundo durante cortos lapsos. Se presentan cuando una eyección de masa solar choca con los polos Norte y Sur de la magnetosfera terrestre y produce una luz difusa proyectada en la ionosfera (véase figura XVIII.11 p. 141).

Conviene explicar aquí que la ionosfera es la parte de la atmósfera terrestre ionizada permanentemente, debido a la fotoionización que provoca la radiación solar. Se sitúa en la termosfera, entre la mesosfera y la exosfera, y se extiende

entre los 80 y los 500 km de altitud. También es conveniente mencionar que la magnetosfera es la parte más externa y amplia de la atmósfera terrestre; se encuentra aproximadamente a 60,000 km de la Tierra en la dirección Tierra-Sol, en la que el campo magnético de la Tierra desvía la mayor parte del viento solar (véanse las siguientes secciones), formando un escudo protector contra las partículas cargadas de alta energía procedentes del Sol.

La magnetosfera no es privativa de la Tierra; todos los planetas con campo magnético, como Mercurio, Júpiter, Saturno, Urano y Neptuno poseen una magnetosfera propia. Algunos científicos piensan que sin la magnetosfera la Tierra habría perdido la mayor parte del agua de la atmósfera y de los océanos, debido al impacto de partículas energéticas que disociarían los átomos de hidrógeno y oxígeno, y permitiría escapar los ligeros átomos de hidrógeno, por lo que la Tierra se parecería más a Marte, que tiene una muy débil magnetización superficial y no posee magnetosfera exterior.

Tormentas solares

El flujo de partículas provenientes del Sol se conoce como viento solar.

Una tormenta solar es una explosión violenta en la atmósfera del Sol; tiene lugar en la corona y en la cromosfera, y produce radiación electromagnética que afecta satélites en órbita y sistemas de comunicación.

Manchas solares

Constan de una parte central oscura (véase figura XVIII.12, p. 142) llamada sombra, rodeada de otra menos oscura llamada penumbra; una sola mancha puede medir hasta 12,000 kilómetros.

Frecuentemente se observan a simple vista grupos de manchas (véase figura XVIII.13, p. 143) que llegan a tener dimensiones 10 o más veces superiores al diámetro de la Tierra. La duración de las manchas es muy variable; algunas no llegan a 24 horas, aunque comúnmente se les puede ver durante tres o cuatro rotaciones del Sol. Es difícil identificarlas por su aspecto, ya que cambian rápidamente de forma; a veces se subdividen en dos o más partes que se van separando para constituir manchas independientes o, por el contrario, dos o más manchas se unen para formar sólo una.

Las manchas solares son perturbaciones de carácter ciclónico en la atmósfera del Sol, que precipitan hacia el interior el hidrógeno de las capas superiores, en forma de vórtice, con velocidades de hasta 350,000 km/h. El número de manchas es muy variable; a veces son muy numerosas y a veces no se observa una sola durante semanas. Las épocas de máxima y mínima actividad solar se suceden con cierta regularidad. Tomando el promedio de un gran número de periodos, las manchas aumentan durante 4.5 años y disminuyen durante 6.6 años, lo que da un periodo total medio de unos 11 años, aunque su duración oscila entre 7 y 17 años.

Las manchas solares lanzan al exterior un gigantesco bombardeo de electrones y crean al-

rededor del Sol un campo electromagnético cuya influencia se percibe en la Tierra. Numerosos fenómenos terrestres son variables con una periodicidad que parece estar estrechamente relacionada con la de la actividad solar. Las auroras polares son más intensas y frecuentes en las épocas de máxima actividad solar, y coinciden siempre con la aparición de las grandes manchas. Al paso de ciertas manchas por el meridiano central del Sol (se conoce como meridiano central de un astro el que está en el centro de la parte visible de ese astro en cierto momento) corresponden en la Tierra las tempestades magnéticas o perturbaciones irregulares que sufre la declinación de la brújula.

También ejercen influencia las manchas solares en las condiciones climáticas. Durante los años de máxima actividad solar, la radiación aumenta en un centésimo de su valor normal. No obstante, la temperatura media de las zonas tórridas y templadas baja de medio a un grado centígrado por cada aumento de 100 manchas, lo que parece indicar que el aumento de temperatura comienza en las altas capas atmosféricas, y con mayor intensidad en la región ecuatorial. Esto provoca una baja de presión, la cual causa una mayor circulación atmosférica que tiende a igualar la temperatura de las distintas zonas y se lleva el calor de las regiones cálidas a las frías, que son las que en definitiva aumentan de temperatura. También influye en esta baja de temperatura de las regiones medias de la Tierra el hecho de que el aumento de radiación solar produce mayor y más

rápida evaporación de los mares intertropicales, mayor número de nubes que reflejan una parte del calor solar y el incremento de las lluvias. Sin embargo, se ha observado que en las épocas de máxima actividad solar, las lluvias aumentan en ciertas regiones y disminuyen en otras; muy cerca del Ecuador aumentan, pero en el norte de América y en Europa disminuyen. En conclusión, resulta difícil definir la influencia de la actividad solar en nuestras condiciones de clima, puesto que resultan de múltiples y complejos factores.

La aparición de las grandes manchas perturba también las comunicaciones radiotelegráficas y radiotelefónicas. Por ejemplo, el 1 y 2 de septiembre de 1859, una intensa tormenta solar afectó a la mayor parte del planeta; las líneas telegráficas de EUA y de Inglaterra quedaron inutilizadas. Además, una impresionante aurora boreal pudo verse en lugares tan alejados entre sí como Roma y Hawai, no obstante que estos fenómenos sólo pueden observarse normalmente en las regiones árticas. Asimismo, al paso de una mancha solar por el meridiano central del Sol el 24 de marzo de 1940, siguió la interrupción de las comunicaciones entre Europa y América; enmudecieron todas las radiodifusoras, especialmente las de onda corta. Al mismo tiempo, las brújulas “enloquecieron” en todo el mundo. Otro ejemplo es que el 13 de marzo de 1989, la ciudad de Quebec, Canadá, fue azotada por una fuerte tormenta solar que afectó a seis millones de personas por la ocurrencia de un gran apagón que duró 90 segundos; además, la

red eléctrica de Montreal estuvo paralizada durante nueve horas.

Luz zodiacal

A veces, inmediatamente después del crepúsculo, se observa en el firmamento un resplandor de luz que se extiende en forma lenticular o triangular por donde pasa la eclíptica, hasta unos 50° del Sol y con un ancho de unos 20°. Se le llama luz zodiacal por hallarse siempre en la faja del Zodiaco; las condiciones para su observación son tanto mejores cuanto más cercano a los 90° sea el ángulo que forma la eclíptica con el horizonte del lugar (véase figura XVIII.14, p. 143).

Este fenómeno se atribuye a la luz solar reflejada en multitud de partículas sólidas aglomeradas en el mismo plano que los demás astros del Sistema Solar, las cuales son tan pequeñas que sólo podemos verlas por su efecto de conjunto; también se atribuye a polvo electrizado que las radiaciones luminosas del Sol repelen hacia afuera del astro, a partir de las capas bajas de la corona. En las latitudes medias del hemisferio norte, se observa mejor viendo hacia el Oeste en primavera después del crepúsculo, o mirando hacia el Este en otoño. Es necesario buscarla en noches sin Luna, y es responsable del 60% de la luz natural.

Aberración de la luz

James Bradley (Inglaterra, 1692-1762) descubrió que la posición de una estrella parecía variar con respecto a una posición media, y que esta variación

era debida a la dirección de nuestro planeta en su traslación alrededor del Sol, ya que aparentemente la estrella se desplazaba en la misma dirección. Esta desviación aparente de la luz de las estrellas se llama aberración de la luz.

Para comprender el fenómeno, supongamos que viajamos en un automóvil al mismo tiempo que cae una lluvia intensa en dirección vertical. Debido al movimiento del auto, nos parecerá que la lluvia cae con cierta inclinación y veremos sus gotas caer en el parabrisas con tanta más inclinación cuanto mayor sea la velocidad con que viajamos. Si esa velocidad fuera muy fuerte, digamos 500 km/h o más, las trayectorias de las gotas serían paralelas al plano en que nos movemos.

Si nuestro vehículo corre hacia el Norte, nos parecerá que la lluvia viene del Norte, es decir, todo sucede como si las gotas estuvieran animadas, además de su velocidad propia, por otra velocidad igual y contraria a la nuestra, y parecerán llegarnos en la dirección de la resultante de dos velocidades: la de la lluvia y la del auto. El ángulo formado por la vertical y la dirección aparente de la lluvia es la aberración (aberración significa “desviación”).

Algo similar sucede con una estrella y la Tierra. Si en lugar de la lluvia se considera un rayo luminoso dimanado de aquélla, y en vez del auto se considera la Tierra, el ángulo formado por la normal al plano de la eclíptica, esto es, al plano de la órbita terrestre, y por el rayo de luz que llega al pie de dicha normal, se llama aberración de la luz.

Sean E y T (véase figura XVIII.15) las posiciones respectivas de una estrella y de la Tierra. Si ésta se desplaza en la dirección TT’ nos parecerá que la luz nos llega en la dirección E’T, resultante de la combinación de la velocidad de la luz y otra velocidad igual a la de la Tierra, pero de sentido contrario.

donde ν es la velocidad de traslación de la Tierra y V es la velocidad de la luz.

El valor de este ángulo, deducido de múltiples observaciones muy precisas, es de 20.5’’ o, más precisamente, de 20.47’’ y se llama constante de aberración. Así, nos parece que una estrella cuya posición coincide con el polo de la eclíptica describe en el transcurso de un año una pequeña circunferencia con centro en dicho polo y de radio igual a la cuerda que subtiende un arco de 20.47’’.

Si la estrella no se encuentra en el polo de la eclíptica, en su desplazamiento aparente describe una elipse en vez de una circunferencia; el eje mayor es la cuerda que subtiende un arco de 20.47’’ × 2 = 41’’.

Este fenómeno de la aberración no sólo confirma que la transmisión de la luz no es instantánea (velocidad de la luz ≠ ∞), sino que es, además, la prueba más convincente de la traslación de la Tierra alrededor del Sol.

Utilizando la ecuación (2) se puede calcular la velocidad de la luz; en efecto, admitiendo como circular la órbita de la Tierra y que su radio es de 149.5 × 106 km, es posible calcular su velocidad de traslación y deducir la velocidad de la luz.

Figura XVIII.15

Se tiene que:

Así pues, de la ecuación (2) se puede escribir lo siguiente:

V = = Además, ν = = 29.8 km/s

∴ V= = 300,000 km/s

Fuerza de gravitación de la Luna

Se sabe que la densidad de la Luna es de 3.4 t/m3 y la de la Tierra, de 5.52 t/m3. El radio de la Luna es de 1,740 km y el de la Tierra, de 6,378 km, por lo que el volumen de la Luna es de 1/49 del de la Tierra. Antes de continuar, definamos algunos términos:

γ = ; m = masa; r = radio de un astro

Los subíndices T y L se refieren a la Tierra y a la Luna. Así: = = × = = 1.6235

∴ 1.6235 = ×

∴ mL = = mT

Aplicando la Ley de Gravitación Universal de Newton: = × = × = 0.168 ≅

Así, la atracción lunar en la superficie es 1/6 de la atracción en la superficie de la Tierra, es decir, que un cuerpo que en ésta pesa 80 kg, en la superficie lunar pesaría sólo 13 kilogramos.

Por otra parte, la atracción que la Luna ejerce sobre la parte ensanchada de la región ecuatorial terrestre tiende a llevar el plano de nuestro Ecuador a coincidir con el plano de la órbita lunar y a provocar la nutación de la que se habló en la sección de ese nombre en el capítulo XI.

Otro efecto de la atracción lunar es el de las mareas, que se definen como el movimiento alternativo de elevación y descenso de las aguas oceánicas. Dos veces al día ascienden e invaden las tierras que colindan con el mar, y dos veces al día retroceden. La elevación máxima alcanzada se llama pleamar o marea alta, y la mínima, bajamar

El nivel del mar oscila alrededor de una posición media denominada nivel medio del mar, al cual se refieren las altitudes.

El tiempo que transcurre entre dos pleamares o entre dos bajamares es, en promedio, de 12 h 25 min. El lapso que separa dos pleamares consecutivas es igual al que media entre dos pasos, el superior y el inferior, de la Luna por el meridiano del lugar.

∴ FL = FT

El Sol también influye en las mareas, aunque solamente con cuatro décimas de la atracción lunar, dada la enorme distancia a que se encuentra de nuestro planeta, a pesar de tener una masa sumamente superior a la de la Luna; la masa del Sol equivale a 26 millones de veces la masa de la Luna.

Analicemos las fuerzas de la Luna que provocan las mareas: en la figura XVIII.16, sea L la Luna, T el centro de la Tierra y A una partícula líquida.

El vector es la fuerza atractiva sobre A; , menor que , es la atracción ejercida sobre T. El vector es igual y paralelo a . La fuerza atractiva AE se puede descomponer en dos: = + .

El vector , paralelo a y de la misma dirección, representa la intensidad de la fuerza

perturbadora que tiende a levantar la partícula A hacia L’ , es decir, hacia la Luna.

Si se considera otra partícula B (véase figura XVIII.17) del lado opuesto a la Luna, B y T son atraídos hacia ella con una intensidad representada, respectivamente, por los vectores y , en que es mayor que . Trazando por B el vector , igual y paralelo a , puede considerarse a como una de las componentes de y a como la otra componente, esto es:

= + , de donde:

Figura XVIII.16

Figura XVIII.17

Si se traza por B el vector , igual y de la misma dirección y sentido que , representará la fuerza que tiende a separar la partícula líquida B.

La componente no produce perturbación en B, mientras que hace que la partícula B se mueva hacia L’, y por eso se le considera como la fuerza perturbadora que hace que el agua tienda a elevarse en la dirección opuesta a la Luna.

Los efectos de las atracciones del Sol y de la Luna en las mareas se suman en la conjunción y en la oposición. Así, en las sizigias la marea alcanza su altura máxima y se llama “aguas vivas”. En cambio, los efectos se restan en las cuadraturas, y es cuando las pleamares tienen su altura mínima y se llaman “aguas muertas”.

Otra fuerza que influye en las mareas es la que se explica a continuación: ya se vio que la masa de la Luna es relativamente considerable con respecto

a la de la Tierra; por ello, el centro de gravedad del sistema Tierra-Luna no coincide con el centro de la Tierra. En efecto, por un principio de mecánica, se tiene que la razón de la masa de la Tierra a la de la Luna es igual a la razón de las distancias de los centros de nuestro planeta y su satélite al centro de gravedad G. Siendo la masa de la Luna 1/80 de la terrestre, la distancia del centro de gravedad G al centro de la Tierra T (véase figura XVIII.18) debe ser 1/80 de la distancia de G al centro de la Luna, es decir:

(3)

Si x es la distancia de T a G, y sabiendo que TL es igual a 60 radios terrestres, sustituyendo en (3) se tiene:

Figura XVIII.18

∴ x = 0.75 r

Este resultado indica que el centro de gravedad se encuentra en el interior de nuestro planeta. Así, el centro de la Tierra gira alrededor del centro de gravedad durante el mismo tiempo que la Luna da una revolución sideral. Este movimiento de la Tierra desarrolla una fuerza centrífuga que contribuye a comunicar mayor elevación a las aguas situadas en el hemisferio opuesto a la Luna.

Entonces hay dos ondas de marea: una que depende directamente de la acción de la Luna y otra, en el hemisferio opuesto a ella, debida a la menor atracción del satélite y a la fuerza centrífuga desarrollada por el movimiento del centro de la Tierra alrededor del centro de gravedad G, común a los dos astros.

La onda de la marea está influida por dos impulsos: el de la rotación de la Tierra, de Oeste a Este, y el causado por el movimiento de la Luna alrededor de nuestro planeta, que es en el mismo sentido que la rotación de la Tierra. Pero dado que el movimiento de traslación de la Luna es mucho más lento que el de rotación de la Tierra, la onda de marea aparentemente corre hacia el Poniente. Estos dos impulsos en dirección opuesta dan como resultado una fricción entre dicha onda y la parte líquida restante de nuestro globo. Esta fricción tiene como consecuencia un retardo muy pequeño (22 segundos de arco cada siglo, según el astrónomo inglés Airy) que sufre la Tierra en

su movimiento de rotación, porque la onda de la marea actúa a manera de freno sobre la parte líquida restante.

Cosmología

La cosmología es el estudio del Universo en su conjunto, en el que se incluyen teorías sobre su origen, su evolución, su estructura a gran escala y su futuro. Tiene una larga historia y en ella quedan involucradas la física, la astronomía, la filosofía, el esoterismo y la religión.

El nacimiento de la cosmología se sitúa en 1700 con la hipótesis de que las estrellas de la Vía Láctea pertenecen a un sistema estelar de forma de disco, del cual forma parte el propio Sol; asimismo, que existen otros sistemas nebulosos (galaxias) similares a la Vía Láctea y visibles con el telescopio, aunque muy lejanos.

La cosmología física es el estudio del origen, la evolución y el destino del Universo, utilizando los modelos de la física. Se desarrolló como ciencia durante la primera mitad del siglo XX.

1915-1916. Albert Einstein formula la Teoría General de la Relatividad, en la que presenta el primer modelo matemático del Universo y establece que éste es homogéneo e isótropo a gran escala, lo cual significa que tiene la misma apariencia general observado desde cualquier lugar.

1920-1921. Se realiza el debate entre los astrónomos Heber Curtis y Harlow Shapley, en el que se asentó la naturaleza extragaláctica de las

nebulosas espirales cuando se pensaba que la Vía Láctea constituía todo el Universo.

1922-1924. Alexander Friedmann publica la primera solución matemática a las ecuaciones de Albert Einstein de la relatividad general, que representan a un Universo en expansión.

1930. Georges Lemaître esboza su hipótesis del átomo primitivo en la que sugería que el Universo había nacido con la explosión de un solo átomo primigenio de energía (quanto), lo que más tarde se denominó Big Bang.

1933. Fritz Zwicky publica un estudio de la distribución de las galaxias, sugiriendo que estaban permanentemente ligadas por su mutua atracción gravitacional.

1948. Ralph Alpher y Robert Herman hacen la primera predicción de la existencia de la radiación de fondo de microondas.

1965. Arno Allan Penzias y Robert Wilson descubren la señal de radio, la cual fue rápidamente interpretada como la radiación de fondo de microondas, lo cual supondría una observación crucial que convertiría al modelo del Big Bang en el modelo físico estándar para describir el Universo.

Durante el resto del siglo XX se produjo la consolidación de este modelo y se establecieron los siguientes hechos fuera de cualquier duda razonable:

• El Universo está en expansión, la distancia entre cualquier par de galaxias lejanas se incrementa con el tiempo.

• La dinámica de la expansión está descrita con muy buena aproximación por la Teoría General de la Relatividad de Einstein.

• El Universo se expande a partir de un estado inicial de alta densidad y temperatura donde se formaron los elementos químicos ligeros, estado a veces denominado Big Bang o Gran Explosión.

Según la teoría del Big Bang, el Universo se originó en una singularidad espaciotemporal de densidad infinita, paradójica matemáticamente. El espacio se ha expandido desde entonces, por lo que los objetos astrofísicos se han alejado unos respecto de los otros.

En las diversas observaciones realizadas entre 1970 y 1990 se mostró que no había suficiente materia visible en el Universo para explicar la intensidad de las fuerzas gravitacionales que se dan en las galaxias y entre ellas. Esto condujo a la idea de que hasta 90% de la materia en el Universo no es materia común sino materia oscura. Dicha materia se ha detectado únicamente a través de su huella gravitacional; no se ha observado en laboratorio ninguna partícula. Sin embargo, hay muchos candidatos a materia oscura en física de partículas, y se están llevando a cabo diversos proyectos para detectarla.

En los años noventa, mediciones detalladas de la densidad de masa del Universo revelaron que ésta sumaba 30% y quedaba 70% de densidad de energía sin contar, por lo que se cree que la energía oscura

constituye ese 70%. Actualmente se están haciendo observaciones que podrían aclarar este punto.

A pesar de que el modelo del Big Bang es ampliamente aceptado entre la comunidad científica, hay aspectos que aún no se resuelven:

• No existe un modelo definitivo de la formación de las estructuras actuales a partir del Big Bang.

• Se ignora a qué se debe el hecho de que el Universo se expanda con aceleración.

• No se sabe cuál es el destino final del Universo.

• Se desconoce en su mayor parte la naturaleza de la materia y de la energía oscuras.

De la cosmología filosófica sólo se dirá aquí que tiene que ver con la metafísica espacial, lo que no debe entenderse en el sentido de que pertenezca a esta parte de la metafísica tratar de todas las cosas o seres que constituyen el mundo, sino del Universo considerado como colección de seres finitos con su esencia, origen, propiedades generales, leyes y caracteres más importantes y generales del mundo sensible.

En cuanto a la cosmología religiosa, ésta es un delicado debate abierto entre religiosos, en el que se tratan temas como el creacionismo, el diseño inteligente y la cosmogonía; esta última es una narración mítica que pretende dar respuesta al origen de los dioses, del Universo y de la propia humanidad.

Las cosmogonías griegas narran el origen del mundo a partir del caos y la intervención divina que impone el orden. Para la cosmogonía judeo-

cristiana, el origen del mundo se encuentra en el Génesis.

Eras geológicas

Son las distintas etapas en las cuales ocurrieron fenómenos importantes en nuestro planeta, incluyendo la evolución de distintos tipos de vida para adaptarse al medio en el que actualmente nos encontramos. Se resumirán aquí las cuatro eras principales: Precámbrico, Paleozoico, Mesozoico y Cenozoico.

Precámbrico

Comenzó hace 4,600 millones de años, es decir, desde que se formó nuestro planeta, y concluyó hace 542 millones de años. Simbolizaremos esto como 4,600-542. El Precámbrico se divide en tres periodos:

• Hadeico (4,600-3,800). En este periodo se formaron la Tierra y la Luna.

• Arcaico (3,800-2,500). Comprende una máxima actividad de impactos meteoríticos y las primeras formas de vida unicelular.

• Proterozoico (2,500-542). Aparece la vida multicelular, ocurre una glaciación global; aparecen las primeras esponjas, animales blandos y los trilobites.

Paleozoico (542-251)

Tiene seis periodos:

• Cámbrico (542-492). Se desarrollan los trilobites, hongos y algas.

• Ordovícico (492-445). Aparecen los animales invertebrados, las estrellas de mar y las primeras plantas verdes; ocurre otra glaciación al final de este periodo.

• Silúrico (445-418). Aparecen los primeros peces y moluscos diversos.

• Devónico (418-374). Aparecen las primeras plantas con semilla, los árboles y los primeros insectos sin alas; surgen también los primeros tiburones.

• Carbonífero (374-300). Primeros vertebrados terrestres, tiburones diversificados; los trilobites declinan, surgen los insectos alados y los primeros reptiles; aparecen los bosques, existen niveles elevados de oxígeno.

• Pérmico (300-251). Emergen terrenos y se forma el supercontinente Pangea (véase figura XVIII.19, p. 143); evolucionan los escarabajos y las moscas. Se extingue 95% de la vida en la Tierra.

Mesozoico (251-65)

Se divide en tres periodos:

• Triásico (251-200). Aparecen los dinosaurios en tierra, los ictiosaurios en el mar y los pterosaurios en el aire; primeros mamíferos y peces.

• Jurásico (200-150). Más dinosaurios, primeras aves y lagartos, erizos y estrellas de mar, separación de la Pangea en dos partes: Gondwana y Laurasia (véase figura XVIII.20, p. 144).

• Cretácico (150-65). Cocodrilos y tiburones actuales, marsupiales. Ruptura de Gondwana

(véase figura XVIII.21, p. 144). Desaparecen los dinosaurios al final de este periodo.

Cenozoico (65 millones de añosla actualidad)

En esta era se trasladan los continentes a sus posiciones actuales. Tiene tres periodos:

• Paleógeno (65-25). Aparecen las plantas actuales, los primeros mamíferos grandes como los osos e hipopótamos, y las primeras ballenas. Aparecen capas de hielo en la Antártida.

• Neógeno (25-2.6). Evolucionan los mamíferos, se diversifican caballos y mastodontes; aparecen los primeros simios y varios géneros de mamíferos. Aparecen los primeros homínidos bípedos y el Australopithecus.

• Cuaternario (2.6 millones de años-la actualidad). Se extinguen muchos grandes mamíferos; aparece el Homo habilis hace 2.5 millones de años; hace 230,000 años vestigios del Neanderthal, y del Homo sapiens hace 200,000 años. Comienza la Edad de Hielo, que finaliza en este periodo. Surge la civilización humana. Este periodo se subdivide en dos épocas: el Pleistoceno (2.6 millones de años-11,800 años) y el Holoceno (11,800 años-la actualidad).

Agujeros negros

Un agujero u hoyo negro es una región del espacio-tiempo provocada por una gran concentración de masa en su interior, con enorme aumento de la densidad, lo que genera un campo

gravitatorio tal que ninguna partícula material, ni siquiera los fotones de luz, pueden escapar de dicha región ni salir de ella. Los agujeros negros proceden de un proceso de colapso gravitatorio que comienza después de la muerte de una gigante roja (estrella de gran masa), entendiéndose por muerte la extinción total de su energía. Tras varios miles de millones de años, la fuerza gravitatoria de dicha estrella comienza a ejercer fuerza sobre sí, origina una masa concentrada en un pequeño volumen, y se convierte en una enana blanca. El proceso puede proseguir hasta el colapso de dicho astro por la autoatracción gravitatoria que termina por convertir a esta enana blanca en un agujero negro. Este proceso acaba por reunir una fuerza de atracción tan fuerte que atrapa hasta a la luz.

El concepto de un cuerpo tan denso que ni la luz pudiese escapar de él fue descrito en 1783 por el geólogo inglés John Michell. Sin embargo, hasta hoy es imposible describir lo que sucede en el interior de un agujero negro.

En 1995, un grupo de investigadores de la UCLA demostró la posibilidad de la existencia de agujeros negros supermasivos en el núcleo de las galaxias. Poco después se verificó que algo deformaba los rayos de luz emitidos desde el centro de nuestra galaxia (la Vía Láctea). Tal deformación se debe a un agujero negro supermasivo que ha sido denominado Sagitarius A, al que se le calcula una masa 4.5 millones de veces mayor que la del Sol y una distancia de 26,000 años luz de nuestro planeta.

El agujero negro más pequeño conocido hasta ahora ha sido denominado J-1650; se ubica en la constelación Altar de la Vía Láctea, en la que se encuentra la Tierra. Tiene una masa cuatro veces la del Sol y tan sólo 24 km de diámetro.

Tamaños aparentes

Un fenómeno que se atribuye a la atmósfera, pero que no es más que una ilusión óptica, es el aumento de los tamaños del Sol, de la Luna y de las constelaciones cuando se hallan cerca del horizonte. Esta ilusión se explica por la comparación que se hace subconscientemente con los objetos terrestres colocados en el campo visual. Además, cuando la Luna está cerca del horizonte, su luz se degrada y nos parece más lejana, por lo que se antoja más grande. Es algo similar a lo que nos pasaría si viéramos en la calle dos coches, uno a 100 metros de distancia y el otro a 500: si los viéramos del mismo tamaño aparente, el más lejano nos parecería gigantesco.

En realidad, se han hecho medidas cuidadosas que demuestran que el fenómeno en cuestión es sólo una ilusión óptica; cuando se ve un objeto de frente, parece mayor que cuando se le ve formando un ángulo importante, digamos mayor de 30°, con el horizonte. Ello, según un estudio realizado en la Universidad de Harvard, se debe a una peculiaridad del cerebro y los ojos humanos. Si el observador se pone en posición horizontal, le parece mayor la Luna en el meridiano que en el horizonte.

Algoritmo para calcular el día de la semana

Tiene por objeto saber el día de la semana en que cae una fecha cualquiera. Los pasos iniciales son los siguientes:

1. Enumerar los días de la semana, comenzando con el 0 para el domingo, el 1 para el lunes y así sucesivamente hasta llegar al 6, sábado.

2. Buscar o calcular mediante una regla en qué día de la semana comenzó un siglo.

3. Buscar o calcular en qué día de la semana comenzó un año dado.

4. Buscar o calcular en qué día comienza un mes dado, sabiendo el año.

Meses correspondientes

Pertenecen a este grupo los meses que comienzan el mismo día de la semana; por ejemplo, los meses de septiembre y diciembre son correspondientes porque el 1 de septiembre cae en el mismo día de la semana que el 1 de diciembre, ya que el número de días entre ellos es múltiplo de 7.

En efecto, son 30 días de septiembre, 31 días de octubre y 30 días de noviembre, los que sumados dan 91, número que es múltiplo de 7. De igual manera, febrero y marzo son correspondientes en un año no bisiesto, puesto que 28 es múltiplo de 7.

Meses correspondientes en un año no bisiesto:

• Enero y octubre

• Febrero, marzo y noviembre

• Abril y julio

• Septiembre y diciembre

Mayo, junio y agosto no se corresponden con ningún mes.

En un año bisiesto son meses correspondientes:

• Enero, abril y julio

• Febrero y agosto

• Marzo y noviembre

• Septiembre y diciembre

Mayo, junio y octubre no se corresponden con ningún mes.

Para determinar el día de la semana de una fecha del calendario gregoriano, se procede como sigue:

1. Se calcula la cantidad de días transcurridos hasta la fecha de interés.

2. Se calcula el módulo con respecto a 7.

Lo anterior se expresa así:

d = [(A – 1) 365 + – (4) + DM +D ] mod7

(en las divisiones sólo se consideran los enteros; por ejemplo, si A = 1,960 entonces (A – 1)/4 = 1,959/4 = 489)

donde d = día de la semana buscado.

A = año correspondiente.

DM = días transcurridos hasta antes del primer día del mes.

D = día de la fecha de interés.

mod7 = módulo de 7; por ejemplo, x mod7 implica dividir x entre 7, y el resultado es el residuo; así, 1,981 mod7 = 0; 1,993 mod7 = 5.

Debemos conocer el módulo correspondiente a cada inicio de mes. Por ejemplo, si buscamos una

fecha de julio, el módulo es, empezando por enero:

X = (31 mod7 + 28 mod7 + 31 mod7 + 30 mod7 + 31 mod7 + 30 mod7)mod7 = = (3 + 0 + 3 + 2 + 3 + 2) mod7 = 13 mod7 = 6.

Puede elaborarse una tabla que contenga los módulos acumulados por mes, como la de abajo.

En realidad no es necesario calcular el número total de días, sino únicamente los módulos con respecto a 7; así, la expresión (4) se reduce a: d = [(A – 1) mod7 + 〈 – 〉 mod7 + M + Dmod7 ] mod7 (5)

donde M = módulo del mes.

Velocidad de escape Es la velocidad que debe adquirir o rebasar un proyectil que quisiera lanzarse al exterior de la

no bisiesto

bisiesto

Ejemplo 1. ¿En qué día de la semana cayó el 15 de noviembre de 2012?

Datos: A = 2012, M = 4, D=15.

d = [(A – 1) mod7 + 〈 – 〉 mod7 + M + Dmod7 ] mod7

(A – 1) mod7 = 2011 mod7 = 2 〈 – 〉 mod7 = 〈 – 〉 mod7 =

= 〈 502 – 15 〉 mod7 = 487 mod7 = 4

M = 4; D mod7 = 15 mod7 = 1.

∴ d = (2 + 4 + 4 + 1) mod7 = 4, que corresponde a jueves.

Ejemplo 2. Calcular el día de la semana en que cayó el 8 de junio de 1966.

Datos: A = 1966; M = 4; D = 8

d = [(A – 1) mod7 + 〈 – 〉 mod7 + M + Dmod7 ] mod7

(A–1) mod7 = 1,965 mod7 = 5 〈 – 〉 mod7 = 〈 – 〉 mod7 =

〈 490 – 15 〉 mod7 = 6.

M = 4 D mod7 = 8 mod7 = 1

∴ d = (5 + 6 + 4 + 1) mod7 = 16 mod7 = 2, que corresponde a martes.

Tierra y que permanezca fuera de la influencia de su campo de gravitación.

Para obtener la fórmula que permita calcular la velocidad de escape, estudiemos lo siguiente: se sabe que la fuerza con la que se atraen dos masas m y m’ situadas entre sí a una distancia d está dada por la expresión:

F = N

en la que N es la constante de Newton o de Gravitación Universal (vale 6.67 × 10–8 dinas), esto es, la fuerza con que se atraen dos unidades de masa situadas a la unidad de distancia. Esto significa que la aceleración que la masa M del Sol comu-

nica a la unidad de masa de un planeta situado a una distancia D es NM/D2, mientras que la que la masa m del planeta comunica a la unidad de masa del Sol es Nm/D2. Entonces, la aceleración relativa es:

+ = (6)

En mecánica, se sabe que la fuerza necesaria para que un cuerpo describa con movimiento uniforme un círculo alrededor de un punto es igual a la masa del cuerpo multiplicada por el cuadrado de la velocidad y dividida entre el radio del círculo.

Así, la fuerza de gravitación está dada por la expresión:

f =

Tratándose de un movimiento uniforme y circular, y llamando T al tiempo de una revolución, la velocidad es:

v = entonces f =

Si m = 1 y haciendo r = D, resulta que la aceleración relativa es:

(7)

Igualando (6) y (7):

NT2 (M + m) = 4π2D3 (8)

Para otro planeta de masa m’ situado a la distancia D’ , tenemos:

NT’ 2 (M + m’ ) = 4π2D’ 3 (9)

Dividiendo (8) entre (9), resulta que:

T 2 (M + m) = D 3 (10)

T’ 2 (M + m’ ) = D’ 3

La ecuación (10) presenta en forma más exacta, deducida por Newton, la tercera ley de Kepler o ley armónica.

Así, el enunciado de Kepler sólo puede ser verdadero cuando las masas de dos planetas se consideren despreciables comparadas con la del Sol, o cuando se aplique a dos planetas de igual masa.

La velocidad con la que se mueve un cuerpo en torno de otro está dada por:

v2 = N(M + m)( – ) (11)

donde r = distancia entre los centros de ambos cuerpos en un instante dado, y a = distancia media entre los cuerpos o semieje mayor de la órbita relativa elíptica.

Si la órbita relativa es parabólica, el cuerpo satélite se mueve con velocidad parabólica. La parábola puede considerarse como el límite hacia el que tiende una elipse, uno de cuyos focos y el centro se alejan indefinidamente del otro foco y del vértice contrario, que permanecen fijos.

Así, en la ecuación (11) el término a se hace infinito, por lo que ésta se convierte en:

v2 = 2N ( )

En este caso parabólico, el cuerpo satélite pasa una vez cerca del foco (centro gravitacional) y no vuelve jamás, y por eso la velocidad se llama de escape.

Para el caso de un cuerpo de masa insignificante en comparación con la de la Tierra y que se mueva cerca de la superficie de ésta, tenemos:

v = ( )1/2 (12)

Esta es la velocidad que tendría que adquirir o rebasar un proyectil que quisiera lanzarse fuera de la Tierra, como el ideado por Julio Verne en su novela De la Tierra a la Luna, publicada en el año 1865.

Giovanni Papini

Para concluir, no quiero dejar de mencionar unos pasajes de dos de las más famosas y laureadas obras del escritor italiano Giovanni Papini (18811956), Gog y El libro negro, que envuelven frases filosóficas alusivas a la astronomía, con gran sentido del humor:

Fragmentos de Gog (1931), capítulo “Contra el cielo”:

Odio al cielo [...] para sufrir la humillación de mi pequeñez bastaba la Tierra [...] Aquellos millones de soles que aparecen a mis ojos como átomos desordenados de luz eléctrica, ¿qué tienen que ver conmigo? [...] ¿para qué me sirven? ¿Por qué vuelven todas las noches, llamas milenarias, a insultar la brevedad de mis días?

Considerando que la masa de la Tierra es de 5.97 × 10 27g (véase apartado “Tierra”, capítulo XIV), que su radio r = 6.37 × 108 cm y que N = 6.67 × 10-8 dinas, de la ecuación (12) resulta que:

v = ( )1/2

= (124.4836 × 1010 )1/2 = 11.16 × 105 = 11.16 km/s = 40,176 km/h

[...] Cuando he sabido a cuántos millones de años luz distan de mí [...], no he hecho más que dar forma aritmética a mi rabia [...] Por eso prefiero no verlo. Me gustan las regiones y las estaciones donde el cielo está siempre cubierto, donde la noche es muda y total, y te sientes bajo una colcha próxima de niebla familiar. Envidio a los habitantes de Venus porque, según se dice, su planeta está casi siempre envuelto por vapores [...] se les evita la vista del irritante chispo-

rroteo de las inútiles constelaciones y de aquella odiosa Vía Láctea que atraviesa el firmamento como una humareda de burla fosforescente. Los poetas, idiotas como niños, se extasían ante las luciérnagas errantes del infinito. Para mí, que por fortuna o desgracia no soy versificador ni místico, el cielo es únicamente el telón siniestro donde leo todas las noches la sentencia de mi nulidad irremediable.

Fragmentos de El libro negro (1951), capítulo

“El astrónomo desilusionado”:

Hasta hace algunos años la astronomía me parecía la más divina de las ciencias, fue mi primer amor intelectual, apasionado y fuerte. Hoy en día, después de haber conocido más de cerca el cielo por medio del telescopio más poderoso del mundo, me siento perplejo, turbado, dudoso, a veces hasta atemorizado. La astronomía me ha desilusionado [...], como ciencia exacta es uno de los más maravillosos edificios levantados por la mente humana en los últimos siglos, pero, en cambio, me ha desilusionado su objeto: el universo sideral [...]; el cielo que vemos no es el de

hoy, el de este momento, en algunas partes es el cielo de hace varios siglos, en otras partes es el cielo de hace milenios. Parece que las nebulosas más lejanas se esfuerzan por alejarse cada vez más de la Vía Láctea, pero jamás sabremos por qué huyen y a dónde van [...] ¿Es posible que una inteligencia superior y perfecta haya querido esa dilapidación enorme, perenne y completamente inútil? ¿Para qué sirven esos innumerables y pavorosamente grandes fuegos huidizos, que continuamente nacen y arden, destinados a consumirse vanamente aun cuando demoren millones de años? [...] Algo semejante sucedería si los hombres iluminaran todas las noches, con millones de lámparas y reflectores, el desierto del Sahara o los océanos árticos, lugares donde nadie habita y por donde nadie anda.

Cierro este capítulo con la reproducción de una obra del caricaturista estadounidense Herblock publicada en la edición 37 de The Washington Post, el 19 de abril de 1955, ante la noticia del fallecimiento de Albert Einstein, quizá el más grande genio del siglo XX.

A 1955 Herblock Cartoon, © The Herb Block Foundation

CAPÍTULO XVIII. TEMAS DIVERSOS

CAPÍTULO XIX

Prontuario de información general

En lo tocante a la ciencia, la autoridad de un millar de hombres no es superior al humilde razonamiento de una sola persona. gAlileo gAlilei (1564-1643)

Unidades de temperatura y conversiones

La siguiente tabla permite convertir temperaturas dadas en cualquier sistema: grados Celsius o centígrados (° C), grados Farenheit (° F) y Kelvin (K); este último se llama Kelvin, sin el término “grados”.

Recordemos que las escalas Celsius y Farenheit son relativamente arbitrarias, a diferencia de la escala Kelvin, la cual se refiere o inicia con el cero absoluto, que es la mínima temperatura a obtener; debido a ello, no existen valores negativos de Kelvin.

Fórmulas útiles y equivalencias

Área del círculo = πr2, r es el radio

Perímetro de la circunferencia = 2πr

Volumen de la esfera = 4/3 πr3

Superficie de la esfera = 4πr

Área de la elipse = πab, a y b son los semiejes mayor y menor, respectivamente.

1 dina = 1 newton =

Dimensiones de los planetas del Sistema

Solar en km y su número de satélites

Planeta Diámetro ecuatorial Diámetro polar Número de satélites

Mercurio 4,879 4,879 0

Venus 12,104 12,104 0

Tierra 12,756 12,714 1

Marte 6,787 6,750 2

Júpiter 142,800 133,708 63

Saturno 120,536 108,728 200

Urano 51,118 49,946 27

Neptuno 49,528 48,681 13

Dimensiones

Diámetro medio del Sol = 1,393,720 km

Diámetro medio de la Tierra = 12,742 km

Diámetro medio de la Luna = 3,476 km

Distancias entre astros

Luna-Tierra: 60.3 radios terrestres (de 55.90 a 63.86 r t) = 384,616 km

De la Tierra al Sol: 23,439 r t = 149.5 millones de km = 1 ua

De los planetas al Sol:

Distancia al Sol (ua)

Velocidades de traslación

De la Tierra alrededor del Sol: = 108,000 km/h = 30 km/s

Velocidad del Sol alrededor de nuestra galaxia = 778,000 km/h = 216 km/s

De la Luna alrededor de la Tierra: 1 km/s

Ángulos de paralaje

Del Sol = 8.8’’

De la Luna = 57’ 2.7’’

Semidiámetros aparentes

Del Sol = 16’ 01.5’’

De la Luna = 15’ 34’’

Edad estimada

Del Sol = 5,000 millones de años

De la Tierra = 4,600 millones de años

De la Luna = 4,550 millones de años

Algunas propiedades de los planetas

Temperaturas del Sol

y sus planetas

De la superficie del Sol = 6,000 K.

Del núcleo del Sol = 13,000,000 K

De la superficie de Mercurio = 440 K = 167° C

De la superficie de Venus = 730 K = 457° C

De la superficie de la Tierra = 288 K = 15° C

De la superficie de Marte = 230 K = –43° C

De la superficie de Júpiter = 152 K= –121° C

De la superficie de Saturno = 134 K= –139° C

De la superficie de Urano = 76 K = –197° C

De la superficie de Neptuno = 53 K = –220° C

= 1)

Mercurio Venus Tierra Marte Júpiter Saturno Urano Neptuno

Periodo de rotación (días

Densidad (agua = 1)

= 1)

*Los valores con asterisco del periodo de rotación indican que el planeta gira en sentido opuesto al de su órbita alrededor del Sol.

TABLAS

Tabla I

Posiciones geográficas de las principales ciudades mexicanas

Entidad federativa Ciudad Latitud N Longitud WG Δ Altitud (m)

Aguascalientes Aguascalientes

B. California Sur La Paz

Ciudad del Carmen 18° 38’ 22”

Coahuila Saltillo 25° 25’ 33”

50’ 16” 7 min 21 s

Chiapas San Cristóbal de Las Casas 16° 44’ 18”

Gutiérrez

Chihuahua C. Juárez 31° 44’ 16”

11’ 06”

s

38’ 17” 10 min 33 s

06’ 46” 12 min 27 s

29’ 00” 1 h 5 min 36 s 1,144 Chihuahua 28° 38’ 12”

04’

Colima

Observatorio Tacubaya

Ciudad

Celaya

Hidalgo

Miguel Allende

Entidad federativa Ciudad

Querétaro Querétaro

San Juan del Río

Quintana Roo Cozumel

Felipe Carrillo Puerto

Mujeres

San Luis Potosí Catorce

Guaymas 27° 55’ 30” 110° 53’ 34” 1 h 23 min 31 s

Coatzacoalcos 18°08’56” 94° 24’ 40” 17 min 39 s

S.A. Tuxtla 18°26’42” 95° 11’ 53” 20 min 48 s 361 Tuxpan 20°57’18” 97° 23’ 59” 29 min 36 s 14

Veracruz 19°12’02” 96° 08’ 13” 24 min 33 s

Yucatán Acanceh 20°48’50” 89° 27’ 11” –2 min 11 s Espita 21°00’36” 88° 18’ 27” –6 min 46 s

Izamal 20°56’17” 89° 01’ 02” –3 min 56 s

Maxcanú 20°35’11” 89° 59’ 55” –0 min 0.3 s Mérida 20°58’05” 89° 37’ 25” –1 min 29.7 s

Peto 20°07’36” 88° 55’ 30” –4 min 18 s

Progreso 21°17’00” 89° 39’ 51” –1 min 21 s

Ticul 20°23’10” 89° 34’ 31” –1 min 46 s

Valladolid 20°41’24” 88° 12’ 83” –7 min 10 s

Zacatecas Fresnillo 23°10’29” 102° 52’ 50” 51 min 31 s

Zacatecas 22°46’35” 102° 34’ 15” 50 min 17 s

Hora sideral

A. Hora sideral a las 0 h del meridiano 90° WG el día 1 de cada mes (*)

Mes Año bisiesto

Años que siguen a uno bisiesto

(*) Corresponde al periodo 1948-1951. Agréguese 0.1 min por cada cuatrienio que pase.

B. Corrección por la fecha del mes

Tabla II

C. Corrección por la hora oficial

Ts = hora sideral

T = hora oficial

To, Tf y Th: datos tomados de las tablas A, B y C

L = longitud del lugar, menos 6 h (véase tabla I)

Tabla III

Catálogo de estrellas

(Coordenadas para 1950)

Núm. Estrella

Núm. Estrella

Nombre en español

Núm. Estrella

Nombre en español Magnitud

Ascensión recta Declinación

Tabla IV

Catálogo de estrellas (Coordenadas para 2011)

Estrella Ascensión recta (α) Declinación (δ)

Tabla V

Julio Agosto Septiembre

Nota: Las coordenadas están calculadas para la hora del paso del Sol por el meridiano de Tacubaya.

VI

Epacta (año gregoriano)

Tabla

Nota: La epacta sirve para calcular la edad de la Luna en una fecha cualquiera, con auxilio de la tabla VII.

Tabla VII. Número N para calcular la edad de la Luna

* En año bisiesto, agréguese 1 del 1 de marzo al 31 de diciembre. En todos los casos, réstese 30 si se puede.

Ejemplo 1. ¿Cuál era la edad de la Luna el 27 de abril de 1962?

En la tabla VI hallamos que la epacta de 1962 es 24. En la VII, para el 27 de abril hallamos N = 28.

La suma es 52. Restando 30, nos queda 22. La Luna tenía 22 días y se hallaba, por tanto, en cuarto menguante.

Ejemplo 2. ¿En qué día de agosto de 1925 hubo Luna llena?

La edad lunar que se requiere es 14. La epacta de 1925 es 5. Por sustracción obtenemos: 14 – 5 = 9.

En esta tabla, en la columna del mes de agosto buscamos 9; y recorriendo el renglón hacia la izquierda, vemos que corresponde al día 4: el 4 de agosto de 1925 hubo Luna llena.

Tabla VIII

Reglas para el uso del calendario perpetuo

Supongamos que se quiere conocer el día de la semana en que cayó una fecha cualquiera del siglo XX. En ese caso, se busca en la tabla IX la fecha del mes, el nombre del mes y las dos últimas cifras del número del año, anotando en cada caso la cifra que encabeza la columna respectiva (en negrita). A continuación se suman estas cifras y se resta del resultado el mayor múltiplo de 7 que contenga. Se busca el resto en las cabezas de columna y encima se hallará el día de la semana.

Ejemplo. Averiguar en qué día de la semana cayó el 5 de febrero de 1964.

En la tabla IX vemos que el año 64 se halla entre paréntesis, que indica que ese año fue bisiesto; tomemos también el mes de febrero entre paréntesis, y entonces:

Encabezando la columna en que se halla el día 5, tenemos 5.

Encabezando la columna en que se halla febrero entre paréntesis, 2.

Encabezando la columna en que se halla el año, 3.

Suma = 10

Restando 10 – 7 = 3, y viendo la columna que encabeza el 3, vemos que corresponde a un miércoles.

Ahora bien, si se trata de otro siglo cualquiera, además de sumar las cifras como en el ejemplo anterior, añadiremos otra tomada de las tablas X u XI, según sea el caso.

Ejemplo. ¿En qué día de la semana cayó el 24 de diciembre de 2012?

En la tabla IX, el año 12 está entre paréntesis, por lo que fue bisiesto.

Encabezando la columna en que se halla el 24, tenemos 3.

Encabezando la columna en que se halla diciembre, 5.

Encabezando la columna en que se halla el año 12 entre paréntesis, 1.

De la tabla XI, para los dos primeros dígitos del año (20), 6.

Suma = 15

Restando 15 – 14 = 1, vemos que corresponde a un lunes.

Tabla IX

Calendario para el siglo XX

Día de la semana Domingo

28 29 30 31

Mes Enero Mayo Agosto Febrero Junio Septiembre Abril Octubre (Febrero) Marzo Diciembre Julio Noviembre (Enero)

Año 1 2 3 - (4) 5

Tabla IX (Continúa)

Los años que están entre paréntesis son bisiestos. En ellos, los meses de enero y febrero deben tomarse también entre paréntesis

Tabla X

Para el calendario juliano

(Hasta el 4 de octubre de 1582)

Tabla XI

Para el calendario gregoriano

(Desde el 15 de octubre de 1582)

Tabla XII

Domingo de Pascua en el calendario gregoriano (Siglos XVI a XIX) Año 0

Tabla XIII

Domingo de Pascua en el calendario gregoriano

(Siglos XX y XXI)

Año 0 1 2 3 4 5 6 7 8 9

1900 15 Abr 7Abr 30 Mar 12 Abr 3 Abr 23 Abr 15 Abr 31 Mar 19 Abr 11 Abr

1910 27 Mar 16 Abr 7 Abr 23 Mar 12 Abr 4 Abr 23 Abr 8 Abr 31 Mar 20 Abr

1920 4 Abr 27 Mar 16 Abr 1° Abr 20 Abr 12 Abr 4 Abr 17 Abr 8 Abr 31 Mar

1930 20 Abr 5 Mr 27 Mar 16 Abr 1° Abr 21 Abr 12 Abr 28 Mar 17 Abr 9 Abr

1940 24 Mar 13 Abr 5 Abr 25 Abr 9 Abr 1°Abr 21 Abr 6 Abr 28 Mar 17 Abr

1950 9 Abr 25 Mar 13 Abr 5 Abr 18 Abr 10 Abr 1° Abr 21 Abr 6 Abr 29 Mar

1960 17 Abr 2 Abr 22 Abr 14 Abr 29 Mar 18 Abr 10 Abr 26 Mar 14 Abr 6 Abr

1970 29 Mar 11 Abr 2 Abr 22 Abr 14 Abr 30 Mar 18 Abr 10 Abr 26 Mar 15 Abr 1980 6 Abr 19 Abr 11 Abr 3 Abr 22 Abr 7 Abr 30 Mar 19 Abr 3 Abr 26 Mar 1990 15 Abr 31 Mar 19 Abr 11 Abr 3 Abr 16 Abr 7 Abr 30 Mar 12 Abr 4 Abr

23 Abr

12 Abr 4 Abr 17 Abr 9 Abr 31 Mar 20 Abr 5 Abr 28

21 Abr 13 Abr 28 Mar 17 Abr 9 Abr 25 Mar 13 Abr 5 Abr 25 Abr 10 Abr 2040 1° Abr 21 Abr 6 Abr

Fiestas religiosas que dependen de la Pascua

Martes de Carnaval: fecha de la Pascua menos 47 días

Miércoles de Ceniza: fecha de la Pascua menos 46 días

Domingo de Ramos: fecha de la Pascua menos 7 días

Viernes Santo: fecha de la Pascua más 39 días

Domingo de Pentecostés: fecha de la Pascua más 49 días

La Trinidad: fecha de la Pascua más 56 días

Corpus Cristi (jueves): fecha de la Pascua más 60 días

Tabla XIV

Conjunciones

A continuación se enumeran las fechas recientes de conjunciones inferiores de los planetas interiores.

Mercurio

Revolución sinódica: 116 días.

Conjunciones inferiores: 9 de abril de 2011, 17 de agosto de 2011, 4 de diciembre de 2011, 21 de marzo de 2012, 28 de julio de 2012 y 17 de noviembre de 2012.

Venus

Revolución sinódica: 584 días =1 año 219 días

Conjunciones inferiores: 27 de marzo de 2009, 29 de octubre de 2010 y 6 de junio de 2012.

Oposiciones

Las fechas recientes de oposiciones de los planetas exteriores se enumeran a continuación.

Marte

Revolución sinódica: 780 días = 2 años 50 días.

Oposiciones: 13 de junio de 2001, 28 de agosto de

2003, 7 de noviembre de 2005, 24 de diciembre de 2007, 29 de enero de 2010 y 3 de marzo de 2012.

Júpiter

Revolución sinódica: 399 días = 1 año 34 días.

Oposiciones: 14 de agosto de 2009, 21 de septiembre de 2010, 29 de octubre de 2011 y 3 de diciembre de 2012.

Saturno

Revolución sinódica: 378 días = 1 año 13 días.

Oposiciones: 8 de marzo de 2009, 22 de marzo de 2010, 4 de abril de 2011, 15 de abril de 2012.

Urano

Revolución sinódica: 370 días = 1 año 5 días.

Oposiciones: 17 de septiembre de 2009, 21 de septiembre de 2010, 26 de septiembre de 2011, 29 de septiembre de 2012.

Neptuno

Revolución sinódica: 367.5 días =1 año 2.5 días.

Oposiciones: 17 de agosto de 2009, 20 de agosto de 2010, 22 de agosto de 2011 y 24 de agosto de 2012.

BIBLIOGRAFÍA

Ancona Albertos, Joaquín, El Universo. Nuevas lecciones de Cosmografía, Editores Unidos, 1948.

Blanchard, Alain et al., Frontiers of cosmology, Springer,-Verlag 2005.

Bretón, Nora. et al., The early universe and observational cosmology, Springer-Verlag, 2004.

Charola, Florencio, Elementos de cosmografía, Kapelusz, 1957.

Colpi, M. et al., Joint evolution of black holes and galaxies, Taylor & Francis, 2006.

Danby, J. M. A., Fundamentals of celestial mechanics, Willmann-Bell, 1992

French, A. P. (ed.), Einstein, a Centenary Volume, Harvard University Press, 1980.

Gallo, J., A. Anfossi y F. Meyer, Curso de cosmografía, Progreso, 1950.

Glendenning, Norman K., After the beginning, Imperial College Press, 2004.

Hogan, Craig, The little book of the Big Bang, Copernicus, 1998.

Hutchison, Robert, Meteorites, Cambridge University Press, 2004.

Kuhn, Karl F., In quest of the universe, Jones and Bartlett, 1998.

Luminet, Jean-Pierre, El tesoro de Kepler, Ediciones B, 2009.

Mark, Hans, Encyclopedia of space science and technology, vol. 2, Wiley Interscience, 2003.

Medina Peralta, Manuel, Elementos de astronomía de posición, Limusa, 1986.

Papini, Giovanni, Gog, Época, 1931. , El libro nego, Época, 1951.

Saint-Exupéry, Antoine de, El principito, Leyenda, 1943.

Schloser, W. et al., Challenges of astronomy, Springer-Verlag, 1989.

Solar system evolution, Cambridge University Press, 2001.

Spinrad, Hyron, Galaxy formation and evolution, Praxis, 2005.

Woods y Bailey, Geometría analítica y cálculo infinitesimal, UTEHA, 1960.

RESPUESTAS A LOS EJERCICIOS PROPUESTOS

Ejercicios del capítulo IV

1. 115° 34 ’30’’

2. 2 horas 28 minutos 39 segundos

Ejercicios del capítulo V

1. 81° 39’.

2. –(27° 10’).

3. a) 247° 39’

b) 337°4 2’

c) 137° 18’

4. a) S39° 20’ 34’’W

b) N78° 30’ 00’’W

c) S00° 00’ 01’’E

Ejercicios del capítulo VI

1. Declinación polo celeste boreal= 90° 00’ 00’’

Declinación polo celeste austral= –90° 00’ 00’’

2. Ascensión recta punto vernal= 00° 00’ 00’’

3. 70° 33’ 55’’

4. 20° 56’ 17’’

5. a) Las circumpolares están entre los límites 70° ≤ δ ≤ 90°.

b) Las estrellas que salen y se ponen están entre los límites –70° ≤ δ ≤ +70°

c) Las que están medio día sideral sobre el horizonte son las de δ = 0°(ecuador)

d) Las que permanecen sobre el horizonte más de doce horas están entre los límites 0° ≤ δ ≤ 90°.

e) Las que no pueden verse desde ese lugar están entre los límites -70° ≤ δ ≤ -90°.

6. a) Kachab, β de la Osa Menor (δ = 74° 21’ 36’’)

b) Alioth, ε de la Osa mayor (δ = 56°13’21’’)

c) Mintaka, δ de Orión (δ = –0° 20’ 04’’)

d) Dubhe, α de la Osa Mayor (δ = 62° 01’ 17’’)

e) Miaplacidus, β de Carinae (δ = –69° 30’ 39’’)

Ejercicios del capítulo VII

1. 11 h 27 min 13 s

2. 5 h 49.5 min

3. 5 h 57.8 min

Ejercicios del capítulo VIII

1. 8 h 59 min 57 s

2. 3 h 54 min 08 s

3. En el círculo ecuatorial H, el ángulo 28° 23’ 42’’ y en el círculo D, el ángulo 31° 59’ 59’’

4. a) 37° 33’ 18’’

b) 36° 00’ 00’’

5. a = 11.537° = 11° 32’ 13’’

U = 66° 54’ 36’’

6. 130° 19’ 12’’

Ejercicios del capítulo IX

1. a) 47 min 15.2 s

b) 1 h 00 min 00 s

2. 1 h 22 min 53.3 s

3. Longitud = 100° 15’

4. Latitud = 20° 12’

Ejercicios del capítulo XI

1. Declinación de la estrella = 23° 27’

2. Primera fecha: 5 de junio

Segunda fecha: 7 de julio

3. 24 de mayo.

4. Equinoccio de primavera: α = 0° y δ = 0°

Equinoccio de otoño: α = 180° y δ = 0°

5. Polo norte de la eclíptica: α = 270° y δ = 66° 33’.

Polo sur de la eclíptica: α = 90° y δ= 66° 33’.

Ejercicios del capítulo XII

1. Epacta del año 2013 = 17

Epacta del año 2016 = 21

2. Edad de la Luna el 24 de diciembre de 2013 = 20.

3. El 21 de marzo de 2014 la fase de la Luna estará entre plenilunio y cuarto menguante (edad = 20)

4. El 2 de mayo de 2015 habrá luna llena.

5. El 12 de abril de 2020 será el domingo de Pascua de Resurrección.

6. El 31 de diciembre de 2018 la edad de la Luna será de 23, por lo que no será plenilunio, esto es, no estará en oposición. Así, no puede haber eclipse de Luna en esa fecha.

Ejercicios del capítulo XIII

3. La luz del Sol tarda en llegar a la Tierra 8 min 18 s. En llegar a Neptuno tarda 4 h 10 min

Ejercicios del capítulo XVII

1. Duración de la revolución sideral de Urano = 84.13 años siderales

2. Distancia media del cometa Halley al Sol = 17.9422 ua

3. Distancia máxima del cometa Halley al Sol = 35.297 ua

La última órbita planetaria que rebasa es la de Neptuno, cuya distancia media al Sol es de 30.071 ua. Como dato interesante, la distancia media del planetoide Plutón al Sol es de 39.56 ua.

PRINCIPIOS DE COSMOGRAFÍA

El ánimo que inspira este libro nació del recuerdo recuperado por el autor de su época de estudiante preparatoriano, hace más de 40 años; concretamente, el texto El Universo. Nuevas lecciones de cosmografía, escrito en 1940 por el ingeniero yucateco Joaquín Ancona Albertos y revisado por Monforte en la actualidad, se convirtió en el impulso para emprender la tarea de escribir Principios de cosmografía.

De la mano del autor, el lector podrá determinar las coordenadas horizontales, ecuatoriales o eclípticas para localizar y observar astros a simple vista o con telescopio; conocer las propiedades, características y antigüedad de los cuerpos celestes del Sistema Solar; calcular la fecha exacta de cada fase de la Luna y entender los eclipses solares y lunares, totales y parciales, entre otros muchos temas.

El objetivo fundamental de la cosmografía –asienta Arturo Monforte en el segundo capítulo– es mirar el Universo en conjunto para comprender la posición que en él tiene el ser humano. A tal objetivo abona este trabajo.

Arturo Manuel Monforte Ocampo es ingeniero civil egresado de la Universidad de Yucatán (1970), con especialidad en Vías Terrestres por la UNAM y maestría en Ingeniería Hidráulica (Medalla “Gabino Barreda”).

Es perito profesional en Vías Terrestres desde 2003, certificado por el Colegio de Ingenieros Civiles de México.

Ha impartido clases en la UNAM, la Universidad Autónoma de Guerrero y las universidades de Chihuahua y Campeche, así como en las universidades del Cauca en Colombia y Católica de Guayaquil, Ecuador. Es miembro emérito del CICM.

Sobre el autor