Manual de socavación de puentes. FASCICULO I

MANUAL DE SOCAVACIÓN DE PUENTES FASCÍCULO I

Comité Técnico de Puentes

MANUAL DE SOCAVACIÓN DE PUENTES

FASCÍCULO I. SOCAVACIÓN GENERAL, SOCAVACIÓN POR ESTRECHAMIENTO Y ESTUDIOS HIDROLÓGICOS

Arturo M. Monforte Ocampo Claudia Rojas Serna

Subcomité de Socavación

ASOCIACIÓN MEXICANA DE INGENIERÍA DE VÍAS TERRESTRES, A.C. XX MESA DIRECTIVA

“POR UNA RED DEL CONOCIMIENTO DE LAS VÍAS TERRESTRES”

Manual de Socavación de Puentes FASCÍCULO I. SOCAVACIÓN GENERAL, SOCAVACIÓN POR ESTRECHAMIENTO Y ESTUDIOS HIDROLÓGICOS

Comité Técnico de Puentes de la Asociación Mexicana de Vías Terrestres, A.C.

© Asociación Mexicana de Ingeniería de Vías Terrestres, A.C.

Primera edición, 2015

Edición: Helios Comunicación, S.A. de C.V.

Av. Insurgentes Sur 4411, 7-3

Col. Tlalcoligia 14430 Tlalpan

México, D.F.

Foto de portada: SCT

MANUAL DE SOCAVACIÓN DE PUENTES

FASCÍCULO I. SOCAVACIÓN GENERAL, SOCAVACIÓN POR ESTRECHAMIENTO Y ESTUDIOS HIDROLÓGICOS

Asociación Mexicana de Ingeniería de Vías Terrestres

XX Mesa Directiva

Presidente

Luis Rojas Nieto

Vicepresidentes

Carlos Bussey Sarmiento

Luis Humberto Ibarrola Díaz

Miguel Ángel Vega Vargas

Secretario

Óscar Enrique Martínez Jurado

Prosecretario

Aarón Ángel Aburto Aguilar

Tesorero

Carlos Alberto Correa Herrejón

Subtesorero

José Mario Enríquez Garza

Vocales

Alejandro Alencaster González

Amado de Jesús Athié Rubio

Germán Francisco Carniado Rodríguez

Héctor Armando Castañeda Molina

Jorge Colonia Albornoz

José María Fimbres Castillo

Belisario García Name

José Roberto Vázquez González

Jesús Felipe Verdugo López

Coordinadores

Héctor Manuel Bonilla Cuevas

Ernesto Cepeda Aldape

Julio César Chacón Vivanco

Verónica Flores Déleon

Bernardo José Ortiz Mantilla

Gerente General

Miguel Sánchez Contreras

Comité Técnico de Puentes

Presidente

Rubén Frías Aldaraca

Secretario

Abraham Morales Linares

Jorge Arriola Aguilar

Gabriel Atala Barrero

Amílcar Galindo Solórzano

Ángel García García

Ignacio E. Hernández Quinto

Héctor Hernández Sánchez

Fernando Isunza Mohedano

Manuel Jara Díaz

José M. Jara Guerrero

Arturo M. Monforte Ocampo

Salvador Ortiz Tapia

Alberto Patrón Solares

Arturo Pérez Aguilar

Guillermo B. Pérez Morales

Vicente Robles Jara

Ismael Rodríguez Bonilla

Luis Rojas Nieto,

Claudia Rojas Serna

Fernando Romero Magaña

Jesús Sánchez Argüelles

Pericles Sánchez Leal

Juan Téllez Muñoz

Andrés Torres Acosta

El fascículo II contendrá los temas: Socavación local, Obras de protección contra la socavación, Estudios topohidráulicos y Ejemplos

PRESENTACIÓN

Desde su fundación, la Asociación Mexicana de Ingeniería de Vías Terrestres (AMIVTAC) tiene por objetivo primordial la transferencia de conocimientos para las nuevas generaciones de ingenieros en vías terrestres en todo el país, razón por la cual se incrementó el interés en la creación de comités técnicos que generen intercambio de conocimientos y la constante actualización de información en cuanto a ingeniería se refiere.

Las innovaciones en la ingeniería y el crecimiento de México en materia de infraestructura obligan a nuestra asociación a brindar actualización en la tecnología y un fácil acceso a la información para todos nuestros miembros, especialmente los estudiantes, que son el futuro de nuestro país.

En el Comité Técnico de Puentes de la AMIVTAC, del cual orgullosamente formo parte, nos fijamos la meta de actualizar los conocimientos en materia de puentes. La socavación es un problema importante en México y en todo el mundo por causa del cambio climático; de ahí que el comité lo haya seleccionado como un tema primordial de estudio, para dar pie al presente Manual de Socavación de Puentes

Toda la información aquí recabada está basada en conocimientos, experiencias, investigación y métodos de trabajo de grandes especialistas que con ética y compromiso han logrado impulsar esta rama tan importante de la ingeniería y lo que representa para un país como el nuestro, expuesto a eventos climáticos como los que hemos vivido en los últimos años: el conservar y mantener en servicio todas nuestras carreteras durante estos eventos.

Uno de los compromisos de la AMIVTAC y sus comités técnicos se cumple con la publicación de este manual. Por ello agradezco ampliamente la participación de todos los involucrados, principalmente a la SCT, el Comité de Puentes y el Subcomité de Socavación por su gran esfuerzo, con el deseo de que los objetivos que se han fijado se vayan cumpliendo por el bien de nuestra ingeniería.

Ing. Luis Rojas Nieto Presidente de la XX Mesa Directiva “Por una Red del Conocimiento de las Vías Terrestres”

PRÓLOGO

El Comité Técnico de Puentes de la Asociación Mexicana de Ingeniería de Vías Terrestres se integró en el año 2013 con especialistas en el área cuyo propósito es contribuir con la asociación en sus principales objetivos, uno de los cuales es difundir conocimientos y experiencias.

Para ello, durante las reuniones de trabajo se decidió llevar a cabo dos trabajos escritos por los integrantes del comité: el Manual de Socavación de Puentes y el Manual de Proyecto de Puentes, además de realizar un seminario internacional de puentes, una visita técnica al puente San Marcos de la carretera México-Tuxpan y elaborar algunos artículos técnicos sobre puentes para su publicación en la revista de la AMIVTAC.

El trabajo que aquí se presenta es la primera parte del Manual de Socavación de Puentes, elaborado con el propósito de crear un material de apoyo para los profesionales de las diversas dependencias gubernamentales y empresas privadas dedicadas al proyecto de puentes.

La idea de este proyecto nace de la experiencia de haber visto numerosos puentes colapsados en nuestra red carretera debido a la ocurrencia de fenómenos naturales, y la causa principal de los colapsos es el fenómeno de la socavación. Ello ha permitido catalogar como imperiosa la necesidad de fomentar mayores conocimientos del fenómeno de la socavación que conduzcan a mejores diseños de la cimentación de los puentes del país.

Por lo anterior, este volumen contempla una descripción de la socavación, su origen, los diferentes factores que intervienen en su ocurrencia, los conceptos que deben considerarse para calcular su magnitud y los métodos que existen para ello

Este fascículo abarca únicamente la socavación general, la socavación por estrechamiento y estudios hidrológicos. La socavación local y otros aspectos serán considerados en la segunda parte de este manual, en la que el Comité Técnico de Puentes continuará trabajando, al igual que en la elaboración del Manual de Proyecto de Puentes

Ing. Rubén Frías Aldaraca Presidente del Comité de Puentes AMIVTAC

CAPÍTULO I

EL FENÓMENO DE LA SOCAVACIÓN

I.1. Introducción

La socavación es un fenómeno que consiste en el descenso del fondo del cauce de una corriente natural de agua durante el paso de una creciente, al ser arrastrados por el flujo los materiales que constituyen el lecho de dicho cauce. Ello puede provocar daños importantes a la cimentación de los puentes, desde una erosión menor en las márgenes adyacentes del cauce o en los terraplenes de acceso hasta el colapso de la estructura del puente o de sus accesos.

Tanto en México como en otros países –desarrollados o en vías de desarrollo–, la causa principal de los colapsos de los puentes, por no decir que casi la única causa, es el fenómeno de la socavación. Con esta afirmación puede vislumbrarse la importancia de conocer, estudiar y entender tal fenómeno causante de la falla de muchos puentes, que son estructuras estratégicas de comunicación y elementos indispensables de las diversas vías terrestres de comunicación, como las carreteras, las vialidades urbanas y los ferrocarriles.

El fenómeno que nos ocupa es muy complejo, y por consiguiente muy difícil de predecir; sin embargo, se ha avanzado mucho en los últimos 40 años y la metodología ofrecida por los diversos investigadores cada vez es menos incierta y más confiable.

En este manual se proporcionan los elementos necesarios para calcular o, mejor dicho, para estimar la profundidad total de socavación que puede ocurrir en los puentes. Tal profundidad tiene diversos componentes en función de los tipos de socavación que existen: la socavación general en sus diversas modalidades, la socavación por contracción y la socavación local.

Para la predicción de algunos de los tipos de socavación general, como la provocada en las curvas de los cauces, o la que ocurre por la confluencia de dos corrientes y por las formas que adquiere el fondo de los cauces, se requiere aún más investigación, al igual que para predecir la migración lateral de los cauces.

En este Manual de Socavación de Puentes se recogen los más recientes avances en la materia alcanzados por los más importantes investigadores del mundo; especial mención merecen los trabajos desarrollados por Bruce W. Melville y Stephen E. Coleman en su libro Bridge Scour, editado por Water Resources Publications, LLC, 2000.

CAPÍTULO II

TIPOS DE SOCAVACIÓN

II.1. Introducción

El diseño estructural de un puente tiene bases teóricas muy confiables. En cambio, la mecánica de flujo y erosión en cauces no está bien definida y no es posible estimar con alto grado de confianza los cambios que pueden ocurrir en los ríos y en su intersección con puentes sujetos a una cierta avenida o creciente. Ello se debe no solamente a la extrema complejidad del problema, sino también al hecho de que las características de los ríos, la geometría de l cauce bajo al puente y las interacciones entre suelo y agua son diferentes para cada puente y para cada avenida.

Al ocurrir la socavación, la elevación del nivel del fondo del río disminuye a causa de la erosión del agua, por lo que puede quedar expuesta la cimentación de un puente. Tal disminución respecto al nivel natural del fondo del río que existe al inicio de la erosión se llama profundidad de socavación. Los tipos de socavación que pueden ocurrir en el cauce de un puente son:

a) socavación general

b) socavación por estrechamiento

c) socavación local

En la figura II.1 se ilustran los tres tipos de socavación, que ocurren simultáneamente.

en un puente.

Figura II.1 Tipos de socavación que pueden ocurrir

II.2. Socavación general

Ésta ocurre independientemente de la existencia de un puente, y puede desarrollarse a largo o a corto plazo. La de corto plazo se desarrolla durante una o varias avenidas que ocurren con separaciones temporales breves. En general, esta socavación es transitoria y ocurre sólo durante la creciente; en la mayor parte de los casos se recupera el nivel del fondo al disminuir la creciente. La socavación de largo plazo tiene una mayor escala de tiempo, que puede ser de varios años, e incluye degradación progresiva y erosión de los márgenes. La degradación progresiva es la disminución casi permanente de la elevación del fondo, debida a cambios hidrometeorológicos (por ejemplo, flujos altos y prolongados), cambios geomorfológicos (por ejemplo, disminución del fondo debido a fuertes ajustes geomorfológicos en la cuenca) o actividades humanas (por ejemplo, construcción de presas). La erosión marginal puede provocar que el puente sea flanqueado por el río al cortarse los accesos, o que fallen por socavación sus estribos; se debe a migración de meandros, a la intervención humana en el control del río o a un cambio repentino del curso del río, por ejemplo causado por el corte de un meandro.

La socavación general incluye también aquélla debida a cambios en la forma del cauce y la causada por migración de las formas de fondo.

II.3. Socavación por estrechamiento

A diferencia de la socavación general, la socavación por estrechamiento y la socavación local (llamadas juntas socavación localizada) se deben a la existencia del puente. El flujo usualmente converge a medida que se aproxima al puente, ya que éste o sus accesos estrechan el flujo; este último se acelera y provoca una socavación adicional a la natural, que se llama socavación por estrechamiento.

II.4. Socavación local

Ocurre por la interferencia de pilas y estribos en el flujo, y se caracteriza por la formación de una poza alrededor de tales elementos o adyacente a ellos. También es socavación local la que ocurre en espigones y otras obras en los ríos.

La socavación por estrechamiento y la local sumadas se conocen como socavación localizada, y puede ocurrir tanto en aguas claras (las que no llevan sedimentos) como en aguas que arrastran sedimentos (fondo vivo). La primera ocurre cuando el material del fondo aguas arriba del área de socavación queda en reposo; en este caso, la máxima profundidad de socavación se alcanza cuando el flujo ya no puede remover el material del fondo del área de socavación. La socavación en aguas que arrastran sedimentos ocurre cuando existe transporte

generalizado de sedimentos en el río. La profundidad de socavación de equilibrio se alcanza cuando el ritmo de transporte de material de fondo en la poza de socavación es igual al ritmo con que dicho material es extraído de ella.

Es necesario asegurarse de que la profundidad de socavación de diseño incluya todas las causas posibles de socavación. Debe suponerse, en general, que las profundidades de socavación, considerando todos sus tipos, son acumulativas, lo que conducirá a una estimación conservadora.

CAPÍTULO III

LA

PROFUNDIDAD DE SOCAVACIÓN EN PUENTES

III.1. Introducción

Son muchos los factores que afectan la profundidad de socavación en puentes. Los más importantes son los que se mencionan a continuación, que se han dividido en cuatro grupos (véase tabla III.1).

III.2. Factores geomorfológicos

Pueden dividirse en a) características de la cuenca y b) características del río, y son más importantes para la socavación general que para la socavación localizada. Las características de la cuenca influyen en los factores topográficos, de vegetación, de suelo y climáticos. La fuente principal de los cuerpos flotantes como troncos y ramazón que se atoran y acumulan en los puentes es la erosión marginal, aunque también inciden en esto los deslizamientos en zonas montañosas.

Las características del río son la orografía, la forma de la sección del cauce, su alineamiento horizontal y las propiedades del material del cauce. Los ríos en regiones montañosas son empinados (de pendiente fuerte), con cauces bien definidos y material grueso en el fondo. Desde el punto de vista de su alineamiento horizontal, los ríos pueden ser rectos, sinuosos, con meandros y ramificados (con cauce muy amplio, dividido en varios canales, el flujo generalmente acarrea mucho sedimento). Los ríos con meandros se caracterizan por un continuo desarrollo de curvas, de modo que tienen un alto potencial de problemas relativos a erosión marginal y migración del cauce. En los ríos ramificados, los canales más profundos pueden tener una fuerte erraticidad durante avenidas.

III.3. Transporte del flujo

Se refiere al transporte de agua, sedimentos, de troncos y ramazón. Son importantes para determinar la socavación general y la localizada. El transporte de sedimentos determina si las condiciones son de socavación de fondo vivo o de aguas claras. En condiciones de fondo vivo, son importantes los factores de gasto sólido y de forma del fondo. La socavación en el puente puede ser fuertemente incrementada por la acumulación de cuerpos flotantes en las pilas.

Características de la cuenca

Geomorfológicos / hidrológicos

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Tabla III.1. Factores que influyen en la profundidad de socavación en puentes

Factores que influyen en la socavación general

Factores que influyen en la socavación localizada

Hidráulicos

Precipitación Frecuencia de avenidas

Características físicas

-Topografía /Pendiente

-Dimensión -Forma Hidrograma

Velocidad de flujo

Vegetación

Suelos: -Tipo -Erosionabilidad

Características del río

Tirante

Sedimentos del fondo

Mediana de los diámetros d!"

Gasto Q Desviación estándar geométrica �!

Media v Estratificación vertical

Longitud

Geometría del puente

Grado de contracción

Sumergencia de la superestructura

Duración T Cohesión c Pilas Tipo

Posición en el cauce de avenidas y en el principal

Distribución lateral Distribución espacial forma Sh

Corrientes secundarias

Fondo rocoso:

-Erosionabilidad -Profundidad

Dimensiones, longitud, ancho (diámetro) l, b, D

Tirante en el cauce principal y Alineamiento �

Distribución lateral

Gasto sólido �!

Cauce: -Variabilidad del ancho -Ancho a cauce lleno -Ancho de las planicies de inundación -Forma de la sección transversal -Pendiente del cauce -Grado de labrado del cauce

Controles hidráulicos

Transporte de sedimentos

Magnitud de las formas de fondo

Forma del transporte de sedimentos

Cuerpos flotantes Ramazón y basura

Estribos Tipo

Posición en el cauce de avenidas y en el principal

En zona plana Forma Sh

Altura y longitud l

Alineamiento �

Localización respecto a curvas

Medidas de protección

Revestimientos, espigones represas, canalizaciones modificaciones de puentes, etc.

Forma en planta:

-Recto

-Sinuoso/meandros -

Trenzado/ramificad o -Desarrollo de barras

Paredes y fondo del cauce

-Material de las márgenes

-Estabilidad de las márgenes

-Cubierta vegetal

III.4. Material del fondo

Incluye el tipo, el tamaño y la distribución de las partículas del fondo. Para suelos no cohesivos, es importante la distribución espacial, tanto horizontal como vertical, de los diámetros del material. La susceptibilidad a la socavación de los suelos cohesivos no puede evaluarse con base en los tamaños de las partículas, debido a la compleja interacción físico-química entre las partículas coloidales, los efectos de presión de poro y los efectos de precarga. Muchos de estos factores no solamente varían grandemente con el tiempo en un sitio particular, sino también de un sitio a otro, aun en el mismo depósito de finos. Un estrato rocoso determina el límite probable de socavación en la cimentación de un puente. Las cimentaciones en roca pueden estar sujetas a socavación si la roca es erosionable.

III.5. Factores geométricos

Los factores geométricos del puente son importantes en la evaluación de la socavación localizada. Incluyen el grado de estrechamiento del flujo, la geometría de la cimentación, la ubicación del puente respecto a las curvas del cauce y la presencia de obras de protección contra la socavación. El estrechamiento puede ser lateral debido a un puente que no cubra todo el ancho del cauce y vertical si el agua rebasa la superestructura. La geometría de las pilas del puente puede describirse por su tipo, forma, longitud, ancho y alineamiento respecto a la dirección del flujo. Similarmente, la geometría de los estribos se describe por su tipo, la forma de su extremo, su longitud y alineamiento, incluyendo el terraplén de acceso. Las posiciones de las pilas y estribos en el cauce son importantes. Por ejemplo, las cimentaciones ubicadas en el cauce de avenidas pueden estar sujetas a socavación en aguas claras, mientras que las condiciones de las cimentaciones en el cauce principal generalmente son de fondo vivo. Las

MANUAL DE SOCAVACIÓN

pilas localizadas cerca de un estribo merecen una atención especial, ya que pueden sufrir una socavación más profunda. También las pilas localizadas en la orilla del cauce principal pueden experimentar un flujo lateral significativo, y ser susceptibles a una mayor socavación debida al esviaje del flujo.

III.6. Medidas de protección

Pueden ser clasificadas de acuerdo con el tipo de socavación que se intente controlar. Las obras de protección contra la erosión marginal incluyen revestimientos con enrocamiento, espigones, diques, tetrápodos y siembra de árboles como rompedores de energía. La degradación puede controlarse con el empleo de represas y con protección local en pilas y estribos. Las medidas de control de depósitos o azolvamiento incluyen trabajos de canalización de ríos y compensación de áreas hidráulicas que hayan sido reducidas; esta compensación se logra elevando el puente o ampliando su longitud. Más adelante se dan detalles.

III.7. Mecanismo de falla de los puentes

Además de la suspensión temporal de acceso a un puente por sumersión del tablero, el agua y los cuerpos de arrastre pueden causar diversos daños a la estructura. Al quedar una pila al descubierto por socavación, pierde capacidad de soporte, con los subsecuentes daños en la superestructura. Las pilas y la superestructura pueden ser dañadas o destruidas por el impacto de cuerpos flotantes, troncos principalmente, o de arrastre, particularmente boleos. Las fuerzas laterales y verticales sobre un puente, debidas a cargas provocadas por cuerpos flotantes y de arrastre, pueden ser magnificadas por los efectos del atoramiento de éstos en el puente. Los sedimentos pueden provocar acumulación de azolve bajo un puente y causar un incremento en la frecuencia de los casos en que la superestructura es sobrepasada por el agua. La erosión del pie o de la cara de un estribo puede provocar la pérdida de capacidad de soporte de su cimentación y sufrir su colapso. Los puentes pueden quedar aislados cuando el terraplén de acceso es deslavado, y aunque resulten sin daños no cabe duda de que por un tiempo tienen una utilidad nula. Este proceso se conoce como “flanqueo del puente”.

CAPÍTULO IV ESTUDIOS

HIDROLÓGICOS*

IV.1. Introducción

Este capítulo tiene como objetivo servir de guía metodológica para la realización de los estudios hidrológicos necesarios en el análisis y revisión de la socavación de puentes en carreteras federales y autopistas.

El concepto fundamental en la elaboración de los estudios hidrológicos es la unidad hidrológica o cuenca hidrográfica superficial, definida como una zona de la superficie terrestre delimitada por los puntos topográficos más altos y donde la lluvia que cae es drenada por un sistema de drenaje hasta un punto en la red hidrográfica, o bien hasta la desembocadura a otro río, a un lago o al mar. En adelante se utilizará la palabra “cuenca” para referirse a la cuenca hidrográfica superficial.

Para el cálculo de la socavación es fundamental conocer el gasto que estaría llegando al puente. El gasto es el volumen de agua que escurre en el río durante un intervalo de tiempo; generalmente se expresa en metros cúbicos por segundo. La metodología del estudio hidrológico para determinar este gasto depende de la información disponible en la cuenca. En este capítulo se sugieren algunos métodos aplicables a dos tipos de cuencas que disponen de diferente información. El primer tipo de cuencas se refiere a las “aforadas”, es decir, a las cuencas que disponen de alguna estación de aforo. El segundo tipo de cuencas son las “no aforadas”, ya que no tienen estación que registre sus escurrimientos.

IV.2.Cálculo de gastos en cuencas con estación de aforo

La cuenca aforada dispone de alguna estación hidrométrica o estación de aforo. Para que los registros de aforo sean considerados en el cálculo del gasto, la estación hidrométrica debe estar localizada en el mismo punto de la red hidrográfica en el que se ubica el puente en estudio. Si la estación de aforo no está localizada en el sitio del puente, se pueden utilizar los registros sólo si se cumple con lo siguiente: considerar un factor de escala para el área drenada, que la estación de aforo se localice sobre el mismo río y que su distancia hasta el sitio del cruce no exceda el 25% de la longitud total del cauce. El factor de escala se calcula con una simple regla de interpolación entre las dos áreas de aportación; una es el área de la cuenca hasta el sitio del cruce y la otra es el área de la cuenca hasta la ubicación de la estación de aforo. Los datos de aforo se deben multiplicar por el factor de escala antes de ser utilizados para calcular el gasto.

* En el desarrollo de este capítulo participaron Mayra Olivia Sánchez Martínez y Jaime Alejandro Romano Cervantes, alumnos del último año de la licenciatura en Ingeniería hidrológica de la UAM, Unidad Iztapalapa.

En el Banco Nacional de Datos de Aguas Superficiales de la Comisión Nacional del Agua se puede consultar la localización de las estaciones hidrométricas del país y obtener sus registros históricos de aforos. Al final de este capítulo se presenta la localización de las 2,070 estaciones de aforo que conforman actualmente la red hidrométrica nacional.

IV.2.1.Análisis estadístico de los datos de aforo

De la estación de aforo se deben extraer los registros de gastos máximos anuales. Ha de disponerse al menos de 10 registros para utilizar la serie de datos anuales.

Primeramente se debe definir si la serie de gastos máximos anuales puede ser utilizada para obtener los gastos necesarios para el cálculo de la socavación. Para esto se tienen que revisar sus parámetros estadísticos y realizar pruebas de homogeneidad e independencia. Una vez que se ha aceptado que la serie de datos es homogénea e independiente, se aplica la teoría de análisis de frecuencias.

Revisión de los parámetros estadísticos de la serie de aforos

Se calculan los siguientes parámetros estadísticos: media, mediana, moda, desviación estándar, coeficiente de asimetría y coeficiente de curtosis. La serie de gastos máximos anuales deberá tener coeficiente de asimetría igual a cero y coeficiente de curtosis igual a 3.

En hidrología se recomienda el uso de los estadísticos muestrales, ya que generalmente se trabajan con muestras relativamente pequeñas.

Media: � = ! ! �! ! ! !! :

Varianza poblacional: �!! = ! ! �! � ! ! ! !!

Varianza muestral: �! ! = ! ! ! �!! = ! ! ! �! � ! ! ! !!

Desviación estándar poblacional: �! = �!!

Desviación estándar muestral: �! = �! !

Coeficiente de asimetría poblacional: �! = !! ! ! ! !!! ! !! !

Coeficiente de asimetría muestral: �! = !! ! ! ! ! �! = ! !! ! ! ! !!! ! ! ! ! !! !

Coeficiente de curtosis poblacional: �! = !! ! ! ! !!! ! !! !

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Coeficiente de curtosis muestral: �! = !! ! ! ! ! ! ! �! = !! !! ! ! ! !!! ! ! ! ! ! ! !! !

Coeficiente de variación: �� = ! !

Revisión de la independencia de la serie de aforos

La prueba de independencia consiste en determinar si una serie es independiente con respecto a otra población o a sí misma, es decir que la serie esté compuesta por variables aleatorias. La prueba de independencia de Anderson (Salas et al., 1988) se expresa por medio del coeficiente de autocorrelación �!

donde

Si al menos el 90% de los datos de la serie quedan dentro de los límites de confianza, entonces se asegura la independencia de la serie. Los límites de confianza se expresan como sigue:

�! = �! ± �! �!

donde:

�! : límites de confianza superior e inferior

�! : evento obtenido a partir de la función de distribución para cierto periodo de retorno

�! : desviación normal estándar para un nivel de confianza �

� = 0.05: parámetro para límites de confianza de 95%

�! = 1.960395: parámetro para límites de confianza de 95%

�! : desviación estándar de los eventos estimados para un periodo de retorno T

Revisión de la homogeneidad de la serie de aforos

La prueba de homogeneidad permite identificar alteraciones en el registro de gastos, las cuales puede deberse a diferentes circunstancias, tales como: cambios en la localización de la estación de aforo, deforestación, construcción de embalses, nuevas áreas de cultivo, etc. Los parámetros

estadísticos de referencia para la prueba de independencia corresponden a la media y a la desviación estándar. Las pruebas sugeridas para las series de tiempo son las siguientes: t de Student, Helmert y Cramer.

Prueba estadística de Helmert. Consiste en analizar el signo de las desviaciones de cada gasto máximo registrado de la serie respecto a su valor medio. Si una desviación de un cierto signo es seguida por otra del mismo signo, entonces se dice que se forma una secuencia S; de lo contrario se considera un cambio (C). La serie se considera homogénea si se cumple:

Prueba estadística � de Student. La prueba estadística t de Student indica que una muestra es homogénea cuando td es menor o igual al estadístico tc de la distribución t de Student de dos colas, para n1+n2–2 grados de libertad.

donde:

X! : media de la primera muestra

X ! : media de la segunda muestra

S1: varianza de la primera muestra

S2: varianza de la segunda muestra

n1: número de datos de la primera muestra

n2: número de datos de la segunda muestra

Prueba estadística de Cramer. Esta prueba se utiliza con el propósito de verificar la homogeneidad en el registro �! ! de la serie j para � = 1,2,3, … , �! y también para determinar si el valor medio no varía significativamente de un periodo a otro. Con este propósito se consideran tres bloques: el primero del tamaño total de la muestra �! ; el segundo de tamaño �!" (60% de los últimos valores de la muestra �! ) y el tercero de tamaño �!" (30% de los últimos valores de la muestra �! ). La prueba compara el valor de � ! del registro total con cada una de las medias de los bloques elegidos �!" ! y �!" ! . Para que se considere la serie analizada

como estacionaria en la media, se deberá cumplir que no exista una diferencia significativa entre las medias de los dos bloques.

IV.2.2. Análisis de frecuencia de gastos máximos anuales

El análisis de frecuencia de gastos máximos anuales se emplea para calcular la magnitud de un gasto � , asociado a cierto periodo de retorno � Se aplican diferentes funciones de distribución de probabilidad FDP y se selecciona la que mejor se ajuste a la serie registrada de gastos máximos anuales. El objetivo de las FDP es relacionar la magnitud de un evento extremo con su probabilidad de ocurrencia. En hidrología se utilizan diversas FDP, siendo fundamental seleccionar la que mejor se ajuste a nuestros datos y con ella determinar los eventos de diseño. La selección de la función o distribución de probabilidad que mejor se ajusta a los datos se realiza calculando el error estándar de ajuste (EEA). La función de probabilidad cuyo EEA sea el de menor valor será la que mejor se ajusta a la serie de gastos

máximos, y con esta función se calcularán los gastos de diseño asociados a cierto periodo de retorno. El periodo de retorno se define como el número de años que transcurren en promedio para que un evento de una magnitud dada sea igualado o excedido, por lo menos una vez, en ese periodo.

��� = �! ! �! ! ! !! ! !! �! �� ! !

donde:

�! ! son los gastos máximos anuales �!! ordenados de mayor a menor con un periodo de retorno asignado � = !! !! ! y una probabilidad � de no excederse � = 1 ! !

�! es la longitud de años del registro de gastos máximos anuales

� es el número de orden del registro

� = 1 para el gasto anual más grande

� = �! para el gasto anual más chico

�! ! son los gastos máximos calculados por la función de probabilidad para cada periodo de retorno � asignado a la serie original y ordenada �!!

�� es el número de parámetros de la función de probabilidad

Las funciones de probabilidad FDP más utilizadas son las siguientes: Normal, LogNormal, Gamma, Log-Pearson III y Gumbel. El cálculo de los parámetros respectivos a estas distribuciones de probabilidad se puede realizar aplicando métodos distintos, entre los que se hallan los siguientes: mínimos cuadrados, momentos, máxima verosimilitud, momentos de probabilidad pesada, momentos L y máxima entropía. En este manual se sugiere utilizar la técnica de momentos, ya que es la más simple; sin embargo, puede utilizarse cualquier otra técnica de estimación de parámetros.

Método de momentos. El método de momentos consiste en igualar los momentos de la población de datos con los momentos de la muestra. Los momentos poblacionales pueden ser con respecto al origen o con respecto a la media. Los momentos muestrales (estadísticos) se obtienen con las siguientes expresiones.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Distribución normal. La función de densidad de probabilidad (FDP) es:

� = 1 � 2� � ! ! ! ! ! !

Estimadores por momentos:

Esta función no tiene inversa, por lo que no se puede estimar el evento directamente. Para estimar los eventos se recurre a una solución aproximada.

= � + ��!

Para el cálculo de �! se tiene la siguiente expresión para 0 < � (� ) ≤ 0.5:

donde:

Para una probabilidad � � > 0.5 se cambia � (� ) por 1 � (� ) en el cálculo de V y se le cambia el signo a �! .

Distribución log-normal de dos parámetros. Función de densidad de probabilidad (FDP):

Para � > 0

Los estimadores por momentos son:

Los eventos se estiman con la siguiente expresión:

Distribución gamma de dos parámetros. La función de distribución de probabilidad (FDP) para esta función es:

donde � � es la función gamma completa

Estimadores por momentos

Distribución log Pearson tipo III. La función de distribución de probabilidad (FDP) para esta función es:

Para � > 1

Los estimadores por el método indirecto son:

Los eventos se estiman con la siguiente expresión:

Distribución Gumbel. La función de densidad de probabilidad (FDP) es:

Estimadores por momentos: � = � 0.45 � � = 0.78 �

Software para análisis de frecuencia

Existen diversos programas para realizar análisis de frecuencias; un ejemplo es el programa AX, utilizado por el Centro Nacional de Prevención de Desastres (Cenapred). Con este programa se pueden ajustar 6 FDP a la muestra e identificar la mejor función de se ajuste a los datos, ya que calcula el EEA de cada FDP. Las funciones de probabilidad disponibles en AX son: Normal, Log-Normal, Gumbel, Exponencial, Gamma y Doble Gumbel. Este programa requiere Windows XP.

IV.3. Cálculo de gasto en cuencas sin estación de aforo

En el caso de que en la cuenca de estudio no exista alguna estación de aforo o que el periodo de registros hidrométricos sea menor a 10 años, el gasto asociado a cierto periodo de retorno se puede calcular aplicando algún modelo lluvia-escurrimiento. El modelo lluviaescurrimiento representa la transformación de la lluvia que cae en la cuenca a su escurrimiento superficial. Este escurrimiento se calcula en unidades de volumen por unidad de tiempo, es decir, en gasto en metros cúbicos por segundo. Para aplicar un modelo lluvia-escurrimiento es necesario determinar las características físicas y climáticas de la cuenca. Las principales características físicas que son necesarias para los métodos más sencillos son: área de la cuenca, pendiente del cauce y su longitud, tipo de suelo y su uso.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO

Tabla IV.1. Valores de coeficientes de escurrimiento (Aparicio, 1992)

Tipos de área drenada

Zonas comerciales

Coeficiente de escurrimiento Mínimo Máximo

Zona comercial 0.75 0.95

Zona mercantil 0.70 0.90

Vecindarios 0.50 0.70

Zonas residenciales

Unifamiliares 0.30 0.50

Multifamiliares espaciados 0.40 0.60

Multifamiliares compactos 0.60 0.75

Semiurbanas 0.35 0.40

Casa habitacíon 0.50 0.70

Zonas industriales

Espaciado

0.50 0.80

Compacto 0.60 0.90

Cementerios y parques 0.10 0.25

Campos de juego 0.20 0.35

Patios de ferrocarril y terrenos sin construir 0.20 0.40

Zonas suburbanas 0.10 0.30

Calles

Asfaltadas 0.70 0.95

De concreto hidráulico 0.80 0.95

Adoquinadas o empredados, junteados con cemento 0.70 0.85

Adoquín sin juntear 0.50 0.70

Terracerías 0.25 0.60

Estacionamientos 0.75 0.85

Techados 0.75 0.95

Praderas

Suelos arenosos planos (pendientes: 0.02 o menos) 0.05 0.10

Suelos arenosos con pendientes medias (0.02-0.07) 0.10 0.15

Suelos arenosos escarpados ( 0.07 o más) 0.15 0.20

Suelos arcillosos planos (0.02 o menos) 0.13 0.17

Suelos arcillosos con pendientes medias (0.02-0.07) 0.18 0.22

Suelos arcillosos escarpados (0.07 o más) 0.25 0.35

La principal característica climática que es necesaria es la altura promedio de la lluvia y su altura efectiva. Es necesario conocer el coeficiente de escurrimiento, el cual se puede identificar de acuerdo con el tipo de cuenca en estudio (véase tabla IV.1).

Principales características físicas de la cuenca

Área de la cuenca

El área drenada es probablemente la característica más importante de la cuenca, ya que refleja el volumen de agua que puede generar la lluvia que cae sobre la zona de estudio y hasta el sitio del puente. El área drenada es delimitada por las cotas topográficas más altas que rodean toda la red hidrográfica de la corriente en estudio, esto es, el parteaguas de la cuenca. Actualmente los sistemas de información geográfica facilitan la delimitación, ya que permiten integrar la información de las cartas topográficas, modelos digitales de relieve y cualquier otro mapa temático, por ejemplo de uso de suelo, geología, etcétera.

Pendiente media del cauce

El método de Taylor-Schwarz es el más utilizado para determinar la pendiente del cauce �!

Este método considera calcular la pendiente del cauce como la de un canal de sección transversal uniforme que tenga la misma longitud y tiempo de recorrido que la corriente en estudio.

donde:

�! es la pendiente media del cauce principal de la cuenca, adimensional

� es la longitud total del cauce principal

�! es la longitud del tramo � , donde � = 1,2,3, … , �

�! es la pendiente del tramo � , donde � = 1,2,3, , �

Característica climática: precipitación máxima

La precipitación máxima en la cuenca se puede determinar con los polígonos de Thiessen. Este método delimita con mediatrices las áreas de influencia de las estaciones climatológicas. El procedimiento para el cálculo es el siguiente:

• Se unen las estaciones climatológicas adyacentes con líneas rectas.

• Se trazan mediatrices a las líneas que unen las estaciones.

• Se prolongan las mediatrices hasta el límite de la cuenca o hasta su intersección con otra mediatriz.

• Se calcula el área formada por las mediatrices para cada estación. Esta área es la zona de influencia de la estación climatológica analizada.

Los registros de precipitación máxima de la estación climatológica se consideran sólo para la zona de influencia.

Modelos lluvia-escurrimiento

Método racional

El método racional es una fórmula matemática que relaciona el gasto pico �! con el área de la cuenca �, la intensidad de la lluvia � y el coeficiente de escurrimiento � Únicamente tiene validez de aplicación en cuencas pequeñas urbanas y suburbanas con áreas entre 2.5 y 3 ��!

�! = 0.278���

El coeficiente de escurrimiento depende de las características del suelo y su cubierta vegetal (véase tabla IV.1); la intensidad de lluvia está expresada en milímetros por hora y el área de la cuenca se expresa en kilómetros cuadrados.

La intensidad de la lluvia debe ser la intensidad de la precipitación asociada al periodo de retorno para el cual se quiere determinar el gasto. La intensidad de la lluvia se puede obtener de las isoyetas editadas por la SCT y considerando la duración de la lluvia, igual al tiempo de concentración. La intensidad de la lluvia también se puede determinar aplicando análisis de frecuencias a los registros de precipitaciones máximas de las estaciones climatológicas, considerando la lluvia de influencia de acuerdo con los polígonos de Thiessen. El tiempo de concentración se puede determinar con la fórmula de Kirpich.

�! = 0 06636 �! � ! !"#

donde:

�! es el tiempo de concentración en horas

� es la longitud del cauce principal en kilómetros

� es la pendiente del cauce principal

Hidrograma unitario

El hidrograma unitario HU de una cuenca se define como el hidrograma de escurrimiento directo producido por unidad de lluvia en exceso –generalmente se considera 1 mm de lluvia en exceso– que cae con una intensidad uniforme sobre toda la cuenca durante un tiempo conocido como duración en exceso, y con su aplicación se puede predecir la forma del hidrograma de la avenida del gasto máximo. Generalmente es utilizado para cuencas que tienen áreas entre 30 y 30,000 km2

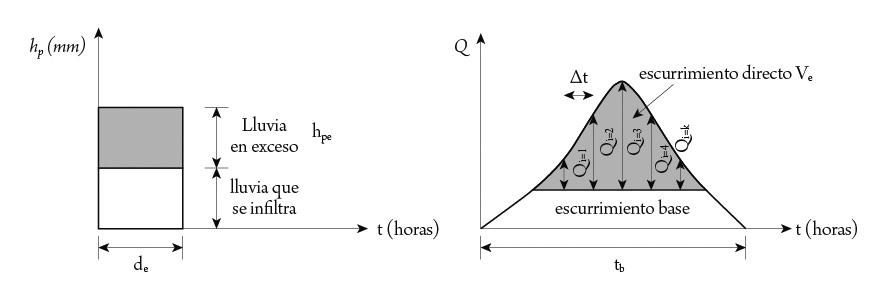
Figura IV.1. Características del hidrograma unitario.

Se debe conocer el área de la cuenca !, la avenida máxima registrada en ella y la tormenta que la produce. Es importante conocer la duración de la avenida y definir un intervalo de tiempo !! para identificar el gasto !! correspondiente a cada incremento de dicho !! . A partir de esto se determina el volumen del escurrimiento directo !! , su tiempo base !! , la altura de precipitación efectiva !!" y la duración en exceso !! Las ecuaciones matemáticas para determinar cada una de estas variables son las siguientes:

! !! !! ! ! !!

donde ! es el número de incrementos del intervalo de tiempo !! en que se dividió el hidrograma de la avenida analizada.

! !! !

El HU se calcula dividiendo el escurrimiento directo calculado entre la altura de precipitación efectiva !!" .

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

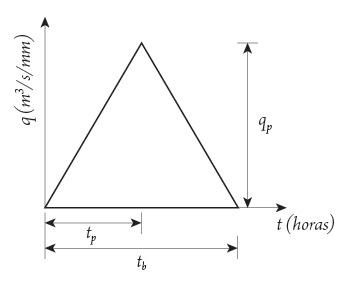
Hidrograma unitario triangular

El hidrograma unitario triangular (HUT) se aplica en cuencas pequeñas y su forma es triangular (véase figura IV. 2). El gasto pico se obtiene con la siguiente ecuación:

!! ! !!!"# ! !!

donde !! es el gasto pico en !! !!!!!

A es el área de la cuenca en !"!

!! es el tiempo pico en horas

El tiempo pico !! y el tiempo base !! se evalúan con las siguientes expresiones:

!! ! !! ! ! !!!

!! ! !!!" !!

donde !! es el tiempo de concentración de la cuenca hidrológica de estudio. El hidrograma de escurrimiento directo se calcula multiplicando cada una de las ordenadas del HUT por la lluvia efectiva !! que se considera en milímetros.

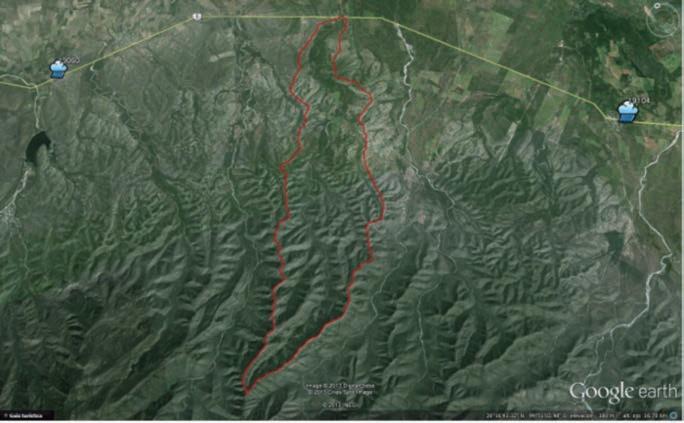
Figura IV.3 Cuenca visualizada a través de Google Earth La línea roja es el parteaguas de la cuenca; la línea blanca es la carretera federal donde está el puente en estudio. Se observan las estaciones 19060 y 19104.

Figura IV.2. Hidrograma unitario triangular.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Método de Chow

Este método permite conocer el gasto máximo del hidrograma de escurrimiento directo asociado a cierto perio-do de retorno. Sólo se aplica a cuencas no urbanas y con área menor a 25 km2.

El gasto pico del escurrimiento directo se calcula con la siguiente ecuación: !! ! ! !"#!" !! !!

donde:

! es el área de la cuenca en km2

!! es la duración en exceso en horas

!! es la lluvia efectiva en milímetros

! es el factor de reducción del gasto p ico que está en función del cociente !! !!

!! es el tiempo de retraso, es decir, tiempo que transcurre del centro de masa de la precipitación al pico del hidrograma !! ! ! !!"

Figura IV.4. Curvas de nivel y red hidrográfica de la cuenca en estudio.

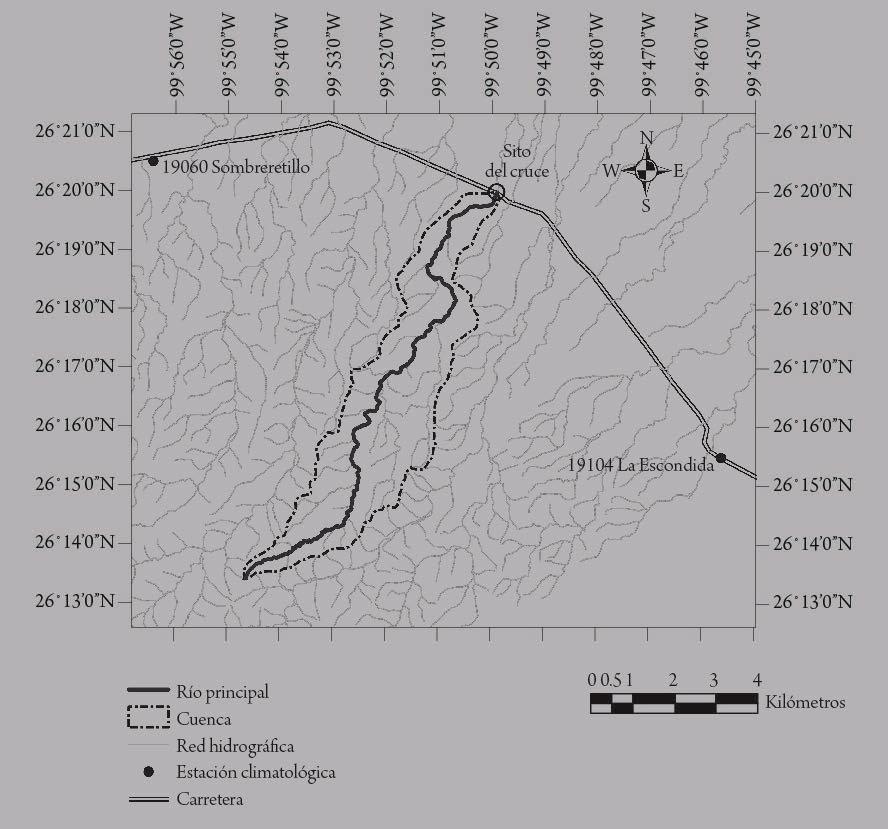
Ejemplo de aplicación: cuenca sin estación de aforo

La cuenca en estudio se ubica en el estado de Nuevo León y el sitio del puente está localizado en las coordenadas 29° 16’ 37.92’’ N y 99° 52’ 05.00’’ O. Se requiere calcular el gasto asociado a los siguientes periodos de retorno: 2, 5, 10, 50, 100, 500 y 1,000 años.

Datos generales y metodología

La identificación del sitio de estudio se realizó en Google Earth (figura IV.3). En este caso, se trata de una cuenca sin estación de aforo, por lo cual se aplicarán modelos lluvia-escurrimiento para de-terminar el gasto de diseño. Las cartas topográficas digitales con escala 1:50000 utilizadas son G14A87 y G14A77 (véase figura IV.4). Estas cartas son obtenidas de la base de datos del Instituto Nacional de Estadística y Geografía En las figuras IV.5 y IV.6 se muestran la edafología y el uso de suelo

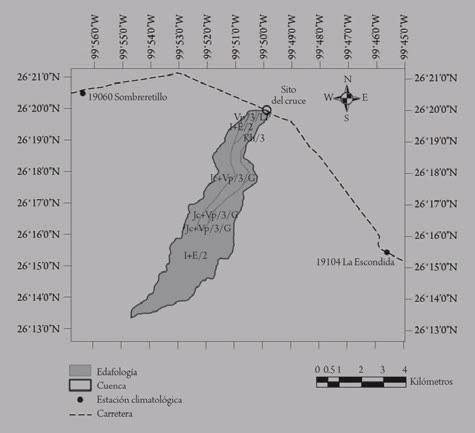
Figura IV.5. Edafología de la zona de estudio. En la tabla IV.2 se presentan los datos de uso de suelo y edafología.

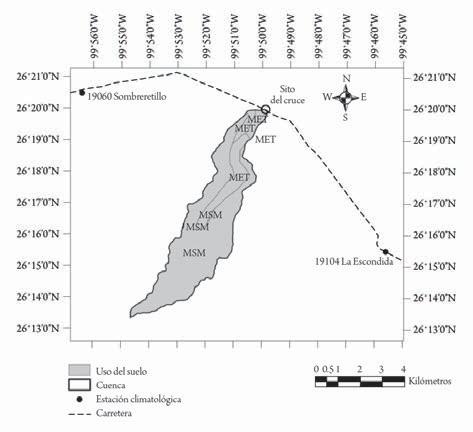
Figura IV.6. Uso de suelo de la zona de estudio. En la tabla IV.2 se presentan los datos de uso de suelo y edafología.

El área de influencia que tiene cada estación en la cuenca se calcula mediante polígonos de Thiessen. Con esto se conocen los valores de precipitación máxima correspondientes a la cuenca (véase la figura IV.7).

Uno de los indicadores más importantes del grado de respuesta de una cuenca a una tormenta es la pendiente del cauce principal. La pendiente media se calcula con el método de Taylor-Schwarz (véase la tabla IV.3).

Tabla VII.2. Edafología y uso de suelo Edafología

Clave Suelo 1 Subsuelo 1 Suelo 2 Subsuelo 2 Textura Fase física

I+E/2 Litosol Rendzina Media

I+E/2 Litosol Rendzina Media

Vp/3/LP Vertisol Pélico Fina Lítica profunda

Kh/3 Castañozem Háplico Fina

Jc+Vp/3/G Fluvisol Calcárico Vertisol Pélico Fina Gravosa

Jc+Vp/3/G Fluvisol Calcárico Vertisol Pélico Fina Gravosa

Uso de suelo

Clave Tipo de información Tipo ecológico Tipo de vegetación Área (km2)

MSM Ecológica-florística-fisonómica Matorral xerófilo

MET Ecológica-florística-fisonómica Matorral xerófilo Matorral espinoso tamaulipeco

MET Ecológica-florística-fisonómica Matorral xerófilo Matorral espinoso tamaulipeco 0.80

MET Ecológica-florística-fisonómica Matorral xerófilo Matorral espinoso tamaulipeco 0.01

MSM Ecológica-florística-fisonómica Matorral xerófilo Matorral submontano 0.19

MET Ecológica-florística-fisonómica Matorral xerófilo Matorral espinoso tamaulipeco 3.76

De acuerdo con el uso del suelo y su clasificación se obtiene un número de escurrimiento ponderado.

Con la fórmula de Kirpich se calcula el tiempo de concentración. Las principales características de la cuenca son las siguientes:

Área = 28.47 km2

Longitud del cauce principal = 20.26 km

Pendiente del cauce principal = 0.01367

Coeficiente de escurrimiento = 77

Tiempo de concentración = 3.5 h

Figura IV.7. Polígonos de Thiessen para la cuenca en estudio.

MANUAL

Tabla IV.3. Cálculo de la pendiente media del cauce con el método de Taylor-Schwarz

1.0212

1.2323

1.1459

1.5994

1.9055

2.2207

2.2908

1.8640

1.0042

14302.7311

18599.1113

suma = 20.2600 180889.48

S= 0.013

El análisis de frecuencia se realiza con el software AX. En las figuras IV.8 a IV.10 se muestran los ajustes para la estación 19060. Este mismo procedimiento se realiza para la estación 19104. En la tabla IV.4, para la estación 19060, se presentan los valores de precipitación máxima para diferentes periodos de retorno y para las funciones de distribución de probabilidad mencionadas Longitud (km)

IV.3.1. Anlálisis de frecuencia para las precipitaciones máximas

Figura IV.8. Ajuste probabilístico para la distribución Normal de la estación 19060.

Figura IV.9. Ajuste probabilístico para la distribución Log Normal de la estación 19060

De la observación de las figuras anteriores y de la tabla IV.3 se desprende que el mejor ajuste se realiza con la función Log Normal, ya que el error estándar de ajuste es de 9.27.

En la figura IV.11 se observan los valores registrados y los valores calculados con las funciones de probabilidad utilizadas.

Tabla IV.4. Lluvias máximas asociadas a diferentes periodos de retorno Tr, obtenidas a través del ajuste de diferentes funciones de distribución de probabilidad, para la estación 19060

Figura IV. 10.- Ajuste probabilístico para la distribución Gumbel de la estación 19060

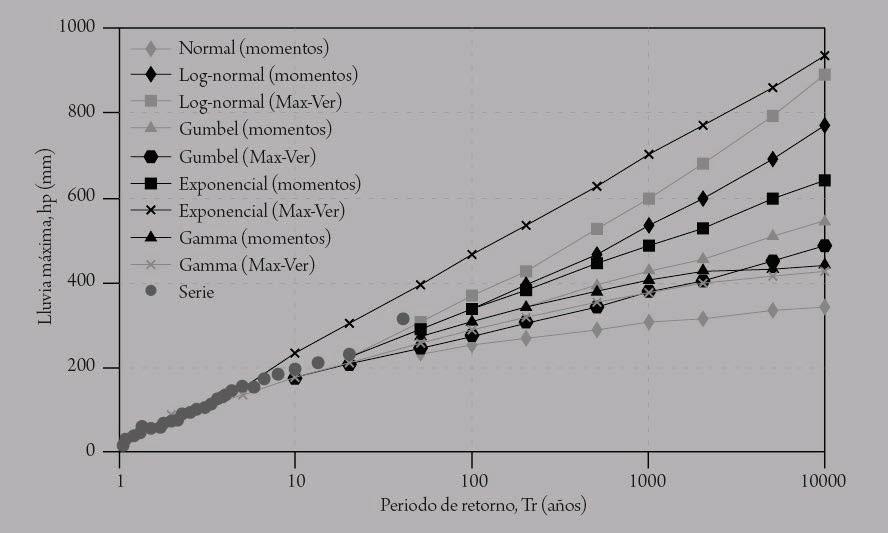
Figura IV.11. Funciones de distribución de probabilidad ajustadas a la serie de lluvias máximas de la estación 19060.

Cálculo del gasto de diseño

El cálculo del gasto máximo se realiza aplicando el método racional, el método del HUT y el método de Ven Te Chow. Los gastos para diferentes periodos de retorno se muestran en la tabla 5; allí también se presentan la lluvia máxima a 24 horas !!!!! 24, y la lluvia media.

Tabla IV.5. Gastos máximos de modelos lluvia- escurrimiento

MANUAL

Figura IV. 12. Hidrogramas para diferentes periodos de retorno, con base en el Hidrograma Unitario Triangular.

El cálculo del hidrograma conforme al gasto pico se realiza mediante el HUT; en la figura IV.12 el hidrograma adimensional del SCS tiene un tiempo al gasto pico igual a 2.99 horas.

IV.4. Censo de estaciones de aforo

La Conagua cuenta con una base de datos –oficial y disponible de forma gratuita – de 1,127 estaciones hidrométricas repartidas espacialmente en todo el país. En la figura IV.13 se muestra la localización de estas estaciones de aforo. En la tabla IV.6 se presenta el censo de las 1,127 estaciones de aforo y se indica para cada estación la siguiente información: clave, río o corriente que afora, cuenca hidrológica y coordenadas geográficas de localización.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Figura 13. Ubicación de estaciones de aforo en el país.

CENSO DE ESTACIONES DE AFORO

Tabla IV.6. Censo de estaciones de aforo en el país

57 09070 Las Pilas

58 09072 Abraham González

59 09076 Chanate Carretera

60 09077 Seris Carretera

61 09078 Km 0+400

62 09079 Hermosillo extracciones

63 09087 Abraham González

64 09088 Abraham González

65 09089 Cocoraque

66 10018 Puente Sudpacífico

67 10020 Puente Cañedo

68 10021 Tierra Blanca

69 10022 Bocatoma

70 10023 Puente Nuevo

71 10026 Picachos

72 10027 El Bledal

73 10029 Naranjo

74 10031 Guamúchil

75 10033 Palos Blancos

CENSO DE ESTACIONES DE AFORO

Canal Tesia

Río Papigóchic

Canal Chanate

Canal Viejo de Seris

Canal Bajo

Canal ppal. del DR Hermosillo

Canal Margen Derecha

Canal Margen Izquierda

Arroyo Cocoraque

Río Culiacán

Río Tamazula

Río Humaya

Canal Canedo

Canal Rosales marg. der.

Río Tamazula

Arroyo El Bledal

Arroyo Ocoroni

Río Mocorito

Río Humaya

Río Mayo -109.358333 27.168055

Río Aros -107.475000 28.500000

Río Sonora -110.920833 29.066666

Río Sonora -110.920833 29.058333

Río Yaqui -109.900000 27.816666

Río Sonora -110.920833 29.083333

Río Papigóchic -107.473333 28.490833

Río Papigóchic -107.473333 28.490833

Arroyo Cocoraque -109.628333 27.415000

Río Culiacán -107.404166 24.805555

Río Culiacán -107.391666 24.811111

Río Culiacán -107.400000 24.829166

Río Culiacán -107.412500 24.798611

Río Culiacán -107.416666 24.805555

Río Culiacán -107.147222 24.812500

Río Tamazula -107.145833 24.804166

Arroyo Cabrera -108.469444 25.802777

Río Mocorito -108.091666 25.469444

Río Culiacán -107.384722 24.925000

76 10034 Zopilote Arroyo Cabrera Río Sinaloa -108.359722 25.741666

77 10035 Naranjo Canal Trinidad Arroyo Ocoroni -108.469444 25.791666

78 10036 Jaina Río Sinaloa Río Sinaloa -108.013888 25.900000

79 10037 Huites Río Fuerte Río Fuerte

80 10038 San Blas Río Fuerte Río Fuerte

81 10040 Santa Cruz

26.883333

Río San Lorenzo Río San Lorenzo -106.952777 24.484722

82 10041 Sanalona II Río Tamazula Río Culiacán -107.162500 24.800000

83 10045 Km 0+710.60

84 10046 Lateral A

85 10048 Bomba Sufragio km 0+660

86 10049 Km 12+290

87 10050 Miguel Hgo Vidal

88 10051 Las Cañas

89 10052 Km 24+140

90 10053 Álamos

91 10054 Km 1+732.6 Puente Gato

92 10055 Km 0+680 (Ant. Puente Gato)

Canal Sufragio

Río Fuerte

26.041666

Canal Lateral Derecho Río Fuerte -108.939444 25.908333

Canal Bomba Sufragio

Canal Sicae

Canal Miguel Hidalgo

Río Fuerte

Canal Sicae

Arroyo Álamos

Canal Tastes

Canal Tastes

Río Fuerte -108.814444 26.043611

Río Fuerte -108.876944 25.970833

Río Fuerte -108.933333 25.904166

Río Fuerte -108.588888 26.472222

Río Fuerte -108.943611 25.912500

Río Fuerte -108.741666 26.393055

Río Fuerte

Río Fuerte

-108.942222 25.920000

-108.933333 25.920833 93 10056 Km 46+780

Canal Sicae

Río Fuerte

25.908333 94 10057 Bamícori

Arroyo Barotén Río Fuerte

26.375000 95 10058 Bocatoma Sufragio

Río Fuerte

Río Fuerte -108.779166 26.073611 96 10060 Km 2+310

Canal Cahuinahua

Río Fuerte -108.879166 26.008333 97 10061 Puente Dren

10062 Santa Rosa

10063 Batopilas

Canal Principal marg. izq.

Canal Santa Rosa

Río Batopilas

Río Culiacán

Fuerte

24.788888

25.901944

10091 Km 0+700

CENSO DE ESTACIONES DE AFORO

124 10112 Guatenipa II Río Humaya

125 10113 La Huerta

126 10117 Km 0+700

127 10118 Puente Las Cabras

128 10119 Jesús Cruz

129 10120 Guasave puente carr.

130

11008 San Felipe

Humaya

Valle del Carrizo

Álamos

11014 Acaponeta

11015 Caboraca

Peñasco Prieto

173 12022 Reforma núm. 1

174 12023 Reforma num. 2

175 12034 Maravatio

176 12067 Emenguaro

177 12093 Zinzimeo

178 12102 Las Islas

179 12109 Batanes

180 12113 Molinos de Caballero

181 12114 La Rosa

182 12115 Pateo

183 12117 Maravatío

184 12120 Huaracha

185 12121 San Nicolás II

CENSO DE ESTACIONES DE AFORO

Canal Reforma

Canal Ardillas

Canal Maravatío

Río Lerma

Río Queréndaro

Canal Islas

Canal San Isidro

Río Lerma

Canal Paquisihuato

Canal Tungareo

Río Lerma -100.883333 20.191666

Canal Reforma -100.883333 20.195833

Río Lerma

Río Lerma

-100.904166 20.198333

-100.875000 20.170833

Lago Cuitzeo -100.976388 19.870833

Río Lerma -101.066666 20.283333

Río Lerma

-100.904166 20.204166

Río Lerma -100.214444 20.069444

Río Lerma -100.304166 19.923611

Río Lerma

Arroyo Cachivi Río Lerma

19.904166

Canal Huaracha Río Lerma -100.300000 19.922222

Canal San Nicolás Río Lerma -100.904166 20.200000

186 12128 Corona Río Santiago Río Santiago -103.083333 20.404166

187 12131 Armadillo Río Lerma

188 12139 Ziritzícuaro

189 12140 Ziritzícuaro

190 12145 Zempoala

191 12148 Ziritzícuaro

192 12162 Compuertas Chicas

193 12192 Compuertas Grandes

194 12194 Ojuelos

195 12209 El Tambor

196 12210 Vertedor Potrerillos

197 12213 Puente FC Chicalote

198 12214 Emenguaro

199 12218 El Águila

200 12219 Cointzio

201 12221 Atapaneo

202 12224 Chiquito

203 12227 Tizcareno

204 12232 Paso de Ovejas

205 12233 Corrales

206 12234 Brisenas

207 12237 Munguía (Zatemaye)

208 12238 Pericos

209 12239 Sn Pedro Piedra Gorda

210 12249 Pateo

211 12254 San Isidro

212 12257 Tarandacuao

213 12258 Lavaderos

214 12268 Excamé I

215 12271 Palmitos

216 12274 Monterrubio

217 12277 San Bartolo

218 12278 Atoyac

219 12280 Túnel núm. 2

220 12281 Km 1+400 (presa Jocoque)

221 12283 Zacapendo

222 12288 Zapotlanejo

223 12310 La Estanzuela

224 12312 Cointzio

225 12314 Queréndaro

226 12315 Calera

227 12323 Salidas de Malpaís

228 12328 Guaracha

229 12331 El Pueblito

230 12335 La Estanzuela

Río Lerma -101.050000 20.279166

Canal Puroagua Río Lerma

Canal San Lorenzo Río Lerma

Canal Extracciones

-100.494444 20.020833

-100.429166 19.954166

Laguna de Yuriria -101.075000 20.316666

Canal Peña Blanca Río Lerma

Canal Extracciones

Canal Alimentador

Río Lerma

Río Lerma

Río Pabellón

Río Chicalote

Canal Eménguaro

Río Santiago

Río Grande de Morelia

Río Grande de Morelia

Río Chiquito

Río Morcinique

Río Lerma

Río Lerma

Río Lerma

Río Tigre

Río de la Laja

Río San Pedro

Río Tlalpujahua

Canal San Isidro

Arroyo Tarandacuao

Río Grande de Morelia

Río Tlaltenango

Río Santiago

Canal La Huerta

Canal San Bartolo

Río Atoyac

Túnel Derivación

Canal Principal

-100.427777 19.955555

Laguna de Yuriria -101.075000 20.295833

Río Lerma -101.065277 20.279166

Río Lerma

Río Lerma

-100.987500 20.262500

-100.237500 19.994444

Río San Pedro -102.435277 22.234722

Río Aguascalientes -102.254166 22.006111

Río Lerma

-100.879166 20.137500

Río Aguascalientes -102.410000 22.136388

Lago Cuitzeo -101.258333 19.641666

Lago Cuitzeo -101.176388 19.725000

Río Grande de Morelia

-101.190277 19.695833

Río Aguascalientes -102.425000 21.920833

Río Lerma

Río Lerma

-100.456944 19.991666

-101.804166 20.195833

Río Lerma -102.558333 20.275000

Río Lerma

Río Lerma

Río Aguascalientes

Río Lerma

Río Lerma

Río Lerma

Lago Cuitzeo

Río Bolaños

-100.559722 20.111111

-101.108333 20.525000

-102.350833 22.445833

-100.316666 19.890277

-100.908333 20.208333

-100.512500 19.994444

-101.072222 19.848611

-103.357500 21.651111

Río Aguascalientes -102.412222 22.137500

Río Grande de Morelia

Río Grande de Morelia

-101.238888 19.654166

-101.011111 19.815277

Laguna de Sayula -103.483333 20.016666

Río Pabellón

-102.442777 22.234722

Río Santiago -102.345000 22.133055

Canal Zacapendo Río Grande de Morelia

Canal Zapotlanejo

Río Duero

Canal La Huerta

Río Queréndaro

Río Teocaltiche

Río Queréndaro

Canal Guaracha

Río del Pueblito

Canal San Simón

-101.004166 19.815277

Río Santiago -103.087500 20.404166

Río Lerma

Río Grande de Morelia

-102.370833 20.116666

-101.256944 19.637500

Lago Cuitzeo -100.889444 19.811666

Río Verde

-102.595833 21.490277

Lago Cuitzeo -100.875555 19.831944

Río Sahuayo -102.579166 19.958333

Río Apaseo

Río Duero

-100.437500 20.512500

-102.362500 20.120833

12347 Santiago Undameo

CENSO DE ESTACIONES DE AFORO

12355 Agostadero Río San Matías

12369 Cuarenta

12370 San Gaspar

de Lagos

12378 Presa Calles

263 12395 Urepetiro

264 12396 Camécuaro

265 12397 Camecuaro

266 12400 Las Juntas

267 12402 Km 0+262

268 12403 Km 2+500

269 12404 Puente Canal

270 12405 El Tecomate

271 12408 El Aguila

272 12409 Chaparaco

273 12410 Platanal

274 12411 La Calzada

275 12412 Jaripo

276 12415 Puente San Isidro

277 12417 La Estancia

278 12418 Los Castillos

279 12422 Cuarenta II

280 12423 Puente Atlacomulco

281 12424 Puerta del Monte

282 12425 Ajojúcar

283 12427 Puente San Isidro

284 12428 Bolaños

285 12436 Las Américas

286 12438 La Yesca

287 12439 Orandino II

288 12440 Puente San Isidro

Tlazazalca

Desagüe del Lago Lago de Camñecuaro -102.216666 19.916666

Río Santiago Río Santiago -103.275000 20.731944

Canal Principal Tepetitlán

Canal Tepetitlán

Canal Enyege

Río Juchipila

Canal Águila Viejo

Canal Calvario

Río Jaltepec -99.951944 19.659722

Canal principal Tepetitlán -99.930555 19.650000

Canal principal Tepetitlán -99.933333 19.648611

Río Santiago -103.050000 21.543055

Canal Principal marg. der. -102.258333 19.979166

Canal Principal marg. der. -102.266666 19.970833

Canal Principal marg. der. Río Duero -102.254166 19.945833

Río de los Gómez

Río Jaripo

Río de la Patera

Canal Alto

Arroyo Los Castillos

Río de Lagos

Río Lerma

Río Turbio -101.683333 21.087500

Río Sahuayo -102.600000 19.958333

Río Angulo -101.525000 19.858333

Manantial La Estancia -102.354166 19.979166

Río de los Gómez -101.679166 21.175000

Río Verde -101.752777 21.488888

Río Lerma -99.893055 19.788888

Canal Alimentador Río Lerma -101.033888 20.264444

Canal Principal

Canal del Banadero

Río Bolaños

Río Guanajuato

Río Santiago

Desagüe del Lago

Canal de la Peñita

Río Aguascalientes -102.437500 21.543055

Río de la Patera -101.533333 19.858333

Río Santiago -103.783333 21.825000

Río Lerma -101.316666 20.850000

Río Santiago -104.090277 21.193055

Río Duero -102.329166 19.966666

Río de la Patera -101.529166 19.858333

289 12443 La Estancia

290 12451 Puente Carretera II

291 12452 Achoquén

292 12454 Lagos

293 12456 Peñuelitas

294 12466 Jerécuaro

295 12469 Cuixtla

296 12470 Huaynamota

297 12471 San Cristóbal

298 12472 Arcediano

299 12473 Santa Rosa

300 12474 El Sauz

301 12476 Km 0+340

302 12477 Jaral

303 12479 Guanajal

304 12483 Canal núm. 1

305 12484 El Platanito

306 12485 El Zapote

307 12486 Capitiro

308 12487 La Florida

CENSO DE ESTACIONES DE AFORO

Canal Bajo

Río Lerma

Salidas Presa

Río de Lagos

Río de la Erre

Río Tigre o Coroneo

Río Cuixtla

Río Huaynamota

Río Santiago

Río Santiago

Río Santiago

Río Santiago

Canal Principal

Canal Extracciones

Río Pedrito

Manantial La Estancia -102.354166 19.979166

Río Lerma

-99.523611 19.279166

Arroyo San Nicolás -103.076388 21.521388

Río Verde -101.913888 21.362500

Río de la Laja -100.879166 21.108333

Río Lerma -100.522222 20.141666

Río Santiago -103.441666 21.051388

Río Santiago -104.711111 21.843055

Río Santiago -103.443055 21.048611

Río Santiago -103.280555 20.741666

Río Santiago -103.718055 20.913888

Río Santiago -104.709166 21.835277

Río de Lagos -101.741666 21.481944

Laguna de Yuriria -101.058333 20.341666

Río de los Gómez -101.879166 21.079166

Canal Principal Río Tlaltenango -103.363055 21.652777

Río San Juan Capistrano

Río Tlaltenango

Río Huaynamota -104.063055 22.568055

Río Bolaños -103.398611 22.065555

Canal Ing. Antonio Coria Río Lerma -101.020833 20.287500

Río Valparaíso Río Tlaltenango -103.603611 22.686388

309 12488 La Gloria Río Colotlán Río Bolaños -103.396388 22.068055

310 12489 Teocaltiche

311 12490 San Nicolasito

312 12493 Castillos

313 12496 Capomal

314 12499 La Patiña

315 12504 La Cuna

316 12505 Achimec I

317 12507 Despeñadero

318 12508 Boquilla Tenasco

319 12510 Obregón

320 12511 Orandino

321 12512 Silao

322 12513 Vertedor Castillos

323 12514 El Caimán

324 12515 la Aurora

325 12516 Mololoa

326 12517 Control

327 12520 Huaynamota II

328 12521 Santa Rosa II

329 12522 El Niágara II

330 12523 Nanchi

331 12525 El Tule

332 12526 Yurécuaro II

333 12527 Ibarrilla

334 12529 Laborio

Río Teocaltiche Río Verde -102.580000 21.441666

Río Lerma

Canal Los Castillos

Río Santiago

Arroyo La Patiña

Río Verde

Río Tepetongo

Río Santiago

Río Chico

Río de la Laja

Canal Alto

Río Silao

Arroyo Los Castillos

Río Bolaños

Canal La Aurora

Río Tepic

Extracciones presa Alemán

Río Huaynamota

Río Santiago

Río Aguascalientes

Canal Principal marg. izq.

Río Tule

Río Lerma

Arroyo Ibarrilla

Río Lerma -100.406111 19.919444

Arroyo Los Castillos -101.666666 21.191666

Río Santiago -105.118055 21.825000

Río de los Gómez -101.700000 21.175000

Río Santiago -102.833055 21.004166

Río Jerez

-103.223333 22.324166

Río Santiago -104.720833 21.843055

Río Colotlán -103.229166 22.172222

Río Lerma -101.108333 21.333333

Manantial Orandino -102.325000 19.966666

Río Guanajuato -101.441666 20.958333

Río de los Gómez -101.666666 21.194444

Río Santiago

Río Santiago

Río Santiago

-104.080555 21.201388

-103.169444 20.516666

-104.879166 21.502777

Río Tlaltenango -103.364444 21.650000

Río Santiago

-104.715277 21.854166

Río Santiago -103.726388 20.922222

Río Verde

Río Santiago

Río Zula

Río Lerma

-102.375000 21.801388

-105.054166 21.797222

-102.433333 20.716666

-102.258333 20.337500

Río de los Gómez -101.641666 21.183333

Canal Laborío Río Lerma -101.062500 20.375000 335 12532 San Cristóbal II

336 12533 Urepetiro II

337 12534 Atotonilco II

338 12535 Cinco Señores

Río Santiago

Río Tlazazalca

Río La Gavia

Río Santiago -103.429166 21.038888

Río Duero -102.154166 19.950000

Río Lerma -99.776388 19.452777

Arroyo San Damián Río de la Laja

20.958333 339 12537 El Sifón

Canal Zanja Sur Presa Malpaís

19.826388 340 12539 San Bernabé

341 12540 La Villita (exced. p La Villita)

Río Lerma

Arroyo La Villita

Río Lerma -99.720000 19.472777

Río Tlaltenango -103.352500 21.583333 342 12541 La Red

343 12543 Calixtlahuaca

344 12544 Agua Blanca

345 12545 El Niágara III

Río Calderón

Río Tejalpa

Salidas presa El Chique

Río Aguascalientes

Río Santiago -102.798611 20.719444

Río Lerma -99.687500 19.338888

Río Juchipila -102.900000 21.991666

Río Verde -102.375000 21.779166 346 12546 González

Arroyo Tlaxcalilla

Río de la Laja -100.845833 20.887500

347 12548 Peñuelitas

348 12549 Yurécuaro

349 12553 Canal núm. 1

350 12554 Canal núm. 2

CENSO DE ESTACIONES DE AFORO

Canal Extracción

Canal marg. izq.

Canal Margen Derecha

Canal Margen Izquierda

351 12556 Cerro Blanco Río Mojarras

352 12557 Cuquio

353 12558 El Batán

354 12559 Lagunillas

de la Erre

Lerma

Lerma

Santiago

Río Gigantes

Río del Pueblito Río Apaseo

Río Tepatitlán

355 12560 Xoconole Canal Xoconole

356 12561 Temascalcingo

Río Lerma

357 12562 La Trinidad Arroyo Temascatío

358 12568 El Tejocote

Río Chiquito

359 12570 La Codorniz Río La Labor

360 12572 La Experiencia

361 12573 La Experiencia

Canal La Experiencia

San Juan de Dios

362 12574 Los Velázquez Río El

12579 El Pinito

366 12581 San Bartolo del Llano Río Sila

12585 Calerita

368 12586 Cuixtla

12587 Cuixtla

12588 El Plan

372 12592 Santa María del Llano

Verde

Grande de Morelia

Lerma

Calvillo

San Juan de Dios

núm. 2 marg. der.

Grande de Morelia

Santo Domingo Río Lerma

373 12601 El Pescado núm. 2 Río El Pescado

Santo Domingo

19.779166 374 12602 Boca del Tesorero Río Jerez

376 12605 Temascales II

20.062500

377 12606 Santa Ana Arroyo de Los Ocotes Río Lerma -101.958333 20.379166

378 12607 La Yerbabuena

379 12608 Los Fresnos

380 12609 Urepetiro

381 12611 Hacienda de Sánchez

382 12612 Angamacutiro

383 12613 Angamacutiro

384 12615 Palomas (salidas p. Palomas)

385 12618 Los Gómez

386 12619 Km 0+050

387 12620 Tarimbaro

388 12621 La Boquilla

389 12622 La Boquilla

390 12623 La Boquilla

391 12624 Derivadora de Toxi

392 12625 Derivadora de Toxi

393 12628 La Boquilla

394 12648 La Yerbabuena

395 12649 La Yerbabuena

396 12652 La Begoña

Río de Los Morales Río Zula -102.750000 20.583333

Río Andamácuaro Río Lerma

Canal Margen Izquierda Río Tlazazalca -102.154166 19.950000

Canal Gugorrones Río Lerma -100.900000 20.220833

Canal Margen Izquierda

Canal Margen Derecha

Río Palomas

Río Angulo -101.704166 20.133333

Río Angulo -101.700000 20.125000

Río Juchipila -102.806944 22.345000

Río de Los Gómez Río Turbio -101.758611 21.061944

Canal Principal Presa La Codorniz -102.681944 21.991666

Arroyo Guadalupe Río Grande de Morelia -101.223611 19.789444

Canal núm. 1 marg. der. Río Juchipila -103.397222 21.058333

Canal núm. 2 marg. der. Río Juchipila -103.402777 21.052777

Canal núm. 3 marg. der. Río Juchipila -103.402777 21.052777

Canal núm. 1 marg. der. Río Lerma -99.915277 19.844444

Canal núm. 2 marg. izq. Río Lerma -99.918611 19.848611

Canal Margen Izquierda Río Juchipila -103.397222 21.058333

Canal Margen Derecha Río de los Morales

Canal Margen Izquierda Río de los Morales -102.750000 20.583333

405 12671 Achimec

406 12673 Guanajal II

407 12693 El Carrizal

408 12700 Achimec II

409 12710 Yurécuaro II

410 12711 El Mezquite

411 12712 El Zapote

412 12713 Angamacutiro II

413 12716 Ibarrilla II

414 12717 El Chapín

415 12718 Ameche

416 12719 Tres Guerras

417 12720 San Nicolás III

418 12728 Tepalcates

419 12729 Trojes

420 12731 Agostadero

421 12732 Agostadero

422 12734 El Sifón

423 12735 El Sifón

CENSO DE ESTACIONES DE AFORO

Canal Principal

Río Pedrito

Río Santiago

Río Tepetongo

Canal marg. izq. núm. 2

Canal principal marg. der.

Canal Margen Derecha

Río Angulo

Arroyo Ibarrilla

Río La Sauceda

Río Querétaro

Río de la Laja

Canal San Nicolás

Canal Tepalcates

Río Temoaya

Canal Margen Derecha

Canal Margen Izquierda

Río Tepetongo -103.224166 22.324722

Río de los Gómez -101.841666 21.020833

Río Santiago -104.774722 21.842222

Río Jerez

-103.223333 22.323055

Canal Principal marg. der. -102.252222 20.333333

Río Lerma

-102.246388 20.340000

Canal Principal marg. der. -102.248888 20.336111

Río Lerma -101.708333 20.137500

Río de los Gómez -101.637500 21.194444

Río Guanajuato -101.235555 20.871388

Río de la Laja -100.587500 20.558333

Río Lerma -100.772222 20.520833

Río Lerma -100.889444 20.202222

Río Guanajuato -101.370833 20.740277

Río Lerma -99.611944 19.428333

Río San Matías -102.347222 21.366111

Río San Matías -102.346666 21.365000

Canal Zanja Sur marg. der. Río Queréndaro -100.881111 19.835277

Canal Zanja Sur marg. izq. Río Queréndaro -103.087500 20.404166 424 12737 Zona Industrial

Canal Desagüe Oriente Río Verdiguel

425 12738 Universidad Río Verdiguel

426 12739 Miltepec

427 12740 Tlacopa

428 12741 La Loma

429 12742 Melchor Ocampo

Canal Desagüe Norte Río Verdiguel -99.656388 19.324166

Canal Principal Desagüe N Río Verdiguel -99.633333 19.317222

Canal Desagüe Oriente Río Verdiguel -99.556666 19.288333

Canal vertedor presa M Ocampo Río Lerma -101.780000 20.166666

430 12743 San Juan Temascatío Arroyo Temascatío Río Lerma -101.224166 20.733333

431 12744 Copalillo

Río Guanajuato Río Lerma -101.346666 20.721666

432 12748 El Sauz Arroyo Zarco Río Guanajuato -101.333055 20.777222

433 12749 Atequiza II

434 12750 Urepetiro

435 12751 Tlacopa núm. 1

436 12752 Tlacopa núm. 2

437 12753 Tlacopa núm. 3

438 12754 Sauces Chicos

439 12755 Angamacutiro II

440 12756 Angamacutiro II

441 12758 El Colorado

442 12759 El Cubo

443 12760 Sauces Chicos

444 12761 La Yerbabuena

445 12762 El Tigre

446 12764 Atemajac

447 12765 San Andrés

448 12767 La Sauceda

449 12769 Amado Nervo

450 12908 Arandas

451 12932 Zinzimeo

452 13001 Paso de Arocha

453 13002 El Refilión

454 14003 Los Rosillos

455 14007 Las Gaviotas II

456 14008 La Desembocada

457 14010 Puente Ameca

458 14011 Puente FFCC II

459 14014 El Colomo

460 14015 La Vega

461 14016 La Vega

462 14017 El Salitre

Canal Atequiza Río Santiago -103.094444 20.398333

Canal marg. der. núm 2 Río Tlazazalca -102.154166 19.950000

Canal Desagüe NE marg. der. Río Lerma -99.633333 19.317500

Canal Desagüe NW Canal ppal Desagüe Norte -99.633333 19.317500

Canal Desagüe NE marg. izq.

Canal Principal

Canal Margen Derecga

Canal Margen Izquierda

Canal ppal Desagüe Norte

Río Encarnación

Río Angulo

Río Angulo

Arroyo Colorado Río Turbio

Dren Tarimoro

Río Encarnacion

Arroyo La Yerbabuena

Arroyo El Tigre

Arroyo Atemajac

Arroyo San Andrés

Río de la Sauceda

Canal Principal marg. izq.

Río de la Llave

Canal Zinzimeo

Río Huicicila

Río Huicicila

Canal Los Rosillos

Río Ameca

Río Mascota

Río Ameca

Río Ahualulco

Canal Principal marg. der.

Río Lerma

Río Aguascalientes

Río Silao

Río Silao

-93.633333 19.317500

-102.144722 21.613611

-101.704166 20.133333

-101.704166 20.133333

-101.882500 20.650000

-100.899444 20.280277

-102.142777 21.611111

-101.363611 21.062500

-101.463333 21.071388

Río San Juan de Dios -102.340000 20.723055

Río Santiago -103.281666 20.715000

Río Lagos -101.851111 21.351388

Río Santiago -105.036666 21.730555

Río Guanajuato -101.370833 20.712500

Canal Zacapendo -101.008333 19.825555

Río Huicicila -105.075000 21.283333

Río Huicicila -104.900000 21.300000

Laguna Colorada -103.987500 20.758333

Río Ameca

20.908333

Río Ameca -105.158333 20.733333

Río Ameca -104.050000 20.550000

Río Ameca -103.858333 20.591666

Río Ameca -105.116666 20.900000

Canal Principal marg. der. Río Ameca -103.850000 20.591666

Canal Principal marg. izq.

Río Cocula

Río Ameca -103.866666 20.583333

Río Ameca -103.866666 20.533333

15007 Cajón de Peña

Zopilota

CENSO DE ESTACIONES DE AFORO

Arroyo La Zopilota

476 15010 Tecomates Arroyo Tecomates

15011 Cihuatlán

15014 Higuera Blanca II

15015 Cajon

La Resolana

La Resolana

San Nicolás

16022 Callejones

487 16026 El Grullo

Canal El Grullo marg. izq. Río Armería

19.850000 488 16027 El Grullo

Canal El Grullo marg. der.

16029 Tacotán II

490 16030 Tacotan D. A. Derrames y arroyo Chapala

16031

494 16034 Peñitas

495 16035 Callejones

Tuxcacuesco Río Armería -103.991666 19.666666

Canal Principal marg. izq. Río Armeria -103.816666 19.316666

496 16036 Las Peñitas II Río Armería

497 16040 Las Piedras

499 18005 San Jacinto Río Atoyac

18089 El Rodeo II

Armería

alimentador Perritos

Rodeo

18094 Cotija Río Cotija

18095 El Puerto Río Cotija

504 18129 Los Granjenos

Río Quitupan

Itzícuaro

Itzícuaro

Tepalcatepec -102.879166 19.930000 505 18131 Los Filtros Canal Los Filtros marg. der.

506 18135 Panotla Río Zahuapan

507 18137 San Juan Molino

508 18140 Xicotzingo

509 18141 El Carmen

510 18148 Echeverría

511 18151 San Francisco

Balsas

Río Atoyac Río Balsas -98.379166 19.287500

Río Zahuapan

Río Atoyac -98.250000 19.166666

Río Atoyac Río Zahuapan -98.450000 19.312500

Río Atoyac

Río Poblano -98.283333 18.970833

Río Alseseca Río Atoyac -98.183333 18.966666

515 18167 Ahuatepec (km 24+769) Canal principal Valsequillo

517 18175 Oacalco Canal Cuarta Toma

518 18176 El Zapote Canal El Zapote

519 18177 El Almeal

Canal El Almeal

521 18182 Cuarta Toma

522 18187 Tercera Toma

523 18188 Quinta Toma

524 18189 Segunda Toma

525 18192 Agua Dulce

526 18193 Yautepec

527 18195 Ziritzícuaro

528 18197 Itzamatitlán

529 18198 Las Minas

530 18199 Oaxtepec

531 18200 Cocoyoc

532 18201 El Cajón

533 18202 El Mentidero

534 18203 Taza Chica

535 18204 Taza Grande

536 18210 Valle de Juárez

537 18219 Perritos núm. 2

538 18223 Ticumán

539 18225 Cuautla

540 18232 Amacuzac

541 18237 Portezuelo

542 18240 Arroyo del Chivo

543 18252 Chamacua II

544 18253 Chamacua

545 18255 Placeres del Oro

546 18257 San José Quesería

547 18261 Aratichanguío

548 18264 Zacatepec

549 18269 Alpuyeca

550 18270 Alpuyeca

551 18271 Temixco

552 18272 Temixco

553 18277 San Andrés

554 18280 San Diego

555 18287 A-12 La Comunidad

556 18288 A-1 César Matadero

557 18291 A-10 Texcaltitlán

558 18292 A-3 San Miguel Ayala

559 18293 A-4 Alpanocan

560 18294 A-8 Totolmajac

561 18295 A-9 El Molino

562 18296 A-11 Real de Arriba

563 18303 A-2 Huilango

564 18311 El Gallo

565 18316 la Cuera

566 18317 Palos Altos I

567 18319 Toma Tecomatapec

568 18322 Tlax

569 18323 Tetlama

570 18324 Atlanga km 0+220

571 18325 Atlanga km 0+060

572 18327 Oropeo

573 18329 Pinzán Morado

574 18335 Acatlán

575 18337 Camotlán

576 18338 Xatán

577 18339 El Pejo

578 18340 San Lucas

CENSO DE ESTACIONES DE AFORO

Barranca Amatzinac Río Balsas -98.770833 18.779166

Barranca Amatzinac Río Balsas -98.762500 18.800000

Barranca Amatzinac Río Balsas -98.770833 18.779166

Barranca Amatzinac Río Balsas -98.737500 18.829166

Canal Agua Dulce Manantial Agua Dulce -98.933333 18.808333

Río Yautepec

Río Amacuzac -99.050000 18.895833

Río de la Parota Río El Marquez -101.973333 19.091666

Canal Tercera Toma Río Itzamatitlán -99.020833 18.904166

Filtraciones presa MA Camacho Río Balsas -98.075000 18.895833

Canal Segunda Toma Río Cacahuatitla -98.966666 18.900000

Canal Primera Toma

Río El Cajón

Río El Cajón

Barranca Cacahuatitla -98.966666 18.900000

Río Tepalcatepec -102.752777 18.968055

Río Tepalcatepec -102.669444 19.055555

Canal Taza Chica Manantiales Cuautla -98.954166 18.837500

Canal Taza Grande Manantiales Cuautla -98.954166 18.837500

Canal de Extracciones

Canal Perritos

Río Yautepec

Río Cuautla

Río Amacuzac

Río Quitupan -102.930555 19.938888

Río Tembembe -99.329166 18.779166

Río Amacuzac -99.104166 18.791666

Río Amacuzac -99.950000 18.808333

Río Mezcala -99.370833 18.600000

Canal Portezuelo Río Atoyac -98.279166 18.958333

Arroyo El Chivo

Río Amuco

Canal Principal marg. izq.

Río Placeres del Oro -101.009722 18.401388

Río Balsas -100.688888 18.265277

Río Amuco -100.700000 18.265277

Río Placeres del Oro Río Balsas -100.994444 18.422222

Río Cuirio

Río Balsas -100.730555 18.261111

Arroyo Barrillos Río Balsas -101.358333 18.488333

Río Apatlaco

Río Tetlama

Canal Xoxocotla

Río Apatlaco

Canal Segunda Toma

Río Ajuchitlán

Río Quitupan

Río Verde

Río César Matadero

Río Texcaltitlán

Río Ahuitzoc

Río Amacuzac

Río San Gaspar

Río Ixtlahuaca

Río El Vado

Río Huitzilac

Río Cutzamala

Río de la Cuera

Río Poliutla

Río Tequimilpa

Río Zahuapan

Río Tetlama

Canal Principal Atlanga

Canal Lateral Atlanga

Río San Pedro

Río Placeres del Oro

Río Acatlan

Río Huajuapan

Río Xatán

Arroyo El Pejo

Arroyo San Lucas

Río Yautepec -99.195833 18.650000

Río Apatlaco -99.258333 18.733333

Río Tetlama -99.258333 18.733333

Río Yautepec -99.220833 18.854166

Río Apatlaco -99.225000 18.850000

Río Balsas

-100.520833 18.047222

Río Tepalcatepec -102.822222 19.893333

Río Cutzamala -99.931944 19.140000

Río Huitzilac -98.550000 18.866666

Río Almoloya -99.941666 18.929166

Río Huitzilac -98.533333 18.908333

Río Balsas -98.716666 18.875000

Río Potrero -99.683333 18.933333

Río Chontalcuatlán -99.820833 18.916666

Río Temascaltepec -100.030000 19.041666

Río Nexapa -98.583333 18.850000

Río Balsas

-100.680555 18.687500

Río Cuautla -98.916666 18.683333

Río Balsas -100.266666 18.391666

Río San Jerónimo -99.716666 18.945833

Río Atoyac -98.241666 19.320833

Río Apatlaco -99.279166 18.833333

Río Zahuapan -98.195833 19.558333

Río Zahuapan -98.200000 19.550000

Río Tepalcatepec -101.806944 18.833333

Río Balsas -100.887500 18.160555

Río Mixteco -98.050000 18.200000

Río Mixteco -97.687500 17.908333

Río Mixteco -97.700000 17.783333

Arroyo Petachícuaro -100.943055 18.687500

Río Balsas -100.798611 18.538888

579 18341 Tezoatlán

580 18342 Teponahuazo

581 18344 Mariscala

582 18347 Los Molinos

583 18348 Tonalá

584 18349 Huamantla

585 18350 Santa Fe

586 18351 Piritícuaro

587 18352 San Mateo

588 18354 Huajuapan de Leon

589 18356 Petachícuaro

590 18360 La Estancia

591 18361 Tonahuixtla

592 18364 Zocoteaca

593 18365 Las Huertas

594 18369 El Mirador

595 18370 El Orégano

596 18371 Tarétaro

597 18372 Coatepequito

598 18374 La Huertilla

599 18375 La Calera

600 18376 Camotlán

601 18379 La Angostura

CENSO DE ESTACIONES DE AFORO

Río Salado Río Mixteco

Río Tlapaneco

Río Mixteco

Río Nexapa

Río Grande -98.512500 17.604166

Río Balsas

Mixteco

Río Salado Río Mixteco -97.945833 17.687500

Río de Guadalupe

Río Amuco

Arroyo Chihuero

Río Mixteco

Río Huajuapan

Arroyo Petachícuaro

Río Tacámbaro

Río Tizaa

Laguna Totolcingo -97.854166 19.316666

Río Balsas -100.680555 18.095833

Río Huetamo -100.888888 18.675000

Río Mixteco -97.983333 17.558333

Río Salado -98.916666 18.683333

Río Huetamo -100.933333 18.688888

Río Balsas -101.115277 18.561666

Río Acateco -97.891666 18.195833

Canal Zocoteaca Río Mixteco

Río Salado Río Mixteco

Barranca de Alchichica Río del Muerto

Barranca de Alchichica Río del Muerto

Río Tarétaro

Cuirio

Río San Jerónimo Río Amacuzac -99.566666 18.741666

Río Tototaya

Canal Principal marg. izq.

Canal Margen Derecha

Río Juxtlahuaca

602 18380 La Laguna Manantial La Laguna

603 18381 Los Molinos

Canal San Félix

Placeres del Oro

Mixteco

Nexapa

615 18404 El Centenario

616 18406 Las Estacas

617 18407 Toma Ixtapan II

618 18411 Buenavista

619 18416 Charapendo

620 18420 Corondiro

621 18421 Corondiro

622 18424 Parácuaro núm. 1

623 18425 Parácuaro núm. 2

624 18426 Parácuaro núm. 3

625 18427 Parácuaro núm. 4

626 18428 Parácuaro núm. 5

627 18429 Parácuaro núm. 6

628 18450 Palos Altos Ii

629 18452 El Charco

Arroyo Ajejela Río Atoyac

Canal Las Estacas Manantial Las Estacas -99.112500

Canal Derivadora Ixtapan Río Tequimilpa -99.708333 18.941666

Canal Buenavista Río Buenavista -102.583333 19.210555

Canal Charapendo Río Cupatitzio -102.081944 19.280555

Canal Antúnez Arroyo Coróndiro -102.120000 18.987500

Canal Para Arroyo Coróndiro -102.116666 18.987500

Canal Núm. Uno Manantial Parácuaro -102.218055 19.151388

Canal Núm. Dos Manantial Parácuaro -102.219444 19.148611

Canal Núm. Tres Manantial Parácuaro -102.226388 19.147222

Canal Núm. Cuatro Manantial Parácuaro -102.225000 19.151666

Canal Núm. Cinco Manantial Parácuaro -102.225000 19.151388

Canal Núm. Seis Manantial Parácuaro -102.225000 19.151666

18454 Zicuirán Canal Zicuirán

631 18455 Tamácuaro

632 18485 La Junta

633 18486 La Angostura

Zicuirán

Río Huajuapan

Río Huetamo Río Balsas -100.897222 18.605555

634 18496 El Carrizo Río Taixtan o Ticuilucan

635 18497 Piedras Blancas

636 18502 El Zopilote

Tepalcatepec

Canal El Zopilote

El Cajón -102.986111 19.036111

637 18504 Enmedio

638 18506 El Carrizo

639 18511 Zimanca

640 18513 Las Burras

641 18525 Guarandicho

642 18527 Punta de Agua

643 18528 Punta de Agua

644 18538 Tezoatlán II

645 18539 Arceo

646 18540 Temascaltepec

647 18541 Balcon del Diablo II

648 18543 Palos Altos

649 18544 Palos Altos

650 18547 Chamacua

651 18548 La Comunidad

652 18549 La Comunidad

653 18550 Nuevo Galeana

654 18553 Obregón

655 18554 El Mirador

656 18555 Chontalcuatlán

657 18557 El Túnel

658 18571 Los Olivos

659 19002 Coyuca de Benítez

CENSO DE ESTACIONES DE AFORO

Corriente

Canal Enmedio

Canal Carrizo

Canal Zimanca

Canal Las Burras

Canal Guarandicho

Canal Dolores

Canal Pinzándaro

Río Salado

Arroyo Las Cruces

Río Verde

Río Atoyac

Canal ppal V. Gro marg. izq

Río Cancitas -102.200000 19.202777

Río Cancitas -102.201388 19.198611

Río Buenavista -102.561111 19.141666

Río Cancitas -102.206944 19.156666

Arroyo Buenavista -102.455555 19.134722

Arroyo Dolores -102.666666 19.098611

Arroyo Dolores -102.663888 19.100833

Río Mixteco -97.791666 17.666666

Río Tepalcatepec -102.268888 18.720000

Río Temascaltepec -100.065833 19.037777

Río Poblano -98.095833 18.908333

Río Poliutla -100.270833 18.363888

Canal lat marg. der. San Antonio Canal ppal Vicente Gro -100.271666 18.379166

Canal Principal Río Amuco -100.691666 18.255555

Canal Margen Izquierda

Canal Margen Derecha

Río Ajuchitlán -100.515277 18.129166

Río Ajuchitlán -100.529166 18.125000

Canal Principal marg. der. Río Cutzamala -100.612500 18.547222

Río Taixtán

Río Almoloya

Río Otates -103.045833 19.002222

Río Chontalcuatlán -99.766666 18.806111

Río Chontalcuatlán Río Amacuzac -99.563888 18.661111

Canal El Túnel Barranca Amanalco -99.236111 18.937500

Canal Los Olivos

Río Coyuca

Río de los Otates -102.866666 19.212500

Río Coyuca -100.095833 17.004166

660 19003 Coyuquilla II Río Coyuquilla Río Coyuquilla -101.058333 17.375000

661 19005 Tecpan

662 19006 San Luis

663 19008 Km 21+000

664 19009 Petatlán

665 19010 La Loma

666 19011 San Pedro

667 19012 Coyuca

668 19013 San Jerónimo

669 19014 San Jeronimito

670 19015 Coyuquilla

671 19016 La Unión

672 19017 Coyuquilla

673 19018 Tuncingo

674 19022 La Salitrera

675 20005 Oax

676 20016 Quetzala

677 20017 Paso de la Reyna

678 20018 Marquelia

679 20019 Nexpa

680 20021 Ixtayutla

681 20022 San Cristóbal

682 20023 Zimatlán

683 20024 El Tomatal II y III

684 20025 Las Juntas

685 20026 Tlapacoyan

686 20027 Oax

687 20028 Nexpa II

688 21002 La Ceiba

689 21003 La Hamaca

690 22007 Las Cuevas

691 22008 Boquilla núm. 1

692 22015 Tequisistlán

693 22016 Chicapa

694 22017 Ixtepec

Río Tecpan

Río San Luis

Río de la Sabana

Río Petatlán

Canal La Loma

Canal San Pedro

Canal Principal

Río Atoyac

Río San Jeronimito

Canal Margen Derecha

Río La Unión

Canal Margen Izquierda

Río de la Sabana

Río Ixtapa

Río Atoyac

Río Quetzala

Río Atoyac

Río Marquelia

Río Nexpa

Río Yolotepec

Río San Miguel

Río Atoyac

Río Cortijos

Río Santa Catarina

Río Atoyac

Río Salado

Río Nexpa

Río Colotepec

Río Copalita

Río Tehuantepec

Río Tehuantepec

Río Tequisistlán

Río Chicapa

Río de los Perros

Río Tecpan -100.620833 17.250000

Río San Luis -100.891666 17.270833

Río de la Sabana -99.793055 16.941666

Río San Jeronimito -101.283333 17.536111

Río San Luis -100.895833 17.283333

Río San Luis -100.887500 17.279166

Río Coyuca -100.100000 17.037500

Río Atoyac -100.466666 17.141666

Río San Jeronimito -101.341666 17.558333

Río Coyuquilla -101.062500 17.379166

Río La Union -101.820833 17.991666

Río Coyuquilla -101.061111 17.377777

Río de la Sabana -99.783333 16.833333

Río Ixtapa -101.583333 17.731666

Río Verde -96.729166 17.048611

Río Ometepec -98.506944 16.658333

Río Verde -97.608333 16.275000

Río Marquelia -98.825000 16.608333

Río Nexpa -99.183333 16.787500

Río Verde -97.566666 16.558333

Río Papagayo -99.941666 17.279166

Río Verde -96.752777 16.870833

Río Ometepec -98.112500 16.494166

Río Ometepec -98.266666 16.704166

Río Atoyac -96.833333 16.730555

Río Atoyac -96.709722 17.027777

Río Nexpa -99.166666 16.821944

Río Colotepec -97.005000 15.857500

Río Copalita -96.184166 15.889166

Río Tehuantepec -95.337500 16.425000

Río Tehuantepec -95.929166 16.647222

Río Tequisistlán -95.597222 16.413888

Río Chicapa -94.808333 16.570833

Río de los Perros -95.091666 16.554166

695 22018 Ostuta

696 22019 Km 2+780

697 22026 Zanatepec

22027 Km 3+000

22028 Niltepec

22029 Santo Domingo

CENSO DE ESTACIONES DE AFORO

Niltepec

Santo Domingo

22030 Las Cuevas II Río Tehuantepec

22032 Km 2+400

22034 Las Pilas

753 24234 Km 106+000

754 24242 Conchos

755 24259 Km 1+500

756 24271 la Boca

757 24282 Rosario

758 24283 Paraíso

759 24291 Icamole

760 24301 Tepehuaje

761 24304 Parshall Huasteca

762 24313 El Rejón

763 24326 la Arena

764 24327 Cadereyta II

765 24331 Chuvíscar

766 24333 Sabinas Hgo.

767 24339 El Granero

768 24346 Parral

770 24351 Los Aldamas

771 24353 Búfalo

772 24361 Filtraciones p. Marte R. Gómez

773 24380 Túnel Topo Chico

774 24383 Los Herreras III

775 24384 Monterrey II

776 24385 Calles (Congregación)

777 24387 Los Lermas

778 24388 Peguis

779 24399 Canadá

780 24400 Llanitos

781 24503 Sacramento

782 25009 San Fernando

783 25010 Pablillo

784 25013 San Francisco

785 25015 Padilla

786 25025 Pilón

787 25027 Camacho

788 25028 Santo Domingo

789 25029 Santo Domingo

790 25030 Cabezones

791 25033 La Sonadora

792 25034 Puerto de Valles

793 25036 Las Norias

794 25037 La Esperanza

795 25038 Corona

796 25039 Paso del Aura

797 25040 Magueyes

798 25042 Cerro Prieto

799 25043 El Tomaseno

800 25044 Purísima de Conchos

801 25062 Padilla II

802 25064 El Nogal

803 25068 El Llano

804 25080 Pilón II

805 25085 Pilón Ill

806 25087 Paso de Molina II

807 25089 La Vega núm. 3

808 25090 Cruz

809 25091 El Barretal II

810 25092 Barberena

811 25093 La Pamona

CENSO DE ESTACIONES DE AFORO

Canal principal San Pedro

Río Conchos

Canal Paso de Piedra

Río San Juan

Canal Rosario

Río Ramos

Río Salinas

Río San Juan

Acueducto Huasteca-Monterrey

Arroyo El Rejón

Río Pesquería

Río Santa Catarina

Río Chuvíscar

Río Sabinas

Río Conchos

Salidas Presa

Río San Pedro -105.597222 28.168333

Río Bravo

-105.191666 27.718055

Río San Pedro -105.605555 28.158333

Río Bravo -100.119444 25.441666

Río Florido -105.633333 26.487500

Río San Juan -100.045833 25.227777

Río Pesquería -100.733333 25.916666

Río Bravo -99.766666 25.495833

Tanque Obispado -100.437500 25.670833

Río Chuvíscar -106.100000 28.616666

Río San Juan -99.966666 25.766666

Río San Juan -99.975000 25.590277

Río Conchos -106.100000 28.625000

Río Salado -100.116666 26.491666

Río Bravo -105.293055 28.958333

Río Parral

Río San Juan Río Bravo

Río Parral Río Florido -105.194444 27.252777

Río San Juan

Acueducto Mina-Monterrey

Río Pesquería

Río Santa Catarina

Río Blanquillo

Río de la Silla

Río Conchos

Río Pesquería

Río Balleza

Río Sacramento

Río San Fernando

Río Pablillo

Canal San Francisco

Río Purificación

Río Pilón

Río Camacho

Canal Santo Domingo

Río Pablillo

Río Potosí

Río Soto la Marina

Río Blanco

Arroyo Chorreras

Río San Rafael

Río Corona

Río Palmas

Río Pilón

Río Pablillo

Río San Antonio

Río Conchos

Río Purificación

Canal El Naranjito marg. der.

Río San Lorenzo

Río Pilón

Río Pilón

Arroyo Grande

Río Soto la Marina

Canal Cruz y Cruz

Río Purificación

Río Barberena

Arroyo La Pamona

Bravo

Río San Juan -100.320833 25.745833

Río San Juan -99.408333 25.897222

Río San Juan -100.351666 25.671666

Río Ramos -99.940000 25.220000

Río Santa Catarina -100.188333 25.680000

Río Bravo -104.714444 29.503888

Río San Juan -100.271666 25.801666

Río Conchos -106.220000 26.683333

Río Chuvíscar -106.066666 28.664444

Río San Fernando -98.158333 24.843888

Río Potosí -99.555555 24.856944

Río Purificación -99.120833 24.083333

Río Soto la Marina -98.772222 24.012500

Río Purificación -98.729166 24.033333

Río Pablillo -99.575000 24.877777

Río Pablillo -99.616666 24.800000

Río Potosí -99.602777 24.790277

Río Conchos -99.741666 24.990277

Río Soto la Marina -98.662500 23.961111

Río Purificación -99.595833 24.155555

Río San Fernando -98.298611 24.608333

Río San Rafael -97.937222 23.162222

Río Purificación -98.951944 23.941666

Río Soto la Marina -98.079166 23.641666

Río Purificación -99.558333 24.569444

Río Potosí -99.383333 24.943055

Río Purificación -99.436111 24.251388

Río San Fernando -99.256944 24.923611

Río Soto la Marina -98.891666 24.036111

Río Pilón -99.554166 24.562500

Río Conchos -98.600000 25.186111

Río Purificación -98.841666 24.095833

Río Purificación -98.901666 24.138333

Río Corona -98.739444 23.756111

Río Soto la Marina -98.469444 23.949444

Río Purificación -99.213055 24.103055

Río Soto la Marina -99.134166 24.112500

Río Barberena -98.120833 22.625000

Río Potosí -99.206666 24.992222

CENSO DE ESTACIONES DE AFORO

812 25098 Mariano Matamoros Canal ppal del DR 86

813 25115 Vega núm. 4

de Tequisquiac

Río Soto la Marina Río Soto la Marina

816 26022 Paso de Tablas Río San Juan

817 26030 El Salto

Río El Salto

819 26032 Molino Blanco Río de los Remedios

26053 El Molinito

827 26054 San Juan Ixhuatepec

Río Hondo

de los Remedios

870 26242 El Morro

871 26243 Requetemu

872 26244 El Higo

873 26245 Potosí

874 26246 Amajac

875 26247 Las Rosas

876 26248 Tempoal

877 26252 Alcholoya

878 26254 Desfogue presa Guadalupe

879 26255 Las Adjuntas

880 26260 Potrero de Palos I

881 26262 San José

882 26263 Santa Rosa

883 26266 El Capulín

884 26267 Gallinas

885 26268 Tansabaca

886 26270 Tierra Blanca

887 26272 El Pujal

888 26273 El Salitre

889 26274 San Mateo

890 26275 San Lucas

891 26276 San Marcos

892 26277 Los Hules

893 26278 El Choy

894 26281 Ventorrillo

895 26282 El Alamo

896 26285 Micos

897 26286 El Cardón

898 26289 Terrerillos

899 26291 Tancuilín

CENSO DE ESTACIONES DE AFORO

Río Moctezuma

Río Axtla

Río Tempoal

Río Moctezuma

Río Amajac

Río Rosas

Río Tempoal

Río Alcholoya

Río Cuautitlán

Río Pánuco

Canal Potrero de Palos

Canal alim Constitución 1857

Río Valles

Canal El Capulín

Río Gallinas

Río Pánuco

Río Axtla

-98.783472 21.266666

-98.883333 21.418055

Río Moctezuma -98.433333 21.763888

Río Pánuco -98.451388 21.768055

Río Moctezuma -98.768055 21.250000

Río Tula -99.347777 20.058333

Río Tempoal -98.383333 21.533333

Río Meztitlán -98.445833 20.212500

Río Tula -99.249166 19.635555

Río Pánuco -98.566666 25.983333

Río Tampaón -100.083333 21.884722

Río San Juan -100.000000 20.362500

Río Tampaón -99.050000 22.016666

Manantial Media Luna -100.020833 21.857777

Río Tampaón -99.250000 21.934722

Río Tampaón Río Tampaón -99.200000 21.651388

Río Moctezuma Río Pánuco -98.884722 21.218055

Río Tampaón

Río El Sifón

Río Tampaón -99.918055 21.834722

Río Tlalnepantla -99.298055 19.503055

Río San Bernardino Lago de Texcoco -98.877777 19.476944

Río de la Compañía Lago de Texcoco -98.856944 19.284722

Río San Francisco Río de la Compañía -98.869444 19.291666

Río Los Hules Río Tempoal -98.266805 21.166666

Río Choy

Río Tampaón -98.866666 21.966666

Túnel Ventorrilo Río Tepatlaxco -99.250555 19.525833

Río Santa María Río Meztitlän -98.625000 20.512500

Río El Salto Río Tampaón -99.166666 22.116805

Río San Pedro Río Tempoal -98.468055 21.384722

Río Calabozo Río Tempoal -98.133472 21.033472

Río Tancuilín

Río Axtla -98.868055 21.384722 900 26292 Tanlacut

901 26293 Temamatla

902 26294 El Álamo

Río Verde Río Tampaón -99.284722 21.668055

Río Amajac

Canal núm. 1

Río Amajac -98.750138 21.233472

Río Santa María -98.625000 20.512500 903 26295 El Álamo

904 26307 Km 14+000

905 26308 Km 2+120 Bombas

Canal núm. 2

Río Santa María -98.625000 20.512500

Filtraciones Canal de Sales Lago de Texcoco -99.016666 19.568055

Desfogue del Lago Lago de Texcoco -99.011944 19.564444

906 26309 San Luis Ameca II Río Ameca Lago de Texcoco -99.870000 19.183888

907 26310 Alcholoya

Canal núm 1

Río Alcholoya -98.445833 20.212500 908 26311 Alcholoya

Canal núm 2

Río Alcholoya -98.445833 20.212500 909 26312 El Manantial

Río de las Avenidas de Pachuca Lago de Zumpango -98.940277 19.851388 910 26313 Km 27+250

Gran Canal Gran Canal -99.053611 19.641388 911 26315 Puente de Vigas

Río de los Remedios Gran Canal -99.211111 19.511666 912 26316 El Manantial

Canal marg. der. Río de las Avenidas de Pachuca -98.940000 19.852777 913 26320 Tepetitlán

Canal Tepetitlán Río Tula -99.359722 20.161111 914 26322 Binola

Canal Binola marg. der. Río Tula -99.352777 20.162500 915 26323 El Manantial

Canal Margen Izquierda Río de las Avenidas de Pachuca -98.940000 19.850833 916 26324 Vertedor Milpa Alta

Río Milpa Alta Lago de Tláhuac -99.183333 19.016666 917 26327 Fernández

Canal Fernández Manantial Media Luna -100.031666 21.870833 918 26328 Río Verde

Canal Río Verde Manantial Media Luna -100.066666 21.884722 919 26329 San José

Canal San José Manantial Media Luna -100.068055 21.883333 920 26331 Km 0+286 (km 0+393)

Emisor Poniente Vaso del Cristo -98.216666 19.516666 921 26332 Los Anteojitos

Canal Los Anteojitos Manantial Los Anteojitos -100.002500 21.878888 922 26337 Nogal Obscuro

Río Verde Río Tampaón -100.183472 22.016805 923 26341 Ojo Caliente

Río Santa María Río Tampaón -100.800000 21.850000 924 26342 Tezontepec

Río Salado Río Tula -99.254166 20.186111 925 26344 Laguna de Apan

Canal Salidas Laguna de Apan -98.508333 19.708333 926 26346 Puente Colgante

Canal Desfogue Lago Tecocomulco -98.485833 19.813888

Río Cuautitlán Río Tula -99.185000 19.763888 927 26347 San Jerónimo

939 26390 Del Pueblo

940 26391 La Romera

CENSO DE ESTACIONES DE AFORO

del Pueblo

La Romera

941 26392 Binola II Río Tula

942 26395 Jasso II Río Tula

943 26402 La Draga Canal La Draga

944 26406 Ixmiquilpan II Río Tula

945 26407 Cañada Rica Río Chicayán

Tepeji

Moctezuma

Pánuco

946 26412 El Conde Río de los Remedios Vaso del Cristo

947 26414 Salidas p. Constitución 1917

948 26415 San Vicente

Moctezuma

949 26416 Tamesí Río Tamesí

26417 Galindo II

951 26422 Clavo de Oro

Galindo

Río Tantuán

952 26423 El Refugio Río Santa Clara Río Guayalejo

Pánuco

954 26429 Guadalupe

Río Pánuco

El Cojo

Guayalejo

971 26501 Potrerito

972 26502 Golondrinas Canal Margen Derecha

Tizar

Alfajayucan

986 28040 El Tejar

987 28057 Km 2+200

988 28069 Capulines

989 28082 Apoala

990 28086 Km 0+300

CENSO DE ESTACIONES DE AFORO

Corriente

Río Jamapa

Canal Lateral Cardel

Río Cotaxtla

Río Apoala

Canal principal Santa Rosa

Río Jamapa -96.160000 19.068333

Río La Antigua -96.405000 19.326666

Río Jamapa -96.305000 18.865000

Río Papaloapan -87.000000 14.000000

Río Actopan -96.463333 19.466666 991 28092 Km 2+150

Canal Principal

Río La Antigua -96.408333 19.320000 992 28105 Km 0+200

993 28106 Úrsulo Galvan

Canal principal la Esperanza

Río Actopan

Río Actopan -96.550000 19.481111

Río Actopan -96.361666 19.405000 994 28108 El Naranjillo

995 28111 Ídolos

Río Actopan

Río Ídolos

Río Actopan -96.381666 19.422222

Río Actopan -96.553333 19.403333 996 28112 Ayotla

Canal Ayotla

Río Salado -87.000000 14.000000 997 28119 Santa Anita

Río Atoyac

Río Cotaxtla -96.821666 18.915000 998 28125 Carrizal

Río La Antigua

Río La Antigua -96.626666 19.320000 999 28127 Santa Anita

1000 28131 Parián

Canal Principal

Río Parián

Río Atoyac -96.820000 18.910000

Río Papaloapan -87.000000 14.000000 1001 28135 Chacaltianguis

Río Papaloapan

Río Papaloapan -87.000000 14.000000 1002 28149 Estanzuela

1003 28152 Paso Cabrito

1004 28173 San Nicolás

1005 29005 Las Perlas

1006 29006 Jesús Carranza Ii

1007 29007 Paso Arnulfo

1008 30002 Gaviotas

1009 30003 La Pigua

1010 30004 El Dorado

1011 30005 Samaria

1012 30006 El Muelle

1013 30012 El Marín

1014 30014 Puente Colgante

1015 30015 Las Peñitas

1016 30016 Pueblo Nuevo

1017 30019 Boca del Cerro

1018 30020 El Boquerón II

1019 30021 Vertedor Chacona

Río Estanzuela

Río Rancho Cabras

Río San Juan

Río Coatzacoalcos

Río Jaltepec

Río del Corte

Río Grijalva

Río de la Pigua

Río Mezcalapa

Río Rompido

Río Grijalva

Río Mezcalapa

Río Grijalva

Río Mezcalapa

Río de la Sierra

Río Usumacinta

Río Suchiapa

Manantial Chacona

Río Papaloapan -87.000000 14.000000

Río Papaloapan -87.000000 14.000000

Río Papaloapan -87.000000 14.000000

Río Coatzacoalcos -94.866666 17.438055

Río Coatzacoalcos -95.054166 17.391666

Río Coatzacoalcos -94.700000 16.900000

Río Grijalva -92.916666 17.966666

Río Carrizal -92.909722 18.020833

Río Grijalva -93.350000 17.900000

Río Mezcalapa -93.291666 17.979166

Río Grijalva -92.916666 17.990277

Río Grijalva -93.250000 17.983333

Río Grijalva -93.033333 16.741666

Río Grijalva -93.450000 17.408333

Río Viejo Mezcalapa -92.879166 17.854166

Río Usumacinta -91.483333 17.433333

Río Santo Domingo -93.150000 16.504166

Río Sabinal -93.175000 16.783333 1020 30024 San Agustín

Manantial San Agustín

Río Sabinal -93.216666 16.791666 1021 30030 Arco de Piedra

Río Grijalva

Río Grijalva -92.650000 16.187500 1022 30031 Puyacatengo

Río Puyacatengo

Río de la Sierra -92.937500 17.566666 1023 30032 Teapa

Río Teapa

Río de la Sierra -92.966666 17.566666 1024 30033 San Francisco

Río Custepeques

Río Concordia -92.883333 16.033333 1025 30036 El Burrero

Río Hondo

Río Grijalva -92.883333 16.816666 1026 30037 San Pedro I

Río San Pedro

Río El Dorado -93.066666 16.150000 1027 30038 Puente Parque Madero

Río Sabinal

Río Grijalva -93.116666 16.750000 1028 30039 La Mesilla

Río San Vicente

Río Blanco -92.300000 16.183333 1029 30040 Argelia

Río San Miguel

Río Grijalva -92.200000 15.950000 1030 30041 La Escalera

Río Santo Domingo

Río Grijalva -92.950000 16.533333 1031 30042 Salto de Agua

Río Tulija

Río Tepetitán -92.350000 17.566666 1032 30048 El Salvador

Río San Gregorio

Río Grijalva -92.166666 15.916666 1033 30049 El Toro

Río de la Venta

Río Grijalva -93.750000 17.162500 1034 30050 Los Berros

Salidas manantiales Los Berros

Arroyo El Próspero -92.912500 16.820833 1035 30051 Reforma

Río Mezcapala

Río Grijalva -93.183333 17.958333 1036 30052 Concepción

Arroyo Concepción

Río Custepeques -92.791666 16.108333 1037 30053 Santa Isabel

Río El Dorado

Río Grijalva -92.883333 16.266666 1038 30055 Macuspana

Río Macuspana

Río Tulija -92.600000 17.766666 1039 30056 La Concordia

Río La Concordia

Río Grijalva -92.633333 16.083333 1040 30057 Pichucalco

Río Pichucalco

Río Viejo Mezcalapa -93.108333 17.558333 1041 30058 Puente Morelos

Río Amarillo

Sumidero Santa Rosa -92.650000 16.719444 1042 30059 Puente Saavedra

Río Amarillo

Río Carrizal

Río Grijalva -93.000000 17.975000

Río Amarillo -92.633333 16.733333 1043 30062 González

CENSO DE ESTACIONES DE AFORO

1045 30065 Las Mercedes Río Viejo Mezcalapa

30067 San Pedro Chis. II

1048 30068 Peje de Oro Río Amarillo

1052 30072 Las Flores II

1057 30088 San Pedro Tab.

1058 30091 San Francisco II

1060 30094 Platanar

1061 30096 Paredón

1063 30098 Grijalva Río Grijalva

1064 30102 Aquespala Río Rincón

Canasayab

1102 36044 El Palmito II

1103 36047 Santa Rosa

1104 36048 Santa Rosa

1105 36049 El Sauz II

1106 36053 Cazadero

1107 36054 Cazadero

1108 36056 Cazadero II (salidas presa)

1109 36058 Km 1+747.41

1110 36059 Santa Rosa Tlahualilo

CENSO DE ESTACIONES DE AFORO

Río Nazas

Canal Margen Derecha

Canal Margen Izquierda

Río de los Lazos

Canal Col Presa El Cazadero

Río Aguanaval

Río Aguanaval

Canal Nuevo Tlahualilo

Canal Nuevo Tlahualilo

Río Nazas -105.025000 25.600000

Arroyo El Arenal -103.108333 22.916666

Arroyo El Arenal -103.108333 22.916666

Río Trujillo -103.225000 23.166666

Río Aguanaval -103.075000 23.658333

Río Aguanaval -103.075000 23.658333

Río Aguanaval -103.075000 23.666666

Río Nazas -103.541666 25.508333

Río Nazas

-103.541666 25.508333 1111 36060 Los Ángeles

Río Nazas

Río Nazas

-103.566666 25.508333 1112 36061 Cazadero izq. (p. El Cazadero)

1113 36067 Cañon Fernández II

1114 36070 Relámpago medidor Parshall

1115 36071 Sardinas

1116 36072 San Antonio II

1117 36075 Puente provisional Morelos

1118 36076 Agustín Melgar

Canal General Izquierdo

Río Nazas

Canal Relámpago

Río del Oro

Canal Nuevo San Antonio

Río Nazas

Río Nazas

Río Aguanaval -103.075000 23.666666

Río Nazas -103.775000 25.283333

Río Nazas -103.483333 25.541666

Río Nazas -105.570000 26.083333

Río Nazas

Río Nazas

25.508333

25.275000

Río Nazas -104.068055 25.264166 1119 36078 Km 0+520

1120 36079 Sardinas

1121 36080 San Francisco

Canal Nuevo Coyote

Canal Sacramento -103.465833 25.570833

Arroyo Sardinas Río de Oro -105.570000 26.083333

Río Aguanaval

Río Aguanaval -102.885000 24.313888 1122 37005 Los Pilares

1123 37006 El Grito

1124 37007 Los Pilares

1125 37008 El Tule

1126 37011 Salida Túnel

1127 37012 Tula

Arroyo La Parada

Arista-Matehuala -101.036111 22.491666

Arroyo Grande Arroyo La Parada -101.120000 22.666666

Canal Principal marg. der. Arroyo La Parada -101.019444 22.491666

Arroyo El Tule

Canal Toma Única

Río Tula

Arroyo Moctezuma -101.179166 22.836666

Arroyo Alaquines -99.630555 22.183333

Cuenca Cerrada Tula -99.712500 23.001388

CAPÍTULO V

INGENIERÍA BÁSICA PARA EL CÁLCULO DE LA SOCAVACIÓN

Para calcular las profundidades de socavación es necesario cuantificar, si es posible, los factores que la afectan, los cuales se enlistan en la tabla III.1. Se discuten en las siguientes secciones los datos requeridos para ello. En la tabla V.1 se presenta el resumen de los datos requeridos para el cálculo de la socavación. El tipo de datos requeridos y su detalle depende mucho de la relativa inestabilidad del río analizado y de la profundidad del estudio. Sin embargo, lo fundamental en cualquier cálculo de socavación es el análisis adecuado de la velocidad y del tirante a lo largo del río.

Tabla V.1. Datos requeridos para el análisis de la socavación

Tipo de análisis Tipo de socavación Etapa

Datos requeridos y sus fuentes

Inspección de campo Todos los tipos Todas las etapas Colección de datos

Hidrológico Todos los tipos Cuenca

Hidráulico Todos los tipos

Sección del cauce en perfil detallado y de construcción

Características de la cuenca y su análisis con mapas, fotos aéreas, observaciones de campo, registro, etc. Datos de precipitación y de aforos de la corriente.

Características hidráulicas para el gasto de diseño. Observaciones de campo y registros. Secciones transversales del cauce con rugosidad, alineamiento, pendiente, etc.

Propósitos

Reconocimiento general de la cuenca, del río y del sitio del puente, así como de la posible inestabilidad del cauce, erosión marginal, indicios de socavación general y localizada, transporte de troncos, ramazón y basura. Observación de sitios con depósito, degradación o movimiento lateral. También de la localización del puente con respecto a los parámetros hidráulicos y a otras estructuras. Inspección de parámetros de flujo en el sitio del puente y huellas de avenidas. Medición de las propiedades del material de fondo y márgenes.

Determinación de los hidrogramas de diseño.

Determinación de la hidráulica del cauce: perfiles de la superficie del agua y pendiente de energía.

Transporte de sedimentos

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Todos los tipos

Cuenca y sección del cauce

Sección del cauce en perfil detallado y perfil de construcción

Información de las características de la cuenca, suelos, uso de la tierra, condiciones geológicas, dimensiones de los sedimentos, etc., a partir de mapas, fotos, observaciones de campo, análisis de muestras de sedimentos, etc.

Análisis hidráulico del cauce. Propiedades de los materiales del fondo y márgenes, a partir de mapas, fotos, observaciones de campo, análisis de muestras de sedimentos, datos de campo sobre gasto sólido estimado.

Determinación de la aportación de sedimentos.

Socavación en el puente

Socavación general de largo plazo: degradacióndepósito, inestabilidad lateral. Información sobre la existencia de bancos de extracción de materiales del cauce en la proximidad del cruce

Cuenca, sección del cauce en perfil detallado y perfil de construcción

Diseño del puente, construcción, mantenimiento e inspección, planos, reportes, registros, experiencia. Fotos y registros tomados por residentes del lugar al río y a la cuenca.

Obras de protección contra la socavación, localización y diseño; mapas históricos y actuales de la región, del sitio, del uso de la tierra, geológicos, de suelos, topográficos. Fotografías aéreas históricas y actuales. Cauces históricos y actuales, secciones transversales de la planicie de inundación; elevación del fondo a lo largo del cauce. Parámetros hidráulicos, propiedades de los materiales del fondo y márgenes, incluyendo registros de sondeos.

Aportación de sedimentos y análisis del gasto sólido.

Observaciones y mediciones de campo de la profundidad de socavación, incluyendo la de otros puentes cercanos.

Determinación del gasto sólido.

Análisis de las características e historia de la cuenca, sección del cauce fuera del puente y bajo éste, incluso clasificación de la corriente: dimensiones, tipo, alineamiento en planta, etc.

Identificación de inestabilidad del cauce, controles en el cauce e influencia de otras estructuras y de fenómenos hidráulicos.

Determinación de migración de curvas, corte de meandros, barras, formas de fondo, etc. Determinación de tipos de suelo, su distribución, su erosionabilidad, cubierta vegetal, disponibilidad de aporte de sedimentos y de troncos, ramazón y basura. Identificación de eventos geomorfológicos, avenidas extraordinarias y cambios provocados por el ser humano (presas, bancos de materiales, cana-lizaciones, etc.) que hayan inducido o modificado la inestabilidad del cauce. Investigación sobre proyectos de ingeniería que puedan influir en el sitio.

Estimación de la socavación general de largo plazo.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Diseño del puente, construcción, mantenimiento e inspección, planos, reportes, registros, experiencia. Fotos y registros tomados por residentes del lugar al río y a la cuenca.

Socavación general de corto plazo

Puente en planta detallada y planta general

Obras de protección contra la socavación, localización y diseño. Mapas históricos y actuales de la región, del sitio, del uso de la tierra, geológicos, de suelos, topográficos. Fotografías aéreas históricas y actuales. Cauces históricos y actuales, secciones transversales de la planicie de inundación y elevación del fondo a lo largo del cauce. Parámetros hidráulicos, propiedades de materiales del fondo y márgenes, incluyendo registros de sondeos. Aportación de sedimentos y análisis del gasto sólido. Características de las formas de fondo. Observaciones y medición de campo de la profundidad de socavación, incluyendo la de otros puentes cercanos.

Determinación de la profundidad de socavación general de corto plazo.

Socavación por contracción

Planta detallada del puente

Socavación local

Planta detallada del puente. Socavación local.

Diseño del puente, su geometría, construcción, mantenimiento e inspección, dibujos, reportes, registros, fotos, experiencia e inspección de campo: grado de contracción, geometría de llegada del cauce, de la cimentación, ubicación de ésta en el cauce, etc. Fotos y registros tomados por residentes del lugar al sitio del puente, al cauce y a la cuenca.

Obras de protección contra la socavación, localización y diseño. Secciones transversales históricas y actuales del cauce y de la llanura de inundación y elevación del fondo a lo largo del cauce.

Hidráulica del cauce, incluyendo la distribución lateral del flujo. Propiedades del material de fondo y márgenes: si el sedimento es cohesivo, no cohesivo o roca; distribución de tamaños, distribución espacial, estratificación, etc. Análisis del gasto sólido, características de las formas de fondo. Acumulación de troncos y ramazón en la cimentación del puente. Medición de la profundidad de socavación en el sitio y en puentes cercanos.

El análisis de la socavación comprende cinco tipos de actividades:

Determinación de la profundidad de socavación por contracción.

Determinación de la profundidad de socavación local.

§ Inspección de campo para evaluar las características de la cuenca y del cauce, así como su evolución.

§ Análisis hidrológico para determinar la avenida de diseño.

§ Análisis hidráulico para determinar los parámetros de diseño.

§ Análisis de transporte de sedimentos.

§ Análisis de socavación para determinar la profundidad total.

V.1. Inspecciones de campo y colección de datos

Se recopilan los datos y se registran las características del sitio del puente, del cauce del río y de la cuenca. Se hacen observaciones de los patrones de flujo en el sitio del puente, de huellas dejadas por el agua y de la inestabilidad de la corriente en la planta detallada, incluyendo zonas de depósito, degradación o de movimiento lateral. Se registra la localización del puente con respecto a otros puentes existentes en la zona, confluencias, tributarios, controles hidráulicos y otras variables que pudieran afectar a la socavación en el puente.

Se registran en algún puente existente, o en otros de la zona, evidencias de erosión marginal y de socavación general y localizada. Se considera la historia del río, incluyendo los efectos de influencias externas tales como la extracción de material del cauce cerca del puente en estudio y cualquier rasgo de inestabilidad del río, como migración de curvas. Se determinan las propiedades del material de fondo y márgenes. Se hacen sondeos para definir la estratigrafía.

V.2. Datos hidrológicos y su análisis

Los principales datos hidrológicos requeridos son las características de la cuenca, como su topografía, cobertura vegetal, tipos de suelo y geología; asimismo, los registros de precipitación y escurrimiento, y la determinación de los hidrogramas de diseño. El análisis hidrológico para obtener el hidrograma de la avenida de diseño es un prerrequisito para analizar la socavación en un puente. Incluye la evaluación de duración del flujo y su frecuencia con base en un análisis regional de registros de aforo. También incluye el cálculo del gasto dominante (gasto a cauce lleno en caso de que no sea posible hacer un análisis detallado del gasto dominante).

Aquí conviene recordar el concepto de gasto formativo y dominante: el gasto formativo es aquel que, de escurrir en forma constante, produce las mismas dimensiones promedio de la sección transversal y la pendiente que el hidrograma anual. También puede definirse como aquel gasto máximo que fluye por el cauce principal sin desbordar, y como el gasto correspondiente a un periodo de retorno de 1.4 años. El gasto dominante es aquel hipotético que, al fluir en forma constante durante un año, transporta el mismo volumen de sedimentos

que el transportado por el río durante un año. Diversos investigadores han propuesto expresiones varias para estimar el valor del gasto dominante.

Aunque el desarrollo de un sistema fluvial se correlaciona a menudo con la ocurrencia de una tormenta aislada, también puede ser resultado de procesos acumulados que conducen a condiciones geomorfológicas inestables. Los cambios en un sistema pueden estar más relacionados con la ocurrencia de una secuencia de tormentas durante un periodo de lluvias arriba del promedio, que con un gran evento aislado. Es por ello que a veces un puente falla con una avenida cuya frecuencia es, por ejemplo, de unos cuatro años.

V.3. Datos hidráulicos y su análisis

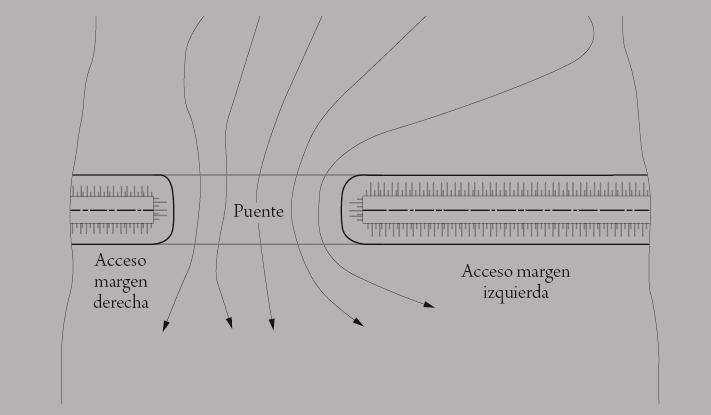
Figura V.1 Terraplenes que invaden parte del cauce.

Incluyen parámetros de la sección transversal del cauce, rugosidad y parámetros de alineamiento del cauce. Se requiere la evaluación de niveles de control de la superficie del agu a, el perfil de ésta y los tirantes y velocidades para el flujo de diseño. Conocido el gasto de diseño, el medio más simple para cuantificar el flujo es en términos de la velocidad media, v, y del tirante medio y, que pueden determinarse con la ecuación de Manning, cuya variable de rugosidad se puede obtener con Chow (1959). Pueden utilizarse también modelos numéricos unidimensionales para el tirante medio, a fin de predecir las elevaciones de la superficie del agua y las velocidades respectivas. Sin embargo, en corrientes naturales el flujo es fuertemente tridimensional y variable, por lo que las velocidades y tirantes medios sólo dan una idea vaga del potencial erosivo del río, especialmente cuando el puente está situado en una curva o cuando el terraplén invade una buena parte del cauce, como se ilustra en la figura V.1. En cauces amplios y ramificados en los que los gastos bajos ocupan sólo un pequeño canal, el cauce principal puede además moverse sustancial e impredeciblemente durante avenidas. En tal caso, la velocidad y el tirante medio serán engañosos para estimar la socavación local.

La forma de la sección transversal del cauce y la distribución lateral del flujo tienen efectos importantes en la socavación. Aunque la socavación local en pilas se obtiene con los valores del tirante y de la velocidad de agua arriba, la local en estribos y en contracciones puede depender del ancho del canal y del gasto. Por ejemplo, si un estribo y su terraplén de acceso abarcan una parte importante del cauce de avenidas (véase figura V.1), la socavación local en el estribo dependerá de la distribución de gastos en el cauce principal y en el de avenidas.

También la socavación por estrechamiento y las pozas de socavación local en estribos se pueden traslapar y afectarse mutuamente, y formarse una geometría compleja de socavación.

Para determinar las distribuciones laterales de la velocidad de flujo, pueden utilizarse modelos numéricos bidimensionales aplicados a la planta general y detallada del puente.

V.4. Datos y análisis del transporte de sedimentos y desechos

La socavación es un proceso de transporte de sedimentos; para evaluar la aportación de sedimentos de la cuenca es necesario conocer las fuentes de los sedimentos y los tipos de erosión más importantes. Los procesos físicos que causan la erosión pueden clasificarse como movimientos en masa, e incluyen deslizamientos de tierra, flujos de lodo y de material granular, erosión de suelos, erosión en surcos y en cárcavas, y erosión en arroyos o ríos.

La evaluación de la aportación de sedimentos y su respuesta a los cambios en la cuenca pueden ser factor importante en la determinación de la estabilidad del cauce. La cantidad de sedimentos aportados a un cauce depende de la intensidad de lluvia y su distribución, así como de varios componentes de la cuenca tales como el clima, el uso del suelo, el manejo de la cuenca, la cobertura vegetal, el tipo de suelo, la topografía, la pendiente del terreno, etc. También depende de la rapidez de la erosión en la parte alta, que es función del tipo de la fuente de erosión. Estas fuentes incluyen erosión del suelo, de surco y de cárcavas. Los cambios en la aportación de sedimentos pueden provocar cambios en la entrada de sedimentos al cauce, lo que por el principio de continuidad resulta en depósito de sedimentos (azolve) o degradación, con los consecuentes cambios del cauce en planta y en perfil. La cuantificación de la aportación de sedimentos no es ciencia exacta y sólo se estiman los cambios cualitativamente. Los materiales del fondo, los de las márgenes y los que están en suspensión varían entre arcillas, limos, arena, grava y boleos. Los del fondo suelen tener una granulometría compleja y estar estratificados. Es común dividirlos en cohesivos y no cohesivos. También suelen clasificarse como aluviales (materiales que son transportados por el flujo), y no aluviales (materiales que constan de grava gruesa y de boleos, que solamente son transportados durante avenidas muy grandes, y fondo rocoso).

MANUAL

El tamaño es la propiedad más importante del sedimento, ya que su velocidad de caída y su forma tienden a ser función de su tamaño. Además, es fácil de medir. Así, los sedimentos aluviales pueden describirse en función de la mediana de los diámetros, �!" (en peso).

Para materiales uniformes el �!" es el adecuado, pero no lo es para no uniformes, pero que pueden describirse por medio de la desviación estándar de sus diámetros, �! =(!!" !!" ) ! ! donde �!" � �!" son los diámetros para los cuales el 84% y el 16% de las partículas, respectivamente, son menores, en peso.

Un lecho de un cauce puede estar compuesto por una serie de estratos con diferente resistencia a la socavación. Cuando un estrato relativamente resistente sobreyace a uno menos resistente, puede ocurrir una profundidad de socavación muy grande si el estrato más resistente es erosionado en todo su espesor. Inversamente, si existe un material muy resistente a una cierta profundidad, podría ser innecesario llevar el nivel de desplante de la cimentación abajo de esa profundidad, si la profundidad de socavación del estrato de arriba no es muy grande. La variación del tipo de material no está restringida a la estratificación vertical, sino que también puede ser horizontal en el sitio del puente, lo que influiría en el proceso de socavación localizada. La socavación general puede ser afectada por variaciones del material en una extensión relativamente grande. En cambio, la socavación por estrechamiento depende de la distribución del material del fondo en la zona del puente.

Los puentes pueden también cimentarse en roca, dependiendo de la profundidad de ésta y de su erosionabilidad. En muchos casos la roca es resistente a la erosión, aunque algunas no lo son, como las sedimentarias blandas (lutita, limolita, etc.) y en algunos casos aun rocas volcánicas altamente intemperizadas.

Para evaluar las condiciones límite del flujo para el movimiento de un sedimento dado puede utilizarse el análisis de movimiento incipiente basado en el diagrama de Shields, el cual indica que, para condiciones por debajo de cierto parámetro función del diámetro representativo del sedimento, el cauce es estable, es decir, no hay movimientos del sedimento. Por arriba de ese parámetro, el sedimento se incorporará al flujo. En función de la continuidad de la aportación de sedimentos al cauce a lo largo de su trayectoria, el transporte de sedimentos no necesariamente significa erosión del fondo.

CAPÍTULO VI

ANÁLISIS DE LA SOCAVACIÓN

VI.1. Introducción

La socavación en un puente es el resultado de una compleja interacción del flujo del río, del material del cauce y, en el caso de la socavación localizada, de la estructura del puente. Los diferentes tipos de socavación ocurren a diferentes escalas de espacio y de tiempo. Por ejemplo, el flujo tridimensional que ocurre en la vecindad de la cimentación del puente es muy importante para la socavación local, pero es mucho menos importante para la socavación general de largo plazo.

Figura VI.1 Diagrama de Shields que define el inicio del movimiento de sedimentos. La banda somb reada indica la difusión de los datos utilizados por Shields.

La socavación localizada (por estrechamiento + local) puede ocurrir en condiciones de aguas claras o de fondo vivo.

Puesto que tanto la socavación máxima como el tiempo para que se produzca difieren en los dos casos, es importante identificar las condiciones de movimiento del material del fondo, en términos del llamado “esfuerzo cortante adimensional” ! / !! ! !"# , conocido también como parámetro de Shields, θ, que puede utilizarse para determinar si las condiciones del flujo de diseño son de aguas claras (θ < límite θc del diagrama de Shields, véase figur a VI.1), o de socavación con fondo vivo (θ > θc). Más adelante se da el significado de las literales.

VI.2. Repaso de hidráulica fluvial

Dediquemos unos párrafos a repasar algunos conceptos de hidráulica fluvial. Se sabe que el esfuerzo cortante ! producido por el agua en el fondo de un cauce vale:

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

donde � = esfuerzo cortante (kg/�! )

γ = peso volumétrico del agua (kg/�! )

R = radio hidráulico de la sección (m)

S = pendiente hidráulica (decimales)

Ahora recordemos algunas definiciones:

Velocidad de corte

siendo ρ la densidad, es decir, la masa por unidad de volumen.

Además, γ, el peso específico, es el peso por unidad de volumen. Por la segunda ley de Newton, γ= �� Entonces,

El número de Reynolds asociado al diámetro d del material del fondo es:

donde

V = velocidad de flujo

d = diámetro del material del fondo

� = viscosidad cinemática

Conviene recordar que la viscosidad de un fluido es una medida de su resistencia a fluir. Según Newton, el esfuerzo tangencial que se produce entre dos láminas separadas una distancia dy, y que se desplazan con velocidades (V) y [V+(� V/� y)dy], es:

donde � es la viscosidad dinámica del fluido, con dimensiones FT/�!

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

La viscosidad cinemática es igual a:

! = ! !

Sus dimensiones son !! !!

Hasta aquí el breve repaso de algunos conceptos de hidráulica fluvial.

VI.3. Análisis del transporte de sedimentos

De acuerdo con el diagrama de Shields (figura VI.1), !! ! !!! ! !! ! !" ! En la figura

VI.2 se muestra la curva que representa las ecuaciones de la velocidad de corte crítica, que son:

!!! ! !!!""# ! !!!"#$!!" ! ! , para 0.1 mm! !!" ! ! !!!

!!! ! !!!"!#!!" ! ! !!!!"#!!"! , para 1 mm! !!" ! !"" !!

En estas ecuaciones !!! está en m/s y !!" en mm

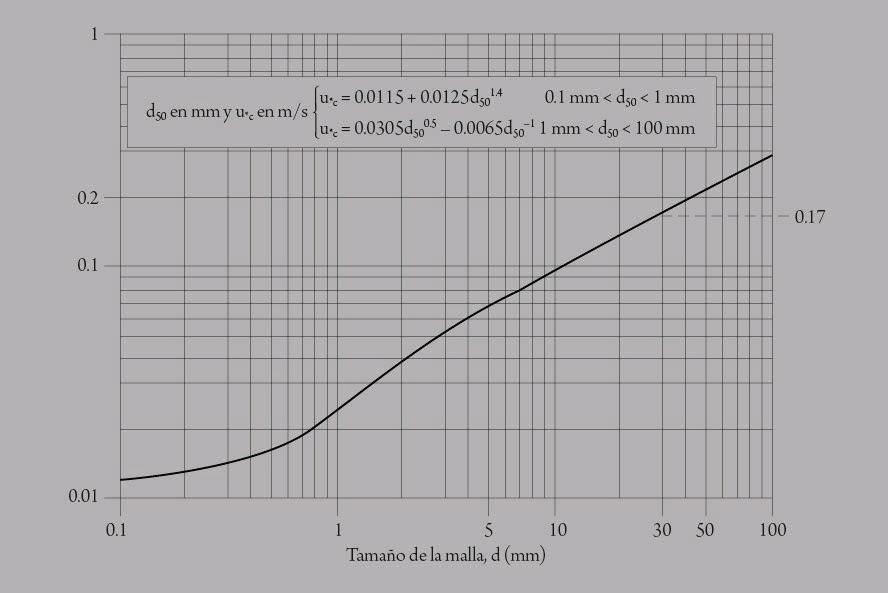
VI.2. Carta de la velocidad de corte para sedimentos de cuarzo en agua a 20° C.

Figura

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

El diagrama de Shields describe las condiciones de flujo incipiente en función de un esfuerzo cortante crítico �! =ρ�! ∗ ! , asociado a un movimiento incipiente de los sedimentos del fondo. Si se prefiere utilizar la velocidad media crítica para describir el movimiento incipiente del sedimento, ésta puede determinarse a partir de la velocidad de corte crítica, utilizando la ecuación:

donde R es el radio hidráulico del cauce y la � de Manning es el valor para condiciones límite que pueden determinarse con la ecuación de Strickler, o

donde y es el tirante

Existen varias relaciones empíricas para la velocidad media crítica bajo condiciones límite de movimiento de sedimentos. Un ejemplo es la siguiente ecuación dada por Neill (1968):

= 1.41 (�! 1)��!" ! ! ! !!" !/! (VI.6)

La ecuación (VI.6) puede obtenerse utilizando las ecuaciones de Manning y de Strickler, y el parámetro de Shields. Con Ss = 2.65 para sedimentos de cuarzo, la ecuación (VI.6) puede simplificarse a

= 5.67� !/! �!"!/! (VI.7)

En la ecuación (VI.7), �! es la velocidad media crítica en m/s de un flujo que transportará material de fondo de diámetro �!" en metros y menores, y � es el tirante en metros. Si la velocidad real � < �! , las condiciones serán de aguas claras, y viceversa.

La velocidad media crítica es aproximadamente igual a la velocidad competente de un sedimento, que se define como la velocidad media máxima del flujo que no erosiona el fondo

del cauce (posiblemente incluyendo un margen de seguridad). Neill (1973), Harris (1988) y Neill (1987) presentan cartas que definen la velocidad competente.

Figura VI.3 Carta de la velocidad competente para rendimientos no cohesivos (Neill, 1987)

En la figura VI.3 se muestra la carta para material no cohesivo que proporciona Neill (1987); es una versión actualizada de la presentada en su primer manual (Neill, 1973). En esta última, Neill sugiere que los materiales de fondo no uniformes pueden representarse utilizando el !!" Alternativamente, la velocidad media crítica para materiales no u niformes, !!" ! puede estimarse como se muestra más adelante.

En la tabla VI.1 se muestran los valores de la velocidad media competente para suelos cohesivos que propone Harris (1988), quien además hace las siguientes recomendaciones para la evaluación de la velocidad competente:

! Para subsuelos variables, elegir la velocidad competente para el material más socavable.

! Para un estrato socavable sobreyaciendo a u n estrato resistente a la socavación, utilizar la velocidad competente del estrato de arriba, a menos que la velocidad en la parte superior del estrato de abajo sea capaz de socavarlo, en cuyo caso debe utilizarse la velocidad competente para el estrato inferior.

! Para un estrato resistente a la socavación, sobreyaciendo a un estrato socavable, debe usarse la velocidad competente para el estrato de abajo, a menos que el estrato de arriba no sea socavado hasta la profundidad donde inicia el estrato de abajo.

! Para una condición de coraza natural, adoptar la velocidad competente para el !!"

! Para un fondo parcialmente protegido, utilizar la velocidad competente del material natural, aunque los cálculos necesitan también tomar en cuenta cualquier reducción de área de la sección transversal, debida a los elementos de protección.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Tabla VI.1. Velocidad media competente para suelos cohesivos (Harris, 1988)

Suelo de alta

(Arcillas de muy suaves a suaves) (Arcillas de firmes a duras) (Arcillas de duras a muy duras)

VI.4. Geomorfología de cauces y su análisis

Las geometrías hidráulicas de canales pueden estimarse de manera conceptual con base en las ecuaciones de régimen. Estas ecuaciones expresan generalmente variaciones aguas abajo (conforme aumentan la cuenca y el gasto) de los parámetros geométricos de un canal, como funciones exponenciales del gasto, sea el medio anual o el que corresponde a cauce lleno, Q:

W = �! � !

y = �! � ! (VI.8)

v = �! � !

�! = �! � !

donde W, y, v, �! son el ancho superficial, el tirante medio, la velocidad media y la pendiente de energía (pendiente de la superficie libre del agua), respectivamente

a, b, c, d, �! , �!, �! � �! son constantes

�! �! �! = 1

a + � + � = 1

Chang (1988) indica que los valores de los exponentes a, b y c parecen ser independientes del gasto; sus rangos son, de acuerdo con varios estudios:

a = 0.39 a 0.60

b = 0.29 a 0.40

c = 0.09 a 0.28

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO

Los coeficientes !! ! !! ! !! están relacionados con el gasto y con las propiedades del canal y del sedimento.

Griffiths (1980) presenta las siguientes ecuaciones con base en seis ríos de Nueva Zelanda con grava en el fondo:

W = 7.09 ! ! !"

y = 0.21 ! ! !" (VI.9)

v = 0.61 ! !!!!

!! ! !!!" ! ! !"

Richardson y otros (1990) presentan las siguientes relaciones empíricas para los parámetros de meandros estables, con todas las unidades en metros:

! ! !!!! ! !!!" h ! !!! ! !!! (VI.10) ! ! !!! !!! !"

donde W es el ancho del cauce lleno; ! , h y !! son, respectivamente, la longitud de onda del meandro, la amplitud de cresta a valle y el radio de curvatura al centro del cauce (véase figura VI.4). Suponiendo que todos los exponentes son iguales a 1.0, resulta que !! ! ! ! !

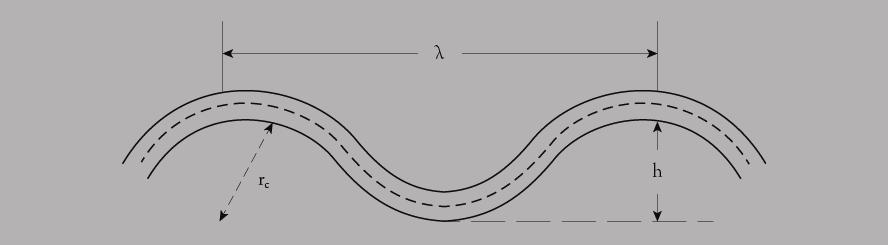
Figura VI.4. Meandro, su longitud y amplitud de onda, y el radio de curvatura.

CAPÍTULO VII

SOCAVACIÓN GENERAL

VII.1. Introducción

La socavación general es aquella que ocurre independientemente de la presencia de alguna estructura construida por el ser humano. En la evaluación de la socavación general tienen que considerarse los procesos fluviales y geomorfológicos, ya que pueden influir en la estructura durante su vida de diseño, generalmente fijada en 50 o 100 años para puentes de caminos rurales o de carreteras troncales, respectivamente.

La socavación es un fenómeno complejo que requiere una evaluación inicial cualitativa, y para cuya solución definitiva deben considerarse todos los factores que intervienen en su determinación, tales como el escurrimiento desde la cuenca (hidrología), la aportación de sedimentos al cauce (erosión en la cuenca), la capacidad de transporte de sedimentos de la corriente (hidráulica) y la respuesta de la corriente a estos factores (geomorfología y mecánica de ríos).

En este capítulo se presentan los procesos de azolvamiento y degradación, la socavación en el cauce principal, la socavación en curvas, la socavación en confluencias, la socavación causada por las formas de fondo y la erosión lateral, incluyendo la erosión en márgenes, el ensanchamiento de canales, la socavación lateral en curvas y la migración

Figura VII.1 Relación entre la forma del río (en planta) y su pendiente (Richard son et al., 1990).

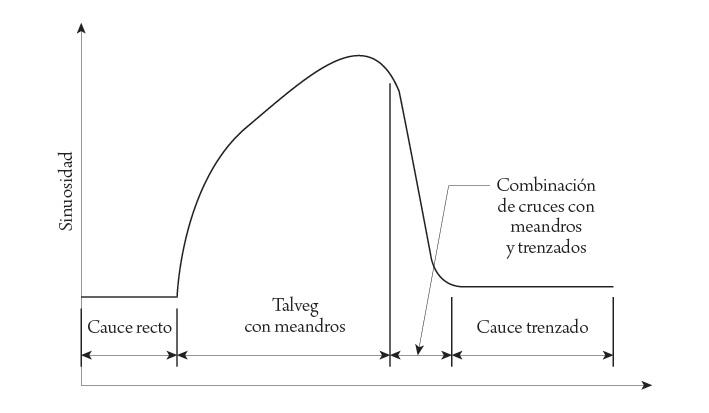
VII.2. Relaciones cualitativas

La relación entre la forma y la pendiente de un cauce se ilustra en la figura VII.1. De esta figura puede concluirse que una variación en la pendiente puede modificar el patrón del flujo; un incremento en la pendiente por el corte de un meandro puede provocar un cambio, pasando de un patrón tranquilo de meandros a un patrón de ramificación que varía rápidamente con el tiempo, con altas velocidades, subdivisiones en barras y carga importante de sedimentos. En cambio, una disminución de la pendiente puede provocar una transición que va de un cauce ramificado inestable a uno de meandros con mayor estabilidad.

Las relaciones cuantitativas entre la forma del cauce, su pendiente !! y el gasto medio Q son analizados por Lane (1957). Se prevé que un cauce con fondo arenoso tenga meandros cuando (!! en m/m y Q en !! /s): !! ! !!!" ≤ 0.00070 (VII.1)

Puede predecirse que un cauce arenoso es ramificado cuando: !! ! !!!" ≥ 0.0041 (VII.2)

En la figura VII.2 se muestran las ecuaciones VII.1 y VII.2.

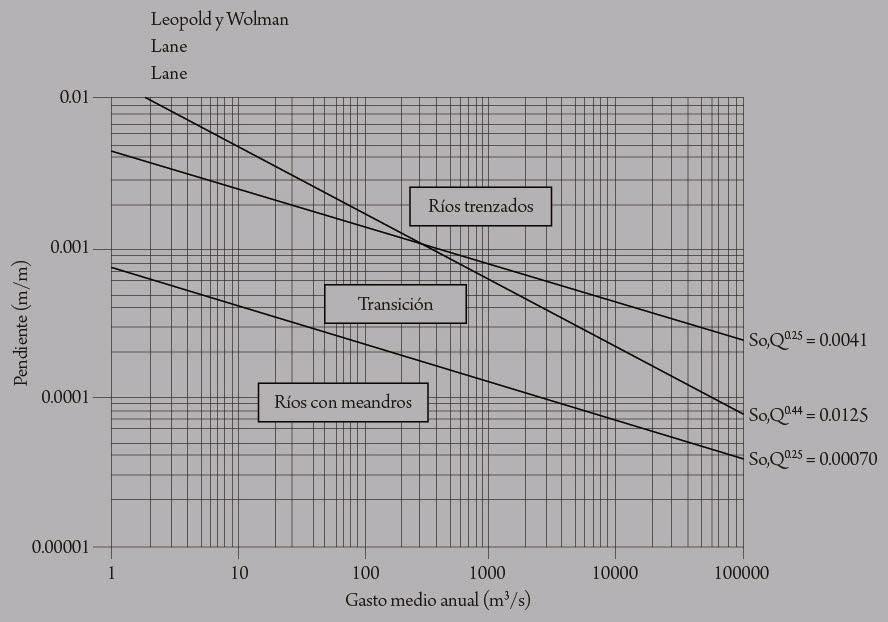
Figura VII.2 Relación entre la forma del río (en planta), pendiente del fondo y gasto medio (después de Lane, 1957).

Hay una zona de transición en que la corriente puede cambiar rápidamente de una a otra condición. Leopold y Wolman (1960), basándose en una variedad de corrientes naturales, encontraron que para corrientes con meandros:

�! � ! !! ≤ 0.00125 (VII.3a)

y que para corrientes ramificadas:

�! � !.!! ≥ 0.00125 (VII.3b)

La sinuosidad se define como la relación entre la longitud del centro de línea del cauce principal y la longitud del centro de línea del cauce de avenidas. Varía entre 1.0 para corrientes rectas y 4.0 para muy sinuosas. Las corrientes con meandros tienen sinuosidades de más de 1.5.

Puede hacerse una predicción cualitativa de la respuesta de una corriente a cambios climatológicos o de la cuenca, basándose en la ecuación de balance:

donde Q es el caudal o gasto líquido, �! la pendiente de energía, �! es el gasto sólido o sedimentos arrastrados y �!" es la mediana de los diámetros del sedimento.

Fue propuesta originalmente por Lane (1955), basándose en un estudio de cambios de la morfología de la corriente causados por modificaciones en el gasto líquido y sólido. Si una o más de las variables de la ecuación (VII.4) se alteran, la expresión indica que una o más de las otras variables se ajustarán para restablecer el balance. Así, esta simple relación proporciona una valiosa herramienta en el comportamiento del sistema, que puede revelar una potencial socavación. También puede ser útil la ecuación (VII.4) para revisar análisis subsecuentes y modelos numéricos o físicos.

Ejemplo de aplicaciones de relaciones cualitativas

Una corriente principal que se encuentra en proceso de degradación gobierna sobre los niveles del fondo de sus tributarios, los cuales son obligados a degradarse y contribuyen con carga adicional de sedimentos hacia la corriente principal. La respuesta de ésta, suponiendo que el gasto líquido y el diámetro de los sedimentos permanecen constantes, puede determinarse con la ecuación de balance (VII.4):

en la que los superíndices indican variaciones en los parámetros que los tienen. Es de esperarse que el cauce principal tenga un incremento en su p endiente debido a la carga adicional de sedimentos. Entonces, la degradación del cauce principal se hará más lenta, y posiblemente se detenga o se invierta si la carga adicional de sedimentos es suficientemente grande. La degradación de los tributarios con tinuará para ajustarse de acuerdo con las variaciones de los niveles de aguas abajo, y eventualmente el sistema adoptará un nuevo equilibrio.

La extracción de sedimentos o la construcción de una presa provocan una reducción de la aportación de sedimentos aguas abajo del sitio. Si Q y !!" permanecen constantes, la ecuación (VII.4) indica que una disminución en la aportación de sedimentos provocará una disminución de la pendiente aguas abajo del sitio. Entonces ocurrirá una degradación asociada aguas abajo del sitio de extracción o de la presa, ya que habrá falta de aportación de sedimentos en esta región (véase figura VII.3).

Figura VII.3 Disminución de la pendiente, junto con la degradación que ocurre aguas debajo de una presa, que causa disminución en el aporte de rendimientos.

!! Q ! !! ¯ !!"

El punto de control de una presa previene cualquier degradación hacia arriba de ella.

Para la situación más probable en que tanto el gasto líquido como el aporte de sedimentos se reducen aguas abajo de una presa, la respuesta del cauce aguas abajo para un mismo diámetro del sedimento se indica por la ecuación (VII.4) como:

!!! ! ! !! !!"

Los cambios consecuentes de la pendiente dependerán de las magnitudes relativas de los cambios de las otras variables.

En el extremo de aguas arriba del vaso formado por la presa, la capacidad de transporte de sedimentos se reduce conforme la corriente entra al vaso. El balance de respuesta del río es:

!! Q ! !! !!"

Esto indica una disminución de la pendiente aguas arriba del vaso, con depósito de sedimentos en el vaso, en el extremo de aguas abajo del tramo, ya que existe una reducción de la capacidad de transporte en ese punto.

Comentarios sobre la evaluación cualitativa de la estabilidad de cauces

Cuando el cauce ha sido, es o será cambiante, su respuesta puede evaluarse utilizando la relación (VII.4) de balance, así como las figuras VII.1, VII.2 y VII.4 y la tabla VII.1. Con base en estos análisis y con un buen juicio ingenieril se puede evaluar la estabilidad vertical y lateral del sistema.

Figura VII.4 Relación entre el tipo de cauce, factores hidráulicos y de pendientes, y estabilidad relativa (después de Shen y Alros, 1980).

Tabla VII.1. Ejemplo de las relaciones proceso-respuesta con base en la ecuación (VII.4) y en las relaciones de régimen

Proceso Descripción

Sólo aumenta

Sólo disminuye

Sólo aumenta

Sólo disminuye

Sólo aumenta

Sólo disminuye

Aumentan � y

; por ejemplo, durante una construcción urbana o en etapas tempranas de deforestación.

Disminuyen

y

; por ejemplo, aguas abajo de una presa.

Aumenta � y disminuye �! ; por ejemplo, cuando aumenta la humedad en una zona inicialmente poco húmeda.

Disminuye � y aumenta �! ; por ejemplo, mayor uso del agua, combinado con mayor uso de la tierra.

Aumentan

Disminuyen

Respuesta

� , �, � , �, �! , � representa, respectivamente, el ancho del cauce, el tirante, la relación (ancho-tirante), la longitud de onda de los meandros, la pendiente de energía y la sinuosidad.

Se requiere un buen juicio ingenieril basado en la experiencia para interpretar cada indicador del potencial de socavación, para determinar la importancia relativa de cada indicador y para consolidar los resultados en un marco general de posibilidades de depósito, degradación o inestabilidad lateral.

VII.3. Depósito y degradación general

Los depósitos de corto y largo plazo serán designados como relleno y depósito progresivo o general, respectivamente. El depósito progresivo puede desarrollarse aguas arriba o aguas abajo.

La degradación es el descenso del nivel del fondo, generalmente en una región extensa, y puede desarrollarse en dirección aguas arriba o aguas abajo. A la degradación de largo plazo se le designará degradación progresiva o general.

El depósito progresivo puede, en general, atribuirse a una aportación de sedimentos que excede la capacidad de la corriente para transportarlos, o bien, a un ascenso del nivel base. El aporte de los sedimentos a un cierto tramo viene de la cuenca y de alguna erosión que ocurre en el cauce. La capacidad de transporte de sedimentos es función del diámetro de éstos, del gasto de la corriente y de las propiedades geométricas e hidráulicas del cauce. Cuando la capacidad de transporte (salida) de un tramo es igual a la aportación de sedimentos (entrada), el tramo está en equilibrio.

El depósito progresivo puede provocar que un puente sea enterrado por el material, debido a lo cual sería necesario reubicarlo, o que la carga sobre la estructura se vea incrementada, principalmente durante avenidas; puede ocurrir falla del puente o erosión de los accesos debido a un mayor ancho del canal provocado por el depósito, y puede haber mayor probabilidad de que el puente sea sobrepasado por el agua, debido a la reducción del área hidráulica. El mayor ancho del cauce, provocado por el depósito, puede aumentar la cantidad de ramazón y basura que ingresa al flujo (hay mayor erosión lateral), lo que aumenta la posibilidad de atoramiento y bloqueo de obras existentes aguas abajo, con la consiguiente mayor carga hidráulica y mayor socavación en los puentes de aguas abajo.

La degradación progresiva puede colapsar tablestacados, así como otras estructuras de control y protección de márgenes; puede causar erosión en estribos y pilas; puede llevar a la necesidad de reubicar algún puente y puede causar el colapso de puentes por exposición de la cimentación (pilotes o zapatas) o por migración del cauce principal además de la degradación, o bien por ensanchamiento del cauce. La consecuente erosión marginal puede aumentar la cantidad de basura aportada a la corriente, con lo que se tendrán problemas como los citados en el caso de depósito de sedimentos.

El principio básico en la evaluación de los cambios que sufre la elevación del fondo es el concepto de la continuidad de los sedimentos. Para un tramo dado, el sedimento no se pierde ni se gana. En un periodo dado, la cantidad de sedimento que entra por el extremo de aguas arriba del tramo, menos aquella que abandona el extremo de aguas abajo, es igual al cambio en la cantidad de sedimento almacenada en el tramo. La entrada de sedimento o aportación a un tramo de cauce es proporcionada por la cuenca y por la erosión que ocurre en la sección. La capacidad de transporte de sedimentos de un tramo, que puede ser evaluada con base en ecuaciones de caudal de sedimentos, determina la salida de sedimentos del tramo. Si la entrada excede a la salida, entonces ocurre depósito en dicho tramo. Si no existen controles que limiten la erosión, la salida excede a la entrada y entonces ocurre degradación.

VII.3.1. Evaluación cualitativa de depósito y de degradación

Neill (1973) comenta que la degradación progresiva del perfil de un cauce, debida a procesos geológicos o cambios de régimen provocados por el ser humano, no puede calcularse sino que debe estimarse con base en tendencias pasadas o en proyectos futuros. Para la evaluación de la socavación general, típicamente los ingenieros han recurrido a un reconocimiento de la zona y a técnicas cualitativas para evaluar problemas potenciales de inestabilidad del cauce (Richardson et al., 1990; Richardson y Davis, 1995; Lagasse et al., 1995). Estos análisis facilitan una comprensión aceptable de los procesos físicos involucrados y proporcionan un sustento para análisis subsecuentes y decisiones adecuadas.

Una vez recopilada la información de campo necesaria, podrá evaluarse el depósito o la degradación, con base en las medidas cualitativas delineadas en párrafos anteriores. Además de estas evaluaciones, debe recordarse que el perfil del fondo a largo plazo en el sitio de un puente puede cambiar durante la vida útil de la estructura, en función de los cambios del cauce y de la cuenca. Los periodos de depósito o degradación pueden ir alternándose si ocurren los disturbios necesarios para ello.

VII.3.2. Evaluación cuantitativa de depósito y degradación

Como se dijo, la estimación cualitativa del depósito o de la degradación requiere un gran conocimiento del transporte de sedimentos y de mecánica de ríos. Esto es también cierto para el análisis cuantitativo. Richardson y Davis (1995) afirman que los cambios de largo plazo en el perfil del fondo de los cauces son generalmente difíciles de evaluar.

La determinación de las condiciones de frontera para el movimiento de sedimentos basada en el diagrama de Shields (figura VI.1) puede orientar en las condiciones de flujo necesarias para movilizar el fondo y afectar la estabilidad del canal. Más adelante, en esta sección, se presenta un procedimiento para estimar la profundidad de degradación necesaria para formar la coraza suficiente para detener la degradación vertical. También se discute la predicción numérica de la socavación general.

Richardson y Davis (1995) presentaron el siguiente procedimiento de diseño para la evaluación cuantitativa del depósito y de la degradación:

Cuando el análisis cualitativo indique que es probable que ocurra depósito o degradación, estimar los cambios en la elevación del fondo en los próximos 100 años, utilizando uno o más de los siguientes criterios:

§ Extrapolación en línea recta de la tendencia actual (cuando la información recabada del perfil del fondo lo permita).

§ Buen juicio ingenieril.

§ Análisis del peor escenario, por ejemplo, que el gasto de diseño ocurra con o sin remanso.

§ Programas de cómputo con tránsito de sedimentos o continuidad de sedimentos.

Si el fondo se está degradando, la socavación total se determina sumando a las elevaciones estimadas de degradación del fondo la socavación por estrechamiento y la socavación local. Si hay depósito, entonces la elevación actual del fondo debe ser la línea básica a la cual se sumen la socavación por estrechamiento y la local, ya que una tendencia de depósito puede ser revertida con la ocurrencia de una avenida importante.

Además de la extrapolación en línea recta, se han propuesto extrapolaciones exponenciales. Por ejemplo, Johnson y Simon (1995) indican que la degradación puede describirse usando una relación exponencial simple como:

E= a� ! (VII.5)

donde E es la elevación del fondo en (m), t es el tiempo en años y a y b son coeficientes de regresión. El uso de esta expresión requeriría que no hubiera ningún disturbio del sistema en el periodo de análisis. Simon (1995) sugiere una función exponencial como base física para describir tanto el depósito como la degradación, con la expresión.

E / E₀ = a+be !" (VII.6)

donde E₀ es la elevación del fondo en el tiempo t = 0, en años k es un coeficiente de regresión que indica la razón de cambio del nivel del fondo por unidad de tiempo a y b son coeficientes adimensionales (a + b =1)

Para E₀ > 0 y k > 0, la degradación se indica por a > 1 (nivel relativo del fondo) y b < o (cambio relativo del nivel del fondo). Similarmente, a < 1 y b > 0 indican depósito. Con tres observaciones del nivel del fondo, la ecuación (VII.6) puede ser aplicada al sitio en cuestión y utilizada para predecir las elevaciones futuras del fondo y las alturas máximas de las márgenes, si el fondo se está degradando.

Uso de mediciones de campo

Las mediciones históricas de la sección transversal y de las elevaciones del fondo serían muy útiles en la estimación de la profundidad máxima de socavación general; pueden extrapolarse las tendencias claras para determinar valores futuros. Los sondeos y las investigaciones subsuperficiales pueden proporcionar una idea aceptable de los estratos resistentes que limitan la socavación. Se requiere una amplia experiencia para hacer la evaluación de estos últimos datos; sin embargo, se requiere aun más experiencia para utilizarlos como base para predecir los límites de socavación.

VII.3.3. Métodos para el cálculo de la socavación general

Fórmula de Régimen de Lacey (1930)

Si se conoce la relación entre los niveles del agua y los gastos, Neill (1973) indica que los niveles del fondo pueden determinarse en un puente sin estrechamiento con la fórmula de Lacey (1930).

�!" = 0 47 ! ! !/! (VII.7)

donde �!" es el tirante medio de socavación, medido desde el NADI hasta el fondo socavado, en m, que se define como el área hidráulica dividida entre el ancho de la superficie

Q (�! /� ) es el gasto del diseño f es el factor de Lacey

Tabla VII.2. Factor “f” de Lacey en función del diámetro medio de sedimentos no cohesivos

Diámetros medio de los gramos �! (mm)

Factor de Lacey � !

Diámetros medio de los gramos �! (mm)

Factor de Lacey � !

-f puede expresarse como f = 1.76 �! ! ! , donde �! está en mm (Adaptado del Congreso de Carreteras de la India, 1966)

Los valores de f presentados por Neill y reproducidos aquí como la tabla VII.2 han sido adaptados de los valores dados por el Congreso Indio de Carreteras (1966).

El método fue diseñado para canales sin estrechamiento y con arenas aluviales. Neill (1973) comenta que f debe ser de 1.0 para materiales arenosos, a menos que la experiencia

indique otra cosa. La fórmula es igualmente aplicable a ríos aluviales que a canales con fondo arenoso influidos por mareas, pero pueden dar profundidades excesivas en materiales más resistentes.

La ec. VII.7 predice el tirante medio de socavación a través de una sección de canal sin contracción; puede ser modificado si existe contracción, si el cauce principal es profundo o si existe alguna curva o efecto de confluencia, como se indica adelante.

Método de Lischtvan-Lebediev (1959)

Consiste en determinar la condición de equilibrio entre la velocidad media de la corriente, Vr, y la velocidad requerida para erosionar un material de diámetro y densidad conocidos, Ve.

Hipótesis del método de Lischtvan-Lebediev:

B = constante durante la avenida

!Q = constante mientras dura el proceso de erosión. !Q es el gasto unitario que pasa por cualquier franja de la sección, de ancho !B.

Las ecuaciones del método de LischtvanLebediev son:

donde

! es el parámetro auxiliar

Q es el gasto de diseño (m3/s)

!! es el tirante medio = área hidráulica / ancho efectivo, Be

Be es el ancho efectivo de la superficie libre del agua (m)

µ es el coeficiente de contracción (adimensional); depende de la longitud de los claros del puente y de la velocidad media del flujo (véase tabla VII.3).

Figura VII.5. Variables a considerar en el cálculo Vur

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

VII.3. Cálculo de socavación general. Método de Lischtvan-Lebediev

Tabla

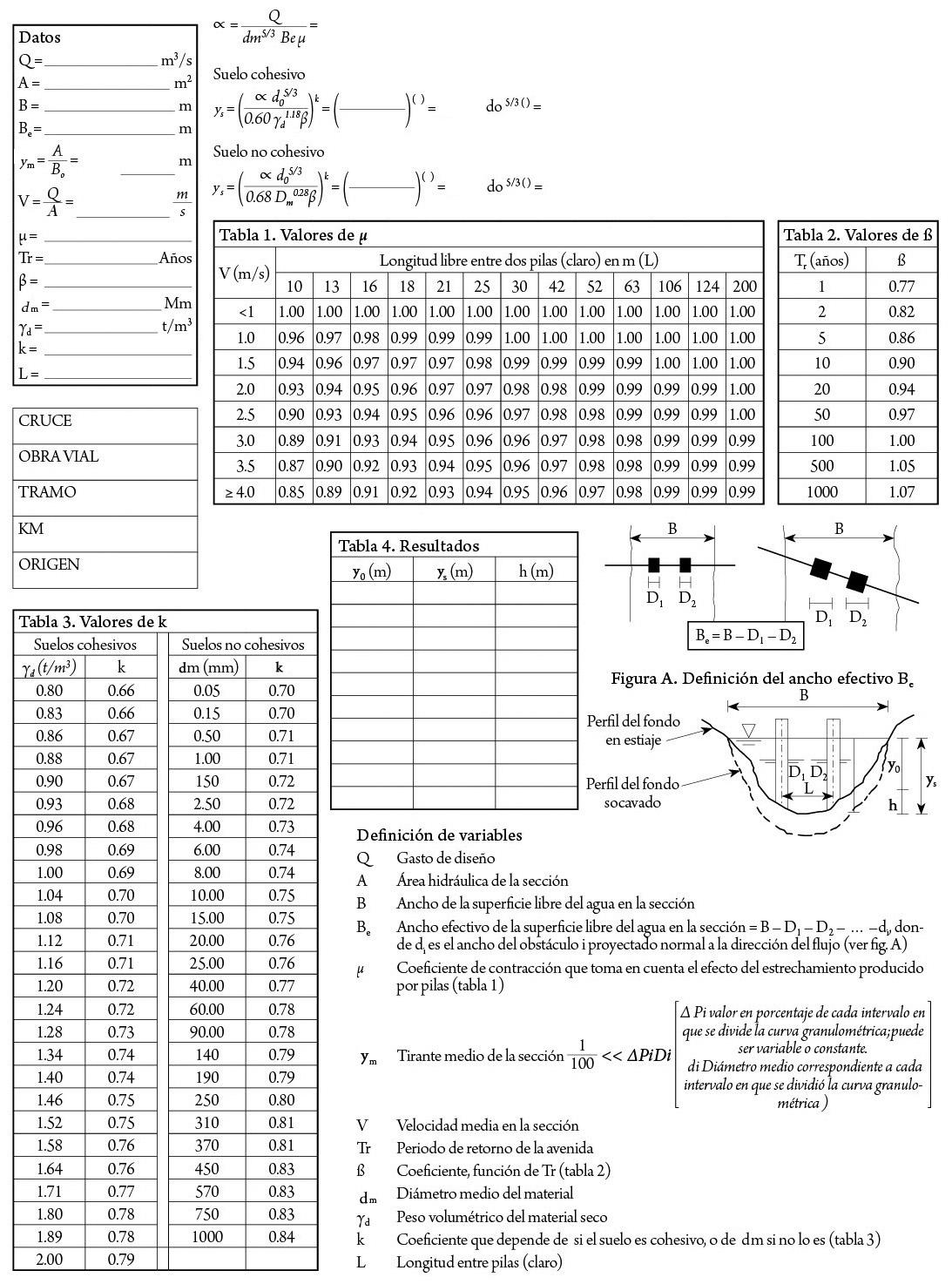
Cauces formados por material granular:

!! ! ! !! !!! !!!!" !!! !" ! ! !

donde

!! es el tirante después de la socavación máxima en el punto considerado de la sección (m)

!! es el tirante en el mismo punto antes de que ocurra la socavación (m)

!! es el diámetro medio del material del cauce (mm)

" es el coeficiente que depende del valor de Tr de la avenida de diseño (adimensional)

Tr es el periodo de retorno de diseño (años)

k es el exponente función de Dm (adimensional, véase tabla VII.3)

Cauces formados por material cohesivo:

!! ! ! !! !!! !! !" !! ! !" ! ! !

donde

!! es el tirante después de la socavación máxima en el punto considerado de la sección (m)

!! es el tirante en el mismo punto antes de que ocurra la socavación (m)

!! es el peso volumétrico seco del material del cauce (t/m 3)

! es el coeficiente que depende del valor de Tr de la avenida de diseño (adimensional)

k es el exponente función de !! (adimensional, véase tabla VII.3)

Si existe un puente, el ancho efectivo Be se puede calcular empleando la ecuación (véase

figura VII.6): Be = ( B - # bi ) cos $ - ( c + 1 – N ) a sen $ donde

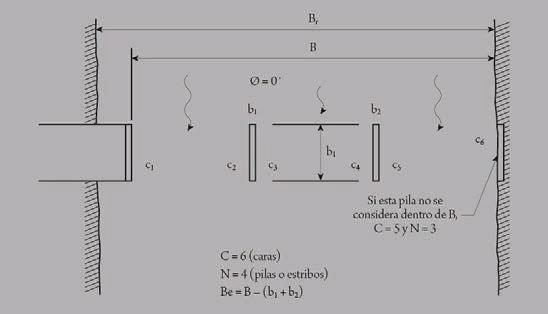
Figura VII.6. Ancho efectivo Be en puentes cuando las pilas están alineadas con respecto al flujo.

B es el claro total del puente en estudio (m)

# bi es la suma de los anchos de las pilas dentro del claro total B (m)

c es el número de caras de las pilas o estribos dentro y en los límites de B

N es el número de pilas o estribos considerados al tomar en cuenta a c

MANUAL

$ es el ángulo que forma la dirección del flujo con el eje longitudinal de las pilas (grados) a es la longitud de los apoyos (m)

Figura VII.7. Ancho efectivo Be en puentes cuando las pilas están esviajadas respecto a la dirección del flujo.

Formulación de Régimen de Blench (1969)

El tirante medio de socavación !!" en m abajo de la superficie libre del agua puede determinarse con base en el gasto por unidad de ancho del canal: !!" ! ! ! ! ! !!! !!"!!! ! para arenas con 0.06 < !!" (mm) ≤ 2 (VII.8)

o bien: !!" ! !!!" ! ! !!! !!"!!!" ! para gravas con !! ! !!!" y !!" > 2 mm (VII.9) donde ! !! ! !! es el gasto por unidad de ancho del cauce principal, si el cauce tiene llanuras de inundación

�! (adimensional) es la gravedad específica de las partículas del sedimento, es decir, su peso específico [F/�! ] dividido entre el peso específico del agua �!" (mm) es el diámetro del sedimento tal que el 50% es menor.

Conociendo el nivel de la superficie del agua correspondiente a q, puede determinarse el nivel del fondo socavado, el cual podría después ser modificado por estrechamiento del cauce, por socavación local, por un cauce principal profundo, por curvas o por efectos de confluencia, como se verá más adelante.

La ecuación (VII.8) se obtuvo para cauces reales en régimen con gasto permanente, y con transporte de sedimentos permanente muy pequeño como para aparecer explícitamente en la ecuación; también para fondos arenosos con dunas y distribución de tamaños tales que 0.1 < �!" (��) ≤ 0.6 con muy pocos sedimentos en suspensión que no alteran las ecuaciones, con bordos cohesivos verticales comportándose como hidráulicamente lisos, canales rectos en planta, de modo que el fondo con dunas lisas está al mismo nivel en toda la sección, pendiente y sección uniforme, y viscosidad constante del agua. Esta ecuación es aplicable a la mayoría de los sistemas de canales de riego de fondo arenoso con mantenimiento adecuado, con una relación de ancho a tirante mayor de 5, y con tirante mayores de 0.4 m.

La ecuación (VII.9) fue obtenida con base en estudios realizados en ríos grandes con fondo de grava.

Métodos basados en la velocidad competente y fuerza tractiva Los métodos de la velocidad competente se basan en la hipótesis (ecuación de continuidad) de que la socavación ocurrirá hasta que se alcancen las condiciones límite; la velocidad competente es aproximadamente equivalente a la velocidad media para las condiciones de movimiento incipiente del material del fondo, esto es, �! (capítulo VI).

Los métodos de la fuerza tractiva pueden utilizarse para indicar el máximo tirante para el cual el material será estable, para una pendiente dada (Raudkivi, 1990; Henderson, 1966). En este concepto se basa la ecuación (VII.17) de más adelante para predecir la socavación por estrechamiento en aguas claras.

Métodos de velocidad competente de Williman (1970), Neill (1973, 1987) y Harris (1988) Con estos métodos se calcula el descenso medio del fondo con base en la velocidad competente. El área socavada se estima por tanteos hasta que la velocidad me dia en la sección socavada (para la elevación constante de la superficie del agua) sea igual a la velocidad media competente para el material expuesto del fondo.

Figura VII.8. Redistribución de la socavación promedio, de acuerdo con Neill (1973).

La profundidad máxima de socavación en una sección transversal, considerando talveg (línea imaginaria que une los puntos más bajos de un valle), curvas y efecto de variaciones de la sección transversal, se evalúa con una redistribución gráfica del área socavada. Esta metodología requiere un buen juicio, pero quizá pueda llevarse a cabo más fácilmente dibujando la sección socavada (véase figura VII.8). Harris (1988) establece que la sección socavada puede ser de forma rectangular o trapezoidal para tramos rectos, pero puede ser triangular para puentes ubicados en una curva del río. Neill, por su parte (1973), indica que en un tramo recto de un río aluvial, la forma de la sección transversal será parabólica, y que para ríos con grava será más rectangular.

Los procedimientos propuestos por Neill (1973) para redistribuir el área socavada en forma triangular se ilustran en la figura VII.8, que presenta dos opciones; una en que la redistribución del área socavada es abajo del nivel original del fondo, y la otra, abajo del nivel de la superficie del agua durante la avenida. Otra opción recomendada por Neill (1973) es redistribuir el área socavada por debajo del nivel de aguas ordinarias.

El método de Williman (1970) es muy similar al de Neill (1973), aunque recomienda utilizar el !!" en la evaluación de la velocidad competente (ecuaciones VII.5, VII.6 y VII.7). El Ministerio de Obras y Desarrollo de Nueva Zelanda (1979) propone opciones para la redistribución del área socavada en tramos rectos y curvos, reconociendo que en tramos

rectos de un río aluvial la sección transversal será parabólica, mientras que en una curva pronunciada será triangular. También reconoce que los ríos con grava presentan forma rectangular. Ese ministerio indica que el método de Williman (1970) puede utilizarse para revisar los resultados obtenidos con otros métodos, de la socavación general y por estrechamiento. Yeo (1991) recomienda utilizar el método de Neill (1973) en forma similar. Watson (1990) comenta, sin embargo, que el método de Neill (1973) subestima el efecto de coraza que ocurre en ríos con grava, y por consiguiente da valores muy conservadores de la socavación en estos ríos. El método de Harris (1988) es recomendado para puentes en Ontario, Canadá.

Método de la velocidad competente d e Maza Álvarez y Echavarría Alfaro (1973) El tirante medio de socavación en un cauce recto sin estrechamiento se estima con:

(VII.10)

donde (véase figura VII.9):

!!" es el tirante medido desde el nivel de aguas de diseño hasta el nivel medio de socavación del fondo

!! (m) es el tirante máximo de socavación

!! (m) es el tirante antes de la socavación en el punto más bajo del cauce

!!" (m) es el tirante medio antes de la socavación

Q (!! / s) es el caudal

W (m) es el ancho de la superficie libre para el gasto de diseño

!!" (m) es la media de los diámetros del sedimento

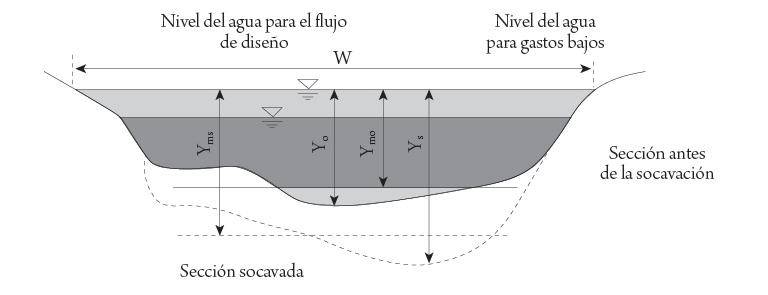
Figura VII.9. Parámetros de la sección transversal para el método de la velocidad competente de Maza Álvarez y Echavarría Alfaro (1973).

Este método empírico fue desarrollado con base en pruebas realizadas por diversos autores y en datos de campo en ríos de América; también en mediciones de la socavación en ocho puentes y en otros ríos. Los diámetros del sedimento variaron desde limos finos hasta arenas gruesas (generalmente con �!" < 6 mm). El método es aplicable a ríos amplios. Si el canal no es lo suficientemente ancho (cuando el área de la sección socavada difiera mucho de aquélla obtenida con �! = W�!" , entonces �!" se sustituye en la ecuación (VII.10) por el radio hidráulico R= �! / P, donde P es el perímetro mojado de la sección socavada. Los autores aclaran que la ecuación (VII.10) es válida para arenas y gravas. No se dispone de datos para calibrar materiales más gruesos, y los valores calculados para materiales más finos difieren de los observados.

Los autores permiten variaciones en el nivel del fondo a través de la sección transversal (debidas a falta de uniformidad del fondo y efecto de talvegs), y proponen calcular el tirante máximo de socavación con la siguiente expresión:

�! = 0.365 ( !! !!" ) ( ! !.!"#

que vale para arenas o gravas con �!" < 6 mm.

(VII.11)

Para efectos de curva y de estrechamiento, los resultados obtenidos con la expresión anterior pueden ajustarse con los métodos que se presentan en capítulos posteriores.

Las expresiones (VII.10) y (VII.11) se basan en la velocidad media mínima para la cual inicia la erosión del fondo, cuya expresión es: �! = 3.62 �!" ! ! �!" ! !"# (VII.12)

que vale para arenas o gravas con �!" < 6 mm.

Neill (1987) comenta que la lógica de la base física de las ecuaciones de Maza Álvarez y Echavarría Alfaro es cuestionable. Otros autores comentan que el método, que se usa actualmente en Nueva Zelanda, podría ser útil para obtener una primera estimación de la socavación general esperada. Watson (1990) reporta el uso generalizado de este método para ríos con fondo de gravas en Nueva Zelanda.

Método de ferrocarriles de Nueva Zelanda, de Holmes (1974)

Este método fue desarrollado para estimar la socavación total en un puente, es decir, la combinación de la socavación general y la socavación por estrechamiento, y debe elegirse el mayor valor entre:

�! = �

o bien

�! = !! !! ! (! !)

donde �! = C (! ! ) ! !/! !/!

K = ! ! !"! ! ! ≤ 1

� (�) es el tirante antes de la socavación

(VII.13)

�! � es el incremento del nivel del agua, de aguas ordinarias a aguas de la creciente de diseño

A (�! ) es el área hidráulica antes de la socavación

W (m) es el ancho del área hidráulica para flujo en llanura de inundación, y es igual a 1.25 �!"

�!" (�) es el ancho del área hidráulica que lleva el 80% del gasto

�! (� �) es la velocidad de llegada

C es un coeficiente igual a 1.2 cuando convergen flujos como el caso de flujo ramificado. De otra manera, C = 1

Q (�! � ) es el gasto

K es un factor que depende del ancho de la sección hidráulica y del ancho de régimen de Lacey.

Este método se basó en datos de campo recabados en Nueva Zelanda para casos de fallas por socavación en varios puentes de ferrocarriles. Los datos cubren un amplio rango de tamaños de sedimentos, y no incorpora factor de seguridad debido al uso histórico de gastos conservadores de diseño en su análisis.

Neill (1987) comenta que la ecuación (VII.13) no parece tener una base física que sea lógica. Yeo (1991) indica que este método no incluye efectos de material del fondo. Sin embargo, este método ha sido utilizado por muchos años en los ferrocarriles de Nueva Zelanda. Varias otras instituciones de ese país usan también este método, aunque Yeo (1991) afirma que ello puede ser más una consecuencia de la simplicidad del método que de su confiabilidad o validez. Watson (1990) reporta predicciones conservadoras para cauces profundos con fondo de grava.

Metodología de diseño basada en la “coraza”

Cuando la corriente es incapaz de mover todos los diámetros de un sedimento con graduación amplia, los granos más grandes del sedimento pueden formar una capa “coraza” en la superficie del fondo y sólo son movidas las partículas más finas de la superficie. Esta coraza inhibe la erosión y protege de ella a la subsuperficie más fina. La degradación de un fondo de río puede ser reducida en forma importante si se forma la coraza. Si la capa “coraza” es estable para un cierto flujo de diseño, es razonable concluir que no ocurrirá degradación del fondo para un caudal menor o igual que el de diseño.

El diámetro del sedimento que estará al límite para un flujo de diseño puede evaluarse con base en el análisis de movimiento incipiente presentado en el capítulo VI. Si en el fondo sujeto a la erosión no existen cantidades importantes de sedimento con diámetro mayor al que corresponde al movimiento incipiente, no se formará la coraza y el fondo se erosionará hasta que las condiciones de flujo alcancen aquellas para las cuales el sedimento es estable.

Es posible el acorazamiento de un fondo erosionable cuando el diámetro límite es menor que el �!" del material del fondo; frecuentemente se encuentra que el tamaño de las partículas que forman la coraza es el �!" o el �!" de dicho material. La profundidad de socavación abajo del nivel original del fondo, � �!" , necesaria para que se forme tal capa coraza puede ser estimada con:

� �!" = �! ! !! 1 (VII.14)

donde �! es la fracción decimal del material que es mayor que el tamaño limite, �! �! es el espesor de la capa coraza, que varía de 2�! a 3�! , dependiendo del valor de �!

La ecuación (VII.14) no contempla variaciones de �! ni de �! al incrementarse la profundidad de socavación, y puede arrojar errores importantes para profundidades más grandes de socavación (menor �! ). Es importante recordar que el análisis de la formación de la coraza es adecuado para cierto flujo de diseño y que el acorazamiento no necesariamente brinda una estabilidad de largo plazo al fondo de un río.

Método basado en la coraza, de Pemberton y Lara (1984) Pemberton y Lara (1984) adoptan la metodología de la coraza calculando el diámetro de acorazamiento para las condiciones del flujo de diseño con base en varios métodos, incluyendo el diagrama de Shields (figura VI.1). El análisis supone que el cauce degradado

tiene las mismas condiciones hidráulicas que el cauce existente, y que la pendiente del cauce permanece constante durante la degradación. Estas condiciones implican que el perfil del cauce desciende como un cuerpo completo. Se supone que la coraza se forma si el fondo contiene más del 10% de material grueso que no puede ser arrastrado bajo condiciones del flujo dominante (�! ≤ �!" ). La profundidad de socavación abajo del nivel original del fondo, � �!" , necesaria para que se forme la capa coraza puede calcularse con la ecuación (VII.14).

Debe recordarse que el uso de (VII.14) para estimar la degradación es limitado, como se indicó arriba. Es posible que ocurra erosión lateral simultáneamente con la formación de la coraza.

Método basado en la coraza, de Borah (1989) Borah (1989) evalúa la profundidad de socavación abajo del nivel original del fondo, � �!" , necesaria para que se forme la coraza, usando una variación de la ecuación (VII.14):

�!" = �! ! ! ! !! 1 (VII.15)

donde e es la porosidad del material del fondo y �! ! �! es el diámetro más pequeño de la coraza

Se supone que la capa de la coraza está bien mezclada, con todas sus partículas teniendo la misma gravedad específica. Debido a que algunas partículas pequeñas quedan atrapadas en la coraza, el autor comenta que la profundidad de socavación puede multiplicarse por un factor de seguridad similar al que propone Einstein (1950), mayor que 1.0. Sin embargo, tal factor no fue aplicado en el análisis que como ejemplo presentó Borah (1989). Puede utilizarse el diagrama de Shields (figura VI.1) para determinar el diámetro �! ! �! , o alternativamente las relaciones desarrolladas por Alonso et al. (1981), basadas en el diagrama de Shields (sus unidades son del sistema kg-m-s): (para �∗ �!" � ≤ 10), �! = 68 ( ! !! !! ! )!

(!∗ ! )! !" (VII.16) (para 10 < �∗ �!" � ≤ 500), �! = 27 ( ! !! !! ! )! !" ( ! !∗ )! !" (VII.17) (para �∗ �!" � > 500), �! = 17( !!! !! !) (VII.18)

donde

y es el tirante (que puede calcularse con la ecuación de Manning)

�∗ es la velocidad de corte = (g��! )! !

�! es la pendiente de fricción

�! es la gravedad específica del sedimento

�!" es la mediana de los diámetros del sedimento

� es la viscosidad cinemática del fluido

�! , � � �!" pueden obtenerse de muestras del material del fondo.

La porosidad puede también estimarse utilizando la relación empírica (Komura y Simons, 1967):

� = 0 245 + ! !"#$ (! ! !!" )! !" (VII.19)

donde �!" está en milímetros

El método de Borah (1989) ha sido validado con datos de laboratorio de Little y Mayer (1972) (se ha cuestionado la confiabilidad de estos datos), y con un gasto de 1,303 �! � ,

�!" > 0.297 mm y una n de Manning = 0.030. Es importante recordar que para este método la profundidad de socavación abajo del nivel original del fondo, � �!" , se calcula con una variación de la ecuación (VII.14). Ya fueron discutidas las limitaciones de esta ecuación.

Resumen y comentarios sobre la evaluación cuantitativa

Se han presentado los siguientes métodos principales para ser utilizados en la predicción de depósito y degradación general:

§ Extrapolación basada en medición de tendencias (ecuaciones VII.5 y VII.6).

§ Formulación de régimen de Lacey (1930) con la predicción de �!" (ecuación VII.7 y tabla VII.2).

§ Formulación de régimen de Blench (1969) con la predicción de �!" (ecuaciones VII.8 y VII.9).

§ Metodología de diseño con la velocidad competente y fuerza tractiva, con la predicción de �!" con base � = �! , y de la profundidad máxima de socavación basada en la redistribución gráfica de la profundidad promedio de socavación (figura VII.8 y ecuaciones VII.10, VII.11 y VII.12 de Maza Álvarez y Echavarría Alfaro).

§ Formulación de Holmes (1974) para ferrocarriles de Nueva Zelanda, con la predicción del tirante de socavación, �! , para la combinación de la socavación general y por estrechamiento (ecuación VII.13).

§ Metodologías de diseño basadas en la coraza, prediciendo la profundidad de socavación, � �!" , abajo del nivel original del fondo necesaria para que se forme la capa coraza (ecuaciones VII.14 y VII.15), aunque la coraza no puede proporcionar estabilidad de largo plazo al fondo del cauce.

Para utilizar los métodos anteriores debe tenerse cuidado en que las expresiones sean aplicables a las características del sitio de estudio (flujos, parámetros del cauce y sedimento), y establecer las limitaciones de su uso antes de su aplicación. Por ejemplo, los métodos que no incluyen los efectos de la pendiente del cauce son de generalidad limitada. Es muy importante la identificación de posibles situaciones de depósito o degradación ante algún disturbio del cauce, para cualquier predicción de futuros cambios de éste.

La aplicación de los métodos citados arriba, junto con observaciones cuidadosas de campo y de la subsuperficie del fondo, y un buen juicio, proporcionan la mejor forma de hacer una evaluación inicial cuantitativa del depósito o degradación.

VII.3.4. Evaluación cuantitativa de la degradación aguas abajo de una presa

La degradación del fondo aguas abajo de una presa puede estimarse utilizando la metodología general basada en la coraza (páginas anteriores de este capítulo). Sin embargo, es difícil determinar la distancia L a la que se extenderá la degradación hacia aguas abajo cuando la coraza sea un factor que la limita. En una primera aproximación y para una pendiente local constante del cauce durante la degradación, puede predecirse que la degradación se extenderá hacia aguas abajo hasta que el volumen degradado más las aportaciones tributarias, �! , sea igual al volumen anual estimado del material, �! , interceptado por la presa, multiplicado por el tiempo requerido de T años:

En contraste con la suposición de la pendiente constante, Pemberton y Lara (1984) comentan que la degradación se reduce hacia aguas abajo, y disminuye la profundidad de socavación en proporción a la carga de sedimentos recogida aguas abajo de la presa. Conforme el tramo de aguas arriba se acoraza, la degradación y el sedimento levantado se reducen ahí, y la degradación aumenta en la siguiente sección hasta que se acoraza, continuando este proceso con el tiempo, hacia aguas abajo.

Pemberton y Lara (1984) presentan un método que describe la degradación aguas abajo de la presa, que es aplicable en ausencia del acorazamiento, y se supone que la degradación continúa hasta que se establece una pendiente límite o estable, con un transporte de sedimentos nulo o despreciable. Dicha pendiente puede obtenerse por diferentes medios, incluido el diagrama de Shields (figura VI.1). La obtención de una pendiente más fuerte que la actual indica que el fondo permanecerá estable o que el método de evaluación de la pendiente no es aplicable para el caso en estudio. Los autores afirman que, dependiendo de las condiciones de campo, la pendiente estable podría considerarse de un medio de la actual.

Para ver con detalle los métodos que permiten estimar la degradación debajo de una presa, véase Yeo (1991).

VII.4. Alteración de la elevación del fondo causada por el talveg

Aunque no es tan evidente el movimiento del talveg (línea de más baja elevación del fondo a lo largo de un cauce) como sí lo es el movimiento del cauce en un río trenzado, aquél puede también hacer variar la elevación del fondo y cambiar el punto o el ángulo de ataque del flujo. Esto puede incrementar sustancialmente la socavación en pilas o estribos. Brice (1984) hace notar que el talveg migrante se presenta más en ríos sinuosos.

Sostiene Lacey (1930) que los tramos de ríos estables presentan con frecuencia una sección transversal semielíptica, con un tirante máximo, �!á! , para una sección semielíptica sobre un tramo recto (véase figura VII.10), igual al tirante medio multiplicado por 1.27 (tabla VII.4). El autor confirma la validez de esta relación para dos casos en que las relaciones medidas del tirante máximo al medio fueron de 1.26 y 1.23. El autor indica que el tirante medio es igual al radio hidráulico R= �/� , donde A es el área hidráulica y P el perímetro mojado. Sin embargo, en los ejemplos presentados por él no queda claro si el tirante medio es R o es el promedio de las profundidades verticales, y. Las diferencias entre y y R se reducen conforme aumenta el ancho. Para un cauce muy estrecho, Lacey (1930) afirma que el �!á! es equivalente al tirante medio (tabla VII.4).

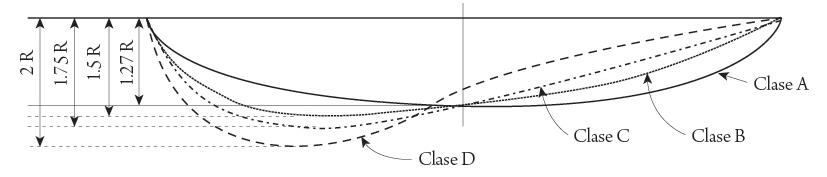
Figura VII.10. Tirante máximo en función de la curvatura (Lacey, 1930).

Tabla VII.4. Efecto de la curvatura en el tirante máximo (!!" es el tirante máximo en una curva y R es el radio hidráulico)

Curvatura Lacey (1930) !!" ! Neill (1973) !!" !

Sección muy contraída

en ángulo recto

Curva con márgenes altas y empinadas 2.25

Williams y Cozakos (1994), al determinar las profundidades de socavación para la protección de diques, consideraron la formación de talvegs con base en “la relación de Lacey del 25% del tirante para tramos rectos”.

Si se considera que el cauce tiene una sección tran sversal cosenoidal (véase figura VII.11), el tirante máximo para un ángulo de reposo del sedimento de Ф! !"# es de 1.69 R o 1.58 y, según Raudkivi, donde y se obtiene dividiendo el área de la sección transversal entre el ancho superior del cauce.

Figura VII.11. Secciones a límite y cosenoidal para la misma pendiente y arrastre de fondo (Vigilar y Diplas, 1997).

La relación propuesta por Lacey proporciona una estimación razonable del descenso del fondo debido a la presencia del talveg. La obtención del tirante medio con los diferentes tirantes de la sección en dicha relación proporciona valores algo conservadores de la profundidad de socavación, en comparación con predicciones equivalentes realizadas utilizando R. Con base en estas consideraciones, una primera estimación del tirante en el talveg, �!" , es:

�!" =1.27 y (VII.21)

donde y es, en efecto, el tirante obtenido con base en el nivel promedio del fondo.

Mahmood y otros (1988) presentan las ecuaciones siguientes para la predicción de la longitud de onda media, �! , y la amplitud (cresta a valle), ℎ! , para un talveg en meandro y en cauce recto con fondo arenoso (véase figura VII.12a):

�! = 8� (VII.22)

ℎ! = !!" !! !"#$!!" (VII.23)

donde W es el ancho de la superficie libre del agua (m), y=A/W es el tirante medio (m)

A es el área de la sección transversal (�! ), �! es la pendiente de energía (en decimales) �!" es la mediana de los diámetros del sedimento (m) se ha supuesto que la gravedad específica de la arena de cuarzo es �! = 2 65

Estas ecuaciones fueron obtenidas con base en datos de talvegs en meandros, medidos en once canales. La profundidad de socavación del talveg es entonces igual a la mitad de la amplitud del talveg en meandro, es decir, ℎ! /2, por lo que el tirante total en el talveg es:

�!" = � + !! ! = � 1 + !!!! !"#$!!" (VII.24)

Mahmood y otros (1988) presentan datos de mediciones en el canal Qadirabad-Balloki Link (véase figura VII.12b) que pueden utilizarse en una evaluación de las predicciones de las ecuaciones (VII.22) y (VII.23). Los datos indican que W = 114 m, y = 3.2 m, v = 0.81 m/s,

!! !0.000112, !!" ! 0.26 mm, y !! ! 1.3 para este canal, donde v es la velocidad media y !! es la desviación estándar geométrica de la distribución de los diámetros de las partícul as (recordar que !! puede estimarse con la ecuación !! ! !!" !!!" !

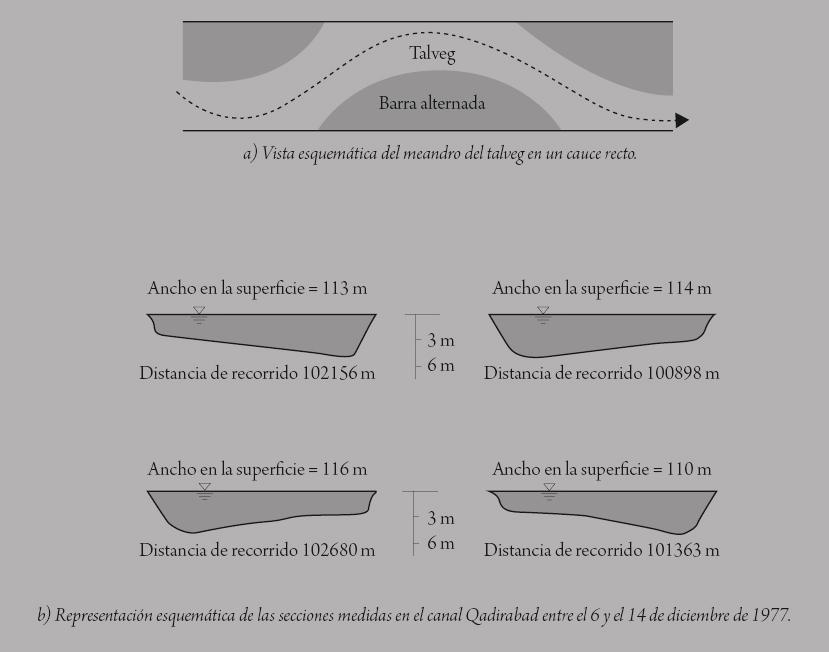
VII.12.

de talveg en un cauce recto (Mahmood et al., 1988).

Para estos datos, las ecuaciones (VII.22) y (VII.23) predicen las magnitudes de la longitud de onda y de la amplitud en el talveg, dando !! = 912 m y !! = 0.76 m, los que se asemejan razonablemente a los valores medios que fueron medidos: longitud de onda de 878 m y amplitud de 1.1 m. Se obtuvo que el tirante en el talveg fue de (y + !! /2) = 3.58 m o 1.12 y. Esto es menor de lo que arroja la ecuación (VII.21), lo que confirma que ésta da resultados conservadores.

Si el talveg en meandro coincide con la presencia de barras alternadas en el fondo, entonces, de acuerdo con las ecuaciones (VII.45) y (VII.46) de Yalin (1992), la longitud de onda y la amplitud de estas formas resultan de 684 m y de 0.30 m, respectivamente.

Figura

Variación

Adoptando �!" ≈ �! �!" para este análisis, las ecuaciones (VII.47), (VII.48) y (VII.49) de Ikeda (1984) arrojan valores de 4,380 m y 0.41 m. La predicción de Ikeda para la longitud de onda es muy superior a la de 878 m que fue la que se midió. En cambio, la predicción de Yalin es muy semejante a los datos medidos. Ambas predicciones para barras son del orden de la mitad de la amplitud medida del talveg (cresta a valle). Una predicción de la altura de la forma de fondo de h = y = 3.2 m (sección VII.7.2) es mucho mayor que la amplitud medida, aunque la altura promedio máxima de la duna (sección VII.7.1) de y/3 = 1.1 m sugerida por Nordin y Algert (1965) es igual que el valor de la amplitud medida de 1.1 m.

Resumen y comentarios

Con base en las discusiones anteriores, el tirante máximo en un talveg puede estimarse para un tramo recto como: �!" = 1.27 � o �!"

donde la amplitud h es la máxima de las amplitudes del talveg, ℎ! , obtenida de la ecuación (VII.19), o la altura de la barra alternada, ℎ! , estimada con las ecuaciones (VII.46) y (VII.49).

En la sección VII.3 se presentaron metodologías alternativas que utilizan procedimientos gráficos para redistribuir la socavación media a través de una sección transversal para considerar los efectos de talvegs y de curvas, y corresponden a los métodos de velocidad competente para estimar la degradación general. Adicionalmente, puede emplearse el método sugerido por Maza Álvarez y Echavarría Alfaro (1973) presentado en la propia sección VII.3.

Este método, que toma en cuenta la no uniformidad (tirantes variables) de la sección transversal del cauce, evalúa la máxima profundidad de socavación (presumiblemente incorporando efectos de talvegs) ajustando el tirante medio de socavación con la relación entre los tirantes máximo y medio del cauce antes de socavarse.

VII.5. Socavación en curvas

El flujo en un tramo curvo provoca interacción entre el gradiente vertical de velocidad y la curvatura del flujo principal, lo que produce corrientes secundarias que a su vez propician tirantes, velocidades y esfuerzos cortantes mayores en el lado exterior de la curva; esto termina por generar una socavación incrementada en la parte exterior de la curva, con mayor material depositado en los flujos más lentos del lado interior.

VII.5.1. Cuantificación de la socavación en curvas

Adoptando una sección transversal semielíptica, Lacey (1930) consideró las diferentes clases de secciones transversales que puede asumir un río con curvatura variable. La sección semielíptica fue mantenida para que el perímetro mojado y el área hidráulica se conservaran sin cambio al variar la curvatura, misma que imponía diferentes grados de traslación lateral en la frontera del canal (figura VII.10). Lacey (1930) hace un resumen de la influencia de la curvatura de un cauce en el tirante máximo (tabla VII.4), donde �!" es el tirante máximo en la curva y R es el radio hidráulico. Neill (1973) presenta los coeficientes (tabla VII.4) que recomienda el Congreso de Carreteras de India (1966) para estimar el tirante natural máximo, a partir del tirante de la sección media. Neill comenta que estos coeficientes, que se basan principalmente en consideraciones de la forma de la sección transversal, se derivan del trabajo de Lacey (1930). Para determinar las profundidades de socavación de diseño con el fin de proteger el pie de un dique, Williams y Kozacos (1994) analizaron la socavación en curva con base en los factores de Lacey de la tabla VII.4.

Neill (1973) supone que los términos “moderada” y “severa” de la tabla VII.4 toman en cuenta tanto el ángulo de deflexión como la relación entre el ancho del canal y el radio de curvatura; no se dispone de más datos que ofrezcan mayor precisión.

En línea con tales comentarios de Neill (1973), Galay et al. (1987) encontraron que el tirante máximo en curvas resistentes (margen exterior no erosionable) con ángulos de 60° en ríos con fondos de grava pueden estimarse con:

! = 1.2 + � /�! (VII.26)

donde y se define como A/W

A es el área de la sección transversal

W es el ancho de la superficie del agua

�! es el radio al centro de línea de la curva del río

También encontraron que los tirantes equivalentes en curvas con ángulos de 100° pueden describirse por:

! = 0 9 + 3 7� /�! (VII.27)

Galay et al. (1987) son los únicos investigadores en presentar relaciones empíricas que incluyen un complemento que considera la influencia del ángulo de la curva en el tirante máximo. Comentan que para ángulos internos de menos de 60°, la profundidad de socavación es muy pequeña. En contraste, para ángulos internos mayores de 100° se observaron grandes profundidades de socavación. Notaron los autores que las profundidades de socavación en curvas erosionables no eran tan grandes como aquéllas en curvas no erosionables, ya que el material erosionado en la margen aporta sedimentos a la hoya de socavación y limita su profundización.

Apmann (1972) hace referencia a la expresión de Chatley (1931): !!" ! = 1 + 2(! !! ) (VII.28)

donde �! es el radio exterior de la curva. Como puede verse, esta expresión es de la misma forma que las de Galay et al. (1987), y es intermedia entre ambas.

Thorne (1988) encontró que la socavación en curva para 70 curvas de un tramo del río Rojo, ubicado entre Arkansas y Louisiana, en Estados Unidos, puede describirse razonablemente por la ecuación (véase figura VII.13):

!!" !! = 2 07 0 19 �� �! /� 2 (VII.29)

donde �! es el tirante medio (A/W) aguas arriba de la curva. Thorne et al. (1995) reportan una comparación de la ecuación (VII.25) con ocho datos de laboratorio y con 257 curvas de ríos de gran diversidad en tipo y dimensiones, y localizados en diferentes partes del mundo. Se encontró que la ecuación (VII.29) concuerda razonablemente con los datos, y todas las predicciones cayeron en ± 50% de los valores observados, con la gran mayoría en la banda de +30% � ( 25%)

El Cuerpo de Ingenieros de la Armada de Estados Unidos (1994), con base en los datos de socavación en curva derivados de estudios realizados en el río Mississippi (Maynord y Hubard, 1993; Thorne y Abt, 1993), sin incluir los datos de laboratorio de estos últimos, presenta una curva “segura” de diseño para los tirantes máximos en curva:

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Figura VII.13. Predicción del tirante máximo de socavación en una curva, ybs, con base en la ecuación VII.32, sin factor de seguridad.

Se le llama una curva “segura” de diseño porque solamente el 5% de los datos utilizados para derivar la curva caen arriba de las predicciones conservadoras de la curva. Una expresión equivalente con mejor ajuste de los datos para derivar la ecuación (VII.30) es la propuesta por Maynord (1966) (véase figura VII.13):

Las ecuaciones de mejor ajuste (VII.29) y (VII.31) dan un grado pobre de ajuste a los datos medidos de socavación en curvas presentados por Maynord (1996). El autor supone que ello se debe a que, para todas las expresiones previas, la profundidad máxima de socavación en curvas es únicamente función de �! /� . Maynord (1996) opina que la ecuación (VII.30) es conservadora para la mayoría de los datos medidos, en particular para corrientes relativamente pequeñas que tienen avenidas de menor duración. Al incorporar la relación W/�! en las expresiones de socavación en curvas, el análisis de regresión de los datos de Thorne y Abt (1993) y de Maynord y Hubard (1993) indica una ecuación con mejor ajuste (figura VII.13):

Para 1.5 < !! ! < 10 y 20< � /�! < 125, !!"

= 1.8 0.051 �! � + 0.0084 � /�! (VII.32)

En la utilización de esta ecuación para fines de diseño, dentro del rango indicado, Maynord (1996) recomienda la adopción de un factor de seguridad igual a 1.19 si se desea que sólo el 2% de las predicciones no sean conservadoras; o 1.08 para un 10% de predicciones no conservadoras; si el factor de seguridad se elige de 1.0, las predicciones no conservadoras se elevan a un 25%. También recomienda Maynord (1996) que para un valor de �! /� < 1.5 se utilice �! /� = 1.5 . Asimismo, para W/ �! < 20 se utilice W/ �! = 20 . Los análisis de Maynord están dirigidos a corrientes arenosas, aunque también valen para gravas. Además, son aplicables a ríos con meandros naturales.

VII.5.2. Recomendaciones

Cuando sea aplicable, se recomienda utilizar la ecuación (VII.32) para estimar la socavación en curvas. Si falla, entonces debe usarse la (VII.29) o la (VII.31) si se prefiere.

VII.6. Socavación en confluencia

En particular, en ríos trenzados pueden ocurrir cambios del cauce en la confluencia de los brazos o ramas de un mismo río. En general, los flujos de dos cauces convergentes del mismo río se encuentran en el centro de línea de la confluencia, atacan el fondo del cauce y regresan a la superficie del agua por los costados de la confluencia; las corrientes helicoidales inducidas por el choque producen una poza de socavación con paredes empinadas. El flujo en una confluencia se asemeja al provocado por dos curvas colocadas de modo que coincidan sus

lados exteriores para formar un solo cauce; la poza de socavación de la confluencia se asemeja a la que ocurre en la parte exterior de las curvas (Chan, 1986). Estas confluencias se pueden formar aleatoriamente en tiempo y espacio para tramos trenzados.

Mosley (1982) reportó pozas de socavación con medición de tirantes en confluencias trenzadas del río Ohau (fondo de grava) en Nueva Zelanda. Estos tirantes llegaron a ser de dos a cinco veces el tirante medio de socavación de aguas arriba. Fahnestock y Bradley (1973) reportaron tirantes de socavación en confluencias, de hasta tres a cuatro veces los tirantes de aguas arriba, en el río Knick, en Alaska. Ashmore y Parker (1983) reportaron tirantes de socavación de más de seis veces el tirante de socavación de aguas arriba, en la confluencia de cauces ramificados. Las mediciones de socavación en el río Jamuna en Bangladesh muestran tirantes máximos de socavación en confluencias de ríos ramificados, de hasta cinco a seis veces el de aguas arriba (Klaasen y Vermeer, 1988). Con base en estas últimas mediciones, los autores comentan que los tirantes máximos de socavación en confluencias para ríos arenosos con una carga considerable de sedimentos en suspensión son men ores que para ríos con gravas.

La confluencia de los cauces puede provocar socavación marcadamente incrementada en pilas y estribos, debido a un aumento en la capacidad de transporte de sedimentos, por la concentración del flujo que ahí se produce; este aumento se debe a que se provoca en fuerte ángulo de ataque a causa del flujo combinado sobre esas estructuras.

Los parámetros que más influyen en la socavación por confluencia son: el ángulo de confluencia, los caudales, los tirantes, la pendiente del cauce, el diámetro del material del fondo y las características del cauce en la confluencia.

VII.6.1. Predicción cuantitativa de la socavación por confluencia

La complejidad de la socavación por confluencia condujo a Chow (1959) a sugerir que la generalización de este fenómeno no era ni posible ni deseable, y que el único método posible para el diseño sería el de estudios en modelos.

Mosley (1981), basado en datos de campo medidos en el río Ohau, en Nueva Zelanda, presenta criterios de diseño para la socavación en confluencias: �!" = 0.531 �!! !"! (VII.33) donde �! = �! + �! = la suma de los gastos de las respectivas ramas izquierda y derecha.

No se presentan diámetros del sedimento, aunque se nota que el río es de fondo con grava. Tampoco se incluye en la ecuación (VII.33) al ángulo de confluencia, �

Ashmore y Parker (1983) dan la siguiente ecuación para fondos de arena y grava y para ángulos de confluencia de � = 30° a 90°: !!"

! = 2.24 + 0.031 � (VII.34)

donde � es el tirante medio de las ramas, �!" es el tirante máximo de socavación y � es el ángulo de confluencia, en grados. Esta relación se obtuvo con regresión lineal por mínimos cuadrados, de datos que muestran mucha dispersión, y se derivó de datos de campo y de laboratorio con pendientes de 0.010 a 0.016, para sedimentos de diámetro uniforme con �!" = 1 1 �� y sedimentos de diámetro no uniforme con el mismo �!" de 1.1 mm.

Ashmore y Parker indican que para un mismo diámetro medio del material del fondo, el mal graduado sufre menor socavación que el bien graduado. Con base en mediciones de Mosley (1977), los mismos autores presentan una relación equivalente para socavación por confluencia en material cohesivo:

!!" ! = 1.01 + 0.030 � (VII.35)

Como puede notarse en las dos ecuaciones anteriores, la socavación por confluencia es esencialmente una función del ángulo de confluencia, aunque los autores indican que las relaciones son ligeramente modificadas por el gasto relativo de los dos cauces cuando éste es grande.

Con base en los trabajos de Ashmore y Parker, Amoafo (1985) presenta la siguiente fórmula para ángulos de confluencia de 30° a 90°:

Esta ecuación se basa en diámetros que varían de �!" = 0 95 �� para sedimentos no uniformes a �!" = 1.8 �� para uniformes.

Klaasen y Verneer presentan una ecuación basada en datos del río Jamuna, en Bangladesh, para ríos trenzados con fondo arenoso y mucho material en suspensión:

MANUAL

Esta ecuación es válida cuando la relación entre el gasto menor !! y el mayor !! se encuentran en el rango !!! ! !! !! ! !. Si !! !! ! !!!" ya no influye ! . Estos autores atribuyen la diferencia entre (VII.34) y (VII.37) a la diferencia entre los sedimentos trasportados.

La figura VII.14 muestra las variaciones de las ecuaciones (VII.34), (VII.35) y (VII.37) en función de los sedimentos transportados.

(VII.37)

Figura VII.14. Predicción del tirante máximo de socavación en una confluencia.

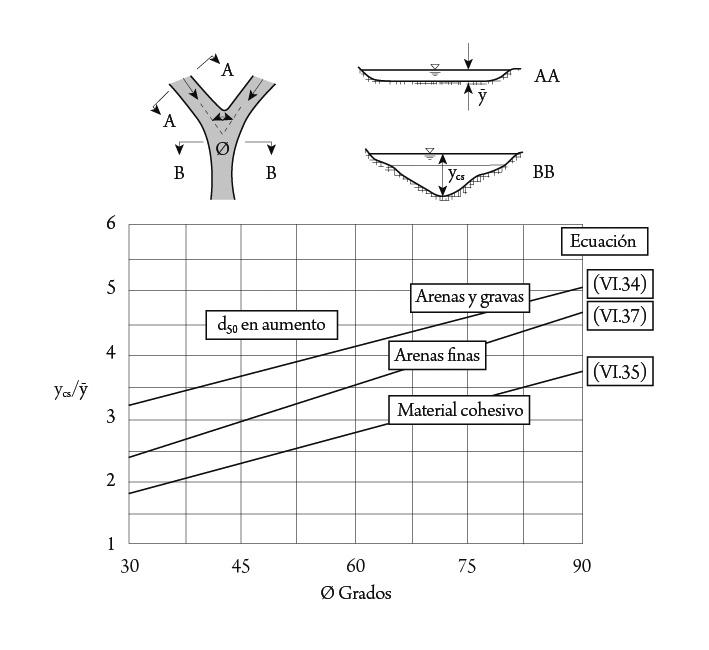
VII.6.2. Comentarios

El tirante máximo de socavación en una confluencia, �!" , puede calcularse con las ecuaciones (VII.34), (VII.35) o (VII.37), dependiendo de los sedimentos transportados (figura VII.14), con el ángulo de confluencia dado en grados. Debe notarse que las predicciones de estas ecuaciones se basan en tirantes obtenidos en la poza de socavación y que son medidos a partir de la superficie del agua, misma que generalmente está sobreelevada (Ashmore y Parker, 1983). Se ha notado, asimismo, que el material mal graduado presenta una socavación por confluencia menor que el material bien graduado para sedimentos del mismo diámetro medio.

Ashmore y Parker (1983) observan que los ángulos de confluencia en la naturaleza rara vez exceden los 100º. Para este ángulo, las ecuaciones (VII.34), (VII.35) y (VII.37) predicen un valor máximo de �!" � de 5.34. Este valor concuerda con las observaciones de campo y de laboratorio discutidas antes.

VII.7. Descenso del nivel del fondo por la formación de ondas

Para la mayoría de los caudales que provocan el movimiento general de sedimentos, se forman dunas u ondas que migran a través del sitio en estudio. La magnitud de tales ondas influye en la socavación de puentes, debido a que las depresiones de éstas causan que las elevaciones del fondo disminuyan momentáneamente y en forma local, conforme dichas ondas se propagan. La rugosidad del fondo determinada por las dunas afecta también en forma importante la relación gasto-tirante durante las avenidas.

Los perfiles que se forman en fondos arenosos (figura VII.15) se clasifican en fondo plano, rizos, dunas, fondo de transición, antidunas y charcas y vertederos (ASCE Task Force on Bed Forms in Alluvial Channels, 1966). En la figura VII.16 se ilustra la influencia típica que sobre la socavación local en pilas tiene la migración de las dunas.

En ríos con gravas, la migración de las formas del fondo ocurre cuando se da el movimiento de barras o dunas de grava. Las barras son depósitos relativamente grandes que se presentan generalmente en ríos trenzados o con meandros. En cruces de puentes, esta migración de barras puede reducir su área hidráulica y desviar el flujo, con lo que puede incrementarse la profundidad de socavación.

VII.7.1. Predicción cuantitativa del descenso del nivel del fondo por las dunas del sedimento

La predicción de la socavación por las formas del fondo es un proceso de dos etapas que requiere primero la estimación del tipo de forma de fondo, y después la altura de dicha forma.

Figura VII.16. Evolución típica de la socavación local en el tiempo, en una pila cilíndrica para condiciones de fondo vivo (Lauchlan, 1999).

Se dispone de métodos para predecir los tipos de perfil del fondo que ocurren en fondos arenosos, basados en la combinación del flujo y de los parámetros del sedimen-to (figuras VII.17 y VII.18).

La figura VII.17 (Simons y Richardson 1966) es quizá la más directa para predecir formas del fondo, donde la potencia de flujo Ω=!! V; el esfuerzo cortante del fondo !! =ρgy !! ; y y V son el tirante y la velocidad medios; ρ es la densidad del flujo; g es la aceleración de la gravedad; y !! es la pendiente del cauce. Esta figura sólo es aplicable a fondos arenosos y se basa en muchos datos de laboratorio y de varios ríos y canales. Definamos “diámetro de caída” como el diámetro de una esfera con una gravedad especifica !! = 2.65 que se asienta con la misma velocidad que la partícula en cuestión, aislada y en reposo, en agua destilada de extensión infinita a 24º C.

La figura VII.18 de Van Rijn (1984), que se basa en datos de laboratorio y de campo, utiliza los parámetros adimensionales:

Figura VII.15. Formas de fondo que ocurren al aumentar la resistencia al flujo en cauces aluviales (Simons y Richardson, 1966).

Figura VII.17. Ocurrencia de formas de fondo en función de la potencia unitaria de flujo y la mediana de los diámetros de caída (Simons y Richardson, 1966).

Figura VII.18. Clasificación de las formas de fondo en términos de parámetros adimensionales de flujo y del sedimento (Van Rijn, 1984).

En las ecuaciones anteriores, T es un parámetro de transporte; !! ! es la velocidad de corte relativa a la rugosidad de los granos; !!! es la velocidad de corte crítica determinada con el diagrama de Shields (figura VI.1); !! es una representación adimensional del diámetro de las partículas; !!" es la mediana del diámetro del sedimento; !! es la gravedad específica del sedimento; ! es la viscosidad cinemática del fluido; V es la velocidad media del flujo; C’ es el coeficiente de Chezy debido a la rugosidad de los granos (!! ! ⁄s); R es el radio hidráulico del cauce, y !!" es el tamaño de partícula para el cual el 90% es más fino, en peso.

La figura VII.15 quizá sea más aplicable que la VII.14 para los regímenes de flujo bajo y de transición, toda vez que se basó en un gran número de datos de campo con tirantes pequeños y grandes. Julien y Klaasen (1995) recomiendan se tenga cuidado en la aplicación de la figura VII.15 para ríos grandes, particularmente al considerar formas de fondo correspondientes a

regímenes de flujo superiores, que la propia figura predice que ocurrirán para T > 25. Para ríos grandes, el régimen bajo está en contraste, ya que también ocurre para T > 25, con datos medidos de regímenes bajos que presentan los autores para T ≤ 50.

Se ha notado que las arenas forman fondos con tamaños de granos bastante uniformes, mientras que los fondos con gravas presentan un rango más amplio de diámetros, variando de arenas finas a boleos grandes. Como se vio antes, se dispone de métodos para predecir la ocurrencia de formas de fondo en arenas, con base en la combinación de resistencia de flujo y de los sedimentos.

Yalin (1992) presenta las siguientes expresiones para predecir las magnitudes promedio de las longitudes y alturas de rizos, dunas y barras alternas:

Longitud de rizo �! , para ��∗ <10 (��∗ es el número de Reynolds de los granos): !! !! !í! = 4� 1 � ! (VII.41)

en que �! !í! = 2650 ! !! !!

d es el diámetro representativo del material

�! = ��! � ! �� !

�! es la densidad del sedimento

ρ es la densidad del agua

� es la viscosidad cinemática del agua

� = � /21 !.!

η= � /�!

� y �! son los parámetros adimensionales de Shields. Recuérdese que

� = �/ �! 1 ���

Altura de rizo ℎ! , para ��∗ <10

ℎ! = 0.14 �! �� � ! ! (VII.42)

� = 1 para ε≤ 1

� = � 2 � para 1 < � < 2

� = � 1 /10

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Longitud de duna �! , para ��∗ >25

�! = 6��! (VII.43)

y es el tirante

�! = 1 + 0.01 � 40 � 400 � !

z = y/d

� = 0 055 � !.! + 0 04 ��∗

Altura de duna ℎ! , para ��∗ >25

ℎ! = 0.06�! � � ! ! 1 � !.!"# (VII.44)

� = � 1 / �! 1

�! = 14 1 � !.!!"! + 2

Longitud de barra �! = 6W (VII.45)

W es el ancho del canal

Altura de barra ℎ! = 0.18� � ! !" (VII.46)

z = y ⁄ d

Ikeda (1984) proporciona otras expresiones para la longitud y la altura de barras alternadas en una sola línea:

Longitud de barra �! , para Fr= � / �� !.! < 8

�! = 5 ��/�! !.! (VII.47)

donde �! = 0.0293 �/�!" ! !"

Si Fr≥0.8, y 4<(W ⁄ y)<70, entonces

�! =181 W�! � /� !.!! (VII.48)

Altura de barra ℎ! , para 6<(W ⁄ y)<40

ℎ! = 1.51 � �! � /� ! !" (VII.49)

Ikeda (1984) hace notar que las barras alternadas de una sola hilera desaparecen para W/y > 70 a 100, dando lugar a barras alternadas de doble hilera conforme W/y aumenta. Las ecuaciones VII.47 a VII.49 son válidas para la mayoría de las condiciones en las que se observan barras alternadas de una sola hilera.

El método de Van Rijn (1984) para predecir las dimensiones de las formas de fondo no es válido para rizos, sino que está restringido a dunas en los regímenes bajo y de transición. Van Rijn obtuvo las siguientes ecuaciones para la altura media de las dunas y su longitud, basado en parámetros adimensionales de campo y de laboratorio:

Para 0 < T < 25 (véase ecuación VII.38),

También para 0 < T < 25,

(VII.50)

de acuerdo con las ecuaciones (VII.50) y (VII.51), �! =7.3 y, expresión que se parece a la de Yalin (1964), basada en campo y laboratorio, que afirma que �! = 5� para dunas. Nordin y Algert (1965) comentan que la longitud de las dunas es, en general, mayor que 5y. Julien y Klaassen (1995) concluyen que el método de Van Rijn generalmente subestima la altura de las dunas. Para ríos grandes, el régimen inferior ocurre para T > 25. Además, en contraste con las indicaciones de las ecuaciones (VII.50) y (VII.51) en cuanto a que la altura y la longitud de las dunas disminuyen en el rango 10 < T < 25, la altura y la longitud aumentan con el gasto y con T, mientras que el valor de ℎ! /�! permanece relativamente constante. La validez de usar T para describir la variación de los parámetros de las formas de fondo también parece ser cuestionable en un sentido más general. Los citados autores presentan ecuaciones alternas para régimen inferior:

!! ! = �! !!" ! ! ! , � !! !! = �! ! !!" ! ! (VII.52)

donde �! � �! son coeficientes tales que el 95% de los datos usados permanecen en los rangos 0.8 < �! < 8 y 0.5< �! < 8. Las magnitudes medias de los parámetros de las dunas caen en �! = �! = 2.5. Así,

ℎ! = 2.5� ! ! �!" ! ! (VII.53) y �! = 6.25� (VII.54)

Las longitudes de onda observadas para las antidunas, �! , coinciden razonablemente bien con una relación propuesta por Kennedy (1963): �! = 2� ! ! ! (VII.55)

Para flujo supercrítico, la relación ℎ! /�! para las antidunas no excede a aquélla de las ondas superficiales asociadas. Con las olas superficiales rompiendo sobre las antidunas para velocidades altas, tal relación para las antidunas puede predecirse conservadoramente con base en Kennedy (1963):

ℎ! /�! = 0.14 (VII.56) donde ℎ! es la altura de las antidunas.

La experiencia en laboratorio de Shen y otros (1969) propone que, para estimar las variaciones en la profundidad de socavación debida a dunas moviéndose a través de la poza de socavación, se agregue a la profundidad máxima de socavación la mitad de la altura esperada de las dunas.

Con excepción de la ecuación (VII.52), las demás, desde la (VII.41) hasta la (VII.56), estiman las magnitudes promedio de las formas de fondo cuando ya están equilibradas.

Para tomar en cuenta las variaciones en magnitud de las formas de fondo, deben considerarse en el diseño de pilas y estribos las máximas dimensiones de dichas formas. Con base en razonamientos teóricos junto con datos empíricos, Yalin (1964) concluye que las alturas de las dunas en promedio no pueden exceder un sexto del tirante. Nordin y Algert (1965) sugieren que es más apropiada una altura máxima de duna igual a y/3. Neill (1973) comenta que las alturas de dunas y barras migrantes en ríos aluviales pueden ser hasta de la mitad del tirante. Williams y Cozakos (1994) adoptaron una altura de forma de fondo de y/3 para calcular la profundidad de socavación de diseño para la protección del pie de un dique. Lagasse y otros (1995) consideran que la altura máxima de una duna es igual al tirante promedio. Julien y Klaassen (1995) notaron que en el río Rhine la altura promedio de las dunas era de un medio a dos tercios de la altura máxima. Los rangos de �! � �! mostrados con la ecuación (VII.52) reflejan la gran dispersión en las magnitudes medidas de las formas de fondo (�! entre 0.8 y 8, y �! entre 0.5 y 8). Así, las dimensiones máximas serían:

ℎ! = 8� !.! �!" ! ! (VII.57)

�! = 64� (VII.58)

VII.7.2. Revisión y comentarios

El tirante máximo debido a la migración de las formas de fondo a través del sitio del puente, �!" , puede estimarse como el mayor entre

�!" = y+(y/2) o �!" = y+(h/2) (VII.59)

donde y es el tirante en ausencia de formas de fondo, y h es la máxima altura de las formas de fondo, calculada con las ecuaciones (VII.41) a (VII.58), para los tipos esperados de las formas de fondo (figuras VII.17 y VII.18). Esta metodología es más aplicable a la migración de dunas, barras o antidunas. Los rizos son muy pequeños y no afectan las magnitudes de socavación. Se requiere criterio para aplicar la ecuación (VII.59), ya que en muchas ocasiones el uso de la primera de las expresiones (�!" = 1.5 y) puede llevar a predicciones demasiado conservadoras –por no decir fuera de la realidad– de la profundidad de socavación.

Vale la pena mencionar que Raudkivi (1990) comenta que las dunas desarrolladas en un fondo con sedimentos bien graduados son muy diferentes que aquéllas formadas en un fondo con sedimentos uniformes. Las formas de fondo en los flujos con fuerte carga de sedimentos coloidales (arcillas) en suspensión son de dimensiones menores, su desarrollo es tardado y la transición a fondo plano ocurre más pronto que en flujos sin arcillas en suspensión.

VII.8. Erosión lateral

Los ríos son dinámicos y presentan zonas cambiantes de concentración de flujo; la línea de las márgenes también es cambiante; existe migración de meandros, tanto lateralmente como a lo largo del cauce, y hay ríos trenzados con cauces variables que interactúan.

La variabilidad en la trayectoria del flujo puede tener graves consecuencias si no se toma en cuenta para el diseño de puentes, que son estructuras fijas. La inestabilidad lateral puede cambiar el ángulo o el punto de ataque de un río en un cruce, acentuando probablemente la socavación local y por contracción; puede socavar pilas y estribos localizados fuera del cauce principal; puede atacar y erosionar los taludes de los estribos redondeados; puede cortar terraplenes de acceso, dando por resultado el flanqueo de los puentes; puede obstruir el área hidráulica de un puente en una curva, con el desarrollo de barras en el interior de las curvas; o simplemente puede aumentar la socavación de las pilas en el cauce principal. Cuando la falla

de una margen es por deslizamiento rotacional, las presiones laterales sobre las pilas en la zona de deslizamiento pueden desplazar la cimentación de las pilas o fracturar pilas y pilotes.

Los cambios de los ríos pueden ser graduales o ser el resultado de una sola creciente. Las direcciones y magnitudes de tales cambios son muy difíciles de predecir. Sin embargo, debe incorporarse en el diseño de puentes la evaluación de cambios potenciales para asegurar su comportamiento satisfactorio durante su vida de diseño. Por ejemplo, para identificar la erosión de la cimentación ubicada fuera del cauce principal, debe efectuarse el análisis de la erosión de las márgenes y de la migración lateral.

La inestabilidad lateral puede ser por a) erosión de las márgenes, b) socavación en curva, c) ensanchamiento natural del cauce y d) movimiento de los cauces.

a) La erosión general de las márgenes puede ser causada por el flujo; por la acción de las ondas generadas por el viento o por el hombre; por mecanismos climáticos tales como heladas o deshielo, desecación, filtraciones y escurrimiento superficial, o por mecanismos de falla masiva como deslizamientos a lo largo de una falla profunda, deslizamientos superficiales y fallas de bloques.

Cuando un cauce se degrada, el río puede atacar sus márgenes, o la propia degradación puede provocar la remoción del material de soporte de los bordos y aumentar la presión de poro durante la rama de declinación del hidrograma de la avenida, lo que a su vez puede conducir a la falla de los bordos y al ensanchamiento del c auce.

La disminución del aporte de sedimentos puede también provocar erosión marginal. Esto fue lo que sucedió en el río Five Mile en Wyoming, EUA (Lane 1955 b); al aumentar considerablemente el caudal, ocurrió degradación hasta que los fragmentos de roca fueron descubiertos y los bordos atacados. El ancho del cauce se volvió muy variable: de 10 m en secciones rocosas (cañón) a 300 m en secciones erosionables. También, con el aporte de sedimentos de las márgenes puede reducirse la velocidad de descenso del fondo.

b) La socavación en curvas provoca, como ya se vio, inestabilidad lateral.

c) El ensanchamiento de un cauce puede estar acompañado de un depósito o azolvamiento; el flujo va incrementando el ancho conforme ocurre el depósito y los tirantes disminuyen.

Figura VII.19.Tipos de desarrollo de los meandros (se indica la dirección del flujo con las líneas discontinuas tendiendo hacia líneas continuas): a) extensión; b) traslación; c) rotación; d) conversión a una gasa compuesta; e) corte en cuello por cierre; f) corte diagonal por desplazamiento; g) corte en cuello por desplazamiento (Brice y Bodgett, 1978).

El ensanchamiento puede llevar a varios efectos adversos en cuanto a socavación en puentes: aumento de la socavación en los estribos o su flanqueo; c ambio de alineamiento del flujo respecto a los ejes de las pilas; socavación mayor en las pilas que originalmente no estaban ubicadas en el cauce principal, y aumento de cuerpos flotantes por la erosión marginal, que es la fuente principal de dichos cuerp os.

Los cauces pueden clasificarse de la siguiente manera:

! Con meandros

! Trenzados, con islas pequeñas y cauces entrelazados

! Divagantes, con tramos de meandros alternando con tramos trenzados y con islas semipermanentes.

Los cauces ramificados pueden considerarse un subconjunto de los trenzados, aunque con islas más grandes.

d) Para cada uno de los tres tipos de ríos existen movimientos del cauce que se manifiestan a lo largo de la cuenca, pero podrían no hacerlo en la vecindad de un puente. El incremento de los movimientos, que puede tomar décadas para llegar a las cercanías del puente, puede ser acelerado por actividades humanas, tales como el uso de la tierra, extracción de grava y arena, o la remoción de la vegetación adyacente al río. En tramos trenzados, la dirección de los cambios del cauce puede variar dramáticamente. Para tramos de meandros, el cambio típico del cauce está dirigido hacia afuera o hacia aguas abajo (figura VII.19), aumentando la sinuosidad del tramo. Esta sinuosidad provoca periódicamente el corte de meandros para balancear los efectos de los cambios continuos del cauce.

VII.8.1. Comentarios

Los factores que influyen en la inestabilidad lateral pueden ser clasificados en función de la geomorfología del cauce; de la localización, en su caso, del cruce con respecto al cauce; de las características del flujo y de las características de los materiales de las márgenes y del fondo. Neill (1983) afirma que para una curva de un río con meandros, el límite superior de la rapidez de la erosión marginal está controlado por el transporte medio anual de sedimentos en el fondo. Hooke (1979) asocia la erosión y el derrumbe de las márgenes con la influencia de los niveles de las crecientes y condiciones previas de precipitación. El propio Hooke (1980) concluye que la rapidez de la erosión marginal depende más de la duración de las avenidas que de las magnitudes de los caudales, y que esta rapidez es proporcional a la raíz cuadrada del área de la cuenca.

VII.8.2. Predicción cualitativa

La evaluación cualitativa de la inestabilidad lateral y de la velocidad de erosión de un cauce puede hacerse con base en:

§ Fotografías aéreas o mapas topográficos que indiquen la variación de la línea marginal en un periodo determinado.

§ Serie histórica de secciones transversales levantadas.

Además, la forma de los meandros cambia en respuesta a las variaciones de aportación de sedimentos y a la capacidad de transporte de sedimentos (sección VII.2). Un incremento del gasto líquido o una disminución del gasto sólido puede provocar una reducción de la pendiente, que provoca a su vez un incremento de la tendencia a divagar.

VII.8.4. Predicción cuantitativa de la velocidad de erosión lateral en curvas

La estabilidad de un río puede ser inferida de sus características vistas en planta. Brice (1982), basado en datos de campo, encontró una fuerte correlación entre la variabilidad del ancho del cauce (figura VII.20) en una serie de meandros, y la rapidez de la migración lateral. Los cauces de ancho constante con depósitos angostos de sedimentos (barras puntuales) o sin ellos en la parte interior de las curvas son los más estables. En cambio, un cauce con meandros y ancho variable, con barras amplias e irregulares en el lado interior de las curvas, tienden a ser muy inestables. La línea punteada de la figura VII.21 separa la mayoría de los cauces de ancho constante, de aquéllos más anchos en curvas y en cauces trenzados, para los datos mostrados. Los cauces trenzados sin barras son relativamente anchos y por ello quedan abajo de la curva arbitraria (datos marcados como rombos en la propia figura VI.18.).

Excluyendo los cauces trenzados con y sin barras, Richardson y otros (1990) indican que los resultados obtenidos de la figura VII.21 proporcionan una primera idea de la rapidez de la migración lateral de una curva, sin considerar las condiciones hidráulicas ni las características del sedimento. El hecho de que algunos cauces en curva de ancho considerable no exhiban migración lateral, refleja que ésta puede ocurrir cíclicamente, lo cual debe tomarse en cuenta en la evaluación de la estabilidad lateral de un cauce.

Las indicaciones de la figura VII.19 pueden ser utilizadas para evaluar las posibles direcciones de los movimientos de las curvas.

La línea discontinua de la figura VII.21 tiene la ecuación:

� = 0.01 � (VII.62)

donde � � �ñ� es la rapidez de la migración lateral y � � es el ancho del cauce. Con base en datos de campo, Hooke (1980) obtuvo una relación entre la velocidad de migración de un meandro, � � �ñ� , y el área drenada, � ��! :

� = 0 0245 �!.!" (VII.61)

Puesto que es de esperarse que el ancho de un cauce varíe con la raíz cuadrada de A, la ecuación (VII.61) implica que � es aproximadamente proporcional al ancho del cauce, que es lo que indica la ecuación (VII.62).

Después de investigar la relación entre � � y varios parámetros que se supone influyen en la rapidez de migración del cauce, Hooke (1980) encontró que el porcentaje de limos y arcillas en los materiales de las márgenes fue el factor dominante para 11 cauces en Devon. Sin

embargo, se encontró que la erosión puede ser influenciada por una compleja combinación d e otros factores. Los otros parámetros que influyen en la rapidez de migración considerados por Hooke (1980) incluyen la longitud del tramo del cauce, su pendiente, su radio de curvatura, la altura de la margen y la existencia de estratos de grava.

En la aplicación de métodos de dendrocronología para los árboles que se desarrollan en las barras del río Beatton en Columbia Britanica, Hickin y Nanson (1975 y 1983) señalan que:

para 0 125 < � �! ≤ 0 32 , � = 2 0 � �! (VII.62a)

para � �! > 0.32, � = 0.2 �! � (VII.62b)

donde �! es el radio de curvatura promedio para la margen interior de la curva.

Con base en el análisis de troncos de árboles y de fotografías aéreas, Hickin y Nanson (1984) presentan datos de rapidez de migración lateral para 189 curvas de 21 ríos con meandros de una sola hebra (sin trenzas), con arcillas, arena y grava, ubicados en el oeste de Canadá. Estos datos muestran que las expresiones obtenidas en el río Beatton (ecuaciones VII.62) no pueden generalizarse (véase figura VII.22, en que la rapidez de migración se expresa como � � ). No obstante, Hickin y Nanson (1984) muestran que la velocidad máxima de migración lateral en curvas ocurre cuando �! � vale de 2 a 3. Para valores mayores o menores que éstos, la velocidad de migración en la curva se reduce f uertemente; para !! ! < 2 � 3, aumenta la posibilidad de que haya un corte de meandros.

Es interesante notar que la velocidad máxima de migración lateral ocurre para geometrías de meandros ( �! � ) atribuidas nominalmente a meandros plenamente desarrollados (sección VI.4). Además, los autores encontraron que muchas curvas no migraron durante el periodo de investigación, lo que refleja aquello que indican los datos que se muestran en la figura VII.21. Tales datos destacan la naturaleza intermitente del proceso de migración de los cauces. Así, cualquier evaluación de velocidad de migración de curvas individuales podría requerir la consideración de escalas importantes de tiempo si se pretende determinar la velocidad de migración de largo plazo; sin embargo, puede determinarse una velocidad media de migración de curvas a lo largo de un tramo de cauce con longitud razonable, con base en registros más cortos.

Hickin y Nanson (1984) transformaron velocidades de migración no nulas a una curvatura de referencia (�! � = 2.5, donde W se mide de cresta a cresta de las márgenes) y

demostraron que �! ! (rapidez de migración lateral para �! � = 2.5) es una función simple de la potencia del cauce por unidad de longitud del mismo � (� = �� � = ����� = ������ = ������ = ���� ), de la altura de la margen exterior (del cauce más profundo a la cresta de la margen) ℎ , y de un coeficiente de resistencia a la migración lateral �! (figura VII.23), donde:

! ! ! = Constante para una resistencia dada de la margen = ! !! ,

El coeficiente �! es, a su vez, función de un rango de variables de resistencia de la margen, siendo que a mayor valor de �! , mayor resistencia a la erosión. Los autores seleccionaron la textura (rango de diámetro de los granos en vez del más preciso pero quizá menos apropiado diámetro de los gramos) de los materiales de la margen exterior como la principal variable que influye sobre �! , y demuestran que �! varía en forma similar a la función de movimiento de Shields (figura VII. 24).

Puede hacerse una evaluación de la textura de la margen para obtener el coeficiente �! , el cual puede indicar la velocidad de migración lateral de una curva dada, para una potencia dada del cauce y una altura de la margen (bordo). Este procedimiento, sin embargo, no ha sido utilizado ampliamente debido quizá a que las relaciones de las figuras VII.23 y VII.24 requieren ser confirmadas como de uso general, con base en datos adicionales que puedan validarlas. Es claro que dichas relaciones, obtenidas con base en ríos de Canadá occidental, quizá no sean aplicables a otros ríos fuera de esta región, a menos que sean similares en cuanto a hidrología y geomorfología. Además, continúa el debate acerca de la influencia de la fuerza tractiva sobre la rapidez de la erosión marginal, en comparación con el papel de los mecanismos de falla, por ejemplo. Con esto en mente, el método puede utilizarse con criterio para tener idea de las tendencias en cuanto a la velocidad de migración de un río dado.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

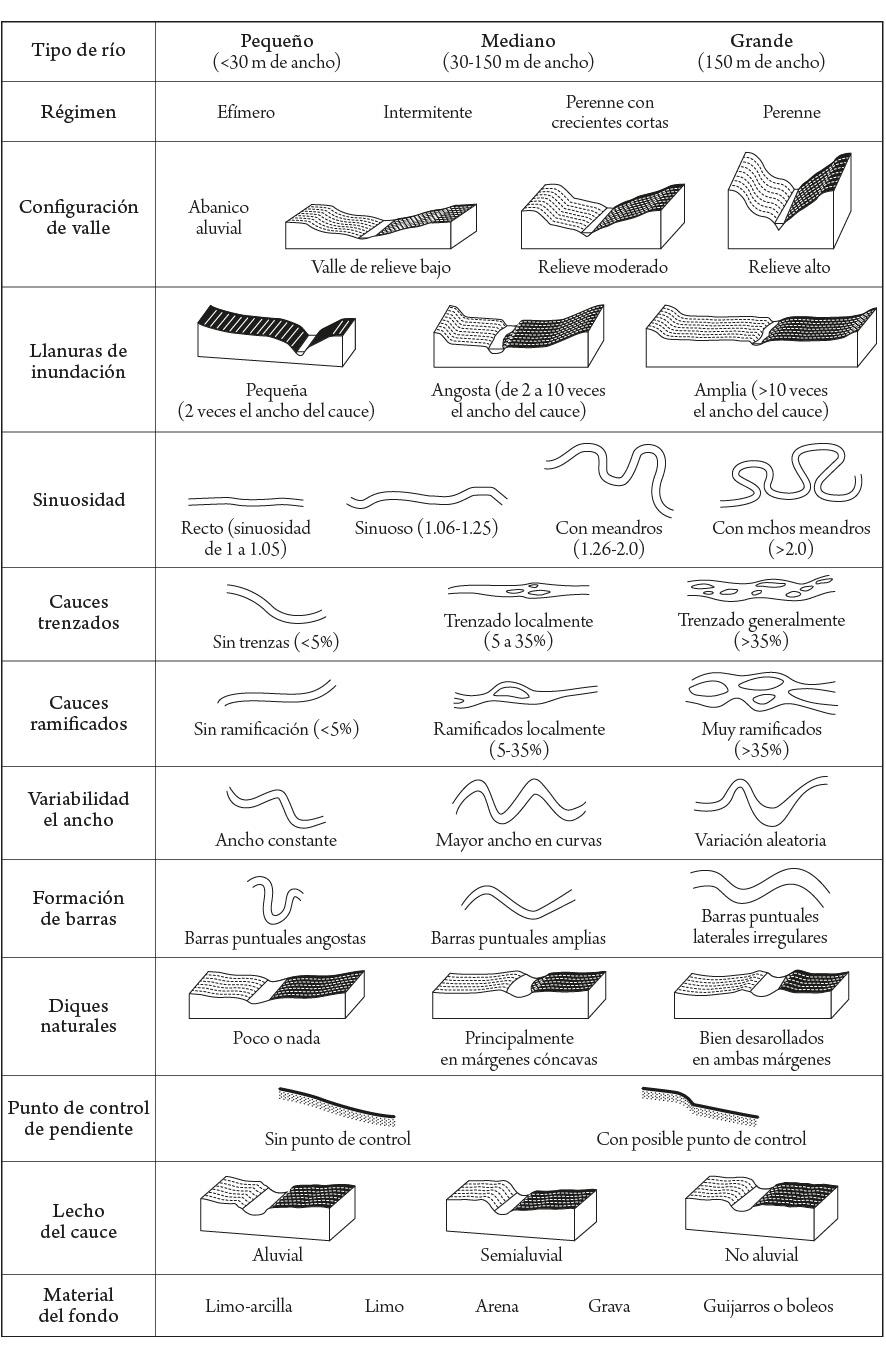
Figura VII.20. Características fluviales que influyen en la estabilidad de los cauces (adaptado de Brown et al., 1981, y Lagasse et al., 1995).

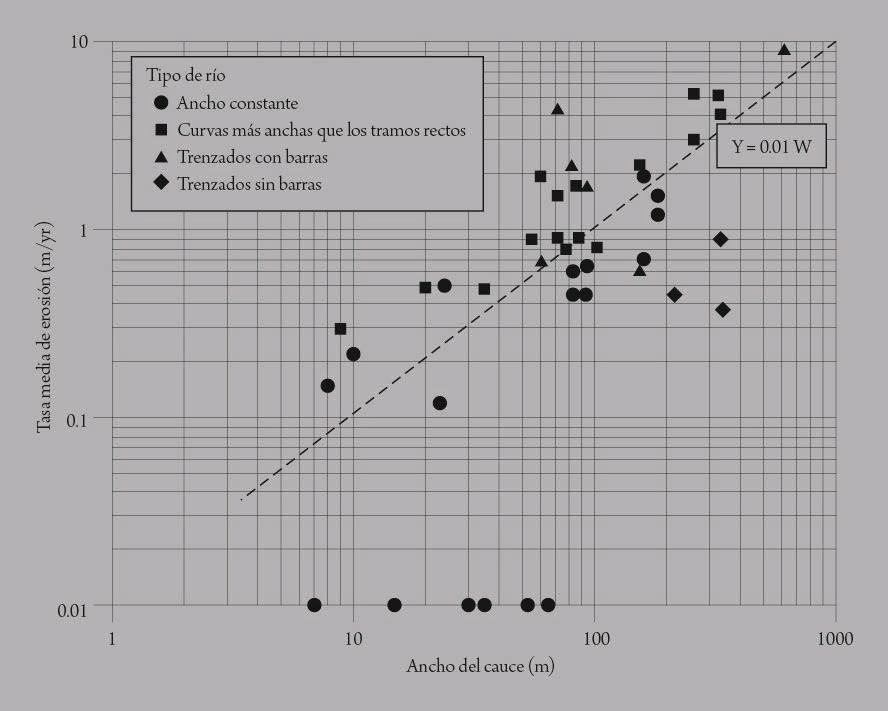
VII.21. Rapidez media de erosión marginal en función del ancho del cauce para diferentes tipos de ríos (Brice, 1982).

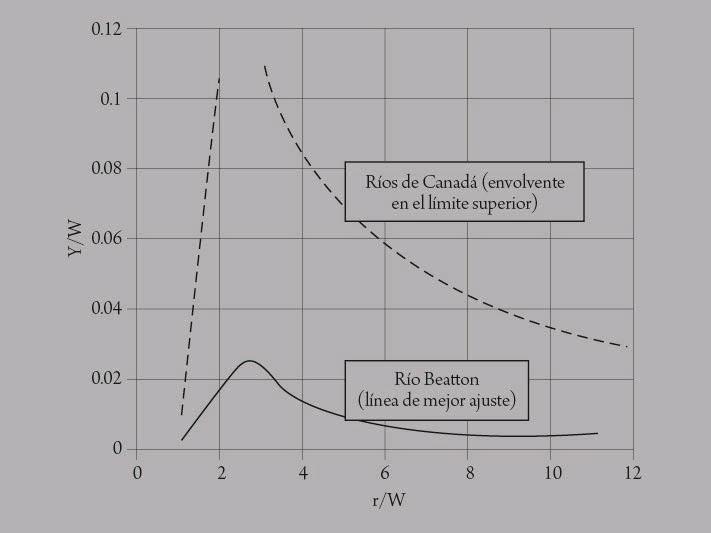
Figura VII.22. Rapidez de migración de una curva (en ancho del cauce/año) en función de su curvatura relativa (Hickin y Nanson, 1984).

Brown et al. (1981) comentan que la extensión de la migración lateral de un cauce depende principalmente del ancho del meandro, de la rapidez y dirección de la migración lateral del cauce, y del posible cambio de alineamiento provocado por el desarrollo de cortes de meandros aguas arriba y aguas abajo del sitio de estudio.

Pueden estimarse cuantitativamente las tendencias de migración lateral con base en las relaciones de morfología de meandros presen-tadas en la sección VI.4. Una vez determinado el ancho máximo probable del cauce con sus márgenes al tope para la avenida de diseño, pueden evaluarse la máxima longitud de onda del meandro, la amplitud de onda y el radio de curvatura del meandro, con base en las ecuaciones (VI.10).

Figura

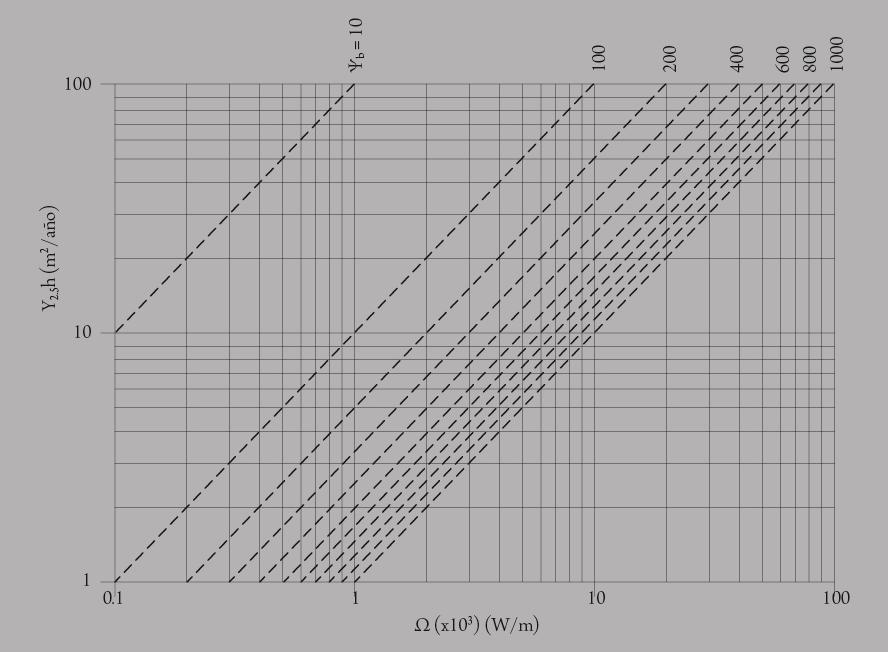
Figura VII.23. Rapidez de migración lateral en función de la curvatura del cauce, de su ancho, de la altura de la margen exterior, de la potencia de flujo y de un coeficiente de resistencia a la migración lateral (Hichin y Nanson, 1984).

Tales longitudes pueden utilizarse junto con fotografías aéreas para evaluar los posibles impactos de las tendencias de migración del rio sobre proyectos de ingeniería.

La comparación de las sinuosidades teóricas con las existentes puede indicar alguna tendencia del cauce, ya sea para que tome un curso recto o para que desarrolle curvas. Los anchos teóricos y los existentes de los meandros pueden compararse para determinar cuánto podrían moverse. Una comparación de las longitudes de onda teóricas y existentes puede dar una idea de la posible migración de las curvas de los meandros a lo largo del cauce.

VII.8.5. Predicción cuantitativa de la velocidad de erosión lateral por ensanchamiento de cauces

Una vez que se han determinado la pendiente de un cauce y su tirante para un fondo alterado por degradación o por depósito, puede evaluarse el ensanchamiento del cauce asociado a la degradación o depósito utilizando la ecuación de continuidad. Maza Álvarez y Echavarría Alfaro (1973) proponen calcular de esta manera el ensanchamiento del cauce asociado con la degradación (sección VII.3.3), ajustando el ancho para el tirante de socavación o btenido, hasta que la velocidad media del cauce coincida con la velocidad límite para el material de las márgenes. Posiblemente este método sea particularmente apropiado para estimar el ensanchamiento del canal asociado con el depósito.

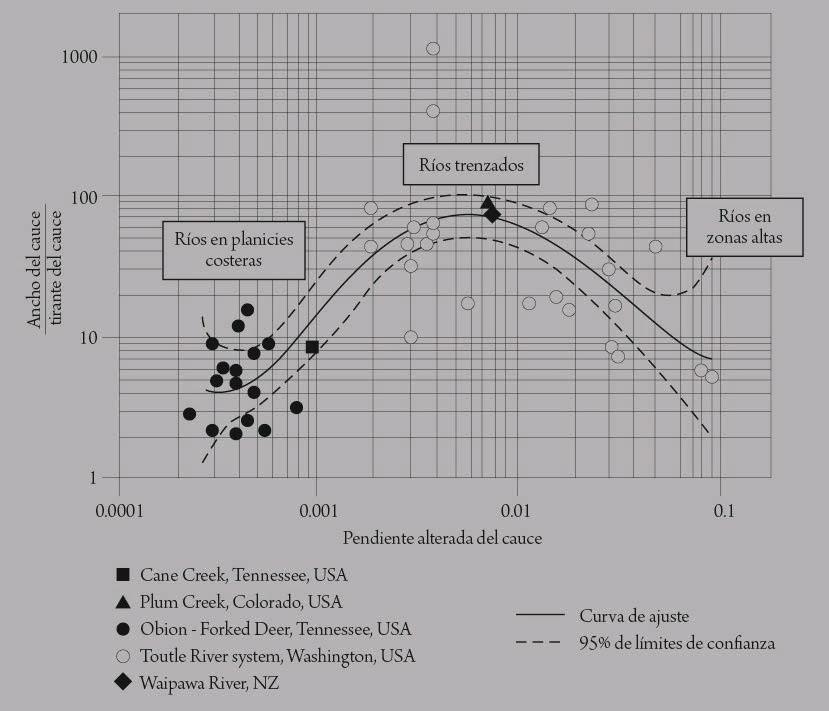
VII.24. Coeficiente de resistencia a la erosión lateral en función de la textura del sedimento de la margen exterior de la curva (Hickin y Nanson, 1984).

Otra forma de estimar el ensanchamiento futuro del cauce es proyectar desde el pie del bordo hasta la elevación de la llanura de inundación, el ángulo de las superficies estables vegetadas que se forman en los bordes a lo largo del cauce.

El ensanchamiento asociado a la degradación puede estimarse con base en el análisis de estabilidad de los bordos. Utilizando las mediciones de la cohesión efectiva del material, c’ (kPa), y el ángulo de fricción efectiva, Ф’ (grados), puede estimarse la altura critica del bordo, !! ! , para una superficie de falla plana (Simon, 1995; Simon y Darby, 1997) con:

Figura

donde � es el peso unitario del material del bordo �� �! , � es el ángulo (grados) de la superficie del bordo. La posibilidad de que el bordo sea inestable, y cuándo podría ocurrir su falla conforme el fondo se degrade, puede saberse comparando la ℎ! de la ecuación (VII.64) con las alturas máximas esperadas de los bordos y con los ángulos que se desarrollen conforme vaya progresando la degradación esperada (con base en las ecuaciones VII.5 o VII.6, por ejemplo). Cuando se espera que un bordo sea estable, puede determinarse el talud estable para la máxima altura del bordo, con el que se define el ensanchamiento esperado. Cuando el bordo tiene una grieta de tensión, Simon y Darby (1997) indican que se modifica la altura crítica del bordo por la profundidad de la grieta, z, de la siguiente manera:

ℎ!" = ℎ! �

donde z = 2�′ � ��� 45° + Ф′ 2 (VII.65)

Una guía más sobre el ensanchamiento de las márgenes es la que se proporciona en la figura VII.25 (Simon, 1995), que indica el cambio del ancho del canal en relación con el cambio que se espera del tirante durante el ajuste del cauce para una pendiente alterada del cauce. El contenido de esta figura no está plenamente probado ni aplicado, pero da una idea del ensanchamiento relativo del cauce, que sin duda es útil en las evaluaciones de inestabilidad futura de los cauces.

VII.8.6. Comentarios

Brice (1983) afirma que “la diversidad en la forma de los meandros y sus dimensiones a lo largo de un tramo típico de un cauce se explica por las diferentes circunstancias en las que se originan los meandros, así como por la evolución tan cambiante de su forma con el tiempo y por la erosión variable de los bordos”. Así, para contar con una metodología que permita predecir el desarrollo y movimiento de los meandros, deben incorporarse a ésta las características detalladas del sitio específico.

Para evaluar la velocidad de la migración lateral pueden compararse la morfología existente del meandro y la de régimen, esta última con base en las ecuaciones (VI.10). También pueden combinarse las ecuaciones (VII.63) con las figuras VII.23 y VII.24, lo que ayuda a predecir la velocidad de migración con base en el material del bordo, forma del cauce y flujo en general. Asimismo la figura VII.21, que relaciona la velocidad de erosión lateral con el ancho del cauce.

La dirección de la migración del meandro puede determinarse con base en proyecciones de tendencias históricas.

Además de la extrapolación de los datos obtenidos con mediciones de campo, el ensanchamiento de los cauces puede predecirse con base en la ecuación de continuidad para el nuevo nivel del fondo, particularmente cuando ocurre depósito de sedimentos; también con base en la proyección de los ángulos estables de los bordos y en la figura VII.25, que relaciona el cambio del ancho del canal con el cambio del tirante para una pendiente modificada del cauce; y finalmente con base en el análisis de estabilidad de los bordos para un fondo degradado.

Figura VII.25. Cambio del ancho del cauce en relación con el tirante durante el ajuste del cauce (Simon, 1995).

CAPÍTULO VIII

SOCAVACIÓN POR ESTRECHAMIENTO

La socavación por estrechamiento o contracción ocurre cuando la cimentación o los terraplenes de acceso de los puentes reducen el área hidráulica de la corriente. Este tipo de socavación puede ocurrir también si el puente está situado en un estrechamiento natural del ancho del río.

El grado de estrechamiento puede considerarse en términos de la relación de estrechamiento, � , dada por � = !! !! (VIII.1)

donde �! es el ancho de la sección de llegada (sin estrechamiento) y �! es el ancho de la sección del puente (con estrechamiento), que es el ancho neto de la abertura del cruce del puente. Por ejemplo, para una reducción del 10% del ancho del cauce debida a la presencia de las pilas, estribos y terraplenes de acceso, se obtiene que � = 1.11 = ( �! /0.9�! ). La reducción del ancho provoca que la socavación se incremente, como resultado del incremento del esfuerzo cortante en el fondo. La mayor parte de los estudios publicados acerca de la socavación por estrechamiento consideran el caso especial de la socavación en la sección estrechada de un canal rectangular, con un estrechamiento gradual lo suficientemente largo para poder suponer que el flujo es uniforme tanto en la entrada como en la sección contraída, y de aquí la frase “estrechamiento rectangular largo”.

VIII.1. Estrechamiento rectangular largo

En la figura VIII.1 se define el problema básico de flujo uniforme a través de un estrechamiento rectangular largo. Los parámetros del flujo son el tirante y, el ancho W, y la velocidad V. Los subíndices 1 y 2 se refieren a las secciones de entrada y a la contraída (sección del puente), respectivamente. Suponiendo que los cambios de carga de velocidad a través del estrechamiento y todas las pérdidas de carga sean despreciables, la profundidad de socavación de equilibrio �!" está dada por:

Figura VIII.1. Flujo uniforme en una contracción rectangular larga.

Straub (1934) presenta un análisis unidimensional simplificado del estrechamiento largo. Su trabajo fue posteriormente complementado por Laursen (1958,1960, 1962 y 1963), Komura (1966), Ashida (1964) y Gill (1981). La teoría del estrechamiento rectangular largo constituye la base de varios de los métodos disponibles para estimar la socavación por estrechamiento. Se han derivado muchas ecuaciones para diferentes casos de socavación por contracción, usando el método de Straub (1934). En la tabla VIII.1 se presentan algunas de ellas (la mayoría de los parámetros son adimensionales; sin embargo, cuando no lo son, las unidades corresponden al Sistema Internacional de Unidades (SIU), es decir, metros, kilogramos, segundos, a menos que se especifique otro sistema). Varias de tales ecuaciones incluyen el exponente ! , que aparece en la siguiente relación generalizada para el transporte de sedimentos, expresada con base en el SIU:

donde !! = gasto unitario sólido !! = gravedad especifica del material del fondo !!" = mediana de los diámetros del material del fondo ! = esfuerzo cortante en el fondo

Entre las fórmulas empíricas conocidas de la forma de la ecuación (VIII.3), ! varía de 1.5, como en la fórmula de Meyer-Peter (Meyer-Peter y Muller, 1948), a 3, como en la fórmula de Einstein-Brown (Brown 1950). Las ecuaciones VIII.4 y VIII.7 (tabla VIII.1) aparecen graficadas en la figura VIII.2 en función de !!" !! (= !! !! - 1) para ! = 2 (como en la fórmula de Du

Boys [Brown, 1950]), donde la ecuación VIII.4 es aplicable cuando !! !! ! ! y la ecuación

VIII.7 cuando !! !! ! !

Figura VIII.2. Gráfica de las ecuaciones VIII.4, VIII.6 y VIII.7 de Gill (1981).

En la gráfica de la figura

VIII.2 se muestra que la dependencia de la profundidad de socavación respecto a !! !! (el transporte relativo del material del fondo en la entrada) es mínima para la socavación con fondo vivo, aun para valores altos de ! . Por el contrario, la socavación por estrechamiento en aguas claras depende mucho de !! !!

Las tendencias descritas son similares a las de la socavación local (en un fascículo próximo se ilustrará este fenómeno).

En la figura VIII.3 se grafican las ecuaciones VIII.9 y VIII.10 en función de !!! !! En el rango mostrado, la figura indica una dependencia casi lineal de la profundidad de socavación respecto a la relación de gastos y a la relación de contracción, tanto para el cauce de avenidas como para el flujo del cauce principal, y un efecto relativamente pequeño de !! (tabla VIII.2). El factor C de la ecuación (VIII.14) puede ser significativo para valores bajos de ! !! , situación para la que !! será mayor que !! , y la relación de tirantes puede ser del orden de un 10% mayor que para valores más altos del gasto sólido. Así, para la socavación con fondo vivo, la profundidad de socavación disminuye ligeramente conforme aumenta la relación ! !! (y la velocidad del flujo y el transporte de sedimentos). Esta disminución, también evidente en la figura VIII.2, fue confirmada con mediciones de laboratorio realizadas por Alawi (1981) y Laursen (1988).

Referencias

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

Tabla VIII.1 Ecuaciones para socavación en estrechamientos con contracciones rectangulares largas

Ecuación

Gill (1981)

Laursen (1958, 1960, 1962, 1963)

Aplicabilidad

Socavación de fondo vivo en el cauce de llegada (τc/τ1 <1)

(5.4)

Socavación en fondo vivo en el cauce de llegada ((τc/τ1 <1), con fuerte transporte de sedimentos

(5.5)

(τc/τ1 → 0), m = 2

Condición límite en el cauce de llegada (τc/τ1 = 1)

(5.6)

Condición de aguas claras en el cauce de llegada

(τc/τ1 = 1)

(5.7)

Socavación en fondo vivo

Corrientes con cauce principal y cauce de avenidas

(5.8)

Socavación en fondo vivo

(5.9)

W1 = W2 (estrechamiento del flujo solamente en el cauce de avenidas)

Socavación en fondo vivo

Q2=Q1m (estrechamiento del cauce principal) Y n1 = n2

(5.10)

Socavación en aguas claras

Ecuación en (m, s)

Socavación en aguas claras

Komura (1966)

Laursen y Alawi (1989)

Parker (1981)

Símbolos

β = relación de estrechamiento

τc = esfuerzo cortante crítico del fondo

τ1 = esfuerzo cortante del fondo en el tramo de llegada

m = exponente en la ec. 5.3 que es la relación generalizada del transporte de sedimentos

Q2 = gasto en el tramo estrechado (Q2 = gasto total, a menos que se reduzca por puentes de alivio o que el agua sobrepase los terraplenes de acceso

Q1m = gasto con transporte de sedimentos en el cauce de aguas arriba, normalmente el cauce principal

n1 y n2 = valores de los coeficientes de Msnning en el tramo de llegada y en el contraído

k1 y k2 = coeficientes (tabla 5.2) que dependen de la velocidad de corte u* y de la velocidad de caída ω

V1 = velocidad de llegada d50 mediana de los diámetros del sedimento (m)

σg = desviación estándar del material de fondo

σg = d84/d16)0.5

Socavación en fondo vivo

Socavación en fondo vivo con transporte moderado de sedimentos

Fr1 = número de Froude en el cauce de llegada

(5.14)

(5.15)

Socavación en fondo vivo en cauces con gravas

C = factor de corte en el fondo, se obtiene expresando el término (τ/τc–1) en la ec (5.3) en la forma C τ/τc k1, k3 = coeficientes (tabla 5.2)

k4 = exponente que puede variar de 0.675 a 0.825

Figura VIII.3. Gráfica de las ecuaciones de Laursen (VIII.9) y (VIII.10).

Parker (1981) investigó la socavación en una contracción larga para una corriente con fondo de grava. En general, los cauces con fondo de grava tienen material mal graduado en la superficie del fondo. Sin embargo, debido a la amplia variación de diámetros de los granos, los cauces con grava se caracterizan por la formación de corazas protectoras que podrían limitar la socavación en un estrechamiento. Al contrario, Parker (1981) encontró que la coraza no limita la socavación por estrechamiento en cauces con fondo de grava. Propuso una ecuación, basada en el método de Straub, la cual aparece como la ecuación (VIII.15) en la tabla VIII.1, que es de la misma forma que la ecuación (VIII.10). El exponente !! de la ecuación (VIII.15) tiene valores un poco más altos (de 0.675 a 0.825) que !! de la ecuación (VIII.10). Recuérdese que los valores de !! ! !! ! !! de las ecuaciones (VIII.8), (VIII.10) y (VIII.14) aparecen en la tabla VIII.2.

A la entrada de una contracción larga ocurre una socavación localizada más grande en la región donde el flujo no es uniforme. La socavación más profunda es análoga a la socavación local que ocurre en un estribo de un puente, y es causada por un fenómeno similar de flujo. Sin embargo, no son iguales, a menos que el puente constituya una contracción larga, lo cual es raro, ya que generalmente los estrechamientos provocados por los puentes son cortos y abruptos.

En resumen, los métodos analíticos para estimar la socavación en estrechamientos largos rectangulares cuentan con ecuaciones de formas similares, con solamente pequeñas diferencias en la influencia de algunos parámetros. Se conoce poco sobre la aplicabilidad de los

métodos de contracciones rectangulares largas a la socavación por estrechamiento de puentes, que generalmente provocan contracciones cortas y abruptas, aunque los datos de Ashida (1964) sugieren que estos métodos son conservadores cuando se utilizan para estimar la socavación por estrechamiento causado por los puentes.

VIII.2. Socavación por estrechamiento más socavación local

Figura VIII.4. Socavación por estrechamiento más socavación local en puentes (Laursen y Toch, 1956).

En la práctica, la socavación por estrechamiento y la socavación local pueden ocurrir juntas y es difícil distinguirlas. Los datos de Laursen y Toch (1956) son útiles para entender la independencia entre ellas; definieron curvas, con base en mediciones de laboratorio, de socavación en pilas de un puente de muchos claros, con pilas circulares espaciadas uniformemente a través del flujo. En la figura VIII.4 aparecen tales curvas, en las que ! considera la obstrucción del flujo causada por las pilas, y b es el ancho de cada pila. En esta figura se muestra tam-bién la solución de Straub (1940) para la socavación en una contracción larga rectangular. Las mediciones de Laursen y Toch (1956) indican que la profundidad de socavación es función de !! ! y de ! , es decir, que comprende ambas socavaciones, la local y la de estrecha-miento Para flujos poco profundos con !! ! ! !, la influencia de la razón de contracción es mínima, por lo que la socavación obtenida es solamente la local. Conforme aumenta el tirante, la influencia de ! se incrementa progresivamente. Para !! ! ! ! , por ejemplo, la profundidad de socavación local es casi independiente de los efectos de la contracción del ancho si !! !! ! ! !!!! es decir, si ! ! !!!!. En cambio, para la misma relación !! ! ! ! y un 50% de contracción del ancho ! ! ! , la profundidad de socavación resulta de poco más del doble

que para una contracción nula. En este caso, la socavación obtenida incluye la socavación local y la socavación por estrechamiento o contracción.

Para contracciones severas, la profundidad de socavación en flujos más profundos tiende a ser igual a la que resulta de una contracción larga rectangular, y la mayor parte de la socavación medida sería por contracción.

VIII.3. Métodos para estimar la profundidad de socavación por estrechamiento

Han sido propuestos muchos métodos para estimar la socavación por estrechamiento. Se verán en esta sección los más aceptados.

VIII.3.1. Inferencia directa de mediciones de campo

Este procedimiento, descrito por Neill (1973), contempla la medición de la socavación en puentes existentes en curvas pronunciadas, en contracciones, o en otros sitios en que la configuración del cauce sea comparable al lugar de estudio. Idealmente, las mediciones deberían efectuarse en condiciones similares de flujo y en sitios en que el material del fondo sea también similar.

VIII.3.2. Solución de la contracción rectangular larga

Se dispone de varios procedimientos para estimar la socavación con la solución de la contracción rectangular larga. En EUA, los procedimientos recomendados se dan en el HEC18 (Richardson y Davis, 1995) y se basan en las ecuaciones de Laursen. Los procedimientos recomendados en Austroads (1994) se derivan del HEC-18. De acuerdo con estos documentos, es común encontrar varios casos de socavación por contracción; dos de ellos incluyen puentes de alivio; los demás, que se tratan enseguida y que se ilustran en la figura

VIII.5, son:

Caso 1, que involucra planicies con flujos que son forzados por los accesos del puente a regresar al cauce principal. Las condiciones del caso 1 incluyen: el cauce principal se contrae debido ya sea a los estribos del puente o a que el puente se localiza en una sección estrecha del río (caso 1a); no se contrae el cauce principal, aunque el flujo de la planicie es completamente obstruido por los terraplenes de acceso (caso 1b); y (caso 1c) los estribos sólo obstruyen el cauce de avenidas.

Caso 2, en que sólo existe cauce principal, es decir, no hay cauce de avenidas. El ancho normal del cauce se hace más estrecho, ya sea por el puente mismo (caso 2a) o porque el cauce se localiza en un tramo más estrecho del río (caso 2b).

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO I

VIII.5. Casos de socavación por estrechamiento en puentes.

Figura

El tirante de socavación por contracción se estima de acuerdo con condiciones de fondo vivo o de aguas claras.

Para fondo vivo, Richardson y Davis (1995) y Austroads (1994) recomiendan la siguiente versión modificada de la ecuación VIII.8 de Laursen (1960):

donde !!! tirante medio en el cauce principal de llegada

!!! tirante medio en el cauce principal de la sección contraída !! ! ancho del fondo del cauce principal de llegada !!! ancho del fondo del cauce principal en la sección contraída !!!! gasto en el cauce prin-cipal de llegada, con sedi-mentos !!! gasto total que pasa por el puente !!! coeficiente (véase tabla VIII.2)

Figura VIII.6. Gráfica de la ecuación VIII.16 para socavación con fondo vivo (Laursen, 1960).

En la figura VIII.6 se grafica la ecuación (VIII.16) en función de !!" !! (= !! !! - 1), para !! !!! ! ! ! ! y para ! (= !!! !!! ) = 1 a 2.

La figura VIII.6 muestra que cuando ocurren juntas una contracción severa del ancho del cauce principal (! grande) y una contracción del cauce de avenidas ( !! !!! grande) pueden generarse fuertes profundidades de socavación por contracción.

Para el caso 1c, es difícil estimar tirantes y gastos debido a que el proceso de socavación depende de la distribución lateral del flujo aguas arriba y en el sitio del puente, siendo difícil de definir �! . Austroads (1994) hace hipótesis simplificatorias, recomendando que �! sea igual que �! y que los parámetros del flujo se definan como sigue: �! = tirante promedio en el área de los cauces principal y de avenidas ocupados por el puente (en la etapa normal y sin socavación); �! = tirante promedio en el puente (incluida la socavación); y �!� ! gasto a través del área de los cauces principal y de avenidas ocupados por el puente (en la etapa normal y sin remanso). Estas definiciones parecen ser inadecuadas. El HEC-18 recomienda el uso de un modelo de flujo (WSPRO) para determinar la distribución del flujo; el modelo 1-D recomendado, sin embargo, puede arrojar resultados engañosos.

Para socavación en aguas claras se recomienda en HEC-18 la siguiente ecuación, basada en la (VIII.11):

�! = 1.48 !! !!!/! !! !/!

donde �! = tirante medio en el puente, incluyendo la socavación (m)

�! = gasto total que pasa por el puente ( �! � )

�� = diámetro medio efectivo (mm) del material del fondo (≡ 1.25 �!" )

�! = ancho del fondo en el puente (m)

La constante 1.48 tiene dimensiones de [L] !/!

(VIII.17)

En la obtención de (VIII.17) se supone que la socavación continúa en la sección contraída del puente hasta que se alcanzan las condiciones de frontera (una velocidad competente de llegada, véase sección VII.3.3.). Esta suposición, así como el diagrama de Shields y la ecuación de Manning-Strickler, conducen directamente a la forma de la ecuación (VIII.17). El valor de la constante en esta ecuación depende del valor del parámetro de Shields en condiciones límite, �! . Laursen utilizó la expresión �! ! 4 �!" (unidades pie-libra), que es equivalente a �! ! 0.039. Como alternativa de la ecuación (VIII.17), Austroads (1994) sugiere utilizar la ecuación (VIII.16) sin el último término (relacionado con � ) para socavación en aguas claras. Para determinar cuál de las ecuaciones anteriores es aplicable para un caso particular, esto es, si las condiciones son de aguas claras o de fondo vivo, se recomienda en HEC-18 la siguiente ecuación:

�! = 6.2 �! !/! �!" !/! (VIII.18)

donde �! = velocidad crítica (� � ) que puede transportar el material del fondo de diámetro �!" o menor.

Si � < �! , las condiciones serán de aguas claras. La ecuación (VIII.18) es similar a la (VI.7).

Richardson y Richardson (1994) afirman que las ecuaciones VIII.16 y VIII.17 son conservadoras cuando se aplican a puentes, ya que las contracciones son generalmente más cortas que las contracciones largas para las que fueron obtenidas las ecuaciones. No se conocen datos que sustenten tal afirmación, aunque la encuentran consistente los resultados obtenidos por Wong (1982) y Ashida (1964).

VIII.3.3. Limitaciones de los métodos para el cálculo de la socavación por contracción

Los métodos disponibles para estimar la socavación por contracción tienen limitaciones que requieren ser tomadas en consideración cuando son utilizadas. Se discuten en seguida tales limitaciones:

Falta de verificación

Se dispone de pocos datos de laboratorio o de campo para verificar los métodos, aunque los disponibles sustentan la validez de los resultados. Entre los pocos datos experimentales están los de Sharma (1972), quien concluye de los datos de campo que la profundidad de socavación por contracción entre pilas de puente (excluyendo la socavación local) es razonablemente bien estimada por las ecuaciones de régimen. También está el estudio de Norman (1975), que afirma de los datos de campo que tanto el método de Laursen como el de Straub ofrecen resultados satisfactorios para puentes en ríos con fondo de grava o de boleos. Asimismo, Wong (1982) encuentra que la profundidad de socavación por contracción obtenida con el método de Laursen (VIII.11) coincide razonablemente con la profundidad medida en el laboratorio para contracciones constituidas por estribos y aleros. La comparación de la ecuación (VIII.13) para la socavación en contracción con fondo vivo de Komura con los datos de Ashida (1964) para la socavación en una contracción corta (relación largo-ancho ≈ 1.0) muestra que la constante de la ecuación (VIII.13) necesita reducirse de 1.45 a 1.22.

Aplicabilidad de las soluciones para la contracción larga rectangular Generalmente, los puentes provocan contracciones cortas y abruptas. La aplicabilidad de la contracción larga rectangular a la predicción de la socavación por contracción es incierta. Sobre la base de sus mediciones, Webby (1984) definió una contracción larga como aquella

cuya longitud es por lo menos dos veces el ancho del cauce de aguas arriba de la contracción. Keller (1977), Gill (1981) y Webby (1984) realizaron en laboratorio mediciones de profundidades de socavación en contracciones rectangulares largas, y compararon los resultados con las profundidades de socavación estimadas con la ecuación (VIII.11). En la tabla VIII.3 se presenta un resumen de sus resultados, que muestran que la ecuación (VIII.11) subestima la profundidad de socavación por contracción, al menos en un 20% en el tramo uniforme, y en mucho más en la sección no uniforme cerca de la entrada de la contracción; esto último es de esperarse, ya que las profundidades de socavación a la entrada incluirían la socavación local. Keller (1977) concluye también que la ecuación (VIII.11) es en general más confiable que la (VIII.12) para el rango de sus experimentos. Gole y Chitale (1967) encontraron, con base en dos puentes de India, que la profundidad total de socavación por contracción obtenida con las ecuaciones para contracciones largas rectangulares no se desarrollaba totalmente en un puente en que el hidrograma era de corta duración. Por el contrario, la socavación por contracción prevista sí se desarrolló en un puente sobre el río Ganges, el cual condujo gastos importantes durante varios meses.

Socavación en aguas claras

Las ecuaciones para la socavación por contracción han sido desarrolladas para materiales uniformes, principalmente para granos finos. Para las áreas contraídas cuando hay condiciones de aguas claras, los estudios se han realizado con base en el cálculo de la fuerza tractiva, cuando existen arenas sin material cohesivo, sin vegetación ni formación de coraza. En cambio, si se dan estas últimas tres condiciones, es de esperarse que las ecuaciones arrojen resultados conservadores.

Distribución lateral de la socavación

Los diversos métodos para calcular la socavación por contracción suponen que la socavación calculada se distribuye uniformemente a través de la sección del río. En puentes en que la socavación se concentre en alguna parte de la sección transversal, se podrá estimar cualitativamente su distribución como se discutió en la sección VII.3.3. En la figura VIII.7 se ilustran gráficamente las posibles variaciones en la distribución de la socavación por contracción, en función de las variaciones de la distribución de las velocidades de llegada.

MANUAL DE SOCAVACIÓN DE PUENTES. FASCÍCULO

Figura VIII.7. Ilustración gráfica de la variación de la distribución de la socavación por estrechamiento, en función de la distribución del flujo de llegada.

El fascículo I del Manual de Socavación de Puentes se terminó de imprimir en los talleres de Drokerz Impresiones de México, S.A. de C.V.

Av. Insurgentes 100, int. 304-O

Col. Juárez, Cuauhtémoc 06600 México, Distrito Federal Se imprimieron 1,000 ejemplares

Asociación Mexicana de Ingeniería de Vías Terrestres, A.C.

XX Mesa Directiva

Comité Técnico de Puentes