Predicción de la velocidad de onda de cortante de arenas de la bahía de Campeche donde Vs está en m/s, ASF = 1.41 para suelos del Pleistoceno, Pa o presión atmosférica en kPa, σ’v esfuerzo vertical efectivo en kPa y qc1 es la resistencia de punta de cono normalizada, dada por: qc1 =
( σ’P ) a
v
0.5
qc Pa
(11)
6. BASE DE DATOS DE LA BAHÍA DE CAMPECHE
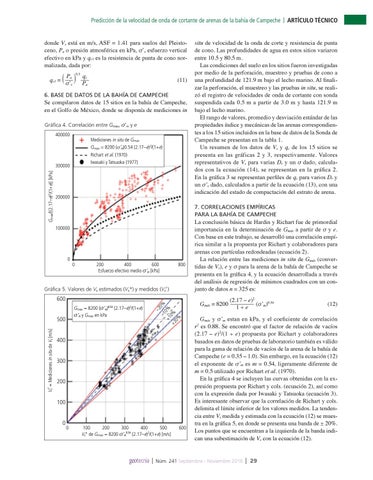
Se compilaron datos de 15 sitios en la bahía de Campeche, en el Golfo de México, donde se disponía de mediciones in Gráfica 4. Correlación entre Gmáx, σ’m y e 400000
Mediciones in situ de Gmáx Gmáx = 8200 (σ’m)0.54 (2.17–e)2/(1+e) Richart et al. (1970) Iwasaki y Tatsuoka (1977)
Gmáx/[(2.17–e)2/(1+e)] [kPa]
300000
200000
ARTÍCULO TÉCNICO
situ de velocidad de la onda de corte y resistencia de punta de cono. Las profundidades de agua en estos sitios variaron entre 10.5 y 80.5 m. Las condiciones del suelo en los sitios fueron investigadas por medio de la perforación, muestreo y pruebas de cono a una profundidad de 121.9 m bajo el lecho marino. Al finalizar la perforación, el muestreo y las pruebas in situ, se realizó el registro de velocidades de onda de cortante con sonda suspendida cada 0.5 m a partir de 3.0 m y hasta 121.9 m bajo el lecho marino. El rango de valores, promedio y desviación estándar de las propiedades índice y mecánicas de las arenas correspondientes a los 15 sitios incluidos en la base de datos de la Sonda de Campeche se presentan en la tabla 1. Un resumen de los datos de Vs y qc de los 15 sitios se presenta en las gráficas 2 y 3, respectivamente. Valores representativos de Vs para varias Dr y un σ dado, calculados con la ecuación (14), se representan en la gráfica 2. En la gráfica 3 se representan perfiles de qc para varios Dr y un σ’v dado, calculados a partir de la ecuación (13), con una indicación del estado de compactación del estrato de arena. 7. CORRELACIONES EMPÍRICAS PARA LA BAHÍA DE CAMPECHE
100000
0
0
200 400 600 Esfuerzo efectivo medio σ'm [kPa]
800
Gráfica 5. Valores de Vs estimados (Vs*) y medidos (Vsf ) Gmáx = 8200 (σ'm) σ'm y Gmáx en kPa
0.54
500
–2 –1 0% 0 +1 % +2 0% 0%
600
Vsf = Mediciones in situ de Vs [m/s]
❘
(2.17–e) /(1+e) 2
400 300 200 100 0
0
100 200 300 400 500 Vs* de Gmáx = 8200 σ'm0.54 (2.17–e)2/(1+e) [m/s]
❘
600
La conclusión básica de Hardin y Richart fue de primordial importancia en la determinación de Gmáx a partir de σ y e. Con base en este trabajo, se desarrolló una correlación empírica similar a la propuesta por Richart y colaboradores para arenas con partículas redondeadas (ecuación 2). La relación entre las mediciones in situ de Gmáx (convertidas de Vs), e y σ para la arena de la bahía de Campeche se presenta en la gráfica 4, y la ecuación desarrollada a través del análisis de regresión de mínimos cuadrados con un conjunto de datos n = 325 es: Gmáx = 8200
(2.17 – e)2 (σ’m)0.54 1+e
(12)
Gmáx y σ’m estan en kPa, y el coeficiente de correlación r2 es 0.88. Se encontró que el factor de relación de vacíos (2.17 – e)2/(1 + e) propuesta por Richart y colaboradores basados en datos de pruebas de laboratorio también es válido para la gama de relación de vacíos de la arena de la bahía de Campeche (e = 0.35 – 1.0). Sin embargo, en la ecuación (12) el exponente de σ’m es m = 0.54, ligeramente diferente de m = 0.5 utilizado por Richart et al. (1970). En la gráfica 4 se incluyen las curvas obtenidas con la expresión propuesta por Richart y cols. (ecuación 2), así como con la expresión dada por Iwasaki y Tatsuoka (ecuación 3). Es interesante observar que la correlación de Richart y cols. delimita el límite inferior de los valores medidos. La tendencia entre Vs medida y estimada con la ecuación (12) se muestra en la gráfica 5, en donde se presenta una banda de ± 20%. Los puntos que se encuentran a la izquierda de la banda indican una subestimación de Vs con la ecuación (12).
Núm. 241 Septiembre - Noviembre 2016
❘
29