
8 minute read
Real Life Application Of Complex Numbers
Real Life Applications of Complex Numbers
Josiah Wu
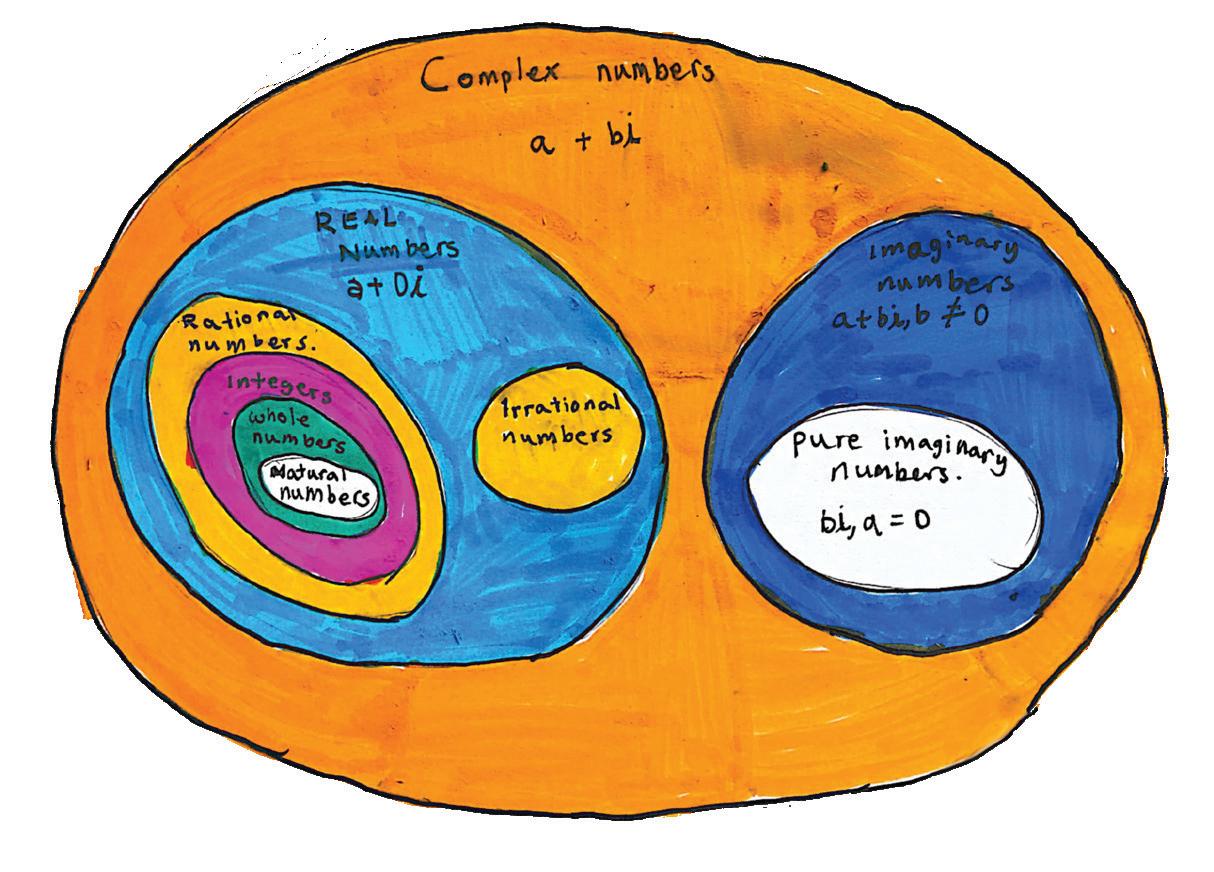
Let’s start with the basics. At a young age, we were taught how to count with positive numbers, such as one, two or three. Later in primary school, we were also introduced to negative numbers: for example, -19 is a negative number. I’m also going to assume that you are familiar with square roots (if not, you should revise). It is commonly taught to students that one cannot take the square root of negative numbers. But what if we could?
You may be wondering, “How is it possible to take the square root of a negative number?” In fact, mathematicians before the 16th century would’ve thought so as well. This was until Italian mathematician Gerolamo Cardano broke the convention by inventing imaginary numbers, in a desperate attempt to solve cubic equations. Throughout history, mathematicians have always loved to break their own rules: apart from taking the square root of a negative number, Ramanujan once proved that 1 + 2 + 3 + 4… all the way up to infinity is equal to -1/12. Another mathematician, Georg Cantor, proved that there are as many even numbers as positive integers. Therefore, what Cardano did was not uncommon (at least in historical records).


So what is an imaginary number? An imaginary number is a multiple of i = √-1. For example, √-25 is an imaginary number because it can be rewritten as √-25 = √25 × -√1 =5i. Furthermore, one can add a real number to an imaginary number to form a complex number. To demonstrate this, one can add 3, a real number, to 3i, an imaginary number, to form the complex number 3+3i.
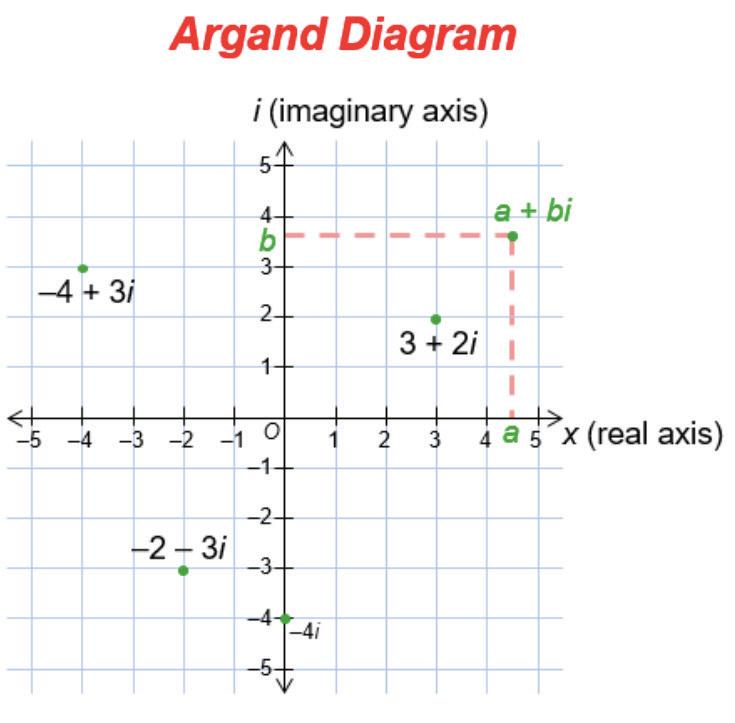
Illustration by Ethan Lan
A common visualisation of complex numbers is the use of Argand Diagrams. To construct this, picture a Cartesian grid with the x-axis being real numbers and the y-axis being imaginary numbers.
An important property of complex numbers is the Euler’s formula: it states that every complex number, can be rewritten in the form of re =r(cos + i sin ), where e=2.71828... is the Euler’s constant, r is the ‘distance’ of the complex number from the origin and is the angle of the complex number from the positive real axis (anticlockwise, in radians). On the left is an illustration of this.
Euler’s formula is described to be the most beautiful mathematical result in history by many mathematicians. Its aesthetic beauty lies in the fact that it implies a magical relationship between real numbers and imaginary numbers. Although I would like to demonstrate the elegant proof for this formula, it is unfortunately outside the scope of this article.
Applications

1.
Signal Processing
Suppose a pianist is recording in a music studio. He invites you to a game - to guess what musical notes he plays without looking at the piano. As someone who doesn’t have perfect pitch (the ability to tell what musical note it is just by hearing), how would you win this game?
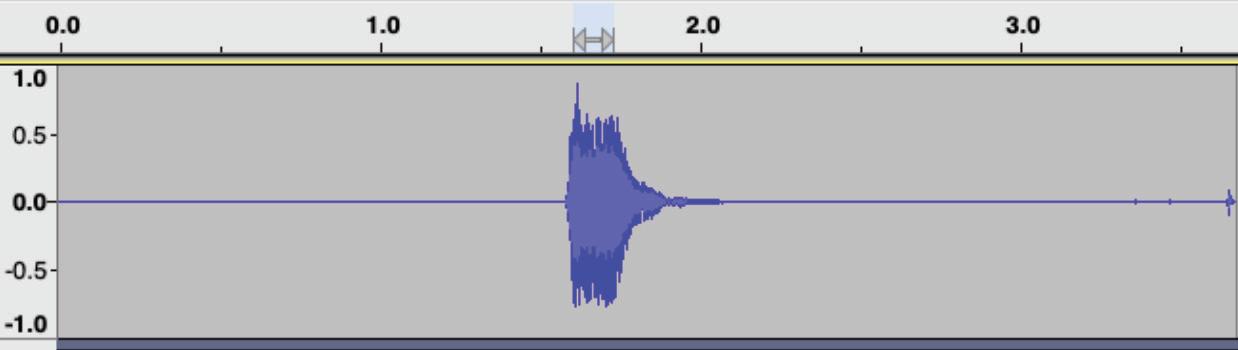
It turns out, there is a way to always deduce what notes he is playing without cheating. Firstly, record his playing in an audio-editing software. The software will store the recording in a waveform.

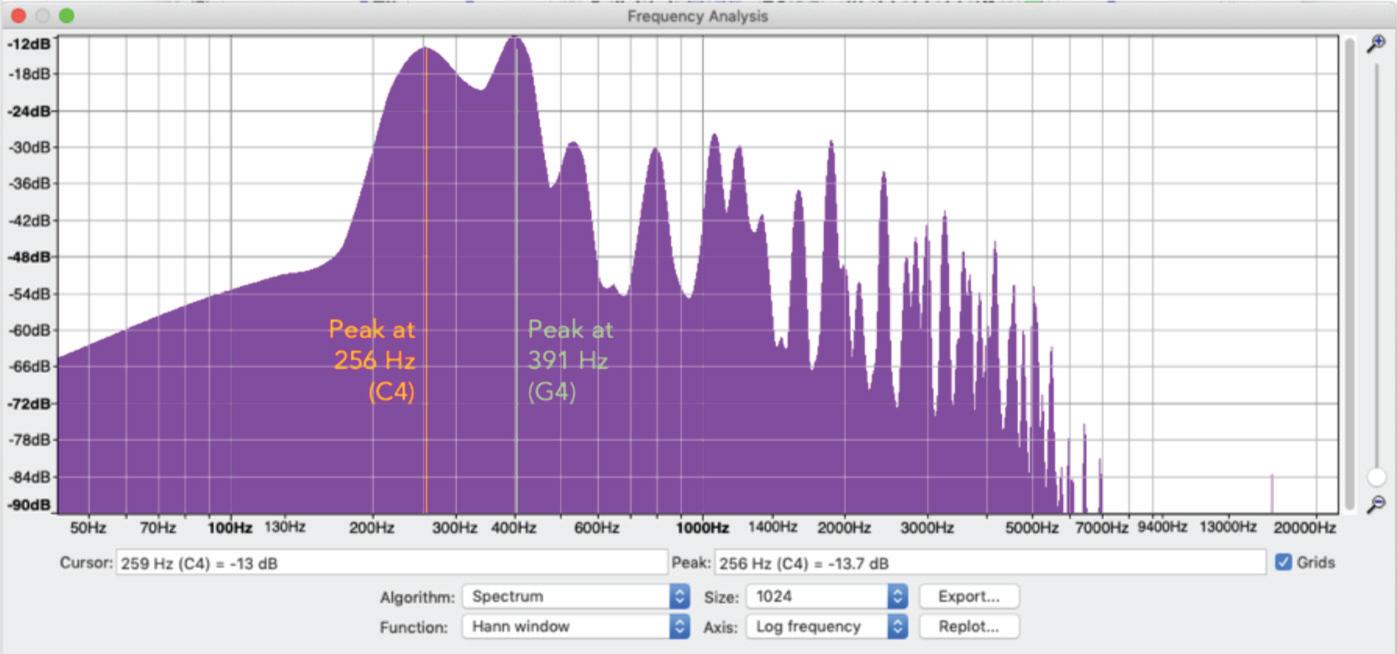
One can then apply Fourier Transform to the waveform signal to figure out which frequencies are the most prevalent within the recording. This can be shown by deducing the ‘peaks’ in the resulting frequency distribution after Fourier Transform has been applied. As there are evident peaks at 256 Hz and 391 Hz (which correspond to C4 and G4, respectively), we can therefore deduce that the pianist must have played C and G on the piano.
Knowing the locations of peaks is incredibly important to audio-editors and music producers. They can not only derive the source of any background noise but also use its frequency as a reference to eliminate them through the means of Equalisation (EQ).
The idea behind the Fourier Transform is rather genius; it proposes that any complicated wave can be decomposed into multiple sinusoidal waves with varying frequencies. What Fourier Transform does is that it predicts which frequency is likely to be equivalent to one of such sinusoidal waves. It does this by ‘wrapping’ the wave around the origin in the complex plane and computing the sum of complex coordinates of all possible points on the wrapped wave.
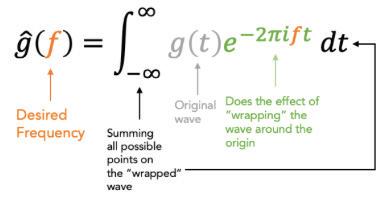
2. AC Circuit Analysis
Complex numbers are also utilised in calculations of current, voltage or resistance in AC circuits (AC stands for Alternating Current, which is a current that changes magnitude and direction over time). A common application of complex numbers (more specifically, Euler’s formula) is to compute the potential difference across two AC power supplies with respect to time. On the right is an example of such a calculation.
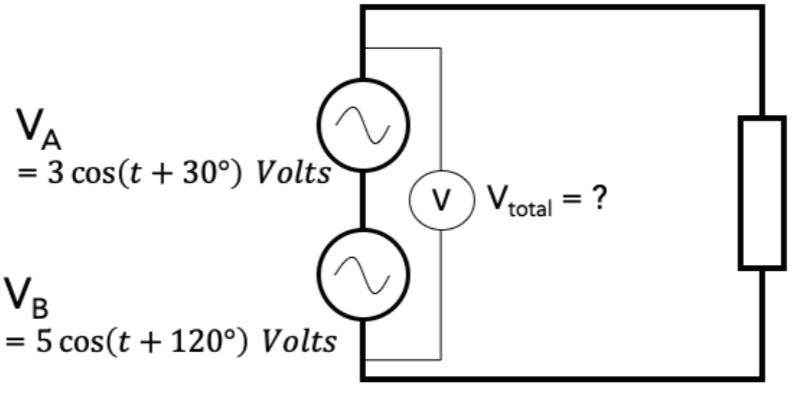
To find the combined potential difference, simply adding VA and VB together will not work. However, we can express both voltages as the Real Part (x-coordinate on the Argand Diagram) of a complex number.
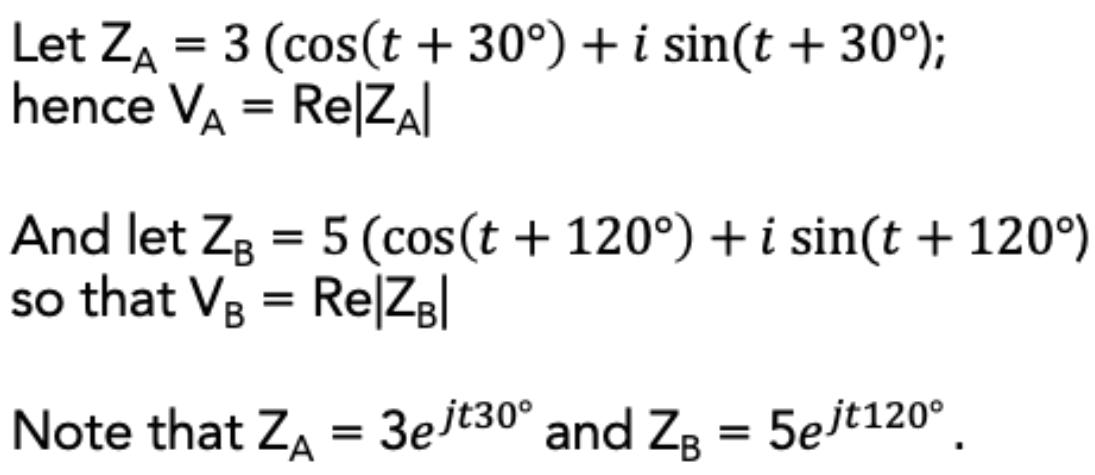
*It is conventional to use j instead of i to represent imaginary numbers in circuit analysis, to avoid confusion with current (which its symbol is i or I).

We can then add the complex numbers and factorise:

Furthermore, complex numbers are also used to express the magnitude and phase of impedance in an AC circuit. Impedance is very similar to resistance - it slows down the electrons in the circuit. The distinction is that impedance causes a phase shift on the electrical current, while resistance does not. Impedance takes place in common electrical components such as inductors and capacitors, and so having a complex number representation is crucial. In general, complex numbers serve as a representation of phase, which is essential to analysing AC circuits.
3. Quantum Mechanics
Quantum Mechanics is a field of Physics that deals with the motions and interactions between subatomic particles - mainly Bosons (e.g. a photon) and Fermions (e.g. a neutron). It provides a mathematical description of their behaviour in terms of probabilities. In fact, complex numbers form the fundamental basis of Quantum Mechanics. The importance of the Schrödinger Equation to Quantum Mechanics is analogous to that of Newton’s Second Law to Classical Physics; they both provide a sensible mathematical prediction of a particle’s position and momentum. The system of complex numbers is essential to the field because it is a convenient language for expressing wave functions without breaking the rules. Furthermore, a direct application of Quantum Mechanics is that it accelerated the expansion of Chemistry. In 1927, Walter Heitler (not Hitler!) and Fritz London formulated the Valence Bond Theory One main area of concern in Quantum Mechanics is to find the wave function of a subatomic particle. A wave function, simply put, is a complex probability distribution indicating the possible positions of the particle on a specific time. A fundamental formula in Quantum Mechanics, in which the role of the wave function is significant,

is the Schrödinger Equation: using the Schrödinger Equation mentioned above. By using the formula, they proved that the two atoms in a hydrogen molecule are, in fact, ‘sharing’ electrons to form what we know as a covalent bond. Immediately after this, several other chemists continued developing their theory of bonding, such as Linus Pauling’s discovery of resonance and orbital hybridisation. In summary, without the development of Quantum Mechanics, scientists wouldn’t be able to discover the electronic structure of atoms, nor be able to come up with the concept of bonding between atoms.
Illustrat i o n b y Ethan Lan
Bibliography
Signal Processing (Fourier Transform)
Star, Zach. “The Mathematics Of Signal Processing | The Z-Transform, Discrete Signals, And More”. www.youtube. com, 2019, https://www.youtube.com/ watch?v=hewTwm5P0Gg&t=1350s&ab_ channel=ZachStar.
“Fourier Analysis”. En.Wikipedia.Org, 2020, https://en.wikipedia.org/wiki/ Fourier_analysis. Accessed 9 Nov 2020.
Chan, Justin. “Application Of Fourier Transform : Signal Processing”. www. youtube.com, 2017, https://www. youtube.com/watch?v=9uv3-m8jkVg&ab_ channel=JustinChan. Accessed 9 Nov 2020.
Conclusion
Although we cannot physically visualise complex numbers, it is difficult to deny its importance to the scientific community. Complex numbers perfectly demonstrate the role of mathematics in science - it acts both as a powerful language to describe complicated phenomenons, and a comprehensive toolkit to solve difficult problems.
AC Circuit Analysis
Star, Zach. “The Real World Uses Of Imaginary Numbers”. Www.Youtube.Com, 2018, https://www.youtube.com/watch?v=_ h49ilnTmW4&t=630s&ab_channel=ZachStar.
“Complex Numbers And Phasors”. Https:// Www.Electronics-Tutorials.Ws/, 2020, https://www.electronics-tutorials.ws/ accircuits/complex-numbers.html.
Johnson, Robert. “Using Complex Numbers In Circuit Analysis And Review Of The Algebra Of Complex Numbers”. 2020, http://www.its.caltech.edu/~jpelab/ phys1cp/AC%20Circuits%20and%20 Complex%20Impedances.pdf
Quantum Mechanics
DeCross, Matt et al. “Schrödinger Equation | Brilliant Math & Science Wiki”. Brilliant. Org, 2020, https://brilliant.org/wiki/ schrodinger-equation/ Accessed 9 Nov 2020.
Karam, Ricardo, ed. by. Why Are Complex Numbers Needed In Quantum Mechanics? Some Answers For The Introductory Level. University Of Copenhagen, 2020,
https://www.ind.ku.dk/english/research/ didactics-of-physics/Karam_AJP_Complex_ numbers_in_QM.pdf.
Trejo, Miguel. “The Math Behind Schrödinger Equation: The Wave-Particle Duality And The Heat Equation.”. Medium, 2020, https://towardsdatascience.com/themath-behind-schr%C3%B6dinger-equationthe-wave-particle-duality-and-the-heatequation-d5837bf4b13f.

