Manuel de calcul mental

Écrit par C HARLES- A IMÉ C apcarrère

Illustrations de Florian Thouret

SOMMAIRE

Introduction 12

I. PRÉREQUIS

15

1. Apprentissage par cœur 16 a) Tables de multiplication (dans l’ordre : 11, 5, 2, 4, 3, 9, 6, 7, 8, 12, 15, 14 et 13) 16 b) Moitiés (de 1 à 19) 23 c) Complémentaires à 10, à 9 et à 5 24

2. Abacus finger : un système original pour compter jusqu’à 99 sur ses doigts 26 a) Intérêt 26 b) Principes 26 c) Notation des nombres entiers relatifs 29 d) Prolongement 29 e) Complémentaires à 100 32

3. Quelques techniques à maîtriser préalablement 33 a) Décomposition d’un nombre 33 b) Multiplication par une puissance de 10 34 c) Division par une puissance de 10 35 d) Modulo 9 36

4. Quelques astuces pour faciliter le calcul mental rapide 38 a) Formation spécifique des chiffres pour l’écriture automatique 38 b) Formulation orale des résultats 39 c) Mémorisation d’un nombre...................................................................................................................................... 39 d) Gestuelle pour des opérations simples 46

II. TECHNIQUES DE BASE

PREMIÈRES TECHNIQUES

47 1. Moitié 47 a) Pour les petits nombres (2 chiffres) : la « décomposition gestuelle » (en attendant l’apprentissage par cœur) 48 b) Pour les grands nombres (autant de chiffres que l’on veut), la méthode Trachtenberg 48 2. Multiplication par 5, 50, 500, etc. 49 a) Multiplication par 5 52 b) Multiplication par 50, 500, etc. 52 3. Multiplication par 11 (méthode Trachtenberg) 54 4. Soustraction dont le premier terme est une puissance de 10 55

Addition « Flansburg » 58 6. Division à la française avec diviseur dont la table est connue 60

Division par 3 avec partie décimale 61

63 TECHNIQUES SUIVANTES 64

Multiplication en base 100 (avec deux facteurs supérieurs à la base) 65

Multiplication en base 1000 (avec deux facteurs supérieurs à la base) 67 10. Multiplication de deux nombres entiers compris entre 11 et 19 69 11. Multiplication « arc-en-ciel » 71 12. Double 74 13. Division par 5, 50, 500, etc. 77 a) Division par 5 77 b) Division par 50, 500, etc. 79 14. Carré des nombres se terminant par 5 80 15. Somme d’une suite arithmétique de 1er terme 1 et de raison 1 84 Révisions 86

III. TECHNIQUES INTERMÉDIAIRES

PREMIÈRES TECHNIQUES 87

1. Division par 4 88 2. Multiplication par 25 90 3. Soustraction avec 1er terme multiple d’une puissance de 10 92 4. Multiplication par 9, 99, 999, etc. d’un nombre de même taille 95

5. Division à la française avec diviseur dont la table est inconnue 99 6. Division par 7 avec partie décimale 101 7. Multiplication en base 100 (avec deux facteurs inférieurs à la base) 103 8. Multiplication en base 1000 (avec deux facteurs inférieurs à la base) 106 Révisions........................................................................................................................................................................... 108

TECHNIQUES SUIVANTES 109 9. Multiplication par 4 110 10. Division par 25 113 11. Multiplication de deux facteurs se terminant par 1 114 12. Multiplication par 15 118 13. Multiplication de deux facteurs dont les dizaines sont égales et les unités complémentaires (34 x 36, 78 x 72, etc.) 120 14. Somme d’une suite arithmétique......................................................................................................................... 122 15. Division par 11 124 Révisions 125

IV - TECHNIQUES AVANCÉES

PREMIÈRES TECHNIQUES

126

1. Division par 8 127 2. Multiplication par 125 128 3. Multiplication par 9, 99, 999, etc. d’un nombre de taille supérieure 130 4. Multiplication par 99, 999, etc. d’un nombre de taille inférieure 134 5. Division par 9 avec partie décimale 138 6. Multiplication en base 100 (avec un facteur supérieur à la base et un facteur inférieur à la base) 142 7. Multiplication en base 1000 (avec un facteur supérieur à la base et un facteur inférieur à la base) 145

Révisions........................................................................................................................................................................... 148

TECHNIQUES SUIVANTES 149 8. Multiplication par 8 150 9. Division par 125 151 10. Multiplication de deux facteurs dont les dizaines sont consécutives et les unités complémentaires (32 x 48, 23 x 37, etc.) 153 11. Multiplication d’un nombre (dont la somme des deux chiffres est 10) par un multiple de 11 .............. 155 12. Multiplication de deux facteurs se terminant par 5 (45 x 75, 25 x 85, etc.) 157 13. Multiplication d’un nombre quelconque par un multiple de 11 161 14. Division par 13 164 Révisions............................................................................................................................................................................ 166 Révisions générales 167

Introduction

Pourquoi un ouvrage de calcul mental rapide ?

Depuis quelques années, les mathématiques en général, et le calcul mental de façon plus particulière, sont délaissés. Et la France ne cesse de dégringoler dans les classements internationaux évaluant l’enseignement de ces matières (CÈDRE, TIMSS, PISA, etc.) Plus grave encore, les élèves prennent de moins en moins de plaisir à l’apprentissage des mathématiques !

Fort de ce constat, l’auteur de cet ouvrage a cherché et compilé des techniques efficaces pour donner à ses élèves des outils et leur permettre de progresser dans leurs apprentissages.

Ce manuel de calcul mental rapide est le fruit de ses recherches et de son expérience. Il présente des techniques accessibles à tous, qui permettent d’effectuer « de tête » toutes sortes d’opérations.

Pourquoi spécifiquement le calcul mental rapide et pas les mathématiques en général ?

Le calcul mental sert de porte d’entrée pour l’ensemble des mathématiques. Il facilite la familiarité avec les nombres, la conscience des ordres de grandeur et la réalisation des différentes opérations. De plus, la pratique du calcul mental rapide est une base solide pour la mise en équation des problèmes et leur résolution.

Est-ce qu’apprendre toutes ces techniques n’est pas un peu rébarbatif ?

Les techniques présentées dans cet ouvrage ont un côté « tour de magie » qui séduit les élèves par leur côté spectaculaire. Certes, l’apprentissage d’une nouvelle technique demande un peu de travail. En général, deux à trois jours suffisent et ensuite, cela devient vraiment un jeu. L’idée est de présenter aux élèves chaque nouvelle technique comme un défi, et l’âpreté de l’apprentissage en est adoucie.

Faut-il faire beaucoup de calcul mental rapide pour réussir à maîtriser les techniques ?

Il ne faut pas en faire beaucoup, mais souvent ! C’est la répétition qui est nécessaire à un bon apprentissage. Pour progresser, 15 à 20 minutes quotidiennes sont recommandées. Une semaine sur deux, une nouvelle technique sera étudiée et mise en application, tandis que les anciennes techniques seront revues durant l’autre semaine, pour permettre au cerveau de ne pas les oublier !

Flashez pour le cours

Nous conseillons de vous procurer les cahiers d’exercices pour vous entraîner. Les exercices proposés sont de difficulté progressive pour ne pas mettre en difficulté les élèves et leur permettre d’assimiler les différentes techniques. Vous retrouverez dans les cahiers d’exercices les personnages de ce manuel, avec leurs ceintures de couleur qui marquent la progression.

L’année 1 propose de « passer » les ceintures jaune et orange, qui correspondent aux techniques de base de ce manuel.

L’année 2 propose de « passer » les ceintures verte et bleue, qui correspondent aux techniques intermédiaires.

L’année 3 propose de « passer » les ceintures marron et noire, qui correspondent aux techniques avancées.

Le calcul mental rapide est-il réservé aux élèves surdoués ?

Pas du tout ! Avec un peu d’entraînement, tout le monde y arrive ! Et l’expérience des classes de Charles-Aimé Capcarrère le confirme !

Comment se présente cet ouvrage ?

11. MULTIPLICATION « ARC-EN-CIEL »

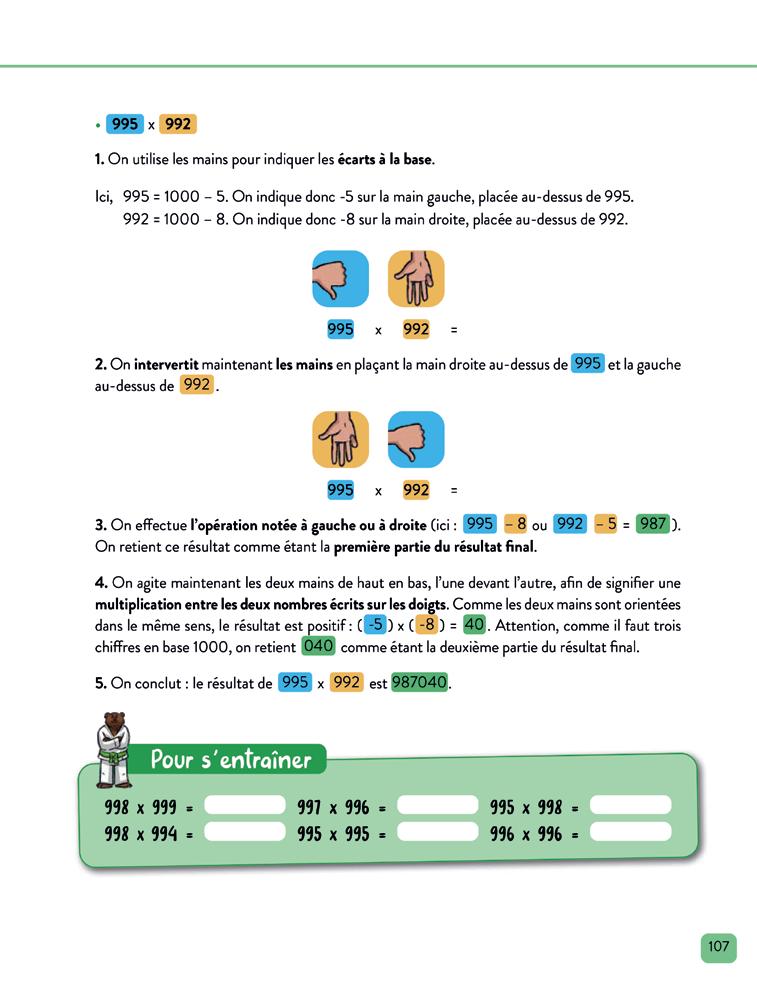
Les multiplications « arc-en-ciel » sont ainsi appelées à cause de la représentation graphique des produits croisés qui fait penser à un arc-en-ciel (ou à un parapluie). Cette technique, qui mêle calcul mental et utilisation des doigts, exige de la pratique et doit donc être abordée assez tôt dans la progression afin de permettre un entraînement fréquent.

Les multiplications « arc-en-ciel » permettent de multiplier n’importe quel nombre de 2 chi res par n’importe quel autre nombre de 2 chi res. Attention, dans cette technique, les mains, qui servent à stocker les résultats intermédiaires, s’utilisent presque comme vu dans le chapitre I.2c, à une di érence près : la main de droite sert à noter les dizaines du résultat final et la main de gauche les centaines du résultat final. Les couleurs aident beaucoup les élèves : on leur fera remarquer que du bleu et du jaune donnent du vert. On peut, pour simplifier, leur parler de « main verte » (pour noter les dizaines du résultat) et de « main bleue » (pour noter les centaines du résultat).

Multiplions 35 par 42.

On commence par chercher

Un QR code permet de retrouver la vidéo de la leçon.

Les vidéos viennent en complément de la leçon. Le professeur réexplique la leçon et un élève montre comment utiliser la technique. Toutes les vidéos sont à retrouver en ligne, à l’adresse www.mameeditions.com/ressources/MM02575_ Calcul_mental/total.php

En raison du nombre de vidéos, le chargement peut être un peu long. Le QR code de chaque vidéo est numéroté pour permettre de retrouver rapidement la vidéo dont il est question.

Certains outils sont accessibles en ligne sur le site editionscriterion.fr, à l’onglet « Ressources pédagogiques ».

II.

Une leçon détaillée, présentée de façon claire, avec de nombreux exemples.

11. Multiplication « arc-en-ciel »

On e ectue ensuite les produits croisés, c’est-à-dire que l’on additionne les 2 produits « bleu par jaune » ( 3 x 2 + 4 x 5 = 6 + 20 = 26 ), en décrivant une sorte d’arc-en-ciel. 6 + 8

1 0 3 5 x 4 2 = Chi re des unités de mille Chi re des centaines Chi re des dizaines Chi re des unités

On « écrit 23 » sur nos mains, le « 3 » se plaçant dans la case verte (bleu et jaune = vert), donc sur la main droite (verte) et le « 2 » se plaçant en retenue dans la case bleue suivante, donc sur la main gauche (bleue). Comme il y a déjà « 1 » en retenue sur la case verte, on fait 23 + 1 = 24 et on « écrit 24 » sur nos mains.

6 + 20

1 0 + 2 6

3 5 x 4 2 = Chi re des unités de mille Chi re des centaines Chi re des dizaines Chi re des unités

On e ectue finalement le produit « bleu par bleu » ( 3 x 4 = 12 ). 1 0 12 + 2 3 3 5 x 4 2 = Chi re des unités de mille Chi re des centaines Chi re des dizaines Chi re des unités

On « écrit 12 » sur la main gauche (bleue), mais il y a déjà « 2 » sur cette main ; on e ectue donc mentalement 12 + 2 = 14, et l’on inscrit « 4 » sur la main gauche (bleue), le « 1 » étant mémorisé. 1 0 + 2 6 + 1 2 3 2 x 4 5 = Chi re des unités de mille Chi re des centaines Chi re des dizaines Chi re des unités 1 4 7 0

70

L’écriture des chiffres

On énonce maintenant le résultat final chi re à chi re (de la gauche vers la droite) : 1 (mémorisé), 4 (« lu » sur la main gauche – bleue), 4 (« lu » sur la main droite – verte), 0 (mémorisé, ou, si besoin, retrouvé en calculant 2 x 5 = 10 et en ne donnant que les unités).

Cette technique est basée sur la distributivité. 32 x 45 = (30 + 2) x (40 + 5)

= 30 x 40 + (30 x 5 + 40 x 2) + (2 x 5)

= 3 x 10 x 4 x 10 + (30 x 10 x 5 + 4 x 10 x 2) + (2 x 5)

= 100 x 3 x 4 + 10 x (3 x 5 + 4 x 2) + (2 x 5)

= 100 x 12 + 10 x 23 + 10

= 100 x 12 + 10 x (2 x 10 + 3) + 1 x (10 + 0)

= 100 x 12 + 2 x 10 x 10 + 3 x 10 + 1 x (10 + 0)

= 100 x 12 + 2 x 100 + 3 x 10 + 1 x 10 + 1 x 0

= 100 x (12 + 2) + 10 x (3 + 1) + 1 x 0

= 100 x 14 + 100 x 4 + 1 x 0

Pour s’entraîner

54 x 66 = 70 x 95 = 28 x 83 = 45 x 63 = 18 x 87 =

= 1 4 4 0 25 x 62 = 47 x 86 = 49 x 18 = 21 x 74 = 33 x 97 =

98 x 99 = 56 x 71 = 24 x 43 = 92 x 37 = 65 x 38 =

39 x 79 = 48 x 35 = 23 x 76 = 92 x 51 = 33 x 27 =

71

Une série d’exercices, de difficulté progressive pour mettre en pratique les techniques étudiées.

Le parti pris dans cet ouvrage est de mettre en avant la technique de calcul. Pour cela, on n’utilise pas de séparateur de milliers dans l’écriture des chiffres. En effet, le résultat est d’abord une série de chiffres : une fois le résultat écrit, l’élève pourra le lire en donnant éventuellement les millions, les milliers, les unités.

I. Prérequis

1. Apprentissage par cœur ....................................................... 16

2. Abacus finger : un système original pour compter jusqu’à 99 sur ses doigts 26

3. Quelques techniques à maîtriser préalablement 33

4. Quelques astuces pour faciliter le calcul mental rapide 38

1. Apprentissage par cœur

I. Prérequis

1. APPRENTISSAGE PAR CŒUR

Le calcul mental rapide passe nécessairement par une phase d’apprentissage par cœur, qui servira de base pour toutes les formes de calcul.

a Tables de multiplication (dans l’ordre

: 11, 5, 2, 4,

L’ordre d’apprentissage

3, 9, 6, 7, 8, 12, 15, 14 et 13)

Pour apprendre les tables de multiplication, on commence par la table la plus facile pour aller graduellement vers les tables les plus ardues. L’idéal est de ne passer à la table supérieure qu’une fois les précédentes parfaitement maîtrisées. L’ordre le plus convenable, avec le recul, me semble être : 11, 5, 2, 4, 3, 9, 6, 7, 8, puis 12, 15, et enfin 14 et 13.

Le support

J’utilise depuis plusieurs années le support ci-contre pour les tables de multiplication. Il suffit de le découper selon les pointillés, de classer les tables dans l’ordre croissant de 2 à 15, puis d’agrafer les parties blanches ensemble.

Premier principe

Il faut que l’enfant apprenne chaque ligne de la table choisie comme un bloc unique. On assiste trop souvent à des récitations de tables lors desquelles les enfants peinent à assembler l’énoncé (6 x 7, par exemple) et la réponse (42). Cela est dû, en grande partie, au fait que l’enfant a appris chaque ligne de sa table trop lentement, ce qui revient à stocker deux informations différentes dans le cerveau pour ensuite les réassembler. C’est un processus long et inutile : en effet, 6 x 7 ne sera jamais associé à un autre résultat que 42 ; pour cette raison, il vaut mieux apprendre directement 6 x 7 = 42 sous la forme d’une seule information que l’on nommera par la suite « bloc logique ».

Pour retenir un bloc logique sous la forme d’une seule information, il suffit de l’apprendre rapidement, en un seul bloc de mots, sans aucune pause, un peu comme on apprendrait à dire « abracadabra » et non pas « abra… ca… dabra ». Plus la ligne sera lue rapidement, plus le but recherché sera atteint ; le cerveau ne pourra, avec la vitesse, privilégier d’autres voies que celle du stockage en un seul bloc, le plus succinct possible. Ainsi, on ne fera pas dire à l’enfant « 6 fois 7 égale 42 », mais juste « 6 fois 7 42 ».

Second principe

Il faut entraîner le cerveau à stocker les informations à long terme. Au fur et à mesure des répétitions, le stockage se fera plus efficace, jusqu’à devenir un réflexe. Ainsi, on commencera par faire répéter à l’enfant le bloc logique à apprendre avant de venir perturber cette répétition quasi-automatique du bloc logique en le distrayant ; pour cela on fera appel alternativement à son imagination, à sa mémoire et à l’humour.

Apprentissage par cœur

LA MÉTHODE COMPLÈTE

Les 5 premiers blocs logiques

On demande à l’enfant, avec le papier ouvert sous les yeux, de lire à voix haute et le plus rapidement possible le 1er bloc logique de la table choisie. Pour cela, il doit inspirer calmement tout en préparant mentalement la prononciation du 1er bloc logique, puis prononcer ce bloc logique le plus vite possible, de manière explosive, à la limite de l’articulation, en expirant et en suivant avec son doigt la ligne lue.

On lui demande ensuite d’inspirer calmement tout en préparant la prononciation du 2e bloc logique (ce temps de pause est très important, c’est ce qui permet au cerveau de segmenter les blocs logiques), et ainsi de suite jusqu’à la moitié de la table environ.

On lui fait recommencer ce travail plusieurs fois de suite, en cherchant la plus grande vitesse possible de prononciation sur chaque bloc, mais jamais sur l’enchaînement d’une ligne à l’autre. Quand l’enfant semble prêt à pouvoir se passer du temps d’inspiration permettant de préparer la ligne suivante, on arrête l’exercice portant sur ces premières lignes et on demande à l’enfant de bien vouloir plier le papier au niveau des signes égal, les résultats n’étant ainsi plus visibles.

On lui demande alors de recommencer comme auparavant, sans rien changer : il doit lire mentalement en inspirant et en préparant sa phrase qu’il dit ensuite d’un jet (le plus rapidement possible en suivant la ligne avec le doigt, comme si le résultat était toujours écrit, en expirant) puis respirer calmement tout en préparant la ligne suivante et ainsi de suite. À la moindre hésitation ne permettant pas à l’enfant de dire son bloc logique de manière explosive, on demandera à l’enfant d’ouvrir à nouveau son papier afin de revoir les résultats. On recommencera ainsi jusqu’à ce que l’enfant soit capable d’enchaîner facilement (mais toujours avec une lente respiration entre deux lignes) les blocs logiques 1 à 5, avec les résultats cachés.

Flashez pour le cours

Les 5 derniers blocs logiques

On passe alors, toujours avec la même technique, aux 5 blocs logiques suivants sans se soucier des 5 premiers : on ne fera répéter à l’enfant que les blocs 6 à 10.

L’enchaînement complet

On demande maintenant à l’enfant de prononcer, toujours avec la même technique, tous les blocs logiques de 1 à 10, en prenant bien, c’est important, une pause entre deux lignes. Il ne faut vraiment chercher la vitesse que lors de la prononciation d’une seule ligne.

Les blocages

Il arrive toujours, quelle que soit la table, que l’enfant bute sur un bloc logique qu’il a du mal à retenir. Dans ce cas, on va perturber son cerveau pour l’obliger à stocker le résultat sur plus long terme. Pour cela, on fait répéter à l’enfant, après le lui avoir énoncé oralement, le bloc logique qui lui pose problème, plusieurs fois et au signal convenu exécuté par l’adulte. Ce signal peut être un geste du doigt, un claquement de doigt, une frappe de la pointe d’un stylo sur la table… peu importe, pourvu que l’enfant attende le signal et que celui-ci ne soit pas toujours donné avec la même cadence. À chaque répétition fausse, l’adulte doit prononcer à nouveau le bloc logique en entier et demander à l’enfant de recommencer.

Au bout de quatre à cinq répétitions correctes, on interrompt ce travail en posant une question. Cette première question fait appel à la mémoire de l’enfant : « Qu’as-tu mangé ce matin au petit déjeuner ? » ; « Sans regarder tes chaussettes, saurais-tu te rappeler leur couleur ? » ; « Quel est le prénom de ton frère ? » ; « Quelle est la couleur de la voiture de tes parents ? », etc. Quand l’enfant cherche la réponse, ses yeux devraient se déplacer dans un sens (variable selon les enfants), signe qu’il utilise sa mémoire. On peut alors lui redemander le bloc logique travaillé ; la réponse est souvent un peu fastidieuse : l’enfant, s’étant concentré sur autre chose, a perdu le résultat. On reprend alors exactement le même travail sur le même bloc (on ne travaillera jamais deux blocs à la fois, tout au moins dans un premier temps).

Au bout de quatre à cinq répétitions convenables d’affilée, on interrompt à nouveau l’enfant pour lui poser une question faisant appel, cette fois, à son imagination : « Quel métier aimeraistu faire plus tard ? » ; « Préférerais-tu habiter à la mer ou à la montagne ? » ; « Si un génie t’offrait d’exaucer un seul vœu, lequel ferais-tu ? » ; « Que voudrais-tu manger ce soir ? », etc. En général, l’enfant devrait avoir les yeux dirigés dans la direction opposée à celle correspondant à la première question. On lui redemande alors de réciter le bloc logique. La réponse devrait être déjà plus rapide qu’après la première question.

Apprentissage par cœur

On recommence le même travail et, après quatre ou cinq répétitions correctes, on lui pose une question amusante : « Quel était l’âge de Napoléon ? » ; « Quelle est la couleur préférée de Barbie ? » ; « Quel était le prénom de Louis Pasteur ? » ; « T’est-il déjà arrivé de venir à l’école en chaussons ? », etc. Et on redemande le bloc logique. La réponse devrait être nettement plus rapide. On recommence ainsi plusieurs fois jusqu’à ce que le bloc logique semble parfaitement su. On demande alors à l’enfant de reprendre son papier et de tout recommencer depuis le bloc 1 jusqu’au bloc 10, en prenant soin de le rassurer et de l’encourager. Normalement, cela fonctionne mais, si cela bloque, il ne faut pas hésiter à reprendre la même technique de répétitions et de questions. Certains enfants sont plus rapides que d’autres, mais tous y arrivent.

La vitesse Quand l’enfant sera capable de réciter deux ou trois fois d’affilée sa table sans erreur, mais en prenant une pause entre chaque ligne, on lui proposera de recommencer mais, cette fois, sans pause entre deux blocs logiques. On pourra alors le chronométrer. L’enfant devrait être capable de réciter sa table en une petite dizaine de secondes. Si ce n’est pas le cas, il suffit d’identifier le problème (en général, un problème de bloc logique mal mémorisé) et de reprendre la méthode pour lever les blocages. Dans mes classes, tous les élèves de CM1 et de CM2 récitent leurs tables en moins de dix secondes. Deux fois par semaine, ils sont interrogés. Ils partent de 20/20 s’ils récitent en dix secondes ou moins, les CM1 perdant 1 point par seconde supplémentaire et les CM2, deux points par seconde supplémentaire. Ils adorent ce petit jeu : mesurer sa performance est la meilleure façon de se voir progresser.

Pour compliquer un peu

Pour les élèves réussissant l’exercice, je propose généralement trois variantes.

• Variante 1 : la table à réciter est tirée aux dés et l’enfant doit la commencer moins de trois secondes après avoir entendu le nom de la table.

• Variante 2 : l’enfant doit réciter sa table à l’envers du bloc 10 au bloc 1 (j’augmente le temps de base de 4 secondes par table).

• Variante 3 : l’enfant enchaîne ses tables de 2 à 9, sans s’arrêter entre deux tables (Le temps attendu est 1 minute 20 secondes ; les meilleurs élèves se contentent de 50 secondes).

b Moitiés (de 1 à

entiers entre 1 et 19 (et donc les doubles nombres décimaux qui se terminent par des ,5 de 0,5 à 9,5).

Ce fichier est disponible en téléchargement sur le site www.editionscriterion.fr, onglet « Ressources pédagogiques ».

donnant

Apprentissage par cœur

c Complémentaires à 10, à 9 et à 5

Pour la suite de ce manuel, les élèves devront maîtriser les complémentaires à 10, à 9 et à 5. Comme pour les moitiés et les doubles, pas de technique particulière, on fera juste apprendre les trois tableaux suivants.

COMPLÉMENTAIRES À 10 COMPLÉMENTAIRES À 9 COMPLÉMENTAIRES À 5

Les tableaux de complémentaires à 10

Disponibles en téléchargement sur le site www.editionscriterion.fr, onglet « Ressources pédagogiques ».

Le but est que l’enfant qui cherche, par exemple, des complémentaires à 10 « flashe » immédiatement un 9 et un 1, que la vue du 9 entraîne immédiatement à chercher un 1.

Pour travailler ce type de réflexe, je donne à mes élèves des tableaux de plus en plus grands, avec des complémentaires à regrouper pour trouver rapidement la somme totale. On peut en réaliser très simplement avec un tableur quelconque. En voici un exemple (avec les résultats).

L’enfant doit trouver la somme totale des chiffres écrits sur fond blanc, puis celle des chiffres sur fonds jaune, orange, vert, bleu, marron et noir. Le temps est de deux minutes en CM2 ; certains enfants n’ont le temps de résoudre que trois couleurs, d’autres arrivent jusqu’au noir. Sur les fonds blanc et jaune, il n’y a que deux types de complémentaires (5 + 5 et 8 + 2) ; sur les fonds orange et vert, il y a trois types de complémentaires (5 + 5, 8 + 2 et 9 + 1) ; sur les fonds bleu et marron, il y a quatre types de

complémentaires (5 +

+

9 + 1 et 6 + 4) ; enfin, sur fond noir, on trouve tous les complémentaires. Le nombre de chiffres à additionner étant toujours impair, l’enfant devra, pour gagner du temps, grouper les complémentaires à 10 et additionner ensuite le chiffre restant : pour le orange, par exemple, il calculera (8 + 2) + (8 + 2) + (9 + 1) + (5 + 5) + 2 = 42. L’enfant s’habitue ainsi à regrouper très rapidement des complémentaires à 10, ce qui lui fera gagner du temps lors des additions « Flansburg », par exemple.

Pour s’entraîner

2. « ABACUS FINGER » : UN SYSTÈME ORIGINAL POUR COMPTER JUSQU’À 99 SUR SES DOIGTS

a Intérêt

Habituellement, on utilise les doigts pour compter avec l’idée que chaque doigt vaut 1. Ce système, certes très simple à comprendre, présente l’inconvénient de ne permettre de compter sur ses doigts que jusqu’à 10, ce qui est très limité.

Il existe un système indien, parfois appelé « abacus finger », qui permet de compter sans difficulté, après un petit temps d’entraînement, jusqu’à 99. Ce système a l’avantage d’être compatible avec le soroban (le boulier japonais), puisqu’il utilise le même principe. Le plus grand intérêt de ce système est qu’il permet de stocker des résultats intermédiaires lors de calculs complexes, de noter les retenues lors des multiplications posées, d’effectuer rapidement des additions, des soustractions ou même de trouver immédiatement des complémentaires à 100.

b Principes

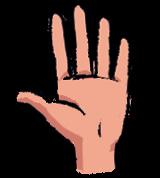
Dans le système « abacus finger », le pouce vaut 5 et les autres doigts valent tous 1.

Il faut préciser à l’enfant de toujours garder les deux mains collées et orientées paumes vers lui, comme montré ci-contre ; ce sera à l’adulte de s’adapter. De même, pour montrer un nombre à l’enfant, il faudra bien penser à se placer dans le même sens que lui ; en général, je place mes deux mains au-dessus de ma tête, tournant le dos aux élèves. On expliquera à l’enfant, qui aura préalablement bien compris le fonctionnement avec une seule main, qu’on ne peut pas faire 10 avec une main : pour cela on utilisera les deux mains, celle de droite indiquant les unités et celle de gauche indiquant les dizaines. Pour écrire 10, on note 1 sur la main de gauche et 0 sur la main de droite, exactement comme on le fait dans un tableau de numération ; les correspondances mains/tableau de numération et mains/écriture du nombre deviennent évidentes. 32, par exemple, s’écrira avec 3 sur la main de gauche (la main des dizaines) et 2 sur la main de droite (la main des unités).

I.

« Abacus finger » : un système original pour compter jusqu’à 99 sur ses doigts

Flashez pour le cours

Il est important d’entraîner le plus tôt possible l’enfant à compter ainsi. On apprendra à l’enfant à reconnaître des figures de base (par exemple, 9, c’est la main complète ; 7, c’est le pistolet de James Bond 007) jusqu’à ce que l’enfant soit capable de lire (et d’écrire) instantanément sur ses mains n’importe quel nombre sans compter. Pour cela on pourra, chaque jour, lui faire des dictées de nombres (on lui donne un nombre à l’oral et il doit l’écrire sur ses doigts, le plus vite possible) ou, à l’inverse, lui demander d’écrire sur son ardoise plusieurs nombres qu’on lui montrera sur nos doigts (toujours en se plaçant dans le même sens que lui, afin de ne pas perturber sa représentation spatiale). Il faut créer un réflexe : écrire sur ses doigts doit devenir un langage supplémentaire pour l’enfant.