Tecno CAT by ELI Publishing

A. Zanin G. Baldisseri M. Bignardi A. Pietrafitta

Tecnologie e tecniche di rappresentazione grafica

tecno

EDUCAZIONE

ORIENTAMENTO Il ruolo del geometra

VIDEOTUTORIAL Dal CAD al cantiere

Zanin G. Baldisseri M. Bignardi A. Pietrafitta

Tecnologie e tecniche di rappresentazione grafica

Gruppo Editoriale

ELi

Il piacere di apprendere

Costruire il futuro insieme

Il Gruppo Editoriale ELi

offre proposte editoriali che coprono tutti i gradi e i rami scolastici, all’insegna della qualità, del rigore e dell’innovazione.

INTELLIGENZA

ARTIFICIALE

Percorsi didattici con attività pratiche che mirano ad approfondire i principali strumenti di IA generativa per favorirne un utilizzo critico e il tool VELIA a disposizione dei docenti per personalizzare l’attività didattica.

EQUILIBRI

Progetto di ricerca costante che mira a eliminare gli stereotipi di genere nei testi scolastici ponendo particolare attenzione alla scelta dei contenuti, a una valutazione iconografica ragionata e all’utilizzo di un linguaggio testuale inclusivo.

INCLUSIONE

Sviluppo di una cultura dell’inclusione attraverso contenuti accessibili e adeguati ai diversi stili di apprendimento.

ORIENTAMENTO

Approccio educativo e formativo volto a favorire la conoscenza di sé, delle proprie attitudini e delle proprie capacità, oltre a sviluppare le competenze non cognitive e trasversali necessarie per le scelte del futuro.

EDUCAZIONE

CIVICA secondo le NUOVE Linee guida

Aggiornamento e ampliamento dei nuclei tematici attorno ai quali si articolano le competenze e gli obiettivi di apprendimento: Costituzione, Sviluppo economico e sostenibilità, Cittadinanza digitale

STEM/STEAM, CLIL

Attivazione del pensiero scientifico e computazionale, approccio interdisciplinare e laboratoriale, sviluppo della competenza multilinguistica, attraverso attività STEM, STEAM e CLIL.

DIGITALE

Acquisizione delle competenze digitali e dell’alfabetizzazione informatica come aiuto all’inclusione sociale e alla cittadinanza attiva.

EDUCAZIONE ALLE RELAZIONI

Percorsi incentrati sullo sviluppo di competenze relazionali che arricchiscono la consapevolezza del vissuto personale in relazione con la realtà circostante.

Gruppo Editoriale

ELi

Gruppo Editoriale

ELi

TECNOCAT è il corso pensato come uno strumento di lavoro completo e progressivo per gli Istituti Tecnici a indirizzo Costruzioni, Ambiente e Territorio. La prima parte affronta i fondamenti del disegno tecnico, dalle costruzioni geometriche alle proiezioni, fornendo le basi della rappresentazione grafica. La seconda parte è invece dedicata alla figura del geometra e collega il disegno alle applicazioni professionali: dalla rappresentazione di edifici e abitazioni, allo studio degli spazi interni, fino ai temi dell’arredo urbano e del territorio. L’obiettivo è fornire un percorso coerente che unisca teoria e pratica, aiutando studenti e studentesse a leggere, interpretare e realizzare elaborati grafici utili sia nello studio sia nella futura attività

tecno

Tecnologie e tecniche di rappresentazione grafica

VANTAGGI

Riciclabilità: molti metalli, come l’acciaio e l’alluminio, possono essere riciclati all’infinito senza perdere qualità.

Durabilità: la loro resistenza permette una lunga vita utile delle strutture, riducendo i consumi di materiali nel lungo periodo.

Efficienza: possono essere utilizzati per prefabbricati. In questo modo si riducono gli sprechi e si ottimizzano i tempi di costruzione.

I metalli hanno avuto un ruolo fondamentale nella storia dell’architettura. Agli inizi si utilizzava lo zinco per le coperture, il rame per le decorazioni e dettagli artistici. Con la Rivoluzione Industriale, però, la funzione del metallo cambia radicalmente grazie all’introduzione della ghisa e, in seguito, dell’acciaio, che resero i metalli i protagonisti delle strutture portanti. Un’opera simbolo di questa trasformazione è la Torre Eiffel, costruita nel 1889 con una struttura metallica ideata da Gustave Eiffel, destinata a diventare un’icona mondiale. Da quel momento il metallo si diffuse in ponti, stazioni, grattacieli, ma anche in elementi di design e architettura leggera. Le sue caratteristiche di resistenza, leggerezza e flessibilità consentono di realizzare grandi luci e forme innovative. Può essere lucido, ossidato, liscio o lavorato, adattandosi a diversi linguaggi fino al mondo contemporaneo. Oggi i metalli sono utilizzati in un’ottica di sostenibilità, anche grazie a tecnologie avanzate e processi di riciclo che riducono l’impatto ambientale. Nell’edilizia moderna trovano applicazione sia nelle strutture portanti che negli elementi di finitura come coperture, facciate e infissi. La possibilità di prefabbricare componenti metallici assicura montaggi rapidi e precisi, migliorando tempi e qualità costruttiva. Tra le soluzioni recenti , apprezzato per la sua resistenza naturale alla corrosione e per la durabilità senza trattamenti aggiuntivi. Grazie a queste qualità, il metallo rimane un materiale centrale, capace di unire innovazione tecnica, estetica e sostenibilità.

Le competenze fondamentali includono: → la progettazione e realizzazione di strutture metalliche; → la scelta dei materiali e controllo della corretta posa in opera; → la gestione di rilievi tecnici e la capacità di saper leggere disegni e computi metrici; → la collaborazione con ingegneri strutturisti e aziende specializzate; → la gestione del cantiere; → l’analisi della sostenibilità dell’opera orientamento

SVANTAGGI AMBIENTALI E CRITICITÀ

CIVICA

Consumo: elevato consumo energetico per l’estrazione e la lavorazione dei metalli. Sostenibilità: significative emissioni di CO2 durante i processi industriali.

Alterabilità: sensibili alla corrosione, possono essere richiesti trattamenti protettivi o l’uso di leghe speciali.

risoluzione grafica, indispensabile strumento per imparare a leggere gli elaborati. L’utilizzo di tre colori guida nei segni, nero, rosso e azzurro, permette di evidenziare al meglio le tre diverse fasi nella costruzione del disegno

SPAZI SEZIONE

HERZOG & DE MEURON

EDUCAZIONE

LA PERCEZIONE VISIVA

D Il linguaggio del DISEGNO TECNICO

COMPENETRAZIONI

SVILUPPO DI SOLIDI

ZAHA HADID

Dal CAD al cantiere sostenibile

SEZIONE

A

PERCEZIONE VISIVA E COMUNICAZIONE GRAFICA

CAPITOLO 1 LA PERCEZIONE VISIVA

CAPITOLO 2 IL LINGUAGGIO MULTIMEDIALE

Álvaro Siza

è un architetto

portoghese noto per la sua capacità di integrare l’architettura

nel contesto urbano, utilizzando forme semplici e materiali locali.

Nei suoi edifici, spesso con le murature rifinite con intonaco bianco, la costruzione “dialoga” con l’ambiente in modo silenzioso ma preciso.

La luce è un elemento fondamentale nei

suoi progetti: entra negli spazi con aperture studiate, creando atmosfere tranquille e accoglienti.

Le sue opere si distinguono per la cura dei dettagli costruttivi, come i muri spessi, gli infissi incassati, le scale e le rampe dolcemente inclinate.

Ogni edificio è il risultato di un attento studio del luogo, sia dal punto di vista topografico che culturale

Álvaro Siza Vieira

Vincitore del Pritzker

Piscine di Leça da Palmeira

Complesso balneare sulla costa atlantica, perfettamente integrato nella scogliera naturale.

ÁLVARO SIZA VIEIRA

Prize nel 1992

Le architetture di Álvaro Siza mostrano l’importanza di curare ogni dettaglio, scegliere bene i materiali e rispettare l’ambiente circostante. Per un geometra studiare queste opere significa imparare a lavorare con grande precisione senza trascurare nulla, capire come unire tecnica, estetica e rispetto del territorio.

Le sue competenze includono: → conoscere i materiali da costruzione e capire come si comportano, per inserirli al meglio negli spazi; → leggere il paesaggio e adattare i progetti in modo che gli edifici non lo rovinino, ma lo valorizzino;

→ trasformare un progetto in spazi funzionali, sicuri e ben integrati con l’ambiente e capire come i materiali dialogano con l’ambiente; → collaborare con architetti e ingegneri, contribuendo in modo concreto alla realizzazione delle idee progettuali.

Lo spirito con cui l’architetto Alvaro Siza ha progettato le sue opere insegna che costruire non significa solo realizzare edifici, ma anche rispettare il paesaggio e la comunità dimostrando che l’architettura può essere al servizio delle persone. Un buon progettista deve creare spazi semplici, utili e civili, pensando al bene comune e non solo all’interesse personale. Costruire in questo modo diventa un atto di educazione civica, perché contribuisce a migliorare la qualità della vita e a prendersi cura del territorio.

1 LA PERCEZIONE VISIVA

1 Il funzionamento dell’occhio

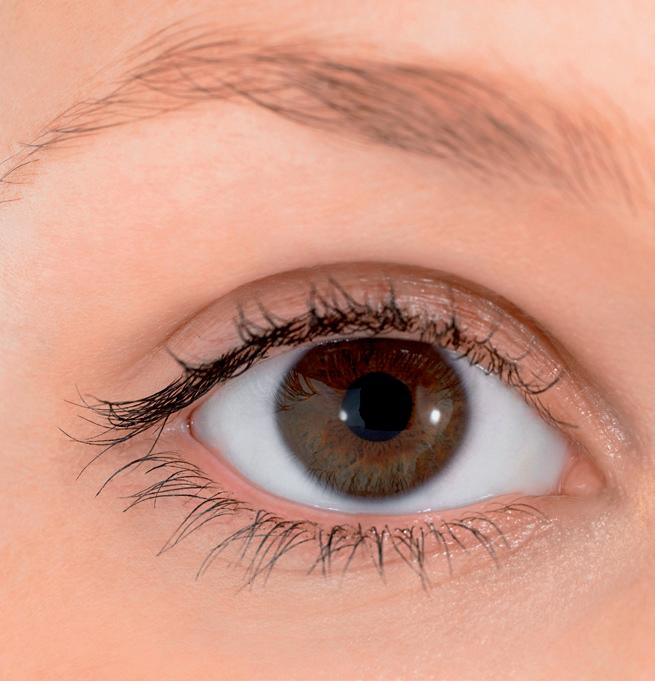
Gli occhi ricevono le onde luminose riflesse dagli oggetti e le convogliano sulle terminazioni del nervo ottico. È possibile comprendere il funzionamento dell’occhio paragonandolo alla macchina fotografica digitale. Gli elementi fondamentali di una macchina fotografica digitale sono la lente e il sensore CCD, che è l’elemento elettronico composto da minuscoli sensori che generano una differenza elettrica analogica proporzionale all’intensità di luce che li colpiscono. Le loro funzioni corrispondono a quelle svolte nell’occhio dal cristallino e dalla rètina.

Per eseguire una fotografia si orienta l’obiettivo verso l’oggetto da fotografare, si inquadra e si scatta, cioè si preme il pulsante che permette ai raggi luminosi di entrare nell’apparecchio e colpire il sensore CCD il quale trasmette gli impulsi elettrici (➜ Fig. 1a).

Un processo simile avviene nel nostro occhio: l’oggetto che osserviamo riflette i raggi luminosi che entrano nell’occhio attraverso il foro della pupilla e vengono captati dal cristallino che li invia alla retina. I recettori posti sulla retina trasformano i segnali luminosi in segnali chimici, che vengono raccolti dal nervo ottico, che a sua volta li invia al cervello. Quest’ultimo decodifica gli impulsi e li trasforma nelle immagini che vediamo (➜ Fig. 1b).

Il cristallino si comporta come una lente per la “messa a fuoco”. Se gli oggetti sono posti a una distanza superiore a 7 metri, i raggi inviati agli occhi giungono paralleli al cristallino, che è costretto, con l’aiuto della cornea, a deformarli per inviarli alla retina. Se invece gli oggetti sono posti a una distanza

CI OCCUPEREMO DI...

1. Il funzionamento dell’occhio

2. La percezione visiva: osservazioni generali

3. La teoria cognitivista

4. La teoria della Gestalt

5. Articolazione gura-sfondo

6. La percezione della profondità

7. La costanza percettiva

8. Le illusioni ottiche

9. La percezione del colore

minore, i raggi luminosi divergono e il cristallino si ispessisce per metterli a fuoco sulla retina.

A questo punto il paragone con la macchina fotografica si esaurisce in quanto entra in azione il cervello, che compie un’elaborazione dei dati ricevuti per la formazione dell’immagine.

lente

➜ Fig. 1a

sensore CCD

umore acqueo retina

cristallino

➜ Fig. 1b

➜ Fig. 1 • L’occhio e la macchina fotogra ca presentano un’analoga struttura. Il corpo diottrico, formato nell’occhio da cornea, umore acqueo e cristallino, e nella macchina fotogra ca dalle lenti dell’obiettivo, ha la funzione di far convergere i raggi luminosi in una zona interna ove sono catturate le immagini: nell’occhio dalla retina, nella macchina fotogra ca dal sensore CCD.

MESSA A FUOCO

Fotografare mantenendo i contorni nitidi di ciò che si intende evidenziare.

La percezione visiva

2 La percezione visiva: osservazioni generali

La percezione visiva

l’attività del cervello sia nel riconoscere cose note che nel registrare cose nuove.

La percezione visiva

1.2 La percezione visiva: osservazioni generali

La percezione visiva

L’essere umano percepisce l’ambiente attraverso i propri sensi che eseguono, per mezzo dei recettori sensoriali, una lettura-descrizione di una grande quantità di informazioni captate dall’ambiente stesso. Queste informazioni giungono al cervello che le seleziona ed elabora, in tempi molto brevi, compiendo un confronto con le tracce di altri stimoli uguali o simili depositate nella memoria. Si ha così una doppia attività di lettura-descrizione e di confronto in cui ha una preponderante importanza

1.2 La percezione visiva: osservazioni generali

L’uomo percepisce l’ambiente attraverso i propri sensi, che eseguono, per mezzo dei ricettori sensoriali, una lettura-descrizione di una grande quantità di informazioni captate dall’ambiente stesso. Queste informazioni giungono al cervello che le seleziona ed elabora, in tempi molto brevi, compiendo un confronto con le tracce di altri stimoli uguali o simili depositate nella memoria. Si ha così una doppia attività di lettura-descrizione e di confronto in cui ha una preponderante importanza l’attività del cervello sia nel riconoscere cose note che nel registrare cose nuove.

1.2 La percezione visiva: osservazioni generali

1.2 La percezione visiva: osservazioni generali L’uomo percepisce l’ambiente attraverso i propri sensi, che eseguono, per mezzo dei ricettori sensoriali, una lettura-descrizione di una grande quantità di informazioni captate dall’ambiente stesso. Queste informazioni giungono al cervello che le seleziona ed elabora, in tempi molto brevi, compiendo un confronto con le tracce di altri stimoli uguali o simili depositate nella memoria. Si ha così una doppia attività di lettura-descrizione e di confronto in cui ha una preponderante importanza l’attività del cervello sia nel riconoscere cose note che nel registrare cose nuove.

Questo succede anche nella percezione visiva in cui, oltre a ciò che percepiamo con la parte biologica della percezione e fisica dello stimolo (intensità, lunghezza d’onda, frequenza spaziale ecc.), c’è la interpretazione della realtà fatta dal nostro cervello. Esso, infatti, con la memoria visiva che deriva dalla cultura visiva e dalle esperienze percettive vissute, dà significato a ciò che si osserva.

Questo succede anche nella percezione visiva, in cui, oltre a ciò che percepiamo con la parte biologica della percezione e fisica dello stimolo (intensità, lunghezza d’onda, frequenza spaziale ecc.), c’è la interpretazione della realtà fatta dal nostro cervello. Esso, infatti, con la memoria visiva che deriva dalla cultura visiva e dalle esperienze percettive vissute, dà significato a ciò che si osserva.

L’uomo percepisce l’ambiente attraverso i propri sensi, che eseguono, per mezzo dei ricettori lettura-descrizione di una grande quantità di informazioni captate dall’ambiente stesso. Queste giungono al cervello che le seleziona ed elabora, in tempi molto brevi, compiendo un confronto altri stimoli uguali o simili depositate nella memoria. Si ha così una doppia attività di lettura-descrizione confronto in cui ha una preponderante importanza l’attività del cervello sia nel riconoscere cose registrare cose nuove.

L’uomo percepisce l’ambiente attraverso i propri sensi, che eseguono, per mezzo dei ricettori lettura-descrizione di una grande quantità di informazioni captate dall’ambiente stesso. giungono al cervello che le seleziona ed elabora, in tempi molto brevi, compiendo un confronto altri stimoli uguali o simili depositate nella memoria. Si ha così una doppia attività di lettura-descrizione confronto in cui ha una preponderante importanza l’attività del cervello sia nel riconoscere registrare cose nuove.

La prova che il nostro cervello elabora le informazioni integrandole con ipotesi a volte anche errate si può ottenere osservando ad esempio questa serie di figure.

Nella ➜ Fig. 2 si tende a percepire un triangolo bianco non trasparente che copre parzialmente tre dischi neri e un altro triangolo bianco col perimetro nero. In realtà si tratta di tre settori circolari neri e tre angoli disposti secondo un certo ordine gli uni rispetto agli altri.

Questo succede anche nella percezione visiva, in cui, oltre a ciò che percepiamo con la parte percezione e fisica dello stimolo (intensità, lunghezza d’onda, frequenza spaziale ecc.), c’è della realtà fatta dal nostro cervello. Esso, infatti, con la memoria visiva che deriva dalla cultura esperienze percettive vissute, dà significato a ciò che si osserva.

La prova che il nostro cervello elabora le informazioni integrandole con ipotesi a volte anche errate si può ottenere osservando ad esempio questa serie di figure.

Questo succede anche nella percezione visiva, in cui, oltre a ciò che percepiamo con la parte percezione e fisica dello stimolo (intensità, lunghezza d’onda, frequenza spaziale ecc.), c’è della realtà fatta dal nostro cervello. Esso, infatti, con la memoria visiva che deriva dalla esperienze percettive vissute, dà significato a ciò che si osserva.

La prova che il nostro cervello elabora le informazioni integrandole con ipotesi a volte anche ottenere osservando ad esempio questa serie di figure.

Nella ➜ Fig. 3 si hanno 8 linee parallele inclinate di 45° intersecate da una serie di segmenti che le fanno apparire leggermente divergenti.

La prova che il nostro cervello elabora le informazioni integrandole con ipotesi a volte anche errate si può ottenere osservando ad esempio questa serie di figure.

Nella ➜ Fig. 4 i triangoli variamente disposti non fanno percepire l’appartenenza alla stessa retta dei puntini.

➜

Il fenomeno della percezione visiva e stato ed è oggetto di molti studi che hanno prodotto alcune teorie, come la cognitivista e la teoria della Gestalt (“forma” in tedesco), e hanno analizzato i fenomeni dell’articolazione figura-sfondo , della percezione della profondità e della costanza percettiva.

Nella ➜ Fig. 5 la distanza AB sembra maggiore della CD quando invece sono congruenti.

Nella ➜ Fig. 6 il segmento EF sembra maggiore di EG mentre invece sono congruenti.

C D B A

Triangolo di Kanizsa

Illusioni di Zoellner

Illusione di Muller-Lyer

Rottura di rettilineità (Giovanelli)

Illusione di Sander

Triangolo di Kanizsa

Illusioni di Zoellner

Illusione di Muller-Lyer

Rottura di rettilineità (Giovanelli)

Illusione di Sander

Triangolo di Kanizsa

Illusioni di Zoellner

Illusione di Muller-Lyer

Rottura di rettilineità (Giovanelli)

Illusione di Sander

Triangolo di Kanizsa

Illusioni di Zoellner

Illusione di Muller-Lyer

Rottura di rettilineità

Illusione di Sander

C D B A F G E

Triangolo di Kanizsa

Illusioni di Zoellner

Illusione di Muller-Lyer

Rottura

Illusione di Sander

Fig. 2 • Triangolo di Kanizsa.

➜ Fig. 3 • Illusioni di Zoellner.

➜ Fig. 5 • Illusione di Muller-Lyer. ➜ Fig. 6 • Illusione di Sander.

➜ Fig. 4 • Rottura di rettilineità (Giovanelli).

I teorici della Gestalt sostenevano che la percezione è un unico insieme dato dall’organizzazione dei singoli elementi in relazioni tra loro secondo il principio del “tutto è più della somma delle parti” e rifiutavano la teoria secondo la quale essa è data dalla somma di sensazioni elementari integrate da associazioni legate alla memoria, al giudizio, al ragionamento ecc. Nell’esempio a fianco (fig.7) è sintetizzata la differenza tra la visione del tutto nella prima figura rispetto alla visione delle parti (a destra).

Nel 1923 Wertheimer, esponente di tale scuola, ha classificato e descritto come “leggi della forma” le modalità secondo le quali si costituiscono le forme.

3 La teoria cognitivista

Questa teoria sostiene che l’uomo dà significato a quello che osserva utilizzando la memoria visiva che proviene dalla sua cultura e dalle sue esperienze percettive acquisite. La sua mente cioè confronta l’immagine con una serie di propri modelli mentali e analizza il contesto in cui essa è collocata ricavando ulteriori informazioni utili per verificare le ipotesi fatte.

Legge del destino comune

Secondo questa legge, detta anche della somiglianza di comportamento, gli elementi che hanno un movimento solidale tra di loro, e differente da quello degli altri elementi, sono uniti in forme.

In figura 8 abbiamo un gruppo di puntini che si leggono spontaneamente su due colonne distinte. Se due puntini rossi e quattro puntini bianchi si muovono contemporaneamente nel senso delle frecce, si tenderà a leggere ancora due gruppi di puntini, ma secondo la logica del gruppo che si è spostato e del gruppo che è rimasto fermo (fig.9).

LEGGE DELLA PREGNANZA

Legge della pregnanza

Secondo la legge della pregnanza della buona

Gestalt, in pratica ciò che si coglie delle forme sono le caratteristiche “pregnanti” da esse possedute: cioè, quanto più regolari, simmetriche, semplici, omogenee, equilibrate, ordinate, coerenti strutturalmente, di carattere unitario esse sono, tanto maggiore è la probabilità che hanno d’imporsi alla nostra percezione.

Se accostiamo tra loro le tre figure di sinistra in figura10 otteniamo la figura di destra, in cui non leggiamo le figure originarie bensì una circonferenza che interseca un esagono regolare.

Secondo la legge della pregnanza della buona Gestalt, in pratica ciò che si coglie delle forme sono le caratteristiche “pregnanti” da esse possedute: cioè quanto più regolari, simmetriche, semplici, omogenee, equilibrate, ordinate, coerenti strutturalmente, di carattere unitario esse sono, tanto maggiore è la probabilità che hanno d’imporsi alla nostra percezione. Se accostiamo tra loro le tre figure di sinistra ➜ Fig. 10 otteniamo la figura di destra in cui non leggiamo le figure originarie bensì una circonferenza che interseca un esagono regolare.

percezione visiva è stato ed è oggetto di molti studi che hanno prodotto alcune teorie, come della Gestalt (“forma” in tedesco), e hanno analizzato i fenomeni dell’ArticolaziPercezione della profondità e della Costanza percettiva.

Gestalt sostenevano che la percezione è un unico insieme dato singoli elementi in relazioni tra loro secondo il principio del delle parti” e rifiutavano la teoria secondo la quale essa è sensazioni elementari integrate da associazioni legate alla ragionamento ecc. Nell’esempio a fianco (fig.7) è sintetizvisione del tutto nella prima figura rispetto alla visione

esponente di tale scuola, ha classificato e descritto come modalità secondo le quali si costituiscono le forme.

I teorici della Gestalt sostenevano che la percezione è un unico insieme dato dall’organizzazione dei singoli elementi in relazione tra loro secondo il principio del “tutto è più della somma delle parti” e rifiutavano la teoria secondo la quale essa è data dalla somma di sensazioni elementari integrate da associazioni legate alla memoria, al giudizio, al ragionamento ecc.. Nell’esempio qui sotto ( ➜ Fig. 7) è sintetizzata la differenza tra la visione del tutto nella prima figura rispetto alla visione delle parti (a destra). Nel 1923 Wertheimer, esponente di tale scuola, ha classificato e descritto come “leggi della forma” le modalità secondo le quali si costituiscono le forme.

LEGGE DEL DESTINO COMUNE

comune detta anche della somiglianza elementi che hanno un movidifferente da quello uniti in forme. gruppo di puntini che si su due colonne distinte. quattro puntini bianchi si contemporaneamente nel senso delle ancora due gruppi di logica del gruppo che si è è rimasto fermo (fig.9).

Legge della pregnanza

Cognitivista l’uomo dà significato a quello che osserva utilizzando la memoria visiva che proviene esperienze percettive vissute in precedenza. La sua mente cioè confronta l’immagmodelli mentali e, inoltre, analizza il contesto in cui essa è collocata ricavando ulteriverificare le ipotesi fatte.

LEGGE DELLA VICINANZA

A parità delle altre condizioni, tendono a essere vissuti come costituenti una unità, elementi vicini piuttosto che elementi lontani. Nelle ➜ Fig. 11 e 12 si tende a leggere quattro coppie di segmenti verticali vicini e cinque linee orizzontali anziché otto linee verticali di puntini.

➜ Fig. 7

Secondo questa legge, detta anche della somiglianza di comportamento, gli elementi che hanno un movimento solidale tra di loro, e differente da quello degli altri elementi, sono uniti in forme.

Secondo la legge della pregnanza della buona Gestalt, in pratica ciò che si coglie delle forme sono le caratteristiche “pregnanti” da esse possedute: cioè, quanto più regolari, simmetriche, semplici, omogenee, equilibrate, ordinate, coerenti strutturalmente, di carattere unitario esse sono, tanto maggiore è la probabilità che hanno d’imporsi alla nostra percezione.

Se accostiamo tra loro le tre figure di sinistra in figura10 otteniamo la figura di destra, in cui non leggiamo le figure originarie bensì una circonferenza che interseca un esagono regolare.

In ➜ Fig. 8 abbiamo un gruppo di puntini che si leggono spontaneamente su due colonne distinte. Se due puntini rossi e quattro puntini bianchi si muovono contemporaneamente nel senso delle frecce si tenderà a leggere ancora due gruppi di puntini ma secondo la logica del gruppo che si è spostato e del gruppo che è rimasto fermo (➜ Fig. 9).

fig.8 fig.9 fig.8 fig.9 4 La teoria della Gestalt

➜ Fig. 8 ➜ Fig. 9

➜ Fig. 11

LEGGE DELLA SOMIGLIANZA

A parità delle altre condizioni, si tende a unire tra loro gli elementi che hanno una qualche somiglianza. Nelle ➜ Fig. 13 e 14 si tende ad accoppiare i segmenti dello stesso colore e i cerchi e i quadrati si leggono per linee verticali cioè per elementi congruenti.

➜ Fig. 13

GELSTAT

➜

Corrente psicologica nata e sviluppatasi agli inizi del XX secolo in Germania tra gli anni Dieci e gli anni Trenta.

➜ Fig. 10

➜ Fig. 12

Fig. 14

LEGGE DELLA CHIUSURA

Le linee che formano delle figure chiuse tendono a essere viste come unità formali.

Si tende a preferire le forme chiuse rispetto a quelle aperte, pertanto in presenza di una forma che appare incompleta si tende a leggerla completa e continua.

Nelle ➜ Fig. 15 e 16 si tendono a leggere tre rettangoli e nove circonferenze anziché quattro coppie di c specchiate o nove coppie di x.

La percezione visiva

1.5 Articolazione figura-sfondo

5 Articolazione figura-sfondo

Lo studioso E. Rubin ha dimostrato che, in un campo visuale, tra probabilità il ruolo di figura, rispetto alle altre zone, quella che obbedisce più importanti sono: la grandezza relativa, i rapporti topologici, semplicità e la simmetria.

Lo studioso E. Rubin ha dimostrato che in un campo visuale, tra le zone che lo compongono, assumerà con più probabilità il ruolo di figura, rispetto alle altre zone, quella che obbedisce a determinate condizioni delle quali le più importanti sono: la grandezza relativa, i tipi dei loro margini, l’orientamento spaziale, i rapporti topologici, la semplicità e la simmetria.

La grandezza relativa: si tende a far emergere come figura la zona più piccola oppure quella circondata da altre aree.

La percezione visiva

La grandezza relativa: si tende a far emergere come figura la zona più piccola oppure quella circondata da altre aree.

1.5 Articolazione figura-sfondo

La percezione visiva

➜

figura-sfondo

Nel primo quadrato figura 19 si potrebbe leggere indifferentemente una croce bianca oppure una nera, nel secondo e nel terzo quadrato si percepiscono rispettivamente una croce bianca e una croce nera.

Nel primo quadrato ➜ Fig. 19 si potrebbe leggere indifferentemente una croce bianca oppure una nera, nel secondo e nel terzo quadrato si percepiscono rispettivamente una croce bianca e una croce nera.

La convessità leggere piuttosto quadrati quelle 21 percepiamo “colonnette

Lo studioso E. Rubin ha dimostrato che, in un campo visuale, tra le zone che lo compongono, probabilità il ruolo di figura, rispetto alle altre zone, quella che obbedisce a determinate condizioni più importanti sono: la grandezza relativa, i rapporti topologici, i tipi dei loro margini, l’orientamento semplicità e la simmetria.

LEGGE DELL’ESPERIENZA PASSATA

1.5 Articolazione figura-sfondo

Elementi che per la nostra esperienza passata sono abitualmente associati tra di loro tendono ad essere uniti in forme.

dimostrato che, in un campo visuale, tra le zone che lo compongono, assumerà con più figura, rispetto alle altre zone, quella che obbedisce a determinate condizioni delle quali le grandezza relativa, i rapporti topologici, i tipi dei loro margini, l’orientamento spaziale, la simmetria.

Lo studioso E. Rubin ha dimostrato che, in un campo visuale, tra le zone che lo compongono, assumerà con più probabilità il ruolo di figura, rispetto alle altre zone, quella che obbedisce a determinate condizioni delle quali le più importanti sono: la grandezza relativa, i rapporti topologici, i tipi dei loro margini, l’orientamento spaziale, la semplicità e la simmetria.

In ➜ Fig. 17 sono rappresentate le lettere E ed H che sono facilmente riconoscibili per coloro che conoscono l’alfabeto, mentre risultano incomprensibili per chi utilizza altre forme di scrittura.

La grandezza relativa: si tende a far emergere come figura la zona più piccola oppure quella circondata da altre aree.

➜ Fig. 19

La grandezza relativa: si tende a far emergere come figura la zona più piccola oppure quella circondata da altre aree.

: si tende a far emergere piccola oppure quella aree.

figura 19 si potrebbe leggere croce bianca oppure una terzo quadrato si percepisuna croce bianca e una croce

La grandezza relativa: si tende a far emergere come figura la zona più piccola oppure quella circondata da altre aree. Nel primo quadrato figura 19 si potrebbe leggere indifferentemente una croce bianca oppure una nera, nel secondo e nel terzo quadrato si percepiscono rispettivamente una croce bianca e una croce nera.

La convessità o la concavità dei margini tendono a far leggere come figura l’area con margini convessi piuttosto che quella con margini concavi; nei quattro quadrati ➜ Fig. 20, prevalgono le forme bombate e quelle a freccia pur invertendo i colori e nella ➜ Fig. 21 percepiamo delle “colonnette panciute” anziché “colonnette a spigoli vivi”.

La convessità o la concavità dei margini tendono a far leggere come figura l’area con margini convessi piuttosto che quella con margini concavi; nei quattro quadrati figura 20, prevalgono le forme bombate e quelle a freccia, pur invertendo i colori, e nella figura 21 percepiamo delle “colonnette panciute” anziché “colonnette a spigoli vivi”.

La convessità o la concavità dei margini leggere come figura l’area con margini piuttosto che quella con margini concavi; quadrati figura 20, prevalgono le forme quelle a freccia, pur invertendo i colori, 21 percepiamo delle “colonnette panciute” “colonnette a spigoli vivi”.

La convessità o la concavità dei margini leggere come figura l’area con margini piuttosto che quella con margini concavi; quadrati figura 20, prevalgono le quelle a freccia, pur invertendo i colori, 21 percepiamo delle “colonnette “colonnette a spigoli vivi”.

LEGGE DELLA CONTINUITÀ DI DIREZIONE

Gli elementi sono uniti in forme in base alla loro continuità di direzione.

Ad esempio si tende a leggere le due linee in ➜ Fig. 18 come la somma della spezzata AC e della curva BD e non delle spezzate AD e BC.

L’orientamento spaziale: tendono ad essere percepite come figura le aree i cui assi coincidono con le direzioni principali, verticale e orizzontale, dello spazio. Nell’esempio di figura 22 si legge più facilmente la croce verticale che non quella inclinata.

➜ Fig. 20

I rapporti geometriche): 23, la queste

➜ Fig. 18

➜ Fig. 21

I rapporti topologici (rapporti tra geometriche): tenderà ad emergere, 23, la zona più piccola o circondata queste ultime assumeranno il carattere

I rapporti topologici (rapporti tra le caratteristiche geometriche): tenderà ad emergere, come in figura 23, la zona più piccola o circondata da altre aree, e queste ultime assumeranno il carattere di sfondo.

Fig. 16

Fig. 15

➜ Fig. 17

fig.19

fig.22

fig.23

fig.20

fig.19

fig.20 fig.21

fig.19

fig.20

fig.21

fig.19

fig.20

fig.21

fig.19

fig.20

fig.21

fig.20

fig.21

L’orientamentospaziale:tendonoadessereperce-pitecomefiguraleareeicuiassi coincidonoconledirezioniprincipali,verticaleeorizzontale,dello spazio.Nell’esempiodifigura22sileggepiùfacilmentelacroceverticalechenonquellainclinata.

L’orientamento spaziale: tendono ad essere percepite come figura le aree i cui assi coincidono con le direzioni principali, verticale e orizzontale, dello spazio. Nell’esempio di ➜ Fig. 22 si legge più facilmente la croce verticale che non quella inclinata.

La simmetria: le forme simmetriche (più pregnanti) sono percepite come figura. Nell’esempio in ➜ Fig. 26 le figure simmetriche, rispetto all’asse verticale, prevalgono sulle sagome più irregolari che sono percepite come sfondo anche quando si invertono i colori.

I rapporti topologici (rapporti tra le caratteristiche geometriche): tenderà ad emergere, come in ➜ Fig. 23, la zona più piccola o circondata da altre aree, e queste ultime assumeranno il carattere di sfondo.

6 La percezione della profondità

La percezione visiva

La semplicità: le forme più semplici o pregnanti tendono a prevalere come figura.

PUNTO DI FISSAZIONE

Si memorizzano più facilmente forme semplici e regolari ➜ Fig. 24 mentre difficilmente riusciamo a memorizzare una forma irregolare come ad esempio una macchia ➜ Fig. 25.

Gran parte degli studiosi sono arrivati alla conclusione che noi non vediamo le distanze nella terza dimensione bensì le pensiamo o ce le rappresentiamo Vediamo cioè degli indizi che, confrontati con i nostri ricordi di esperienze passate, ci permettono di giudicare la collocazione nello spazio degli oggetti e le loro relative distanze. L’esempio classico è quello del bambino che nell’afferrare il biberon le prime volte annaspa incerto mentre successivamente, dopo varie esperienze, riesce ad associare il movimento della mano all’immagine retinica e a compiere l’atto al primo tentativo e con gesto sicuro. Si hanno due gruppi di indizi che permettono la percezione della profondità: i binoculari, che richiedono l’uso contemporaneo dei due occhi, e i monoculari cioè con un solo occhio.

Gli indizi binoculari sono: j la tensione dei muscoli che regolano la convergenza dei globi oculari quando si osservano gli oggetti vicini. Essi mediante i recettori sensoriali situati nei muscoli stessi e nei tendini trasmettono al cervello il grado di contrazione ➜ Fig. 27;

PUNTO DI FISSAZIONE

fig.23

La percezione visiva

fig.23

fig.20 fig.21

➜ Fig. 22

➜ Fig. 23

➜ Fig. 24 ➜ Fig. 25

➜ Fig. 26 ➜ Fig. 27

fig.29 fig.30

Gli indizi monoculari sono: Il movimento dei muscoli interni all’occhio, quando accomodano il cristallino per mettere a fuoco l’immagine, la cui contrazione è trasmessa al cervello mediante i ricettori sensoriali situati nei muscoli stessi e nei tendini (fig.29).

La prospettiva dimensionale per cui due oggetti della stessa forma ma di diverse dimensioni appaiono collocati a distanze differenti (fig.32).

quando accomodano il cristallino per mettere a fuoco l’immagine, la cui contrazione è trasmessa al cervello mediante i ricettori sensoriali situati nei muscoli stessi e nei tendini (fig.29).

j la differenza tra le due immagini dello stesso oggetto date dai due occhi nella visione binoculare che ci permette di avere una visione tridimensionale fino alla distanza di circa 100 metri ➜ Fig. 28.

La percezione visiva

➜ Fig. 28

fig.32

Gli indizi monoculari sono: j il movimento dei muscoli interni all’occhio , quando accomodano il cristallino per mettere a fuoco l’immagine, la cui contrazione è trasmessa al cervello mediante i recettori sensoriali situati nei muscoli stessi e nei tendini (➜ Fig. 29);

che sentato L’esempio neo parallele,

j la prospettiva cromatica, che ci fa apparire più vicini gli oggetti maggiormente contrastati o che abbiano colori “caldi” (rosso, giallo, arancio) anziché “freddi” (azzurro, verde, grigio) come in ➜ Fig. 31;

La prospettiva cromatica, che ci fa apparire più vicini gli oggetti maggiormente contrastati o che abbiano colori “caldi” (rosso, giallo,arancio) anziché “freddi” (azzurro, verde, grigio), come in figura 31

L’effetto che ci sentato L’esempio neo di parallele,

MUSCOLI RILASSATI

VISIONE DA LONTANO

fig.35

➜ Fig. 29

fig.31

L’effetto prospettico, cioè quel particolare fenomeno che ci fa percepire lo spazio così come viene rappresentato col metodo della prospettiva (fig.30).

La prospettiva dimensionale per cui due oggetti della stessa forma ma di diverse dimensioni appaiono collocati a distanze differenti (fig.32).

➜ Fig. 31

La prospettiva dimensionale per cui due oggetti della stessa forma ma di diverse dimensioni appaiono collocati a distanze differenti (fig.32).

L’altezza nel campo visivo che tende a far percepire più lontane le immagini collocate nelle zone superiori del campo visivo (fig.35).

MUSCOLI CONTRATTI

VISIONE DA VICNO

La prospettiva dimensionale per cui due oggetti della stessa forma ma di diverse dimensioni appaiono collocati a distanze differenti (fig.32).

j l’effetto prospettico, cioè quel particolare fenomeno che ci fa percepire lo spazio così come viene rappresentato col metodo della prospettiva (➜ Fig. 30). L’esempio classico lo si ha osservando il tratto rettilineo di una linea ferroviaria dove le rotaie, che sono parallele, sembrano convergere in un punto;

L’esempio classico lo si ha osservando il tratto rettilineo di una linea ferroviaria dove le rotaie, che sono parallele, sembrano convergere in un punto.

j la prospettiva dimensionale per cui due oggetti della stessa forma ma di diverse dimensioni appaiono collocati a distanze differenti (➜ Fig. 32);

fig.32

➜ Fig. 32

L’effetto prospettico, cioè quel particolare fenomeno che ci fa percepire lo spazio così come viene rappresentato col metodo della prospettiva (fig.30).

j l’altezza nel campo visivo che tende a far percepire più lontane le immagini collocate nelle zone superiori del campo visivo (➜ Fig. 33);

L’altezza nel campo visivo che tende a far percepire più lontane le immagini collocate nelle zone superiori del campo visivo (fig.35).

L’esempio classico lo si ha osservando il tratto rettilineo di una linea ferroviaria dove le rotaie, che sono parallele, sembrano convergere in un punto.

L’altezza nel campo visivo che tende a far percepire più lontane le immagini collocate nelle zone superiori del campo visivo (fig.35).

La prospettiva vicini abbiano “freddi”

➜ Fig. 30

altezza nel campo visivo che tende a far percepire più lontane le immagini collocate nelle zone superiori del campo visivo (fig.35).

➜ Fig. 33

fig.35

fig.29

fig.30

fig.31

fig.32

VISIONE DA LONTANO

MUSCOLI RILASSATI

VISIONE DA VICNO

MUSCOLI CONTRATTI

fig.29

fig.31

fig.32

fig.35

VISIONE DA LONTANO

MUSCOLI RILASSATI

VISIONE DA VICNO

MUSCOLI CONTRATTI

fig.29

La vicini abbiano “freddi”

La percezione visiva

Le ombre portate che fanno percepire in posizione avanzata un oggetto rispetto ad un altro quando il primo proietta la sua ombra sul secondo (fig.34).

j le ombre portate che fanno percepire in posizione avanzata un oggetto rispetto a un altro quando il primo proietta la sua ombra sul secondo (➜ Fig. 34);

Le ombre portate che fanno percepire in posizione avanzata un oggetto rispetto ad un altro quando il primo proietta la sua ombra sul secondo (fig.34).

j l’interposizione in cui un soggetto che ci appare incompleto, perché nascosto da un altro, ci fa desumere che il primo sia dietro e quindi più lontano del secondo ➜ Fig. 35.

L’interposizione in cui un soggetto che ci appare incompleto, perché nascosto da un altro, ci mere che il primo sia dietro e quindi più lontano secondo (fig.35).

L’interposizione in cui un soggetto che ci appare incompleto, perché nascosto da un altro, ci fa desumere che il primo sia dietro e quindi più lontano del secondo (fig.35).

fig.34

fig.35

1.7 La costanza percettiva

7 La costanza percettiva

1.7 La costanza percettiva

Quando ci muoviamo o muoviamo gli occhi le immagini degli oggetti che ci circondano, e che si determinano sulla retina, cambiano di forma, grandezza, colore e luminosità. Nonostante ciò la capacità di riconoscere gli oggetti rimane invariata. Questo fenomeno è detto costanza percettiva ed è dato dalle costanze di dimensioni, di forma, di chiarezza e colore e dall’invariabilità della posizione.

Quando ci muoviamo o muoviamo gli occhi le immagini degli oggetti che ci circondano, e che si determinano sulla retina, cambiano di forma, grandezza, colore e luminosità. Nonostante ciò la capacità di riconoscere oggetti rimane invariata. Questo fenomeno è detto costanza percettiva ed è dato dalle costanze di dimensioni, di forma, di chiarezza e colore e dall’invariabilità della posizione.

La costanza di dimensioni ci permette di percepire come costanti le dimensioni di un oggetto che, allontanandosi o avvicinandosi, proietta sulla retina rispettivamente un’immagine più piccola o più grande (fig. 36).

j La costanza di dimensioni ci permette di percepire come costanti le dimensioni di un oggetto che allontanandosi o avvicinandosi proietta sulla retina rispettivamente un’immagine più piccola o più grande (➜ Fig. 36);

fig.36

La costanza di chiarezza e colore ci fa percepire il colore di un oggetto anche se si varia la luminosità dell’ambiente.

La costanza di forma ci fa percepire la forma di un oggetto anche se collocato in diverse posizioni e che quindi proietta sulla retina immagini diverse: ad esempio la scacchiera in figura 37 che, inclinata, da quadrata ci appare trapezoidale.

La costanza di forma ci fa percepire la forma oggetto anche se collocato in diverse posizioni quindi proietta sulla retina immagini diverse: ad esempio la scacchiera in figura 37 che, inclinata, quadrata ci appare trapezoidale.

j La costanza di forma ci fa percepire la forma di un oggetto anche se collocato in diverse posizioni e che quindi proietta sulla retina immagini diverse: ad esempio la scacchiera in ➜ Fig. 37, che inclinata da quadrata ci appare trapezoidale;

fig.37

j La costanza di chiarezza e colore ci fa percepire il colore di un oggetto anche se si varia la luminosità dell’ambiente;

L’invariabilità della posizione fa sì che i cambiamenti delle immagini sulla retina, quando ci muoviamo o muoviamo gli occhi, non ci facciano percepire in movimento l’ambiente in cui siamo.

j L’invariabilità della posizione fa sì che i cambiamenti delle immagini sulla retina, quando ci muoviamo o muoviamo gli occhi, non ci facciano percepire in movimento l’ambiente in cui siamo.

La costanza di chiarezza e colore ci fa percepire il colore di un oggetto anche se si varia la luminosità dell’ambiente.

L’invariabilità della posizione fa sì che i cambiamenti delle immagini sulla retina, quando ci muoviamo o muoviamo gli occhi, non ci facciano percepire in movimento l’ambiente in cui siamo.

L’invariabilità della posizione fa sì che i cambia menti delle immagini sulla retina, quando ci muoviamo o muoviamo gli occhi, non ci facciano percepire movimento l’ambiente in cui siamo.

fig.37

fig.35

fig.37

fig.36

fig.35

fig.34

fig.37

fig.36

fig.35

fig.34

➜ Fig. 37 ➜ Fig. 36

➜ Fig. 34

➜ Fig. 35

Nella figura la metà del cerchio superiore appare per contrasto più scura

inferiore.

Fig. 38

1.8 Illusioni ottiche

8 Le illusioni ottiche

1.8 Illusioni ottiche

In figura all’incrocio delle fascie bianche compaiono delle macchie scure che svaniscono appena si porta losguardo su di esse.

Fig. 39

In questa trama di linee producono l’effetto di cerchi. effetto è chiamato illusione stein.

Illusione diHering. Le linee parallele orizzontali subiscono l’influsso delle linee inclinate e sembrano restringersi o dilatarsi al centro.

C’è la tendenza del cervello a valutare le dimensioni di figure basandosi su effetti prospettici o confrontandoli con oggetti vicini.

Sono illusioni cognitive che fanno percepire l’immagine o parte di essa in modo errato. Ad esempio linee che sono parallele sono percepite come divergenti, convergenti o curve. Oppure due elementi della stessa dimensione sono percepiti con dimensione differente. C’è la tendenza del cervello a valutare le dimensioni di figure basandosi su effetti prospettici o confrontandoli con oggetti vicini.

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

Fig. 41

Nell’illusione gialle diversa

Fig.

Nella figura la metà del cerchio superiore appare per contrasto più scura della metà inferiore.

C’è la tendenza del cervello a valutare le dimensioni di figure basandosi su effetti prospettici o confrontandoli con oggetti vicini.

Nella figura la metà del cerchio superiore appare per contrasto più scura della metà inferiore.

Fig. 39

In figura all’incrocio delle fascie bianche compaiono delle macchie scure che svaniscono appena si porta losguardo su di esse.

Illusione diHering. Le linee parallele orizzontali subiscono l’influsso delle linee inclinate e sembrano restringersi o dilatarsi al centro.

In questa trama di linee gli estremi producono l’effetto di cerchi. Questo effetto è chiamato illusione di Ehrenstein.

Fig. 40

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

diHering. Le linee parallele subiscono l’influsso delle e sembrano restringal centro.

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

fanno percepire l’immagine o parte di essa in modo errato. Ad esempio linee che percepite come divergenti, convergenti o curve. Oppure due elementi della stessa dimendimensione differente. a valutare le dimensioni di figure basandosi su effetti prospettici o confrontandoli

Fig. 41

che fanno percepire l’immagine o parte di essa in modo errato. Ad esempio linee che percepite come divergenti, convergenti o curve. Oppure due elementi della stessa dimendimensione differente. cervello a valutare le dimensioni di figure basandosi su effetti prospettici o confrontandoli

cerchio contrasto più

cerchio contrasto più inferiore.

In figura all’incrocio delle fascie bianche compaiono delle macchie scure che svaniscono appena si porta losguardo su di esse.

In figura all’incrocio delle fascie bianche compaiono delle macchie scure che svaniscono appena si porta lo sguardo su di esse.

Illusione diHering. Le linee parallele orizzontali subiscono l’influsso delle linee inclinate e sembrano restringersi o dilatarsi al centro.

In figura all’incrocio delle fascie bianche compaiono delle macchie scure che svaniscono appena si porta losguardo su di esse.

Illusione diHering. Le linee parallele orizzontali subiscono l’influsso delle linee inclinate e sembrano restringersi o dilatarsi al centro.

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

In un ambiente che abbia le superfici orizzontali decorate come in figura, la superficie di fondo sembra dilatarsi al centro come nell’illusione di Hering.

In questa trama di linee gli estremi producono l’effetto di cerchi. Questo effetto è chiamato illusione di Ehrenstein.

di essa in modo errato. Ad esempio linee che curve. Oppure due elementi della stessa dimenbasandosi su effetti prospettici o confrontandoli

ambiente che abbia le orizzontali decorate figura, la superficie di dilatarsi al centro nell’illusione di Hering.

linee parallele l’influsso delle sembrano restring-

fascie macchie appena si

In questa trama di linee gli estremi producono l’effetto di cerchi. Questo effetto è chiamato illusione di Ehrenstein.

In un ambiente che abbia le superfici orizzontali decorate come in figura, la superficie di fondo sembra dilatarsi al centro come nell’illusione di Hering.

Nell’illusione di Ponzo gialle sembrano di lunghezza diversa quando invece

In un ambiente che abbia le superfici orizzontali decorate come in figura, la superficie di fondo sembra dilatarsi al centro come nell’illusione di Hering. Illusione rossi appaiono quando

Nell’illusione di Ponzo le due fascie gialle sembrano di lunghezza diversa quando invece sono uguali.

Fig. 42

Fig. 44

Fig.

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

In un ambiente che abbia le superfici orizzontali decorate come in figura, la superficie di fondo sembra dilatarsi al centro come nell’illusione di Hering.

Nell’illusione di Ponzo le due fascie gialle sembrano di lunghezza diversa quando invece sono uguali.

Illusione di Ebbinghaus. I due cerchi rossi appaiono di diametro diverso quando invece sono tra loro uguali.

Nell’illusione di Ponzo le due fascie gialle sembrano di lunghezza diversa quando invece sono uguali.

Illusione di Ebbinghaus. I due cerchi rossi appaiono di diametro diverso quando invece sono tra loro uguali.

Illusione di Ebbinghaus. I due cerci rossi appaiono di diametro diverso quando invece sono tra loro uguali.

Le parallele

Le linee grigie orizzontali parallele appaiono storte.

Le linee grigie orizzontali tra loro parallele appaiono storte.

le decorate superficie di

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

In questa trama di linee gli estremi producono l’effetto di cerchi. Questo effetto è chiamato illusione di Ehrenstein.

Illusione di Ebbinghaus. I due cerchi rossi appaiono di diametro diverso quando invece sono tra loro uguali.

In un ambiente che abbia le superfici orizzontali decorate come in figura, la superficie di fondo sembra dilatarsi al centro come nell’illusione di Hering.

Nell’illusione di Ponzo le due fascie gialle sembrano di lunghezza diversa quando invece sono uguali.

I lati del quadrato appaiono incurvati e ciò è prodotto dalla lettura inconscia dell’immagine in chiave prospettica.

Le linee grigie orizzontali tra loro parallele appaiono storte.

Fig. 45

Illusione di Ebbinghaus. I due cerchi rossi appaiono di diametro diverso quando invece sono tra loro uguali.

Nell’illusione

Illusione di Ebbinghaus. I due cerchi rossi appaiono di diametro diverso quando invece sono tra loro uguali.

Nell’illusione di Ponzo le due fascie gialle sembrano di lunghezza diversa quando invece sono uguali. parallele l’influsso delle restring-

Nell’illusione di Ponzo le due fascie gialle sembrano di lunghezza diversa quando invece sono uguali.

Le linee grigie orizzontali tra loro parallele appaiono storte.

Fig. 46

Le linee grigie orizzontali tra loro parallele appaiono storte.

Fig.

Fig. 44

Fig.

Fig. 40

Fig. 42

Fig. 43

Fig. 38

Fig. 39

Fig. 40

Fig. 42

Fig. 41

Fig. 43

Fig. 45

Fig. 44

Fig. 46

Fig. 38

Fig. 39

Fig. 40

Fig. 42

Fig. 41

Fig. 43

Fig. 45

Fig. 44

Fig. 46

Fig.

Fig. 42

Fig. 43

Fig. 40

di Ponzo le due fascie gialle sembrano di lunghezza

Fig. 38

Fig. 39

Fig. 40

Fig. 42

Fig. 41

Fig. 43

Fig. 45

Fig. 44

Fig. 46

8.1 LE ILLUSIONI OTTICHE NELL’ARCHITETTURA GRECA

Nella costruzione dei templi, gli architetti greci adottarono alcuni accorgimenti per correggere l’errata percezione di ”deformazioni” che il rigido rispetto dell’esatta geometria (ortogonalità e orizzontalità) degli elementi costruttivi avrebbe generato. Ad esempio davano, ai frontoni dei Templi, una leggera inclinazione verso l’interno per ridurre la sensazione di incombenza su chi si trovava a ridosso dell’edificio (➜ Fig. 38), oppure inclinavano le colonne più esterne verso l’interno così da compensare la percezione di

➜ Fig. 38 • Leggera inclinazione verso l’interno per ridurre la sensazione di incombenza.

➜ Fig. 40 • Curvatura verso l’alto delle linee orizzontali, come lo stilobate e la trabeazione.

una loro divaricazione verso l’esterno (➜ Fig. 39); curvavano verso l’alto le linee orizzontali, come lo stilobate e la trabeazione (➜ Fig. 40), per correggere così l’impressione di una loro leggera curvatura verso il basso (➜ Fig. 41) e ottenere pertanto la sensazione di una perfetta rettilineità; inoltre, più accentuata nei templi dorici, creavano l’èntasi cioè un rigonfiamento del fusto della colonna a circa 1/3 della sua altezza (➜ Fig. 42) per correggere la percezione di restringimento della colonna stessa al centro (➜ Fig. 43; Fig. 44).

➜ Fig. 39 • Inclinazione delle colonne più esterne verso l’interno così da compensare la percezione di una loro divaricazione verso l’esterno.

Colonna come si voleva percepita

Colonna con rigonfiamento entasi

Percezione di restringimento

Colonna come si voleva percepita

entasi

Colonna con rigonfiamento entasi

Colonna come si voleva percepita

Percezione di restringimento

entasi

Percezione di restringimento

Colonna come si voleva percepita

Percezione di restringimento

➜ Fig. 41 • impressione di una loro leggera curvatura verso il basso.

Colonna come si voleva percepita

Colonna con rigonfiamento

Percezione di restringimento

Colonna con rigonfiamento

Colonna come si voleva percepita entasi

➜ Fig. 42 ➜ Fig. 43 ➜ Fig. 44

Colonna con rigonfiamento

Colonna con rigonfiamento entasi

Percezione restringimento

Come si vede la psiche tende a “vedere” la situazione più consueta. Applicazioni di questa fenomeno sono frequenti in campo scenografico teatrale, vedi il Teatro Olimpico del Palladio, ma sono state utilizzate anche in campo architettonico per ottenere particolari effetti spaziali come nella Piazza del Campidoglio da Michelangelo, oppure nella piazza adiacente alla Basilica di S. Pietro dal Bernini oppure per il finto coro a Santa Maria presso S. Satiro dal Bramante ecc.

➜ Fig. 48 • Pianta del teatro Olimpico di A. Palladio. Dagli ingressi di un monumentale proscenio rettangolare si dipartono a raggiera sette scene che ra gurano le vie di Tebe e furono progettate da V. Scamozzi per lo spettacolo inaugurale.

Pianta del teatro Olimpico di A. Palladio. Dagli ingressi di un monumentale proscenio rettangolare si dipartono a raggiera sette scene che raffigurano le vie di Tebe e furono progettate da V. Scamozzi per lo spettacolo inaugurale.

➜ Fig. 50 • Piazza del campidoglio di Michelangelo. Esempio di prospettiva accorciata.

Piazza del campidoglio di Michelangelo. Esempio di prospettiva accorciata.

➜ Fig. 52 • Finto coro a Santa Maria presso S. Satiro del Bramante visto lateralmente da destra e di fronte. Esempio di prospettiva accelerata.

per ottenere particolari effetti spaziali come nella Piazza del Campidoglio da Michelangelo (➜ Fig. 50), oppure nella piazza adiacente alla Basilica di S. Pietro dal Bernini (➜ Fig. 51) oppure per il finto coro a Santa Maria presso S. Satiro dal Bramante (➜ Fig. 52) ecc.

➜ Fig. 49 • Il grandioso proscenio del teatro Olimpico che si apre nell’arco trionfale centrale e in due aperture laterali da cui si scorgono le scene dello Scamozzi esempio di prospettiva accelerata.

Il grandioso proscenio del teatro Olimpico che si apre nell’arco trionfale centrale e in due aperture laterali da cui si scorgono le scene dello Scamozzi esempio di prospettiva accelerata.

➜ Fig. 51 • Piazza S. Pietro con il Sagrato di forma trapezoidale del Bernini. Esempio di prospettiva accorciata.

Piazza S. Pietro con il Sagrato di forma trapezoidale del Bernini. Esempio di prospettiva accorciata.

Finto coro a Santa Maria presso S. Satiro del Bramante visto lateralmente da destra e di fronte. Esempio di prospettiva accelerata.

CAVEA

violetto.

11. 2 La retina del nostro occhio ha due tipi di fotoricettori i coni bastoncelli (Fig.2).

9 La percezione del colore

9.1 SINTESI ADDITIVA

coni, che consentono una visione nitida e tricromatrica, si attivano presenza di fonti luminose come la luce del giorno o le luci artificiali. Sono di tre tipi, sensibili ciascuno a differenti lunghezze d'onda nello spettro del visibile. Per i coni sensibili al blu la massima percezione è di 440 nm, per quelli che sensibili al verde è di 540 nm per i quelli sensibili al rosso è di 570 nm. bastoncelli, che sono molto sensibili alla luce, permettono di vedere con una bassa intensità luminosa come avviene nella penombra o di notte. Non danno una visione nitida e non distinguono i colori ma consentono solamente la percezione in bianco in nero e nella scala di grigi.

1. 11 La percezione del colore

Il colore esiste perché c’è la luce che è una forma di energia assorbita o riflessa da tutto ciò che ci circonda. Isac Newton dimostrò sperimentalmente, mediante un prisma triangolare ( ➜ Fig. 53), come si possa scomporre la luce bianca nello spettro dell’iride che va dalle lunghezze d’onda λ = 700nm (nanometri) per il rosso e λ = 400nm per il violetto. Successivamente Thomas Yung elaborò la teoria, ripresa e approfondita da Helmholtz, che riconduce la percezione dei colori alla presenza sulla retina di tre strutture nervose, sensibili rispettivamente al rosso, al verde e al blu-violetto.

11. 3 Il colore che si percepisce è dato dalla sintesi, cioè dalla unione, di tre colori primari da cui si ottengono tutti gli altri colori. Esistono due tipi di sintesi: la sintesi additiva e la sintesi sottrattiva.

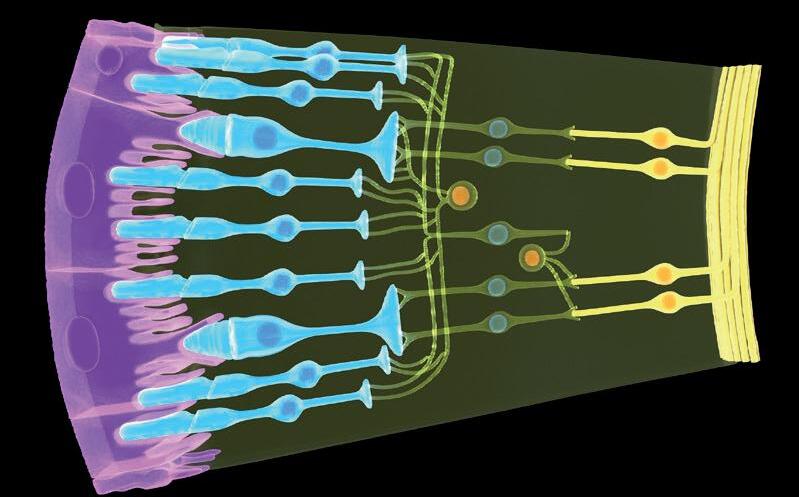
La retina del nostro occhio ha due tipi di fotoricettori i coni e i bastoncelli (➜ Fig. 54).

1. 11. 1 Il colore esiste perché c’è la luce che è una forma di energia assorbita o riflessa da tutto ciò che ci circonda. Isac Newton dimostrò sperimentalmente, mediante un prisma triangolare (Fig.1), come si possa scomporre la luce bianca nello spettro dell’iride che va dalle lunghezze d’onda λ = 700nm (nanometri) per il rosso e λ = 400nm per il violetto. Successivamente Thomas Yung elaborò la teoria, ripresa e approfondita da Helmholtz, che riconduce la percezione dei colori alla presenza sulla retina di tre strutture nervose, sensibili rispettivamente al rosso, al verde e al bluvioletto.

Fig.1 Con un prisma triangolare Newton scompose la luce bianca nei colori dello spettro

Consiste nella mescolanza di tre luci monocromatiche, corrispondenti alle radiazioni assorbite dai tre tipi di coni della retina, cioè il rosso il verde e il blu che mescolati nelle giuste proporzioni danno tutti i colori percepibili (➜ Fig. 55). Dalla sintesi di due colori primari si ottengono i secondari (il giallo= rosso+verde, il magenta= rosso+blu e il ciano= blu+verde) (➜ Fig. 56) e dei tre colori primari, nelle stesse quantità, si ha luce bianca. Il nero è assenza di luce. La sintesi additiva è identificata con la sigla RGB (R= red, G= green, B= blu). Suoi esempi sono le immagini colorate sul video del computer o sul televisore che sono date dalla composizione di tanti puntini (pixel) di color rosso, verde o blu.

Fig.2 Particolare della retina con evidenziati i coni e i bastoncelli.

11. 3. 1 Sintesi additiva

I coni, che consentono una visione nitida e tricromatrica, si attivano in presenza di fonti luminose come la luce del giorno o le luci artificiali. Sono di tre tipi, sensibili ciascuno a differenti lunghezze d’onda nello spettro del visibile. Per i coni sensibili al blu la massima percezione è di 440 nm, per quelli che sensibili al verde è di 540 nm e per i quelli sensibili al rosso è di 570 nm.

Consiste nella mescolanza di tre luci monocromatiche, corrispondenti alle radiazioni assorbite dai tre tipi di coni della retina, cioè il rosso il verde e il blu che mescolati nelle giuste proporzioni danno tutti i colori percepibili (Fig.3). Dalla sintesi di due colori primari si ottengono i secondari (il giallo= rosso+verde, il magenta= rosso+blu e il ciano= blu+verde) (Fig.4) e dei tre colori primari, nelle stesse quantità, si ha luce bianca. Il nero è assenza di luce. sintesi additiva è identificata con la sigla RGB (R= red, G= green, B= blu). Suoi esempi sono le immagini colorate sul video del computer o sul televisore che sono date dalla composizione di tanti puntini (pixel) di color rosso, verde o blu.

1. 11. 2 La retina del nostro occhio ha due tipi di fotoricettori i coni e i bastoncelli (Fig.2).

I coni, che consentono una visione nitida e tricromatrica, si attivano in presenza di fonti luminose come la luce del giorno o le luci artificiali. Sono di tre tipi, sensibili ciascuno a differenti lunghezze d'onda nello spettro del visibile. Per i coni sensibili al blu la massima percezione è di 440 nm, per quelli che sensibili al verde è di 540 nm e per i quelli sensibili al rosso è di 570 nm.

➜ Fig. 55 • Esempio della sintesi additiva data da tre proiettori con i tre colori primari.

I coni, che consentono una visione nitida e tricromatrica, si attivano in presenza di fonti luminose come la luce del giorno o le luci artificiali. Sono di tre tipi, sensibili ciascuno a differenti lunghezze d'onda nello spettro del visibile. Per i coni sensibili al blu la massima percezione è di 440 nm, per quelli che sensibili al verde è di 540 nm e per i quelli sensibili al rosso è di 570 nm.

Fig.1 Con un prisma triangolare Newton scompose la luce bianca nei colori dello spettro

1. 11. 3 Il colore che si percepisce è dato dalla sintesi, cioè dalla unione, di tre colori primari da cui si ottengono tutti gli altri colori. Esistono due tipi di sintesi: la sintesi additiva e la sintesi sottrattiva

11. 3. 2 Sintesi sottrattiva

1. 11. 3. 1 Sintesi additiva

I bastoncelli, che sono molto sensibili alla luce, permettono di vedere con una bassa intensità luminosa come avviene nella penombra o di notte. Non danno una visione nitida e non distinguono i colori ma consentono solamente la percezione in bianco in nero e nella scala di grigi. Il colore che si percepisce è dato dalla sintesi, cioè dalla unione, di tre colori primari da cui si ottengono tutti gli altri colori. Esistono due tipi di sintesi: la sintesi additiva e la sintesi sottrattiva

➜ Fig. 53 • Con un prisma triangolare Newton scompose la luce bianca nei colori dello spettro.

Fig.2 Particolare della retina con evidenziati i coni e i bastoncelli.

Particolare della retina con evidenziati i coni e i bastoncelli.

Consiste nell’assorbimento o nella riflessione, tutto o in parte, dei tre colori-luce primari, rosso, verde e blu, da parte del colore della superficie del corpo illuminato. quella cui normalmente ci si riferisce quando parliamo di dipinti, di stampa, del colore degli oggetti, ecc. A differenza della sintesi additiva, che riguarda l’emissione di luce, la sintesi sottrattiva riguarda la riflessione o la sottrazione di luce. I tre colori fondamentali in sottrattivo sono i secondari in additiva (Fig.5).

Consiste nella mescolanza di tre luci monocromatiche, corrispondenti alle radiazioni assorbite dai tre tipi di coni della retina, cioè il rosso il verde e il blu che mescolati nelle giuste proporzioni danno tutti i colori percepibili (Fig.3). Dalla sintesi di due colori primari si ottengono i secondari (il giallo= rosso+verde, il magenta= rosso+blu e il ciano= blu+verde) e dei tre colori primari, nelle stesse quantità, si ha luce bianca. Il nero è assenza di luce. La sintesi additiva è identificata con la sigla (R= red, G= green, B= blu). Suoi esempi sono le immagini colorate sul video del computer o sul televisore che sono date dalla composizione di tanti puntini (pixel) di color rosso, verde o blu.

Consiste nella mescolanza di tre luci monocromatiche, corrispondenti alle radiazioni assorbite dai tre tipi di coni della retina, cioè il rosso il verde e il blu che mescolati nelle giuste proporzioni danno tutti i colori percepibili (Fig.3). Dalla sintesi di due colori primari si ottengono i secondari (il giallo= rosso+verde, il magenta= e dei tre colori primari, nelle stesse quantità, si ha luce bianca. Il nero è assenza di luce. La sintesi additiva è identificata con la sigla RGB (R= red, G= green, B= blu). Suoi esempi sono le immagini colorate sul video del computer o sul televisore che sono date dalla composizione di tanti

1. 11. 3. 2 Sintesi sottrattiva

Consiste nel in tutto o in parte, dei tre colori-luce primari, rosso, verde e blu, da parte del colore della superficie del corpo illuminato

➜ Fig. 54 • Particolare della retina con evidenziati i coni e i bastoncelli.

l’assorbimento o nella riflessione, in tutto o in parte, dei tre colori-luce primari, rosso, verde e blu, da parte del colore della superficie del corpo illuminato

E’ quella cui normalmente ci si riferisce quando parliamo di dipinti, di stampa, del colore degli oggetti, ecc. A differenza della sintesi additiva, che riguarda l’emissione di luce, la sintesi sottrattiva riguarda la rifles sione o la sottrazione di luce. fondamentali in sottrattivo sono i secondari in additiva

9.2 SINTESI SOTTRATTIVA

Fig.3 Esempio della sintesi additiva data da tre proiettori con i tre colori primari.

blu ciano rosso bianco magenta verde giallo

Consiste nell’assorbimento o nella riflessione, in tutto o in parte, dei tre colori-luce primari, rosso, verde e blu, da parte del colore della superficie del corpo illuminato. È quella cui normalmente ci si riferisce quando parliamo di dipinti, di stampa, del colore degli oggetti, ecc. A differenza della sintesi additiva, che riguarda l’emissione di luce, la sintesi sottrattiva riguarda la riflessione o la sottrazione di luce. I tre colori fondamentali in sottrattivo sono i secondari in additiva (➜ Fig. 57).

Fig.3 Esempio della sintesi additiva data da tre proiettori con i tre colori primari.

Fig.3 Esempio della sintesi additiva data da tre proiettori con i tre colori primari. blu ciano rosso nero magenta verde giallo

colore degli oggetti, ecc. A differenza della sintesi additiva, che riguarda l’emissione di -

fondamentali in sottrattivo sono i secondari in

Fig.5 Sintesi sottrattiva

Fig.4 Sintesi additiva

Fig.5 Sintesi sottrattiva

Fig.4 Sintesi additiva

Fig.2

Fig.5 Sintesi sottrattiva

Fig.4 Sintesi additiva

➜ Fig. 56 • Sintesi additiva ➜ Fig. 57 • Sintesi sottattiva.

VERIFICA LE CONOSCENZE

1. La retina ha la funzione di:

a mettere a fuoco l’immagine.

b trasmettere l’immagine.

c trasformare i segnali ottici.

2. L’immagine dal cristallino viene:

a ingrandita.

b messa a fuoco.

c deformata.

3. Le onde luminose:

a assorbono gli oggetti.

b riflettono gli oggetti.

c emettono gli oggetti.

4. Nell’occhio la funzione della lente nella macchina fotografica è svolta da:

a la retina.

b l’umore acqueo.

c il cristallino.

5. La teoria cognitivista sostiene che l’uomo dà significato a quello che osserva utilizzando: a l’istinto.

b la sensibilità.

c la memoria visiva.

6. La teoria della Gestalt dice che il tutto:

a è la somma delle parti.

b è più della somma delle parti.

c è la somma di sensazioni.

7. Quale legge dice che gli elementi che hanno un movimento solidale tra loro, e differente da quello di altri, sono uniti in forme:

a legge della somiglianza.

b legge del destino comune.

c legge della vicinanza.

8. Quale legge dice che gli elementi si tende a unirli quando possiedono una qualche somiglianza a parità delle altre condizioni:

a legge della vicinanza.

b legge della continuità di direzione.

c legge della chiusura.

Test interattivi

9. Quale legge dice che gli elementi si tende a unirli in forme quando nella nostra esperienza passata sono abitualmente associati tra loro:

a legge della vicinanza.

b legge della esperienza passata.

c legge della somiglianza.

10. Ciò che tende a farci percepire come figura le aree i cui assi coincidono con le direzioni verticale e orizzontale è:

a la semplicità.

b la simmetria.

c l’orientamento spaziale.

11. È un indizio binoculare nella percezione della profondità:

a la differenza tra le due immagini.

b l’effetto prospettico.

c la prospettiva cromatica.

12. È un indizio monoculare:

a l’interposizione.

b la tensione dei muscoli.

c la differenza tra le due immagini.

13. Ciò che ci fa percepire il colore di un oggetto anche al variare della luminosità è:

a la costanza di chiarezza e colore.

b la memoria.

c l’onda luminosa.

14. Ciò che ci consente una visione nitida e tricomatrica sono:

a i bastoncelli.

b la luminosità.

c i coni.

15. Nella sintesi sottrattiva i colori primari sono:

a il rosso, il giallo e il verde.

b il verde, il blu e il magenta.

c il giallo, il ciano e il magenta.

La percezione

visiva

2 IL LINGUAGGIO MULTIMEDIALE

CI OCCUPEREMO DI...

1. Il linguaggio gra co: la segnaletica

2. Il linguaggio gra co: il disegno cartogra co

3. Il linguaggio gra co: i disegni scienti ci e tecnici

4. Il linguaggio infogra co: il diagramma, l’istogramma, l’areogramma

5. Il linguaggio infogra co: il diagramma di usso

1 Il linguaggio grafico: la segnaletica

IL LINGUAGGIO MULTIMEDIALE

Il linguaggio grafico: la segnaletica

Gli esseri umani, per comunicare tra di loro, usano vari linguaggi, tra i quali il linguaggio grafico, quello infografico e quello multimediale, che sono molto efficaci poiché si avvalgono di figure, segni e immagini che facilitano la descrizione e la comprensione di ciò che si vuole comunicare. Il termine “multimediale” (dove media deriva dal latino medium, qui inteso come mezzo di comunicazione) ha il significato di “con molti mezzi di comunicazione”: quindi, il linguaggio multimediale è il linguaggio che utilizza contemporaneamente più mezzi – le immagini, i filmati, i video, la musica e il testo scritto – per comunicare informazioni. Il prodotto che così si ottiene è un qualche cosa che è più della somma dei singoli elementi che lo compongono.

IL LINGUAGGIO GRAFICO

Il linguaggio grafico: la segnaletica

Il linguaggio multimediale

Gli esseri umani per comunicare tra di loro usano vari linguaggi, tra i quali il grafico, quello infografico e quello multimediale,che sono molto efficaci poiché si avvalgono di figure, segni e immagini che facilitano la descrizione e la comprensione di ciò che si vuole comunicare.

Gli esseri umani per comunicare tra di loro usano vari linguaggi, tra i quali il linguaggio grafico, quello infografico e quello multimediale,che sono molto efficaci poiché si avvalgono di figure, segni e immagini che facilitano la descrizione e la comprensione di ciò che si vuole comunicare.

Il termine “multimediale” ( dove media deriva dal latino medium, qui inteso come mezzo di comunicazione) ha il significato di “con molti mezzi di comunicazione”: quindi, il linguaggio multimediale è il linguaggio che utilizza contemporaneamente più mezzi – le immagini, i filmati, i video, la musica e il testo scritto... - per comunicare informazioni. Il prodotto che così si ottiene è un qualche cosa che è più della somma dei singoli elementi (immagini, video, testi, musica ...) che lo compongono.

Il linguaggio grafico

Il linguaggio grafico permette la trascrizione di un pensiero, di una informazione, sotto la forma di segni e di colori codificati secondo un preciso criterio. Esso comprende molti linguaggi riguardanti la segnaletica stradale, la segnaletica di sicurezza, il disegno cartografico, il disegno scientifico, il disegno tecnico, ecc. Questi, perché siano efficaci, devono rispettare determinate norme che ne uniformano il significato sia che si tratti di linguaggi specialistici, come il disegno tecnico, sia che siano rivolti all’intera popolazione come ad esempio la segnaletica di un aeroporto o di una stazione ferroviaria. Vediamo alcuni esempi.

Normalmente le comunicazioni umane si basano sull’espressione verbale che è la più naturale e diretta. In determinate situazioni essa però si può rivelare insufficiente o troppo complicata come quando si vuole descrivere un disegno, un oggetto, un ambiente, ecc.. Si provi ad esempio a far eseguire un semplice disegno, formato da poche linee, che vede solo colui che lo esegue. Successivamente fatevelo descrivere a parole e cercate di riprodurlo su un foglio seguendo le descrizioni. Confrontate quindi quanto da voi prodotto con l’originale. Vedrete che difficilmente riuscirete a riprodurre lo stesso disegno se non dopo lunghe e dettagliate indicazioni. Il linguaggio grafico permette la trascrizione di un pensiero, di una informazione, sotto la forma di segni e di colori codificati secondo un preciso criterio, il cui senso generale è fornito dal titolo e la chiave di lettura da una legenda. Esso comprende molti linguaggi riguardanti la segnaletica stradale, la segnaletica di sicurezza , il disegno cartografico, il disegno scientifico, il disegno tecnico, ecc. Questi, perché siano efficaci, devono rispettare determinate norme che ne uniformano il significato sia che si tratti di linguaggi specialistici, come il disegno tecnico, sia che siano rivolti all’intera popolazione come ad esempio la segnaletica di un aeroporto o di una stazione ferroviaria. Vediamo alcuni esempi.

LA SEGNALETICA STRADALE

Il linguaggio grafico permette la trascrizione di un pensiero, di una informazione, sotto la forma di segni e di colori codificati secondo un preciso criterio, il cui senso generale è fornito dal titolo e la chiave di lettura da una legenda. Esso comprende molti linguaggi riguardanti la segnaletica stradale, la segnaletica di sicurezza , il disegno cartografico, il disegno scientifico, il disegno tecnico, ecc. Questi, perché siano efficaci, devono rispettare determinate norme che ne uniformano il significato sia che si tratti di linguaggi specialistici, come il disegno tecnico, sia che siano rivolti all’intera popolazione come ad esempio la segnaletica di un aeroporto o di una stazione ferroviaria. Vediamo alcuni esempi.

La segnaletica stradale

La segnaletica stradale è pressoché uguale in tutta Europa. Prevede che i segnali di pericolo siano di forma triangolare con una fascia rossa lungo il perimetro, i segnali di divieto rotondi con bordo e banda trasversale rossi e segnali di obbligo rotondi con fondo azzurro ecc. Questo tipo di schema è rispettato anche dalla segnaletica di sicurezza fig.1.

Normalmente le comunicazioni umane si basano sull’espressione verbale che è la più naturale e diretta. In determinate situazioni essa però si può rivelare insufficiente o troppo complicata. Si provi ad esempio a far eseguire un semplice disegno, formato da poche linee, che vede solo colui che lo esegue. Successivamente fatevelo descrivere a parole e cercate di riprodurlo su un foglio seguendo le descrizioni. Confrontate quindi quanto da voi prodotto con l’originale. Vedrete che difficilmente riuscirete a riprodurre lo stesso disegno se non dopo lunghe e dettagliate indicazioni.

La segnaletica stradale è pressoché uguale in tutta Europa. Prevede che i segnali di pericolo siano di forma triangolare con una fascia rossa lungo il perimetro, i segnali di divieto rotondi con bordo e banda trasversale rossi e i segnali di obbligo rotondi con fondo azzurro ecc. (➜ Fig. 1) Questo tipo di schema è rispettato anche dalla segnaletica di sicurezza.

L’ACCESSO AI NON ADDETTI AI LAVORI

PERICOLO CADUTA MASSI

DIVIETO DI SVOLTA A DESTRA

VIETATO L’ACCESSO AI NON ADDETTI AI LAVORI

TENSIONE ELETTRICA PERICOLOSA

PERICOLO CADUTA MASSI

DIVIETO DI SVOLTA A DESTRA

VIETATO

PERICOLO CADUTA MASSI

DIVIETO DI SVOLTA A DESTRA

TENSIONE ELETTRICA

CATENE PER NEVE OBBLIGATORIE

2 Il linguaggio grafico: il disegno cartografico

Comprende carte di varie scale: piante (➜ Fig. 2), che rappresentano i centri urbani, e mappe (➜ Fig. 3), che rappresentano le aree rurali. Sono a grandissima scala, quindi con denominatore molto piccolo e cioè di 1:5.000 o 1:10.000. Sono molto dettagliate nel riportare il terreno con costruzioni, tracciati stradali, piantumazioni ecc. e hanno un utilizzo prettamente tecnico come la stesura di piani regolatori, e quanto altro riguarda l’organizzazione del territorio;

carte topografiche hanno una scala da 1:10.000 a 1:200.000 e riportano le costruzioni edili, l’andamento del terreno, i corsi fluviali ecc. e hanno anch’esse un uso prettamente tecnico (➜ Fig. 4);

Fig. 4

carte corografiche (a media scala) da 1:200.000 a 1:1.000.000 rappresentano regioni o territori abbastanza estesi, sono meno particolareggiate delle precedenti e danno una conoscenza generale del territorio (➜ Fig. 5):

Fig. 5

carte geografiche che sono a piccola e piccolissima scala, quindi col denominatore molto grande, cioè oltre 1:1.000.000 sono una rappresentazione simbolica, su una superficie, del globo terrestre o di una parte di esso (➜ Fig. 6).

➜ Fig. 2 • Pianta settecentesca della città di Brescia.

Fig. 6

Fig. 3 • Mappa di area rurale.

A volte le carte topografiche sono eseguite in modo schematico e fuori scala come le carte che rappresentano le linee della metropolitana di Londra ( ➜ Fig. 7 ). Ciò nasce dalla necessità di rappresentare una vasta estensione in una carta di piccole dimensioni. Essa infatti diventa sempre più densa di indicazioni mano a mano che ci si avvicina al centro città con il risultato che le indicazioni e le scritte, relative alle stazioni centrali, risulterebbero troppo vicine le une alle altre da sovrapporsi. Il problema è stato risolto non adottando una scala precisa ma seguendo la logica della più facile lettura e quindi la zona del centro, che è più congestionata da stazioni, è rappresentata a una scala maggiore rispetto alla periferia e anche l’andamento dei tracciati, a volte tortuoso, è rappresentato rettilineo.

3 ll linguaggio grafico: i disegni scientifici e tecnici

I DISEGNI SCIENTIFICI

I disegni scientifici sono molto accurati e permettono di mettere in risalto, e quindi descrivere spesso meglio di una fotografia, l’oggetto in esame. Infatti mentre la fotografia riporta indiscriminatamente tutto ciò che è inquadrato (➜ Fig. 8), anche cose che possono non interessare o addirittura ostacolare la perfetta lettura, il disegno consente di sottolineare od omettere i vari elementi (➜ Fig. 9).

I DISEGNI TECNICI

Sono disegni che rappresentano in modo dettagliato oggetti, organi, costruzioni con indicazioni precise per la loro descrizione o per la loro realizzazione. Essi sono eseguiti rispettando norme precise e spesso sono accompagnati da una Legenda che specifica il significato di eventuali simboli utilizzati nella rappresentazione. In questa e nelle pagine seguenti sono riportati alcuni esempi: in ➜ Fig. 10 è riportato lo schema di una caldaia, in ➜ Fig. 11 lo schema di un impianto oleodinamico, in ➜ Fig. 12 una planimetria catastale, in ➜ Fig. 13 una mappa catastale, in ➜ Fig. 14 la pianta di una abitazione e in ➜ Fig. 15 lo schema dell’impianto elettrico di un appartamento.

Il linguaggio grafico: i disegni scientifici

➜ Fig. 7

I disegni scientifici sono molto accurati e permettono di mettere in risalto, e quindi descrivere spesso meglio di una fotografia, l’oggetto in esame. Infatti mentre la fotografia riporta indiscriminatamente tutto ciò che è inquadrato fig.2, anche cose che possono non interessare o addirittura ostacolare la perfetta lettura, il disegno consente di sottolineare od omettere i vari elementi fig.3.

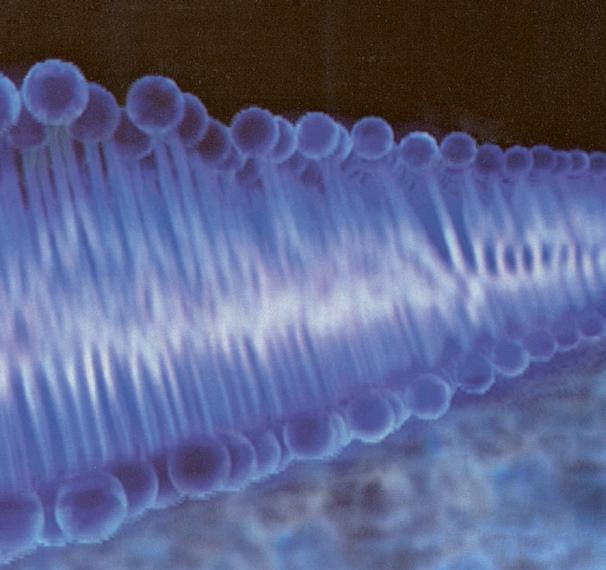
Sono disegni che con opportuni simboli danno indicazioni estremamente precise sugli impianti, sugli organi, sulle loro dimensioni, sui materiali, sui trattamenti superficiali, sulle finiture, sulle lavorazi

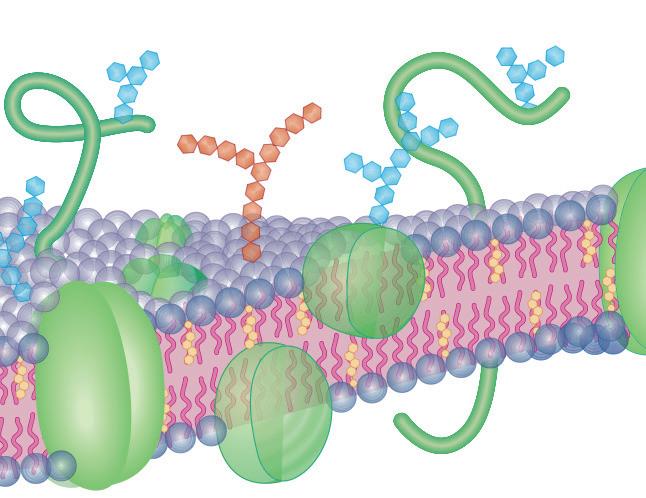
➜ Fig. 8

In fig.4 è riportato lo schema di una caldaia e in fig.5 è riportato lo schema di un impianto oleodinamico.

➜ Fig. 9

➜ Fig. 10

➜ Fig. 11

Fig. 13

➜ Fig. 12

LEGENDA: muratura portante in c.a. muratura portante in laterizio 0m 1 2 3 4

Pianta piano primo

Punto luce a soffitto

Punto luce a parete

Lampada a fluorezenza

Lampada di segnalazione

Pulsante di chiamata

Pulsante di chiamata a tirante

Suoneria

Ronzatore

Collegamento di messa a terra

Citofono Apparecchio

Fig. 15

4 Il linguaggio infografico: il diagramma, l’istogramma, l’areogramma

Il linguaggio infografico permette di comunicare informazioni e dati in forma grafica e cioè mediante diagrammi, istogrammi, areogrammi, schemi, tabelle, diagrammi di flusso.

DIAGRAMMA CARTESIANO

È dato da un sistema di assi cartesiani in cui su un asse si riporta la variabile indipendente e sull’altro asse la variabile dipendente. Descrive sinteticamente l’andamento di un fenomeno, di un processo, di una funzione matematica ecc. Un esempio è il diagramma carichi–allungamenti di materiali metallici (➜ Fig. 16).

ISTOGRAMMA

Usa come riferimento un sistema di assi cartesiani e può essere a colonne o a barre a seconda che i rettangoli che lo costituiscono siano verticali o orizzontali. Nell’istogramma a colonne si riportano sull’asse delle ascisse le basi delle colonne le cui altezze fanno riferimento all’asse delle ordinate.

Gli istogrammi sono particolarmente indicati per la rappresentazione di dati di cui è più importante il confronto diretto. Nel caso in cui invece sia necessario collegare i dati, per ottenere una linea che ne sottolinei l’andamento caratteristico, si ricorre al diagramma. L’istogramma in figura mette a confronto il numero di navigatori internet su rete mobile in Italia negli ultimi anni (➜ Fig. 17).

AREOGRAMMA

È detto anche diagramma a settori. È particolarmente efficace per rappresentare la ripartizione di un tutto. Per creare un areogramma si parte normalmente da un cerchio che rappresenta il 100% di ciò che si vuole analizzare e lo si suddivide in tanti settori circolari il cui numero dipende dai soggetti che partecipano a formare il tutto e la cui ampiezza dipenderà dalla rispettiva importanza. Ad esempio per rappresentare la distribuzione delle valutazioni in disegno (➜ Fig. 18) in una classe formata da 26 allievi di cui 2 gravemente insufficienti,

➜ Fig. 18

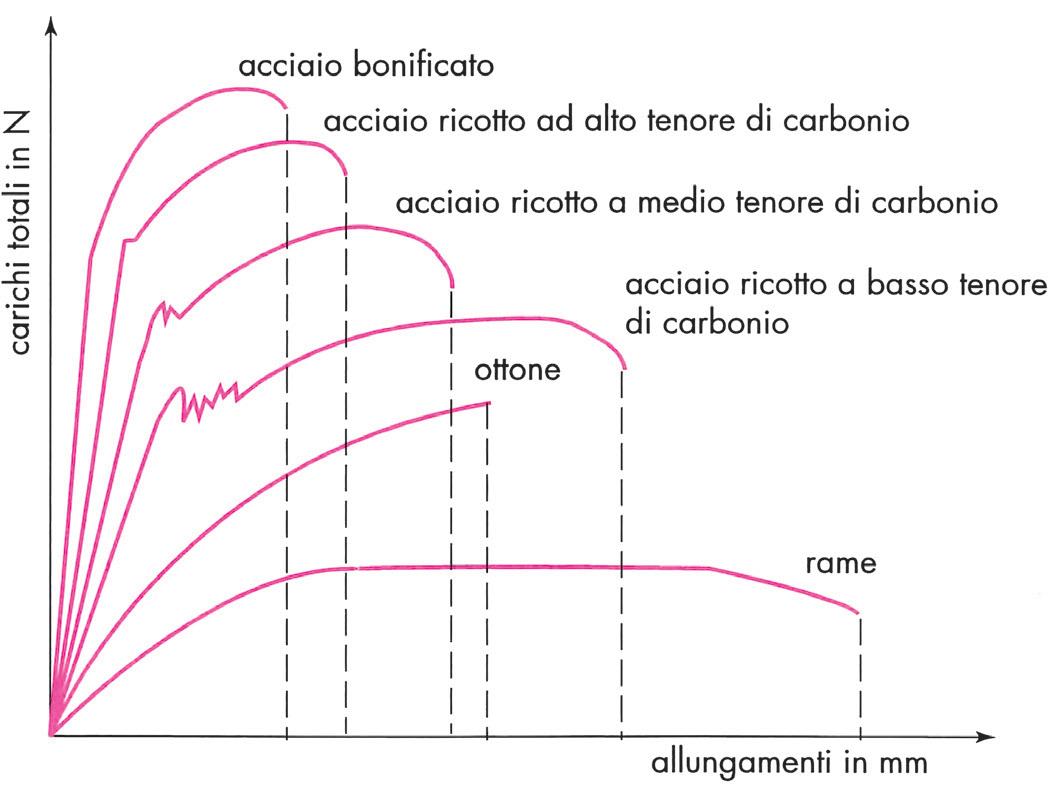
➜ Fig. 16

➜ Fig. 17

4 insufficienti, 6 sufficienti, 6 buoni, 5 distinti e 3 ottimi, si calcolano le percentuali dei vari gruppi e si moltiplica l’angolo di 360° per ciascuna percentuale ricavando l’apertura angolare di ciascun settore.

Inizio sequenza istruzioni

Inserimento ed emissione dati

Il linguaggio infografico: il diagramma di flusso

Diagramma di flusso E’ il metodo più usato per rappresentare un algoritmo (cioè una sequenza ordinata di istruzioni che porta alla soluzione di un problema). Nella tabella sono descritti i vari elementi che possono costituire un diagramma di flusso col relativo significato. A fianco, con un diagramma di flusso, sono indicati i passi da seguire prima di iniziare un disegno.

5 Il linguaggio infografico: il diagramma di flusso

È il metodo più usato per rappresentare un algoritmo (cioè una sequenza ordinata di istruzioni che porta alla soluzione di un problema). Nella tabella sono descritti i vari elementi che possono costituire un diagramma di flusso col relativo significato. A fianco, con un diagramma di flusso, sono indicati i passi da seguire prima di iniziare un disegno.

Inizio sequenza istruzioni

INIZIO FINE

Inizio sequenza istruzioni

Inserimento ed emissione dati

Istruzione da eseguire

Inserimento ed emissione dati

Istruzione con scelta tra due possibili percorsi a seconda della valutazione di una certa condizione

Istruzione da eseguire

Fine sequenza istruzioni

Istruzione con scelta tra due possibili percorsi a seconda della valutazione di una certa condizione

CONTROLLA SE IL TAVOLO È PULITO È PULITO?

SÌ

PRENDI UN FOGLIO DA DISEGNO

CONTROLLA SE IL TAVOLO È PULITO È PULITO?

SÌ

PROCURATI UNO STRACCIO E PULISCILO

Fine sequenza istruzioni

PROCURATI UNO STRACCIO E PULISCILO

PRENDI UN FOGLIO DA DISEGNO

FISSALO SUL TAVOLO COL NASTRO ADESIVO

SÌ NO SÌ NO È DELLA

DIMENSIONE GIUSTA? SAI COME ORIENTARLO? SÌ

CHIEDI ALL’INSEGNANTE

PREPARA SUL TAVOLO L’ATTREZZATURA PER IL DISEGNO È IN ORDINE SUL TAVOLO C’È SOLO LO STRETTO NECESSARIO PER DISEGNARE?

FISSALO SUL TAVOLO COL NASTRO ADESIVO

SÌ NO SÌ NO È DELLA DIMENSIONE GIUSTA? SAI COME ORIENTARLO?

COMPILA IL FOGLIO CON COGNOME, NOME, DATA, CLASSE E N° TAVOLA

PREPARA SUL TAVOLO L’ATTREZZATURA PER IL DISEGNO È IN ORDINE SUL TAVOLO C’È SOLO LO STRETTO NECESSARIO PER DISEGNARE?

AFFILA LE MINE DELLA MATITA E DEL COMPASSO E PULISCI LE SQUADRE NO

CHIEDI ALL’INSEGNANTE

RIPONI CIÒ CHE NON SERVE: ASTUCCIO, CUSTODIE, NASTRO ADESIVO ECC. NO

AFFILA LE MINE DELLA MATITA E DEL COMPASSO E PULISCI LE SQUADRE NO

RIPONI CIÒ CHE NON SERVE: ASTUCCIO, CUSTODIE, NASTRO ADESIVO ECC. NO

ORA SEI PRONTO PER INIZIARE L’ESERCITAZIONE

COMPILA IL FOGLIO CON COGNOME, NOME, DATA, CLASSE E N° TAVOLA

ORA SEI PRONTO PER INIZIARE L’ESERCITAZIONE

VERIFICA LE CONOSCENZE

La comunicazione grafica: Esercizi

1. I segnali rotondi con bordo e banda trasversale rossi sono segnali di: a obbligo. b pericolo. c divieto.

comunicazione grafica: Esercizi

La comunicazione grafica: Esercizi

Test interattivi

1893-1903 24,1°; 1903-1913 24,8°; 1913-1923 23,9°; 1923-1933 26,2°; 1933-1943 23,8°; 1943-1953 26,2°; 1953-1963 24,7°; 1963-1973 25,1°; 1973-1983 24,2°; 1983-1993 26,7°; 1993-2003 25,9°

2. Le carte geografiche sono in scala: a tra 1:10.000 e 1:200.000. b oltre 1:1.000.000. c tra 1:200.000 e 1:1.000.000.

3. Volendo un carta che rappresenti solo la tua regione sceglieresti: a una carta corografica. b una carta topografica. c una carta geografica.

4. Traccia un diagramma cartesiano con i seguenti dati relativi alla temperatura massima a Torino nel mese di luglio tra il 1893 e il 2003 con cadenza decennale:

1893-1903 24,1°; 1903-1913 24,8°; 1913-1923 23,9°; 1923-1933 26,2°; 1933-1943 23,8°; 1943-1953 26,2°; 1953-1963 24,7°; 1963-1973 25,1°; 1973-1983 24,2°; 1983-1993 26,7°; 1993-2003 25,9°

5. Costruisci un istogramma che metta a confronto le ore settimanali di lezione nella tua classe nelle varie materie:

6. Costruisci un areogramma che descriva la suddivisione degli studenti di una scuola basata sui tempi di percorrenza da casa a scuola sapendo che ce ne sono: 45 da 1’ a 10’; 82 da 11’ a 15’; 145 da 16’ a 20’; 231 da 21’ a 30’; 319 più di 30’.

SEZIONE

B

GLI STRUMENTI PER IL DISEGNO TECNICO

CAPITOLO 3 STRUMENTI TRADIZIONALI E LORO USO

CAPITOLO 4 STRUMENTI ATTUALI: IL COMPUTER

CAPITOLO 5 CENNI SULLE NORME UNI

Tadao Ando

è un architetto giapponese autodidatta.

È famoso per usare il cemento a vista, che è diventato il suo segno distintivo. I suoi edifici sono caratterizzati da forme semplici come cubi, cilindri e superfici lisce, che sembrano dialogare con la luce naturale, studiata sempre con grande attenzione. Per ottenere queste superfici perfette, Ando usa stampi in legno molto curati.

Nei suoi progetti spesso si trovano acqua, cortili e percorsi che rendono gli spazi tranquilli e adatti alla riflessione. Le finestre e le aperture non servono solo a far entrare la luce, ma anche a collegare l’interno con l’esterno. In molte sue opere, la luce diventa quasi un “materiale architettonico” vero e proprio, capace di creare contrasti tra chiaro e scuro e di dare forma allo spazio.

Museo d’Arte di Naoshima

del Pritzker

Complesso museale sotterraneo sull’isola giapponese di Naoshima. I volumi in cemento armato, vetro e legno emergono dal terreno e dialogano con l’ambiente naturale.

TADAO ANDO

Tadao Ando

Vincitore

Prize nel 1995

Le opere di Tadao Ando insegnano al geometra che la precisione è fondamentale in ogni costruzione. Studiare le sue opere aiuta il geometra a capire che dietro un edificio essenziale e silenzioso ci sono competenze tecniche e scelte consapevoli.

Le sue competenze includono:

→ conoscere materiali semplici come il cemento, trasformandoli in edifici di qualità.

→ valorizzare la luce nei progetti non solo come fonte

EDUCAZIONE CIVICA

di illuminazione, ma come strumento in grado di rendere gli spazi più belli e funzionali.

→ attenzione ai dettagli tecnici, come giunzioni pulite e superfici lisce, che richiedono controllo e accuratezza.

L’analisi delle opere di Tadao Ando insegna che costruire non vuol dire solo alzare muri. L’integrazione di elementi naturali come la luce e l’acqua con elementi e materiali tipici delle costruzioni mostra che l’architettura può aiutare a vivere meglio creando spazi silenziosi che invitano alla calma e alla riflessione. Le sue opere mostrano come si possa costruire in modo sostenibile, valorizzando quello che c’è già senza sprechi e senza rovinare il paesaggio.

3 STRUMENTI TRADIZIONALI E LORO USO

1 Descrizione degli strumenti principali

L’uomo è l’unico essere vivente che sa progettare e costruire oggetti, utensili, macchine ecc. Egli ha iniziato con il vasellame, le armi, gli attrezzi, giungendo successivamente alla costruzione di manufatti più complessi, la cui realizzazione implicava la stesura preventiva di un progetto in cui fossero studiate tutte le fasi costruttive. Il disegno tecnico è stato ed è un mezzo indispensabile per la progettazione di un’opera, perché permette di rappresentare sia l’idea globale sia le caratteristiche costruttive di ogni singolo componente. Di seguito presentiamo le principali caratteristiche degli strumenti impiegati per l’esecuzione di disegni tecnici.

1.1 LA CARTA

La carta è costituita principalmente da cellulosa, trattata chimicamente, ottenuta dagli alberi di legno tenero come la betulla, il pioppo, il pino. Una carta meno comune, in quanto costosa e più pregiata, è ottenuta dal cotone, il lino e la canapa. Esistono vari tipi di carta, tra cui quella per il disegno, con caratteristiche diverse a seconda dell’uso a cui è adibita.

1.2 LA CARTA PER IL DISEGNO

La carta per il disegno normalmente è fornita in fogli oppure in rotoli come la carta da lucido (trasparente e usata principalmente per i disegni a china) e la carta da spolvero detta anche da scena (per usi particolari in pittura e disegno).

1. Descrizione degli strumenti principali

2. Uso corretto degli strumenti tradizionali

3. Squadratura del foglio e uso delle squadre

4. Il disegno a mano libera CI OCCUPEREMO DI...

permette l’esecuzione di disegni di precisione. Può essere di varia grammatura e spessore, e la scelta dell’uno o dell’altro tipo dipenderà dall’uso che se ne intende fare. Per il disegno tecnico si consiglia l’uso di una carta con grammatura di 220 gr/m2 in quanto fornisce una buona resistenza all’eventuale azione della gomma e allo strofinio delle squadrette. Per il disegno a mano libera, soprattutto nei primi tempi, conviene utilizzare carta quadrettata o anche millimetrata.

I fogli bianchi o già utilizzati conviene conservarli in cartelline rigide così da evitare piegature e arrotolamenti che ne comprometterebbero l’aspetto.

1.3 MATITE

Per il disegno si usano i portamine, più adatti al disegno tecnico delle matite tradizionali di legno (➜ Fig. 1). In ogni caso l’importante è che la punta sia lunga e non tozza e, nel caso del portamine (➜ Fig. 2), sporgente almeno 10 mm in modo da poter vedere bene dove si appoggia (➜ Fig. 3).

Per il disegno tecnico la carta più indicata è la carta liscia bianca, in fogli di varie dimensioni, perché ➜

Sia nella matita in legno sia nel portamine ciò che lascia il segno è la mina che è costituita principalmente da grafite con l’aggiunta di argilla. La proporzione di grafite e di argilla rende più o meno dura la mina. Ci sono mine morbide (da 9B a 2B), medie (B-HB-F), dure (da H a 9H) (➜ Fig. 4). Più le mine sono morbide più carico ne risulta il segno, ma è anche più facile sporcare il foglio. Viceversa più sono dure meno il segno risulta visibile ma è più facile incidere il foglio. Le più adatte per il disegno tecnico sono le HB, F e H e per eseguire i disegni a mano libera la B e la 2B.

9B 8B 7B 6B 5B 4B 3B 2B B HB

F H 2H 3H 4H 5H 6H 7H 8H 9H

➜ Fig. 4

Per eseguire un disegno è importante impugnare in modo corretto la matita. Pertanto nel caso in cui si avesse qualche difficoltà nel farlo, si consiglia l’uso di matite in legno a sezione triangolare oppure l’uso di opportuni correttori (➜ Fig. 5) da applicare alla matita o al portamine.

1.5 GOMME

Per il disegno a matita si usano gomme bianche morbide (➜ Fig. 9); eventualmente per pulire un disegno particolarmente sporco, si usa la gommapane (➜ Fig. 10). Per il disegno a china su carta da lucido si usa una gomma specifica traslucida di colore bianco o giallo (➜ Fig. 11).

1.6 SQUADRE, RIGHE E RIGHELLI

Per tracciare le linee rette si usano squadre, righe e righelli.

➜ Fig. 5

1.4 AFFILAMINE

Per affilare le mine sono usati la carta smeriglio (➜ Fig. 6), le campane (➜ Fig. 7) e i girelli (➜ Fig. 8). Questi ultimi permettono di ottenere velocemente una corretta affilatura grazie anche a due regolatori di lunghezza, uno per ottenere una punta affilata, l’altro per ottenere una punta un po’ più grossa.

➜ Fig. 6

Le squadre sono a forma di triangolo rettangolo isoscele (con angoli di 45° e 90°) (➜ Fig. 12) e di triangolo rettangolo scaleno (con angoli di 30°, 60° e 90°) (➜ Fig. 13), di varie dimensioni. Si sconsiglia l’uso di squadrette troppo piccole, perché insufficienti, o troppo grandi, perché ingombranti. Nell’uso si deve fare attenzione a non spostarle trascinandole, bensì sollevandole per non sporcare il foglio.

CARTA SMERIGLIO

Foglio di tela o carta ricoperta da materiale abrasivo.

CARTA DA LUCIDO

Carta a bassa opacità che consente di vedere in trasparenza. Usata, con matita o china, per riprodurre una figura posta al di sotto di essa.

➜ Fig. 7

➜ Fig. 9

➜ Fig. 10 ➜ Fig. 11

➜ Fig. 8

Le righe servono per tracciare linee di dimensioni tali da non poter essere eseguite con le squadrette, come ad esempio le linee della squadratura, mentre i righelli servono per rilevare misure e sono meno ingombranti delle squadrette. Ne esistono di varie lunghezze (➜ Fig. 14). Quando si acquistano squadre, righe e righelli è bene controllare che non siano arcuate e che i bordi siano perfettamente lisci. Nel caso poi delle squadrette in plastica, è opportuno verificare che non presentino residui dovuti a uno stampaggio mal realizzato.

1.8 GONIOMETRI

Il goniometro è uno strumento che serve per misurare l’ampiezza degli angoli. È formato da un disco graduato su cui sono riportate 360 tacche (ogni tacca corrisponde a 1°) (➜ Fig. 16), oppure da un semidisco con 180 tacche (➜ Fig. 17).

1.7 PARALLELOGRAFI

Il parallelografo (➜ Fig. 15) è una riga, guidata da due cavetti, che si sposta sempre parallelamente a se stessa. In commercio se ne trovano di già montati su tavolette.

1.9 COMPASSI

Il compasso è uno strumento, formato da due aste incernierate tra loro e con una apertura regolabile, che viene usato per tracciare circonferenze o per riportare misure. In commercio ne esistono di diversi tipi, ma quelli che ci interessano sono il balaustrone (➜ Fig. 18) e il normale compasso ad aste (➜ Fig. 19).

➜ Fig. 16

➜ Fig. 17

➜ Fig. 14

➜ Fig. 18

➜ Fig. 15 ➜ Fig. 19

Nell’uso del compasso è importante controllare che la punta di grafite sia sempre bene affilata e alla stessa altezza della punta metallica o un po’ più sporgente. Nel compasso tradizionale è bene controllare che l’apertura o la chiusura delle aste non sia né troppo difficoltosa nè troppo facile. Nel caso lo fossero, si deve regolare il serraggio delle viti che collegano le aste con la cerniera e che sono accessibili svitando il perno zigrinato e togliendo la copertura.

1.10 MASCHERINE, CURVILINEI, NORMOGRAFI

Le mascherine servono per tracciare rapidamente le principali figure geometriche (➜ Fig. 20) (cerchi, ellissi, poligoni ecc.) e i simboli ricorrenti nei disegni meccanici, come dadi esagonali (➜ Fig. 21), negli schemi elettrici, come lampade, spine ecc., o nell’arredamento, come mobili o apparecchi sanitari (➜ Fig. 22).

I curvilinei (➜ Fig. 23) sono mascherine atte al tracciamento delle curve. Col disegno a matita è consigliato l’uso di curvilinei con bordi dritti per poterli capovolgere qualora si dovessero eseguire curve simmetriche.

I normografi (➜ Fig. 24) sono mascherine usate per scrivere caratteri in stampatello. Sono dotati di supporti laterali, che li tengono sollevati dal foglio per la scrittura con penne a china, che sono rimossi quando si usano con la matita.

PERNO ZIGRINATO

Perno posto sulla sommità del compasso, per poterlo ruotare agevolmente, reso rugoso mediante zigrinatura cioè per mezzo di solchi (vedi p. 382).

➜ Fig. 20

➜ Fig. 21

➜ Fig. 22

➜ Fig. 23

➜ Fig. 24

2 Uso corretto degli strumenti tradizionali

2.1 INDICAZIONI PER UN USO CORRETTO: MATITA E COMPASSO

Indicazioni per un uso corretto: matita e compasso

Indicazioni per un uso corretto:

matita e compasso

1. MATITA

Matita

Indicazioni per un uso corretto: matita e compasso

Matita

- punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia fig.1;

- impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio; - perpendicolare al foglio fig.2 e non inclinata nè verso la squadretta fig.3 nè contro essa fig.4;

- impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio;

- punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia fig.1; - impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio; - perpendicolare al foglio fig.2 e non inclinata nè verso la squadretta fig.3 nè contro essa fig.4; - inclinata, se vista di fronte fig.5, e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse fig.4.

- perpendicolare al foglio fig.2 e non inclinata nè verso la squadretta fig.3 nè contro essa fig.4;

- inclinata, se vista di fronte fig.5, e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse fig.4.

punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia (➜ Fig. 25); impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio; perpendicolare al foglio (➜ Fig. 26) e non inclinata né verso la squadretta (➜ Fig. 27) né contro essa (➜ Fig. 28); inclinata, se vista di fronte (➜ Fig. 29), e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse (➜ Fig. 29).

- punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia fig.1;

Compasso

2. COMPASSO

Compasso

- usare la punta in acciaio a spillo anziché quella conica fig.6; - punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente fig.7; - le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine);

- usare la punta in acciaio a spillo anziché quella conica fig.6;

- punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente fig.7;

- nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica fig.8;

- le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine);

- nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica fig.8; - se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio fig.9.

- se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio fig.9.

- nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica fig.8;

usare la punta in acciaio a spillo anziché quella conica (➜ Fig. 30); punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente (➜ Fig. 31); le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine); nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica (➜ Fig. 32); se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio (➜ Fig. 33).

- se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio fig.9.

fig.3

fig.6

fig.9

fig.4

fig.2

fig.1

fig.5

fig.3

fig.4

fig.2

fig.1

fig.5

fig.3

fig.6 fig.7 fig.8

fig.9

fig.4

fig.2

fig.1

fig.5

Strumenti per il disegno: uso delle squadrette

Strumenti per il disegno: uso

delle squadrette

2.2 STRUMENTI PER IL DISEGNO: USO DELLE SQUADRETTE

Uso delle squadrette per tracciare linee parallele e perpendicolari

1. USO DELLE SQUADRETTE PER TRACCIARE LINEE PARALLELE E PERPENDICOLARI

Uso delle squadrette per tracciare linee parallele e perpendicolari

Accostando due squadrette e facendole scorrere l’una sull’altra si possono tracciare linee tra loro parallele o perpendicolari.

2. USO DELLE SQUADRETTE PER COSTRUIRE ANGOLI MULTIPLI DI 15°

Uso delle squadrette per costruire angoli multipli di 15°

Appoggiando le ssquadretta a una riga, accostandole e ruotandole opportunamente si può ottenere una serie di angoli multipli di 15°.

Appoggiando le squadrette a una riga, accostandole e ruotandole opportunamente si può ottenere una serie di angoli multipli di 15°.

Appoggiando le ssquadretta a una riga, accostandole e ruotandole opportunamente si può ottenere una serie di angoli multipli di 15°.

2.3 INDICAZIONI PER UN USO CORRETTO: CERCHIOGRAFO E CURVILINEO

Indicazioni

Indicazioni per un uso corretto: cerchiografo e curvilineo

1. CERCHIOGRAFO

per un uso corretto: cerchiografo

e curvilineo

Indicazioni per un uso corretto: cerchiografo e curvilineo

Cerchiografo

Indicazioni per un

Indicazioni per un uso corretto: cerchiografo e curvilineo

Cerchiografo

tracciare gli assi del cerchio che si vuole disegnare (➜ Fig. 34); posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi (➜ Fig. 35); tracciare la circonferenza con la matita perpendicolare al foglio (➜ Fig. 36).

- tracciare gli assi del cerchio che si vuole disegnare fig.1;

uso

corretto: cerchiografo e curvilineo

- tracciare gli assi del cerchio che si vuole disegnare fig.1;

Indicazioni per un uso corretto: cerchiografo e curvilineo

- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;

- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.

Cerchiografo

- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;

Cerchiografo

- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.

- tracciare gli assi del cerchio che si vuole disegnare fig.1;

- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.

- tracciare gli assi del cerchio che si vuole disegnare fig.1; - posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.

- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.

Fig. 34

- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.

2. CURVILINEO

Curvilineo determinare i punti per cui deve passare la curva fig.1;

Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;

Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2; - appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); - traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; - se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.

- abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;

Curvilineo determinare i punti per cui deve passare la curva fig.1;

Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;

Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2; - il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);

- abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;

- traccia solo una parte di curva fig.3;

- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); - traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; - se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.

- traccia solo una parte di curva fig.3;

- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.

- traccia solo una parte di curva fig.3;

- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;

- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);

- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; - tenere la matita perpendicolare al foglio.

- tenere la matita perpendicolare al foglio.

- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.

- il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; - se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.

- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;

- tenere la matita perpendicolare al foglio.

determinare i punti per cui deve passare la curva (➜ Fig. 37); abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento (➜ Fig. 38); appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); tracciare solo una parte di curva (➜ Fig. 39); il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) (➜ Fig. 40) così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare (➜ Figg. 41-42); cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; tenere la matita perpendicolare al foglio.

- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;

- tenere la matita perpendicolare al foglio.

Fig. 40

- tenere la matita perpendicolare al foglio.

- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; - tenere la matita perpendicolare al foglio.

Fig. 41

Fig. 42

fig.4 fig.5

fig.2

fig.1

fig.9

fig.3

fig.6

fig.3

fig.7 fig.8

fig.2

fig.1

fig.9

fig.3

fig.6

fig.2

fig.1

fig.9

fig.3

fig.6

fig.2

fig.1 fig.9

fig.3

fig.6

fig.4

fig.5 fig.7

fig.8

fig.2

fig.3

fig.6

fig.2 fig.1

fig.3

fig.6

fig.2 fig.1 fig.9 fig.3

fig.6

3 Squadratura del foglio e uso delle squadre

3.1 STRUMENTI PER IL DISEGNO: SQUADRATURA DEL FOGLIO

Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.

Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .

Strumenti per il disegno: squadratura del foglio

1. ESEGUIRE LA SQUADRATURA DI UN FOGLIO

Eseguire la squadratura di un foglio

Strumenti per il disegno: squadratura del foglio

Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:

Eseguire la squadratura di un foglio

Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:

Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.

Da O si riportano su golo (squadratura)

Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.

squadratura del foglio

disegnare su di esso disegno, si

Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.

Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.

Strumenti per il disegno: squadratura del foglio

Eseguire la squadratura di un foglio

Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D. foglio

Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.

Ripetendo la stessa cale si tracciano le completando la costruzione.

Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.

Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:

Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .

Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.

Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .

C, D con una otto archetti E, F, G, H. Si passano per O, assi del foglio.

Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.

Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .

Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.

all’asse orizzonfacendola scorrere passanti per I e M.

Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.

Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .

Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.

Il disegno a mano libera

4.1 DISEGNO A MANO LIBERA DI QUADRATI E CIRCONFERENZE

Il disegno a mano libera è certamente la più importante tra le tecniche utilizzate per eseguire un elaborato grafico. Richiede, infatti, una strumentazione molto scarna (matita, foglio di carta e gomma) e pertanto può essere utilizzato ovunque, anche nelle situazioni più disagevoli. Questa sua facoltà di utilizzo permette quindi in ogni momento di integrare spiegazioni verbali, non sempre facilmente comprensibili, con schizzi, o di apportare correzioni a un elaborato grafico, lasciando in tal modo traccia di quanto discusso. È comunque importante tenere presente che si tratta di un disegno tecnico: pertanto, nell’eseguirlo, si devono sempre rispettare le norme relative. Di seguito sono proposte alcune costruzioni geometriche, utili per acquisire dimestichezza con questa tecnica. Per eseguire un disegno a mano libera si consiglia di utilizzare una matita morbida (B o 2B) e fogli quadrettati, sia perché si possono usare le quadrettature come guide nella tracciatura di linee, sia perché i quadretti sono d’aiuto per rispettare le proporzioni.

Disegno a mano libera di quadrati e circonferenze

Il disegno a mano libera è certamente la più importante tra le tecniche utilizzate per eseguire un elaborato grafico. Richiede, infatti, una strumentazione molto scarna (matita, foglio di carta e gomma) e pertanto può essere utilizzato ovunque, anche nelle situazioni più disagevoli. Questa sua facoltà di utilizzo permette quindi in ogni momento di integrare spiegazioni verbali, non sempre facilmente comprensibili, con schizzi, o di apportare correzioni ad un elaborato grafico, lasciando in tal modo traccia di quanto discusso. E’ comunque importante tenere presente che si tratta di un disegno tecnico: pertanto, nell’eseguirlo, si devono sempre rispettare le norme relative. Di seguito sono proposte alcune costruzioni geometriche, utili per acquisire dimestichezza con questa tecnica. Per esegire un disegno a mano libera si consiglia di utilizzare una matita morbida (B o 2B) e fogli quadrettati, sia perché si possono usare le quadrettature come guide nella tracciatura di linee, sia perché i quadretti sono d’aiuto per rispettare le proporzioni.

Le costruzioni proposte, in tutto il testo, sono scandite da disegni che ne illustrano le fasi. Ciò che le differenzia tra loro sono i colori dei segni: il nero è utilizzato per ciò che fa parte del disegno finale, come lati, assi ecc., il rosso per ciò che si deve eseguire in quella fase e l’azzurro per ciò che è stato eseguito nella fase precedente.

Le costruzioni proposte, in tutto il testo, sono scandite da disegni che ne illustrano le fasi. Ciò che le differenzia tra loro sono i colori dei segni: il nero è utilizzato per ciò che fa parte del disegno finale, come lati assi ecc., il rosso per ciò che si deve eseguire in quella fase e l’azzurro per ciò che è stato eseguito nella fase precedente.

1. DISEGNARE A MANO LIBERA UN QUADRATO

Disegnare a mano libera un quadrato

1a. Si tracciano due assi tra loro perpendicolari che si intersecano nel punto O e si fissano i punti A, B, C, D equidistanti da O. Si tracciano per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato (➜ Fig. 43).

1a Si tracciano due assi tra loro perpendicolari che si intersecano nel punto O e si fissano i punti A, B, C, D equidistanti da O.

1b Si traccino per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato. Si completa la costruzione evidenziando il perimetro del quadrato.

1b. Si completa la costruzione evidenziando il perimetro del quadrato (➜ Fig. 44).

1b Si traccino per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato. Si completa la costruzione evidenziando il perimetro del quadrato.

2. DISEGNARE A MANO LIBERA UNA CIRCONFERENZA

Primo metodo

➜ Fig. 43

➜ Fig. 44

Disegnare a mano libera una circonferenza

2a. Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e siano A, B, C, D i punti di tangenza tra la circonferenza e i lati del quadrato. Con la maggior precisione possibile si traccia un quarto di circonferenza e si individuano su di esso due punti di intersezione tra la curva e la quadrettatura (➜ Fig. 45).

Disegnare a mano libera una circonferenza

Primo metodo

Disegnare a mano libera una circonferenza

Primo metodo

2a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e siano A, B, C, D i punti di tangenza tra la circonferenza e i lati del quadrato. Con la maggior precisione possibile si tracci un quarto di circonferenza e si individuino su di esso due punti di intersezione tra la curva e la quadrettatura.

2b. Si tracciano gli altri tre quarti di circonferenza riportando simmetricamente rispetto agli assi i punti individuati precedentemente (➜ Fig. 46).

Secondo metodo

2b Si traccino gli altri tre quarti di circonferenza prendendo come riferimento i punti individuati precedentemente.

Secondo metodo

3a. Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e si tracciano le sue diagonali (➜ Fig. 47).

Partendo da O, si riporta su queste ultime il raggio, valutandone la misura ad occhio con la miglior approssimazione possibile. Si determinano così i punti E, F, G, H, che appartengono alla circonferenza.

3a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e si tracciano le sue diagonali. Partendo da O, si riporta su queste ultime il raggio, valutandone la misura ad occhio con la miglior approssimazione possibile. Si determinano così i punti E, F, G, H, che appartengono alla circonferenza.

3b Si traccia ora la curva passante per i vari punti completando la costruzione.

3b. Si traccia ora la curva passante per i vari punti completando la costruzione (➜ Fig. 48).

➜ Fig. 45

➜ Fig. 46

➜ Fig. 47

➜ Fig. 48

Disegno a mano libera di circonferenze e triangoli equilateri

Terzo metodo

4a. Si costruisce il quadrato T, U, V, Z col lato pari al diametro della circonferenza.

4a Si costruisce il quadrato T, U, V, Z col lato pari al diametro della circonferenza. Si tracciano gli assi dei lati che si intersecano in O (centro della circonferenza) e determinano i punti A, B, C, D.

Si tracciano gli assi dei lati che si intersecano in O (centro della circonferenza) e determinano i punti A, B, C, D (➜ Fig. 49).

a mano libera di circonferenze e triangoli equilateri

4b Si congiunge B con V e Z e D con T e U.

4b. Si congiunge B con V e Z allo stesso modo D con T e U (➜ Fig. 50).

4b Si congiunge B con V e Z e D con T e U.

costruisce il quadrato T, U, V, Z col diametro della circonferentracciano gli assi dei lati che si O (centro della circondeterminano i punti A, B, C,

4c Si tracciano le congiungenti di D con R e con S, punti medi di VC e AZ, che intersecano BZ in H e BV in G. Si ripete la costruzione con BP e BQ che intercettando DT e DU determinano E e F.

4c. Si tracciano le congiungenti di D con R e con S, punti medi di VC e AZ, che intersecano BZ in H e BV in G. Si ripete la costruzione con BP e BQ che intercettando DT e DU determinano E e F (➜ Fig. 51).

congiunge B con V e Z e D con T e

4d I punti così determinati assieme a A, B, C, D permettono di tracciare la circonferenza.

4d. I punti così determinati assieme a A, B, C, D permettono di tracciare la circonferenza (➜ Fig. 52).

4d I punti così determinati assieme a A, B, C, D permettono di tracciare la circonferenza.

le congiungenti di D con punti medi di VC e AZ, che BZ in H e BV in G. Si ripete con BP e BQ che interDU determinano E e F.

così determinati assieme a permettono di tracciare la

➜ Fig. 49

➜ Fig. 50

➜ Fig. 51

Disegnare a mano libera un triangolo equilatero

4.2 DISEGNO

5a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e un segmento orizzontale passante per M, punto medio di OB, che determina sulla circonferenza i punti E e F.

A MANO LIBERA DI UN TRIANGOLO EQUILATERO

➜ Fig. 52

1. DISEGNARE A MANO LIBERA UN TRIANGOLO EQUILATERO

5a. Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e un segmento orizzontale passante per M, punto medio di OB, che determina sulla circonferenza i punti E e F (➜ Fig. 53).

5b. Si completa la costruzione congiungendo tra loro E, F e D vertici del triangolo (➜ Fig. 54).

mano libera un triangolo equilatero

5b Si completa la costruzione congiungendo tra loro E, F e D vertici del triangolo.

una circonferenza (ad tracciandone una quarto con il e completandola con il metodo) e un segmento orizzonper M, punto medio di determina sulla circonferenza i

5b Si completa la costruzione congiungendo tra loro E, F e D vertici del triangolo.

completa la costruzione congiunE, F e D vertici del trian-

Fig. 53 ➜ Fig. 54

Disegno a mano libera di poligoni regolari

4.3 DISEGNO A MANO LIBERA DI POLIGONI REGOLARI

Disegno a mano libera di poligoni regolari

1. DISEGNARE A MANO LIBERA UN ESAGONO REGOLARE

6a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per M e N, punti medi di DO e OB, che determinano sulla circonferenza i punti E, F, G, H.

6b Si completa la costruzione congiungendo tra loro i vertici.

6a. Si traccia una circonferenza (ad esempio tracciandone un quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per M e N, punti medi di DO e OB, che determinano sulla circonferenza i punti E, F, G, H. (➜ Fig. 55). 6b. Si completa la costruzione congiungendo tra loro i vertici. (➜ Fig. 56).

6b Si completa la costruzione congiungendo tra loro i vertici.

7a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e le diagonali del quadrato in cu è inscritta determinando su di essa E, F, G, H che con A, B, C, D sono i vertici dell’ottagono.

2. DISEGNARE A MANO LIBERA UN OTTAGONO REGOLARE

Fig. 55

7b Si completa la costruzione congiungendo tra loro i vertici.

7a. Si traccia una circonferenza (ad esempio tracciandone un quarto con il terzo metodo e completandola con il primo metodo) e le diagonali del quadrato in cui è inscritta determinando su di essa E, F, G, H che con A, B, C, D sono i vertici dell’ottagono (➜ Fig. 57).

7b Si completa la costruzione congiungendo tra loro i vertici.

7b. Si completa la costruzione congiungendo tra loro i vertici (➜ Fig. 58).

8a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per R e S, punti medi di DO e OB, e due verticali passanti per P e Q che determinano sulla circonferenza i otto punti che con A, B, C, D sono i vertici del dodecagono.

3. DISEGNARE A MANO LIBERA UN DODECAGONO REGOLARE

8b Si completa la costruzione congiungendo i tra loro i vertici.

8a. Si traccia una circonferenza (ad esempio tracciandone un quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontali passanti per R e S, punti medi di DO e OB, e due verticali passanti per P e Q che determinano sulla circonferenza gli otto punti che con A, B, C, D sono i vertici del dodecagono (➜ Fig. 59).

8b. Si completa la costruzione congiungendo tra loro i vertici (➜ Fig. 60).

➜ Fig. 57 ➜ Fig. 59

➜ Fig. 58 ➜ Fig. 60

➜

➜ Fig.

Esercitazione

SVILUPPA LE ABILITÀ

Esercitazione sull’uso di strumenti tradizionali per il disegno

Si traccino quattro serie di linee parallele come indicato nella figura a fianco.

1. Traccia quattro serie di linee parallele come indicato nella figura a fianco.

Dopo aver suddiviso il foglio in quattro quadranti, si riportano nei quadranti 1, 2, 4 le tacche segnate in rosso alla distanza di 5mm. Quindi posizionando le squadrette come nelle figure e facendole scorrere nel senso indicato dalle dalle frecce si traccino le linee. Si faccia attenzione a far scorrere le squadrette non sulle linee appena tracciate in quanto raccoglirebbero la polvare di grafite che rimane sul foglio sporcandolo e sporcandosi.

Dopo aver suddiviso il foglio in quattro quadranti, si riportano nei quadranti 1, 2, 4 le tacche segnate in rosso alla distanza di 5 mm. Quindi posizionando le squadrette come nelle figure e facendole scorrere nel senso indicato dalle frecce si tracciano le linee. Si deve fare attenzione a far scorrere le squadrette non sulle linee appena tracciate in quanto raccoglierebbero la polvere di grafite che rimane sul foglio sporcandolo e sporcandosi.

di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si proceda quindi secondo le indicazioni in fig.1.

Tracciare alcune serie di linee parallele e alcuni archi di circonferenza come indicato in fig. 2.

Nell’esecuzione si presti attenzione a non commettere gli errori evidenziati in fig.3, 4, 5, 6.

Esercitazione sull’uso di strumenti tradizionali per il disegno

2. Traccia alcune serie di linee parallele e alcuni archi di circonferenza come indicato in ➜ Fig. 2

Esercitazione sull’uso di strumenti tradizionali per il disegno

linee parcirconferenza

quattro traccino le sole interdeterminarne il assi. Nel 4° orizzontaposizioni dei punti piccoli segni seguendo le quindi secondo

attenzione a non evidenziati in fig.3, sull’uso di

attenzione a non evidenziati in fig.3,

Dopo aver squadrato e diviso in quattro quadranti un foglio UNI A3 si traccino le diagonali nel 1° quadrante e le sole intersezioni nel 2° e 3° per determinarne il centro per cui passeranno gli assi. Nel 4° quadrante si traccino le tre linee orizzontali. Quindi si riportino le posizioni dei punti di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si proceda quindi secondo le indicazioni in fig.1.

sull’uso di strumenti tradizionali per il disegno

Dopo aver squadrato e diviso in quattro quadranti un foglio UNI A4 si tracciano le diagonali nel 1° quadrante e le sole intersezioni nel 2° e 3° per determinarne il centro per cui passeranno gli assi. Nel 4° quadrante si tracciano le tre linee orizzontali. Quindi si riportano le posizioni dei punti di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si procede quindi secondo le indicazioni in ➜ Fig. 1

Tracciare alcune serie di linee parallele e alcuni archi di circonferenza come indicato in fig. 2. Dopo aver squadrato e diviso in quattro quadranti un foglio UNI A3 si traccino le diagonali nel 1° quadrante e le sole intersezioni nel 2° e 3° per determinarne il centro per cui passeranno gli assi. Nel 4° quadrante si traccino le tre linee orizzontali. Quindi si riportino le posizioni dei punti di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si proceda quindi secondo le indicazioni in fig.1.

Nell’esecuzione si presti attenzione a non commettere gli errori evidenziati in fig.3, 4, 5, 6.

➜ Fig. 1

➜ Fig. 2

Nell’esecuzione si presti attenzione a non commettere gli errori evidenziati in fig.3, 4, 5, 6.

Nell’esecuzione si deve prestare attenzione a non commettere gli errori evidenziati in ➜ Figg. 3-4-5-6.

fig.1

fig.3 fig.4

fig.2

fig.1

fig.2

fig.1

fig.2

fig.1

fig.3

fig.4 fig.5

fig.2

Disegno a mano libera su carta quadrettata

Disegno a mano libera: esercizi

3. Riproduci a mano libera su carta quadrettata i disegni proposti.

Riprodurre a mano libera su carta quadrettata i disegni proposti

Fase preliminare di preparazione

Disegno a mano libera: esercizi

Disegno a mano libera su carta non quadrettata

Disegno a mano libera: esercizi

Disegno a mano libera su carta non quadrettata

4. Disegna a mano libera il supporto in Fig. 1.

Disegno a mano libera: esercizi

Disegno a mano libera su carta non quadrettata

Disegnare a mano libera il supporto in fig.1

Disegno a mano libera su carta non quadrettata

Disegnare a mano libera il supporto in fig.1

La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione quella più piccola in quanto più facile da eseguire.

Disegnare a mano libera il supporto in fig.1

La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.

Disegnare a mano libera il supporto in fig.1

La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto (➜ Fig. 2). Quindi per ciascun centro si costruisce il quadrato con la trama per tracciare la circonferenza corrispondente (➜ Fig. 3). Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.

La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.

➜ Fig. 1

➜ Fig. 2

➜ Fig. 3

Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6

Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate avendo cura di mantenersi da esse a un distanza costante (➜ Fig. 4). Si tracciano quindi anche le tangenti e si ripassano gli archi (➜ Fig. 5). Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei (➜ Fig. 6).

➜ Fig. 4

➜ Fig. 5

➜ Fig. 6

Disegno a mano libera: esercizi

5. Riproduci a mano libera su carta quadrettata i disegni proposti.

Riprodurre a mano libera su carta quadrettata i disegni proposti