Prove Nazionali INVALSI Matematica 2024 - Classe 5° - Primaria

Pronti per la PROVA

Invalsi 5

• Prove ufficiali commentate • Prove di allenamento

Prove digitali

MATEMATICA

LIBRO DIGITALE INTERATTIVO - Versione studente

Il Libro digitale, sfogliabile e interattivo, contiene esercizi interattivi, con correzione immediata.

Scaricare il Libro digitale è molto semplice. Vai alla pagina www.gruppoeli.it/libridigitali, segui le indicazioni e inserisci il codice:

Inquadra il QR code per accedere al video tutorial

Guarda e ascolta sullo smartphone o sul tablet

tutti i contenuti multimediali del tuo libro con la App

Scarica la App da App Store per iOS e su Google Play per Android.

Inquadra la pagina del tuo libro.

Accedi ai contenuti e scaricali.

Inquadra il QR code per accedere al video tutorial

ESERCIZI con il tablet

Invalsi 5

NUOVA EDIZIONE

NUOVA EDIZIONE

Pronti per la prova Invalsi 5 Matematica

Testi : Elena Costa, Lilli Doniselli, Alba Taino

Responsabile editoriale : Beatrice Loreti

Art director: Marco Mercatali

Responsabile di produzione : Francesco Capitano

Progetto grafico e impaginazione : Carlo Mella

Copertina: Curvilinee

Illustrazioni : Gianluca Martini

Revisione Testi : Mattia Rugiano

Foto : Shutterstock

© 2023 ELI – La Spiga Edizioni Via Brecce, 100 – Loreto tel. 071 750 701

info@elilaspigaedizioni.it www.gruppoeli.it

Stampato in Italia presso Tecnostampa – Pigini Group Printing Division –Loreto – Trevi 23.83.444.0

ISBN 978-88-468-4423-1

Le fotocopie non autorizzate sono illegali. Tutti i diritti riservati. È vietata la riproduzione totale o parziale così come la sua trasmissione sotto qualsiasi forma o con qualunque mezzo senza previa autorizzazione scritta da parte dell’editore.

PRESENTAZIONE

Le prove Invalsi servono per monitorare le competenze raggiunte dagli alunni e dalle alunne al termine del percorso nella scuola primaria, quando devono essere consolidate le abilità di operare con i numeri e risolvere situazioni problematiche che attengono alle differenti aree della matematica.

Esse sono anche un ottimo strumento per:

• programmare e strutturare il lavoro;

• favorire l’acquisizione e lo sviluppo delle competenze nell’area logico-matematica.

Il testo presenta:

• una prova guidata per poter aiutare gli allievi e le allieve nei primi passi;

• due prove graduate per complessità dei quesiti posti;

• le prove ufficiali degli ultimi tre anni. Queste prove sono commentate e aiutano gli alunni e le alunne a trovare i punti su cui dovranno concentrarsi maggiormente;

• una prova finale, simile alle prove ministeriali per numero di item e difficoltà, per poter controllare le competenze e le abilità raggiunte al termine del percorso.

Consigliamo di somministrare agli alunni e alle alunne queste prove scandendole durante tutto l’anno scolastico. In questo modo la preparazione per affrontare le prove ufficiali sarà graduale e aiuterà i bambini e le bambine a superare l’ansia della prova Invalsi.

Le prove contenute in questo testo danno la possibilità ai bambini e alle bambine di acquisire una forma mentale che li aiuta nel percorso per raggiungere il vero scopo finale: acquisire competenze in matematica.

L’insegnante ha a disposizione un percorso propedeutico online con esercizi specifici per comprendere le consegne. C’è poi una parte che riguarda le dimensioni della matematica (conoscere – risolvere problemi – argomentare) e i suoi ambiti (numeri – spazio e figure – dati e previsioni – relazioni e funzioni). Questo percorso aiuta a individuare il tipo di lavoro che si può proporre per ciascun ambito e dimensione, anche esportandolo in altre situazioni di lavoro.

Le esercitazioni proposte permettono inoltre di monitorare durante tutto l’anno scolastico i successi e le eventuali difficoltà di alunne e alunni.

Questa pagina offre gli strumenti per aiutare i bambini e le bambine ad affrontare le prove Invalsi con maggiore serenità.

MINDFULNESS

Presta attenzione leggendo con calma la consegna.

LIFE SKILLS

Consapevolezza di sé : sai che come tutti hai punti deboli, ma anche punti di forza. Fai leva su questi ultimi per sentirti forte.

Concentrati per capire che cosa ti sta chiedendo la consegna e non pensare subito alla risposta.

Gestione delle emozioni : non puoi cancellare l’emozione, ma cerca di reagire in modo positivo e con fiducia.

Metti in azione la curiosità per conoscere quali sono le risposte proposte o per capire come puoi dare tu una risposta.

Gestione dello stress: è normale sentirsi stressati di fronte ad una prova importante. Cerca di mantenere la calma e sappi che sei pronto/a a risolvere i problemi che ti vengono presentati.

Sfida te stesso/a convinto/a che sei in grado di “uscire vincitore”.

Pensiero creativo : a volte la curiosità e un’idea originale ti possono aiutare a trovare la soluzione.

Pensa positivamente perché “ce la puoi fare”.

Prendere decisioni : quando sei sicuro/a dai la tua risposta senza incertezze. Rivedendo poi le tue risposte puoi sempre correggere.

Prova 1 È una prova guidata. Svolgila autonomamente. Leggi con attenzione le indicazioni che ti possono aiutare.

Prova 2 e Prova 3

In queste prove le difficoltà sono in progressione : dal più facile al più difficile.

Prova 4, Prova 5 e Prova 6 Sono le “vere” prove Invalsi che i bambini e le bambine come te hanno affrontato nelle prove ufficiali degli anni 2021 – 2022 – 2023. I suggerimenti possono aiutarti a comprendere quale procedimento devi seguire.

Prova 7 È una prova molto simile alle prove ufficiali. Metti in atto tutto ciò che hai imparato.

Come ti prepara questo testo ad affrontare bene le prove Invalsi?

In queste prime tre prove e nella prova 7 sono evidenziati gli ambiti:

numeri dati e previsioni

spazio e figure relazioni e funzioni

1

Questa è l’ora che segnava l’orologio dell’automobile di Emma quando è partita. 9:25

Emma è giunta a destinazione dopo tre quarti d’ora. Quale orologio segna l’orario di arrivo?

A. 9:40

B. 10:00

C. 10:10

D. 12:25

A quanti minuti corrispondono tre quarti d’ora? Quanti minuti ci sono in un’ora? Ricordarlo ti servirà per calcolare il passaggio all’ora successiva.

2 In un deposito sono arrivate 88 casse di mattonelle. A lan le sposterà dal camion al capannone utilizzando un muletto che trasporta 10 casse per volta.

Qual è il numero minimo di viaggi che farà Alan?

A. 8

B. 8,8

C. 9

D. 10

Con un viaggio il muletto trasporta 10 casse, con 2 viaggi 20 casse e così via.

Però le ultime casse che rimangono avranno bisogno di un altro viaggio, anche se sono meno di 10.

3 Le frazioni 12 15 e 3 15 sono complementari?

Leggi queste risposte. Segna quella che indica l’argomentazione che giustifica la risposta corretta.

No, perché… Sì, perché…

A. i numeratori sono diversi. C. i denominatori sono uguali.

B. il numeratore della seconda frazione è minore di quello della prima.

D. la somma dei numeratori è uguale ai denominatori.

Ricorda che due frazioni sono complementari quando la loro somma forma l’intero.

4 Il serbatoio dell’auto di Marisa può contenere 60 l di benzina. Ora è pieno per 1 3 . Quanti litri di benzina deve aggiungere Marisa per riempire completamente il serbatoio?

Risposta: Deve aggiungere ………………. litri di benzina

Sai quanti litri di benzina contiene ora il serbatoio? Puoi calcolarlo?

5 Scrivi sulla linea dei numeri al posto giusto il numero 220. 0 100

Se trovi il numero che devi scrivere sotto ciascuna tacca da 0 a 100, troverai anche dove posizionare il numero 220.

6

Vasco vuole comprare un libro. 11 monete da 50 centesimi non sono sufficienti, 12 monete da 50 centesimi sono troppe.

Quanto potrebbe costare il libro?

A. 5,50 euro

B. 5,80 euro

C. 11,12 euro

D. 11,50 euro

Trova il valore di ciascuno dei due gruppi di monete.

8 cm

4 cm

Quanto misura il perimetro della figura?

A. 24 cm

B. 28 cm

C. 30 cm

D. 32 cm

Quale relazione c’è tra la lunghezza dei lati della figura?

Rifletti e ricava le misure di ciascun lato.

Poi ricorda che devi calcolare il perimetro e non l’area.

7 Osserva questa figura.

8 Se dal punto A si traccia una retta parallela alla linea blu il rettangolo rimane diviso in: A

A. tre triangoli.

B. un triangolo, un trapezio e un parallelogramma.

C. un triangolo, un trapezio e un pentagono.

D. due triangoli e un trapezio.

Traccia la linea richiesta. Poi osserva le figure in cui il rettangolo viene diviso dalle due linee. Presta molta attenzione alla figura centrale.

9 La seguente figura è formata da 10 quadrilateri.

Scrivi:

• R nei rettangoli

• P nei parallelogrammi non rettangoli

• Q in tutti gli altri quadrilateri

Osserva un quadrilatero alla volta. Ricorda che un rettangolo rimane tale in qualsiasi modo sia orientato. Ricorda le caratteristiche dei parallelogrammi.

In una scuola si insegnano due lingue: inglese e cinese. Le persone iscritte al primo livello sono 60, tante quante quelle iscritte al secondo livello.

Completa la tabella di frequenza con il numero di persone.

Primo livello ....................... .......................

Secondo livello

Dal primo grafico puoi facilmente ricavare quante persone studiano inglese e quante studiano cinese (primo livello).

Per conoscere i dati del secondo livello dovrai tenere conto dell’indicazione che ti danno le frazioni del grafico a torta e del numero totale di persone al secondo livello.

11 In un luna park c’è questo tiro a segno:

Per ciascuna affermazione indica se è vera (V) o falsa (F).

a. Ci sono le stesse probabilità di colpire un settore con il sole o un settore con la stella.

b. È più probabile colpire un settore con la stella che un settore con la luna.

c. Ci sono le stesse probabilità di colpire un settore con il sole o un settore con la nuvola.

d. È meno probabile colpire un settore con il sole che un settore con la luna.

Devi contare quante volte ciascuna figura compare nel tiro a segno.

12 Tre bottiglie di salsa uguali contengono complessivamente 1,2 l di prodotto. Quanti litri di salsa contengono 12 bottiglie dello stesso tipo?

Risposta: …………….. litri di salsa. 1,2 l è il contenuto di 3 bottiglie. Perciò prima devi trovare quanta salsa contiene una sola bottiglia.

13

Un treno impiega esattamente 12 minuti per spostarsi da una stazione all’altra. In ogni stazione si ferma per 3 minuti.

Stazione 1 Stazione 2 Stazione 3 Stazione 4 Stazione 5

Se il treno è partito dalla stazione 1 alle ore 8:30, a che ora arriverà alla stazione 5?

A. 8:42

B. 9:27

C. 9:30

D. 9:35

14

Il tempo di cui tenere conto è quello impiegato dal treno per raggiungere ogni stazione e quello in cui si ferma nelle stazioni. Per l’ultima stazione non devi considerare il tempo di fermata.

Due alberi nello stesso momento proiettano così la loro ombra.

albero A

albero B

L’albero B è alto il quadruplo dell’albero A.

In questo momento l’ombra dell’albero B è lunga 2,2 m. Quanto è lunga l’ombra dell’albero A?

A. 1,1 m perché è più corta dell’ombra dell’albero B.

B. 0,55 m perché è 1 4 dell’ombra dell’albero B.

C. 4,8 m perché è più lunga dell’ombra dell’albero B.

D. 2,2 m perché siamo nello stesso momento della giornata.

Se l’albero B è alto il quadruplo dell’albero A, anche le loro ombre mantengono la stessa proporzione.

1 Completa le frasi inserendo i numeri o le parole giusti. Scegli tra questi.

il triplo – 125 – 5 – 10, 5 – 42 – la terza parte

a) 25 è un quinto di …………….. .

b) è la metà di 21.

c) 3,6 è di 1,2.

d) 0,04 è di 0,12.

2 In quale delle figure la parte colorata rappresenta la metà dell’intero?

A. Solo nella figura 4.

B. Nella figura 2 e nella figura 4.

C. Nelle figure 1 e 2.

D. In tutte le figure.

3 Quale tra le seguenti scritture non corrisponde al numero ventiquattromilatrenta?

A. 24 030

B. 2403 decine

C. 20 000 + 4000 + 30

D. 24 migliaia + 3 centinaia

Figura 1

Figura 2

Figura 3

Figura 4

4

Osserva questi due numeri.

Quale frase è giusta?

5

18,89 18,9

A. I numeri hanno la stessa parte decimale.

B. 18,89 è maggiore perché è composto da 4 cifre.

C. Tutti e due i numeri hanno una cifra che vale 9 decimi.

D. 18,9 corrisponde a 189 decimi.

Questa è la quantità di acqua che occorre a un bambino o a una bambina per

Segna sul contenitore quanta acqua occorre per 4 bambini e bambine.

7

Osserva il poligono.

Disegna il poligono simmetrico ad esso rispetto all’asse r.

Quale tra i seguenti numeri corrisponde a 75 decimi?

A. 0,075

B. 0,75

C. 7,5

D. 75

8

a) Nello spazio quadrettato disegna un poligono che abbia queste caratteristiche:

• 4 lati di cui solo una coppia paralleli tra di loro

• solo una coppia di lati uguali

• gli angoli uguali a due a due

b) Quale poligono hai disegnato?

Risposta: …………………………………………

c) Nella figura colora con lo stesso colore gli angoli uguali

9 A un numero aggiungo la metà di 5 e ottengo 4,5. Qual è il numero iniziale?

A. 2

B. 2,5

C. 5

D. 6,5

10

Osserva i seguenti triangoli e leggi ciò che dice Gloria.

I tre triangoli hanno la stessa area e lo stesso perimetro.

Gloria

A. ha ragione.

B. ha torto perché i triangoli hanno la stessa area, ma non lo stesso perimetro.

C. ha torto perché i triangoli hanno lo stesso perimetro, ma non la stessa area.

D. ha torto perché i triangoli sono tutti diversi.

11 Il grafico mostra i punti ottenuti dalle prime quattro squadre nel campionato regionale. Le Tigri sono arrivate al terzo posto.

Disegna la barra che manca.

Leopardi

Tartarughe

Gloria

12

La seguente figura è formata da due triangoli rettangoli isosceli e un rettangolo.

Per ciascuna affermazione indica se è vera (V) o falsa (F) V F

a. La figura è un quadrilatero.

b. L’angolo colorato in grigio misura 135°.

c. La figura ha 2 angoli ottusi e 2 angoli retti.

d. L’altezza è uguale al lato obliquo.

13 Questa è la fotografia di un modellino di automobile.

3,6 cm

Nella realtà questa automobile è lunga 3,60 m. Qual è la scala del modellino?

A. 10 : 1

B. 1 : 10

C. 1 : 100

D. 1 : 1000

14 Osserva con attenzione.

1978 1987 1996 2005

Quale operatore è indicato dalla freccia?

A. + 11

B. – 11

C. + 9

D. – 9

15 Gli alunni e le alunne della 5a C hanno scritto le lettere della parola AMICIZIA, ognuna su un cartoncino. I cartoncini sono tutti uguali.

Gli 8 cartoncini sono stati messi in una scatola e vengono estratti uno alla volta. A M I C I Z

I A

Completa le frasi.

a) La lettera che ha più probabilità di essere estratta è ……………………

b) Le lettere che hanno meno probabilità di essere estratte sono

c) La lettera che ha due probabilità su otto di essere estratta è

1 Filippo abita a Trento.

Sul cellulare legge che la temperatura nella sua città in quel momento è di –2°. Questo è il termometro nella sua stanza.

2

Quanti gradi di differenza ci sono tra la temperatura esterna e quella interna?

Risposta: ……………..

Osserva questa moltiplicazione.

2,9 x 100,2

Quale tra queste moltiplicazioni dà il risultato più vicino a quello dell’operazione nel riquadro?

A. 2 x 100

B. 2,5 x 100

C. 3 x 100

D. 3 x 101

Questa è la manopola del forno di Luciano.

Luciano regola il forno alla temperatura di 250 gradi. Per passare dalla posizione iniziale alla posizione di 250 gradi la manopola è stata ruotata in senso orario di:

A. 250°

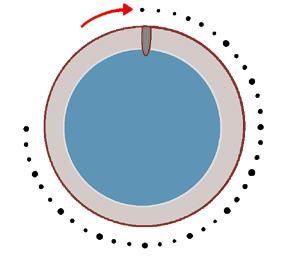
B. 225°

C. 180°

D. 125°

4 In un sacchetto ci sono stelline bianche o nere.

Che cosa occorre fare perché la probabilità di pescare una stellina nera sia il doppio di quella di pescare una stellina bianca?

A. Togliere una stellina nera.

B. Togliere due stelline nere.

C. Aggiungere una stellina nera.

D. Aggiungere due stelline nere.

5

Quale numero è la metà di 0,1?

A. 0,05

B. 0,2

C. 0,25

D. 0,5

6 Il campeggio Sole e mare è aperto da aprile ad ottobre.

Questo grafico rappresenta il numero di persone presenti nei bungalow o nelle tende.

LEGENDA: R presenze nei bungalow presenze in tenda

a) In quali mesi è stata maggiore la presenza nei bungalow rispetto alle tende? ……………………………………………………………………………………………..

b) In quali mesi o quale mese le presenze nei bungalow e nelle tende sono uguali? ……………………………………………………………………………………………..

c) In quali mesi o quale mese le presenze totali sono state maggiori di 300?

Fausto costruisce una sequenza di casette usando bastoncini tutti uguali.

1 casetta 2 casette

3 casette

a) Quanti bastoncini utilizzerà Fausto per costruire 5 casette?

Risposta: ……………………

b) Quante casette costruirà con 36 bastoncini?

A. 6

B. 7

C. 8

D. 9

c) La sequenza potrebbe comprendere una figura formata 20 bastoncini?

Sì, perché

No, perché …………………………………………………………………………… ………………………………………………………………………..……………… ……………………………………………………………………………………..… 8

Inserisci un numero al posto dei puntini in modo che l’uguaglianza sia vera.

x 0,3 = 1,2

9 Gli alunni e le alunne della 5a A rappresentano con questo diagramma i luoghi in cui hanno trascorso le vacanze. Ciascun simbolo indica un alunno o un’alunna.

Indica se le seguenti affermazioni sono vere (V) oppure false (F).

a. Gli alunni e le alunne che sono andati in montagna sono 7.

b. Gli alunni e le alunne che sono andati al mare sono 9.

c. 4 alunni e alunne sono andati sia al mare sia in montagna.

d. Nessuno/a è andato/a al mare, in montagna e in campagna.

10 Ripassa 4 lati tratteggiati per formare un quadrato.

11 Al termine della cena in pizzeria su un tavolo sono rimasti questi avanzi.

Chi tra queste persone ha mangiato 5 8 di pizza?

A. Paola

B. Elfrid

C. Olga

D. Tullio

12 Nella sua azienda Valentina produce block notes di tre formati. In tutti i formati il lato più corto è pari a 5 7 del lato più lungo.

Completa

Paola Elfrid Olga Tullio

13 È stata organizzata una corsa campestre. I/Le concorrenti dovranno percorrere tutti i sentieri, seguendo il senso indicato dalle frecce e passando su ogni sentiero una sola volta.

Da quale punto devono partire i/le concorrenti?

A. Dal punto A.

B. Dal punto B.

C. Dal punto C.

D. Da qualsiasi punto.

14 Fulvio per fare il pane ha comprato 3 kg di farina e alcuni cubetti di lievito da 30 g. Un cubetto di lievito è sufficiente per 600 g di farina.

Quanti cubetti di lievito servono per poter utilizzare tutta la farina?

A. 3

B. 5

C. 9

D. 18

Osserva questo mandala.

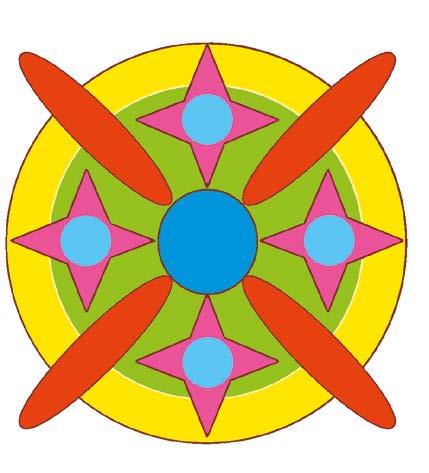
Quanti assi di simmetria ha?

Risposta: …………….. assi di simmetria

16 Completa le frasi inserendo queste unità di misura.

Mg kg hg g

Puoi usare più volte la stessa unità di misura.

a) Per merenda mangio 50 di cioccolato

b) Il fratello di Sveva, appena nato, pesava 3,5

c) Il camion di Olaf pesa 10

d) Per fare la macedonia per 6 persone uso 8 di frutta

e) La mia matita pesa 15

17

L’insegnante scrive alla lavagna la seguente moltiplicazione.

135 x 30

Per trovare il risultato quattro bambini fanno calcoli diversi. 135

18

Chi ha sbagliato?

A. Anja

B. Diego

C. Luca

D. Daniela

Osserva il triangolo ABC.

Il segmento DE è un lato di un rettangolo che ha la stessa area del triangolo ABC. Completa il rettangolo.

19

45 e 90 sono entrambi multipli di 15. Tutti i numeri multipli di 15 sono anche multipli di...

A. 6 e 5

B. 3 e 5

C. 10 e 5

D. 9 e 4

20

In questo diagramma sono riportati i dati relativi al numero di alunni e alunne che hanno frequentato la scuola primaria in Lombardia dal 2015 al 2019. I dati sono arrotondati ed espressi in migliaia.

Riferendoti al grafico completa le frasi.

a) Dal 2015 al 2018 la popolazione scolastica della scuola primaria in Lombardia è

b) Nel 2019 gli iscritti alla scuola primaria erano …………….……., in numero rispetto all’anno precedente.

c) L’anno in cui il numero degli iscritti è stato maggiore è stato il ……….…….

d) Nel 2018 gli iscritti erano un migliaio in più del ……….…….

21 Osserva questi sacchetti di biscotti.

2 euro 5,50 euro

a) Quale tipo di biscotti ha un costo minore a parità di peso?

Stelle Lune

b) Scrivi il procedimento che hai seguito per trovare la risposta.

PROVE UFFICIALI DAL 2023 AL 2021

COMMENTATE

ISTRUZIONI

Troverai nel fascicolo 34 domande di matematica. La maggior parte delle domande ha quattro possibili risposte, ma una sola è quella giusta. Prima di ogni risposta c’è un quadratino con una lettera dell’alfabeto: A, B, C, D.

Per rispondere, devi mettere una crocetta nel quadratino accanto alla risposta (una sola) che ritieni giusta, come nell’esempio seguente.

Esempio 1

Quanti giorni ci sono in una setti mana?

A. X Sette

B. Sei

C. Cinque

D. Quattro

Se ti accorgi di aver sbagliato, puoi correggere: devi scrivere NO accanto alla risposta sbagliata e mettere una crocetta nel quadratino accanto alla risposta che ritieni giusta, come nell’esempio seguente:

Esempio 2

Quanti minuti ci sono in un’ora?

NO A. X 30

B. 50

C. X 60

D. 100

In alcuni casi le domande chiedono di scrivere la risposta o il procedimento, oppure prevedono una diversa modalità di risposta. In questo caso il testo della domanda ti dice come rispondere. Leggilo dunque sempre con molta attenzione.

Puoi usare il righello, la squadra e il goniometro ma non la calcolatrice. Non scrivere con la matita, ma usa soltanto una penna nera o blu.

Ricordati che puoi disegnare o scrivere sulle figure e puoi usare gli spazi bianchi del fascicolo per fare calcoli, se ti serve.

Per fare una prova, ora rispondi a questa domanda:

In quale delle seguenti sequenze i numeri sono scritti dal più piccolo al più grande?

A. 2; 5; 4; 8

B. 8; 5; 4; 2

C. 2; 4; 8; 5

D. 2; 4; 5; 8

Hai a disposizione un’ora e quindici minuti (75 minuti) per rispondere alle domande. L’insegnante ti dirà quando cominciare a lavorare. Quando l’insegnante ti comunicherà che il tempo è finito, posa la penna e chiudi il fascicolo.

Se finisci prima puoi controllare le risposte che hai dato. Poi puoi chiudere il fascicolo e aspettare la fine.

D1. Quale numero devi addizionare a 8,44 per ottenere 9?

A. 1,66

B. 1,56

C. 0,66

D. 0,56

Il numero che devi addizionare è maggiore o minore di 1?

Quanti centesimi devi addizionare a 44 centesimi per ottenere una unità?

D2. La griglia è formata da rettangoli congruenti.

Disegna sulla griglia una retta parallela alla retta r.

Ricorda quando due rette sono parallele. Per disegnare la retta segna due punti che siano alla stessa distanza dalla retta r (dalla stessa parte).

La griglia ti aiuta a trovarli.

D3. Osserva questa relazione.

Un vale come:

vale come

A.

B.

C.

D.

Nel secondo gruppo quanti cerchi ci sono in più del primo gruppo? Quanti triangoli in meno?

D4. Se moltiplichi per 0,5 un numero compreso tra 20 e 30, il risultato sarà un numero compreso

A. tra 5 e 20

B. tra 20,5 e 30,5

C. tra 40 e 60

D. tra 100 e 150

Ricorda che moltiplicare un numero per 0,5 vuol dire trovare la sua ..............................

Tra quali delle opzioni indicate è compresa la .............................. dei numeri 20 e 30?

D5. Il seguente grafico rappresenta il numero di iscritti ai corsi di inglese, spagnolo e francese organizzati da una scuola di lingue. I dati sono suddivisi tra uomini e donne.

a. A quale corso è iscritto il maggior numero di donne?

Risposta: al corso di ................................

b. Qual è la differenza tra il numero degli uomini e il numero delle donne iscritti al corso di inglese?

Risposta: la differenza è .................. iscritti

c. Quanti sono in tutto gli uomini iscritti ai tre corsi?

Risposta: .................. uomini

Il grafico indica con chiarezza il numero degli uomini, ma non quello delle donne. Il numero delle donne va calcolato.

CORSO INGLESE CORSO SPAGNOLO CORSO FRANCESE

D6. Chiara ha 5 euro e vuole spenderli per comprare il maggior numero possibile di vasetti di yogurt uguali a quello che vedi in figura.

0,80 euro

Qual è il numero massimo di vasetti che può comprare Chiara?

A. 4

B. 5

C. 6

D. 7 Trova quanto costano 4,5,6,7 vasetti.

D7. Cerchia i due poligoni con quattro angoli retti.

Ricorda che gli angoli retti possono assumere differenti posizioni sul piano. Devi trovare due poligoni, non uno solo.

D8. Osserva questa scrittura.

(14 x 3) – 2 = (11 x 4) – 4

È corretta?

A. Sì, perché ci sono una moltiplicazione e una sottrazione sia prima sia dopo il segno “uguale”

B. Sì, perché il risultato di (14 x 3) – 2 è uguale al risultato di (11 x 4) – 4

C. No, perché il risultato di (14 x 3) – 2 non è uguale al risultato di (11 x 4)

D. No, perché dopo il segno “uguale” ci sono altri numeri

Il segno uguale ti indica che le operazioni alla sua destra e alla sua sinistra hanno lo stesso valore, perciò ciò che conta è il .............................. delle due espressioni.

D9. La tabella indica le temperature registrate alle ore 8:00 in una settimana del mese di dicembre.

Giorno Lunedì Martedì Mercoledì Giovedì Venerdì Sabato Domenica

Facendo riferimento alla tabella, completa il grafico con le temperature mancanti.

Temperature della settimana

Lunedì Martedì Mercoledì Giovedì Venerdì Sabato Domenica

Aiutati ripassando nel grafico la linea corrispondente alla temperatura di zero gradi.

D10. Durante un viaggio in Egitto, Livia vuole comprare un profumo al gelsomino.

Due negozi diversi mostrano questi prezzi per lo stesso profumo.

NEGOZIO B

Gelsomino 50 euro

NEGOZIO A Gelsomino 760 sterline egiziane

Un euro vale circa 19 sterline egiziane.

In quale negozio il profumo costa meno?

Rispondi e spiega perché confrontando i prezzi.

Risposta: Il profumo Gelsomino costa meno al negozio .................. perché ........... .......................................................................................................................................... ..........................................................................................................................................

Per essere confrontati, i prezzi devono essere espressi nella stessa valuta, cioè nella stessa moneta.

D11. Quale numero ottieni se addizioni 40 decine e 20 centinaia?

A. 420

B. 4020

C. 240

D. 2400

Pensa a quali numeri corrispondono, rispettivamente, 40 decine e 20 centinaia.

D12. Osserva l’immagine.

A quale frazione del rettangolo corrisponde tutta la parte colorata in grigio?

Puoi arrivare alla soluzione con differenti procedimenti. Ad esempio conta quanti sono i quadretti grigi e quanti quelli bianchi. Fai attenzione ai mezzi quadretti.

D13. Osserva queste uguaglianze.

Quale numero devi mettere al posto dell’esagono perché tutte le uguaglianze siano vere?

Risposta: = ..................

Quale operazione devi eseguire per trovare il valore del triangolo?

D14. La Torre degli Asinelli a Bologna è alta 97,20 metri e ha una scalinata interna

di 498 gradini. Lavinia ha già percorso 1 3 della scalinata.

Quanti gradini ha salito Lavinia?

Risposta: .................. gradini

Tutti i dati del problema ti servono per risolverlo?

D15. L’immagine mostra i dati sulla popolazione residente in Italia nel 2019.

a. Sulla base dei dati riportati nell’immagine, indica se ciascuna delle seguenti informazioni è vera (V) o falsa (F).

1. Nell’immagine è indicata la percentuale di donne straniere

2. La percentuale delle persone con almeno 65 anni è il doppio della percentuale delle persone di età compresa tra 0 e 14 anni

3. Le persone che hanno più di 100 anni sono meno di 15 000

4. L’età media della popolazione è 63,8 anni

b. Quante sono all’incirca le donne residenti in Italia nel 2019?

A. Circa 14 milioni

B. Circa 30 milioni

C. Circa 51 milioni

D. Circa 60 milioni

a) Le informazioni che ti servono sono tutte contenute nel grafico. Leggi un’affermazione per volta. Poi con molta calma e attenzione cerca nel grafico la parte a cui si riferisce.

b) Questo dato non è contenuto nel grafico, ma puoi ricavarlo con un calcolo. Non viene chiesto un dato preciso, perciò puoi arrotondare.

Fonte: https://www.ideegreen.it/popolazione-istruzione-stranieri-i-nuovi-dati-del-censimento-istat-138870.html

D16. Ludovica ha preso un tubo di cartone e ha fatt o un taglio con le forbici in questo modo:

Ludovica apre il tubo di cartone. Quale fi gura otti ene?

D. Osserva bene il verso del taglio. Immagina di fare tu la stessa azione di Ludovica e “vedi” nella tua mente che cosa ottieni.

A.

B.

C.

D17. Sara vuole disegnare un rettangolo con il perimetro di 24 cm e un lato di 13 cm. Sara non può disegnare questo rettangolo. Perché?

A. Perché 13 è un numero dispari mentre il perimetro corrisponde a un numero pari

B. Perché 24 – 13 = 11 e il numero 11 non è divisibile per 2

C. Perché la somma delle misure di due lati è 26 cm e 26 è maggiore di 24

D. Perché il perimetro è 24 cm e il numero 24 non è multiplo del numero 13

Ricorda come puoi trovare il perimetro del rettangolo. Se un lato è lungo 13 cm, il perimetro sarà più lungo del doppio di 13 cm.

D18. Osserva attentamente questa sequenza di cinque figure. La figura 4 non è stata disegnata.

La regola per passare da una figura alla successiva è sempre la stessa. Quanti sono i quadratini della Figura 4?

Risposta: .................. quadratini

Per aiutarti puoi disegnare la figura 4 o colorarla nella figura 5.

Figura 1

Figura 2

Figura 3

Figura 4

Figura 5

D19. In un videogioco il robot AVAC dice sempre il vero e il robot AFRU dice sempre il falso.

AVAC Dice sempre il vero

AFRU Dice sempre il falso

AVAC e AFRU osservano una stessa figura geometrica e dicono:

C’è almeno un angolo retto

Non ha tre lati

Qual è la figura osservata dai robot?

Tutti i lati sono uguali

Ha quattro lati

Cerca la figura che abbia le caratteristiche indicate da Avac e non abbia quelle indicate da Afru.

D20. La tabella indica i dati e gli orari di partenza di ogni atleta in una prova a cronometro di ciclismo.

Osserva la tabella e rispondi:

a. Quanto tempo trascorre tra la partenza di un atleta e quella dell’atleta successivo?

Risposta: .................. secondi

b. Quanto tempo trascorre tra la partenza del primo atleta italiano (ITA) e la partenza dell’ultimo atleta italiano (ITA)?

Risposta: .................. minuti

Per rispondere ai quesiti ti servono i dati della seconda colonna?

Presta attenzione al fatto che gli orari sono indicati in ore, minuti e secondi.

D21. Lucia arriva con il treno alle ore 13:05 nella località dove trascorrerà le vacanze.

Il suo viaggio in treno è durato 45 minuti.

A che ora è partita Lucia con il treno?

Risposta: alle ore ...........................

Leggi con molta attenzione il testo e rappresenta nella tua mente la situazione.

D22. Mauro ha incollato un triangolo grigio sopra al quadrato che vedi in figura.

Mauro vuole ricoprire completamente il quadrato con triangoli uguali a quello grigio, senza sovrapporli.

Quanti triangoli uguali a quello grigio mancano per ricoprire completamente il quadrato?

Risposta: .................. triangoli

Disegna i triangoli nel quadrato, prestando attenzione alla griglia sottostante. Ricorda che non devi conteggiare il triangolo grigio già disegnato.

D23. Gianni ha moltiplicato tra loro i numeri 2,25 e 0,5 con la calcolatrice.

La stellina nasconde una cifra del risultato.

La cifra nascosta è

A. 0

B. 1

C. 2

D. 4 Ricorda che cosa si ottiene moltiplicando un numero per 0,5.

D24. Mario è un atleta professionista. Mario si allena cinque giorni alla settimana e segna su una tabella le ore di allenamento che fa ogni giorno.

Ha già segnato le ore fatte durante i primi tre giorni della settimana.

LUNEDÌ MARTEDÌ MERCOLEDÌ GIOVEDÌ VENERDÌ

ORE DI ALLENAMENTO 4 5 2

Quante ore di allenamento dovrebbe fare giovedì e venerdì per ottenere una media giornaliera di 4 ore esatte sui 5 giorni?

A. 3 e 6

B. 6 e 5

C. 4 e 4

D. 4 e 6

Quante ore di allenamento in tutto deve fare Mario in 5 giorni per avere una media giornaliera di 4 ore?

D25. Marco ha costruito un quadrilatero usando come lati i segmenti che vedi qui sotto.

Quale di questi quadrilateri ha costruito Marco?

A. Rettangolo

B. Parallelogramma

C. Rombo

D. Trapezio isoscele

Ricorda le caratteristiche dei lati dei 4 quadrilateri indicati nelle risposte.

D26. Emily sta cercando un numero che ha tutte queste proprietà:

• è un numero compreso tra 85 e 105

• la cifra al posto delle unità è uguale alla cifra al posto delle decine

• non è un numero multiplo di 11

Qual è il numero?

Risposta: È il numero ..................

Il numero può essere di sole due cifre uguali senza essere multiplo di 11?

Il numero non può essere maggiore di 105, ma le cifre al posto delle decine e delle unità devono essere uguali.

D27. Negli ultimi sei mesi, un negozio di sport ha venduto gli articoli sportivi riportati in tabella.

Il seguente grafico rappresenta la distribuzione delle magliette da calcio suddivise per taglie e vendute dal negozio negli ultimi sei mesi. Il grafico è

tu il grafico.

Taglia

Ti occorre un solo dato tra quelli riportati nella tabella. Poi dovrai fare semplici calcoli.

D28. Disegna la figura simmetrica della Figura A rispetto all’asse.

asse

Figura A

Per disegnare una figura simmetrica bisogna tenere conto della distanza di ciascun punto dall’asse di simmetria.

D29. Osserva il rettangolo EFGH.

Immagina un quadrato con il lato lungo 1 4 del lato EF del rettangolo. L’area del rettangolo è

A. 4 volte l’area del quadrato

B. 8 volte l’area del quadrato

C. 16 volte l’area del quadrato

D. 32 volte l’area del quadrato

Disegna nel rettangolo un quadrato con la caratteristica richiesta.

D30. Hai a disposizione queste tre cifre. 4 3 7

Utilizza tutte e tre le cifre una sola volta per scrivere un numero minore di cinquecento e divisibile per 2.

Risposta: ..................

Per la richiesta “divisibile per 2” devi fare attenzione alla cifra delle unità; per la richiesta “minore di 500” alla cifra delle centinaia.

D31. Traccia due linee per dividere questa figura in un rettangolo e due triangoli.

Questa figura è un ……………………………

Se in questo tipo di poligono tracci due altezze, come viene suddiviso?

D32. Due dei numeri che vedi qui sotto possono essere scritti nella posizione indicata dal triangolino sulla retta. Cerchia i due numeri.

___ 3 2,3 5 ___ 2 2,5

Quale numero si trova a metà tra 2 e 3? A quale frazione corrisponde quel numero?

D33. Il triplo di un numero è uguale alla metà di 24. Il numero è

A. 3

B. 4

C. 8

D. 12

Prima calcola la metà di 24. Poi chiediti qual è il numero che moltiplicato per 3 dà la metà di 24.

D34. Linda propone un indovinello ai compagni: “Ho pensato un numero, l’ho raddoppiato, ho tolto 3 e ho ottenuto 7”. Quale numero ha pensato Linda?

A. 20

B. 10

C. 5

D. 8

Parti dal numero ottenuto da Linda e procedi “al contrario”.

D1. Osserva i prezzi delle tre tazze rappresentate in fi gura e vendute in tre citt à diverse lo scorso anno.

I valori del cambio erano:

• 1 sterlina valeva 1,17 euro

• 1 dollaro valeva 0,89 euro

Quale tazza costava di più in euro?

A. La tazza in vendita a Roma

B. La tazza in vendita a Londra

C. La tazza in vendita a New York

D. Le tre tazze avevano lo stesso costo

Quale moneta vale più dell’euro?

D2. Mantenendo una velocità costante, Riccardo ha percorso con la sua automobile 180 chilometri in due ore.

Se viaggiasse con la stessa velocità senza fermarsi, quante ore impiegherebbe per percorrere un tragitto di 270 chilometri?

Risposta: .................. ore

Per sapere quante ore impiega Riccardo per percorrere 270 km, prima devi trovare la velocità oraria.

D3. L’immagine rappresenta un campo da pallavolo.

La linea tratteggiata indica dove è posizionata la rete che divide il campo in due parti di uguali dimensioni.

Il campo è lungo 18 m.

Qual è il perimetro del campo da pallavolo?

Risposta: .................. m

Non farti confondere dai dati inutili. Per trovare il perimetro devi conoscere quanto è lungo e quanto è largo il campo.

D4. Due sacchetti contengono due tipi di gettoni, alcuni bianchi, altri neri.

Tutti i gettoni hanno stessa forma e stesso peso.

Si estrae a occhi chiusi un solo gettone da uno solo dei due sacchetti. C’è un sacchetto dal quale è più probabile estrarre un gettone nero?

A. Sì, il sacchetto 1 perché contiene un numero maggiore di gettoni neri

B. Sì, il sacchetto 2 perché contiene un numero minore di gettoni bianchi

C. No, perché i gettoni si estraggono a occhi chiusi da entrambi i sacchetti

D. No, perché in ogni sacchetto i gettoni neri sono tanti quanti i gettoni bianchi

Non ti interessa sapere quanti gettoni in tutto ci sono nei sacchetti, ma la proporzione tra neri e bianchi. In ogni sacchetto sono di più i gettoni bianchi o quelli neri?

Sacchetto 1

Sacchetto 2

D5. Giovanni ha preso un treno che doveva arrivare a Roma alle ore 13:45, ma che invece è arrivato con 110 minuti di ritardo.

A che ora è arrivato a Roma il treno preso da Giovanni? Scrivi il procedimento che fai per trovare la risposta e poi riporta sotto il risultato.

Risultato: ..................................

A quanto corrispondono 110 minuti? Ricorda che il ritardo indica “tempo in più”.

D6. Osserva la seguente figura.

Quale tra le seguenti misure rappresenta la stima migliore dell’area della figura?

A. 20 cm2

B. 24 cm2

C. 26 cm2

D. 30 cm2

La figura non è un poligono. La “punta” in basso corrisponde circa al “vuoto” in alto. I quadretti ti aiutano a calcolare l’area approssimata.

1 cm

D7. Il grafico qui sotto rappresenta le temperature medie di tre capitali europee nei primi otto mesi dell’anno 2016.

Sulla base dei dati riportati nei grafico, indica con una crocetta se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).

a. Le temperature medie registrate a Parigi sono sempre state maggiori di quelle registrate a Vienna

b. In marzo la temperatura media di Oslo è stata la stessa di quella di Vienna in aprile

c. In agosto la temperatura media di Parigi è stata la stessa di quella di Vienna

d. Da gennaio a giugno la temperatura media di Oslo

è aumentata di più di 16 gradi

Per rispondere alle domande “a” e “b” devi cercare i dati sul grafico e confrontarli.

La risposta alla domanda “c” è visualizzata dal grafico.

Per rispondere alla domanda “d” tieni conto dei numeri negativi o positivi.

Confezioni Peso complessivo delle confezioni

7 kg

16 kg

13 kg

Quanto pesa questa confezione?

Confronta i dati e trova:

• prima il peso complessivo della confezione con il manico e di quella con lo spago;

• poi il peso della confezione con il manico.

Risposta: .................. kg

D9. Tommaso ha 23 figurine.

Diego ha 10 figurine in più del triplo delle figurine di Tommaso.

Quante figurine ha Diego?

Risposta: .................. figurine

Per prima cosa pensa a che cosa significa “il triplo”.

D8. Osserva la tabella.

Ricorda che l’immagine simmetrica è come un’immagine vista allo specchio, perciò immagina di ribaltare la figura.

Quale tra i seguenti numeri corrisponde alla posizione della tacca indicata dalla freccia?

A. 830

B. 875

C. 870

Qual è la differenza tra 800 e 900? Quanti spazi hai su questa linea dei numeri tra 800 e 900? Quanto vale ogni spazio? prova 5 • Prova Ufficiale 2022 P ROVAUFFI C I ALE 2022 FACSIMILE Tratto da www.invalsi.it

D10. Disegna la figura simmetrica a quella data rispetto alla retta r.

D11. Osserva la seguente retta dei numeri.

800 900

D12. Osserva il rubinetto rappresentato nella fotografia.

La maniglia del rubinetto viene ruotata nel verso indicato dalla freccia fino alla posizione seguente.

Di quanti gradi è stata ruotata la maniglia?

A. Circa 90 gradi

B. Circa 120 gradi

C. Circa 240 gradi

D. Circa 340 gradi

Osserva la freccia che indica la rotazione. La rotazione è maggiore di un angolo retto?

È maggiore di un angolo piatto?

È maggiore o minore di 3 angoli retti?

D13. Completa la seguente frase con i numeri mancanti.

Con 6 litri di acqua si possono riempire completamente …………… bottigliette da mezzo litro oppure …………. bottiglie da un litro e mezzo.

Trova quante bottigliette da mezzo litro si possono riempire. Un litro e mezzo a quanti mezzi litri corrisponde?

D14. Osserva l’immagine.

Qual è la lunghezza dell’accendino?

A. Circa 5,5 cm

B. Circa 6,5 cm

C. Circa 7,5 cm

D. Circa 13 cm

D15. In un articolo di giornale si legge:

Conta quanto misura la distanza tra “l’inizio” e la “fine” dell’accendino.

“Un quarto della popolazione mondiale non fa abbastanza sport.”

Una delle seguenti affermazioni ha lo stesso significato della frase scritta sopra. Quale?

A. Nel mondo 4 persone su 10 non fanno abbastanza sport

B. Il 25% della popolazione mondiale non fa abbastanza sport

C. Il 40% della popolazione mondiale non fa abbastanza sport

D. Più della metà della popolazione mondiale non fa abbastanza sport

Se non ricordi come si trasforma una frazione in percentuale, per trovare a quale percentuale corrisponde un quarto dividi 100 in 4 parti.

D16. Il bidone della spazzatura rappresentato è alto nella realtà 90 cm.

Stima l’altezza del lampione nella realtà. Completa la frase.

Il lampione nella realtà è alto circa …………………… centimetri

Riporta la misura del bidone sul lampione per capire quante volte il lampione stesso è più alto. Puoi aiutarti con le dita, con un righello, con una matita…

D17. Osserva la seguente retta di numeri. 62,5 64 65,5

Collega con una freccia il numero scritto nel riquadro alla tacca corrispondente alla sua posizione sulla retta dei numeri.

Devi capire a quanto corrisponde l’intervallo tra una tacca e l’altra.

D18. Ai 21 alunni di una classe è stato chiesto: “Qual è la tua materia preferita?” Ogni alunno ha dato una sola risposta.

I dati sono stati registrati in questo grafico.

NUMERO ALUNNI

ITALIANO MATEMATICA INGLESE

Quanti alunni della classe preferiscono INGLESE?

A. 2

B. 4

C. 6

D. 10

Gli alunni sono 21 e sono rappresentati da 3 colonne che in tutto sono alte 7 “parti”. A quanto corrisponde ciascuna “parte”?

D19. Lungo un viale sono stati piantati 10 alberi tutti alla stessa distanza di 4 metri l’uno dall’altro.

Qual è la distanza tra il primo e l’ultimo albero del viale?

Risposta: .................. metri

Gli alberi sono 10, ma gli spazi tra il primo e l’ultimo albero sono in tutto 9.

D20. Su un piano cartesiano è stato costruito il quadrato OPTR che vedi in figura.

Il punto E ha coordinate (6;0). Il punto P è il punto medio del segmento OE.

R T

O P E

a. Quali sono le coordinate del punto T?

A. (6;6)

B. (0;6)

C. (3;3)

D. (0;3)

b. Marta vuole disegnare il rettangolo OEFR. Deve ancora posizionare il punto F.

Quali sono le coordinate del punto F?

Risposta: (……;…...).

a) Ti può aiutare trovare prima le coordinate del punto P.

b) Disegna il rettangolo OEFR.

D21. Per andare a scuola, Mara percorre complessivamente 1100 metri in bicicletta, seguendo il percorso indicato.

CASA DI LUCIA

200 METRI

CASA DI MARA

SCUOLA PARCO

La distanza tra la scuola e il parco è il doppio della distanza tra la casa di Lucia e il parco. Qual è la distanza tra la casa di Lucia e il parco?

Risposta: ....................... metri

Prima trova quanto misura il percorso dalla casa di Lucia alla scuola. Poi ricorda che uno dei due tratti che formano questa parte di percorso è doppio dell’altro.

D22. Osserva le due uguaglianze.

20 × = – 15 = 65

Quali numeri devi sostituire ai simboli per rendere vere entrambe le uguaglianze?

Al simbolo devo sostituire il numero ……......

Al simbolo devo sostituire il numero ……......

La seconda operazione ti consente di trovare il valore di Se conosci il valore di puoi trovare anche il valore di .

D23. Per la sua collezione, Mattia compra un raccoglitore e 8 pacchetti di carte dello stesso tipo. Spende in totale 55 euro.

Se il raccoglitore costa 23 euro, quanto costa ogni pacchetto di carte?

Risposta: .................. euro

Per risolvere il problema devi eseguire 2 semplici operazioni. Prima trova il costo complessivo di 8 pacchetti. Poi trova il costo di un singolo pacchetto.

D24. Nel seguente distributore ci sono 80 palline colorate: 40 sono rosse, 20 sono verdi e 20 sono gialle. Alice e Marco discutono su quale sia la percentuale di palline rosse dentro il distributore.

Alice dice: “Il 50% delle palline nel distributore è rosso”.

Marco dice: “Il 40% delle palline nel distributore è rosso”.

Chi ha ragione? Scegli una delle due risposte e completa la frase spiegando perché ha ragione.

Alice ha ragione perché ........................................................................................... .....................................................................................................................................

Marco ha ragione perché ........................................................................................ ......................................................................................................................................

Pensa a quale frazione corrisponde 40 (palline rosse) su 80 (palline colorate).

La frazione ti permette di trovare la percentuale giusta.

D25. La seguente immagine riporta i consigli d’uso scritti sulla confezione

del detersivo per lavatrice che Carlo utilizza per fare il bucato.

4-5 kg TOGLIERE 20 mL dalla dose consigliata per sporco normale

6-8 kg TOGLIERE 35 mL dalla dose consigliata per sporco normale POCO SPORCO

La durezza dell’acqua di casa di Carlo è media.

a. Carlo vuole lavare in lavatrice 7 kg di bucato “Molto sporco”.

Quanti millilitri (mL) di detersivo deve utilizzare?

Risposta: ....................... mL

b. Carlo deve lavare 4 kg di bucato “poco sporco”.

Quanti millilitri di detersivo deve utilizzare?

A. 20 mL

B. 95 mL

C. 115 mL

Prima cerca la riga che indica la durezza dell’acqua della casa di Carlo. Poi cerca la colonna relativa al peso e allo sporco. Per rispondere alla seconda domanda fai lo stesso procedimento come se il bucato fosse “sporco normale”. Tieni presente poi ciò che viene indicato in caso di bucato poco sporco. prova 5 • Prova Ufficiale 2022 P ROVAUFFI C I ALE 2022 FACSIMILE Tratto da www.invalsi.it

D26. Qui sotto è raffigurato un plastico dei monumenti di Piazza dei Miracoli di Pisa.

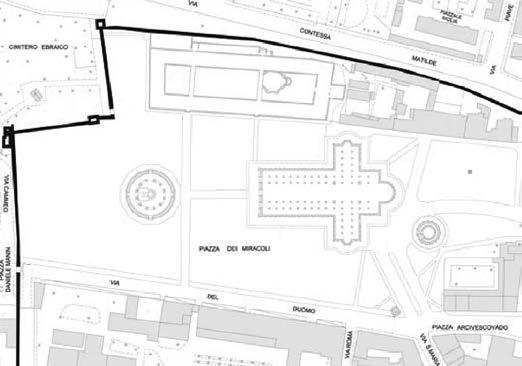
Camposanto

Museo dell’Opera del Duomo Museo delle sinopie

Quale monumento sul plastico corrisponde al numero 5 sulla piantina?

Individua nella piantina la cattedrale, il battistero e la torre, tenendo presente la loro forma e grandezza. Troverai poi la posizione di tutti gli altri monumenti.

Torre

Cattedrale Battistero

Palazzo dell’Opera del Duomo Battistero ottagonale

La stessa piazza è rappresentata in questa piantina. Ogni monumento è indicato con un numero.

A. Camposanto

B. Museo delle sinopie

C. Cattedrale

D. Museo dell’opera del Duomo

D27. Al supermercato c’è questa offerta su un particolare tipo di formaggio.

OFFERTA

300 g costano

7,50 euro

Maria ha acquistato una certa quantità di quel formaggio in offerta e ha speso 30 euro. Quanti grammi di formaggio ha acquistato Maria?

Risposta: ....................... grammi

Con 30 euro quanti pezzi da 7,50 euro si possono comperare? Quanto pesano complessivamente?

D28. Osserva la Figura A e la Figura B: ciascuna è composta da sei rettangoli congruenti.

Figura A Figura B

Completa le seguenti frasi inserendo al posto dei puntini una delle espressioni che vedi sotto la riga dei puntini.

L’area della Figura A è ………………………………….. area della Figura B. (maggiore dell’/ minore dell’/ uguale all’)

Il perimetro della Figura A è ………………………………….. perimetro della Figura B. (maggiore del/ minore del/ uguale al)

Due rettangoli congruenti sono perfettamente sovrapponibili perché hanno la stessa forma e la stessa grandezza. La figura A e la figura B sono formate dalle stesse parti, perciò l’area cambia? La figura B però non ha la stessa forma di A. Osserva attentamente da quali lati è formato il perimetro delle due figure.

D29. Osserva la seguente tabella che riporta i fabbisogni energetici giornalieri di uomini e donne a diverse età.

Come cambia il fabbisogno energetico giornaliero*

(dati in kcal)

uomo

altezza metri 1,70

normopeso (kg 65)

età

25 anni 2420

4 5 anni 2350

65 anni 2060

8 0 anni 1910

donna

altezza metri 1,60

normopeso (kg 57,6)

età

25 anni 2010

4 5 anni 1900

65 anni 1700

8 0 anni 1660

* Si è considerato uno stile di vita sedentario.

Fonte: Tabelle LARN, IV revisione. Società Italiana di Nutrizione Umana. Valori da intendersi come esemplificativi

Completa il testo utilizzando le informazioni riportate nella figura.

Un uomo di 80 anni ha un fabbisogno giornaliero di …………. kcal.

Un uomo di 45 anni ha un fabbisogno giornaliero di …………. kcal in più rispetto a un uomo di 65 anni.

Una donna di ……... anni ha come fabbisogno giornaliero all’incirca le stesse kcal di un uomo di ……... anni.

Puoi trovare:

• il primo dato richiesto nella tabella

• il secondo calcolando la differenza tra due dati nella tabella

• il terzo confrontando i dati dei due gruppi e cercando i due che più si avvicinano.

D30. 26 chilometri e 37 metri equivalgono a:

A. 26 037 metri

B. 26 370 metri

C. 2,6037 chilometri

D. 26,37 chilometri

Osserva il valore di ciascuna cifra di ciascuna misura.

Oppure trasforma i chilometri in metri e sommali a 37 m.

Calcola il perimetro dell’esagono ABCDEF.

Risposta: ....................... cm

Osserva bene i 6 triangoli che formano l’esagono ABCDEF. Che tipo di triangoli sono?

D31. La figura qui sotto è ottenuta sovrapponendo tre esagoni con lo stesso centro O.

D32. Luisa ha costruito quattro ruote della fortuna. Ha diviso i cerchi in parti uguali e ha colorato alcuni spicchi in bianco e altri in grigio; poi ha fissato nel centro di ogni cerchio una freccia in modo che possa ruotare.

Qui sotto sono rappresentate le ruote costruite da Luisa.

Una sola delle ruote è colorata in modo tale che la probabilità che la freccia si fermi sul bianco sia il doppio della probabilità che si fermi sul grigio.

Quale?

A. Ruota 1

B. Ruota 2

C. Ruota 3

D. Ruota 4 In quale figura gli spicchi bianchi sono in numero doppio dei grigi?

Ruota 1

Ruota 2

Ruota 3

Ruota 4

D33. Osserva il rettangolo ABCD.

In una delle seguenti figure sono stati colorati di grigio i 3 4 del rettangolo ABCD.

In quale?

In quante parti è stato diviso il rettangolo? A quante parti corrispondono 3 4 ?

D34. Uno dei seguenti numeri è compreso tra 1,1 e 1,2. Quale?

A. 1,05

B. 1,5

C. 1,19

D. 1,21

L’area del quadrato ACEF è

A. 2 volte l’area del quadrato ABCD

B. 3 volte l’area del quadrato ABCD

C. 4 volte l’area del quadrato ABCD

D. 5 volte l’area del quadrato ABCD

Quale tra i 4 numeri indicati è maggiore di 1,1 ma minore di 1,2?

Quanti triangoli uguali formano il quadrato grigio? Quanti triangoli come quelli del quadrato grigio formano il quadrato ACEF?

D35. Il lato AC del quadrato ACEF è uguale alla diagonale del quadrato grigio ABCD.

D1. Osserva questa striscia graduata.

Quale numero corrisponde alla posizione indicata dalla freccia?

A. 8,9

B. 8,5

C. 8,2

D. 8,1

Pensa: quale numero decimale è esattamente a metà tra 8 e 9?

D2. Teresa vuole incollare tre stelle su ogni faccia rettangolare di un parallelepipedo di legno e una stella su ogni faccia quadrata. Ha già incollato tre stelle su una faccia rett angolare. Quante stelle deve ancora incollare?

A. 4

B. 7

C. 11

D. 14

Nel disegno non si vedono tutte le facce. Ma tu pensa a quante facce rettangolari e quante facce quadrate ha questo parallelepipedo. Poi fai un semplice calcolo: ricorda che su una faccia le stelle sono già state incollate. Se vuoi puoi disegnare lo sviluppo del solido.

D3. La seguente tabella riporta informazioni sulle partenze di alcuni treni dalla stazione di Milano Centrale.

Utilizza le informazioni riportate in tabella per rispondere alle seguenti domande.

a. Qual è il numero del treno che ha un ritardo di 15’?

Risposta: ..................................

b. Da quale binario parte il treno R 2154?

Risposta: ..................................

a) Nella quarta colonna dello schema trovi l’informazione relativa al ritardo, nella prima quella necessaria per rispondere.

b) Nella prima colonna dello schema trovi l’informazione relativa al numero del treno, nella quinta quella necessaria per rispondere.

D4. Una carta geografica è in scala 1 : 250 000.

Un centimetro sulla carta a quale lunghezza corrisponde nella realtà?

A. 25 m

B. 250 m

C. 2500 m

D. 25 000 m

La scala ti dice che 1 cm sulla carta corrisponde a 250 000 cm nella realtà.

Esegui l’equivalenza per trovare la risposta giusta.

D5. Dario vuole disegnare un triangolo rettangolo isoscele su un reticolo regolare. Ha già disegnato il lato AB. Completa tu la figura.

Ricordi le caratteristiche del triangolo rettangolo isoscele? Quale angolo formano i due lati uguali in questo particolare tipo di triangolo? Puoi considerare il lato già disegnato come uno dei lati uguali, o come il terzo lato.

D6. L’uguaglianza che vedi non è completa.

110 × ….... = 11

Qual è il numero che messo al posto dei puntini rende vera l’uguaglianza?

A. 10

B. 11

C. 0,11

D. 0,1

Il risultato della moltiplicazione è più piccolo del numero moltiplicato. Ciò significa che il moltiplicatore è maggiore o minore di 1? Tra i due numeri nelle risposte che hanno questa caratteristica, qual è quello giusto? Dopo aver scelto, verifica eseguendo l’operazione.

D7. La seguente tabella indica la dose giornaliera di sciroppo per peso corporeo, ma mancano alcuni dati.

a. Completa tu la tabella.

corporeo (kg)

b. Questo è il misurino che si usa per prendere lo sciroppo.

Luca deve prendere 15 millilitri (mL) di sciroppo. Quanti misurini di sciroppo dovrà bere?

A. Due misurini e mezzo

B. Due misurini

C. Un misurino e mezzo

D. Un misurino

a) Per completare la prima colonna, osserva: i numeri sono progressivi. Qual è l’intervallo tra i due numeri?

Per completare la seconda colonna osserva di quanti millilitri aumenta la dose per ciascun differente peso.

b) Calcola a quanto corrisponde un intero misurino. Ricorda che le tacche sono 4 e ogni tacca segna 2,5 mL.

D8. Nel seguente diagramma sono riportati i dati relati vi al numero di visitatori dei musei italiani negli anni dal 2013 al 2017. I dati sono espressi in milioni.

VISITATORI MUSEI ITALIANI

a. Indica se ciascuna delle seguenti informazioni relati ve ai dati espressi in milioni si può ricavare o non si può ricavare dal diagramma. Metti una crocett a per ogni riga.

Si può ricavare Non si può ricavare

1.

2.

3.

4.

La differenza tra il numero di visitatori dei musei italiani nel 2017 e quello nel 2013

Il numero dei visitatori dei musei italiani

nei giorni festivi

Il numero totale dei visitatori dei musei italiani negli anni 2014 e 2015

La differenza tra il numero di visitatori dei musei italiani nel 2012 e quello nel 2016

a) Il grafico ti dice chiaramente qual è il numero dei visitatori complessivo in ciascun anno dal 2013 al 2017. Non fornisce però altre informazioni.

b. Con gli stessi dati è stato costruito un diagramma a barre. Scrivi al posto dei puntini i valori mancanti.

b) Non è necessario confrontare i dati con quelli forniti dal grafico precedente. È sufficiente osservare che 45 milioni corrispondono a 9 spazi. A quanto corrisponderà ciascuno spazio?

D9. Gino, Alice e Marco abitano lungo la stessa strada che porta a scuola. Le loro case e la scuola sono disposte lungo la strada come vedi nella rappresentazione qui sotto.

Casa di Gino

Casa di Alice Casa di Marco Scuola

La casa di Gino dista 3,7 chilometri dalla casa di Alice e 6,7 chilometri dalla scuola. La casa di Marco si trova a metà tra la casa di Alice e la scuola.

Quanto dista la casa di Marco dalla casa di Gino?

A. 1,5 chilometri

B. 3 chilometri

C. 5,2 chilometri

D. 10,4 chilometri

Con i dati a disposizione puoi calcolare

• prima la distanza tra la casa di Alice e la scuola;

• poi quella tra la casa di Alice e la casa di Marco;

• infine quella tra la casa di Gino e la casa di Marco.

D10. Osserva il seguente piano cartesiano.

a. Una delle seguenti affermazioni è vera. Quale?

A. Sia il punto A sia il punto B hanno coordinate (8;1)

B. Solo il punto A ha coordinate (8;1)

C. Solo il punto B ha coordinate (8;1)

D. Sia il punto A sia il punto B hanno coordinate (1;8)

b. Nicola vuole costruire un triangolo rettangolo su questo piano cartesiano usando A e B come vertici e disegnando un altro punto C. Quali delle seguenti coordinate può avere il punto C?

A. (8;7)

B. (8;8)

C. (9;8)

D. (2;1)

a) Ricorda che nelle coordinate il primo numero indica la posizione sull’asse orizzontale.

b) Segna sul piano cartesiano i punti indicati nelle soluzioni e osserva qual è quello che stai cercando.

D11. Nello scontrino della rosticceria Mangiabene non appare l’importo in euro che Lucia deve pagare per il suo acquisto.

ROSTICCERIA MANGIABENE

kg 15,00

31/03/2020 12:37

L’importo che Lucia deve pagare è compreso tra

A. 19 e 20 euro

B. 14 e 15 euro

C. 11 e 12 euro

D. 7 e 8 euro

Arrotonda il peso. Se fosse stato 0,8 kg (8 hg), allora Lucia avrebbe pagato...

Poiché il peso reale è un po’ inferiore a 8 hg, allora Lucia ha pagato....

D12. Tra dieci anni Elisa avrà 12 anni. Marina 4 anni fa aveva gli anni che ha ora Elisa. Quanti anni ha ora Marina?

Risposta: .................................. anni

Pensa a quanti anni ha Elisa oggi e a quanti anni ha Marina più di Elisa.

D13. Scrivi un numero che sia maggiore di 18,62 e minore di 18,63.

Risposta: ..................................

La differenza tra i due numeri è di un solo centesimo. Perciò il numero che stai cercando dovrà avere anche la cifra dei ..................

D14. Osserva il poligono grigio. r

Disegna il suo simmetrico rispetto all’asse r.

Ricorda: i rispettivi punti delle parti simmetriche hanno la stessa distanza dall’asse di simmetria. L’orientamento delle linee sarà a specchio.

D15. Carlo fa un viaggio in auto di quattro giorni.

Il primo giorno percorre 96 km, il secondo giorno 72 km, il terzo giorno altri 72 km e il quarto giorno percorre 60 km.

Cosa deve fare Carlo per calcolare la media dei chilometri percorsi nei quattro giorni?

A. Addizionare 96 e 60 e dividere il risultato per 2

B. Addizionare 96, 72 e 60 e dividere il risultato per 3

C. Addizionare 96, 72, 72 e 60 e dividere il risultato per 4

D. Considerare il valore più frequente, cioè 72

Ricorda come si calcola la media.

D16. Maria ha utilizzato 40 grammi di lievito per preparare il pane. La quantità di lievito utilizzata da Maria corrisponde al 25% di tutto il lievito che c’era nel frigorifero. Quanti grammi di lievito c’erano nel frigorifero?

A. 10 grammi

B. 25 grammi

C. 160 grammi

D. 1000 grammi

A quale frazione dell’intero corrisponde 25%? Se lo sai, ti sarà facile calcolare il peso del lievito.

D17. Anna e Carlo giocano con un dado a 6 facce non truccato. Lo lanciano una sola volta.

Anna vince se uscirà il numero 3 oppure il numero 5. Carlo vince se uscirà un numero pari. Chi ha più probabilità di vincere?

Anna perché ........................................................................................................ ................................................................................................................................ ................................................................................................................................

Carlo perché ........................................................................................................ ................................................................................................................................ ................................................................................................................................

Quanti sono i numeri pari tra 1 e 6?

D18. Il bagnino ha iniziato a sistemare in file ordinate gli ombrelloni numerati come vedi in figura.

a. Che numero avrà l’ombrellone posizionato in terza fila, nella colonna degli ombrelloni numero 8 e 20?

Risposta: ..................................

b. Il bagnino continua a disporre gli ombrelloni nello stesso modo per formare altre file con uguale numero di ombrelloni. In quale fila si trova l’ombrellone 60?

Risposta: ..................................

a) Scrivi i numeri nelle caselle vuote e troverai facilmente il numero richiesto.

b) In ogni fila ci sono 12 ombrelloni. Quante file occorrono per avere 60 ombrelloni?

D19. Una libreria nel mese di gennaio ha venduto 1000 libri. Nel mese di febbraio il numero di libri venduti è diminuito di 240 unità rispetto a gennaio. Nel mese di marzo il numero di libri venduti è aumentato di 180 unità rispetto a febbraio.

Completa il diagramma a barre con i dati mancanti, in base alle informazioni presenti nel testo.

Trova a quanti libri corrisponde ciascuno spazio. Disegna prima la colonna relativa a febbraio, tenendo conto di quanti spazi in meno dovrà essere lunga, poi quella relativa a marzo.

D20. Uno dei seguenti numeri corrisponde a 115 centesimi. Quale?

A. 1,15

B. 11,5

C. 0,115

D. 1,015

Presta attenzione al valore posizionale delle cifre.

D21. Al Parco dei divertimenti c’è questo cartello.

TIRO AL BERSAGLIO

OGNI 5 BERSAGLI COLPITI RICEVI

1 GETTONE OMAGGIO

CON 1 GETTONE OMAGGIO VINCI

2 GIRI GRATUITI SULLA GIOSTRA PANORAMICA

Paolo gioca al Tiro al bersaglio e vince 6 giri gratuiti sulla giostra panoramica. Qual è il numero minimo di bersagli che ha colpito?

A. 3

B. 6

C. 15

D. 30

Prima dovrai trovare quanti gettoni ha vinto Paolo. Presta attenzione a quanti bersagli corrisponde un gettone.

D22. Su una griglia sono disegnati due esagoni regolari A e B. B A

Il lato dell’esagono grigio B misura 2 cm.

Quanto misura il perimetro dell’esagono A?

Risposta: .................................. cm

D23. Osserva i seguenti numeri.

Qual è la relazione tra il lato dell’esagono A e quello dell’esagono B?

Elimina con una crocetta i numeri che hanno almeno una delle seguenti

caratteristiche:

• sono minori di 5 decine

• sono maggiori di 80

• sono pari

Quale numero è rimasto?

Risposta: ..................................

Segui le indicazioni e procedi con ordine. Sarà facilissimo trovare la risposta.

D24. Un giardiniere vuole realizzare delle aiuole quadrate utilizzando delle piante di rose. Il disegno rappresenta le prime tre aiuole.

Aiuola n° 1 4 piante

* * * * * * * * *

Aiuola n° 2 9 piante

* * * * * * * * * * * * * * * *

Aiuola n° 3 16 piante

A ogni nuova aiuola, il giardiniere aumenta il numero di piante usate secondo la stessa regola: aggiunge una riga e una colonna di piante, come vedi per le prime tre aiuole.

a. Quante piante di rose utilizzerà il giardiniere per l’aiuola n° 5?

A. 5

B. 10

C. 25

D. 36

b. In quale aiuola utilizzerà 81 piante di rose?

Risposta: nell’aiuola n° .................................

a) Continua la progressione e pensa a quante file e a quante piante per fila ci saranno nell’aiuola n. 5. Se vuoi puoi anche fare il disegno.

b) Per trovare quante file e quante piante per fila ci sono, cerca il numero che moltiplicato per se stesso dà 81. Presta attenzione: il numero di file non corrisponde al numero dell’aiuola!

D25. Una delle figure non rappresenta lo sviluppo piano della superficie di un cubo. Quale?

Lo sviluppo di un cubo è formato da 6 facce: 4 laterali e 2 di base. Le facce di base possono stare dalla stessa parte?

D26. Sono le ore 16:25. Alice mette in forno una torta. La torta deve cuocere per tre quarti d’ora. A che ora Alice deve spegnere il forno?

Risposta: alle ore ................................

Pensa a quanti minuti corrispondono tre quarti d’ora e poi sommali all’orario di partenza. Ricorda che 60 minuti diventano un’ora.

A.

B.

C. D.

D27. Osserva la mappa di una piazza rett angolare evidenziata dal rett angolo grigio chiaro.

Quale fra le seguenti è la sti ma migliore dell’area della piazza?

Calcola con una moltiplicazione quanti quadretti all’incirca compongono l’area. Poi sapendo a quanti m2 corrisponde ciascun quadretto, puoi ottenere la stima.

D28. Questo grafico rappresenta le temperature massime e minime registrate a Parigi nei primi sette giorni di marzo.

a. In quale giorno la differenza tra la temperatura massima e la temperatura minima è stata maggiore?

Risposta: .................................. marzo

b. Il 3 marzo qual è stata la temperatura minima?

Risposta: .................................. gradi

I dati richiesti si possono “leggere” sul grafico con facilità.

Se vuoi puoi scrivere la differenza tra le temperature per ciascun giorno.

D29. Nella stessa cartoleria Ilaria e Giovanni comprano del materiale per la scuola. Giovanni compra tre gomme uguali.

Paga con una banconota da 20 euro e riceve 14 euro di resto.

Ilaria compra 3 matite uguali e una gomma come quella di Giovanni.

Ilaria spende 6,50 euro.

Completa la frase che segue inserendo al posto dei puntini i numeri corretti. Una gomma costa …………….. euro e una matita costa …………………. euro.

Con i dati a disposizione puoi calcolare quanto costa una gomma.

Potrai poi trovare il costo di 3 matite ricordando quanto costa una gomma.

Infine troverai il costo di una sola matita.

D30. Osserva la figura.

Completa la frase inserendo al posto dei puntini una delle espressioni scritte sotto.

il doppio della il triplo della la metà della uguale alla

La misura della superficie della parte grigia è ………………………….. misura della superficie della parte bianca.

Presta attenzione: devi confrontare la parte bianca e la parte grigia, non una parte e l’intero. Conta da quanti quadretti sono formate le due parti.

D31. In una delle seguenti fi gure la parte colorata in grigio NON rappresenta 1 4 dell’area della fi gura.

Quale?

Anche solo a colpo d’occhio puoi individuare l’unico rettangolo in cui la parte grigia non rappresenta 1/4 della figura.

D32. Osserva l’orologio.

In questo momento l’orologio segna le 9:00. Dopo che la lancett a dei minuti avrà descritt o un angolo di 270°, che ore saranno?

A. 6:00

B. 8:15

C. 9:45

D. 9:15

A quanti angoli retti corrispondono 270°?

Disegna la lancetta lunga nella nuova posizione e leggi l’ora.

A.

1 Osserva i seguenti numeri.

A. tutti dispari.

B. tutti divisibili per 3.

C. tutti divisibili per 4.

D. tutti maggiori di 30 decine.

2 Nella hall di un albergo di New York sono esposti tre orologi che indicano l’ora di diverse città del mondo. Completa la tabella.

3 Osserva la figura.

A quale frazione dell’area dell’esagono corrisponde la parte colorata?

A.

B. 2

C. 2

D.

4 Sul foglio è stata disegnata la base minore di un trapezio rettangolo. Completa il disegno.

5 Osserva questa divisione.

10 : = 20

Quale numero devi scrivere sui puntini perché il risultato della divisione sia 20?

A. 0,2

B. 0,5

C. 1

D. 2

6 Camilla ha disegnato questi tre pini.

Per ciascuna affermazione indica se è vera (V) o falsa (F). V F

a. Le tre figure hanno forma diversa.

b. Gli angoli corrispondenti delle tre figure non hanno la stessa ampiezza.

c. Il pino più piccolo rispetto al pino più grande è in scala 1 : 3.

7 Il grafico rappresenta le presenze odierne di automobili in un parcheggio multipiano.

Il guardiano, osservando il grafico, afferma:

Il numero delle auto a pianterreno è il doppio di quelle nel primo sotterraneo

Il guardiano ha ragione? Scegli la risposta e completa la frase.

Sì, ha ragione perché

Non ha ragione perché

8 Filippo ha fatto questo disegno.

La sua compagna Claudia compone un altro disegno ruotando ogni volta di 90° in senso orario il disegno iniziale. Qual è il disegno che ha ottenuto Claudia?

3

9 Giulio Cesare è nato nel 100 a.C. ed è morto nel 44 a.C.

L’imperatore Augusto è nato nel 63 a.C. ed è morto nel 14 d.C.

a) Chi tra i due è nato prima? .........................................

b) Quanti anni ha vissuto Giulio Cesare?.......................

c) Quanti anni ha vissuto Augusto? ...............................

A. Disegno 1

B. Disegno 2

C. Disegno

D. Disegno 4

10

La pasticciera Lina deve preparare 6 crostate. Per ognuna servono 350 g di farina. Lina ha a disposizione 2 kg di farina. La farina sarà sufficiente?

A. Sì, perché 350 g sono meno di 2 kg.

B. No, perché 350 è maggiore di 2.

C. No, perché 2100 g sono più di 2 kg.

D. Sì, perché i chilogrammi sono più grandi dei grammi.

11

Una società autostradale controlla l’andamento del traffico nell’ultima settimana.

Numero di automobili circolanti

Per ciascuna affermazione indica se è vera (V) o falsa (F). Ricava le informazioni dal grafico.

a. Da martedì a giovedì il traffico è aumentato.

b. Il picco massimo di traffico si è rilevato venerdì.

c. Giovedì sono transitati meno di 119 000 veicoli.

d. Da lunedì a domenica il traffico è diminuito.

Il barman Diego prepara i suoi famosi aperitivi analcolici.

Per ciascun aperitivo utilizza 1 6 di succo di limone, 2 6 di acqua tonica e 3 6 di succo di pesca.

Diego vuole preparare 4,8 l di questo aperitivo.

a) Completa la tabella

Succo di limone 1 6 Acqua tonica 2 6 Succo di pesca 3 6 Totale 1,6 l 4,8 l

b) Considerate le proporzioni, quale potrebbe essere la giusta composizione di un aperitivo?

A. Succo di limone 50 ml - Acqua tonica 100 ml - Succo di pesca 150 ml.

B. Succo di pesca 50 ml - Acqua tonica 100 ml - Succo di limone 150 ml.

C. Succo di limone 100 ml - Acqua tonica 100 ml - Succo di pesca 100 ml.

D. Succo di limone 6 ml - Acqua tonica 12 ml - Succo di pesca 36 ml.

13 Pino e Carla hanno insieme 45 euro.

a) Se Carla ha 5 euro più di Pino, quanti euro ha Pino?

A. 20

B. 25

C. 30

D. 40

b) Spiega come hai fatto a trovare la risposta. …………………………………………………………………………………………… ……………………………………………………………………………………………

14

Marino vuole ricoprire una scatola a forma di parallelepipedo.

Ha già preparato 4 dei 6 rettangoli che occorrono parte superiore parte inferiore

parte laterale parte laterale

Disegna i due rettangoli che mancano

15 Nel parco giochi c’è un percorso formato da cerchi colorati in fila uno dietro l’altro.

Matilde salta nei cerchi a due a due. Enrico salta nei cerchi a tre a tre. Partono insieme dall’inizio, fuori dal primo cerchio. In questo modo arrivano insieme all’ultimo cerchio. Da quanti cerchi potrebbe essere formato il percorso?

A. 15

B. 16

C. 18

D. 21

16

Alla sua festa di compleanno Simone distribuisce i lecca lecca tra i 21 bambini e bambine presenti.

Ognuno ne riceve due.

Quanti lecca lecca riceverebbe ognuno se i bambini e le bambine che se li dividono fossero 6?

A. 3

B. 4

C. 6

D. 7

17

Igor usa la calcolatrice per eseguire questo calcolo

95 x 25

Si sbaglia e digita

95 x 26

Quanto dovrà togliere al risultato della calcolatrice per correggere l’errore?

A. 1

B. 25

C. 26

D. 95

Osserva le due figure.

Le due figure hanno la stessa area?

A. No, perché la figura A è un quadrato e la figura B è un rettangolo.

B. Sì, perché i poligoni che formano la figura A sono congruenti a quelli che formano la figura B.

C. Sì, perché entrambe sono formate da 5 poligoni.

D. No, perché la figura B ha perimetro maggiore della figura A.

19 È tempo di saldi. Il tablet Alfa 24 ha il prezzo di listino di 250 euro. Due negozi espongono questi cartelli.

In quale negozio il tablet costa meno?

A. Nel negozio Supermedia.

B. Nel negozio Il computer.

C. Il tablet ha lo stesso costo nei due negozi perché lo sconto è uguale.

D. Non si può sapere perché non si possono confrontare gli sconti.

Figura A

Figura B

20 Nel grafico è rappresentata la presenza del team italiano a cinque edizioni delle Olimpiadi.

a) Riferendoti al grafico indica quali informazioni puoi ricavare e quali non puoi ricavare.

1. Il numero delle medaglie vinte.

2. Lo sport in cui ha gareggiato il maggior numero di atleti/atlete.

3. In quale anno, nelle ultime 5 edizioni, il team italiano era più numeroso.

4. Il rapporto numerico tra atleti e atlete presenti.

b) In quale anno la differenza tra il numero degli atleti e quello delle atlete è stato maggiore?

Risposta: ……………………

c) In quale anno è stato minore?

Risposta: ……………………

a) Quali sono le coordinate del punto A?

Risposta: ……………………

Le due linee che vedi sul piano cartesiano sono due lati di un rettangolo.

b) Disegna sul piano cartesiano il punto D in modo che unendolo ai punti A e C completerai il rettangolo.

22 Alice decide di trascorrere una vacanza di 8 giorni a Londra. Al suo ritorno

cambia le sterline avanzate in euro.

10 sterline corrispondono a circa 12 euro. La banca, per le sterline consegnate, le dà 180 euro.

Quante sterline circa le erano avanzate?

A. 50 sterline

B. 100 sterline

C. 150 sterline

D. 200 sterline

Su questo piano cartesiano sono stati segnati 3 punti.

23

Al bar Cin Cin hanno fatto un’indagine per rilevare quanto spendono i/le clienti per il pranzo.

a) Ricava i dati dal grafico e completa il testo.

L’indagine ha preso in considerazione ………… clienti Nessun/nessuna cliente ha speso più di ……………………

I/le clienti che hanno speso 11 euro sono …………

9 clienti hanno speso …………………… a testa

b) Quanti/quante clienti hanno speso più di 13 euro?

Risposta: ……………………

c) Qual è il valore della moda?

Risposta: ……………………

24

Sulla retta dei numeri scrivi al posto giusto i seguenti numeri.

25

Questa è la pianta della camera di Dario.

Scala 1 : 100

Dario vorrebbe collocare sul lato più corto della sua camera questo armadio.

Potrà farlo?

Sì, perché

Scala 1 : 50

No, perché

Quale criterio è stato utilizzato per suddividere queste figure in due gruppi?

Gruppo A Gruppo B

A. Nel gruppo A le figure sono tutti poligoni, nel gruppo B sono tutti non poligoni.

B. Nel gruppo A tutte le figure hanno angoli concavi, nel gruppo B tutte le figure hanno angoli convessi.

C. Nel gruppo A le figure hanno tutte un solo asse di simmetria, nel gruppo B le figure hanno più di un asse di simmetria.

D. Nel gruppo A alcune figure sono quadrilateri, nel gruppo B nessuna figura è un quadrilatero.

27 Aggiungi nel riquadro i tulipani necessari affinché la frase sia vera.

“Il 30% dei fiori sono tulipani”

Il pastore Stefan ha 48 tra capre e pecore. Le capre sono 16 più delle pecore. Quale di questi schemi rappresenta in modo corretto la situazione?

A.

B.

C.

D.

29 Osserva queste cifre.

0 3 4 4 5 6

Utilizza tutte le cifre una sola volta per ottenere un numero che:

• sia divisibile per 10

• abbia la stessa cifra alle decine e alle centinaia

• sia minore di 360 000

30 I segni delle operazioni sono stati coperti da due macchie.

2500 100 = 2,5 10

Scrivi tu gli operatori corretti per rendere vera l’uguaglianza.

2500 ……… 100 = 2,5 ……… 10