Direzione Discipline - Risorse Didattiche - Matematica Classe 4

RISORSE DIDATTICHE

MATEMATICA

Prove di ingresso

Schemi per la progettazione per UA

Didattica partecipata: strumenti e schede

Interdisciplinarità: strumenti e schede

Compiti di realtà

Classe capovolta

LOGICA MATEMATICA: strumenti e schede

STEAM: strumenti e schede

Gruppo Editoriale

2 Prove di ingresso

1 Logica e problemi 7 Didattica partecipata

Schede operative 8 Che problema il problema! • Schede operative

Compito di realtà

La classe capovolta 14 UA 2 Progettazione dell’UA 16 UA 2 I numeri

classe capovolta

28

3 Progettazione dell’UA 30

3 La misura 32 Didattica partecipata • Schede operative 34 Interdisciplinarità • Schede operative 38 Compito di realtà 39 La classe capovolta

40 UA 4 Progettazione dell’UA

42 UA 4 Spazio e figure 44 Didattica partecipata

52 UA 5 Progettazione dell’UA

53 UA 5 Relazioni, dati e previsioni 56 Didattica partecipata • Schede operative 58 Interdisciplinarità

61 Compito di realtà

62 La classe capovolta

63 LOGICA MATEMATICA

64 Lo sviluppo intellettivo nella Scuola Primaria •

La logica: un mezzo, non un fine

65 Logica matematica

66 La metodologia

67 Programmazione

68 Primo step

70 Schede operative

94

95

Secondo step

Schede operative

119 Soluzione degli esercizi

123 STRUMENTI COMPENSATIVI

131 LA DIDATTICA STEAM

132 Che cos’è la didattica STEAM?

133 Le caratteristiche di una didattica STEAM

134 Che cos’è il Tinkering? • Che cos’è l’ingegneria?

135 Dalla realizzazione manuale all’invenzione

137 Gli ingegneri e il processo di progettazione ingegneristica

140 Schede operative

145 Le fasi del processo di progettazione ingegneristica

145 Identificare il problema

146 Schede operative

150 Raccogliere informazioni

151 Schede operative

154 Immaginare

156 Schede operative

163 Pianificare

164 Schede operative

166 Creare

169 Schede operative

172 Verificare sul campo

173 Schede operative

177 Migliorare

178 Schede operative

186 Condividere

191 Schede operative

Numeri

1 Colora in azzurro la cifra delle unità, in rosa quella delle decine, in verde quelle delle centinaia.

2 Colora in rosa la cifra delle decine, in giallo quelle delle migliaia.

3 Esegui la catena di operazioni.

4 Scrivi l’operatore mancante.

5 Trova gli operatori mancanti che determinano la sequenza. Poi continua tu.

6 I risultati di queste operazioni sono tutti sbagliati. Cerca di capire di quanto è sbagliato il risultato. Poi:

• modifica un addendo per ottenere il risultato indicato.

15 + 5 + 6 = 23

• modifica il sottraendo per ottenere il risultato indicato.

40 – 11 = 38

15 + 5 + = 23 4 + 7 + 9 = 30 + + = 30 102 – 92 = 20

40 – = 38

• modifica il minuendo per ottenere il risultato indicato.

30 – 15 = 10 – 15 = 10

– = 20 90 – 1 = 85 – 1 = 85

Misura

1 Utilizza il righello e scrivi la misura di ciascuna linea.

2 Scrivi la misura di ciascuna linea, utilizzando il millimetro come unità di misura.

3 Confronta le misure e inserisci il segno >, < o =

4 Completa.

5 Osserva le immagini. Colora il pallino in rosso se sono figure piane, in blu se sono figure piane ma non sono poligoni, in giallo se non sono figure piane.

Prodotto finale atteso: classe capovolta

OBIETTIVI FORMATIVI

LOGICA E PROBLEMI

• Costruire un gioco, da proporre alla classe, che si risolva attraverso un percorso logico.

• Acquisire un atteggiamento di osservazione e problematizzazione della realtà.

• Favorire lo sviluppo delle attività metacognitive attraverso la costruzione e l’utilizzo di modelli e schemi.

• Commentare, individuare collegamenti, operare inferenze, proporre ipotesi esplicative.

• Argomentare le proprie scelte.

COMPETENZE

Competenze di Educazione Civica

Competenze chiave (europee)

Competenze mirate (traguardi di competenze disciplinari)

OBIETTIVI DI

• Lavorare insieme per raggiungere uno scopo comune.

• Competenza matematica e competenza in Scienze, Tecnologie e Ingegneria.

• Competenza personale, sociale e capacità di imparare a imparare.

L’alunno/a:

• legge e comprende testi che coinvolgono aspetti logici e matematici;

• risolve situazioni problematiche utilizzando formule, tecniche e procedure di calcolo.

APPRENDIMENTO

Conoscenze (sapere)

• Leggere e decodificare un problema.

• Individuare i dati necessari per risolvere un problema.

• Individuare i dati utili, inutili, sovrabbondanti, mancanti.

• Individuare la domanda nascosta.

• Verificare il risultato.

• Descrivere il procedimento seguito per risolvere i problemi.

Contenuti

Attività e metodologia

Abilità (saper fare)

• Risolvere problemi con l’uso di diagrammi.

• Trovare differenti strategie di risoluzione dei problemi.

• Analisi di differenti situazioni problematiche.

• Problemi con dati sovrabbondanti e/o mancanti.

• Problemi graduati con una o più domande.

Logica e soluzione di problemi sono alla base di qualsiasi apprendimento, non solo quelli concernenti la Matematica.

Perciò la metodologia, le proposte didattiche, le modalità operative adottate in questa UA potranno essere “esportate” anche nelle altre discipline.

Poiché la “soluzione dei problemi” è parte integrante dell’agire quotidiano e va oltre il tempo e lo spazio attribuiti a questa parte della Matematica nelle ore di curricolo scolastico, le attività di logica e risoluzione dei problemi avranno un deciso carattere di trasversalità disciplinare.

Le attività trarranno spunto da situazioni problematiche concrete e dalla necessità di risolvere situazioni pratiche derivanti dalle esperienze reali del bambino e della bambina. Si allargherà poi il contesto a situazioni “fantastiche”, ma emotivamente coinvolgenti.

INTERDISCIPLINARITÀ

Compito di realtà Trova i problemi intorno a te, pag. 12. Raccolta dati osservando una realtà strutturata (supermercato) e formulazione autonoma di problemi.

Tempi L’intero anno scolastico.

Destinatari Tutta la classe.

MATEMATICA

LOGICA E PROBLEMI

L’argomento che tratteremo

La risoluzione dei problemi

Nel Sussidiario di Matematica non vi è una sezione specifica dedicata alla logica: riteniamo infatti che la logica sia permeante e sottesa a tutte le discipline e debba pertanto rappresentare un modo di vedere e insegnare la Matematica, piuttosto che un “argomento” da trattare solo in un periodo particolare dell’anno scolastico, per poi essere abbandonata.

Le categorie di pensiero che costruiscono la base della Matematica (seriare, classificare, porre in relazione, collocare nello spazio, congetturare…) si apprendono essenzialmente attraverso l’azione e la riflessione su quanto fatto, procedendo per prove ed errori, argomentando per esplicitare il ragionamento o la procedura adottati. È necessario quindi che talvolta l’insegnante si “metta da parte” e lasci i ragazzi e le ragazze liberi di sperimentare autonomamente la ricerca di soluzioni ai problemi, procedendo attraverso il metodo dell’osservazione, della scoperta e della spiegazione reciproca delle conclusioni alle quali si è giunti o si potrebbe giungere.

Nel testo, pertanto, vengono spesso proposte attività che pongono agli allievi e alle allieve quesiti formulati in modo non standardizzato e richiedono l’attivazione di differenti strategie per essere risolti.

Risulta sicuramente più proficuo far risolvere queste situazioni problematiche in gruppo. Nel confronto con i pari l’alunno/a impara a rispettare le idee altrui, a confrontarsi e a cercare in team la soluzione. Il lavoro in gruppo non è facile: talvolta possono sorgere conflitti, possono manifestarsi situazioni di subalternità. L’insegnante dovrà perciò intervenire nei gruppi, quando necessario, non per suggerire la risposta al quesito, ma per indicare la metodologia di lavoro più adatta, gli spunti da prendere in considerazione e che possono aiutare a giungere a una conclusione.

Nel testo i quesiti esplicitamente di logica sono presentati come situazioni vissute da Zic e Zac, due giovani alieni, con i quali gli allievi/le allieve possono entrare in empatia, riconoscendoli come loro pari.

In questa Guida l’insegnante troverà le soluzioni ai quesiti presenti nel volume e proposte di lavoro per implementare le capacità logiche degli allievi/delle allieve. Ricordiamo che le ragazze e i ragazzi amano essere sfidati, trovano stimolante cercare una soluzione a problemi anche solo per il gusto di farlo, senza che ciò venga collegato alla risoluzione di un compito e soprattutto a una valutazione. Per questa ragione le schede di logica che vengono proposte in questa Guida non sono necessariamente collegate a situazioni che il bambino/la bambina può vivere direttamente, ma coinvolgono la sua fantasia e il suo desiderio di immaginare situazioni nuove.

Se talvolta i ragazzi e le ragazze possono sperimentare in piena autonomia percorsi personali per risolvere compiti autentici o situazioni problematiche proposte dall’insegnante, è altrettanto vero che hanno, invece, bisogno di essere aiutati ad acquisire gli strumenti per diventare competenti in Matematica. Perciò nel Sussidiario è proposto un percorso didattico relativo ai “problemi” che aiuta a identificare le tappe necessarie per il percorso risolutivo degli stessi e ad approcciarsi a una situazione problematica con differenti strategie.

Come introdurre l’argomento “problemi”

L’insegnante può chiedere agli allievi e alle allieve di dare un significato alla parola “problema”.

• Quando la parola “problema” entra nel linguaggio di tutti i giorni?

• Quando la usano le perosne adulte? Quando la usano i bambini e le bambine?

• Che cos’è per voi un vero problema? I problemi hanno una soluzione?

• Tutti i problemi hanno una soluzione che si trova utilizzando i numeri?

La scheda di didattica partecipata fornita di seguito può essere di aiuto per stimolare risposte.

Il concetto di problema e la soluzione

1 Osserva le situazioni e rispondi.

Qual è il problema?

Come si può risolvere?

Come faccio?

Non ho abbastanza soldi!

Qual è il problema?

Come si può risolvere?

E adesso?

La biro non funziona!

Qual è il problema?

Come si può risolvere?

Non ho capito proprio nulla!

Qual è il problema?

Come si può risolvere?

Dalla situazione problematica al testo

Osserva le immagini e per ciascuna scrivi il testo di un problema possibile.

PARCHEGGIO

GALATTICO

TARIFFE

1 ora = 25

Paga lei per tutti?

3 ore 1 ora 2 ore 5 ore

3 ore 1 ora 2 ore 5 ore

PARCHEGGIO

PARCHEGGIO

40 posti

40 posti

Ci sono posti liberi?

Ci sono 8 astronavi nella zona gialla, 4 nella zona blu, 7 nella zona verde e 9 nella zona rossa.

L’ordine dei dati e delle domande

Hai difficoltà a risolvere i problemi? Prima di pensare alla soluzione impara a prestare attenzione ad alcuni particolari: l’ordine dei dati e delle domande. Non sempre i dati del problema vanno utilizzati nell’ordine in cui sono presentati nel testo.

Leggi i problemi e rispondi.

1 Il signor Guerrini usa la macchina solo per andare in ufficio. Alla fine della settimana il contachilometri della sua automobile segna 35 234. Questa settimana è andato al lavoro per 5 giorni. Guerrini percorre 15 km all’andata e 18 km al ritorno. Quale cifra indicava il contachilometri all’inizio della settimana?

• Quali sono i due dati che devi utilizzare per primi?

2 Il signor Guerrini ogni settimana spende 50 euro di benzina per andare in ufficio. Ogni giorno paga 3 euro per il pedaggio dell’autostrada all’andata e 4 al ritorno. Fa colazione al bar e spende 2 euro. Quanto spende in tutto in una settimana, tenendo conto che lavora per 5 giorni?

• Quale dato devi utilizzare per ultimo?

3 Per le fotocopie nell’ufficio del signor Guerrini oggi sono a disposizione 4 risme da 500 fogli ciascuna. Il signor Guerrini deve stampare 12 copie di una relazione di 48 pagine e 23 copie di tabelle e grafici per 14 pagine.

• Numera le domande per ordinarle nella sequenza da utilizzare per la risoluzione del problema.

Quanti fogli rimangono a disposizione?

Quanti fogli servono in tutto?

Quanti fogli vengono utilizzati per la stampa della relazione?

Quanti fogli ha a disposizione il signor Guerrini?

Quanti fogli vengono utilizzati per la stampa dei grafici?

L’importanza delle parole

Quando devi risolvere il problema, a volte ti capita di non riuscire perché ti sembra che manchino dei dati?

Presta sempre attenzione alle parole del problema: a volte nascondono un dato, altre volte possono trarre in inganno!

Leggi i problemi, rispondi e risolvi.

1 In un castello in Transilvania vivono le famiglie di due vampiri, Vamp e Vomp. Vamp ha 350 anni e Vomp ne ha 320.

Quanti anni ha Vamp più di Vomp?

• Sei sicuro che la parola “più” indichi che devi eseguire un’addizione?

Soluzione:

2 Nonna Vimp ha regalato a Vampiretto 50 candele per giocare, 5 in meno di quanto ne ha regalate a Vampiretta. Quante candele ha avuto Vampiretta?

• Sei sicuro che la parola “meno” indichi che devi eseguire una sottrazione?

Soluzione:

3 Vamp in una settimana utilizza mezza dozzina di lenzuola bianche e Vomp 3 paia di lenzuola color panna. Chi utilizza più lenzuola?

• I dati sono tutti espressi con i numeri?

• Quali dati sono nascosti nelle parole?

Soluzione:

4 Vump, il primo antenato di Vomp, è nato una decina di secoli fa e ha avuto il suo primo figlio dopo un paio di secoli.

Quanti anni fa è nato Vump? A che età ha avuto il primo figlio?

Quanti anni fa è nato il primo figlio di Vump?

• Si può risolvere questo problema che non contiene alcun numero?

• Quali dati sono nascosti nelle parole?

Soluzione:

Soluzioni diverse

Hai mai pensato che il problema possa avere una soluzione diversa dalla tua? A volte un problema può avere più soluzioni, tutte giuste!

Leggi i problemi e risolvi.

1 Al centro sportivo “Mira e misura” si svolgono tornei di molti sport. Remo ha tirato 4 frecce a questo bersaglio, totalizzando 16 punti.

• Scrivi 4 combinazioni possibili per raggiungere il punteggio di Remo.

2 La signora Adele vuole comperare delle freccette per allenarsi a casa. Nello shop del centro sportivo c’è questo espositore. La signora Adele ha speso 100 euro e ha comperato più di 4 scatole. Quali e quante scatole potrebbe aver comperato la signora Adele?

• Scrivi 4 soluzioni possibili.

3 Il signor Guglielm O’ Tell ha bisogno di 54 mele di polistirolo per allenarsi al tiro con l’arco. Allo shop incontra la signora Adele e le chiede un consiglio sulle confezioni da acquistare, perché vuole acquistare solo 5 scatole.

• Scrivi almeno 2 soluzioni possibili.

Compito di realtà

Trova i problemi intorno a te

I problemi non sono solo sui libri di testo, ma ovunque attorno a te. Vai al supermercato con una persona adulta. Porta con te una penna e un block notes oppure lo smartphone. Preparati a suggerire problemi per i tuoi/le tue insegnanti. Questa è l’unica situazione in cui non dovrai risolvere problemi, ma inventarli. Il difficile compito spetterà ai tuoi compagni e alle tue compagne, se l’insegnante è d’accordo!

Formula i seguenti problemi.

1 Scrivi a che ora parti da casa, a che ora arrivi al supermercato, a che ora esci dal supermercato, a che ora torni a casa.

• Riporta qui i dati che hai rilevato.

Ora di partenza:

Ora di arrivo al supermercato:

Ora di uscita:

Ora di arrivo a casa:

• Ora, su un foglietto, formula il testo del problema.

2 Sei nel supermercato. Scegli una corsia: per esempio quella della pasta e dei sughi. Annota da quanti piani è composto ciascuno scaffale. Controlla il prezzo di tre tipi di pasta in confezioni da 500 g e 3 in confezioni da un chilogrammo. Scegli un tipo di pasta e annota quante confezioni di quella pasta ci sono sullo scaffale.

Annota i prezzi di tre tipi diversi di sughi pronti e controlla quante porzioni di pasta ognuno di essi condisce. Chiedi a chi ti accompagna per quante persone è sufficiente, in media, mezzo chilogrammo di pasta.

• Riporta qui i dati che hai rilevato.

Numero piani di uno scaffale:

Prezzo della pasta in scatole da 500 g:

Prezzo della pasta in scatole da 1 kg:

Prezzo dei sughi pronti:

Confezioni di pasta su uno scaffale:

500 g di pasta sono sufficienti per persone

• Con i dati che hai rilevato, formula uno o più problemi. Per esempio puoi calcolare quanto costa preparare le penne con il pesto per 8 persone.

Consegna all’insegnante i problemi che hai formulato.

Costruire un gioco di logica

Osserva e gioca.

• L’extraterrestre per uscire dal labirinto deve seguire un percorso rispettando questa sequenza che si ripete in continuazione:

• Segna l’unica strada possibile: l’extraterrestre può muoversi solo in alto, in basso, a destra o a sinistra, ma non in diagonale.

Trova ora tu un’altra situazione e disegna nel riquadro gli elementi necessari affinché ci sia una sola strada possibile per attraversare il labirinto.

Prodotto atteso

Costruzione di un gioco che si risolva attraverso un ragionamento logico.

Prodotto finale atteso: classe Capovolta

OBIETTIVI FORMATIVI

I NUMERI

• Costruzione di un calcolatore da polso.

• Acquisire un atteggiamento di osservazione e problematizzazione della realtà.

• Favorire lo sviluppo delle attività metacognitive attraverso la costruzione e l’utilizzo di modelli e schemi.

• Commentare, individuare collegamenti, operare inferenze, proporre ipotesi esplicative.

• Argomentare le proprie scelte.

COMPETENZE

Competenze di Educazione Civica

Competenze chiave (europee)

Competenze mirate (traguardi di competenze disciplinari)

• Lavorare insieme per raggiungere uno scopo comune.

• Competenza matematica e competenza in Scienze, Tecnologie e Ingegneria.

• Competenza personale, sociale e capacità di imparare a imparare.

• Competenza in materia di Educazione Civica.

• Competenza alfabetica funzionale.

L’alunno/a:

• si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali;

• conosce i numeri decimali e opera con essi.

OBIETTIVI DI APPRENDIMENTO

Conoscenze (sapere)

• Leggere e scrivere i numeri interi e decimali.

• Riconoscere il valore posizionale delle cifre per numeri fino alla classe delle centinaia di migliaia.

• Comporre e scomporre i numeri.

• Ordinare i numeri in senso progressivo e regressivo.

• Conoscere le proprietà delle operazioni e saperle applicare.

• Conoscere e operare con i numeri decimali.

• Acquisire il concetto di intero e di frazione.

• Riconoscere frazioni proprie, improprie, apparenti, equivalenti, complementari.

• Saper confrontare frazioni con uguale denominatore o uguale numeratore.

• Acquisire il concetto di frazione di un numero.

Contenuti

• La storia dei numeri.

Abilità (saper fare)

• Eseguire le 4 operazioni con sicurezza.

• Eseguire la divisione con il divisore di 2 cifre.

• Saper applicare le proprietà delle operazioni.

• Operare con le frazioni.

• Saper calcolare la frazione di un numero.

• Trasformare frazioni decimali in numeri decimali e viceversa.

• La numerazione in base dieci.

• I grandi numeri.

• Le operazioni e le loro proprietà.

• La divisione con il divisore di due cifre.

• I multipli e i divisori.

• Concetto di frazione e unità frazionaria.

• Frazioni complementari.

• Frazioni proprie, improprie, apparenti, equivalenti, decimali.

• Confronto di frazioni.

• La frazione come operatore.

Attività e metodologia Poiché la Matematica è costruzione del pensiero, essa non può essere appresa meccanicamente, come un insieme di regole e formule, ma attraverso l’attivazione di processi mentali che portino alla capacità di ordinare, quantificare, mettere in relazioni i dati…

Perciò anche l’apprendimento dell’aritmetica sarà fondato sull’operatività, base per giungere all’astrazione. Nella proposizione degli argomenti si terrà conto dei principi di gradualità e ciclicità: cioè gli argomenti saranno proposti in successione graduale di difficoltà, ma saranno anche riproposti ciclicamente per comprenderli meglio, approfondire e progredire.

INTERDISCIPLINARITÀ

Discipline coinvolte

Matematica, Storia, Italiano, Geografia, Educazione Civica.

La connotazione posizionale e decimale del nostro sistema di misurazione risulterà di più facile comprensione se sarà confrontata con altri sistemi di numerazione, facendo notare che la necessità di adottare simboli per rappresentare la realtà è stata presente fin dagli inizi della civiltà e il modo di organizzare i simboli aveva un preciso fondamento: le dita della mano, di due mani, le falangi delle dita…

Anche in questa UA si privilegerà il brain storming per ascoltare le conoscenze pregresse, il cooperative learning e la didattica partecipata e attiva che rende il bambino/la bambina protagonista del proprio apprendimento.

Nuclei tematici

• Storia: L’abaco, pag. 22.

Fin dall’inizio della sua storia, l’essere umano ha sentito la necessità di registrare le quantità; ha sviluppato però diversi segni per indicare le quantità e differenti modi di organizzare le numerazioni; anche gli strumenti che lo hanno aiutato nei calcoli si sono modificati nel corso del tempo.

• Italiano: I segni e la lingua, pag. 23.

Matematica e Italiano, segni e lingua, sono profondamente correlati ed entrambi sono codici comunicativi.

• Geografia, Educazione Civica: La frazione in geografia, pag. 24.

Le parole della Matematica si ritrovano anche in altre discipline dove assumono significati talvolta simili, talvolta profondamente diversi.

Compito di realtà

Numeri e cifre intorno a te, pag. 25.

Rilevazione di quantità numeriche nella realtà che ci circonda, valutando la differenza anche molto elevata di valore assoluto.

Tempi L’intero anno scolastico.

Destinatari

Tutta la classe.

L’argomento che tratteremo

I NUMERI

Nell’Unità di Apprendimento relativa ai numeri gli alunni e le alunne:

• cominciano a conoscere numeri sempre più grandi fino alla classe delle migliaia;

• riflettono sul significato delle quattro operazioni ed operano con esse, rilevandone le principali proprietà e riconoscendo le relazioni tra le operazioni stesse;

• operano con le frazioni per capire che anche esse sono numeri, se pure espressi in modo differente.

Le bambine e i bambini, giunti in classe quarta, conoscono già i numeri, anche grandi, hanno compreso il valore posizionale delle cifre, hanno compreso a quali processi mentali corrispondono le quattro operazioni. Non sempre, però, hanno riflettuto bene sulla relazione che intercorre tra le operazioni: probabilmente non tutti colgono la relazione tra operazioni inverse.

Sarà perciò necessario operare molto con i numeri utilizzando il calcolo mentale e soffermandosi sul valore dello zero e dell’1 nelle quattro operazioni.

Il calcolo mentale

I grandi numeri

Nella Scuola Primaria il calcolo mentale è fondamentale. Esso è il fondamento di quello scritto. Prima di effettuare calcoli scritti i bambini e le bambine devono saper operare con il calcolo mentale e la prima “calcolatrice” sono le dita. Perciò è necessario dedicare al calcolo mentale almeno 5 minuti ogni giorno e non pretendere che abbandonino l’uso delle dita se non hanno ancora interiorizzato bene la formazione del 10, anche in classe quarta.

I numeri non sono collegati a concetti che si possono apprendere e/o consolidare utilizzando solo, o principalmente, i canali verbali.

I meccanismi cardine per l’acquisizione di una intelligenza numerica si basano sulla visuo-spazialità e sulla composizione dei numeri.

Perciò, anche in quarta, è bene proporre continui esercizi orali di composizione del numero:

• partendo da una triade (Qual è il numero composto da 3 h 4 da 6 u?);

• mescolando la triade (Qual è il numero composto da 2 da 7 u 5 h?);

• lavorando su una triade in cui una quantità è rappresentata dallo zero (Qual è il numero composto da 3 h e 6 u?).

Man mano, poi, si passa a numeri sempre più grandi. Le bambine e i bambini non solo saranno coinvolti e troveranno divertenti questi “giochi”, ma impareranno meglio, perché:

• potranno elaborare strategie personali di composizione dei numeri;

• avranno meno paura di sbagliare (l’errore orale lascia una traccia più labile di quello scritto) e quindi saranno stimolati a provare senza farsi bloccare dal timore di non essere capaci di rispondere.

La presentazione dei grandi numeri potrebbe causare problemi a chi non ha ancora interiorizzato il valore posizionale delle cifre e non ha ancora imparato a rappresentarle mentalmente.

Fino a non molti anni fa si usava inserire un puntino (separatore delle migliaia) per dividere le classi di numeri, per facilitarne sia la scrittura sia la lettura. Ora questa scrittura è stata abbandonata, perché il puntino era anche utilizzato in alcune circostanze come separatore della parte intera del numero da quella decimale (è, ad esempio, in uso come separatore decimale negli Stati Uniti e in molte calcolatrici). Perciò il Sistema Internazionale raccomanda l’uso dello spazio per separare le classi di numeri. Nulla vieta di utilizzare comunque il puntino, spiegando agli allievi e alle allieve perché esso andrà poi abbandonato. Raggruppare per 3 è infatti un modo proficuo per il nostro cervello per rappresentare le quantità.

Le frazioni

Come introdurre l’argomento e didattica partecipata

Il concetto di frazione è molto ampio.

Generalmente nella Scuola Primaria esso viene collegato alla partizione di una quantità continua (un oggetto: torta, pizza, figura piana…) o discreta (un gruppo di oggetti).

La frazione afferisce anche ad altri significati, che è necessario ricordare:

• è un rapporto o una proporzione (per ogni parte di tempera colorata si aggiungono 2 parti di acqua; l’apotema e il lato del poligono sono in proporzione indicata da un numero fisso…);

• è un operatore (i 2 3 dei 300 partecipanti alla gara);

• è una divisione ( 1 4 significa 1 : 4);

• è un modo in cui si possono esprimere le percentuali ( 75 100 = 75%).

Se i bambini e le bambine riescono a intuire alcuni dei molteplici significati della frazione sarà più facile operare con esse.

Consigliamo inoltre di introdurre fin da subito il concetto di frazione come divisione in parti equivalenti, non solo in parti congruenti

Ogni intero, infatti, può essere frazionato suddividendolo o in parti di forma e grandezza uguale o in parti di forma e grandezza diversa, ma equivalenti.

Questo intero, per esempio, è diviso in quarti, anche se le parti non hanno la stessa forma. Questo concetto sarà sicuramente approfondito in classe quinta, ma, tenendo conto delle competenze di ciascuno/a, può essere introdotto con esempi pratici già in classe quarta.

È importante che i ragazzi e le ragazze operino a lungo concretamente con le frazioni, utilizzando prima piegature del foglio, per passare poi alla rappresentazione grafica autonoma.

È molto più difficile per gli allievi e le allieve comprendere il concetto di frazione se l’hanno osservata solo su interi già suddivisi. È anche raccomandabile far suddividere gli interi in parti, utilizzando forme differenti.

Si passerà poi alla rappresentazione della frazione anche su una linea (entità più astratta di una figura geometrica piana) e al frazionamento anche di quantità discrete (un gruppo di oggetti).

Per meglio comprendere il sistema di numerazione decimale posizionale che oggi utilizziamo può essere interessante conoscere la storia che ha accompagnato l’evoluzione dei sistemi di numerazione. Nel Sussidiario essa viene descritta a grandi linee, pertanto in questa Guida forniamo una scheda per approfondire l’argomento. In essa viene analizzato il sistema di numerazione in uso presso i Maya. Era un sistema basato sull’uso di 3 segni (il chicco di valore 1, il legnetto di valore 5, la conchiglia di valore 0) che avevano un valore diverso a seconda della posizione che prendevano. I Maya utilizzavano sia la base 5 sia la base 20. Può essere interessante, dopo aver proposto la scheda di pag. 18 chiedere agli allievi e alle allieve perché, secondo loro, noi utilizziamo la base 10 e i Maya la base 5 e la base 20. Gli studiosi considerano queste le risposte più accreditate: la base 5 corrispondeva a una mano e la base 20 alle dita delle mani e dei piedi.

Per far svolgere la seconda scheda è necessario procurarsi un gomitolo di spago che verrà utilizzato per eseguire l’esercitazione.

Antichi sistemi di numerazione

I Maya sono un antico popolo vissuto in America Centrale. Non vennero mai in contatto con i popoli della Mesopotamia, con i Greci o con i Romani.

Anche loro avevano un sistema di numerazione che, come il nostro, si basava su precisi segni e sulla loro posizione.

Per contare utilizzavano i fagioli o i chicchi di mais (valore 1) e i legnetti (valore 5). Avevano anche un simbolo, la conchiglia, per rappresentare lo zero (sembra siano stati i primi a utilizzarlo).

Ecco i loro numeri fino a 19.

1 Come avranno rappresentato il numero 20?

Fai un’ipotesi, scegli uno tra questi segni e motiva la tua scelta. Discuti anche con i compagni e le compagne per confrontare le risposte. Infine, leggi la risposta giusta.

Il simbolo usato dai Maya per il numero 20 è il quarto.

Pensa a come scriviamo noi il numero 10. 1 decina e 0 unità

I Maya scrivevano 1 ventina (un puntino che cambiava posizione perché si spostava verso l’alto) e zero. Noi usiamo la base 10, cioè raggruppiamo per gruppi di 10; i Maya invece raggruppavano in base 5 (sostituivano 5 unità con un legnetto) e in base 20 (arrivati a 20, formavano una ventina e la spostavano verso l’alto).

I numeri più grandi si scrivevano così:

Le frazioni su una linea

Di seguito ti proponiamo alcune attività per imparare a rappresentare le frazioni anche su linee. Procurati alcuni pezzi di corda lunghi 10 cm e alcuni lunghi 5 cm: li utilizzerai per svolgere in modo concreto gli esercizi n. 1 e 2.

1 Dividi prima la corda da 10 cm nelle parti indicate, poi ciascuna linea (sempre nelle parti indicate). Infine, colora con i pennarelli l’unità frazionaria.

Dividi in 4 parti e colora 1 4

Dividi in 5 parti e colora 1 5

Dividi in 10 parti e colora 1 10 .

2 Dividi prima la corda da 5 cm nelle parti indicate, poi ciascuna linea (sempre nelle parti indicate). Infine, colora con i pennarelli l’unità frazionaria.

Dividi in 5 parti e colora 3 5

Dividi in 4 parti e colora 4 4

Dividi in 10 parti e colora 8 10 .

3 Osserva la linea dei numeri. Suddividi lo spazio tra 0 e 1 e tra 1 e 2 nelle parti indicate. Poi colora la frazione indicata.

Dividi in 5 parti + 5 parti. Colora 5 5

Dividi in 5 parti + 5 parti. Colora 7 5 .

Dividi in 2 parti + 2 parti. Colora 1 2 .

Dividi in 2 parti + 2 parti. Colora 3 2

Suddividere utilizzando forme differenti

1 Suddividi ciascun intero in 4 parti uguali, utilizzando 3 modi diversi, come negli esempi. Colora l’unità frazionaria e scrivila.

2 Suddividi ciascun intero in 8 parti uguali, utilizzando 3 modi diversi. Colora l’unità frazionaria e scrivila.

3 Suddividi ciascun intero in 6 parti uguali, utilizzando 3 modi diversi. Colora l’unità frazionaria e scrivila.

4 Suddividi ciascun intero in 10 parti uguali, utilizzando 3 modi diversi. Colora l’unità frazionaria e scrivila.

Suddividere utilizzando frazioni differenti

1 Colora l’unità frazionaria e scrivila.

3 Colora l’unità frazionaria e scrivila.

2 Su ciascuna parte, scrivi quale frazione rappresenta dell’intero.

5 Colora l’unità frazionaria e scrivila.

4 Su ciascuna parte, scrivi quale frazione rappresenta dell’intero.

6 Su ciascuna parte, scrivi quale frazione rappresenta dell’intero.

L’abaco

Fin dall’antichità l’essere umano utilizzava le mani per contare. Quando i calcoli diventarono più complicati, ha cercato degli strumenti che lo aiutassero.

1 Il primo strumento utilizzato dall’essere umano per velocizzare i calcoli fu l’abaco. Osserva le immagini, leggi e collega ciascuna spiegazione al disegno, scrivendo il nome dell’abaco rappresentato.

• I primi abachi erano delle tavolette di argilla, legno o marmo, ricoperte da polvere o sabbia: erano abachi a polvere. I segni venivano incisi con uno stilo.

• L’abaco a colonne rappresentava in maniera visiva i numeri e veniva utilizzato per le operazioni più semplici: addizioni e sottrazioni. Sassolini, gettoni o anelli erano allineati su colonne parallele per rappresentare i numeri. I sassolini erano chiamati “calculi”, perciò eseguire le operazioni, si dice anche “calcolare”.

• In Cina era in uso un particolare tipo di abaco, il suan pan. È formato da una serie di asticelle parallele fissate a un supporto. In ogni asticella sono infilati sette anelli. Un’altra asticella divide le palline in gruppi di 5 e 2.

2 Osserva ora questo abaco: probabilmente ne avrai uno uguale o simile in classe. Descrivilo rispondendo alle domande.

hkdakukhdauhkdakukhdau

• Quante sono le asticelle verticali? A che cosa corrispondono?

• Quante palline possono essere inserite al massimo in ciascuna asticella?

I segni e la lingua

Quando non erano ancora stati inventati i segni della Matematica, per indicare le operazioni si usavano delle parole in latino, la lingua da cui deriva l’italiano.

1 Segna con una X

In un libretto di aritmetica stampato a Treviso nel 1478 e intitolato “L’arte dell’abaco per la preparazione dei giovani che intendono darsi al commercio”, si trovano queste parole: et, de, fia, intra. Come potresti tradurre:

• la parola “et” (è una parola che ha a che fare con l’addizione)?

E

È

Sta

• la parola “fia” (è una parola che ha a che fare con la moltiplicazione)?

Volta

Facile

Meno

• la parola “de” (è una parola che ha a che fare con la sottrazione)?

Da

Intorno

Per

• la parola “intra” (è una parola che ha a che fare con la divisione)?

Fuori

Entro

Lontano

2 Collega ciascuna parola latina al segno matematico che l’ha sostituita.

intra fia de et : × +

3 Osserva le antiche operazioni. Poi, completa scrivendo quale termine e quale segno usi oggi nelle operazioni indicate dalle parole latine.

5 et 6 11

1 de 1 0

3 fia 2 6

5 intra 15 3

9 et 4

3 de 3

4 fia 5

2 intra 20

6 et 5

5 intra 25

e 4

+ 4

3

5

5

La frazione in geografia

La parola “frazione” si usa anche in geografia, non solo in Matematica, ma ha un significato diverso.

1 Solo una di queste affermazioni è giusta. Quale? Segnala con una X

La frazione è una parte di un Comune. Il Comune è una parte della frazione.

2 Leggi i cartelli stradali e completa.

SAN ROCCO

frazione di CAMOGLI

PAGNANO

frazione di MERATE

PORTISCO

frazione di OLBIA

• Nome del Comune:

• Nome della frazione:

3 Rispondi.

• Nome del Comune:

• Nome della frazione:

• Nome del Comune:

• Nome della frazione:

• Bollate è un comune in provincia di Milano. Ha quattro frazioni:

Cassina Nuova, Cascina del Sole, Ospiate, Castellazzo. Questo significa che il comune di Bollate è stato suddiviso in quattro parti uguali?

• Il Sindaco è il “capo” del Comune. Sarà anche il “capo” delle frazioni che appartengono al suo Comune?

Per le elezioni comunali voteranno anche gli abitanti delle frazioni?

Le frazioni si trovano in periferia o nel centro di un Comune?

4 Completa.

• L’espressione “frazione aritmetica” indica:

• L’espressione “frazione geografica” indica:

Numeri e cifre intorno a te

Leggi e completa la tabella.

Pensa alle situazioni indicate nella tabella. Scrivi da quante cifre, secondo te, è formato ciascun numero che indica la quantità. Poi confronta le tue risposte con quelle della classe. Se sono molto discordanti, cercate luoghi o oggetti come quelli nominati per verificare quale sia la risposta più corretta.

Persone che abitano in un condominio di 6 piani.

Pesci sul banco della pescheria al mercato o al supermercato.

Libri nella biblioteca scolastica (o di zona).

Costo di un’automobile di lusso.

Matite colorate presenti nella tua aula.

Bambini e bambine che frequentano la tua scuola.

Bambini e bambine che frequentano la Scuola Primaria nel tuo Comune.

E ora... si gioca!

Tanti anni fa un programma televisivo proponeva ai telespettatori di indovinare quanti fagioli erano contenuti in un barattolo.

Voi farete lo stesso gioco. Fatevi comperare da una persona adulta alcuni sacchetti di fagioli secchi.

• Dividete la classe in due gruppi. Un gruppo preparerà 3 barattoli di dimensioni diverse e li riempirà in questo modo:

– barattolo 1 = numero di fagioli inferiore a 3 cifre; – barattolo 2 = numero di fagioli di 3 cifre;

– barattolo 3 = numero di fagioli superiore a 3 cifre.

• Chiedete ai componenti del secondo gruppo di indovinare il numero dei fagioli contenuti in ciascun barattolo (naturalmente voi dovete sapere con esattezza quanti ve ne sono).

• Per ogni risposta, voi dovete suggerire se i fagioli contenuti sono di più o di meno. Segnate quante risposte occorrono per terminare il quiz.

• Poi, procedete invertendo nuovamente i ruoli!

Numero di cifre

Il vostro abaco da polso!

Occorrente

• Rotolo di cartone della carta da cucina.

• Righello, forbici, pennarello nero a punta fine.

• Tempera del colore che preferite.

• Pennello.

• Filo di nylon e ago.

• Perline colorate: 36 in 4 colori diversi (9 per ciascun colore).

• Nastro adesivo trasparente.

Procedimento

1. Tagliate dal rotolo di cartone un pezzo alto 5 cm.

2. A 0,5 cm da entrambi i bordi, segnate un punto con il pennarello. Avete bisogno di 4 punti per lato.

Costruite un ingegnoso calcolatore da polso come questo... potrebbe essere utile! 5cm 0,5cm0,5cm

3. Tagliate in verticale il bracciale di cartone per poterlo aprire.

4. Colorate il bracciale del colore che più vi piace.

5. Infilate in un ago un filo di nylon lungo almeno 20 cm.

LA CLASSE CAPOVOLTA

6. Con il nastro adesivo fissate un’estremit à del filo all’interno del bracciale.

7. Passate il filo nel primo punto dall’interno. Infilate 9 perline dello stesso colore e passate sul punto corrispondente sull’altro lato del bracciale.

8. Da sotto infilate l’ago in corrispondenza del punto successivo. Infilate altre 9 palline di un altro colore e proseguite in questo modo per tutti e quattro i gruppi.

9. Fissate all’interno il filo con il nastro adesivo. Attenzione! Il filo deve essere ben teso, ma non in modo eccessivo, perché le palline devono poter scivolare in orizzontale.

10. Chiudete il bracciale fissandolo con del nastro adesivo.

• Nel libretto delle istruzioni che accompagnerà la vostra geniale invenzione scrivete brevemente:

– i tipi di abaco conosciuti nell’antichità; – il tipo o i tipi di abaco in uso nella vostra scuola; – quali ordini di grandezza indicano gli abachi che utilizzate in classe;

– quale colore corrisponde nel vostro abaco da polso alle unità, alle decine, alle centinaia, alle migliaia.

Prodotto atteso Costruzione di un calcolatore/abaco da polso.

Prodotto finale atteso: classe capovolta

OBIETTIVI FORMATIVI

LA MISURA

• Costruire il time table di un itinerario complesso utilizzando gli strumenti necessari adatti (orari di autobus, treni, app…).

• Acquisire un atteggiamento di osservazione e problematizzazione della realtà.

• Commentare, individuare collegamenti, operare inferenze, proporre ipotesi esplicative.

• Argomentare le proprie scelte

COMPETENZE

Competenze di Educazione Civica

Competenze chiave (europee)

Competenze mirate (traguardi di competenze disciplinari)

• Lavorare insieme per raggiungere uno scopo comune.

• Competenza matematica e competenza in Scienze, Tecnologie e Ingegneria.

• Competenza personale, sociale e capacità di imparare a imparare.

• Competenza in materia di Educazione Civica.

• Competenza multilinguistica.

• Competenza imprenditoriale.

• Competenza digitale.

L’alunno/a:

• comprende che cosa significa misurare;

• determina misure utilizzando misure convenzionali e non;

• utilizza i più comuni strumenti di misura.

OBIETTIVI DI APPRENDIMENTO

Conoscenze (sapere)

• Comprendere il concetto di misura convenzionale.

• Conoscere le unità di misura convenzionali.

Contenuti

• La storia delle misure.

• Le misure di lunghezza.

• Le equivalenze.

• Le misure di peso.

Abilità (saper fare)

• Ipotizzare quale unità di misura sia più adatta per misurare quantità differenti.

• Usare correttamente le unità di misura convenzionali, operando conversioni tra di esse.

• Risolvere problemi con le unità di misura.

• Operare con l’euro.

• Risolvere problemi sulla compravendita.

• Le misure di capacità.

• L’euro.

• La compravendita.

• Le misure di tempo.

Attività e metodologia

• Peso lordo, peso netto, tara.

L’Unità di Apprendimento dovrà iniziare indagando le conoscenze pregresse degli allievi e delle allieve riguardo i concetti di misurazione, unità di misura e unità di misura convenzionale.

L’approccio sarà laboratoriale affinché i bambini e le bambine riescano a comprendere che le quantità misurabili sono molte e diverse, e per ognuna di esse occorre una particolare unità di misura.

È importante anche sviluppare la capacità di valutare le misure “a occhio”. Questa abilità, però, può essere conseguita solo dopo molte esperienze concrete. Perciò saranno invitati/e a operare non solo con le misure di lunghezza, peso, capacità, che sono quelle su cui ci si sofferma maggiormente nella scuola primaria, ma anche, ad esempio, sul valore che viene dato a figurine particolarmente rare. Operando concretamente i bambini e le bambine giungeranno a comprendere che esistono alcune situazioni in cui si possono utilizzare unità di misura convenzionali uguali per tutti e altre in cui l’unità di misura è condivisa solo da un piccolo gruppo.

INTERDISCIPLINARITÀ

Discipline coinvolte

Matematica, Storia, Italiano, Geografia, Inglese.

È bene ricordare che nel passato venivano utilizzate differenti unità di misura e che esistono ancora oggi nazioni in cui è in uso un differente sistema di misurazione. È importante che gli allievi e le allieve comprendano che la necessità di misurare è presente da tempo immemorabile, ma solo da circa 2 secoli si è sentita la necessità di misure comuni.

Nuclei tematici

• Storia: La storia delle misure, pag. 34.

La necessità di misurare le merci era presente già nelle prime civiltà: è nata infatti con la specializzazione del lavoro.

• Italiano: I prefissi nelle misure, pag. 35.

Le “parole” della Matematica hanno un preciso significato etimologico: conoscerlo aiuta a capire meglio il significato dei termini matematici e delle loro abbreviazioni attraverso simboli.

• Geografia: Le unità di misura anglosassoni, pag. 36. Le diversità geografiche nelle unità di misura permangono in alcune aree geografiche di influenza anglosassone. Conoscerle aiuta a comprendere come le unità di misura siano nate da “accordi” tra persone che vivevano nello stesso territorio.

• Inglese: “Misurare” negli USA, pag. 37. Utilizzare la L2 in situazioni concrete.

Compito di realtà Il time table, pag. 38.

La misurazione del tempo scandisce la giornata di tutti. Riflettere sulle possibili forme di organizzazione della giornata aiuta a utilizzare il tempo in modo responsabile.

Tempi

Destinatari

L’intero anno scolastico.

Tutta la classe.

L’argomento che tratteremo

LA MISURA

Misurare significa confrontare le grandezze ed esprimerle utilizzando un’unità di misura convenzionale.

È evidente dunque che le misurazioni sono strettamente collegate alla geometria e allo studio delle relazioni (la misura non è altro che la relazione che intercorre tra una grandezza e l’unità di misura scelta).

Anche nelle Indicazioni Nazionali, infatti, l’esperienza del “misurare” non viene presentata come attività autonoma, ma è sempre collegata allo studio delle relazioni e della geometria.

Nonostante ciò, abbiamo ritenuto importante dedicare alla misura, nel sussidiario Direzione Discipline, una unità didattica specifica per centrare l’apprendimento sulla specificità di una misura e dunque avere le conoscenze che permetteranno poi di esportare la misura stessa in ambiti differenti.

L’importanza delle esperienze concrete

La necessità di unità di misura convenzionali

Riteniamo infatti che sia molto importante, anche in classe quarta, dedicare molto tempo per effettuare esperienze concrete di misurazioni di lunghezze, capacità, peso, superficie e, in seguito, anche di volumi e tempi. Molto spesso viene sottovalutata la necessità di esperienze concrete utilizzando anche campioni non convenzionali, mentre è proprio dalla sperimentazione di misure arbitrarie che si giunge alla consapevolezza della necessità della convenzionalità. Le bambine e i bambini sono abituati fin da piccoli all’uso di tecnologie anche molto avanzate: con il GPS dell’auto di un familiare sono in grado di conoscere in modo preciso distanze molto grandi, gli orologi digitali mostrano immediatamente ore, minuti e secondi, le bilance elettroniche misurano pesi anche di pochi grammi. È, però, solo con la manipolazione concreta che il bambino e la bambina imparano che la misurazione è il confronto tra una grandezza e l’unità di misura scelta, imparano che misurare significa “vedere quante volte ci sta” il campione scelto nella grandezza da misurare. Le misurazioni concrete sono necessarie anche per sviluppare la capacità di osservare e, in seguito, di imparare a valutare “a occhio” quantità relative a lunghezze, pesi, capacità. I bambini e le bambine potrebbero anche scegliere unità di misura particolari, valide solo per la loro classe, per misurare le grandezze: l’ombrello di Stefania (lunghezze), il bicchiere di Matteo (capacità), il libro di lettura (pesi), comprendendo il valore delle misure correlato al gruppo che le utilizza.

È altrettanto importante che i ragazzi e le ragazze capiscano che le misure sono unità convenzionali, frutto di accordi tra le persone. In quasi tutto il mondo sono in uso le unità di misura stabilite dal Sistema Internazionale, ma esso è in vigore da circa 60 anni, quindi da un tempo relativamente breve. Unificare i sistemi di misurazione si è reso necessario a causa dell’aumento degli scambi e del commercio.

Così come è necessario utilizzare una lingua conosciuta da tutti per comunicare con persone di altri Paesi e l’inglese si è affermato come lingua transnazionale, allo stesso modo è necessario utilizzare unità di misura per pesi, lunghezze, capacità, tempo… uguali per tutti, per poter commerciare e confrontare le quantità con facilità. Quando, invece, le comunicazioni tra i popoli erano scarse e i commerci erano limitati, le unità di misura erano differenti da un luogo a un altro; assolvevano, però, alla loro funzione: visualizzare la grandezza di ciò di cui si stava parlando tra persone che vivevano nello stesso gruppo e comunicavano tra di loro.

Può essere perciò interessante approfondire l’evoluzione delle unità di misura.

Tutto (o quasi) si può misurare

Come introdurre l’argomento

È fondamentale anche che il bambino/la bambina capisca che sono innumerevoli le grandezze che possono essere misurate (non solo quelle “classiche” presentate a scuola), ma per ognuna di esse occorrono un’unità di misura e strumenti adatti. Perciò sarà importante scoprire insieme agli allievi e alle allieve il maggior numero di grandezze misurabili (la velocità del vento, l’intensità di un suono, la forza di un terremoto, la potenza di una lampadina, la temperatura di un forno acceso…) valutando quali strumenti siano necessari e quale potrebbe essere l’unità di misura adatta. Non è necessario che i bambini e le bambine imparino già da ora che cosa indicano i termini watt, hertz, ampere, candela, grado Celsius, ma è necessario che comprendano che ogni grandezza deve avere una sua particolare unità di misura.

L’insegnante potrà introdurre l’argomento sollecitando la discussione con domande stimolo.

• Secondo voi, che cosa si può misurare?

• Quali unità di misura conoscete?

Gli alunni e le alunne potranno preparare un cartellone con le grandezze che secondo loro sono misurabili, scrivendo accanto l’unità di misura che viene utilizzata (se la conoscono), arricchendolo nel corso dell’anno scolastico con le nuove conoscenze.

Si può chiedere agli allievi e alle allieve se hanno mai sentito parole quali miglio, yarda, gallone, libbra… che afferiscono a unità di misura non utilizzate in Italia, a quali grandezze misurabili le associano e in quali occasioni le hanno sentite. In modo analogo, si possono proporre parole che afferiscono a unità di misura non più in uso: pertica, spanna, cubito, staio, oncia, barile, moggio. Anche in questo caso gli allievi e le allieve saranno invitati a elencare in quali situazioni hanno sentito utilizzare queste unità di misura, ricostruendo la loro storia. Si può infine proporre di “cercare” i più recenti termini “aboliti”: quintale e tonnellata. Dove ritrovano ancora queste unità di misura? (Sono presenti ancora in alcuni segnali o segnalazioni stradali, sono in uso per i prodotti dell’agricoltura…).

Didattica partecipata

Per sviluppare la capacità di misurare, dopo aver compiuto molte esperienze pratiche di misurazioni con campioni arbitrari e convenzionali e di valutazione a occhio delle misure, si può proporre di scegliere un’unità di misura di lunghezza che sia valida solo per il loro specifico gruppo classe: un’unità di misura personale e unica a cui daranno il nome che preferiscono e che abbrevieranno con un simbolo scelto da loro. Con questa unità di misura si compiranno e registreranno misurazioni di oggetti, si effettueranno drammatizzazioni di situazioni di compravendita. Per esempio, i bambini e le bambine potranno utilizzare una bacchetta presente in classe (le bacchette fermafogli), il dorso di un libro della biblioteca di classe, la cintura di un/a alunno/a, un nastro recuperato da qualche regalo… Sceglieranno un nome (quartabino, quartacino, lunghetto, pinferlo…) e una marca (qb, a4, lg…). L’esperienza può anche essere confrontata con quella svolta da altre classi, se in esse è stato effettuato un lavoro analogo.

In tal modo si abitueranno a capire che la misura non è altro che l’espressione scritta del rapporto tra una grandezza e l’unità campione adottata. Per meglio comprendere come misurare sia stata una necessità dell’essere umano fin dagli albori della sua storia, l’insegnante può invitare a formulare ipotesi su come i nostri antenati abbiano risolto il problema di misurare oggetti personali o merci da scambiare prima che fossero in uso unità di misura convenzionali.

Misurare il valore

Nella tua classe c’è qualche collezionista? Collezionare significa raccogliere una serie di oggetti: figurine, pupazzi, braccialetti…

1 Lavora in gruppo o in autonomia. Tra queste figurine, scegliene una che sarà “l’unità campione”, cioè quella su cui baserai il valore delle altre per gli scambi. Assegna un valore alle altre figurine, poi rispondi.

Uomo Ragno Batman Captain America

Wonder Woman Hulk Catwoman

Iron Man Thor Daredevil Flash

• Qual è la figurina che hai scelto come unità campione?

• Quali figurine hanno valore minore dell’unità campione?

• Quali figurine hanno valore maggiore dell’unità campione?

• Il valore delle monete che noi utilizziamo e della nostra numerazione è decimale, cioè ogni moneta o ogni ordine è 10 volte maggiore o minore di quello che lo precede o lo segue. Qual è l’ordine di valore delle tue figurine?

Valutare le misure

1 Visualizza nella tua mente l’oggetto di cui si parla e segui le istruzioni.

Colora il quadratino:

• in verde se la misura è maggiore di 1 m;

• in rosso se la misura è minore di 1 m;

• in blu se la misura è circa di 1 m.

larghezza di una porta

altezza di un banco

lato più lungo della cattedra larghezza della finestra

altezza di un bambino che frequenta la classe prima distanza tra il pavimento e la finestra

2 Osserva l’ambiente intorno a te. Valuta a occhio la lunghezza di alcuni oggetti. Scegli tra le lunghezze date quella che ritieni si avvicini di più a quella reale, sottolineandola. Poi misura e calcola la differenza tra misura presunta e misura reale.

lato lungo del banco

altezza del cestino della carta 30 cm • 40 cm •

lato più lungo del sussidiario 20 cm • 25 cm • 30 cm

lunghezza dell’avambraccio di un/a compagno/a 10 cm • 25 cm • 35 cm altezza dello zaino 50 cm • 60 cm • 70 cm

3 Per ciascun oggetto, sono indicate 3 misure relative ad alcune sue caratteristiche misurabili. Una, però, è impossibile. Quale? Segnala con una X.

La storia delle misure

Il più antico sistema di misurazione riguarda i pesi.

1 Osserva queste immagini e cerca di dare una spiegazione al fatto illustrato.

Nell’antichità lo scambio di merci riguardava soprattutto cibo e metalli, tutte quantità che andavano pesate!

Anche nel linguaggio comune è presente questa attenzione al “peso” tra le caratteristiche misurabili. Si dice, infatti: “queste informazioni hanno lo stesso peso”, “non dare peso a ciò che senti”, “utilizzare gli stessi pesi e le stesse misure”. Le prime unità di peso erano le pietre, i chicchi di cereali, i semi di legumi e frutti. Per esempio la parola carato, utilizzata ancora oggi in gioielleria, deriva proprio dal nome dei semi di carrubo.

2 Secondo te, quando è stato possibile cominciare a misurare i liquidi in modo abbastanza preciso? Osserva l’immagine e spiega brevemente.

I prefissi nelle misure

I prefissi nelle misure si ripetono sempre uguali: per esempio, decagrammo, decalitro, decametro…

1 Collega ciascun prefisso al suo significato etimologico, cioè della parola, non matematico. Questi prefissi derivano dal greco.

Chilo

Etto

Deca

Giga

Mega

Mille Grande Gigante

Cento

Dieci

2 I seguenti prefissi, invece, derivano dal latino e indicano le piccole quantità. Scrivi tu che cosa indicano.

• Deci:

• Centi:

• Milli:

3 E adesso leggi alcuni prefissi “particolari”. Per capire quale numero indicano, aggiungi ogni volta tre zeri (un ordine composto da centinaia, decine, unità). Completa scrivendo i due nomi adatti.

Le unità di misura anglosassoni

Non in tutto il mondo si utilizzano le unità di misura del Sistema Internazionale di Unità di Misura, cioè quelle che adottiamo anche noi in Italia.

Fin quasi alla fine del secolo scorso era in uso in molti paesi il Sistema Imperiale Britannico; poi anche nel Regno Unito è stato adottato il Sistema Internazionale e altri Paesi di lingua anglosassone hanno cambiato le loro unità di misura.

Alcune unità di misura appartenenti a questo particolare Sistema sono ancora adottate negli Stati Uniti, anche se con caratteristiche diverse, e rimangono nell’uso comune di altri Paesi.

1 Leggi le frasi e colora il cerchiolino: in rosa se si riferiscono a unità di misure di lunghezza, in verde se si riferiscono a unità di misure di peso, in blu se si riferiscono a unità di misure di capacità.

L’atleta si allena su una pista di 600 yarde.

Ho comperato 4 libbre di pane.

Per eliminare gli insetti infestanti dell’orto ho utilizzato un grano di antiparassitario.

Le dimensioni della finestrella del ripostiglio sono 2 piedi x 3 piedi.

Ho due pollici di spazio tra l’armadio e lo stipite della porta.

Il papà ha comperato un gallone di vino bianco da consumare alla grigliata con gli amici.

Luca ha regalato a sua madre una collana da un’oncia d’oro.

Alla festa della birra di Monaco si usavano boccali da due pinte.

Le bottiglie grandi di aranciata contengono circa un quarto di liquido.

2 Le frasi che hai letto rappresentano tutte situazioni possibili. Immagina le situazioni, deduci il valore dell’unità di misura e copia i nomi delle unità di misura del Sistema Imperiale Britannico al posto giusto nella tabella.

“Misurare” negli USA

Per esprimere in lingua inglese un peso, una lunghezza, una capacità occorre prima di tutto sapere il nome corretto in quella lingua!

1 Osserva le immagini e collega ciascuna situazione alla didascalia corrispondente, numerando.

Thomas e sua sorella Sonia si sono trasferiti con i genitori negli Stati Uniti e, oltre alla lingua, hanno dovuto imparare anche a usare le unità di misura “americane”.

1. My bracelet is eight inches long.

2. My friend John, a fisherman, finds a one-once gold nugget in the creek.

3. Granny uses two pounds of flour to make my birthday cake.

4. The school corridor is ten yards long.

5. Dad put fifteen gallons of gasoline in his car.

6. My sister Sonia and I drink a pint of milk every day.

Compito di realtà

Il time table

Il time table è una tabella che contiene le indicazioni di una serie di eventi o attività e l’orario in cui si svolgono.

Completa il time table della tua giornata scolastica, indicando i tempi e le attività.

Giorno

Orario Attività Luogo Insegnanti presenti

8:30

Ora completa il time table delle tue attività pomeridiane non scolastiche dal lunedì al sabato.

Giorno Attività Orario Luogo

Lunedì

Martedì

Mercoledì

Giovedì

Venerdì

Sabato

Sul tuo quaderno costruisci poi il time table di una domenica tipo. Confronta le attività che svolgi nelle ore della domenica con quelle svolte nello stesso orario durante la settimana.

LA CLASSE CAPOVOLTA

Leggere un time table

Gaia deve partire per Roma insieme alla sua amica Irene. Si sono date appuntamento alle ore 12 davanti al Comune di Novate Milanese, dove abita Irene.

Gaia abita a Milano e dovrà prendere l’autobus n. 89 per arrivare all’appuntamento.

Osserva il time table e rispondi.

Autobus n. 89

Orario

Dalle ore 6 alle ore 9 ogni 15 minuti alle:

00 15 30 45

Dalle ore 9 a fine servizio ogni 20 minuti alle:

00 20 40

Per compiere il tragitto l’autobus impiega circa 25 minuti. Poi Gaia dovrà anche camminare a piedi per altri 10 minuti.

• A che ora dovrà prendere l’autobus?

Le due amiche hanno fatto una ricerca per sapere come raggiungere la stazione Centrale di Milano dal Comune di Novate.

• Possono utilizzare una app? Quale?

• A che cosa serve?

• Colora sulla schermata in azzurro il tragitto che faranno a piedi, in blu quello che faranno in treno, in verde il tragitto in metropolitana.

• Per quanto tempo le due amiche dovranno camminare, “spostarsi a piedi”?

• A che ora prenderanno il treno da Novate Milanese?

• A che ora prenderanno la metropolitana da Cadorna?

12:09 12:13 12:28 12:41 12:49

Comune di Novate Milanese A piedi

Circa 4 minuti, 250 m

Novate Milanese

Stazione Trenord 15 min (4 fermate)

Stazione Ferroviaria Cadorna A piedi

Metropolitana Cadorna

M2 direzione Gessate 8 min (5 fermate)

Stazione Centrale di Milano

Lavora con uno/a o più compagni/e. Dopo aver “aiutato” Gaia e Irene, stabilisci una destinazione che vuoi raggiungere partendo dalla tua scuola.

Prodotto atteso

Utilizzare gli strumenti necessari adatti (orari di autobus, treni, app…) per “costruire” un itinerario, indicando tempi e mezzi di trasporto.

Prodotto finale atteso: classe Capovolta

OBIETTIVI FORMATIVI

SPAZIO E FIGURE

• Compilazione di una tabella che compari l’area di figure isoperimetriche per comprendere la relazione tra isoperimetria ed equiestensione.

• Acquisire un atteggiamento di osservazione e problematizzazione della realtà.

• Favorire lo sviluppo delle attività metacognitive attraverso la costruzione e l’utilizzo di modelli e schemi.

• Commentare, individuare collegamenti, operare inferenze, proporre ipotesi esplicative.

• Argomentare le proprie scelte

COMPETENZE

Competenze di Educazione Civica

Competenze chiave (europee)

Competenze mirate (traguardi di competenze disciplinari)

• Lavorare insieme per raggiungere uno scopo comune.

• Competenza matematica e competenza in Scienze, Tecnologie e Ingegneria.

• Competenza personale, sociale e capacità di imparare a imparare.

• Competenza digitale.

L’alunno/a:

• riconosce e rappresenta forme del piano e dello spazio;

• descrive, denomina e classifica figure in base a caratteristiche geometriche, ne determina misure;

• utilizza strumenti per il disegno geometrico (riga, squadra) e i più comuni strumenti di misura (metro, goniometro...).

OBIETTIVI DI APPRENDIMENTO

Conoscenze (sapere)

• Saper confrontare linee, figure piane, solidi.

• Riconoscere, classificare e misurare angoli.

• Conoscere le caratteristiche dei poligoni.

• Riconoscere i vari tipi di poligoni, classificandoli in base alle analogie e alle differenze.

• Individuare e riconoscere le isometrie: simmetria, rotazione, traslazione.

• Calcolare perimetro e area di quadrilateri e triangoli.

• Conoscere le misure di superficie.

• Risolvere problemi relativi a perimetri e aree delle figure piane.

Contenuti

Abilità (saper fare)

• Calcolare perimetro e area di quadrilateri e triangoli.

• Operare con le misure di superficie.

• Risolvere problemi relativi a perimetri e aree delle figure piane.

• Differenza tra solidi, figure piane, linee.

• Le caratteristiche delle linee e degli angoli.

• Le isometrie: simmetria, traslazione, rotazione.

• I poligoni e le loro caratteristiche.

• Il perimetro e la superficie.

• Le misure di superficie.

• L’area dei quadrilateri e del triangolo.

Attività e metodologia Se è vero che la Matematica si impara “facendo”, ciò è ancor più vero per quanto riguarda lo studio dello spazio e delle figure geometriche. Troppo spesso la geometria viene proposta in modo teorico, invitando il bambino/la bambina solo a “studiare” le caratteristiche degli oggetti e le formule per calcolare perimetro e area.

Se invece lo studio delle figure prevederà la partecipazione attiva dei bambini e delle bambine, se partirà dall’osservazione della realtà e dalla manipolazione di oggetti concreti, sarà molto più facile comprendere quali sono le caratteristiche geometriche delle figure.

INTERDISCIPLINARITÀ

Discipline coinvolte

Matematica, Storia, Scienze, Tecnologia.

Il concetto di linea, ad esempio, è talvolta presentato in modo molto astratto, ma può essere facilmente compreso se allieve e allievi saranno invitati a operare con corde per creare tutti i tipi di linea possibili.

Anche l’acquisizione dei concetti di angolo e figura piana sarà molto più agevole se i bambini/le bambine potranno operare concretamente: intuiranno che si forma un angolo ogni volta che qualcosa che si sta muovendo in linea retta cambia direzione. In tal modo saranno reali protagonisti/e della loro conoscenza, imparando a imparare.

Nuclei tematici

• Storia: Le misure agrarie, pag. 47.

La misura delle superfici è stata per lungo tempo correlata al lavoro dei campi. Alcune misure agrarie sono utilizzate ancora oggi.

• Scienze: I frattali, pag. 48.

L’osservazione della natura dimostra quanto l’organizzazione delle parti segua precisi rapporti matematici.

• Tecnologia: Il triangolo nelle costruzioni, pag. 49.

Le caratteristiche delle differenti forme geometriche vengono sfruttate dalla tecnologia per la costruzione di palazzi, monumenti, grandi opere…

Compito di realtà

Tempi

Destinatari

Pavimenti e mattonelle, pag. 50.

La realtà che ci circonda mostra come sia possibile concretamente ricoprire delle superfici con campioni differenti.

L’intero anno scolastico.

Tutta la classe.

L’argomento che tratteremo

SPAZIO E FIGURE

Il concetto di spazio si costruisce in ognuno di noi fin dalla nascita. Possiamo dire che i bambini e le bambine sono diversi/e proprio perché hanno avuto esperienze spaziali differenti (luogo in cui sono cresciuti, interazione con gli oggetti e con lo spazio, possibilità di muoversi e di giocare…). Nella Scuola Primaria gli allievi e le allieve devono prendere coscienza dello spazio che li circonda: perciò la geometria e la misura devono diventare esperienze di vita, non solo studio delle misure e delle forme geometriche.

A che cosa serve la geometria

L’importanza dell’operatività

Il concetto di linea

L’analisi dello spazio e delle figure che ci circondano aiuta a:

• osservare la realtà da punti di vista differenti, utilizzando punti di riferimento non univoci;

• padroneggiare sempre meglio l’organizzazione dello spazio;

• individuare spostamenti e situazioni statiche sul piano e nello spazio;

• acquisire progressivamente una terminologia sempre più specifica per descrivere gli elementi e le relazioni spaziali.

Per l’acquisizione delle competenze relative allo spazio è imprescindibile l’operatività: la concezione di spazio di ciascuno di noi, infatti, si costruisce attraverso il movimento e la manipolazione.

I concetti di linea (curva, spezzata, mista), angolo, cambiamento di direzione vengono percepiti e compresi con facilità se sperimentati attraverso percorsi prima attuati direttamente dal bambino/dalla bambina e solo in una seconda fase riportati a livello grafico. Operare concretamente richiede tempo, ma non è ”perdere tempo”. Se le conoscenze sono realmente patrimonio personale, rimarranno per il bambino/la bambina un bene a cui attingere per costruire le conoscenze future.

È bene ricordare che il concetto di retta è molto difficile da assimilare, perché la retta è diritta e illimitata, ma tutto ciò che ci circonda ha limiti ben precisi. Perciò, l’insegnante terrà conto di questa difficoltà, considerando che l’acquisizione del concetto di retta come ente geometrico infinito avverrà negli anni successivi. Per facilitare la comprensione del concetto di retta è opportuno realizzarla graficamente sempre utilizzando agli estremi il tratteggio, che ne indica la prosecuzione all’infinito.

Per acquisire i concetti di linea retta, curva, spezzata, sono utili esercizi svolti in classe o in palestra e che prevedono differenti tipologie di percorsi.

Angoli e figure piane

Anche l’acquisizione dei concetti di angolo e di figura piana risulterà molto più facile, se collegata a esperienze concrete.

I bambini e le bambine posseggono già un concetto intuitivo di angolo e utilizzano la parola stessa nel linguaggio quotidiano (calcio d’angolo, il negozio all’angolo, il foglio è piegato e ha fatto un angolo...). L’acquisizione precisa del concetto di angolo è, però, complessa. Anche per una persona adulta è difficile comprendere come l’ampiezza dell’angolo non dipenda dalla lunghezza dei lati che lo racchiudono.

L’angolo può essere definito in due modi:

• come concetto “statico”, cioè come spazio compreso tra due semirette che hanno la stessa origine;

• come concetto “dinamico”, cioè come spazio descritto da una semiretta che ruota attorno alle sua origine.

Come introdurre l’argomento e didattica partecipata

È bene, perciò, presentare agli allievi e alle allieve entrambe le definizioni:

• osservando diversi angoli presenti nella realtà (lo spazio tra due lati del pavimento, tra due lati della superficie del banco..);

• ottenendo angoli attraverso la rotazione.

Per fare esperienza concreta degli angoli, i bambini e le bambine possono utilizzare una bacchetta: ne segneranno la posizione su un foglio disegnandone il contorno e la faranno ruotare, tenendo fermo un estremo. Per evidenziare meglio l’angolo si può stendere un leggero strato di colore sulla bacchetta, in modo che esso venga distribuito sul foglio durante la rotazione.

I bambini e le bambine potranno costruire un semplicissimo strumento unendo con un fermacampioni due striscioline di carta. Quando sono sovrapposte l’angolo è nullo. Tenendo ferma una strisciolina e ruotando l’altra si ottengono angoli sempre più grandi, fino a ottenere l’angolo di ampiezza maggiore: l’angolo giro. Nella presentazione delle figure piane è consigliabile far costruire molte figure, utilizzando cannucce da bibita, piegando la carta o anche semplicemente disegnando e ritagliando. Attraverso la manipolazione, gli alunni e le alunne impareranno non solo le caratteristiche delle figure piane, ma anche l’uso di strumenti semplici, ma importantissimi: la matita e il righello!

Uno degli argomenti più importanti della classe quarta è costituito dallo studio dei poligoni e dall’apprendimento delle tecniche per calcolare aree e perimetri. Affinché i bambini e le bambine abbiano ben chiaro il concetto di area e perimetro si può introdurre l’argomento nel seguente modo.

Dopo aver osservato alcuni solidi che i bambini/le bambine possono ritrovare nell’ambiente attorno a sé, si osserverà come essi siano chiusi da facce che sono figure piane.

Per analizzare poi la figura piana si appoggeranno i solidi su uno strato di sabbia o di farina di mais, osservando l’impronta che essi lasciano e proponendo alcune domande stimolo.

• Quale impronta lascia una scatola?

• Quale impronta lascia la stessa scatola se la appoggio su un’altra faccia? Si inviteranno a passare la mano sull’impronta lasciata dalla scatola, e si stimoleranno ulteriori riflessioni.

• È possibile usare solo un dito per “accarezzare” tutto lo spazio dell’impronta?

Infine, si chiederà agli alunni e alle alunne di ripassare il contorno dell’impronta con il dito, sottoponendo altre semplici domande.

• Il dito ha descritto una linea o ha “accarezzato” uno spazio?

• Quante volte il dito ha cambiato direzione?

È importante che i bambini/le bambine comprendano la differenza tra il contorno e lo spazio che esso racchiude: spesso i concetti di perimetro e area risultano di difficile comprensione perché i bambini/le bambine hanno operato poco con oggetti concreti.

È consigliabile ripassare il contorno di figure che sembrano figure piane perché hanno uno spessore sottile (i blocchi logici sottili, i pezzi sottili delle costruzioni), facendo osservare e valutare le differenze tra il disegno e l’oggetto. Il disegno è la rappresentazione “astratta” sul piano della faccia. Non ha spessore (o almeno è talmente sottile che è trascurabile).

• Se si ripassa il contorno di un pezzo rotondo quale figura si ottiene?

• Quante volte la matita ha cambiato direzione? (Le risposte più corrette sono “infinite volte” o “in continuazione”. Se i bambini/le bambine facessero fatica a rendersene conto, si può chiedere loro di tracciare il contorno di una figura che ha come base un rettangolo utilizzando il righello e di ripetere poi l’operazione per il contorno del pezzo rotondo. Perché nel secondo caso non sono riusciti a utilizzare il righello?).

Oggetti, impronte, contorni

1 Osserva l’immagine e rispondi.

• Questa agendina è un solido, una figura piana o una linea?

– Osservala ancora con attenzione: ti accorgerai che ha 6 facce, uguali a due a due.

– Se viene appoggiata sulla faccia che sta davanti, su quella laterale e su quella che sta sopra o sotto si ottengono tre impronte, come vedi nel disegno sottostante.

• Usa tre colori, uno per ciascuna impronta, e colora nell’oggetto stilizzato la faccia che l’ha prodotta.

• Per colorare le impronte hai utilizzato una riga continua? A B C

2 Ripassa il contorno delle tre impronte prima con il dito, poi utilizzando una matita colorata e il righello. Infine rispondi.

• Il dito ha cambiato direzione descrivendo il contorno della figura?

• Hai potuto tracciare una sola linea con il righello attorno alla figura o hai dovuto tracciare più linee? Quante?

3 Immagina di appoggiare i solidi sulla sabbia e rispondi.

• Quale impronta lascia la piramide se viene appoggiata sulla sua faccia di base?

• E se viene appoggiata di lato?

• Quale impronta lascia il prisma se viene appoggiato sulla sua faccia di base?

• E se viene appoggiato di lato?

• Quale impronta lascia il cilindro se viene appoggiato sulla sua faccia di base? piramide cilindro prisma

Piegare le figure

1 Esegui e rispondi.

• Disegna un quadrato e ritaglialo. Piegalo a metà, sovrapponendo un lato su quello opposto, poi aprilo.

Quali e quante figure hai ottenuto?

Sono tutte uguali?

• Ora piega il quadrato come ha fatto prima e poi piegalo ancora sovrapponendo i due lati più corti, poi aprilo.

Disegna le piegature sulla figura e rispondi. Quali e quante figure hai ottenuto? Sono tutte uguali?

• Che cosa succede se oltre alle due piegature che hai fatto prima, pieghi il tuo foglio lungo la diagonale?

Disegna le piegature sulla figura e rispondi. Quali e quante figure hai ottenuto? Sono tutte uguali?

2 Ora ripeti l’esperienza usando un rettangolo. Disegna le piegature sulla figura e completa.

• Dopo una sola piegatura hai ottenuto , tra loro.

• Dopo 2 piegature hai ottenuto , tra loro.

• Dopo 3 piegature hai ottenuto , tra loro.

3 Utilizza di nuovo un quadrato. Piegalo a metà lungo la diagonale e aprilo. Disegna le piegature sulla figura e rispondi.

• Quali e quante figure hai ottenuto? Sono tutte uguali?

• Ripeti la piegatura che hai fatto prima, poi piega a metà lungo l’altra diagonale.

• Quali e quante figure hai ottenuto? Sono tutte uguali?

4 Ora continua tu utilizzando altre figure piane e piegando il foglio come vuoi e quante volte vuoi. Osserva le figure che si vengono a formare.

I punti di vista diversi

Usando pezzi di costruzioni, costruisci un cubo. Osservalo da diversi punti di vista, poi svolgi l’esercizio successivo.

1 Due bambini/e (A e B) osservano un cubo come questo, mettendosi nelle posizioni che vedi. Rispondi.

• A e B vedono l’oggetto nello stesso modo o in modo diverso?

A

B

• Se un terzo bambino osservasse il cubo dall’alto, lo vedrebbe come lo vedono A e B?

• Se un terzo bambino osservasse la scatola dall’alto, la vedrebbe come la vedono A e B? A B

2 Due bambini/e (A e B) osservano una scatola come questa, mettendosi nelle posizioni che vedi. Rispondi.

B

B

A

A• A e B vedono l’oggetto nello stesso modo o in modo diverso?

3 Claudia, Francesca e Fabio, affascinati dalla civiltà sumera, hanno costruito con il cartoncino un modellino di ziggurat e ora lo osservano da punti di vista differenti. Disegna come vedono il solido.

Francesca lo osserva dal basso.

Fabio lo osserva di lato.

Claudia lo osserva dall’alto.

Le misure agrarie

Per misurare le superfici, oggi si utilizzano il metro quadrato e i suoi multipli e sottomultipli.

Per le grandi superfici, come i terreni agricoli, si prendono in considerazione anche le misure agrarie, cioè utilizzate solo a questo scopo. Andando indietro nel tempo, poi, si incontrano unità di misura ancora più strane.

Queste sono le misure utilizzate per la misurazione dei terreni agricoli: ettaro, ara, centiara. Corrispondono, rispettivamente, all’ettometro quadrato, al decametro quadrato e al metro quadrato. Ancora oggi le puoi ritrovare nei documenti del catasto, l’ufficio dove sono registrati tutti i proprietari dei terreni.

1 Completa le equivalenze.

1 ha (ettaro) = 1

1 a (ara) = 1

1 ca (centiara) = 1

1 ha = a

1 a = ca

1 ha = ca

2 Segna con una X, in base alle tue conoscenze o al tuo ragionamento.

• Tra le misure agricole la più utilizzata è l’ettaro. Secondo te, perché?

Perché sono misure antiche usate quando non si conoscevano i numeri decimali.

Perché i terreni agricoli sono generalmente vasti.

Perché i contadini non sapevano misurare superfici piccole.

• L’unità di misura principale delle misure agricole è l’ara.

Da che cosa lo puoi dedurre?

È scritta in stampato minuscolo.

È l’unica che non ha un prefisso.

• Che cosa indica il simbolo “ca”?

Un centesimo di ara.

Un centinaio di are.

3 Rispondi.

Gli antichi Romani utilizzavano come unità di misura lo iugero: corrispondeva alla quantità di terreno che una coppia di buoi poteva arare in una giornata. In latino “jugum” significa “giogo”. In Lombardia invece si usava un’unità di misura di superficie detta “piò di terra”, dal nome dato all’aratro: “piò” (in antico longobardo “plom”). Che cosa avrà indicato questa unità di misura?

I frattali

Il frattale è una figura geometrica dalla forma particolare: non cambia aspetto se lo si osserva a occhio nudo o con il microscopio, perché ripete sempre la stessa forma, ma in scala differente. La parola frattale deriva dal latino “fractus”, che significa “rotto”, “spezzato”, “frammentato”.

I frattali sono perciò forme spezzate e ognuna è uguale a tutte le altre: una parte del frattale ha la stessa forma dell’intero frattale.

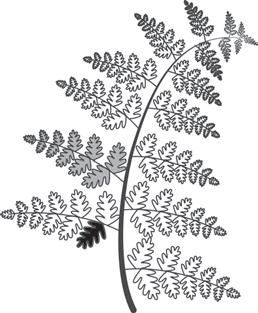
1 In natura puoi osservare molte forme di frattali. Osserva un cavolo romano e una felce, poi rispondi.

• Riesci a vedere come la forma dell’intero cavolo sia ripetuta in ciascuna “rosetta” che lo forma?

• Come sono l’intera felce, la piccola foglia nera e la parte grigia scura?

2 Continua tu a disegnare i rami dell’albero.

Il triangolo nelle costruzioni

Se costruisci alcuni poligoni con le cannucce, ti accorgerai che è facile schiacciare un quadrato o un rettangolo; invece, i triangoli reggono bene la pressione. Questa caratteristica del triangolo è stata utilizzata nella costruzione di strutture grandi e piccole.

1 Osserva una sezione di un foglio di cartone e descrivila.

2 Fai questa esperienza per capire perché il cartone ha quella struttura particolare.

Appoggia un foglio tra due scatole. Appoggia sul foglio una matita alla volta fino a quando il foglio riuscirà a sorreggerle. Ora piega il foglio a fisarmonica e ponilo ancora tra le due scatole.

Appoggia sul foglio una matita alla volta. Prova anche con oggetti più pesanti.

• Che cosa succede?

• Perché?

3 Osserva queste costruzioni. In esse ricerca la presenza di triangoli e colora il contorno di alcuni di essi.

Traliccio dell’alta tensione

Torre Eiffel a Parigi in Francia

Biosfera dell’Expo di Montreal, in Canada

Compito di realtà

Pavimenti e mattonelle

Lavora in gruppo.

• Ognuno/a di voi dovrà osservare nella realtà che lo circonda (a casa, per strada, a scuola, in biblioteca…) il maggior numero possibile di pavimentazioni.

• Ognuno/a fotograferà le tre pavimentazioni che lo/la hanno maggiormente incuriosito/a.

• A gruppi, osservate le immagini portate. Numerate le immagini e compilate uno schema simile a questo.

n. immagine Pavimento interno o esterno? Mattonelle tutte uguali? Forma delle mattonelle 1 2

• Tra le pavimentazioni che avete osservato ve ne sono alcune che sono formate da mattonelle della stessa forma, ma poste in modo differente, come ad esempio queste?

• Osservando queste due pavimentazioni, in quale si sono dovute tagliare un maggior numero di mattonelle?

• Tra tutte le immagini che avete portato sceglietene alcune che vi piacciono maggiormente e riproducetele, lavorando a coppie, su fogli quadrettati. Osservate con quali forme è più facile ricoprire l’intero foglio. Infine, colorate come preferite ed esponete le vostre “opere”!

Isoperimetria ed equiestensione

Leggi con i compagni e con le compagne i dialoghi e rispondete.

Prendo uno spago e lo tengo tra le mani in questo modo. Ora allontano un po’ le mani tra loro, avvicinando le dita. Come sono i due rettangoli che ho formato con lo spago?

Naturalmente hanno lo stesso perimetro e la stessa area. Lo spago è sempre lo stesso e anche lo spazio che c’è dentro: mica può scappare fuori dallo spago!

• Che cosa ne pensate? Siete d’accordo con la risposta data dal secondo ragazzo?

• Come avreste risposto voi?

Provate anche voi a “lavorare” con lo spago, come il primo ragazzo. Osservate i risultati e discutete tra di voi.

Poi, passate a una fase “astratta”. Disegnate più rettangoli possibili isoperimetrici e stabilite se l’area varia oppure no. Compilate una tabella che evidenzi le variazioni delle misure dei lati con il perimetro e l’area delle figure ottenute.

Prodotto atteso

Compilazione di una tabella che compari l’area di figure isoperimetriche per comprendere la relazione tra isoperimetria ed equiestensione.

Prodotto finale atteso: classe capovolta

OBIETTIVI FORMATIVI

RELAZIONI, DATI E PREVISIONI

• Organizzazione di una gita per rilevare nella realtà le variabili statistiche e i rapporti numerici, le misure, le forme geometriche.

• Acquisire un atteggiamento di osservazione e problematizzazione della realtà.

• Favorire lo sviluppo delle attività metacognitive attraverso la costruzione e l’utilizzo di modelli e schemi.

• Commentare, individuare collegamenti, operare inferenze, proporre ipotesi esplicative.

• Argomentare le proprie scelte.

COMPETENZE

Competenze di Educazione Civica

Competenze chiave (europee)

Competenze mirate (traguardi di competenze disciplinari)

• Lavorare insieme per raggiungere uno scopo comune.

• Competenza matematica e competenza in Scienze, Tecnologie e Ingegneria.

• Competenza personale, sociale e capacità di imparare a imparare.

• Competenza in materia di Educazione Civica.

L’alunno/a:

• ricerca dati per ricavare informazioni e costruisce rappresentazioni (tabelle e grafici);

• ricava informazioni anche da dati rappresentati in tabelle e grafici;

• riconosce e quantifica, in casi semplici, situazioni di incertezza.

OBIETTIVI DI APPRENDIMENTO

Conoscenze (sapere)

• Classificare e interpretare classificazioni mediante diagrammi di Eulero–Venn, di Carroll, ad albero.

• Acquisire la capacità di raccogliere dati.

• In situazioni concrete valutare il grado di probabilità del verificarsi di un evento.

Contenuti

• Le relazioni.

• Le classificazioni.

Abilità (saper fare)

• Saper mettere in relazione.

• Leggere e interpretare i dati di un’indagine.

• Calcolare la moda e la media.

• Rappresentare dati mediante grafici.

• I diagrammi di Venn, di Carroll, ad albero.

• Le indagini statistiche.

• I grafici.

• La probabilità.

Attività e metodologia La capacità di classificare è fondamentale per lo sviluppo del pensiero logico. È importante far rilevare agli allievi e alle allieve che anche nello studio delle altre discipline si operano classificazioni (in Scienze quando si classificano gli esseri viventi, in Geografia quando si classificano gli elementi del territorio….).

I bambini/Le bambine dovranno imparare non solo a classificare materiale concreto, ma anche a rappresentare le classificazioni con adeguati diagrammi. Anche lo studio dei grafici è fondamentale: grafici e tabelle di differente tipo sono utilizzati quotidianamente per trasmettere le informazioni.

Il bambino/La bambina dovrà perciò imparare l’importanza della raccolta dei dati e della loro classificazione. Il passo successivo sarà ricercare un’adeguata strategia per rendere immediatamente visibili e fruibili le informazioni attraverso l’uso di diversi tipi di grafico.

Ci si soffermerà anche sul concetto di enunciato. I bambini/Le bambine dovrebbero già aver chiaro che non a tutte le frasi è possibile attribuire un valore di verità, ma sarà necessario controllare che tale competenza sia stata acquisita con sicurezza.

Come sempre la metodologia adottata privilegerà il cooperative learning e la didattica partecipata e attiva.

INTERDISCIPLINARITÀ

Discipline coinvolte

Matematica, Scienze, Geografia, Educazione Civica

Compito di realtà

Nuclei tematici

• Scienze: La classificazione delle piante, pag. 58. Gli strumenti della Matematica aiutano gli scienziati nella classificazione degli esseri viventi.

• Geografia: La popolazione in Italia, pag. 59. Dai grafici si possono ricavare informazioni utili per comprendere meglio la situazione passata, presente e futura della popolazione in Italia.

• Educazione Civica: I gratta e vinci, pag. 60. Ragionare in termini matematici su situazioni concrete aiuta a comprenderne meglio le implicazioni e le ricadute anche sociali.

Quale grafico è più adatto?, pag. 61.

Diagrammi e grafici sono molto utilizzati, ma è necessario anche capire quale sia meglio utilizzare in base alla situazione: questo si può comprendere meglio in situazioni concrete.

Tempi L’intero anno scolastico.

Destinatari

Tutta la classe.

L’argomento che tratteremo Perché sono importanti le rappresentazioni attraverso diagrammi?

Quali tappe seguire

RELAZIONI, DATI E PREVISIONI

Il disegno è la prima forma di astrazione della realtà: attraverso di esso il bambino rappresenta ciò che vede, cogliendone gli aspetti essenziali.

Fin dalle prime classi il disegno è utilizzato in Matematica per rappresentare visivamente le quantità, per visualizzare la situazione descritta nei problemi, per stabilire corrispondenze biunivoche e non. Man mano che i bambini e le bambine crescono, però, al disegno viene data sempre meno importanza. È invece fondamentale incoraggiare i ragazzi e le ragazze a rappresentare le situazioni osservate attraverso disegni simbolici, che non devono necessariamente essere “belli”, ma devono essere efficaci, devono cioè sintetizzare in modo chiaro la situazione per poterla comunicare ad altri/e.

La rappresentazione simbolica implica un processo mentale molto importante: cogliere l’essenzialità del concetto, tradurlo in una rappresentazione visiva chiara, efficace, fruibile da tutti al di là delle parole. La rappresentazione grafica e simbolica è dunque sintomo della “proprietà” del concetto e della capacità di esporlo.

Le rappresentazioni simboliche sono propedeutiche all’uso dei diagrammi, tra i quali i più utilizzati sono i diagrammi di Venn, di Carroll e le tabelle a doppia entrata. Talvolta alle attività di classificazione viene data poca importanza, valutandole come troppo semplici per bambini e bambine delle ultime classi di Scuola Primaria. È bene però ricordare che imparare a classificare, cioè a riconoscere uguaglianze, similitudini e differenze, è fondamento di qualsiasi attività scientifica.

Imparare sia a classificare sia a rappresentare le classificazioni attraverso i diagrammi è importante, perché aiuta il bambino e la bambina a:

• scoprire analogie e differenze;

• scegliere quali caratteristiche sono molto rilevanti e quali lo sono in misura inferiore;

• argomentare le proprie scelte.

Per aiutare bambini e bambine a classificare, anche utilizzando i diagrammi, è necessario seguire le seguenti tappe:

• dare spazio all’osservazione diretta e alla descrizione di gruppi di oggetti o di persone;

• portare il bambino e la bambina a essere capaci di descrivere in tutte le loro caratteristiche gli oggetti presi in considerazione: per esempio, non solo la forma, ma anche il colore, la funzione, il materiale da cui sono composti… (sviluppo del linguaggio);

• abituare all’uso della negazione (i bambini e le bambine spesso descrivono un oggetto elencando solo le caratteristiche che possiede, non quelle che “non possiede”);

• comprendere il significato e l’uso dei connettivi;

• rappresentare le situazioni utilizzando tutti i tipi di connettivi.

L’importanza degli enunciati e delle parole chiave

In questo lavoro è importante far riflettere gli alunni e le alunne su che cosa sia un enunciato: si definisce enunciato una frase di cui sia possibile stabilire con certezza il suo valore di verità.

Per esempio:

• Milano è una città del Piemonte. è un enunciato falso, ma è un enunciato, perché è possibile dire con certezza se la frase è falsa o vera.

• Milano è una città della Lombardia. è un enunciato vero.

• Milano è una bella città. non è un enunciato, perché il valore di verità non è universale.

È importante far capire agli allievi e alle allieve l’importanza di poter definire con certezza il valore di verità, distinguendo gli enunciati dai “non enunciati”. Infatti, spesso i bambini e le bambine confondono l’enunciato falso con un non enunciato.

È altrettanto importante abituarli/e all’uso corretto di alcune parole chiave (connettivi e quantificatori): solo, almeno, tutti, non di più, al massimo, non meno di, e, o, se... allora…

I connettivi e i quantificatori

1 Osserva gli ombrelli e rispondi.

• Qual è l’ombrello che: non è aperto, non è a pallini, non ha il puntale, ha il manico ricurvo ed è nuovo? È l’ombrello

• Qual è l’ombrello che: non è aperto, non è a pallini, ha il puntale, non ha il manico ricurvo e non è nuovo? È l’ombrello

2 Disegna quattro ombrelli che abbiano le caratteristiche date.

• Tutti sono aperti.

• Almeno uno è a pallini.

• Non più di due hanno il puntale.

• Solo uno ha il manico ricurvo.

Gli enunciati e le classificazioni

1 Solo alcune di queste frasi sono enunciati. Colorale in azzurro.

Ora sta piovendo. Domani pioverà. Mauro ha quindici anni.

Elisa è la più alta della classe.

Nadia è la più simpatica della classe. 8 + 10 = 11

2 Leggi i seguenti enunciati con attenzione, individua i posti a tavola e scrivi i nomi.

• Giada, Raul, Leo, Tino e Nadia sono seduti attorno a un tavolo rotondo.

• Nadia siede tra Leo e Raul.

• Giada è vicino a Raul, ma non vicino a Leo.

3 Leggi il problema e rispondi.

Un gruppo di amici si trova al ristorante. 4 di loro ordinano solo il primo, 4 ordinano solo il secondo, 3 hanno poca fame e mangiano solo un’insalata.

• Da quante persone è formato questo gruppo di amici?

• Segna con una X quale diagramma rappresenta la situazione.

4 Leggi il problema e rappresenta la situazione nel diagramma di Venn. Disegna una X per ciascun/a bambino/a.

Alcuni/e bambini/e della classe 4aB hanno partecipato alla festa di un compagno.

6 bambini/e hanno mangiato solo la torta, 5 solo il gelato, 4 hanno mangiato sia il gelato sia la torta.

Nadia Raul

La classificazione delle piante

In tutte le discipline è importante classificare per mettere ordine tra le informazioni: in particolare nelle scienze, i biologi hanno cercato di classificare piante e animali seguendo criteri collegati a particolarità delle specie viventi.

1 Osserva questo diagramma che illustra un modo possibile per classificare i vegetali.

La pianta possiede radici, fusto, foglie?

È una pianta acquatica?

Possiede fiori o semi?

I semi sono contenuti in un frutto?

Il seme è intero o diviso in due parti?

2 Riporta al posto giusto nel diagramma il simbolo che contraddistingue le seguenti piante. Fai riferimento a quanto studiato in scienze e alle informazioni che puoi leggere.

Alghe

Pino

Muschi

Felci

Palma

(ha fiori, frutti e semi non divisi)

Melo

(ha fiori, frutti e semi divisi in due parti)

La popolazione in Italia

Oggi la popolazione italiana è di circa 60 milioni: quante sono le persone giovani? Quante quelle anziane? Come è cambiata la popolazione?

Come sarà probabilmente in futuro?

Possiamo rispondere a queste domande consultando i dati.

1 Osserva con attenzione i grafici.

2 Rispondi e completa.

• Quali tra questi grafici riportano dati reali?

• Quali tra questi grafici riportano dati possibili?

• Nel 1950 la fascia con il maggior numero di persone è: 0-5 anni. 5-10 anni.

30-35 anni.

• Nel 2017 la fascia con il maggior numero di persone è: 35-40 anni.

40-45 anni.

45-50 anni.

• Nel 2050, rispetto agli anni precedenti, le persone con età compresa tra 80 e 100: aumenteranno. diminuiranno.

• Nel 2050, rispetto al 2100, le persone con età compresa tra 80 e 100: sono in numero minore. sono in numero maggiore.

• La popolazione con età inferiore a 20 è maggiore nel: 1950. 2017. 2050. 2100.

I gratta e vinci

Ti è mai capitato di “grattare” un “gratta e vinci”? Questi “foglietti” sembrano un bel gioco, ma per molte persone sono diventate un gran problema!

I “gratta e vinci” sono tagliandi venduti dai Monopòli di Stato (“un mercato” in cui è solo lo Stato che produce e vende un prodotto). L’acquirente può controllare subito se il biglietto che ha comperato comporta una vincita: per questo motivo sono chiamati anche “lotteria istantanea”.

Furono introdotti in Italia nel 1994.

1 Il grafico indica quanti biglietti sono stati venduti dal 1994 al 2016. Osserva e rispondi.

Numero biglietti venduti: dati espressi in milioni.

19941995199619971998199920002001200220032004200520062007200820092010201120122013201420152016

• Qual è stato, tra questi, l’anno in cui è stato venduto il maggior numero di biglietti?

• Quanti ne sono stati venduti in quell’anno?

2 I biglietti venduti hanno prezzo diverso: ve ne sono da 1, 2, 3, 5, 10, 20 euro. Calcola la media del prezzo dei biglietti venduti.

1 + 2 + + + + = : 6 =

3 Se moltiplichi il prezzo medio per il numero dei biglietti venduti puoi avere un’idea di quanti soldi circa vengono spesi in un anno per questi acquisti.

Anno 2009 : Biglietti acquistati × Prezzo medio = Valore della vendita

4 Hai ottenuto un numero veramente enorme: però esso ti dice circa quanto è stato speso. Perché il dato non può essere considerato preciso? Segna con una X

Perché non si conosce con precisione quanti biglietti sono stati venduti.

Perché il calcolo è stato fatto sul prezzo medio.

Perché i numeri sono molto alti e potrei aver commesso errori di calcolo.

Compito di realtà

Quale grafico è più adatto?

Davide ha fatto un’indagine sui luoghi in cui i suoi compagni e le sue compagne hanno trascorso le vacanze. Poiché però temeva di essere poco chiaro, ha riportato i risultati attraverso 4 grafici diversi.

Discuti con i compagni e con le compagne e rispondete.

• Secondo voi tutti i grafici utilizzati da Davide sono adatti?

• Quale o quali rappresentano in modo più chiaro la situazione?

• Da tutti si può ricavare il numero di bambini/e coinvolti/e nell’indagine?

• Tra i grafici scelti da Davide manca l’ideogramma: secondo voi sarebbe stato un grafico adatto alla situazione?

Ora, a gruppi, svolgete un’indagine, avendo come riferimento la vostra classe.

• Scegliete un argomento che volete indagare. Ve ne suggeriamo alcuni, ma sarete voi a decidere quale vi interessa di più: numero di fratelli/sorelle, materia preferita, programma televisivo preferito, sport preferito, sport praticati…

• Ciascun gruppo raccoglierà i dati relativi all’argomento da indagare scelto e li illustrerà attraverso due tipi diversi di grafico.

• Valutate insieme il lavoro svolto da vari gruppi. Verificate se i tipi di grafici scelti sono i più adatti a illustrare con chiarezza i dati raccolti.

LA CLASSE CAPOVOLTA

Una gita al la scoperta della Ma tema tica

Alla fine dell’anno scolastico proponete agli/alle insegnanti di effettuare una “gita di Matematica”.

Probabilmente nel corso dell’anno avrete visitato un museo o una bella località, arricchendo le vostre conoscenze e competenze in geografia, storia, arte…

Ora, senza dovervi spostare molto, organizzate una gita per scoprire quanta

Matematica c’è intorno a voi.

Organizzatevi e procedete in questo modo.

• Scegliete un luogo facilmente raggiungibile dalla vostra scuola.

• Preparate un time table in cui segnare l’orario di partenza da scuola, quello di arrivo, i tempi di percorrenza e il tempo che volete dedicare all’osservazione del luogo.

• Giunti sul luogo annotate tutto ciò che potete osservare che sia legato alla Matematica.

• Suddividetevi in gruppi e registrate le vostre osservazioni.

• Dovrete cercare non solo la numerosità, ma anche ciò che vi ricorda la misura, la geometria e la statistica. Dunque, tenete conto dei seguenti suggerimenti.

– Relazioni, dati e previsioni: quante automobili bianche passano in un minuto? Quante rosse? È più probabile che in un’ora intera passino più automobili rosse o bianche? È probabile o certo?

– Numeri: quante persone vi sono nel luogo che state osservando? Da quanti anni esiste il monumento (la piazza, il campo giochi..)?

– Misura: quanto è grande il posto in cui vi trovate?

– Spazio e figure: quali forme geometriche potete osservare attorno a voi?

Prodotto atteso

Organizzare una gita; rilevare nella realtà i rapporti numerici, le misure, le forme geometriche, le variabili statistiche. Relazionare agli altri/alle altre le proprie osservazioni.

LOGICA LOGICA MATEMATICA MATEMATICA

Il vero banco di prova per verificare se siamo stati/e in grado di “tessere bene” conoscenze e abilità.

Un percorso per sviluppare capacità logiche esportabili in tutte le discipline.

Le attività proposte in ogni unità sono collegate da un filo conduttore presentato in forma di narrazione.

Coding della didattica

Primo e secondo step:

• giocare con i numeri;

• osservare attentamente e dedurre;

• risolvere problemi.

Dal gioco alla formazione del pensiero

LO SVILUPPO INTELLETTIVO NELLA SCUOLA PRIMARIA

I bambini e le bambine che frequentano la Scuola Primaria sono in una fase molto delicata della loro crescita sia dal punto di vista fisico sia dal punto di vista intellettivo.

La crescita intellettiva ha bisogno di stimoli adatti e diversificati tanto quanto lo sviluppo fisico: una corretta alimentazione, l’attività fisica e la salubrità dell’ambiente sono indispensabili per un armonioso ed equilibrato sviluppo fisico. Meno immediato è identificare gli stimoli più adatti per una crescita intellettiva che diventi uno strumento per capire a fondo la realtà e agire su di essa.

Un ritardo nello sviluppo fisico del bambino o della bambina è facilmente individuabile da parte delle persone adulte che con lui/lei sono a contatto (genitori, insegnanti, educatori), ma la necessità di un’opportuna stimolazione delle attività mentali e intellettive è talvolta sottovalutata.

Proprio perché in questa fase della crescita i bambini e le bambine sperimentano e sviluppano molte delle loro abilità e conoscenze che formeranno la base delle future strategie di apprendimento è non solo opportuno, ma indispensabile, favorire un approccio critico e personale all’esplorazione della realtà.

Attraverso il gioco, i bambini e le bambine imparano: il gioco è la prima palestra della mente, dell’osservazione e dell’intervento sulla realtà.

È dunque importante proporre giochi che facciano acquisire strategie per costruire un apprendimento significativo, giochi che affinino le capacità logiche, giochi che permettano di arrivare a una soluzione attraverso un percorso intellettivo personale, cioè che si adatti alla propria struttura mentale. Le abilità mentali che vanno conseguite sono quelle di saper osservare, descrivere, rappresentare, interpretare, simulare, modellizzare, saper fare collegamenti

Le persone adulte hanno il compito di stimolare i bambini e le bambine all’osservazione per cogliere le analogie e le differenze, per porre in relazione, per manipolare oggetti fisicamente. Le attitudini progettuali e di costruzione di nuove conoscenze si sviluppano attraverso la capacità di modificare la realtà dopo aver imparato a osservarla e ad agire su di essa in modo consapevole e utile al raggiungimento di un obbiettivo.

LA LOGICA: UN MEZZO, NON UN FINE

La logica non può rappresentare un fine da raggiungere, ma un mezzo per sviluppare capacità esportabili in tutte le discipline

La logica permette non solo di apprendere, ma anche di manifestare e applicare le proprie conoscenze esportandole in ambiti diversi, perciò è fondamentale per ogni disciplina. Attraverso la logica, le conoscenze si trasformano in competenze e le abilità si consolidano.

Uno dei maggiori psicologi contemporanei, Max Wertheimer, esamina il processo attraverso cui il pensiero riesce ad affrontare i problemi e a trovare delle soluzioni. Egli afferma che il pensiero produttivo non procede per prove ed errori, ma escogita altre soluzioni: prende in considerazione i dati a disposizione, li esamina, li confronta, li mette in relazione e con essi scopre le soluzioni al problema. È questa strutturazione del pensiero che va favorita nella Scuola Primaria attraverso giochi logici di vario tipo.

LA LOGICA MATEMATICA

La Matematica, almeno apparentemente, è la disciplina che più di altre dovrebbe sviluppare l’acquisizione di capacità logiche. Purtroppo non sempre ciò accade. I problemi e i quesiti matematici sono generalmente formulati in modi molto simili tra loro. Il bambino/La bambina interiorizza così una capacità di risolvere i problemi solo quando la richiesta è conforme ai classici schemi cui è abituato, ma non è in grado realmente di decodificare il testo di un problema.

I libri propongono tipologie di quesiti e di problemi che sono ripetitivi.

Questa metodologia è valida per acquisire e consolidare le abilità e le strumentalità di base, ma non per affinare le capacità logiche utili per creare una struttura mentale duttile.

Seppur sia vero che la capacità di trovare convergenze e divergenze per affrontare in modo diverso uno stesso apprendimento è analoga in tutti gli ambiti della conoscenza, è altrettanto vero che i contenuti delle discipline sono differenti e divergono le modalità di applicazione.

Da qui la necessità di offrire uno strumento didattico specifico che favorisca l’applicazione delle capacità logiche in campo strettamente matematico, ma con modalità che consentano di formare un habitus mentale.

Le situazioni problematiche poste in questo percorso scaturiscono da storie graduate per complessità e difficoltà che inducono il bambino/la bambina ad analizzare la situazione cercando di comprendere i nessi e, se necessario, trovare la soluzione al problema o comunque il modo più coerente per intervenire nella situazione.

La maggior parte degli errori compiuti dai bambini e dalle bambine della Scuola Primaria in Matematica nasce da operazioni effettuate in modo meccanico, senza dare significato a ciò che si sta facendo.

È importante, quindi, far nascere e strutturare nel bambino/nella bambina processi mentali che lo abituino a ricavare da solo la soluzione e a ricercare le strategie più adatte.

L’acquisizione di una competenza Matematica parte anche da conoscenze necessarie (gli algoritmi delle operazioni, la conoscenza delle tabelline ecc.), ma si fonda soprattutto sull‘acquisizione di procedure riutilizzabili in contesti differenti. In questo percorso, il contesto, pur essendo inserito in un mondo fantastico, non è mai artificioso; il bambino/la bambina viene coinvolto nelle storie di cui deve diventare protagonista egli stesso. Il ruolo attivo, la creazione di momenti coinvolgenti che assecondano la naturale curiosità del bambino/della bambina lo/la portano a “fare” Matematica, non solo a impararla. Se i bambini e le bambine si accostano alla Matematica comprendendo che essa non è un corpo di conoscenze già predisposto, ma un modo di interpretare la realtà, costruiranno autonomamente la propria conoscenza, che rimarrà un patrimonio solido e duraturo.

Se i giochi proposti sono situazioni problematiche ricche di contenuti e aperte all’indagine, allora ogni risposta porterà a una nuova scoperta; se il bambino o la bambina “fa” Matematica essendo coinvolto/a in prima persona, come questo percorso propone, si mette in gioco, prova a trovare strategie, diventa disponibile ad assumere un ruolo attivo e soprattutto… ricorda quanto ha imparato.

I giochi logici sono perciò una grande opportunità per dare significato ai concetti matematici, sia per il metodo di lavoro che fa recuperare un rapporto “sano” con la Matematica, spesso materia non molto amata dai bambini e dalle bambine, sia perché perseguono l’acquisizioni di competenze indispensabili per stabilizzare ed esportare la conoscenza.

LA METODOLOGIA

All’inizio di ogni serie di Unità di Apprendimento, l’insegnante troverà alcune indicazioni metodologiche per realizzare meglio il lavoro proposto.

In tutti i casi, i concetti logici sono introdotti gradualmente attraverso giochi che tengono conto sia delle conoscenze pregresse dei bambini e delle bambine sia della realtà in cui vivono, ma che stimolano anche il mondo della fantasia, che è parte integrante della realtà di bambini e bambine in età scolare.

Gli esercizi sono sempre preceduti da una storia e da una spiegazione che ambientano l’esercizio per indurre il bambino e la bambina a viverlo come “situazione” e non come esercitazione. Le attività non sono accompagnate da una consegna precisa, perché l’alunno/a deve imparare ad attivare capacità interpretative più che di semplice comprensione: deve esser invitato/a a osservare la situazione del protagonista e a svolgere le sue stesse azioni, a entrare nella situazione rappresentata. Nel proporre il lavoro, l’insegnante terrà ben presente che alcuni esercizi non sono facili e potrebbe succedere che alcuni/e alunni/e, se non sono abituati/e a risolvere quesiti logici, non riescano a comprendere il lavoro da svolgere o non siano in grado di rispondere alle richieste, sviluppando atteggiamenti di delusione e di sfiducia in se stessi/e. Ciò può essere evitato facilmente procedendo in modo graduato.

In qualsiasi caso occorre spiegare agli alunni e alle alunne che è importante anche solo provare a risolvere i problemi posti. Il fine non è trovare la soluzione ai quesiti, ma imparare a mettere in atto processi risolutivi diversificati e adatti alla situazione problematica.

PROGRAMMAZIONE

OBIETTIVI GENERALI

• Saper osservare, discriminare e dedurre.

• Distinguere, riconoscere, classificare le caratteristiche di un oggetto, di un evento, di una storia.

• Ordinare secondo criteri (quantitativi e qualitativi).

• Stabilire e riconoscere relazioni e rapporti tra oggetti e tra situazioni.

• Sviluppare le abilità logiche.

• Favorire la crescita del senso critico.

• Saper rappresentare situazioni e procedimenti mentali.

OBIETTIVI SPECIFICI

NUMERI

SPAZIO E FIGURE

• Cogliere nella realtà elementi ricorrenti.

• Classificare numeri, figure, oggetti, a seconda dei contesti e dei fini.

• Conoscere le caratteristiche dei numeri.

• Eseguire calcoli mentali.

• Saper fare previsioni sui risultati di un’operazione.

• Conoscere numeri palindromi.

• Eseguire operazioni tra numeri in contesti differenti.

• Comprendere la regolarità in una sequenza.

• Trasformare i simboli in quantità.

• Riconoscere in una situazione problematica il rapporto simbolo-valore e saperlo utilizzare.

• Comprendere e utilizzare i connettivi logici.

• Cogliere analogie, differenze e comprendere le relazioni causali.

• Riconoscere le relazioni tra numeri.

• Conoscere il grado di probabilità del verificarsi di un evento.

• Riconoscere le combinazioni possibili tra numeri.

• Saper operare in basi numeriche diverse.

• Riconoscere le figure in contesti diversi.

• Classificare utilizzando i connettivi logici.

• Realizzare percorsi in base a variabili date e saperli confrontare.

• Osservare con attenzione per cogliere i particolari, le differenze, le incongruenze.

• Riconoscere che gli oggetti possono apparire da vari punti di vista.

• Percepire e rappresentare forme, relazioni e strutture.

• Saper ricostruire una figura scomposta.

• Confrontare e seriare figure geometriche diverse.

• Utilizzare il piano cartesiano in modo autonomo e creativo.

• Cogliere rapporti di simmetria.

• Riconoscere figure equiestese.

• Saper misurare utilizzando modelli adatti.

• Comprendere i rapporti, spaziali e non, tra gli elementi osservati.

• Cogliere i significati nascosti.

• Operare con le coordinate polari.

PROBLEMI

• Leggere con attenzione un testo per cogliere i dati.

• Utilizzare rappresentazioni adeguate.

• Utilizzare le rappresentazioni per ricavare dati.

• Imparare a costruire ragionamenti.

• Descrivere e classificare in base a una o più caratteristiche.

• Leggere con attenzione e collegare le informazioni.

• Riconoscere e discriminare i dati di un problema.

• Analizzare i dati di un problema per trovare una soluzione.

• Risolvere problemi utilizzando diverse strategie.

• Interpretare i dati e ricavarne informazioni.

• Risolvere quesiti e problemi utilizzando più soluzioni.

• Rendersi conto che i processi risolutivi possono essere diversi e molteplici.

Prima unità

Primo Step

INDICAZIONI METODOLOGICHE

Il percorso proposto in questa Guida è suddiviso in due sezioni. In ognuna di esse sono contenute tre unità didattiche che vertono su tre temi portanti: il numero, l’osservazione, la soluzione dei problemi.

Nelle tre unità, le differenze sono date dalla tipologia degli esercizi, ma le abilità che vengono stimolate sono le stesse: l’osservazione attenta, la deduzione, la capacità di riconoscere e stabilire relazioni, lo sviluppo delle abilità logiche, la capacità di rappresentare le situazioni attraverso personali procedimenti mentali. Per questo motivo a volte l’insegnante troverà esercizi che perseguono il medesimo obiettivo anche in sezioni differenti.

La prima unità, che vede protagonista la fata Gigliola, invita a esaminare il rapporto simbolo-quantità (schede 1 e 4): essi dovranno riflettere sul valore del simbolo per riuscire a svolgere gli esercizi. L’insegnante potrà utilizzare questa prima unità come spunto per spiegare altri sistemi di numerazione in uso presso antichi popoli (Sumeri, Romani, Cinesi, Maya…) e per invitarli a lavorare con simboli numerici diversi.

Altre schede della prima unità sono utili per riflettere sulle caratteristiche dei numeri stessi. La scheda 3 propone di giocare con i numeri palindromi, generalmente non conosciuti da bambini e bambine: così, giocando, il bambino/la bambina apprende come si formano i numeri.

Seconda unità

Terza unità

La seconda unità, con protagonista il mago Barnabà, è incentrata su esercizi di osservazione e deduzione. Uno di essi (scheda 1) prevede anche il confronto tra figure per stabilirne l’area. La scheda può essere proposta anche se la classe non ha ancora affrontato nel programma curriculare tale argomento. Le piantine sono riportate su fondo quadrettato per aiutare il confronto, ma l’insegnante potrà anche suggerire di riprodurre le impronte su un foglio a quadretti, ritagliare in parti le figure e provare se possono essere sovrapposte.

La terza unità, di cui è protagonista la streghetta Fliggy, propone problemi di tipo diverso.

La mancanza di una consegna di lavoro precisa invita il bambino/la bambina ad attivare maggiormente le sue capacità di decodificazione della realtà, comprensione del problema e scelta della risposta. Nel caso in cui qualche bambino/a dovesse presentare difficoltà nell’individuare il compito da svolgere, l’insegnante lo inviterà a osservare e a leggere con maggiore attenzione e porrà delle domande stimolo atte a fargli comprendere la

Didattica

consegna. È bene che l’insegnante abbia un ruolo “discreto” di aiuto e di stimolo, indirizzando l’alunno/a verso la comprensione del problema.

L’insegnante inviterà a utilizzare qualsiasi metodo ritengano utile per trovare la soluzione: schemi, disegni, operazioni…

Può essere utile suggerire loro di risolvere i problemi in gruppo, in modo che ognuno possa confrontare con i compagni e le compagne le proprie idee e capire che le strategie di risoluzione possono essere diverse.

Per lo stesso motivo, è indispensabile correggere collettivamente i lavori: si metterà in luce che non vi è un solo sistema per giungere alla soluzione e anche il procedere per prove ed errori può essere proficuo.

BACCHETTE MAGICHE

Se non si osserva attentamente, dalla strada, è difficile vedere quella bellissima villa immersa nel parco dalla cui torre, ogni mattina, Gigliola osserva il sole che sorge e illumina ogni cosa. Ma chi è Gigliola? Gigliola è una fata furbetta, ma molto simpatica. A un primo sguardo, non sembra proprio una fata; tutti sanno che di solito le fate sono alte, slanciate, belle… Lei, invece, è un po’ diversa; ad esempio, non riesce a liberarsi di quei chiletti di troppo. Dovrebbe mangiare meno dolci e muoversi un po’ di più. Ma perché fare tanta fatica quando è così piacevole starsene distesa sotto gli alberi del parco a inventare tanti giochi?

In questo momento Gigliola sta giocando al Gioco delle Bacchette Magiche. Funziona così:

• Gigliola sa che per ogni magia ha bisogno di 16 punti.

• Deve fare 4 magie.

• Ogni volta utilizza lo stesso numero di bacchette, che valgano 16 in tutto.

• Le combinazioni devono essere tutte diverse.

PERCORSO A OSTACOLI

Gigliola ha un’amica. Naturalmente anche lei è una fata, si chiama Nerina e abita in una piccola casa in mezzo a un grande bosco. Nerina è una cara amica e Gigliola le vuole molto bene, anche se, alle volte, anzi spesso, combina dei guai: è proprio una pasticciona! L’altro giorno, aveva deciso di sistemare degli ostacoli magici su tutti i sentieri che, attraverso il bosco, portano alla sua casetta. Solo un sentiero sarebbe stato percorribile, ma… qual era la formula che consentiva l’accesso? – Pronto? Gigliola, ho bisogno del tuo aiuto! Non ricordo più che cosa si deve fare per percorrere il sentiero senza ostacoli.

Gigliola con pazienza osserva la cartina su cui sono visibili gli ostacoli posti su ogni strada, riflette un po’ e poi esclama: – Ma certo! Basta percorrere i tratti di strada in cui il risultato dà 25.

PARTENZA

IL GIOCO DEI NUMERI PALINDROMI

Oggi Gigliola è un po’ agitata perché nel pomeriggio verranno a trovarla Nerina e altri amici e lei deve preparare un gioco-indovinello da sottoporre loro. Ecco! Il librone di nonno Aristide le suggerisce un’idea geniale: il gioco dei numeri palindromi. Che cos’è un numero palindromo?!

Semplice: è un numero che non cambia sia che venga letto da destra a sinistra sia che venga letto da sinistra a destra, come ad esempio 45254. Ma nel librone di nonno Aristide le addizioni per formare numeri palindromi sono in parte cancellate. Che disdetta!

Ma ora Gigliola le completa.

Gigliola osserva attentamente gli addendi delle addizioni e fa una scoperta: nel primo e nel secondo numero ci sono le stesse cifre, ma le cifre

Gigliola si mette alla prova con un altro gioco. In questo caso i due addendi che, insieme, formano il numero palindromo sono anch’essi palindromi, ma sarà possibile scoprire quali sono?

LE CIFRE SONO SPARITE!

Gigliola sta passeggiando nel parco ed è tutta assorta nei suoi pensieri. Strano, che cosa sarà successo?

Di solito a quest’ora se ne sta sdraiata sull’amaca… Ha in mano il librone delle formule magiche di nonno Aristide e osserva sconsolata gli strani segni che compaiono in due pagine. Ieri aveva prestato il libro a Nerina, che voleva utilizzare alcune formule per trasformare quell’antipatico topo che le aveva rubato il formaggio. Ma qualcosa è andato storto e, invece di trasformare il topo, ha confuso le formule del libro.

Come farà adesso Gigliola a sistemare le formule?

Nella pagina a fianco dovrà sostituire i simboli con i numeri.

I NUMERI FATATI

Il salone della villa di Gigliola è stato addobbato a festa. Accanto al camino c’è un tavolo strapieno di panini, salatini, pizzette, torte e dolci di ogni tipo. Nel salone ci sono fate che chiacchierano, mangiano e giocano, perché è il compleanno di Gigliola e tutte le sue amiche sono venute a festeggiarla.

A un tratto la fata Nerina chiede a tutte le altre di fare silenzio e propone a Gigliola dei quesiti. Riuscirà la fata a risolverli?

Qual è il numero di 3 cifre, compreso tra 900 e 700, in cui ogni cifra è la metà di quella che la precede?

C’è un numero in cui il numero delle lettere che formano il suo nome corrisponde al valore del numero stesso. Qual è?

Qual è il numero più piccolo possibile formato da 3 cifre tutte diverse?

Qual è il più grande numero possibile di 4 cifre?

Qual è il numero più grande possibile, senza zeri, in cui le cifre diano come somma 4?

VIA DEI GELSOMINI, NUMERO…

Gigliola non si sorprende quando, rispondendo al telefono, sente la voce preoccupata di Nerina che le racconta di aver combinato un altro guaio. – Raccontami che cosa è successo.

E così Nerina le dice che quella mattina era andata al villaggio e, mentre percorreva la via dei Gelsomini, ha inciampato nella radice di un albero.

È caduta e ha rotto la bacchetta dei numeri. Risultato: in quattro strade sono spariti parte dei numeri civici delle case.

Il problema è che nel villaggio delle fate i numeri con cui vengono contrassegnate le case seguono ordini diversi e… particolari.

Per fortuna Gigliola, ragionando su quelli rimasti, è in grado di dire a Nerina quali sono i numeri scomparsi.

LE BOTTEGHE DELLE FATE

Non molto distante dalla dimora di Gigliola sorge il villaggio delle fate. Qui i negozi non sono come li conosciamo noi: hanno più l’aspetto di piccole botteghe, un po’ buie e strapiene di merce; ma la cosa più strana di questi negozi è proprio la merce che viene venduta. Le fate, infatti, per le loro magie, hanno bisogno di prodotti molto, molto particolari e li possono comperare solo nel loro villaggio. Ma, ancora una volta, Nerina ne ha combinata una delle sue! Ha fatto sparire le insegne delle botteghe e, al loro posto, ha fatto comparire dei numeri.

Adesso, per rimetterle in ordine, Gigliola dovrà consultare il librone, capire a quale numero corrisponde ogni insegna e scriverla.

Cappellaio

Il numero delle gobbe di 50 cammelli meno le zampe di 8 cammelli.

Stellaio

I mesi di 30 giorni in cinque anni.

Animali magici

Le zampe di 6 leoni meno le zampe di 4 vermi.

Ampollificio

Le ali di 15 aerei e 6 elicotteri.

Campanellini

Il triplo della metà dei giorni di aprile.

Polveri luminose

Il numero delle settimane che ci sono tra Capodanno e Natale.

Bacchettaio

I mesi con la Z.

Fibbie colorate

Il doppio di 53 meno la metà di 140.

UNA LETTERA MISTERIOSA

Nella casella delle lettere c’è una busta misteriosa. Gigliola la prende, la apre e inizia con calma a leggerla. Ma, a un tratto, fa un balzo sulla sedia e, scapicollandosi, sale in camera, dove inizia a preparare la valigia.

– Le bacchette, il libro di nonno Aristide, le polverine magiche, i vestiti con le stelline: c’è tutto?

È raro vedere fata Gigliola affannarsi così, ma ha una buona ragione. Ogni secolo, in una località segreta, si tiene il raduno di Fate, Maghi e Streghe; è un evento molto importante perché è in questa occasione che si prendono le decisioni che riguardano riti e formule magiche.

Gigliola sposta un vecchio armadio dietro al quale si cela il nascondiglio della mappa. Ci sono molte strade: per arrivare bisogna seguire quella indicata dai multipli di 4.

IL MAGO BARNABÀ METTE SU CASA…

Barnabà è un mago vero, ma se lo incontri per la strada non te ne accorgi: è un ragazzone sempre allegro e pieno di energia. Da poco tempo si è laureato in SMO&A (Scienze Magiche Occulte & Affini) con 220 e lode, passando dal grado di Apprendista a quello di Vero Mago con diritto ad avere, a sua volta, un apprendista. La casa nella quale è appena andato ad abitare è un modernissimo loft. Sul fondo, nascosta da un pannello in acciaio, c’è una scala che scende el laboratorio sottostante.

Barnabà deve arredare la casa e così studia la piantina su cui sono segnate le impronte di due armadi di forma diversa. Poiché ha poco spazio, compererà l’armadio più piccolo. Quale?

A Barnabà serve anche una grande scrivania. Sulla piantina ci sono le impronte di due originali scrivanie. Qual è più grande? A B C D

IL QUADRATO MAGICO

Dietro alla casa di Barnabà c’è un ampio cortile e, in un angolo, proprio sotto le finestre del mago, c’è un grande mosaico che dicono risalga all’epoca dei castelli. È una specie di “quadrato magico”; la superficie, suddivisa in esagoni, ha tanti bei disegni. È davvero bello, ma ha una particolarità: se un oggetto cade su un esagono, questo se lo inghiotte e l’oggetto sparisce! Barnabà, però, ha una speciale polvere con cui colora il riquadro nel quale sparisce l’oggetto e l’esagono lo restituisce subito! È grazie a questa polverina che Barnabà ha ancora il suo cappello da mago e la sua bacchetta magica. Infatti, uscendo precipitosamente dal suo laboratorio, questi due oggetti preziosissimi gli erano caduti ed erano spariti immediatamente. Il mago ricordava quali erano i riquadri e, dopo averli individuati nel “quadrato magico”, li ha cosparsi con la polvere colorata per farli riapparire.

UN’APPRENDISTA DISORDINATA

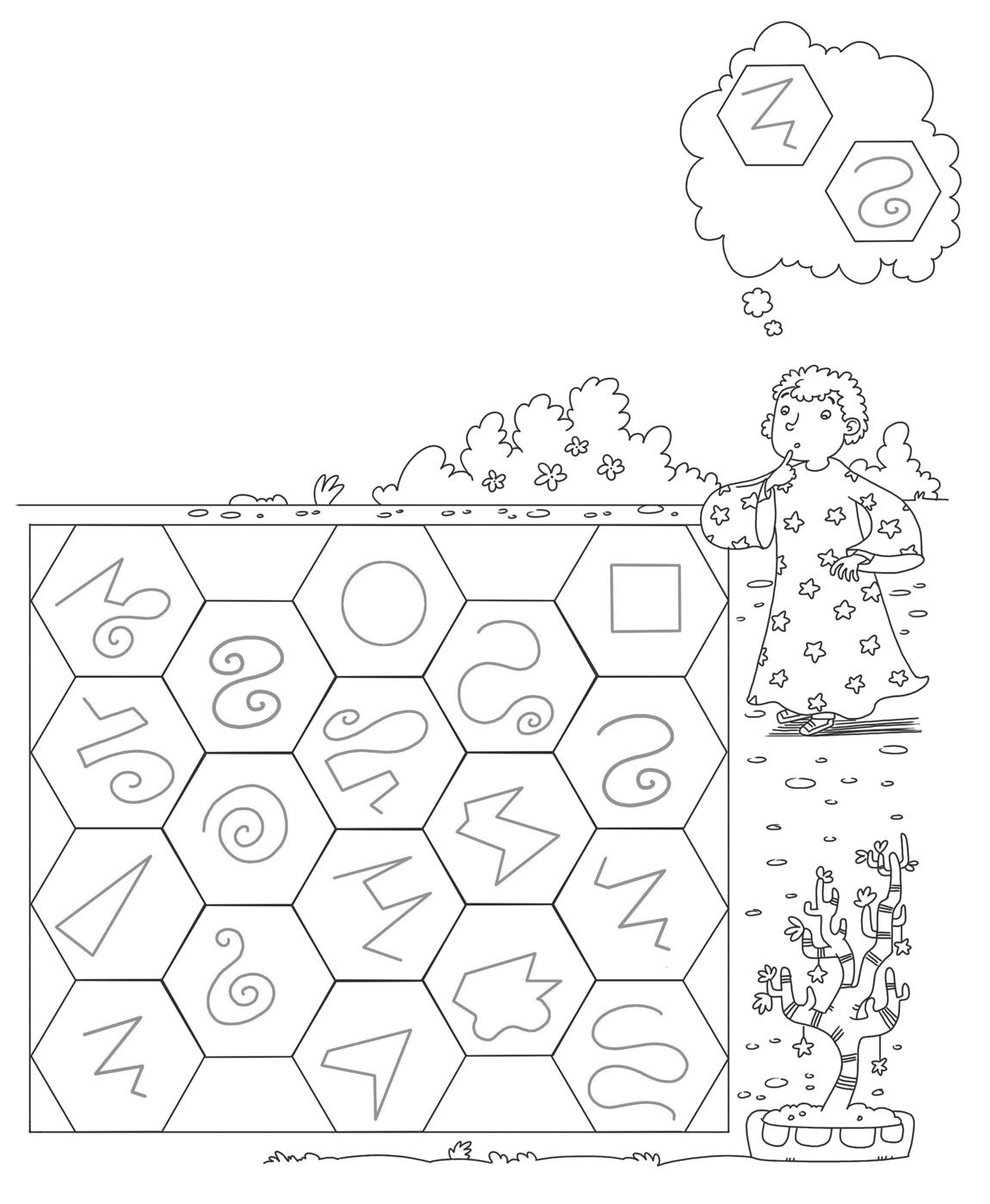
Finalmente dal mago Barnabà sta per giungere l’apprendista, che, per la verità, è in ritardo… Drrriinn! Il mago apre la porta e si trova davanti 3 bauli, 8 valigie, 14 borse, un’infinità di pacchetti e, dietro a tutta questa montagna di bagagli, compare… Virginia. – Salve, mago Barnabà, sono la tua apprendista. Scusa il ritardo, ma con tutti questi bagagli… Il mago, un po’ perplesso, le mostra il laboratorio: – Uno dei tuoi compiti più importanti sarà quello di tenere in ordine il laboratorio. – Non c’è problema, fidati di me! – risponde Virginia. Ma quando Barnabà ritorna per controllare il lavoro dell’apprendista, rimane senza fiato… ma con molta rabbia! Che pasticcio! È tutto un gran disordine. Virginia è in angolo mortificata e sussurra: – Otto oggetti si sono rotti e devono essere aggiustati.

Barnabà si guarda intorno e li cerca. Quali sono?

PARETI… INTERATTIVE!

Virginia e Barnabà si sono accomodati sul grande divano e stanno osservando le pareti del loft. Discutono animatamente.

– Queste pareti sono troppo vuote, guarda come sono tristi – afferma Virginia. – Non posso metterci i soliti quadri: nella casa di un mago serve qualcosa di… diverso. Barnabà si concentra, si alza, si avvicina a una parete, china la testa, poi si volta di scatto verso la sua apprendista. Ha avuto un’idea geniale! Corre nel suo laboratorio e prepara dei cartelloni fatti con vari materiali: carta, plastica, acciaio, legno. Poi li appende.

Accanto a ciascuno lascia un riquadro bianco in cui gli ospiti della casa dovranno scrivere delle frasi per definire ciò che è rappresentato. Uno, che serva come esempio, lo ha già preparato Barnabà.

Alcuni hanno il risvolto. Tutti hanno le stelle. Non tutti sono scuri.

UN MESSAGGIO MISTERIOSO

C’è aria di mistero oggi a casa di Barnabà. All’alba è arrivato uno strano personaggio avvolto in un mantello scuro e con un cappello calato sul volto; ha depositato una serie di buste sullo zerbino e se n’è andato senza dire una parola. Il mago ha raccolto le buste; dopo essersi accertato che nessuno lo guardasse, è entrato in casa e ha chiuso la porta a chiave. Insieme a Virginia ha aperto le buste e dentro a ciascuna c’era un messaggio cifrato di quelli che arrivano una volta ogni cento anni.

Barnabà, però, sa come decifrarlo e lo spiega alla sua apprendista:

• a ogni lettera si dovrà sostituire quella che la precede nell’alfabeto;

• poi si dovranno mettere in ordine le lettere partendo da quelle contenute nella busta più grande fino ad arrivare a quelle contenute nella busta più piccola;

• infine bisognerà trascrivere il messaggio in chiaro sullo schema sottostante.

BARNABÀ AL RADUNO DEI MAGHI

– Dai, Virginia, non abbiamo molto tempo e dobbiamo preparare tutto stando attenti a non dimenticare nulla!

– Hai ragione, Barnabà, non possiamo fare brutte figure al nostro primo Raduno dei Maghi, delle Fate e delle Streghe.

Preparati i bagagli, Barnabà e Virginia salgono a bordo di una potente auto. Dopo un lungo viaggio, finalmente ecco il villaggio in cui si tiene il raduno. Che strano posto: è un groviglio di viuzze e piazzette e non è facile orientarsi. Per fortuna hanno indicazioni precise per ritrovare i punti importanti e giungere così a destinazione. Il mago riesce a individuarli tutti e al suo passaggio i posti, per magia, si colorano.

• La casa del mago Gherardo è verde e ha le tendine a tutte le finestre.

• L’ufficio del mago Teodoro ha una pianta azzurra davanti alla porta.

• La casa dove è previsto il raduno è gialla e ha il campanello a forma di drago.

• La locanda è rosa, non ha balconi e ha un gufo sul tetto.

• L’emporio magico è arancione e si trova tra la fontana e il grande pino.

LA STANZA DEGLI SPECCHI

Barnabà il mago e Virginia l’apprendista sono emozionati: non succede tutti i giorni di partecipare a un evento così importante! Si sono dati appuntamento maghi di prim’ordine e anche gli apprendisti sembrano veramente in gamba. Virginia vuole fare una sorpresa a Barnabà per dimostrargli che anche lei è diventata una vera maghetta. Ha pensato a qualcosa che possa impressionare favorevolmente i maghi, i quali, si sa, sono vanitosi e, se nessuno li ammira, amano farlo… da soli! Così, nel salone in cui si svolge il raduno, ha costruito una stanza degli specchi; già immagina la sorpresa dei partecipanti quando, entrando nel salone, vedranno la propria immagine riflessa. Purtroppo, però, ha fatto pasticci e gli specchi riflettono in modo sbagliato. In ogni specchio si producono 6 errori. Per fortuna Barnabà li vede prima che facciano il loro ingresso i suoi illustri colleghi. Si specchia, e, per rimediare agli errori di Virginia, segna con la bacchetta i particolari sbagliati.

SI METTE IN ORDINE!

Quante cose interessanti ha scoperto Barnabà e quanti nuovi amici si è fatto! Ma il Raduno dei Maghi, purtroppo, finisce. È il momento dei saluti, degli arrivederci e poi tutto sarà smontato e non sembrerà neppure che in quel luogo ci sia stata così tanta gente. Come vuole la tradizione, sarà il partecipante più giovane con il suo apprendista a rimettere tutto in ordine. Così questa volta tocca a Barnabà e Virginia, perché sono i “pivellini”.

Sul pavimento del salone sono rimasti molti oggetti.

Loro li raccolgono formando delle coppie logiche e poi, per divertirsi, colorano nello stesso modo i due oggetti che stanno insieme. Cinque oggetti, però, non si accoppiano con nessun altro.

Virginia scrive in stampatello i nomi degli oggetti che rimangono e capisce qual è la caratteristica che li accomuna.

La caratteristiche che li accomuna è .

FLIGGY, UNA STREGA BIZZARRA

All’ultimo piano di un antico palazzo, proprio sotto il tetto, c’è una bella mansarda in cui abita Fliggy, una strega giovane e moderna. Si veste con i jeans, in testa porta una specie di cilindro con un nastro viola e per fare le magie usa un telecomando.

Quando deve uscire di casa, apre una finestra sul tetto e, con la sua scopa volante a motore, sorvola tutta la città. A Fliggy non piacciono le cose semplici: ha l’abitudine di rispondere con dei quesiti alle domande che le vengono poste. Ieri si è incontrata sul tetto del condominio di fronte con la sua amica Trillina che, vedendole addosso degli abiti nuovi, le ha chiesto il prezzo di ogni indumento.

– Che bel cappello, ti sarà costato almeno 40 pirilli! Fliggy risponde: – Non esattamente, però il prezzo avrebbe superato i 40 pirilli se fosse costato 6 pirilli in più, mentre, in realtà, l’ho pagato meno di 36 pirilli.

Trillina è perplessa, ma insiste: – E la gonna quanto ti è costata? Fliggy ci pensa un po’, poi dice: – Meno di 58 pirilli, ma se non mi avesse fatto lo sconto di 4 pirilli avrebbe superato i 60 pirilli.

– E i guanti? – chiede Trillina ormai stremata. – Meno di 10 pirilli – risponde Fliggy, –ma se avessi comperato quelli con il bottone di madreperla avrei pagato 5 pirilli in più e ne avrei pagati più di 13.

Ma Trillina ha capito quanto sono costati il cappello, la gonna e i guanti di Fliggy e annota i prezzi sul suo taccuino.

cappello:

gonna:

guanti:

L’ERBA TREMOLINA

Le streghe hanno deciso di ritrovarsi nel parco a mezzanotte di venerdì prossimo, il 17 novembre, per festeggiare la nuova scoperta di Fliggy: l’erba tremolina.

Si tratta di una pianta molto potente in grado di trasformare i sogni in realtà.

– Ma può essere anche molto pericolosa – osserva la saggia Milli.

Nel pieno della notte sei streghe sono sotto la quercia al centro del parco.

Si devono disporre in cerchio, ma la cosa non è affatto semplice: le streghe sono capricciose e superstiziose e i desideri di ciascuna vanno rispettati.

Perciò Fliggy scrive i nomi delle sue amiche sui cartellini segnaposto.

• Gelinda non vuole stare vicino a una strega con il cappello a punta.

• Fliggy vuole stare a destra di Gelinda.

• Milli si siede di fronte a Fliggy.

• Viperella non vuole essere vicino a Fliggy.

• Solo Trillina non dice nulla.

Trillina Rosaspina Milly Fliggy Gelinda Viperella

Dopo aver parlato di come si deve usare l’erba tremolina, Fliggy racconta che la sera precedente si era recata in pizzeria e, al tavolo accanto al suo, c’erano degli amici: due padri e due figli. Hanno ordinato tre pizze e ognuno ne ha mangiata una. Come è stato possibile?

La sua amica Trillina lo ha capito e ora lo svela alle altre.

QUANTI FIORI!

Fliggy ha molti amici sparsi per il mondo, che le scrivono spesso. Perciò, quasi ogni giorno, la strega scende in portineria e, oltre a ritirare la sua posta, si ferma a chiacchierare con il suo amico Berto, il portinaio.

Oggi la novità è costituita dai balconi fioriti di Viperella al terzo piano e di Gelinda al primo.

Fliggy sta spiegando a Berto quali fiori ci sono sui balconi. – Sul balcone di Viperella ci sono 10 fiori, margherite o primule, blu o gialle. Il numero dei fiori blu è lo stesso di quelli gialli. Le margherite sono 3 blu e 4 gialle. Allora mi sai dire come sono le primule?

Berto ci prova, ma… no, proprio non riesce a capire. Fliggy, allora, lo aiuta con il disegno.

Berto racconta a Fliggy che sul balcone di Gelinda, invece, ci sono 15 fiori, di cui 6 sono gialli e gli altri sono tutti rossi. I gerani sono 8 e gli altri sono tutti rose rosse.

Fliggy, in fretta e furia, fa il disegno dei vasi e in pochissimo tempo riesce a dire a Berto come sono i fiori di Gelinda.

GATTI PICCOLI, GRANDI E MEDI

È notte, ma le streghe non vanno a dormire, anzi, questo è il momento migliore per uscire, incontrarsi e chiacchierare. Basta svolazzare qua e là e trovare un tetto tranquillo o un vecchio rudere pieno di splendidi pipistrelli… Questa notte è proprio sul tetto di Fliggy che si incontrano le streghe e ognuna porta con sé il proprio gatto. Se le streghe sono strane, i loro gatti non sono da meno!

Rubasalsicce, il gatto di Rosaspina, è lungo 40 cm. La testa e la coda del gatto hanno la stessa lunghezza. La testa è la metà del corpo. Rosaspina chiede alle amiche: – Avete capito quanto misura la coda del mio gatto?

Il gatto di Gelinda, Lungobaffo, è invece piccolino, ma ha la coda molto lunga. La coda misura 12 cm ed è lunga come il corpo. La testa è 1 4 del corpo.

Gelinda dice: – Sicuramente non riuscite a dirmi quanto è lungo il mio gatto!

Miagolando arriva Pistacchio, il gatto di Trillina, che ha la testa lunga come 1 3 del corpo

e la coda che è il doppio della testa. Il gatto di Trillina è lungo 60 cm. – Chi di voi sa dire quanto misurano le varie parti di Pistacchio? – chiede la sua padrona.

Fliggy ha calcolato tutte le misure richieste:

L’IRA DI VIPERELLA

L’amica di Fliggy, Viperella, è una strega simpatica, che racconta sempre storie divertenti: con lei non ci si annoia mai.

Ma… è molto irascibile e quando si arrabbia lancia fulmini e saette tutto intorno e trasforma in pipistrello chi la fa arrabbiare. Tuttavia non è tremendissima come sembra: dopo un po’ si pente di quel che ha fatto e si lascia facilmente convincere ad annullare il maleficio. Certo, l’incantesimo dura di più se l’hanno fatta arrabbiare molto!

Ieri Fliggy ha lanciato la sua scopa a motore a tutto gas per andare da Viperella e tentare di farla ragionare. Aveva combinato un bel guaio: aveva trasformato in pipistrello:

• il mago Pepito per 3 quarti d’ora;

• lo gnomo Polifemo per 5 quarti d’ora;

• il folletto Martello per 2 ore e un quarto;

• l’orco Barabù per 2 mezz’ore;

• la fata Birbella per 8 quarti d’ora.

Fliggy, dopo aver calmato la rabbia di Viperella, le ha chiesto: – Toglimi una curiosità, ma chi ti ha fatto arrabbiare di più?

– Sono sicura che se ci pensi e ci ragioni un po’, lo capisci da sola – le ha risposto Viperella.

In effetti Fliggy ci ragiona e…

– Certo – risponde, – chi ti ha fatto arrabbiare di più è stato

Picco del Diavolo

LE VACANZE DI FLIGGY

Fliggy ha deciso di concedersi una rilassante vacanza e sta preparando l’itinerario del suo viaggio. “Partirò da Fiorevelenoso dove tornerò dopo aver visitato: Picco del Diavolo, Orridonero, Grotta tenebrosa e Vallestregata“ pensa la strega. Vuole trovare la strada più breve che le consenta di arrivare in tutti questi luoghi, però non deve passare due volte per la stessa strada e sa che il tratto che va da Orridonero a Fiorevelenoso è a senso unico. Infine, dopo aver stabilito quale sarà il percorso da fare, Fliggy carica i bagagli sulla scopa a motore, saluta Rubasalsicce, che lascia in custodia a Berto il portinaio e, spensierata, se ne va! Prima, però, segna la strada più breve sulla mappa.

Grotta tenebrosa Vallestregata

Orridonero

Fiorevelenoso

BUGIA O VERITÀ?

Berto è uno strano personaggio perché (ma solo Fliggy ne è a conoscenza) mente sempre nei giorni di domenica, lunedì e martedì, mentre dice la verità negli altri giorni.

Oggi ha detto: – Domani mentirò!

Però Berto, che è anche uno smemorato, non ricorda che giorno è oggi, ma sa con certezza che non è sabato perché il sabato passa sempre il corvo postino e oggi non è passato.

Adesso è lì, seduto sulla sedia in portineria, che si chiede: – Ma che giorno sarà mai oggi?

Fliggy ha capito.

– Ma certo – dice, – oggi è .

Alcuni giorni fa Berto, smemorato come sempre, era sempre lì a domandarsi quale giorno fosse. Sapeva che non era martedì perché il martedì sua moglie fa la torta di mele e quel giorno, invece, era andata dalla sua amica.

Ma pare che sia di moda mentire, infatti la strega Milli, che dice la verità nei giorni di sabato, domenica, lunedì e martedì, ma mente negli altri giorni, gli aveva detto: – Domani mentirò.

Che confusione, povero Berto! Ma, alla fine, se non era martedì, che giorno era?

AL RADUNO DEI MAGHI

Berto sale faticosamente le scale fino alla mansarda di Fliggy e brontola tra sé e sé: “È una raccomandata espresso urgente, con timbro segreto! Sbuff! Devo consegnargliela subito. Sbuff!”.

Da dove arriverà questa busta misteriosa?

A Fliggy tremano le mani per l’emozione mentre la apre: – Lo sapevo! Che bello, finalmente ho ricevuto l’invito a partecipare al secolare Raduno dei Maghi, delle Fate e delle Streghe… ma… e questo biglietto che cos’è?

Per partecipare all’importante Raduno devi risolvere esattamente questi quesiti.

Un contadino ha 12 animali tra cui mucche, una chioccia e dei pulcini.

Se le zampe sono in tutto 32, quante sono le mucche e quanti sono i pulcini?

Su un albero ci sono 11 ciliegie.

Un passerotto ne mangia 2 al giorno.

Ogni 2 giorni matura una nuova ciliegia. Quanti giorni impiegherà a mangiarle tutte?

Ci sono 3 pipistrelli messi in questo modo:

• 2 pipistrelli sono dietro a un pipistrello;

• 2 pipistrelli sono davanti a un pipistrello;

• 1 pipistrello è tra 2 pipistrelli.

Se al convegno vuoi partecipare, i pipistrelli devi disegnare!

6 streghe fanno 6 pozioni in 12 minuti. Quanti minuti impiegano 12 streghe per fare 12 pozioni?

Secondo Step

INDICAZIONI METODOLOGICHE

Questo secondo gruppo di tre unità riveste le finalità di quelle del primo gruppo, ma con una difficoltà crescente.

Nella prima unità, lo sceriffo Lucky Jo propone attività che invitano a giocare con i numeri per scoprirne le peculiarità. Gli esercizi prevedono calcoli mentali, riflessioni sulla struttura del numero e mettono in gioco non solo capacità di calcolo, ma soprattutto capacità logico-deduttive.

Se gli allievi e le allieve mostrassero difficoltà nel risolvere le schede 2 e 7, l’insegnante li inviterà a costruire una tabella per trovare le combinazioni possibili. È probabile, infatti, che i bambini e le bambine non possiedano ancora gli strumenti necessari per organizzare in modo logico i numeri, senza dimenticare qualche combinazione possibile. L’insegnante, però, non si sostituirà agli alunni e alle alunne, ma cercherà di stimolarli affinché trovino un loro modo personale per risolvere i problemi.

La seconda unità, che ha come protagonista il capo indiano Grande Bisonte, propone esercizi basati anche sulle proprietà delle figure geometriche. Per risolvere le schede 1 e 2 sarà opportuno far copiare e sovrapporre ai bambini e alle bambine le due figure per comprendere meglio l’equiestensione delle stesse. L’insegnante potrà poi far costruire il maggior numero possibile di figure equiestese utilizzando il tangram, facilmente costruibile anche in classe.

La terza unità ha come protagonista il pirata Thomas e propone agli allievi e alle allieve problemi di diverso tipo.

È molto importante che i bambini e le bambine si abituino a risolvere problemi formulati in modo differente dai classici problemi scolastici. Una diversa formulazione invita il bambino/la bambina a leggere con attenzione, a decodificare i dati e a utilizzare solo quelli veramente rilevanti. È utile che il bambino/la bambina si abitui a usare schemi e tabelle in modo da “visualizzare” il problema (come ad esempio nella scheda 7).

L’insegnante troverà in fondo a ogni pagina un obiettivo di apprendimento. Occorre tenere conto, però, che in ogni scheda sono richieste al bambino e alla bambina abilità diverse e molteplici.

Anche per gli esercizi di queste unità si consiglia di far svolgere i lavori più complessi in gruppo, affinché i bambini e le bambine riescano a discutere tra di loro e comprendano che i processi risolutivi possono essere molteplici e che le strategie risolutive devono adattarsi alla situazione. È anche necessario consigliare di utilizzare il maggior numero di volte possibile tabelle e schemi, perché aiutano a visualizzare il procedimento risolutivo.

Prima unità

Seconda unità

Terza unità

LUCKY JO

Nelle vaste praterie dell’Arizona, lo sceriffo Lucky Jo dà la caccia alla banda del feroce Black Jack, noto svaligiatore di banche. Nonostante siano in tanti a cercarlo, ancora nessuno ha scoperto notizie certe. Anche il numero di rapinatori che formano la banda è sconosciuto a tutti, tranne allo sceriffo. L’aiutante di Lucky Jo, Little Boy, è un tipo abbastanza sveglio, ma lo sceriffo vuole metterlo alla prova per capire se è in grado di seguirlo nelle sue avventure.

Lucky Jo dice a Little Boy: – Io so quanti sono i componenti della banda di Black Jack, vediamo se lo scopri anche tu.

Pensa un numero e scrivilo:

Aggiungi 15: Togli 6:

Togli il numero che hai pensato all’inizio e il risultato finale sarà sicuramente 9.

Proviamo ancora.

Pensa un numero e scrivilo: Aggiungi 22: Togli 13:

Togli il numero che hai pensato all’inizio e il risultato finale sarà sicuramente 9.

Little Boy ha capito che questo accade perché

Alunno/a

Data Classe

LA RAPINA IN BANCA

Lo sceriffo e Little Boy hanno cavalcato tutto il giorno sulle tracce della banda di Black Jack; ma, mentre i bravi rappresentanti della legge sono lontani, il pericoloso bandito irrompe nella banca di Silver City e vuole aprire le due casseforti, una blu e una gialla, piene di dollari.

Black Jack sa che la combinazione delle casseforti è un numero di 3 cifre tutte diverse e senza lo zero: in quella blu sono tutte dispari e la somma dei tre numeri è 9; in quella gialla sono tutte pari e la somma è 12.

Black Jack scrive tutte le combinazioni possibili per aprire la cassaforte gialla…

… e per aprire quella blu.

QUIZ INTORNO AL FALÒ

La banda di Black Jack sembra imprendibile. Lucky Jo ha dovuto arruolare altri aiutanti per poterla catturare. Da giorni perlustrano la zona. Oggi si sono spinti fino al passaggio tra le montagne, ma, purtroppo, non ci sono stati risultati positivi. Ormai è sera e bisogna fermarsi e far riposare i cavalli. Little Boy ha acceso il falò e tutti si sono seduti intorno. L’atmosfera è triste perché, nonostante l’impegno dei banditi, non si vedono le tracce.

Lucky Jo, per sollevare il morale degli uomini, propone un gioco: – In 60 secondi dovrete rispondere a queste domande.

• Sono di più i multipli del numero 3 o quelli del numero 4?

• Qual è la cifra delle unità nella moltiplicazione 456782 x 456782?

• Quanto fa 4 x 5 x 7 x 0 x 12 x 6 x 9?

• Il risultato di 345671 x 345671 è un numero pari o dispari?

• Il risultato di 897999 – 876842 è un numero pari o dispari?

• Il risultato di 245666 + 456244 è un numero pari o dispari?

• Quante cifre decimali ci sono nel risultato della moltiplicazione 8,25 x 12,68?

• Il risultato di 340 x 50 dà un numero maggiore o minore di 1000?

• Il risultato di 7500 : 65 dà un numero maggiore o minore di 100?

STORIE DA SALOON

La caccia a Black Jack si fa sempre più aspra e, intanto, nel saloon di Silver City non si parla d’altro: le imprese di Black Jack vengono mitizzate; il vecchio Bill racconta storie inverosimili. Persino Tom, il credulone, si mette a ridere.

Sam, a un tratto, si alza e propone una scommessa: – Chi riesce a dare la risposta esatta alle mie domande sulla vita di Black Jack, potrà mangiare e bere gratis!

• La barca su cui Black Jack si è imbarcato per sfuggire alla cattura aveva una scaletta per salire a bordo formata da 9 gradini, ognuno alla distanza di 20 cm l’uno dall’altro. 3 gradini erano sott’acqua.

Quando la marea si alzava di 40 cm, quanti gradini rimanevano fuori dall’acqua?

• Black Jack è stato in prigione 6 volte più di Pink Jack.

Pink Jack è stato in prigione il triplo di volte di Yellow Jack.

Yellow Jack è stato in prigione 8 volte. Black Jack è stato in prigione .

• Nella spartizione del bottino dell’ultima rapina

Black Jack ha dato a suo fratello Red Jack un terzo della metà del bottino e all’altro fratello la metà di un terzo del bottino. Chissà chi dei due avrà avuto la parte più grossa?

• Dopo la razzia nel ranch di Tobia sono rimasti pochi animali. Tobia, disperato, li guarda e si accorge che gli animali rimasti sono tutte pecore, tranne 3 che sono capre, e tutte capre, tranne 3 che sono pecore.

Quanti animali, tra pecore e capre, sono rimasti nel ranch di Tobia?

ALLA SCOPERTA DEI NUMERI

MISTERIOSI

Al saloon arrivano anche Lucky Jo e Little Boy, che raccontano la loro avventura alla ricerca della banda di rapinatori. Il loro racconto viene interrotto dal vociare di un gruppo di cow-boy seduti al tavolo di Sam, il giocatore che questa sera propone agli amici un gioco divertente che richiede, soprattutto, intelligenza e concentrazione.

Lucky Jo si rivolge al suo aiutante: – Per aiutarci, Sam ha detto che la somma dei tre numeri fa 75. Dai, Little Boy, proviamo anche noi!

• È un divisore di 70. Perciò potrebbe essere

• Ma è un numero pari. Perciò potrebbe essere .

• Però è anche multiplo di 7 e minore di 20.

Perciò è .

• È un multiplo di 13 più piccolo di 100. Perciò potrebbe essere

• Ma è un numero dispari. Perciò potrebbe essere .

• La somma delle sue cifre è 12. Perciò è .

• È un multiplo di 11 più piccolo di 120. Perciò potrebbe essere

• Ma è un numero divisibile per 2. Perciò potrebbe essere

• È un numero di 2 cifre. Perciò potrebbe essere .

• Tra quelli rimasti è la metà del successivo. Perciò è .

LA SFIDA DI BLACK JACK

Black Jack e i suoi banditi si sentono al sicuro. C’è stato un momento in cui lo sceriffo stava per raggiungerli, ma poi ha attraversato il fiume e si è allontanato. Così sono tutti molto allegri, ridono e si rilassano giocando a dadi.

Black Jack tira due dadi e li copre con la mano, poi sfida il Guercio, Carson e il Gringo: – Mille dollari in più a chi indovina la somma dei numeri sulle due facce superiori dei dadi. Il Guercio dice 12, Carson 7 e il Gringo 3.

Improvvisamente nel campo dei banditi cala il silenzio: mille dollari sono tanti, chi ha più probabilità di vincerli?

È ora il turno di Carson di porre una domanda. Tira i dadi e poi chiede: – Tenendo conto che in tutti i dadi la somma del valore delle facce opposte è uguale a 7, quel è il punteggio della faccia che vi sto indicando?

giallo

verde

verde

Per Black Jack è evidente: il dito di Carson indica la faccia con il numero giallo rosso rosso

LA CATTURA

Black Jack è molto astuto, ma ha una mania: quella dei cavalli. Ne ha tre: uno nero, uno bianco, uno grigio; e li tiene in tre recinti di colore diverso: nero, bianco e grigio. Ogni giorno mette i cavalli nei tre recinti in modo che la combinazione sia diversa da quella del giorno precedente.

Li osserva e si chiede: – Riuscirò, dopo una settimana a fare una combinazione diversa? Per quanti giorni riuscirò a fare combinazioni diverse?

La risposta non è difficile: Black Jack

È una mania che costa cara a Black Jack; infatti lo sceriffo vede i cavalli, è incuriosito dal loro movimento nei recinti ed è così che scopre il nascondiglio di Black Jack e lo cattura con tutta la sua banda.

Alunno/a

FESTEGGIAMENTI

Dopo la cattura della banda del famigerato Black Jack, si organizzano grandi festeggiamenti a Silver City. Naturalmente i protagonisti di questa festa sono Lucky Jo e Little Boy.

Nel covo di Black Jack, è stato trovato il bottino della rapina alla banca e un foglio con degli strani segni. Lo sceriffo lo osserva con attenzione, capisce quali sono le cifre che stanno al posto dei simboli, ma… che cosa significa?

Little Boy ha capito: – È la suddivisione del bottino. Rappresenta la quantità di dollari che doveva essere data a ogni componente della banda!

GRANDE BISONTE

La tribù indiana dei Piedi Scalzi si è accampata nella pianura non molto distante dalla Montagna Sacra.

Tutti scaricano dai cavalli le loro masserizie e iniziano a montare i tepee del villaggio. Il Grande Capo e lo sciamano sono impegnati a decidere in quale punto sarà sistemato il Totem. A un tratto alte grida attirano l’attenzione di tutti. Due indiani stanno litigando: Becco d’Aquila sostiene che 4 tende grandi come quella grigia occupano meno spazio di una tenda grande come quella azzurra. Cavallo Stanco, invece, sostiene il contrario. Il capo Grande Bisonte si avvicina ai due litiganti, ascolta pazientemente le loro ragioni e scuote la testa. – Nessuno di voi ha ragione – spiega, – provate a ragionare e ve ne accorgerete da soli.

Grande Bisonte è molto saggio e si è accorto che

L’OMBRA DELLO SCIAMANO

Lo sciamano del villaggio si è svegliato molto preoccupato perché ha fatto un sogno che lo ha turbato: due ombre nere volteggiavano nel cielo proprio sopra l’accampamento.

È un cattivo presagio e lui lo sa bene; bisogna fare un rito per evitare che un maleficio si abbatta sui Piedi Scalzi. Dopo aver meditato a lungo, si siede sotto il Totem e disegna sulla sabbia le forme che ha visto in sogno; poi, da una scatola che maneggia con cura, estrae dei pezzi con i quali deve ricomporre le figure che ha disegnato.

Lo sciamano sa che un errore potrebbe essere fatale, perciò disegna sulle figure i 7 pezzi che le compongono e, per non sbagliare, scrive anche i numeri corrispondenti.

NELLA TENDA DEGLI ANZIANI

La sera scende presto nella prateria e gli indiani si ritirano nelle loro tende. Le squaw preparano la zuppa e gli anziani si ritrovano nella tenda di Grande Bufalo a discutere delle cose importanti successe durante la giornata e a fare uno strano gioco che assomiglia vagamente agli scacchi. Su una scacchiera vengono posizionati due cavalli: uno nero per lo sciamano e uno azzurro per il capo. I cavalli, come negli scacchi, si possono spostare solo muovendosi ad elle. Così:

Gli altri anziani osservano e chiedono:

– Quali oggetti il cavallo dello sciamano raggiunge in 3 mosse?

Quali oggetti il cavallo di Grande Bufalo raggiunge in 3 mosse?

Ci sono oggetti raggiungibili in 2 mosse?

Quali? Da quali cavalli?

Grande Bisonte sa rispondere a tutte le domande.

GIALLO ALL’ACCAMPAMENTO INDIANO

C’è grande subbuglio tra gli indiani della tribù di Grande Bufalo; lo sciamano alza le braccia al cielo e piange come un bambino, le squaw si sono strette intorno a Dolce Luna, la moglie del capo, e sono spaventate. Dal tepee dello sciamano sono spariti tre oggetti dai poteri magici: una penna, un’ascia, un calumet.

Ciò è proprio una sciagura per la comunità. Ma Dolce Luna, che durante la notte era uscita dal suo tepee perché aveva sentito strani rumori, sa chi è il colpevole. Infatti punta il dito contro Penna Avvelenata e lo costringe a confessare. Gli oggetti sono stati nascosti nel Totem, basta solo trovarli.

I CAVALLI RUBATI

Una mattina gli indiani Piedi Scalzi si svegliano e trovano una brutta sorpresa: il recinto dei cavalli è aperto e i cavalli sono spariti. Sicuramente sono stati rubati. Grande Bufalo chiama Volpe Astuta e gli mostra alcune impronte sul terreno. – Queste sono impronte di stivali, dobbiamo trovare a chi appartengono e avremo trovato il ladro. Su una pelle l’indiano disegna l’impronta e inizia le indagini.

Volpe Astuta sa che quegli stivali appartengono a un bianco; così si reca al villaggio e osserva attentamente le impronte fuori dal saloon.

“Lo sapevo, non poteva essere stato che Black Jack” pensa e, con un legnetto, circonda la scarpa del ladro di cavalli.

SCENE DI VITA INDIANA

All’accampamento è arrivato un pittore che ha dipinto sei quadri, ritraendo la vita degli indiani. I dipinti sono in successione, ma, tornando in città, il pittore ha mescolato i quadri.

Basta però osservare attentamente i particolari per ritrovare la giusta successione.

IL RITO SACRO

Ieri Grande Bufalo era inquieto. Da qualche giorno succedevano cose inspiegabili: il suo copricapo di piume era stato trovato sul recinto dei cavalli, Penna Avvelenata non aveva ancora combinato guai, i cacciatori che erano andati a caccia di bufali non ne avevano trovato neanche uno. – Forse qui intorno ci sono degli spiriti maligni; è meglio che lo sciamano metta le pietre. E così lo sciamano ha sistemato, tutto intorno all’accampamento, delle pietre dipinte che tengono lontani gli spiriti cattivi. Penna Avvelenata, però, era in agguato e, mentre nessuno lo vedeva, ha cancellato i disegni da tre pietre. Bisogna ridisegnarle in fretta altrimenti gli spiriti potrebbero entrare nell’accampamento.

CAVALLO STANCO

È stato avvistato un branco di bisonti che si stanno spostando nella prateria; i cacciatori della tribù dei Piedi Scalzi partono all’inseguimento sotto il sole cocente. A un certo punto Cavallo Stanco comincia a boccheggiare: – Se non faccio una sosta scoppio! Così si ferma all’ombra di un grande albero e si addormenta senza accorgersi di avere compagnia.

Per scoprire che cosa pensa il bisonte bisogna ricostruire la scena e trascrivere nelle caselle bianche le lettere corrispondenti a ciascun tassello.

IL PIRATA THOMAS

Il pirata Thomas, con la sua nave Terrore dei Sette Mari, è a capo di una ciurma di terribili bucanieri e assalta le navi cariche di oggetti preziosi che navigano vicino alla sua isola segreta. Thomas è un tipo preciso e ordinato e tiene il conto di tutte le losche operazioni che compie. Ha un’apposita agenda in cui numera le navi che assalta; quella di oggi è la numero 101. Il pirata osserva con attenzione questo numero e scopre che si può leggere, senza che cambi il valore, da destra verso sinistra e da sinistra verso destra. – È un numero palindromo – gli dice Gambastorta, l’intellettuale del gruppo.

“E adesso quali saranno le prossime cinque navi che potrò indicare con numeri palindromi?” pensa Thomas e prova a scriverli.

A Thomas è venuta la fissa dei numeri palindromi. Nella cambusa ci sono tante fiaschette di rum, ognuna rigorosamente numerata. Ieri ne è arrivato un altro carico che è da sistemare; il numero della prima bottiglia è 1001: un altro numero palindromo…

E i prossimi cinque quali saranno?

QUIZ

– Bucanieri, oggi si deve pulire il ponte del Terrore dei Sette Mari. Chi si offre volontario? – grida Thomas. C’era da aspettarselo, nessuno ha voglia di fare del lavoro extra. Thomas ha un’idea: tutti coloro che risponderanno esattamente ad almeno una delle domande che lui stesso farà potranno andare a riposarsi. Gli altri prenderanno secchio e spazzolone e puliranno il ponte fino a farlo brillare.

1. Se in una gara superi il secondo, in quale posizione arrivi?

2. Il dottore ti dà tre pillole da prendere, una ogni mezz’ora. In quanto tempo le prenderai tutte?

3. Il padre del pirata

Barbanera ha 5 figli:

Lai

Lei

Lii

Loi

Come si chiama il 5° figlio?

4. Il pirata divide il suo bottino con il fratello Pirata Rosso. Poi divide la metà che gli rimane con un altro. Poi ancora la metà che gli rimane con un altro e alla fine gli restano solo 5 dobloni. Quanti dobloni aveva all’inizio?

LA TAVERNA DEL GATTO NERO

Thomas, Uncino Spuntato e altri loschi figuri sono andati alla Taverna del Gatto Nero a fare baldoria.

Ma, alla fine della serata, quando arriva il momento di pagare e l’oste dice che il conto totale

è di 32 dobloni, salta fuori che:

• due pirati non hanno soldi,

• uno ha soltanto 3 dobloni,

• un altro soltanto 1 doblone,

• i rimanenti devono sborsare 7 dobloni ciascuno.

L’oste li guarda con aria torva e si chiede:

Ma… quanti sono in tutto i pirati?

L’oste ha sistemato sul bancone 10 bicchieri di rum per i pirati; alcuni sono pieni, altri sono ancora vuoti. L’oste li osserva con attenzione e dice a Thomas che, “usando” uno solo dei bicchieri di destra, può ottenere lo stesso ordine dei bicchieri posti sulla sinistra del bancone. – Hai capito in che modo?

IL FORZIERE SEGRETO

Ogni tanto Thomas, assieme al suo amico fidato

Uncino Spuntato, controlla segretamente la sua riserva di denaro. Questa sera ha aperto il forziere e ha contato 15 monete che, però, non hanno tutte lo stesso valore. Ce ne sono da 5 scudi, da 10 scudi e da 20 scudi.

Tuttavia il pirata osserva che è come se tutte le monete fossero da 10 scudi; in realtà quelle da 10 sono solo 9.

Thomas vuole mettere alla prova l’intelligenza di Uncino Spuntato, così gli chiede: – Mi sai dire, senza guardare, quanti sono i pezzi da 5 scudi e quanti quelli da 20?

Uncino Spuntato, che è furbo, si aiuta disegnando le monete.

L’ASSALTO DEI PIRATI

È stato avvistato un convoglio di navi appartenenti al re di Spagna e che trasportano forzieri pieni di monete e stoffe preziose. Thomas fa dipingere la sua nave di nero e parte immediatamente all’assalto delle navi spagnole. Purtroppo per lui anche altri sei corsari hanno avuto la stessa informazione e la stessa idea. Ognuno ha dipinto la propria nave di un colore diverso. Che traffico che c’è sul mare!

La nave Blu è stata più veloce della nave Verde e la nave Verde è stata più veloce di quella Marrone. Il veliero Giallo è arrivato immediatamente prima del veliero Arancione e immediatamente dopo di quello Blu.

La nave Nera di Thomas è arrivata subito dopo quella Verde e prima dei velieri Marrone e Rosso. Il veliero Rosso non è stato l’ultimo.

Ma alla fine… ecco qual è stato l’ordine di arrivo:

1ª nave:

2ª nave:

3ª nave:

4ª nave:

5ª nave:

6ª nave:

7ª nave:

A CACCIA DI ACQUA

Il Terrore dei Sette Mari getta l’ancora nella baia di un’isola piccola e deserta. Thomas ha deciso di nascondere lì il tesoro accumulato assaltando le navi spagnole. Appena sbarcati, i pirati si accorgono di avere terminato la riserva d’acqua; così Thomas manda tre corsari, con dei barilotti, alla ricerca di una sorgente. Quando fanno ritorno al campo, Uncino Spuntato ha un barilotto pieno, uno con l’acqua a metà e due con un quarto d’acqua. Testa di Legno ha due barilotti a metà e due con un quarto d’acqua. Barbagialla ha un barilotto a metà e uno con un quarto d’acqua. Thomas li osserva e dice: – Chi ha la maggiore quantità d’acqua riceverà 3 dobloni. Chi ne ha la minore dovrà tornare indietro a riempire un altro barile.

segnate la quantitA ‘ di acqua che contengono.

Ha raccolto più acqua .

Ha raccolto meno acqua

CHE ORA È?

Il tesoro dei pirati di Thomas è stato nascosto in una profonda caverna; in un forziere sono stati trovati tanti orologi. I pirati, che non ne avevano mai posseduto uno, si divertono a usarli.

1. L’orologio di Salomon segna le 19.07 ed è in anticipo di 15 minuti rispetto a quello del Capo, che aveva regolato il suo con quello di Mano di Velluto. L’orologio di Mano di Velluto ha 10 minuti di ritardo sull’ora esatta, che è stata vista sull’orologio della torre cinque minuti prima. Ma che ora sarà mai adesso?

2. Due pirati regolano i loro orologi guardando quello della torre. È mezzogiorno. Però l’orologio di un pirata ogni ora va avanti di 10 minuti e l’orologio dell’altro pirata ogni ora va indietro di 10 minuti. Che ora sarà sull’orologio della torre quando gli orologi dei due pirati segneranno esattamente un’ora di differenza tra loro?

3. La pendola che Thomas ha sistemato nella sua cabina ogni 10 minuti perde 1 minuto. Quanto tempo impiega per perdere un’ora intera?

4. Il vecchio orologio che è nella cambusa, ogni quarto d’ora perde mezzo minuto. Quanto tempo impiega per perdere un’ora intera?

PIRATI SULLA DILIGENZA

Alcuni pirati sono sbarcati dalla nave e, su ordine di Thomas, stanno visitando i villaggi della costa. Per muoversi più rapidamente usano la diligenza.

1. Due pirati prendono la stessa diligenza; uno parte ogni due giorni, l’altro ogni 5 giorni.

Oggi è martedì 2 gennaio. In quale giorno prenderanno di nuovo la diligenza insieme?

3. Tre pirati prendono la stessa diligenza, uno parte ogni cinque giorni, uno ogni quattro giorni, uno ogni tre giorni.

Oggi è domenica 30 giugno e tutti e tre hanno preso la diligenza. Quando la prenderanno di nuovo tutti e tre insieme?

2. Tre pirati prendono la stessa diligenza; uno parte ogni tre giorni, uno ogni quattro giorni; uno ogni due giorni. Oggi è lunedì 1 aprile e tutti e tre hanno preso la diligenza. Quando la prenderanno di nuovo tutti e tre insieme?

Pagina 70

SOLUZIONI DEGLI ESERCIZI

(7 + 3 + 5 + 1) • (1 + 5 + 5 + 5) • (7 + 3 + 3 +3 ) • (1 + 1 + 7 + 7)

Pagina 71

(50 : 2) • (25 x 1) • (90 – 65) • (5 x 5) • (31 – 6) • (18 + 7)

Pagina 72

24033 + 33042 = 57075 • 12365 + 56321 = 68686 • 72441 +14427 = 86868 • 31215 + 51213 = 82428

1342 + 2431= 3773 (oppure 1432 + 2341 = 3773)

14351 + 15341 = 29692 21433 + 33412 = 54845 (oppure 12424 + 42421 = 54845) 12011 + 11021 = 23032 (oppure 12021 + 11011 = 23032)

Pagina 73

98 – 82= 16 43 + 45 + 14 = 102

45 + 33 = 78 64 : 8 = 8

12 : 2= 6 327 – 222 = 105

34 x 2= 68 15 x 5 = 75

Pagina 74

• Numero di 3 cifre, compreso tra 900 e 700, in cui ogni cifra è la metà di quella che la precede: 842.

• Numero più grande possibile di 4 cifre: 9999.

• Numero più piccolo possibile formato da 3 cifre tutte diverse: 102.

• Numero in cui il numero delle lettere che formano il suo nome corrisponde al valore del numero stesso: 3.

• Numero più grande possibile, senza zeri, in cui le cifre diano come somma 4: 1111.

Pagina 75

3 • 6 • 12 • 24 • 48 • 96 • 192 • 384 (il comando è “x 2”)

512 • 256 • 128 • 64 • 32 • 16 • 8 • 4 (il comando è “: 2”)

6561 • 2187 • 729 • 243 • 81 • 27 • 9 • 3 (il comando è “: 3”)

2 • 5 • 11 • 23 • 47 • 95 • 191 (il comando è “x 2 + 1” oppure “+ 3 + 6 + 12 + 24 + 48 + 96”)

Pagina 76

Cappellaio 68 [50 (cammelli) x 2 (gobbe) – 4 (zampe) x 8 (cammelli)]

Stellaio 20 [4 (mesi: aprile, giugno, settembre, novembre) x 5 (anni)]

Animali magici 24 (6 x 4 – i vermi non hanno zampe)

Ampollificio 30 (15 x 2 – gli elicotteri non hanno ali)

Campanellini 45 (30 x 3 : 2)

Polveri luminose 51 [52 (settimane anno) – 1 (settimana tra Natale e Capodanno)]

Bacchettaio 1 (marzo)

Fibbie colorate 36 (53 x 2 – 140 : 2)

Pagina 77

8 • 48 • 20 • 12 • 24

4 • 44

Pagina 78

• Le figure A e B sono equiestese.

• È più grande la figura D perché ha 60 quadretti, mentre la figura C ne ha 53.

Pagina 79

Pagina 80

tendina • occhiali • manico della tazza • paralume • stivale • racchetta da tennis • gamba della sedia più in alto • bacchetta magica

Pagina 81

• Alcuni (oppure non tutti) hanno la carota.

Tutti hanno il fiocco.

Non tutti (oppure alcuni) hanno le orecchie abbassate (oppure alzate).

• Non tutti sono a righe (oppure a forma di cilindro…).

Alcuni sono a forma di cono (oppure di cilindro, a punta…).

Tutti hanno una stellina.

Soluzioni degli esercizi

Pagina 82

Tra tre giorni comincerà il grande raduno.

USB TRA

USF TRE

HLPSOL GIORNI

DPNLO COMIN

DFSB` CERÀ

LM IL

HSBOEF GRANDE

SBE RAD

VOP UNO

Pagina 83

• La casa del mago Gherardo è quella in basso a sinistra.

• Quella del mago Teodoro è in basso a destra.

• La casa dove è previsto il raduno è dietro quella del mago Teodoro.

• La locanda è quella più alta dietro la casa del mago Gherardo.

• L’emporio è la seconda casa (partendo dal basso) al centro.

Pagina 84

• Particolari sbagliati nell’immagine a sinistra: orecchio destro del coniglio, orecchio sinistro del coniglio, farfallino, orologio, orecchio del mago, piede del mago.

• Particolari sbagliati nell’immagine a destra: cappello, naso, bacchetta, bottone, stellina, coda del frac.

Pagina 85

• Accoppiamenti: cane – osso, paletta – scopa, candela – portacandele, pilota – automobile da corsa, bicicletta – ruota, balena – Pinocchio, forchetta – coltello, uccello – nido, matita – temperino.

• Oggetti che rimangono: nave, topo, casa, mela, mago. La caratteristica che li accomuna è che sono tutti formati da 4 lettere.

Pagina 86

cappello: 35 pirilli • gonna: 57 pirilli • guanti: 9 pirilli

Pagina 87

Rosaspina Fliggy

Gelinda Viperella

• Le persone erano tre: il nonno, il papà e il figlio, quindi due padri e due figli. Il papà è anche figlio (del nonno).

Pagina 88

• Le primule sono 3, due blu e una gialla. In questo modo ci sono 10 fiori, di cui 5 blu (2 primule e 3 margherite) e 5 gialli (una primula e 4 margherite).

• Ci sono 7 rose rosse, 6 gerani gialli e 2 gerani rossi.

Pagina 89

• Rubasalsicce ha la testa lunga 10 cm, il corpo lungo 20 cm e la coda lunga 10 cm.

• Lungobaffo è lungo 27 cm, determinati da 12 cm di coda, 12 cm di corpo, 3 cm di testa.

• Pistacchio ha la testa lunga 10 cm, il corpo 30 cm, la coda 20 cm: in totale 60 cm.

Pagina 90 Il folletto Martello.

Pagina 91

La strada più corta è: Fiorevelenoso • Picco del Diavolo • Vallestregata • Grotta tenebrosa • Orridonero • Fiorevelenoso.

Pagina 92

• Oggi è martedì. Lo si desume in questo modo: se Berto sta dicendo una bugia, allora può essere solo martedì. Se invece sta dicendo la verità, può essere solo sabato. Poiché non è sabato, ne consegue che è martedì.

• Era venerdì. Lo si deduce in questo modo: se Milli sta dicendo una bugia, l’unico giorno possibile è venerdì; se invece sta dicendo la verità, può essere solo martedì. Poiché non è martedì, ne consegue che è venerdì.

Pagina 93

• Le mucche sono 4, 1 è la chioccia e 3 sono i pulcini: infatti, per avere 32 zampe e 12 animali l’unica combinazione possibile è 4 animali a quattro zampe e 8 a due zampe.

• Il passerotto impiegherà 7 giorni.

Lo si può dedurre da questo schema in cui C indica le ciliegie che c’erano all’inizio e Nc le ciliegie nate durante il periodo:

C C C Nc C C C Nc C C C Nc C C

1° e 2° giorno: 11 – 4 + 1 = 8

3° e 4° giorno: 8 – 4 + 1 = 5

5° e 6° giorno: 5 – 4 + 1 = 2

7° giorno: 2 – 2 = 0

• Le streghe impiegano sempre 12 minuti, perché ogni strega impiega 12 minuti per fare una pozione, e le streghe fanno la loro pozione contemporaneamente.

• I tre pipistrelli vanno disegnati in fila uno dietro l’altro.

Trillina

Milly

Pagina 95

Accade così perché il numero iniziale viene tolto e quindi non influisce sul risultato finale. Il risultato delle altre operazioni dà come risultato, in entrambi i casi, 9.

Pagina 96

• Combinazioni possibili per aprire la cassaforte gialla sono sei: 246, 264, 462, 426, 642, 624.

• Combinazioni possibili per aprire la cassaforte blu sono sei: 135, 153, 315, 351, 513, 531.

Pagina 97

• Sia i multipli di 3 sia quelli di 4 sono infiniti.

• 4 (perché il prodotto delle cifre delle unità fa 4  2 x 2 = 4).

• 0. Nella moltiplicazione lo zero è l’elemento annullante.

• Dispari (perché il prodotto delle cifre delle unità è dispari  1 x 1 = 1).

• Dispari (perché la differenza delle cifre delle unità è dispari  9 – 2 = 7).

• Pari (perché la somma delle cifre delle unità è pari  6 + 4 = 10).

• Quattro, perché ci sono due cifre decimali nel primo fattore e due nel secondo.

• Maggiore  340 x 100 : 2 = 1700

• Maggiore  115,38

Pagina 98

• Rimanevano 3 gradini fuori dall’acqua perché, se si alzava la marea, si alzava anche la barca.

• 30 volte (3 x 8 + 6).

• Nessuno, le parti sono uguali.

• Sono rimasti 6 animali: 3 pecore e 3 capre.

Pagina 99

• È un divisore di 70. Perciò potrebbe essere 1, 70, 2, 5, 7, 10, 14, 35.

• Ma è un numero pari. Perciò potrebbe essere 2, 10, 14, 70.

• Però è anche multiplo di 7 e minore di 20. Perciò è 14.

• È un multiplo di 13 più piccolo di 100. Perciò potrebbe essere 13, 26, 39, 52, 65, 78, 91.

• Ma è un numero dispari. Perciò potrebbe essere 13, 39, 65, 91.

• La somma delle sue cifre è 12. Perciò è 39.

• È un multiplo di 11 più piccolo di 120. Perciò potrebbe essere 11, 22, 33, 44, 55, 66, 77, 88, 99, 110.

• Ma è un numero divisibile per 2. Perciò potrebbe essere 22, 44, 66, 88, 110.

• È un numero di 2 cifre. Perciò potrebbe essere 22, 44, 66, 88.

• Tra quelli rimasti è la metà del successivo. Perciò è 22.

Pagina 100

• Carson ha più probabilità di vincere, perché tirando due dadi ci sono più probabilità che esca il 7 (6 possibilità) piuttosto che il 3 (2 possibilità) o il 12 (1 possibilità).

• Il dito di Carson indica la faccia con il numero 2 perché si trova di fronte alla faccia di colore rosso che ha come punteggio 5.

Pagina 101

Le combinazioni possibili sono sei. Quindi Black Jack non potrà fare combinazioni diverse per sette giorni, ma solo per sei.

Pagina 102

1. 22 + 22 + 22 + 22 = 88 2. 51 + 8 – 8 = 51

3. 444 – 44 = 400 4. 75 – 55 = 20

5. 13 x 31 = 403 6. (24 + 14) x 4 = 152 7. 10 : 10 = 1

8. (66 : 6) + 6 = 17

Pagina 103

Grande Bisonte si è accorto che la tenda grande ha un’estensione 4 volte maggiore di quella piccola, perciò 4 tende piccole occupano lo stesso spazio di una tenda grande.

Pagina 104

Pagina 105

• Il cavallo dello sciamano raggiunge in tre mosse la tenda o il bisonte.

• Anche il cavallo di Grande Bufalo raggiunge in tre mosse la tenda o il bisonte.

• Il cavallo dello sciamano raggiunge in due mosse il totem o il copricapo.

• Il cavallo di Grande Bufalo raggiunge in due mosse il totem.

Soluzioni degli esercizi

Pagina 106

Pagina 107

L’impronta corrisponde alla scarpa in basso, in centro.

Pagina 108

prima riga: 2 – 5 • seconda riga 4 – 1 • terza riga 6 – 3

Pagina 109

Nei tre riquadri vanno disegnati, rispettivamente:

Pagina 110

Per fortuna è pigro.

Pagina 111

111 • 121 • 131 • 141 • 151

1111 • 1221 • 1331 • 1441 • 1551

Pagina 112

1. Arrivi secondo, perché se superi il secondo eri terzo.

2. Le prenderai tutte in un’ora (all’inizio dell’ora la prima, dopo mezz’ora la seconda, dopo un’ora la terza).

3. Si chiama Barbanera.

4. All’inizio aveva 40 dobloni.

Pagina 113

• I pirati sono 8. I 32 dobloni vengono pagati in questo modo: 4 dobloni dai due pirati che hanno pochi dobloni; i rimanenti 28 dobloni da 4 pirati; sommando i due pirati che non hanno soldi, si deduce che i pirati sono 8.

• L’oste travasa il primo bicchiere del secondo gruppo nel terzo bicchiere del secondo gruppo.

Pagina 114

Le monete sono: 9 da 10, 2 da 20, 4 da 5. Poiché il valore totale delle 15 monete è 150 e quelle da 10

sono 9, le rimanenti 6 monete devono avere un valore complessivo di 60 scudi. L’unico modo per ottenere 60 con 6 monete da 20 o da 5 è 2 da 20 e 4 da 5.

Pagina 115

1ª nave: blu • 2ª nave: gialla • 3ª nave: arancione • 4ª nave: verde • 5ª nave: nera • 6ª nave: rossa • 7ª nave: marrone

Pagina 116

• Ha raccolto più acqua Uncino Spuntato.

• Ha raccolto meno acqua Barbagialla. Uncino Spuntato raccoglie in tutto 2 barilotti di acqua (1 + 1 2 + 1 4 + 1 4 )

Testa di Legno raccoglie in tutto 1 barilotto e mezzo

di acqua ( 1 2 + 1 2 + 1 4 + 1 4 )

Barbagialla raccoglie 3 4 di un barilotto di acqua ( 1 2 + 1 4 ).

Pagina 117

1. Adesso sono le 19.02. Infatti, dall’orario segnato dall’orologio vanno tolti 15 minuti (anticipo rispetto all’orologio del Capo e di Mano di Velluto) e aggiunti 10 minuti (ritardo rispetto alla torre). Il fatto che l’orologio fosse stato regolato cinque minuti prima è un dato inutile.

2. Saranno le 15. Infatti, dopo un’ora l’orologio di un pirata segnerà le 13.10 e l’altro le 12.50; dopo 2 ore 14.20 e 13.40; dopo 3 ore 15.30 e 14.30 ed avranno un’ora di differenza. Tre ore dopo mezzogiorno sono le 15.

3. Impiega 10 ore. Un’ora è formata da 60 minuti. Perciò per perdere un’ora la pendola impiegherà 10 x 60 = 600 minuti, cioè 10 ore.

4. Impiega 30 ore. Un’ora è formata da 120 mezzi minuti. Perciò per perdere un’ora l’orologio impiegherà 15 x 120 = 1800 minuti, cioè 30 ore.

Pagina 118

1. Il 12 gennaio (venerdì): il multiplo più piccolo comune a 2 e 5 è 10, perciò i pirati si incontreranno dopo 10 giorni.

2. Il 13 aprile (sabato): il multiplo più piccolo comune a 2, 3 e 4 è 12, perciò i pirati si incontreranno dopo 12 giorni.

3. Il 29 agosto (giovedì): il multiplo più piccolo comune a 3, 4 e 5 è 60, perciò i pirati si incontreranno dopo 60 giorni.

STRUMENTI STRUMENTI COMPENSATIVI COMPENSATIVI

I MULTIPLI DEI NUMERI FINO AL 10

Per eseguire le moltiplicazioni e le divisioni puoi utilizzare la tabella dei multipli. Segui le istruzioni.

• Incolla la pagina su un cartoncino.

• Con l’aiuto di un adulto, ritaglia le due figure. Taglia le linee interne tratteggiate.

• Inserisci i due pezzi.

• Spostando il cursore, potrai leggere il risultato delle moltiplicazioni.

I MULTIPLI DEI NUMERI DA 10 A 20

Per eseguire le moltiplicazioni e le divisioni puoi utilizzare la tabella dei multipli. Segui le istruzioni.

• Incolla la pagina su un cartoncino.

• Con l’aiuto di un adulto, ritaglia le due figure. Taglia le linee interne tratteggiate.

• Inserisci i due pezzi.

• Spostando il cursore, potrai leggere il risultato delle moltiplicazioni.

Numero

GRIGLIA PER INSERIRE

I NUMERI INTERI

hG daG uG hM daM uM hk dak uk h da u

Numero

hG daG uG hM daM uM hk dak uk h da u

Numero

hG daG uG hM daM uM hk dak uk h da u

Numero

hG daG uG hM daM uM hk dak uk h da u

Numero

hG daG uG hM daM uM hk dak uk h da u

Numero

hG daG uG hM daM uM hk dak uk h da u

Numero

GRIGLIA PER INSERIRE

I NUMERI DECIMALI

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

Numero

k h da u , d c m

ADDIZIONI E SOTTRAZIONI

CON I NUMERI INTERI

hk dak k h da u

hk dak k h da u

dak k h da

h da u

h da u

ADDIZIONI E SOTTRAZIONI

CON I NUMERI DECIMALI

SCOMPOSIZIONE ED EQUIVALENZA

Mariagrazia Bertarini

Gianluca Agnello

DIDATTICA DIDATTICA STEAM STEAM

Indicazioni metodologiche

Schede operative

4/5 4/5

Valentina Falanga

CHE COS'È LA DIDATT ICA STEAM?

 Science Scienze, lo studio del mondo e dei fenomeni della natura.

 Technology Tecnologia, non solo digitale, che comprende qualsiasi artefatto o opera che derivi da un processo trasformativo intenzionale da parte dell’essere umano. Per questo motivo, ogni prodotto creato dai ragazzi e delle ragazze per la risoluzione di un problema è tecnologia.

 Engineering Ingegneria, il processo di progettazione che i ragazzi e le ragazze mettono in atto per risolvere un problema.

 Art Arte, intesa sia come espressione della creatività presente in qualsiasi processo di invenzione e innovazione, tecnica, scientifica o letteraria, sia come estetica della produzione.

 Math Matematica, il linguaggio dei numeri, delle forme, dei grafici, delle quantità e delle formule.

Le discipline STEAM comprendono Scienze, Tecnologia, Ingegneria, Arte e Matematica; tuttavia, queste non sono considerate materie di studio indipendenti e l’approccio STEAM non è la somma delle loro parti, bensì è una meta-disciplina che consente la risoluzione di problemi contestualizzati.

La didattica STEAM si basa sull’integrazione e sull’applicazione di conoscenze matematiche e scientifiche con lo scopo di creare, attraverso le fasi del metodo scientifico, del processo ingegneristico di invenzione e costruzione o della programmazione informatica, soluzioni a problemi reali. Per raggiungere questo obiettivo vengono chiamate in gioco competenze globali – o life skills – tra cui pensiero critico, problem solving, creatività e innovazione, collaborazione e imprenditorialità.

Negli ultimi tempi alcune scuole di pensiero hanno aggiunto una R (per reading) all’acronimo STEAM, trasformandolo in STEAM. A questa stregua, tuttavia, si dovrebbe inserire anche una W per writing, in modo che sia coinvolta anche la scrittura. Ma se si riflette sull’immagine di scienziati intenti a fare esperimenti o di matematici davanti a una lavagna piena di numeri e formule, ci si accorge facilmente che sono stereotipi molto più affascinanti dell’immaginare uno studioso con una scrivania sommersa di libri e davanti a un computer impegnato a scrivere un saggio. Lettura e scrittura, però, sono competenze di base che appartengono a ogni disciplina.

LE CARATTERIST ICHE

DI UNA DIDATT ICA STEAM

1 La base di una didattica STEAM è il sul pensiero computazionale ovvero un’attitudine mentale che permette di risolvere problemi di varia natura seguendo metodi specifici. Il pensiero computazionale è un processo logico-creativo che consente di scomporre un problema complesso in problemi più semplici, quindi più gestibili se affrontati uno dopo l’altro. Trovando una soluzione a ciascuno di essi è possibile risolvere il problema originario.

2 Il contesto è motivante, coinvolgente e apre le porte della scuola al mondo reale. Esplicitando il senso e lo scopo di ciò che si fa in classe, aiuta ad abbattere la barriera del drop out scolastico di cui ogni insegnante è tenuto a occuparsi fin dai primi anni di scuola.

3 Il lavoro di gruppo, la comunicazione efficace e le abilità interpersonali hanno un’importanza fondamentale e preludono a quella che sarà la vita sociale e lavorativa dei ragazzi e delle ragazze del ventunesimo secolo, nel quale la quantità e diversità di informazioni rende poco plausibile, se non impossibile, lo svolgimento di qualsiasi lavoro in totale autonomia.

4 Il programma è fortemente inclusivo, per l’importanza che ogni membro riveste all’interno del gruppo, in dipendenza dalle proprie peculiari abilità.

5 Il pensiero critico, il problem solving, la capacità di prendere decisioni, di essere creativi e innovativi, sono una palestra significante che allena i ragazzi e le ragazze all’approccio con qualsiasi branca del sapere, sia essa umanistica o scientifica, e alla vita sociale.

6 L’errore assume il significato positivo di crescita personale. Sbagliare è considerata come possibilità sia di nuove scoperte sia di rimettersi in gioco in un ambiente sicuro e protetto, per allenarsi alla resilienza

7 In un percorso STEAM non esiste la soluzione giusta o corretta, perché innovazione e creatività sono sempre al primo posto.

8 La classe lavora in gruppi e l’insegnante assume il ruolo di guida applicando la metodologia dell’Inquired Based Learning, ovvero una metodologia didattica basata sull’investigazione, volta a stimolare nello studente la formulazione di domande e azioni per risolvere problemi e capire fenomeni.

9 Il nucleo della didattica STEAM consiste nell’applicazione del metodo scientifico, del Tinkering, della progettazione ingegneristica e del Coding

CHE COS'È IL T INKERING?

Il Tinkering, che in lingua originale vuol dire armeggiare, trafficare con, darsi da fare, nasce più di dieci anni fa negli Stati Uniti e precisamente nel Museo delle Scienze di San Francisco, dove un gruppo di educatori apre il Tinkering Studio. In questo spazio creativo i bambini e le bambine hanno la possibilità di investigare fenomeni scientifici e creare, con i più disparati materiali messi a disposizione, invenzioni completamente originali. Nato inizialmente con lo scopo di appassionare i bambini e le bambine alla scienza, alla tecnologia e alla matematica, il Tinkering si è sviluppato rapidamente in moltissimi Paesi del mondo ed è menzionato nel Piano Nazionale Scuola Digitale come uno strumento importante per lo sviluppo delle competenze del XXI secolo e per l’educazione alle discipline STEAM Lo scopo del Tinkering è costruire oggetti di vario genere e meccanismi funzionanti, utilizzando materiali di recupero, facilmente reperibili anche in casa, e lavorando in gruppo. Vasetti, scatole, tappi, bicchieri, carta, pezzi di legno, fili metallici sono solo alcuni esempi di ciò che serve per iniziare a creare e costruire di tutto e di più: circuiti elettrici, giochi meccanici, semplici robot…

CHE COS'È L'INGEGNERIA?

Nell’Enciclopedia Treccani leggiamo che l’ingegneria è l’insieme di studi e tecniche che utilizzano le conoscenze delle varie branche delle scienze (fisica, chimica ecc.), unite a quelle tecnologiche (per es. materiali), per risolvere problemi applicativi e per progettare e realizzare opere di diversa natura come quelle edili o meccaniche. I campi di applicazione dell’ingegneria si sono allargati da quelli tradizionali della costruzione di manufatti e di trasformazione della materia alla soluzione di problemi aventi per oggetto sia la materia organica e inorganica sia processi di carattere più teorico e astratto, per cui ingegneria economica, ingegneria finanziaria, ingegneria costituzionale, ingegneria della gestione aziendale sono solo alcune delle nuove discipline.

Parlare di bambini, bambine e ingegneria può quindi sembrare un azzardo. Tuttavia, in ambiente didattico il Tinkering è associato a una didattica appropriata alle bambine e ai bambini piccoli ed è considerato un approccio informale alle discipline STEAM, mentre l’ingegneria propone una procedura precisa e delineata che dà ai ragazzi e alle ragazze la possibilità di agire in modo più ponderato e permette soprattutto di sistematizzare le fasi di creazione e di intraprendere un percorso metacognitivo. Il processo che è alla base della progettazione ingegneristica porta, infatti, non solo all’applicazione del pensiero critico, del problem solving e delle competenze globali o trasversali, ma anche a un’analisi e un’appropriazione di tali concetti.

DALLA REALIZZAZIONE MANUALE

ALL'INVENZIONE

Se l’applicazione del processo di progettazione ingegneristica è uno dei nuclei dell’approccio STEAM, il punto di inizio è la risoluzione di un problema e la creazione di qualcosa che soddisfi lo scopo. Ma quali sono le differenze tra la metodologia STEAM e la realizzazione di un artefatto, attività normalmente svolta nella maggior parte delle aule scolastiche? E quali sono i vantaggi dell’applicare questo metodo?

Gli scaffali dei negozi di giocattoli e dei supermercati, le librerie, Internet e perfino i testi scolastici offrono tantissime idee dettagliate di bricolage o di costruzione; tuttavia, non danno altrettanti spunti per mettere in atto il pensiero critico o creativo. Al contrario, impegnano i ragazzi e le ragazze nella comprensione di un testo regolativo e a seguire passo passo un set di istruzioni.

Certo, tradizionalmente questi tipi di attività sono definiti creativi, ma non c’è molto spazio perché il ragazzo possa mettere in pratica l’immaginazione. Al contrario, se non seguirà le istruzioni pedissequamente, il lavoro (o lavoretto, termine detestabile) non avrà il risultato atteso, illustrato o fotografato e quindi non soddisferà chi lo ha realizzato. La metodologia STEAM non dà istruzioni, non prescrive che cosa realizzare e come, ma propone una sfida che la classe, divisa in gruppi, deve risolvere.

Solitamente in riviste, libri o anche in programmi televisivi troviamo testi quali: Come costruire una catapulta, seguiti dai materiali e dalle fasi per la costruzione. In un approccio STEAM, al contrario, leggeremo: In un orto circondato da un alto steccato, la fata madrina e Cenerentola sono perplesse. Il ballo al castello sta per iniziare, ma perché la fata riesca a fare la super magia ci vuole una zucca. Ma, accipicchia... non ce n’è nemmeno una! Fortunatamente, tu hai una zucchetta e puoi aiutare Cenerentola. Veramente hai una pallina di carta arancione, ma con tutta questa fretta non è il caso di fare gli schizzinosi...

SF IDA

La tua sfida è lanciare la zucchetta al di là dello steccato, in modo che la fata possa trasformarla e Cenerentola possa andare al ballo.

VINCOLI

Non puoi lanciare la zucchetta né con le mani né con i piedi. La zucchetta deve superare un ostacolo (lo steccato) alto almeno 50 cm per almeno 3 volte.

MATERIALI

Puoi usare qualsiasi materiale, ma ti potrebbe servire un pezzo di cartone per realizzare lo steccato e un metro per misurarne l’altezza.

Ai ragazzi e alle ragazze non viene quindi suggerito che cosa costruire e, per quanto sia naturale pensare a una catapulta, nel momento in cui ne abbiamo parlato qualche riga sopra, saranno liberi di realizzare qualsiasi marchingegno, dalla catapulta all’elevatore al razzo o chissà che cos’altro, e saranno liberi di farlo con i materiali che preferiscono.

In questo modo, ogni partecipante del gruppo dovrà:

 identificare il problema attivando il pensiero logico e il pensiero critico;

 raccogliere informazioni su come un problema simile può essere stato risolto;

 immaginare, attivando tutta la propria creatività, che cosa può risolvere il problema;

 pianificare le fasi di costruzione mettendo in moto processi logici e metacognitivi;

 predisporre una lista di strumenti e materiali necessari;

 decidere e distribuire i ruoli all’interno del gruppo;

 realizzare l’invenzione, seguendo le fasi e mettendo in gioco la propria abilità manuale;

 verificare sul campo l’efficacia e l’efficienza della realizzazione e, se necessario, produrre un grafico;

 accettare l’errore come input di miglioramento;

 condividere il proprio risultato con gli altri gruppi;

 autovalutare le proprie azioni e il proprio comportamento.

Per fare tutto questo, il gruppo seguirà una procedura che non è altro che l’esemplificazione del processo di progettazione ingegneristica

Il nostro ruolo di insegnanti assume quindi una valenza molto diversa, poiché presuppone la disponibilità ad assistere all’autoapprendimento senza interferire nelle scelte logiche o illogiche della classe. Dovremo porci come chi allenerà i ragazzi e le ragazze nel prendere sempre più familiarità con una procedura che darà loro la possibilità di scoprire i propri talenti.

Ciascuna fase del processo sottende ad abilità di pensiero e di relazione con gli altri che esemplificheremo man mano attraverso numerose schede e riflessioni.

All’interno di questo volume l’insegnante troverà poi delle griglie di valutazione e, al termine, una serie di “diplomi” che potranno essere fotocopiati, distribuiti o appesi in classe.

I migliori maestri sono quelli che ti indicano dove guardare, ma non ti dicono che cosa vedere.

Alexandra K. Trenfor

GLI INGEGNERI E IL PROCESSO DI

PROGETTAZIONE INGEGNERIST ICA

Gli ingegneri sono uomini e donne che utilizzano le conoscenze e le scoperte fatte dagli scienziati per inventare ciò che può migliorare la vita e il mondo intorno a noi.

Per svolgere il loro lavoro, gli ingegneri:

 si fanno molte domande;

 pensano a ciò che può servire per migliorare la vita degli esseri umani (e non solo);

 si informano sulle continue scoperte scientifiche;

 studiano come funzionano le cose per migliorarle;

 immaginano macchine e tecniche che ancora non esistono per migliorare il futuro;

 lavorano in gruppo

Gli ingegneri lavorano in gruppi/squadre/team/equipe perché esistono molti tipi di ingegneri e tutti molto specializzati, quindi alla costruzione di una macchina o di un edificio partecipano più ingegneri esperti in materie specifiche.

Il termine “ingegnere“ risale all’Alto Medioevo, deriva dal latino ingenium, che significa “congegno, creatore e capacità mentale“.

Il più antico documento italiano in cui appaia il termine “ingegnere“ è datato 19 aprile 1195. Da allora la parola diventò di uso frequente in Italia e, in forme simili, anche in Francia. Generalmente il termine “ingegneria“ era applicato a macchine, fortificazioni e simili.

Leonardo da Vinci è ricordato come il più grande ingegnere, architetto e visionario di tutti i tempi. Ha previsto cose come l’elicottero, il serbatoio e il sottomarino.

Parlando di ingegneria, i grandi enigmi scientifici da lui posti e risolti attraverso grandi opere, hanno dato spunti significativi al processo di avanzamento tecnologico dell’essere umano.

La prima donna ingegnere italiana fu Emma Strada, laureata nel 1908 al Politecnico di Torino con il massimo dei voti. Nel 1957 fondò l'AIDIA (Associazione Italiana Donne Ingegnere e Architetto) con l’intento di promuovere e tutelare il lavoro delle donne nel campo della scienza e delle tecniche, favorire l’assistenza reciproca nel campo della professione, coltivare legami culturali e professionali con analoghe associazioni italiane ed estere. Morì nel 1970, pochi mesi prima di presiedere, a Torino, la III Conferenza internazionale di donne ingegneri e scienziate.

Sempre parlando di ingegneria non possiamo non citare Jules Verne Se fosse vivo avrebbe più di 180 anni e potrebbe vedere realizzate molte delle sue fantastiche invenzioni.

Esempi ne sono il Nautilus, il grande sottomarino elettrico pro tagonista di “Ventimila leghe sotto i mari”, pubblicato nel 1870 e scritto quando l’elettricità era considerata poco più di una magia.

Da grande visionario qual era, in “Dalla Terra alla Luna”, scritto nel 1865, Verne descrive navicelle spaziali alimentate dalla luce solare. Oggi questa tecnologia esiste: sono vele solari come la sonda orbitante Nanosail-D della NASA. Nello stesso romanzo, lo scrittore racconta di proiettili sparati da un grosso cannone con tale forza da vincere la gravità terrestre e usati per trasportare passeggeri fino alla Luna, quelli che oggi chiamiamo moduli lunari, inoltre immagina un’astronave che atterra e galleggia nell’oceano.

In “La giornata di un giornalista americano nel 2889”, scritto nel 1889, Verne descrive quotidiani impensabili: giornali che vengono ‘detti’ ogni mattina agli abbonati; in pratica, parla del giornale radio che, però, iniziò a essere trasmesso circa 30 anni più tardi. Nello stesso libro, descrive il “fonotelefoto”, ovvero, l’apparecchio e la tecnologia che è alla base delle teleconferenze di oggi.

Tuttavia, come spiega Rosalind Williams, storica della tecnologia al Massachusetts Institute of Technology, “Jules Verne predisse molte cose che poi si sono avverate, ma non per magia, solo perché leggeva molto, parlava con gli esperti e sapeva quel che stava succedendo nel mondo”.

L’idea da cui si sviluppa il processo di progettazione è il pensiero computazionale che, come già accennato, è un processo logico-creativo che consente di scomporre un problema complesso in problemi più semplici. Trovando una soluzione a ciascuno di questi “problemi scomposti” è possibile risolvere il problema originario. Per quanto la storia di questo tipo di pensiero sembri risalire agli anni ’50, il termine pensiero computazionale è stato utilizzato per la prima volta da Seymour Papert solo nel 1980 nel suo libro “Mindstorms” e, successivamente, formalizzato dalla psicologa Americana Jeanette Wing in un articolo del 2006.

In realtà è un modo di pensare assolutamente naturale e le sue analisi e applicazioni sono delle proficue attività metacognitive già utilizzate spontaneamente sia nella vita quotidiana sia da tecnici e inventori.

IL PROCESSO DI PROGETTAZIONE INGEGNERIST ICA

Identificare il problema

Raccogliere informazioni

Condividere

Immaginare

Migliorare

Pianificare

Verificare sul campo

Creare

CHI SONO GLI INGEGNERI?

1 Segna con una X solo le frasi corrette.

Gli ingegneri sono uomini e donne che utilizzano le conoscenze e le scoperte fatte dagli scienziati per inventare ciò che può migliorare la vita e il mondo intorno a noi.

• Per svolgere il loro lavoro, gli ingegneri: si fanno molte domande. lavorano sempre nei cantieri. pensano a ciò che può servire per migliorare la vita di esseri umani e animali. si informano sulle continue scoperte scientifiche. parlano poco. lavorano in gruppo. studiano come funzionano le cose, per poterle migliorare. immaginano macchine e tecniche che nel nostro presente non esistono ancora. sono inventori. studiano la natura intorno a noi.

2 Utilizza le frasi che hai segnato come corrette e scrivi la tua definizione di “ingegnere”.

3 Secondo te, come lavorano gli ingegneri? Colora la tua scelta e motivala.

Ciascuno per conto proprio. In gruppo.

Perché

TANT I T IPI DI INGEGNERI

1 Di che cosa si occupano questi tipi di ingegnere? Collega correttamente.

Costruzione di navi e di imbarcazioni in generale.

Ingegnere informatico

Ingegnere aerospaziale

Ingegnere delle costruzioni

Ingegnere ambientale

Ingegnere meccanico

Ingegnere navale

Ingegnere robotico

Costruzione di veicoli, sonde e satelliti che viaggiano nello spazio.

Realizzazione di ponti ed edifici in generale.

Progettazione e controllo di strumenti, motori, macchine e altre attrezzature meccaniche.

Studio e sviluppo di metodi che permettono a un robot di eseguire compiti specifici, riproducendo in modo automatico il lavoro umano.

Studio e progettazione di soluzioni per la salvaguardia dell’ambiente.

Sviluppo di componenti hardware e programmazione di software.

2 Conosci altri tipi di ingegnere? Se sì, scrivi i loro nomi.

IL PROCESSO DI PROGETTAZIONE

INGEGNERIST ICA

1 Completa le fasi del processo. Collega correttamente.

Mi chiedo:

1 Quale problema deve essere risolto?

Identifico il problema

Pianifico

Verifico sul campo

Condivido

Creo

Raccolgo informazioni

Rifletto

Immagino

2 Chi ha quel problema?

3 Perché è importante risolverlo?

4 Quali sono i vincoli?

Mi informo sull’argomento e sui modi in cui un problema simile è già stato risolto.

Disegno le mie idee, poi ne scelgo una.

Faccio una lista dei materiali che mi servono e delle fasi di lavorazione.

Realizzo l’idea seguendo la mia pianificazione.

Faccio una serie di test per vedere se l’idea funziona.

Se non funziona, rifletto e ci riprovo. Se funziona, cerco di migliorare.

Presento la mia soluzione del problema alla classe.

LE SCHIAPPE NON ESISTONO!

1 Osserva e rispondi.

Sentire

Essere in sintonia

Prendersi cura

Conoscersi

Scegliere

Riflettere

Condivider Insegnare

Collaborare Interagire

INTELLIGENZE MULTIPLE

L e ggereScrivere

Parlare

Rappare

Ritmare Suonare

• Quali sono le cose che sai fare meglio?

TICA

• Quali sono quelle che sai fare “così e così”?

Quantificare

Pensare criticamente

Ragionare Sperimentare

Vedere Disegnare Colorare SVisualizzare chematizzare

Cos Recitare Muoversi Ballare

• Quali vorresti migliorare?

• Quali cose ti piacerebbe imparare a fare?

IL MIO GRUPPO IDEALE

1 Completa.

Pensa di dover progettare un’invenzione e forma il tuo gruppo ideale. Ricorda che ognuno di noi ha dei talenti e ognuno di noi è un campione in uno specifico campo. Nel progettare qualcosa ci sono tante fasi: serve capacità di analizzare i problemi, creatività, ma anche manualità, serve saper organizzare e pianificare, serve chi ha una vena artistica e sa rendere un oggetto bello, oltre che funzionale. Ma è necessario anche essere logici, serve saper spiegare bene e saper presentare l’invenzione alla classe. E serve, anche e soprattutto, qualcuno che incoraggi e tiri su il morale quando le cose non funzionano come dovrebbero!

SCEGLIEREI

PERCHÉ

CONSULENTI ESTERNI

PERCHÉ

LE FASI DEL PROCESSO

DI PROGETTAZIONE INGEGNERISTICA

Identificare il problema

Identificare un problema significa innanzitutto trovare la causa originaria di un effetto. È un’operazione complessa, poiché spesso consideriamo istintivamente solo l’ultima causa e non quella di origine. In altri casi, poi, si tende a confondere la causa del problema con la sua spiegazione.

Un esempio da raccontare alla classe, citato da G. Nardone, psicologo e psicoterapeuta italiano, in ‘’Problem Solving Strategico’’, può essere il seguente.

Ora ci sono computer e tablet, ma negli anni ’60, quando la NASA diede il via al programma di conquista dello spazio, gli astronauti si accorsero che le penne a sfera nello spazio non funzionavano. Per risolvere il problema, gli Americani spesero circa 12 miliardi di dollari, oltre al tempo e alle energie di chi lavorava all’invenzione. Infatti, gli esperti si concentrarono su come far funzionare la biro nello spazio, mentre il vero problema era scrivere nello spazio. Se lo avessero individuato correttamente, avrebbero risolto il problema in un attimo e a costo zero, come fecero i Russi, che decisero semplicemente… di usare le matite!

Prima di valutare se una risposta è esatta si deve valutare se la domanda è corretta.

Immanuel Kant

La maggioranza dei problemi non deriva dalle risposte che ci diamo ma dalle domande che ci poniamo.

Giorgio Nardone

È importante, quindi, che i ragazzi e le ragazze utilizzino del tempo per identificare il vero problema. Il lavoro sarà reso più semplice se svolto attraverso alcune domande chiave.

1

Quale problema deve essere risolto?

2 Chi ha il problema che deve essere risolto?

3 Perché è importante risolvere questo problema?

4 Quali sono i vincoli?

LA CAUSA ORIGINARIA

1 Il diagramma a lisca di pesce ti sarà d’aiuto per trovare la causa originaria di un problema.

Oggi il tuo problema sono... le formiche attratte da mezzo biscotto sulla scrivania in camera tua. Quante cause sai trovare per questo problema? Completa il diagramma.

Perché

Perché

Perché

Perché

Perché

Perché

Problema: formiche

2 Qualcun altro ha trovato una causa a cui tu non avevi pensato? Quale?

CHE PROBLEMI!

Gli ingegneri sono inventori e inventrici che costruiscono cose nuove o che migliorano quelle esistenti. Per esempio, a un ingegnere si potrebbe chiedere di costruire una casa pieghevole da poter spostare rapidamente da un posto all’altro, ma anche un pastello la cui mina non si spezza mai o un’automobile che può restringersi per entrare in garage piccolissimi.

1 Scrivi due problemi che incontri nella vita di tutti i giorni.

PROBLEMA NUMERO 1

Chi ha questo problema?

PROBLEMA NUMERO 2

Chi ha questo problema?

Perché è importante risolverlo?

Perché è importante risolverlo?

2 Scegli uno dei due problemi e immagina alcune invenzioni che potrebbero risolverlo.

SAREBBE MEGLIO...

1 Scegli un oggetto elettrico o meccanico che hai in casa e analizzalo.

Incolla qui la sua foto o disegnalo

• Che cos’è?

• A che cosa serve?

• Come funziona? Scrivi o disegna.

• È elettrico o meccanico?

2 Qual è la cosa che ti sorprende di più di questo oggetto?

3 Secondo te, come è fatto all’interno? Scrivi o disegna.

4 Cerca il libretto delle istruzioni o guarda su Internet. Avevi indovinato come era fatto all’interno?

5 Come miglioreresti questo oggetto?

Raccogliere informazioni

Gli alunni e le alunne, una volta identificato il problema o l’argomento, cercheranno informazioni utilizzando più fonti

Le fonti che presumibilmente i ragazzi e le ragazze hanno a disposizione sono:

 libri di testo, libri di varia o divulgazione, giornali, riviste, enciclopedie;

 video, tutorial, programmi televisivi;

 Internet;

 esperti (parenti, conoscenti, insegnanti);

 i propri sensi;

 la propria esperienza;

 associazioni e analogie con oggetti e funzioni conosciuti.

Nonostante le numerose possibilità, solitamente gli alunni e le alunne si fermano a una sola fonte, evitando di controllarne l’affidabilità o la veracità. Pericolosamente, la fonte primaria di informazioni è Internet e quindi varrà la pena evidenziare che trovare dati in rete non è un problema, la cosa difficile è essere sicuri che siano informazioni corrette

Un semplice trucco da suggerire alla classe è quello di controllare più di un sito

Fate notare che anche in questo modo si può tuttavia correre il rischio di essere ingannati. Se, infatti, si trova la stessa identica informazione, scritta con le medesime parole, su due siti diversi, sicuramente un web writer ha copiato dall’altro e non sempre è possibile stabilire se l’informazione è corretta e veritiera.

A volte è proprio così che dati falsi, informazioni sbagliate e fake news fanno il giro del mondo. Purtroppo, infatti, capita spesso che gli scrittori del web si copino l’un l’altro, senza chiedersi se la cosa che si sta scrivendo sia vera oppure no.

Incitate gli alunni e le alunne a non cadere in tali trappole. La rete non è la verità assoluta e dobbiamo imparare la fondamentale arte del dubbio. Usare gli strumenti che abbiamo con ASTUZIA e CERVELLO è l’unico modo per non farci ingannare e per non cadere… nella rete!

COME E DOVE RACCOGLIERE INFORMAZIONI

1 Rispondi.

• Quando sei in classe, sei una persona curiosa? Perché? Fai un esempio.

• Secondo te, essere curiosi in classe è una cosa positiva o negativa?

• Quando devi fare una ricerca o desideri sapere qualcosa, dove cerchi le informazioni che ti servono?

• Esistono altre fonti di informazioni? Quali conosci?

• Credi alle informazioni che trovi o controlli sempre anche un’altra fonte?

• Perché?

• Hai mai trovato in rete un’informazione sbagliata? Se sì, racconta.

I 5 TRUCCHI PER UNA BUONA

RICERCA IN RETE

1 CHIARISCIT I LE IDEE

• Che cosa stai cercando?

• Formula la domanda in modi diversi.

• Pensa alle parole chiave e ai sinonimi.

2 CERCA

• Inizia la ricerca con le parole chiave.

• Rendi la domanda sempre più specifica.

3 APPROFONDISCI

• Non fermarti ai primi risultati.

4 VALUTA

• Non credere a tutto ciò che leggi.

• Verifica controllando almeno tre fonti diverse.

5 CITA

• Riscrivi le informazioni con le tue parole.

• Scrivi la fonte (il sito o il nome dell’autore).

OSSERVARE UN OGGETTO

1 Sei in classe oppure a casa tua. Guardati intorno e scegli un oggetto qualsiasi: un tavolo, una sedia, una biro... Completa e rispondi.

• Nome dell’oggetto:

• Dove si trova?

• In quali ambienti si può trovare?

Di che colore è? È lucido, opaco...

Quali sono le sue dimensioni? Se puoi, misuralo, altrimenti descrivilo usando aggettivi appropriati.

A che cosa serve?

Può avere altre funzioni?

È indispensabile per qualcosa?

Da che cosa può essere sostituito?

È un pezzo unico o è composto da più parti? Se sì, da quante e quali?

Di quali materiali è fatto?

Può essere fatto di altri materiali? Quali?

Com’è al tatto?

2 Applica lo stesso metodo di osservazione ad altri oggetti.

Immaginare

In questa fase le alunne e gli alunni solo liberi di immaginare le proprie personali soluzioni del problema e quindi la realizzazione di un manufatto originale.

Essere creativi è una facoltà innata di ogni essere umano, ma a generare idee e a valutarne la qualità si impara. Ci sono molte tecniche utilizzate dai creativi di tutto il mondo per espandere e affinare le capacità creative, e molte di queste comprendono combinare, assemblare, separare, ribaltare idee per crearne di nuove, originali e sorprendenti.

Il nostro consiglio in questa fase è di lasciare liberi gli alunni e le alunne e di non indicare esempi, poiché inevitabilmente questi tenderanno a imitare ciò che vedono per paura di sbagliare o per essere coerenti con quello che si fa a scuola, in cui la maggior parte delle volte il compito dello studente è replicare un’esemplificazione dell’insegnante. Tuttavia, questo annullerebbe alcuni grandi benefici della didattica STEAM che, vogliamo ricordare, permette di:

 applicare il pensiero critico;

 lavorare in modo creativo;

 pensare in modo originale e anticonvenzionale.

Invitate tutti i componenti, lavorando in gruppo o in autonomia, a disegnare le proprie idee.

Non dovranno fare un elaborato grafico completo, bensì uno schizzo, avendo cura di scrivere i materiali occorrenti per la realizzazione. Rassicurateli, dicendo che non è importante che il disegno sia bello o brutto. Quello che conta è che il disegno dovrà:

 essere comprensibile;

 risolvere il problema;

 rispettare i vincoli;

 avere etichette con scritti i materiali di cui è fatta ogni parte.

Se poi ci sarà qualcuno che vorrà descrivere l’invenzione, lasciatelo fare, anche se uno schizzo è più semplice di una descrizione.

Evidenziate, però, che scrivere i materiali impiegati per le diverse parti dell’invenzione è fondamentale per ricordarli in seguito.

Bastoncini da gelato Tappo di plastica

Elastici

Esempio di disegno di catapulta.

Una volta che tutti i membri del gruppo avranno realizzato lo schizzo della loro invenzione, ogni partecipante esporrà la propria idea e insieme verrà deciso quale progetto realizzare attraverso un brainstorming, dapprima individuale, poi all’interno di ogni gruppo.

Le competenze che entrano in gioco in questa fase, oltre alla creatività e alla capacità di problem solving, sono di tipo relazionale

Sarà dunque necessario illustrare ai componenti di ogni gruppo le regole per un buon brainstorming

1 Restare nell’argomento e non divagare.

2 Non si parla contemporaneamente.

3 Tutti possono esprimere la propria idea.

4 Tutti ascoltano le idee degli altri.

Quando si lavora in gruppo bisogna ricordare che un’idea sciocca può essere geniale... e due teste pensano meglio di una!

Ci vogliono due pietre focaie per accendere un fuoco.

Louisa May Alcott

DAI CERCHIETT I ALL'IMMAGINE

1 Trasforma ogni coppia di cerchi in un’immagine speciale.

2 Rispondi.

• Quale tra le tue creazioni ti soddisfa maggiormente?

• Perché?

• Quale ha stupito maggiormente la tua classe?

• Perché?

CREARE CON LE PAROLE

1 Completa il titolo e continua il racconto.

LA MACCHINA

Mio nonno è un tipo bizzarro, dicono i vicini.

Mio nonno è un inventore, dico io.

La settimana scorsa il nonno era uscito a comprare il giornale, quando la nonna mi ha chiesto se le andavo a prendere un barattolo di salsa di pomodoro in cantina. Cercando il barattolo, però, ho trovato una strana macchina con un sacco di pulsanti, ingranaggi, leve, manopole e interruttori. Su un interruttore rosso c’era la scritta “ON”.

PRESENTARE UN'IDEA

1 Prepara una scaletta che ti aiuti a presentare la tua idea al resto del gruppo, per fare in modo che tutti capiscano chiaramente che cosa hai intenzione di realizzare.

I materiali che servono sono

Risolve il problema perché

VALUTAZIONE DELLE IDEE DEL GRUPPO

1 Rifletti e rispondi.

• Quale idea pensi che sia la migliore?

• Perché?

• È perfetta in tutto o c’è qualche aspetto che si può migliorare?

• L’aspetto che vorresti migliorare può essere sistemato utilizzando l’idea di un altro partecipante del gruppo?

• In che cosa consiste?

• Perché le altre idee non ti convincono? Scrivi un pro e un contro per ogni idea.

CAPACITÀ DI RELAZION

I INTERPERSONALI

Essere capaci di mantenere buone relazioni sociali significa comportarsi in modo che alle persone piaccia stare con te. Al contrario, non essere in grado di mantenere relazioni sociali significa comportarsi in modo che le persone ti sfuggano.

1 Per ogni atteggiamento, scrivi “SUPER!” se fa avvicinare le persone, “BOO!” se le fa allontanare.

Pensare a quello che vuoi dire prima di parlare.

Guardare negli occhi chi ti sta parlando.

Non coprirti la bocca quando starnutisci.

Congratularti con qualcuno che ti ha battuto in una gara.

Toccare le cose degli altri senza chiedere il permesso.

Dire “per favore” e “grazie”.

Ridere quando qualcuno sbaglia una risposta.

Accettare di aver sbagliato.

Interrompere qualcuno mentre sta parlando.

Ringraziare chi ti invita a giocare.

Arrabbiarti quando qualcuno non è d’accordo con le tue idee.

Voler avere sempre il primo turno di gioco.

Non stare troppo vicino alle persone con cui si sta parlando.

Avere una scarsa igiene personale.

PARLARE E AGIRE IN UN GRUPPO

1 Essere un gruppo vuol dire imparare a parlare e ad agire nel modo giusto. Leggi e rispondi.

SITUAZIONE n. 1

Stai raccontando al tuo gruppo STEAM come risolveresti un problema, quando uno del gruppo dice che è una grande sciocchezza. Come ti comporti?

SITUAZIONE n. 2

Tu e il tuo gruppo STEAM siete al terzo incontro. Oggi è arrivato un ragazzo nuovo che fa un po’ fatica a sintonizzarsi con voi. Però, disegna benissimo. Che cosa proponi per farlo sentire a suo agio?

SITUAZIONE n. 3

Nel tuo gruppo STEAM sembra che non ti sopporti nessuno, perché sai molte più cose di loro. Come ti comporti per creare un buon rapporto con gli altri?

SITUAZIONE n. 4

Uno dei componenti del tuo gruppo STEAM dice che suo zio è ingegnere e che potrebbe aiutarvi. Come reagisci?

SCEGLIERE UN'IDEA

1 Tutti i giorni dobbiamo prendere decisioni e farlo non è sempre facile. Utilizzare uno schema può aiutarti a decidere in modo più semplice ed efficace.

• Per prima cosa, identifica il problema e scrivi tre possibili soluzioni.

• Scrivi gli aspetti positivi e quelli negativi (i pro e i contro) di ogni soluzione.

• Decidi qual è la soluzione migliore e quella sarà la tua decisione.

Ricorda: lo schema ti può aiutare a prendere decisioni, ma esiste comunque la possibilità di commettere degli errori. Tutti ne commettiamo, tutti i giorni.

Ricordati che non casca il mondo quando si sbaglia, ed è sempre possibile rimediare e trovare una nuova soluzione.

Qual è il problema?

Soluzione 1

Conseguenza positiva

Conseguenza negativa

Soluzione 2

Conseguenza positiva

Conseguenza negativa

Soluzione 3

Valutazione e, infine, DECISIONE

Conseguenza positiva

Conseguenza negativa

Pianificare

In questa fase gli alunni e le alunne faranno un elenco di materiali e di strumenti necessari per la realizzazione dell’idea scelta. Ne esemplificheranno poi le fasi di realizzazione attraverso la stesura di un testo regolativo che potrà essere scritto, illustrato, scritto e illustrato, schematizzato in mappa, scaletta o tabella.

Il magazzino degli ingegneri

Per inventare e costruire abbiamo bisogno di materiali. I materiali che possono essere utilizzati nella classe STEAM saranno, oltre al normale corredo scolastico, materiali di recupero che le ragazze e i ragazzi raccoglieranno a casa. Tappi, bottigliette, spago, contenitori e tutto quello che riterranno utile e ispirante costituiranno il materiale di base che potrà essere arricchito di volta in volta a seconda di specifiche richieste dell’attività che verrà affrontata. Se in classe sarà disponibile una zona o un armadio nel quale conservare i materiali, potranno essere disposti in scatole etichettate secondo il contenuto.

I ruoli nel gruppo

Per evitare che il lavoro venga monopolizzato dagli alunni e dalle alunne più intraprendenti, è opportuno che i ruoli all’interno del gruppo siano ben definiti

Ci saranno quindi:

 i costruttori, che lavoreranno manualmente;

 i ricercatori, che eseguiranno le ricerche e raccoglieranno le informazioni;

 i responsabili dei materiali, che cercheranno i materiali necessari o decideranno sostituzioni;

 i responsabili di magazzino, forse i più timidi o chi fatica a mettersi in gioco, che consegneranno i materiali richiesti dai responsabili del magazzino;

 i supervisori del progetto, che controlleranno che le fasi vengano seguite nel modo corretto;

 i responsabili ambientali, che terranno pulito il piano di lavoro;

 i responsabili dei test, che verificheranno i risultati delle varie prove;

 i reporter, che registreranno le azioni compiute;

 i supporter, che inciteranno positivamente il gruppo;

 gli speaker, che presenteranno il progetto;

 gli artisti, che renderanno il prodotto finito più attraente…

…e così via.

Con ogni probabilità qualcuno si offrirà volontario, mentre altri diventeranno assegnatari di un compito per elezione (vostra). Alla fine, ciascun membro del gruppo avrà uno o più ruoli da svolgere. Se avete a disposizione dei porta-badge potrete fare in modo che ognuno, all’interno del gruppo, sia identificabile dalla targhetta appropriata.

COME SI FA?

1 Osserva attentamente l’immagine e rispondi.

• Secondo te, quali materiali sono stati utilizzati per costruire la giraffa?

Testa:

Collo:

Corpo:

Coda:

Zampe:

• Quali strumenti sono stati utilizzati?

2 Descrivi le fasi di realizzazione.

1 Descrivi tutte le azioni che si devono compiere per lavarsi correttamente i denti. Scrivi una sola istruzione per riga, fino a quando non darai l’istruzione finale, e cioè: esci dal bagno.

1 Se la porta del bagno è chiusa, aprila o ti procurerai un bel bernoccolo.

2 Entra in bagno.

3 Cammina fino a quando sei davanti al lavabo.

Creare

La realizzazione vera e propria è il gli alunni e le alunne, il momento in cui vedono materializzarsi le loro idee e la loro immaginazione.

Tuttavia, dobbiamo considerare il fatto che la fase del “fare e co struire” è di notevole impegno, poiché ha come presupposto un’ tensa attività di riflessione sui processi cognitivi in gioco molteplici competenze do i principi dell’imparare a imparare imprenditorialità

L’attività manuale è infatti il riflesso visibile di un processo che coinvolge:

 la comprensione di un testo

 la formulazione di ipotesi

 la progettazione;

 la pianificazione;

 l’organizzazione;

 la previsione di risultati intermedi e di quello finale;

 il continuo adattamento alla realtà contingente, il relativo problem solving e lo sviluppo della creatività (mi serve un tappo per fare una ruota; se non ho il tappo, che cosa posso usare?);

 la riorganizzazione delle proprie abilità e conoscenze;

 l’ottimizzazione delle procedure e l’imparare a imparare (per ottenere questo risultato compio una serie di azioni, ma ora so che posso seguire un percorso più breve o più semplice);

 la verifica del proprio elaborato in termini funzionali (funziona, non funziona, dove ho sbagliato?);

 l’autovalutazione del risultato in termini di gradevolezza, soddisfazione personale e gratificazione (il risultato ottenuto mi soddisfa?);

 l’autovalutazione della procedura seguita.

Prima di iniziare, sarà opportuno che la squadra prepari tutto il materiale e gli strumenti necessari e si prepari a lavorare con attenzione e concentrazione, seguendo le istruzioni precedentemente stabilite e svolgendo ognuno il ruolo che gli è stato assegnato.

concentrazione, fondamentali in questa fase del processo, sono parole chiave per l’approccio a qualsiasi tipo di apprendimento. Tuttavia, riflesso fisiologico innato, la concentrazione implica volontà e soprattutto abilità che vanno allenate. Avrete certamente chiara la differenza tra attenzione e concentrazione, dal momento che la sperimentate ogni giorno in classe. Pensate a quando richiamate a stare attento qualcuno che si è distratto, a come immediatamente si ricompone e vi guarda e a come un minuto dopo è nuovamente immerso nei propri pensieri. Beh, gli avete chiesto di stare attento, e lui lo ha fatto! I fattori che differenziano attenzione e concentrazione sono la volontà, ma anche il tempo.

L’ATTENZIONE:

• è una funzione del corpo;

• è un evento momentaneo;

• non ha bisogno di essere insegnata.

LA CONCENTRAZIONE:

• è formata da un susseguirsi di attimi;

• è volontaria;

• si impara;

• si insegna.

GIOCHI E ATT IVITÀ PER LO SVILUPPO

DELLA CAPACITÀ DI CONCENTRAZIONE

1 PAROLE NASCOSTE

Cercate un breve testo con una parola ricorrente, che può essere un verbo, un nome, una preposizione, e comunicatela alla classe. Leggete il testo ad alta voce e invitate gli alunni e le alunne a fare una X ogni volta che sentono la parola stabilita. La lunghezza e la difficoltà del testo sarà proporzionale sia all’età degli alunni e delle alunne sia alla familiarità con il gioco proposto.

2 CALZINO PUZZOLENTE

Comunicate alla classe che farete una serie di domande a catena, una domanda a ciascun componente. Indipendentemente dalla domanda, la loro risposta dovrà essere: “Calzino puzzolente”. Iniziate con domande anche abbastanza difficili, come per esempio: “Quante città ci sono in Italia?”, “Qual è il vulcano più alto del mondo?” ecc. All’inizio, e soprattutto se si tratta di una domanda complicata, per loro sarà semplice rispondere “Calzino puzzolente”; tuttavia, dopo qualche minuto, qualcuno avrà già perso la concentrazione e se intercalerete domande difficili a domande più immediate e semplici, come per esempio: “Quanti anni hai?”… vi risponderanno la verità!

3 NESSUN SÌ E NESSUN NO

Fate a ogni componente della classe una serie di domande a cui si dovrà rispondere senza dire sì o no. Il gioco è più difficile di quanto possa sembrare, ed esige una grande concentrazione. Le sequenze classiche in cui si perde la concentrazione sono:

– Da dove vieni?

– Da Milano.

– Milano in Italia?

4 CIAK!

– Qual è il tuo colore preferito?

– Il rosso.

– Non il blu?

Impartite una serie di ordini. La classe dovrà eseguirli solo se al termine dell’ordine batterete le mani.

ALLENARSI ALLA PRECISIONE

1 Completa le simmetrie.

ORGANIZZAZIONE!

1 Rispondi.

• Sei una persona organizzata?

• Da che cosa si capisce?

• Com’è il tuo diario scolastico dal punto di vista dell’organizzazione?

2 Ora pensa di avere avuto il permesso di andare a dormire una notte da un amico o da un’amica. Prepara mentalmente il tuo zaino e scrivi che cosa ti porti.

3 Confrontati con il resto della classe. Hai dimenticato qualcosa? Che cosa?

PARTY T IME!

1 Hai la possibilità di organizzare una festa e naturalmente hai un sacco di cose a cui pensare: dove farla, a che ora iniziare, a che ora finire, chi invitare, quale musica mettere, quali giochi fare, che cibo e bevande procurarti (chiaramente ti serviranno piattini, bicchieri...). Realizza una mappa per avere tutto sotto controllo.

Verificare sul campo

Dopo aver svolto tutte le precedenti fasi del processo di progettazione, gli alunni e le alunne raccoglieranno i dati, attraverso alcune misurazioni necessarie e realizzeranno grafici che potranno essere di diversa natura, a seconda dei dati raccolti.

Di seguito, sono proposte alcune attività per rivedere i principali tipi di grafici che servono per registrare i dati raccolti durante i test.

Ideogramma

L’ideogramma è una rappresentazione grafica che usa disegni più o meno stilizzati. Ogni disegno prende il nome di “unità grafica”. Ogni unità grafica ha un valore stabilito in precedenza e la sua ripetizione dà il valore complessivo.

È utile quando si vuole dare un’idea immediata dell’argomento trattato. Nonostante piaccia molto agli alunni e alle alunne, i dati espressi in questo modo non sono precisi e il grafico non è utilizzabile per quantità molto grandi da registrare.

Istogramma

L’istogramma, detto anche ortogramma o diagramma a strisce, è una rappresentazione grafica a colonne di uguale larghezza e di altezza variabile in dipendenza del dato da rappresentare. L’istogramma può essere a colonne verticali o a righe orizzontali.

Diagramma cartesiano

Il diagramma cartesiano è una rappresentazione grafica che utilizza un piano cartesiano in cui vengono inseriti i valori, uniti da una linea continua che mostra chiaramente l’andamento dei dati

Areogramma

L’areogramma, o diagramma circolare, è una rappresentazione grafica formata da un cerchio diviso in settori. L’ampiezza di ogni settore corrisponde al dato con siderato. Per quanto le percentuali siano visivamente immediate, difficilmente sono precise.

LEGGERE UN IDEOGRAMMA

1 Nella classe IV A è stata condotta un’indagine per scoprire quale sia il tempo atmosferico preferito. Osserva e rispondi.

• A quanti piace il sole?

• Sono di più quelli a cui piace la pioggia o quelli a cui piace il temporale?

• A quanti piace la neve?

• Quanti sono in tutto i componenti della IV A?

2 Osservando l’ideogramma, formula e scrivi una domanda da sottoporre alla tua classe.

LEGGERE UN ISTOGRAMMA

1 La classe di Alberto ha lavorato per un mese intero per creare il “magazzino delle STEAM”. Ciascun componente della classe ha raccolto: tappi di plastica, rotoli terminati di carta igienica, contenitori per le uova, scatole di cartone. Dopo un mese, i dati della raccolta sono stati registrati in un istogramma. Osserva e rispondi.

• La classe ha raccolto più rotoli vuoti o più contenitori per le uova?

• La classe ha raccolto più o meno di 20 scatole di cartone?

• La classe ha raccolto più o meno di 30 tappi?

• Quanti tappi di plastica sono stati raccolti?

LEGGERE UN DIAGRAMMA CARTESIANO

1 A Elisa piace moltissimo giocare a calcio. Decide di lanciare da metà campo ogni giorno per un’ora per vedere quanti gol riesce a fare. Alla fine, raccoglie i dati in un diagramma cartesiano. Osserva e rispondi.

mercoledì martedì giovedì venerdì sabato domenica

• Qual è il giorno in cui Elisa ha fatto più gol?

• E quello in cui ne ha fatti meno?

• Ci sono giorni in cui ha fatto lo stesso numero di gol?

• Quanti gol ha fatto lunedì?

• Quanti ne ha fatti giovedì?

• Quanti gol fa Elisa in media, in una settimana?

GLI AREOGRAMMI

= film horror = film comici

• Qual è il tipo di film preferito?

• Quale tipo di film piace di meno?

• Piacciono di più i film horror o i film d’avventura?

• Piacciono di meno i film di fantascienza o quelli d’amore?

2 Nella classe di Martina si praticano diversi sport. Leggi con attenzione i dati e registrali in un areogramma.

1 Osserva l’areogramma dei tipi di film preferiti nella classe di Mauro, poi rispondi. = 13 = film d’avventura = film d’amore

= film gialli = film di fantascienza = 7

= 1 = 5

Migliorare

Dopo aver eseguito i test, i gruppi di lavoro sono invitati a riflettere attentamente sulla propria invenzione per migliorarla oppure, se non funziona, per ricominciare con una nuova progettazione.

Se il miglioramento dovrà essere estetico, il gruppo accetterà volentieri di apportarlo, ma nel momento in cui dovesse essere funzionale, potrebbero nascere dei problemi. Ci sono persone sbrigative che tendono a vivere ogni cosa in modo troppo affrettato e che quindi riportano lo stesso comportamento anche in classe; ci sono persone insicure che nascondono questa loro caratteristica dietro a un eccessivo perfezionismo.

Inoltre, nel caso in cui l’invenzione non funzioni e sia necessario rimaneggiare il progetto, potrà esserci chi non accetterà l’errore, per cui è necessario allenare la classe alla resilienza, che non è una qualità innata dell’essere umano: si impara, di conseguenza si può insegnare.

Avere un alto livello di resilienza non vuol dire essere infallibili, vuol dire invece essere disposti a pensare di poter sbagliare

La resilienza, termine che viene proprio dall’ingegneria e dalla biologia, è la proprietà che hanno alcuni materiali di adattarsi e resistere a forze di deformazione o all’usura, conservando o riacquistando la propria forma originaria. In psicologia, il termine definisce la capacità delle persone di far fronte agli eventi traumatici o stressanti e di riorganizzarsi cogliendo le opportunità positive che la vita offre. Le persone resilienti sono quelle che riescono nonostante le circostanze non siano favorevoli, sono quelle che contro ogni previsione ce la fanno e che raggiungono mete importanti credendo in ciò che fanno, senza abbattersi.

Per questa ragione, le schede successive sono un punto di partenza per allenare la classe a un atteggiamento resiliente, che contempla l’errore e non lo demonizza.

CHI SBAGLIA, IMPARA!

1 Rispondi.

• Pensa a una volta in cui hai fatto un errore.

Che cosa è successo?

• Che cosa hai imparato da quell’errore?

• Che cosa hai fatto quando hai capito di avere sbagliato?

QUANDO CAPITA DI SBAGLIARE

1 Rispondi.

• Ti capita spesso di sbagliare?

• Quando te ne accorgi, come ti senti?

• E come ti comporti?

• Che cosa dici a te stesso/a quando ti rendi conto di aver sbagliato qualcosa?

• Quando fai un errore, chi è la prima persona a cui lo dici?

• Che cosa vorresti che ti dicessero le persone, quando sbagli?

Vorrei che i miei cari mi dicessero Vorrei che i miei amici mi dicessero

MIT ICI SUPER ERRORI

1 Molte invenzioni sono nate da clamorosi errori. Non ci credi? Leggi con attenzione.

Post-it

Spencer Silver lavorava in un’azienda di prodotti chimici. Un giorno fu incaricato di creare un adesivo super forte da utilizzare nell’industria aeronautica. Si mise al lavoro e nel 1968 produsse una colla... super debole! Il prodotto aveva il vantaggio che poteva essere rimosso senza lasciare residui e poteva essere riutilizzato più volte. Tuttavia, non era quello che gli avevano chiesto: i suoi capi non ne furono contenti e il progetto fu considerato un errore. Solamente diversi anni dopo si accorsero dell’importanza di questa debole colla e dal 1980 i Post-it sono venduti in tutto il mondo.

Coca cola

Una delle bevande più conosciute del mondo è nata per sbaglio. Il farmacista di Atlanta John Pemberton nel maggio del 1886 stava cercando un rimedio per curare il mal di testa che lo affliggeva a causa di una ferita subìta in battaglia. In effetti, il miscuglio che creò fu un fallimento, poiché non faceva passare il mal di testa e non era neppure buono da bere. Tuttavia, anni dopo provò a mischiare la sua pozione ad acqua gassata, e così nacque la famosa bevanda.

2 E tu, hai mai scoperto qualcosa per sbaglio? Racconta.

CHI SI FERMA... NON ARRIVA

DA NESSUNA PARTE!

1 A volte prima di raggiungere un successo bisogna superare molti fallimenti, senza arrendersi. Leggi gli esempi di costanza di questi ingegneri e rispondi.

La lampadina

Thomas Edison è stato uno tra i più grandi inventori ed è famoso in tutto il mondo per avere inventato la lampadina. Tuttavia, prima di trovare un buon filamento per la sua invenzione, Edison ne sperimentò 1600 diversi. Tutti bruciarono in pochi minuti. Ma l’inventore non si scoraggiò: – Non ho fallito, ho solo trovato 1600 soluzioni che non funzionano. Grazie a una fibra di bambù carbonizzata, la soluzione numero 1.601 fu quella giusta. Il 21 marzo 1879 la lampadina funzionò e grazie alla costanza del suo inventore da quel giorno abbiamo la luce artificiale.

L’auto volante

Per ora nessuno ha inventato l’auto volante. Esistono progetti, ma di flying car funzionanti non se ne vedono. Ci sono prototipi con eliche pieghevoli, che però faticherebbero a passare per una strada cittadina, ce ne sono altri con eliche interne, più adatti alle strade del centro, ma che hanno bisogno di dieci motori e causano un grande inquinamento. Rafi Yoeli, un ingegnere aeronautico israeliano, sta lavorando a questo progetto da più di vent’anni e ora sta mettendo a punto un’auto volante a idrogeno, che non inquina.

2 Rispondi.

• Secondo te, quali sono le qualità che hanno in comune questi due inventori?

CAMPIONI SI DIVENTA

1 Leggi e completa.

MICHAEL JORDAN

è considerato il più grande giocatore di pallacanestro di tutti i tempi.

Di sé stesso dice: – Nella mia vita ho sbagliato più di novemila tiri, ho perso quasi trecento partite, trentasei volte i miei compagni mi hanno affidato il tiro decisivo e l’ho sbagliato. Ho fallito molte volte. Ed è per questo che alla fine… ho vinto tutto.

Posso accettare la sconfitta, tutti falliscono in qualcosa. Ma non posso accettare di rinunciare a provarci. Per imparare ad avere successo, devi prima imparare a fallire.

Le sconfitte mi hanno sempre motivato per fare di più la volta successiva.

Se ci si arrende una volta, diventa un’abitudine. Mai arrendersi!

Se lavori duramente, sarai ricompensato. Non ci sono scorciatoie nella vita.

• Secondo me, quello che dice Michael Jordan dà il coraggio di continuare e di sognare anche quando le cose non sembrano andare benissimo perché…

IL MIO MOTTO

1 A volte per superare un momento difficile può essere utile avere un “motto”, cioè una propria frase di incoraggiamento. Leggi le frasi e colora quella che preferisci. Poi motiva la tua scelta.

2 Ora, inventa un motto per la tua squadra STEAM, poi rispondi. Gli errori sono la prova che ci stai tentando. 1

Volere è potere. 2

Non mollare mai. Le grandi conquiste richiedono tempo. 3

Se lo puoi sognare, lo puoi fare. 4

Non ho fallito, ho scoperto qualcosa che non funziona. 5

• La frase che preferisco è la numero perché

• Il motto è piaciuto ai componenti della tua squadra?

• E tu, quali preferisci tra i motti scritti dalla tua squadra?

CONSIGLI

1 Leggi il racconto, poi scrivi ad Andrea alcuni consigli per farlo stare meglio.

Oggi Andrea è veramente a pezzi!

3 a 3. L’arbitro fischia la fine della partita. Si va ai supplementari, ma ancora niente di fatto: la vittoria si gioca ai rigori.

Andrea! Andrea! Andrea!

La squadra grida forte il suo nome.

È un cannoniere, non sbaglia mai un tiro.

Iniziano gli avversari ed è... GOL!

Tocca ad Andrea e... Sììì. Il cannoniere non si smentisce.

1 a 1.

I tiri si susseguono e la partita non si risolve.

5 a 4. Ultimo tiro di nuovo per Andrea e...

Clamoroso! Impossibile, ma Andrea sbaglia l’angolazione.

La vittoria è della squadra avversaria.

Caro Andrea,

LA MIA VITA COME UN F ILM DELL'ERRORE''

Capita spesso di aver commesso errori, sbagli o distrazioni che al momento ci sono sembrati vere e proprie catastrofi. Poi, ripensandoci tempo dopo, beh, risultano essere fatti buffi o incredibili scoperte.

1 Ripensa ai tuoi errori e completa.

Che ridere, quella volta!

Wow, che scoperta!

Condividere

Al termine del percorso, ogni gruppo (o ogni persona, in caso di esperimento da svolgersi individualmente), condividerà i risultati con i compagni e le compagne. La presentazione dell’esperimento e dei risultati ottenuti potrà essere fatta oralmente o attraverso slide.

Parlare in pubblico è una delle paure più diffuse e, secondo le statistiche, affligge un italiano su quattro, comprese quindi persone dello spettacolo, politici e manager. Tuttavia, quasi ogni giorno noi chiediamo ai nostri alunni e alunne di farlo, considerando raramente le tensioni psicologiche a cui sono sottoposti. Soprattutto, non dedichiamo spazio sufficiente all’insegnamento del parlare in pubblico o, come si chiama solitamente a scuola, del sapersi esprimere. Quante volte sarà capitato di aver sentito dire o di aver detto la classica frase: – Si vede che hai studiato, ma non sai esprimerti.

Sì, saper parlare è proprio considerata, dai più, una dote innata, naturale. Tutti sanno parlare, questo è vero, ma quanti sanno parlare bene? A scuola si dedica molto tempo e impegno allo scrivere testi narrativi, descrittivi, espositivi, regolativi, argomentativi, e certamente questo è apprezzabile e necessario; tuttavia, la stessa quantità e qualità di tempo non viene dedicata alla competenza comunicativa orale, anche se è fuor di dubbio che sia parte integrante del vivere sociale.

Spendiamo quindi qualche riga per ricordare che, in un atto comunicativo, che cosa si dice ha un’influenza pari al 7%, contro il 93% rappresentato da come lo si dice

È fondamentale conoscere ciò di cui si parla, in caso contrario spesso non vi sarebbe nemmeno bisogno di esporlo; tuttavia, il 38% della nostra comunicazione è influenzato dagli elementi paraverbali e passa quindi attraverso il tono, il timbro, il volume e l’inflessione della voce, mentre il 55% è veicolato dalla mimica, dalla gestualità e dalla postura del nostro corpo.

Verbale

Paraverbale

Non-verbale

Nelle pagine seguenti proponiamo alcuni giochi e schede che non hanno la presunzione di esaurire l’argomento, ma cercano di essere un punto di partenza per gli alunni e le alunne – e perché no, anche per gli/le insegnanti – con cui poter allenarsi a parlare in pubblico attraverso esercizi per la voce, per il viso e per il corpo.

Dal momento che i risultati possono essere condivisi anche attraverso la proiezione di immagini, le ultime schede sono dedicate a come realizzare buone slide.

GIOCHI PER LA VOCE

Parlare mantenendo il corretto volume non è semplice.

Parlare a un volume molto basso può essere utile in determinate occasioni, ma certamente non quando si presenta un lavoro alla classe. Normalmente è indizio di insicurezza oppure al contrario di arroganza e presunzione, poiché si obbliga l’interlocutore a un silenzio innaturale e contemporaneamente a uno sforzo uditivo tale per cui è molto difficile che ci si possa concentrare sul contenuto.

Parlare a voce molto alta, invece, può essere indispensabile in occasioni quali la richiesta d’aiuto o di attenzione nei confronti di un pericolo, ma in conversazioni normali produce nell’interlocutore un senso di fastidio che offusca il contenuto.

Entrambe le modalità quindi, ovvero il parlare a voce troppo bassa o troppo alta, sono da ritenersi socialmente inappropriate in situazioni quali lo scambio comunicativo quotidiano o la presentazione orale in classe.

Per allenarsi all’uso del corretto volume di voce, sono qui proposte alcune attività che permetteranno di interiorizzare il concetto di volume adeguato alla circostanza.

1

SU, SU, SU! GIÙ, GIÙ, GIÙ!

Seduti in semicerchio, chiedete ai componenti della classe di alzarsi, a turno, e di recitare una filastrocca, uno scioglilingua, una poesia o un breve testo che conoscono a memoria. In una seconda fase, chiedete di ripetere l’esercizio iniziando con un volume molto basso, ma udibile da tutti, e aumentando via via il volume (senza esagerare).

Ora chiedete di fare il contrario, ovvero di iniziare con un volume alto fino ad arrivare a un sussurro.

2 MI SENT I?

A coppie, gli alunni e le alunne reciteranno un breve dialogo come se urlassero.

Dite loro di pensare di essere per esempio su marciapiedi opposti di una strada.

Domande da rivolgere alla classe:

 In quali occasioni è necessario parlare a voce molto alta?

 C’è qualcuno che lo deve fare per lavoro?

 Che cosa provi quando senti qualcuno urlare?

 Quando, di solito, le persone urlano? Ipotizza due situazioni.

esempio di dialogo:

– Ehi, Elena!

– Ciao, Marco.

– Come va?

– Bene, ma sono di fretta.

– Dove vai di bello?

– Sto andando a giocare da Luca.

– Posso venire anch’io?

– Certo, fai attenzione quando attraversi la strada!

Come nell’esercizio precedente, gli alunni e le alunne lavoreranno a coppie, ma immaginando di confidare un segreto o comunque di essere in una situazione in cui non si possa parlare a voce alta.

Nel recitare la scenetta, dovranno tener conto che la classe deve sentire ciò che si stanno confidando.

Domande da rivolgere alla classe:

 In quali occasioni è necessario parlare a voce molto bassa?

 C’è qualcuno che lo deve fare per lavoro?

 Che cosa pensi quando senti qualcuno parlare a voce molto bassa?

 Quando, di solito, le persone parlano a voce molto bassa? Ipotizza due situazioni.

esempio di dialogo:

(Al cinema)

– Non hai sete?

– No, perché?

– Perché io ho sete.

– Aspetta l’intervallo!

– Ma se ho tanta, tanta sete?

– Ti alzi, vai fuori e mi lasci vedere il film. Ok?

Il tono e l’inflessione della voce sono molto difficili da gestire. Tuttavia, presentando un lavoro in classe è fondamentale mantenere un certo controllo. Un modo per farsi ascoltare è trasmettere curiosità e interesse riguardo a ciò che diciamo. Certamente ci vuole allenamento, ma svolgere il seguente esercizio può essere una buona palestra.

4 SINTONIZZAT I?

Invitate i componenti della classe a pronunciare alcune frasi con un tono che voi sceglierete.

In seguito chiedete a ognuno di scegliere un’intonazione e di proporla alla classe.

Sapranno essere abbastanza espressivi da comunicare quello che davvero vogliono?

I compagni e le compagne riusciranno a indovinare? Incitateli a mettersi alla prova.

ESEMPI DI FRASI:

Hai copiato il compito da un compagno?

Tono seccato, divertito, arrabbiato, di richiesta, deluso.

Mi fai paura!

Tono spaventato, divertito, ironico (non mi fai paura), irritato.

Perché non hai cenato?

Tono stupito, di rimprovero, freddo e scostante, triste, divertito.

GIOCHI PER IL VISO

Anche l’espressione del viso è importante, perché quando si parla davanti ad altre persone le emozioni che traspaiono condizionano chi ci ascolta. Inoltre, mentre è facile mentire con le parole, è estremamente difficile mentire con la mimica o la gestualità. Esercitarsi a controllare la mimica facciale può essere davvero divertente e coinvolgente.

1 COME STO?

Insieme alla classe, scrivete su un foglio tutte le diverse emozioni a cui riuscite a pensare: stupore, paura, dubbio, felicità, tristezza, disgusto e così via.

Fate sedere la classe in cerchio.

A turno, ciascuno sceglierà un’emozione, si alzerà e cercherà di riprodurre solo con le espressioni del viso l’emozione scelta.

La classe dovrà indovinare di quale emozione si tratta.

2 CAMBIO D'UMORE

A rotazione, ogni alunno/a dovrà scegliere tre espressioni diverse e presentarle una alla volta alla classe. I compagni e le compagne dovranno ricordare la sequenza e riproporla a loro volta.

GIOCHI PER IL CORPO

Il nostro corpo è un importante mezzo di comunicazione, per questo è bene imparare a usarlo anche quando si presenta un lavoro alla classe o semplicemente si parla in pubblico.

1 VERO O FALSO?

Invitate due alunni/e a lavorare insieme a voi e chiedete alla classe di osservare che cosa accade. Rivolgetevi a uno dei due e dite: – Che bello vederti! – poi sorridete e dategli una pacchetta sulla spalla.

Ora ripetete la frase rivolgendovi all’altro, ma incrociate le braccia e battete un piede sul pavimento. Invitate la classe a interpretare il vero messaggio di ciò che avete detto. La frase era la stessa, eppure… che cosa avete trasmesso utilizzando gesti diversi?

2 L'ATTORE SILENZIOSO

Fate sedere la classe in cerchio. A turno, ognuno si alzerà e si siederà su una sedia posta al centro del cerchio.

Dovrà assumere una posizione in modo da risultare: pensoso, assonnato, nervoso, impaziente, annoiato… La classe dovrà comprendere lo stato d’animo interpretato.

3 LA SCENETTA

Dividete la classe in piccoli gruppi. Chiedete loro di scegliere una situazione, come per esempio un viaggio in autobus, una partita di basket, una festa di compleanno.

I componenti del gruppo dovranno muoversi e atteggiarsi come se fossero in quella particolare situazione e il resto della classe dovrà indovinarla.

4 LA BUFERA

In piedi, con le gambe un po’ divaricate e gli occhi chiusi, dite alla classe di immaginare di essere su una nave in mezzo a una bufera e di muoversi di conseguenza.

5 SECONDO ME, È...

Come cammina un egoista? E un timido? E uno spaccone? E un pauroso?

Invitate gli alunni e le alunne, a turno, a mimare l’andatura e la postura di persone caratterialmente diverse o che provano differenti stati d’animo. La classe riuscirà a indovinare?

PRIMA, DURANTE E DOPO

1 Rispondi.

• Che cosa provi quando ti dicono che dovrai presentare una ricerca alla classe?

• C’è qualcosa che ti preoccupa? Se sì, di che cosa si tratta?

• Che cosa provi quando sei davanti a tutta la classe e devi iniziare la tua presentazione?

• Come ti senti mentre parli?

• Che cosa vorresti che facessero i tuoi compagni e le tue compagne?

• Che cosa vorresti che NON facessero?

• Che cosa vorresti che facesse l’insegnante?

• Che cosa vorresti che NON facesse?

• Di solito, come ti senti alla fine della presentazione?

LA MAPPA SALVA–TUTTO!

1 Per non correre il rischio di incappare nell’ansia da prestazione orale, prepara una mappa dell’argomento e dei sotto-argomenti, scrivendo solo le parole chiave. Aggiungi a ogni punto un materiale da mostrare alla classe. Può essere un oggetto, un disegno, un grafico, una foto o qualsiasi cosa che c’entri con l’argomento. Mostrare qualcosa serve per incuriosire e per mantenere l’attenzione. Ricordati di terminare la presentazione con una conclusione efficace.

Titolo argomento

Punto 1

Punto 2

Punto 3

I 10 TRUCCHI PER SENT IRSI A PROPRIO

AGIO DAVANTI ALLA CLASSE

1 Leggi, prova e non dimenticare!

Stai in piedi con le gambe leggermente aperte, per non dondolare da un lato all’altro o avanti e indietro. 1

Ogni tanto, spostati da un punto all’altro. 2

Evita di toccarti i capelli, i braccialetti ecc... per non distrarre chi ti ascolta. 3

Se hai in mano un foglio o un oggetto, tienilo all’altezza della vita. 4

Pronuncia le parole chiaramente. 5

Parla alla giusta velocità. Fai una breve pausa tra un argomento e l’altro.

Usa il giusto volume.

Parla in modo espressivo.

Cerca di avere anche un viso espressivo.

Mentre parli, guarda i compagni e le compagne.

SLIDE PERFETTE

1 Se vuoi preparare delle slide da complimenti assicurati, prova a seguire questi semplici consigli.

PRIMA SLIDE O COPERT

La prima slide è molto importante, perchè è quella che farà esclamare il primo WOW!

Quindi, ci saranno:

 il TITOLO della tua presentazione;

 il TUO NOME scritto con una dimensione più piccola rispetto a quella del titolo;

 una GRANDE IMMAGINE. Più l’immagine è scenografica, più interessante sarà la slide.

L'ORANGO

ricerca di Elisa Quadri

Una cosa molto importante da ricordare è che si fa fatica a leggere caratteri scuri su uno sfondo scuro o caratteri brillanti su uno sfondo brillante. Quindi, mentre prepari le tue slide controlla sempre di aver creato il CONTRASTO giusto.

Ciao, io sono una slide che non leggerà nessuno.

Io, invece, sono una slide che fa venire il mal di testa!

Ciao, io sono una slide perfetta!

DE PERFETTE

NTERNE O SUCCESSIVE

Per realizzare le tue pagine interne, segui la mappa che hai preparato per la tua presentazione orale. Ricorda che sulle slide devi scrivere solo le parole chiave, non tutto quello che dirai, e che è meglio una slide in più che una slide troppo piena. Ecco alcuni suggerimenti.

Carattere

1 tipo di carattere

2 colori

2 dimensioni

Testo

Immagini

Scrivi al massimo 6 righe su ogni slide. Non aggiungere testo sopra alle immagini.

Usa immagini grandi.

Un altro consiglio che non devi mai dimenticare è il seguente: una slide per essere efficace deve essere semplice!

HABITAT

Gli oranghi abitano in del Borneo e di loro il nome comune: costituisce circa il orango di Sumatra

Per l’orango la foresta è di vitale importanza: trascorre la sua giornata passando da un albero all’altro.

HABITAT

Slide non efficace Slide efficace