Thethreebasicengineeringtasks
Thefundamentaltaskofanengineeringassignmentistofindqualitativelypossiblesolutionstoagivenproblemandtoanswerthequantitative questionaboutitstechnicalfeasibilityandeconomicadvantage.
Thequalitativesolutionusuallyleansonthesearchofthescientific,commercial,andpatentliteraturebut,inthefirstplace,onone’sownexperience combinedwithone’sowncapabilityofcombinationsandfantasy.
Whenaquantitativesolutionisrequiredthentheengineerisaskedto applythethreebasicengineeringtasks,oftenusingsimple,butmoreoften sophisticatedmathematicalmethods.
Thefirsttask isbasedonsimple,andinthesimplifiedworldofreallife, undisputedprinciplesof naturalsciences,suchasthelawofconservation ofmass,thelawofconservationofvariouskindsofenergy,andthestoichiometriclawsofchemistry;alsoincludedaresimplerulesfortheconversionof quantitiessuchasthemassandvolumes.Usingtheserulesonecanreliably perform massandenergybalances ofaparticularprocess.
Thesecondtask followsaquestionhowfarcanacertainprocessproceed,orunderwhatcircumstanceswilltheprocesschangequalitatively.In thiscase,onecanmakeuseofknown processequilibrium.Thequantities thatenterintothecalculationsherearemorecomplexparametersfromthe domainof statics and thermodynamics thatcanhavetheformofconstants,functions,orcomplexmathematicalobjects,thevaluesofwhichmust bedeterminedexperimentally.Alternatively,thevaluesofsome(suchasthe meltingpoints,vaportensions,solubilities,interfacialtensions,andbonding enthalpies)canbefoundwithsufficientaccuracyinatabularforminthe appropriateliterature.Insomecases,onecanuserelativelyreliableformulas fortheestimationofthesequantitiesintowhichoneneedstosubstitute quantitiesthatareeasiertoobtain.
Thethirdtask dealswiththe kinetics ofaprocess,i.e.,whatisitsrate. Inthecaseofchemicalandphysicalprocessesthatproceedoutsidetheequilibrium,therateisdeterminedbythesetofdrivingforcesopposedbyasetof resistancesthatactagainsttheequalizationofthepropertiesindifferentparts ofthesystem.Thethreemostsignificantresistancesarethosethatopposethe transferofmomentum, thetransferofheat,and thetransferofmass. Theseresistanceshave,toacertaindegree,alinearcharactersoitis
advantageoustostudythemtogetherunderacommontitleof transport phenomena.Aseparatetaskisthestudyofthe chemicalkinetics that, asarule,isnotlinearand,therefore,mustbestudiedindependently.
Transportphenomena:Thecontinuum andtheinterfaces
Underordinarycircumstancesweperceivethroughoursensesanymassas beinga continuum orasasetofcontinuaseparatedbysimple geometrical interfaces.Inreality(unlessonewantstoimmersedeeperintonuclear physics),themassisratherasetofmovingparticles(vibrating,sometimes rotating,andevenmutuallyexchangingtheirpositions).Despiteofthat, itisusefultoconsideralargesetofparticles(betheymolecules, nanoparticles,orevenparticlesvisiblebybareeye)tobeacontinuumto whichonecanassign averagedquantities toeverypointofthesystem. Intensivequantities areratiosofdirectlymeasurableextensivequantities (e.g.,thedensityistheratioofmassandvolumeatagivenpoint).
Amongthe statisticallyaveragedquantities,thelocalvelocityisthe statisticalaverageofparticlepathscuttingtheimaginaryplaneinthevicinity ofthepointinquestionperunitoftime)orthetemperature(expressing meanenergyoftheoscillatingmolecules).
Todescribesuchanapproach,the classicalphysics developedmathematicaltools;theanalysisofcontinuousfunctions(Newton,Leibnitz)lead tousual differentialandintegralcalculus
Theequilibriumstates inhomogeneousphasesarecharacterizedbyinvariabilityofquantitiesthatcanbecalledthe measuresofequilibrium,forexample,thetemperature.Whenthetemperatureisconstant,thereisnolocalheat transport,whentheconcentration(activities,fugacities)areconstant,thereis nomasstransport,etc.Thedisciplineofphysicsthatdealswiththeusualequilibriumprocessesiscalledstatics;inphysicalchemistryitiscalledthermodynamics.
Whenthesystemis notinequilibrium thenthevariabilityofthose quantitiesthatmeasuretheequilibriumleadtopositionchanging, regrouping,andtransformationsofbothmassandenergy.Toevaluate theratewithwhichthesystemmovestowardtheequilibrium,theso-called transportprocesses,itisusefultointroducequantitiesthatcharacterizethe basictransportphenomena: momentumtransfer,heattransfer,and masstransfer.Therelevanttransfercoefficientsare viscosity,thermal conductivity,anddiffusivity.
Inthepast,theindividualphenomenawerestudiedinseparatescientific disciplines,suchasthefluidmechanics,hydrodynamics,andthescience ofheatandmasstransfer.Later,itturnedout,howeverthatthesethree processesareanalogousandthattheycanbetreatedwiththesame mathematicaltools.
Asarule,theindividualstepsofanengineeringsolutionusuallyareas follows:
•Thedefinitionofaspatialandtemporalregioninwhichtheprocessin questiontakesplace.
•Theapplicationofamathematicalmodeltothetransportinquestion includingboundaryandinitialconditions.
•Ananalysisofpossiblesolutionsofthemodel,firstinasimplifiedform.
•Theevaluationofallpossiblesolutions,insimplecases,iscarriedout.
•Thepresentationoftheresultsinausefulform.
Thetransportacrossaphaseboundaryisaspecialcase.Thedifference betweenthetransportcoefficientsindifferentmediumsresultsinadiscontinuitythatmodifiesvelocityfields,velocitygradients,temperaturegradients,concentrationgradients,etc.Theopposinglimitsatthephase boundaryareusuallyrelatedbyasimplemathematicalformulathatisfortunatelynotmodifiedbythetransportitself.Therefore,thecommonrulesof physicsandphysicalchemistrydescribingtheequilibriumsatphaseboundaryremainvalid.Thus,theknowledgeofsurfacephenomenaisessentialfor thestudyofcomplextransportphenomena.
Thehistoryofthisdiscipline
Aperfunctoryopeningofanymonographtitled“TransportPhenomena”(possiblyexpandedin“Transportofmomentum,heat,andmass”) mightleadthereadertoerroneousconclusions.Thosewhoarenottoofond ofmathematicsarefrightenedbythemassofformulasandrelationshipsfrom thedomainofdifferentialequationsandthosefromthevectorcount.Onthe otherhand,mathematicalgeeksseeafascinatingplayingfield.
Thisshouldnotbeverysurprisingsincethisdisciplinegrewoutofthe workofsuch physicists (Newton,Bernoulli,Euler,Cauchy,Stokes,and others)whoareknownbytheirdiscoveriesinmathematicsneededforsolutionstospecificphysicalproblems.Itisevenpossibletoclaimwithacertain degreeofexaggerationthat mathematics initstimeoweditsprogress moretothestudyoftransportphenomenathanthescienceoftransport
phenomenatomathematics.Uptotheendofthe19thcentury,thesedisciplinesformedrelativelyspecialandnottooemphasizedpartofphysics.
Nextcametheperiodcharacterizedbytheprogressinshiptransportation,upswingofaviation,steamenergygeneration,andchemicalengineering,whenthisdisciplinebecomesthesubjectofinterestofexperimentalists andmathematicallytrainedengineerssuchasNusselt,Kirchhoff,Reynolds, Grashof,Zhoukovsky,Prandtl,Karman,Luikov,Kolmogoroff,andothers.
In1956,ProfessorHansKramersfromtheTechnicalUniversity,Delft (TheNetherlands)forthefirsttimeconnectedandorganizedtheexisting knowledgeaboutthetransportsofmomentum,heat,andmassinaseries oflectures“FysischeTransportverschijnselen”sothatmethodshithertoused onlyinparticularcasescouldnowbeusedgenerally.Thisideawasfurther expandedbyhisdiscipleR.B.Bird,laterprofessorofchemicalengineering attheUniversityofWisconsin,USA,andhiscolleaguesProfessorsW.E. StewartandE.N.Lightfootintheseminalmonograph“TransportPhenomena”publishedin1960.
Inthenexttwodecades,thedisciplinebecameadomainof theoreticians fromuniversitieswhograduallyfilledanyremaininggapsinalready solvedtasks.Inmostcases,theseweretheoreticalcomputationalworkseven thoughsomeofthemwerejustinsignificantproblems.Still,theappearance ofnewadvancedexperimentalmethodsmadeitpossibletocarryoutaseries ofnewmeasurementtechniques.Theinclusionoftransportphenomena coursesinengineeringcurriculaatuniversitiesbecamecommon.
Withtheexponentialgrowthoftheperformanceofthecomputational techniques,withtheexpansionofpersonalcomputers,andwiththeappearanceofuser-friendlysoftwarehasdiminishedthepressureonthe mathematical skillsofthesubmitter.Transportphenomenabecomeagainavailableto engineers andgenerallyforchemicalengineerswhoneedtounderstandthe processestakingplaceundermorecomplexconditionssincetheyhaveto designtheseprocesses.Thetemptingavailabilityofready-madesolutions shouldnot,however,distractfromasensibledefinitionoftheproblemand fromtherationalspecificationofthemaingoalofthecalculations.
Thestructureofthisbook
ThisbookoriginatedfromthelecturesgivenattheTechnicalUniversityOstrava(CzechRepublic)in1995forgraduatestudentsofchemical engineering.Thelectureswerealsoattendedbygraduatestudentsof
materialengineering,environmentalengineering,safetyengineering,and nanotechnology.Therefore,thebookisdividedintothreeparts:
Inthefirstpartnamed“FundamentalsofTransportPhenomena”the focusisongeometricallysimplesetupsinwhichthetransportoccurs.Some morecommonproblemsthatareoftenencounteredbyphysicalchemists, materialengineersandtechnologists(metallurgists,plasticsengineers, ceramicists,foodprocessingengineers,etc.)areexpanded.Toalargeextent, thispartisonlyqualitativebutitdefinescertainfundamentalconceptsofthis disciplinethatarelaterusedinmorecomplexsituations.
Thesecondpartnamed“BalancesofTransportPhenomena”isintended forpracticinghydrodynamicists,heattechnologists,andgenerallytochemicalengineerswhoneedtounderstandtheprocessesundermorecomplex conditionsanddesignsuchprocesses.Thesolutiontothesetasksusually requiresmorecomplexmathematicalapparatus.Therefore,itisthebasic priorityofthisworktogetthestudentformulateaspecifictasktosuch anextentthattheactualsolutioncanbeperformedwiththehelpofthecomputationalmethodsbyaspecialistwhodoesnotneedtoknowmuchabout thephysicalnatureoftheproblem.Acompletesolutionusuallyleadstothe descriptionofthevelocity,temperature,orconcentrationfieldsbutthe engineerneedstoobtainoutoftheseonlyrelativelysimpleresults,forexample,onlysomelocalvaluesorthosesuitablyaveraged.Thefinalaimisthusis tosuitablyspecifythetaskandsuitablyinterprettheresults.
Thethirdparttermed“MathematicalMethodsforSolvingtheTransports”conciselyelucidatesthemathematicalmeansusedtosolvethetransports:vectorandtensorcountandtheselectedapproachestosolvingpartial andordinarydifferentialequationsthatdonotbelongtothecommon widelytrainedgearofcollegestudentsoftechnicalandsciencefaculties.
Theaimofthistextwasnotthecreationofanencyclopedictreatmentof thesubjectneithertostaywithasimplemanualforthesolutionofafew standardtasks.Theaimistodemonstratehowthenecessaryconceptsand methodsofthedisciplinewerecreatedandtoshowwhataretheyuseful for.Thestudentshouldbecomecompetentinunderstandingoriginalworks dealingwiththetransferofmomentum,heat,andmassandorienthim/herselfinnumerousmonographsthatsystematicallydealwiththesubjectinvariousdepthsandextentandwithmiscellaneousorientationandapplication.
Forthepriceofacertaininconsistencyitwillbeattemptednottooverwhelmthestudentwithanexcessofformalisms.Rightfromthebeginning thetextissandwichedbetweennotesreferringtopracticalproblemsin whichthediscussedtheoreticalconceptsareapplied.
Otherbooks
VandenAkker,H.,Mudde,R.F.,2014.TransportPhenomena—TheArtofBalancing, firsted.DelftAcademicPress/VSSD,Delft,TheNetherlands.
Asano,K.,2006.MassTransfer:FromFundamentalstoModernIndustrialApplications. Weinheim,WileyVCH,Germany.
Astarita,G.,Ocone,R.,2002.SpecialTopicsinTransportPhenomena.Elsevier,Amsterdam,NewYork,UnitedStates.
Baukal,C.E.,2000.HeatTransferinIndustrialCombustion.CRCPress,BocaRaton, UnitedStates.
Beek,W.J.,Muttzall,K.M.K.,VanHeuven,J.W.,1999.TransportPhenomena,seconded. JohnWiley&Sons,Inc.,NewYork,UnitedStates.
Belfiore,L.A.,2003.TransportPhenomenaforChemicalReactorDesign.J.Wiley,New York,UnitedStates.
Bennett,C.O.,Meyers,J.O.,1982.Momentum,HeatandMassTransfer,McGraw-Hill Collegesubsequented.NewYork,UnitedStates.
Bergman,T.L.,2011.IntroductiontoHeatTransfer.JohnWiley&Sons,Inc.,Hoboken, NJ,UnitedStates.
Bird,R.B.,Stewart,W.E.,Lightfoot,E.N.,2006.TransportPhenomena,revisedseconded. JohnWiley&SonsInc.,NewYork,UnitedStates.
Bird,R.B.,Stewart,W.E.,Lightfoot,E.N.,Klingenberg,D.,2015.IntroductoryTransport Phenomena.JohnWiley&SonsInc.,NewYork,UnitedStates.
Brodkey,R.S.,Hershey,H.C.,2003.TransportPhenomena:AUnifiedApproach.Brodkey Publishing,Columbus,UnitedStates.
Carslaw,H.S.,Jaeger,J.C.,1959.ConductionofHeatinSolids.ClarendonPress, Oxford,UK.
C¸engel,Y.A.,Ghajar,A.J.,2015.HeatandMassTransfer:Fundamentals&Applications. McGraw-Hill,NewYork,UnitedStates.
Cussler,E.L.,2009.Diffusion:MassTransferinFluidSystems.CambridgeUniversityPress, Cambridge,NewYork,UnitedStates.
Das,M.K.,Mukherjee,P.P.,Muralidhar,K.,2018.ModelingTransportPhenomenain PorousMediaWithApplications.SpringerInternationalPublishing.
Deen,W.M.,1998.AnalysisofTransportPhenomena.OxfordUniversityPress,Oxford, England,UK.
Faghri,A.,Zhang,Y.,2006.TransportPhenomenainMultiphaseSystems.Elsevier,New York,UnitedStates.
Farmer,R.C.,Pike,R.W.,Cheng,G.C.,Chen,Y.-S.,2009.ComputationalTransportPhenomenaforEngineeringAnalyses,firsted.CRCPress,NewYork,UnitedStates. Fournier,R.L.,2017.BasicTransportPhenomenainBiomedicalEngineering,fourthed. CRCPress,BocaRaton,UnitedStates.
Geankoplis,CH.J.,1993.TransportProcessesandUnitOperations,thirded.PTRPrenticeHall,Inc.,ASimon&SchusterCompany,EnglewoodCliffs,NewJersey,UnitedStates.
Geankoplis,CH.J.,Hersel,A.A.,Lepek,D.H.,2018.TransportProcessesandSeparation ProcessPrinciples,fifthed.PrenticeHallInternationalSeries,NewJersey,UnitedStates. Geiger,G.H.,Poirier,D.R.,1973.TransportPhenomenainMetallurgy,firsted.AddisonWesley,Reading,UnitedStates.
Greenkorn,R.,1999.Momentum,Heat,andMassTransferFundamentals,firsted.CRC Press,NewYork,UnitedStates.
Griskey,R.,2006.TransportPhenomenaandUnitOperations.ACombinedApproach. JohnWiley&SonsInc.,NewYork,UnitedStates.
Hanjalic,K.,Kenjeres,S.,Tummers,M.J.,Jonker,H.J.J.,2009.AnalysisandModellingof PhysicalTransportPhenomena.VSSD,Delft,TheNetherlands.
Hauke,G.,2008.AnIntroductiontoFluidMechanicsandTransportPhenomena.Springer, Netherlands.
Incropera,F.P.,2007.FundamentalsofHeatandMassTransfer/FrankP.Incropera [etal.],JohnWiley,Hoboken,NJ,UnitedStates.
Jakobsen,H.A.,2014.ChemicalReactorModeling:MultiphaseReactiveflows.Springer, Berlin,Germany.
Jiji,L.M.,2009.HeatConvection.Springer-Verlag,Berlin,Heidelberg,Germany.
Jiji,L.M.,2009.HeatConduction.Springer-Verlag,Berlin,London,Germany.
Kou,S.,1996.TransportPhenomenainMaterialsProcessing.JohnWiley&SonsInc., NewYork,UnitedStates.
Leal,G.L.,2007.AdvancedTransportPhenomena,FluidMechanicsandConvective TransportProcesses.CambridgeUniversityPress,Cambridge,England,UK. Levenspiel,O.,2014.EngineeringFlowandHeatExchange.Springer,NewYork.
Lue,L.,2014.Momentum,Heat,andMassTransfer.Bookboon(Bookboon.COM).
Mashelkar,R.A.,1989.TransportPhenomenainPolymericSystems,vol.2.Balaji International,India.
McComb,W.D.,1990.ThePhysicsofFluidTurbulence.OxfordUniversityPress, NewYork,UnitedStates.
Plawsky,J.,2014.TransportPhenomenaFundamentals,thirded.CRCPress,NewYork, UnitedStates.
Poirier,D.R.,Geiger,G.H.,2016.TransportPhenomenainMaterialsProcessing.Springer InternationalPublishers,Switzerland.
Suryavanshi,B.M.,Dongre,L.R.,2006.TransportPhenomenaforChemical,Petrochemical andPolymerEngineering.NiraliPrakashan,Puna,India.
Ramachandran,P.A.,2014.AdvancedTransportPhenomena:Analysis,Modeling,and Computations,firsted.CambridgeUniversityPress,Cambridge,England,UK.
Rebay,M.,Kakac ¸,S.,Cotta,R.M.,2016.MicroscaleandNanoscaleHeatTransfer:Analysis, DesignandApplication.CRCPress,BocaRaton,FL,UnitedStates.
Rohsenow,W.M.,Choi,H.Y.,1961.Heat,Mass,andMomentumTransfer.Prentice-Hall, EnglewoodCliffs,NewJersey,UnitedStates.
Rorrer,G.L.,Foster,D.G.,Welty,J.,2014.FundamentalsofMomentum,Heat,andMass Transfer,revisedsixthed.JohnWiley&SonsInc.,NewYork,UnitedStates.
Ruocco,G.,2018.IntroductiontoTransportPhenomenaModeling.SpringerInternational Publishing.
Saatdjian,E.,2000.TransportPhenomena:EquationsandNumericalSolutions.JohnWiley &SonsInc.,NewYork,UnitedStates.
Sa ´ ez,A.E.,Baygents,J.C.,2014.EnvironmentalTransportPhenomena,firsted.CRCPress, BocaRaton,UnitedStates.
Sharma,K.R.,2010.TransportPhenomenainBiomedicalEngineering:ArtificialOrgan DesignandDevelopmentandTissueEngineering.McGraw-Hill,NewYork,United States.
Slattery,J.C.,1972.Momentum,EnergyandMassTransferinContinua.McGrawHillBook Co.,NewYork,UnitedStates.
Soto,R.,2016.KineticTheoryandTransportPhenomena.OxfordUniversityPress, Oxford,England,UK.
Thomas,W.J.,2000.IntroductiontoTransportPhenomena.PrenticeHall,UpperSaddle River,NewJersey,UnitedStates.
Tosun,I.,2007.ModelinginTransportPhenomena:AConceptualApproach,seconded. Elsevier,Amsterdam,TheNetherlands.
Truskey,G.,Yuan,F.,Katz,D.,2007.TransportPhenomenainBiologicalSystems: Internationaledition.Pearson,London,England,UK.
Venerus,D.C., Ottinger,H.Ch.,2018.AModernCourseinTransportPhenomena. CambridgeUniversityPress,Cambridge,England,UK.
Welty,J.R.,Wicks,Ch.E.,Wilson,R.E.,1976.FundamentalsofMomentum,Heat,and MassTransfer,seconded.JohnWiley&Son,NewYork,UnitedStates.
Welty,J.R.,Rorrer,G.L.,Foster,D.G.,2014.FundamentalsofMomentum,Heat,andMass Transfer,revisedsixthed.JohnWiley&Sons,NewYork,UnitedStates.
Yang,W.-J.,Mochizuki,S.,Nishiwaki,N.,1994.TransportPhenomenainManufacturing andMaterialsProcessing,aVolumeinTransportProcessesinEngineering.Elsevier Science.Amsterdam,TheNetherlands.
Definitionsofunidirectional steadytransport
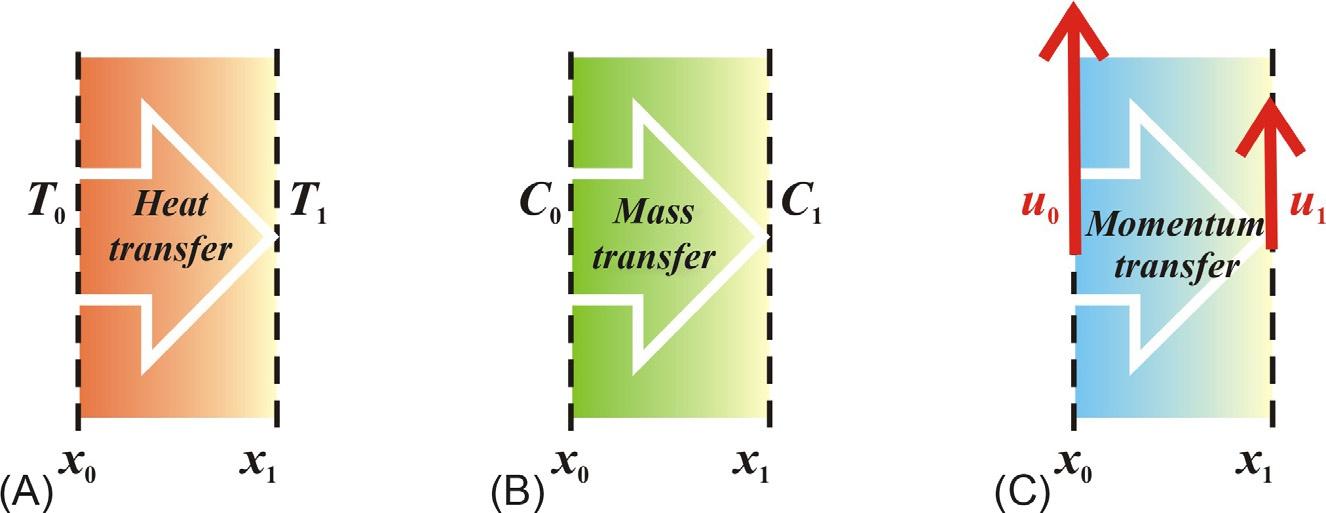
Thesimplestcasesoftransportsaredemonstratedinthoughtexperiments whenthereisonlyoneimbalancemanifesteditselfbychangesinonly onepropertyinonedirection.Thenacoordinatesystemcanbesetupin suchawaythattheequilibriummeasureshaveaconstantvaluein x0 and x1 planes,whichisshownschematicallyin Fig.1.1A.ThenaCartesiancoordinatesystem x,y,z canbesetuptocarryoutthetransportonlyinthe z directionbetween x0 and x1 throughthearea ΔS ¼ Δy Δz.Forthetime being,letusignorethewaythisstatushasbeenreachedandmaintained andwhatisgoingonoutsidethesystemjustdefined.
Dailyexperienceshowsthat,atleastforsometransports,itispossibleto finda linearrelationship betweenthe intensityofthetransfer (i.e.,the transferthroughaunitareaoveraunitoftime)andthe drivingforce (i.e., thedifferencebetweenthemeasuresofaparticularbalance).Thiscanbefirst demonstratedforthetransferofheatenergy.
1.1Steadyunidirectionaltransportofheat byconduction
Inthecaseshownin Fig.1.1A,therewillbetwoconstant,timely invariabletemperatures T0 and T1 intheplanes x < x0 and x > x1.Thehistoryofhowthisstatewasarrivedataswellaswhatisgoingonat x > x0 and
Fig.1.1 Transportphenomena:(A)heat,(B)mass,(C)momentum.
x < x1 willbeignored.Shouldthetemperatures T0 and T1 bearebothdifferentthenenergytransportintheformof heat Q (theunitbeingJouleJ) willoccuratarate(heattransport) dQ/dt (theunitbeingJ/s,i.e.,Watt,W).
Itisobviousthatthistransportwillbedirectlyproportionaltothesizeofthe area ΔS.Itisthereforeusefultointroduceaquantity q bythedefinition
where q istheheattransportedthroughaunitareaduringaunittime [J/(m2s),i.e.,W/m2]calledthe intensityoftheheatflow,alternatively the densityoftheheatflow.Theintensityoftheheatflowdependson the drivingforce (T0 T1).Thereareseveralmechanismsbywhichthe heatcanbetransported.Inthecaseofsmalltemperaturedifferencesina stationarymatter,thekeymechanismisthe conductionofheat,where q isdirectlyproportionaltothedrivingforceandindirectlyproportional tothe thickness ofthematerial h (x1 x0),thus
wheretheconstant k definedbythisrelationisoneofthe materialconstants thatdependsonlyonthematerialproperties,i.e.,onthe composition andthe structure ofthematerialaswellasonthe physicochemical stateofaggregation ofthematter.Thismaterialconstantthatiscalled thermalconductivity hasthedimensionofW/(mK).The relation (1.2) canbeexpressedalsoinadifferentialformas
knownasthe Fourierlaw ofunidirectionalthermalconductivity.The minussignindicatesthattheheatmovesfromwarmerplanetocoolerone.
1.2Steadyunidirectionaltransferofmassbydiffusion
Ananalogoussituationisshownin Fig.1.1Bwherethecontrolareas arekeptatdifferent concentrations.Also,forthiscase,alinearrelationship canbeformulatedbetweenthe intensity (density)ofthetransfer(i.e.,the flowthroughaunitofareaoveraunitoftime)anda drivingforce (i.e.,the differencebetweenthemeasuresofaparticularbalance).
Severaldifferentunitscanbeusedtoexpressthetransferofmass(material orvolume).Inthesimplestcase,materialunitscanbeusedtoexpressthe transferofmaterial A.Ifthe materialamount isdenotedas N (thebasic unitis1mol)thenthematerialflow(rate)is dN/dt (theunitbeingmol/s).
Thenthe intensityofthematerialflow [measuredinmol/(m2s)]is expressedas
whichisdirectlyproportionaltothedrivingforcethat,inthiscase,willbe the concentrationdifference (C0 C1)(measuredinmol/m3).Itisobviousthattheflowofthematerialwillbeindirectlyproportionaltothe thickness ofthelayer h.Theconstantofproportionality D knownasthe diffusivity isamaterialconstant,thedimensionofwhichism2/s.
Itwouldbemorecorrecttouseactivitiesratherthanconcentrationsbut, inmostpracticalsituations,activitiesarealmostequaltoconcentrations.Partialpressures(orratherfugacities)aremoresuitableformasstransferingases then,however,stateequationsoughttobeemployedtocalculatethedriving force.Similarly,ifitismoreusefultoexpresstheintensityofflowinother quantitiesthanarethemassamounts,thentherelevantcorrelationsaretobe usedtoobtainthemassfloworthetransferofvolumes.Forthese recalculations,thefundamentalequationsintermsofmassconcentrations andflowshavetobeused.
The diffusioncoefficient isamorecomplexmaterialconstantsinceit dependsonthepropertiesofbothcomponents,thatis,the diffunding molecule aswellasthe medium inwhichthemoleculemoves.Byanalogy withtheconductionofheat,thedefiningrelationshipfortheunidirectional diffusioncanbeexpressedas
whichisknownas Fick’slaw.
1.3Steadyunidirectionaltransferofmomentum byviscousfrictioninfluids
Somewhatmorecomplexisthesituationdepictedin Fig.1.1Cina layeroffluid.Inthiscase,therearedifferenttangentialvelocitiesonthe twoboundaries uy inthe y direction.Thisconfigurationiscalledthesimple tangentialflowandthetransferofmomentumismediatedbyatangential force Fxy thathasatendencytospeeduptheslowerlayerwhileslowing upthefasterone.Accordingtothesecondlawofmotion,thechangeof momentumwillbe
Itisamatterofconvention,whichofthetwoactionswillbetakenasthe positiveone.Intheclassicalmechanics,thetraction(thepull)ischosenas thepositiveforcesothatthe intensityofthemomentumtransfer isequalto
Thus,thetransferofmomentumisthenegativevalueoftheforceactingona unitofarea,theso-called tangentialtension τyx,theunitofwhichisthe sameastheunitofpressure,whichisN/m2 orPa.ItwasNewtonwhofor thefirsttimeexpressedaconjecturethatthereisaproportionality
Thisrelationshipknownas Newton’slawofviscosity definesamaterial constant μ,theunitofwhichisPasorkg/ms,whichiscalledthe dynamic viscosity.Theterm(duy/dx)iscalled shearrate orthe rateofdeformation.Theoftenusedterm“velocitygradient”shouldbeavoidedbecause theshearvelocityissameasthevelocitygradientonlyinthesimplestconstellations(asexplainedin Chapter8).
1.4Similaritiesanddifferences
1.4.1Commonfeaturesofsometransportphenomena
Itwasshownthatthemathematicalmodelsoftheunidirectionaltransports ofheat,mass,andmomentumaresimilar.Thereasonforthissimilarityis thatthemotionofmoleculesplaysakeyroleinthesetransportsasshown inthe Chapter2.Eveninrathercomplexcasesinwhichmorecomplicated mathematicaltoolshavetobeused,somesimilaritiesdoexist.Solutions developedforoneofthesetransportscanbeusuallyusedfortheotherones.
1.4.2Othertransportphenomena
Othertransportphenomena,takingplaceoveraperiodoftime,areencounteredbothinthenatureaswellasinengineeringpractice.Letusmentionin thefirstplacethe transferofpressure.Thistransfertakesplaceatthespeed ofsoundsoitis,withtheexceptionofacousticandshockwaves,rarelyperceivable.Evenfasteristhe transferofenergybyradiation thattakesplace atthespeedoflight.Radiationtransportdoesnotneedthepresenceofmoleculessoittakesplaceeveninvacuum.Laterinthisbook,the radiationof heat isbrieflytreatedbecauseitmightbecomecomparablewithheat conduction.
Therearealargenumberofphenomenaduetothe transferofan electriccharge.Thistransferisrealizedeitherbythemotionofelectrons thathavenegligibleinertialmasssotheycanbeputtomotioninelectric conductorsatainfinitesimallyshorttimeorbysignificantlyslowermotion ofionsinelectrolytesthatiscomparabletodiffusion.Theirmotion(electric currentduetothedifferenceinelectricpotentials)islimitedbytheimpedanceofthemediumthatismadeofelectricresistanceand,inparticularat thetransitionbetweenconductorsandelectrolytes,byinductanceand capacity.
1.5Summary
Thischapterdealswiththreetransferphenomena:momentum,heat, andmass.Thesetransfersarecharacterizedbytransfercoefficientsthatdeterminetherelationshipbetweentheflowandthedrivingforce.Thesetransfer coefficientsaredynamicviscosity,thermalconductivity,anddiffusivity, respectively.Thetransfercoefficientsarematerialconstantsinthatthey dependonlyonthenatureofthemedia,whichisviewedasacontinuum.
Inunidirectionaltransfersitholdsthat
Flow ¼ transfercoefficient drivingforce:
Table1.1 summarizestheindividualcases.
Table1.1 Transportanddrivingforce.
PhenomenaFlow Transfer coefficientDrivingforce
Momentum transfer Tangentialstress Tensor (Tangentialforceon unitarea) τ [Pa]
HeattransferIntensityofheatflow
Dynamicviscosity
Scalar μ [Pas]
Vector q [W] Thermal conductivity
MasstransferIntensityofmassflow
Vector n [mol/(m2 s)]
Scalar k [W/mK]
Diffusivity
Scalar D [m2/s]
Shearrate Tensor γ (—u+u—)[s 1] (Equaltothe velocitygradient γ —u [s 1]onlyin thesimplestcase!)
Temperature gradient Vector —T [K/m]
Concentration gradient vector —C [mol/m4]