Theoryandmodelingofdispersedmultiphase turbulentreactingflowsZhou
https://ebookmass.com/product/theory-and-modeling-ofdispersed-multiphase-turbulent-reacting-flows-zhou/
Physical
K. S. Verma
https://ebookmass.com/product/physical-chemistry-for-jee-advancedpart-1-3rd-edition-k-s-verma/
ebookmass.com
Butterworth-HeinemannisanimprintofElsevier
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright r 2018ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicor mechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem,without permissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthe Publisher’spermissionspoliciesandourarrangementswithorganizationssuchastheCopyrightClearance CenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher (otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary. Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingand usinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationor methodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhomthey haveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliability foranyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,or fromanyuseoroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress ISBN:978-0-12-813465-8
ForInformationonallButterworth-Heinemannpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher:MatthewDeans
AcquisitionEditor:GlynJones
EditorialProjectManager:NaomiRobertson
ProductionProjectManager:VijayarajPurushothaman
CoverDesigner:MilesHitchen
TypesetbyMPSLimited,Chennai,India
Preface
Multiphase,turbulent,andreactingflowsarewidelyencounteredinengineeringandthenaturalenvironment.Thebasictheory,phenomena,mathematicalmodels,numericalsimulations,andapplicationsofmultiphase(gas orliquidflowswithparticles/dropletsorbubbles),turbulentreactingflows arepresentedinthisbook.Thespecialfeatureofthisbookisincombining themultiphasefluiddynamicswiththeturbulencemodelingtheoryand reactingfluiddynamics(combustiontheory).Thereareninechaptersinthis book,namely:“FundamentalsofDispersedMultiphaseFlows”;“Basic ConceptsandDescriptionofTurbulence”;“FundamentalsofCombustion Theory”;“BasicEquationsofMultiphaseTurbulentReactingFlows”; “ModelingofSingle-PhaseTurbulentFlows”;“ModelingofDispersed MultiphaseTurbulentFlows”;“ModelingofTurbulentCombustion”;“The SolutionProcedureforModelingMultiphaseTurbulentReactingFlows”; and“SimulationofFlowsandCombustioninPracticalFluidMachines, CombustorsandFurnaces.”Themaindifferencebetweenthisbookandpreviousbookswrittenbytheauthoristhatmoremuchbetterdescriptionsof basicequationsandclosuremodelsofmultiphaseturbulentreactingflows areintroduced,andrecentadvancesmadebytheauthorandotherinvestigatorsbetween1994and2016areincluded.
Thisbookservesasareferencebookforteaching,research,andengineeringdesignforfacultymembers,students,andresearchengineersinthe fieldsoffluiddynamics,thermalscienceandengineering,aeronautical, astronautical,chemical,metallurgical,petroleum,nuclear,andhydraulic engineering.
TheauthorwishestothankProf.F.G.Zhuang,H.X.Zhang,andC.K.Wu fortheirvaluablecommentsandsuggestions.Thanksalsogotocolleagues andformerstudents:Prof.W.Y.Lin,R.X.Li,X.L.Wang,J.Zhang,B. Zhou,Y.C.Guo,H.Q.Zhang,L.Y.Hu,Y.Yu,F.Wang,Z.X.Zeng,K.Li, Y.Zhang;Drs.GeneX.Q.Huang,T.Hong,C.M.Liao,W.W.Luo,K.M. Sun,Y.Li,T.Chen,Y.Xu,G.Luo,M.Yang,L.Li,H.X.Gu,X.L.Chen, X.Zhang,andY.Liu.Theirresearchresultsunderthedirectionandcooperationoftheauthorcontributedtothecontextofthisbook.
xiv Nomenclature
w reactionrate
x, y, z coordinates
X combinedmassfraction;molefraction
Y massfraction
GREEKALPHABETS
α volumefraction
μ dynamicviscosity
ν kinematicviscosity
λ heatconductivity
ε dissipationrateofturbulentkineticenergy;emissivity
φ generalizeddependentvariable
θ dimensionlesstemperature
τ shearstress
σ Stefan-Boltzmannconstant;generalizedPrandtlnumber
SUBSCRIPTS
A, a air
c rawcoal,reaction
ch reaction;char
d diffusion
e effective;exit
F, fu fuel
f flame;fluid
g gas
h char;heterogeneous
hr heterogeneous
i, in initial;inlet
i, j, k coordinatedirections
k k-thparticlegroup
l liquid
m mixture
Introduction
Dispersedmultiphaseturbulentreactingflowsarewidelyencounteredin thermal,aeronautical,astronautical,nuclear,chemical,metallurgical,petroleum,andhydraulicengineering,andinwaterandatmosphereenvironments. Asearlyasthe1950s,VonKarmanandH.S.Tsiensuggestedusingcontinuummechanicstostudylaminargasreactingflowsandcombustion,called “aerothermochemistry”or“dynamicsofchemicallyreactingfluids.” MultiphasefluiddynamicswasfirstproposedbyS.L.Soointhe1960sfor studyingnonreactingmultiphaseflows.Theclassicalreactingfluiddynamics andmultiphasefluiddynamicsdonotincludethetheoryofturbulence modeling.Ontheotherhand,thetheoryofturbulencemodelingwasfirst proposedbyP.Y.Chouinthe1950s,andwasfullyrealizedbyB.E.Launder andD.B.Spaldinginthe1970s.Withinthelast40years,throughworldwide studyandapplication,ithasbecometheonlyreasonableandeconomical methodtosolvecomplexturbulentflowsinengineeringproblems.However, upuntilthe1980s,thetheoryofturbulencemodelingwaslimitedtoonly single-phasefluidflowsthemselves,anddidnotconcernthedispersedphase, i.e.,particles/droplets/bubblesinmultiphaseflows.
Sincethe1980s,theauthorhascombinedmultiphasefluiddynamicswith thetheoryofturbulencemodeling,andproposedtheconceptofmultiphase (two-phase)turbulencemodels,inparticulartheturbulencemodelsofthe dispersedphase,i.e.,particles/droplets/bubbles.Furthermore,wedeveloped theturbulence-chemistrymodelsforsingle-phaseandtwo-phasecombustion usingamethodsimilartoturbulencemodeling.Hence,thedynamicsofmultiphaseturbulentreactingflowswasdeveloped,wherethemodelingtheory, numericalsimulation,measurements,andtheirapplicationincombustion systemsweresystematicallystudied.Thecomprehensivemodels,basicconservationequations,therelationshipsbetweenslipanddiffusion,theenergy distributionbetweenthecontinuumanddispersedphases,thefluid-particle/ droplet/bubbleturbulenceinteractions,theinteractionsbetweenparticle turbulenceandparticlereaction,thegas-phaseturbulence-chemistryinteraction,andtheparticle wallinteractionwerethoroughlystudied.Aseriesof newclosuremodelswereproposed,many2-Dand3-Dcomputercodeswere developedbasedontheproposedmodelsandsomeofthesimulationresults
combustors,andfurnaces,areturbulentflowsduetothesizeofthe geometricsystem,thevelocityrangea ndthepresenceofvariousbarriers orexpansionsleadingtoflowsepar ation,andfrequentlytheyarecomplexturbulentflows,suchasrecirculatingflows,swirlingflows,and buoyantflows.
MULTIPHASETURBULENTREACTINGFLOWS ANDCOMBUSTION
Inmanycaseswearedealingwithnonisothermalmultiphaseturbulent flowswithheatandmasstransferandchemicalreactions(exothermicor endothermic),andevenelectrostaticeffects(forgasflowsladenwithfine particlesinelectrostaticdustseparators,ormetalorplasticpipes)ormagneticeffects(forgasflowsinplasmatorchandmagneto-hydrodynamic (MHD)generators).Sprayorpulverized-coalcombustionisatypicalcase ofmultiphaseturbulentreactingflows.
Theword“combustion”denotesaclassofchemicalreactionswithhigh heatreleaseandlightradiation.Thesereactionsinthefirstplaceareoxidationofsolidfuel(nonmetalsormetals),liquidfuelorgaseousfuel,butchlorination,fluoridation,nitridation,dissociation,andsubstitutionreactions (e.g.,sodium waterreaction)andself-propagatingreactionsinthesynthesis ofsolidmaterialscanalsobeconsideredascombustion,iftheyhaveahigh heatingeffect.Asamatteroffact,combustionisnotsimplyreactionsthemselves,butacomplexprocessofgasflowsorgas particleflowswithheat andmasstransferandchemicalreactions.Justtheinteractionsbetweenheat andmasstransferandchemicalreactionscontroltheprocessesofignition, extinction,flamepropagation,andcombustionrate.
Frequently,“flame”isconsideredasthehigh-temperaturecombustion products.Theword“flame”initsscientificsensecanbedefinedasazone withasharpchangeoftemperatureandconcentration.Animportantflame propertyisthattheflamezonecanpropagateautomatically.Theflame propagationvelocityistheflamevelocityrelativetothatofthecoldfresh combustiblemixture,whichisequaltothedifferencebetweentheflame displacementvelocityandthemixtureflowvelocity,suchasthatobserved inflamepropagationinalongtubewithoneclosedend.Forstationary flamessuchasthoseinBunsenburnersorflatburners,thedisplacement velocityiszeroandthepropagationvelocityshouldbeequaltotheflow velocity.Twopossibleregimesofflamepropagationwereobservedin experiments:deflagrationwithflamevelocityof0.2 1m/sanddetonation withflamevelocitynear3000m/s.Otherflamepropertiesarecarbonformation,flameradiation(duetocarbonorsootparticles),ionizationwith concentrationupto1012 ions/cm3 inlaminarpremixedflamesandnoisein turbulentflames.
DIFFERENTFLOWREGIMESOFDISPERSEDMULTIPHASE TURBULENTREACTINGFLOWS
Tounderstandphysicallythegeneralfeaturesofdispersedmultiphaseturbulentreactingflows,itispropertojudgetheirflowregimes.Atfirst,thefollowingcharacteristictimesandnondimensionalnumbersaredefinedas:
Flowtime(residencetime)
Particlerelaxationtime
Particlerelaxationtimeformeanmotion
Fluidfluctuationtime(diffusiontime)
Particlecollisiontime
Stokesnumber St
Hinze Tchennumber
Soonumber Sl
FirstDamkohlernumber D1 5
SecondDamko ¨ hlernumber
Accordingtothemagnitudeofnondimensionalnumbers,thefollowing regimesforlimitingcasesofdispersedmultiphaseturbulentreactingflows canbeidentifiedas:
St ,, 1No-slipordynamicequilibriumflows
St .. 1Strong-slipordynamicfrozenflows
Ht ,, 1Diffusion-equilibriumflows
Ht .. 1Diffusion-frozenflows
Sl ,, 1Dilutesuspensionflows
Sl .. 1Densesuspensionflows
D1 ,, 1Reacting-frozenflows
D1 .. 1Reacting-equilibriumflows
D2 ,, 1Kinetics-controlledcombustion
D2 .. 1Diffusion-controlledcombustion
DEVELOPMENTOFVARIOUSDISPERSED-PHASEMODELS
Therearetwobasicapproachestostudyingdispersedmultiphaseturbulent flows.OneistheEulerian Eulerianormultifluid(two-fluid)approach,in whichthefluidphase(liquid/gas)istreatedasacontinuumandthedispersed phase(particles/droplets/bubbles)istreatedasapseudo-fluid(PF)orpseudocontinuum.Differentphasesoccupythesamespace,interpenetrateintoeach other,andallaredescribedintheEuleriancoordinatesystem.Theotheris theEulerian Lagrangianapproach,inwhichonlythefluidphaseistreated asacontinuumintheEuleriancoordinatesystemandtheparticles/droplets/ bubblesaretreatedasadispersedsystemintheLagrangiancoordinatesystem.Thisapproachforthedispersedphaseisalsocalledthetrajectory approach.Earlystudiesarelimitedtoparticle/droplet/bubblemotionina
beendeveloped.However,duetothelargecomputationtime,DNSismainly usedforunderstandingtheturbulenceandflamestructureandvalidatingthe LESandRANSmodeling.Itstillcannotbedirectlyusedtosolveengineeringproblems.
Chapter1
SomeFundamentalsof DispersedMultiphaseFlows
1.1PARTICLE/SPRAYBASICPROPERTIES
Tocharacterizegas-particleorgas-sprayflows,itisnecessaryfirstto describetheparticle/spraybasicproperties [1 4] asfollows.
1.1.1Particle/DropletSizeandItsDistribution
Theparticle/dropletsizedistributionisfrequentlyexpressedbythesemiempiricalRosin Rammlerformulaas:
where R(dk)istheweightfractionofparticleswithsizeslargerthan dk, n is theindexofnonuniformness,and d isacharacteristicsize.Both n and d are determinedbyexperiments.Thederivativeof R(dk)is
whichexpressesthedifferentialparticlesizedistribution,and R(dk)isthe integralsizedistribution.Themeanparticlesizescanbedefinedas: d10 5 X nk dk = X nk d20 5 X nk d 2 k = X nk 1=2
30 5 X nk d 3 k = X nk 1=3
32 5
where d10 ; d20 ; d30 ; and d32 arediameter-averaged,surface-averaged, volume-averaged,andSautermeansizes,respectively.TheSauterdiameter ismostwidelyusedinengineering.Thetypicalparticlesizesare:
Coalparticlesinfluidizedbeds1 10mm Liquidspray 10 200 μm
Pulverizedcoal 1 100 μm Sootparticles 1 5 μm
1.3.2MotionofaSingleParticleinaUniformFlowField
Assumingaparticlewithinitialvelocity vP0 andStokes’draglaw,moving inauniformflowfield(Fig.1.1),whenneglectingthegravitationalforce, theparticlemomentumequationinthe x directionis
where τ r 5 d 2 p ρp =ð18μÞ.Integrationof Eq.(1.12) withaninitialconditionof up 5 up0 at t 5 0givestheparticlelongitudinalvelocity
Theparticlelateralvelocitycanbeobtainedinasimilarwayas
Integrationof Eqs.(1.13)and(1.14) withrespectto t givestheparticle trajectoryequationsas
Similarequationscanalsobederivedfornon-Stokes’particledrag. Eqs.(1.13,1.14,1.15) pointoutthatasthetimeapproaches N,theparticlelongitudinalvelocityapproachesthefluidvelocity,theparticlelateralvelocity approacheszeroandtheparticle lateraldisplacementapproaches y 5 vp0 τ r .When t 5 τ r,wehave vp 5 vp0 =τ r .Hencethephysicalmeaningoftheparticlerelaxationtimeisthetimeneededforthefluid-particlevelocitysliptodecreaseto1/e ofitsinitialvalue.Itexpressestheeasinesswithwhichparticlesfollowthefluid.
1.3.3ParticleGravitationalDeposition
ForaninitiallystagnantparticleactingonlybyStokes’dragandgravity,the motionequationis:
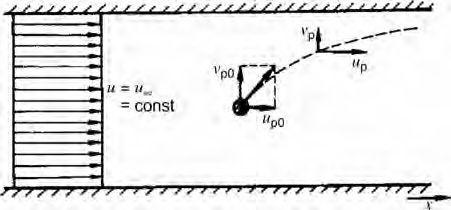
FIGURE1.1 Motionofasingleparticleinuniformflowfield.
Fortheinitialconditionof vp0 5 0at t 5 0,itssolutionis: vp 5 τ r gð1 e t =τ r Þð1 17Þ
Asthetimeapproachesinfinity, vp approaches τ rg 5 vpr,theparticle accelerationbecomeszeroandthegravityanddragforcewillbeinequilibrium.Inthiscasetheparticlevelocityiscalledtheterminalvelocity.
1.3.4ForcesActingonParticlesinNonuniformFlowField
1.3.4.1MagnusForce
Asanonsphericalparticlemovesintheflowfieldwithvelocitygradient,in particularafteritsimpactonthewall,itmayrotate,causingaliftingforce perpendiculartothedirectionofrelativevelocity,calledtheMagnusforce. Itsmagnitudeis:
where ω p istheangularvelocityofparticlerotation,and Ω isthehalf offluidvorticity.IthasbeenestimatedthattheratioofMagnusforce tothedragforceis0.04fora1- μmparticleand3fora10- μmparticle. However,experimentalstudieshaveshownthatinmostregionsofthe flowfield,particlesdonotrotate duetofluidviscosity.Therefore, exceptintheregionadjacenttothewall,theMagnusforceisnot important.
1.3.4.2SaffmanForce
Iftheparticleissufficientlylargeandthereisalargevelocitygradientinthe flowfield(forexample,nearthewall),therewillbeaparticle-liftingforce calledtheSaffmanforce.Itsmagnitudeis
TheratiooftheSaffmanforcetotheMagnusforceismuchgreaterthan unity;hencetheSaffmanforcemayplayanimportantrole,inparticularin theregionofalargevelocitygradient,suchasintherecirculationregionand thenear-wallregion.
1.3.4.3ParticleThermophoresis,Electrophoresis, andPhotophoresis
Tinyparticlessmallerthan1 μmmaymoveundertheeffectsofso-called “thermophoresis,”“electrophoresis,”and“photophoresis,”causedbyalarge
8 TheoryandModelingofDispersedMultiphaseTurbulentReactingFlows
[13]E.E.Michaelides,Transientequationsforthemotion,heatandmasstransferofbubbles, dropsandparticles.In:MatsumotoYEd.,Proceedingsof5thInternationalConferenceon MultiphaseFlow,Yokohama,Japan,2004-05-30-06-04,2004,Abstracts,PaperNo.K11.
[14] L.S.Fan,C.Zhu,PrinciplesofGas-SolidFlows.,CambridgeUniversityPress, Cambridge,1998.
[15] C.T.Crowe,M.Sommerfeld,Y.Tsuji,MultiphaseFlowswithDropletsandParticles., CRCPress,Florida,1998.
FURTHERREADING
L.X.Zhou,CombustionTheoryandReactingFluidDynamics.,SciencePress,Beijing,1986.
Chapter2
BasicConceptsandDescription ofTurbulence
2.1INTRODUCTION
Asthisbookisrelatedtomultiphaseturbulentreactingflows,someknowledge ofthefundamentalconceptsanddescriptionofturbulenceareintroduced.More than100yearsago,OsbornReynolds(1883 94)firstindicatedthatflowscan beeitherlaminarorturbulentbyobservinginjecteddyedwaterflowinatube.A parametercalledtheReynoldsnumberRe 5 vd =ν (where v isthevelocity, d is thesize,and ν isthekinematicviscosity)isusedtoidentifythesetwoflow regimes.Hefirstsuggestedthedecompositionoftheflowvariablesintotimeaveragedandfluctuationquantitiesformathematicallyanalyzingturbulentflows.
Turbulentflowswidelyoccurinnatureandengineering,particularin astronomyandnaturalwaterbodies.Inengineeringfacilities,turbulentflows areencounteredinfluidmachines,heatexchangers,andcombustors,because frequentlyinthesefacilitiesthefluidvelocityishigher,andthegeometrical sizesarelarge,inotherwords,theReynoldsnumberislarge.However,in somecases,eveniftheRenumberisnotlarge,butthereareroughwallsand flowseparationbyobstacles,turbulencemayalsobeproduced.
Examplesofturbulentflowsarethedischargeofsmokefromastack,asshown in Fig.2.1,andaturbulentgasjetflame,asshownin Fig.2.2.Theflowsofsmall sootparticlesandcombustionproductsshowononehandtheirregularbehaviorof instantaneousgasflows,butontheotherhand,someorganizedstructures—thesocalled“coherentstructures.”Therefore,turbulentflowshavebothrandomand organizedstructures. Fig.2.3 showsthevorticitymapofasudden-expansionflow bylarge-eddysimulation(LES).Itgivesthe detailedturbulencestructures.Itcan beseenthattherearedifferentlengthscalesofeddiesinturbulentflows.
2.2TIMEAVERAGING
Letusconsideravariable ~ aðx; t Þ changingwithtimeatagivenspatiallocationoftheturbulentflowfield.O.Reynoldsfirstintroducedtheconceptof timeaveragingofavariable φ [1] as: