https://ebookmass.com/product/statistics-for-ecologists-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
eTextbook 978-0134173054 Statistics for Managers Using Microsoft Excel
https://ebookmass.com/product/etextbook-978-0134173054-statistics-formanagers-using-microsoft-excel/
ebookmass.com
Advances in Business Statistics, Methods and Data Collection Ger Snijkers
https://ebookmass.com/product/advances-in-business-statistics-methodsand-data-collection-ger-snijkers/
ebookmass.com
Using Statistics in the Social and Health Sciences with SPSS Excel 1st…
https://ebookmass.com/product/using-statistics-in-the-social-andhealth-sciences-with-spss-excel-1st/
ebookmass.com
Oral Pathology for the Dental Hygienist E Book 7th Edition, (Ebook PDF)
https://ebookmass.com/product/oral-pathology-for-the-dental-hygieniste-book-7th-edition-ebook-pdf/
ebookmass.com
Polar Organometallic Reagents - Synthesis, Structure, Properties and Applications Wheatley Andrew E.H. (Ed.)
https://ebookmass.com/product/polar-organometallic-reagents-synthesisstructure-properties-and-applications-wheatley-andrew-e-h-ed/
ebookmass.com
The Stormbringer Isabel Cooper [Cooper
https://ebookmass.com/product/the-stormbringer-isabel-cooper-cooper/
ebookmass.com
The Bourgeois and the Savage: A Marxian Critique of the Image of the Isolated Individual in Defoe, Turgot and Smith Iacono Alfonso Maurizio
https://ebookmass.com/product/the-bourgeois-and-the-savage-a-marxiancritique-of-the-image-of-the-isolated-individual-in-defoe-turgot-andsmith-iacono-alfonso-maurizio/
ebookmass.com
Surfeit of Suspects George Bellairs
https://ebookmass.com/product/surfeit-of-suspects-george-bellairs/
ebookmass.com
Interviewing and Change Strategies for Helpers 8th Edition
Sherry Cormier
https://ebookmass.com/product/interviewing-and-change-strategies-forhelpers-8th-edition-sherry-cormier/
ebookmass.com
Communicating Across Cultures and Languages in the Health Care Setting: Voices of Care 1st Edition Claire Penn
https://ebookmass.com/product/communicating-across-cultures-andlanguages-in-the-health-care-setting-voices-of-care-1st-editionclaire-penn/
ebookmass.com
6.3 Graphs to illustrate differences
6.4 Graphs to illustrate correlation and regression
6.5 Graphs to illustrate association
6.6 Graphs to illustrate similarity
6.7 Graphs – a summary
7. Tests for differences
7.1 Differences: t-test
7.2 Differences: U-test
7.3 Paired tests
8. Tests for linking data – correlations
8.1 Correlation: Spearman’s rank test
8.2 Pearson’s product moment
8.3 Correlation tests using Excel
8.4 Correlation tests using R
8.5 Curved linear correlation
9. Tests for linking data – associations
9.1 Association: chi-squared test
9.2 Goodness of fit test
9.3 Using R for chi-squared tests
9.4 Using Excel for chi-squared tests
10. Differences between more than two samples
10.1 Analysis of variance
10.2 Kruskal–Wallis test
11. Tests for linking several factors
11.1 Multiple regression
11.2 Curved-linear regression
11.3 Logistic regression
12. Community ecology
12.1 Diversity
12.2 Similarity
13. Reporting results
13.1 Presenting findings
13.2 Publishing
13.3 Reporting results of statistical analyses
13.4 Graphs
13.5 Writing papers
1.2 Types of experiment/project
As part of the planning process, you need to be aware of what you are trying to achieve. In general, there are three main types of research:
• Differences: you look to show that a is different to b and perhaps that c is different again. These kinds of situations are represented graphically using bar charts and box–whisker plots.
• Correlations: you are looking to find links between things. This might be that species a has increased in range over time or that the abundance of species a (or environmental factor a) affects the abundance of species b. These kinds of situations are represented graphically using scatter plots.
• Associations: similar to the above except that the type of data is a bit different, e.g. species a is always found growing in the same place as species b. These kinds of situations are represented graphically using pie charts and bar charts.
Studies that concern whole communities of organisms usually require quite different approaches. The kinds of approach required for the study of community ecology are dealt with
in detail in the companion volume to this work (Community Ecology, Analytical Methods Using R and Excel, Gardener 2014).
In this volume you’ll see some basic approaches to community ecology, principally diversity and sample similarity (see Chapter 12). The other statistical approaches dealt with in this volume underpin many community studies.
Once you know what you are aiming at, you can decide what sort of data to collect; this affects the analytical approach, as you shall see later. You’ll return to the topic of project types in Chapter 5.
1.3 Getting data – using a spreadsheet
A spreadsheet is an invaluable tool in science and data analysis. Learning to use one is a good skill to acquire. With a spreadsheet you are able to manipulate data and summarize it in different ways quite easily. You can also prepare data for further analysis in other computer programs in a spreadsheet. It is important that you formalize the data into a standard format, as you’ll see later (in Chapter 2). This will make the analysis run smoothly and allow others to follow what you have done. It will also allow you to see what you did later on (it is easy to forget the details).
Your spreadsheet is useful as part of the planning process. You may need to look at old data; these might not be arranged in an appropriate fashion, so using the spreadsheet will allow you to organize your data. The spreadsheet will allow you to perform some simple manipulations and run some straightforward analyses, looking at means, for example, as well as producing simple summary graphs. This will help you to understand what data you have and what they might show. You’ll look at a variety of ways of manipulating data later (see Section 3.2).
If you do not have past data and are starting from scratch, then your initial site visits and pilot studies will need to be dealt with. The spreadsheet should be the first thing you look to, as this will help you arrange your data into a format that facilitates further study. Once you have some initial data (be it old records or pilot data) you can continue with the planning process.
1.4 Hypothesis testing
A hypothesis is your idea of what you are trying to determine. Ideally it should relate to a single thing, so “Japanese knotweed and Himalayan balsam have increased their range in the UK over the past 10 years” makes a good overall aim, but is actually two hypotheses. You should split up your ideas into parts, each of which can be tested separately:
“Japanese knotweed has increased its range in the UK over the past 10 years.”
“Himalayan balsamhas increased its range in the UK over the past 10 years.”
You can think of hypothesis testing as being like a court of law. In law, you are presumed innocent until proven guilty; you don’t have to prove your innocence.
In statistics, the equivalent is the null hypothesis. This is often written as H0 (or H0) and you aim to reject your null hypothesis and therefore, by implication, accept the alternative (usually written as H1 or H1).
The H0 is not simply the opposite of what you thought (called the alternative hypothesis, H1) but is written as such to imply that no difference exists, no pattern (I like to think of it as the dull hypothesis). For your ideas above you would get:
“There has been no change in the range of Japanese knotweed in the UK over the past 10 years.”
“There has been no change in the range of Himalayan balsam in the UK over the past 10 years.”
So, you do not say that the range of these species is shrinking, but that there is no change. Getting your hypotheses correct (and also the null hypotheses) is an important step in the planning process as it allows you to decide what data you will need to collect in order to reject the H0. You’ll examine hypotheses in more detail later (Section 5.2).
1.4.1 Hypothesis and analytical methods
Allied to your hypothesis is the analytical method you will use to help test and support (or otherwise) your hypothesis. Even at this early stage you should have some idea of the statistical test you are going to apply. Certain statistical tests are suitable for certain kinds of data and you can therefore make some early decisions. You may alter your approach, change the method of analysis and even modify your hypothesis as you move through the planning stages: this all part of the scientific process. You’ll look at ways to choose which statistical test is right for your situation in Section 5.3, where you will see a decision flow-chart (Figure 5.1) and a key (Table 5.1) to help you. Before you get to that stage, though, you will need to think a little more about the kind of data you may collect.
1.5 Data types
Once you have sorted out more or less what your hypotheses are, the next step in the planning process is to determine what sort of data you can get. You may already have data from previous biological records or some other source. Knowing what sort of data you have will determine the sorts of analyses you are able to perform. In general, you can have three main types of data:
• Interval: these can be thought of as “real” numbers. You know the sizes of them and can do “proper” mathematics. Examples would be counts of invertebrates, percentage cover, leaf lengths, egg weights, or clutch size.
• Ordinal: these are values that can be placed in order of size but that is pretty much all you can do. Examples would be abundance scales like DAFOR or Domin (named after a Czech
botanist). You know that A is bigger than O but you cannot say that one is twice as big as the other (or be exact about the difference).
• Categorical (sometimes called nominal data): this is the tricky one because it can be confused with ordinal data. With categorical data you can only say that things are different. Examples would be flower colour, habitat type, or sex.
With interval data, for example, you might count something, keep counting and build up a sample. When you are finished, you can take your list and calculate an average, look to see how much larger the biggest value is from the smallest and so on. Put another way, you have a scale of measurement. This scale might be millimetres or grams or anything else. Whenever you measure something using this scale you can see how it fits into the scheme of things because the interval of your scale is fixed (10 mm is bigger than 5 mm, 4 g is less than 12 g). Compare this to the ordinal scales described below.
With ordinal data you might look at the abundance of a species in quadrats. It may be difficult or time consuming to be exact so you decide to use an abundance scale. The Domin scale shown in Table 1.2, for example, converts percentage cover into a numerical value from 0 to 10.
Table 1.2 The Domin scale; an example of an ordinal abundance scale.
The Domin scale is generally used for looking at plant abundance and is used in many kinds of study. You can see by looking at Table 1.2 that the different classifications cover different ranges of abundance. For example, a Domin of 8 represents a range of values from about half to three-quarters coverage (51–74%). A value of 6 represents a range fromabout a quarter to a third coverage (26–33%). The first three divisions of the Domin scale all represent less than 4% coverage but relate to the number of individuals found. The Domin scale is useful because it allows you to collect data efficiently and still permits useful analysis. You know that 10 is a
greater percentage coverage than 8 and that 8 is bigger than 6; it is just that the intervals between the divisions are unequal.
Table 1.3 An example of a generalized DAFOR scale for vegetation, an example of an ordinal abundance scale.
There are many other abundance scales, and various researchers have at times worked out useful ways to simplify the abundance of organisms. The DAFOR scale is a general phrase to describe abundance scales that convert abundance into a letter code. There are many examples. Table 1.3 shows a generalized scale for vegetation analysis.
There are other letters that might be used to extend your scale. For example C for “common” might be inserted between Aand F (ACFOR is a commonly used ordinal scale). You might add E and/or S for “extremely abundant” and “super abundant”. You might also add N for “not found”. The DAFOR type of scale can be used for any organism, not just for vegetation.
When you are finished, you can convert your DAFOR scale into numbers (ranks) and get an average, which can be converted to a DAFOR letter, but you cannot tell how much larger the biggest is fromthe smallest – the interval between the values is inexact.
Many of the abundance scales used are derived from the work of Josias Braun-Blanquet, an eminent Swiss botanist. Table 1.4 shows a basic example of a Braun-Blanquet scale for vegetation cover.
Table 1.4 The basic Braun-Blanquet scale, an ordinal abundance scale. There are many variations on this scale.
With categorical data it is useful to think of an example. You might go out and look to see what types of insect are visiting different colours of flower. Every time you spot an insect, you record its type (bee, fly, beetle) and the flower colour. At the end you can make a table with numbers of how many of each type visited each colour. You have numbers but each value is uniquely a combination of two categories.
Table 1.5 shows an example of categorical data laid out in what is called a contingency table. The rows are one category (colour) and the columns another category (type of insect).
Table 1.5 An example of categorical data. This type of table is also called a contingency table. The rows and columns are each sets of categories. Each cell of the table represents a unique combination of categories.
1.6 Sampling effort
Sampling effort refers to the way you collect data and how much to collect. For example, you have decided that you need to determine the abundance of some plant species in meadows across lowland Britain. How many quadrats will you use? How large will the quadrats need to be? Do you need quadrats at all?
Sample is the term used to describe the set of data that you have. Because you generally cannot measure “everything”, you will usually have a subset of stuff that you’ve measured (or weighed or counted). Think about a field of buttercups as an example. You wish to know how many there are in the field, which is a hectare in size (i.e. 100 m × 100 m). You aren’t really
Each method is suitable for certain situations, as you’ll see now.
Random sampling
In a random sampling method, you use predetermined locations to carry out your sampling. If you were looking at plants in a field, for example, you could measure the field and use random numbers to generate a series of x, y co-ordinates. You then place your quadrats at these coordinates. This works nicely if your field is square. If your field is not square you can measure a large rectangle that covers the majority of the field and ignore co-ordinates that fall outside the rectangle. For other situations you can work out a method that provides co-ordinates to place your quadrats. Basically, the locations are predetermined before you start, which is more efficient and saves a lot of wandering about.
In theory, every point within your area should have an equal chance of being selected and your method of creating random positions should reflect this. What happens if you get the same location twice (or more)? There are two options:
• Random sampling without replacement. If you get duplicate locations you skip the duplicate and create another randomco-ordinate instead.
• Random sampling with replacement. If you get duplicate locations you use themagain.
In random sampling without replacement you never use the same point twice, even if your randomnumber generator comes up with a duplicate.
In random sampling with replacement you use whatever locations arise, even if duplicated. In practice, this means that you use the same data and record it both times. It is important that you do not ignore duplicate co-ordinates. If you have ten co-ordinates, which include duplication, then you will still need to get ten values when you have finished. Obviously you do not need to place the quadrat a second time and count the buttercups again, you simply copy the data.
Randomsampling is good for situations where there is no detectable pattern. In other cases a pattern may exist. For example, if you were sampling in medieval fields you might have a ridge and furrow system. The old methods of ploughing the field create high and low points at regular intervals. These ridges and furrows may affect the growth of the plants (you assume the ridges are drier and the furrows wetter for instance). If you sampled randomly, you may well get a lot more data from ridges than from furrows. Consequently, you are introducing unwanted bias.
In other cases you may be deliberately looking at a situation where there is an environmental gradient of some sort. For example, this might be a slope where you suspect that the top is drier than the bottom. If you sample randomly then you may once again get bias data because you sampled predominantly in the wetter end of the field (or the drier end). You need to alter your sampling strategy to take into account the situation.
Systematic sampling
In some cases you are deliberately targeting an area where an environmental gradient exists. What you want is to get data from right across this gradient so that you get samples from all
parts. Random sampling would not be a good idea (by chance all your observations could be fromone end) so you use a set systemto ensure that you cover the entire gradient.
Systematic sampling often involves transects. A transect is simply the term used to describe a slice across something. For example, you might wish to look at the abundance of seaweed across a beach. The further up the beach, the drier it gets because of the tide so what you do is to create a transect that goes from the top of the beach (high water) to the bottom of the beach (low water). In this way you cover the full range of the gradient from very dry (only covered by water at high tides) to very wet (in the sea).
There are several kinds of transect:
• Line: this is exactly what it sounds like. You run a line along your sampling location and record everything along it.
• Belt: this kind of transect has definite width! This may be a quadrat or possibly a line of sight (used in butterfly or bird surveys). The transect is sampled continuously along its entire length.
• Interrupted belt: this kind of transect is most commonly used when you have quadrats (or their equivalent). Rather than sample continuously you sample at intervals. Often the intervals are fixed but this is not always necessary.
You take your samples along the transect, either continuously (line, belt) or at intervals (interrupted). You do not necessarily have to measure at regular fixed intervals along the transect (although it is common to do so).
One transect might not be enough because you may miss a wider pattern (Figure 1.1). You ought to place several transects and combine the data from them all. In this way you are covering a wider part of the habitat and being more representative of the whole, which is the point.
Figure 1.1 One transect may not be enough to see the true pattern. In this case several transects would give a truer representation.
You also need to determine how long the transect should be. You might, for example, be looking at a change in abundance of a plant species along a transect, which may relate to an environmental factor. You need to make sure that you make the transect long enough to cover the change in abundance but not so long that you over-run too far.
• It is extremely powerful and will handle very complex analyses as easily as simple ones.
• It will handle a wide variety of analyses. This is one of the most important features: you only need to know how to use R and you can do more or less any type of analysis; there is no need to learn several different (and expensive) programs.
• It uses simple text commands. At first this seems hard but it is actually quite easy. The upshot is that you can build up a library of commands and copy/paste them when you need them.
• Documentation. There is a wealth of help for R. The CRAN site itself hosts a lot of material but there are also other websites that provide examples and documentation. Simply adding CRAN to a web search command will bring up plenty of options.
1.8.1 Getting R
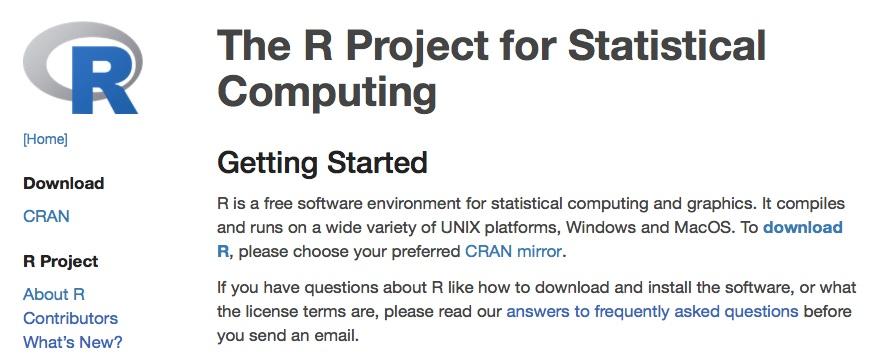
Getting R is easy via the Internet. The R Project website is a vast enterprise and has local mirror sites in many countries. The first step is to visit the main R Project webpage (http://www.r-project.org) where you can select the most local site to you (this speeds up the download process a bit).
Figure 1.2 Getting R from the R Project website. Click the download link and select the nearest mirror site.
Once you have clicked the download link (Figure 1.2), you have the chance to select a mirror site. These mirrors sites are hosted in servers across the world and using a local one will generally result in a speedier download.
Once you have selected a mirror site, you can click the link that relates to your operating system(Figure 1.3). If you use a Mac then you will go to a page where you can select the best option for you (there are versions for various flavours of OSX). If you use Windows then you will go to a Windows-specific page. If you are a Linux user then read the documentation; you generally install R through the terminal rather than via the web page.
Now the final step is to click the link and download the installer file, which will download in the usual manner according to the setup of your computer.
Figure 1.3 Getting R from the R Project website. You can select the version that is specific to your operating system.
1.8.2 Installing R
Once you have downloaded the install file, you need to run it to get R onto your computer. If you use a Mac you need to double-click the disk image file to mount the virtual disk. Then double-click the package file to install. If you use Windows, then you need to find the EXE file and run it. The installer will copy the relevant files and you will soon be ready to run R. Now R is ready to work for you. Launch R using the regular methods specific to your operating system. If you added a desktop icon or a quick launch button then you can use these or run R fromthe Applications or Windows Start button.
1.9 Excel
There are many versions of Excel and your computer may already have had a version installed when you purchased it. The basic functions that Excel uses have not changed for quite some while so even if your version is older than is described here, you should be able to carry out the same manipulations. You will mainly see Excel 2013 for Windows illustrated here. If you have purchased a copy of Excel (possibly as part of the Office suite) then you can install this following the instructions that came with your software. Generally, the defaults that come with the installation are fine although it can be useful to add extra options, especially the Analysis ToolPak, which you will see described next.
Figure 1.7 The Analysis ToolPak provides a range of analytical tools.
Each tool requires the data to be set out in a particular manner; help is available using the Help button.
1.9.2 Other spreadsheets
The Excel spreadsheet that comes as part of the Microsoft Office suite is not the only spreadsheet; of the others available, of particular note are the Open Office and Libre Office programs. These are available from www.openoffice.org and www.libreoffice.org and there are versions available for Windows, Mac and Linux.
Other spreadsheets generally use the same functions as Excel, so it is possible to use another program to produce the same result. Graphics will almost certainly be produced in a different manner to Excel. In this book you will see Excel graphics produced with version 2013 for Windows.
EXERCISES
Answers to exercises can be found in Appendix 1.
1. In a project looking for links between things you would be looking for or , depending on the kind of data.
2. Arrange these levels of measurement in increasing order of “sensitivity”: Ordinal, Interval, Categorical.
3. Domin, DAFOR and Braun-Blanquet are all examples of scales, whereas red, blue and yellow would be examples of .
4. Which one of the following is not a kind of transect?
A. Line. B. Belt.