PrefacetotheSecondEdition
Thissecondeditionof“SignalProcessingforNeuroscientists” includesthepartlyrevisedandupdatedmaterialofthereprintedfirst editionanditscompanionvolume.Attherequestofmystudents, colleagues,andreaders,Ihaveextendedseveralchaptersandadded newones.Asaresult,thiseditioncontainsafewadditionaladvanced topics(theimagingsectionofChapters7,8,and13),anintroductionto differentialequationsandmodelingdynamics(Chapters9,10,and23), andanoverviewofmodelingactivityofsingleneuronsandneuronal networks(Chapters29and30).Theselasttwochapterssummarize approachestomodelingofneuralactivitywithaflavorofahistorical overviewofmodelinginneuroscience.Duetothereviewaspectofthe modelingcomponent,thesechaptersincludeamuchlongerreference listthantheothers.AtmultiplerequestsIhavealsoincludedaseries ofexerciseswitheachchapter.Answerstoasubsetoftheseexercises areavailableon http://booksite.elsevier.com/9780128104828/ . Overall,theendresultofthissecondeditionisfairlyclosetowhatI hadinitiallyhopedtoproduceforthefirsteditionaboutadecadeago butcouldn’tfinishwithintheavailabletime.However,althoughthistext appearsmuchlaterthanIhadenvisioned,Inowhavetheadditional advantageofhavingtaughtthesignalanalysisandmodelingtopics multipletimestodifferentgroupsofstudents,givingmeamuchbetter insightintohowtopresentandexplainthematerial.Inaddition,the currenttext,figures,andexerciseswereextensivelyevaluatedandtested bystudentsandreaders.Threeyearsago,someofthelectureswere madeavailableonYouTubeforaworldwideaudience,andthistriggered usefulfeedbackandsuggestionsthatwereincludedinthisedition.The overallgoalofthetextremainstopresentthemathematicalbackground ofdifferenttypesofsignalanalysisandmodelinginneuroscience,andto illustratethiswithpracticalexamplesintheformofMATLAB scripts thatareavailableon http://booksite.elsevier.com/9780128104828/. UltimatelyIhopethisendresulthelpsthereaderwhenstudyingthe materialinthistext.
Iwanttoincludeafewsuggestionsforthosewhoplantousethis textand/oritsfigures(http://booksite.elsevier.com/9780128104828/) intheirlectures.Mostchaptersarebasedonmaterialandexamples thatcanbecoveredina1 1½hlecture.However,dependingonthe backgroundofthestudents,Chapters9,10,15,16,21and22maybe
combinedinsingle1½hlectures,whileChapters7and13,aswellasthe overviewinChapter30,aremoresuitableformultiplelecturesofthat length.InadditiontotheMATLAB material,somechaptersalso includeelementsthatcanbeusedforlabsessions.Afilterlabcanbe basedontheRC-circuitdescribedinChapter15.Forsettingupmore advancedlabsessions,Idescribemembranemodelsusingtheintegrate-and-firecircuitandtheNagumoequivalentcircuitinChapter29 andAppendix29.2.
Itisdifficulttothankeveryonewhocontributeddirectlyorindirectly tothisbook,butIwilltry(withanapologytothoseIforgettoinclude). InadditiontoallIalreadyacknowledgedinthepreviouseditionandits companionvolume,IwanttothankmycollaboratorsattheUniversityof Chicagoandelsewhere:Drs.MichelJ.A.M.vanPutten,StephanA.van Gils,CatherineA.Schevon,AndrewK.Tryba,CharlesJ.Marcuccilli, andJan-Marino(Nino)Ramirez.IalsothankDrs.StevenSmall,Ahmed Shereen,andJustinJurellerfortheircriticalinputwhilewriting thematerialonimaging.SpecialthankstoDr.JackD.Cowanfor hisinspiringguestlecturesontheWilson Cowanequations,and who(inthemanyconversationswehad)mademeappreciatethe populationmodelapproachinneuroscience.IalsothankmyTeaching AssistantsAlexSadovsky,ArupSarma,KylerBrown,AlbertWildeman, JamesGoodman,GrahamFetterman,andJoeDecheryfortheiruseful suggestions.Thefeedbackofthe(under)graduatestudents,Mark Saddler,TahraEissa,JyothsnaSuresh,AlbertWildeman,andJeremy Neuman,inmylaboratorywasveryhelpful.Ialsothankthepeopleat Elsevier,Dr.NatalieFarra,KristiAnderson,andPoulouseJosephfor theirsupportandsuggestions.LastbutnotleastIthankIngridforher ongoingfabuloussupport!
PrefacetotheFirstEdition
Thistextbookisanintroductiontosignalprocessingprimarilyaimedat neuroscientistsandbiomedicalengineers.Thetextwasdevelopedfora one-quartercourseIteachforgraduateandundergraduatestudentsat theUniversityofChicagoandtheIllinoisInstituteofTechnology.Thepurposeofthecourseistointroducesignalanalysistostudentswithareasonablebutmodestbackgroundinmathematics(includingcomplexalgebra, basiccalculus,andintroductoryknowledgeofdifferentialequations)and aminimalbackgroundinneurophysiology,physics,andcomputerprogramming.Tohelpthebasicneuroscientisteaseintothemathematics, thefirstchaptersaredevelopedinsmallsteps,andmanynotesareadded tosupporttheexplanations.Throughoutthetext,advancedconceptsare introducedwhereneeded,andinthecaseswheredetailswoulddistract toomuchfromthe“bigpicture,”furtherexplanationismovedtoan appendix.Mygoalsaretoprovidestudentswiththebackgroundrequired tounderstandtheprinciplesofcommerciallyavailableanalysessoftware, toallowthemtoconstructtheirownanalysistoolsinanenvironment suchasMATLAB , 1 andtomakemoreadvancedengineeringliterature accessible.Mostofthechaptersarebasedon90-minlecturesthatinclude demonstrationsofMATLAB scripts.Chapters7and8containmaterial fromthreetofourlectures.Eachchaptercanbeconsideredasastandaloneunit.Forstudentswhoneedtorefreshtheirmemoryonsupporting topics,Iincludereferencestootherchapters.Thefigures,equations,and appendicesarealsoreferencedindependentlybychapternumber.
TheCDthataccompaniesthistextcontainstheMATLAB scriptsand severaldatafiles.Thesescriptswerenotdevelopedtoprovideoptimized algorithmsbutserveasexamplesofimplementationofthesignalprocessingtaskathand.Foreaseofinterpretation,allMATLAB scriptsarecommented;commentsstartingwith%providestructureandexplanationof proceduresandthemeaningofvariables.Togainpracticalexperiencein signalprocessing,Iadvisethestudenttoactivelyexploretheexamples andscriptsincludedandworryaboutalgorithmoptimizationlater.All scriptsweredevelopedtoruninMATLAB (Version7)includingthetoolboxesforsignalprocessing(Version6),imageprocessing(Version5),and wavelets(Version3).However,asidefromthosethatuseadigitalfilter, theFourierslicetheorem,orthewavemenu,mostscriptswillrunwithout
1MATLAB isaregisteredtrademarkofTheMathWorks,Inc.
Mostcurrenttechniquesinsignalprocessinghavebeendeveloped withlineartime-invariant(LTI)systemsastheunderlyingsignal generatororanalysismodule(Chapters9 14).Becauseweareprimarily interestedinthenervoussystem,whichisoftenmorecomplicatedthan anLTIsystem,wewillextendthebasictopicswithanintroductioninto theanalysisoftimeseriesofneuronalactivity(spiketrains , Chapter20), analysisofnonstationarybehavior(waveletanalysis , Chapters21and 22),modelingandcharacterizationoftimeseriesoriginatingfrom nonlinearsystems (Chapters23 27), decompositionofmultichannel data (Chapter28),andfinallyhowtoapplythisto neuralsystems (Chapters29and30).
1.2BIOMEDICALSIGNALS
Duetothedevelopmentofavastarrayofelectronicmeasurement equipment,arichvarietyofbiomedicalsignalsexist,rangingfrom measurementsofmolecularactivityincellmembranestorecordings ofanimalbehavior.Thefirstlinkinthebiomedicalmeasurementchain istypicallya transducer or sensor,whichmeasuressignals(suchasa heartvalvesound,bloodpressure,orX-rayabsorption)andmakes thesesignalsavailableinanelectronicformat.Biopotentialsrepresenta largesubsetofsuchbiomedicalsignalsthatcanbedirectlymeasured electricallyusingan electrode pair.Somesuchelectricalsignalsoccur “spontaneously”(e.g.,theelectroencephalogram,EEG);otherscanbe observeduponstimulation(e.g.,evokedpotentials,EPs).
1.3BIOPOTENTIALS
Biopotentialsoriginatewithinbiologicaltissueaspotentialdifferencesthatoccurbetweencompartments.Generally,thecompartments areseparatedbya(bio)membranethatmaintainsconcentrationgradientsofcertainionsviaanactivemechanism(e.g.,theNaþ/Kþ pump). HodgkinandHuxley(1952) werethefirsttomodelabiopotential (theactionpotentialinthesquidgiantaxon)withanelectronic equivalent(Fig.1.1).Acombinationofordinarydifferentialequations (ODEs)andamodeldescribingthenonlinearbehaviorofionic conductancesintheaxonalmembranegeneratedanalmostperfect descriptionoftheirmeasurements.Thephysicallawsusedtoderivethe baseODEfortheequivalentcircuitare: Nernst, Kirchhoff, and Ohm’s laws (Appendix1.1).Anexampleofhowtoderivethedifferential
FIGURE1.3 Asomatosensory-evokedpotentialrecordedfromthehumanscalpasthe averageresultof500electricalstimulationsoftheleftradialnerveatthewrist.Thestimulus artifact(attime0.00)showsthetimeofstimulation.Twomeasurementsaresuperimposedto showreproducibility.The arrow indicatestheN20peakat w20mslatency. FromSpiegel,J., Hansen,C.,Baumgartner,U.,Hopf,H.C.,Treede,R.-D.,2003.Sensitivityoflaser-evokedpotentialsversussomatosensoryevokedpotentialsinpatientswithmultiplesclerosis.Clin.Neurophysiol. 114,992 1002.
(AEPs,VEPs,andSSEPs,respectively).Thesesignalsrepresentthebrain’s responsetoastandardstimulussuchasatoneburst,click,lightflash, changeofavisualpattern,oranelectricalpulsedeliveredtoanerve. Whenthebrainrespondstospecificstimuli,theevokedelectrical responseisusuallymorethan10timessmallerthantheongoingEEG backgroundactivity.Signalaveraging(Chapter4)iscommonlyapplied tomakethebrain’sevokedactivityvisible.Anexampleofanaveraged SSEPisshownin Fig.1.3.Theaveragingapproachtakesadvantageof thefactthattheresponseistime-lockedwiththestimulus,whereasthe ongoingEEGbackgroundisnottemporallyrelatedtothestimulus.
1.4.2Electrocardiogram
Theactivityoftheheartisassociatedwithahighlyorganizedmuscle contractionprecededbyawaveofelectricalactivity.Normally,onecycle ofdepolarizationstartsatthesino-atrialnodeandthenmovesasawave throughtheatriumtotheatrio-ventricularnode,thebundleofHis, andtheremainderoftheventricles.Thisactivationisfollowedbya repolarizationphase.Duetothesynchronizationoftheindividual cellularactivity,theelectricalfieldgeneratedbytheheartissostrong thattheelectrocardiogram(ECG;thoughsometimestheGerman abbreviation“EKG”[elektrokardiogram]isused)canbemeasuredfrom almostanywhereonthebody.TheECGisusuallycharacterizedby severalpeaks,denotedP-QRS-T(Fig.1.4B ).TheP-waveisassociated withtheactivationoftheatrium,theQRS-complexandtheT-wavewith
Ascanbeseenin Fig.1.6,theresolutionofthecompleteADCprocess expressedinthepotentialstepperdigitizerunit(e.g., mV/bit)isnot uniquelydeterminedbytheADC,butalsodependsontheanalog amplification.Afterthemeasurementsareconverted,thedatacanbe storedindifferentformats:integer,real/float,orASCII.Itiscommonto referto8bitsasabyteandacombinationofbytes(e.g.,4bytes)asaword.
1.6MOVINGSIGNALSINTOTHEMATLAB ANALYSIS ENVIRONMENT
Throughoutthiscoursewewillexploresignalprocessingtechniques withrealsignals.Therefore,itiscriticaltobeabletomovemeasurements intotheanalysisenvironment.Herewegivetwoexamplesofreading recordingsofneuralactivityintoMATLAB .Togetanoverviewoffile typesthatcanbereaddirectlyintoMATLAB ,youcansearchthe MATLAB documentationfor“DataImportandExport.”Mostfiles
Header: Names,Dates,etc.
SampleRate,DataStructure
orbySample#)
Header:
Names,Dates,etc.
DATAFILE HEADERFILE
SampleRate,DataStructure
AdministrativeInformation: TechnicalInformation: (InterleavedbyChannel orbySample#)
FIGURE1.7 Datafiles.(A)Anintegratedfileincludingbothheaderinformationand data.Sometimestheheaderinformationisattheendofthefile(tailer).(B)Separateheader anddatafiles.
recordedwithbiomedicalequipmentarenotdirectlycompatiblewith MATLAB andmustbeeditedand/orconverted.Usuallythisconversion requireseitheranumberofstepstoreformatthefile,orreadingthefile usingthelow-level fopenand freadcommands.SinceA/Dconverters typicallygenerateintegervalues,mostcommercialdataformatsfor measurementfilesconsistofarraysofintegerwords.Suchafilemay containsomeadministrativeinformationatthebeginning(header)orend (“tailer”);inothercases,thistypeofmeasurement-relatedinformationis storedinaseparatefile(sometimescalledaheaderfile;see Fig.1.7).
Asanexercisewewillmovedatafromtwoexampledatasetsinto MATLAB .Thedatasetsandassociatedfilesandscriptcanbedownloadedfrom http://booksite.elsevier.com/9780128104828/;onesetisan EEGrecording(consistingoftwofilesdata.eeganddata.bni)andthe otherisameasurementofaneuron’smembranepotential(Cell.dat).Like manybiomedicalsignalsthesedatasetswereacquiredusingaproprietaryacquisitionsystemwithintegratedhardwareandsoftwaretools. Aswewillsee,thiscancomplicatetheprocessofimportingdataintoour analysisenvironment.
Themembranepotentialrecording(Cell.dat)canbedirectlyread withAxoScopeoranysoftwarepackagethatincludestheAxoScope reader(AxonInstruments,Inc.).Ifyouhaveaccesstosuchapackage,you canstoreaselectionofthedatainatextfileformat(*.atf).This fileincludesheaderinformationfollowedbythedataitself(Fig.1.7A). Ifyoudonothaveaccesstotheproprietaryreadersoftware,youcanwork withanoutputtextfileofAxoScopethatisalsoavailableontheCD (Action_Potentials.atf).Inordertobeabletoloadthisfile(containingthe singlecelldata)inMATLAB ,theheadermustberemovedusingatext editor(suchasWordPadinaWindowsoperatingsystem).Thefirstfew linesofthefileasseeninWordPadareshownhere:
ATF1.0 74
"AcquisitionMode¼GapFree"
"Comment¼ "
"YTop¼10,100,10"
"YBottom¼-10,-100,-10"
"SweepStartTimesMS¼72839.700"
"SignalsExported¼PBCint,neuron,current"
"Signals¼""PBCint""neuron""current" "Time(s)""Trace#1(V)""Trace#1(mV)""Trace#1(nA)"
72.83970.90332-58.59380.00976563
72.84 0.898438-58.59380
72.84030.90332-58.7402-0.00976563
Afterdeletingtheheaderinformation,thefilecontainsonlyfourcolumnsofdata.
72.83970.90332-58.59380.00976563
72.84 0.898438-58.59380
72.84030.90332-58.7402-0.00976563
72.84060.898438-58.6914 0.00488281
72.84090.90332-58.6426-0.00488281
Thiscanbestoredasatextfile(Action_Potentials.txt)containing therecordeddata(withoutheaderinformation)beforeloadingthe fileintoMATLAB .TheMATLAB commandtoaccessthedatais loadAction_Potentials.txt-ascii.Theintracellulardataareinthe thirdcolumnandcanbemadedisplayedwiththecommand plot(Action_Potentials(:,3)).Theobtainedplotresultshouldlooksimilar to Fig.1.5 .ThevaluesinthegrapharetherawmeasuresofthemembranepotentialinmV.Ifyouhaveabackgroundinneurobiology,you mayfindthesemembranepotentialvaluessomewhathigh;infactthese valuesmustbecorrectedbysubtracting12mV(theso-calledliquid junctionpotentialcorrection).
Incontrasttotheintracellulardata,theexampleEEGmeasurement datawepresentbelowconsistofaseparateheaderfile(data.bni)anddata file(data.eeg),correspondingtothediagramin Fig.1.7B.Asshowninthe figure,theheaderfileisanASCIItextfile,whilethedigitizedmeasurementsinthedatafilearestoredina16-bitintegerformat.Sincethedata andheaderfilesareseparate,MATLAB canreadthedatawithout modificationofthefileitself,thoughimportingthiskindofbinarydata requirestheuseoflower-levelcommands(aswewillshow).SinceEEG filescontainrecordsofanumberofchannels,sometimesoveralong periodoftime,thefilescanbequitelargeandthereforeunwieldyin MATLAB .Forthisreason,itmaybehelpfultouseaspecialreview applicationtoselectsmallersegmentsofdatawhichcanbesavedin separatefilesandreadintoMATLAB inmoremanageablechunks.In thisexamplewedonothavetofindasubsetoftherecordingbecausewe havealreadypreselecteda10-sEEGepoch.Ifyoudon’thaveaccessto specialEEGreadersoftware,youcanseewhatthedisplaywouldlooklike inthejpgfiles:data_montaged_filtered.jpganddata.jpg.Thesefilesshow thedisplayinanEEGreaderapplication(EEGVue,NicoletBiomedical Inc.)ofthedata.eegfileinamontagedandfilteredversionandinaraw dataversion,respectively.
ThefollowingMATLAB scriptshowsthecommandsforloadingthe rawdatafromdata.eeg:
%pr1_1.m
sr¼400;%SampleRate
Nyq_freq¼sr/2;%NyquistFrequency
fneeg¼input('Filename(withpathandextension):' , ' s ');
t¼input('HowmanysecondsintotalofEEG?: ');
ch¼input('HowmanychannelsofEEG?: ');
le¼t*sr; %LengthoftheRecording
fid¼fopen(fneeg, ' r ' , 'l');
EEG¼fread(fid,[ch,le],'int16');
% *) Openthefiletoread(‘r’)and little-endian(‘l’)
%ReadData-> EEGMatrix fclose('all');
%CloseallopenFiles
*) Thelittle-endianbyteorderingisonlyrequiredinafewspecialcases,in straightforwardPCtoPCdatatransferthe ’l’ optioninthe fopenstatementcanbeomitted.
ExecutingtheabovecommandsinaMATLAB commandwindowor viatheMATLAB scriptthatcanbedownloadedfrom http://booksite. elsevier.com/9780128104828/ (pr1_1.m)generatesthefollowingquestions:
Filename(withpathandextension): data.eeg
HowmanysecondsintotalofEEG?: 10
HowmanychannelsofEEG?: 32
Theanswerstothequestionsareshowninbold.Youcannow plotsomeofthedatayoureadintothematrixEEGwith plot(-EEG(1,:)), plot(-EEG(16,:)),or plot(EEG(32,:)).Thefirsttwoplotcommandswill displaynoisyEEGchannels;thelasttraceisanECGrecording.The (minus)signsinthefirsttwoplotcommandsareincludedinorderto followtheEEGconventionofshowingnegativedeflectionsupward.To comparetheMATLAB figuresoftheEEGwiththetracesinthe proprietaryEEGVuesoftware,seethejpegfileshowingtherawdata data.jpg.Alternativelyyoucanquicklyverifytheintegrityofyourresult bycheckingchannel32fortheoccurrenceofQRScomplexessimilarto theoneshownin Fig.1.4B.
Likethefirstfewlinesofheaderinformationinthesinglecelldatafile above,thefirstfewlinesoftheseparateEEGheaderfile(data.bni)contain
similarhousekeepinginformation.Again,thisASCII-formattedfilecanbe openedwithatexteditorsuchasWordPad,revealingthefollowing:
FileFormat ¼ BNI-1
Filename ¼ f:\anonymous_2f1177c5_2a99_11d5_a850_00e0293dab97\ data.bni
Comment ¼
PatientName ¼ anonymous
PatientId ¼ 1
Usuallythefileformatsofmeasurementsinneurosciencearespecific tothemanufactureroreventherecordingdevice.Therefore,each instrumentmayrequireitsown,oftennontrivial,customprocedureto exportrecordingsacrossdifferentsoftwareapplications.Oneexception istheso-calledEuropeanDataFormat(EDF)thatwasdevelopedasa genericfileformatofthetypeshownin Fig.1.7A.Itwasinitiallyintroducedinthe1990sforstoringsleepandEEGdataandmorerecently updatedtoEDFþ toalsoincludeothermodalitiessuchasEKG,electromyography,andEPmeasurements( Kempetal.,1992;Kempand Olivan,2003 ).Fortunately,severalins trumentmanufacturersnow supportEDFasoneoftheirfileformats.
APPENDIX1.1
Thisappendixprovidesaquickreferencetosomebasiclawsfrequently usedtoanalyzeproblemsinneurobiology,andwhicharecited throughoutthistext(Fig.A1.1-1).Furtherexplanationoftheselawscanbe foundinanybasicphysicstextbook.
FIGUREA1.1-1 Overviewofbasicphysicslaws.
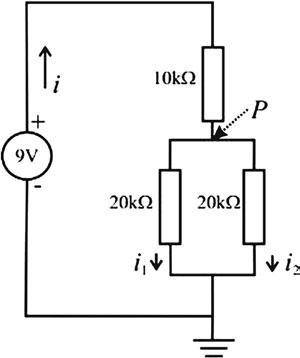
FIGUREE1.5 Athree-resistornetworkconnectedtoa9-Vbattery.
1.5Forthecircuitin Fig.E1.5,answerthefollowingquestions.
a.Whatresistorsareparallel?
b.Whatresistorsareinseries?
c.UseOhm’slawtocomputetotalcurrent i.
d.UseKirchhoff’sfirstlawtocomputecurrents i1 and i2
e.UseKirchhoff’ssecondlawtocomputethepotentialatpoint P. [Recallthattheequivalentresistor R fortwoparallelresistors R1 and R2 canbedeterminedwith 1 R1 þ 1 R2 ¼ 1 R].
References
Hodgkin,A.L.,Huxley,A.F.,1952.Aquantitativedescriptionofmembranecurrentandits applicationtoconductionandexcitationinthenerve.J.Physiol.117,500 544. AseminalpaperdescribingtheHodgkinandHuxleyequations.
Kemp,B.,Olivan,J.,2003.Europeandataformat‘plus’(EDFþ),anEDFalikestandard formatfortheexchangeofphysiologicaldata.Clin.Neurophysiol.114(9),1755 1761.
Kemp,B.,Varri,A.,Rosa,A.C.,Nielsen,K.D.,Gade,J.,1992.Asimpleformatforexchangeof digitizedpolygraphicrecordings.Electroencephalogr.Clin.Neurophysiol.82(5), 391 393.
Oostenveld,R.,Praamstra,P.,2001.Thefivepercentelectrodesystemforhigh-resolution EEGandERPmeasurements.Clin.Neurophysiol.112,713 719. DefinitionoftheelectrodeplacementinhumanEEGrecording.
Spiegel,J.,Hansen,C.,Baumga ¨ rtner,U.,Hopf,H.C.,Treede,R.-D.,2003.Sensitivityoflaserevokedpotentialsversussomatosensoryevokedpotentialsinpatientswithmultiple sclerosis.Clin.Neurophysiol.114,992 1002.
Anexampleoftheapplicationofevokedpotentialsinclinicalelectrophysiology.