RIEMANNIAN GEOMETRIC STATISTICSIN MEDICALIMAGE ANALYSIS
Editedby
XAVIERPENNEC
STEFANSOMMER TOMFLETCHER
AcademicPressisanimprintofElsevier 125LondonWall,LondonEC2Y5AS,UnitedKingdom 525BStreet,Suite1650,SanDiego,CA92101,UnitedStates 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom
Copyright©2020ElsevierLtd.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical,including photocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwritingfromthepublisher. Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangementswith organizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions.
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanasmaybe notedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenourunderstanding, changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation, methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbemindfuloftheir ownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityforanyinjury and/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromanyuseoroperationof anymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-814725-2
ForinformationonallAcademicPresspublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MaraConner
AcquisitionEditor: TimPitts
EditorialProjectManager: LeticiaM.Lima
ProductionProjectManager: KameshRamajogi
Designer: MilesHitchen
TypesetbyVTeX
4.3Thediffeomorphismgroupinshapeanalysis..................138
5.1Introduction...
5.4Left,right,andbiinvariantRiemannianmetricsonaLiegroup..191
5.5StatisticsonLiegroupsassymmetricspaces..
5.6Thestationaryvelocityfields(SVF)frameworkfor
5.7ParalleltransportofSVFdeformations........................213
5.8Historicalnotesandadditionalreferences.....................223
StephenM.Pizer,JunpyoHong,JaredVicory,ZhiyuanLiu,J.S.Marron, Hyo-youngChoi,JamesDamon,SungkyuJung,BeatrizPaniagua, JörnSchulz,AnkurSharma,LiyunTu,JiyaoWang
6.1Introductiontoskeletalmodels.
6.2Computingans-repfromanimageorobjectboundary
6.7Howtocomparerepresentationsandstatisticalmethods...
6.8Resultsofclassification,hypothesistesting,andprobability
6.9Thecodeanditsperformance................................265
6.10Weaknessesoftheskeletalapproach..........................266
Contributors
MartinBauer
FloridaStateUniversity,DepartmentofMathematics,Tallahassee,FL,UnitedStates
RudrasisChakraborty
UniversityofFlorida,CISEDepartment,Gainesville,FL,UnitedStates
BenjaminCharlier
IMAG,Univ.Montpellier,CNRS,Montpellier,France
InstitutduCerveauetdelaMoëlleÉpinière,ARAMIS,Paris,France
NicolasCharon
JohnsHopkinsUniversity,CenterofImagingSciences,Baltimore,MD,UnitedStates
Hyo-youngChoi
UNC,ChapelHill,NC,UnitedStates
JamesDamon
UNC,ChapelHill,NC,UnitedStates
LoicDevilliers
UniversitéCôted’AzurandInria,Epioneteam,SophiaAntipolis,France
AasaFeragen
UniversityofCopenhagen,DepartmentofComputerScience,Copenhagen,Denmark
TomFletcher
UniversityofVirginia,DepartmentsofElectrical&ComputerEngineeringandComputer Science,Charlottesville,VA,UnitedStates
JoanGlaunès
MAP5,UniversitéParisDescartes,Paris,France
PolinaGolland
MassachusettsInstituteofTechnology,ComputerScienceandArtificialIntelligenceLab, Cambridge,MA,UnitedStates
PietroGori
TélécomParisTech,LTCI,équipeIMAGES,Paris,France
JunpyoHong
UNC,ChapelHill,NC,UnitedStates
SarangJoshi
UniversityofUtah,DepartmentofBioengineering,ScientificComputingandImagingInstitute, SaltLakeCity,UT,UnitedStates
SungkyuJung
SeoulNationalUniversity,Seoul,RepublicofKorea
ZhiyuanLiu
UNC,ChapelHill,NC,UnitedStates
MarcoLorenzi
UniversitéCôted’AzurandInria,Epioneteam,SophiaAntipolis,France
J.S.Marron
UNC,ChapelHill,NC,UnitedStates
StephenMarsland
VictoriaUniversityofWellington,SchoolofMathematicsandStatistics,Wellington, NewZealand
NinaMiolane
UniversitéCôted’AzurandInria,Epioneteam,SophiaAntipolis,France
StanfordUniversity,DepartmentofStatistics,Stanford,CA,UnitedStates
JanModersitzki
InstituteofMathematicsandImageComputing,UniversityofLübeck,Lübeck,Germany
FraunhoferMEVIS,Lübeck,Germany
KlasModin
ChalmersUniversityofTechnologyandtheUniversityofGothenburg,Departmentof MathematicalSciences,Göteborg,Sweden
MarcNiethammer
DepartmentofComputerScience,UniversityofNorthCarolinaatChapelHill,ChapelHill,NC, UnitedStates
BiomedicalResearchImagingCenter(BRIC),ChapelHill,NC,UnitedStates
TomNye
NewcastleUniversity,SchoolofMathematics,StatisticsandPhysics,NewcastleuponTyne, UnitedKingdom
BeatrizPaniagua
UNC,ChapelHill,NC,UnitedStates
XavierPennec
UniversitéCôted’AzurandInria,Epioneteam,SophiaAntipolis,France
StephenM.Pizer
UNC,ChapelHill,NC,UnitedStates
ThomasPolzin
InstituteofMathematicsandImageComputing,UniversityofLübeck,Lübeck,Germany
LaurentRisser
InstitutdeMathématiquesdeToulouse,CNRS,UniversitédeToulouse,UMRCNRS5219, Toulouse,France
PierreRoussillon
ENSCachan,CNRS,UniversitéParis-Saclay,CMLA,Cachan,France
JörnSchulz
ArcticUniversityofNorway,Tromsø,Norway
AnkurSharma
UNC,ChapelHill,NC,UnitedStates
StefanSommer
UniversityofCopenhagen,DepartmentofComputerScience,Copenhagen,Denmark
AnujSrivastava
FloridaStateUniversity,Tallahassee,FL,UnitedStates
LiyunTu
UNC,ChapelHill,NC,UnitedStates
BabaC.Vemuri
UniversityofFlorida,CISEDepartment,Gainesville,FL,UnitedStates
François-XavierVialard
Laboratoired’informatiqueGaspardMonge,UniversitéParis-EstMarne-la-Vallée,UMRCNRS 8049,ChampssurMarne,France
JaredVicory
UNC,ChapelHill,NC,UnitedStates
JiyaoWang
UNC,ChapelHill,NC,UnitedStates
WilliamM.WellsIII
HarvardMedicalSchool,DepartmentofRadiology,Boston,MA,UnitedStates
MiaomiaoZhang
WashingtonUniversityinSt.Louis,ComputerScienceandEngineering,St.Louis,MO, UnitedStates
RuiyiZhang
FloridaStateUniversity,Tallahassee,FL,UnitedStates
Introduction
Introduction
Overthelasttwodecades,therehasbeenagrowingneedin themedicalimagecomputingcommunityforprincipledmethodstoprocessnonlineargeometricdata.Typicalexamplesofdata inthisdomainincludeorganshapesanddeformationsresulting fromsegmentationandregistrationincomputationalanatomy, andsymmetricpositivedefinitematricesindiffusionimaging. Inthiscontext,Riemanniangeometryhasgraduallybeenestablishedasonethemostpowerfulmathematicalandcomputational paradigms.
Thisbookaimsatbeinganintroductiontoandareference onRiemanniangeometricstatisticsanditsuseinmedicalimage analysisforresearchersandgraduatestudents.Thebookprovides bothdescriptionsofthecoremethodologyandpresentationsof state-of-the-artmethodsusedinthefield.Wewishtopresentthis combinationoffoundationalmaterialandcurrentresearchtogetherwithexamples,applications,andalgorithmsinavolume thatiseditedandauthoredbytheleadingresearchersinthefield. Inaddition,wewishtoprovideanoverviewofcurrentresearch challengesandfutureapplications.
Beyondmedicalimagecomputing,themethodsdescribedin thisbookmayalsoapplytootherdomainssuchassignalprocessing,computervision,geometricdeeplearning,andotherdomains wherestatisticsongeometricfeaturesappear.Assuch,thepresentedcoremethodologytakesitsplaceinthefieldof geometric statistics,thestatisticalanalysisofdatabeingelementsofnonlineargeometricspaces.Wehopethatboththefoundationalmaterialandtheadvancedtechniquespresentedinthelaterpartsof thebookcanbeusefulindomainsoutsidemedicalimagingand presentimportantapplicationsofgeometricstatisticsmethodology.
Contents
Part 1 ofthiseditedvolumedescribesthefoundationsofRiemanniangeometriccomputingmethodsforstatisticsonmanifolds.Thebookhereemphasizesconceptsratherthanproofswith thegoalofprovidinggraduatestudentsincomputersciencethe
mathematicalbackgroundneededtostartinthisdomain.Chapter 1 presentsanintroductiontodifferential,Riemannianand Liegroupgeometry,andchapter 2 coversstatisticsonmanifolds. Chapters 3–5 presentintroductionstogeometryofSPDmatrices, shapeanalysisthroughtheactionofthediffeomorphismgroup, andgeometryandstatisticalanalysisbeyondtheRiemanniansettingwhenanaffineconnection,notametric,isavailable.
Part 2 includescontributionsfromleadingresearchersinthe fieldonapplicationsofstatisticsonmanifoldsandshapespaces inmedicalimagecomputing.Inchapter 6,StephenPizer,Steve Marron,andcoauthorsdescribeshaperepresentationviaskeletalmodelsandhowthisallowsapplicationofnonlinearstatisticalmethodsonshapespaces.Chapter 7 byRudrasisChakraborty andBabaVemuriconcernsestimationoftheiterativeRiemannian barycenter,acandidateforthegeneralizationoftheEuclidean meanvalueonselectedmanifolds.Inchapter 8,AasaFeragenand TomNyediscussthestatisticsonstratifiedspacesthatgeneralize manifoldbyallowingvariationofthetopologicalstructure.Estimationoftemplatesinquotientspacesisthetopicofchapter 9 byNinaMiolane,LoicDevilliers,andXavierPennec.StefanSommerdiscussesparametricstatisticsonmanifoldsusingstochastic processesinchapter 10.Inchapter 11,RuiyiZhangandAnujSrivastavaconsidershapeanalysisoffunctionaldatausingelastic metrics.
Part 3 ofthebookfocusesondiffeomorphicdeformationsand theirapplicationsinshapeanalysis.NicolasCharon,Benjamin Charlier,JoanGlaunès,PierreRoussillon,andPietroGoripresent currents,varifolds,andnormalcyclesforshapecomparisonin chapter 12.Numericalaspectsoflargedeformationregistration isdiscussedinchapter 13 byThomasPolzin,MarcNiethammer, François-XavierVialard,andJanModersitzki.Francois-Xavierand LaurentRisserpresentspatiallyvaryingmetricsforlargedeformationmatchinginchapter 14.Chapter 15 byMiaomiaoZhang, PolinaGolland,WilliamM.Wells,andTomFletcherpresentsa frameworkforlow-dimensionalrepresentationsoflargedeformationsanditsuseinshapeanalysis.Finally,inchapter 16,Martin Bauer,SarangJoshi,andKlasModinstudydensitiesmatchingin thediffeomorphicsetting.
Weareextremelygratefulforthisbroadsetofexcellentcontributionstothebookbyleadingresearchersinthefield,andwehope thatthebookinitsentiretywillinspirenewdevelopmentsand researchdirectionsinthisexcitingintersectionbetweenapplied mathematicsandcomputerscience.
Theeditors: XavierPennec UniversityCôted’AzurandInria,SophiaAntipolis,France StefanSommer
DIKU,UniversityofCopenhagen,Copenhagen,Denmark TomFletcher UniversityofVirginia,Charlottesville,VA,UnitedStates February,2019
Introductiontodifferentialand Riemanniangeometry
StefanSommera ,TomFletcherb ,XavierPennecc
a UniversityofCopenhagen,DepartmentofComputerScience,Copenhagen, Denmark. b UniversityofVirginia,DepartmentsofElectrical&Computer EngineeringandComputerScience,Charlottesville,VA,UnitedStates.
c UniversitéCôted’AzurandInria,Epioneteam,SophiaAntipolis,France
1.1Introduction
Whendataexhibitnonlinearity,themathematicaldescription ofthedataspacemustoftendepartfromtheconvenientlinear structureofEuclideanvectorspaces.Nonlinearitypreventsglobal vectorspacestructure,butwecanneverthelessaskwhichmathematicalpropertiesfromtheEuclideancasecanbekeptwhilestill preservingtheaccuratemodelingofthedata.Itturnsoutthatin manycases,localresemblancetoaEuclideanvectorspaceisone suchproperty.Inotherwords,uptosomeapproximation,thedata spacecanbelinearizedinlimitedregionswhileforcingalinear modelontheentirespacewouldintroducetoomuchdistortion.
TheconceptoflocalsimilaritytoEuclideanspacesbringsus exactlytothesettingofmanifolds.Topological,differential,and Riemannianmanifoldsarecharacterizedbytheexistenceoflocal maps,charts,betweenthemanifoldandaEuclideanspace.These chartsarestructurepreserving:Theyarehomeomorphismsinthe caseoftopologicalmanifolds,diffeomorphismsinthecaseofdifferentialmanifolds,and,inthecaseofRiemannianmanifolds, theycarrylocalinnerproductsthatencodethenon-Euclideangeometry.
Thefollowingsectionsdescribethesefoundationalconcepts andhowtheyleadtonotionscommonlyassociatedwithgeometry:curves,length,distances,geodesics,curvature,paralleltransport,andvolumeform.InadditiontothedifferentialandRiemannianstructure,wedescribeoneextralayerofstructure,Liegroups thataremanifoldsequippedwithsmoothgroupstructure.Lie groupsandtheirquotientsareexamplesofhomogeneousspaces. Thegroupstructureprovidesrelationsbetweendistantpointson thegroupandtherebyadditionalwaysofconstructingRiemannianmetricsandderivinggeodesicequations.
RiemannianGeometricStatisticsinMedicalImageAnalysis https://doi.org/10.1016/B978-0-12-814725-2.00008-X
Topological,differential,andRiemannianmanifoldsareoftencoveredbyseparategraduatecoursesinmathematics.Inthis muchbrieferoverview,wedescribethegeneralconcepts,often sacrificingmathematicalrigortoinsteadprovideintuitivereasons forthemathematicaldefinitions.Foramorein-depthintroductiontogeometry,theinterestedreadermay,forexample,refer tothesequenceofbooksbyJohnM.Leeontopological,differentiable,andRiemannianmanifolds[17,18,16]ortothebookon RiemanniangeometrybydoCarmo[4].Moreadvancedreferences include[15],[11],and[24].
1.2Manifolds
Amanifoldisacollectionofpointsthatlocally,butnotglobally,resemblesEuclideanspace.WhentheEuclideanspaceisof finitedimension,wecanwithoutlossofgeneralityrelateitto Rd forsome d> 0.Theabstractmathematicaldefinitionofamanifoldspecifiesthetopological,differential,andgeometricstructurebyusingcharts,mapsbetweenpartsofthemanifoldand Rd , andcollectionsofchartsdenotedatlases.Wewilldiscussthisconstructionshortly,however,wefirstfocusonthecasewherethe manifoldisasubsetofalargerEuclideanspace.Thisviewpointis oftenlessabstractandclosertoournaturalintuitionofasurface embeddedinoursurrounding3DEuclideanspace.
Letusexemplifythisbythesurfaceoftheearthembeddedin R3 .Weareconstrainedbygravitytoliveonthesurfaceoftheearth. Thissurfaceseemslocallyflatwithtwodimensionsonly,andwe usetwo-dimensionalmapstonavigatethesurface.Whentravelingfar,wesometimesneedtochangefromonemaptoanother. Wethenfindchartsthatoverlapinsmallparts,andweassume thatthechartsprovideroughlythesameviewofthesurfacein thoseoverlappingparts.Foralongtime,theearthwasevenconsideredtobeflatbecauseitscurvaturewasnotnoticeableatthe scaleatwhichitwasobserved.Whenconsideringtheearthsurfaceasatwo-dimensionalrestrictionofthe3Dambientspace,the surfaceisanembeddedsubmanifoldof R3 .Ontheotherhand, whenusingmapsandpiecingtheglobalsurfacetogetherusing thecompatibilityoftheoverlappingparts,wetaketheabstract viewusingchartsandatlases.
1.2.1Embeddedsubmanifolds
Arguablythesimplestexampleofatwo-dimensionalmanifold isthesphere S2 .Relatingtothepreviousexample,whenembeddedin R3 ,wecanviewitasanidealizedmodelforthesurfaceof
theearth.Thespherewithradius 1 canbedescribedasthesetof unitvectorsin R3 ,thatis,theset S2 ={(x 1 ,x 2 ,x 3 ) ∈ R3 | (x 1 )2 + (x 2 )2 + (x 3 )2 = 1} . (1.1)
Noticefromthedefinitionofthesetthatallpointsof S2 satisfythe equation (x 1 )2 + (x 2 )2 + (x 3 )2 1 = 0.Wecangeneralizethisway ofconstructingamanifoldtothefollowingdefinition.
Definition1.1 (Embeddedmanifold).Let F : Rk → Rm beadifferentiablemapsuchthattheJacobianmatrix dF(x) = ( ∂ ∂x j F i (x))ij hasconstantrank k d forall x ∈ F 1 (0).Thenthezero-levelset M = F 1 (0) isanembeddedmanifoldofdimension d
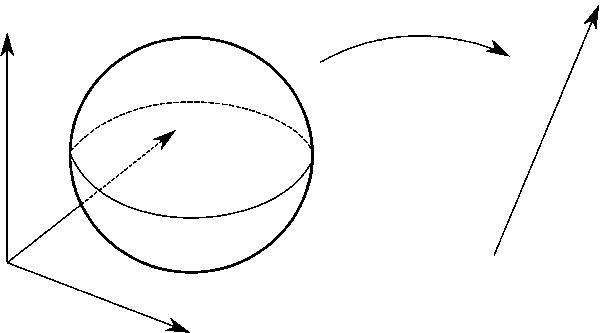
Figure1.1. Anembeddedmanifoldarisesasthezero-levelsubset M = F 1 (0) of themap F : Rk → Rm .Here F : R3 → R isgivenbythesphereequation x → (x 1 )2 + (x 2 )2 + (x 3 )2 1,andthemanifold M = S2 isofdimension 3 1 = 2
Themap F issaidtogiveanimplicitrepresentationofthe manifold.Inthepreviousexample,weusedthedefinitionwith F(x) = (x 1 )2 + (x 2 )2 + (x 3 )2 1 (seeFig. 1.1).
Thefactthat M = F 1 (0) isamanifoldisoftentakenasthe consequenceofthesubmersionlevelsettheoreminsteadofa definition.Thetheoremstatesthatwiththeaboveassumptions, M hasamanifoldstructureasconstructedwithchartsandatlases. Inaddition,thetopologicalanddifferentiablestructureof M isin acertainwaycompatiblewiththatof Rk lettingusdenote M as embedded in Rk .Fornow,wewillbesomewhatrelaxedaboutthe detailsandusetheconstructionasaworkingdefinitionofwhat wethinkofasamanifold.
Themap F canbeseenasasetof m constraintsthatpoints in M mustsatisfy.TheJacobianmatrix dF(x) atapointin x ∈ M linearizestheconstraintsaround x ,anditsrank k d indicates
IntroductiontodifferentialandRiemanniangeometry howmanyofthemarelinearlyindependent.Inadditiontothe unitlengthconstraintsofvectorsin R3 defining S2 ,additionalexamplesofcommonlyoccurringmanifoldsthatwewillseeinthis bookarisedirectlyfromembeddedmanifoldsorasquotientsof embeddedmanifolds.
Example1.1. d -dimensionalspheres Sd embeddedin Rd +1 .Here weexpresstheunitlengthequationgeneralizing(1.1)by
Thesquarednorm x 2 isthestandardsquaredEuclideannorm on Rd +1 .
Example1.2. Orthogonalmatrices O(k) on Rk havetheproperty thattheinnerproducts Ui ,Uj ofcolumns Ui , Uj ofthematrix U ∈ M(k,k) vanishfor i = j andequal 1 for i = j .Thisgives k 2 constraints,andO(k) isthusanembeddedmanifoldinM(k,k) bythe equation O(k) = U ∈ M(k,k)
withIdk beingtheidentitymatrixon Rk .WewillseeinSection 1.7.3 thattherankofthemap F(U) = UU Idk is k(k +1) 2 on O(k),anditfollowsthatO(k) hasdimension k(k 1) 2 .
1.2.2Chartsandlocaleuclideaness
Wenowdescribehowcharts,localparameterizationsofthe manifold,canbeconstructedfromtheimplicitrepresentation above.Wewillusethistogiveamoreabstractdefinitionofadifferentiablemanifold.
Whennavigatingthesurfaceoftheearth,weseldomuse curvedrepresentationsofthesurfacebutinsteadrelyoncharts thatgiveaflat,2Drepresentationofregionslimitedinextent.It turnsoutthatthisanalogycanbeextendedtoembedmanifolds witharigorousmathematicalformulation.
Definition1.2. Achartona d -dimensionalmanifold M isadiffeomorphicmapping φ : U → U fromanopenset U ⊂ M toan openset ˜ U ⊆ Rd .
Thedefinitionexactlycapturestheinformalideaofrepresentingalocalpartofthesurface,theopenset U ,withamappingtoa Euclideanspace,inthesurfacecase R2 (seeFig. 1.2).
Whenusingcharts,weoftensaythatwework incoordinates.Insteadofaccessingpointson M directly,wetakeachart