https://ebookmass.com/product/relativity-in-modern-physics-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
University Physics with Modern Physics (15th Edition)
https://ebookmass.com/product/university-physics-with-modernphysics-15th-edition/
ebookmass.com
University Physics with Modern Physics 14th Edition, (Ebook PDF)
https://ebookmass.com/product/university-physics-with-modernphysics-14th-edition-ebook-pdf/
ebookmass.com
University Physics with Modern Physics (Third Edition) Wolfgang Bauer
https://ebookmass.com/product/university-physics-with-modern-physicsthird-edition-wolfgang-bauer/
ebookmass.com
Advances in Aerogel Composites for Environmental Remediation 1st Edition Aftab Aslam Parwaz Khan (Editor) https://ebookmass.com/product/advances-in-aerogel-composites-forenvironmental-remediation-1st-edition-aftab-aslam-parwaz-khan-editor/ ebookmass.com
Savage Covenant: Part of the Gallo Mafia Empire Jade Marshall & Sofa Aves
https://ebookmass.com/product/savage-covenant-part-of-the-gallo-mafiaempire-jade-marshall-sofa-aves/
ebookmass.com
(eBook PDF) Universe Solar System, Stars and Galaxies 8th Edition
https://ebookmass.com/product/ebook-pdf-universe-solar-system-starsand-galaxies-8th-edition/
ebookmass.com
Studies in Natural Products Chemistry Volume 52 1st Edition Edition Atta-Ur-Rahman (Eds.)
https://ebookmass.com/product/studies-in-natural-products-chemistryvolume-52-1st-edition-edition-atta-ur-rahman-eds/
ebookmass.com
Late Europeans and Melancholy Fiction at the Turn of the Millennium Ian Ellison
https://ebookmass.com/product/late-europeans-and-melancholy-fictionat-the-turn-of-the-millennium-ian-ellison/
ebookmass.com
Financial Accounting 9th Edition Robert Libby
https://ebookmass.com/product/financial-accounting-9th-edition-robertlibby-2/
ebookmass.com
https://ebookmass.com/product/wings-of-stars-fallen-destinybook-1-r-l-caulder-m-sinclair/
ebookmass.com
RelativityinModernPhysics RelativityinModernPhysics Jean-PhilippeUzan
NathalieDeruelle
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
EnglishEdition c OxfordUniversityPress2018
Anearlierversionofthisbookhasappearedas Th´eoriesdelaRelativit´ e by NathalieDeruelleandJean-PhilippeUzan c EditionsBelin,2014
Themoralrightsoftheauthorshavebeenasserted
FirstEditionpublishedin2018
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2018933841 ISBN978–0–19–878639–9
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Thisbookisdedicatedtothosewhohavedevelopedrelativity inFrance,inparticular,HenriPoincar´e,PaulLangevin, ´ ElieCartan, Andr´eLichnerowicz,YvonneChoquet-Bruhat,andThibaultDamour
Foreword Thephysicscommunityhasrecentlycommemoratedthecentenaryofthebirthofgeneral relativity,developedbyAlbertEinsteinbetween1907and1915.Thismagnificenttheory, whichunitesrelativityandgravitywithintheframeworkofnon-Euclideangeometry,haslong beenviewedasauniquefeatureinthephysicslandscape.Itsloftyheighthasintimidated themajorityofphysicists,andfewhaveventuredtoclimbitsmathematicallysteepslopes, especiallywhiletheconnectionofthistheorytoobservablerealityremainedtenuous.
Thaterahasvanished,becausegeneralrelativityhasnowcometoplayanessentialrole intheremarkablerecentadvancesinastrophysicsandcosmology.Astrophysicshasrevealed theexistenceof‘compact’starslikeneutronstars,whosematterissoconcentratedthat thedeformationoftimeandspacepredictedbygeneralrelativitybecomestangible.And thentherearethecelebratedblackholes,whichhaveoutgrowntheboundsofmathematical abstractionandsciencefictiontobecomepartofthedailylifeofastrophysicists.Adefinitive proofoftheirexistencehasrecentlybeenprovidedbythedetectionofthegravitationalwaves emittedwhentheymerge,thusopeninganewwindowinastronomy.
Onthecosmologicalside,generalrelativityliesattheheartofourcurrentunderstandingoftheexpansionoftheuniverse.Cosmologicalobservationshaverecentlyrevealedthe presenceofamysterious‘darkenergy’whichmaycorrespondtothecosmologicalconstant initiallyintroducedbyEinsteintoobtainastaticuniverse,andthenquicklyabandoned, beforeitscurrentrevivaltoexplaintheobservationaldata.Owingtotheenormousprogress whichhasbeenmadeinmeasurementaccuracy,relativityhasevenbecomeapartofthe dailylifeofanordinaryperson:theaccuratefunctioningoftheGPSactuallyrequiresthe inclusionofeffectsduetospecialandgeneralrelativity.
Allthesefascinatingaspectsofrelativity,andothers,arepresentedandexplainedrigorouslyandaccuratelyinthisbookbyNathalieDeruelleandJean-PhilippeUzan.Thetheory ofgeneralrelativityconstitutestheclimaxofthisimpressivework,whichassemblesand summarizes,inacoherentandextremelydeepmanner,thevariousrelativisticaspectsof ‘classical’(thatis,non-quantum)theoreticalphysics,startingfromthedescriptionofNewtonianmechanicsandgravitation.
Oneofthestrengthsofthisbookisitsrevelationofthecontinuedrelevanceofanumberof principlesandmathematicaltoolsbeyondtheconceptualrupturewhichrelativityrepresents comparedtothetheoriesofclassicalphysics.Forexample,theauthorsstudyNewtonian physicsinanacceleratedreferenceframeandarbitrarycoordinatesusingthesameformalism asthatusedtodescribespacetimeingeneralrelativity.Theechoesbackandforthbetweenthe chaptersonelectromagneticwavesandgravitationalwavesemphasizeboththeconceptual differencesandthesimilaritiesinthetreatmentofthesetwoconcepts.Thesimultaneous embraceofNewtoniangravity,specialrelativity,andgeneralrelativityallowsthereaderto beledgraduallyfromfamiliar,gentleterraintothehighestpeaks.
Manyofthesectionsinthisbookareenrichedbyresearchtopics,andpresentviewpoints andresultswhichthereaderwillfindonlyrarely,ifatall,inothertextbooksonthese
viii Foreword
subjects.Thisbookthereforeconstitutesaremarkablereferencework,fromwhichthereader canextractagreatvarietyofinformationaswellasmanycalculationtechniques,anditcan serveasapointofentrytoresearcharticles.Itiswrittenequallyforthestudentpassionate abouttheoreticalphysicsandfortheresearcherwishingtoacquireadeeperunderstanding ofrelativity,aswellasforthecuriousreaderwithascientificbackgroundwhowishesto independentlyexplorevariousfacetsofrelativityunderthetutelageofexperiencedguides.
Ihavehadtheprivilegeofsharingmyprofessionallifewiththetwoauthorsofthis book,andofbeingawitnesstotheirinsatiablecuriosityandpassionfortransmittingtheir knowledgetoothers.IhavealsohadthegreatfortunetosharewithNathalieDeruelle manyyearsofteachinggeneralrelativity,andithasbeenapleasuretorediscoverinthis bookvariouspathswhichsheexploredduringourpedagogicaladventure.Thisbookattests admirablytoapassionateencounterbetweenademandingbutfascinatingscientificdomain andtwoscientistswhoaresimultaneouslyparticipantsinthecontinuingdevelopmentofthe fieldandtransmittersoftheirknowledgetofuturegenerations.
DavidLanglois June2018
PARTIIIELECTROMAGNETISM PARTIVELECTRODYNAMICS PARTIVFRIEDMANN–LEMAˆıTRESOLUTIONSANDCOSMOLOGY PARTVELEMENTSOFRIEMANNIANGEOMETRY Space,time,andgravityin Newton’stheory PARTIIDYNAMICS PartI Kinematics Idonotdefine Time, Space, Place and Motion,asbeingwellknowntoall.OnlyImust observe,thatthevulgarconceivethosequantitiesundernoothernotionsbutfromtherelation theybeartosensibleobjects.Andthencearisecertainprejudices,fortheremovingofwhich, itwillbeconvenienttodistinguishtheminto Absolute and Relative, True and Apparent, Mathematical and Common
AbsoluteSpace,initsownnature,withoutregardtoanythingexternal,remainsalways similarandimmovable.
Absolute,True,andMathematicalTime,ofitself,andfromitsownnatureflowsequably withoutregardtoanythingexternal,andbyanothernameiscalledDuration...
SirIsaacNewton, PhilosophiæNaturalisPrincipiaMathematica,London,1687;English translationbyAndrewMotte, TheMathematicalPrinciplesofNaturalPhilosophy, London,1729
1 Cartesiancoordinates InthisfirstchapterwegiveanelementaryandbriefpresentationofEuclideangeometry,which providesthemathematicalframeworkinwhichthelawsofNewtonianphysicsareformulated.
1.1Absolutespaceandtime InNewtonianphysics,‘space’and‘relative,apparent,andcommon’placearerepresented byamathematicalensembleofpoints,the‘absolute’space E3 ,whichispostulatedtobe Euclidean.
Eachpointofthisspaceisthuscharacterizedbythreerealnumbers,itscoordinates, whichdefineitsposition.Inaddition,thereexistsystemsofcoordinatescalledCartesian coordinatessuchthatthe distance r12 betweentwopointswithcoordinates(X1 ,Y1 ,Z1 )and (X2 ,Y2 ,Z2 )isgivenbythePythagoreantheorem
Itvanishesonlyifthetwopointscoincide.
The lengthelement,thatis,thesquareofthedistance dl (≥ 0)betweentwoinfinitesimally separatedpointswithCartesiancoordinates(seeFig.1.1) X i and X i + dX i ,whichisusedto measurelengthsofcurvesandtodisplaythemetricpropertiesoffigures,isthenwrittenas
Fig.1.1 Cartesiancoordinatesandframeintwodimensions.
Book1.PartI:Kinematics
Thesecondequalitydefinesthe Kroneckerdelta δij ;inthisgeometricalcontextitssix components(δij =1if i = j , δij =0otherwise)arereferredtoasthecoefficientsofthe EuclideanmetricinCartesiancoordinates.Thethirdequalitydefinesthe Einsteinsummation convention,accordingtowhichrepeatedindicesaresummedover(theyarethenreferredtoas dummyindices).Theoriginwithcoordinates(0, 0, 0)andthethreeaxes(X,Y,Z )constitute a Cartesianframe S
Asforthe‘apparent’time,itisrepresentedbyarealnumber,the‘absolute’oruniversal time t ∈ R.
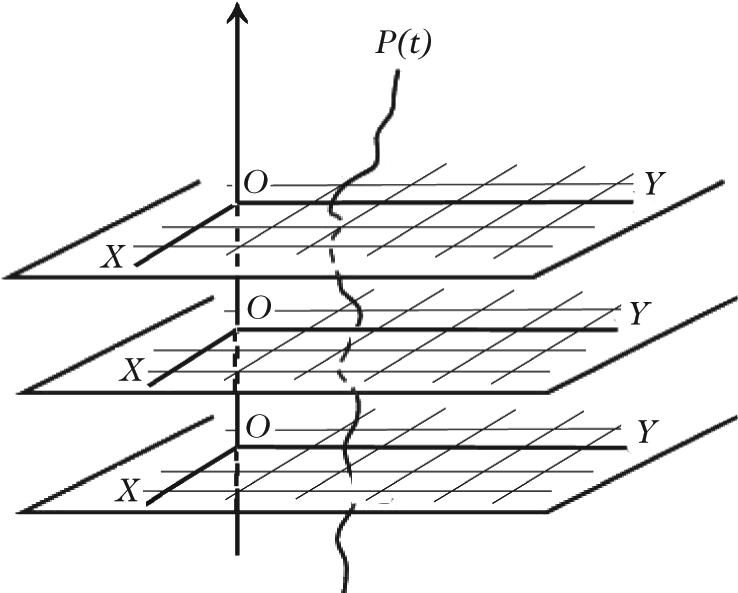
Fig.1.2 Absoluteframeandmotion.
ItisthereforepossibletorepresentNewtonianspacetime N4 asa‘foliation’,thatis,a stackofcopiesofEuclideanspace E3 orderedbyincreasingtime t: N4 = E3 × R.Theensemble ofcopiesofapointin E3 thenbecomesa‘fiber’of N4 representingapointatabsoluterest. InthiskinematicalcontexttheensembleofCartesianframesindexedby t isreferredtoas anabsoluteframe.1 (SeeFig.1.2.)
Themotionofaphysicalobjectwithoutextentorinternalstructure,calledapointparticle,isrepresentedbyacurveinspacetimecalleda worldline or,equivalently,a trajectory, thatis,acurvein E3 : t → P (t) ∈E3 ,wheretheparameter t istheabsolutetime.
1.2Theabsolutereferenceframe Theabsolutetime t ismadeconcretebyclocksandwatches,thatis,byrepetitivephenomenanumberedinincreasingorder.Agoodclockisultimatelyadevicewhichmeasures,no matterwhatsortofmotionitundergoes,timeintervals,expressedforexampleinseconds, inaccordancewiththepredictionsofthelawsofdynamicswrittenasafunctionofabsolute time.
ACartesianframeofabsolutespaceismaterializedin‘relative,apparent,andcommon’ spacebya referenceframe.Specifically,thisreferenceframeisasolidtrihedron,thatis, anensembleofphysicalobjectswhoserelativedistancesareconstantintimeandforwhich anorientationoftheaxeshasbeenchosen(byusingtheright-handrule,forexample). Itisconstructedbymeansofinstrumentswhichqualifyasrigid(i.e.,theyarealsosolids)
1 Wenotethat t belongstotherealline R andnottothecircle S 1 :inNewtonianmechanicstimehasno beginningandnoend.
Chapter1:Cartesiancoordinates 13 throughoutrepeatedusesuchasrulers,compasses,andsoon,usingthePythagoreantheorem anditsconsequences.Finally,alengthstandard,forexample,themeter,ischosen.This referenceframe,whichestablishesagridonphysicalspace,is‘good’ifalltheEuclidean propertiesoffiguresareverifiedtowithinthemeasurementaccuracy.2
The absolutereferenceframe whichmaterializestheabsoluteframeofNewtonianspacetimeisareferenceframewhichmustbeatrestinorderforittobepossibletoidentify thefibersof N4 withphysicalobjectsatrest.ForNewton,theabsolutereferenceframewas formedbythesolarsystemandthestarsfarenoughawaytoappearfixed,whichhepostulatedtobeatabsoluterest.Wenotethatsincetheuniverseappearstobeessentiallyempty, thepointsof E3 areforthemostpartonly‘virtuallymaterialized’,acontradictioninterms whichshockedDescartesandKant.Beginningintheseventeenthcentury,thisdifficultywas circumventedbyintroducingtheconceptofthe aether,anebulousmediumresponsiblefor materializing E3
IfspaceandtimedoactuallyembodythestructureattributedtothembyNewton,we canpredictanelementarybutimportantresult.Letusimaginetwotravelers A and B who simultaneouslydepartfromacertainplaceandreturntothesameplaceaftertheirseparate peregrinations.Thedurationsofthetripsmeasuredby A and B mustbethesame, i.e., theirwatches,whicharesynchronizedwhentheystartout,mustindicatethesametimeat arrival.3
1.3ChangeofCartesiancoordinates Wepostulatethatifthelabelingofthepointsof E3 ischanged,thedistancebetween twopointsremainsunchanged.Here,werestrictourselvestotransformations X i → X i whichpreservethe form ofthelengthelement,thatis,transformationssuchthat dl 2 ≡ δij dX i dX j = δij dX i dX j .Then,bydefinition,thenewcoordinates X i arealsoCartesian, andthetransformationsaregivenby
WeimposetheconditiondetR =+1,wheredetR isthedeterminantoftherotationmatrix R i j (i numbersthelinesand j thecolumns);thetransformationthereforepreserves theorientationoftheaxes.Suchtransformationsformthe(proper)groupoftransformationsofCartesianframes,agroupwith n(n +1)/2parameters, n ofthemtranslationaland n(n 1)/2rotational,where n isthedimensionofthespace.4
2 IfmeasurementsgiveresultswhichsystematicallycontradicttheEuclideanpredictions(e.g.,ifthesum oftheanglesofatriangleisnotequalto π ),itcanbededucedthattherepresentationoftheactualspace(the surfaceoftheEarth,forexample)byaEuclideanplaneisinadequate.Foramasterfulandconciseexposition oftheinterplaybetweenphenomenaandtheirmathematicalrepresentationseetheletterofA.Einsteinto M.Solovinein, e.g.,J.Eisenstaedt(2002).
3 Ifinasingleexperimentthiswerenotthecase,itwouldmostlikelyindicatethattheirwatchesarenot accurate.However,ifalargenumberofcarefullyperformedexperimentsgavearesultsystematicallydifferent fromtheprediction,onewouldconclude,inagreementwithEinstein,thattheabsolutespacetimeofNewton doesnotadequatelyrepresenttheactualuniverse.
4 Notethatwealwaysassumethatthe topology oftheabsolutespaceistrivialandthataglobalorientation exists,therebyexcludingspacesoftheM¨obius-striptypeintwodimensionsortheKlein-bottletypeinthree dimensions.