PolymersforVibration DampingApplications
B.C.Chakraborty
DebdattaRatna
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
©2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicor mechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem,without permissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthe Publisher’spermissionspoliciesandourarrangementswithorganizationssuchastheCopyrightClearance CenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(other thanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation, methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbemindfulof theirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityforanyinjury and/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromanyuseor operationofanymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN978-0-12-819252-8
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionEditor: EdwardPayne
EditorialProjectManager: JohnLeonard
ProductionProjectManager: AnithaSivaraj
CoverDesigner: VictoriaPearson
TypesetbySPiGlobal,India
Preface
Thisbookisdedicatedtopolymerscientistsassociatedwithvibrationdamping.Vibrationsinstructures andmachinescausecomponentfatigueandhumandiscomfortiftheyarenotproperlycontrolled. Forwarshipsandsubmarines,controllingvibrationofhullstructureisaveryimportantaspectofunderwateracousticstealthtechnology.Oneofthemosteffectivemethodsofvibrationdampingis passivemethod,wherein,asuitablepolymersystemwithappropriateviscoelasticpropertyisused accordingtotheapplicationenvelope.Thisrequiresunderstandingthebasicsofshockandvibration, developmentofsuitablematerialsthroughsynthesis,modification,formulation,andfinally,engineeringdesignofdampingtreatmentofthemachineryorstructure.Therefore,acombinedeffortof physicists,mechanicalengineers,materialsscientists,andchemistsisabsolutelynecessaryforthesuccessfuldevelopmentofvibrationdampingsystems.
Wehavedoneextensiveworkinthefieldofmaterialsanddevelopedseveralproductssuitable forcivilanddefenceapplications.Whileworkinginthisareaforalongtime,wefeltthenecessity ofaself-sufficientbookinthisfield.Therefore,wedecidedtocompileourfundamentalunderstanding andlongresearchexperienceinthedevelopmentofpolymersandcompositesforvibrationdamping andpresentintheformofabook.
Thisbookisdividedintosixchapters.Itstartswithageneralintroductiontovibrationin Chapter1. Inthischapter,basicmathematicalexpressionsonfreeandforcedvibrationofobjects,bothundamped andwithviscoelasticdampinginsingledegreeoffreedom,arediscussed.Examplesofnumerical calculationofundampedanddampedfreeandforcedvibrationareprovidedwithgraphicalrepresentations.Anappendixisaddedtodemonstratetheselectionofanappropriateelastomerfromseveral compositionsformachinerymount.
Chapter2 includesfundamentalmathematicalexpressionsofshockpulseandshockresponse spectraforasingledegreeoffreedomsystem.Graphicalrepresentationsofvariousresponsespectra (calculatedbysimpleequationsofresponse)areincluded.
Viscoelasticpropertiesarecoveredin Chapter3.Onlylinearviscoelasticityisdiscussedinthis chapter.Variousphysicalandmathematicalmodelsforpolymersarediscussedwithexamples.Dynamicviscoelasticityisdealtwithsomedetailsincludingphenomenologicalrelaxationtheorywithnumericalexamplesoffrequencyandtemperaturedependenceandtime–temperaturesuperpositionsas well.Abriefdiscussiononthecomparisonofstaticanddynamicpropertiesisincludedwithnumerical examples.
Chapter4 dealswiththedesignofpolymersystemforvibrationdampingapplicationsandreviewof recentadvancesinthefield.Thischapterincludesthevariousclassificationofpolymers,basicprinciplefortheselectionofpolymersanddesignofpolymersystemsforvibrationdampingapplications. Variousstrategies,whicharetobeadoptedtoachievevibrationdampinginabroadfrequencyrange, havebeenelaborated.
Themodeofdampingandthecorrespondingdesignrulesrequiredtobeadoptedforefficientvibrationdampingwithsomeexampleshavebeenpresentedin Chapter5.Variousmathematicalexpressionsforconstrainedandunconstrainedlayerdampingaredescribedwithexamples.
Chapter6 describesequipment,instruments,andmethodsofcharacterisationandtesting,whichare relevanttothedevelopmentandselectionofpolymersforvibrationandshockdamping.
Withsuchbroadtechnicalcontentscoveringthebasicconcepts,practicalexamples,andrecent advances,wearesurethatthisbookwillserveasausefultextbook-cum-handbookforthestudents, researchers,engineers,R&Dscientistsfromacademia,researchlaboratories,andindustriesrelated totheapplicationofpolymersforvibrationandshockdamping.
Wewouldliketodedicatethisbooktoourlateparents.Weareindebtedtothemembersofour familiesfortheirpatienceandforalwaysbeingthesourceofinspiration,withoutwhichthisbook wouldnothavebeenareality.Dr.Chakrabortythankshiswife(Mitali),son(Abhishek),anddaughter (Anwesha)fortheirencouragementandsupport.Dr.Ratnawouldliketoplaceonrecordhissincere thankstohiswife(Sujata)andsons(SaptarshiandDebarshi).Althoughithasbeenourendeavourto makethebookcomprehensiveandofahighstandard,errorsthatmaycreepinaresincerelyregretted.
WearethankfultothepublicationteamofM/sElsevier,UnitedKingdom,fortheircooperation andencouragement.WearealsothankfultoDr.M.Patri,Director,andothercolleaguesofNMRL, especiallySriPraveenSrinivasan,fortheircooperationandsuggestionandSriRamakantKhushwaha forhishelpinpreparingthebook.
DebdattaRatna BikashChandraChakraborty
1.2 Importanceofthestudyofvibration
Thestudiesofsoundandvibrationarecloselyrelated.Soundwaves,inturn,canalsoinducethevibrationofobjects,forexample,tuningfork.Inmanyoccasions,soundandvibrationarerequired.Asan example,soundisnecessaryfortheformofmusic,speeches,verbalcommunication,signalling,etc. Vibrationsarerequiredformaterialhandlingsizeseparation,sieving,mechanicaloperationssuchas pneumaticdrilling,medicaltreatmentsandhealthcare,physiotherapy,etc.Inmanyothercases, vibrationandsoundareundesirable.Undesirablesoundistermedas‘noise’andthequalityofanacousticsignalisdecidedbythe‘signaltonoiseratio’.Sincesoundisaresultofmaterialvibration,primarily, attempttoreducenoiseisrelatedtocontrollingthevibrationatthesource.Vibrationsarecloselyassociatedwiththemanandmachinery.Thevibrationsofthemachineryarearesultoftheimbalanceof rotationalmovements(eccentricity)suchasformotors,engines,turbines,etc.Machineryvibrations cancauseseriousdamagestothemachineduetoexcessivedynamicdisplacementsapartfrom undesirableradiatednoiseintheatmosphere.Heavymachineryundervibrationcanbedamaged permanentlyduetofatigueresultingfromthecyclicvariationofinducedstresses.Furthermore,the vibrationcausesmorerapidwearofmachinepartssuchasbearingsandgearsandalsocreatesexcessive noise.Inmachines,vibrationcanloosenfastenerssuchasnuts,etc.Inmetalcuttingprocesses, vibrationcancausechatter,whichleadstoapoorsurfacefinish.Vibrationinducedbytheexternal
sourceoninstrumentsandmachineryisdetrimentalasitmightaffecttheperformance.Anexampleis opticalrecordingandexperiments,whereeveryminutevibrationoftheopticaltablewouldcauseopticaldistortions.Similarly,vibrationduetotransportationofequipmentmaycausedamage.Therefore, studyofexternallyinducedvibrationonobjectsisalsoimportant.
Anotherconcernforthevibrationofmachineryandradiatednoiseistheenvironmentalproblem. Probably,thenoisepollutioncreatedbyvehiclesisthemostseriousprobleminurbanlife.Withrapid urbanisationandrandomuseofautomobilesonstreets,railandairtraffic,loudpublicaddresssystems, constructionmachinery,etc.,theenvironmentissubjectedtoahighlevelofnoisepollution.The excessivesoundintheatmospherecancausepermanentdamagetooureardrum,orpartiallossofhearing [1].Noisecancauseischemicheartdisease,hypertension,cardiovascularproblems,etc. [2] Increasednoiselevelscancreatestress,increasedaggressionandworkplaceaccidentrates,andpossiblyenhanceantisocialbehaviours [3].Loudnoisemayaffectthenervoussystemofthebrainand createpsychologicaldisorders [1–3].Birthdefectssuchasharelip,cleftpalate,anddefectsinthespine arealsopossiblefromhigh-intensitysoundssuchasairportenvironment.Typicalnoiselevelsofsound originatedfromnormalhumanconversationcanbe60dB,whilenoiseofgroundvehiclescanbe80–90dBandjetengineattake-offcanbe120dB [4].However,continuousnoiselevel80dBisdangerous forhumanhealth.InIndia,thenoiseintensitylimitinthedaytimeis75dB(A)inindustrialareas, whereas55dB(A)inresidentialareasasperthenoisepollutionrules [5].
Earthquakesarethemostimportantexampleoftheilleffectofvibration.Itisaseismicwaveonthe earthsurfaceanditsdevastatingeffectiswellexperiencedbymankind.Itresultsfromasuddenrelease ofhugeenergyintheearth’scrust.Thesewavescanbeviolentcausinglossoflifeandcanevendestroy anentirecivilisationaround.Theintensitiesofsuchseismicwavesaremeasuredinacomparativescale called‘Richter’,namedaftertheseismologistCharlesFrancisRichter.Itisalogarithmicscale,where, amagnitudeof3ontheRichterscaleisnotdangerous,while7onthescalecancauselarge-scale devastation.Richterscaleisdevelopedasanempiricalformulausingthelogarithmofamplitudes attherecordingseismometer,arbitraryvalue,andtheepicentraldistanceoftherecordingstationas parameters [6].
Soundandvibrationarealsoimportantsubjectsofstudyforunderwaterobjects.Acousticsignals areusedforbathymetricseabedmappingstudies,todetectandidentifyunderwaterobjectslikerocks, submarines,mines,andeventodetectmarineanimalssuchasaclusteroffishes,sharks,whales,etc., usingadevicecalledsoundnavigationandranging(SONAR).Therearetwomethodsforthedetection ofanunderwaterobject,namelyactiveandpassivedetections.Inactivedetectionsystem,theSONAR sendsasoundpulsetogetareflectionfromanyobjecthavingadifferenceinspecificacousticimpedancecomparedtowaterandanalysethereflectedsignaltodeterminethetypeofobjectandits coordinates(location),whilepassiveSONARonlyreceivestheunderwaternoiseradiatedfromany objectnearby.Forthedefenceforces,navalshipsandsubmarinesneedtobeassilentaspossible toavoiddetectionbythepassiveSONAR.Vibrationsofmachineryinsidethevesselsaretransmitted tothehullofthevesselthroughinternalstructuresandinturntransmittedtotheseawaterasradiated noise,whichispickedupbythepassiveSONAR.Sincethereisanumberofsuchmachineryina submarine/ship,therewouldbeaparticularunderwateracousticsignatureoftheship/submarine. Thevibrationspectrumwoulddependonthetypeofmachinery,theirdesign,manufacturingprocess, installationmethodologies,andalsoonageingeffects.Ingeneral,vibrationsofheavymachinerysuch asdieselalternatorsandturbinesinashiporsubmarineproducelow-frequencyradiatednoiseinthe sea.Thecavitationduetorotationofpropellersofships/submarinesalsoproducessoundlikenoisein
theseawater.Thecavitationnoisespectrumwoulddependonthenumberofblades,rpmofthe propeller,cavitationvolume,skinfrictionoftheblades,thethrust,andpropellerloading [7].Both theradiatednoiseduetomachineryandthecavitationcanbedetectedbypassiveSONARs.
Thestudyofvibrationandsoundpropagationindifferentmediaisveryimportantforpredictionand enhancingthefatiguelifeofanequipment,prediction,andmitigationofcatastrophicfailureofmachineries,reductionofenvironmentalacousticpollution,studiesonacousticnoise-relatedhealthhazardof thesociety,andfordesignofacousticallystealthystrategicobjectsofdefenceforces.
1.3 Simpleharmonicmotion(SHM)
Asimpleandperiodicoscillationofapointobjectiscalledharmonicmotionifitpassesthrougha referencepointafteradefiniteintervalandfollowsthesamelocusperiodically.Thenumberofsuch motionperunittimeistermedas‘frequency’andtheintervalisthe‘timeperiod’,whilethelength betweentwoconsecutivepointshavingthesamephaseiscalledthe‘wavelength’.Itisexplainedin Fig.1.1AandB.Letusimagineapointrotatinginacircularpathrepeatedlyataconstantangularspeed. Therefore,thepointwouldcrossanyreferencepointonthecircleataregularinterval.Thelocusofthe pointisthecircleasshownin Fig.1.1A,andwhenthemovementofthepointisplottedagainsttime, thelocusdescribesaperfectsinusoidalcurveasin Fig.1.1B.From Fig.1.1B,thewavelengthisthe distanceAB,thetimetakentocoverthisdistanceis‘timeperiod’,andnumberofsuchdistance travelledinonesecondisthe‘frequency’ofthewave.Itmeans,onewaveisequivalenttoonerotation ofthepointonthecircleandcorrespondinglythedistancetraveledbythewaveisAB,whichis thewavelength.Thespeedofthewavepropagationisthustheproductofthefrequencyandthe wavelength.Theconventionofsymbolsandunitsforwavepropertiesaregivenin Table1.1.Simple vibration,inthebasicanalysis,isassumedtobeharmonicmotion,thatis,asinusoidalwave,thoughthe actualvibrationsignaturemaycontainvariousperiodicities(frequency).Anonharmonicvibrationisa randomvibrationwithnoregularityinperiodicity.

FIG.1.1
SHM:(A)locusofapointinSHM,(B)time-dependentdisplacementofthepoint.
Table1.1Propertiesofawave:symbolsandunits
1.3.1 Displacement,velocity,andacceleration
ASHMcanberepresentedbyasinusoidalwavewhichalsorepresentstheexpressionfortimedependentdisplacement:
wheretheangularfrequencyisgivenby: ω ¼ 2π f and f isthefrequencyincyclespersecondorHzof thedynamicdisplacement.Onecommonterminacircularmotionisrevolutionperminute(rpm), whichisusedforrotatingmachinelikeamotor.Thecorrespondingfrequencyisthen f ¼ (rpm/60)Hz. ThevelocityandaccelerationcanbederivedfromEq. (1.1) as
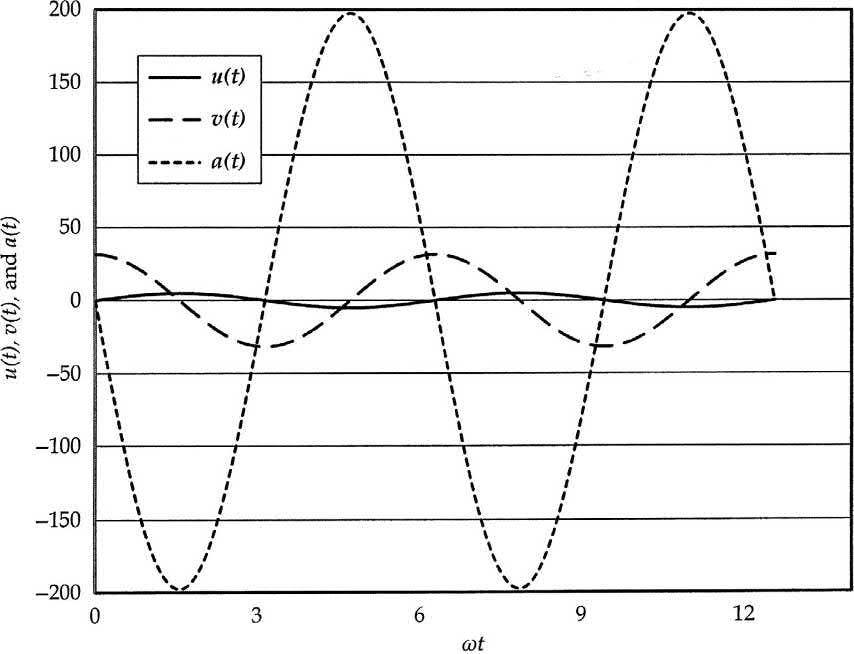
Graphicalrepresentationofdisplacement,velocity,andaccelerationisshownin Fig.1.2.Itcanbeseen fromEqs (1.2), (1.3),and Fig.1.2:
(i) Theratiosofvelocitiesoraccelerationsarethesameasthedisplacementratio.Thisisusedinthe calculationofvibrationsensitivityofobjectsinacomparativeevaluation.
(ii) Thevelocitychangeswiththefirstpoweroffrequencyandthephasedifferencebetweenthe displacementandthevelocityis90°,whichmeansthatwhenthedisplacementisateitherpositive ornegativemaximum,thevelocityiszeroandvice-versa.
(iii) Theaccelerationincreaseswiththesecondpoweroffrequencyandthephasedifferencebetween thedisplacementandaccelerationis180°,whichmeansthattheaccelerationispositivemaximum whenthedisplacementisatnegativemaximumandvice-versa.Also,attheneutralpoint, bothaccelerationanddisplacementarezero.
(iv) Thedisplacement,thevelocity,andthedynamicforcecanbecalculatedfromtheabove expressionsatanygiventimebymeasuringtheamplitudeoftheaccelerationcorrespondingtoa frequencywhenthemassoftheobjectisknown.
Itcanbeseenfrom Fig.1.2 thatthenumericalvalueofaccelerationamplitudeisquitehighcomparedto displacement.Atthesamedynamicforce,avibrationamplitudereduceswithincreasingfrequency,but theaccelerationincreaseswiththesquareofthefrequency.Thisisusedinthemeasurementofvibration studieswheretestprotocolsdefineaccelerationbothasinputandmeasuringparameters.
Inaddition,forthestudyofstructuralvibrationandtransients(shock),theaccelerationisconventionallyrepresentedasmultipleofaccelerationduetogravity(g)andinSIunit,thevalueof‘g’istaken
FIG.1.2
Displacement,velocity,andaccelerationofasimpleharmonicmotion.
as9.81m/s2.Secondly,allvibrationintensitiesareexpressedasaratioofaccelerationnormalisedby theforce[a(t)/F0].
1.3.2 Freevibrationandnaturalfrequency
Ifabodyisallowedtovibratebyaninitialimpactforce,thevibrationiscalledfreevibrationandthe frequencyofthevibrationistermedasthenaturalfrequencyofthebody.Everymatterorobjecthasa naturalfrequencyofvibrationdependingonitsphysicalcharacteristicssuchaselasticmodulus,mass, size,andshape [8,9].Asanexample,ifastringwithafixedlengthinaguitarisplucked,therewillbea soundofaparticularfrequencyandeverytimethesametunewillbeheard.Therecanbesubsequent higherharmonicswhicharemultiplesofthefirstnaturalfrequencyoftheobject.Inthecaseofathin beam,modesintheaxialdirectionisenoughtostudyvibration,foraflatplateofnegligiblethickness, twodirectionsaretobeconsidered,andforathree-dimensionalbody,therewillbenaturalfrequencies andmodalsinthreedirections,forexample,acylinderwillhaveaxial,circumferential,andradialnaturalfrequenciesandhighermodesofeachtoo.
1.3.3 Forcedvibrationandresonance
Whenanexternaldynamicforceisappliedtoanobjectforaperiodgreaterthanitsowntimeperiodof oscillation,thevibrationistermedasforcedvibration.Theobjectvibratesatthesamefrequencyas isimposedbytheexternalforce.Runningmachinery(suchasmotor,engine,pump,centrifuge, etc.)issubjectedtoforcedvibration.
Whenthefrequencyofanexternaldynamicforcecoincideswiththenaturalfrequencyofthebody, therewillbeaverylargeamplitudeofdisplacementandthephenomenonistermedasresonance.Itis alsothefrequency,atwhichthepotentialenergyoftheobjectistotallyconvertedtokineticenergy. Therefore,atresonance,thevibrationamplitudeattainsamaximumvalue.Therecanbeseveralmodes ofresonances,whicharehigherharmonicsofthefirstnaturalfrequency.Ineachmode,theintensity peaksareobserved.Systemresonanceformachinerywithverylargeamplitudemaycausesevere damageorcatastrophicfailure.Thus,thestudyofthevibrationresponseofastructurewithrespect totimeandfrequencyisveryimportanttotakemeasurestoavoidsuchdamagesorfailures.
1.4 Randomvibration
Ifthemagnitudeofexternaldynamicforceatagiventimeisknown,thenthevibrationisdeterministic vibration.Whenthemagnitudescannotbedeterminedatagiventime,thenitisrandomvibration.Ina randomvibrationscenario,aclusterofvibrationintensitiesandfrequencieswouldexist.Therefore, whateverbethecomplexityofarandomvibrationsignature,itcanbeassumedasasumofmanypure sinewavesofdifferentamplitudeswithcorrespondingharmonicfrequenciessuchas
Generally,therecordingofarandomvibrationspectrumisdonewithrespecttotime(timedomain). FourierTransformisappliedtofindtheindividualintensitiesinthefrequencyscaleafterselectionofa timedomainwindowoftherandomsignal.Theexampleofrandomvibrationiswindvelocity,earthquakes,etc.Iflargedataisavailable,astatisticalanalysismaybedonetodeterminethedifferentmagnitudesandfrequenciesoftherandomvibration [10,11].TypicalFouriertransformofrandom vibrationintimedomainandfrequencydomaintakingthelimitsof ∞ to+∞ forfrequencyandtime areexpressedmathematicallyas
Theinfinitelimits,however,isonlytheoretical,andthelimitscanbedecidedwheretheintensityisbelow 1%ofthehighestintensityinthefrequencyscale.Present-dayFastFourierTransform(FFT)analysisof vibrationandshockspectraiscomputerisedasstandardsoftwareavailablewithallvibrationanalysers.
1.5 Undampedanddampedvibration
Afreeorforcedvibrationmayormaynotexperienceresistanceslikeinternalfrictionorinelasticdeformationoftheobject.Anundampedvibrationisacasewherethereisnoresistancetothevibration andthevibrationisnotdampedorattenuatedwithtime,whichimpliesthatthedynamicdeformationis perfectlyelasticinnature.Therefore,inanundampedsystem,thereisnolossofmechanicalenergyin thesystem.
Ifthevibratingbodyexperiencesfrictionalorothertypesoflossofmechanicalenergy,thevibration intensityisattenuatedordampedwithtime.Thetimedependenceofresponsecausesaphaseshiftfor thestatevariablesuchasstrainandismathematicallyexpressedasacomplexquantity.Thephaseshift representstheextentofdampingorlossofenergyinadampedoscillatorysystem.Thelossmechanism couldbeinelastic(dashpot)orviscoelasticdamping,magneto-rheologicalorelectro-rheologicaldamping,oractivecontrolorshearthinning-typedamping.
1.5.1 Expressionsforfree,undampedvibration
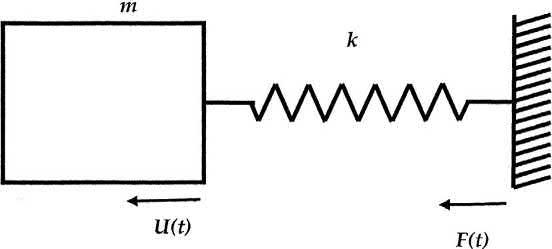
AnSDOFsystemofamassattachedtoaspringisshownin Fig.1.3.Therotatingoroscillatorymachinesandmanysuchreal-lifesystemscanbemodelledasamass-springsystemasshowninthefigure. Mostmetallicobjects,suchasmachinesandequipment,haveverylowinherentlossesandthevibrationsareapproximatelyundamped.
Thekeyassumptionsfortheabovesystemarethatthespringhasverylowmass,andcanbe neglectedanditsbehaviourisHookean,thatis,theforceislinearlyproportionaltothedeflection ofthespring.Theproportionalityconstantistermedas SpringConstant,denotedby‘k’.Theresponse ofthespringisinstantaneous,whichmeansthereisnotimelagbetweentheforceanddeformationand alsothespringcomestoitsundeformedstateinstantlyonwithdrawaloftheforce.Therefore,thereisno lossofenergyduetodeformationandretractioncycle.
Consideringtheforcebalance,theforceexertedbythestretchingofthespringisbalancedbythe forceduetotheaccelerationofthemass:
Onesolutiontotheabovesecond-orderdifferentialequationcanbe
where u0 istheinitialdisplacement, v0 istheinitialvelocity,and ωn isthe NaturalAngularFrequency ofthespring-masssystemandisgivenby
FIG.1.3
Spring-massarrangementinanSDOFsystem:undampedfreevibration.
Unitofnaturalangularfrequency(ωn)isradian/s.Theexpressionofnaturalfrequencyissignificantfor thedesignofmachinerymountsincethestiffnessofthemountandthemassofthemachinewould decidethesystemresonance.Asystemofhighstiffnessandlowermasswouldhaveahighnatural frequency,andthedampingsystemshouldbetunedtocaterforhighdampingatsuchfrequencyto reducethehighvibrationintensityatresonance.
Inanelasticvibrationsystem,whenthemassisplacedoverthespring,andthereisastaticdeflection δs asaresultoftheweightofthemass,theresonancefrequencyofsuchavibratingsystemcanbe expressedas
where‘g’isaccelerationduetogravity.
Theaboveexpressionfornaturalfrequencyisonlyvalidforasystemwhichisbothlinearandelasticinbehavioursincestaticanddynamicstiffnessofanelasticmaterialaresameanddoesnotdepend onthefrequencyofvibration.Theexpressionisnotvalidforhighdampingmaterialssincetheyare neitherlinearnorelasticinbehaviour.
AnothersolutiontoEq. (1.4) canbeofgeneralexpressionas
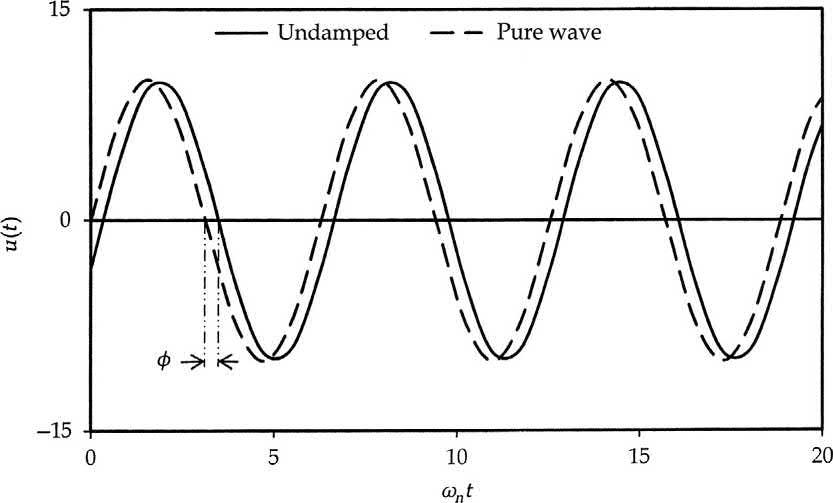
Thewaverepresentsasinusoidalcurvewithaphaseoffsetof‘φ’andthedisplacementvariesfrom A to +A asshownin Fig.1.4.
Theamplitude A andphase φ arerelatedtotheinitialconditions u0 and v0 as
FIG.1.4 Undampedvibrationcomparedtoapuresinusoidalwave.
Thephaseangle(φ)canbeverysmallincaseofasystemwithahighnaturalfrequency,orinanother way,highstiffnessandlowmass.
1.5.2 Expressionsforfreedampedvibration
Continuingwiththeundampedsystemasaspring-masscombination,aviscousdashpotcanbeintroducedtorepresentadampedvibration.Aviscouspotconsistsofacylinderfilledwithaviscousfluid suchassiliconeoilandapistoninthecylinder.Theviscousdissipationtakesplaceforaforceappliedto thepistonduetoshearingoftheviscousfluid.Theforceisproportionaltothevelocityofthepiston:
where λ iscalled Dampingcoefficient oftheviscousdashpot.
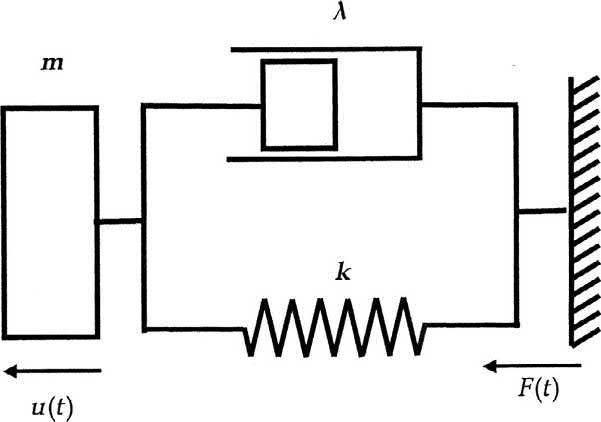
Thedampedvibratingsystemisassumedtobeacombinationofspring,mass,andadashpot.A typicalsketchofthespring-mass-dashpotsystemisshownin Fig.1.5.TheforcebalanceofsuchasystemwithanSDOF,underfreevibration,wouldbe [12]
Thesolutiontothisequationdependsonthevalueofthedampingcoefficient‘λ’.Ifthedampingis small,asformetallicbeams,thesystemwillcontinuetooscillatebutwithdiminishingamplitudewith time.Thesystemissaidtobe Underdamped.Ifthedampingisjustenoughtostoptheoscillation,thenit istermedas CriticallyDamped.Whenthedampingexceedsthecriticalvalue,thesystemiscalled Overdamped.Thevalueofcriticaldampingis
FIG.1.5
AschematicrepresentationofafreevibrationwithdampingsystemforSDOF.
Undampedanddampedvibration
Dampingisoftenexpressedbyadimensionlessquantitycalled DampingFactor ‘ξ’definedastheratio ofthedampingcoefficienttothecriticaldamping:
Thesolutionsforthethreecasesofdampedvibrationaredescribedbelowwithexamples.
1.5.2.1 Case(1)—Underdampedsystem
Intheaboveexpression,wecanidentifyamodifieddampednaturalfrequency ωd definedas
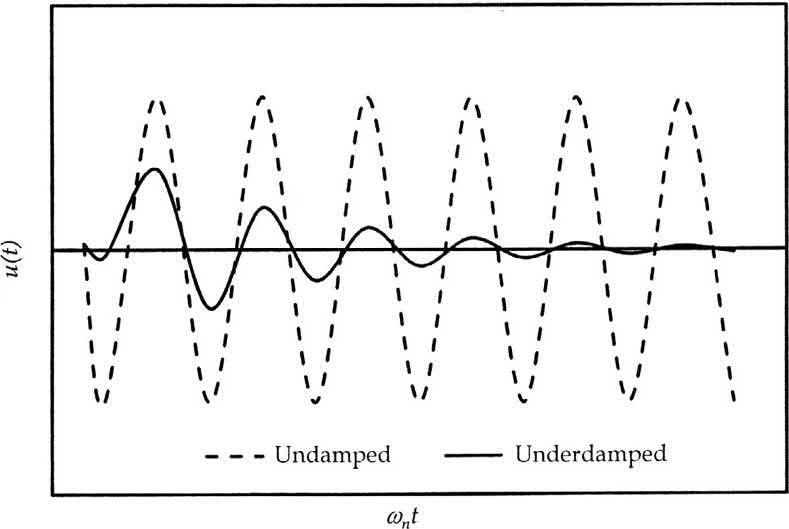
Thenatureofthecurveissinusoidalwithanexponentialdecaywithaphaseshiftof φ comparedtoan undampedsystemasshownin Fig.1.6
Eq. (1.15) oftheunderdampedsystemsuggeststhatathighfrequency(beyond10Hz),thedamping isveryfast,inafractionofasecondatadampingfactorofeven0.1.Itwillbeseeninconsecutive chaptersthatthedampingfactorofmostmountsandvibrationdampingmaterialsarelowatlow frequenciesexceptforactivevibrationdampingorsmartdamping,wheredampingcanbeenhanced byasmartoractivesystematevenverylowfrequencies.
FIG.1.6
Underdampedandundampedsysteminfreevibration.
Thetimeperiodofdampedoscillation, Td ismodifiedsincethedampedresonancefrequencyis expressedbyEq. (1.16). Td isdefinedas
Thedecayofthewavecanbeexpressedbytakingtheratiooftwoconsecutiveamplitudesas
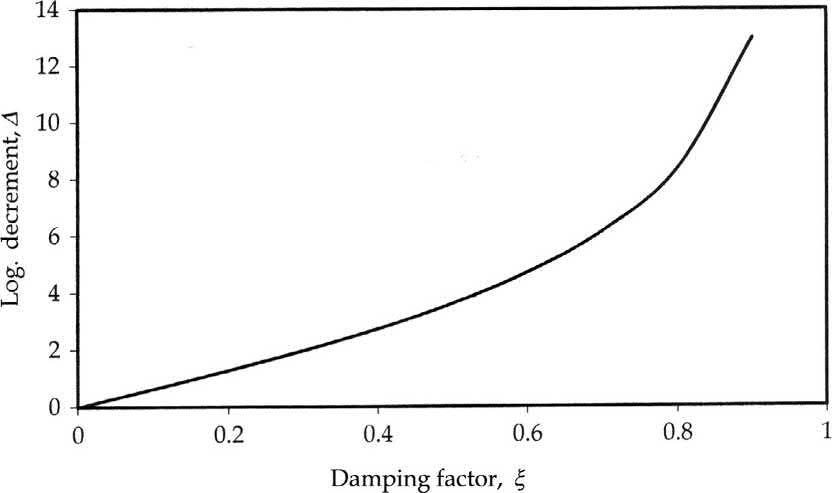
Thenaturallogarithmoftheamplituderatioalsotermedaslogarithmicdecrement(Δ)expressedas
ThisgivesusanimportantconclusionthatinanunderdampedfreevibrationwithanSDOF,thelogarithmicdecrementdependsonlyonthedampingfactor. Fig.1.7 showsthevariationinlogarithmic decrement Δ, ondampingfactor ξ.
1.5.2.2 Case(2)—Criticallydampedsystem
Inthiscase, λ ¼ λC ¼ 2 kmp and ξ ¼ 1.
ThesolutiontotheEq. (1.12) couldbe
Solvingfor C1 and C2,usinginitialconditionsas:
FIG.1.7
Dependenceoflogarithmicdecrementondampingfactor.
1.5 Undampedanddampedvibration
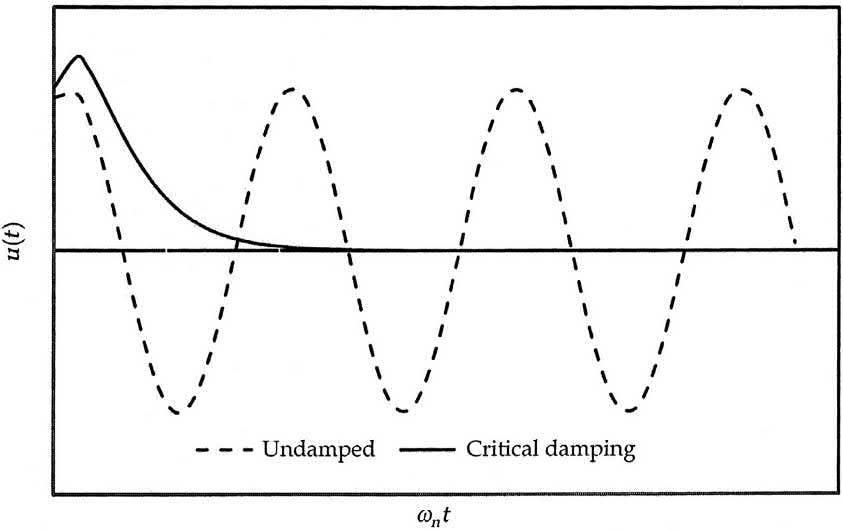
FIG.1.8
FreevibrationofanSDOFsystem,undampedandcriticallydamped.
Itcanbeseenthatthedisplacementcanhaveoneovershootcomparedtotheundampedinitialdisplacement. Fig.1.8 depictsthenatureofthedecay,whichisanexponentialcurvehavingnosinusoidal component.
1.5.2.3 Case(3)—Overdampedsystem
Thevibrationresponseisoverdampedwhenthedampingfactoris >1,thatis, λ/λC or ξ > 1.The solutiontoEq. (1.12) canbe
where C1 and C2 arethecoefficientsofintegrationandcanbefoundoutbysolvingtheequationusing initialconditions u0 and v0.Thesolutionbecomes
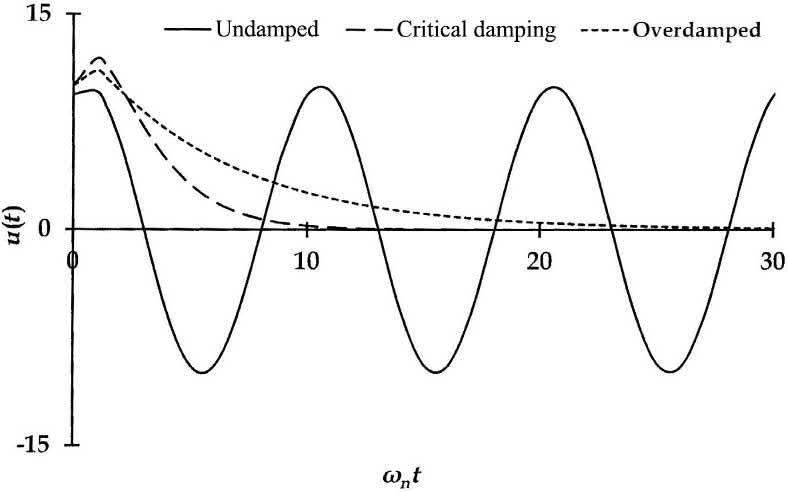
Thisisalsoauniformexponentialdecaycurvewithoutanyvibrationcharacteristics.Atypicalresponse curveisgivenin Fig.1.9.Exampleofanunderdampedsystemiscommon,includingcuredrubber bushesandmounts,whileatypicalexampleofanoverdampedsystemistheunvulcanisedbutyl rubberlatex.
FIG.1.9
OverdampedSDOFsysteminfreevibration,comparedwithundampedandcriticallydampedsystems.
1.5.3 Forcedvibration
Whenanexternaloscillatoryexcitationforceisappliedontoabody,theresultingvibrationistermedas forcedvibration.Intheeventofafrequencysweepbyanexternalexciter,whenthesweepingfrequency coincideswiththatofthenaturalfrequencyofthesystem,thephenomenoniscalledresonanceandat thatpoint,theamplitudeofvibrationwouldbemaximum.Inarandomvibration,suchasarunning turbine,therecanbemanysubsequenthighermodes.
1.5.3.1 Frequencyresponseinundampedforcedvibration
Let F0sin(ωt)betheexternaloscillatingforceonabodywithoutdamping(mass-springsystem).
Theforcebalancewouldbe
Solutiontotheaboveequationatsteadystateis
where ωn isthenaturalfrequencyofthesystem,definedbyEq. (1.6).
Inareal-worldapplicationofforcedvibration,itisimportanttostudytheforcetransmittedtothe foundationduetoavibratingmachineorviceversa.Thetransmissibilityofoutputforcecomparedto inputforcecanbecalculatedandcanbemeasuredforavibratingsystem.Theforcetransmissibility(ε) insuchaspring-masssystemisdefinedbytheratioofexciterforceamplitudetotheresultingforce amplitude.FollowingEq. (1.24),weget,transmissibility, ε:
Theratioofforceisnumericallythesameastheratioofaccelerationorvelocityordisplacement amplitudesandhencethedisplacement,velocity,acceleration,andforcetransmissibilityisexpressed bythesameEq. (1.25).
Thetransmissibilityexpressionabovesuggeststhatthedisplacementamplitudeofvibrationwill assumeinfinitevalueattheresonance,thatis,whentheforcingfrequencyequalsthenaturalfrequency ofthemachine(ω ¼ ωn).
Incaseofmachinesinstalledonfoundations,andhavingarotationaloroscillatorymovementlike anengineormotor,thefirstnaturalfrequency f0 canbederivedfromEq. (1.7) andisgivenby
Fig.1.10 showsthetypicaltransmissibilityasatheoreticalcurveforanundampedforcevibrationinan SDOFsystem.Here, ω0 istakenasthefirstnaturalangularfrequencyofthesystemhaving rad/s asthe unit,and ω0 ¼ 2π f0.
From Fig.1.10,itisobservedthatthetransmissibilityincreasesinfinitelyattheresonance,thatis, whentheimposedfrequency(ω)coincideswiththefirstnaturalfrequency(ω0).Secondly,thetransmissibilitydecreaseswiththefrequencybeyondresonance.Atafrequencyof √ 2timestheresonance frequency,thatis,at ω ¼ √ 2ω0,thevalueoftransmissibilityis1,meaningtheimposedforceisthe sameastheoutputascanbecalculatedfromEq. (1.25).Beyondthispoint,thevibrationisdamped monotonically.Atveryhighfrequencies,beyondresonance,thetransmissibilityisinversely
FIG.1.10
AtypicaltransmissibilitycurveforanSDOFundampedforcedvibration.
proportionaltothesquareoftheimposingfrequency.However,inpractise,therewillbepeaksof highermodesalsointhevibrationspectrumbeyondthefirstresonancefrequencyforallvibratingplatformsandmachines.Thehighermodeswillshowsharplyincreasedintensitiesofvibration.Ifthese highermodesareintheregionof‘mostdisturbingfrequency’domain,theyshouldbeattenuated byadampingmechanismwhichcantakecareofallmodesaseffectivelyaspossible.
1.5.3.2 Frequencyresponseindampedforcedvibration
NowconsideradampedforcedvibrationinSDOFsystem.Theclassicalmechanicaldampersystem consistsofamass,spring,andaviscousdashpot.Thedashpotisacylinder-pistonassemblyhavinga viscousliquidinside,which,onpistonmovement,convertsthetotalenergyintoviscousenergyand ultimatelytoheat.Therefore,thispartoftheenergyconsumedbythedashpotisirrecoverable.It is,inreality,amachinemountedonshockandvibrationmounts,havingonlyonedirectionofvibration. ThemountismadeofaVEMandisassumedtobeacombinationofaspringandadashpotforboth physicalandmathematicalrepresentation.Thespringrepresentstheelasticpartoftheviscoelastic responseandthedashpotrepresentstheviscousdissipationcharacteroftheVEM.Themachine undergoesvibrationduetooscillatoryorrotationalmotionandthevibrationforceisreduceddueto thedashpotactionofthemount.
Theequationofmotioncanberepresentedas
Forthefirstnaturalfrequencyofthemachine ω0 andwithadampingfactor ξ,weobtain
Theforcetransmittedtothefoundationofavibratingmachineisofimportanceinthestudyofreduction ofstructuralvibration.Forafloatingfoundationorbaseplatesofavessel,thevibrationtransmittedto thebaseisimportantfromthepointofviewofacousticnoisereduction.Theforcetransmittedtothe foundationcanbegivenby
Sincetheforceissinusoidal,theforceforviscousdampingandforceforspringdeflectionasgiven inEq. (1.29) are90° outofphasetoeachother.
Thesteady-stateratiooftransmittedforce(onthefoundation)totheappliedforce(bythemachine) canbegivenas
where εd istheforetransmissibility,andgivenby
andthephaseangleisgivenby
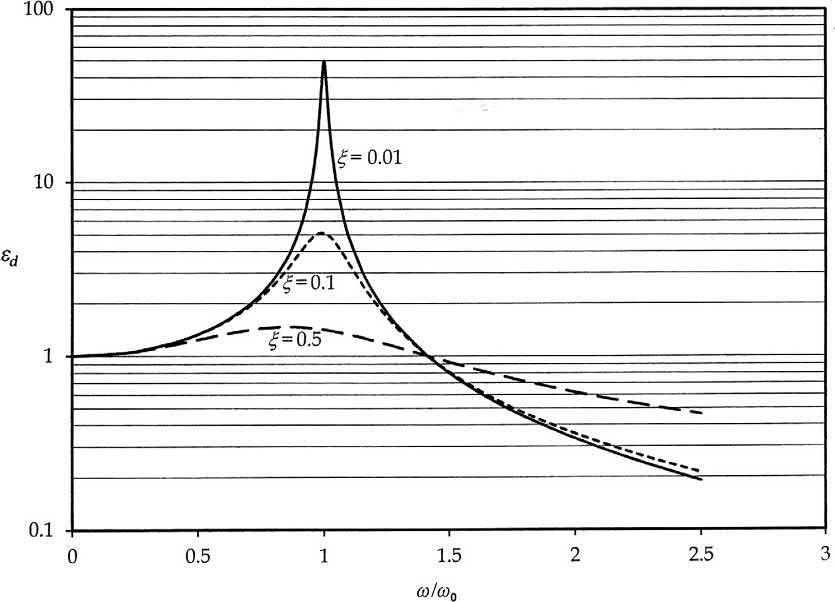
Thephaseangle(Eq. 1.32)isnotcommonlyusedinmountdesign.Thetransmissibilitiesfordisplacement,velocity,andaccelerationarenumericallythesameastheforcetransmissibility. Fig.1.11 shows thetransmissibilitycurvesasafunctionoffrequencyratioforseveraldampingfactors.
Thefirstnaturalfrequencyofamachinecanbefoundoutbythedeflectionduetotheweightofthe machine.ReferringtoEq. (1.26),thedeflectionofthebasemountduetothemachineweightdecides thenaturalfrequency.Thedeflectionoftheamountisdecidedbytheelasticmodulus,thenumberof mounts,contactareaofeachmount,andthetotalload.Eq. (1.26) isonlyvalidwhenthedampingfactor isverysmall,typicallybelow0.1andthedynamicstiffnessofthemountisnotmuchdifferentfromthe staticstiffness.Formostmounts,thedynamicstiffnessvarieswithfrequencyandtemperature.
From Fig.1.11,itcanbeseenthatusingvariousdampingfactorsof0.01,0.1,and0.5,thedecayin transmissibilitybeyond ω ¼ √ 2ω0 ismuchfasterwithfrequencyforlowdampingfactorthanthatfor thehigherdampingfactor.Thereductionoftransmissibilitydependsonthedampingpropertyofthe system.Forinstance,whenamachineisinstalledonashockandvibrationdampingmount,supposedly madeofanelastomer,thedamping,whichisadynamicviscoelasticlosspropertyoftheelastomer, stronglydependsonthefrequencyandenvironmenttemperature.Similarbehaviourwouldbe expectedfromdampersmadeofshearthickeningordilatantfluids.Hence,theextentofreduction
FIG.1.11
TransmissibilityofdampedforcedvibrationcasesforanSDOFsystemwithdifferentdampingfactors(0.01,0.1, and0.5).
intransmissibilitymaynotbethesameasatheoreticalcurvecalculatedasin Fig.1.11,sinceitisassumedinthiscase,thatthedampingfactoristhesamefortheentirefrequencyband.
However,progressivelyhigherdampingfactorwithfrequencyisnecessaryforshockandvibration mountsformachinesafetyandtoreducethepeaksofhighermodes.Atypicalmachinesuchasadiesel alternatormaycauseavibrationspectrumof10–5000Hzwithvaryingintensitiesatthefoundation.It isobviousthattomakethemachinerelativelysilentinthesonicrange,vibrationintensitiesaretobe reducednotonlyatfirstresonancefrequencybutatallhighermodesalso.Theradiatednoisedueto machinevibrationshouldbereducedfornotonlystealthpurposebutalsoforhumancomfortinindustriesbywayofreducingintensitiesofnoiseatafrequencyrangeof3000–6000Hz,whichareconsidereddisturbingfrequencyrange,mostdisturbingbeing4000Hzforhumanear [13]
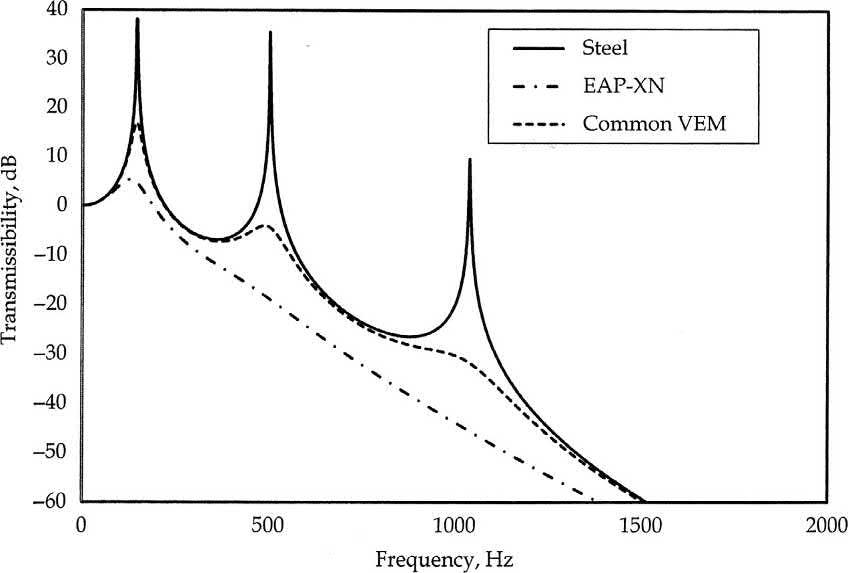
Ifamaterialhasadampingfactorwhichgraduallychangeswithfrequency,thenatureofthecurve willbedifferent.Asanexample,twoVEMsareselected,oneacommonVEMhavingvariablebutlow dampingfactorinfrequencyscaleandahighdampingVEM(EAP-XN,energyabsorbingpolymerXN)developedbyus.Theirviscoelasticlossfactorsaregivenin Fig.1.12.Arotatingmachineis assumedtobemountedontheseVEMsseparately.Themachinetransmitsthevibrationtoafoundation. Hence,thefoundationresponseistakenasgivenbyEq. (1.31).Thevibrationdampingbythesetwo VEMsiscomparedastransmissibility(inpowerratio,dB)againstaseeminglyrigidmountingonsteel blockwithanassumeddampingfactorof0.002.Thetransmissibilitywithfrequencyiscalculatedwith threemodesofresonancesat145,500,and1036HzofthemachineusingEq. (1.31).Thetransmissibility(indB)curvesforeachmountareaddeduptogetthemodalsforeachmount.Thecombined responseinfrequencyscaleisshownin Fig.1.13.ItcanbeseenthattheadvantageofusingaVEMwith higherdampingisthatitreducessuccessiveintensitiesofhigherresonancesquiteeffectivelyifits dampingfactorfurtherincreaseswithfrequency,whichistrueformanytailor-madeVEMs.

FIG.1.12
DynamicviscoelasticlossfactorofacommonVEMandEAP-XNinfrequencyscaleat30°C.
FIG.1.13
AcomparisonofvibrationtransmissibilityofahighdampingVEM(EAP-XN)versusacommonVEMasmounts forfirstthreenaturalfrequenciesof145,500,and1036Hz.
Inthecaseofsuspensiondesignofautomobiles, Fig.1.11 canbeexaminedtoreducevibrationintensity.Ifwecanmake ω/ω0 ≫ 1,byreducingthesuspensionspringstiffness(softspring)andwith increasedmass,thenaturalfrequency(ω0)oftheunitisrenderedlowerandattheworkingfrequency (ω),theattenuationinvibrationwillbebetter.However,lowerstiffnessmayresultinmorechancesof transversedeflectioninarubber-basedmount,causingmorevibrationsinotherdirections.Alargereductioninvibrationamplitudeisalsopossiblebeyondresonancebyalowerdampingfactor.However, lowdampingfactorhastwomajorproblems,one,thatatanyextratransientforce,whichisvery oftenpossibleforvehicles,thenaturaldecaywilltakealongtime,andsecondly,neartheresonance frequency,thevehiclemaybedamagedduetohighamplitudeofvibration.Athirdproblemwouldbe radiatednoiseathighermodes.Thedesignofasuspensionis,therefore,abalancedselectionofspring anddamper,whichrequiresanoptimumVEMdesign.
Whenamachineisvibratingduetothebaseexcitationwithaviscoelasticdampingmount,the amplitudeofvibrationisrepresentedby
where F/k isthestaticdeflection(δST)ofthemount.Thisexpressionisactuallyacomparisonofthe vibrationamplitudeateveryfrequencypointtothestaticdeflection.Thereductionofamplitudeissubjecttotwoparameters,thefrequencyratioandthedampingfactor.Higherthefrequencyratio,higheris thereductioninamplitude.However,theintensityatresonance(ω ¼ ω0)isinfiniteintheabsenceofa dampingmount.
1.5.3.3 Propertiesofasystemfromforcedvibrationresponse
Thevibrationresponsecurveforamachineisusedtodetermineseveraldynamicpropertiesofasystem.Inanexperimentofrecordingvibrationspectraofamachinewithrespecttofrequency,therewill beabandofthefrequencywithpeaksasdifferentmodesofresonances.Fromthenatureofthepeaks, thebandwidth,quality,anddampingfactorcanbedetermined.
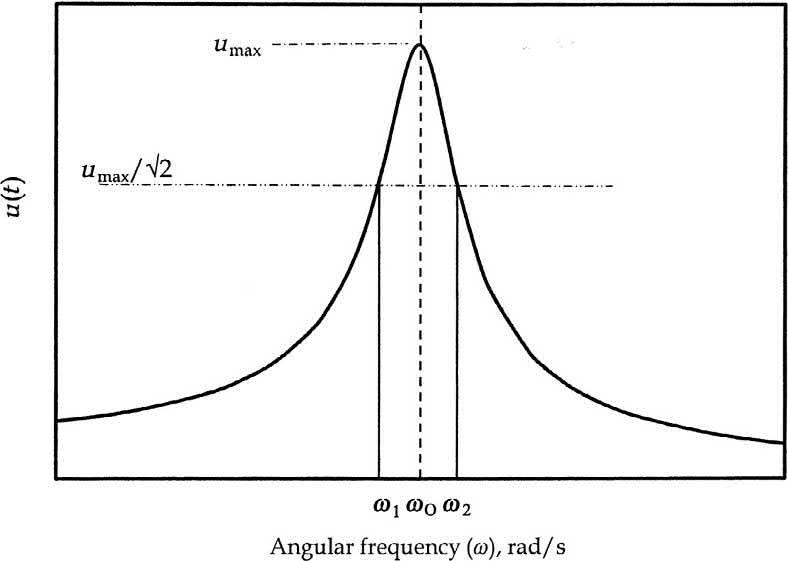
Letusexaminethefirstresonancepeakofaforcedvibrationasdepictedin Fig.1.14.Fromthe figure,letustakethevalue umax whichisthepeakvalue.FollowingEq. (1.31),itcanbeseenthat at ω ¼ 0,thetransmissibility ¼ 1andalso,at ω ¼ √ 2ω0,thetransmissibilityisagain ¼ 1andbeyond thiscut-offfrequency,thetransmissibilityis <1,meaningthattheisolationofvibrationoccurscontinuouslyasthefrequencyincreasesfurther.Thevibrationenergy,representedbypowerintermsofdB, ishalfwhentheintensityis1/√ 2timesthepeakintensityatresonance.Therefore,athalfpower,the amplitudeofvibrationis ¼ umax/√ 2.
Ifwedrawahorizontallinealongavalueof umax/√ 2,wegettwofrequencyvaluesatwhichthis conditionprevails, ω1 and ω2 asshownin Fig.1.14.Wenotethevaluesoffrequencies ω1 and ω2 from theintersectionsofthedrawnlinewiththeresponsecurve.Thedifferencebetweenthesetwofrequenciesisthe‘frequencybandwidth’atwhichband,thetransmittedvibrationpowerisequaltohalfthe peakpower.Itiscustomarytorelatehalf-powerbandwidthwiththequalityoftheresonancepeak.
Thehalf-powerbandwidthofthecurveis
Thequalityfactor,whichissimilartothatinsoundandelectricalcircuits,isdefinedas
FIG.1.14
Firstresonancepeakforaforcedvibrationwithasmalldampingfactor.