PHASEDIAGRAMSAND THERMODYNAMIC MODELINGOF SOLUTIONS
ARTHURD.PELTON
Dep’tChemicalEngineering,CentredeRechercheen CalculThermochimique,EcolePolytechniquedeMontreal
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
# 2019ElsevierInc.Allrightsreserved.
Covercredit:A.D.Pelton,“ThermodynamicsandPhaseDiagrams”in“PhysicalMetallurgy 5thedition”,D.E.LaughlinandK.Hono(eds.),Elsevier,pp.203-303(2014)
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronic ormechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem, withoutpermissioninwritingfromthepublisher.Detailsonhowtoseekpermission,further informationaboutthePublisher’spermissionspoliciesandourarrangementswithorganizations suchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatour website: www.elsevier.com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedical treatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluating andusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuch informationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,including partiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assume anyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability, negligenceorotherwise,orfromanyuseoroperationofanymethods,products,instructions,orideas containedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN978-0-12-801494-3
ForinformationonallElsevierpublicationsvisitour websiteat https://www.elsevier.com/books-and-journals
Publisher: SusanDennis
AcquisitionEditor: KostasKI.Marinakis
EditorialProjectManager: CarlyDemetre
ProductionProjectManager: OmerMukthar
CoverDesigner: GregHarris
TypesetbySPiGlobal,India
1
Fig.1.1 Temperature-compositionphasediagramat P ¼ 1baroftheFe-Mosystem (Pelton,2014).
Fig.1.2 Isothermalphasediagramsectionat25°Cand P ¼ 1baroftheZn-Mg-Al system(Pelton,2014).
Chapter2 providesareviewofthefundamentalsofthermodynamicsasrequiredfortheinterpretationandcalculationofphase diagramsofalltypes.In Chapter3,theGibbsphaseruleisdevelopedinageneralformsuitablefortheunderstandingofphase diagramsinvolvingawiderangeofvariablesincludingchemical potentials,enthalpy,andvolume. Chapter4 providesareviewof
(Gamma + Phi + Tau)
(Liquid + Tau)
+ Phi + MgZn hcp + MgZn
+ Gamma + MgZn
(fcc + Laves + Mg2Zn11 (fcc + Mg 2Zn11 + hcp)
Fig.1.3 Isoplethalphasediagramsectionat XZn ¼ 0.1and P ¼ 1barofthe Zn-Mg-Alsystem.(A)Temperatureversuscomposition;(B)enthalpyversus composition(Pelton,2014).
thethermodynamicsofsolutions. Chapter5 beginswithadiscussionofthethermodynamicoriginofbinary T-compositionphase diagrams,presentedintheclassicalmannerinvolvingcommon tangentstocurvesofGibbsenergy. Chapter5 continueswitha thoroughdiscussionofallfeaturesof T-compositionphasediagramsofbinarysystemswithparticularstressontherelationship betweenthephasediagramandthethermodynamicpropertiesof thephases.Asimilardiscussionof T-compositionphasediagrams ofternarysystemsisgivenin Chapter6.Isothermalandisoplethal sectionsandpolythermalliquidusandsolidusprojectionsare discussed.
(mnprth) (eactuj) (gvaonqsui) (dobrsk) (fvcbpql)
bcc + fcc + MC fcc + MC bcc + M23C6 bcc + MC + M23C6 fcc + M7C3 fcc + M23C6
+ MC + M7C3 bcc + MC + M7C3 + M23C6 bcc +MC+M
Fig.1.4 PhasediagramsectionoftheFe-Cr-V-Csystemat850°C,0.3wt%C,and P ¼ 1bar(SGTE).
Spinel + Fe2O3
Spinel
+ Monoxide
Spinel + Monoxide
+ fcc
+ fcc
Fig.1.5 PhasediagramoftheFe-Ni-O2 systemat1200°Cshowingequilibrium oxygenpressureversusoverallmetalratio(Pelton,2014).
In Chapter7,thegeometryofgeneralphasediagramsections isdevelopedindepth.Inthischapter,thefollowingarepresented: thegeneralrulesofconstructionofphasediagramsections,the properchoiceofaxisvariablesandconstantsrequiredtogivea single-valuedphasediagramsectionwitheachpointofthediagramrepresentingauniqueequilibriumstate,andageneral bcc + MC
Pyrrhotite + FeCr2S4
Pyrrhotite + fcc
Pyrrhotite + bcc
fcc + M2O3
bcc
bcc + M2O3
925∞C, Molar ratio Cr/(Fe+Cr) = 0.5 log10p(O2) (bar)
Spinel fcc + Spinel
Fig.1.6 PhasediagramoftheFe-Cr-S2-O2 systemat925°CshowingequilibriumS2 andO2 partialpressuresatconstant molarratioCr/(Cr+Fe) ¼ 0.5(Pelton,2014).
Triple point
Fig.1.7 (A) P-T and(B) V-T phasediagramsofAl2SiO5 (Pelton,2014).
Kyanite
Sillimanite
Andalusite
Sillimanite + Kyanite
Andalusite + Sillimanite
Sillimanite
Andalusite Kyanite
Andalusite
algorithmforcalculatingallsuchphasediagramsections thermodynamically.
Chapter8 beginswithadiscussionofthecourseofequilibrium solidificationofbinary,ternary,andmulticomponentsystemsand includesaclassificationofinvariantreactions.Next,nonequilibriumScheil-Gulliversolidificationisdiscussedinwhichsolids, onceprecipitated,ceasetoreactwiththeliquidorwitheachother. Scheil-Gulliverconstituentdiagramsareintroducedfromwhich onecanvisualizethecourseofScheil-Gullivercoolingastemperatureandcompositionarevaried.Thecalculationandtheoryof thesediagramsarediscussed.
Chapter9 treatsparaequilibriuminwhich,duringcooling,rapidlydiffusingelementsreachequilibriumbutmoreslowlydiffusingelementsremainessentiallyimmobile.Paraequilibriumphase diagramsareintroduced,andtheapplicationofthePhaseRuleto thesediagramsisdeveloped.
Chapter10 providesanintroductiontophasediagramswith second-orderphasetransitionsandtoferromagneticandorder/ disordertransitions.
In Chapter11,phasediagramsforsystemsinvolvinganaqueousphaseincludingevaporationdiagrams,classicalEh-pHdiagrams(whicharenottruephasediagrams),andtrueaqueous phasediagramsarediscussed.
Finally, Chapter12 providesasurveyofphasediagramcompilationsandtextsontherelationshipbetweenthermodynamics andphasediagrams.
References
Pelton,A.D.,2014.In:Laughlin,D.E.,Hono,K.(Eds.),(Chapter3).PhysicalMetallurgy.fifthed.Elsevier,NewYork.
ListofWebsites
SGTE,ScientificGroupThermodataEurope, www.sgte.org.
2
introductorytreatiseonthesubject.Thedevelopmentofthe thermodynamicsofphasediagramswillbecontinuedinthe succeedingchapters.
2.1TheFirstandSecondLawsof
Thermodynamics
Ifthethermodynamic system underconsiderationispermitted toexchangebothenergyandmasswthits surroundings,thesystemissaidtobe open.Ifenergybutnotmassmaybeexchanged, thesystemissaidtobe closed.Thestateofasystemisdefinedby intensiveproperties,suchastemperatureandpressure,whichare independentofthemassofthesystem,andby extensiveproperties,suchasvolumeandinternalenergy,whichvarydirectlyasthe massofthesystem.
2.1.1Nomenclature
Extensivethermodynamicpropertieswillberepresentedby uppercasesymbols.Forexample, G ¼ GibbsenergyinJ.Molar propertieswillberepresentedbylowercasesymbols.Forexample, g ¼ G/n ¼ molarGibbsenergyinJmol 1 where n isthetotalnumberofmolesinthesystem.
2.1.2TheFirstLaw
The internalenergy ofasystem, U,isthetotalthermaland chemicalbondenergystoredinthesystem.Itisanextensivestate property.
Consideraclosedsystemundergoingachangeofstatethat involvesanexchangeofheat,dQ,andwork,dW,withitssurroundings.Sinceenergymustbeconserved,
ThisistheFirstLaw.Theconventionisadoptedwherebyenergy passingfromthesurroundingstothesystemispositive. ThesubscriptondUn indicatesthatthesystemisclosed(constant numberofmoles.)
ItmustbestressedthatdQ anddW arenotchangesinstate properties.Forasystempassingfromagiveninitialstatetoa givenfinalstate,dUn isindependentoftheprocesspathsinceit isthechangeofastateproperty;however,dQ anddW are,ingeneral,path-dependent.
2.1.3TheSecondLaw
ForarigorousandcompletedevelopmentoftheSecondLaw, thereaderisreferredtostandardtextsonthermodynamics.The entropy ofasystem, S,isanextensivestatepropertythatisgiven byBoltzmann’sequationas
S ¼ kB ln t (2.2)
where kB isBoltzmann’sconstantand t isthe multiplicity ofthe system.Somewhatloosely, t isthenumberofpossibleequivalent microstatesinamacrostate,thatis,thenumberofquantumstates ofthesystemthatareaccessibleundertheapplicableconditions ofenergy,volume,etc.Forexample,forasystemthatcanbe describedbyasetofsingle-particleenergylevels, t isthenumber ofwaysofdistributingtheparticlesovertheenergylevels,keeping thetotalinternalenergyconstant.Atlowtemperatures,mostof theparticleswillbeinornearthegroundstate.Hence, t and S will besmall.Asthetemperatureandhence U increase,moreenergy levelsbecomeoccupied.Consequently, t and S increase.Forsolutions,anadditionalcontributionto t arisesfromthenumberof differentpossiblewaysofdistributingtheatomsormolecules overthelatticeorquasi-latticesites(see Section4.6).Againsomewhatloosely, S canbesaidtobeameasureofthedisorderofa system.
Duringanyspontaneousprocess,thetotalentropyoftheuniversewillincreaseforthesimplereasonthatdisorderismore probablethanorder.Thatis,foranyspontaneousprocess,
dStotal ¼ dS +dSsurr ðÞ 0(2.3)
wheredS anddSsurr aretheentropychangesofthesystemandsurroundings,respectively.Theexistenceofastateproperty S that satisfiesEq. (2.3) istheessenceoftheSecondLaw.
Eq. (2.3) isanecessaryconditionforaprocesstooccur.However,evenifEq. (2.3) issatisfied,theprocessmaynotactuallybe observediftherearekineticbarrierstoitsoccurrence.Thatis,the SecondLawsaysnothingabouttherateofaprocessthatcanvary fromextremelyrapidtoinfinitelyslow.
Itshouldbenotedthattheentropychangeofthesystem,dS, canbenegativeforaspontaneousprocessaslongasthesum (dS +dSsurr)ispositive.Forexample,duringthesolidificationof aliquid,theentropychangeofthesystemisnegativeingoing fromtheliquidtothemoreorderedsolidstate.Nevertheless,aliquidbelowitsmeltingpointwillfreezespontaneouslybecausethe entropychangeofthesurroundingsissufficientlypositivedueto thetransferofheatfromthesystemtothesurroundings.Itshould
alsobestressedthatinpassingfromagiveninitialstatetoagiven finalstate,theentropychangeofthesystemdS isindependent oftheprocesspathsinceitisthechangeofastateproperty. However,dSsurr ispath-dependent.
2.1.4TheFundamentalEquationof Thermodynamics
Consideranopensystematequilibriumwithitssurroundings andatinternalequilibrium.Thatis,nospontaneousirreversible processesaretakingplace.Supposethatachangeofstateoccurs inwhich S, V (volume),and ni (numberofmolesofcomponent i in thesystem)changebydS,dV,anddni.Suchachangeofstate occurringatequilibriumiscalleda reversible process,andthecorrespondingheatandworktermsaredQrev anddWrev.Wemaythen write
μi isthe chemicalpotential ofcomponent i whichwillbediscussed in Section2.8.
Theabsolutetemperatureisgivenas
Weexpectthattemperatureshouldbedefinedsuchthatheat flowsspontaneouslyfromhightolow T.Toshowthat T as givenbyEq. (2.6) is,infact,suchathermalpotential,consider twoclosedsystems,isolatedfromtheirsurroundingsbutinthermalcontactwitheachother,exchangingonlyheatatconstant volume.Letthetemperaturesofthesystemsbe T1 and T2,and let T1 > T2.Supposethatheatflowsfromsystem1tosystem2, thendU2 ¼ dU1 > 0.Therefore,fromEq. (2.6),
Thatis,theflowofheatfromhightolowtemperatureresultsinan increaseintotalentropy,andhence,fromtheSecondLaw,itis spontaneous.
ThesecondterminEq. (2.4) is( PdV ),theworkofreversible expansion.FromEq. (2.6),thefirstterminEq. (2.4) isequalto TdS, andthisisthenthereversibleheat:
Thatis,intheparticularcaseofaprocessthatoccursreversibly, (dQrev/T )ispath-independentsinceitisequaltothechangeof astatepropertydS.Eq. (2.8) isactuallythedefinitionofentropy changeintheclassicaldevelopmentoftheSecondLaw.
Eq. (2.4) maynowbewrittenas
Eq. (2.9),whichresultsfromcombiningthefirstandsecondlaws,is calledthe fundamentalequationofthermodynamics.Wehave assumedthattheonlyworktermisthereversibleworkofexpansion (sometimescalled“PVwork”).Ingeneral,inthisbook,thiswillbethe case.Ifothertypesofworkoccur,thennon-PVterms,dWrev(non-PV), mustbeaddedtoEq. (2.6).Forexample,iftheprocessisoccurring inagalvaniccell,thendWrev(non-PV) isthereversibleelectricwork intheexternalcircuit.Eq. (2.9) canthusbewrittenmoregenerallyas
U ¼ T dS P dV + Xμ
2.2Enthalpy
Enthalpy, H,isanextensivestatepropertydefinedas H ¼ U + PV (2.11)
Consideraclosedsystemundergoingachangeofstatethatmay involveirreversibleprocesses(suchaschemicalreactions). Althoughtheoverallprocessmaybeirreversible,weshallassume thatanyworkofexpansionisapproximatelyreversible(i.e.,the externalandinternalpressuresareequal)andthatthereisno workotherthantheworkofexpansion.Then,fromEq. (2.1), dUn ¼ dQ P dV (2.12)
FromEqs. (2.11),(2.12),itfollowsthat dHn ¼ dQ + V dP (2.13)
Furthermore,ifthepressureremainsconstantthroughoutthe process,then dHp ¼ dQp (2.14)
IntegratingbothsidesofEq. (2.14) gives ΔHp ¼ Qp (2.15)
Thatis,theenthalpychangeofaclosedsysteminpassingfroman initialtoafinalstateatconstantpressureisequaltotheheat
exchangedwiththesurroundings.Hence,foraprocessoccurring atconstantpressure,theheatispath-independentsinceitisequal tothechangeofastateproperty.Thisisanimportantresult.Asan example,supposethattheinitialstateofasystemconsistsof 1.0molofCand1.0molofO2 at298.15Kat1.0barpressureand thatthefinalstateis1.0molofCO2 atthesametemperature andpressure.Theenthalpychangeofthisreactionis.
(wherethesuperscripton ΔH298.15 o indicatesthe standardstate reactioninvolvingpuresolidgraphiteandCO2 andO2 at1.0bar pressure).Hence,anexothermicheatof 393.52kJwillbe observed,independentofthereactionpath,providedonlythat thepressureremainsconstantthroughouttheprocess.For instance,duringthecombustionreaction,thereactantsandproductsmayattainhighandunknowntemperatures.However,once theCO2 producthascooledbackto298.15K,thetotalheatthat hasbeenexchangedwiththesurroundingswillbe 393.52kJ independentoftheintermediatetemperatures.
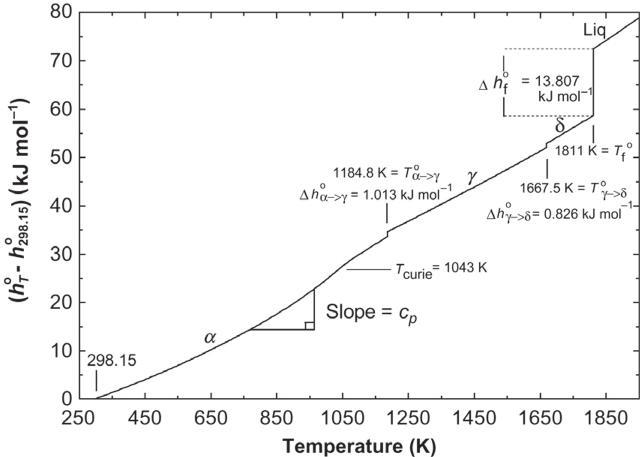
In Fig.2.1,thestandardmolarenthalpyofFeisshownasa functionoftemperature.The y-axis,(hT o h298.15 o ),istheheat requiredtoheat1.0molofFefrom298.15Ktoatemperature T atconstantpressure.Asusual,thesuperscripts“o”indicatethe standardstate ofpureFe.Theslopeofthecurveisthemolarheat capacityatconstantpressure:
Fig.2.1 StandardmolarenthalpyofFe(FactSage).
C+O2 ¼ CO2 ΔH o 298:15 ¼ 393 52kJ(2.16)
Heatcapacitiesareoftenrepresentedasfunctionsoftemperature bythesemiempiricalequation:
where a, b,and c areconstantsand T isinkelvins.Empiricalterms withotherpowers Ti areoftenalsoused.
FromEq. (2.17),weobtainthefollowingexpressionfortheheat requiredtoheat1.0molofasubstancefromatemperature T1 toa temperature T2 atconstant P (assumingnophasechangesinthe interval):
Theenthalpycurvecanbemeasuredbythetechniqueofdrop calorimetry,ortheheatcapacitycanbemeasureddirectly byadiabaticcalorimetry.
Thestandardequilibriumtemperatureoffusion(melting) ofFeis1811Kasshownin Fig.2.1.Thefusionreactionisa first-orderphasechange sinceitoccursatconstanttemperature. Thestandardmolarenthalpyoffusion Δhf o is13.807kJmol 1 asshownin Fig.2.1 .Itcanalsobeseenin Fig.2.1 thatFe undergoestwootherfirst-orderphasechanges,thefirstfrom α (bcc)to γ (fcc)Feat T α!γ o ¼ 1184.8Kandthesecondfrom γ to δ (bcc)at1667.5K.Theenthalpychangesare,respectively, 1.013and0.826kJmol 1.TheCurietemperature, Tcurie ¼ 1045K, whichisalsoshownin Fig.2.1,willbediscussedinChapter10. Hence,forexample,theenthalpychangeuponheating1.0mol ofpureFefrom298.15Ktoatemperature T abovethemelting pointisgivenas
where cP α , cP γ , cP δ ,and cPliq arethemolarheatcapacitiesofthe individualphases,eachexpressedbyanequationsimilarto Eq. (2.18).InthecaseofFeandothermagneticmaterials,additionaltermsmustbeaddedto cP α aswillbediscussedin Chapter10.
2.2.1“Absolute”Enthalpy
Nonaturalzeroexistsfortheenthalpybecausethereisnosimplenaturalzerofortheinternalenergy(seeEq. (2.11)).However, byconvention,the“absolute”enthalpyofapureelementinits stablestateat P ¼ 1.0barand T ¼ 298.15Kisoftensettozero. Hence,underthisconvention,the y-axisof Fig.2.1 couldbe labeledsimplyas hT o .
2.2.2StandardEnthalpyofFormation
The standardmolarenthalpyofformation ofacompoundis definedastheenthalpyofformationof1.0molofthepurecompoundinitsstablestatefromthepureelementsintheirstable statesat P ¼ 1.0baratconstanttemperature.So,forexample, ΔH298.15 o ofthereactioninEq. (2.16) isthestandardenthalpyof formationofCO2 at298.15K.
Undertheconventionthatthestandardenthalpiesofthe elementsarezeroat298.15K(Section2.2.1),itthenfollowsthat the“absolute”standardenthalpyofacompoundat298.15Kis equaltoitsstandardenthalpyofformationfromtheelements. Thatis, hCO2(298.15) o ¼ 393.52kJmol 1 .
2.3GibbsEnergy
TheGibbsenergy(alsocalledtheGibbsfreeenergyorsimply thefreeenergy), G,isdefinedas
Asin Section2.2,weconsideraclosedsystemandassumethatthe onlyworktermistheworkofexpansionandthatthisisreversible. FromEqs. (2.13),(2.21),
Consequently,foraprocessoccurringatconstant T and P ina closedsystem,
Considerthecasewherethe“surroundings”aresimplyaheatreservoiratatemperatureequaltothetemperature T ofthesystem. Thatis,noirreversibleprocessesoccurinthesurroundingswhich receiveonlyareversibletransferofheat( dQ)atconstanttemperature.Therefore,fromEq. (2.8),
SubstitutingintoEq. (2.23) andusingEq. (2.3) yields
dGT,P,n ¼ TdS surr T dS ¼ T dStotal 0(2.25)
Eq. (2.25) maybeconsideredtobeaspecialformoftheSecond Lawforaprocessoccurringinaclosedsystematconstant T and P.FromEq. (2.25),suchaprocesswillbespontaneousifdG isnegative.
Forourpurposesinthisbook,Eq. (2.25) isthemostusefulform ofthesecondlaw.
AnobjectionmightberaisedthatEq. (2.25) appliesonlywhen thesurroundingsareatthesametemperature T asthesystem. However,ifthesurroundingsareatadifferenttemperature,we simplypostulateahypotheticalheatreservoirthatisatthesame temperatureasthesystemandthatliesbetweenthesystemand surroundings,andweconsidertheirreversibletransferofheat betweenthereservoirandtherealsurroundingsasasecond separateprocess.
SubstitutingEqs. (2.8),(2.24) intoEq. (2.25) gives
GT,P,n
InEq. (2.26),dQ istheheatoftheactualprocess,whiledQrev isthe heatthatwouldbeobservedweretheprocessoccurringreversibly.Iftheactualprocessisreversible,thatis,ifthesystemisat equilibrium,thendQ ¼ dQrev,anddG ¼ 0.
Asanexample,considerthefusionofFein Fig.2.1.At Tf o ¼ 1811K,solidandliquidareinequilibrium.Thatis,atthis temperature,meltingisareversibleprocess.Therefore,at1811K,
g o f ¼ dho f Tds o f ¼ 0(2.27)
where,again,thesuperscriptsindicatethestandardstateofpure Feat P ¼ 1.0bar.
Therefore,themolarentropyoffusionat1811Kisgivenby
s o f ¼ Δho f =T when T ¼ T o f (2.28)
Similarequationsapplytootherfirst-orderphasechanges.For example,forthe α ➔ γ transitionofFein Fig.2.1,
when
¼ 1184:8K(2.29)
Eq. (2.28) appliesonlyattheequilibriummeltingpoint.Attemperaturesbelowandabovethistemperature,theliquidandsolid arenotinequilibrium.Abovethemeltingpoint, Δgf o < 0,andmeltingisaspontaneousprocess(liquidismorestablethansolid). Belowthemeltingpoint, Δgf o > 0,andthereverseprocess (solidification)isspontaneous.Asthetemperaturedeviates
progressivelyfurtherfromtheequilibriummeltingpoint,the magnitudeof Δgf o,whichisthemagnitudeofthedrivingforce, increases.Weshallreturntothissubjectin Section5.1.
2.4EquilibriumandChemicalReactions
Considerfirstthequestionofwhethersilicafibersinanaluminummatrixat500°Cwillreacttoformmullite,Al6Si2O13:
Ifthereactionproceedswiththeformationof dξ molesofmullite, thenfromthestoichiometryofthereaction,dnSi ¼ (9/2)dξ, dnAl ¼ 6dξ,anddnSiO2 ¼ 13/2dξ.Sincethefoursubstances areessentiallyimmiscibleat500°C,theirGibbsenergiesareequal totheirstandardmolarGibbsenergies, gio (alsoknownasthestandardchemicalpotentials μi o asdefinedin Section2.8),thestandardstateofasolidorliquidcompoundbeingthepure compoundat P ¼ 1.0bar.TheGibbsenergyofthesystemthenvariesas
where ΔGo iscalledthestandardGibbsenergychangeofthereactionEq. (2.30) at500 °C.Since ΔG° < 0,thereactionwillproceed spontaneouslysoastominimize G.Equilibriumwillneverbe attained,andthereactionwillproceedtocompletion.
2.4.1EquilibriaInvolvingaGaseousPhase
An idealgas mixtureisonethatobeysthe idealgasequationof state:
where n isthetotalnumberofmoles.Further,thepartialpressure ofeachgaseousspeciesintheidealmixtureisgivenby
where n ¼ P ni and P ¼ P pi (Dalton’slaw foridealgases). R isthe idealgasconstant.The standardstate ofanidealgaseouscompoundisthepurecompoundatapressureof1.0bar.(See Section2.4.2 forthecaseofnonidealgases.)Itcaneasilybeshown thatthepartialmolarGibbsenergy gi (alsocalledthechemical potential μi asdefinedin Section2.8)ofaspeciesinanideal
(2.34)
gasmixtureisgivenintermsofitsstandardmolarGibbsenergy gi o (alsocalledthestandardchemicalpotential μi o)by gi ¼ g o i + RT ln pi
ThefinalterminEq. (2.34) ispurelyentropic.Asagasexpandsat constanttemperature,itsentropyincreases.
ConsideragaseousmixtureofH2,S2,andH2Swithpartialpressures pH2, pS2,and pH2S.Thegasescanreactaccordingto 2H2 +S2 ¼ 2H2 S (2.35)
Ifthereaction(Eq. 2.35)proceedstotherightwiththeformation of2dξ molesofH2S,thentheGibbsenergyofthesystemvariesas
ΔG,whichistheGibbsenergychangeofthereactioninEq. (2.35), isthusafunctionofthepartialpressures.If ΔG < 0,thenthereactionwillproceedtotherightsoastominimize G.Inaclosedsystem,asthereactioncontinueswiththeproductionofH2S, pH2S willincrease,while pH2 and pS2 willdecrease.Asaresult, ΔG will becomeprogressivelylessnegative.Eventually,anequilibrium statewillbereachedwhendG/dξ ¼ ΔG ¼ 0.
Fortheequilibriumstate,therefore,
where K,the equilibriumconstant ofthereaction,istheone uniquevalueoftheratio( pH2S 2 pH2 2pS21)forwhichthesystemwill beinequilibriumatthetemperature T.Iftheinitialpartialpressuresaresuchthat ΔG > 0,thenthereactioninEq. (2.35) willproceedtotheleftinordertominimize G untiltheequilibrium conditionofEq. (2.37) isattained.
Asafurtherexample,considerthepossibleprecipitationof graphitefromagaseousmixtureofCOandCO2.Thereactionis 2CO ¼ C+CO2 (2.38)
Proceedingasabove,wecanwrite
dG =dξ ¼ gC + gCO2 2gCO ¼
g o C + g o CO2 2g o CO + RT ln pCO2 p 2 CO ¼
ΔG o + RT ln pCO2 p 2 CO ¼ ΔG ¼ RT ln K + RT ln pCO2 p 2 CO (2.39)