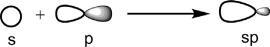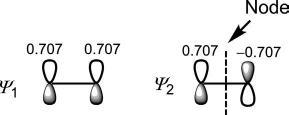MolecularOrbitals
Abasicandpictorialknowledgeofmolecularorbitals(MOs)isessentialfora mechanisticdescriptionofpericyclicreactions.Inthiscontext,asimplified andnonmathematicaldescriptionofMOtheory1–4 ispresentedinthischapter.WeshalldealwiththreekindsofMOs—σ, π and ω withmajoremphasis on π MOs,anddiscusstheirpropertieswithreferencetoorbitalsymmetry, energyandcoefficient.
1.1ATOMICORBITALS
Anatomicorbital(AO)isdescribedbyawavefunction ϕ,where ϕ2 denotes theprobabilityoffindinganelectronatanypointinathree-dimensional space.Thealgebraicsignof ϕ maybepositiveornegative,whichindicates thephaseoftheorbital(cf.thepeaksandtroughsofatransversewave).An orbitalcanhavenodeswhere ϕ ¼ 0.Onoppositesidesofanode, ϕ has oppositesigns.AnAOasagraphicaldescriptionof ϕ showslobeswith a+ora sign(theoppositesignsoftwolobesarealsoindicatedbyunshaded andshadedlobes).Ontheotherhand, ϕ2 isalwayspositivewhether ϕ is positiveornegative.Assuch,therepresentationofAOintermsof ϕ2 is madebydrawinglobeswithoutaphasesign.Thisdrawingreferstothe probabilitydistributionofAOs,andisindicatedinthistextassimplyorbital picture.
1.1.1s,pandHybridOrbitals
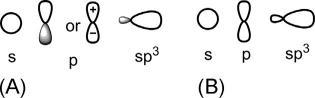
1sorbitalissphericallysymmetricalaboutthenucleusandhasasinglesignof ϕ.Itisrepresentedasacircle,beingonecross-sectionofthesphericalcontour.The2sorbitalisalsosphericallysymmetricalbutpossessesaspherical node.Thenodeisclosetothenucleusandhencetheinnersphereisnot importantforbondingoverlap.The2sorbitalisusuallydrawnasasingle circlewithasinglesignomittingtheinnersphere.
Unlikeansorbital,theporbitalsaredirectional,andorientedalongthe x-, y-and z-axis.Eachporbitalhastwolobeswithoppositesignsandone node(nodalplane).
PericyclicChemistry © 2018ElsevierInc. https://doi.org/10.1016/B978-0-12-814958-4.00001-5 Allrightsreserved.
CarbonhasfourAOs(2s,2px,2py and2pz)thatareavailableforbonding. Thoughthismodelofonesandthreeporbitalsisveryuseful,thereisan alternativemodeloffourAOsofcarbon,basedonPauling’sideaofhybridization.Thehybridizationinvolvesmixingof2sand2porbitalsinvarious proportionstoproduceanewsetofAOs.Mathematically,themixingis takentobethelinearcombinationofatomicorbitals(LCAOs).Such LCAOsonthe sameatom arecalledhybridorbitals.Thecombinationof 2swithone,twoorthreeporbitalscanbeusedindifferentwaystoproduce differentsetsofhybridorbitals,designatedasspn wherenmaybeawhole numberorafraction.Forexample,acombinationof2sandthree2porbitals canbeusedtogeneratefourequivalenthybridorbitalscalledsp3 hybrids. Eachsp3 hybridorbitalhastwolobeswithoppositesigns,butunlikeap orbital,thetwolobesofahybridorbitalhavedifferentsizes.
Theschematicrepresentationsofs,pandsp3 hybridorbitalsareshownin Fig.1.1.In Fig.1.1A,theorbitalsaredrawnasgraphicaldescriptionofwave function(ϕ)showingaphasesignwhile Fig.1.1Bshowstheorbitalpicture intermsof ϕ2 withnophasesign.
Fig.1.1 (A)Sketchofatomicorbitalsintermsof ϕ withaphasesign;(B)orbitalpicturein termsof ϕ2 withoutaphasesign.
Theunequalsizeoftwolobesofahybridorbital,saysp,arisesfrom themixingofsorbitalwithaporbitalonthesameatom(Fig.1.2).The twolobesofporbitalhavethesamesize,butoppositesigns(unshaded andshaded),andthesorbitalhasasinglesign(unshaded).Thecombinationgivesin-phase(samesign)mixingononesideofthenucleus andout-of-phase(differentsigns)mixingontheotherside,leadingto alargelobeontheleftsideandasmalllobeontherightsideofthehybrid orbital.
Fig.1.2 Unequalsizeoftwolobesofahybridorbital.
Table1.1 Energiesofsandpatomicorbitals
1.1.2AtomicOrbitalsofNitrogenandOxygen
Nitrogenandoxygenhavesimilarsetsofs,pandhybridorbitalsasforcarbon.However,theenergiesaredifferent.TherelativeenergiesofanAOon differentatomsfollowtheirpatternofelectronegativity.Anorbitalona moreelectronegativeatomwillhavelowerenergy(Table1.1).5
1.2MOLECULARORBITALS
AnMOisalsodescribedbyawavefunction ψ whichcanbeexpressedasan LCAOs.ThesetofAOschosenforthelinearcombinationiscalledthe basis set.ThetotalnumberofMOswillbeequaltothetotalnumberofAOscombined.ThecalculationofMOsusingallAOsofamoleculepresentsmassive computationalproblems.However,theessentialqualitativefeaturesof bondingcanbeunderstoodifthebasissetisrestrictedjusttothoseAOsthat areinvolvedinaparticulartypeofbonding.MOsaredesignatedbythesymbols σ, π and ω reflectingthetypeofbondingthatoccurs.
NowconsiderthelinearcombinationoftwoAOs ϕ1 and ϕ2 onatoms1 and2.(Notethatthelinearcombinationusesonlythefirstpowerofwave function;cf.equationofastraightline.)TwoMOs ψ 1and ψ 2 areproduced whichareexpressedas
where c1 and c2 arethemixingcoefficientswhichdenotetherelativecontributionsoftheAOs ϕ1 and ϕ2 toanMO.Thecoefficientsmaybepositive, negativeorevenzero.
ThegeometryofapproachofthetwoAOsleadstodifferenttypesof MOs.Thisisillustratedbelowtaking,forexample,theoverlapoftwop AOscentredontwoidenticalatoms(homonuclear),when c1 ¼ c2.
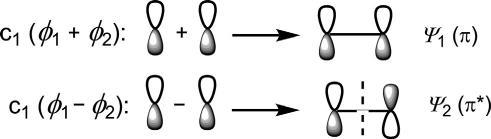
End-onapproach:End-onoverlapoftwoporbitalsgivestwoMOs(ψ 1 and ψ 2)thatarecylindricallysymmetricalabouttheinternuclearaxis(Fig.1.3).
Thesearecalled σ MOs.Here,‘+’combinationsignifiesin-phase(same sign)overlapwhen ψ 1 hasnonode.Incontrast,‘ ’combinationdenotes out-of-phase(oppositesign)overlapleadingtoanode(nodalplane)in ψ 2. TheMO ψ 1 haslowerenergythanpAOandiscalledbonding σ orbital (symbolized σ),while ψ 2 hashigherenergyandiscalledanantibonding σ orbital(σ*).
Fig.1.3 End-onoverlapoftwoporbitalstoproduce σ MOs.
Side-onapproach:Side-on(lateral)overlapoftwoporbitalsproducestwo MOs(ψ 1 and ψ 2)thatarenotcylindricallysymmetricalabouttheinternuclearaxis,andarecalled π MOs(Fig.1.4). ψ 1 haslowerenergywithnonode andisabondingMO(π),while ψ 2 withonenode(nodalplane)isofhigher energyandisanantibondingMO(π*).
Fig.1.4 Side-on(lateral)overlapoftwoporbitalstoproduce π MOs.
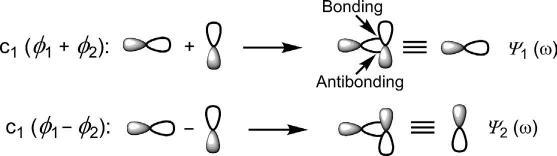
Orthogonalapproach:Fororthogonal(perpendicular)approachoftwop orbitals,bondingoverlapofthesamesigniscancelledbyanantibonding overlapoftheoppositesign(Fig.1.5).Thenetinteractionisthereforenonbonding. ψ 1 and ψ 2 havethesameenergyandareequivalenttoindividualp orbitals.ThesenonbondingMOsarecalled ω MOs.
Fig.1.5 Orthogonalapproachoftwoporbitalstoproduce ω MOs.
Itmaybementionedherethatbesidesnonbonding ω MOs,therearealso nonbonding π MOsthatcanariseinconjugated π systems(seelater).
1.2.1EnergyDiagram
Ingeneral,theinteractionoftwoAOsleadstoapairofbondingandantibondingMOs.Considertheformationof σ and σ* MOsforhydrogenmolecule.Fromquantummechanicalcalculation,theenergy(E )ofanelectron in σ and σ* orbitalisexpressedintermsofthreeintegrals(α, β and S)as
where α istheCoulombintegralwhichdenotestheenergyofanelectronin anisolatedAO; β istheresonanceintegralwhichrepresentstheenergyof interactionbetweentwoAOs;and S istheoverlapintegralwhichindicates theextentofoverlapoftheAOs.
NowwefocusonthenumeratoranddenominatortermsinEqs (1.1), (1.2) α and β arenegativequantities.Therefore,(α + β ) < α (indicatingloweringofenergyof σ)and(α β ) > α (raisingofenergyof σ*).Theoverlap integral S isafunctionofinternucleardistanceandthevalueof S rangesfrom 0to1.Fortwointeractingorbitals, S > 0.Hence,thedenominator(1+ S) > (1 S).Thus,theenergyincreaseassociatedwithantibonding σ* orbitalis slightlygreaterthantheenergydecreaseforbonding σ orbital.Theseresults arepresentedqualitativelyintheMOenergydiagram(Fig.1.6).
Fig.1.6 MOenergydiagramforatwo-orbitalinteraction. x and y indicate,respectively, theenergydecreaseforthebondingorbitalandenergyincreasefortheantibonding orbital.
For π and π* orbitals,asimilarpatternfollows;however,thevalueof S for π overlapismuchsmaller.Ifweassume S ¼ 0,weobtain
where α istheenergyofanelectroninanisolatedporbitaland β represents theenergyofinteractionbetweentwoadjacentporbitals.
1.2.1.1Remarks
TheaboveMOenergydiagramservesqualitativelyageneralpatternfora two-orbitalinteractionthatmayinvolveanyAOsorMOs.Itcanbeseen from Fig.1.6 thatifeachinteractingorbitaliscompletelyfilledproviding atotaloffourelectrons,bothbondingandantibondingorbitalswouldbe completelyfilled.Thenetinteractionwouldthusberepulsivebecause theincreaseinenergyintheantibondingcombinationisgreaterthanthe decreaseinenergyinabondingcombination.Thisrepulsivefilled orbital/filledorbitalinteractionistheunderlyingreasonforthestericstrain (repulsionbetweenclosed-shellmoleculesorgroups),andisincludedinthe firsttermoftheSalem–Klopmanequation(see Section4.1).
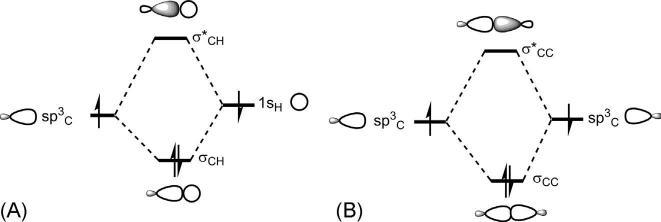
1.2.2C HandC C σ Bonds
AC Hbondisformedbytheinteractionofahybridorbital(say,sp3)of carbonwiththe1sorbitalofhydrogen.Thistwo-orbitalinteractionleadsto bonding σCH andantibonding σ* CH asshownin Fig.1.7A.Notethatthe energyofsp3C ( 16.1eV)issomewhatlowerthanthatof1sH ( 13.6eV).
AC C σ bondisformedbytheend-onoverlapoftwohybridorbitals,one fromeachcarbon. Fig.1.7Bshowstheformationofabonding σCC andan antibonding σ* CC fromtwosp3 hybridorbitals.(Notetheconventional MOsketcheswiththeAOsinsteadofthedelocalizedsketchesofMOs.) Thebonding σ MOhasnonodebetweenlobesofthesamesign,butantibonding σ* MOhasonenodebetweenlobesofoppositesign(shadedand unshaded).
Fig.1.7 BondingandantibondingMOsfor(A)C Hbondand(B)C Cbond.
Weshallseelaterthatthemoreimportantorbitalsinconnectionwith reactivityarethehighestoccupiedmolecularorbital(HOMO)andthelowestunoccupiedmolecularorbital(LUMO).Thesearecalledthefrontier MOs.Thus,forthe σ component(C HorC C),theHOMOis σ andtheLUMOis σ*
BesidesMOs,orbitalpicturerepresentation(withoutphasesign)ofa σ-componentisusedinthemechanisticanalysisofpericyclicreactions.
Fig.1.8 showstheorbitalpicturesofC HandC C σ components. The σ componentislabelledas σ2(2isthenumberofelectronsinthe component).
Fig.1.8 OrbitalpicturesofC HandC C σ components.
1.3H € UCKELMOLECULARORBITAL(HMO)THEORY FORACYCLICCONJUGATED π SYSTEMS
H € uckeltheory1,6 treatsa π systemindependentlyofthe σ framework(the π and σ orbitalsbeingorthogonaltoeachother).TheHMOtheoryassumes thefollowing:
(1) EachCoulombintegral(α)hasthesamevalue.
(2) Theresonanceintegral(β )issameforanytwoadjacentatomsbutzero fortwoatomsnotdirectlybonded.
(3) Theoverlapintegral(S)iszerofortheinteractionbetweentwo porbitals.
Itmightbesurprisingthat S isassumedtobezero,whilethewholeconcept ofchemicalbondingisbasedontheoverlapoforbitals(!).Infact,overlapis notreallyneglectedbecauseitisimplicitlyincludedinotherparameterssuch as β whichisroughlyproportionalto S.Theassumptionthat S ¼ 0greatly simplifiesthecalculation.
The π MOwavefunction(ψ j)isdescribedbyalinearcombinationofp AOs(ϕr)as
where n isthetotalnumberofporbitalsinvolvedand j ¼ 1,2,3,…,n.
Here,weshallconsiderthelinearconjugatedsystemsandobtaintheir π MOsandenergiesusingCoulsonequations7 asfollows:
1.3.1LinearConjugatedSystemWithEvenNumber ofpOrbitals
1.3.1.1Ethylene
Thesimplestsystemisethyleneinwhichtwoporbitals(n ¼ 2)areconjugatedtoeachotherinforminga π bond.AccordingtoEq. (1.3),the MOwavefunctionsare
ThecoefficientsareevaluatedusingEq. (1.4).Thus c11 ¼
0.707.Similarly,
¼
c22 ¼ 0.707.Substitutingthesevalues, weobtain
(Notethatthesignsofcoefficientsarearisingfromthecalculationusing Eq. 1.4.)
Thewavefunctions(π MOs)cannowbesketchedas
Therelativemagnitudesofthecoefficientsareusuallyindicatedbytherelativesizesofthelobes.Herethetwocoefficientshavethesamesizeforboth ψ 1 and ψ 2.For ψ 1,thecoefficientshavethesamesignindicatingin-phase (bonding)overlap.For ψ 2,thecoefficientshaveoppositesignsindicating out-of-phase(antibonding)overlapwhichcreatesanode(nodalplane).
Theenergiesofthe π MOsareestimatedusingEq. (1.5) as
Fig.1.9 showstheMOenergydiagramwhere ψ 1 isabondingMO(π)as ithaslowerenergythantheenergyofporbital(α)and ψ 2 isanantibonding MO(π*)havinganenergyhigherthan α.
Fig.1.9 MOenergydiagramofethylene.
Thegroundstate π electronconfigurationofethyleneis π 2 π*0.Therefore, π isHOMOand π* isLUMO.Athermalpericyclicreactionisa groundstateprocesswhereasaphotochemicalreactionisafirstexcitedstate process.Onphotochemicalexcitationbyabsorptionoflight,oneelectronis promotedfrom π (HOMO)to π* (LUMO)withtheconservationofspin, andtheresultingexcitedstateisasingletwithsinglyoccupied π (formerly HOMO)andsinglyoccupied π* (formerlyLUMO)(Fig.1.10).
Fig.1.10 Frontierorbitalsinthegroundstateandintheexcitedstateofethylene.
Ausefulconvention8 istodesignatethesinglyoccupiedexcitedstate orbitalsofamoleculebyitsformergroundstateHOMO/LUMOlabels.This excitedstatefrontierorbitalconventionasshownin Fig.1.10 willbeused whiledealingwiththefrontierorbitalanalysisofphotochemicalreactions. (Analternativeexcitedstatenomenclaturethatspecifies π* asHOMOand π asNHOMO,nextlowerHOMO,willnotbeusedinthistext.)
Attheinstantofexcitation,thenucleiretaintheplanargroundstate geometry(Frank–Condonprinciple).The π bondorder[½ (no.ofbonding electrons no.ofantibondingelectrons)]intheexcitedstateiszero.The initialplanarexcitedstatethenquicklyrelaxestotheminimumenergy geometryinwhichthetwosp2 carbonsaretwistedbyabout90degrees whenthereisno π overlap(Fig.1.11).Thistwisted,excitedstate,sometimes calledthe pstate,permitsthepossibilityofreturningtoeither E or Z configurationofthegroundstatealkene.
Fig.1.11 Orbitalpicturesofthegroundstateandexcitedstateofethylene.
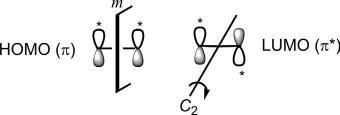
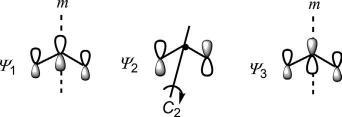
Weshallseelaterthatthephaserelationshipofterminalporbitalsin HOMO/LUMOisimportantinthemechanisticanalysisofpericyclicreactions.Thisphaserelationshipischaracterizedbyorbitalsymmetry. Fig.1.12 showstheorbitalsymmetriesofHOMOandLUMOofethylene.The HOMO(π)hasthesamephaseatthetwoendsandpossessesaplaneofsymmetry(symbolizedby m)sincealobe(labelled *)reflectstoalobeofthesame sign.Notethatthemirrorplane(m)bisectstheC Cbondandisperpendiculartotheplaneofthemolecule.Ontheotherhand,theLUMO(π*)has oppositephasesatthetwoendsandischaracterizedby C2 symmetryasthe C2 operationbringsalobe(labelled *)toapositionofalobewiththesame sign.Notethatthe C2 axisbisectstheC Cbondandislyingintheplaneof themolecule.
Fig.1.12 OrbitalsymmetriesofHOMOandLUMOofethylene.
1.3.1.2Butadiene
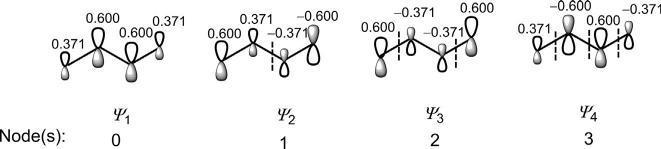
Thebasissetorbitalsofbutadiene(ϕ1–ϕ4)arefourporbitals(n ¼ 4).The wavefunctions(ψ 1–ψ 4)representingfour π MOsarewrittenas
UsingEq. (1.4),
othercoefficientsarecalculatedsimilarly.Weobtain
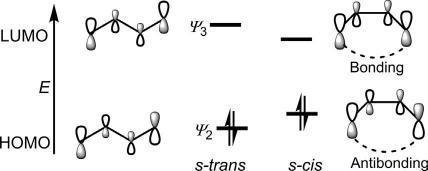
Thewavefunctions(π MOs)ofbutadienecanbesketchedin s-trans or s-cis conformation. Fig.1.13 showsthebutadiene π MOsinmorestable s-trans conformation.(Weshallseelaterthatitisthe s-cis formwhichis thereactivecomponentinmostpericyclicprocesses.)Therelativesizesof thelobesindicatequalitativelytherelativevaluesofthecoefficients.The numberofnodes(indicatedbydashedline)in ψ 1, ψ 2, ψ 3 and ψ 4 is0,1, 2and3,respectively.Thisindicatesthatanorbital ψ j has( j 1)nodes.
Fig.1.13 Sketchesof π MOsofbutadienein s-trans conformation.
Asthenumberofnodesincreases,theenergyoftheorbitalincreasesin theorder: ψ 1 < ψ 2 < ψ 3 < ψ 4.Inanotherfashion,ifwecountthenumberof bonding/antibondinginteractionsbetweentheadjacentporbitals,itisseen that ψ 1 withthreebondingoverlapsand ψ 2 withtwobondingandoneantibondinginteractionsbecomebondingMOswhereas ψ 3 withtwoantibondingandonebondinginteractionsand ψ 4 withthreeantibondinginteractions
becomeantibondingMOs.TheMOenergythereforeincreasesinthesame orderasshownabove.
Theenergiesofthe π MOscanhoweverbeestimatedusingEq. (1.5). Forexample, E1 ¼ α +2β cos π 5 ¼ α +1 618β .Theestimatedenergiesofall π MOsareshownintheMOenergydiagram(Fig.1.14).Notethatthemore positiveorlessnegative β valuesimplyadecreaseinenergy;lesspositiveor morenegative β valuesindicateanincreaseinenergy.
Fig.1.14 MOenergydiagramofbutadiene.
Thebonding/antibondingclassificationofthe π MOsisnowclearlyevident. ψ 1 and ψ 2 haveenergieslowerthantheenergy(α)ofaporbitalandare thereforebondingMOswhereas ψ 3 and ψ 4 areantibondingMOsastheir energiesarehigherthan α. (SincethedecreaseorincreaseinenergyofanMOisconsideredrelative totheenergyoftheAO, α canbearbitrarilyassumedtobezeroandtheMO energycanbeexpressedinonly β terms;howeverinthistextMOenergyis expressedinboth α and β terms,asobtainedfromtheenergyexpression.)
Thegroundstate π electronconfigurationofbutadieneis ψ 1 2 ψ 2 2.Thus, ψ 2 isHOMOand ψ 3 isLUMO.Inthefirstexcitedstate,oneelectronispromotedfrom ψ 2 (HOMO)to ψ 3 (LUMO).Asperthefrontierorbitalconventionusedinthistext(seep.10),thesinglyoccupied ψ 2 and ψ 3 also representHOMOandLUMOinthefirstexcitedstate.
TheHOMO/LUMOenergiesin s-trans and s-cis conformationsofbutadienearenotthesame.In s-cis conformation,theHOMOenergyisraised andtheLUMOenergyisloweredrelativetothoseinthe s-trans form (Fig.1.15).Unlikethe s-trans form,the s-cis conformationhasapossible interactionbetweenthetwoterminalporbitals.Anantibondinginteraction raisestheHOMOenergy,whileabondinginteractionlowerstheLUMO energyin s-cis conformation.
Fig.1.15 Relativeenergiesoffrontierorbitalsin s-trans and s-cis conformationsof butadiene.
Infrontierorbitalanalysis,thehigherenergyHOMOandlowerenergy LUMOwouldmakethe s-cis-butadienemorereactivethan s-transbutadieneinpericyclicreactions.Itmaybementionedherethatthelower HOMO/LUMOenergygapin s-cis conformationleadstoUVabsorptionat alongerwavelength(253nm)forahomoannulardienelockedin s-cis conformationcomparedwitha λmax of215nmforanacyclicoraheteroannular dieneexistingpredominantlyorexclusivelyin s-trans conformation.
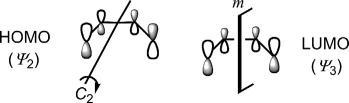
Theorbitalsymmetryoffrontierorbitalsisimportantinthecontextof mechanismofpericyclicreactions. Fig.1.16 showsthattheHOMOhasthe oppositephaserelationshipatthetwoterminiandischaracterizedby C2 symmetrywhiletheLUMOwiththesamephaserelationshipatthetwo endsexhibits m symmetry.
Fig.1.16 Orbitalsymmetriesof ΗΟΜΟ andLUMOofbutadiene.
1.3.1.3Hexatriene
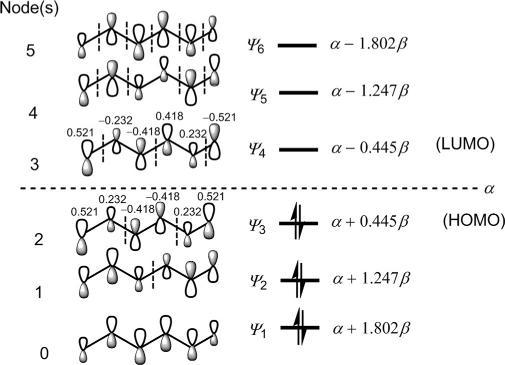
1,3,5-Hexatrieneisaconjugated π systemofsixporbitals(n ¼ 6).UsingEqs (1.3),(1.4),thewavefunctions(ψ 1 – ψ 6)forsix π MOsareobtainedasfollows:
Notethepatterninthesize(notsign)ofcoefficients:thefirstthreeand lastthreevaluesineachMOholdamirrorimagerelationship.Theenergies ofthe π MOsareestimatedusingEq. (1.5).Forinstance, E3 ¼ α +2β cos 3π 7 ¼ α +0 445β .Thesketchesofsix π MOs,theirnodal propertiesandenergiesareshownin Fig.1.17.Itisevidentthatthesix π MOsconstitutethreebondingandthreeantibondingMOs.
Inthegroundstate,the π electronconfigurationofhexatrieneis ψ 1 2 ψ 2 2 ψ 3 2 . Thus, ψ 3 isHOMOand ψ 4 isLUMO.Inthefirstexcitedstate, ψ 3 and ψ 4 alsorepresentHOMOandLUMOwheneachishalf-filled.(OnlyHOMO andLUMOarelabelledwithcoefficientvaluesinthefigure.)
MOenergydiagramandsketchesofthe π MOsof1,3,5-hexatriene.
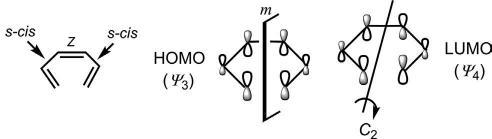
Inpericyclicreactions,thetwoterminiofthehexatrienecomponent oughttobegenerallyclosetoeachother.Thisisachievedwhenthemiddle doublebondis Z andthemoleculeadopts s-cis conformation.Thesymmetry ofthefrontierorbitalsofhexatrieneisshownin Fig.1.18.TheHOMOhas m symmetrywhiletheLUMOischaracterizedby C2 symmetry.
Fig.1.18 Orbitalsymmetriesof ΗΟΜΟ andLUMOof1,3,5-hexatriene.
Fig.1.17
1.3.2LinearConjugatedSystemWithOddNumber ofpOrbitals
Wehaveseenthatthe π MOsofaconjugatedsystem(n ¼ even)comprise equalnumberofbondingandantibondingMOs.When n ¼ odd,theconjugated π systemisareactiveintermediate(carbocation,carbanionorcarbon radical)whenthe π MOswillcontainanonbondingMObesidesbonding andantibondingorbitalsasdescribedbelow.
1.3.2.1AllylSystem
Theallylsystem(cation,radicaloranion) representsaconjugated systemofthreeporbitals(n ¼ 3).Thewavefunctions(ψ 1–ψ 3)forthree π MOsare,accordingtoEq. (1.3),givenby
ThecoefficientsareevaluatedusingEq. (1.4).Forinstance, c21 ¼
¼ 0.Withthecalculatedvaluesof thecoefficients,thewavefunctionsare
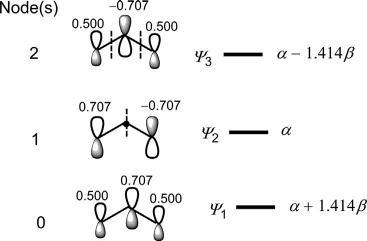
In ψ 2,thecoefficientof ϕ2 iszerowhichindicatesthatthereisnocontributionof ϕ2 to ψ 2.Physically,thisimpliesthat ϕ2 isorthogonalto ϕ1 and ϕ3 in ψ 2.Theenergiesofthe π MOscanbeestimatedusingEq. (1.5).The sketchesoftheMOs,theirnodalpropertiesandtheestimatedenergiesare shownin Fig.1.19.Thenodalpropertiesindicatethat ψ j hasagain( j – 1) nodes,asobservedforthesystemwithevennumberofporbitals.Incase of ψ 2,anodepassesthroughthemiddlecarbonC-2.Theenergyof ψ 2 is α,whichissameastheenergyofaporbital,andhence ψ 2 isanonbonding MO.Itisseenthat ψ 1 isbondingand ψ 3 isantibonding.Thus,thethree π MOsofanallylsystemcompriseabonding,anonbondingandan antibondingMO.
Thefrontierorbitalsofanallylsystemdependonwhetheritisacation,a radicalorananion.Thenumberof π electronsinallylcation,radicaland anionis2,3and4,respectively.Thefrontierorbitalsaregivenbelow:
Fig.1.19 Thecoefficients,nodalpropertiesandenergiesofthe π MOsofanallylsystem.
ψ 1 2) Allylradical(ψ 1 2 ψ 2 1)Allylanion(ψ 1 2 ψ 2 2)
1
2
2
2 ψ 3
Thefrontierorbitalforanallylradicalis ψ 2 whichisasinglyoccupied molecularorbital(SOMO).Thesymmetrypropertiesofthe π MOsare shownin Fig.1.20
Fig.1.20 Orbitalsymmetriesof π MOsofanallylsystem.
Problem1.1
Derivethe π MOsofapentadienylsystemusingCoulsonequations.Sketch theMOsin s-cis conformationofthemoleculeshowingnode(s).Indicate thefrontierorbitalsforcation,anionandradicalspecieswithsymmetry.
Answer
Thepentadienylsystem(cation,radicaloranion)is The π MOs(ψ 1 – ψ 5)andtheirenergiesarederivedas
Allylcation(
Theenergiesindicatethat ψ 1 and ψ 2 arebondingMOs; ψ 3 isa nonbondingMO;and ψ 4 and ψ 5 areantibondingMOs.
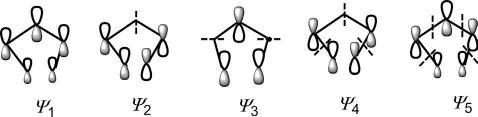
Thesketchesofthe π MOsareshownbelow.Itisseenthatanorbital ψj has( j – 1)nodes.
Thefrontierorbitalsforthepentadienylcation,radicalandanion,and theirsymmetryaregivenbelow:
1.3.2.2AShort-CutMethodforSketching π MOs
Thesketchesofthe π MOscanbesimplifiedbyignoringthedifferenceof coefficients,wherethecoefficientsarenotimportantinamechanistic descriptionofpericyclicreactions.Ashort-cutmethodtodrawingsucha simplifiedpictureof π MOsistousethenodalpropertieswhichindicatethat anMO ψ j has(j – 1)nodes.Theprocedureisillustratedforthedrawingof frontierorbitalsin Fig.1.21.Notethatthenodesaretobeplacedinthemost symmetricalmannerintheprospectiveMO.
Thesymmetrypropertiesofthe π MOscanbesummarizedasfollows:
ψ j ( j ¼ odd) ) m symmetry;
ψ j ( j ¼ even) ) C2 symmetry.
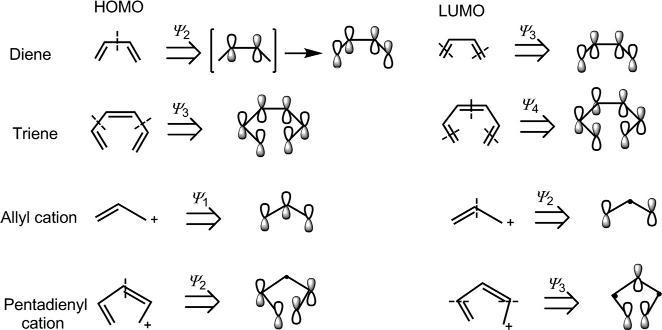
BesidestheMOs,orbitalpicturerepresentation(withoutphasesign)of the π componentsisalsousedinmechanisticanalysisofpericyclicreactions. Theorbitalpicturesofthedieneandtrienecomponentsaresketchedas
Fig.1.21 Sketchesoffrontierorbitalsfromnodalproperties.
1.4CARBONYL π SYSTEM
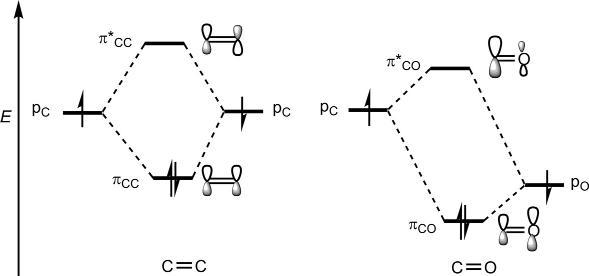
Thesymmetrypropertiesof π MOsofthecarbonylsystemaresimilarto thoseofalkenes;however,theenergyandcoefficientpatternsdiffer.The energyofaporbitalonoxygen( 15.9eV)ismuchlowerthanthatoncarbon( 10.7eV)(see Table1.1).Thiswouldleadtoloweringofenergyof both πCO and π* CO comparedwiththoseforalkene(Fig.1.22).
Forthecarbonylgroup,thelowerenergypO wouldcontributemoreto thelowerenergy πCO andthehigherenergypC wouldcontributemoreto thehigherenergy π*CO.Asaresult,therewillbealargercoefficientonoxygenin πCO andalargercoefficientoncarbonin π* CO asshownin Fig.1.22 πCO isHOMOand π* CO isLUMO,thepolarizationofHOMOand
Fig.1.22 Energydiagramof π MOsofcarbonylgroupvis-a-visalkene π MOs.
LUMObeingopposite.Thepresenceoflow-lyingLUMOwithalarge coefficientoncarbonmakesthecarbonylgroupaparticularlyimportant electron-withdrawingsubstituentorareactivecomponentinpericyclic reactions.
1.5EFFECTOFSUBSTITUENTSONFRONTIERORBITAL ENERGIESANDCOEFFICIENTSOF π SYSTEMS
Aqualitativepictureoftheperturbationeffectsofdifferenttypesofsubstituentsonthefrontierorbitalenergiesandcoefficientsof π systemsisnecessary torationalizethefeaturesofreactivityandselectivityincycloadditions andotherpericyclicprocesses.Thesubstituentsaregenerallyclassifiedas follows:
•c-Substituents:Thesearesimpleconjugatingsubstituentssuchasvinyl, Phetc.Theycanactas π donorsoras π acceptorsbasedontheelectron demandoftheparent π system.
•z-Substituents:Theseindicateconjugatingandelectron-withdrawing substituentssuchasCOR,CO2R,CN,NO2,SiR3,BR2 etc.They actas π acceptors.
•x-Substituents:Thesedenotetheelectron-donatingsubstituentssuchas OR,NR2,R(alkyl)etc.Theyactas π donors.
1.5.1HOMO/LUMOEnergiesandCoefficients ofSubstitutedAlkenes
Theunsubstitutedalkene(ethylene)isthereferenceorunperturbedalkene. Aperturbedalkenesystemisrepresentedbyc-,z-orx-substitutedalkene. Thepatternsoffrontierorbitalenergiesandcoefficientsfortheperturbed systemsvis-a-visunperturbedalkenecanbedeterminedbychoosingareasonablemodelforeachsubstitutedalkene.Anall-carbonmodelforwhich HMOenergiesandcoefficientsareknownisthepreferredchoicetodrawa qualitativeinference.
1.5.1.1Perturbationbyc-Substituents
Sinceac-substituentisaneutralconjugatingsubstituent(e.g.CH]CH2),a reasonablemodelforac-substitutedalkeneisbutadiene: