PERICYCLIC CHEMISTRY
OrbitalMechanismsand Stereochemistry
DIPAKK.MANDAL
FormerlyofPresidencyCollege/University Kolkata,India
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
© 2018ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyany means,electronicormechanical,includingphotocopying,recording,oranyinformation storageandretrievalsystem,withoutpermissioninwritingfromthepublisher.Detailson howtoseekpermission,furtherinformationaboutthePublisher’spermissionspolicies andourarrangementswithorganizationssuchastheCopyrightClearanceCenterandthe CopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions.
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyright bythePublisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchand experiencebroadenourunderstanding,changesinresearchmethods,professionalpractices, ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledge inevaluatingandusinganyinformation,methods,compounds,orexperimentsdescribed herein.Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafety andthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors, assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterof productsliability,negligenceorotherwise,orfromanyuseoroperationofanymethods, products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary ISBN:978-0-12-814958-4
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: JohnFedor
AcquisitionEditor: EmilyMcCloskey
EditorialProjectManager: BillieJeanFernandez
ProductionProjectManager: PaulPrasadChandramohan
CoverDesigner: MarkRogers
TypesetbySPiGlobal,India
Dedicatedtothememoryofmyparents.
PREFACE
Itisabout50yearssincetheappearanceofthepioneeringworkof R.B.WoodwardandR.Hoffmannonthetheoryofconservationoforbital symmetryinconcertedreactions.Thewordpericyclicwasintroducedin1969 andtheapplicationoftheconceptoforbitalsymmetrytopericyclicreactions provedtobeamajorturningpointinunderstandingorganicreactionmechanisms.The1981NobelPrizeinChemistrywasawardedtoK.Fukuiand R.Hoffmannfordevelopingtheoriesofpericyclicreactions(Woodwarddied in1979attheageof62andcouldnotsharethisprize;however,hewonthe NobelPrizein1965forhisworkonorganicsynthesis).Pericyclicreactions havearemarkablequalityofbeingmanifold,extremelyelegant,andhighly useful;theyrevealstereochemicalintricaciesandidiosyncrasiesandremain asanintegralpartofchemistryteachingandresearch.
Pericyclicchemistryiscoveredineverygraduatecourseandinadvanced undergraduatecoursesinorganicchemistry.Ergo,thisbookisaddressed principallytoanaudienceofgraduateandadvancedundergraduatestudents. Thepurposeofwritingthisbookisentirelypedagogic,keepinginview thatourstudentscraveunderstanding,notfactualknowledgealone.The bookevolvesfromaseriesoflecturenotesandstudents’feedbackduring myteachingthiscoursetograduatestudentsformorethan20years.The mechanisticdescriptionsandthestereochemistryresultingfromorbital mechanismsareattheheartofthisbook;thesynthesisofspecifictarget moleculeshasbeengenerallygivenshortshrift.
Thebookcontainselevenchapters.Anintroductiontomolecularorbital theory(Chapter1)andrelevantstereochemicalconcepts(Chapter2)have beenprovidedasabackgroundaidtofollowthechaptersonpericyclic chemistry.Intheintroductorychapter(Chapter3),Ihaveintroducedall fourclassesofpericyclicreactionsinvolvingthreemechanisticapproaches linkedthroughorbitalpicturerepresentation.Thisunifyingandintegrated stylewouldhelpenhancethepedagogyofthistext.Thequalitativeperturbationmolecularorbitaltheoryhasbeenincorporatedasthemostaccessible andusefulapproachtounderstandingmanyaspectsofreactivityandselectivity.Threechapters(Chapters4–6)havebeendevotedtocycloadditions, themostversatileclass,onetoelectrocyclicreactions(Chapter7),twoto sigmatropicrearrangements(Chapters8and9),andonetogrouptransfer reactions(Chapter10).Aseparatechapter(Chapter11)isincludedto
illustratetheconstructionofcorrelationdiagramsinapractical, ‘how-to-do-it’manner.
Besidestheunifyingapproachofmechanisticdiscussion,themost importantdifferencebetweenthisbookandothersistheemphasisonstereochemistry,specificallyhowtodelineatethestereochemistryofproducts. Ihavefoundthatstudentsarenotoftenquitecomfortabletoworkstereochemistryforthemselves.Afterall,reactionstereochemistryisnoteasy! Studentsneedsomemorehelp.Toaddresstheirconcerns,Ihavealways beenlookingforinnovativeapproachestostereochemicalissues.Myefforts haveresultedinformulatingsimplestereochemicalrules/guidelines,someof whichhavebeenpublishedinthe JournalofChemicalEducation.Thesepublished(alsosomeunpublished)rules/mnemonicshavebeenusedextensively intherelevantchaptersasanaidtowritequicklyandcorrectlytheproduct stereochemistryinpericyclicreactions.
Usually,theproblemsetsaregivenattheendofchapterswithoutorwith answerkeys.OnepedagogicaldecisionIhavemadewithrespecttoproblem setsisthatmorethan130problemsareinsertedwithinthechapterswith detailedworkedsolutions,reinforcingthemainthemesinthetext.Itis hopedthatstudentscouldtesttheirlearningimmediatelywhilereading throughthechapters.Theseproblemsetsshouldbeconsideredanintegral partofthecourse.Alistofselectivereferencestoprimaryandreviewliteratureisincludedattheendofeachchapter.Thesereferences(about550) wouldenablethestudentsattheadvancedlevelstosupplementthematerials coveredinthechapters.
Theapproachpresentedinthisbookisdistinctandclass-tested.Ihope thisbookwillbeofvalueandinteresttothestudents,teachers,and researchersoforganicchemistry.Iencouragethereaderstocontactme (dm.pcchem@gmail.com)withcomments,corrections,andwithsuggestionsthatmightbeappropriateforfutureeditions.
Iwouldliketothankthereviewersforhelpfulsuggestions.Specialthanks areduetomyundergraduate,graduate,andresearchstudentsfortheirloving insistence,help,andencouragementinwritingthisbook.Iamgratefultothe editorialmembersEmilyM.McCloskeyandBillieJeanFernandez,productionmanager,andotherpeopleatElsevierfortheirexcellentsupportand cooperation.Finally,Ithankmyfamily,inparticularmydaughterSudipta, forhercontinuoussupportandmysonTirthaforhisactivehelpinreferencing.
MolecularOrbitals
Abasicandpictorialknowledgeofmolecularorbitals(MOs)isessentialfora mechanisticdescriptionofpericyclicreactions.Inthiscontext,asimplified andnonmathematicaldescriptionofMOtheory1–4 ispresentedinthischapter.WeshalldealwiththreekindsofMOs—σ, π and ω withmajoremphasis on π MOs,anddiscusstheirpropertieswithreferencetoorbitalsymmetry, energyandcoefficient.
1.1ATOMICORBITALS
Anatomicorbital(AO)isdescribedbyawavefunction ϕ,where ϕ2 denotes theprobabilityoffindinganelectronatanypointinathree-dimensional space.Thealgebraicsignof ϕ maybepositiveornegative,whichindicates thephaseoftheorbital(cf.thepeaksandtroughsofatransversewave).An orbitalcanhavenodeswhere ϕ ¼ 0.Onoppositesidesofanode, ϕ has oppositesigns.AnAOasagraphicaldescriptionof ϕ showslobeswith a+ora sign(theoppositesignsoftwolobesarealsoindicatedbyunshaded andshadedlobes).Ontheotherhand, ϕ2 isalwayspositivewhether ϕ is positiveornegative.Assuch,therepresentationofAOintermsof ϕ2 is madebydrawinglobeswithoutaphasesign.Thisdrawingreferstothe probabilitydistributionofAOs,andisindicatedinthistextassimplyorbital picture.
1.1.1s,pandHybridOrbitals
1sorbitalissphericallysymmetricalaboutthenucleusandhasasinglesignof ϕ.Itisrepresentedasacircle,beingonecross-sectionofthesphericalcontour.The2sorbitalisalsosphericallysymmetricalbutpossessesaspherical node.Thenodeisclosetothenucleusandhencetheinnersphereisnot importantforbondingoverlap.The2sorbitalisusuallydrawnasasingle circlewithasinglesignomittingtheinnersphere.
Unlikeansorbital,theporbitalsaredirectional,andorientedalongthe x-, y-and z-axis.Eachporbitalhastwolobeswithoppositesignsandone node(nodalplane).
PericyclicChemistry © 2018ElsevierInc. https://doi.org/10.1016/B978-0-12-814958-4.00001-5 Allrightsreserved.
Thesearecalled σ MOs.Here,‘+’combinationsignifiesin-phase(same sign)overlapwhen ψ 1 hasnonode.Incontrast,‘ ’combinationdenotes out-of-phase(oppositesign)overlapleadingtoanode(nodalplane)in ψ 2. TheMO ψ 1 haslowerenergythanpAOandiscalledbonding σ orbital (symbolized σ),while ψ 2 hashigherenergyandiscalledanantibonding σ orbital(σ*).
Fig.1.3 End-onoverlapoftwoporbitalstoproduce σ MOs.
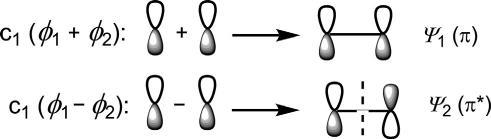
Side-onapproach:Side-on(lateral)overlapoftwoporbitalsproducestwo MOs(ψ 1 and ψ 2)thatarenotcylindricallysymmetricalabouttheinternuclearaxis,andarecalled π MOs(Fig.1.4). ψ 1 haslowerenergywithnonode andisabondingMO(π),while ψ 2 withonenode(nodalplane)isofhigher energyandisanantibondingMO(π*).
Fig.1.4 Side-on(lateral)overlapoftwoporbitalstoproduce π MOs.
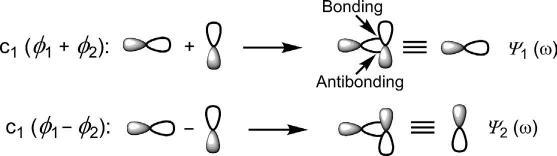
Orthogonalapproach:Fororthogonal(perpendicular)approachoftwop orbitals,bondingoverlapofthesamesigniscancelledbyanantibonding overlapoftheoppositesign(Fig.1.5).Thenetinteractionisthereforenonbonding. ψ 1 and ψ 2 havethesameenergyandareequivalenttoindividualp orbitals.ThesenonbondingMOsarecalled ω MOs.
Fig.1.5 Orthogonalapproachoftwoporbitalstoproduce ω MOs.
Itmaybementionedherethatbesidesnonbonding ω MOs,therearealso nonbonding π MOsthatcanariseinconjugated π systems(seelater).
Weshallseelaterthatthemoreimportantorbitalsinconnectionwith reactivityarethehighestoccupiedmolecularorbital(HOMO)andthelowestunoccupiedmolecularorbital(LUMO).Thesearecalledthefrontier MOs.Thus,forthe σ component(C HorC C),theHOMOis σ andtheLUMOis σ*
BesidesMOs,orbitalpicturerepresentation(withoutphasesign)ofa σ-componentisusedinthemechanisticanalysisofpericyclicreactions.
Fig.1.8 showstheorbitalpicturesofC HandC C σ components. The σ componentislabelledas σ2(2isthenumberofelectronsinthe component).
Fig.1.8 OrbitalpicturesofC HandC C σ components.
1.3H € UCKELMOLECULARORBITAL(HMO)THEORY FORACYCLICCONJUGATED π SYSTEMS
H € uckeltheory1,6 treatsa π systemindependentlyofthe σ framework(the π and σ orbitalsbeingorthogonaltoeachother).TheHMOtheoryassumes thefollowing:
(1) EachCoulombintegral(α)hasthesamevalue.
(2) Theresonanceintegral(β )issameforanytwoadjacentatomsbutzero fortwoatomsnotdirectlybonded.
(3) Theoverlapintegral(S)iszerofortheinteractionbetweentwo porbitals.
Itmightbesurprisingthat S isassumedtobezero,whilethewholeconcept ofchemicalbondingisbasedontheoverlapoforbitals(!).Infact,overlapis notreallyneglectedbecauseitisimplicitlyincludedinotherparameterssuch as β whichisroughlyproportionalto S.Theassumptionthat S ¼ 0greatly simplifiesthecalculation.
The π MOwavefunction(ψ j)isdescribedbyalinearcombinationofp AOs(ϕr)as
where n isthetotalnumberofporbitalsinvolvedand j ¼ 1,2,3,…,n.
Here,weshallconsiderthelinearconjugatedsystemsandobtaintheir π MOsandenergiesusingCoulsonequations7 asfollows:
1.3.1LinearConjugatedSystemWithEvenNumber ofpOrbitals
1.3.1.1Ethylene
Thesimplestsystemisethyleneinwhichtwoporbitals(n ¼ 2)areconjugatedtoeachotherinforminga π bond.AccordingtoEq. (1.3),the MOwavefunctionsare
ThecoefficientsareevaluatedusingEq. (1.4).Thus c11 ¼
0.707.Similarly,
¼
c22 ¼ 0.707.Substitutingthesevalues, weobtain
(Notethatthesignsofcoefficientsarearisingfromthecalculationusing Eq. 1.4.)
Thewavefunctions(π MOs)cannowbesketchedas
Therelativemagnitudesofthecoefficientsareusuallyindicatedbytherelativesizesofthelobes.Herethetwocoefficientshavethesamesizeforboth ψ 1 and ψ 2.For ψ 1,thecoefficientshavethesamesignindicatingin-phase (bonding)overlap.For ψ 2,thecoefficientshaveoppositesignsindicating out-of-phase(antibonding)overlapwhichcreatesanode(nodalplane).
1.3.1.2Butadiene
Thebasissetorbitalsofbutadiene(ϕ1–ϕ4)arefourporbitals(n ¼ 4).The wavefunctions(ψ 1–ψ 4)representingfour π MOsarewrittenas
UsingEq. (1.4),
othercoefficientsarecalculatedsimilarly.Weobtain
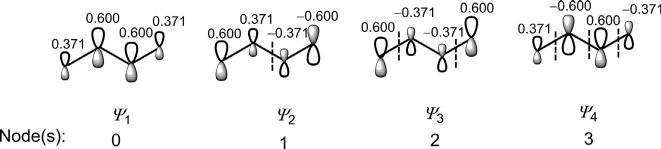
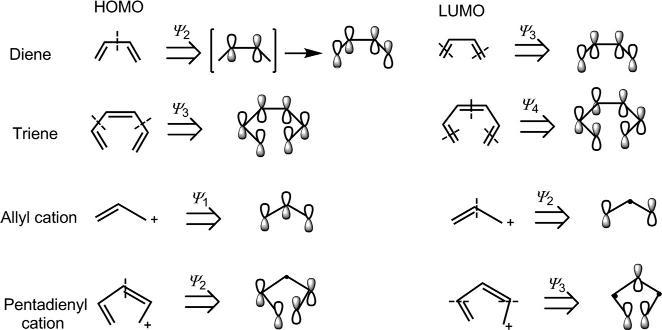
Thewavefunctions(π MOs)ofbutadienecanbesketchedin s-trans or s-cis conformation. Fig.1.13 showsthebutadiene π MOsinmorestable s-trans conformation.(Weshallseelaterthatitisthe s-cis formwhichis thereactivecomponentinmostpericyclicprocesses.)Therelativesizesof thelobesindicatequalitativelytherelativevaluesofthecoefficients.The numberofnodes(indicatedbydashedline)in ψ 1, ψ 2, ψ 3 and ψ 4 is0,1, 2and3,respectively.Thisindicatesthatanorbital ψ j has( j 1)nodes.
Fig.1.13 Sketchesof π MOsofbutadienein s-trans conformation.
Asthenumberofnodesincreases,theenergyoftheorbitalincreasesin theorder: ψ 1 < ψ 2 < ψ 3 < ψ 4.Inanotherfashion,ifwecountthenumberof bonding/antibondinginteractionsbetweentheadjacentporbitals,itisseen that ψ 1 withthreebondingoverlapsand ψ 2 withtwobondingandoneantibondinginteractionsbecomebondingMOswhereas ψ 3 withtwoantibondingandonebondinginteractionsand ψ 4 withthreeantibondinginteractions
becomeantibondingMOs.TheMOenergythereforeincreasesinthesame orderasshownabove.
Theenergiesofthe π MOscanhoweverbeestimatedusingEq. (1.5). Forexample, E1 ¼ α +2β cos π 5 ¼ α +1 618β .Theestimatedenergiesofall π MOsareshownintheMOenergydiagram(Fig.1.14).Notethatthemore positiveorlessnegative β valuesimplyadecreaseinenergy;lesspositiveor morenegative β valuesindicateanincreaseinenergy.
Fig.1.14 MOenergydiagramofbutadiene.
Thebonding/antibondingclassificationofthe π MOsisnowclearlyevident. ψ 1 and ψ 2 haveenergieslowerthantheenergy(α)ofaporbitalandare thereforebondingMOswhereas ψ 3 and ψ 4 areantibondingMOsastheir energiesarehigherthan α. (SincethedecreaseorincreaseinenergyofanMOisconsideredrelative totheenergyoftheAO, α canbearbitrarilyassumedtobezeroandtheMO energycanbeexpressedinonly β terms;howeverinthistextMOenergyis expressedinboth α and β terms,asobtainedfromtheenergyexpression.)
Thegroundstate π electronconfigurationofbutadieneis ψ 1 2 ψ 2 2.Thus, ψ 2 isHOMOand ψ 3 isLUMO.Inthefirstexcitedstate,oneelectronispromotedfrom ψ 2 (HOMO)to ψ 3 (LUMO).Asperthefrontierorbitalconventionusedinthistext(seep.10),thesinglyoccupied ψ 2 and ψ 3 also representHOMOandLUMOinthefirstexcitedstate.
TheHOMO/LUMOenergiesin s-trans and s-cis conformationsofbutadienearenotthesame.In s-cis conformation,theHOMOenergyisraised andtheLUMOenergyisloweredrelativetothoseinthe s-trans form (Fig.1.15).Unlikethe s-trans form,the s-cis conformationhasapossible interactionbetweenthetwoterminalporbitals.Anantibondinginteraction raisestheHOMOenergy,whileabondinginteractionlowerstheLUMO energyin s-cis conformation.
1.3.2LinearConjugatedSystemWithOddNumber ofpOrbitals
Wehaveseenthatthe π MOsofaconjugatedsystem(n ¼ even)comprise equalnumberofbondingandantibondingMOs.When n ¼ odd,theconjugated π systemisareactiveintermediate(carbocation,carbanionorcarbon radical)whenthe π MOswillcontainanonbondingMObesidesbonding andantibondingorbitalsasdescribedbelow.
1.3.2.1AllylSystem
Theallylsystem(cation,radicaloranion) representsaconjugated systemofthreeporbitals(n ¼ 3).Thewavefunctions(ψ 1–ψ 3)forthree π MOsare,accordingtoEq. (1.3),givenby
ThecoefficientsareevaluatedusingEq. (1.4).Forinstance, c21 ¼
¼ 0.Withthecalculatedvaluesof thecoefficients,thewavefunctionsare
In ψ 2,thecoefficientof ϕ2 iszerowhichindicatesthatthereisnocontributionof ϕ2 to ψ 2.Physically,thisimpliesthat ϕ2 isorthogonalto ϕ1 and ϕ3 in ψ 2.Theenergiesofthe π MOscanbeestimatedusingEq. (1.5).The sketchesoftheMOs,theirnodalpropertiesandtheestimatedenergiesare shownin Fig.1.19.Thenodalpropertiesindicatethat ψ j hasagain( j – 1) nodes,asobservedforthesystemwithevennumberofporbitals.Incase of ψ 2,anodepassesthroughthemiddlecarbonC-2.Theenergyof ψ 2 is α,whichissameastheenergyofaporbital,andhence ψ 2 isanonbonding MO.Itisseenthat ψ 1 isbondingand ψ 3 isantibonding.Thus,thethree π MOsofanallylsystemcompriseabonding,anonbondingandan antibondingMO.
Thefrontierorbitalsofanallylsystemdependonwhetheritisacation,a radicalorananion.Thenumberof π electronsinallylcation,radicaland anionis2,3and4,respectively.Thefrontierorbitalsaregivenbelow:
Fig.1.19 Thecoefficients,nodalpropertiesandenergiesofthe π MOsofanallylsystem.
ψ 1 2) Allylradical(ψ 1 2 ψ 2 1)Allylanion(ψ 1 2 ψ 2 2)
1
2
2
2 ψ 3
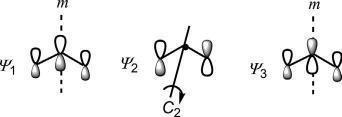
Thefrontierorbitalforanallylradicalis ψ 2 whichisasinglyoccupied molecularorbital(SOMO).Thesymmetrypropertiesofthe π MOsare shownin Fig.1.20
Fig.1.20 Orbitalsymmetriesof π MOsofanallylsystem.
Problem1.1
Derivethe π MOsofapentadienylsystemusingCoulsonequations.Sketch theMOsin s-cis conformationofthemoleculeshowingnode(s).Indicate thefrontierorbitalsforcation,anionandradicalspecieswithsymmetry.
Answer
Thepentadienylsystem(cation,radicaloranion)is The π MOs(ψ 1 – ψ 5)andtheirenergiesarederivedas
Allylcation(
Fig.1.21 Sketchesoffrontierorbitalsfromnodalproperties.
1.4CARBONYL π SYSTEM
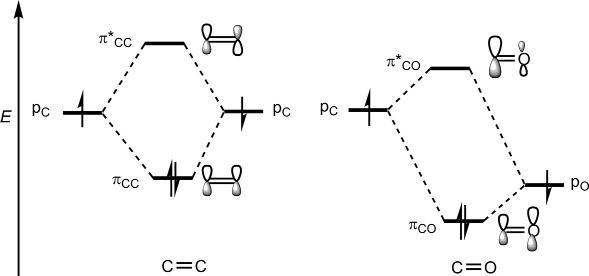
Thesymmetrypropertiesof π MOsofthecarbonylsystemaresimilarto thoseofalkenes;however,theenergyandcoefficientpatternsdiffer.The energyofaporbitalonoxygen( 15.9eV)ismuchlowerthanthatoncarbon( 10.7eV)(see Table1.1).Thiswouldleadtoloweringofenergyof both πCO and π* CO comparedwiththoseforalkene(Fig.1.22).
Forthecarbonylgroup,thelowerenergypO wouldcontributemoreto thelowerenergy πCO andthehigherenergypC wouldcontributemoreto thehigherenergy π*CO.Asaresult,therewillbealargercoefficientonoxygenin πCO andalargercoefficientoncarbonin π* CO asshownin Fig.1.22 πCO isHOMOand π* CO isLUMO,thepolarizationofHOMOand
Fig.1.22 Energydiagramof π MOsofcarbonylgroupvis-a-visalkene π MOs.
LUMObeingopposite.Thepresenceoflow-lyingLUMOwithalarge coefficientoncarbonmakesthecarbonylgroupaparticularlyimportant electron-withdrawingsubstituentorareactivecomponentinpericyclic reactions.
1.5EFFECTOFSUBSTITUENTSONFRONTIERORBITAL ENERGIESANDCOEFFICIENTSOF π SYSTEMS
Aqualitativepictureoftheperturbationeffectsofdifferenttypesofsubstituentsonthefrontierorbitalenergiesandcoefficientsof π systemsisnecessary torationalizethefeaturesofreactivityandselectivityincycloadditions andotherpericyclicprocesses.Thesubstituentsaregenerallyclassifiedas follows:
•c-Substituents:Thesearesimpleconjugatingsubstituentssuchasvinyl, Phetc.Theycanactas π donorsoras π acceptorsbasedontheelectron demandoftheparent π system.
•z-Substituents:Theseindicateconjugatingandelectron-withdrawing substituentssuchasCOR,CO2R,CN,NO2,SiR3,BR2 etc.They actas π acceptors.
•x-Substituents:Thesedenotetheelectron-donatingsubstituentssuchas OR,NR2,R(alkyl)etc.Theyactas π donors.
1.5.1HOMO/LUMOEnergiesandCoefficients ofSubstitutedAlkenes
Theunsubstitutedalkene(ethylene)isthereferenceorunperturbedalkene. Aperturbedalkenesystemisrepresentedbyc-,z-orx-substitutedalkene. Thepatternsoffrontierorbitalenergiesandcoefficientsfortheperturbed systemsvis-a-visunperturbedalkenecanbedeterminedbychoosingareasonablemodelforeachsubstitutedalkene.Anall-carbonmodelforwhich HMOenergiesandcoefficientsareknownisthepreferredchoicetodrawa qualitativeinference.
1.5.1.1Perturbationbyc-Substituents
Sinceac-substituentisaneutralconjugatingsubstituent(e.g.CH]CH2),a reasonablemodelforac-substitutedalkeneisbutadiene: