OptimalStateEstimationfor ProcessMonitoring,Fault DiagnosisandControl
Ch.Venkateswarlu
ChiefScientist(Retd.),IndianInstituteofChemicalTechnology(CSIR-IICT),Hyderabad,India
RamaRaoKarri
PetroleumandChemicalEngineering,FacultyofEngineering,UniversitiTeknologiBrunei,Gadong, BruneiDarussalam
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2022ElsevierB.V.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical,including photocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwritingfromthepublisher. Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangements withorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions .
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanasmaybe notedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenourunderstanding, changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation, methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbemindfuloftheir ownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityforanyinjury and/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromanyuseoroperationof anymethods,products,instructions,orideascontainedinthematerialherein.
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
ISBN:978-0-323-85878-6
ForInformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: SusanDennis
EditorialProjectManager: SamYoung
ProductionProjectManager: SruthiSatheesh
CoverDesigner: GregHarris
TypesetbyMPSLimited,Chennai,India
PartI
Basicdetailsandstateestimation algorithms1
1.Optimalstateestimationandits importanceinprocesssystems engineering3
1.1Introduction3
1.2Significanceofstateestimation3
1.3Roleofstateestimationinprocesssystems engineering4
1.4Outlineofthisbook4 1.5Summary4
2.Introductiontostochasticprocesses andstateestimationfiltering5
2.1Introduction5
2.2Probabilityandstochasticvariables5
2.2.1Probabilitytheorems6
2.2.2Conditionalprobability7
2.3Probabilitydistributionsanddistribution functions7
2.3.1Discreterandomvariablesand discreteprobabilitydistributions8
2.3.2Continuousrandomvariablesand continuousprobabilitydistributions10
2.4WhiteGaussiannoiseandcolorednoise13
2.5Stochastic/randomprocesses14
2.5.1Stochasticmodelscheme15
2.5.2Stochasticrepresentationofreal processes16
2.5.3Stochasticrepresentationofgeneral dynamicmodels18
2.6Filtering,estimation,andprediction problem18
2.6.1Filtering,prediction,andsmoothing18
2.6.2Bayesfilteringapproachforstate estimation19
2.6.3Stochasticfilteringapproachfor stateestimation19
2.7Summary20 References20
3.Linearfilteringandobservation techniques21
3.1Introduction21
3.2Representationofasystemand associatedvariables21
3.2.1Definitionofsystemstate21
3.2.2Systemvariables21
3.2.3Statespacerepresentationof linearsystems22
3.2.4Outputequations22
3.2.5Discretetimerepresentationof linearsystems23
3.3Conceptsofobservabilityand controllability24
3.3.1Observabilityofacontinuoussystem24
3.3.2Observabilityofadiscretesystem25
3.3.3Controllabilityofacontinuoussystem25
3.3.4Controllabilityofadiscretesystem25
3.4Recursiveweightedleastsquares estimator27
3.4.1Estimationprocedure30
3.5Luenbergerobserverforstateestimation31
3.5.1Discreteformofobserverdesign32
3.5.2Discreteobserverbasedstate feedbackcontrol32
3.5.3Continuousformofobserver37
3.5.4Continuousobserverbasedstate feedbackcontrol38
3.6ReducedorderLuenbergerobserver forstateestimation41
3.7Kalmanfilterforstateestimation44
3.7.1DiscreteKalmanfilter44
3.7.2Filtercovariancematrices46
3.7.3ContinuousKalmanfilter52
3.8Stateestimationapplicationsoflinear filteringandobservationtechniques56
3.9Summary56 References56
4.Mechanisticmodel-basednonlinear filteringandobservationtechniques foroptimalstate/parameter estimation59
4.1Introduction59
4.2Generalnonlinearsystemandsystem models59
4.2.1Mechanistic/firstprinciplemodels59
4.2.2Generalrepresentationofdynamic models61
4.3Observabilityofnonlinearsystems61
4.3.1Localobservability62
4.3.2Globalobservability64
4.4ExtendedKalmanfilter65
4.4.1Processrepresentationforstate estimation66
4.4.2Processrepresentationforstateand parameterestimation66
4.4.3ExtendedKalmanfilterfor continuoustimenonlinearsystems66
4.4.4ExtendedKalmanfilterfordiscrete timenonlinearsystems68
4.4.5Emphasisoncovariancematricesof extendedKalmanfilter68
4.5SteadystateextendedKalmanfilter73
4.6Two-levelextendedKalmanfilter74
4.6.1Stateestimationfilter74
4.6.2Parameteridentificationfilter75
4.7AdaptivefadingextendedKalmanfilter75
4.8UnscentedKalmanfilter76
4.9SquarerootunscentedKalmanfilter78
4.10EnsembleKalmanfilter80
4.11Particlefilter81
4.12ReducedorderLuenbergerobserver84
4.12.1Determinationofobserver coefficientmatrices84
4.13ReducedorderextendedLuenberger observer85
4.14Nonlinearobserver86
4.15Stateestimationapplicationsofnonlinear filteringandobservationtechniques88
4.16Summary88 References88
5.Data-drivenmodelingtechniquesfor stateestimation91
5.1Introduction91
5.2Principalcomponentanalysis91
5.2.1Basicprinciples91
5.2.2GeometricinterpretationofPCA92
5.2.3Eigenstructurefordatamatrix92
5.2.4PCAmodelestablishment93
5.3Projectiontolatentstructures94
5.3.1Theregressionproblem94
5.3.2Scalingandcenteringthedata94
5.3.3PLSmodel94
5.4Artificialneuralnetworks95
5.4.1ANNstructureanditscomponents95
5.4.2Neuronprocessingfunctions97
5.4.3Learningparadigms97
5.4.4Learningalgorithmsandtraining procedure97
5.4.5Informationprocessing100
5.4.6ANNarchitectures100
5.5Radialbasisfunctionnetworks102
5.5.1StructureofRBFN103
5.5.2AutomaticconfigurationofRBFN105
5.5.3Implementationprocedure106
5.6Nonlineariterativepartialleastsquares107
5.6.1NIPALSalgorithmforPLS107
5.6.2NonlinearPLSwithinPLS framework108
5.6.3NIPALSalgorithmforRBFN108
5.7Stateestimationapplicationsof data-drivenmodelingtechniques110
5.8Summary110 References110
6.Optimalsensorconfiguration methodsforstateestimation113
6.1Introduction113
6.2Briefreviewonsensorconfiguration methods113
6.3Optimalsensorconfiguration:classical methods114
6.3.1Sensitivityindex114
6.3.2Singularvaluedecomposition114
6.3.3Principalcomponentanalysis115
6.4Optimalsensorconfiguration: gramian-basedmethodsforlinear systems116
6.4.1Observabilitygramianforlinear systems116
6.4.2Observabilitygramian-basedsensor selectionprocedure117
6.5Optimalsensorconfigurationfor nonlinearsystems117
6.5.1Empiricalobservabilitygramianfor nonlinearsystems118
6.5.2Empiricalobservabilitygramian metrics119
6.5.3Empiricalobservabilitygramian-based sensorselectionprocedure119
6.6Summary119 References121
PartII
Optimalstateestimationfor processmonitoring123
7Applicationofmechanistic model-basednonlinearfilteringand observationtechniquesforoptimal stateestimationinmulticomponent batchdistillation125
7.1Introduction125
7.2Batchdistillationprocessandits dynamicmodel125
7.3Simplifieddynamicmodelofbatch distillation128
7.3.1Equilibriumrelations128
7.4Theapplicationsystem128
7.5Measurementsconfigurationforstate estimation129
7.6Performancecriteria132
7.7ExtendedKalmanfilterforcompositions estimation132
7.7.1DesignofEKFestimator132
7.7.2EKFimplementationresults134
7.8SteadystateKalmanfilterfor compositionsestimation136
7.8.1DesignofSSKFestimator136
7.8.2SSKFimplementationresults136
7.9AdaptivefadingextendedKalman filterforcompositionsestimation137
7.9.1DesignofAFEKFestimator137
7.9.2AFEKFimplementationresults137
7.10Comparativeperformanceof compositionestimators137
7.11Summary139 References140
8Applicationofmechanistic model-basednonlinearfilteringand observationtechniquesforoptimal stateestimationinmulticomponent reactivebatchdistillationwith optimalsensorconfiguration141
8.1Introduction141
8.2Reactivebatchdistillationprocessandits dynamicmodel142
8.2.1Equilibriumrelations144
8.2.2Enthalpyrelations144
8.3Simplifieddynamicmodelofreactive batchdistillation144
8.4Theapplicationsystem145
8.5Sensorconfigurationforstateestimation145
8.5.1Sensorconfigurationusing sensitivityindex146
8.5.2Sensorconfigurationusing singularvaluedecomposition147
8.5.3Sensorconfigurationusing principalcomponentanalysis149
8.6Performancecriteria152
8.6.1Meanintegralsquarederror152
8.7ExtendedKalmanfilterforcompositions estimation152
8.7.1DesignofextendedKalmanfilter estimator154
8.7.2ExtendedKalmanfilter implementationresults155
8.8Summary160 References161
9Applicationofmechanistic model-basednonlinearfilteringand observationtechniquesforoptimal stateestimationincomplex nonlineardynamicalsystems163
9.1Introduction163
9.2NonlineardynamicalCSTR164
9.2.1Mathematicalmodel164
9.2.2Stabilityanalysis165
9.2.3Bifurcationanalysis166
9.3Optimalstateestimationinnonlinear dynamicalCSTR166
9.3.1Stateestimatordesign166
9.3.2Stateestimationresults170
9.4Nonlineardynamical homopolymerizationreactor170
9.4.1Mathematicalmodel171
9.4.2Stabilityanalysis173
9.4.3Steadystatesolution174
9.4.4Bifurcationanalysis177
9.5Optimalstateestimationinnonlinear dynamicalhomopolymerizationreactor177
9.5.1Stateestimatordesign179
9.5.2Stateestimationresults181
9.6Summary181 References183
10Applicationofmechanistic model-basednonlinearfilteringand observationtechniquesforoptimal stateestimationofakraftpulping digester185
10.1Introduction185
10.2Experimentalsystemanddynamic modeling186
10.2.1Batchpulpingprocess186
10.2.2Developmentofadynamic modelforkraftpulpingdigester188
10.3Optimalstateestimationofkraft pulpingdigester191
10.3.1DesignofEKF191
10.3.2Designofnonlinearobserver193
10.4Stateestimationresults193
10.5Summary196 References198
11Applicationofmechanistic model-basednonlinearfilteringand observationtechniquesforoptimal stateestimationofacontinuous reactivedistillationcolumnwith optimalsensorconfiguration201
11.1Introduction201
11.2Theprocessanditsmathematical model202
11.2.1Totalmassbalance202
11.2.2Componentbalance202
11.2.3Energybalance203
11.2.4Trayhydraulics203
11.3Optimalsensorconfigurationusing empiricalobservabilitygrammians204
11.3.1Significanceofoptimalsensor configurationinareactive distillationcolumn204
11.3.2Measurementspecificempirical observabilitygrammians204
11.3.3Optimalsensorconfiguration usingempiricalobservability grammians206
11.4Stateestimatordesign207
11.5Estimatorperformancemeasurefor optimalityofsensorconfiguration210
11.6Analysisofresults211
11.7Summary214 References215
12Applicationofmechanistic model-basednonlinearfilteringand observationtechniquesforoptimal stateestimationofacatalytictubular reactorwithoptimalsensor configuration217
12.1Introduction217
12.2Theprocessanditsmathematicalmodel218
12.2.1Process218
12.2.2Mathematicalmodel218
12.3Methodofsolution219
12.4Resultsofnumericalsolution221
12.5Optimalsensorconfigurationin acatalytictubularreactor222
12.5.1Significanceofsensor configurationinatubular reactor223
12.5.2Empiricalobservability Grammians223
12.5.3Optimalsensorconfiguration usingempiricalobservability Grammians223
12.5.4Sensorconfigurationresults224
12.6Optimalstateestimationusing unscentedKalmanfilter226
12.6.1Stateestimatordesign227
12.6.2Stateestimationresults227
12.7Summary229 References229
13Applicationsofdata-driven model-basedmethodsforprocess stateestimation231
13.1Introduction231
13.2Projectiontolatentstructures model-basedcompositionsestimator formulticomponentbatch distillation231
13.2.1Stateestimatordevelopment232
13.2.2Stateestimationresults234
13.3Artificialneuralnetworkmodel-based compositionsestimatorfor multicomponentbatchdistillation236
13.3.1Stateestimatordevelopment236
13.3.2Stateestimationresults238
13.4Radialbasisfunctionnetwork model-basedcompositions estimatorformulticomponentbatch distillation238
13.4.1Stateestimatordevelopment238
13.4.2Stateestimationresults239
13.5NIPALS RBFNmodel-based compositionsestimatorfor multicomponentbatchdistillation243
13.5.1Stateestimatordevelopment243
13.5.2Stateestimationresults243
13.6Summary246 References246
PartIII
Applicationofdatadriven model-basedmethodsfor processstateestimation247
14Optimalstateandparameter estimationforfaultdetectionand diagnosisincontinuousstirred tankreactor249
14.1Introduction249
14.2Generalstructureofmodel-based faultdetectionanddiagnosis250
14.3Generalprocessdescriptionforfault detectionanddiagnosis251
14.4NonlinearCSTR,itsmathematical modelandfaultcasesconsidered252
14.5MethodofextendedKalmanfilter253
14.5.1Designstrategy253
14.5.2Analysisofresults255
14.6Methodofreducedorderextended Luenbergerobserverandextended Kalmanfilter257
14.6.1Designstrategy257
14.6.2Analysisofresults260
14.7Methodoftwo-levelextendedKalman filter261
14.7.1Designstrategy261
14.7.2Analysisofresults263
14.8Methodofadiscreteversionof extendedKalmanfilterand sequentialleastsquares264
14.8.1Designstrategy264
14.8.2Analysisofresults266
14.9Methodofdiscreteversionof extendedKalmanfilterand simultaneousleastsquares267
14.9.1Designstrategy267
14.9.2Analysisofresults269
14.10Summary269 References270
15Optimalstateandparameter estimationforfaultdetectionand diagnosisofanonlinearbatchbeer fermentationprocess271
15.1Introduction271
15.2Generalstructureandgeneralprocess descriptionformodel-basedfault detectionanddiagnosis271
15.3Batchbeerfermentationprocess,its mathematicalmodelandfaultcases272
15.3.1Mathematicalmodel272
15.3.2Faultcasesinbatchbeer fermentation273
15.4MethodofextendedKalmanfilter273
15.4.1Designstrategy273
15.4.2Analysisofresults274
15.5Methodofreduced-orderextended Luenbergerobserverandextended Kalmanfilter276
15.5.1Designstrategy276
15.5.2Analysisofresults279
15.6Methodoftwo-levelextended Kalmanfilter279
15.6.1Designstrategy279
15.6.2Analysisofresults282
15.7Methodofdiscreteversionofextended Kalmanfilterandsequentialleast squares284
15.7.1Designstrategy284
15.7.2Analysisofresults284
15.8Methodofdiscreteversionof extendedKalmanfilterand simultaneousleastsquares285
15.8.1Designstrategy286
15.8.2Analysisofresults287
15.9Summary287 References287
16Optimalstateandparameter estimationforfaultdetectionand diagnosisofahigh-dimensional fluidcatalyticcrackingunit289
16.1Introduction289
16.2Processrepresentation290
16.3Fluidcatalyticcrackingunit290
16.4Mathematicalmodeloffluidcatalytic crackingunit291
16.4.1Feedandpreheatsystems291
16.4.2Reactor292
16.4.3Regenerator296
16.4.4Airblowers300
16.4.5Catalystcirculation302
16.4.6Nomenclatureandnumerical data303
16.5Fluidcatalyticcrackingunitsystem variables305
16.5.1Statevariables305
16.5.2Algebraicvariables305
16.5.3Measuredvariables305
16.6Faultcasesconsideredinfluid catalyticcrackingunit306
16.7Designofdiscreteversionofextended Kalmanfilter306
16.8DesignofunscentedKalmanfilter307
16.9Analysisofresults308
16.10Summary310 References311
PartIV
Optimalstateestimationfor processcontrol313
17Optimalstateestimator-based inferentialcontrolofcontinuous reactivedistillationcolumn315
17.1Introduction315
17.2Processandthedynamicmodel315
17.2.1Processdescription316
17.2.2Thedynamicmodelofthe process317
17.3Theprocesscharacteristics317
17.3.1Nonlinearityanalysis317
17.3.2Interactionandstabilityaspects317
17.4Classicalproportional-integral/ proportional-integral-derivative controllersfordistillationcolumn319
17.5Briefdescriptionofgeneticalgorithms319
17.6Designofgeneticallytuned proportional-integralcontrollers320
17.6.1Controllertuning320
17.6.2Formulationoftheobjective function320
17.6.3Desiredresponsespecifications forgenetic-algorithmtuning321
17.7Designofcompositionestimator322
17.8Analysisofresults325
17.9Summary330 References330
18Optimalstateestimationfor nonlinearcontrolofcomplex dynamicsystems333
18.1Introduction333
18.2Optimalstateestimationand estimator-basedcontrolofchaotic chemicalreactor333
18.2.1Chaoticchemicalreactorandits mathematicalmodel333
18.2.2Estimatordesignandestimation results334
18.2.3Controlleralgorithm334
18.2.4Controllerdesign334
18.2.5Analysisofresults335
18.3Optimalstateestimationand estimator-basedcontrolof homopolymerizationreactor338
18.3.1Homopolymerizationreactor anditsmathematicalmodel338
18.3.2Estimatordesignandestimation results338
18.3.3Controllerdesign338
18.3.4Analysisofresults339
18.4Summary342 References342
19Optimalstateestimatorbased controlofanexothermicbatch chemicalreactor343
19.1Introduction343
19.2Experimentalsystemandits mathematicalmodel343
19.2.1Experimentalbatchreactor344
19.2.2Analysisofreaction components345
19.2.3Esterificationreactormodel345
19.3State/parameterestimation347
19.4Controlalgorithms348
19.4.1ExtendedKalmanfiltercontrol348
19.4.2Genericmodelcontrol349
19.4.3Modelpredictivecontrol349
19.5Designofestimatorbasedcontrollers fortheesterificationreactor350
19.5.1ExtendedKalmanfiltercontrol350
19.5.2Genericmodelcontrol350
19.5.3Modelpredictivecontrol351
19.6Analysisofresults352
19.7Summary356 References357
Optimalstateestimationfor onlineoptimization359
20Optimalstateandparameter estimationforonlineoptimization ofanuncertainbiochemical reactor361
20.1Introduction361
20.2Theprocessanditsmathematical model362
20.3Stateandparameterestimationusing extendedKalmanfilter362
20.4Stateandparameterestimationusing two-levelextendedKalmanfilter362
20.5Onlineoptimizationproblem363
20.6Functionalconjugategradientmethod363
20.7ExtendedKalmanfilter-assistedonline optimizingcontrolofthebiochemical reactor364
20.7.1Designingthestrategy364
20.7.2Analysisofresults365
20.8Two-levelextendedKalman filter-assistedonlineoptimizing controlstrategy366
20.8.1Designingthestrategy366
20.8.2Analysisofresults367 20.9Summary368 References371
21Overview,opportunities,challenges, andfuturedirectionsofstate estimation373
21.1Overview373
Introductiontostochasticprocessesand stateestimationfiltering
2.1Introduction
Inmanyautonomoussystems,theknowledgeofthesystemstateisessentiallyrequiredtomonitorthestatusofthe process.Inarealisticsituation,thestateofaprocessisoftennotdirectlyobtainablebutitisusuallyinferredorestimatedbased onthesystemoutputsmeasuredbyinstruments(sensors)alongwiththesupportofadynamicmodelrepresentingthesystem.In mostcases,buildingaperfectmodelto captureallthedynamicphenomenonisnotpossible.Tocompensatefortheunmodelled dynamics,processnoiseisoftenaddedtothedynamicmodel.Moreover,toaccountthemeasurementerrorsinrealisticsituation, propermeasurementnoiseisaddedtothemeasurementmodel.Processesthatareassociatedwithsucharandomnoisephenomenonaredefinedasstochasticorrandomprocesses.Formostengineeringapplications,theprocessnoiseandmeasurementnoise areassumedtofollowzero-meanGaussian ornormaldistribution.Thegeneralideaoffilteringandestimationproblemisto establishthebestestimateforthetruevariableofasystemfromanincompleteandnoisysetofobservationsofthesystem.
Thischapterdescribesandelaboratesthebasicconceptsrelatingtostochastic variables,noise,probability,probability distributions,randomprocesses,stochasticrepresentationofgeneraldynamicmodels,filtering,prediction,andestimation. Theconceptsanddefinitionspresentedinthischapterprovideabasicframeworkforotherchaptersofthisbook.
2.2Probabilityandstochasticvariables
Aprobabilityvariableisarandomvariable,whereasastochasticvariableisachancevariable.Theprobabilityvariableisusuallydenotedbyacapitalletter X or Y.Thenamesuggeststhatthevariablehassomethingtodowiththeconceptofprobabilities.Suppose,adieisrolledand X istheoutcome,thentheoutcomevariesforeveryturn.Thus X representsarandom variable.Thepossiblevaluesof X are1,2,3,4,5,and6.Occurrenceofeachofthesevalueshasaprobabilityof1/6.Inastatisticalsense,probabilityrepresentstherelativefrequencyofanevent,whenitisobservedformorenumberoftimes.Assume thatadiscreterandomvariable X takesonthevalues x1, x2, , xk asaresultofanexperiment.If X takesthevalue xi for m observationsandthetotalnumberoftrialsis n,thentheratio m/n iscalledtherelative frequencyoftheevent X 5 xi.Therelativefrequency m/n itselfisarandomnumberandchangesaccordingtothenumberoftrialsperformed.Asanexampleofrelativefrequency,considerthetossingofacoin.Heretheevents areheadsandtails.Consideringboththeeventsoccurequally likely,thatimpliesthecoinisunbiasedanditistossedalargenumberoftimessuchthattheeventheadsappearexactlyhalf thenumberoftails.Therelativefrequencyofoccurrenceofheadsisthus0.5.Similarly,theprobabilityoftailsis0.5.
Ingeneral,theprobabilityisanonnegativenumberanditsvaluesliebetween0and1.Avalueof“zero”indicates thattheeventwillnotoccurand“one”signifiesthattheeventcertainlyoccurs.Supposewehaveacaseof n possible events, x1, x2, ..., xn,whicharemutuallyexclusiveinthesensethattheoccurrenceofoneeventexcludestheother. Considertheprobabilitiesofoccurrenceoftheseeventsas p1, p2, , pn,respectively,suchthatthecombinedprobabilityofalltheeventsisunity,thatis, p1 1 p2 1 ? 1 pn 5 1.
Probabilitymeasure: Theprobabilityofaneventismeasuredbyassigninganumericalvalueforeachevent.Considera samplespace S with n(S)outcomesinwhichtheevent A occurs n(A)times.Theprobabilitymeasureisexpressedas
Numberoffavorableoutcomes
Probabilityofanevent 5
Numberofpossibleoutcomes
Ifthesamplespace S has n equallylikedoutcomes,then
Thisiscalledauniformdistributionon S.
Example1: Considerrollingafairdie3times,findtheprobabilitywhenallthenumbersarethesameineachtrail.
Solution
Whenthedieisrolledthreetimes,thesamplespacehas216orderedtripletsas(i, j, k).Sincethedieisfair,the eventofinterestistheequalprobabilityofthesamenumberswithsixoutcomes:
Thuswehaveauniformprobabilitydistribution.Here n(A) 5 6and n(S) 5 216. Thus, P(A) 5 6/216 5 1/36.
2.2.1Probabilitytheorems
Theadditionandmultiplicationtheoremsofprobabilityarebriefedasfollows:
Additiontheorem: Let A and B aretwoindependenteventsinthesamplespaceofanexperiment.
If A and B aremutuallyexclusiveevents, A - B 5 nullset.Thus
Ifthesamplespaceconsistsof n eventssuchthat
Thus,accordingtotheadditiontheorem,
Multiplicationtheorem:Let A and B aretwoindependenteventsinthesamplespaceofanexperiment.According tothemultiplicationtheorem,
If A1, A2,..., An areindependenteventsinthesamplespace,then
Example2: Considerthrowingofasinglediewithsamplespace S 5 {1,2,3,4,5,6}.Whatistheprobabilityof gettinganoddnumber , 3andevennumber . 3?
Solution
Thesamplespace S isrepresentedby S 5 1; 2; 3; 4; 5; 6 fg
Let A and B aremutuallyexclusiveeventsinthesamplespace.
2.2.2Conditionalprobability
Itisaprobabilitymeasurethatdealswithdependentevents.Suppose A and B aretwodependentevents;the P(A/B) definestheprobabilityofevent A aftertheoccurrenceof B.Then P(A/B)canbeinterpretedasaprobabilityof A given B.Similarly, P(B/A)definestheviceversa.Thisconceptisknownasconditionalprobabilitysinceaconditiononthe occurrenceof B or A isspecified.
Themeasureforconditionalprobabilityisgivenasfollows:
If A and B areindependentevents,then
Itisoftenrequiredtofindtheprobabilityofevent B aftertheoccurrenceofevent A.Thisprobabilityiscalledthe conditionalprobabilityof B given A anddenotedas P(B/A).Theprobabilitymeasureforthiscaseisgivenby
Incaseiftheevents A and B occurinasamplespace S,and P(A) ¼ 0, P(B) ¼ 0,then
If A and B areindependentevents,then
If P(A) ¼ 0, P(B) ¼ 0,then
Thismeansthattheprobabilityof A doesnotdependontheoccurrenceornonoccurrenceoftheprobabilityof B, andviceversa.
Example3: Aprobleminanengineeringsubjectisgiventothreestudents A, B,and C.Thechancesofsolvingthe problembythestudentsare1/3,1/4,and1/5,respectively.Whatistheprobabilitythattheproblemissolved?
Solution
Theprobabilitythat A cansolvetheproblem, P(A) 5 1/3.
Theprobabilitythat A cannotsolvetheproblem 5 1 1/3 5 2/3
Theprobabilitythat B cansolvetheproblem, P(B) 5 1/4.
Theprobabilitythat B cannotsolvetheproblem 5 1 1/4 5 3/4
Theprobabilitythat C cansolvetheproblem, P(C) 5 1/5.
Theprobabilitythat C cannotsolvetheproblem 5 1 1/5 5 4/5
Theprobabilitythat A, B,and C cannotsolvetheproblem 5 2/3 3 3/4 3 4/5 5 2/5
Theprobabilitythattheproblemissolvedbyatleastonestudent 5 1 2/5 5 3/5
2.3Probabilitydistributionsanddistributionfunctions
Theprobabilityfunctionsandtheprobabilitydistributionsaredescribedasfollows:
2.3.1Discreterandomvariablesanddiscreteprobabilitydistributions
Randomvariablescanbediscreteorcontinuous.Ifarandomvariabletakesafinitesetofcountablevalues,itiscalled adiscreterandomvariable.Let X beadiscreterandomvariable.Ourinterestistocomputetheprobabilitiesoftheform P(X 5 xk)forvariousvaluesof xk intherangeof X.As xk variesas x1, x2, ,etc.,intherangeof X,theprobability P (X 5 xk)alsovaries.Thus P(X 5 xk)isafunctionof xk.Theprobabilityfunctionisrepresentedby
(2.16)
Theprobabilityfunctionisalsocalleda probabilitydistribution whichisgivenby
For x 5 xk,thisfunctionfollows Eq.(2.16);whileforothervaluesof x, f(x) 5 0.
Ingeneral, f (x)isaprobabilityfunctionif
(i) f (x) $ 0 (ii) P f ðxÞ 5 1,wherethesumistakenastheoverallpossiblevaluesof x.
(2.17)
Example4: Supposethatacoinofthehead(H)andtail(T)istossedtwice,thesamplespacebecomes S 5 {HH, HT, TH, TT}.Let X betherandomvariablerepresentingthenumberofheadsthatcancomeupinthesamplespace.Find theprobabilityfunctioncorrespondingtotherandomvariable X.
Solution
Wehave X isarandomvariablerepresentingeachofthesamplepoint HH, HT, TH,and TT inthesamplespace. Thus,wehave PHHðÞ 5 1=4; PHTðÞ 5 1=4; PTHðÞ 5 1=4 ; and PTTðÞ 5 1=4:
Then
5 0 ðÞ 5
PX 5 2 ðÞ 5 PHHðÞ 5 1=4
Theprobabilityfunctionisgivenin Table2.1
Example5: Findwhetherthefollowingfunctions f1(x) and f2(x) representtheprobabilitydistributionfunctionsfordiscreterandomvariables.
;
Solution
Thefunction f1(x)takesnonzerovalues3/4and1/4atthepoints x 52 2and3,respectively,and x takesallother valueswithzeroprobability,thatis, f1( 2) 5 3/4, f1(3) 5 1/4,and f1(x) 5 0,elsewhere.Condition(i)issatisfiedsince f1(x) $ 0forallvaluesof x.Condition(ii)isalsosatisfiedbecause3/4 1 1/4 1 0 5 1.Hence f1(x)representsaprobabilityfunctionforadiscreterandomvariable x
TABLE2.1 Probabilityfunctionforexample4. x 012 f(x)1/4 1/2 1/4
Similarly,inthecaseof f2(x), Px f2 ðxÞ 5 1,thuscondition(ii)issatisfied.However, f2(x)at x 5 4,thatis, f2(4) 52 1/3, whichisnegative.Hencecondition(i)isviolated.Therefore f2(x)cannotbetheprobabilityfunctionofanyrandomvariable. Cumulativedistributionfunction: Thedistributionfunctionorcumulativedistributionfunctionforadiscrete randomvariable X canbeobtainedfromitsprobabilityfunctionbynotingthat,forall x in(2~ , ~ ),
wherethesumistheoverallvaluesof u takenonby X forwhich u # x If X takesononlyafinitenumberofvalues x1, x2, ..., xn,thenthedistributionfunctionisgivenby
Example6: Findthedistributionfunctionfortherandomvariable x inExample4.
Solution
Thedistributionfunctionis
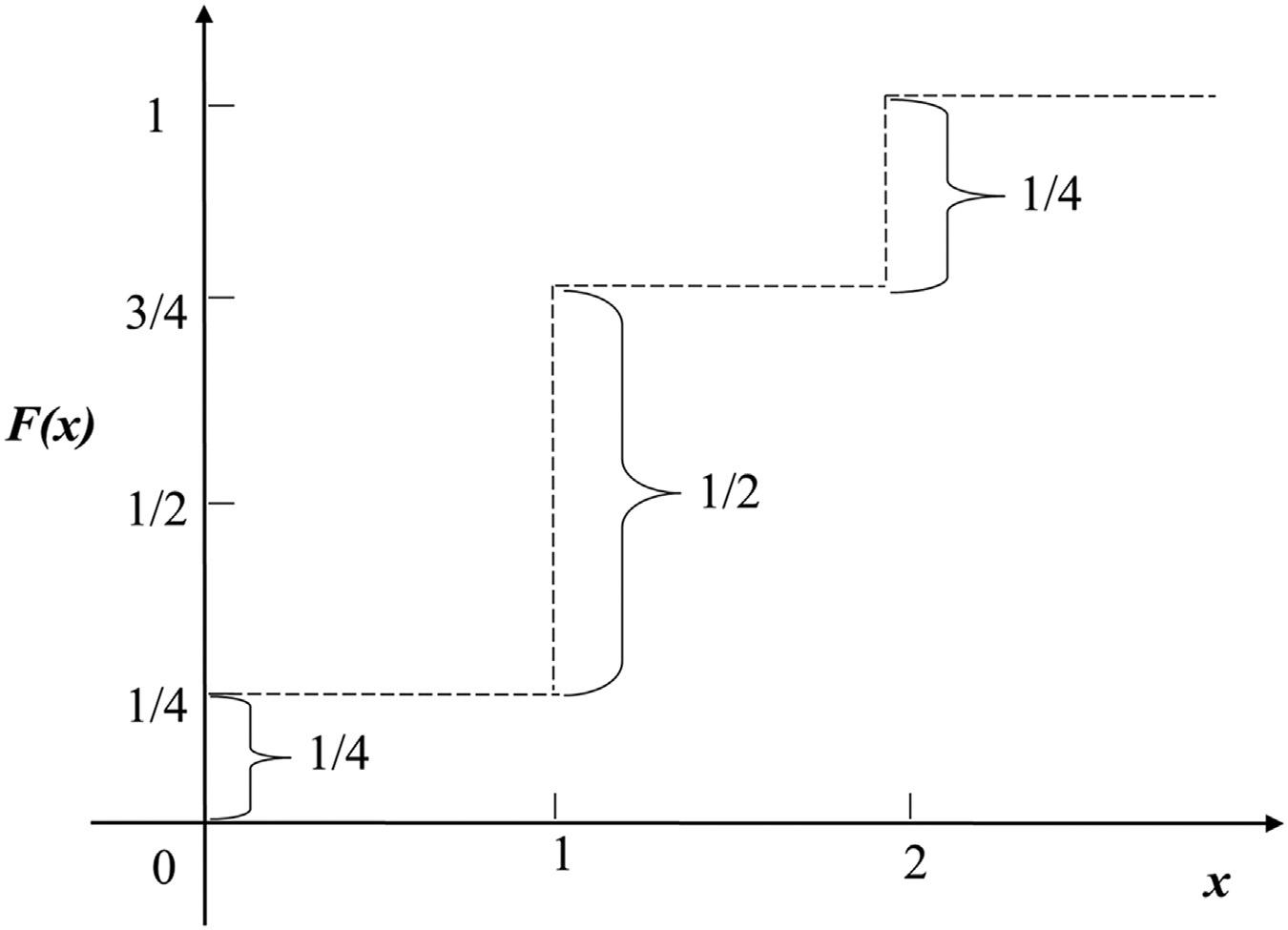
Thedistributionfunction [1] issketched,asshownin Fig.2.1.
Fromthedistributionfunction(Fig.2.1),itcanbeobservedthatthemagnitudeofjumpsat0,1,and2aretheprobabilitiesgivenin Table2.1.Thisshowsthattheprobabilityfunctioncanbeobtainedfromthedistributionfunction. Accordingly,theprobabilityfunctionofadiscreterandomvariableobtainedfromthedistributionfunctionisgivenby:
FIGURE2.1 Plotofthedistributionfunction.
2.3.2Continuousrandomvariablesandcontinuousprobabilitydistributions
Arandomvariablethatassumesaninfinitenumberofvaluesiscalledacontinuousrandomvariable.Thedistribution functionofacontinuousrandomvariable X isdefinedas
The F(x)iscalledtheProbabilityDistributionFunctionoftherandomvariable X.Thefollowingaretheproperties oftheprobabilitydistributionfunction:
Theconditionalprobabilitydistributionfunctionoftherandomvariable X forevent A isdefinedas
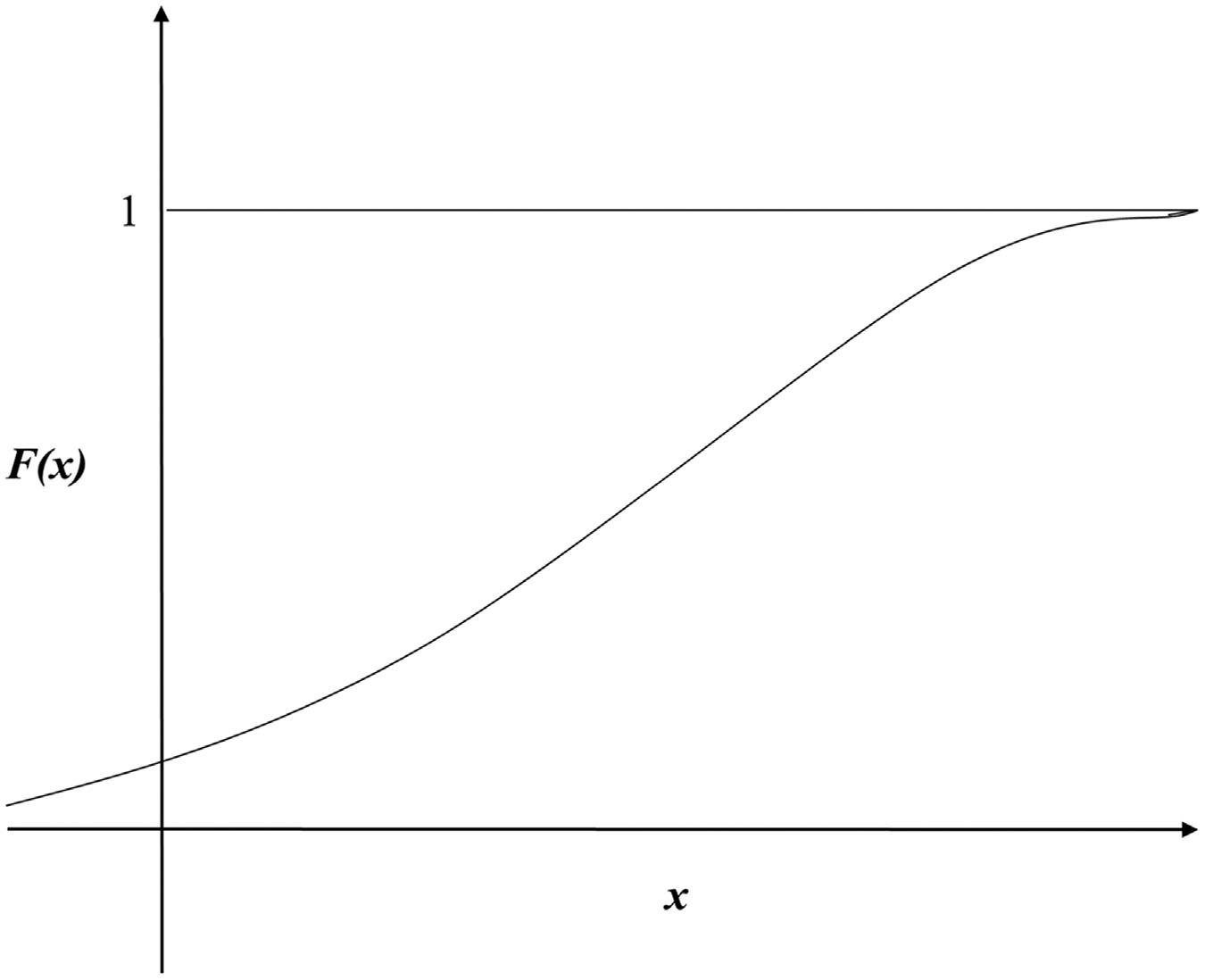
Thedistributionfunction F(x) 5 P(X # x)canbeconsideredasamonotonicallyincreasingfunctionwhich increasesfrom0to1andisrepresentedasshownin Fig.2.2.
Onthebasisofintegralcalculus,theprobabilitydistributionfunctioncanbedefinedasthederivativeof F(x)as
Thefunction f (x)hastheproperties
FIGURE2.2 Monotonicallyincreasingfunctionfrom0to1.
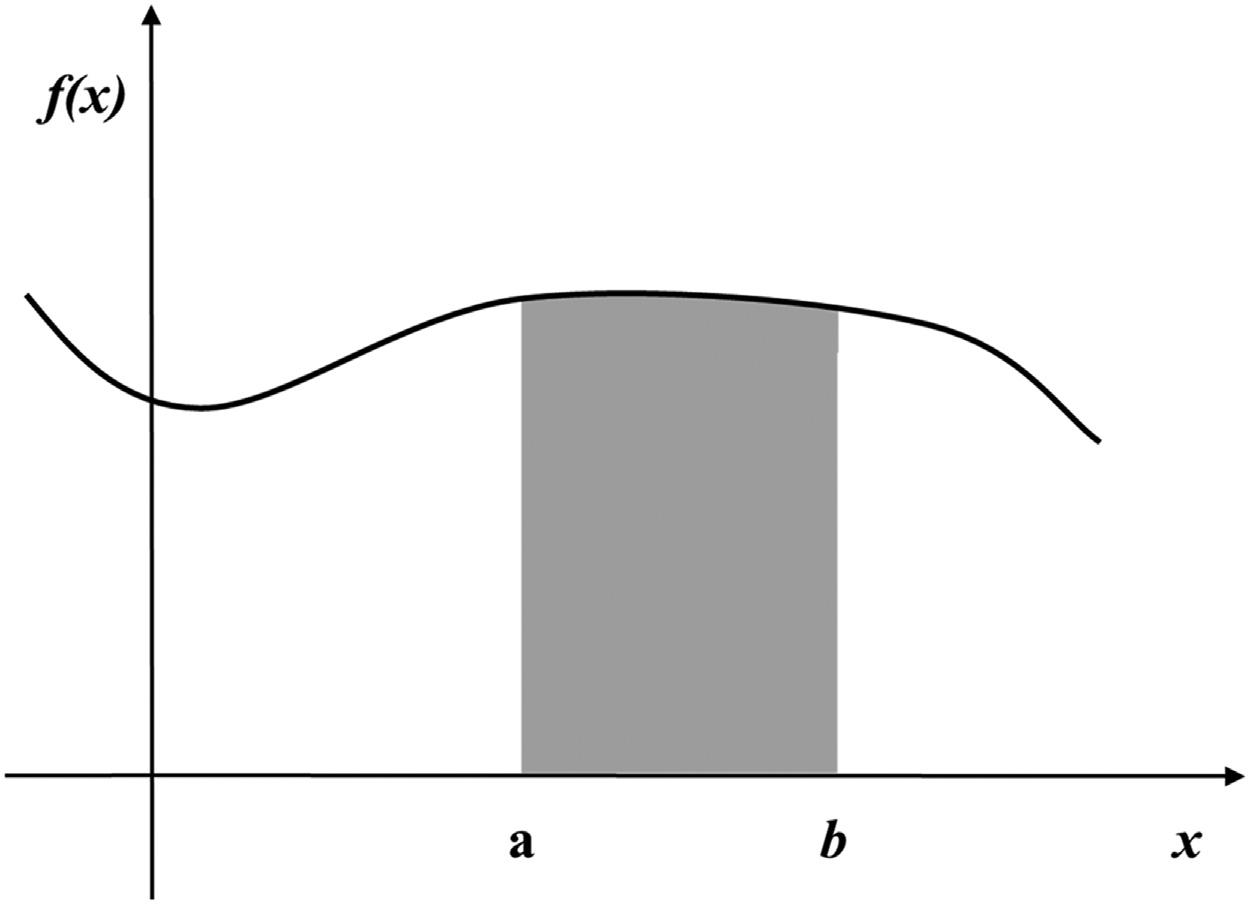
Thefunction f(x)isalsocalleda probabilitydensityfunction(PDF) orsimply densityfunction ofacontinuousrandomvariable.If f(x)isthedensityfunctionforarandomvariable X,thenwecanrepresent y 5 f(x)graphicallybya curveasin Fig.2.3.Since f(x) $ 0,thecurvecannotfallbelowthe x-axis.Theentireareaboundedbythecurveand the x-axismustbe1.Geometricallytheprobabilitythat X isbetween a and b,thatis, P(a , X , b),isthenrepresented bytheareashownshadedin Fig.2.3.
TheconditionalPDFoftherandomvariable X forevent A isdefinedas
Supposewehavetworandomvariables X1 and X2,theconditionalprobabilitydensityofthefirstgiventhatthesecondtakesonthevariable x2 as
where f(x1, x2)and f(x2)arethejointprobabilitydensityofthetworandomvariablesandthemarginaldensityofthe secondvariable.
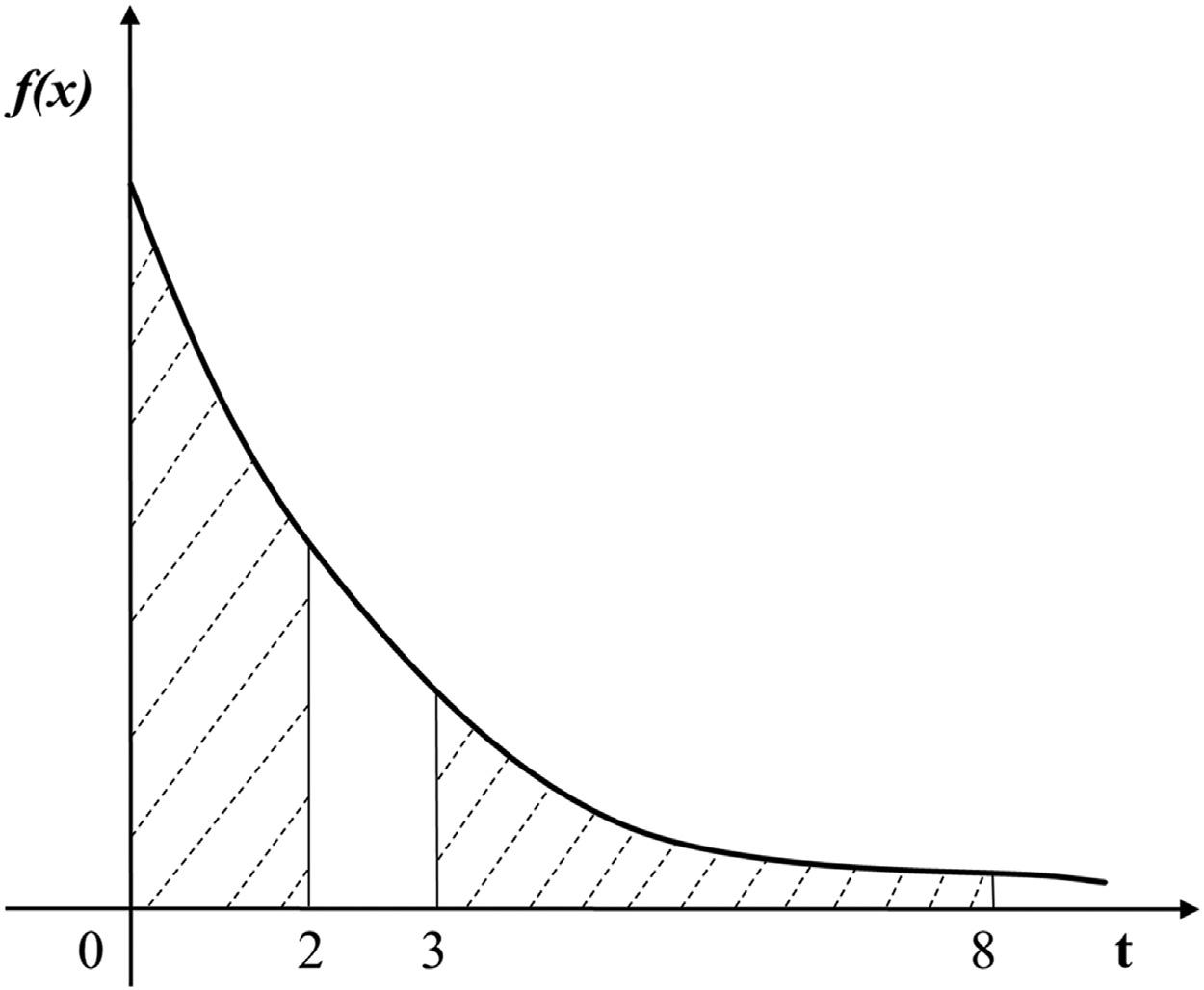
Example7: Theprobabilitydensityisrepresentedbyanexponentialdecayfunctionoftheform
Computetheprobabilities(i) P(0 # t # 2),and(ii) P(3 # t # 8).
Solution
Probabilitiesarecalculatedastheareasunderthedensitycurvebetweenthecorrespondingordinatesortheintegral ofthedensityoverthegiveninterval.
(i)Theprobability P(0 # t # 2)isgivenby
FIGURE2.3 Probabilitythat X isbetween a and b
(ii)Theprobability P(3 # t # 8)isgivenby
Theprobabilitiesareshownintheshadedareascoveredbydottedlinesasshownin Fig.2.4
Example8: Considerthefollowingdensityfunction
(a) Findtheconstant k
(b) Compute P(2 , X , 3)
Solution
Thefunction f (x)hasthepropertiessuchas f (x) $ 0,and Ð ~ 2~ f ðxÞdx 5 1.
(a) f (x) $ 0if k . 0
Sincethismustbeequalto1,whichmeans64k 5 1 . k 5 1/64.
(b) P 2 , X , 3 ðÞ
If f(x)iscontinuous,weknowtheprobabilityof X isequaltoanyparticularvalueiszero.Insuchacase,wecan replaceeitherorbothofthesigns , in Eq.(2.25) by # .Thus,forthisexample,
FIGURE2.4 Probabilitiesoftheexponentialfunction.
Example9: Iftworandomvariableshavethejointprobabilitydensity
Findtheconditionalprobabilitydensityofthefirstvariable,giventhatthesecondvariabletakesonthevalue x2 Solution
First,wefindthemarginaldensityofthesecondrandomvariablebyintegratingthefunctionwithrespectto x1.
and f(x2) 5 0,otherwise.
Hence,bydefinition,theconditionalprobabilityofthefirstrandomvariablegiventhatthesecondtakesonthevalue x2 is
and f(x1, x2) 5 0,otherwise.
2.4WhiteGaussiannoiseandcolorednoise
Infilteringandestimationproblems,mostofthephysicalsystemsunderconsiderationarenoisy.Thenoisemayarisein anumberofways.Forexample,theinputstothesystemmayassociatewithnoisewhichisunknown/unpredictable. Theoutputsfromthesystemmaybenoisyduetosensorsignalmeasurementinaccuracies.Whitenoiseandcolored noiseareimportantsignalsinstochasticsystems.
Whitenoise: Insignalprocessing,whitenoiseisarandomsignalhavingequalintensityatdifferentfrequencies, givingitaconstantpowerspectraldensity.Whitenoisedrawsitsnamefromwhitelight,althoughlightthatappears white,generallyitdoesnothaveaflatpowerspectraldensityoverthevisibleband.Indiscrete-time,whitenoiseisa discretesignalwhosesamplesareregardedasasequenceofseriallyuncorrelatedrandomvariableswithzeromeanand finitevariance.Ifeachsamplehasanormaldistributionwithzeromean,thesignalissaidtobeadditivewhite Gaussiannoise.
Considerthediscretemodelofatypicalsystemisrepresentedbythefollowingequations:
where xARn denotethestatevariables, θ denotesystemparameters,and yARm denotestheoutputs. H is m 3 n measurementmatrix, G isstatenoisecoefficientmatrix,andthesymbols w and v refertoGaussianwhitenoises.White noisesaresomeuncertaintiesthatareindependenttimeseriesanddistributedidentically,whichmeansnoautocorrelationbetweenthem.Inaparticularcase,the“Gaussianwhitenoise”hasanormaldistributionwithzeromeanandstandardvariation σ .
Forthesystemin Eq.(2.28),theGaussianwhitenoise{w}onstatesandGaussianwhitenoise{v}onoutputhasthe followingstatisticalexpectationswithrespecttotheirmeanandautocorrelations.Themeanvectorandautocorrelation matrixof w and v are:
where E istheexpectedvalueoperatorand I isanidentitymatrix.
Colorednoise:Colorednoisesaresomeuncertaintiesthataredependentontheirpaststatesandhaveanautocorrelation.Inparticular,passinga“Gaussianwhitenoise”fromfirst-orderfilterresultscolorednoise.