https://ebookmass.com/product/optics-of-chargedparticles-2nd-edition-hermann-wollnik/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Encyclopedia of modern optics 2nd Edition Duncan G. Steel (Editor)
https://ebookmass.com/product/encyclopedia-of-modern-optics-2ndedition-duncan-g-steel-editor/
ebookmass.com
Nonlinear optics 4th ed Edition Boyd
https://ebookmass.com/product/nonlinear-optics-4th-ed-edition-boyd/
ebookmass.com
Charged Elemental (The Zeita Chronicles Book 2) Embry Fox
https://ebookmass.com/product/charged-elemental-the-zeita-chroniclesbook-2-embry-fox/
ebookmass.com
Modality: A History (Oxford Philosophical Concepts)
Yitzhak Y. Melamed
https://ebookmass.com/product/modality-a-history-oxford-philosophicalconcepts-yitzhak-y-melamed/
ebookmass.com
Valuation Workbook 7th Edition Mckinsey & Company Inc. https://ebookmass.com/product/valuation-workbook-7th-edition-mckinseycompany-inc/
ebookmass.com
The Spirit of Inquiry : How One Extraordinary Society
Shaped Modern Science 1st Ed. Edition Susannah Gibson
https://ebookmass.com/product/the-spirit-of-inquiry-how-oneextraordinary-society-shaped-modern-science-1st-ed-edition-susannahgibson/ ebookmass.com
Geographical Models with Mathematica 1st Edition Edition André Dauphiné (Auth.)
https://ebookmass.com/product/geographical-models-withmathematica-1st-edition-edition-andre-dauphine-auth/
ebookmass.com
The Massachusetts Eye and Ear Infirmary Illustrated Manual of Ophthalmology 5th Edition Neil J. Friedman
https://ebookmass.com/product/the-massachusetts-eye-and-ear-infirmaryillustrated-manual-of-ophthalmology-5th-edition-neil-j-friedman/
ebookmass.com
Hitler’s Allies: The Ramifications of Nazi Alliance
Politics in World War II 1st Edition John P. Miglietta
https://ebookmass.com/product/hitlers-allies-the-ramifications-ofnazi-alliance-politics-in-world-war-ii-1st-edition-john-p-miglietta/
ebookmass.com
Cultural Dana Walrath
https://ebookmass.com/product/cultural-anthropology-the-humanchallenge-15th-edition-dana-walrath/
ebookmass.com
OPTICSOF CHARGED PARTICLES OPTICSOF CHARGED PARTICLES SecondEdition HERMANNWOLLNIK
NewMexicoStateUniversity,LasCruces, NM,UnitedStates
AcademicPressisanimprintofElsevier 125LondonWall,LondonEC2Y5AS,UnitedKingdom 525BStreet,Suite1650,SanDiego,CA92101,UnitedStates 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom
Copyright©2022ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorageand retrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowtoseek permission,furtherinformationaboutthePublisher’spermissionspoliciesandour arrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyright LicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightby thePublisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchand experiencebroadenourunderstanding,changesinresearchmethods,professionalpractices, ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribed herein.Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafety andthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,or editors,assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatter ofproductsliability,negligenceorotherwise,orfromanyuseoroperationofanymethods, products,instructions,orideascontainedinthematerialherein.
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
ISBN:978-0-12-818652-7
ForInformationonallAcademicPresspublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: SusanDennis
AcquisitionsEditor: CharlotteCockle
EditorialProjectManager: SusanIkeda
ProductionProjectManager: BharatwajVaratharajan
CoverDesigner: VictoriaPearson
TypesetbyMPSLimited,Chennai,India
Forewordtosecondeditionxi Forewordxiii
1.Gaussianopticsandtransfermatrices1
1.1 Themethodoftransfermatrices1
1.1.1 Thedescriptionofstraightraysinopticalsystems1
1.1.2 Propertiesofthinlenses3
1.2 Anopticalsystemthatcontainsonethinlens4
1.2.1 Theformationofarealimageorofavirtualimage6
1.3 Generalopticalsystems8
1.3.1 Thesignificanceofthedisappearanceofelementsof transfermatrices10
1.4 Transfermatricesoflensmultiplets11
1.4.1 Thetransfermatrixofadoubletoftwothinlenses12
1.5 Roundlensesforchargedparticles18 References19
2.Generalrelationsforthemotionofchargedparticlesin electromagneticfields21
2.1 Energy,velocity,andmassofacceleratedchargedparticles21
2.2 Forcesonchargedparticlesinelectromagneticfields22
2.2.1 Themagneticrigidity25
2.2.2 Theelectrostaticrigidity26
2.3 Thedescriptionofabundleofparticlesofdifferentkinetic energiesandmasses28
2.4 Therefractiveindexoftheelectromagneticfield29
2.5 TheEuler Lagrangeequations32 Appendix33 Hamilton’svariationalprincipleandtheLagrangeequations33 Themotionofchargedparticlesintime-independent magneticandelectrostaticfields35 References37
3.Quadrupolelenses39
3.1 Theelectricandmagneticfieldsinquadrupolelenses40
3.1.1 Fieldsinelectricquadrupolelenses41
3.1.2 Fieldsinmagneticquadrupolelenses42
3.2 Particletrajectoriesinquadrupolelenses43
3.2.1 Theequationsofmotion43
3.2.2 Focusingpropertiesofsinglequadrupolelenses46
3.3 Thedesignofquadrupolemultiplets49
3.3.1 Quadrupoledoublets50
3.3.2 Quadrupolemultiplets56
3.4 Thin-lensapproximationsforquadrupolemultiplets59
3.4.1 Doublypoint-to-parallelfocusingthin-lensquadrupole multiplets60
3.4.2 Stigmaticfocusingthin-lensquadrupolemultiplets63
3.4.3 Thinlensquadrupolemultipletsforwhich ðx jaÞ and ðbjbÞ vanishsimultaneously65
3.4.4 A “beamrotator” 65 References66
4.Sectorfields67
4.1 Homogeneousmagneticsectorfields68
4.1.1 Particletrajectoriesinhomogeneousmagneticsectorfields68
4.1.2 Focusinganddispersingpropertiesofhomogeneousmagnetic sectorfields72
4.1.3 Obliqueentranceandexitofparticlebeamsinsectormagnets81
4.2 Inhomogeneousmagneticsectorfieldsformedbyinclinedplanarpole faces(wedgemagnets)86
4.2.1 Particletrajectoriesinwedgemagnets87
4.2.2 Focusinganddispersingpropertiesofwedgemagnets90
4.3 Radiallyinhomogeneoussectorfieldsformedbyconicalpolefacesor toroidalelectrodes92
4.3.1 Theequationsofmotioninradiallyinhomogeneoussectorfields93
4.3.2 Particletrajectoriesinradiallyinhomogeneousmagneticor electrostaticsectorfields98
4.3.3 Focusinganddispersingpropertiesofradiallyinhomogeneous sectorfields100
4.3.4 Examplesofradiallyinhomogeneoussectorfields104
4.4 Particleflighttimesinradiallyinhomogeneoussectorfields, quadrupoles,andfield-freeregions106 Appendix109 Paraxialtrajectoriesinwedgemagnets109 References112
5.Chargedparticlebeamsinphasespace113
5.1 Liouville’stheoremandfirst-ordertransfermatrices114
5.2 Phase-spaceareasofparticlebeamspassingthroughopticalsystems115
5.2.1 Phase-spaceareasofparticlebeamsinfield-freeregions116
5.2.2 Phase-spaceareasofparticlebeamsinimage-formingsystems117
5.2.3 Thevirtualthinobjectlens118
5.3 Beamenvelopes120
5.3.1 Envelopesofbeamswithparallelogram-likephase-spaceareas122
5.3.2 Envelopesofbeamswithoctagon-likephase-spaceareas123
5.3.3 Envelopesofbeamswithellipticalphase-spaceareas123
5.4 Positionsandsizesofenvelopeminima129
5.4.1 Imagesandpupils129
5.4.2 Beamwaists130
5.4.3 Pupilsandwaistsforpoint-to-parallelfocusingsystems131
5.5 Minimalbeamenvelopesatpostulatedlocations131
5.6 Liouville’stheoremanditsapplicationtowide-anglebeams134
5.6.1 Abbe’ s “SineLaw” foratwo-dimensionalphasespace135
5.6.2 Thecurrentdensity136
5.7 Beamswithspacecharge137
5.7.1 Thecompensationofspacechargeinparticlebeams138
5.7.2 Thecalculationoftransporteffectsinconstantdiameter ionbeams139
5.7.3 Thedesignofbeamlinesforhigh-intensitybeams141 References143
6.Particlebeamsinperiodicstructures145 6.1 Single-particletrajectoriesandbeamenvelopes146
6.1.1 Systemswithpostulatedopticalproperties149
6.1.2 Opticalsystemsthathaveidenticalentranceandexitbeams151
6.2 Ringsofunitcells158
6.2.1 Lateralbeamdeviations158
6.2.2 Longitudinalbeamdeviations159 References160
7.Fringefields161 7.1 Particletrajectoriesinthefringefieldsofdipolemagnets161
7.1.1 Positionsofeffectivefieldboundariesindipolemagnets163
7.1.2 Fringe-fieldshuntsfordipolemagnets165
7.1.3 Fringe-fieldshuntsforhomogeneousandinhomogeneous dipolemagnets169
7.1.4 y-Focusinginthefringefieldsofdipolemagnets169
7.1.5 Transfermatricesofrealisticmagneticsectorfields174
7.2 Particletrajectoriesinfringefieldsofelectrostaticdeflectors174
7.2.1 Electrostaticdeflectorsbiasedsymmetricallytoground175
7.2.2 Electrostaticdeflectorsbiasedasymmetricallytoground176
7.2.3 Transfermatricesofrealisticelectrostaticsectorfields178
7.3 Particletrajectoriesinthefringefieldsofquadrupolelenses179 References182
8.Imageaberrations183
8.1 Systematicsofimageaberrations183
8.2 Originofimageaberrations190
8.2.1 Geometricaberrations191
8.2.2 Chromaticaberrations196
8.3 RelationsbetweencoefficientsofEq.(8.2)duetotheconditionof symplecticity201
8.3.1 Canonicaltransformationswithtimebeingtheindependentvariable201
8.3.2 Canonicaltransformationswithpositionbeingthe independentvariable202
8.3.3 Theconditionofsymplecticity204
8.4 Imageaberrationsof nth order211
8.4.1 Overallimageaberrations213
8.4.2 Theaberrationdrivingtermsofallorders217
8.4.3 Imageaberrationsduetofringefields217 Appendix222
Coefficientsofimageaberrationsof nthorder222
Equationsofmotionintime-independentfields223
Explicitparticletrajectoriesinradiallyinhomogeneouselectromagnetic sectorfields224 References228
9.Designofparticlespectrometersandbeamguidelines229
9.1 Single-sectormagneticspectrometers229
9.1.1 Ionbeamsfrompoint-likeandslit-likeionsources232
9.1.2 Asectormagnetionanalyzerassistedbyonequadrupolelens233
9.1.3 Aphase-spaceadapterforionbeamsinsectormagnets234
9.2 Aqualityfactorforparticlespectrometers235
9.2.1 Arigidity-or QΔ -value236
9.2.2 Anenergy QK -valueandamass Qm -value240
9.2.3 A Q-valuefor N cascadedspectrometers241
9.2.4 Achromaticsystems242
9.3 Time-of-flightparticlespectrometers245
9.3.1 A Qt -valuefortime-of-flightmassanalyzers247
9.3.2 Isochronousopticalsystems248
9.3.3 Angleandenergy-focusingisochronousopticalsystems249
9.4 Thealignmentofanopticalsystemandthecorrectionofits aberrations251
9.4.1 Thecorrectionofthesecond-orderapertureaberrationsin magneticsystems253
9.4.2 Thecorrectionofimageaberrationsinelectrostaticsystems263 References265
10.Time-of-flightmassspectrographs267
10.1 Time-of-flightmassspectrographsthatusesectorfields269
10.1.1 Time-of-flightmassspectrographsthatusemagnetic sectorfields269
10.1.2 Acceleratorstorageringsusedastime-of-flightmass spectrographs270
10.1.3 Determiningthepassagetimeforhigh-energyions271
10.2 Time-of-flightmassspectrographsthatuseelectrostaticsectorfields272
10.3 Low-energyionbeamsintime-of-flightmassspectrographs275
10.3.1 Ioncoolinginaquadrupoleiontrap275
10.3.2 Coolingionsinandextractingthemoutofaflattrap277
10.3.3 RF-carpetstointroduceionsintocoolers277
10.4 Acceleratingandbunchingofionsinpulsedelectricfields278
10.4.1 Acceleratingandbunchingbyasinglepulsedfield279
10.4.2 Ionbunchingtoadesiredposition281
10.4.3 Delayedionextraction283
10.5 Energy-isochronoustime-of-flightmassspectrographsthatuse ionmirrors285
10.5.1 Energy-isochronoustime-of-flightmassspectrographsthat usegriddedionmirrors285
10.5.2 Energy-isochronoustime-of-flightmassspectrographsthat usegrid-freeionmirrors287
10.5.3 Energy-isochronoustime-of-flightmassspectrographsthat useseveralionmirrors287
10.6 Amultireflectiontime-of-flightmassspectrograph288
10.6.1 MovingionsintoandextractingthemoutofaMRTOF-MS290
10.6.2 Determiningthenumberoflapsthationshaveperformed inamultireflectiontime-of-flightmassspectrograph291
10.6.3 ThedesignofaMRTOF-MSforprecisemassdeterminations292
10.6.4 Achievablemassresolvingpowers293
10.6.5 ORBITRAP:asmallhighfrequencymultireflectiontime-of-flight massspectrograph296
References297 Index 301
Forewordtosecondedition Thesecondeditionof OpticsofChargedParticles followsthefirstedition aftermorethan30yearsandattemptstooutlineagainhowchargedparticlesmoveinmagneticandelectricfields.Inthissecondedition,newly arisenquestionsareaddressedas,forinstance,thoseofnewtime-of-flight measurements,andoldexplanationsareimprovedinsimplicityandcompletenessdescribinghowchargedparticlesmovethroughthemainand thefringefieldsofopticalsystemsandthroughindividualopticalelements. Also,itusesthesametypeofformulationandnomenclaturethroughout thebook.
Aswiththefirstedition,thesecondeditiondoesnotrequirethe readertohaveanyspecialpreknowledgeofchargedparticleoptics. However,itrequiresthatthereaderhassomebasicunderstandingofthe physicsandmathematicsequivalenttoanundergraduateeducation.The intentionofthesecondeditionisalsonottoleadthereadertoindividual mountaintopsofscientificfindings,butrathertoahighplateauofunderstandingfromwherethemountaintopscanbeseenandreachedbyhisor herownstrengthandskill.
Ihavetriedtosupplyacomprehensivesetofreferences,whichinclude theearliestpublicationsaswellasthemostimportantones.However,not allpossiblereferencesarelisted,asthiswouldhaveexceededtheavailable space.
Atthispoint,Iwouldliketoacknowledgethemanyfruitfuldiscussions andinsightsabouttheobjectofchargedparticleopticswithmycolleagues M.Berz,K.Brown,S.Dodonov,K.Halbach,A.Kalimov,H.Matsuda, T.Matsuo,S.Schepunov,P.Schury,D.Vieira,andM.Wada.Ialso extendmythankstomywifeAnnettewhoconstantlysupportedmyefforts oversomanyyears.
SantaFe,03-05-2021 HermannWollnik
Foreword Someintroductorybooksaswellasseveralarticlesinscientificjournals andresearchreportshavebeenpublishedonthesubjectofchargedparticleoptics.However,exceptforbasicaspects,itisverydifficulttoobtaina generaloverviewfromthesesources,asmostconcentrateonisolatedproblemsandnormallyusedifferentmathematicalformalisms.Furthermore, astheresultsareappliedtoquitedifferentproblems,thesolutions obtainedareoftenincompatible.Thisbookunifiessuchapproaches, resultinginadescriptionofhowchargedparticlesmoveinthemainand fringingfieldsofmagneticorelectrostaticdipoles,quadrupoles,hexapoles, etc.,usingthesametypeofformulationandconsistentnomenclature throughout.Besidesthedescriptionofparticletrajectoriesandbeam shapes,guidelinesaregivenfordesigningparticleopticalinstruments.
Thisbookdoesnotrequirethereadertohaveanyknowledgeof chargedparticleoptics;however,theequivalentofanundergraduateeducationinphysicsandmathematicsisneeded.Itiswrittenneithertocarry everyonetothemountaintopsofscientificfindingsnortostopatthe foothillsofthemountainrange.Rather,itshouldleadtheinterested readertoahighplateauofunderstandingfromwhichhecanreachthe mountaintopsbyhisownstrength.
Ihavetriedtosupplyacomprehensivesetofreferenceswitheach chapter,normallyquotinganearlyandarecentpublicationforanygiven problem.However,notallpossiblereferencesaregivensincethiswould haveexceededtheavailablespace.
Atthispoint,IwouldliketoacknowledgethemanyfruitfuldiscussionsIhavehadwithM.Berz,H.Matsuda,T.Matsuo,andH.Nestle. IamalsogreatlyindebtedtoR.Kosempelfortheskilledandcareful drawingofthemanyfiguresinthisbookandtoM.Gowansfortheexperiencedandpatienttypingandretypingofthemanuscript.
Gaussianopticsandtransfer matrices Chargedparticleopticsisverysimilartolightoptics.Therefore,inthis chapter,wemainlydescribetheeffectspresentinlight-opticalsystems. Theresultsobtainedcanlaterbeappliedtothediscussionofoptical systemsforchargedparticles.
1.1Themethodoftransfermatrices Forgeometriclightoptics,ithasbeencustomarysincethetimeof Newtontouseanalgebraicformulationforallequationsinvolved;however,inrecentyearsthismethodhasatleastpartiallybeenamendedby theuseof transfermatrices.Forsimpleopticalsystems,theuseoftransfer matriceshasnoparticularadvantage.Forcomplexsystems,ontheother hand,itoffersanunexcelledsimplicityandclarity,ashasbeenshown forparticleopticsby Cotte(1938), Penner(1961), Brownetal.(1964), and Wollnik(1967) aswellasby Herzberger(1958) or Halbach(1964) forlightoptics.
1.1.1Thedescriptionofstraightraysinopticalsystems Assumethe z-axisofaCartesiancoordinatesystemtorepresenttheoptic axisofabundleofraysinwhichcasethedeviationfromtheoptic axis-the z-axis-ofanystraightrayofthisbundlecanbedescribed (see Fig.1.1)by
OpticsofChargedParticles
DOI: https://doi.org/10.1016/B978-0-12-818652-7.00004-7
with l 5 z2 z1 .Thoughnotimportanthere,itisgenerallyusefulto describenotonlythedeviations xzðÞ; yðzÞ butalsotheanglesof 1
optic axis z
profile-plane-1 at profile-plane-2 at
Figure1.1 Thedeviationofastraightrayfromtheopticaxispassingobliquely throughtwoprofile-planeslocatedat z1 and z2 from x1 ; y1 to x2 ; y2 .
inclinations α z ðÞ; β ðzÞ ofarayrelativetotheopticaxis.Inaregionofa constantrefractiveindextheseinclinationsstayconstant
tanα z2 ðÞ 5 tanα z1 ðÞ orabbreviatedtanα2 5 tanα1 (1.1c) tanβ z2 ðÞ 5 tanβ z1 ðÞ orabbreviatedtanβ 2 5 tanβ 1 (1.1d)
The Eqs.(1.1) canalsobewritteninamatrixnotationandsodescribe astraightrayasitmovesthrougharegionoflength l 5 z2 z1 ofconstantrefractiveindex:
Herein a tanα and b tanβ denoteinclinationsofrayswithrespectto theopticaxis,whereintheseinclinationsareonlyusedasabbreviationsfor tanα andtanβ .Onlyin Section1.3,moredetailsareoutlined.
Thematrixnotationsasusedin Eqs.(1.2) provideagoodoverview overthedetailsofanopticalsystemandprovideacompactdescription.In detailthefactisexpressedthatthereare
Position-vectorsX1 (x1, a1)and Y1 (y1, b1)inprofile-plane1, thatis,atposition z1,aretransformedby x-and y-transfermatricestonewposition-vectors X2 (x2,a2)andY2 (y2, b2)inprofile-plane2,thatis,atposition z2.
asisillustratedin Fig.1.1.Incaseofrotationallysymmetricsystems,the x-and y-transfermatricesareidentical.Asinthischapter,onlyrotationally symmetricsystemsaredescribed,itissufficienttodescribeonlytheprojectionofraysontothe xz-plane,asisdoneherein Eq.(1.2a) oronto the yz-planeasisdoneherein Eq.(1.2b)
1.1.2Propertiesofthinlenses Athinlensisdefinedasaninfinitesimallythindevicethatcausesabundleofparallelrays,thatis,abundleoflightrays,tobefocusedtoasocalledfocalpoint(see Fig.1.2 ).Indetail,araythatarrivesatthe profile-plane-2at z2 justupstreamofathinlensadistance x2 5 xðz2 Þ awayfromtheopticaxiswithaninclination a2 5 az2 ðÞ tanα2 and movestotheprofile-plane-3at z3 ,itkeepsthepositionx 2 ,butisbent byanangle x2 =f towardtheopticaxisincaseofafocusinglens(see Fig.1.2 ),sothat
Herein f istheso-calledfocallengthofthethinlens. Eq.(1.3) canalsobe writteninamatrixnotationas
Figure1.2 Athinlensthatfocusesabundleofparallelstraightraystoapointis shown.Incasetheincomingraysareaxis-parallel,theraysarefocusedtoapointon theopticaxis,theso-calledfocalpoint.Incasetheincomingraysareobliquetothe opticaxis,thispointisoffthe z-axisandlocatedapproximatelyinthefocalplane, whichisperpendiculartotheopticaxisandincludesthefocalpoint.
Thetransfermatrixof Eq.(1.4) describestheactionofathinlens, whentheinitialraysareparalleltothe z-axis.However,thistransfer matrixisalsocorrectforthecasethattheinitialraysareinclinedrelative totheopticaxis.Inthiscasethebend Δα issimplyaddedtotheinitial inclination a2 asisshowninthesecondpartof Fig.1.2
Noteherethatthetransfermatrixof Eq.(1.4) expressesallpropertiesof athinlenstofirstorderin x andin a andthatthefocallength f orbetter therefractivepower1=f istheonlyquantitythatcharacterizesthepropertiesofthethinlens.Notealsothataray,thatpassesthroughthemiddleof thethinlens,passesunbentsothatfor x2 5 0 Eq.(1.4) yields a3 5 a2 .
1.2Anopticalsystemthatcontainsonethinlens Asimpleopticalsystemconsistsofonethinlens(see Eq.1.5)of focallength f anddriftregions(see Eqs.1.2) oflengths l1 upstreamand l2 downstreamofthethinlens.Suchanopticalsystemissketchedin Fig.1.3 characterizedby6position-vectors:
1. X1 ðx1 ; a1 Þ at z1 ; thatis,adistance w1 upstreamofthefocal-plane1
2. X2 ðx2 ; a2 Þ at z2 ,thatis,atthepositionofthefocal-plane1
3. X3 ðx3 ; a3 Þ at z3 ; thatis,ontheupstreamsideofthethinlens
4. X4 x4 ; a4 ðÞ at z4 ; thatis,onthedownstreamsideofthethinlens
5. X5 x5 ; a5 ðÞ at z5 ; thatis,atthepositionofthefocal-plane2
6. X6 x6 ; a6 ðÞ at z6 ; thatis,adistance w2 downstreamofthefocal-plane2
profile-plane 1
profile-plane 2 =focal-plane 1
profile-plane 6
optic axis z
profile-plane 5 =focal-plane 2
3 profile-plane 4
Figure1.3 Sketchedisanarbitraryraythatpassesthrougharegionthatincludesa thinlens.Shownarealsotheray’s x -positionsand a-inclinationsatdifferent z-positionsalongtheopticaxis.
Theseposition-vectors X1 ; X2 ; X3 ; X4 ; X5 ; X6 describeanarbitraryray (see Fig.1.3)byusingrepeatedly Eqs.(1.2a) and (1.4):
Asknownfromclassicalmatrixalgebra,itispossibletoobtainthe positionvector X6 x6 ; a6 byapplyingtheposition-vector X1 x1 ; a1 to theproductofthelisted5transfermatricessothat:
orexplicitly
Advantageously,themiddlethreetransfermatricesarecombinedtoa singlematrixthatdescribestheionmotionfromthefocal-plane1, upstreamofthethinlens,tothefocal-plane2,downstreamofthethin lens,(see Fig.1.3):
Usingthetransfermatrix Tff Eq.(1.5) canberewrittenas x6 a6 5 x
For w1 w2 5 f 2 thematrixelement ðxjaÞ vanishesandallraysthatstart fromapoint x1 5 xðz1 Þ underdifferentinclinations a1 meetagaininone point x6 5 xjx ðÞx1 .Inthiscaseonespeaksofan “object-image relationbetweentheprofileplanesat z1 and z6 ”.Thisrelation,the so-called “lensequation” isknownsincealongtimeandhasbeen reportedalreadyinNewton’sPRINCIPIAin1685.
Noteherethatthedeterminantsofallsofarshowntransfermatrices havethemagnitudeof1,thatis
orexplicitly xjx ðÞ aja ðÞ xja ðÞ ajx ðÞ 5 1.Thispropertyholdsverygenerallyfor anytransfermatrixthatdescribestrajectoriesofchargedparticlesmoving throughanopticalsystem,inwhichtherefractiveindexforlightopticalsystemsortheelectricpotentialforsystems ofchargedparticlesisidenticalatthe beginningandattheend.ThereasonforthispropertyisthatparticletrajectoriesarealwaysdeterminedfromHamiltonianequationsofmotion,inwhich casetheobtainedsolutionsforparticlemotionsarecalledtobesymplectic.
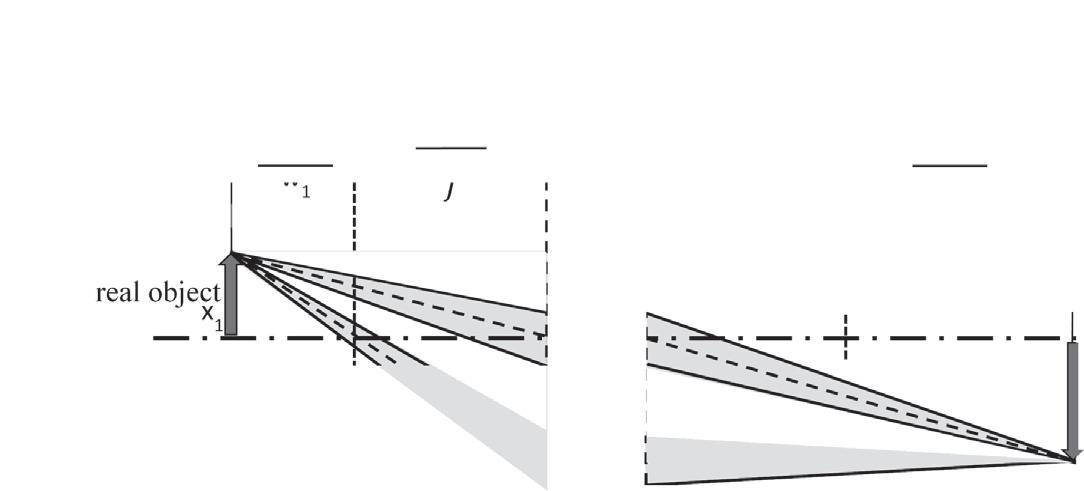
1.2.1Theformationofarealimageorofavirtualimage Fromthecondition xja ðÞ 5 0in Eq.(1.7),whichestablishesanobjectimagerelationbetweentheprofileplanesat z1 and z6 in Eq.(1.7) or z1 and z2 in Fig.1.4,theso-called lensequation: w1 w2 5 f 2 or 1 l1 1 1 l2 5 1 f (1.9) isderived,forwhich w1 w2 isalsoreplacedby(l1 f Þðl2 f)asonemay takefrom Fig.1.4
2
Figure1.4 Theformationoftherealimageofanobjectbyathinlensoffocal length f .Notethatthecenterrayofonegroupofrayspassesunbentthrough thecenterofthethinlensandthatthecenterrayofanothergrouppasses throughthefirstfocalpointandthenisparalleltotheopticaxisdownstreamof thethinlens.
Forthecasethatthe Eq.(1.9) arevalidthe Eqs.(1.5) and (1.7) transformto
describingthattheimage x6 is xjx ðÞ timeslargerthantheobjectofsize x1 .Noteherethat xjx ðÞ 52 w2 =f 5 1 l2 =f isthesocalledlateralmagnification Mx ,whichisalwaysnegativeaslongas l2 . f .Inotherwords, theimage x6 isalwaysupsidedownwithrespecttotheobject x1 asis shownin Fig.1.4
Incaseofafocusingthinlenswith f . 0,onecanreadfrom Eq.(1.10b) that,whentheobjectislocatedat l1 with 1. l1 , f avirtualmagnifieduprightimageisformed,locatedat l2 . f Incaseoflightrayssuchopticalsystemsarecalled “loups” or “magnifyingglasses.”
2. 2f . l1 . f arealmagnifiedupside-downimageisformed,locatedat l2 . 2f
3. l1 . 2f arealdemagnifiedupside-downimageisformed,locatedat 2f . l2 . f (see Fig.1.5).
2
Figure1.5 Theformationofavirtualimageofanobjectbyalightopticthinlensof focallength f isshown.Noteherethatanobliqueraythatstartsfromx1 canpass unbentthroughthecenterofthethinlensandthatanaxis-parallelraythatstarts fromx1 isbentbythethinlenssothatitpassesthroughthedownstreamfocal point.Inthiscaseallraysseemtooriginatefromanenlargedvirtualimagelocated inbackoftheobject.
1.3Generalopticalsystems Therelationbetweenpositionvectors Xm1n and Xm inprofile planesat zm1n and zm canbewrittenforanarbitraryopticalsystemas
1n
(1.11) with xm and xm1n describinghowmucharayisapartfromtheopticaxis andfurthermorewhatinclinations am and am1n ithasrelativetotheoptic axis.Suchatransfermatrixalsodescribestheactionofagenerallens system,inwhichraysarebenttowardtheopticaxisincaseoffocusing lensesorawayfromitincaseofdefocusinglenses.Whenspeakingof inclinations,itisirrelevantforallfirst-orderdiscussions,whetheronetalks ofinclinations a; b oroftanα; tanβ with α; β beinganglesofinclinations. However,itisgoodtounderstandthattheinclinationsaredefinedas ratiosofcomponentsofparticlevelocitiesorincaseoflightraysofvelocitiesofshortpulsesoflight:
Herein v isthevelocityofaparticleorofashortlightpulseand vx ; vy ; vz arecomponentsthereof.Explicitlytheserelationscanbewrittenas
Also,itissufficienttoconsiderthatlensesdeflectparticletrajectories orlightraysproportionallytothedistancetheyhavefromtheopticaxis atthepositionofthelens,thatis,theproportionalityconstantto x is1. However,verygenerallythisproportionalitycouldalsobenonlinear.
Definingittobe k2 wouldyield:
wherein kðzÞ canalsovarywith z.Thisgeneralpropagationequationis namedaftertheastronomerGeorgeHill1 asHill’sequation.Assuming that kðzÞ ispiecewiseconstant,andthatthedifferential Eq.(1.14) issolved foreachsectionof z withconstant k2 . 0,itisfoundthat xzðÞ 5 c ðÞcos kz ðÞ 1 ðd Þsin kz ðÞ
Introducingtheinitialconditions xz1 ðÞ 5 x1 and az1 ðÞ 5 a1 intothese relationsthecoefficients c and d aredeterminedandthe Eqs.(1.15) can bewrittenfor k2 . 0with k 5 kðzÞ: xðzÞ aðzÞ 5 cosðkzÞ ksinðkzÞ k 1 sinðkzÞ cosðkzÞ x1 a1 (1.16)
Noteherethatfor k2 , 0thefunctionssinðkzÞ andcosðkzÞ arereplaced bysinh kz ðÞ andcosh kz ðÞ
Thetransfermatricesof Eq.(1.16) aresolutionsofHill’sequationund thusthemostgeneralfirst-orderdescriptionsoftrajectoriesofcharged
1 Throughoutthisbookanequation d 2 x=dz2 52 k2 ðzÞx willbecalledHill’sequation,thoughin mostpublicationsHill’snameisonlyusedif kðzÞ isperiodicwith z
particlespassingthroughvaryingpotentialsaslongasthepotentialsat z1 and z2 areidentical.
1.3.1Thesignificanceofthedisappearanceofelementsof transfermatrices
Tounderstandthemeaningofthedifferentmatrixelementsforageneral opticalsysteminmoredetail,itisusefultodiscuss,whattheirindividual disappearanceimplies(Halbach,1964).Noteherethatthedeterminantof anytransfermatrixequalsunity(see Eq.1.8)sothatnevermorethantwo diagonalmatrixelementscanvanishsimultaneously,thatis,either xjx ðÞ 5 aja ðÞ 5 0oralternatively xja ðÞ 5 ajx ðÞ 5 0.
1.3.1.1Theconditions x ja ðÞ 5 0and/or ðajx Þ 5 0inatransfermatrix
For xja ðÞmn 5 0 thefirstrowof Eq.(1.11) reads xm1n 5 xjx ðÞmn xm describing that xm1n doesnotdependon am .Consequently,allraysthatstartedunder differentinclinations am fromonepointontheprofileplaneat zm ,meet againatonepointontheprofileplaneat zm1n .Thismeansthatthereisan object-imagerelationbetweenprofileplanesat zm and zm1n withalateral magnification Mx 52 xjx ðÞmn .Thissituationisillustratedin Fig.1.6A,where thestartandtheendpointsaresituatedonthe z-axis.
the case ( | ) =0
(B) the case ( | ) =0
the case ( | ) =0
(D)the case ( | ) =0
Figure1.6 Schematicrepresentationsofopticalsystems,whicharereferredtoas(A) beingparallel-to-pointfocusing,when x jx ðÞmn 5 0,(B)beingpoint-to-pointfocusing, when x ja ðÞmn 5 0,(C)havingnofocusingpower,when ajx ðÞmn 5 0,(D)beingpointto-parallelfocusing,when aja ðÞmn 5 0.
(C)
(A)
For ajx ðÞmn 5 0 thesecondrowof Eq.(1.11) reads am1n 5 aja ðÞmn am describingthat am1n doesnotdependon xm .Consequently,abundleof parallelrays,whichattheprofileplaneat zm areallinclinedbytheangle am relativetothe z-axis,aretransformedtoabundleofparallelraysat theprofileplaneat zm1n withallraysbeinginclinedbyanangle am1n 5 aja ðÞmn am orinotherwordsmagnifiedbyanangularmagnification Ma 52 aja ðÞmn .Thissituationisillustratedin Fig.1.6B,inwhichinitial andfinalbundlesofparallelraysareshown.
1.3.1.2Theconditions x jx ðÞ 5 0 and/or ðajaÞ 5 0 inatransfermatrix
For xjx ðÞmn 5 0 thefirstrowof Eq.(1.11) reads xm1n 5 xja ðÞmn am describingthat xm1n doesnotdependon xm .Consequently,abundleofparallel rays,whichattheprofileplaneat zm formsabundleofparallelraysareall inclinedbythesameangle am relativetothe z-axisandwillbefocusedto thesamepointintheprofileplaneat zm1n : Thismeansthattheprofile planeat zm1n isthesecondfocalplaneoftheopticalsystem.Thissituation isillustratedin Fig.1.6C,forthecasethattheinitialraysareallparallelto the z-axis,sothatthefinalfocusissituatedonthe z-axis.
For aja ðÞmn 5 0 thesecondrowof Eq.(1.11) reads am1n 5 ajx ðÞmn xm describingthefactthat am1n doesnotdependon am .Consequentlyallrays, thatstartedfromonepointunderdifferentanglesofinclination am fromthe profileplaneat zm ; willbeparallelafteradistance f downstreamoftheprofile planeat zm1n .Thissituationmayalsobeunderstoodastheprofileplaneat zm beingthefirstfocalplaneofthecorrespondingopticalsystem.Thissituationis illustratedin Fig.1.6D forthecasethatallraysstartedfromonepointonthe z-axis,sothattheraysofthefinalbundleareallparalleltothe z-axis.
1.4Transfermatricesoflensmultiplets Lensmultipletscanconsistoftwo,three,four....individuallenses,and itspropertiescanbedeterminedfromtheproductofthetransfermatricesof allsubparts.Thefirststepininvestigatingsuchlensmultipletscanbetoestablishatransfermatrixthatconnectsthemultiplet’sentrancefocal-plane-1toits exitfocal-plane-2(seealso Fig.1.7)as xjx ðÞff ajx ðÞff xja ðÞff aja ðÞff 5 1 0
principal-plane 1 principal-plane 2
focal-plane 1
2
Figure1.7 Apoint-to-pointfocusinglensmultipletisshown,inwhichthedistance betweenthetwofocalplanesis2f 1 dpp ,with dpp beingthedistancebetweenthe twoprincipleplanesofalensmultiplet.
Hereinthecentermatrixdescribesthepropertiesofthelensmultipletandthe driftlengths r1 ; r2 mustbechosensothat xjx ðÞff 5 aja ðÞff 5 0.Thisresultsin
(1.18a)
Experimentally r1 ; r2 couldbeobtainedforanexistinglensmultiplet bysendingaparallelbeamthroughthemultipletfromtheleftandfrom therightsideandobservethepositionsofthefocuspointsontheopposite sideofthelensmultiplet.
1.4.1Thetransfermatrixofadoubletoftwothinlenses Incaseofathinlensdoublet(see Fig.1.8),theoveralltransfermatrix fromanobjecttoanimageisdescribedby Eq.(1.17),whereinthemiddle transfermatrixof Eq.(1.17) is
Introducingtheelementsofthistransfermatrixintothe Eqs.(1.18) onefindsthefocallength fd ofthequadrupoledoubletandthedistances r1 ; r2 betweenthedoubletfocallengthand(see Fig.1.8)thepositionsof thefocalplanesoflens-1andoflens-2
with d 5 f1 1 f2 1 dff asonemaytakefrom Fig.1.8.Noteherethat fd can bevariedbyvaryingthedistance d betweenthelenses.Notefurtherthatfor fd tobepositiveoneorallthreeofthequantities dff ; f1 ; f2 mustbenegative.
planes-lens-1 principle-planes of doublet focal-planes of
planes-lens-2
Figure1.8 Alensdoubletconsistingoftwofocusingthinlenses.
Thedistances l1fd and l2fd betweenthefocalplanesofthedoubletand thepositionsofthefirstandthesecond thinlenses,respectively,arefoundas
andthedistances l1pd and l2pd betweentheprincipleplanesofthethin lensdoubletandthefocalplanesarefoundas
Importantisalsothatthedistance dppd betweenthetwoprinciple planesofthedoubletis
1.4.1.1Thetelescopeaspeciallensdoublet
Awell-knownlensdoubletisatelescope,whichbecameimportant alreadyseveral100yearsagotoobserveobjectsthatarelongdistances away.Suchdevicesformasmallrealimageofadistantobject,whichis
observedthroughaloupeormagnifyingglass(see Fig.1.5).Thus,the twolens-systemachievesanobject-imagerelationbetweenthedistant objectandthevirtualimage,whichrequires xja ðÞff 5 0forthetransfer matrixofthelensdoublet.Also,asisshownin Fig.1.9,theincoming lightraysthatoriginatedfromonepointofthedistantobjectforma quasi-parallelbeam,whichshouldbetransformedbythetelescopeintoan outgoingparallelbeam,sothattheincominglightiscompletelypassedto theobserver.Suchasituationwasalreadyshownin Fig.1.6B and discussedasbeingcausedby ajx ðÞff 5 0.
axis
Figure1.9 Twotelescopesareshowneachoneofwhichconsistsoftwolenses,a firstso-calledobjectivelensandasecondsocalledeyepieceorocular.Thereisa Keplertelescope,whichhasanegativeangularmagnification a2 =a1 andforwhich bothlensesarefocusing,andaGalileantelescope,whichhasapositiveangularmagnification a2 =a1 andforwhichoneofthelensesisfocusingwhiletheotherisdefocusing.NotethatforhighperformanceapplicationstheKeplertelescopeispreferred whileGalileantelescopesareused,whencompactdevicesaredemanded.
Applyingtheconditionthattheoutgoingraysformaparallelbeam, whentheincomingbeamisaparallelbeamto Eq.(1.19) resultsin dff 5 0,whichisthesameasstatingthatthesecondfocalplaneofthe objectlensandthefirstfocalplaneoftheeye-pieceorocularcoincide. Forasystemtoobservefarawayobjectsthetelescopemustenlargethe
inclination a1 oftheincomingbeamtoamagnifiedinclination aja ðÞa1 of theoutgoingbeamwiththeratioofthetwoinclinationsbeing
Toachieveahighangularmagnification, f1 mustbelargeand f2 mustbesmall. Noteherethatthediameteroflens-1,theobjectlens,limitsthe diameter D1 oftheincomingparallelbeamandthatthetelescopeshould bedesignedsothatthediameter D2 ofthefinalparallelbeamissmaller thanthediameteroftheobserver’seyepupil.Notefurtherthatthe amountoflightthatiscollectedbytheeyeoftheobserverisincreasedby thetelescope’ s ðD1 =D2 Þ2 ,whichmakesitadvantageoustochooselarge diametersfortheobjectlens.
Therearetwosolutionsforatelescope.Thereistheso-calledastronomicalorKeplertelescopeforwhich f1 . 0and f2 . 0and Ma isnegative,thatis,theobjectisseenupsidedown.ThereisalsotheDutchor Galileantelescope,forwhich f1 . 0and f2 , 0and Ma ispositive,thatis, theobjectisseenupright.Inbothcasestheusedlensesshouldbewell designedlensmultiplets,sothattheimageaberrationsofthelensesdonot limittheresolvingpowerofthetelescope.
1.4.1.2Lensesoflongandshortfocallengthsforphotographic cameras
Forsomeapplicationsoflensdoubletsonedefocusingandonefocusing lensarecombined,sothatthefocallength fd ofthelensdoubletispositive onlyfor dff , 0accordingto Eq.(1.20a).Consequently,thetwolenses arerelativelyclosetoeachotherandaccordingto Eq.(1.21c) theprincipleplanesareshiftedtowardthesideofthepositivelensasisshownin Fig.1.10.Thispropertyofadoubletcanbeusedtoconstructlensesfor whichtheprincipalandthefocalplanesareshiftedtosuitablepositions relativetothephysicaldimensionsofthelenses.Oneexampleofsucha designisatele-lensthatcanbeusedforaphotographiccamera.Insucha cameratheimageofaverydistantobject,thatis, w1fd N,issituated ataposition w2fd 5 f 2 d =w1fd closebyanddownstreamofthefocal-plane-2 ofthecameralens.Theimageofadistantobjectislocatedatthesecond focalpaneofthedoubletanditssizeisthemagnitudeoftheobject multipliedbythelateralmagnification Mx 5 fd =w1fd ofthedoublet. Tokeepthismagnificationwithinlimitsandstillallowtoobservedetails oftheimage,itisadvantageoustousealensoflongfocallength fd .On theotherhand,suchalensislargeandinconvenienttocarry.Asolution