NONLINEAR DIFFERENTIAL EQUATIONSIN
MICRO/NANO
MECHANICS
Applicationinmicro/nanostructures andelectromechanicalsystems
ALIKOOCHI
DepartmentofMechanicalEngineering UniversityofTorbatHeydarieh TorbatHeydarieh,Iran
MOHAMADREZAABADYAN
DepartmentofMechanical&AerospaceEngineering RamsarBranch,IslamicAzadUniversity Ramsar,Iran
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2020ElsevierLtd.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicor mechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem,without permissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthe Publisher’spermissionspoliciesandourarrangementswithorganizationssuchastheCopyrightClearanceCenter andtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions.
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(other thanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusingany information,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodsthey shouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessional responsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliability foranyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,or fromanyuseoroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-819235-1
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: SimonHolt
EditorialProjectManager: GabrielaD.Capille
ProductionProjectManager: NirmalaArumugam
Designer: AlanStudholme
TypesetbyVTeX
TomywifeFatemeh, mydaughterKousar, andmysonKiarash.
AliKoochi
ToO.B.
ForO.B.wasaninspiringfriendeventhoughwe’venevermet. O.B.knewthesecretsofseasons, Andlivesfaraway,whereonemightmisshome.
...Ifallthesereasonsarenotenough,IwilldedicatethebooktoKOOCHIfromwhom O.B.grew... AndsoIcorrectmydedication:ToO.B.whenO.B.wasKOOCHI. MohamadrezaAbadyan
Preface ix Acknowledgments xi
1.Differentialequationsinminiaturestructures1
1.1. Introductiontominiaturestructures1
1.2. Physicsofsmall-scalestructures4
1.3. Modelingofsmall-scalestructures17
1.4. Conclusion 26 References 26
2.Semianalyticalsolutionmethods31
2.1. Introduction31
2.2. Homotopyperturbationmethod31
2.3. Adomiandecompositionmethods43
2.4. Green’sfunctionmethods63
2.5. Differentialtransformationmethod77
2.6. Variationiterationmethods84
2.7. Galerkinmethodforstaticproblems90
2.8. Conclusion100 References 100
3.Numericalsolutionmethods107
3.1. Introduction107
3.2. Generalizeddifferentialquadraturemethod107
3.3. Finitedifferencemethod124
3.4. Finiteelementmethod136
3.5. Conclusion156 References 156
4.Dynamicandtime-dependentequations161
4.1. Introduction161
4.2. Reduced-orderapproaches161
4.3. Runge–Kuttamethod195
4.4. Homotopyperturbationmethodfortime-dependentdifferentialequations217
4.5. Energybalancemethod227
4.6. Methodofmultiplescales237
4.7. Conclusion248 References 248 Index 253
Preface
Introduction
Withthenewadvancesinmicro-andnanotechnology,ultrasmallstructureshave beenincreasinglyconsideredinvariousengineeringandsciencebranches.In-depth knowledgeoftheminiaturestructuresundervariousphysicalphenomenacan significantlyreducethetimeandcostofdesigning,developing,andoptimizingthese structures,comparedtorepetitivefabricationandtestinginthelaboratory.
Thepurposeofthisbookistobringtogetherthevariousconcepts,methods, andtechniquesneededtoattackandsolveawidearrayofproblems,including modeling,simulation,analysis,anddesignofsmall-scalestructuressuchasmicro-and nanoelectromechanicalsystems(NEMS/MEMS).
Generally,accuratemodelsarecrucialfornanostructuredesignandanalysisdue tothehighcostsandcomplexityofexperimentalsetupsandfabricationprocesses. Ontheotherhand,reliablesimulationofminiaturesystemsrequiresacomprehensive understandingofthemechanicalbehaviorsofdevices,aswellastheinteractionbetween thesystemandexternalforcefields.Inthisway,newphysicalphenomenawillemergein thecaseofdecreasingthedimensionsofastructurefrommicroscaletonanoscale.The precisesimulationofMEMS/NEMSneedsacomprehensiveknowledgeofnanoscale phenomenaandefficientmethodstoincludetheseissuesinthefinalmodel.The mechanicalperformanceofnanostructurescanbemodeledusingvarioustechniques suchasmoleculardynamics/mechanics,multiscalemodeling,modifiedmechanics models,andthelike.Inthisregard,theuseofnonclassicalcontinuummechanicsis regardedasoneofthepowerfultechniquesformodelingminiaturestructures.The continuummechanicdoesnotrequirecomputationalequipmentasthemolecular dynamicsorab-initiomethodsandprovidessufficientlyaccurateresultsforsimulating nanostructures.However,continuummechanicsusuallyleadstoahighlynonlinear differentialequationthatcannotbesolvedusingconventionaltechniques.
Thisbookattemptstoapplyvariousefficientnumericalandsemianalyticalmethods forsolvingthenonlineargoverningequationsofmicro/nanostructuresthatemerged fromthemodifiedcontinuummechanicsmodels.Theproposedsolutionmethodsare employedtoevaluatethestaticanddynamicbehaviorsofmicro/nanostructuresthrough someappropriateexamples.Tothisaim,wesimulatedvariousstructures,including beamtypeMEMS/NEMS,carbonnanotubeactuators,nanotweezers,nanobridges, plate-typemicrosystems,nanoresonators,androtationalmicromirrors.Thebookalso includesthemodelingprocessneededforsimulatingnumerousnonlinearitiesinmicroandnanostructuresduetophysicalphenomenasuchasdispersionforces,dampingeffect,
nonclassicboundaryconditions,fluid–solidinteractions,electromechanicalinstability, surfaceenergies,nonlocalandsize-dependency.
Thematerialofthecurrentbookisorganizedasfollows.Chapter 1 introduces theessentialconceptsforthemodelingofultrasmallstructuresandexplainsthe physicalphenomenaemergingonthenano-andmicroscale.Chapter 2 discusses somesemianalyticalapproachestosolvenonlineardifferentialequations,inadditionto investigatingthebehaviorofvariousmicro-andnanostructuresbasedonsemianalytical methods.Chapter 3 presentsavarietyofnumericalapproachestosolvethenonlinear differentialequationsforevaluatingthebehaviorofsomemicro-andnanostructures. Finally,Chapter 4 providessomemathematicalapproachestosolvethenonlinearpartial differentialequationdescribingthedynamicperformanceofmicro/nanostructures.
Itshouldbeacknowledgedthatnomatterhowmanytimesthematerialisreviewed andhowmanyeffortsarespenttoguaranteethehighestquality,theauthorscannot ensurethatthemanuscriptisfreefromminorerrorsandshortcomings.Weare lookingforwardtoreceivingeveryone’sfeedbackandcommentsontheerrorsor subjectofthebook.Pleasesendyourcommentstothefirstauthor’semailatthe DepartmentofMechanicalEngineering,UniversityofTorbatHeydarieh,withthe address: A.koochi@gmail.com (AliKoochi).
Audience
Thisbookisacomprehensivetextonnonlineardifferentialequationsinmicroandnanostructures,andithasbeenpreparedforawiderangeofreaders,especially academics,whoneedtolearnhowtosolvenonlinearordinaryandpartialdifferential equations,andprofessionalresearcherswhoinvestigateinthefieldofnanostructuresand NEMS/MEMSmodeling.Theproposedmethodsareappropriateformultidisciplinary researchersinthefieldofmicro/nano-computations.Tobemoreprecise:
• Thebookissuitableforstudentsparticipatinginthecoursesandresearchesonthe nonlineardifferentialequationandanalyticalmethodsinmicro-andnanostructures.
• Thebookcanbeusefulforprofessionals,duetotheconsiderationofdifferent physicalphenomenaandvariousnano/microstructures.
• Thesolutionmethodsofthedifferentialequationsarepresentedpracticallyand straightforwardly.Therefore,thebookwillbesuitableforbothundergraduate andpostgraduatelevels,i.e.,forBachelorstudentsandMaster/PhDstudentsand lecturers.
• Thisbookcanalsobeadaptedforashort-termprofessionalcourseonthesubject matter.Engineersandappliedscienceresearcherswillbeabletodrawuponthe bookinselectinganddevelopingmathematicalmodelsforanalysisanddesign purposesinappliedconditions.
Differentialequationsinminiature structures
1.1.Introductiontominiaturestructures
Today,theapplicationofminiaturestructureshasincreaseddramaticallyinvariousindustriesbecauseoftheincreasingneedforpreciseinstrumentsandextensiveeffortsto reducethevolumeandweightofequipment.Thediminutivesize,lowpowerconsumption,highprecision,andreliabilityofthesesystemsmakethemattractive.Miniature structuresmightrefertomicrostructureornanostructures.The UnitedStatesNational NanotechnologyInitiative definesnanotechnologyas“theunderstandingandcontrolof matteratthenanoscale,atdimensionsbetweenapproximately1and100nanometers”[1].Referringtothisdefinition,ananostructurecanbedefinedasastructure thathasatleastonedimensionintherangeof1to100nm.Becauseananostructuremustbuildfromatomsandmolecules,thelowerlimitisfixedbythesizeofthe moleculesandatoms.Forinstance,thediameterofanH2 moleculeisabout0.25nm, andthefullerene(C60 )ballouterdiameterisabout1nm.Theupperlimitisroughly contractual.However,100nmisapproximatelythesizeatwhichnanoscalephenomena cannotbeobservedorarenegligible.Similarly,amicrostructurecanbedescribedasa structurewithatleastonedimensionsizedfrom1to100micrometers[2].
Microelectromechanicalandnanoelectromechanicalsystems(MEMS/NEMS)are well-knownultrasmallstructureswithbroadapplicationsinscienceandtechnology. ReferringtotheappellationofNEMS/MEMSmightbeasimplewaytorecognize theirmeanings:thefirstpartofMEMSsignifies“micro,”andthefirstpartofNEMS signifies“nano.”Thesetermsspecifytheirscales.HenceMEMSandNEMSaredevices onthe“micro”and“nano”scale,respectively.Thesubsequentpartsaresimilar.The “electro”componentspecifiesthatNEMSandMEMSuseelectronicsorelectricpower. “Mechanical”referstomechanicalactionormotion.The“system”indicatesthatthese devicesareasetofintegratedcomponents,notindividualparts.
NEMSandMEMShavedistinguishedpropertiesanduniquecharacteristics,such aseasyfabrication,highefficiency,lowpowerconsumption,andquickresponse.These devicescanbeutilizedassensorsandactuators.Therearedifferentactuationtechniques, suchasthepiezoelectric,thermal,piezoresistive,optical,electromagnetic,andelectrostaticmethods.Whiletheactuationmethodisdependentupontheapplicationofthe device,electrostaticsisthemostpopularactuatingandsensingmethod[3].
NEMS/MEMSandmicrostructures/nanostructureshavebeenusedwidelyindifferentbranchesofscienceandtechnologyassensorsandactuators.Theapplicationof
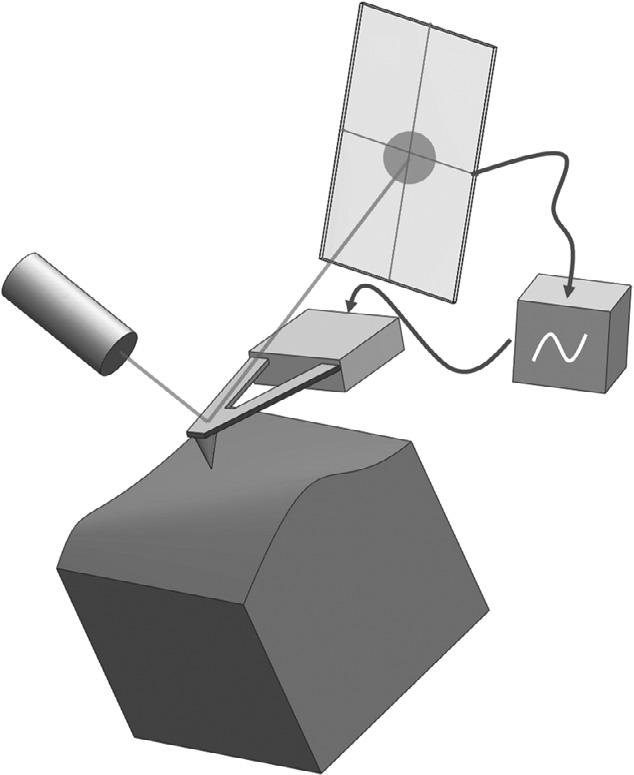
Figure1.1 Atomicforcemicroscopysensor[12]:(A)schematicview,(B)SEMimage.
thesesystemsincludes,butisnotlimitedto,atomicforcemicroscopy(AFM)[4],microandnanoswitches[5],micro-andnanoresonators[6],pressuresensors[7],accelerometers[8],micro-andnanotweezers[9],neuronalrecordingsdevice[10],andmicro-and nano-opticalswitches[11].Fig. 1.1 showsthescanningelectronmicroscope(SEM)imageandschematicviewofanatomicforcemicroscope(AFM)sensor.Ascanbeseen, theAFMsensorcanbemodeledasacantilevermicro/nanobeam.TheSEMimageofa radiofrequency(RF)microswitchandamicroresonatorarepresentedinFigs. 1.2 and 1.3,respectively.Aclamped–clampedmicro/nanobeamhungoverafixedsubstratewith adielectricin-betweencanmodelthesestructures.Fig. 1.4 demonstratestheSEMimageofanaccelerometermicrosensor.Thesesensorscanbesimulatedasacantileverbeam withaconcentratedmassonthetip.TheSEMimageofmicrotweezersisillustratedin Fig. 1.5.Thisstructurecanbemodeledasatwoparallelcantilevermicro/nanobeams witharectangular,orcircularcross-sectiondependsonthemanufacturingmethod.
Figure1.2 SEMimageofanRFmicroswitch[13].
Figure1.3 Amicroresonator[6].
Figure1.4 AnMEMSaccelerometersensor[14].
AtypicalopticalswitchisillustratedinFig. 1.6.ThistypeofNEMS/MEMScanbe simulatedasaplatesupportedbytorsionalarms.Acarbonnanotubeprobeusedinthe tipofanatomicforcemicroscopyisshowninFig. 1.7.
1.2.Physicsofsmall-scalestructures
Whendimensionsofasystemarereducedtosubmicronscale,somephysicalaspects appear,whichmaynotexistatthemacroscale.Inthissection,theessentialphysical phenomenaofNEMSandMEMSarediscussed.Theimpactoftheproposedphenomenaontheperformancesofmicro-andnanostructuresarediscussedthroughseveral examplesinthesubsequentsections.
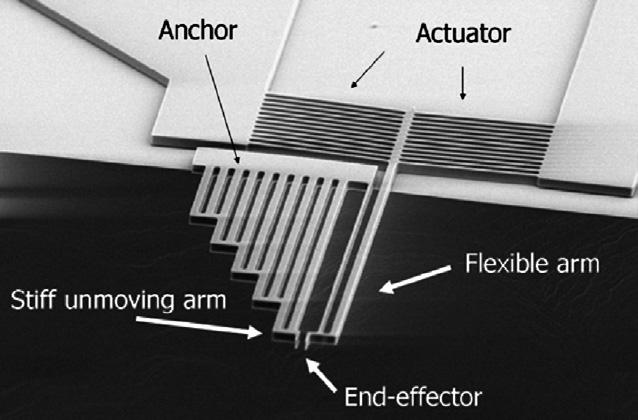
Figure1.5 SEMimageofnanotweezers[15].
Figure1.6 SEMimageofanopticalmicroswitch[16].
Figure1.7 SEMimageofacarbonnanotubeprobe[17].
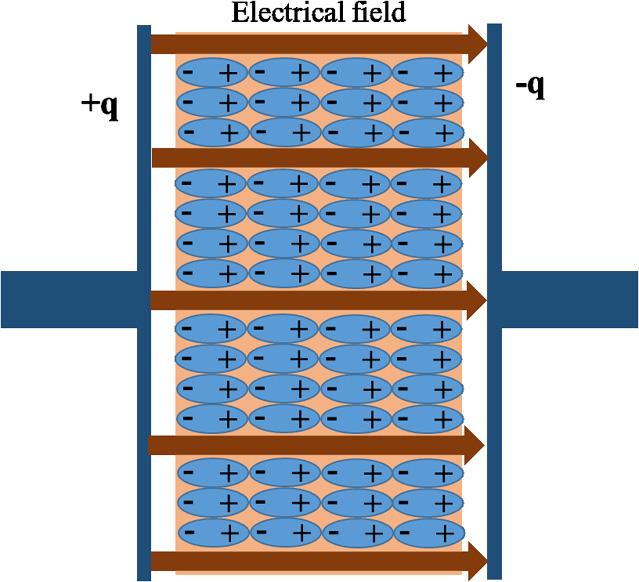
Figure1.8 Theidealelectricfieldbetweenparallelplates’capacitors.
1.2.1Electrostaticactuation
Asmentionedpreviously,electrostaticactuationisthemostpopularactuationmethod inMEMSandNEMS.BecauseawidespreadgroupofNEMSandMEMScanbe consideredasparallelbeamsorplates,theelectricalfieldbetweentwoparallelplates isintroduced.Whenavoltagedifferenceisappliedbetweentwoparallelplates,the platesconstructacapacitor.Theelectricalforceactingonthepartscanbeachieved bydifferentiatingthestoredpotentialenergyofthecapacitor.Fortwoinfiniteparallel plates,theelectricalfieldisuniform,asshowninFig. 1.8.Forthisidealcase,the capacitanceoftwoparallelplatesisdirectlyproportionaltotheplates’areaandinversely proportionaltotheseparationordistancebetweentheplates.Hence,thecapacitance canbeformulatedas[18]
where ε isthepermittivityofvacuum.Theelectricalenergyperunitlengthisdeterminedas
Therefore,theelectricalforcebetweentwoinfiniteparallelplatesisachievedas
TheelectricalforceexplainedinEq.(1.3)isfortwoinfiniteparallelplates.Inthisequation,theelectricalfieldisassumedtobeideallyuniform,andtheeffectoftheplate’s
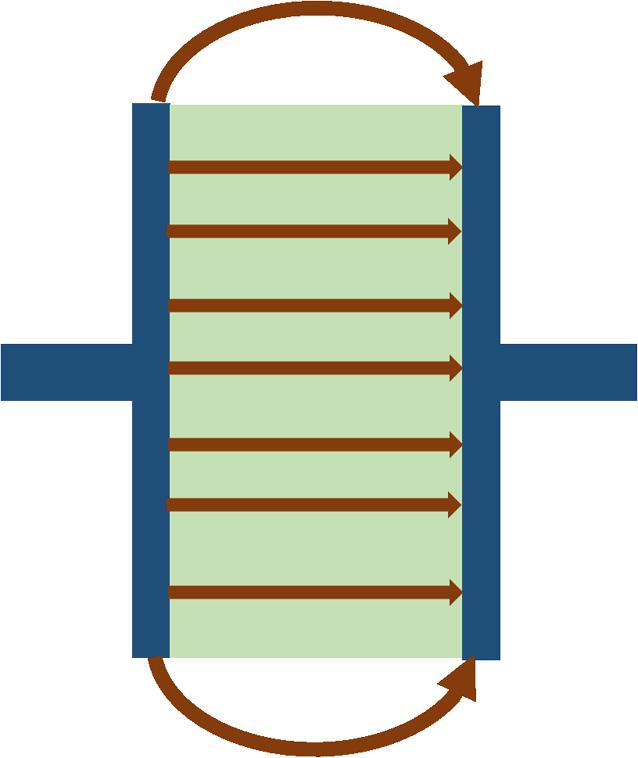
Figure1.9 Fringingfieldeffectinparallelplates’capacitors.
thicknessisneglected.However,forafiniteplate,theimpactofthenonuniformelectricalfieldintheedges(i.e.,flingingfield)mightaffectthecapacitance(seeFig. 1.9). Toincorporatethefringingfieldinthesimulationoftheelectricalforce,severalmodifiedmodelshavebeendeveloped.Forafiniteplate(beam)withthickness h,width b, andlength L ,paralleltoaninfiniteplateatdistance g ,themodelsforcapacitanceby consideringfringingfieldeffectaresummarizedinTable 1.1.
1.2.2Pull-ininstability
NEMSandMEMSarewidelyappliedassensorsandactuators.WhiledetectionmethodsrequireforNEMS/MEMSsensors,theactuationtechniquesareessentialinthe applicationofNEMS/MEMSasactuators.Asensingordetectionmethodisatransforminaphysicalquantitysuchasforce,pressure,acceleration,ortemperatureinto ameasurableelectricalsignal.Conversely,anactuationmethodisthetransformation ofelectricalpotentialtothemechanicalmovement,whichcanbeusedformotion, applyingforce,andswitching.Therearedifferentsensingandactuationtechniquesin NEMSandMEMS,includingelectro-thermal[26,27],electromagnetic[28,29],electrostatic[30,31],piezoelectric[32,33],andpiezoresistive[34,35]methods.Whilethe actuationmethodstronglydependsonthepracticalapplicationofthedevices,theelectrostaticactuationschemeisthemostcommonlyusedinMEMSandNEMSbecause ofitsnumerousinherentbenefits[3].However,thismechanismresultsinhighlynonlinearinstabilitybehaviorcalled“pull-ininstability.”Theelectricvoltageactsonan NEMS/MEMS,leadingtoanelectrostaticforcefollowedbythedeflectionofthemoveablecomponentsintoanewequilibriumposition.Theelectricalforcehasanupper
Table1.1 Capacitancemodelsbyconsideringthefringingfieldeffect. ModelCapacitanceperunitlength
Palmer[19]
Chang[20]
YuanandTrick[21]
SakuraiandTamaru[22]
VanderMeijsandFokkema[23]
Elliott[24]
Batraetal.[25]
c0 =−5 40
c1 = 4 60
c2 = 0 325
c3 = 0 126
c4 =−0.554
c5 =−0.00388
c6 = 0.891
c7 = 3.47
c8 = 0.118
Batraetal.[25] C = ε b g + c0 + c1 b g c2 + c3 h g c4
c0 =−0.36
c1 = 0.85
c2 = 0.2
c3 = 2.5
c4 = 0 24
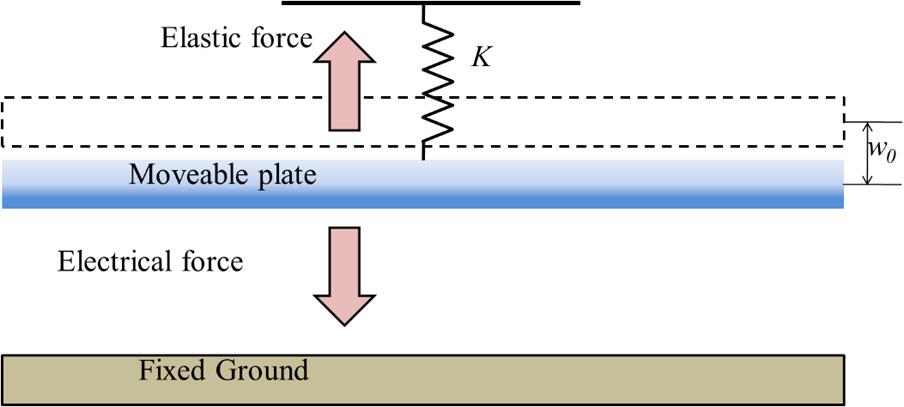
Figure1.10 Aparallelplatecapacitor(theupperplatehungbyaspring).
limit.Iftheelectricalforcepassesthislimit,itovercomesthemechanicalresistance, therebyincreasingthemoveablecomponentdeflection.Accordingly,theelectrostatic forceisenhancedinapositiveloop.Thisphenomenonisknownas“pull-in,”andits pertinentvoltageisknownasthe“pull-involtage”[36].Sometimesthepull-inphenomenonistheessentialaspectfortheproperperformanceofNEMS.Forexample,the pull-ininstabilityorganizesthebasisoftheRFswitchoperation[37,38].Conversely, thekeypointinthedesigningofmicronanoresonatorsandmicromirrorsareavoiding thepull-inphenomena[39,40].
Toexplainthisphenomenonmoreclearly,consideraparallelplatemicrocapacitor. Thisstructurecanbeconsideredasamovableplatehungoverafixedgroundbya spring,asdemonstratedinFig. 1.10.Itshouldbenotedthatthissimplemodel,known asthe“lumpedparametermodel,”issometimesusedtomodelthebehaviorofbeamtypeMEMSandNEMS[41].Thelumpedparametermodelisdiscussedindetailin Section 1.3.1.Theplate’sareaisassumedtobe0.16mm2 ,theinitialgapbetweenthe platesis4 µm,andthespringconstantis0.816N/m.Byapplyingthevoltagedifference betweentwoplates,themoveableplatemovestowardthefixedoneuntiltheelectrical forceisequaltothespringforce.Theelectricalandspringforcesfordifferentvalues ofexternalvoltageareplottedinFig. 1.11.Theinteractionpointbetweentheelectricalandspringforcesistheequilibriumpoint.Whentheappliedvoltageislowerthan thepull-invalue,therearetwoequilibriumpoints(Fig. 1.11A–B);byincreasingthe appliedvoltage,thespringforceistangenttotheelectricalforceatthepull-involtage (Fig. 1.11C).Iftheappliedvoltagerisesmore,thereisnointersectionbetweenthe electricalandspringforces.Inotherwords,theelectricalforceisalwayshigherthanthe springforce.Therefore,thespringforcecannotovercometheelectricalforce,andthe upperplatefallstothefixedground,i.e.,instabilityoccurs.
ItisworthnotingthatwhentheDCvoltageleadstopull-in,theinstabilityiscalled “staticpull-in”orjust“pull-in.”However,inthecaseofACloadingortransientDC voltage,theinstabilityisknownas“dynamicpull-in”[42].
Figure1.11 Electricalandspringforcesfordifferentappliedvoltages:(A) V = 2volts;(B) V = 3volts; (C) V = 3 3057volts(pull-in);and(D) V = 3 4volts.
Figure1.11 continued
1.2.3Dispersionforces
Thedispersionforcesaretheforcesthatactlikegravitybetweenallatomsandmolecules, evenbetweentwounchargedbodiesinavacuum.LifshitzdevelopedthecohesivetheoryofthevanderWaalsandCasimirforcesassubdivisionsofdispersionforces[43]. Basedonthistheory,thedispersioninteractionbetweentwoparallelplatesisrelatedto thefrequency-dependentdielectricpermittivitiesandmagneticpermeabilitiesofplates’ materials.Whenthedistancebetweenthebodiesissmallerthantheretardationlength, thevanderWaalsforceshouldbeconsidered.ThevanderWaalsattractionbetween twoinfiniteparallelplatesisproportionaltotheinverse-cubeofthedistancebetween theplates[44].ThevanderWaalsattractionperunitareabetweentwoidealparallelflat platesisdefinedas[45]
where g isthedistancebetweentheplatesand A istheHamaker’sconstant.
AnappropriatemethodforcalculatingthevanderWaalsforcebetweentwoarbitrary bodiesistoemploytheLennard-Jonespotential,whichexpressesthepotentialbetween twoatomsas
where C12 istherepulsiveconstant, C6 istheattractiveconstant,and rij isthedistance oftheatoms.Fordistancesgreaterthan3.4Å,therepulsivetermisnegligibleincomparisonwiththeattractiveterm.Areliablecontinuummodelhasbeenestablishedto computethevanderWaalsenergyusingthedouble-volumeintegraloftheLennard-
Jonespotential,whichis[46]
where υ1 and υ2 representthetwodomainsofintegration,and ρ1 and ρ2 arethedensitiesofatomsinthesedomains.Thedistancebetweenanytwopointson υ1 and υ2 is r (υ1 ,υ2 )
AnothersubdivisionofdispersionforceistheCasimirforce.Thisforceactsatlarger separationsthanthevanderWaalsforce.Indeed,whentheseparationbetweenthe twobodiesisgreaterthantheretardationlength,theCasimirforceisdominant.The Casimirattractionperunitareabetweentwoparallelconductingplatesisnotaffectedby thematerial’spropertiesandisproportionaltotheinversefourthpowerofdistance.For twoinfiniteconductingparallelsseparatedbyadistance, g theCasimirforceisdefined as[47]
where c = 2.9979 × 108 m/sisthelightspeedand h = 1.0546 × 10 34 J.sisthereduced Planck’sconstant.
1.2.4Sizedependency
Experimentalobservationdemonstratedthatthestiffnessofmetal-basedultra-small structuresisscale-dependent.Forexample,empiricalobservationofthebendingof nickelmicrobeamscarriedoutbyStolken,andEvans[48]confirmedthatwhenthe beamthicknessdecreases,themicrobeamplasticworkhardeningisenhancedconsiderably.Flecketal.[49]investigatedthetorsionalhardeningofcopperwires.Theydetected thehardeningofa12-µmdiameterwiretobeaboutthreetimesgreaterthanthehardeningofasimilar170-µmdiameterwire.Thisphenomenonhasalsobeendiscovered insomepolymers.ChongandLam[50]demonstratedthatadecreaseinthethickness ofepoxybeamsresultsintheenhancementoftheirnormalizedbendingstiffness.They determinedthatthebendingrigidityofanepoxybeamwitha20-µmthicknessisabout 2.4timesgreaterthanthebendingstiffnessofasimilarbeamwitha115-µmthickness. McFarlandandColton[51]evaluatedthestiffnessofpolypropylenemicrocantilevers anddeterminedittobeatleastfourtimesgreaterthanthevaluesexpectedwiththe classicalelasticitytheory.Thissize-dependentbehaviorofmaterialsandstructurescannotbesimulatedthroughclassicalcontinuumelasticity.Tobridgethegapbetweenthe theoreticalsimulationandtheexperimentalresults,varioussize-dependentcontinuum theorieswereproposed.
In1962,Mindlindevelopedthecouplestresselasticitytheoryforsimulatingthe scale-dependentbehaviorofminiaturestructures[52].Forthispurpose,ahigher-order
Figure1.12 Simpleillustrationofincreasingthesurfacetovolumeratiobyreducingthesize.
stresstensor(i.e.,couplestresstensor)wasintroducedinadditiontotheclassicalstress tensor.Thecouplestresstensorcomponentswereexpressedintermsofthegradientof elementsrotationandnewmaterialconstants,whichwerepertinenttotheconventional materialconstantsbythemateriallengthscale.Yangetal.[53]modifiedtheMindlin couplestresstheory.Theydevelopedthecouplemomentsequilibriumratherthanclassicalforcesandmomentsequilibrium.Thisadditionalequilibriumconditiondictated thatthecouplestresstensormustbesymmetric.Thereby,twomateriallength-scaleparametersofageneralcouplestresstensorwerereducedtoonematerialparameterinthe modifiedcouplestresstensor.
ThemostcomprehensivestraingradientmodelwasexpressedbyMindlin[54].This theoryincludesfiveaddedmaterialparameters,andtheotherstraingradienttheories canextractfromtheMindlingeneralstraingradienttheoryLametal.[55]expressed amodifiedstraingradient.Theydecomposedthesecond-orderdeformationgradient tensorintothestretchgradienttensorandtherotationgradienttensor.Thisdecompositionreducedthemateriallength-scaleparameterfromfiveinthegeneralstraingradient theorytothreeinthemodifiedstraingradienttheory.
Eringendevelopsthenonlocaltheoryinthe1970s[56].Intheclassicalorlocal continuummechanics,thestressateachpointdependsonthestrainsatthatpoint.In contrast,inthenonlocalcontinuummechanic,thestressatareferencepointinthe domaindependsnotonlyonthestrainsatthatpointbutalsoonthestrainfieldatevery pointinthebody.Inthisregard,scale-dependentparameters(internalcharacteristic length)appearintheconstitutiveequationswhichcansimulatethesizedependencyof theminiaturestructures.
1.2.5Surfaceeffects
Reducingthestructuresizeenhancesitssurfacearea-to-volumeratio.AsimpledemonstrationoftheenhancementofthesurfacetovolumerationisillustratedinFig. 1.12.As seenbyreducingthevolumefrom9tooneunit,thesurfacetovolumeratioincreases from2to6.Toclarifythisfact,thesurface-to-volumeratioasafunctionofthebasicdi-
Figure1.13 Surface-to-volumeratioasafunctionofbasicdimension.
mensionisillustratedinFig. 1.13.Thisfiguredemonstratesthatthesurface-to-volume ratioofa1nmwidthcubeis109 timesgreaterthanthesurface-to-volumeratioofa 1mwidthcube.Thesamecanbeobservedforananoscalesphere.
Formechanicalelementswithahighsurface–volumeratio,thesurfaceenergiescan significantlyaffecttheirmechanicalproperties.Tosimulatethesurfaceenergies,the moleculardynamicmethodcanbeemployed.However,thismethodishighlytimeconsumingandrequireshigh-performancecomputers.Toovercometheinefficiencyof themoleculardynamicsprocedureforstructures,thesurfaceelasticitytheorydeveloped byGurtinandMurdoch[57]canbeemployed[58].Itiscapableofsimulatingboththe residualsurfacestressandthesurfaceelasticity.
1.2.6DampinginNEMS/MEMS
TheresourcesforenergydissipationinNEMS/MEMScanbeclassifiedintointrinsic andenvironmentaleffects.Theintrinsicenergylossresourcesincludethermoplasticdampingandsurfacephononscattering.Also,themostcommonenvironmental resourcesofenergylossinNEMSandMEMSareanchors,acoustic,andviscousdamping[36].Intheultrasmallstructures,theintrinsicenergylossisnegligibleincomparison withtheexternalresources.Nevertheless,theintrinsiceffectshouldbeconsideredwhen achievingahigh-qualityfactorisdesired.Todeterminetheeffectofallenergydissipationresources,eachsourcecanbedefinedintermsofacorrespondingqualityfactor (Qi ).Thetotalqualityfactorisgivenby
Table1.2 Parameter α inEq.(1.10)[36].
BoundaryconditionVibratingmode
Thequalityfactorhasaninverserelationshipwiththedampingratio(ξ )andtheenergy lossofthesystem.Therefore,ahigherqualityfactorindicatesalowerrateofenergyloss relativetothestoredenergy.Incontrast,alowerqualityfactorindicatesahigherrateof energylossrelativetothestoredenergy:
Energylossinthesupportsinknownasanchorloss.Thislossisduetouncanceledshear forcesandmomentsintheendsupports.Amongthese,theshearforceshaveamore dominanteffectonenergyloss.Therefore,byneglectingtheimpactoftheuncanceled moment,thequalityfactorforcantileverandclampedbeamsisgivenby[59]
where L isthebeamlength, h isthebeamthickness,and α isaparameterthatdepends ontheboundaryconditions,modeofvibration,andPoisson’sratio.Theparameter α forcantileverandclampedboundaryconditionbyconsideringthePoisson’sratioequal to0.28isdemonstratedinTable 1.2.
1.2.6.1Dragforce
Dragforceactingistheresistanceforceoppositetotherelativemotionofabodymoved throughthefluid.Inmicro-andnanostructures,thedragforcemightresultinenergyloss.Therefore,thedragforcecanbeconsideredasadampingresource.Some researchersinvestigatedthedragforceofcomplexsystemsbydividingthemintosimple shapes.Forexample,thebeamhasbeensimulatedasaseriesofspheres,andthesphere dragforceisusedtofindthedragforceoverabeam[60,61].Byneglectingtheeffectof addingmass,thedragforceoveraspherewithradius R andvelocity u isgivenby
Intheaboveequation,thedampingcoefficientofasphereforthefrequency ω isdefined as
Figure1.14 Squeezedfilmbetweentwoplates.
where μ isthefluidviscosityand ρ isthefluiddensity.Also,abeamcanbesimulated asastringofdisheswiththediameterofthedishesequaltothewidthofthebeam.By usingthisapproach,Bao[62]determinedthedampingcoefficientofabeamequalto 8μ
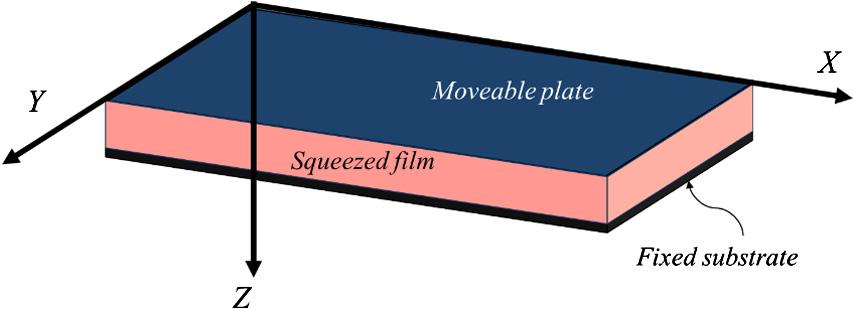
1.2.6.2Squeezedfilmdamping
Thedynamicofsmallpartsinanultrasmallsystemcanbeaffectedbythemovement ofthefluidtrappedunderneaththeplate,whichisknownassqueezedfilmdamping (seeFig. 1.14).ForNEMS/MEMSwithamoveableplate,squeezefilmdampingcan affectthesystemfrequencyresponse.Squeezefilmdampingisthemostcommonand dominantenergylossmechanisminNEMS/MEMS.Ingeneral,thedynamicofthe squeezefilmisgovernedbybothviscousandinertialeffectsonfluid.However,for ultrasmallstructures,theinertialeffectcanbenegligible.Insuchacase,assumingideal gaslawandisothermalconditions,thebehaviorofaNewtonianfluidcanbeexpressed bytheReynoldsequationas
where P isthepressure, m istheviscosity, t isthetime,and g indicatestheseparation betweenthemoveableandfixedplate.Itshouldbenotedthatthevariationofpressure acrossthefilmthickness(i.e., Z direction)isignoredinderivingtheReynoldsequation.
NEMS/MEMSmightoperateinlow-pressureconditions.Inthissituation,thefluid cannotconsiderasacontinuum.Therefore,Eq.(1.13)mightnotpredictthebehavior ofsqueezedfilmcorrectly.However,bymodifyingtheviscosity,moreaccurateresults canbeachievedfromEq.(1.13).Variousmodelshavebeenproposedfor“effective viscosity,”whichdependsdirectlyontheKnudsennumber.Somemodelsforeffective viscosityarepresentedinTable 1.3
Forincompressiblegas,thederivativeofpressurewithrespecttotimeiszero.Also, forbeamtypeNEMS/MEMS,thelengthofthebeamisconsiderablymoresignificantthanthebeamwidths.Therefore,thepressureinthelongitudinaldirection(x)