Multi-Objective Passing Vehicle Search algorithm for structure optimization
Sumit Kumar a, 1 , Ghanshyam G. Tejani b, * , 2 , Nantiwat Pholdee c , Sujin Bureerat c
a Department of Mechanical Engineering, GPERI, Gujarat Technological University, Gujarat, India
b Department of Mechanical Engineering, School of Technology, GSFC University, Vadodara, Gujarat, India
c Sustainable and Infrastructure Research and Development Center, Department of Mechanical Engineering, Faculty of Engineering, Khon Kaen University, 40002, Thailand
ARTICLE INFO
Keywords:
Metaheuristic
Multi-objective optimization
Structural design
Discrete variables
Constraint optimization
ABSTRACT


A novel Multi-Objective Passing Vehicle Search (MOPVS) algorithm is proposed for structural design optimization. MOPVS is inspired by the two-lane highway passing vehicle mechanism. This multi-objective version is modified and further improved from the single-objective version of passing vehicle search through a Pareto dominance-based approach. For performance evaluation of MOPVS, five daunting benchmark structural design problems have been used. Two conflicting objectives i.e. structure weight minimization and minimization of maximum nodal displacement along with discrete design variables have been considered to ensure its real-world applications. For fitness and efficiency evaluation of the proposed algorithm, the results obtained from the new algorithm are compared with four other state-of-the-art multi-objective algorithms. Moreover, two performance indicators test called Hypervolume and Spacing-to-Extent were performed for the rigorous evaluation of the performance and feasibility of the proposed algorithm. The findings demonstrate the superiority of the MOPVS algorithm over the others while the potential to find a non-dominated solution set with diverse individual solutions. Present work considers the Friedman’s rank test for the statistical investigation of the experiment work. The solutions and convergence behavior achieved by MOPVS show its high efficiency in solving challenging design problems.
1. Introduction
Real-world engineering design problems are typically complicated and multidimensional, thus, finding its solution is a very challenging job. All such sectors are mainly linked to many goals which are called Multi-objective (MO). More often, those objectives are conflicting and demand a trade-off between them (Blondet, Duigou, & Boudaoud, 2019; Wu et al., 2020; Chinchuluun, Pardalos, Migdalas, & Pitsoulis, 2008). This leads to a set of two or more solutions rather than a single optimal solution as with a problem with one objective function (Anita, Yadav, & Kumar, 2020). Optimization is an integral part of any system design as it works to maximize/minimize the system outcomes by making the least use of resources possible. In the case of a structure optimization, these conflicting objectives are generally minimization of cost or weight and,
* Corresponding author.
at the same time, maximization of strength or performance which, by itself, is a very challenging design issue (Kumar, Tejani, & Mirjalili, 2019). From the last three decades, there have been lots of methodologies like deterministic optimization techniques developed for solving such kind of design issues; however, they are struggling to find optimal solutions due to their limitations like premature convergence, complex programming approach, inefficiency in solving non-linear, and the issues of non-convex functions and regions (Pardalos, Zilinskas & ˇ Zilinskas, 2017). Often, an inaccurate derivative calculation can lead the optimizers to wrong solutions and may cause linear and quadratic programming sub problems being ill-conditioned.
The above demerits make most scholars turn towards more robust and gradient-free algorithms for solving challenging design problems, particularly Metaheuristics (MHs). The MHs are the algorithms which
E-mail addresses: sumit21sep1990@gmail.com (S. Kumar), p.shyam23@gmail.com (G.G. Tejani), nantiwat@kku.ac.th (N. Pholdee), sujbur@kku.ac.th (S. Bureerat).
1 ORCID ID: 0000-0003-3042-3779.
2 ORCID ID: 0000-0001-9106-0313.
https://doi.org/10.1016/j.eswa.2020.114511
Received 7 June 2020; Received in revised form 5 October 2020; Accepted 14 December 2020
0957-4174/©2020ElsevierLtd.Allrightsreserved.
are inspired by natural events in our surroundings and have advantages like simplicity, almost parameter-free ability, and flexibility. Owing to those advantages, the algorithms have been implemented to a wide range of applications in engineering and industrial sectors for solving real-word optimization problems (Tejani, Kumar, & Gandomi, 2019). Moreover, from the last two decades, MHs have seen a rise in their applications in structural optimization problems for investigation of its potential to solve many objectives with conflicting nature. As opposed to the single-objective design problem which has only one solution, the MO design issue has a set of optimal solutions traditionally called the Paretooptimal set (Ho-Huu et al., 2018; Kumar, Tejani, Pholdee, & Bureerat, 2020). Generally, there are two steps in dealing with a design problem with more than one objective function. The first one is to explore all possible Pareto optimal solutions by using a powerful optimizer. In the second task, the selection of one solution from the obtained Pareto optimal set is performed usually employing a decision-making process. Therefore, the best solution must be from the Pareto optimal set, and at the same time, it should be the chosen one or more from the designer (Kaveh & Laknejadi, 2011).
Meanwhile, as metaheuristics (initially named evolutionary algorithms) have been established for single-objective optimization, their MO versions can be created exploiting the nature of MH search, which is based on a population or set of design solutions and randomization (Pardalos & Romeijn, 2013). The so-called non-dominated sorting operator is a key to upgrade existing single-objective MHs to become MO ones. At the very beginning, they were termed multi-objective evolutionary algorithms (MOEAs) and later multi-objective metaheuristics (MOMHs) to cover all possible philosophical aspects of MH search. Some of the first generation MOMHs are MO genetic algorithms (MOGA) (Fonseca & Fleming, 1993), non-dominated sorting genetic algorithms (NSGAII) (Deb, Pratap, Agarwal, & Meyarivan, 2002), and strength Pareto evolutionary algorithms (SPEA2) (Zitzler, Laumanns, & Thiele, 2001). Then, there have been numerous MOMHs invented in parallel to their single-objective counterparts. The concepts for upgrading singleobjective MHs to be MO versions include, for example, a nondominance approach (Tejani, Pholdee, Bureerat, & Prayogo, 2018; Tejani, Savsani, Patel, & Mirjalili, 2018; Tejani, Savsani, Patel, & Savsani, 2018), a decomposition-based approach (Zhang & Li, 2007), and an elitism strategy (Deb, Agrawal, Pratap, & Meyarivan, 2000), a gridbased approach (Knowles & Corne, 1999), a preference-based approach (Bureerat & Srisomporn, 2010), a guided population-based approach (Got, Moussaoui, & Zouache, 2020), and an oppositionbased learning approach (Gupta, Deep, Heidari, Moayedi, & Wang, 2020). The most outstanding feature of MOMHs is that they can explore a Pareto front within one optimization run. Nevertheless, to achieve such a feat, the reproduction must be very powerful for both exploitation and exploration. It is even more difficult when the number of objective functions is higher than 3, which is usually called many-objective optimization. As a result, the seek for new better MOMHs is still a challenging task.
One of the newly developed state-of-the-art algorithms is Passing Vehicle Search (PVS) which was proposed by Savsani and Savsani (2016). This algorithm is typically a human action-based system in which the behavior of passing vehicles on the two-lane highway has been mathematically modelled. This is one of the population-based global optimization algorithms which is designed for finding global optima. It is motivated by the overtaking mechanism of vehicles and has advantages like controlling parameter-free and fast convergence in comparison to other MHs. This novel algorithm is investigated by a few researchers in numerous design problems for its performance evaluation. Sheth et al. (2019) investigated PVS for parametric optimization of the Wire Electric discharge machine on Mg-Zn-RE-Zr alloy. Results were compared with a standard GA code while outstanding performance was noticed which can be explored in the aerospace industry. To control the network flow, PVS was used and the results show the least time delay of the vehicles at the traffic signals. Furthermore, the basic version of PVS
was modified, improved, and hybridized with other algorithms by a few scholars to check its performance. Savsani, Tejani, Patel, and Savsani (2017) modified PVS based on random mutation and applied for topology optimization of structures with static and dynamic constraints. The results demonstrate the superiority of the modified PVS algorithm over other compared MHs. Tejani, Pholdee, Bureerat, Prayogo, and Gandomi (2019) and Tejani, Savsani, Bureerat, Patel, and Savsani (2019) modified the PVS based on a parallel run mechanism with the incorporation of simulated annealing methodology which is used for prevention from local optima trap and enhancement of population diversity. In a similar study, to improve the exploration and exploitation potential of the basic PVS algorithm, Tejani, Pholdee, et al. (2018), Tejani, Savsani, Patel, and Mirjalili (2018) and Tejani, Savsani, Patel, and Savsani (2018) incorporated a mutation-based search technique for the optimization of the truss under dynamic bounds. The results were compared with other popular MHs and proved the dominance of the improved PVS version over the others. Literature also witnessed few hybridizations like enhanced PVS algorithm for wind farm layout optimization (Patel, Savsani, Patel, & Patel, 2019), and fuzzy-based symbiotic organism search with PVS for optimization of automatic generation control (Nayak, Shaw, & Sahu, 2020) which proves the better performance characteristics of PVS in challenging design issues.
A very few scholars extended PVS to MO design issues. Parsana et al. (2018) in their study applied the PVS algorithm for the parametric MO optimization of Electric Discharge Machine (EDM) on Mg–RE Alloy. The obtained Pareto front was better and the performance metric results were found to be acceptable. In a similar parametric study of EDM, Ram Prabhu et al. (2018) investigated the performance of PVS with MO in different mathematical models and also compared it with other intelligent MHs. The findings show better results. However, as per the knowledge of the authors, the PVS has limited investigation so far especially in the case of MO structural design issues. Moreover, PVS is a novel population-based algorithm which was just suggested, thus, there is room for even more research and need to explore its potential in different analyses. Furthermore, as per the no free lunch (NFL) theorem (Wolpert & Macready, 1997), one MH cannot be efficient for all design problems. Thus, there is always a need for a novel efficient algorithm for more challenging design problems posed every year. PVS, with its successful implementation to many engineering applications, is a new metaheuristic that deserves this attention.
Therefore, this study suggests a Multi-Objective Passing Vehicle Search (MOPVS) algorithm for structure optimization. The two objectives are mass minimization and minimization of maximum nodal deflection which are diverse in nature and simultaneously optimized. Five challenging constrained test examples i.e. the 10-, 25-, 60-, 72-, and 942-bar trusses have been examined in this investigation for the performance measurement of the proposed MOPVS algorithm. Also, the findings of MOPVS are compared with other noteworthy algorithms for efficiency verification.
The rest of the article is convened as follows: Section 2 provides the details about the fundamental PVS algorithm and the proposed MOPVS algorithm description has been shared in Section 3; Section 4 presents the mathematical formulation of the MO design problem; the findings and detail discussion of all the test examples are presented in Section 5; Section 6 puts forward the concluding remarks with prospects of the proposed algorithm.
2. The Passing Vehicle Search algorithm
PVS is a novel single-objective population-based MH suggested by Savsani and Savsani (2016) as a global optimization algorithm that is inspired by a certain natural occurrence. Like other population-based algorithms, PVS also initializes its search mechanism with a random set of solutions traditionally called a population, and updates the current population as per the other searched solutions and finally end with the optimized set of solutions. PVS mimics the two-lane highways
overtaking or passing behavior of vehicles which is simplified into a mathematical model. It is a simple, efficient, and parameter-free algorithm and modifies the population-based on three simple mathematical conditions of passing vehicles with numerous probabilities. Having a safe passing opportunity is the most significant criterion for the overtaking mechanism of two-lane. This overtaking mechanism depends on various criteria like the gap between the vehicles, individual vehicle velocity, road, driver skills, traffic behaviors, and weather which are highly interrelated and have complex characteristics.
Three sets of conditions will arise when a slow vehicle is approached by a vehicle:
(a) the fast vehicle will overtake the slower vehicle;
(b) until a suitable opportunity arises, the vehicle will follow the slow vehicle;
(c) without the objective of overtaking, the vehicle continues to follow the slower vehicle.
If the vehicle is not able to overtake other slower vehicles then platoon rise to form which affects the desired speed of the vehicle again. This makes mathematical modeling of the overtaking mechanism of two-lane traffic more challenging. However, Savsani and Savsani (2016) suggested a simplified model for easy understanding as illustrated in Fig. 1.
In this PVS algorithm, three different vehicles i.e. Front vehicle (FV), Back vehicle (BV), and Oncoming vehicles (OV) are considered which are engaged in the mechanism of overtaking of the vehicle on the highway. The process of overtaking will be executed only when the BV velocity will become greater than the speed of FV and if not then the overtaking process of vehicles will not be possible. This feature clearly illustrates the dependency of the overtaking process on the speed and the position of OV and the distance between each vehicle and their corresponding velocities. This generates different conditions of the overtaking process on the two-lane highway as follows:
Assume,
s– Distance between Back vehicle and Front vehicle
k – Distance between Front vehicle and Oncoming vehicles
S1 , S2 , S3 – Distance from the reference line v1 , v2 , v3 – Velocities of Back vehicle, Oncoming vehicles, and Front vehicle, respectively,
At any instant, the velocity of the BV, OV, and FV vehicles are v1 ,
, and v3 respectively on the two-lane highway. Thus, based on the velocity of FV, two specific conditions will arise i.e. FV is slower than BV and vice versa. At this particular condition, the overtaking phenomena possibly mean BV can pass the FV. Passing is only feasible in that state when the distance from FV at which passing takes place is shorter than
Fig. 1. Two-lane highway vehicle overtaking mechanism.
the distance covered by OV. However, if the BV speed is slower than FV, BV cannot overtake the FV and it only moves with its speed. Thus, based on the three selected vehicles, the following conditions will arise:
Case1. When FV is slower than BV (v3 < v1 ) (termed as Primary condition-1)
(a) (k k1 ) > s1 (Secondary condition-1)
(b) (k k1 ) < s1 (Secondary condition-2)
Case 2. FV is faster than BV (v3 > v1 ) (termed as Primary condition-2)
2.1. Primary condition-1
This is the case when FV has a slower velocity than BV which further leads to two sub-cases i.e. secondary conditions (1) and (2). The details are in the following mathematical formulation form:
2.1.1. Secondary condition-1
It is assumed that after traveling distance s1 by FV the BV can catch the FV and simultaneously pass it and the corresponding time is ‘t ’ to execute this passing mechanism which is depicted in Fig. 1.
Hence, in time interval ‘t ’ the distance travelled by FV is
s1 = v3 t (1)
Similarly, in time ‘t ’ the distance covered by BV will be
s + s1 = v1 t (2)
On substitution of Eq. (1) in Eq. (2), the following result will generate
s1 = v3 s v1 v3 (3) and t = s v1 v3 (4)
At the same time, ‘t’ OV covered the distance of
k1 = v2 t (5)
After replacing the value of ‘t’ from Eq. (4) in Eq. (5), one can have
y1 = v2 x v1 v3 (6)
The corresponding change in positions of BV is
BV c1 = s + s1 (7)
After putting the value of s1 from Equation (3),
BV c1 = s( v1 v1 v3 ) (8)
The value of s that relates the reference line is
s = S3 S1 (9)
Thus,
BV c1 = (S3 S1 )( v1 v1 v3 ) (10)
The change in the position of BV from the reference line is
S1 + BV c1 = S1 + (S3 S1 )( v1 v1 v3 ) (11)
2.1.2. Secondary condition-2
This case pertains to two separate possibilities, one being positive and the other being negative which is represented in Fig. 1. In case of the existence of any one of these possibilities, the passing of FV by BV cannot occur before OV passes BV. A motor vehicle accident can, therefore, be
prevented if BV does not switch lanes before OV passes BV. The encounter between BV and OV will happen at distance somewhere located in between BV and OV initial positions.
The BV has the position changed as
BV c2 = rand (s + k ) (12)
In the above equation, rand is a uniform random number, rand ∈ [0, 1]
The change of BV location from the line of reference is
2.2. Primary condition-2
As per Fig. 1, BV cannot overtake FV when FV is faster than BV. Thus, the BV position change can be written as:
S1 + BV c3 = S1 + rands = S1 + rand (S3 S1 ) (14)
In the PVS algorithm, two-lane highway different vehicles are assumed to correspond to different solutions set. Vehicle velocities are corresponding to objective function or fitness values where the vehicle with the highest velocity is assumed as the best fitness value. The vehicle’s position on a motorway is analogous to design variables. Thus, PVS initializes its search with the vehicle population (set of solutions). In the reproduction phase, three vehicles (solutions) are randomly selected. BV corresponds to the current solution out of the three selected vehicles while FV and OV are other two different solutions. Depending on the size of the population and its fitness values, the relative distances between the vehicles and their corresponding velocities are allocated. Then the overtaking conditions are inspected after velocity and distance allocation. Subsequently, vehicles alter their positions on the highway based on the condition applied. The detailed explanation of the PVS algorithm is shown in Fig. 2
3. The Multi-Objective Passing Vehicle Search (MOPVS) algorithm
MO engineering design problems simulate the more practical conditions and that is why they are more widely applied and investigated. However, because of the challenges like diverse objectives, nonlinearity, stringent bounds, and multi-modal search domains, it becomes difficult for a designer to find the best solutions (Tejani, Kumar, et al., 2019). MHs emerged as arguably the best alternative for solving these intricate MO design issues. MHs are the remarkably efficient and robust algorithms that mimic the basic physical and biological phenomena and have widely been applied for solving several industrial, science, and engineering design problems.
MHs pose several advantages over traditional algorithms i.e. gradient-free, can handle any kind of variables, free from problemspecific knowledge, least setup time, and objective convexity requirement. However, they face problems like premature convergence, lack of population diversity, and local optima trap which needs to be addressed properly (Kumar et al., 2019). For large-scale problems, their performance does not scale well and usually crumbled in the aspect of both computing time and quality of the solution. Moreover, most of the MHs required controlling parameters that require proper tuning, which makes them inefficient for global optimization design issues.
Another aspect for MHs which plays a crucial role in governing their efficiency in finding the optimal solution is the proper balance between two key components i.e. local intensification (exploitation) and global diversification (exploration) (Yang, Deb, & Fong, 2014). Diversification implies the production of heterogeneous and diverse solutions to explore the global search space whereas intensification denotes the focusing on searching in an immediate territory via exploiting the current found good solution knowledge. The interaction between these two key components will help in finding the best feasible solution out of all possible

solutions within acceptable computational time. However, there is no predefined set of conditions to balance these two performance defining parameters. Thus, it is required to find an algorithm that can find a good quality solution most of the time and simultaneously efficient and practical (Blum & Roli, 2003). In general, for efficient MHs two potentials are a must. The first one is the potential of new solution generation which has a greater chance to replace the existing or previous solution along with the ability to search all-important arena where the global optimum solution possibility lies. The second potential is to escape from any local optima solution so that the MH can avoid the local mode trap.
However, the previous MHs studies and analyses of their convergence behavior, advocate that mere diversification leads to convergence rate reduction whereas only intensification results in the enhancement of convergence speed (Kumar et al., 2019). Notwithstanding, excessive diversification enhances the likelihood of the global optimal solution, however, it reduces the efficiency of an algorithm. Whereas too much intensification has an inclination toward the local optima trap of the algorithm. Thus, it is required for powerful MHs to have a good harmony between the fine level of local intensification and well magnitude of global diversification (Tejani, Kumar, et al., 2019; Yang et al., 2014).
In MO problems, there are a set of optimal solutions called Paretooptimal set instead of a single solution as in single objective design problems. In the absence of any prior knowledge, it is difficult for the designer to find which one is the best solution out of all. As MO design
issues are challenging, thus a high-performance algorithm is always in demand. Also, the NFL theorem (Wolpert & Macready, 1997) states that an MH cannot solve all design issues competently. That means one algorithm may be seen effective in solving one particular design problem, however, it may fail in another kind of optimization issue. Thus, there is a need for a successful MH which can solve MO design issues and has the potential to find the global or near optimum solution with high accuracy.
Hence to resolve all aforementioned problems, in the proposed study authors applied a highly efficient population-based novel PVS algorithm for solving MO structural optimization problems named MOPVS. The dominance approach is incorporated into PVS to create a new MO version of PVS. Given that design solutions X1 and X2 result in function vectors f1 and f2 respectively, X1 is said to dominate X2 (for minimization) if i) all elements in f1 are less than or equal to their corresponding elements in f2 and ii) at least one element of f1 is strictly less than its corresponding element in f2. With the definition of dominance, having had a population of solutions, those who are not dominated by any solution in the set are said non-dominated solutions. Thus, MOMHs work by iteratively reproducing a population, classifying non-dominated solutions, and saving them to the so-called Pareto archive. The set of nondominated solutions at the final iteration is regarded as an approximate Pareto optimal set. MOPVS works on the overtaking mechanism of the vehicles on the freeway which helps in updating the population-based
Fig. 2. Flowchart of fundamental PVS algorithm.
on vehicle velocity and the relative distance between the vehicles. It is a highly efficient algorithm that poses a good convergence rate which helps in finding globally optimal solutions with less computational time.
At the initial stage, an initial population with function evaluations is created at random while the non-dominated solutions are sorted and saved to the initial Pareto archive. The PVS reproduction operator is then activated to produce a new set of offspring. The offspring and the members in the Pareto archive are combined to sort for new nondominated solutions. The population and the archive are iteratively updated until reaching a termination criterion. In cases that the archive size is larger than a predefined size, some non-dominated solutions are removed from the Pareto archive by using the normal line method
(Kanyakam & Bureerat, 2007). The normal line method is one of the archiving techniques used to screen out some non-dominated solutions from the archive in order to save computer memory. This is because it is usual that MOMHs can explore an excessively large number of nondominated solutions often leading to insufficient memory for the used computer. The concept is to screen out some solutions whilst maintaining as high as possible diversity of the remaining solutions. The detailed process of the MOPVS algorithm is illustrated in Fig. 3.
In this study, MOPVS is applied for solving five challenging benchmark structure design examples i.e. the 10-bar, 25-bar, 60-bar, 72-bar, and 942-bar trusses with discrete sections as design variables, to evaluate the performance of the algorithm. MOPVS algorithm creates a
Fig. 3. Flow chart of the MOPVS algorithm.
S. Kumar
balance between intensification and diversification of the search and simultaneously results in non-dominated solutions keeping the diversity in the Pareto fronts. For comparison purposes, the optimal Pareto front obtained by the proposed MOPVS algorithm is compared with the other five distinct MHs i.e. MO ant system (MOAS), MO ant colony system (MOACS), MO symbiotic organism search (MOSOS), and MO heat transfer search (MOHTS). Moreover, two performance indicators called Hypervolume and Spacing-to-Extent were performed for the exact evaluation of the performance and feasibility of the proposed algorithm. The present work also considers the Friedman’s rank test for the statistical investigation of the experiment work. Finally, the comparison is made based on the ranking and the nature of the best Pareto front obtained by all considered algorithms for all test examples.
4. The Multi-objective optimization problem formulation
Realistic industry and engineering design issues are relevant to modeling as MO problems having conflicting objectives. These MO challenging issues have characteristics like non-linearity, large search domain, and sometimes multi-modal functions. Moreover, instead of a single best solution as in the case of single objectives, MO has an optimal solution set which makes the decision process more intricate for a designer. Out of all solutions in the set (also known as a Pareto optimal set), a designer has to choose one best solution based on predefined rules. For any specific design issue, these optimal Pareto solutions are usually unexplored. Therefore, it is essential to search for more optimal solutions rather than being limited to a single solution.
The mathematical formulation for the MO structure optimization problem is as follows:
Find, Z = {Z1 , Z2 , .., Zm } (15)
to minimize, the structure mass and maximum nodal deflection
Subjected to :
Behavior constraints:
g(Z ) : Stress constraints, |σ i | σmax i ≤ 0
Side constraints:
Cross sectional area constraints, Z min i ≤ Zi ≤ Z max i
where, i = 1, 2, , m; j = 1, 2, , n
Here,Zi is a design variable vector; ρi and Li are the mass density and length of the elements respectively;Ei and σ i corresponds to the ‘i’ element Modulus of elasticity and stress respectively. Moreover, the allowable upper and lower bounds are represented by superscripts ‘max’ and ‘min’ respectively.
4.1. The dynamic penalty function
For processing the constrained problems like Eq. (7), one of the best ways is to transform these design issues into dynamic unconstrained optimization problems using a dynamic penalty approach. Considering that in the design arena all the objective function values being positive, the multiplication-based penalty function (Tejani, Savsani, & Patel, 2016) is among the most effective penalty functions.
(16)
where pi is the dimension of requirement infringement having the bound as p * i The parameter q is the number of constraints. The factors ε1 and ε2 are pre-specified by a user. In this investigation, the estimations of both ε1 and ε2 are set at 3, which were obtained from testing their impact on the parity of the investigation balance (Tejani, Pholdee, et al., 2018, 2019; Tejani, Savsani, Patel, & Mirjalili, 2018; Tejani, Savsani, Patel, and Savsani, 2018; Tejani, Kumar, et al., 2019; Tejani, Savsani, et al., 2019; Kumar et al., 2020).
5. Test examples, results, and discussion
The performance evaluation of the considered algorithms is made by the application in five challenging structure examples which are being investigated by many scholars (Angelo, Bernardino, & Barbosa, 2015; Tejani, Pholdee, et al., 2018, 2019; Tejani, Savsani, Patel, and Mirjalili, 2018; Tejani, Savsani, Patel, and Savsani, 2018; Tejani, Kumar, et al., 2019; Tejani, Savsani, et al., 2019; Kumar et al., 2020). Also, some multi-objective standard convex test functions are used to examine the search performance of the considered algorithm. The population size is taken as 100 and functional evaluations are considered 50,000 in this investigation according to previous studies. Each algorithm tested with
Fig. 4. The 10-bar truss.
Design considerations of the truss problems.
Design variables
Young
Size variables
Loading conditions
S = [1.62,1.8,1.99,2.13,2.38, 2.62,2.63,2.88,2.93,3.09, 3.13, 3.38,3.47,3.55,3.63,3.84,3.87, 3.88,4.18,4.22,4.49,4.59,4.8,4.97, 5.12, 5.74, 7.22,7.97, 11.5,13.5,13.9,14.2, 15.5,16,16.9,18.8,19.9,22,22.9,26.5,30, 33.5] in2 S = [1,0.2,0.3,0.4,0.5,0.6,0.7,0.8, 0.9,1,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8, 1.9,2,2.1,2.2,2.3,2.4,2.5,2.6,2.8,3,3.2, 3.4] in2
2:F1z = F2z = F3z = F4z = 5 kips Px3 = 0 5 Klb, Px6 = 0 6 Klb
3:Px22 = 20 Klb and Py22 = 10 Klb
At each node: vertical loading:
Section 1; Pz = 3kips
Section 2; Pz = 6kips
Section 3; Pz = 9kips
Lateral loading: Right-hand side; Px = 1.5kips
Left-hand side; Px = 1 0kips
Lateral Loading: Py = 1 0kips
Table 2
The hypervolume values of results obtained for the 10-bar truss.
Table 3
The front Spacing-to-Extent values of results obtained for the 10-bar truss.
Algorithms
100 independent runs to find the solutions. The Pareto front Hypervolume (PFHV) test is conducted for all algorithms where the mean value is treated as equivalent to the rate of convergence and the standard deviation (STD) value is taken as the measure of reliability.
A blend of two testing indicators, i.e. a front spacing (S) scale and Extent called the Front Spacing-to-Extent (FSTE) (Tejani, Pholdee, et al., 2018, 2019; Tejani, Savsani, Patel, and Mirjalili, 2018; Tejani, Savsani, Patel, and Savsani, 2018; Tejani, Kumar, et al., 2019; Tejani, Savsani, et al., 2019; Kumar et al., 2020) is used to measure algorithm performance. The lower value of FSTE specifies the superior result. Friedman’s rank test is considered to rank the algorithms statistically.
5.1. 10-bar test example
The first test example taken into account for investigation in this study is a 10-bar structure which was widely applied in numerous researches. The details about this benchmark are illustrated in Fig. 4 which also represents the loading conditions, constraints, nodes, and structure dimensions. The design consideration of all the benchmarks is depicted in Table 1.
The statistical results obtained for the 10-bar test example are represented in Table 2 in the PFHV value form. Here the mean and STD optimal values are considered as the measure of performance for all the considered algorithms. The optimal mean PFHV values of MOAS,

MOACS, MOSOS, MOHTS, and MOPVS algorithms are 52094.31, 54864.00, 57352.53, 58491.60, and 58684.42 respectively. Similarly, the STD of the PFHV values for the MOAS, MOACS, MOSOS, MOHTS, and MOPVS algorithms are 1304.90, 321.26, 241.81, 81.86, and 27.57 respectively. These results show that the proposed MOPVS algorithm has better values of mean and STD than others in terms of convergence and search consistency. The Friedman’s rank test is performed for statistical analysis for each algorithm based on their PFHV values. The Friedman test values obtained by MOAS, MOACS, MOSOS, MOHTS, and MOPVS are 100, 200, 300, 400, and 500 respectively. At a 95% significance level of Friedman’s rank test, MOPVS is found to be the best algorithm that justifies the Hypervolume results. MOHTS and MOSOS followed the MPOVS and ranked second and third respectively among all.
Table 3 demonstrates the FSTE metric values which signify the relative spacing between the solutions in the non-dominated set for the 10-bar example. The corresponding mean values for MOPVS and MOHTS are 0.0059 and 0.0058. The best values of STD are obtained by MOPVS i.e. 0.0001 followed by that of MOHTS and MOSOS, which are 0.0004 and 0.0010 respectively. As per the Friedman’s test ranking, it is evident that MOHTS and MOPVS are the best performers.
The obtained median Pareto fronts for the 10-bar example from all the considered algorithms are illustrated in Fig. 5 which is obtained from 100 independent runs of each optimizer. It is understood from the figure that the solutions for MOAS and MOACS are scattered and noncontinuous. However, MOPVS, MOHTS, and MOSOS Pareto fronts are smooth, well-distributed, and steady. Also, these algorithms have an array of heterogeneous solutions. Considering all aspects, we can say that MOPVS is the superior algorithm in comparison to other considered algorithms in solving the MO 10-bar structure design problem.
5.2. 25-bar test example
The second test example considered in this investigation for performance evaluation of the considered algorithms is the 25-bar 3D structure which is shown in Fig. 6 with all the dimensional conditions. The design consideration of this truss is depicted in Table 1 Based on the symmetry about planes x–z and y–z, all the 25 elements of the structure are divided into 8 groups.
The PFHV test optimal results for the 25-bar example is presented in Table 4. In this test problem, the mean and STD values are considered as the performance evaluation parameters. The mean values obtained for MOAS, MOACS, MOSOS, MOHTS, and MOPVS algorithms are 1881.80, 1893.66, 1942.58, 1947.23, and 1950.25 respectively. Likewise, the obtained STD values from the PFHV test are 9.79, 14.43, 0.54, 0.51, and 0.21 for the MOAS, MOACS, MOSOS, MOHTS, and MOPVS algorithms respectively. MOPVS shows better results in terms of convergence rate and search consistency. Moreover, for a fair comparison of all the
Fig. 5. Median Pareto fronts of the 10-bar truss.
4
The hypervolume values of results obtained for the 25-bar truss. Algorithms
algorithms, a statistical test is performed (Friedman rank test) at a 95% significant level. The test values obtained by MOAS, MOACS, MOSOS, MOHTS, and MOPVS are 123, 177, 300, 400, and 500. As per the rank, MOPVS outperforms other followed by MOHTS and MOSOS algorithm. Also, the results values of all the five algorithms are different from each other.
Table 5 shows the FSTE results obtained from all examined algorithms for the 25-bar test example. The algorithms MOHTS and MOPVS have the best values of mean and STD values i.e. 0.0065 and 0.0004, 0.0067, and 0.0001 respectively. Based on the Friedman rank values MOHTS and MOPVS are the best algorithms in terms of the relative spacing between the solutions in a non-dominated set for the 25-bar example.
The median Pareto fronts for the 25-bar example from all the considered algorithms are illustrated in Fig. 7 which is obtained after 100 independent runs. It is understood from the figure that solutions from MOAS and MOACS are scattered and non-continuous. However, MOPVS, MOHTS, and MOSOS Pareto fronts are smooth, welldistributed, and steady. Also, these algorithms have an array of heterogeneous solutions. Considering all we can say that MOPVS is the superior algorithm in comparison to other considered algorithms in solving the MO 25-bar structure design problem.
5.3. 60-bar test example
For performance evaluation of all five considered algorithms, the third benchmark test example examined is the 60-bar truss, which is depicted in Fig. 8 All the details of the design consideration are
Table 5
The front Spacing-to-Extent values of results obtained for the 25-bar truss.
Algorithms
presented in Table 1 Motivated by the previous studies, 60 elements of the structure are grouped into 25 members.
The PFHV test results for the 60-bar test example is demonstrated in Table 6 The mean and STD values are considered as the parameters of efficiency measurement. The STD values obtained by the MOAS, MOACS, MOSOS, MOHTS and MOPVS algorithms are 166.65, 74.18, 5.92, 2.04, and 1.38 respectively. The PFHV mean values obtained from
Fig. 6. The 25-bar space truss.
Table
Fig. 7. Median Pareto fronts of the 25-bar truss.
using the MOAS, MOACS, MOSOS, MOHTS, and MOPVS algorithms are 3179.88, 3106.68, 4293.25, 4316.10, and 4323.02 correspondingly. MOPVS and MOHTS algorithm obtained the Friedman test values of 500 and 400. The ranks allotted to algorithms conclude the dominance of MOPVS over other algorithms. MOHTS and MOSOS are ranked second and third respectively in the Friedman ranking.
The second test i.e. FSTE is performed for comparative analysis of algorithms and the obtained results are depicted in Table 7 The MOPVS achieves the best mean value 0.0060 followed by MOHTS and MOSOS i. e. 0.0062 and 0.0120 respectively. Also, in terms of STD, MOPVS outperforms the others with a value of 0.0001. The Friedman’s rank test is performed for all algorithms and the results show the ascendancy of MOPVS among all others whereas the MOHTS and MOSOS settled at second and third ranks individually.
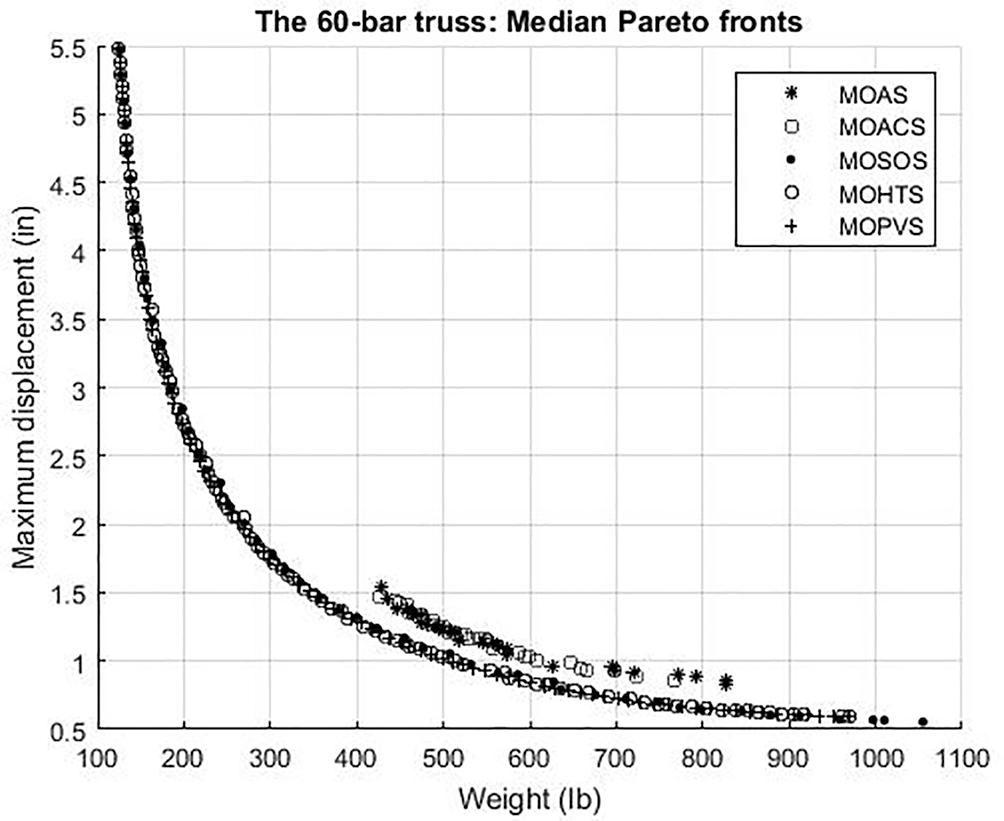
The median Pareto fronts of the third test example are illustrated in Fig. 9 that is obtained from 100 independent runs of all algorithms. The Pareto fronts obtained by MOAS and MOACS are broken and also discontinuous whereas that from MOPVS is uniform and steady with well-diverged solutions. Hence the MOPVS is the better algorithm in terms of non-dominated solutions.
5.4. 72-bar test example
This subsection comprised the 72-bar 3D test example as the fourth benchmark (Fig. 10), which was evaluated according to five algorithms. Table 1 represents all the loading, elements, and dimension details of this example. From 72 elements of the structure, 16 groups were formed based on structural symmetry.
The PFHV values of the 72-bar example obtained by the various algorithms are reported in Table 8 Similar to the previous examples, the
Table 6
The hypervolume values of results obtained for the 60-bar truss.
Algorithms
mean and STD values are the point of interest in the performance evaluation. As per the PFHV test, the mean values obtained from the algorithms MOAS, MOACS, MOSOS, MOHTS, and MOPVS are 2140.24, 2142.38, 2270.93, 2282.66, and 2285.46 respectively. The STD values are 10.17, 19.50, 1.81, 0.63, and 0.90 respectively for MOAS, MOACS, MOSOS, MOHTS, and MOPVS algorithms. The MOPVS algorithm presents better results in terms of convergence and search consistency. Also, for a fair comparison of all the algorithms, a statistical test is performed (Friedman rank test) at a 95% significant level. The test values obtained by MOAS, MOACS, MOSOS, MOHTS, and MOPVS are 145, 155, 300, 403, and 497. As per the rank, MOPVS dominates the others followed by the MOHTS and MOSOS algorithms. Also, the results values of all the five algorithms are different from each other.
Table 9 demonstrates the FSTE metric values which signify the relative spacing between the solutions in the non-dominated set for the 72-bar example. The corresponding mean values for MOPVS and MOHTS are the same i.e. 0.0072. The best values of STD are obtained by MOPVS i.e. 0.0002 followed by MOSOS and MOHTS which are 0.0004 and 0.0005 respectively. As per the Friedman’s test ranking, it is evident that MOPVS is the best performer.
The obtained best Pareto fronts for the 70-bar example are illustrated in Fig. 11 which is obtained from running the algorithms 100 times. The figure demonstrates that the solutions from MOAS and MOACS are scattered and non-continuous. However, MOPVS and MOHTS Pareto fronts are smooth, well-distributed, and steady. Also, these algorithms have an array of heterogeneous solutions. Considering all, we can say that MOPVS is the superior algorithm in comparison to other considered algorithms in solving the MO 72-bar structure design problem.
5.5. 942-bar test example
The tower structure problem (942-bar) is the fifth benchmark example considered in this study depicted in Fig. 12 with its geometric parameters. All accounted design aspects are presented in Table 1 for this test example. From a total of 200 structural elements, 59 groups were formed depending on the structural symmetry.
The PFHV results for the 942-bar example are presented in Table 10. The mean values obtained from the MOAS, MOACS, MOSOS, MOHTS and MOPVS algorithms are 60795099.20, 61174938.07, 71950729.01, 76064884.48, and 76279259.43 respectively. Likewise, the obtained STD values from the PFHV test are 4084186.41, 1116525.94, 696707.86, 113801.21, and 122569.23 for the MOAS, MOACS, MOSOS, MOHTS, and MOPVS algorithms respectively. MOPVS shows better results in terms of convergence rate and consistency. Moreover, for a fair comparison of all the algorithms, a statistical test is performed (Friedman rank test) at a 95% significant level. The test values obtained by MOAS, MOACS, MOSOS, MOHTS, and MOPVS are 152, 148, 300, 413, and 487. As per the rank, MOPVS outperforms the others followed by the MOHTS and MOSOS algorithms. Also, the results values of all the five algorithms are different from each other.
Table 11 presents the FSTE results obtained from all examined algorithms for the 942-bar test example. The algorithms MOHTS and MOPVS have the best values of mean and STD values i.e. 0.0066 and 0.00038, 0.0068, and 0.00040 respectively. Based on the Friedman rank values MOHTS and MOPVS are the best algorithms in terms of the relative spacing between the solutions in the non-dominated set.
The median Pareto fronts for the 942-bar example from all the
Fig. 8. The 60-bar ring truss.
Table 7
The front Spacing-to-Extent values of results obtained for the 60-bar truss. Algorithms
considered algorithms are illustrated in Fig. 13 which is obtained from the 100 runs. It is understood from the figure that the solutions for MOAS, MOACS, and MOSOS are scattered and non-continuous. However, MOPVS and MOHTS Pareto fronts are smooth, well-distributed, and steady in nature. Also, these algorithms have an array of heterogeneous solutions. Comprehensively, MOPVS outperforms the other considered algorithms in solving the MO large structure design problem. Fig. 14 shows the convergence plot based on the mean hypervolume values against the number of function evaluations. Only the top three best algorithms are considered. From the figure, MOPVS and MOHTS performances are equally good. When zooming into the figure at an early stage, it was found that MOPVS is slightly better than MOHTS at the number of function evaluations (FEs) before 2000. This paves the way for further improvement of the algorithm through hybridization.
5.6. Multi-objective convex test functions
Further performance investigation has been made. Rather than the five real engineering applications of truss optimisation problems, six traditional convex test functions; ZDT1, ZDT3, ZDT4 (Zitzler, Deb & Thiele, 2000), Four Bar Truss design, Hatch Cover design, and Reinforced Concrete Beam design (Tanabe & Ishibuchi, 2020) are also
Fig. 9. Median Pareto fronts of the 60-bar truss.
Fig. 10. The 72-bar 3D truss. S.
Table 8
The hypervolume values of results obtained for the 72-bar truss.
Table 9
The front Spacing-to-Extent values of results obtained for the 72-bar truss. Algorithms
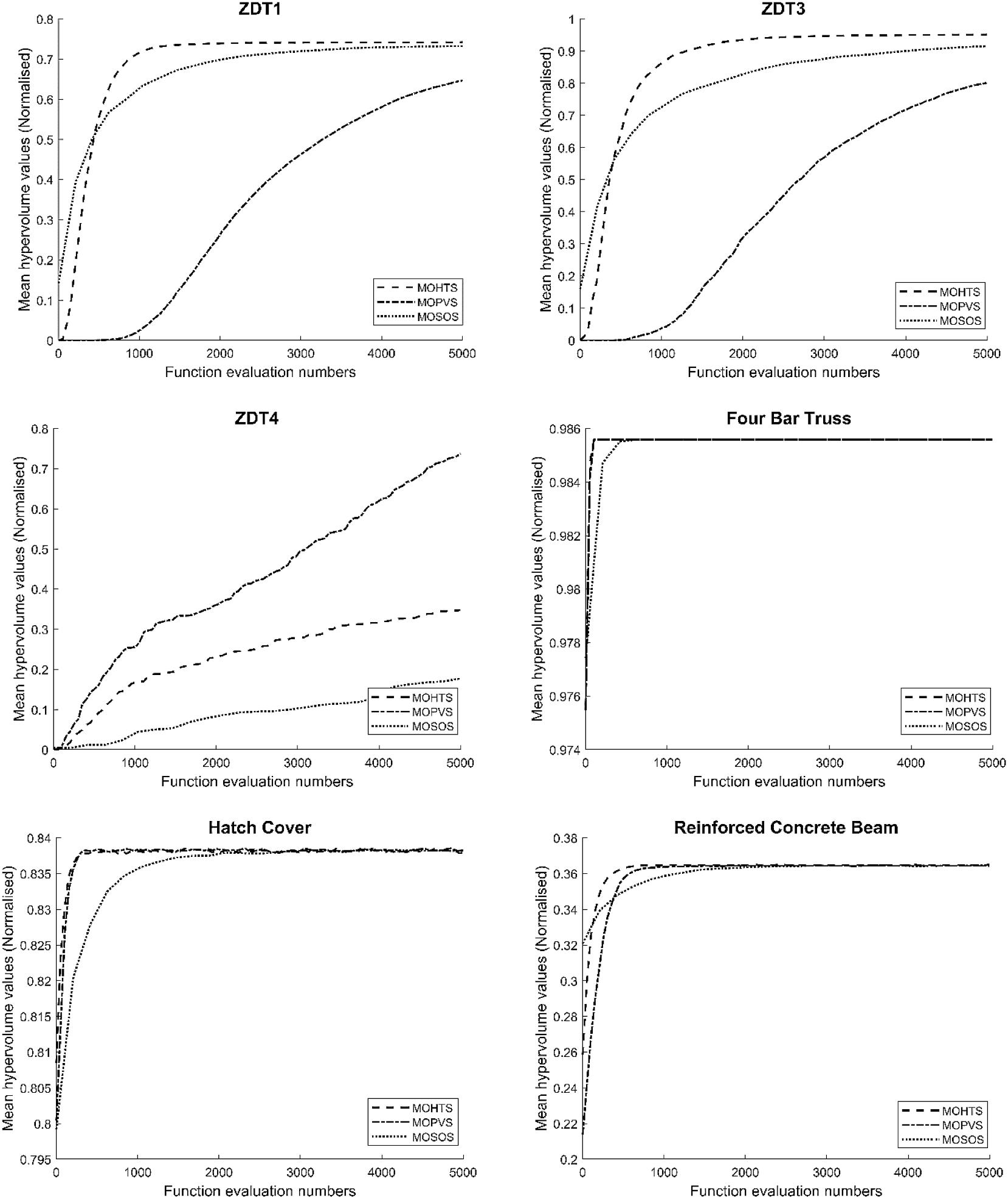
employed for performance investigation. For each problem, population size and the number of iterations is set to be 50 and 100, respectively. For the algorithm using different population sizes, they will be terminated at 50 × 100 FEs. The top three algorithms from the truss optimisation problems; MOSOS, MOHTS, and MOPVS are used to solve the standard test functions for 20 optimization runs while the results based on hypervolume are reported in Table 12 From the table, the most efficient optimizer for the ZDT1, ZDT3, and Reinforced Concrete Beam design is MOHTS while the most efficient method for the ZDT4 and Hatch Cover design is MOPVS. For the Four Bar truss design, all optimisers perform similar mean hypervolume values while the MOSOS gives a slightly better standard deviation.
Fig. 15 shows the search history based on the normalised mean hypervolume indicator versus FEs for all test functions. For ZDT1 and ZDT3, MOHTS and MOSOS are said to be fast at the beginning while MOSOS slows down in the second half of the run. Meanwhile, MOHTS remains consistent and converges to the final values after about 200 function evaluations. For the ZDT4, MOPVS shows its clearly fastest convergence rate from the beginning until reaching the termination criterion while the second fastest is MOHTS. MOPVS and MOHTS show a somewhat similar convergence rate to the final values for the Four Bar Truss design and the Hatch Cover design problems while, for the Reinforced Concrete Beam problem, the MOHTS has the fastest convergence rate at the beginning while the MOPV can later converge and catch up
Fig. 11. Median Pareto fronts of the 72-bar truss.
Fig. 12. The 942-bar tower truss.
Table 10
The hypervolume values of results obtained for the 942-bar truss.
Table 11
The front Spacing-to-Extent values of results obtained for the 942-bar truss.
fronts of the 942-bar
Table 12
The comparison of standard test convex problems based on hypervolume indicator.
Bold value signifies the best solution.
MOHTS. This implies that the proposed MOPVS is acceptable for general-purpose multi-objective optimization.
6. Conclusions
A novel MOPVS algorithm is developed and investigated for multiobjective structure optimization design issues. Inspired from the fundamental two-lane highway overtaking mechanism of the vehicles, the MOPVS is a global optimization algorithm. For performance evaluation,
Fig. 13. Median Pareto
truss.
Fig. 14. The 942 bar search history based on mean hypervolume indicator (a) original view
five challenging structure test examples are accounted with discrete cross-sections under multiple loading conditions. Also, six convex test functions are added for further performance investigation. For the comparative analysis, the outcomes of the MOPVS can be compared with four distinguished algorithms. Moreover, for measuring the effectiveness of the proposed strategy, PFHV and FSTE tests were conducted. Simultaneously for statistical analysis of considered algorithms, the Friedman rank test is performed. Outcomes of this test demonstrated the superiority of MOPVS over the other accounted algorithms in terms of obtaining a good balance between global diversification and local intensification. Moreover, MOPVS results are significantly diverse from the other MHs, especially for large-scale truss design problems. From the proposed investigation, it is understood that MOPVS achieves the better nondominated Pareto front with a diverse optimal solution set in contrast to MOAS, MOACS, MOSOS, and MOHTS algorithms.
In the future, one can investigate this algorithm for higher dimensions and intricate engineering design problems. As this algorithm is
relatively new in this field, more research is needed for prediction of its global optimization behavior which can be contrasted with other prominent algorithms.
authorship contribution statement
Sumit Kumar: Conceptualization, Methodology, Writing - original draft. Ghanshyam G. Tejani: Conceptualization, Methodology, Software, Formal analysis, Data curation, Writing - original draft, Writingreview & editing, Supervision, Project administration. Nantiwat Pholdee: Conceptualization, Methodology, Software, Formal analysis, Data curation, Writing - original draft, Writing - review & editing, Supervision, Project administration. Sujin Bureerat: Funding acquisition, Conceptualization, Methodology, Software, Formal analysis, Data curation, Writing - original draft, Writing - review & editing, Supervision, Project administration.
CRediT
Fig. 15. Multi-objective standard convex test functions search history based on mean hypervolume indicator (Normalised).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper
Acknowledgement
The authors are grateful for the support from the Thailand Research Fund (RTA6180010).
References
Angelo, J. S., Bernardino, H. S., & Barbosa, H. J. C. (2015). Ant colony approaches for multiobjective structural optimization problems with a cardinality constraint. Advances in Engineering Software, 80(C), 101–115. https://doi.org/10.1016/j. advengsoft.2014.09.015
Anita, Yadav, A., & Kumar, N. (2020). Artificial electric field algorithm for engineering optimization problems. Expert Systems with Applications, 149 https://doi.org/ 10.1016/j.eswa.2020.113308, 113308.
Blondet, G., Duigou, J Le, & Boudaoud, N. (2019). A knowledge-based system for numerical design of experiments processes in mechanical engineering. Expert Systems with Applications, 122, 289–302. https://doi.org/10.1016/j.eswa.2019.01.013
Blum, C., & Roli, A. (2003). Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM Computing Surveys, 35(3), 268–308. https://doi.org/ 10.1145/937503.937505
Bureerat, S., & Srisomporn, S. (2010). Optimum plate-fin heat sinks by using a multiobjective evolutionary algorithm. Engineering Optimization, 42(4), 305–323. https:// doi.org/10.1080/03052150903143935
Chinchuluun, A., Pardalos, P. M., Migdalas, A., & Pitsoulis, L. (2008). Pareto optimality, game theory and equilibria Springer
Deb, K., Agrawal, S., Pratap, A., & Meyarivan, T. (2000). A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II. In International conference on parallel problem solving from nature (pp. 849–858). Berlin, Heidelberg: Springer Berlin Heidelberg Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197. https://doi.org/10.1109/4235.996017
Fonseca, C. M., & Fleming, P. J. (1993). Genetic algorithms for multiobjective optimization: formulation discussion and generalization. In Proceedings of the 5th International Conference on Genetic Algorithms (pp. 416–423). San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
Got, A., Moussaoui, A., & Zouache, D. (2020). A guided population archive whale optimization algorithm for solving multiobjective optimization problems. Expert Systems with Applications, 141 https://doi.org/10.1016/j.eswa.2019.112972, 112972.
Gupta, S., Deep, K., Heidari, A. A., Moayedi, H., & Wang, M. (2020). Opposition-based learning Harris Hawks optimization with advanced transition rules: principles and analysis. Expert Systems with Applications https://doi.org/10.1016/j. eswa.2020.113510
Ho-Huu, V., Hartjes, S., Visser, H. G., & Curran, R. (2018). An improved MOEA/D algorithm for bi-objective optimization problems with complex Pareto fronts and its application to structural optimization. Expert Systems with Applications, 92, 430–446. https://doi.org/10.1016/j.eswa.2017.09.051
Kanyakam, S., & Bureerat, S. (2007). Passive vibration suppression of a walking tractor handlebar structure using multiobjective PBIL. In 2007 IEEE Congress on Evolutionary Computation (pp. 4162–4169)
Kaveh, A., & Laknejadi, K. (2011). A novel hybrid charge system search and particle swarm optimization method for multi-objective optimization. Expert Systems with Applications, 38(12), 15475–15488. https://doi.org/10.1016/j.eswa.2011.06.012
Knowles, J., & Corne, D. (1999). The Pareto archived evolution strategy: a new baseline algorithm for Pareto multiobjective optimisation. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406) (pp. 98–105). https://doi. org/10.1109/CEC.1999.781913
Kumar, S., Tejani, G. G., & Mirjalili, S. (2019). Modified symbiotic organisms search for structural optimization. Engineering with Computers, 35(4), 1269–1296. https://doi. org/10.1007/s00366-018-0662-y
Kumar, S., Tejani, G. G., Pholdee, N., & Bureerat, S. (2020). Multi-objective modified heat transfer search for truss optimization. Engineering with Computers https://doi. org/10.1007/s00366-020-01010-1
Nayak, J. R., Shaw, B., & Sahu, B. K. (2020). Novel application of optimal fuzzy-adaptive symbiotic organism search-based two-degree-of-freedom fuzzy proportional integral
derivative controller for automatic generation control study. International Transactions on Electrical Energy Systems, 30(5). https://doi.org/10.1002/20507038.12349
Pardalos, P. M., & Romeijn, H. E. (2013). Handbook of global optimization Springer Science & Business Media
Pardalos, P. M., Zilinskas, A., & Zilinskas, J. (2017). Non-convex multi-objective optimization Springer International Publishing
Parsana, S., Radadia, N., Sheth, M., Sheth, N., Savsani, V., Prasad, N. E., & Ramprabhu, T. (2018). Machining parameter optimization for EDM machining of Mg–RE–Zn–Zr alloy using multi-objective Passing Vehicle Search algorithm. Archives of Civil and Mechanical Engineering, 18(3), 799–817. https://doi.org/10.1016/j. acme.2017.12.007
Patel, J., Savsani, V., Patel, V., & Patel, R. (2019). Layout optimization of a wind farm using geometric pattern-based approach. In Energy Procedia (pp. 940–946). Elsevier Ltd. https://doi.org/10.1016/j.egypro.2019.01.233.
Ram Prabhu, T., Savsani, V., Parsana, S., Radadia, N., Sheth, M., & Sheth, N. (2018). Multi-objective optimization of EDM process parameters by using passing Vehicle Search (PVS) algorithm. Defect and Diffusion Forum, 382, 138–146. https://doi.org/ 10.4028/www.scientific.net/DDF.382.138
Savsani, P., & Savsani, V. (2016). Passing Vehicle Search (PVS): A novel metaheuristic algorithm. Applied Mathematical Modelling, 40(5–6), 3951–3978. https://doi.org/ 10.1016/j.apm.2015.10.040
Savsani, V. J., Tejani, G. G., Patel, V. K., & Savsani, P. (2017). Modified meta-heuristics using random mutation for truss topology optimization with static and dynamic constraints. Journal of Computational Design and Engineering, 4(2), 106–130. https:// doi.org/10.1080/0305215X.2016.1150468
Sheth, M., Sheth, N., Radadia, N., Parsana, S., Savsani, V., Mishra, R. K., Prabhu, T. R. (2019). Optimization of WEDM parameters for Mg-Zn-RE-Zr alloy using Passing Vehicle Search algorithm. Materials Research Express, 6(12). https://doi.org/ 10.1088/2053-1591/ab66f9
Tanabe, R., & Ishibuchi, H. (2020). An easy-to-use real-world multi-objective optimization problem suite. Applied Soft Computing, 89 https://doi.org/10.1016/j. asoc.2020.106078
Tejani, G. G., Kumar, S., & Gandomi, A. H. (2019). Multi-objective heat transfer search algorithm for truss optimization. Engineering with Computers https://doi.org/ 10.1007/s00366-019-00846-6
Tejani, G. G., Pholdee, N., Bureerat, S., & Prayogo, D. (2018). Multiobjective adaptive symbiotic organisms search for truss optimization problems. Knowledge-Based Systems, 161, 398–414. https://doi.org/10.1016/j.knosys.2018.08.005
Tejani, G. G., Pholdee, N., Bureerat, S., Prayogo, D., & Gandomi, A. H. (2019). Structural optimization using multi-objective modified adaptive symbiotic organisms search. Expert Systems With Applications, 125, 425–441. https://doi.org/10.1016/j. eswa.2019.01.068
Tejani, G. G., Savsani, V. J., & Patel, V. K. (2016). Adaptive symbiotic organisms search (SOS) algorithm for structural design optimization. Journal of Computational Design and Engineering, 3(3), 226–249. https://doi.org/10.1016/j.jcde.2016.02.003
Tejani, G. G., Savsani, V. J., Bureerat, S., Patel, V. K., & Savsani, P. (2019). Topology optimization of truss subjected to static and dynamic constraints by integrating simulated annealing into passing vehicle search algorithms. Engineering with Computers, 1–19. https://doi.org/10.1007/s00366-018-0612-8
Tejani, G. G., Savsani, V. J., Patel, V. K., & Mirjalili, S. (2018). Truss optimization with natural frequency bounds using improved symbiotic organisms search. KnowledgeBased Systems, 143, 162–178. https://doi.org/10.1016/j.knosys.2017.12.012
Tejani, G. G., Savsani, V. J., Patel, V. K., & Savsani, P. V. (2018). Size, shape, and topology optimization of planar and space trusses using mutation-based improved metaheuristics. Journal of Computational Design and Engineering, 5(2), 198–214. https://doi.org/10.1016/j.jcde.2017.10.001
Wolpert, D. H., & Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1), 67–82. https://doi.org/10.1109/ 4235.585893
Wu, J., Wang, Y.-G., Burrage, K., Tian, Y.-C., Lawson, B., & Ding, Z. (2020). An improved firefly algorithm for global continuous optimization problems. Expert Systems with Applications, 149. https://doi.org/10.1016/j.eswa.2020.113340, 113340.
Yang, X. S., Deb, S., & Fong, S. (2014). Metaheuristic algorithms: Optimal balance of intensification and diversification. Applied Mathematics and Information Sciences, 8 (3), 977–983. https://doi.org/10.12785/amis/080306
Zhang, Q., & Li, H. (2007). MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11(6), 712–731. https://doi.org/10.1109/TEVC.2007.892759
Zitzler, E., Deb, K., & Thiele, L. (2000). Comparison of multiobjective evolutionary algorithms: Empirical results. Evolutionary Computation, 8(2), 173–195. https://doi. org/10.1162/106365600568202
Zitzler, E., Laumanns, M., & Thiele, L. (2001). SPEA2: improving the strength Pareto evolutionary algorithm. In Evolutionary methods for design optimization and control with applications to industrial problems (pp. 95–100). https://doi.org/10.1.1.28.7571






























