Modeling
Vincent Richefeu Pascal Villard
First published 2016 in Great Britain and the United States by ISTE Press Ltd and Elsevier Ltd
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Press Ltd
27-37 St George’s Road
Elsevier Ltd
The Boulevard, Langford Lane London SW19 4EU Kidlington, Oxford, OX5 1GB UK UK
www.iste.co.uk
www.elsevier.com
Notices
Knowledge and best practice in this field are constantly changing. As new research and experience broaden our understanding, changes in research methods, professional practices, or medical treatment may become necessary.
Practitioners and researchers must always rely on their own experience and knowledge in evaluating and using any information, methods, compounds, or experiments described herein. In using such information or methods they should be mindful of their own safety and the safety of others, including parties for whom they have a professional responsibility.
To the fullest extent of the law, neither the Publisher nor the authors, contributors, or editors, assume any liability for any injury and/or damage to persons or property as a matter of products liability, negligence or otherwise, or from any use or operation of any methods, products, instructions, or ideas contained in the material herein.
For information on all our publications visit our website at http://store.elsevier.com/
© ISTE Press Ltd 2016
The rights of Vincent Richefeu and Pascal Villard to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988.
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library Library of Congress Cataloging in Publication Data
A catalog record for this book is available from the Library of Congress
ISBN 978-1-78548-076-8
Printed and bound in the UK and US
cases.So,thecurrentcomputationsinlabsinvolveatbestafew hundredthousandgrainsand,forspecificproblems,afewmillion.Let usnote,however,thattheparallelizationofDEMcodeshasgivenrise tosomecomputationsinvolving10billiongrains,significantly broadeningthefieldofapplicationsforthefuture.
Inaddition,thissetofbookswillalsopresentrecentdevelopments inmicromechanics,appliedtogranularassemblies.Theclassical schemesconsiderarepresentativeelementvolume.Theseschemes proposetogofromthemacro-straintothedisplacementfieldbya localizationoperator,thenthelocalintergranularlawrelatesthe incrementalforcefieldtothisincrementaldisplacementfield,and eventuallyahomogenizationoperatordeducesthemacro-stresstensor fromthisforcefield.Theotherpossibilityistopassfromthe macro-stresstothemacro-strainbyconsideringareversepath.So, somemacroscopicconstitutiverelationscanbeestablished,which properlyconsideranintergranularincrementallaw.Thegreatest advantageofthesemicromechanicalrelationsisprobablytoconsider onlyafewmaterialparameters,eachonewithaclearphysical meaning.Thissetofaround20bookshasbeenenvisagedasan overviewofallthepromisingfuturedevelopmentsmentionedearlier.
FélixD ARVE
July2016
balanceoftheforceworks,andthekineticschangesasaresult.In otherword,thedissipationconcernsthecontacts/collisionsandnot entireblocks;thisisdifferentfromthetrajectoryanalysisthatusually treatstheblockasapointwherethemasshasbeenlumped.Without sayinganythingaboutthephysicsconcretelyimpliedatthecollision (e.g.localdamageorbreakage,elasticwaveabsorption,viscosity),two inputsaredistinguishedinthedissipatedenergyforagivencollision: thedissipationduetotheforcesactinginthedirectionnormaltothe contactandthedissipationofthetangentialforces.Athirdtypeof dissipationinvolvesaresistancemomentatthecontactpointwhena blockcollideswithasoftsubstratum.Allthesedissipationtermsare trackedbymeansoftheworksofthecontactforces(ormoment)by assumingthattheworksoftheelasticcomponentsarenegligible(this isindeedaweakassumption).Whenconsideringtheevolutionofthe forcesactingateachcontactinaDEMsimulation,acompletemapping ofthelossofenergycanbedrawnbothinspaceandduringtime.The DEMassociatedwiththisanalysisframeworkprovidesapowerfultool witharichdatabaseforanalysis.
Inadditiontothedissipationanalysis,thecoreoftheapproachrelies ontheshapeoftheblocksand,forasecondtime,onthetopologyof thepropagationterrain.Itisbelievedthatthesegeometricfeaturesare keyelementsthatplayacrucialroleintheglobalbehaviorofagranular flow.Wewillsee,throughoutthereading,thatthisisindeedthecase. However,noattempttocharacterizetheshapewillbeproposed.Instead, theanalysiswillbebuiltuponmoreevocativedescriptionssuchas“the propensityofablockforrollingorforsliding”orthe“disturbanceofa granularflowduetothebumpynessoftheterrain”.
Anothernotableaspectoftheworkisthefactthatallsimulations aredeterministic.Indeed,webelievethattheexplicitconsiderationof geometries(forboththeblocksandtheterrain)eliminatestheneedfor usingsomestochasticinputstypicallyusedinrockfallsimulations.For example,theexplicituseofacomplexshapewillnaturallyinvolvea statisticaldistributionofthedeviationanglesafterablockcollisionona slope;therateofenergydissipationwillalsoobeyacertaindistribution asafunctionoftheconfigurationofcollision(inparticular,theangular
xviModelingGravityHazardsfromRockfallstoLandslides
velocityandpositionoftheblockrelativetotheslope)withnoneedto explicitlydefinethisdistribution.Onceagain,theroleofgeometryis showntobedecisiveandthebiasistosaythat“anaccurategeometryis betterthanlotsofparameters”.
DespiteallrecognitionenjoyedbyDEM,thisapproachmainlyfaces twodifficulties:(1)themechanicalparameterscanbedifficulttoassess and(2)thecomputationdurationbecomesprohibitivewhenthenumber ofelementsistoolarge.Thislatterissueiscanceledwhenassumingthe granularmediumasacontinuum.Althoughmanybenefitsarelost,the modelbecomesusableintheframeworkofengineering.Forthatreason, thebookalsodealswiththe materialpointmethod (MPM),whichisa relativelynewandpromisingapproach.
Itisimportant,whenreadingthisbook,tofosteramindsetoftruth seekingratherthantargetingtheapplicabilityofthedifferentmodels depicted.Certainly,thisattitudeofcuriosityishelpfulforabetter appreciationofthemessagesdelivered–theauthorsareevidentlywell awareaboutthesimplificationsmade.
Thisbookiscomposedoffivechapters.Chapter1providesa descriptionoftheemployedmodels.ThevalidityofthespecificDEM developedwillthenbedealtwith–inChapter2–bymeansof comparisonswithreleaseexperiments.Theframeworkoftypical analysiswillalsobepresented.Chapter3discussestheinfluencesof severalmechanicalandgeometricalparametersthatcanbeinvolvedin thepropagationprocesses.Chapter4willpresentthreeconcretecases ofmediumrockavalanchesthatimplementsophisticated digital surfacemodels togetherwithblockshapesissuedfromnatural discontinuityplans(orblasting).Finally,acomparisonofmass releasessimulatedbyDEMandMPMwillbeintroducedinChapter5.
Theauthorswouldliketoinsistupononepointverystrongly:the studiespresentedinthebookresultfromtheworkofseveralkey players–so-calledco-workers–whoarecolleaguesorstudents.The namesoftheseco-workershavebeenmentionedatthebeginningof thechapterswheretheirworkhasbeeninvolved.
Inthischapter,computationalmethodswillbedescribedwitha particularfocusonthediscreteelementmethod(DEM).Thequestion ofknowingwhichmethodismostappropriateforoneoranother situationisnotdirectlyaddressedhere.Instead,thefundamental methodsarediscussedfromboththephysicalandthecomputation pointofview.
1.1.Trajectoryanalysis
Theaiminthissectionistoprovidethebasicconceptsofthe approachwithoutgoingtoodeepintoconsiderations.Inreality,there aresomanyvariantsthatonecannotfocusonaparticularone.
Basically,themainstrategytoconductatrajectoryanalysisisthe lumpedmass approachthattreatsablockasapointwithamass [RIT63,PIT76,HUN88].Morerecentapproachesdealwithshaped blocks[FAL85,DES87];theyarenotreportedhereforthesakeof brevity.Atrajectoryanalysisconsistsofgeneratingahighnumberof trajectoriesbyvaryingtheinitialconditionsandbyintroducingsome controlledrandomnessinthecollisionswiththeterrain.Nowadays, thisrandomnessisalmostalwaysaccountedforinthetrajectory
4ModelingGravityHazardsfromRockfallstoLandslides
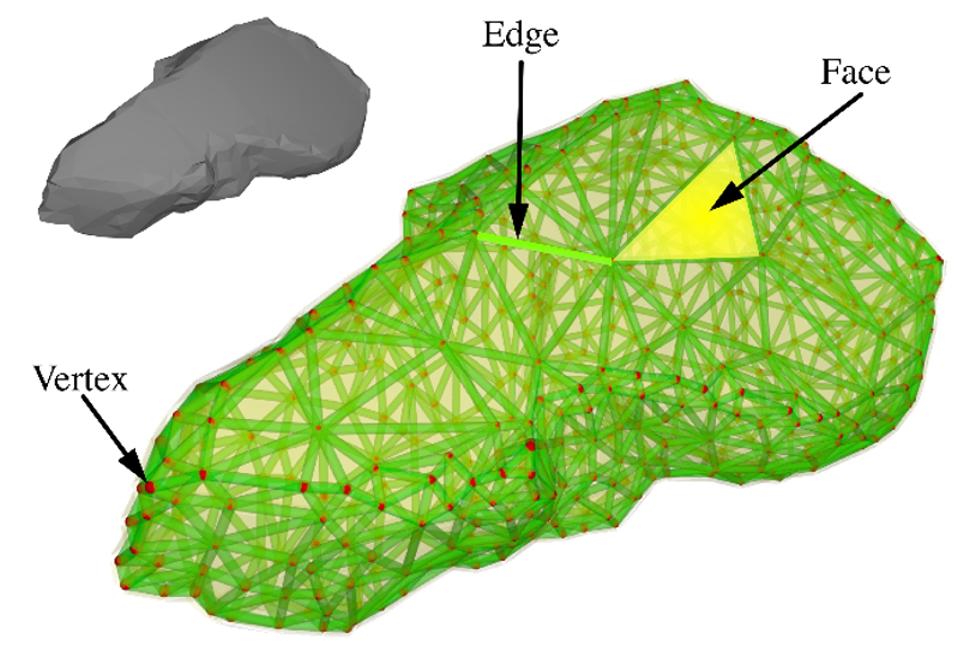
issimilartothatof“clumps”wherespheresareassembledtoforma rigidobjectofcomplexshape.WithSP,inadditiontospheres,two extraformsareassembled:cylinderstoformtheedgesandplanar polygonstoformthefaces.Thevertexesareformedbyspheres. Figure1.1providesanoverviewofanSPrepresentingapebble,which hastheparticularityofbeingnon-convex.Thebodyshapeisactually definedbysweepingasphereoveralledgesandfaces.Froma mathematicalviewpoint,theseblockshapescanbeseenasthe Minkowskisumofapolyhedronandasphere[BER03].
Figure1.1. Definitionofasphero-polyhedronillustratedinthecaseofa non-convexpebble.Thevextexesarespheres,theedgesarecylinders andthefacesarethick3Dpolygons(trianglesinthispicture)
SPofferseveraladvantagesincludinghighlysimplifiedcontact detection(i.e.findingcontactlocationsandassociatedlocal frameworks)[ALO08].Indeed,allthecontactconfigurationsbetween twoSPcanbereducedtoasetofonlyfourtypesofelementary contactsconfigurations: vertex–vertex, vertex–edge, vertex–face and edge–edge.Onecanbetterappreciatethebenefitofthisapproachwhen considering,forinstance,theface–faceintersectiontest:thelattercan simplybereplacedbyasetofedge–edgeandvertex–faceintersection tests.Amongthemanyotherbenefits,theSPapproachallowsthe shapestobeconcaveand/orhollow.Also,thenormalvectorsatcontact aredefinedwithoutambiguity.
1.2.2. Massproperties
ThemasspropertiesoftheSPhavetobeprecomputedinorderto integratetheirdynamicmotions.Theyarethecenterofmass,themass (orvolume)andtheinertiamatrixexpressedintheprincipalframe.To estimateallthesepropertiesforblocksthatmayhaveanygeometries (concave,convex,hollow),MonteCarlo(MC)numericalintegrations areperformed(see[PRE07]).Thebasicpremiseofthemethodrelies ontheapproximationoftheintegralofafunction f onavolume V :
wherethesymbol ... correspondstoanarithmeticmeanofasample of N points.
Theintegrationprocedureisconductedbyfirstsettingan axis-alignedboundingbox (AABB)thatcloselywrapsthebody.Aset ofpositionswithinthisAABBisrandomlygeneratedbymeansofa Sobolsequence(forafasterMCintegration).Toassesswhetherornot thispoint x standsinsidetheSP,afunction ϕ(x) isdefinedsothatitis 1whenthepointisinsidetheshapevolume V ,and0otherwise.In practice,thisisverifiedquitetriviallyatthevertexes(sphere),atthe edges(cylinder)andatthefaces(thickthree-dimensional[3D] polygon).Then,ontheinsidepolyhedron(i.e.withouttheMinkowski radius)thisisverifiedwithanalgorithmbasedontheoddnessofthe amountintersectionbetweenasemiinfiniteray(startingfromthepoint) andeachface.Finally,inmoreformalterms:
Itthenbecomeseasytonumericallyintegrateanyquantityon V AABB volumeusingequation[1.5].Thevolumeofthebodyisfirst estimate:
Byassumingavolumedensity ρ uniformlydistributed,themassof thebodyis m = ρV ,anditsinertialcenter xG canbeobtainedbymeans ofanMCintegration:
Thesymmetricmatrixofinertiarelativetothepoint xG isalso computedusingMCintegrationsforeachofthesixcomponents:
Ixx (xG )= γ ϕ(x)(δy 2 + δz 2 )
Iyy (xG )= γ ϕ(x)(δx2 + δz 2 )
Izz (xG )= γ ϕ(x)(δx2 + δy 2 )
Ixy (xG )= γ ϕ(x) δxδy
Ixz (xG )= γ ϕ(x) δxδz
Iyz (xG )= γ ϕ(x) δyδz [1.9] where T(δx,δy,δz )=(x xG ) andthecommonprefactoris γ = V AABB V [1.10]
Tosavememoryandcomputingtime,onlytheeigenvalues extractedfromtheinertiamatrixwillbestoredas I ∗ 1 /m, I ∗ 2 /m and I ∗ 3 /m.Thevertexpositionsareexpressedinthebodyframeworkgiven bytheeigenvectorsoftheinertiamatrix,withtheoriginplacedatthe masscenteroftheSP.Thepositionandorientationofthelatteristhus defined.
Theuseofregularshapeissometimesrequired(small-scale laboratoryexperiments,characterizationoftheinfluenceoftheshape, etc.).Itisinthiscaseadvantageoustohavealibraryofshapeswith
theirinertiaproperties(inertiaandvolume)precalculatedeitherby handorbynumericalintegrationdependingonthecomplexityofthe form.Suchalibrarywasaddedtothecode DEMbox bysettingeach forminitsownframeworkwithchosendimensions.Thescalingis donethroughascalingfactor H .Forexample,thepositionsofthe elementsconstitutingacubearedefinedrelativetothecenterofthe cube,themainaxesbeingthoseoftheedgeshavingaunitlength.Ifa cubeof1.8cmsquarehastobetakenfromthelibrary,ascalingfactor H =0.18 willbeused(theunitoflengthbeingthemeter).The volumewillbescaledbymultiplyingthe“unitvolume”by H 3 andthe eigenvaluesofinertia(dividedbythebodymass)by H 2 .
1.2.3. Blockmotions
SinceanSPisarigidbody,onlythetimeevolutionofthemass centerpositionandoverallrotationiscomputed.Themovementofthe entitiesthatcomposetheSP(namelytheslavebodies)isgovernedby therelationsofrigidmotion.
ThealgorithmfortheclassicalDEMinvolvestwostagesforeach rigidbody i:(1)thecomputationoftheresultantforces Fi andmoment Mi fromvolumeandcontactforces(seesection1.2.6);and(2)the timeintegrationofNewton’ssecondlaw(fortranslations)andEuler’s equations(forrotations).Thismovementintegrationisperformedby meansofthevelocityVerletscheme[ALL89],whichisasatisfactory compromisebetweentheaccuracyoftheblockvelocities(forboth translationsandrotations)andmemorysaving.
Eachbody i iskinematicallydefinedintheglobalframeworkbyits mass-centerposition xi ,itsmass-centervelocity vi ,itsangular positiongivenbyaunitquaternion ˘ Qi anditsangularvelocity Ωi . Unitquaternionsprovideaconvenientmathematicalnotationfor representingorientationsandrotationsofobjectsinthreedimensions. ComparedtoEulerangles,theyaresimplertocomposeandmayavoid theproblemofgimballock.Comparedtorotationmatrices,theyare morenumericallystableanduselessmemory.Somehow,unit quaternionscanbeinterpretedasrotationmatricesbuttheyonlyhold
8ModelingGravityHazardsfromRockfallstoLandslides
onescalarvalueandonevector: ˘ Qi ≡ [si , Vi ].Thereexistsalargely developedmathematicalbackgroundconcerningquaternions,butall thisknowledgeisnotabsolutelynecessarywhendealingwith rotations.
Fortranslationmotion,thevelocityVerletalgorithmcanbe summarizedasfollowsforeachtimestep Δt:
with ai = Fi mi g z,
where mi isthemassofthebody i and g z isthegravityacceleration.
Forrotationmotion,thevelocityVerletalgorithmisalsousedto determinetheangularpositionsandvelocitiesofthebodies.Itformally reads:
Inthisscheme,thefirstandsecondtimederivativeofthequaternion canbeexpressedintermsoftheangularvelocityvectoras:
where ˘ Ω denotesforthequaternion [0, Ω],andoperator isthe Hamiltonproductdefinedby
inamodule DEMbox.Itisimportanttokeepinmindthatafamilyof discontinuitiesisdefinedby(1)anormalvectorcommontoall discontinuityplanes,(2)apointbelongingtothefirstplane,(3)apoint belongingtothelastplaneand(4)thedistance(chosenconstant) betweentheplanes.Theextentoftheplanesofdiscontinuityare infinite,whichimpliesthateachcutpassesthroughthemassfromone endtotheother,whichisnotnecessarythecasewith discretefracture models.
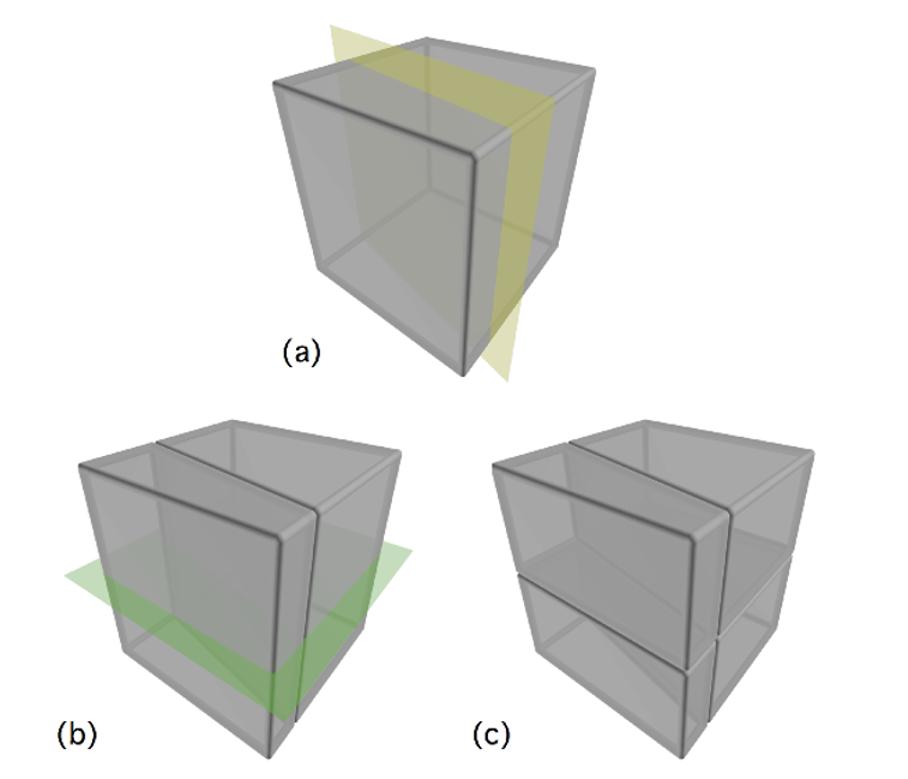
Figure1.2. Aschematicillustrationofthecuttingprocedurealongfamiliesof discontinuityplanes.Theinitialvolume,representedhereasacube,isaspheropolyhedron:a)itisfirstcutalongthefirstfamilyofdiscontinuities(onlyasingle yellowplaneisshown);b)eachresultingblockwillbecutalongthefollowing familyofdiscontinuities(onlyasinglegreenplaneisshown);c)whenallthe cutsaremade,theresultisanassemblyofblocksthatwillbeabletointeract whentheywillbedestabilizedbygravity
Thisproceduregivesrisetorealisticgeometriesofblocks.Theyare issuedfroma3Ddigitalmodeloftheunstablevolume(inthestandard STLformatforexample)andadetailedknowledgeofthefracturing resultingfromasiteinvestigationorfromgeologicaldatabases.Some applicationstorealsitesareshowninChapter4.
1.2.5. Digitalterrainmodel
Thetopologyoftheterraincanbeassessedbymeansofdifferent techniques(aerialLIDARscans,stereocorrelationofphotographic images,etc.).Suchascanoftheterraingenerallyresults,aftersome postprocessing,inatriangularmeshformingthe digitalsurfacemodel (DSM)oftheterrain.Fromthepointofviewof DEMbox model,each triangleisaspherotrianglehavingallitsdegreesoffreedomblocked. AlltheadvantagesofSPstillexistforboththeterraintopologyandits interactionswiththemovingblocks.However,thequestionofthe sensitivitytothesizeresolution(relatedsomehowtothebumpynessof theterrain)remains,eveniftheuseofMinkowskiradiismoothsthe surface.
Figure1.3showsanexampleofDSM.Inthisexample,therelief hasbeenscannedbymeansoftheLIDARtechnique,anddifferent digitaltreatmentshaveresultedinatriangulationwiththedesired fineness.Theinsetinthetop-rightcornerillustrateshowthe spherotrianglesaresuperimposedontotheDSM.
Figure1.3. Digitalsurfacemodelusedtomodelthespread ofarockavalanchetriggeredartificiallyaspartofapreventive purgeofunstablerockyshellofNeronmountnear Grenoble(France)in2011Imagefrom[BOT14]
1.2.6. Contactforcelaws
Thegoodnessofamodelcanbeevaluatedfromitsabilitytoreflect concretephysicalphenomena,butalsobytheeasinesswithwhichthe requiredparametersareaccessible.Inotherwords,thecurrentstakesin modelinggravityhazardsconcernnotonlythedevelopmentof powerfulnumericaltoolscapableofsimulatingcomplexrheologiesbut alsotheabilityofanoperatortoidentifyandassignmodelparameters. Withthisinmind,adissipativemodelofcontact–collisionisdepicted. Themodelisintentionallyminimalist.Forrockfallmodeling,itis believedthatitincludestheminimumnumberoffeaturesnecessaryto takeaccountof(1)thedeformabilityofthecontactzones,(2)a dissipationrelatedtonormalcollisionsand(3)adissipationassociated withtangentialrelativedisplacements.
Themodeldepictedhereisbasedonbodyshapesthataremore realisticthanspheres,asseenpreviously.Thisisactuallyacrucial featureofthemodel.Theothercrucialfeatureconcernscollision(or contact)forcelaws.Asimpleformulationhasbeenused;nevertheless, itincorporatestheenergydissipationduetoblockcollisions. Consideringthehugeamountofuncertaintiesrelatedtoanaturalevent, itseemedtotallyimpossibletopredicttheexacttrajectoryofeach particleintheflow.Thus,itwasdecidedtofocusontheenergyloss associatedwitheachimpact,ratherthantoreproduceinsmallest detailstheexactphysicalphenomenarelatedtothisimpact.Theenergy lossmayresultfromverycomplexphysicalmechanisms(heat production,wavepropagation,microcracking,blockchipping,etc.)for whichitisreasonabletoadmitthattheyarebeyondunderstandingof collectivebehavioroftheblocksinaflow.Moreover,thelocal mechanismsdonotneedtobepreciselyidentified,especiallysinceit willbenecessarytoidentifytheparametersinvolved.Minimalistlaws wereoptedfor,whereonlytherateofenergylossandthefrictionare requiredtodissipatethekinematicenergyoftheblocks.Inother words,acoarserscalehasbeenconsideredtotakeintoaccountforce transmissionanddissipationmechanismsinagranularassemblythat flowsandthenstops.Itisimportanttostressherethatthiscoarserscale isnotnon-physicalbutignoressomephysicalmechanismsthatare
14ModelingGravityHazardsfromRockfallstoLandslides
involvedatsmallerscales.Itwillbeseeninthefollowingchaptersthat thelawsproposedherearesufficienttosatisfactorilydescribethemain reboundpatterns–eventhemosterratic–providedthattheminimum timeresolutionofinterestislongerthanacollisionduration. Obviously,themodelhereshouldnotbeusedwhendealingwithsome otherfeaturesforwhichtheforceevolutionduringthecontact/ collision,suchacousticwavepropagationinconfinedgranularsystems [SOM05](anyway,itisnotwhyitisdesignedfor).
Rockavalanchesinvolvedynamicblockmovements.Forthis reason,dampingmodels,whichaffectblockmovementswithan artificialparachute,cannotbeusedsinceitwouldleadtonon-physical behavior.Anothersolutionistoaccountforalocalviscousdampingat acontactlevel.Thissolutionwasalsorejectedbecause,althoughit introducesaviscosityparameterthatcanbeconnectedtoa well-defineddissipationrateinthecaseofsinglecontact[TSU92],it isill-definedintheparticularcaseofthemultiplecontactsinvolvedin theinteractionsofSP.Moreprecisely,theeffectivemass meff involved inthecriticalviscosity 2√meff kn isnotwelldefinedforcomplex shapesandshoulddependonthepositionsofthecontactpointsand theirnumber.
1.2.6.1.
Normalforce
Thesimplestformulationforthenormalforce fn makesuseofa linearelasticlawwithtwodifferentstiffnessesinthecaseofloadingor unloading(respectively, k + n and kn )[BAN09].Whentheoverlap hn increases(i.e. Δhn ≥ 0),thenormalforceincrementreads:
Δfn = k + n Δhn [1.22]
Otherwise,if Δhn < 0 and hn > 0,theforce fn isgivenby: fn = kn hn [1.23]
Figure1.4(a)isaplotofthisforcelaw,whichillustratestheroleof incrementalloading.Itshouldbenotedthattheliteratureprovides othercontactlawsthatalsointroduceenergydissipationbymeansofa