Modeling and analysis of passive vibration isolation systems 1st edition sudhir kaul - Download the by Education Libraries

ModelingandAnalysisofPassiveVibration IsolationSystems1stEditionSudhirKaul

https://ebookmass.com/product/modeling-and-analysis-ofpassive-vibration-isolation-systems-1st-edition-sudhir-kaul/

Instant digital products (PDF, ePub, MOBI) ready for you

Download now and discover formats that fit your needs...

Modeling and analysis of modern fluid problems Zhang

https://ebookmass.com/product/modeling-and-analysis-of-modern-fluidproblems-zhang/ ebookmass.com

Modeling and Simulation of Dynamic Systems 1st Edition

Robert L. Woods

https://ebookmass.com/product/modeling-and-simulation-of-dynamicsystems-1st-edition-robert-l-woods/

ebookmass.com

Embedded Mechatronic Systems, Volume 2: Analysis of Failures, Modeling, Simulation and Optimization 2nd Edition Abdelkhalak El Hami

https://ebookmass.com/product/embedded-mechatronic-systemsvolume-2-analysis-of-failures-modeling-simulation-andoptimization-2nd-edition-abdelkhalak-el-hami/ ebookmass.com

Art Through the Ages - A Concise Global History 4th Edition Fred

S. Kleiner

https://ebookmass.com/product/art-through-the-ages-a-concise-globalhistory-4th-edition-fred-s-kleiner/ ebookmass.com

Consequences of Maritime Critical Infrastructure

Accidents: Environmental Impacts Modeling-IdentificationPrediction-Optimization-Mitigation Magdalena Bogalecka

https://ebookmass.com/product/consequences-of-maritime-criticalinfrastructure-accidents-environmental-impacts-modelingidentification-prediction-optimization-mitigation-magdalena-bogalecka/ ebookmass.com

A Textbook of Data Structures and Algorithms, Volume 2: Mastering Nonlinear Data Structures Vijayalakshmi Pai

https://ebookmass.com/product/a-textbook-of-data-structures-andalgorithms-volume-2-mastering-nonlinear-data-structures-vijayalakshmipai/ ebookmass.com

Adams And Victor’s Principles Of Neurology 11th Edition Edition Allan H. Ropper

https://ebookmass.com/product/adams-and-victors-principles-ofneurology-11th-edition-edition-allan-h-ropper/ ebookmass.com

Digital Transformations in the Challenge of Activity and Work: Understanding and Supporting Technological Changes

Marc-Eric Bobillier Chaumon

https://ebookmass.com/product/digital-transformations-in-thechallenge-of-activity-and-work-understanding-and-supportingtechnological-changes-marc-eric-bobillier-chaumon/ ebookmass.com

The Chorus of Drama in the Fourth Century BCE: Presence and Representation Lucy C. M. M. Jackson

https://ebookmass.com/product/the-chorus-of-drama-in-the-fourthcentury-bce-presence-and-representation-lucy-c-m-m-jackson/ ebookmass.com

Stochastic Modeling: A Thorough Guide to Evaluate, PreProcess, Model and Compare Time Series with MATLAB Software First Edition Hossein Bonakdari

https://ebookmass.com/product/stochastic-modeling-a-thorough-guide-toevaluate-pre-process-model-and-compare-time-series-with-matlabsoftware-first-edition-hossein-bonakdari/ ebookmass.com

MODELINGAND ANALYSISOF

PASSIVEVIBRATION ISOLATIONSYSTEMS

MODELINGAND ANALYSISOF PASSIVEVIBRATION ISOLATIONSYSTEMS

SUDHIRKAUL

AssociateProfessor,SchoolofEngineeringandTechnology, WesternCarolinaUniversity,Cullowhee,NC,USA

Elsevier

Radarweg29,POBox211,1000AEAmsterdam,Netherlands

TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates

Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorage andretrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowto seekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandour arrangementswithorganizationssuchastheCopyrightClearanceCenterandthe CopyrightLicensingAgency,canbefoundatourwebsite:www.elsevier.com/permissions.

Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyright bythePublisher(otherthanasmaybenotedherein).

Notices

Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchand experiencebroadenourunderstanding,changesinresearchmethods,professionalpractices, ormedicaltreatmentmaybecomenecessary.

Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribed herein.Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafety andthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.

Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,or editors,assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatter ofproductsliability,negligenceorotherwise,orfromanyuseoroperationofanymethods, products,instructions,orideascontainedinthematerialherein.

BritishLibraryCataloguing-in-PublicationData

AcataloguerecordforthisbookisavailablefromtheBritishLibrary

LibraryofCongressCataloging-in-PublicationData

AcatalogrecordforthisbookisavailablefromtheLibraryofCongress

ISBN:978-0-12-819420-1

ForInformationonallElsevierpublicationsvisitourwebsiteat https://www.elsevier.com/books-and-journals

Publisher: MatthewDeans

AcquisitionsEditor: DennisMcGonagle

EditorialProjectManager: HilaryCarr

ProductionProjectManager: PrasannaKalyanaraman

CoverDesigner: designerChristianBilbow

TypesetbyAptara,NewDelhi,India

3.Vibrationisolationsystemmodeling

6.4

7.1

Preface

Passivevibrationisolatorsarewidelyusedinareassuchasautomotive, aerospace,manufacturing,heavymachinery,andcivilstructures.Ontheone hand,thedesignanddevelopmentofpassivevibrationisolatorsisamature technology.Ontheotherhand,analyticalmodelingofsuchisolationsystems isstillevolvingduetothemultifacetedintersectionofdifferentdisciplines. Theaimofthisbookistoserveasareferenceforengineersandresearchers involvedinthedesign,development,modeling,analysis,andtestingofpassive vibrationisolationsystems.

Thisbookhasbeendividedintosevenchapters.Chapter1presentsabrief reviewofvibrationanalysisandterminology.Theaimofthischapteristo serveasarefresher;thischaptercanbeusedinconjunctionwithAppendix AandAppendixBtorecapitulatethecontentfromanintroductorycourse invibrationanalysis.Chapter2presentsseverallinearviscoelasticrheological modelsthatcanbeusedforasingle-degree-of-freedomanalysisofvibration isolationsystems.Themainattributesofeachmodelarediscussedinthis chapteralongwiththegoverningrelationshipsbetweencriticalmodeland designparameters.Chapter3presentslinearviscoelasticmodelsforplanar (two-andthree-degree-of-freedom)andspatial(six-degree-of-freedom) vibrationisolationsystems.Additionalmodelsforpiecewisebehaviorand hystereticsystemsarealsopresentedinthischapter.Chapter4presents nonlinearmodelsforsingle-degree-of-freedomsystemsaswellasmultipledegree-of-freedomsystemsthatcanbeusedfortheanalysisofpassive vibrationisolation.Althoughnonlinearitiescanbeattributedtomultiple sources,thischapterprimarilyfocusesonanalyticalmodelsforafewspecific nonlinearitiesassociatedwithstiffnessanddampingcharacteristics.Chapter 5presentsmodelsthataretypicallyusedfortheanalysisofelastomeric vibrationisolators.Modelsthatcanbeusedtorepresentsuchphenomena asMullinseffect,Payneeffect,hyperelasticity,aging,andcreephavebeen discussedinthischapter.Chapter6presentsmodelsthatcanbeusedto accountfortheinertiaeffectthatistypicallyobservedinvibrationisolation systemsthatneedtowithstandveryhighexcitationfrequencies.These modelsallowanevaluationofvibroacousticcharacteristicswellabove1 kHzwhilecapturinginternalresonanceandwaveeffects.Chapter7presents examplesandcasestudiesthatintegrateconceptsfromthemodelspresented inthepreviouschaptersofthebookwhiledemonstratingtheinfluenceof

thevibrationisolationsystemonoverallsystemdynamics.Therearetwo briefappendicesthatmaybeusedasarefresheronordinarydifferential equationsandmatrixalgebra.Eachchapterhasafewexerciseproblemsthat canbesolvedtotesttheunderstandingofthecontentpresentedinthe chapter.

Themodelsdiscussedinthisbookencompassawiderangethatcan beusefulfortheanalysisofpassivevibrationisolationsystems.Whilesome ofthemodelspresentedinthisbookhavebeenusedforquitesometime, othersarerelativelynewandofferusefuloptionsforgainingananalytical insightthatcanbeusedfordesign.Furthermore,someofthemodelsare phenomenological,whileothersaresemi-empirical;thereforeallowinga designoranalysisengineertocustomizethemodelsduringtheproduct developmentprocess.Someofthemodelsforelastomericmaterialsand nonlinearbehaviorthathavebeendiscussedinthisbookareactiveareas ofresearchandcontinuetobediscussedandinvestigatedintheexisting literature.Asurgeintheuseofelectricpowertrainshasresultedinnew requirementsforpassivevibrationisolationsystems,afewmodelspresented inthisbookarepossibleoptionsfortheanalysisofinternalresonancein suchsystems.Ihopethatthevarietyofmodelsdiscussedinthisbookis usefulinthedesignanddevelopmentofpassivevibrationisolationsystems byholisticallyaccountingforvibrationresponse,systemdynamics,design parameters,andisolatordesign.

Dedication

Dedicatedtomymother,whoselifewasabeaconofperseverance,resilience, humility,andkindness.

Dedicatedtomyfather,whoselifecontinuestoinspiremewithaninsatiable loveforlearning.

Acknowledgments

Iwouldliketoacknowledgethehelpreceivedfromtheentirepublishing teamatElsevier.Ialsowanttoacknowledgethesupportreceivedfrom WesternCarolinaUniversityandallmycolleagues,students,peers,and collaboratorsovertheyears.Whilemanyindividualshavehelpedinshaping myunderstandingofthecontentofthisbook,twoindividualsmerit specialmention.Iwanttoexpressmygratitudetomygraduateadvisor attheUniversityofWisconsin-Milwaukee,Dr.AnoopDhingra,andmy supervisoratHarleyDavidsonMotorCompany,Dr.TimHunter,for introducingmetodifferentaspectsofpassivevibrationisolation.Finally,I wanttothankmywifeforherlove,patience,andunderstandingduringthis endeavor.

Iwouldberemissinfailingtoacknowledgethecontributionofmany individualswhohaveshapedmyacademicjourney,thisincludesmany teachersfrommyschoolandprofessorsfromtheuniversitiesIattended. Ialsowanttothankmysisterforbeingmyveryfirstteacherandmentor.

CHAPTER1

Vibrationisolation— background

1.1Introduction

Theuseofvibrationisolatorsandvibrationisolationsystemsiswidely prevalentinmultipleapplicationssuchasautomotive,railroad,aerospace, heavymachinery,civilstructures,etc.Someofthemainreasonsforusing avibrationisolatorincludemitigationofresonancepeaks,reductionof transmissibility,enhancementoffatiguelife,improvementinergonomics, etc.inthepresenceofexternalorinternalsourcesofdynamicexcitation. Thedesignofavibrationisolatorrequiresacloseexaminationofmultiple considerationssuchasthesourceofdynamicexcitation,rangeofexcitation frequency,excitationamplitude,allowabledisplacement,accelerationlimits oftheisolatedsystem,availabledesignenvelope,etc.Additionally,considerationsofenvironmentalconditions,manufacturability,andmaterialchoice arealsoimportant.Alltheseconsiderationsaccentuatetheimportanceof atheoreticalmodelthatcanreasonablypredicttheperformanceofthe isolationsystembeforefinalizingthedesignandbeforemanufacturing prototypesthatcanbeusedfortesting.Therefore,itiscriticaltoselecta suitablemodelthatcanbecorrelatedtotestresultsandeventuallyusedto finalizedesigndetails.

1.2Isolatormaterials

Vibrationisolationcanbeachievedbyusingmaterialscapableofproviding acombinationofhighlyelasticbehaviorinconjunctionwithdamping properties.Pneumatic,hydraulic,elasticmetal,andelastomericdesignsare commonlyusedincommercialvibrationisolationapplications.Elastomeric materialsarearguablymostcommonandareextensivelyusedintheindustry withaverycommonlyuseddesignconsistingofelastomericmaterial bondedtometalplatesorametalcore.Suchisolatorsaretypicallycalled elastomericmounts.Naturalrubber,neoprene,andbutylrubberaresomeof thecommonlyusedelastomersincommercialvibrationisolators.Elastomers provideadesignerwitharangeofstiffnessanddampingcharacteristics aswellasanabilitytowithstanddifferentenvironmentalconditions.This abilitytosatisfyperformancerequirementsoverawiderangeofrugged conditionsalongwiththeeaseofmanufacturingthroughamoldingprocess makeelastomersacommonchoiceforisolatorsduringthedesignprocess. Table1.1listssomeofthecommonlyusedelastomersformanufacturing passivevibrationisolatorswithalistingofsomeoftheircharacteristics thatcanbeconsideredduringdesign.Inadditiontothecommonlyused elastomers,manufacturersoftendevelopproprietaryelastomericrecipes toservetheneedsofaspecificdesignthatmayrequireacombination ofpropertiesfromdifferentmaterials.Propertiesofelastomericmaterials canbechangedsignificantlybychangingtheircompositionorbyusing differentblends.Atypicalmanufacturingprocessoftherawmaterialinvolves vulcanizationbyaddingsulfurandbytheadditionofaccelerators,fillers,and plasticizers(Mark,Erman,&Roland,2013).Therawmaterialisthenused inamoldingprocesstoproduceavibrationisolatorofthedesignedshape andsizetodeliverthenecessarystiffnessanddampingproperties.While therearemanycharacteristicsthataresoughtfromthedesignofavibration isolator,someofthecommontechnicalpropertiesthatadesignerseeksto comprehendaredamping,dynamicstiffness,environmentalresistance,and someoftheinherentnonlinearities.

Metalspringshavebeencommonlyusedforvibrationisolationapplicationsastheycanbedesignedtoofferarangeofstiffnessproperties inheavymachineryapplications.Mostofthesedesignsdonotallow muchflexibilitywithdampingasmostmetalspringsofferrelativelylow materialdamping.Coilsprings,discsprings,slottedsprings,etc.aresome examplesofmetalspringscommonlyusedinvibrationisolationapplications (Rivin,2003).

Table1.1 Commonlyusedelastomericmaterials.

Material

Naturalrubberor polyisoprene(NR)

Neopreneor polychloroprene

Nitrileoracrylonitrile butadiene

Styrenebutadiene

Ethylene-propylene-diene terpolymer

Keycharacteristics

Goodprocessability,highelongation,high tensilestrength,relativelylowdamping ratio,goodbondingtometals, moderate-to-lowoilresistance, moderate-to-lowchemicalresistance, operatingtemperature: 30to160°F.

Goodabrasionresistance,goodtearstrength, mechanicalpropertiessimilartoNR, moderateoilresistance,moderatechemical resistance,flameretarding,operating temperature: 20to180°F.

Goodabrasionresistance,highoilresistance, resistancetoswelling,conductorof electricity,operatingtemperature: 30to 250°F

Highabrasionresistance,moderate-to-high oilresistance,moderate-to-highchemical resistance,goodelectricalinsulator, operatingtemperature: 20to210°F

Highabrasionresistance,relativelyhigher dampingratio,moderatetearresistance, lowoilresistance,lowchemicalresistance, operatingtemperature 40to300°F

Insomecases,itiscommontouseaseparatedampertoaugment dampingofthevibrationisolationsystem.Viscousdampersaredesigned toofferresistancetorelativemotionbetweentwosurfacesthataretypically separatedthroughafluidfilm.Someofthesedamperscanexhibitnonlinear behaviorduetostrongtemperaturedependence.Sincetheearly1990s, magnetorheological(MR)dampershavebeendevelopedbyresearchersand manufacturerstoprovidesmartdampingpropertiesthatcanbecontrolled throughinputcurrenttoanelectromagnetthatinturngovernsthebehavior ofthedamper.MRfluidsconsistofmicron-sizedparticlesinacarrier fluid,anMRdamperallowscontrolovertheapparentviscosityofthe fluidbycontrollingthemagneticfluxoftheelectromagnet.Suchadamper isconsideredtobeasemi-activesystemthatcanbeusedforvibration isolationandcontrol(Choi&Wereley,2008;Dominguez,Sedaghati,& Stiharu,2004).Frictiondampersandelectromagneticdampersareother

examplesofdampersthathavebeenusedinsomevibrationisolation applications.

Ahydraulicmount,alsocalledahydromount,isanothervibrationisolatorthathasbeenusedinautomotiveapplications.Suchanisolatorprovides propertiesthatareamplitudedependentaswellasfrequencydependent.The isolatortypicallyconsistsoftwochambersconnectedthroughachannelthat allowsfluidpassagefromonechambertotheother.Thisdesignallowsthe vibrationisolatortoexhibitlowstiffnessandhighdampingfordynamic excitationswithlargeamplitudeandlowfrequencywhiledemonstrating lowdampingatsmallamplitudeandhighfrequencyvibrations(Truong &Ahn,2010).Differentdesignsofhydromountshavebeenusedinsome automotiveapplicationstoprovidedynamiccharacteristicsthatcanbetuned toprovideafrequency-dependentbehavior.

1.3Commonelastomericisolatordesigns

Someofthecommondesignsofpassivevibrationisolatorsinvolveelastomericmaterialbondedtometalplatesorametalcorewithastaticmember thatisassembledtoarigidframeandadynamicmemberthatseparates theisolatedcomponentsfromthesourceofdynamicexcitation.Thereare somedesignsthatconsistofelastomericmaterialswithoutbeingbondedtoa metalplateorametalcore,suchdesignstypicallydonotneedtowithstand highstaticloads.Passiveelastomericisolatorsaregenerallydesignedtobe undercompressionloadingorshearloadingwithcircularorrectangular crosssectionsbeingthemostcommonlyused.Grommets,bushings,etc. arealsocommonexamplesofpassiveelastomericisolators.Someofthe commonlyuseddesignconfigurationsofelastomericisolatorsareshownin Table1.2.

Mostelastomericisolatorsexhibitvaryingamountsofcreep.Creepisexhibitedintheformofanincreasingdeformationevenwhentheloadisstatic. Creepbehaviorisexponentialandtimedependent.Uponremovalofthe staticload,creepismostlyreversiblebutleavessomeresidualstrainorpermanentsetintheelastomer.Dynamicloadscanalsoresultinanincreasing deformationinelastomericisolatorswitheveryloadingcycle,thispropertyis oftenreferredtoasthedynamicset.Inelastomericisolatordesign,itiscommontoallowfor10%deflectiontoaccountforcreepanddynamicset.Some specificcharacteristicsofelastomericisolatorswillbediscussedindetailin Chapter5.

Table1.2 Examplesofpassiveelastomericisolatordesigns.

1.4Stiffnessanddamping

Stiffnessanddampingaretwomaincharacteristicssoughtfromavibration isolatorandareusedforcharacterizingadynamicmodel.Stiffnessidentifies theabilityofamaterialtowithstandappliedforce.Thestiffnessconstant orthespringconstant(k)ofanisolatorisdefinedastheforceperunit deflection,expressedasfollows:

InEq.(1.1), F istheforceand x isthecorrespondingdeflection.A relativelyhigherstiffnessindicatesahighervalueof k,inturnimplyingthata higherforceisnecessarytoobtainthesameamountofdeflection.Forlinear elasticbehavior,thestiffnessconstantisdirectlyrelatedtothemodulusof elasticityofthematerial.Themodulusofelasticityofelastomericmaterials issignificantlylower,andthematerialregainsitsoriginalshapeandsizevery quicklyafterundergoingsignificantdeformation.Eq.(1.1)identifiesalinear relationship,someofthepassiveisolatordesignsmaynotberepresentedby thisstiffnessmodel.Suchcaseswillbediscussedinthechapteronnonlinear vibrationisolators.Often,anequivalentstiffnessiscomputedfordeveloping adynamicmodelwhenmultipleisolators(orspringelements)areconnected together.Anexampleofcalculatingtheequivalentstiffnessispresentedin Example1.1.

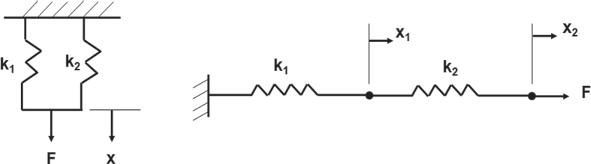
Example1.1: Findtheequivalentstiffnessforthesystemofspringsin(A) paralleland(B)seriesshowninFig.1.1.

Forthetwospringsinparallel F = (k1 + k2 )x,thiscanbeidentified fromthefree-bodydiagramasanexternalforcecausesthesamedeflection inboththesprings.Thisrelationshipcanbeusedtowritetheratioofforce

Figure1.1 Springsinparallelandspringsinseries.

anddeflectionas F x = k1 + k2 . Therefore,forthetwospringsinparallel, theequivalentspringconstantcanbeexpressedasthesumofthespring constants: keq = k1 + k2 ,therebyexpressingtheforce-deflectionratioas F x = keq .Itcanbeseenthattheequivalentspringconstant(keq )ofthe springsinparallelishigherthanthespringconstantofeachspring.Ingeneral, theequivalentspringconstantforanynumberofspringsinparallelcanbe calculatedas keq = i ki .Forthetwospringsinseries, F = k1 x1 = k2 x2 = keq x

astheforceinboththespringsremainsthesame.Theoveralldeflection, x, isthesumoftheindividualdeflection x1 and x2 ofeachspring, x1 + x2 = x

Substitutionfromtheforceequationresultsinthefollowing: F k1 + F k2 = F keq . Thesetwoequationscanbeusedtocalculatetheequivalentspringconstant ofthetwospringsinseriesas keq = 1 1 k1 + 1 k2 . Theoverallequivalentspring constant keq ofthespringsinseriesislesserthanthespringconstantofeach spring.Ingeneral,theequivalentspringconstantforanynumberofsprings inseriescanbecalculatedas keq = 1 1 ki . Itmaybenotedthatspring elementsmaybeconnectedthroughacombinationofseriesandparallel configurations.However,theequivalentspringconstantofthesystemcan becalculatedbyusingaterm-by-termreductionoftheseriesandparallel configurations.

Asvibrationisolationsystemscanbesubjecttoawiderangeofexcitation frequencies,itiscommontorepresenttheforce-deflectionrelationshipin termsofcomplexstiffness.Foraninputdisplacementof x = Xejω t andan outputforceof f = Fej(ω t + ϕ ) ,complexstiffnessistheratiobetweentheforce andthecorrespondingdisplacementandisexpressedas

InEq.(1.2), k∗ iscomplexstiffnessthatisoftenexpressedintermsofthe magnitudeandphasefromEq.(1.2)as

InEq.(1.3),|k∗ |isthemagnitudeofcomplexstiffness,oftencalled dynamicstiffness,and η iscalledthelossfactorthatisdirectlyrelatedto thephaseangle, ϕ ,asseeninEq.(1.4).Thisformofstiffnessiscommonly

usedincaseofhystereticdamping,withalagbetweentheappliedforceand theresultingdeformation.

Dampingisacomplexphenomenonthatcanbeusedtoindirectly representtheenergydissipatedbythevibrationisolationsystemduring repeatedorcyclicloading.Viscousdampingiscommonlyusedtomodel thedampingofmanyvibrationisolators.Insomecases,hystereticdampingis moresuitabletorepresentthedampingofavibrationisolator,whichwillbe discussedfurtherinsubsequentchapters.Threevariablesusedtocharacterize viscousdampingarethedampingconstant,thecriticaldampingconstant, andthedampingratio(alsocalledthedampingfactor).Thedamping constant(c)isdefinedasappliedforceperunitrelativevelocity

InEq.(1.5), v istherelativevelocitycorrespondingtotheappliedforce, F. Criticaldampingisdefinedtoidentifythelimitingcasebetweenoscillatory andnonoscillatorymotion,andthecriticaldampingconstantisdefined as

InEq.(1.6), k isthestiffnessconstantand m isthemassofthesystem. Thedampingratioisdefinedastheunitlessratiobetweenthedamping constantandthecriticaldampingconstant.

InEq.(1.7), ξ isthedampingratio.Asystemissaidtobeundamped whenthedampingratioiszero,thisisanidealizationthatissometimes usedinpreliminarymodelingofanisolationsystem.Asystemissaidtobe underdampedwhenthedampingratioisbetweenzeroandone,thisisthe mostcommoncaseinvibrationisolationmodeling.Asystemissaidtobe overdampedwhenthedampingratioisaboveone.Ifthedampingratiois equaltoone,thesystemissaidtobecriticallydamped.Vibrationisolatorsare mostcommonlymodeledasspring-damperunitswithstiffnessanddamping characteristicsthatareusedtoisolateasystemfromanexcitationsourceor toisolateonesubsystemfromanother.

Forhystereticdamping,anequivalentdampingratio, ξ eq ,andanequivalentdampingconstant, ceq ,aredefinedas

InEqs.(1.8)and(1.9), η isthelossfactordefinedinEq.(1.4).Itmay benotedthattheequivalentdampingratioandtheequivalentdamping constantassumeaharmonicresponse,withfrequency ω ,toaharmonic excitation.Thevariables k and k arethevariablesassociatedwithcomplex stiffness,asseeninEqs.(1.2)and(1.3).Itmaybenotedthatsomesystemsmay exhibitfrictiondamping,detailsaboutsuchdampingcanbefoundinvarious studies(Balachandran&Magrab,2019;Inman,2014;Thomson&Dahleh, 1998;Inman,2014;Meirovitch,1997;Rao,20072017;Tongue,2002).

1.5Single-degree-of-freedomsystem

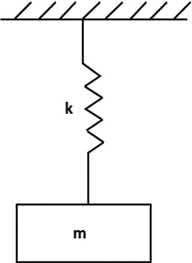
Degreeoffreedom(DOF)isdefinedastheminimumnumberofindependentparametersneededtolocatearigidbodyinspace.AsingleDOF (SDOF)systemisthesimplestformofavibratingsystemoftenusedasa preliminarymodelforvibrationisolation.Suchamodelconsistsofarigid bodyconnectedtooneormultiplespringsoraspring-damperunit.The systemissaidtobeundampedifitismodeledwithoutdamping.Thissection presentsthesolutionofanSDOFsystemthatwillbeusedinsubsequent chapters.Theequationofmotion(EOM)foranundampedSDOFsystem withoutanyexternalexcitation,showninFig.1.2,canbeexpressedas

InEq.(1.10), m isthemassofthesystemand k isthestiffnessconstant, while x isthedeflectionduetoanyexternalperturbationthatthesystemmaybesubjectto(fromitsstateofstaticequilibrium).Eq.(1.10)is ahomogeneoussecond-orderdifferentialequationwiththefollowing solution: x (t ) = c1 cos( ωn t ) + c2 sin( ωn t ) (1.11)

InEq.(1.11), c1 and c2 aretwoconstantsthatcanbedeterminedfrom theinitialconditionsofthesystem,and ωn = k m isthenaturalfrequency

Figure1.2 UndampedSDOFsystem-freevibration.

ofthesystem.Eq.(1.11)providesthetime(t)historyofdisplacementfor theundampedsystemwhenitisperturbedfromitsstaticequilibrium.The stepsinthedevelopmentofthesolutioninEq.(1.11)arenotpresentedhere. AppendixAprovidesabriefintroductiontothesolutionofthesecondorderdifferentialequations.

TheEOMforanundampedSDOFsysteminthepresenceofan excitationinputcanbeexpressedas

InEq.(1.12), f istheexcitationforce.ThesolutiontotheEOMin Eq.(1.12)isacombinationofthehomogeneousandtheparticularsolution forageneralexcitationforce, f = f0 ejω t ,withanexcitationfrequencyof ω , andcanbewrittenas

ThesolutioninEq.(1.13)canbeexpressedindifferentformsdepending ontheratiobetweentheexcitationfrequencyandthenaturalfrequencyof thesystem.

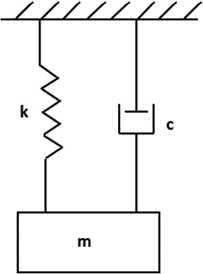
TheEOMforadampedSDOFsystemwithviscousdampingand withoutanyexternalexcitation,showninFig.1.3,canbeexpressedas

ThesolutionfortheEOMofthedampedsysteminEq.(1.14)is

Figure1.3 DampedSDOFsystem—freevibration.

InEq.(1.15), c1 and c2 aretwoconstantsthatcanbedeterminedfrom theinitialconditions.Also,thesolutionvarieswiththenatureof λ1 and λ2 , λ1,2 =− c 2m ± c 2m 2 k m ,todeterminewhetherthesystemis underdamped,overdamped,orcriticallydamped.Thestepsneededfor solvingthegoverningdifferentialequationinEq.(1.14)areprovidedin AppendixA.

Forvibrationisolation,underdampingisthespecificcaseofinterest.For underdamping,0 <ξ< 1andthesolutioninEq.(1.15)canbemodifiedas follows:

InEq.(1.16), c1 and c2 aretwoconstantsthatcanbedeterminedfrom theinitialconditions,and ωd = ωn 1 ξ 2 isthedampedfrequency,while ω n istheundampednaturalfrequency.Itmaybenotedthatfor ξ = 0,the solutioninEq.(1.16)becomesidenticaltothesolutionoftheundamped systeminEq.(1.11).

TheEOMforadampedSDOFsysteminthepresenceofanexcitation inputcanbeexpressedas

InEq.(1.17), f istheexcitationforce.ThesolutiontotheEOMin Eq.(1.17)isacombinationofthehomogeneousandtheparticularsolution forageneralexcitationforce, f = f0 ejω t ,withanexcitationfrequencyof ω ,

andcanbeexpressedas

InEq.(1.18), ϕ isthephaseanglebetweenexcitationforceandthe resultingdisplacementandcanbefoundas

ExamplesoftheresponseofundampedanddampedSDOFsystemsare presentedinExample1.2.

Althoughtheclosed-formsolutionofEq.(1.17)isreadilyavailable,itis commontoexpressthesecond-orderequationasasystemofthefirst-order equationsasfollows:

InEqs.(1.20)and(1.21), x1 = x and x2 = x ThesysteminEqs.(1.20)and (1.21)isequivalenttoEq.(1.17).Themainadvantageofexpressingthe second-orderdifferentialequationasasystemofthefirst-orderdifferential equationsistheuseofnumericalmethods.Thisisparticularlybeneficialfor anonlinearsystemasaclosed-formsolutionmaynotbereadilyavailablefor suchasystem.ThesysteminEqs.(1.20)and(1.21)canalsobeexpressedin amatrixformas

TheformulationinEq.(1.22)iscommonlycalledthestate-spaceform ofthesystem.

Thesolutioninthissectionislimitedtoharmonicexcitation.The excitationforcemaynotalwaysbeharmonic.Insuchcases,alternative methodsareusedtosolvethegoverningEOM.MethodssuchasFourier series,convolution,Laplacetransform,etc.canbefoundinintroductorytext bookssuchas(Rao,2017)(Thomson&Dahleh,1998).Abriefreviewof someofthepropertiesoftheLaplacetransformandtheFouriertransform isprovidedinAppendixA.

Figure1.4 UndampedSDOF—freevibrationresponse.

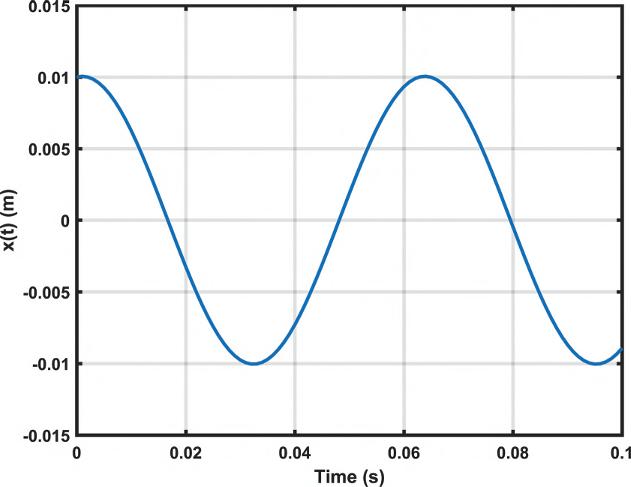
Example1.2a: ForanundampedSDOFsystem,asshowninFigure1.2, withamass(m)of1kg,astiffnessconstant(k)of10,000N/m,andthe giveninitialconditions,plotthefreevibrationresponse.Thegiveninitial conditionsareasfollows: x (0) = 0.01mand x (0) = 0.1m/s. Usingthe solutionfromEq.(1.11)andapplyingtheinitialconditions,thetwoconstants canbefoundas c1 = 0.01and c2 = 0.001. Freevibrationresponsecanbe expressedas

x (t ) = 0.01cos(100t ) + 0.001sin(100t )(E1.2.1)

Thenaturalfrequencyofthesystemis100rad/sor15.9155Hzandthe naturaltime-periodisthereciprocalofthenaturalfrequency,0.0628s.The firstfewcyclesoffreevibrationresponseareshowninFig.1.4byplotting theresponse, x(t)

Example1.2b: ForadampedSDOFsystem,asshowninFig.1.3,with amassof1kg,astiffnessof10,000N/m,aviscousdampingconstantof 50N-s/m,andthegiveninitialconditions,plotthefreevibrationresponse.

Thegiveninitialconditionsareasfollows: x (0) = 0 01 m and x (0) = 0.1 m/s.Thecriticaldampingconstantforthesystemis200N-s/m.This