Acknowledgments
Iamindebtedtonumerouspeoplewhomadethisbookpossible.
First,Ithankallchapterauthorswhodiligentlyfinishedtheirchaptersandprovidedreviewsontime andwithquality,andDr.MingqingChenof Siemenswhoreviewedachapter.
MyspecialthanksgotoProf.JamesDuncanfromYaleUniversity,whowrotetheforewordforthe book.
Further,Iextendmygratitudetothebest-everElsevierpublisherteam,especiallymyeditor,Tim Pitts,editorialprojectmanager,CharlotteKent,andproductionprojectmanager,MelissaReadwho providedeveryhelpwhenneededandkeptthebookproductiononschedule.
IamgratefultoallmypastandcurrentcolleaguesatSiemensCorporateTechnology,including Dr.DorinComaniciu,Dr.BogdanGeorgescu,Dr.ZhuowenTu,Dr.JingdanZhang,Dr.Yefeng Zheng,Dr.MichalSofka,Dr.ShaoleiFeng,Dr.HaibinLing,Dr.NeilBirkbeck,Dr.TimoKohlberger, Dr.DirkBreitenreicher,Dr.DavidLiu,Dr.Jin-HyeongPark,Dr.DijiaWu,Dr.NathanLay,Dr.LeLu, Dr.AdrianBarbu,Dr.DaguangXu,etc.,forthegreatteamworkandstimulatingbrainstorming.Ialso thanksmanySiemenscolleaguesandclinicalcollaboratorsfortheirsupport.
Finally,Ithankmywife,son,andparentsfortheirendlesslove!
S.KevinZhou
Contributors
M.D.Abràmoff
IowaInstituteforBiomedicalImaging,UniversityofIowa,IowaCity,IA,USA
M.A.GonzálezBallester
DepartmentofInformationandCommunicationTechnologies,PompeuFabraUniversity,and CatalanInstitutionforResearchandAdvancedStudies,Barcelona,Spain
A.Barbu
DepartmentofStatistics,FloridaStateUniversity,Tallahassee,FL,USA
N.Birkbeck
Google,MountainView,CA,USA
H.Bogunovi ´ c
IowaInstituteforBiomedicalImaging,UniversityofIowa,IowaCity,IA,USA
A.Carass
DepartmentofElectricalandComputerEngineering,TheJohnsHopkinsUniversity,Baltimore, MD,USA
M.Chen
ComputerEngineeringDepartment,StateUniversityofNewYork,Albany,NY,USA
D.J.Collins
CancerResearchUKCancerImagingCentre,InstituteofCancerResearchandRoyalMarsden Hospital,London,UnitedKingdom
D.Comaniciu
ImagingandComputerVision,SiemensCorporateTechnology,Princeton,NJ,USA
S.Doran
CancerResearchUKCancerImagingCentre,InstituteofCancerResearchandRoyalMarsden Hospital,London,UnitedKingdom
B.Georgescu
ImagingandComputerVision,SiemensCorporateTechnology,Princeton,NJ,USA
B.Glocker
BiomedicalImageAnalysisGroup,ImperialCollegeLondon,London,UnitedKingdom
S.Grbic
ImagingandComputerVision,SiemensCorporateTechnology,Princeton,NJ,USA
J.Feulner
Giesecke&DevrientGmbH,Munich,Germany
D.R.Haynor
DepartmentofRadiology,UniversityofWashington,Seattle,WA,USA
G.Hermosillo
SiemensMedicalSolutionsUSA,Inc.,Malvern,PA,USA
R.Ionasec
SiemensHealthcare,Forchheim,Germany
T.Kanade
RoboticsInstitute,CarnegieMellonUniversity,Pittsburgh,PA,USA
S.Kashyap
IowaInstituteforBiomedicalImaging,UniversityofIowa,IowaCity,IA,USA
B.M.Kelm
SiemensHealthcareGmbH,Forchheim/Erlangen,Germany
M.Kim
DepartmentofRadiologyandBRIC,UniversityofNorthCarolinaatChapelHill,ChapelHill, NC,USA
A.P.Kiraly
SiemensCorporateTechnology,Princeton,NJ,USA
E.Konukoglu
MartinosCenterforBiomedicalImaging,MGH,HarvardMedicalSchool,Boston,MA,USA
N.Lay
SiemensCorporateTechnology,Princeton,NJ,USA
M.O.Leach
CancerResearchUKCancerImagingCentre,InstituteofCancerResearchandRoyalMarsden Hospital,London,UnitedKingdom
C.Ledig
DepartmentofComputing,BiomedicalImageAnalysisGroup,ImperialCollegeLondon,London, UnitedKingdom
D.Liu
SiemensCorporateTechnology,Princeton,NJ,USA
T.Mansi
ImagingandComputerVision,SiemensCorporateTechnology,Princeton,NJ,USA
D.N.Metaxas
DepartmentofComputerScience,RutgersUniversity,Piscataway,NJ,USA
C.L.Novak
SiemensCorporateTechnology,Princeton,NJ,USA
B.L.Odry
SiemensCorporateTechnology,Princeton,NJ,USA
I.Oguz
IowaInstituteforBiomedicalImaging,UniversityofIowa,IowaCity,IA,USA
M.Orton
CancerResearchUKCancerImagingCentre,InstituteofCancerResearchandRoyalMarsden Hospital,London,UnitedKingdom
Z.Peng
SiemensMedicalSolutionsUSA,Inc.,Malvern,PA,USA
J.L.Prince
DepartmentofElectricalandComputerEngineering,TheJohnsHopkinsUniversity,Baltimore, MD,USA
D.Rueckert
DepartmentofComputing,BiomedicalImageAnalysisGroup,ImperialCollegeLondon,London, UnitedKingdom
G.Sanroma
DepartmentofRadiologyandBRIC,UniversityofNorthCarolinaatChapelHill,ChapelHill,NC, USA,andDepartmentofInformationandCommunicationTechnologies,PompeuFabraUniversity, Barcelona,Spain
D.Shen
DepartmentofRadiologyandBRIC,UniversityofNorthCarolinaatChapelHill,ChapelHill, NC,USA
H.-C.Shin
NationalInstitutesofHealth,Bethesda,MD,USA
M.Sofka
SecurityBusinessGroup,CiscoSystems,andDepartmentofComputerScience,CzechTechnical University,Prague,CzechRepublic
M.Sonka
IowaInstituteforBiomedicalImaging,UniversityofIowa,IowaCity,IA,USA
R.M.Summers
ImagingBiomarkersandComputer-AidedDiagnosisLaboratoryandClinicalImageProcessing Service,RadiologyandImagingSciencesDepartment,ClinicalCenter,NationalInstitutesofHealth, Bethesda,MD,USA
I.Voigt
ImagingandComputerVision,SiemensCorporateTechnology,Princeton,NJ,USA
A.Wimmer
SiemensHealthcareGmbH,Forchheim/Erlangen,Germany
G.Wu
DepartmentofRadiologyandBRIC,UniversityofNorthCarolinaatChapelHill,ChapelHill, NC,USA
X.Wu
IowaInstituteforBiomedicalImaging,UniversityofIowa,IowaCity,IA,USA
D.Xu
MedicalImagingTechnologies,SiemensHealthcareTechnologyCenter,Princeton,NJ,USA
D.Yang
Rutgers,NewBrunswick,NJ,USA
J.Yao
ImagingBiomarkersandComputer-AidedDiagnosisLaboratoryandClinicalImageProcessing Service,RadiologyandImagingSciencesDepartment,ClinicalCenter,NationalInstitutesofHealth, Bethesda,MD,USA
Y.Zhan
Computer-AidedDiagnosisandTherapyResearchandDevelopment,SiemensHealthcare,and SiemensMedicalSolutionsUSA,Inc.,Malvern,PA,USA
S.Zhang
DepartmentofComputerScience,UniversityofNorthCarolinaatCharlotte,Charlotte,NC,USA
Y.Zheng
ImagingandComputerVision,SiemensCorporateTechnology,Princeton,NJ,USA
S.KevinZhou
MedicalImagingTechnologies,SiemensHealthcareTechnologyCenter,andSiemensCorporate Technology,Princeton,NJ,USA
X.S.Zhou
SiemensMedicalSolutionsUSA,Inc.,Malvern,PA,USA
S.KevinZhou
1.1 INTRODUCTION
Medicalimagerecognition,segmentation,andparsingareessentialtopicsofmedicalimageanalysis. Medicalimagerecognitionisaboutrecognizingwhich objectsareinsideamedicalimage.Inprinciple, itisnotnecessarytodetectorlocalizetheobjectsforobjectrecognition;butinpractice,oftenit S.KevinZhou(Ed):MedicalImageRecognition,SegmentationandParsing. http://dx.doi.org/10.1016/B978-0-12-802581-9.00001-9 Copyright©2016ElsevierInc.Allrightsreserved.
isbeneficialtoassociateobjectrecognitionwithobjectdetectionorlocalization.Oncetheobject isrecognizedordetectedusing,say,aboundingbox,medicalimagesegmentationfurtherconcerns findingtheexactboundaryoftheobjectinamedicalimage.Whentherearemultipleobjectsinthe images,segmentationofmultipleobjectsbecomesmedicalimageparsingthat,inthemostgeneral form,assignssemanticlabelstopixelsina2Dimageorvoxelsina3Dvolume.Bygroupingthepixels orvoxelswiththesamelabel,segmentationisrealized.
Effectiveandefficientmethodsformedicalimagerecognition,segmentation,andparsingbringa multitudeofimportantclinicalbenefits.Below,wehighlightthebenefitstoimagingscanner,image reading,andadvancedquantificationandmodeling.
• Scanner. Becausethecomputertomography(CT)ormagneticresonanceimaging(MRI)scanneris equippedwithmanyconfiguration possibilitiesorimagingprotocols,itischallengingtoproduce consistentandreproducibleimagesofhighquality acrosspatientsandthisisonlypossibleifthe scanningispersonalizedwithrespecttoapatient.Highscanningthroughputisalsoofinterestfor costsaving.ProtectingpatientsfromunnecessaryradiationfromtheCTscannerisofmajor concern.AnidealdiagnosticCTscanshouldbepersonalizedtoimageonlythetargetregionofa givenpatient,nomore(toreducedose)ornoless (toavoidmissinginformation).Therefore, efficientdetectionoforgansfromascoutimageenablespersonalizedscanningatareduceddose, savesexamtimeandcost,andincreasesconsistencyandreproducibilityoftheexam.
• Imagereadingfordiagnosis,therapy,andsurgeryplanning. Duringimagereading,when searchingfordiseaseinaspecificorganorbodyregion,aradiologistneedstonavigatethevolume totherightlocation.Further,aftercertaindiseaseisfound,heorsheneedstoreportthefinding. Medicalimageparsingenablesstructuredreadingandreportingforastreamlinedworkflow, therebyimprovingimagereadingoutcomeintermsofaccuracy,reproducibility,andefficiency. Finally,inradiationtherapy,interventionprocedures,andorthopedicsurgery,medicalimage parsingisprerequisiteintheplanningphase.
• Advancedquantificationandmodeling. Clinicalmeasurementssuchasorganvolumesare importantforquantitativediseasediagnosis.But itistime-consumingforaphysiciantoidentify thetargetobjectespeciallyin3Dandperformquantitativemeasurementswithouttheaidofan intelligentpostprocessingsoftwaresystem.Automaticimageparsingalsoovercomesthedifficulty inreproducingthemeasurementevenwhenreadingthesameimageforthesecondtime.Finally, with3Dobjectssegmentedas boundaryconditions,moreadvancedmodelingthatsimulates biomechanicalorhemodynamicalprocessesisfeasible.
Theholygrailofamedicalimageparsingsystemisthatitsparsingcomplexitymatchesthatof FoundationalModelofAnatomy(FMA)ontology,a whichisconcernedwiththerepresentationof classesortypesandrelationshipsnecessaryforthesymbolicrepresentationofthephenotypicstructure ofthehumanbodyinaformthatisunderstandabletohumansandisalsonavigable,parsable,and interpretablebymachine-basedsystems.Asoneofthelargestcomputer-basedknowledgesourcesin thebiomedicalsciences,itcontainsapproximately75,000classesandover120,000terms,andover 2.1millionrelationshipinstancesfromover168relationshiptypesthatlinktheFMAclassesinto acoherentsymbolicmodel.AlesscomplexrepresentationisTerminologicaAnatomica,b whichis theinternationalstandardofhumananatomicterminologyforabout7500humangross(macroscopic) anatomicalstructures.
Currentmedicalimagerecognition,segmentation,andparsingmethodsarefarbehindtheholygrail, concerningmostlythefollowingsemanticobjects:
• Anatomicallandmarks. Ananatomicallandmarkisadistinctpointinabodyscanthatcoincides withanatomicalstructures,suchaslivertop,aorticarch,pubissymphysis,tonameafew.
• Majororgans. Examplesofmajororgansincludeliver,lungs,kidneys,spleen,prostate,bladder, rectum,etc.
• Majorbones. Examplesofmajorbonesincluderibs,vertebrae,pelvis,femur,tibia,fibula,skull, mandible,handandfootbones,etc.
• Lesions,nodules,andnodes. Examplesincludeliverandkidneylesions,lungnodules,lymph nodes,etc.
1.2 CHALLENGESANDOPPORTUNITIES
Medicalimagerecognition,segmentation,andparsingconfrontalotofchallengestoobtainresultsthat canbeusedinclinicalapplications.Themainchallengeisthatanatomicalobjectsexhibit significant shapeandappearancevariations causedbyamultitudeoffactors:
• Sensornoise/artifact. Asinanysensor,medicalequipmentgeneratesnoise/artifactinherenttoits ownphysicalsensorandimageformationprocess.Theextentoftheartifactdependsonimage modalityandimagingconfiguration.Forexample,whilehigh-doseCTproducesimageswith fewerartifacts,low-doseCTisquitenoisy.Also,metalobjects(suchasimplants)cangeneratea lotofartifactsinCT.InMRIscans,artifactsaregeneratedduetoinhomogeneousmagneticfield, gradientnonlinearity,etc.
• Patientdifferenceandmotion. Differentpatientsexhibitdifferentbuildforms:fatorslim,tallor short,adultorchild,etc.Asaresult,theanatomicalstructuresalsoexhibitdifferentshapes.Also, patientsundergomotionsfromrespiration,cardiaccycle,bloodandcerebrospinalfluidflow, peristalsisandswallowing,andvoluntarymovement,allcontributingtothecreationofdifferent images,causinganatomicalshapedeformation.
• Pathology,surgery,andcontrastagents. Pathologycangiverisetohighlydeformedanatomical structuresorevenmissingoneswithvaryingappearancesandshapes.Thismakesstatistical modelingverydifficult.Tobetterunderstandthepathologicalconditions,contrastagentsare utilizedtobettervisualizetheanatomicalmorphology.Imageappearancesunderdifferentcontrast phasesaredifferent.Finally,asurgicalresectioncompletelychangestheshapeandimage appearanceofanatomicalobject(s)inanunexpectedmanner.
• Partialscanandfieldofview.DoseradiationisamajorconcerninCT.Inanefforttominimizethe doseradiation,onlythenecessarypartofthehumanisimaged.Thiscreatespartialscansand narrowfieldofview,inwhichtheanatomicalcontextishighlyweakenedortotallygone.Asa result,thelandmarksororgansaremissingorpartiallyvisible.InMRI,thescanrangeisoften minimizedforfastacquisition.
• Softtissue.Anatomicalstructuressuchasinternalorgansaresofttissueswithsimilarproperties. They(suchasliverandkidney)mighteven toucheachother,formingaveryweakboundary betweenthem.But,itisamustthatthesegmentedorgansbenonoverlapping.
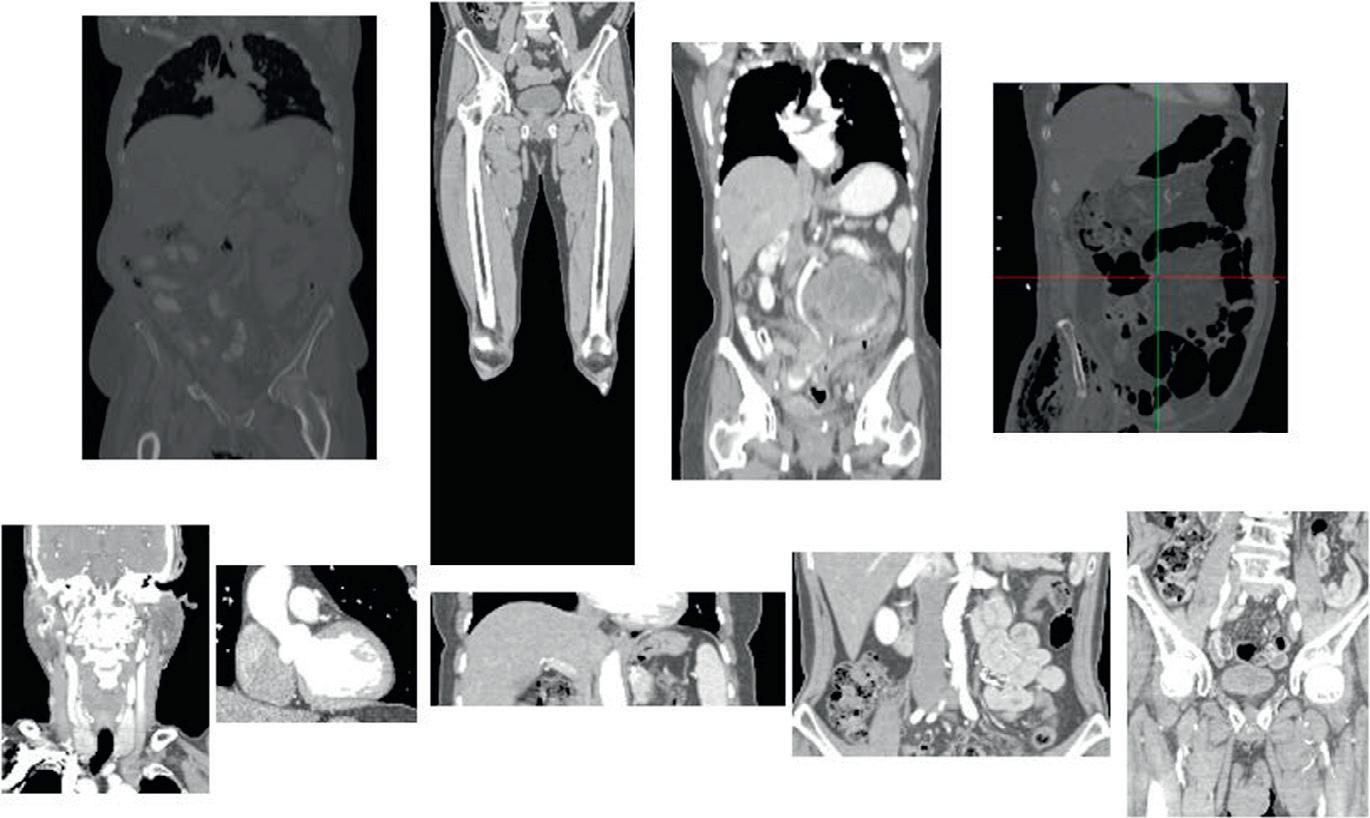
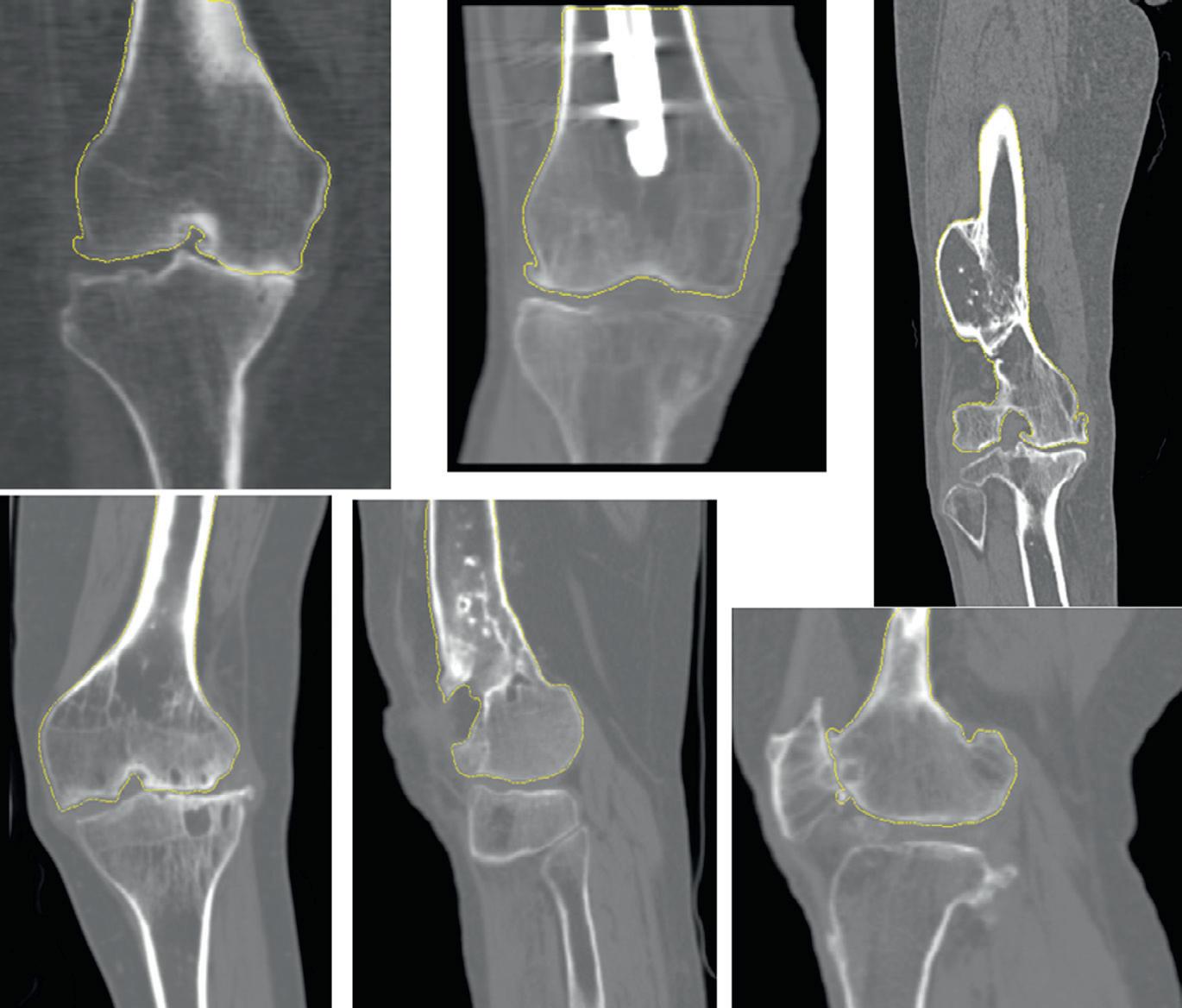
Figure1.1(a)shows3DCTscanswithdifferentsourcesofappearancevariationand Figure1.1(b) displaysCTexamplesofvariouspathologiesandconditionsassociatedwithakneejoint.
Anotherchallengeliesinstringent accuracy,robustness,andspeed requirementsarisingfromreal clinicalapplications.Imagereadinganddiagnosisallowalmostnoroomformistakes.Despitethehigh accuracyandrobustnessrequirements,thedemandforspeedyprocessingdoesnotdiminish.Aspeedy workflowiscrucialtoanyradiologylabthatstrivesforhighthroughput.Fewradiologistsorphysicians canwaitforhoursorevenminutestoobtaintheanalysisresults.
Tobuildeffectiveandefficientalgorithmstotacklethesechallenges,onehastoexploitthe opportunitieswithleverage.Therearetwomainopportunities:
• Largedatabase. Thereisadelugeofmedicalscans.TakeCTscans,forexample.In2005, approximately57millionindividualsintheUSAreceivedCTexams.By2012,thenumberof annualCTexamsrosetoover85million.c Thehypothesisthatalargedatabaseexhibitsthe appearancevariationscommonlyfoundinpatientsisstatisticallysignificant.
• Anatomicalcontext. Unlikenaturalsceneimages,medical imagesmanifeststrongcontextual information,suchasalimitednumberofanatomicalobjects(sayonlyoneleftventricle), constrainedandstructuredbackground,therelationshipbetweendifferentanatomies,strongprior informationabouttheposeparameter,etc.
Inlightoftheseopportunities,statisticalmachinelearningmethodsthatexploitsuchcontextual informationexemplifiedbyalargenumberofdatasetsarehighlydesired.Thiswholebookis dedicatedtoapproachesbasedonmachinelearning.Italsocoversapproachesthatcopewithmultiple objects.
1.3 ROUGH-TO-EXACTOBJECTREPRESENTATION
Anyintelligentsystemstartsfromasensibleknowledgerepresentation(KR).Themostfundamental rolethataKRplays(Davisetal., 1993)isthat“itisasurrogate,asubstituteforthethingitself.This leadstotheso-calledfidelityquestion:howcloseisthesurrogatetotherealthing?Theonlycompletely accuraterepresentationofanobjectistheobjectitself.Allotherrepresentationsareinaccurate;they inevitablycontainsimplifyingassumptionsandpossiblyartifacts.”
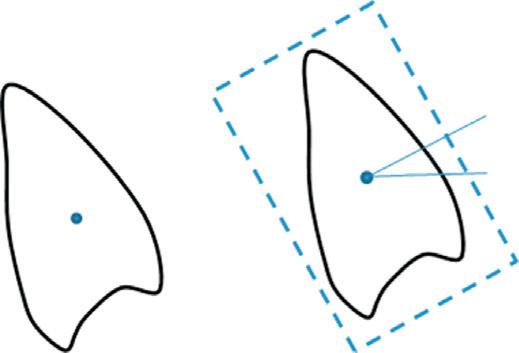
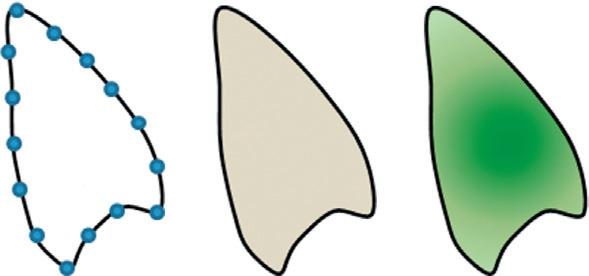
Intheliterature,therearemanyrepresentationsthatapproximateamedicalobjectoranatomical structureusingdifferentsimplifyingassumptions. Figure1.2 showsavarietyofshaperepresentations commonlyusedintheliterature.d
• Rigidrepresentation. Thesimplestrepresentationistotranslateatemplatetotheobjectcenter t =[tx , ty , tz ] asshownin Figure1.2(a).Inotherwords,onlytheobjectcenterisconsidered.A completerigidrepresentationin Figure1.2(b)consistsoftranslation,rotation,andscale parameters θ =[t, r, s].Whenthescaleparameterisisotropic,thisreducestoasimilarity transformation.Anextensionofrigidrepresentationisaffinerepresentation.
• Free-formrepresentation. Commonfree-formrepresentations,shownin Figure1.2(c-e),include point-basedpresentation(2Dcurve S or3Dmesh M),maskfunction φ (x, y, z),levelsetfunction φ (x, y, z),etc.
(a)ExampleofCTimageswithdifferentbodyregions,severepathologies,contrastagents,weakcontrast,etc.
(b)ExampleofCTimageswithvariouskneepathologiesandconditions.Fromlefttoright,toptobottom:Touch betweenfemurandtibia,metallicimplantinsidefemur,femurwithmajordefects,osteoporosis,osteoporosis withminorfemurdefects,andtouchbetweenfemurandpatella.
(a)
(b)
FIGURE1.1
FIGURE1.2
Agraphicalillustrationofdifferentshaperepresentationsusing2Dshapeasanexample.(a)Rigid representation:translationonly t =[tx , ty ].(b)Rigidrepresentation: θ =[tx , ty , r , sx , sy ].(c)Free-form representation: S =[x1 , y1 , , xn , yn ].(d)Free-formrepresentation:a2Dbinarymaskfunction φ (x , y ).
(e)Free-formrepresentation:a2Dreal-valuedlevelsetfunction φ (x , y )(onlytheinteriorpartisdisplayed).
(f)Low-dimensionalparametricrepresentation:PCAprojection S = S0 + M m =1 λm Sm
• Low-dimensionalparametricrepresentation. Theso-calledstatisticalshapemodel(SSM) (HeimannandMeinzer, 2009)shownin Figure1.2(f)isacommonlow-dimensionalparametric representationbasedonprincipalcomponentanalysis(PCA)ofapoint-basedfree-formshape.
Otherlow-dimensionalparametricrepresentationsincludeM-rep(Pizeretal., 2003),spherical harmonics(SPHARM)(Shenetal., 2009),sphericalwavelets(Nainetal., 2006),etc.
AKRalsoisamediumforpragmaticallyefficientcomputation(Davisetal., 1993).Therefore, itisbeneficialtoadoptahierarchical, rough-to-exact representationthatgraduallyapproximatesthe objectitselfwithincreasingprecision,whichalsomakescomputationalreasoningmoreamenableand efficientasshownlater.
Acommonrough-to-exact3Dobjectrepresentation(Zhengetal., 2008; Zhou, 2010; Kohlberger etal., 2011; Wuetal., 2014)consistsofarigidpartfullyspecifiedbytranslation,rotation,andscale
parameters θ =[t, r, s],alow-dimensionalparametricpartsuchasfromthePCAshapespacespecified bythetopPCAcoefficients λ =[λ1:m ] andafree-formnonrigidpartsuchasa3Dshape S ,a3Dmesh M,ora3Dmaskorlevelsetfunction φ .
ThePCAshapespacecharacterizesashapebyalinearprojection:
where S0 isthemeanshapeand Sm isthe mthtopeigenshape.ThisPCAshapemodelingformsthe basisofthefamousactiveshapemodel(ASM)(Cootesetal., 1995).Inthishierarchicalrepresentation, thefree-formpartcanberough-to-exacttoo.Fora3Dmesh,themeshvertexdensitycanbeacontrol parameter,fromsparsetodense.Foralevelsetfunction,itdependsontheimageresolution,from coarsetofine.
1.4 SIMPLE-TO-COMPLEXPROBABILISTICMODELING
Tohandleasingleobject O froma3Dvolume V,theposteriordistribution P(O|V) offersthecomplete characterizationoftheobject O giventhevolume V.Once P(O|V) isknown,inferringtheobjectcanbe donebytakingtheconditionalmean,whichistheminimummeansquareerrorestimator,orconditional mode,whichisthemaximumaposterioriestimator,orafunctionoftheposterior.Bythesametoken, theposteriordistribution P(O1:n |V) completelycharacterizesthemultipleobjects O1:n inastatistical sense.
1.4.1CHAINRULE
Whentherough-to-exactrepresentationforasingleobject O isused,jointmodelingofthefullobjectis challengingandoftenlesseffective.Totacklethis challenge,acommonstrategyistoperformsimpleto-complexmodelingbybreakinga complextaskintoafewsimpletasks.Foreachsimpletask,effective modelingismorefeasible.
Onewayistoutilizethechainrulethatpermitsthecalculationofajointprobabilityusing conditionalprobabilities.
Thisbreakstheoveralltaskintothreesimplertasks.Thefirsttaskistoinfertherigidobject,also knownasobjectdetectionorrecognition,using P(θ |V);thesecondtaskistoinferboththerigidand low-dimensionalshapemodelparametersusing P(λ|V, θ );andthelastisfullobjectinferenceusing P(S |V, θ , λ),solvingthesegmentationproblem.
Infact,forasingleobject O,effectivemodelingofits3Dposepartalone θ =[t, r, s] isdifficult. Thesimple-to-complexmodelingisappliedheretoo.
Marginalspacelearning(MSL)(Zhengetal., 2008)leveragessuchastrategy. Whendealingwithmultipleobjects O1:n ,thechainrulealsoapplies.
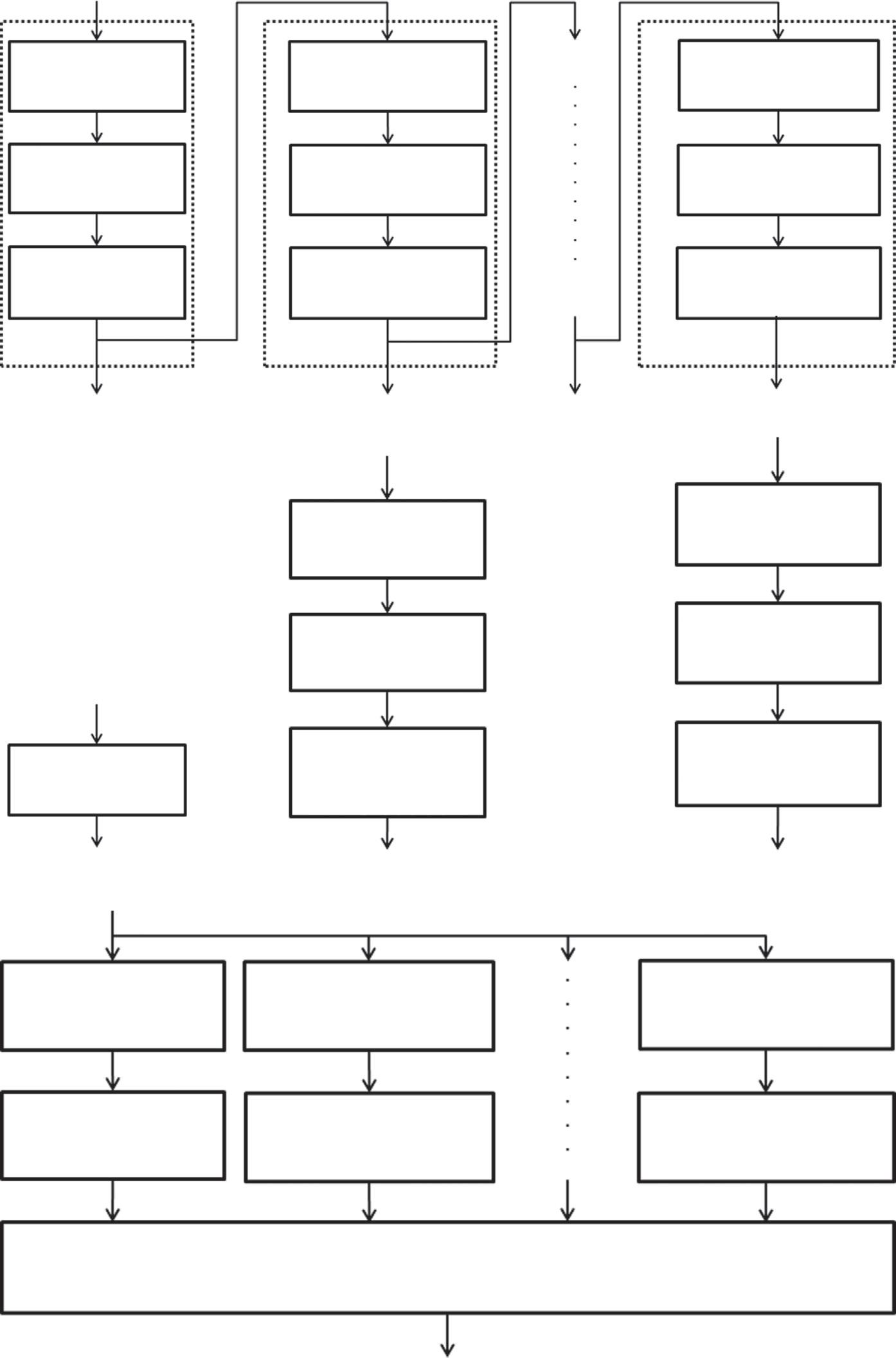
InEq.(1.5),eachconditionalprobabilityspellsasimpler task,whichcanbefurtherdecomposedusing Eqs.(1.3)and(1.4).IntegratingEqs.(1.3)–(1.5)endowsageneral-purposecomputationalpipelineas shownin Figure1.3(a),inwhichaseriesofsimpletasksareconnected.
1.4.2BAYES’RULEANDTHEEQUIVALENCEOFPROBABILISTICMODELING ANDENERGY-BASEDMETHOD
AccordingtotheBayes’rule,theposteriorprobability P(O|V) isproportionaltotheproductofthe likelihood P(V|O) andtheprior P(O),
Energy-basedmethods(MumfordandShah, 1989; ChanandVese, 2001)oftenminimizeanenergy function E (O; V),consistingoftwoparts.Thefirstenergyfunction E1 (O; V) relatestheimage V with theobject O andthesecondenergyfunction E2 (O) representsthepriorbeliefabouttheobject.
Byletting
thentheprobabilisticmodelisequivalenttotheenergy-basedmethod.Inthepreviousdiscussion,we usethewholeobject O forillustration,butthederivationsholdevenwhenapartialobjectrepresentation isused.
WhenthisBayes’ruleisintegratedintothechainrule,completemodelingofobjectappearancesand priorbeliefsabouttheobjectatdifferentrepresentationlevelsandusingdifferentmodelsisprovided.
1.4.3PRACTICALMEDICALIMAGERECOGNITION,SEGMENTATION,ANDPARSING ALGORITHMS
Ingeneral,practicalalgorithmsformedicalimagerecognition,segmentation,andparsingarespecial examplesofthiscomputationalpipeline.They,however,differdependingontheirspecializationinthe followingtwoaspects:
• Thechangestothecomputationalarchitecture. Dependingonindependenceassumptionsthey makeortherepresentationtheychoose,practicalalgorithmsmodifyorsimplifythearchitecture accordingly.Forexample,ifdetectingonlyoneobjectisconcerned, thepipelinereducestotheone shownin Figure1.3(b). Figure1.3(c)showstheMSLpipeline(Zhengetal., 2008)for3Drigid objectdetection.In Figure1.3(d),acompletepipelineforsegmentingasingleobjectispresented, goingfromdetectingorrecognizingtherigidpart,todeformableshapesegmentation,tothe freeformshapesegmentation. Figure1.3(e)presentsanarchitecturethatdealswithmultiple
Rigid object detection/recognition using P (q1|V)
Parameterized object segmentation using P(l1|V, q1)
Freeform object segmentation using P (S1|V, q1,l1)
FIGURE1.3
Rigid object detection/recognition using P(q |V)
Rigid object detection/recognition using P (q2|V, O1)
Parameterized object segmentation using P (l2|V, q2, O1)
Freeform object segmentation using P (S2|V, q2, l2, O1)
Rigid object detection/recognition using P (q n|V, O1:n–1)
Parameterized object segmentation using P (l2|V, q n, O1:n–1)
Freeform object segmentation using P (Sn|V, q n, l n, O1:n–1)
Object translation detection using P(t |V )
Object translation and rotation detection using P (r |V, t )
Object translation, rotation, and scale detection using P (s |V, t, r )
Rigid object detection/recognition using P (q1|V )
Rigid object detection/recognition using P (q2|V )
Parameterized object segmentation using P (l1|V, q1)
Parameterized object segmentation using P (l2|V, q2)
Rigid object detection/recognition using P (q |V )
Parameterized object segmentation using P (l|V,q )
Freeform object segmentation using P (S|V, q, l) q n, l
Rigid object detection/recognition using P (q n|V )
Parameterized object segmentation using P (λn|V, q n)
Freeform joint object segmentation using P (S1:N|V, q1:n, l1:n)
(a)Ageneral-purposecomputationalpipelineformedicalimagerecognition,segmentation,andparsingbased onrough-to-exactobjectrepresentationandsimple-to-complexmodeling.(b-e)Specialrealizationsofthe computationalpipeline.
objects,whichisusedin Kohlbergeretal. (2011), Luetal. (2012),and Wuetal. (2014).Here,the conditionaldependencyamongdifferentobjectsisassumedfortherigidandlow-dimensional parametricparts;henceeachobjectisprocessedindependently.Finally,thejointfreeform segmentationisappliedforsegmentingmultipleshapestogether.
• Themodelingchoicesoftheconditional probabilities. Goodalgorithmperformanceneeds effectivemodelingoftheconditionalprobabilities.Formedical imagerecognitionordetection, machinelearningmethodsareprevalenttoleverageanatomiccontextembeddedinthemedical images. Section1.5 definestheconceptofanatomiccontextandbrieflyreviewsseveralmachine learningmethodsthatmodeltheanatomiccontext.Afterobjectdetection,objectsegmentation follows. Section1.6 listsafewclassicalimagesegmentationmethods,eachhavingitsown modelingchoicebasedonitsparticularobjectrepresentation.Throughoutthewholebook,each bookchapterwilldiscussitsownchoicesofmodeling,eitherfromageneraltheoreticperspective orinaparticularapplicationsetting.
1.5 MEDICALIMAGERECOGNITIONUSINGMACHINELEARNINGMETHODS
1.5.1OBJECTDETECTIONANDCONTEXT
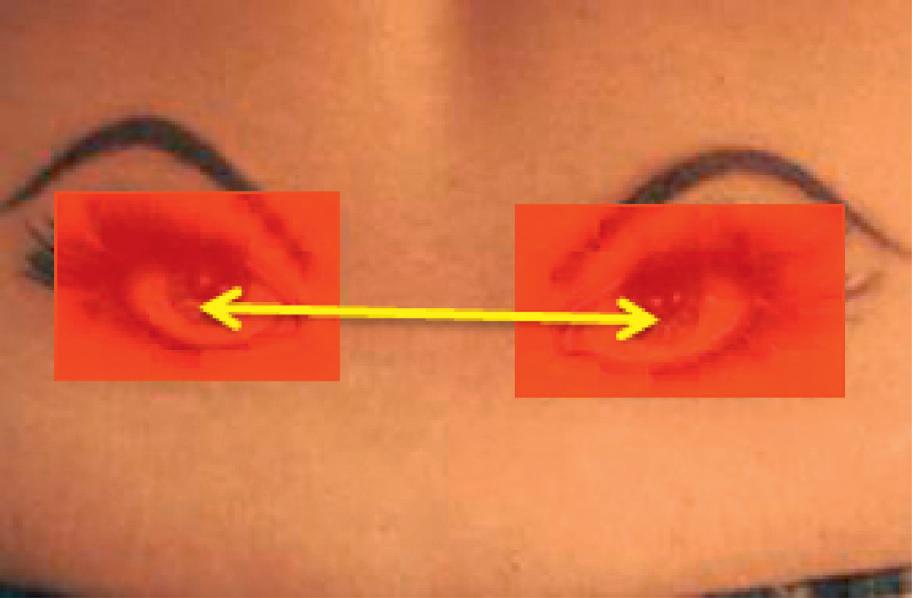
Considerthetaskofdetectinghumaneyesfromthethreeimagesin Figure1.4.Todetectthehuman eye(s)in Figure1.4(a)inwhichalldifferentobjectsarejuxtaposedrandomly,oneislikelytoscrutinize theimagepixelsrowbyrow,columnbycolumntilltheeyeislocated.However,todetecttheeye(s) in Figure1.4(c)inwhichaperfecthumanfaceispresented,itiseffortlessbecausetheimageisso structuredorfullofcontext.Amedicalimageisthekindofimagewithcontextualinformationwith respecttoanatomies.Suchcontextisreferredtoas anatomicalcontext.Todetectthetwoeyesin Figure 1.4(b),therelationshipbetweenthem canbeuseful.Once,say,thelefteyeisdetected,thedetectionof therighteyebecomeslesscomplicated.
Asshownin Figure1.4,thecontextcanberoughlycategorizedintothreetypes,namely unitaryor local, pairwiseorhigher-order,and holisticorglobal context.
•The unitaryorlocalcontext referstothelocalregularitysurroundingasingleobject.
•The pairwiseorhigher-ordercontext referstothejointregularitiesbetweentwoobjectsoramong multipleobjects.
•The holisticorglobalcontext goesbeyondtherelationshipsamongacohortofobjectsandrefers tothewholerelationshipbetweenallpixels/voxelsandtheobjects:inotherwords,regardingthe imageasawhole.
Differentdetectionmethodsbasicallyoperatewithdifferenttrade-offsbetweenofflinemodel learningcomplexityandonlinecomputationalcomplexity,dependingon howtoleveragewhich context(s).Forexample,abinaryclassifierthatseparatestheobjectinstancesfromnonobjectinstances islearnedtomodelthelocalcontext.Givenatestimagelike Figure1.4(a),exhaustivescanningofthe imageusingthelearnedclassifierisneededtolocalizetheobject(eye).Toleveragetheglobalcontext, aregressionfunctioncanbelearnedtopredicttheobjectlocationdirectlyfromanypixel.Givenatest imagelike Figure1.4(c),theregressionfunctionisusedforafewsparselysampledpixellocationsto reachaconsensuspredictiondecisionabouttheobject location.Learningabinaryclassifieriseasier
FIGURE1.4
Threetypesofcontext:(a)unitaryorlocalcontext;(b)pairwiseorhigher-ordercontext;and(c)holistic orglobalcontext.
thanaregressionfunction,butexhaustivescanningismorecomputationallyintensivethantestinga fewlocations.Below,wereviewseveralmodernmachinelearningmethodsforbinaryclassification, multi-classclassification,andregression.Thesubsequentbookchapterspresentdifferentrecognition methodsthatemploymachinelearning.
1.5.2MACHINELEARNINGMETHODS
Statisticalmachinelearningmodelsthestatisticaldependenceofanunobservedvariable y onan observedvariable x viatheposteriorprobabilitydistribution P(y|x).Suchadistributioncanbeusedto predicttheunobservedvariable y.Modeling P(y|x) canbedoneintwoways,namelydiscriminative learningandgenerativelearning.Whilegenerativelearningmodels P(y|x) indirectlyviathejoint
(a)
(b)
(c)
distribution P(x, y),discriminativelearninginsteaddirectlymodelstheposterior.Discriminativemodels areeffectiveforsupervisedlearningtaskssuchasclassificationandregressionthatdonotnecessarily requirethejointdistribution.
1.5.2.1Classification
Thegoalofbinaryclassificationistolearnafunction F (x) thatminimizesthemisclassification probability P{yF (x) < 0},where y istheclasslabelwith +1forpositiveand 1fornegative.Thereare manyinfluentialbinaryclassificationmethodssuchaskernelmethods( Hofmannetal., 2008),ensemble methods(Polikar, 2006),anddeeplearningmethods(Bengio, 2009).Supportvectormachine(SVM) (Vapnik, 1999)isaclassicalkernelmethod.Ensemblemethodsincludeboosting(FreundandSchapire, 1997; Friedmanetal., 2000)andrandomforest(RF)(Breiman, 2001).Deeplearningmethodsarebased onartificialneuralnetworks(ANNs)(Bishopandetal., 1995).
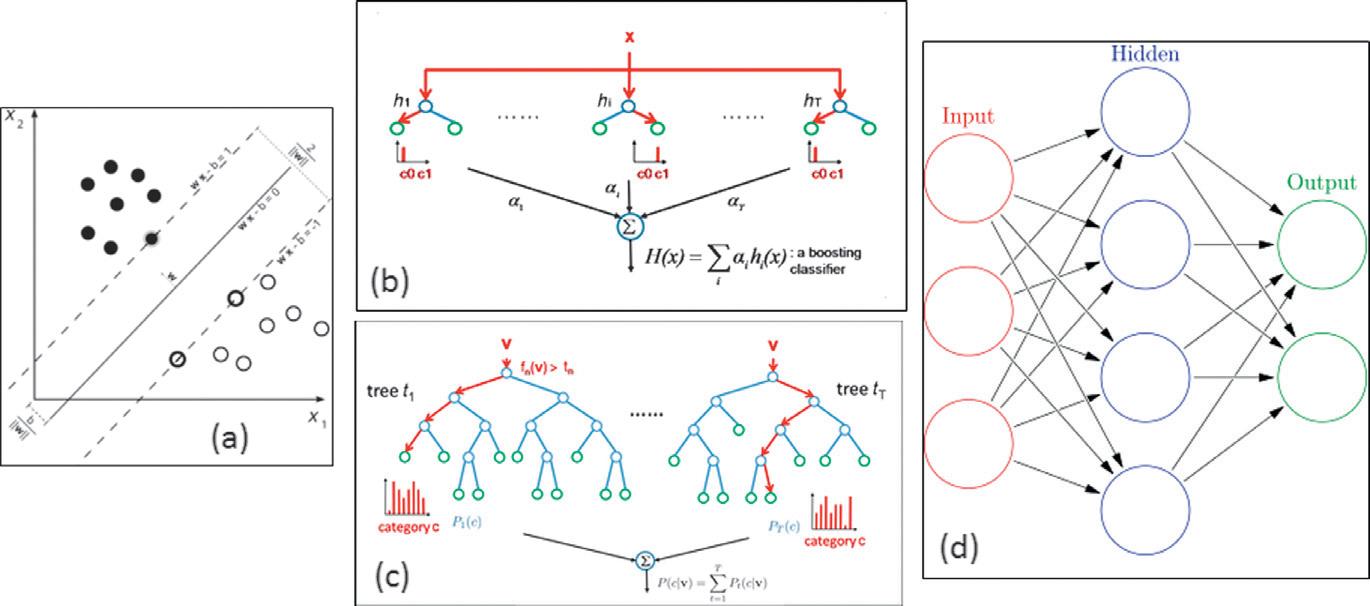
SVMseeksaseparatinghyperplanewithamaximummargin.Asshownin Figure1.5(a),the hyperplaneisdefinedas w · x + b,where x istheinputvector, w istheslopevector,“·”meansthe dotproduct,and b istheintercept.Themax-marginplaneisobtainedbysolvingthefollowingtask:
Thesolutionis F (x) = j αj yj (xj · x) + b,where xj saresupportvectors.Oftenthenumberofsupport vectorsismuchsmallerthanthatofinputtrainingdata.Thekerneltrick K (xj , x) = φ (xi ) · φ (x) iswidely usedtomodeldatanonlinearity,hencethename kernelmethod. Anensemblemethodcombinesmultiplelearnersintoacommitteeforfinaldecision.Inboosting (FreundandSchapire, 1997; Friedmanetal., 2000),insteadofminimizing themisclassification probability,itminimizesitsupperbound E {exp(yF (x))} as
FIGURE1.5
Binaryclassificationmethods:(a)supportvectormachine,(b)AdaBoosting,(c)randomforest,and(d)neural network.ImagecourtesyofWikifor(a,d)andofICCV2009tutorialentitled“Boostingandrandomforest”for (b,c).
Theclassificationfunction F (x) inboostingtakesanadditiveformasin Figure1.5(b):
where Fn (x) isastronglearnerthatiswellcorrelatedwiththetrueclassificationand hm (x) isaweak learnerthatisonlyslightlycorrelatedwiththetrueclassification(betterthanrandomguessing).This minimizationisdoneiteratively.Atthe nthiteration,itselectstheminimizingweaklearner hn (x) and thenadjuststheweightsfortrainingexamples,weighingmoreonmisclassifiedexamples.Theposterior P(+1|x) isapproximatedas
TheRF(Breiman, 2001)classifierconsistsofacollectionofbinaryclassifiersasin Figure1.5(c), eachbeingadecisiontreecastingaunitvoteforthemostpopularclasslabel.Tolearna“random” decisiontree,eitherthetrainingexamplesforeachdecisiontreeareindependent,identicallydistributed (i.i.d.)sampledfromthefulltrainingsetorthefeaturesusedinthetreenodesarei.i.d.sampledfrom thefullfeaturesetorboth.Itisshownin Breiman (2001)thattheRFaccuracyiscomparableto boostingwiththeaddedbenefitsofbeingrelativelyrobusttooutliersandnoiseandamenabletoparallel implementation.
Whentheseensemblemethodsareappliedtoimageapplications,theweaklearnersinboostingare associatedwithimagefeatures(ViolaandJones, 2001; Tu, 2005)andthedecisiontreeinRF(Criminisi etal., 2009)usesanimagefeatureinatreenode.Oftenahighlyredundantfeaturepoolisformedto coverlargeappearancevariationintheobject.Learningtheweaklearnerorthedecisiontreehence becomesa featureselection process.
AnANNconsistsofaninterconnectedgroupofnodesasshownin Figure1.5(d),eachcircular noderepresentinganeuronandanarrowrepresentingaconnectionfromtheoutputofoneneuronto theinputofanother.AdeeplearningmethodconcernsanANNwithmultiplehiddenlayers.Often aneurontakesthefollowingform σ (w · x + b),where x istheinputvectortotheneuron, y isthe outputoftheneuron, w istheweightvector, b isthebiasterm,and σ isanonlinearfunctionsuchasa sigmoidfunction.ThefinaloutputfromtheANN(saywithonehiddenlayerandonenodeintheoutput layer)is
where wh istheweightvectorfortheinputvectortothenode h inthehiddenlayer, αh istheweight coefficientfromthehiddennode h totheoutputnode.Typically,theweightsforallneuronsarelearned
usingstochasticgradientdescent.Sincecombiningtheinputusingweightedlinearcoefficientsamounts tofeaturecomputation,ANNtrainingperformsfeaturelearning.
Thegoalofmulti-classclassificationistoclassifyaninput x intooneof J > 2classlabels. TheLogitBoostalgorithm(Friedmanetal., 2000)fitsanadditivesymmetriclogisticmodelvia themaximum-likelihoodprinciple.Thisfittingproceedsiteratively byselectingweaklearnersand combiningthemintoastrongclassifier.TheoutputoftheLogitBoostalgorithmisasetof J response functions {F j (x); j = 1, ... , J },whereeach F j (x) isalinearcombinationofasubsetofweaklearners:
where f j m (x) isaweaklearnerand n isthenumberofweaklearners.“LogitBoost”providesanatural waytocalculatetheposteriordistributionofclasslabel:
TousetheLogitBoostforimageclassification,theweakclassifiersareassociatedwithimagefeatures. Referto Zhouetal. (2006)formoredetails.
1.5.2.2Regression
Regression(Hastieetal., 2001)findsthesolutiontothefollowingminimizingproblem:
where {(xn , yn )}N n=1 aretrainingexamples, L(◦, ◦) isthelossfunctionthatpenalizesthedeviationofthe regressoroutput g(x) fromthetrueoutput y, λ> 0isthe regularizationcoefficient thatcontrolsthe degreeofregularization,and K (g) istheregularizationtermthatcombatsoverfitting.Regularization oftenimposesacertainsmoothnessconstraintontheoutputfunctionorreflectssomepriorbeliefabout theoutput.Therearemanyregressionapproaches(Hastieetal., 2001)intheliterature;herewebriefly reviewboostingregressionandregressionforest,whichareoftenusedforobjectdetection.
Asinanyboostingprocedure(FreundandSchapire, 1997; Friedmanetal., 2000),boosting regressionassumesthattheregressionoutputfunction g(x) takesanadditiveform: gt (x) = gt 1 (x) + ht (x).Boostingisaniterativealgorithmthatleveragestheadditivenatureof g(x).Atthe tthiteration, onemoreweakfunction ht (x) isaddedtothetargetfunction g(x) tomaximallyreducethecostfunction asfollows:
1
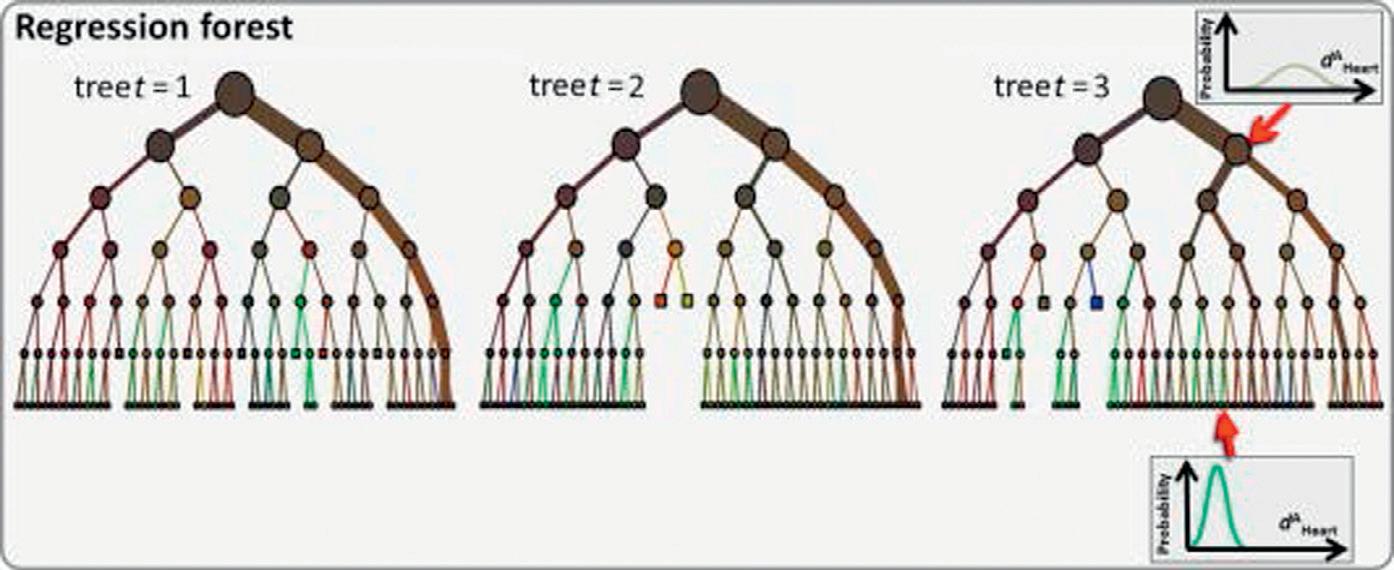
FIGURE1.6
Graphicalillustrationsofregressionforestproposedin Criminisietal. (2013).Reprintedwithpermission, ©2013Elsevier. where rt (xn ) = yn gt 1 (xn ) istheresidualandthe L2 lossfunctionisused.ToderiveEq.(1.16),the regularizationterm K (g) ischosentotakeanadditiveform: K (gt ) = K ( t i=1 hi ) = t i=1 Ki (hi ).In Zhou (2010),theridgeregressionprinciple(alsoknownasTikhonovregularization)isincorporated intoaboostingframeworktopenalizeoverlycomplexmodelsandtheimagefeaturesareconnected withweaklearners.Thisleadstotheimage-basedboostingridgeregressionframework.
SimilartoRFforclassification,regressionforest(Breiman, 2001; Criminisietal., 2013)isa collectionofregressiontreesthatjointlypredictcontinuousoutput(s).Tolearna“random”regression tree,eitherthetrainingexamplesforeachregressiontreearei.i.d.sampledfromthefulltrainingsetor thefeaturesusedinthetreenodesarei.i.d.sampledfromthefullfeaturesetorboth.Trainingthenode ofaregressiontreeistypicallydonebymaximizinganinformationgainmeasure,variancereduction, oroptimizingothersplittingcriteria.Unliketheboostingregressionthatisablackboxtopredictthe output,theregressionforestcarriesaprobabilisticnaturethatprovidesaconfidencemeasurewiththe predictedoutput. Figure1.6 showsagraphicalillustrationofregressionforest.
1.6 MEDICALIMAGESEGMENTATIONMETHODS
Assumingtheobjectisrecognizedorlocalized,thenextstepistoperformpreciseimagesegmentation againusingthelocalcontextbetweentheshapeandappearance.Medicalimagesegmentationisabout partitioningamedicalimageintomultiplesegmentsorregions,eachsegmentationorregioncomposed ofasetofpixelsorvoxels.Often,segmentscorrespondtosemanticallymeaningfulanatomicalobjects. Herewereviewafewimagesegmentationmethodsforsegmentingasingleobject.Theremaining