MeanCurvatureFlow:ProceedingsoftheJohnH. BarrettMemorialLecturesheldattheUniversity ofTennessee,Knoxville,May29–June1,2018 TheodoraBourni(Editor)
https://ebookmass.com/product/mean-curvature-flowproceedings-of-the-john-h-barrett-memorial-lectures-held-atthe-university-of-tennessee-knoxvillemay-29-june-1-2018-theodora-bourni-editor/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
A3N2M: Approximation, Applications, and Analysis of Nonlocal, Nonlinear Models: Proceedings of the 50th John H. Barrett Memorial Lectures Tadele Mengesha
https://ebookmass.com/product/a3n2m-approximation-applications-andanalysis-of-nonlocal-nonlinear-models-proceedings-of-the-50th-john-hbarrett-memorial-lectures-tadele-mengesha/ ebookmass.com
Trapped: Brides of the Kindred Book 29 Faith Anderson
https://ebookmass.com/product/trapped-brides-of-the-kindredbook-29-faith-anderson/
ebookmass.com
Patristic Theology: The University Lectures of Fr. John Romanides Romanides
https://ebookmass.com/product/patristic-theology-the-universitylectures-of-fr-john-romanides-romanides/
ebookmass.com
Work, Retire, Repeat: The Uncertainty of Retirement in the New Economy Ghilarducci
https://ebookmass.com/product/work-retire-repeat-the-uncertainty-ofretirement-in-the-new-economy-ghilarducci/
ebookmass.com
Our Forever Place Maren Hill
https://ebookmass.com/product/our-forever-place-maren-hill/
ebookmass.com
Human Resource Management in the Pornography Industry: Business Practices in a Stigmatized Trade 1st ed. Edition
David M. Kopp
https://ebookmass.com/product/human-resource-management-in-thepornography-industry-business-practices-in-a-stigmatized-trade-1st-ededition-david-m-kopp/ ebookmass.com
Bratva Beauty (The Ivankov Brotherhood Book 4) Sabine Barclay & Celeste Barclay
https://ebookmass.com/product/bratva-beauty-the-ivankov-brotherhoodbook-4-sabine-barclay-celeste-barclay/
ebookmass.com
Careless (Bastards of Grove Hill Book 2) Zepphora .
https://ebookmass.com/product/careless-bastards-of-grove-hillbook-2-zepphora-4/
ebookmass.com
Wicked Heiress (Princes of Devil's Creek Book 5) Jillian Frost
https://ebookmass.com/product/wicked-heiress-princes-of-devils-creekbook-5-jillian-frost/
ebookmass.com
Pentecostal Politics in a Secular World: The Life and Leadership of Lewi Pethrus 1st ed. Edition Joel Halldorf
https://ebookmass.com/product/pentecostal-politics-in-a-secular-worldthe-life-and-leadership-of-lewi-pethrus-1st-ed-edition-joel-halldorf/
ebookmass.com
Theodora Bourni, Mat Langford (Eds.)
Mean Curvature Flow
De Gruyter Proceedings in Mathematics Mean Curvature Flow Proceedings of the John H. Barrett Memorial Lectures held at the University of Tennessee, Knoxville, May 29 – June 1, 2018
Edited by Theodora Bourni
Mat Langford
Editors
Prof. Dr. Theodora Bourni
University of Tennessee Department of Mathematics
1403 Circle Drive
Knoxville TN 37996-1320
USA
Prof. Dr. Mat Langford
University of Tennessee Department of Mathematics 1403 Circle Drive
Knoxville TN 37996-1320
USA
ISBN 978-3-11-061818-1
e-ISBN (PDF) 978-3-11-061836-5
e-ISBN (EPUB) 978-3-11-061822-8
Library of Congress Control Number: 2020933595
Bibliographic information published by the Deutsche Nationalbibliothek The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.
© 2020 Walter de Gruyter GmbH, Berlin/Boston Printing and binding: CPI books GmbH, Leck www.degruyter.com
Foreword TheJohnBarrettMemorialLectureswereestablishedin1970asatributetoDr.John H.Barrett,anexpertonoscillationanddisconjugacytheoryoflinearordinarydifferentialequationsandinfluentialMathematicsDepartmentHeadattheUniversity ofTennessee.OriginallydedicatedtotopicsinBarrett’sfield,ordinarydifferential equations,thelectureshavebeenheldannuallysince1970.Sincethe1980’s,however, thelecturethemeshavetraversedthemathematicallandscape—frommathematics educationthroughcomputationalandappliedmathematics,discretemathematicsand stochasticstogeneralrelativity,nonlinearpartialdifferentialequationsandtopological quantumfieldtheory.
Duringtheirhistory,theBarrettLectureshavebeengracedbyasuccessionof highlydistinguishedmathematicians,withlecturesgivenbyGarrettBirkoff(1972);Sir MichaelAtiyah,IsadoreSingerandKarenUhlenbeck(1989);SirJohnBallandLawrence C.Evans(1991);SergiuKlainerman,Fang-HuaLinandMichaelStruwe(1995);Alice Chang,TobiasColdingandKarstenGrove(2000);JohnBaez(2006);RichardSchoen, RobertWaldandIgorRodnianski(2011);andFernandoMarquesandAndréNeves (2013)tonameafew.
Inrecentyears,geometricanalysishasalsobeenrepresented,withworkshopson generalrelativityin2011andtheproofoftheWillmoreconjecturein2013.Marques andNevesacknowledgedtheimportantroleplayedbytheBarrettLecturesindisseminatingtheirproofoftheWillmoreconjecturetothemathematicalcommunityintheir InternationalCongressofMathematiciansaddressesin2014.
TheLectureshavebeenpartiallysupportedbyagrantfromtheMathematicsDepartmentoftheUniversityofTennesseesincetheirinauguration.Inrecentyears,theyhave alsobeensupportedbytheCollegeofArtsandSciencesandtheOfficeofResearchand EngagementatUTKand,since2017,havereceivedsupportfromtheBarrettMemorial Endowment,anendowmentfundstartedbyformerUniversityofTennessee,Knoxville mathematicsdepartmentheadJohnBradleyandhiswifeBeverley.TheLectureshave alsobeenconsistentlysupportedbytheNationalScienceFoundation¹.
2018JohnH.BarrettMemorialLectures: Geometricanalysisisoneofthemostactiveandexcitingareasinpuremathematics todayandgeometricflowsinparticularhaveprovedtobeapowerfultoolintheanalysis ofalargenumberofimportantproblemsindifferentialgeometry,imageprocessing
1 The 2018 Lectures were supported partly by the NSF grant DMS-1812058.
https://doi.org/10.1515/9783110618365-202
andmathematicalphysics,leadingtoaprofoundimpactoneachofthesefields.They alsoarisenaturallyinvariousphysicalcontextssuchasthermomechanics,annealing metals,crystalgrowth,flamepropagation,wearingprocessesandconformalfield theory. Meancurvatureflow,thethemeofthe2018JohnBarrettMemorialLectures,is inmanywaystheprototypicalgeometricflowequation.
TheLecturestookplaceduringthefourdayperiod29May-1June,2018atthe UniversityofTennessee,Knoxville.Theyhadtheformatofaworkshoponrecent developmentsintheareaofmeancurvatureflowaimedprimarilyatgraduatestudents andearlycareerresearchers.Furthertalksweregiveninthebroaderareaofgeometric flows(whichincludes,forexample,theRicci,YamabeandGausscurvatureflows) includingaseriesofshorttalksbygraduatestudentsandearlycareerresearchers.
Theintroductoryone-dayworkshop,consistingof300minutesoflecturesandadditionalinformaldiscussion,introducedparticipants(overhalfofwhomweregraduate orundergraduatestudents)tobasicmethodsinthefieldofmeancurvatureflow,and geometricflowsmoregenerally.Duringthefollowingthreedays,participantsheard surveylecturesintroducingrecentdevelopmentsandmajorresearchtrendsinthe meancurvatureflow,deliveredbyleadingexpertsinthefield.Thesupplementaryinvitedandshorttalksprovidedfurtherinsightintocurrentresearchtrends.TheBradley Lecturer,BruceKleiner,presentedhisrecentresolution,withRichardBamler,ofthe generalizedSmaleconjecture(apartfromthecaseof ℝP3).
UniversityofTenneseeKnoxville,June2018TheodoraBourniandMatLangford
Contents Foreword | V
BrianAllen
IntroducingMeanCurvatureFlow 1
JacobBernstein
Self-similarsolutionsofmeancurvatureflow | 26
SigurdAngenentandNatasaSesum Ancientsolutionsingeometricflows | 47
IanM.Adelstein
AnextensiontotheMorseenergygradientflow 67
BeomjunChoi
Regularityofnon-compactinversemeancurvatureflow | 71
FriederikeDittberner
Areapreservingcurveshorteningflow | 75
ChristineGuenther
SecondOrderRenormalizationGroupFlow 81
Siao-HaoGuo
AnalysisofVelàzquez’ssolutiontothemeancurvatureflowwithatypeII singularity | 92
RobertHaslhofer
Somerecentapplicationsofmeancurvatureflowwithsurgery 93
BrettKotschwar
Identifyingshrinkingsolitonsbytheirasymptoticgeometries 99
SajjadLakzian
GeometricsingularitiesundertheGigli-Mantegazzaflow | 109
StephenLynch
Pinchedancientsolutionstohighcodimensionmeancurvatureflow | 116
AlexanderMramor
Ontheunknoteddnessofselfshrinkersin ℝ3 120
XuanHienNguyen
Gluingconstructionsforself-translatingandself-shrinkingsurfacesundermean curvatureflow | 123
ShengwenWang(jointworkwithJacobBernstein)
Thelevelsetflowofahypersurfacein ℝ4 oflowentropydoesnotdisconnect 132
KaWaiWong
ApplicationofMeanCurvatureFlowforsurfaceparametrizations 135
BrianAllen
IntroducingMeanCurvatureFlow Abstract: WewillstartbydefiningMeanCurvatureFlow(MCF)andlookingatmany importantexamples.Thenwewillmoveontodiscusstheavoidanceprinciple,scaling properties,evolutionequationsandfirstconsequences,convergencetoaroundpoint forconvexsolutions,Huisken’smonotonicityformula,singularityanalysis,anda surveyofresultsforTypeIandTypeIIsolutions.Emphasiswillbeongivingproof ideaswithreferencesratherthanshowingallofthedetailsinordertobeabletosurvey asmanyimportantpropertiesofMCFaswecanatacomfortablepace.
MSC 2010: 53C44, 53A10, 35K40
1 DefinitionofMCFandExamples WestartbydefiningthenotionofaMeanCurvatureFlowwhichwillbethemainobject ofstudyforthisentireintroduction.
Definition1.1. Let Σn beasmooth,orientedmanifoldandlet
beaoneparameterfamilyofsmoothembeddings(immersions)thatsatisfy
wherewechoose ν tobetheoutwardpointingnormalvectorto Σt = φ(Σ, t).Asolution to (1.1) iscalledaMeanCurvatureFlow(MCF)where Σ0 istheinitialembeddingof Σ fortheflow.
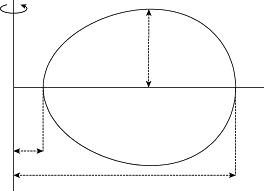
MeanCurvatureFlow(MCF)isanalogoustotheheatequationonaclosedhypersurface. Forinstance,wecanconsiderheatflowonacirclewhichcanbemodeledbyafunction u : [ L, L]×[0, T]→ℝ withperiodicboundaryconditions u(L)= u( L) and ux (L)= ux ( L).Inthiscasethesolutionwillexistforalltime,theheatwillbecomeuniformover time,andequaltotheaveragetemperatureattime t = 0.Insteadofthetemperature becominguniformovertimetheexpectationunderMCFisthattheprincipalcurvatures willbecomeuniformovertime.Seefigure1foranexampleofanellipsoidwhich becomesmoresphericalovertimeunderMCF.
MCFisanonlinearequationandhencewewillfindthatforcertaininitialhypersurfacestheflowwillencountersingularities,whichcausetheflowtonolongerbe defined,beforetheflowhashadachancetocausethecurvaturetobecomeuniform.
Brian Allen, United States Military Academy, e-mail:Brian.Allen@usma.com https://doi.org/10.1515/9783110618365-001
Inthecasewheresingularitiesoccurourgoalwillbetoclassifythegeometryofthe singularitiesthatcanoccur.Thisisdonebyzoominginonthesingularityviaarescaling andobtainingdetailedestimatesontheflowbehavior.Afteradetailedunderstanding ofsingularitiesareobtainedthenwecanhopetodefineawaytocontinuetheflow throughasingularity.Inthisintroductionwewillgetaglimpseofhowtomakethese intuitiveideasandexpectationsaboutthebehaviorofMCFrigorousbysurveying classicresultsinthefield.
Fig.1: ApillshapedsurfaceevolvingunderMCFwhichbecomesmoresphericalovertime.
Remark 1.2. When Σ = S1 thenDefinition1.1iscalledCurveShorteningFlow(CSF).
Remark 1.3. SometimesMCFisdefinedasasolutionto
where ⊥ representsorthogonalprojectionto Σt insideof ℝn+1.Thedifferencebetween (1.1) and (2) isthat (2) allowsformotionindirectiontangentto Σt whichproduces reparameterizations.Fromageometricpointofviewthesetwosolutionsarethesame butfromananalyticalpointofviewthesetwodefinitioncanproducesubtledifferenceswhichwewillhavetobecarefultokeeptrackof.Wewillseeinexample1.4the importanceofthisdistinctionforgraphsover ℝn .
Let {x1 ,..., xn } belocalcoordinateson Σ withcorrespondingbasisvectors { ∂ ∂x1 ,..., ∂ ∂xn }. Forafixedtime t ∈ [0, T] wecandefinethepushforwardvectorsthroughthemap φ(⋅, t) by { ∂φ ∂x1 ,..., ∂φ ∂xn }.Nowifwelet ⟨⋅, ⋅⟩ denotetheusualinnerproducton ℝn+1 we candefinedtheinducedmetricon Σt by,
(3) andthesecondfundamentalform,
Thisallowsustodefine,
Example1.4. Let Σ = ℝn andconsiderthefunction u : ℝn ×[0, T] → ℝ sothat
φ(x1 ,..., xn , t)=(x1 ,..., xn , u(x1 ,..., xn , t) isagraphoveraplanein ℝn+1.Onecan showthat Σt willremainagraphoveraplaneforatleastashorttimeandforthe solutionsof(2)areequivalenttosolutionsofthescalarPDE,
where D and div representthegradientanddivergencein ℝn+1.Equation (7) follows fromformulasfor gij , ν, Aij , H forgraphs.Againboth (1) and (2) wouldgivethesame geometricsolutionbutinthiscase (2) allowsustoreparameterizesothat Σt remains thegraphofthesolutionof (7).Studying (7) givesustheadvantageofapplyingPDE resultsandtechniquesforscalarPDEson ℝn .
EckerandHuisken[9,10]wereabletoshowthatif Σ0 isalocallyLipschitzgraph over ℝn thenasmooth,longtimesolutionexists Σt , t ∈[0, ∞) whichremainsagraph over ℝn .Thisisparticularlyinterstingsincetheydontorequiregrowthassumptions ontheinitialfunction u(⋅, 0) whicharenecessaryundertheheatequation.Under additionalassumptionsontheinitialhypersurface,EckerandHuiskenwereableto studythelongtermbehaviorofthesolution.
Remark 1.5. ShorttimeexistencetoMCFcanbeshownbywriting Σt asagraphover theinitialhypersurface Σ0 andobtainingascalarPDEdefinedon Σ.Withcareful attentiontodetailonecanthenappealtostandardPDEresultsforshorttimeexistence ofquasilinear,parabolicPDE.See[23]forthedetails.
1.1 SelfShrinkingSolutions InthissubsectionwewillseeourfirstexamplesofexplicitsolutionsofMCF.
Example1.6. Let Σ = Sn beasphereandconsider Σ0 = Sn r0 ⊂ ℝn+1 isasphereof radius r0 > 0.Onecanobservethat Σt willremainasphereunderMCFwithradius solvingthefollowingdifferentialequation: { { { dr dt =− n r , r(0) = r0 .
Noticethat(8)isseparableandhasthesolution, r(t)=√r2 0 2nt,
Fig.2: AspherecontractingtoapointinfinitetimeunderMCF.
Fig.3: Aselfshrinkingcylindercontractingtoaline.
fromwhichwecanobservethatthefinalexistencetimeis,
Wecanalsonoticethat
Itisimportanttonote (10), (11) and (12) sincewewillseethesequantitiesshowup againwhenestimatingmoregeneralsolutions.
Example1.7. Let Σ =ℝk × Sn k , n > k ≥ 1 beacylinderandconsider Σ0 =ℝk × S
⊂ ℝn+1 isacylinderofradius r0 > 0.Onecanobservethat Σt willremainacylinderunder MCFwithradiussolvingthefollowingdifferentialequation:
Noticethat(13)isseparableandhasthesolution,
fromwhichwecanobservethatthefinalexistencetimeis,
BoththesphereandthecylinderareexamplesofspecialsolutionstoMCFcalledself shrinkers.
Fig.4: Aselfshrinkingtoruswhichendsatapoint.
Definition1.8. WesaythatasolutiontoMCF, Σt ,isa selfshrinker if, Σt =√T tΣ0 , t ∈[0, T]. (16)
Noticethatbedefinitionaselfshrinkermustendinasingularityattime T.Nowwe willseethatselfshrinkerscanbefoundbystudyingaparticularellipticPDE.
Theorem1.9. Onecanshowthat Σt isaselfshrinkerifandonlyifthemeancurvature of Σ0 satisfiestheequation,
Σ0 (p)=−
φ(p, 0) x0 , ν0⟩ 2 , (17) where x0 ∈ℝn+1 , p ∈ Σ0,and ν0 istheoutwardpointingnormalto Σ0.
Equation17isanellipticPDEincoordinatesandexistenceofsolutionsisimportant tounderstandingspecialsolutionsofMCF.Byimposingvarioussymmetriesonthe equationforaselfshrinkerwecanoftenreducetheobjectiveoffindingselfshrinkers downtostudyinganODEaswewillseeinExample1.11.
Remark 1.10. Sincewecanalwaystranslatetime,i.e.define s = T t, s ∈( ∞, 0],and translatein ℝn+1,i.e.move x0 totheorigin 0 ∈ℝn+1,wecanequivalentlydefineaself shrinkerbythepropertythat,
withdefinedequation,
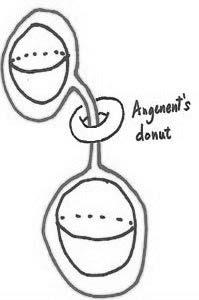
Example1.11. In[3],Angenentfoundaselfshrinkingtoruswhichisrotationally symmetricbysolvingtheODEwhichresultsfromimposingrotationalsymmetryon theselfshrinkerequation (1.9).Thequalititativebehaviourofthissolutionisdepicted infigure4andthecurvewhichisrotatedinordertogeneratethisspecialtorusis depictedinfigure5.In[3],Angenentalsofoundafamilyofimmersedselfshrinking torussolutionsofMCF.
Example1.12. Infigure6weseeanexampleofarotationallysymmetrictorusin ℝ3 whichshrinkstoacircleatthefinaltime T.ThisisanexampleofasolutionsofMCF whichdoesnothavenon-negativemeancurvatureeverywhere.
Fig.5: ThecurvewhichisrotatedaroundtheverticalaxisinordertoproduceAngenent’storus (Figurefrom[7]).
Fig.6: Torusshrinkingtoacircle.
1.2 AvoidancePrinciple NowthatwehavegatheredausefulcollectionofexamplesolutionsofMCFwewill nowseetheirusefulnessforstudyinggenericsolutionsofMCF.
Theorem1.13 (AvoidancePrinciple). Anytwosmooth,compactsolutionsofMCFwhich areinitiallydisjointwillremaindisjointunderMCF.
OneshouldseeEcker’sbook[8]orMantegazza’sbook[23]foradiscussionoftheproof ofTheorem1.13.Animportantconsequenceoftheavoidanceprincipleisthatcompact solutionstoMCFmustexistforafinitetime T <∞.Onecanseethisbychoosing r0 > 0 largeenoughsothat Σ0 ⊂ Sn r0 andhencebetheavoidanceprinciple Σt ⊂ Sn r(t) which implies T ≤ r2 0 2n .Thisrealizationmotivatesthequestionofwhatthesesingularitiesof MCFwilllooklikefordifferentcompactinitialhypersurfaces Σ0?
Fig.7: Adumbellshapedinitialsurfacedevelopinganeckpinchsingularity[2].
Example1.14. Onecanusetheavoidanceprinciple,thespheresolution,andthe angenenttorusinordertoshowthataneckpinchmustoccurforadumbellshapeas giveninfigure7.ThisargumentwasgivenbyAngenentin[3]whereoneplacestwo spheresinsidethebulbsofthedumbellandplacesanAngenenettorusontheoutside oftheneck.Iftheradiiofthebulbsandneckofthedumbellarechosenproperlythen onecanshowthattheexistencetimefortheself-shrinkingtorusisstrictlylessthan thatofthespheres.Bytheavoidanceprinciple,allfoursolutionsofMCFmustremain disjointandhencethesphereswillensurethatthebulbsremainun-collapsedwhereas theneckmusthaveshrunktoapointatthesametimeorbeforetheshrinkingtorus. HenceaneckpinchlikeinExample1.14musthaveoccurred.
Fig.8: AdumbellwithspheresinsidethebulbsofthedumbellandaAngenenttorussurroundingthe neckwhichcanbeusedtoshowasingularitymustoccur(Figurefrom[6]).
Inthecaseoftheneckpinchexample1.14itseemsreasonablethatifoneweretozoom inonthesingularityas t → T onewouldseeahypersurfacewhichlooksmoreand morelikeacylinder.Oneveryimportantresearchdirectionistoclassifysingularities ofMCFbyrescalingtheflowinordertozoomin.Wenowdescribeoneveryimportant waytorescaleasolutionofMCF.
1.3 RescalingMCF Ifwedefine φ(p, t)= λφ(p, t), λ ∈ℝ then
Itisagoodexerciseingeometricanalysiscalculationstochecktherescaledequations givenabove.
Ifwedefinetheparabolicrescaling,
then,
(27) andhence φ isalsoasolutionofMCF.
Remark 1.15. Noticethatforlargeλ,ifthesingularityfor Σt occurredat p ∈ℝn+1 then therescaling,
(28)
hastheeffectofzoominginonthesingularitythatisoccurringat p overalargerportion oftime.Thisisnottheonlywaytorescalesolutionsinordertoclassifysingularities andwewillseeanothercommonrescalinglater.
1.4 TranslatingSolutions InthissubsectionwewilllookatanotherspecialfamilyofsolutionstoMCFwhich evolveinasimpleway.Westartwithanexampleofthegrimreapersolution.
Example1.16. ThegrimreapersolutionofMCF, Γ1 t ⊂ℝ2,isgivenasthegraphofthe function u : ( π/2, π, 2)×ℝ→ℝ definedas, u(y, t)=− log(cos(y))+ ty ∈( π/2, π/2). (29)
Thissolutionevolvessimplybytranslating Γ0 ⊂ℝ2 inthe x-directionofthe xy-plane andisdefinedforallvaluesof t ∈ℝ.Wecanusethegrimreapersolutiontodefine higherdimensionalsolutionsofMCFbydefining Σn t = Γt ×ℝn 1 whichalsoevolvesby translating.
Fig.9: Grimreapercurveboundedbyapairofhorizontallines.
Ifwelet Πt bethegrimreaperthenwecanconstructothertranslatingsolitons
n t = Πt ×ℝn 1 . (30)
ThegrimreaperisanexampleofaspecialsolutiontoMCFcalledatranslatingsoliton.
Definition1.17. WesayasolutiontoMCFisatranslatingsolitonif,
t = Σ + tv, (31) for v ∈ℝn+1 , t ∈ℝ.
Similartoselfshrinkingsolutions,translatingsolitonscanalsobecharacterizedbyan ellipticequation.
Theorem1.18. Σt isatranslatingsolitonifandonlyif HΣ0 =⟨ν0 , v⟩. (32)
Example1.19. Anotherexampleofatranslatingsolitonisgivenbythebowlsoliton whichisarotationallysymmetric,paraboloidshapedhypersurfacewhichevolvesby translating(Seefigure10).
WewillseethattheselfshrinkersandthetranslatingsolitonsareimportantforclassifyingsingularitiesofMCF.
Fig.10: Paraboloidshapedbowlsolitonwhichevolvesbytranslation.
2 EvolutionEquationsandFirstConsequences Inthissectionwewilllookatimportantevolutionequationsforgeometricquantities underMCF.Whentheseevolutionequationsarecombinedwiththemaximumprinciple wewillbeabletoderiveimportantgeometricestimateswhichallowustocontrolMCF solutionsforspecifiedclassesofinitialhypersurfaces.
Tobeginwecancalculatetheevolutionofsomebasicgeometricobjectsunder MCF.Byusingthedefinitionof,
,wecanderivethefollowingtime derivatives:
where ∇ isthecovariantderivativeof Σt .Oneshouldseetheappendixof[8]fora derivationofthesetimederivatives.Itisalsoagoodexercisetoderivetheseequations byusingthedefinitionofMCF.
2.1 GradientFlowofArea Ifwelet φ : Σ ×( ε, ε) → ℝn+1 beaoneparameterfamilyofsmoothembeddings whichsatisfiestheequation
forsomespeedfunction f : Σ ×( ε, ε)→ℝ.Thenwecancalculatethefirstvariation ofarea
Oneshouldsee[22]foradetailedderivationofthevariationofareaformula.Notice thatthecriticalpointsfortheareafunctionalsatisfytheequation H = 0 whichare calledminimalsurfaces.MinimalsurfacesaretrivialexamplesofsolutionsofMCF whichdonotchangethroughouttheirevolution.
Bypluggingin f =−H wefindtheevolutionforareaunderMCF,
andhencewenoticethatMCFalwaysdecreasesareaandisthegradientflowforthe areafunctional.
Remark 2.1. CommonrescalingsoftheMCFaimtokeeptheareaorenclosedvolume of Σt fixedalongtheevolution.Noticethatifwechoosethespeedin(5)tobe,
thenunderthecorrespondingflowwewouldfind,
Hencetheflowdefinedbythespeed (8) wouldkeeptheareaof Σt fixedalongthe evolutionandcanbeshowntobecloselyrelatedtoMCF.Asimilarrescalingwasused byHuiskeninhisoriginalMCFpaper[16]studyingconvexsolutionstoMCF.
2.2 Hamilton’sMaximumPrinciple InordertofurtherunderstandhowgeometricquantititesevolveunderMCFwewill usethemaximumprincipleinordertoderiveestimates.WenowintroduceHamilton’s maximuprinciplewhichisparticularlyimportantwhenquantitiesareeasiertocontrol atamaximumoraminimum.
Theorem2.2 (Hamilton’sMaximumPrinciple). Assume g(t), t ∈ [0, T] isasmooth familyofRiemannianmetricsonaclosedmanifold M.Let f : M ×[0, T)→ℝ beasmooth
functionsatisfying,
where X isacontinuousvectorfieldand b isalocallyLipschitzfunction.Setting,
wehavethat umax islocallyLipschitz,hencedifferenriableatalmosteverytime t ∈[0, T), andateverydifferntiabletimesatisfies,
Thisimpliesthatif g : [0, T)→ℝ isasolutionto
OneshouldseeHamiltonswork[14, 15]andMantegazza’sbook[23]fortheproof ofthistheorem.Oneimportantaspectofthismaximumprincipleisthatyouonly needtomakethecomparisontotheODEfor g atpointsofmaximumfor f .Thisis importantsincethereisoftenaspecialgeometrythatcanbeexploitedatmaximums ofgeometricquantities.Wewillillustratethisbyprovingthefollowingweakerversion oftheavoidanceprincipleTheorem1.13.
Theorem2.3. If Σ0 ⊂ Sn r0 for r0 > 0 then Σt ⊂ Sn r(t) where r(t)=√
Proof. Considerthefunction
andcompute,
Nowwenotethatatamaxfor φ onecanshowthat φ and ν areparellelvectorsand H ≥ n |
| whichyieldsthesimplerequation
Nowbyintegrating(16)wefind,
whichyieldstheestimate,
fromwhichtheresultfollows.
2.3 MaximumPrincipleEstimates Inordertoobtainfurtherestimatesofgeometricquantitiesviathemaximumprinciple wewillneedafurtherlistofevolutionequations.
Wenotethatif T and J aretensorsthen T ∗ J representssomeundeterminedtraceof T and J.Oneshouldsee[8]and[23]fordetailedderivationsoftheseevolutionequations. Asafirstconsequenceoftheseevolutionequationsweseethatmeanconvexityis preservedunderMCF.Wesayahypersurface Σ ⊂ℝn+1 ismeanconvexif H ≥ 0.
Theorem2.4. If Σ0 ismeanconvexthen Σt remainsmeanconvexunderMCF.
See[23]foraproofofthisclaim.Nowthatweknowthat H ≥ 0 ispreservedwecanuse thisinformationtogetamoredetailedestimateofmeancurvature.
Theorem2.5. If Σ0 ismeanconvexwith H0 = minΣ0 H > 0 then
(25) If H0 = 0 thenasimilarestimateholdswith H0 replacedwith H = min
H for t
∈[0, ε).
Proof. Notethat |A|2 ≥ H2 n andsobycombiningwiththeevolutionequationfor H we find,
Henceatalmostevery t ∈[0, T] wefind,
whichbyintegratingyields,
Theorem2.6. If Σ0 satisfies |A|≤ CH forsome C > 0 then |A|≤ CH on Σt for t ∈[0, T).
Thisresultfollowsbycombiningtheevolutionequationfor |A|2 withtheevolution equationfor H2.Oneshouldsee[16]or[23]forthedetails.Theorem2.6impliesthatif |A| blowsupatacertainratethen H wouldalsoblowupwithatleastthatsamerate. Thenextresultsaysthatif A isnotboundedthen maxΣt |A| mustblowupwithsome minimumrate.
Theorem2.7. If A isnotboundedas t → T <∞, Σ0 compact,thenthesolutionofMCF, Σt ,mustsatisfy,
(29) forall t ∈[0, T).
WecanobtainfurtherestimatesforsolutionsofMCFbyintroducingHamilton’stensor maximumprinciple.Webeginwithanimportantdefinitionwhichwillbeusedasan assumptioninthemaximumprinciple.
Definition2.8. Let A beasymmetric 2-tensorand g aRiemannianmetricon M.Let B beasymmetric 2-tensorsothat B = B(A, g).Wesaythat B satisfiesthe nulleigenvector assumption ifforanynullvector V for A,i.e. A(V, ⋅)= 0,wehavethat B(V, V)≥ 0.
Theorem2.9. Let M beaclosedmanifoldand g(t) asmoothfamilyofRiemannian metricson M.Let T beasymmetric 2-tensorwhichsatisfiestheevolutioninequality,
(30) where X(t) isatimedependentvectorfieldand
(31)
isasymmetric 2-tensorwhichislocallyLipschitz.Supposethat B satisfiesthenulleigenvectorassumptionand T isnonnegativedefiniteon Σ0.Then T isnonnegativedefiniteon Σt forall t ≥ 0.
OneshouldseethebookofChow,Lu,andNi[4]foraproofofthisresultaswell asapplicationstoRicciflow.Wenowsurveyafewgeometricconditionswhichare preservedunderMCFwhichcanbeshownbyusingthetensormaximumprinciple.
Theorem2.10. If A isnonnegativedefinite(convex)on Σ0 then A isnonnegativedefinite (convex)on Σt .
Proof. TheproofthatconvexityispreservedfollowsfromHamilton’stensormaximum principle,Theorem2.9,appliedtotheevolutionequationfor Aij .Inthiscasewesee that,
Nowassumethat v ∈ Tp Σt isanulleigenvectorfor A,i.e. Aij vi = 0 incoordinates.Then wecancalculate,
andhence B satisfiesthenulleigenvectorassumptionwhichimpliesthat A remains nonnegativedefinitealongtheflow.
Thisresultsaysthatconvexityof Σ0 ispreservedalongasolutionofMCFwhichwas usedbyHuiskeninhisoriginalMCFpaper[16].
Theorem2.11. If A ≥ αHg, α > 0 on Σ0 then A ≥ αHg on Σt .
ThisresultshowsthateigenvaluepinchingispreservedunderMCFwhichwasalso provedandusedbyHuiskenin[16].
Theorem2.12. Let λ1 ,..., λn betheeigenvaluesof A inincreasingorder.If λ1+...+λk ≥ 0 on Σ0 then λ1 + ... + λk ≥ 0 on Σt .
Thisresultshowsthat k-convexityispreservedalongsolutionsofMCF.Huiskenand Sinestrari[21]usedthefactthat 2-convexityispreservedunderMCF,combinedwith importantestimatesof 2-convexsolutions,inordertodefineasurgeryprocedurewhich allowsonetoclassifythetopologyof 2-convexhypersurfacesof ℝn+1 .
2.4 ContinuationCriterion Inthissectionwewouldliketogiveacriterionfor T tobethefinalexistencetime. Tothisendwefirstshowthatif |A| isboundedon [0, T) thenallofitshigherorder covariantderivativesareboundedaswellonthesametimeinterval.
Theorem2.13. If Σ0 isclosedand |A|2 isboundedon Σt forall t ∈[0, T) then, |∇k A|2 ≤ Ck , (34) on Σt forall t ∈[0, T) forall k ∈ℕ.
Proof. Onewaytoprovethisresultisbyinductionon k,thenumberofcovariant derivativesof A.Inthiscasethebasecaseisassumedinthestatementsince |A|2 ≤ C. Fortheinductivestepweassumethat |∇j 1 A|2
andnote thatwehavetheevolutionequationfor |∇k A|2 ,
wherewehaveusedtheinductionhypothesisin (37).Nowwenoticethattheevolutionequationfor |∇k 1 A|2 hasagoodnegative |∇k A|2 term.Hencewecandefine f
andcalculate,
Nowbyapplyingthemaximumprincipleto(38)wefindthat,
Thisresultallowsustoproveacontinuationcriterionfortheflowwhichimpliesthat T canonlybeasingulartimeforMCFif max Σt |A| blowsupas t → T.
Theorem2.14 (ContinuationCriterion). If Σ0 iscompactand |A|≤ C on
t for t ∈[0, T), T <∞ then T cannotbeasingulartimeforthemeancurvatureflow Σt .
ProofIdea. Assumethat T isasingulartimefortheflow Σt .Byassumptionweknow that |A| isboundedon [0, T) andhencebyTheorem2.13weknowthat |∇k A| isbounded forall t ∈[0, T) and k ∈ℕ.Theboundon |A| alsoimpliesthat H isboundedwhich impliesthatforevery 0 ≤ s < t < T
Thisshowsthatthemaps φ(⋅, t) areLipschitzintimeandhenceuniformlyconvergeto acontinuousmap φT : Σ →ℝn+1 as t → T.
Nowwecanusethehigherorderboundson |∇k A| toarguethat φT isasmooth immersionandhencebyshorttimeexistencewecanextendthesmoothflowpast T
whichcontradictsthefactthat T wasasingulartimefortheflow.Oneshouldnotethat alotoftechnicalworkgoesintothislaststepwhichwehavesimplysketchedtheidea ofhere.Oneshouldsee[23]or[16]formoredetails.
2.5 SurveyofFirstMCFResults InthissectionwesurveyresultsforMCFinthecasewheretheoriginalintuitionthat MCFshouldcausethecurvaturetobecomeuniformovertimeplaysoutperfectly.In thesecasesthesingularitiesarewellbehavedandcanbeuniformlyrescaledaway.
Theorem2.15 (GageandHamilton[11,12]). UndertheCurveShorteningFlow(CSF)a convex,closedcurvein ℝ2 smoothlyshrinkstoapointinfinitetime.Afterrescalingin ordertokeepthelengthconstantthesolutionsmoothlyconvergestoacircle.
Theorem2.16 (Husiken[16]). UnderMCFacompact,convexhypersurfacein ℝn+1 , n ≥ 2 smoothlyshrinkstoaroundpointinfinitetime.Afterrescalinginordertokeep areaconstantthesolutionsmoothlyconvergestoasphere.
Theorem2.17 (Grayson[13]). Let γt betheCSFofaclosed,embedded,smoothcurvein ℝ2 withmaximalintervalofsmoothexistence [0, T).Then ∃τ < T suchthat γτ isconvex.
NoticethatbycombiningTheorem2.15withTheorem2.17weseethatanyCSFofa closed,embedded,smoothcurvein ℝ2 willshrinktoaroundpointinfinitetime.This isasurprisingresultandisspecialtothecaseofcurves.Inthecaseofanon-convex hypersurfacein ℝn+1 weknowthatsingularitiescandevelopingeneralandwillbethe focusofthenextsection.
Remark 2.18. ItisinterestingtonotethattheproofofTheorem2.16givenbyHuisken in[16]doesnotapplytothecaseofcurvesin ℝ2.ThisisbecauseHusikenleverages theevolutionequationforthetracefreesecondfundamentalform A∘ = A 1 n Hg.If onelets λ1 ,..., λn betheeigenvaluesof A thenonecanshowthat, |A∘|2 = 1 2 n ∑ i<j (λi λj )2 , (43)
andhenceifonecanshowthat |A∘|2 → 0 as t → T thenonewillconcludethatthe principalcurvaturesarebecomingasymptoticallyidenticalas t → T.Noticethatif n = 1 thenthetracefreesecondfundamentalformistrivialandhenceitisonlyuseful for n ≥ 2.
3 SingularityAnalysis Oneshouldrememberthedumbellexample1.14whereasingularityoccursonacylindricalneck.OurgoalnowistostudysolutionsofMCFwherewewillbeabletoshow thattheonlytypeofsingularitiesthatcanoccurarespheresorgeneralizedcylinders afterrescaling.
3.1 TypeIvs.TypeIISolutions RememberTheorem2.7whichstatesthatforcompactsolutionsofMCF, Σt ,wehave that
Wewillnowrestrictoutattentiontosolutionswhose maxΣt |A| isboundedabove bythesamerate.
Definition3.1. Let T bethemaximumexistencetimeforthesolutionofMCF, Σt .We willsaythat Σt is TypeI if ∃C > 1 sothat
Wesaythat Σt is TypeII ifinstead
NowthatwehavedefinedthenotionofTypeIandTypeIIsolutionsofMCFitisnatural toask:DoesaTypeIIsolutionofMCFexist?
BymodifyingthedumbellexampleonecanshowthatindeedaTypeIIsolution doesexist.Wewillgiveaninformaldiscussionoftheidea.Imagineadumbellwith onebulbofradius r1,theotherbulbofradius 1,andaneckofradius r2.
Ifwechoose r1 relativelysmalland r2 closeto 1 thenoneexpectstheMCFto eventuallybecomeconvexandeventuallyconvergetoaroundspherebyHuisken’s result[16].Ifwechoose r1 closeto 1 and r2 relativelysmallthenoneexpectstheMCF todevelopaneckpinchasinexample1.14whichwewillbeabletoshowisTypeI. Onecanshowthatthereisasolutioninbetweenthefirsttosituations,withcarefully chosen r1 and r2 value,sothattheMCFdevelopsaTypeIIsolution.
InthissectionwewillfocusonTypeIsolutionsofMCF.Oneshouldnoticethatin theexampleabovehowwehadtofinetunetheparametersinordertofindaTypeII solutionofMCF.Thisraisesthequestion:HowgenericareTypeIIsolutionsofMCF? ThisquestionhasbeenextensivelystudiedbyColdingandMinicozzi[5]wherethey showthatTypeIsolutionsofMCFaregeneric.Fortheprecisemeaningofgeneric solutionsoneshouldsee[5].