Curriculum: From Theory to Practice 2nd Edition
https://ebookmass.com/product/curriculum-from-theory-to-practice-2ndedition/
ebookmass.com
Graphs, Orders, Infinites and Philosophy
First published 2023 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Ltd
John Wiley & Sons, Inc.
27-37 St George’s Road 111 River Street London SW19 4EU Hoboken, NJ 07030
UK USA
www.iste.co.uk
www.wiley.com
© ISTE Ltd 2023
The rights of Daniel Parrochia to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s), contributor(s) or editor(s) and do not necessarily reflect the views of ISTE Group.
Library of Congress Control Number: 2022948075
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
ISBN 978-1-78630-897-9
Chapter1.Graphs .....................................1
1.1.Graphtheory:abriefhistory.............................1
1.2.Basicdefinitions...................................6
1.3.Differenttypesofgraphs...............................6
1.4.Moreonthelistofgraphs..............................9
1.5.Graphsandvertices..................................11
1.6.Someoperationsongraphs.............................13
1.7.Graphisomorphisms.................................15
1.7.1.Self-complementarygraphs...........................15
1.7.2.Propertiesofself-complementarygraphs...................16
1.8.Symmetricandasymmetricgraphs.........................17
1.9.Extremalgraphs...................................20
1.10.Independence,non-separability,reconstructionconjecture. ..........23
2.1.Ancientmappings..................................29
2.2.Chinesetetragrams..................................33
2.3.Pythagorismandpentagram.............................33
2.4. n-gramsandsomefiguresoftheworld.......................35
2.5.Graphsandclassicalsystematicity.........................41
2.6.Towardsanewkindofsystematicity........................52
2.6.1.Non-Hamiltonianandnon-Eulerianphilosophies ...............52
2.6.2.PancyclicgraphsandMetahegelianism....................57
2.7.Non-pythagorismandarrangementoflines....................58
2.7.1.Levigraphsoflinearrangements........................62
2.7.2.Linearrangementsofcurvelines........................65
2.7.3.Hyperbolicgraphs................................67
Chapter3.OrderandItsPhilosophicalUse
3.1.Themathematicalnotionoforder:abriefhistory.................74
3.2.Theideaof“well-ordering”.............................76
3.3.Quasiorders(orpreorders)..............................79
3.4.Partialorders.....................................81
3.4.1.Thenotionofwellpartialorder.........................84
3.4.2.Linearextensionofaposet...........................84
3.4.3.Wellpartiallyorderings.............................85
3.5.Trees..........................................85
3.5.1.Azooofinfinitetrees..............................86
3.5.2.Ordinalinfiniteclassifications.........................87
3.6.Moralproblemsinafiniteworld..........................87
3.7.Orderversuscircularity...............................92
3.8.Conclusion......................................96
Chapter4.TowardsaFormalPhilosophy
4.1.Asenjo’ssystemsandDubarle’sformalizationofHegelianism..........99
4.1.1.Asenjo’ssystemsandDubarle’scase......................100
4.1.2.Dubarle,Parmenides’thoughtandHegel ...................102
4.1.3.Projectivealgebras................................103
4.2.Somecriticisms ....................................106
4.3.Porphyryandtheneoplatonistmodeofthought... ...............107
4.4.AvariantofDubarle’sformalism..........................109
4.5.Quasi-Hegeliansystems...............................112
4.6.Philosophicalthinkingandfiniteprojectivegeometry ...............114
4.7.Otheralgebrasforphilosophicalthinking. ....................116
4.8.Modelsderivedfromgeometryandalgebraicgeometry..............117
4.9.Conclusion......................................120
Chapter5.PhilosophicalTransformations
5.1.Theparadoxofametasystem............................121
5.2.Insearchofanalgebra................................137
Chapter6.ConceptsandTopology ..........................141
6.1.Formalconcepts...................................141
6.2.Fuzzyconcepts....................................143
6.3.Thecaseofphilosophicalconcepts .........................144
Chapter7.TheProblemoftheInfinite ........................155
7.1.Thearithmeticofinfinitecardinals.........................156
7.2.Thequestionoflargecardinals...........................158
7.3.Woodin’sprogram... ...............................163
7.3.1.WoodinI:CHwouldbefalse. .........................163
7.3.2.WoodinII:CHmaybetrue.. .........................165
7.3.3.Ultimate L andCH...............................167
7.4.Infiniteandphilosophy. ...............................167
Chapter8.InSearchforaNewPhilosophy .....................171
8.1.Thefinitecase.....................................171
8.2.Theinfinitecase...................................176
Chapter9.ExtensionofStructuralismandNegativeTheology ........181
9.1.Complementaritygraphs...............................182
9.2.Orderrelation,orderedset..............................184
9.3.Graphsassociatedwithapartiallyorderedset...................185
9.4.Complementarityandincomparabilitygraphsofaposet... ..........187
9.5.Booleanrepresentationofaposet..........................187
9.6.Caseoflattices....................................189
9.6.1.CaseofBooleanlattices.............................191
9.6.2.Generalization:Booleanlatticesas n-cubes..................193
9.7.Consequencesfornegativetheology........................196
Chapter10.FromFuzzyGraphstoNeutrosophicGraphs ...........201
10.1.Fuzzysets......................................201
10.2.Fuzzygraphs....................................204
10.3.Intuitionisticfuzzysettheory...........................206
10.4.Neutrosophy. ....................................208
10.5.Single-valuedneutrosophicsetsandgraphs ....................211
Infact,mathematicsisoneofthemainsourcesofintelligibilityofreality. Butitsroledoesnotstopthere.Itcanalsoprovidephilosophywithmoreprecise conceptsthantheonesweordinarilyusetointerpretthesensibleworld.Aswe shallsee,discoveriesinmathematicssometimeslimitordisputetheclaimsofpast doctrines,buttheymayalsosuggestnewwaysofposingproblems.
Wefirstwishtoillustratetheseaffirmationsbysomereflectionsongraph’s problems,asthemathematicianstodayconceivethem.Wewillgoonby someconsiderationsonorder,pre-orderandpartialorder,thencarryoutmore geometricandtopologicalinvestigations.Intheend,wetacklethequestionof infinityandcometopossibleapplicationsinourdomainofsomeparticular graphs(incomparability,fuzzy,neutrosophicorpolyhedral graphs).Weonlyuse commonnotationsandremain,themostofthetime,asclearaspossible,in ordertogivethephilosophicalreadersomeusefultoolsfordevelopingtheirown thought.
Letusnowdefinewhata“philosophicalsystem”isforus,i.e.the“unit”on whichphilosophicalconsiderationsarebased.Iemphasizethispoint:thehistory ofthought,thesociologyofknowledgemaybeconcernedwithphilosophical ideas.Buttheproperhistoryofphilosophyisconcernedwith systems,or,atleast, philosophicalconstructionswhichmustexplicitlyexplainwhytheyarenot–or cannotbe–systems.
Definition: Wewillcalla philosophicalsystem atheory,expressedinthe commonlanguageorasaturatedextensionofit,whichtriestogiveaconceptual imageofthewholeworld,oreventuallyexplainswhysuchanimageisimpossible toconstruct.
Commentary: Thesentence“expressedinthecommonlanguageorasaturated extensionofit”allowsustodistinguishbetweenphilosophyandscience. Generally,philosophyiswritteninalanguageveryclosetothenaturallanguage andthatmaybereadbyeveryone.Forexample,thisisthecaseinPlato’s dialogues,intheworksofFrenchauthorsfromthe18thcenturysuchasRousseau andDiderot,orintheessaybyFichteentitled Thedestinationofman.However, inamoreelaboratedform,philosophycanmakeuseofmoreorlessabstract conceptsandsometimesreferstoscientificlanguage(see,forinstance,the LogicalInvestigations byHusserl).Theexpression“saturatedextension”comes fromlogicandwasintroducedbyJeanLadrière(seeLadrière1972) 2 .
2Tokeepitsimpleandnotgetintotootechnicalconsiderationsofmodeltheory,wecansaythat alogicalsystemis saturated ifanyadditionofasupplementary thesismakesitcontradictory or,ifittoleratescertainformsofcontradictioninitself,inconsistentwithrespecttoaparticular operationdifferentfromclassicalnegation.
Moreover,inordertocompletethisdistinctionbetweenscienceand philosophy,theterm“world”hastobeinterpretedinalargersensethanthe term“universe”.Thenwecanseparatephilosophyfromthisbranchofphysics called“cosmology”.Classicalphilosophyisakindofexistentialcosmology supportingthenon-physicaldimensionsoftheworld.Foraclassicalphilosopher, theuniverseor,afortiori,theobserveduniverse,isonlyasmallpartofalarger entitythattheGerman-SwissphilosopherKarlJaspers(1883–1969)named“the Encompassing” 3 .
Inthiscontext,theclassicphilosophicaloperationconsistsofpostulatingthat thereexistsamapping:
φ : W → S
betweenametaphysicalentity W ,whichissupposedtorepresentthewholeworld initscomplexity 4,andaphilosophicalsystem S ,whichcapturesitsmainfeatures.
Whenaphilosopherthinksthatthisoperationisimpossible,thenthey generallytrytoshowthat,insomeparticularsystem SP writtenbyaphilosopher P ,thereexistssomelinguisticexpression x towhich P didnotgiveanysense,so wecannotexhibitanycorrespondingconcreteentityin W .Insymbols:
Commentary: FollowingthesuggestionsofHume,Kantwasprobablythe firstphilosopherwhoappliesthismethod.Heprovesthatwecannothaveany knowledgeofentitiesaboutwhichwegetnoinformation(inhislanguage,no empiricalorpureintuitions),sothatthethreegreatmetaphysical“objects”named God,WorldandSoulhavenocorrespondingrealityintheconcreteexperience. Wittgensteinpursuethistaskinhis Tractatuslogico-philosophicus andbeganto huntdownallthelinguisticexpressionsthatphilosophersusedinanaivewayand thatwereinthesamesituation.Thisproject,inamoreorlessstrongform,was thereaftercontinuedbyallso-called analyticalphilosophy.
3Becauseofthesubject–objectsplit,whichalwaysplacesourconsciousnessoutsidetheworld ofobjects,beingasawholecanbeneitherobjectnorsubject.AccordingtoJaspers,itmustbe the“encompassing”thatmanifestsinthissplit.Objectsassubjectsthereforeariseagainstthe backgroundofthisencompassing,whichremainspartlyobscure.Itisclarifiedonlybyobjects, anditbecomesallthemoreclearastheobjectsaremoreclearlypresenttoconsciousness.But, forallthat,itdoesnotitselfbecomeanobject.Itisthereforebasicallywhat,throughthought, onlyannouncesitself.Wenevermeetititself,buteverythingwedomeet,wemeetinit.
4Thiscomplexityisassumed,butitisnotyetknownwhenthephilosopherbeginstheirwork. Inordertojustifythepossibilityofthisoperation,somephilosopherslikeM.Gueroulthave spokenofthisentity W asa“commonreal”(seeGueroult1979).Othershavesimplypostulated thatthereis,ineveryone,a“thoughtofaframeofreference”(see,forexample,Granier1977).
Inthisbook,wewanttoexploretheactualpossibilityofconstructingtoday’s philosophiesbystudyingthedifferentformsoforganizationsthattheycantake. Wewillshowthatmathematicsgivesalotoftoolstobuildrobustconceptual architecturessothatwemayhopethatsystematicphilosophyisalwayspossible 5
Thisundoubtedlyrestsonseveralpostulateswhichcanbelistedasfollows:
–(P1 )Itispossibletorepresentwithoutbias,inasingleformandoflimited dimension–whatiscalleda“philosophicalsystem”–theessentialofwhat constitutesourexperienceoftheworld.
–(P2 )Aphilosophicalsystemisusefulandevennecessary(ifnot,whywaste timebuildingit?).
–(P3 )Therelationalstructure(generallyexpressedasagraph 6)ofa philosophicalsystemisconnectedinsomesensetotherelationalstructureofthe world.Butthecorrespondencebetweenthemisnotanisomorphism–“themap isnottheterritory”,asKorzybskisaid(seeKorzybski1933,p.58)–butprobably notevenahomomorphism.Forexample,thestructureoftheworldmaybean asymmetricgraph,whilethestructureofthesystemissymmetric.However,we requirethesystemtorepresent,withoutnoticeabledistortion,themainfeatures oftheworldofwhichitissupposedtobeanimage.
Thefirsttwopostulateshaveamethodologicalcharacter.Thelatterisclearly ontological.
Thislatterisprobablythemostproblematic.Ithasbeenwidelydiscussed, sincethefamousarticlebytheAmericanmathematicianandphilosopherRandal RoyDipert(1997),ofwhichwewouldliketosayafewwordshere.
ThefirstpartofDipert’sarticle(“theshortcomingsoflogicandlogical metaphysics”)isoneofthebestarguedrefutationsofanalyticalphilosophy thatcanbefound.Thesecondpartarguesforawell-tempered“relationalism”. Butitisespeciallythethirdpart(“structure,asymmetricgraphsandAristotle refuted”)andthefourthpart(“theworldasasymmetricgraph”)whicharethe mostinterestingforourpurpose 7 .
5Thisprojectmustnotbeconsideredasanutopyoranold-fashioneddream.FromWhitehead toRescher,theideaofcognitivesystematizationhascontinued,as,moreover,itpersistsinour everydaylifewhenwetrytounderstandthisoneinallitsaspects.
6Letusjustsayhere,tofixideas,thatitisasetofverticesconnectedbyarcsoredges, dependingonwhetherthegraphisdirectedornot.
7Thereadercanfindthecompletedefinitionofsymmetricandasymmetricgraphsin section1.8.
impossible,isperfectlyaboutanobjectjustwhenitsinternal graphicalstructureisthesameastheobject’s,andwhentheobject occupiesalocationinthesystemofallobjectsthatislikethe thought’slocationinthesystemof(thatmind’s)thought(Dipert1997, p.357).
Wemightthinkthenthat,insuchatheory,thereisnoroomforminds, consciousnessandothermentalphenomena,unless,precisely,everythingis mental,whichfinally,Dipert,followinginthisLeibniz,ifnotSpinoza,does notentirelyexclude,becausetheverticesofthegraphcould,afterall,onlybe “feelings”.
Thisremarkablearticlesurelyunleashedthehostilityofthephilosopherswho preferAristotelianmattertoformalstructuresandthesentimentalillusionof humanwarmthtotheobjectiverelationshipsdepictedinthiscoldgraph.Butthe strongestobjection,developedinashortarticlebyOderberg(2011,pp.6–9), wasbasedonamathematicalargumentthatShackel(2011,p.11)verywell summarizedasfollows:
1)supposetheworldisagraph;
2)ifitisagraph,itisanasymmetricgraph;
3)anyasymmetricgraphcanbeturnedintosymmetricgraphbytheremoval ofedges;
4)thelossoflessthanalltheedgesoftheworld(specifically,thelossofall thosenotpartofsomesymmetricsubgraph,alossconsequentoncertainnodes goingoutofexistence)metaphysicallyentailsthenon-existenceoftheentire world(1,2,3);
5)Therefore,theworldisnotagraph(1,4,reductioadabsurdum).
Infact,thismathematicalargumentisquitespecious:whyimaginethatthe asymmetricgraphoftheworldcouldbecomesymmetrical?AsShackelwrites, “it’simpossiblefortheworldgraphtobeotherthanitisandhenceanychangeat allentailsnon-existence”(Shackel2011,p.13),soOderberg’sobjectionisnota validargument:“itisimpossibletogetridofthenodesandedgesofaworldand theargumenttotheabsurdinexistenceisblocked”(Shackel2011,p.14).
ThefactremainsthatthenecessityofDipert’sstructuremayseem troublesome.However,reducingthepropertiestosimplepotentials,asBirdcould havedoneinanothermodel(seeBird2007),wouldnotremovetheproblem accordingtoOderberg.Becauseifthereisonlypotentialandnoactualization,
thennothingcanreallymanifestitself,ashealsoexplainsinanotherarticle (seeOderberg2012).But,asShackelshows,therearepotencygraphsfor whichadiffusionprocessgraduallyupdatessome(orall)ofthepotentials.The phenomenonisa“snowball”andwecandemonstratethat,inthistypeofgraph (snowflakegraphs),wecanalwayschooseanodefromwhichallthepotentials canbeactualized.
Inconclusion,Dipert’sgraphisperfectlyplausibleandthispossiblereduction oftheworldtoagraphmakesitpossible,aswell,tosomehowontologically basetheattemptsofphilosophersovertime.Ifitisrejected,however,itcannotbe deniedthattheseattemptscanbemethodologicallydescribedusingtheformalism ofgraphtheory.Sowedonotabsolutelyneedtheassumption P3 tojustifywhat follows.
However,ifweaccepttoconsidertheworldasagraph,then,iftheworldis finite,thereisagoodchancethatitsgraphisasymmetric.Indeed,theproportion ofgraphson n verticeswithnon-trivialautomorphismstendstozerowhen n grows,whichinformallymeansthatalmostallfinitegraphsareasymmetric. Incontrast,almostallinfinitegraphsaresymmetricand,morespecifically, countableinfiniterandomgraphsintheErdös–Rényimodelare,withprobability 1,isomorphictothehighlysymmetricRadograph(seeErdösandSzekeres1935).
Inthistext,usingthelanguageofgraphs,ordersandsometimesinfinites,we trytorepresentmathematicallythisentitythatJasperscalled“theencompassing”, andwhichhethoughtitwas,bydefinition,impossibletoobjectify.
Infact,mathematicshasoftentaughtusthatitispossibletoobtaingood characterizationsofanobjectwithouthavingtobringitinanyexteriority.As Gaussshowedinthecaseofsurfaces(theoremaegregium),itisveryremarkable thatthecurvatureofageometricalobjectcanbedescribedintrinsically,i.e. withoutanyreferencetoa“spaceofembedding”inwhichtheconsideredobject wouldbelocated.Forexample,thefactthatanordinarysphereisasurfacewith constantpositivecurvatureiscompletelyindependentofthefactthatweusually seethissphereasbeingimmersedinourthree-dimensionalEuclideanspace. Thecurvatureofthisspherecouldverywellbemeasuredbytwo-dimensional intelligentbeingslivingonthesphere(kindsof“two-dimensionalants”),from measurementsoflengthsandanglescarriedoutonthesphere.
Wemustimaginethatweare,withrespecttotheencompassing,inthesame situationastwo-dimensionalantswithrespecttothesphere.Inprinciple,nothing preventsusfrombeingabletodescribeitifwehavethenecessaryinformation.
Thischapterisanintroductiontooursubject.Afterafewwordsaboutthe historyofgraphs,weexplainwhatwenowcalla“graph”inmathematicsand introducethemaindefinitionsusefultounderstandwhatfollows.Then,westudy someparticularclassesofgraphsthatwecanmeetinphilosophyandgivesome examplesofthem.
1.1.Graphtheory:abriefhistory
Theoriginofgraphdrawingsisnotwellknown,butwehavealreadyfound someoftheminancientChina.
Asintheterrestrialorder,wheretheancientChineseusedcryptographyto restrictthetransmissionofcertainmessagestotheinitiates,communication withtheheavenlyforcesrequiredinChinaaformadaptedtotheaddressee, andconverselythemessageofcelestialforcescouldnottakeovertheform ofaterrestrialmessage.Thuscamethe fu,thesegraphs,mostoftenDaoist, whichallowedfollowerstoenterintocommunicationwithspiritsandspiritsto communicatewiththeearthlyworld(seeFigure1.1).
Inthisregionoftheworld,somegraphicconstructionsmayalsobefoundin decorativemotivesofarchitectureorjails(seeFigure1.2)whichfollowcertain logics(HeandSchnabel,2018).
1Foracolorversionofallthefiguresinthischapter,seehttp://www.iste.co.uk/parrochia/ graphs.zip.
2Graphs,Orders,InfinitesandPhilosophy
Figure1.1. TaoistFusurmountedbyaconstellationof5stars(right);officialof fate(left)(BNF,Coins,MedalsandAntiques-CFA-135)(source:BNF)
Chinesedecorativegraphs(photo:Z.Guo)
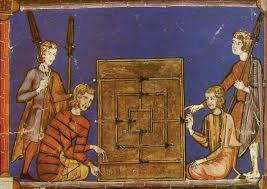
Itseemsthatoneoftheearliestformsoftheminwesterncountriesare probablythatofMorrisandMillgames,asshowninFigure1.3,wherethenodes ofthegraphdrawingarethepositionsthatgamecounterscanoccupy,theedges indicatinghowgamecounterscanmovebetweennodes(seeKruskal1960,pp. 272–286).
Summer Palace (Beijing) - photo Z. Guo
Lingering Garden (Suzhou)
Forms of motives
Figure1.2.
Figure1.3. DepictionofMorrisgameboards
4Graphs,Orders,InfinitesandPhilosophy
paper,aswellastheonewrittenbyVandermondeontheknightprobleminchess, carriedonwiththedreamoftheso-called“analysissitus”initiatedbyLeibnizand theancestoroftopology.
Euler’sformularelatingthenumberofedges,verticesandfacesofaconvex polyhedronwasstudiedandgeneralizedbyCauchy(1813)andL’Huillier (1812-1813)andrepresentsthebeginningofthisnewbranchofmathematics: algebraicaltopology.
MorethanonecenturyafterEuler’spaperandwhileListingwasintroducing theconceptoftopology,Cayleywasledbyaninterestinparticularanalytical formsarisingfromdifferentialcalculustostudyaparticularclassofgraphs, thetrees(seeCayley1857).Thisstudywaspartlymotivatedbyimportant problemsintheoreticalchemistry.ThetechniquesCayleyusedmainlyconcerned theenumerationofgraphswithspecificproperties.Enumerativegraphtheory thenarosefromhisresultsandalsothefundamentalresultspublishedbetween 1935and1937.ThesewerethengeneralizedbyDeBruijnin1959.Thelinks establishedbyCayleybetweenhisresultsontreesandcontemporarystudiesof chemicalcomposition(seeCayley1875)influencedthedevelopmentofastandard terminologyingraphtheory.
Forexample,theterm“graph”wasintroducedbySylvesterinapaper publishedin1878in Nature,wherehedrawsananalogybetween“quantic invariants”and“co-variants”ofalgebraandmoleculardiagrams(seeSylvester 1878):
Everyinvariantandco-variantthusbecomesexpressiblebyagraph preciselyidenticalwithaKekuléandiagramorchemicograph.Igivea ruleforthegeometricalmultiplicationofgraphs,i.e.forconstructing agraphtotheproductofin-orco-variantswhoseseparategraphsare given.
Thefirsttextbookongraphtheorywas writtenbyDénesKönigandpublished in1936(seeKönig1990).AnotherbookbyFrankHarary,publishedin1969, was“consideredtheworldovertobethedefinitivetextbookonthesubject”(see Gardner1992,p.203)andenabledmathematicians,chemists,electricalengineers andsocialscientiststotalktoeachother.InFrance,ClaudeBerge(seeBerge 1970)hasalsopublishedinthe1970saveryimportantbookaboutgraphsand hypergraphs.
Letusnowentersomeparticularproblemsingraphtheory.
Oneofthemostfamousandstimulatingproblemsinthisfieldisthefourcolor problem:“Isittruethatanymapdrawnintheplanemayhaveitsregionscolored withfourcolors,insuchawaythatanytworegionshavingacommonborder havedifferentcolors?”Thisproblem wasfirstposedbyFrancisGuthriein1852 anditsfirstwrittenrecordisinaletterofDeMorganaddressedtoHamiltonthe sameyear.Manyincorrectproofshavebeenproposed,includingthosebyCayley, Kempeandothers.ThestudyandthegeneralizationofthisproblembyTait, Heawood,RamseyandHadwigerledtothestudyofthecoloringsofthegraphs embeddedonsurfaceswitharbitrarygenus.Tait’sreformulationgeneratedanew classofproblems,thefactorizationproblems,particularlystudiedbyPetersen andKönig.TheworksofRamseyoncolorationsandmorespeciallytheresults obtainedbyTuránin1941wereattheoriginofanotherbranchofgraphtheory, extremalgraphtheory.
Thefour-colorproblemremainedunsolvedformorethanacentury.In1969, HeinrichHeesch(seeHeandSchnabel2018)publishedamethodforsolving theproblemusingcomputers.Acomputer-aidedproofproducedin1976by KennethAppelandWolfgangHakenmakesthefundamentaluseofthenotion of“discharging”developedbyHeesch(seeAppelandHaken1977a,1977b). Theproofinvolvedcheckingthepropertiesof1,936configurationsbycomputer, andwasnotfullyacceptedatthetimeduetoitscomplexity.Asimplerproof consideringonly633configurationswasgiven20yearslaterbyRobertsonetal. (1997).
Theautonomousdevelopmentoftopologyfrom1860to1930fertilizedgraph theorybackthroughtheworksofJordan,KuratowskiandWhitney.Another importantfactorofcommondevelopmentofgraphtheoryandtopologycame fromtheuseofthetechniquesofmodernalgebra.Thefirstexampleofsuchause comesfromtheworkofthephysicistGustavKirchhoff,whopublishedin1845his Kirchhoff’scircuitlawsforcalculatingthevoltageandcurrentinelectriccircuits.
Theintroductionofprobabilisticmethods ingraphtheory,especiallyinthe studyofErdösandRényioftheasymptoticprobabilityofgraphconnectivity, gaverisetoyetanotherbranch,knownas randomgraphtheory,whichhasbeen afruitfulsourceofgraph-theoreticresults.
Theconsiderationofflowsandnetworksandthedevelopmentofthe Ford–Fulkersonmethodprovideanewapproachingraphtheory,combinatorics andthenalgorithmics.
Wewillfirstexplorethealreadylargeuniverseofgraphs.
1.2.Basicdefinitions
Letusbeginwithsomedefinitions.
D EFINITION 1.1.– Initsmodernmathematicalsense,agraphisanorderedpair G(V,E ) comprisingaset V ofverticesornodesorpointstogetherwithaset E ofedgesorarcsorlines,whichare2-elementsubsetsof V (i.e.anedgeis associatedwithtwovertices,andthatassociationtakestheformoftheunordered paircomprisingthosetwovertices).Thisisnotexactly,indeed,themostgeneral definition.Toavoidambiguity,wewillseelaterthatthistypeofgraphmaybe describedpreciselyasundirectedandsimple.Thischaracteristicsaresufficient forthemoment.
R EMARK 1.1.– Theverticesbelongingtoanedgearecalledtheendsorend verticesoftheedge.Avertexmayexistinagraphandnotbelongtoanedge.
R EMARK 1.2.– Thesets V and E areusuallytakentobefinite,andmanyofthe well-knownresultsarenottrue(orareratherdifferent)forinfinitegraphsbecause manyoftheargumentsfailintheinfinitecase.
D EFINITION 1.2.– Theorderofagraphis |V |,itsnumberofvertices.Thesize ofagraphis |E |,itsnumberofedges.Thedegreeorvalencyofavertexisthe numberofedgesthatconnecttoit,whereanedgethatconnectsavertextoitself (aloop)iscounted.
Foranedge {x,y },graphtheoristsusuallyusethesomewhatshorternotation xy
1.3.Differenttypesofgraphs
Aswehaveseen,manygraphshavebeendiscoveredthroughoutthehistory ofthediscipline,sothattoday,evenrestrictingustointerestingorwell-known graphs,whicharealreadyverynumerous,wearedealingwithanextremelylarge set,infactaverybushyforest,nottosayarealjungle.
Exploringthiscollectionsupposesthatwehaveidentifiedsomedistinctive featuresthatcanguideusandallowustodefineclassificationcriteria.
Thereare,infact,varioustypesofgraphsdependinguponthenumberof vertices,thenumberofedges,theirinterconnectivityandtheiroverallstructure. Wewilldiscussonlyacertainfewimportanttypesofgraphsinthischapter.
8Graphs,Orders,InfinitesandPhilosophy
D EFINITION 1.10(C YCLEGRAPH ).– Asimplegraphwith n vertices(n ≥ 3)and n edgesiscalledacyclegraphifallitsedgesformacycleoflength n
R EMARK 1.4.– Ifthedegreeofeachvertexinthegraphistwo,thenitiscalleda cyclegraph.
Philosophicalexample: AsinthesystemofHegel,thesequenceofthemain conceptsofthephilosophyofEricWeilformsacyclegraph.
D EFINITION 1.11(W HEELGRAPH ).– Awheelgraphisobtainedfromacycle graph Cn 1 byaddinganewvertex.ThatnewvertexiscalledaHubwhichis connectedtoalltheverticesof Cn .
Philosophicalexample: InLeibnizianphilosophy,Godisa Hub becauseHeis connectedtoallthemonads.Conversely,eachmonadisconnectedtoallaspects oftheworld.So,theLeibniziansystemis,fromagraphicpointofview,awheel ofwheels.
D EFINITION 1.12(C YCLICGRAPH ).– Agraphwithatleastonecycleiscalleda cyclicgraph.
Philosophicalexample: Therearealotofcyclesintheclassicphilosophical systemsofLeibnizorHegel.
D EFINITION 1.13(ACYCLICGRAPH ).– Agraphwithnocyclesiscalledan acyclicgraph.
Philosophicalexample: InDescartes’philosophy,the“longchainsofreasons” areexamplesofacyclicgraphs.ButDescartes’systemitselfisnotacyclic(see Beyssade1979;Parrochia1993b,p.183,2012,pp.114–115).
D EFINITION 1.14(B IPARTITEGRAPH ).– Asimplegraph G =(V,E ) witha vertexpartition V = {V1 ,V2 } iscalledabipartitegraphifeveryedgeof E joins avertexin V1 toavertexin V2
Philosophicalexample: AccordingtoGillesDeleuze(seeDeleuze2003, pp.42–43),inthewholegraphofSpinoza’s Ethics,wecanmakeapartition intotwobigclassesofverticesassociatedwithstatements:ontheonehand,the propositions,corollariesandproofs,whichformthedeductivepartofthebook; ontheotherhand,thescholia,adiscontinuousbrokenchainwhichdonotbelong tothededuction.However,scholiaareconnectedtopropositionsandcorollaries (ortheirproofs)bysomeedges.Allthatdonotconstitutereallyabipartitegraph.