IntroductiontotheTheory ofComplexSystems
StefanThurner,RudolfHanel,andPeterKlimek
MedicalUniversityofVienna,Austria
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregistered trademarkof OxfordUniversityPressintheUKandincertainothercountries
©StefanThurner,RudolfHanel,andPeterKlimek2018
Themoralrightsoftheauthorshavebeenasserted
FirstEditionpublishedin2018
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeof the aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2018947065
Dataavailable
ISBN978–0–19–882193–9
DOI:10.1093/oso/9780198821939.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibility forthematerials containedinanythirdpartywebsitereferencedinthiswork
Preface
Thisbookisforpeoplewhoareinterestedinthescienceofcomplexadaptivesystems andwishtohavemorethanjustacasualunderstandingofit.Aswithallthesciences, understandingofcomplexadaptivesystemsisreachedsolelyinaquantitative,predictive, andultimatelyexperimentallytestablemanner.Complexadaptivesystemsaredynamical systemsthatareabletochangetheirstructure,theirinteractions,and,consequently, theirdynamicsastheyevolveintime.Thisisnotabookaboutcomplicatedsystems, eventhoughmostcomplexsystemsarecomplicated.Indeed,overthelast300years, scientistshaveusuallydealtwithcomplicatedsystemsthat areneithercomplexnor adaptive.
Thetheoryofcomplexsystemsisthetheoryofgeneralizedtime-varyinginteractions betweenelementsthatarecharacterizedbystates.Interactionstypicallytakeplaceon networksthatconnectthoseelements.Theinteractionsinvolvedmaycausethestates oftheelementsthemselvestoalterovertime.Theessenceofa complexsystemisthat theinteractionnetworksmaychangeandrearrangeasaconsequenceofchangesin thestatesoftheelements.Thus,complexsystemsaresystemswhosestateschange asaresultofinteractionsandwhoseinteractionschangeconcurrentlyasaresultof states.Duetothischicken–egg-typeproblem,complexsystemsshowanextremely richspectrumofbehaviour:theyareadaptiveandco-evolutionary;theyshowpathdependence,emergence,powerlaws;theyhaverichphasediagrams;theyproduce anddestroydiversity;theyareinherentlypronetocollapse;theyareresilient,andso on.Thetheoryofcomplexsystemstriestounderstandthesepropertiesbasedonits buildingblocksandontheinteractionsbetweenthosebuildingblocksthattakeplace onnetworks.Itcombinesmathematicalandphysicalprincipleswithconceptsborrowed frombiologyandthesocialsciences;itusesnewcomputationaltechniquesand,with theadventofcomprehensivelarge-scaledatasets,isbecomingexperimentallytestable. Thegoalofthetheoryofcomplexsystemsistounderstandthedynamical systemic outcomesofinterconnectedsystems,anditsultimategoalistoeventuallycontroland designsystemicpropertiesofsystemssuchastheeconomy,thefinancialsystem,social processes,cities,theclimate,andecology.Thetheoryofcomplexsystemsbuildspartly onpreviousattemptstounderstandsystemsthatinteractinnon-trivialways,suchas gametheory,cybernetics,orsystemstheory.However,initscurrentstate,thescience ofcomplexsystemsgoeswellbeyondtheseearlierdevelopments,insomanyways, infact,thatitcanberegardedasanindependentscientificbranch,which—duetoits quantitative,predictive,andtestablenature—isanaturalscience.
Eventhoughitisfairtosaythatthetheoryofcomplexsystems isnotyetcomplete, inrecentyears,ithasbecomequiteclearjustwhatthetheoryisgoingtolooklike. Itselementsandstructureareemerging.Thecurrentstateofthetheoryofcomplex
vi Preface systemsiscomparableperhapstothestateofquantummechanicsinthe1920s,before thefamousCopenhagenmeetingsandWernerHeisenberg’sbook.Atthattime,quantum mechanicswasacollectionofexperimentalandtheoreticalbitsandpieces,which hadnotyetbeenseenwithinafullycomprehensiveframework.Nevertheless,itwas clearthat,onedaysoon,suchaframeworkwouldexist.Thepresentsituationcan becomparedtoanarchaeologicalproject,whereamosaicfloorhasbeendiscovered andisbeingexcavated.Whilethemosaicisonlypartlyvisibleandthefullpictureis stillmissing,severalfactsarebecomingclear:themosaicexists;itshowsidentifiable elements(forinstance,peopleandanimalsengagedinrecognizableactivities);there arelargepatchesmissingorstillinvisible,butexpertscanalreadytellthatthemosaic representsascenefrom,say,Homer’s Odyssey.Similarly,fordynamicalcomplexadaptive systems,itisclearthatatheoryexiststhat,eventually,canbefullydeveloped.There arethosewhosaythatcomplexsystemswillneverbeunderstoodorthat,bytheirvery nature,theyareincomprehensible.Thisbookwilldemonstratethatsuchstatementsare incorrect.Theelementsofatheoryofcomplexsystemsarebecomingclear:dynamical multilayernetworks,scaling,statisticalmechanicsofalgorithmicdynamics,evolution andco-evolution,andinformationtheory.Theessenceofthisbookistofocusonthese components,clarifytheirmeaninginthecontextofcomplex systems,andenablethe readerwithamathematicalskillsettoapplythemtoconcrete problemsintheworldof complexsystems.
Thebookiswritteninmathematicallanguagebecausethisis theonlywayto expressfactsinaquantitativeandpredictivemannerandto makestatementsthatare unambiguous.Weaimforconsistency.Thebookshouldbecomprehensiblesothatnoonewithanunderstandingofbasiccalculus,linearalgebra,andstatisticsneedrefer tootherworks.Thebookisparticularlydesignedforgraduatestudentsinphysicsor mathematics.Wetrytoavoidambiguousstatementswhile,at thesametime,beingas generalaspossible.Thehopeisthatthisworkwillserveasatextbookandasastarting pointforjourneysintonewandunexploredterritory.
Manycomplexsystemsareoftensensitivetodetailsintheir internalsetup,toinitial andtoboundaryconditions.Conceptsthatprovedtobeextremelyrobustandeffectivein non-complexsystems,suchasthecentrallimittheorem,classicalstatisticalmechanics,or informationtheory,losetheirpredictivepowerwhenconfrontedwithcomplexsystems. Extremecareisthusneededinanyattempttoapplytheseotherwisedistinguished conceptstocomplexsystems:doingsocouldendinconfusionandnonsensicalresults. Inseveralconcreteexamples,wewilldemonstratetheimportanceofunderstandingwhat thesemethodsmeaninthecontextofcomplexsystemsandwhethertheycanorcannot beapplied.Wewilldiscusshowsomeoftheseclassicalconceptscanbegeneralizedto becomeusefulforunderstandingcomplexsystems.
Thebookisalsoastatementaboutourbeliefthattheexactsciencesmaybeentering aphaseoftransitionfromatraditionalanalyticaldescriptionofnature,asusedwith tremendoussuccesssinceGalileoandNewton,towardsan algorithmic description. Whereastheanalyticaldescriptionofnatureis,conceptually,basedlargelyondifferential equationsandanalyticalequationsofmotion,thealgorithmicviewtakesintoaccount evolutionaryandco-evolutionaryaspectsofdynamics.Itprovidesaframeworkfor
Preface vii
systemsthatcanendogenouslychangetheirinternalinteractionnetworks,rulesof functioning,dynamics,andevenenvironment,astheyevolveintime.Algorithmic dynamics,whichischaracteristicofcomplexdynamicalsystems,maybeakeytothe quantitativeandpredictiveunderstandingofmanynaturalandman-madesystems.In contrasttophysicalsystems,whichtypicallyevolveanalytically,algorithmicdynamics describecertainlyhowliving,social,environmental,and economicsystemsunfold. ThisalgorithmicviewisnotnewbuthasbeenadvocatedbyauthorslikeJosephA. Schumpeter,StuartKauffman,andBrianArthur.However,ithas not,todate,been pickedupbymainstreamscience,andithasneverbeenpresentedinthecontextofthe theoryofcomplexsystems.
Thisbookisbasedonatwo-semestercourse,thathasbeenheldattheMedical UniversityofViennasince2011.WearegratefultoourstudentsandtoKathrynPlatzer andAnitaWanjekforhelpinguswiththemanuscript.
STViennaJanuary2018
1IntroductiontoComplexSystems
1.1Physics,biology,orsocialscience?
1.2Componentsfromphysics
1.2.1Thenatureofthefundamentalforces 2
1.2.2Whatdoespredictivemean? 3
1.2.3Statisticalmechanics—predictabilityonstochasticgrounds5
1.2.4Theevolutionoftheconceptofpredictabilityinphysics5
1.2.5Physicsisanalytic,complexsystemsarealgorithmic6
1.2.6Whatarecomplexsystemsfromaphysicspointofview?7
1.2.7Anoteonchemistry—thescienceofequilibria9
1.3Componentsfromthelifesciences 10
1.3.1Chemistryofsmallsystems 10
1.3.2Biologicalinteractionshappenon networks—almostexclusively 12
1.3.3Evolution 13
1.3.4Adaptiveandrobust—theconceptoftheedgeofchaos16 1.3.5Componentstakenfromthelifesciences19
1.4Componentsfromthesocialsciences 19
1.4.1Socialsystemscontinuouslyrestructuringnetworks 20
1.5WhatareComplexSystems? 21
1.5.1Whatisco-evolution? 24
1.5.2Theroleofthecomputer 25
1.6Thestructureofthebook
1.6.1Whathascomplexitysciencecontributedtothehistoryofscience?27
2ProbabilityandRandomProcesses
2.1Overview
2.1.1Basicconceptsandnotions
2.1.2Probabilityandinformation
2.2.1BasicprobabilitymeasuresandtheKolmogorovaxioms39
2.2.2Histogramsandrelativefrequencies 41
2.2.3Mean,varianceandhighermoments 41
2.2.4Morethanonerandomvariable 44
2.2.5AnoteonBayesianreasoning
2.2.6Bayesianandfrequentistthinking
x Contents
2.3Thelawoflargenumbers—addingrandomnumbers53
2.3.1Thecentrallimittheorem 55
2.3.2Generalizedlimittheoremsand α-stableprocesses59
2.4Fat-taileddistributionfunctions 65
2.4.1Distributionfunctionsthatshowpowerlawtails66
2.4.2Otherdistributionfunctions 69
2.5Stochasticprocesses 75
2.5.1Simplestochasticprocesses 76
2.5.2History-orpath-dependentprocesses84
2.5.3Reinforcementprocesses 85
2.5.4Drivendissipativesystems 86
2.6Summary 89
2.7Problems 90
3Scaling 93
3.1Overview 93
3.1.1Definitionofscaling 95
3.2Examplesofscalinglawsinstatisticalsystems96
3.2.1Anoteonnotationfordistributionfunctions98
3.3Originsofscaling 100
3.3.1Criticality 101
3.3.2Self-organizedcriticality 105
3.3.3Multiplicativeprocesses 106
3.3.4Preferentialprocesses 108
3.3.5Samplespacereducingprocesses 110
3.3.6Othermechanisms 119
3.4Powerlawsandhowtomeasurethem 120
3.4.1Maximumlikelihoodestimatorforpowerlawexponents λ< 1 120
3.4.2Maximumlikelihoodestimatorforpowerlawsforallexponents122
3.5Scalinginspace—symmetryofnon-symmetricobjects,fractals124
3.5.1Self-similarityandscale-invariance 125
3.5.2Scalinginspace:fractals 125
3.5.3Scalingintime—fractaltimeseries 129
3.6Example—understandingallometricscalinginbiology131
3.6.1Understandingthe3/4powerlaw 133
3.6.2Consequencesandextensions 136
3.7Summary 137
3.8Problems 139
4Networks 141
4.1Overview 141
4.1.1Historicaloriginofnetworkscience 143
4.1.2Fromrandommatrixtheorytorandomnetworks143
4.1.3Smallworldsandpowerlaws 144
4.1.4Networksinthebigdataera 145
4.2Networkbasics 145
4.2.1Networksorgraphs? 146
4.2.2Nodesandlinks 146
4.2.3Adjacencymatrixofundirectednetworks146
4.3Measuresonnetworks 151
4.3.1Degreeofanode 151
4.3.2Walkingonnetworks 153
4.3.3Connectednessandcomponents 154
4.3.4Fromdistancesonnetworkstocentrality155
4.3.5Clusteringcoefficient 156 4.4Randomnetworks 159
4.4.1Threesourcesofrandomness 160
4.4.2Erd˝os–Rényinetworks 161
4.4.3PhasetransitionsinErdos–Rényinetworks163
4.4.4Eigenvaluespectraofrandomnetworks165
4.5BeyondErdos–Rényi—complexnetworks167
4.5.1GeneralizedErd˝os–Rényinetworks168
4.5.2Networksuperpositionmodel 170
4.5.3Smallworlds 171
4.5.4Hubs 173 4.6Communities 178
4.6.1Graphpartitioningandminimumcuts179
4.6.2Hierarchicalclustering 180
4.6.3DivisiveclusteringintheGirvan–Newmanalgorithm181
4.6.4Modularityoptimization 182
4.7Functionalnetworks—correlationnetworkanalysis184
4.7.1Constructionofcorrelationnetworks186
4.7.2Filteringthecorrelationnetwork 190
4.8Dynamicsonandofnetworks 194
4.8.1Diffusiononnetworks 195
4.8.2Laplaciandiffusiononnetworks 196
4.8.3Eigenvectorcentrality 199
4.8.4Katzprestige 200
4.8.5PageRank 200
4.8.6Contagiondynamicsandepidemicspreading201
4.8.7Co-evolvingspreadingmodels—adaptivenetworks205
4.8.8Simplemodelsforsocialdynamics206
4.9Generalizednetworks 208
4.9.1Hypergraphs 209
4.9.2Powergraphs 209
4.9.3Multiplexnetworks 210
4.9.4Multilayernetworks 211
4.10Example—systemicriskinfinancialnetworks212
4.10.1Quantificationofsystemicrisk 213
4.10.2Managementofsystemicrisk 218
4.11Summary
5.1Overview
5.1.1Scienceofevolution 225
5.1.2Evolutionasanalgorithmicthree-stepprocess227
5.1.3Whatcanbeexpectedfromascienceofevolution?230
5.2Evidenceforcomplexdynamicsin evolutionaryprocesses 232
5.2.1Criticality,punctuatedequilibria,andtheabundanceof fat-tailedstatistics 232
5.2.2Evidenceforcombinatorialco-evolution234
5.3Fromsimpleevolutionmodelstoageneral evolutionalgorithm 236
5.3.1Traditionalapproachestoevolution—the replicatorequation 237
5.3.2Limitstothetraditionalapproach 241
5.3.3Towardsageneralevolutionalgorithm242
5.3.4Generalevolutionalgorithm 244
5.4Whatisfitness? 246
5.4.1Fitnesslandscapes? 247
5.4.2Simplefitnesslandscapemodels 247
5.4.3Evolutionarydynamicsonfitnesslandscapes249
5.4.4Co-evolvingfitnesslandscapes—TheBak–Sneppenmodel261
5.4.5Theadjacentpossibleinfitnesslandscapemodels263
5.5Linearevolutionmodels 264
5.5.1Emergenceofauto-catalyticsets—the Jain–Krishnamodel 265
5.5.2Sequentiallylinearmodelsandtheedgeofchaos271
5.5.3Systemicriskinevolutionary systems—modellingcollapse 277
5.6Non-linearevolutionmodels—combinatorialevolution 281
5.6.1Schumpetergotitright 282
5.6.2Genericcreativephasetransition 282
5.6.3Arthur–Polakmodeloftechnologicalevolution286
5.6.4Theopen-endedco-evolvingcombinatorialcritical model—CCCmodel 288
5.6.5CCCmodelinrelationtootherevolutionarymodels298
5.7Examples—evolutionarymodelsforeconomicpredictions299
5.7.1Estimationoffitnessofcountriesfromeconomicdata300
5.7.2Predictingproductdiversityfromdata304
5.8Summary 308
5.9Problems 311
6StatisticalMechanicsandInformationTheoryforComplexSystems 313
6.1Overview 313
6.1.1Thethreefacesofentropy 314
6.2Classicalnotionsofentropyforsimplesystems318
6.2.1Entropyandphysics 321
6.2.2Entropyandinformation 328
6.2.3Entropyandstatisticalinference 343
6.2.4Limitsoftheclassicalentropyconcept348
6.3Entropyforcomplexsystems 349
6.3.1Complexsystemsviolateergodicity 350
6.3.2Shannon–Khinchinaxiomsforcomplexsystems352
6.3.3Entropyforcomplexsystems 352
6.3.4Specialcases 356
6.3.5Classificationofcomplexsystemsbasedontheirentropy358
6.3.6Distributionfunctionsfromthecomplexsystemsentropy361
6.3.7Consequencesforentropywhengivingupergodicity363
6.3.8Systemsthatviolatemorethanthecompositionaxiom365
6.4Entropyandphasespaceforphysicalcomplexsystems365
6.4.1Requirementofextensivity 365
6.4.2Phasespacevolumeandentropy 366
6.4.3Someexamples 369
6.4.4Whatdoesnon-exponentialphasespacegrowthimply?373
6.5Maximumentropyprincipleforcomplexsystems374
6.5.1Path-dependentprocessesandmultivariatedistributions374
6.5.2Whendoesamaximumentropyprincipleexistfor path-dependentprocesses? 375
6.5.3Example—maximumentropyprincipleforpath-dependent randomwalks 380
6.6Thethreefacesofentropyrevisited 382
6.6.1ThethreeentropiesofthePólyaprocess383
6.6.2Thethreeentropiesofsamplespacereducingprocesses 387
6.7Summary 393
6.8Problems 395
7TheFutureoftheScienceofComplexSystems? 397
8SpecialFunctionsandApproximations 399
8.1Specialfunctions 399
8.1.1Heavisidestepfunction 399
8.1.2Diracdeltafunction 399
xiv Contents
8.1.3Kroneckerdelta
8.1.4TheLambert-Wfunction
8.1.5Gammafunction
8.1.6IncompleteGammafunction
8.1.7Deformedfactorial
8.1.8Deformedmultinomial
8.1.9Generalizedlogarithm
8.1.10Pearsoncorrelationcoefficient
8.1.11Chi-squareddistribution
8.2Approximations
8.2.1Stirling’sformula
8.2.2Expressingtheexponentialfunctionasapower404 8.3Problems
IntroductiontoComplexSystems
1.1Physics,biology,orsocialscience?
Thescienceofcomplexsystemsisnotanoffspringofphysics,biology,orthesocial sciences,butauniquemixofallthree.Beforewediscusswhatthescienceofcomplex systemsisorisnot,wefocusonthesciencesfromwhichithas emerged.Byrecalling whatphysics,biology,andthesocialsciencesare,wewilldevelopanintuitivefeelfor complexsystemsandhowthissciencediffersfromotherdisciplines.Thischapterthus aimstoshowthatthescienceofcomplexsystemscombinesphysics,biology,andthe socialsciencesinauniqueblendthatisanewdisciplineinitsownright.Thechapter willalsoclarifythestructureofthebook.
1.2Componentsfromphysics
Physicsmakesquantitativestatementsaboutnaturalphenomena.Quantitativestatementscanbeformulatedlessambiguouslythanqualitativedescriptions,whichare basedonwords.Statementscanbeexpressedintheformofpredictionsinthesense thatthetrajectoryofaparticleortheoutcomeofaprocesscanbeanticipated.If anexperimentcanbedesignedtotestthispredictionunambiguously,wesaythatthe statementisexperimentallytestable.Quantitativestatementsarevalidatedorfalsified usingquantitativemeasurementsandexperiments.
Physicsistheexperimental,quantitative,andpredictive scienceofmatterandits interactions.
Pictorially,physicsprogressesbyputtingspecificquestionstonatureintheformof experiments;surprisingly,ifthequestionsarewellposed,theyresultinconcreteanswers thatarerobustandrepeatableforanarbitrarynumberoftimesbyanyonewhocan dothesameexperiment.Thismethodofgeneratingknowledge aboutnature,byusing experimentstoaskquestionsofit,isuniqueinthehistoryofhumankindandiscalledthe scientificmethod.Thescientificmethodhasbeenatthecoreofalltechnologicalprogress sincethetimeoftheEnlightenment.
IntroductiontotheTheoryofComplexSystems.StefanThurner,RudolfHanel,andPeterKlimek, OxfordUniversityPress(2018).©StefanThurner,RudolfHanel,andPeterKlimek. DOI:10.1093/oso/9780198821939.001.0001
IntroductiontoComplexSystems
Physicsdealswithmatteratvariousscalesandlevelsofgranularity,rangingfrom macroscopicmatterlikegalaxies,stars,planets,stones, andprojectiles,tothescaleof molecules,atoms,hadrons,quarks,andgaugebosons.There arefourfundamentalforces atthecoreofallinteractionsbetweenallformsofmatter:gravity,electromagnetismand twotypesofnuclearforce:theweakandthestrong.Accordingtoquantumfieldtheory, allinteractionsinthephysicalworldaremediatedbytheexchangeofgaugebosons.The graviton,thebosonforgravity,hasnotyetbeenconfirmedexperimentally.
1.2.1Thenatureofthefundamentalforces
Thefourfundamentalforcesareverydifferentinnatureand strength.Theyare characterizedbyanumberofpropertiesthatarecrucialfor understandinghowandwhy itwaspossibletodevelopphysicswithoutcomputers.These propertiesaresetouthere.
Usually,thefourfundamentalforcesarehomogeneousandisotropicinspace(and time).Forcesthatarehomogeneousactinthesamewayeverywhereinspace;forces thatareisotropicarethesame,regardlessofthedirection inwhichtheyact.Thesetwo propertiesdrasticallysimplifythemathematicaltreatmentofinteractionsinphysics.In particular,forcescanbewrittenasderivativesofpotentials,two-bodyproblemscan effectivelybetreatedasone-bodyproblems,andtheso-calledmeanfieldapproach canbeusedformany-bodysystems.Themeanfieldapproachistheassumptionthat aparticlereactstothesinglefieldgeneratedbythemanyparticlesaroundit.Often, suchsystemscanbefullyunderstoodandsolvedevenwithout computers.Thereare importantexceptions,however;onebeingthatthestrongforceactsasifinteractionswere limitedtoa‘string’,whereflux-tubesareformedbetweeninteractingquarks,similarto typeIIsuperconductivity.
Thephysicalforcesdiffergreatlyinstrength.Comparedto thestrongforce,the electromagneticforceisaboutathousandtimesweaker,the weakforceisabout1016 timesweaker,andthegravitationalforceisonly10 41 ofthestrengthofthestrongforce [405].Whenanyphysicalphenomenonisbeingdealtwith,usuallyonlyasingleforce hastobeconsidered.Alltheothersaresmallenoughtobesafelyneglected.Effectively, thesuperpositionoffourforcesdoesnotmatter;foranyphenomenon,onlyoneforce
Characteristic MatterInteractiontypeslengthscale
macroscopicmattergravity,electromagnetismallranges moleculeselectromagnetismallranges atomselectromagnetism,weakforce ∼ 10 18
quarksandgaugebosonselectromagnetism,weakandstrongforce10
Componentsfromphysics 3 isrelevant.Wewillseethatthisisdrasticallydifferentincomplexsystems,wherea multitudeofdifferentinteractiontypesofsimilarstrengthoftenhavetobetakeninto accountsimultaneously.
Typically,physicsdoesnotspecifywhichparticlesinteractwitheachother,as theyinteractinidenticalways.Theinteractionstrengthdependsonlyontherelevant interactiontype,theformofthepotential,andtherelativedistancebetweenparticles. Incomplexsystems,interactionsareoften specific.Notallelements,onlycertainpairsor groupsofelements,interactwitheachother.Networksareusedtokeeptrackofwhich elementsinteractwithothersinacomplexsystem.
1.2.2Whatdoespredictivemean?
Physicsisanexperimentalandapredictivescience.Letusassumethatyouperforman experimentrepeatedly;forexample,youdropastoneandrecorditstrajectoryovertime. Thepredictiveortheoreticaltaskistopredictthistrajectorybasedonanunderstanding ofthephenomenon.SinceNewton’stime,understandingaphenomenoninphysics hasoftenmeantbeingabletodescribeitwithdifferentialequations.Aphenomenon isunderstooddynamicallyifitsessencecanbecapturedina differentialequation. Typically,thefollowingthree-stepprocessisthenfollowed:
1.Findthedifferentialequationstoencodeyourunderstandingofadynamical system.Intheexampleofourstone-droppingexperiment,we wouldperhapsapply Newton’sequation,
where t istime, x(t) isthetrajectory, m ismassofthestone,and F isforceonthe stone.Inourcase,wewouldhopetoidentifytheforcewithgravity,meaningthat F = gm.
2.Oncetheequationisspecified,trytosolveit.Theequationcanbesolved usingelementarycalculus,andweget, x(t) = x0 + v0t + 1 2 gt2.Tomakeatestable predictionwehavetofixtheboundaryorinitialconditions; inourcasewehave tospecifywhattheinitialposition x0 andinitialvelocity v0 areinourexperiment. Oncethisisdone,wehaveapredictionforthetrajectoryofthestone, x(t).
3.Comparetheresultwithyourexperiments.Doesthestonereallyfollowthis predictedpath x(t)?Ifitdoes,youmightclaimthatyouhaveunderstood somethingonaquantitative,predictive,andexperimental basis.Ifthestone (repeatedly)followsanothertrajectory,youhavetotryhardertofindabetter prediction.
Fixinginitialorboundaryconditionsmeanssimplytakingthesystemoutofits context,separatingitfromtherestoftheuniverse.Therearenofactors,otherthan theboundaryconditions,thatinfluencethemotionofthesystemfromtheoutside.That
IntroductiontoComplexSystems
suchaseparationofsystemsfromtheircontextisindeedpossibleisonereasonwhy physicshasbeensosuccessful,evenbeforecomputingdevicesbecameavailable.For manycomplexsystems,itisimpossibletoseparatethedynamicsfromthecontextin aclearway.Thismeansthatmanyoutsideinfluencesthatarenotunderexperimental controlwillsimultaneouslydeterminetheirdynamics.
Inprinciple,thesamethinkingusedtodescribephysicalphenomenaholdsfor arbitrarilycomplicatedsystems.Assumethatavector X (t) representsthestateofa systematagiventime(e.g.allpositionsandmomentaofitselements),wethengeta setofequationsofmotionintheform,
where G isahigh-dimensionalfunction.Predictivemeansthat,inprinciple,these equationscanbesolved.Pierre-SimonLaplacewasfollowingthisprinciplewhenhe introducedahypotheticaldaemonfamiliarwiththeNewtonianequationsofmotionand alltheinitialconditionsofalltheelementsofalargesystem(theuniverse)andthusableto solveallequations.Thisdaemoncouldthenpredicteverything.Theproblem,however, isthatsuchadaemonishardtofind.Infact,theseequationscanbedifficult,even impossible,tosolve.Alreadyforthreebodiesthatexertagravitationalforceoneachother, thefamousthree-bodyproblem(e.g.Sun,Earth,Moon),thereisnogeneralanalytical solutionprovidedbyalgebraicandtranscendentalfunctions.Thiswasfirstdemonstrated byHenriPoincaréandpavedthewayforwhatistodaycalledchaostheory.Infact, thestrictNewton–Laplaceprogramofapredictableworldin termsofunambiguously computabletrajectoriesiscompletelyuselessformostsystemscomposedofmany particles.Aretheselargesystemsnotthenpredictable?Whataboutsystemswithan extremelylargenumberofelements,suchasgases,whichcontainoftheorderof O(1023) molecules?
Imaginethatweperformthefollowingexperimentoverandoveragain:weheatand coolwater.Wegaintheinsightthatifwecoolwaterto0oCandbelow,itwillfreeze, thatifweheatitto100oCitwillstarttoboiland,understandardconditions,ultimately evaporate.Thesephasetransitionswillhappenwithcertainty.Inthatsense,theyare predictable.Wecannotpredictfromtheequationsofmotion whichmoleculewillbethe firsttoleavetheliquid.Givenappropriateinstrumentation,wecanperhapsmeasurethe velocityofafewsinglegasmoleculesatapointintime,butcertainlynotall1023.What canbemeasuredistheprobabilitydistributionthatagasmoleculeisobservedwitha specificvelocity v,
where T istemperature,and k isBoltzmann’sconstant.Giventhisprobabilitydistribution,itispossibletoderiveanumberofpropertiesofgases thatperfectlydescribetheir macroscopic behaviourandmakethempredictableonamacroscopic(orsystemic)level.
Componentsfromphysics 5
Fornon-interactingparticles,thesepredictionscanbeextremelyprecise.Thepredictions immediatelystarttodegenerateassoonastherearestronginteractionsbetweenthe particlesorifthenumberofparticlesisnotlargeenough.Notethatthetermprediction nowhasamuchweakermeaningthanintheNewton–Laplaceprogram.Themeaning hasshiftedfrombeingadescriptionbasedontheexactknowledgeofeachcomponent ofasystemtoonebasedonaprobabilisticknowledgeofthesystem.Eventhoughone canstillmakeextremelyprecisepredictionsaboutmultiparticlesystemsinaprobabilistic framework,theconceptofdeterminismisnowdiluted.Theframeworkforpredictions onamacroscopiclevelaboutsystemscomposedofmanyparticlesonaprobabilistic basisiscalledstatisticalmechanics.
1.2.3Statisticalmechanics—predictability onstochasticgrounds
Theaimofstatisticalmechanicsistounderstandthemacroscopicpropertiesofasystem onthebasisofastatisticaldescriptionofitsmicroscopic components.Theideabehind itistolinkthemicroscopicworldofcomponentswiththemacroscopicpropertiesofthe aggregatesystem.Anessentialconceptthatmakesthislink possibleisBoltzmann–Gibbs entropy.
Asystemisoftenpreparedinamacrostate,whichmeansthataggregateproperties likethetemperatureorpressureofagasareknown.Thereare typicallymanypossiblemicrostatesthatareassociatedwiththatmacrostate.Amicrostateisapossible microscopicconfigurationofasystem.Forexample,aparticularmicrostateisonefor whichallpositionsandvelocitiesofgasmoleculesinacontainerareknown.Thereare usuallymanymicrostatesthatcanleadtooneandthesamemacrostate;forexample,the temperatureandpressureinthecontainer.Instatisticalmechanics,themaintaskisto computetheprobabilitiesforthemanymicrostatesthatleadtothatsinglemacrostate.In physics,themacroscopicdescriptionisoftenrelativelysimple.Macroscopicproperties areoftenstronglydeterminedbythephaseinwhichthesystemis.Physicalsystemsoften haveveryfewphases—typicallysolid,gaseous,orliquid.
WithintheNewton–Laplaceframework,traditionalphysics workswithextreme precisionforveryfewparticlesorforextremelymanynon-interactingparticles,where thestatisticalmechanicsofBoltzmann–Gibbsapplies.Inotherwords,theclassof systemsthatcanbeunderstoodwithtraditionalphysicsisnotthatbig.Mostsystemsare composedofmanystronglyinteractingparticles.Often,theinteractionsareofmultiple types,arenon-linear,andvaryovertime.Veryoften,suchsystemsarecomplexsystems.
1.2.4Theevolutionoftheconceptofpredictabilityinphysics
Theconceptofpredictionandpredictabilityhaschangedin significantwaysoverthe pastthreecenturies.Predictionintheeighteenthcentury wasquitedifferentfromthe conceptofpredictioninthetwenty-first.Theconceptofdeterminismhasundergoneat leastthreetransitions[300].
IntroductiontoComplexSystems
Inthe classicalmechanics oftheeighteenthandnineteenthcenturies,predictionmeant theexactpredictionoftrajectories.Equationsofmotionwouldmakeexactstatements aboutthefutureevolutionofsimpledynamicalsystems.The extensiontomorethan twobodieshasbeencausingproblemssincetheverybeginningofNewtonianphysics; see,forexample,thefamousconflictbetweenIsaacNewtonandJohnFlamsteedonthe predictabilityoftheorbitoftheMoon.Byabout1900,wheninterestinunderstanding many-bodysystemsarose,theproblembecameapparent.ThetheoryofLudwigBoltzmann,referredtonowadaysasstatisticalmechanics,waseffectivelybasedonthethen speculativeexistenceofatomsandmolecules,anditdrasticallychangedtheclassical conceptofpredictability.
In statisticalmechanics,basedontheassumptionthatatomsandmoleculesfollow Newtoniantrajectories,thelawoflargenumbersallowsstochasticpredictionstobe madeaboutthemacroscopicbehaviourofgases.Statisticalmechanicsisatheoryof themacroscopicorcollectivebehaviourofnon-interactingparticles.Theconceptsof predictabilityanddeterminismweresubjecttofurtherchangeinthe1920swiththe emergenceofquantummechanicsandnon-lineardynamics.
In quantummechanics,theconceptofdeterminismdisappearsaltogetherdueto thefundamentalsimultaneousunpredictabilityofthepositionandmomentumofthe (sub-)atomiccomponentsofasystem.However,quantummechanicsstillallowsusto makeextremelyhigh-qualitypredictionsonacollectivebasis.Collectivephenomena remainpredictabletoalargeextentonamacro-orsystemiclevel.
In non-linearsystems,itbecameclearthateveninsystemsforwhichtheequationsof motioncanbesolvedinprinciple,thesensitivitytoinitialconditionscanbesoenormous thattheconceptofpredictabilitymust,forallpracticalpurposes,beabandoned.Afurther crisisintermsofpredictabilityaroseinthe1990s,wheninterestinmoregeneralforms ofinteractionsbegantoappear.
In complexsystems,thesituationisevenmoredifficultthaninquantummechanics, wherethereisuncertaintyaboutthecomponents,butnotaboutitsinteractions.For manycomplexsystems,notonlycancomponentsbeunpredictable,buttheinteractions betweencomponentscanalsobecomespecific,time-dependent,non-linear,andunpredictable.However,thereisstillhopethatprobabilisticpredictionsaboutthedynamics andthecollectivepropertiesofcomplexsystemsarepossible.Progressinthescienceof complexsystemswill,however,beimpossiblewithoutadetailedunderstandingofthe dynamicsofhowelementsspecificallyinteractwitheachother.Thisis,ofcourse,only possiblewithmassivecomputationaleffortandcomprehensivedata.
1.2.5Physicsisanalytic,complexsystemsarealgorithmic
Physicslargelyfollowsan analytical paradigm.Knowledgeofphenomenaisexpressed inanalyticalequationsthatallowustomakepredictions.Thisispossiblebecause interactionsarehomogeneous,isotropic,andofasingletype.Interactionsinphysics typicallydonotchangeovertime.Theyareusuallygivenand fixed.Thetaskistowork outspecificsolutionsregardingtheevolutionofthesystem foragivensetofinitialand boundaryconditions.
Componentsfromphysics 7
Thisisradicallydifferentforcomplexsystems,whereinteractionsthemselvescan changeovertimeasaconsequenceofthedynamicsofthesystem.Inthatsense,complex systemschangetheirinternalinteractionstructureastheyevolve.Systemsthatchange theirinternalstructuredynamicallycanbeviewedas machines thatchangetheirinternal structureastheyoperate.However,adescriptionoftheoperationofamachineusing analyticalequationswouldnotbeefficient.Indeed,todescribeasteamenginebyseeking thecorrespondingequationsofmotionforallitspartswouldbehighlyinefficient. Machinesarebestdescribedas algorithms—alistofrulesregardinghowthedynamicsof thesystemupdatesitsstatesandfutureinteractions,whichthenleadtonewconstraints onthedynamicsatthenexttimestep.First,pressurebuilds uphere,thenavalveopens there,vapourpushesthispiston,thenthisvalveclosesand opensanotherone,driving thepistonback,andsoon.
Algorithmicdescriptionsdescribenotonlytheevolutionofthestatesofthecomponentsofasystem,butalsotheevolutionofitsinternalstates(interactions)thatwill determinethenextupdateofthestatesatthenexttimestep. Manycomplexsystemswork inthisway:statesofcomponentsandtheinteractionsbetweenthemaresimultaneously updated,whichcanleadtothetremendousmathematicaldifficultiesthatmakecomplex systemssohardtounderstand.Thesedifficultiesintheirvariousformswillbeaddressed timeandagaininthisbook.Wheneveritispossibletoignorethechangesinthe interactionsinadynamicalsystem,analyticdescriptions becomemeaningful.
Physicsisgenerallyanalytic,complexsystemsarealgorithmic.Quantitativepredictionsthatcanbetestedexperimentallycanbemadewithintheanalyticorthe algorithmicparadigm.
1.2.6Whatarecomplexsystemsfromaphysicspointofview?
Fromaphysicspointofview,onecouldtrytocharacterizecomplexsystemsbythe followingextensionstophysics.
• Complexsystemsarecomposedofmanyelements,components, orparticles. Theseelementsaretypicallydescribedbytheirstate,such asvelocity,position, age,spin,colour,wealth,mass,shape,andsoon.Elementsmayhavestochastic components.
• Elementsarenotlimitedtophysicalformsofmatter;anythingthatcaninteract andbedescribedbystatescanbeseenasgeneralizedmatter.
• Interactionsbetweenelementsmaybespecific.Whointeractswithwhom,when, inwhatform,andhowstrongisdescribedbyinteractionnetworks.
• Interactionsarenotlimitedtothefourfundamentalforces,butcanbeofamore complicatedtype.Generalizedinteractionsarenotlimitedtotheexchangeof gaugebosons,butcanbemediatedthroughexchangeofmessages,objects,gifts, information,evenbullets,andsoon. continued
• Complexsystemsmayinvolvesuperpositionsofinteractionsofsimilarstrengths.
• Complexsystemsareoftenchaoticinthesensethattheydependstronglyonthe initialconditionsanddetailsofthesystem.Updateequationsthatalgorithmically describethedynamicsareoftennon-linear.
• Complexsystemsareoftendrivensystems.Someobeyconservationlaws,some donot.
• Complexsystemscanexhibitarichphasestructureandhavea hugevarietyof macrostatesthatoftencannotbeinferredfromthepropertiesoftheelements.This issometimesreferredtoas emergence.Simpleformsofemergenceare,ofcourse, alreadypresentinphysics.Thespectrumofthehydrogenatomortheliquidphase ofwaterareemergentpropertiesoftheinvolvedparticlesandtheirinteractions.
Withtheseextensions,wecanderiveaphysics-baseddefinitionforwhatthetheory ofcomplexsystemsis.
Thetheoryofcomplexsystemsisthequantitative,predictiveandexperimentally testablescienceofgeneralizedmatterinteractingthroughgeneralizedinteractions.
Generalizedinteractionsaredescribedbytheinteraction typeandwhointeractswith whomatwhattimeandatwhatstrength.Iftherearemorethantwointeractingelements involved,interactionscanbeconvenientlydescribedbytime-dependentnetworks,
Mα ij (t),
where i and j labeltheelementsinthesystem,and α denotestheinteractiontype. Mα ij (t) arematrixelementsofastructurewiththreeindices.Thevalue Mα ij (t) indicates thestrengthoftheinteractionoftype α betweenelement i and j attime t. Mα ij (t) = 0 meansnointeractionofthattype.Interactionsincomplexsystemsremainbasedonthe conceptofexchange;however,theyarenotlimitedtotheexchangeofgaugebosons.In complexsystems,interactionscanhappenthroughcommunication,wheremessagesare exchanged,throughtradewheregoodsandservicesareexchanged,throughfriendships, wherebottlesofwineareexchanged,andthroughhostility, whereinsultsandbulletsare exchanged.
Becauseofmorespecificandtime-varyinginteractionsandtheincreasedvarietyof typesofinteraction,thevarietyofmacroscopicstatesand systemicpropertiesincreases drasticallyincomplexsystems.Thisdiversityincreaseof macrostatesandphenomena emergesfromthepropertiesbothofthesystem’scomponents anditsinteractions. Thephenomenonofcollectivepropertiesarisingthatare,a priori,unexpectedfrom theelementsaloneissometimescalled emergence.Thisismainlyaconsequenceofthe presenceofgeneralizedinteractions.Systemswithtime-varyinggeneralizedinteractions canexhibitanextremelyrichphasestructureandmaybeadaptive.Phasesmayco-exist inparticularcomplexsystems.Thepluralityofmacrostatesinasystemleadstonewtypes
Componentsfromphysics 9 ofquestionsthatcanbeaddressed,suchas:whatisthenumberofmacrostates?Whatare theirco-occurrencerates?Whatarethetypicalsequencesofoccurrence?Whatarethe life-timesofmacrostates?Whataretheprobabilitiesoftransitionbetweenmacrostates? Asyet,therearenogeneralanswerstothesequestions,andtheyremainachallengefor thetheoryofcomplexsystems.Formanycomplexsystems,the frameworkofphysicsis incomplete.Someofthemissingconceptsarethoseofnon-equilibrium,evolution,and co-evolution.Theseconceptswillbeillustratedinthesectionsthatfollow.
1.2.7Anoteonchemistry—thescienceofequilibria
Inchemistry,interactionsbetweenatomsandmoleculesare specificinthesensethat noteverymoleculebindsto(interactswith)anyothermolecule.Sowhyischemistry usuallynotconsideredtobeacandidateforatheoryofcomplexsystems?Toalarge extent,chemistryisbasedonthelawofmassaction.Manyparticlesinteractinwaysthat leadtoequilibriumstates.Forexample,considertwosubstances A and B thatundergo areactiontoformsubstances S and T,
where α, β , σ , τ arethestoichiometricconstants,and k+ and k aretheforwardand backwardreactionrates,respectively.Theforwardreactionhappensataratethatis proportionalto k+{A}α {B}β ,thebackwardreactionisproportionalto k {S}σ {T }τ .The bracketsindicatetheactive(reacting)massesofthesubstances.Equilibriumisattained iftheratioofthereactionratesequalsaconstant K,
Notethatthesolutiontothisequationgivesthestationary concentrationsofthe varioussubstances.Technically,theseequationsarefixed pointequations.Incontrastto chemicalreactionsandstatisticalmechanics,manycomplexsystemsarecharacterized bybeingout-of-equilibrium.Complexsystemsareoftenso-calleddrivensystems,where thesystemis(exogenously)drivenawayfromitsequilibriumstates.Ifthereisno equilibrium,thereisnowayofusingfixed-point-typeequationstosolvetheproblems. Themathematicaldifficultiesindealingwithout-of-equilibriumornon-equilibrium systemsaretremendousandgenerallybeyondanalyticalreach.Onewaythatoffers ahandleonunderstandingdrivenout-of-equilibriumsystemsistheconceptofselforganizedcriticality,whichallowsessentialelementsof thestatisticsofcomplexsystems tobeunderstood;inparticular,theomnipresenceofpowerlaws.
Manycomplexsystemsaredrivensystemsandareout-of-equilibrium.
IntroductiontoComplexSystems
Bycomparingthenatureofcomplexsystemsandbasicequilibriumchemistry,we learnthatthemerepresenceofspecificinteractionsdoesnotautomaticallyleadus tocomplexsystems.However,cyclicalcatalyticchemicalreactions[22,113,205],are classicprototypesofcomplexsystems.
1.3Componentsfromthelifesciences
Wenowpresentseveralkeyfeaturesofcomplexsystemsthathavebeenadoptedfrom biology.Inparticular,wediscusstheconceptsofevolution,adaptation,self-organization, and,again,networks.
Thelifesciencesdescribetheexperimentalscienceoflivingmatter.Whatisliving matter?Areasonableminimalanswerhasbeenattemptedbythefollowingthree statements[223]:
• Livingmattermustbeself-replicating.
• ItmustrunthroughatleastoneCarnotcycle.
• Itmustbelocalized.
Lifewithoutself-replicationisnotsustainable.Itis,of course,conceivablethatnonself-replicatingorganismscanbecreatedthatliveforatimeandthenvanishandhaveto berecreated.However,thisisnothowweexperiencelifeontheplanet,whichisbasically asingle,continuous,livinggermlinethatoriginatedabout3.5billionyearsago,andhas existedeversince.ACarnotcycleisathermodynamiccyclicalprocessthatconverts thermalenergyintowork,orviceversa.Startingfromaninitialstate,afterthecycleis completed,thesystemreturnstothesameinitialstate.The notionthatlivingmattermust performatleastoneCarnotcycleismotivatedbythefactthatalllivingorganismsuse energygradients(usuallythermal)toperformworkofsomekind.Forexample,thiswork couldbeusedformovingorcopyingDNAmolecules.Thisviewalsopaystributetothe factthatalllivingobjectsareout-of-equilibriumandconstantlydrivenbyenergygradients.If,afterperformingwork,asystemwerenotabletoreachitspreviousstates,itwould behardtocallitalivingsystem.Bothself-replicationand Carnotcyclesrequiresome sortoflocalization.Onthisplanet,thislocalizationtypicallyhappensatthelevelofcells.
Livingmatterusesenergyandperformsworkonshorttimescaleswithoutsignificantlytransformingitself.Itisconstantlydrivenbyenergygradientsandisout-ofequilibrium.Self-replicationandCarnotcyclesrequirelocalization.
1.3.1Chemistryofsmallsystems
Livingmatter,asweknowitonthisplanet,isaself-sustainedsequenceofgeneticactivity overtime.Bygeneticactivitywemeanthatgenes(locations ontheDNA)canbeturned
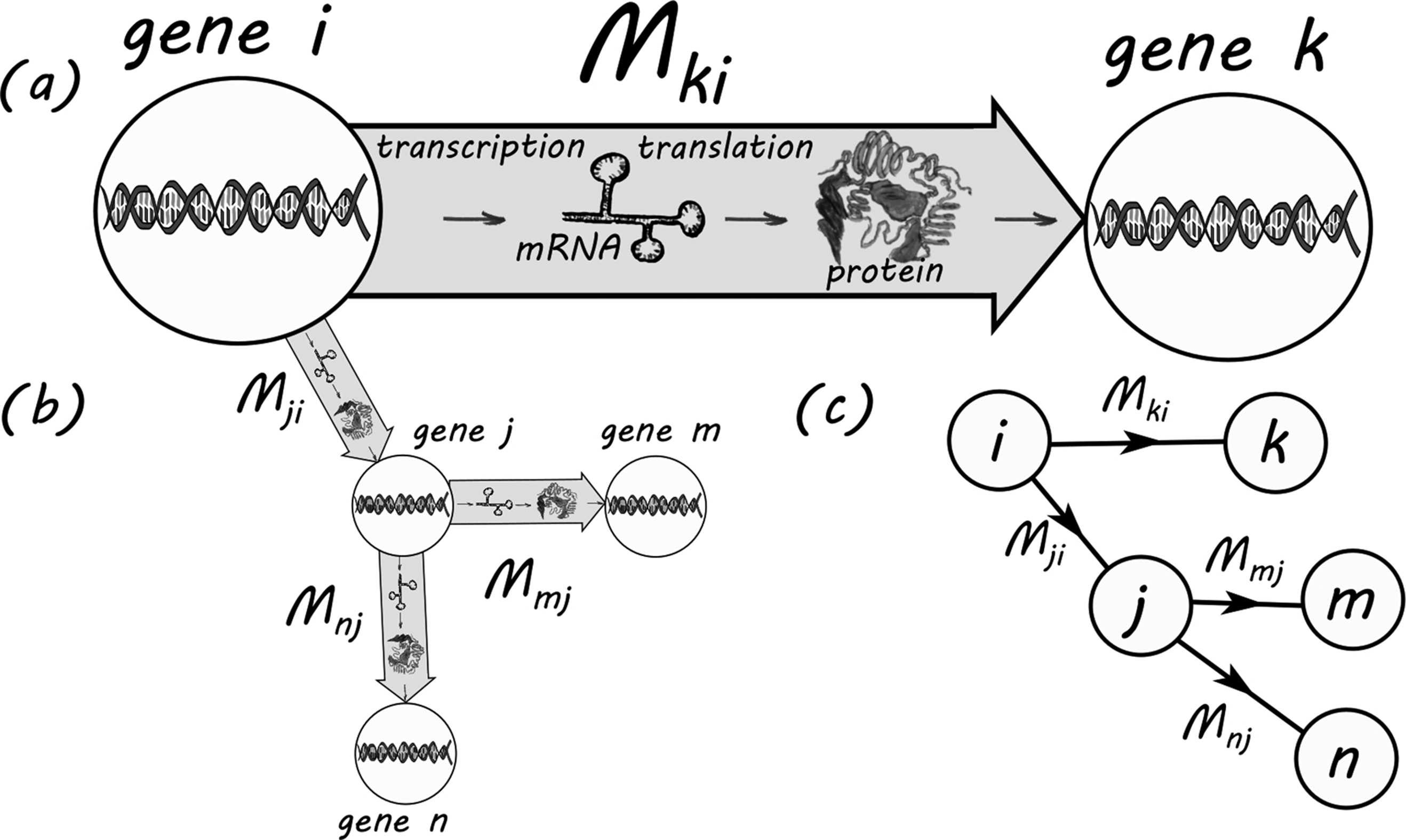
Figure1.1 SchematicviewofgeneticactivityandwhatalinkMki meansinageneticregulatory network.(a)Geneiactivatesgenekifsomethinglikethefollowingprocesstakesplace:theactivityof geneimeansthataspecificsub-sequenceofthedeoxyribonucleicacid(DNA)(gene)iscopiedintoa complementarystructure,anmRNAmolecule.ThismRNAmoleculefromgenei,mightget‘translated’ (copiedagain)intoaproteinoftypei.Thisproteincanbindwithotherproteinstoformaclusterofproteins, a‘complex’.SuchcomplexescanbindtootherregionsoftheDNA,say,theregionthatisassociatedwith genek,andtherebycausetheactivationofgenek.(b)Geneicausesgenejtobecomeactive,whichactivates genesmandn.(c)Theprocess,wheretheactivityofgeneitriggerstheactivityofothergenes,canbe representedasadirectedgeneticregulatorynetwork.Complexescanalsodeactivategenes.Ifgenejis active,acomplexmightdeactivateit.
‘on’and‘off’.Ifageneison,ittriggerstheproductionofmolecularmaterial,suchas ribonucleicacid(RNA)thatcanlaterbetranslatedintoproteins.Ageneistypically turnedonbyaclusterofproteinsthatbindtoeachothertoformaso-called‘complex’. IfsuchaclusterbindstoaspecificlocationontheDNA,thiscouldcauseacopying processtobeactivatedatthisposition;thegeneisthenactiveor‘on’;seeFigure1.1. Geneticactivityisbasedonchemicalreactionsthattakeplacelocally,usuallywithin cellsortheirnuclei.However,thesechemicalreactionsarespecialinthesensethatonly afewmoleculesareinvolved[341].Intraditionalchemistry,reactionsusuallyinvolve billionsofatomsormolecules.Whathappenswithinacellis chemistrywitha few molecules.Thisimmediatelyleadstoanumberofproblems:
• Itcannolongerbeassumedthatmoleculesmeetbychancetoreact.
• Withonlyafewmoleculespresentthatmightnevermeettoreact,theconceptof equilibriumbecomesuseless.
• Withoutequilibrium,thereisnolawofmassaction.
IntroductiontoComplexSystems
Ifthereisnolawofmassaction,howcanchemistrybedone?Classicalequilibrium chemistryisinadequatefordealingwithmolecularmechanismsinlivingmatter.In cells,moleculesareoftenactivelytransportedfromthesiteofproduction(typically,the nucleus,fororganismsthathaveone)towheretheyareneededinthecell.Thismeans thatdiffusionofmoleculesnolongerfollowstheclassical diffusionequation.Instead, moleculartransportisoftendescribablebyananomalousdiffusionequationoftheform,
where p(x, t) istheprobabilityoffindingamoleculeatposition x attime t, D isthe diffusionconstant,and µ and ν areexponentsthatmakethediffusionequationnonlinear.
Chemicalbindingoftendependsonthethree-dimensionalstructureofthemolecules involved.Thisstructurecandependonthe‘state’ofthemolecules.Forexample,a moleculecanbeinanormaloraphosphorylatedstate.Phosphorylationhappensthrough theadditionofaphosphorylgroup(PO2 3 )toamolecule,whichmaychangeitsentire structure.Thismeansthatforaparticularstateofamoleculeitbindstoothers,but doesnotbindifitisintheotherstate.Afurthercomplicationinthechemistryofa fewparticlesariseswiththereactionrates.Bydefinition, thetermreactionrateonly makessenseforsufficientlylargesystems.Thespeedofreactionsdependscruciallyon thestatisticalmechanicsoftheunderlyingsmallsystemandfluctuationtheoremsmay nowbecomeimportant[122].
1.3.2Biologicalinteractionshappenon networks—almostexclusively
Geneticregulationgovernsthetemporalsequenceoftheabundanceofproteins,nucleic material,andmetaboliteswithinanylivingorganism.Toalargeextent,geneticregulation canbeviewedasadiscreteinteraction:ageneisactiveorinactive;aproteinbindsto anotheroritdoesnot;amoleculeisphosphorylatedornot.Discreteinteractionsare well-describedbynetworks.Inthecontextofthelifesciences,threewell-knownnetworks arethemetabolicnetwork,theprotein–proteinbindingnetwork,andtheBooleangeneregulatorynetwork.Themetabolicnetwork1 isthesetoflinkedchemicalreactions occurringwithinacellthatdeterminethecell’sphysiologicalandbiochemicalproperties. Themetabolicnetworkisoftenrepresentedinnetworksofchemicalreactions,where nodesrepresentsubstancesanddirectedlinks(arrows)correspondtoreactionsor catalyticinfluences.Theprotein–proteinnetworksrepresentempiricalfindingsabout protein–proteininteractions(binding)innetworkrepresentations[102].Nodesare proteins,andlinksspecifytheinteractiontypebetweenthem.Differentinteractiontypes includestable,transient,andhomo-orhetero-oligomerinteractions.
1 Foranexampleofwhatmetabolicnetworkslooklike,seehttp://biochemical-pathways.com/#/map/1
1.3.3Whatisevolution?
‘Nothinginbiologymakessenseexceptinthelightofevolution’.Theodosius Dobzhansky
Evolutionisanaturalphenomenon.Itisaprocessthatincreasesanddestroysdiversity, anditlookslikebotha‘creative’anda‘destructive’process.Evolutionappearsinbiological,technological,economical,financial,historical,andothercontexts.Inthatsense, evolutionarydynamicsisuniversal.Evolutionarysystems followcharacteristicdynamical andstatisticalpatterns,regardlessofthecontext.These patternsaresurprisinglyrobust and,asanaturalphenomenon,theydeserveaquantitativeandpredictivescientific explanation.
Whatisevolution?Geneticmaterialandtheprocessofreplicationinvolveseveral stochasticcomponentsthatmayleadtovariationsintheoffspring.Replicationand variationaretwoofthethreemainingredientsofevolutionaryprocesses.Whatevolution meansinabiologicalcontextiscapturedbytheclassicDarwiniannarrative.Consider apopulationofsomekindthatisabletoproduceoffspring.Thisoffspringhassome randomvariations(e.g.mutations).Individualswiththeoptimalvariationswithrespect toagivenenvironmenthaveaselectionadvantage(i.e.higherfitness).Fitnessmanifests itselfbyhigherreproductivesuccess.Individualswithoptimalvariationswillhavemore offspringandwillthuspasstheirparticularvariationson toanewgeneration.Inthis way‘optimal’variationsareselectedovertime.Thisiscertainlyaconvincingdescription ofwhatisgoingon;however,inthisformitmaynotbeusefulforpredictivescience. Howcanwepredictthefitnessofindividualsinfuturegenerations,giventhatlifein futureenvironmentswilllookverydifferentfromwhatitis today?Exceptoververy shorttimeperiods,thisisatrulychallengingtaskthatisfarfromunderstood.Thereisa goodprospect,however,ofthe statistics ofevolutionarysystemsbeingunderstood.The Darwinianscenariofailstoexplainessentialfeaturesaboutevolutionarysystems,suchas theexistenceofboomandcrashphases,wherethediversityofsystemsradicallychanges withinshortperiodsoftime.Anexampleisthemassivediversification(explosion)of speciesandgeneraabout500millionyearsagointheCambrianera.Itwillalmostcertainlyneverbepossibletopredictwhatspecieswillliveon Eartheven500yearsfromnow, butitmaybeperfectlypossibletounderstandthestatisticsofevolutionaryeventsandthe factorsthatdeterminethestatistics.Inparticular,statisticalstatementsaboutexpected diversity,diversificationrates,robustness,resilience,andadaptabilityarecomingwithin reach.InChapter5wewilldiscussapproachestoformulatingevolutionarydynamicsin waysthatmakethemaccessiblebothcombinatoriallyandstatistically.
Theconceptofevolutionisnotlimitedtobiology.Intheeconomy,theequivalentof biologicalevolutionisinnovation,wherenewgoodsandservicesareconstantlybeing producedbycombinationofexistinggoodsandservices.Somenewgoodswillbe selectedinmarkets,whilethemajorityofnoveltieswillnotbeviableandwillvanish. Theindustrialrevolutioncanbeseenasoneresultofevolutionarydynamics,leading, asitdid,toanongoingexplosionofdiversificationofgoods,services,andinnovations.