ToallonthequestfortheTruth
Chapter1:TheMagicofQuantumMechanics....................................1
1.1Historyofarevolution.........................................................5 1.2Postulatesofquantummechanics.............................................18 1.3TheHeisenberguncertaintyprinciple.........................................41 1.4TheCopenhageninterpretationoftheworld..................................46
1.5HowtodisprovetheHeisenbergprinciple?TheEinstein–Podolsky–Rosen’s recipe...........................................................................47
1.6ThelifeanddeathofSchrödinger’scat...
Chapter2:TheSchrödingerEquation.............................................69
2.1SymmetryofthenonrelativisticHamiltonianandtheconservationlaws...72
2.1.1Invariancewithrespecttotranslation....................................77
2.1.2Invariancewithrespecttorotation.......................................79
2.1.3Invariancewithrespecttopermutationofidenticalparticles (fermionsandbosons)....................................................80
2.1.4Invarianceofthetotalcharge.............................................80
2.1.5Fundamentalandlessfundamentalinvariances....... ..................81
2.1.6Invariancewithrespecttoinversion–parity............................81
2.1.7Invariancewithrespecttochargeconjugation...........................85
2.1.8Invariancewithrespecttothesymmetryofthenuclearframework....86
2.1.9Conservationoftotalspin................................................86
2.1.10Indicesofspectroscopicstates...........................................87
2.2Schrödingerequationforstationarystates....................................87
2.2.1WavefunctionsofclassQ................................................90
2.2.2Boundaryconditions. .....................................................93
2.3Thetime-dependentSchrödingerequation...................................96
2.3.1Evolutionintime..........................................................96
2.3.2Timedependenceofmechanicalquantities..............................97
2.3.3Meanenergyisconserved................................................99
2.3.4Symmetryisconserved...................................................99
2.3.5Energy-timeuncertaintyprinciple.......................................100
2.3.6Meditationsatwaterspring...............................................103
2.3.7Linearity...................................................................104
2.4Evolutionafterswitchingaperturbation......................................104
2.4.1Time-independentperturbation–thetwo-statemodel..................106
2.4.2Oscillatingperturbation–thetwo-statemodel..........................108
2.4.3Short-timeperturbation–thefirst-orderapproach......................110
2.4.4Time-independentperturbationandtheFermiGoldenRule............112
2.4.5OscillatingperturbationandtheFermiGoldenRule....................114 Chapter3:BeyondtheSchrödingerEquation.....................................123
3.1Aglimpseofclassicalrelativitytheory... ....................................127
3.1.1Thevanishingofapparentforces........................................127
3.1.2TheGalileantransformation.............................................130
3.1.3TheMichelson–Morleyexperiment....
3.1.4TheGalileantransformationcrashes.....................................133
3.1.5TheLorentztransformation..............................................134
3.1.6Newlawofaddingvelocities....
3.1.7TheMinkowskispace–timecontinuum..................................138
3.1.8Howdoweget E = mc 2 ?................................................142
3.2Towardsrelativisticquantummechanics......................................144
3.3TheDiracequation.............................................................147
3.3.1Theelectronicseaandthedayofglory..................................147
3.3.2TheDiracequationsforelectronandpositron..........................151
3.3.3Spinorsandbispinors.....................................................151
3.3.4Whatnext?................................................................153
3.3.5Largeandsmallcomponentsofthebispinor............................153
3.3.6HowtoavoiddrowningintheDiracsea.................................154
3.3.7FromDiractoSchrödinger–howtoderivethenonrelativistic Hamiltonian?..............................................................156
3.3.8Howdoesthespinappear?...............................................157
3.3.9Simplequestions..........................................................159
3.4Thehydrogen-likeatominDiractheory.. ....................................159
3.4.1Stepbystep:calculationofthehydrogen-likeatomgroundstate withinDiractheory.......................................................160
3.5Largersystems.................................................................166
3.6BeyondtheDiracequation.... .................................................170
3.6.1TheBreitequation........................................................171
3.6.2Afewwordsaboutquantumelectrodynamics...........................173
Chapter4:ExactSolutions–OurBeacons.......................................185
4.1Freeparticle ....................................................................188
4.2Boxwithends(andthemusic)................................................189
4.3Cyclicbox......................................................................193
4.3.1Comparisonoftwoboxes:hexatrieneandbenzene.....................196
4.4Carbonnanotube...............................................................200
4.5Singlebarrier ...................................................................203
4.5.1Tunnelingeffectbelowthebarrierheight................................203
4.5.2Surprisesforenergieslargerthanthebarrier............................207
4.6Themagicoftwobarriers .....................................................210
4.6.1Magicenergeticgates(resonancestates)................................211
4.6.2Strangeflightovertwobarriers..........................................215
4.7Harmonicoscillator ............................................................217
4.8Morseoscillator..
4.9Rigidrotator....................................................................229
4.10Hydrogen-likeatom ............................................................232
4.10.1Positroniumanditsshortlifeinmolecules..............................242
4.11Whatdoallthesesolutionshaveincommon?................................242
4.12Hookeheliumatom(harmonium).............................................243
4.13Hookemolecules...............................................................244
4.14CharmingSUSYandnewsolutions...........................................249
4.14.1SUSYpartners............................................................250
4.14.2RelationbetweentheSUSYpartners....................................251
4.15Beaconsandpearlsofphysics.................................................255
Chapter5:ThreeFundamentalApproximateMethods............................263
5.1Variationalmethod.............................................................265
5.1.1Variationalprinciple......................................................265
5.1.2Variationalparametersleadtothevariationalmethod..................269
5.1.3LinearvariationalparametersortheRitzmethod.......................271
5.2Methodofmoments............................................................273
5.3Perturbationalmethod.........................................................274
5.3.1Rayleigh–Schrödingerapproach.........................................274
5.3.2Hylleraasvariationalprinciple...........................................280
5.3.3Hylleraasequation........................................................281
5.3.4Degeneracy................................................................282
5.3.5Convergenceoftheperturbationalseries................................284
5.4Virialtheoremasaprobeofwavefunctionquality ..........................287
5.4.1Classicalmechanics–thevirial..........................................287
5.4.2Lookingatstars–thediscoveryofdarkmatter.........................288
5.4.3Quantummechanics......................................................288
5.4.4Areviewofexamples.....................................................290
5.4.5Whataboutthemeanvaluescalculatedwithanapproximatesolution?292
5.4.6Quantumchemistry:howusefulisthevirialtheorem?.................297
Chapter6:AKeyConceptofMolecular3DStructure–SeparationofElectronic andNuclearMotions.................................................305
6.1Separationofthecenter-of-massmotion......................................311
6.2Exact(nonadiabatic)theory.. .................................................315
6.3Adiabaticapproximation.......................................................318
6.4Born–Oppenheimerapproximation...........................................320
6.5Vibrationsofarotatingmolecule..............................................321
6.5.1Onemoreanalogy........................................................323
6.5.2Whatvibrates,whatrotates?.............................................324
6.5.3Thekeymessage:thepotentialenergysurface(PES)and molecularshape...........................................................326
6.6Basicprinciplesofelectronic,vibrationalandrotationalspectroscopy.....332
6.6.1Electronicandvibrationalstructure......................................332
6.6.2Rotationalstructure.......................................................332
6.7Approximateseparationofrotationsandvibrations..........................335
6.8UnderstandingtheIRspectrumofadiatomic:HCl..........................336
6.8.1Selectionrulesareconsequencesofconservationlaws.................337
6.8.2Microwavespectrumgivestheinternucleardistance...................339
6.8.3IRspectrumandisotopiceffect..........................................339
6.8.4Internucleardistance......................................................341
6.8.5Whywehaveaspectrum“envelope”....................................341
6.8.6Intensityofisotopomers’peaks. .........................................342
6.9Aquasiharmonicapproximation..............................................342
6.10Polyatomicmolecules..........................................................344
6.10.1Kineticenergyexpression................................................344
6.10.2Quasirigidmodel–simplifyingbyEckartconditions..................346
6.10.3Approximation:decouplingofrotationsandvibrations................348
6.10.4Spherical,symmetric,andasymmetrictops.............................348
6.10.5Separationoftranslational,rotational,andvibrationalmotions........350
6.11Typesofstates..................................................................351
6.11.1Repulsivepotential........................................................351
6.11.2“Hook-like”curves.. .....................................................351
6.11.3Continuum...
6.11.4Wavefunction“measurement”...........................................355
6.12Adiabatic,diabatic,andnonadiabaticapproaches ............................358
6.13Crossingofpotentialenergycurvesfordiatomics............................361
6.13.1Thenoncrossingrule .....................................................361
6.13.2SimulatingtheharpooningeffectintheNaClmolecule................363
6.14Polyatomicmoleculesandtheconicalintersection...........................367
6.14.1Branchingspaceandseamspace.........................................369
6.14.2Conicalintersection.......................................................369
6.14.3Berryphase................................................................371
6.14.4Theroleoftheconicalintersection–nonradiativetransitionsand photochemicalreactions.. ................................................373
6.14.5Whatisthenumberofconicalintersections?...........................375
6.15Atravelbeyondtheadiabaticapproximation .................................377
6.15.1Vibroniccoupling.........................................................377
6.15.2Consequencesforthequestofsuperconductors.........................381
6.15.3PhotostabilityofproteinsandDNA......................................383
6.15.4Muon-catalyzednuclearfusion. .........................................386
6.15.5“Russiandolls”–oramoleculewithinmolecule.......................388
7.1Rovibrationalspectra–anexampleofaccuratecalculations: atom–diatomicmolecule.......................................................401
7.1.1CoordinatesystemandHamiltonian.....................................401
7.1.2Anisotropyofthepotential V ............................................403
7.1.3Addingtheangularmomentainquantumphysics.... ..................404
7.1.4ApplicationoftheRitzmethod..........................................405
7.2Forcefields(FFs)...............................................................406
7.3Localmolecularmechanics....................................................411
7.3.1Bondsthatcannotbreak.. ................................................411
7.3.2Bondsthatcanbreak ......................................................413
7.4Globalmolecularmechanics..................................................413
7.4.1Multipleminimacatastrophe .............................................413
7.4.2Isittheglobalminimumwhichcounts?.................................414
7.5Smallamplitudeharmonicmotion–normalmodes..........................416
7.5.1Theoryofnormalmodes.................................................417
7.5.2Zero-vibrationenergy.....................................................426
7.6Moleculardynamics ...........................................................427
7.6.1Whatdoesmoleculardynamicsofferus?................................429
7.6.2Whattoworryabout?. ....................................................431
7.6.3Moleculardynamicsofnonequilibriumprocesses......................431
7.6.4Quantumclassicalmoleculardynamics.............
7.7Simulatedannealing...........................................................434
7.10Car–Parrinellodynamics. ......................................................443 7.11Cellularautomata..............................................................446
Chapter8:OrbitalModelofElectronicMotioninAtomsandMolecules..........457
8.1Hartree–Fockmethod–abird’seyeview....................................463
8.1.1Spinorbitalsastheone-electronbuildingblocks.......................464
8.1.2Variables...................................................................465
8.1.3Slaterdeterminant........................................................465
8.1.4WhatistheHartree–Fockmethodallabout?............................468
8.2TowardstheoptimalspinorbitalsandtheFockequation....................469
8.2.1Diracnotationforintegrals...............................................469
8.2.2Energyfunctionaltobeminimized......................................470
8.2.3Energyminimizationwithconstraints...................................471
8.2.4Slaterdeterminantsubjecttoaunitarytransformation..................475
8.2.5The ˆ J and ˆ K operatorsareinvariant.....................................476
8.2.6DiagonalizationoftheLagrangemultipliers............................477
8.2.7OptimalspinorbitalsaresolutionsoftheFockequation (generalHartree–Fock[GHF]method) ..................................478
8.2.8“Unrestricted”Hartree–Fock(UHF)method............................479
8.2.9TheclosedshellsystemsandtherestrictedHartree–Fock (RHF)method.............................................................479
8.2.10Iterativesolution:theSelf-ConsistentField(SCF)method.............488
8.3TotalenergyintheHartree–Fockmethod.....................................490
8.4Computationaltechnique:atomicorbitalsasbuildingblocksofthe molecularwavefunction.......................................................492
8.4.1Centeringoftheatomicorbital...........................................494
8.4.2Slater-typeorbitals(STOs)...............................................494
8.4.3Gaussian-typeorbitals(GTOs)...........................................495
8.4.4Linearcombinationofatomicorbitals(LCAO)method................499
8.4.5Basissetsofatomicorbitals..............................................504
8.4.6TheHartree–Fock–Roothaanmethod(SCFLCAOMO)...............504
8.4.7Somepracticalproblems.................................................507
8.5Backtofoundations ............................................................510
8.5.1WhendoestheRHFmethodfail?........................................510
8.5.2Fukutomeclasses.. .......................................................514
RESULTSOFTHEHARTREE–FOCKMETHOD
8.6Mendeleevperiodictable......................................................521
8.6.1Allatomsaresimilartothehydrogenatom–theorbitalmodelofan atom.......................................................................521
8.6.2Shellsandsubshells.......................................................522
8.6.3Educatedguessofatomicorbitals–theSlaterrules....................528
8.6.4Atomicradii...............................................................529
8.7Thenatureofthechemicalbond–quantummakesadifference............531
8.7.1Thesimplestchemicalbond:H+ 2 intheMOpicture....................531
8.7.2Canweseeachemicalbond?..... .......................................536
8.8Excitationenergy,ionizationpotential,andelectronaffinity (RHFapproach)................................................................537
8.8.1Approximateenergiesofelectronicstates...............................537
8.8.2Singletortripletexcitation?..............................................539
8.8.3Hund’srules.. .............................................................540
8.8.4Hund’srulesfortheatomicterms ........................................541
8.8.5Ionizationpotentialandelectronaffinity(Koopmans’theorem).......544
8.9Towardsachemicalpicture–localizationofmolecularorbitals............547
8.9.1Canachemicalbondbedefinedinapolyatomicmolecule?...........548
8.9.2Theexternallocalizationmethods .......................................549
8.9.3Theinternallocalizationmethods........................................550
8.9.4Examplesoflocalization.................................................552
8.9.5Localizationinpractice–computationaltechnique.....................554
8.9.6Thechemicalbondsof σ,π,δ symmetry................................555
8.9.7Electronpairdimensionsandthefoundationsofchemistry............558
8.9.8Hybridizationormixingone-centerAOs................................561
8.10Aminimalmodelofamolecule...............................................571
8.11Theisolobalanalogy...........................................................578
AppendixG:VectorandScalarPotentials........................................673
AppendixH:OptimalWaveFunctionfortheHydrogen-LikeAtom................683
AppendixI:TheVirialTheorem...................................................685
AppendixJ:Space-andBody-FixedCoordinateSystems...........................691
AppendixK:Orthogonalization...................................................697
AppendixL:DiagonalizationofaMatrix.........................................703
AppendixM:SecularEquation
AppendixN:Slater–CondonRules................................................707
AppendixO:LagrangeMultipliersMethod.......................................719
AppendixP:PenaltyFunctionMethod............................................725
AppendixQ:MolecularIntegralswithGaussian-TypeOrbitals
AppendixR:SingletandTripletStatesforTwoElectrons.........................731
AppendixS:TheHydrogenMolecularIonintheSimplestAtomicBasisSet.......735
AppendixT:DipoleMomentofaLonePair.......................................741
Quantumscimusguttaest,ignoramusmare
Whatweknowisadrop,whatwedonotknowisasea (Latinsentence)
Thisbook(volume1)isabouthowtounderstandthereasonforexistenceofmolecules,which theEarth,Nature,andourselvesarecomposedof.
Realityanditsimages
HaveyoueverseentheMilkyWayonthenightsky?Anexceptionalandbreathtakingexperience!Youfeelyourselflookingatagreatmystery,asifstandingontheshoresoftheUniverse, ofsomethingbeyondourimaginationofspaceandtime.Thewarmthofthecampfireflames andthecoldofthenight,theMoon,theMilkyWay,andthestars–allthatofferedawonderful, unique,andpuzzlingspectaclethat,formillennia,challengedourancestors’imaginationand posedtheBigQuestions: whatdowesee and whoarewe?
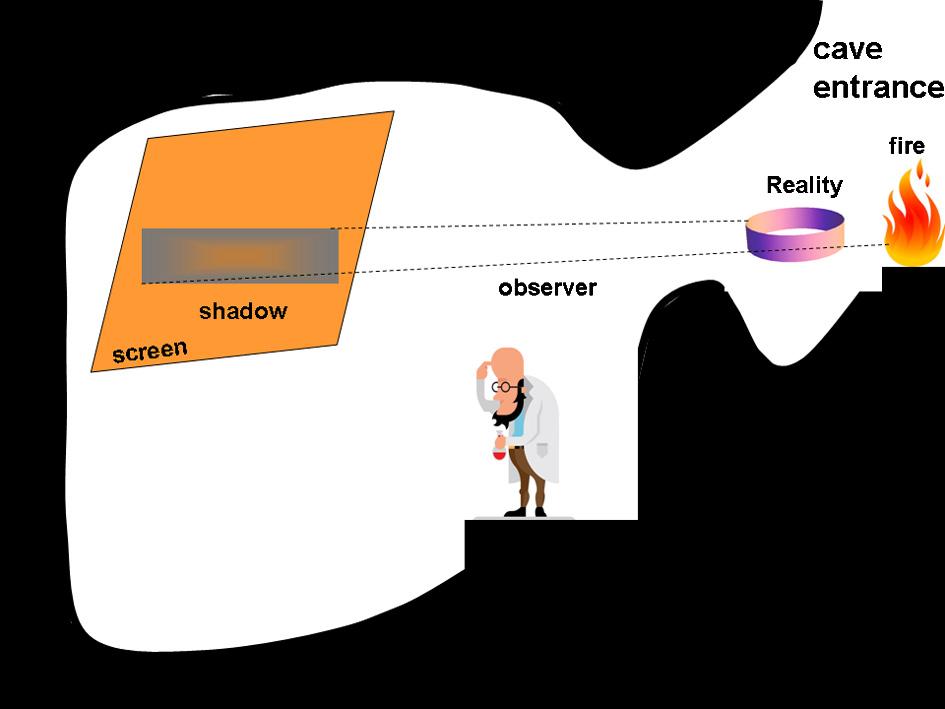
TheGreekphilosopherPlato(427–347BC)wasalreadyawarethatlookingattheskyislike lookingatshadowsofsomeunknownRealityseenonthewallofacave(litbyacampfire atitsentrance),Fig. 0.1.Itisoursensesthatconnectusandthe“shadows”somehowtothis mysteriousReality,whichwecalltheUniverse.WefeeltheUniverse’spresence,whileatthe sametimewe arepartofit –afascinatingthingbyitself.Canweunderstandwhathappens aroundusandinus?Manypeople,amongthemPlato,suspectedthatwhatweseeexhibitsa kindoforderorregularity,andthatmaybewe can understandit.Itismovingformetofeelthe spirituallinkbetweentheAcademiafoundedbyPlatointhesacredpieceoflandofAcademos inAthensandallofusinalluniversitiesoftheworld,whoareseekingthetruth,amongthem you,myfriend,whoarereadingthesewords.Usuallyafterpainfulwork,ifwearelucky,ina flashofenlightenmentasecretofNaturemaybedisclosedbeforeoureyes,agreatfeeling–ourprize,themostpreciousone.
Sensoryoperationsarethedirectresultofinteractions,bothbetweenmoleculesandbetween lightandmatter. All ofthesephenomenadealwithchemistry,physics,biology,andevenpsychology.Inthesecomplexeventsitisimpossibletodiscernpreciselywherethedisciplinesof
Fig.0.1. Plato’scave.Acavemanisabletoseeonlysomeshadowsonthecavewall.Theshadowsare producedbyanunknownRealityandafireoutsidethecave.
chemistry,physics,biology,andpsychologybeginandend.Anyseparationofthesedomainsis artificial.Theonlyreasonformakingsuchseparationsistofocusourattentionon some aspects ofoneindivisiblephenomenon.Sight,hearing,smell,taste,andtouch–aretheseouronlylinks andinformationchannelstotheUniverse?Howlittleweknowaboutit!Tofeelthat,justlook upatthesky.Amyriadofstarsarounduspointtonewworlds,whichwillremainunknownforever(becauseofdistance).Itistruethatbyingeniousspectrometrywehaveseriousgroundsto believethesestarsarebuiltfromthesamekindofmatterwehavearoundus.Thisboldconclusionwasquestionedquiterecently,sincewedonothavetheslightestideawhatkindofparticles represent90%ofthematterthatdoesnotshine(blackmatter).Thispertainstothemacroscale. Ontheotherend,imaginehowincrediblycomplicatedthechemistryof(unconditional)maternallovemustbe,themostbeautifulphenomenonintheUniverse!Scienceisacertainresponse ofhumanstoreducetheUnknown,butitcannotansweralllegitimatequestionsahumanbeing mayaskwhensittingatacampfire.ScienceisabletodiscoverlawsofNature,butisunable toansweraquestionlike: whydoesourworldconformtoanylawsatall1 ?Suchquestionsgo beyondscience.
Wetrytounderstandwhatmightbereallyaroundusbyconstructinginourmindsakind ofsimplifiedpicture,whichrepresentstosomeextentReality.Itcontainsseeminglyessential elements,beingdevoidofthoseelementsthatwethinkareirrelevant.Thesepictureswecall models.Anymodelreliesontheonehandonourperceptionofreality(ontheappropriatescale ofmassesandtime)emanatingfromourexperience,andontheotherhandonourabilityto
1 “Themostincomprehensiblethingabouttheworldisthatitisatallcomprehensible”(AlbertEinstein).
abstractbycreatingidealbeings.Theseidealbeingsseemtobeclosetotheconceptofideas (“forms”)thatPlatolovedmost.Manysuchmodelswillbedescribedinthisbook.
Itisfascinatingthatmanisabletomagnifytherealmofhissensesbyusingsophisticatedtools, e.g.,toseequarkssittinginaproton2 ortodiscoveranamazinglysimpleequationofmotion3 thatdescribesbothcosmiccatastrophes,withintensitybeyondourimagination,andtheflight ofabutterfly.AwatermoleculehasexactlythesamepropertiesinthePacificOceanason Marsorinanothergalaxy.Theconditionsovertheremaybequitedifferentfromthoseinour laboratory,butwe assume thatiftheseconditionscouldbeimposedinthelab,themolecule wouldbehaveinexactlythesameway.Weholdouthopethatasetofuniversalphysicallaws applyfortheentireUniverse.
Themodelofthesebasiclawsisnotyetcompleteorunified.Thankstotheprogressandimportantgeneralizationsofphysics,muchiscurrentlyunderstood.Forexample,forceswith seeminglydisparatesourceshavebeenreducedtoonlythreekinds:
• thoseattributedto stronginteractions (actinginnuclearmatter),
• thoseattributedto electroweakinteractions (thedomainofchemistry,biology,aswellas β -decay),
• thoseattributedto gravitationalinteractions (showingupmainlyinastrophysics).
Manyscientistsbelieveotherreductionsarepossible,perhapsuptoasinglefundamentalinteraction,onethatexplainsEverything(quotingFeynman:“thefrogsaswellasthecomposers”). Thisassertionisbasedontheconviction,whichseemstobesupportedbydevelopmentsin modernphysics,thatthelawsofNaturearenotonlyuniversal,butalsosimple.
Whichofthethreebasicinteractionsisthemostimportant?Thisisanill-conceivedquestion.Theanswerdependsontheexternalconditionsimposed(pressure,temperature)andthe magnitudeoftheenergyexchangedamongsttheinteractingobjects.Ameasureoftheenergyexchanged( E )maybetakentobethepercentageoftheaccompanyingmassdeficiency ( m)accordingtoEinstein’srelation E = mc 2 .Atagivenmagnitudeofexchangedenergiessomeparticlesarestable.Stronginteractionsproducethehugepressuresthataccompany thegravitationalcollapseofastarandleadtotheformationofneutronstars,wherethemass deficiency m approaches40%.Atsmallerpressures,whereindividualnucleimayexistand
2 Aprotonis1015 timessmallerthanahumanbeingandneverthelessin1970JeromeFriedman,HenryKendall, andRichardTaylorwereabletotakeaproton’sphotograph.Theyhaveshownusthreequarksandunknown electricallyneutralmatterthatbindsthequarkstogether(“gluons”)!
3 Accelerationisdirectly proportional toforce.Higherderivativesofthetrajectorywithrespecttotimedonot enterthisequation,neitherdoesthenatureorcauseoftheforce.Theequationisalsoinvariantwithrespecttoany possiblestartingpoint(position,velocity,andmass).Whataremarkablesimplicityandgenerality(withinlimits; seeChapter 3)!
Introduction
undergonuclearreactions(stronginteractions4 ),themassdeficiencyisoftheorderof1%. Atmuchlowerpressurestheelectroweakforcesdominate,nucleiarestable,andatomicand molecularstructuresemerge.Life(asweknowit)becomespossible.Theenergiesexchanged aremuchsmallerandcorrespondtoamassdeficiencyoftheorderofonlyabout10 7 %.The weakestofthebasicforcesisgravitation.Paradoxically,thisforceisthemostimportantonthe macroscale(galaxies,stars,planets,etc.).Therearetworeasonsforthis.Gravitationalinteractionssharewithelectricinteractionsthelongestrangeknown(bothdecayas1/r ).However, unlikeelectricinteractions5 thoseduetogravitationarenotshielded.ForthisreasontheEarth andtheMoonattracteachotherbyahugegravitationalforce6 whiletheirelectricinteraction isnegligible.ThisishowDavidconquersGoliath,sinceat anydistance electronsandprotonsattracteachotherbyelectrostaticforces,about40ordersofmagnitudestrongerthantheir gravitationalattraction.
Gravitationdoesnothaveanymeasurableinfluenceonthecollisionsofmoleculesleadingto chemicalreactions,sincereactionsareduetomuchstrongerelectricinteractions.7
Tendegreesonly
Duetostronginteractions,protonsovercomemutualelectrostaticrepulsionandform(togetherwithneutrons)stablenuclei,leadingtothevarietyofchemicalelements.Therefore, stronginteractionsaretheprerequisiteofanychemistry(excepthydrogenchemistry).However, chemistsdealwithalreadypreparedstablenuclei8 andthesestronginteractionshaveavery smallrange(ofabout10 13 cm)ascomparedtointer-atomicdistances(oftheorderof10 8 cm). Thisiswhyachemistmaytreatnucleiasstablepointchargesthatcreateanelectrostatic field. Testtubeconditionsallowforthepresenceofelectronsandphotons,thuscompletingthe setofparticlesthatonemightexpecttosee(someexceptionsarecoveredinthisbook).Thishas todowiththeorderofmagnitudeofenergiesexchanged;undertheconditionsofourchemical reactions,theenergiesexchangedexcludepracticallyallnuclearreactions.
4 Withacorrespondinglargeenergyoutput;theenergycomingfromthefusionD + D → Hetakingplaceonthe Sunmakesourexistencepossible.
5 Inelectrostaticinteractionschargesofoppositesignattracteachotherwhilechargesofthesamesignrepeleach other(Coulomb’slaw).Thisresultsinthefactthatlargebodies(builtofahugenumberofchargedparticles)are nearlyelectrically neutral andinteractelectricallyonlyveryweakly.Thisdramaticallyreducestherangeoftheir electricalinteractions.
6 HugetidesanddeformationsofthewholeEartharewitnesstothat.
7 Itdoesnotmeanthatgravitationhasnoinfluenceonreactants’concentrations.Gravitationcontrolstheconvection flowinliquidsandgases(andevensolids)andthereforeachemicalreactionorevencrystallizationmayproceed inadifferentmannerontheEarth’ssurface,inthestratosphere,inacentrifuge,orinspace.
8 Atleastonthetimescaleofchemicalexperiments.Instabilityofsomenucleiisusedbynuclearchemistryand radiationchemistry.
Onthevastscaleofattainabletemperatures9 chemicalstructuresmayexistinthenarrowtemperaturerangeof0KtothousandsofK.Abovethisrangeonehasplasma,whichrepresents asoupmadeofelectronsandnuclei.Nature,initsvibrantlivingform,requiresatemperature rangeofabout200–320K,amarginofonly120K.Onedoesnotrequireachemistforchemicalstructurestoexist.However,todevelopachemicalscienceonehastohaveachemist.This chemistcansurviveatemperaturerangeof273 ± 50K,i.e.,arangeofonly100K.Thereader hastoadmitthatachemistmaythinkofhisjobonlyinthenarrowrangeof290–300K,only 10K.
Grandunificationandmissionofchemistry
Supposeourdreamcomestrueandthegrandunificationofthethreeremainingbasicforces isaccomplishedoneday.WewouldthenknowthefirstprinciplesofconstructingEverything. Oneoftheconsequencesofsuchafeatisacatalogofalltheelementaryparticles;maybethe catalogwillbefinite,10 hopefullyitwillbesimple.Wemighthaveacatalogoftheconserved symmetries(whichseemtobemoreelementarythantheparticles).Ofcourse,knowingsuch firstprincipleswouldhaveanenormousconceptualimpactonallthephysicalsciences.Itcould createanimpressionthateverythingisclear,becausescienceiscomplete.Eventhoughsuch structuresandprocessesaregovernedbyfirstprinciples,itwouldstillbeverydifficulttopredict theirexistencebysuchprinciplesalone.Theresultingstructureswoulddependnotonlyonthe principles,butalsoontheinitialconditions,complexity,self-organization,etc.11 Therefore,if itdoeshappen,theGrandUnificationwillnotchangethegoalsofchemistry.
Organizationofthebook
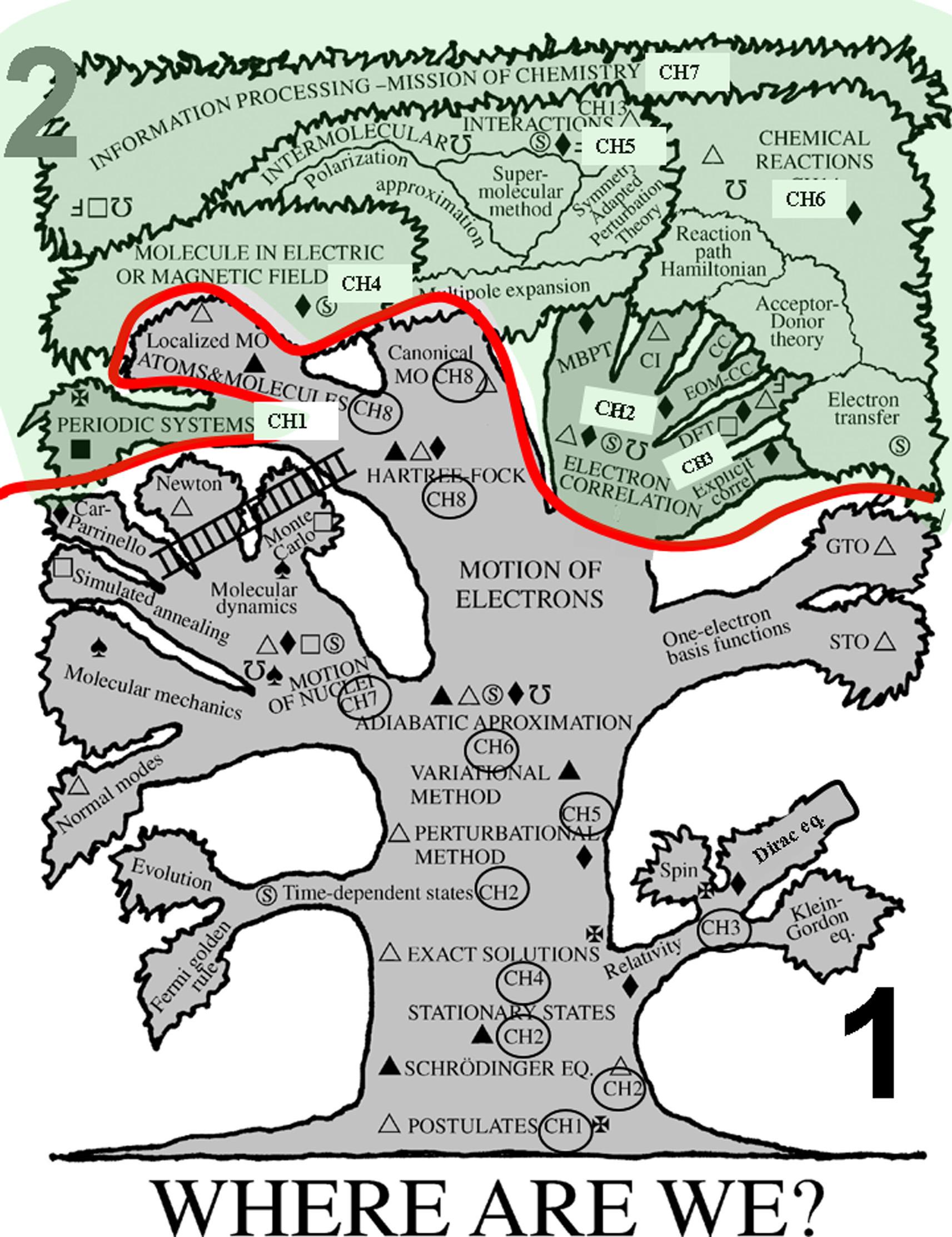
TREE
Anybookhasalinearappearance,i.e.,thetextgoespageafterpageandthepagenumbers remindusofthat.However,the logic ofvirtuallyanybookis nonlinear,andinmanycasescan bevisualizedbyadiagramconnectingthechaptersthat(logically)followfromoneanother.
9 Millionsofdegrees.
10 Noneofthisiscertain.Muchofelementaryparticleresearchreliesonlargeparticleaccelerators.Thisresearch resemblesdiscerningthecomponentsofacarbydroppingitfromincreasingheightsfromalargebuilding. Droppingitfromthefirstflooryieldsfivetiresandajack.Droppingfromthesecondfloorrevealsanengine and11screwsofsimilarappearance.Eventuallyaproblememerges:afterlandingfromaveryhighfloornew componentsappear(havingnothingtodowiththecar)andrevealthatsomeofthecollisionenergyhasbeen convertedtothenewparticles!
11 ThefactthatUncleJohnlikestodrinkcoffeewithcreamat5p.m.possiblyfollowsfromthefirstprinciples,but itwouldbeverydifficulttotracethatdependence.
Introduction
Suchadiagramallowsformultiplebranchesemanatingfromagivenchapter,particularlyif thebranchesareplacedlogicallyonanequalfooting.Suchlogicalconnectionsareillustrated inthisbookasaTREEdiagram(beginningofthebook).ThisTREEdiagramplaysavery importantroleinourbookandisintendedtobeastudyguide.Itisusedtoleadthereader inacertaindirection;fromtheTREEdiagram,thereadercanobservewhatthisdirectionis, whyhe/sheneedsthisdirection,whatwillfollow,andwhatbenefitshe/shewillgainafter suchstudy.Ifstudyingwereeasyanddidnotrequiretime,aTREEdiagrammightbeoflittle importance.However,theoppositeisusuallytrue.Inaddition,knowledgerepresentsmuch morethanaregistryoffacts.Anyunderstandinggainedfromseeingrelationshipsamongthose factsandmethodsplaysakeyrole.12 TheprimaryfunctionoftheTREEdiagramistomake theserelationshipsclear.
AthicklineinthecenteroftheTREEdiagramseparatesvolume1(bottompart)fromvolume2 (upperpart).
Theuseofhypertextininformationscienceissuperiortoatraditionallinearpresentation.It reliesonatreestructure.However,ithasaseriousdrawback.Sittingonabranch,wehave noideawhatthatbranchrepresentsinthewholediagram,whetheritisanimportantbranch oraremotetinyone,whetheritleadsfurthertoimportantpartsofthebookorwhetheritis justadeadend,andsoon.Atthesametime,aglimpseattheTREEdiagramshowsusthat thethicktrunkisthemostimportantstructure.Whatdowemeanbyimportant?Atleasttwo criteriamaybeused.Importantforthemajorityof readers,orimportantbecausethematerial isfundamentalforanunderstandingofthe lawsofNature.Ihavechosenthefirst.13 Thus,the trunkoftheTREEdiagramcorrespondstothepragmaticwaytostudythisbook. Thetrunkisthebackboneofthisbook.
• Itbeginsbypresentingpostulates,whichplayavitalroleinformulatingthefoundationof quantummechanics.
• Next,itcontinueswiththeSchrödingerequationforstationarystates,sofarthemostimportantequationinquantumchemicalapplications,and
• theseparationofnuclearandelectronicmotion(throughtheadiabaticorBorn–Oppenheimer approximation, thecentralideaofthepresentbookandchemistryingeneral).
12 Thisadvicecomesfromantiquity:“knowledgeismorepreciousthanfacts,understandingismorepreciousthan knowledge,wisdomismorepreciousthanunderstanding.”
13 Forexample,relativitytheoryplaysapivotalroleasafoundationofthephysicalsciences,butforthevast majorityofchemistsitspracticalimportanceandimpactaremuchsmaller.Shouldrelativityberepresented thereforeasthebaseofthetrunk,orasaminorbranch?Contemporaryinorganicchemistryandmetallo-organic chemistryconcentratecurrentlyonheavyelements,whererelativityeffectsareimportant.Wehavedecidedto makethesecondchoice,to not createtheimpressionthatthistopicisabsolutelynecessaryforthestudent.