HydrodynamicLubricationof Non-NewtonianFluids
PINGHUANG
SchoolofMechanicalandAutomotiveEngineering,SouthChina UniversityofTechnology,Guangzhou,China
QIANQIANYANG
SchoolofMechatronicEngineering,GuangdongPolytechnicNormal University,Guangzhou,China
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2023TsinghuaUniversityPressLimited.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorageand retrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowtoseek permission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangements withorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency, canbefoundatourwebsite: www.elsevier.com/permissions .
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchand experiencebroadenourunderstanding,changesinresearchmethods,professionalpractices, ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribedherein. Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafetyandthesafety ofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors, assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproducts liability,negligenceorotherwise,orfromanyuseoroperationofanymethods,products, instructions,orideascontainedinthematerialherein.
ISBN:978-0-323-99477-4
ForInformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: GlynJones
EditorialProjectManager: NaomiRobertson
ProductionProjectManager: AnithaSivaraj
CoverDesigner: ChristianJ.Bilbow
TypesetbyMPSLimited,Chennai,India
PartIUniversalequationofnon-Newtonianhydrodynamic lubrication1
1.Viscosityoffluid5
1.1 Overview 5
1.2 ViscosityofNewtonianfluid6
1.2.1 Definitionofviscosity6
1.2.2 Unitsofviscosity7
1.3 Rheologicalpropertyofnon-Newtonianfluid8
1.3.1 Typesofnon-Newtonianfluids8
1.3.2 Viscosityofnon-Newtonianfluid11
1.4 Factorsinfluencingviscosity17
1.4.1 Relationshipbetweenviscosityandtemperature17
1.4.2 Relationshipbetweenviscosityandpressure18
1.4.3 Combinationalrelationshipofviscosity,temperatureandpressure19
1.5 Commonrheologicalexperimentdevices19
1.5.1 Coaxialcylinderrheometer19
1.5.2 Cone-platerheometer20
1.5.3 Parallelplaterheometer20 References 21 Furtherreading 22
2.Basicequationsofhydrodynamiclubrication23
2.1 Basicequationsandassumptionsofhydrodynamiclubrication23
2.1.1 Basicequations23
2.1.2 Basicassumptions24
2.2 Continuityequation25
2.3 Equilibriumequations27
2.3.1 Expressionofequilibriumequations27
2.3.2 Derivationofequilibriumequations27
2.4 Fluidconstitutiveequation29
2.4.1 Newtonianfluidconstitutiveequation29
2.4.2 Non-Newtonianfluidconstitutiveequations30
2.5 Boundaryconditionsofhydrodynamiclubrication35
2.5.1 Boundaryconditionsbetweenfluid-solidinterface35
2.5.2 Pressureboundaryconditions36
Reference 37
3.Reynoldsequationandnon-Newtonianhydrodynamiclubrication39
3.1 DerivationofReynoldsequation39
3.1.1 Analysisofbasicequations39
3.1.2 Eliminationofshearstress40
3.1.3 Eliminationofflowvelocities41
3.2 Generalnonlinearproblems43
3.2.1 Linearproblems43
3.2.2 Nonlinearproblems44
3.2.3 Non-Newtonianhydrodynamiclubrication45
3.3 DifficultiesduringderivationofReynoldsequationofnon-Newtonianhydrodynamic lubrication 46
3.3.1 Reynoldsequationofpowerconstitutiveequation46
3.3.2 DifficultiestoderiveageneralReynoldsequationofnon-Newtonianfluid49
Reference 52
4.Universalhydrodynamiclubricationequation53
4.1 Separatedflowvelocitymethod53
4.1.1 Basicprinciplesofseparatedflowvelocitymethod53
4.1.2 Stepstosolvenon-Newtonianhydrodynamiclubricationproblems withseparatedflowvelocitymethod55
4.1.3 Theoreticalbasisoftheseparatedflowvelocitymethod58
4.2 Derivationofuniversalhydrodynamiclubricationequation59
4.2.1 Derivationstepsofuniversalhydrodynamiclubricationequation60
4.2.2 Simplifieduniversalhydrodynamiclubricationequation62
4.2.3 Solutionofuniversalhydrodynamiclubricationequation63
4.3 Determiningconditionsofseparatedflowvelocitymethod65
4.3.1 Separatedflowvelocitymethodsatisfiesallbasicequations65
4.3.2 Boundaryconditions66
4.4 Commonnon-Newtonianuniversalhydrodynamiclubricationequations67
4.4.1 Powerconstitutiveequation67
4.4.2 Universalhydrodynamiclubricationequationsofcommonlyused non-Newtonianfluids68 PartIILubricationfailureduetolimitshearstress73
5Experimentalstudyonrheologicalpropertiesoffluids75
5.1 Non-Newtonianfluidexperimentsunderatmosphericpressure75
5.1.1 Preparationofnon-Newtonianfluids75
5.1.2 Experimentalresultsofnon-Newtonianfluids76
5.1.3 Viscosity-temperaturerelationshipofpolyethyleneoxidesolutions82
5.2 Experimentaldevicesoffluidrheologicalpropertyunderhighpressureand highshearrate84
5.2.1 Doubledisctype84
5.2.2 Impacttype86
5.2.3 Sheartype87
5.2.4 Capillarytype87
5.2.5 Puresheartype87
5.2.6 Impactandsheartype89
5.2.7 Impactandsqueezetype90
5.2.8 Fallingcolumntype91
References 94
6Interfaceslipmodelsandslipmeasurement95
6.1 Interfaceslipmodels95
6.1.1 Sliplengthmodel95
6.1.2 Limitshearstressslipmodel98
6.2 Experimentalstudyoninterfaceslip99
6.2.1 Interfaceslipmeasurement100
6.2.2 Influencingfactorsofinterfaceslip102
References 107
7Lubricationfailureofnon-Newtonianfluid109
7.1 Interfaceslipanditsconditions109
7.1.1 Interfaceslip109
7.1.2 Slipboundaryconditions111
7.1.3 Flowvelocitydistributionatslipzone112
7.2 Differenceofrollingandslidingforlubricationfailure114
7.2.1 Slide-rollratio114
7.2.2 Reynoldsequationofpurerolling115
7.2.3 One-dimensionalReynoldsequationofpurerolling115
7.2.4 Shearstressofhydrodynamiclubricationinpurerolling118
7.2.5 Lubricationfailureofnon-Newtonianfluidinsliding119
7.3 Criterialpointoflubricationfailure120
7.3.1 Stribeckcurveandlubricationfailure120
7.3.2 Frictioncoefficientofhydrodynamiclubrication121
7.3.3 Relationshipbetweenfrictioncoefficientandlubricationfailure122
7.3.4 Influenceoffrictioncoefficient123
Reference 127
8Analysisoflubricationfailureofnon-Newtonianfluidwithlimitshearstress129
8.1 Lubricationfailureofviscos-plasticfluid129
8.1.1 Constitutiveequationofviscos-plasticfluid129
8.1.2 Basicequationsofviscos-plasticfluid132
8.1.3 Numericalanalysisoflubricationfailureofviscos-plasticfluid137
8.2 Lubricationfailureofbucklingfluid140
8.2.1 Constitutiveequationofbucklingfluid140
8.2.2 Basicequationsofbucklingfluid142
8.2.3 Numericalanalysisoflubricationfailureofbucklingfluid144
8.3 Lubricationfailureofcircularfluid149
8.3.1 Circularconstitutiveequation150
8.3.2 Basicequationsofcircularfluid150
8.3.3 Numericalanalysisoflubricationfailureofcircularfluid151 References 153 PartIIICalculationmethodandprogram155
9Calculationmethodandprogramofhydrodynamiclubricationof non-Newtonianfluids157
9.1 Basicequations,numericalmethodandprogramofone-dimensional hydrodynamiclubrication157
9.1.1 Basicequations157
9.1.2 Numericalmethod159
9.1.3 Calculationprocedure160
9.2 Basicequations,numericalmethodandprogramoftwo-dimensional hydrodynamiclubrication165
9.2.1 Basicequations165
9.2.2 Numericalmethod167
9.2.3 Calculationprocedure167
10Calculationmethodandprogramofelastohydrodynamiclubrication ofnon-Newtonianfluid175
10.1 Basicequations,numericalmethodandprogramofnon-NewtonianEHLinlinecontact175
10.1.1 Basicequations175
10.1.2 Numericalmethod179
10.1.3 Calculationprocedure180
10.2 Basicequations,numericalmethodandprogramofnon-NewtonianEHLinpointcontact188
10.2.1 Basicequations188
10.2.2 Numericalmethod189
10.2.3 Calculationprocedure191 References 198
11Temperaturecalculationmethodandprogramofhydrodynamiclubrication199
11.1 Basicequationsofhydrodynamiclubrication199
11.1.1 Basicequations199
11.1.2 Flowcontinuityequation201
11.2 Energyequationandcalculationmethod202
11.2.1 Energyequation202
11.2.2 Numericalcalculationofenergyequation204
11.2.3 Temperaturecalculationflowchart210
11.3 CalculationprogramofthermalhydrodynamiclubricationofNewtonianfluid210
11.3.1 One-dimensionaltemperaturecalculationprogram211
11.3.2 Two-dimensionaltemperaturecalculation213 Reference 218
12CalculationmethodandprogramofthermalhydrodynamiclubricationofnonNewtonianfluids219
12.1 Equations,numericalmethodandprogramofone-dimensionalthermalhydrodynamic lubricationofnon-Newtonianfluids219
12.1.1 Basicequations219
12.1.2 Numericalmethod221
12.1.3 Calculationprogram222
12.2 Equations,numericalmethodandprogramoftwo-dimensionalthermalhydrodynamic lubricationofnon-Newtonianfluids227
12.2.1 Basicequations227
12.2.2 Numericalmethod230
12.2.3 Calculationprogram231 Reference 238
13Calculationmethodandprogramofthermalelastohydrodynamiclubricationof non-Newtonianfluids239
13.1 Basicequations,numericalmethodandprogramofnon-NewtonianTEHLinlinecontact239
13.1.1 Basicequations239
13.1.2 Numericalmethod245
13.1.3 Calculationprogram245
13.2 Basicequations,numericalmethodandprogramofnon-NewtonianTEHLinpoint contact 264
13.2.1 Basicequations264
13.2.2 Numericalmethod270
13.2.3 Calculationprogram270 References 287
14Calculationmethodandprogramoflubricationfailure289
14.1 Lubricationfailurecalculationofviscos-plasticfluid289
14.1.1 Basicequations289
14.1.2 Discreteiterativeformula291
14.1.3 Calculationflowchart292
14.1.4 Sourceprogram293
14.1.5 PressuredistributionsofNewtonianfluidandviscos-plasticfluid295
14.2 Lubricationfailurecalculationofbucklingfluid295
14.2.1 Basicequations295
14.2.2 Discreteiterativeformula296
14.2.3 Calculationflowchart297
14.2.4 Sourceprogram299
14.2.5 PressuredistributionofNewtonianfluidandbucklingfluid301
14.3 Lubricationfailurecalculationofcircularconstitutivefluid302
14.3.1 Basicequations302
14.3.2 Sourceprogram303
14.3.3 PressuredistributionsofNewtonianfluidandcircularfluid306
Preface
Inhydrodynamiclubrication,non-Newtoniancharacteristicsoflubricantarevery common.However,duetothenonlinearityofconstitutiveequations,obtainingsolutionsfornon-Newtonianhydrodynamiclubricationproblemsisverydifficult.Even throughnumericalanalysis,itisnoteasytoobtainaconvergentsolution.Therefore non-Newtonianhydrodynamiclubricationhasalwaysbeenadifficultyinlubrication theory.
Foralongtime,noeffectivemethodhasbeenfoundtosolvethelubricationcalculationofnon-Newtonianfluids.Althoughavarietyofconstitutiveequationsof non-Newtonianfluidshavebeenobtainedinpractice,theyareusuallysimplifiedas Newtonianfluidsforanalysisandcalculation.Aquasilinearizednon-Newtonian hydrodynamiclubricationproblemoftenleadstodeviationssothattheresultsmaydistortdesignandevenhavehiddenerrors.Therefore,findinganeffectivemethodto solvehydrodynamiclubricationproblemsofnon-Newtonianfluidsisanimportant taskoflubricationtheory.
Twodifficultiesinsolvingnon-Newtonianhydrodynamiclubricationare:(1) Non-Newtonianfluidbringsagreatobstacletoderivateananalyticalequationbecause ofthenonlinearityofitsconstitutiveequation;(2)EvenifaReynolds-likeequation hasbeenobtained,aconvergencesolutioncannotbeeasilyobtainedbecauseofnonlinearity.Inthepast,whensolvinganyhydrodynamiclubricationproblem,people alwayswanttodeduceaReynolds-likeequationsimilartoNewtonianfluid,andthen solveitwithonlyonepressurevariable.InordertodeduceaReynolds-likeequation ofnon-Newtonianfluid,exceptforsomespecialnon-Newtonianfluids,itsexpression isusuallynotsuitableforobtainingastablenumericalsolution.
Thisbookisdividedintothreeparts.Thefirstpartisthebasictheories,including Chapters1 4.First,viscosityofnon-Newtonianfluidisanalyzedindetail,andthe conceptsoftheincrementalviscosityandthetotalviscosityareputforward.TheoriginaldefinitionofviscositycomesfromNewtonianfluidandisnotsuitablefornonNewtonianfluids,sowemustclearlyunderstandthedifferencesbetweenNewtonian fluidviscosityandnon-Newtonianfluidviscosity.Otherwise,itisdifficulttostudy themindepth.
TheseparatedflowvelocitymethodisaneffectivemethodforsolvingnonNewtonianhydrodynamiclubricationproblems.AfteranalyzingthestepstosolvehydrodynamiclubricationofaNewtonianfluid,explainingdifficultiesofnon-Newtonian hydrodynamiclubricationandconsideringthe particularitiesofhydrodynamiclubrication problems,weproposetheseparatedflowvelocitymethodforsolvingnon-Newtonian
hydrodynamiclubricationproblems.Thus,theuniversalequationsforsolvinghydrodynamiclubricationproblemsofnon-Newtonianfluidsarederived.
Thesecondpartisaboutlubricationfailure,including Chapters5 8. Theoretically,Newtonianfluidwillnotbringaboutlubricationfailure,butthisis inconsistentwiththeactualsituationinpractice.Thisprovokespeopletosearchfor thecausesoflubricationfailure.Thenon-Newtoniannatureisoneoftheseimportant causes.Basedontheanalysisofconstitutiveequationsofnon-Newtonianfluidwith limitshearstress,alubricationfailuremechanismcausedbylimitshearstresshasbeen discussedindepth.First,wegiveanimportantconclusionthatpurerollingdoesnot havelubricationfailurewhichiscausedbylimitshearstress,andonlyslidingcauses suchlubricationfailure.Thisconclusionishelpfultodeeplyunderstandtheinfluence ofthenon-Newtonianproperty.Moreover,relationshipsbetweenfrictioncoefficient, load,filmthicknessandlubricationfailurearealsodiscussedbyanalyzingvariationof loadcarryingcapacityofhydrodynamiclubricationfilm.Finally,sometestersfor experimentallymeasuringlimitshearstressareintroducedin Chapter8
Thethirdpartcoverscalculationmethodsandprograms,including Chapters9 14 Calculationformulas,numericalmethodsandsolutionprogramsofcommonnonNewtonianhydrodynamiclubricationproblemsarepresentedbyusingtheabove method.Thecalculationresultsobtainedbytheseprogramsshowthattheuniversal equationbasedontheseparatedflowvelocitymethodcanbesuccessfullyappliedto thecalculationofpressuredistribution,filmthicknessandtemperatureriseofnonNewtonianhydrodynamiclubricationproblems.Comparedwiththepastcalculation methodsfornon-Newtonianhydrodynamiclubricationproblems,thepresentmethod hasadvantagesofaunifiedformat,simplecalculationsteps,goodconvergenceand accuracy.
ThisbookcanprovidetheoreticalandnumericalanalysisforresearchonnonNewtonianhydrodynamiclubrication.ItwaswrittenbyPingHuangandQianqian Yang.PingHuangwrote Chapters1to8and14.QianqianYangwrote Chapters 9 13.Theresearchcontentofthisbookisfinanciallysupportedby “Computational Tribology” (No.51575190)oftheNationalNaturalScienceFoundationofChina. Moreover,thebookquotestheexcellentachievementsofmanytribologists. Dr.WanglongZhanalsoprovidedgreathelpwithdatacollectionduringcompletion ofthebook.Theauthorsthankallofyouverymuch!
Duetocomplexityofnon-Newtonianhydrodynamiclubricationandlimitationof theauthors,itisinevitablethatsomemistakesexistinthebook.Wehopethereaders willnothesitatetoputforwardvaluableopinionsandsuggestions.
PingHuangandQianqianYang March,2022,Guangzhou
Introduction
Theprimarygoalofthisbookistodeduceauniversalhydrodynamiclubrication equationforsolvingnon-Newtonianhydrodynamiclubricationproblemsbasedonthe separatedflowvelocitymethod,whichsolvesthedifficultiesofderivingaReynoldslikeequationofnon-Newtonianhydrodynamiclubrication.Theuniversalequation canbeusedtosolvethehydrodynamiclubricationproblemsofbothNewtonianand non-Newtonianfluids.Inaddition,inthisbookwealsocarryoutadetailedanalysis ofviscosityofnon-Newtonianfluidsandputforwardtheconceptsoftheincremental viscosityandthetotalviscosity.Thenon-Newtonianpropertyoffluidisoneofthe primaryreasonsforlubricationfailure.Wehaveanalyzedloadcarryingcapacitiesof hydrodynamiclubricationfilmofdifferentfluidsandpointoutthatthelubrication failuremechanismofnon-Newtonianfluidsisrelatedtothelimitshearstress.We havealsointroducedvarioustestinginstrumentsformeasuringlimitshearstress. Finally,somenumericalmethodsandcalculationprogramsusingtheseparatedflow velocitymethodarepresented.Withtheseprograms,hydrodynamiclubrication,elastohydrodynamiclubrication,thermalelastohydrodynamiclubricationandlubrication failureofcommonnon-Newtonianfluidscanbecalculatedandanalyzed.
Thisbookcanbeusedasteachingmaterialorasateachingreferencebookfor postgraduatesorstudentsmajoringinmechanicalengineeringorrelated.Itcanalsobe usedasareferenceforengineersandtechniciansengagedinthecalculation,analysis andresearchofnon-Newtonianhydrodynamiclubrication.
Thispageintentionallyleftblank
1.2ViscosityofNewtonianfluid
1.2.1Definitionofviscosity
Fluidlubricantgenerallydoesnothaveafixedshapeanditcanflow.Oneofthemost importantpropertiesofafluidlubricantisitsviscosity.Whenitflows,duetotherelativemotionbetweenmoleculesoffluidorontheinterfaceoffluidandsolid,shear ratewillbeproduced;theviscosityoradhesionisthereasonforresistancetofluid flowsoastoproduceshearstress.
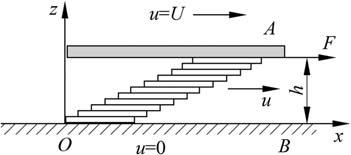
Newtonproposedamodelforviscousfluids,inwhichheproposedthattheviscousfluidmotionrelativelyslidesinmanyverythinlayers,asshownin Fig.1.1.In thefigure,aflatplatewithanarea A onthetopofthefluidmovesatavelocity U undertheactionoftheforce F.Acrossthefilmthickness h,anothersurfaceisfixedat thebottomofthefluid.Thetwosurfacesareparallel.Duetotheviscosityofthefluid, internalfrictionalactionwillexistbetweeneachslidinglayer.Motionwillbetransmitted totheadjacentlayersthroughthisaction,whichcausesthefastermovinglayertodecelerate,andtheslowermovinglayertoaccelerate.Aflowvelocitydistributioniseventuallyformed.IfthefluidisNewtonian,theflowvelocity u willchangeinastraightline asshowninthefigure.
Aconstitutiveequationisusuallyusedtodescribetherelationshipbetweenshear stressandshearrateofafluid.Iftheshearstress τ isproportionaltotheshearrate _ γ , wesaythatthefluidobeysNewton'slaw.Itsdynamicviscosity η isequalto:
or
where, τ istheshearstress,whichthetangentforceperarea, τ 5 F/A; F isthetangent force; γ 5 du dz istheshearrate,thatis,theshearstrainchangeswithtime t; u isthefluid velocity; z istheverticalcoordinate,whichisperpendicularto u,theratioofshear stresstoshearrateisdefinedastheviscosity η offluid,ordynamicviscosity;and U is
Figure1.1 Newtonianfluidmodel.
thevelocityoftheuppersurface.Allfluidsthatobey Eq.(1.1) arereferredtoas Newtonianfluids.Thosethatdonotarecallednon-Newtonianfluids.
Inengineering,theratioofthedynamicviscosity η ofafluidtoitsdensity ρ is oftenused,whichiscalledthekinematicviscosityandiscommonlyexpressedas ν Theexpressionofthekinematicviscosityis:
1.2.2Unitsofviscosity
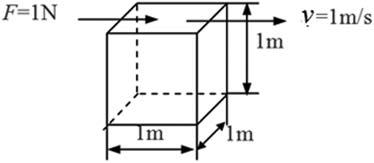
Theunitofthedynamicviscositycanbeobtainedfromitsdefinition.Asshownin Fig.1.2, iftheunitoftheforce F isnewton,thelengthandwidthoftheelementare1meterand theunitoftimeisseconds,thentheunitofthedynamicviscosityisN s/m2 orPa s.
Therangeofdynamicviscositiesoffluidsisquitewide.Forexample,thedynamic viscosityofairisabout0.02mPa s,thatofwateris1mPa s:thedynamicviscosities ofcommonlubricantsarefrom2to400mPa s,whilethedynamicviscosityof meltedasphaltisupto700mPa s.
Inengineering,thecentimeter-gram-second(CGS)systemisoftenused,wherethe unitofthedynamicviscosityisPoise,simplyPorcP(onepercentofP).
Iftheimperialunitsareused,theunitofthedynamicviscosityisReyn,thatis:
Theunitofthekinematicviscosity ν ism2/sintheinternationalunitsystem. Becausethedensity ρ ofmineraloilisoftenfrom0.7to1.2g/cm3,thetypicaldensity isabout0.85g/cm3.Thereforethekinematicviscosityanddynamicviscositycanbe approximatelyconvertedbythefollowingequation:
Figure1.2 Unitofdynamicviscosity.
IntheCGSunitsystem,theunitofthekinematicviscosityisStokeorSt,thatis:
Infact,onepercentofStorcStiscommonlyused,wherecStis1mm2/s. ThefluidsthatobeyNewton'slawarereferredtoasNewtonianfluids.Thosethat donotconformtoNewton'slawsarecallednon-Newtonianfluids.Theactualviscosityoffluidsisoftenaffectedbyvariousexternalfactors(temperature,pressure,etc.)so thatitisnotaconstant.However,thechangesofviscositycausedbytheexternalfactorsdonotaffectthepropertiesoffluid.Thereforetheoutsidefactorsdonotchange thepropertiesoffluid,thatis,whetherafluidisNewtonianornon-Newtonianis onlydeterminedbyitsinternalproperties.
Ifviscosityvarieswiththeshearrateorshearstress,itnolongermeetstheviscosity definitionoftheNewtonianfluid.Thereforeitsfluidmodelorconstitutiveequationis non-Newtonian.
1.3Rheologicalpropertyofnon-Newtonianfluid
Non-NewtonianfluidreferstoafluidthatdoesnotmeetNewton'slaw,thatis,the relationshipofitsshearstressandshearrateisnotlinear.Suchfluidswidelyexist.The viscosityofaNewtonianfluidisaconstant.However,theviscosityofanonNewtonianfluidisnotaconstant,butanonlinearfunction,whichdescribestherelationshipbetweenshearstressandshearrate.Thefunctioniscalledtheconstitutive equationandtheconstitutiveequationofaNewtonianfluidisaconstant.
1.3.1Typesofnon-Newtonianfluids
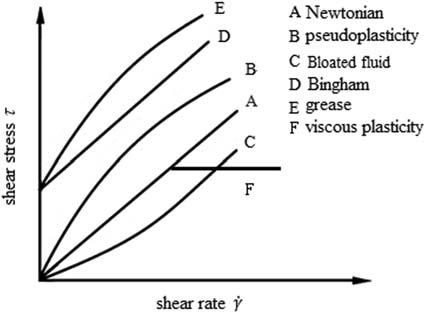
Theconstitutivecurvesofseveralcommonfluids,whichindicatetherelationship betweenshearstressandshearrate,areshownin Fig.1.3.Amongthem,LineAisthe Newtonianfluid.FortheNewtonianfluid,itsrelationshipbetweenshearstressandshear rateislinearevenifitsviscosity, η sometimesisnotaconstant.Forexample,itmay changewithvariationoftemperature,pressureandotherenvironmentalparameters.
Therelationshipbetweenshearstressandshearrateofnon-Newtonianfluidsis nonlinear.Itmayhaveayieldshearstresssothatthecurvestartsatanonzeropointas inCurveDorE.Furthermore,somerelationshipsofshearstressversusshearratemay changewithtime.Experimentalmeasurementsshowthatnon-Newtonianfluidsoften exhibitpseudoplasticity,expansion,viscous-elasticity,yieldandotherdifferentforms, asinCurveBtoFin Fig.1.3
Wewillbrieflyintroducesomecommonlyusednon-Newtonianfluidsandtheir characteristicsasfollows.
Figure1.3 Shearstress-shearratecurvesforcommonfluidtypes.
1.3.1.1Pseudoplasticfluid
Pseudoplasticity,alsoknownasshearthinning,isamajormanifestationofnonNewtonianfluids,asseeninCurveBin Fig.1.3.Mostsyntheticlubricantsareshear thinningfluids.Theviscosityofthiskindoffluidwilldecreasewithincreasingshear rate.Underthesameconditions,thefilmofashear-thinninglubricantisthinnerto carrythesameloadthanthatofnone.
1.3.1.2Bloatedfluid
Bloatedisalsoknownasshearthickening,asinCurveCin Fig.1.3.Incontrastto shear-thinningfluids,theviscosityofthiskindoffluidwillincreasewithincreasing shearrate.Thereforeunderthesameconditions,thefilmthicknessofashearthickeninglubricantisthickerthanthatofashear-thinninglubricant.
1.3.1.3Binghamfluid
AsshowninCurveDin Fig.1.3,BinghamfluidisnamedafterE.C.Bingham,who proposedthiskindofmaterial.Binghamfluidislikearigidmaterialifshearstressis lowsothatshearratecanbeconsideredzero.However,thefluidwillyieldwhen whentheshearstressislargeenough.Theshearstressyieldingiscalledtheyieldstress. Afteryielding,itislikeaviscousfluidandtheshearrateincreaseslinearlywithincreasingshearstress.Thusitsconstitutivecurveisastraightlinebutdoesnotstartfromthe origin.Theyieldstressisafunctionofitsperformancesaswellasitspressureandtemperature.ExperimentsshowthattheyieldstressofBinghamfluidsisfrom4 3 105Pa to2 3 107Pa.
1.3.1.4Grease
AsshowninCurveEin Fig.1.3,thegreasecanbethoughtofasanoverlayof Binghamfluidandpseudoplasticfluid,whichhasbothyieldstressandshearthinning characteristics.SimilartotheBinghamfluid,greasekeepstheoriginalshapeasasolid whenthesurfaceisstationary.Whilethesurfacemoves,greaseactslikeapseudoplastic fluid.
1.3.1.5Viscos-plasticfluid
AsinCurveFin Fig.1.3,theviscos-plasticfluidisasimplificationofcommonnonNewtonianfluids.Itissimilartoanelastoplasticmaterial.Atasmallshearrate,the viscos-plasticfluidcanbeconsideredaNewtonianfluid.However,withincreasing shearrate,plasticitybecomesthemainfactor,especiallyattheinterfacebetweenfluid andsolid.Whenthefluidshearstressonasolidsurfacecannotincreasewithan increaseinshearrateanymore,interfaceslipoccurs.Themaximumshearstressis calledthelimitshearstress, τ L.Inelastohydrodynamiclubrication,thelubricantwill showsolid-likecharacteristicsduetotheexistenceoftheviscosity-pressureeffectand thesurfaceeffect.Moreover,becauselubricantflowsthroughthecontactareafora veryshortperiodoftimeandthelubricantfilmisverythin,thefluidwillbehaveasa viscos-plasticfluid.
1.3.1.6Thixotropyfluidandrheopexyfluid
Theshearrateofathixotropyfluidisthefunctionoftime.Theincrementofitsshear stresswillgraduallydecreasewithincreasingshearrate.Incontrast,inarheopexyfluid shearstressneedstograduallyincreasetokeeptheshearrateasaconstant.Athixotropyfluidcanbethoughtofasatime-sensitiveshearthinningfluid.Butitsviscosity couldnotrespondimmediatelyaccordingtotheshearrate.However,theviscosityof ashearthinningfluiddecreaseswithanincreaseoftheshearrate,andthisresponseis immediateandrepeatable.Theviscosityofathixotropyfluidnotonlyvarieswith shearrate,butalsowithtime.Becausethefluidstructurecanbedamagedbyshear stress,iftheshearstressislargeenough,thestructurecanbecompletelydestroyed.At thispoint,thethixotropyfluidcanexhibitthepropertiesofNewtonianfluidovera periodoftime.Suchastructurecanberestoredtoitsoriginalcondition,thatis,itcan recoverafteralongenoughtimeunderalowshearstress.Experimentsshowthat greasehasthixotropy.
1.3.1.7Viscoelasticfluid
Theviscoelasticfluidshowsboththeelasticpropertiesofsolidsandtheviscouspropertiesoffluids,anditsmainperformancesarecreepandrelaxation.Thestudyofthe viscoelasticmaterialfornon-Newtonianhydrodynamiclubricationisusefulforsome speciallubricantsinpractice.Althoughthereisnodetailedexperimentalverification,it
Table1.1 Classificationsandcharacteristicsofmainnon-Newtonianfluids.
ClassificationTypeCharacteristicsApplications
ViscousfluidShearthinningdecreasesastheshearrate increases
Shearthickeningincreasesastheshearrate increases
Viscos-plastic fluid
Timedependent fluid
Binghamwithyieldstress,like viscousfluidwhenthe shearstressisgreaterthan theyieldstress
Greasewithyieldstress,likeshear thinningfluidwhenthe shearstressisgreaterthan theyieldstress
Thixotropyviscosityincreasesasthe shearstressisappliedfor anextendedperiodof time
Rheopexyviscositydecreasesasthe shearstressisappliedfor anextendedperiodof time
Viscoelastictime-relatedstresswith relaxationandcreep
Siliconeoil,most synthetic lubricants
Cornmealaqueous solution,etc.
Porcelain,graphite, paint
Grease,some emulsions
Printerink, gypsumpaste
Castoroil,slip, mud
Somespecial lubricants
isgenerallybelievedthattheeffectofviscoelasticityonfilmthicknessofhydrodynamic lubricationisnotsignificant.
In Table1.1,classificationsandcharacteristicsofcommonnon-Newtonianfluids havebeengiven.
1.3.2Viscosityofnon-Newtonianfluid
Viscosityisnaturallythemostimportantcharacteristicoflubricant.Itistheparameter todescribefluidresistance.ThedefinitionofviscosityforNewtonianfluidsisvery clear,thatis,theratioofshearstresstoshearrate,asshownin Eq.(1.8).
However,thedefinitionofviscosityofanon-Newtonianfluidisnotdefinitively given.ItisoftenassumedthatthefluidsotherthanCurveAarenon-Newtonianfluids