Handbookof ProbabilisticModels
Editedby PijushSamui
DepartmentofCivilEngineering,NITPatna,Bihar,India
DieuTienBui
DepartmentofBusinessandIT,SchoolofBusiness UniversityofSouth-EasternNorway(USN),Telemark,Norway
SubrataChakraborty
DepartmentofCivilEngineering,IndianInstituteof EngineeringScienceandTechnology,Howrah,India
RavineshC.Deo
UniversityofSouthernQueensland Springfield,QLD,Australia
Butterworth-HeinemannisanimprintofElsevier
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorage andretrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowto seekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandour arrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyright LicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions . Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightby thePublisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthis fieldareconstantlychanging.Asnewresearchand experiencebroadenourunderstanding,changesinresearchmethods,professional practices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribed herein.Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafety andthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility. Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,or editors,assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatter ofproductsliability,negligenceorotherwise,orfromanyuseoroperationofanymethods, products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-816514-0
ForinformationonallButterworth-Heinemannpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionEditor: MatthewDeans
EditorialProjectManager: JoshuaMearns
ProductionProjectManager: KameshRamajogi
CoverDesigner: MilesHitchen
TypesetbyTNQTechnologies
Dedicatedtomygrandfatherandgrandmother
Contributors
FaridWajdiAkashah,CentreforBuilding,ConstructionandTropicalArchitecture (BuCTA),FacultyofBuiltEnvironment,UniversityofMalaya,KualaLumpur, Malaysia
HassanZ.AlGarni,DepartmentofElectricalandElectronicEngineeringTechnology, JubailIndustrialCollege,JubailIndustrialCity,SaudiArabia
MumtazAli,SchoolofAgriculturalComputationalandEnvironmentalSciences, UniversityofSouthernQueensland,Springfield,QLD,Australia;Deakin-SWU JointResearchCentreonBigData,SchoolofInformationTechnology,Deakin University,Burwood,VIC,Australia
ArmandoA.Apan,SchoolofCivilEngineeringandSurveying,UniversityofSouthern Queensland,Toowoomba,QLD,Australia
AnjaliAwasthi,ConcordiaUniversity,CIISE,Montreal,QC,Canada
RahimAzadnia,DepartmentofAgriculturalMachineryEngineering,Universityof Tehran,Tehran,Iran
HamoonAzizsoltani,DepartmentofComputerScience,NorthCarolinaStateUniversity,Raleigh,NC,UnitedStates
MouradBelgasmia,DepartmentofCivilengineering,SetifUniversity,Setif,Algeria
OmidBozorg-Haddad,DepartmentofIrrigationandReclamationEngineering,FacultyofAgriculturalEngineeringandTechnology,CollegeofAgricultureand NaturalResources,UniversityofTehran,Tehran,Iran
TanmoyChatterjee,CollegeofEngineering,SwanseaUniversity,BayCampus, Swansea,UnitedKingdom;DepartmentofCivilEngineering,IndianInstituteof TechnologyRoorkee,Roorkee,Uttarakhand,India
SouravChoudhary,DepartmentofCivilEngineering,NationalInstituteofTechnologyPatna,Patna,Bihar,India
RajibChowdhury,DepartmentofCivilEngineering,IndianInstituteofTechnology Roorkee,Roorkee,Uttarakhand,India
XuefengChu,DepartmentofCivilandEnvironmentalEngineering,NorthDakota StateUniversity,Fargo,ND,UnitedStates
KavinaS.Dayal,SchoolofAgriculturalComputationalandEnvironmentalSciences, UniversityofSouthernQueensland,Springfield,QLD,Australia
MichaelDelichatsios,FireSafetyEngineeringResearchandTechnologyCentre (FireSERT),UniversityofUlster,Newtownabbey,UnitedKingdom
RavineshC.Deo,SchoolofAgriculturalComputationalandEnvironmentalSciences, UniversityofSouthernQueensland,Springfield,QLD,Australia
S.Dey,DepartmentofMechanicalEngineering,NationalInstituteofTechnology Silchar,Silchar,Assam,India
NathanJ.Downs,SchoolofAgricultural,ComputationalandEnvironmentalSciences, UniversityofSouthernQueensland,Springfield,QLD,Australia
SubhrajitDutta,AssistantProfessor,DepartmentofCivilEngineering,National InstituteofTechnologySilchar,Silchar,Assam,India;NationalInstituteofTechnologySilchar,DepartmentofCivilEngineering,Silchar,Assam,India
AmirH.Gandomi,FacultyofEngineeringandInformationTechnology,Universityof TechnologySydney,Ultimo,NSW,Australia;SchoolofBusiness,StevensInstitute ofTechnology,Hoboken,NJ,UnitedStates
J.RamonGaxiola-Camacho,DepartmentofCivilEngineering,AutonomousUniversityofSinaloa,Culiacan,Sinaloa,Mexico
AboubakerGherbi,DepartmentofCivilengineering,ConstantineUniversity,Constantine,Algeria
AchintyaHaldar,DepartmentofCivilandArchitecturalEngineeringandMechanics, UniversityofArizona,Tucson,AZ,UnitedStates
SoheilSadatHosseini,DepartmentofElectricalEngineering,CapitolTechnology University,Laurel,MD,UnitedStates;DepartmentofElectricalEngineeringand ComputerScience,TheUniversityofToledo,Toledo,OH,UnitedStates
PravinJagtap,DepartmentofCivilEngineering,IndianInstituteofTechnology(IIT) Delhi,NewDelhi,India
MohsinM.Jamali,CollegeofEngineering,TheUniversityofTexasofthePermian Basin,Odessa,TX,UnitedStates
MadanK.Jha,AgriculturalandFoodEngineeringDepartment,IndianInstituteof TechnologyKharagpur,Kharagpur,WestBengal,India
ShahjahanKhan,SchoolofAgricultural,ComputationalandEnvironmentalSciences, CentreforAppliedClimateSciences,UniversityofSouthernQueensland,Toowoomba,QLD,Australia
AnoopKodakkal,ChairofStructuralAnalysis,DepartmentofCivil,GeoandEnvironmentalEngineering,TechnischeUniversitatMu ¨ nchen(TUM),Munich,Germany
R.R.Kumar,DepartmentofMechanicalEngineering,NationalInstituteofTechnology Silchar,Silchar,Assam,India
YuankaiLi,UniversityofElectronicScienceandTechnologyofChina,Chengdu, China
NeharMandal,DepartmentofCivilEngineering,NationalInstituteofTechnology Patna,Patna,Bihar,India
TekMaraseni,SchoolofAgricultural,ComputationalandEnvironmentalSciences, UniversityofSouthernQueensland,Springfield,QLD,Australia
SamanMaroufpoor,DepartmentofIrrigationandReclamationEngineering,Faculty ofAgriculturalEngineeringandTechnology,CollegeofAgricultureandNatural Resources,UniversityofTehran,Tehran,Iran
VasantMatsagar,DepartmentofCivilEngineering,IndianInstituteofTechnology (IIT)Delhi,NewDelhi,India
AnkeMeyer-Baese,DepartmentofScientificComputing,FloridaStateUniversity, Tallahassee,FL,UnitedStates
BehshadMohebali,DepartmentofScientificComputing,FloridaStateUniversity, Tallahassee,FL,UnitedStates
TanmoyMukhopadhya,DepartmentofAerospaceEngineering,IndianInstituteof TechnologyKanpur,Kanpur,India
ShahbazMushtaq,CentreforAppliedClimateSciences,UniversityofSouthern Queensland,Toowoomba,QLD,Australia
S.Naskar,SchoolofEngineering,UniversityofAberdeen,Aberdeen,UnitedKingdom
ThongNguyen-Huy,SchoolofAgricultural,ComputationalandEnvironmentalSciences,CentreforAppliedClimateSciences,UniversityofSouthernQueensland, Toowoomba,QLD,Australia
WeiNing,SchoolofCivilEngineering,ChongqingUniversity,Chongqing,China
RachidOuache,SchoolofEngineering,FacultyofAppliedScience,Universityof BritishColumbia,Okanagancampus,Kelowna,BC,Canada
K.M.Pandey,DepartmentofMechanicalEngineering,NationalInstituteofTechnologySilchar,Silchar,Assam,India
ThendiyathRoshni,DepartmentofCivilEngineering,NationalInstituteofTechnologyPatna,Patna,Bihar,India
ZhangRunhong,SchoolofCivilEngineering,ChongqingUniversity,Chongqing, China
VikasKumarSharma,InstituteofInfrastructuteTechnologyResearchandManagement(IITRAM),DepartmentofMathematics,Ahmedabad,Gujarat,India
S.Sriramula,SchoolofEngineering,UniversityofAberdeen,Aberdeen,United Kingdom
AmirhessamTahmassebi,DepartmentofScientificComputing,FloridaStateUniversity,Tallahassee,FL,UnitedStates
AnthonyTeckCheeGoh,SchoolofCivilandEnvironmentalEngineering,Nanyang TechnologicalUniversity,Singapore
S.MohsenVazirizade,DepartmentofCivilandArchitecturalEngineeringand Mechanics,UniversityofArizona,Tucson,AZ,UnitedStates
FranciscoJavierVillegas-Mercado,DepartmentofCivilandArchitecturalEngineeringandMechanics,UniversityofArizona,Tucson,AZ,UnitedStates Contributors
xxii Contributors
ZhangWengang,KeyLaboratoryofNewTechnologyforConstructionofCitiesin MountainArea,ChongqingUniversity,Chongqing,China;SchoolofCivilEngineering,ChongqingUniversity,Chongqing,China;NationalJointEngineering ResearchCenterofGeohazardsPreventionintheReservoirAreas,Chongqing University,Chongqing,China
LiYongqin,SchoolofCivilEngineering,ChongqingUniversity,Chongqing,China
JianpingZhang,FireSafetyEngineeringResearchandTechnologyCentre(FireSERT),UniversityofUlster,Newtownabbey,UnitedKingdom
Fundamentalsofreliability analysis
AchintyaHaldar
DepartmentofCivilandArchitecturalEngineeringandMechanics,UniversityofArizona,Tucson, AZ,UnitedStates
1.Introduction
Thepresenceofuncertaintyineveryaspectofengineeringanalysisanddesign hasbeenunderconsiderationoveralongperiodoftime.Infact,afamous mathematicianPierre-SimonLaplace(1749 1827)wrote“. theprincipal meansofascertainingtruth induction,andanalogy arebasedonprobabilities;sothattheentiresystemofhumanknowledgeisconnectedwiththe theory(ofprobability). .Itleavesnoarbitrarinessinthechoiceofopinions andsidestobetaken;andbyitsusecanalwaysbedeterminedthemost advantageouschoice.Therebyitsupplementsmosthappilytheignoranceand weaknessofthehumanmind.”(Laplace,1951).
Theaforementionedstatementsbyawell-knownscholarclearlyjustifythe needforthishandbook.Morerecently, Freudenthal(1956),AngandTang (1975),Shinozuka(1983),and HaldarandMahadevan(2000a) madesimilar commentsjustifyingtheneedsforstructuralsafetyandreliabilityanalyses. Therelatedareasgrewexponentiallyinthe1970sand1980s.Itappearsthat mostofthedesignguidelinesandcodeseitherhavebeenorareintheprocess ofincorporatingtherisk-baseddesignconcept,atleastintheUS.This handbookisexpectedtobeextremelyvaluableinmovinginthatdirection.
However,beforemovingforward,itisimportanttofigureoutwhatisthe conceptofuncertainty,probability,reliability,stochasticity,etc.andhowthey implicatetheengineeringanalysisanddesign.StochosisaGreekwordfor stochasticityoruncertainty.Ingeneral,mostobservablephenomenaofinterest toengineersproducemultipleoutcomesandcannotbepredictedwith certainty.Multipleoutcomesmaynothaveanypattern,andsomeoutcomes mayoccurmorefrequentlythanotherscoveringdifferentregionsofinterest. Testingofidenticalspecimensmaynotproduceidenticaloutcomes.The designwindvelocityorrainfallatasiteduringthelifetimeofastructure
cannotbepredictedwithcertainty.Wemayknowtheirupperandlowerlimits orboundsandthemostlikelyvaluebutnotthedesignvalueforwhicha specificstructureneedstobedesigned.Thistypeofunpredictabilityis generallyrepresentedbyuncertaintyorrandomness.Complexityofaproblem maynothaveanythingtodowithuncertainty.Thereisnodoubtthatlanding onthemoonconsistsofnumerouscomplicatedandcomplexprocesses,butwe nevermissedthemoonwhenweattemptedtolandonit.Eventheoutcomeof averysimpletaskoftossingacoincannotbepredictedwithcertainty. Uncertaintyisassociatedwithmostoftheanalysisanddesignofinterestto engineers.Consideringtheunpredictabilityofmostofthedesignvariables,the basicchallengeistoassuresatisfactoryperformanceofengineeringsystemsin thepresenceofuncertainty.Thepresenceofuncertaintycannotbecompletely eliminated,butwithreasonableefforts,itsimpactonthedesigncanbe appropriatelymanaged.Thisobservationclearlyindicatesthatengineering systemscannotbedesigned“full-proof”or“risk-free.”Therewillalwaysbe someriskorprobabilityoffailure.Foracceptabledesign,theamountofunderlyingriskneedstobeminimizedtoanacceptablelevelormitigated appropriately.Riskandreliabilityarecomplementarytermsandneedtobe mathematicallyestimatedusingprobabilitytheory.Probabilityandstatistics arenotsynonymousterms.Statisticsisthemathematicalquantificationof uncertainty.Probabilitytheoryusesstatisticalinformationtoestimatethe likelihoodofspecificevents.Withthisintroduction,fundamentalsof reliabilityanalysisarebrieflydiscussedinthisintroductorychapter.
2.Importantstepsinreliabilityevaluation
Mostengineeringproblemsconsistofmultiplerandomvariables(RVs).The firststepisthenthequantificationofrandomnessinthem,onevariableata timeandjointlywhenpossible.TheuncertaintyinanRVisgenerally describedpictoriallyintermsofhistogramandfrequencydiagramsorprobabilitydensityfunction(PDF)andanalyticallywiththehelpofmean,variance,standarddeviation,coefficientofvariation(COV),skewness,etc.They aresometimescollectivelydenotedasthestatisticsofanRV.FormultipleRVs, itisdescribedasjointPDF,correlationcoefficients,etc.Meanisthecentral tendency,varianceandstandarddeviationindicatethedispersionfromthe mean,COVistheratioofstandarddeviationandmeanandrepresents theamountofuncertaintyinanondimensionalway,andskewnessrepresents thesymmetryinthedata,generallyexpressedintermsofskewnesscoefficient. ForaknownPDF,meanisthecentroidaldistancefromtheorigin;itisalso knownasthefirstmoment.VarianceisthemomentofinertiaofthePDFabout themean;itisalsoknownasthesecondmoment.Skewnessisthethird momentofthePDFaboutthemean.Forsymmetricdata,theskewness coefficientwillbezero;morespreadinthedataabovethemeanwillhave positiveskewnesscoefficient,etc.Inthecontextofquantifyingrandomnessin
oneRV,threeadditionalparametersarecommonlyused.Theyaremode, median,andpercentilevalueofanRV.ThemodeormodalvalueofanRVis thevalueofthehighestPDF.ThemedianvalueofanRVisthevalueforwhich itisequallylikelytobeaboveorbeloworthe50thpercentilevalue.The percentilevalueistheprobability,expressedasapercentage,thevalueofthe RVwillbelessthanthespecifiedvalue.Formorecompletediscussionson thetopics,readersarerequestedtoreferto HaldarandMahadevan(2000a). WhendealingwithmultipleRVs,theinformationoncovarianceandcorrelationisveryimportant.ThecovarianceoftwoRVs X and Y,denotedasCov (X,Y),isthesecondmomentabouttheirrespectivemeans.Normalizingthe covariancewithrespecttothestandarddeviationsofthetwoRVswillresult thecorrelationcoefficient.Thecorrelationcoefficientrepresentsthelinear dependencybetweentwoRVs.Itvariesbetween 1.0andzerowhentwoare uncorrelated.Thevalueofcorrelationcoefficientexactlyzeroisrarely obtainedfromobserveddata. HaldarandMahadevan(2000a) suggestedthatif itislessthan 0.3,thetwovariablescanbeconsidereduncorrelated.
Thesecondstepinthereliabilityanalysiswillbetheperformance requirementsthatneedtobesatisfied.Theperformanceofengineering systemswilldependontheuncertaintyintheRVspresentintheformulation; however,theywillnotaffecttheperformanceequally.Thepropagationof uncertaintyfromthevariableorparametertosystemleveldependsonmany factorsincludingtheindividualnatureofuncertaintyinanRV,functional relationshipbetweenvariables,typesofanalysis;linearversusnonlinear,load pathtofailure,etc.Ingeneral,asystemneedstobedesignedsatisfyingperformancerequirementsattheelementandsystemlevels,andtheyareexpected tobefunctionsofoneormultipleRVs.Thiswillrequiretopropagatethe uncertaintiesinRVstothecorrespondinglevelofinterest.Onlythen,the underlyingriskortheprobabilityoffailurecorrespondingtoaspecificperformancerequirementcanbeestimated.Theuncertaintyinsomeofthevariablesmaybeamplifiedatthesystemlevel,someofthemmaybedeamplified, andsomeotherwillhaveveryminoreffect.Reliability-basedengineering analysisanddesignareexpectedtobemoreinvolvedorcomplicatedin comparisonwiththedeterministicapproachescommonlyusedbytheprofessioninthepastwithoutchangingthebasicunderlyingmathematicalprinciples.Itisamajorchallengetothereliabilitycommunitytomakesurethat whattheyaredoingissimilartopracticesfollowedbythedeterministic community.Themostrecenttrendistoextractthereliabilityinformationby conductingmultipledeterministicanalyses.However,tomaintainthebasic simplicityintheformulation,effortshouldbeexercisedtoreducethesizeof theproblemasmuchaspossiblebyconsideringlesssignificantRVsas deterministicattheirmeanvalues.Itneedstobepointedoutthatinatypical deterministicanalysisanddesign,nominalvalues(severalstandarddeviations abovethemeanfortheload-relatedvariablesandseveralstandarddeviations belowthemeanvaluefortheresistance-relatedvariables)areused,indirectly
introducingthesafetyfactorconcept.Ifformulatedproperly,itmayalso satisfytherequiredunknownunderlyingrisk.Intherisk-baseddesign,the uncertaintyinavariableisexplicitlyexpressedintermsofthestatistical information(mean,varianceorstandarddeviation,PDF,etc.).
Theperformancelevelcanbeattheelementorsystemlevel,asmentioned earlier.Element-levelperformancerequirementsaregenerallystrengthrelated. Thesystemlevelrequirementsgenerallyreflectserviceability-relatedperformancescausingexcessivelateral(interstoryoroverall)deflectionordrift causedbyfailureofstructuralelementsorinadequatestiffnessofelements, etc.Theperformancerequirementsaregenerallyexpressedintheformof performanceorlimitstatefunctions/equations.Atypicalperformancefunction consistsofallload-andresistance-relatedRVspresentintheformulation. Performancerequirementsaregenerallysuggestedinthedesignguidelinesor specifiedbytheowner.Sometimes,performancefunctionscanbeexplicit,but inmostcasesofpracticalinterest,theyareimplicitinnature.
Thethirdstepistheestimationofrisk/reliabilitycorrespondingtoaperformancerequirement.Someoftheestimationprocedureswillbediscussedin moredetaillaterinthischapter.Essentially,theinformationinformsthe designertheunderlyingriskforthespecificdesign.Iftheriskisnotacceptable evenwhenalldesignrequirementsweresatisfied,thedesignneedstobe alteredtosatisfytheownerorthestakeholder.Thisstepmakesthereliabilitybasedanalysisanddesignmoreattractivethantheconventionaldeterministic evaluation.Ithelpstocomparedifferentdesignalternatives.Usinginformation onriskoftwodesignalternatives,themostdesirableorappropriateoptioncan beselected.
3.Elementsofsettheory
Essentialstepsinestimatingriskhavebeendiscussedintheprevioussection. Itisnownecessarytoquantifytheriskassociatedwithadesign.Forthe reliabilityevaluation,theconceptofsettheoryinsteadofconventionalalgebra needstobeused.Theconceptofsettheoryisverybrieflydiscussedinthis section.
Atypicalengineeringproblemmusthaveasamplespace,discreteor continuous,consistingofmutuallyexclusivesamplepoints.Aneventof interestmustcontainatleastonesamplepoint.Eventscanbecombinedusing unionorintersectionoperation,andtheycanbemutuallyexclusive,statisticallyindependent,orcorrelated.Theinformationonriskorreliabilitycanbe extractedwiththehelpofsettheoryandthethreeaxiomsofprobability.Three axiomsofprobabilityare(1)theprobabilityofanevent E,generallywrittenas P(E), willalwaysbenonnegative,(2)theprobabilityofthesamplespace, S,or P(S), willbe1.0;thus,theprobabilityofaneventwillbebetweenzeroand one,and(3)ifthetwoevents E1 and E2,aremutuallyexclusive,theprobability
oftheirunionwillbethesummationoftheirindividualprobability.Itis generallyexpressedas
Thecomplementofanevent,denotedas E ,canbeshowntobe
Eq.(1.2) indicatesthattheprobabilityofsurvivalcanbeestimatedas1.0 risk Ingeneral,eventsarenotmutuallyexclusive.Inthatcase, Eq.(1.1) canbe showntobe
Theprobabilityofintersectionorjointoccurrenceofevents, P(E1E2)asin Eq.(1.3),needstobecalculatedusingthemultiplicationrule.Thegeneral multiplicationrulefortwoeventscanbeshowntobe
P(E1jE2)or P(E2jE1)isgenerallyknownastheprobabilityoftheconditional eventsindicatingtheoccurrenceofoneeventgiventheoccurrenceoftheother event.Itreducesthesizeoftheoriginalsamplespace.Toestimatetheprobabilitywithrespecttotheoriginalsamplespace,theconditionalprobability needstobemultipliedbytheprobabilityoftheeventconditionedonwith respecttotheoriginalsamplespace.
Iftheeventsarestatisticallyindependent,indicatingtheoccurrenceofone doesnotdependontheother, Eq.(1.4) becomes
Iftheeventsaremutuallyexclusive,i.e.,iftheoccurrenceofoneprecludes theoccurrenceoftheother,theprobabilityofjointoccurrencesofthemwillbe zero.Iftheunionsofalltheeventsconstitutethesamplespace,theyarecalled collectivelyexhaustiveevents.Morediscussionsonsettheory,axiomsof probability,multiplicationrules,andotheroperationscanbefoundinthestudy by HaldarandMahadevan(2000a).
4.Quantificationofuncertaintiesinrandomvariables
Thenextessentialtaskinthereliabilityestimationisthequantificationof uncertaintiesinalltheRVspresentintheformulation.Thequantificationof uncertaintyinanRVrequiresthecollectionofdataonitfromasmanysources aspossible.Thesamplesizeisveryimportantintheuncertaintyquantification. Largersamplesizeisalwayspreferable.Itmaybeimpracticaltocollectdata fromavailablesourcesfromallovertheworld.Thecollecteddatacanbe graphicallyrepresentedwiththehelpofthehistogramandPDF.PDFisa
histogramwiththeareaof1.0.Inmostcases,aPDFcanbegeneratedbyfitting apolynomialwhoseparameterscanbeestimatedfromthesamplesusedto generateit.Inmostengineeringapplications,two-parameterPDFsare routinelyused.Itcanbeshownthattheseparameterscanbeestimatedfrom thefirsttwomoments,themeanandvariance,ofthesamples.Themost encouragingpartofreliability-basedanalysisanddesignisthatmostofthe designvariablesusedinroutineengineeringapplicationsarealready researchedandwidelyavailableintheliterature.TheinformationonthePDF anditsparametersofanRVofinterestcanbeeasilyobtainedwithacasual literaturesearch.
Forthecompletenessofthisdiscussion,commonlyusedcontinuousRVs arerepresentedbynormal,lognormal,Beta,Rayleigh,andexponentialdistributions.AnormaldistributionwillbevalidwhenanRVisvalidfromminus infinitytoplusinfinity.AlognormaldistributionisusedwhenanRVisvalid fromzerotoplusinfinity.ABetadistributioncanbeusedwhenanRVisvalid betweenalowerandupperlimits.SomeofthecommonlyuseddiscreteRVs arebinomial,geometric,Poisson,etc.ParametersrequiredtodefinetheseRVs aretabulatedinmanybooks(AngandTang,1975;HaldarandMahadevan, 2000a).
5.Transformationofuncertaintyfromparametertothe
systemlevel
Aswillbediscussedlater,ifaperformanceorlimitstateequation(LSE)or functionisalinearfunctionofoneRV,itwillberelativelysimpletoestimate theriskusingtheavailablestatisticalinformationontheRV.However,inmost casesofpracticalinterest,theperformanceofastructuralelementmaydepend onnonlinearfunctionofoneRVormultipleRVs.Forastructuralsystem consistingofnumerousstructuralelements,theLSEwillbeafunctionof numerousRVs.Theunderlyingriskwilldependontheformulationsandthe statisticalcharacteristicsofalltheRVsinvolvedintheformulation.Forthe sakeofdiscussion,theaxialloadcarryingcapacityofasteelcolumnwillbe denotedastheresponsevariableandwilldependontheloadactingonit,grade ofsteelused,cross-sectionalarea,radiusofgyration,lengthofthecolumn, supportconditions,etc.Collectively,theywillbedenotedhereafterasthe basicRVs.Uncertaintiesinthesebasicvariableswilldictatetheoverall uncertaintyintheaxialloadcarryingcapacity.Functionalrelationship betweenthesedesignvariablestotheloadcarryingcapacityisgenerally suggestedindesigncodesorguidelinesorcanbemathematicallyderived. WhenthefunctionalrelationshipofallRVsandtheappropriateperformance requirementisavailable,itwillbeconsideredasanexplicitLSE.Asteelframe mayconsistofnumeroussuchcolumns.Thelateraldeflectionatthetopofthe frame(responsevariable)willdependonthepropertiesofthesecolumnsand otherstructuralelementspresentintheframe,essentiallyallthevariables
involvedintheestimationofthelateraldeflectionandtheloadsactingonit. However,anexplicitexpressionforthelateraldeflectionintermsofallthe RVsmaynotbepracticaltodevelop;itmaybeavailableinanalgorithmic form,foranexample,intheformoffiniteelementsrepresentation.Inthis situation,theLSEcanbeconsideredasimplicitinnature.
TransformationofuncertaintyfromthebasicRVstotheresponsevariable willdependonmanyfactorsincludingthetypesofthefunctionalrelationship, linearornonlinear,thetotalnumberofRVspresentintheformulation,their statisticalandcorrelationcharacteristics,etc.Obviously,theunderlyingrisk estimationprocedurewillbedifferentforeachsituation.Eachscenariowill producedifferenttypesofchallengesandwillrequiredifferentlevelsof sophisticationorexpertisetoextractthereliabilityinformation.Onlyinfew cases,thepropagationofuncertaintiesfromthevariabletosystemlevelcanbe accomplishedexactly.Insomecases,thepropagationcanbeachieved partially;insomeothercases,thepropagationcanbeachievedapproximately; insomeothercases,theinformationcanbegeneratednumerically;andin somecases,theunknownrelationshipneedstobegeneratedfromtheavailable data.Theyarediscussedbrieflyinthefollowingsections.
Fortheeaseofpresentationandconsideringthespacelimitation,the discussionsaresubdividedintotwoparts:whenfunctionalrelationshipis availableandwhenitisnot. HaldarandMahadevan(2000a) discussedmany relatedissuesinmoredetailandshouldbereferencedifdesired.
5.1Explicitfunctionalrelationship
Evenwhenexplicitfunctionalrelationshipsareavailable,theymaybeof differentforms.Someofthemarediscussedinthefollowingsections.
5.1.1Exactsolution
Supposethefunctionalrelationshipislinear,theresponsevariable Y isa functionofonebasicrandomvariable X.Therelationshipcanbeexpressedas
where a and b areknownconstants.Itcanbeshownthatthedistributionof Y willnotchange,butitsmean E(Y)andvarianceVar(Y) needtoberecalculatedas
Supposetheknownfunctionalrelationshipisnonlinear,responsevariable Y isafunctionofonebasicrandomvariable X.Therelationshipcanbe expressedas
ThePDFof Y canbeshowntobe
where x ¼ g 1(y)and n isthenumberoftermsaftertheinversion; n willbe twoforaquadraticrelationship.
Suppose Y isaknownfunctionofmultipleRVs,theexactsolutioncanbe obtainedonlyforfewspecialcases.Someofthemarediscussedinthe following.
Case1 MultipleRVswithknownjointPDF
Thiscaseisexpectedtoberare,buttheprocedurediscussedforthesingle basicRVusing Eq.(1.10) canbefollowed,asdiscussedin Haldarand Mahadevan(2000a).
Case2 SumofIndependentnormalvariables
Forthiscase,theresponsevariable Y canbewrittenas
where c0 i s areknownconstantsand X 0 i s arestatisticallyindependentnormal RVswithmeanandstandarddeviationof mXi and sXi ,respectively.
Themeanandvarianceof Y canbeshowntobe
Case3 Productofindependentlognormalvariables
Inthiscase,
Where X 0 i s arestatisticallyindependentlognormalRVswithparameters lXi and xXi .
Itcanbeshownthat
Case4 SumofindependentPoissonRVs
Suppose X 0 i s arestatisticallyindependentPoissonRVswithparameters yXi , theyarerelatedto Y as
Itcanbeshownthat Y isalsoaPoissonRVwithparameter
Case5 Centrallimittheorem
Theaforementioneddiscussionswillnotbecompletewithoutbriefly discussingthecentrallimittheorem.Itstatesthatthesumofalargenumberof RVs,ifnoneofthemdominatethesum,regardlessoftheirinitialdistributions, tendstothenormaldistributionasthenumberincreases.Similarly,theproduct ofalargenumberofRVs,ifnoneofthemdominatetheproduct,regardlessof theirinitialdistributions,tendstothelognormaldistributionasthenumber increases.
5.1.2PartialSolutions
Theexactsolutionsdiscussedintheprevioussectioncanbeverylimitedfrom theapplicationpointofview.Forsomeofthecasesnotdiscussedpreviously, itwillbedesirableifpartialsolutionscanbeobtainedtopropagate uncertaintiesfromthevariabletothesystemlevel.
PartialSolutions linearfunctionofmultipleRVs
Consider Eq.(1.11) again.Supposetheinformationondistributionof X 0 i s isunknownortheyhavedifferentdistributions,itwillnotbepossibleto determinetheexactdistributionon Y. However,itsmeanandvariancecanbe obtainedas
5.1.3Approximatesolutions generalfunctionofmultipleRVs
Ifapartialsolutionisnotpossible,itwillbereasonabletoobtainan approximatesolution.Someofthemarediscussedinthefollowingsections.
Supposetherelationshipbetween Y and X 0 i sisknown,themeansand varianceof X 0 i sareknownwithouttheirdistributioninformation.Therelationshipcanberepresentedas
Itwillnotbepossibletoobtainthedistributioninformationon Y;however, theapproximatemeanandvariancecanbeobtainedbyexpandingthefunction inTaylorseriesaboutthemeanvaluesof X 0 i s.
Theapproximatefirst-orderandsecond-ordermeans,denotedas E(Y 0 )and E(Y 00 ),canbeshowntobe
Inmostcases,onlythefirst-ordervariance,denotedas Var(Y 0 ),canbe estimatedas
where Ei and Ej arepartialderivatives vg=vXi and vg=vXj ,respectively,evaluatedatthemeanvaluesof X 0 i s.Theyareconstants.Thecoefficients E 0 i scanbe consideredasamplificationordeamplificationfactorsbasedontheirnumerical values.TheywillshowtheroleofeachRVinpropagatinguncertaintyfromthe variabletothesystemlevel.Iftheyareverymuchsmallerthan1.0,theycanbe consideredasdeterministicconstantsevaluatedattheirmeanvalues.Ifthey aremuchlargerthan1.0,resourcesshouldbeinvestedtoreducetheiruncertaintieswiththehelpofqualitycontrolandmoreinspections.
5.2Multiplerandomvariableswithunknownrelationship
Inmanypracticalcases,theexactfunctionalrelationshipof Y and X 0 i smaynot beknown;itmayonlybeknowninanalgorithmicform,forexample,withthe helpofthefiniteelementalgorithm.Inthissituation,thefirst-ordermeanand varianceof Y,withoutcalculatingthepartialderivativesasin Eqs.(1.24)and (1.25),canbeobtainedusingtheTaylorseriesfinitedifferenceprocedure. Inthiscase, Y valuesneedtobecalculatedtwomoretimesforeachRVas
and
Eq.(1.26) suggeststhat Y þ i tobeestimatedatthemeanvaluesofallthe RVsexceptthe ithone;ithastobeatthemeanplusonestandarddeviation value.Similarly, Eq.(1.27) suggeststhat Yi tobeestimatedatthemeanvalues ofalltheRVsexceptthe ithone;ithastobemeanminusonestandarddeviationvalue.Usingthecentraldifferenceapproximation,itcanbeshownthat Ei in Eq.(1.25) canbeestimatedas
Thecorresponding Var(Y 0 )canbecalculatedas
5.3Regressionanalysis
RegressionanalysisisgenerallyconductedtodevelopprobabilisticrelationshipbetweentheresponsevariableandoneormultiplebasicRVs.Developing alinearrelationshipbetweentheresponsevariableandonebasicRViscalled thesimplelinearregressionanalysis.Whenlinearrelationshipisrequiredfor multipleRVs,itiscalledthemultipleregressionanalysis.Whennonlinear relationshipisrequired,itiscallednonlinearregressionanalysis.Theconcept behindregressionanalysisisrelativelysimple;however,thereisapotentialfor misuse.Thebasicconceptisbrieflydiscussedinthefollowingsectionfor simplelinearregression.Theinterestedreadersaresuggestedtoreferto HaldarandMahadevan(2000a) and Montgomeryetal.(2012) formore advanceddiscussionsonregressionanalysis.
5.3.1Simplelinearregression
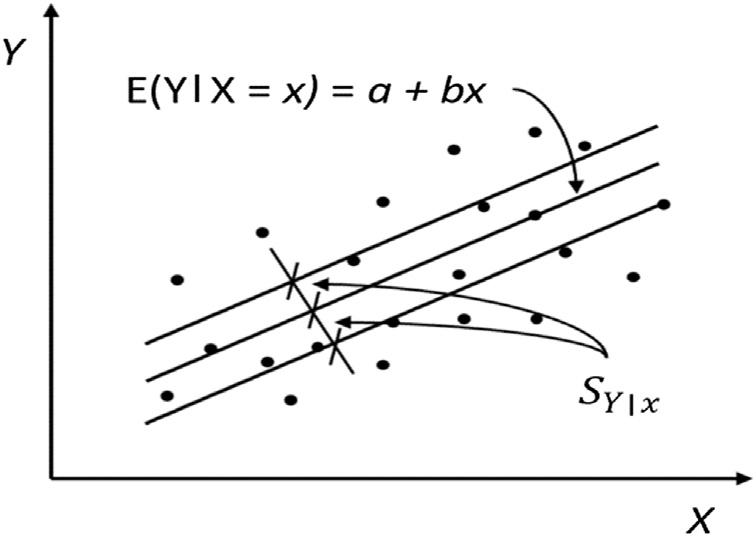
Denoting Y astheresponsevariableand X asthebasicRV, n pairsofdata (x1, y1),(x2, y2), .,(xn, yn)areavailabletodevelopalinearregression-based probabilisticrelationship.Atypicalscatterdiagramofthedataisshownin Fig.1.1.Itcanbeexpressedas
where b0 and b1 aretheinterceptandtheslopeoftheline,respectively,and theyareknownastheregressioncoefficients. Eq.(1.30) representsthemean valueoftherelationship.Someofthebasicassumptionsoftheregression analysisrepresentedby Eq.(1.30) arethatthescatterdiagramindicatesthe relationshipislinear,thespreadofthedataabouttheequationisuniform representedbyanerrorterm ε withazeromeanandunknownbutconstant variance,andtheerrorsareuncorrelatedandnormallydistributed.Thebasic assumptionsinregressionanalysisareshownin Fig.1.1
Generally,theregressioncoefficientsareestimatedusingthemethodof leastsquares.Theyareestimatedbyminimizing ε2,alsoknownastheerror sumofsquares(SSE)representingthedifferencesbetweentheobservedand predictedvaluesusingtheregressionequation. Eq.(1.30) representsthemean valueoftherelationship.Ithasalsoavariance,denotedas Var ðY jX ¼ xÞ¼ S2 Y =x ,knownastheerrormeansquareortheresidualmean square(MSE).Itcanbeestimatedas
whereSSE canbeestimatedas
FIGURE1.1 Scatterdiagramofthedata.
Theappropriatenessoftheregressionequationisevaluatedbyestimating thecoefficientofdetermination, R2.Denotingthetotalvariabilityin Y as Syy andtheamountofuncertaintyaccountedforbytheregressionequation, SSR, thefollowingrelationshipcanbeobtained:
Then, R2 canbeshowntobe
R2 willhaveavaluebetween0and1.Whenitiscloseto1.0,itrepresentsthat theregressionequationisappropriateorreasonable.Itisimportanttomention thattheextrapolationoftheequationbeyondtherangeoftheobserveddatais notrecommended.
Formultipleornonlinearregressionanalyses,theinterestedreadersare referredtothereferencescitedearlier.
6.Fundamentalsofreliabilityanalysis
Itisexpectedthatthereadersnowdevelopedthebasicunderstandingofhowto quantifyuncertaintyinanRVandhowtopropagateitfromthevariablelevel tothesystemlevel.Asmentionedearlier,thebasicintentionistoestimatethe underlyingriskorreliabilityofengineeringdesigns.Theconcepthasbeen developedovertime,anditisconsideredtobematuredatpresent.Severalrisk estimationprocedureswithvariouslevelsofsophisticationandcomplexityare available.However,beforediscussingthem,thefundamentalsofreliability analysisarebrieflydiscussedinthefollowingparagraph.
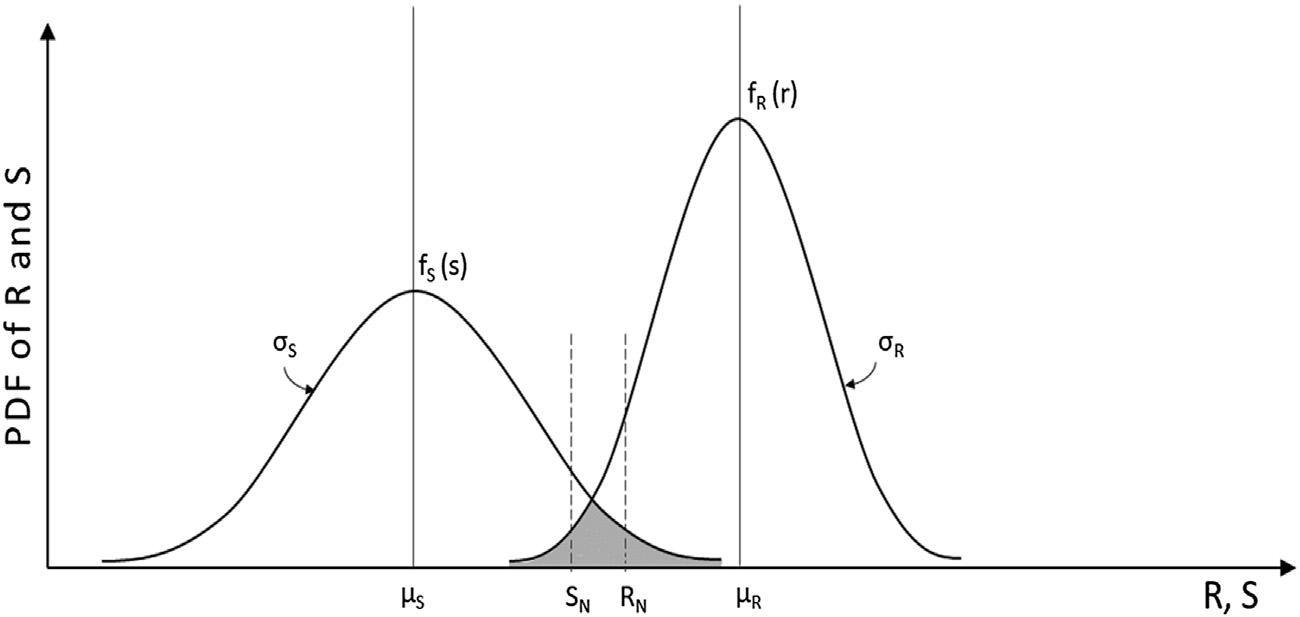
Thebasicintentofanyengineeringdesignisthattheresistance R isgreater thanthemostcriticalloadeffect S duringthelifetimeofastructure.Because both R and S cannotbepredictedwithcertainty,theyarerandominnature. RepresentinguncertaintyinthemwiththehelpoftheircorrespondingPDFsin termsofmean m andstandarddeviation s,thebasicconceptisgraphically shownin Fig.1.2.Theshadedareaisrelatedtothepossibilityof R lessthan S, indicatingtheunderlyingriskofthedesign.Obviously,itshouldbeassmallas possiblesatisfyingtheintentofthedesignguidelines.Thefigurealsoindicates thattheoverlappedtailendsof R and S cannottotallybeeliminated,indicating itwillbedifficultifnotimpossibletodesign“fail-proof”systems.
Thefigurealsoindicatesseveralwaystoreducethesizeoftheoverlapped area.Thereductioncanbeachievedbyincreasingthedistancebetweenthe twoPDFsorseparatingthemeanvaluesofthetwoRVsbyreducingthe uncertaintyinthemintermsof s value(maybewiththehelpofadditional inspectionsorqualitycontrol),orbychangingtheshapeofthetwoPDFs representingthenatureofuncertaintyinthem.Thenominalvaluesof R and S areindicatedinthefigureas RN and SN,respectively.Thenominalvalueswere
usedinthepastbythedeterministiccommunity.Thenominalvalueofthe resistance RN isseveralstandarddeviationsbelowthemean,indicatingthe amountofunderestimationofit.Ontheotherhand,thenominalloadeffect SN isseveralstandarddeviationsabovethemean,indicatingtheamountof overestimationofthem.Accordingtodeterministicpractices,iftheratio of RN/SN isgreaterthan1.0,itisanacceptabledesignandifitislessthan1.0, sayeven0.999,itisnotacceptable.Byunderestimatingtheresistanceand overestimatingtheloadeffect,thedeterministiccommunityintroducedthe safetyfactorconceptwithoutestimatingtheunderlyingrisk.Thefigureclearly indicatesthebasicweaknessintheoldpractice.
Thesamedesigncodesorguidelinesforsteel,concrete,orothermaterials areusedtodesignnuclearpowerplants,hospitals,firestations,buildings,etc. intheUS.However,theengineeringprofessionclaimsthatanuclearpower plantismuchsaferthananordinarybuilding.Itistruebecausefornuclear powerplants, RN and SN areselectedmuchmoreconservativelybyconsidering themseveralstandarddeviationsbelowandabovethemeancorrespondingto differentreturnperiods,respectively.Denoting p astheannualprobabilityof occurrenceofanevent,thereturnperiod, T,canbedefinedas T ¼ 1/p (HaldarandMahadevan,2000a).For50yearsofreturnperiod,onanaverage, theannualprobabilityofoccurrencewillbe p ¼ 1/50 ¼ 0.02.Inroutine applications,ordinarystructuresaredesignedfor50-yearreturnperiodevents, butnuclearpowerplantsaredesignedforthousandsofyearsreturnperiod events.
Incorporatingthepresenceofuncertaintyinthedesign,andreferringto Fig.1.2,theprobabilityoffailure, pf, canbedefinedas P(R < S)andcanbe estimatedas
FIGURE1.2 Fundamentalconceptofriskevaluation.PDF,probabilitydensityfunction. Adopted fromHaldar,A.,Mahadevan,S.,2000.Probability,Reliability,andStatisticalMethodsinEngineeringDesignNewYork,NY.WithpermissionfromJohnWileyandSons,Inc.
Numericalevaluationof Eq.(1.35) canbeverychallenginginmostcases. Ingeneral,both R and S areexpectedtobefunctionsofmultipleRVs,andtheir jointPDFsmaynotbeavailable.When R and S areassumedtohavespecific knownPDFsandtheinformationonthecorrespondingparameterstodefine themisavailable,closed-formnumericalsolutionof Eq.(1.35) mayrequire considerableeffort.However,forfewcases, pf canbediscussedinthe following.
R and S areassumedtobenormalRVswithknownparameters,i.e., N (m R , s R )and N ( m S , s S ),respectively.Itisreasonabletoassumethattheyare statisticallyindependent.Then, p f canbeestimatedas
Intheaforementionedequation, V isthecumulativedistributionfunction (CDF)ofthestandardnormaldistributionand b isgenerallyknownasthe reliabilityindex.Theaforementionedequationindicatesthatwhen b islarge, theunderlyingriskwillbesmaller.Inmostdesigns,thevalueof b between 3and5isexpected.
If R and S arestatisticallyindependentlognormalRVswiththesame meansandvariances, pf canbeapproximatelyestimatedas
where d istheCOVofRVs.Intheaforementionedequation,COVofanRVis consideredtobenotlarge,sayitislessthan0.3(HaldarandMahadevan, 2000a).Forthelognormaldistribution,thereliabilityindex b istheterminthe squarebracket.
Inmostcases, R and S arenotexpectedtobenormalorlognormalvariables.Evenoneofthemcouldbenormal,andtheothercouldbelognormal. Ingeneral, R and S areexpectedtobefunctionsofmultipleRVs,andthe functionalrelationshipcouldbeofanyform.Then,theevaluationofriskusing Eq.(1.35) canbeverychallenging.Forthesecases,severalriskevaluation techniqueswithvariousdegreesofsophisticationwereproposed.However, beforediscussingthem,theconceptoflimitstateneedsadditionaldiscussions.
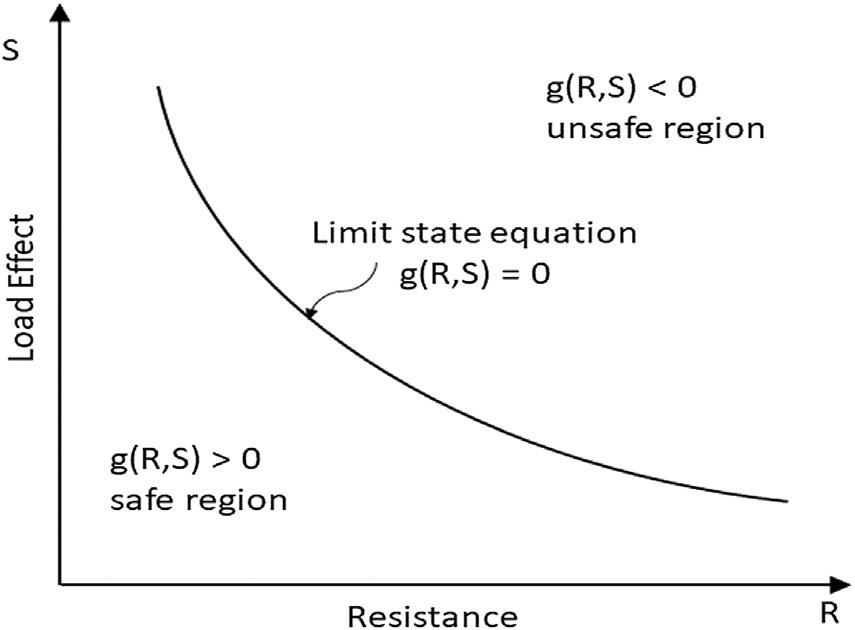
6.1Limitstateequationsorfunctions
Riskisalwaysestimatedforaspecific limitstatefunctionorequation,itwill bedenotedhereafterasLSE.Asmentionedearlier,theyarefunctionsof
load-andresistance-relatedparametersandtherequiredperformancelimitor acceptablebehavior.Theconceptisgraphicallyshownin Fig.1.3.
AtypicalLSEcanbeanexplicitorimplicitfunctionofthedesignvariables andthedesignrequirementsexplicitlysuggestedindesignguidelinesorcodes. Theyaregenerallyrelatedtothestrengthand/orserviceabilityrequirements. Inmostcases,multipleLSEsneedtobesatisfied,indicatingmultiple requirementsneedtobesatisfiedunderthesamedesiredrisk.Thisisvery importanttoeliminatetheweakest-linkfailuremode.Therequirementsmay beatthestructuralelementlevelorbasedontheoverallwholestructural behavior.Forframedstructures,someofthecommonlyusedLSEsarepure bendingofmembers,combinedaxialandcompression,andbendingofframe members,sideswayatthetopoftheframe,interstorydrift,maximumdefectionalongthelengthofamember,etc.Itisextremelyimportanttoformulate theappropriateLSEproperly.
6.1.1Serviceabilitylimitstateequationorfunction
TheserviceabilityLSEfortheinterstory,overall,orthemaximumdeflection alongthelengthofamembercanbeexpressedas
where dallow istheallowablevalueofthespecificdeflectionofinterestmostof thetime;suggestedindesignguidelinesorcommonlypracticedand dmax(X)is themaximumvalueobtainedbytheanalysisusingtheunfactoredloads.Itis interestingtonotethatsomedesignguidelinespermitusinghigher dallow valuesdependingontheproceduresusedtoestimatethem.Forexample, ASCE/SEI7 10permitsincreasingitby125%ifitisestimatedforthe seismicloadingapplyingtheexcitationintimedomain.
FIGURE1.3 Limitstateconcept.
6.1.2Strengthlimitstateequationorfunction
SupposeastrengthLSEofasteelmemberofaframeneedstobedefined,the followinginteractionequationsareusedtodesignthemaccordingtotheload andresistancefactordesign(LRFD)guidelinesfortwo-dimensionalelements oftheAmericanInstituteofSteelConstruction(AISC)’s(AISC,2011):
where f istheresistancefactor, Pu istherequiredtensile/compressive strength, Pn isthenominaltensile/compressivestrength, Mu istherequired flexuralstrength,and Mn isthenominalflexuralstrength. Pu and Mu arethe criticalfactoredloadeffects.ThecorrespondingLSEscanbeexpressedas
where b P u and M _ ux areunfactoredloadeffects.Itisimportanttonotethatin LSEs,theloadandresistancefactorsarenotused.
6.2Reliabilityevaluationmethods
Thestageisnowsettoestimateriskorreliability.Toevaluate Eq.(1.35), severalreliabilityevaluationmethodswithdifferentlevelsofsophistication wereproposed.Initially,thedevelopmentswerelimitedtolinearortangentto thenonlinearlimitstateorperformancefunction,leadingtothedevelopment ofthefirst-orderreliabilitymethods(FORMs).In Eqs.(1.36)and(1.37),the limitstateequations(LSEs)aredefinedas Z ¼ R S and Z ¼ R/S,respectively. Ingeneral, R and S arefunctionsofmultiplerandomvariables.Togeneralize thediscussions,atypicalLSEcanberepresentedas
¼ gðXÞ¼ gðX1 ; X2 ; ; Xn Þ (1.43)
Because Xi ʹ shavedifferentstatisticalcharacteristics,itwillbedifficultto estimateexactlythestatisticalinformationon Z.However,asdiscussedearlier, theapproximatemeanandvarianceof Z canbeestimatedbyexpanding Z in TaylorseriesaboutthemeanofRVs.Thesafetyindex b canbecalculatedby takingtheratioofthemeanandthestandarddeviation.However,becausethe TaylorseriesexpansionismadeatthemeanvaluesofalltheRVs,itisknown
asthemeanvaluefirst-ordersecondmoment(FOSM)orsimplyMVFOSM. Mostofthefirst-generationreliability-baseddesignguidelinesarebasedon thisconcept.
Theaforementionedconcepthasseveralmajorweaknessesasdiscussedby HaldarandMahadevan(2000a).Theprocedurefailstoincorporatethe informationondistributionofRVsevenwhenitisavailable.BecausetheLSE representedby Eq.(1.43) islinearizedatthemeanvaluesoftheRVs,itcan introducesignificanterrorbynotconsideringthehigherorderterms.Itwas documentedinthestudyby HaldarandMahadevan(2000a) thatforthesame mechanicallyequivalentLSEsdefinedas(R S < 0)or R=S < 1 ,theproceduredoesnotgivethesamereliabilityindex.Itneedsimprovements.
6.2.1AdvancedFOSMforstatisticallyindependentnormal variables(Hasofer Lindmethod)
Duringthisphaseofdevelopment, HasoferandLind(1974) gaveageometric definitionofthereliabilityindex.Theyobservedthatinthereducedvariable space,asdefinedinthefollowing,thereliabilityindex,denotedas bHL,isthe shortestdistancefromtheorigintotheLSE.Thisobservationisvalidwhenall RVsarenormal.Thereducedvariableof Xi,denotedas X 0 i ,canbedefinedas
TheclosetpointonanLSEinthereducedvariablespacefromtheoriginis generallydenotedasthedesignorcheckingpoint.Ifitscoordinatesare expressedinavectorialformas x 0 *,itcanbeshownthat
Theconceptisshownin Fig.1.4.
Thesignificanceof HasoferandLind(1974) observationcanbeeasily demonstratedwiththehelpalinearLSEconsistingoftwoindependentRVs,as shownin Fig.1.5.Consider Fig.1.5A first.TheLSEisplottedintheoriginal coordinatesystem.Itwillbeastraightlineata45degreesangle.Thesafeand unsaferegionsarealsoshowninthefigure.InMVFOSM,thefunctionis evaluatedatthemeanvaluesofRVs,indicatingthecoordinatesofthemost probablefailurepoint(MPFP)orcheckingpointordesignpoint.Itisnoton LSEandisamajorsourceoferrorintheriskestimation.Thecoordinatesof theMPFP,denotedas(r*, s*),arealsoshowninthefigure.ItisonLSE.The authorobservedthaterrorintheriskestimationincreaseswiththeseparation distancebetweentheMPFPandthemeanvalues.
Consider Fig.1.5B now.ThesameLSEisnowplottedinthereduced coordinatesinthefigurebylineAB.ThecoordinatesofPointAare