FUNDAMENTALSOF
MULTISCALEMODELING OFSTRUCTURAL MATERIALS
Editedby
WENJIEXIA
AssistantProfessor,NorthDakotaStateUniversity,USA
LUISALBERTORUIZPESTANA
AssistantProfessor,UniversityofMiami,USA
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2023ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronic ormechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem, withoutpermissioninwritingfromthepublisher.Detailsonhowtoseekpermission,further informationaboutthePublisher’spermissionspoliciesandourarrangementswithorganizationssuch astheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedical treatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluating andusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuch informationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,including partiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assume anyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability, negligenceorotherwise,orfromanyuseoroperationofanymethods,products,instructions,or ideascontainedinthematerialherein.
ISBN:978-0-12-823021-3
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: DennisMcGonagle
EditorialProjectManager: IsabellaC.Silva
ProductionProjectManager: PrasannaKalyanaraman
CoverDesigner: MilesHitchen
TypesetbySTRAIVE,India
Introduction
In2011,theUSGovernmentpresentedtheMaterialsGenomeInitiative (MGI),oneofthemostsignificanteffortsinhistoryfocusedonaccelerating thedesignanddevelopmentofthenextgenerationofadvancedmaterialsfor globalcompetitiveness.Thetraditionalparadigmofmaterialsdiscoveryprimarilyreliesontrial-and-errorexperimentation,andtheepitomeofthis approachwasEdison’sassertion:“Ihaven’tfailed.I’vejustfound10,000 waysthatwon’twork.”Thetraditionalparadigmisneitherefficientnor cost-effective,renderingitinsufficienttocurrentdemands.
ThelaunchoftheMGIseededaparadigmshiftinthewaymaterialsare discoveredandoptimized.Inthenew“materials-by-design”paradigm, quantitativetheoreticalandcomputationalpredictionsprecedemanufacturingandexperimentaltesting.Asaresult,computationalmodelingmethods, whichareideallysuitedtopredictmultiscalestructure-propertyrelations, tookcenterstage.Inthecomputer,onecanmodelenvironmentalconditionsthatarechallengingtoexplorethemexperimentally.Moreimportantly,simulationsprovideanidealtestbedofmaterialsthatdonoteven yetexistnecessarily.Multiscalemodelingmethodsandsimulationtools, whichrangefromquantummechanicalmethodsthatcanrevealtheelectronicpropertiesofmaterialstocontinuummodelsthatcanshedlighton theirmacroscopicbehaviorasparts,haveemergedasthefoundationof the“materials-by-design”paradigm.Inthelastdecade,data-driven approachesbasedonartificialintelligencemethodsarealsobecoming increasinglyimportant,andtheprospectofcombiningphysics-based simulationsanddata-drivenmethodsisparticularlyenticing.
Itwouldbehardtooveremphasizethepotentialimpactonsocietyby applyingsuchacomputationalframeworktostructuralmaterialssuchas steel,aluminum,orconcrete,whicharecharacterizedbymultiscalecomplex structuresandareamongthemostusedman-madematerialsworldwide. Predictingtheemergentresponseofstructuralmaterialsthereforerequires amultiscalemodelingframeworktoinvestigatephenomenaatdifferent multipletimeandlengthscales.Anessentialstepinthediscoveryofthenext generationofsustainable,resilient,andenvironmentallyfriendlystructural materialsistotrainscientistsandengineersincomputationalmultiscale modelingmethods,theoverarchingaimofthisbook.
Thecontentofthisbookisaimedprimarilyatupper-levelundergraduates,graduatestudents,andactiveresearcherswithinterestinstructural materialsbutwhomaynotbeexpertsincomputationalmodeling.Thebook providesacomprehensiveintroductiontomainstreammultiscalemodeling methods(PartOne)andofferspracticalguidelinesspecifictoavarietyof structuralmaterials(PartTwo). Chapter1 introducesdensityfunctionaltheory(DFT),arguablythemostpopularelectronicstructuremethodinmaterialsscience.In Chapter2,weintroduceatomisticmolecularmodeling methods,withanemphasisonmoleculardynamics(MD)simulations, wheretheelectronsarenotexplicitlymodeled,andtheinteratomicinteractionsarecapturedbyempiricalfunctions. Chapter3 focuseson particle-basedmesoscalemodelingtechniquesandcoarse-grainedmethods, which,atthecostofchemicalaccuracy,canreachmicroscopictimeand lengthscaleswithmodelsystemsthatstillretainsomemolecularfeatures ofamaterial. Chapter4 focusesonreduced-ordermodels(ROMs)thattake advantageofdata-drivenapproaches. Chapter5 coversadvancesincomputationalcontinuummechanicsbasedonanimmersogeometricformulation forlarge-scalemodelingoffree-surfaceflows. Chapter6 providesan introductoryoverviewofmachinelearninganddata-driventechniques formaterialsmodelinganddesign.Thesecondpartofthebookisfocused onthemodelingandpropertiesofspecificclassesofmaterialsystems. Chapter7 discussestheuseofbottom-upmultiscalemodelstostudythefailurebehaviorofcarbonfiber-reinforcedpolymer(CFRP)composites.
Chapter8 examinesthemolecularandmultiscalemechanismsofelasticity ofbiopolymersthatexhibitexceptionalelasticityinvivowiththeaimof deducingdesignprinciplesandmechanismsthatcanbeusedtodevelop novelelasticbiopolymersformedicalandengineeringapplications. Chapter9 focusesonmultiscalemodelingapproachestostudymetaladditive manufacturing,fromthemanufacturingprocessestomicrostructureevolutionandfinallymechanicalproperties.Finally, Chapter10 overviewsthe mechanicalbehaviorofsupramolecularassembliesoftwo-dimensional materialssimulatedusingcoarse-grainedmodelingapproaches.
LuisAlbertoRuizPestana
Contributors
AmirhadiAlesadi
DepartmentofCivil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo, ND,UnitedStates
FranciscoManuelAndradePires
DepartmentofMechanicalEngineering,FacultyofEngineering,UniversityofPorto,Porto,Portugal
AmaraArshad
MaterialsandNanotechnology,NorthDakotaStateUniversity,Fargo,ND,UnitedStates
MiguelAnı´balBessa
FacultyofMechanical,MaritimeandMaterialsEngineering,DelftUniversityofTechnology,Delft,The Netherlands
JaneBreslin
DepartmentofMechanicalEngineering,ClemsonUniversity,Clemson,SC,UnitedStates
Fatima
DepartmentofMathematics,ComputerScienceandPhysics,RoanokeCollege,Salem,VA;Departmentof Civil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo,ND,UnitedStates
BernardoProenc ¸ aFerreira
DepartmentofMechanicalEngineering,FacultyofEngineering,UniversityofPorto,Porto,Portugal;Faculty ofMechanical,MaritimeandMaterialsEngineering,DelftUniversityofTechnology,Delft,TheNetherlands
DaijunHu
DepartmentofMechanicalEngineering,NationalUniversityofSingapore,Singapore
KamrunN.Keya
DepartmentofCivil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo, ND,UnitedStates
GenevieveKunkel
DepartmentofMechanicalEngineering,UniversityofConnecticut,Storrs,CT,UnitedStates
ZhaofanLi
DepartmentofCivil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo, ND,UnitedStates
YangchaoLiao
DepartmentofCivil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo, ND,UnitedStates
MohammadMadani
DepartmentofMechanicalEngineering;DepartmentofComputerScience&Engineering,Universityof Connecticut,Storrs,CT,UnitedStates
ZhaoxuMeng
DepartmentofMechanicalEngineering,ClemsonUniversity,Clemson,SC,UnitedStates
WenjianNie
DepartmentofCivil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo, ND,UnitedStates
LuisAlbertoRuizPestana
DepartmentofCivilandArchitecturalEngineering,UniversityofMiami,CoralGables,FL,UnitedStates
QingpingSun
CollegeofAerospaceandCivilEngineering,HarbinEngineeringUniversity,Harbin,China
AnnaTarakanova
DepartmentofMechanicalEngineering;DepartmentofBiomedicalEngineering,UniversityofConnecticut, Storrs,CT,UnitedStates
SaraA.Tolba
MaterialsandNanotechnology,NorthDakotaStateUniversity,Fargo,ND,UnitedStates
LuWang
DepartmentofMechanicalEngineering,NationalUniversityofSingapore,Singapore
YangWang
SchoolofMaterialsScienceandEngineering,UniversityofScienceandTechnologyBeijing,Beijing,China
WenjieXia
DepartmentofCivil,ConstructionandEnvironmentalEngineering;MaterialsandNanotechnology,North DakotaStateUniversity,Fargo,ND,UnitedStates
JinhuiYan
DepartmentofCivilandEnvironmentalEngineering,UniversityofIllinoisatUrbana-Champaign,Urbana,IL, UnitedStates
WentaoYan
DepartmentofMechanicalEngineering,NationalUniversityofSingapore,Singapore
ChengengYang
DepartmentofBiomedicalEngineering,UniversityofConnecticut,Storrs,CT,UnitedStates
ZhangkeYang
DepartmentofMechanicalEngineering,ClemsonUniversity,Clemson,SC,UnitedStates
YefengYu
DepartmentofMechanicalEngineering,NationalUniversityofSingapore,Singapore
GuoweiZhou
DepartmentofEngineeringMechanics,SchoolofNavalArchitecture,OceanandCivilEngineering,Shanghai JiaoTongUniversity,Shanghai,China
QimingZhu
DepartmentofCivilandEnvironmentalEngineering,UniversityofIllinoisatUrbana-Champaign,Urbana,IL, UnitedStates
Preface
Imagineaworldwhereonecouldaccuratelypredict,withouttheneedfor manufactureorexperimentaltesting,thecomplexbehaviorofamaterial, whichmaynotevenexistyet.Insuchaworld,itwouldbepossibletorationallydevelopnewmaterialswithtailored,optimalpropertiesinasmall fractionofthetimethatitcurrentlytakes.Reachingthatpointistheoverarchinggoalofmultiscalematerialsmodeling.Infact,multiscalemodeling hasalreadycontributedtothemomentousshiftofthematerialsdiscovery paradigmawayfromtheinefficientexperimental“trial-and-error”(also knownasEdisonian)approach.Thisbook,whichprimarilyfocuseson materialswithmechanicalorstructuralapplications,isthusmotivatedby thepivotalrolethatmultiscalemodelinghasandcontinuestoplayinthe discoveryandoptimizationofthenextgenerationofmaterials.
Themotivationtowriteandeditthebookoriginatedfromthescarcityof pedagogicalmaterialsforself-instructiononthebasicsandapplicationsof multiscalemodelingofstructuralmaterials.Simulatingandgaininginsight intothebehaviorofstructuralmaterialsacrossmultipletimeandlength scalesisacomplexinterdisciplinaryaffairthatrequiresnotonlyadeep understandingofthespecificnuancesassociatedwithdifferentclassesof materials,frombiologicalstructuralmaterialstometalsandalloys,butalso knowledgeofdiversescientificfieldsrangingfromalgorithmsandcomputationalmethodstofoundationalareasofphysicsandchemistry,suchas quantumorstatisticalmechanics.Whilethedevelopmentanduseofstructuralmaterialsoftenfallunderthepurviewofengineers,mostoftheareasof knowledgerelevanttomultiscalemodelingareseldomcoveredinthetraditionalengineeringcurriculum.Furthermore,whileanabundanceoftexts existsthatextensivelycovereachofthoseareas,separately,indetail,veryfew books,ifany,offeranintegrated,introductorytreatmentofmultiscale modelingofstructuralmaterials,togetherwithapplicationsofthosemodelingtoolstosolvechallengingproblems.
Thisbookisourhumblebutambitiousattempttofillinthegrayarea betweentheoryandpractice,betweennoviceandexpert,andbetween methodsandapplications.Overall,astheeditorsandcoauthorsofseveral chaptersofthisbook,wehavetriedtoprovideaconcise,coherentsetof notesaimedatupper-levelundergraduates,graduatestudents,andactive researcherswhoareinterestedinstructuralmaterialsandwanttogetstarted
inthefieldofmultiscalemodeling.Thebookwasdesignedtohavetwo parts:thefirstpartfocusesonthebasiccomputationalmethodsthatcan bebroadlyappliedtodifferentmaterialssystemsandthesecondpartisdedicatedtohowtomodelspecificimportantclassesofstructuralmaterials. Giventhebroadscopeofthebook,itwasnotpractical,orevenbeneficial toourintendedreadership,toundertakeacomprehensivecoverageofeach andeverytopic.Instead,wehavetriedtoincludepertinentreferences throughoutthebook,withthegoaltoprovideasomewhatstructured frameworktofurtherself-learning.Weviewthebookasafirststopfor someonewhoisunfamiliarwithmultiscalemodelingofmaterials,butwants togobeyondtypicalintroductorytextsonsimulation,butdoesnothave timetoscreenthevastliteratureortostudymultipletextbooksinparallel.
Althougheachofushasover10yearsofexperienceusingmultiscale modelingtopredictandunderstandmaterialsatmultiplescales—anadventurethatstartedduringourPhDinDr.SinanKeten’slabatNorthwestern University—abooklikethiswouldnothavebeenpossiblewithoutthe amazingcontributionsofworld-classacademicsandcolleagues,expertsin thedifferentrelevantfields.
WenjieXia
LuisAlbertoRuizPestana
Electronicstructureanddensity functionaltheory
Fatimaa,b,YangchaoLiaob,SaraA.Tolbac,LuisAlbertoRuizPestanad, andWenjieXiab,c
aDepartmentofMathematics,ComputerScienceandPhysics,RoanokeCollege,Salem,VA,UnitedStates bDepartmentofCivil,ConstructionandEnvironmentalEngineering,NorthDakotaStateUniversity,Fargo, ND,UnitedStates cMaterialsandNanotechnology,NorthDakotaStateUniversity,Fargo,ND,UnitedStates dDepartmentofCivilandArchitecturalEngineering,UniversityofMiami,CoralGables,FL,UnitedStates
1.Abriefintroductiontoelectronicstructuremethods
Understandingthecomplexbehaviorofmatteratthelevelsofindividualatomsandmoleculesisafirststepinthequesttoexploitandeventuallydesign,fromthebottom-up,advancedmaterialswithpropertiesthat areinaccessiblethroughconventionalbulkdesign.Quantummechanics
(QM)iscurrentlyourbesttheorytodescribethephysicalbehaviorofmaterialsattheatomicandsubatomicscales.
Inclassicalmechanics,systemsaredefinedasadeterministiccollectionof interactingparticleswhosepositionsandvelocitiesevolveaccordingto Newton’sequationsofmotion.Incontrast,inquantummechanicssystems aredescribedbyamathematicalobjectknownasthewavefunction,which dependsonthepositionsofalltheelectronsandnucleiinthesystem.The wavefunction,morespecificallythesquareofthewavefunction,represents theprobabilityoffindingtheelectronsinparticularquantumstates.The wavefunctionoftheelectronevolvesovertimeaccordingtotheSchr € odinger equation.Unfortunately,computationallysolvingthemany-body,timedependentSchr € odingerequationremainsunfeasiblebeyondtrivialsystems.
TomaketheproblemofsolvingSchrodingerequationtractable,afirst approximationistodecouplethewavefunctionoftheelectronsandthe nuclei,whichisknownastheBorn-Oppenheimer(BO)approximation. ThevalidityoftheBOapproximationliesinthefactthatbecausetheatomic nucleiaremuchheavierthantheelectrons,electronicrelaxationtakesplace atamuchfasterratethanthetimescaleofnuclearmotion.Afurthersimplificationistofocusonsolvingthetime-independentprobleminstead,which isreasonablegiventhatmostmaterialpropertiesofinterestareassociated withtheequilibriumorgroundstateofthesystemandthusdonotdepend ontime.Undertheassumptionofequilibrium,thescopeofmostelectronic structurecalculations(asweareonlysolvingforthewavefunctionofthe electrons)isreducedtosolvingthetime-independentSchr € odinger equationforasystemofelectronsundertheexternalpotentialcreated bythe“frozen”nuclei.However,solvingeventhissimplifiedproblem (i.e.,electronicandtime-independent)forsystemsofpracticalimportance remainschallengingduetothehighdimensionalityoftheelectronic wavefunction(threespatialdimensionsplusspinforeachelectroninthe system),whichmakesthecomputationalcostofthecalculationincrease exponentiallywiththenumberofelectronsinthesystem.
Manyelectronicstructuremethodshavebeendevelopedoverthelast severaldecades,basedondifferentapproximationstothemany-bodyelectronicproblem,aimedattacklingproblemsofpracticalimportance.These abinitioorfirst-principlesmethods,astheyarealsoknown,canbebroadly classifiedintotwofamilies:wavefunctionmethodsanddensityfunctional theory(DFT).Modernwavefunctionmethods,suchasMøller-Plessetperturbationtheory [1] orcoupledclustertheory [2],aregenerallyfavoredby computationalchemistsduetotheirhighaccuracybutaretooexpensiveto
simulatesystemsinthecondensedphase,which,however,arecentralto mostmaterialsscienceandengineeringapplications.InDFT,thewavefunctionisreplacedbytheelectrondensityasthefundamentalvariableto solveforinthecalculations(hencetheterm“density”inthename).Because theelectrondensityisonlyathree-dimensionalscalarfield,thecomputationalcostofthecalculationsisdramaticallyreduced.Thegreatbalance betweencomputationalcostandaccuracyhasmadeDFTthemostpopular electronicstructuremethodtostudymaterials.
Inthischapter,weprovideabeginner’sguidetoDFT.Wewillcoverthe basicunderlyingtheoreticalprinciples,outlinesomeofitsmainadvantages andshortcomings,andprovidesomepracticalguidelinestouseDFTtocalculatebasicmaterialpropertiesbasedonsimpleexamples.Weassumethe readerhassomebasicknowledgeofquantummechanics.Foramoreindepththeoreticaltreatmentofelectronicstructuremethods,wereferthe readertoR.M.Martin’sbook [3] onelectronicstructure,andforamore practicalintroductiontoDFT(morecomprehensivethanwhatispresented inthischapter),werecommendthebookbyD.S.ShollandJ.A.Steckel [4]
2.Thetheoreticalframeworkbehinddensity functionaltheory
2.1WheredoesDFTcomefrom?
Themainpremisethatdrivesthedevelopmentofdensityfunctional methodsisthereplacementofthemany-bodyelectronicwavefunction bythethree-dimensionalscalarelectronicdensity.This,ofcourse,isnot aneasytask.Thefirstmethodforcalculatingtheelectronicstructureof atomsbasedontheelectronicdensityalonewasindependentlyproposed byThomasandFermiin1927 [5,6].Althoughpromising,Thomas-Fermi modelhadaseriesofdrawbacks,suchastheinaccuraterepresentationof kineticenergyandexchangeenergy.Specifically,itcompletelyignored contributionstotheenergyofthesystemduetoelectroncorrelations (relatedtothePauliexclusionprincipleforsame-spinelectrons);asaresult, itsufferedfromself-interactionerrors(electronsinteractingwiththeirown contributiontotheelectrondensity)andcrudelyapproximatedthekinetic energyoftheelectronicsystembythatofauniformelectrongaswhenthe electrondensitycanrapidlyvaryinrealsystems.Despitethefactthatthose approximationspredictablyresultinverypoorquantitativepredictionsfor molecularsystems,theseearlyDFTapproachesfoundsomeholdinsolidstateapplicationswherethematerialsystemsaremorehomogeneous.
Itwasonlyinthemid-1960sthatDFTtookaturntowardstardom.In 1964,HohenbergandKohn [7] provedthattheproblemofsolvingthe Schr € odingerequationcouldberecast exactly astheproblemoffindingthe electrondensitythatminimizestheenergyofthesystem(avariationalprincipleforDFT).Inthegroundstate(i.e.,equilibrium),theenergyisaunique functionaloftheelectrondensity(hencetheterm“functional”inDFT). TheHohenberg-Kohntheoremsdidnot,however,offeranyguidanceon howtofindtheelectrondensityofthegroundstateorwhattheformof theuniqueenergyfunctionaloftheelectrondensitymightbe.Justayear later,in1965,KohnandShamofferedapracticalbreakthroughbyformulatingtheproblemasasetofself-consistentequationscorrespondingtoafictitioussystemofnoninteractingelectronswhosedensityis,remarkably,the sameground-stateelectrondensityofthefullyinteractingsystem [8].The Hohenberg-KohnandKohn-Shamtheoremssetthestageformodern DFTapproachesbyprovidingbotharigoroustheoreticalfooting(avariationalprinciple)andapracticalpathforward(i.e.,theKohn-Shamequations) tosolveelectronicstructureproblems.ForhisfoundationalworkonDFT, WalterKohnwonthe1998NobelPrizeinChemistry,whichheshared withJohnPoplewhocontributedtremendouslytothedevelopmentof computationalmethodsinquantumchemistry.
ThereisacatchtoDFT,however.DespitethatDFTisinprinciplean exacttheory,thepreciseformoftheenergyfunctional(i.e.,howtheenergy inthegroundstatedependsontheelectrondensity)isunknown.Asaresult, DFTisonlyanapproximatemethodinpractice,andamultitudeofDFT modelsexistdependingonhowtheenergyfunctionaloftheelectrondensity isdescribed.
2.2AformulationofDFT ala Kohn-Sham
ThegoalofaDFTcalculationistofindtheelectrondensity n r ðÞ associated withtheground-stateenergyofasystemofelectronsinanexternalpotentialofpositivelychargedfrozennuclei.Thetime-independentelectronic Schrodingerequationcanbewrittenas: b H ψ ¼ E ψ ,where b H istheHamiltonianofthesystem(anoperatorthatactsonthewavefunction), ψ r1 , r2 , …, rN ðÞ istheelectronicwavefunctionwhichdependsonthespatialcoordinates r1 ,r2 , ,rN ofalltheelectrons,and E istheenergyofthe system.Therelationshipbetweentheelectronicdensityandthe wavefunctionis n r ðÞ¼ ψ r ðÞ jj2.ThefirststepinDFTistotrytoformulate
theSchrodingerequationasafunctionoftheelectrondensity, n r ðÞ ,instead ofthewavefunction ψ r1 , r2 , …, rN ðÞ.
Usingatomicunits,wherethereducedPlankconstant ħ ¼ 1,themassof theelectron m ¼ 1,andthechargeoftheelectronis1,theelectronicHamiltoniancanbewrittenas:
wherethefirsttermcorrespondstothekineticenergyoftheelectrons,the secondtermtotheclassicalelectron-electronrepulsioninteractions,andthe lasttermrepresentstheattractiveCoulombicinteractionsbetweeneachof the N electronsandtheexternalpotentialcreatedbythe M nucleiwith charge Zk atfixedpositions Rk.Theenergyofthesystem,whichisthe expectationvalueoftheHamiltonianoperator,canbewrittenasthesum ofthosethreecontributionscorrespondingtothekineticenergy, Ekin, theelectron-electronrepulsion, Eee,andelectron-nucleiinteractions, Eext:
where ψ ∗ isthecomplexconjugateofthewavefunction.Thetheoremsby HohenbergandKohnstatethatauniversaldensityfunctionalexistsuchthat: E[n(r)] ¼ Ekin[n(r)]+ Eee[n(r)]+ Eext[n(r)].Theeasiesttermisthecontributiontotheenergyfromtheelectron-nucleiinteractions,whichcanbewrittenwithoutapproximationsas:
TheclassicalCoulombicrepulsiveinteractionsbetweenelectronscanbe writtenas E Coul
,whereelectronexchangeandcorrelationeffects(i.e.,quantumeffects)areneglected.Furthermore, ECoul also includesunphysicalself-interactionsbetweentheelectronsandtheirown contributiontotheelectrondensity.Inordertoaccountforallnonclassical effectsandtoremovethecontributionfromtheself-interactions,wecanadd acorrectionterm, ΔEee,whichresultsinthefollowingexpressionforthe electron-electroninteractions:
Thekineticenergycontributionisthemostproblematictermtoapproximate.“Pure”or“orbital-free”DFTmethods,suchastheThomas-Fermi model,exist,butremaininaccurate,mostlyduetothepoordescription oftheelectronickineticenergy.Alternatively,wecancalculatethekinetic energyofasystemofnoninteractingelectronsasafunctionofthesingle electronwavefunctions, φi,knownasmolecularorbitals(MOs),exactly andthenaddacorrectionterm, ΔEkin,toaccountfortheinteractingnature oftheelectrons:
WhilethekineticenergyterminEq. (5) isnotcompletelysatisfactoryasnot exclusivelyexpressedintermsoftheelectrondensity,theelectrondensity canbeeasilycalculatedfromthesingle-electronMOs:
wherethefactorof2arisesfromthefactthattwoelectronswithopposite spinscanoccupythesameMO.
PuttingtogetherEqs. (2)–(5),thetotalenergyofthesystemasafunction oftheelectrondensity(andthemolecularorbitalsinthecaseofthekinetic energy)becomes:
where Exc ¼ ΔEee + ΔEkin istheexchange-correlationenergy,which includesthecorrectiontermsthataccountforthenonclassicalelectroncorrelations,theself-interactionsintroducedbytheCoulombicterm,andthe differenceinkineticenergybetweenthesystemofnoninteractingelectrons andtherealinteractingone.Thebiggestcaveatofthisformulation,known asKohn-ShamDFT,isthat Exc isnotformallyknown.Despitethat,
approximationstotheexchange-correlationfunctionalare,generally,much moreaccuratethananydirectapproximationstothekineticenergyofthe interactingsystemofelectrons(e.g.,intheThomas-Fermimodel).ThedifferentexistingflavorsofDFTarisefromthedifferentwaysofapproximating theexchange-correlationfunctional Exc,whichembodiesourignoranceof theunique,exactfunctionaloftheenergy.
Havingthefunctionalexpressionoftheenergyofthesystem(Eq. 7),the nextstepistofindtheelectrondensitythatminimizesit.KohnandSham,in aremarkablestrokeofgenius,showedthattheoriginalsystemofinteracting electronscanbereplacedbyasystemofself-consistentsingle-electron,timeindependentSchrodingerequationsthatrepresentafictitioussystemof noninteractingelectronswhoseelectronicdensityisthesameasthatof theoriginalsystem [8].TheKohn-Shamequations(oneforeachelectron) readas:
where VKS(r)isknownastheKohn-Shampotential(thesameforallthe electrons),and φi and εi arethemolecularorbitalandthesingle-electron contributiontothetotalenergyofthesystem,respectively,corresponding toelectron i.Thetotalenergyofthesystemisjust E ¼ P εi.TheKohnShampotential, VKS(r) ¼ δE[n]/δn,whichisthefunctionalderivativewith respecttotheelectrondensityoftheenergyfunctionalgiveninEq. (7),containsthefollowingterms:
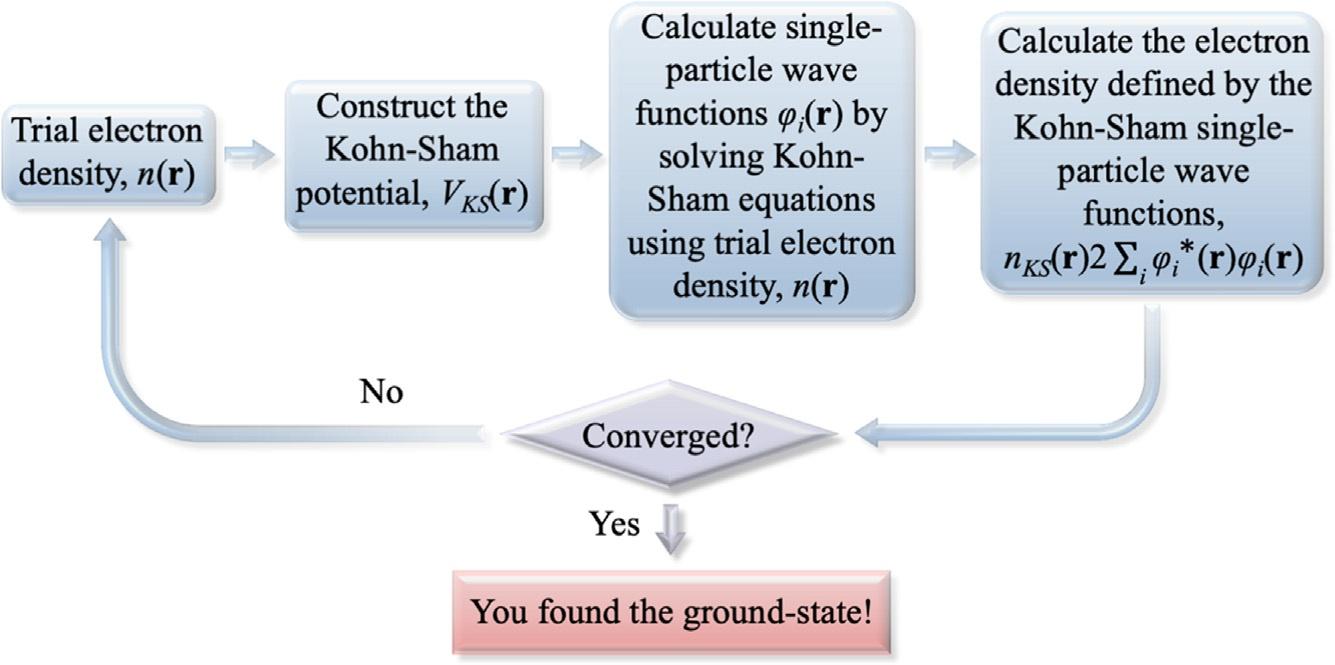
Thefirsttermontheright-handsideofEq. (9) iscommonlyknownasthe Hartreepotential.TofindtheMOsthatminimizetheenergyofthesystem, theKohn-Shamequations(inwhichthereisoneforeachelectron)needto besolvedsimultaneously.Tobeabletowriteeachoftheequations,weneed toconstruct VKS(r)(Eq. 9)anddeterminetheHartreepotentialrequiring knowingtheelectrondensity n(r),whichinturndependsonthesame MOs(Eq. 6)thatwearetryingtofind.Toescapethiscircularity,wesolve thesystemofequationsthroughaniterativeprocessusingaself-consistent field(SCF)methodfollowingthestepsschematicallyillustratedin Fig.1.
Self-consistentfield(SCF)proceduretofindthegroundstateofthesystem.
2.3DFTlevelsoftheoryandthezooofexchange-correlation functionals
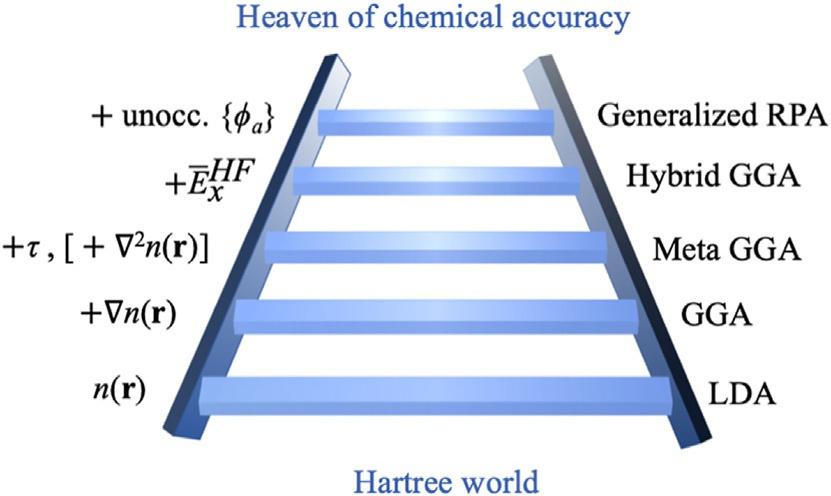
Theexactexchange-correlationenergyfunctionalisunknown.This functionalshouldaccountforallnonclassicalelectroncorrelations, electron-electronself-interactionsarisingfromtheHartreepotential,and thedifferencesinthekineticenergybetweenthenoninteractingsystem ofelectronsandtheoriginalinteractingsystem.TheaccuracyofaDFTcalculation,therefore,hingesonhowweapproximate Exc[n(r)](typically referredtoasjustthe functional).OnewayofclassifyingtheexchangecorrelationfunctionalsinDFTisbasedon“levelsoftheory,”whichcan bepictoriallyarrangedliketherungsinaladder(Fig.2).Eachhigherrung intheladderincorporatesfurtherphysicalingredientstotheapproximation, generallymakingthemmoreaccurate(inprinciplebutnotalwaysinpractice)andmorecomputationallyexpensive.Thisrepresentationwasfirst illustratedbyJohnPerdewandcoworkersusingananalogytothebiblical Jacob’sladder [9].Becauseofthespeed-accuracytradeoff,understanding thestrengthsandlimitationsofthedifferentapproximationsisessentialto beabletochoosetherightfunctionalfortherightapplication.Inthissection,webrieflyexaminethefirstfourrungsoftheladder,whicharetypically usedinmostengineeringandmaterialsscienceapplications.
AllthedifferentlevelsoftheoryinDFT(orrungsintheladder)arebuilt basedonthesimpleuniformelectrongas(UEG)model,alsoknownas jellium.IntheUEG,theinteractingelectronsexperienceapositivechargethat isuniformlydistributedinspace,thusresultinginauniformelectrondensity.
Fig.1
Fig.2 Jacob’sladder ofdensityfunctionalapproximationstotheexchange-correlation energywhichlinksHartreeWorldofIndependentElectronsandChemicalAccuracy [9]. Here, n(r), r n(r), τ, EXC HF,and ϕa presentstheelectrondensity,densitygradient,the kineticenergydensity,Hartree-Fockexchange,andunoccupiedKohn-Shamorbitals, respectively.The plussigns nexttothequantitiesintheleftoftheladderindicatethat thoseareextraingredientsintherespectiverung.
ThereasonUEGoccupiessuchaprominentplaceinDFTisthatitisthe onlysystemforwhichtheexchangeandcorrelationenergyfunctionals areeitherexactoratleastcanbecalculatedwithveryhighaccuracy [10] Inrealmaterialsystems,however,theelectrondensityisnotuniformin spaceandwecannotapplytheUEGmodeldirectlyandexpectgood results.Afirstapproximationistoassumethatthecontributiontothe exchange-correlationenergyofeachdifferentialvolumeelementofspace isequaltowhatwouldbeexpectedfromtheUEGmodelattheelectron densityinthatparticularpointinspace, εXC UEG[n(r)],whichisknownas thelocaldensityapproximation(LDA):
Themoreuniformtheelectrondensityofthesystemis(e.g.,bulkmetals), thebettertheaccuracyofLDAcalculations.Inmostmolecularsystems, however,theelectrondensitycanchangerapidlyinspace,makingLDA apoorchoice.Intheearlydays,LDAwastheonlyapproximationavailable, soDFTwasmostlyemployedinsolid-statephysics(i.e.,extendedperiodic systems)andhadaverymoderateimpactinproblemsinvolvingchemistry (i.e.,molecules).
Rungs2and3arebuiltupontheLDAbutincorporatethedescriptionof theenergyfunctionalhigherordertermsoftheelectrondensitysuchasthe gradient r n(r)ortheLaplacian r2 n(r),whichresultsinbetteraccuracy.
Becauseofthat,functionalsinRungs2and3,whichcanbeconsideredasthe workhorseofDFTapplications,areknownas semilocal.Thefirstsuccessful attempttoimprovetheLDAwasintheearly1980s [11–14],byincorporatinginformationaboutthegradientoftheelectrondensity, r n(r),aclassic functionalapproximationknownasthegeneralizedgradientapproximation (GGA).Becausetherearenumerouswaysofincorporatinginformation aboutthegradientoftheelectrondensityintotheexchange-correlation, avastnumberofGGAfunctionals(withnamesakintoStarWarsdroidcharacters)existintheliterature.PopularexamplesofGGAfunctionalsinclude thePerdew-Burke-Ernzerhof(PBE) [15],Perdew-Wang-1991(PW91) [16],orBecke-Lee-Yang-Parr(BLYP) [17,18],whicharenamedaftertheir creators.GGAfunctionalscapture(toadegree)thenonhomogeneous natureoftheelectrondensityinrealmaterialsandarerelativelyaccurate whenthedensityofthesystemisslowlyvaryinginspace.Forexample, GGAsarenotparticularlyaccurateforquantifyingenergybarriersofchemicalreactions,whichinvolvesharpvariationsintheelectrondensity.The acceptableaccuracyandcomputationalefficiencyofGGAs,however,make themoneofthemostwidelyusedclassesoffunctionalsinmanyareasof physics,chemistry,andengineering,wherethesystemsizeisofparamount importance.
ThenextrungintheladderabovetheGGAscorrespondstometaGGAfunctionals,whichincorporate,inadditiontothelocaldensity andthedensitygradient,theLaplacianoftheelectrondensity, r2 n(r), orthekineticenergydensity, τ(r) ¼ P jr φi(r)j2.Despitehistoricallyhavingplayedarelativelydiscreteroleduetothefactthattheextracomputationalcostdidnotjustifythemodestgaininaccuracy(ifany)ofearlier meta-GGAs,someofthenewlydevelopedfunctionals,suchasB97M-rV [19] andSCAN [20],arguablyoffertodaythebesttradeoffbetweenaccuracyandcomputationalefficiencyacrosstheboard [21].Infact,both B97M-rVandSCANhavebeenrecentlyusedwithsignificantsuccess tosimulatewaterinthecondensedphase(asystemnotoriouslyhardto model)usingabinitiomoleculardynamics(AIMD)simulations,which employDFTtocalculatetheforcesbetweenatoms,andmoleculardynamics(see Chapter2)tointegratetheequationsofmotion,andthustimedependentbehavior [22–25].
MovinguptoRung4,abovethemeta-GGAswehavehybridGGA functionals,whichwerepioneeredbyA.D.Beckeinthe1990s [26].Itis worthmentioningatthispointthattheelectronexchangeenergycanbe
calculated exactly usingHartree-Fock(HF)theory,avariationalwavefunctionmethoduponwhichmanymodernquantumchemistrymethods havebeenbuilt.However,thequalityoftheelectrondensitypredicted byHFmethodsisrelativelypoor,andthebestresultsare,inpractice, achievedbymixingafractionoftheexactHartree-Fockexchangewith somesemilocaltreatmentofexchangeandcorrelation [10],whichiswhat hybrid-GGAfunctionalsdo.Wewillnotdwellonithere,butthesuccess ofcombiningHFandDFTexchangeenergiescanbejustifiedtosome extentusingtheadiabaticconnectionformula [27,28].Justasanexample, theB3LYPfunctional [18,29],arguablythemostpopularhybridfunctional, combinesthefollowingdifferentfractionsandcontributionstoexchange andcorrelationenergy:
ForB3LYP,andforotherempiricalhybridfunctionals,theoptimal mixingcoefficientsareusuallydeterminedbyfittingtoabenchmark datasetofmolecules.Onenoteworthyhybrid-GGAfunctionalthat,similarlytoitsGGApredecessor,attemptstoremovesomeoftheempiricism involvedinthedeterminationofthemixingparametersofthedifferent contributionstotheexchangeandcorrelationenergiesisPBE0,where EXCPBE0 ¼ 0.25EXHF +0.75EXPBE + ECPBE.Hybrid-GGAfunctionalsareparticularlyusefultodetermineenergybarriersinchemicalprocesses,where covalentbondscanbebrokenandformed.Theyalsotypicallypredict moreaccuratebandgapsthanGGAs(toonarrow)orHartree-Fock (toowide).Hybrid-GGAshavebeenthegoldstandardforapplications inmolecularchemistry.Onthedownside,thenonlocalcharacterofthe exactHFexchangetermmakeshybridfunctionalsmorecomputationally expensivetocompute.
TheoptimalchoiceofDFTfunctionalisanontrivialmatterandultimatelydependsonthespecificchemicalsystemandapplicationofinterest. ForanexhaustivereviewofrecentDFTfunctionalsandtheirperformance ondifferenttests(e.g.,barrierheights,thermochemistry,noncovalentbonding,etc.)thereaderisreferredtotheexcellentreviewbyN.Mardirossian andM.Head-Gordon [21].Forotherinterestingdiscussionsonthistopic, wereferthereadertothepaperbyK.Burkeandcoworkers [30] andto Section10.2inShollandSteckel’sbook [4].
2.4WherearetheVanderWaalsinteractionsinDFT?
VanderWaalsordispersioninteractions,alsoknownasLondonforces,arise frominteractionsbetweenaninstantaneousdipolemomentcausedbyspontaneousfluctuationsoftheelectrondistributioninsomeatomormolecule andthetemporarydipoleinducedbytheelectricfieldoftheinstantaneous dipoleonanotheratomormolecule(i.e.,aninstantaneousdipole-induced dipoleinteraction) [31].Dispersioninteractionsexistbetweenallmolecules (evennonpolaroneswheretheaveragedipolemomentovertimeiszero), areattractiveinnature,andareessentialtoawiderangeofphenomena,from thedynamicsofliquidcarbohydratestotheself-assemblyofsupramolecular materials [13].Londonshowedthattwosphericallysymmetricatomsinteractwitheachotheraccordingto VvdW ¼ C/r6,where r isthedistance betweentheatoms,and C isaconstantthatdependsonthechemicalidentity oftheatoms.Dispersionforces,beingsignificantoverevennanometer lengthscales,areconsideredlong-rangeandareparticularlyimportantfor moleculeswithlargesurfaceareas(e.g.,2Dmaterials).
Dispersioninteractions,whicharetheresultofnonlocalcorrelations betweenelectronscharacterizedbylargedensitygradientsinregionswhere theelectrondensityissmall,cannotbecapturedbysemilocalDFTfunctionals,nomatterhowsophisticated.Themostcommon(alsosimpleand efficient)strategytoamelioratethisshortcomingistoaddtoanempirical correctiontermthataccountsforthedispersionenergybetweeneachpair ofatomsinthesystem: EDFT D ¼ EDFT + Edisp,aschemeknownas dispersion-correctedDFTorsimplyDFT-D.Althoughtheexactformof thedispersioncorrectiondependsontheexactflavororformulationof theusedDFT-D(e.g.,DFT-D2andDFT-D3) [32,33],aroughapproximationtothedispersioninteractionbetweenapairofatoms ij,canbewrittenas E disp s f damp r ij C ij =r ij 6,where s isascalingfactorthatdependsonthe XCfunctionalused, fdamp(rij)isadampingfunctiontoavoidunphysicalinteractionsatveryshort-range,and Cij arecoefficientsparameterizedapriori thatdependonthetypeofatomsinteracting.
Analternativetosimpleempiricalcorrectionsforcapturingdispersion interactionsisarelativelynewerclassofDFTfunctionalsthatincludenonlocalelectroncorrelations,whichareessentialtocapturelong-range,vander Waalsinteractions.NonlocalcorrelationDFTfunctionalshavebeenprimarilydevelopedoverthelastdecade,andsomenotableexamplesinclude thedifferentversionsofvdW-DF [34] aswellasVV10 [35] andsubsequent improvements [36],amongothers.Someofthesenonlocalfunctionalshave
beencombinedwithpowerfulsemilocalfunctionals,e.g.,SCAN-rVV10 [37] orB97M-rV [38],toformtrulyformidablefunctionals.
2.5Basissets
ThegoalofDFTsimulationistocalculatetheelectrondensityandthe energyofasysteminthegroundstatebysolvingtheKohn-Shamequations (Eq. 8),whichareformulatedintermsofsingle-electronmolecularorbitals. Inpractice,tosolvethissystemofequations,weexpandthemolecular orbitalsasasumofpredeterminedfunctions(thebasisset)multipliedby unknowncoefficients.OncetheMOshavebeenexpanded,thegoalof theDFTcalculationbecomestodeterminethoseexpansioncoefficients. Therearetwomajortypesoffunctionsorbasissetsthatareusedinthe expansionoftheMOs:localizedandextendedfunctions.Localizedbasissets areparticularlyusefultodescribeisolatedmoleculesbecausetheir wavefunctionactuallydecaystozeroatlongrange,andthus,theyhavetypicallybeenpreferredbythechemistrycommunity.Ontheotherhand, extendedfunctionsareidealtodescribebulkperiodicsystems,whichhave typicallyattractedtheattentionofthephysicscommunity.
2.5.1Localizedbasissets
AcommonpracticetodaywhichwasfirstintroducedbyRoothaaninthe contextofHartree-Focktheory [39] istoexpandtheMOsasalinearcombinationofatomicorbitals(LCAO):
where{Cμi}arecoefficientsfoundbysolvingtheKSequations,and ημ(r)are theatomicorbitals,whicharepredeterminedbasisfunctionscenteredatthe nucleioftheatomsandareknownasthebasisset(BS).Backinthe1950s, whentheLCAOmethodwasfirstdeveloped,basisfunctionswerechosento mimictheeigenfunctions(i.e.,atomicorbitals)ofthehydrogenatom, whichareknownasSlater-typeorbitals(STO).BecausenumericalintegrationusingSTOsisdifficultandtheatomicorbitalsofthehydrogenatomare somewhatlimiting,today,basisfunctionsarechosenusingmorepragmatic criteriabasedonthetypeofsystem,thephenomenaoneneedstostudy,and thecomputationalefficiency.Accordingtothevariationalprinciple,the moreflexibletherepresentationoftheMOsis,themoreaccuratethe DFTcalculationswillbe.Popularinthequantumchemistrycommunity
are Gaussian-type-orbitals (GTO),whichallowforefficientnumericalintegration,andtaketheform:
where α determineshowcompacttheorbitalis(e.g.,large α correspondstoa morediffuseorbital), N isanormalizationfactorwhichensuresthat hημ j ημi¼ 1,and L ¼ l + m + n categorizestheGTOass-functions(L ¼ 0), p-functions(L ¼ 1),d-functions(L ¼ 2),etc.GTOscanbefurthercombined toform contractedGaussianfunctions (CGFs),whicharethefoundationof mostbasissetscurrentlyavailableinquantumchemistrysoftware.Besides thesizeofthebasisset,dependingonthesystemstudied,itmaybeimportant (ornot)toincludeorbitalpolarizationordiffusedfunctionsintheBS.Two ofthemostbroadlyusedbasissetstodayarethesplit-valenceBSdeveloped byPopleandcoworkers(e.g.,thebasisset6-311+G) [40],andthe correlation-consistentBScreatedbyDunningandothers(e.g.,aug-ccpVDZ) [41].BotharetypicallyavailableinmostDFTprograms.
Despitethefactthatanyconceivablemolecularorbitalcanbe,inprinciple,representedbyEq. (12) ifenoughtermsareincluded(knownasthe completebasissetlimit),inpractice,thebasissetmustbefiniteduetocomputationallimitations.Thefinitenatureofthebasissetlimitsthecomplexity oftheelectrondensitythatcanbedescribedandthusitcanbeanimportant sourceoferrorinDFTcalculations.Ingeneral,largerbasissetsaremore accuratebutmorecomputationallyexpensive.Ifpossible,agoodpractice istostudytheconvergenceoftheenergyorotherpropertiesofthesystem withrespecttobasissetsize,asthetruegroundstatecanonlybereally achievedinthebasissetlimit.Anothersignificantsourceoferrorthatarises fromthefinitenatureofthebasisset,whichisparticularlyproblematicwhen computinginteractionenergiesbetweentwomolecules,isknownasthe basissetsuperpositionerror(BSSE).Let’ssaythat EAB istheenergyofasystemwherebothmonomerAandmonomerBareinteracting.Inthiscombinedsystem,eachofthemonomersinthecomplexABcan borrow the overlappingbasisfunctionsoftheothermonomer(whichisnotpossible whentheyareinisolation),thuseffectivelyincreasingtheflexibilityof thedescriptionofthewavefunction,which,consistentwiththevariational principle,canleadtoalowerenergyofthecombinedsystem.Inother words,thebasissetforthecomplexABisartificiallyenhancedwithrespect tothatforthemonomersAorB,whichultimatelyleadstoanartificialstabilizationofthecomplex.Themostcommonapproachtoestimatingthe
BSSEisknownasthecounterpoisemethodintroducedbyBoysand Bernardi [42].Forarecentreviewonthetopic,wereferthereaderto Ref. [43].
2.5.2Planewaves
Tounderstandwhyplanewavebasissetsarethenaturalchoicetodescribe extendedperiodicsystemssuchasmetals,wefirstneedtointroducetheconceptsofcrystalstructureandreciprocalspace,whicharefundamentalconceptsinsolid-statephysics.Foramorein-depthtreatmentofthematter beyondwhatwillbepresentedinthissection,werecommendtheintroductorytextbyS.H.Simon [44].
ABravaislatticeisaninfinitearrayofpointsgeneratedbydiscretetranslationoperationsofaunitcelldefinedbysomeprimitivevectors.ThestructureofaBravaislatticeiscapturedbythreeprimitivevectors a1, a2,and a3 (Fig.3),andalatticevectorintheextendedsystemisdefinedas: R ¼ m1a1 + m2a2 + m3a3,where m1, m2,and m3 areintegernumbers.The simplestprimitivecellofaBravaislatticeisknownastheWigner-Seitzcell, whichcontainsjustoneatom,anditisconstructedbyapplyingaVoronoi tessellationaroundanatominthecrystallattice.Thereare14differentpossibleBravaislatticesorsymmetrygroupsinthree-dimensionalspace.Of those,threearecubiccrystalsystems(i.e.,haveaunitcellintheshapeof acube):simplecubic(SC),body-centeredcubic(BCC),andface-centered cubic(FCC).
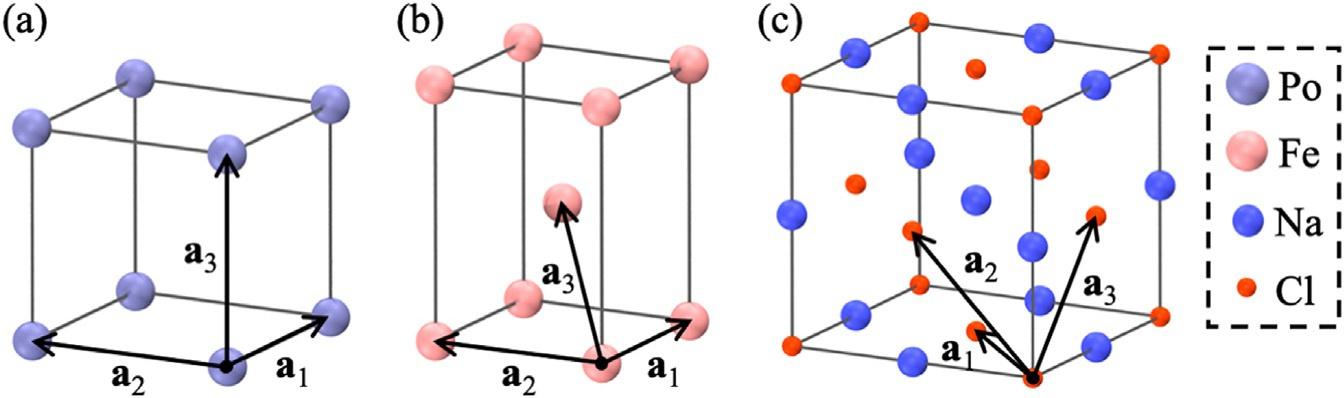
Fig.3 Examplesofcubiccrystalstructures.Theunitvectorsinthe x, y,and z Cartesian coordinatesare i, j,and k,respectively.(a)Poloniumhasasimplecubic(SC)latticestructurewithalatticeconstantof | a1 | ¼ | a2 | ¼ | a3 | ¼ 3.359Å.(b)Ironhasabody-centered cubic(BCC)latticestructure, a1 ¼ ai, a2 ¼ aj, a3 ¼ (i + j + k)a/2,withalatticeconstantof | a1 | ¼ | a2 | ¼ | a3 | ¼ 2.8665Å.(c)Sodiumchloride(NaCl)hasaface-centeredcubic (FCC)latticestructure, a1 ¼ (i + j)a/2, a2 ¼ (j + k)a/2, a3 ¼ (i + k)a/2withalatticeconstant | a1 | ¼ | a2 | ¼ | a3 | ¼ 5.6402Å.