https://ebookmass.com/product/free-surface-flow-shallow-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Free-surface flow: environmental fluid mechanics Katopodes
https://ebookmass.com/product/free-surface-flow-environmental-fluidmechanics-katopodes/ ebookmass.com
Geophysical fluid dynamics : understanding (almost) everything with rotating shallow water models First Edition Zeitlin
https://ebookmass.com/product/geophysical-fluid-dynamicsunderstanding-almost-everything-with-rotating-shallow-water-modelsfirst-edition-zeitlin/
ebookmass.com
Surface Process, Transportation, and Storage Qiwei Wang
https://ebookmass.com/product/surface-process-transportation-andstorage-qiwei-wang/
ebookmass.com
Pinch of Nom Express : Fast, Delicious Food Kate Allinson
https://ebookmass.com/product/pinch-of-nom-express-fast-deliciousfood-kate-allinson/
ebookmass.com
https://ebookmass.com/product/maniacs-imp-iron-punishers-mcbook-3-ciara-st-james/
ebookmass.com
Make Me Burn Marie Harte
https://ebookmass.com/product/make-me-burn-marie-harte-2/
ebookmass.com
Solid Waste Landfilling: Concepts, Processes, Technology
Raffaello Cossu
https://ebookmass.com/product/solid-waste-landfilling-conceptsprocesses-technology-raffaello-cossu/
ebookmass.com
The Barn: An Extraordinary True Story David Hill
https://ebookmass.com/product/the-barn-an-extraordinary-true-storydavid-hill/
ebookmass.com
Brokerage and Networks in London’s Global World: Kinship, Commerce and Communities Through the Experience of John Blackwell David Farr
https://ebookmass.com/product/brokerage-and-networks-in-londonsglobal-world-kinship-commerce-and-communities-through-the-experienceof-john-blackwell-david-farr/
ebookmass.com
Second Edition Jay Dorfman
https://ebookmass.com/product/theory-and-practice-of-technology-basedmusic-instruction-second-edition-jay-dorfman/
ebookmass.com
Free-SurfaceFlow Shallow-WaterDynamics Free-SurfaceFlow Shallow-WaterDynamics NikolaosD.Katopodes Butterworth-HeinemannisanimprintofElsevier
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2019ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicor mechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem,without permissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationabout thePublisher’spermissionspoliciesandourarrangementswithorganizationssuchastheCopyright ClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher (otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedicaltreatment maybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingand usinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformation ormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesfor whomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeany liabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligence orotherwise,orfromanyuseoroperationofanymethods,products,instructions,orideascontainedin thematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-815487-8
ForinformationonallButterworth-Heinemannpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionEditor: KenMcCombs
EditorialProjectManager: SerenaCastelnovo/JoshuaMearns
ProductionProjectManager: SuryaNarayananJayachandran
Designer: MatthewLimbert
TypesetbyVTeX
Dedicatedtotheonethatmastersitall, andmakesmeproudeveryday
HerculescombatingtheRiverAcheloos. StatuebyBosio,LouvreMuseum,Paris
Prologue Nomaneverstepsinthesamerivertwice,foritisnotthesameriverand heisnotthesameman.
Heraclitus;circa750B.C.
Motivation Thelengthscalescoveredbyenvironmentalfree-surfaceflowsareoftensodissimilarthatresolvingthemwithequalfidelityleadstonoadvantagealthough incursamajorcost.Mostnaturalandman-madechannelshavealengththatis considerablylargerthantheirdepthandwidth.Theobjectiveofanyanalysisof free-surfaceflowsalsovariessignificantlydependingontheassociatedapplication.Thus,knowledgeofsecondarycurrentsinariverisoftenunimportant ifthegoalistopredictpotentialfloodingofamunicipality.Itisthereforewise toseekanapproximationtofree-surfaceflowbyaveragingtheflowproperties alongthedirectionscorrespondingtothesmallerscalesoftheproblem.Historically,theseapproximationsweredevelopedlongbeforewewereabletosolve thecompletehydrodynamicequationsoffree-surfaceflow,thusitisnosurprise thatthesemethodscontainempiricalelementsthatareoftenofquestionablescientificvirtue.Ontheotherhand,averagedflowmodelsarepowerfultoolsfor solvingpracticalproblemsthatarenotamenabletosolutionbymoreelegant modelsoffluidmechanics.
Thebest-knownapproximationoffree-surfaceflowisobtainedbyintegratingthehydrodynamicequationsoverthedepthofflow,whichleadstothe conceptof shallow-waterflow.Whenthegoverningequationsareaveragedin theverticaldirection,theconceptofair-waterinterfacedegenerates.Thepositionofthefreesurfaceisrepresentedbythedepthofflow,whichisindependent oftheverticalcoordinate,andnolongerdeterminestheextentofthesolution domain.Therefore,three-dimensional,incompressiblefree-surfaceflowisconvertedtoatwo-dimensional,depth-averagedflowthatisphysicallyanalogous tocompressiblegasflowsincethedepthassumesthesameroleasthegasdensity.Thus,an elevationwave onthefreesurfaceisabsorbedbythedepthlikea compressionwave bythegasdensity.Similarly,a depressionwave onthefree surfaceistreatedlikea rarefactionwave inthegas.Thedepthandthedepthaveragedvelocitiesarethenewdependentvariablesoftheproblem,andthe verticaldimensiondisappearsfromtheanalysis.Furthermore,thehorizontaldimensionsoftheproblemarepermanentlyfixedexceptwhenwavespropagate onadrybed,asinthecaseoftidalflatsandfloodplains.
Thephysicsofshallow-waterflowissodrasticallydifferentfromthatof free-surfaceflowthatitisarguablewhetherornotthesecondbookinthisseries shouldbeincludedunderthetitle Free-SurfaceFlow.However,thepractical usageofthesetwotheoriesissocloselyintertwinedthatitisimpossibleto masteronewithoutunderstandingtheother.Fortheiradvantagesandlimitations combinetocreateaninseparableapproachtosolvingenvironmentalproblems associatedwithsurfacewaters.
Whenthegeometryoftheproblemallowsit,shallow-waterflowcanbeintegratedoverthewidthofawell-definedconduit,whichleadstotheconcept of open-channelflow.Inthiscase,attentionisfocusedonfindingthedepthof flowandthevolumeofwatercarriedbythestreamperunittime.Thecalculationofthevolumetricflowrateisbasedontheintegraloflocalvalues,thus
takingintoaccountthevariationofthevelocityvectoroverthestream’scross sectionalarea.Thisareaisafunctionofthedepthofflow,which,togetherwith theaveragevelocitysufficetocompletelydescribetheproblem.Thedepthand theflowratearefunctionsonlyoftimeanddistancealongthechannel’slongitudinalaxis,thusthesolutiondoesnotdependontheverticalortransverse coordinates,whichresultsinamajorsimplification.Thisso-called hydraulic descriptionofflowproblemsformsthebasisforone-dimensionalmodelingof avarietyofflowsinvolvingafreesurface.Theword hydraulic originatesfrom theGreek ύδωρ,(water),andeither αυλός (pipe)or αύλαξ (flume).Bothof theseconduitsguidetheflowalongtheirlongitudinalaxiswhilelimitingany transverseorverticalvelocitycomponents.Therefore, hydraulics isabranchof hydrodynamics thatimpliesa scaling ofthegeneralflowconditionswhenthe lengthofflowismuchlargerthanthedepthorwidth.
Ofcourse,notalltypesoffree-surfaceflowaresuitableforthistypeof averaging,asanumberofconditionsmustbemetfortheapproximationtobe valid.Intruefree-surfacehydrodynamics,thedomainoftheproblemconstantly changesaspartofthesolutioninunsteadyflow.Insteadyflow,thedomainis fixed,butthepreciseconfigurationoftheboundarygeometryisnotknowna priori,thusagainitmustbedeterminedaspartofthesolution.
Ontheotherhand,furthersimplificationsareoftenpossiblebytruncationof theopen-channelflowequationsatvariouslevels,arrivingfinallyattheso-called hydrologic formulation,whichallowsforthesimplest,albeitcrudest,solutionof free-surfaceflowproblems.Yet,thecomplexityofthegeometryandsurfaceresistanceinoverlandflow,forexample,allowsustoaddresssuchproblemswith lessrigorousmathematicalformulationswhileachievingsatisfactoryaccuracy. Thehydraulicsofopenchannelswasapparentlyknownintheantiquity whenmajorstructureswerecompletedforconveyingwatertomajorcenters ofcivilization.Themodernhistoryofopen-channelflowbeginswiththework ofChézy(1776),whoestablishedthefirstequationsdescribinguniformchannelflow.Afewyearslater,Monge(1807)laidthefoundationofthetheory ofwavepropagationinacompressiblegasthatalsodescribesshallow-water waves.Atapproximatelythesametime,Bélanger(1828)developedthefirst numericalsolutionfornon-uniformflowinopenchannels,andlaterGauckler (1867)andManning(1891)furtherdevelopedtheflowresistanceequations.The descriptionofunsteadyflowwascompletedbyBarrédeSaint-Venant(1871), thustheone-dimensionalshallow-waterequationsareoftencalledthe Saint Venantequations.AcomprehensivetreatiseonthesubjectwaswrittenbyDarcy andBazin(1865)whocombinedanalyticalandexperimentaltechniquesintwo beautifulvolumes.Finally,anenhancementofshallow-watertheorywasmade byBoussinesq(1903),whoincludedhigher-ordertermsthataccountforwave dispersion.
Thefirstformaltreatiseonopen-channelflowwaswrittenbyBakhmeteff (1932)andwasfollowedbyWoodwardandPosey(1941).Thesubjectwas enlightenedbytheclassictextofStoker(1957),whointroducedtheterm Mathe-
maticalHydraulics,andreviewedallpreviousworkonwavesinopenchannels. Almostsimultaneously,atreatiseonthesubjectappearedthatremainseven todaythemostcomprehensivereferenceonopen-channelflow.Chow(1959) coveredalltechnicaldetailsforanalysisanddesignofopenchannels.However, thebookthatreallycapturedthemindsandheartsofyoungengineerswasthe brilliantbookbyHenderson(1966).Hisphysicalinsightofferedapedagogical approachtotheconceptsofchannelflowthathasnotbeenmatchedtothisday. Manyworthycontributionstothesubjectofshallow-waterwavesweremade duringthefirstpartofthetwenty-firstcentury,andcontinueatarapidrate. Alistofcurrentbooksonrelatedtopicscanbefoundinthegeneralbibliography section,astheyhaveallbeeninvaluableinthedevelopmentofthistext.At thesametime,arevolutioninnumericalmathematicsanddigitalcomputation hastakenplacethatbroughtunprecedentedchangetoallfieldsofscienceand engineering.
ApproachofThisText ThesecondbookintheFree-SurfaceFlowseriesattemptstobridgethegapbetweenenvironmentalfluidmechanicsandopen-channelhydraulicsbyproviding arigoroustransitionbetweentheNavier-StokesandShallow-Waterequations. Aspecialefforthasbeenmadetoprovideaseamlessintegrationofvarying ordersofapproximation,fortheyallrepresentdifferentviewsofessentially thesameproblem.Asaresult,theunderlyingphilosophyoftheentirebookis that,regardlessofthedevelopmentsinnumericalmethods,scientificcomputationmustbebasedonappropriateapproximationsofthegeneralmathematical descriptionoffree-surfaceflow.Theseshouldbedeterminedbyathoroughunderstandingofthephysicalaspectsofflowmotion,whichvarysignificantlyat eachapproximationlevel.Onlybykeepingthesimplifiedmodelsinperspective cantheirlimitationsbeexplained,andtheirfailuresbeanticipated.
Anotherobjectiveofthesecondbookoftheseriesistolaythefoundationof theconstructingofcomputationalmethodsforsolvingtheshallow-waterequations.Theyareshowntobepartialdifferentialequationsofthehyperbolictype, thusgenuinesolutionsarefoundusingthemethodsofcharacteristicsintwoand threeindependentvariables.Bypresentingacomprehensivedescriptionofthis method,itisexpectedthatthecomputationalmethodsoutlinedinthethirdbook oftheserieswillbedevelopedonsoundprinciples.
Finally,thisbookpresentsanintroductiontosensitivityanalysis,parameter estimation,andcontrolofchannelflowbyboundaryactuators.Thismaterialis anextensionofthesolutemasscontrolpresentedinthefirstbookoftheseries, andallowstheefficientmanagementofhydraulicstructures.
Outline Thematerialisdividedinchaptersthatrepresentcompleteentitieswhileleading sequentiallyfromgeneraltospecificformulationsoffree-surfaceflowproblems.
Chapter 1 describestheelementsofphysicsandmathematicsneededtodevelopthetheoryofshallow-waterwaves.Thisincludesthefundamentals ofsurfacedifferentialgeometry,andthecurvatureofsurfaces.Geometric relationsofcurvesandsurfacesinspacearedeveloped,andtheconcept ofmeancurvatureisdiscussedindetail.Explicitandimplicitsurfacesare defined,andEuler’stheoremisproved.Furthermore,aformaldescriptionofinitialandboundaryvalueproblems,astheyapplytofree-surface flow.Thedivergencerepresentationtothecurvatureofthefreesurfaceis presented,intheformthatisusedinmoderncomputermodels.Finally, aclassificationofpartialdifferentialequationsisgiven,thusproviding anearlyencounterwiththemethodofcharacteristics.Theclassification includesfirstordersystemsofequations,andhigher-orderequations.
Chapter 2 isdedicatedtothedescriptionoftheair-waterinterface.Surfacetensionisintroduced,andtheYoung-Laplaceequationisderived.Themeniscusprofileofafluidnexttosolidboundaryisanalyzed.TheMarangoni effectisintroducedandtheimportanceofBondnumberisexplained.The dynamicsoffloatingbodies,andthecircularhydraulicjumpareanalyzed. Implicitsurfacedescriptionisusedtoformulatethekinematicanddynamicconditionsatthefreesurface.Free-streamlinetheoryisusedto obtainexactsolutionsforfree-surfaceflowproblems.Boundaryconditionsforcontactlinesareintroduced,andsimpleviscousflowproblems withafreesurfacearesolvedanalytically.Flowdrivenbywindshear isexamined,andthesurfacedragcoefficientiddetermined.Significant waveheightisdefined,followedbyarandomwaveanalysis.Theatmosphericsurfacelayerisalsodiscussed,andtheMonin-Obukhovsimilarity theoryisintroduced.Theconceptofstormsurgeisdeveloped,andwave set-upisquantified.
Chapter 3 introducesthetheoryoflinearoscillatorywaves.HarmonicmotionandAiry’stheoryforgravitywavesarediscussed,andtheconceptof wavedispersionisintroduced.Thedispersionofawavepacketisstudied.Standingwavesandseichesarediscussed,andamphidromicpoints areidentified.Massandenergytransportbygravitywavesareanalyzed, andtheconceptofgroupvelocityisintroduced.Waverefractionand diffractionareanalyzedinrelationtocoastalproblems.Wavebreaking isaddressed,andtheconceptofradiationstressesisexplained.Finally, methodsforthepredictionofwaveset-uparepresented.
Chapter 4 introducestheShallow-Waterapproximation.Followingascale analysisofchannelflow,thegeneralequationsareintegratedoverthe verticaltoyieldvariouslevelsoflong-waveapproximation.Thekinematicfree-surfaceandbottomboundaryconditionsareemployed,andthe conceptsofflowdepthanddepth-averagedvelocityaredefined.Higherordershallow-watertheoryisalsopresented,andequationsfornonlinear dispersivewavesarederived.Vorticitytransportinshallowwaterisstudied,andthegasdynamicsanalogyisoutlined.GravitywavesofPoincaré,
Kelvin,andRossbytypearedescribed.Dispersionofnonlinearwavesis outlined,andtheBoussinesqequationsarederived.TheSerreequations forfullynonlinearwavesarederived,andtheKorteweg-deVriesequation ispresentedalongwiththesolitarywavesolution.Finally,aHamiltonian approachtowaterwavesispresented,aimingatconstructionmorerobust modelsfornonlineardispersivewaves.
Chapter 5 investigatesthecauseoftidalforcesandtheireffectonriversandestuaries.Theequilibriumanddynamictheoriesoftidesareintroduced,and standingtidalwavesareanalyzed.Kelvinwavesandamphidromicpoints aredefined,andtheharmonicdescriptionoftidesisbrieflydiscussed.
Chapter 6 dealswiththelowestordershallow-waterapproximationinone spacedimension,representingwhatiscommonlyknownasopen-channel flowtheory.TheequationsofdeSaint-Venantarederivedforchannels ofarbitrarycross-sectionalshape.Non-prismaticchannels,lateralflow, andtheeffectoffloodplainintegrationinthecrosssectionarediscussed. Conservationformsandalternativeformulationsofthegoverningequationsarealsopresented.Furthertruncationoftheequationsispursued, andthesimplestpossiblemodelsoffree-surfaceflowareestablished.Extensionsoftheequationstononlineardispersivewavesandwave-current interactionarealsopresented.Theconceptofradiationstressesisintroducedandtheshallow-waterequationmodelsaremodifiedtoaccountfor shortwaves.
Chapter 7 simplifiesmattersfurtherbyfocusingonsteadyopen-channelflow. Graduallyandrapidly-variedflowaredefined,andindependentmethods ofanalysisareproposed.Bakhmeteff’sconceptofspecificenergyisintroduced,andtheconditionsforcriticalflowarediscussed.Theconceptof specificforceisintroducedintheprocessofmomentumconservation,and thephenomenonofthehydraulicjumpisanalyzed.Variousapplications ofchannelconstrictionsandexpansionsarepresented,andtheinterplay betweentheconservationandofmomentumandenergyisusedtosolve avarietyofrapidly-variedflowproblems.
Chapter 8 describesthefundamentalconceptsofflowresistance.Thebasic ideasofskinandformresistancearepresented,andequationsforlaminar andturbulentflowanalysisarederived.Approximatemodelsforturbulenceareconstructedandappliedtofree-surfaceflow.Theprofilesof velocitydistributionadjacenttosmoothandroughwallsaredeveloped, andapproximatetheoriesforconstructingfrictioncoefficientsarestudied.Furtherdevelopmentofturbulentflowmodelsismadeforlaterusein relatednumericalsolutions.Uniformflowconditionsaredeveloped,and channelslopeclassificationispresentedinconnectiontodesignconsiderations.
Chapter 9 isdedicatedtosteady,non-uniformflow.Thedifferentialequationforgradually-variedchannelflowisderived,andsomeanalytical solutionsaredevelopedforsimplifiedchannelconditions.Acomplete
classificationoffree-surfaceprofilesispresented,andsomeelementsofa numericalsolutionaregiven.Techniquesarealsopresentedforhydraulic jumplocation,spatially-variedflow,andthelake-dischargeandtwo-lake problems.
Chapter 10 isanintroductiontothemethodofcharacteristicsasitapplies toshallow-waterflow.Partialdifferentialequationsareclassifiedand physicalproblemsareassociatedwithcharacteristiccurves.Thepaths alongwhichwavestravelinspaceandtimeareexamined,andcompatibilityrelationsalongthemarederived.Thecharacteristicsofkinematic anddynamicwavesareconstructedmathematicallyandgraphically,and boundaryconditionsforlongwavesinopenchannelsarespecified.Twodimensional,supercriticalflowisanalyzed,andsteady-statewavefronts inchanneltransitionsarecomputed.
Chapter 11 Themethodofbicharacteristicsisintroducedfortwo-dimensional, unsteadyflow,andthecorrespondingcompatibilityequationsarederived. Boundaryconditionsfortwo-dimensionalflowareestablishedandassociatedwiththegeometryofthecharacteristicconoid.
Chapter 12 describessimplewaves,surges,andshocksinone-dimensional flow.Depressionandelevationwavesandhydraulicboresaredefined.By usingcharacteristicanalysis,thespontaneousformationofshockwavesis studied.Weaksolutionsofconservationlawsareconstructedforanalyzingsurgesandbores.Shockinteraction,reflection,andenergydissipation arealsodiscussed.
Chapter 13 Dam-breakanalysisoninitiallydryandflowingstreamsisperformedusingthemethodofcharacteristics.Theeffectsofslopeand frictiononthedam-breakwavearepresented.Acomplete,albeitonedimensional,analysisofpartialclosingandopeningofasluicegateis presented,andtheresultingsystemofalgebraicequationsaresolved.
Chapter 14 introducestheconceptofadjointsensitivity,anddiscussesparameterestimationandmodelvalidation.Themethodsofsteepestdescentand conjugategradientareintroducedandusedtoidentifythebasicparametersoffree-surfaceflow.Adjointequationsarederivedforopen-channel flow,andmulti-dimensionalshallow-waterflow.Boundaryconditionsand solutionmethodsforadjointequationsarepresented.Thefundamental conceptsofactivefloodcontrolareintroduced,andtechniquesforfocusingdepressionwavesonthepeakoffloodwavesarepresented.Adjoint equationsaredevelopedleveebreachcontrol,andnon-reflectingboundaryconditionsareconstructedformulti-dimensionalsensitivitywavesin openchannels.
Acknowledgments Thisbookhasdemandedalongtimetocomplete,thusmanystudentshave contributedtoitsdevelopment.Iamindebtedtoallofthem,andespeciallyto thosewhosubsequentlyhaveusedthebookwhileteachingtheirownclasses,
xxvi Prologue afterleavingtheUniversityofMichigan.Theirvaluablesuggestionshavemade thisagratifyingproject.Iamalsogratefultomyownmentors,GeorgeTerzidis andTheodorStrelkoff,whointroducedmetothesubject,andguidedmethrough someofitstortuouspaths.Ithasbeenawonderfulvoyageofexplorationand learning.
N.D.Katopodes AnnArbor REFERENCES Bakhmeteff,BorisAlexandrovi ˇ c,1932.HydraulicsofOpenChannels.McGraw-Hill,NewYork. BarrédeSaint-Venant,A.J.C.,1871.Théorieetequationsgénéralesdumouvementnonpermanent deseauxcourantes.ComptesRendusdesSéancesdel’AcadémiedesSciences73,147–154. Bélanger,J.B.,1828.EssaisurlaSolutionNumériquedequelquesProblémesRelatifsauMouvementPermanentdesEauxCourantes.Carilian-Goeury,Paris.
Boussinesq,JosephValentin,1903.ThéorieAnalytiquedelaChaleur.Vol.II.Gauthier-Villarset Fils,Paris.
Chézy,Antoine,1776.FormulepourTrouverlaVitessedel’EauConduitdanuneRigoledonnée (Formulatofindtheuniformvelocitythatthewaterwillhaveinaditchorinacanalofwhich theslopeisknown).Dossier847,Ms.1915,ofthemanuscriptcollectionoftheÉcoleNational desPontsetChaussées,Paris.Reproducedin:Mouret,G.,1921.AntoineChézy:histoired’une formuled’hydraulique.AnnalesDesPontsEtChaussées61,165–269.
Chow,VenTe,1959.Open-ChannelHydraulics.McGraw-Hill,NewYork.
Darcy,M.H.,Bazin,M.H.,1865.RecherchesHydrauliques,Premièrepartie:RecherchesExpérimentalessurl’Écoulementdel’EaudanslesCanauxDécouverts.E.Dunod,Éditeur,Paris, p.1865.
Gauckler,P.G.,1867.EtudesThéoritiquesetPratiquessurl’EcoulementetleMouvementdesEaux. ComptesRendusdel’AcadémiedesSciences64,818–822. Henderson,FrancisM.,1966.OpenChannelFlow.Macmillan,NewYork. Manning,R.,1891.OntheFlowofWaterinOpenChannelsandPipes.TransactionsInstituteof CivilEngineersofIreland20,161–209.
Monge,Gaspard,1807.Applicationdel’AnalyseàlaGéométrie.Àl’usagedel’Ecoleimpériale polytechnique,Paris.
Stoker,JamesJ.,1957.WaterWaves:TheMathematicalTheorywithApplications.WileyInterscience,NewYork.
Woodward,S.M.,Posey,C.J.,1941.HydraulicsofSteadyFlowinOpenChannels.JohnWiley& Sons,Inc.,London.
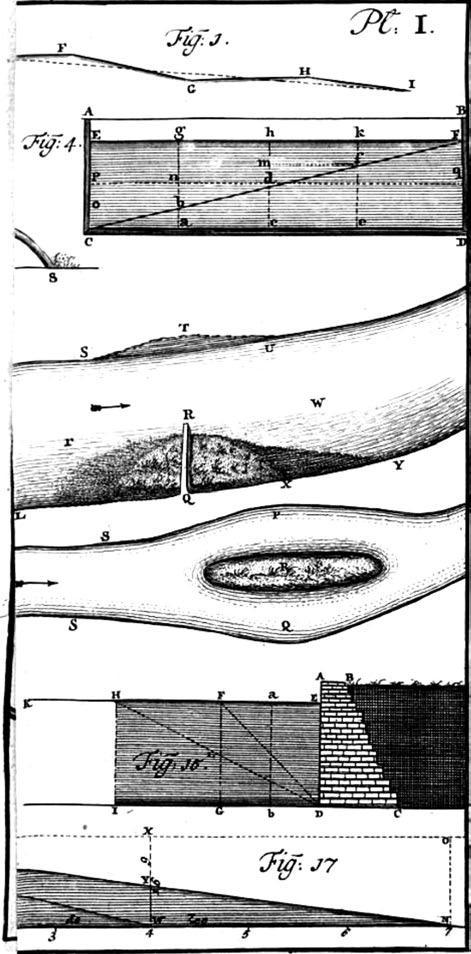
Velsen’shydraulicdesigndrawings.Reproducedfrom RivierkundigeVerhandeling,AfgeleidUit WaterwigtEnWaterbeweegkundige byCornelisVelsen,1749,Amsterdam
Chapter1 BasicConcepts ...thetruthisthatthedeclinationoftheheavenlybodiesbringsafierydisasterupontheearth.Then,thosewholiveonhighaltitudessufferagreater disasterthanthoselivingnearriversorbythesea.However,theNilewho isoursaviorforeverything,savesusfromthisconundrumbyflooding. Plato.Timaeus–AboutAtlantisandNature.Circa360B.C.
1.1INTRODUCTION Infree-surfaceflow,theanalyticaldescriptionoftheflowconditionsisachieved bydeterminingthevelocityvectorfieldandthescalarfieldcorrespondingto thepressureintensity.Inaddition,thepositionofthefreesurfacemustbedeterminedbyimposingthekinematicanddynamicboundaryconditionsonthefree surface.Forflowonanunevenbottom,thekinematicconditionalsoneedstobe appliedtothechannelbed,asexplainedinChapter 2.Iftheanalysisisbased ontheturbulentNavier-Stokesequations,theresultingsolutionyieldsthemost completeinformationabouttheflowproblem.However,physicalreasoningand observationsconfirmthatwhenthedepthofflowisconsiderablysmallerthan thehorizontaldimensionsoftheproblem,theflowpatternisaltereddrastically.
Observationsshowthatastheflowbecomesmoreshallow,particleorbits andstreamlinesunderagravitywavearegraduallytransformedfromcircles toellipses.Therefore,theverticalcomponentofthevelocitybecomesnegligiblecomparedtothehorizontalcomponents.Furthermore,asexplainedin section I-6.4.3,thepiezometricheadremainsconstantnormaltostreamlines withminimalcurvature.Thisimpliesthatthepressuredistributioncanbedirectlydeterminedoncethedepthofflowisknown,thusthepressureisnolonger adependentvariableintheproblem.Therefore,theshallow-waterequations,i.e. thevertically-averagedcontinuityandhorizontalmomentumequations,suffice todeterminethesolutionoftheflowproblemwithaccuracy.Suchasolutionis nearlyidenticaltotheoneobtainedbysolvingthecorrespondingfree-surface flowproblem,providedthattheassumptionsassociatedwiththeshallow-water limitoftheflowaresatisfied.
Thereductioninthephysicaldimensionsoftheproblemandthenumberof dependentvariablesrepresentsadefiniteimprovementinefficiency.Inthelimit, asthedepthapproacheszero,theshallow-waterapproximationactuallyyields perfectresults.However,therealvalueofshallow-watertheoryisfoundinapplicationsofpracticalinterestwherethedepthisfinite.Intheseproblems,the resultsarealmostperfect,especiallywhenoneconsidersthesourcesofothererrorsencounteredinpredictionsofflowinrivers,lakes,andestuaries.Therefore, themainchallengeforthewaterscientistandengineerisnottheimplementationofthetheoryinpractice,buttheassessmentoftheinformationhiddenby theshallow-waterapproximation.Thisisafascinatingstatementbecausewe areaccustomedtobelievingthatasymptoticapproximationshavenoimplicationsonthephysicaldescriptionofaproblem.However,thisisfarfromtruefor shallow-waterwaves.Boththemathematicsandthephysicsdifferfromthose fordeep-waterwaves,andtheapproximationcreatesanewbranchofenvironmentalfluidmechanics.
1.1.1Shallow-WaterModels Theobjectiveofthisbookistodevelopmathematicalmodelsbasedonthe shallow-waterapproximation.Asalreadymentioned,theseareapproximations
withreducedspatialdimensions,thusitisimportanttodistinguishshallowwaterfromgenuinefree-surfaceflowmodels.Asanexample,considertheflow patterncreatedbya sluicegate operatinginanopenchannel,asshownin Fig. 1.1.
Forthereaderunfamiliarwiththisdevice,Fig. 1.1 showsatypicalsetupina laboratoryflume,underflowconditionsthataretimeinvariant.Thegateslides verticallyinguidesmountedonthechannelsidewalls,andhelpsregulatethe flowbychangingthesizeofthegateopening.TheflowpatternshowninFig. 1.1 correspondstoafreeflowinggate,asopposedtoonethatissubmergedonthe downstreamside.Specifically,theleftfaceofthegateisincontactwiththefluid whiletherightfaceiscompletelyexposedtoair.Furthermore,ontheupstream side,theflowappearstobetranquilwiththeexceptionofaminordisturbance onthefreesurfacenearthesidewallofthechannel,whichisassociatedwith vortexstretching,asdescribedinFig. I-7.17 ofsection I-7.6.Thereisaslight super-elevationofthefreesurfaceatitspointofcontactwiththegate,whichis aresultofthefluidcomingtoanabruptstopagainstthemetalplate.
Onthedownstreamside,thepictureischaracterizedbyrapidflow,forming acurvilinearfreesurfacethatglidessmoothlyunderthegate.Thestreaksofair entrainmentarevisibleonthefreesurface,andtheyindicatethehighvelocity withwhichthewateremergesfromthegateopening.Finally,asmalldistance away,andonbothsidesofthegate,thefreesurfacebecomesparalleltothe channelbed.
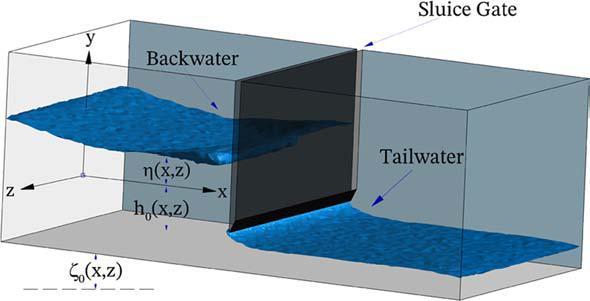
Thegeometricelementsoftheflowaregivenbythebedelevation, ζ0 (x,z) , thedepthoftheundisturbedwatersurface, h0 (x,z) ,theCartesiancoordinates, (x,y,z) ,ofthegateandsidewallsofthechannel,andthepositionofthefree
FIGURE1.1 Laboratory-scalesluicegate
surface, η(x,z) .Noticethat η(x,z) isnotknownapriori,butinsteaditmust becomputedaspartofthesolution.Thebasicelementsofafree-surfaceflow modelfortheflowunderasluicegateareshowninFig. 1.2
FIGURE1.2 Definitionofflowregimesforasluicegate;free-surfaceflow
Ontheupstreamside,oftencalledthe backwater region,thefluidcomesto anabruptstopor stagnationpoint onthefaceofthegate.Atthesametime,the fluidbelowacceleratestopassthroughthereducedflowopening.Theelevation ofthefreesurfaceincreasesgraduallytoitsmaximumheightatthestagnation point,i.e.whereitmeetsthegateonitsupstreamface.Onthedownstreamside, alsocalledthe tailwater region,thetipofthegateguidesthefreesurfacetoa smooth,stronglycurvilinearprofileuntiltheinfluenceofthegatediminishes furtherdownstream.
Thereareseveraldirectobservationsthatcanbemadeabouttheflowconditions.First,inthevicinityofthegatethevelocityisnotuniforminthevertical direction,andneitheristheacceleration,asthefluidisforcedtochangefrom horizontaltoverticalmovement.Second,thepiezometricheadisnotconstant sincethepressuremustbeatmosphericatthefreesurfaceonbothsidesofthe gate.Third,althoughtheflowisdirectedalongthechannelaxis,thefreesurface, andconsequentlythevelocity,arenotperfectlyuniforminthetransverseflow direction.NoticethattheimageshowninFig. 1.2 isthe true,three-dimensional solutiondomainoftheproblem.
Whentheshallow-waterapproximationisimplemented,theimageshownin Fig. 1.2 collapsesontothehorizontalplane,andthefreesurfacedisappearsas aphysicalelementoftheflowdomain.Thegeometricelementsofthefloware givenbythebedelevation, ζ0 (x,z) ,andtheCartesiancoordinates, (x,z) ,ofthe gateandsidewallsofthechannel.AsshowninFig. 1.3,thesolutionisdefined bythedepthandthehorizontalcomponentsoftheflowrate,thusthephysical representationsofthetwoproblemsarequitedifferentalthoughthesolutions maybeidentical.Noticethatthepresenceofthesluicegateontheflowpattern
createsadiscontinuityinthedepthandvelocityofflow,thusthegateneedsto betreatedasaninternalboundarycondition.
FIGURE1.3 Definitionofflowregimesforasluicegate;shallow-waterflow
Whentheopen-channelflowapproximationisappropriate,thechannelimagecollapsesonthe x axis,asshowninFig. 1.4.Thegeometricconfiguration isreducedtothebedelevation, ζ0 (x),andthelocationofthegate, (x),along thechannelaxis.Ifthechanneldoesnothavearectangularcrosssection,the topwidth, B(y) ,andsectionarea, A(y),mustbegivenaswell.Nowaunique solutioncanbefoundbydetermining A ,andtheflowrate, Q ,ateverypoint alongthechannel.
FIGURE1.4 Definitionofflowregimesforasluicegate;open-channelflow
Theflowunderafree-flowingsluicegateisaproblemofbothdidacticand practicalvalue.TheconfigurationsshowninFig. 1.2,Fig. 1.3,andFig. 1.4 representseveralalternativeflowmodelsassociatedwiththeflowunderasluice gate.Dependingonthelevelofdetaildemandedbytheapplication,thequestionofcomplexityversusreliabilityisofgreatimportanceinchoosingthe appropriatemathematicalmodel.Theincorporationofdetailedfeaturesofthe free-surfaceprofilemayormaynotresultinincreasedaccuracyoftheresults althoughthedecisiontoincludethedetailsmayincreasetherequiredeffortdramatically.
Throughoutthisbook,numeroussketchesofshallow-waterandopenchannelflowaredrawnthatpotentiallymisrepresentthetheorybehindthe methodsbeingdiscussed.Forexample,asshowninFig. 1.5,wemayusea sketchforopen-channelflowthatshowsthe“freesurface”andchannelbedprofiles.Thisisdonetohelpbettervisualizetheproblem,asthesketchinFig. 1.4
doesnotgiveameaningfulpictureofthesolutionoftheproblem.Notice,however,thattheverticalandhorizontalscalesinFig. 1.5 maybequitedifferent, thusthefreesurfacemayappeartohavestrongercurvaturethanitistrue.
FIGURE1.5 Definitionofflowvariablesforopen-channelflow
ThecorrectreadingofthesketchinFig. 1.5 istointerpretthesolidline asthedepthprofileplottedagainstthechannelaxis.Thesumof h + ζ0 gives theelevationofthefreesurfaceasafunctionof x ,butdoesnotcoincidewith upperboundaryoftheproblem’sdomainintheverticaldirection,asisthecase inFig. 1.2.Instead,thesketchdepictsthevariationofoneofthedependent variablesofaone-dimensionalproblem,afterthesolutionhasbeencompleted. Therefore,thedefinitionsketchesintheremainderofthebookshouldnotbe interpretedasrepresentingthetruedomainoftheflow,butasvisualaidesto helpdescribethesolutionoftheproblemunderconsideration.
Oneoftheobjectivesofthisbookistoconstructmathematicalmodelsat theshallow-waterandopen-channellevelsofapproximationforproblemslike thefree-surfaceflowunderasluicegate.Suchmodelsallowforanaccurateand efficientdesignofflowcontrolstructuresthatisverydifficulttoachievebylaboratorystudiesalone.Theamountofinformationthatbecomesavailablethrough amathematicalmodel,andtheeaseoftransferabilitytootherflowstructures isthedrivingforceofmodernanalysis,design,andcontroloffluidflow.Once validated,amathematicalmodelprovidesinformationatanydesiredresolution, isscalable,applicableuniversally,andtransferabletoavarietyofpracticalapplications.
1.2SURFACESINTHREE-DIMENSIONALSPACE Theair-waterinterfacegeneratesatwo-dimensionalsurfacethatdefinesthediscontinuityofpropertiesbetweentwofluids,determinestheirdomainofsolution andtheirdynamicandchemicalinteractions.Aspreviouslyexplained,thesolutiontoanyfree-surfaceflowproblemdependsonthepreciseidentificationof thegeometriccharacteristicsofthisinterface.Two-dimensionalsurfaceshave beenthesubjectofstudyindifferentialgeometry,thusawealthofinformation ontwo-dimensionalsurfacescanbefoundinrelevanttextslikeSpivak(1999), Topogonov(2006),andPressley(2012).
1.2.1AnalyticRepresentationofSurfaces Therearevariouswaytodescribeatwo-dimensionalsurfacemathematically. Themostintuitiveapproachistoexpressitasan explicitsurface,inwhichone oftheCartesiancoordinatesofapointonthesurfacecanbefoundasafunction oftheothertwo,i.e.
Thus,ifthegraphofthefunction f(x,z) isdefinedateverypointinspace, y generatesa regularsurface
Example1.2.1. Considerthesurface y = √x 2 + z2 thatdescribesthesurface ofaconewithvertexattheorigin,similartotheoneshowninFig. I-1.26 Notice,however,thatinthiscase y isnotaregularsurfacebecausetheoriginis asingularpoint.
Themainadvantageoftheexplicitrepresentationofasurfaceistheease intracingit.Forexample,Eq.(1.1)permitsarelativelyeasycomputationof thesurfaceheightfromanarbitrarydatum.However,therelationinEq.(1.1)is axisdependent,thusitmaybedifficulttotransformifnecessary.Furthermore, theexplicitrepresentationinherentlyexcludessurfaceswithfolds,overhangs, oreventhosethatareparalleltothe y axis.ThesurfacedepictedinFig. I-1 showsatypicalexampleofthesedifficulties.Finally,theexplicitrepresentation doesnotallowaneasyidentificationoflocalsurfacepropertiesormethodsfor predictingthebehaviorofothersurfacesintheneighborhood.
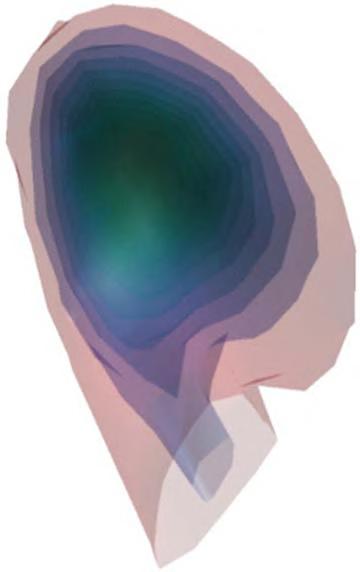
1.2.2ImplicitSurfaces Considertheinstantaneousreleaseofatraceratapointlocateddeepina lake.Asthedyespreadsduetolakecurrentsandturbulentdiffusion,itisusefultovisualizetheplumebyplottingiso-concentrationsurfaces,asshownin Fig. 1.6
Theconcentrationiscontinuousinthree-dimensionalspace;however,we canvisualizeiso-surfaces,i.e.thinbandsofconstantconcentrationthatform two-dimensionalsurfacesofequalconcentration.Todefinethesesurfaces,we constructafunction F(x,y,z) suchthatwhen
= 0(1.2) thenthepointwithcoordinates (x,y,z) liesonthesurface.Noticethat F is moregeneralthannecessarytodescribeatwo-dimensionalsurface.Infact, F isathree-dimensionalfunctionthatinherentlydescribesavolume.If F> 0, thepoint (x,y,z) liesoutsidethesurfacewhileif F< 0,thepointliesinside thesurfaceinthree-dimensionalspace.Onlywhen F = 0thepointliesonthe surface, F ,andthisdefinesan implicitsurface.
Itmayfirstappearthatthisdefinitionofasurfaceismorecomplicatedthan theexplicitrepresentationofatwo-dimensionalsurface,however,Eq.(1.2)has certainsignificantadvantages.Forexample,itcaneasilydeterminewhethera point (x,y,z) isinsideoroutsidethesurfacebysimplycheckingthesignof
FIGURE1.6 Implicitsurfaces
F(x,y,z)
the implicitsurfacefunction F .Furthermore,computationoftheunitnormal vectoratanypointofanimplicitsurfaceisstraightforward,providedthat F is differentiable.Then,thegradientof F determinesthenormaldirectionsincethe unitnormalisgivenby
Example1.2.2 (ASphericalDroplet). Considerasphericaldropletofradius equaltounity.Ifitscenterislocatedattheorigin,theimplicitsurfacefunction
F(x,y,z) = x 2 + y 2 + z 2 1
separatesthree-dimensionalspaceintoaninteriorandanexteriorsub-domain dependingonthesignof F .When F = 0,thecorrespondingiso-surfacedefines thesurfaceofthedroplet,asshowninFig. 1.7.
FIGURE1.7 Implicitdropletsurfaceandnormalvectors
Theimplicitsurfaceiscomputednumericallybyevaluating F ona20 × 20 × 20gridalongwiththenormalvectorfieldgivenbyEq.(1.3).Iso-surfaces of F arethenconcentricspheres,andallnormalsaredirectedalongtheradiusof thespheres.Noticethatforclarityonlytheiso-surfacecorrespondingto F = 0 isshowninFig. 1.7