Prologue
...donotreadfastthebookofHeraclitus...itisaverydifficultpathtowalk. Itislikenightandlightlessdarkness.If,however,somemysticguidesyou, itshouldbeclearerthanthebrightestsun.
Skythinos(Iambicpoet;circa500B.C.)
Motivation
Thisbookseriesisdesignedasacomprehensiveintroductiontothetheoryand computationoffree-surfaceflow.Thefundamentalsofmasstransport,numericalmodeling,parameteridentification,andcontroloffree-surfaceflowarealso covered.However,thesubjectmatterisnotasbroadasitinitiallyappearsto be,asemphasisisplacedprimarilyonenvironmentalflows.Nevertheless,these threetextsrepresentanambitiousattempttolaythefoundationfortheconstructionofmathematicalmodelsforenvironmentalflowswithafree-surfacebased onsoundphysicalreasoning.Themotivationforwritinganintroductoryseries onfree-surfaceflowatthegraduateleveloriginatesbothfromtheabsenceof asimilartreatise,andtheneedforbetterunderstandingofthephysicalprinciplesbehindthecomputermodelsoffree-surfaceflowthatarecurrentlyusedin practice.Mostofthechallengesassociatedwiththesemodelsareofconceptual ratherthannumericalnature,thusabetterunderstandingofthefundamental conceptsistheonlyavenuetoaccurateandreliablesimulationoffree-surface flows.
Free-surfaceflowisabranchoffluidmechanicsthatfocusesontheinterfacebetweenairandwateralthoughotherfluidsmaybeconsideredwithout majorconceptualdifficulties.Thelengthscalesinvolvedinfree-surfaceflow varywidely,andtheapplicationsrangefrompredictingseal-levelrisetobubble formationandcollapse.Predictingchangesofthefreesurfaceinrivers,lakes, estuaries,andtheoceanisaproblemdirectlyaffectinghumanlifeandproperty, guidingthedesignofstructuresthatcontrolsurfacewaters,andplanningforthe allocationoffresh-waterresourcesinasustainablemanner.Controlofthefree surfaceatsmallerscalesaffectsthetransferofchemicalsthroughtheliquid-gas interface,preventsmaterialfatigueduetolargepressurechangesduringbubblecollapse,andimprovestheefficiencyoflubrication,thusminimizingenergy losses.
Thisfirstbookisdevotedtothestudyoffluidflowinthenaturalenvironment,alsoknownas EnvironmentalFluidMechanics.Itcovers,eitherdirectlyor indirectly,thefieldsofhydrology,riverdynamics,coastalprocesses,limnology, oceanography,fateandtransportofcontaminants,meteorology,climatechange, andmanyothers.Thefieldisundoubtedlyverybroadanddifficulttocoverin asinglebookorcourseofstudy.Noticethattheforegoinglistdidnotattempt toincludeenvironmentalflowsinporousmediaorsedimentationanderosion. Thisnarrowsthefieldtofree-surface,rigid-boundaryenvironmentalflows.Furthermore,onlynaturalflowsofwaterandairareconsideredinthisbook,thus excludingbiologicalflows,andanyflowsthatinteractwithman-mademachineryandstructures,exceptthosethatareusedforcontrollingfree-surface flows.
Besidesthisratheradhocselectionoftopicsthatcomprisefree-surfaceenvironmentalflows,therearealsosomephilosophicalreasonsthatjustifyplacing moreemphasisonsometopicswhilementioningothersonlyindirectly.For example,thereisananalogybetweenchannelflowandcompressiblegasdy-
namics,butflowintheatmosphericboundarylayerseldomrequiresustotreat airasacompressiblegas.Similarly,thetheoryofpressurizedpipeflowhas manycommonelementswiththatofchannelflow,butthelattercanbedevelopedindependently.Finally,thedrivingforcesbehindenvironmentalflows aredifferentfromthoseingeneralfluidsengineering.Thus,althoughinfiltrationandboundarysuctionmayappearatfirsttorepresentthesameboundary condition,theyaredifferentphenomenathatarecontrolledbytotallyunrelated processes.Yetthelinesofseparationareoftenblurred,asforexample,inthe caseofsuctionusedtoeliminateacontaminantfromaconduitcarryingwater toamunicipality.
Thepurposeofmathematicalmodelinghaschangedovertheyearsandso havethefocalpointsofeducationinfree-surfaceflow.Suchflowisdominated bygravity,andiscommonlyencounteredinnature.Free-surfaceflowisalsodifficulttoexplain,andhasthuschallengedphilosophersandscientistssincethe beginningofcivilization.Airentrainmentinafoamingriver,flowreversalina tidalestuary,andcoastalupwellinghavepuzzledphysicistsandmathematicians forcenturies.Acenturyago,thedesignofchannels,damsandcontrolstructures dominatedtheapplicationsofsurfacewaterflows.Presently,itisstreamrestoration,flowmonitoringandcontrol,andimpactofclimatechangethatattractthe headlines.Ineithercase,however,thefundamentalsremainthesame.
Itisdifficulttogiveabriefhistoryofthephilosophyandmathematicsbehind thebranchofsciencewenowcallfluidmechanics.Thereishighuncertaintyas towhencontributionsworthyofrecordwerefirstmade.Thereisalsouncertainty astowhatinformationshouldbeincluded.Inthepresentcontext,aneasyescape isfoundbyfocusingoncontributionstoflowsdrivenbygravity,andbyseeking acommonthemeamongcontributors.Thecommonthemethatemergesreflects thosewhoworshipedmathematicsataveryyoungage,thensoughttoexplain physicalphenomenausinganalyticalmeans,andfinallyendedtheirliveswhile writingmetaphysicaltreatises,failingtoexplainalltheenigmasofthecosmos bymathematicsalone.Shortbiographiesandanecdotaldetailsregardingthese individualsarepresentedthroughoutthetextinthevicinityofthematerialthat theyhavecontributedtofree-surfaceflow.
Inthemethodintroducedbythesescholars,knowledgewascreatedandaugmentedbyafellowshipofteachingandlearning,masterfullyencapsulatedin Raphael’sfresco TheSchoolofAthens.Throughouthistory,agatheringofgreat mindstodebateandforgenewideasseemedtogeneratehighlevelsofenergy thatwerenotpossiblebysolitarythinkers.Thismaster-apprenticemodel,in whichthestudenteventuallysurpassestheteacher,istheLydianstoneofWesterncivilization.Explainingthebasicprinciplesgivestheteacheranunparalleled understandingofthematerialwhilethequestionsofthestudentsgenerateunpredictabledeparturesfromthenormthatleadtotransformativesolutionsnever foreseenbytheteacher.Inthatsense,theSchoolofAthenswasthefirst University,andremainsthemodelofscientificdebateandscholarship(Haas, 2012). Yet,thesparkofgeniusbyanobscurephilosophercouldopenhorizonsnever
Prologue anticipatedbyorganizedschools.HeraclitusofEphesuswasthefirsttocapturetheessenceof flow anditsconsequencesontheuniverse,andisrightfully consideredtobethefatheroffluidmechanics.
TheGreekphilosophersofantiquityknewthatanswerstomostproblemsin ourworldrelyongoodphysicsandrigorousmathematicalformulation.Unfortunately,thisknowledgewaslostinthedarkages,thusaneweraofenlightenmentwasneededtorevivephysicalscience.Itsfoundationswerelaidinthe 17thcenturybyIsaacNewton.However,itrequiredyearsofscientificargumentbeforeNewton’slaws,andinparticularthelawofuniversalgravitation, wereaccepted.Thedebateofwhetherforcewastransmittedthroughaninvisiblemediumorvacuumwentonfordecades,andlongexplorationstotheNorth PoleandtheEquatorhadtobeundertakentovalidatetheoblatespheroidshape oftheearththatwaspredictedbyIsaacNewton.
Thefirstbookoftheseriesaimsatbuildingafoundationonclassicalmechanics,andthenarticulatingtheadvancesinenvironmentalfluidmechanics madeduringthelastcentury.Theinfusionoffluidmechanicsintothephysics offree-surfaceflowcoincideswiththepublishingofthebrilliantbooksbyVennard(1940),Rouse(1946)andStreeter(1951)inthemid20thcentury.This wasfollowedbyRouse’s AdvancedMechanicsofFluids (Rouse, 1959),which presentedthefirstcomprehensivetreatmentofenvironmentalfluidmechanics. Finally,theeleganttextwrittenbyChia-ShunYihentitled FluidMechanics: AConciseIntroductiontotheTheory (Yih, 1969)emphasizedtheneedtointegratemathematicsandphysicsinthestudyoffree-surfaceflow.
Manyworthycontributionstothesubjectoffree-surfaceflowwerealso madeduringthefirstpartofthetwenty-firstcentury,andcontinueatarapid rate.Alistofcurrentbooksonrelatedtopicscanbefoundinthegeneralbibliographysection,astheyhaveallbeeninvaluableinthedevelopmentofthistext. Atthesametime,arevolutioninnumericalmathematicsanddigitalcomputationhastakenplacethatbroughtunprecedentedchangetoallfieldsofscience andengineering.ManyofthemodernmethodsallowintegrationofthethreedimensionalNavier-Stokesequationsforflowswithafreesurface.Notonlyis thisatruebreakthroughincomputationalfluiddynamics,butforthefirsttime itgivesustheopportunitytoestablishthetruelimitsofapplicabilityofthe approximatemethodsthatweredevelopedoverthelastonehundredyears.Of course,thesemethodsremainpowerfultoolseventoday,asdiscretemodelsare stillcomputationallyintensive,thustheyarenotallreadilyapplicabletolargescaleproblemsliketheonesencounteredinenvironmentalflows.Furthermore, allnumericaltechniquesinvolveapproximationsthatareoftenthesourceofnew difficulties,thustherightapproachtothesolutionoffree-surfaceflowproblems remainsaquestionofjudgment,anddependsstronglyontheapplicationand scopeofthesolution.

HeraclitusofEphesus
HeraclitusofEphesus(535–475B.C.)wasa Greekphilosopherwhobelievedinthepower ofobservationandexperimentation.Heleda lifeofsolitude,andoftenmadecontemptuousstatementsabouthisfellowcitizens.Only fragmentsofhisworkssurvive,butPlutarch reportsthatHeraclitusdedicatedhiscryptic book OnNature tothetempleofArtemis.The contentsofHeraclitus’bookbecamefamous inantiquityalthoughmostofitsstatementsweredifficulttounderstand. Heraclitusdeliberatelywrotethetextsoobscurelythatonlyanenlightened readercouldcomprehendit.
Heraclitusbelievedthatthereexistsareason(λόγος)thatrulestheuniverse.Healsoarguedthatmostpeopleareunabletounderstandthisreason evenafterithasbeenexplainedtothem.Inaccordancetothisreason, everythingflows intheuniverse(πάνταρει).Thewordrheo(ρέω)means tofloworformastreaminGreek,andisalsofoundintheetymologyof theterm rheology.Furthermore,Heraclitusbelievedthatthereareopposingforcesintheuniverse.Whentheseforcesareunbalanced,theirsum, whichhecalled strife (έρις)producesflow.Incontrast,whentheforces areinequilibrium, harmony (δίκη)prevails,andfluidsrestinequilibrium. Thiswasthefirstrecordedstatementregardingconservationofmomentum,aprinciplere-discoveredtwothousandyearslaterbyIsaacNewton.
ApproachofThisText
Free-surfaceflowencompassesspatialscalesrangingfromplanetarytomicroscopiclevels.Itisalsocharacterizedbytemporalscalesrangingfromafraction ofasecondtodecades.Thisbookdoesnotmakeanattempttocoverallthese scales.Ratheritaimsatgivingthereaderthebasicskillstomakethenecessary jumpsacrossscaleswhennewproblemsareencountered.Presently,themajorityoftheleadinggraduateprogramsinenvironmentalscienceandengineering includecoursesinenvironmentalfluidmechanics,open-channelflow,mixing inriversandestuaries,andcomputationalmethods.Thereisasignificantinterdependenceamongthesesubjectssincemostenvironmentalproblemsarenonlinear,andthereforerequireanumericalsolution.Furthermore,mostofthese problemsareassociatedwithturbulentflowsovercomplexterrain,andpossess multiplelengthscalesthatoftenallowsomeveryefficientapproximations.At thesametime,thesefundamentalsubjectssufferfromanevolutionarydisconnect.Formulationsinfluidmechanicsderivedirectlyfromthethree-dimensional Navier-Stokesequations;open-channelflowisfoundedonone-dimensionalhydraulicsandsemi-empiricalresistanceequations;mixinganddispersionhas evolvedfromapproximatemodelsofturbulence;finally,computationalmethodscoursesintroducetheconceptsofsignalpropagation,numericaldissipation
Prologue
anddispersion,withoutadirectreferencetothephysicalcounterpartsofthese topics.
Thepresentbookseriesattemptstobridgethesegapsinlearningunderthe umbrellaofamodernapproachtofree-surfaceflow.Specifically,theultimate goaloftheseriesistoprovidenumericalsolutionsoftheturbulentNavierStokesequationsinthreespacedimensions,includingtheexplicitdetermination oftheinterfacebetweenairandwater.Foraseamlesspresentation,BookIlays thefundamentalsoffluidmechanicswithemphasisonenvironmentalproblems. BookIIdescribesthepropagationofwavesinshallowwater,includingmethods formonitoringenvironmentalflows,sensitivityanalysis,andcontrol.Finally, BookIIpresentsmethodsforthecomputationoftheair-waterinterface,starting withsimplescalartransportandconcludingwithmulti-dimensionaltechniques fortrackingtheinterface.
Fromtheforegoingdiscussion,itshouldbenosurprisethattheprecise choiceoftheseries’titlehasbeenitselfadifficulttask.Althoughtheultimate goalistheanalysisandsimulationofflowwithafreesurface,manyofthe methodspresentedhereintreatthefreesurfaceindirectlybymeansofsuitable approximations.Thisisdonepurposefullybyfirstconductinganorderofmagnitudeanalysis,andtheresultsareadoptedonlywhenfieldvalidationvindicates theoriginalapproximation.Thereader’sconfidenceinthisasymptoticapproach isthenstrengthenedbycomparisontothefullproblemsolutionanddiscussion ofcasestudiesofsuccessfulapplications.Thus,whenthepreciselimitationsof eachsimplifiedmethodaredocumented,itsadoptionismadenotforexpediency,butforefficiency.Aspecialefforthasbeenmadetosmoothlyintegrate thesevaryingordersofapproximation,fortheyallrepresentdifferentviewsof essentiallythesameproblem.Asaresult,theunderlyingphilosophyoftheentireseriesisthat,regardlessofthedevelopmentsineitherhardwareorsoftware,
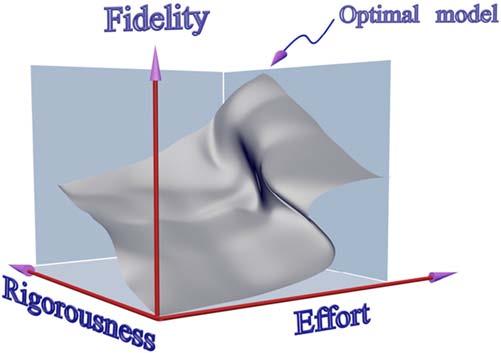
FIGURE1 Catastrophetheoryforfree-surfaceflow
scientificcomputationmustbebasedonappropriateapproximationsofthegeneralmathematicaldescriptionoftheproblem.Theseshouldbedeterminedbya thoroughunderstandingofthephysicalaspectsofflowmotion,whichvarysignificantlyateachapproximationlevel.Onlybykeepingthesimplifiedmodelsin perspectivecantheirlimitationsbeexplained,andtheirfailuresbeanticipated.
Theinterconnectionbetweentherigorousnessofthemethodofsolution andtheeffortrequiredtoconstructtheoptimalfree-surfaceflowmodelrepresentsthemainthesisofthisbookseries.Forifthefundamentallawsoffluid mechanicsarenotenforced,anoptimalmodelcanneverbereached,regardlessoftheeffortmade.Anadaptationof catastrophetheory (Arnold, 1992)to mathematicalmodeldevelopmentmakesthistransparentbythegraphicalrepresentationshowninFig. 1.Modelfidelitymaybevisualizedasacomplex, two-dimensional performancesurface thatcontainsafold.Ifthebasiclawsof physicsareignored,thereisnolevelofeffortthatcanleadtooptimality.Thisis trueevenformoderatelevelsofrigorousness,becausethecatastrophefoldmay continuetotheinteriorofthesurface.Incontrast,increasingthephysics-based contentofthemodel,increasestheefficiencyoftheeffortinput,andallows theconstructionofoptimummodels.Thishypothesisactuallysuggeststhatthe higherthescientificstrictnessoftheapproach,theeasiertheachievementofan optimalmodelis.
Emphasishasbeenplacedonmakingthepresentationatanintroductory levelthatisself-contained.Althoughthisisintendedtobeatextforgraduateand advancedundergraduatestudentswithsomeexperienceinboth FluidMechanics and NumericalMethods,allbasicmaterialisderivedfromelementaryconceptsinthemaintext.Noassumptionsaremadeonthereader’sknowledgeof Open-ChannelHydraulics,whichrepresents,however,anaturalprecursorofthe materialinthisbook.Inaddition,considerablepainshavebeentakentoreduce thecomplexityofthemathematicalformulations.Elegancehasbeensacrificed whereverpossible,andemphasishasbeenplacedonthephysicaldescription ratherthantheformalityofthepresentation.Whenithasbeenimpossibleto avoidcertaincomplicatedderivationsbecausetheyaredeemedessentialforthe developmentofvariousmodels,allstepsaregivenindetail,eveniftheyseem trivial.Thismaybetiresomeforsomereaders,but“twotrivialitiesomittedcan adduptoanimpasse”(Littlewood, 1953).
Thebasicapproachthroughoutthistextisforthereaderstolearntherules wellenoughinordertobendthem,andevenbreakthem.Thereisadelicate pathinthisprocessthatrequiresrespectforexistingknowledgewithoutdependenceorunquestionableacceptance.Someofthefundamentalconceptsof free-surfaceflowarecenturiesold.Someoftheapplicationsremainthesame. Butothershavechangedoraltogetherdisappearedwhilenewchallengeshave emerged.Shouldweuseouroldapproachtothesenewchallenges?Woulda modernmindderivetodaythesameequationsthatgovernedfree-surfaceflowin theseventeenthcentury?Shouldsomeonethathasaccesstohigh-performance computingpersistondeterminingthelocationofthefreesurfaceusing confor-
malmapping?Howshouldwemodelfree-surfaceflowonaplanetthathasa thousandtimesEarth’sgravity?And,tostretchthispointtotheextreme,what istheprobabilitythattheinhabitantsofaplanetinafarawaygalaxywilluse thesesametheoriestosolvetheirfree-surfaceflowproblems?
Thegoalofthisbookseriesistoaskprovocativequestionswhilepresenting thefundamentalsoftheacceptedtheoryoffree-surfaceflow.Thebookwillnot necessarilyprovidenewmethodsofsolution,butrathergivethereadersenough confidencetoseektheirown.Evenbetter,byexposingthetentativenessofthe presentstate-of-the-art,thebookhopestopromoteliberationfromestablished methodologyandconservatism.Thetextisintendedforandhasevolvedfroma three-courseseriestaughtinthegraduateprogramofEnvironmentalandWater ResourcesEngineeringattheUniversityofMichiganoverthelastthirtyyears. Asignificantfractionofthestudentshavecomefromotherdisciplines,suchas Chemical,Marine,Mechanical,OceanicEngineering,andtheSchoolofNatural ResourcesandtheEnvironment.Everyefforthasbeenmadetomakethebook ausefulsourceofinformationforapplicationsotherthanenvironmentalflows, andindeedmanyofthetechniquesdiscussedaredirectlyapplicabletoseveral otherproblemsofengineeringimportance.Insummary,thepresentbookseries isateachingaidbasedonthehypothesisthat knowledgeofcauses, rigorousness ofpresentation,and fellowshipoflearning providethemeanstounderstanding thelawsgoverningsurfacewaterdynamics.
Outline
Thematerialisdividedinchaptersthatrepresentcompleteentitieswhileleading sequentiallyfromgeneraltospecificformulationsoffree-surfaceflowproblems.
Chapter 1 dealswithbasicconceptsofmechanicsandanalysisthatareneeded forthedescriptionofenvironmentalflows.Somebasicpropertiesoffluids arereviewedanddiscussedinthecontextoffree-surfaceflow.Reductionismisintroducedastheunderlyingphilosophyforthedifferentialmodels offluidflow.Newton’slawsofmotionandgravitationarereviewed. AsymptoticapproximationandtheTaylorseriesexpansionareusedfor predictionintimeandspace.Simpleharmonicmotionisdescribedand connectedtowavemotionandtheFouriertransform.Areviewofspectral analysisispresented,andbasicconceptsofCartesianvectorsareoutlined. Fluxandthescalarproductaredefinedinthecontextoffluidmechanics.Anintroductiontotensoranalysisisgivenwithemphasistostress influids.Uniformshearflowisexamined,andNewton’slawofviscosityisderived.Theno-slipconditiononsolidboundariesisdescribedand theconditionsofitsapplicabilityarediscussed.Ageneralizationtoother flux-gradientmethodslinksviscousfluidflowtoheatconductionandsimilarmacroscopiclawsofphysics.
Chapter 2 dealswithfluidkinematics,composition,andthermodynamics. Scalarandvectorfieldsareintroducedandrelatedtostandardflowpatterns.Theconceptsofgradient,divergence,andcurlofscalarandvector
fieldsaredevelopedinCartesianandcurvilinearcoordinates.Materialcoordinatesandderivativesareintroducedandlinkedtoenvironmentalflow problems.Streamlines,pathlines,andstreaklinesaredifferentiatedand drawnforsomesimpleflowpatterns.TheLagrangianandEulerianframes ofreferenceareintroduced,andtheuseofmaterialcoordinatesishighlighted.Spacecurvesaredescribedmathematically,andtheexpression forcurvatureisderived.Integraltheoremsforvectorfieldsarepresented, andthegeneralconservationlawsareintroduced.Issuesofthermodynamicsandcompositionarealsodiscussed.Thisbriefreviewislimited totopicsrelevanttotheanalysisoffree-surfaceflow.Entropyisdefined bothinclassicalandstatisticalframeworks.Theequationofstateforperfectsgasesandsaltwaterarepresented.Thelawsofthermodynamicsare derived,andfluidcompressibilityisdefined.
Chapter 3 introducesthebasicconceptsofdiffusionalmasstransferinsurfacewaterflow.Fick’slawofdiffusionisformulated,andvalidatedby theEinstein-Kolmogorovtheory.ThemechanicsofBrownianmotionis presented,andLangevin’sequationofmotionislinkedtomasstransfer. ConservationofmassiscoupledwithFick’slawtoderivethediffusion equation.Thesolutionofthelock-releaseproblemisobtainedusinga similaritytransform.Theimpulseresponsefunctionofdiffusionisdefined,andlinkedtotheGaussiandistributionofsoluteparticles.Practical solutionsareobtainedbysuperpositionandconvolution.Diffusion,adsorption,andreactionarecoupled,andavarietyofanalyticalsolutionsare presented.FourierandLaplacetransformsareintroducedforthesolution ofboundary-valueproblems.Inertia-moderateddiffusionisdefined,and solutionsofthetelegraphequationareobtained.Themethodofimagesis usedtoconstructrealisticsolutionsinthepresenceofrealboundaries.
Chapter 4 dealswithmasstransportbyadvection.Conservationofmassis establishedforthree-dimensionalpureadvection.Depth-averagedand cross-sectionaveragedequationsarederived,andthemethodofcharacteristicsisappliedtothesolutionoflinearadvection.AFourieranalysis oftheadvectionequationforvariousinitialconditionsisperformed.The physicsofadvectionisanalyzedinthefrequencydomain.Point,line, andareasourcesareintroduced,andtherelativeimportanceofadvectionversusdiffusionisexamined.Theconceptofscalingthespreading ofaplumeisintroduced.Thedistanceandtimeforaplumetospread horizontallyandverticallyareestablishedbysemi-analyticalmeans.The Streeter-Phelpsequationisintroduced,anditslimitationsarediscussed. Solutionsforpoint,line,andplanesourcesarederived,andtheconditions forcompletemixingintheverticalandtransversedirectionsareobtained.
Chapter 5 presentsthedifferentialandintegralconservationlawsoffluidmotionandtheconditionsfortheirapplicability.Theincompressibilityconstraintisdefined,andthestreamfunctionisusedtoidentifythestreamlinesoftheflow.Equationsfortheconservationofmomentumandenergy
arederived,andthevelocitygradienttensorisanalyzed.TheStokeshypothesisforviscousflowisintroduced,theNavier-Stokesequationsare derived,andtheimportanceofthePoissonpressureequationisemphasized.TheNavier-Stokesequationsarescaled,andvariousdimensionless numbersareintroduced.Thegoverningequationsofflowaresimplified andusedtosolvesimpleflowproblems.Theapproximationoftheseequationsbymeansofasymptoticanalysisleadstotheconceptofcreeping flow.Exactsolutionsarepresentedforflowaroundasphere,andHeleShawflowiscomparedtoviscousandidealflow.
Chapter 6 dealswiththedynamicsoffluidflowintheabsenceofrotation. Thebasicconceptsofclassicalhydrodynamicsareintroduced,andequationsforthevelocitypotentialandstreamfunctionarederived.AsolutionoftheDirichletproblemfortheLaplaceequationispresented.The equationsofEulerandBernoulliarederivedandusedforthesolution ofsimpleproblems.Analyticalsolutionsforseveralstandardflowpatternsarepresented,andtheresultsareshowngraphicallyintermsofthe correspondingflownet.Superpositionofsimplesolutionsleadstomore complicatedflowpatterns,includingtheflowaroundasphere.Conformal mappingisintroduced,andCauchy’sintegralformulaisderived.Free streamlinetheoryisusedtoderiveanexactsolutionforthefree-surface flowexitingasharporifice,andanexactvalueofthecontractioncoefficientiscalculated.
Chapter 7 presentsthedynamicsofvorticityanditsrelationtoturbulence. Vortexlines,tubes,sheets,andconcentratedvorticesareanalyzed,and thefundamentalvorticitytheoremsareformulated.Concentratedvortex modelsarediscussed,includingtheforced,free,andRankinevortices. Cellularflowsareintroduced,andlinkedtothermalflowinstability.Vorticityinshearflowisdiscussed,andtheconditionsforflowinducedby vorticityareexamined.Thevorticitytransportequationisderived,and eachtermisexaminedforitsphysicalmeaning.Vortexstretching,vortex rings,andvortexlinesfrozeninthefluidareexplained.Diffusionofvorticityandvortexsheddingareintroduced,andStokes’stheoremisproved. Enstrophyandhelicityaredefinedandrelatedtoenvironmentalflows. Kelvin’scirculationtheoremisestablished,andconservationofhelicity isproven.
Chapter 8 focusesontheinterplayofinertiaandviscosity,andtheproduction ofturbulenceinchannelflow.Thescalesofturbulentflowsarepresented togetherwithsomeclassicalmodelsofturbulentflowapproximationsuch asReynoldsaveragingandmixinglengththeory.Theequationsformean velocitydistributioninchannelflow,andthetransportofturbulentstresses aredevelopedandcomparedwithexperimentaldata.Theinstabilityof laminarflowisexamined,andtheconditionsleadingtoturbulentfloware established.Averagingmethodsandtheintegralscaleofeddiesarepresented.Thekineticenergyanddissipationspectraarepresented,andthe
conceptofuniversalequilibriumisintroduced.Turbulenceclosuremodelsarepresented,andvonKarman’ssimilarityhypothesisisexamined. Thekineticenergy-dissipationmodelispresented,anditslimitationsare discussed.Large-eddysimulationisintroduced,andthefilteredNavierStokesequationsarederived.TheSmagorinskyanddynamicmodelsare compared,andtheirrelativemeritsareanalyzed.
Chapter 9 presentsthefundamentalsofboundary-layertheory.Usingascalingapproach,theapproximateequationsdescribinglaminarandturbulent boundary-layerflowarederived.Asimilaritysolutionfortheboundarylayerequationsisobtained,andthevelocitydistributioninthestreamwise andtransversedirectionsisconstructed.Boundary-layerseparationisdiscussed,anditsimportanceinflowresistanceisexplained.Skinfrictionis introducedandcomparedtoformdrag.Theeffectofwallsuctiononseparationisanalyzed,andtechniquesforthereductionofdragarediscussed. Integralrelationsfortheboundary-layerthicknessandthedragcoefficient areintroduced.Freeshearflows,includingjetsandwakesaredescribed, andthecorrespondingvelocityprofilesarederived.Flowaroundasphere isstudied,andexpressionsfortheassociateddragcoefficientarepresented.
Chapter 10 focusesontheeffectsandassociatedscalesofgeophysicalphenomena.TheEarth’srotationonflowpatternsareexaminedindetail, andtheroleoffictitiousforcesintheconservationlawsisdescribedboth physicallyandmathematically.TheimportanceoftheCoriolisaccelerationinrelationtoinertialandviscousforcesisalsodiscussed.Hydrostatic equilibriumandthevariationoftemperatureintheverticalareanalyzed. Theconditionofincompressibilityisdescribedindetail.Boussinesq’sapproximationofcontinuouslystratifiedflowisstudied,andthelimitsofits applicabilityarepresented.Scalesofgeophysicalflowsarepresented,and variousdimensionlessnumbersareintroduced.Thegoverningequations aresimplified,andthesolutiontovariousgeophysicalflowsisobtained analytically.TheTaylor-Proudmanphenomenonisexplained,anditsimportancetoenvironmentalflowsidentified.TheEkmanlayerisstudied, andthecorrespondingvelocityprofilesareconstructed.Ekmanpumping isintroduced,andcoastalupwellingexplained.
Chapter 11 examinestheeffectsofstratificationonenvironmentalflows.Discretelayerandcontinuouslystratifiedflowsareanalyzed.Theimportance oftheRichardsonnumberisexplained.Interfacialstabilityisexamined, andtheonsetofRayleigh-Taylorinstabilityisanalyzed.Continuously stratifiedflowisanalyzedandexpressedintermsofthestratification frequency.Internalwavesandseichesareintroduced,andthecorrespondingpropagationpropertiesarestudied.Densitycurrentsaredescribed, andtheirpropagationunderstratifiedflowconditionsisquantified.The interplaybetweenstratificationandturbulenceisdiscussed,andtheimportanceofthecollapseofturbulenceinstratifiedflowinlakes,estuaries
andtheatmosphericboundarylayerisexplained.TheReynolds-averaged Boussinesqequationsarederived,andvariousapproximationsarepresented.
Chapter 12 focusesonturbulentmixinginfree-surfaceflows.Modelsaredevelopedformulti-dimensionalflows,andmethodsfortheestimationof theassociatedmixingcoefficientsarepresented.TheLagrangiantime scaleforchannelflowisusedtodeterminethelimitsofapplicabilityof turbulenttransportintermsofthestandarddiffusionequation.Dispersionisdefined,anditsvariousformsidentified.Sheardispersionunder shallow-waterconditionsisanalyzed.Dispersioncoefficientsarederived forvertically-integratedflowunderbothlaminarandturbulentflowconditions.Dispersionanalysisforarea-integratedchannelflowisalsopresented,andtheimplicationsofthegeneralizeddiffusionequationinenvironmentalflowsarediscussed.
Chapter 13 developsthefundamentalsofflowcontrol,astheyapplytomass transportandflowswithafreesurface.Basicconceptsofoptimizationmethodsareintroduced,focusingongradient-basedapproaches.The methodsofsteepestdescent,Newton’siteration,andtheBFGSalgorithm areintroduced.Theconjugategradientmethodisderivedforfastandrobustapproachtooptimization.Adjointequationsaredevelopedformass transport,andLagrange’sdualitytheoremisproven.Applicationstooptimalsourceplacementinastreamarepresented,andtheconceptof sensitivityisintroduced.Uncertaintyanalysisisconductedbasedonthe adjointequation.Themethodisusedtoidentifydispersioncoefficients, andtheoptimumreleasestrategyfromtreatmentplants.Sourceinversionisstudiedbymeansofoptimizationmethods,andtheconditionsof sourceobservabilitybywall-mountedsensorsareexamined.Activecontrolofsoluteplumesisintroduced,andresultsareobtainedforreal-time mitigationofcontaminants.
Acknowledgments
Thisbookserieshasdemandedalongtimetocomplete,thusmanycolleagues andstudentshavecontributedtoitsdevelopment.Iamindebtedtoallofthem, andespeciallytothosewhohaveusedthebookwhileteachingtheirownclasses, afterleavingtheUniversityofMichigan.Theirvaluablesuggestionshavemade thisagratifyingproject.Iamalsogratefultomyownmentors,GeorgeTerzidis andTheodorStrelkoff,whointroducedmetothesubject,andguidedmethrough someofitstortuouspaths.Ithasbeenawonderfulvoyageofexplorationand learning.
REFERENCES
Arnold,VladimirIgorevich,1992.CatastropheTheory,thirdedition.Springer-Verlag,Berlin. Haas,R.,2012.Raphael’sschoolofAthens:atheoreminapainting?JournalofHumanisticMathematics2(2).
Littlewood,JohnEdensor,1953.AMathematician’sMiscellany.CambridgeUniversityPress,London.
Rouse,Hunter,1946.ElementaryMechanicsofFluids.JohnWiley&SonsInc.,NewYork. Rouse,Hunter,1959.AdvancedMechanicsofFluids.JohnWiley&SonsInc.,NewYork. Streeter,V.L.,1951.FluidMechanics.McGraw-Hill,NewYork.
Vennard,J.K.,1940.ElementaryFluidMechanics.JohnWiley&SonsInc.,London:Chapman& Hall,Limited.
Yih,Chia-Shun,1969.FluidMechanics:AConciseIntroductiontotheTheory.McGraw-Hill,New York.
SketchinNewton’s PhilosophiaeNaturalisPrincipiaMathematica,SECTVIII,DeMotuperFluida propagato,depictingthepassageofawavethroughaslit.ThesourceisatpointA;Theslitis definedbypointsBandC;Lowercasesymbolsdescribethecrestsofwavesradiatingfromthe slit. Imagesource:[PD-art],viaWikimediaCommons: http://commons.wikimedia.org and https: //www.flickr.com/photos/internetarchivebookimages/14596023408/
BasicConcepts
Becauseinquiryandcomprehensioninalldisciplinesthathaveprinciples, conditionsorelementsisobtainedthroughexplorationofthem(foritisthen thatweclaimthatweunderstandeachsubjectwhenwehavemasteredits fundamentalfactsorfirstprinciples,andhaveresolveditintoitselements) itisobviousthatforthescienceofNaturetooourfirsttaskshouldbetotry todetermineitsbasicprinciples.
Aristotle.Physics,BookA
1.1INTRODUCTION
Undertheinfluenceofmechanicalforces,mostobjectsundergoadeformation, i.e.analterationinshapeorsize. Flow isdefinedasachangeinthisdeformation thatcontinuesaslongastheforceisapplied.ThetermderivesfromtheLatin fluere andtheOldEnglish flowan,whichwasprobablyofGermanicorigin.The effectofmechanicalforcesonanobjectisbetterinterpreted,iftheyaredivided bytheareaofthesurfaceonwhichtheyact.Theresultisknownasa stress actingonthesurfaceunderconsideration.Furthermore,wedistinguishbetween normal and tangentialstresses dependingontheorientationofthestressinrelationtothesurface.Undertheinfluenceofanormalstress,solidmaterialsare eithercompressedorstretched.Incontrast,ashearstresscausesanangulardeformationofasolidobject.Basedonthisexperience,a fluid isdefinedasa materialthatisunabletowithstandastaticshearstress.Equivalently,afluidis asubstancethatdeformscontinuously,i.e.flows,underanappliedshearstress, regardlessofhowsmallitis.Therefore,fluidsbehaveradicallydifferentfrom solids,andthebranchofphysicsthatstudiesthebehavioroffluidsisknownas FluidMechanics.
1.1.1Reductionism
Thesuccessfulapplicationofmodernfluidmechanicsisduetothemathematical formulationofphysicallawsatthemostelementaryleveloffluidflow,where simpleforcescausesimplereactions.Thequestforelementaryconstituentsof matterdatesbacktotheGreekphilosophers,whosetheoriesof reductionism postulatedthatifasystemisdescribedwiththehighestpossibleresolution,the physicallawsyieldunambiguouspredictionsforthestateofmatter.
Theremarkableattributeofreductionismisthatonlyahandfulofphysical lawsandforcesdescribeallsystems.Thisallowsthedevelopmentofuniversal conservationlawsformass,energy,andmomentumthatdescribepreciselythe behaviorofasystematanelementarylevel.Findingthesmallestelementof matterwasarealchallengethroughoutantiquity.Earth,wind,water,andfire werealltestedandfailed,untilalltheoriesconvergedtothe atom.
Theunderstandingoftheinteractionsbetweentheelementaryandobservablestatesofaflowproblemallowstheconstructionofa mathematicalmodel, i.e.atheoreticalreplicathatrepresentsindetailtherealfluid.Amathematical modelcanaccountforinhomogeneityoranisotropyofthefluid,asproperties ofmatterarecapturedlocallyatamicroscopicscale.Themodelisalsoscalable becausefluidparcelsofallsizesareofthesameelementarymatter.Finally,the mathematicalmodeliseasilytransferablebecausedifferentsystemsdifferonly intheirmacroscopicgeometryandexternalinputs,butnotintheirelementary buildingblocks.
Reductionismisanattractivetheorythatisgettingeverclosertoreality,as moderninstrumentsyieldmoreaccuratemeasurements,andcomputersperform massivecalculations.Formanyimportantproblems,however,theconstruction
ofmathematicalmodelsbasedonthemostelementaryconstituentsofmatter isstillimpractical.Wethereforeagreetorepresentrealitybyresolvingmatter atsomeintermediatelevel,andthentopostulatethedetailedinteractionofthe modelandthemicroscopicscales.Theobjectiveistoresolvethesysteminthe smallestscalethatcanbeaffordedinordertocapturethespatialandtemporal variabilityoflocalproperties,andtosupplementthephysicallawsbyadditional, oftenempirical,statementsregardingthebehaviorofmatterbelowtheresolved scale.Thesearecalled constitutivelaws,butothernamessuchas phenomenological or observationallaws areoftenusedintheliterature.
Theprocessdescribedintheprecedingparagraphisknownasa mathematicalmodelhypothesis implyingthatthephysicallawsareaccuratelyresolved atsomeappropriatescalewhilefinerscalesaremodeled.Occasionallytheterm model isusedtodescribethefundamentalbehaviorbelowtheresolvedscalein adiscretesolution.Thismayleadtosomeconfusion,butoneneedstorealize thatinthiscontexttheresolvedscaleisassumedtobetrulyidentifiedbythe numericalmodel,thus“modeling”isonlyneededbelowtheresolvedscale.
Themathematicalmodelhypothesisfurtherstatesthatcarefulassessment ofthedominantforcesinagivenproblemnecessitatestheinclusionofcertain forceswhilepermittingtheomissionofothers.Thistypicallyyieldsasimpler modelwithoutanylossofaccuracy.Onceadecisionismade,however,nofurthercompromiseisallowed,andthemathematicalformulationandsolution shouldbecarriedtotheendwithoutanyadditionalreductionofeitheraccuracy orconsistencywithregardtotheoriginalproblem.
Theforegoingargumentrepresentsacriticalviewthatwillberepeatedmany timesthroughoutthisbook.Amodelhypothesisismadeonlyonce,andinparticular,duringtheinitialstepsoftheformulation.Thestepsthatfollowshould thentreatthegoverningequationsasappropriateforthesolutionoftheproblem, providedofcoursethattheoriginalhypothesisisvalidated.Ifafluidisassumed, forexample,tohavenoviscosity,thehydrodynamicbehaviorofanyresulting flowmayseemunrealisticcomparedtolaboratoryobservations.Theanalysis, however,mustbecarriedthroughwithouttemptationtore-introduceviscosity atalaterstageforthesakeofagreementwithmeasureddata.Iftheresultsare indeedpoor,thehypothesisshouldbeabandonedasinappropriate;thereshould benoattempt,however,to“improve”thehypothesisbymeansofalternative solutiontechniques,especiallyofnumericaltype.
Theselectionoftheproperapproximationlevelisofparamountimportance, butitiscomplicatedbythefactthatthesolutionofthegoverningequationsfor mostenvironmentalflowsmustbeobtainedalmostexclusivelynumerically.The algorithmiccharacteristicsofthenumericalmethodofteninteractwiththemathematicalapproximationinthegoverningequations,whichonoccasioncreate spurioussolutionsthatshouldbestudiedcarefullyuntiltheiroriginandgeneralbehaviorareunderstood.Themostdelicateissueinthenumericalsolution offree-surfaceflowproblemsis modelconsistency.Specialattentionshouldbe paidtothosecaseswherethenumericalsolutionyieldsresultsthatappeartobe
closertomeasureddatathantheexactsolutionofthegoverningequations.This includesthetheoreticallyanticipatedformofthesolution,incaseananalytical versionisnotpossible.
Themathematicalmodelhypothesis,i.e.allthephysicalapproximations neededtoarriveatthegoverningequations,shouldbekeptseparatefromthe numericalapproximationsmadetoachievea discretesolution oftheseequations.Ifanumericalerrorworksfortuitouslyinsomecasestocounteractor masktheeffectsofthephysicalapproximations,itshouldstillbeconsidered unacceptable.Attemptstomanipulatenumericalerrorstoobtainanadvantage overtheexactsolutionofthegoverningequationshouldbemadewithextreme caution.Ofcourse,theintroductionof“newphysics”bythenumericalsolutionisnotalwaysbad.Inmanyoccasions,thediscretesolutionleadstoabetter understandingofthetruephysicsoftheproblem,especiallyincomplexflow systems.
1.1.2Free-SurfaceFlowModels
Inareviewofbasicconcepts,itiswisetorelyaslittleaspossibleonthereader’s previousknowledgeoffree-surfaceoropen-channelflow.However,thepresentationbecomesmorefocused,ifitislinkeddirectlytothesubjectofthisbook. Manyoftheexamplesinthischapterarechosenfromcommonapplicationsin surfacewaterflow,forexample,theflowpatterncreatedbythrowingarock inashallowpond.Lestthereaderconsiderthisexampletootrivial,Fig. 1.1 showsthesequenceofeventsfollowingtheinitialdisturbancetothesurfaceof thepond.Theresultisacomplexdeformationoftheair-waterinterfacethat dependsonthesizeandshapeoftherock,theangleofpenetration,andfinal velocityoftherockatthetimeofentry.Next,theensuingsplashgeneratessecondarywaveswhiletheinitialdisturbancespreadsoutinacircularfront.As timeelapses,awavetrainisformedradiatingfromthepointofdisturbance.The leadingwaveappearsflatterandsmootherfornoapparentreason.Noticethat thephotographsdonotrevealanyinformationregardingthewaveproperties belowthefreesurface.
Oneoftheobjectivesofthisbookistoconstructmathematicalmodelsatvariouslevelsofapproximationforproblemsinvolvingfree-surfacewaves.Such modelsallowforanaccurateandefficientdesignofflowcontrolstructuresthat isverydifficulttoachievebylaboratorystudiesalone.Theamountofinformationthatbecomesavailablethroughamathematicalmodel,andtheeaseof transferabilitytootherflowstructuresisthedrivingforceofmodernanalysis, design,andcontroloffluidflow.Oncevalidated,amathematicalmodelprovidesinformationatanydesiredresolution,isscalable,applicableuniversally, andtransferabletoavarietyofpracticalapplications.
Ontheotherhand,amathematicalmodelintroduceserrorsanduncertaintiesthatmayunderminethereliabilityandrobustnessofthepredictedresults. Ineverymathematicalformulation,thereareassumptionsandapproximations
thatforcethemodeltodeviatefromreality.Eitherforexpediencyorefficiency, thelevelorapproximationisoftenreducedtotheminimumallowablelevel.Undersuchconditions,theperformanceofthemodelisdeemedsatisfactoryifan applicationofthemodeltoacertainclassofproblemsyieldsresultsthatare compatiblewiththedemandsoftheproblem.However,itisalsotruethatthe nextapproximationlevelmaycontainmorethanjustanimprovementinaccuracy.

Therearenumerousexamplesinfluidmechanicswhereinfactthenextapproximationlevelrevealsanentirelydifferentbehavioroftheflowconditions. Forexample,itiscommonlyassumedbysomemodelsthatthecurvatureof thefreesurfaceinlakes,rivers,andestuariesissmall,andthereforecanbeneglected.However,whenthisconditionisviolated,theassociatedmathematical modeldoesnotsimplysufferacommensuratelossofaccuracy,butinsteadit producesresultsthataretotallyunrealistic.Similarproblemsareencountered whentheviscosityofafluidisneglected,whentheamplitudeofawaveisconsideredsmall,andwhenmanyothersimilarsimplificationsaremade.Validation ofthemodelwithfieldorlaboratoryobservationsisthereforenecessaryevenfor thesimplestproblems.Noticethattheforegoingdiscussionmakesnoreference toerrorsinvolvedinthenumericalapproximationofthemathematicalmodel itself.Thatisanothersourceofuncertaintythatwillbediscussedextensivelyin thethirdbookofthisseries.
FIGURE1.1 Propagationofsurfacewavesinshallowpond