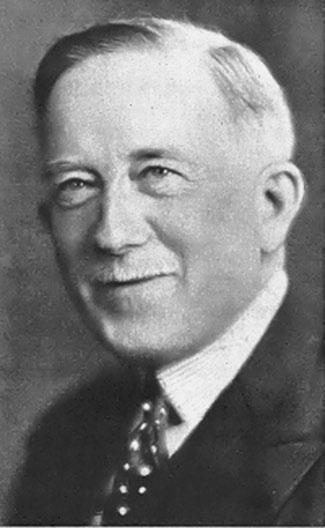FOUNDATIONSOF
GEOPHYSICAL ELECTROMAGNETIC THEORYANDMETHODS
SecondEdition
MICHAELS.ZHDANOV
UniversityofUtah, SaltLakeCity,UT,UnitedStates
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2018ElsevierB.V.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical,including photocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwritingfromthepublisher.Detailson howtoseekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangementswithorganizationssuchas theCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanasmaybenoted herein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenourunderstanding,changes inresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation, methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbemindfuloftheirownsafety andthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityforanyinjuryand/or damagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromanyuseoroperationofanymethods, products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-444-63890-8
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: CandiceJanco
AcquisitionEditor: MarisaLaFleur
EditorialProjectManager: HilaryCarr
ProductionProjectManager: PunithavathyGovindaradjane
Designer: ChristianJ.Bilbow
TypesetbyVTeX
Preface to the Second Edition
PART 1 INTRODUCTION TO FIELD THEORY
CHAPTER 1 1.1 Differential Calculus of Vector Fields and Differential Forms The Basic Differential Relationships of Field Theory
1.1.1 Concept of the Physical Field
1.1.2 Dot (Scalar) and Cross (Vector) Products of Vectors
1.1.3 Vector Differential Operators
1. 1.4 Differentiation of the Products of Scalar and Vector
2.1 Field
2. 1.1 Hannonic Functions; Liouville's Theorem
2. 1.2 Uniqueness of Determination of the Scalar Field by Its Gradient and the Vector Field by Its Divergence and Curl........................
2.1.3 Field Generation Conditions
2.1.4 Sources of the Field and Their Physical Meaning
2.1.5 Vortices of the Field and Their Physical
2.1.6
2.2 Stationary Field Equations and Methods of Their Solutions
2.2.1 Poisson's Equations for Scalar and Vector Fields
2.2.2 Point Source; Dirac Singular Function...........................
2.2.3 Fundamental Green's Function for the Laplace Equation
2.3 Scalar and Vector Potentials of the Stationary Field.
2.3.1
PART 2 FOUNDATIONS OF ELECTROMAGNETIC THEORY
CHAPTER 3
3.2 3.3 Electromagnetic Field Equations
and Boundary
3.1.1 Basic Equations in the Theory of Electromagnetic Fields
3.1.2 Physical Interpretationof MaxweWs Equations
3.1.3 Boundary Conditions for the Vector Field
3.1.4 The Field in a Homogeneous Medium Time-Hamlonic Electromagnetic Field .. Electromagnetic E
3.3.1
rgy and Poynting's The
3.3.2 Poynting's Theorem in the Time Domain. .
3.3.3 Energy Inequality in the Time Doma in
3.3.4 Poynting's Theorem in the Frequency Domain
3.4 Electromagnetic Green's Tensors
3.4.1 Green'sTensorsin the Frequency Domain
3.4.2 Green's Tensors in the Time Domain
3.5 Reciprocity Relations
3.5.1 Lorentz LCln.lna .
3.5.2 Reciprocity Relations for the Green's Tensors and Electrom
3.5.3 Electromagnetic Green ' s TensorRepresentation Theorems .
, References and Recommended Reading to Chapter 3 ,.,
CHAPTER 4 4.1 4.2 Models of Electromagnetic Inducti on in the Earth
Models of Electromagnetic Fields
Static Ele
4.2.1 Electrostatic Fields and Electrostatic Potentials
4.2.2 Boundary Conditions for Electrostatic Potential
4.2.3 Calculation of the Electrostatic Field of a SpecifiedCharge Distribution ..
4.2.4 Analogy Between Constant Current Fjelds and Electrostatic Fields 98
4.2.5 Direct Current Flow, Associated Magnetic Field, and the Biot-Savan Law 101
4.2.6 Point and Dipole Sources on a Uniform Ealth ...
4.2.7 DC Potential in an Anisotropic Earth.
4.3 Electromagnetic Field Diffusion in Conductive Media
]03
5.2.2
5.2.3
5.2.4
5.2.5 Expressions for Electric Fields in a Horizontally Layered
Using the Hankel Transform ....................................... 163
5.3 Electromagnetic Field of an Arbitrary System of Magnetospheric Currents in a Horizontally Homogeneous Medium
5.3.1 Spatial Frequency-Domain (SFD) Representation of the Electromagnetic Field in a Horizontally Layered Medium ....... .
5.3.2 Lipskaya-Vanyan Formulas Concerning Impedance Ratios.........
5.3.3 Horizontal Polarization of the Electric Field in a Horizontally Homogeneous Earth, and the Reduced Spatial Wave Number Spectrum
5.4 Electromagnetic FjeJds Generated in Layered Earth by Electric and Magnetic Djp ole Transmitters
5.4.1 Spectral Representation of the Field of a Horizonta l Current Dipole on the Surface of a Horizontally Layered Medium
5.4.2 Electromagnetic Field of a Horizontal Current Dipole at the Surface of a Homogeneous HaJf-Space
5.4.3 Frequency Domain Representation of the Field of a Vertical Magnetic Dipole Above a Horizonta lly Stratified Medium
5.4.4 The Magnetic Field of a Ve11ical Magnetic Dipole on the Surface ofa Uniform Half-Space .. .
5.4.5 Near and Far Fields ........... .
5.4.6 Frequency Domain Method for Computing Transient Fields . .. . . . .
5.4.7 Transi ent Fields of a Dipole Source Observed in a Homogeneous Medium and on the Surface of a Homogeneous Conducting Half-Space; Fields in the Near and Far Zones ......................................... .
and Recommended Reading
CHAPTER 6 Electromagnetic Fields in Inhomogeneous Media
6.1 Integral Equation Method .......
6.1.1 Background (Nonnal) and Anomalous Parts of the Electromagnetic Field 203
6.1.2 Poynting ' s Theorem and Energy In equality for an Anomalous Fi
6.1.3 Integral Equation Method in Two Dimensions.
6.1.4 Calculation of the First Variation (Frechet Derivative) of the
Electromagnetic Field for 2-D Models
6.1.5 Integral Equation Method in Three Dimensions
6.1.6 Contraction Integral Equation Method
6.1.7 Calculation of the First Variation (Frechet Derivative) of the Electromagnetic Fjeld for 3-D Models
6.1.8 Integral Equation Method in Anisotropic Medium
6.1.9 Disc rete Form of the Anisotropic IE Forward Modeling Method ......
6.1.10 Contraction Integral Equation as the Preconditioned Conventional Integral Equation
6.2 Integral Equation Method ill Models With Inhomogeneous Background
Model With Inhomogeneous Background Conductivity
6.2.2 Accura
6.3
6.3.1 Born and Extended Born Approximations
6.3.2 Quasi-Linear Approximation and Tensor
Quasi-Analytical
s for a 3-D Electromagnetic
6.3.5 Quasi.Analytical and Quasi.Bom Approximations for a Model With Variable Background ...........
6.3.6 Quasi-Analytical Solutions for 2-D
6.3.7 Localized
6.3.8 Localized Quasi-Linear Appro
6.4 Differential Eq
6.4.1 Field Equations and Boundary Conditions
6.4.2 Electromagnctk Potential Equations and Boundary Conditions
6.4.3
6.4.4
6.4.5 Finite Difference Approximation of Boundary-Value Pr
Discretization of Maxwell's Equations Using a Staggered Grid Contraction Preconditioner for a System ofFD Eq
6.4.6 Discretization of the Electromagnetic PotentiaJ Differential Equations,. , 25]
6.4.7 Finite Element Solution of Boundary-Value Problems
6.4.8 Edge·Based Finite Element Method
and Recommended
PART 3 INVERSION AND IMAGING OF ELECTROMAGNETIC FIELD DATA
CHAPTER 7 Principles of III-Posed Inverse Problem Solution ................•.....
7.1 ILL-Posed Inverse Problems. .
7.1.1 FOimulation of Well-Posed and lII-Posed Problems
7.1.2 Correctness Set ................... ....... ..•.....•. .
7.1.3 Quasi-Solution of the III-Posed Problem
7.2 Foundations of Regularization Theory
7 2 1 Definition of Misfit Functional
7.2.2
7.2.3
7.24 Regularizing Operators . _ ... Stabilizing Functjonals Tikhonov Parametric Functional
7.3 Regularization Parameter ...
7.3.1 Tikhonov Method of Regularization Parameter Selection ........•...
7.3.2 L-Curve Method of Regularization Parameter Selection ......•..•... References and Recommended Reading to Chapter 7
CHAPTER 8 Electromagnetic Inversion .......
8.1 Linear Inversions . .
8.1.1 Born Inversion
8.1.2 Discrete Linear EM Inverse Problem
8.1.3 The Tikhonov Regularization .Method of Linear Inversion
8.104 Definition of the Weighting Matrices for Model Parameters and Data
8.1.5 Approximate Regularized Solution of Linear Tnverse Problem
8.1.6 The Levenberg-Marquardt Method
8.1.7 Conductivhy Imaging by the Born Approximation
8.1.8 lterative Born lnversions
8.2 Nonlinear [nversion
8.2.1 Formulation of the Nonlinear EM Inverse Problem
8.2.2 Regularized Solution of Nonlinear Discrete EM Inverse Problem ..... .
8.2.3 The Steepest Descent Method for Nonlinear Regularized Least-Squares [nversion
8.2.4 The Newton Method for Nonlinear Regularized Least-Squares Inversion .
8.2.5 Numerical Schemes of the Newton Method for Nonlinear R
ularized Least-Squares Inversion , .. .. ... .... . , ...... .... . ....
8.2.6 Nonlinear Least-Squares Inversion by the Conjugate Gradient Method
8.2.7 The Numerical Scheme of the Regularized Conj ugate Gradient Method for
8.2.9
9.3.t 2-0 Finite Difference Migration
9.3.2 Finite Difference Migration of a 3-D EM Fiel
9.4 Visual ization of Geoelectric StructuresbyUseof Migration.in theFrequency and TimeDomains
9 4 1 Migration Imaging Condition in the Freq
Migration ImagingCondition in the Time Domain
9.5 Migration Versus Inversion
9.5.t Fonnulation of the Inverse Problem. .
9.5.2 General Concept of the Migration Anomalous Field
9.5.3 General Migration Imaging Conditions
9.5.4 Regularized Iterat ive Migration
of Heterogeneous Medium
10.4 Properties in an Existential Sense
Longitudinal Conductance and Transverse Resistance ofthe H
10.5 Properties of Large-Scale Geoelectric Structures.
G
The Oceans.
12.3.6 Fundamental IP Model II: Effective Resistivi ty of the Multiphase Heterogeneous Medium Filled With Elliptical Inclusions
12.4 Nonlinear Regularized Inversion of IP Data Based on the GEMTIP Model ...
12.4.1 Regularized Integral Equation (IE)-Based Inversion for Complex
12.4.2 Regularized Inversion for the GEMTIP Model Parameters _
Quantitative Interpretation of TP Data - the Road Ahead
13.2
rd Model of the MT Field
Tikhonov-Cagniard M
Concepts of Apparent
13.2.3 Relationships Between the MT Sounding Curve and the Actual I-D
13.3 T
13.3.1 Magnetotelluric Operators: I
13.3.2 Induction Vectors and Mag ne
and
13.4.1 Concepts of External and Internal, Normal and Anomalous Parts ofan Electromagnetic Fjeld . . . .,............,..............,...... 525
13.4.2 Anomalous Electromagnetic Fields and Their Classification . ,., ... . . . 527
13.4.3 Fields in Two-Dimensionally Inhomogeneous Media and the Concepts of E and H Polarization
Magnetotelluric and MagnetovariationaL Surveys
13.5.I The MTS, MTP, and TCM Methods
13.5.2 MVS and MVP Survey Methods
13.5.3 CGDS Survey Method
Processing and Analysis of MT and MV Data
13.6.1 The Least-Squares Method
13.6.2 Remote Reference Method
13.6.3 Robust Estimation of Magnetotelluric and Induction Matrices
13.4 Magnetotelluric Fields in Horizontally Inhomogeneous Media .... .... 525 13.5 13.6 13.7
13.6.4 Graphical Presentation of Magnetotelluric and Induction Matrices _ . One-Dimensional Interpretation of MT Data
13.7.I An alysis of Distorted MTS Curves
13.7.2 Quick and Dirty MTS Analysis
13.7.3 Quantitat.ive Interpretation of MTS Curves With One-Dimensional Models
13.8 Interpretation of MVP and ODS Data. .
13.8.1 Separation of Fields Into Internal and External Parts .......•.......
13.8.2 Separation of Fields Into Normal and Anomalous Parts .............
13.9 3-D Magnetotelluric Inversion
13.9.1 Tikhonov Regularization in the Full MT Impedance Tensor Inversion
13.9.2 Princip les of the Re-weighted Regularized Inversion . .
13.9.3 Minimum Support Nonlinear Parameterization .
13.9.4 Foochet Operator and Its Adj oint for Two·Component Impedance Inversion.
13.9.5 Foochet Operator for the Full Magnetotelluric Impedance Tensor Inversion.
13.9.6 Frechet Derivative Calcu lation Using Quasi-Analytical Approximation for a Variable Background (QAVB)
13.10 3D Inversion of Magnetotelluric Phase Tensor
13.10.1 MT Phase Tensor .......................•...
13.10.2 Frechet Derivative of the Phase Tensor
References and Recommended Reading to Chapter 13
CHAPTER 14 Electrom agnetic Methods in the Frequency and Time Domains
14.1 Electromagnetic Sounding in the Frequency and Time Domains ...
14.1.1 Mutual Coupling
14.1.2 Theoretic al Curves for EM Sounding in the Frequency D
14.1.3 Time-Domain El
14.1 4 Properties ofTOEM Sounding Curves .
14.2 Int
15.3 MCSEM Method With Arrays of Fixed Ocean Bottom Receivers and Towed Transmitters
15.3.1 General Survey Configuration of the MCSEM Method ....•..•..•.
15.3.2 Interpretation of MCSEM Data ...................
15.4 Towed Streamer Electromagnetic Method ................
15.4.1 General Principles of the Towed Streamer EM Method ...•..•..•.
15.4.2 Interpretation of Towed Streamer EM Data ............•..•....
15 .4. 3 Moving Sensitivity Domain Approach
References and Recommended Reading to Chapter 15
CHAPTER 16 Airborne Electromagnetic Methods ............
16.1 Frequency Domain Ajrborne Surveys .
16.2 Time Domain Airborne Surveys ..
16.3 3-D Modeling and lnversion of Airborne EM Data .........
16.4 Ground-Based Transmitter and Natural EM Field Airborne Surveys .. .....
16.4. 1 Far Field AEM Methods ........
16.4.2 ZTEM Method ......
References and Recommended Reading to Chapter 16
CHAPTER 17 Case Histories ..... ................
17.1 Tectonic Studies - EarthScope MT Survey in the Northwestern United States . .
17.2 Crustal Studies -the Khibini Experiment ..........
17.3 Minerals Exploration - IP Survey in Mongolia
17.4 Minerals Exploration - Airborne Survey in Reid-Mahaffy Site, Canada
17.5 Hydrocarbon Exploration - Off-Shore EM Survey in North Sea .....
17.5.1 The Acquisition COIlfiguration and Survey Layout
17.5.2 3D Anisotropic Inversions of the Towed Streamer EM Data ...
17.6 Marine MagnetoteJlurics In the Gulf of Mexico
References and Recommended Reading to Chapter 17
Appendix A Algebra of Differential Forms
A.l Differential Forms in Three-Dimensional Space
1-. 2-. and 3-Forms
A.1.2 A 1.3 Exterior Product ofthe Differential Forms Basis of Differential Forms ....................
A.2 Differential Forms in Multidimensional Spaces
B.2
PREFACE
Geophysicalmethodsarebasedonstudyingthepropagationofthedifferentphysicalfieldswithinthe earth’sinterior.Oneofthemostwidelyusedfieldsingeophysicsistheelectromagneticfieldgeneratedbynaturalorartificial(controlled)sources.Electromagneticmethodscompriseoneofthethree principletechnologiesinappliedgeophysics(theothertwobeingseismicmethodsandpotentialfield methods).Inthisbooktheauthorpresentsboththefoundationsandthemostrecentachievementsof electromagneticgeophysicalmethodsintheframeworkofaunifiedsystematicexposition.
Thebookisdividedintofourpartscoveringthefoundationsoffieldtheoryanditsapplications toappliedelectromagneticgeophysics,includingnewemergingmethodsofmarineelectromagnetic exploration.Thefirstpartisanintroductiontofieldtheoryrequiredforunderstandingthebasicsof geophysicalelectromagnetictheory.Thesecondpartcontainsalltheprincipalelementsofgeophysical electromagnetictheoryfromadescriptionofthefundamentalMaxwell’sequationstomodernmethodsofmodelingelectromagneticfieldsincomplex3-Dgeoelectricalformations.Thefollowingpart, Part 3,dealswithimportantaspectsoftheelectromagneticmethods,whichincludeprinciplesofthe regularizedsolutionofill-posedinverseelectromagneticproblems,one-dimensionalandmultidimensionalimagingandinversionofelectromagneticdata,andgeneralinterpretationtechniques.Thefinal part,Part 4,coversspecificgeophysicalelectromagneticmethods.
Whilethefoundationsofelectromagnetictheory,usedingeophysicalmethods,wereestablished morethanacenturyandahalfagointheworksofAmpere,Faraday,Maxwell,Gauss,andmanyother greatscientists,themostremarkableadvancesingeophysicalexplorationtechnologyweremadeatthe endofthe20thcenturyandarecontinuingtobemadeinthe21stcentury.InthisbookIemphasizethe linkbetweenthegreatdiscoveriesinphysicsandmathematicsandpracticaladvancesinexploration methods.Ialsowouldliketoattracttheattentionofthereaderstothefactthatourunderstandingof thebasiclawsofelectromagnetismhasbeenchangingrecently.
Thefundamentalsystemofelectromagneticfieldequations,Maxwell’sequations,wasdevelopedas ageneralizationofthebasiclawsofelectromagnetismestablishedinthefirsthalfofthe19thcentury. Intheframeworkofclassicaltheory,theelectromagneticfieldisdescribedbytheelectricandmagnetic vectorfields,andMaxwell’sequationsrepresentasystemofdifferentialequationswithrespecttothese vectorfields.
Duringthelastdecade,analternativeapproachtotheformulationofMaxwell’sequationshasbeen developed.Thisapproachisbasedonthealgebraictheoryofdifferentialforms,anditresultsina verycompactandsymmetricsystemofdifferentialformequationswhichisalsopresentedinthebook (Chapters 1 and 2,Appendices A and B).Thisnewapproachtotheformulationandunderstandingof thebasicpropertiesofthelawsofelectromagnetismhasastrongpotentialtostimulatethefuturedevelopmentofelectromagneticgeophysics.ThatiswhyIfounditusefultoincludethisadvancedmaterial inthemanuscript.Atthesametime,inChapter 3,Ipresentaclassicaldescriptionofelectromagnetic theory,usingthetraditionalGibbsianvectorformofMaxwell’sequations.Thereaderwhoismore interestedinpracticalapplicationsthaninanewtheoreticaldevelopmentinelectromagnetismmay skipthesectionsofChapters 1 and 2 dedicatedtodifferentialformrepresentation,andbeginreading directlywiththetraditionaltheoryofMaxwell’sequations,presentedinChapter 3.
Anothercriticaldevelopmentofelectromagneticgeophysicsduringthepastseveraldecadeshas beentakingplaceinthecomputationalmethodsassociatedbothwithforwardmodelingandwiththe inversionofgeophysicaldata.WeconsiderdifferentaspectsofforwardmodelinginChapters 4, 5,and 6,startingwithsimplemodelsofelectromagneticinductionintheearth,examiningfieldpropagation inhorizontallystratifiedmedia,anddevelopingadvancedmethodsofnumericalcomputersimulation oftheelectromagneticfieldincomplexinhomogeneousgeoelectricalstructures.InChapters 7, 8,and 9 wewilldiscussimportantaspectsoftheinversionandimagingofelectromagneticdatawhicharecommontoallgeophysicalmethods.Theseaspectsincludetheformulationoftheprinciplesofregularized inversionofill-posedgeophysicalinverseproblemsandthedevelopmentofeffectivenumericalinversionalgorithms.Idemonstratethatthisapproachprovidesaneffectivetoolforcomprehensiveinversion ofelectromagneticdata.However,inversionmeetssignificantdifficultiesbecauseoftheenormous amountofcomputationsrequiredinthecaseofthemultitransmitterandmultireceiverdataacquisition systemstypicalformodernelectromagneticgeophysicalsurveys.Thereexists,however,analternative approachtothesolutionofthisproblembasedontheprinciplesofelectromagneticholography/migration,whichextendstoelectromagneticcasesthemethodsofopticalandradioholographyandof seismicmigration.Ireviewthephysicalandmathematicalprinciplesofelectromagneticmigrationin Chapter 9
Thus,thefirstthreepartsofthebookcomprisethetheoreticalfoundationofappliedelectromagnetic geophysics.Theyarefollowedbythefinalpart, 4,whichexposesthemajorgeophysicalelectromagneticmethods.Part 4 openswithChapter 10 outliningtheelectromagneticpropertiesofrocksand mineralsinboththeparametricandexistentialsenses.InChapter 11,Iconsiderthepracticalaspectsof thegenerationandmeasurementofelectromagneticfieldsingeophysicalapplications.Thesechapters arefollowedbyfourchaptersdescribingthemostwidelyusedgeophysicalmethods–directcurrent andinducedpolarizationmethods,magnetotelluricandcontrolled-sourcemethods,aswellasmarine, airborne,andothertechniques.Thesechaptersalsocontainsomeupdatedmaterialfromthebook“The GeoelectricalMethodsinGeophysicalExploration,”byM.S.ZhdanovandG.W.Keller,publishedin 1994.Inparticular,Part 4 includesseveralsectionsformulatingthefoundationsandprinciplesofmodernIPmethods,airborneelectromagneticinductionmethods,andmarineMTandcontrolled-source electromagneticmethodsofhydrocarbonexploration.Notethateachchapterinthebookconcludes withalistofreferences.Amasterbibliographyisgivenattheendofthetext,forconvenience.
Insummary,thegoalofthisbookistobringtogetherthefundamentaltheoryofelectromagnetic fieldsandthepracticalaspectsofgeophysicalexplorationformineralandenergyresources.
Inthisbook,Ipresentalsosomeoftheresearchresultscreatedbytheauthorwiththesupport oftheConsortiumforElectromagneticModelingandInversion(CEMI),aresearchandeducational programinappliedgeophysicsbasedattheDepartmentofGeologyandGeophysics,Universityof Utah(http://www.cemi.utah.edu/).CEMIisanindustry-sponsoredconsortiumformedbymanymajor nationalandinternationalpetroleumandminingexplorationcompaniesandgeophysicalorganizations. IamverygratefultothemembersoftheCEMIconsortiumfortheircontinuingsupportofthisresearch.
Theauthorisalsoindebtedtoagreatnumberofhisteachers,colleagues,andstudentsatboth MoscowStateUniversityandtheUniversityofUtah.Amongmany,Iwouldliketosingleoutmy long-termfruitfulcollaborationwithmyteacher,ProfessorMarkN.Berdichevsky,whostimulatedmy earlyinterestinelectromagneticgeophysics.
IalsowishtoacknowledgemygratitudetoProfessorVladimirI.DmitrievofMoscowStateUniversityandtoProfessorGeorgeV.KelleroftheColoradoSchoolofMinesfortheircontributionto someofthematerialpresentedinthisbook.
IalsothankProfessorFrankBrownandothercolleaguesintheDepartmentofGeologyandGeophysics,UniversityofUtah,forcreatingasupportiveenvironmentformyresearch.Iamthankfultoall mypastandpresentgraduatestudentsandresearchassociates,whohaveworkedtogetherwithmeon manyexcitingprojectsinelectromagneticgeophysics.Thanksareexpressedparticularlytomyformer graduatestudent,Dr.LeifCox,whoreadthemanuscriptwithgreatcareandmadeanumberofuseful suggestionsandcorrections.
Inconclusion,Iwishtoexpressmydeepgratitudetomywife,OlgaZhdanov,forherconstant encouragementduringtheworkonthemanuscript.
SaltLakeCity,Utah October,2008
MichaelS.Zhdanov
INTRODUCTION
Manyofthetheoriesandmethodsofmodern-dayEMgeophysicsarebasedonafewfundamentallaws developedinthenineteenthcentury,suchasOhm’slaw,Ampere’slaw,andFaraday’slaw.
GeorgSimonOhm(Fig.1),bornonMarch16,1787,inErlangen,Bavaria,contributedthekey conceptofthetheoryofelectricity,whichisnowfamouslyknownastheOhm’slaw,whichforms thefoundationofthemoderngeoelectricalmethodsofexploration.Afterbecomingaprofessorof mathematicsattheageof30intheJesuit’sCollegeinKolnin1817,hespentmanyyearsstudyingthe relationshipbetweenvoltageandcurrent.Hisrecognitionofwhatwenowacceptasbeingsoobvious, thatvoltageandcurrentarelinearlyrelated,definingaquantitywecallresistance,wasverycoolly receivedbyhispeers.Infrustrationoverthislackofrecognition,hefinallyresignedhispositionand movedtothePolytechniqueSchoolatNurnbergin1833.Afterlongyearsofeffort,hisworkbecame acceptable,andin1841hewasawardedtheCopleyMedaloftheRoyalSocietyofLondon.Hedied onJuly7,1854,inMunichattheageof67.
Weshouldnotethat,untiltheearly19thcentury,electricityandmagnetismweretreatedbyscientistsastwodifferentnaturalphenomena,whichwerenotrelatedtoeachother.Andre’MarieAmpere (Fig.2)wasthefirstwhoexperimentallyobservedthattherewasalwaysamagneticfieldassociated withcurrentflow,andthestrengthofthemagneticfieldwasproportionaltotheamountofcurrentflow-
FIGURE1
GeorgSimonOhm.(https://en.wikipedia.org/wiki/Georg_Ohm#/media/File:Georg_Simon_Ohm3.jpg)
Andre’MarieAmpere.(https://en.wikipedia.org/wiki/Andr%C3%A9-Marie_Amp%C3%A8re#/media/ File:Ampere_Andre_1825.jpg)
ing.Thiswasafundamentalcontributiontothescienceofelectromagnetism,whichbecameknownas Ampere’slaw.
AmperewasFrench,borninPolemieux,nearLyons,inJanuary,1775.Hetookpassionatedelight inlearningfromhisearlyinfancy,andissaidtohaveworkedoutlengthysumsusingpebblesand biscuitcrumbsevenbeforeheknewfigures.Helaterclaimedthatheknewasmuchaboutmathematics atageeighteenasheeverknew.
DuringAmpere’seighteenthyear,LyonswasoccupiedbytheArmyoftheConvention,andhis father,whohadbeenopposedtotheRevolution,wasthrownintoprison,andlater,hanged.Ampere wentintodeepdepression,andforayearwasmentallyincompetent.However,by1796,hewasgiving privatelessonsinmathematicsandlanguages,andby1801hehadbecomeaprofessorofphysicsand chemistryatBourg,butaftertwoyearsreturnedtotheLyceuminLyonsasProfessorofMathematics. HemovedtothePolytechnicSchoolatParisin1805,andwaselectedProfessorofAnalysisin1809. Onthe18thofSeptember,1820,hepresentedapaperbeforetheAcademyofSciences,definingthe magneticforceaccompanyingcurrentflow,aphenomenonnowknownasAmpere’slaw.Hediedin MarseillesinJune,1836,attheageof61.
Ampere’sdiscoverythatamagneticfieldcanbegeneratedbytheflowofanelectriccurrentwas fascinatingand,forthefirsttimeinthehistoryofscienceprovidedalinkbetweenelectricityand magnetism.However,thequestionremainedwhetherornotthereverserelationhold,inotherwords, whetheramagneticfieldcouldbethesourceofanelectriccurrent.Thescientist,whodedicatedmany yearsofresearchtryingtoanswerthisfundamentalquestion,wasMichaelFaraday(Fig.3).Faraday
FIGURE2
FIGURE3
MichaelFaraday.(https://en.wikipedia.org/wiki/Michael_Faraday#/media/File:Faraday-Millikan-Gale-1913.jpg) wasbornonSeptember22,1791,atNewington,Surrey,whichwasthenlocatedinthecountryside southofLondon.Hisfatherwasablacksmith.
Michaelreceivednoformaleducation,butwasapprenticedtoabooksellerandbookbinderin1805, attheageof14.Inthisshop,hedevelopedakeeninterestinreadingscience.In1812,attheage of21,heattendedaseriesoflecturesgivenbySirHumphreyDavyattheRoyalInstitutionofGreat Britain.HesenthisnotesofthelecturestoHumphreyDavywithapetitionforemployment,persuading HumphreyDavytohirehimasaresearchassistantattheRoyalInstitution.Hisfirstgreatexperiment wasdonein1821,inwhichhecausedacurrent-carryingwiretorotateinthefieldofahorseshoe magnet.Hecontinuedwiththiseffortdespitethecriticismsoffellowscientistswhowereunsuccessful inreproducingthisearlyexperiment,andfinally,overaperiodoftendaysin1831,hecarriedouta convincingdemonstrationofthephenomenonofelectromagneticinduction–Faraday’slaw.
Inlateryears,hemetwithconsiderabledifficultiesincontinuinghisresearch,probablybecauseof theeffectofmercurypoisoningresultingfromworkinglonghoursinthepoorlyventilatedbasement roomsoftheRoyalInstitution.Faradayusedapurelyintuitiveapproachtoscience,eschewinganyuse ofmathematics,butplacingstrongdemandsonthementalprocesses.Heretiredin1858toaroyal palace,HamptonCourt,madeavailabletohimatthesuggestionofthePrinceConsort,Albert.After hediedonAugust25,1867,acollectionofninety-fivediplomasoflearnedsocieties,boundwithhis ownhand,wasfoundinhispersonaleffects.
Thesethreefundamentalphysicallawswerediscoveredquiteindependently,basedonphysical experiments,andreflecteddifferentaspectsofelectromagneticphenomena.Atthetime,itwasnotclear ifandhowtheselawswererelated.ItrequiredthegeniusofanotherEnglishmanofgreatdistinction,
FIGURE4
JamesClerkMaxwell.(https://en.wikisource.org/wiki/Popular_Science_Monthly/Volume_17/May_1880/ Sketch_of_James_Clerk_Maxwell#/media/File:PSM_V17_D008_James_Clerk_Maxwell.jpg)
JamesClerkMaxwell(Fig.4)torecognizethatOhm’slaw,Faraday’slaw,andAmpere’slawwere propertiesofagreatwhole,thatwholenowbeingcalledthe electromagneticfield.
JamesClerkMaxwellwasbornonJune13,1831inEdinburgh.HispatronymwasactuallyClerk, withtheaddednameMaxwellbeingderivedfromhismother’sfamilyname.Hewasraisedona countryestate,Glenlair,inKirkcudbright.Hisfamilyprovidedhimwiththebesteducationthathis timeoffered.ThisincludedfirsttheEdinburghAcademy,wherehiscountrywayswerenotreadily acceptedbyhisclassmates;hecametobeknownbythenickname“Dafty.”Afterspendingthreeyears attheUniversityinEdinburgh,MaxwellwenttoCambridgeintheAutumnof1850.But,beforeleaving Edinburghattheageof19,JameshadalreadyhadtwopaperspublishedbytheRoyalSociety.In1860, hewasappointedtoKing’sCollege,London,wherehespentthemostproductiveyearsofhislife.In 1855,henotedthatFaradayhadseeninhismind’seyelinesofforcetraversingalloverspace,while thegreatmathematicians(Gauss,Weber,Rieman,theNeumans)hadseenonlycentersofforceacting throughdistance.AftertranslatingFaraday’sresultsintomathematicalform,Maxwellsawthatallthe earlierresultscoincidedtoformauniformtheoryofelectromagneticphenomena.Maxwellnotedthat severalofthemostfertilemethodsofresearchdiscoveredbythemathematicianscouldbeexpressed muchbetterintermsofideasderivedfromFaradaythanintheiroriginalform.Maxwell’s“Treatiseon ElectricityandMagnetism”appearedin1873,definingtheunificationofopticsandelectrodynamics. Then,afterabriefteachingengagementinAberdeen,Maxwellbecamethefirstdirectorofthenewly foundedCavendishLaboratoryatCambridge.HediedonNovember5,1879,attheageof47.
Maxwell’sequationsarethequintessenceofthedevelopmentofelectromagnetictheory;aftertheir statement,furtherdevelopment,includingthatusedinthegeoelectricalmethods,wasonlyamatterof performingtheappropriatemathematicalmanipulations.
Theearlystudyofelectricalandelectromagnetic(EM)phenomenainrelationtotheproblemsof findingoreandothermineraldepositswasstimulatedbyagrowingdemandfromtheminingindustry.
FIGURE5
ConradSchlumberger.(CourtesyofDGGfrom https://ro.wikipedia.org/wiki/Conrad_%C8%99i_Marcel_ Schlumberger#/media/File:Schlumberger.jpg)
RobertFox(1830)wasprobablythefirstscientistwhoconsideredapossibleapplicationofspontaneous polarizationphenomenainlocatingorebodies.Thefirstexperimentsmeasuringelectricalconductivity tolocatecopper-bearingloadswereconductedbyJamesFisherinMichigan,U.S.A.,in1893(Jakosky, 1940).From1912to1914,theSchlumbergerbrothers,MarcelandConrad,conductedthefirstdirect current(DC)geophysicalsurveysinFrancefortectonicstudy.In1916,Wenneradvancedamethod formeasuringearthresistivity(Wenner,1928)thatwastakenupfororeprospectingby Lundberg (1922), GishandRooney(1925),and Heiland(1926).Wennermadesignificanteffortsindeveloping theprinciplesofinterpretingDCdata.However,theDCmethoddidnotgainmuchpracticalground untiltheconceptofapparentresistivitywasintroducedbytheSchlumbergerbrothersin1922,which madedataanalysisandinterpretationmuchmoregeologicallymeaningfulandeasiertoconduct.
TheintriguingsagaoftheSchlumbergerfamilyistoldinprobablythemostcomprehensivewayin therecentbookby OristaglioandDorozynski(2009).Theexcitingideaofusinganelectricfieldfor “seeing”throughthegroundwasconceivedofbyConradSchlumbergerasearlyas1912.However, theadventofWorldWarIin1914delayedthepracticalimplementationoftheidea.Onlyin1919did PaulSchlumbergerofferfinancialsupporttohissons,ConradandMarcel(Figs.5and6),todevelop
FIGURE6
MarcelSchlumberger.(http://wiki.seg.org/wiki/File:Marcel_Schlumberger_headshot.png#filelinks)
therevolutionarynewtechnologyofelectricalprospecting.On12November1919,thefatherandsons formalizedtheiragreement,markingthebeginningofanewerainexplorationgeophysics.
Initially,theSchlumbergerbrothers’fieldexperimentstouseelectricalmeasurementstomapsubsurfaceformationsdidnotresultinsignificantdiscoveries.Thefirstmajorcommercialsuccesscame inthe1930swhenthefirmfoundedbytheSchlumbergerbrotherswasinvitedtoworkintheformer SovietUnion.ItwasintheAzerbaijanoilfieldsandtheCaucasusMountainsthatresistivitywellloggingstarteditstriumphantmarchovertheplanet.ThepioneeringworkoftheSchlumbergerbrothers stimulatedthecreationanddevelopmentoftheRussianschoolofEMgeophysicists,whichproduced asignificantnumberofdistinguishedgeophysicistsandledtomajorgeologicdiscoveriesintheUral MountainsandeasternSiberiainthe1940sand1950s.
Withthepracticalapplicationofelectricalmethodsinexplorationofthesubsurface,theneedfor mathematicalsolutionsforthebehaviorofelectromagneticfieldsinteractingwithreasonablemodelsof theearthbecameapparent.Inthisrespect,SabbaS.Stefanescu(Fig.7)builtthemathematicalbasisfor electromagneticmodeling.StefanescuwasborninBucharestonthe20thofJuly,1902,toafamilyof distinguishedintellectuals,beingthethirdsonofProfessorSabbaStefanescu,acorrespondingmember oftheRomanianAcademy.Hisinterestinmathematicswasrecognizedearly,whileheattendedhigh schoolclassesattheSt.SavaLycee.DuringWorldWarI,whilehisfatherwasassignedtoadiplomatic postinFrance,heandhisfamilyescapedfromRomania,crossingthewholeofRussiafromwestto eastduringtheearlydaysoftheRussianCivilWar,finallyreachingParisbycrossingtheArcticOcean fromeasternmostRussia.
SabbaStefanescucontinuedhisschoolinginParis,completinghispreparatorystudiesatSaint LouisLyceein1918,completinghisstudiesfortheB.Sc.degreeinScienceattheSorbonnein1919,