Thermodynamicfundamentals
Nomenclature
A area(m2)
d difference
e specificenergy(kJ/kg)
ex specificexergy(kJ/kg)
E energy(kJ)
Ex exergy(kJ)
Ex exergyrate(kg/s)
g gravitationalacceleration(m/s2)
h specificenthalpy(kJ/kg)
^ h specifictotalenergy(kJ/kg)
H enthalpy(kJ)
ke specifickineticenergy(kJ/kg)
KE kineticenergy(kJ)
m massflowrate(kg/s)
M molarmass(kg/mol)
pe specificpotentialenergy(kJ/kg)
PE potentialenergy(kJ)
q specificheattransfer(kJ/kg)
Q heattransfer(kJ)
Q heattransferrate(kg/s)
R gasconstant(kJ/kmolK)
s specificentropy(kJ/kgK)
S entropy(kJ/K)
T temperature(°CorK)
u specificinternalenergy(kJ/kg)
U internalenergy(kJ)
V velocity(m/s);volume(m3)
w specificwork(kJ/kg)
W work(kJ)
_ W workrate(kg/s)
Greekletters
d difference
D difference
h energyefficiency
c exergyefficiency
Subscripts
1,2 statepoints
cv controlvolume
e exit
gen generation
i inlet
Exergy https://doi.org/10.1016/B978-0-12-824372-5.00001-4 © 2021ElsevierLtd.Allrightsreserved.
si sink
so source
surr surroundings
sys system
Acronyms
FLT firstlawofthermodynamics
SLT secondlawofthermodynamics
1.1Introduction
Energy,entropy,andexergyconceptsstemfromthermodynamicsandapplytoallfieldsofscienceandengineering.This chapterprovidesthenecessarybackgroundforunderstandingtheseconcepts,aswellasbasicprinciples,generaldefinitions,andpracticalapplicationsandimplications.Illustrativeexamplesareprovidedtohighlighttheimportantaspectsof energy,entropy,andexergy.
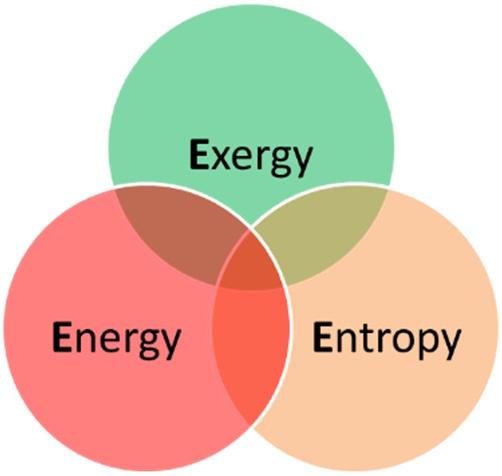
Thescopeofthischapterispartlyillustratedin Fig.1.1,wherethedomainsofenergy,entropy,andexergyareshown. Thischapterfocusesontheportionofthefieldofthermodynamicsattheintersectionofenergy,entropy,andexergyfields. Notethatentropyandexergyarealsousedinotherfields(suchasstatisticsandinformationtheory);therefore,theyarenot subsetsofenergy.Also,someformsofenergy(suchasshaftwork)areentropy-free;thus,entropysubtendsonlyapartof theenergyfield.Likewise,exergysubtendsonlyapartoftheenergyfieldassomesystems(suchasairatatmospheric conditions)possessenergybutnoexergy.Mostthermodynamicsystems(suchassteaminapowerplant)possessenergy, entropy,andexergyand,thus,appearattheintersectionofthesethreefields.
1.2Energy
Energycomesinmanyforms.Thermodynamicsplaysakeyroleintheanalysisofprocesses,systems,anddevicesinwhich energytransfersandenergytransformationsoccur.Theimplicationsofthermodynamicsarefar-reaching,andapplications spantherangeofthehumanenterprise.Throughoutourtechnologicalhistory,ourabilitytoharnessenergyanduseitfor society’sneedshasimproved.Theindustrialrevolutionwasfueledbythediscoveryofhowtoexploitenergyonalarge scaleandhowtoconvertheatintowork.Natureallowstheconversionofworkcompletelyintoheat,butheatcannotbe entirelyconvertedintoworkanddoingsorequiresadevice(e.g.,acyclicengine).Enginesattempttooptimizetheconversionofheattowork.
1.2.1Applicationsofenergy
Mostofourdailyactivitiesinvolveenergytransferandenergychange.Thehumanbodyisafamiliarexampleofabiologicalsysteminwhichthechemicalenergyoffoodorbodyfatistransformedintootherformsofenergy,suchasheatand work.Engineeringapplicationsofenergyprocessesarewide-rangingandincludepowerplantstogenerateelectricity, enginestorunautomobilesandaircraft,refrigerationandairconditioningsystems,etc.
Manyexamplesofsuchsystemsarediscussedhere.Inahydroelectricpowersystem,thepotentialenergyofwateris convertedintomechanicalenergythroughtheuseofahydraulicturbine.Themechanicalenergyisthenconvertedinto
electricenergybyanelectricgeneratorcoupledtotheshaftoftheturbine.Inasteampowergeneratingplant,chemicalor nuclearenergyisconvertedintothermalenergyinaboilerorareactor.Theenergyisimpartedtowater,whichvaporizes intosteam.Theenergyofthesteamisusedtodriveasteamturbine,andtheresultingmechanicalenergyisusedtodrivea generatortoproduceelectricpower.Thesteamleavingtheturbineisthencondensed,andthecondensateispumpedbackto theboilertocompletethecycle.Breederreactorsuseuranium-235asafuelsourceandcanproducesomemorefuelinthe process.Asolarpowerplantusessolarconcentrators(parabolicorflatmirrors)toheataworkingfluidinareceiverlocated onatower,whereaheatedfluidexpandsinaturbogeneratorasinaconventionalpowerplant.Inaspark-ignitioninternal combustionengine,thechemicalenergyofthefuelisconvertedintomechanicalwork.Anair-fuelmixtureiscompressed andcombustionisinitiatedbyasparkdevice.Theexpansionofthecombustiongasespushesagainstapiston,whichresults intherotationofacrankshaft.Gasturbineengines,commonlyusedforaircraftpropulsion,convertthechemicalenergyof fuelintothermalenergythatisusedtorunagasturbine.Theturbineisdirectlycoupledtoacompressorthatsuppliestheair requiredforcombustion.Theexhaustgases,uponexpandinginanozzle,createthrust.Forpowergeneration,theturbineis coupledtoanelectricgeneratoranddrivesboththecompressorandthegenerator.Inaliquid-fuelrocket,afuelandan oxidizerarecombined,andcombustiongasesexpandinanozzlecreatingapropulsiveforce(thrust)topropeltherocket. Atypicalnuclearrocketpropulsionengineoffersahigherspecificimpulsewhencomparedtochemicalrockets.Afuelcell convertschemicalenergyintoelectricenergydirectlymakinguseofanion-exchangemembrane.Whenafuelsuchas hydrogenisionized,itflowsfromtheanodethroughthemembranetowardthecathode.Thereleasedelectronsattheanode flowthroughanexternalload.Inamagnetohydrodynamicgenerator,electricityisproducedbymovingahigh-temperature plasmathroughamagneticfield.Arefrigerationsystemutilizesworksuppliedbyanelectricmotortotransferheatfroma refrigeratedspace.Low-temperatureboilingfluids,suchasammoniaandrefrigerant-12,absorbthermalenergyasthey vaporizeintheevaporator,causingacoolingeffectintheregionbeingcooled.
Theseareonlysomeofthenumerousengineeringapplications.Thermodynamicsisrelevanttoamuchwiderrangeof processesandapplicationsnotonlyinengineeringbutalsoinscience.Agoodunderstandingofthistopicisrequiredto improvethedesignandperformanceofenergy-transfersystems.
1.2.2Conceptofenergy
TheconceptofenergywasfirstintroducedinmechanicsbyNewtonwhenhehypothesizedaboutkineticandpotential energies.However,theemergenceofenergyasaunifyingconceptinphysicswasnotadopteduntilthemiddleofthe 19thcenturyandisconsideredoneofthemajorscientificachievementsofthatcentury.Theconceptofenergyissofamiliar toustodaythatitseemsintuitivelyobvioustounderstand,yetweoftenhavedifficultydefiningitprecisely.
Energyisascalarquantitythatcannotbeobserveddirectlybutcanberecordedandevaluatedbyindirectmeasurements. Theabsolutevalueoftheenergyofasystemisdifficulttomeasure,whereastheenergychangeisrelativelyeasyto evaluate.
Examplesofenergyuseinlifeexperiencesareendless.Thesunisthemajorsourceoftheearth’senergy.Itemitsa spectrumofenergythattravelsacrossspaceaselectromagneticradiation.Energyisalsoassociatedwiththestructure ofmatterandcanbereleasedbychemicalandatomicreactions.Throughouthistory,theemergenceofcivilizationshas beencharacterizedbythediscoveryandeffectiveapplicationofenergytohelpmeetsociety’sneeds.
1.2.3Formsofenergy
Energymanifestsitselfinmanyforms,whichareeitherinternalortransient.Itcanbeconvertedfromoneformtoanother. Inathermodynamicanalysis,theformsofenergycanbeclassifiedintotwogroups:macroscopicandmicroscopic.
Macroscopicformsofenergy arethosewhichanoverallsystempossesseswithrespecttoareferenceframe,e.g., kineticandpotentialenergies.Forexample,themacroscopicenergyofarisingobjectchangeswithvelocityandelevation. Themacroscopicenergyofasystemisrelatedtomotionandtheinfluenceofexternaleffectssuchasgravity,magnetism, electricity,andsurfacetension.
Theenergythatasystempossessesasaresultofitsmotionrelativetosomereferenceframeis kineticenergy.Kinetic energyreferstotheenergyofthesystembecauseofits“overall”motion,eithertranslationalorrotational.Here,theterm “overall”isusedtospecifythatwerefertothekineticenergyoftheentiresystem,notthekineticenergyofthemoleculesin thesystem.Ifthesystemisagas,forexample,thekineticenergyistheenergyduetothemacroscopicflowofthegas,not themotionofindividualmolecules.
The potentialenergy ofasystemisthesumofthegravitational,centrifugal,electrical,andmagneticpotentialenergies. Theenergythatasystempossessesasaresultofitselevationinagravitationalfieldiscalledgravitationalpotentialenergy
(orcommonly,justpotentialenergy).Forexample,a1kgmass,100mabovetheground,hasgreaterpotentialenergythan thesamemassontheground.Potentialenergycanbeconvertedintootherformsofenergy,suchaskineticenergyifthe massisallowedtofall.
Kineticandpotentialenergydependsontheenvironmentinwhichthesystemexists.Inparticular,thepotentialenergy ofasystemdependsonthechoiceofazerolevel.Forexample,ifgroundlevelisconsideredtobeatzeropotentialenergy, thenthepotentialenergyofthemass100mabovethegroundhaspositivepotentialenergyequaltothemass(1kg)multipliedbythegravitationalconstant(g ¼ 9.807m/s2)andtheheightabovetheground(100m).Itspotentialenergywillbe 980.7(kgm2)/s2 (or980.7Newton-meters(Nm),or980.7J).Thedatumplaneforpotentialenergycanbechosenarbitrarily. Ifithadbeenchosenat100mabovethegroundlevel,thepotentialenergyofthemasswouldhavebeenzero.Ofcourse,the differenceinpotentialenergybetweenthemassat100mandthemassatgroundlevelisindependentofthedatumplane.
Microscopicformsofenergy arethoserelatedtothemolecularstructureofasystemandthedegreeofmolecular activity,andtheyareindependentofoutsidereferenceframes.Thesumofallthemicroscopicformsofenergyofasystem isits internalenergy.Theinternalenergyofasystemdependsontheinherentqualities,orproperties,ofthematerialsinthe system,suchascompositionandphysicalform,aswellastheenvironmentalvariables(temperature,pressure,electricfield, magneticfield,etc.).Internalenergycanhavemanyforms,includingmechanical,chemical,electrical,magnetic,surface, andthermal.Someexamplesareconsideredforillustration:
l Aspringthatiscompressedhashigherinternalenergy(mechanicalenergy)thanaspringthatisnotcompressedbecause thecompressedspringcandoworkonchanging(expanding)totheuncompressedstate.
l Twoidenticalvessels,eachcontaininghydrogenandoxygen,thathavedifferentchemicalenergiesareconsidered.In thefirst,thegasesarecontainedintheelementalform,purehydrogenandpureoxygen,inaratioof2:1.Thesecond containsanidenticalnumberofatomsbutintheformofwater.Theinternalenergiesofthesesystemsdiffer.Aspark maysetoffaviolentreleaseofenergyinthefirstcontainer,butnotinthesecond.
Thestructureofthermodynamicsinvolvestheconceptofequilibriumstatesandpostulatesthatthechangeinthevalueof thermodynamicquantities,suchasinternalenergy,betweentwoequilibriumstatesofasystemdoesnotdependonthe thermodynamicpaththesystemtakestogetfromonestatetotheother.Thechangeisdefinedbythefinalandinitialequilibriumstatesofthesystem.Consequently,theinternalenergychangeofasystemisdeterminedbytheparametersthat specifythesysteminitsfinalandinitialstates.Theparametersincludepressure,temperature,magneticfield,surfacearea, mass,etc.Ifasystemchangesfromstate1tostate2,thechangeininternalenergy DU is(U2 U1),theinternalenergyinthe finalstateislessthanthatintheinitialstate.Thedifferencedoesnotdependonhowthesystemgetsfromstate1to2.The internalenergy,thus,isreferredtoasastatefunction,orapointfunction,thatis,afunctionofthestateofthesystemonly, andnotitshistory.
Thethermalenergyofasystemistheinternalenergyofasystem,whichincreasesasthetemperatureisincreased.For instance,wehavetoaddenergytoanironbartoraiseitstemperature.Thethermalenergyofasystemisnotreferredtoas heat,asheatisenergyintransitbetweensystems.
1.2.4Thefirstlawofthermodynamics(FLT)
Thefirstlawofthermodynamicsisthe lawoftheconservationofenergy,whichstatesthat,althoughenergycanchange form,itcanbeneitherbecreatednordestroyed.TheFLTdefinesinternalenergyasastatefunctionandprovidesaformal statementoftheconservationofenergy.
However,itprovidesnoinformationaboutthedirectioninwhichprocessescanspontaneouslyoccur,thatis,thereversibilityaspectsofthermodynamicprocesses.Forexample,theFLTcannotindicatehowcellscanperformworkwhile existinginanisothermalenvironment.TheFLTprovidesnoinformationabouttheinabilityofanythermodynamicprocess toconvertheatfullyintomechanicalworkoranyinsightintowhymixturescannotspontaneouslyseparateorunmixthemselves.Aprincipletoexplainthesephenomenaandcharacterizetheavailabilityofenergyisrequiredtodothis.Thatprincipleisembodiedinthesecondlawofthermodynamics,whichweexplainlater.
1.2.5Energyandthefirstlawofthermodynamics
Foracontrolmass,theenergyinteractionsforasystemmaybedividedintotwoparts: dQ,theamountofheat,and dW,the amountofwork.Unlikethetotalinternalenergy dE,thequantities dQ and dW arenotindependentofthemanneroftransformation,sowecannotspecify dQ and dW simplybyknowingtheinitialandfinalstates.Hence,itisnotpossibletodefine
afunction Q,whichdependsontheinitialandfinalstates,i.e.,heatisnotastatefunction.TheFLTforacontrolmasscanbe writtenasfollows:
WhenEq. (1.1) isintegratedfromaninitialstate1toafinalstate2,itresultsin
where E1 and E2 denotetheinitialandfinalvaluesoftheenergy E ofthecontrolmass, Q1-2 istheheattransferredtothe controlmassduringtheprocessfromstate1tostate2,and W1-2 istheworkdonebythecontrolvolumeduringtheprocess fromstate1tostate2.
Theenergy E mayincludeinternalenergy U,kineticenergy KE,andpotentialenergy PE termsasfollows:
Forachangeofstatefromstate1tostate2withaconstantgravitationalacceleration g,Eq. (1.3) becomes
where m denotesthefixedamountofmasscontainedinthesystem, V thevelocity,and Z theelevation.
Thequantities dQ and dW canbespecifiedintermsoftheratelawsforheattransferandwork.Foracontrolvolume,an additionaltermappearsfromthefluidflowingacrossthecontrolsurface(enteringatstateiandexitingatstatee).TheFLT foracontrolvolumecanbewrittenas
where m ismassflowrateperunittime, ^ h istotalspecificenergy,equaltothesumofspecificenthalpy,kineticenergy,and potentialenergy,i.e., ^ h ¼ h + V2/2+ gZ.
1.2.6Economicaspectsofenergy
Althoughallformsofenergyareexpressedinthesameunits(joules,megajoules,gigajoules,etc.),thefinancialvalueof energyvariesenormouslywithitsgradeorquality.Typically,electricalandmechanicalenergyarethemostcostly,followedbyhigh-gradethermalenergy.Attheotherextreme,thermalenergy,whichisonlyafewdegreesfromambient,has virtuallynocommercialvalue.Theseexampleshighlighttheweaknessoftryingtoequatetheenergycontainedinsteamor theheatcontentofgeothermalfluidswiththehigh-gradeenergyobtainablefromfossilfuelsornuclearpower.Economics usuallysuggeststhatoneshouldavoidusingenergyatasignificantlyhighergradethanneededforatask.Forexample, electricalenergy,whichhasahighenergygrade,shouldbeusedforsuchpurposesasmechanicalenergygeneration,productionoflight,sound,andveryhightemperaturesinelectricalfurnaces.Electricspaceheating,ontheotherhand,inwhich electricityisusedforraisingthetemperatureofambientaironlytoabout20°C,isanextremelywastefuluseofelectricity. Thisobservationappliesinbothdomesticandindustrialcontexts.Inmanyjurisdictions,thereisexcesselectricitygenerationcapacityatnight;therefore,someofthenighttimeelectricityissoldatreducedpricesforspaceheatingpurposes,even thoughthisisinherentlywasteful.Itisoftenmoreadvantageousandefficientinsuchsituationstoutilizeenergystorage, suchasflywheels,compressedair,orpumpedwater,whichleadstoreducedthermodynamicirreversibility.
Inindustrysettings,tasksoftenrequireenergybutatdifferentgrades.Theopportunityoftenexiststousethewasteheat fromoneprocesstoservetheneedsofanotherinaneffectiveandefficientmanner.Sometimes,acascadeoftaskscanbe satisfiedinthismanner,Forexample,atypicalglassworksreleaseswasteheatatbetween400°Cand500°C,whichissufficientforraisingintermediate-pressuresteamforrunningback-pressureturbinestoproduceelectricityorraisinglowpressuresteamatabout120°Cforotherpurposesorheatingoperationsattemperaturesashighas400–500°C.Theheat exhaustedfromasteamturbinecan,inturn,beusedtoevaporatemoisturefromagriculturalproducts.Thewatervapor obtainablefromsuchprocessescanbecondensedtoprovidewarmwateratabout60°C,whichcanbeemployedforspace heatingorforthesupplyofheattofishfarmsorgreenhouses.Inthisexample,theoriginalsupplyofhigh-gradeenergy obtainedbyburningcoal,oil,ornaturalgasperformsfourseparatetasks:
l Thevariousglassconstituentsaremeltedafterbeingheatedtoabovetheirsolidificationtemperature(about1500°C).
l Medium-pressuresteamisusedtoproduceelectricity(500°C).
l Theexhauststeamfromtheback-pressureturbineisusedforcropdrying(120°C).
l Thecondensedwatervaporheatswaterforuseinspaceheating,fishfarms,orgreenhouses(60°C).
1.2.7Energyauditmethods
Energymanagementopportunitiesoftenexisttoimprovetheeffectivenessandefficiencywithwhichenergyisused.For instance,energyprocessesinindustrial,commercial,andinstitutionalfacilities,includingheating,cooling,andairconditioning,canoftenbeimproved.Manyoftheseopportunitiesarerecognizableduringawalk-throughauditoramore detailedexaminationofafacility.Suchanauditisusuallymoremeaningfulifsomeonefromoutsidethefacilitybut,generally,familiarwithenergymanagementisinvolved.Typicalenergy-savingitemsnotedduringawalk-throughaudit includesteamandwaterleaksatconnectionsandotherlocations,damagedinsulation,excessivelighting,etc.Alertmanagementandoperatingstaffandgoodmaintenanceprocedurescan,withlittleeffort,reduceenergyusageand,thereby, savemoney.
Notallitemsnotedinawalk-throughauditareeasytoanalyze.Forexample,astreamofcoolingwatermaybedirected toadrainafterbeingusedforacoolingapplication,eventhoughsomethermalenergyremainsinthewater.Theeconomics ofrecoveringthisheatneedstobeinvestigatedtodetermineifitisworthrecovering.Somerelevantquestionstoconsiderin suchanassessmentincludethefollowing:
l Howmuchthermalenergyisavailableinthewastestream?
l Isthereauseforthisenergy?
l Whatarethecapitalandoperatingcostsinvolvedinrecoveringtheenergy?
l Willtheenergyandassociatedcostsavingspayfortheequipmentrequiredtorecovertheenergy?
Adiagnosticauditisrequiredtodeterminethethermalenergyavailableinawastestream,howmuchenergycanbe recovered,andifthereisauseforthisrecoveredenergywithinoroutsidethefacility.Thecostsavingsassociatedwith recoveringtheenergyaredetermined,andalongwiththecosttosupplyandinstalltheheatrecoveryequipment,thesimple paybackperiodcanbeevaluatedforthemeasuretoestablishitsfinancialviability.
1.2.8Energymanagement
Energymanagementreferstotheprocessofusingenergycarefullysoastosavemoneyorachieveotherobjectives.Energy managementmeasurescanbedividedintothefollowingcategories:maintenance(orhousekeeping),low-cost(orsimple), andretrofit.Manyenergymanagementmeasuresareoutlinedherealongwiththeirpotentialenergysavings.Thislistisnot intendedtobecomprehensive(e.g.,itdoesnotcoverallopportunitiesavailableforheating,cooling,andairconditioning equipment),buttohelpthoseinvolvedinmanagement,operations,andmaintenancetoidentifyenergysavingsopportunitiesspecifictoaparticularfacility.Otherenergymanagementopportunitiesexist.
Energymanagementisbestapproachedinanopenmannerthatallowspreviouslyacceptedinefficientpracticestobe explored.Improvedawarenessonthepartofthestaffmanaging,operating,ormaintainingafacility,combinedwithimaginationand/orexpertassistance,canyieldlargedividendsintermsofenergyuseandcostreductions.Severalpractical energymanagementmeasuresarecoveredbelow.
Maintenanceopportunities.Maintenancemeasuresforenergymanagementarethosecarriedoutregularly,normally nomorethanannually,andincludethefollowing:
l Sealingleaksatvalves,fittings,andgaskets.
l Repairingdamagedinsulation.
l Maintainingtemperatureandpressurecontrols.
l Maintainingsteamtraps.
l Cleaningheattransfersurfaces.
l Ensuringsteamqualityisadequatefortheapplication.
l Ensuringsteampressureandtemperaturerangesarewithinthetolerancesspecifiedfortheequipment.
l Ensuringsteamtrapsarecorrectlysizedtoremoveallcondensate.
l Ensuringheatingcoilsslopefromsteaminlettosteamtraptopreventcoilsfromfloodingwithcondensate.
Low-costopportunities. Low-costenergymanagementmeasuresarenormallyonce-offactionsforwhichthecostisnot consideredgreat:
l Shuttingequipmentwhennotrequired.
l Providinglockablecoversforcontrolequipment,suchasthermostats,topreventunauthorizedtampering.
l Operatingequipmentatornearcapacitywheneverpossibleandavoidingrunningmultipleunitsatreducedcapacity.
l Addingthermostaticairvents.
l Addingmeasuringandmonitoringequipmenttoprovidetheoperatingdataneededtoimprovesystemoperation.
l Assessingthelocationofcontroldevicestoensurethebestoperation.
Retrofitopportunities. Retrofitenergymanagementmeasuresarenormallyonce-offactionswithsignificantcoststhat involvemodificationstoexistingequipment.Manyofthesemeasuresrequiredetailedanalysisandarebeyondthescope ofthischapter.Workedexamplesareprovidedforsomeofthelistedenergymanagementopportunities,whileinothercases thereisonlycommentary.Typicalenergymanagementmeasuresinthiscategoryfollow:
l Convertingfromdirecttoindirectsteam-heatedequipmentandrecoveryofcondensate.
l Installing/upgradinginsulationonequipment.
l Relocatingsteam-heatedequipmentfromcentralbuildingareastoareaswithexteriorexposuressothatheatlossfrom theequipmentcanassistinheatingthearea.
l Reviewinggeneralbuildingheatingconceptsasopposedtotaskheatingconcepts.
l Modifyingprocessestostabilizeorreducesteamorwaterdemand.
l Investigatingtheschedulingofprocessoperationsinanattempttoreducepeaksteamorwaterdemands.
l Evaluatingwastewaterstreamsexitingafacilityforheatrecoveryopportunities.
1.3Entropy
Inthissection,basicphenomenalikeorderanddisorderaswellasreversibilityandirreversibilityarediscussed.Entropy andthesecondlawofthermodynamicsarealsocovered,alongwiththeirsignificance.
1.3.1Orderanddisorderandreversibilityandirreversibility
Withinthelast80years,ourviewofnaturehaschangeddrastically.Classicalscienceemphasizedequilibriumandstability. Now,weobservefluctuations,instability,andevolutionaryprocessesonalllevelsfromchemistryandbiologytocosmology.Everywhere,weobserveirreversibleprocessesinwhichtimesymmetryisbroken.Thedistinctionbetween reversibleandirreversibleprocesseswasfirstintroducedinthermodynamicsthroughtheconceptof“entropy.”
Theformulationofentropyisinthemoderncontextfundamentalforunderstandingthermodynamicaspectsofselforganizationandtheevolutionoforderandlifethatweobserveinnature.Whenasystemisisolated,theentropyofasystem continuallyincreasesduetoirreversibleprocessesandreachesthemaximumpossiblevalue,whenthesystemsattainastate ofthermodynamicequilibrium.Inthestateofequilibrium,allirreversibleprocessescease.Whenasystembeginsto exchangeentropywithitssurroundingsthen,ingeneral,itisdrivenawayfromtheequilibriumstatethatitisreachedwhen isolated,andentropyproducingirreversibleprocessesbegin.Anexchangeofentropyisassociatedwiththeexchangeof heatandmatter.Whennoaccumulationofentropywithinasystemoccurs,theentropyflowingoutofthesystemisalways largerthantheentropyflowingin,thedifferencearisingduetotheentropyproducedbyirreversibleprocesseswithinthe system.Asweshallseeinthefollowingchapters,systemsthatexchangeentropywiththeirsurroundingsdonotsimply increasetheentropyofthesurroundingsbutmayundergodramaticspontaneoustransformationsto“self-organization.” Irreversibleprocessesthatproduceentropycreatetheseorganizedstates.Suchself-organizedstatesrangefromconvection patternsinfluidstoorganizedlifestructures.Irreversibleprocessesarethedrivingforcethatcreatesthisorder.
Muchoftheinternalenergyofasubstanceisrandomlydistributedaskineticenergyatthemolecularandsubmolecular levelsandasenergyassociatedwithattractiveorrepulsiveforcesbetweenmolecularandsubmolecularentities,whichcan moveclosertogetherorfurtherapart.Thisenergyissometimesdescribedasbeing“disordered,”asitisnotaccessibleas workatthemacroscopiclevelinthesamewayasisthekineticenergyorgravitationalpotentialenergythatanoverall systempossessesduetoitsvelocityorpositioninagravitationalfield.Althoughsomeenergyformsrepresentthecapacity todowork,itisnotpossibledirectlytoaccesstheminutequantitiesofdisorderedenergypossessedatagiveninstantbythe entitieswithinasubstancesoastoyieldmechanicalshaftworkonamacroscopicscale.Thetermdisorderreferstothelack ofinformationaboutexactlyhowmuchandwhattypeofenergyisassociatedatanymomentwitheachmolecularorsubmolecularentitywithinasystem.
Atthemolecularandsubmolecularlevel,therealsoexists“orderedenergy”associatedwiththeattractiveandrepulsive forcesbetweenentitiesthathavefixedmeanrelativepositions.Partofthisenergyis,inprinciple,accessibleasworkatthe macroscopiclevelunderspecialconditions,whicharebeyondthescopeofthisbook.
Temperatureisthepropertythatreflectswhetherasystemthatisinequilibriumwillexperienceadecreaseorincreasein itsdisorderedenergyifitisbroughtintocontactwithanothersystemthatisinequilibrium.Ifthesystemshavedifferent temperatures,disorderedenergywillberedistributedfromthesystematthehighertemperaturetotheoneatthelower
temperature.Theprocessreducedtheinformationaboutpreciselywherethatenergyresides,asitisnowdispersedoverthe twosystems.
Heattransfertoasystemincreasesitsdisorderedenergy,whileheattransferfromasystemreducesitsdisordered energy.Reversibleheattransferischaracterizedbyboththeamountofenergytransferredtoorfromthesystemand thetemperatureatwhichthisoccurs.Thepropertyentropy,whosechangebetweenstatesisdefinedastheintegralof theratioofthereversibleheattransfertotheabsolutetemperature,isameasureofthestateofdisorderofthesystem.This “stateofdisorder”ischaracterizedbytheamountofdisorderedenergyanditstemperature.Reversibleheattransferfrom onesystemtoanotherrequiresthatbothsystemshavethesametemperatureandtheincreaseinthedisorderofoneisexactly matchedbyadecreaseinthedisorderoftheother.Whenreversibleadiabaticworkisdoneonorbyasystem,itsordered energyincreasesordecreasesbyexactlytheamountoftheworkand,correspondingly,thetemperaturechanges,depending onthesubstancesinvolved.Reversibleworkischaracterizedbytheamountofenergytransferredtoorfromthesystem, irrespectiveofthetemperatureofthesystem.Irreversiblework,suchasstirringworkorfrictionworkbetweensubsystems, involvesachangeinthedisorderofthesystemand,likeheattransfertoasystem,hastheeffectofincreasingtheentropy.
1.3.2Characteristicsofentropy
Wenowintroducethethermodynamicpropertyentropy,whichisameasureoftheamountofmoleculardisorderwithina system.Asystempossessingahighdegreeofmoleculardisorder(suchasahigh-temperaturegas)hashighentropyandvice versa.Thevaluesforspecificentropyarecommonlylistedinthermodynamictablesalongwithotherpropertydata(e.g., specificvolume,specificinternalenergy,specificenthalpy).Afundamentalpropertyrelatedtothesecondlawofthermodynamics,entropyhasthefollowingcharacteristics:
l Theentropyofasystemisameasureofitsinternalmoleculardisorder.
l Asystemcanonlygenerate,notdestroy,entropy.
l Theentropyofasystemcanbeincreasedordecreasedbyenergytransportsacrossthesystemboundary.
Heatandworkaremechanismsofenergytransfer.Theycancausechangesintheinternalenergyinabodyasenergyis transferredtoorfromit.Workisaccomplishedbyaforceactingthroughadistance.Heatrequiresadifferenceintemperatureforitstransfer.Thedefinitionofheatcanbebroadenedtoincludetheenergystoredinahotgasastheaveragekinetic energyofrandomlymovingmolecules.Thisdescriptionhelpsexplainthenaturalflowofheatfromahottoacoolersubstance.Theconceptofrandommotioncanbetranslatedintothenotionoforderanddisorderandleadstoarelationbetween orderanddisorderandprobability.Energytransfersassociatedwithasystemcancausechangesinitsstate.Thenatural directionofthechangeinthestateofasystemisfromastateoflowprobabilitytooneofhigherprobability.Sincedisorderedstatesaremoreprobablethanorderedones,thenaturaldirectionofchangeofstateofasystemisfromorderto disorder.Entropyisameasureoforderthathelpsexplainthenaturaldirectionforenergytransfersandconversions.The entropyofasystemataspecificstatedependsonitsprobability.Thus,thesecondlawofthermodynamicscanbeexpressed morebroadlyintermsofentropyinthefollowingway:
Inanytransferorconversionofenergywithinaclosedsystem,theentropyofthesystemincreases.Theconsequencesof thesecondlawcan,thus,bestatedas(1)thespontaneousornaturaldirectionofenergytransferorconversionistoward increasingentropyor(2)allenergytransfersorconversionsareirreversible.Moreloosely,theFLTimplies“Youcan’twin” becauseenergyisconservedsoyoucannotgetmoreenergyoutofasystemthanyouputin,whiletheSLTstates“Youcan’t breakeven”becauseirreversibilitiesduringrealprocessesdonotallowyoutorecovertheoriginalqualityofenergyyouput intoasystem.
Low-entropyenergysourcesarenormallydesiredandusedtodriveenergyprocessesaslow-entropyenergyis“useful.” Energysourcescanberatedonanentropyorusefulnessscale,withzero-entropyenergyformslikeworkandkineticand gravitationalpotentialenergybeingthemostuseful,andhigh-entropyformslikeheatbeinglessuseful.
ThisbroaderinterpretationoftheSLTsuggeststhatreal“energyconservation”shouldconsidertheconservationofboth energyquantityandquality.Forhighthermodynamicefficiency,energytransfersorconversionsshouldbearranged,all elsebeingequal,sothatthechangeinentropyisminimum.Thisrequiresthatenergysourcesbematchedinentropyto energyend-use.
1.3.3Significanceofentropy
Theentropyofasystematsomestateisameasureoftheprobabilityofitsoccurrence,withstatesoflowprobabilityhaving lowentropyandstatesofhighprobabilityhavinghighentropy.Fromtheprevioussection,itisseenthattheentropyofa
systemmustincreaseinanytransferorconversionofenergybecausethespontaneousdirectionofthechangeofstateofa closedsystemisfromalesstoamoreprobablestate.Consequently,asimplestatementofthesecondlawis“Inanyenergy transferorconversionwithinaclosedsystem,theentropyofthesystemincreases.”
Inopensystems,energyconversionscanoccur,whichcausetheentropyofpartorallofasystemtodecrease.Charginga storagebattery,freezingicecubes,andthegrowthoflivingentitiesareexamples.Ineachoftheseexamples,theorderofthe systemincreasesandtheentropydecreases.Ifthecombinationofthesystemanditssurroundingsisconsidered,however, theoverallneteffectisalwaystoincreasedisorder.Tochargeabattery,wemustprovideacertainminimumamountof externalenergyofacertainqualitytoreformthechemicalcombinationsinthebatteryplates.Inthecaseofthebattery,the inputenergycanbeintheformofelectricity.Someofthislow-entropyelectricalenergyislostasitisconvertedintohighentropyheatinthecurrent-carryingwires.Infreezingice,weincreasetheorderbydecreasingtheentropyofthewaterinthe icecubetraysthroughtheremovalofheat.Theremovedheatistransferredintoasubstancethatisatalowertemperature, increasingitsentropyanddisorder.Thenetchangeinentropyispositive.Foricecubesinafreezer,wealsosupplytothe motorlow-entropyelectricalenergy,whichultimatelyisdegradedtoheat.Inlifeprocesses,highlyorderedstructuresare builtfromsimplerstructuresofvariouschemicals,buttoaccomplishthis,livingentitiestakeinrelativelylow-entropy energy—sunlightandchemicalenergy—andreleasehigh-entropyheatandotherwastes.Theentropyoftheoverallsystem againincreases.
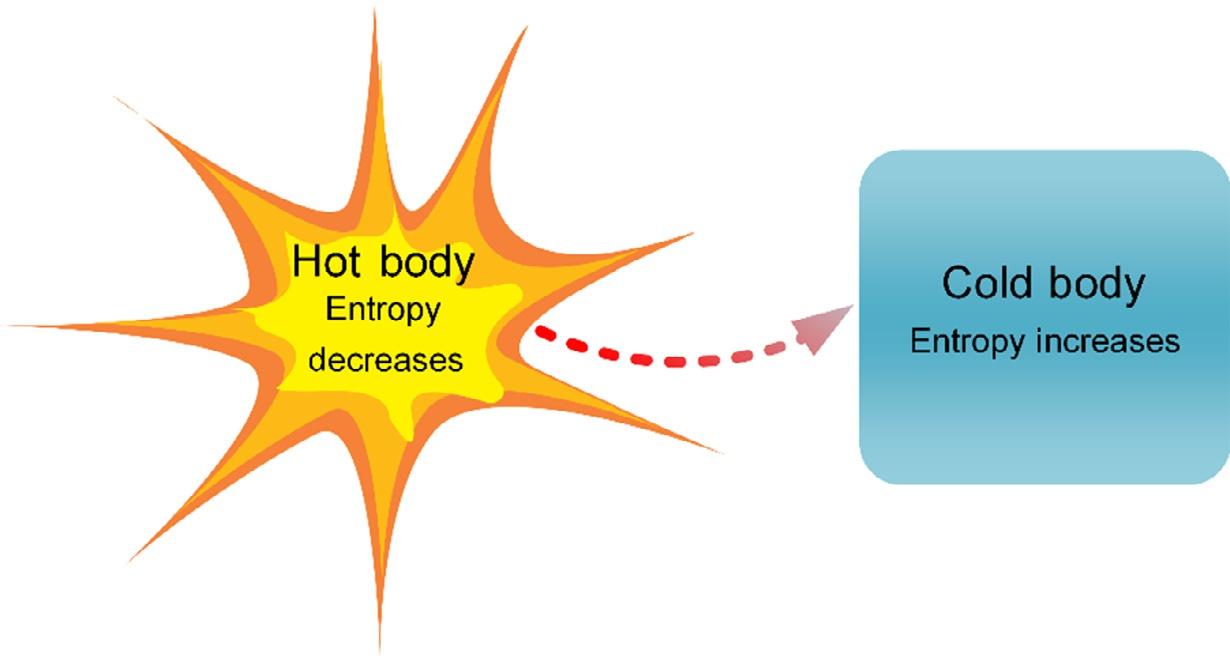
Fig.1.2 illustratesaheattransferprocessfromtheentropypointofview.Duringtheheattransferprocess,thenet entropyincreases,withtheincreaseinentropyofthecoldbodymorethanoffsettingthedecreaseinentropyofthehot body.ThismustoccurtoavoidviolatingtheSLT.Moregenerally,processescanoccuronlyinthedirectionofincreased overallentropyordisorder.Thisimpliesthattheentireuniverseisbecomingmorechaoticeveryday.
AnotherwayofexplainingthisconsequenceoftheSLTistostatethatallenergytransfersorconversionsareirreversible.Absentexternalenergyinputs,suchprocessesoccurspontaneouslyinthedirectionofincreasingentropy.Ina powerplant,forexample,althoughsomeofthelossescanbereduced,theycannotbeentirelyeliminated.Entropymust increase.Usualmechanismsforlow-entropyenergytobeconvertedtohigh-entropyheatareirreversibilitieslikefrictionor electricalresistanceorleakageofhigh-temperature,low-entropyheattoalowertemperatureregion,anditssubsequent degradation.
1.3.4Carnot’scontribution
AnotherstatementoftheSLTwasdevelopedmorethanonehundredyearsago.Oneofthemostbrilliantcontributionswas madebyayoungFrenchphysicist,SadiCarnot,inthe19thcentury.Carnot,studyingearlysteamengines,wasableto abstractfrompumpingpistonsandspinningwheelsthattheconversionofheattomechanicalworkrequiresadifference intemperature.Thepurposeofaheatengine,ashedescribedit,istotakeheatfromahigh-temperaturesource,convert someofittomechanicalwork,andthenrejecttherestoftheheattoalower-temperatureheatreservoir.Carnotdescribed heatenginesusingasimpleanalogytowaterwheels.Theenergyavailableforconversioninawaterwheelisthegravitationalenergycontainedinwaterasitflowsfromsomeheight(behindadamorfromamountainlake)downthroughthe wheel.Theamountofenergyavailabledependsonthedifferenceinheight—the“head”asitiscalled—betweenthesource andthepoolbelowthewheel.Theenergyavailabletoaheatenginedependsonthe“temperaturehead.”Justasahighdam
FIG.1.2 Illustrationofentropyincreaseanddecrease forcoldandhotbodiesduringheattransfer.
canprovidemoreenergythanalowone,alargetemperaturedifferencecanprovidemoreenergytobeconvertedbyaheat enginethancanasmalltemperaturedifference.Intheexampleofaheatengine,thehigh-temperaturereservoiristhehot steamproducedinthepowerplantfurnace.
Forasteamturbineandcondenserassembly,thelow-temperaturereservoirtowhichthedevicerejectstheunconverted energyisthecondensercoolingwater.Theimportanttemperaturedifferenceis,thus,thedifferenceintemperaturebetween theincomingsteam,usuallyabout700°C,andthewaterinthecondenser,whichistypicallybetweenenvironmentalconditions(around0–25°C)andtheboilingtemperatureofwater(100°C).The“temperaturehead”inthisexamplewould, therefore,be600–700°C.Carnot’sexplanationofheatenginesledtothesecondlaw.Onceenergyisintheformofheat, itcannotbeconvertedentirelyintomechanicalenergy.Someheatwillalwaysbeexhaustedorlostaccordingly.
1.3.5Thesecondlawofthermodynamics(SLT)
Althoughaspontaneousprocesscanproceedonlyinadefinitedirection,theFLTgivesnoinformationaboutdirection;it merelystatesthatwhenoneformofenergyisconvertedtoanother,thequantitiesofenergyinvolvedareconserved regardlessofthefeasibilityoftheprocess.Thus,processescanbeenvisionedthatdonotviolatetheFLTbutdoviolate theSLT,e.g.,transferofacertainquantityofheatfromalow-temperaturebodytoahigh-temperaturebody,withoutthe inputofanadequateexternalenergyformlikework.However,suchaprocessisimpossible,emphasizingthattheFLTis itselfinadequateforexplainingenergyprocesses.
TheSLTestablishesthedifferenceinthequalityofdifferentformsofenergyandexplainswhysomeprocessescan spontaneouslyoccurwhileotherscannot.Itisusuallyexpressedasaninequality,statingthatthetotalentropyaftera processisequaltoorgreaterthanthatbefore.Thisequalityonlyholdsforidealorreversibleprocesses.TheSLThasbeen confirmedexperimentally.
Itdefinesthefundamentalquantityentropyasarandomizedenergystateunavailablefordirectconversiontowork.The SLTalsostatesthatallspontaneousprocesses,bothphysicalandchemical,proceedtomaximizeentropy,thatis,tobecome morerandomizedandconvertenergytoalessavailableform.Adirectconsequenceoffundamentalimportanceistheimplicationthatatthermodynamicequilibrium,theentropyofasystemisatarelativemaximum,thatis,nofurtherincreasein disorderispossiblewithoutchangingthethermodynamicstateofthesystembysomeexternalmeans(suchasaddingheat). AcorollaryoftheSLTisthestatementthatthesumoftheentropychangesofasystemandthatofitssurroundingsmust alwaysbepositive.Inotherwords,theuniverse(thesumofallsystemsandsurroundings)isconstrainedtobecomeforever moredisorderedandproceedtowardthermodynamicequilibriumwithsomeabsolutemaximumvalueofentropy.Froma biologicalstandpoint,thisisintuitivelyreasonable,asunlessgradientsinconcentrationandtemperatureareforciblymaintainedbytheconsumptionofenergy,organismsproceedspontaneouslytowardthebiologicalequivalentofequilibriumdeath.
TheSLTisgeneral.However,whenintermolecularforcesarelong-range,asinthecaseofparticlesinteractingthrough gravitation,therearedifficultiesbecauseourclassificationintoextensivevariables(proportionaltosize)andintensive variables(independentofsize)doesnotapply.Thetotalenergyisnolongerproportionaltosize.Fortunately,gravitational forcesareveryweakcomparedwithshort-rangeintermolecularforces.Itisonlyontheastrophysicalscalethatthisproblem becomesimportant.ThegeneralityoftheSLTprovidesapowerfulmeanstounderstandthethermodynamicaspectsofreal systemsthroughtheuseofidealsystems.AclassicexampleisPlanck’sanalysisofradiationinthermodynamicequilibrium withmatter(blackbodyradiation);inwhich,Planckconsideredidealizedsimpleharmonicoscillatorsinteractingwithradiation.Planckconsideredsimpleharmonicoscillatorsnotmerelybecausetheyaregoodapproximationsofmoleculesbut becausethepropertiesofradiationinthermalequilibriumwithmatterareuniversal,regardlessoftheparticularnatureofthe matterwithwhichtheradiationinteracts.Theconclusionsonearrivesatusingidealizedoscillatorsandthelawsofthermodynamicsmustalsobevalidforallotherformsofmatter,nomatterhowcomplex.
WhatmakesthisstatementoftheSLTvaluableasaguidetoformulatingenergypolicyistherelationshipbetween entropyandtheusefulnessofenergy.Energyismostusefultouswhenitisavailabletodoworkorwecangetittoflow fromonesubstancetoanother,e.g.,towarmahouse.Usefulenergy,thus,musthavelowentropysothattheSLTwillallow transferorconversionstooccurspontaneously.
1.3.6Secondlawofthermodynamicsstatements
AlthoughtherearevariousformulationsoftheSLT,twokeystatementsareparticularlywell-known:
l Clausiusstatement.Itisimpossibleforheattomovebyitselffromalowertemperaturereservoirtoahighertemperaturereservoir.Thatis,heattransfercanonlyoccurspontaneouslyinthedirectionoftemperaturedecrease.For example,wecannotconstructarefrigeratorthatoperateswithoutanyworkinput.
l Kelvin-Planckstatement.Itisimpossibleforasystemtoreceiveagivenamountofheatfromahigh-temperature reservoirandprovideanequalamountofworkoutput.Whileasystemconvertingworktoanequivalentenergytransfer asheatispossible,adeviceconvertingheattoanequivalentenergytransferasworkisimpossible.Alternatively,aheat enginecannothaveathermalefficiencyof100%.
1.3.7TheClausiusinequality
TheClausiusinequalityprovidesamathematicalstatementofthesecondlaw,whichisaprecursortosecondlawstatements involvingentropy.GermanphysicistR.J.E.Clausius,oneofthefoundersofthermodynamics,stated
wheretheintegralsymbol Þ showstheintegrationshouldbedonefortheentiresystem.Thecyclicintegralof dQ/T is alwayslessthanorequaltozero.Thesystemundergoesonlyreversibleprocesses(orcycles)ifthecyclicintegralequals zero,andirreversibleprocesses(orcycles)ifitislessthanzero.
Eq. (1.6) canbeexpressedwithoutinequalityas
where Sgen ¼ DStotal ¼ DSsys + DSsurr
Thequantity Sgen istheentropygenerationassociatedwithaprocessorcycle,duetoirreversibilities.Thefollowingare casesforvaluesof Sgen:
l Sgen ¼ 0forareversibleprocess
l Sgen > 0foranirreversibleprocess
l Sgen < 0fornoprocess(i.e.,negativevaluesfor Sgen arenotpossible)
Consequently,onecanwriteforareversibleprocess
Foranirreversibleprocess,itresultsin
duetoentropygenerationwithinthesystemasaresultofinternalirreversibilities.Hence,althoughthechangeinentropyof thesystemanditssurroundingsmayindividuallyincrease,decrease,orremainconstant,thetotalentropychangeorthetotal entropygenerationcannotbelessthanzeroforanyprocess.
1.3.8Usefulrelationships
Itishelpfultolistsomecommonrelationsforaprocessinvolvingapuresubstanceandassumingtheabsenceofelectricity, magnetism,soliddistortioneffects,andsurfacetension.Thefollowingfourequationsapply,subjecttothenoted restrictions:
l dq ¼ du + dw (aFLTstatementapplicabletoanysimplecompressibleclosedsystem)
l dq ¼ du + pdv (aFLTstatementrestrictedtoreversibleprocessesforaclosedsystem)
l Tds ¼ du + dw (acombinedstatementoftheFLTandSLT,with Tds ¼ dq)
l Tds ¼ du + pdv (acombinedstatementoftheFLTandSLTvalidforallprocessesbetweenequilibriumstates)
1.4Exergy
Averyimportantclassofproblemsinengineeringthermodynamicsconcernssystemsorsubstancesthatcanbemodeledas beinginequilibriumorstableequilibriumbutarenotinmutualstableequilibriumwiththesurroundings.Forexample,
withintheearth,therearereservesoffuelsthatarenotinmutualstableequilibriumwiththeatmosphereandthesea.The requirementsofmutualchemicalequilibriumarenotmet.Anysystematatemperatureaboveorbelowthatoftheenvironmentisnotinamutualstableequilibriumwiththeenvironment.Inthiscase,therequirementsofmutualthermalequilibriumarenotmet.Anylackofmutualstableequilibriumbetweenasystemandtheenvironmentcanbeusedtoproduce shaftwork.
WiththeSLT,themaximumworkthatcanbeproducedcanbedetermined.Exergyis,therefore,consideredthemost usefulquantitythatstemsfromtheSLTandhelpsinanalyzingenergyandothersystemsandprocesses.
1.4.1Thequantityexergy
Theexergyofasystemisdefinedasthemaximumshaftworkthatcanbedonebythecompositeofthesystemandaspecifiedreferenceenvironment.Thereferenceenvironmentisassumedtobeinfinite,inequilibrium,andtoencloseallother systems.Typically,theenvironmentisspecifiedbystatingitstemperature,pressure,andchemicalcomposition.Exergyis notsimplyathermodynamicpropertybutisapropertyofbothasystemandthereferenceenvironment.
ThetermexergycomesfromtheGreekwords ex and ergon,meaningfromandwork.Theexergyofasystemcanbe increasedifexergyisinputtoit(e.g.,workisdoneonit).Thefollowingaresometermsfoundintheliteraturethatare equivalenttoornearlyequivalenttoexergy:availableenergy,exergy,utilizableenergy,availableenergy,andavailability.
1.4.2Exergyanalysis
Exergyhasthecharacteristicthatitisconservedonlywhenallprocessesoccurringinasystemandtheenvironmentare reversible.Itisdestroyedwheneveranirreversibleprocessoccurs.Whenanexergyanalysisisperformedonaplantsuchas apowerstation,achemicalprocessingplant,orarefrigerationfacility,thethermodynamicimperfectionscanbequantified asexergydestructions,whichrepresentlossesinenergyqualityorusefulness(e.g.,wastedshaftworkorwastedpotential fortheproductionofshaftwork).Likeenergy,exergycanbetransferredortransportedacrosstheboundaryofasystem.For eachtypeofenergytransferortransport,thereisacorrespondingexergytransferortransport.
Exergyanalysistakesintoaccountthedifferentthermodynamicvaluesofdifferentenergyformsandquantities,e.g., workandheat.Theexergytransferassociatedwithshaftworkisequaltotheshaftwork.Theexergytransferassociatedwith heattransfer,however,dependsonthetemperatureatwhichitoccursinrelationtothetemperatureoftheenvironment.
1.4.3Characteristicsofexergy
Someimportantcharacteristicsofexergyaredescribedandillustrated:
l Asystemincompleteequilibriumwithitsenvironmentdoesnothaveanyexergy.Nodifferenceappearsintemperature, pressure,concentration,etc.sothereisnodrivingforceforanyprocess.
l Theexergyofasystemincreasesthemoreitdeviatesfromtheenvironment.Forinstance,aspecifiedquantityofhot waterhasahigherexergycontentduringthewinterthanonahotsummerday.Ablockoficecarrieslittleexergyin winterwhileitcanhavesignificantexergyinsummer.
l Whenenergylosesitsquality,exergyisdestroyed.Exergyisthepartoftheenergythatisusefuland,therefore,has economicvalueandisworthmanagingcarefully.
l Exergy,bydefinition,dependsnotjustonthestateofasystemorflowbutalsoonthestateoftheenvironment.
l Exergyefficienciesareameasureofapproachtoideality(orreversibility).Thisisnotnecessarilytrueforenergyefficiencies,whichareoftenmisleading.
Exergycangenerallybeconsideredavaluableresource.Therearebothenergyornonenergyresourcesandexergyis observedtobeameasureofvalueforboth:
l Energyformswithhighexergycontentsaretypicallymorevaluedandusefulthanenergyformswithlowexergy.Fossil fuels,forinstance,havehighenergyandenergycontents.Wasteheatatanearenvironmentalcondition,ontheother hand,haslittleexergy,eventhoughitmaycontainmuchenergy,and,thus,isoflimitedvalue.Solarenergy,whichis thermalradiationemittedatthetemperatureofthesun(approximately5800K),containsmuchenergyandexergy.
l Aconcentratedmineraldeposit“contrasts”withtheenvironmentand,thus,hasexergy.Thiscontrastandexergy increasewiththeconcentrationofthemineral.Whenthemineralismined,theexergycontentofthemineralisretained, andifitisenrichedorpurified,theexergycontentincreases.Apoor-qualitymineraldepositcontainslessexergyand
can,accordingly,beutilizedonlythroughalargerinputofexternalexergy.Today,thissubstitutionofexergyoften comesfromexergyformssuchascoalandoil.Whenaconcentratedmineralisdispersed,theexergycontentis decreased.
Anengineerdesigningasystemmakestrade-offsamongcompetingfactors.Theengineerisexpectedtoaimforthehighest reasonabletechnicalefficiencyatthelowestreasonablecostundertheprevailingtechnical,economic,andlegalconditions aswellasaccountingforethical,ecological,andsocialconsequencesandobjectives.Exergyanalysisisatoolthatcan facilitatethiswork.Exergymethodsprovideuniqueinsightsintothetypes,locations,andcausesoflossesandcan,thereby, helpidentifypossibleimprovements.Forinstance,theExergeticLifeCycleAssessmentissuggestedasamethodtobetter meetenvironmentalobjectivesasstudiedindetailin Chapter18
Beforediscussingindetaillinkagesbetweenenergyandexergyandtherelationsbetweenexergyandboththeenvironmentandsustainabledevelopment,somekeypointsthathighlighttheimportanceofexergyanditsutilizationareprovided.Specifically,exergyanalysisisaneffectivemethodandtoolfor
l combiningandapplyingtheconservationofmassandconservationofenergyprinciplestogetherwiththesecondlawof thermodynamicsforthedesignandanalysisofenergysystems.
l improvingtheefficiencyofenergyandotherresourceuse(byidentifyingefficienciesthatalwaysmeasuretheapproach toidealityaswellasthelocations,types,andtruemagnitudesofwastesandlosses).
l revealingwhetherornotandbyhowmuchitispossibletodesignmoreefficientsystemsbyreducingtheinefficiencies inexistingsystems.
l addressingtheimpactontheenvironmentofenergyandotherresourceutilizationandreducingormitigatingthat impact.
l identifyingwhetherasystemcontributestoachievingsustainabledevelopmentorisunsustainable.
1.4.4Thereferenceenvironment
Asthevalueoftheexergyofasystemorflowdependsonthestateofboththesystemorflowandareferenceenvironment,a referenceenvironmentmustbespecifiedbeforetheperformanceofexergyanalysis.
Theenvironmentisoftenmodeledasareferenceenvironmentsimilartotheactualenvironmentinwhichasystemor flowexists.Thisabilitytotailorthereferenceenvironmenttomatchtheactuallocalenvironmentisoftenanadvantageof exergyanalysis.
Some,however,considertheneedtoselectareferenceenvironmentadifficultyofexergyanalysis.Tocircumventthis perceiveddifficulty,somesuggestthata“standardenvironment”bedefinedwithaspecifiedchemicalcomposition,temperature,andpressure.Apossiblechemicalstandardenvironmentforglobalusecould,forinstance,bebasedonastandard atmosphere,astandardsea,andalayeroftheearth’scrust.However,thedefinitionofsuchareferenceenvironmentis usuallyproblematicasthesesystemsarenotinequilibriumwitheachother.
Inaccountingforlocalconditions,areferenceenvironmentcanvaryspatiallyandtemporally.Theneedtoaccountfor spatialdependenceisclearifoneconsidersanairconditioningandheatingsystemoperatinginthedifferentclimatesacross theearth.Inaddition,anaircraftorrocketexperiencesdifferentenvironmentalconditionsasitascendsthroughtheatmosphere.Theimportanceofaccountingfortemporaldependenceishighlightedbyconsideringatechnologylikeaseasonal thermalenergystorageunit,inwhichheatingorcoolingcapacitycanbestoredfromoneseason,whenitisavailableinthe environment,toanotherseason,whenitisunavailablebutindemand.
1.4.5Exergyvsenergy
Energyanalysisisthetraditionalmethodofassessingthewayenergyisusedinanoperationinvolvingthephysicalor chemicalprocessingofmaterialsandthetransferand/orconversionofenergy.Thisusuallyentailsperformingenergybalances,whicharebasedontheFLT,andevaluatingenergyefficiencies.Thisbalanceisemployedtodetermineandreduce wasteexergyemissionslikeheatlossesand,sometimes,toenhancewasteandheatrecovery.
However,anenergybalanceprovidesnoinformationonthedegradationofenergyorresourcesduringaprocessand doesnotquantifytheusefulnessorqualityofthevariousenergyandmaterialstreamsflowingthroughasystemandexiting asproductsandwastes.
TheexergymethodofanalysisovercomesthelimitationsoftheFLT.TheconceptofexergyisbasedonboththeFLT andtheSLT.Exergyanalysisclearlyindicatesthelocationsofenergydegradationinaprocessandcan,therefore,leadto improvedoperationortechnology.Exergyanalysiscanalsoquantifythequalityofheatinawastestream.Themainaimof
TABLE1.1 Comparisonofenergyandexergy. EnergyExergy
dependentonpropertiesofonlyamatterorenergyflowand independentofenvironmentproperties
hasvaluesdifferentfromzerowheninequilibriumwiththe environment(includingbeingequaltomc2 inaccordance withEinstein’sequation)
conservedforallprocesses,basedontheFLT
canbeneitherdestroyednorproduced
appearsinmanyforms(e.g.,kineticenergy,potentialenergy, work,andheat)andismeasuredinthatform
ameasureofquantityonly
dependentonpropertiesofbothamatterorenergyflowandthe environment
equaltozerowheninthedeadstatebyvirtueofbeingincompleteequilibriumwiththeenvironment
conservedforreversibleprocessesandnotconservedforreal processes(whereitispartlyorcompletelydestroyedduetoirreversibilities),basedontheSLT
canbeneitherdestroyednorproducedinareversibleprocess, butisalwaysdestroyed(consumed)inanirreversibleprocess
appearsinmanyforms(e.g.,kineticexergy,potentialexergy, work,andthermalexergy)andismeasuredbasedonworkor abilitytoproducework
ameasureofquantityandquality
exergyanalysisistoidentifymeaningful(exergy)efficienciesandthecausesandtruemagnitudesofexergylosses. Table1.1 presentsageneralcomparisonofenergyandexergy.
Itisimportanttodistinguishbetweenexergyandenergyinordertoavoidconfusionwithtraditionalenergy-based methodsofthermalsystemanalysisanddesign.Energyflowsintoandoutofasystemwithmassflows,heattransfers, andworkinteractions(e.g.,workassociatedwithshaftsandpistonrods).Energyisconserved,inlinewiththeFLT.Exergy, althoughsimilarinsomerespects,isdifferent.Itlooselyrepresentsaquantitativemeasureoftheusefulnessorqualityof energyormaterialsubstance.Morerigorously,exergyisameasureoftheabilitytodowork(ortheworkpotential)ofthe greatvarietyofstreams(mass,heat,andwork)thatflowthroughasystem.Akeyattributeofexergyisthatitmakesit possibletocompareoncommonbasisinteractions(inputsandoutputs)thatarequitedifferentinaphysicalsense.Another benefitisthatbyaccountingforalltheexergystreamsofthesystem,itispossibletodeterminetheextenttowhichthe systemdestroysexergy.Thedestroyedexergyisproportionaltothegeneratedentropy.Exergyisalwaysdestroyedinreal processes,partiallyortotally,inlinewiththeSLT.Thedestroyedexergy,orthegeneratedentropy,isresponsibleforthe less-than-idealefficienciesofsystemsorprocesses.
1.4.6Exergyefficiencies
The exergyefficiency isanefficiencybasedontheSLT.Inthissection,wedescribetheuseofexergyefficienciesin assessingtheutilizationefficiencyofenergyandotherresources.
Engineersmakefrequentuseofefficienciestogaugetheperformanceofdevicesandprocesses.Manyoftheseexpressionsarebasedonenergyandare,thus,FLT-based.Alsousefularemeasuresofperformancethattakeintoaccountlimitationsimposedbythesecondlaw.EfficienciesofthistypeareSLT-basedefficiencies.
ToillustratetheideaofaperformanceparameterbasedontheSLTandtocontrastitwithananalogousenergy-based efficiency,consideracontrolvolumeatsteady-stateforwhichenergyandexergybalancescanbewritten,respectively,as
Energyin ðÞ¼ Energyoutputinproduct ðÞ + Energyemittedwithwaste ðÞ (1.10)
Exergyin ðÞ¼ Exergyoutputinproduct ðÞ
Intheseequations,thetermproductmightrefertoshaftwork,electricity,acertainheattransfer,oneormoreparticularexit streams,orsomecombinationofthese.Thelattertwotermsintheexergybalance(Eq. 1.11)combinetoconstitutethe exergylosses.Lossesincludesuchemissionstothesurroundingsaswasteheatandstackgases.Theexergydestruction termintheexergybalanceiscausedbyinternalirreversibilities.
Fromenergyorexergyviewpoints,agaugeofhoweffectivelytheinputisconvertedtotheproductistheratioofproduct toinput.Thatis,energyefficiency canbewrittenas
andtheexergyefficiency c as
Theexergyefficiency c frequentlygivesafinerunderstandingofperformancethanenergyefficiency .Inevaluating ,the sameweightisassignedtoenergywhetheritisshaftworkorastreamoflow-temperaturefluid.Also,theenergyefficiency centersattentiononreducingenergyemissionstoimproveefficiency.Theparameter c weightsenergyflowsbyaccounting foreachintermsofexergy.Itstressesthatbothwasteemissions(orexternalirreversibilities)andinternalirreversibilities needtobedealtwithtoimproveperformance.Inmanycases,itistheirreversibilitiesthataremoresignificantandmore difficulttoaddress.
Efficiencyexpressionseachdefineaclassofefficienciesbecausejudgmenthastobemadeaboutwhatistheproduct, whatiscountedasaloss,andwhatistheinput.Differentdecisionsabouttheseleadtodifferentefficiencyexpressions withintheclass.
OtherSLT-basedefficiencyexpressionsalsoappearintheliterature.Oneoftheseisevaluatedastheratioofthesumof theexergyexitingtothesumoftheexergyentering.Anotherclassofsecondlawefficienciesiscomposedoftask efficiencies.
1.4.7Solarexergyandtheearth
Mostenergyinthethintoplayeroftheearth’ssurface,wherelifeisfound,derivesfromthesun.
Sunlight,richinexergy,isincidentontheearth.Muchisreflectedbytheatmosphere,whilesomeisabsorbedbyatmosphericconstituentsorreachesthesurfaceoftheearth,whereitisabsorbed.Mostoftheabsorbedsolarradiationisconvertedtothermalenergy,whichisemittedatthetemperatureoftheearth’ssurfaceandatmosphereandleavestheearthas thermalradiation(heat)withnoexergyrelativetotheearth.Thus,whilealmostalltheenergyinputtotheearthwithsolar energyisre-emittedtospaceasthermalenergy,theexergyassociatedwithsolarradiationisdeliveredtotheearth.
Thenetexergyabsorbedbytheearthisgraduallydestroyed,butduringthisdestruction,itmanagestodrivetheearth’s waterandwindsystemsandtosupportlife.Greenplantsabsorbexergyfromthesunlightandconvertitviaphotosynthesis intochemicalexergy.Thechemicalexergythenpassesthroughdifferentfoodchainsinecosystems,frommicro-organisms topeople.Thereexistsnomaterialwaste.
1.5Illustrativeexamples
Weprovidefourillustrativeexamplestohighlighttheconceptsdiscussedinthischapterandtheirimportanceandtodemonstratetheirapplicationinengineeringsettings.Theexamplescoverentropygenerationduringheattransferprocesses, entropygenerationinawallduetoheattransfer,andsensibleenergystorage.Thefollowingthreeexamplesareadapted fromexamplesofCengelandBoles [1].
1.5.1Illustrativeexample1
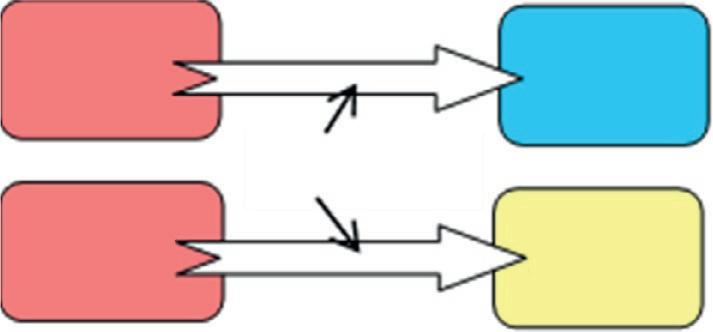
Aheatsourceat800Kloses2000kJofheattoasinkat(a)500Kand(b)750K.Determinewhichheattransferprocessis moreirreversible.
Solution:Asketchofthereservoirsisshownin Fig.1.3.Bothcasesinvolveheattransferthroughafinitetemperaturedifferenceandare,therefore,irreversible.Themagnitudeoftheirreversibilityassociatedwitheachprocesscanbedetermined bycalculatingthetotalentropychangeforeachcase.Thetotalentropychangeforaheattransferprocessinvolvingtwo reservoirs(asourceandasink)isthesumoftheentropychangesofeachreservoir,asthetworeservoirsformanadiabatic system.
Ordothey?Theproblemstatementgivestheimpressionthatthetworeservoirsareindirectcontactduringtheheat transferprocess.Butthiscannotbethecaseasthetemperatureatapointcanhaveonlyonevalue;thus,itcannotbe800Kon onesideofthepointofcontactand500Kontheotherside.Inotherwords,thetemperaturefunctioncannothaveadiscontinuity.Therefore,itisreasonabletoassumethatthetworeservoirsareseparatedbyapartitionthroughwhichthe
Source
Source
K
2000 kJ
FIG.1.3 Schematicfortheexampleofentropygenerationduringheattransferforaheatsinkat(A)500Kand(B)750K.
temperaturedropsfrom800Kononesideto500K(or750K)ontheother.Therefore,theentropychangeofthepartition shouldalsobeconsideredwhenevaluatingthetotalentropychangeforthisprocess.However,consideringthatentropyisa propertyandthevaluesofpropertiesdependonthestateofasystem,wecanarguethattheentropychangeofthepartitionis zeroasthepartitionappearstohaveundergonea steady processand,thus,hasexperiencednochangeinitspropertiesatany point.Webasethisargumentonthefactthatthetemperatureonbothsidesofthepartitionand,thus,throughoutremain constantduringthisprocess.Therefore,wearejustifiedtoassumethat DSpartition ¼ 0,astheentropy(aswellastheenergy) contentofthepartitionremainsconstantduringtheprocess.
Aseachreservoirundergoesaninternallyreversible,isothermalprocess,theentropychangeforeachreservoircanbe determinedfrom DS ¼ Q/T,where T istheconstantabsolutetemperatureofthesystemand Q istheheattransferforthe internallyreversibleprocess.
(a) Fortheheattransferprocesstoasinkat500K:
DSsink ¼ Qsink/Tsink ¼ 2000kJ/500K ¼ 4.0kJ/Kand Sgen ¼ DStotal ¼
Therefore,1.5kJ/Kofentropyisgeneratedduringthisprocess.Notingthatbothreservoirsundergointernallyreversible processes,theentireentropygenerationoccursinthepartition.
(b) Repeatingthecalculationsinpart(a)forasinktemperatureof750K,weobtain
DSsource ¼ 2.5kJ/K DSsink ¼ 2 7kJ
Thetotalentropychangefortheprocessinpart(b)issmaller;therefore,itislessirreversible.Thisisexpectedastheprocess in(b)involvesasmallertemperaturedifferenceand,thus,smallerirreversibility.
Discussion:TheirreversibilitiesassociatedwithbothprocessescanbeeliminatedbyoperatingaCarnotheatengine betweenthesourceandthesink.Inthiscase,itcanbeshownthat
1.5.2Illustrativeexample2
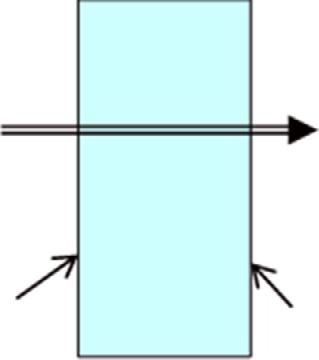
Considersteadyheattransferthrougha5m 6mbrickwallofahouseofthickness30cm.Onadaywhenthetemperature outdoorsis0°C,thehouseismaintainedat27°C.Thetemperaturesoftheinnerandoutersurfacesofthebrickwallare measuredtobe20°Cand5°C,respectively,andtherateofheattransferthroughthewallis1035W.Determinetherateof entropygenerationinthewallandtherateoftotalentropygenerationassociatedwiththisheattransferprocess.
Solution:Wefirsttakethe wall asthesystem(Fig.1.4).Thisisa closedsystem asnomasscrossesthesystemboundary duringtheprocess.Wenotethattheentropychangeofthewalliszeroduringthisprocess,asthestateand,thus,theentropy
FIG.1.4 Schematicfortheexampleonentropygenerationinawallduetoheattransfer.
ofthewalldonotchangeanywhereinthewall.Heatandentropyenterfromonesideofthewallandleavefromthe otherside.
Assumptions: (i)Theprocessissteady;thus,therateofheattransferthroughthewallisconstant.(ii)Heattransferthrough thewallisone-dimensional.
Analysis:Therateformoftheentropybalanceforthewallsimplifiesto
Therefore,therateofentropygenerationinthewallis0.191W/K.
Notethatentropytransferbyheatatanylocationis Q/T atthatlocation,andthedirectionofentropytransferisthesame asthedirectionofheattransfer.
Todeterminetherateoftotalentropygenerationduringthisheattransferprocess,weextendthesystemtoincludethe regionsonbothsidesofthewallthatexperienceatemperaturechange.Then,onesideofthesystemboundarybecomes roomtemperaturewhiletheothersidebecomesthetemperatureoftheoutdoors.Theentropybalanceforthis extended system (systemanditsimmediatesurroundings)willbethesameasthatgivenabove,exceptthetwoboundarytemperatures willbe300Kand273Kinsteadof293Kand278K,respectively.Then,therateoftotalentropygenerationbecomes 1035W=300K ðÞ 1035W=273K ðÞ + S gen,total ¼ 0 ) S gen,total ¼ 0 341W=K
Discussion:Notethattheentropychangeofthisextendedsystemisalsozeroasthestateofairdoesnotchangeatanypoint duringtheprocess.Thedifferencebetweenthetwoentropygenerationratesis0.150W/Kandrepresentstheentropygenerationrateintheairlayersonbothsidesofthewall.Theentropygenerationinthiscaseisentirelyduetoirreversibleheat transferacrossafinitetemperaturedifference.
1.5.3Illustrativeexample3
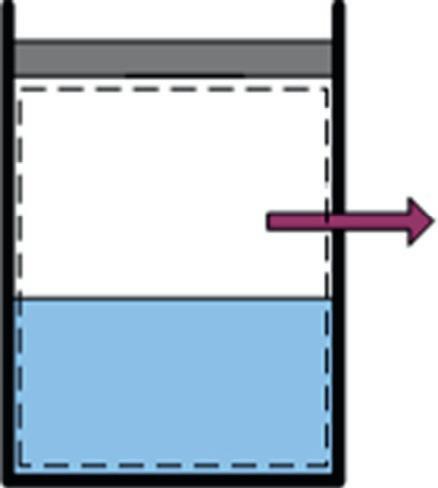
Considerafrictionlesspiston-cylinderdevicecontainingasaturatedliquid-vapormixtureofwaterat100°C.Duringa constant-pressureprocess,600kJofheatistransferredtothesurroundingairat25°C.Asaresult,partofthewatervapor containedinthecylindercondenses.Determine(a)theentropychangeofthewaterand(b)thetotalentropygeneration duringthisheattransferprocess.
Solution:First,wetakethe waterinthecylinder asthesystem(Fig.1.5).Thisisa closedsystem asnomasscrossesthe systemboundaryduringtheprocess.Notethatthepressureand,thus,thetemperatureofwaterinthecylinderremainconstantduringtheprocess.Also,theentropyofthesystemdecreasesduringtheprocessbecauseofheatloss.
Assumptions: (i)Therearenoirreversibilitiesinvolvedwithinthesystemboundaries;thus,theprocessisinternally reversible.(ii)Thewatertemperatureremainsconstantat100°Ceverywhere,includingattheboundaries.
Analysis:(a)Notingthatwaterundergoesaninternallyreversibleisothermalprocess,itsentropychangecanbedetermined from
Schematicfortheexampleofentropygenerationassociatedwithheattransferfromapiston-cylinderdevice.
DSsystem ¼ Q=Tsystem ¼
(b)Todeterminethetotalentropygenerationduringthisprocess,weconsiderthe extendedsystem,whichincludeswater, thepiston-cylinderdevice,andtheregionimmediatelyoutsidethesystemthatexperiencesatemperaturechangesothatthe entireboundaryoftheextendedsystemisatthesurroundingtemperatureof25°C.Theentropybalanceforthis extended system (systemanditsimmediatesurroundings)yields
or
Theentropygenerationinthiscaseisentirelyduetoirreversibleheattransferthroughafinitetemperaturedifference. Notethattheentropychangeofthisextendedsystemisequivalenttotheentropychangeofthewaterasthepistoncylinderdeviceandtheimmediatesurroundingsdonotexperienceanychangeofstateatanypointand,thus,anychange inanyproperty,includingentropy.
Discussion:Forillustration,considerthereverseprocess(i.e.,thetransferof600kJofheatfromthesurroundingairat25°C tosaturatedwaterat100°C)andseeiftheincreaseofentropyprinciplecandetecttheimpossibilityofthisprocess.This time,heattransferistothewater(heatisgainedinsteadoflost);thus,theentropychangeofwateris1.61kJ/K.Also,the entropytransferattheboundaryoftheextendedsystemhasthesamemagnitudebutoppositedirection.Thisprocessresults inanentropygenerationof 0.4kJ/K.Anegativeentropygenerationindicatesthatthereverseprocessis impossible.
Tocompletethediscussion,considerthecasewherethesurroundingairtemperatureisadifferentialamountbelow100°C (say99.999…9°C)insteadofbeing25°C.Thistime,heattransferfromthesaturatedwatertothesurroundingairoccurs throughadifferentialtemperaturedifferencerenderingthisprocess reversible.Itcanbeshownthat Sgen ¼ 0forthisprocess. Rememberthatreversibleprocessesareidealized,andtheycanbeapproachedbutneverreachedinreality.
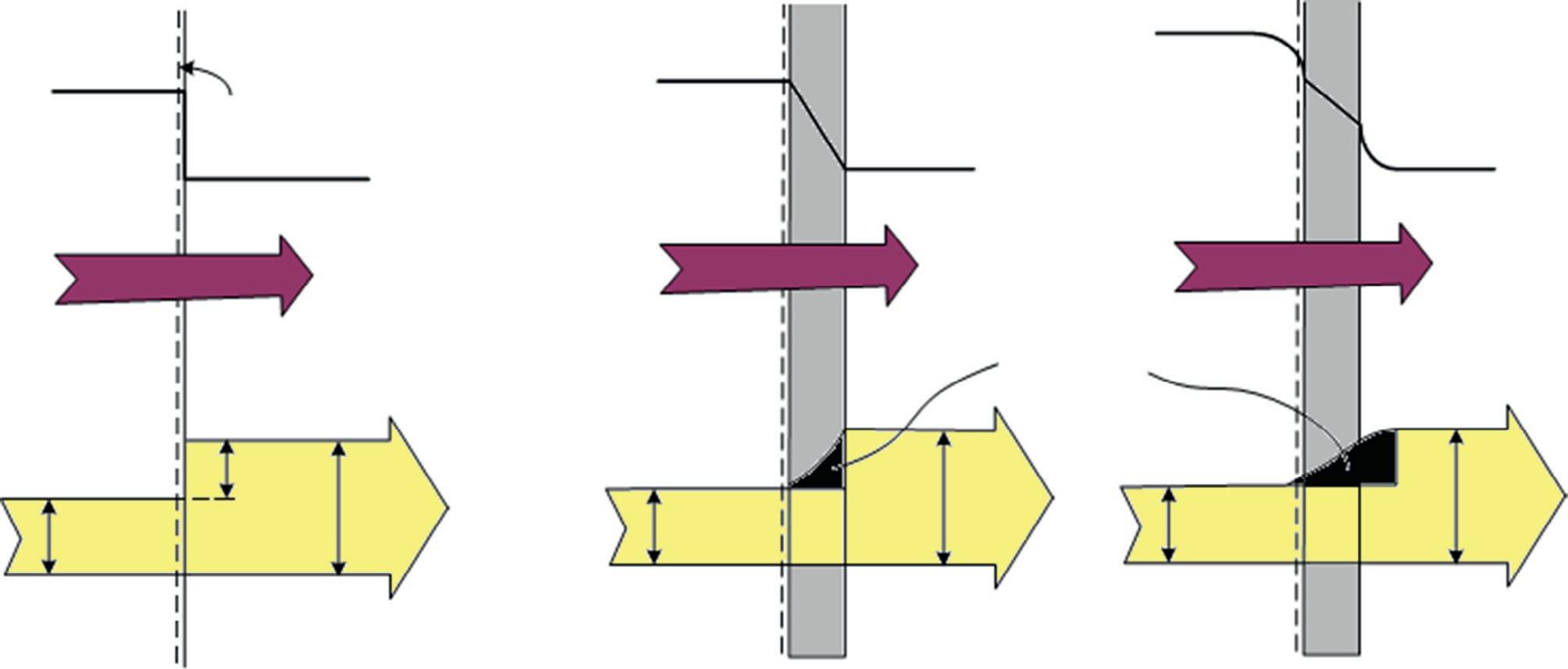
FurtherDiscussiononEntropyGenerationAssociatedwithHeatTransfer:
Intheexampleabove,itisdeterminedthat0.4kJ/Kofentropyisgeneratedduringtheheattransferprocess,butitisnot clearexactlywheretheentropygenerationtakesplace,andhow.Topinpointthelocationofentropygeneration,weneedto bemorepreciseaboutthedescriptionofthesystem,itssurroundings,andthesystemboundary.
Intheexample,weassumedboththesystemandthesurroundingairtobeisothermalat100°Cand25°C,respectively. Thisassumptionisreasonableifbothfluidsarewell-mixed.Theinnersurfaceofthewallmustalsobeat100°Cwhilethe outersurfaceisat25°C,astwobodiesinphysicalcontactmusthavethesametemperatureatthepointofcontact.Consideringthatentropytransferwithheattransfer Q throughasurfaceatconstanttemperature T is Q/T (asshownin Fig.1.6A), theentropytransferfromthewatertothewallis Q/Tsys ¼ 1.61kJ/K.Likewise,theentropytransferfromtheoutersurfaceof thewallintothesurroundingairis Q/Tsurr ¼ 2.01kJ/K.Clearly,entropyintheamountof(2.01 1.61) ¼ 0.4kJ/Kisgeneratedinthewall,asillustratedin Fig.1.6B.
Identifyingthelocationofentropygenerationenablesustodeterminewhetheraprocessisinternallyreversible.A processisinternallyreversibleifnoentropyisgeneratedwithinthesystemboundaries.Therefore,theheattransferprocess discussedintheexampleaboveisinternallyreversibleiftheinnersurfaceofthewallistakenasthesystemboundary;thus,
T =100°C Tsurr=25°C
FIG.1.5
of
(A)(B)(C)
FIG.1.6 Schematicrepresentationofentropygenerationduringaheattransferprocessthroughafinitetemperaturedifference.
thesystemexcludesthecontainerwall.Ifthesystemboundaryistakentobetheoutersurfaceofthecontainerwall,thenthe processisnolongerinternallyreversibleasthewall,whichisthesiteofentropygeneration,isnowapartofthesystem.
Forthinwalls,itistemptingtoignorethemassofthewallandregardthewallastheboundarybetweenthesystemand thesurroundings.Thisseeminglyharmlesschoicehidesthesiteofentropygenerationandisasourceofconfusion.The temperature,inthiscase,dropssuddenlyfrom Tsys to Tsurr attheboundarysurface,andconfusionarisesastowhichtemperaturetouseintherelation Q/T forentropytransferattheboundary.
Notethatifthesystemandthesurroundingairarenotisothermalasaresultofinsufficientmixing,thenpartofthe entropygenerationoccursinboththesystemandthesurroundingairinthevicinityofthewall,asshownin Fig.1.6C.
1.5.4Illustrativeexample4
Considertwosensiblethermalenergystoragesystems,XandY,inanenvironmentatatemperatureof25°C.Eachstorage receivesaquantityofheatfromastreamof500kgofwater,whichiscooledfrom80°Cto30°C.Therecoveryoperationand thestoragedurationforthetwostoragesdiffer.Determine(a)theenergyrecovery,loss,andefficiencyforeachstorageand (b)thecorrespondingexergyparameters.Comparethestorages.
Solution:Assumption:Thethermalstoragesystemisassumedtobecomprisedofthreeprocesses:charging,storing,and discharging(Fig.1.7).Thissimplemodelisusedinordertodistinguishenergyandexergyconceptsclearlyandhighlight theimportanceofexergyasatoolforpracticalthermodynamicsystems.
(a) BothsensiblethermalstoragesystemsXandYreceiveaquantityofheatfromastreamof500kgofwater,whichis cooledfrom80°Cto30°C.Therefore,theheatinputtoeachstorageduringthechargingperiodis
i ¼ mi cp DT ¼ 500 4:186 80 30 ðÞ¼
ForsystemX:
After1day,94,185kJofheatisrecoveredduringthedischargingperiodfromstoragesystemXbyastreamof4500kg ofwaterbeingheatedfrom30°Cto35°C.Thatis,
o ¼ mo cp DT ¼ 4500 4:186 35 30 ðÞ¼ 94,185kJ
Therefore,theenergyefficiencyforsensiblethermalstorageXbecomes