EngineeringReliabilityand RISKASSESSMENT
Editedby HARISHGARG
SchoolofMathematics,ThaparInstituteof EngineeringandTechnology,DeemedtobeUniversity, Patiala,Punjab,India
MANGEYRAM
GraphicEraDeemedtobeUniversity,Dehradun, Uttarakhand,India;PetertheGreatSt.Petersburg PolytechnicUniversity,SaintPetersburg,Russia
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright © 2023ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronic ormechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem, withoutpermissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangementswithorganizationssuchas theCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions .
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthis fieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluating andusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuch informationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,including partiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assume anyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability, negligenceorotherwise,orfromanyuseoroperationofanymethods,products,instructions,orideas containedinthematerialherein.
ISBN:978-0-323-91943-2
ForinformationonallElsevierpublicationsvisitour websiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: BrianGuerin
EditorialProjectManager: ClodaghHolland-Borosh
ProductionProjectManager: KameshR
CoverDesigner: MarkRogers
TypesetbyTNQTechnologies
Contributors
DanielO.Aikhuele
FacultyofEngineeringandBuiltEnvironment,UniversityofJohannesburg,Johannesburg,South Africa
JoydipDhar
ABV-IndianInstituteofInformationTechnologyandManagement,Gwalior,MadhyaPradesh, India
LongDing
StateKeyLaboratoryofFireScience,UniversityofScienceandTechnologyofChina,Hefei, Anhui,China
AhmedEl-Awady
DepartmentofEnvironmentalEngineeringSciences,FacultyofGraduateStudiesand EnvironmentalResearch,AinShamsUniversity,Cairo,Egypt
AmenehFarahani
DepartmentofIndustrialEngineering,OojInstituteofHigherEducation,Qazvin,Iran
ZawarHussain
DepartmentofStatistics,FacultyofComputing,TheIslamiaUniversityofBahawalpur, Bahawalpur,Pakistan
DesmondE.Ighravwe
FacultyofEngineeringandBuiltEnvironment,UniversityofJohannesburg,Johannesburg,South Africa
JieJi
StateKeyLaboratoryofFireScience,UniversityofScienceandTechnologyofChina,Hefei, Anhui,China
Komal DepartmentofMathematics,SchoolofPhysicalSciences,DoonUniversity,Dehradun, Uttarakhand,India
GirishKumar
DelhiTechnologicalUniversity,Delhi,India
MohitKumar DepartmentofBasicSciences,InstituteofInfrastructureTechnologyResearchandManagement, Ahmedabad,India
AjayKumar
ABV-IndianInstituteofInformationTechnologyandManagement,Gwalior,MadhyaPradesh, India
M.K.Loganathan
KazirangaUniversity,Jorhat,Assam,India
ReetuMalhotra
ChitkaraUniversityInstituteofEngineeringandTechnology,ChitkaraUniversity,Punjab,India
A.J.NakhalAkel
DepartmentofMechanicalandAerospaceEngineering,SapienzaUniversity,Rome,Italy
RamNiwas
DepartmentofStatistics,GoswamiGaneshDuttaSanatanDharmaCollege,Chandigarh,India
N.Paltrinieri
DepartmentofMechanicalandIndustrialEngineering,NorwegianUniversityofScienceand Technology,Trondheim,Norway
R.Patriarca
DepartmentofMechanicalandAerospaceEngineering,SapienzaUniversity,Rome,Italy
KumaraswamyPonnambalam
DepartmentofSystemsDesignEngineering,FacultyofEngineering,UniversityofWaterloo, Waterloo,ON,Canada
VishalPradhan
ABV-IndianInstituteofInformationTechnologyandManagement,Gwalior,MadhyaPradesh, India
AnumSha fiq
SchoolofMathematicsandStatistics,NanjingUniversityofInformationScienceand Technology,Nanjing,China
AhmadShoja
DepartmentofMathematicsandStatistics,RoudehenBranch,IslamicAzadUniversity, Roudehen,Iran
TabassumNazSindhu
DepartmentofStatistics,Quaid-i-AzamUniversity,Islamabad,Pakistan
ZhaojunStevenLi
DepartmentofIndustrialEngineeringandEngineeringManagement,Spring fi eld,MA,United States
HamidTohidi
DepartmentofIndustrialEngineering,SouthTehranBranch,IslamicAzadUniversity,Tehran, Iran
HuiminWang
SchoolofMechanicalandElectricalEngineering,UniversityofElectronicScienceand TechnologyofChina,Chengdu,China
OmYadav
NorthDakotaUniversity,Fargo,UnitedStates
Bayesiannetworksforfailureanalysis ofcomplexsystemsusingdifferent datasources
AhmedEl-Awady1 andKumaraswamyPonnambalam2
1DepartmentofEnvironmentalEngineeringSciences,FacultyofGraduateStudiesandEnvironmentalResearch,AinShams University,Cairo,Egypt; 2DepartmentofSystemsDesignEngineering,FacultyofEngineering,UniversityofWaterloo, Waterloo,ON,Canada
1.Introduction
Failureanalysisisanimportantandchallengingaspectofthestudyofcomplexsystems.A systemisdefinedtobeconsistingofcomponents,subsystems,inputs,andoutputswithin systemboundaries.Theinputsprovidephysicalresourcesandinformationtothesubsystems,whichareinteractingamongeachothertoproducesomeoutputs.Allinteractions areassumedtotakeplacewithinsystemboundaries.Acomplexsystemcanbedefinedasa systemstructurethatiscomposedofusuallyalargenumberofcomponentsthathave complexinteractions,[1].Anyfailureinperformingtherequiredinteractionsamongsystemcomponents,oranyfailureingettingtheexpectedoutput/result,isconsideredtobe contributingtosystemfailure[2].Thus,analysisofasystemwithitscomponentsisa crucialstepindeterminingthedifficultiesandcomplexitiesthatthesystemwillexperienceatanystage.However,intherealworld,performanceofbothinputsandsubsystems isaffectedbyprobabilisticuncertainty,andhence,afailuremaycomewithanassociated probability.Themaingoalofthischapteristoevaluatetheprobabilityoffailureofcomplexsystems,while findingthefailurecausesusingBayesianNetworks(BNs).Forany givensystemwithitsinputsandsubsystems,probabilisticfailureanalysisdependson findingtheprobabilityofnotgettingtherequiredorestimatedoutputofthatsystem. TherequiredoutputoftheBNanalysismaybetheeffectthatisproducedfromcertain causes(i.e.,predictionreasoning),orthedeterminationofthecauseresponsiblefor certainresultsandeffects(i.e.,diagnosticreasoning),bothinprobabilisticmeasures. Thus,determiningthecause effectrelationisanimportant firststepintheprobabilistic failureanalysis,whichallowsforbetterunderstandingtoenhancethesystemreliability andtakedecisionsformitigatingthenegativeeffectsorbetterenhancingthecauses.In thischapter,thegraphrepresentationofsystemsisconductedusingBNs,whichallow forrepresentingmarginal,conditional,andjointprobabilitymeasuresaffectingsystem components;BNanalysisprovidestheabilitytodecomposealargesystemintoamanageablenumberofsubsystemsfortheirownanalysisandintheendaggregatingtheseresults
toprovidethewholesystemresults.RepresentingsystemsofengineeringapplicationsusingBNsisaffectedbymultiplefactorsthataffecttheprobabilisticquantificationprocess. Theaimofthischapteristorevealthedifferentapproachesthatfacilitatetheprobabilistic quantificationofBNsandhence,facilitatepredictionofsystemfailures.
2.Risk,reliability,anduncertainty
Therearemanydefinitionsofrisk.Twocommondefinitionsofriskare:(i)probabilityof failureand(ii)theproductoftheprobabilityofanundesiredoutcome(failure)andthe consequencesofthatoutcome[3 12].ThedevelopmentofriskestimatesorthedeterminationofrisksinagivencontextiscalledRiskAnalysis,whileRiskAssessmentisthe processofevaluatingtherisksanddeterminingthebestcourseofaction.Uncertaintyof outcomesisacommonconceptinalldefinitionsofrisk.Uncertaintymaybedefinedas thestateofhavinglimitedknowledgesurroundingexistingeventsandfutureoutcomes, orimperfectabilitytoassignacharacterstatetoaprocessthatformsasourceofdoubt,[3]. Thus,uncertaintyisanintrinsicpropertyofriskandispresentinallaspectsofriskmanagementincludingriskanalysisandriskassessment[4].Generally,riskanalysisisasystematictoolthatfacilitatestheidentificationoftheweakelementsofacomplexsystemand thehazardsthatmainlycontributetotherisk.InRef.[13],hazardanalysisisdescribedas “investigatinganaccidentbeforeitoccurs,” withtheaimofidentifyingpotentialcauses ofaccidentsthatcanleadtolosses.
AccordingtoRefs.[11,12,14,and 15],availabilityistheabilityofacomponentor systemtofunctionataspecifiedintervaloftime.Thisiscloselyrelatedtowhatiscalled “Reliability,” whichdescribestheabilityofasystemorcomponenttofunctionunder statedconditionsforaspecifiedperiodoftime.Reliabilityengineeringisasubdiscipline ofsystemsengineeringthatemphasizesdependabilityinthelifecyclemanagementofa product.Inreliabilityengineeringprograms wherereliabilityplaysakeyroleinthe costeffectivenessofsystems testability,maintainability,andmaintenancearepartsof theseprograms.Inreliabilityengineering,estimation,prevention,andmanagementof highlevelsoflifetimeengineeringuncertaintyandrisksoffailurearecommonareasto bedealtwith.Theoretically,reliabilityisdefinedastheprobabilityofsuccess(Probability ofsuccess ¼ 1-Probabilityoffailure).Sometimes,probabilisticstabilityanalysisisreferred toas “reliabilityanalysis.” Duringfailureprobabilityestimation,reliabilityanalysiscannot beusedsolely,andtheresultsofsuchanalysismustbemoderatedusingengineeringjudgmentandappropriatemodelsasusefultoolsinestimatingconditionalprobabilities.
Insomeliterature,accordingtoRefs.[6,12,16,and 17],uncertainty whichisa commonconceptforexpressinginaccuracies meansthatanumberofdifferentvalues canexistforaquantity,whileriskmeansthepossibilityoflossasaresultofuncertainties. Accordingly,anyuncertainvariable,whichcantakevariousvaluesoverarange,should beprovidedwithanuncertaintyanalysisthatisusedtoassessoutputuncertaintyandto
identifythemostefficientwaystoreducethatuncertaintyaccordingtothecontributing variables.Hence,intermsofstatisticalconcepts,uncertaintycanbethoughtaboutasa statisticalvariableandcanbecalculatedusingwell-verifiedstatisticalprocedures.Ina broadappliedstatisticalsense,thevaluereportedforameasurementdescribesthecentral tendency(mean);whiletheuncertaintydescribesthestandarddeviation(deviationfrom themean).Ideally,thismeasureofuncertaintyiscalculatedfromrepeatedtrialsortobe takenfromestimatesinwholeorpartinmanyengineeringtestsorresearchexperiments. Thus,riskanalysisforcestheengineertoconfrontuncertaintiesdirectlyandtousebest estimatesandpredictions,especially,whiletakingdecisionsregardingthesafetyoflarge technological(complex)systems.Increasingly,suchdecisionsarebeingbasedontheresultsofprobabilisticriskassessments,whichmustbeassociatedwithadequatequantificationoftheuncertainties.Uncertainparameterscanbetreatedasrandomvariableswith appropriateprobabilitydistributions.Suchdistributionsareassignedonthebasisofavailabledata(whichisoftenscarce),combinedwiththejudgmentofexperts(whichcanvary widely),addinganotherelementofuncertaintyintotheuncertaintyanalysisitself.This meansthattheremightbedifferentsourcesofuncertaintyduetodataavailable,limited knowledge,andsubjectivejudgment,anduncertaintyhereisassumedtobeavailablein probabilistictermseitherfromdataorfromexpertjudgmentorlogicalinference,[3,16].
Acomplexsystemhasasystemstructurethatiscomposedofamanycomponentsthat havecomplexinteractionsandmayberepresentedasanetworkwherethenodesrepresentsystemcomponentsandtheedges(links)aretheirinteractions.Givenanycomplex systemthatincludesinputs,outputs,subsystems,andboundaries,itisreasonabletoassumethatallofthesesystemcomponentsareinteractingeitherdirectlywithoneanother orindirectly.Inordertoestimatetheprobabilityoffailureforsuchsystem,theinteractionsshouldberepresentedmathematicallyincludinganyprobabilitymeasures.Afull representationofthesystemfacilitatesitsanalysisfromthefailurepointofview.The mainobstacleinfailureanalysisofcomplexsystemsishowtorepresentthesystemcomponentsandtheirbasicandconditionalprobabilities.BNsarefoundtosolvethisproblem.BNprovidesagraphicalrepresentationofanysystemusingbasicprobabilities,for systeminputs,andconditionalprobabilities,forsubsystemsandtheirinteractions.One ofthemainadvantagesofusingBNsistheabilityofintegratingalltypesofdata(social, environmental,technical,etc.)seamlesslyinonerepresentation.Thisisbecauseofthe probabilisticnatureoftheBNs,aseverythingisrepresentedasaprobability.
3.Bayesiannetworks(BNs)
AccordingtoRefs.[18 22],BNs,orbeliefnetworks,areprobabilisticgraphicalmodels usedtorepresentknowledgeaboutanuncertaindomainusingacombinationofprinciplesfromgraphtheory,probabilitytheory,computerscience,andstatistics.Inthegraph, nodes(vertices)arerepresentingrandomvariables,andtheedges(arcs)representthe
interrelationships(conditionalprobabilisticdependencies)amongthesevariables,which canbeestimatedusingknownstatisticalandcomputationalmethods.BNscanmodelthe quantitativestrengthoftheinterrelationshipsamongvariables(nodes),allowingtheir probabilitiestobeupdatedusinganynewavailabledataandinformation.BNisagraphicalstructureknownasadirectedacyclicgraph(DAG),whichispopularinsome fieldsof learning(statistics,machinelearning,andartificialintelligence).Thismeansthatasetof directededgesareusedtoconnectthesetofnodes,wheretheseedgesrepresentdirect statisticaldependenciesamongvariables,withtheconstraintofnothavinganydirected cycles(i.e.,cannotreturntoanynodebyfollowingdirectedarcs).Thus,thedefinition ofparentnodesandchildnodesisobvious.Thedirectededgeisoftendirectedfroma parentnodetoachildnode,whichmeansthatanychildnodedependsonitsparent node(s).BNsaremathematicallyrigorous,understandable,andefficientincomputing jointprobabilitydistributionoverasetofrandomvariables,alongwithbeingusefulin riskanalysis.Also,BNs duetotherequirementsofbeingDAGs aremoreeasilysolvablethanMarkovnetworks.InBNs,therearetwomaintypesofreasoning(inference support):one predictivereasoning(top-downorforwardreasoning),inwhichevidencenodesareconnectedthroughparentnodes(causetoeffect),andtwo diagnostic reasoning(bottom-uporbackwardreasoning),inwhichevidencenodesareconnected throughchildnodes(effecttocause).Firstly,thetopologyoftheBNshouldbespecified (structuringofgraphicalcausalitymodel),then,theinterrelationshipsamongconnected nodesshouldbequantified,i.e.,conditionalprobabilitydistributionsusingconditional probabilitytables(CPTs).Also,thebasicprobabilitiesofbasic(evidence)nodesshould bedeterminedusingbasicprobabilitytables(BPTs).Asthenumberofparentnodes, and/ortheirstates,increases,theCPTsgetverylarge. Fig.1.1 introducesthedifferent
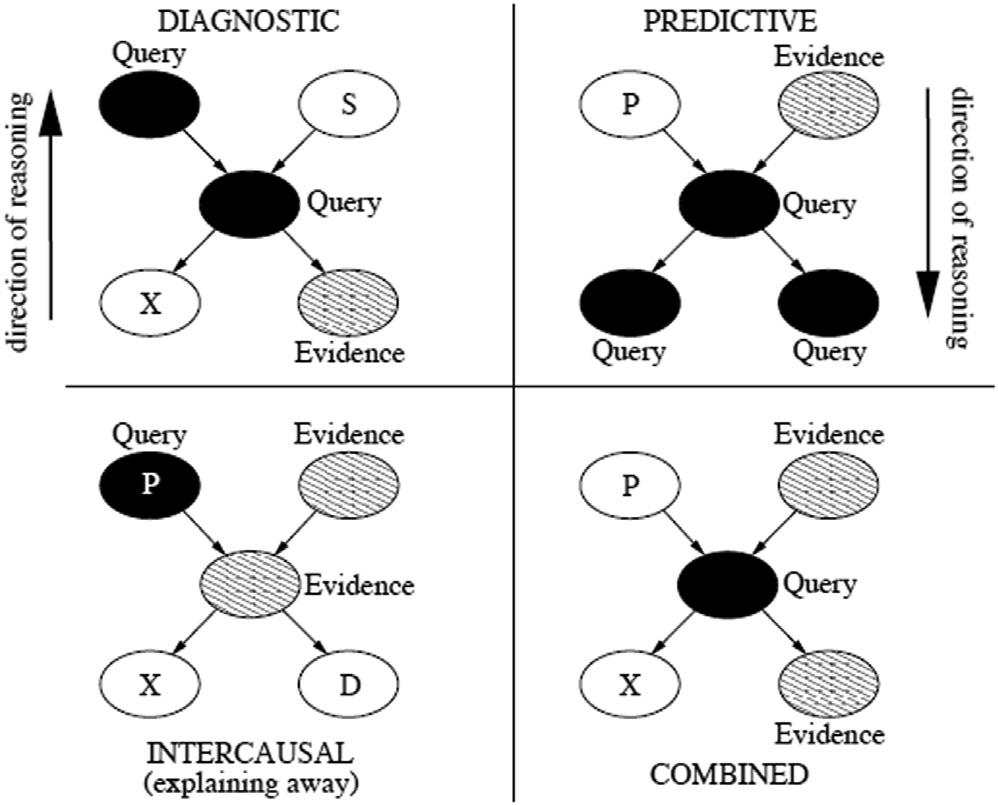
Figure1.1 TypesofreasoninginBNs[22].
typesofreasoninginBNs.Nodeswithoutanyarrowsdirectedintothemarecalledroot nodes,andtheyhaveprior(basic)probabilitytables,whilenodeswithoutchildrenare calledleafnodes.Nodeswitharrowsdirectedintothemarecalledchildnodes,while nodeswitharrowsdirectedfromthemarecalledparentnodes.Thepriorbasicprobability tables,fortherootnodes,andtheconditionalprobabilitytables,fortheparentandchild relationships,maybeobtainedfromhistoricaldatabasecurrentlyavailable,whichcanbe updatedincaseofhavinganynewdataorinformation.Generally,quantifyingBNsdependsonfoursourcesofdata: statisticalandhistoricaldata,judgmentbasedon experience(i.e.expertjudgment),existingphysicalmodels(orempirical models),andlogicinference. Wherenosuchsufficientdataexist,eithersubjective probabilitiesfromexpertsordetailedsimulationmodelscanbeusedtoestimateconditionalprobabilities,whichisdiscussedindetailslaterinthischapter.
ThemainchallengeinBNsisthatstatisticaldatamustbeavailableinordertoestimate probabilities.Whenthesystemisfullyrepresented,thefailureprobabilitycouldbeestimatedusingBayesianequations.AnalternativeuseoftheBNistoevaluatetheperformanceofthesystemcomponentsandtheirinteractionstogetsomeinformationabout thefailurecauses.Ifthepostfailureanalysisstageistakenintoconsideration,determinationofcausesandmitigationortreatmentactionsshouldbeconsideredinorderto improvetheperformanceandlimittheoverallsystemfailure.
AnexampleofBNwithsevenvariablesisshownin Fig.1.2.Thejointprobability functionofrandomvariablesinaBNcanbeexpressedasshownin Eq.(1.1):
Figure1.2 AnexampleofBNwithsevenvariables[23].
Where P ðx₁; ..; xn Þ isthejointprobabilityofvariables x1,x2,x3,.. xn,and Pa(xi) isthe parentsetof xi.If xi hasnoparents,thenthefunctionreducestotheunconditional probabilityof P(xi).FormoreillustrationofBNsandtheirapplications,including mathematicalrelationsandequations,seeRefs.[18 26].
Thejointprobabilitycanbederivedaccordingto Eq.(1.1),withtheconditional probabilitiesbeingquantifiedusingavailableinformation(e.g.,statisticalandhistorical data,expertjudgment,andphysicalandempiricalmodels),[24].Oneofthefeatures thatBNallowsisenteringevidenceasinput,resultinginupdatingprobabilitiesinthe networkwhennewinformationisavailable.Thisinformationwillpropagatethrough thenetworkandtheposteriorprobabilitiescanbeestimated.
PosteriorProbability ¼ Likelihood* PriorProbability Evidence
Theconceptofposteriorprobabilityallowsforidentifyingtheevents,whichhave highercontributingimpactsontheundesired/failureevent,andthenthedecisionmakermaypaymoreattentiontotheseimportantfactors,[27].InBNs,themainconcern isthecause effectrelationships,andderivingcausalinferencesfromacombinationof diverseassumptions.Generally,theuseofBNshelpstoanswerqueriesevenwhenno experimentaldataareavailable.
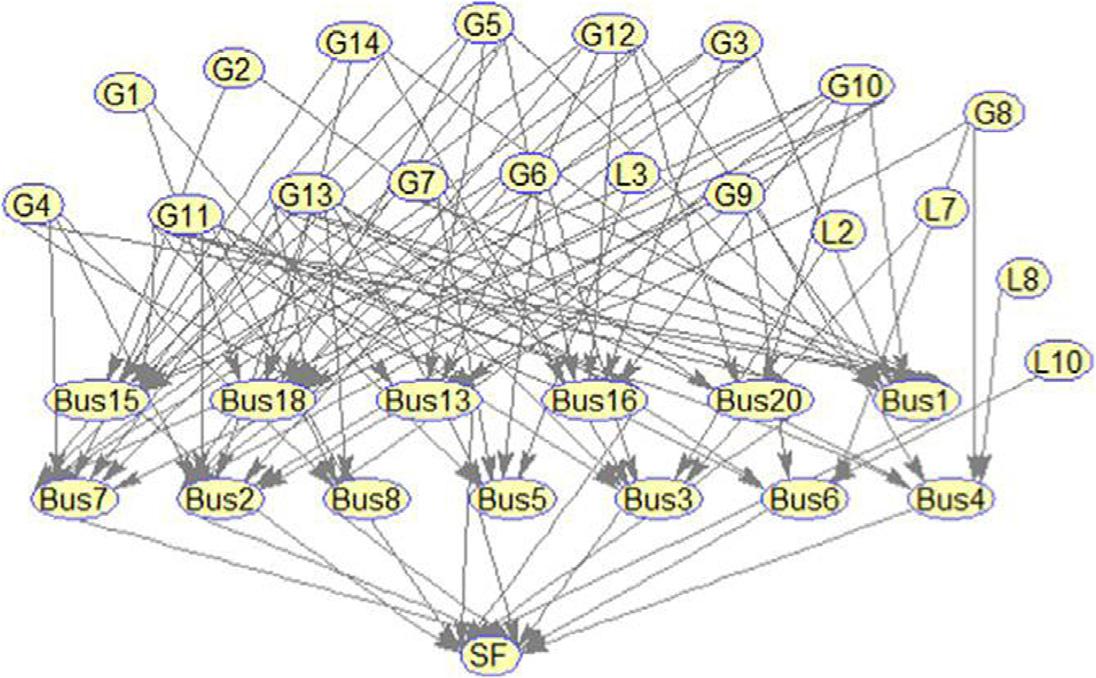
ThestructureofarelativelycomplexBNoftheIEEE-RTSsystemisshownin Fig.1.3 fromRef.[28].Thisshowshowcomplicatedthesysteminterrelationshipscould
Figure1.3 TheBNstructureoftheIEEE-RTSsystem[28].
bewhenrepresentedasaBN,especiallywhenlargenumberofsystemcomponents/ nodesneedtoberepresented.ThisalsorevealsthatBNmaybeusedtorepresentdifferent applicationsduetoitsprobabilisticnature.
Asthemainpurposeistopredicttheprobabilityoffailure,thewayofrepresentation shouldbeprobabilistic.BNshavethedistinctiontorepresentthedifferentcomponentsof thesystemwiththeirinterrelationships,alongwithdefiningthedifferentcausesleading tocertaineffect(s)inaprobabilisticrepresentation.OneofthemainadvantagesofBNsis thattheycanincorporateanykindofdatabecauseallofthemarerepresentedintermsof theirprobabilitiesofoccurrence,nottheirvalues.Itwouldbecrucialtohaveasimplified representationthatincludesallthesystemvariablesandfactorstomaketheprobabilistic representationoftheBNuseful.BNs,asDirectedAcyclicGraphs(DAGs),havetheabilitytorepresentanynetwork quantitatively (usingprobabilitymeasures)and qualitatively (usingsimplerepresentationanddependencystructure).
4.Probabilisticfailureanalysisofhydropowerdams
Damsandreservoirsystemsarecomplexcivilengineeringsystems[29].Studyingsafetyof damsneedsacomprehensivemultidisciplinaryanalysisthatshouldconsideralltherelevantfactorsandtheirinterrelationships.ItisshowninRefs.[29,30]howcomplexthe decision-makingprocessiswhiledealingwiththechallengingproblemofdamsafety. Althoughpastcasesofdamfailuresaretakentodiagnosethecausesoffailure;thisis notenoughforpredictingotherdams’ failureprobabilitiesaseverydamisdifferentin termsofhuman,environmental,design,andtechnicalinfluentialfactors.Someofthe shortcomingsassociatedwithtraditionalriskanalysisandassessmentapproachesarelisted inRef.[30].ThecurrentavailableapproachessuchasMonte-Carlosimulationare computationallyexpensiveastheyrequiredetailedexhaustivesystemsimulations.Therefore,theyareinefficientforcomplexsystemshavingalargenumberofelementsand highlynonlinearrelationships,andanyimprovedpracticalapproachtodamsafetyanalysis andprediction,notjustdiagnosis,isofsignificantvalue.Inthisline,aparadigmshifthas beensuggestedinRefs.[31,32]todealwithdisastermanagementbyquantifyingdisaster resilienceinsteadofthetraditionalrisk-basedtechniques.Withthesenewapproaches, systemanalysiswillcontinuetobeaprimaryapproachtounderstandingthesystem behaviorunderuncertaintyandothermeasuresthatneedtobetakenintoconsideration. Thisisanattempttoaddresssomeoftheseshortcomings,especiallyinenhancingtheway ofpredictingtheprobabilityofsystemfailureusingsystemsanalysiswhiledealingwith datascarcityinsomeengineeringapplications.
Itcanbeshownin Fig.1.4 thatdamoperationandcontrolsystemmodelsincorporate multipleinterrelatedsubsystems.High-leveldecision-makersmayhavedifficultyinunderstandingsuchrepresentations.Decision-makers,ashumans,focuson “whatisimportant” whenfacingsuchcomplexsystemsinthecaseoflackofsureness[29].Theyneeda
simplifiedsystemrepresentationtoincludeallthesystemcomponents,variables,andsubsystemswhileaccountingfordifferentinteractions.Whentheytrytoevaluatetherisk situationandtakeacontrol/mitigationaction,theybecomeawareofthesituationof othersystemcomponents.Thiskindofsystemrepresentationshouldbeathighlevel, whichallowsforanalyzingthesystemtosubnetworkshavinglessnumberofstatesinstead ofdealingwiththeentirenetworkcomponents.Andifneeded,thesesubnetworks shouldhavetheabilitytobedisaggregatedtoitselementalcomponents.BNshaveshown potentialsinthisdirection.
Indamsafetystudies,threeprincipalapproachesarewidelyused:failuremodesand effectsanalysis(FMEA),eventtreeanalysis(ETA),andfaulttreeanalysis(FTA). Recently,BNanalysishasdrawnattentionasanotheralternativefordamsafetystudies. BasedontheinformationinRefs.[19]and[33]attemptstoextendthetechniqueofBNs tothediagnosisofaspecificdistresseddam.Themainobjectiveof[19]istodevelopa probability-basedtoolusingBNsforthediagnosisofembankmentdamdistressesat thegloballevelbasedonpastdamdistressdata.Historicaldatafordamdistressesare usedtoquantifytheinterrelationsamongsystemparameters.
Thecriticalstepindealingwithsafetyofdamsisthattherepresentationmustinclude thetechnicalfactorsbesides,atleast,thehumanfactors.Onerecentimportantexampleis whathappenedinOrovilledam,California,inFebruary2017,[34].Thedamsuffered fromsomehydrologic,economic,andoperational,strategic,andtacticalproblems, whichputthedamstructureinacriticalsituation,andputlivesofhundredsofthousands ontheedge.Itwasn’tapuretechnicalprobleminthedamdesign,butrather,theoperationplanandstrategyperformedbyhumanswerepartofthedisaster.Tobetterpresent
Figure1.4 Exampleofadamsystemmodel[29].
suchcasesforfutureprevention,morethanjusttechnicalfactorsshouldbeconsideredin thefailureanalysis.
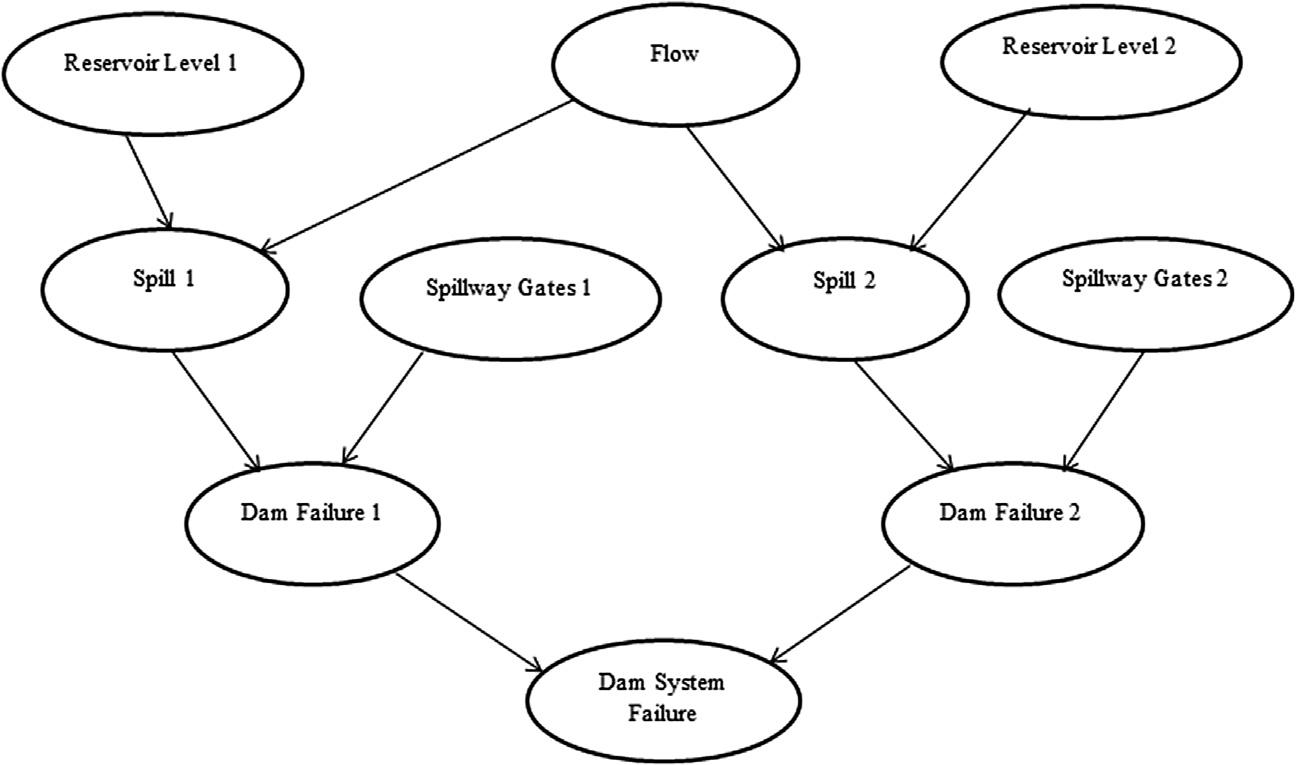
AsimpleexampleforapplyingtheBNrepresentationonthesafetyofhydropower dams,topredictthefailureprobability,isillustratedin Figs.1.5and1.6 Twodamsare connectedinseriesorinparallel,andtheinflowsofbothdamsarestatisticallydependent (andcanbeindependentinotherconfigurations),[35].Theinflowandthereservoirlevel ofeachdamareaffectingthespillevent(i.e.,tohaveexcesswatermorethanthereservoir capacity),andifthespillwaygatesfailedtoopenatthespillevent(duetoanyelectromechanicalfailures),thedamwillexperienceanovertoppingfailure,andaffectingthesystemfailureaccordingtotheconnectionbetweenbothdams(serialorparallel).Forthis kindofsystems,itissupposedtohavethebasicandconditionalrelationsamongsystem components/nodesfromhistoricalandoperationaldata,ifavailable,inordertofeedthe basicandconditionalprobabilitytables(i.e.,BPTsandCPTs)oftheBNtopredictthe failureprobability.Thiscanbeusedforthesakeofpreventionofanyfuturefailure thatmayaffectthedamsorthepopulationatrisk(PAR)livingarounddams.
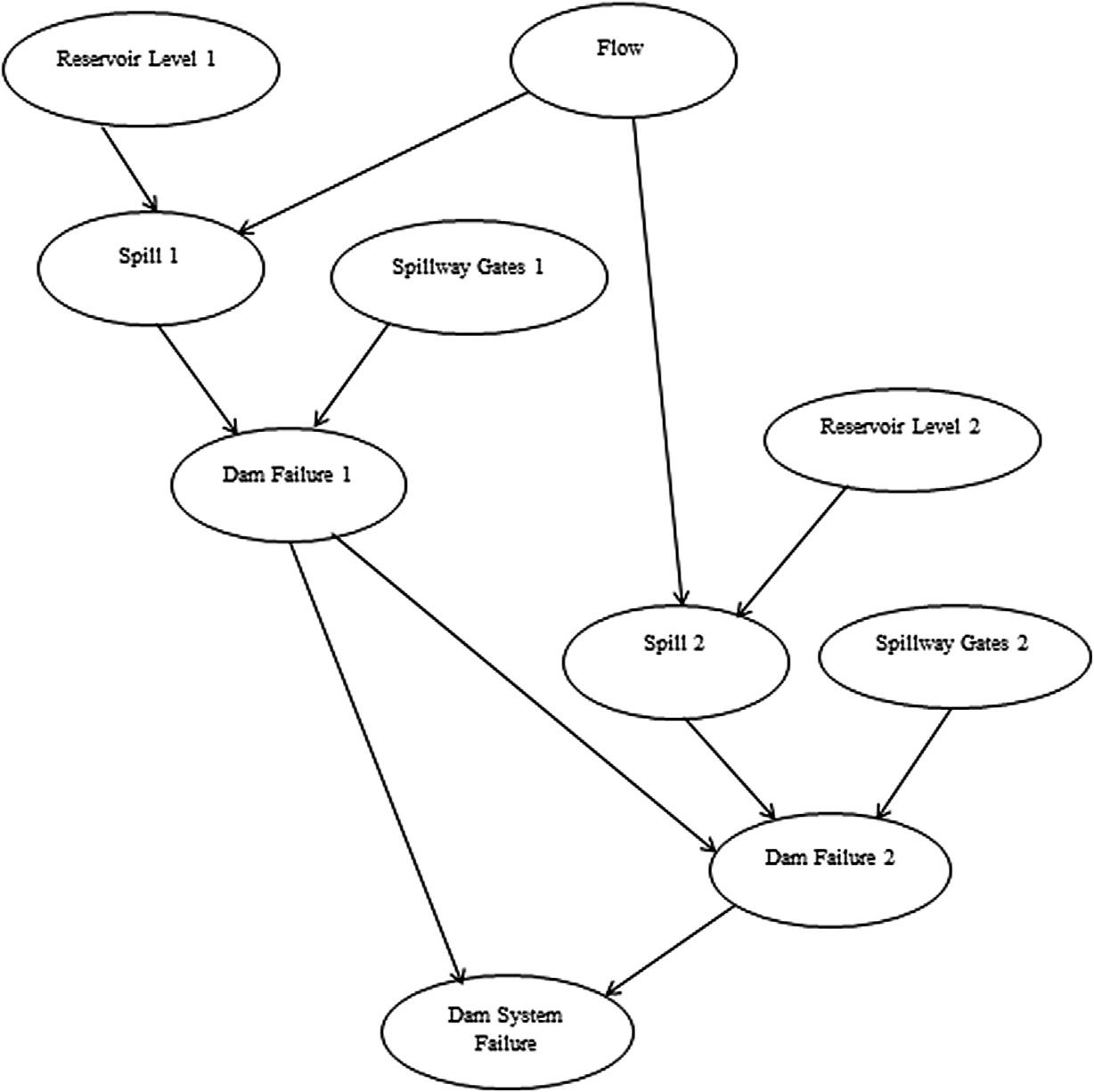
Figure1.5 BNoftwoseries-dependentdams/reservoirs.
Inpreexistingsystems,suchashydropowerdams,theoperational,historical,andstatisticaldatacanbeestimatedtoquantifytheBNsthatrepresentthesesystems.Thequestionis:cansimulationbeusedasanothersourceofinformationtoquantifythecomplex systemsrepresentedbyBNs?
In[36],reassessmentofdamsafetyeventsusingBNsisillustrated.TheBNsarebuilt basedontheeventtreeanalysisandweresupplementedwithMonteCarlosimulations. Thiscombination,BN-Simulation,withenoughnumberofsampleruns,canbeaneffectivetooltonarrowdowntherangeofprobabilitiesandmaycoverawiderangeofuncertaineventsleadingtofailures.However,itcanbeseenintheapproachof[36]that simulationisperformedforrelativelysmallnetworks(notthatcomplex).Moreover, thebasicdataandstatisticsareknownfromthebeginningforthesystemunderstudy. So,ifweareupdating(reassessing)thenetworkusingsimulationmodels,whynotwe providethenetworkwiththeprobabilityestimatesusingsimulationfromthebeginning?
Ifsufficienthistoricalandstatisticaldataareavailable,thereshouldbenoneedfor simulation.Suchdataarenotavailableintwocases:infuturesystems(i.e.,blueprintprojects),orfornetworksthatdon’thaveanefficientmonitoringsystemtosavetheoperationaldatawithtime.Inbothcases,relyingonlogicinferencing,expertjudgment,or empiricalmodelsmaybemisleadingandmayaddmoreuncertainty,especiallyinvery complexsystems.Thatiswhysimulationmaybeintegratedasausefulsourceofdata. Butthechallengeisthatsimulatingaverycomplexsystemmaybecomputationally expensiveforthepurposeofidentifyingtheprobabilisticinterrelationshipsamongsystems’ variablesandsubcomponents.Ontheotherhand,simulationresultsofdecomposedsubsystemsmayprovidetheBNwithprobabilityestimatesthatareusedto
Figure1.6 BNoftwoparallel-dependentdams/reservoirs.
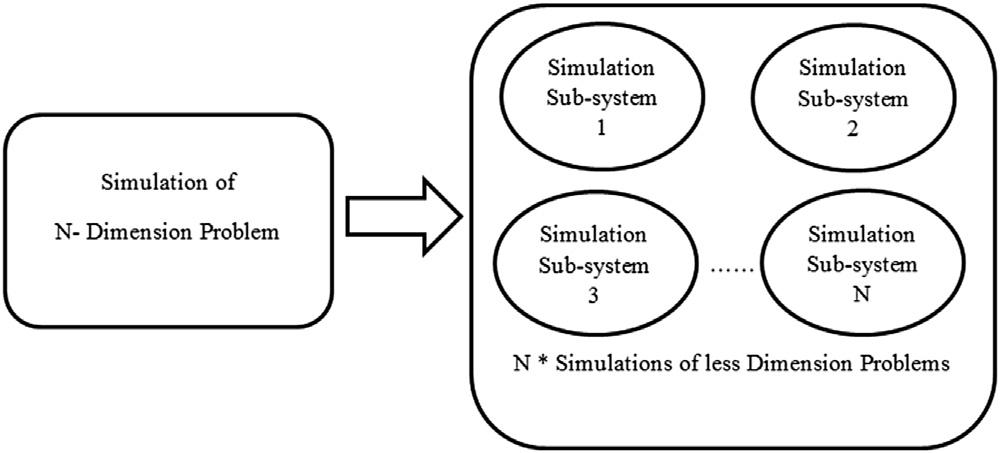
estimateprobabilitiesofwholesystems.AproposedmethodologyinRef. [35] SimulationSupportedBN(SSBN)foracomplexsystem issummarizedin Fig.1.7.Thesimulationwillbecomputationallycomplicatedifperformedfortheentire network,especiallyincomplexnetworkswithalargenumberofstates.Forthatreason, SSBNproposestohavethenetworkdecomposedintosmallersubnetworks(subtrees). Eachsubnetworkwillhaveitsownsimulationaccordingtothedataavailable,orfrom randomsamplingincaseonlybasicdataareavailable(e.g.,lowerandupperbounds). Foreverysubnetwork,simulationresultsareallaboutprobabilisticquantificationof thissubnetwork’sBN.Thus,probabilityvaluesareestimatedfromsimulationandfed intotheBNofthesubnetwork.
OnceallBayesiansubnetworksareprobabilisticallyquantifiedwiththeirbasicand conditionalprobabilityvalues,thesubnetworksarereadytoberecombinedasonewhole networkrepresentation.SSBNmakesthecomplexsystemmorereadableforboththe operatorsanddecision-makers.SSBNovercomesthefollowingobstacles:
• Complex,time-consumingsimulationmodels,
• Complexrepresentationofsystems,
• Propagationofuncertaintymeasuresinacomplexnetwork,and
• Theintegrationamongdifferentsourcesofdata,includingsimulation.
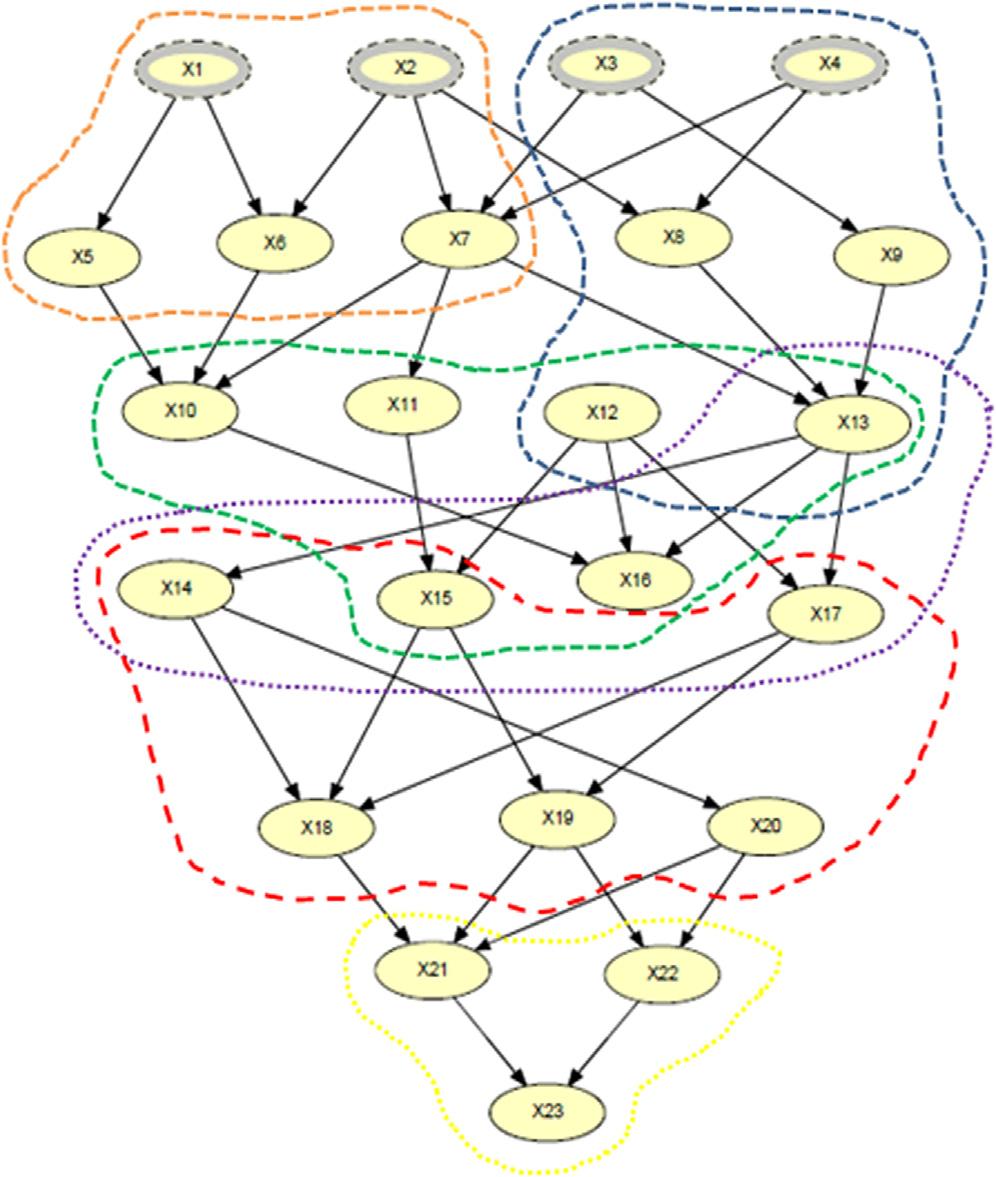
Asanexample,in Figs.1.8aand1.8b,a23-nodeBNisrepresentedtoshowhow complexsystemcomponentscanbeinterrelated.Eachnodeisassumedtoincludeatleast twostates,whichmeansatleast223 statesinthatsystem.Themorestatesthenodeshave, themorecomplexthesystemis.Whentheanalysisofthesystemisenhancedusingthe SSBNmethod,ratherthansimulatingtheentiresystem(in Fig.1.8a),smallersubsystems maybesimulatedinstead.In Fig.1.8b,theBNisdecomposedtosixdifferentsubentities (subsystems,subnetworks,orsubtrees).Eachsubsystemislesscomplexthanthewhole system,whichmeanslessnumberofstates.Ingeneral,asystemof N nodes/components, twostateseach(i.e., 2N possiblestates)canbedecomposedto n subsystemsandthenumberofpossiblestatesbecomes n*(2N/n),whichismuchlessthan 2N [i.e.,ifN ¼ 12, n ¼ 4,2N ¼ 4096,andn*(2N/n) ¼ 32].Thesubsystemcomponentsareinterrelated,
Figure1.7 ProposedmethodologyofSSBN.
andthesubsystemsmayalsohaveinterrelationsamongeachother.ByapplyingtheSSBN concept,everysubsystemissimulatedseparately,usingtheappropriatemethods,toget theprobabilityestimatesneededforquantifyingtheBN.
Inordertoquantifytheconditionalinteractionsamongsubsystemdecompositions, domainknowledgeandexpertjudgmentmayberequired.Ifthiskindofjudgmentis notavailable,assumingdifferentscenarios/statescanbeusedwithsensitivityanalysis instead.Thismeansthatdifferentinteractionsamongsubsystemdecompositionarequantifiedbyassumingworst-casescenarios,best-casescenarios,andnormal-casescenariosin ordertoestimatethesystemfailureprobabilitiesindifferentsituations.
AccordingtoRef.[34],theAmericanSocietyofCivilEngineers(ASCE)issueda reporttitled “GuidingPrinciplesfortheNation’sCriticalInfrastructure.” Riskmanagementofcriticalinfrastructuredependsonfourinterrelatedguidingprinciples,identified asfollows:
1. Toquantifyandcommunicaterisk,
2. Toemployanintegratedsystemsapproach,
Figure1.8a A23-nodeBNusingHuginsoftware.
Figure1.8b A23-nodeBNdecomposedtosixsubentitiesreadytobesimulated.
3. Toexerciseleadership,management,andstewardshipindecision-makingprocesses, 4. Toadaptcriticalinfrastructureinresponsetodynamicconditionsandpractices.
Wearefocusingmainlyonthe firsttwoguidingprinciples,whichisofhowtorepresentallinterrelatedsystemcomponentsinacombinedrepresentation(integratedsystems approach),whileenhancingtheabilitytoquantifythiskindofsystemrepresentationinordertobetterpredictthefailuresformanypurposes(riskmanagement,riskreduction,etc.).
Anexampleofareal-worldcasestudyisshownin Figs.1.9aand1.9b byrepresenting theproposedBNforprobabilisticfailureanalysisofMountainChutehydropowerdamin Ontario,Canada,operatedbyOntarioPowerGeneration(OPG).Inthisnetwork,there are21nodesrepresentingsystemcomponentsforthepurposeofanalyzingthefailureof thissystem.ThisincludesProbableMaximumPrecipitation(PMP),iceloading,earthquakeandseismicactions,waterpressure,geologyandrocktype, floodseverity,adequacyofdischargecapacity,sluicegates,drainage,vegetationcontrol,seepage,and othercomponents.Ifmorethantwostatesaredefinedforeverynode,thesystemwill turntobeahugecomplexnetworktoanalyze.However,themorestatesthesystem componentshave,themoreaccuratetheresultsare.But,themainproblemfacedis
Figure1.9a BNforprobabilisticfailureanalysisofMountainChuteDam.
Figure1.9b BNofMountainChuteDamdecomposedtosubentitiesreadytobesimulated.
havinglimitedhistorical,operational,andmonitoringdata.Onlybasicdataoflowerand upperboundsofinflows,outflows,and floodingeventsmaybeavailable,alongwith expertopinionsandlogicinferencing,andsomeacceptedempiricalmodelsofreservoir systemanalysis.Insuchcases,mathematicalmodelingandsimulationmaybea firststepto getprobabilisticestimates.TheadvantageofthedecompositionalBNapproachis obviouswhendealingwithsuchnetworks.Decomposingthesystemtonewentitiesis shownin Fig.1.9b,andSSBNmethodcanbeappliedasdemonstratedinRef.[35]. Accordingly,simulationresults,logicinference,andexpertjudgmentmayprovideprobabilisticdatathatcanbefedtotherecompositionoftheentirenetwork(in Fig.1.9a)to estimate/predicttheprobabilityoffailurefortheentiresystem.
InRefs.[37,38],MountainChutedam’sBNisquantifiedwithlogicallyinferreddata, whichhavehigheruncertainty,andthencomparedwiththeresultsofquantifyingthe BNwithexpertopinions.Herethelogicallyinferreddataplaytheroleoftheworstcasescenario,andtheexpertopinionsplaytheroleofthebest-casescenariofortheconditionsthataremostprobabletohappenatpresent.Ifsufficientdataandmathematical modelsareavailablefortheentiresystemvariablesandtheirinteractions,simulationusing SSBNdecompositionalapproachmaybeusedforthepurposeofenhancingtheprobabilisticresultsandgeneratingscenariosoftakingdifferentdecisionsforthenetwork.
5.Summaryandconclusions
Failureanalysisofcomplexsystemshavingahugenumberofinteractingsystemcomponentsischallenging,especiallywhilehavingprobabilisticeventsthataffectthesystems performance.Aprobabilisticmultifactorrepresentationthatrepresentsdifferenttypes offactors(i.e.,technicalandnontechnical)andeventsmaybehelpfulinperformingfailureanalysisofcomplexsystems.Itcanbeconcludedthattheengineeringcomplexsystemshavemanywaystoberepresented;however,BNshaveshownadvantagesin representingsuchsystemsintermsofdefiningtheinterrelationshipsamongsystemcomponents.ThequantificationofBNsdependsondifferentsourcesofdatasuchaslogic inference,expertengineeringjudgment,empiricalmathematicalmodels,historicaland operationaldata,and/ordetailedsimulation.Complexsystems,ifsimulated,willhave complexandexhaustivesimulations,whiletheaimistofacilitatetheprocessofpredicting theprobabilityoffailureofcomplexsystems.Thus,theSSBNdecompositionalapproach isillustratedandhowitcanbeappliedtooneofthecomplexsystems,i.e.,hydropower dams.Areal-worldcasestudy,i.e.,MountainChuteDam,isalsoexplainedandhowthe BNcanbequantifiedindifferentways.TheposteriorcapabilityoftheBNmayalsobe helpfulinidentifyingthemaincontributingcomponentstosystemfailure.Thismaybe usefulinthedesign,operation,ordecision-makingstages.
References
[1]Y.Bar-Yam,Generalfeaturesofcomplexsystems,EncyclopediaofLifeSupportSystems(EOLSS)1 (2002).
[2]J.Berk,SystemsFailureAnalysis,ASMInternational,2009,pp.1 9.
[3]OfficeoftheGeneTechnologyRegulator,DepartmentofHealthandAging,AustralianGovernment, “RiskAnalysisFramework”,January,2005.
[4]H.P.Berg,Riskmanagement:procedures,methodsandexperiences,RT&A#21(17)(June,2010) 79 95.
[5]I.H€aring,Introductiontoriskanalysisandriskmanagementprocesses,in:RiskAnalysisandManagement:EngineeringResilience,SpringerScienceþBusinessMedia,Singapore,2015,pp.9 26.
[6]C.Rodger,J.Petch, “Uncertainty&RiskAnalysis,APracticalGuidefromBusinessDynamics,” PricewaterhouseCoopers,MCS,BusinessDynamics,UnitedKingdom,April,1999.
[7]G.L.S.Babu,A.Srivastava,Riskandreliabilityanalysisofstabilityofearthendams,in:IGC,Guntur, India,2009.
[8]FAO(FoodandAgricultureorganization),IntroductiontoRiskAnalysis BasicPrinciplesofRisk Assessment,RiskManagementandRiskCommunication,Yerevan,Armenia,October,2010.
[9]U.S.Armycorpsofengineers&U.S.Departmentoftheinterior,bureauofreclamation,BestPractices inDamandLeveeSafetyRiskAnalysis(July,2015).
[10]U.S.Armycorpsofengineers&U.S.Departmentoftheinterior,bureauofreclamation,BestPractices inDamandLeveeSafetyRiskAnalysis(February26,2015).
[11]L.King,Reliabilityof flow-controlsystems,BCHydroforGenerations(May12,2014).
[12]D.N.D.Hartford,G.B.Beacher,RiskandUncertaintyinDamSafety,ThomasTelfordLtd.,2004.
[13]N.G.Leveson,EngineeringaSaferWorld,SystemsThinkingAppliedtoSafety,TheMITPress,2011.
[14]S.Bernardi,etal.,Dependabilityanalysistechniques,in:Model-DrivenDependabilityAssessmentof SoftwareSystems,Springer-Verlag,2013,pp.73 90.
[15]U.S.Armycorpsofengineers&U.S.Departmentoftheinterior,bureauofreclamation,Probabilistic StabilityAnalysis(ReliabilityAnalysis)(March,2015).
[16]D.C.Cox,P.Baybutt,Methodsforuncertaintyanalysis:acomparativesurvey,SocietyforRiskAnalysis1(4)(1981)251 258.
[17]S.J.Kline,Thepurposesofuncertaintyanalysis,JournalofFluidsEngineering,ASME107(June,1985) 153 160.
[18]M.Peng,L.M.Zhang,Analysisofhumanrisksduetodam-break floods part1:anewmodelbased onBayesiannetworks,NaturalHazards64(2012)903 933.Springer.
[19]L.M.Zhang,Y.Xu,J.S.Jia,C.Zhao,DiagnosisofembankmentdamdistressesusingBayesiannetworks.PartI.Global-levelcharacteristicsbasedonadamdistressdatabase,CanadianGeotechnical Journal48(2011)1630 1644.NRCResearchPress.
[20]C.J.Lee,K.J.Lee,ApplicationofBayesiannetworktotheprobabilisticriskassessmentofnuclearwaste disposal,ReliabilityEngineering&SystemSafety91(2005)515 532.ElsevierLtd.
[21]I.BEN-GAL,Bayesiannetworks,in:EncyclopediaofStatisticsinQuality&Reliability,Wiley& Sons,2007,pp.1 6.
[22]K.B.Korb,A.E.Nicholson,Introducingbayesiannetworks,in:BayesianArtificialIntelligence, seconded.,Chapman&Hall/CRCPressLLC,2004,pp.29 54.
[23]S.Hosseini,K.Barker,ModelinginfrastructureresilienceusingBayesiannetworks:acasestudyof inlandwaterwayports,ComputersandIndustrialEngineering93(2016)252 266.ElsevierLtd.
[24]F.Nadim,Z.Q.Liu,Quantitativeriskassessmentforearthquake-triggeredlandslidesusingBayesian network,in:Proceedingsofthe18thInternationalConferenceonSoilMechanicsandGeotechnical Engineering,Paris,2013.
[25]P.Li,C.Liang,Riskanalysisforcascadereservoirscollapsebasedonbayesiannetworksunderthe combinedactionof floodandlandslidesurge,MathematicalProblemsinEngineering(2016)1 13. HindawiPublishingCorporation.
[26]M.Smith,Damriskanalysisusingbayesiannetworks,in:EngineeringConferencesInternational, GeohazardsLillehammer,Norway,2006.
[27]X.Zheng,Y.Wei,K.L.Xu,H.M.An,Riskassessmentoftailingsdambreakduetoovertopping,EuropeanJournalofGovernmentalandEconomics21(7)(2016)1641 1649.
[28]T.Daemi,A.Ebrahimi,M.Fotuhi-Firuzabad,ConstructingtheBayesianNetworkforcomponents reliabilityimportancerankingincompositepowersystems,ElectricalPowerandEnergySystems 43(1)(2012)474 480.ElsevierLtd.
[29]D.N.D.Hartford,G.B.Baecher,P.A.Zielinski,R.C.Patev,R.Ascila,K.Rytters,OperationalSafety ofDamsandReservoirs,UnderstandingtheReliabilityofFlow-ControlSystems,InstitutionofCivil Engineering(ICE)Publishing,2016.
[30]L.M.King,S.P.Simonovic,D.N.D.Hartford,Usingsystemdynamicssimulationforassessmentof hydropowersystemsafety,WaterResourcesResearch(2017)7148 7174.AmericanGeophysical Union,no.53.
[31]S.P.Simonovic,Fromriskmanagementtoquantitativedisasterresilience aparadigmshift,InternatioanlJournalofSafetyandSecurityEng6(2)(2016)85 95.
[32]A.Schardong,S.P.Simonovic,H.Tong,Useofquantitativeresilienceinmanagingurbaninfrastructureresponsetonaturalhazards,InternatioanlJournalofSafetyandSecurityEng9(1)(2019)13 25.
[33]Y.Xu,L.M.Zhang,J.S.Jia,DiagnosisofembankmentdamdistressesusingBayesiannetworks,in: PartII.DiagnosisofaSpecificDistressedDam,vol.48,NRCResearchPress,2011,pp.1645 1657.
[34]R.G.Bea,T.Johnson, “RootCausesAnalysesoftheOrovilleDamGatedSpillwayFailuresandOther Developments,” UniversityofCalifornia,CenterforCatastrophicRiskManagement,Berkeley,July, 2017.
[35]A.El-Awady,K.Ponnambalam,IntegrationofsimulationandMarkovchainstosupportbayesiannetworksforprobabilisticfailureanalysisofcomplexsystems,ReliabilityEngineeringandSystemSafety 211(2021).Elsevier.
[36]Z.Q.Liu,F.Nadim,U.K.Eidsvig,S.Lacasse,ReassessmentofDamSafetyUsingBayesianNetwork, Geo-Risk,ASCE,2017,pp.168 177.
[37]A.Verzobio,A.El-Awady,K.Ponnambalam,J.Quigley,D.Zonta,Anelicitationprocesstoquantify bayesiannetworksfordamfailureanalysis,CanadianJournalofCivilEngineering(2020), https:// doi.org/10.1139/cjce-2020-0089.
[38]A.El-Awady,ProbabilisticFailureAnalysisofComplexSystemswithCaseStudiesinNuclearand HydropowerIndustries,UWSpace,UniversityofWaterloo,2019.
Failuremodesandeffectanalysis modelforthereliabilityandsafety evaluationofapressurizedsteamtrap
DanielO.AikhueleandDesmondE.Ighravwe FacultyofEngineeringandBuiltEnvironment,UniversityofJohannesburg,Johannesburg,SouthAfrica
1.Introduction
Pressuresteamlinetrapsareoneofthevitalpartsoftheengineroomofashippingvessel; theycontrolandconnectseveralunitsintheengineroomincludingtheboilerandturbinesystemsthatpoweredtheship[1].Thesteamtrap,whichensuresthesteamusedas thedrivingforceandforheatinginthevesselisnotwasted,canbedescribedasanautomaticvalvethat filtersoutcondensedsteamandnoncondensablegasessuchasairfrom thesteamlinewithoutlettingthesteamescape[2].
Shippingvessels,asweknowthem,areoftenoperatedinthemostextremecondition. Astheyareexploitedundertheseconditionsovertime,thehighlypressurizedsteamline trapbecomesweakerandpronetofailureordamage[3].Thisfailureordamagethat couldhappenwellbeforeexpectedmayoccurnotonlybecauseoftheinternalpressure andtemperaturebutbecauseoftheloadsgenerated,whichmaybeduetobaddesignand insufficientmaintenance.Thiscouldalsohappenduetothefrequenton offswitching oftheboiler,aswellasthemisuseofthestartdiagram.
Withthecomplexityinthedesignsofthecomponentsandmaterialsemployedinthe engineroom,especiallythepressuresteamlinetrap,andthehighriskinvolvedwhenever anyofthesesystemsfailedonboardship,thereisaneedtoconstantlymonitorandmaintainthesystemdesignarchitecture[4].Thereliabilityofthepressuresteamlinetrap shouldbeatitsoptimallevelallthetime,toresistextremestress,pressure,temperature, andtocatertotheothermanydemandsofthesystem.Also,anyreliabilityfailuresdiscoveredonboardcouldresultinthesystem/componentnotabletoperformitsintended functionsuccessfully,whichinsomecasescouldendangerthelivesoftheshipoperators, andresultinacostlyandstrategicissueandcanleadtotheneedforanexpensiveredesigningofthepartaltogethershouldbeavoidedatallcost.Onewayofachievingthatisto addressthereliabilityfailureissuesbeforetheyoccurandimprovesafetyonboardshipby developingasystematicframework,model,andstrategytokeepthecomponentsonboardtheshipupandrunning.
Topreventaccidentsandriskysituationsonboard,safetyprotocolandassessment methodshavebeenproposedandimplementedtoevaluate,improve,andpreventfailure ofthedifferentcomponentsintheengineroomofashippingvessel.Amongthem include,theuseofhardwaresuchastheultrasonictestinginstrumentforidentifyingpressuresteamlinetrapfailures[5],theultrasonictestinginstrument,whichisanextensive andexpensivemethod,requiresreferencecalibrationforitseffectiveuse.Analytical methodsuchastheDecision-MakingTrialandEvaluationLaboratory(DEMATEL) modelproposedbyBashanandDemirel[6]hasalsobeenusedfortheevaluationof thecriticaloperationalfaultsinamarinedieselgenerator.Themodelcontributesto thesafetyoftheshipatseaaswellaspreventstheeffectofhazardousmachineryinthe engineroom;however,uncertaintiesintheuseofthemodelwerenotconsidered.Jeon etal.[7]appliedthefailuremodeandeffectsanalysis(FMEA)evaluationmethod,which reliesontheriskprioritynumber(RPN)approachfortheevaluationofthesafetyand reliabilityofthefuel-cell-basedhybridpowersystem,usedonboardship,theRPN approachasweknowitisnotcomprehensiveforcomplexreliabilityassessment[8].
Lazakisetal.[9]deployedapredictivemaintenanceapproachforthereliabilityand criticalityanalysisofthedieselgeneratorsystemofamotoredcruiseshipvessel.Thepredictivemaintenanceapproach,whichusesthefailuremodes,effects,andcriticalityanalysis(FMECA)methodalso,implementsthefaulttreeanalysis(FTA)methodaswellas thereliabilityimportancemeasures(IMs)fortheestimationofthereliabilityofthesystem.Vizentinetal.[10]reviewedthefailuresassociatedwiththepropulsioncomponent/ systemsonboardamarinecargovessel.Theconsequencesofsuchfailure,whichcould resultin financiallosses,delayindeliverytimeofthecargo,orathreattothesafetyof thepeopleandoperatoronboardwerestudied.Furthermore,experimental,analytical, andnumericalmethodswereusedintheevaluationofthefailureofthepropulsionsysteminthevessel.
Anantharamanetal.[11]presentsamodelfortheestimationofthereliabilityofthe mainpropulsionengineofamerchant’svessel.Themodelthatisbasedontheintegration oftheMarkovmodelisusedfortheconstantfailurecomponents,whileaWeibullfailure modelwasusedforwearingoutcomponentsinthevessel.Similarly,Aikhueleetal.[12] presentedamodelforthedetectionofafailureinamarinedieselengineauxiliarysystem, themodelthatisbasedonaninterval-valuedintuitionisticfuzzyTOPSISmodelandan improvedscorefunctionusesagroupofexperts’ opinionstodetecttherootcauseofthe failure.Thoughtheabovemodelsprovideamorerealisticandpracticalapproachforthe reliabilityestimation,however,themodelswerepropulsionanddieselenginespecific.
Ahybridrisk-assessmentmodelthatusestheconceptsofFMEAaswellasthatofthe multiple-criteriadecision-making(MCDM)theorywasproposedbyLoetal.[13]forthe identificationofpotentialfailuremodes(FMs)inapowersupplyequipment.Theproposedmodelconsidereduncertaintiesintheinformationprovidedbyanalysts,which weredrawnfromvariedbackgroundsaswellasusetheentropyweightsintheriskindex.
Jeonetal.[7]proposedanFMEAevaluationmethodthatisbasedonanRPNforshipbuildingprocess.Themethod,whichisaimedatsecuringsafeoperationoftheship,examinesthesuitabilityfromthedesignstageoftheship,bysettingupapreliminaryreview andcountermeasuresforfailuresanddefectsthatmayoccurduringtheconstructionprocess.Maetal.[14]proposedaquantifiableriskassessmentmethodthatisbasedonFMEA forimprovingtheaccuracyofbrakingdistancemeasurementandforreducingtheimpact ofhumanfactorsonbrakeriskassessmentofescalatorsystems.Thequantifiablerisk assessmentmethod,whichallowsforfailuremodes,failuremechanism,andconsequencesofthefailureoftheelevatorsystemstobeanalyzed,usesaspecialriskindex assessmentsystem.
Aikhuele[15]improvedtheconceptsofFMEA,byproposingamulticriteria decision-makingmodelthatisbasedonatriangularintuitionisticfuzzyhammingdistance anda flexibilityfunctionfortheidentification,analysis,andrankingoftherootcauseof failureinaslewinggearsystem.ThemodelusedcriteriasuchasSeverity,Occurrence, Detection,Maintenance,andEnvironmentalconditionsintheevaluationprocess.The model,however,wasslewinggearsystemspecific.Similarly,withthehelpof fieldexperts,Liangetal.[16]developedadynamicheterogeneoussocialnetworkconsensus reachingmodel(DHSNCRM)withminimumadjustmentdistanceasareplacement fortheconventionalFMEAmodel,whichhelpsinthereachingofconsensuswhenevaluatingtoobtainconsentientpriorityoffailuremodes.Themodel,whichisatwo-stage feedbackprocess,isusedforreliabilitymanagementofmedicalequipment.
Fromtheforegoing,itisnothardtoseethatnotmuchconsiderationhasbeengiven totheevaluationofthereliabilityandsafetyofthepressuresteamlinetraponboardship andnoglobalorganizationworldwidehasgatheredreasonabledataonitsfailureincidents includingrelatedcomponentsdespitethemanyrisksassociatedwiththefailureofthesystem.Themodelsreviewedinthispaperfortheassessmentofthereliabilityandsafetyof thedifferentcomponentsintheengineroomofashippingvesselcanbeconcludedto haveonemajorshortcomingortheother.Amongthemincludetheinabilityofthe modelstoaddressandaccountforuncertaintyintheevaluationprocess,theexclusion ofkeyreliabilityparameterssuchasthefailurerate,meantimebetweenfailure,and thehazardrateintheevaluationprocess,and finally,theexclusionoftheimportance ofprobability,maintainability,andseverityintheevaluationprocess.Thus,itisworthwhileandpurposefultodevelopamethodologyandprotocolfortheevaluationofthe failuremodes,aswellastoimprovethesystemreliability,preventexpensivesteamleakages,waterhammersinthesteamlines,andenhanceitsoperationalsafetyconceptsonboardtheship.
Inthispaper,however,ananalyticalmodel hybridfailuremodesandeffectsanalysis model whichconsistsofamulticriteriadecision-makingtoolthatusesanIntervalvaluedIntuitionisticFuzzyNumber(IVIFN)inacomplexintuitionisticfuzzysethas beenproposedforthereliabilityandsafetyevaluationofthepressuresteamlinetrap
onboardship.Theuseofthemulticriteriadecision-makingtoolisaimedattheidentificationofthemostcriticalfailuremodesthatcouldcausehighriskandreliabilityconcerns inthepressuresteamlinetrapwhenusedasavalveintheengineroomoftheshipping vessel.Hence,thestudycontributestothereliabilityevaluationliteraturebyaddressing andaccountingforsomeoftheshortcomingsinthereviewedliterature,someofwhich includeuncertaintiesintheevaluationprocess,whichhavebeenaddressedbytheuseof fuzzy-basednumbersintheevaluationprocess.Theuseofreliability-basedcriteriasuch asseverityandmaintainabilityintheevaluationprocessaswellastheintegrationofparameterssuchasthefailurerateandmeantimebetweenfailureofthepressuresteamline trapinthemulticriteriadecision-makingmodel,whichtothebestofmyknowledge havenotbeenusedorintroducedinanyofthecurrentlyexistingreliabilityliterature.
Thecomplexintuitionisticfuzzysettheoryisageneralizedinnovativeconceptdevelopedfromthetraditionalcomplexfuzzyset(CFS)theorybyintroducingthenonmembershiptermtothedefinitionofCFS.Thenoveltyofthecomplexintuitionisticfuzzyset usedinthischapterliesinitsabilityformembershipandnonmembershipfunctionsto achievemorerangeofvalues.Therangesofvaluesareextendedtotheunitcircleincomplexplaneforbothmembershipandnonmembershipfunctionsinsteadof[0,1]asinthe traditionalintuitionisticfuzzyfunctions.Otherbenefitsfromtheuseoftheconceptof thecomplexintuitionisticfuzzysettheoryareintheabilityofthesettoindicateand representboththepresenceandabsenceofassociation,interaction,orinterconnectedness inonesetofthecomplexintuitionisticfuzzysetinsteadoftwosetsascontainintheconventionalCFS.Thecomplexintuitionisticfuzzysethasamembershipandnonmembershipfunctionsthatcanoperateinthesameset,whereasfortheCFS,onlythe membershipfunctionsareusedtoindicatethepresenceorabsenceofassociation,interaction,orinterconnectednesswhenmakingcriticaldecisions.
Therestofthepaperisorganizedasfollows:in Section2,thehybridfailuremodes andeffectsanalysismodelanditsalgorithmareintroduced,thisisfollowedbythepresentationofnumericalimplementationofthemodel,observation,anddiscussionsin Section3.Finally,in Section4,someconcludingremarksaboutthestudyarepresentedas wellastheauthors’ futureresearch.
2.Hybridfailuremodesandeffectsanalysismodel
Intheevaluationofthereliabilityandsafetyofthehigh-pressuresteamtraponboardship, ahybridfailuremodesandeffectsanalysismodel,whichisbasedonamulticriteria decision-makingmodelthatusesanIVIFS,hasbeenproposed.Theevaluationofthe reliabilityandsafetyofthehighlypressurizedsteamtrapisachievedbyprioritizingthe failuremodesthatcouldresultinthemaincriticalreliabilityissuesinthesystem.The model,whichcanbelikenedtothereliability-centeredmaintenanceconcept,isdesigned