ElementsofNumericalMathematicalEconomicswith Excel:staticanddynamicoptimization.Romeo
https://ebookmass.com/product/elements-of-numericalmathematical-economics-with-excel-static-and-dynamicoptimization-romeo/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Static and Dynamic Analysis of Engineering Structures: Incorporating the Boundary Element Method Levon G. Petrosian
https://ebookmass.com/product/static-and-dynamic-analysis-ofengineering-structures-incorporating-the-boundary-element-methodlevon-g-petrosian/ ebookmass.com
Numerical Methods and Optimization in Finance [2nd ed.]
Manfred
Gilli
https://ebookmass.com/product/numerical-methods-and-optimization-infinance-2nd-ed-manfred-gilli/
ebookmass.com
Mathematical optimization terminology: a comprehensive glossary of terms First Edition Keller
https://ebookmass.com/product/mathematical-optimization-terminology-acomprehensive-glossary-of-terms-first-edition-keller/ ebookmass.com
Clean Sweep: VIII Fighter Command against the Luftwaffe, 1942–45 Thomas Mckelvey Cleaver
https://ebookmass.com/product/clean-sweep-viii-fighter-commandagainst-the-luftwaffe-1942-45-thomas-mckelvey-cleaver/
ebookmass.com
The Watcher (Men of Hidden Justice Book 4) Melanie Moreland
https://ebookmass.com/product/the-watcher-men-of-hidden-justicebook-4-melanie-moreland/
ebookmass.com
A Cowboy Christmas Legend Linda Broday
https://ebookmass.com/product/a-cowboy-christmas-legend-lindabroday-3/
ebookmass.com
The Poverty of Critical Theory in International Relations Davide Schmid
https://ebookmass.com/product/the-poverty-of-critical-theory-ininternational-relations-davide-schmid/
ebookmass.com
5 Steps to a 5: AP U.S. Government & Politics 2024 Pamela K. Lamb
https://ebookmass.com/product/5-steps-to-a-5-ap-u-s-governmentpolitics-2024-pamela-k-lamb/
ebookmass.com
Corporate spirit: religion and the rise of the modern corporation Amanda Porterfield
https://ebookmass.com/product/corporate-spirit-religion-and-the-riseof-the-modern-corporation-amanda-porterfield/
ebookmass.com
Alessandro Terenzi
https://ebookmass.com/product/flow-analysis-for-hydrocarbon-pipelineengineering-alessandro-terenzi/
ebookmass.com
ELEMENTSOFNUMERICAL MATHEMATICALECONOMICS WITHEXCEL Thispageintentionallyleftblank
ELEMENTSOF NUMERICAL MATHEMATICAL ECONOMICSWITH EXCEL STATICANDDYNAMIC OPTIMIZATION GIOVANNI ROMEO IndependentFinancialAdvisor
AcademicPressisanimprintofElsevier 125LondonWall,LondonEC2Y5AS,UnitedKingdom
525BStreet,Suite1650,SanDiego,CA92101,UnitedStates
50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom
Copyright © 2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicor mechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem,without permissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthe Publisher’spermissionspoliciesandourarrangementswithorganizationssuchastheCopyrightClearance CenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions.
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher (otherthanasmaybenotedherein).
Notices Knowledgeandbestpracticeinthis fieldareconstantlychanging.Asnewresearchandexperiencebroaden ourunderstanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecome necessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationor methodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhom theyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceor otherwise,orfromanyuseoroperationofanymethods,products,instructions,orideascontainedinthe materialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-817648-1
ForinformationonallAcademicPresspublicationsvisitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: BrianRomer
AcquisitionEditor: BrianRomer
EditorialProjectManager: DevlinPerson
ProductionProjectManager: PaulPrasadChandramohan
CoverDesigner: MarkRogers
TypesetbyTNQTechnologies
I Excelandfundamentalmathematics foreconomics 1.ExcelVBA,solver,andotheradvanced worksheettools
1.1VBAintroductionandmainstatements3
1.2TheExcelSolver:simplexLP,Generalized ReducedGradient,andevolutionary21
1.3What-ifanalysis:scenariomanager,GoalSeek, DataTable,andcontourlines29
1.4Scatterchartsandtrendlines40
2.Univariateandmultivariatecalculus 2.1Numericalmethodsforunivariate differentiation45
2.2Numericalmethodsforunivariate integration58
2.3Numericalpartialdifferentiation66
2.4Applicationsineconomics75 Exercises83
3.Elementsoflinearalgebra 3.1Built-inExcelmatrixfunctionsandbasic operations88
3.2LinearsystemsandresolutionmethodsinExcel: Cramer,Solver,Inverse95
3.3Eigenvaluesandeigenvectorssearch:analytical andgraphicalapproach107
3.4Quadraticformsanddefi nitenessofasymmetric matrix115
3.5Leontiefopenmodel121
3.6Equilibriuminnmarkets124
3.7Economicpolicymodeling:objectivesand instruments129 Exercises134
4.Mathematicsfordynamiceconomic models
4.1Ordinarydifferentialequationsandnumerical methods:EulerandRunge-Kutta140
4.2Forceofinterest,Walrasianstability,utility functions,andcapitalformationwithordinary differentialequation147
4.3Differenceequationsandphasediagrams159
4.4Cobwebmodelofpriceadjustmentandother economicmodelswithdifference equations170
4.5Systemsoflineardifferentialequations181
4.6Tourism fightbetweentwocompeting regions202
4.7Walrasianadjustmentwithentry206 Exercises209
II Staticoptimization 5.Classicalstaticnonlinearoptimization theory
5.1Classicalunconstrainedoptimizationofa univariatefunction220
5.2Classicalunconstrainedoptimizationofa multivariatefunction232
5.3Someeconomicapplicationsofthenonlinear unconstrainedoptimization247
5.4Numericalsteepestdescentmethodappliedto theunconstrainedoptimization withVBA256
5.5NonlinearproblemsinRn withequality constraints:Lagrangemultipliersand Solver264
5.6NonlinearproblemsinR2 withequality constraints:contourlines272
5.7Nonlinearproblemswithinequality constraints285
Exercises288
6.Microeconomictheoryinastatic environment 6.1Theconsumerproblem:cardinalversusordinal utilityapproach296
6.2Consumeroptimizationandderivationof thedemandcurveinthecardinal approach297
6.3Consumeroptimizationandderivationofthe demandcurveintheordinalapproach307
6.4The firmproblem319
6.5One-inputclassicalproductionfunction320
6.6Two-inputsproductionfunctions322
6.7Isoquantsandtheconstrainedproduction optimizationwithtwoinputs331
6.8ProductionEdgeworthbox,contract curve,andthepossibilityfrontier construction335
6.9Short-run,long-runcostsandtheenvelope averagetotalcostsderivation340
6.10Perfectcompetitivemarkets:short-run,long-run supplycurvesandmarketequilibrium350
6.11Monopolisticmarketequilibrium:the Chamberlinmodel356
6.12Marketswithhigh-entrybarriers:monopolyand theCournotduopolymodel360
6.13Gametheory.Zero-sumgamesand minimaxcriterion:matrixandgraphical resolutions370
Exercises376
7.Linearprogramming 7.1Standardformulationofalinearprogramand resolutionmethods383
7.2Applicationstothestaticproductionplanning andcapitalbudgeting389 Exercises408
8.Nonlinearoptimizationappliedtothe portfoliotheory
8.1Portfoliomodelingandtheefficientfrontier construction417
8.2Investor’sutilityandtheoptimalportfolio choice427 Exercises432
Dynamicoptimization 9.Calculusofvariations
9.1ThefundamentalproblemoftheCalculusof Variations438
9.2DiscreteapproximateCalculusofVariations: Lagrangemultipliersandcontourlines solutions442
9.3SetupoftheExcelworksheetforCalculusof Variationsproblems:theSolversolution451
9.4GeneralcasesdevelopedinExcelwith fixedand variableterminalpoints453
9.5Dynamicoptimizationforamonopolist469
9.6Unemploymentandinflation471
9.7TheEisner Strotzmodel475
9.8TheoptimalconsumptionRamseymodel479
9.9Inventorydynamicoptimization481
9.10Optimalcapitalstructureandthe firmcostof capital482
9.11ContourlinessolutionforCalculusofVariations usingtheVBAcode487
9.12CalculusofVariationswithfunctionals involvingtwoindependent functions494
9.13CalculusofVariationsconstrainedproblems497
9.14CheckingtheSecond-OrderConditionsin Excel505 Exercises511
10.Theoryofoptimalcontrol 10.1Theoptimalcontrolproblemandthe Pontryagin’smaximumprinciple522
10.2NonlinearHamiltonianandlinearHamiltonian (bang-bangcontrol)523
10.3SetupoftheExcelworksheetforoptimal controlproblems525
10.4Bang-bangcontrolproblems542
10.5Consumptionmodel547
10.6Investmentmodel554
10.7Inventoryoptimization561
10.8Twostatevariablescontrol problems563
10.9Current-valueHamiltonian571
10.10Constraintsonthestatevariable:alinearcase withaninventoryapplicationwithVBA576
10.11Steepestdescentnumericalapproachfor optimalcontrolproblemsusingVBA587
10.12Checkingthesufficientconditionsin Excel593
Exercises600
11.Discretedynamicprogramming 11.1Bellman’sprinciple,discreteshortestpath problems,andtheExcelMINIFS function612
11.2Discretedynamicsystems:tabularmethod, Exceldatatable,andSolver619
11.3Cargoloadingallocationproblems:tabular methodandtheExcelSolver629
11.4MultistageallocationproblemsusingtheExcel Solver632
11.5Equalityconstrainedoptimizationproblems usingtherecursiveBellman’sapproach636
11.6Dynamiceconomicproblemssolvedwith DiscreteDynamicProgramming639
11.7DiscreteDynamicProgramming,Optimal Controltheory,andCalculusofVariations:a synthesis649
Exercises652
IV Specialtopics 12.Dynamicproductionplanningand inventorymodeling
12.1Multiperiodproductionmodelswithlinear programming661
12.2Wagner Whitinalgorithmforinventory dynamicmodeling669
12.3EliezerNaddorstochasticsingle-period inventorymodels677 Exercises687
13.Dataanalysisforbusinessand economics
13.1Asimplewaytoorganizeaspreadsheetusing theVBAcodeandbookmarks696
13.2Pivottables,Pivotcharts,anddynamic dashboardsformanagerialdataanalysis697
13.3Basicdescriptivestatistics711
13.4Somenumericalcalculusappliedtocontinuous densities721
13.5Univariate,multivariateregressionanalysisand theANOVAtables727
Exercises756
14.EssentialMonteCarloanalysis
14.1TheMonteCarlomethodandthegeneration ofrandomnumbers764
14.2TheMonteCarlomethodforbusiness decisions773
14.3Numericalintegration788 Exercises792
Thispageintentionallyleftblank
Excelandfundamental mathematicsforeconomics PartIofthisbookaimsatgivingtothereaderthefundamentaltoolsof someimportantadvancedworksheetcapabilities,includingtheExcelVBA, aswellasthefundamentaltoolsofthemathematicaleconomicsapplied withinaspreadsheet.Thesearealltoolsthatwillbeneededwithinthe courseofthewholebookandtoolsthatanyeconomistanalystshouldmaster withinacomputerlanguageframework.
Chapter1willreviewsomeVBAcodes,whosepriorknowledgewouldbe somehowrequiredfromthereader,inordertooptimallyutilizetheworksheetsthatwillbeimplementedwithinthebook.TheExcelmacrosused withinthebookarenotataveryadvancedlevel,butstill,theywillrequire (besidethemathematicalknowledge)acertaindegreeofVBAprogramming languagemastery.
Otheradvancedfeatures,liketheExcelSolver,the what-ifdatatableanalysis (thesetwowillbeusedalotinthebook), contourdiagrams, scattercharts,and trendlines willbeintroducedandthendevelopedindetailwithinthebook.
Chapters2 4willinsteadgivetheessentialelementsofthemathematical economicsappliedwithExcel.
Threeimportantareasofthemathematicaleconomicsarecoveredhere.
Chapter2willcovertheessentialelementsofthestandardcalculus (numericaldifferentiationandintegration)appliedwithinaspreadsheet.
Chapter3isdedicatedtotheessentialelementsofthelinearalgebra.
Chapter4isinsteaddevotedtothedynamicalmathematics(ordinary differentialanddifferenceequations,aswellasthesystemsofdifferential equations).Thisisachapterofparamountimportanceasmanyofthetechniqueswewilldevelopinthischapterwillbeusedwithinthedynamicoptimizationsectionandalsobecausethedifferentialanddifferenceequations representthekeyconstituentareaoftheeconomicdynamicmodeling.
Inallthesethreechapters,someeconomicapplicationsarealsoproposed.
Thispageintentionallyleftblank
1 ExcelVBA,solver,andother advancedworksheettools OUTLINE 1.1VBAintroductionandmain statements3
TheVBAEditorandthemodules3 1VisualBasicMacros6 UsingtheMacroRecorder9 MainVBAstatementsusedwithinthe book(theloopingstructures)10
EXAMPLE 1(CONSTRAINEDOPTIMIZATION IN <2 WITH LAGRANGEMULTIPLIERS USINGTHE VBA DO UNTIL)13 ForNextLooping16
EXAMPLE 2(HEATSHEETHIGHLIGHTING THEBESTPERFORMINGFUNDSWITHIN THEIRPEERGROUP)17
2UserDefinedFunctions(orfunction procedures)19
EXAMPLE 3(NUMERICAL INTEGRATION)19
1.2TheExcelSolver:simplexLP, GeneralizedReducedGradient,and evolutionary21 NonlinearGeneralizedReduced Gradient21 SimplexLinearProgramming26 Evolutionary27
1.3What-ifanalysis:scenariomanager, GoalSeek,DataTable,and contourlines29 EXAMPLE 1(WHAT-IFANALYSISON NPV AND IRR CALCULATION)31
1.4Scatterchartsandtrendlines40 .
1.1VBAintroductionandmainstatements
TheVBAEditorandthemodules
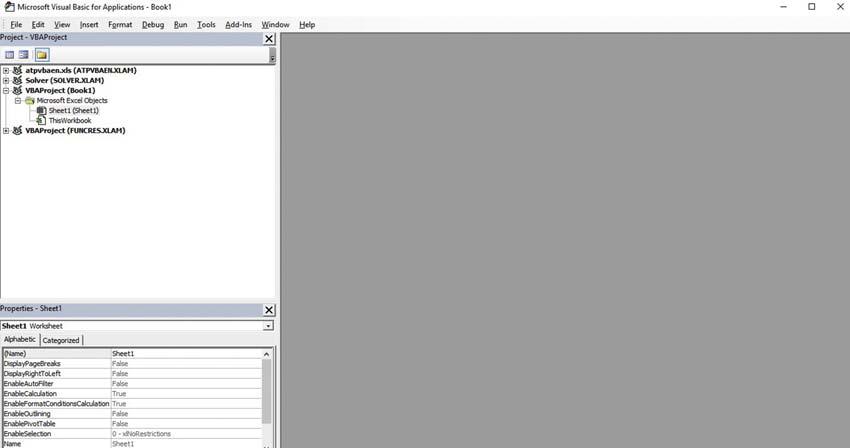
WhenwritingaVBAcode,the VBEditor needstobeusedinExcel.TheVBEditoristhe workingareawherewewillwritea Macro anditisaccessiblefromthetabDeveloperofthe Ribbonbar,asshownin Fig.1.1-1.Then, Fig.1.1-2 willappear.
1.ExcelVBA,solver,andotheradvancedworksheettools
Ontheleft-handsideof Fig.1.1-2,wehavethe ProjectExplorer (atthetop)andasecond panel(atthebottom)whichcontainsthe Properties (modifiablebytheuserwhennecessary) referredtoany ExcelObject weselectinthe VBAProject window:aworksheet,aworkbook, oramoduleitself.
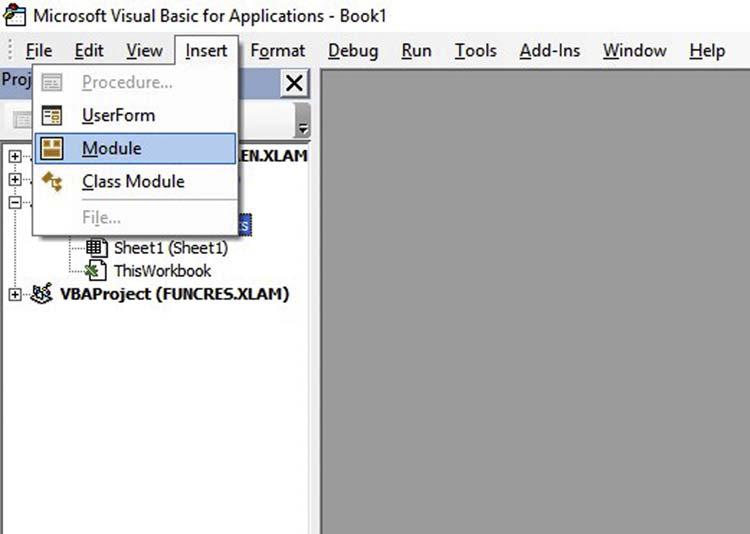
Now,whatwehavetodoistoopentheactualworkingareawheretowriteourVBAcode, andthisisdonebyinsertinga Module,asin Fig.1.1-3
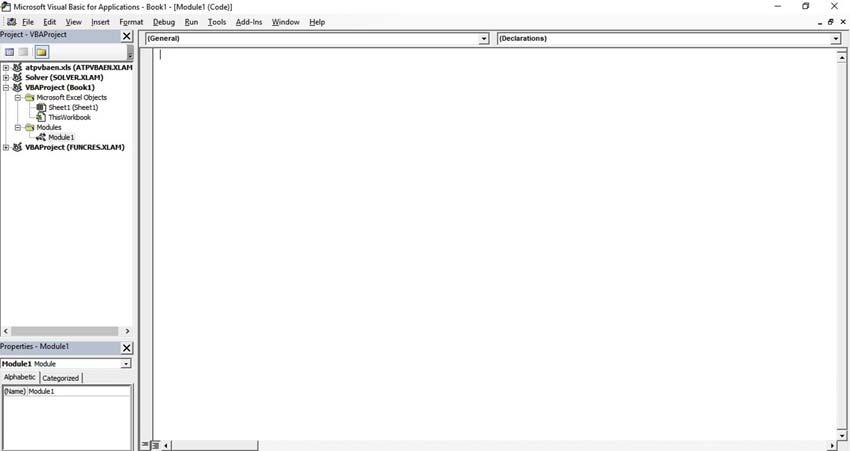
Amodulecanbeinserted,forexample,byclickingonInsertonthe MenuBar andthenselectingModule,and finallytheVBEditorwillbecompletedwiththeModuleinsertedasin Fig.1.14.Ifwewant,wecanrenameaModuleusingthepropertieswindowatthebottomofthescreen of Fig.1.1-4.Whenrenamingit,wejustneedtopayattentiontospaces,whicharenotaccepted, andtheunderscorecharactershouldbeusedinplaceofaspace.Nowthatwehaveamodule,we canbeginwritingacode.Thisiscalleda Macro (orprocedure,orroutine).
ExcelVBAalsoallowstocreatea UserDefinedFunction,whichwillenrichthelibraryof thebuilt-infunctions.
FIGURE1.1-2 VBAProjectExplorer(withExcelObjects)andthePanelPropertiesatthebottom.
FIGURE1.1-1 TheVBEditorintheExcel2019.
FIGURE1.1-3 InsertingaModulefromtheMenubar.
FIGURE1.1-4 ModuleInsertedwheretowriteaVBAprogram.
1.ExcelVBA,solver,andotheradvancedworksheettools
1VisualBasicMacros InExcel,theroleofaMacroisessentiallythatofgettinganactionautomated,without manualinterventionontheExcelsheet.ItisacommandwegivetoExcel,suchthatitperformssomethingwewanttodo(e.g.,arepeatedcalculationuntilaspecifiedcellisequal tozero).Thewaytodothatistocreatea Sub procedureintheModule.
Theprocedureisinthefollowingform:
VBAStatements
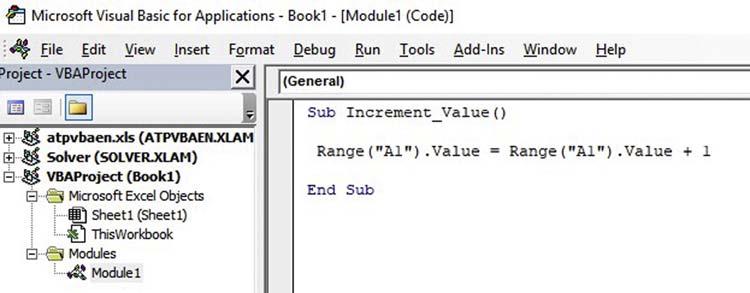
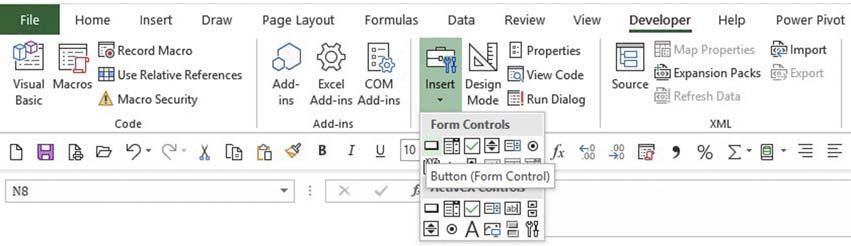
Supposewewanttoincrementthevaluein CellA1ofaworksheetby1.Thecodewouldbe asin Fig.1.1-5.Nowaquestionarises.Howcanwegetthecodeactivatedintheworksheet? Inotherwords,howcanwemakethemacrorun?Thisisnormallydoneinsertinga Button in theworksheet,whichisthenassociatedtothespecificcodewehavecreated.Thebuttonwe arereferringtoisthe FormControl,asshownin Fig.1.1-6
FIGURE1.1-5 IncrementingthevalueofaCell.
FIGURE1.1-6 FormControlButtontorunaSub.
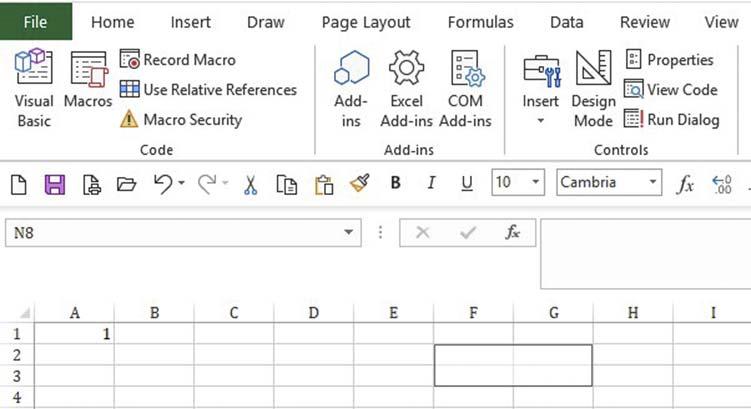
FIGURE1.1-7 InsertingaButton(formControl)inaworksheet.
UsingtheAlt-KeytofacilitatetheButtonpositioningonthesheet,wedecidetoposition theButtonasin Fig.1.1-7
Releasingthemouse,ExcelwillaskustoassociateaMacrotothisButton,andwechoose theonlyMacroavailablesofar,whichisthe SubIncrement Value asin Figs.1.1-8.Then,the
FIGURE1.1-8 AssigningamacrotoaButton.
1.ExcelVBA,solver,andotheradvancedworksheettools
FIGURE1.1-9 NamingtheButtonforthemacro “Increment_Value”
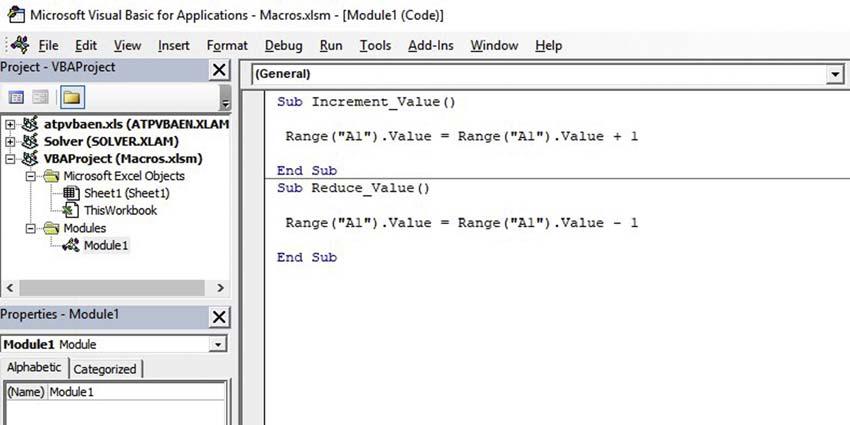
macroisavailabletoberunthroughtheButton “IncrementValue,” asin Fig.1.1-9.Wecan createasecondMacrocalled “Reduce_Value ” asin Fig.1.1-10,insertingasecondButtonasin Fig.1.1-11
FIGURE1.1-10 Secondmacro “Reduce_Value.”
UsingtheMacroRecorder TheMacrocanbealsorecordedinExcelusingthe RecordMacro optionunderthe DeveloperTab.
Forexample,supposewewanttoaddnew sheetstoaworkbook;wecansimplyrecordamacrotodothat.Whatwedoisjustclickingonthe RecordMacro optionaddinganewsheet;then,whenwe fi nishrecording,weclickonthelittlesquare Stop Recording shownin Fig.1.1-12 .Themacrowillbeavailableinanewmoduleofthe ProjectExplorer.
Recordingamacroisusefulwhenwearenotsureabouttheexactcodetouseandwe lookforsomehintssuggestedbyExcelregardingaspecificoperationwewanttoperform. Wecanrecordasimilaroperation,thenmodifyitobtainingthe finalinstructionwewere lookingfor.
Theresultingmacro(tobefoundintheVBEditor)wouldbeasfollows:
SubAdd New SheetsðÞ
Sheets AddAfter : ¼ ActiveSheet
FIGURE1.1-11 SecondButtonforthemacro “Reduce_Value.”
StopRecording. 1.ExcelVBA,solver,andotheradvancedworksheettools
Ifwewanttoaddfoursheetsinoneshotthemacrowouldbemodifiedasfollows:
SubAdd 4 New SheetsðÞ
Sheets:AddAfter : ¼ ActiveSheet; Count : ¼ 4
EndSub MainVBAstatementsusedwithinthebook(theloopingstructures)
ManyoftheVBAsubproceduresneedtobeenteredmanuallyintheVBEditor,andwe willshowherethemainstatementsusedwithinthebook.
Thesearethe Looping structures,whichareVBASubsthatare finalizedat:
1. repeatingasetofinstructions,untilaspeci ficgoalisreached,forexample,untilthe Excelsetsaspeci ficcellequaltozero,oruntilaspecifictargetcellislessthanadesired ε (theSteepestDescentVBAcodeshowninSection5.4isanexample)or
2. finalizedatrepeatingasetofinstructionsforacertainnumberoftimes.
A looping structurebelongingtothe firstcategoryisthe DoUntil statement,sometimes usedinconjunctionwiththe ExcelSolver,tooptimizeaspecificobjectivefunction.
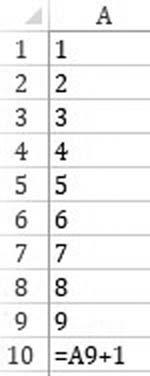
Supposewehavealistof10numberslikein Fig.1.1-13,wherethelastoneineffectcontainsaformula.Inthiscase,itisjustaformulathataddsthevalue1tothepreviouscell. Theobjectiveistoaddautomaticallyanewrowinanewupdatingsheetround,including thecountingformulaandremovingtheformulafromthepenultimatecell(whichwasthelast cellinthepreviousupdatinground).
Todothatusingthe DoUntil statementcanbeaperfectsolution.Thefollowingwouldbe thestatementwhichmakesExcelselectthe CellA1asa firststepandthenmoveforwarduntil thecellisempty:
Rangeð}A1}Þ:Select
DoUntil IsEmptyðActiveCellÞ
FIGURE1.1-12
ActiveCell:Offsetð1; 0Þ:Select Loop
Excelmovesforwardfrom CellA1alongthesamecolumnusingtheinstruction:
ActiveCell Offsetð1; 0Þ Select
insertedbetween DoUntil and Loop (thisisalwaysinsertedbelowtheinstructionwewantto repeat).
Thecompletecodeofwhatwewanttoachieveisshownin Fig.1.1-14.Wecanfollowstep bystepthemacrobypressing F8onthekeyboard.Thisisuseful,especiallywhensomething doesnotworkasplannedandwewanttostudythemacroindetail,investigatingatwhich lineofthecodethemistakecouldbelocated.Thiscanbedonealsousingthe Debug option fromtheMenuBarasshownin Fig.1.1-15.
Therearesomeotheralternativestotestforablankcell,notonlyusingthe DoUntil Is Empty(ActiveCell);forexample,wemayalsousethefollowing: DoUntil ActiveCell Value ¼ }}
Also,averyslightlydifferentcodewouldbethe LoopUntil statement,asdescribedas follows
FIGURE1.1-13 Listofnumbersfrom1to10.
1.ExcelVBA,solver,andotheradvancedworksheettools
FIGURE1.1-14 AddinganewRowtoanArray.
FIGURE1.1-15 SteppingthroughaVBAcode.
I.Excelandfundamentalmathematicsforeconomics
ActiveCell:Offsetð1; 0Þ:Select
LoopUntil IsEmptyðActiveCellÞ
wherewehavemovedthe Until,withtheconditiontobemet,after Loop.
Anothersimilarstatement,the DoWhile statement,wouldalsoreachthesamesolution withthecodeexpressedasfollows:
Rangeð}A1}Þ:Select
DoWhile ActiveCell:Value <> }}
ActiveCell:Offsetð1; 0Þ:Select Loop
Inthiscase,wehavereplacedthetestingconditionoftheemptycell,toexittheloop, testingwhetherthecellisdifferentfromzero.
Anotheralternativeistousethe if statementinsidethe Loop asfollows: Do If ActiveCell:Value ¼ }} ThenExit Do
ActiveCell Offsetð1; 0Þ Select Loop
EXAMPLE 1(CONSTRAINEDOPTIMIZATIONIN <2 WITH LAGRANGEMULTIPLIERS USINGTHE VBA DO UNTIL)
LetustrytosetupaVBAcodeusingthe DoUntil Loopingstatement,fortheapproximate solutionofthefollowingconstrainedoptimizationproblem(thesameexampleinsolvedusingtheExcelSolverinSection5.5):
TheLagrangianfunctionis:
1.ExcelVBA,solver,andotheradvancedworksheettools
FIGURE1.1-16 Example1:constrainedoptimizationexcelsetup.
fromwhichweobtainthesystemof(3) first-ordercondition equations:
Fromthethirdequation,weobtain l1 ¼ 5andthestationarypoint x*(4.5,5.5).
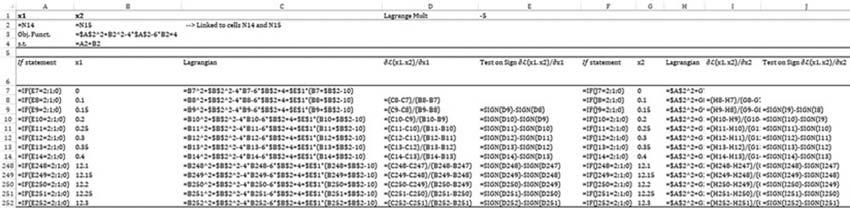
Thewaywecansolvetheproblemis firstsettingupinExceltheequations Lðx1 ; x2 ; l1 Þ;
vLðx;lÞ vx1 ,and vLðx;lÞ vx2 asin Fig.1.1-16,where:
CellA2 CellB2 ¼ x1 and x2,respectively,linkedtotheoptimizationresultsof Fig.1.1-17.
CellB3 ¼ ObjectiveFunction
CellB4 ¼ Constraint
CellE1 ¼ LagrangeMultiplier l1
(Itisthisvaluethatwillbeincrementedordecremented via theVBAcodeof Fig.1.1-18, untilthesolutionisfound)
FIGURE1.1-17 TestConditionfortheoptimization.
FIGURE1.1-18 VBALoopingstructureforthenonlinearconstrainedoptimization(withLagrangemultipliers).
SincebeforetheoptimizationwedonotknowwhichsigntheLagrangemultiplierwilltake on,wewilljusttryapositivevalue(thismustallowachangeinthesignofthepartialdifferentialunder ColumnD and ColumnI).
IftheMacrostopswithout findingthesolution,thenwetrywithanegativevalueinthe Lagrangemultiplier(again,thismustallowachangeinthesignofthepartialdifferentialunder ColumnD and ColumnI).
Theworksheetlimitsthechoiceuptoamaximumvalueof3fromaminimumvalue of 10,usingadrop-downlist.
Thesolutionwillbefoundwhen CellN18isequaltozero.See Fig.1.1-17 and Table1.1-1.
ColumnA ¼ ifstatementthatreturnsx1
TABLE1.1-1
ColumnB ¼ x1
ColumnC ¼ Lagrangianasafunctionofx1 holdingx2 constant
ColumnD ¼ partialdifferential vLðx; lÞ vx1
Whenthedifferentialchangessign,thevalueof2isreturned.Atthesamerowthestationarypointwillbefound.
ColumnF ¼ ifstatementthatreturnsx2
ColumnG ¼ x2
ColumnH ¼ Lagrangianasafunctionofx2 holdingx1 constant
ColumnI ¼ partialdifferential vLðx; lÞ vx2
ColumnJ ¼ testconditiononthesignof vLðx; lÞ vx2 :
Whenthedifferentialchangessignthevalueof2isreturned.Atthesamerowthestationarypointwillbefound.
Beginningwithapositivevaluein CellE1ofLagrangemultipliertheVBALoopof Fig.1.118 reducesthisvaluerepeatedly(thisisbecauseoftheVBA DoUntil)by0.5untiltheoptimizationisreached;i.e.,when CellN18 ¼ 0(andconstraint x1 þ x2 ¼ 10issatisfied);when optimizationisreached CellN20s0mustalsoresult,whichmeansthatthetwopartialdifferentialshavechangedsignsomewherealongtherangeoftheindependentvariables.
Otherwise,ifthe CellE1reachesthevalueofzerowithoutanyoptimization(namely, Cell N18isstilldifferentfromzero)theVBAexitstheLoopandreturnsa MessageBox.Therefore, weneedtoreoptimizeinputtingin CellE1anegativevalue,makingthemacroincreasethis valueuntiltheoptimizationisreached.
Table1.1-1 isthe finaloptimizationresult.Inthiscase,theoptimizingLagrangemultiplier turnsouttobenegative(i.e., l1 ¼ 5)ascalculatedbythetheoreticalsolution.
ForNextLooping Anotherloopingstructureisthe ForNext. InVBA,thisloopingstructurerepeatsasetof instructionsacertainnumberoftimes.
Whatweneedhereisa variable whichallowstocountthroughtheloop.Thisisthe Loop Counter,anditisnormallydenotedwithaletter.
InVBA,itisdefinedasanintegerasfollows:
DimiAsInteger The ForNext statementthenbegins,recallingthe LoopCounteri andstatinghowmany times(e.g.,100)weneedtorepeatasetofinstructions:
Fori [ 1 to 100 whichmeansthatthe loop willcount100times.
Whatmakestheloopgoforwardistheword Next.Between For and Next wehavethereforetoinsertthesetofinstructionstoberepeated.
EXAMPLE 2(HEATSHEETHIGHLIGHTINGTHEBESTPERFORMINGFUNDSWITHINTHEIR PEERGROUP)
Letusconsideraninvestmenthousethathasgatheredthedataof Table1.1-2 onthefunds theymanage,where:
% Change ¼ performanceoftheperiod ðOneweek ; OneMonth; etc Þ
Rank ¼ RankpositionwithinthePeer Group
Count ¼ NumberofFundswithinthePeer Group
Qrtl ¼ InwhichQuartile ðfrom 1 to 4Þ thefundispositionedwithinthePeer Group
Forexample,Fund1hasaperformanceof 3.79%overamonth,withinitspeergroup (e.g.,EuroEquity)madeof55funds(Count)anditappearstobeinthe firstquartile,as it’sbeenrankedintheeighthposition.
Now,usingtheVBA ForNext statement,wewanttoperformaconditionalformatting changingthecolortotheFundsforeachperformanceperiod(OneWeek,OneMonth,Three
TABLE1.1-2 PerformanceandRankingforeachfundwithineachPeerGroup.