ElectronicStructureandSurfacesofSulfide Minerals:DensityFunctionalTheoryand ApplicationsJianhuaChen
https://ebookmass.com/product/electronic-structure-andsurfaces-of-sulfide-minerals-density-functional-theory-andapplications-jianhua-chen/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Chemistry of Functional Materials Surfaces and Interfaces: Fundamentals and Applications Andrei Honciuc
https://ebookmass.com/product/chemistry-of-functional-materialssurfaces-and-interfaces-fundamentals-and-applications-andrei-honciuc/
ebookmass.com
Fluid Inclusion Effect in Flotation of Sulfide Minerals 1st Edition Shuming Wen
https://ebookmass.com/product/fluid-inclusion-effect-in-flotation-ofsulfide-minerals-1st-edition-shuming-wen/
ebookmass.com
Structure in the Sea: The Science, Technology and Effects of Purpose-Built Reefs and Related Surfaces William Seaman
https://ebookmass.com/product/structure-in-the-sea-the-sciencetechnology-and-effects-of-purpose-built-reefs-and-related-surfaceswilliam-seaman/
ebookmass.com
Liquid-phase Extraction Poole Colin F. (Ed.)
https://ebookmass.com/product/liquid-phase-extraction-poole-colin-fed/
ebookmass.com
Securities Industry Essentials Exam 2023-2024 For Dummies with Online Practice Steven M. Rice
https://ebookmass.com/product/securities-industry-essentialsexam-2023-2024-for-dummies-with-online-practice-steven-m-rice/
ebookmass.com
The Norton Field Guide to Writing (Fifth Edition)
https://ebookmass.com/product/the-norton-field-guide-to-writing-fifthedition/
ebookmass.com
The Maiden Kate Foster
https://ebookmass.com/product/the-maiden-kate-foster/
ebookmass.com
Radiotherapy and the Cancers of Children, Teenagers and Young Adults (Illustrated Edition) Tom Boterberg
https://ebookmass.com/product/radiotherapy-and-the-cancers-ofchildren-teenagers-and-young-adults-illustrated-edition-tom-boterberg/
ebookmass.com
Language Change, Variation, and Universals Culicover https://ebookmass.com/product/language-change-variation-anduniversals-culicover/
ebookmass.com
Psychology Fifth Edition Daniel L. Schacter https://ebookmass.com/product/psychology-fifth-edition-daniel-lschacter/
ebookmass.com
ElectronicStructureandSurfaces ofSulfideMinerals DensityFunctionalTheoryandApplications
JianhuaChen
ZhengheXu
YeChen
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom
50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2020CentralSouthUniversityPress.PublishedbyElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical, includingphotocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwritingfrom thepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthePublisher ’spermissionspoliciesand ourarrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency,can befoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanas maybenotedherein).
Notices
Knowledgeandbestpracticeinthis fieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbe mindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessional responsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityfor anyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromany useoroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-817974-1
ForinformationonallElsevierpublicationsvisitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher:CandiceJanco
AcquisitionsEditor:AmyShapiro
EditorialProjectManager:EmeraldLi
ProductionProjectManager:SruthiSatheesh
CoverDesigner:MilesHitchen
TypesetbyTNQTechnologies
Preface Flotationisaprocessofseparatingfinevaluablemineralparticlesfromtheirassociated gangues.Inflotation,hydrophobicmineralsofinterestareattachedtoairbubbles,floated underthebuoyancyforceofbubblestothetopofpulp,andcollectedasproductsreferredto asconcentrate,leavinghydrophilicparticlesinthepulpastailings.Flotationhasbeenused inlarge-scalemineralprocessingindustrysincethe1920s.In1921,Perkinsfirstpatented theslightlysolublethiocarbamateasanonoilchemicalcollectorforsulfidemineral flotation,followedbyKellerwhoinventedin1925water-solublexanthatesandWhitworth whodevelopedin1926dithiophosphate,whichrevolutionizedflotation.During1930s,the applicationofsoapsandcationicaminecollectorsindustrializedprocessingofnonmetallic ores.Duetoitshighefficiencyandlowcost,flotationiscurrentlyusedtoprocessannually overbillionsoftonsofores,inadditiontoitswidelyexpandingapplicationtowastewater treatmentandrecyclingofvarioustypesofvaluablesfromelectronicwastes,metallurgical slugs,usedbatteries,etc.Theimportanceofthefrothflotationtotheeconomyofthe industrialworldhasbeenconsideredtobeenormous.
Manyearlyeffortsatunderstandingflotationweredirectedtowardexplainingdifferential flotationintermsoftherelativeocclusionofgases.In1916,bubbleswereconsideredtobe attheheartofflotationscience.
TheroleofinterfacesinflotationhadbeenconsideredbySulmanby1912.Thefirstdirect applicationofthermodynamicstosystemssimilartoflotationwasthatofvonReinders,who deducedhowfinesolidparticleswouldbedistributedbetweenoilandwaterphasesbased onMaxwell’scapillarityequationsin1913.In1915,Ralstonsuggestedthatflotationmight resultfromtheelectricalattractionbetweennegativelychargedairbubblesandpositively chargedmineralparticles.In1917,TaggartandBeachfairlylucidlyapplied thermodynamicsconceptsdirectlytoflotation.Atpresent,thermodynamicshasbecomea fairlywidelyusedtoolfortheanalysisofflotationphenomena.
In1917,Andersonsuggestedthatadsorptionmightplayadominantroleinflotationand usedtheGibbsadsorptionequationtodiscussthefrotheradsorptionattheair water interface.In1920,Langmuirfoundthecorrelationbetweenadsorptionandhydrophobicity. Hereportedthatoleicacidcreatedlargecontactanglesoncleavedcalciteandgalenabut onlysmallanglesoncleanglassandcleavedmica.In1928,Taggartdescribedtheresultsof adsorptiontestsonsulfidemineralsthatrelatedthestructureoftheadsorbatetoitsabilityto
actasaflotationcollector.Taggartformulatedthedefinitionofthemolecularstructure neededforasolubleflotationcollector,namely,thatitmustpossessbothapolargroupthat bindsittothesurfaceandanonpolargroupthatcanorientawaywhenadsorbedata mineral waterinterface.AlthoughsuchearlyresearchersasFahrenwald,Sulman,and Taggartcarriedoutanumberofexperimentstoelucidateflotationphenomena,thefounder ofthescientificbasisofflotationwasA.M.Gaudinandhiscolleagues,whoopenedthe beginningofthemodernapproachtoresearchinflotationchemistry.Majoradvances, particularlystartinginthe1950s,wereachievedtoflotationsystemsthroughbetter understandingandapplicationofthefundamentalprinciplesofsurfaceandcolloid chemistry,particularlyelectricaldouble-layerphenomena.
Sincemostofnaturalmineralsareoriginallynotsufficientlyhydrophobicforeffective attachmenttoairbubbles,akeyforseparatingvaluablemineralsfromganguemineralsis thereforetorenderthetargetmineralshydrophobicbyselectiveadsorptionofadded chemicalsknownascollectorsinmineralprocessing.Collectorscanadsorbonmineral surfacesbyelectrostaticattraction,electrochemicalreaction,chemicalbinding,hydrogen bonds,etc.Toachieveselectiveadsorptionofcollectorsontargetmineralsrequires designingspecialstructuresofcollectorstosuitparticularmineralsurfaces.Anumberof theorieshavebeenproposedtoexplaintheselectivityofcollectoradsorptionatmineral surfacesinflotation.In1930,forexample,thesolubilityproducttheoryofsolutionswas suggestedbyTaggartthatthesmallerthesolubilityproductofthecompoundsformedby reagentandmetallicionsis,thestrongeristheadsorptionofthereagentsonthe correspondingminerals,hencethemoreeffectiveflotation.Thistheoryhasprovided satisfactoryexplanationonsomeflotationphenomena,suchasstrongflotationofcalcium mineralsandweakerornegligiblecollectingpowerofsilicatemineralsbyoleicacids. Similarly,theproductsolubilitytheoryhasbeenusedtoexplainselectiveflotationofmetal sulfidemineralsfromganguemineralsbyxanthate.Othertheoriesbasedonchemical reactions,chelation,andcoordinationofcollectorswithmetalionsinsolutionshavealso beenproposedtoexplainselectiveflotation.Inthesetheories,thepotencyofmetalionsto reactwithcollectorsinbulksolutionsisusedtoinfertheirinteractionsonmineralsurfaces. Clearlytheinfluenceofthemineralsurfacestructureandthepropertiesofadjacent coordinationatomsontheirinteractionswithcollectorsarenotconsideredinthesetheories. Therefore,theycannotexplainwhycopper,lead,andironsulfidescanbeeffectivelyfloated byxanthate,butnottheircorrespondingoxidizedminerals.Theatoms(ions)inmineral crystalstructureandonmineralsurfacesareknowntointeractwitheachother,which greatlyaffectstheirreactivitywithcollectors.Forexample,thereactivityofironinhematite (Fe2O3)andinpyrite(FeS2)withcollectorsisdrasticallydifferent,leadingtotheuseof completelydifferentcollectorsforhematiteflotationandpyriteflotation.Pradipsuggested thattheselectivityofflotationreagentsdependsgreatlyonthe“structural/stereochemical compatibility”betweenthemoleculararchitectureoftheadsorbingcollectorandthe specificstructureofmineralsurface.Moreaccuratepredictionofinteractionsbetweenthe flotationreagentmoleculeandthemineralsurfacerequiresbetterunderstandingofspatial effectofmineralsurfaces.AlthoughLangmuirnoticedtheeffectofsolidsurfacestructure onadsorptionasearlyas1917,actualeffectofmineralsurfacestructureoncollector
adsorptionremainsunknown.M.C.Furstenauetal.wroteinTheFrothFlotationCentury that“Wearenowatastagewherethefurtherimprovementoftheflotationprocessrequires adeeperunderstandingofitsfundamentaltheory.”
In1925,Schrodingerputforwardthewavefunctionequationofelectronstodescribethe behaviorofmicroscopicparticles.In1927,HitlerandLondonmadethefirstattemptto describethestructureofhydrogenmoleculesusingtheSchrodingerequation,whichlaidthe foundationofmodernquantumchemistry.In1991,K.Takahashicalculatedtheelectronic propertiesofreagentmoleculesbyadoptingextendedHukelmolecularorbital(EHMO) methodtopredicttheirreactivity.D.Z.Wangfocusedonthestructure activityrelationship ofthereagentbyusingsemiempiricalLCAO-MOmethod.However,thecalculationusing atomicorbital-basedMOmethodisverydifficult.Foramoleculeof100electrons,for example,resolvingtheRHFequationusingMOmethodsrequiresintegrationof100million double-electronequations.Itisthereforealmostimpossibletocalculatemineralsurfacesby MOapproach.Densityfunctionaltheory(DFT)usingelectrondensitydistributionasabasic variableisanewrevolutionaryapproachforstudyingthegroundstatepropertiesof multi-particlesystems,whichgreatlyreducetheintensityofcalculations.Withtherecent developmentofsupercomputingpower,awiderangeofsoftwareforDFTcalculationhas beendevelopedandavailableforvariousapplications.Asaresult,DFTisnowbeingrapidly usedtocalculatethecrystalstructureofminerals,latticeimpurity,mineralsurfaceand interfaceproperties,andreagentadsorption.
Thesolidphysicalpropertiesofmineralsareofparticularimportanceforsulfideflotation. First,sulfidemineralshavesemiconductingproperties,andtheflotationofsulfidemineralis anelectrochemicalprocess.Electrochemistryisthebasicfeatureofsulfidemineralflotation. Secondly,electrochemicalreactionsorelectrochemicalinteractionsarecommoninthe sulfideoreprocessingfromgrindingtoflotationseparation,suchasgalvanicinteraction betweensulfidemineralsandgrindingmedia,theelectrochemicalinteractionsbetween flotationreagentsandsulfidemineralsurfaces,thegalvaniccorrosionbetweendifferent sulfidemineralparticles,andtheelectrochemicalreactionbetweenthesulfidemineral surfaceandtheoxygenandwatermedium,allofwhichinvolvethesemiconductorband structureandelectronicpropertiesofsulfideminerals.Therefore,thesemiconducting propertiesofsulfidemineralsarethefoundationofelectrochemistryofsulfidemineral flotation.Studyingthesolidphysicalpropertiesofsulfideminerals(energybandstructure, electronstate,andelectrontransfer)couldprovidetheoreticalexplanationtotheelectron transfermechanismsduringsulfidemineralflotation.Thisbooksystematicallysummarizes theresearchresultsoftheauthorsinrecentyearsandexpoundstherelationshipbetweenthe crystalpropertiesandthefloatabilityofsulfidemineralsfromsolidphysics,crystal chemistry,surfacescience,andquantummechanics.
TheresearchworksofthisbookhavebeenfundedbytheNationalNaturalScience FoundationofChina(50864001,51164001,51864003,51304054).Theauthorsarethankful forthesesupports.WewouldalsoliketothankDr.LiYuqiong,Dr.ZhaoCuihua,Dr.Lan Lihong,andothersfortheircontributionstothisbook.
Prologue Thisbooksystematicallystudiestheelectronicstructureofsulfideminerals,surface properties,andinteractionofreagentswithmineralsurfaces.Thebookisstructuredin sevenchapters.Thefirstchapterintroducesdensityfunctionaltheory(DFT),andsome importantconceptsofsolidstatephysicsarealsointroduced.Thesecondchapterdealswith thecrystalstructureandelectronicpropertiesofsulfidemineralsandtheirapplicationsin flotation.Therelationshipsbetweenthefloatabilityandtheircrystalstructure,band structure,densityofstates,andfrontierorbitalsareprovided.Thethirdchapterpresentsthe surfacerelaxationandelectronicstructureofsulfidemineralssurfaces.Thedifferencein chargedistributionbetweensurfaceatomsandbulkatoms,aswellasthecorrelation betweensurfaceatomiccoordinationandreactivityisdiscussed.Inthefourthchapterthe adsorptionofflotationreagentsonmineralsurfacesatthesolid liquidinterfacewas studied.Inaddition,theeffectofwaterandoxygenmoleculeonthesurfacepropertiesand reagentadsorptionarediscussed.Thefifthchapterexplorestheelectronicpropertiesof flotationreagentsbyDFT,andstructure activityofreagentsisdiscussed.Inthesixth chapterthemechanismofflotationreagentinteractingwithmineralsurfaceswasstudiedby DFTcalculationandmicrocalorimetrytests.Theseventhchapterreportstheeffectsof latticedefectsonthepropertiesofsulfideminerals,surfacestructure,andadsorption behaviorsofreagents.
Introductionofdensityfunctionaltheory 1.1Introduction In1926and1927,physicistsSchrodingerandHeisenberg,respectively,putforwardthe Schrodingerequationanduncertaintyprinciple,whichmarkedthebirthofquantum mechanics.Afterthat,anewworldthatiscompletelydifferentfromclassicalphysicswas showninfrontofthephysicist.Meanwhile,anewtheoreticaltoolforunderstandingthe chemicalstructureofmatterwasprovidedforthechemisttoo.In1927thephysicists HeitlerandLondonappliedtheapproachofquantummechanicstoatomicstructureto studyH2 molecule[1],successfullyexplainingthebondingmechanisminahomonuclear molecule.Theirsuccessmarkedtheinterdisciplinaryscienceofquantummechanicsand chemistry:thebirthofquantumchemistry.
AfterHeitlerandLondon,chemistshavealsobeguntoapplyquantummechanicstheory tostudy.Onthebasisofthestudyofhydrogenmoleculebythetwophysicists,three theoriesofmolecularstructurewereestablishedbychemists,namelyvalencebondtheory, molecularorbitaltheory,andligandfieldtheory.Paulingdevelopedthevalencebond theoryonthebasisoftheearliesthydrogenmolecularmodel[2]andwontheNobelPrize inChemistryin1954.In1928,thephysicistMullikenputforwardtheearliestmolecular orbitaltheory[3 5].In1931,Hu ¨ ckeldevelopedthemolecularorbitaltheoryofMulliken andappliedittoconjugatedandaromatichydrocarbons[6].In1929,Betheproposedthe theoryofligandfieldandappliedittothetheoreticalresearchonthetransitionmetal complexes[7].Later,thetheoryofligandfieldandmolecularorbitaltheorydeveloped intoamodernligandfieldtheory.Thevalencebondtheory,molecularorbitaltheory,and ligandfieldtheoryarethethreebasictheoriesofquantumchemistryusedtodescribe molecularstructure.Intheearlystages,duetothelimitationofcalculationmethodand relativelysmallcalculationamount,themoreintuitivevalencebondtheorydominatedthe studyofquantumchemistry.Afterthe1950s,withtheinventionandrapiddevelopmentof thecomputer,ahugeamountofcomputationbecameaneasytask.Theadvantagesof molecularorbitaltheorywerehighlightedatthisbackground,whichgraduallyreplacedthe valencebondtheory.
In1928,HartreeproposedtheHartreeequation[8],whichassumedthatthecharge distributionofeachelectronwasthesolutionoftheSchrodingerequationforanelectron inapotential n(r),derivedfromthefield.In1930,Hartree’sstudents,FockandSlater, proposedaself-consistentfielditerativeequationconsideringthePauliprinciple,calledthe Hartree-Fockequation,whichfurtherimprovedtheHartreeequation[9 11].Tosolvethe Hartree-Fockequation,in1951,Roothaanfurtherproposedthatmolecularorbitalscould beexpressedasthelinearcombinationofatomicorbitalsthatcomposedthemoleculeand developedthefamousRoothaan-Hartree-Fock(RHF)equation[12].Thisequationalong withthemethodbasedonthefurtherdevelopmentofthisequationisthefundamental methodofmodernquantumchemistry.
In1952,JapanesechemistKenichiFukuiproposedafrontiermolecularorbitaltheory[13]. In1965,theAmericanorganicchemistWoodwardandthequantumchemistHoffmann jointlyproposedthetheoryofconservationofmolecularorbitalsymmetryinorganic reactions.ThetheoriesproposedbyFukui,Woodward,andHoffmanusesimplemodels thatarebasedonthesimplemolecularorbitaltheorytoavoidcomplexmathematical operationsandapplyquantumchemistrytheorytoqualitativetreatmentofchemical reactionsinanintuitiveform.Throughtheirtheory,experimentalchemistscanintuitively understandtheabstractconceptsofmolecularorbitalwavefunctions.In1981,Fukuiand HoffmanwontheNobelPrizeinChemistryfortheircontributions.
Althoughthequantumtheoryhadbeenestablishedasearlyasthe1930s,theSchrodinger equationisverycomplexandstilldifficulttoobtaintheexactsolution.Evenforthe approximatesolutionbymolecularorbital,therequiredcomputationsareenormous.For example,forasmallmoleculewith100electrons,thereareover100millionofthe double-electronintegralsintheprocessofsolvingtheRHFequation.Thiscalculationis obviouslyimpossibletocompletebyhumans.Hence,inthenextdecades,quantum chemistryprogressedslowly,andwasevenrejectedbyexperimentalchemists.Inthestudy ofsolidstatephysics,itisalmostimpossibletocalculatethecrystalandthesurfacefrom theclassicalmolecularorbitalduetotheperiodicstructureofthecrystaland1023 order magnitudeofnucleiandelectronspercubiccentimeter,thusthetheoreticalcalculationof solidphysicshasbeendevelopingslowly.Itwasnotuntilthe1990sthatthematurityof densityfunctionaltheory(DFT)andthedevelopmentofcomputerhardwareprovidedan effectivetheoreticaltoolforthecalculationofsolidsandtheirsurfaces.
DFTisoneofthesolutionsbasedonquantummechanicsandtheabinitiomethodof Born Oppenheimerapproximation.Distinguishedwithmanymethodsbasedon molecularorbitaltheory,whichconstructswavefunctionsofmultielectronsystems (e.g.,Hartree Fockmethods),thismethodisbasedonelectrondensityfunctionand solvesthesingle-electronmany-bodySchrodingerequationbyKohn Sham
self-consistentfield(KS-SCF)iterationtoobtaintheelectrondensitydistribution.This operationreducesthenumberoffreevariablesandthedegreeofsystematicoscillation, thusimprovingtherateofconvergence.
In1964,HohenbergandKohnputforwardanimportantcomputationalideaandproved thattheelectronenergywasdeterminedbytheelectrondensity[14].Thus,theelectronic structurecanbeobtainedbyelectrondensitywithoutdealingwithcomplexmany-body electronwavefunctions.Theelectronicstructurecanbedescribedbyonlythreespatial variables.Thismethodiscalledasdensityfunctionaltheory(DFT).Accordingtothis theory,theHamiltonianoftheparticleisdeterminedbythelocalelectrondensity,andthe localdensityapproximation(LDA)methodisderived.Thismethodhasachievedgreat successinthesimulationofsolidmaterialssuchasmetalandsemiconductorsthroughthe combinationofmetalelectrontheory,periodicboundarycondition,andenergyband theory.LDAwaslaterextendedtoseveralotherfields,inparticulartostudytheproperty ofmoleculesandcondensedmatter.Nowitisoneofthemostcommonlyusedmethodsin thefieldofcondensedmatterphysicsandcomputationalchemistry.WalterKohnreceived theNobelPrizeinChemistryforthegreatcontributionsinthedevelopmentsofdensity functionaltheory.InviewoftheextensiveapplicationandgreatachievementsofDFT,this theoryistakenasthesecondrevolutionofquantumchemistry.Atpresent,DFTisthe mainmethodtocalculatethestructureandelectronicpropertiesofsolids,andtheselfconsistentcalculationbasedonthismethodiscalledthefirstprinciplemethod.
Since1970,DFThasbeenwidelyusedinthecalculationofsolidstatephysics.Inmost cases,DFTwithLDAgivesverysatisfyingresultscomparedwithothermethodsof solvingthemany-bodyproblemofquantummechanics,andthecomputationalcostisless thanthatoftheexperiment.Itwasgenerallyconsideredthatquantumchemistry calculationscannotgivesufficientpreciseresults,untilthe1990s,whentheapproximation usedintheDFTwasrefinedintoabetterexchangecorrelationmodel.
However,DFTisstillnotperfect.DFTismainlyachievedthroughtheKohn-Sham method.IntheframeworkofKohn-ShamDFT,theintractablemany-bodyproblem(dueto theinteractingelectronsinastaticexternalpotential)issimplifiedtoatractableproblem ofnon-interactingelectronsmovinginaneffectivepotential.Theeffectivepotential includestheexternalpotentialandtheeffectofCoulombinteractionsbetweenthe electrons,e.g.,theexchangeandcorrelationinteractions.Modelingthelattertwo interactionsbecomesthedifficultywithinKohn-ShamDFT.Atpresent,thereisnoprecise solutiontocalculatetheexchangecorrelationenergy;thesimplestapproximationisthe local-densityapproximation(LDA).LDAapproximationusesasimplehomogeneous electrongasmodeltocalculatetheexchangeenergyofthesystem,andthecorrelation
energyistreatedbyfittingfreeelectrongas.AlthoughDFThasbeengreatlyimproved,it ishardtoaccuratelydescribetheintermolecularinteractions,especiallyvanderWaals forcesandincalculationsofthebandgapinsemiconductors.Forexample,the experimentalbandgapofzincsulfide(ZnS)isof3.6eV,butthecalculatedresultbasedon DFTisonly2.0eV,whichisfarawayfromtheexperimentalvalue.
1.2Thomas¡Fermimodel Asearlyas1927,ThomasandFermifirstrealizedthatstatisticalmethodscouldbeusedto approximatethedistributionofelectronsinanatom[15,16].Theyproposeda homogeneouselectrongasmodelbasedonthekineticenergyasanelectrondensity functionalexpression,whichiscalledastheThomas Fermimodel.
AccordingtotheThomas Fermimodel,thetotalkineticenergyoftheelectrons(TTF)can beexpressedasshownin Eq.(1.1):
where CF ¼ 3 10
Theintegrand rðr Þ isanundeterminedfunction,so TTF ½r isafunctional.Forthemanyelectronsystem,inconsideringonlytheinteractionsbetweennucleiandelectronsand betweenelectronsandelectrons,thetotalenergyoftheelectronscanbeexpressedas shown:
Eq.(1.2) needstobesolvedunderequivalentperiodicconditions:
TheThomas Fermimodeldoesnotconsidertheatomicexchangeenergy,sothe calculationaccuracyislowerthanothermethods.Althoughthetreatmentofmoleculesby theThomas Fermimethodisnotsuccessful,theThomas Fermimethodopensanew methodforDFT.Sincethen,thecalculationaccuracyofthemodelhasbeenthefocusof researchinthisfield,buttheresultsarenotunsatisfactory.Thissituationkeepsunchanged untiltheemergenceofHohenberg Kohn’stheorem.
1.3Hohenberg Kohntheorem In1964,basedontheinhomogeneouselectrongastheory,HohenbergandKohnproposed amulti-electronsysteminanexternalpotential V ðr Þ,whosegroundstatephysical propertiescanbedeterminedbytheelectrondensitydistributionfunction rðr Þ.Thistheory proposedthattheenergyofthesystemisthefunctionaloftheelectrondensitydistribution function,andthegroundstateistheminimum[14].
J ½r istheclassicelectronrepulsionenergy, Vne isthepotentialenergybetweennuclear andelectrons,and Vee isthepotentialenergybetweenelectronsandelectrons. Nonclassicaltermveryimportantbutdifficulttounderstandquantity.Inthisnonclassical term,exchange-correlationenergy(Exc ½rðr Þ )isthemainpartofit.
Hohenberg Kohn’stheoremisaboutthevariationalprincipleof EV ½rðr Þ .Itisassumed that EV ½r inthisequationisdifferentiable.Undertheconditionthatthenumberof particlesisconserved,theconditionfortheextremevalueoffunctional EV ½r isas follows:
Substituting Eq.(1.4) into Eq.(1.9) yieldsthis:
Eq.(1.10) istheEuler Lagrangeequationof EV ½r .Where FHK isindependentof externalpotential V ðr Þ,itisauniversalfunctionalof rðr Þ.Ifwecanfinditsapproximate form,theEuler Lagrangeequationcanbeappliedtoanysystem.Therefore, Eq.(1.10) is thebasicequationoftheDFT.
However,althoughtheHohenberg Kohntheoremclearlystatesthatthetotalenergyofthe systemcanbeobtainedbysolvingthegroundstateelectrondensitydistributionfunction, itdoesnotindicatehowtodeterminetheelectrondensitydistributionfunction rðr Þ,the kineticenergyfunctional T ½rðr Þ ,andtheexchange-correlationenergyfunctional Exc ½rðr Þ . ItwasnotuntiltheKohn Shamequationwasproposedin1965thatDFTwasintroduced intopracticalapplication.
1.4Kohn¡Shamequation KohnandShamproposedin1965thattheelectrondensityfunctionofamultiparticle systemcanbeobtainedbyasimplesingle-particlewaveequation[17].ThissimplesingleparticleequationistheKohn Shamequation(K Sequationforshort).
IntheKohn Shamequation,theelectrondensityfunctionofthesystemcanbeexpressed bythesumofthesquaresofthesingleelectronwavefunctions:
andtheKohn Shamequationcanbewrittenas:
Theproblemofthegroundstateeigenvaluesofthemulti-electronsystemcanbe transformedintoasingleelectronproblem.TheKohn Shamequationfindsitsselfconsistentsolutionobtainedthroughaniterativeequation.
1.5Exchange-correlationenergyfunctional Theexchange-correlationfunctional EXC ½r isveryimportantinDFT,butsofar,thereis noaccurateexpressionfor EXC ½r .Ifamoreaccurateexpressioncanbefound,theDFT calculationwillbemorepractical.Variousapproximationmethodshavebeenproposed, includingLDA,LSDA(localspindensityapproximation),GGA(generalizedgradient approximation),andBLYP(hybriddensityfunctional).Atpresent,LDAandGGAare widelyused.
1.5.1Localdensityapproximation ThebasicideaofLDAproposedbyKohnandShamin1965istodividetheentire inhomogeneouselectronregioninthesystemintomultiplesmallregions,andto approximatethesesmallregionsasahomogeneouselectrongas.Thespecificformofthe systemnonuniformelectrongasexchange-correlationfunctionalisobtainedbythedensity function rðr Þ oftheuniformelectrongas,andthentheself-consistentcalculationis performedbytheK Sequationandthe VKS equation:
where εXC ½rðr Þ istheexchange-correlationenergyofeachparticleinauniformelectron gasofdensity.
TheLDApotentialfunctionistheexchangecorrelationpotentialbasedonthelocalcharge densityinthesystem.TheLDAhasbeenverysuccessfulindealingwiththeelectronic energybandsandrelatedphysicochemicalpropertiesofmetalsandsemiconductors,but therearealsodeficienciesincalculatingthemetald-bandandthebandgapof semiconductor.ConsideringtheelectronspinstateonthebasisoftheLDA,LSDAis developed.Itsexchange-correlationenergyiscalculated:
Where, r[ ðr Þ and rY ðr Þ arethespin-upelectrondensityandthespin-downelectron density,respectively,and εxc r[ ; rY istheexchange-correlationenergyequivalenttothe homogeneouselectrongassingleelectroninthepresenceofspinpolarization,whichis relatedtothespinorientation.
1.5.2Generalizedgradientapproximation BasedonLDA,PerdewandWangproposedin1986thatinadditiontoelectrondensity, theexchangeenergyandcorrelationenergyofthesystemalsodependonthedensity gradient[18].Basedonthistheory,theexchange-correlationfunctionalcanbeexpressed asafunctionofchargedensityandgradient:
Duetoitsrationalityandaccuracy,manyfunctionalssuchasPBE,RPBE,andPW91have beendevelopedundertheframeworkofGGA[19 23].
Atpresent,LDAandGGAhavebeenwidelyusedinthecalculationofsolidphysicsand materialchemistryandhaveachievedgreatsuccess.
1.6Energybandtheory 1.6.1Bloch’stheorem
Bloch’stheoremisthefoundationofenergybandtheoryofsolidphysics.Itisbasedona basicassumptionthattheatomsinthecrystalareperiodicallyarrangedandthatthe potentialfieldinthecrystalistranslational.Intheperiodicpotential,thesingle-electron Schrodingerdifferentialequationcanbewrittenas:
where V ðxÞ istheperiodicpotential,whichistranslational
Here, a1, a2,and a3 arethethreelatticebasisvectorsofthecrystal.TheBlochtheorem statesthattheelectronicstatesinthecrystalhavethefollowingproperties:
where k istherealwavevectorof k-space,andfunction Jðk ; xÞ isalsocalledBloch functionorBlochwave,whichisthemostbasicfunctioninmodernsolidstatephysics.
Inordertomaketheeigenfunctionandeigenvalue,one-to-onecorrespondence,whichis theelectronicwavevectorkandtheintrinsicvalueofE(k),mustlimitthewavevectork valuesinaninvertedprimitive cellinterval,andtheinterval iscalledthefirstBrillouin zone.TheelectronicwavevectornumberinthefirstBrillouinzoneisequaltothe primitivecellnumberofthecrystal.
When k changesintheBrillouinzone,theenergyofthecorrespondingBlochwave,i.e., theeigenvalueEoftheequation (1.17),alsochangeswithinacertainrange.These allowableenergyrangesarecalledenergybands,oritcanbewrittenas En ðk Þ (where n is theenergybandindicator),andtheycanbearrangedinorderofincreasingenergy:
Thecorrespondingeigenfunctionscanberepresentedby Jn ðk ; xÞ,whichcanbewrittenas follows:
where k isthewavevectorand un ðk ; xÞ isthefunctionwiththesameperiodicityasthe lattice:
Theenergybandformedbycrystalvalenceelectronsplaysanimportantroleinthe physicalpropertiesofthecrystalandthephysicalprocessesinvolved.Thecrystalhasa bandgapbetweenitshighestoccupiedenergybandandthelowestunoccupiedenergy band.Thecrystalhasonlyasmallnumberofconductiveelectronsatlowtemperatures, whichisasemiconductororaninsulator,dependingonthebandgap.Ifacrystalhasno bandgapbetweenitshighestoccupiedbandandthelowestunoccupiedband,therewill stillbeasignificantnumberofconductiveelectrons,evenatverylowtemperatures, whichismetal.Thebandtheoryofcrystalsexplainstheconductivityofsolidswell,and thehypothesisisreasonable.Thebandtheoryhasbeenvaluedbysolidphysicists. Althoughtherearestillsomeproblemsthatcannotbeexplainedwell,thebandtheoryis stillthemosteffectivemeansofstudyingsolidstatephysics.
1.6.2ThefirstBrillouinzone Brillouinzoneisapartofspacecenteredontheorigininthereciprocallattice.Thefirst Brillouinzonecanbeobtainedbybisectingwithperpendicularplanesnearestneighbors reciprocallatticevectors,secondnearestneighbors,andconsideringthesmallestvolume enclosed.Similarly,thesecondBrillouinzoneisobtainedbycontinuingthebisecting operationsanddelimitingthesecondvolumeenclosed.Thevolumeadjacenttothesecond BrillouinzoneandequalinvolumetothefirstBrillouinzoneisthethirdBrillouinzone. ThefirstBrillouinareaisalsocalledasthesimplyBrillouinzone,referredtoasthe Brillouinzone(BZ).Brillouinzoneisasymmetricprimitivecellinwavevectorspace, whichhasallthesymmetriesofthepointgroupofthereciprocallattice.
Theshapeofthereciprocallatticeofcrystallatticeofsimplecubeisstillsimplecube,and itsshapeoftheBrillouinzoneisstillsimplecube.Theshapeofthereciprocallatticeof crystallatticeofbody-centeredcubeisface-centered,anditsshapeoftheBrillouinzoneis rhombicdodecahedron.Theshapeofthereciprocallatticeofcrystallatticeoffacecenteredcubeisbody-centered,anditsshapeoftheBrillouinzoneistruncated octahedron.ThevolumeoftheBrillouinzoneisequaltothevolumeoftheprimitiveunit cell.
Theprimitivetranslationvectorsofatwo-dimensionallatticeare a1 ¼ ai, a2 ¼ aj;then theprimitivetranslationvectorsofreciprocallatticeare:
Therearefourreciprocalpointsclosesttotheorigin:b1, b1,b2, b2.Thespaceenclosed bytheirperpendicularbisectorsisthesimplyBrillouinzone,thatis,thefirstBrillouin zone.Asshownin Fig.1.1,thesquareinthisreciprocallatticespaceisthefirstBrillouin zoneofthesquarelattice.
Byconnectingthecoordinateoriginwiththesecondnearestneighborreciprocalpoints anddrawingtheverticalbisectoroftheselines,thespaceadjacenttothefirstBrillouin zoneandequalinvolumetothefirstBrillouinzoneisthesecondBrillouinzone,whichis theshadedareaofthefourisoscelesrighttrianglesasshownin Figure1.1.
Byconnectingthecoordinateoriginwiththethirdnearestneighborreciprocalpointsand drawingtheverticalbisectoroftheselines,thespaceadjacenttothesecondBrillouinzone andequalinvolumetothesecondBrillouinzoneisthethirdBrillouinzone,whichisthe regionoftheeightisoscelesrighttrianglesin Figure1.1.
Figure1.1
Two-dimensionalsquarelatticeBrillouinzone.
ThefirstBrillouinzoneoftheface-centeredcubiclattice.
ThefirstBrillouinzoneoftheface-centeredcubiclatticeismorecomplex.Itisa tetrakaidecahedronwitheightregularhexagonsandsixsquares,oftencalledtruncated octahedron. Fig.1.2 showstheshapeofthistruncatedoctahedron. ThecoordinatesofthetypicalsymmetrypointinthefirstBrillouinzoneofthefacecenteredcubiclatticeareasfollows:
References [1]HeitlerW,LondonF.WechselwirkungneutralerAtomeundhomo ¨ opolareBindungnachder Quantenmechanik.ZPhys1927;44(6 7):455 72.
[2]PaulingL.Thenatureofthechemicalbond.CornellUniversityPress;1960.
[3]MullikeRS.Theassignmentofquantumnumbersforelectronsinmolecules,I.PhysRev 1928;32(2):186 222.
[4]MullikeRS.Theassignmentofquantumnumbersforelectronsinmolecules.II.Correlationofmolecular andatomicelectronstates.PhysRev1928;32(5):761 72.
[5]MullikeRS.Theassignmentofquantumnumbersforelectronsinmolecules.III.Diatomichydrides.Phys Rev1929;33(5):730 47.
[6]Hu ¨ ckelE.QuanstentheoretischeBeitra ¨ gezumBenzolproblemII.Quantentheoriederinduzierten Polaritaten.ZPhys1931;72(5 6):310 35.
[7]BetheH.Splittingoftermsincrystals.AnnPhys1929;3:133.
[8]HartreeDR.Thewavemechanicsofanatomwithanon-Coulombcentralfield.PartI.Theoryand methods.ProcCambPhilosSoc1928;24(01):89.
G XKL
Figure1.2
[9]FockV.NaherungsmethodezurLosungdesquantenmechanischenMehrkorperproblems.ZPhys 1930;61(1 2):126 48.
[10]SlaterJC.NoteonHartree’smethod.PhysRev1930;35(2):210 1.
[11]SlaterJC.Atomicshieldingconstants.PhysRev1930;36(1):57 64.
[12]RoothaanCCJ.Newdevelopmentsinmolecularorbitaltheory.RevModPhys1951;23(2):69 89.
[13]FukuiK,YonezawaT,ShinguH.Amolecularorbitaltheoryofreactivityinaromatichydrocarbons. JChemPhys1952;20:722.
[14]HohenbergP,KohnW.Inhomogeneouselectrongas.PhysRev1964;136(3B):B864 71.
[15]ThomasLH.Thecalculationofatomicfields.ProcCambPhilosSoc1927;23:542.
[16]FermiE.Unmetodostatisticoperladeterminazionedialcunepriorietadell’atome.Rend.AccadNaz Lincei1927;6:602 7.
[17]KohnW,ShamLJ.Self-consistentequationsincludingexchangeandcorrelationeffects.PhysRev 1965;140(4A):A1133 8.
[18]PerdewJP,WangY.Accurateandsimpledensityfunctionalfortheelectronicexchangeenergy: generalizedgradientapproximation.PhysRevB1986;33(12):8800 2.
[19]PerdewPJ,BurkeK,EmezerhofM.Generalizedgradientapproximationmadesimple.PhysRevLett 1996;77(18):3865 8.
[20]HammerB,HansenLB,NorskovJK.Improvedadsorptionenergeticswithindensityfunctionaltheory usingrevisedPBEfunctionals.PhysRevB1999;59:7413.
[21]WuZ,CohenRE.Moreaccurategeneralizedgradientapproximationforsolids.PhysRevB 2006;73(23):235116 21.
[22]PerdewJP,ChevaryJA,VoskoSH,JacksonKA,PedersonMR,SinghDJ,FiolhaisC.Atoms,molecules, solids,andsurfaces:applicationsofthegeneralizedgradientapproximationforexchangeandcorrelation. PhysRevB1992;46(11):6671 87.
[23]VanderbiltD.Softself consistentpseudopotentialsinageneralizedeigenvalueformalism.PhysRevB 1990;41(11):7892 5.
Electronicpropertiesofsulfideminerals andfloatability Sulfidemineralsarecharacteristicofsemiconducting,andelectrontransferand electrochemicalreactionswouldoccurintheprocessofflotation.Theelectronic propertiesofsulfidemineralsdeterminethebasicflotationbehaviors.The electrochemicalreactionisnotonlycarriedoutonthesurfaceofsulfideminerals,butit alsoisinvolvedinbulkelectrons.Forexample,therestpotentialisabulkparameter, whichcanbeusedtoexplainthecollector’sproductsonthesulfidesurface.Thestudyof theelectronicstructureandpropertiesofsulfidemineralscangiveaninsightto understandtheelectrochemicalbehaviorofflotation.Thischapterdiscussestheeffectsof crystalstructureandelectronicpropertiesofsulfidemineralsandattemptstoestablish therelationshipbetweenelectronicstructureandfloatabillityofsulfideminerals.
2.1Crystalstructureandelectronicpropertiesofcoppersulfide minerals
2.1.1Crystalstructureofcoppersulfides
Coppersulfideore,whichaccountsfor80%ofthecopperresource,isthemajorsource forthemetalliccopper[1].Themajorcoppersulfideorescontainchalcopyrite(CuFeS2), bornite(Cu5FeS4),covellite(CuS),andchalcocite(Cu 2S).Theconcentratesofcopper fromsulfidesoresaregenerallyperformedbyflotationandthenprocessedby pyrometallurgicorhydrometallurgicroutestoextractcopperfromtheconcentrates. Althoughthepyrometallurgicprocessisthemajorroutetoproducecopper,moreand moreattentionhasbeenpaidtohydrometallurgicandbioleachingprocessingroutesdue totheireconomicandenvironmentalbenefits,especiallyforthelow-gradeoresand copper-richtailings[ 2].
Itiswellacceptedthatthehydrometallurgy,bioleaching,andflotationofmetalsulfides areelectrochemicalprocesses,whicharedependentonthecompositionandmorphology ofthemineral.Thedifferencesincrystalstructurebetweencoppersulfidesleadto differencesindissolution,oxidative,andflotationbehaviors.Forexample,thedissolution ofmetalcomponentsfromchalcopyriteisslowinbothchemicalandbiologicleaching reaction[3,4].Thebioleachingratesofothercoppersulfidessuchascovellite(CuS)and chalcocite(Cu2S)arerelativelyhighinthepresenceofironoxidizingbacteria[ 5].
Borniteisknowntooxidizerapidlyonexposuretoairatroomtemperature[6]. Therefore,thedifferencesincrystalstructureofthesecoppersulfidescouldresultin differentelectronicproperties,andconsequentlyhavegreatinfluenceonthe electrochemicalandoxidativebehaviors.
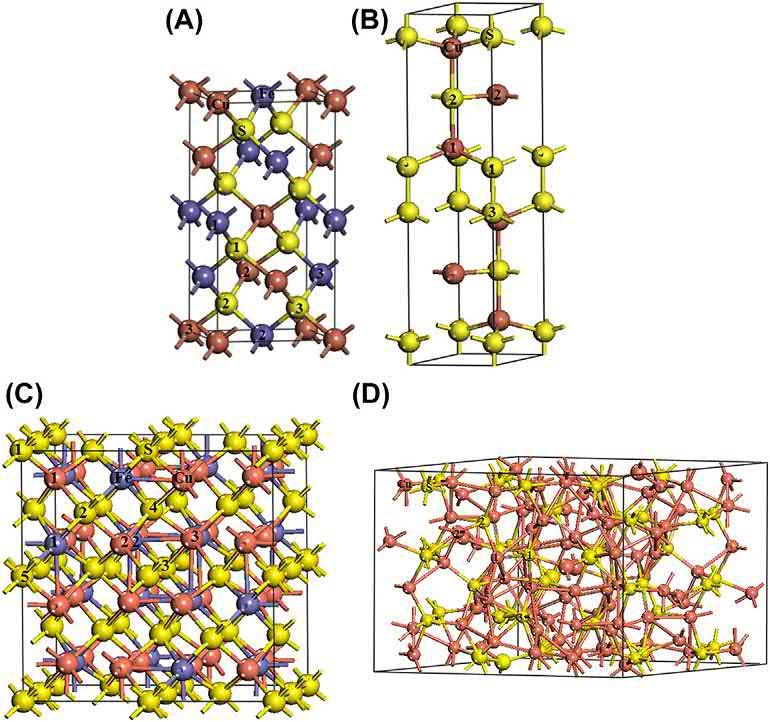
Differentcoppersulfidemineralsareofsimilarchemicalcomposition,butoftotally differentcrystalstructure,andconsequentlydifferentcharacteristics.Themodelsfor crystalstructuresofthefourkindsofcoppersulfidesareshownin Fig.2.1.
Chalcopyritecrystallizesinthetetragonalsystem,andtheunitcellisCu4Fe4S8 (Fig.2.1A).Eachmetalatom(CuandFe)iscoordinatedbyatetrahedronofSatoms,and eachSatomiscoordinatedbytwoCuandtwoFeatoms.Thecalculatedbondlengthsare asfollows:dCu S ¼ 2.323A ˚ ,dFe‒S ¼ 2.216A ˚ ,dCu
‒
¼ 3.695A ˚ , dCu Fe ¼ 3.695A ˚ ,anddS S ¼ 3.631/3.853A ˚ ,whichareinagoodagreementwiththe experimentalvaluesof2.302,2.257,3.713,3.740,and3.685/3.795A ˚ [7].
Covellitebelongstoahexagonalcrystal,andtheunitcellformulaisCu6S6 (Fig.2.1B). ThecovelliteCuatomsarethree-andfourfoldcoordination,andSatomsarefourand
Figure2.1
Schematicviewsofthestructurefor(A)chalcopyrite(Cu4Fe4S8),(B)covellite(Cu6S6), (C)bornite(Cu32Fe16S32),and(D)chalcocite(Cu96S48).(Numbersarethecoordinationvalueof theatom.)
fivefoldcoordination.Thefour-coordinatedCuatombondstothefour-coordinatedSatom, andthethree-coordinatedCubondstothefive-coordinatedSatomwiththebondlengths of2.340and2.181A ˚ [8],respectively.
Bornite,Cu5FeS4,occursinthreepolymorphicforms:low-,intermediate-,andhightemperaturestructuralforms[9].Thehighformisstableabove228 Candhascubic symmetrywitha ¼ 5.50A ˚ andspacegroupFm3m;andthelowformistetragonalwith a ¼ 10.94andc ¼ 21.88A ˚ andspacegroup P421c [10].Theintermediateformoccurs below228 Candhasthespacegroup Fd3m witha ¼ 10.94A ˚ [11].Sulfuratomsforman idealface-centeredcubicclosestpacking,andmetalatomsaredistributedstatisticallyin thetetrahedralsitesofsulfuratoms.ThesuperstructurecellforborniteisCu32Fe16S32 (Fig.2.1C),andSatomhasfour-coordinateCuatomwiththebondlengthof2.234A ˚ and eight-coordinateFeatomwiththebondlengthof2.230A ˚ .
Thecrystalstructureofchalcocite(Cu2S)iscomplexwiththreephases[12],amonoclinic phasecalledlowchalcocitebelow103.5 C,ahexagonalphasecalledhighchalcocite betweentheprevioustemperatureand436 C,andacubicphaseabovethistemperature. Theunitcelloflowchalcocitecontains48Cu2Swith144atoms(Fig.2.1D). ThecoordinationnumberofchalcociteCuatomvariesfromthreetosix.TheSatomsare mainlyinsixfoldcoordinationandpartlyinfivefoldcoordination.Thefourfoldand threefoldcoordinatedCuatomsarecoordinatedwithsixfoldSatoms,andthefivefoldand sixfoldcoordinationCuatomsarecoordinatedwithsixfoldandfivefoldSatoms.
2.1.2Computationalmethods Thefourcoppersulfideshaveseveralpolymorphs;here,wechoosethecommon polymorphinnaturetosimulate.Chalcopyrite(CuFeS2)crystallizesinthetetragonal group(spacegroupofI42d)withthelatticeparametersofa ¼ b ¼ 5.289A ˚ and c ¼ 10.423A ˚ [13].Thespacegroupofbornite(Cu5FeS4)is Fd3m andthelattice parametersarea ¼ b ¼ c ¼ 10.940A ˚ and a ¼ b ¼ g ¼ 90 [10].Covellite(CuS)hasa spacegroupofP63/mmc witha ¼ b ¼ 3.794A ˚ andc ¼ 16.341A ˚ [8].Chalcocite(Cu2S) crystallizesinspacegroupof P21/c withlatticeparametersofa ¼ 15.246A ˚ ,b ¼ 11.884A ˚ , c ¼ 13.494A ˚ ,and b ¼ 116.35 [14].
GeometryoptimizationsoffourcoppersulfideswereperformedusingtheCambridge SerialTotalEnergyPackage(CASTEP)[15]andDMol3 [16],whicharefirst-principle pseudopotentialmethodsbasedondensityfunctionaltheory(DFT).Theinteractions betweenvalenceelectronsandtheioniccorewererepresentedbyultrasoft pseudopotentials.Aftertesting,theexchangecorrelationfunctionandthecutoffenergyof theplanewavebasisweredetermined,andtheoptimizedresultsoffourcoppersulfides areshownin Table2.1.Itisfoundthatthecalculatedlatticeparametersagreewellwith theexperimentalvalues.
Table2.1: Latticeparametersofthebulkcoppersulfide.
Bornite(Cu32Fe16S32)GGA-PW91(280eV)a
Covellite(Cu6S6)GGA-WC[18] (270eV)
Chalcocite(Cu96S48)GGA-PW91(300eV)a ¼
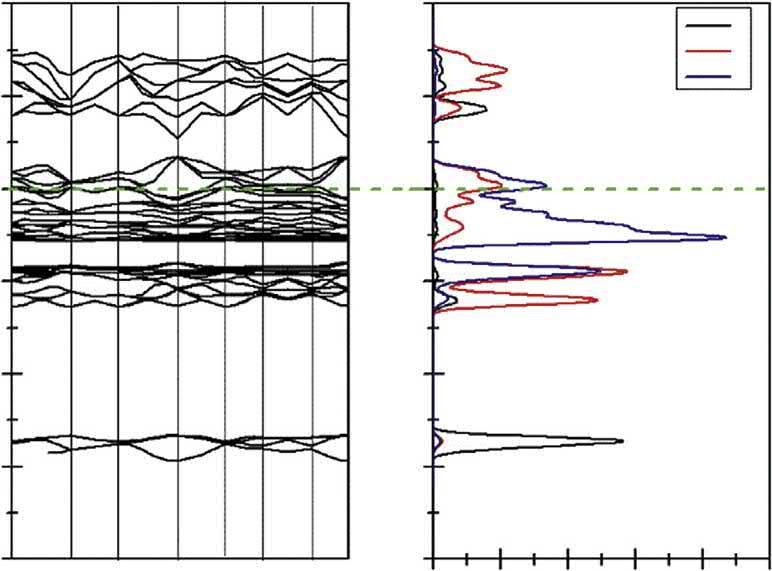
2.1.3Theelectronicpropertiesofcoppersulfide Thebandstructuresanddensityofstates(DOS)forthefourkindsofcoppersulfidesare shownin Figs.2.2 2.5,andtheFermilevel(EF)issettothezeropoint.Thecalculated resultindicatesthatthereisnospinDOSforchalcopyriteandbornite.
Forchalcopyrite,itisfoundfrom Fig.2.2 thatboththevalencebandmaximumand conductionbandminimumoftheidealchalcopyritearelocatedattheGpoint,which suggeststhatchalcopyriteisap-typesemiconductor.AstheFermilevelentersintothe valenceband,itindicatesthatchalcopyriteisadegeneratesemiconductor,whichis consistentwiththereportofFujisawa[19].
Figure2.2 BandstructureandDOSofchalcopyrite.
Figure2.3
BandstructureandDOSofcovellite.
Figure2.4
BandstructureandDOSofbornite.
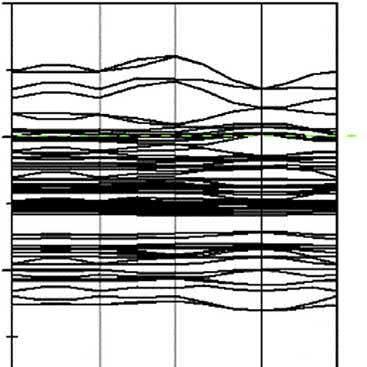
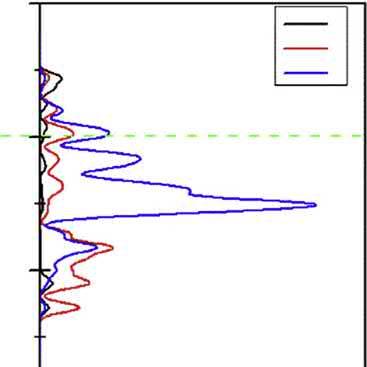
Figure2.5
BandstructureandDOSofchalcocite.
TheDOSshownin Fig.2.2 indicatesthattheconductionbandsofchalcopyritearederived fromCu4sandFe4sstates.Thelowervalencebandslocatedfrom 14.5to 12.5eVare composedofS3sstates,andtheupperpartsfrom 6.5to2.4eVaremainlycomposedof Cu3dstates,mixedwithFe3dandS3pstates.
TheDOSofcovelliteisshownin Fig.2.3.Thedeepvalencebandsconsistofthreeparts: (a)bandsfrom 16.3to 12.3eVarecontributedbythe3sstatesofS2f andS3f atoms; (b)bandsfrom 7.6to1.1eVarecomposedmainlyofCu3dstates,mixedwithS3p states;and(c)bandsfrom2.6to7.4eVarederivedfrom4sstatesofCu1atomand3p statesofS2atom.Thebandslocateat1.1 2.7eVconnectingtheconductionandvalence bandsarecomposedmainlyof3pstatesmixedwith2sstatesofS2atom,whichgreatly improvestheelectricalconductivityofcovellite.
ThebandstructureandDOSofborniteareshownin Fig.2.4.Inthevalenceband, thebandsfrom 16.7to 11.9eVarederivedfromS3sstates,andthebandsfrom 8.7 to 3.9eVarederivedfromS3pstates.Inaddition,thebandsfrom 3.9to1.8eV mainlyconsistofCu3dandFe3dstatesandpartlyofS3pstates.Theconductionbands arefrom1.8to4.5eV.
Aspreviouslypointedout,thecopperatomsintheunitcellofchalcocitehavefivefoldand sixfoldcoordination,calledasCu1andCu2,respectively.Itisfoundfrom Fig.2.5 thatthe lowerpartofthevalencebandsfrom 8.7to0eVisderivedfromS3sstates.Theupper valencebandsfrom 15.4to12.9eVaremainlycomposedofthehybridizationstateof Cu23d,Cu13d,andS3pstates.TheconductionbandsconsistofCu4sandS3pstates.
Thecalculatedbandstructuresofchalcocite,covellite,andborniteshowthattheir conductionbandandthevalencebandintersect,indicatingthattheyareconductorswith goodelectricalconductivity[6,14,20,21],whilechalcopyriteisanarrowbandgap semiconductorexhibitingasimilarpropertywithmetallic.Theresearch[22]showsthat electronsneartheFermilevelaremoreactive,andtheimportantphysicalandchemical reactionsoftenoccurneartheFermilevel.
ItisnotedthatforchalcopyritethebandsneartheFermienergylevelarecontributedbyS 4pandFe3dorbital,forcovellitethataremainlycomposedofS3pstatesmixedwithCu 3dstates,forbornitethatarederivedfromCu3dandS3pstates,andforchalcocitethat aremainlycomposedofCu4sstatesmixedwithS3pstates.Itcouldbeconcludedthatin chalcopyrite,ironandsulfuratomsexhibitmorereactivitythancopperatom,andin chalcocite,copperatomwillshowthegreatestreactivity,andincovellitethemostreactive atomisthesulfuratom,andinbornite,copperandsulfuratomsarethemostreactive atoms.
2.1.4Bondinganalysisofcoppersulfideminerals ThebondingenergylevelgenerallyappearsaroundtheFermilevel,andthecontribution ofdeeperenergyleveltothebondingisrelativelyweak.Inaddition,itisobservedthat dorbitalsplitsintot2g andeg orbitalsinthecrystalfield,especiallyattheFermilevel. Therefore,theanalysisoftheDOSneartheFermilevelwouldgiveabetterunderstanding oftheinteractionbetweenorbitalsandthestrengthofthebonding.
Forchalcopyrite,theDOSforCu SandFe Sbondingareshownin Fig.2.6.The tetrahedralfieldresultsinthesplitofCu3dandFe3dorbitalsintotwoterms,eandt2, andthesplitofCu3dorbitalisweakerthanthatofFe3dorbitalasthebandsofCu3d orbitalarelocatedfarawayfromtheFermilevel,whilebandsofFe3dorbitalare concentratedattheFermilevel.
FortheCu Sbonding,thelowervalencebands,from 6.71to 3.74eV,aretheCu4s andS3pbondingstates.TheresonanceofCu3d(e)withS3porbitalisweakatenergies between 4.0and4.5eV,andthebondingofCu3d(e)andS3pisweakened.Theupper valencebandsfrom 3.38to 1.0eVaretheCu3d(t2)andS3pstates,andbandsfrom 1.0to 0.4eVaretheCu3d(e*)andS3pantibondingstates.
FortheFe Sbonding,theFe3d(eg)andS3pbondingstatesappearfrom 6.63to 3.72eV,andahybridizedpeaklocatedat 4.5eVstrengthensthebondingeffect betweenFe3d(eg)andS3porbitals.Bandsfrom 3.01to 0.37eVaretheweakFe3d (t2g)andS3pbondingstates.ThestrongantibondingstatesofFe3d(eg*)andS3pare observedfrom 0.37to1.56eV.