EARTH’SCORE
GeophysicsofaPlanet’s DeepestInterior
VERNON F.CORMIER
ProfessorofPhysicsandGeophysics,UniversityofConnecticut,Storrs,CT,UnitedStates
MICHAEL I.BERGMAN
ProfessorofPhysics,BardCollegeatSimon’sRock,GreatBarrington,MA,UnitedStates
PETER L.OLSON
AdjunctProfessor,UniversityofNewMexico,Albuquerque,NM,UnitedStates
Elsevier Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2022ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicor mechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem,without permissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthe Publisher’spermissionspoliciesandourarrangementswithorganizationssuchastheCopyrightClearance CenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher (otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecome necessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusing anyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethods theyshouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhavea professionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliability foranyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,or fromanyuseoroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-811400-1
ForinformationonallElsevierpublications visitourwebsiteathttps://www.elsevier.com/books-and-journals
Publisher: CandiceJanco
AcquisitionsEditor: AmyShapiro
EditorialProjectManager: LenaSparks
ProductionProjectManager: BharatwajVaratharajan
CoverDesigner: MarkRogers
TypesetbySTRAIVE,India
Abouttheauthorsvii Prefaceix
1.RadialstructureofEarth’score
1.1Geophysicalevidence1 1.2Referencemodels3
1.3Analysisoftheseismicwavefield4 1.4Viscoelasticattenuation11 1.5Scattering12
1.6Anisotropy14 1.7Viscosity15
1.8Summary17
Appendix1.1Momentofinertia18 Appendix1.2Elasticequationofmotion19 Appendix1.3Seismicnomenclature21 Appendix1.4Adams-WilliamsonequationandtheBullen parameter23
Appendix1.5Viscoeleasticattenuationparameterization24 Appendix1.6Birch’slawandseismicvelocity/density relations26
Appendix1.7Compositeelasticmodulianddensity27 Appendix1.8Elasticanisotropy28 Appendix1.9Equationsofstate30 References31
2.Chemicalandphysicalstateofthecore
2.1Compositionofthecore33
2.2Temperatureinthecore38
2.3Transportpropertiesofthecore40
2.4Thermodynamicsofthecore46
2.5Innercoremineralogy57
2.6Summary64
Appendix2.1Constructionofphasediagramsandthe partitioncoefficient64 Appendix2.2ThermodynamicrelationsandtheGruneisen parameter67 Appendix2.3ThefreeelectronFermigas,phonons, andtheDebyemodel68 Appendix2.4Millerindicesandpolefigures69 References71 Furtherreading73
3.Geodynamoandgeomagneticbasics
3.1Preliminaries75
3.2Thegeomagneticfieldinthecore78
3.3Thegeodynamoprocess91
3.4Geomagneticimagesofthecoreflow104
3.5Summary109
Appendix109 References111 Furtherreadingsandresources112
4.Outercoredynamics
4.1Theoutercoreenvironment115
4.2Dimensionlessparameters118
4.3Thermochemicaltransportandbuoyancy121 4.4Steadylaminarflows124
4.5Wavesintheoutercore135
4.6Outercoreconvection143
4.7Numericaldynamos151
4.8Summary168 Appendix169 References175 Furtherreadingsandresources176
5.Boundaryregions
5.1D00 (lowermostmantleregion)179 5.2CMBtopography186
5.3E0 region(uppermostoutercore)187 5.4Fregion189
5.5ICBtopography190 5.6Summary191 References192
6.Innercoreexploredwithseismology
6.1Elasticanisotropy195
6.2Attenuationandscattering197
6.3Hemisphericaldifferences201
6.4Differentialrotation204
6.5Shearmodulus,density,andviscosity207
6.6Summary212 References213
7.Innercoredynamics
7.1Solidificationoftheinnercore215
7.2Deformationintheinnercore223
7.3Annealing:Recovery,recrystallization,graingrowth, andcoarsening234
7.4Grainsizeandthedeformationmechanismmapofthe innercore239
7.5Innercoreviscosity240
7.6Innercoreelasticanisotropy,attenuation,andisotropic heterogeneity242
7.7Summary244 References245 Furtherreading246
8.Formationandevolutionofthecore
8.1Formationofthecore247
8.2Coreevolution259
8.3Thegeodynamointhedeeppast271 8.4Seedingtheearlygeodynamo273 8.5Summary276 Appendix276 References278
9.Futureresearchgoals
9.1Introduction281
9.2Seismology281 9.3Mineralphysics283 9.4Coredynamics286 References289
Notationtables291 Corepropertiesandparameters297 Glossary301 Index309
RadialstructureofEarth’score
1.1Geophysicalevidence
Earth’score,asweknowittoday,extendstoabouthalfofEarth’sradius.Itconsistsofaliquidoutercoreofiron alloyedwithnickelandotherunknownlightelementsandapredominantlyFe-Nisolidinnercorewithlesseramounts oflighterelements.Inmostpartsofthisbook,weexamineEarth’scoreasasnapshotintime,whenithasbeenpossible forhumanstomeasureorestimateitsinternalpropertiesfromitsmagneticandgravitationalfields,itselasticstructure fromseismicwavefields,itsvariationsinrotation,anditschemistryfromrocksbroughttoitssurfacebyitsinternal dynamicsordepositedasmeteorites.Itscurrentchemistry,state,anddynamicshaveevolvedoveramuchdeeper periodoftime,startingfromtheoriginofthesolarsystem.Wesaveaglimpseofthatdeepertimeperiodfor Chapter8.
Inthischapter,webrieflyreviewgravity,magnetic,andseismicevidenceofgrosscorestructure.Weemphasize seismicobservationsbecausetheyarecapableofimagingitsdeepinteriorinthreedimensionsatspatialscales approaching10kmorless.Thesesmallscalesarethoseofelasticvelocityvariations.Elasticvelocities,whicharecombinedfunctionsofelasticmodulianddensity,areonlyweaklysensitiveto viscosity andcanhavecomplexandoften unknowncorrelationswithchemistryandotherphysicalpropertiesimportanttothegeodynamosuchaselectricaland thermalconductivity.Nonetheless,manyusefulrelationsexistforpredictinghowseismicvelocitieschangedueto variationsinrheology,composition,temperature,andpressure(seeAppendices1.4–1.9).
1.1.1Momentofinertiaandgravity
Evenchemicallyhomogeneousplanetscanbeexpectedtoexhibitsomedensitystratification,withdensityincreasingwithdepthduetovolumetriccompressionfromtheeffectsofincreasingpressuretowardtheircenters.TheuncompressedbulkdensityofEarth(4050kg/m3),however,ismuchhigherthanthatpredictedfortheuncompresseddensity ofmantlesilicates(3000kg/m3).Thisinescapablyleadstotheconclusionthattheexistenceofthedensitystratification mustbealsoaccompaniedbyacompositionalstratification.
Afirst-orderrepresentationofaplanet’sstratificationindensityisgivenbyitsmeasuredmomentsofinertia.Two momentsofinertiaofEarthcanbemeasuredfromthespatialvariationofitsgravitationalpotential,determinedfrom observationsofthepathofEarth-orbitingsatellites,andfromthemeasuredprecessionalperiodofitsaxisofrotation aboutanormaltoitsorbitalplaneaboutthesun(Appendix1.1).Thesetwomeasurementsaresubstitutedintotwo equationsandfortwounknowns,themomentofinertiaaboutEarth’saxisofrotationandthatforanaxislyinginits equatorialplane.Theequatorialmomentofinertiaisslightlylargerthanthepolar,representingtheeffectsofflattening fromEarth’srotation.Withintwosignificantdigitsbothmomentsofinertiaare0.32MR2,where M and R arethemass andaverageradiusoftheEarth,respectively.Sincethemomentofinertiaofahomogeneoussphereis0.4MR2,itisclear thatdensermaterialmustexistneareritscenter.Sincethecompressionofsilicatemineralswithincreasingpressureat depthisnotsufficienttoexplainthislowmomentofinertia,thisprovidesevidenceforironconcentratedinacore beginningatadepthapproximatelyhalfwaytoitscenter.
1.1.2Magneticfield:Spatialspectrumandtimevariation
ThespatialandtemporalbehaviorofEarth’smagneticfieldprovidesadditional,indirectevidence,forthelocation, state,andphysicalpropertiesofEarth’soutercore.Downwardextrapolation(Chapter3)ofthespatialspectrumof
Earth’smagneticfieldpredictsawhitenedspatialspectrumoflow-orderspatialharmonicsabouthalfwaytoEarth’ s center.Thisagreeswiththebehaviorexpectedforadynamoconsistingofanelectricallyconductingfluidinconvective motion,drivenbyvigorousflowsoverawiderangeofscales.FromthetimevariationsofEarth’smagneticfield,the magnitudesoftheconvectivevelocitiesofthisfluidareinferredtobeontheorderof10–20km/year,morethan5 ordersofmagnitudelargerthantheconvectivevelocitiesofEarth’smantleandobservedplatemotionsatitssurface (cm/year).FromtheobservationsofEarth’sgravity,rotationalmotion,andmagneticfieldalone,wecanthusconclude thatithasadense,electricallyconducting,lowviscosityfluid,outercore,witharadiusabouthalfofEarth’s.Thatitis enrichedinironcanbeinferredfromtheknownchemistryanddensityofsurfaceigneousrocksandironmeteorites,in combinationwithmeasuredsolarabundances,strippedofhydrogenandhelium.
1.1.3Seismology:Bodywavesandnormalmodes
Solutionstotheseismicequationofmotion(Appendix1.2)canestablishstrongconstraintsoncompositionfromthe elasticmodulianddensitiesofEarth’scorefromthemeasurementofelasticvibrationsobservedasbodywavesabove 0.01Hzinfrequencyandnormalmodesinthemillihertzband.Solutionsinthehigh-frequencybandpropagateas bodywaves(compressionalPandshearS)outwardfromanearthquake,explosion,orimpactinquasi-spherically shapedwavefronts,samplingtheelasticwavespeedoftheEarthalongraypathsnormaltothewavefront.Solutions inthelow-frequencybandaredescribedbytheelasticnormalmodesofEarth.Modespectraareidentifiedandmeasuredinthefrequencydomain,whereasbodywavevelocitiesareinferredfromthetraveltimesofwavesobservedin seismogramsrecordedinthetimedomain.
EmilWiechertin1896wasthefirstphysicistandseismologisttoquantifytheexistenceofametalliccore.Timingof seismicbodywavesbeginningintheearly20thcenturywiththeworkofOldhamandLehmannprovidedestimatesof itsinternalelasticpropertiesandstatewithdepth,addingconstraintstoitsdensitystructure,andmorepreciselylocatingtheradiioftheboundariesoftheliquidouterandsolidinnercores(Fig.1.1).Bythe1930s,globalseismometer coveragewassufficienttorevealtheexistenceoftheinnercore.Withcurrentcoverage,thesignaturesofthesharp discontinuitiesoftheouterandinnercorescanbeeasilyobserved(Fig.1.2).Evidenceoftheoutercorecamefrom theobservationofashadowzone,inwhichnodirectPandSwavesareobservedbeginningaroundagreatcirclerange of95°.ThisisconsistentwithastrongsharpdecreaseinPwavevelocityandtheabsenceofdirectSwavesbeneatha radiusof3480km,duetothefluidityoftheoutercore.Evidenceforaninnercoreoriginatedfromtheidentificationofa Pwavemultipath,associatedwitha traveltimetriplication ofPwaves(differentcorewavesarriveatthesamedistance fromdifferentanglesasexplainedin Section1.3.1)arrivinginthegreatcirclerangeof120–155°.Thisispredictedbya sharpincreaseinPwavevelocityatradius1215–1220km.
FIG.1.1 Thepioneeringseismologistswho determinedthebasicstructureofthecore.Left toright,withdateofseminalpublicationson Earth’score:Emil Wiechert(1896),Richard Oldham(1906),andInge Lehmann(1936).

Knowledgeofthestate(liquidorsolid)ofthecorehasbeenobtainedfromseismologyinboththebodywaveand free-oscillationfrequencybands.ThelackofSwavespropagatingthroughtheoutercoreisinferredfromthetravel timeandpolarizationofSKSwaves,whichpropagateasSwavesinthemantleandcompressionalwavesintheliquid outercore(Fig.1.3).Directobservationofshearwavespropagatinginthesolidinnercore(PKJKP)hasbeendifficult becausetheamplitudeofthiswaveisquiteweak.WeakPKJKPamplitudeisduetothesmallcoefficientofconversion ofPtoSwavesattheinnercoreboundaryforpossibleanglesofincidenceontheinnercoreboundary.FurtherweakeningofPKJKPisalsopossibleduetothepossibilityofshearwavesplittingfromthe elasticanisotropy oftheinnercore, whichwillwidenasinglepulseintotwointerferingPKJKPpulsesonbothverticalandradialcomponentsofmotion. Freeoscillation eigenfrequencies areconsistentwithaliquidoutercoreandasolidinnercorewithabulkaveragedshear velocityof3.5km/s.Usingcorrelationwavefields, TkalcicandPham(2018) reportedavalueof3.42km/satthe ICB
risingto3.58km/satEarth’scenter.Thesevalueshavebeenproblematictoreconcilewithestimatesfromlikelyinner corecompositions,whicharepredictedtoapproach5km/sfornearlypureironatthetemperaturesandpressuresof theinnercore(see Chapter6).
FIG.1.2 Bodywavetraveltimecurvescreatedbystacking90,673seismogramsfrom3648shallowearthquakes(<50kmdepth)from Sheareretal. (2011).(NomenclatureoflabeledwavesisassociatedwiththeirraypathsinEarthandisexplainedinAppendix1.3.)Asignatureoftheoutercoreis thePwaveshadow,wherethedirectPwavefadesintoawavediffracted(Pdiff)aroundthecore-mantleboundary.Asignatureoftheinnercoreis thebifurcatedPKPcurveevidentbetween150° and180°,consistingofafasterPKIKPwave,havinganearhorizontalslope,transmittedthroughthe innercoreandaslowerPKPwave,havingasteeperslope,transmittedthroughonlytheoutercore.Theshearwavetravelingthroughthesolidinner core(PKJKP)cannotbeeasilydetected.
FIG.1.3 PandSwavepolarizationsensitivitiestothesolid/liquidstatesoftheinner/outercores.Left:theshearwavetransmittedthroughthe innercorewaveispredictedtoexistasonlyan SVpolarized Swavewithinasolid,isotropicinnercore.Right:theliquidstateoftheoutercorecanbe confirmedbythepolarizationoftheSKSwave,inwhichonlytheSVpolarizedcomponentoftheSwaveincidentonthecore-mantleboundarycanbe convertedtoaPpolarizedwaveintheliquidoutercore(K)andthenconvertedtoanSVpolarizedwaveonexit.
1.2Referencemodels
WhendeterminingthedetailedstructureofEarth’sinterior,itisusefultoseekdeviationsfromreferenceEarth models,whichassumeanaverage,radiallysymmetric,elastic,anddensitystructure.TwosuchmodelsarePREM (DziewonskiandAnderson,1981)andAK135-F(Kennettetal.,1995)asshownin
Fig.1.4.Theseandotherreference modelsareavailableascomma-separated(CSV)spreadsheetfilesfromwebpagesoftheDataManagementCenterof theIncorporatedResearchInstitutionsforSeismology(IRISDMC,2011).ThecoremodelofPREMassumesa
chemicallyhomogeneousandneutrallybuoyantouterandinnercore.PREMisdesignedtofitasuiteofelastic-free oscillationsandacatalogoftraveltimesofbodywaves.SincebodywavesinteractingwiththeboundariesofEarth’ s innerandoutercorehavearelativelycomplexstructure(Figs.1.5and1.6),PREMignoresfittingcatalogedtraveltimes indistancerangeswherethetraveltimecurvesofbodywavesexhibitthiscomplexity.Hence,bodywavestudiesfrequentlychooseAK135-FratherthanPREMasthebestreferencemodelforcorestructure.AK135-Faddsdetailsinthe formofchangesingradientstoelasticvelocityanddensityabovethecore-mantleboundaryandoneithersideofthe innercoreboundary.Inlaterchapters,wewillseethatchangesinvelocityanddensitygradienthaveimportantconsequencesforchemistryandstablestratificationoftheoutercore.Itisthusnotsurprisingthattheirexistenceandlateralvariationisstilloneofthemoreactiveareasofcoreresearch.
ReadersofseismologicalliteraturewillencounterreferencestoahistoricalschemeofletteredregionsoftheEarthA–FdevelopedbyK.Bullentoclassifydepthregionsdifferinginelasticvelocityand/oritsgradientindepth.Extensions ofBullen’sclassificationschemehaveledtoidentifyingaregionD00 (theregion200–300kmabovethecore-mantle boundary)andregionsE0 andFofsimilarthicknessesintheliquidoutercorejustbelowthecore-mantleboundary andjustabovetheinnercoreboundary,respectively.Modernresearchconcentratesoninterpretingtheseismic observationsthatbestconstrainsmallerscalestructuresofBullen’sD00 ,E0 ,andFregions.Changesincomposition andthevelocitygradientsneartheboundariesoftheouterandinnercores(CMBandICB),toosmalltoberepresented in Fig.1.4,andtheexistenceofscatterersinD00 andtheuppermostinnercoreareimportantforunderstandingthe dynamicsandevolutionoftheinnerandoutercores.Evidenceforandmodelsofsmallperturbationsnearthe CMBandICBaretreatedin Chapter5
FIG.1.4 Plottedstarting120kmabovethecore-mantleboundary(CMB)atradius3480kmarereferencemodelsPREM(solid)andAK135-F (dashed)forPwavevelocity(blue,blackinprintversion),density(red,darkgrayinprintversion),andSwavevelocity(green,lightgrayinprint version)fromthelowermostmantletothecenterofEarth’sinnercore.Theinnercoreboundary(ICB)atradius1220kmseparatestheliquidoutercore fromthesolidinnercore.ThelocationofBullen’s( JeffreysandBullen,1940)depthregionsD00 (lowermostmantle),E0 (uppermostoutercore),and F(lowermostoutercore)aremarked.
1.3Analysisoftheseismicwavefield
ObservableelasticvibrationsofEarthsensitivetocorestructureoccuroverabroadspectrumoffrequencies,from lessthan1mHztogreaterthan10Hz.Thesolutionoftheequationofmotionofthesevibrationsandtheirobservations arecommonlydividedintoeitherarepresentationasbodywavesornormalmodes.Bodywavespropagateoutward fromanearthquake,explosion,orimpactsourceasquasi-sphericalwavefrontswhosenormalsarecalledrays.Fora normalmodeofoscillation,thewholeEarthvibratesatadiscretefrequency,withanamplitudethatexponentially decayswithtimefromitsinitialexcitation.Thevibrationsformaquiltedpatternofasmallnumberofnodesofzero amplitudeatitssurface,similartothespatialpatternofthemodesofadrumheadin2Dorastringedinstrumentin1D.
Therepresentationeitherastravelingbodywavesornormalmodesofvibrationbeginswiththetreatmentoftheelastic equationofmotion(Appendix1.2).Abodywaverepresentationisaccuratewhengravityandthepseudo-forcesof rotationcanbeneglectedintheequationofmotionatsufficientlyhighfrequency.Atlowerfrequencies,anormalmode representationisrequiredbecausethemagnitudeoftheforcesofgravityandrotationalpseudo-forces(centrifugal and Coriolis)canbeclosetothemagnitudeoftheelasticcontactforces.
1.3.1Bodywaves
Bodywaveconstraintsondensitiesarerelativelyweak,beingonlysensitivetothesharpchangesintheproductof velocityanddensityorseismicimpedanceatsteepanglesofincidencetomaterialdiscontinuities.The bulkmodulus or incompressibilityobtainedfromjointPandSwavevelocitiesconstrainsthedensitygradientthroughtheAdamsWilliamsonequation(Appendix1.4).Inthefree-oscillationband,however,gravitybecomesarestoringforceinthe equationofmotion,andmodeeigenfrequenciescanestablishadditionalconstraintsoncoredensity.Densityprofiles ofthecorehavebeendeterminedfromcombinedinversionsofbodywavevelocities,modeeigenfrequencies,andmass andmomentofinertiaofEarth,togetherwiththeassumptionofneutrallybuoyantstratification.
Thebodywavescommonlyusedtostudycorestructurearesubjecttotwodiscontinuouschangesinelasticwave velocitiesanddensities,oneatthecore-mantleboundaryandoneattheinnercoreboundary.Anyrapidordiscontinuousdecreaseinelasticvelocityproducesa caustic andtwopathsinalitzone,eachhavingoppositesignofcurvatureintheirassociatedtraveltimecurves.Acausticisasurface,line,orpointinspacewherebodywavesare stronglyfocusedandfrequency-independent raytheory breaksdown.Anyrapidordiscontinuousvelocityincrease producesatriplicationofthetraveltimecurve.Atriplicationisaregionofdistancesinwhichthreebodywaveshaving differentraypaths(multipaths)canarriveatthesameseismicstation,forexample,thetraveltimecurvesforPwaves interactingwiththeinnercoreboundaryatdistancesgreaterthan145° in Fig.1.5.Thepointswherethecurvatureof traveltimecurveschangessignarethedistancesatwhichthecausticsintersecttheEarth’ssurface.
TheinteractionwiththecoreboundariesofPwaves,whosepolarizationdirectioniscoincidentwiththedirectionof theirrays,provideanexampleofthewaveformcomplexityinducedbyadiscontinuousvelocitydecreaseatthecoremantleboundary,followedbyadiscontinuousvelocityincreaseattheinnercore-mantleboundary.Itistheexistence ofthiscomplexityintraveltimecurvesthatenablesanestimateofthedepthsofbothEarth’souterandinnercoresto within10kmorless.AshadowzoneandcausticareinducedinPwavesbyadiscontinuousPvelocitydecreaseatthe core-mantleboundary,andatriplicationisinducedbyadiscontinuousPvelocityincreaseattheinnercoreboundary.
FIG.1.5 Pwaveseismograms(left)observedfromadeepfocusearthquakeat140° emphasizeseveralcomplexinteractionswithboththeinner core(PKIKP+PKiKP)andtheoutercoreandthecore-mantleboundary(PKP,diffractionfromtheBcausticandCcusp,andCMBscattering).AhighpassfilteremphasizesaprecursortoPKIKP+PKiKPscatteredfromtheCMBregion,whileinthebroadbandrecordingthelow-frequencydiffraction fromtheBcausticbecomesvisible.Thetraveltimecurve(right)showsray-theoreticalwavesasblacklines,low-frequencydiffractedwavesasdashed redlines,andhigh-frequencyscatteredwavesfromtheCMBasdottedbluelines.
FIG.1.6 Left:raypathsandtraveltimecurves ofcorePwaves,identifyingkeydistanceranges sensitivetoinnercorestructure:aprecritical reflection,wherePKiKPamplitudesaresmall, andapostcriticalreflectionPKiKP,where Pwavesaretotallyreflected.Right:synthetic recordsectionofPwavedisplacementfroman explosivesourceillustratinghowthecomplexity ofthetraveltimecurveisexpressedbycomplexityinthePbodywaves.Twofrequencydependentwaves,notpredictedbyraytheory, arevisibleinthewavefield:adiffractionfrom theinnercoreboundary(PKP-Cdiff)andthediffractionfromtheoutercorecaustic(PKP-Bdiff). ThechangeinshapeofPKP-ABwavevisibleas thelatestarrivingpulseafter152° isduetoa π/2,phaseshiftrelativetothePKIKPwave.
ThetriplicationisdenotedbylinesconnectingpointsA,B,andCinthetraveltimecurvesshownin Figs.1.5and1.6 ThePwavestransmittedthroughtheoutercorearesometimesdenotedaseitherPKP-ABorPKP-BCaccordingtothe branchoftheirtraveltimecurve.
Thevelocitydecreaseatthecore-mantleboundarygeneratesareversalofthetraveltime-distancecurveplottedfora seriesofincreasingverticaltakeoffangles.AstrongfocusingofPKPwavesoccursatthecausticdistanceB.Instandard referenceEarthmodels,thecoreshadowzonestartsat95° andthecausticdistanceatpointBiscloseto145°.Thediscontinuousincreaseinvelocityattheouter-innercoreboundarygeneratesthetriplicationC-D-F.Frequency-dependent diffraction occursalongtheextensionofBCtolongerdistances.Aloweramplitudepartialreflectionalongthedashed segmentextendsfromDtoshorterdistances.Inadditiontotheeffectsinducedbyradiallysymmetricstructure,lateral heterogeneitynearthecore-mantleboundarycanscatterhigherfrequencybodywavesinalldirections,detectablebya high-frequency(>1Hz)codathatarrivesbeforePKIKPatdistancesthatprecedetheBcaustic,ridingontopofalowfrequencysignaldiffractedfromthecaustic.Scatteringatthecore-mantleboundarycanalsoinduceahigh-frequency arrival,less-frequentlyobserved,betweenPKIKP(PKP-DF)andPKP(PKP-AB)atrangesbeyondcuspC.Thecurved dashedlineextendedtoshorterdistancesfrompointBin Fig.1.5 representstheminimumarrivaltimeofthesehighfrequencyPKIKPprecursorsscatteredfromeitherheterogeneitynearortopographyonthecore-mantleboundary.The combinedeffectsofthePwavescatteredbyheterogeneitiesneartheCMBandtheBcausticdiffractionarebestseenin broadbandseismogramsspanningadistancerangeofPwavecoreinteractionbetween130° and145° (Figs.1.5and1.6). TheamplitudeofthePKiKPwavevariesfromsmallvaluesatshortdistancesandnearverticalincidencetoatotal reflectionasitapproachesgrazingincidenceontheinnercore.PKiKPcorrespondingtotherangeoftotal(critical) reflectionisthetraveltimebranchlabeledPKP-CDin Figs.1.5and1.6.ThetransitioninamplitudeofPKiKPfrom precritical to postcriticalreflection isagradual,frequency-dependenttransitionsurroundingthedistanceofpointD.
UnlikethemotionofPwavespolarizedparalleltothedirectionoftheirrays,themotionofSwavesispolarized perpendiculartothedirectionoftheirrays,similartothepolarizationofelectromagneticwaves.Assumingelastic isotropy,theorientationofthetransversepolarizationofanSwaveisfixedbytheorientationoftheslipvectorsalong anearthquakefaultplane.ThispolarizationiscommonlydecomposedintoanSVcomponentintheplanecontaining thesource,receiver,andcenterofEarth,andanSHcomponentperpendiculartothatplane.TheSHcomponentof SpolarizationcannotbeconvertedtoacompressionalwaveinEarth’sliquidoutercorebecauseSHparticlemotion hasnocomponentinthepropagationdirectionoftheconvertedPwave.Hence,itsinteractionwiththeoutercore producesonlyapure SHpolarized ScSandadiffractedS.SVpolarizedwavescanconverttoPwavesandviceversa atthecore-mantleboundary.SincecompressionalwavesinthecorearefasterthantheSwavesonthemantlesideof
1020104010601080
FIG.1.7 SVinteractionswiththecore-mantle boundaryregioninwhichanSPdiffKSwaveis excited(Rondenayetal.,2010).
thecore-mantleboundary,thetraveltimecurvesofSVpolarizedS,ScS,andSKSwavesareexamplesofatriplication equivalenttoadiscontinuousvelocityincrease.TheSKSwaveshouldbeapurelySVpolarizedwave(Fig.1.3).Thisis indeedthecase,exceptforcasesinwhichsignificantanisotropyoccursinthemantlealongthepathexitingtheouter coretothereceiver. Fig.1.7 showsanexampleobservationofSVpolarizedSwavesinteractingwithboththeouterand innercoreboundaries.ItillustratesanotherimportantSinteractionwiththeCMBinwhichatsomeanglestheSV polarizedSKSwavecanexciteaPwavediffractedalongtheCMBbeforeitconvertstoacompressionalKwaveat theoutercore.Thiscanhappenateitherthereceiverend,sourceend,orbothendsofapath,andhasbeenuseful inresearchonthestructureandlateralvariationofstructureintheD00 regionatthebaseofthemantle.
Similartothesequenceofundersidereflectionsthatareexcitedbythevelocityincreaseattheinnercoreboundary (PKIIKP,PKIIIKP+..)shownin Fig.1.7 traveltimecurves,thereisasequenceofundersidereflectionsoftheoutercore boundary(SKKS+SKKKS+…)excitedbytheequivalentincreaseofSvelocityonthemantlesideoftheCMBtothe highercompressional(K)velocityontheoutercoresideoftheCMB.Thesecollectionsofundersidemultiplesareexamplesofinterferenceheadwavesorwhisperinggallerywaves.TheamplitudesandtraveltimesoftheSmKSmultiples areespeciallysensitivetothecompressionalwavevelocityanditsgradientinBullen’sE0 regionoftheuppermostinner core,andhavebeenusedtodetermineifthereexistsastablystratifiedlayeratthetopoftheoutercorethatdoesnot participateintheprimaryconvectiondrivingthegeodynamo(Chapter5).
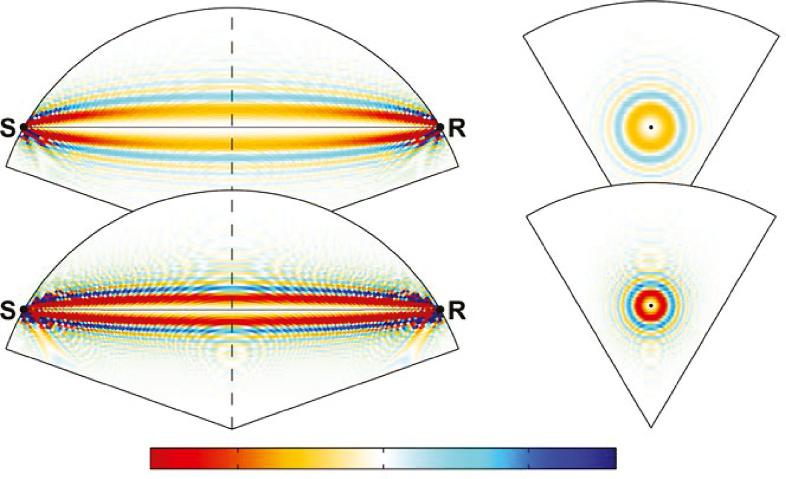
Foragivenfrequencycontentthesensitivityofbodywavetraveltimesandamplitudestoelasticvelocitystructure canberepresentedbyabanana-shapedvolumesurroundingtheirraypaths,thelowerthefrequency,thewiderthe waistofthebanana(Fig.1.8).Midwayalongtherayconnectingasourceandreceiver,thediameterofthezoneof
FIG.1.8 3DsensitivitykernelsforanSHwaveinahomogeneoussphereatanepicentraldistanceof120° calculatedin narrowfrequencybandscenteredat25mHz(top)and50mHz (bottom).Intheseexamples,thesensitivitykernelsarecalculatedusinganapproximateray-theoreticalapproach describedin Zhaoetal.(2000)
highestsensitivityisroughlythesizeofthesquarerootofthelengthoftheraypathtimeswavelength(Noletand Dahlen,2000).ThiszoneofsensitivitycanmoreaccuratelybeestimatedfromthevolumeofthefirstFresnelzone surroundingaraypath.ThefirstFresnelzonecontainsallSnellraysconnectingasourcelocation,apointscatterer location,andareceiverlocation,suchthatthedifferencebetweenthatpathandtheleast-timeSnellraypathisless thanahalfperiod.Moreprecisemeasuresofazoneofsensitivitycanbedeterminedfromasuperpositionofthenormal modeeigenfunctionsthatcorrespondtoarepresentationofspecificbodywaves.Calculatedeitherfromraysornormal modes,thesensitivitykernelKisafunctionofbothfrequencyandspace.Itisdefinedbyintegratingovervolumea3-D perturbation δVP, S VP, S toseismicvelocitythatisneededtomodeltheobserveddifferenceintraveltime δtP,S between thatpredictedfromareferenceandtruevelocitystructure:
Bodywaves,whoseraypathsturnfromdownwardtoupwardpropagation,areespeciallysensitivetostructurenear theirturningpoints.Areasofthisenhancedsensitivityareofspecialinterestforstructuresnearthecore-mantleboundaryandinnercoreboundary,wherephaseandchemistrychangeeitherdiscontinuouslyoroveradepthtransition whosewidthismuchlessthanthedominantwavelengthofthebodywave.ExamplesincludecoregrazingPand Swavesobservedbeforetheshadowofthecore-mantleboundaryandbeyondtheshadowasfrequency-dependent diffractions,PdiffandSdiff.Anotherimportantcore-grazingwaveisPKP-ABobservedatdistancesfarfromthePKP-B caustic.
SKSandSKnKSarestronglysensitivetostructureonbothsidesofthecore-mantleboundary.ThecollectionofSKS, SKKS,S3KS, atdistancesgreaterthan110° hasbeenusedasatestfortheexistenceofachemicallydistinctregionof stablestratificationatthetopoftheoutercore.InnercoreboundarygrazingPKiKPatpostcriticalincidenceatranges betweenDandC,togetherwithPKIKPinthesamedistancerange,hasbeenusedtoinferstructureintheuppermost innercore.ThedistanceofthePKP-Ccusp,togetherwiththeamplitude,traveltime,andpulsedispersionofPKP-Cdiff diffractedaroundtheinnercorehasbeenimportantinconstrainingstructureatthebottomoftheoutercore(Bullen’ s Fregion)aswellasdeterminingboundsoninnercoretopography.
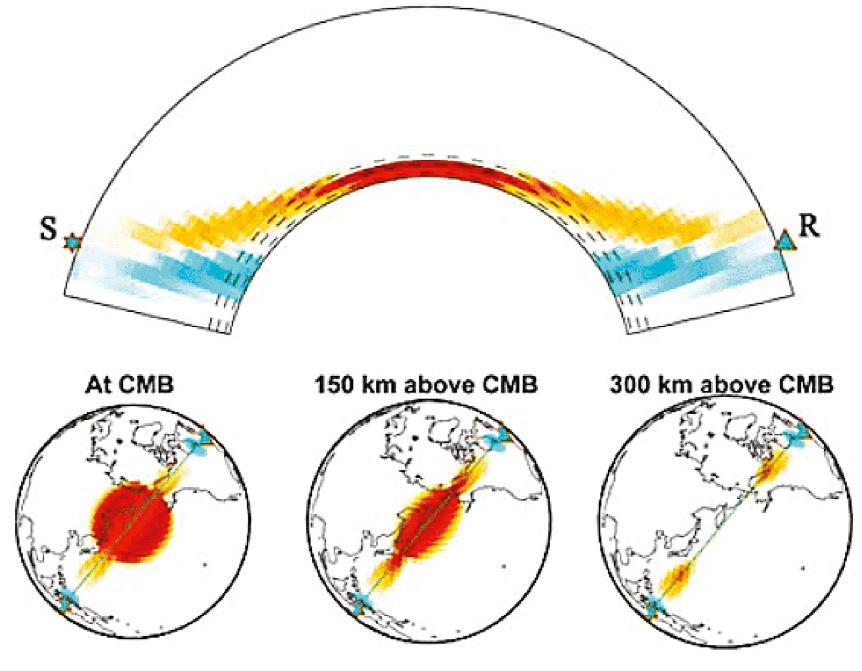
Differentialtraveltimesmeasuredbycross-correlatingthewaveformsoftwobodywavesthathavenearlyidentical raypathsinshallowerregionshaveprovedtobeapowerfulapproachinremovingtheeffectsofshallowerheterogeneousstructurewherethesensitivitykernelsofthetwowavesoverlap. Fig.1.9 showstheeffectivesensitivityof
FIG.1.9 SensitivitykernelforPKP-DF Pdiffdifferentialtimesatlowfrequency.SandRdenotesourceandreceiverlocations,respectively. From Karason,H.,vanderHilst,R.,2001.Tomographicimagingofthelowermostmantlewithdifferentialtraveltimesofrefractedanddiffractedcorephases.J.Geophys. Res.106,6559–6588.
thedifferencebetweenthetraveltimeofaPwavetransmittedthroughtheinnercoreandthetraveltimeofaPwave diffractedaroundtheoutercore.Theeffectofthenearidenticalraypathsthroughtheuppermantleisminimized,and theresultantsensitivityisfocusedonD00 structurenearthecore-mantleboundary.Asimilarapproachcanbeusedto imagestructureoftheE0 regionoftheuppermostoutercoreusingthedifferencebetweenthetraveltimeSKKS andSKS.
Withincreaseddensityofdigitallyrecordedandtelemeteredseismicnetworks,ithasbecomepossibletoextract weakerbodywavessensitivetocorestructureusingtechniquesofstackingandcross-correlation.Amongtheseare PcP,PKiKP,andPKIIKPatnearverticalanglesofincidenceonthecore-mantleandinnercoreboundaries.Atnear verticalangles,thesePwavesaresensitivetoonlytothePvelocityanddensitychangesatdiscontinuities.Frequency dependenceandcomplexityoftheirwaveformsmayrevealthenatureofanytransitionzonestructuresintheboundaryregion.ThemostelusiveoftheseweakwavesisthePKJKPwave,whichisacompressionalwavethatconvertsto anSwaveinEarth’ssolidinnercore,andconvertsbacktoacompressionalwaveintheoutercore.Theconversion coefficientofthecompressionalKwaveintheoutercoreintotheSVpolarizedwaveinthesolidinnercoreisvery smallforallpossibleanglesofincidence.MakingtheobservationofPKJKPevenmoredifficultisthatforsomeincidenceanglesandtypesofelasticanisotropy(Appendix1.8)theenergyoftheinnercoreSwavemaybesplitintotwo interferingSwaves,differinginpolarizationfromeitherSHorSV,andarrivingatslightlydifferenttimes.
Pwavescanbeobservedfromreflectionsbytheoutercoreboundary(PcP)orinnercoreboundaryfromeither above(PKiKP)orbelow(PKIIKP).Atmoregrazinganglesofincidence(precriticalPKiKP)andPKIIKPatrangesless than180°,theiramplitudesareaffectedbybothPandSvelocitydiscontinuitiesanddensitydiscontinuities.For Pwavesatnearverticalanglesincidence,theamplitudesofreflectedandtransmittedPwavesdependonlyonthe Pvelocityanddensitydiscontinuitiesandarenearlyindependentoftheshearvelocityjumpsattheouterandinner coreboundaries.Atnearverticalincidence,alloftheCMBandICBreflectedwavesareataprecriticalangleofincidenceandarepartiallyreflectedandhenceareweakandrelativelydifficulttodetectinthepresenceofambientnoise andotherscatteredwaves.Whenthesepartialreflectionsareobservable,theiramplitudesincombinationwith Pvelocityestimatesfromwaveformandtraveltimemodelingcanpotentiallyprovidebetterestimatesofthedensity jumpattheinnercoreboundary.Thisdensityjumpisimportanttodrivingacoredynamopoweredbycompositional convection.
1.3.2Freeoscillations
Anearthquake,explosion,oranimpactsourcecanexcitethefreeoscillations(normalmodes)ofEarth.Theyarebest observedinthefrequencydomain,Fouriertransformingaseismogramrecordedinthetimedomain.Structurenearthe boundariesoftheouterandinnercores,wherechemicalheterogeneityandphasechangesaremostlikely,isanimportantgoalofcurrentresearch.StructureneartheseboundariescanideallybeinvertedfromStoneleytypemodes,whose energyisconcentratedneareitherthecore-mantleboundaryorinnerthecoreboundary.Unlikebodywaves,which providerelativelyweakconstraintsondensitygradientsanddensityjumpsneardiscontinuities,normalmodeoscillationsaremeasurablyaffectedbyagravitationalrestoringforce.Thus,theycanprovideconstraintsontheaverage densitythroughoutadepthregion.
Theeigenfrequenciesoffreeoscillationsareclassifiedaseither spheroidal (nSlm)or toroidal (nTlm)modes.Themotions ofspheroidalmodesareperpendiculartoEarth’ssurface;thoseoftorroidalmodesaretangenttoEarth’ssurface. SuperpositionsofspheroidalmodescorrespondtoP-SVbodywavesandRayleighsurfacewaves;thoseoftoroidal modescorrespondtoSHbodywavesandLovewaves.Thesubscript l in nSl and nTl istermedastheangularorder numberanditsvalueisrelatedtothewavelength λ betweenpeaksindisplacementofthemodeattheEarth’ssurfaceat radius R bytherelation l ¼ 2π R λ .Thesubscript n istermedastheradialordernumberandalsotheovertonenumber.The radialordernumber n correspondstothenumberofnodeswithdepthintheEarthwherethedisplacementofthemode iszeroandundergoesareversalinthesignofitsmotion.Eachangularordernumber l canhave2 l +1possibleazimuthalordernumber m ofmodeshavingslightlydifferenteigenfrequenciesclusteredaboutacenterfrequency.Modes havinglowradialordernumber n andsmallangularordernumber l aremostsensitivetouppermantlestructure. ThesemodeslargelycomprisetheelasticenergymakingupLoveandRayleighsurfacewaves.Modeshavinglarge radialordernumber n andsmallangularordernumber l aremostsensitivetodeepmantleandcorestructure,comprisingenergythatmakesupdeeplypenetratingbodywaves.Modenomenclature,thesensesofmotion,andsubscripts n and l andsuperscript m aredescribedindetailinAppendix1.3.
The2 l +1eigenfrequenciespossiblefordifferentazimuthalordernumbersmwouldallbeequal(degenerate)ina sphericallysymmetric,nonrotating,elastic,isotropicEarth.Degeneracyisremoved,makingeachmhaveslightly
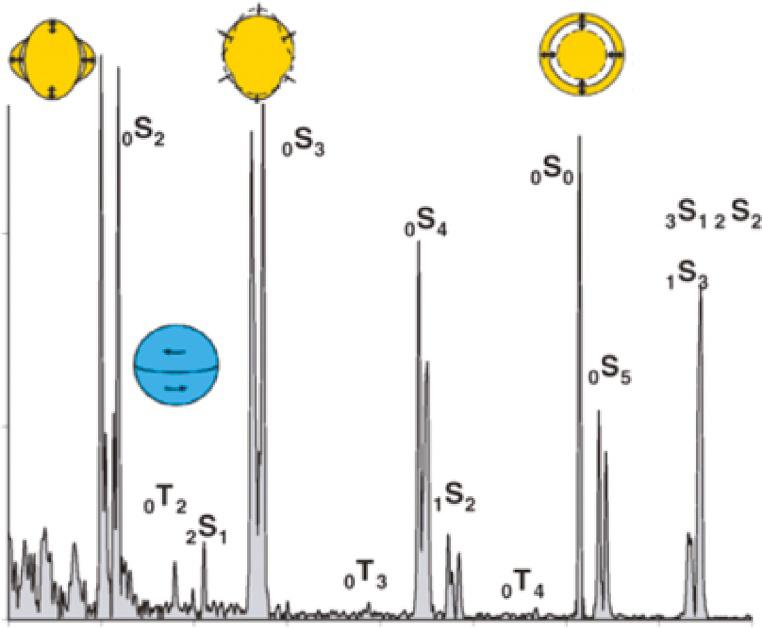
FIG.1.10 ExamplespectrumofEarth’snormal modes,withillustrationsshowingsensesofdisplacementforselectedspheroidal(yellow)andtoroidalmodes (blue)(Parketal.,2005).
differentfrequency,duetotheeffectsofEarth’srotation,ellipticity,lateralheterogeneity,intrinsicattenuation,and anisotropy.Theexistenceofthesedifferenteigenfrequenciesorsingletsistermedasmodesplittingandtheeffect ofthesuperpositionofthesesplitmodesistobroadenthespectrumofthemodepeaksseenin Fig.1.10 thatwould otherwisebenarrowerbecauseeach2 l +1eigenfrequencywouldbeidentical.Thebroadeningofaspectralpeakassociatedwiththeconstructiveinterferenceof m’shavingslightlydifferentfrequencyforaspecific n and l istermedselfcoupling.Somemodeidentificationscanbemadedifficultbecauseofcross-coupling.Stronglycross-coupledmodes arethosewhose n’sand/or l’sdifferbutwhoseeigenfrequenciesaresufficientlyclosetogetherthattheirobservation mustbeinterpretedandmodeledjointly.
Thestructuralsensitivityofnormalmodescanbedisplayedinvariousways.Thesimplestapproachistodisplaya componentofdisplacementassociatedwithamode,showingnodelinesordirectionsofdisplacementvaryingwith depthorlatitudeandlongitudeatthesurface,e.g.,Appendix1.3andinsetsin Fig.1.10
ToprovidemoreinsightintowhichregionsofEarthsignificantlycontributetotheobservedsplittingofamodeone cancalculateastructurefunction.Structurefunctionscanbemeasuredfromsyntheticseismogramsforareference Earthmodelandexploitedinaniterative,linearized,inversionofobservedseismogramstodetermineperturbations tothestructureofthereferencemodel(Woodhouse,1980).Usuallynomorethantwoiterationsareperformed,starting fromareferenceEarthmodelthatincludesthesplittingeffectsofellipticityandrotation.Theprocedurecomputesa structurecoefficient cst anda splittingfunctionfE,where
Ms(r)isakernelfunctiondependingonthecomponentsofmotionofthemodeeigenfunctionand δmst(r)isa3-Dstructuralperturbationwithrespecttoareferencemodelexpandedin sphericalharmonicsYs t (θ , φ).
InEq. (1.3) thestructurecoefficientsaresummedoversphericalharmonicstodefineasplittingfunctionthatcanbe projectedontothesurfaceoftheEarthtoobtainanimageoflateralstructuralsensitivityofaspecificmode.Torepresentperturbationstovelocitydiscontinuities,anadditionaltermcanbeaddedtothedefinitionofthestructure
S20RTS
+
CRUST
5.1
Elastic 9S4 Re part
Anelastic 9S4 Re part
9S4 f(μHz) f(μHz)
smax = 4 for Re
smax = 2 for Im
9S4 Im part
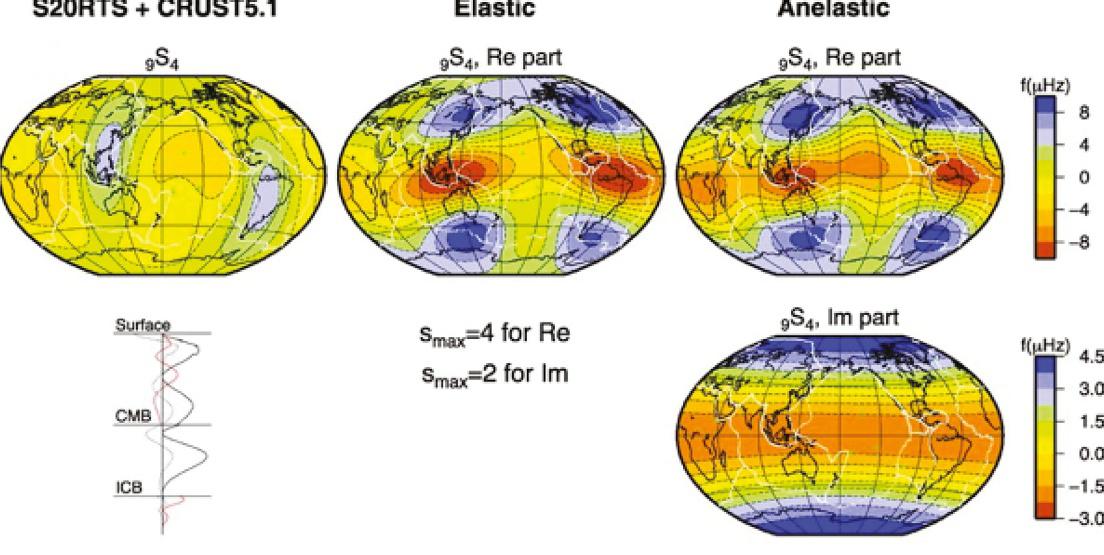
FIG.1.11 Splittingfunctionsplottedforthespheroidalmode 9S4.Leftcolumn:predictedsplittingfunctionfromamodelthatincludesonlythe effectsof3Dvelocityanddensityvariationsinthecrustandmantleestimatedfromatomographicmodel.Lowerleft:verticaldisplacementsensitivityof 9S4 toPvelocity(solidblackline),Svelocity(dashedredline),anddensity(dottedblackline).Middleandrightcolumns:splittingfunctions obtainedfrominvertingmodedataforamodelassumingeitherpureelasticoranelasticstructuralperturbationsinEarth’sinnercore(Makinenand Deuss,2013).
coefficient cst inEq. (1.2).Anadditionalfunction fA(θ , φ)canalsobedefinedtorepresentthesplittingeffectsofanelasticity(viscoelasticattenuation),resultinginacomplexsplittingfunction,
Arelativelycompletesenseofboththeradialsensitivityofamodeandthelateralperturbationsinstructurerequiredto matchitsspectralshapecanbeobtainedbyplottingitsradialeigenfunctionversusdepthanditssplittingfunctionwith latitudeandlongitude. Fig.1.11 comparesthesensitivityofamodesinglettothatpredictedfroma3Dmodelofelastic velocitiesanddensityinthecrustandmantlewiththepredictionsforthesplittingfunctionsobtainedfrominverting modedata.Anelasticanisotropyintheinnercoreisrequiredtoachievethebestmatchtoobservedmodalspectra.The anelasticanisotropyhasastrongzonalpattern,withfastpolarregionscorrelatingwithhighattenuationcompared withslowervelocitiescorrelatingwithlowerattenuationintheequatorialregion.Thissenseofcorrelationisopposite towhatiscommonlyobservedinEarth’smantle,whichisdiscussedinmoredetailin Chapter6.
1.4Viscoelasticattenuation
Theobservedattenuationoftheseismicwavefieldwithtimeandspaceandthecomplexityofbodywavepulses assistinunderstandingthethermalstate,microstructure,andlargerscaletextureofEarth’scores.Elasticwavessuffer littleornoattenuationintheliquidoutercore,similartothehighefficiencyofacousticwavespropagatinginlowviscosityfluids.InEarth’ssolidinnercore,Pwavesareobservedtosuffermuchhigherattenuation.Thisattenuation islikelyacombinationofviscoelasticdissipationduetotheinternalfrictionassociatedwiththemotionsofcrystal dislocationsorincludedpartialmeltand/orscatteringattenuationduetotheeffectsof0.1–50kmscaleheterogeneities thatredistributeelasticenergyintolatertimewindowsandlocationsfromobservedPKIKPwaveforms.
Seismicviscoelastic,orintrinsicattenuation,istheenergylosttoheatandinternalfrictionduringthepassageofan elasticwave.Themicroscopicmechanismsofintrinsicattenuationhavebeendescribedinseveraldifferentways, includingtheresistiveandviscouspropertiesofoscillatormodelsoftheatomsincrystallinelattices,themovement ofinterstitialfluidsbetweengrainboundariesandcracks,andthefrictionalslidingofcracks.
Forelasticwavestheexistenceofviscoelasticattenuationrequiresthatphaseandgroupofelasticbodywavesare notexactlyequalandmustbeweaklydispersive.Thisdispersionisdifficulttodetectintypicallynarrowbandseismograms(Chapter6)butisimportanttoincludeincomparingtheelasticmoduliorvelocitiesdeterminedinthebody wavebandaround1HzwiththosedeterminedinthemHzbandoffreeoscillations.ThereferenceEarthmodel
FIG.1.12 Left:raypathsofP4KP(solid)and P7KPsamplingtheoutercore.Right:estimatedbulk Q factorsforattenuationintheoutercorefromthe spectralratioP7KP/P4KP(CormierandRichards, 1976).
TABLE1.1 Seismicviscoelasticattenuationestimatesreportedfrom Q parametersofreference modelsat1HzforEarth’slowermostmantle(D00 ),outercore,andinnercore.
D00 72527336227357,823372840372 OC57,822057,822057,823057,8230 IC626853388513278544885
SubscriptsKand μ refertobulkandshearattenuation,respectively;PandStoPandSwaveattenuation, respectively.
velocitiesplottedin Fig.1.4 areshownfor1Hzelasticwaves.InthemHzfrequencyband,appropriateforfreeoscillationobservations,thephasevelocitiesandelasticmoduliareslightlysmaller.Amodelofviscoelasticattenuationparametersincludingtheirfrequencydependence,termedasthe relaxationspectrum (Appendix1.5),mustbe knownandappliedtoproperlycomparetheelasticvelocitiesandmoduliestimatedinthebodywavebandtothose estimatedinthefreeoscillationband.
Inestimatesofglobalaverages,referencemodelsshowincreasedattenuationinthelowermostmantleD00 region, associatedwithincreasedtemperatureinthethermalboundarylayerclosetothecore-mantleboundaryand/orthe presenceofpartialmelt.Referencemodelsincorporateevidenceforlowornear-zeroattenuationintheliquidouter core,consistentwiththebehaviorofmostlow-viscosityfluids.Inordertoexplaintheobservationsofhigh-frequency PnKPwaves(Fig.1.12)thattravellongdistancesintheoutercore,multiplyreflectingalongtheundersideofthecoremantleboundary,attenuationintheoutercoreinbothbulkandshearmustbeverynearlyzero(Q’snearinfinity).
Attenuationincreasesagainintheinnercore,consistentwithasolidironclosetoitsmeltingtemperature.Midway intotheinnercoresomemodelsshowasharpdecreaseinattenuation.Referencemodelsgenerallyagreeonthevalues ofPwaveattenuationinD00 ,theinnercore,andonthelowbulkattenuationoftheliquidoutercore.Thedetailed behaviorofinnercoreattenuation,however,iscomplex,exhibitinganisotropy,depthdependence,andfrequency dependence.Becauseofthis,referencemodelsforinnercoreattenuationhavebeendifficulttoconstruct,illustrate, orbeofmuchuseexceptoverbroadregionsofdepth.Referenceattenuationmodelsin Table1.1 aregivenfor Q values inD00 ,theoutercore,andinnercore.Wewillreturntoadiscussionofinnercoreseismicattenuationin Chapter6.
1.5Scattering
ThefabricortextureofEarth’ssolidcrust,mantle,andinnercoresconsistsofassemblagesofpolycrystallinemineralsorganizedintocompositionallydifferentpatchesoforganizedcrystalsandcrystallinephases,sometimes
includinglensesofpartialmelt.Ifthevelocityand/ordensitiesofthesepatchessufficientlydifferacrosstheirboundaries,theycanscatterelasticwaveswhosewavelengthisontheorderoforlessthanthesizeofthepatch.Seismic observationshavefoundthatthisisespeciallytrueinEarth’slowermostmantleneartheCMBandinitsinnercore,e.g., Shearer(2015).Scatteringredistributesenergyintodifferentdistancesandtimewindows,removingitfromthefirst arrivingpulseofabodywave.Theshapeandfrequencycontentofthescatteredcodathatarrivesfollowingthefirst breakofabodywavepulsecanbemodeledtodetermineastatisticaldescriptionoftheheterogeneityscalelengthsand percentvelocityanddensityperturbationsresponsibleforthescatteredcoda.
Scatteringeffectsofbodywavecodaarequantifiedbydomainsdefinedbytheproduct ka ofwavenumber k times scalelength a ofthescatterer.Realisticfabricsofmanyheterogeneousmaterialsarewellcharacterizedbyapower spectrumofvelocityand/ordensityfluctuation ε aboutabackgroundaveragevalueplottedasafunctionof ka. Thescalingsbetween ε fluctuations(ΔVP/VP, ΔVS/VS,and Δρ/ρ)areoftenassumedfrom Birch’s(1960) empirical observationsforthebehaviorofPvelocityanddensityasafunctionofmeanmolecularweight(Appendix1.6). AcommonlyassumedshapeforthespectrumofheterogeneityisthevonKármánspectrum,whichisflatuptoacorner of ka ¼ 1andthendecaysatanegativepowerof ka,termedaHurstnumber(Fig.1.13).Thewaveformeffectsofscatteringcanbedividedintodifferentbehaviorsdependingonthemagnitudeof ka (Satoetal.,2012).
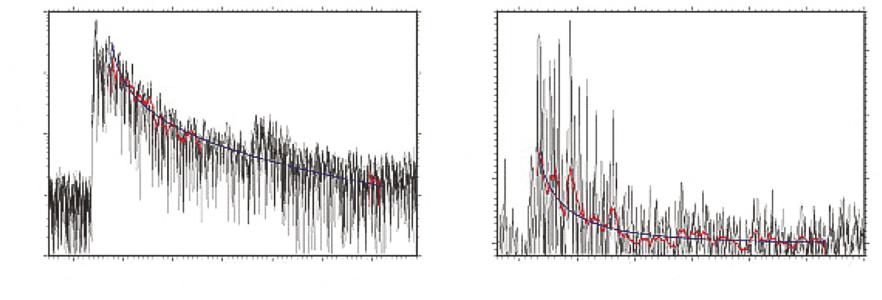
Anysharp(relativetowavelength)contrastinPvelocity,Svelocity,and/ordensityandanytopographyonthe innerandoutercoreboundariescancontributetoscatteredcodaofbodywaves.TheD00 regioncorenearthemantle boundaryisawell-documentedregionofincreasedscatteringfromobservationsofahigh-frequencyprecursorycoda toPKIKPinthe110–140° range(broadbandseismogramin Fig.1.5),confirmedfromseismogramssynthesizedassumingstatisticalmodelsoftopographyonandheterogeneityabovetheCMB.Theuppermantle,mid-mantle,lowermantleD00 region,andtheinnercorecanallcontributetothescatteredcodaobservedinhigh-frequencyseismogramsof PwavesinteractingwithEarth’souterandinnercores.Aftercorrectingforscatteringinthemantle,the heterogeneity spectrum oftheinnercoreandtopographyonitsboundarycanbeestimatedfrommodelingthecodaofPKiKP,a PwavereflectedbytheICB(Fig.1.14).

FIG.1.13 Randomwalkinwhichdeterministicraypathsconveyingpacketsofelasticenergyareinterruptedbyscatteringeventsinaheterogeneousmedium,contributingtothecoda(e.g., Fig.1.14)followingthedirectarrivalpredictedfromalong-wavelength,equivalentmedium.Top left:2DvonKármánheterogeneityspectrumasafunctionofcorrelationwavenumber k;spectralpowerisflatupto kcorner 1/a,afterwhichsmaller spatialscalesdecaywithfalloffratecontrolledbyHurstparameter κ.Bottom:examplespatialrealizationsofheterogeneityspectraforvarious κ ata magnificationleveloftenscalelengths a. FromSanborn,C.J.,Cormier,V.F.,Fitzpatrick,M.,2017.Combinedeffectsofdeterministicandstatisticalstructure onhigh-frequencyregionalseismograms.Geophys.J.Int.210(2),1143–1159, https://doi.org/10.1093/gji/ggx219
FIG.1.14 Left:codaenvelopesofPcP +PKiKPfromanearthquakeat82° (Leyton andKoper,2007).Right:thesmoothedenvelope ofPcPshownatleftissubtractedfromtheenvelopeofPKiKPtoemphasizescatteringfromthe innercore.
Improvedobservationsandinterpretationsoftheheterogeneityspectrumofthelowermostmantlemayeventually aidindiscriminatingamongvariousprocessesthathavebeenproposedforincreasedscatteringinD00 ,includingremnantmaterialfromsubductedslabs,partialmelt,apostperovskitephasechange,andproductsofchemicalreactions betweenthesilicatemantleandliquidironandlightelementsintheoutercore.Modelingtheheterogeneityspectrum intheinnercoremayassistindeterminingwhetheritisduetolensesofpartialmeltorboundariesbetweenorganized patchesofintrinsicallyanisotropicironcrystals.
1.6Anisotropy
Onlytwoelasticconstantsarerequiredtorepresentanisotropicelasticregioninwhichthestress-strainrelation doesnotdependonthechoiceofcoordinateaxes.Forcomparisonwithlaboratorymeasurementsandthespatially simplestformsofstress,thebestchoicesforreportingthesetwoconstantsarethebulkmodulusKandshearmodulus μ.Twotypesofbodywavesexist,PandS,withdifferentvelocitiesandpolarizations,withStransversetotheray directionanddecomposedintoSHandSVcomponentsrelatedtothesource-receivergeometry.Theassumptionof anisotropicmediumisappropriateforEarth’sliquidoutercore.Mineralscharacterizedbyanarrangementofatoms inaunitcellrepeatedoveravolumeinaregularlatticestructure,however,arenearlyalwaysbothelasticallyaswellas electromagneticallyanisotropic,requiringupto21differentelasticmodulitodescribethestress-strainrelation.Inthe solidmantleandinnercore,theassumptionofelasticisotropymaystillbeappropriateforapolycrystalaggregate whenindividualsilicateorFecrystalsaresufficientlydisorganizedinorientationorshape.Thevalidityofthisassumptionweakensincaseswhereprocessesalignortexturecrystallographicaxesorwherethereisashapeanisotropy.Severaltheoriesexistforestimatingtheelasticmoduliforcompositemixturesofintrinsicallyanisotropicmineralshavinga statisticallyvariableorientation.Themostadvancedofthese(Appendix1.7)incorporateinformationonthestatistics oftheorientationofintrinsicallyanisotropiccrystals.Fortunatelynomorethanfiveseparateelasticmodulithatcanbe confidentlymeasuredinlaboratorycrystalsandnomorethanthreeseparatewaveswithdifferentelasticvelocitiescan theoreticallyexistinananisotropicelasticsolid(Appendix1.8).ThesethreewavesareaPwaveandtwoquasi-S waves.Thequasi-Swavesarepolarizedtransversetotheirraybutaremutuallyperpendiculartoeachotherandtravel atdifferentvelocities.TheirpolarizationissetbythemediumelasticconstantsratherthandecomposedintoSVandSH directionsthataregovernedbysourceandreceiverpositions.Withthesedifferentspeedsandpolarizations,the Swaveistermedassplit.
WeakanisotropyistreatedbyperturbationtheoriesintheanalysisofPwavesinthehigh-frequencybandandfree oscillationsinthelow-frequencyband.ObservationofanisotropicSwavesplittingmanifestsitselfasaninterferenceof thetwoquas-SwavesonbothSHandSVresolvedcomponentsofmotion.InthecaseofSKSwaves,generalandweak anisotropymanifestsitselfbymakingobservationsoftheSKSwaveformonthetransverse(SH)componentofmotion visibleandapproximatelyequaltothetimederivativeoftheSKSwaveformobservedontheradial(SV)componentof motion.AzimuthalvariationinPwavevelocityduetoanisotropycantradeoffwithlateralvariationinisotropybut observationofshearwavesplittingisprimafacieevidenceofanisotropy.
Evidenceexistsforanisotropyintheregionofthelowermostmantle(D00 )andintheinnercore.InD00 anisotropy maybeassociatedwithlensesofanisotropicsilicates,orientationsofsubductedslabs,andconvectivefloweitherparalleltothecore-mantleboundaryorinupward-projectingzonesabovetheCMBfromupwellingplumes.Givenall thesescenarios,itisnotsurprisingthatinvestigationsofD00 anisotropyarecharacterizedbystronglateralvariations andbydifficultiesinassessingtheirresolution.
FIG.1.15 FractionaltraveltimeanomalyasafunctionofrayanglewithrespecttoEarth’srotationaxis,showingfitstoaninnercore-sensitive traveltimeanomalyassumingtransverseisotropywithanaxisofsymmetrycoincidentwiththerotationaxis.Thefitsaretodifferentialtraveltimes ofbodywavesPKP-DF-PKP-ABandthepredictionstothoseobservationsfromseparatefitstonormalmodeeigenfrequencies. AdaptedfromSong,X., Jordan,T.H.,2017.Stochasticrepresentationsofseismicanisotropy:transverselyisotropiceffectivemediamodels.Geophys.J.Int.209(3),1831–1850, https://doi. org/10.1093/gji/ggx112
Evidenceofanisotropyintheinnercorehasbeenfoundbothinbodywavetraveltimesandfreeoscillations,consistentwithafastPwavevelocityinpolardirectionscomparedtoequatorialdirections(Fig.1.15).Themechanismfor explaininginnercoreanisotropyisintimatelyconnectedtotheprocessesofsolidificationanddeformationoftheinner coreandthelatticestructureofiron.Becauseoftheimportanceforinnercoresolidificationtoadynamodrivenby compositionalconvection,wewillreturntothistopicin Chapter6 onobservationalseismologyappliedtotheinner coreand Chapter7 oninnercoredynamics.
1.7Viscosity
Oneofthemostimportantphysicalpropertiesfortheoperationofaplanetarydynamoistheviscosityoftheelectricallyconductingfluid,whoseconvectivemotionsustainsthedynamo.Theformofviscositythatappearsinaviscous rheology (theequationthatdefinestherelationbetweenstressandstrain)istermedthedynamicviscosity. ViscositiesaresaidtobeNewtonianiftherheologyissuchthatstressissimplylinearlyproportionaltostrainrate, withviscosity η definedasthecoefficientofproportionality,i.e.,
Notethatboththestressandstrainarenormallyassumedtobeinshear,andatensorrelationisnotneeded.TheSI unitsofdynamicviscosityarePascal-sec (Pas).Kinematicviscosity,whichistheformusuallyshownintheequations forthemotionoffluidcoresinthedescriptionsofplanetarydynamos,isjustthedynamicviscositydividedbydensity. TheMKSunitsofkinematicviscosityarem2 s.
Theviscosityoftheoutercorehasbeenestimatedboththeoreticallyfromabinitiocalculationsandobservationally fromtheattenuationofbodywaves,freeoscillations,andlengthofdayvariationssensitivetotherheologyofthe uppermostoutercore.AbinitiocalculationsconsidertheCoulombforceinteractionsbetweenelectronsandatom nucleitoestimatephysicalproperties.Dynamicviscosity η isobtainedfromtheestimateoftheself-diffusioncoefficient DdeterminedfromthetheoryofBrownianmotionforthediffusionofsphericalparticlesthroughaliquidwithlow Reynoldsnumber(laminarflow).TherelationisknownastheStokes-Einsteinequation,withDdefinedfrom
where kB isBoltzmann’sconstant, T temperature,and r theradiusofthesphericalparticle.Mostabinitiocalculations haveassumedapureironliquidoutercoreandavolumecontaininganorderofabout100atoms.Atthetemperature andpressureconditionsofEarth’soutercore,theabinitioestimatesof AlfèandGillan(1998) predictanoutercore
FIG.1.16 Viscosityestimatesfortheliquidoutercore.Absoluteupperboundsaredeterminedfromobservedlengthofday(LOD)variations, observed2HzPnKPwaveshavingmraylegswithintheoutercore,andobserved6HzPwavesscatteredatthecore-mantleboundarywhose raysturnneartheinnercoreboundary(P *KP-BC+PK*P-BC,wherethesymbol * indicatesscatteringattheCMBofthewaveprecedingthe symbol.)
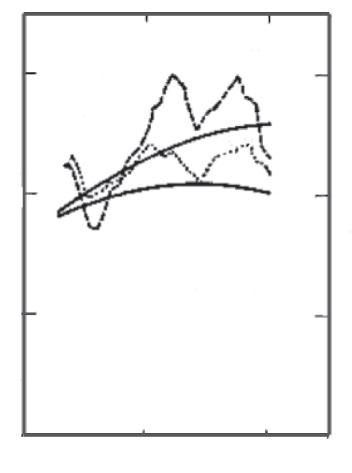
shearviscosityof10 2 Pas.Atfirstglanceestimatesofviscosityfromgeophysicalobservationspresentaconfusionof resultsscatteredacross11ordersofmagnitude(Fig.1.16).Whenidentifiedwiththeirdepthregionofsensitivityand consideredasupperbounds,theyareconsistentwithaviscositythatmayexponentiallyincreasewithincreasingpressureordepthintheinnercore(Smylieetal.,2009).
AttheCMB, MoundandBuffett(2007) estimatetheupperboundof102 Pasfromthecouplingbetweenthefluid outercoreandmantle,whichaffectsEarth’srotationobservedinvariationsofthelengthofday.Thefourordersof magnitudedifferencebetweenMoundandBuffett’supperboundandthatobtainedfromestimatesofself-diffusion coefficientsinironmeltsmayarisefromtheeffectsofnonlaminarflowinaturbulentoutercore.Otherupperbounds canbedeterminedfrommeasurementsoftheattenuationofPnKPbodywavessamplingthemid-outercoreanddirect andscatteredPwavessamplingtheloweroutercore.Theseupperboundscanbedeterminedfromthetheoryforbulk soundattenuation QK 1 influids(Lautrup,2011).Theseassumethatthereexistsaneffectivebulkviscosity ς roughly equaltotheshearviscosity η.Thebulkattenuationisgivenby.
Calculatingthebulkmodulus K fromthePvelocityanddensityatmid-outercoredepthandsubstituting8π forthe radianfrequency ω forthe2HzmaximumfrequencyofobservedPnKPwaves(CormierandRichards,1976)resultsin anupperboundestimateof η equalto4 106 Pas.Similarlyanupperboundof109 Pascanbestestimatedfromthe attenuationofinnercoregrazingPwaves(Cormier,2009).Consideredassimplyupperbounds,however,thenotuncommonobservationofevenhigherfrequency(upto6Hz)seismicwavestransmittedorscatteredintotheouter coreareentirelyconsistentwithanoutercorehavinganear-infinite Q valueandanear-zeroviscosityfromtheCMBto theICB,agreeingwiththelowestimatesfromLODobservationsandself-diffusion.
In Chapter4 oncoredynamicsandthedynamo,wewillseethat viscositycontrolstheEkmannumber,whichis theratioofviscoustoCoriolisforcesimportantforpredic tingthecharacteroftheoutercoreflowthatdrivesthe dynamo.ThelowabinitiovaluesestimatedforoutercoreviscositypredictEkmannumbersthatareconsistentwith highlyturbulent,complexflow.Theattenuationofhigh -frequencyPwavesintheoutercorearealsoeasilyconsistentwitheitheraviscositynearzeroorthehigherviscositieswithintheupperboundsshownin Fig.1.16 .If theupperboundsofviscosityareaccepted,however,theEkmannumbersinalargevolumeoftheoutercorewill beintherangeofthosecommonlyaccessiblebynumericalsimulationsofthedynamo.Sincetheseupperbound viscositiesaremuchhigherthanabinitioestimates,theirvaluesaresometimestermedashyperviscosities.Anunansweredquestionrequiringexperimental,observational,andcomputationaladvancesiswhethertheassumptionof