DYNAMICSOF MOLECULAREXCITONS
SEOGJOOJ.JANG
QueensCollege,CityUniversityofNewYork DepartmentofChemistryandBiochemistry Queens,NY,UnitedStates
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2020ElsevierLtd.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical,including photocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwritingfromthepublisher. Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangementswith organizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanasmaybe notedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenourunderstanding, changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusinganyinformation, methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodstheyshouldbemindfuloftheir ownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityforanyinjury and/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfromanyuseoroperationof anymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-08-102335-8
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: SimonHolt
EditorialProjectManager: LindsayLawrence
ProductionProjectManager: PrasannaKalyanaraman
Designer: GregHarris
TypesetbyVTeX
Tomywife
5.4Harmonicoscillatorbathwithlinearcoupling..
B.4Interactionwithaplanewaveradiationanddipole
Abouttheauthor
SeogjooJ.Jang isaProfessorofChemistryatQueensCollegeof theCityUniversityofNewYork(CUNY),andisadoctoralfacultyofbothChemistryandPhysicsPhDprogramsattheGraduate CenterofCUNY.HeobtainedhisBS(1989)andMS(1993)degrees inChemistryfromSeoulNationalUniversity,andaPhDdegree (1999)inChemistryfromtheUniversityofPennsylvania.Hethen workedasapostdoctoralassociateatMIT(1999–2002)andasa GoldhaberDistinguishedFellow(2003–2005)atBrookhavenNationalLaboratorybeforestartinghisfacultypositionatQueens College,CUNYin2005.Hisresearchexpertiseisinquantumdynamicstheoriesandcomputationalmodeling.Inparticular,he haspioneeredmoderntheoriesofresonanceenergytransferthat arenowbeingincorporatedintotheoreticalanalysesofexperimentaldataoncomplexmolecularsystems,andhasmadekey contributionstounderstandingtheroleofdelocalizedexcitons inphotosyntheticlightharvestingcomplexes.Heisarecipientof theNationalScienceFoundationCAREERAward(2009)andthe CamilleDreyfusTeacherScholarAward(2010).
Preface
Writingabookonexcitonisanactofsignificantcouragegiven thattherearealreadymanyauthoritativeclassicbooksonthis topicthatarehardtomatch.However,whenProf.DavidAndrews invitedmetowriteabookonmolecularexcitonsasoneofthe NanophotonicsSeries,Iacceptedtheofferwithoutmuchhesitation.Ihopedwritingsuchabookwouldbeagreatchanceto organizetheinformationandknowledgeIhavecumulatedover abouttwodecadesofresearch.Inaddition,throughoutmyinteractionswithcolleaguesandstudents,Ihaveindeedexperienced thenecessityforanewkindofmonographonexcitonsthatcan addresscurrentcomputationalandexperimentalneed,inparticularconcerningthedynamics.
Thisbookisintendedforgeneralreaderswhohavecompleted standardgraduatelevelquantummechanicsorquantumchemistrycourses.Itriedtomakethisbookasakindofselfcontained theoreticalreferenceforthosewhotrytounderstandtheoriesof excitondynamics.Thisbookcanhelpnon-expertswhowould liketogetintothisfieldofresearchandalsoexpertsbyoffering newdetailsandperspectivesthatarenotoftendiscussedexplicitly.Itriedtoalsoaddressapplicationsasmuchaspossible,butI shouldadmitthattheaccountofapplicationsinthisbookisquite limited.
Therearethreemajorissuesthisbookisparticularlyfocused on.Thefirstistounderstandtheassumptionsandapproximationsimplicitinconventionalmodelsformolecularexcitonsand theirinteractionswithenvironments.Mostofconsiderationisat formallevel,whichwillformthebasisformoredetailednumerical investigationsinthefuture.Inaddition,thispartcanbeconsideredasanextensionofstandardmolecularquantummechanics, andcanbeusedassupplementalreadingforaquantumchemistryclass.Thesecondistoofferascomprehensivedescription aspossibleofmostdynamicstheoriesofmolecularexcitons.The mainfocuswasonexplainingthederivationofthesetheoriesand methods.Theratetheoriesandquantumdynamicsmethodsdescribedhereareinfactmuchmoregeneralandareapplicableto otherquantumdynamicalprocesses.Finally,detailedtheoretical descriptionisprovidedforthespectroscopyofexcitons.Again,the majorfocusisontheoreticalaspectsofthesespectroscopicmeth-
odsandunderstandingtheircapabilityasatoolforprobingthe excitondynamics.
NewYork
December6,2019
SeogjooJ.Jang
Acknowledgments
IthankthelateBobSilbeywhotaughtmeagreatdealabout molecularexcitonswhenIwasapostdoctoralresearcheratMIT. Healsocontinuedinspiringmeformanyyearsafterwardsasa colleague.Interactionswithhimwerealwaysspecial.Hecould easilyexplainimportantideasandissuesinafewminutes,which helpedmeunderstandtheirimplicationssoquicklyandpursue newideasefficiently.Writingthisbookgavemeanotherchance tointeractwithhimindirectlythroughhispublications,andIam stilllearningfromworkshehascompleteddecadesago.
Althoughnotdirectlyrelatedtothistopic,IamheavilyindebtedtoMarshallNewton,oneofthebestcriticalthinkerand theoreticianIamawareof.Hisbroadknowledgeandexpertisein electrontransfertheorieshelpedmeenvisionaroadmapfordevelopingtheoriesofexcitontransferanddynamics,whichhave remainedrelativelyunexploredincomparisontothefieldofelectrontransfertheories.Communicationsandinteractionswithhim helpedmeevolvethroughmyearlyformativeperiodasanindependenttheoretician.
TherearealsomanyothersthatIshouldnotforgetmentioningnamesforvariouscontributionsrelatedtothisbook.Iam indebtedtomymentorsatSeoulNationalUniversity,Sangyoub LeeandKookJoeShin,whofirstintroducedmetoFörstertheory andguidedmyfirstresearchonthistopic,andtomyPhDmentor GregoryVothfromwhomIlearnedthefundamentalsofquantum dynamics.IwouldliketothankJeffCina,DavidReichman,Chris Bardeen,Yuan-ChungCheng,BenedettaMennucci,JoeSubotnik, DortheEisele,GregScholes,YoungMinRhee,DavidCoker,JianshuCao,JasperKnoester,GrahamFleming,andK.BirgittaWhaley fordiscussionsandhelpatvariousstagesleadingtothiswork, andFrankSpano,AriChakraborty,QiangShi,andAndrewMarcusforallowingmeusetheirimages.SupportfromNationalScienceFoundation,theDepartmentofEnergy,andCamilleDreyfus Foundationhavemadeitpossibletocontinueprojectsthatconstitutevariouspartsofthisbook.
IamgratefultotheeditoroftheNanophotonicsSeries,Prof. DavidAndrews,andtheeditorialofficeofElsevierforsupport.Finally,Icannotthankenoughmywifewhohasbeentrulysupportiveofwritingthisbook.Iamhappytodedicatethisbooktoher.
SeogjooJ.Jang January28,2020
Introduction
Contents
1.1 Motivationandobjective 1
1.2 FrenkelandWannierexcitons 3
1.2.1 Abriefoverview 3
1.2.2 ModelHamiltoniansforFrenkelexcitons 6
1.2.2.1 Linearchain 7
1.2.2.2 Circularchain 11
1.2.3 SemiclassicalmodelHamiltoniansforWannierexcitons 15
1.3 Disorder,fluctuations,andmeasureofdelocalization 16
1.4 Utilityandlimitationsofexcitonmodels 18
1.1Motivationandobjective
Anexcitonrepresentsaquantummechanicalstateofelectronicexcitationoraboundpairofanelectronanditshole.1 Anyelectronicexcitationofamoleculecanbeviewedasanexcitonconfinedwithinthemolecule.However,therealbenefitof theconceptofexcitonisthatithelpsgeneralizingtheexcitation beyondmolecularboundariesinasimplemanner.Forexample, excitonscanbeformedacrosstheconfinesofmoleculesandexist inquantummechanicalsuperpositionstates.Theserepresentcollectivequantumstatesdistinctivefromindependentsumsofelementarymolecularexcitations,whichcanexhibituniquequantummechanicalpropertiesofcollectivenature.Onewell-known exampleisthesuper-radiance,acollectiveemissionphenomenon thatappliestoanyatomic[1]ormolecularsystems[2–6].
Directexperimentalconfirmationofmolecularexcitonswas difficultinearlydaysofquantummechanics.Althoughwellestablishedconceptually,theirpracticalsignificancewasnot clearlyrecognizedeither.Throughdecadesofresearchanddevelopment,excitonshavesteadilybecomeestablishedasessential objectsforsolarlightharvesting,imaging,sensing,lasing,and light-emittingdevices.Applicationsofexcitonsforquantuminformationprocessingdevicesandnovelphotonicmaterialsarealso emergingareasofresearch.Thankstotheseadvances,excitons arenowwellsupportedbymanycomputationalandexperimental
1 Theholeitselfisaquasi-particleandreferstotheabsenceofelectron.
data,andareperceivedasimportantobjectsforafewkeyapplications.However,whiledatainformingtheexistenceandcontributionofexcitonsabound,accurateandcompleteinformationon excitonsisstilldifficulttogetingeneral.Inparticular,accurate measurementofbothspatialpatternsandtemporaldynamicsof excitons,whichiscrucialforsatisfactorymicroscopiccharacterization,remainsachallengingareaofresearcheventodate.
Thedifficultyindetailedmicroscopiccharacterizationofexcitonsstemsinpartfromtheirindefinitespatialextents(in nanometerlengthscales)andtransientdynamicalnature(intime scalestypicallyasshortastensoffemtoseconds).Resolvingthis issuerequiresexperimentaltoolsthatcansimultaneouslyprobe nanometerlengthscalesatfemtosecondtimeresolution,which remainchallengingdespiterecentadvances.Theotherreason,althoughlessappreciated,isthefactthatexcitonhasoftenbeen perceivedbyexperimentalistsasalooselydefinedsimpleobjectof semi-empiricalnature.Thisisincontrasttothecurrentstatusof computationalmolecularquantummechanics,whichhascomea longwayofconstructingsophisticatedmethodsandrigorousmicroscopicformulationsthatcanaccountforvariousmany-body quantumeffects.Thegapbetweenthesemodernpracticesof molecularquantummechanicsandtheconceptualbasisofmost experimentalinvestigationbasedonoldexcitontheories,isoften thesourceofconfusionandmiscommunication.
Forbothpracticalandfundamentalreasons,thereisincreasingdemandforaccuratecharacterizationandcontrolofexcitons incomplexenvironments.However,formanyinterestingsystems, thescaleandaccuracyofcalculationsnecessaryforreliablecomputationofexcitonicpropertiesisingeneralbeyondthereachof rigorouscomputationalmethodsatpresent.Significanttheoreticalprogressisneededformoreaccurateandmicroscopicdescriptionofexcitonsaswellasforfurtheradvancesinexperimental probetechniques.Inpromotingthetheoreticalprogress,itisimportanttoestablishageneraltheoreticalframeworkforexcitons thatisbothrigorousandpractical.Thisisoneofthemainmotivationsforthisbook.
Thefirstobjectiveofthisbookistohelpconsolidatingmany versionsandideasofexcitonsintoasingletheoreticalformalism. Whilethisisanambitiousobjectivedifficulttoachieveatpresent, thisbookcansetthestageforinitiatingalongtermeffortofsuch nature.Inaddition,manyassumptionsandapproximationsclarifiedinthisbookwillhelpgainbetterunderstandingofthedynamicsandspectroscopicdata.Thesecondobjectiveistooffer comprehensivedescriptionofvarioustheoriesofexcitondynamicsalongwiththeirapplications.Therearemultipleapproaches
possibleforachievingthisgoal.Theapproachtakeninthisbook istobeginwithmolecularHamiltonians.Thisapproachmakes itstraightforwardtoclarifyassumptionsandapproximationsimplicitindifferentformsofexcitonsfromtheoutset.Theformal foundationforthiswillbeprovidedinthenextchapter.Inthe restofthischapter,formotivationalpurposes,abriefoverviewof FrenkelandWannierexcitonsispresented.Thisisthenfollowed byintroductionofsimplemodelHamiltoniansusedfordescribingsuchexcitons.
Afewwordsontheconventionofnotations.Forexcitonstates andHamiltonians,thefirstorderquantizationandtheDiracnotationforstatesandoperatorswillbeusedinmostcases.Thesecondquantizationwillbeprimarilyreservedonlyforthedescriptionofelectromagneticradiationwithinthequantumelectrodynamicsformalism.Whenappropriate,semiclassicaldescription ofelectromagneticradiationwillalsobeusedforthedescription ofmatter-radiationinteraction.
1.2FrenkelandWannierexcitons
1.2.1Abriefoverview
Frenkel[7–9]andWannierexcitons[10,8]representtwowellknownformsofcollectiveexcitationsthatareapplicableintwo opposinglimitsandareamenableforsimplequantummechanicaldescription.
Frenkelexcitontheoryhasbeensuccessfulfordescribingthe spectroscopyofmolecularcrystalsandaggregates[8,11,12],where moleculesareboundtogetherbyweakinteractions.Inthiscase, electronicpropertiesofindividualmoleculesremainmostlyintact.Thus,collectiveexcitationprocessescanbedescribedstill intermsofpropertiescharacterizingtheexcitationofindividual molecules.ApplicationoftheFrenkelexcitontheoryhassince beenexpandedtomacromolecularandsupramolecularsystems. Mostrecently,Frenkelexcitonswereshowntoplayamajorrolein naturalphotosyntheticlightharvestingcomplexes[13].
Ontheotherhand,Wannierexcitons[10,8]areappropriatefor inorganicinsulatingorsemiconductingsolidmaterialswherethe bandtheoryservesasasuccessfulframeworktodescribedelocalizedelectronsandholes.TheconceptofWannierexcitonplayed akeyroleinthedevelopmentofinorganicphotovoltaicandsolid statelaserdevices.Toacertainextent,Wannierexcitonscanbe usedtodescribeelectronicexcitationprocessesinhighlyconfined systemssuchasquantumdots.
ThebasissetofquantummechanicalstatesusedforFrenkel excitonisthedirectproductofindividualmolecularorbitals, whicharetypicallyassumedtobeorthogonaltoeachother.Tobe morespecific,consideranexampleof N aggregatesofmolecules, wherethe j thmoleculehasthegroundelectronicstate |gj ,and asingleexcitedstate |ej .Then,thegroundelectronicstateofthe aggregateis
where ⊗ representsdirectproduct.Onecanthenintroduce N orthogonalstatesformingthebasisofsingleexcitonstates,eachof whichisdenotedas |sj .Thisrepresentsastatewhereonlythe j thmoleculeisintheexcitedstate |ej whileallothersareinthe groundelectronicstate.Thus,
Higherorderexcitonssuchasdoubleandtripleexcitonscanalso bedefinedinasimilarmanner.
TheoriginalformulationofFrenkelexciton[7,9]usedasingle orbitaltodefineeachstate |ej .However,thisisnotinfactanessentialassumption.Eachelectronicstateatmolecule j canbeany generalmolecularelectronicstateaccountingforallmany-body electroniccorrelationswithinthemoleculeashasbeensuggested byAgranovich[14].TheonlyassumptionnecessaryfortheconstructionofFrenkelexcitonbasis,aswillbecomeclearinthenext chapter,isthat ej |ek = 0 for j = k .Consequently,
Despitetheassumptionofweakinteractionsimplicitin Eq.(1.3),theelectronicexcitation |ej atthemolecule j canstill causeperturbationofelectronsinthegroundelectronicstate |gk ofanothermolecule k .SuchinteractionisdominatedbyexchangeinteractionatshortrangeandbecomesmainlyCoulombic atmoderatetolongdistances.Theseinteractionscoupletheexcitationofelectronsatthe j thmoleculewiththatofelectronsat the k thmolecule,andareoftencalledresonanceinteractions.In otherwords,giventheelectronicHamiltonianoftheaggregate ˆ He , thereisanon-vanishingresonanceterm
= sj | ˆ He |sk , for j = k. (1.4)
Theseresonanceinteractions, Jjk ’s,causeeigenstatesof ˆ He tobe coherentsuperpositionsof |sj ’s.Theresulting N eigenstatesform
the excitonbasis,whichisdifferentfromthesiteexcitationbasis. Theexcitonstatesarefullydelocalizedandalsoformabandofvirtuallycontinuousstatesinthelimitoflarge N .Thisexcitonband ishoweverconstructedoutoftwoelectronprocessesandisdifferentfromtheconductionandvalancebandofthesingleelectron picturethatformthebasisoftheWannierexcitonsasdescribed below.
TheconceptofWannierexcitonisbuiltonthebandtheory ofelectronicstatesinsemiconducting/insulatingsolidmaterials, whichrepresentalmostcontinuumstatesofdelocalizedelectrons (conductionband)andholes(valanceband).Namely,itisbased onthefollowingeffectiveelectronicHamiltonian:
where Ec (k) and Ev (k) areenergiesofconductionandvalance bandscorrespondingtowavevector k,
)and
(
)are creation(annihilation)operatorsofanelectronandhole,respectively. Nt isthetotalnumberoflatticesitesand V(p, k, k ) isthe Coulombpotentialbetweenelectronandholerepresentedinthe momentumspace.
Forelectronsandholeslocalizednearthebandedges,semiclassicalwavepacketsconsistingofthesuperpositionofthe nearbybandstatescanprovidereasonabledescriptionoftheir properties.Thesewavepacketsbehaveinalmostclassicalmannerwitheffectivemassesreflectingthedispersionrelationships ofrespectivebands.Giventhatthedistancebetweenthecentersofelectronandholewavepacketsismuchlargerthanlattice spacingsofthesolids,theireffectiveinteractioncanbemodeled bysimpleCoulombattractionscreenedbytheaveragedielectric constantofthemedium.Withinthispicture,theenergylevelsof excitons(inthesimplestcase)havethesamestructureastheelectronicenergyofthehydrogenatom,butwitheffectivecharges andmassesthataredifferentfrombareones.Inthepresence ofconfinementorboundaryeffects,theeffectivepotentialdeviatessignificantlyfromasimpleCoulombicbehavior.Accurate theoreticalunderstandingofsuchdeviationisnecessaryforthe determinationoftheexcitonbindingenergy.
Themanneroflocalization/delocalizationisdifferentfor FrenkelandWannierexcitons.Intheformercase,thedelocalizationoccursonlythroughquantummechanicalsuperposition
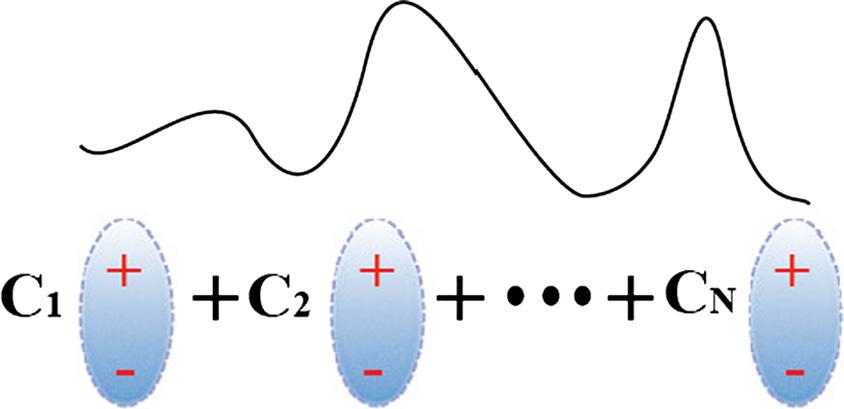
Figure1.1. IllustrationoftheformationofaFrenkelexciton.Eachellipsewith + and representsintramolecularexcitation,andthewholeexcitonstate(black line)isformedasalinearcombinationoftheselocalizedexcitations. C1 , , CN arecomplexcoefficientssuchthat
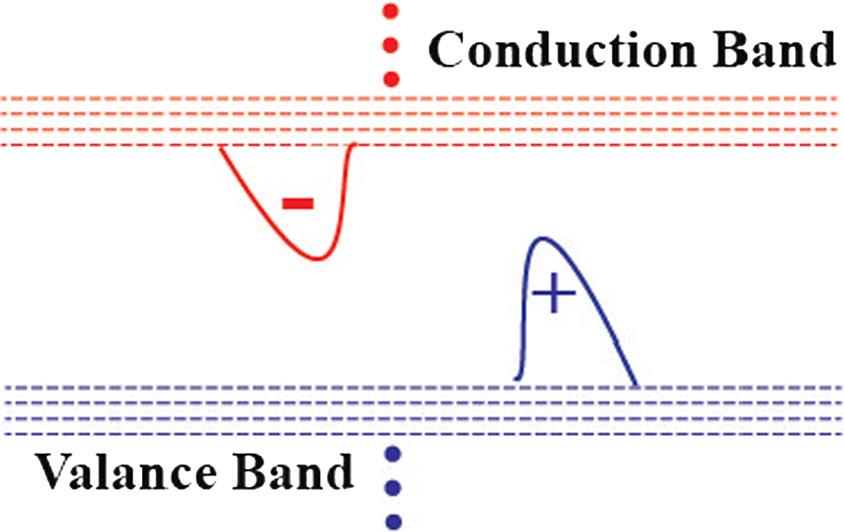
Figure1.2. IllustrationoftheformationofWannierexciton.Localized wavepacketsofelectronintheconductionbandandholeinthevalancebandare formedandareboundtoeachotherviaCoulombinteraction.
oforiginallylocalizedexcitationstates,namely,formationof delocalizedexcitonstates.Fig. 1.1 providesillustrationofsuch states.Ontheotherhand,inthelattercase,formationofexcitonsamounttopartiallocalizationofbandstates,whicharefully delocalizedeffectivesingleelectronandholestates.Fig. 1.2 depictsthisprocess.Thesourcesoflocalizationcanvarybutare mostlikelythecombinationofdisorder,dynamicrelaxation,and thermalizationeffect.TheCoulombicbindingpotentialbetween electronandholealsocontributestothelocalizationaswell.
1.2.2ModelHamiltoniansforFrenkelexcitons
Formoreconcreteunderstanding,itisinstructivetoconsider twowell-knownmodelsofFrenkelexcitonsformedby N identical molecularunits.Oneisalinearchainwithonlynearestneighborinteractions.Theotherisacircularchainwitharbitrarynon-
nearestneighborinteractionssatisfyingcyclicsymmetry.Inthe absenceofanydisorderordynamicalfluctuations,thesemodels havesimpleanalyticexpressionsfortheireigenvaluesandeigenstates.Detailedconsiderationofthesestatescanbeusedtoillustratekeyconceptsandlanguagesofmolecularexcitons.Inthetwo modelsdescribedbelow,itisassumedthatthelevelspacingsof excitedstateswithineachmolecularunitaremuchlargerthanthe resonancecoupling.Underthiscondition,onecanfocusononly oneexcitedstateofeachmoleculewithenergy E asfarassingle excitonisconcerned.
1.2.2.1Linearchain
Consideralinearchainof N identicalmolecules,withonlythe nearestneighborresonanceinteractiondenotedas J .Then,the singleexcitonHamiltonianinthebasisof |sj ,with j = 1, ··· ,N , canberepresentedas
TheeigenstatesandeigenvaluesofthisHamiltonianareasfollows:
where p = 1, ··· ,N .Detailedmathematicalstepsleadingtothese expressionsareprovidedinAppendix A.
For J< 0,thelowestvalueoftheexcitonenergyanditseigenstatecorrespondto p = 1 inEqs.(1.7)and(1.8)asfollows:
Ontheotherhand,thehighestvalueoftheexcitonenergyandthe correspondingeigenstatecorrespondto p = N asfollows:
Therefore,theenergiesofalltheexcitonstatesarewithinaband ofthefollowingwidth:
whicharedistributedsymmetrically2 around E .Thus,theexciton bandwidthischaracteristicofthenearestneighborcoupling. For J> 0,theorderofeigenstatesisreversed.Inotherwords, Eq.(1.11)becomesthelowestexcitonenergyandEq.(1.9)the highestexcitonenergy.Exceptforthis,otherfeaturesremainthe sameasinthecaseof J< 0. Letusnowconsideramoreconcretemodelfortransition dipoles.Assumethatthe j thmolecularunithasthefollowing transitiondipolemoment:
whereitisassumedthatthelinearchainisalongthe z-direction. Thus, θj istheaxialangleand φj istheazimuthalangleofthedirectionofthetransitiondipole μj .Letusalsoassumethat J is givenbyasumofconstantnearestneighbortermandaneffective transitiondipoleinteractionasfollows:
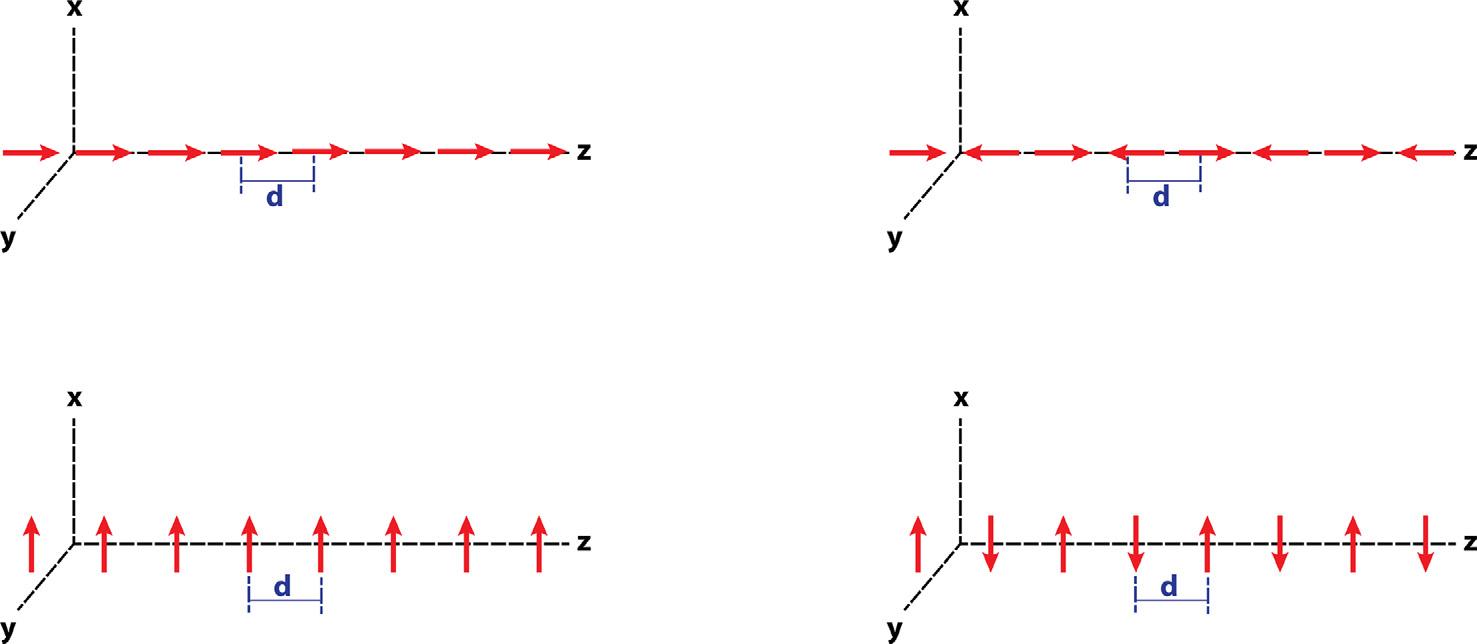
where isaneffectiveopticaldielectricconstantand d isthedistancebetweennearestneighbors.Thisassumptionisreasonable ifthedistance d islargeenoughsuchthat μ2 /(8 d 3 )<< |J0 |.Here, J0 representsallthehigherorderCoulombandexchangeinteractionsthataresignificantonlybetweennearestneighbors. InorderforEq.(1.15)tobeindependentof j , φj φj +1 = δφ . For θj ,therearetwopossibilities, θj = θj +1 or θj + θj +1 = π .As representativeexamples,itisusefultoconsiderthefollowingfour cases: (i) φj = 0, θj = 0; (ii) φj = 0, θ2j 1 = 0, θ2j = π ; (iii) φj = 0, θj = π/2; (iv) φj +1 φj = π with φ1 = 0, θj = π/2,whicharedepictedinFig. 1.3.Detaileddescriptionofeachcaseisprovided below.
2 Thissymmetrygetsbrokeniftherearenon-nearestneighborinteractions.
Figure1.3. Depictionoffourexamplesoflinearaggregates.
(i) Inthiscasewhereallthetransitiondipolesarealongthe z directioninhead-to-tail,Eq.(1.15)simplifiesto J = J0 2μ2 /( d 3 ).Assumethat J0 < 0.Then, J< 0,andEqs.(1.9) and(1.10)representthelowestexcitonenergyandeigenstate.Thecorrespondingtransitiondipoleofeachexciton statehaszerocomponentsalongthe x and y directions,but onlythefollowing z-component: μp,z = μ N j =1 ϕp |sj = μ 2 N + 1 1/2 N j =1 sin pjπ N + 1 = μ (1 ( 1)p ) √2(N + 1) cot pπ 2(N + 1) , (1.16) where p = 1, ··· ,N .Inthelarge N limitandfor p<<N ,this approaches μp,z ≈ μ√2(N + 1)(1 ( 1)p )/(pπ). (ii) Inthisconfigurationofanalternatinghead-to-headand tail-to-tailconfigurationalongthe z direction,Eq.(1.15) simplifiesto J = J0 + 2μ2 /( d 3 ).Dependingonthesignof J0 anditsmagnituderelativeto 2μ2 /( d 3 ),theorderofexcitonenergylevelsmayormaynotbethesameascase (i).Let usassumefornowthat J> 0.Then,Eqs.(1.11)and(1.12) representthelowestsingleexcitonenergyandeigenstate. Asincase (i),thetransitiondipoleofeachexcitonstatehas zerocomponentsalongthe x and y directions,andhasthe
followingcomponentalongthe z-direction: μp,z = μ N j =1 ( 1)j 1 ϕp |sj
μ 2 N + 1 1/2 N j =1 sin pjπ N + 1 + (j 1)π
Byintroducing p = N + 1 p ,itiseasytofindthatthiscase becomesnearlyequivalentto (i).Inthelarge N limitandfor N p<<N ,Eq.(1.17)approaches ˜ μp,z ≈ μ√2(N + 1)(1 ( 1)p )/((N + 1 p)π).Foreven N ,thelowestexcitonlevel (p = N )haszerointensity,whereasthesecondlowestexcitonstatehasthemaximumintensity.Ontheotherhand, forodd N ,thelowestexcitonstatehasthemaximumintensity,butthesecondlowestonehaszerointensity.Except forthesefinedetailsdependingonevenorodd N ,thelevel spacingsandthefactthatmajorintensitiesareinthelower excitonstatesarethesameasincase (ii). (iii) Inthiscasecorrespondingtoaparallelarrangementoftransitiondipolesalongthe x -direction,Eq.(1.15)simplifiesto J = J0 + μ2 /( d 3 ).Letusassumethat J> 0 asincase (ii). Then,Eqs.(1.11)and(1.12),thecasewith p = N ,representthelowestexcitonenergyandeigenstate.Thetransitiondipoleofeachexcitonstatehaszerocomponentsalong the y and z directions,buthasthefollowing x -component:
NotethatthishasthesameexpressionasEq.(1.16)except thatthedirectionisnowalongthex-direction.Thisisexpectedbecausethetransitiondipolesareparallelinboth casesandexactlythesameexpressionisusedforsumming upthecontributiontothetransitiondipoleoftheexciton state.However,thereismajordifferencefromcase (i) inthat theorderofexcitonstateisreversedhere,asincase (ii).For even N ,thetransitiondipoleofthelowestexcitonstateis zero.Forodd N ,thetransitiondipoleofthelowestexciton stateisfinitebutoftheminimummagnitude.Inthelimitof largeodd N ,itapproaches μN,x ∼ π √2μ/(N + 1)3/2 ,whichis vanishinglysmall.Thus,thelowestsingleexcitonstatehas eitherzerooralmostzerotransitiondipoleinthiscase.
(iv) Inthiscasecorrespondingtoantiparallelarrangementof transitiondipolesalongthe x -direction,Eq.(1.15)simplifiesto J = J0 μ2 /( d 3 ).Letusassumethat J< 0.Then, Eqs.(1.9)and(1.10)representthelowestexcitonenergyand eigenstate.Thetransitiondipoleofeachexcitonstatehas zerocomponentsalongthe y and z directions,buthasthe following x -component:
NotethatthishasthesameexpressionasEq.(1.17)except thatitisnowalongthex-direction.However,notethedifferenceofexcitonenergyorderinginthiscase.Whilethe transitiondipoleofthelowestexcitonstateisnonzero,its valueis π √2μ/(N + 1)3/2 ,whichisvanishinglysmall. Thedetailsdescribedaboveforthecases (i) and (ii) arealmostequivalentexceptforthephasefactor,whichcanbeincorporatedintothedefinitionofeachstate |sj .Thesameistruefor thecases (iii) and (iv).Thus,boththecases (i) and (ii) correspond to J -aggregates[8,15,16]inthesensethatthemajoroscillator strengthareconcentratedonthelowestexcitonstate.Ontheother hand,thecases (iii) and (iv) correspondto H -aggregates[8,15,16] inthesensethelowestexcitonstatehasvirtuallyzerooscillator strength.Thesealsoserveascounterexamplesforoftenreferred simplepicturefor J -and H aggregates, i.e.,theformerasresultingfrom“head-to-tail”andthelatterfrom“parallel”configurationoftransitiondipoles.Forexample, (ii) isnotin“head-to-tail” butthepatternoftransitiondipoleswillempiricallyclassifyitas J -aggregate.Ontheother, (iv) isnot“parallel”butitspatternof transitiondipolesalsomakesitanexampleof H -aggregate.
Thesummaryprovidedaboveisofcoursebasedontheassumptionthatthesignof J0 isthesameasthatofthetransition dipoleinteraction.Ifthesignof J0 isdifferentandplaysadominantrole,theclassificationgivenaboveshouldbealtered.Inaddition,formoregeneralvaluesof θj and φj φj +1 = δφ ,thedivision into J or H aggregateswillbelessclear.
1.2.2.2Circularchain
Asthesecondexample,consideraringofidentical N molecularunitswiththefollowingexcitonHamiltonian:
where J(j k) satisfiesthecyclicboundaryconditionwithperiod N and J(0) = E ,whichistheenergyofeachstate |sj .Thiscyclic symmetryleadstothefollowingstatestobeeigenstatesof ˆ He .
where p = 0, ··· ,N 1.Thiscanbedemonstratedeasilybythe followingidentity:
wheretheindex k = j j wasintroducedinthethirdlineandthe factthat J(j) = J(j + N) and e 2πipj/N = e 2πip(j +N)/N wasusedto replace j< 0 with N + j inthesummation.Asaresult,theexciton Hamiltonianandeigenvaluecanbeexpressedas
Equivalently, p canberearrangedtobecenteredaroundzero, whichisoftenmoreconvenient.Forodd N , p = 0, ±1, , ±(N 1)/2 canbeused.Foreven N , p = 0, ±1, ··· , ±(N 2)/2,N/2, canbeused.
Letusnowconsideramoredetailedspecificationofthepositionsandtransitiondipolesofmoleculesformingthering.Assumethattheringisinthe xy -planeandthatitsradiusis R .Then, assumethatthepositionandtransitiondipoleofthe nthmolecule
aregivenby
rj = R (cos(2πj/N), sin(2πj/N), 0) , (1.25) μj = μ sin θμ cos φμ + 2πj/N , sin θμ sin φμ + 2πj/N , cos θμ , (1.26)
where θμ and φμ arefixedreferenceanglesofthetransition dipoles.Then,assumingadditionalnon-transitiondipoleinteractiononlyfornearestneighbors,itisstraightforwardtoshowthat J(j k) for j = k canbeexpressedas
J(j k) = J0 δ[(j k)/N ],±1 + μ 2 2cos2
where [(j k)/N ] inthesubscriptofthedeltafunctiondenotes modfunctionof j k withrespect N .Insertingthisexpressioninto Eq.(1.24)andutilizingthefactthat J(k) = J(N k),weobtainthe followinggeneralexpression:
Notethattheenergylevelsof ±|p |’saredegenerate. Ontheotherhand,forthedefinitiongivenbyEq.(1.26),the transitiondipoleofthe p thexcitonstatebecomes
Unlikethecasewiththelinearchain,non-zerovaluesoftransition dipolesinthismodelareconfinedtoonly p = 0 and ±1.Whether thesecorrespondtolow-lyingorhigh-lyingexcitonstatesdepend ondetailssuchas J0 , θμ , φμ ,and N .