https://ebookmass.com/product/dynamics-and-stochasticity-in-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Logistics Transportation Systems Sarder
https://ebookmass.com/product/logistics-transportation-systems-sarder/
ebookmass.com
Logistics Transportation Systems Md Sarder
https://ebookmass.com/product/logistics-transportation-systems-mdsarder/
ebookmass.com
Transportation Cyber-Physical Systems Lipika Deka
https://ebookmass.com/product/transportation-cyber-physical-systemslipika-deka/ ebookmass.com
Living in Words: Literature, Autobiographical Language, and the Composition of Selfhood Garry L. Hagberg
https://ebookmass.com/product/living-in-words-literatureautobiographical-language-and-the-composition-of-selfhood-garry-lhagberg/ ebookmass.com
Fundamentals of Nuclear Science and Engineering 3rd Edition
https://ebookmass.com/product/fundamentals-of-nuclear-science-andengineering-3rd-edition/
ebookmass.com
Wicked Highland Ways Wine Mary
https://ebookmass.com/product/wicked-highland-ways-wine-mary/
ebookmass.com
Personality Psychology, Ideology, and Voting Behavior: Beyond the Ballot Ben F. Cotterill
https://ebookmass.com/product/personality-psychology-ideology-andvoting-behavior-beyond-the-ballot-ben-f-cotterill/
ebookmass.com
Hot Conduit (Hot Under the Collar Book 2) Katherine Mcintyre
https://ebookmass.com/product/hot-conduit-hot-under-the-collarbook-2-katherine-mcintyre/
ebookmass.com
Sex Blood (Blood Splatter Books) Rick Wood
https://ebookmass.com/product/sex-blood-blood-splatter-books-rickwood/
ebookmass.com
The Four Day Fakeout (West Oaks Heroes Book 3) Hannah Shield
https://ebookmass.com/product/the-four-day-fakeout-west-oaks-heroesbook-3-hannah-shield/
ebookmass.com
Dynamicsand Stochasticityin Transportation Systems Dynamicsand Stochasticityin Transportation Systems ToolsforTransportation
NetworkModelling
GiulioErbertoCantarella
DavidPaulWatling
StefanodeLuca
RobertaDiPace
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
# 2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronic ormechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem, withoutpermissioninwritingfromthepublisher.Detailsonhowtoseekpermission,furtherinformation aboutthePublisher’spermissionspoliciesandourarrangementswithorganizationssuchasthe CopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher (otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedicaltreatment maybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluating andusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuch informationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,including partiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assume anyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability, negligenceorotherwise,orfromanyuseoroperationofanymethods,products,instructions,orideas containedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary ISBN:978-0-12-814353-7
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: JoeHayton
AcquisitionEditor: BrianRomer
EditorialProjectManager: AleksandraPackowska
ProductionProjectManager: NirmalaArumugam
CoverDesigner: ChristianJ.Bilbow
TypesetbySPiGlobal,India
Contributors GiulioErbertoCantarella
UniversityofSalerno,Salerno,Italy
RobertaDiPace
UniversityofSalerno,Salerno,Italy
StefanodeLuca UniversityofSalerno,Salerno,Italy
DavidPaulWatling
InstituteforTransportStudies,UniversityofLeeds,Leeds,UnitedKingdom
Preface Dissidenceandcontroversyarewhatbringscienceforward. Agreementandacceptancerarelystimulateexperimentsandprogress. ThorHeyerdahl.
Outline. Inthischapterthereadermayfindthecontentsandthepurposeofthisbook, andaframeworkgeneralenoughtoencompassalmostallTTTtools.Besidethereader mayfindaproposalofnomenclature.Mainemphasisinthisbookisonthemathematicalfeaturesofmodelsandalgorithmsfortraveldemandassignmenttoatransportation network.Implementationandapplicationissueswillbethetopicsofafuturecompanion book(possiblybyotherauthors)aswellascontrolanddesigntools.
Sincehuntinggatheringerahumanbrainshaveevolvedtobemoresensitivetovariationsinspaceand/ortimeofthesurroundingenvironmentratherthanregularity anduniformity;(mostlyunconscious)representationsoflocationoverspaceand evolutionovertimeallowedhumanbeingstosurviveinchallengingconditions.This isstillthecase:apedestrianwishingtocrossaurbanstreettriestoanticipateevolutionovertimeofthelocationsofthesurroundingvehicles.
Developinga(mathematical)modelofrealsystems,ascommoninmodern appliedsciences,isamoreconsciouswaytofollowthatancestralattitude.
Eventhoughfuturewereperfectlydeterminedbypast,accordingtoBeowulf’s wellknownstatement“Fatewillunwindasitmust!”(butnottoauthors’opinion), stillitmaynotbeperfectlyforecastedduetolackofenoughinformationaboutpast, touncertaintyaffectingforecastingmethods, ….Thus,howeverdesirable,inseveral casesaprecisemodelprovidingdeterministicdescriptionandforecastingofsystem statecannotbedeveloped,andthemostgeneralmodellingtoolsincludeboth dynamicandstochasticfeaturestogetherwithspacecharacterisation.
Itshouldberemarkedthatanykindofrepresentationormodelmentionedabove is,asbeauty,inthemindofthebeholder;thereforedynamicsorstochasticityare featuresof(mathematical)modelsonly,asortofsocialconstructionsagreedby themodellercommunity,notbeconfusedwiththeobjectoftheirapplications,such variationsinspaceand/ortimeinarealsystem.Alongthislineofreasoning observationsofrealworldarefacts,whilstmodelsareopinionsaboutthem.
Thefocusofthisbookistheuseofmathematicalmodellingmethodstoassist intheunderstanding,prediction,policy assessmentanddesign oftransportation systems;butwhatisa“transportationsystem”,ormostpertinentlywhatdowe meanbyitforthepurposesofthisbook?Firstly,itcontainstheinfrastructure, thepavementstowalkon,theroadsonwhichwecycle,driveormayuseabus
ortaxi,thetraintracks,aswellasthefleetsofbuses,airplanesandtrainsthatare usedtorunservicesandtransportgoods .Secondly,itcontainstheusersofthe transportationsystem,namelythepeoplewhochoosewhere,whenandhowto travel,aswellasthegoodsoperatorsandsupplierswhodecidehowandwhere totransporttheirgoods.Thirdly,itcontainsthevarious publicandprivateorganisationsresponsibleforplanning,operating,pricingandprovidinginformationon theinfrastructure.
Sucha“system”containsmanyinteractingelements.Atravellermaydecideto drivetotheirnormalplaceofworkduring amorebusy(congested)periodofthe daythantheywouldnormally,andbydoingsocontributesadditionallytothe congestionforthatday.Thiscongestionmaydelayotherroaduserswhoareusing someofthesameroads,butperhapstravelli ngbetweenanentirelydifferentorigin anddestinationtothefirsttraveller.Theadditionaldelayexperiencedmay,onthe otherhand,holdbackthesecondtravellersothattrafficisinfactmorefreely runningthatitmightbeonsomedownstreamstretchofroadontheirintended route.Thismaycausetheresponsivetra fficsignalsatanintersectiontotrigger atadifferenttime,andsoinfluencesomeothertravellers.Ontheotherhand, oursecondtravellerhassuchabadexperienceoftravellingthatdaythatthey decidestotryadifferentroutewhentheymakethattripnexttime,whereasthefirst travellerdecidesthatre-adjustingtheirdeparturetimewouldbewiseinthefuture. Asthishappening,aprivatetransportoperatordecidestointroduceanewhighspeedtrainserviceinthearea,whichourfirsttravellerthendecidestouseonsome subsequentday,thusalleviatingsomeofthepressureonroadcapacity.Atthesame timeasalltheseinteractionsareon-going,eachminuteofeveryday,atransport plannerisdecidingonhowtomakeadjustmentstoachievesomepolicyobjective, andasaresultintroducesonsomesubsequentdayanewhigh-occupancyvehicle laneforcertainhoursoftheday.
Thisisonlyoneexample.Makingsenseofsuchsystemsisnosimpletask. Mathematicalmodelsareatoolforcaptu ringatleastsomeofthiscomplexity, assistingthosewhoareresponsibleforpl anninganddesigningsuchsystemsfor the‘publicgood’.Theyallowlocation-specificdatatobesystematicallyusedto calibrateamodeltoparticular locale. Importantly,themodelsthatwillinterest usinthisbookhaveaclearforecastingc apability,allowingthemodellertostudy “what-if”scenarios.Thesescenariosm ayrange,forexample,fromstudyingthe impactofpotentialfuturechangestotrav eldemandpatterns,theeffectofalternativecontrolmeasures,ortheimpactofpolicymeasuresontravellers’experience andnetworkperformance.
Thesemodelsare,insomerespect,alwayswrong,asalwaysthecaseinall appliedsciences.Theyalwaysomitorover-simplifyorincorrectlycapturesome phenomenon,andsowhenusingthemitisalwaysimportanttobeasclearaspossible onthelimitationsofthemodel,whatitisnotabletocaptureaswellaswhatitis representing.Themodellerhastheresponsibilitytocommunicatethistothe decision-maker,howevermuchthedecision-makermaynotliketohearit.Todothis effectively,webelieveweneedaclear,standardreferencesystem’fordynamic
transportationanalysis,inorderthatparticularmodelsandmodelassumptionsfit intosuchaunifiedframework.Developingsuchaconsistentandsystematictreatmentisamajorgoalofthisbook,andthereforewetakesometimeandcareindefiningandexplainingourterminology,assumptionsandconcepts,andhowtheserelate toboththereal-worldandtocommonmethodsusedformodellingdynamictransportationsystems.
1 Purposeofthisbook Travelandtransportationplayacentralroleinthelivesofmostoftheworld’spopulation.Transportationprovidesbotha meansoftradeinmovinggoods,andaway ofmovingpeopletoengageinemployment, education,socialandotheractivities. Ifwehadobservedthesamegeographicalareaoveraperiodofpastdecades,we wouldlikelyhaveseenthatthesizeandstructureofemployment,productionand residentialareashadchangedovertime, andthesechangeshadinturnchangedthe requirementsandpressuresonthetransportationsystem.Atthesametime,these changeswillhavemadeenvironmenta l,socialandeconomicimpacts,some positiveandsomenegative,withsomewinnersandsomelosers.Itisnaturalthen toaskwhetherwecanholdamirrortothepast,anduseittoseeintothefuture;at leastthenwemaybeabletoreactinabe tterwaytotheinevitablechangesthe mirrorshowsus,andtherebyasasociety expendresourcesmor eefficiently(in thesenseoflessnegativeandmorepositiveimpacts).Itisonlyonemorestep tothenrealisethatthemirroranalogyis limited,thatunlesswebelievethefuture ispre-determinedwemayinfluenceitby ouractions,bothasindividualsandas organisations.Understandingsuchinflu encesandtheirlikelyconsequencesthen providesawayofnotonly‘managing’atransportationsystemmoreeffectively, butalsopositivelyengineeringittoimprovethelivesofthepeopleusingit. Thecurrentbookfitsintothiswideareaof ‘transportationplanning’,andparticularlythefieldoftransportationmodellingwhichaimstopostulatemathematical systemsthatbroadlyapproximatethe changesandprocessesunderlyingsuch phenomena.
Spaceandtimearetwointrinsicallyimportantaspectstounderstandingtravellers’needsandwhattransportationsystemscansupply.Letusfirstlyconsiderspace. Thetypeanddensityofactivitiesarenotdistributedevenlyacrossacityorregion, andtherearefixedgeographicalfeatures(rivers,mountains,valleys,etc.)thatinfluencethefeasibilityofdifferenttransportationoptionsacrossanarea.Dense,‘vertical’residentialareasprovideverydifferentchallengestomoresparselydistributed ones.Therealsocomplexinteractionsthatplayoutinthetransportinfrastructure;a congestedroadorovercrowdedbusmaybepartiallytheresultoftravellersavoiding overloadedfacilities,meaningthatagoodsolutionwillnotbeunderstoodwithout consideringsystem-levelinteractionsbetweenthevarioustravelneedsofpeople/ organisationsandtheservicesandfacilitieswhichareprovided.Overthelast 50yearsthetransportationcommunityhasdevelopedrathersophisticatedwaysof
representingthesekindsofspatialinteractions,typicallybyrepresentingtheinfrastructureasanetwork(mathematical‘graph’),andbyconsideringvariouslevels ofsophisticationinrepresentingthebehaviouralresponsesoftravellers(e.g.from theperfectlyinformedtravellertorandomutilityapproaches).Atthesametime, however,itshouldbementionedthatwhiletheindividualfieldshavedeveloped toahighlevel,itisrelativelyraretofindaconsistentintegrationofdemandmodellingandnetworkmodelling.
Thereareratherwelldeveloped(ifnotalwaysconsistent)methods,then,forconsidering‘space’;sowhatabout‘time’?Whiletraveltime,asadisincentiveinmaking travelchoices,isacentralaspectoftransportationplanning,bytheword‘time’we areinsteadreferringheretochangesthatoccurovertime(“dynamics”).Asthereis considerablepotentialforconfusion,letusveryearlyonmakeacleardistinction: changesona‘within-day’time-scalearethekindofchangesthatwewouldexpect toseeaswemadeajourneyonaparticularday,orifwecomparedourtravelexperiencewithsomeonetravellingbythesameroute/servicebutatadifferenttimeon thatday(therearemanyotherwaystocharacterisethiskindoftime,buttheseexamplessufficefornow).Ontheotherhand,changesona‘between-day’time-scaleconcern,forexample,thewayinwhichwemightadaptourtravelchoicenexttimewe makeajourney,basedonourtravelexperiencestoday.Whileresearchershavebeen awareofboth‘within-day’and‘between-day’effectsforseveraldecades,itisonly relativelyrecentlythataconcertedefforthasbeenmadetodeveloptoolsand methodstoexplicitlymodelthem.Onthewithin-dayscale,thishasbeenachieved byintroducingandadaptingmethodsfromtrafficflowtheoryforuseinnetwork models.Onthebetween-dayscale,ithasinvolvedbringinginnewtechniquesfrom bothappliedmathematics(fordeterministicdynamicalsystems)andprobabilitytheory(forstochasticprocesses).
Thenewstudenttothisfieldisfacedwithanextremelychallengingtasktodigest andassimilatethesedevelopments,withtheirvariousassumptions,approachesand needtodrawondifferentaspectsofmathematics.Infact,itisalsoachallengeforthe experiencedresearchertokeepfullyabreastofdevelopmentsinthisfield,aswithout detailedreadingitisoftenunclearwhereanewpaperfitswithintheliterature,and howitcomplementsoradvancespreviousdevelopments.Theintentionofthisbook istobringtogetherthetheoreticalworkinthisfieldinaninternallyconsistentway. Thismeansunifyingtransportationnetworkmodellingtheory,travelchoicetheory andtrafficflowtheory,whiledrawingonrelevantmathematicalconceptsfromoperationsresearch,matrixalgebra,dynamicalsystems,statisticsandsimulation.Our intentionisthatthebookisself-contained,sodoesnotrequireadditionalreading, althoughwesuggestfurtherreadingforthoseinterested.Inordertoassistusinthis goalofbeingself-contained,wesupplyamathematicalsupplementwhichoutlines themainmathematicalideasthatwewilldrawon.
Apartfromthepedagogicalaim,toassistnewcomerstothefield,itmightbe asked:whydowewishtosetoutaconsistenttheoreticalapproachtosuchproblems? Whatadvantagedoesitgive?Oneanswermightthatitisapurelyaestheticobjective, thathavingasingleunifyingtheoreticalframeissatisfyingpurelyinitsownright.
Certainlywewouldadmitthatpersonallywedofindsatisfactioninthisaesthetic quality,howeverwefeelthatithasmuchgreatersignificancethanthis,forseveral reasons.Firstly,asweshallshow,itprovidesawayofusingtheorytoassesswhatwe mightexpectfromapplyingsuchamodellingapproachtoanycase-study,forexampleintermsofuniqueness,stabilityorreproducibilityofitspredictions.Thesehave importantimplicationsforprojectevaluation,andmaynotbeself-evidentfromcomputationalapplicationalone,especiallygiventhecomplexnatureandinteractions involvedinsuchmodels.Secondly,ourbookisanattempttointegratethestateof-the-artinawaythatwehopegeneratesakindoffeedbackeffectwiththeacademiccommunity,wherebyourworkprovokesareactioneitherintermsofdisagreementswithourmethodofintegration,orthestimulusfornewresearchdirections, whichinturnwillimpactonthefuturestate-of-the-art.Thirdly,weintendthat ourapproachleadstoakindoftaxonomyofmodelsthatfacilitateeasiercommunicationofassumptions,byreferencetoacommonmodellingframe.Thisisimportant inorderthatforecastingisnotseenasakindofsupernaturaldivination,akinto‘reading’tarotcards,butsothatuncertaintyoverassumptionsmadeandtrendsassumed canbeproperlycommunicatedtodecision-makers.
Giventhetasktobringtogetherseveraltheoreticalfields,ithasbeennecessaryto keepthefocusofthebookfirmlyonthedevelopmentofforecastingmethods.In orderthatthebookbeofamanageablesize,wethereforedonotconsidertwoactivitiesthatmightbesaidto‘bookend’thetaskofforecasting,namelycalibrationand design.Weshouldmention,however,thattheapproachesdescribedare,webelieve, especiallysuitedtothesetwoactivities.Inthecaseofcalibration,aswewritethis bookweareinaperiodofunprecedenteddataavailability,rangingfromvarious kindsof‘tracking’data(frommobilephoneactivity,GPSorBluetooth,forexample),toarchiveddetectordataoverlongperiods,andothermeansofinferringactivity patterns(e.g.shoppingtransactiondata,videosurveillance).Suchdatarevealsa complex,time-of-day-varying,daily-varying,heterogeneouspatternoftravelbehaviourthatisnotonlypoorlycapturedbysteady-stateapproaches,butisactuallyrather difficultto‘project’ontotheconventionalideologies.Moreovertheapproachespresentedthataredevelopedfromprobabilitytheoryprovideameansofcalibrating suchmodelsusingformalstatisticalinference.Intermsofdesign,theprocess approachwedevelopallowsustoexaminehowlikelyitisthatthesystemcould beinfluencedtoattainandoperateunderverydifferenttransportationsystemdesigns tothepresent.Thetraditional,‘comparativestatics’approach,ontheotherhand, onlyallowsustoassessalternativedesignsonthepremisetheyareattainablefrom thepresent.
Evengivenourdecisiontofocusonthetheoreticaldevelopmentofforecasting methods,spacelimitationsmeanthatithasstillbeennecessarytobeselectivein termsofthekindsofproblemconsidered.Thismeansweexcludemanyimportant areas,suchastheroutingoffreightvehicles,theuseoftaxis(ortaxi-likevehicles), andthebehaviourofpedestriansincontinuousspace,suchasasquare.Givenits ratherlongassociationwithdynamicprocesses,andthepracticaluseofdisequilibriumforecasts,itwouldhavebeeninterestingtohaveincludedaconsiderationof
land-useandtransportinteractionmodels.Methodologically,itwouldhavebeen veryrelevanttoincludeaconsiderationoftour-basedandactivity-basedapproaches, giventheirnaturalassociationwithschedulingduringtheday,andamorethorough studyofmicroscopicapproaches,giventheirnaturalrelationwithstochasticprocess models.Perhapsthemostnaturalextensiontoourworkwouldhavebeentoinclude modechoice(integratedwithroute/serviceandtime-of-daychoice)inafullymultimodalmodellingapproach.Thelistcouldcontinue,andwewouldhavesufficientto writeseveralbooks.Nodoubtwewillirritatemanypeoplebytheproblemswe decidedtoincludeandexclude,butintheendwesatisfiedourselvesthatourchoice ofwhattoincludewasakindofmetaphorforhowamodellerinpracticemust approachareal-lifestudy:ultimately,notallprocessesmayberepresentedinachosenmodeller,andsothemodellermustalwaysaccept(oftenunwillingly)thatthere arepotentiallyimportantaspectsthatareoutsidetheremitofthemodelchosen.Ifthe taskofamodelleristoprovidethetoolsforamodellingtool-box,thenwehopethat wecanbeconsideredtohaveprovidedagoodselectionofscrewdriversandchisels, andhopethatothersinthefuturecanaddtothisboxwiththeirownselectionofsaws andhammers.
Lookingtothefuture,modellingfacesunprecedentedchallengesandopportunities.Ontheonehand,itmustrisetothechallengeofrepresenting‘new’formsof transportation,suchasautonomousand/orconnectedvehicles,electricbicycles andsharedmobilityservices,andtheseeminglyevermorecomplexwaysthatlives areorganised;forexample,ifweplanabusinessmeetinginanautonomousvehicle insuchawaythatthetripendsatasocialmeetingpointatsomeprescribedtime (greaterthantheminimumtimetoreachthatpoint),whatdoweconsiderthepurpose anddestinationofthetriptobe,andwhatvalue-of-timeandroutingprinciplemaybe consideroperating?Howmightwemodelpopulationsofindividualsbeingtransportedaroundacityincoordinated,sharedtransportation?
Thesechallengesarebalancedbynewopportunitiesintermsoftherichnessand extentofthedatawemayexpect.Somehavearguedthatsuchdatamaybeof suchextentthatmodelsarenolongerr equired,sincewemightexpecttohave almostcompleteobservationoftravelmovementsandrelatedphenomena.Actually,webelievethecontrarytobetrue;t hisisexactlywhenmodelsareneeded most.Thequantityofdatafromsuchsour cesispotentiallyoverwhelmingand diverse,andmodelsmaythenbeusedtoextractkeypatternsfromthismorass ofinformation.Furthermore,evenwithperfectobservationofthepast,wereturn toouroriginalquestionofwhetherwewillsimplyuseitasamirrorforthefuture. Withoutforecastingtoolswewillbeunabletoconsiderhowthefuturemight changeandhowwemightinfluenceitinabeneficialdirection.Inaneraof “bigdata”,weneedevenmorethanbeforesimplified,abstractedmodelsthat areabletoprovideanindicationofthelikely futuretrajectoryofourtransportation system,andtheinfluencethatindividuals ,organisationsandpolicy-makersmay haveonsuchatrajectory.
2 Contributionofthisbook Mostbranchesofengineeringwerefoundedonphysics(and/orchemistry)developed fromlate19thcentury,andnowarewell-established.Thisactuallyisthetraditional imagetocommonfolksofanengineer:apersonabletosolvepracticalproblemsthat arewellrootedonaspecificbackground,forinstanceelectronics,hydraulics,etc., throughspecialisedmathematicaltools.Goodexampleswithintransportationengineeringareanalysisanddesignofcomponentssuchasvehicles(andtheirengines), facilities,etc.,andtrafficengineering,developedbyapplyingametaphorderived fromfluiddynamics,whichdealswiththebehaviourofseveralvehiclessharing thesamefacilityandthedesignoftrafficcontroldevices,suchastrafficlights, ATC,etc.,.
Atthebeginningof50softhelastcenturyanewparadigmwasintroduced,by linkingtogetherthecontributionsofseveralauthors,leadingtothe(abstract)systems engineering,whereemphasisisonmathematicalrepresentationofaproblemrather thanitsphysicalbackground.Thisisanewtypeofengineer:apersonabletosolvea practicalproblemconsideringitasawholethroughaneverincreasingboxofnon specialisedmathematicaltools.
Forwhatmaynowbeconsideredacharmingsynchronicity,JohnG.Wardrop,in hisseminalpresentationheldon24January1952,andpublishedinJune(Wardrop, 1952),foundedtransportationsystemsengineering,includingbothanalysisand design.Inhispaper,heproposedawideandcomprehensivereviewoftrafficengineering,butatthesametime,heunderstoodthattrafficengineeringtechniquescan beusedonlytoanalysetheperformanceofasinglecomponent(cfrp.344).Healso statedthatatransportationsystemcannotbestudiedonasingleelementbasis,butas awholesystemindeed(notethatheactuallyusedtheword“system”).
Hence,startingfromasmallexample,heproposedhisnowwidelyknowntwo principlestomodeltraveldemanddistributionoveralternativeroutesinatransportationnetworks(cfrp.345).Then,hestatedthatthesetwocriteriamustbeextended todealwithawholenetwork,whereroutearebrokenintolinkspossiblysharedby otherroutes,eventhough(cfrp.348)inthecaseofanetworkofroadsthetheoretical problembecomesverycomplicated.Thisway,JohnG.Wardropintroducedthemain elementsofanyeffectivemodelofatransportationsystem:
•auserbehaviourmodel,whichsimulatehowlevel-of-service,sayjourneytimes, affectsuserchoices,asexpressedinhispaperbythetwocriteria(traveldemand); •aperformancemodel,whichsimulatehowuserchoices,sayflows,affectlevelof service,sayjourneytimes;itismadeupbyanetworkmodelrepresenting topologicalfeaturesand,atalinklevel,byperformance – flowrelationsderived byapplyingtrafficengineeringtechniques(transportationsupply).
Besides,hegreatlystressed TheValueofaTheoreticalApproach (cfrp.326)asthe onlyeffectiveone,thusstatingthatmodelswithinaspecifictheoryshouldbedeveloped.Thesemodels,nowreferredtoastraveldemandassignmenttotransportation
networks,arethebasictoolstosimulateatransportationsystem.Itisalsoworthnotingthat,pointingoutthattheuserbehaviourislikelyselfishanddoesnotlead towardsthemostefficientpattern,hestatedtheneedofsupplynetworkdesign.
FromtheseedplantedbyJ.G.WardropthestillgrowingtreeofthemodernTrafficandTransportationTheory(TTT)emerged.AgeneraloverviewofexistingproblemsandtoolsofTTTisgivenbelowinordertopointoutthecontributionofthis book.TTTstudiestheinteractionsbetweenthelevelofserviceprovidedbytransportationsystemsandtheresultsofseveraltypesofuserchoicebehaviour,which mayregardinahierarchicalorderfrombottomtotop:
•driving,concerninginteractionsbetweenuserstravellingonthesamefacilityand theireffectsontraveltime, …;
•routing,concerningconnectionsbetweenoriginanddestinationofthejourney, parkinglocationandtype,possiblydepartingtime, …;
•travelling,concerningtransportationmode,time-of-day,destination,frequency, …;
•mobility,concerningcarownership,drivinglicenceacquisition,
Ontopoftheabovehierarchytherearethekindsofuserbehaviouraddressedby land-use/transportinteractiontheories.
ToolsofTTThavereachedaveryadvancedandsophisticatedlevel,andlargescaleapplicationsareacurrentpractice.Mostofthesetoolsarebasedonexplicitly behaviouralmodellingapproaches,whichgrantclearinterpretationofparameters.A taxonomyisgivenin Table1 belowwhereforbrevity’ssake kindsofchoicebehaviourothersthanroutinganddrivinghavenotbeexplicitlyconsidered.Abriefreview ofthesetoolsisgiveninthefoursectionsbelowtointroducethenomenclatureused inthisbookandthecontentsofthechaptersofthisbook. (inroundparenthesisthenumberofthecorrespondingsectionbelow.)
2.1 Trafficanalysis Thissectionbrieflydiscussesmethodsfortrafficanalysis,whichaddressesthe effectsofdrivingchoicebehaviour,andareusuallyderivedfromTrafficTheory, describedindetailsinAppendixB,alsodiscussingQueuingTheoryforbottlenecks.
Table1 ToolsofTTT.
Understeady-stateconditions(introducedin Chapter1)themostcommonlyused modeltodescribevehiclesflowingalongastreet(railway,airway, …)isthesocalledfundamentaldiagram(FD)describingtherelationsamongdensity,flow and(spaceaverage)speed.Inparticular,inthestableregimespeedisadecreasing functionofflow,thatcanbeusedtospecifytraveltimefunctions.
Whensteadystateconditionsdonothold,within-daydynamics(introducedin Chapter1)inalinkshouldexplicitlybetakenintoaccountthroughthreekindsof macroscopicmodels,describedindetailsinAppendixB:
•continuousinspaceandtime;
•discreteinspaceandcontinuousintime;
•discreteinspaceandtime.
Thefullspecificationofalltheabovemodelsrequiresanequationdescribingtherelationbetweenspeedandfloworbetweenspeedanddensity,tobederivedfromtheFD, aswellsomenetworkequationstoleadtowithin-daydynamicassignmentmodels. InappendixBmesoscopicandmicroscopicmodellingapproacheswillalsobe described.
2.2 Transportationsystemsanalysis Thissectionbrieflydiscussesmethodsfortransportationsystemsanalysis,whichcan bedistinguishedintomethodsfor:
•traveldemandanalysis, •transportationsupplyanalysis, •demand–supplyinteractionanalysis,orassignment.
Beforeapplyinganyoftheabovemethodssomepreliminarystepsshouldbecarried out.Thestudyareaisdelimitedanddividedintozones,whereajourneystartsorends, andmaininfrastructuresandservicesaresingledouttosupportjourneysbetweenany pairofthem.Then,usersaredistinguished,followinga5Wapproach,withrespectto.
WHO:socio-economiccharacteristicsandgroupedintocategories(orinto commoditiesforfreight),
WHY:trippurpose,
WHAT:tripfrequency,
WHERE:triporiginanddestination[forsimplicity’ssakewewillassumethat eachjourneyisdefinedbyasingletrip,thustrip-chainsortoursarenot considered],
WHEN:timeofday(morningvs.afternoonpeakperiod,dayofweekvs. weekenddays,wintervs.summer,specialevents,usualvs.emergency conditions, ).
Oncetriporiginsanddestinationshavebeensingledout,itinerariesbetweeneach pairoforiginanddestinationcanbedefined,possiblydistinguishedbycategory, purpose, ….Then,eachitinerarycanbebrokendownintolinks,eachlinkbeing
astretchofstreet,railway,airway, …,withcommoncharacteristics.Inthemostgeneralcaseanitineraryisaroutingstrategyincludingbothpre-tripanden-routechoices dependingoninformationavailabletousers.
2.2.1Traveldemandanalysis Duringeachtime-of-day,usersbelongingtodifferentusercategories,withdifferent trippurposes,andjourneyingbetweendifferentorigin–destinationpairsinteracteach otherandcompetetoaccesssameinfrastructuresandservices,thusforeasyreferenceanycombinationsofusercategory,trippurpose,origin–destinationpairis calledauserclass(u.c.).Givenatime-of-day,foreachuserclassthetraveldemand flowdefines.
HOWMANYusersaremovinginthestudyarea.
Traveldemandflowscanbeestimatedthroughstatisticmethodsgivingthesocalledorigin–destinationtraveldemandflowmatrices(oro-dmatricesforshort). Theyareassumedconstantinthefollowing,since,asalreadystatedabove, kinds ofchoicebehaviourothersthanroutinganddrivingarenotexplicitlyconsidered inthisbook.Thus,thetraveldemandmodeldescribes:
HOWusersreachtheirdestinationsfromtheirorigins.
Travellingchoicebehaviourcanbemodelledthroughanydiscretechoiceanalysistheory(e.g.RandomUtility,FuzzyUtility,Prospect, … theory),asdescribedin AppendixA.Underwithin-daydynamicconditions,userdeparturetimechoice behaviourshouldalsobetakenintoaccountthroughpre-fixedproportionsorthrough afurtherchoicemodel,wheretheutilityfunctionincludespenaltyforearlyorlate arrivalwithrespecttodesiredarrivaltime.
2.2.2Transportationsupplyanalysis Methodsfortransportationsupplyanalysiscombinemethodsfortrafficflowanalysis, withmethodsderivedfromtheTheoryofCongestedNetworks,includingsynchronic anddiachronicnetworks,describedindetailsin Chapter1.Inthisbooktoolsfor modelling continuoussupply, e.g. pedestriansmovinginasquare,arenotconsidered
Theconnectionsbetweentriporiginsanddestinationsaredescribedbyanorientedgraph,suchthateachlinkisdescribedbyanorientedarcbetweentwonodes andeachitineraryisdescribedbyaroute,withnodesmodellingjunctions.Moreover, eachoriginandeachdestinationismodelledthroughafurthernodeconnectedtothe mainnetworkthroughconnectingarcs(orconnectors)notcorrespondingtolinks (see Section1.2).
Understeady-stateconditionsaflowandatransportationcostareassociatedto eacharc;usuallycostisacombinationofseveralattributesregardingtime(on-board, waiting,delayduetojunctions, …),money(fuelcost,tolls,fees, …),andreliability (dispersionindicesoftraveltime, …
Thetransportationsupplymodeldescribes: HOWMUCHitcoststousersreachtheirdestinationfromtheirorigins. Within-daydynamicsgreatlyaffectsthetransportationsupplymodel,sincearc flowsandcostsdependontime,moreovertheflowofanarcalsodependsonthe
positionwithinthearc.Theflowenteringanarcatagiventimedependsontravel timetoreachthearc,generallythroughdifferentpaths,thetraveltimeofeachof thesepathsdependsonthetraveltimeofeacharcspreviouslytraversed,whichin turndependontheflowthathastraversedthem.Therefore,within-daydynamic modelsrequirethatHOWLONGittakestouserstoreachtheirdestinationfromtheir originsisexplicitlymodelled(iftraveltimeisdifferentfromtransportationcost).
2.2.3Assignment Traditionalequilibriumassignmentsearchesformutuallyconsistentarcflowsand costs.Itwasfirstintroducedundersteady-stateconditionsby Wardrop(1952), whonameditUserEquilibrium(UE).
Equilibriumassignmentmayeffectivelybeformulatedthroughfixed-point modelswhichcanbeeasilyextendedtodealwithseveraltypesofassignment Fixed-pointmodelscaneasilybespecifiedcombiningtogetherthethreeequations ofthetransportationsupplymodelandthethreeequationsofthetraveldemand model,asdescribedin Chapter3,startingfromassignmenttouncongestednetworks describedin Chapter2.
Equilibriumassignmentmayberegardedasaspecialcaseofday-to-day dynamics(see Chapter1)thatmainlyaffectsthetraveldemandmodel,inthiscase indeedboththeutilityfunctionandthech oicefunctionarespecifiedthroughrecursiveequations.Thisapproachallowstoexplicitlymodellingevolutionovertime throughdeterministicandstochasticprocessmodels,asdescribedin Chapters4 and5 .
Methodsforwithin-daydynamicequilibriumassignment(traditionallycalled DynamicTrafficAssignment)followthesamestructureofsteady-stateequilibrium assignment.Stilluserdeparturetimechoicebehaviourshouldalsobetakeninto account;moreover,theflowandcostconsistencyrelationsarenon-linearasdiscussedabove;therefore,severalresultsavailableforsteady-stateequilibriumnolongerapply.Moreover,eachofthethreekindsofmacroscopicmodelsdescribedin Section2.1 leadstodifferentassignmentmethodsthatcanhardlybeputundera commonframeworktohighlighttheirmutualrelationships,letalonemesoscopic andmicroscopicmodels.Within-daydynamicsmaybecombinedwithday-to-day dynamicsleadingtoso-calleddoublydynamicassignment.Thesetopicsare describedin Chapter6.
2.3 Trafficcontrol Mostmethodsfortrafficflowcontrolarebasedonthedescriptionandpredictionof trafficflowswithoutanymodellingofroutingchoicebehaviour. Theyincludefixedsignstrategies,suchaspriorityjunctionsorroundabouts designedoff-line,aswellvariablesignstrategies,suchasrampmeteringortraffic lights.Thelattermaybeappliedoff-linetosupporttransportationplanningorinsimplecaseswhenthereisnoneedofadaptivecontroloron-linetosupportreal-time trafficmanagement.
On-lineapplicationsrequiressensorsforflowmonitoringandwithin-day dynamicmodelsforflowprediction,suchasthosedescribedin Section2.1,orsimple data-drivenmethods,suchasmethodsfromtimeseriesanalysis,Bayesiannetworks, ArtificialNeuralNetworks(ANN).
Allthesetopicsareoutofthescopeofthisbook.
2.4 Transportationsystemscontrolanddesign Methodsfortransportationsystemscontrolanddesignprovideoptimalfeaturesof transportationinterventionstakingintoaccounttheireffectsontraveldemand, sayonuserroute(anddeparturetime,ifthecase)choicebehaviour(quiteoftenunder theassumptionofconstantdemandflows).Thisisusuallyachievedbyconsidering anymodelforequilibriumassignmentasaconstraintembeddedwithinthewhole optimizationmodelunderlingthedesignmethod.
Methodsfortransportationsystemsorbettertransportationsupplycontroland designmaybegroupedinto:
•Methodsfortransportationsystemscontrolortransportationnetworkcapacity design,orforContinuousNetworkDesign,suchasnetworksignalsetting designwithequilibriumconstraints,busfrequencydesign, ; •Methodsfortransportationnetworktopologydesign,orforDiscreteNetwork Design,suchasUrbanNetworkDesign,includingbothsignalsettingdesign andlaneallocationwithequilibriumconstraints[laneallocationcannot consistentlybecarriedoutwithoutincludingsignalsettingdesigntoo],designof buslines, … .
On-linetransportationsystemscontrolmethodscanalsobecombinedwithIntelligentTransportationSystems(ITS)suchasAdvancedTransportationInformation Systems(ATIS),whichmayprovideinformationorindications.Inthiscaseany informationorindicationprovidedtousersshouldbeconsistentwiththecontrol strategyandtheuserreactionleadingtoclosed-loopsystems;satisfactorymodels ofsuchsystemsarestillanopenissue.Currentlynomethodisavailabletodesign allfeaturesofatransportationsystem,possiblyincludingaITS.
Accordingtoanarguablebutlongsinceestablishedtradition,measuresregarding restrictedareaaccesspolicy,parkingpolicy,tolls,congestioncharge,andthelike, arecollectivelyknownasTravelDemandManagement(TDM)measures.Needless tosaytraveldemandresultingfromthefreechoicesmadebyuserscannotbecentrallymanaged,butonlybedescribed.Thesekindsofinterventionsshouldbeconsideredpartoftransportationsupplydesignwithinaconsistentplanalsoincluding kindsofinterventionsmentionedabove.
Allthesetopicsareoutofthescopeofthisbook.
3 Scopeofthisbook Ondecidingonthescopeofthebook,wedecidedtomakeseveralrestrictions,omittingexplicittreatmentofseveralimportanttopics,onthegroundsthatwewishthe contentofthebooktobeofamanageablesizeforthereadertoappreciate.Thisisnot, however,intendedtosuggestaboundaryofwhatispossiblewiththepresented framework;onthecontrary,wehopethatourworkencouragesothertocastfuture modellingadvanceswithinthepresentedconceptualframe.Whiletherearemany limitationsofourwork,whichwediscussasthedetailedtreatmentunfolds,there areseveralaspectsthatdeserveparticularmentionattheoutset.Firstly,wewill consideronlyjourneysthatoccurfromasingleorigintoasingledestination.This excludestours,forexampleahome-shop-workjourneywithmultipledestinations, aswellasgooddeliveriestomultiplelocations.Secondly,weconsideronlynetworks consistingofasinglemode,andmakenoexplicittreatmentofinter-modality(e.g. park-and-ride,oragoodsdeliverycombiningtruckwithlast-miledeliveryby bicycle).Bothoftheseexclusionsaresignificant,butwehavemadethischoice inordertokeepthematerialmoremanageable,andinanycasethestudyofsuch issueswithinafullydynamictransportationsystemsistoourknowledgeanopen researchquestion.
Through Chapters1–4 mainemphasisisonmacroscopicmodelling,thenmicroscopicmethodsarediscussedin Chapter5 ontime-drivenStochasticProcessmodels forDay-to-dayDynamicassignment,andin Chapter6 wheremacroscopic,mesoscopicand(event-driven)microscopicmodellingapproachestoWithin-DayDynamicsarediscussed.Data-drivenmethodsarenotdiscussedforbrevity’ssake;anyhow theyseemmoreusefultosolvespecificproblems,suchshort-termtrafficforecasting, incident-detection, …,ratherthanprovidingawideinsightoftrafficandtransportationsystems.
4 Summary 4.1 Majorfindings Travelandtransportationplayacentralroleinthelivesofmostoftheworld’spopulation.Thustraveldemandandtransportationsupplyaswellastheirinteraction shouldcarefullybeanalysedtoeffectivelyassesstheeffectsoftransportationplanningpoliciesandtrafficcontrolstrategies.Thisbookdealswithtraveldemand assignmenttoatransportationnetwork,themaintoolfortransportationsystemanalysisandplanning.Thisprefacedescribesthepurposeandthecontributionofthis bookwithrespecttothecurrentliteratureaboutthetoolsofTrafficandTransportationTheory.
4.2 Furtherreadings AwidedescriptionofmostofthetoolsofTTTmaybefoundinthebooksby Cascetta(2001,2009) ;assignmenttoolsarealsodesc ribed,butwithoutacomplete andcomprehensiveanalysisofmathematicalfeatures,ontheotherhandimplementationisalsodiscussed.Anotherwidelyusedbookisby deDiosOrtuzarand Willumsen(2011) ,whereimplementationandappl icationissuesarediscussed withgreatdetails.
References Cascetta,E.,2001.TransportationSystemsEngineering:TheoryandMethods.KluwerAcademicPublisher,p.2001.
Cascetta,E.,2009.TransportationSystemsAnalysis:ModelsandApplications.Springer. deDiosOrtuzar,J.,Willumsen,L.G.,2011.ModellingTransport,fourthed.Wiley. Wardrop,J.G.,1952.Sometheoreticalaspectsofroadtrafficresearch.Proc.Inst.Civ.Eng. 2(1),325–378.
Acknowledgements Besidesthecolleaguesalreadymentionedabove,Iwishtothankthecolleaguesand friends,toomanytobeenlistedhere,aswellasallmystudentswhomIdiscussed withthetopicsofthisbookovertheyears.IalsowishtothankFulvioSimonelli whocarefullyreviewed Chapters1–3.Iwishtothanksmyuniversityaswellfor thefinancialsupportthroughseveralresearchprojectsovertheyears.Aspecialthank goestoAleksandraPackowskawhogentlybutfirmlykeptpushingandpullingme untilthisbookwascomplete,toNirmalaArumugam,whogentlytriedtomeetallmy specialrequirementsaboutstyles,andwiththemtoalltheElsevier’sstaffwho supportedme.
ThisbookisdedicatetoRose(whomImarriedmanyyearsago)whobroughtand keepbringingartsandbeautyinmylife,evenwhenIwasbusywritingthisbook.
Introduction 1 GiulioErbertoCantarella
UniversityofSalerno,Salerno,Italy
Theknowledgeoffirstprinciples,asspace,time,motion,number, isassureasanyofthosewhichwegetfromreasoning. Andreasonmusttrusttheseintuitionsoftheheart, andmustbaseonthemeveryargument.
BlaisePascal,Pensees(translatedbyW.F.Trotter) Outline. Inthischapterthereadermayfindthebasicdefinitionsandassumptions usedtodevelopthemodelspresentedinthenextchapters.Thisisconsistentwith themethodologycommontoappliedscienceswhosefirststepsareapreliminary analysisaimedatprovidingasimplifiedd escriptionofthesystemunderstudyanda statementofassumptionsaboutspaceandtimemodellingpossiblyincludingstochasticapproaches.
Amodelfortransportationsystemanalysistriestodescribethestateofatransportationsystemasresultingfromtheinteractionbetweentravellerswillingtotraveland transportationsupplysystemsprovidingopportunitiestothem.Inthethissectionand thefollowingonesweoutlinethemethodology,commontoallmodernappliedsciencessuchasengineeringandeconomics,appliedinthisbookandthemainassumptionsupportingit.Readerofthisbookisassumedfamiliarwithfundamentalsof Calculus,ofTheoryofProbability,andofInferentialStatistics.
Throughallthisbookwekeepclearlyseparatedfeaturesoftherealworld,say (datafrom)observations,andthoseofthemodellingtoolstryingtousedifferent wordsasfaraswecan;forinstancelocationoverspaceandevolutionovertimecome fromobservationsoftherealword,whilespatialanddynamicareadjectivesonly usedtodenotemodelstryingtodescribethesephenomena.Similarconsiderations holdwithregardstoobservedvariationsorfluctuationsoverspaceortimeinreal worldandtoadjectivessuchasrandomorstochasticonlyusedtodenotemodelstryingtodescribethesevariationsaswellasothersourcesofuncertainty.Thefollowing examplesmayhelpunderstandingthispointandtointroducesomebasicelementsof modellingtheory.
Supposethatyouarewalkingapathinawoodlookingforseedsofhorse-chestnut treestoplayconkerswithafriendyouexpectwillpayyouavisitinthenearfuture(or
foranyotherreason).Youmayobservethenumberofseedsatthefootofeachtree alongthepathinagivenday,locationoverspace,and/oratthefootofatreeinconsecutivedays,evolutionovertime.Thesampleofobservationscanbecollectedinan arrayofvariables,suchthattheindexdescribesthetree(space)ortheday(time).
Ifthenumberofobservationsistoo largetobeeasilyrememberedyoumay computetheobservedmeantohavearoughlyideaofthenumberseedsyou mayfindtogetherwiththeobservedvariancetodescribehowdispersedtheobservationsarearoundtheobservedmean.Boththesevalues,aswellasothers indicatorsfromdescriptivestatistics,aretobeconsideredasobservationssincetheycan becomputedfromthemthrough(simpleal gebraic)equations.[Thisaggregation procedureintroducesasourceofuncertaintysomehowdifferentfromtheonediscussedbelow.]
Amoresophisticatedapproachisbasedon probabilisticmodels basedonrandom variables,suchthatthemodelmeanandthemodelvariancetrytoreproducethe observedmeanorvariance,andmoregenerallytheprobability(density)functiontries tomimictheobservedfrequencydistribution;anexamplearemodelsbasedonthe Poissonrandomvariable,popularmodelsforbothlocationoverspaceandevolution overtime.Thesemodelsarenotconsideredproperspatialordynamicmodelssince theylackanexplicitdescriptionoflocationoverspaceorofevolutionovertime.
Spatialordynamicmodels arethoseusedtoexplicitlyforecastthelocationover space(inafutureday)oroftheevolutionovertime(inagivenlocation).Models includingrandomvariablesareusedwhenforecastingisaffectedbyuncertainty duetothelackofenoughinformationandpossiblyothersourcesofuncertainty, seebelowsothateffectivedeterministicmodelscannotbespecified;accordingto theseconsiderationsdynamicmodelsarenamed deterministic or stochasticprocesses.[Thissourceofuncertaintyduetolackofenoughinformationissomehow differentfromtheoneduetotheaggregationprocedurediscussedabove.]
Afteritsspecification,anykindofmodelshouldbecalibratedagainstobserved data,sayitsparametersshouldbeestimatedthrough inferencestatisticsmethods, beforeapracticalapplicationispossible.Thisissueisoutofthescopeofthisbook.
Themodellingapproachdiscussedabovecanbeextended multi-classmodels whichalsotakeintoaccountthedistributionoverotherquantitativefeatures,thesize ofseedsbesidestheirnumber,orqualitativefeatures,saydifferenttypesofitemsto collectsuchaswalnutseedsormushrooms. Multi-typemodels occurwhenthedistributionofthesefeaturesisdulymodelled,usuallythroughaprobabilisticmodel.
Alltheaboveconsiderationsholdinotherfieldsofapplicationaswell:ifwechange thepathwithalongurbanstreet,theseedswithcars,andthetreeswithlinkswegetthe mainelementsofTrafficTheory,brieflypresentedinAppendixBtothisbook.
Beforeany(mathematical)modelcanbedevelopedapreliminaryanalysis shouldbecarriedoutaimingathighlightingthemostrelevantfeaturesandprovidingasimplified(verbalqualitative)descriptionofthesystemunderstudy,asbriefly reviewedinthebeginningof Section2.2 inthePrefacefortransportationsystems. Mainelementsarerepeatedbelowforreader’sconveniencetogetherwithnew considerations.
Userscanbetravellers,orpersons,andfreight,orgoods.Thisbookmainemphasisisontravellers,butmostdescribedmodelscanrelativelyeasilyadaptedtofreight transportation.Inthefollowingausermaymeanawalkingperson,apersonridinga bicycle,avehicle,atonoffreight,a(20ftlong)container, …,thuspronoun“it”is utilised.
Severaltypesofuserchoicebehaviouroccurinreallife;thisbookmostlyfocuses ontwoofthemonly[HYP ①]:
•driving,concerninginteractionsbetweenusersmovingonthesamefacility (calledcongestion)andtheireffectsontraveltime, …; •routing,concerningconnectionsbetweenoriginanddestinationofthejourney, parkinglocationandtype,possiblydepartingtime, … .
Userdrivingbehaviourisusuallymodelledwithinthetransportationsupplymodels, whichdescribe(ifand)howroutinguserchoicesaffectlevelofservice,saytravel time,delayatjunctions,monetarycost, ….Ontheotherhand,userroutingbehaviour isusuallymodelledwithinthetraveldemandmodels,whichdescribehowprovided levelofserviceaffectsroutinguserchoices.
Transportationsupplysystemscanbedistinguishedbetweenthoseproviding continuous overspaceandtime services (walk,bicycles,cars,vans,trucks, …)or discreteservices (buses,trains,airplanes,ferries, …),oftenrequiringquitedifferent modellingapproaches;thegeographicalscale,urban/metropolitanareasvs.extraurbanconnections,isalsoarelevantfeatures.Discreteservicetransportationsystems operatinginurbanareasareoftencalledtransitsystems.
Makingasharpdistinction,adiscreteservicesystemmaybecalled:
• frequency-based:mostusersarriveatrandomatstopswithoutanypre-trip planningsincetheydonotpreciselyknowthetimetableorthefrequencyis sohighthatitdoesnotmatter,thususersperceivethesystemasasetoflines withagivenfrequencyovertime,(oftenurbanservices,likebuses,metrolines, …),
• schedule-based:mostusersarriveatstopsatachoseninstantoftimeaftersome pre-tripplanningsincetheypreciselyknowthetimetablethususersperceivethe systemasasetofscheduledconnections(mostoftenextra-urbanservices,intercitytrains,airflights, …).
Presentedmodellingapproachescanbeappliedtoeithercaseabove.
Foreachtimeofdayperiodrelevantforthestudyatthehand,usersareassumed groupedintouserclasses(multi-userclassmodels)withrespecttoorigin-destination pairandpossiblytousercategoryandtrippurpose.Eachgroupbeingassociateda traveldemandflow,assumedconstantinthefollowing,andacommonsetofitineraries,aswellasofbehaviouralparameters.Eachitineraryisbrokendownintolinks, eachlinkbeingastretchofstreet(railway,airway, …),possiblysharedbyothers itineraries.Bothitinerariesandlinksaremodelledfollowingadiscretespace approachthroughtheelementsofagraphasdescribedinthenextsection[HYP ②].
[Inthisbook,asalreadystatedinthepreface,toolsforcontinuouslymodelling space,e.g.fordealingwithpedestriansmovinginasquare,arenotconsidered.]
Manymodelspresentedthroughthisbookfollowamacroscopicapproach[HYP ③]describingtheaggregateresultsofdecisionsofalltheusersthroughflowvariables,measuredbynumberofuserspertimeunit,ratherthantracingthejourneyof eachsingleuserasinmesoscopicormicroscopicmodellingapproach;somemesoscopicandmicroscopicarealsodiscussed,butwithlessdetails.
1.1 Spacemodelling:Graphsandnetworks Inthisbook,assaidabove,thespaceismodelledinadiscretewaythroughgraphs andnetworks;whilethesetwowordsareoftenusedassynonymouswewishto givethemdifferentmeaningsasshownbelow; Section1.1.1 reviewsbasicdefinitions(understeadystateconditions)u sefulforthisbook(formoredetailsand applicationsofgraphsandnetworkstooth erappliedsciencestoo,seeforinstance Baraba ´ si,2016 ).Thewaytoapplythesemodelsto transportationsystemsanalysis willbrieflybediscussedin Section1.1.2 .Algebraicdetailswillbeintroducedin Chapter2 .
1.1.1 Basicelementsofgraphandnetworktheory A graph, G,ismathematicalobjectdefinedbyanorderpairof(finite)sets, G =(N, A),thefirstoneusuallycalledthesetof nodes (orvertices), N,andthesecondone usuallycalledthesetof arcs, A,asubsetoftheCartesianproductbetweenthefirst oneanditself, A N N,withelements a =(n1, n2) 2 A where n1, n2 2 N.
Ifanyelementinset A isanunorderedpair,(n1 , n 2 )=(n 2 , n 1 ),thegraphis calledundirectedanditsarcsareoftencallededges.Viceversa,ifalltheelements ofset A areorderedpairs,arcs( n 1, n 2)and( n2 , n 1 )aredifferent,thegraphis calleddirected,oradigraph;inthiscasethefirstnode n 1 ,iscalledthetailof arc( n 1, n2 )exitingfromnode n1 ,whilethesecondnode n 2 istheheadofarc ( n 1, n2 )enteringtonode n 2
Ifneededwemayassumethatagraphdoesnotcontainparallelarcs,saydifferent arcswithsameheadandtailwithnolossofgenerality;indeedifthegraphcontains someparallelarcs,itsufficestointroducefurthernodestogetanew(equivalent) graphwithoutparallelarcs.Therefore,ifthenumberofnodesisfinitethenumber ofarcsisfiniteaswell.
Graphsusedinallapplicationstomodelspaceintransportationsystemsanalysis arealwaysdirected,thusforsimplicity’ssakewewillfurtherrefertothiskindof graphsonly,omittingtheworddirected.
Fig.1.1 showsa(directed)graphwith4nodes:A,B,C,D,and5arcs:1=(A,C), 2=(B,D),3=(B,C),4=(A,B),5=(C,D).
A path fromoriginnode no todestinationnode nm is(agraph)definedbya sequenceof m arcssuchthattheheadofanarcisthetailofthesuccessiveone
FIG.1.1
Adirectedgraphwith4nodesand5arcs.
(adjacentarcs),thatis(nO, n1),(n1, n2), ,(nm-1, nm),asinglearcbeingaspecial case;theoriginnode, nO,andthedestinationnode, nm,areassumeddifferent.On theotherhand,iftheoriginandthedestinationarethesamenodethepathiscalled aloop.Inan elementarypath nonodeappearstwice,thuseachnode,butthedestination,istailofonearcandheadofonearc,withtheexemptionoftheorigin;hence anelementarypathdoesnotcontainloops,andisalsocalledloop-less.Thus,ifthe numberofarcsisfinitethenumberofelementarypathsisfiniteaswell.Ina simple path noarcappearstwice,Thus,ifthenumberofarcsisfinitethenumberofsimple pathsisfiniteaswell.
There12pairsofnodesingraphin Fig.1.1;6ofthem—(B,A),(C,A),(C,B),(D,A), (D,B),(D,C)—arenotconnectedbyanypath,3ofthem—(A,B),(B,C),(D,C)—are connected,eachbyonepathmadebyonearconly;last3pairsofnodes—(A,C),(A,D), (B,D)—areconnectedbymorethanonepath,atleastoneofthemcomposedbymore thanonearc.
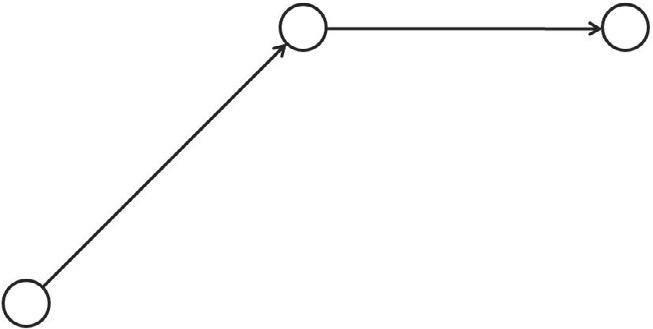
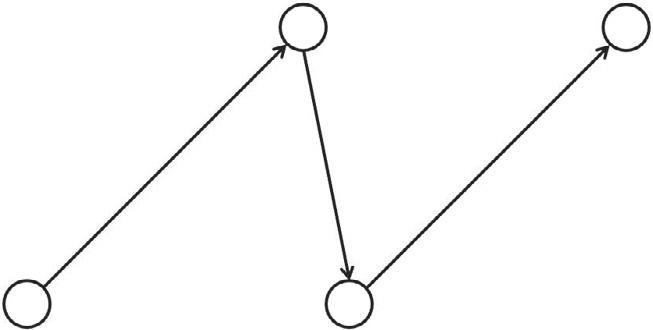
Inparticular,thepairofnodes(A,D)isconnectedby3paths:1=(ACD), 2=(ABD)and3=(ABCD),shownin Fig.1.2A–C,respectively.[Pathsarenumbered afterarcs1,2,3,respectively.]
An elementaryhyperpath isanextensionofelementarypathwheresome(possiblyall)nodes,called diversionnodes,maybethetailofoneormorearcs,called diversionarcs,eachofwhichisgivenapositiveweightsumminguptoone,called diversionproportion;accordingtothisdefinitionanelementarypathisanelementaryhyperpathwherethereisnodiversionnode.Anelementaryhyperpath(with somediversionnodes)reducestoanelementarypathwhenalldiversionproportions areequaltoone,anditiscalled simple;otherwiseitiscalleda composed elementary hyperpath,madeupbyseveraloverlappingelementarypaths,eachgivenatraversing probabilityobtainedfromdiversionproportions.Itisworthnotingthatapathmay wellbelongtoseveralhyperpaths,withdifferenttraversingprobabilities.Thus,ifthe number, mP.,ofelementarypathsisfinitethenumberofhyperpathsisfiniteaswell, atmost2mp -1.
LetnodesAandBbediversionnodesin Fig.1.1.BetweennodesAandBthere are3simplehyperpathsgivenbypaths:1=(ACD),2=(ABD)and3=(ABCD), shownin Fig.1.2A–C.Furthermorethereare4composedhyperpaths:
FIG.1.2
(A)Path1 ¼ (ACD)betweennodesAandD.(B)Path2 ¼ (ABD)betweennodesAandD. (C)Path3 ¼ (ABCD)betweennodesAandD.
•4madebypaths1and2,assumingthatadiversionmayoccuratnodeAonly;
•5madebypaths1and3,assumingthatadiversionmayoccuratnodeAonly;
•6madebypaths2and3,assumingthatadiversionmayoccuratnodeBonly;
•7madebypaths1,2and3,assumingthatadiversionmayoccurbothatnodeA and/ornodeB.
Composedhyperpaths4,5,6,and7areshownin Fig.1.3A–D,respectively.[They arenumberedbythesumoftheindicesofthepathscomposingthemplus1.]
Anorderedpairof(different)nodes,(n O, n D )iscalled connected ifthereisat leastone(hyper-)pathfromthefirstnode, nO ,tothesecondnode, n D, single-connected ifthereisexactlyone(hyper-)path,and multi-connected ifthereareatleast two(hyper-)paths;itisworthnotingthattheinversepair( n D, n O)maynotbe connected.