CONTACT MECHANICSWITH APPLICATIONSIN TRIBOLOGY
IRINAGORYACHEVA
IshlinskyInstituteforProblemsinMechanicsofthe RussianAcademyofSciences,Moscow,Russia
YULIAMAKHOVSKAYA
IshlinskyInstituteforProblemsinMechanicsofthe RussianAcademyofSciences,Moscow,Russia
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright © 2022ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyany means,electronicormechanical,includingphotocopying,recording,oranyinformation storageandretrievalsystem,withoutpermissioninwritingfromthepublisher.Details onhowtoseekpermission,furtherinformationaboutthePublisher’spermissions policiesandourarrangementswithorganizationssuchastheCopyrightClearance CenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier. com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedunder copyrightbythePublisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthis fieldareconstantlychanging.Asnewresearch andexperiencebroadenourunderstanding,changesinresearchmethods,professional practices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledge inevaluatingandusinganyinformation,methods,compounds,orexperiments describedherein.Inusingsuchinformationormethodstheyshouldbemindfulof theirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhavea professionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,or editors,assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasa matterofproductsliability,negligenceorotherwise,orfromanyuseoroperationof anymethods,products,instructions,orideascontainedinthematerialherein.
ISBN:978-0-12-821799-3
ForinformationonallElsevierpublicationsvisitourwebsite at https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: DennisMcGonagle
EditorialProjectManager: CatherineCostello
ProductionProjectManager: KameshRamajogi
CoverDesigner: VickyPearsonEsser
TypesetbyTNQTechnologies
1.Normaldiscretecontactofelasticsolids1
1.1 Formulationofthediscretecontactproblem1
1.2 Periodiccontactproblems5
1.3 Approximatesolutionoftheperiodiccontactproblembasedon themethodoflocalization12
1.4 Contactproblemswithboundednominalcontactregion32
1.5 Conclusion39 References40
2.Effectofadhesioninnormaldiscretecontact43
2.1 Adhesionofadifferentnature:molecularandcapillary43
2.2 Approachtostudythenormaldiscreteadhesivecontact49
2.3 Effectofmolecularadhesioninnormaldiscretecontact57
2.4 Effectofcapillaryadhesioninnormaldiscretecontact60
2.5 Conclusion63 References63
3.Additionaldisplacementduetomicrogeometryofcontacting bodies67
3.1 Additionaldisplacementfunction(2-Danalysis)68
3.2 Additionaldisplacementfunction(3-Danalysis)73
3.3 Additionaldisplacementduetomicrogeometryandadhesion76
3.4 Effectiveworkofadhesionforsurfaceswithmicrogeometry81
3.5 Two-scaleanalysisofthecontactproblems86
3.6 Conclusions98 References99
4.Movingcontactofelasticbodieswithsurfacemicrogeometry101
4.1 Adhesivemechanismofenergydissipationin approach-retractioncycleoftwoindividualasperities101
4.2 Modelingofslidingfrictionforce115
4.3 Modelingofrollingfrictionforce121
4.4 Conclusion132 References132
5.Microgeometryeffectinslidingcontactofviscoelasticsolids135
5.1 Hystereticmechanismofenergydissipation135
5.2 Effectofmicrogeometryandthinviscoelasticlayerinslidingcontact ofelasticsolids(2-Danalysis)138
5.3 Slidingcontactofapunchwithperiodicmicrogeometryoverthe viscoelastichalf-plane(2-Danalysis)148
5.4 Slidingcontactofarigidcylinderovertheviscoelasticlayerwith periodicsurfacemicrogeometry159
5.5 Slidingcontactofapunchwithperiodicmicrogeometryoverthe viscoelasticfoundation(3-Danalysis)170
5.6 Combinedeffectofhysteresisandadhesioninslidingofawavysurface177
5.7 Frictionofamultiscalewavysurfacetakingintoaccountadhesion189
5.8 Effectof fluidinthegapinslidingcontactofapunchwith periodicmicrogeometryovertheviscoelastichalf-space197
5.9 Conclusions201
Preface
Tribologyisbothafundamentalandanappliedscienceaimedtoexplain thephenomenaoffrictionandwearofmaterialsincontactinteractionas wellastocontroltheseprocessesbasedonthedeepunderstandingofthem. Tribologydevelopmentisbasedonboththetheoreticalandexperimental study.
Thedevelopmentoffundamentaltribologyisstronglyconnectedwiththe progressincontactmechanicsandfracturemechanicsaswellasphysicsand chemistry.Mechanicscontributessignificantlytothestudyoffrictionand fractureofsurfaces,sinceallprocessesofvariousnaturesoccurringduring frictioninthesurfacelayersofcontactingbodiesaregreatlyinfluencedbythe magnitudeofstressesactingthere.Highrealpressuresandslidingvelocitiesat andnearcontactspotscausesignificanttemperatureriseintheseareas,which changesthepropertiesofsubsurfacelayers.Theyalsocausemechanicaland temperaturestressesthere,whichfacilitatechemicalreactionsandactivate interdiffusion.Inthesurfacelayerundergoinghighdeformations,crackinitiationanddevelopmentoccur,whichresultsinfracture(wear)ofthematerial.
Explanationofthemechanismsoffrictionandwearofmaterialsunder variouscontactconditions,whichisoneofthekeyissuesoffundamental tribology,isimpossiblewithoutformulatingandsolvingcontactproblems takingintoaccountnotonlythemacrogeometryofinteractingsurfaces,but alsotheirmicrogeometry.
Asurfacemicroreliefintheformofwavinessandroughnesscausesa discretecontactregion.Asaresult,highpressuresariseontherealcontact spots,leadingtothestressconcentrationinathinsurfacelayer,thethickness ofwhichiscomparablewiththecharacteristicsizeofacontactspot.The distributionofstressesinthislayerlargelydeterminesthenatureofits fracture,i.e.,itssurfacewear.
Thecharacteristicsofcontactinteractionandthemagnitudeofthe frictionforceareinfluencedbyboththeparametersofthesurfacemicroreliefofinteractingbodiesandtheirmechanicalcharacteristics,aswellasby thephysicalpropertiesofthesurfacesandthemediumbetweenthem. Adhesiveattractionbetweenthesurfaces,causedbyintermolecularforces andcapillarypressureinliquidbridges,leadstoaredistributionofcontact pressureatthemicroscopiclevelandincreasestherealcontactarea,which significantlyaffectsthefrictionandwearbehavior.Thecombinedeffectof
thesurfacemicroreliefandadhesionleadstoadhesionhysteresisand irreversibilityoftheprocessofformationanddestructionofcontactspots, whichisoneofthemainmechanismsoffrictionforce(itsadhesive component).
Anotherimportantcontributiontothefrictionforceisthedeformation (hysteresis)componentassociatedwiththeenergylossthatoccurswhen surfacelayersofanimperfectlyelasticmaterialaredeformedbyasperitiesof acounterbodyduringrelativemotionofthesurfaces.Themicroreliefand discretenessofcontactplayanimportantroleinthismechanismoffriction: they,togetherwiththevelocityofrelativemotionofthesurfaces,define thefrequencyandamplitudeofmaterialdeformation,whichdeterminethe hysteresislosses.
Inthisbook,modelsofcontactinteractionarepresented,whichare developedtostudythedistributionofcontactstressesinnormaland tangentialcontactsofelasticandviscoelasticbodieswithgivenmacroshapes ofthecontactingsurfaces,alsotakingintoaccountasurfacerelief(waviness, roughness)atmicroscale.Adistinctivefeatureofallthedevelopedmodelsis theuseofanalyticalmethodsbasedonsolvingmixedproblemsofcontact mechanicsforasystemofcontactspots,takingintoaccounttheirmutual influence.Theresultsobtainedallowonetoanalyzetheinfluenceofboth theshapeofasperitiesanddensityoftheirlocationonthecontact characteristics(distributionofrealcontactpressure,realcontactarea, approachofbodiesatgivenvaluesofnominalpressure,etc.)innormal approachandretractionofthesurfaces,aswellasonthefrictionforceinthe relativecontactmotion.
Inthe firstthreechapters,modelsaredevelopedforstudyingthenormal contactofelasticbodiestakingintoaccounttheirsurfacemicrogeometry. Chapter1 studiesthenormalapproachofelasticbodieswithnominally flat surfaceshavingaregularmicrorelief.Anapproximatemethodforsolving periodiccontactproblemsbasedontheprincipleoflocalizationisproposed. Byusingthismethod,itispossibletoanalyzetheinfluenceofnotonlythe shapeofanindividualasperity,butalsothedensityoftheirlocationonthereal contactareaandadditionaldisplacementofelasticbodiesduetothepresenceof aroughlayerontheirsurfaces.Thismethodisusedin Chapter2 tosolve contactproblemsforelasticbodieswithnominally flatsurfaces,takinginto accounttheirmicrogeometryandadhesiveinteractionsofadifferentnature (molecularandcapillaryadhesion).Inaddition,in Chapter 1,anapproximate analyticalsolutionoftheproblemofindentationofaboundedsystemof asperitiesintoanelastichalf-spaceisconstructed,andtheroleoftheedgeeffect
onthedistributionofforcesbetweentheasperitiesisstudied,takinginto accounttheirmutualinfluence.Theadditionaldisplacementfunction associatedwiththepresenceofaroughlayeronthesurfaceisanalyzedindetail in Chapter3,includingtheeffectoftheadhesiveforcesbetweenthesurfaces. Takingintoaccounttheadditionaldisplacementfunction,theformulation andthemethodofsolutionofcontactproblemsforbodiesofagivenmacroandmicrogeometryarealsopresentedin Chapter3.Theobtainedsolutionsof themodelproblemsmadeitpossibletoanalyzetheinfluenceofthesurface roughnessparameters(shape,densityandheightdistributionofasperities)on thenominalcontactpressuredistributionatmacrolevel,aswellasonthesizeof thenominalcontactarea.
Chapters4and5 aredevotedtomodellingtheadhesiveanddeformation (hysteresis)components,respectively,ofthefrictionforceinthesliding contactofdeformablebodies.In Chapter4,ananalyticalmodelisdeveloped forcalculatingtheenergylossinanapproach-retractioncycleoftwo asperities,whichisusedtocalculatetheadhesivecomponentofthefriction forceduringrelativeslidingoftwoelastichalf-spaces,whosesurfacesare coveredwithasperitiesofagivenshape.Thedependenceoftheadhesive frictionforceinslidingcontactontheparametersofmicrogeometry, adhesion,andelasticpropertiesofthecontactingbodiesisanalyzed.The adhesivecomponentoftherollingfrictionforceisalsocalculated,andits dependenceontheheightdistributionofasperitiesonthesurfaceofthe rollingbodyisstudied.
In Chapter5,amodelisdevelopedforcalculatingthefrictionforce causedbyhysteresislossesduringcyclicdeformationofthesurfacelayerof animperfectlyelasticbodywhenaroughcounterbodyslidesoverit.Based ontheobtainedanalyticalandnumerical-analyticalsolutionsofdiscrete contactproblemsforaviscoelastichalf-space(orviscoelasticlayer)under conditionsofuniformslidingofasurfacewithmicrogeometryoverit,the influenceofthemicrogeometryparameters(roughnessshape,densityof location),viscoelasticcharacteristicsofthebody,andslidingvelocityonthe contactcharacteristicsandhysteresiscomponentofthefrictionforceis studied.Thisapproachisusedtoanalyzethecombinedeffectofmicrogeometryandadhesiveforces,aswellasliquidcontainedinthegap betweenthesurfacesonthehysteresiscomponentofthefrictionforce.
Thus,thedevelopedanalyticalmodelsmakeitpossibletostudythe effectofsurfacemicrogeometryonthecontactcharacteristicsforvarious typesofinteractionofdeformablebodies(normalapproach,relativesliding, androlling),andforvariouscontactconditions(dryandlubricatedsurfaces,
x Preface
liquidinthegap,etc.),aswellastoanalyzethefrictionforceasafunctionof themechanicalandsurfacepropertiesofthecontactingbodiesandtheir microgeometry.
ThesestudieswerecarriedoutintheIshlinskyInstituteforProblemsin MechanicsoftheRussianAcademyofSciencespartlyunderthe financial supportoftheRussianFoundationforBasicResearch(grant20-01 00400).
Normaldiscretecontactofelastic solids
Theclassicalcontactproblemisusuallyformulatedfortopographically smoothcontactingsurfaces,sothecontactregioniscontinuous.Butitis wellknownintribologythatarealcontactregionconsistsofcontactspots distributedwithinthenominal(average)contactregion.So,therealcontact areaisasmallfractionofthenominalcontactarea.
Themainreasonofthecontactregiondiscretenessistheroughnessand wavinessofthecontactingsurfaces.Inthegeneralcase,surfacetopography isrepresentedbyacombinationofdeterministicandrandomfunctions (Whitehouse,1994)determinedbynaturalfactorsortechnologicaltreatmentofthesurface.Deterministiccomponentsareformedeitherasaresult ofimperfectionsintheoperationoftechnologicalequipmentorinstationaryoperatingconditions,forexample,thesteadyshapeofaworn surface(Goryacheva,1998).Inaddition,aregularmicrogeometryonthe surfacecanbecreatedtocontroltheoperationalpropertiesoffriction pairs,inparticulartheirtribologicalcharacteristics(Goryachevaand Tsukanov,2020a).
Notethatthediscretecontactproblemalsoarisesinstudyofthecontact interactionofcompositematerialsandinhomogeneousbodieswithinclusions.Thecontactdiscretenesscanbealsoformedbyaspecialsurface treatment,duetostructuralinhomogeneity,byusingdiscontinuous coatings,andsoon.
Inthischapter,wepresenttheapproachestostudythecontactcharacteristicsofasystemofthe finitenumberofasperitiespenetratingintothe elastichalf-spaceandthecharacteristicsofanelasticcontactofnominally flatsurfaces(atmacrolevel),oneofwhichhasaregularmicrogeometry.
1.1Formulationofthediscretecontactproblem
Wegiveherethegeneralformulationofthediscretecontactproblem.Let usconsideracontactinteractionofadeformablehalf-spaceandacounter
DiscreteContactMechanicswithApplicationsinTribology ISBN978-0-12-821799-3
https://doi.org/10.1016/B978-0-12-821799-3.00002-9
2 DiscreteContactMechanicswithApplicationsinTribology
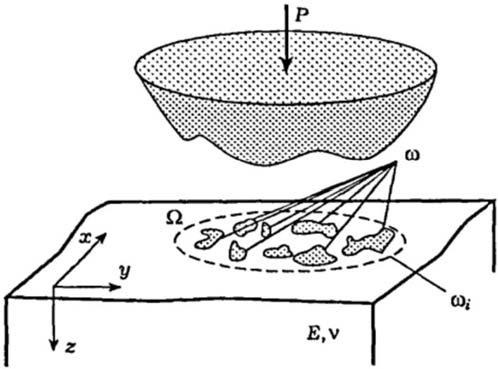
body,theshapeofwhichisdescribedbythefunction z ¼ F ðx; yÞ inthe systemofcoordinatesconnectedwiththehalf-space(theplane Oxy coincideswiththehalf-spacesurfaceintheundeformedstate,andthe z-axisis directedintothehalf-space).Afterdeformation,a finitenumber N oran infinitenumberofcontactspots ui occuratthesurface z ¼ 0ofthehalfspacewithinthenominalcontactregion U (Fig.1.1).If N /N,theregion U coincideswiththeplane z ¼ 0.
Therealcontactpressure pi ðx; yÞ actsateachcontactspot ðx; yÞ ˛ ui Weassumeherethatshearstressesarenegligiblysmall.Thecontactpressure providesthedisplacementofthehalf-spacesurfacealongthe z-axis.This displacement uz ðx; yÞ dependsonthepressures pi ðx; yÞði ¼ 1; 2;:::N Þ appliedtoallcontactspots:
Theoperator A isdeterminedbythemodelofthedeformablebodiesin contact.Forthecontactbetweenarigidbodywitharoughsurfaceandan elastichalf-space,therelationis
Figure1.1 Schemeofthecontactofarigidbodywithroughsurfaceandtheelastic half-space.
Here, E and n aretheYoung’smodulusandPoisson’sratioofthehalfspace,respectively.
Thecontactconditionateachcontactspot ui is
where D isthedisplacementoftherigidbodyalongthe z-axis.If D isnot giveninadvance,butthetotalload P appliedtothebodiesanddirected alongthe z-axisisknown,theequilibriumequationmustbeaddedto Eqs.(1.1)and(1.3):
Thesystemof Eqs.(1.2) (1.4) canbeusedtodeterminetherealcontact pressure pi ðx; yÞ withinthecontactspots ui .However,thesolutionofthis contactproblemisverycomplicated,evenifthesizesandthearrangement ofcontactspotsareknown.Inthegeneralcase,wemustdeterminealsothe number N ,andthepositionsandshapesofthecontactspots ui forany valueoftheload P .Foradifferentiablefunction F ðx; yÞ; wecanusethe condition pi ðx; yÞjx;y˛vui ¼ 0todeterminetheregion ui ofanindividual contact.Notethatthecontactproblemwithunknowncontactregions ui is nonlinear,soitisnotpossibletousethesuperpositionmethodforits solution.
Oneofthemethodsdevelopedtosolvethediscreteproblemistheuse oftheknownexactsolutionsforthecompletecontactwithinthe nominalcontactregion U andthenthestep-by-stepmodificationofthe contactregiontogetthepositivecontactpressureswithintherealcontact spots ui andzeropressuresoutsidethem(ChekinaandKeer,1999).This methodisbasedontheexactanalyticalsolutionsofthecontactproblemsin 2-D(Muskhelishvili,1953)and3-Dformulations(Galin,1953,2008).
Thecontactproblemformulatedabovecanbesolvednumericallybased onthegeometricdescriptionofthecontactingsurfacesobtainedfrom measurements(Lubrecht,1991; Stanley,1997).Inthiscasethefaithfulness ofthestress-strainstatesodetermineddependsontheaccuracyofthe numericalprocedure.
Itisworthnotingthatthereislittlepointindevelopinganexactsolutionofthediscretecontactproblembecausethefunction F ðx; yÞ is usuallydeterminedapproximatelybymeasurementsofsomesmallsurface
elementbeforedeformation.Therearebasicconstraintsontheaccuracyof measurementsofasurfacemicrogeometrybydifferentdevices.Thefunction F ðx; yÞ mayvaryfromelementtoelement.Inaddition,thefunction F ðx; yÞ canchangeduringcontactinteraction(forexample,inawear process).Notonlydosuchnumericalsolutionsconsumecomputertime, buttheyarenotuniversal.Asolutionforonesetofcontactcharacteristics andenvironment(load,temperature,etc.)cannotbeusedforanotherset.
So,itismoreimportanttodevelopanalyticalmethodstostudythe discretecontactsundervariousinterfaceconditions.Itallowsustoanalyze theinfluenceofdifferentmicrogeometryparameters(densityofcontact spots,asperitiesheightdistribution)onthecontactcharacteristics,friction force,heatconduction,adhesion,wear,andsoon,andalsotocontrolthe frictionandwearprocessesbasedonthesurfaceengineering.
Forthesereasons,thediscretecontactproblemisusuallyinvestigatedin asimplifiedformulation.Firstofall,somemodelofarealroughsurfaceis considered.Themodelandtherealsurfaceareassumedtobeadequateif chosencharacteristicsoftherealsurfacecoincidewiththecorresponding characteristicsofthemodel.
Itistraditionalfortribologytomodelaroughsurfaceasasystemof asperitiesofaregularshape,thespacedistributionofwhichreflectsthe distributionofmaterialinthesurfaceroughlayer.Researchersusevarious shapesofasperitiesintheirmodels.Acompletelistofasperityshapes,with theiradvantagesanddisadvantages,isgivenby Kragelskyetal.(1982).The shapeofeachasperityisdeterminedbyanumberofparameters(asphereby itsradius,anellipsoidbythelengthsofitsaxes,etc.).Theseparametersare calculatedfromthemeasurementdataofthesurfacemicrogeometry.The spacingoftheasperitiesiscalculatedusingthechosenasperityshapeandthe characteristicsofthesurfacemicrogeometryobtainedfromthemeasurements(Demkin,1970).
Inadditiontotheapproximatedescriptionofthesurfacemicrogeometry(itsroughness),approximatemethodsofsolutionof Eqs.(1.1), (1.3),and(1.4) areusedtoanalyzethediscretecontactproblem.The first studiesinthemechanicsofdiscretecontactdidnotaccountfortheinteractionbetweencontactspots;thatis,thestress-strainstateofbodiesinthe vicinityofonecontactspotwasdeterminedbytheloadappliedtothis contact,neglectingthedeformationcausedbytheloadsappliedtothe remainingasperities.Underthisassumption,theoperator A in Eq.(1.1) dependsonlyonthefunction pi ðx; yÞ,if ðx; yÞ ˛ ui .Thisassumptiongives goodagreementbetweentheoryandexperimentforlowcontactdensity,
i.e.,forlowratiooftherealcontactareatothenominalone.However, undercertainconditions,therearediscrepanciesbetweenexperimental resultsandpredictions.Forexample,investigatingthecontactareaof elastomers, BartenevandLavrentiev(1972) revealedtheeffectofsaturation; thatis,therealcontactarea Ar isalwayssmallerthanthenominalcontact area Aa ,howevergreatacompressionloadisused.Basedontheexperimentaldata,theyobtainedthefollowingrelation:
where lA ¼ Ar=Aa istherelativecontactarea, b istheparameterofroughness, p isthenominalcontactpressure,and E istheelasticitymodulusofthe elastomers.Itfollowsfrom Eq.(1.5) that lA < 1for finitevaluesof p.To describethesaturationeffect,themutualinfluenceofthecontactspotsmust betakenintoaccount.
Indiscretecontactmechanics,theapproachdevelopedby Greenwood andWilliamson(1966) iswidelyused.Theyconsideredamodelofarough surfaceconsistingofasystemofsphericalasperitiesofequalradii,theheight ofanasperitybeingarandomfunctionwithsomeprobabilitydistribution. ThedeformationofeachasperityobeyedtheHertzequation.Theadditionaldisplacementofthesurfacebecauseoftheaverage(nominal)pressure distributionwithinthenominalcontactareawasalsotakenintoaccountin thismodel.Sothecontactpressurescalculatedfromthemodeldonot satisfy Eqs.(1.2)and(1.3),butthemodelallowsonetoestimateapproximatelythemutualinfluenceeffectonthediscretecontactcharacteristics (radiusofcontactspots,additionaldisplacement,etc.).
1.2Periodiccontactproblems
Ifasurfacehasclearlydefineddirectionandperiodicityofroughness(e.g., at finishingpolishing,millingorturning),itsmicroshapecanbemodeledby regularwavinessofvariousshapes.Asurfacewavinessingeneralcasecanbe representedbyperiodicfunctions.Sincefor finishingprocessingtheperiod ofwavinessismuchhigherthanitsamplitude,thelinearelasticitycanbe appliedtosolvetheperiodiccontactproblem.Forsurfaceswithregular microgeometry(forexample,wavysurfaces)themethodsofsolutionof periodiccontactproblemscanbeusedtoanalyze Eqs.(1.1),(1.3),and(1.4). Periodiccontactproblemsplayanimportantroleinstudyingtheeffectof
mutualinfluenceofcontactspotsonthecharacteristicsofcontactinteraction(contactpressuredistribution,contactarea),andalsoinanalyzingthe effectofmicrogeometryparametersontheapproachofthecontacting bodies.
1.2.12-Dperiodiccontactproblems
Forasystemofrigidpuncheswith flatbasepenetratingintoanelastichalfplane,the2-Dperiodiccontactproblemwas firstsolvedby Sadowsky (1928) usingacomplexstressfunction.Thefollowingexpressionwas derivedforthecontactpressure:
where P istheappliednormalloadperunitlength, L isthedistancebetweenthepunches,and a isthehalf-widthofapunch.
Thesolutionoftheperiodiccontactproblemfortheinclinedpunches withthe flatbaseinthecaseofthecompletecontactwasobtainedby Block andKeer(2008).Thecontactpressurewasgivenbythefollowing expression(BlockandKeer,2008):
Thenormalload P ,whichactedoneachpunchandprovidedthe completecontactbetweenthepunchesinclinedattheangle ε andthehalfspace,satisfiedtheinequality
Inthesimplestcasethewavinesscanbedescribedbysinusoid,i.e., F ðxÞ¼ Dð1 cosð2px =l ÞÞ,where D isanamplitudeand l isaperiod.The
contactproblemforsuchasurface,penetratingintoanelastichalf-plane, was firstsolvedby Westergaard(1939) undertheassumptionofnofriction withinthecontactspots.Thecontactpressure p(x)forthistypeof modelroughnessisdescribedbythefollowingperiodicfunction (Westergaard,1939):
Here E * isthereducedelasticmodulusofthecontactingbodies,which isdeterminedbytheformula:
Here Ei and ni aretheelasticmodulusandthePoissonratiooftheelastic half-space(i ¼ 1)andthewavyelasticcounterbody(i ¼ 2).
Thehalf-width a ofthecontactzonein Eq.(1.9) isrelatedtothe nominalpressure p bythefollowingexpression(Westergaard,1939):
Asimilarsolutionforcalculatingthecontactpressureinindentationofa wavysurfacedescribedbytheperiodicfunctionwasobtainedby Staierman (1949).Later,byusingthemethodofpairedsummationequation,the normalcontactproblemforabodywithsinusoidalwavysurfaceandthe elastichalf-planewassolved(Dundursetal.,1973),andthefollowing relationshipbetweenthemaximumcontactpressure pmax andtheapplied nominalpressure p wasderived:
where p * ¼ pE * D l isthenominalpressurerequiredforthecompletecontact oftheinteractingbodies.
Thegeneralmethodforsolvinga2-Dperiodiccontactproblemfor elasticbodiesundertheassumptionofnofrictioninthecontactzonewas proposedby BlockandKeer(2008).Itwasbasedonthereductionofthe integralequationoftheperiodiccontactproblem,whichhadthefollowing form(Staierman,1949):
where g 0 ðxÞ isthederivativeoftheinitialgapfunction,totheequationcorrespondingtotheproblemwithaunitcontactregion:
where u ¼ tan x=2 ; v ¼ tan x=2 and a ¼ tan a=2 :
Usingthismethod,thecontactproblemfortheelastichalf-planeand therigidbodywiththewavysurfacedescribedbythefunction
where m istheshapeparameter ðm < 1Þ,wasanalyzedin(Tsukanov, 2018a).Theresultingexpressionforthecontactpressureisageneralization oftheWestergaardsolutionforasinusoidalwavysurface:
Theeffectoftheshapesofwavysurfaceonthecontactpressurehasbeen analyzed(Tsukanov,2018a, 2018b)basedon Eq.(1.16) forarigidbody withtwo-levelwavysurfacepenetratingintoanelastichalf-plane.In particular,itwasshownthatthepresenceofasmall-amplitudehighfrequencysinusoidalharmonic(secondlevel)onthefundamentalone (firstlevel)leadstoanoscillatingcharacternotonlyofthecontactpressure, butalsooftheintegralcontactcharacteristics(inparticular,thedependence oftherealcontactareaonthenominalpressure).
Kuznetsov(1976) wasthe firsttoobtainanexactsolutionofthe2-D periodiccontactproblemwithfrictionforarigidwavyindenterandan elastichalf-plane.TheKolosov Muskhelishvilimethodandthetheoryof automorphicfunctionswereusedtosolvethecontactproblem.Foran indenterwithasurfaceprofile
where l isaperiod, R istheprofileradiusattheinitialpointofcontact,and g isthecontactshift,thefollowingexpressionforthecontactpressure withinthecontactregion ð a g; a gÞ hasbeenderived(Kuznetsov andGorohovskii,1977):
Here a isthehalf-widthofthecontactzone, G and n aretheshear modulusandPoissonratio,respectively, a istheparametercalculatedfrom therelationship
and m isthefrictioncoefficient.Thecontactshift g iscalculatedfromthe followingexpression:
Thecombinedeffectofthefrictioncoefficientandcontactdensity a/l onthecontactpressuredistribution,aswellasonthesizeandpositionof thecontactregions,wasanalyzed(KuznetsovandGorohovskii,1977). Basedonanapproximatesolutionofthisproblem(KuznetsovandGorokhovsky,1978),thestress-strainstateofthesubsurfacelayersofcontacting bodieswasstudiedatdifferentvaluesofthefrictioncoefficientandwidthof thecontactregion(KuznetsovandGorokhovsky,1981).
Similarproblemsforanelastichalf-planeinfrictionalcontactwitha sinusoidalpunchandwithaperiodicsystemofpuncheshavinga flatbase wereconsideredby BlockandKeer(2008).Theproblemsweresolvedby reducingthebasicequationtoanintegralequationofthesecondkindwith theCauchykernel.Forasinusoidalpunch,theyobtainedthefollowing expressionforthecontactpressureatawavinessperiod l ¼ 2p:
Heretheeccentricity g ofthecontactregioniscalculatedfromthe expression
In Eqs.(1.22)and(1.23),tan
¼
,l ¼ (p
f(2m 1)),and tan f ¼ 1/j.
Foraperiodicsystemofpuncheswitha flatbase(a isthehalf-widthof thepunchbase),thecontactpressuredistributionisobtainedintheform (BlockandKeer,2008):
ðxÞ¼
Ageneralformulationandamethodforsolvingvariouscontactproblems,includingperiodicones,consideringadhesionandslippageby reducingthemtoavectorRiemannproblem,wereproposedby Antipov andArutyunyan(1991).Inthisandtheirearlierstudies,itwasshownthat themathematicalformulationoftheproblemstakingintoaccountfriction incontactregionscanbereducedtoacoupledsystemofintegralequations forthenormalandshearcontactstresses.Inaspecialcaseofequalelastic constantsofthecontactingmaterials,thesystemisuncoupled.
1.2.23-Dperiodiccontactproblems
3-Dperiodiccontactproblemsareofconsiderableinterestbecausemost roughsurfacesinnatureandtechnicalapplicationsareisotropic;i.e.,the
heightandstepparametersoftheroughnessprofilesinthelongitudinaland transversedirectionsarecomparableinmagnitude.Inaddition,3-Dperiodiccontactproblemsarisewhenthereisaspecialtextureonthecontacting surfaces,asarule,formedbyphysicalandchemicaltreatment,e.g.,bylaser orpressure.Fromtheviewpointofelasticitytheory,the3-Dperiodic contactproblemismuchmorecomplicatedthanthe2-Doneduetothe absenceofadirectresolventofthebasicintegralequationfollowedfrom Eqs.(1.2)and(1.3).Often Eqs.(1.1)and(1.3) aresolvedusingiterative proceduresortheboundaryelementmethod.Withcompletecontactbetweenthebodies,theproblembecomeslinearandmuchsimpler.
Johnsonetal.(1985) developedamethodofanalysisofadiscrete contactproblemforanelasticbody,thesurfaceofwhichintwomutually perpendiculardirectionswasdescribedbytwosinusoidalfunctions;the counterbodyhadasmoothsurface.Basedonthesuperpositionprinciple,it wasshownthat,foraregularreliefdescribedbythefunction
thecontactpressureatcompletecontactisexpressedas
modulusdeterminedby Eq.(1.10).Toprovidethecompletecontact,the followingconditionforthenominalpressuremustbesatisfied: p p * x þ p * y .Forlowervaluesofthenominalpressure p,incompletecontactoccurs. Asymptoticmethodstosolvethecontactproblemweredevelopedforlow valuesof p basedontheHertztheoryandforvaluesclosetothelimited value p * x þ p * y (butnotexceedingthislimit)basedontheellipticcrackstheory(Johnsonetal.,1985).Forintermediatevaluesof p thesolutionwas constructednumericallybasedonseekingtheFouriercoefficientswith minimizingthetotaladditionalenergy(similartothecaseofthe2-Dproblemforsinusoidalwaviness).
Usingthe finiteelementmethod,relationshipsforintegralcontact characteristics,whichareclosetotheresultsof Johnsonetal.(1985),were obtainedin(RostamiandJackson,2013);inaddition,expressionsthat approximatetherealcontactareaandmeangapbetweenthecorrugated surfaceandthehalf-spacefortheentirerangeofappliednominalpressures
wereproposed.Theresultsof Johnsonetal.(1985) onthecontactproblem forawavysurface (1.25) wererefinedin(Yastrebovetal.,2014)byusing theboundaryelementmethodandthefastFouriertransform.Inflection pointswerefoundontherealcontactareaasafunctionofthenominal pressure.The firstpointcorrespondstothetransformationofthecontact region’scontourfromacircletoasquarewithroundedcorners.The secondonecorrespondstothemergingofadjacentcontactregions.
Basedontheexpansionoffunction (1.25) inadoubleFourierseriesin polarcoordinates,theasymptoticdependencesobtainedby Johnsonetal. (1985) wererefinedby Tsukanov(2019).Theobtainedrelationshipsforthe realcontactareaandthemeangapasfunctionsofthenominalpressure correlatewellwiththeresultsofnumericalsimulation(Rostamiand Jackson,2013; Yastrebovetal.,2014).
1.3Approximatesolutionoftheperiodiccontact problembasedonthemethodoflocalization
Inthissection,anapproachtoderiveanapproximatesolutionofthe discretecontactproblemforperiodicsystemsofindentersbasedonthe localizationmethodispresented.
1.3.1Problemformulationforone-levelperiodicsystemof axisymmetricsmoothindenters
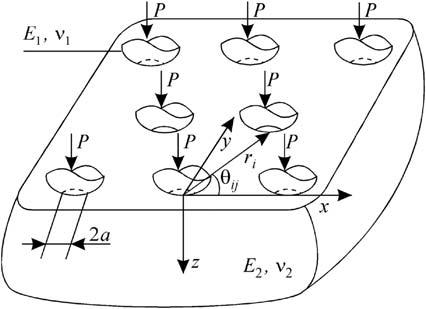
Aperiodiccontactproblemforasystemofaxisymmetricsmoothindenters, thecontactingsurfaceofwhichisdescribedbyanaxisymmetricfunction z ¼ f ðr Þ,thatinteractswithoutfrictionwithanelastichalf-spaceis considered(Fig.1.2).
Theaxesoftheindentersareperpendiculartothehalf-spacesurface z ¼ 0andintersectthissurfaceatpointsthataredistributeduniformlyoverthe plane z ¼ 0.Asanexampleofsuchasystem,wecanconsiderindenters locatedatthesitesofaquadraticorhexagonallattice.
Letus fixanarbitraryindenterandlocatetheorigin O ofapolarsystem ofcoordinates ðr ; qÞ intheplane z ¼ 0atthepointofintersectionofthe axisofthisindenterwiththeplane z ¼ 0(see Fig.1.2).Thetopsofthe indentershavethecoordinates ri ; qij (i ¼ 1; 2; . j ¼ 1; 2; .; mi )where mi isthenumberofindenterslocatedatthecircumferenceoftheradius ri (ri < riþ1 ).
Duetotheperiodicityoftheproblem,eachcontactoccursunderthe sameconditions.Weassumethatcontactspotsarecirclesofaradius a
Figure1.2 Schemeoftheperiodiccontactbetweensmoothindentersandahalfspace.
(itimposescertainrestrictionsonthedensityoftheindentersarrangement), andthatonlynormalpressure pðr ; qÞ actsateachcontactspot ðr aÞ (the shearstressisnegligiblysmall).Todeterminethepressure pðr ; qÞ actingat anarbitrarycontactspotwithacenter O ,weusethesolutionofacontact problemforanaxisymmetricindenterwithsurfaceshape z ¼ f(r)andan elastichalf-spacesubjectedtothepressure qðr ; qÞ,distributedoutsidethe contactregion,whichwasderivedby Galin(1953, 2008).Thecontact pressure pðr ; qÞ (r a)isdeterminedbythefollowingrelationship (Galin,1953):
where
and E * isdeterminedby Eq.(1.10).Thefunction c ðqÞ dependsontheshape oftheindenter f ðr Þ.Forexample,iftheindenterissmooth(thefunction f 0 ðr Þ iscontinuousat r a),thenthecontactpressureiszeroat r ¼ a, i.e., pða; qÞ¼ 0,andthefunction c ðqÞ hastheform
ðqÞ¼ Z þN
The firsttermin Eq.(1.27) meansthepressurethatactsunderasingle axisymmetricindenteroftheshapefunction f ðr Þ penetratingintoanelastic half-space,andthelasttwotermsaretheadditionalcontactpressure occurringduetothepressure qðr ; qÞ distributedoutsidethecontactregion. Fortheperiodiccontactproblem,thefunction qðr ; qÞ coincideswith thepressure pðr ; qÞ ateachcontactspotlocatedat ri ; qij ðri > aÞ,andiszero outsidecontactspots.Soweobtainthefollowingintegralequationfrom Eq.(1.27),undertheassumptionthat f 0 ðr Þ isacontinuousfunction (pða; qÞ ¼ 0): pðr ; q
Þ¼
Thekernel K ðr ; q; r 0 ; q0 Þ in Eq.(1.32) isrepresentedasaseries (1.33).A generalterm (1.34) ofthisseriescanbetransformedtotheform:
ðr ; q; r 0 ; q0 Þ¼ 1
Weassumethatfortheperiodicsystemofindentersunderconsideration,eachcontactspotwiththecenter ri ; qij hasapartnerwiththe centeratthepoint ri ; p þqij .Sothesumonthe firstlineof Eq.(1.36) is zero.Hence,thegeneraltermoftheseriesin (1.33) hastheorder O 1 r 2 i ,since mi wri ,andtheseriesconverges.
1.3.2Methodoflocalization
Letusconsiderthefollowingequation:
where N istheaveragenumberofcontactspotsperunitarea,and P isa loadappliedtoeachcontactspot.Thisloadsatisfiestheequilibrium equation
Toobtain Eq.(1.37),wereplacethesummationovertheregion Un ðUn : r An ; 0 q 2pÞ byintegrationover i > n in Eq.(1.33),taking intoaccountthatthecentersofcontactspotsaredistributeduniformlyover theplane z ¼ 0andtheirnumberperunitareaischaracterizedbythe value N .Thefollowingtransformationdemonstrateshow Eq.(1.37) is derived: