Naturalgastechnology
1.1Chemicalcomposition
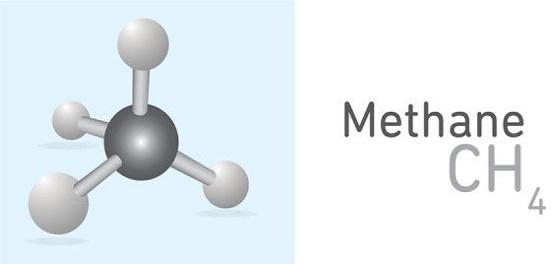
Naturalgas,alsocalled“fossilgas”orjust“gas”forshort,isanon-renewablesource ofenergy.Naturalgasisthecombinationofhydrocarbonandnon-hydrocarbongasses foundintheporousformationcalledthereservoirundertheearth’ssurfacewithoil,and theprincipalcompoundofnaturalgasismethane.Methaneisacolorlessandodorlessgas withthechemicalformulaofCH4 (onecarbonatomandfourhydrogenatoms,asillustratedin Fig.1.1).Itisveryflammable,burnsrapidlyintheair,andformsmainlycarbon dioxideandwatervaporduringcombustion.Althoughmethaneisastablegas,amixture ofasmallpercentageofmethane,between5%and14%,andairisextremelyexplosive. Methanecanbereleasedfromthecoalincoalminesandcauseanexplosionasaresultof mixturewiththeair.Ahydrocarbonisanorganicmoleculecompoundthatismadeof carbonandhydrogen.Hydrocarbonsaredividedintothreemaincategories:alkane, alkene,andalkyne.Alkanehassinglebondsinitsatomicstructure.Alkenehasdouble bondsinitsatomicstructure,andalkynehastriplebonds.Thetenmainhydrocarbons aremethane(CH4),ethane(C2H6),propane(C3H8),butane(C4H10),pentane (C5H12),hexane(C6H14),heptane(C7H16),octane(C8H18),nonane(C9H20),anddecane(C10H22).Allofthesehydrocarbonsarealkane,withasinglebondbetweencarbon andhydrogenatoms,andthegeneralformulaofalkanecompoundsisCnH2n+2.
Naturalgasisacolorless,highlyflammablemixtureofgases.Itisatypeofpetroleum andhydrocarbonthatisproducedasabyproductofoilindeepundergroundreservoirs.
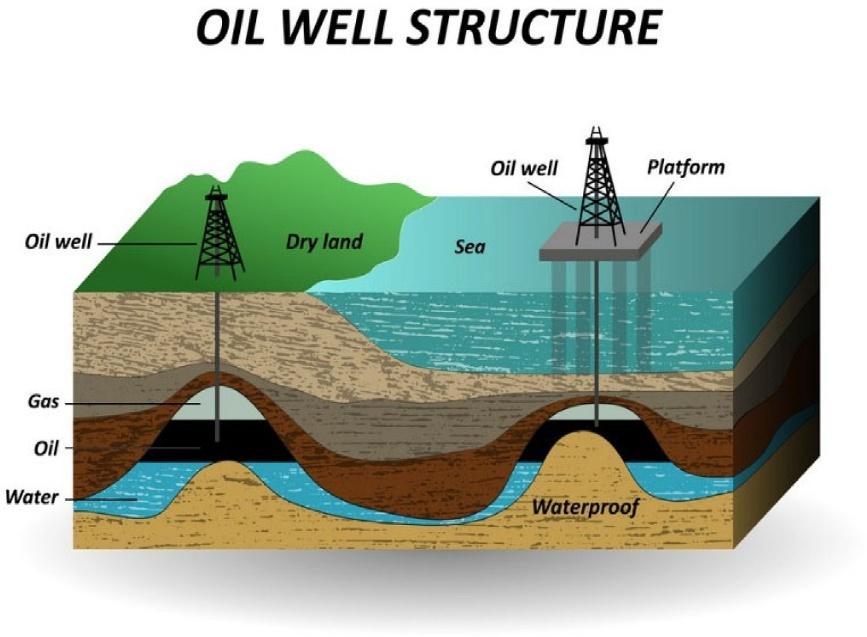
Fig.1.2 illustratestwooilwells,oneinthelandandtheotherinthesea,thataredrilled intoreservoirswheregasistrappedabovetheoilandwater.Thetypicalcompositionof naturalgasincludesbothhydrocarbonandnon-hydrocarboncompounds.Themain hydrocarbongasinnaturalgasismethane,whichcancomprise70–90%ofthenatural gas’svolume.Thenon-hydrocarbongasesinnaturalgasarenitrogen,hydrogen,oxygen, carbondioxide,andhydrogensulfide,whichareminorinpercentageofvolumeand inorganic.Theinorganiccompoundsinnaturalgasarenotdesirablesincetheyare notcombustibleandcausecorrosionandothertypesofproblemsintheproduction andprocessingofnaturalgas.Naturalgasisusedforthegenerationofelectricity,heating, cooking,andasafuelforcertainvehicles. Table1.1 displaysthechemicalcompositionof naturalgas.Itisimportanttoknowthatmethane,ethane,propane,andbutaneexistas
Fig.1.1 Methaneatomstructure. (Courtesy:Shutterstock.)
Fig.1.2 Drillingaland-basedwellandasubseawellintoreservoirswherenaturalgasistrappedabove oilandwater. (Courtesy:Shutterstock.)
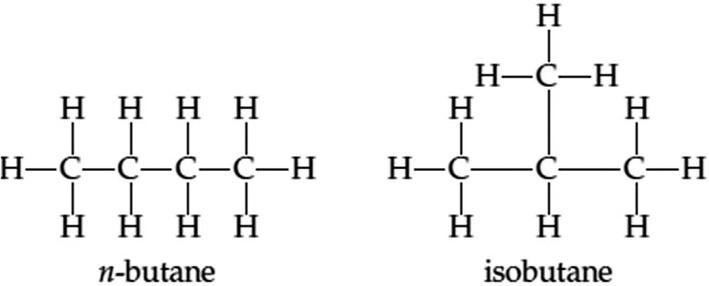
Fig.1.3 Thedifferentatomicarrangementsofn-butaneandisobutane.
Table1.1 Chemicalcompositionofrawnaturalgasbeforeprocessing.
Element/compound
Carbondioxide(CO2)andhydrogensulfide(H2S)0.7 0.1–1%
Oxygen 0.02 0.01–0.1%
Hydrogen TraceamountTraceto0.02%
Noblegasessuchasargon(Ar),helium(He), Neon(Ne),andXenon(Xe)
TraceamountTraceamount
Note1:n-butaneisthesameasbutane,whichisanalkanewithaformulaof(C4H10).Isobutaneisanisomerofbutane. Isomersinchemistryrefertomoleculeswithidenticalformulas,meaningthatisomershavethesamenumberofatomsbut indifferentarrangements. Fig.1.3 illustratesthedifferentatomicarrangementsofn-butaneandisobutane.
Note2:n-pentaneandISOpentanearealsoisomers.
gasesatnormaltemperaturesandpressures,whileotherhydrocarboncompoundsare liquidatnormaltemperaturesandpressures.
1.2Gasdefinitions
Itisimportanttoknowthatrawnaturalgasproducedfromawellmustbeprocessed tobeamarketableproduct.Inshort,processinganaturalgasinvolvestheremovalof watervapor,toxicandcorrosivecompoundssuchashydrogensulfide(H2S),andcarbon dioxide(CO2),aswellastheseparationofthecondensablehydrocarboncompounds. Naturalgascanbeclassifiedintoseveralbroadcategories,whichareexplainedbelow: Wetgas:Wetgascontainsheavy,condensablehydrocarbonssuchaspropane,butane, andpentane.Moreprecisely,ifmorethan5%ofagasiscomposedoftheabovementionedheavyhydrocarbonmoleculesandlessthan95%ismethane,itisclassified asawetgas.Wetgasshouldnotbeconfusedwithsaturatedgas,whichisexplainedin thenextparagraph.
Saturatedgas:Saturatedgasreferstogasbeforethedehydrationprocessinwhichthe gasissaturatedwithwater.Gasdehydrationistheprocessofextractingthemoisture andwaterfromthenaturalgasandgassesmixture.
Leangas:Ingeneral,leangasrepresentsakindofnaturalgaswiththeabsenceofcondensablehydrocarbons.Moreprecisely,leangasistheoppositeofwetgas,containing morethan95%methaneandlessthan5%condensableorheavyhydrocarbon molecules.
Drygas:Watermoistureexistsineverytypeofgas,butthequantityofitvaries.Dry gasisatypeofgaswithnegligiblewatercontent,lessthan7poundsper1million cubicfeetofgas.OnemillioncubicfeetofgasisabbreviatedasMMCF,where thetwoM’smean“onethousandthousand”oronemillion.Arelatedtermis absolutelydrynaturalgas,whichisdefinedasnaturalgaswithzerowatervapor.
Sourgas: Oneoftheundesirablebyproductsofoilandgasishydrogensulfide(H2S). elementalsulfurisanotherundesirablecompoundthatcanmakethegassour.Hydrogensulfideiscolorless,flammable,toxic,andcorrosive.Therefore,hydrogensulfide shouldberemovedfromhydrocarbon.Naturalgasisconsideredsouriftheamountof hydrogensulfideismorethan5.7mg/m3 ofnaturalgas,whichisequivalentto approximately4ppmbyvolumeunderstandardtemperatureandpressure.
Sweetgas:Sweetgasreferstoatypeofnaturalgaswithlessthan4ppmofhydrogen sulfide.However,sweetgascancontaincarbondioxide,whichcreatesasweetand uniformcorrosiontype.
1.3Physicalproperties
Itisessentialforengineerstounderstandthesegaspropertiesinordertobeableto designandanalyzegasproductionandprocessingsystemsandplants.Thephysicalpropertiesofgasarelargelydependentonthechemicalcompositionofthegas.Theproperties ofnaturalgasmaybedeterminedeitherdirectlyfromlaboratorytestsorthroughcalculationsbasedontheknownchemicalcompositionofthegas.Theprocessofcalculating thephysicalpropertiesofnaturalgasbasedonthephysicalpropertiesandcompositionof theindividualcomponentsissometimescalled mixingrules.Thissectionprovidessome informationaboutthepropertiesofnaturalgas.
Thepropertiesofnaturalgasincludethespecificgravity,viscosity,density,compressibilityofthe Z-factor,pseudocriticalpressure,andtemperature;theymustbeknownin ordertodesignandanalyzenaturalgasproductionandprocessingsystems.Asexplained before,naturalgasisacombinationoflighthydrocarbonswithasmallnumberofinorganicelementsorcompounds,suchasnitrogen,carbondioxide,etc.Itisalwaysidealand importanttodeterminethechemicalcompositionofnaturalgasthroughmeasurement. Gascomposition,aswillbeshownindifferentexamplesinthischapter,istypically reportedasthemolefractionsofthedifferentcomponents.Ifthegascompositionis known,itisusuallypossibletocalculatethegaspropertiesthroughcertainrules,formulas, andcorrelations.Thenextsectionfocusesonthecalculationandestimationofthe differentnaturalgaspropertiesmentionedabove.
1.3.1Specificgravityofgas
Specificgravityofgas:Thespecificgravityofagas,parameterSG,isadimensionlessunit thatisdefinedastheratioofthemolecularweightofthenaturalgastothemolecular weightofair.Specificgravityisalsocalled relativedensity.Eq. (1.1) isusedtocalculate thespecificgravityofnaturalgasbasedontheabove-mentioneddefinition.
Equation1.1:Specificgravitycalculation
Where:
γ ¼ SGg ¼ Specificgravityofthegas(dimensionless).
Mg ¼ Molarmassofgas gr mol
Ma ¼ Molarmassofair,whichisequalto28.97 gr mol.
Themoleistheunitofmeasurementfortheamountofasubstanceintheinternational systemofunits.Amoleisusedasaunitinparticlecounting.Amolecontainsapproximately6 1023 particles,whichcanbeatoms,molecules,ions,orelectrons.Themolar massofasubstancereferstothemassorweightof1molofthatsubstance.Themolecular weightofairgiventhattheairisdryandcontainsapproximately79%nitrogenand21% oxygenisequalto28.97 gr mol (molarmass).Butthequestionishowisthemolarmassofair calculated?Oxygen’smolarmassisapproximately15.9994 gr mol,andnitrogenhasamolar massof14.0067 gr mol.Butitisimportanttoknowthatbothnitrogenandoxygenare diatomic,meaningtheycontaintwoatoms,likeO2 andN2.Therefore,themassmolar ofoxygengasinairisapproximately32 gr mol,andthemolarmassofnitrogengasinairis approximately28 gr mol.Themixtureoraverageofmolarmassisthesumofthemole fractionsofeachgasmultipliedbyitsfractionaccordingtoEq. (1.2).
Equation1.2:Averagemolarmasscalculationofgasmixturessuchasair
Where:
Mmg ¼ Molarmassofthemixtureofgassessuchasair gr mol;
Xi ¼ Molefractionorpercentageofeachgasinthemixtureorair(dimensionless);
Mi ¼ Themolarmassofeachgas gr mol;
UsingtheEq. (1.2),itispossibletocalculatethemolarmassoftheairasfollows:
Thespecificgravityofairisapproximatelyequaltoone.Ifthespecificgravityofagasis morethanthatofair,whichisapproximatelyone,thenthatgasisheavierthanair.Onthe
otherhand,ifthespecificgravityofagasislessthanone,thenthatgasislighterthanair. Naturalgasislighterthanair,anditsspecificgravityvalueisusuallyintherangeof0.55to 0.87.Anaturalgasincludingrichgasesorahigherwetgascontentandcondensatestypicallyhashigherspecificgravitycomparedtoleangaswithasmallernumberofcondensatesandhigherratesofmethane.Carbondioxide(CO2)whichcausessweetand uniformcorrosioninnon-corrosionresistantalloys(CRAs)suchascarbonsteel,hasa specificgravityof1.5189.Thismeansthatcarbondioxideisheavierthanairandthe presenceofcarbondioxidecanincreasethespecificgravityofnaturalgas.
Example1.1
Gascompositions,molarfractions,andmolarmassesareprovidedin Table1.2.Calculate therelativedensityorspecificgravityofeachgas.
Answer
Thefirststepistocalculatethemolarweightofthenaturalgas(Mg)usingthedataprovidedinthetableandusingEq. (1.2) asfollows:
Themolarweightoftheairisequalto28.97 gr mol ,soitisnowpossibletocalculatethe specificgravityusingEq. (1.1) asfollows:
Alightgascontainsmainlymethaneandsomeethane.Thespecificgravityofpuremethaneasthelightestgasis0.55.Arichorheavygashasaspecificgravityofapproximately 0.75andinsomecasesmorethan0.9.Basedonthegiveninformation,itcanbeconcluded thatthegivengasinthisexampleislighttomediumweight.
Table1.2 Gaschemicalcomposition.
Therearetwoimportantlawsthatshouldbediscussedhereregardingthepressure, volumeandmolefractionofidealgases:thefirstis Dalton’slaw ,andthesecondis Amagat’slaw .Dalton’slawstatesthatthepartialpressureofagasinamixtureof gasesisdefinedasthepressurethatthegaswouldexertifitalonewerepresentat thesametemperatureandvolumeasthemixture.Dalton’slawstatesthatthesum ofthepartialpressuresofthegasesinamixtureisequaltothetotalpressureof themixture.Thesecondlawisonlytrueforidealgases.Definitionsofidealandreal gasesareprovidedlaterinthischapter.Eq. (1.3) indicatestherelationshipbetween thepartialpressureofagasmixtureandthetotalpressureforidealgasesaccordingto Dalton’slaw.Eq. (1.4) providesacalculationofthepartialpressureofeachgasina mixture.
Equation1.3:Relationshipbetweenthepartialpressureofagasmixture andthetotalpressureforidealgasesaccordingtoDalton
Where:
PTotal:Totalpressureofthegasmixture
PGas1:PartialpressureofGas#1inthegasmixture
PGas2:PartialpressureofGas#2inthegasmixture
PGas3:PartialpressureofGas#3inthegasmixture
PGasn:PartialpressureofGas#ninthegasmixture
X1:molefractionofGas#1
X2:molefractionofGas#2
X3:molefractionofGas#3
Xn:molefractionofGas#n
Equation1.4:Partialpressureofgascalculation
Where:
PGas:Partialpressureofthegas
XGas:Molefractionofthegas
PTotal:Totalpressureofthegas
Example1.2
Aircontains20.95%oxygen,78.08%nitrogen,and0.97%argon.Thepressureofairis equalto14.7psi.Calculatethepartialpressureoftheothergasesinsidetheair.
Answer
Thepercentageofeachelementinairisequaltothemolefraction.Thus,themolefractionsofoxygen,nitrogen,andargonare20.95%,78.08%,and0.97%respectively.The partialpressureofeachgasintheair(amixtureofgases)isobtainedbymultiplyingthe totalpressure,whichisequalto14.7psi,bythemolefractionofeachgas.Thus,thepartial pressuresofeachofthesethreeelementsarecalculatedasfollows:
AccordingtoDalton’slaw,thesumofthepartialpressurevaluesforall3gasescalculated aboveisequaltothepressureofair,meaningthat:
Amagat’slawstatesthatthevolumeofagasinamixtureofgasesisdefinedasthevolume thatthegaswouldoccupyifitalonewerepresentatthesamepressureandtemperatureas themixtureofgases.Foridealgases,thesumofthepartialvolumeofthegasesthatmake upagasisequaltothetotalvolumeofthemaingas.Thisrulecanbestatedinanother way:underthesameconditionsoftemperatureandpressure,equalvolumesofidealgases havethesamenumberofmolecules.Infact,one-poundmoleofanidealgascontains 2.7333 1026 molecules,occupies378.6ft3 at60 °F,andhasapressureequalto14.73psi.
1.3.2Gasviscosity
Gasviscosity (parameter μ)isdefinedasameasurementofagas’sresistancetoflow.“Viscosity”isderivedfromtheLatinword“viscum”meaning“anythingsticky.”Afluidwith lowviscosityiscalled“thin,”whileafluidwithhighviscosityiscalled“thick.”Viscosity describestheinternalfrictionofmovingfluid,andafluidwithahigheramountofviscosityresistsmotionbecausethemoleculesofahighviscosityfluidcreatealotofinternal friction.Lowviscosityfluids,ontheotherhand,flowbetter. Fig.1.4 comparestheviscosityofwaterandhoneywithregardtotheirgravitationalflowrates.Thinkaboutfluid flow,specificallythelayersofmovingmolecules.Theselayersofmoleculesarerubbing againsteachother,andgreaterfrictionmeansslowermovementandhigherviscosity. Honeyismoreviscousthanwater,soitresistsmoreagainstthegravitationalforces andflowsharderandmoreslowlythanwater.Therearetwotypesofviscositiesexplained inthissection: dynamicviscosity and kineticviscosity.
ViscosityissometimesdefinedusingIsaacNewton’sequationforfluids,ormoreprecisely,thesecondlawofmotion.Newton’ssecondlawofmotionstatesthatwhenaforce actsonanobject,itwillcausetheobjecttoaccelerate.Thereisarelationshipbetweenthe forcerequiredforaccelerationandthemassoftheobject,meaningthatagreaterforceis
Viscositycomparisonbetweenwaterandhoney. (Courtesy:Shutterstock.)
requiredtomoveandaccelerateamoremassiveobject.Newton’ssecondlawisformulatedbyEq. (1.5).Thegreatertheforcerequiredtomovethefluid,thehigherthe viscosity.
Equation1.5:Secondlawofnewtonformulation(Relationshipbetween theforceandmass)
Where:
F:Force(Newtonor kg m s2 )
m:Mass(Kilogramorkg)
a:Acceleration m s2 )
Acceleration(parameter a)isdefinedastherateofvelocitychangewithtime.Speeding upincreasestheacceleration,andslowingdownreducestheacceleration.Accelerationis calculatedaccordingtoEq. (1.6) asfollows:
Equation1.6:Accelerationcalculation
Where:
a:Acceleration m s2 )
Fig.1.4
V:Finalvelocity(m s )
Vo:Initialvelocity(m s )
t:Durationortime(s)
Velocity(parameter V)isaquantitythatmeasuresdisplacementorchangeinposition overachangeintimeoroveraspecificperiodoftime.Thisdefinitionisoneofthefundamentalconceptsofmechanics.Eq. (1.7) isusedtocalculatevelocitybasedontwoother importantparameters:distanceandtime.
Equation1.7:Velocitycalculation
Where:
V:Velocity(m s )
d:Distance(m)
t:time(s)
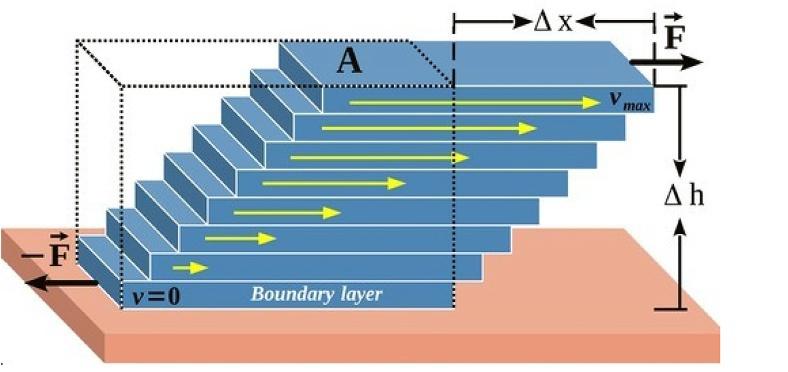
Thereisnocorrelationbetweenforceandviscositybasedontheequationsprovided above.Abetterapproachforthemathematicalformulationof dynamicviscosity isthe useofthetwoterms“ShearStress”and“Shearrate.”Dynamicviscosityisthetangentialforcerequiredtomoveonehorizontallayerorplaneofafluidrelativetoanother layer.Aswillbeexplainedlaterinthissection,dynamicviscosityiscalculatedasaratioof shearstresstoshearrate.Theothernamefordynamicviscosityis absoluteviscosity. Underlyingthetheoryoffluidmovementistheinternalfrictionbetweenmolecules. Shearstress isdefinedasaforce(parameter F)pushingonelayeroffluidflowacross anotherlayerwithinthecross-sectionareaofA.Shearstressisakindofforcethatcauses deformationofamaterialbyslippagealongtheplanesthatrunparalleltotheimposed stress(Fig.1.5).
Shearstressisshownwithparameter τ.ShearstressiscalculatedaccordingtoEq. (1.8), asfollows:
Equation1.8:Shearstresscalculation
Where:
τ:Shearstress( N m2 equaltopascal)or dyn cm2
F:Force(N)or(dyne)
A:Area(m2)or(cm2)
Fig.1.5 Viscosityofafluidwithdifferentlayersoffluidflow. (Courtesy:Shutterstock.)
Theshearratecanalsobedefinedastherateatwhichfluidlayersaremovingpasteach other.Theshearratedependsonbothgeometryandthespeedoftheflow.Theshearrate iscalculatedaccordingtoEq. (1.9),asfollows:
Equation1.9:Shearratecalculation
Where:
γ :Shearrate 1 s
Δ V:Differenceinvelocitybetweentwolayers m s or cm s
Δ h:Thedistancebetweentwofluidlayers(morcm)
Dynamicorabsoluteviscosityiscalculatedbydividingtheshearstressbytheshearrate, accordingtoEq. (1.10):
Equation1.10:Dynamicviscositycalculation
Where:
μ or ŋ:Dynamicviscosity( Ns m2 equaltoPascalsecond)or(dyns cm2 equaltopoise)
Thegivenunitsareinboththeinternationalsystem(SI)andcentimeter-gram-second system(CGS).CGSisavariantofthemetricsystemthatusescentimetersastheunit oflength,gramsastheunitofmass,andsecondsastheunitoftime.TheCGSsystem haslargelybeenreplacedbySI,whichisalsoknownasthemetricsystemorthe
MKSsystem.MKSisanabbreviationformeter,kilogram,second.Inmanyscientific fields,SIistheonlysystemused,buttherearestillsomefieldsinwhichtheCGSsystem isused.InordertoconvertCGSsystemunitstoMKS,theunitconversionfactorsare normallypowersof10,exceptfortheunitoftime,whichissecondsinbothsystems. Forexample,1mintheMKSsystemisequalto100cmintheCGSsystem.TheSIunit offorceisaNewton,whichisequivalentto kg m s2 .TheunitofforceintheCGSsystemisa dyne andisequivalentto g:cm s2 .ThemainquestionishowtoconvertNewtonstodynes.In fact,1Newtonisequalto105 dynes,whichiscalculatedasfollows:
Correspondingly,1dyneisequalto10 5 Newton.
Themostcommonunitofgasviscosityisa poise or centipoise,whichisnamedafter theFrenchphysician,JeanLouiseMariePoiseuille,wholivedfrom1799to1869.Apoise unitistypicallyexpressedusingtheCGSsystem.TheSIunitofviscosityisa Pascal second,abbreviatedas“Pa.s.”APascalisaunitusedtoquantifyinternalpressure,and 1Pascalisequalto(1newton m2 ).
1Pascal ¼ 1newton m2 (1Newtonisequalto kg m s2 ),so1Pascalisequalto kg m∗s2 .Sincethe viscosityunitisaPascalsecond,theSIunitofviscosityis kg m∗s .
Kineticviscosity (parameter Vg)iscalculatedaccordingtoEq. (1.11) bydividingthe dynamicviscositybythedensityofthegas.Kineticviscosityisnottypicallycalculatedfor naturalgasessoitwillnotbediscussedfurther.
Fluidsaredividedintotwocategorieswithregardstoviscosity: Newtonian fluids,in whichshearstressislinearlyconnectedtoshearratesothattheviscosityofafluidhas aconstantvalue,and non-Newtonianfluids,forwhichviscosityissubjecttochange andisadynamicfunctionofcertainvariablessuchastimeandshearrate.Whenshaking anon-Newtonianfluid,theviscositycoulddecreaseorincreaseduringtheshakingprocess.ItiseasiertoworkwithandmodelNewtonianfluidsastheirbehaviorswithregard toviscosityaremorepredictable.Itisworthnotingthatbothairandwaterareconsidered Newtonianfluids.Examplesofnon-Newtonianfluidsareblood,paints,andsome polymers.Inaddition,mostgasesareconsideredNewtonianfluids.
Viscosityingasescomesfromgasmoleculestransferringmomentumbetweeneach other.Theviscosityofnaturalgasismuchlowerthanthatofoilandwater.Thislower
Equation1.11:Kineticviscositycalculation
viscositymeansthatthegasismoremobileandmovesfasterthanoilandwater.Thisis especiallytrueinpetroleumproduction,wherethreephasesofoil,water,andgasare producedfromreservoirs.Animportantpointaboutgasviscosityisthatitismostlyindependentfrompressure.Temperature,however,isthemostinfluentialparameterongas viscosity. Sutherland’slaw or formula isanexpressionofhowagas’sviscosityisdependentontemperature.ThislawwasdiscoveredbyWilliamSutherland,anAustralian physicist,in1893.Asarule,increasingthetemperatureofagasresultsinfastermovement ofthemoleculesandanincreaseintheviscosityofthegas.However,theeffectoftemperatureonaliquidistheopposite:theviscosityofaliquidisdecreasedbyincreasingthe temperature.Eq. (1.12),knownasSutherland’sformula,showshowviscositycanbe changedbymodifyingthetemperatureofagas:
Equation1.12:Effectofgastemperatureongasviscosity(Sutherland’s formula)
Where:
μ:Gasviscosityattemperature T usingtheKelvinscale
μ0:Gasviscosityincentipoiseatareferencetemperatureof T0 inKelvin(K)
T:TemperatureinKelvin(K)
T0:ReferencetemperatureinKelvin(K)
S:Sutherland’sconstanttemperature(equalto110.4K)
FortheconversionoftemperaturesinCelsius(°C)toKelvin(K),Eq. (1.13) shouldbe used:
Equation1.13:ConversionoftemperaturesfromCelsiustoKelvin
:15 (1.13)
Example1.3
Theviscosityofairatareferencetemperatureof0 ºCis1.716 10 5 kg m∗s .Giventhat Sutherland’sconstanttemperatureis110.4K,bywhatpercentagedoestheviscosityof airincreasewhenthetemperatureisincreasedto100 ºC.
Answer
Thereferencetemperatureis0 °C,whichisequalto273.15K.Theviscosityatatemperatureof100 °C,whichisequalto373.15K,canbecalculatedbyusingEq. (1.12) (Sutherland’sformula).
Thiscalculationshowsthattheviscosityofthegasisincreasedby0.454 * 10 5.Thus,the percentageincreaseintheviscosityofthegasiscalculatedasfollows: Gasviscosityincreasesbyincreasingthetemperatureto100
Naturalgasisamixtureofdifferentgaseswithvariousviscosities,molecularweights,and molefractions.Insomecases,naturalgasviscositycanbecalculatedusingtheviscosities, molefractions,andmolecularweightsofthegasesthatcomposeit,asinEq. (1.14):
Equation1.14:Gasviscositycalculationusingviscosities,molecular weights,andmolefractionsoftheconstituentgases
Where:
μg:Viscosityofthegasmixtureatthedesiredtemperatureandatmosphericpressure
yi:Molefractionofthe/thcomposition
μi:Viscosityofthe/thcomponentofthegasmixtureatthedesiredtemperatureandatmosphericpressure
Mgi:Molecularweightofthe/thcomponentofthegasmixture
N:Totalnumberofcomponentsofthegasmixture
ForEq. (1.14),itisimportanttoknowtheviscosityofeachgasinordertocalculatethe viscosityofthegasmixture.Butinsomecases,noinformationisavailableabouttheviscosityofthedifferentgasesinnaturalgas.Insuchcases,followingstepsshouldbe followedtocalculatetheviscosity.Thefirststepistocalculatetheviscosityofthegas atoneatmosphericpressure,representedby μga in Fig.1.6,usingthetemperatureof thegasaswellasthemolecularweightorgravityofthegas.Itisessentialthattheobtained viscosityofthenaturalgasatoneatmosphericpressurefromthechartbecorrectedfor certainnon-hydrocarbonelementsorcompoundsinthegas,suchasnitrogen(N2),carbondioxide(Co2),andhydrogensulfide(H2S).Itispossibletoobtaintheviscosityof nitrogen,carbondioxide,andhydrogensulfidefromthesmallchartsprovidedinthecornersof Fig.1.6.Thecorrectedviscositiesforeachofthesenon-hydrocarbonelementsor compoundscanbeestimatedusingthemolepercentageofnon-hydrocarbonelements andthespecificgravityofthenaturalgas.Themolepercentageiscalculatedbymultiplyingthemolefractionby100.Thevaluesoftheviscositiesofnitrogen,carbondioxide,
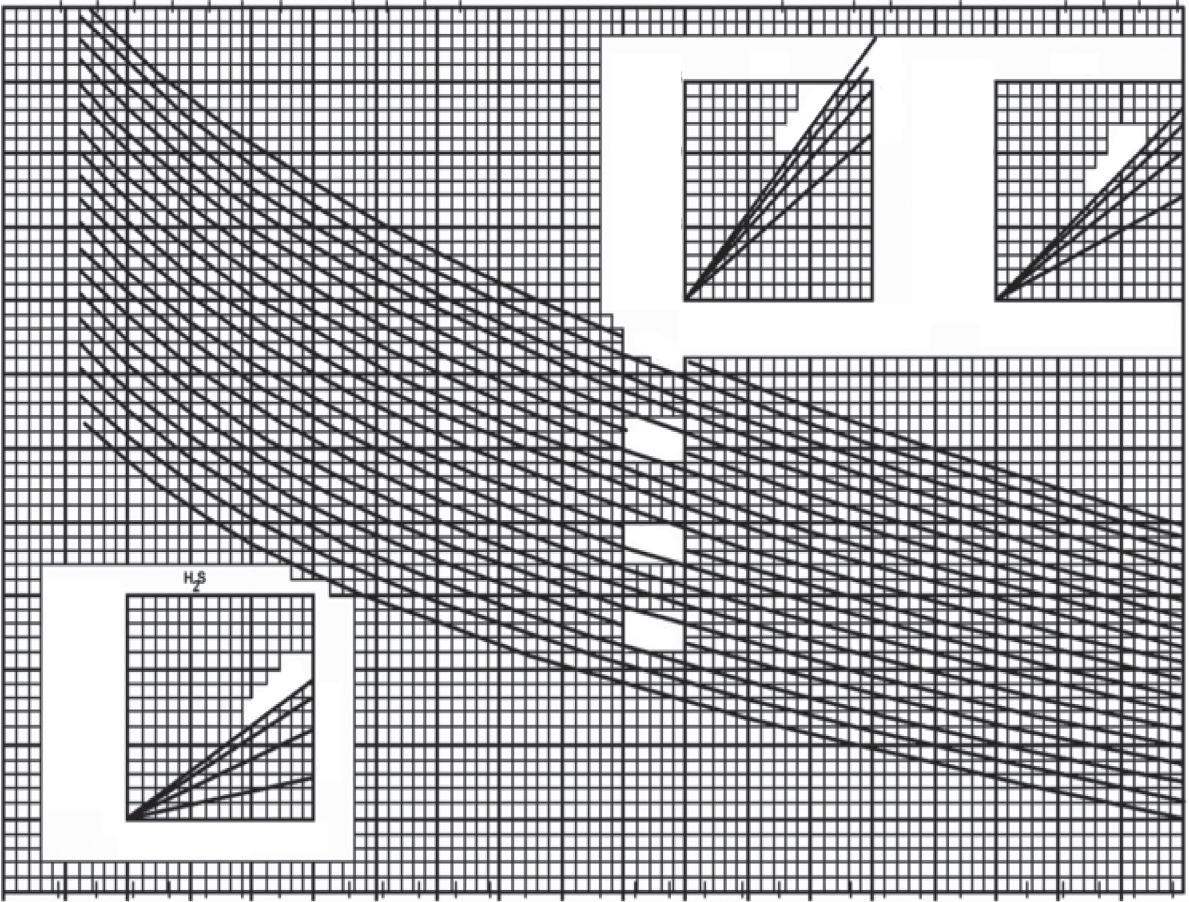
Fig.1.6 Estimatedviscosityofnaturalgasat1atmosphericpressure,parameter μga. (Courtesy:Carr,N.L.,Kobayashi,R.,&Burrows,D.B.(1954). Viscosityofhydrocarbongasesunderpressure.JournalofPetroleumTechnology,6(10),47–55. https://doi.org/10.2118/297-G .)
andhydrogensulfideshouldbeaddedtotheestimatedviscosityofthenaturalgas.The presenceofeachofthenon-hydrocarbonsincreasestheviscosityofthehydrocarbon mixtureornaturalgas.
Example1.4
Table1.3 displaysthechemicalcompositionofnaturalgas,includingthemolarweight andmolefractionofeachcompoundorelement.Assumingthetemperatureofthegas tobe200 °F,whatwouldbetheviscosityofnaturalgasat1atmosphericpressure?
Answer
Thefirststepistocalculatethemolarweightofthegasbyusingthemolefractionsand molarweightofeachcomponentasfollows:
Itisnowpossibletoobtaintheviscosityofthenaturalgas,parameter μga,at1atmospheric pressurefrom Fig.1.6 byusingthemolecularweightofthegas,whichisequalto20.29, andthetemperature,whichisequalto200 °F.Theobtainedviscosity,parameter μga,is approximately0.012CP.Butacorrectionisneededbecausethenitrogencontentisequal toa15%molefraction.Inordertofindtheviscosityofnitrogenasperthesmallcharts providedin Fig.1.6,itisessentialtoknowthespecificgravityofthemaingas,whichis equalto0.7accordingtothefollowingcalculations:
Theestimatedviscosityofthenitrogenisapproximatelyequalto0.0012CP,givena15% molefractionandaspecificgravityofthemaingasof0.7.Theviscosityofthenitrogen shouldbeaddedtotheviscosityofthenaturalgas,whichis0.012CP.Thus,theviscosity ofthenaturalgas,parameter μga,afteraddingthenitrogencorrectionfactoris0.0132CP.
Table1.3 Chemicalcompositionofgas.
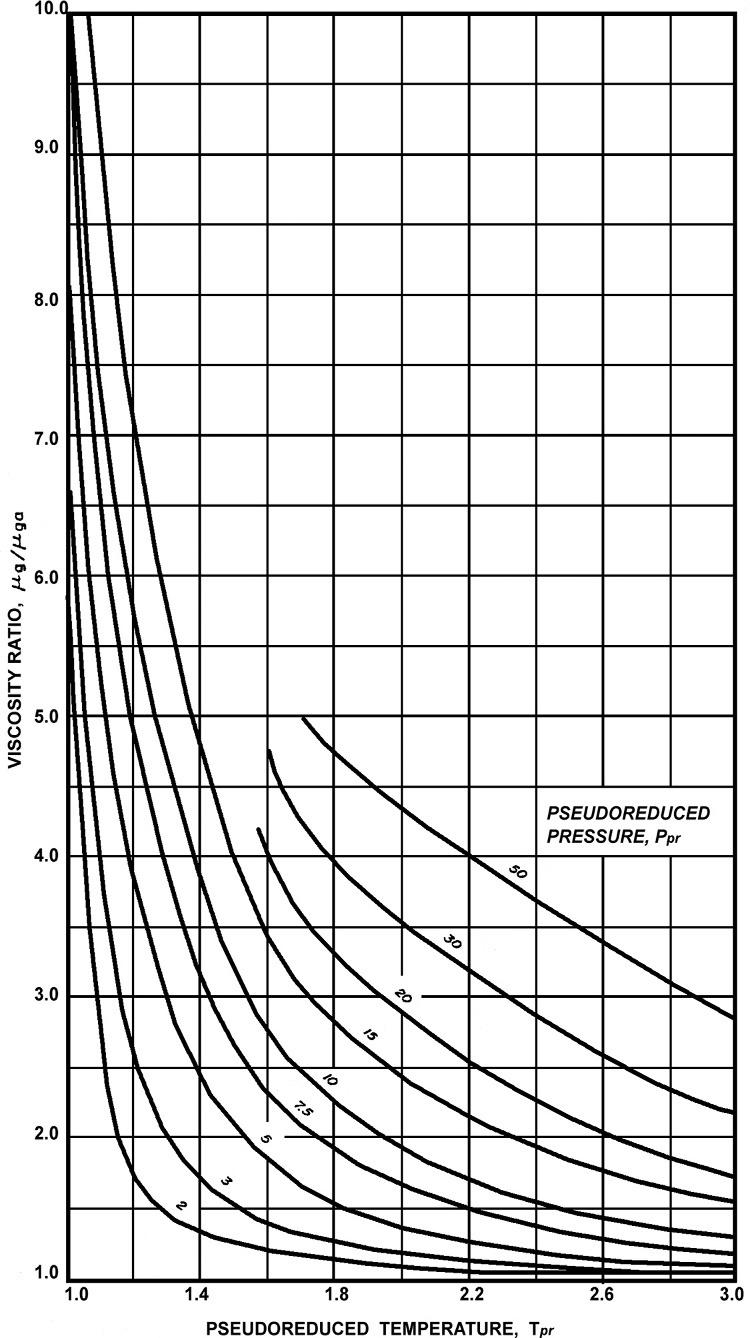
Themainquestionishowtoconverttheviscosityofthenaturalgasatthegiventemperatureandoneatmosphereofpressuretotheviscosityofthegasatotherpressure values. Fig.1.7 isusedtofindthevalueof μg μga fromthevaluesof pseudocriticalreduced
Fig.1.7 Viscosityratioestimationfrompseudocriticalreducedpressureandtemperature(Option1).
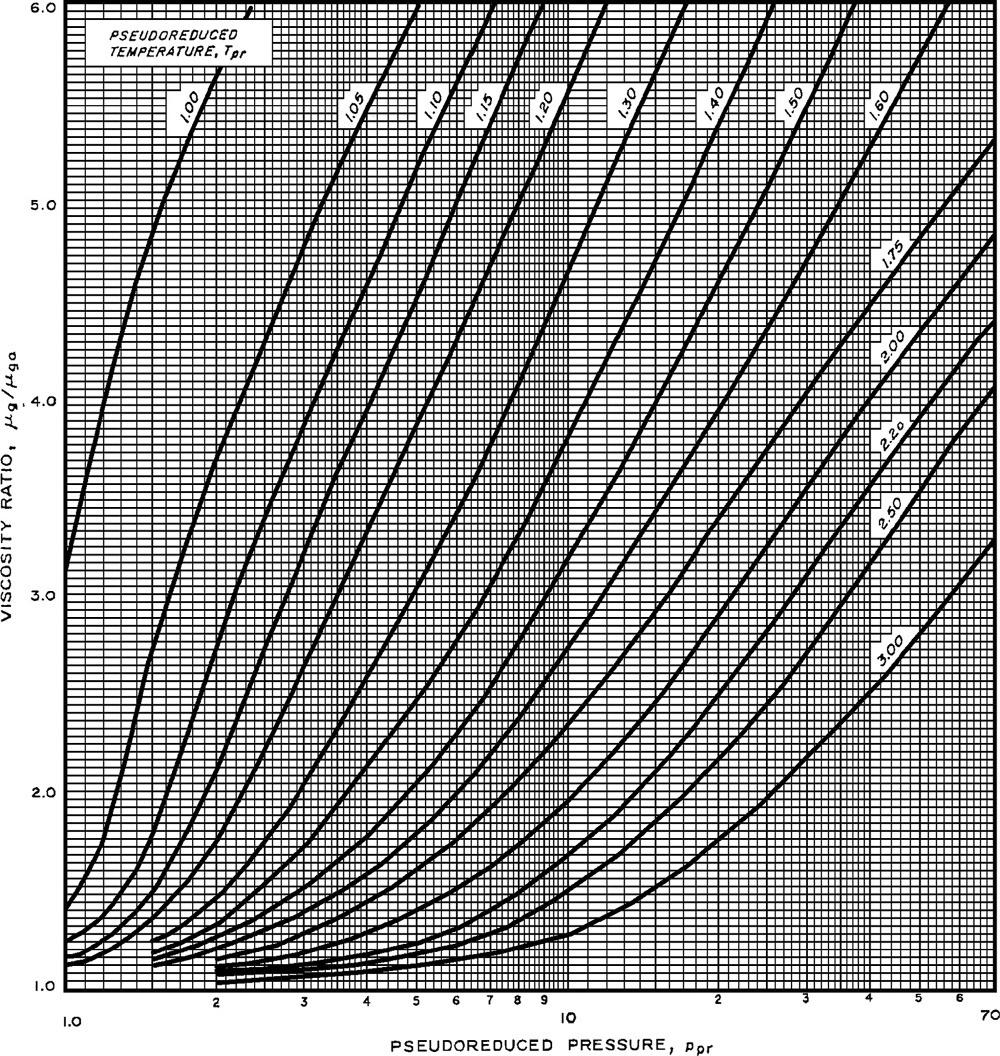
Viscosityratioestimationfrompseudocriticalreducedpressureandtemperature(Option2).
pressureandtemperature. Thereisanalternativechart, Fig.1.8,thatcanalsobeusedto obtainthevalueof μg μga fromthepseudocriticalreducedpressureandtemperature.
Pseudocriticalreducedpressureandtemperatureandhowtocalculatethemarefurtherexplainedinthischapter.Pseudocriticalreducedpressureiscalculatedbydividing thepressureofagasbythepseudocriticalpressure,asinEq. (1.35).Thepseudocritical pressureisequaltothesumofthepseudocriticalpressureofeachgascompound. Thepseudocriticalpressureofeachgascompoundiscalculatedbymultiplyingthe
Fig.1.8
criticalpressure ofeachgascompoundbyitsmolefractionasperEq. (1.31).The pseudocriticalreducedtemperatureiscalculatedbydividingthetemperatureofthe gasbythepseudocriticaltemperature,asinEq. (1.36).Thepseudocriticaltemperature isequaltothesumofthepseudocriticaltemperatureofeachgascompound.The pseudocriticaltemperatureofeachgascompoundiscalculatedbymultiplyingthe critical temperature ofeachgascompoundbyitsmolefractionasperEq. (1.33).Therearealternativewaystocalculatepseudocriticalpressureandtemperaturedirectlyfromthespecific gravity,asdemonstratedbyEqs. (1.32)and(1.34).
Example1.5
Consideringthenaturalgascompositiongiveninthepreviousexample,whatwouldbe theviscosityofthegasat200 °Fand2000psi?
Answer
Theviscosityofthegasatthatatmosphericpressure,parameter μga,wascalculatedtobe 0.0133CP.Thereisnoinformationavailableaboutthecriticalpressureandtemperature ofthegascompounds.Thus,itisnotpossibletocalculatethepseudocriticalreducedpressureandtemperaturefromthecriticalpressureandtemperatureofeachgascompound. Thegasmolecularweight,however,isequalto20.29 gr mol,andthespecificgravityofthe gascanbecalculatedasfollows:
Itisnowpossibletocalculatethepseudocriticalpressureandtemperaturefromgasspecific gravitybyapplyingEqs. (1.32)and(1.34) asfollows:
Usingthevaluespseudocriticalreducedpressureandtemperaturecalculatedaboveand Fig.1.7 providesaviscosityratioapproximatelyequalto1.4.Thus,theviscosityofthe gasatthegivenpressureandtemperaturearegivenasfollows:
1.3.3Gasdensity
Thedensityofagasisdefinedasthemassofthegasdividedbyitsvolume,asper Eq. (1.15).
Equation1.15:Basicgasdensitycalculation
Where:
ρg ¼ Densityofgas kg m3
mg ¼ Massofthegas(kg)
Vg ¼ Volumeofthegas(m3)
A1-poundmolegashasaweightof mg,whichisequaltothemolecularweightofthegas, Mg.Fora2-poundmolegas,thegasweight, mg,wouldbedoublethemolecularweight, Mg,ofthegas.Asageneralrule,thegasweightisequaltothenumberofmolesmultiplied bythemolecularweightofthegas,asperEq. (1.18).Thenextstepistoconvertthe volumeofthegastootherpropertieslikepressureandtemperatureaccordingto Eq. (1.25).Thus,itisnowpossibletoobtainanewcalculationforthegasdensityusing Eq. (1.16).
Equation1.16:Gasdensityalternativecalculation
Where:
R: Gasuniversalconstant,whichisequalto8.31
psift3
Rankine:mol:pound ; P:Gaspressure(Bar,Mpa,psi);
SGg:Gasspecificgravity(Dimensionless);
T:Gastemperature(°C, °F,K,Rankine).
Example1.6
Calculatethedensityofanaturalgaswithapressureof1525psiand75 °F.Themolecular weightofthegasis20.424 gram mole,andthegasisassumedtobeintheidealstate.Assumethat thegasisideal,andtheZfactorisequalto1.
1.4Naturalgaslawsandcalculations
1.4.1Idealgaslaws
Therearecertainimportantlawsthatapplyto idealgases.Thequestioniswhatisan idealgas?Toanswerthisquestion,itshouldbenotedthatgassesinvolvecomplicated compoundsandstructures.Theyaretypicallymadeofbillionsofenergeticgasmoleculesthatareininteractionwitheachother.Therefore,itisverycomplexanddifficulttomodelarealgas.Thus,theconceptofanidealgaswascreatedinorderto simplifythebehaviorofgases.Thetheoryofidealgaseshelpsscientistsandengineers tomodelandpredictthebehaviorofgases.However,thebehaviorofrealgasses matchesthatofidealgasesonlyinsomecases,suchaswhenthepressureisatmosphericandthetemperatureisintherangeofroomtemperature. Roomtemperature isatemperatureatwhichmostpeoplewou ldfeelcomfortableinanindoorsetting. Typically,roomtemperatureisintherangeof20 – 22 °C.Atlowerandhighertemperatures,thecharacteristicsofrealgasesdeviatesignificantlyfromidealgases.There aretwomainrulesassociatedwithidealgases:Thefirstruleisthatthemoleculesof idealgasesdonotattractorrepeleachother,buttheyareconstantlymoving.Infact, intermolecularforcesarenegligibleinidealgases.Theonlytypeofinteraction betweenthemoleculesinanidealgasmodelis elasticcollision ,whichreferstowhen moleculesstrikeagainsteachotherandki neticenergyisexchangedbetweenthem. However,thetotalmolecularkineticener gyinsidethegasisconstant,andthereis nochangeinkineticenergybeforeandafteracollision.Thesecondimportantruleis thatthemoleculesoccupynegligiblevolume.Heliumisknownasatypeofgasthat behavesinaverysimilarwaytoidealgases.
The idealgaslaw demonstratestherelationshipbetweenthepressure(P ),volume (V)andtemperature( T)ofanidealgas.Eq. (1.17) isanexpressionoftheideal gaslaw:
Equation1.17:Idealgaslaw
Where:
P:Pressureofthegas(poundpersquareinch(psi),atmosphere,Pascal)
V:Volumeofthegas(ft3,m3,liter)
n:Moles,orthenumberofmolecules
R: Gasuniversalconstant,whichisequalto8.31
psift3
Rankine mol pound
T:TemperatureofthegasinRankine(R)orKelvin(K)
Thepressure,temperature,andvolumeofgascanbeconvertedasfollows:
Eq. (1.18) isusedtocalculatethenumberofpound-molesinagas.Infact,thenumber ofpound-molesinagasisequaltothemassofthegasdividedbythemolecularweightof thegas.
Equation1.18:Calculationofnumberofmolesinagas
Where:
n:Numberofpound-moles
m:Massofthegas(poundsorgrams)
M:Molecularweightofthegas(poundmoleorgrammole)
Example1.7
Calculatethepressureof1moleofnaturalgasinidealconditionsat0 °Cassumingthatthe volumeofthegasis22.4L.
Answer
TheidealgaslawandEq. (1.17) canbeusedasfollows: