Cowboy Wolf Outlaw Kait Ballenger
https://ebookmass.com/product/cowboy-wolf-outlaw-kait-ballenger-5/ ebookmass.com
COMPUTATIONALGEOELECTROMAGNETICS Methods,Models,and Forecasts
VIACHESLAVV.SPICHAK
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom
50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright 2020ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical, includingphotocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwriting fromthePublisher.Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissions policiesandourarrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyright LicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions .
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthan asmaybenotedherein).
Notices
Knowledgeandbestpracticeinthis fieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusingany information,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodsthey shouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessional responsibility.
Tothefullestextentofthelaw,neitherthePublisher,northeauthors,contributors,oreditors,assumeanyliability foranyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,or fromanyuseoroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-819631-1
ISSN:2468-547X
ForinformationonallElsevierpublicationsvisitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher:CandiceJanco
AcquisitionsEditor:AmyShapiro
EditorialProjectManager:AndreaDulberger
ProductionProjectManager:OmerMukthar
CoverDesigner:ChristianJ.Bilbow
TypesetbyTNQTechnologies
Preface
Themainstreamapproachinthepresent-dayinterpretation ofelectromagnetic(EM)dataistosolvetheoreticallynonunique inverseproblemusingsomeregularizationtechnique.Many examplescouldbefoundinthemonographspublishedinthe past20years(e.g., Zhdanov,2002,2009;SimpsonandBahr,2005; BerdichevskyandDmitriev,2009;ChaveandJones,2012;Spichak,2015).Thesituationisespeciallycomplicatedinthe3-D and4-Dcases,whenthenumberoftheunknownsincreases dramatically(e.g., Spichak,1999;SpiesandOristaglio,1999; ZhdanovandWannamaker,2002; Spichak,2019).Thehugevolumeandhighcomplexityofthedatatobeprocessednecessitatesthedevelopmentandapplicationofefficientquantitative methodsandcomputationaltools,inparticular,parallelization ofappropriatecodes,exploitinghighperformancecomputer resources(whicharenotalwaysathand).
Meanwhile,ourknowledgeoftheEarth’sinterioraswellas theefficiencyofsolutionsofnumerousrelatedproblemsstrongly dependsonaccuracyofEMdatainterpretation.Theapproaches usedtothisendshouldtakeintoaccountthepurposeofthe study,volume,andqualityoftheavailabledata,priorgeological andgeophysicalinformation,scaling,signaltonoiseratio,etc.If onedoesnothavearegulararrayofhighqualityandevenly distributedEMsoundingdata,reliableanduserfriendlysoftware fortheir3-Dinversionandmulti-processorworkstationfor parallelcalculations,readingthisvolumemayhelptoextract maximuminformationfromtheavailabledata.
Incontrarytopreviouslypublishedmonographsongeoelectromagnetics,thisvolumeoffersthetechniquesandappropriatealgorithmsforbuildinggeoelectricalmodelsunderthe conditionsofsparseorirregularlydistributedEMdata,andlack ofpriorgeologicalorgeophysicalinformation.Secondly,itprovidesmethodologicalguidelinesforinterpretationofelectromagneticsoundingdatadependingongoalsofthestudy.Finally, onemayfindcomputationalalgorithmsforusingelectrical resistivityasaproxyparameterforforecastingpetrophysical propertiesofrocksbeyondboreholes.
Accordingly,thebookhasthreeparts.InPartI(Methodology ofEMdatainterpretation)twoalternativeapproachestoEMdata inversionareconsidered:theBayesianstatisticalinversionand neuralnetwork basedalgorithms.Theformeroneprovides flexibletoolsfortakingintoaccountpriorinformationandexpert
estimatesduringEMdatainversionandquantifyingitsresultsin termsofposteriorparameters’uncertainties.Thelatteroneis especiallyusefulinthecaseofconstructing3-Dmodels(in particular,intermsofmacroparameters)fromsparse,irregularly distributedorasingle-profileelectromagneticdata.Finally,a reviewofthemethodsusedforjointanalysisandinversionofEM andothergeophysicaldataispresented.
InPartII(Modelsofgeologicalmedium)theapproaches consideredinthePartIareappliedtostudymethodologicalissues ofEMmodelingvolcanoes(byexamplesofVesuvio,Kilauea, Elbrus,Komagatake,Hengill),geothermalandhydrocarbonreservoirs.ConceptualmodelsoftheIcelandictypecrust,alensin theuppercrustandcopper-porphyryoreformationaresuggested basedonjointanalysisofEMandothergeophysicaldata.
InPartIII(Forecastingpetrophysicalpropertiesofrocks)the techniquesforestimatingtemperature,seismicvelocities,and porosityfromtheelectricalresistivityasproxyparameterare considered.ThispartissupplementedbyAppendix,which includesusefulempiricalrelationsbetweenelectricalresistivity, seismicvelocitiesandporosity.
Thestudiesaddressedinthisvolumeweresupportedby grantsfromRussianFoundationforBasicResearch,Russian AcademyofSciences,OYOCorporation(Japan),BRGM(France), EinsteinConsortium(Italy),INTASandVIFrameworkProgram ofEuropeanCommunity.Iamverythankfulforthefunding supportprovidedbytheseorganizations.Iamdeeplygratefulto Prof.M.Zhdanov(UtahUniversity)whoinitiatedmyinterestin geo-electromagneticsin1979andwasmyPhDthesismentor,I amindeptedtoProf.T.Mogi(SapporoUniversity)forproviding friendlysupportofmystudiesincomputationalgeo-electromagneticsduringalmost30years.,Itismygreatpleasureto acknowledgeDr.H.Shima(OYOCorporation,Tokyo),Dr.M. Mareschale(l’E ´ colePolytechniquedeMontre ´ al),Dr.R.Lewis (HobartUniversity),Prof.D.Patella(UniversityFedericoIIdi Napoli),Prof.A.Siniscalchi(BariUniversity),Prof.M.Menvielle (UniversityParisSud),Prof.T.Harinarayana(InstituteofScience andTechnology,Hyderabad),Dr.A.Manzella(InstituteofGeoscienceandEarthResources,Pisa),Dr.H.Eysteinsson(ISOR, Reykjavik),Dr.G.Gugunava(M.NodiainstituteofGeophysics, Tbilisi)Dr.P.Calcagno(BRGM,Orleans),Dr.A.Genter(ESGeothermie,Electricite ´ deStrasbourg)forfruitfulscientificcollaborationintheframeworkofjointprojects.Whiledeveloping computercodesforEMdataanalysisandinterpretationI
receivedmuchassistancefromformeremployeesofmyLaboratoryDrsE.FomenkoandI.Popova.
IacknowledgeMarinaNazarenkoforpartialEnglishtranslationofthisvolumeandAlexandraGoidinaforassistancewith computergraphics.
ViacheslavV.Spichak Moscow,July,2019
References
Berdichevsky,M.N.,Dmitriev,V.I.,2008.ModelsandMethodsof Magnetotellurics.Springer-Verlag,Berlin.
Chave,A.,Jones,A.(Eds.),2012.Themagnetotelluricmethod:theoryand practice.CambridgeUniversityPress,NewYork.
Simpson,F.,Bahr,K.,2005.Practicalmagnetotellurics.CambridgeUniversity Press,NewYork.
Spichak,V.V.,1999.Magnetotelluricfieldsinthree-dimensionalgeoelectrical models.ScientificWorld,Moscow.
Spichak,V.V.(Ed.),2015.ElectromagneticSoundingoftheEarth’sInterior: Theory,Modeling,Practice.ElsevierB.V.,Amsterdam.
Spichak,V.V.,2019.ElectromagnetictomographyoftheEarth’sinterior.Scientific World,Moscow.
Spies,B.,Oristaglio,M.(Eds.),3DElectromagnetics.SEGPubl.,GD7,Tulsa,USA.
Zhdanov,M.S.,2002.Geophysicalinversetheoryandregularizationproblems. Elsevier,Amsterdam.
Zhdanov,M.S.,2009.Geophysicalelectromagnetictheoryandmethods.Elsevier, Amsterdam.
Zhdanov,M.S.,Wannamaker,P.(Eds.),2002.Three-Dimensional Electromagnetics.Elsevier,Amsterdam.
3-DEMforwardmodeling techniques
1.1Introduction
Tosolvetheforward3-Delectromagnetic(EM)problem(inafrequencydomain)impliestodeterminetheelectromagnetic field(E; H)satisfyingtheMaxwellequations
atagivenfrequency u,fromthedistributionofgeneralized complexelectricalconductivity e sðr; uÞ¼ s i uε (m isamagnetic permeability, ε isapermittivity, jext ðr; uÞ istheexternalcurrent density)specifiedinacertainspatialregionthatincludesan inhomogeneity.Inthischapterweassumeforsimplicitythat j ext ¼ 0; m ¼ m0 ¼ 4p,10 7 H/m,where m0 isthefree-spacemagnetic permeability,andneglectthedisplacementcurrents,i.e., e sh s.In otherwords,wewillconsidermodelingoftheelectromagnetic fieldsinducedin3-Dearthbynaturalsource planewave(socalled “magnetotelluric” (MT) fields)thoughtheissuesdiscussed belowinmostcasesreferequallytocontrolledsourceexcitation.
Variousapproachestothesolutionofthisproblemexist,allof themfallingintotwolargegroupscomprisingintegralequations anddifferentialequationstechniques.Currently,numerical computer-aidedmodelingofelectromagnetic fieldsbecomesa powerfulandrelativelyeasy-of-accesstoolforanalyzing complicatedsituations.Whereasformerlythescopeofgeophysicalconsiderationwascon finedtosimplifiedmodelmedia(1-D 2-D),theadventindesigningpowerfulcomputerfacilities madeitpossibletoposetheproblemofnumericalmodelingof electromagnetic fieldsexcitedby3-Dsourcesinatwo-or three-dimensionalmediumorby2-Dsourcesinathreedimensionalmedium(seereviewpapersby Avdeev(2005, 2015) ; Boerner(2010); Newman(2014) andreferencestherein).
Inthischapter,wewillconsiderbrieflythenumerical(Sections 1.2 1.4)andanalog(Section 1.5)approachestotheforward problemsolution.Numericalmethods,inturn,aresubdivided
intotwolargegroups:integralequationmethods(Section 1.2)and differentialequationmethods(Section 1.3).Acomparativeanalysisofthesetwogroupsofmethodsandhybridapproaches(Section 1.4)basedontheircombinationispresent.
Section 1.6 describesmaincharacteristicfeaturesofabalance techniqueforEM field’scalculationinmediawitharbitrary3-D distributionoftheelectricalconductivity.Atthesametime,ifthe electricalconductivitymodelshowsacertainsymmetrytype,the above-mentionedpurposecanbeachievedusingsmallercomputerresources.Inparticular,for3-Dmodelswithaverticalaxial symmetry,thevectorproblemreducestoascalarone.Section 1.7 addressesanalgorithmfornumericalcalculationofquasistationaryelectromagnetic fieldsin3-Daxiallysymmetricmedia basedona finiteelementmodificationofthebalancemethod.
1.2Methodsofintegralequations
Theintegralequationmethodforthenumericalcomputationof electromagnetic fieldswaspioneeredby Dmitriev(1969).The basicideasofthisapproachweredevelopedby Raiche(1974), Hohmann(1975), Tabarovsky(1975) ,and Weidelt(1975).Subsequently,theintegralequationmethodwassuccessfullyelaborated by DmitrievandFarzan(1980), TingandHohmann(1981), Hohmann(1983) , Wannamakeretal.(1984a,b), Hvozdara(1985), Hvozdaraetal.(1987), Wannamaker(1991), Xiong(1992) , Pankratovetal.(1995), Singer(1995), SingerandFainberg(1995, 1997), XiongandTripp(1995) , Avdeevetal.(1997) , Farquharsonand Oldenburg(1999) , Leeetal.(1999), Portniaguineetal.(1999), Xiongetal.(1999a ,b), HursanandZhdanov(2002), Zhdanov etal.(2000, 2006), Singer(2008), Endoetal.(2009), Avdeev (2015), Kruglyakovetal.(2016).
Paralleltothemethodofvolumeintegralequations(VIE)that involvesintegrationovertheentirevolumeoftheanomalous domain,amethodofsurfaceintegralequations(SIE)implying integrationonlyovertheboundaryofthedomainhasbeendeveloped(OshiroandMitzner,1967; DmitriedandZakharov,1970; Tabarovsky,1971; Smagin,1980; LiuandLamontagne,1999).
Letusconsiderthesetwoapproaches.
1.2.1Themethodofvolumeintegralequations
Volumeintegralequation(VIE)techniqueisbasedonthenumericalsolutionofthesecond-typeFredholmequation,whichcanbe derivedfromMaxwellequationsusingGreenfunctions:
where Eb isabackground fieldcalculatedwiththeassumption that s ¼ sb (backgroundelectricalconductivity), c G e ðr =r0 Þ isthe electrical-typeGreentensor, r and r0 arecoordinatesoftheobservationandsourcepoint,respectively,and V istheregioninquestion.(Hereinafter,forthesakeofde finitenessonlytheequation fortheelectrical field E willbeconsidered.Oncethenumerical solutiontothisequationisobtained,themagnetic field H can bereadilycalculatedfrom,e.g.,thesecondMaxwellequation (seeinthisconnectionSection 1.6.4)).
Thepivotalideaofthisapproachisasfollows.Theanomalous regionisdividedbyaspatialgridintocells.Withineachcell,the fieldisassumedtobeconstant.Therefore,inthesecondtermof (1.2) ,itcanbetakenoutsidetheintegralsign.Toobtainasystem oflinearalgebraicequationsforthe field,onehastoonlycalculate therespectivetensorcoef ficientswithineachunitcell.
Letusdiscussthemainadvantagesanddrawbacksofthis method.Theadvantagescompriseitsgreaterphysicaltransparencycompared,e.g.,tothemethodsofdifferentialequations. Inaddition,asisapparentfrom (1.2),thesecondtermonthe right-handsideisnonzeroonlyif sssb ;i.e.,integrationmustbe carriedoutonlyovertheanomalousregionalone.Finally,thenumericalapproximationof (1.2) doesnotinvolvetheunstableprocedureofnumericaldifferentiation,whichistypicalofmostthe differentialequationmethods.
Ontheotherhand,signi ficantdifficultiesariseinthenumericalapproximationofthesecondtermintheright-handsideof Eq. (1.2).Inparticular,determinationoftheGreentensor G e ^ ðr =r0 Þ componentsisanontrivialcomputationalproblem, solutionofwhichinvolvestheHankeltransforms(Hohmann, 1975; Weidelt,1975; FarquharsonandOldenburg,1999;etc.)or thelinear filtrationtechnique(DasandVerma,1981; Vermaand Das,1982).Computationofthetensorcoefficientscanbeas timeconsumingasitselfsolvingthesystemoflinearalgebraic equations.Therefore,itisa “bottleneck” ofthetechnique,and thesuccessofthewholeapproachthusdependsonhoweffectivelythisproblemissolved.
Anotherdifficultyariseswhilesolvingthesystemoflinear algebraicequations.Densematrixofthesystemmakeslimited computerresourcesacriticalfactor.Inturn,thelimitationon thedimensionalityofalgebraicsystemultimatelyentailslimitationstothemathematicalmodel:wecanonlycomputethe fields
forbodiesthatarenottoolarge. Xiong(1992) overcamethisdrawbackbypartitioningthescatteringmatrixintomanyblocksubmatricesandsolvingthewholesystembyablockiterative method.Thisreducesthecomputermemoryrequirementsand timeofcomputation.(Itisworthmentioninginthisconnection thatmuchmoredrasticreductionofthecomputerresources couldbeachievedbyusingtheso-called “sparsematrixtechnique” (PoggioandMiller,1973)thatimpliesignoringtheinteractionamongsufficientlyremoteareasofthemodelingdomain;the lattercorrespondstozeroingthoseelementsofthematrixthatare smallcomparedtothediagonalones.)Anothersimplification (whichalsoreducestheclassofobjectsbeingmodeled)istosolve theproblemwithinthelong-waveapproximation.Thisenables one, firstly,tosimplifycomputationoftheGreentensor(Hvozdara,1981)and,secondly,touseinthenumericalsolutionof (1.2) theBornapproximation(Torres-Verdin,1985; Torres-Verdin andBostick,1992),localizednonlinearapproximations(Habashy etal.,1993; Torres-VerdinandHabashy,1994),quasilinear approximationandseries(ZhdanovandFang,1996, 1997)and quasianalyticalseries(Zhdanovetal.,2000). Portniaguineetal. (1999) suggestedawayofreducingthetimeofcomputationsby theuseof “compressionmatrix” thatconvertstheoriginaldense matrixintothesparseonebyconstructinganinterpolationpyramidinmultipledimensions.Finally, Endoetal.(2009) suggesteda multidomainapproach,while Zhdanovetal.(2006) proposedan algorithmbasedonusinginhomogeneousbackgroundconductivity,whichincreasecompetitivenessofthisapproachincomparisonwithdifferentialequationtechniques(Zhdanovetal., 2013).
InevaluatingtheadvantagesanddrawbacksoftheVIE methodonawhole,itshouldbenotedthatthismethodseems givingthemostaccurateresults inacomparativelyshorttime foranomaliesthataresmallcomparedtothewavelengthwithin theanomalousregionandhaveasimpleshape.
1.2.2Themethodofsurfaceintegralequations
Surfaceintegralequation(SIE)techniquemakesuseofelectromagnetic fieldrepresentationasanintegraloverthesurfaceof adomainbymeansofStratton Chuformulas(Dmitrievand Zakharov,1970),methodofauxiliary(fictitious)sources(Tabarovsky,1971),methodofpotentials(Smagin,1980),orthemethod employingtheHelmholtzscalarequations(LiuandLamontagne, 1999).Afterpassingtothelimitwiththeobservationpointtending totheboundaryofthedomainfrominsideandfromoutsidein
turn,onecan,usingthecontinuityofthetangentialcomponents ofelectromagnetic fieldontheboundary,obtainthenecessary equationsonlyovertheboundaryofdomain V withrespecttounknown fielddensities.NumericalsolutionoftheseequationsinvolvestheKrylov Bogolyubovmethod,variationalapproaches, Bubnov Galerkin typemethods,etc. SmaginandTsetsokho (1982) haveobtainedthesystemoflinearalgebraicequationsusingthecollocationmethodandthedensitiessoughtforwere approximatedbysmooth finitefunctions,whichforma finite partitionofunityoverthesurfaceofthedomain.
Thistechniquehasanobviousadvantageovertheintegral equationmethod.Numericalsolutiontotheequationswritten overthesurfaceofthedomainratherthanoveritsvolumeinvolvesaconsiderablereductioninthedimensionalityofthesystemoflinearalgebraicequations.Thisisespeciallyimportant whenmodelinglargeinhomogeneitiesbecausetheratioofthedimensionsofrespectivematricesdecreaseswithanincreaseinthe characteristiclineardimension L as 1/L
Despitethisadvantage,however,theuseofSIEtechniqueis limitedtomodelinghomogeneousbodieswithrotationalsymmetry,embeddedinahomogeneousspace(halfspace)(Oshiro andMitzner,1967; LiuandLamontagne,1999).Thisisdueto theimperfectionofthemathematicalapparatusformodeling inhomogeneitieswithanarbitrarydistributionofanomalouselectricalconductivity sa ¼ s(x,y,z) sb(z)embeddedinahorizontally layeredsectionandtothedifficultiesarisingatthestepofnumericalapproximationofsingularintegralequationsandofsolving theresultingsystemoflinearalgebraicequationswithanillconditionedmatrix.
Therefore,integralequationmethodsaremosthelpfulwhen modelinginhomogeneitiesofcomparativelysimpleshapeand smallsize(comparedtothewavelengthwithinthem)embedded inahorizontallylayeredmediumwithasmallnumberoflayers.
1.3Methodsofdifferentialequations
Advancesingeoelectricscallforthcomputing3-Delectromagnetic fieldsincomplicatedsituationswhentheinhomogeneityexhibits anarbitraryshapeanddimensions(inparticular,itmaynotbe local)andtheanomalouselectricalconductivityinthemodel variesarbitrarily,as,e.g.,inregionalmodels.Inthiscase,as pointedoutabove,integralequationmethodsareoflimiteduse.
Theonlyviableapproachtosuchproblemsinvolveseithera directsolutionofdifferentialequationswithpartialderivatives,
ortheuseofso-calleddifferentialequationmethods,ofwhich twomainonesbeingthe finitedifference(FD)techniqueand the finiteelement(FE)technique.Letuslistthemainfeatures oftheirapplicationtotheproblemofnumericalmodelingof 3-Delectromagnetic fields.
1.3.1Thefinitedifferencetechnique
TheFDtechniquebasedonthe finitedifferenceapproximationof derivativesisusedforthenumericalsolutionofadifferential equationwithrespecttotheelectricalormagnetic fieldina certainspatialregionthatcontainsaninhomogeneity:
whichfollowdirectlyfrom (1.1).
Theadvantagesofthistechniqueareitsgreaterversatility comparedtointegralequationmethods,thesimplicityofitsnumericalimplementation,bandstructureofthematrixofresulting systemoflinearalgebraicequations.Thelattercircumstanceis vitalbecauseitsignificantlyreducesthetimeandamountof operationalcomputermemoryrequiredforsolvingtheproblem and,consequently,enablesmodelingthetargetsoflargesizeor withcomplicatedconductivitydistributioninit.
Themainfactorsinfluencingtheeffectivenessofthismethod areasfollows: -choiceoftheappropriategoverningequation; -selectionofthediscretizationscheme; -approximationofthesecondderivativesin (1.3) or (1.4); -specifyingboundaryconditionsthatarevalidatnonindefinite distancefromtheanomaly; -conservationofcurrentsandmagnetic field flux; -accuracywhensolvingtheproblemsatfrequenciesapproachingthestaticlimit(similarproblemismetbytheFE technique);
-accuracywhensolvingtheproblemswithsharpconductivity contrasts.
Sincethe first3-Dmodelingresultswereobtainedwiththis methodbyF.Jones(JonesandPascoe,1972; LinesandJones, 1973; Jones,1974; JonesandLokken,1975; HibbsandJones,
1978),anumberofimprovementsweremadethatsignificantly increasedtheeffectivenessofFDtechnique(ZhdanovandSpichak,1980; Zhdanovetal.,1982; Lametal.,1982; Spichak, 1983a ,b; ZhdanovandSpichak,1989, 1992; MackieandMadden, 1993; Mackieetal.,1993, 1994; DruskinandKnizhnerman,1994; AlumbaughandNewman,1996; Smith,1996a,b; LaBreque,1999; Spichak,1999; Weidelt,1999; Weaveretal.,1999; Xiongetal., 1999b ; Sasaki,2001; WangandFang,2001; FomenkoandMogi, 2002; NewmanandAlumbaugh,2002; WeissandNewman,2002; Streich,2009; Mittet,2010; YavichandZhdanov,2016; Wang andTan,2017; Caoetal.,2018).
ZhdanovandSpichak(1980) suggestedabalancetechniquefor approximationoftheFDequationinelectrical field(seeSection 1.6 later),whichenabledtheaccuracyoftheresultstoincrease duetoreductionfromtheunstablecalculationofthesecondorderderivativestothe first-orderones. Spichak(1983a) proposed touseacurrentdivergence-freeconditioninthebalancetechnique,whichraisedtheaccuracyoftheresultsduetodisappearanceofthesecondterminEq. (1.3) inregionswithzero conductivitygradientandalsoatthestaticlimit. Zhdanovetal. (1982) and Spichak(1985, 1999, 2006) introducedtheasymptotic boundaryconditionsthatgreatlydiminishedthedimensionsof themodelingdomainandreallyincreasedtheaccuracyoftheforwardmodeling. Smith(1996a) proposedtouseastaggeredgrid method(pioneeredby Yee(1966))thatguaranteesautomaticconservationofcurrentsandmagnetic fluxonthegrid(though,atthe costofsomeinconveniencewhencomputingsome fieldcomponentsattheearthsurfaceorthe fieldtransformationsinvolving thecomponentsspecifiedondifferentgrids). Davydychevaand Druskin(1999) , Weidelt(1999),and WangandTan(2017) extendedthisapproachtotheanisotropicmedia.
DruskinandKnizhnerman(1994), Druskinetal.(1999) , Jin etal.(1999) , Zhouetal.(2013) useaspectralLanczosdecompositionmethod(SLDM)withKrylovsubspacesgeneratedfromthe inverseoftheMaxwelloperator.SLDMenablesaccelerationof theforwardmodelingowingtopossibilityofgettingthesolution forthewholefrequencyrangepracticallyatthecostofsolution forasinglefrequency.
Smith(1996b) developedastaticcorrectionprocedurethat explicitlyenforcestheelectricalcurrentandmagnetic field divergence-freeconditionsthat,inturn,increasestheaccuracyof theEM fieldcalculationwhenthefrequencytendstozero.Inorder toacceleratethesolutionoftheforwardproblematlowinduction numbers(LINs), NewmanandAlumbaugh(2002) proposedanLIN preconditioner.Itisbasedonsplittingtheelectrical fieldintocurl-
freeanddivergence-freeprojectionsthatremovesthenullspaceof thediscretecurl-curloperatorinthesolutionprocess.
Anumberofefficientsolversandpreconditionersareused presentlyinordertoachievebothagoodaccuracyandhigh convergencerateoftheiterationprocess,especiallywhenhigh conductivitycontrastsincreasetheconditionnumberofthematrixofthesystemoflinearequations(SLE). Fomenko(1999), Varentsov(1999), Siripunvarapornetal.(2002), GrayverandStreich (2012), VarilsuhaandCandansayar(2018) carriedoutacomparativeanalysisofdifferentpreconditionersandsolvers.
Finally, Zhdanovetal.(1982) and Spichak(1999) constructed internalcriterionsforcontrollingtheaccuracyoftheforward modelingresults(seeSection 1.6.5.1 later).
1.3.2Thefiniteelementtechnique
The finiteelementtechniqueisespeciallyusefulforEMmodeling intheregionswithcomplicatedgeometryorreliefearthsurface. Duetothis finiteelementmethodbecameverypopularincomputationalelectromagnetics(Reddyetal.,1977; Pridmoreetal.,1981; Boyseetal.,1992; Livelybrooks,1993; Mogi,1996; Haber,1999; Sugengetal.,1999; Zunoubietal.,1999; ZysermanandSantos, 2000; Badeaetal.,2001; Jin,2002; MitsuhataandUchida,2004; FarquharsonandMiensopust,2011; MukherjeeandEverett, 2011; Schwarzbachetal.,2011; Silvaetal.,2012; Umetal.,2012, 2013; VieiradaSilvaetal.,2012; Kordyetal.,2013; Persovaetal., 2013; Puzyrevetal.,2013; Renetal.,2013a,b; Rivera-Rios etal.,2013; AnsariandFarquharson,2014; Caietal.,2014; JahandariandFarquharson,2014, 2015; Caietal.,2017a,b; Jahandari etal.,2017; Liuetal.,2018a,b; Xiaoetal.,2019).
Intheframeworkofthisapproach,thesolutionofEq. (1.1) in the finitedomain V isequivalentto findingthestationarypointof theenergyfunctional:
(Notethatwearedealingwiththedeterminationofastationary point,nottheminimumofthefunctional F becausethedifferential operatorontheright-handsideof (1.5) isnotpositivelydefinedand hencedoesnotsatisfytheconditionsoftheMinimumtheorem).
Haber(1999), Badeaetal.(2001), AnsariandFarquharson (2014), JahandariandFarquharson(2015) usetothisenda potential currentformulationoftheinitialproblembasedon theHelmholtzdecomposition.Theresultingmatrixhasaproperty
ofthediagonaldominancethat,inturn,allowsitsefficientsolutionevenforveryhighconductivitycontrasts.
Analternativewaytoovercomethesameproblemisbasedon usingofasinglevectorshapefunctionateachedgeofthegrid insteadofthreescalarfunctionsde finedincornernodes.Due tothis,onehastoonlysolvefortangentialcomponentsofthe electrical fieldalongtheedgesofcells(“edge-based finiteelements”).Thus,avoidingasolutionfornormalcomponentsof the fieldallowsmodelingforhighcontrasts(Sugentetal.,1999; MukherjeeandEverett,2011; Kordyetal.,2013; Rivera-Rios etal.,2013; Caietal.,2014; Xiaoetal.,2018).
JahandariandFarquharson(2014, 2015) haveintroduced mixed “finitevolume” schemesbasedonboththeEM fieldand thepotentialformulationsofMaxwell’sequations(Nedelec, 1986).Comparisonbetweenthreestaggeredgrid finitevolume andtwoedge based finiteelementmodelingschemes(Jahandari etal.,2017)showsthatwhiletheyarecomparableintermsofaccuracyandcomputationresources,the finiteelementsschemes areslightlymoreaccuratebutalsomoreexpensivethanthe finite volumeones.
Itisalsoimportanttooptimizethehexahedralirregular meshes. Persovaetal.(2013) eliminate “ unnecessary” nodes, while Cherevatovaetal.(2013) representsafullgridasavertical stackofsubgridseachofwhichisastandardstaggeredgrid.Itis refinedonlyinthehorizontaldirection,uniformlyacrossthe verticallayers,allowingonlyafactoroftwobetweenvertically adjacentsubgrids. Schwarzbachetal.(2011), Renetal.(2013a), and Liuetal.(2018b) usetothisendadaptiverefinementprocedure,whichiterativelyrefinesthe finiteelementgridguidedby globalposteriorerrorestimators.Basingonnumericalexperiments Renetal.(2013a) concludedthattheerrorestimatorusing facejumpsofnormalcomponentsofcurrentdensityembedded inthegoal-orientedadaptiverefinementprocedureshowsthe mostefficientperformance.
Inordertoreducethetotalcomputationtime, Zysermanand Santos,(2000) proposeda “mixedhybriddomaindecomposed iterativenonconforming” methodthatisbasedontheiterative decompositionofthemodeldomainandsolvingthelocallinear systemsofequations.Thisapproachallowsreductionofmemory andtimerequiredforsolutionoftheappropriatesystemoflinear equations.Noteinthisconnectionthatmoresignificant reductionofthecomputationtime(notonlyintheFEbasedalgorithms)couldbeachievedmymeansofusingparallelization schemes(AlumbaughandNewman,1996; Newmanand
Alumbaugh,1999; Wilsonetal.,1999; Kordyetal.,2013; Puzyrev etal.,2013; Newman,2014; Caietal.,2017a).
Despitethefactthat,theoretically, fi niteelementsarewell suitedtomodelingthegeologicalsectionswithcomplexdistributionsofelectricalconductivity,the fl exibilityofthemethod isattainedthroughconsiderablecomputingeffortsassociated withtheuseofcomplicated fi niteelements.Tocharacterizedifferentialequationmethodsingen eral,itshouldbeemphasized thattheyaregenerallymoreversatilecomparedtointegral equationmethods.However, toincreasetheircomputing ef fi ciency,anumberofproblemsdiscussedabovehavetobe properlysolved.
1.4Hybridschemes
Onewaytorefinethetechniquesofnumericalmodelingof3-D electromagnetic fieldsistoapplyhybrid(“mixed” or “nonclassical ”)approachesthatblendtheadvantagesofthedifferential andintegralequationmethods.Thisimpliesthedifferential equationmethodtobeusedinsidethemodelingdomain,which permitsconsiderationofamodelwithanarbitrarydistributionof theelectricalconductivityandintegralrelationsbetween field componentstobeemployedattheboundary,whichensures thepossibilityoflimitingthemodelingdomaintowithinan areathatonlyslightlyexceedstheinhomogeneityindimensions.
The firststeponthiswaywasmadeby Weidelt(1975) who usedtheGreenfunctionsapparatustoremovefromaconsiderationtheregionsofthenormalsectionaboveandbelowthe inhomogeneities:
where S isthesurfaceofthediscontinuityseparatingthelayers, Ea istheanomalous(secondaryorscattered) field(Ea hE Eb ),and thepoints r0 areselectedintheregiontoberemoved.
Theef fi ciencyofhybridschemeswasfurtherimprovedby reducingthemodelingdomainnotonlyverticallybuthorizontallyaswell.Thus,in(Guptaetal.,1987; Leeetal.,1981; PridmoreandLee,1980 ; Bestetal.,1985 ),anareaoflimiteddimensionsiscoveredoverasmalldistancebya fi niteelement grid.Applyingthe fi niteelementtechniquetotheinnerpartof thedomainandtheintegralequationtechniquetotheouter partgivesrisetotwosystemsofequations:(1) fi niteelement
equationsintheinnernodes,withtherespectivepartofthematrixshowingacharacteristicbandstructureand(2)equations thatrelatetheunknownsontheboundaryandinnernodes (withtherespectivepartofthematrixbeing fi lled)inaccordance withtheformula
where r0 liesontheboundaryofthedomain V.
Renetal.(2014) haveproposeda finiteelementschemewitha hybridboundaryelement(BE),whichenablescompleteremoval ofthevolumediscretizationoftheairspace,which,inturn,providesthecapabilityofsimulatinglarge-scalecomplicatedgeoelectromagneticinductionproblems.Intheframeworkofthis approach,thesurfaceintegralformulaintermsofthereduced electricalvectorpotentialisapproximatedusingthepointcollocationboundaryelementmethod.Numericalexperimentsshow thatatlowfrequencies,wherethequasistaticapproximationis applicable,standardFEmethodsprovetobesuperiortothe hybridBE FEsolutionsintermsofcomputationaltime,because theFEmethodrequiresonlyacoarsediscretizationoftheair domainandoffersanadvantageoussparsityofthesystemmatrix. AtradiomagnetotelluricfrequenciesofafewhundredkHz,the hybridBE FEschemeturnstobesuperiortotheFEmethod becauseitavoidsexplicitstorageofthesystemmatricesaswell asdensevolumediscretizationoftheairdomainrequiredbyFE methodsathighfrequencies.
Hybridschemesarecommonlygroupedintotwotypes:direct anditerative.Indirecthybridtechniques,thematrixofthesystemisinverteddirectly,whereasiniterativetechniques,the valuesoftheunknownsatthedomainboundariesareat first assumedtobeknown,andthenthevaluesintheinnernodes arecomputed,whicharerecalculatedby (1.7) intoboundary values,etc.Asappearsfromtheestimationperformedby Lee etal.(1981),theiterativehybridschemesaregenerallymore sparingintermsoftheoperationalmemoryresourcesandCPU timeused.Similarlytoothernumericalmodelingtechniquestheir furtherreductionrequiresusingparallelcomputing.
Therefore,despitecertainadvantagesofhybridsystems,their practicalapplicationentailsanumberofdifficulties.Inparticular,therequirementsoncomputerresourcesremainrather high,convergenceoftheiterativeprocedureisnotguaranteed (ifthemostresource-savingiterativeschemeisconsidered)and nointernalcriteriafortheaccuracyoftheresultsobtainedare
used(Thelastobservation,whichalsoappliestotherestofthe numericalapproachesjustmentioned,isperhapsmostcritical forhybridschemes).
1.5Analog(physical)modelingapproaches
Analog,orphysical,modelingimpliesaphysicalnatureforthe modeloftheprimary fieldsource,themedium,andtheinhomogeneity.Twobasicapproachesaredistinguishedhere:thecontinuousmediamethodandtheelectricalcircuitmethod(Tetelbaum andTetelbaum,1979).Intheformerapproach,themodelisdeterminedbythe fieldofanelectricalcurrentinacontinuousmedium (Dosso,1966),whilethelatterinvolvestheuseofelectricalcircuits withconcentratedparameters(Brewitt-TaylorandJohns,1980).
Thecontinuousmediamethodisbasedontheuseoftheelectrodynamicsimilitudecriterion(Stratton,1941):
mus L2 ¼ inv ; (1.8)
where L isthecharacteristiclineardimensionofthemodel.Among theadvantagesofthisapproach,oneshouldrecallitssimplicity andlowcost,theuniquenessoftheequipment,andthepossibility ofmodelingthemediawithsharpelectricalconductivitycontrasts (Berdichevskyetal.,1987; Farquharsonetal.,2006).
Someoftheseadvantages,however,provetobedrawbacksif theissueisaddressedinabroadercontext,namely,fromthe standpointofelectromagnetic fieldsmodelinginrealsituations. Theextremelysmallnumberofphysicalmodelinginstallations allovertheworldvirtuallyobviatestheirapplicationasatoolfor analyzingtheobserved fields,letalonetherepeateduseofthe modelingresults,whichisonlypossiblethroughcouplingphysical installationstocomputingfacilities.Inaddition,oneshouldnotea numberoftechnologicdifficulties,suchasthechoiceofmaterials withasufficientlywiderangeofelectricalconductivityvariations butnotsubjecttofrequencydispersion,thepainstakingtechnologicimplementationofmodelsformultilayermedia,thepoorly developedmodelingtechniqueforusewithhardmaterialsand low-meltingmetals,andthedifficultiesarisinginobtainingexperimentalcurvesoverabroadfrequencyrange.
Theotherimportantapproachinphysicalmodelingistheelectricalcircuitmethod,whichinactualpracticeisrealizedintwomodifications.The firstisbasedondiscretizationofthemodeling domainfollowedbytherepresentationoftheelementaryvolumes obtainedbymeansofelementsofanelectricalcircuit(replacement
schemes)andmeasurementofvoltagesandcurrentsinthecircuit, whichmodeltheelectricalandmagnetic fields,respectively.The otherisbasedonobtainingreplacementcircuitsdirectlyfrom finite differenceequationsthatdescribethe fieldbeingmodeled(BrewittTaylorandJohns,1980).
Aswaspointedoutin(TetelbaumandTetelbaum,1979,p. 211), “theprimeadvantageofelectricalcircuitsisthattheyenable onetomodelthree-dimensional fields,whicharedescribedby equationswitharight-handside”.Anotherimportantadvantage ofthisapproachisthatitcanbeusedinhybridanalog/numerical installations.Itisalsoworthwhiletonotethatwiththisapproach, theuseofthediacopticsconceptof Kron(1972) mayprove noteworthy.
Despitetheoutwardmeritsoftheaboveapproach,however,it isnotfreeofthecharacteristic flawsofboththeotherphysical modelingtechniques(measurementerrorsandtechnicaldifficultiesinconstructingthemodels)andmathematicalmodeling approaches(e.g.,errorsensuingfromthediscretizationofthe modelingdomainand fieldequations).
Wehavediscussedthemaintechniquesandapproaches currentlyinuseformodeling3-Delectromagnetic fields. Collatingtheiradvantagesanddrawbacksshowsthedifferential equationmethodstobethemostversatileandbestsuitedfor modelingthebroadestspectrumofpracticalsituations.However, theirapplicationinvolvesanumberoftheoretical,methodological,andcomputingproblemsthataffectthemodelingefficiency. Inthefollowingsections,thesecrucialissueswillbeaddressedin thecontextofthebalancetechnique.
1.6BalancetechniqueforEMfield computation
Inpublications(ZhdanovandSpichak,1980, 1989; Spichak, 1983a , 1985, 1999),basicprincipleswereformulatedofconstructinganalgorithmforthisproblembearingonamoderate-speed computerwithalimitedcorememory(forinstance,minicomputers).Inwhatfollows,wewilldescribethisalgorithmand demonstrateitsapplicationtosolutionoftheforwardproblem in3-Daxialsymmetricsituations.
1.6.1Governingequations
Letsomedomain U intheEarth’scrustoruppermantlebe isotropic,nonmagnetic(mhm0 isthepermeabilityoffreespace),
andtohaveathree-dimensionaldistributionofelectricalconductivity sðx ; y ; z Þ thatcanberepresentedintheform:
sðP Þ¼ 0 @
sðz Þ; P ˛U1
sðx ; z Þ; P ˛U2
sðx ; y ; z Þ; P ˛U3 ;
where U ¼ U1 WU2 WU3 , P ¼ P ðx ; y ; z Þ; with U3 u 0.Theelectromagnetic fieldinthedomain U isinducedbyaplanewaveverticallyincidentontheEarth’ssurface.Thetimedependenceofthe fieldisgivenbyfactor expð i ut Þ.
Giventheconductivitydistribution sðx ; y ; z Þ,itisnecessaryto determineelectricalandmagnetic fieldseverywhereinthe domain P ¼ UWU0 ,where U0 istheloweratmosphereadjacent to U.
Overperiodsofinteresttogeophysics,the fieldinthedomain S isquasistationaryandsatisfiestheMaxwellequations: V H ¼ sE; (1.9) V E ¼ i um0 H (1.10)
Eq. (1.9) (1.10) yieldtheelectrical fieldequations: DE VðV , EÞþ k 2
where k ¼ði um0 Þ1=2 ; Rek > 0
TakingthedivergencefromthetwosidesofEq. (1.8),we derive sðV , EÞþðE; VsÞ¼ 0(1.12)
Withdueaccounttakenof (1.12),Eq. (1.11) takestheform:
E þ VðE; Vln sÞþ k 2 E ¼ 0 (1.13)
Todeterminetheelectromagnetic fieldinthedomain S we havetosolveaboundaryvalueproblemforthe field E satisfying Eq. (1.13) within S andthencalculate H.
1.6.2Boundaryconditions
Letusnowconsiderthechoiceofboundaryconditionsatthe boundariesofthedomain S: Thevaluesofelectrical fieldorof itsnormalderivativearenotknownbeforehand.So,acommon approachisbasedontheassumptionthatanomalous electromagnetic fieldvanishesattheboundarieslocatedat finite distancefromtheanomaly(Dirichlettypeboundaryconditions).
D
However,thiscausestwoproblems: first,itisdifficulttodeterminethisdistancecorrectlyand,second,inordertoensureits correctnessitisnecessarytoplacetheboundariesofthemodeling domainfarenoughfromtheanomaly(especiallyinthenonconductingparts),which,inturn,leadstounnecessaryincreasing ofthecomputationtime.
Oneofpossiblesolutionsmakeuseofintegralboundaryconditions(Weidelt,1972),butitcouldbeverydifficulttousethemin practicebecauseoftheirentailingconsiderablecomputing difficulties.Inthisconnection,itwouldbeinterestingtoconsider anothertypeofboundaryconditionsthatarebasedontheimplicitaccountofthecharacteroftheanomalous fielddecaying farfromthemediumheterogeneities. Spichak(2006) suggested ageneralapproach,whichmaybeusedtoconstructthedifferentialboundaryconditionsforthevector fields,satisfyingthe Helmholtzequation.Itisbasedontheexpansionofthe fieldsin aseriesofmultipolesanduseof “canceling ” operators.
Inparticular,thealgorithminquestionmakesuseofthe asymptoticboundaryconditionsofthe firstorder:
ikr þ r v vr ðE Eb Þ¼ 0; (1.14)
where Eb isthebackgroundelectrical fieldcorrespondingtothe casewhen shsðz Þ forall P ˛ P; r isthedistancebetweenthe pointslyingontheboundaryofthedomain P : andtheorigin ofthecoordinates.
Basingontheresultsofthenumericalmodeling Spichak (2006) hasconcludedthatitispossibletomakethefollowingrecommendationsusefulforapplicationoftheboundaryconditions whensolvingtheexternalboundaryvalueproblemsof geoelectromagnetics:
-theearthresponsesarenotequallyaffectedbytoosmalldistancebetweenthetargetandthemodelingdomainboundaries:theapparentresistivityismoresensitiveinthecaseof theresistivetargetwhilethephasesaremoresensitiveinthe caseoftheconductiveone; -the “safe” distanceforusingtheDirichlet-typeboundaryconditions E !a ¼ 0shouldnotbelessthan0.5 d,where d isaskin depthinthebackgroundstructure.
1.6.3Discretizationscheme
Toobtainasystemoflinearalgebraicequationsanditssubsequent computer-aidedsolution,atransitionfromcontinuoustodiscrete
valuesisrequired.Variousmechanismsforsuchatransitionare mainlybasedon(1)theapplicationofTaylorseries,(2)thevariationalformulation,and(3)integrationoftheprimaryequation. Eachoftheseapproacheshasitsadvantagesandrespective fields ofapplicability.Thus,the firsttechniqueapplicabletodifferential equationsingeneralcaseisusedmostoftenindefiningtheorder ofapproximationindifferenceschemes.Thevariationalformulationisinvitinginthat,initscontext,naturalboundaryconditions areadirectconsequenceoftherelevantfunctionalbeingstationary (Pridmoreetal.,1981).Lastly,thethirdapproach,oftenreferredto asthe “balancetechnique,” isapplicableingeneralcaseandyields particularlysimplediscreteschemeswithinternalboundariesand nonuniformgrids(Spichak,1983a).LetusrefertothislasttechniquetoobtaindiscreteanalogsofEq. (1.13).
Providedthattheelectricalconductivityintheregion variesstepwise,derivativesofthefunctionbeingsoughtfor mayundergobreaks.Itthusisworthwhiletocomputethe valuesofthefunctionitselfatt henodesofacertaingridwhile specifyingvaluesoftheelectricalconductivityfunctionatthe nodesofanintermediategrid( Brewitt-TaylorandWeaver, 1976 )withnoworrytosatisfyinternalboundaryconditions. Similarideaisrealizedinthestaggeredgridsapproach mentionedearlier.
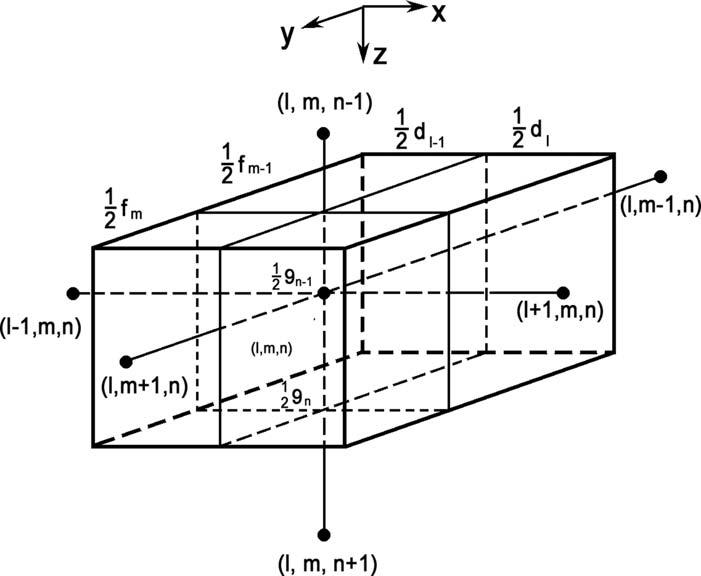
Toderivediscreteequationsforspacegridnodes,letus proceedfromthecontinuousvectorfunction E tothediscrete one Ul ;m;n ,de finedatthenodesofthemaingrid.Integrating Eq. (1.13) withrespecttothevolumeofanelementarycellin thevicinityofthenode(l ; m; n)(Fig.1.1),weobtainanequation forelectricalcurrentbalance:
Substitutingthederivativesof U and s inEq. (1.15) by finite differencesandapproximatingtheintegralsbythetrapezium rule,wearriveatalinearalgebraicequationrelatingthevalues ofthevectorfunctionUonlyinsevenadjacentnodes:
where b Dði Þ l ;m;n (i ¼ 1,2,.6)arethematrixcoefficientshavingasize (3 3)anddeterminedbythegridgeometry,distributionofthe electricalconductivity s andEM fieldfrequency. NotethatnumericalapproximationofEq. (1.13) hasanumber ofadvantagescomparedtotheapproximationofthecorrespondingsecond-orderdifferentialEq. (1.11): -thebalanceofcurrentsisholdwithineachcellofthespatial grid; -theuseofEq. (1.13) makesitpossibletoavoidtheapproximationofmixedsecondderivativesin (1.11) andexplicitlyenforcescurrentdivergence-freeconditionsateachgridnode (comparewithstaggeredgridapproximation(Smith,1996a )); -theapproximationofthethirdterminEq. (1.13) isaccurate enoughinthevicinityofelectricalconductivitycontrastsas well;
Figure1.1 Elementarycellofaspatialgrid.
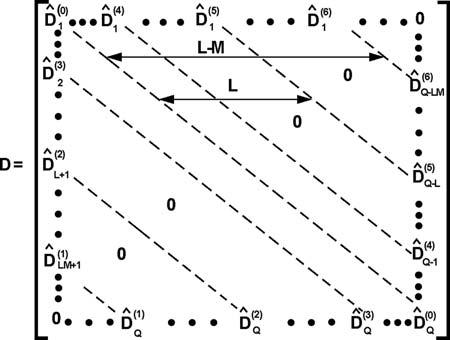
StructureofmatrixD:L,M,N numberofnodesinX,Y,andZ axes,respectively;Q ¼ L M N, b D
Þ (3 3) submatrix.
-intheregionswhere s ¼ 0or Vs ¼ 0thesecondtermofthe equationautomaticallyvanishesandinapproximationof (1.15) thetotalerrordecreases.
ThematrixofacorrespondingSLEhasablock-bandedshape andisverysparse(Fig.1.2).
Suchsystemsaresolvedmoreefficientlybyiterativemethods, whichenablethemosteconomicaluseoftheCPUcorememory. Inparticular,in(Spichak,1999)SLE (1.16) wassolvedusingconjugategradienttechniqueBiCGstab(Steijpenetal.,1994)afterits preconditioningbymeansofthediagonal(Jacobi)scaling.
1.6.4Calculationofthemagneticfield
Themagnetic field H canbedetermineddirectlyfromEq. (1.4) or, asnotedabove,itcanbesimplyrecalculatedfromthedetermined electrical fieldbyitsdifferentiationintermsofthe finitedifference (or finiteelement)approximationofEq. (1.10).Indoingso,we havetoovercomethedifficultyarisinginregionswithlargeconductivitygradients,whichmaycauseblundersinthecalculation oftherelevantelectrical fieldderivativesand,eventually,incorrectvaluesofthemagnetic field.Particularly,inthecalculation ofthehorizontalcomponents Hx and Hy attheEarth’ssurface accordingtoformulas (1.10),theapproximationofderivatives dEx =dz and dEy =dz isnotstable.
Apossiblewaytotacklethisproblemliesinconstructinga splineoverasetofvaluesofthegridfunctionandthenusing theanalyticallyobtainedderivativestocomputethemagnetic
Figure1.2
fieldcomponentsfromEq. (1.10).Thistechniquegivessatisfactoryresultsintwo-dimensionalcasewhenthesolutioninvolves onlyonecomponentoftheelectrical field,butitprovestobeunstableinthree-dimensionalcase(Pridmoreetal.,1981).
Anotherapproachliesincomputingtheanomalousmagnetic fieldbymeansofnumericalintegrationofexcesscurrentscirculatingintheanomalousregion Va :
where Ds ¼ s sb .
Despitethefactthatthisprocedureisstable,inordertodeterminethemagnetic fieldtherelevantGreenstensormustbe known.Iftheelectrical fieldwascalculatedusingoneoftheintegralequationtechniques(seeSection 1.2),thencomputingthe magnetic fieldwouldnotrequireanyadditionalcalculationsof theGreenstensor.However,ifthecomputationisperformedby meansofadifferentialequationtechnique(seeSection 1.3), determiningthemagnetic fieldby Formula(1.16) wouldrequire computingtheGreentensor,whichinvolvesconsiderablecomputationexpenses.
Fromthispointofview,thewayproposedby Spichak(1999) appearstobemorepreferable.Inthisapproach,magnetic field componentsaredeterminedintwosteps.First,inthecentersof thegridcells,theverticalcomponentofthemagnetic field Hz is found,andthen,usingHilberttransforms(see,forinstance, (Zhdanov,1988)),tangentialcomponents Hx and Hy are computedatthegridnodes:
where r ¼½ðx x0 Þ2 þðy y0 Þ2 1=2 ;thevalueof Hz isprecalculatedaccordingto Formula(1.10); H b x and H b y arethebackground magnetic fieldcomponentsattheEarth’ssurface.
Theabovealgorithmfortheforwardproblemsolutionwas realizedasasoftwarepackageFDM3D(Spichak,1983b )and widelyusedformodelingEM fieldsin3-Dmedia(Spichak,1999, 2015).
1.6.5Controllingtheaccuracyoftheresults
1.6.5.1Criteriaforaccuracy
Inmostcases,theaccuracyofmodelingEM fieldscanonlybe evaluatedindirectly,becausetheexistingcontroltechniques provide,asarule,necessarybutnotsuf ficientconditionsfor theaccuracyoftheresults.
“External” and “internal” techniquesareemployedforaccuracycontrol.Externaltechniquesinclude (a) comparisonwiththeresultsofotherauthors; (b) comparisonwiththeresultsobtainedbyothermethods, includinganalyticalones.
Thusfar,thesetwocriteriahavebeenusedmainlyfor checkingthecorrectnessofsolutions.Theresultsofnumerous comparisons,however,clearlyshowtheaboveaccuracycriteria tobeinsufficient.Controltechniquesthatenabletheaccuracy estimationbyaninternalmeansofoneoranothernumerical approachshouldbeapplied.
Aspointedoutby PoggioandMiller(1973), “theideaof numericalevaluationoftheaccuracyofatechniqueattimesappearstobeinternallyinconsistent,becauseitseemsthatnumericalresultscannotbeusedtoconfirmtheirowncorrectness.In reality,thereareseveralapproachesthatenableamanifestincorrectnessofnumericalresultstobedetected.” Suchcriteriainclude testingthefollowing:
-thereciprocitytheorem; -theenergyconservationlaw;
-theaccuracytowhichtheequationsandboundaryconditions aresatisfied; -convergenceofthesolutionwithdecreasingsizeofgridcells, numberofunknowns,etc.
Finally,onemayconsiderasamixedtype(inemployingdifferentialequationtechniques)thecriterionproposedby Zhdanov etal.(1982).Itisbasedonanestimationoftheaccuracytowhich theintegralidentity
issatisfiedbysubstitutinginitthesolutionobtainedbythe finite differenceor finiteelementtechniques.Unfortunately,numerical implementationofthiscriterionrequiresatime-consuming computationofGreentensorforalayeredmedium,whichreducesitspracticalvalue.